AI-Integrated Feature Selection of Intrusion Detection for Both SDN and Traditional Network Architectures Using an Improved Crayfish Optimization Algorithm

1  Introduction

1.1 Research Background

Network intrusion detection system is a crucial component of contemporary network security [1]. It not only effectively protects network resources and data security, but also reduces security operating costs and enhances the active defense capability of the network [2]. As network technology evolves, the significance of intrusion detection systems will increasingly rise.

As a critical technology for realizing network intelligence, providing flexibility and programmability to the network, Software-Defined Networking (SDN) separates the control logic from the data forwarding functions of network equipment, allowing the network to be managed and orchestrated by a centralized software controller [3]. SDN addresses the issues of traditional networks that are difficult to deploy, the non-programmability of devices, and the difficulty of managing the network [4]. Due to the unique advantages of SDN, there are significant differences in security requirements and defense mechanisms between SDN and traditional network structures.

1.2 Current State of Research

Intrusion detection identifies anomalous traffic and attack traffic in network behavior through extensive features. However, extensive redundant data and irrelevant features exist in the raw data, which cause intrusion detection systems to incur unnecessary time and cost overhead. Therefore, feature selection becomes a key technology to improve the performance of intrusion detection systems.

Currently, Artificial Intelligence (AI) techniques, including machine learning and optimization algorithms, are extensively applied in feature selection for intrusion detection. Many AI-integrated feature selection approaches are employed in network intrusion detection. For example, Kareem et al. [5] presented a feature selection model that utilizes a hybrid meta-heuristic algorithm for Internet of Things (IoT) intrusion detection, and experiments proved that the proposed model achieves better convergence performance and generates higher-quality solutions. Zhang et al. [6] created a detection technique that uses multiple-operator cooperative evolution and combines an adaptive parallel quantum genetic algorithm with normalized mutual information for feature selection. Results from experiments on actual datasets demonstrate that this approach performs better than current detection methods. Babu et al. [7] implemented an improved flower pollination algorithm for feature selection and utilized an improved monarch butterfly optimization algorithm to fine-tune the parameters of an attention-based Nested U-Net, thereby enhancing the efficiency of the intrusion detection system. Alkanhel et al. [8] proposed a novel intrusion detection system hybrid optimization algorithm based on the grey wolf algorithm and dipper throated optimization algorithm for application in the IoT, which better balances the exploitation and exploration phase. Our prior work [9,10] applies AI algorithms to promote the performance of intrusion detection for traditional networks or SDN. The most valuable subset of features can be found using an AI-integrated feature selection method, which can eliminate unnecessary features and redundant data to improve intrusion detection system performance.

The Crayfish Optimisation Algorithm (COA) is a novel metaheuristic algorithm that mimics the biological behavior of crayfish to find the optimal solution to a problem. It was first introduced in 2024 [11]. The COA has been applied to engineering problems, and related experiments have shown that the algorithm has strong convergence and optimization-seeking ability [12,13]. Most metaheuristic algorithms face issues such as slow convergence speed, weak optimality searching ability, and easy falling into local optimization. COA faces the same problem. Particle Swarm Optimization (PSO) is prone to falling into local optimality when processing high-dimensional data [14]. Grey Wolf Optimiser (GWO) relies on α, β, and δ wolves to guide the search. If the leading wolf falls into the local optimum, it is difficult for the entire population to jump out, resulting in premature convergence [15]. Genetic Algorithm (GA) has a crossover mutation process and uses a large number of random processes, which will lead to slow convergence [16]. COA has two exploitation stages and uses temperature and food factors to balance the survey and exploration stages, so it has a strong convergence speed and ability. Therefore, this paper selects the COA for feature selection of AI integration.

1.3 Motivation and Innovation

(1)   Differences in network environments: Considering the significant differences in intrusion detection between traditional networks and SDN, the primary motivation of this paper is to design a feature selection technology that can be effective in multiple network environments to improve the efficiency of intrusion detection in different network environments.

(2)   Disadvantages of COA: Wang et al. [17] proposed that COA has good optimization performance, but still suffers from slow convergence speed and sensitivity to local optima. Maiti et al. [18] argue that COA suffers from a lack of exploitation capacity. To solve these problems, this paper introduces Levy flight, crowding factor, elite reverse learning, and parameter modification strategies, and proposes an Improved Crayfish Optimisation Algorithm (ICOA).

(3)   Advantages of AI-integrated feature selection: Combining the ICOA with AI (K-Nearest Neighbours) applied to optimize feature selection for traditional network and SDN intrusion detection, which enhances the performance of intrusion detection.

1.4 Research Objectives and Contributions

(1)   This paper first tries to utilize AI algorithms to solve the integration problem of intrusion detection for both SDN and traditional network architectures and proposes ICOA for AI-integrated feature selection.

(2)   In this paper, four improvement strategies are used to improve COA; elite reverse learning improves the quality of the population, Levy flight improves the ability to jump out of the local optimum, and parameter modification and crowding factor strategies balance the exploration phase and exploitation phase. The convergence ability of ICOA is tested on benchmark functions, the feature selection ability of ICOA is verified on the UCI dataset, the feature selection ability of ICOA to optimize traditional network intrusion detection is verified on the NSL_KDD and UNSW_NB15 datasets, and its feature selection ability to optimize SDN network intrusion detection is verified on the InSDN dataset.

1.5 Paper Organization

The rest of the paper is organized as follows. Section 2 describes the feature selection problem for SDN and traditional network architectures. Section 3 introduces the characteristics and the concept of COA. Section 4 explains four improvement strategies of the proposed ICOA. Section 5 constructs a feature selection optimization model of AI-integrated using ICOA. Section 6 verifies the ability of the ICOA-based AI-integrated feature selection model to optimize feature selection in different network intrusion detection by testing traditional network datasets and SDN datasets. Section 7 provides a summary of this paper and outlines potential directions for future research.

2  Problem Description

Both SDN and traditional network environments have a lot of features. Assuming that a dataset has n features, there are 2n kinds of results for feature selection, which increases the time overhead of network intrusion detection significantly.

Eq. (1) defines the data matrix D and the feature vector L.

D=[d11⋯d1n⋮⋱⋮dm1⋯dmn],Li=(li1,li2,⋯,lin)(1)

As shown in Eq. (1), m indicates the quantity of data, and n denotes the dimension of the data. Therefore, the feature selection problem is to find k features from n features to form a feature subset H, and the data selected by the feature subset H has the same classification effect as the original data.

Eq. (2) describes the feature selection results through the binary vector H and calculates the filtered data matrix D′.

D′=D×(HT,HT,⋯,HT)=[d11d12d21d22d13⋯d1nd23⋯d2n⋮⋮dm1dm2⋮⋮⋮dm3⋯dmn][00110⋯01⋯1⋮⋮11⋮⋯⋮1⋯1]=[d11′d12′d21′d22′⋯d1k′⋯d2k′⋮⋮dm1′dm1′⋮⋮⋯dmk′](2)

Define the feature subset H=(h1,h2,⋯,hn), where the value of hi is 0 either 1, when a feature is chosen, it is represented by 1, and when it is rejected, it is indicated by 0.

Feature selection diminishes data dimensionality and enhances intrusion detection performance by identifying subsets of features that exhibit the strongest correlation. The fitness function used for feature selection plays a crucial role. It is closely related to the classifier’s performance as well as the quantity of features. Therefore, in this paper, the following fitness function is designed by considering both the number of feature subsets and the error rate.

Fit=A×error+FeatureselectedFeatureall∗B(3)

where error denote the error rate of this classification. Featureselected denotes the quantity of selected features. Featureall denote the overall count of features. A and B are the parameters which are 0.99 and 0.01, respectively.

Assume the time required to detect each feature of each sample is tij,(i∈(1,m),j∈(1,n)). Therefore, the detection time cost of this set of data is as shown in the formula.

Time=Sum(tij⋅HT)(4)

Feature selection should take into account not only the validity of the feature subset but also the time factor. Therefore, the evaluation indexes in this paper include both Eqs. (3) and (4)

3  Crayfish Optimization Algorithm (COA)

The COA is a metaheuristic algorithm that simulates the summer resort behavior, competition behavior, and foraging behavior of crayfish. The COA is divided into two phases, which are the exploration phase and the exploitation phase. The exploration phase includes summer resort behavior. The competition behavior and the foraging behavior represent the exploitation phase.

3.1 Summer Resort Stage

When Temp≥30&&rand<0.5, it represents that the temperature is excessively high and the cave is not crowded, crayfish will enter the cave directly. The location of the populations and the cave is updated as follows.

Temp=rand×15+20(5)

Xshade=(Xbestposition+Xglobalposition)/2(6)

C1=2−t/T(7)

Xi,jt+1=Xi,jt+C1×rand1×(Xshade−Xi,jt)(8)

where Xi,jt+1 indicates the location of the ith crayfish in the t + 1 cycle. rand indicates a random value ranging from 0 to 1. Xglobalposition represents the optimal position obtained so far by iterations. Xbestposition indicates the optimal position within the current population. Xshade represents the location of the cave. C1 is a decreasing curve, t represents the number of the current iteration, T represents the maximum number of iterations.

3.2 Competition Stage

When Temp≥30&&rand≥0.5, it represents that the temperature is excessively high and the cave is too crowded, crayfish compete for the position in the cave. The location is updated as follows.

Xi,jt+1=Xi,jt−Xz,jt+Xshade(9)

z=round(rand(N−1))+1(10)

where Xz,jt represents the position of a randomly selected crayfish. z is a generated random integer in the range (1,N). In the competition stage, crayfish compete for cave positions. Cave locations are updated based on randomly selected locations of crayfish z.

3.3 Forage Stage

When Temp<30, crayfish enter foraging phase, and the foraging approach of crayfish is determined by the food size Q. When Q≤(C2+1)/2, crayfish will forge directly. The location is updated as follows.

Q=C2×rand×(fitnessi/fitnessfood)(11)

Xi,jt+1=(Xi,jt−Xfood)×p+p×rand×Xi,jt(12)

Xfood=exp⁡(−1Q)×Xfood(13)

where Xfood indicates the location of the food, p indicates the intake of crayfish, fitnessfood indicates the fitness value of the food, fitnessi represents the fitness of the current individual and C2 shows the food factor and the value is constant 3. Q is determined by the fitness value of the food and the current individual. Xfood obeys the exponential distribution function.

When Q>(C2+1)/2, it implies that the food size is excessively large. Crayfish uses its second and third legs to break down food and forage alternately. The location is updated as follows.

Xi,jt+1=Xi,jt+Xfood×p×(cos⁡(2×π×rand)−sin⁡(2×π×rand))(14)

3.4 Characteristics of COA

The advantages of the COA are as follows. Firstly, the COA has a strong exploitation capability due to its two exploitation phases. Secondly, by altering the temperature, the algorithm moves through several steps. This method more effectively balances the COA’s exploration and exploitation capabilities. The disadvantages of the COA mainly originate from the exploitation phase. Due to the existence of two exploitation phases, the COA is likely to enter a local optimum in the latter iteration, which could result in the issue of sluggish convergence.

4  Improvement Strategies of COA

Aiming at the shortcomings of the COA, this paper introduces four improvement strategies. Through the elite reverse learning strategy, the population’s quality is improved. Introducing the Levy flight strategy in the iteration process increases the step length of random wandering, which can prevent getting stuck in a local optimum. The ICOA uses Euclidean distance to describe the degree of crowding. Finally, the food factor is adjusted to balance the processes of alternate foraging and direct foraging, ensuring a more effective search strategy.

4.1 Elite Reverse Learning Strategy

The elite reverse learning strategy is divided into two stages. Firstly, for the initial population, each Xi obtains its reverse solution X_o through reverse learning [19–21]. The reverse learning formula is as follows.

X_o=k×(L−U)−Xi(15)

where k is a random value ranging between 0 and 1. L and U represent the minimum and maximum values of the feasible solution. After that, the elite strategy compares the fitness values of X and X_o. The optimal individual is selected for updating the position of the population individual. The position update formula is as follows.

Xi={Xiiffitness(Xi→)>fitness(Xi)X_oelse(16)

4.2 Levy Flight Strategy

The Levy flight can explain many random phenomena, such as Brownian motion, random walks, and so on [22]. The Levy flight can be applied to the field of optimization. For example, the Levy flight strategy is used in the cuckoo algorithm for position updating, and PSO also employs this technique to escape from local optima. Levy flight increases the diversity of the population and expands the search range [23,24], so the Levy flight strategy is incorporated into the ICOA. The Levy flight strategy position update formula is as follows.

Xit+1=Xit+α⊕Levy(λ)i=1,2,⋯,n(17)

where α denotes the control step sizes, ⊕ represents the point-to-point multiplication, Levy(λ) represents the search path, and are satisfied as follows.

Levy∼u=t−λ1<λ≤3(18)

s=u|v|1/β(19)

u∼N(0,σu2),v∼N(0,σv2)(20)

σu={Γ(1+β)sin(π×β2)Γ(1+β)×β×2β−12}1β,σv=1(21)

where s represents the step size, u and v follow a normal distribution, and β typically has a value of 1.5.

4.3 Crowding Factor Strategy

The COA employs a random function to choose between the summer resort stage and the competition stage of the crayfish. In the ICOA, a crowding factor is introduced to select the summer resort stage or competition stage. The distance between each individual in the population and the burrow is calculated to derive the crowding factor h. The level of cave crowding is then determined based on the value of h. The crowding factor is defined as follows.

Li=(Xi,1−Xshadei,1)2+(Xi,2−Xshadei,2)2+⋯(Xi,j−Xshadei,j)2(22)

Lmean=1N∑h=1iLh(23)

h=mN(24)

where Li represents the distance from the population to the cave, Lmean represents average distance. m represents the number of populations within a distance of Lmean.

4.4 Parameter Modification Strategy

The crowding judgment of the original algorithm is based on fixed values. In the ICOA, at the beginning of the algorithm, a larger number of individuals are allowed to approach the optimal position to achieve rapid convergence. In the later stages, individuals can jump out of the local range as much as possible to find the optimal, avoiding falling into the local optimum. Therefore, the original crowding judgment is modified. The new crowding judgment is as follows.

h<1−t/T(25)

Parameter Q determines how crayfish feed. In the ICOA, the food size Q judgment is as follows.

Q<(max(fitness)+min(fitness))/2(26)

4.5 Effectiveness of Improvement Strategies

Fig. 1 shows the effect graphs of the four improved strategies. A graph shows that the population after elite reverse learning is closer to the optimal solution, which confirms the effectiveness of the strategy. The b graph represents the iteration curves of the four strategies and the original algorithm in the process of optimization searching. From the figure, it can be seen that each strategy converges faster than the original algorithm, has high convergence accuracy, and is not easy to fall into a local optimum. Therefore, it can be assumed that the four improved strategies have some improvement effect on the original algorithm.

Figure 1: Comparison chart of improvement effects. (a) Comparison of elite reverse learning effectiveness. (b) Convergence trends for different improvement strategies

5  AI-Integrated Feature Selection Using ICOA

5.1 Improved Crayfish Optimisation Algorithm (ICOA)

As explained in Section 4, the ICOA is developed using four improvement strategies, and its pseudo-code is presented in Algorithm 1. First, the elite reverse learning strategy enhances both population quality and convergence speed. Second, introducing both the crowding factor strategy and the modification parameters strategy balances the exploration and exploitation phases. Finally, the Levy flight strategy is employed to prevent getting stuck in local optima during the later stages.

The time complexity of COA is shown in Eq. (27), N indicates the population size, D represents the population dimension, T represents the number of iterations, and C represents the cost of the evaluation function. In each iteration of ICOA, the time complexity of crowding factor strategy and parameter modification strategy is O(1), the elite reverse learning strategy and Levy flight strategy exist at the beginning and end of each iteration, the time complexity is O(N), and the population update time complexity of COA is O(N×D), so 1≪N≪N×D. Therefore, the complexity of time for ICOA is almost the same as for COA.

O(COA)≅O(T×N×(C+D))(27)

Table 1 shows the specific differences between ICOA and the comparison algorithms. Elite reverse learning is used in the initialization phase, and a crowding factor is added in the balancing phase to balance the development and detection phases. ICOA has the same time cost as several other compared algorithms in terms of time complexity.

5.2 Applying ICOA to Utilise AI-Integrated Feature Selection

As to the integration problem of network intrusion detection for both SDN and traditional architectures, the proposed ICOA can be applied to find the optimal value subset of features by utilizing its advantages of fast convergence speed and high convergence accuracy to promote AI-integrated feature selection, as demonstrated in Fig. 2. Initially, ICOA is used to initialize the features, followed by an iterative search conducted through the biological behavior of ICOA. Once the termination condition is satisfied, the optimal subset is then output.

Figure 2: Application of ICOA in utilizing AI-integrated feature selection of network intrusion detection for both SDN and traditional architectures

5.3 AI-Integrated Feature Selection Model

When applying ICOA to optimize feature selection for network intrusion detection, the most valuable subset of features is selected and then combined with the KNN algorithm for classification to construct an AI-integrated feature selection model, which improves the performance of network intrusion detection for both SDN and traditional architectures. The AI-integrated feature selection model is then shown in Fig. 3.

Figure 3: AI-integrated feature selection model of network intrusion detection for SDN and traditional architectures

As demonstrated in Fig. 3, the AI-integrated feature selection model consists of the following steps.

Step 1: Preprocess input SDN and traditional data.

Step 2: Make training and test datasets out of the data.

Step 3: Perform feature selection for the training dataset based on ICOA to obtain the optimal subset of features.

Step 4: Reduce the dimensionality of the test dataset based on the optimal subset of features and use the KNN algorithm for classification.

Step 5: Calculate the evaluation metrics for SDN and traditional networks based on the prediction results.

6  Experimental and Analysis

This section concentrates on the setting and outcomes of the experiment. Firstly, the convergence performance of ICOA is tested using benchmark functions. Secondly, the effect of ICOA on optimizing feature selection is tested on the UCI dataset. Finally, the effectiveness of AI-integrated feature selection using ICOA in optimizing feature selection for different network intrusion detection is validated using the NSL-KDD dataset, the UNSW_NB15, and the InSDN dataset. The NSL-KDD dataset is widely used in network intrusion detection, which was developed to fix problems with the KDD Cup 1999 dataset and enhance data quality by removing redundant records and rebalancing the sample [25]. On one side, the NSL-KDD dataset is a common dataset used in network intrusion detection research. On the other, it does not fully reflect the modern network environment [26]. The UNSW-NB15 dataset contains modern normal cyber activities and current attack behaviors, which better reflect the current network threat environment [27,28]. Moreover, UNSW-NB15 contains rich features and a large amount of data. The InSDN dataset is specially designed for SDN environments and contains various attacks that can occur on SDN controllers and network devices [29,30].

6.1 ICOA Capability Test

6.1.1 Experimental Environment

The experimental tests are conducted in a single environment to ensure the objectivity and fairness of the experiment. The processor, which is the 13th Gen Intel(R) Core (TM) i7-13620H with a speed of 2400 MHz, 10 cores, and 16 logical processors, MATLAB 2022b and the Windows 11 operating system are also used in the experimental configurations. In the experiment, the two learning factors of PSO were set to 1.5, the number of iterations of each algorithm was 500, and the population size was 30. Each experiment was run independently 30 times. Several studies have shown that KNN achieves superior performance in classification tasks compared to other machine learning models. Therefore, this paper also uses the KNN algorithm for experiments. In COA, the authors have confirmed that C2 = 3 has relatively good results on the CEC14_3, CEC14_9, CEC14_24, and CEC14_25 datasets.

6.1.2 Benchmark Function Test

In this part, 6 benchmark functions are used for testing, including 2 single-peak functions (F1–F2) and 4 multi-peak functions (F3–F6). The initial population in each experiment is maintained the same, and different algorithms are used to evaluate the performance of the benchmark functions, which are executed independently multiple times. As shown in Table 2, the benchmark functions are displayed. Table 3 shows the outcomes of the benchmark function tests, and the convergence curves for the four algorithms are demonstrated in Fig. 4.

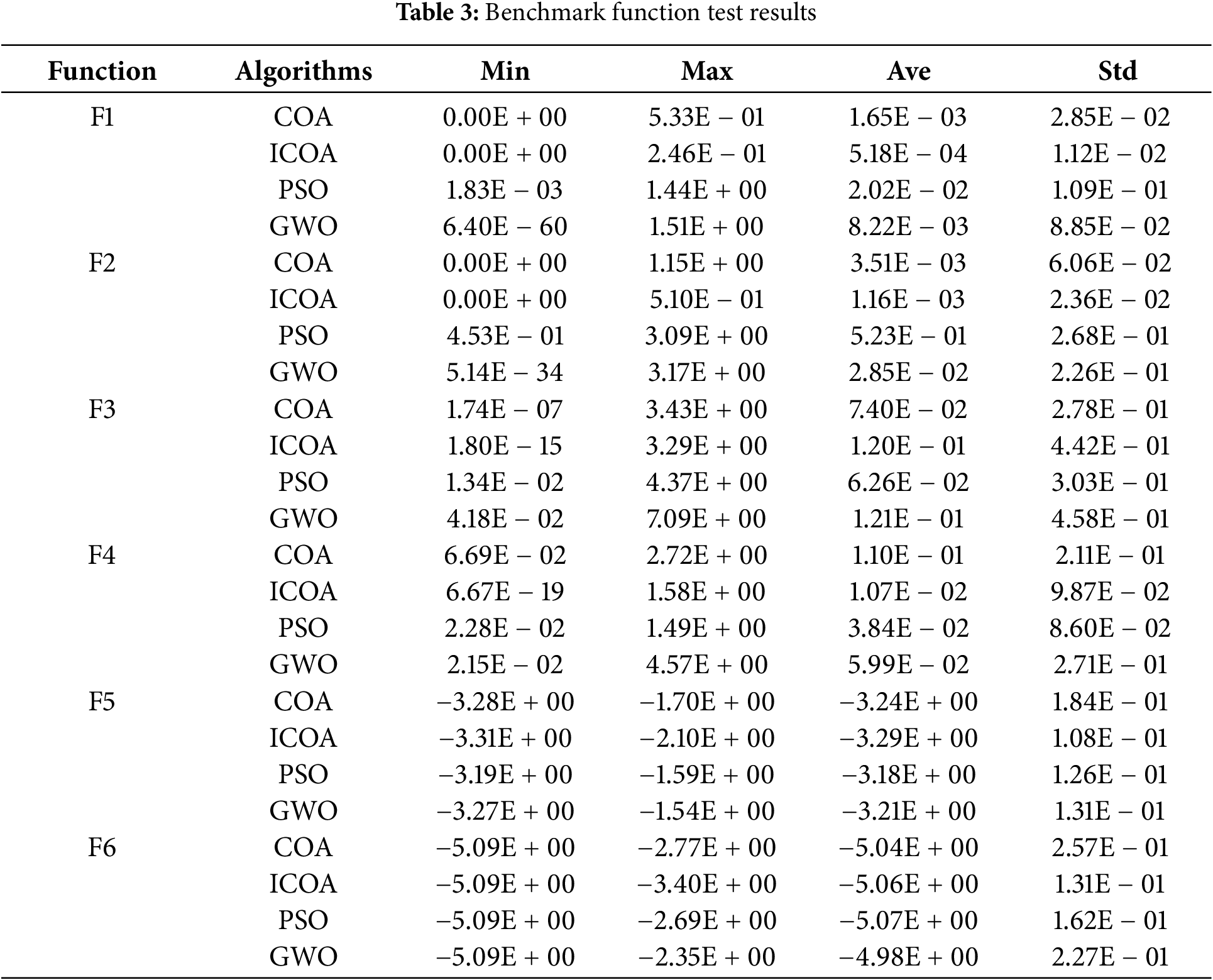
Figure 4: Convergence curves of fitness. (a) F1. (b) F2. (c) F3. (d) F4. (e) F5. (f) F6

As indicated in Fig. 4 and Table 3, when evaluating single-peak functions (F1–F2), the ICOA and the COA demonstrate comparable convergence accuracy in finding the optimal value, whereas the PSO and the GWO show lower convergence accuracy than the COA and the ICOA. Additionally, ICOA exhibits the fastest convergence speed. Therefore, in single-peak function tests, the ICOA outperforms in terms of convergence accuracy and speed. When evaluating multi-peak functions (F3–F6), the ICOA consistently achieves the best convergence accuracy. The ICOA can find values with higher accuracy within the same number of iterations, indicating an advantage in convergence speed as well. Analysis of the convergence curve reveals that the ICOA possesses strong global optimization capabilities and can escape local optima in later iterations. Based on the benchmark function test results, it can be concluded that the ICOA performs better than other algorithms in terms of speed and convergence accuracy.

6.1.3 UCI Datasets

This section uses three UCI datasets (Ionosphere, Heatstatlog, WDBC) for classification performance testing. Table 4 gives specifics on the UCI datasets.

Table 5 presents the test results for the UCI datasets. The ICOA achieves the best results in the Ionosphere and WDBC datasets. In the Heatstatlog dataset, ICOA ranks third lowest in terms of precision. In the other metrics, it scores the highest. The ICOA algorithm demonstrates excellent classification capabilities, as evidenced by the test results across the UCI datasets.

6.2 NSL-KDD Dataset

The NSL-KDD dataset comprises 41 features and a corresponding classification label. First, the dataset is preprocessed, which includes data cleaning, numerical transformation, and normalization. The dataset contains four attack types, which are U2R, Dos, Probe, and R2L. When testing the NSL-KDD data, 50% of the data in KDDTrain+ is used for training, and the data in KDDTest+ is used for testing. Table 6 provides the classification results of the NSL-KDD dataset, and Fig. 5 shows the Fitness and ROC curves of the NSL-KDD dataset.

Figure 5: Fitness and ROC curves of the NSL-KDD dataset. (a) Fitness curve. (b) ROC curve. (c) NSL-KDD result. (d) Confusion matrix

As shown in Table 6, the ICOA is higher than other algorithms by about 0.532% to 5.368% in terms of accuracy. The high accuracy indicates that the ICOA can differentiate the data types better. Similarly, the ICOA is higher than other algorithms in both recall and F1-score. The ICOA has a high recall rate, which indicates that the ICOA is capable of recognizing the attack types of data. The high F1 score suggests that the ICOA can better balance the precision and recall rates. Although in terms of precision rate, the performance of the ICOA is not excellent, it still reaches 94.397%, which is 0.64% less than COA and 0.173% lower than GWO. Regarding the number of features, the ICOA has the fewest number of features. The time test on the selected feature subset showed that ICOA requires the least time, taking only 0.015 s. The fitness curve can better reflect the convergence ability and convergence speed of the algorithm. A higher fitness value means a higher convergence accuracy. Based on the fitness curve in Fig. 5, the ICOA demonstrates a strong ability to find the optimum compared to the COA. It can escape local optima later, improving both the convergence speed and precision. The ROC curve represents the ability to categorize the data, and the ROC curve of the ICOA has the largest area underneath it, which means the ICOA has the best performance in classifying the data and can reduce the rate of false positives. The confusion matrix exhibits the prediction results of ICOA-based intrusion detection, showing that ICOA can categorize the data classes well. From the experimental results, ICOA-based AI-integrated feature selection performs better in network intrusion detection than other AI algorithms.

6.3 UNSW-NB15 Dataset

There are 175,341 network data points in the UNSW-NB15 dataset. This dataset provides the training and testing sets; therefore, after removing redundant features manually from the dataset, data preprocessing and normalization are done. Selected portions of the training and test sets are tested. In total, about 10,000 data are selected for this experiment. The test results are displayed in Fig. 6 and Table 7.

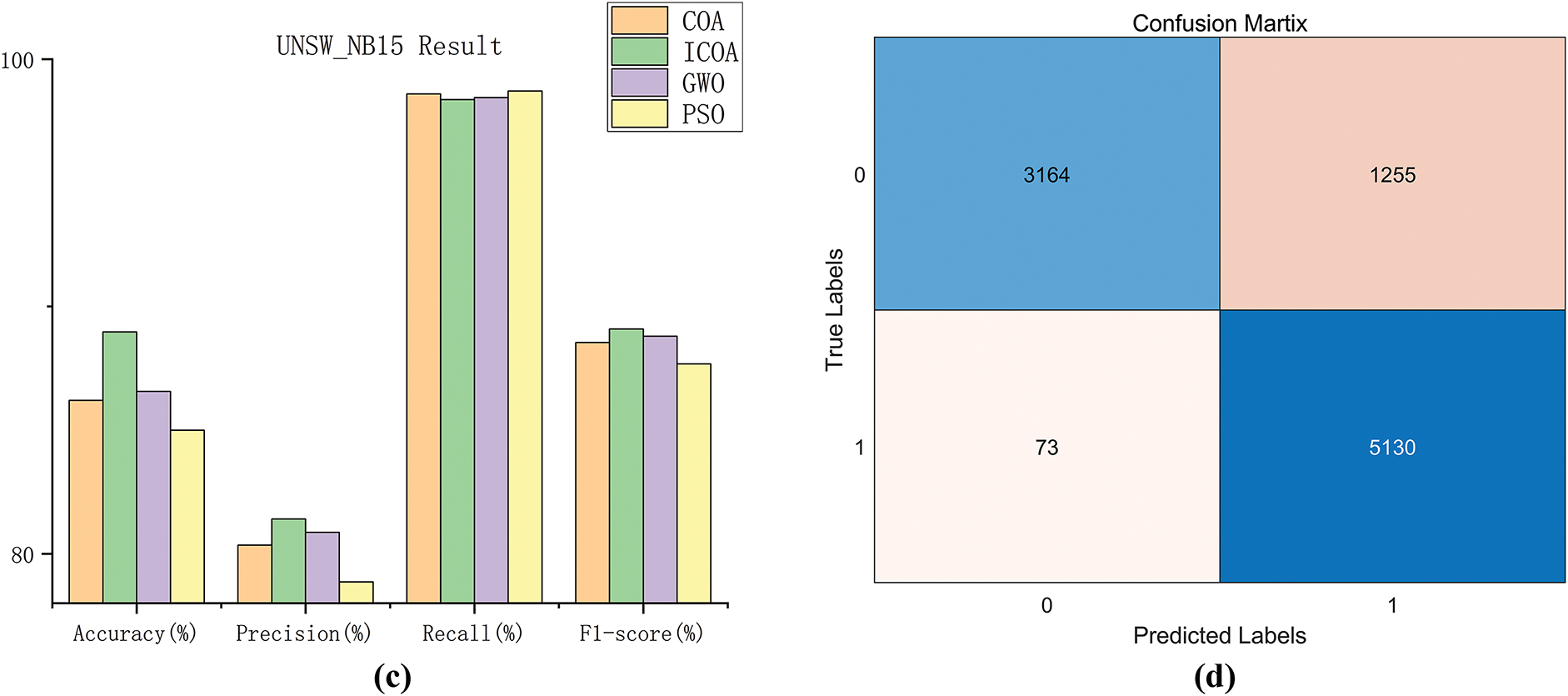
Figure 6: Fitness and ROC curve of UNSW-NB 15. (a) Fitness curve. (b) ROC curve. (c) UNSW_NB15 result. (d) Confusion matrix

From the results in Table 7, it is evident that ICOA is the best in all the metrics except for the number of features and recall. ICOA has one fewer feature than the original algorithm, one more feature than GWO, and three fewer features than PSO, but ICOA takes the least time. In terms of accuracy, ICOA is about 2.405% to 4.004% higher than other algorithms. In precision rate, is 2.548% higher than the PSO algorithm. In the F1-score, ICOA is 0.546% higher than COA, 0.293% higher than GWO, and 1.411% higher than PSO. As can be seen from Fig. 6, the convergence performance and classification performance of ICOA are also optimal. As shown in the confusion matrix, almost all of the attack types are detected, which proves the effectiveness of the ICOA-based intrusion detection approach. Experimental results from the UNSW-NB15 dataset show that ICOA-based AI-integrated feature selection minimizes the number of features while optimizing the performance of traditional network intrusion detection.

6.4 InSDN Dataset

The InSDN dataset contains three files, which are known as Ovs.csv, metasploitable-2.csv, and Normal_data.csv. The InSDN dataset contains seven attack classes and one normal class. After preprocessing the InSDN, manually remove some unnecessary features, such as ID, IP address, and so on. Then, the 7 attack types are binary coded as 1, and normal types are coded as 0. The training set and test set are divided for testing. In this experiment, 11,753 data as the training set and 2000 data as the test set are randomly selected for testing. The experimental results are shown in Table 8 and Fig. 7.

Figure 7: Fitness and ROC curve of InSDN. (a) Fitness curve. (b) Roc curve. (c) InSDN result. (d) Confusion matrix

As seen from Table 8, the test results of ICOA are optimized in all the metrics. The accuracy and precision are about 0.3% higher than those of the PSO. The ICOA is 0.4% higher than the COA and GWO for the recall rate. In the F1-score, ICOA is about 0.2%~0.3% higher than the other three algorithms. The number of features in ICOA is only 4, which is half of COA. The highest number of features is PSO, which has 13 features. ICOA also takes the least time, only 0.024 s. As seen in Fig. 7, the convergence speed and accuracy of ICOA are improved compared to COA. At the later iteration stage, ICOA does not easily fall into local optimality and can find better fitness values. From the ROC curve, the ICOA-based feature selection has better classification performance. As shown in the confusion matrix, the ICOA-based intrusion detection approach can accurately identify the data class in SDN networks with a high level of recognition of both normal and intrusion data. From the experimental results on the InSDN dataset, it is clear that ICOA-based AI-integrated feature selection can better optimize SDN network intrusion detection compared to other comparison algorithms.

6.5 Summary of Experiments

In the NSL-KDD dataset, ICOA has the optimal effect for all metrics except precision rate, with an accuracy of 90.062%, which is 0.532% higher than GWO, and the number of features is only 6. In the UNSW_NB15 dataset, ICOA does not have the least number of features, but the accuracy rate is 2.405% higher than GWO and 2.769% higher than COA. In the InSDN dataset, ICOA has the best results for all metrics, including the number of features and runtime, so it is proven from the experiments that the feature selection of ICOA-based AI-integrated can better optimize network intrusion detection.

7  Conclusions and Future Work

The main contribution of this paper is to utilize the ICOA in enhancing AI-integrated feature selection for both traditional network intrusion detection and SDN intrusion detection. Four improvement strategies of the ICOA are proposed according to the shortcomings of the original COA for AI-integrated feature selection. First, the quality of the population is improved by the elite reverse learning strategy in each iteration to accelerate the convergence speed. Second, the Levy flight strategy is added to randomly expand the wandering step length to avoid falling into the local optimum in the late stage. Finally, the exploration phase and the exploitation phase are balanced by the crowding factor, and parameters are adjusted to improve convergence accuracy. By testing the benchmark functions, ICOA can find the optimal value faster and has better optimality-finding ability on both single-peak and multi-peak functions. The feature selection ability of ICOA-based AI-integrated is tested on the UCI dataset with an accuracy of 95.2% on the Ionosphere dataset, 98.2% on the WDBC dataset, and 86.4% on the Heatstatlog dataset, which demonstrates the feature selection ability of the proposed model on all three datasets. In addition, experiments on different network intrusion detection datasets show that ICOA-based AI-integrated feature selection can reduce the number of features and improve the performance of intrusion detection in both traditional and SDN-based networks. For example, the number of features of the ICOA model is only 6 in NSL-KDD, and the number of features in SDN networks is only 4, which is less than all other algorithms. It can be concluded that AI-integrated feature selection based on the ICOA can promote intrusion detection for both SDN and traditional network architectures in a better way compared to other evaluated AI algorithms.

Although this study demonstrates the effectiveness of ICOA-based AI-integrated feature selection for binary classification in traditional and SDN intrusion detection systems, there are several limitations worth discussing:

1.    Multi-classification and binary classification problems: The current experiment only focuses on binary classification experiments. Although it simplifies the evaluation framework, it cannot fully represent the model performance in the real world. However, the feature selection model we proposed can be extended to multi-classification problems.

2.    Parameter sensitivity analysis: Although we use a comparative study and all common parameters are set the same, the impact of key parameters on model performance needs to be systematically studied.

3.    Dataset constraints: Each dataset has certain limitations. Although some limitations have been solved, problems such as limited dataset samples and failure to reflect the actual network status still exist.

Future directions: Apply the model to multi-classification problems, verify parameter sensitivity through experiments, build a real SDN network environment, and collect SDN datasets for experiments.

Acknowledgement: We would like to take this opportunity to express our sincere gratitude to all the reviewers whose valuable insights greatly contributed to the completion of this manuscript.

Funding Statement: This work has been supported by the National Natural Science Foundation of China under Grant 61602162 and the Hubei Provincial Science and Technology Plan Project under Grant 2023BCB041.

Author Contributions: Study conception and design: Hui Xu, Wei Huang, Longtan Bai; data collection: Wei Huang; analysis and interpretation of results: Wei Huang, Hui Xu; draft manuscript preparation: Hui Xu, Wei Huang, Longtan Bai. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The dataset used in this study is openly accessible and reliable. It can be obtained from the following website: ieee-dataport.org/documents/nsl-kdd-0, research.unsw.edu.au/projects/unsw-nb15-dataset and iotseclab.ucd.ie/datasets/SDN/ (accessed on 05 May 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Doost PA, Moghadam SS, Khezri E, Basem A, Trik M. A new intrusion detection method using ensemble classification and feature selection. Sci Rep. 2025;15(1):13642. doi:10.1038/s41598-025-98604-w. [Google Scholar] [PubMed] [CrossRef]

2. Ahanger AS, Khan SM, Masoodi F, Salau AO. Advanced intrusion detection in Internet of Things using graph attention networks. Sci Rep. 2025;15(1):9831. doi:10.1038/s41598-025-94624-8. [Google Scholar] [PubMed] [CrossRef]

3. Hakiri A, Gokhale A, Berthou P, Schmidt DC, Gayraud T. Software-defined networking: challenges and research opportunities for future Internet. Comput Netw. 2014;75(7):453–71. doi:10.1016/j.comnet.2014.10.015. [Google Scholar] [CrossRef]

4. Sandhya, Sinha Y, Haribabu K. A survey: hybrid SDN. J Netw Comput Appl. 2017;100(6):35–55. doi:10.1016/j.jnca.2017.10.003. [Google Scholar] [CrossRef]

5. Kareem SS, Mostafa RR, Hashim FA, El-Bakry HM. An effective feature selection model using hybrid metaheuristic algorithms for IoT intrusion detection. Sensors. 2022;22(4):1396. doi:10.3390/s22041396. [Google Scholar] [PubMed] [CrossRef]

6. Ling Z, Hao ZJ. Intrusion detection using normalized mutual information feature selection and parallel quantum genetic algorithm. Int J Semant Web Inf Syst. 2022;18(1):1–24. doi:10.4018/ijswis.307324. [Google Scholar] [CrossRef]

7. Suresh Babu K, Narasimha Rao Y. Improved monarchy butterfly optimization algorithm (IMBOintrusion detection using mapreduce framework based optimized ANU-Net. Comput Mater Contin. 2023;75(3):5887–909. doi:10.32604/cmc.2023.037486. [Google Scholar] [CrossRef]

8. Alkanhel R, El-kenawy EM, Abdelhamid AA, Ibrahim A, Abdullah Alohali M, Abotaleb M, et al. Network intrusion detection based on feature selection and hybrid metaheuristic optimization. Comput Mater Contin. 2023;74(2):2677–93. doi:10.32604/cmc.2023.033273. [Google Scholar] [CrossRef]

9. Qiu F, Xu H, Li F. Applying modified golden jackal optimization to intrusion detection for software-defined networking. Electron Res Arch. 2024;32(1):418–44. doi:10.3934/era.2024021. [Google Scholar] [CrossRef]

10. Li F, Xu H, Qiu F. Modified artificial rabbits optimization combined with bottlenose dolphin optimizer in feature selection of network intrusion detection. Electron Res Arch. 2024;32(7):4515–6. doi:10.3934/era.2024204. [Google Scholar] [CrossRef]

11. Jia H, Rao H, Wen C, Mirjalili S. Crayfish optimization algorithm. Artif Intell Rev. 2023;56(2):1919–79. doi:10.1007/s10462-023-10567-4. [Google Scholar] [CrossRef]

12. Fakhouri HN, Ishtaiwi A, Makhadmeh SN, Al-Betar MA, Alkhalaileh M. Novel hybrid crayfish optimization algorithm and self-adaptive differential evolution for solving complex optimization problems. Symmetry. 2024;16(7):927. doi:10.3390/sym16070927. [Google Scholar] [CrossRef]

13. Jia H, Zhou X, Zhang J, Abualigah L, Yildiz AR, Hussien AG. Modified crayfish optimization algorithm for solving multiple engineering application problems. Artif Intell Rev. 2024;57(5):127. doi:10.1007/s10462-024-10738-x. [Google Scholar] [CrossRef]

14. Grazioso M, Gallese C, Vanneschi L, Nobile MS. A survey of modern hybrid particle swarm optimization algorithms. In: Applications of evolutionary computation. Cham, Switzerland: Springer Nature; 2025. p. 107–28. doi: 10.1007/978-3-031-90065-5_7. [Google Scholar] [CrossRef]

15. Chen X, Ye C, Zhang Y. Strengthened grey wolf optimization algorithms for numerical optimization tasks and AutoML. Swarm Evol Comput. 2025;94(3):101891. doi:10.1016/j.swevo.2025.101891. [Google Scholar] [CrossRef]

16. Katoch S, Chauhan SS, Kumar V. A review on genetic algorithm: past, present, and future. Multimed Tools Appl. 2021;80(5):8091–126. doi:10.1007/s11042-020-10139-6. [Google Scholar] [PubMed] [CrossRef]

17. Wang R, Zhang S, Zou G. An improved multi-strategy crayfish optimization algorithm for solving numerical optimization problems. Biomimetics. 2024;9(6):361. doi:10.3390/biomimetics9060361. [Google Scholar] [PubMed] [CrossRef]

18. Maiti B, Biswas S, Ezugwu AE, Bera UK, Alzahrani AI, Alblehai F, et al. Enhanced crayfish optimization algorithm with differential evolution’s mutation and crossover strategies for global optimization and engineering applications. Artif Intell Rev. 2025;58(3):69. doi:10.1007/s10462-024-11069-7. [Google Scholar] [CrossRef]

19. Wang B, Zhang Z, Siarry P, Liu X, Królczyk G, Hua D, et al. A nonlinear African vulture optimization algorithm combining Henon chaotic mapping theory and reverse learning competition strategy. Expert Syst Appl. 2024;236:121413. doi:10.1016/j.eswa.2023.121413. [Google Scholar] [CrossRef]

20. Xie C, Li S, Qin X, Fu S, Zhang X. Multiple elite strategy enhanced RIME algorithm for 3D UAV path planning. Sci Rep. 2024;14(1):21734. doi:10.1038/s41598-024-72279-1. [Google Scholar] [PubMed] [CrossRef]

21. Hu G, Song K, Abdel-salam M. Sub-population evolutionary particle swarm optimization with dynamic fitness-distance balance and elite reverse learning for engineering design problems. Adv Eng Softw. 2025;202(1):103866. doi:10.1016/j.advengsoft.2025.103866. [Google Scholar] [CrossRef]

22. Edwards AM, Phillips RA, Watkins NW, Freeman MP, Murphy EJ, Afanasyev V, et al. Revisiting Lévy flight search patterns of wandering albatrosses, bumblebees and deer. Nature. 2007;449(7165):1044–8. doi:10.1038/nature06199. [Google Scholar] [PubMed] [CrossRef]

23. Jensi R, Jiji GW. An enhanced particle swarm optimization with levy flight for global optimization. Appl Soft Comput. 2016;43(23):248–61. doi:10.1016/j.asoc.2016.02.018. [Google Scholar] [CrossRef]

24. Tang H, Xue F. Cuckoo search algorithm with different distribution strategy. Int J Bio Inspired Comput. 2019;13(4):234–41. doi:10.1504/ijbic.2019.100150. [Google Scholar] [CrossRef]

25. Rama Devi R, Abualkibash M. Intrusion detection system classification using different machine learning algorithms on KDD-99 and NSL-KDD datasets—a review paper. Int J Comput Sci Inf Technol. 2019;11(3):65–80. doi:10.5121/ijcsit.2019.11306. [Google Scholar] [CrossRef]

26. Su T, Sun H, Zhu J, Wang S, Li Y. BAT: deep learning methods on network intrusion detection using NSL-KDD dataset. IEEE Access. 2020;8:29575–85. doi:10.1109/access.2020.2972627. [Google Scholar] [CrossRef]

27. Moustafa N, Slay J. UNSW-NB15: a comprehensive data set for network intrusion detection systems (UNSW-NB15 network data set). In: 2015 Military Communications and Information Systems Conference (MilCIS); 2015 Nov 10–12; Canberra, ACT, Australia; 2015. p. 1–6. doi:10.1109/MilCIS.2015.7348942. [Google Scholar] [CrossRef]

28. Al-Daweri MS, Zainol Ariffin KA, Abdullah S, Md Senan MFE. An analysis of the KDD99 and UNSW-NB15 datasets for the intrusion detection system. Symmetry. 2020;12(10):1666. doi:10.3390/sym12101666. [Google Scholar] [CrossRef]

29. Elsayed MS, Le-Khac NA, Jurcut AD. InSDN: a novel SDN intrusion dataset. IEEE Access. 2020;8:165263–84. doi:10.1109/access.2020.3022633. [Google Scholar] [CrossRef]

30. Kou L, Ding S, Wu T, Dong W, Yin Y. An intrusion detection model for drone communication network in SDN environment. Drones. 2022;6(11):342. doi:10.3390/drones6110342. [Google Scholar] [CrossRef]