SAMI-FGSM: Towards Transferable Attacks with Stochastic Gradient Accumulation

1  Introduction

In recent advancements, neural networks have proven to be highly effective for various complex tasks. Notably, their ability to classify images into multiple categories has been one of the most prominent uses [1,2]. Despite their effectiveness, image classification models are vulnerable to adversarial attacks, where imperceptible perturbations are applied to the input data, leading the models to make erroneous predictions. The process of crafting adversarial examples has garnered increasing attention, as studying these examples helps uncover the weaknesses of models, thereby contributing to improving their robustness. However, adversarial examples have also posed significant security threats, particularly in critical applications such as facial recognition [3,4], autonomous driving [5,6], and 3D target detection [7]. Although these difficulties exist, adversarial examples play a vital role in revealing vulnerabilities within neural networks and are key to enhancing the models’ robustness.

Adversarial attack methods are generally classified into two primary types: white-box and black-box attacks. In the case of white-box attacks, the attacker is granted total control over the internal structure and parameters of the target model, allowing for targeted modifications [8,9]. Powerful attacks can be developed by directly creating adversarial examples that leverage the gradient data from a target model. In contrast, black-box attacks often involve studying multiple models, where adversarial examples generated on a surrogate model are transferred to other target models [10]. The ability of adversarial examples to be more effective in black-box attacks is often linked to boosting their transferability across different models. Given that it is often challenging to obtain specific parameters and structural details of target models in real-world scenarios, research on black-box attacks has become increasingly crucial.

Adversarial examples generated under white-box settings have demonstrated outstanding attack performance against models in such settings. Nevertheless, the transferability of these adversarial examples can usually be poor, particularly when applied to models that employ adversarial training or advanced defenses. Several methods for adversarial attacks have been introduced with the aim of boosting the transferability of adversarial examples in black-box settings. For instance, Wang et al. [11] leveraged gradient variance from previous iterations to stabilize the direction of gradient updates, thereby improving the effectiveness of adversarial attacks. Similarly, Wang et al. [12] combined momentum accumulation methods in both spatial and temporal domains by incorporating contextual gradient information from different regions, significantly boosting the attack success rate on most models. Although these methods have proven effective against normally trained models, there remains significant room for improvement in attacking adversarially trained and defended models. Therefore, this study focuses primarily on attacking models with defense capabilities.

In this paper, we introduce a novel attack method named Stochastic Gradient Accumulation Momentum Iterative Attack (SAMI-FGSM). This technique mitigates the overfitting of adversarial examples and enhances their effectiveness against models that have undergone adversarial training and defense mechanisms, by accumulating the stochastic gradient data from each iteration. Specifically, in [11], uniform sampling over a uniform distribution is used to obtain gradient variance information. However, this uniform sampling method can easily suppress the gradient’s update towards the optimal direction, especially for points farther from the sample, which exhibit greater feature differences. To address this, we employ normal distribution sampling because points sampled from a normal distribution are concentrated around the sample point, having feature information similar to that of the sample. This approach further enhances the attack effectiveness compared to the original method. Although traditional momentum or variance tuning methods such as variance tuning momentum iterative fast gradient sign method (VMI-FGSM) stabilize the update direction by introducing gradient variance, they still use uniform distribution sampling and are prone to fall into local optima near highly nonlinear decision boundaries. The normal distribution sampling proposed in this paper captures key feature changes with a higher probability by sampling neighborhood points closer to the original sample, which effectively reduces noise interference and is easier to jump out of local optimum. As depicted in Fig. 1, the sampling method introduced in this paper achieves better attack success rates than uniform sampling on adversarially trained models. Furthermore, to alter the attack direction of the original sample, we aggregate gradient information from the selected points. Most gradient attack and defense work focuses on input transformation or integration of multiple models to improve the diversity and transferability of adversarial samples, but there is still limited performance in adversarial training or robustness enhanced defense models. By combining the historical accumulated gradient with the current normal sampling gradient, SAMI–FGSM takes into account the sensitive area of the model in the update direction, which significantly improves the success rate of attacking multiple defense models. As illustrated in Fig. 2, since decision boundary of model is highly nonlinear, original attack direction targets only one model. By accumulating the gradient from all sampled points, the attack direction can be modified to target both Model 1 and Model 2, thereby enhancing the transferability of adversarial examples.

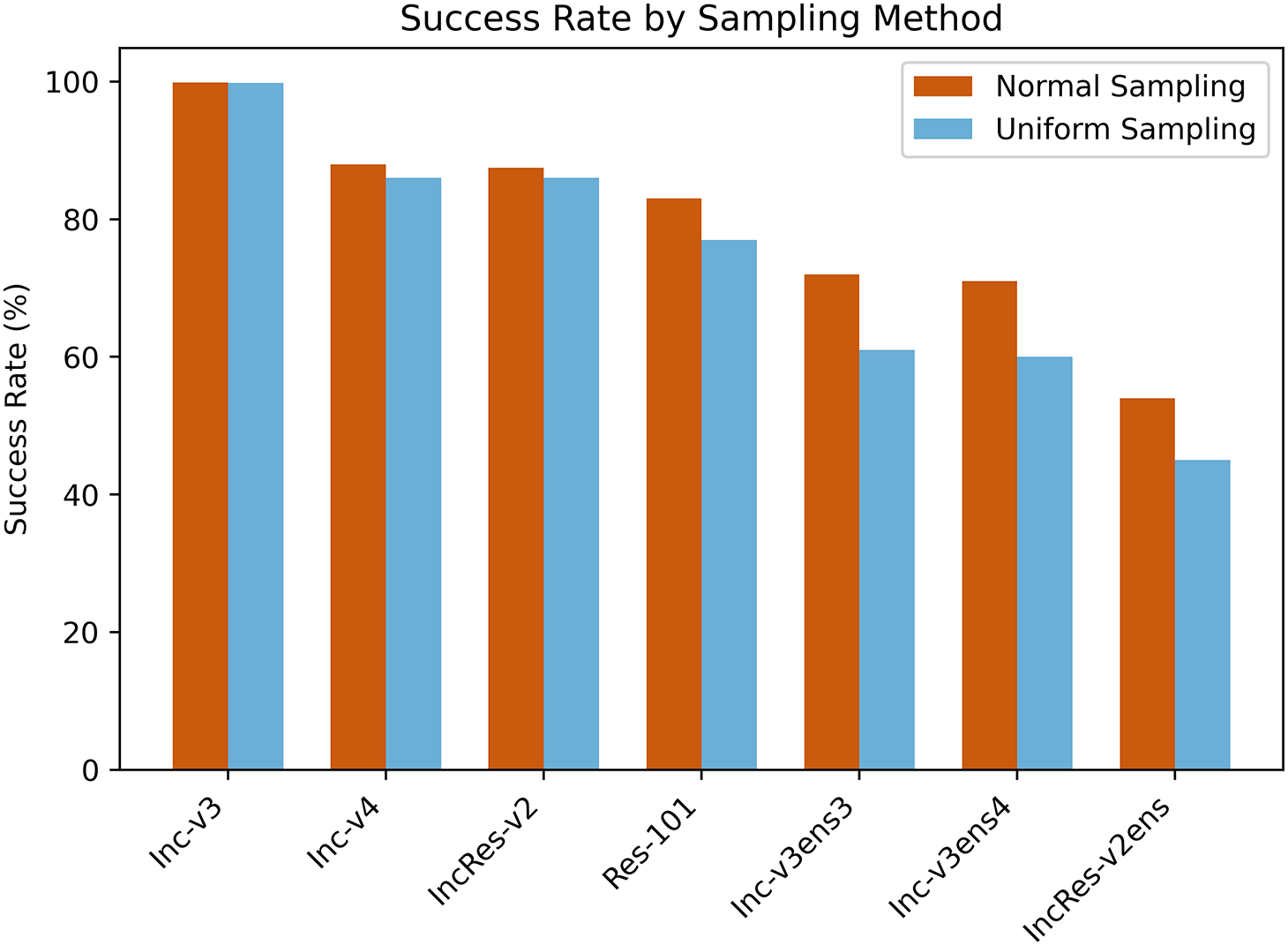
Figure 1: The effectiveness of SAMI-FGSM-based adversarial examples in terms of attack success on the Inc-v3 model. The blue represents uniform sampling, and the red represents normal sampling used in our method. The results clearly demonstrate that normal sampling significantly outperforms uniform sampling

Figure 2: Schematic diagram illustrating our proposed method SAMI-FGSM. The black arrow represents the original attack direction. Our approach optimizes this direction by accumulating gradient information from sampling points near the x samples, enabling simultaneous attacks on both Model 1 and Model 2

The main contributions of this paper are as follows:

•   The traditional uniform sampling approach in variance adjustment often samples features that hinder gradient updates. In this work, we employ normal sampling around the sample points to capture features that enhance attack performance, thereby effectively improving the black-box attack performance of adversarial examples.

•   Additionally, by accumulating the gradient information obtained from stochastic sampling, our method can alter the original attack direction of adversarial examples, steering it closer to the optimal direction. This approach enhances the attack effectiveness of adversarial examples against adversarially trained and defended models.

•   Comprehensive experiments conducted on the ImageNet dataset demonstrate the applicability of our method. The proposed adversarial attack technique outperforms existing methods, as evidenced by the result on various models.

2  Related Work

2.1 Adversarial Attacks

This section classifies gradient-based iterative attacks into two categories: traditional gradient attack methods and those that evolve from gradient-based strategies.

2.1.1 Baseline Based on Gradient Attack

Threats to deep neural networks are typically classified into two types: black-box and white-box attacks. Research into the transferability of adversarial examples is classified as part of black-box attack techniques, where the attacker is unable to access details such as the parameters or structure of the victim model. Additionally, black-box attacks can target multiple other models simultaneously, making black-box transferability methods highly sought after. Fast Gradient Sign Method (FGSM) [13], originally developed for white-box attacks, inspired the creation of iterative gradient-based methods tailored for black-box research. This, in turn, spurred the quick advancement of more effective techniques to improve transferability in black-box settings. Dong et al. [14] integrated momentum in gradient-based iterative attacks, while Liu et al. [15] combined the accelerated gradient of Nesterov with gradient attack methods using a momentum-based approach. Wang et al. [11] addressed the issue of local optima by utilizing the gradient variance from earlier steps in the iteration process, and Wang et al. [12] integrated spatial domain gradients within images with earlier work that concentrated on temporal domain gradients. Global momentum initialization is used by Wang et al. [16] to improve update direction stability.

2.1.2 Gradient Attack-Based Derivation

Since gradient-based adversarial attacks were first introduced, numerous methods have been developed along this baseline. In addition, several methods derived from this baseline have been thoroughly examined, typically combined with the original approaches to create adversarial examples that offer better transferability. As an example, Li et al. [17] successfully used the optimization process of multi-step attacks to produce adversarial examples with higher black-box success rates by predicting induced adversarial losses through linear mapping of intermediate-level discrepancies. In order to create adversarial examples with better transferability against both normally trained and defended models, Long et al. [18] presented a novel spectral simulation attack that applies spectral transformations to the inputs and performs model enhancement in the frequency domain. Large step-size updates were used for adversarial examples by Yang et al. [19], who calculated several samples with small step sizes within each large step and then averaged the gradients of these samples. By reducing the discrepancy between the true update direction and the steepest descent direction, this method improves the transferability of the resulting adversarial examples.

2.1.3 Attacks Based on Feature Destruction

In recent years, attacks on the feature space of models have been extensively studied. For example, Wang et al. [20] proposed the Feature Importance-aware Attack (FIA), which focuses on disrupting important object-related features that play a major role in model’s decision-making, resulting in adversarial examples with improved transferability. Huang et al. [21] focused on augmenting perturbations on designated layers of the source model to adjust existing adversarial examples for better performance in black-box settings. Zhu et al. [22] refine the gradient by averaging it over several nearby data points, and subsequently modify the update gradient with a decay indicator. These methods show that destroying the high-level semantic features of the model or optimizing the middle layer differences can significantly improve the black box attack effect.

2.1.4 Attacks Based on Input Transformation

Diverse Inputs (DI) attack [23] generates diverse input patterns by using arbitrary changes on the input samples at every iteration, where the random transformations consist of a certain probability to perform random resizing and padding, resulting in adversarial examples that exhibit greater randomness and enhanced transferability. Translation-Invariant (TI) attack [24] approximates the gradient by applying a fixed kernel matrix to the gradient of an untranslated image. Each iteration requires a gradient computation as the image is subtly shifted. Thus produced adversarial examples to deceive another model with higher probability. The Scale-Invariant (SI) attack [15] presents scale invariance by scaling a collection of input images by an element of 1/2i (i signifies the hyperparameter), and optimizing the gradient of this set of images with the gradient of input images to create adversarial examples with transferability.

2.2 Adversarial Defense

The threat posed by adversarial examples to deep neural networks has driven the design of more sophisticated defense mechanisms [25]. Tramér et al. [26] proposed separating the generation of adversarial examples from model parameter training, aiming to increase perturbation diversity during training while reducing the dimensionality of the adversarial examples. A fast adversarial training technique was proposed by Shafahi et al. [27], which simultaneously updates the model parameters and image perturbations within one iteration, achieving a training speed 3 to 30 times faster than traditional approaches. In their work, Gokhale et al. [28] developed an adversarial training approach that creates novel samples, maximizing the classifier’s exposure to the attribute space, all without relying on test domain data. The min-max optimization problem is tackled by this adversarial training approach, which first optimizes the loss from adversarial perturbations in the inner maximization phase and then finds the best model parameters in the outer minimization phase.

Currently, one of the best techniques for increasing model robustness is adversarial training; however, it faces challenges related to increased training costs, particularly on large-scale datasets. To address the high computational costs, recent studies have focused on designing efficient methods to enhance model robustness. Naseer et al. [29] developed a NRP model, which uses self-derived supervision to learn to purify images from adversarial interference. To identify hostile examples, Xu et al. [30] developed two feature squeezing methods: Bit Reduction (Bit Red) and Spatial Smoothing. In response to adversarial inputs, Feature Distillation (FD) [31] was introduced as a defense system utilizing JPEG compression.

3  Methodology

This section begins with a definition of adversarial attacks, followed by an introduction to the baseline gradient-based methods. We also explain the underlying motivation for our research and describe the proposed Stochastic Gradient Accumulation Momentum Iterative Attack method, drawing connections to previous attack approaches.

3.1 Explanation of Adversarial Attack

Adversarial attacks involve generating an adversarial example xadv from a clean sample x using a classifier f with parameters θ. The crafted adversarial example xadv causes the classifier f to produce incorrect classifications, i.e., f(x;θ)≠f(xadv;θ), where f(x;θ) represents the output of the deep neural network (DNN), often denoted by y. The loss function of the classifier f is represented as J(x,y,θ). The generated adversarial example must satisfy the constraint ||xadv−x||p≤ϵ, where ϵ is the constraint value, and ||⋅||p denotes the p-norm distance, with p typically being 0, 2, or ∞. In this work, consistent with previous studies [11], we set p=∞. The specific definition is given as:

fθ(xadv)≠y,s.t.||xadv−x||p≤ϵ(1)

3.2 Gradient-Based Attack

Following the introduction of the Fast Gradient Sign Method (FGSM) [13], iterative refinements in gradient-based adversarial attacks have resulted in the creation of advanced techniques, including SM2I-FGSM [12]. All of these methods rely on gradient optimization. The gradient-based optimization family includes FGSM [13], I-FGSM [32], MI-FGSM [14], NI-FGSM [15], VNI-FGSM [11], VMI-FGSM [11], and SM2I-FGSM [12].

Fast Gradient Sign Method (FGSM) [13] as the earliest proposed gradient-based attack, generates adversarial examples by inputting a clean sample x into the network and performing a single update based on the loss function J(xadv,y,θ). The loss function is only calculated once in the adversarial example. The following is the particular generation process:

xadv=x+ϵ⋅sign(∇xJ(x,y,θ))(2)

where ∇x denotes the gradient with respect to x, J(⋅) represents the loss function, sign(⋅) is the function that computes the sign of the gradient ∇x, and ϵ is the perturbation magnitude.

Iterative Fast Gradient Sign Method (I-FGSM) [32] extends the single-step method FGSM to a multi-step attack by introducing a step parameter α:

xt+1adv=xtadv+α⋅sign(∇xtadvJ(xtadv,y;θ))(3)

where x0adv=x, x is a clean sample, α=ϵ/T, ϵ is the perturbation size, and T is the iteration count.

Momentum Iterative Fast Gradient Sign Method (MI-FGSM) [14] introduces the momentum factor μ collects the gradient of every iteration of I-FGSM as momentum in the next gradient calculation:

gt=μ⋅gt−1+∇xtadvJ(xtadv,y;θ)||∇xtadvJ(xtadv,y;θ)||1(4)

xt+1adv=xtadv+α⋅sign(gt)(5)

where  g0=0, μ is the momentum element, and gt is the sum of the current gradient and μ times (t − 1) the next gradient.

Nesterov Iterative Fast Gradient Sign Method (NI-FGSM) [15] introduces the idea of Nesterov Gradient Descent (NAG) by replacing all xtadv in Eq. (4) with xtadv+α⋅μ⋅gt when calculating xt+1adv to additional strengthen the black-box aggressiveness of MI-FGSM.

Variance momentum Iterative Fast Gradient Sign Method (VMI-FGSM) [11] steady the updated guidance of the present gradient by incorporating the gradient variance details from the prior round of iterations:

gt+1=μ⋅gt+∇xtadvJ(xtadv,y;θ)+vt||∇xtadvJ(xtadv,y;θ)+vt||1(6)

xt+1adv=xtadv+α⋅sign(gt+1)(7)

where  vt+1=1N∑i=1N∇xiJ(xi,y;θ)−∇xJ(x,y;θ), xi is a random sample within a specific range of x uniform distribution.

Spatial Momentum Iterative Fast Gradient Sign Method (SM2I-FGSM) [12] considers contextual gradient knowledge in various image regions, introducing a momentum accumulation system from the timing to the spatial domain, with the gradient updated as:

gt+1s=∑i=1nλi∇xJ(Hi(xtadv),y)(8)

xt+1adv=xtadv+α⋅sign(gt+1s)(9)

where Hi(.) represents the random resizing and padding used to transform xtadv, n denotes the number of transformations in the spatial domain, and λi denotes the weight of the gradient.

3.3 Stochastic Gradient Accumulation Method

Deep neural networks often exhibit complex forms when handling high-dimensional classification tasks due to the highly nonlinear and often high-curvature nature of their decision boundaries. Fig. 2 illustrates the high curvature of Model 1 and Model 2’s decision boundaries. To induce misclassification in both Model 1 and Model 2, our goal is to generate an adversarial example x that identifies the optimal attack direction during its creation. The current techniques for generating adversarial examples struggle in transferring attacks to other models because of the pronounced curvature in the decision boundary. In contrast, robust models feature smoother decision boundaries, which significantly weakens the impact of adversarial attacks against defensive and adversarially trained model.

Our goal is to improve the black-box transferability of adversarial examples by refining the attack direction, steering it towards a more aggressive path. Inspired by VMI-FGSM [11], we investigate the gradient information of a uniform distribution around the sample during the iterative process, effectively improving the transferability of the final adversarial example. Building on this, we consider sample feature information closer to the surrounding sample points, which shares similarities with the feature information of the sampling points. By setting the sampling point as the center of a normal distribution, we can sample misleading features near the sample point with maximum probability. Due to the concentration of the normal distribution around the sample point, most sampled points exhibit features that are more closely aligned with the original examples. In adversarial attacks, critical feature variations often occur near the model’s decision boundary. The localized focus of the normal distribution increases the likelihood of sampling points that are closer to these critical regions, thereby providing more informative guidance for gradient optimization. This focus reduces deviations in gradient update directions, resulting in smoother and more stable gradient variations, which enhance the generalization and cross-model transferability of adversarial perturbations. Furthermore, the localized sampling characteristic of the normal distribution mitigates the interference of high-curvature decision boundaries on gradient updates, particularly in adversarially trained models, thereby improving the accuracy of gradient update directions and the overall attack effectiveness. In contrast, uniform distribution sampling generates points randomly across the entire sampling range, which may result in sampled points with features that deviate from the original examples, introducing noise and irrelevant information into the optimization process. As shown in Fig. 1, the comparison of the two sampling methods clearly demonstrates that normal sampling outperforms uniform sampling on adversarially trained models. To boost the attack power of the adversarial example, we add gradient information from the original sample as noise to image. This is achieved by performing random sampling around the sample’s point based on a normal distribution and aggregating the gradients obtained from this sampling.

Based on this, we present a new attack method called Stochastic Gradient Accumulation Momentum Iterative Attack (SAMI-FGSM). At each iteration, the method combines the gradient information from the earlier step to ensure a more stable gradient direction, effectively smoothing the update direction. Additionally, during the calculation of accumulated gradient information, it incorporates sample gradient information from a specific normal distribution range. The specific implementation of the proposed SAMI-FGSM method is as follows:

Definition: Given a classifier f with parameters θ and a loss function J(x′,y;θ), the gradient accumulation can be described as follows:

A(x)=∑i=1N∇xiJ(xi,y;θ) (10)

where xi=x+ri ri∼N(0,(δ⋅ϵ)d), and N(0,(δ⋅ϵ)d) denotes a d-dimensional normal distribution. After obtaining the random gradient information from the (t − 1)-th iteration through the above process, this information is used to adjust the gradient of xtadv in the t-th iteration, thereby stabilizing the gradient update direction more effectively. Specifically, At+1 aggregates the gradients of all sampled points in the current iteration, and this accumulation affects the gradient update in the following ways:

Stable direction: The historical gradient information (At) is combined with the current gradient to smooth the randomness of the single gradient update and avoid falling into local optimum.

Enhanced generalization: The gradient mean of multiple sampling points implies the local geometric characteristics of the decision boundary of the model, so that the attack direction is more suitable for the boundary differences of different models.

The complete process of the proposed stochastic gradient accumulation method is described in Algorithm 1, referred to as SAMI-FGSM. The method proposed here demonstrates optimal performance along the primary path of gradient-based attacks and is compatible with various derivative techniques, such as frequency domain attacks [18] and adaptive targeted attacks [33]. Furthermore, the proposed method is compatible with a variety of existing methods such as DIM attacks, TIM attacks, and SIM attacks.

3.4 Differences from Existing Attacks

Derivative methods based on gradient attacks primarily originate from FGSM. This section provides an overview of the key gradient-based attack techniques, as illustrated in Fig. 3. If the domain upper bound δ is set to 0, SAMI-FGSM degenerates into MI-FGSM. In the same way, setting the decay factor μ to 0 and limiting the number of iterations T to 1 results in these methods returning to the standard FGSM. Moreover, the aforementioned gradient-based attack methods are capable of being integrated with many input transformations, such as DIM, SIM, and TIM, to enhance the transferability of adversarial examples.

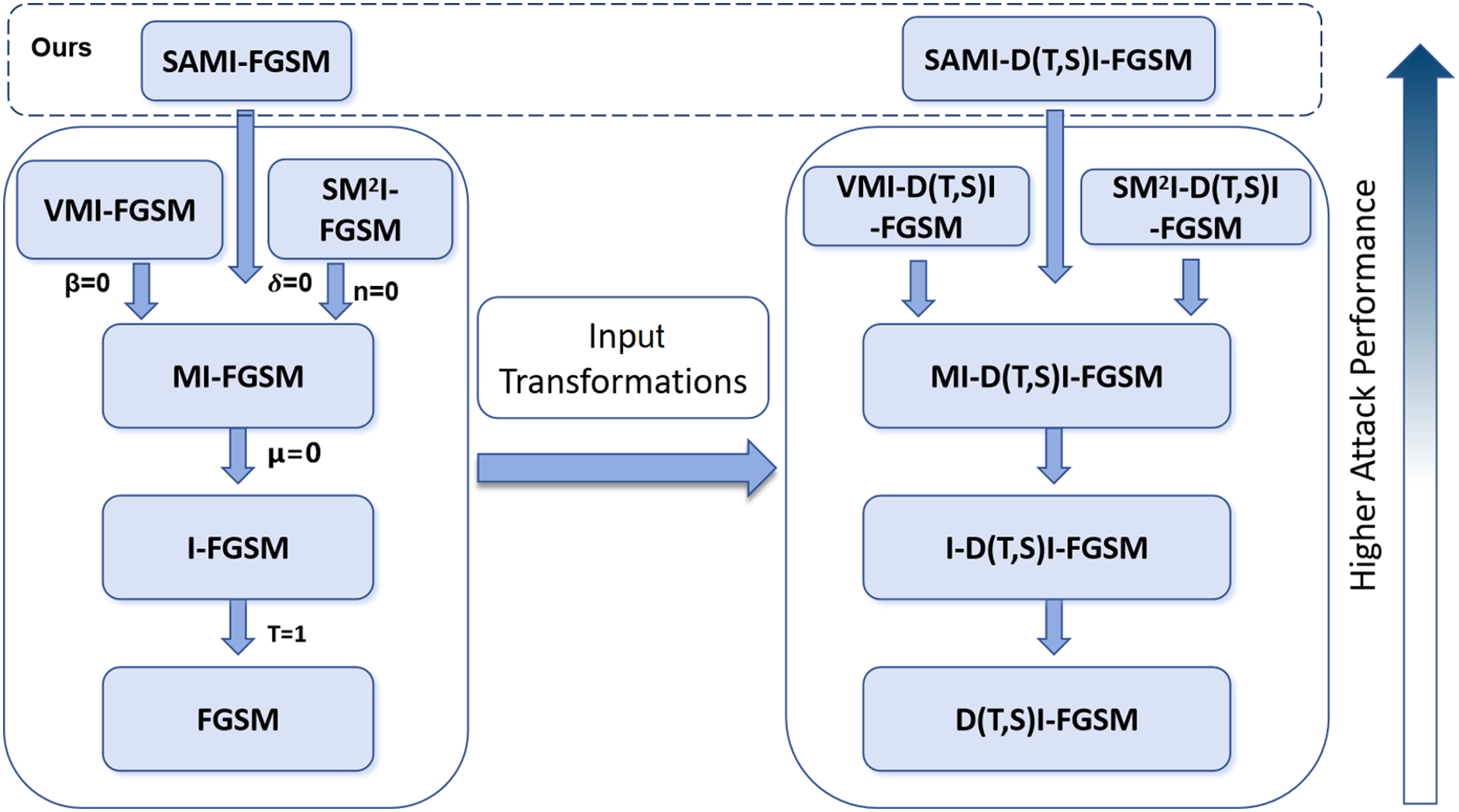
Figure 3: Linkages between various adversarial attacks

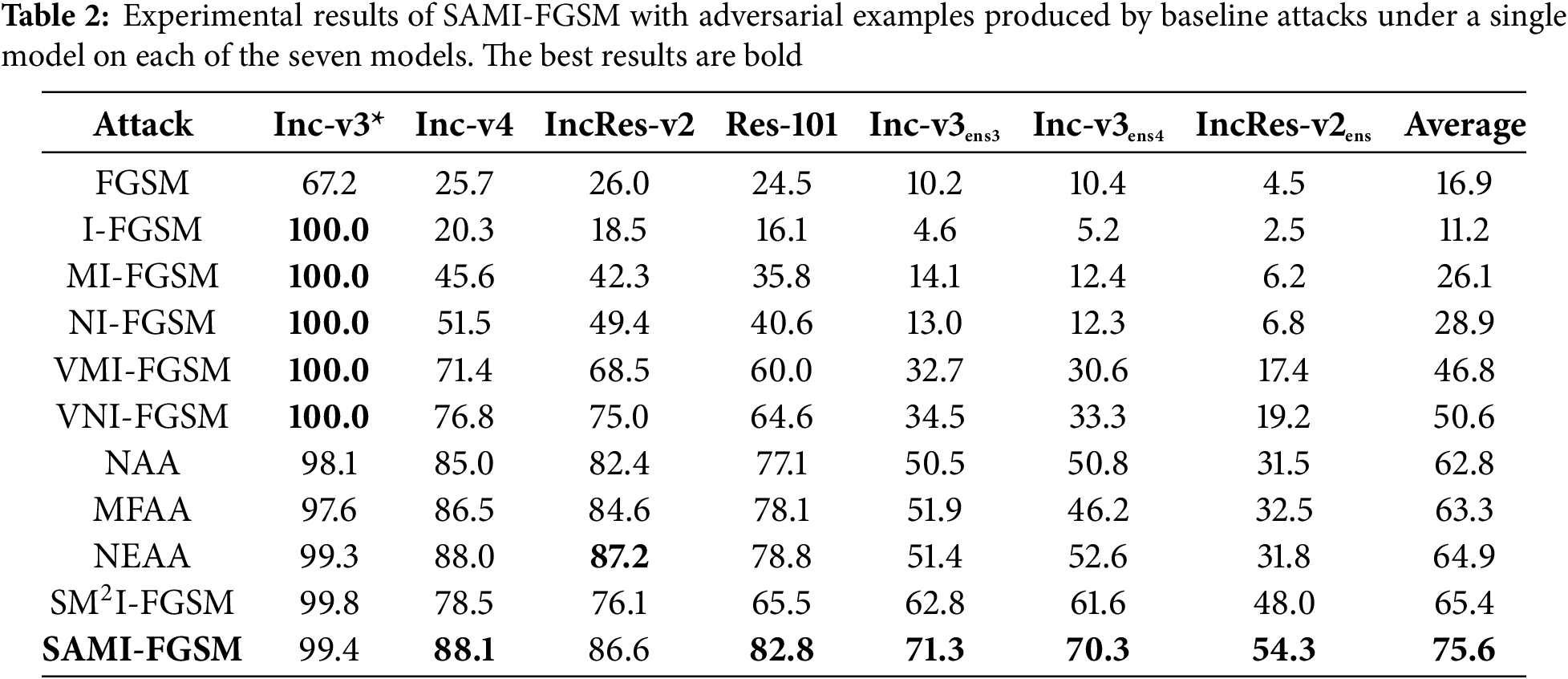
Finally, the framework design of SAMI-FGSM is inspired by VMI-FGSM and inherits the key ideas in VMI-FGSM in design. While SAMI-FGSM and VMI-FGSM are on the same level, SAMI-FGSM simplifies the approach of VMI-FGSM and reduces computational overhead. The contribution of SAMI-FGSM is not a simple combination of existing techniques, but through normal sampling theory and gradient accumulation mechanism, it solves the fundamental limitations of traditional methods in local optimum trap and defense model attack efficiency. As presented in Table 2, the proposed method generates adversarial examples for Inc-v3 that achieve the highest average attack success rate compared to six other models.

4  Experiments

This section begins with a comprehensive description of the datasets and models employed in the experiments. Next, a comprehensive comparison is made between the proposed approach and baseline attacks, focusing on single models and various input transformations. The experimental findings clearly show the advantages of our method. The impact of adversarial examples produced by our approach in comparison to three baseline attacks is shown in Fig. 4. Fig. 5 illustrates the attention heatmaps of the original image and the adversarial examples generated by SAMI-FGSM on the Inc-v3 model. Finally, we discuss the parameter ablation study conducted on the proposed SAMI-FGSM. It is important to remember that the average success attack rates reported in all tables represent black-box attack performance, with (*) indicating the results on white-box models.

Figure 4: The original image is shown in the first column, while the sample effect image of the confrontation created by our SAMI-FGSM method and the three baseline attacks on Inc-v3 model is shown in the remaining column. It is obvious that our method’s attacks have a larger success rate than the baselines, yet the difference in visualization remains minimal

Figure 5: Examples of model attention heatmaps generated by Grad-CAM [34] are used for clean images and for SAMI-FGSM generated adversarial examples

4.1 Experimental Setup

Dataset. Based on earlier works [11,14,15,23], we randomly selected one image from every one of the 1000 categories in the ILSVRC2012 validation set, each selected image was able to be correctly categorized in all models in that paper. We also list other mainstream datasets, as shown in Table 1. In the standardized adversarial attack research, ILSVRC2012 still has the only unified benchmark; Although other large-scale or diverse datasets have more advantages in the number of categories, they have not yet formed a unified evaluation standard in the adversarial attack community or the computational cost is too high.

Models. To better contrast our method with the existing dominant methods, seven naturally trained models are used, four of which are typically trained models are Inception-v3 (Inc-v3) [35], Inception-v4 (Inc-v4) [36], Inception-Resnet-v2 (IncRes-v2) [36], Resnet-v2-101 (Res-101) [37], as well as three adversary-trained models that have been trained using adversarial examples, namely, ens3-adv-Inception-v3 (Inc-v3ens3) [26], ens4-Inception-v3 (Inc-v3ens4) [26], and ens-adv-Inception-ResNet-v2 (IncRes-v2ens) [26]. In the experiment of this paper, every one of these models functioned as a stand-in model to produce adversarial examples. In addition to the above CNNs, we also use transformer-based architectures including ViT [38], PiT [39], Visformer [40], Swin [41]. Besides, we utilized three cutting-edge defensive models to evaluate our strategy’s attack performance: Neural Representation Purifier (NRP) [29], Bit-Reduction (Bit-Red) [30], Feature Distillation (FD) [31], Resize and Padding (RP) [42], HGD [43], and RS [44].

Baseline. We consider eight gradient-based attacks as our baselines, including MI-FGSM, NI-FGSM, VMI-FGSM, SM2I-FGSM, NEAA [45], NAA [46] and MFAA [47]. Additionally, our method can be paired with various common input transformation attacks to test its compatibility and effectiveness.

Hyperparameters. The parameters used in our experiments are consistent with those in the baseline attack methods. Specifically, the number of iterations, maximum perturbation, and step size are set to T = 10, ϵ = 16/255, α = 1.6/255, respectively. For the gradient-based momentum term (decay factor) in the baseline attacks, it is set to 1.0. For the three input transformation methods, the parameter settings are as follows: DIM has a transformation probability of 0.5, SIM involves 5 scale copies, and TIM uses a Gaussian kernel of size 7 × 7, as established in previous studies. For VM(N)I-FGSM, the settings are consistent with the optimal attack performance reported in [11], where the domain upper bound factor β is set to 1.5, and the number of samples for variance adjustment N is set to 20. For the method we propose, based on stochastic gradient accumulation, the sample size drawn from normal distribution is N = 500, and the upper limit for sampling is set to 5/2.

4.2 Attack a Single Model

In this part, we tested several baseline methods and our proposed Stochastic Gradient Accumulation Momentum Iterative Attack (SAMI-FGSM) on individual deep neural network models. Table 2 shows that the Inc-v3 model was initially used to generate adversarial examples for the experiments. The adversarial examples were generated on the Inc-v3, Inc-v4, and IRes-v2 models, and then evaluated on eight different models, comprising one white-box model, two models trained without defenses, two adversarially trained defense models, and three models with advanced defensive techniques. Table 3 demonstrates that our SAMI-FGSM technique surpasses every baseline method in terms of attack success rates.

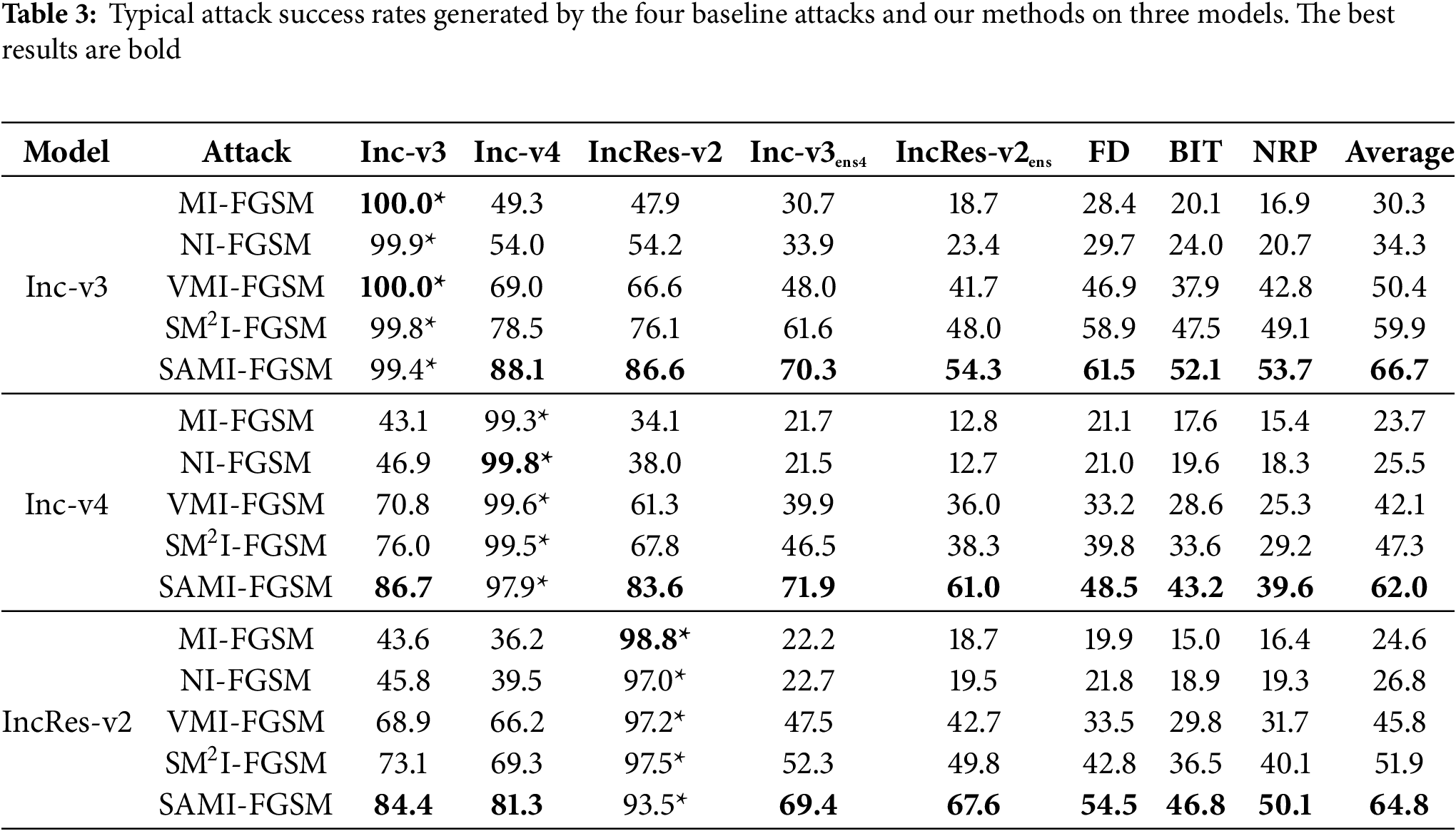
4.3 Attack with Input Transformations

To increase the efficacy of adversarial attacks, Wang et al. [11] demonstrated through experiments that DI (DIM), SI (SIM), and TI (TIM) attacks can be integrated into a composite transformation approach (DTS). This method, which integrates multiple transformations, can be paired with gradient-based attack techniques, resulting in enhanced attack success rates. Our approach, the Stochastic Gradient Accumulation Momentum Iterative method (SAMI-FGSM), focuses on improving the transferability of adversarial examples. We validate that our approach is just as applicable as classical gradient-based methods by combining this method with composite transformation techniques. Table 4 demonstrates that combining our method with different input transformations consistently improves attack performance.

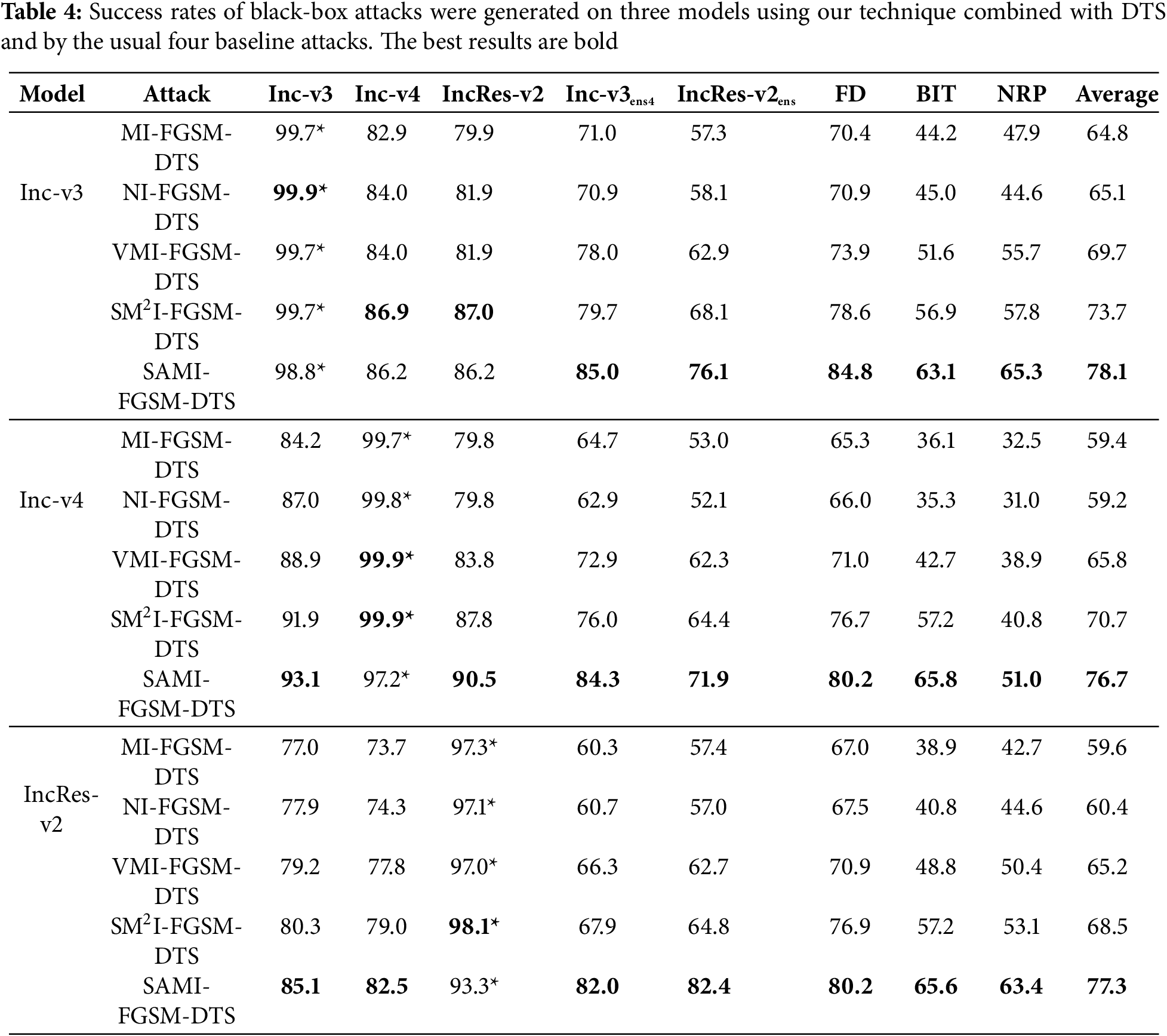
4.4 Attack an Ensemble of Models

Through the integration of multiple models, Liu et al. [48] demonstrated that such an approach boosts the attack performance of adversarial examples, significantly increasing their transferability. Typically, there exist three kinds of ensemble methods: ensemble at the prediction level, ensemble at the logit level, and ensemble within the loss function. In this work, we utilize the logit ensemble method, where we average the logit outputs from the Inc-v3, Inc-v4, and IncRes-v2 models. By making a slight sacrifice in attack performance in white-box attacks, we gain enhanced transferability in black-box attacks, where our proposed method exhibits optimal performance. We conduct experiments on two adversarially trained defense models, and six models with advanced defensive techniques, in Table 5, the upper section reports the success attack rates (%) of four baseline attacks and our proposed method across three ensemble models, while the lower section shows the results when combined with DTS. Additionally, we combine the composite transformation method (DTS) with the ensemble approach to confirm the generality of our proposed approach. Compared to the four standard gradient-based attack techniques, our approach delivers superior performance, achieving an average success rate of 88.9%.

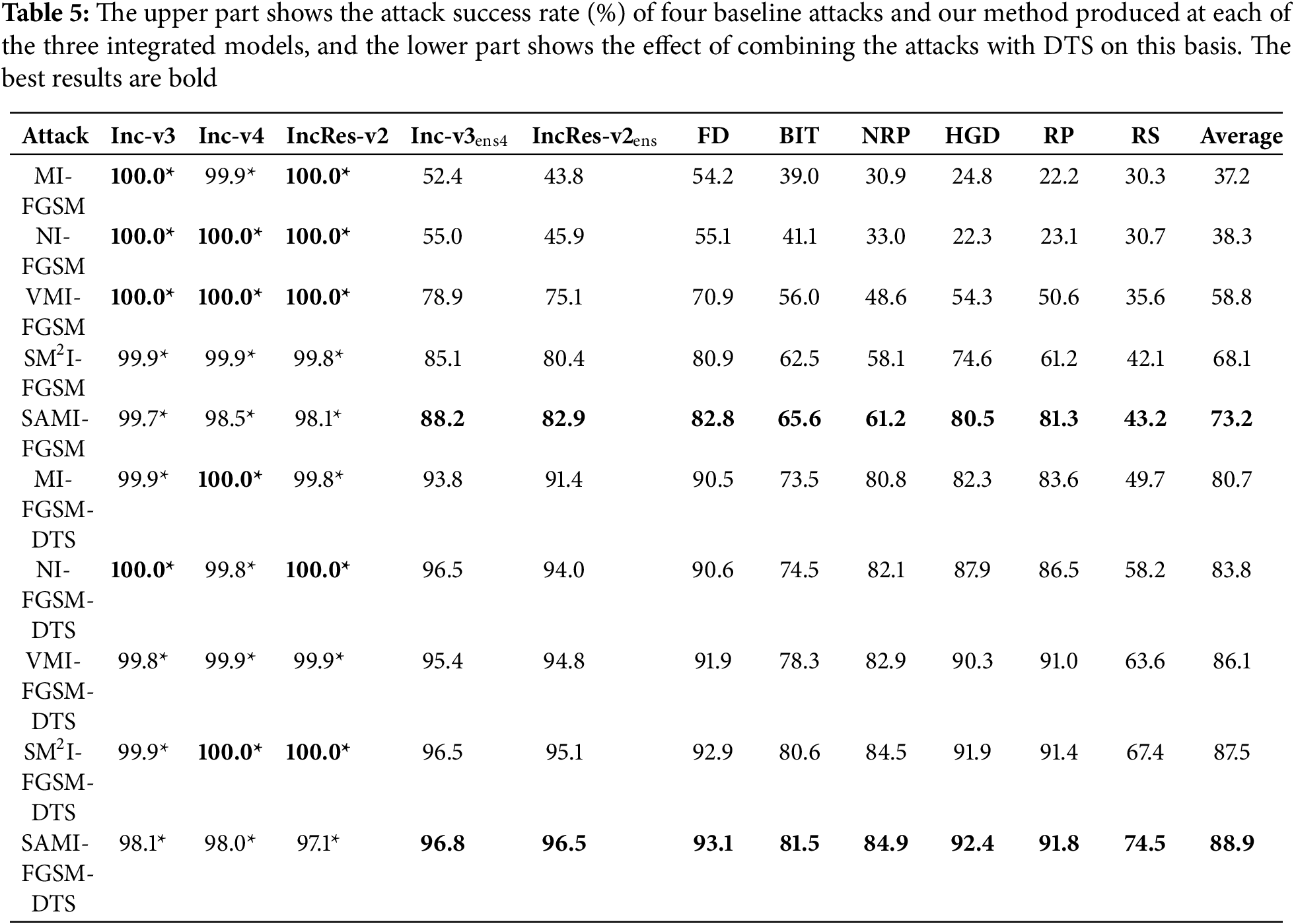
Notably, our method consistently outperforms others on both single and ensemble models, demonstrating its effectiveness and highlighting the vulnerability of current defense models.

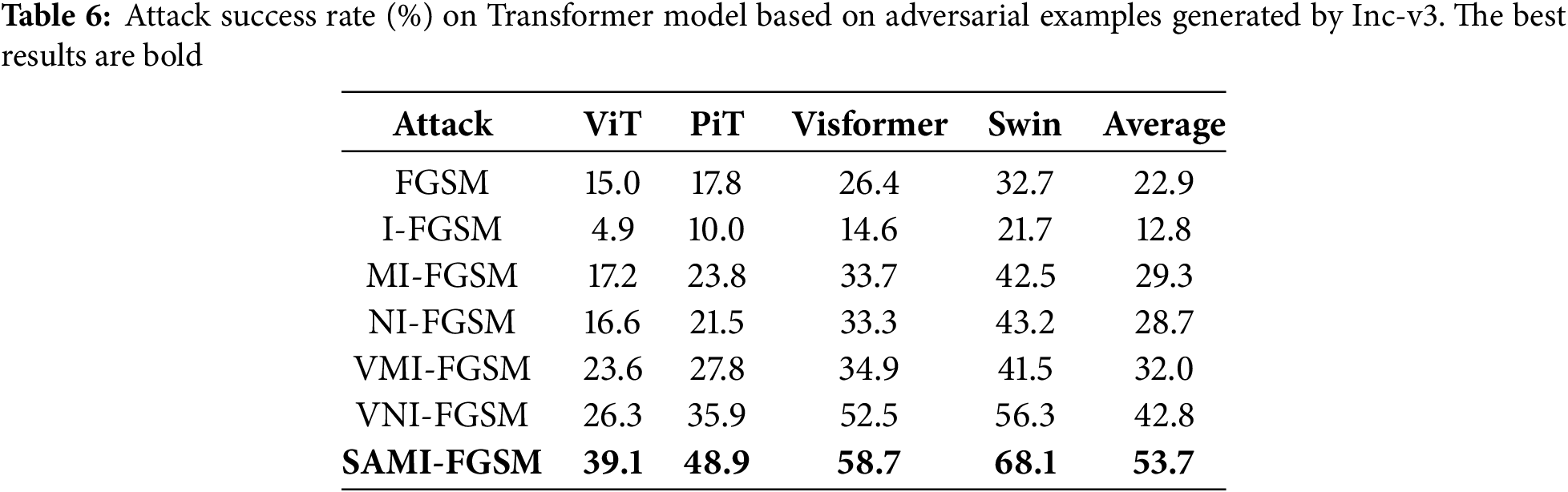
4.5 Attack a Transformer Architecture Model

In order to verify the generalization ability of SAMI-FGSM on Transformer architecture models, four typical vision Transformer models are selected as target models in this section: ViT, PiT, Visformer, and Swin Transformer. The experiment uses Inc-v3 as the source model to generate adversarial samples, and the attack results are shown in Table 6. The average attack success rate of SAMI-FGSM on four Transformer models reaches 53.7%, which is 21.7% and 10.9% higher than the baseline methods VMI-FGSM (32.0%) and VNI-FGSM (42.8%), respectively. Experiments show that SAMI-FGSM has significant advantages on the Transformer architecture model.

4.6 Statistical Significance Test

To ensure the statistical reliability of the results, we performed a paired t-test between SAMI-FGSM and the baseline method, and each attack experiment was independently repeated 10 times. The significance test was performed using a two-sample t-test with significance level α = 0.05 to verify whether the performance difference between SAMI-FGSM and baseline methods was significant. As shown in Table 7, The two-sample t-test shows that SAMI-FGSM has a significantly higher attack success rate than VMI-FGSM on the defense model. In addition, in the cross-model transfer scenario, the average success rate of SAMI-FGSM is 28.8% higher than that of the baseline method, indicating that its performance improvement is highly stable.

4.7 Evaluation of Disturbance Perceptibility and Verification of Robustness to Input Transformations

We invite 20 subjects to blind test 100 pairs of original/adversarial examples. The experimental results show that less than 10% of the samples are correctly distinguished by the subjects, which further verifies the perceptual imperceptibility of SAM I-FGSM under the constraint of ϵ = 16/255. In addition, we also tested the robustness of perturbation to Gaussian noise (σ = 0.1), motion blur (kernel = 5 * 5) and random cropping (20%). As shown in Table 8, the proposed method has strong robustness to noise, blurring and cropping on the premise of maintaining low perception.

4.8 Parameters Ablation Study

This section presents ablation studies on two parameters of SAMI-FGSM to assess its effectiveness. First, we assess the influence of the two parameters, sampling limit δ and sampling number N, on the attack performance of SAMI-FGSM. To evaluate the influence of these hyperparameters, adversarial examples are created Utilizing Inc-v3 as a source model, with default settings of δ = 5/2 and N = 500.

Sampling Limit δ: As shown in Fig. 6, we analyze how the sampling limit δ in the normal distribution affects the performance of black-box transferability. The left plot shows adversarial examples generated using Inc-v3, while the right plot shows results on the Inc-v4 model. The sampling number N is fixed at 500. When δ = 0, SAMI-FGSM degenerates into MI-FGSM, resulting in lower transferability. When δ = 1/5, despite the small sampling limit, SAMI-FGSM exhibits a significant improvement in attack performance. When δ = 5/2, our method achieves optimal attack performance, showing excellent effectiveness even against several defense models. Finally, as δ increases further, the attack performance of the proposed method gradually decreases. δ controls the normal sampling limit, and its value needs to maintain a proportional relationship with the perturbation constraint value ϵ. When δ = 5/2, it ensures that the sampling points not only contain local feature disturbances, but also avoids the introduction of irrelevant noise due to the large range. Therefore, δ = 5/2 is chosen for all experiments in this study.

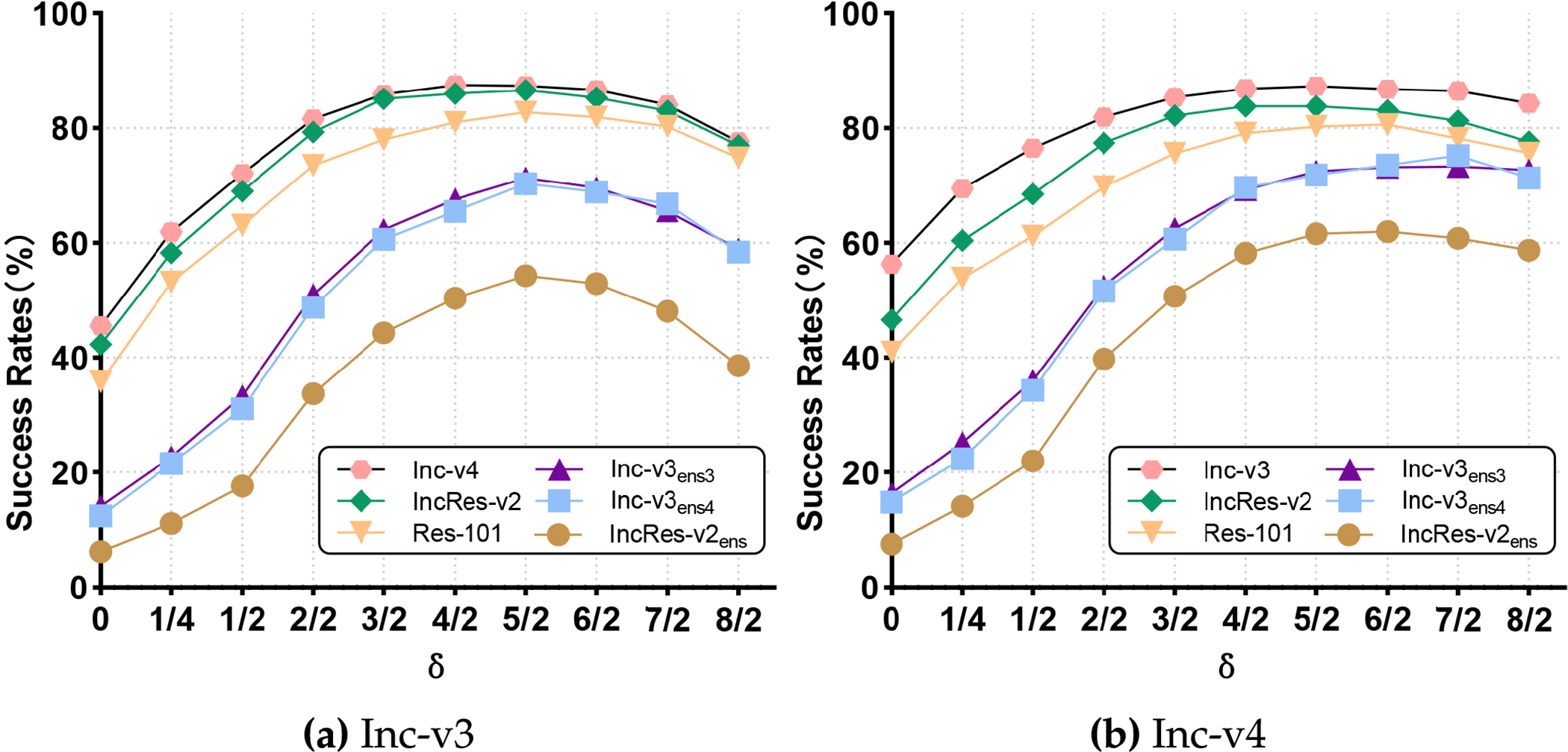
Figure 6: Success rate of transferability attacks on the remaining six models by SAMI-FGSM produced adversarial examples on Inc-v3 or Inc-v4 when δ is changed

Sample Size N: Next, we examine how the number of samples (N) in the neighborhood affects the transferability of adversarial examples. As seen in Fig. 7, the left plot represents adversarial examples created using Inc-v3, while the right plot shows outcomes on the Inc-v4 model. The sampling limit δ is set to 5/2 by default. Our approach also degenerates into MI-FGSM when N = 0. The attack performance of our method will be significantly affected by the sampling number when N = 20, with the effectiveness of the black-box attack increasing significantly as N increases. Our method achieves near-optimal attack performance at N = 500. Although there is a slight increase in success attack rates with further increases in N, each iteration requires extensive sampling and gradient computation. As shown in Table 9, when N increases from 500 to 1000, the average attack success rate increases by 1.9%, but the running time increases by 98.2%. When N > 500, the success rate increases slowly, while the time cost increases significantly. Thus, a larger N results in higher computational costs. In our experiments, we set N = 500 to strike a compromise between attack success and computational efficiency.

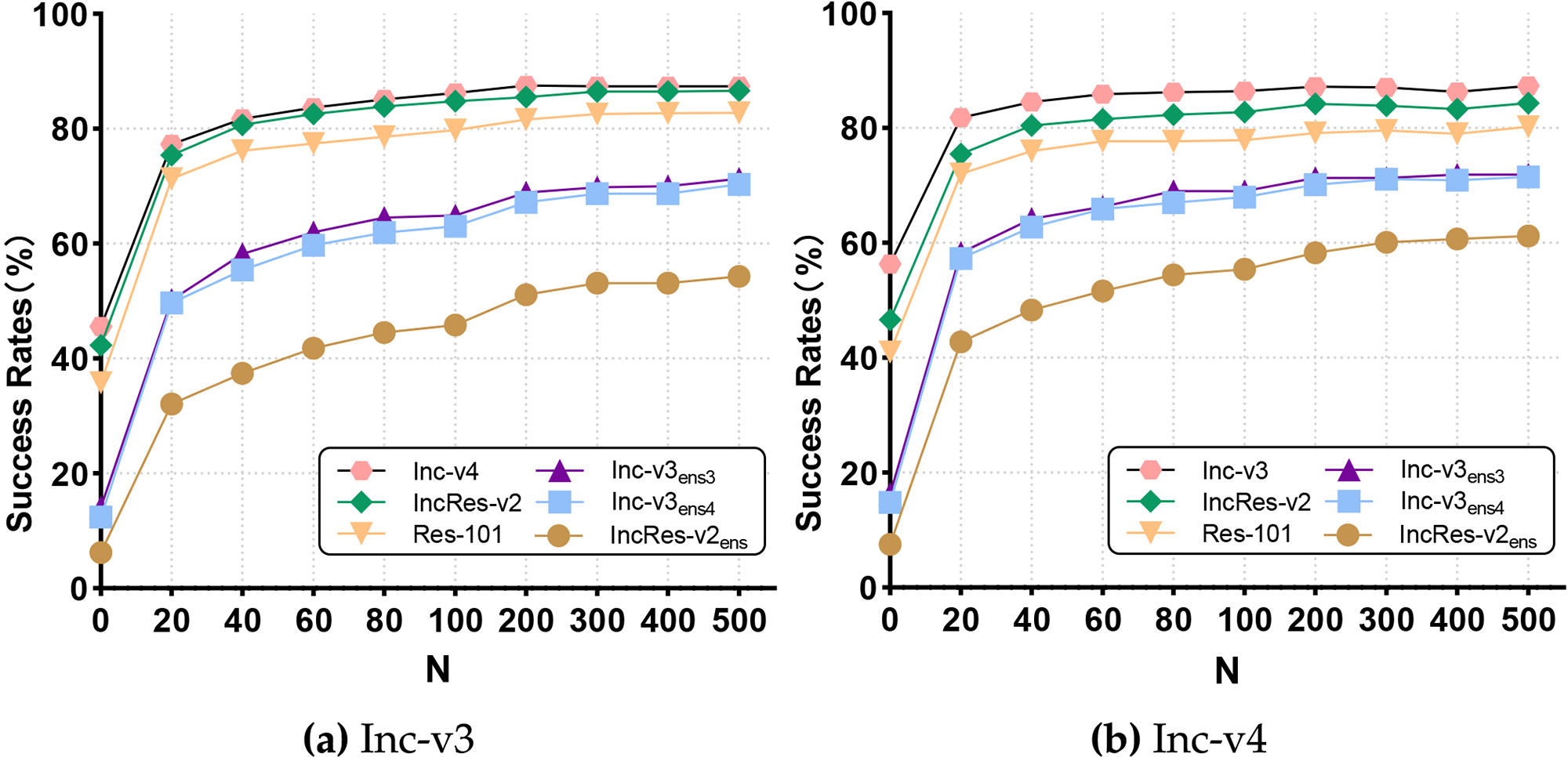
Figure 7: Success rate of transferability attacks on this remaining six models by SAMI-FGSM produced adversarial examples on Inc-v3 or Inc-v4 when sample size (N) is changed

In summary, when N > 500, the impact of N on black-box attack effectiveness gradually diminishes, while the parameter δ has an important impact on the success attack rate. Therefore, for all experiments, we choose δ = 5/2 and N = 500.

5  Conclusion

This paper introduces a novel Stochastic Gradient Accumulation Momentum Iterative Attack (SAMI-FGSM) to enhance the transferability of adversarial examples. This approach stabilizes the gradient update direction by calculating the accumulated gradient of random samples during each iteration, effectively avoiding local optima and achieving higher transferability. The attack efficiency of adversarial examples may also be boosted by integrating this method with other optimization-based attack techniques. Extensive experimental results demonstrate that SAMI-FGSM achieves optimal attack performance under both single-model and multi-model settings. Furthermore, combining our method with various input transformations further enhances attack success rate. Finally, ensemble experiments using three models validate the efficacy of SAMI-FGSM and show that it also achieves superior attack performance. Statistical tests further confirm that the performance improvement of SAMI-FGSM does not fluctuate by chance. This highlights the vulnerabilities of current defense models, underscoring the need to develop more robust defense strategies.

Although our experiments are based on the ImageNet dataset, the design principle of SAMI-FGSM has broad applicability and can be extended to other image modalities: medical images usually contain high-resolution local features and low SNR regions [49]. The normal distribution sampling of SAMI-FGSM can focus on the subtle disturbances in the lesion area, and the gradient accumulation mechanism can alleviate the overfitting problem caused by data scarcity. Satellite images have large-scale spatial heterogeneity and multi-spectral characteristics [50]. The local sampling strategy of SAMI-FGSM can specifically perturb the key areas of ground cover classification, and the cumulative gradient can adapt to the complex decision boundaries of the multi-band model. In the future, we plan to conduct experiments on medical images and satellite images to verify the attack effect of SAMI-FGSM against the scene classification and segmentation model.

When improving adversarial attack performance through stochastic gradient accumulation, although the method based on stochastic gradient accumulation significantly enhances black-box transferability, it is still necessary to explore more distribution sampling methods to determine whether the normal sampling process is optimal. In the gradient accumulation process, as the number of samples increases, the attack success rate also gradually increases. However, the reason why the attack performance reaches a peak at a certain number of samples needs further research and discussion. SAMI-FGSM also has scenarios or potential weaknesses that may perform poorly. When the target model employs random preprocessing such as random cropping and image enhancement to obfuscate the gradients, SAMI-FGSM may suffer from interference in the sampled gradient estimation, thereby reducing the attack success rate. Existing experiments mainly focus on CNN classification models. In object detection or segmentation tasks, there are modules such as anchor box mechanism or self-attention in the model structure, and SAMI-FGSM may not be directly applicable or have poor effects. A key limitation of SAMI-FGSM lies in the computational overhead introduced by the normal sampling process. In comparison to previous methods, generating a high number of samples for gradient accumulation dramatically increases the per-iteration cost. To address the computational overhead, future work will explore adaptive sampling techniques that focus on informative regions to reduce unnecessary computations. Parallel and distributed implementations may further accelerate gradient accumulation, enabling scalability for large-scale tasks. At present, the hyperparameters δ and N of SAMI-FGSM are considered as fixed values, but there may be differences in the optimal values between different models and datasets. In the future, an adaptive tuning framework based on Bayesian optimization or reinforcement learning can be introduced to realize adaptive hyperparameter adjustment in the attack process, so as to improve the attack efficiency and success rate. It is also possible to extend SAMI-FGSM to physical adversarial attacks and multi-modal datasets. In other domains, we will try to adapt SAMI-FGSM to text classification and machine translation tasks in the future. Although experiments show that normal distribution sampling significantly improves the transferability of adversarial examples, its theoretical optimality has not been rigorously proved mathematically. This limitation comes from the high-dimensional non-convex optimization characteristics of adversarial attacks, and its theoretical analysis requires more in-depth functional analysis and probability theory tools. In our future work, we will cooperate with scholars in the mathematical field to give priority to solving this problem and establish a universal theoretical framework for the distributed design of adversarial attacks.

Acknowledgement: Not applicable.

Funding Statement: This research was supported in part by the National Natural Science Foundation (62202118, U24A20241); in part by Major Scientific and Technological Special Project of Guizhou Province ([2024]014, [2024]003); in part by Scientific and Technological Research Projects from Guizhou Education Department (Qian jiao ji [2023]003); in part by Guizhou Science and Technology Department Hundred Level Innovative Talents Project (GCC[2023]018).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Haolang Feng; methodology, Haolang Feng, Yuling Chen, Yang Huang; validation, Yuling Chen, Yang Huang; formal analysis, Yang Huang; investigation, Haolang Feng; resources, Haolang Feng; data curation, Haolang Feng; writing—original draft preparation, Haolang Feng; writing—review and editing, Haolang Feng; visualization, Xuewei Wang; supervision, Haiwei Sang; project administration, Haiwei Sang; funding acquisition, Xuewei Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in https://github.com/FHL000/SAMI-FGSM (accessed on 21 May 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Adv Neural Inf Process Syst. 2012;25(6):84–90. doi:10.1145/3065386. [Google Scholar] [CrossRef]

2. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556. 2014. [Google Scholar]

3. Nguyen XB, Duong CN, Xin L, Susan G, Han-Seok S, Luu K. Micron-BERT: BERT-based facial micro-expression recognition. In: 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2023 Jun 17–24; Vancouver, BC, Canada. p. 1482–92. [Google Scholar]

4. Li Y, Li Y, Dai X, Guo S, Xiao B. Physical-world optical adversarial attacks on 3D face recognition. In: Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2023 Jun 17–24; Vancouver, BC, Canada. p. 24699–708. [Google Scholar]

5. Jiang B, Chen S, Xu Q, Liao B, Chen J, Zhou H, et al. VAD: vectorized scene representation for efficient autonomous driving. In: Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision; 2023 Oct 1–6; Paris, France. p. 8340–50. [Google Scholar]

6. Jia X, Gao Y, Chen L, Yan J, Liu PL, Li H. DriveAdapter: breaking the coupling barrier of perception and planning in end-to-end autonomous driving. In: Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision; 2023 Oct 1–6; Paris, France. p. 7953–63. [Google Scholar]

7. Zhao T, Ning X, Hong K, Qiu Z, Lu P, Zhao Y, et al. Ada3D: exploiting the spatial redundancy with adaptive inference for efficient 3D object detection. In: Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision; 2023 Oct 1–6; Paris, France. p. 17728–38. [Google Scholar]

8. Mao X, Chen Y, Wang S, Su H, He Y, Xue H. Composite adversarial attacks. In: Proceedings of the 2021 AAAI Conference on Artificial Intelligence; 2021 Feb 2–9; Online. p. 8884–92. [Google Scholar]

9. Zhao Z, Liu Z, Larson M. Towards large yet imperceptible adversarial image perturbations with perceptual color distance. In: Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2020 Jun 13–19; Seattle, WA, USA. p. 1039–48. [Google Scholar]

10. Chen Y, Yang H, Wang X, Wang Q, Zhou H. GLH: from global to local gradient attacks with high-frequency momentum guidance for object detection. Entropy. 2023;25(3):461. doi:10.3390/e25030461. [Google Scholar] [PubMed] [CrossRef]

11. Wang X, He K. Enhancing the transferability of adversarial attacks through variance tuning. In: Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2021 Jun 20–25; Nashville, TN, USA. p. 1924–33. [Google Scholar]

12. Wang G, Wei X, Yan H. Improving adversarial transferability with spatial momentum. arXiv:2203.13479. 2022. [Google Scholar]

13. Goodfellow IJ, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. arXiv:1412.6572. 2014. [Google Scholar]

14. Dong Y, Liao F, Pang T, Su H, Zhu J, Hu X, et al. Boosting adversarial attacks with momentum. In: Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition; 2018 Jun 18–23; Salt Lake City, UT, USA. p. 9185–93. [Google Scholar]

15. Lin J, Song C, He K, Wang L, Hopcroft JE. Nesterov accelerated gradient and scale invariance for adversarial attacks. arXiv:1908.06281. 2019. [Google Scholar]

16. Wang J, Chen Z, Jiang K, Yang D, Hong L, Guo P, et al. Boosting the transferability of adversarial attacks with global momentum initialization. Expert Syst Appl. 2024;255(5):124757. doi:10.1016/j.eswa.2024.124757. [Google Scholar] [CrossRef]

17. Li Q, Guo Y, Chen H. Yet another intermediate-level attack. In: Computer Vision–ECCV 2020: 16th European Conference, 2020 Aug 23–28; Glasgow, UK. p. 241–57. [Google Scholar]

18. Long Y, Zhang Q, Zeng B, Gao L, Liu X, Zhang J, et al. Frequency domain model augmentation for adversarial attack. In: European Conference on Computer Vision; 2022; Cham, Switzerland: Springer. p. 549–66. [Google Scholar]

19. Yang X, Lin J, Zhang H, Yang X, Zhao P. Improving the transferability of adversarial examples via direction tuning. arXiv:2303.15109. 2023. [Google Scholar]

20. Wang Z, Guo H, Zhang Z, Liu W, Qin Z, Ren K. Feature importance-aware transferable adversarial attacks. In: Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision; 2021 Oct 10–17; Montreal, QC, Canada. p. 7639–48. [Google Scholar]

21. Huang Q, Katsman I, He H, Gu Z, Belongie S, Lim SN. Enhancing adversarial example transferability with an intermediate level attack. In: Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision; 2019 Oct 27–Nov 2; Seoul, Republic of Korea. p. 4733–42. [Google Scholar]

22. Zhu H, Ren Y, Sui X, Yang L, Jiang W. Boosting adversarial transferability via gradient relevance attack. In: Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision; 2023 Oct 1–6; Paris, France. p. 4741–50. [Google Scholar]

23. Dong Y, Pang T, Su H, Zhu J. Evading defenses to transferable adversarial examples by translation-invariant attacks. In: Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2019 Jun 15–20; Long Beach, CA, USA. p. 4312–21. [Google Scholar]

24. Xie C, Zhang Z, Zhou Y, Bai S, Wang J, Ren Z, et al. Improving transferability of adversarial examples with input diversity. In: Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2019 Jun 15–20; Long Beach, CA, USA. p. 2730–9. [Google Scholar]

25. Zhang H, Yao Z, Sakurai K. Versatile defense against adversarial attacks on image recognition. arXiv:2403.08170. 2024. [Google Scholar]

26. Tramèr F, Kurakin A, Papernot N, Goodfellow I, Boneh D, McDaniel P. Ensemble adversarial training: attacks and defenses. arXiv:1705.07204. 2017. [Google Scholar]

27. Shafahi A, Najibi M, Ghiasi MA, Xu Z, Dickerson J, Studer C, et al. Adversarial training for free! In: Advances in neural information processing systems; 2019. doi:10.48550/arXiv.1904.12843. [Google Scholar] [CrossRef]

28. Gokhale T, Anirudh R, Kailkhura B, Thiagarajan JJ, Baral C, Yang Y. Attribute-guided adversarial training for robustness to natural perturbations. In: Proceedings of the 2021 AAAI Conference on Artificial Intelligence; 2021 Feb 2–9; Online. p. 7574–82. [Google Scholar]

29. Naseer M, Khan S, Hayat M, Khan FS, Porikli F. A self-supervised approach for adversarial robustness. In: Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2020 Jun 13–19; Seattle, WA, USA. p. 262–71. [Google Scholar]

30. Xu W. Feature squeezing: detecting adversarial examples in deep neural networks. arXiv:1704.01155. 2017. [Google Scholar]

31. Liu Z, Liu Q, Liu T, Xu N, Lin X, Wang Y, et al. Feature distillation: DNN-oriented JPEG compression against adversarial examples. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2019 Jun 15–20; Long Beach, CA, USA. p. 860–8. [Google Scholar]

32. Kurakin A, Goodfellow IJ, Bengio S. Adversarial examples in the physical world. In: Artificial intelligence safety and security. Boca Raton, FL, USA: Chapman and Hall/CRC; 2018. p. 99–112 [Google Scholar]

33. Wei Z, Chen J, Wu Z, Jiang YG. Enhancing the self-universality for transferable targeted attacks. In: Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2023 Jun 17–24; Vancouver, BC, Canada. p. 12281–90. [Google Scholar]

34. Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D. Grad-cam: visual explanations from deep networks via gradient-based localization. In: Proceedings of the 2017 IEEE International Conference on Computer Vision; 2017 Oct 22–29; Venice, Italy. p. 618–26. [Google Scholar]

35. Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z. Rethinking the inception architecture for computer vision. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition; 2016 Jun 27–30; Las Vegas, NV, USA. p. 2818–26. [Google Scholar]

36. Szegedy C, Ioffe S, Vanhoucke V, Alemi A. Inception-V4, Inception-ResNet and the impact of residual connections on learning. In: AAAI’17: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence; 2017 Feb 4–9; San Francisco, CA, USA. p. 4278–84. [Google Scholar]

37. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition; 2016 Jun 27–30; Las Vegas, NV, USA. p. 770–8. [Google Scholar]

38. Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, et al. An image is worth 16x16 words: transformers for image recognition at scale. arXiv: 2010.11929. 2020. [Google Scholar]

39. Heo B, Yun S, Han D, Chun S, Choe J, Oh SJ. Rethinking spatial dimensions of vision transformers. In: Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision; 2021 Oct 10–17; Montreal, QC, Canada. p. 11936–45. [Google Scholar]

40. Chen Z, Xie L, Niu J, Liu X, Wei L, Tian Q. Visformer: the vision-friendly transformer. In: Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision; 2021 Oct 10–17; Montreal, QC, Canada. p. 589–98. [Google Scholar]

41. Liu Z, Lin Y, Cao Y, Hu H, Wei Y, Zhang Z, et al. Swin transformer: hierarchical vision transformer using shifted windows. In: Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision; 2021 Oct 10–17; Montreal, QC, Canada. p. 10012–22. [Google Scholar]

42. Xie C, Wang J, Zhang Z, Ren Z, Yuille A. Mitigating adversarial effects through randomization. arXiv:1711.01991. 2017. [Google Scholar]

43. Liao F, Liang M, Dong Y, Pang T, Hu X, Zhu J. Defense against adversarial attacks using high-level representation guided denoiser. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2018 Jun 18–23; Salt Lake City, UT, USA. [Google Scholar]

44. Cohen J, Rosenfeld E, Kolter Z. Certified adversarial robustness via randomized smoothing. In: ICML 2019: 36th International Conference on Machine Learning; 2019 Jun 10–15; Long Beach, CA, USA. p. 1310–20. [Google Scholar]

45. Ke W, Zheng D, Li X, He Y, Li T, Min F. Improving the transferability of adversarial examples through neighborhood attribution. Knowl Based Syst. 2024;296:111909. doi:10.1016/j.knosys.2024.111909. [Google Scholar] [CrossRef]

46. Zhang J, Wu W, Huang JT, Huang Y, Wang W, Su Y et al. Improving adversarial transferability via neuron attribution-based attacks. In: Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022 Jun 18–24; New Orleans, LA, USA. p. 14993–5002. [Google Scholar]

47. Zheng D, Ke W, Li X, Duan Y, Yin G, Min F. Enhancing the transferability of adversarial attacks via multi-feature attention. IEEE Trans Inf Forensics Secur. 2025;20:1462–74. doi:10.1109/tifs.2025.3526067. [Google Scholar] [CrossRef]

48. Liu Y, Chen X, Liu C, Song D. Delving into transferable adversarial examples and black-box attacks. arXiv:1611.02770. 2016. [Google Scholar]

49. Dong J, Chen J, Xie X, Lai J, Chen H. Survey on adversarial attack and defense for medical image analysis: methods and challenges. ACM Comput Surv. 2025;57(3):79–38. doi:10.1145/3702638. [Google Scholar] [CrossRef]

50. Du A, Chen B, Chin TJ, Law YW, Sasdelli M, Rajasegaran R, et al. Physical adversarial attacks on an aerial imagery object detector. In: Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision; 2022 Jan 3–8; Waikoloa, HI, USA. p. 1796–806. [Google Scholar]