 Open Access
Open Access
ARTICLE
Classification of Cyber Threat Detection Techniques for Next-Generation Cyber Defense via Hesitant Bipolar Fuzzy Frank Information
1 Department of Mathematics and Statistics, International Islamic University Islamabad, Islamabad, 44000, Pakistan
2 SK-Research-Oxford Business College, Oxford, OX1 2EP, UK
3 Department of Statistics and Operations Research, Faculty of Science, King Saud University, P.O. Box 2455, Riyadh, 11451, Saudi Arabia
4 Department of Mathematics, University of Management and Technology, C-II, Johar Town, Lahore, 54700, Punjab, Pakistan
5 Transport and Logistics Competence Centre, Vilnius Gediminas Technical University, Vilnius, LT-10223, Lithuania
* Corresponding Author: Dragan Pamucar. Email:
Computers, Materials & Continua 2025, 84(3), 4699-4727. https://doi.org/10.32604/cmc.2025.065011
Received 28 February 2025; Accepted 27 April 2025; Issue published 30 July 2025
Abstract
Cyber threat detection is a crucial aspect of contemporary cybersecurity due to the depth and complexity of cyberattacks. It is the identification of malicious activity, unauthorized access, and possible intrusions in networks and systems. Modern detection methods employ artificial intelligence and machine learning to study vast amounts of data, learn patterns, and anticipate potential threats. Real-time monitoring and anomaly detection improve the capacity to react to changing threats more rapidly. Cyber threat detection systems aim to reduce false positives and provide complete coverage against the broadest possible attacks. This research advocates for proactive measures and adaptive technologies in defending digital environments. Improvements in detection ability by organizations will assist in safeguarding assets and integrity in operations in this increasingly digital world. This paper draws on the categorization of cyber threat detection methods using hesitant bipolar fuzzy Frank operators. Categorization is a step that is necessary for systematic comparison and assessment of detection methods so that the most suitable method for particular cybersecurity requirements is chosen. Furthermore, this research manages uncertainty and vagueness that exists in decision-making by applying hesitant bipolar fuzzy logic. The importance of the work lies in how it fortifies cybersecurity architectures with a formal method of discovering optimal detection measures and improving responsiveness, resulting in holistic protection against dynamic threats.Keywords
Cybersecurity has turned into an essential part of modern digital life as cyber-attack’s frequency and complexity keep rising. Organizations worldwide are increasingly faced with threats like phishing, ransomware, denial-of-service attacks, advanced persistent threats, and others that bring about operations disruption, loss of sensitive data, and possible financial loss. The ability to detect and mitigate these threats in real-time has emerged as a critical requirement to ensure the security and integrity of digital systems. Advances in technology have, in turn, propelled threat detection techniques. Artificial intelligence and machine learning are critical in the sense that they analyze huge volumes of data to find anomalies and detect malicious activities. It can be said that techniques, such as behavior-based detection, signature-based detection, and anomaly detection, enhance the capabilities of cybersecurity systems. Moreover, real-time monitoring, adaptive algorithms, and predictive analytics are an integral part of modern threat detection frameworks. The growth of the cybersecurity market for threat detection is discussed in Fig. 1.
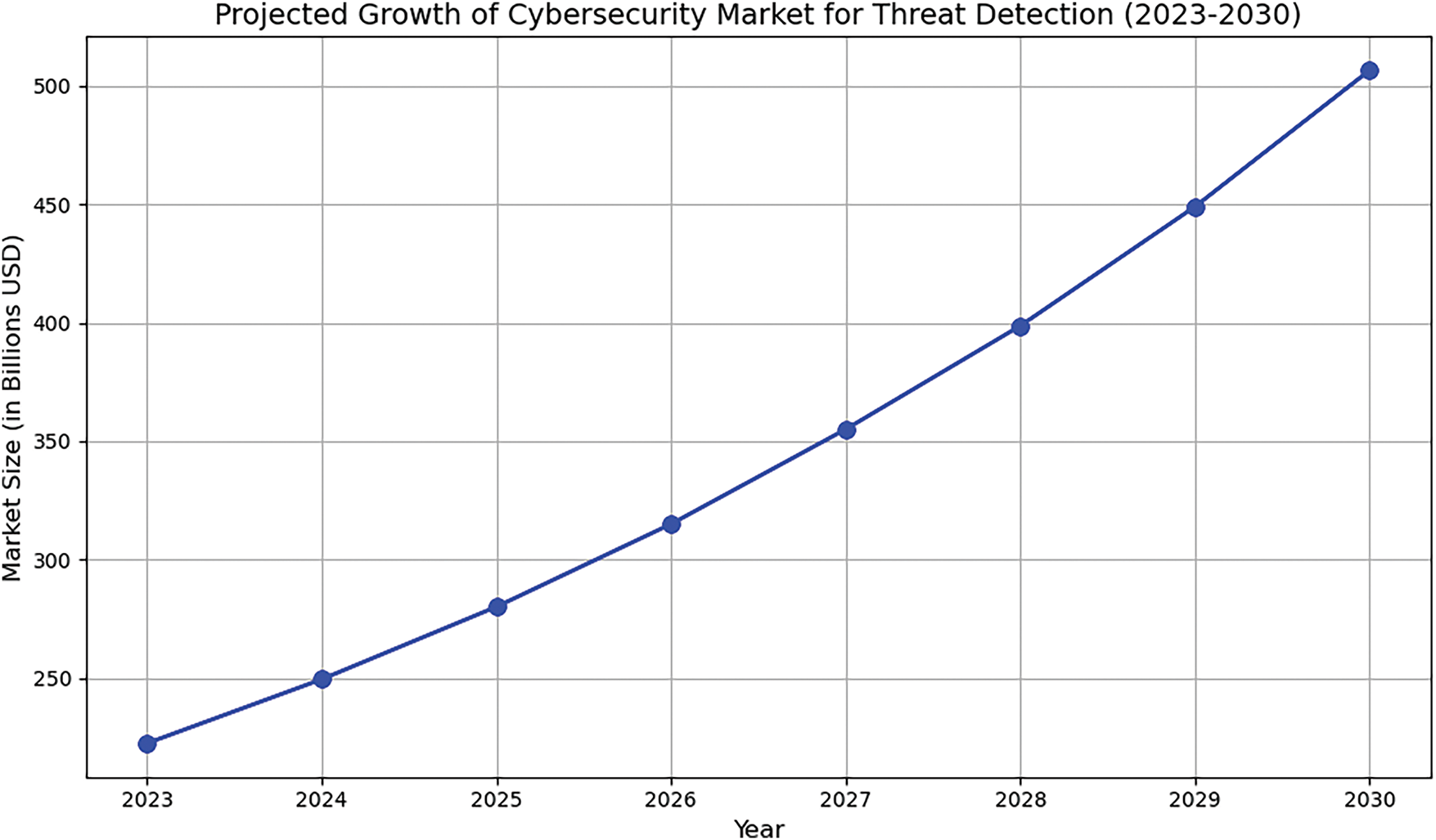
Figure 1: Estimated growth trajectory of the cybersecurity market for advanced threat detection solutions from 2023 to 2030
However, with these advancements and the sheer volume of data, as well as changing cyber threats, it proves to be difficult to design such systems that can detect threats consistently without producing false positives and false negatives. The presence of uncertainty and ambiguity while dealing with complex decision-making often fails to be handled effectively by traditional methods. These reasons have led to searching for more advanced techniques in handling multi-criteria evaluation and providing precise results in an uncertain environment. Classification of detection techniques becomes important in this context to understand the strengths, limitations, and applicability of each method. A well-structured classification framework helps organizations pick the best-suited detection strategy for their needs, which will make their cybersecurity measures efficient and effective. This manuscript presents a new approach to the classification of cyber threat detection techniques based on hesitant bipolar fuzzy (HBF) Frank operators. Using HBF logic, the proposed framework deals with the uncertainty and imprecision that arise in an evaluation process regarding detection techniques. The decision-making process is advanced using Frank operators. This enables an in-depth study of competitive techniques. This research will provide a strong and flexible classification system that will guide the development and deployment of optimized cyber threat detection strategies. Some key steps involved in cyber threat detection are data collection, processing, threat identification, classification or analysis, and mitigation strategy. Data is first collected from the networks and devices. Then it is processed for noise removal before further analysis. Threat identification helps to spot irregular activities or vulnerabilities. They classify or analyze threats, understand their types, and then estimate the probable impact. They finally develop strategies for mitigating threats to neutralize them so that such incidents may not happen in the future. These three steps make for a complete security system against cyber-attacks. Moreover, the cyber threat detection steps are discussed in Fig. 2.
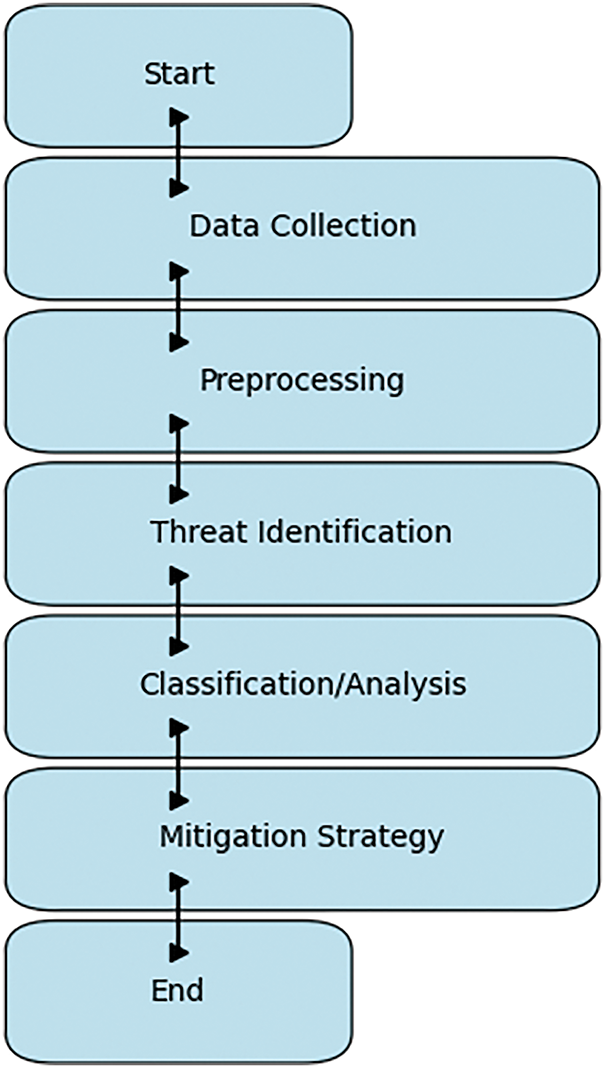
Figure 2: Key stages in the cyber threat detection process, including identification, analysis, mitigation, and response strategies
Q: Why is the classification of cyber threat detection techniques necessary in today’s cybersecurity landscape?
The classification of cyber threat detection techniques is very important in today’s fast-changing cybersecurity landscape, especially with the increasing complexity and frequency of cyberattacks. As organizations face diverse threats, ranging from phishing and ransomware to advanced persistent threats, a structured classification enables the systematic evaluation of detection methods. It identifies the most effective techniques for specific scenarios, ensuring efficient resource allocation and improved protection. This provides an understanding of the existing methods’ shortcomings and strengths, leading to innovative new systems and highly developed and flexible detection mechanisms. Classifications are vital to modern, information technology societies because the loss or exploitation of digital data can cause far-reaching effects, ranging from minor annoyances to financial disasters and other disastrous ends. Moreover, Fig. 3 discusses the classification and rising market adoption of cyber threat detection techniques.
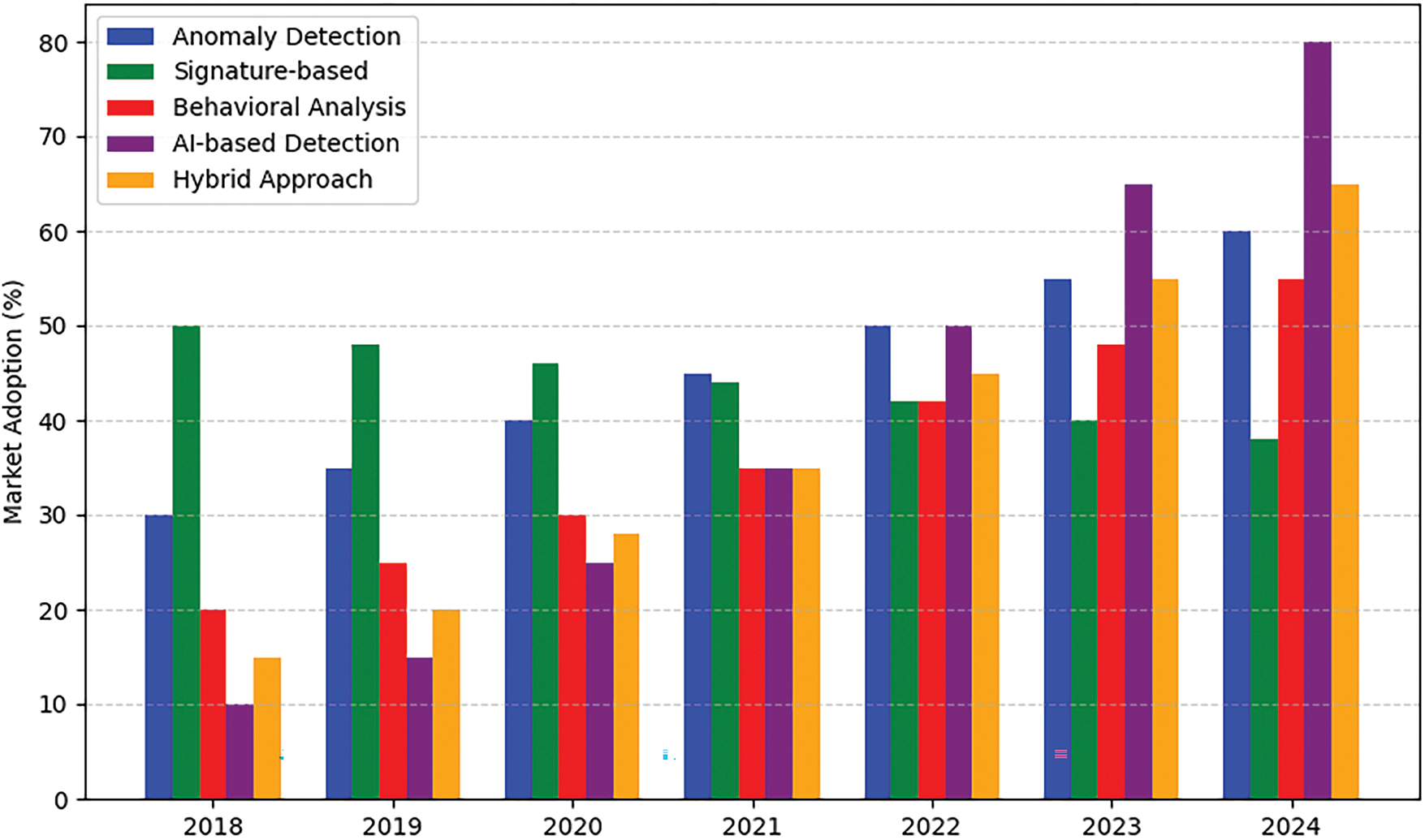
Figure 3: Increasing market adoption of advanced cyber threat detection techniques across industries, demonstrating growth from 2018 to 2024
1.1 Significance of HBF Framework in MCDM
The HBF approach represents a very important issue to MCDM techniques when considering uncertainty and imprecision associated with decision-making activities. Real-world decision-makers regularly meet situations where they are unaware of the exact values or prefer two alternatives in conflict under situations where multiple alternatives exist according to various criteria for evaluating the alternatives. The HBF framework can be used to express both positive and negative membership values and hesitancy. Therefore, the model would be more flexible and realistic for capturing the vagueness and ambiguity involved in decision-making. In MCDM, where one has to compare alternatives with multiple attributes, the HBF framework helps enhance the quality of the decision by being able to incorporate multiple conflicting criteria. It offers a means of articulating uncertain judgments and preferences to present a more subtle appreciation of how alternatives perform concerning one another. Under this framework, MCDM methodologies can generate more robust and more consistent results even when dealing with incomplete, uncertain, or inconsistent information. This also enhances the robustness of decision-making models, ensuring superior outcomes in complex, multi-attribute environments, including cybersecurity, resource allocation, or technological selection. The below Fig. 4 shows the capability and limitations of the proposed theory in MCDM.
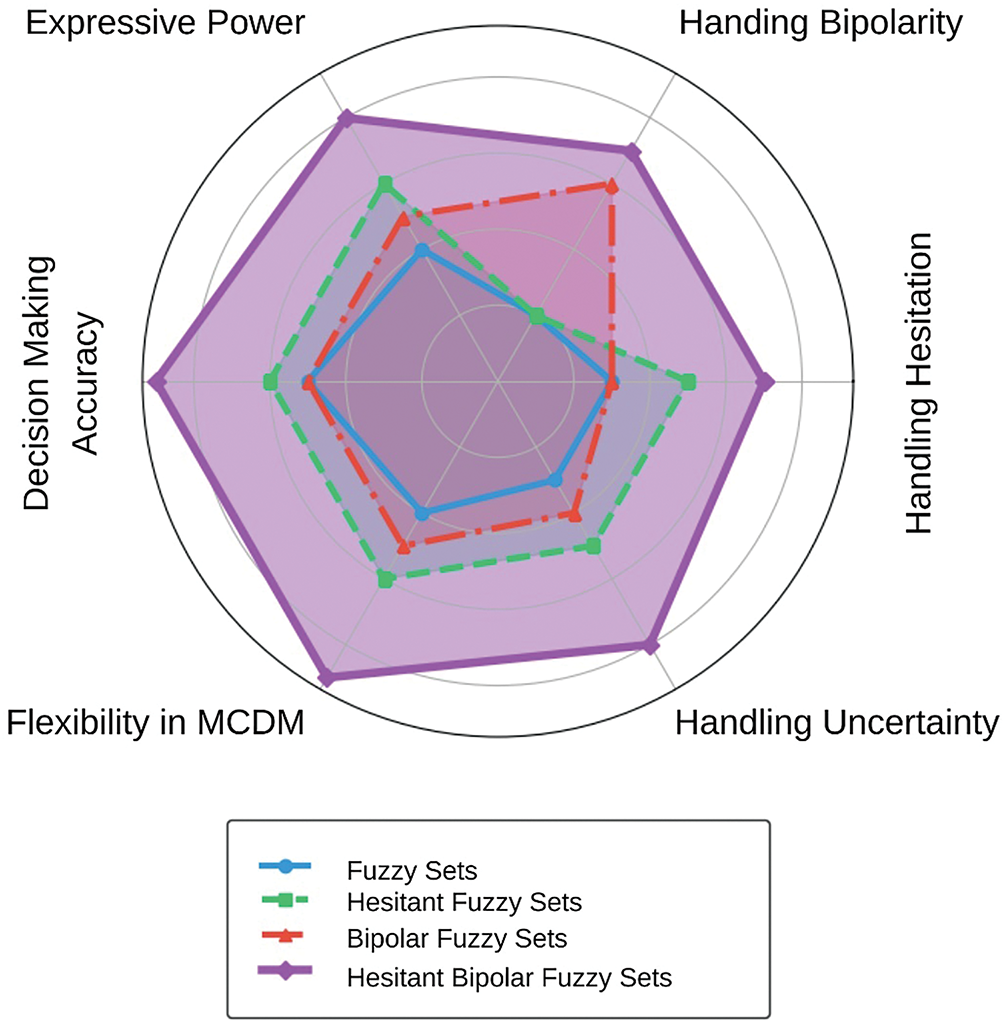
Figure 4: Key advantages and limitations of hesitant bipolar fuzzy sets in MCDM applications
1.2 Taxonomy of Cyberattacks and Detection Methods
Organizations must depend on cyber threat detection as their core security element to spot and manage harmful activities that aim at their computer systems and networks. Information security expert teams use detection approaches that match attack characteristics among the different cyberattacks including malware infections and distributed denial-of-service (DDoS) attacks. System detection success depends on how well detection systems recognize abnormal behaviors that could signal potential malicious activities from typical normal activity patterns. An organization relies on signature-based detection and anomaly detection and behavioral analysis to track and analyze cybersecurity threats. The following part examines standard cyberattack types through a classification system along with detection strategy analysis for specific threat varieties.
(a) DDoS (Distributed Denial-of-Service) Attacks: Attackers execute DDoS attacks through network service flooding with extremely high traffic volumes that blocks access for permitted users. Detection systems for DDoS attacks perform traffic pattern analysis together with anomaly detection algorithm automation. Security solutions compare present traffic data against typical baseline patterns in order to detect unusual spikes or irregular traffic patterns which signal possible DDoS attacks.
Example: The anomaly-based detection method detects the large amount of typical suspicious requests during a DDoS attack through which administrators can take preventive actions to block suspicious IP addresses.
(b) Malware Detection: The goal of malware attacks is to breach and damage systems through various threats like viruses together with worms and ransomware. The detection of known malware through files and behaviors relies on signature-based methods that match database signatures. Behavioral detection methods monitor system activities for malicious behavior, such as unusual file modifications or unauthorized data access.
Example: Security software uses signature detection to recognize familiar malware types but behavioral analysis examines system activities for ransomware through monitoring of abnormal file encryption patterns.
(c) Advanced Persistent Threats (APT): Following extensive durations APTs utilize professional methods to perform their advanced attacks for the theft of confidential information. The detection methods for APTs operate through signature-based detection together with anomaly detection and user behavior analytics (UBA). Recording methods analyze the small deviations between normal network traffic patterns and user behavior means when compared against typical patterns.
Example: Network traffic analysis and detection of users making unexpected file access during abnormal hours can help detect APTs.
(d) Phishing Attacks: Social engineering through phishing tactics makes attackers trick users to hand over sensitive information such as password or financial data. The detection of phishing activities depends on machine learning together with natural language processing (NLP) to recognize abnormal email patterns and text along with unusual communication behaviors.
Example: The detection system analyzes email content for frequent suspicious indicators which include untrusted senders and suspicious links to warn users about possible phishing attempts.
This manuscript is divided into several sections to make the content readable and understandable. In Section 1, we give an overview of the manuscript and explain what it is about and why. Section 2 discusses our research problem and the main contribution of our work in light of that problem. In Section 3, we present a review of previous literature to demonstrate how our work fits into and pushes forward the current research. Section 4 discusses fundamental concepts and operations that support this research. New aggregation operators are introduced and explained to facilitate the research in Section 5. Section 6 has described the MCDM technique used in this work; furthermore, the case study regarding cyber threat detection techniques for next-generation cyber defense systems is presented here. We compare our proposed approach against other related theories to highlight its robustness and effectiveness in Section 7. Finally, in Section 8, the manuscript is concluded by summarizing the key findings and the overall contributions of this work. A graphic representation of the above methodology is discussed in Fig. 5.
Figure 5: Graphical representation of the proposed manuscript
2 Research Problem and Contribution
With the escalating complexity of cyber threats, the most appropriate choice of cyber threat detection technique is a critical challenge for modern cybersecurity systems. Traditional methods of detection, which are mostly based on uncertainties and the dynamic nature of cyber threats, often provide inaccurate results. Existing decision-making models, such as fuzzy sets, hesitant fuzzy sets, or bipolar fuzzy sets, have shortcomings in dealing with conflicting information and the uncertainty involved in multi-criteria evaluations. This manuscript develops a classification framework for cyber threat detection techniques using the HBF framework to enhance the decision-making process by overcoming the shortcomings of conventional fuzzy logic systems. The HBF framework is required to classify cyber threat detection techniques since it is better suited for dealing with uncertainty, imprecision, and conflicting criteria than the traditional fuzzy approaches. Here we discuss underneath why it is particularly relevant to the classification process. Traditional fuzzy sets introduce a possibility of representing vagueness, but an element can have only a degree of membership, which would sometimes be too simple for imprecise information and incompleteness available in the problem. Moreover, in cyber threat detection, there are often quite many attributes to be tested regarding detection speed, accuracy, and scalability, with uncertain or incomplete information for each attribute, in turn making fuzzy sets inapplicable for accurate decision-making. While hesitant fuzzy sets extend fuzzy sets by allowing the possibility of multiple membership values for an element, they cannot still properly deal with situations that contain both positive and negative information. The introduction of positive and negative membership values in bipolar fuzzy sets makes it possible to include both the advantageous and disadvantageous aspects of alternatives. However, it faces the demerit that it cannot capture the entire uncertainty scale of the state of being uncertain. It fails to reveal the importance of criteria when decision-makers are uncertain or in disagreements on the set of criteria. The HBF framework amalgamates the merits of hesitant fuzzy sets and bipolar fuzzy sets. It allows the expression of more than one hesitant value both in positive and negative memberships. Thus, it takes care of inherent uncertainty and imprecision within decision-making processes. It is a framework that represents more accurately the decision environment in which criteria may conflict or are uncertain. This framework enables a more specific categorization in the context of cyber threat detection by considering the positive and negative attributes of the detection techniques involved.
This paper aims to bridge the current gaps in existing frameworks and methodologies for cyber threat detection through a new theory supported by HBF Frank aggregation operators. To improve the classification of cyber threat detection techniques, we develop a set of novel aggregation operators such as hesitant bipolar fuzzy Frank weighted averaging (HBFFWA), hesitant bipolar fuzzy Frank ordered weighted averaging (HBFFOWA), hesitant bipolar fuzzy Frank weighted geometric (HBFFWG), and hesitant bipolar fuzzy Frank ordered weighted geometric (HBFFOWG) operators. These operators are specifically developed to address the challenges of uncertainty and imprecision in decision-making by integrating multiple criteria with both positive and negative evaluations. Using these HBFF operators, we introduce an MCDM methodology tailored for the classification and prioritization of cyber threat detection techniques. This methodology makes possible more precise and credible choices of methods for detection based on inconsistent and uncertain data. The given methodology provides a systematic means to assess the alternatives considering several performance criteria. Besides, we consider the same methodology for an illustrative case study in cyber threat detection techniques and illustrate how such aggregation operators enhance the decision-making capability in real-world scenarios related to cybersecurity. We also provide a comprehensive comparative analysis of the proposed method with existing approaches in the field. Finally, the manuscript concludes with insights into the effectiveness of the proposed framework and its potential for future applications in enhancing cybersecurity measures. The flow chart of main contributions is discussed in Fig. 6.

Figure 6: Main contributions flow chart such as aggregation operators, MCDM, case study and analysis
With the growing intensity of cyber-attacks, the detection as well as mitigation requirements are of high end. Hence, artificial intelligence and machine learning-based approaches to the development of effective as well as precise cybersecurity measures received much attention up till now. The methods proposed to attain better threat detection were neural networks, deep learning, and adaptive defense mechanisms. These studies underscore that the need lies in dynamic adaptation towards combating newer, ever-increasing cyber threats. Different related studies are discussed as; Labu and Ahammed [1] point out second-generation AI-oriented strategies for timely detection and reaction against cyber-attacks, based on the anticipation of intelligent system behavior to better proactively uncover emerging risks beforehand. For discussion, Shaukat et al. [2] have produced a comprehensive analysis that relates to the state-of-the-art techniques in cyber threat detection employing machine learning with insights into comparative performance across multiple scenarios. Bridging the theoretical advancement and application in real scenarios, this is enabling practitioners to choose models apt for specific security needs. Similarly, Balantrapu [3] discusses current trends and future directions in using machine learning for cybersecurity scalable and automated solutions that will be able to address the rising volume and complexity of cyberattacks. This also shows how cybersecurity is evolving from static rule-based systems to dynamic, self-learning algorithms. In addition, Lee et al. [4] propose a model of artificial neural networks through event profiles, showing the system’s ability to process large quantities of data without delay for identifying anomalies. Rajendran et al. [5] develop this type of story using deep learning along with anomaly detection techniques, and bring forth robust frameworks that are excellent at identifying complex and subtle patterns of malicious activity. Aminu et al. [6] work by integrating real-time threat intelligence into adaptive defense mechanisms and thus, a dynamic and responsive system is provided that not only detects threats but also adapts to their evolving nature. In addition to these recent developments, Maddireddy and Maddireddy [7] emphasize the use of deep learning models for the improvement of cybersecurity protocols, which shows how neural network architectures can improve detection accuracy and efficiency. Their study emphasizes the scalability of deep learning solutions in large-scale environments, providing robust defenses against known and unknown threats. Lakhno [8] has been the first to present an adaptive cyber threat detection system based on fuzzy feature clustering, which very effectively manages the uncertainties and incomplete data so often faced in cybersecurity. It thereby reveals the potential usefulness of fuzzy logic to construct robust and adaptable detection algorithms capable of functioning in vaguer than normal environments. Ullah et al. [9] with an innovative hybrid system combining transfer learning with multi-model image representation of cyber threats, that considerably strengthens detection precision as well as robustness of scalability of systems across the range of diversified dynamic landscapes.
The literature on MCDM techniques unfolds as reflective of their evolution, diversity in application, and importance in a multiplicity of domains. Massam [10] delivers a more fundamental survey on MCDM methods in the context of planning, exposing their ability to address complex decision-making scenarios, and accommodating diverse criteria. It reveals early conceptions of the scope of flexibility and adaptability in MCDM techniques in structuring and solving planning problems. On this basis, Zavadskas et al. [11] discuss the application of MCDM in business process information management. They pointed out the importance of integrating MCDM techniques to ensure the effectiveness of decision-making in information systems. Sahoo and Goswami [12] present a thorough review of advances in MCDM methods in their contemporary applications and future research directions. Their work highlighted that these methods keep evolving as more and more practical applications spring forth in everyday fields. Kumar et al. [13] showed how MCDM can contribute toward sustainable renewable energy development by directing critical decisions for resource allocation, technology choice, and policy formation toward accomplishing the long-term goals of sustainability at a global level. Alghamdi et al. [14] presented MCDM within the bipolar fuzzy environment that exposes how the fuzziness involved may be beneficial to the management of uncertainties when dealing with decision-making. Riaz et al. [15] have extended the scope of bipolar fuzzy MCDM by designing new distance measures and operators, which help enhance the accuracy and reliability of decision-making. This methodology maximizes the applicability of MCDM in bipolar assessment problems. Riaz et al. [16] also extended the cubic bipolar fuzzy Dombi aggregation operators to present a strong structure toward resolving the great MCDM complexities with greater degrees of fuzziness. The VIKOR MCDM approach experiences an extension by Gul [17] through his introduction of a bipolar fuzzy preference model based on δ-covering and bipolar fuzzy rough set theory. The research builds upon decision-making processes through its addition of uncertain preference structures that enable higher precision during alternative classification and choice determination. Bhol [18] examines MCDM techniques for cybersecurity applications and demonstrates their ability to handle security operations that include threat detection and risk evaluation. The analysis evaluates diverse MCDM techniques such as AHP and TOPSIS aligned with VIKOR by proving their effectiveness for cybersecurity solution evaluation. Ali [19] develops fairly aggregation operators that operate with complex p, q-rung ortho-pair fuzzy sets for solving real-world decision-making problems. The study develops a new method for combining vague data which results in better delivery of reliable decision outcomes. Kumar and Pamucar [20] conducted an extensive review of MCDM methodologies that have emerged from 2004 to 2024. Their comprehensive study evaluates numerous MCDM methodologies by investigating their basic concepts and their breakthroughs as well as their utilization across numerous sectors. Ali et al. [21] developed a decision-making methodology based on intuitionistic fuzzy soft information and Aczel-Alsina operational laws. A solution combining fuzzy logic elements with decision-making structures increases both flexibility and robustness in their system. The identification of suitable encryption algorithms through hesitant bipolar complex fuzzy Frank aggregation operators forms the basis of Mahmood et al.’s research [22]. MCDM techniques apply fuzzy logic for encryption algorithm selection according to their research because it lets users evaluate multiple performance criteria at once. Aslam et al. [23] use hesitant bipolar complex fuzzy Dombi aggregation operators to apply MCDM techniques during their study on cloud service provider selection. Waqas et al. [24] improve the process of cloud security selection. MCDM methodologies prove adaptable for security analysis through their research which presents structured evaluation methods for security measures. Multiple domains benefit from MCDM technique evolution through these research works which demonstrate widespread applications.
In this section, we discuss the basic notion of HBFSs and their related operations and contributions.
Definition 1: [25] Let
where,
Definition 2: [25] Let
Definition 3: [25] Let
Definition 4: [25] Let
Definition 5: [26] Let
4.1 HBF Frank Operational Laws
In this subsection, we discuss HBF operational laws based on Frank t-norm and Frank t-conorm.
Definition 6: Let
Theorem 1: Let
1.
2.
3.
4.
5.
5 HBF Frank Aggregation Operators
In this section, we proposed several new aggregation operators such as HBFFWA, HBFFOWA, HBFFWG, and HBFFOWG operators.
5.1 HBF Frank Arithmetic Aggregation Operators
Definition 7: Let
where,
Theorem 2: Let
Proof: Based on mathematical induction methodology, for
Hence (7) holds for
Next, we have to show (7) is true for
Hence, (8) is true for
Definition 8: Let
where,
Theorem 3: Let
5.2 HBF Frank Geometric Aggregation Operators
Definition 9: Let
where,
Theorem 4: Let
Definition 10: Let
where,
Theorem 5: Let
Note that the all above-defined operators must satisfy the properties of idempotency, boundedness, and monotonicity.
In this section, we introduce the MCDM approach for the classification of cyber threat detection techniques for next-generation cyber defense based on the proposed HBF Frank operators.
Suppose there are
Next, we have the following algorithm steps to solve the MCDM technique.
Step-1: In this step, we convert the cost type attribute into benefit type and for this, we have the following formula,
Step-2: Use the HBFFWA or HBFFWG operators that are given below to aggregate all the values,
Step-3: Determine the score values as;
Step-4: Rank all the alternatives
Step-5: Choose the best alternative.
In this case study, we are considering the selection of cyber threat detection techniques for a financial institution. The sensitive customer information, transaction integrity, and overall system reliability are at the top of the priority list for this institution. The threats it faces range from insider attacks to fraud, data breaches, and DDoS attacks. The objective is to analyze several types of detection methods concerning their speed of threat identification and responsiveness, along with false positive risks. In light of the high stakes, the detection methods would need to be accurate, dynamically adaptive to emerging threats, and scalable as the load of data grows. The evaluation of these alternatives will be made by using a few performance attributes to identify the technique with the most successful and reliable defense; the detailed cyber threat detection techniques as an alternative are discussed in Table 1.

The criteria for cyber threat detection techniques are discussed in Table 2.

For selecting the best cyber threat detection technique, the financial institution has the following expert decision matrix and attribute weights
The expert decision matrix in the form of HBF information is discussed in Table 3.
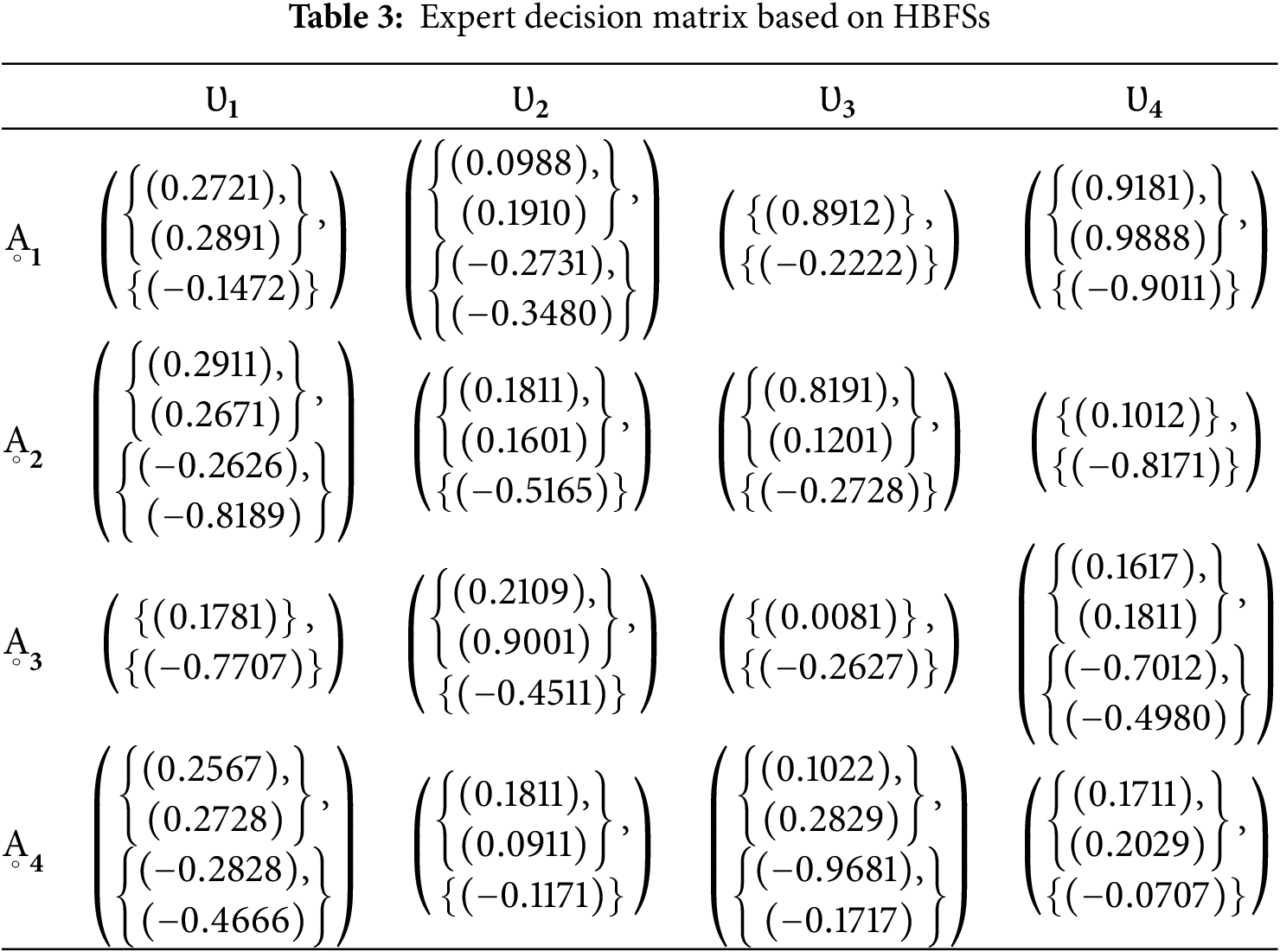
Step 1: Given that Table 3 provides data specific to each type of benefit, normalization is unnecessary
Step 2: For
Step 3: The obtained score values of
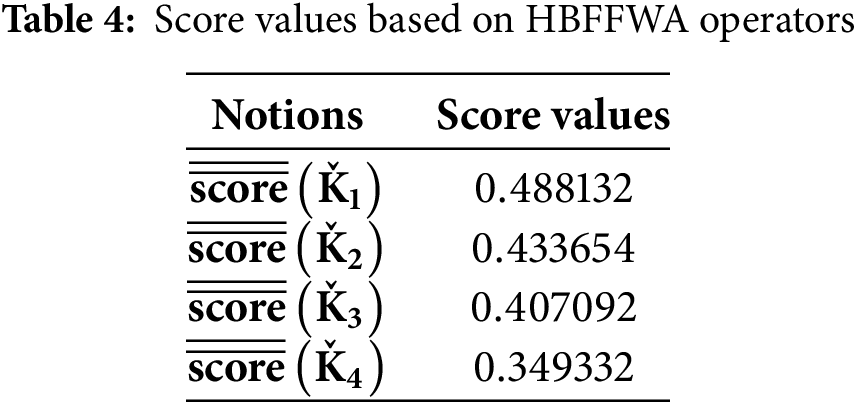
Step 4: Rank all the platform
Step 5:
The graphical representation of the ranking of cyber threat detection techniques for next-generation cyber defense based on HBFFWA operators is discussed in Fig. 7.
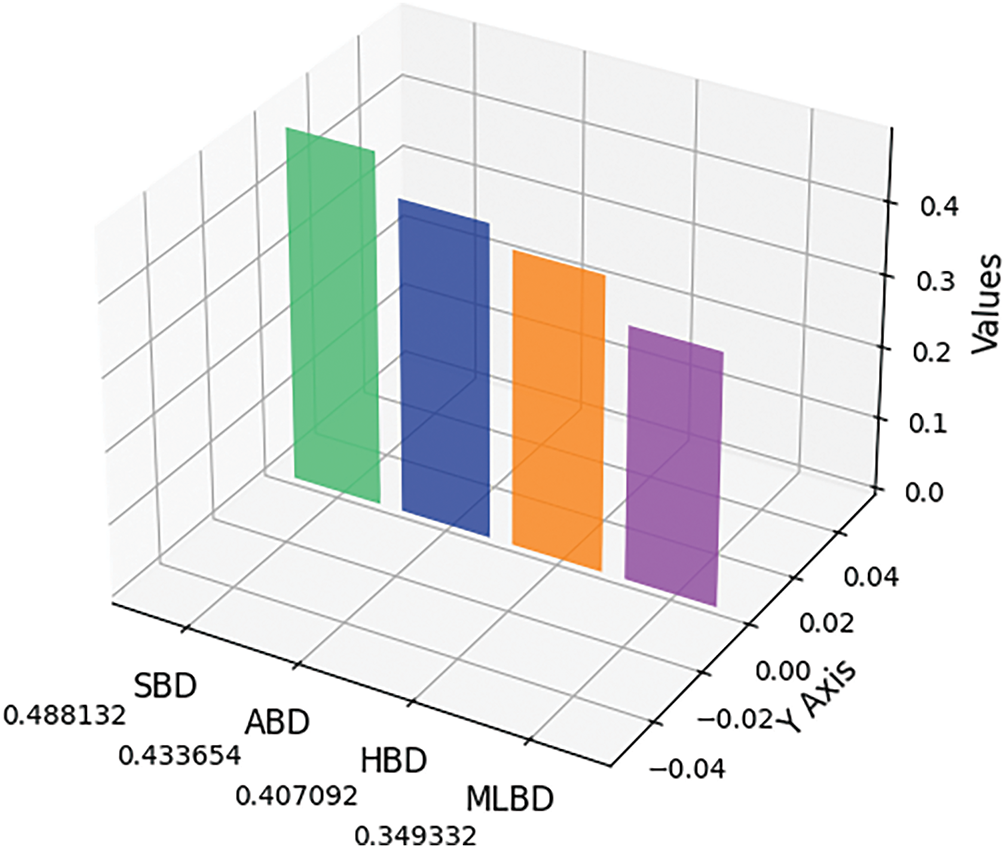
Figure 7: Graphical representation of the ranking of cyber threat detection techniques based on hesitant bipolar fuzzy frank weighted averaging (HBFFWA) operators
If we use the HBFFWG operator instead of the HBFFWA operator then all the above steps are similar to the HBFFWG framework.
Step 1: The given data in Table 3 is benefit type so there is no need to normalize it.
Step 2: For
Step 3: The obtained score values of
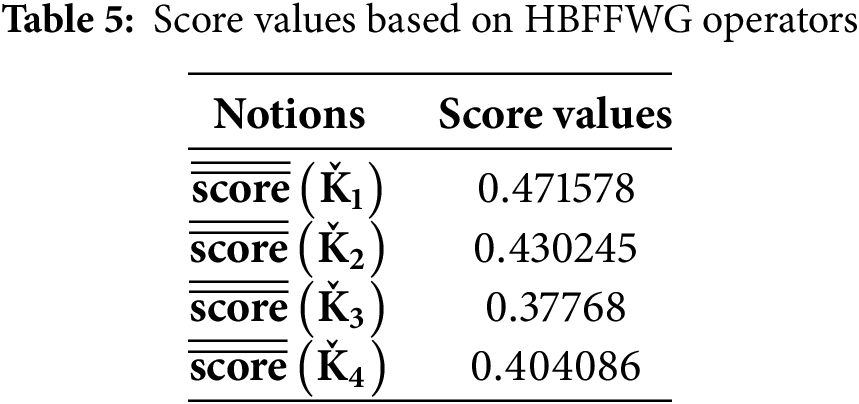
Step 4: Rank all the platform
Step 5:
The graphical representation of the ranking of cyber threat detection techniques for next-generation cyber defense based on HBFFWG operators is discussed in Fig. 8.

Figure 8: Graphical representation of the ranking of cyber threat detection techniques based on hesitant bipolar fuzzy frank weighted geometric (HBFFWG) operators
Sensitivity analysis is an important aspect of decision-making, particularly in the ranking of cyber threat detection methods. In the current research, we perform a sensitivity analysis with Frank aggregation operators to determine the stability and robustness of the proposed HBF approach. By adjusting the input weights and parameters, we investigate how the changes affect the ranking of cyber threat detection methods, thereby ensuring the strength of our methodology. Such a comparison gives stronger insights into how resilient the chosen methods are for various scenarios and further strengthens our model’s validity for future cybersecurity defense.
The aggregated results of HBFFWA and HBFFWG operators based on different variations are discussed in Tables 6 and 7.


Ranking of all the alternatives is discussed in Tables 8 and 9.

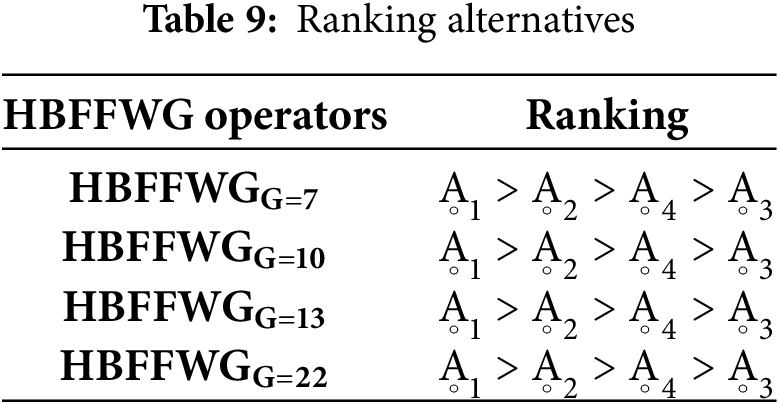
Graphical representation of variations by different parameters is discussed in Figs. 9 and 10.

Figure 9: Sensitivity analysis of cyber threat detection techniques with varying parameter values based on HBFFWA operators
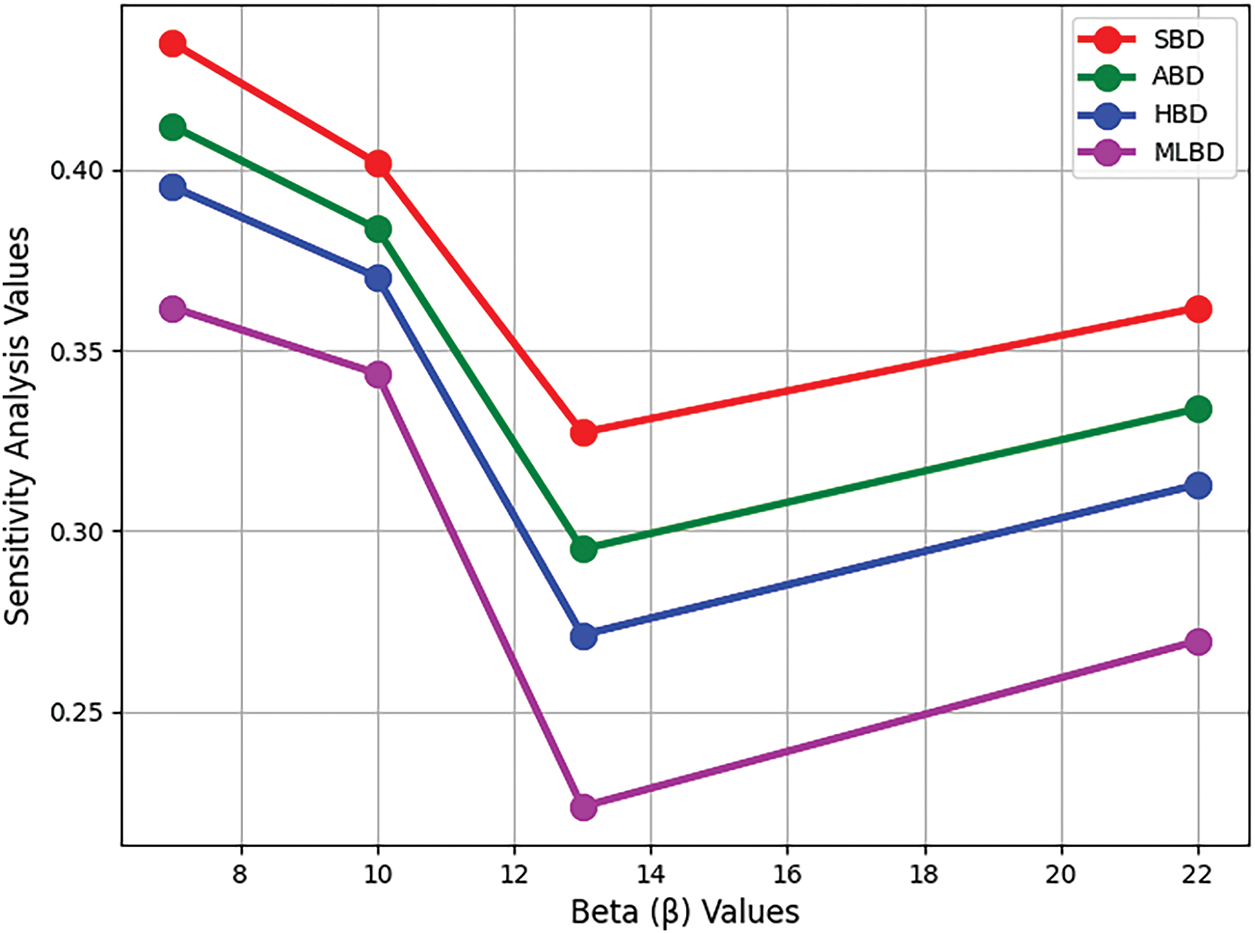
Figure 10: Sensitivity analysis of cyber threat detection techniques with varying parameters based on HBFFWG operators
The above sensitivity analysis presents that changes in parameter values cannot change the rank of cyber threat detection methods, which proves the stability and solidity of the proposed framework. Such consistency reflects the credibility of our solution with the assurance of the decision process not being disturbed by small oscillations in the input parameters. This stability becomes significant in security applications. Moreover, the findings prove the effectiveness of HBF Frank aggregation operators in handling uncertainty and providing credible rankings, which makes them a critical tool for decision-makers in future cyber defense strategies.
The importance of comparative analysis between the proposed theory and existing theories is that one can see the unique advantages and possible applicability of the HBF framework when decisions are complicated. Cyber threat detection techniques require a methodology that can effectively handle both uncertainty and dual-polarity assessments, which is often lacking in conventional approaches. It is only by comparing the proposed theory of HBFSs with the prevailing ones that it can highlight the capability for next-generation cyber defense and withstand the ill-mannered challenges of complex cyberspace threats. A similar comparative study not only strengthens the theory but also emphasizes its practical relevance in the latest contexts of cybersecurity. Moreover, the supposed theories for mathematical comparison are:
• Theory of fuzzy generalized hybrid aggregation operators (FGHAOs) and its application in fuzzy decision-making by Merigo and Casanovas [27].
• The theory of hesitant fuzzy Hamacher aggregation operators (HFHAOs) for multicriteria decision-making by Tan et al. [28].
• The theory of bipolar fuzzy Dombi aggregation operators (BFDAOs) and its application in MCDM by Jana et al. [29].
The detailed comparison and related results are discussed in below Table 10.
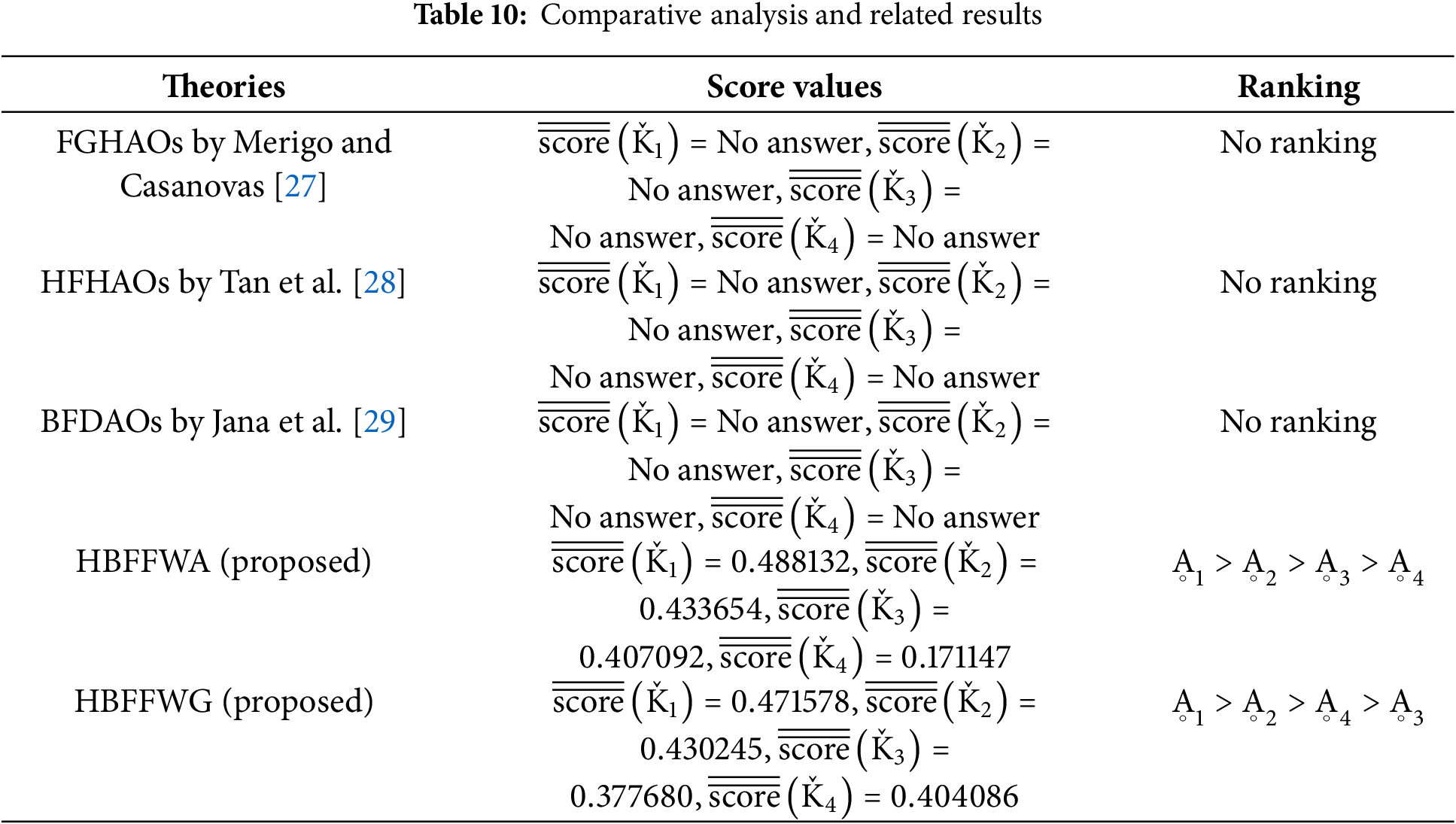
Merigo and Casanovas [27] developed the theory of FGHAOs, which merges different aggregation techniques in the fuzzy domain to tackle decision-making problems with uncertainty. Although this theory offers a versatile framework for the treatment of imprecise data, it works under the traditional fuzzy environment. Such a framework cannot treat hesitation, an important feature of data in cyber threat detection since ambiguity and contradictory evidence are frequently encountered. FGHAOs are effective for general fuzzy decision-making but lack in capturing the layered hesitations and bipolar nature of evaluations required in classifying and prioritizing cyber threats. Tan et al. [28] generalized hesitant fuzzy sets by proposing Hamacher aggregation operators to improve decision-making in multicriteria conditions. The HFHAOs can solve the problems with multiple hesitations as they provide decision-makers with a granular representation of uncertainty. In such a manner, this theory fails to integrate the bipolar perspective required for cyber threat detection techniques that will involve dual assessment of a set of positive criteria (such as threat detection accuracy) and those of negative criteria (such as false alarm rates). The inability of HFHAOs to handle both hesitation and bipolarity at the same time limits their application in the cybersecurity domain, where both dimensions are important in making informed and balanced decisions. Jana et al. [29] introduced BFDAOs and this approach has successfully applied BFDAO in MCDM environments by designing for managing bipolar fuzzy data. Even though the theory encompasses the bipolarity of the data, hesitation does not form part of this account; yet this is the frequent case for the cyber threat classification problem. Cyber threat detection is mostly based on conflicting or incomplete information, and in the process of BFDAOs, because it lacks hesitation modeling, the decision accuracy deteriorates. Therefore, BFDAOs are not feasible in those applications that necessitate a representation of uncertainty along with ambiguity and bipolarity. The proposed theory of HBFSs brings the integration of two principles, one hesitation and the other bipolarity. It fills the gaps left out by the theories above and brings with it an all-inclusive framework that can represent dual-polar opinions and includes uncertainties and conflicts present in cyber threat data. This information, based on HBF Frank, raises further aggregation with a mechanism being more dynamic and adaptive, thus allowing better classification over cyber threat detection techniques. This novel approach is suitably robust, flexible, and precise and, hence, suited to the complex landscape of next-generation cyber defense. Moreover, the proposed theory of HBFSs addresses all these challenges by providing a superior framework to meet the advanced needs of the application in the field of cybersecurity.
7.1 Advantages of the Proposed Approach
• Decision-making uncertainty becomes manageable through the HBFS theory since it allows simultaneous assessment of multiple opinions and values in complex situations.
• HBFS delivers dual viewpoint modeling by handling positive along negative information to exceed traditional fuzzy set functionality. The dual representation mechanism increases its ability to solve complicated decision problems involving conflicting criteria.
• Real-life decisions often involve hesitant information and this theory includes methods to handle this typical situation. HBFS delivers its highest value when knowledge about alternative membership values remains uncertain or unclear to decision-makers.
• Through aggregation operators in HBFS, decision-makers may effectively gather data from multiple criteria along with alternatives. Decision-making becomes both precise and sophisticated thanks to this system when different factors compete against each other.
• This framework enhances decision precision since it presents a refined technique to handle imprecise and uncertain information so judgments become better than traditional crisp and fuzzy approaches.
• The complex management of fuzzy sets in HBFS delivers superior decision-making support systems when formal logic fails to address judgment complexities or information ambiguity.
• The HBFS system offers enhanced alternative ranking precision through the incorporation of hesitant and bipolar information that frequently occurs in practical situations.
Moreover, the characteristics comparison is discussed in Table 11 which shows the significance of HBFSs.
The graphical representation of the comparison of the characteristics is given in Fig. 11.
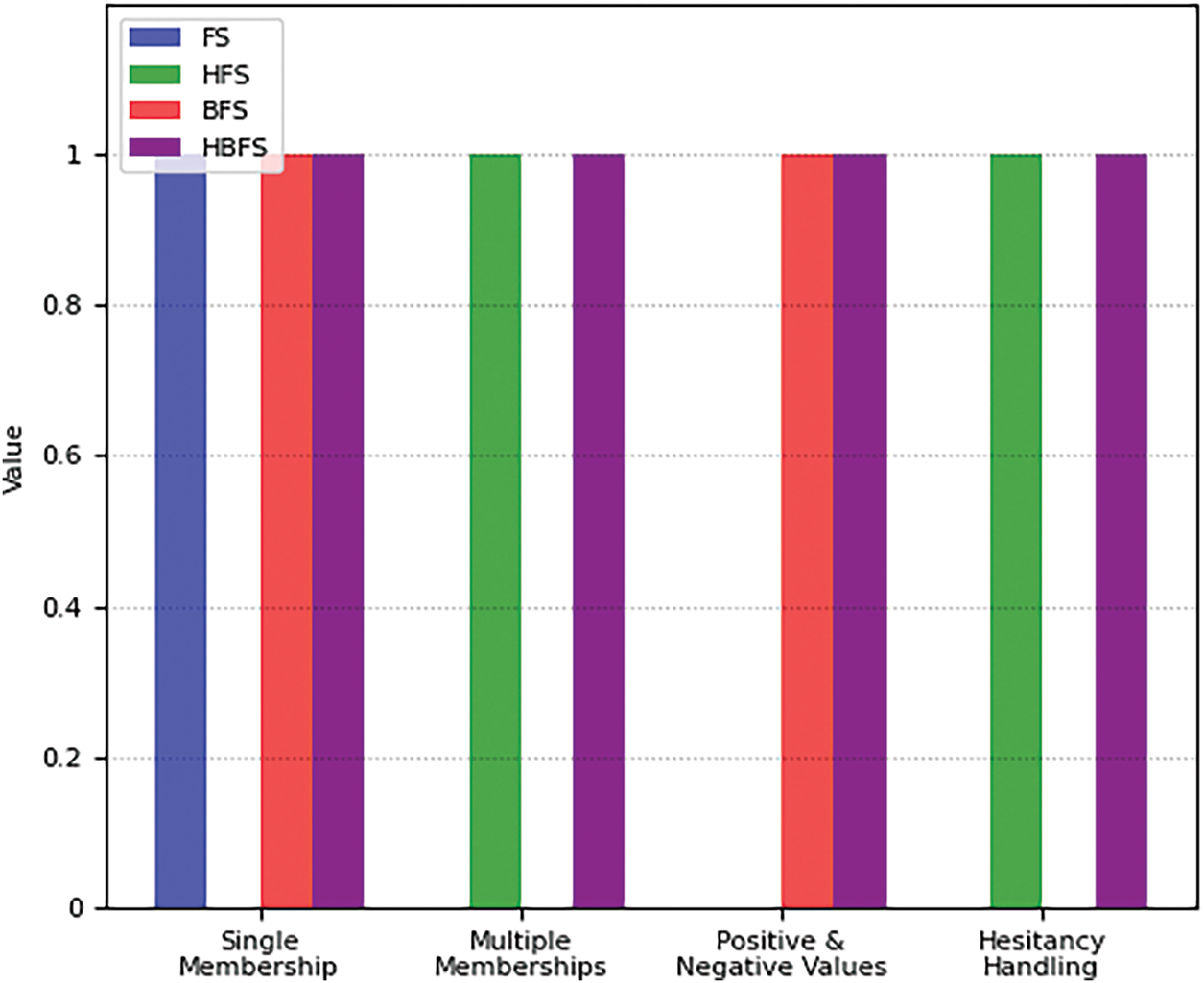
Figure 11: Characteristics comparison between different fuzzy sets
• The complexity of HBFSs makes it challenging for non-experts to apply effectively in real-world scenarios. This increases the need for specialized knowledge to interpret and use the theory.
• The performance of HBFS is highly sensitive to the choice of aggregation operators and other parameters. Small changes in these factors can lead to significant variations in the results.
• Additional testing along with theory improvement is necessary. Such validation and refinement of the theory would enhance its effectiveness in real decision situations.
• The proposed theory shows reduced performance effectiveness when alternatives and decision criteria experience constant changes in dynamic environments. The theory becomes less suitable for swift situations that experience rapid changes.
• The decision-making implications derived from HBFS often remain obscure or unready to use for public officials. Due to its complex nature fuzzy set theory makes it challenging for decision makers to extract direct conclusions from the research results.
• The theory currently lacks empirical validation through case studies or real-world data. Without such validation, its practicality remains uncertain in various applications.
• As the number of criteria and alternatives increases, the computational load grows significantly. This scalability issue limits its use in large, complex decision-making problems.
The most effective method for defending systems against various assaults is to use the appropriate cyber threat detection methodology. Organizations may select the optimal strategy for their requirements by evaluating several approaches based on criteria including accuracy, speed, scalability, and resource usage. While more recent approaches, such as machine learning and anomaly-based detection, can better manage unknown or changing threats, more established strategies, like signature-based detection, are also helpful. By decreasing uncertainty, the application of HBF Frank aggregation operators in decision-making makes it possible to compare different detection methods in a more flexible and trustworthy way. This study highlights the need to take into account a variety of factors when choosing a detection method and how doing so might increase cybersecurity efficacy. Better detection methods are essential to stay up with the ever-increasing cyber threats. This study would be significant since it would shed light on how to choose a suitable detection method to bolster organizational defenses. The findings of this study may help direct future advancements in cyber threat identification, resulting in a more secure online environment. Moreover, we discuss the different comparison results with other existing theories to show the importance of the new proposed approach for classifying the best cyber threat detection technique. In the future, we aim to extend our work with the help of the following theories [30,31].
• The development of a new theory that relies on HBF Frank aggregation operators fills missing gaps in the current cyber threat detection frameworks and methodologies.
• The development of some new aggregation operators such as HBFFWA, HBFFOWA, HBFFWG, and HBFFOWG operators.
• The integration of positive and negative evaluation criteria helps decision-makers manage uncertain and imprecise situations in their decision processes.
• The development of the MCDM approach focuses on classification along with prioritization procedures for cyber threat detection techniques.
• The methodology provides accurate detection method selection capabilities when dealing with unverified data and uncertainties.
• The research presents an application of the methodology through its implementation within a cyber threat detection case study.
• The research presents examples that show how aggregation operators help decision-making procedures in actual cybersecurity situations.
• The manuscript performs an exhaustive evaluation of the new approach compared to traditional research methods within this field.
• A summary highlighting both the success rate of the framework along its anticipated roles in improving cybersecurity protocols follows the analysis.
Acknowledgement: The study was funded by Ongoing Research Funding program (ORF-2025-749), King Saud University, Riyadh, Saudi Arabia.
Funding Statement: The study was funded by the Ongoing Research Funding program (ORF-2025-749), King Saud University, Riyadh, Saudi Arabia.
Author Contributions: Hafiz Muhammad Waqas: Methodology, Investigation, Validation, Software. Tahir Mahmood: Methodology, Investigation, Validation, Software. Walid Emam: Methodology, Validation, Software. Ubaid ur Rehman and Dragan Pamucar: Writing—original draft. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data will be available on reasonable request to the corresponding author or anyone can use the data by just citing the article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Labu MR, Ahammed MF. Next-generation cyber threat detection and mitigation strategies: a focus on artificial intelligence and machine learning. J Comput Sci Technol Studies. 2024;6(1):179–88. doi:10.32996/jcsts.2024.6.1.19. [Google Scholar] [CrossRef]
2. Shaukat K, Luo S, Chen S, Liu D. Cyber threat detection using machine learning techniques: a performance evaluation perspective. In: 2020 International Conference on Cyber Warfare and Security (ICCWS); 2020; Islamabad, Pakistan: IEEE. p. 1–6. [Google Scholar]
3. Balantrapu SS. Current trends and future directions exploring machine learning techniques for cyber threat detection. Int J Sustain Dev Through AI, ML IoT. 2024;3(2):1–15. [Google Scholar]
4. Lee J, Kim J, Kim I, Han K. Cyber threat detection based on artificial neural networks using event profiles. IEEE Access. 2019;7:165607–26. [Google Scholar]
5. Rajendran T, Imtiaz NM, Jagadeesh K, Sampathkumar B. Cybersecurity threat detection using deep learning and anomaly detection techniques. Vol. 1. In: 2024 International Conference on Knowledge Engineering and Communication Systems (ICKECS); 2024 Apr; Chikkaballapur, India: IEEE. p. 1–7. [Google Scholar]
6. Aminu M, Akinsanya A, Dako DA, Oyedokun O. Enhancing cyber threat detection through real-time threat intelligence and adaptive defense mechanisms. Int J Comput Appl Technol Res. 2024;13(8):11–27. [Google Scholar]
7. Maddireddy BR, Maddireddy BR. Advancing threat detection: utilizing deep learning models for enhanced cybersecurity protocols. Rev Esp Doc Cient. 2024;18(2):325–55. [Google Scholar]
8. Lakhno V. Creation of the adaptive cyber threat detection system on the basis of fuzzy feature clustering. East-Europ J Enterp Technol. 2016;2(9):18–25. [Google Scholar]
9. Ullah F, Ullah S, Naeem MR, Mostarda L, Rho S, Cheng X. Cyber-threat detection system using a hybrid approach of transfer learning and multi-model image representation. Sensors. 2022;22(15):5883. doi:10.3390/s22155883. [Google Scholar] [PubMed] [CrossRef]
10. Massam BH. Multi-criteria decision making (MCDM) techniques in planning. Prog Plann. 1988;30(6):1–84. doi:10.1016/0305-9006(88)90012-8. [Google Scholar] [CrossRef]
11. Kazimieras Zavadskas E, Antucheviciene J, Chatterjee P. Multiple-criteria decision-making (MCDM) techniques for business processes information management. Information. 2018;10(1):4. doi:10.3390/info10010004. [Google Scholar] [CrossRef]
12. Sahoo SK, Goswami SS. A comprehensive review of multiple criteria decision-making (MCDM) methods: advancements, applications, and future directions. Decis Mak Adv. 2023;1(1):25–48. [Google Scholar]
13. Kumar A, Sah B, Singh AR, Deng Y, He X, Kumar P, et al. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew Sustain Energ Rev. 2017;69:596–609. [Google Scholar]
14. Alghamdi MA, Alshehri NO, Akram M. Multi-criteria decision-making methods in bipolar fuzzy environment. Int J Fuzzy Syst. 2018;20:2057–64. [Google Scholar]
15. Riaz M, Garg H, Athar Farid HM, Chinram R. Multi-criteria decision making based on bipolar picture fuzzy operators and new distance measures. Comput Model Eng Sci. 2021;127(2):771–800. doi:10.32604/cmes.2021.014174. [Google Scholar] [CrossRef]
16. Riaz M, Habib A, Aslam M. Cubic bipolar fuzzy Dombi averaging aggregation operators with application to multi-criteria decision-making. J Intell Fuzzy Syst. 2021;41(2):3373–93. doi:10.3233/jifs-210667. [Google Scholar] [CrossRef]
17. Gul R. An extension of VIKOR approach for MCDM using bipolar fuzzy preference δ-covering based bipolar fuzzy rough set model. Spec Oper Res. 2025;2(1):72–91. [Google Scholar]
18. Bhol SG. Applications of multi criteria decision making methods in cyber security. In: Cyber-physical systems security. Studies in big data. Vol. 154. Singapore: Springer; 2025. p. 233–58. doi:10.1007/978-981-97-5734-3_11. [Google Scholar] [CrossRef]
19. Ali Z. Fairly aggregation operators based on complex p, q-rung orthopair fuzzy sets and their application in decision-making problems. Spect Oper Res. 2025;2(1):113–31. doi:10.1007/s40314-021-01696-z. [Google Scholar] [CrossRef]
20. Kumar R, Pamucar D. A comprehensive and systematic review of multi-criteria decision-making (MCDM) methods to solve decision-making problems: two decades from 2004 to 2024. Spectr Decis Mak Appl. 2025;2(1):178–97. [Google Scholar]
21. Ali A, Ullah K, Hussain A. An approach to multi-attribute decision-making based on intuitionistic fuzzy soft information and Aczel-Alsina operational laws. J Decis Anal Intell Comput. 2023;3(1):80–9. doi:10.1016/j.jksus.2023.102760. [Google Scholar] [CrossRef]
22. Mahmood T, Waqas HM, Rehman UU. Selection of optimal encryption algorithm based on hesitant bipolar complex fuzzy frank aggregation operators. J Appl Math Comput. 2024;71(2):1–35. doi:10.1007/s12190-024-02239-5. [Google Scholar] [CrossRef]
23. Aslam M, Waqas HM, Rehman UU, Mahmood T. Selection of cloud services provider by utilizing multi-attribute decision-making based on hesitant bipolar complex fuzzy dombi aggregation operators. IEEE Access. 2024;12(2):35417–47. doi:10.1109/access.2024.3369893. [Google Scholar] [CrossRef]
24. Waqas HM, Emam W, Mahmood T, Rehman UU, Yin S. Selection of cloud security by employing mabac technique in the environment of hesitant bipolar complex fuzzy information. IEEE Access. 2024;12(1):123127–48. doi:10.1109/access.2024.3436687. [Google Scholar] [CrossRef]
25. Mandal P, Ranadive AS. Hesitant bipolar-valued fuzzy sets and bipolar-valued hesitant fuzzy sets and their applications in multi-attribute group decision making. Granul Comput. 2019;4(3):559–83. doi:10.1007/s41066-018-0118-1. [Google Scholar] [CrossRef]
26. Frank MJ. On the simultaneous associativity of F(x,y) and x+y−F(x,y). Aequationes Math. 1979;19(1):194–226. doi:10.1007/bf02189866. [Google Scholar] [CrossRef]
27. Merigo JM, Casanovas M. Fuzzy generalized hybrid aggregation operators and its application in fuzzy decision making. Int J Fuzzy Syst. 2010;12(1):15–24. [Google Scholar]
28. Tan C, Yi W, Chen X. Hesitant fuzzy Hamacher aggregation operators for multicriteria decision making. Appl Soft Comput. 2015;26:325–49. [Google Scholar]
29. Jana C, Pal M, Wang JQ. Bipolar fuzzy Dombi aggregation operators and its application in multiple-attribute decision-making process. J Ambient Intell Humaniz Comput. 2019;10(9):3533–49. doi:10.1007/s12652-018-1076-9. [Google Scholar] [CrossRef]
30. Yazdinejad A, Dehghantanha A, Parizi RM, Srivastava G, Karimipour H. Secure intelligent fuzzy blockchain framework: effective threat detection in iot networks. Comput Ind. 2023;144:103801. [Google Scholar]
31. Yazdinejad A, Dehghantanha A, Parizi RM, Epiphaniou G. An optimized fuzzy deep learning model for data classification based on NSGA-II. Neurocomputing. 2023;522:116–28. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools