Secure Medical Image Transmission Using Chaotic Encryption and Blockchain-Based Integrity Verification

1  Introduction

The rapid advancement of the Internet of Things (IoT) has changed how we interact with smart devices, affecting many aspects of our daily lives. This concept facilitates interconnectedness and data exchange among millions of smart devices. It can be conceptualized as a network of physical devices capable of capturing and sharing various types of information in any location, time, medium, or context [1]. With advancements in technologies such as IoT, the healthcare sector is experiencing rapid growth. The primary objective of integrating IoT into healthcare facilities is to enable remote accessibility, facilitating seamless communication between doctors and patients via the Internet, particularly in emergency situations. Advancements in camera technology have brought IoT to a new dimension, but security remains an issue. The centralized storage of sensitive health data might expose personal information to unauthorized access. Moreover, the prevalent IoT architecture heavily relies on centralization, entrusting a single entity with the administration of healthcare data, thereby introducing a single point of failure. Implementing a Blockchain network stands out as one of the most effective approaches, given its role as a distributed database in this scenario. It is suggested that it can serve as a secure and efficient foundation for numerous IoT applications. It offers crucial features including privacy protection, immutability, and decentralization, which greatly enhance the security of data sharing [2–6]. Many existing works rely primarily on the security attribute of Blockchain [7–11]. The authors in [12] address the processing of multimedia data in the context of healthcare systems and present a secure framework for healthcare. leveraging blockchain technology to ensure confidentiality and transparency between patients and intermediaries. Specifically, they proposed a security framework for healthcare utilizing blockchain techniques, where each data is hashed to establish secure chains of records stored across all patient networks. The paper [13] suggested a Blockchain model framework for securing reported patient status health data thereby guaranteeing the security of health data. The method is a (BSDMF): Blockchain-assisted Secure Data Management Framework tailored for health information within the Internet of Medical Things (IoMT). The framework aims to facilitate the exchange of patient data while improving security, scalability, and data accessibility in healthcare environments. It provides secure data management among embedded medical devices, cloud servers, and personal servers. Leveraging the security framework based on IoMT, the authors employed BC technology to guarantee the security of data transmission and effective data management across interconnected nodes. Azbeg et al. [14] introduced BlockMedCare, a secure healthcare system integrating IoT medical devices with BC and IPFS technologies. This solution is constructed with the objective of efficiently collecting and sharing patient data with medical teams, ensuring a high level of security for storing and sharing sensitive information. The system is divided into three key parts. The first part is devoted to data collection, utilizing IoT healthcare devices to ensure accurate and reliable data acquisition. The second part is dedicated to securely sharing data, with blockchain technology ensuring the integrity and confidentiality of shared information. Lastly, the third part handles data storage, utilizing IPFS for efficient and decentralized storage of patient data. Therefore, by primarily leveraging the security attribute of Blockchain, some works may not suffice for certain use cases. However, there has been a lack of extensive research conducted regarding security and privacy within the domain of IoT in healthcare.

Some research efforts have been dedicated to the security domain [15–19]. To ensure security and privacy for telehealth services, Anand et al. [20] proposed a sophisticated technique to enhance the security of medical images in telemedicine by leveraging discrete wavelet transform (DWT) and singular value decomposition (SVD) for watermarking. The method excels in providing enhanced security, robust resistance to various signal processing attacks, and high imperceptibility, which are crucial for ensuring the integrity and confidentiality of medical data. Despite its strengths, the method’s complexity can lead to increased computational demands, potentially limiting its application in real-time environments or when scaling large datasets. Additionally, while robust, the approach may not guarantee comprehensive defense against all novel attack vectors, emphasizing the need for continuous updates. The paper in [21] proposed a medical image encryption scheme combining DNA computing and chaotic maps to enhance security in telemedicine. The method ensures high entropy, low pixel correlation, and strong key sensitivity, making it resistant to brute-force, statistical, and differential attacks. It is computationally efficient and suitable for cloud-based healthcare applications. However, its high computational complexity may limit use in resource-constrained devices, and key management challenges could impact synchronization during decryption. Additionally, it lacks explicit countermeasures against quantum computing threats. Despite these limitations, the method provides robust encryption for securing medical images in modern telemedicine systems. In [22], the authors introduced a novel approach to medical image cryptography within the context of smart IoT healthcare applications, utilizing a Neural Stacked Auto-Encoder (SAE) framework to leverage deep extracted features. The proposed cryptosystem employs the network SAE to generate two chaotic random matrices. They used the first matrix to create a comprehensive shuffling matrix, which alters the location of pixels within the digital input image. Subsequently, the medical image is shuffled using this matrix, resulting in a rearranged image where pixel values are altered based on their corresponding positions in the shuffling matrix. The second set of chaotic random matrices generates independent sequences, which remove the correlation among the shuffled cipher and original images. Each chaotic sequence used to further confuse the permuted medical image. In [23], authors proposed a cryptosystem for enciphering different types of medical images. A hybrid mechanism was created to scramble two plain images in a separate way using chaotic maps and combining them to improve the robustness and security of the cryptosystem. The first image undergoes diffusion and permutation through the Logistic-May map and the Henon map. The second image exhibits a scrambled arrangement of pixels using the Logistic-Sine system. Lastly, a non-linear formula that is based on Cramer’s rule was used for fusing both ciphered images, resulting in two hybrid encrypted images.

Indeed, numerous security solutions have been proposed in the literature, among them encryption and blockchain technology stand out prominently [24–27]. In response to cybersecurity challenges, Doreen Hephzibah Miriam et al. [28] present a novel security enhancement approach involving blockchain-based data sharing within healthcare systems. It introduces the Lionized Golden Eagle-based Homomorphic Elapid Security (LGE-HES) algorithm. This algorithm combines the LGE and HES techniques. The HES technique relies on a confusion process, utilizing S-Box components in both the original and encrypted data. On the other hand, the LGE technique is employed for optimal key selection, aiming to select the most suitable private and public keys for transmission and reception within the blockchain network. Several issues arise in this work, including the overall key size and the computational complexity, which tend to be significant. The work in [29] introduced a Blockchain-based chaotic deep Generative Adversarial Network (GAN) encryption scheme. This scheme leverages blockchain technology to protect personal information and to authenticate the veracity of data. Medical images are ciphered using the chaotic deep GAN based on the principles of confusion, substitution, and diffusion before storing them in the cloud. This scheme generates secret keys that are specific to image with the objective of enhancing the system’s ability against attacks. The data sender sends the ciphered data to the cloud server, signs the ID of the cipher image, and then stores it on the blockchain while the data user requests the data from the cloud and uses the signature to verify the encrypted image’s authenticity. In the paper [30], the authors proposed a Blockchain-based Chaotic Arnold’s Cat Map Encryption Scheme (BCAES). This scheme is used to encrypt the medical image utilizing Arnold’s cat map encryption scheme. Subsequently, the ciphered image is transmitted to the Cloud Server, while the signature of the plain image is stored in the Blockchain. The signature is made using the SHA-256 hash function. The image encryption algorithm goes through three phases: confusion, using the henon, permutation, and lastly, a diffusion phase using a novel Arnold’s cat map, which is XORed with the previous results. This work has used classical chaotic systems while these systems have some limitations including periodicity, vulnerability to phase space destruction, and low Lyapunov exponents. In the article [31], authors have proposed an image encryption model, named Multi-Chaotic Maps and Blockchain (MCBE). The encryption process was divided into two phases. The confusion phase: a random permutation is employed to scramble the original image pixels. The diffusion phase: a logistic map and tent map are applied row-wise and column-wise. Additionally, blockchain is integrated using the SHA-256 hash function, enhancing the model’s efficiency and increasing security. Finally, the encrypted image data blocks are merged to form the entire encrypted image.

In this context, we introduce a novel encryption algorithm that integrates Blockchain technology, intending to enhance the security and privacy of data transmission.

The main purpose of our contribution is:

•   Implementing an innovative block cipher encryption scheme for medical images based on chaos theory.

•   Encrypting the medical images and generating digital signatures utilizing hash functions and storing them to authenticate the cipher image’s authenticity.

•   Proposing a blockchain-based solution that transmits the medical images into the network after encrypting them, and secure communication between the nodes.

•   The remainder of this work is structured as follows. Section 2 presents the necessary background and preliminaries. Section 3 outlines the proposed methodology, followed by the proposed cryptosystem in Section 4. A description of the signature generation is discussed in Section 5. The results analysis is described in Section 6. In Section 7, a comparative study is discussed and finally, conclusions are drawn in Section 8.

2  Preliminaries

After outlining the introduction and organization of the paper, this section begins with an overview of some topics. This serves as a background and a preamble to the concepts utilized in the proposed method.

2.1 Chaotic Maps: Logistic Map (LM)

The LM is presented as a second-order polynomial map, characterized by its one-dimensional discrete-time nonlinear nature [32]. It serves as a thoroughly documented example of a discrete system demonstrating chaotic behaviour. It stands out as one of the simplest and most transparent systems showcasing the transition from order to chaos [33]. The LM is defined by the Eq. (1):

xn+1=rxn(1−xn)(1)

With r presented as a control parameter in the range of [0, 4]. The generated chaotic sequence is presented by xn with values ranging between 0 and 1. The logistic map shows chaotic behavior when the control parameter r varies between 3.57 and 4.

Fig. 1 displays the bifurcation diagram of the one-dimensional LM. The diagram reveals periodic windows appearing at fixed intervals. These periodic windows must be eliminated as their presence prevents the cipher image from behaving randomly, ultimately leading to an inefficient encryption process.

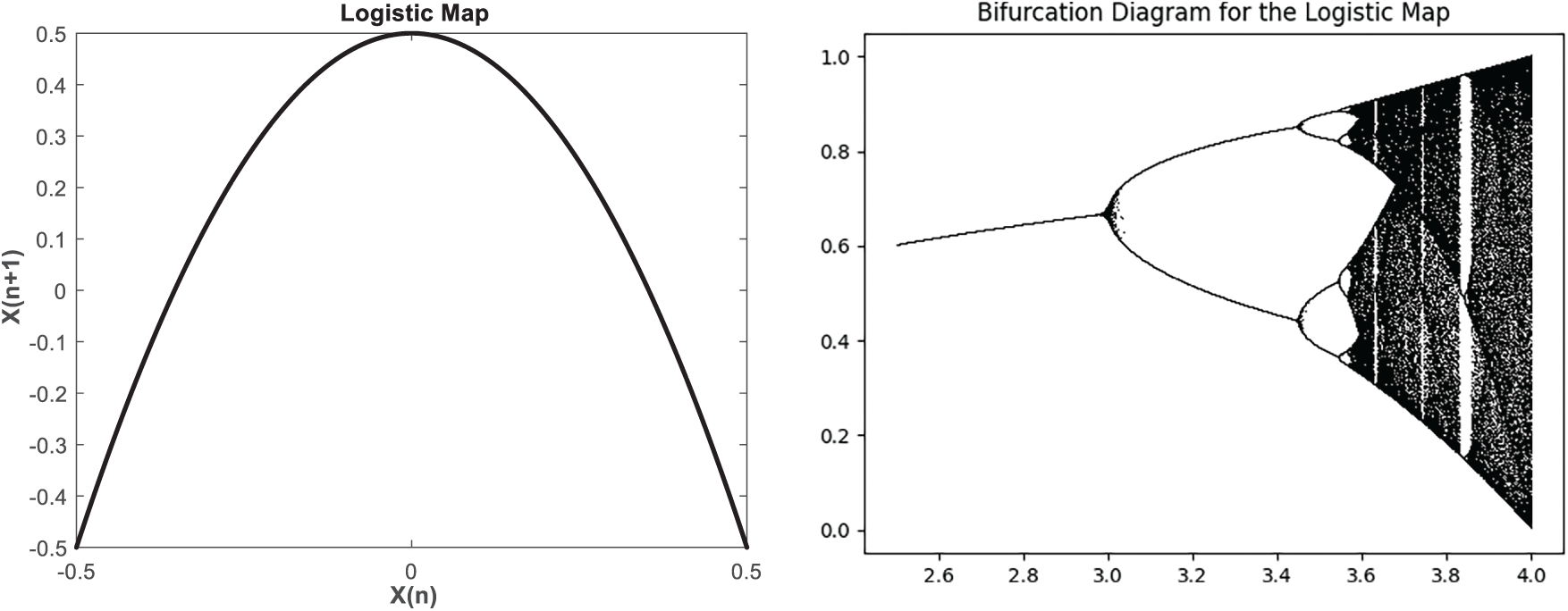
Figure 1: The Logistic Map function and Bifurcation diagram with r between 2.5 and 4

2.2 Chaotic Maps: Tent Map (TM)

The tent map stands out as one of the most straightforward 1-D, non-invertible, piecewise linear discrete maps showing chaotic dynamics [34]. The chaotic tent map equation is denoted by Eq. (2):

xi+1=f(xi,μ)(2)

where f(xi,μ) is defined as:

f(xi,μ)={μ×xiIfxi<0.5,μ×(1−xi)Ifxi≥0.5.(3)

In which, xi∈(0,1)for i≥0 is referred to as the state of the system. It should be noted that μ∈[0,2] is the control parameter and x0 is the initial value.

Fig. 2 illustrates the bifurcation diagram of the Tent map, highlighting its dynamic behavior and broad chaotic regime. The diagram clearly reveals the system’s transition into chaos, with the bifurcation phenomenon indicating its inherently chaotic nature.

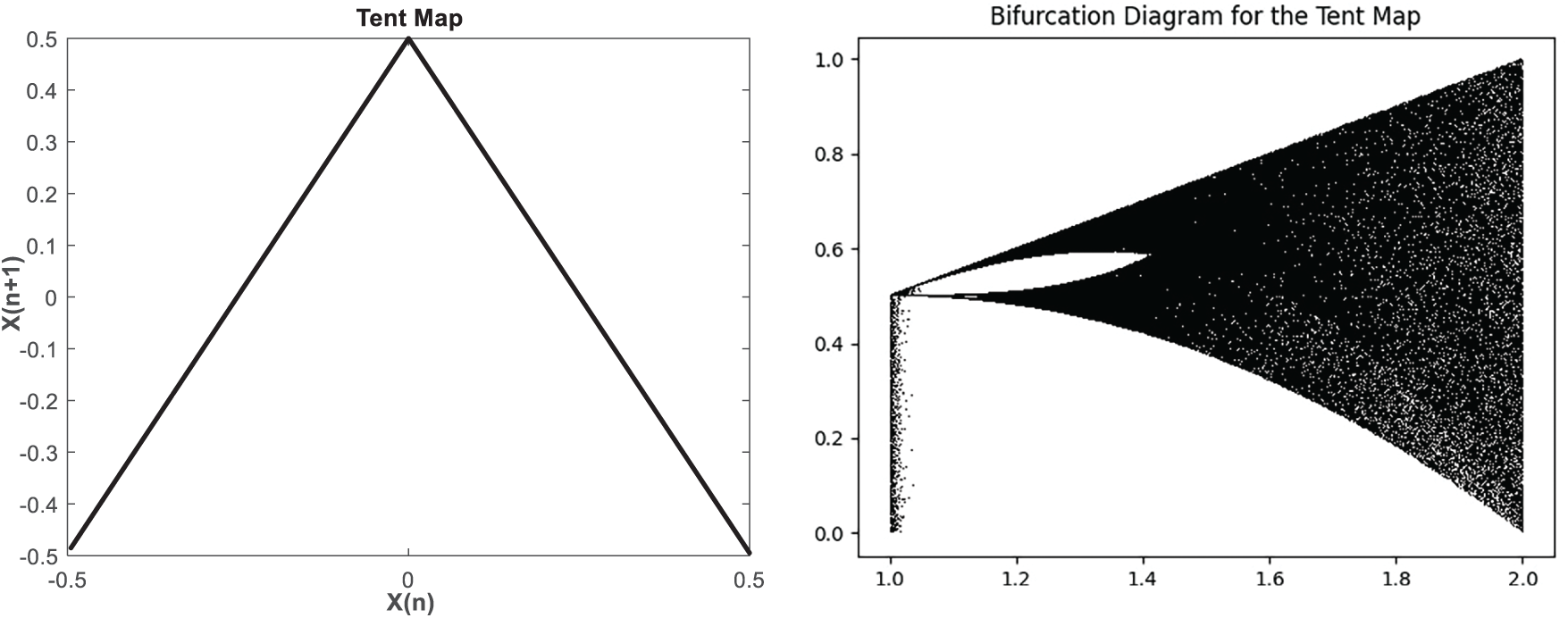
Figure 2: The Tent Map function and Bifurcation diagram with μ between 1 and 2

2.3 Chaotic Maps: Henon Map (HM)

The Henon map, which was first introduced by Michel Henon in 1976, is a straightforward 2D discrete chaotic system [35]. It serves as a discrete dynamic map demonstrating chaotic behavior, being highly sensitive to its initial conditions.

Mathematically, the Henon map is presented as follows:

x(n+1)=1−axn2+yny(n+1)=bxn(4)

The variables (x(n),y(n))∈R2 are presented as the state values of the system, while a and b serve as the control parameters. The Henon Map depends on these two parameters, which are explored across various numerical values. However, the system exhibits chaotic behavior specifically when a = 1.4 and b = 0.3. Fig. 3 illustrates the Henon map attractor on the (x, y) plane.

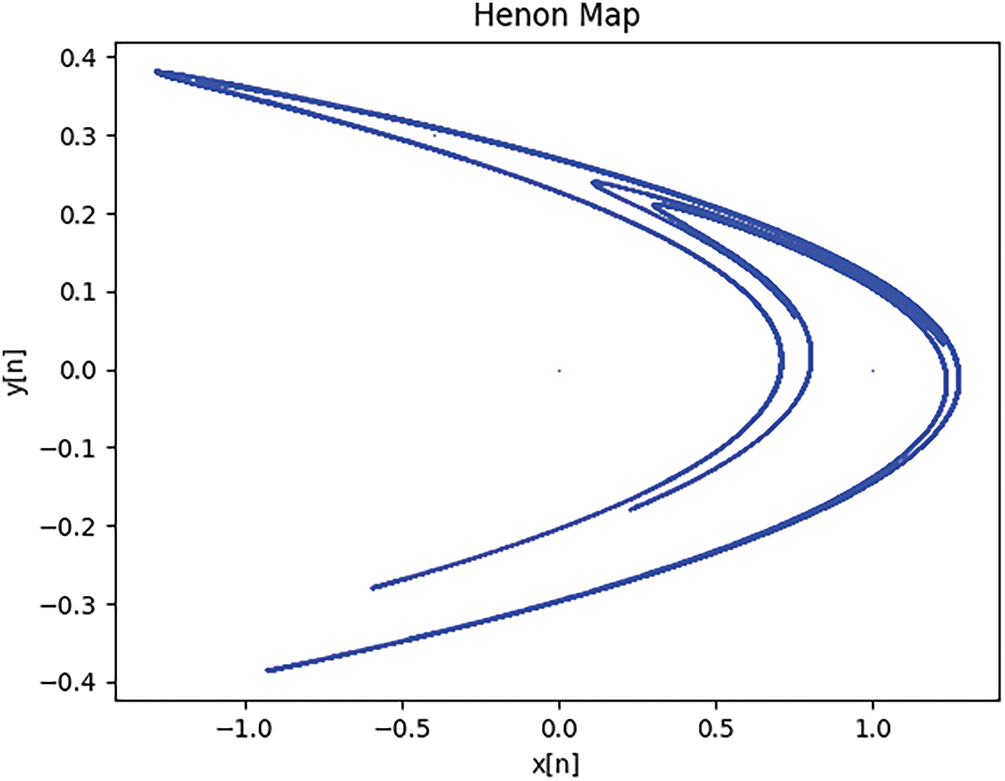
Figure 3: Diagram of henon map for a = 1.4 and b = 0.3

2.4 Scan Pattern Method

The Scan method is a two-dimensional spatial access technique designed to generate diverse scanning trajectories across a matrix of size M × M. It offers a systematic and efficient approach for constructing various scanning paths, which are particularly useful in image processing applications. In the context of image encryption, these scan patterns play a critical role in the pixel scrambling process, enhancing diffusion and security. Fig. 4 presents several commonly employed scan patterns that are frequently integrated into encryption schemes [36,37].

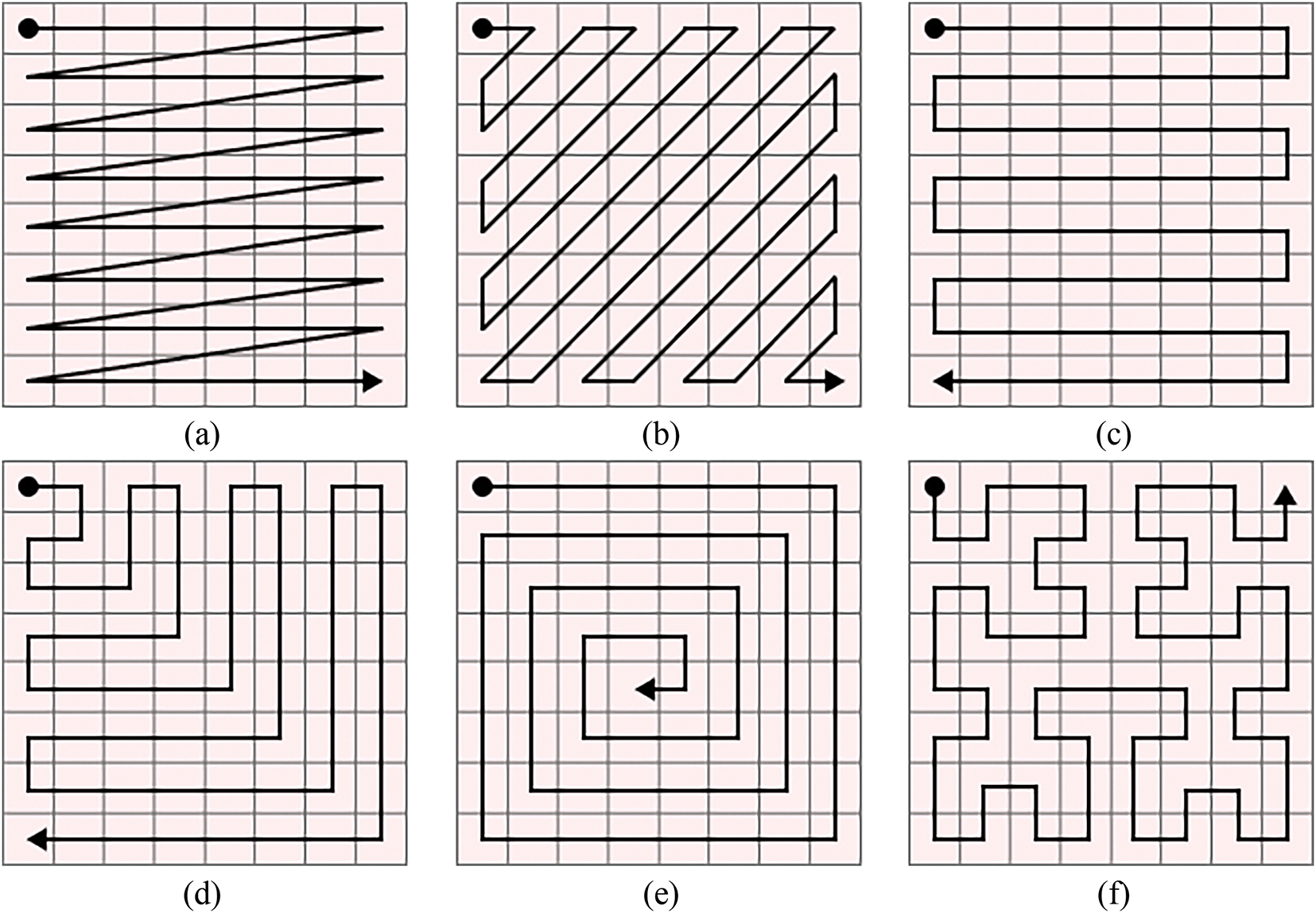
Figure 4: Different scan patterns

In this work, image scrambling is achieved utilizing the Hilbert curve, ensuring only pixel-level permutations. The primary reason for using the Hilbert curve is its easy to generate. Additionally, when applied to the image, it better utilizes the coherence of neighboring pixels compared to the traditional scan-line approach, resulting in greater image confusion. The Hilbert curve is a type of SCAN pattern that scans a 2 m × 2 m array of points as shown in Fig. 4f. The scan path can be constructed starting from the right-top (RT), left-top (LT), right-bottom (RB), or the left-bottom (LB) corners of the square grid. In the scan method, the Hilbert curve is employed to shuffle the pixel positions of the image, resulting in a scrambled image. Fig. 5a–d depicts the Hilbert curves of orders 1, 2, 3, and 4, respectively, corresponding to square grids of sizes 2 × 2, 4 × 4, 8 × 8, and 16 × 16.

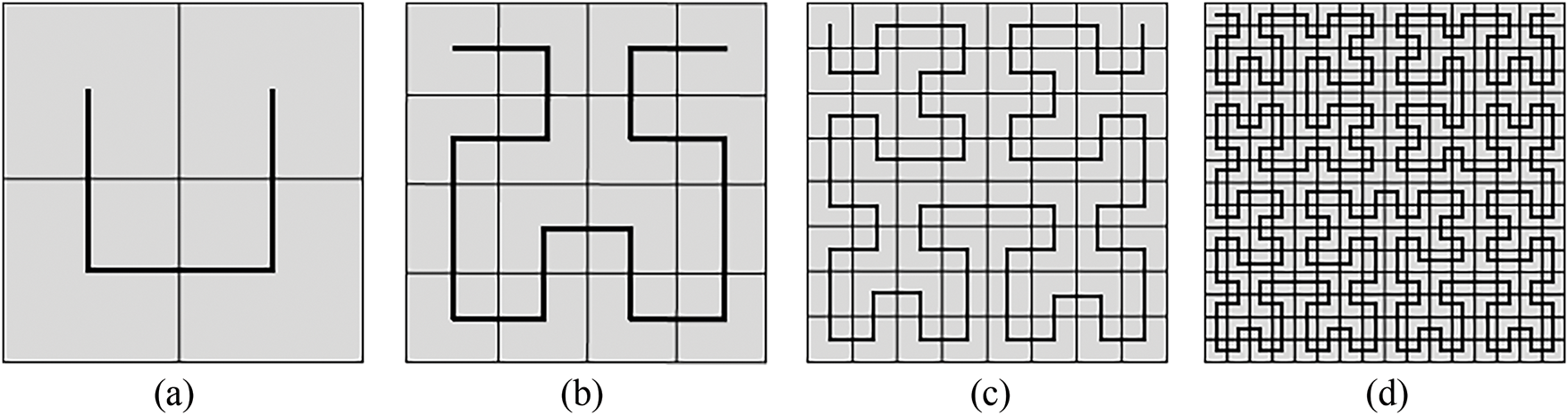
Figure 5: The Hilbert curves of orders 1, 2, 3, and 4 correspond to square grids of sizes 2 × 2, 4 × 4, 8 × 8, and 16 × 16, respectively

2.5 Blockchain Technology

Blockchain technology serves as a mechanism for storing and transmitting data, primarily aimed at facilitating transactions without the necessity of an intermediary, a concept known as decentralization [38]. The blockchain is a technology that enables decentralized and secure storage of data by utilizing blocks that are linked together. Its application extends to ensuring the security and transparency of data gathered by interconnected objects within IoT networks [39]. In Blockchain, information such as transactions is stored within the blocks of the blockchain. Each block serves as a grouping of the most recent transactions that await validation and undergo cryptographic processing [40]. A block is divided into two parts. The first part is the header containing identification information used to prove the block’s authenticity and transactions it contains. The second part is the body that contains all recent transactions.

Fig. 6 illustrates an overview of the fundamental architecture of a blockchain. The header comprises the hash value of the previous block, the current block, and a timestamp. The body section encompasses transactions or data.

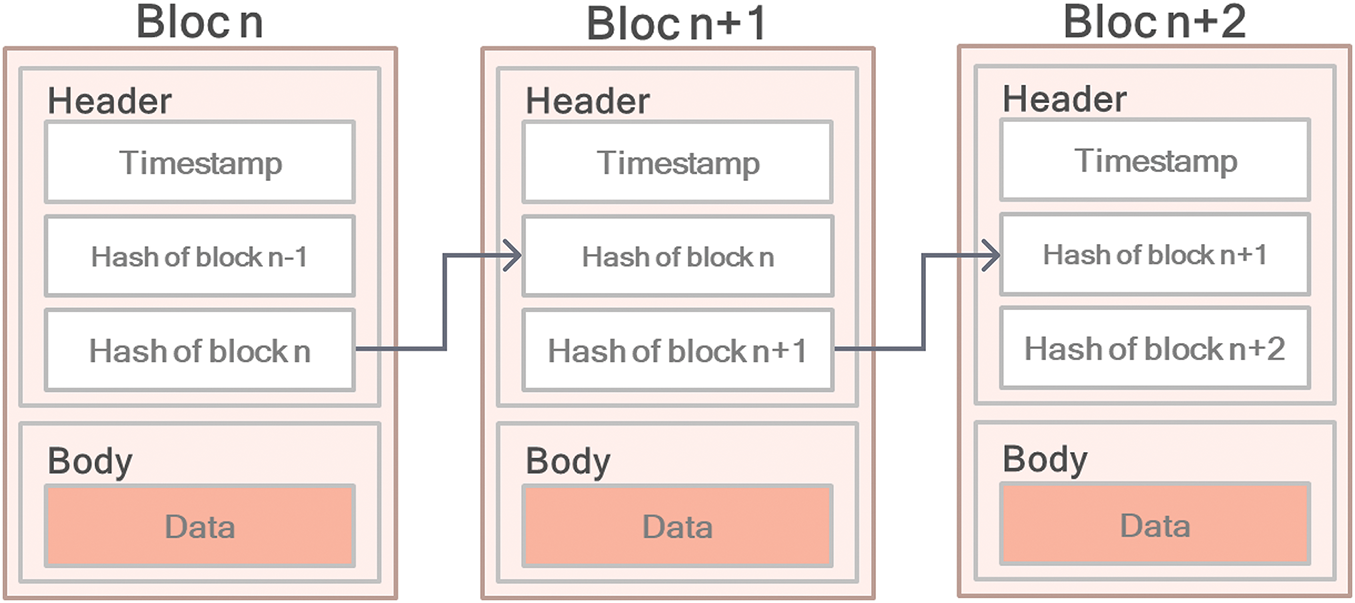
Figure 6: General structure of a blockchain

Blockchain technology relies on cryptography, employing encryption through advanced algorithms to protect data and ensure its integrity. This cryptography guarantees secure communication, even in scenarios where a malicious entity gains access to confidential data on a device. The cryptography primitives used in blockchain are hash functions, asymmetric encryption, and digital signatures.

A hash function is employed to transform data of variable size into fixed-size output data. It is applied to both transactions and blocks. Any modification made to the data will impact the hash of the data, thereby affecting the final hash because the mentioned function merges blocks. This function provides a double layer of protection to the data and renders blockchain blocks resistant to tampering and manipulation.

In asymmetric encryption, a key pair is necessary, comprising a private and a public key. The public one can be exchanged openly, whereas the private one has to remain exclusive to its owner, ensuring that it cannot be derived from the public key.

3  Methodology

The primary objective of this study is to develop a novel encryption framework that incorporates blockchain technology to enhance the security and privacy of data transmission, while ensuring the confidentiality and integrity of medical images. The integration of blockchain is motivated by its decentralized architecture, immutability, and ability to provide a tamper-proof and permanent record of information.

Fig. 7 shows the proposed architecture of a blockchain method used in healthcare systems and enhanced with encryption.

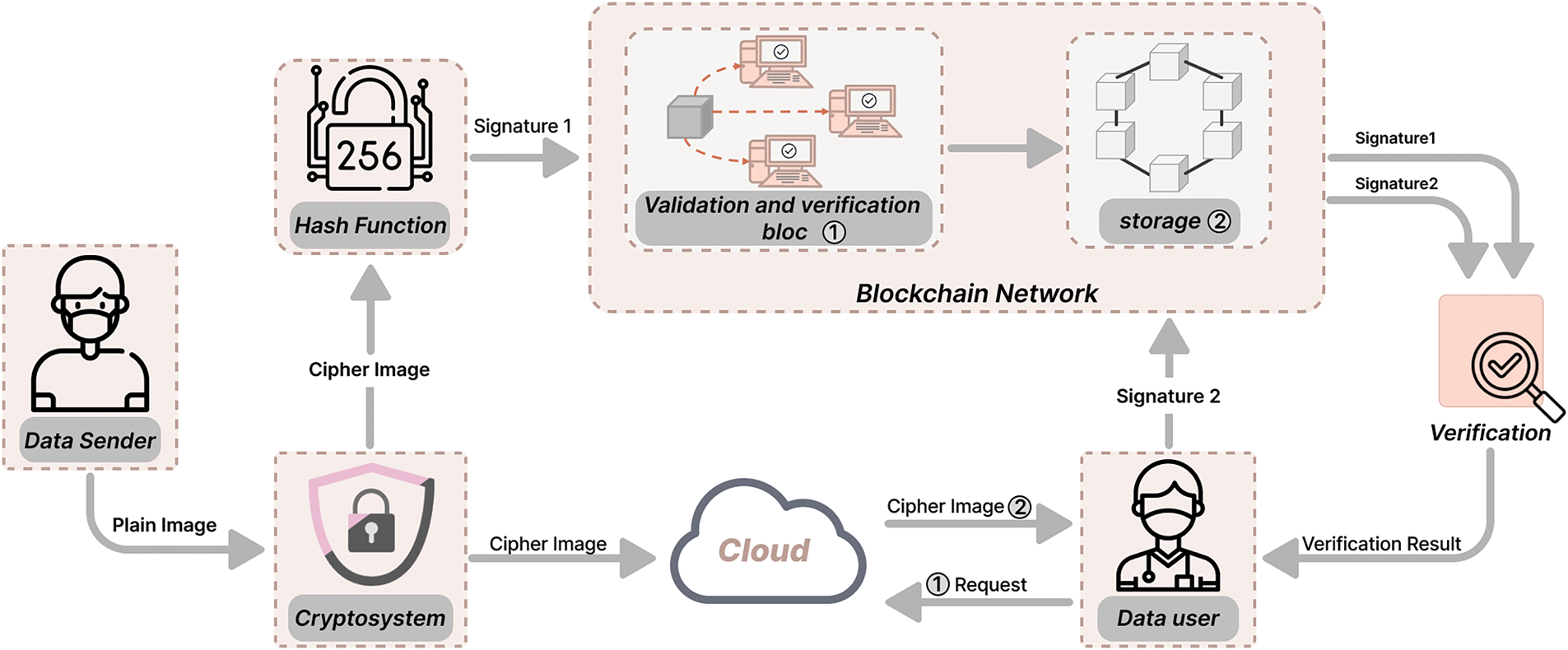
Figure 7: The proposed architecture of the blockchain method used in healthcare systems

Initially, the sender generates a digital signature of the medical image using the SHA-256 hash function and subsequently encrypts the image using the proposed encryption scheme. The resulting ciphertext is uploaded to a cloud server, while the corresponding digital signature is recorded on the blockchain. When a data user requests access to the medical image, the encrypted file is retrieved from the cloud and delivered to the user. Upon receipt, the user applies the decryption algorithm to recover the image. Prior to decryption, the user verifies the integrity and authenticity of the encrypted image by submitting it to the blockchain. The blockchain performs the verification using the stored signature and returns a confirmation message either “yes” or “no” indicating whether the image has maintained its authenticity. The key features of the proposed model are summarized as follows:

•   Data Sender (Patient): Encrypts medical images with the proposed encryption algorithm, sends the obtained data to the Cloud Server, and then signs the ciphered image to finally store it in the Blockchain network.

•   Data User (Health Service): Requests the data from the cloud server to obtain the ciphered image. In addition, the user verifies the authenticity of the cipher image by matching the cipher image’s signature stored in the blockchain.

•   Cloud Server (CS): Stores large amounts of medical image data and searches and sends the associated encrypted images due to the data user’s request.

•   Blockchain: Checks the stored signature when it receives a request from the data user to confirm the validity of the encrypted image. If the condition is true, the result is 1; else, the result is 0.

•   Encryption and Decryption Process: Before transmission to the Cloud Server, the medical image undergoes encryption using our proposed encryption algorithm that is based on chaotic maps. The reverse process, which is for retrieving the medical image, is the decryption process.

4  Proposed Cryptosystem

This section presents the proposed algorithm for image encryption and decryption based on chaotic maps. The algorithm comprises two primary phases. In the first phase, three initial chaotic keys are employed to generate high-quality encryption keys using three distinct chaotic maps: the Logistic map, the Tent map, and the Henon map. The second phase involves the application of the cryptosystem, which leverages the principles of confusion and diffusion to ensure robust security. Fig. 8 illustrates the overall structure of the proposed encryption and decryption framework.

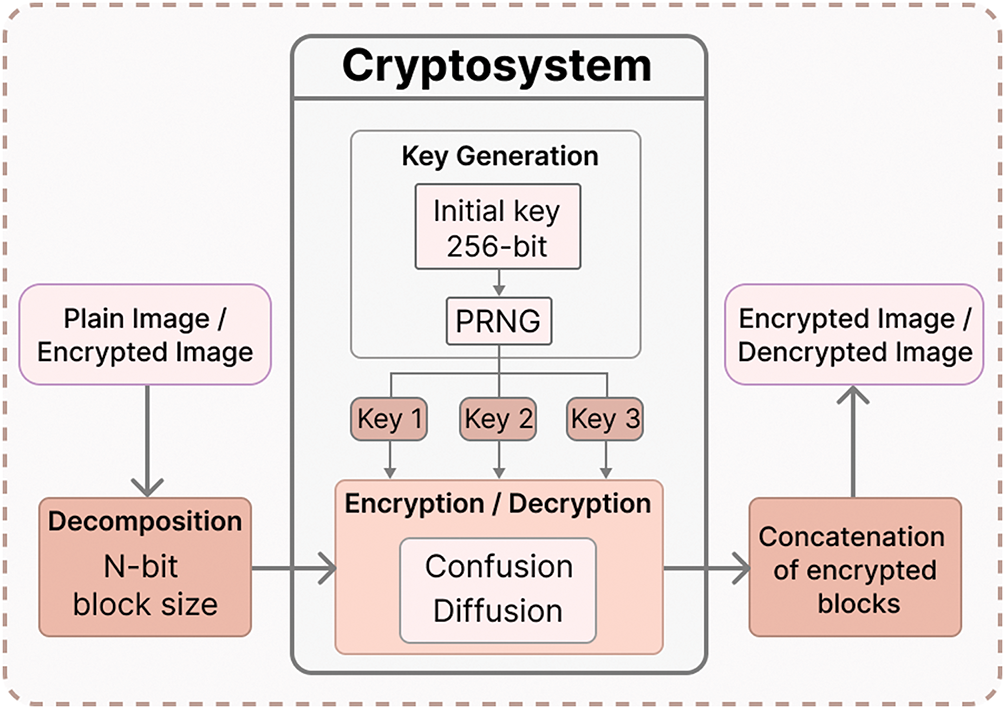
Figure 8: General view of the proposed cryptosystem

4.1 Key Generation

To enhance the robustness of keys against hackers, we have proposed a Pseudo-Random Number Generator (PRNG) that produces deterministic random number sequences based on various chaotic maps. In this paper, we have chosen three distinct chaos maps for analysis and design: the LM, the TM, and the HM. These maps exhibit strong chaotic characteristics, rendering their chaotic orbits highly unpredictable.

The PRNG necessitates initialization with an initial state to generate a set of numbers displaying robust random behavior. The input image’s hash value was generated using SHA-256, producing a 256-bit (32-character) result. This hash value is then divided into four parts. To implement the confusion and diffusion processes, the three chaotic maps are utilized. Each 32 bits of hash value is employed to generate the initial conditions for each chaotic map. Fig. 9 illustrates the block diagram of the key generation procedure.

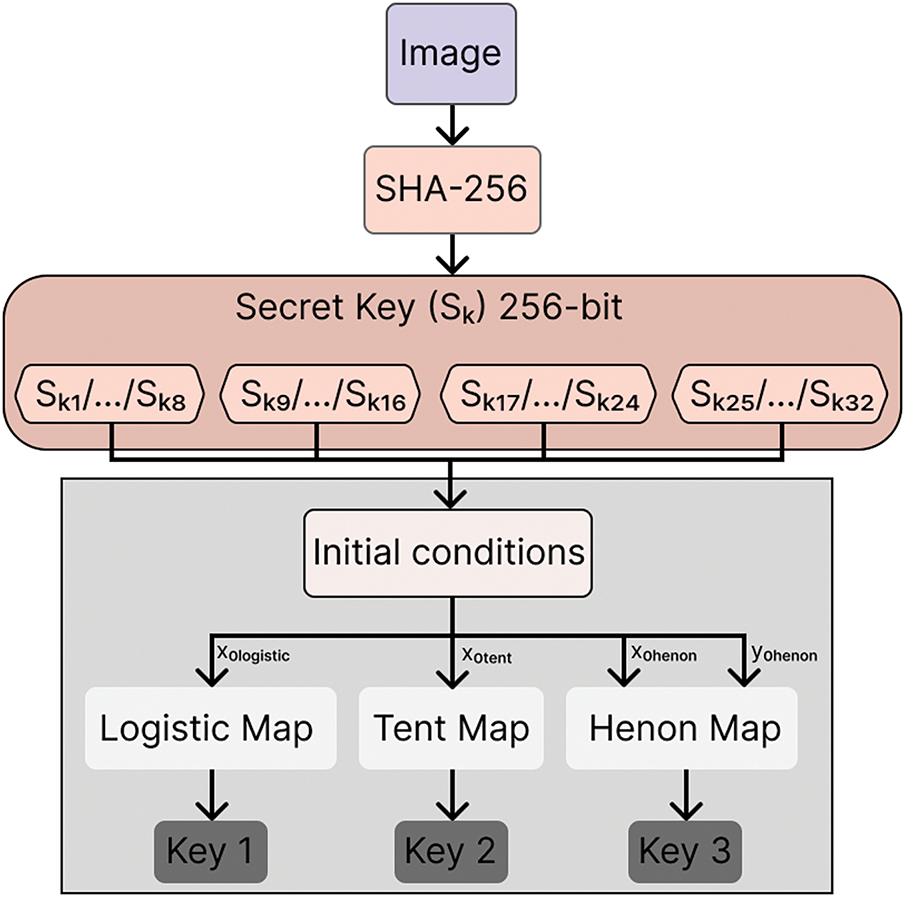
Figure 9: Key generation module used for feeding the encryption process

The generated sequence, referred to as the 256-bit secret key (Sk), is divided into 8-bit blocks (Ski), allowing Sk to be expressed as described in the equation below. These new blocks (Ski) will be utilized to create the initial map values.

Sk=Sk1|Sk2|Sk3|Sk4|…|Sk32(5)

x0log⁡istic=x0log⁡istic′+Sk1⊕Sk2⊕…⊕Sk8256(6)

x0tent=x0tent′+Sk9⊕Sk10⊕…⊕Sk16256(7)

x0henon=x0henon′+Sk17⊕Sk18⊕…⊕Sk24256(8)

y0henon=y0henon′+Sk25⊕Sk26⊕…⊕Sk32256(9)

4.2 Encryption Process

To illustrate the effectiveness and practical applicability of the proposed approach, a basic image encryption algorithm based on confusion and diffusion principles is developed. The input image I, with dimensions M × N × L, undergoes encryption, where L represents the number of channels, and M and N denote the image height and width, respectively. For grayscale images, the encryption is applied directly. In the case of color images, each of the three RGB channels; Red, Green, and Blue is encrypted independently. The resulting encrypted channels are then recombined to produce the final ciphertext image. Prior to encryption, each color component is divided into fixed-size blocks of 512 bits. If the image data does not evenly divide into 512-bit blocks, the final block is zero-padded to meet the required length. Fig. 10 presents an overview of the general architecture of the proposed encryption process.

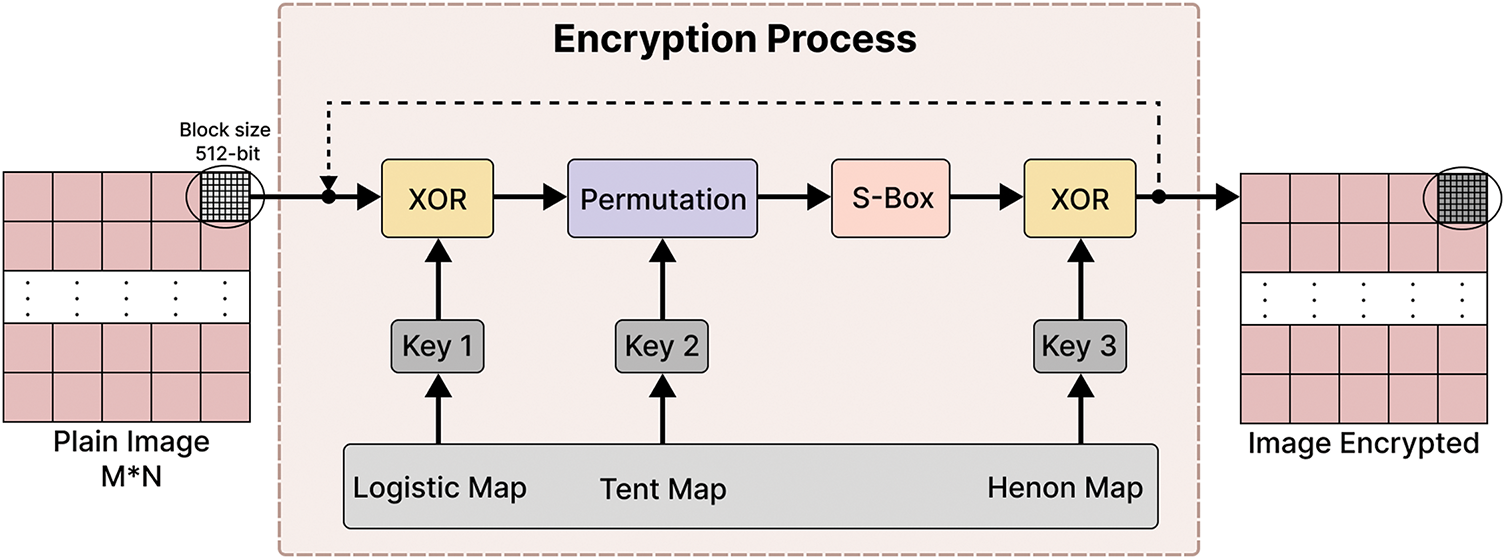
Figure 10: General architecture of our image encryption process

As shown in Fig. 10, the encryption process is split into four operations.

•   Operation 1 (Diffusion): The first operation is an XOR operation in which we applied an XOR between a block of plaintext image and a block of the key ‘key1’ generated by the logistic map. This operation is important for our work because it masks the original pixel values, eliminates the redundant pixels, and equalizes grey levels throughout the image.

•   Operation 2 (Confusion): The next operation is a level-pixel permutation. Permutation is an efficient technique for shuffling the pixel positions, effectively reducing the correlation between adjacent pixels in the original image. That operation utilized the Hilbert curve of order 3 and the ‘key2’ generated by the tent map. Based on the key block’s parity, the medical image’s pixels undergo scrambling by starting the Hilbert curve from the top-left (TL) or the bottom-right (BR).

The process is illustrated in Fig. 11a,b. The Hilbert curve starts from the top-left if the key value is even. Conversely, if the key value is odd, it starts from the top-right:

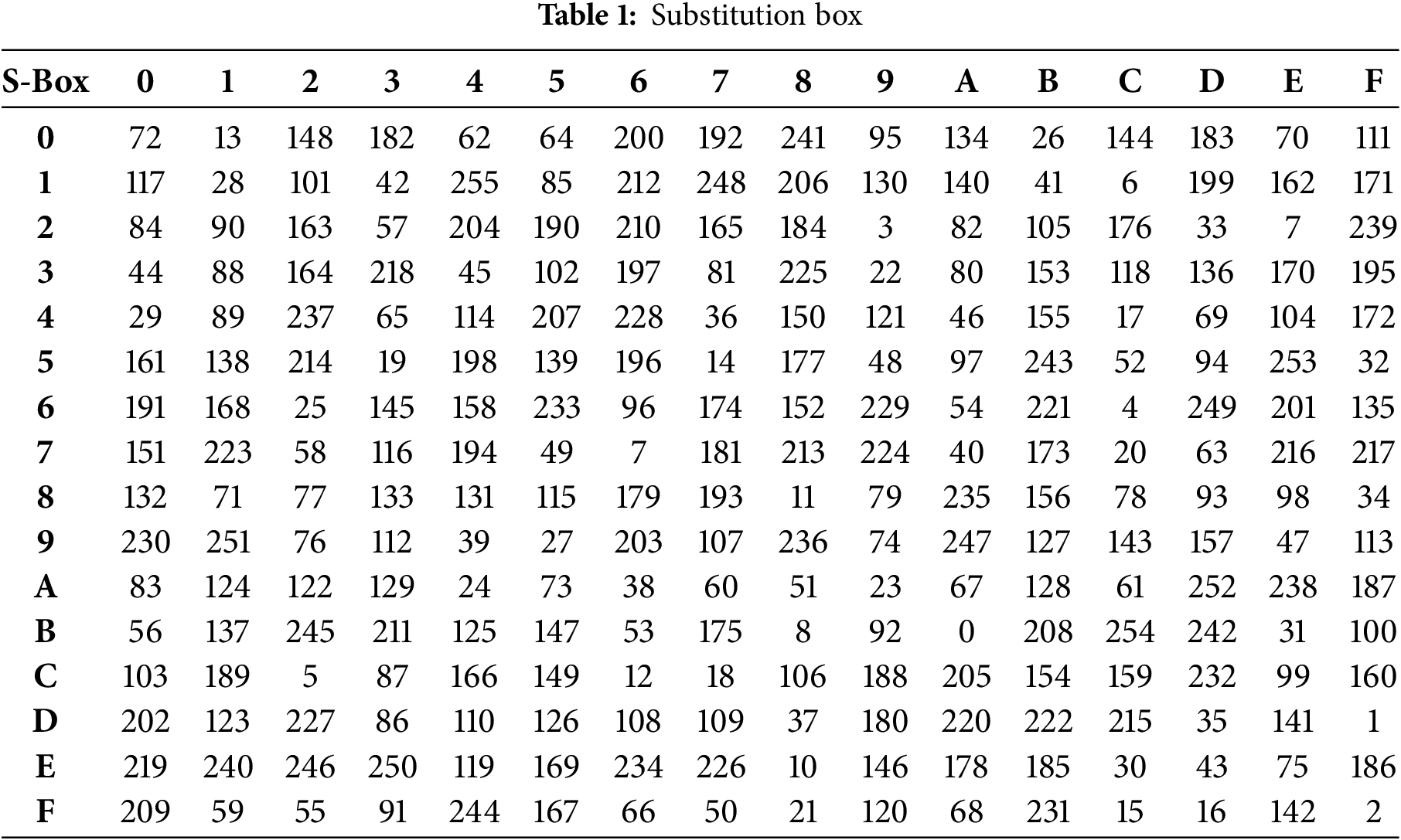
•   Operation 3 (Diffusion): This operation involves substituting all the permuted pixels from the previous stage using an S-Box. We utilized a dynamic S-box generated via the logistic map. This dynamic S-box serves to enhance the security of the proposed system. Therefore, the logistic map is applied iteratively to produce a random vector of size 256. This vector is then arranged in a matrix of size 16 × 16 to create the S-box. Consequently, to enhance the randomness and complexities of the proposed scheme, this S-box is applied to the diffused layer to produce a highly secure cipher image.

Each pixel of the block is replaced by a specific value from the S-Box as mentioned in Eq. (10):

Sp=SBox(Pij)(10)

where Sp represents the substituted pixel, P denotes the pixel obtained from the previous step, and i and j represent the index position. Table 1 illustrates the S-Box generated in the standard 16 × 16 format.

•   Operation 4 (Diffusion): This operation is another XOR operation that is performed among the block obtained in the previous step and the key block ‘key3’ generated by the Henon map. This step conceals all the encryption operations carried out on the image.

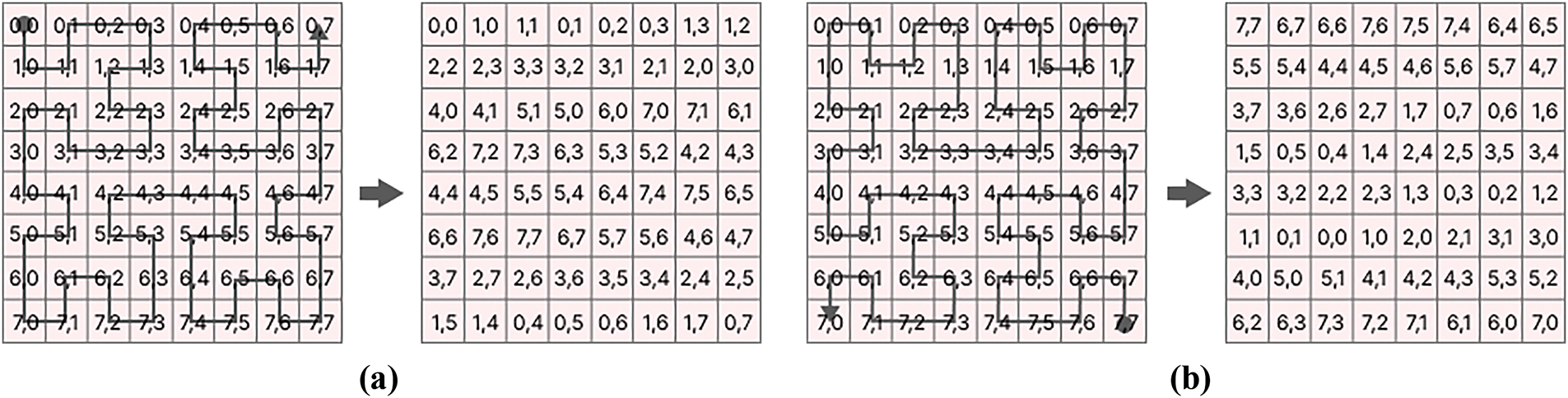
Figure 11: (a) Top-left Hilbert curve process. (b) Bottom-right Hilbert curve process

All these operations are applied until passing by all blocks of the plaintext image. Finally, the last step in this encryption phase involves combining all the ciphered blocks to maintain the final cipher image.

4.3 Decryption Process

To decrypt the encrypted image and recover the corresponding plain image, the reverse of the encryption process is followed. Starting from operation 4 and moving backward to operation 1, the steps are reversed using the correct initial conditions. The detailed decryption process is represented in Fig. 12.

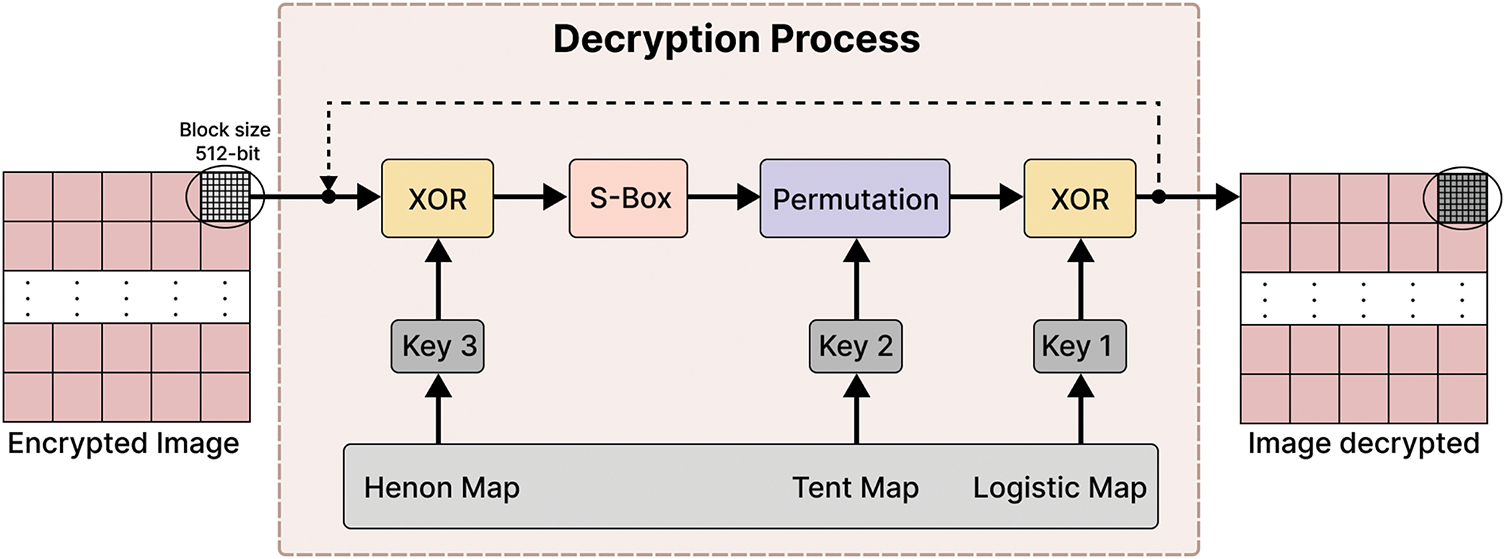
Figure 12: Decryption process

Operation 1 performs a bitwise XOR between the cipher image block and the key block Key3. Operation 2 applies an inverse S-Box substitution to each element of the resulting block from the previous step, enhancing non-linearity. The specific inverse S-Box used is provided in Table 2.

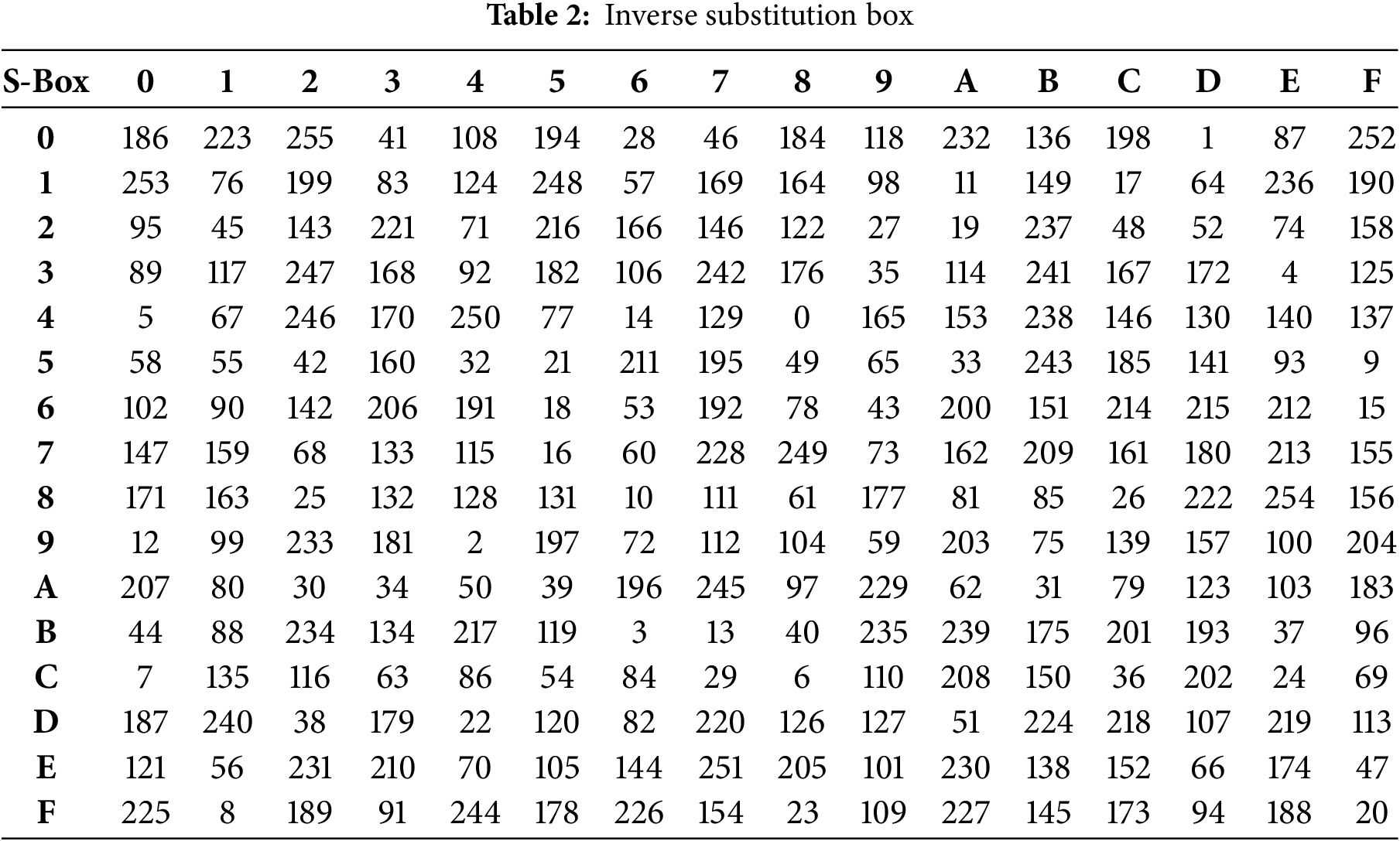
Operation 3 reverses the permutation using a Hilbert curve of order 3, and finally, Operation 4 applies another XOR operation with the key block Key 1.

5  Signature Generation

•   The creation of signature: Once the encryption process is complete, the sender uploads the resulting encrypted data to the cloud and utilizes a hash function to record the hashed value of the image onto the blockchain. That step is essential for ensuring the integrity and authenticity of the cipher image. In the proposed system, we used SHA-256 to produce a hash value, which serves as a signature for the encrypted image. This ensures that attackers can’t access the original image because hashing functions are unidirectional. This makes it impossible to reverse back the hashed value to the original image.

•   The verification of signature: To verify the authenticity of the ciphered image, the data user initiates a signature verification process based on the information stored on the blockchain. This process involves computing the hash value of the received image and comparing it with the original hash value previously recorded on the blockchain by the sender. A successful match confirms the integrity and authenticity of the image, while any discrepancy indicates potential tampering or data corruption. Fig. 13 illustrates the complete signature verification process.

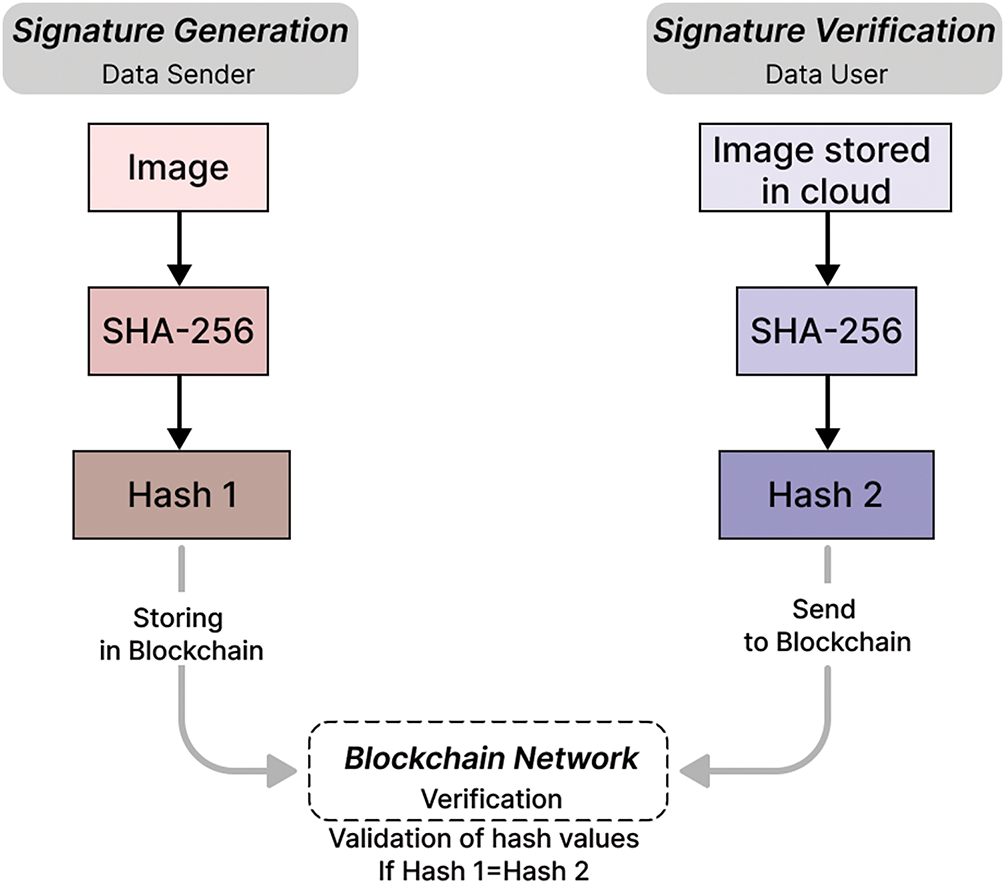
Figure 13: The process of generating and verifying digital signatures

6  Performance and Security Analysis

This section outlines a series of tests suggested to evaluate the security performance of the proposed algorithm. By comparing the encryption results with those of several other researchers using experimental images, which consist of medical images with the same sizes 512 × 512. These images fall into two categories: normal medical images and images depicting diseases. While both types represent the same medical issue, there are slight differences that can only be diagnosed by a specialist (doctor). Despite their close similarity, the encryption results for these images are entirely distinct. The encryption and decryption protocols were tested using multiple gray-scale medical images.

We initialize the parameters as follows: μl = 4.0 for the logistic chaotic sequence, μt = 2.0 for the tent sequence, and a = 1.4 and b = 0.3 for the Henon sequences.

6.1 Experimental Evaluation of the Blockchain Environment

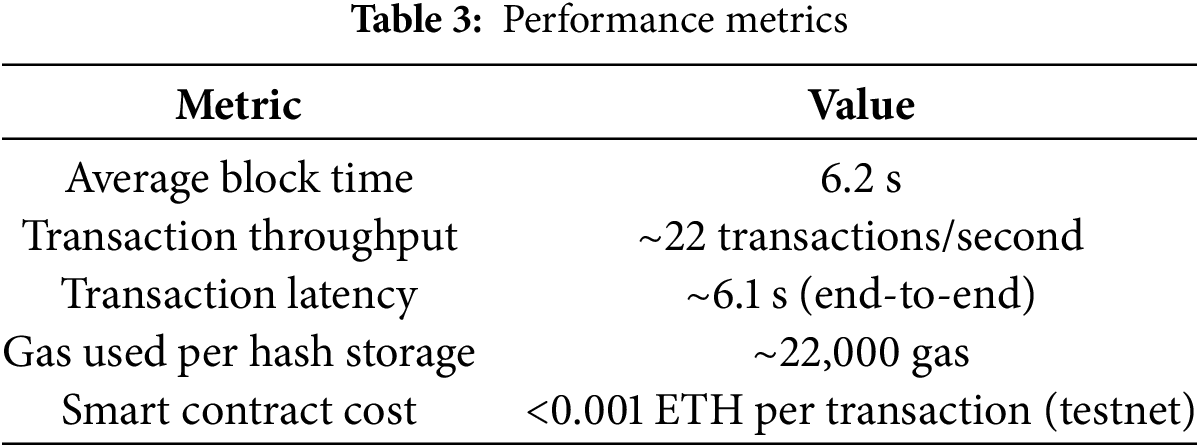
To assess the efficiency and responsiveness of the blockchain component within the proposed framework, a series of tests were conducted on a private Ethereum blockchain environment configured using the Geth client and simulated locally via Ganache, details are shown in Table 3.

The blockchain was tested with the following setup:

•   Environment: Ganache CLI (v7.7.5)

•   Consensus Mechanism: Proof of Authority (PoA)

•   Client: Geth (Go Ethereum)

•   Interaction: Python Web3.py library

•   System: Intel® Core™i5-1035G1 CPU @ 1.19 GHz, 20 GB memory, and 64-bit Windows 10

The blockchain operated smoothly under private conditions, with reliable performance and low latency. Since PoA does not require extensive mining or complex consensus calculations, the network showed predictable and consistent timing, making it suitable for medical applications where integrity is critical and timeliness is essential.

6.2 Execution Time Analysis

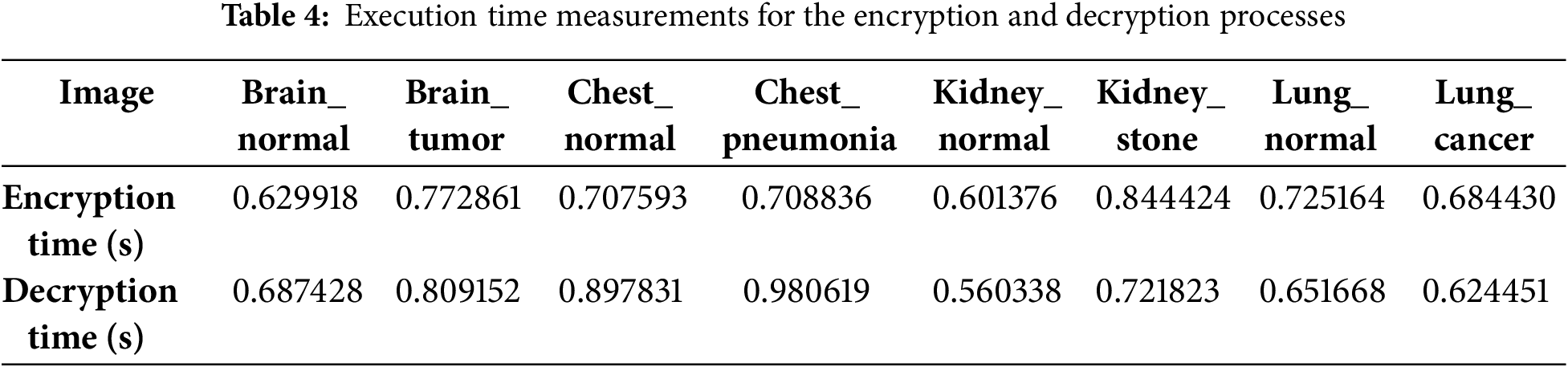
We evaluated the encryption and decryption algorithm’s performance on 8 grayscale images, all sized 512 × 512 pixels. Table 4 details these execution times in seconds, showing an average encryption time of 0.70932525 s.

6.3 Analysis of Key Space

An ideal image encryption scheme should possess a sufficiently large key space and exhibit high sensitivity to its key. The key space size represents the number of possible keys in the cryptographic system. Consequently, the key space must exceed 2100 to ensure that the algorithm is capable of resisting brute force attacks [41]. In the proposed cryptosystem, initial conditions are: x0log⁡istic, x0tent, x0henon, and y0henon and the parameters are: r, μ, a, and b. The xlog⁡istic, xtent, xhenon and yhenon are the key parameters with 10−10 of precision. Thus, the total key space for our proposed algorithm is as follows: 108×10=1080≃2266>2100. That equation meets the security requirements outlined in the standard. Consequently, the encryption algorithm possesses a sufficiently large key space to withstand various brute-force attacks.

6.4 National Institute of Standards and Technology (NIST) Analysis

The NIST test, developed as an effective estimation measure for randomness in encrypted images. It is referred to as the NIST SP 800 analysis.

The NIST test has been utilized for the assessment of the overall quality of the dynamic offset. The random behavior of selected chaotic maps utilized in the suggested system has been confirmed through the National Institute of Standards and Technology. The test comprises 15 statistical tests, each of which yields a p-value (randomness probability). Accordingly, it has been employed to assess the randomness of the chaotic sequences generated by the three utilized maps, as illustrated in Fig. 14. All fifteen tests were successfully completed, as evidenced by the figure. Consequently, it has been demonstrated that the generated sequences by the Logistic map, Tent map, and Henon map achieve a great level of randomness.

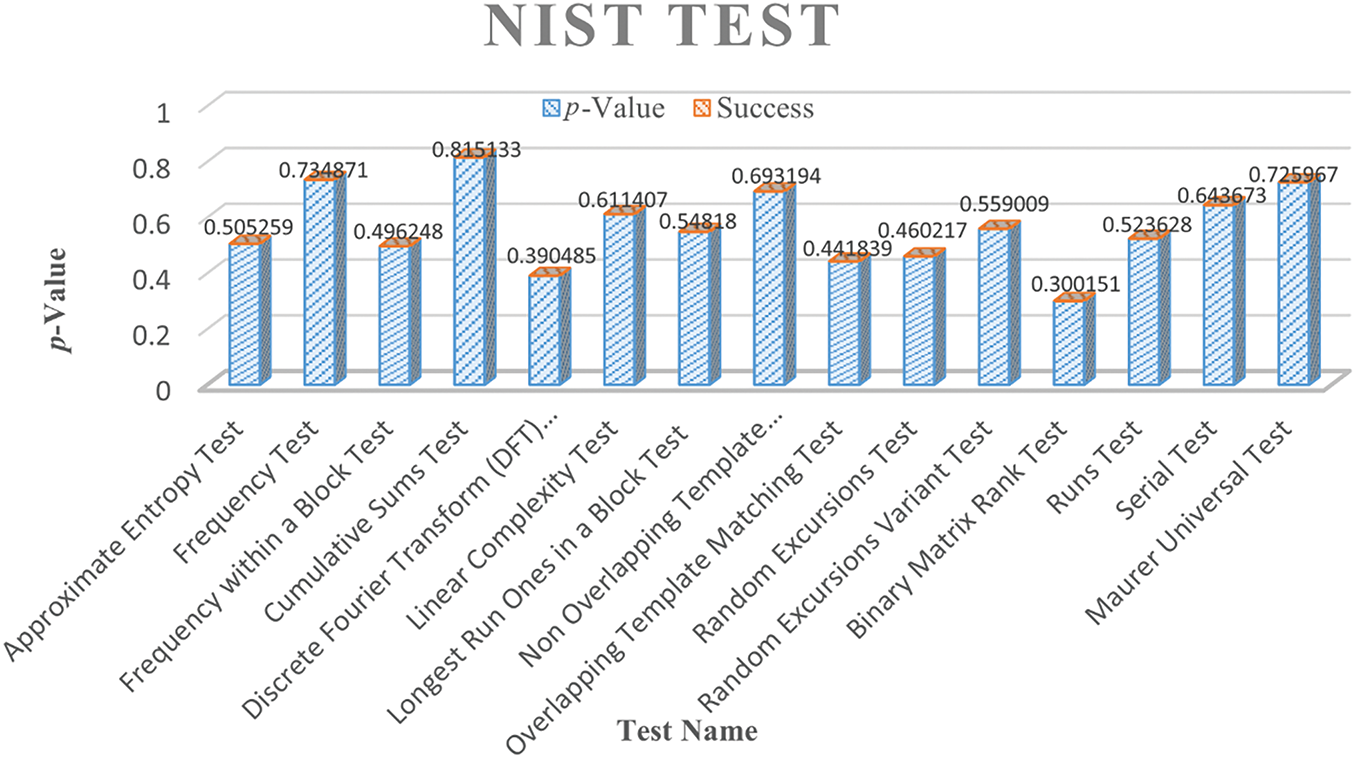
Figure 14: Nist test analysis

6.5 Differential Attack Analysis

The Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI) are essential metrics for assessing an encryption algorithm’s resistance to differential attacks. NPCR reflects the percentage of changed pixels in the cipher image when a single pixel in the plaintext is modified, while UACI measures the average intensity difference. High NPCR and UACI values indicate strong sensitivity to input changes, demonstrating robust security. These metrics are computed using the following equations:

NPCR=∑i,jD(i,j)m×n×100%,UACI=1m×n∑i,j|C1(i,j)−C2(i,j)|255×100%(11)

D(i,j)={1,C1(i,j)≠C2(i,j)0,C1(i,j)=C2(i,j)(12)

where m and n represent the dimensions of the image while C1 and C2 are two encrypted images generated from original images that differ by only one pixel in gray value.

In this paper, an experiment was executed for each test image. To calculate those values, we randomly selected from the original image a pixel value and changed it. The results illustrated in Table 5 indicate that most NPCR values are greater than 99%, and the UACI values are above 33%. This outcome indicates that the algorithm possesses high sensitivity to plaintext variations and demonstrates strong resilience against differential attacks.

6.6 Structural Similarity Index Measure (SSIM)

SSIM Index is a test utilized to measure the degree of resemblance between two images. It is based on the fact that pixels have strong interdependencies, specifically when they are located close together. These dependencies convey vital information about how the visual scene gets structured. The resulting SSIM index ranges from −1 to 1, where 1 is achievable only if the two sets of data are identical. Eq. (13) is utilized to determine the SSIM value for images.

SSIM(x,y)=[l(x,y)a×c(x,y)b×s(x,y)c](13)

This formula is based on three measurements of comparison between samples of x and y: (l) is the luminance (l), (c) is the contrast, and (s) is the structure as shown in Eqs. (14)–(16):

l(x,y)=2μxμy+c1μx2μy2+c1(14)

c(x,y)=2σxσy+c2σx2σy2+c2(15)

s(x,y)=σxy+c3σxσy+c3(16)

Table 6 shows that the results obtained from the SSIM analysis are very close to zero. These results demonstrate that the original and cipher images are not similar. Consequently, no pertinent data can be extracted from the encrypted image to reconstruct the original image.

6.7 Mean Squared Error (MSE) & Peak Signal to Noise Ratio (PSNR)

The quality of the proposed encryption system can be quantitatively evaluated by comparing the original and encrypted images. The Peak Signal-to-Noise Ratio (PSNR) is employed to measure the perceptual difference in quality between the plain and encrypted images, whereas the Mean Squared Error (MSE) quantifies the pixel-level variance between them. Table 7 presents the computed PSNR and MSE values. The formulas for calculating PSNR and MSE are defined as follows:

PSNR=20log⁡(255MSE)(dB)(17)

MSE=1M×N∑y=1M∑x=1N[P(x,y)−C(x,y)]2(18)

where P(x, y) is the plain image, C(x, y) is the cipher image and (M, N) are the dimensions of the images. A lower MSE indicates less error, and due to the inverse relationship between MSE and PSNR, this results in a higher PSNR value. A higher value of PSNR indicates a better quality of the signal relative to the noise.

The greater the PSNR value is, the better the image separation result. In this context, the signal refers to the plain image, while the noise represents the error in reconstruction.

6.8 Histogram Analysis

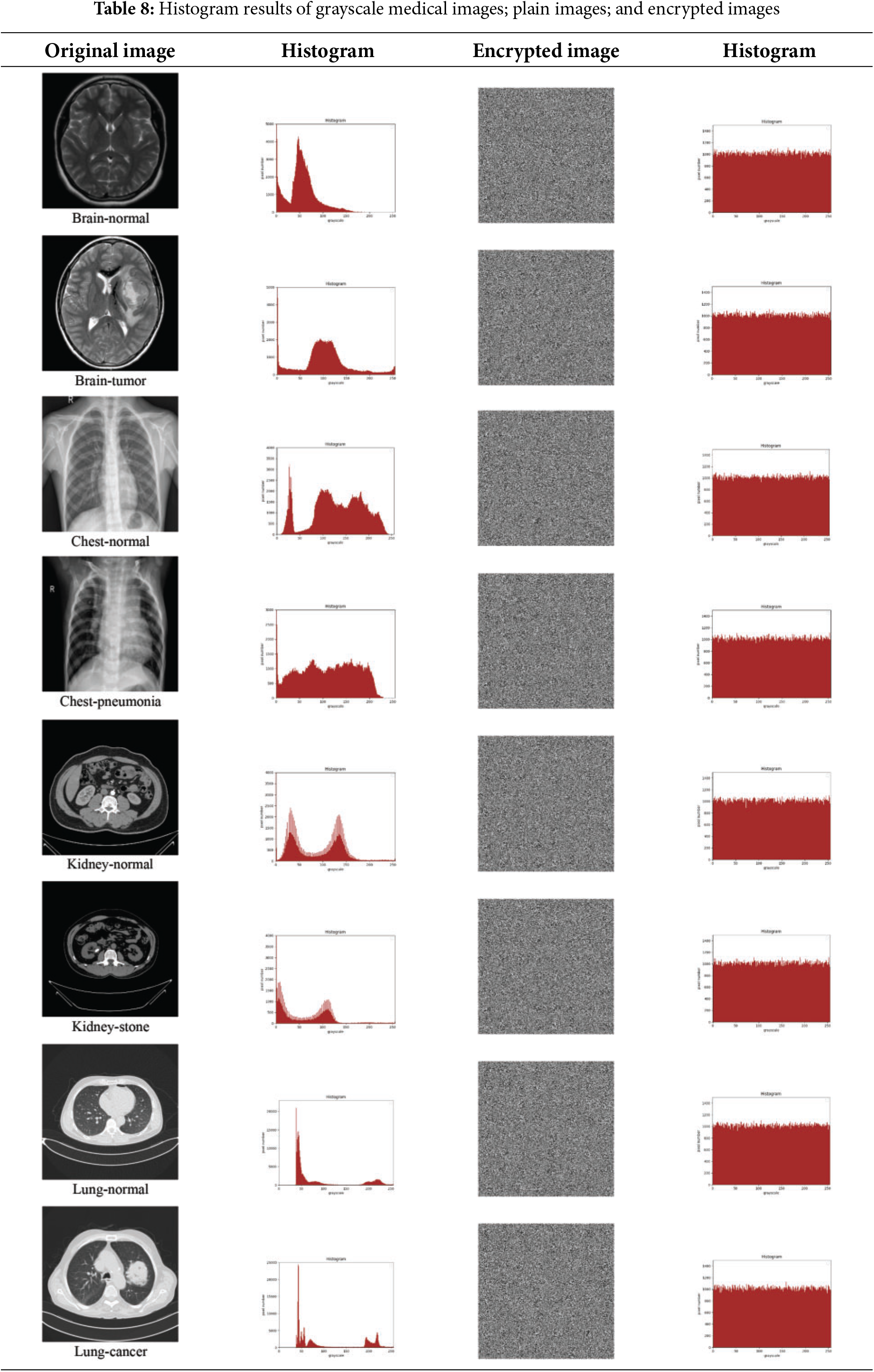
An image histogram represents the distribution of pixel intensities across gray levels and provides valuable statistical insight. For encrypted images, a uniform histogram is essential as it obscures patterns and prevents information leakage. In this study, eight images of identical dimensions were used. As shown in Table 8, plaintext image histograms exhibit distinct peaks and valleys, whereas the histograms of the corresponding ciphered images are uniformly distributed. This uniformity confirms the absence of statistical correlation between plaintext and ciphered images, highlighting the algorithm’s effectiveness in resisting statistical attacks.

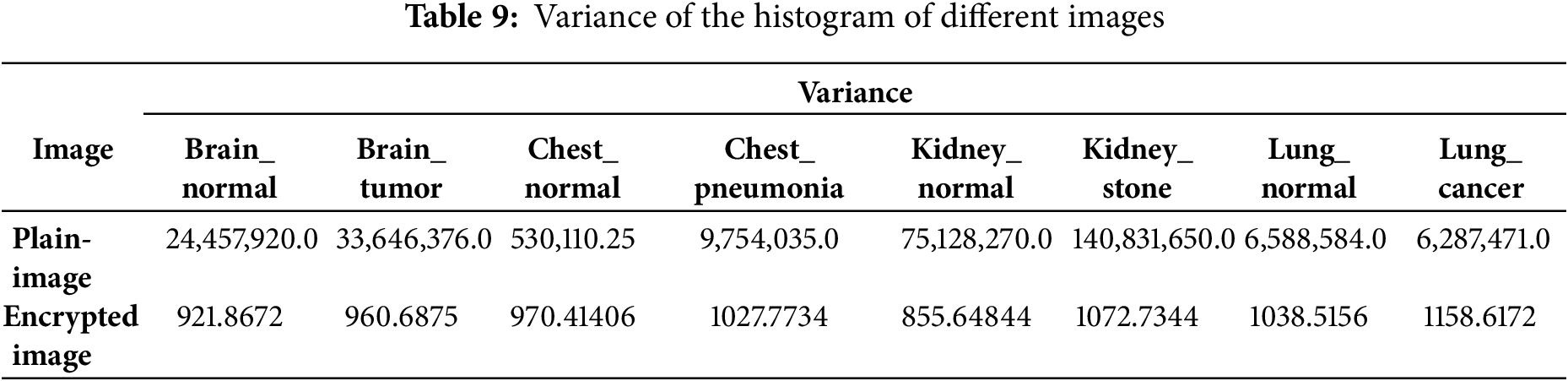
For quantitative analysis of the performance of pixel value distribution, we present histogram variances as a measure to assess the uniformity of encrypted images. The histogram variance is calculated in the Eq. (19):

var(Z)=1p2∑i=1p∑j=1p12(zi−zj)2(19)

The greater the uniformity of encrypted images, the lower the variance values. Here, Z represents the vector of histogram values Z={z1,z2,…,z256}, while ziand zj denote the counts of pixels with gray values equal to i and j, respectively.

Table 9 presents the histogram variance values for both the original images and their corresponding encrypted images, generated using the proposed algorithm.

6.9 Information Entropy

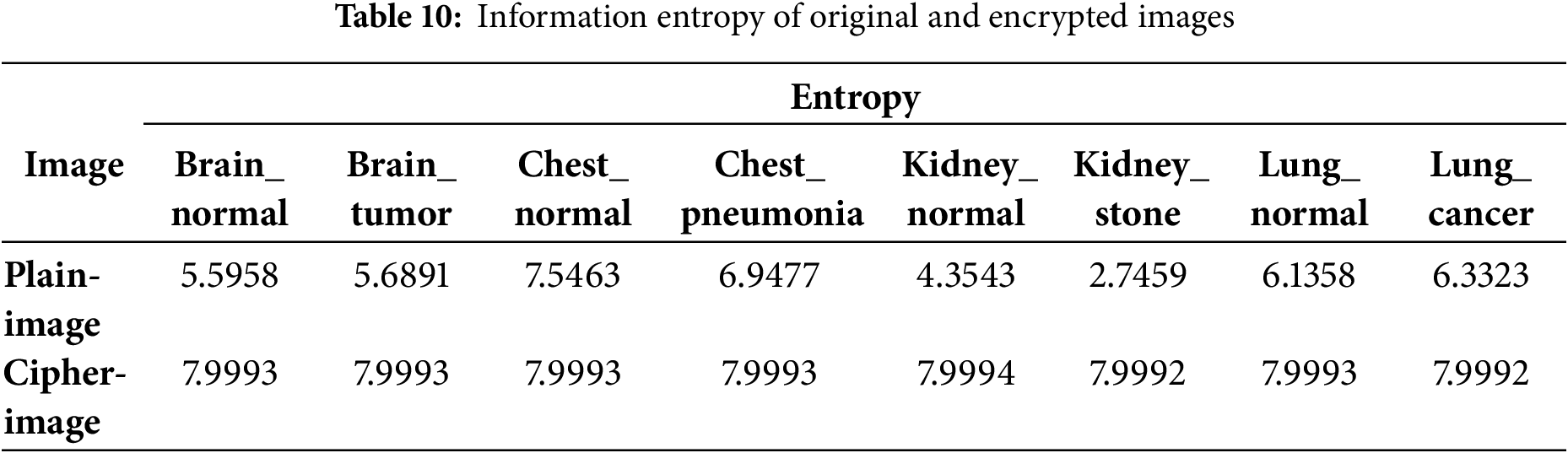
Entropy is a thermodynamic physical quantity that describes the degree of disorder in a physical system. In the context of digital images, information entropy represents the distribution of each grey level. The Eq. (20) is used to calculate information entropy:

E(m)=−∑i=1Mp(mi).log2⁡p(mi)(20)

With m is the information entropy of the gray image, M is the total number of symbols and p(mi) is the probability that the image pixel value appears. For an ideal algorithm, the ciphertext image should appear completely random, with an information entropy value approaching the theoretical maximum of 8. Table 10 presents the entropy values computed for the cipher-images corresponding to the test plaintext images. As shown, the entropy results are consistently close to 8, indicating a high level of randomness in the encrypted images. This suggests that the proposed algorithm effectively minimizes the risk of information leakage through statistical analysis.

6.10 Correlation Analysis

The pixel correlation test is a widely used technique for evaluating the effectiveness of image encryption algorithms. It assesses the degree of correlation between adjacent pixels in an image, where an ideal encryption scheme should significantly reduce this correlation. To perform this analysis, 2000 pairs of adjacent pixels are randomly selected from the horizontal, vertical, and diagonal directions of both the original and encrypted images. The correlation coefficients are then computed to quantify the decorrelation achieved by the encryption process. This test is performed as follows:

Cx,y=Cov(x,y)D(x).D(y)(21)

With:

Cov(x,y)=1K∑i=1K(xi−E(x))(yi−E(y))(22)

E(x)=1K∑i=1Kxi(23)

D(x)=1K∑i=1K(xi−E(x))2(24)

Here, x and y are presented as two adjacent pixels, and N as the sample counts. E(x) donates the mathematical expectation of x, and D(x) denotes the standard deviation.

Fig. 15 represents the distribution of 2000 pixel pairs in different directions for original and encrypted images of the two Brain example. In the original images and in vertical direction, the majority of points cluster near the diagonal line, indicating that vertically adjacent pixels have similar values. Similar distributions are observed for horizontal and diagonal directions. In every direction in the encrypted images, the dots are randomly dispersed throughout the space. This indicates that no relationship exists among the adjacent pixels of the cipher image.

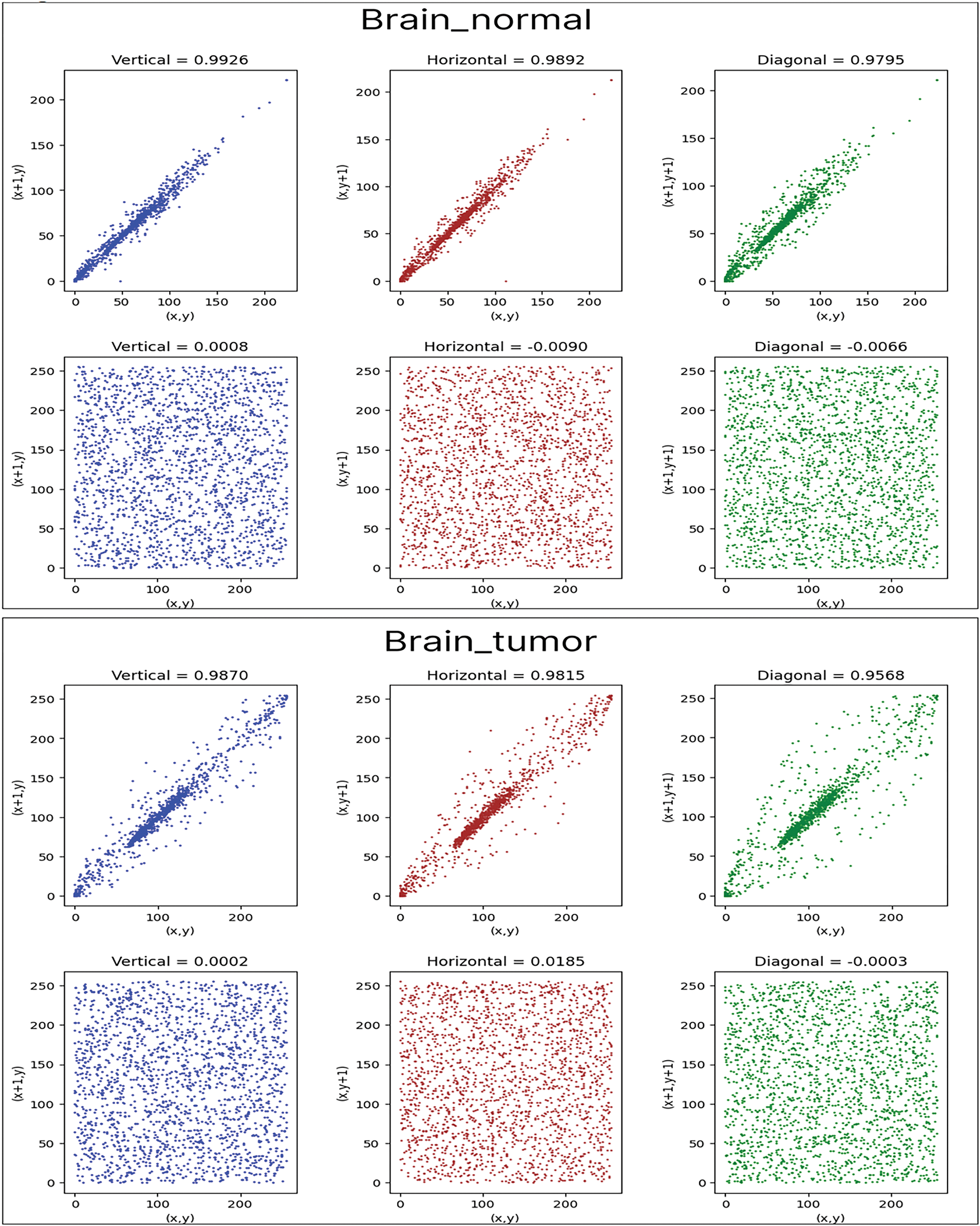
Figure 15: Distribution of 2000 pairs of adjacent pixels randomly selected from the original images in the vertical, horizontal, and diagonal directions

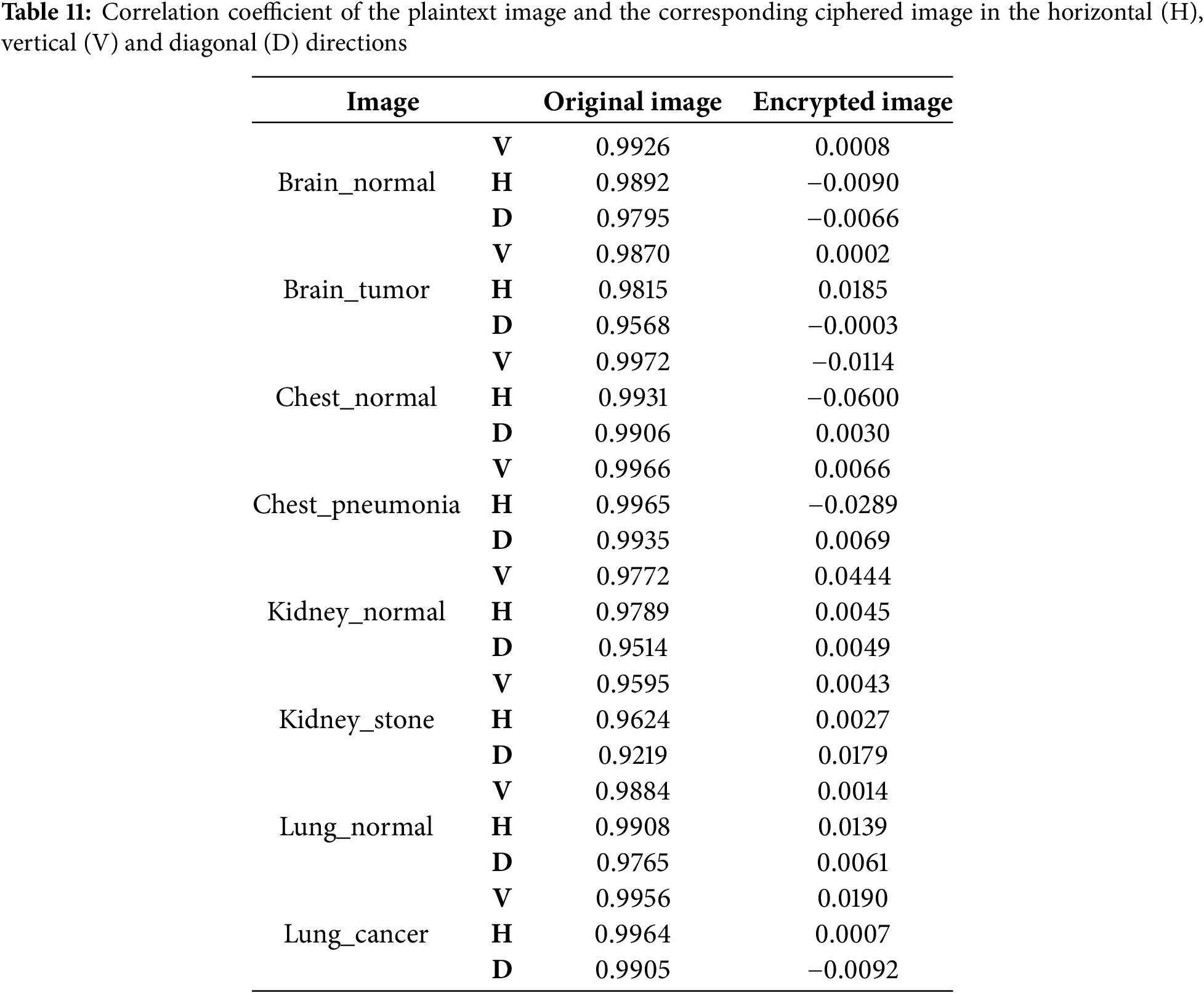
It is shown in Fig. 15 that the correlation coefficients of the plain images are all above 0.5, with the pixel distribution concentrated near the diagonal. This indicates a strong correlation between adjacent pixels in the original image.

However, this strong correlation is disrupted after encryption, and the correlation coefficient approaches 0, indicating that the encrypted image pixels are uncorrelated. Table 11 illustrates the correlation values between neighboring pixels in the horizontal, vertical, and diagonal directions for both the original and encrypted images.

7  Comparative Study

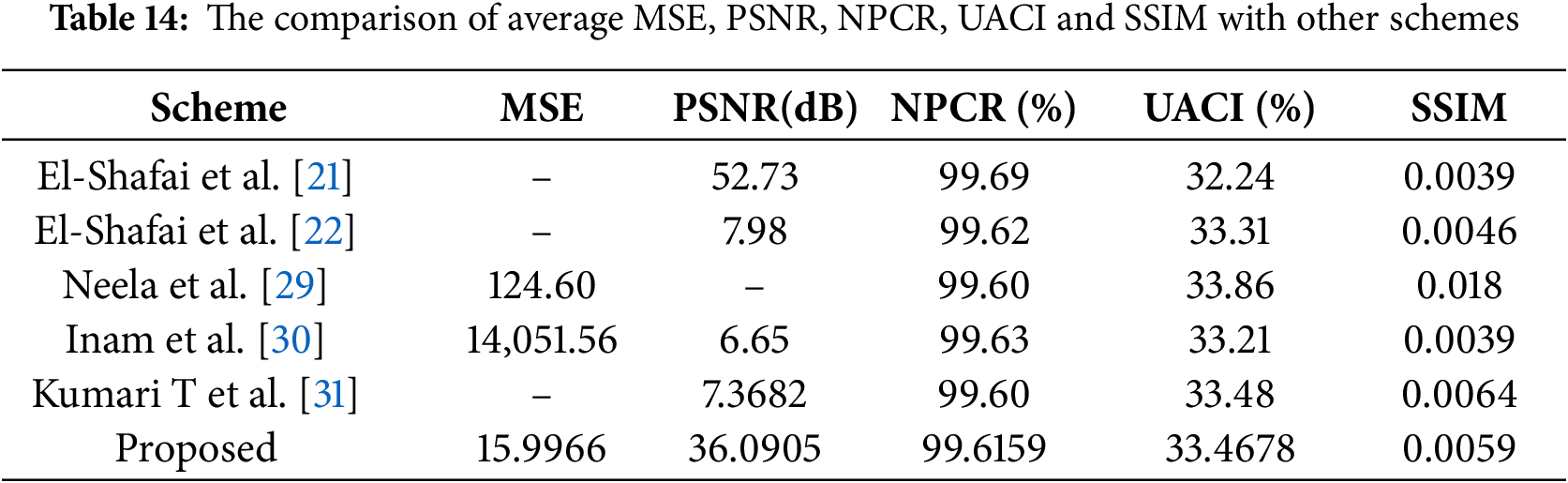
Numerous image encryption techniques have been developed and are used as benchmarks for evaluating the performance of the proposed method. Table 12 presents a comparative analysis of existing encryption schemes. Based on this comparison, a blockchain-based image encryption method tailored for medical images is suggested. The proposed algorithm is evaluated using a dataset of eight medical images, and its average performance is assessed through key metrics including key space, MSE, PSNR, NPCR, UACI, SSIM, and global entropy. The results are summarized in Tables 13 and 14.

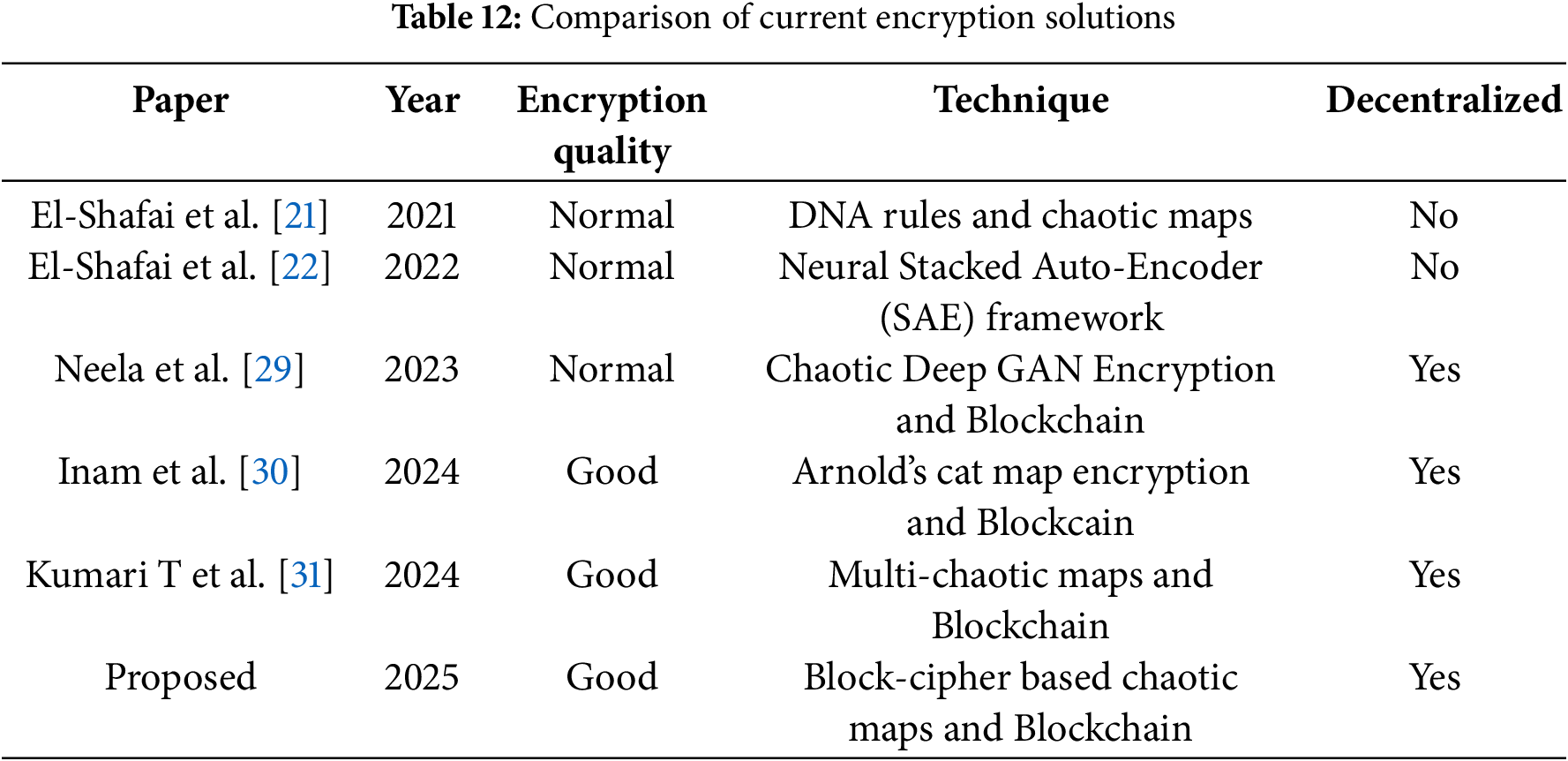
As shown in Table 13, the information entropy values of the encrypted images generated by the proposed cryptosystem are consistently close to 8, indicating a high level of randomness. These values surpass those reported in Refs. [21,22,29,30] and are comparable to those in Ref. [31], suggesting strong resistance to entropy-based attacks. Furthermore, the proposed method demonstrates a larger key space than those in Refs. [21,22,30], though slightly smaller than Ref. [31]; nonetheless, it remains sufficiently large to resist brute-force attacks.

Table 14 highlights the proposed scheme’s efficiency, showing superior PSNR values compared to most existing methods, indicating better image quality retention. Moreover, the NPCR and UACI values confirm the robustness of the proposed algorithm against differential attacks, outperforming several compared schemes, though not all.

The results above demonstrate that the proposed encryption scheme performs as well as or better than other standard schemes. Additionally, it meets the current demands, establishing its high acceptability.

8  Conclusion

This paper presents a Blockchain-based image encryption algorithm utilizing chaos theory to enhance data security, privacy, and authenticity. The sender encrypts the medical image, generates a SHA-256 digital signature, stores the ciphered image in the cloud, and records the signature on the blockchain. Upon request, the user retrieves the encrypted image from the cloud and verifies its authenticity via the blockchain before decryption. Comprehensive security evaluations; including histogram analysis, key space testing, correlation coefficient analysis, entropy measurement, and differential attack resistance demonstrate that the proposed scheme offers robust protection against various cryptographic threats.

Future work will focus on extending this encryption framework to real-time telemedicine applications, enabling secure and efficient transmission of medical images in dynamic healthcare environments.

Acknowledgement: The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Group Project under grant number (RGP2/473/46).

Funding Statement: This work was supported by the Large Group Project under grant number (RGP2/473/46).

Author Contributions: Rim Amdouni designed the algorithm and software implementation. Mahdi Madani analyzed and validated the algorithm. Mohamed Ali Hajjaji and El Bay Bourennane analyzed and validated the results. Mohamed Atri read and evaluated the final manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Material: This study does not include any datasets. No new data were generated or analyzed during this study.

Ethics Approval: This study does not involve human participants or animals; therefore, ethical approval is not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Manju Bala P, Rajmohan R, Ananth Kumar T, Ajagbe SA, Adigun MO. Quantum blockchain-oriented data integrity scheme for validating clinical datasets. In: Exploring intelligent healthcare with quantum computing. Stevenage, UK: IET; 2024. p. 259–78 doi:10.1049/pbhe060e_ch13. [Google Scholar] [CrossRef]

2. Dinh TTA, Liu R, Zhang M, Chen G, Ooi BC, Wang J. Untangling blockchain: a data processing view of blockchain systems. IEEE Trans Knowl Data Eng. 2018;30(7):1366–85. doi:10.1109/tkde.2017.2781227. [Google Scholar] [CrossRef]

3. Khan PW, Byun Y. A blockchain-based secure image encryption scheme for the industrial Internet of Things. Entropy. 2020;22(2):175. doi:10.3390/e22020175. [Google Scholar] [PubMed] [CrossRef]

4. Chen M, Malook T, Rehman AU, Muhammad Y, Alshehri MD, Akbar A, et al. Blockchain-Enabled healthcare system for detection of diabetes. J Inf Secur Appl. 2021;58:102771. doi:10.1016/j.jisa.2021.102771. [Google Scholar] [CrossRef]

5. Ajagbe SA, Florez H, Awotunde JB. AESRSA: a new cryptography key for electronic health record security. In: Applied informatics. Cham, Switzerland: Springer International Publishing; 2022. p. 237–51. doi:10.1007/978-3-031-19647-8_17. [Google Scholar] [CrossRef]

6. Aggarwal S, Chaudhary R, Aujla GS, Kumar N, Choo KR, Zomaya AY. Blockchain for smart communities: applications, challenges and opportunities. J Netw Comput Appl. 2019;144:13–48. doi:10.1016/j.jnca.2019.06.018. [Google Scholar] [CrossRef]

7. Bhardwaj A, Chaudhary R, Aslam AM, Budhiraja I. Blockchain-based robust SDN framework for digital twin-enabled IoT networks. In: IEEE 98th Vehicular Technology Conference (VTC2023-Fall); 2023 Oct 10–13; Hong Kong, China. p. 1–6. doi:10.1109/VTC2023-Fall60731.2023.10333591. [Google Scholar] [CrossRef]

8. Rai HM, Shukla KK, Tightiz L, Padmanaban S. Enhancing data security and privacy in energy applications: integrating IoT and blockchain technologies. Heliyon. 2024;10(19):e38917. doi:10.1016/j.heliyon.2024.e38917. [Google Scholar] [PubMed] [CrossRef]

9. Hosseinzadeh M, Malik MH, Safkhani M, Bagheri N, Le QH, Tightiz L, et al. Toward designing a secure authentication protocol for IoT environments. Sustainability. 2023;15(7):5934. doi:10.3390/su15075934. [Google Scholar] [CrossRef]

10. Liu J, Yang D, Zhou H, Chen S. A digital image encryption algorithm based on bit-planes and an improved logistic map. Multimed Tools Appl. 2018;77(8):10217–33. doi:10.1007/s11042-017-5406-2. [Google Scholar] [CrossRef]

11. Sneha PS, Sankar S, Kumar AS. A chaotic colour image encryption scheme combining Walsh-Hadamard transform and Arnold-Tent maps. J Ambient Intell Humaniz Comput. 2020;11(3):1289–308. doi:10.1007/s12652-019-01385-0. [Google Scholar] [CrossRef]

12. Rathee G, Sharma A, Saini H, Kumar R, Iqbal R. A hybrid framework for multimedia data processing in IoT-healthcare using blockchain technology. Multimed Tools Appl. 2020;79(15–16):9711–33. doi:10.1007/s11042-019-07835-3. [Google Scholar] [CrossRef]

13. Abbas A, Alroobaea R, Krichen M, Rubaiee S, Vimal S, Almansour FM. Blockchain-assisted secured data management framework for health information analysis based on Internet of Medical Things. Pers Ubiquitous Comput. 2024;28(1):59–72. doi:10.1007/s00779-021-01583-8. [Google Scholar] [CrossRef]

14. Azbeg K, Ouchetto O, Jai Andaloussi S. BlockMedCare: a healthcare system based on IoT, Blockchain and IPFS for data management security. Egypt Inform J. 2022;23(2):329–43. doi:10.1016/j.eij.2022.02.004. [Google Scholar] [CrossRef]

15. Naskar PK, Bhattacharyya S, Nandy D, Chaudhuri A. A robust image encryption scheme using chaotic tent map and cellular automata. Nonlinear Dyn. 2020;100(3):2877–98. doi:10.1007/s11071-020-05625-3. [Google Scholar] [CrossRef]

16. Masood F, Boulila W, Alsaeedi A, Khan JS, Ahmad J, Khan MA, et al. A novel image encryption scheme based on Arnold cat map, Newton-Leipnik system and Logistic Gaussian map. Multimed Tools Appl. 2022;81(21):30931–59. doi:10.1007/s11042-022-12844-w. [Google Scholar] [CrossRef]

17. Ibrahim S, Alharbi A. Efficient image encryption scheme using henon map, dynamic S-boxes and elliptic curve cryptography. IEEE Access. 2020;8:194289–302. doi:10.1109/access.2020.3032403. [Google Scholar] [CrossRef]

18. Alexan W, Elkandoz M, Mashaly M, Azab E, Aboshousha A. Color image encryption through chaos and KAA map. IEEE Access. 2023;11:11541–54. doi:10.1109/access.2023.3242311. [Google Scholar] [CrossRef]

19. Singh KN, Singh OP, Singh AK, Agrawal AK. EiMOL: a secure medical image encryption algorithm based on optimization and the Lorenz system. ACM Trans Multimed Comput Commun Appl. 2023;19(2s):1–19. doi:10.1145/3561513. [Google Scholar] [CrossRef]

20. Anand A, Singh AK. An improved DWT-SVD domain watermarking for medical information security. Comput Commun. 2020;152(3):72–80. doi:10.1016/j.comcom.2020.01.038. [Google Scholar] [CrossRef]

21. El-Shafai W, Khallaf F, El-Rabaie EM, El-Samie FEA. Robust medical image encryption based on DNA-chaos cryptosystem for secure telemedicine and healthcare applications. J Ambient Intell Humaniz Comput. 2021;12(10):9007–35. doi:10.1007/s12652-020-02597-5. [Google Scholar] [CrossRef]

22. El-Shafai W, Khallaf F, El-Rabaie EM, Abd El-Samie FE. Proposed neural SAE-based medical image cryptography framework using deep extracted features for smart IoT healthcare applications. Neural Comput Appl. 2022;34(13):10629–53. doi:10.1007/s00521-022-06994-z. [Google Scholar] [CrossRef]

23. Yepdia LMH, Tiedeu A. Secure transmission of medical image for telemedicine. Sens Imag. 2021;22(1):17. doi:10.1007/s11220-021-00340-8. [Google Scholar] [CrossRef]

24. Malika A, Sharma RS. A novel image encryption based on feedback carry shift register and blockchain for secure communication. Int J Appl Eng Res. 2021;16(6):466–77. [Google Scholar]

25. Brabin D, Ananth C, Bojjagani S. Blockchain based security framework for sharing digital images using reversible data hiding and encryption. Multimed Tools Appl. 2022;81(17):24721–38. doi:10.1007/s11042-022-12617-5. [Google Scholar] [CrossRef]

26. Ravi RV, Goyal SB, Verma C, Raboaca MS, Enescu FM, Mihaltan TC. Image encryption using block chain and chaos for secure communication. In: 2022 14th International Conference on Electronics, Computers and Artificial Intelligence (ECAI); 2022 Jun 30–July 1; Ploiesti, Romania. p. 1–6. doi:10.1109/ECAI54874.2022.9847446. [Google Scholar] [CrossRef]

27. Abrar A, Abdul W, Ghouzali S. Secure image authentication using watermarking and blockchain. Intell Autom Soft Comput. 2021;28(2):577–91. doi:10.32604/iasc.2021.016382. [Google Scholar] [CrossRef]

28. Doreen Hephzibah Miriam D, Dahiya D, Nitin, Rene Robin CR. Secured cyber security algorithm for healthcare system using blockchain technology. Intell Autom Soft Comput. 2023;35(2):1889–906. doi:10.32604/iasc.2023.028850. [Google Scholar] [CrossRef]

29. Neela KL, Kavitha V. Blockchain based Chaotic Deep GAN Encryption scheme for securing medical images in a cloud environment. Appl Intell. 2023;53(4):4733–47. doi:10.1007/s10489-022-03730-x. [Google Scholar] [CrossRef]

30. Inam S, Kanwal S, Firdous R, Hajjej F. Blockchain based medical image encryption using Arnold’s cat map in a cloud environment. Sci Rep. 2024;14(1):5678. doi:10.1038/s41598-024-56364-z. [Google Scholar] [PubMed] [CrossRef]

31. Kumari T, Singh D, Singh B. Multi-chaotic maps and blockchain based image encryption. Concurr Comput. 2024;36(14):e8092. doi:10.1002/cpe.8092. [Google Scholar] [CrossRef]

32. Arif J, Khan MA, Ghaleb B, Ahmad J, Munir A, Rashid U, et al. A novel chaotic permutation-substitution image encryption scheme based on logistic map and random substitution. IEEE Access. 2022;10(2):12966–82. doi:10.1109/access.2022.3146792. [Google Scholar] [CrossRef]

33. Phatak SC, Rao SS. Logistic map: a possible random-number generator. Phys Rev E. 1995;51(4):3670–8. doi:10.1103/physreve.51.3670. [Google Scholar] [PubMed] [CrossRef]

34. Kiran Parameshachari BD, Panduranga HT. Medical image encryption using SCAN technique and chaotic tent map system. In: Recent advances in artificial intelligence and data engineering. Singapore: Springer; 2021. p. 181–93. doi:10.1007/978-981-16-3342-3_15. [Google Scholar] [CrossRef]

35. Hénon M. A two-dimensional mapping with a strange attractor. In: The theory of chaotic attractors. New York, NY, USA: Springer New York; 1976. p. 94–102. doi:10.1007/978-0-387-21830-4_8. [Google Scholar] [CrossRef]

36. Jawad LM. A new scan pattern method for color image encryption based on 3D-Lorenzo chaotic map method. Multimed Tools Appl. 2021;80(24):33297–312. doi:10.1007/s11042-021-11295-z. [Google Scholar] [CrossRef]

37. Shahna KU, Mohamed A. A novel image encryption scheme using both pixel level and bit level permutation with chaotic map. Appl Soft Comput. 2020;90(4):106162. doi:10.1016/j.asoc.2020.106162. [Google Scholar] [CrossRef]

38. Tanwar S, Parekh K, Evans R. Blockchain-based electronic healthcare record system for healthcare 4.0 applications. J Inf Secur Appl. 2020;50(10):102407. doi:10.1016/j.jisa.2019.102407. [Google Scholar] [CrossRef]

39. Tariq N, Qamar A, Asim M, Khan FA. Blockchain and smart healthcare security: a survey. Procedia Comput Sci. 2020;175(9):615–20. doi:10.1016/j.procs.2020.07.089. [Google Scholar] [CrossRef]

40. Zhai S, Yang Y, Li J, Qiu C, Zhao J. Research on the application of cryptography on the blockchain. J Phys Conf Ser. 2019;1168:032077. doi:10.1088/1742-6596/1168/3/032077. [Google Scholar] [CrossRef]

41. Alvarez G, Li S. Some basic cryptographic requirements for chaos-based cryptosystems. Int J Bifurcation Chaos. 2006;16(8):2129–51. doi:10.1142/s0218127406015970. [Google Scholar] [CrossRef]