Blockchain Sharding Algorithm Based on Account Degree and Frequency

1  Introduction

Blockchain is a decentralized distributed database technology [1] that employs cryptographic algorithms to ensure the security and immutability of data. Blockchain technology has been widely applied in various fields such as product traceability, financial payments, privacy protection, and identity verification. However, with the development of blockchain technology, blockchain scalability has remained a persistent obstacle and challenge [2], limiting the potential for widespread adoption of blockchain in real-world applications [3,4].

In a blockchain network, as transaction volumes increase, the processing speed and storage capacity of the blockchain often become bottlenecks, leading to longer transaction confirmation times and lower throughput [5]. To address this issue, sharding technology [6] has emerged. It divides the blockchain network into multiple shards, allowing each shard to independently validate and process transactions, thereby the parallel processing of blockchain can reduce the burden of individual nodes and improve the overall processing capacity and efficiency [7]. Sharding technology not only improves the scalability of blockchain but also enables the network to handle more transaction requests while maintaining decentralization and security [8].

Blockchain sharding technology includes network sharding, transaction sharding, and state sharding [9]. Traditional blockchain networks require every node to store the entire blockchain data, which results in nodes having to handle large amounts of data and transactions, thus limiting the system’s scalability [10]. Network sharding addresses this issue by partitioning the entire blockchain network into smaller subnetworks, where each subnetwork only processes transactions within its shard, allowing shards to operate independently. Transaction sharding involves dividing blockchain data and transactions into multiple segments [11], where each shard independently validates and records transactions without relying on a single global node to validate all transactions. This reduces network congestion and enhances transaction throughput and speed. State sharding, on the other hand, splits the blockchain’s state data, with each shard managing a portion of the state, enabling simultaneous state updates across the entire network and improving processing capacity [12]. Network sharding serves as the foundation for transaction and state sharding [13]. However, as the number of nodes per shard decreases after sharding, security risks are introduced. Current network sharding strategies mitigate this risk by randomly selecting nodes to form sub-chains, thus preventing malicious node aggregation and ensuring blockchain security [14]. In transaction sharding, transactions are dispersed across multiple shards, yet dependencies of transactions between different shards may exist, and a large number of cross-shard transactions rush into the blockchain. This leads to a certain delay in transaction confirmation speed [15]. Therefore, how to assign transactions to the appropriate shards to minimize cross-shard transactions is a major challenge in transaction sharding design [16] and is the primary focus of this research.

Sharding technology, as one of the main solutions to address blockchain scalability [17], has many characteristics and advantages, and is being increasingly adopted by various projects. There are already several relatively mature sharding technologies, such as Ethereum 2.0 [18], OmniLedger [19], and Zilliqa [20], which employ random sharding algorithms (RSA) where nodes are randomly assigned to different shards to participate in the consensus process, ensuring network decentralization. In the design of Monoxide [21], accounts are assigned to different blockchain shards based on the modulus operation of the first few digits of their addresses [22], which belongs to the modular sharding algorithms (MSA). Although RSA and MSA can ensure that transactions are uploaded to the chain in real time, in practical applications, transactions between accounts often show a certain degree of correlation, and some accounts frequently conduct transactions. Since both of these sharding algorithms are simple partitions based on node address or other identifiers, they cannot optimize the allocation according to the transaction patterns between accounts, resulting in an excessively high cross-sharding proportion. On this basis, some scholars have proposed sharding schemes that consider transaction relationships between accounts, such as BrokerChain [23], FBTS [24], and CLPA [25]. These schemes analyze transaction frequencies between accounts, assign accounts with frequent transactions to the same shard, and place less active or inactive accounts into different shards. This design can effectively reduce cross-shard transactions, thereby lowering the communication overhead and delays caused by cross-shard transactions. However, these schemes do not take into account the comprehensive characteristics of the accounts and do not analyze the transaction relationships between accounts globally.

The research motivations of this paper mainly have two aspects: On the one hand, considering the comprehensive characteristics of accounts and analyzing the transaction relationships between accounts globally, the aim is to reduce the cross-shard transaction proportion; On the other hand, by adopting redundant storage, some cross-shard transactions are transformed into intra-shard transactions, further reducing the cross-shard transaction proportion. This paper proposes a blockchain sharding algorithm based on account degree and frequency (DFSA). This algorithm abstracts transactions in the blockchain network as an undirected weighted graph, analyzes the relationships between accounts globally, and employs community detection algorithms to cluster active accounts. The main contributions of this paper are as follows:

1.    A blockchain transaction sharding algorithm based on account degree and frequency is proposed in this paper. This algorithm introduces a comprehensive account weight based on the account activity and transaction frequency and uses community detection to aggregate accounts, thereby reducing cross-shard transaction proportion.

2.    This paper designs a random redundancy strategy based on account relationships, which randomly selects a certain proportion of accounts and redundantly stores them into the same shard, so both sides of the accounts originally located in different shards become intra-shard transactions, and cross-shard transactions can be reduced effectively.

3.    Simulation experiments verify the performance of DFSA algorithm. The simulation results show that compared with the existing sharding algorithms, the proposed algorithm performs well in multiple indicators such as delay and throughput, indicating that the proposed algorithm can effectively reduce the proportion of cross-shard transactions and shorten the transaction delay.

The remainder of this paper is structured as follows: Section 2 provides an overview of existing technologies through a literature review. Section 3 presents the sharding design, related definitions, and a detailed description of the DFSA algorithm. Section 4 provides experimental evaluation. Section 5 concludes the paper and outlines future work.

2  Related Work

Blockchain sharding technology is an important scalability solution that aims to enhance the system’s processing capacity and efficiency by dividing the blockchain network into multiple independent shards. With the continuous expansion of blockchain applications, many mature blockchain sharding solutions have been proposed, greatly driving the development of blockchain technology in large-scale application scenarios.

Blockchain systems currently execute transactions using two main types of transaction models: the UTXO (Unspent Transaction Output) model and the account/balance model [26]. In 2016, Luu et al. [27] proposed the earliest sharding model, Elastico, in which nodes are randomly assigned to committees after identity information is confirmed by the PoW mechanism [28]. However, services cannot be provided during identity confirmation, resulting in intermittent system unavailability. Kokoris-Kogias et al. [19] was optimized for Elastico design deficiencies. It uses the distributed random source protocol RandHound combined with VRF (verifiable random function) to replace the energy-intensive PoW (Proof-of-Work) calculation [29]. Wang and Wang [21] uses the formula n=2k to determine which shards the current user belongs to. A similar example of using a simple calculation to determine the shard of a node is Ethereum 2.0 [18]. In Ethereum 2.0, the beacon [30] chain dynamically allocated validators to shards through cryptographic random numbers generated by RANDAO + VDF. Similarly, in Zilliqa [20], all transactions from the same account are processed in the same shard. These sharding protocols rely on relatively simple node allocation principles, resulting in frequently active accounts being distributed across different shards, causing a large number of cross-shard transactions and increasing the time for transaction verification and processing. Therefore, reducing cross-shard transactions is a major challenge for sharding technology.

In the network, the user’s transaction behavior usually has a clear goal and stability, which is manifested as a long-term and high-frequency interaction between specific accounts. This feature provides a thought point for sharding technology, allowing accounts with similar characteristics to be placed in the same shard. For example, Zhang [24] considers the transaction characteristics between accounts, puts the accounts with high transaction frequency into the same shard, and recursively puts their associated accounts into the same shard. Li et al. [25] adopt an improved label propagation algorithm (LPA) to optimize the fragmentation process. Both Zhang and Li et al. take into account the current account and neighboring accounts information. However, the lack of assessment of global account relationships can result in important accounts being split into different shards, often not effectively reducing cross-shard transactions. To improve the impact of local optimization on blockchain performance, Huang et al. [23] proposed to abstract transactions into a state graph using the graph-based segmentation method and divide all accounts in the graph using Metis [31]. Zhang et al. [32] adopted the method of modularity optimization, used the classic Louvain algorithm to preliminarily divide accounts, and then carried out detailed division with the goal of optimizing throughput.

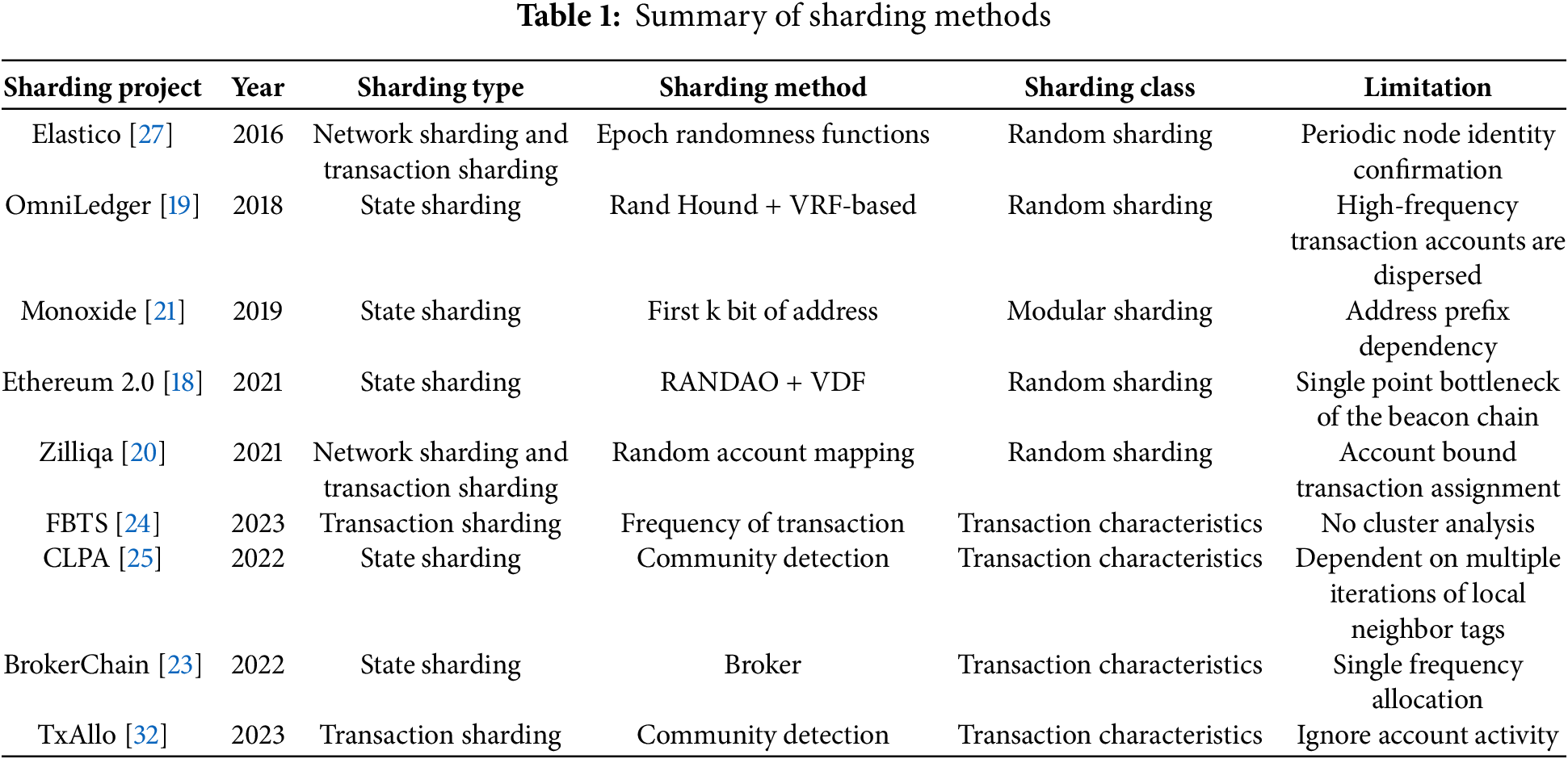
The existing sharding schemes are summarized in Table 1. In a multi-shard blockchain network, cross-shard transactions are inevitable but should be minimized. The existing sharding technology is often unable to comprehensively consider the complex characteristics of accounts based on a global perspective, resulting in insufficient optimization of transaction allocation. In view of the shortcomings of existing sharding strategies in comprehensive features, this paper adopts a community detection algorithm and proposes a transaction sharding algorithm based on account activity and transaction frequency.

3  Methodology

In real-world transactions, the relationships between accounts are complex. Existing sharding schemes typically use transaction frequency between accounts as the basis for sharding when analyzing transaction characteristics [23,24,32]. However, some accounts, despite not having a high transaction frequency, engage in transactions with a large number of other accounts and are highly active within the transaction network. The account activity degrees are also a major factor influencing community clustering. Therefore, the relationship between accounts is mainly reflected in the activity of accounts and the transaction frequency between accounts. Based on the above, we comprehensively consider both the activity of accounts and the transaction frequency between accounts, and propose a blockchain sharding algorithm based on active degree and transaction frequency, which can optimize account sharding and reduce the number of cross-shard transactions.

3.1 Sharding Design

Shard technology has improved blockchain performance to some extent [8], but it also brings challenges such as high cross-shard transaction proportion and long transaction delays. Comprehensively considering the transaction frequency and activity degree of accounts is the key to reducing cross-shard transactions, so a blockchain transaction sharding algorithm based on account degree and frequency is proposed as shown in Fig. 1.

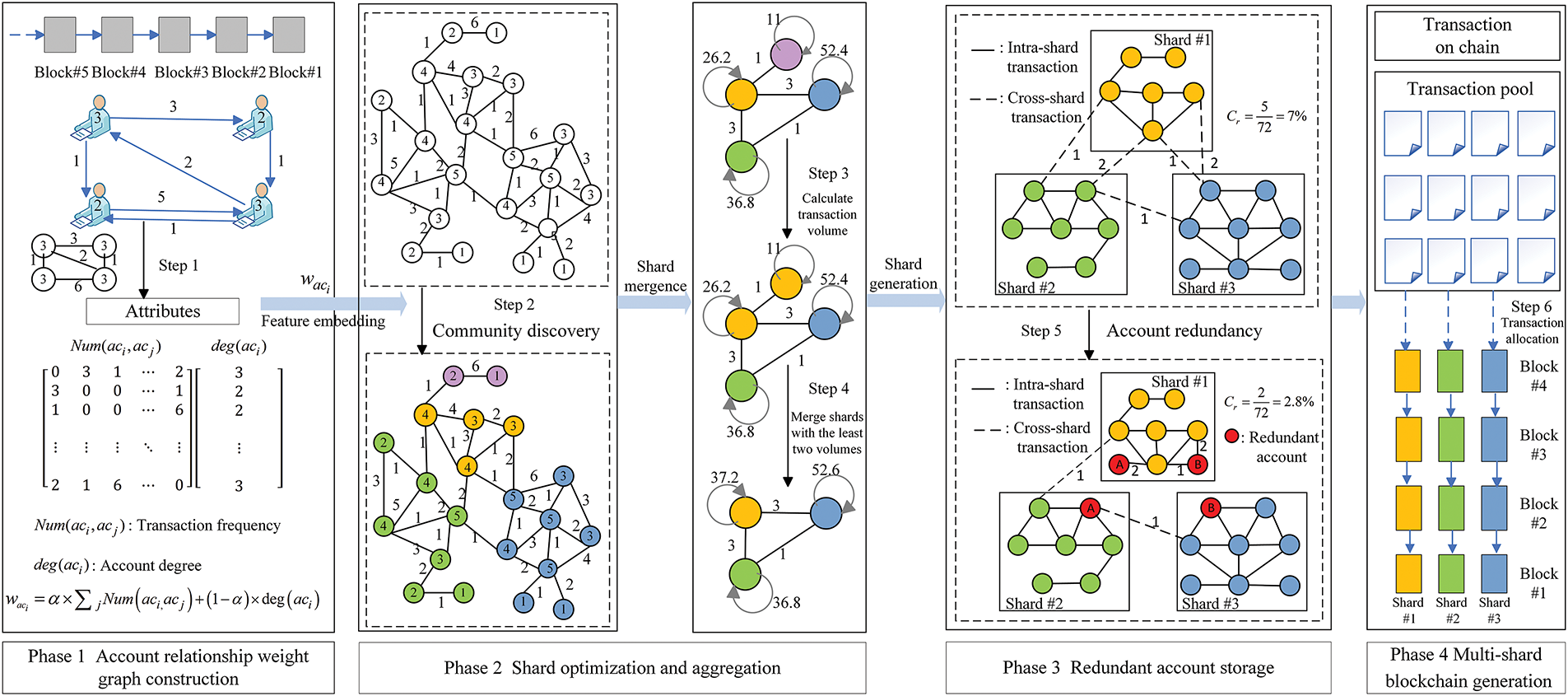
Figure 1: Schematic diagram of DFSA

The working process is summarized as follows:

Phase 1: Account relationship weight graph construction. The real-world transaction relationships are for accounts. For research convenience, the transaction relationships are abstracted as an undirected weighted graph, as shown in Step 1. The undirected weighted graph is composed of a frequency matrix and a degree vector, where Num(aci,acj) represents the total transaction frequency of aci and deg⁡(aci) represents the total number of transaction counterparts. By a weighted average of account frequency and account degree, a comprehensive account weight waci is obtained, which provides an important basis for the next account sharding.

Phase 2: Shard optimization and aggregation. At this phase, the community detection algorithm is applied to initial account segmentation as shown in Step 2. The comprehensive account weight is used as the basis for calculating the modularity of community detection. The associated account with the highest modularity is selected for merging. Through multiple rounds of operations, an initial sharding division result is formed. Based on the initial sharding result, calculate the total transaction volume of each shard as shown in Step 3, and merge the two shards with the smallest transaction volumes as shown in Step 4.

Phase 3: Redundant account storage. To further reduce the number of cross-shard transactions, a certain proportion of accounts are randomly selected and redundantly stored in the shard in which their frequent transaction accounts are located, as shown in Step 5. Selecting redundant accounts randomly can prevent attackers from constructing high-frequency fake transactions and ensure that the account cannot predict which shard it is in. All redundant accounts can be redundant only once in a shard to reduce the difficulty of duplicate maintenance and avoid the cost of duplicate synchronization caused by dynamic redundancy. By using redundant storage, some cross-shard transactions are converted into intra-shard transactions. As a result, the reduction in cross-shard transactions is inevitable.

Phase 4: Multi-shard blockchain generation. After the redundant accounts are completed, a multi-shard blockchain architecture is generated. Based on the above account sharding result, the transactions in the transaction pool are pulled to the corresponding shard as shown in Step 6. Each shard independently processes transactions and packages the transactions into blocks.

3.2 Related Definitions

In order to conveniently describe the relationship in blockchain, the account relationship weight graph G=(Ac,Tn) is constructed, where Tn is defined as the set encompassing all transaction frequencies on the blockchain, Tn={tn1,tn2,…,tns}, tni={aci,acj,Num(aci,acj)}, tni∈Tn, and Num(aci,acj) represents the cumulative frequency of transactions, where aci is the sender of the transaction and acj is the receiver of the transaction. The set of account degrees is represented by Deg={deg⁡(ac1),deg⁡(ac2),…,deg⁡(acn)}, where degree of account aci represents the number of accounts with which transactions are made and is denoted as deg⁡(aci), deg⁡(aci)=|{acj∈Ac|Num(aci,acj)+Num(acj,aci)>0}|. The total transaction frequency of account relationship weight graph G is represented as M, M=1/2∑i,jNum(aci,acj), the multi-shard blockchain network is represented as Shard, Shard={shard1,shard2,…,shardm}, where shardi represents a set of accounts, shardi={ac1,ac2,…,acn}. For any shardi, the internal weights of shardi is represented as wi, wi=∑i,jNum(aci,acj), where aci∈shardi, acj∈shardi. Moreover, the weight between shardi and shardj is denoted as wshardi,j, wshardi,j=∑i,jNum(aci,acj), where aci∈shardi, acj∉shardi. For any given shardi, the associated shards of shardi are denoted as Rshardi, where Rshardi=∪shardj and wshardi,j≠0. The weight of account aci and adjacent shard is represented by Num(aci,shardj).

The comprehensive weight of account aci is represented by waci, where α is weight regulation factor, which is used to balance the importance of account transaction frequency and activity degree in the comprehensive weight calculation, and waci is defined as:

waci=α×∑jNum(aci,acj)+(1−α)×deg⁡(aci)(1)

The modularity Q and the modularity gain ΔQ used in Algorithm 1 can be calculated based on M, wi, wshardi,j and waci. Table 2 gives the relevant formulas and brief descriptions.

Definition 1 (Transaction Volume Redundancy): On blockchain, the transaction volume of account aci as the sender is denoted as snaci, the set of redundant accounts is denoted as Vac, and the transaction volume redundancy is denoted as V.

V=∑i=1i=|Vac|snaci|Tx|(2)

Definition 2 (Cross-Shard Transaction Proportion): For ∀txk in the shard, txk∈Tx, txk={aci,acj,value}, if aci∈shardk, acj∈shardn, and shardk≠shardn, then txk is termed a cross-shard transaction. The overall count of transactions in the blockchain is represented as |Tx|, the overall count of cross-shard transactions is represented as |Txcross|, and the cross-shard transaction proportion is represented as Cr.

Cr=|Txcross||Tx|(3)

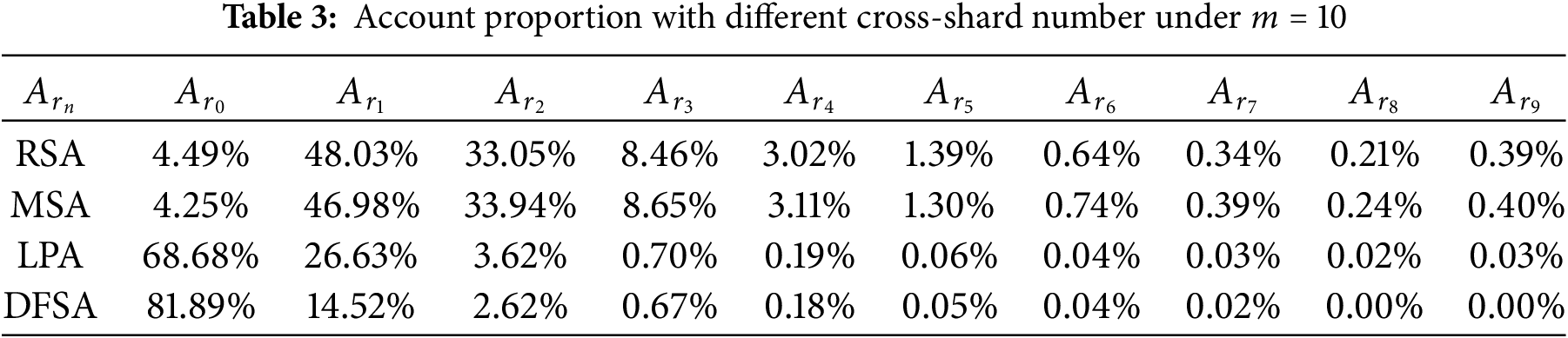
Definition 3 (Accounts Proportion with Different Cross-Shard Number): On a blockchain with a shard granularity of m, N represents the set of across-shard number and N={0,1,…,m−1}. naci represents the cross-shard number of aci. The account set with n cross-shard number is represented as An, An={aci|naci=n}, aci∈Ac, and the proportion of accounts with n cross-shard number is represented as Arn.

Arn=|An||Ac|(4)

Definition 4 (Average Cross-Shard Number): The average cross-shard number is represented as navg.

navg=∑i=1i=|Ac|naci|Ac|(5)

3.3 Algorithm Description

Sharding technology has improved the performance of blockchains to some extent, but it has also introduced issues such as longer transaction latency. The transactional relationships between accounts are the main factors influencing the cross-shard transaction proportion. The DFSA algorithm proposed in this paper is inspired by community detection, optimizes the basis for community division, and redefines account weights. The algorithm includes two parts: (1) optimizing account partition and adjusting shard granularity; and (2) account redundancy strategy.

Algorithm 1 involves optimizing account partition and adjusting shard granularity. The algorithm analyzes the activity degree of accounts and the transaction frequencies. First, each account is treated as an independent shard (Line 1), and adjacent accounts are merged into the same shard based on the modularity gain ΔQ (Lines 2–17). Reconstruct the community and update the modularity until |Q−Qinit|≤10−6 (Lines 18–20). Then, the transaction volume of each shard is calculated. If the current shard granularity exceeds the target value m, the two shards with the least transaction volume are merged. If the shard granularity is insufficient, the shard with the largest transaction volume is split into two, and the cycle is adjusted until the shard granularity is equal to m (Lines 21–34). Finally, the blockchain with shard granularity of m is output (Line 35).

After Algorithm 1 is executed, the strong correlations between accounts are found through community detection, and the strong-correlated and high-frequency accounts are assigned to the same shard. For high-frequency accounts that are not clustered in the same shard, one of them is randomly selected as a redundant account, and its transactions are backed up to the shard where the other account resides. The transactions that originally required cross-shard operations are converted into intra-shard transactions through redundant storage. Therefore, properly redundant storage of strong-correlated accounts can avoid unnecessary cross-shard transactions. But how many redundant accounts are appropriate? Thus, the concept of account redundancy rate r is introduced. The account redundancy rate r is obtained through the experimental results in Section 4. The description of the account redundancy strategy is shown as Algorithm 2. The construction process of redundant account candidates is as shown in Lines 1–6. K is a dynamic threshold that needs to be adjusted according to the characteristics of the data set. Identify the accounts with significantly high comprehensive weights from the dataset. Select the minimum comprehensive weight value of these accounts with relatively high comprehensive weights as the benchmark for division. Divide the value of this benchmark by the total comprehensive weight of all accounts in the dataset. These accounts will not be selected as redundant account candidates because their redundancy would lead to a storage explosion. The K value of this experiment is taken as 0.05. According to the account redundancy rate r, randomly select accounts from the candidate and store them in the shard with the largest transactions (Lines 7–17).

4  Experiment Evaluation

The mainstream sharding schemes (RSA, MSA, and LPA) were analyzed as baselines. To validate the effectiveness of the algorithms, simulation experiments were conducted under different shard granularities. The performance of the four algorithms is comprehensively evaluated based on multiple indicators. Additionally, the optimal redundancy strategy proposed in this paper is verified through experiments, and the influence of different account redundancy rates on system performance is analyzed.

In order to verify the feasibility of the algorithm, the transaction sharding algorithm is designed using the Python language, and experiments were conducted on PyCharm. All experiments were conducted on an Intel Core i7 64-bit Windows operating system with 16 GB of memory. 2 million transactions were extracted from Ethereum, totaling 75,222 accounts.

4.1 Cross-Shard Transaction Proportion under Different Redundancy Strategies

In order to further decrease Cr, the redundant storage of some accounts is considered. However, it is worth considering which account redundancy strategy to choose. Account redundancy can be stored in the shard with the least transaction volume, or it can be stored in the shard where the most frequent account that transacts with the redundant account is located (called strong-correlated account redundant strategy). In order to verify the effectiveness of the redundancy strategy, non-account redundancy is used as a comparative experiment to test Cr of the two strategies under different shard granularities. As shown in Fig. 2, it can be intuitively seen that using the strong-correlated accounts redundant strategy can significantly reduce Cr. With the increase of shard granularity, the strong-correlated account redundant strategy still maintains a low cross-shard transaction, because the strategy takes into account transaction frequency, and converts more cross-shard transactions into intra-shard transactions through account redundancy. Therefore, the subsequent experiments are conducted on the basis of the strong-correlated accounts redundant strategy.

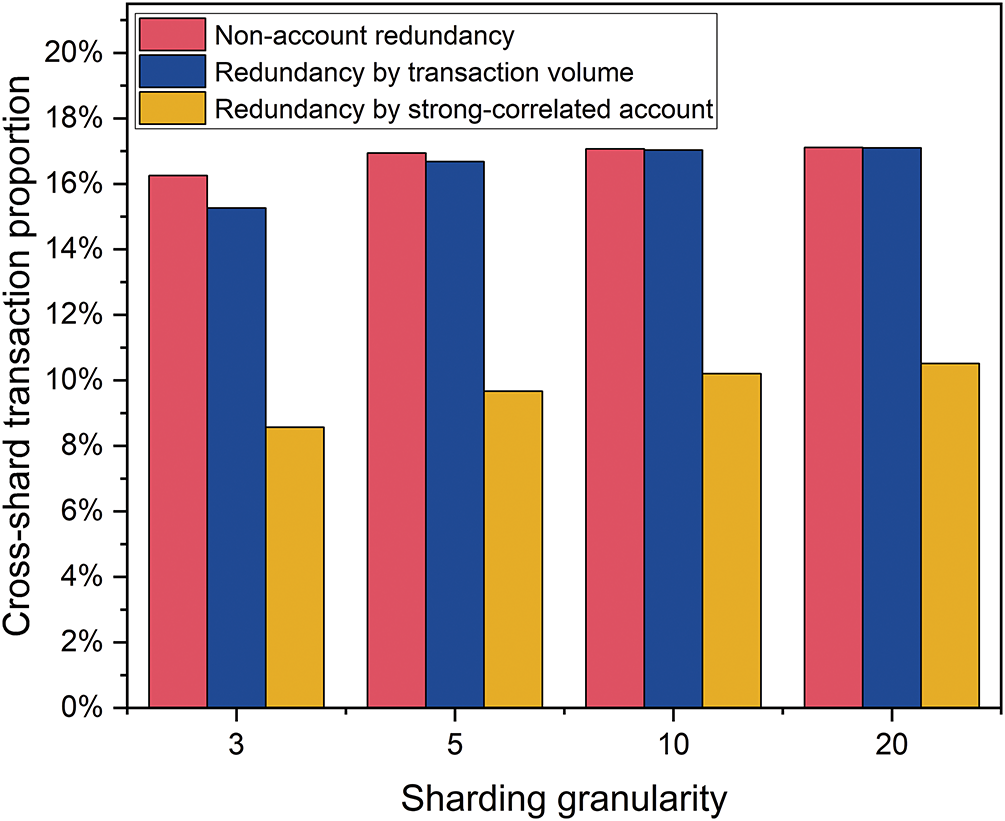
Figure 2: The cross-shard transaction proportion under different redundant strategies

4.2 Cross-Shard Transaction and Transaction Volume Distribution

After determining the account redundancy strategy, the account redundancy rate needs to be considered. As shown in Fig. 3, Cr is inversely proportional to the V. To find a balance between these two factors, this study tests their variations under different account redundancy rates. When the account redundancy rate increased from 5% to 10%, the transaction volume redundancy increased by 3 to 12 percentage points, while the other indicator remained stable at around 10%. When the account redundancy rate further increases to 15%, the transaction volume redundancy surges by 22 to 31 percentage points, far exceeding expectations. Therefore, the account with 10% redundancy is selected as the optimal solution, which is used as account redundancy rate r in Algorithm 2.

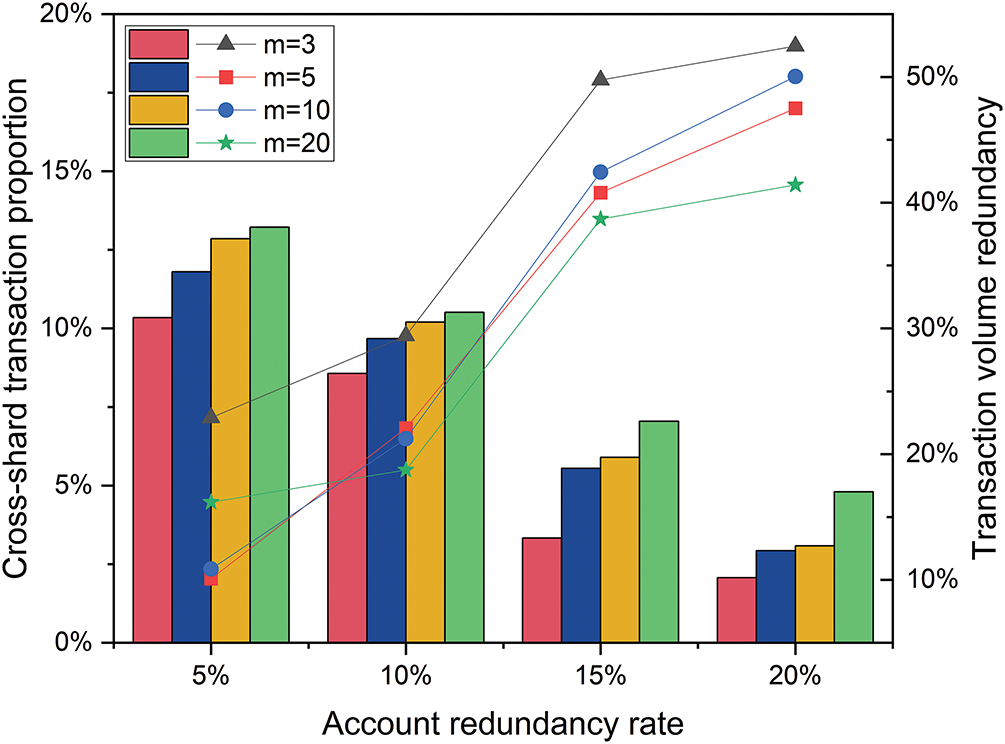
Figure 3: The change of cross-shard transaction proportion and transaction volume redundancy under different account redundancy rates

4.3 Cross-Shard Transaction and Account Distribution

Fig. 4 shows Cr under different shard granularities. The Cr of the four algorithms increases with the increase of shard granularity m. When the sharding granularity of DFSA is 3, 5, 10, and 20, the cross-sharding transaction proportion remains at around 10%, performing the best among the four algorithms. This is mainly because it thoroughly considers the relationships between accounts during the sharding process. It not only analyzes the transaction frequency between accounts, but also takes into account the activity degrees, and ensures that accounts with high correlation are prioritized and located together. Table 3 lists Arn when m is equal to 10. In the case of adopting the DFSA algorithm, 81.89% of the accounts can complete transaction verification without cross-shard, thereby reducing the demand for cross-shard transactions and transaction delays.

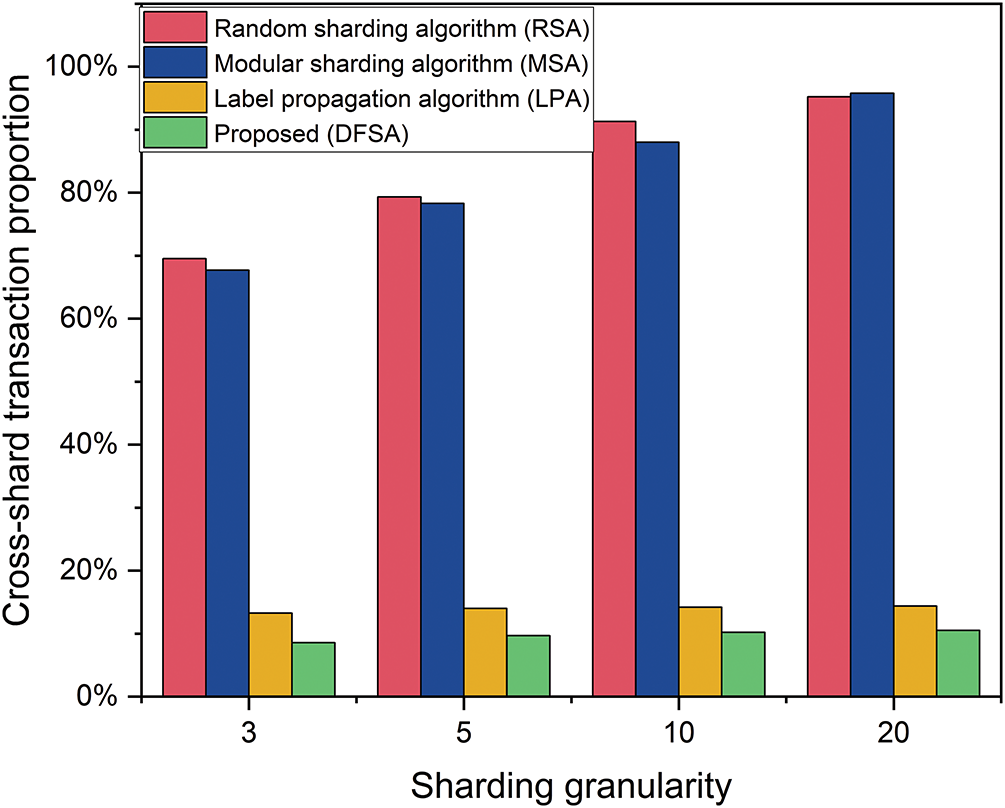
Figure 4: The cross-shard transaction proportion under different sharding granularity

4.4 Transaction Latency

Transaction delay is the core indicator of user concern in practical applications, which directly affects system availability and user experience, and therefore becomes a key standard to measure blockchain performance. In order to comprehensively evaluate the performance of different algorithms in the transaction confirmation process, the transaction delay cumulative distribution function (CDF) under different sharding granularities is plotted, as shown in Fig. 5.

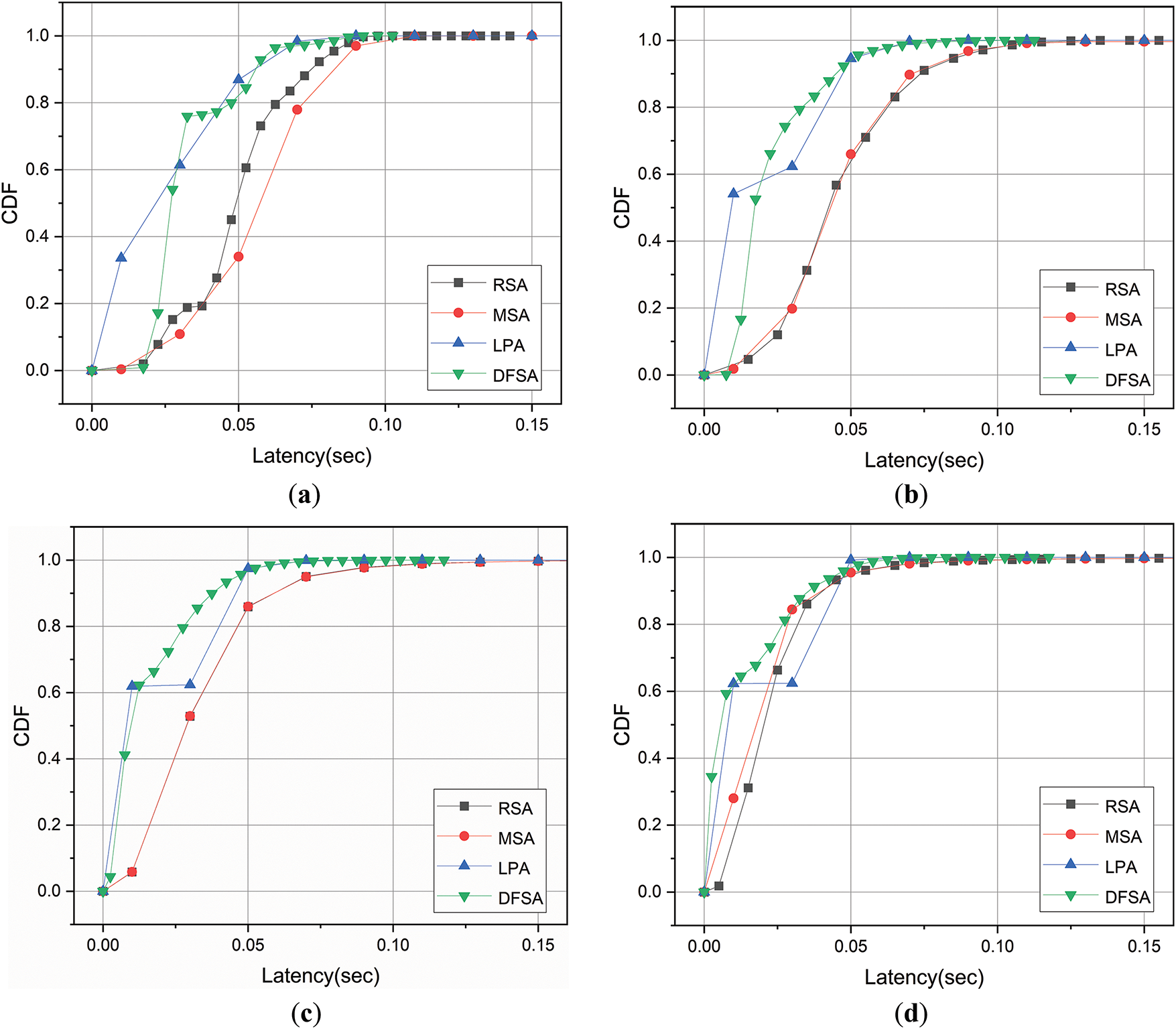
Figure 5: Account transaction delay with different sharding granularity: (a) m = 3, (b) m = 5, (c) m = 10, (d) m = 20

With the increase of sharding granularity, the transaction confirmation time of more than 90% of the four algorithms decreased from 0.1 s to 0.05 s. This is because sharding technology shares the load in the network among multiple independent subnetworks, which allows transactions to be processed and confirmed faster, reducing overall transaction latency. In Fig. 5a, the LPA algorithm can process more transactions than the DFSA algorithm at the same time, because the LPA algorithm relies on the local neighbor information propagation label. When the sharding granularity is small, the more relevant nodes are more likely to propagate to the same label and thus cluster together. In Fig. 5c, the DFSA algorithm enables up to 80% of transactions to be confirmed within 0.03 s, while for other baselines such as LPA, MSA, and RSA only confirm 60%, 51%, and 52% of transactions respectively within the same time. This is because the DFSA algorithm can better capture the global structure and potential community relations between nodes through global optimization, thus improving the quality of the partition. To sum up, at higher sharding granularity, the DFSA algorithm always maintains a low transaction latency4.5 Average Delay.

This study systematically evaluates transaction latency and account cross-shard number based on specific sharding granularity. However, in practical applications, it is necessary to prioritize the global performance of the blockchain rather than a single account. To this end, the concepts of navg and average transaction latency are introduced. It can be seen from Fig. 6a that with the increase of sharding granularity, all four algorithms show an upward trend. In contrast, the DFSA algorithm has fewer cross-shard numbers and a smaller fluctuation range, approximately 0.07 percentage points. Fig. 6b shows the average transaction latency of the four algorithms under different sharding granularities. The delay of all algorithms decreases as the sharding granularity increases. This is because the larger the sharding granularity, the more decentralized the transaction, and the transaction only needs to be verified in the shard where the transaction account is located, speeding up the transaction verification speed. When the sharding granularity is 20, the latency of the DFSA algorithm is still lower than that of other algorithms, decreasing by 27%, 38%, and 41%, respectively. In summary, the DFSA algorithm performs better in all aspects.

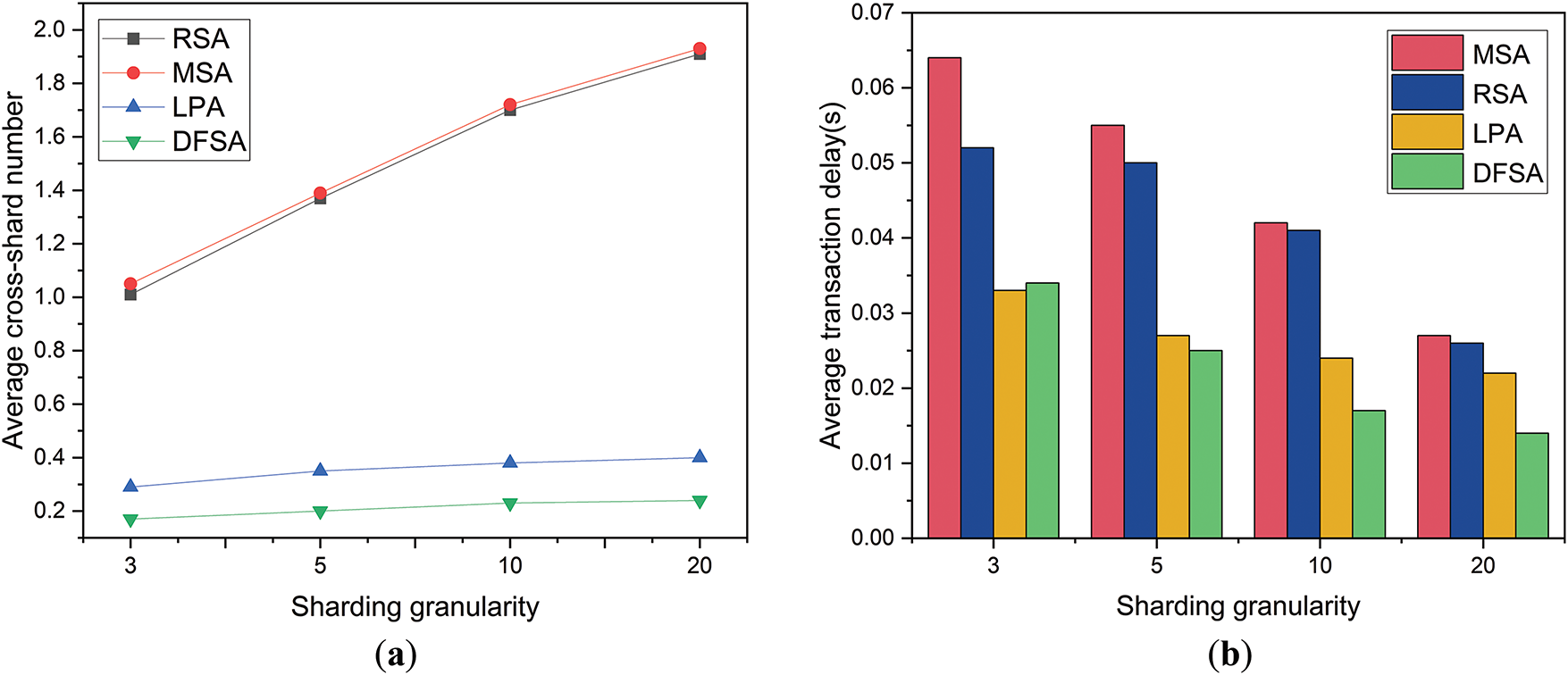
Figure 6: (a) Average cross-shard number and (b) average transaction delay under different sharding granularity

4.5 Transaction Throughput

Transaction throughput is an important index that is paid attention to in practical applications. Fig. 7 shows the transaction throughput at different sharding granularities. With the increase of sharding granularity, the throughput of the four algorithms shows an increasing trend. When m is equal to 20, the DFSA algorithm improves throughput by 34%, 78%, and 82% compared to the LPA, RSA, and MSA algorithms, respectively. The experimental results show that the DFSA algorithm can effectively improve the transaction throughput.

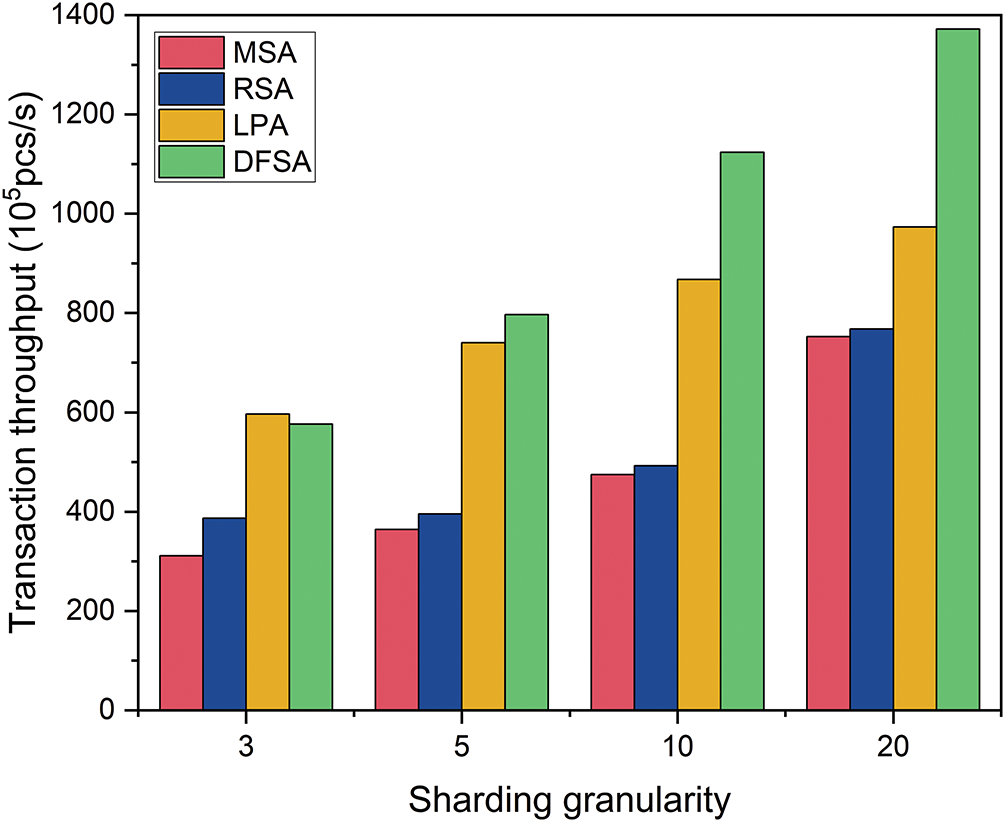
Figure 7: Transaction throughput

5  Conclusion

This paper focuses on solving the problem of an excessively high cross-shard transaction proportion in sharding technology. To address this, the DFSA algorithm is proposed, which calculates the comprehensive account weight based on their activity degrees and transaction frequency. The algorithm uses a community detection approach to partition the network and further reduces the cross-shard transaction proportion by considering a random redundancy strategy based on account relationships. A large number of experimental results show that the DFSA algorithm is significantly superior to the widely adopted RSA and MSA, with less transaction delay and higher throughput. Future work will focus on addressing the issue of shard load balancing to ensure reasonable transaction allocation, prevent certain shards from being overloaded, and further enhance the overall performance of the blockchain.

Acknowledgement: The authors would like to thank the editors and reviewers for their hard work.

Funding Statement: This work has been supported by the National Natural Science Foundation of China (Grant No. 61802301) awarded to J. Li; the Postgraduate Innovation Fund Project of Xi’an Shiyou University (Grant No. YCX2513159).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jiao Li, Xiaoyu Song; data collection, experiment, and analysis: Xiaoyu Song; supervision and discussion: Jiao Li; writing, editing, and reviewing: Jiao Li, Xiaoyu Song. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Khan D, Jung LT, Hashmani MA. Systematic literature review of challenges in blockchain scalability. Appl Sci. 2021;11(20):9372. doi:10.3390/app11209372. [Google Scholar] [CrossRef]

2. Hafid A, Hafid AS, Samih M. Scaling blockchains: a comprehensive survey. IEEE Access. 2020;8:125244–62. doi:10.1109/access.2020.3007251. [Google Scholar] [CrossRef]

3. Huang H, Zhao Y, Zheng Z. tMPT: reconfiguration across blockchain shards via trimmed merkle patricia trie. In: 2023 IEEE/ACM 31st International Symposium on Quality of Service (IWQoS); 2023 Jun 19–21; Orlando, FL, USA. p. 1–10. [Google Scholar]

4. Kustov V, Beksaev N, Ravi R. Sharding in the blockchain or divide and conquer. In: Proceedings of the 16th International Conference on Advanced Technologies, Systems and Services in Telecommunications (TEL-SIKS); 2023 Oct 25–27; Nis, Serbia. p. 223–7. [Google Scholar]

5. Zhang Y. Research on hierarchical sharding based on spectral clustering algorithm. In: Proceedings of the 4th International Conference on Computer Science and Blockchain (CCSB); 2024 Sep 6–8. Shenzhen, China. p. 577–83. [Google Scholar]

6. Liu Y, Xing X, Cheng H, Li D, Guan Z, Liu J, et al. A flexible sharding blockchain protocol based on cross-shard byzantine fault tolerance. IEEE Trans Inf Forensics Secur. 2023;18:2276–91. doi:10.1109/tifs.2023.3266628. [Google Scholar] [CrossRef]

7. Li J, Zhang X, Ning Y. Blockchain sharding method for reducing cross-shard transaction proportion. J Comput Appl. 2024;44(6):1889–96. doi:10.11772/j.issn.1001-9081.2023060757. [Google Scholar] [CrossRef]

8. Yu G, Wang X, Yu K, Ni W, Zhang JA, Liu RP. Survey: sharding in blockchains. IEEE Access. 2020;8:14155–81. doi:10.1109/access.2020.2965147. [Google Scholar] [CrossRef]

9. Tan P, Xu T, Tu R. Review of research on blockchain sharding techniques. Comput Sci. 2024;51(11):307–20. doi:10.11896/jsjkx.231200078. [Google Scholar] [CrossRef]

10. Li H, Wang D, Zhi H, Wang Y, Yang T, Song J. A dynamic sharding scheme for blockchain based on graph partitioning. In: Proceedings of the 2024 IEEE International Conference on Blockchain (Blockchain); 2024 Aug 19–22; Copenhagen, Denmark. p. 286–93. [Google Scholar]

11. Fang P, Zhao F, Wang B, Wang Y, Jiang T. Development, technologies and applications of Blockchain 3.0. J Comput Appl. 2024;44(12):3647–57. doi:10.11772/j.issn.1001-9081.2023121826. [Google Scholar] [CrossRef]

12. Jia L, Liu Y, Wang K, Sun Y. Estuary: a low cross-shard blockchain sharding protocol based on state splitting. IEEE Trans Parallel Distrib Syst. 2024;35(3):405–20. doi:10.1109/tpds.2024.3351632. [Google Scholar] [CrossRef]

13. Huang H, Kong W, Peng X, Zheng Z. Survey on blockchain sharding technology. Comput Eng. 2022;48(6):1–10. doi:10.19678/j.issn.1000-3428.0063887. [Google Scholar] [CrossRef]

14. Quan BLY, Wahab NHA, Al-Dhaqm A, Alshammari A, Aqarni A, Razak SA, et al. Recent advances in sharding techniques for scalable blockchain networks: a review. IEEE Access. 2025;13:21335–66. doi:10.1109/access.2024.3523256. [Google Scholar] [CrossRef]

15. Xu J, Ming Y, Wu Z, Wang C, Jia X. X-shard: optimistic cross-shard transaction processing for sharding-based blockchains. IEEE Trans Parallel Distrib Syst. 2024;35(4):548–59. doi:10.1109/tpds.2024.3361180. [Google Scholar] [CrossRef]

16. Wang Q, Guan Y. TransShard: a dynamic transaction-aware sharding scheme for account-based blockchain. IEEE Access. 2024;12:179797–812. doi:10.1109/access.2024.3505953. [Google Scholar] [CrossRef]

17. Cai Z, Liang J, Chen W, Hong Z, Dai H-N, Zhang J, et al. Benzene: scaling blockchain with cooperation-based sharding. IEEE Trans Parallel Distrib Syst. 2023;34(2):639–54. doi:10.1109/tpds.2022.3227198. [Google Scholar] [CrossRef]

18. Taş R, Tanrıöver Ö. Building a decentralized application on the ethereum blockchain. In: Proceedings of the International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT); 2019 Oct 11–13; Ankara, Turkey. p. 1–4. [Google Scholar]

19. Kokoris-Kogias E, Jovanovic P, Gasser L, Gailly N, Syta E, Ford B. OmniLedger: a secure, scale-out, decentralized ledger via sharding. In: Proceedings of the IEEE Symposium on Security and Privacy (SP); 2018 May 21–23; San Francisco, CA, USA. p. 583–98. [Google Scholar]

20. Aiyar K, Halgamuge MN, Mohammad A. Probability distribution model to analyze the trade-off between scalability and security of sharding-based blockchain networks. In: Proceedings of the 2021 IEEE 18th Annual Consumer Communications & Networking Conference (CCNC); 2021 Jan 9–12; Las Vegas, NV, USA. p. 1–6. [Google Scholar]

21. Wang J, Wang H. Monoxide: scale out blockchains with asynchronous consensus zones. In: Proceedings of the 16th USENIX Symposium on Networked Systems Design and Implementation (NSDI’19); 2019 Feb 26–28; Boston, MA, USA. p. 95–112. [Google Scholar]

22. Wu J, Yuan L, Chen M, Xie T. Blockchain dynamic sharding model based on node trustworthiness. Appl Res Comput. 2024;41(12):3563–71. doi:10.19734/j.issn.1001-3695.2024.04.0243. [Google Scholar] [CrossRef]

23. Huang H, Peng X, Zhan J, Zhang S, Lin Y, Zheng Z, et al. BrokerChain: a cross-shard blockchain protocol for account/balance-based state sharding. In: Proceedings of the IEEE INFOCOM 2022—IEEE Conference on Computer Communications (INFOCOM); 2022 May 2–5; London, UK. p. 1968–77. [Google Scholar]

24. Zhang X. Research on blockchain sharding method based on transaction feature analysis [master’s thesis]. Xi’an, China: Xi’an Shiyou University; 2023. [Google Scholar]

25. Li C, Huang H, Zhao Y, Peng X, Yang R, Zheng Z, et al. Achieving scalability and load balance across block-chain shards for state sharding. In: Proceedings of the 41st International Symposium on Reliable Distributed Systems (SRDS); 2022 Sep 19–22; Vienna, Austria. p. 284–94. [Google Scholar]

26. Li Z, Xu B, Zhou Y. Graph neural network-based address classification method for account balance model blockchain. J Commun. 2023;44(9):115–26. doi:10.11959/j.issn.1000-436x.2023173. [Google Scholar] [CrossRef]

27. Luu L, Narayanan V, Zheng C, Baweja K, Saxena P. A secure sharding protocol for open blockchains. In: Proceedings of the ACM SIGSAC Computer and Communications Security (CCS’16); 2016 Oct 24–28; Vienna, Austria. p. 17–30. [Google Scholar]

28. Zhai D, Liu J, Yang Y, Zhu P. Blockchain dynamic sharding adaptive model. Appl Res Comput. 2024;41(11):3231–8. doi:10.19734/j.issn.1001-3695.2024.03.0069. [Google Scholar] [CrossRef]

29. Wang F, Zhang Q, Liu Y, Liu L, Lu Y. Look at blockchain from a scalability perspective. Appl Res Comput. 2023;40(10):2896–907. doi:10.19734/j.issn.1001-3695.2023.02.0075. [Google Scholar] [CrossRef]

30. Rashid M, Rasool I, Zafar N, Afzaal H. Formal modeling and verification of justification and finalization of checkpoints in Ethereum 2.0 beacon chain. In: Proceedings of the 1st IEEE Karachi Section Humanitarian Technology Conference (KHI-HTC); 2024 Jan 8–9; Tandojam, Pakistan. p. 1–6. [Google Scholar]

31. Echbarthi G, Kheddouci H. Streaming METIS partitioning. In: Proceedings of the IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM); 2016 Aug 18–21; San Francisco, CA, USA. p. 17–24. [Google Scholar]

32. Zhang Y, Pan S, Yu J. TxAllo: dynamic transaction allocation in sharded blockchain systems. In: Proceedings of the IEEE 39th International Conference on Data Engineering (ICDE); 2023 Apr 3–7; Anaheim, CA, USA. p. 721–33. [Google Scholar]