Optimized Attack and Detection on Multi-Sensor Cyber-Physical System

1  Introduction

The deep integration of information technology with industrialization has significantly enhanced the intelligence and networking capabilities of next-generation production systems, establishing higher standards for traditional single-point technologies. In this context, Cyber-Physical Systems (CPS) have emerged as advanced systems that seamlessly integrate the physical environment, communication infrastructure, and computational resources [1,2]. CPS integrate advanced technologies in computing, communications, and control to enable dynamic regulation and real-time perception. These capabilities support the delivery of information-centric services across complex engineering domains, thereby enhancing system reliability, operational efficiency, and responsiveness [3]. These systems have found extensive applications in environmental monitoring, industrial automation, navigation, and target tracking. Furthermore, network communication technology facilitates network-based control of physical processes, streamlining system design and deployment while enabling more flexible and efficient management [4].

Unlike traditional physical systems that operate in relatively isolated environments, modern CPS systems inherently rely on openness and interconnectivity to maximize efficiency and scalability. However, this openness also introduces vulnerabilities, exposing CPS susceptible to cyber threats within the information layer. Such threats can trigger cascading effects, potentially leading to hardware failures and significant system damage. Such as the SQL Slammer worm and the Stuxnet attacks, illustrate the serious risks that CPS security vulnerabilities pose to national security and public safety [5,6].

The CPS attack model is structured into three aspects: the adversary’s apriori system model knowledge, disclosure abilities, and disruption resources [7]. Based on this modeling, attacks are generally grouped into three major types: 1) Denial of Service attack; 2) Replay attack; 3) False Data Injection attack [8]. Wei et al. investigated sequential DoS attacks against finite impulse response (FIR) systems, developing a parameter identification algorithm to formulate optimal attack strategies based on the covariance matrix of estimation error [9]. To mitigate impact of DoS attacks, Zhao et al. proposed an adaptive event-triggered communication mechanism. This mechanism reduces communication resource consumption and alleviates network bandwidth pressure by only transmitting data when necessary, based on specific event triggers rather than continuous transmission. In addition, they developed a combined design method to jointly tune the controller gain, and event-triggered weighting matrix [10]. Mo et al. examined how replay attacks influence system behavior and evaluated whether such attacks can succeed under certain conditions. They further proposed injecting minor variations into the control commands to help the system recognize and detect these attacks [11]. To address periodic replay threats in CPS, Li et al. designed an encryption-based method that ensures complete detection during an attack [12]. Naha et al. propose a detection method for replay attacks that integrates signal watermarking with cumulative sum testing to enhance system resilience. By optimizing the watermark signal’s variance to maximize the KLD, the method significantly shortens the latency in identifying replay attacks [13]. Ni et al. investigated how reset attacks affect CPS, presented basic and advanced reset attacks, and demonstrated validity of these attacks [14]. Remote state estimation with an active eavesdropper, Ding et al. introduced a unified framework such attacks and proposed a stealthiness metric derived from the estimator’s packet reception rate [15]. Pang et al. proposed a partial FDI attack strategy aimed at networked stochastic systems. This strategy degrade the performance of a Kalman filter-based output tracking control system by manipulating certain sensor measurements [16]. Xu et al. addressed event-based remote state estimation attacks by proposing a false data injection strategy aimed at evading the Chi-squared data detector while reducing the impact of the scheduler. They developed a two-channel, scheduler-oriented false data injection method by altering the numerical characteristics of the innovation signal [17]. Taking into account multiple forms of detection feedback, Li et al. proposed a novel estimation framework designed to defend against false data injection attacks [18].

Existing research on stealthy attacks has made substantial progress in the field of CPS security. Anomaly detection techniques have evolved significantly, with advanced methods leveraging deep learning models to enhance adaptability and detection sensitivity. Alzubi proposed a GRU-based detection framework that demonstrates improved performance in dynamic environments by effectively capturing temporal dependencies [19]. Furthermore, Alzubi et al. introduced a deep learning-driven detection scheme that integrates Frechet and Dirichlet distributions to enhance intrusion detection accuracy in industrial wireless sensor networks [20]. Despite recent advances, residual-based detection remains highly relevant for resource-constrained systems, owing to its minimal computational demands and ease of implementation. However, linear deception attack strategies remain limited by strict feasibility constraints, often enforcing tight residual conditions. Guo et al. formulated a linear attack with the condition that residual covariance remains unchanged [21]. An attack strategy aimed at maximizing system degradation was developed by Liu et al, while strictly satisfying constraint Tk𝒫TkT+ℬ=𝒫 [22]. Li et al. extended their research on detecting linear deception attacks in multi-sensor remote state estimation [23]. However, their work did not investigate the impact of relaxing feasibility constraints on attack performance. To address these limitations, this paper proposes a linear deception attack framework with relaxed feasibility constraints, enabling the attacker to introduce controlled statistical deviations into the innovation signal. Furthermore, considering the characteristics of multi-sensor systems, we design an adaptive detection algorithm that compares distributed state estimates, thereby improving detection sensitivity under parameter uncertainty. The primary contributions as follows:

1.   We adopt a linear deception attack form broadly applicable to multi-sensor remote estimation systems and establish the corresponding feasibility constraint. Recognizing the inherent statistical variability of the detection function derived from the χ2 detector, we strategically relax this constraint to allow controlled deviations from the nominal innovation distribution. The recursive formulation of the error covariance under the proposed broadened constraint is rigorously derived using Kalman filtering theory, thereby enabling a precise quantification of the attack’s detrimental effects on the system’s estimation accuracy.

2.   Under the broadened constraint scenario, we incorporate the predefined permissible deviation into the estimation error covariance to construct an optimization-based objective function. Consequently, the determination of attack parameters is transformed into a structured optimization problem. Comparative analysis demonstrates that the proposed attack strategy markedly outperforms existing approaches, yielding significantly larger estimation error covariance and thereby severely degrading system performance.

3.   Since single-sensor detection methods cannot be directly applied to multi-sensor scenarios, we propose a novel adaptive detection algorithm specifically designed for such settings. This algorithm dynamically adjusts detection parameters and leverages discrepancies in inter-sensor state estimation to identify linear deception attacks. Simulation results demonstrate that our adaptive detection approach significantly reduces the missed detection rate compared to traditional fixed-parameter detection algorithms, thereby enhancing the reliability of multi-sensor CPS.

The structure of the remainder of this paper is as follows. Section 2 outlines the setup of CPS and briefly reviews essential concepts. In Section 3, we examine the features of linear attacks and derive a targeted attack strategy. A detailed account of the proposed attack detection method can be found in Section 4. Section 5 illustrates numerical results and simulation experiments. Lastly, Section 6 summarizes the contributions of study then discusses possible directions for future research.

2  Cyber-Physical System Setup

The system configuration designed to support remote state estimation under cyber attack conditions, illustrated in Fig. 1, comprises six core components: physical process, sensors, adversary, wireless communication network, remote estimator, and a false data detection mechanism. Sensors collect data from the physical process and transmit measurements to the remote estimator through the wireless network. In this configuration, the remote estimator transmits a centralized prior estimate to the sensor at each time step through a dedicated feedback channel. Although this design slightly increases communication overhead, it significantly reduces the computational burden requirements for a single sensor. To better support the design of the attack strategies and detection algorithms, it is necessary to review representative classical and emerging CPS attack and detection methods.

Figure 1: System architecture

As shown in Table 1, a range of attack strategies have been proposed to compromise the state estimation of CPS. Replay attack and DoS attack are simple to implement but often limited in their impact. Machine learning-based adversarial attacks demonstrate strong performance, but they generally rely on prior knowledge of training data or model structure, making them difficult to implement in real CPS environments. To address these limitations, this paper proposes a linear attack strategy under relaxed feasibility constraints. This design enables the attacker to degrade estimation performance while remaining undetectable within acceptable statistical bounds.

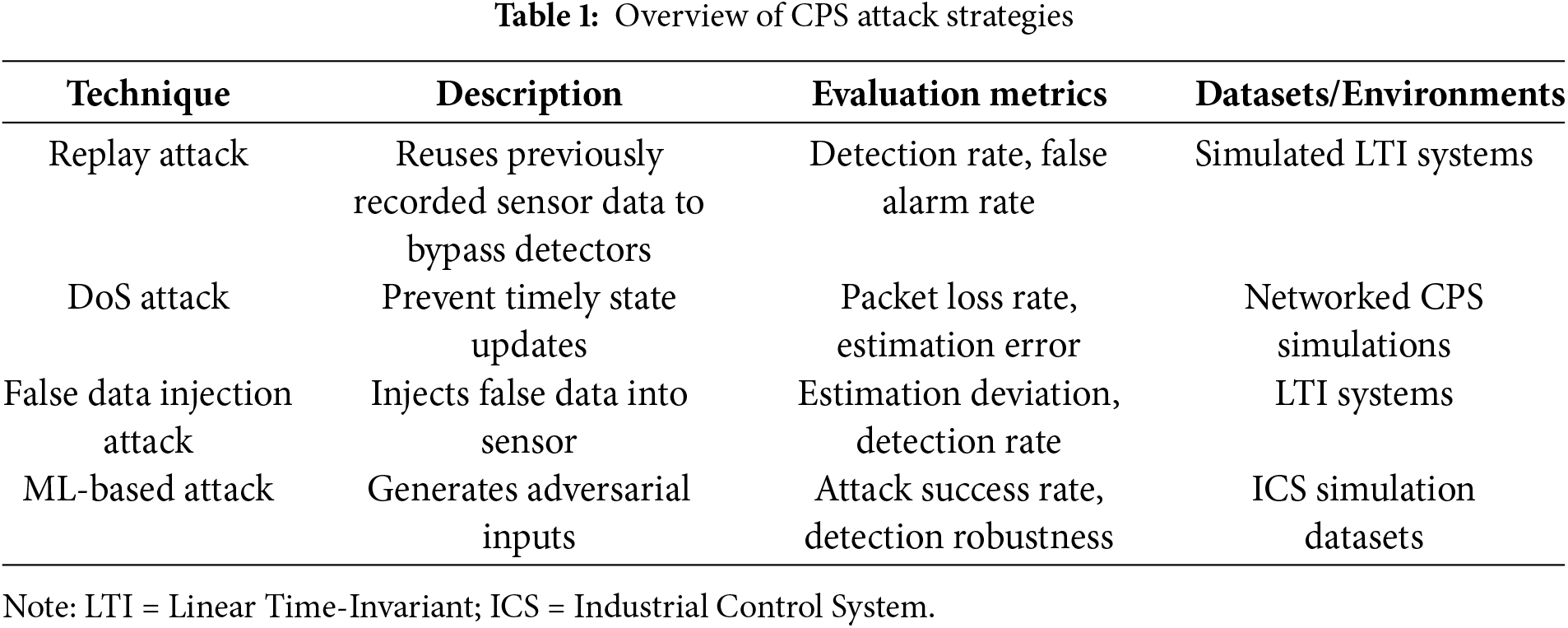
As summarized in Table 2, recent years have seen the development of a variety of detection techniques tailored to CPS.

Despite notable progress, existing detection methods face several limitations. Graph-based approaches can become computationally intensive for large-scale networks. Deep learning models require substantial training data and may struggle with limited generalization. Federated learning introduces communication and synchronization complexity, and Kalman residual methods often fail to detect stealthy or low-magnitude attacks under noisy conditions. To address these challenges, we design a detection mechanism based on adaptive that enhances sensitivity to persistent threats while maintaining a low false alarm rate. Furthermore, the approach avoids large-scale model training or distributed coordination, making it suitable for real-time deployment in noisy and resource-constrained CPS environments.

2.1 Process Model

We consider a networked system consisting of N wireless sensors and a single remote estimator, that communicate in real time. Each sensor i∈𝒩≜{1,2,3,…,N} observes the output of a linear time-invariant process denoted by {x(k)}

xk+1=Axk+wk(1)

yi,k=Cixk+vi,k(2)

k∈N denotes the discrete-time index, xk∈Rn represents system state vector, yi,k∈Rmi indicates the measurement vector collected by sensor i. The system matrix is given by A∈Rn×n and the observation matrix corresponding to sensor i is denoted as Ci∈Rmi×n. The variables wk∈Rn denote the process noise and vi,k∈Rmi denote the measurement noise. Both are zero-mean, independent, and identically distributed (i.i.d.) Gaussian random variables with associated covariance matrices.

E[wkwlT]=δklQ(Q≥0)E[vi,kvj,lT]=δijδklRi(Ri>0)E[wkvi,lT]=0,∀k,l∈N,i,j=1,2,3,…,N

The initial state x0 is a zero-mean Gaussian random vector with a positive definite covariance matrix Π0>0. It is assumed to be statistically independent of both the noise wk and the noise vi,k for all k≥0.

When sensors transmit observations to a centralized fusion unit, the system behaves equivalent to that of a single sensor directly communicating with a remote estimator under real-time conditions [24]. By defining

C≜[C1T C2T C3T ⋯ CNT]Tyk≜[y1,kT y2,kT y3,kT ⋯ yN,kT]Tvk≜[v1,kT v2,kT v3,kT ⋯ vN,kT]TR≜diag{R1,R2,R3,⋯,RN}

The total measurement equation is

yk=Cxk+vk(3)

vk denotes a zero-mean Gaussian noise sequence with covariance matrix R [25]. The system is assumed to satisfy the detectability condition for the pair (A,C), the controllability condition holds for the pair (A,Q).

2.2 Remote Estimation

Given the demands of real-time performance and high accuracy, it is computationally inefficient for each sensor to independently calculate its prior estimate using only local information. Consequently, the centralized prior estimate feedback mechanism employed in this study provides significant advantages that outweigh the minor increase in communication overhead.

At each discrete time step, sensors transmit their local measurements to the remote estimator over a wireless communication network. The estimator employs a Kalman filter to perform real-time state estimation by minimizing mean squared error. This technique operates by recursively updating state estimates through the fusion of prior predictions and incoming measurements The Kalman filtering process involves two key steps: predicting the system state and correcting it using the latest observations.

x^k|k−1=Ax^k−1Pk|k−1=APk−1AT+QKk=Pk|k−1CT(CPk|k−1CT+R)−1x^k=x^k|k−1+Kk(yk−Cx^k|k−1)Pk=(I−KkC)Pk|k−1

where x^k|k−1 and x^k are the a priori and the a posteriori minimum mean squared error (MMSE) estimates of the state xk in the Kalman filter, and Pk|k−1 and Pk are the corresponding estimation error covariances. The recursion is initialized with x^0=0 and P0=Π0>0. The gain matrix Kk determines the weighting of the current measurement in updating the state estimate For notational clarity in the following analysis, we introduce:

h(X)≜AXAT+Qg~i(X)≜X−XCiT(CiXCiT+Ri)−1CiXg~(X)≜X−XCT(CXCT+R)−1CX

Although Kalman filter employs a time-varying gain Kk, both the estimation error covariance and the gain matrix converge exponentially to a unique steady-state solution, irrespective of the initial conditions, provided that the pair (A,C) is detectable and (A,Q) is controllable. The steady-state values corresponding to the local and centralized Kalman filters are defined as follows:

P¯i≜limk→∞Pi,k|k−1,Pi≜limk→∞Pi,kP¯≜limk→∞Pk|k−1,P≜limk→∞Pk

The matrices P¯i, Pi, P¯, P represent the unique solutions to the corresponding equations, each being positive semi-definite:

h∘g~i(X)=X,g~i∘h(X)=Xh∘g~(X)=X,g~∘h(X)=X

The fixed-gain representations for both local and centralized Kalman filter are derived below, without loss of generality:

Ki≜P¯iCiT(CiP¯iCiT+Ri)−1K≜P¯CT(CP¯CT+R)−1

Under these conditions, Kalman filter operates with a fixed gain, recursive update of x^k is given by the following expression.

x^k=x^k|k−1+K(yk−Cx^k|k−1)(4)

In absence of attack, the communication link between sensors and remote estimator is assumed to be ideal, meaning that no packet loss, delay, or quantization distortion occurs under normal conditions. All transmitted innovation sequences are reliably received by the estimator. This assumption guarantees that any anomalies detected in the innovation statistics can be attributed solely to potential malicious attacks, rather than network-related factors.

For local Kalman filters, the innovation corresponding to sensor i is defined as zi,k≜yi,k−Cix^i,k|k−1. In practical scenarios, each intelligent sensor processes its own raw measurement locally and then sends the resulting innovation to remote estimator. In distributed multi-sensor systems, individual sensors are unable to independently compute their local a priori estimates x^i,k|k−1 due to the absence of information from other nodes. To address this, a more efficient strategy involves the remote estimator broadcasting a centralized a priori estimate x^k|k−1 at each time instant, thereby significantly reducing communication overhead [26]. Under this strategy, the innovation for each sensor is redefined as zi,k=yi,k−Cix^k|k−1. During nominal conditions, the innovation sequence follows an independent and identically distributed (i.i.d.) pattern, characterized by a zero-mean Gaussian distribution with a specific covariance structure. In the case of centralized Kalman filtering, the corresponding innovation can be concisely expressed as follows:

zk=yk−Cx^k|k−1

Transmitting innovations instead of raw measurements offers significant advantages, as innovations typically demonstrate lower average signal amplitudes. This leads to reduced communication bandwidth requirements and decreased sensor energy consumption, thereby improving overall communication efficiency [27]. Additionally, because the innovation sequence inherently follows a zero-mean white Gaussian distribution, it offers a statistical foundation for false data detectors to reliably ascertain whether the system is subject to cyber-attacks or data anomalies.

2.3 False Data Detector

Although machine learning-based detection methods have gained popularity in recent years due to their flexibility and adaptability, the χ2 detector remains better suited to the problem addressed in this study. χ2 detector is constructed based on statistical distribution properties of the innovation sequence, with clear mathematical derivations and explicit assumptions and χ2 detection typically computed as gk=zk⊤P−1zk, involves only simple matrix operations, ensuring low computational complexity that is well suited for real-time and embedded system applications. In contrast, machine learning methods generally impose considerable computational burdens, making them less appropriate for resource-constrained environments. Moreover, the Chi-square detector does not require large volumes of training data, thereby avoiding common issues associated with machine learning, such as data availability challenges, overfitting, and generalization errors. Since the innovation sequence itself is a key statistical quantity derived from the Kalman filter, the Chi-square detector naturally integrates with the estimation framework. But machine learning methods require additional feature extraction and data processing steps, which increase system complexity. Therefore, the Chi-square detector offers a more efficient, reliable, and theoretically grounded choice for anomaly detection in multi-sensor remote estimation systems.

Theorem 1. Consider the LTI system governed by Eqs. (1) and (2) under Kalman filtering. In this setting, the innovation zi,k corresponding to the i-th local Kalman filer follows a steady-state Gaussian distribution. 𝒩(0,CiP¯iCiT+Ri) and E[zi,kzi,lT]=0 for all k≠l.

Proof of Theorem 1. Noting e^k=xk−x^k|k−1, according to Eq. (2), rewrite zi,k:

zi,k=yi,k−Cix^k|k−1=Cixk+vi,k−Cix^k|k−1=Cie^k+vi,k

The error covariance becomes

E[zi,kzi,kT]=CiE[e^ke^kT]CiT+E[vi,kvi,kT]=CiP¯iCiT+Ri

□ 

In the same way, in the centralized Kalman filter framework, the innovation term zk=yk−Cx^k|k−1 also follows 𝒩(0,CP¯CT+R) with cross-time expectations E[zkzlT]=0 for all k≠l.

The χ2 detector identifies anomalies by evaluating the cumulative sum of the normalized innovation sequence. The detection procedure adheres to a hypothesis testing criterion at each step k

gk=∑j=k−J+1kzjT𝒫−1zj≶H1H0⁡η(5)

where 𝒫=CP¯CT+R, J represents the detection window size, and η denotes an appropriately chosen detection threshold. With the aim of regulate the false alarm rate of detection strategy, the threshold η is determined according to a predefined significance level α.η is selected as the (1−α) quantile of the Chi-squared distribution χ2(mJ), such that it satisfies the specified confidence requirement

P(gk>η∣H0)=α

Null hypothesis H0 indicates that system operates under normal conditions, whereas alternative hypothesis H1 corresponds to an ongoing attack. The normalized detection statistic defined in Eq. (5) follows the χ2 distribution with mJ degrees of freedom where m=∑i=1Nmi [28]. If the statistic gk exceeds the predefined η, the detector issues an alarm. Otherwise, the measurement is considered normal and passes detector.

3  Linear Attack Strategy

This section formulates a linear deception attack and revisits conventional feasibility constraint. To account for the variability of the χ2 detection statistic, we propose a generalized extension of the original constraint and its impact on system performance is analyzed. Finally, establish an objective function in conjunction with the selected deviation from the distribution of the innovation to determine specific attack parameters.

3.1 Linear Deception Attack

Consider an attacker with full knowledge of the system model and the capability to intercept and modify measurement data in real time. Given this assumption, the attacker can manipulate the innovation sequence to any desired value [29]. The corresponding strategy is expressed as

z~k=fk(zk)+bk

z~k denotes the innovation term that has been altered by the attacker, fk represents a general function defined over a suitable domain, and bk∈Rm is a Gaussian random vector that is independent of zk.

However, if the function fk is nonlinear, it becomes difficult to rigorously analyze the impact of the attack, as statistical properties of modified innovation sequence cannot be precisely characterized. In contrast, adopting a linear attack strategy enables explicit quantification of both the stealthiness constraint and the attack’s effect, thereby facilitating the design of effective stealth attacks. Consequently, this study focuses on linear deception attacks, where fk is defined as a linear operator acting on the innovation signal zk. The corresponding attack mechanism is as follows:

z~k=Tkzk+bk(6)

Tk∈Rm×m denotes a configurable attack matrix. The attacker can compute the steady-state Kalman filter configuration along with the corresponding innovation statistics. Under this assumption, the forged innovation z~k follows an i.i.d. zero-mean Gaussian distribution with covariance Tk𝒫TkT+ℬ. Attacker is capable of intercepting and altering innovation sequences in real time, without incurring observable delays. Given limited disruption capacity, the attacker may only target a subset of sensor channels by imposing structural constraints on Tk. If forged innovation z~k matches statistical profile of nominal innovation zk, then the linear attack defined in Eq. (6) can evade detection, as it satisfies the test condition of Eq. (5). That is to say, z~k must conform to the 𝒩(0,𝒫) which means that attack condition can be defined as

Tk𝒫TkT+ℬ=𝒫(7)

In previous work, the feasibility condition for stealthy attacks was defined as a zero-deviation constraint, indicating that the residual distribution during an attack must precisely align with the normal case. But the detection statistic gk defined in Eq. (5) is a random variable that inherently fluctuates due to its underlying χ2 distribution with mJ degrees of freedom. Even under normal conditions, the statistic exhibits a mean of E[gk]=mJ and a variance of Var(gk)=2mJ, implying that gk does not remain constant but varies within a probabilistic confidence interval. As long as the statistics after the attack satisfy P(g~k≤η)≈P(gk≤η), the purpose of bypassing the detector can be achieved. We express the new constraint as follows:

‖TkPTk⊤+ℬ−𝒫‖F≤ϵ

After attack, 𝒫~=Tk𝒫TkT+ℬ is the covariance of z~k. The expected detection statistics are as follows:

E[g~k]=∑j=k−J+1kE[z~j⊤P−1z~j]=∑j=k−J+1ktr(P−1P~)=J⋅tr(P−1P~)

The deviation can be estimated by the trace inequality

|E[g~k]−mJ|=J⋅|tr(𝒫−1(𝒫~−𝒫))|≤J⋅‖𝒫−1‖F⋅‖𝒫~−𝒫‖F(8)

From Eq. (8), deviation of the expected detection statistic is proportional to the Frobenius norm of the covariance perturbation. Thus, by choosing ε

ε≤2mJJ⋅‖𝒫−1‖F(9)

Eq. (9) ensures that the detection statistics after the attack are still within the fluctuation range of normal system operation, thereby maintaining the concealment of the attack in a statistical sense.

3.2 Performance Analysis

Malicious attackers often formulate strategies aimed at undermining system reliability by introducing substantial estimation errors into the remote estimator. Given the LTI system described in Eqs.(1) and (3), and considering a linear deception attack as specified in Eq. (6), the resulting state estimate evolves as follows:

x~k|k−1=Ax^k−1(10)

x~k=x~k|k−1+Kz~k(11)

When the χ2 detector fails to identify an anomaly, and the system is mistakenly considered to be operating normally, allowing the remote estimator to continue functioning. In such cases, due to the use of compromised data, the estimated state gradually deviates from the true state, ultimately degrading overall system performance.

To quantify this deviation, we define a priori error e~k|k−1 as difference between xk and a priori state estimate x~k|k−1 after an attack, one has e~k|k−1=xk−x~k|k−1. Similarly, the a posteriori error e~k is defined as the deviation between the xk and the updated estimate x~k, given by e~k=xk−x~k.

Then, the a priori error covariance matrix P~k|k−1 can be expressed as P~k|k−1=E[e~k|k−1e~k|k−1T]. And the a posteriori error covariance matrix P~k can be expressed as

P~k=E[e~ke~kT]=E[(xk−x~k)(xk−x~k)T]=E[((xk−x~k|k−1)−Kz~k)((xk−x~k|k−1)−Kz~k)T]=P~k−1+K(Tk𝒫TkT+ℬ)KT−E[Kz~k(xk−x~k|k−1)T]−E[(xk−x~k|k−1)z~kTKT](12)

To obtain the last two terms of Eq. (12), substituting Eq. (11) into e~k|k−1=xk−x~k|k−1, we can obtain

e~k|k−1=xk−x~k|k−1=Axk−1+wk−1−Ax~k−1=A(xk−x~k−1|k−2)−AKz~k−1+wk−1=Ak(x0−x^0|−1)+∑i=1kAi−1wk−i−∑i=1kAiKz~k−i(13)

Introducing the a priori error e^k|k−1 between the xk and the a priori state estimate x^k|k−1, one has

e^k|k−1=xk−x^k|k−1=Axk−1+wk−1−Ax^k−1=Axk−1+wk−1−A(x^k−1|k−2+Kzk−1)=A(I−KC)(xk−1−x^k−1|k−2)+wk−1−AKvk−1(14)

Substituting Eqs. (3) and (14) into Eq. (6) for expansion and iteration, we can get

z~k=Tkzk+bk=Tk(Cxk+vk−Cx^k|k−1)+bk=TkC(A(I−KC)(xk−1−x^k−1|k−2)+wk−1−AKvk−1)+Tkvk+bk=TkC(A(I−KC))k(x0−x^0|−1)+∑i=1kTkC(A(I−KC))i−1wk−i−∑i=1kTkC(A(I−KC))i−1AKvk−i+Tkvk+bk(15)

It is known that E[z~kz~lT]=0 for all k≠l, so the last term of Eq. (13) and z~k are independent of each other. Since x0, wk, vk and bk are mutually independent, the last three terms of Eq. (15) and the first two terms of Eq. (13) are also independent of each other.

Based on the above analysis, the third term of Eq. (12) is obtained

E[Kz~k(xk−x~k|k−1)T]=E[K(TkC(A(I−KC))k(x0−x^0|−1)+∑i=1kTkC(A(I−KC))i−1wk−i)×(Ak(x0−x^0|−1)+∑i=1kAi−1wk−i)T]=KTkC((A(I−KC))k×E[(x0−x^0|−1)(x0−x^0|−1)T](Ak)T+∑i=1k(A(I−KC))i−1E[wk−iwk−iT](Ai−1)T)=KTkC((A(I−KC))kP¯(Ak)T+∑i=1k(A(I−KC))i−1Q(Ai−1)T=KTkCP¯(16)

Similarly, the fourth term of Eq. (12) follows:

E[(xk−x~k|k−1)z~kTKT]=P¯CTTkTKT(17)

Therefore, the error covariance can be expressed as follows:

P~k=AP~k−1AT+Q+K(Tk𝒫TkT+ℬ)KT−KTkCP¯−P¯CTTkTKT(18)

3.3 Computation of the Optimal Attack Strategy

When Tk𝒫TkT+ℬ≠𝒫, to achieve optimal impact, attacker aims to maximize P~k, as defined in Eq. (18), under linear deception attack. Specifically, the objective is to maximize tr(P~k).

Attacker predefines the random variable bk to follow a Gaussian distribution characterized by zero mean and covariance ℬ. By selecting a minor deviation from the innovation distribution, the attack matrix Tk can be determined under the widening constraint by formulating the objective function presented in Eq. (19).

maxTk∈Rm×mtr(P~k)s.t.||Tk𝒫TkT+ℬ−𝒫||F=ε(19)

where ε represents the deviation from the distribution of the innovation chosen by the attacker and given by Eq. (9).

Further analysis of Eqs. (18) and (19), it can be seen that maximizing the trace of the error covariance matrix in Eq. (18) is mathematically equivalent to optimizing the objective function tr(K(Tk𝒫TkT+ℬ)KT−KTkCP¯−P¯CTTkTKT). As a result, the problem of solving the attack strategy under the widening constraint shown in Eq. (19) can be transformed into an optimization problem as follows:

maxTk∈Rm×mtr(K(Tk𝒫TkT+ℬ)KT−KTkCP¯−P¯CTTkTKT)s.t.||Tk𝒫TkT+ℬ−𝒫||F=ε(20)

The attacker through several means, such as insider threats or the leakage of system parameters by staff can obtain system matrices A and C. The noise covariances Q and R can be estimated through statistically analyzing the measurement sequences collected during periods of normal system operation. With knowledge of these parameters, the attacker is able to compute the steady-state covariance matrix P¯ by solving the associated Riccati equation. Additionally, the attacker can derive the innovation sequence, which is modeled as a Gaussian distribution with zero mean and covariance 𝒫. In practical engineering applications, when dimensions of attack matrix Tk∈Rm×n are moderate, obtaining a closed-form solution for the optimization problem can be computationally challenging. Here a gradient-based numerical optimization approach is employed to approximate the optimal solution of the attack matrix.

To facilitate optimization, we present a Lagrangian formulation

ℒ(Tk,λ)=tr(KMK⊤−KTkCP¯−P¯C⊤Tk⊤K⊤)+λ(‖M−𝒫‖F2−ε2)(21)

where M=Tk𝒫Tk⊤+ℬ and E=M−𝒫. The Eq. (21) becomes

ℒ(Tk,λ)=tr(KTkPTk⊤K⊤)−2tr(KTkCP¯)+λ⋅tr(E⊤E)+tr(KℬK⊤)

The gradient is obtained by differentiating the objective function ℒ with respect to Tk

∂ℒ∂Tk=∂∂Tk(tr(KTk𝒫Tk⊤K⊤)−tr(KTkCP¯)−tr(P¯C⊤Tk⊤K⊤)+λ⋅tr(E⊤E))=2K⊤KTk𝒫−K⊤CP¯⊤−K⊤CP¯⊤+2λ(E)𝒫Tk=K⊤KTk𝒫−K⊤CP¯⊤+2λ(Tk𝒫Tk⊤+ℬ−𝒫)𝒫Tk

where E=Tk𝒫Tk⊤+ℬ−𝒫. A gradient descent scheme is then applied, updating Tk iteratively as follows:

Tk(i+1)=Tk(i)−η⋅∇Tkℒ(Tk(i),λ)

The step size η determines the magnitude of each update during the iterative optimization. The procedure is terminated when any of the following conditions is met: Frobenius norm of the gradient satisfies ‖∇Tkℒ‖F<δ; or the constraint ‖TkPTk⊤+ℬ−𝒫‖F≈ε is approximately fulfilled. This design of optimized attack strategies is of broad relevance in CPS security, particularly in domains such as electric vehicle infrastructure [30].

The proposed attack framework does not require simultaneous interference with all sensor channels. Instead, the attacker can selectively target a subset of sensor innovations by strategically combining attack resources. While the attack matrix Tk∈Rm×m is obtained though solving the optimization problem in Eq. (20), the problem formulation itself is under the attacker’s control. Structural constraints can be imposed on Tk to enable structured attacks.

The solution obtained is denoted as Tk∗. The attack algorithm at Algorithm 1.

After solving Eq. (20) to obtain Tk∗ and designing a specific attack strategy based on z~k=Tk∗zk+bk, the attacker can first compute the value of the χ2 detection function under attack using Eq. (5) to determine whether it falls within the normal fluctuation range before deciding to execute the attack. If an attack occurs and the χ2 detection function value remains below the threshold established by the system, the detector will interpret the system as operating normally.

The proposed attack strategy relaxes the traditional strict feasibility constraint by introducing a small deviation bounded by a tolerance parameter ε, as shown in Eq. (20). Traditional detection schemes based on residual monitoring are insufficient, because they assume strict adherence to the nominal distribution and lack mechanisms to detect small but systematic deviations. The attack discussed in this paper precisely exploits this statistical uncertainty. Effective defense would either require significantly tightening the detection thresholds, which would inevitably lead to a higher false alarm rate, or introducing complex multi-dimensional detection frameworks, which increase the risk of missed detections due to difficulties in parameter tuning.

Moreover, the attack formulation explicitly integrates a bounded relaxation of the detection feasibility constraint. As defined in Eq. (20), the objective is to maximize the degradation of remote estimator’s error covariance, subject to the relaxed constraint |Tk𝒫Tk⊤+ℬ−𝒫|F≤ε. The parameter ε explicitly controls the allowable statistical deviation, thus providing a trade-off mechanism: a larger ε permits more powerful attacks but increases the risk of detection, whereas a smaller ε ensures better stealthiness but limits the attack impact. This design enables the attacker to flexibly balance between effectiveness and stealth.

Real-world CPS face several practical constraints, such as communication noise, limited computational resources, and strict real-time requirements. However, the proposed methods remain practical. Matrix operations involved in Eqs. (8) and (21), such as trace evaluations and Frobenius norm calculations, scale quadratically with the number of sensors, which keeps the computational burden manageable for embedded processors typically used in smart grid substations.

4  Detection of Linear Attack

As previously discussed, a linear attack can evade detection by conventional detectors. To determine whether any sensors have been compromised, a Kalman filter can be employed to estimate the measurements of each individual sensor.

At each time k, note Δx^ij,k=x^i,k−x^j,k=(x^i,k−xk)−(x^j,k−xk) where x^i,k represents the a posteriori state estimate of the i-th sensor and x^j,k represents the a posteriori state estimate of the j-th sensor.

In the absence of attacks and under steady-state conditions, we are able to obtain that x^i,k−xk and x^j,k−xk are zero-mean Gaussian. Based on statistical knowledge, Δx^ij,k follows Gaussian distribution 𝒩(0,Pij,k) where the covariance term Pij,k can be obtained in advance through process simulation. However, in presence of an attack, the a posteriori compromised sensor will deviate from its nominal distribution, causing a statistically significant shift in the value of Δx^ij,k. This shift disrupts the expected Gaussian consistency between sensors, allowing anomalies to be detected through inter-sensor discrepancies.

Therefore, we consider the security issues in this case and propose a method to detect whether the system is under attack by comparing the change of a new detection indicator. Specifically, any pair of distinct sensors, denoted as the i-th and j-th sensors (i,j=1,2,…,N, i≠j), can be arbitrarily selected. The corresponding detection indicator is defined as follows:

Gij,k𝒥=∑h=k−𝒥+1k(Δx^ij,h)TPij,h−1(Δx^ij,h)≶H1H0⁡δij,k(22)

Let 𝒥 denote the detection window size, and δij,k denotes the threshold. For the two sensors, the normalized sum in Eq. (22) conforms to a χ2 distribution with n𝒥 degrees of freedom under normal conditions. However, if an attack occurs, the distribution characteristics are expected to deviate from the nominal pattern. Eq. (22) does not directly rely on the innovation sequence, it utilizes the statistical consistency among multiple sensors by comparing the posterior estimates x^i,k and x^j,k obtained from different sensors.

Combined with Eq. (22), we propose a dual-stage detection method to balance these trade-offs by adjusting the detection window length L, the effective rejection threshold M, and the single-sample detection threshold η maintain a low false positive rate while minimizing the probability of missed detections.

Firstly, according to Algorithm 2, we need to set the parameters maximum detection window length L and effective rejection threshold M. The choice of L should reflect the dynamic characteristics of the system. For systems with rapidly varying states, a smaller L enables prompt detection of anomalies to ensure timely detection of anomalies. But systems with higher noise levels require a larger L to effectively smooth out random fluctuations. The optimal value of L can be determined empirically through simulation under the assumed attack model. The parameter M controls the rejection threshold, a lower value (e.g., M = [L/2]) is suitable for systems requiring higher sensitivity. Conversely, for applications that prioritize reliability and low false alarm rates, a more conservative threshold (e.g., M=⌊2L/3⌋ to L−1) is recommended. When L and M are determined, the detection procedure incrementally increases the window length 𝒥 from 1 to L, allowing the detector to adaptively accumulate evidence over multiple time scales.

In contrast to fixed-window χ2 detection, Algorithm 2 dynamically adjusts the window length. Smaller windows provide rapid response to strong anomalies, while larger windows accumulate evidence to capture weak or stealthy deviations. To reduce the risk of misjudgment from a single detection window, a multi-window voting scheme is used. The system is considered under attack only if at least M out of L window-based tests report anomalies. The additional overhead compared to traditional χ2 detectors is minor, making the proposed method suitable for real-time implementation in resource-constrained environments. After obtaining preliminary results, conduct 100 cycles to confirm the final system status.

While the Algorithm 2 improves sensitivity to stealthy linear attacks by aggregating residual decisions over a window, certain real-world scenarios may still limit its effectiveness. If the injected attack signals are correlated, the residual inconsistencies could be masked, violating the statistical assumptions in Eq. (22). Additionally, if an attacker can adapt its strategy based on detection outcomes in real time, the fixed-length window aggregation might not react quickly enough to capture rapid changes. Furthermore, our approach assumes that measurement noise and packet losses across different sensors are independent. In practical systems where disturbances are correlated or bursty failures occur, the detection sensitivity could degrade. Although Algorithm 2 improves the detection rate, it inherently introduces a longer decision window to ensure robustness against random fluctuations. As trade-off between rapid detection and reliable decision-making is observed, and optimizing this trade-off remains a topic for future investigation.

5  Simulation Examples

This section presents simulation results that evaluate the effectiveness of the proposed linear deception attack and its associated detection approach.

5.1 Stable Process under Linear Attack

We consider a dynamic model characterized by the following parameters

A=[0.60.40000.500000.40.30000.2],

C1=[1000],

C2=[0100],

C3=[0010],

C4=[0001],

R1=0.1, R2=0.2, R3=0.3, R4=0.4 and x^0=[1111]T.

When the system operates in a safe and steady state, remote estimator employs Kalman filter to perform state estimation and derives the traces of the system state and its corresponding estimation error covariance, as illustrated in Figs. 2 and 3.

Figure 2: System status

Figure 3: Trace of estimation error covariance

During the interval [0,50], the remote estimator operates under the Kalman filtering framework and attains a steady-state condition. To initiate a cyber attack, the adversary injects falsified innovation signals, specifically z~k=−Izk and z~k=Tk∗zk, over the interval [83,93]. The corresponding simulation results, including the system state estimation and the trace of the error covariance matrix, are illustrated in Figs. 4 and 5.

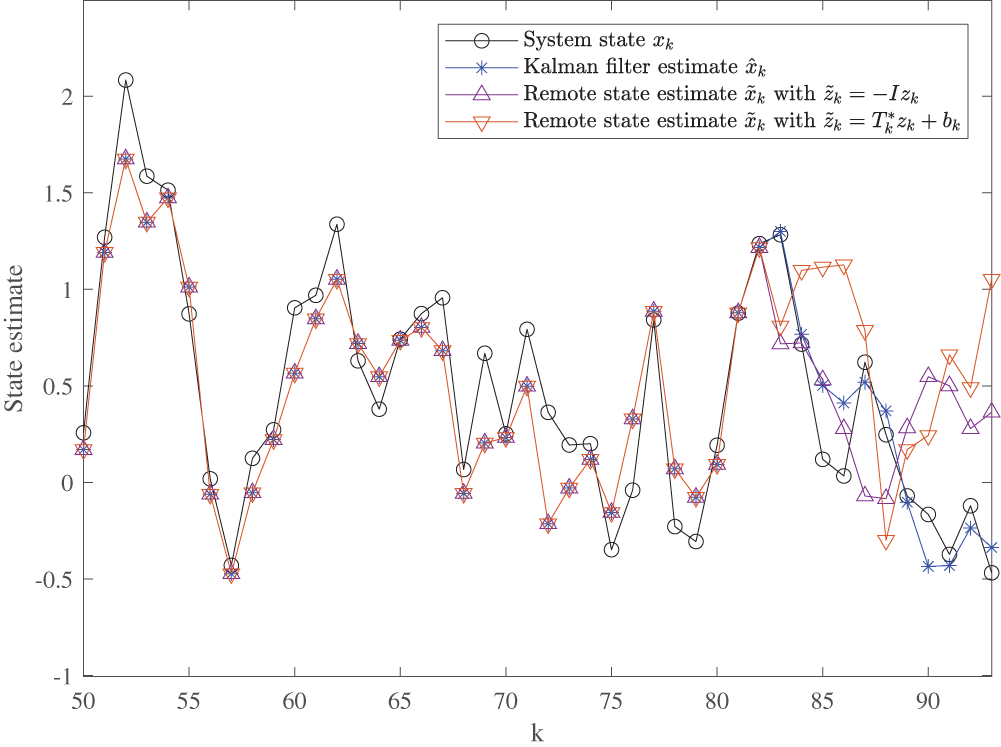
Figure 4: State estimate

Figure 5: The trace of remote estimation error covariance

As shown by the purple and red curves in Fig. 4, it is evident that a linear attack using z~k=−Izk or z~k=Tk∗zk results in the state estimate gradually deviating from both the true system state xk and the Kalman filter estimate x^k. The red and yellow curves in Fig. 5 indicate that under a linear attack, the tr(P~k) exceeds the value observed during normal system operation, and the error covariance will converge. The Figs. 4 and 5 demonstrate that both attack strategies effectively disrupt system performance. Additionally, Fig. 5 shows that tr(P~k) under the attack z~k=Tk∗zk is larger than that corresponding to attack with z~k=−Izk during the same time period. Although the error covariance increases under attack, it remains bounded, indicating that the system maintains practical stability without exhibiting divergent behavior.

Detection statistic values based on the Chi-square detector, calculated according to Eq. (5) under different system operating conditions, are shown in Fig. 6.

Figure 6: Detection function based on Chi-square detector

As shown in Fig. 6, during normal operation, the maximum detection statistic value reaches 18.8346. This value is selected as the detection threshold, i.e., η=18.8346. When an attacker implements the strategy z~k=Tk∗zk during the interval k=83 to k=93, the detection statistic remains below the threshold η. The detector erroneously classifies the system as operating normally and fails to trigger an alarm, allowing the remote estimator to continue updating the state estimates using the Kalman filter. This result demonstrates that, in a stable system, the proposed attack z~k=Tk∗zk can successfully evade the Chi-square detector at certain time steps, thereby verifying the stealthiness of the proposed attack strategy.

5.2 Unstable Process under Linear Attack

We consider a dynamic model characterized by the following parameters

A=[10.10001000010.10001],

C1=[1000],

C2=[0100],

C3=[0010],

C4=[0001],

R1=0.1,R2=0.2,R3=0.3,R4=0.4 and x^0=[1111]T.

During the interval [0,50],the remote estimator runs the Kalman filter and reaches a steady state. The attacker employs false data, specifically z~k=−Izk and z~k=Tk∗zk, during the period [83,93] to execute a cyber attack. The simulation results for the state estimate and the tr(P~k) are shown in Figs. 7 and 8.

Figure 7: State estimate

Figure 8: The trace of remote estimation error covariance

The purple and red curves in Fig. 7 indicate that a linear attack using either z~k=−Izk or z~k=Tk∗zk results in a gradual deviation of the state estimate from the true system state xk and the Kalman filter estimate x^k. The red and yellow curves in Fig. 8 demonstrate that, under unstable conditions, a linear attack results in a trace of the error covariance P~k that exceeds its value under normal system operation, resulting in exponential divergence of the error covariance. Both Figs. 7 and 8 illustrate that both attack strategies effectively disrupt system performance. Furthermore, Fig. 8 reveals that the trace of error covariance P~k for the attack using z~k=Tk∗zk exceeds that observed under the attack z~k=−Izk during the same time period. This observation indicates that, in certain instances, the proposed attack method in this study may lead to a more severe degradation in the performance of the unstable system.

5.3 Detection of Linear Attack

We consider a dynamic model characterized by the following parameters

A=[2101],C1=[1011],C2=[1101],

Q=[0.01000.01],R1=R2=[0.01000.01],

x^0=[11]T,L=6 and M=4.

During the time interval [0,200], the remote estimator operates under the Kalman filtering algorithm and gradually reaches a steady-state condition. It is assumed that the attacker employs the false data z~k to execute a linear attack on the first sensor at time steps k=38, k=39, and k=40. Subsequently, we utilize two different algorithms for detection, each executed 100 times. The first approach involves fixing 𝒥 in Eq. (22) to 1 and conducting direct detection. The second method employs Algorithm 2. A detection output of 0 indicates acceptance of H0, signifying that no attack has occurred. Conversely, a result of 1 indicates acceptance of H1, confirming that the system has been compromised. The simulation results for k=30 and k=40 are presented in Figs. 9 and 10.

Figure 9: Comparison of the two algorithms (k=30)

Figure 10: Comparison of the two algorithms (k=40)

It can be known from the setting of the simulation parameters that when k=30, the system is not actually attacked. From Fig. 9, it can be found that in the 100 tests, the algorithm with 𝒥=1 considers the number of times that the system is attacked at the current moment is 1. Algorithm 2 considers the number of times to be 2. Both are within acceptable limits. This figure also illustrates the feasibility of Table 2 when the system is not attacked. Fig. 10 indicates that when the system is attacked at time 40, Algorithm 2 detects that the system is attacked significantly more times than the algorithm that only uses 𝒥=1 for detection. This proves that Algorithm 2 is more efficient in detection and reduce the missed detection rate when the system is under attack.

6  Conclusion

To address linear attacks, this study proposes a novel attack parameter design method with a broadened traditional feasibility constraint. Simulation comparisons demonstrate that at certain time steps, the attack strategy can successfully evade the χ2 detector, leading to greater deviation in the state estimate of the remote estimator, which consequently results in more significant damage to system performance. The generalized feasibility constraint presented in this paper offers a more realistic foundation for modeling stealthy attacks within real-world detection systems. Furthermore, we propose a new detection algorithm. Analysis through simulation and comparison indicates that the index of the detection method increases only when the system is under attack, thereby validating the effectiveness of this algorithm in detecting the presence of an attack. Future work will focus on enhancing detection efficiency. Additionally, we will explore the system’s performance under various attack strategies and investigate new detection schemes to effectively mitigate these threats.

Acknowledgement: We are grateful to our families and friends for their unwavering understanding and encouragement.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors contributed to the study as follows: study conception and design: Fangju Zhou, Zhu Ren; simulations: Fangju Zhou, Na Ye, Jing Huang; analysis and interpretation of results: Fangju Zhou, Hanbo Zhang, Na Ye, Jing Huang, Zhu Ren; draft manuscript preparation: Fangju Zhou, Hanbo Zhang, Zhu Ren. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Humayed A, Lin JQ, Li FJ, Luo B. Cyber-physical systems security—a survey. IEEE Internet Things J. 2017 Dec;4(6):1802–31. doi:10.1109/JIOT.2017.2703172. [Google Scholar] [CrossRef]

2. Fawzi H, Tabuada P, Diggavi S. Secure estimation and control for cyber-physical systems under adversarial attacks. IEEE Trans Automat Contr. 2014 Jun;59(6):1454–67. doi:10.1109/tac.2014.2303233. [Google Scholar] [CrossRef]

3. Zhang XM, Han QL, Ge XH, Ding L. Resilient control design based on a sampled-data model for a class of networked control systems under denial-of-service attacks. IEEE Trans Cybern. 2020 Aug;50(8):3616–26. doi:10.1109/tcyb.2019.2956137. [Google Scholar] [PubMed] [CrossRef]

4. Gu CY, Zhu JW, Zhang WA, Yu L. Sensor attack detection for cyber-physical systems based on frequency domain partition. IET Control Theory Appl. 2020 Jul;14(11):1452–66. doi:10.1049/iet-cta.2019.1140. [Google Scholar] [CrossRef]

5. Ayas MŞ. A brief review on attack design and detection strategies for networked cyber-physical systems. Turkish J Eng. 2021;5(1):1–7. [Google Scholar]

6. Hasan MK, Habib AKMA, Shukur Z, Ibrahim F, Islam S, Razzaque MA. Review on cyber-physical and cyber-security system in smart grid: standards, protocols, constraints, and recommendations. J Netw Comput Appl. 2023;209(23):103540. doi:10.1016/j.jnca.2022.103540. [Google Scholar] [CrossRef]

7. Teixeira A, Pérez D, Sandberg H, Johansson KH, Acm. Attack models and scenarios for networked control systems. In: 1st ACM International Conference on High Confidence Networked Systems; 2012 Apr 17–19; Beijing, China. p. 55–64. [Google Scholar]

8. Ye D, Zhang TY. Summation detector for false data-injection attack in cyber-physical systems. IEEE Trans Cybern. 2020 Jun;50(6):2338–45. doi:10.1109/tcyb.2019.2915124. [Google Scholar] [PubMed] [CrossRef]

9. Wei JL, Jia RZ, Song Y, Jing FW, Guo J. Binary observation-based FIR system identification under sequence denial of service attacks. Int J Robust Nonlinear Control. 2024 Mar;34(5):3442–63. doi:10.1002/rnc.7146. [Google Scholar] [CrossRef]

10. Zhao N, Shi P, Xing W, Lim CP. Event-triggered control for networked systems under denial of service attacks and applications. IEEE Trans Circuits Syst I: Regular Papers. 2022 Feb;69(2):811–20. doi:10.1109/tcsi.2021.3116278. [Google Scholar] [CrossRef]

11. Mo YL, Sinopoli B. Secure control against replay attacks. In: Proceeding of the 47th Annual Allerton Conference on Communication, Control, and Computing; 2009 Sep; Monticello, IL, USA. [Google Scholar]

12. Li TX, Wang ZD, Zou L, Chen B, Yu L. A dynamic encryption-decryption scheme for replay attack detection in cyber-physical systems. Automatica. 2023;151(1):110926. doi:10.1016/j.automatica.2023.110926. [Google Scholar] [CrossRef]

13. Naha A, Teixeira A, Ahlén A, Dey S. Sequential detection of replay attacks. IEEE Trans Automat Contr. 2023 Mar;68(3):1941–8. doi:10.1109/tac.2022.3174004. [Google Scholar] [CrossRef]

14. Ni YQ, Guo ZY, Mo YL, Shi L. On the performance analysis of reset attack in cyber-physical systems. IEEE Trans Automat Contr. 2020 Jan;65(1):419–25. doi:10.1109/tac.2019.2914655. [Google Scholar] [CrossRef]

15. Ding KM, Ren XQ, Leong AS, Quevedo DE, Shi L. Remote state estimation in the presence of an active eavesdropper. IEEE Trans Automat Contr. 2021 Jan;66(1):229–44. doi:10.1109/tac.2020.2980730. [Google Scholar] [CrossRef]

16. Lu AY, Yang GH. False data injection attacks against state estimation without knowledge of estimators. IEEE Trans Automat Contr. 2022 Sep;67(9):4529–40. doi:10.1109/tac.2022.3161259. [Google Scholar] [CrossRef]

17. Xu QL, Xiong JL. Scheduler-pointed false data injection attack for event-based remote state estimation. Automatica. 2024;162(10):111523. doi:10.1016/j.automatica.2024.111523. [Google Scholar] [CrossRef]

18. Li L, Yang H, Xia YQ, Yang HJ. State estimation for linear systems with unknown input and random false data injection attack. IET Control Theory Appl. 2019 Apr;13(6):823–31. doi:10.1049/iet-cta.2018.5954. [Google Scholar] [CrossRef]

19. Alzubi OA. A deep learning-based frechet and dirichlet model for intrusion detection in IWSN. J Intell Fuzzy Syst. 2022;42(2):873–83. doi:10.3233/JIFS-189756. [Google Scholar] [CrossRef]

20. Alzubi OA, Qiqieh I, Alzubi JA. Fusion of deep learning based cyberattack detection and classification model for intelligent systems. Cluster Comput. 2023;26(2):1363–74. doi:10.1007/s10586-022-03686-0. [Google Scholar] [CrossRef]

21. Guo Z, Shi D, Johansson KH, Shi L. Worst-case stealthy innovation-based linear attack on remote state estimation. Automatica. 2018 Mar;89(1):117–24. doi:10.1016/j.automatica.2017.11.018. [Google Scholar] [CrossRef]

22. Liu H, Ni Y, Xie L, Johansson KH. How vulnerable is innovation-based remote state estimation: fundamental limits under linear attacks. Automatica. 2022 Feb;136(12):110079. doi:10.1016/j.automatica.2021.110079. [Google Scholar] [CrossRef]

23. Li Y, Shi L, Chen T. Detection against linear deception attacks on multi-sensor remote state estimation. IEEE Trans Control Netw Syst. Jan 2017;5(3):846–56. doi:10.1109/TCNS.2017.2648508. [Google Scholar] [CrossRef]

24. Li Y, Yang Y, Zhao Z, Zhou J, Quevedo DE. Deception attacks on remote estimation with disclosure and disruption resources. IEEE Trans Automat Contr. 2023 Jul;68(7):4096–112. doi:10.1109/tac.2022.3202981. [Google Scholar] [CrossRef]

25. Gupta A, Sikdar A, Chattopadhyay A, IEEE. Quickest detection of false data injection attack in remote state estimation. In: IEEE International Symposium on Information Theory (ISIT); 2021 Jul 12–20; Melbourne, VIC, Australia. p. 3068–73. [Google Scholar]

26. Li YZ, Yang YK, Chai TY, Chen TW. Stochastic detection against deception attacks in CPS: performance evaluation and game-theoretic analysis. Automatica. 2022 Oct;144(1):110461. doi:10.1016/j.automatica.2022.110461. [Google Scholar] [CrossRef]

27. Guo ZY, Shi DW, Johansson KH, Shi L. Optimal linear cyber-attack on remote state estimation. IEEE Trans Control Netw Syst. 2017 Mar;4(1):4–13. doi:10.1109/tcns.2016.2570003. [Google Scholar] [CrossRef]

28. Guo ZY, Shi DW, Quevedo DE, Shi L. Secure state estimation against integrity attacks: a gaussian mixture model approach. IEEE Trans Signal Process. 2019 Jan;67(1):194–207. doi:10.1109/tsp.2018.2879037. [Google Scholar] [CrossRef]

29. Liu HX, Ni YQ, Xie LH, Johansson KH. An optimal linear attack strategy on remote state estimation. IFAC-PapersOnLine. 2020;53(2):3527–32. doi:10.1016/j.ifacol.2020.12.1719. [Google Scholar] [CrossRef]

30. Pandey R, Koranga M, Thakur SN, Khan H, Singh SK, Ravikumar RN. Securing vehicle-to-grid communications: a cyber-physical approach. In: Optimized energy management strategies for electric vehicles. Hershey, PA, USA: IGI Global Scientific Publishing; 2025. p. 301–18. [Google Scholar]