Slice-Based 6G Network with Enhanced Manta Ray Deep Reinforcement Learning-Driven Proactive and Robust Resource Management

1  Introduction

5G is expected to facilitate a wide range of applications and use cases that fall under the categories of massive machine-type communications (mMTC), ultra-reliable low-latency communications (uRLLC), and improved mobile broadband (eMBB). Autonomous driving, smart homing, intelligent transportation, etc., are examples of use cases [1], and the main technological enablers are cloud computing, mobile edge computing (MEC), network function virtualization (NFV) [2], and software-defined networking (SDN) [3]. Different radio access network (RAN) topologies, functionalities, and quality of service (QoS) requirements are present in the use cases [4]. Consequently, new methods for network design, building, and maintenance will be required to simplify network operations. One possible way to deal with these issues is by network slicing [5]. Within the same physical network infrastructure, it changes the network build philosophy of earlier generations’ monolithic design to create and operate logical/virtual networks that are customized to meet the unique requirements of certain clients and services. In radio access systems, slice traffic and inter-cell interference become more complicated and dynamic when new networks, including micro cells, are deployed. The creation, modification, and deletion of slices as needed will provide flexible network management and operation [6]. To ensure service level agreements (SLAs), the slices are segregated and can be allocated to a use case with particular QoS requirements [7]. To avoid over-provisioning, the network resources can be distributed to each slice according to specific needs and on-demand [8]. Model-based techniques such as convex optimization and linear programming are weakening when resource management becomes more sophisticated [9]. Reinforcement learning (RL) has been used to handle resource and application management services associated with network slicing in 5G networks [10]. RL is a machine learning (ML) technique that allows a bot to choose the optimal course of action by observing its performance in various scenarios. RL with advanced learning capabilities, such as deep Q-networks, has been used more and more in the management of complex networks [11]. Govern networked resources like storage, computing, and network throughput as slices or discrete units, the majority of these initiatives have focused on implementing adaptive resource allocation.

However, the end-to-end (ETE) resilience and proactive resource management in such slice enable 5G/6G networks is not taken into account by the majority of the effort [12]. Besides, the dynamic nature of network conditions and user demands pose major challenges to maintaining optimal performance and ensuring service continuity. Thereby, innovative methods are needed to dynamically adapt resource allocation for varying traffic loads and potential network disruptions. To overcome this complexity, the incorporation of deep RL (DRL) [13] and convergence of metaheuristic optimization algorithm provides a promising way. Renowned for the capability to explore vast solution space as well as determine near-optimal solutions, the metaheuristic algorithms can be employed to leverage the DRL agents. Meanwhile, the DRL permits the advancement of intelligent resource management tactics that can adapt to real-time network conditions with its ability to learn policies through interaction with the environment. This combination offers a supportive framework for accomplishing ETE resilient and proactive resource management in slice-enable 5G/6G networks. Through the incorporation of the metaheuristic’s global search ability with adaptive learning of DRL, it is possible to introduce a system that not only optimizes current resource allocation but also addresses potential future disruptions. The major contributions of the proposed method are provided below as follows:

To propose an enhanced metaheuristic-DRL model, which offers proactiveness and resilience properties for improving the efficiency of resource allocation in slice-enabled 6G networks. A metaheuristic, improved manta ray foraging optimization algorithm (ImpMRFO) algorithm is incorporated into the proposed model instead of solely relying on DRL to enhance the exploration and exploitation balance in RL training. This improves the learning process and avoids suboptimal convergence. A Chebyshev chaotic map and levy flight are incorporated into a standard manta ray foraging optimization (MRFO) algorithm to address local optima issues and improve convergence performance. To compare the performance of the proposed method with prevailing models for demonstrating the superiority in resource usage, minimization of resilience time and improved performance.

The proposed work’s remaining portions will be organized as follows: The review of relevant literature is provided in Section 2. The proposed design for resource management in slice-enabled 6G network is stated in Section 3. In Section 4, the proposed technique is examined and compared with existing methods Table 1. The conclusion and future scope of the proposed model is exposed in Section 5.

2  Related Works

Khan et al. [14] emphasise security and reliability, this article delivers a comprehensive assessment of resource allocation in integrated computer and networking systems. Based on resource categories, technologies, situations, and solution features, the research groups the body of current work. Comparative study reveals how few works either individually or in groups—address security and reliability. The study emphasizes the need to concurrently evaluate these factors to enable important applications. Results expose flaws in present methods and imply the requirement of intelligent, flexible, and strong allocation mechanisms to improve the dependability of next computing and networking systems. Wang et al. proposed [15] dependable, reasonably priced network slicing in IoT systems, combined with VNF partition and hybrid backup strategy. The approach divides VNFs into smaller pieces to improve dependability with fewer resources and employs a hybrid backup plan mixing local and remote backups. We frame the orchestration, backup, and mapping issue as a dynamic MILP and model as an MDP. Solving the MDP using a multiagent deep reinforcement learning method with action space reduction reduces conventional approaches and simulation findings indicate better latency, dependability and network cost Table 2.

Ghafouri et al. [21] presented a network slicing and resource management strategy using multi-level deep RL for O-RAN networks. To system capacity while ensuring the specified Quality of Service (QoS), this RL-based scheme of O-RAN’s openness to offer two levels of centralized multi-agent decision-making and decentralized single-agent execution for selecting appropriate service types. The simulation results showed this user-experienced data rate, latency, and peak data rate. However, the complexity of this model was higher. Mhatre et al. [22] recommended an Explainable Artificial Intelligence (XAI) framework intended for ORAN architectures to simplify the process of deep RL (DRL). This system tackled the crucial problem of comprehending and optimizing the control of DRL agents for managing and allocating resources by providing network-oriented explanations. The results demonstrated that a DRL agent’s capacity to make well-informed multimodal decisions involving several control parameters significantly enhanced Key Performance Indicator (KPI)-based rewards. However, the model would require more actionable and interpretable resource management actions. Zangooei et al. [23] suggested a flexible RAN Slicing with constrained cooperative multi-agent RL in Open RAN. To train this model, the advantage of a new constrained RL technique that specifically took the SLA limitations was considered to lessen the SLA violation ratio. This method could be implemented in future mobile networks because it was compatible with the Open RAN architecture. For a variable number of slices, it utilized 19% less resources and had 8% fewer SLA violations. However, it was difficult to design reward functions as well as constraint satisfaction mechanisms. The optimization of resource management was examined by Ros et al. [24] using Markow decision problem (MDP)-assisted deep q-network-based priority/demanding resource management, or DQG-PD. The DQG-PD algorithm was used to address energy efficiency and resource management in IIoT devices. The usage of deep Q-network (DQN) simultaneously optimized energy computation and resource consumption for every service request. To effectively adjust to a changing IIoT environment, DQN was separated into target and online networks. Lastly, the experiments demonstrated better performance in terms of average service completion ratio, reliability energy, resources, and cost. The DQG-PD algorithm could face issues in adapting quickly to a dynamic IIoT environment. In multi-tier edge slicing networks, Nouruzi et al. [25] recommended a unique cooperative method resilient to imprecise channel state information (CSI) brought on by the mobility of user equipment (UEs). Here, a smart joint dynamic pricing and resources sharing (SJDPRS) system was employed owing to the network’s limited resources, the UEs’ mobility, and the workload’s dynamic requirement. The multi-objective optimization method was used to design an optimization problem. Further, a deep reinforcement learning (DRL) technique was built depending on the reward function to address the issue. According to the simulation results, the overall profit was improved as opposed to the non-cooperative situation. However, the complex computation involved in this method would tend to be resource-intensive and time-consuming.

Problem statement: In recent days, several existing methods have been introduced for effective resource management in slice-enabled 6G networks. However, the existing models are hindered by various challenges such as dynamic adaptations, scalability issues and complexity owing to rapidly varying network conditions as well as the diversity of user needs. Moreover, they fail to guarantee optimal performance as well as resource allocation, resulting in inefficient network utilization and operational costs. More significantly, the existing models can not proactively manage resources as well as speedily recover from network failures, tending to suboptimal QoS and resilience. The proposed method employs an enhanced metaheuristic DRL model to resolve the existing issues. The proposed model can adapt to dynamic conditions, effectively allocate resources and improve network performance. Besides, the proposed model minimizes resilience time, enhances PSSPr, and guarantees robust QoS. By this means, the proposed method overcomes the issues posed by prevailing techniques and meets the advanced requirements of slice-enabled 6G networks. Deep reinforcement learning and metaheuristic optimization enhance algorithmic complexity, making it computationally costly. Scalability is difficult when managing several slices in big, diverse 6G networks.

3  Proposed Methodology

This section introduces an advanced packet-based ETE resource management system with network slicing support. The model utilizes an enhanced DRL (EDRL) model for allocation of optimal resources in slice-enabled 6G networks. Initially, the system model is discussed, then the proposed EDRL is presented with the optimization strategy.

3.1 System Model

3.1.1 Network and Infrastructure

In the proposed work, an ETE network design that includes transport, RAN, and core domains is discussed. Here, an SDN controller is used to manage the network. Furthermore, it is presumed that the design of this network is slice-enabled. Thereby, represents the set of slices having slices. Represents the collection of users with users. Each time slot is designated to model and formulate the system model according to the time. Let represent a user-slice indicator. The user requests a slice at the time slot. Multiple user slices are created when a user requests over one slice. Consequently, there are always more user slices in the network than the number of users. In this proposed work, “user” is used instead of “user-slice” for the sake of conciseness. Here, indicates the user’s arrival time. Every slice has a unique virtual network function (VNF) and service function chain (SFC), with the set of VNFs for slice having functions denoted by Here, is used to the VNF in SFC s to indicate each function’s order in SFC. For instance, network address translator (NAT) VNFs are always executed before firewalls in a particular service, such as web browsing. Let resembles the VNF of SFC of slice in CPU cycle per bits of packet/flow, which represents the processing requirement for function. The maximum packet size and tolerable delay for each slice are denoted by in [Mbps] and in [ms]. Moreover, the mean in packets per second indicates that the number of incoming packets for each slice follows a Poisson process. Accordingly, gives the probability of creating packets by slice. Furthermore, and signifies the size coefficients for a packet of slices in the transport, RAN, and core domains. RAN domain: Here, represents the set of BSs included in the RAN domain, and indicates the sub-carrier sets having sub-carriers. An SDN controller acts as the agent, coordinating and managing the network’s components, as seen in Fig. 1.

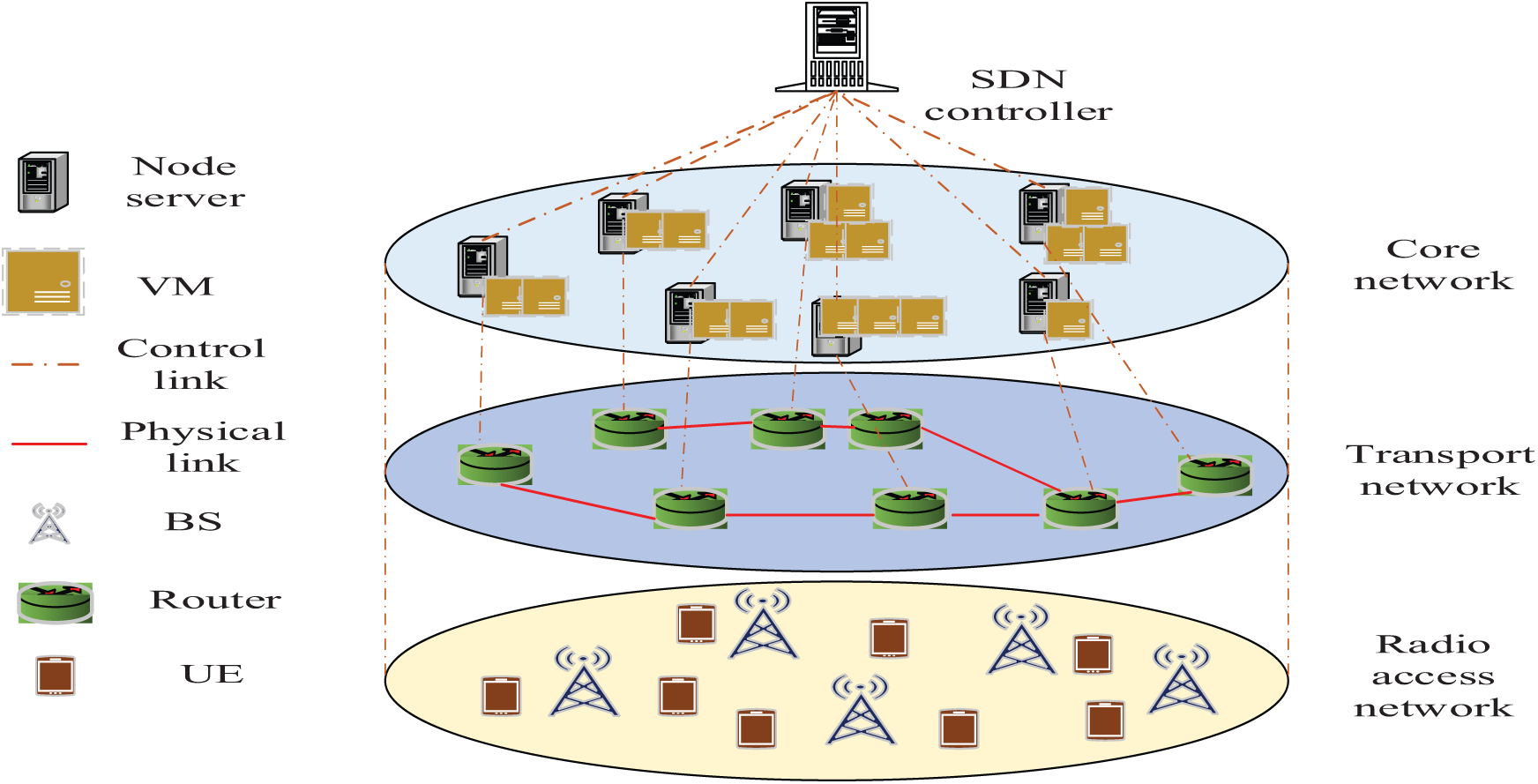
Figure 1: Network with multiple domains based on the suggested system model

RAN Optimization qu,vc,l influence v slot u BS c on the sub-carrier l ϑu,vc,l assigned v and l BS c. In each BS, each sub-carrier can be assigned to a single user using the orthogonal frequency multiple access (OFDMA) approach. Furthermore, it is guaranteed that the total power allotted to the users is less than the maximum preset transmit power of each c, Qmaxc. Let, iu,vc,l the v’s channel gain on sub-carrier k in BS b through u. The uncertainty in the channel gain exists because of factors including hardware limitations, estimate errors, mobility, and feedback channel delay. The channel gain uncertainty model is expressed as follows: i~u,vc,l=iu,vc,l+∈CSI, i~u,vc,l, ∈CSI estimated channel gain and estimation iu,vc,l. For v data rate in bps/Hz is given s~vc,l. The interference between the BSs, the probabilistic constraint is considered as follows:

Pr(J~vc,l,u≤Jth)∈ϕ(1)

where, J~vc,l,u is the intrusion v, ϕ route. In the meantime, Jth is the threshold for the other BSs’ interference v.

3.1.2 Core and Transport Domains

M∗, M^ the set of links in the core and transport networks, P∗ besides P^ nodes in the core and transport (switch/router) networks. To model the transport and core networks, two connected graphs are considered J^(P^,M^) and J∗(P∗,M∗). K^ besides K the adjacency matrices of the network K^=[kp^,p^′]P^×P^, K=[kp^,p^′]P×P′. For the transport network k^p^,p^′=1, if p^, p^′ connected by a link, kp^,p^′=0 fundamental kp^,p^′=1, p besides p′ connected kp^,p^′=0 otherwise. The Abilene from a popular data set SNDlib used to have a unique graph and simulation repeatability for a core and transport network/graph topology with 15 links and 12 nodes. In the core network ep,p′u the link available capacity between s p besides p′, u, zp,p′,vu the bandwidth allotted to this link. It is ensured that the total bandwidth allotted p, p′ than ep,p′u provided by the following ∑v∈U∗zp,p′,vu≥ep,p′u,∀p,p′∈N∗,∀u. e^p,p′u capacity for the p, p^′,(p^,p^′)P^, u system. The zp,p′,vu bandwidth allotted to v, p, p^′ time slot u transport network link. The subsequent ∑v∈U∗z^p,p′,vu≤e^p,p^′u,∀p^,p^′∈N^,∀u is stated for the link between p, p′, p^, p^′ the limitations in the resources available.

Core and transport optimization variables:

The τu,vhm,n′∈{0,1} core hn.,n′ user data n, n′, u. Furthermore, Vm∗n={1m,…,vmn,…,Vmn} denotes the VM sets hosted n∈P∗ through Vmn VMs in the core network. Assume that the ot on virtual machine (VM) vm for v on n, u as ψu,vvm,n,ot. avm,nu in Mbps represents the available processing capacity of VM vm hosted on n, u. Furthermore, in the avm,nu buffer capacity available for p^∈P^ through u. To γvm,n,vu, γ^p^′,vu computational ability and reserved buffer capacity for v, p^, VM vm node p. The following constraints are taken into account owing to the resource boundaries of routers and VMs,

∑v∈U∗γvm,n,vu≤avm,nu,∀u,∑v∈U∗γ^p^′,vu≤a^p^′,∀u.(2)

3.1.3 Failure Model

Here, a failure can be interpreted differently in different network domains. A failure in the RAN domain is an outage caused by CSI uncertainty. It designates router or link congestion in the transport network. It mentions overloaded VMs in the core domain. The product of success probabilities in each area is the probability of successful slice provisioning (PSSPr) because these faults are statistically independent and unique. PSSPr has a multiplying formula since ETE slice provisioning entails successive operations. Also, Pr(m)v the slice probability v and m packs. The outage probability of RAN is expressed as:

℘M−1(μran)≤[ϑu,vc,llog⁡(1+qu,vc,l℘i~vc,l,u−1(1−μranL)∑t∈T∗χv,tubwtrt,ran)](3)

The ϑu,vc,l binary variable (0 or 1) is whether l BS c to v slot u. ρ2 clatter qu,vc,l allocated transmission power to v, l period u. χv,tu demonstrating v, t, u, rt,ran coefficient that normalizes the bandwidth based on RAN’s nature t and bw the size coefficient that normalizes the [.] ceiling function, which rounds the value up to the nearest integer. In the core domain PSSPr can be expressed as,

℘M−1(μcore)≤minn,vm(γvm,n′,vu)∑t∈T∗χv,tubwtrt,core(4)

where, maxn,vm represents the maximum values over virtual machines vm physical e n, γvm,n′,vu the capacity of vm, n to user v, u, as well rt,core coefficient associated the core network characteristics for service t. Further, in the transport network, PSSPr m besides v is defined. The following are the closed forms of an uncongested connection for the user v across the router p^, the link between nodes p^ besides p^′:

℘M−1(μrouter)≤minp^γ^p^,v,p^∈P^(5)

℘M−1(μlink)≤minp^,p^′(z^p^,p^′,vu)∑t∈T∗χv,tubwtrt,tran(6)

where, minγ^p^ the minimum values over all routers in the routers set, minp^,p^′ the minimum values over the node (p^,p^′) and z^p^,p^′,vu bandwidth. Additionally, the constraint |K∗||V∗|ϑu,vc,lqu,vc,l℘iu,vc,l−1((1−ε)1|K∗||V∗|≤Jth which Jth is the inference threshold imposes the conditions on the transmitted power associated the outage probability thresholds.

3.1.4 Delay Model

Two forms of delays namely the processing delay and transmission delay are considered in the proposed work. The model computes the processing delay depending on the VMs engaged in processing network functions, in which the overall processing delay of the summation of the delay over all relevant nodes and VMs. The transmission delay is computed by the data rate in several network domains, comprising the RAN domain, core domain, and transport domain. Besides, the model examines the total transmission delay as an accumulation of delays experienced in these domains conferring to the packet transmission of users and their respective service allocated to them. Accordingly, the total delay experienced by a user is acquired by adding the processing and transmission delays and guaranteeing that the sum of delay does not exceed the permissible limits for every service slice to ensure the desired Quality of Service (QoS) standards. This comprehensive strategy enables efficient resource allocation and management in dynamic network conditions to support proactive network operations.

3.1.5 Time-Based Constraints on Evaluation

In this section, two new constraints are deliberated to assess the network’s performance and guarantee its resilience and proactiveness tendencies. The υ time duration after u the network’s performance. It is important to note that the following restriction is established to guarantee the network’s proactivity:

minu′(Γvu′(m))≥μPSSPrmin,∀u′>u,u′−u≤υ(7)

It indicates the next u′ minimum PSSPr v, m must surpass a minimal threshold μPSSPrmin. In addition, the following restriction defines the network resilience,

|argminu′(Γvu′(m))−u~|≤Ures,u′<u~,u′′−u~<υ(8)

where, u~ indicates the initial time that Γvu(m) is equivalent μPSSPravr where u~=arg⁡maxw′(Γvw′(m)|Γvw′(m)=μPSSPravr) as well μPSSPravr excepted threshold on average of PSSPr, Ures is the longest amount of time that the network may return to its prior performance.

3.1.6 Cost Model

In slice-enabled networks, the cost model involves the evaluation of the economic impact of using network resources, with emphasis on two main cost categories migration cost and utilization cost. Utilization cost encompasses the cost incurred during the deployment of network resources or elements, which may fluctuate depending on parameters transmission speeds for various links and power usage for servers. Every resource category, whether a link, a VM, or a sub-carrier in the RAN has a defined unit cost related to its use. In contrast, the migration cost happens when there is a necessity to reassign resources to accommodate developing network conditions or demands, comprising costs associated scheduling, synchronization, and forwarding data associated with VMs. Through this cost, the model delivers efficiencies and trade-offs of resource management, permitting operators to optimize their allocated resources both in terms of performance and economic goals. Understanding facilitates decision-making intended to progress network performance when reducing operational costs.

3.1.7 Problem Formulation

The RR, route, and VM selection variables are the primary variables of the issue. Since the goal is to minimize the function that contains the imposed cost, the proposed method adds a novel objective function that is stated as follows,

minϑ,q,τ,ψ,γ,γ^,Z,Z^d^1∑t∈T∗v∈V∗Ωutil,v(u)+d^2∑t∈T∗v∈V∗Ωmigr,v(u),∀v∈V∗(9a)

S.T: Dtotal,v(u,m)χv,tu≤dt,∀t∈T∗,∀v∈V∗,∀u,(9b)

minu′(Γvu′(m))≥μPSSPrn,∀u′>u,u′−u≤υ(9c)

|argminu′(Γvu′(m))−u~|≤Ures,u′<u~,u′′−u~<υ(9d)

℘M−1(μlink)≤minp^,p^′(z^p^,p^′,vu)∑t∈T∗χv,tubwtrt,tran(9e)

℘M−1(μrouter)≤minp^γ^p^,v,p^∈P^(9f)

℘M−1(μcore)≤minn,vm(γvm,n′,vu)∑t∈T∗χv,tubwtrt,core(9g)

|K∗||V∗|ϑu,vc,lqu,vc,l℘iu,vc,l−1((1−ε)1|K∗||V∗|≤Jth(9h)

∑v∈U∗z^p,p′,vu≤e^p,p^′u(9i)

∑v∈U∗zp,p′,vu≥ep,p′u(9j)

℘M−1(μran)≤[ϑu,vc,llog⁡(1+qu,vc,l℘i~vc,l,u−1(1−μranL)∑t∈T∗χv,tubwtrt,ran)](9k)

∑v∈U∗γvm,n,vu≤avm,nu,∀u,(9l)

∑v∈U∗γ^p^′,vu≤a^p^′,∀u.(9m)

The coefficient factors for each component of the utilization function are denoted d^1 besides d^2. It is ensured that the overall imposed delay for every user in constraint (9b) must be less than the tolerable delay for every slice. The network’s proactivity property and capacity to maintain PSSPr above the minimal amount needed for the upcoming time slots are guaranteed by constraint (9c). Besides the network can reach the desired PSSPr in a constrained amount of time under constraint (9d). Constraint (9e) guarantees that the threshold μlink under consideration, the ratio of the minimum bandwidth allotted to v the transport network’s connections to the packet size must be larger than the inverse function of the cumulative distribution function (CDF) M. In the same way, constraint (9f) intends to router’s reserved the threshold μrouter bigger than the inverse of CDF M for user v. The μcore (9g) for the core network the ratio of minimum computing resources allotted to v the packet size must be more than the inverse of CDF M. Also, it is confirmed that the derived closed-form of (1) must be less Jth (9h). The bandwidth allotted to users across the transport and core networks’ links is kept below their capability by constraints (9i) and (9j). Eq. (9k) yields the non-outage RAN with μran the ratio of data rate should be bigger than the inverse of the CDF random variable M. Lastly, it is guaranteed that all computing resources are distributed and the user buffer is smaller than the capacity of VMs and buffers under limitations (9l) and (9m).

3.2 Enhanced Deep Reinforcement Learning (DRL) Based Approach

The optimization problem is classified as a MINLP problem, which is known to be computationally because it involves binary integer variables (ϑ and τ) for selecting path and allocating subcarrier, as well as continuous non-linear variables (q) for power allocation. Since joint subcarrier and power allocation issues have exponential complexity because of binary choice variables and non-linear couplings, their NP-hardness has been thoroughly established. Problem (9) inherits the NP-hardness of these scenarios as a special case since it generalizes them by including resource management and routing. Therefore, it is impossible to solve (9) exactly in polynomial time. Furthermore, the proposed method seeks to ensure the network’s proactivity and resilience for the upcoming time windows.

An online approach with proactiveness must be utilized. ML-based techniques perform well in resolving online issues and forecasting behaviour in the future using historical data. As a result, an enhanced DRL model is used in the network and problem. The online optimization problem is solved using an improved manta ray foraging optimization algorithm (ImpMRFO) while preserving its proactive and robust characteristics. The two-phase method assesses the efficacy of proactive and resilient properties across episodes and resolves the resource management optimization problem in each time slot. Main Environment and Agent: The proposed method examines an ETE network that consists of a core network with several servers, a transport network with bandwidth-constrained links, and a RAN with BSs comprising limited sub-carriers and power. Various slices are requested by various users. A deep neural network (DNN) is merged with RL to empower agents to learn optimal networking with the environment. The architecture of Enhanced DRL is provided in Fig. 2.

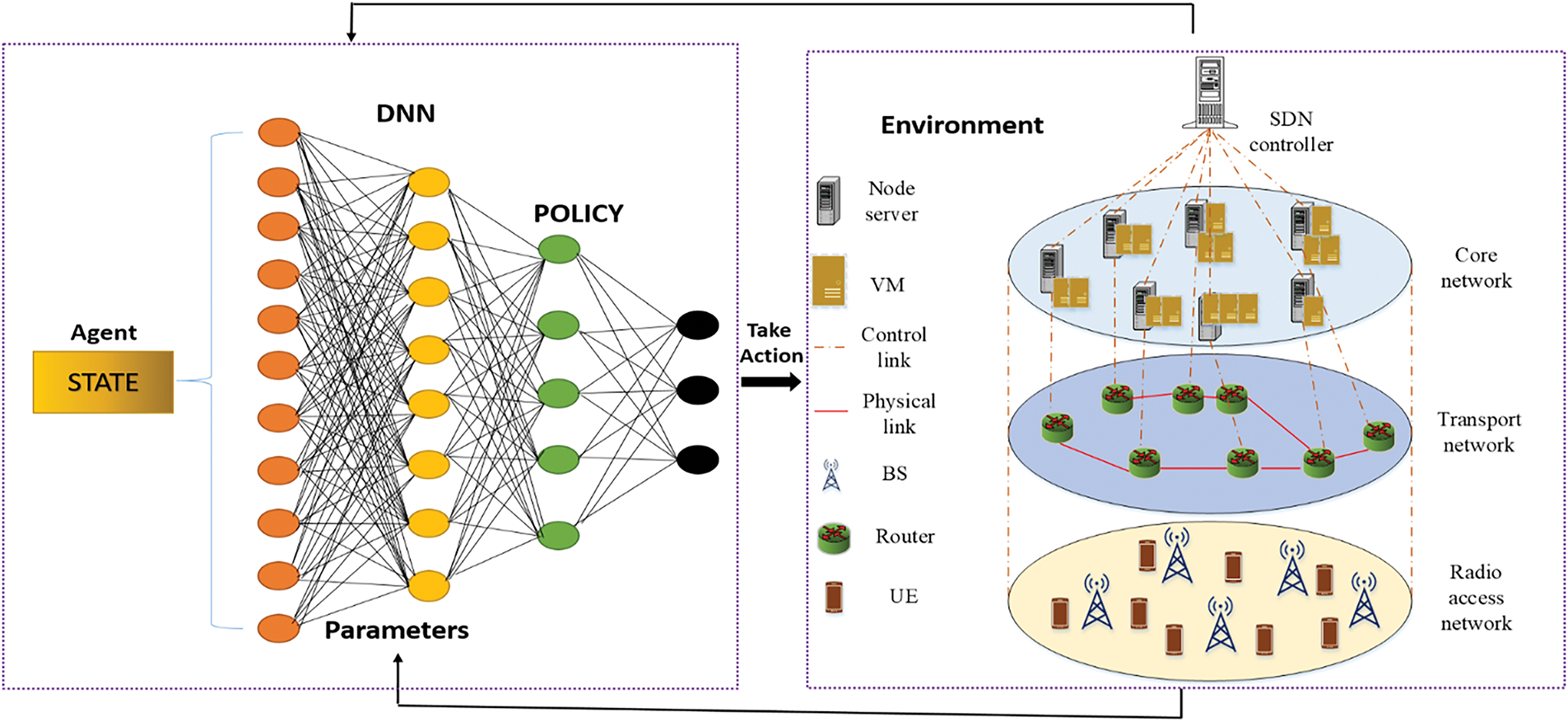
Figure 2: Architecture of enhanced DRL

State: When using DRL techniques, the agent decides which agents or actions to take by considering the system. For each time u network state is defined T∗(u)=[iu,vc,l,ep^,p^′u,e^p^,p^′u,avm,nu,a^p^u],∀u is the network’s available resources and user channel gains. In terms of states, the agent or agents select the proper action by shifting the network state to the subsequent state. The VM selector, path, RR, and resource allocation in the transport and core networks are the optimization factors included in this action A∗(u)={ϑu,qu,τu,ψu,γu,γ^u,Zu,Z^u},∀u.

Reward function: Two categories of reward functions such as episodic reward and instance reward are considered. By A(u) is the objective function and constraints, the instance reward function S(u) is achieved as follows:

Re(u)(S(u),A(u))={d^3Γ~u−(d^1∑vΩutil,v(u)+d^2∑vΩmigr,v(u)),ifconstraint(9)satisfies−ϖ,otherwise(10)

The coefficient factor and the number of successful arrival packet ratio at u, d^3, Γ~u. Furthermore, breaking the limits carries a large penal ϖ. The 0<Γ~u≤1 continuous d^3 is selected (d^1∑vΩutil,v(u)+d^2∑vΩmigr,v(u)). It is important to remember that each time slot the number of packets successfully is determined. However, E, the episodic reward is acquired by,

ReEp(E)={∑u=1URe(u)U,ifconstraint(9c)and(9d) satisfiesineverytimeslotsofepisodeE−ϖ,otherwise(11)

Then, the proposed method examines the specifics of the implemented ImpMRFO algorithm in the following part. It is noted that the learning process is directly impacted by choosing the right value when the constraints are not met. In this regard, the ImpMRFO is set in the proposed method.

3.3 Improved Manta Ray Optimization

In slice-enabled 6G networks, resource management problems can be non-convex. The metaheuristic optimization algorithm is well-suited to overcome such non-convex optimization problems by exploring diverse solutions instead of converging to local optima. In the proposed DRL approach, an improved manta ray foraging optimization algorithm (ImpMRFO) is used for handling the non-convex nature of the optimization problem by optimizing the policy and enabling stable learning. A bio-inspired optimizer, the manta ray foraging optimization algorithm (MRFO) mimics the manta ray’s motion of snatching prey. It makes use of three foraging characteristics of manta rays: chain foraging, cyclone foraging, and somersault foraging. The trials conducted under various test suits demonstrated MRFO’s ability to resolve optimization issues. However, the standard MRFO occasionally encounters problems with local optima and convergence issues. Thus, the concept of the chaotic map and Levy flight is applied by the ImpMRFO algorithm. In ImpMRFO, the manta ray’s positions (potential resource allocations), current resource constraints, QoS requirements and user demand patterns are considered as input. The outputs are the optimized policy, resource allocation decisions for network slices, and mapped resource distribution profiles. The major steps involved in MRFO.

3.3.1 Initialization Stage

The initialization of MRFO is c randomly to construct random locations Z. It initiates the population size Q, maximum iteration IterMaxi, and problem dimension F. The expression of the population initialized in the initialization phase is provided as follows.

Qj=lbk+ubk−t1zj,j∈1,2,....Q(12)

where, tk is the random number in the [0,1] besides ubk addition lbk greater and lower bounds kth component. For every manta ray in the solution space Fitn(Z), which is the maximization of Eq. (9) calculated analytically and compared. Based on the fitness computation, a fitness score has been assigned to each manta ray in the solution space.

3.3.2 Optimization Stage

As previously stated, the optimization phase can be divided into three categories: chain foraging, cyclone foraging, and somersault foraging. To update the global best solution, the MRFO model uses this to calculate and compare the fitness.

Chain foraging: The expression below has been used to update Zm of this foraging operation.

zmu+1={zmu+t∗(zBestu−zmu)+χ(zBestu−zmu)m=1zmu+t∗(zm−1u−zmu)+χ(zBestu−zmu)m=2,3,....,Q(13)

The zmu characterizes mth of the agent in u, t resembles the random vector in [0, 1], χ designates the weight zBestu the high-concentration plankton.

Cyclone foraging: The following expression is used to update the Zm cyclone foraging.

zmu+1={zBestu+t∗(zBestu−zmu)+δ(zBestu−zmu)m=1zBestu+t∗(zm−1u−zmu)+δ(zBestu−zmu)m=2,3,....,Q(14)

where, δ indicates the weight coefficient. Additionally, to enhance the MRFO model’s exploration, the cyclone foraging phase modifies the agents’ locations based on a random position inside the search area. As a result, the agent’s current position can be modified as follows.

zmu+1={zRandu+t∗(zRandu−zmu)+δ(zRandu−zmu)m=1zRandu+t∗(zm−1u−zmu)+δ(zRandu−zmu)m=2,3,....,Q(15)

The zRandu random position in the search space.

Somersault foraging: The food position is perceived as a pivot in this performance. Every individual tendency to swim around the pivot and somersault into a new location. As a result, they constantly update their location to reflect the best location found so far. A mathematical formulation used in this stage can be specified as follows.

The location of the food is thought to be crucial to this performance. Each individual has a propensity to swim around the pivot and somersault into a different area. Therefore, they update their location frequently to reflect the greatest spot found so far. The mathematical formulation utilized in this step to update the agent can be described as follows.

zmu+1=zmu+w∗(t1.zBestu−t2.zmu)(16)

where, t1 and t2 are the random number in the range [0, 1] as well w, the somersault factor equivalent to 2.

3.3.3 Termination Stage

The previous phase steps are repeated until the halting condition is met. Here, the stop condition is the total number of iterations. The MRFO algorithm selects the optimal solution based on the higher fitness function value.

3.3.4 ImpMRFO Based on Levy Flight and Chebyshev Chaotic Map

Chebyshev chaotic map: The convergence feature may be impacted by the random number sequence utilized to differentiate parameters during the MRFO execution. The MRFO lacks specific analytical findings that could improve its effectiveness, in contrast to other swarm-based intelligence algorithms. A random state that rises during the development of a non-linear system is called chaos in deterministic systems. In general, the Chebyshev chaotic map exhibits a greater uniform distribution range. It is distributed in [−1,1] sequence is ergodic, chaotic, and uncorrelated within the range of m≥2 (m being the order). Thereby, the distributed chaotic map is used in MRFO to initialize the position of manta rays. The equation of Chebyshev chaotic map is specified as,

Rz+1=cos⁡(mcos−1⁡rz)rz∈[−1,1](17)

To initialize the manta ray position, MRFO utilizes the above Eq. (12) for generating uniformly dispersed points.

Qj=lbk+Rz+1ubk−t1zj,j∈1,2,...Q(18)

This increases the original population’s capacity for global searches and optimizes the solution performance.

Levy flight, in this subsection, levy flight has been used to enhance the MRFO. Levy flying considerably reduces the early convergence issue of MRFO. Levy suggested approach takes the random walk method provide suitable control over local search. The below equation is a quantification of this mechanism’s representation,

Le(ε)≈ε−1−κ(19)

ε=N|Q|1κ(20)

ρ2={Γ(1+κ)κΓ((1+κ)2)Sin(πκ/2)2(1+κ)/2}2κ(21)

where, 0<κ≤2 and N∼P(0,ρ2) Γ represents the gamma function, κ is describes the index, N/P∼P(0,ρ2) expresses that the sample from Gaussian distribution in which the ρ2 is 0. Here, the value ε=3/2. Eq. (16) has been updated based on flight update MRFO solution. It is provided as follows (Table 3):

zmu+1=zmu+w∗Le(ε)(t1.zBestu−t2.zmu)(22)

Conversely, our methodology utilizes ImpMRFO not just for parameter optimization, but as an adaptive support system coupled with DRL in real-time, specifically for resource allocation in 6G network slicing—a highly dynamic, multi-constraint context. The innovation resides in: The twin function of ImpMRFO: enhancing the initial selection of DRL policies and dynamically directing exploration informed by real-time system status input.

Algorithm 1 can offer the pseudocode of ImpMRFO algorithms.

The use of Chebyshev chaotic initialization and Levy flight-enhanced local search enhances the learning agent’s flexibility and minimizes the risk of local optima entrapment—attributes often absent in previous meta-heuristic and deep reinforcement learning combinations. Focusing on a proactive and resilient solution in delay-sensitive, resource-limited IoT situations, where the majority of current research emphasizes static optimization or single-layer decision-making.

4  Results and Discussion

In this section, the result obtained by the proposed method is discussed in detail. Using the metrics such as PSSPr, utilization cost, migration (cardinality), robustness and relaxation time, the performance of the proposed approach is compared to other baselines.

4.1 Stimulation Setup and Environment

The simulation setup and environment are offered to assess the proposed approach. The Spyder compiler and Python language are utilized. For simulations, an Intel Core i7-10678K CPU with eight cores and 8 GB of RAM is utilized. Initial UE locations are established through random uniform distribution in area with four BSs of 5 W. Besides, in each time slot, there are ten users. For every BS, 16 sub-carriers are considered with a 200 kHz bandwidth. As a primary topology, the Abilene network topology with 15 links and 12 nodes from SNDlib3 is utilized in the core and transport networks. Furthermore, the proposed method has considered the computing capacity of 120 Mbps for every VM in the core domain. Every server node also includes six VMs. In addition, each router buffer can accommodate up to 50 packets, and each link in the transportation network has a 100 Mbps capacity. For each slice, packets per time slot indicate the average number of arriving packets and the maximum acceptable time is fixed 100 (ms). Fixed to slots over a time period with 100 time slots, and is fixed to 0.95. The proposed method deliberates 1000 episodes, each of which spans 100 time slots. The optimizer is used to configure the proposed EDRL-based technique.

4.2 Comparison of Baselines with the Proposed Approach

The experimental outcomes and convergence are among the most crucial criteria for assessing the proposed approach. Enhanced manta ray assisted DRL (EMR-DRL) is the primary algorithm used in the proposed work, whereas the baselines are deep deterministic policy gradient (DDPG), distributed algorithm, greedy, multi-agent DDPG (MADDPG), and soft actor critic-based RL (SAC-RL). In this regard, an individual agent is suggested for directing each domain through an E2E network by modifying MADDPG. Furthermore, each domain handles resource management independently by utilizing the distributed technique. The comparison of average reward achieved for the proposed and baseline methods over the episodes is presented in Fig. 3. The result of the implemented EMR-DRL method is better than the baseline algorithms, as shown in Fig. 4. This is due to the ability of improved MRFO that supports the DRL model to effectively function in dynamic conditions with a high degree of uncertainty. Furthermore, the results obtained indicate that the reward is lower and more variable in the distributed learning and MADDPG methods as a result of the problem being solved disjointedly.

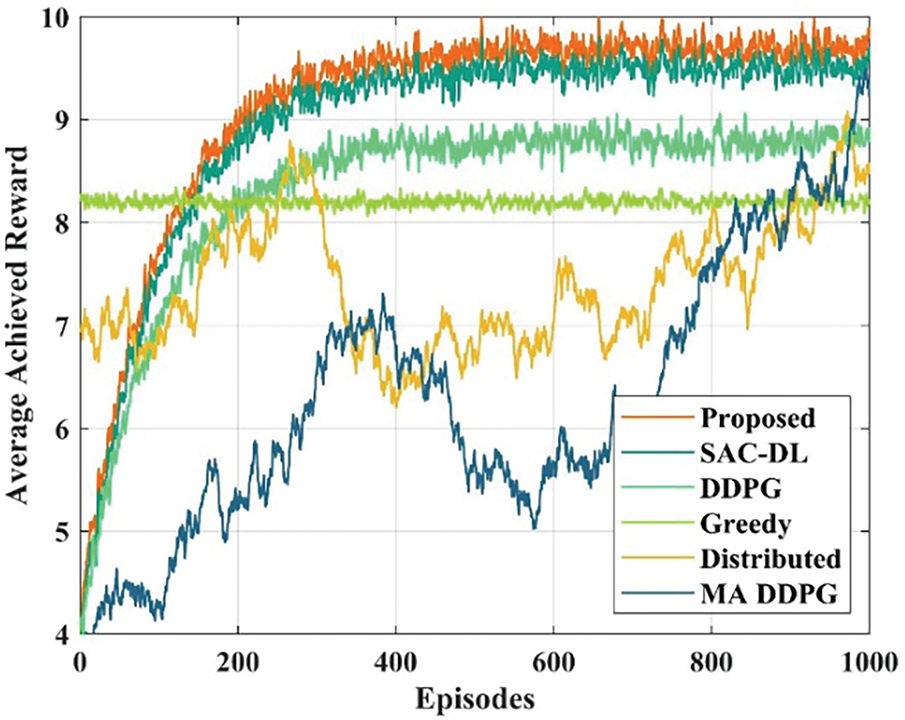
Figure 3: Comparison of average reward achieved

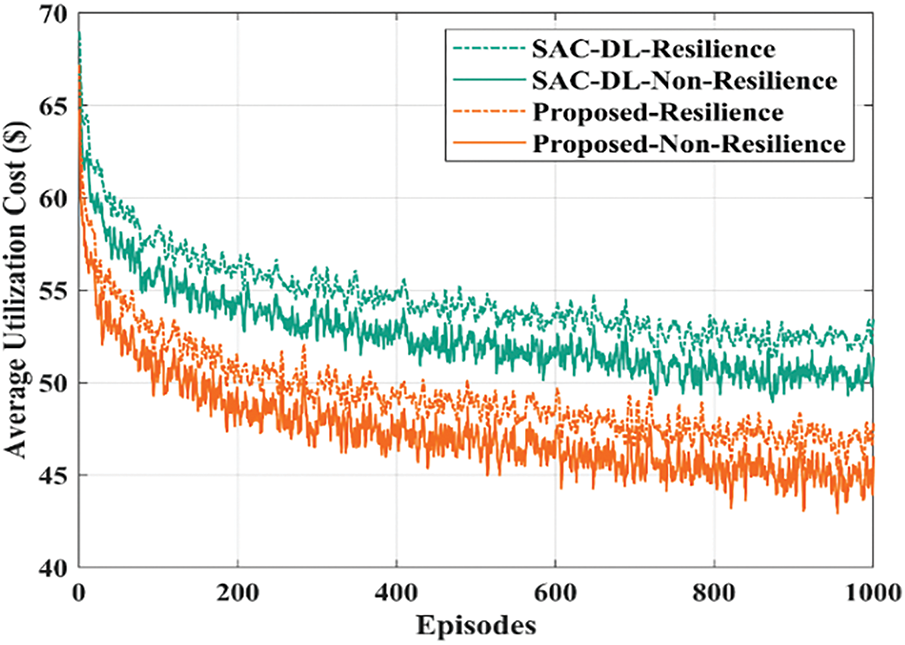
Figure 4: Comparison of utilization cost imposed for scenarios

4.3 Comparison of Baselines with the Proposed Approach

The resilience time or the amount of time taken for the system to return to its intended performance after a failure, is considered in this subsection to assess network performance. To evaluate the impact of network, two scenarios such as resilient and non-resilient are considered. However, the proposed method accounts for relaxation time in the non-resilience situation. The resilience time is different from the return time since it pertains to a resilience, when the system aims to return its intended performance in a constrained amount of time. On the other hand, the former relates to the non-resilience scenario, in which the system’s inherent chance of failure may cause it to gradually return to its predicted performance. In Fig. 5, the saturated time increases and the cardinality cost rises for the resilient and non-resilient scenarios. In comparison to the non-resilient scenario, the resilient scenario’s average cardinality cost rises by up to 7%. Furthermore, the utilization costs of the non-resilience and resilience scenarios are depicted over the number of episodes. In Fig. 6, the average resilient time over the episodes is presented. It demonstrates how the resilience of the system is enhanced with each episode.

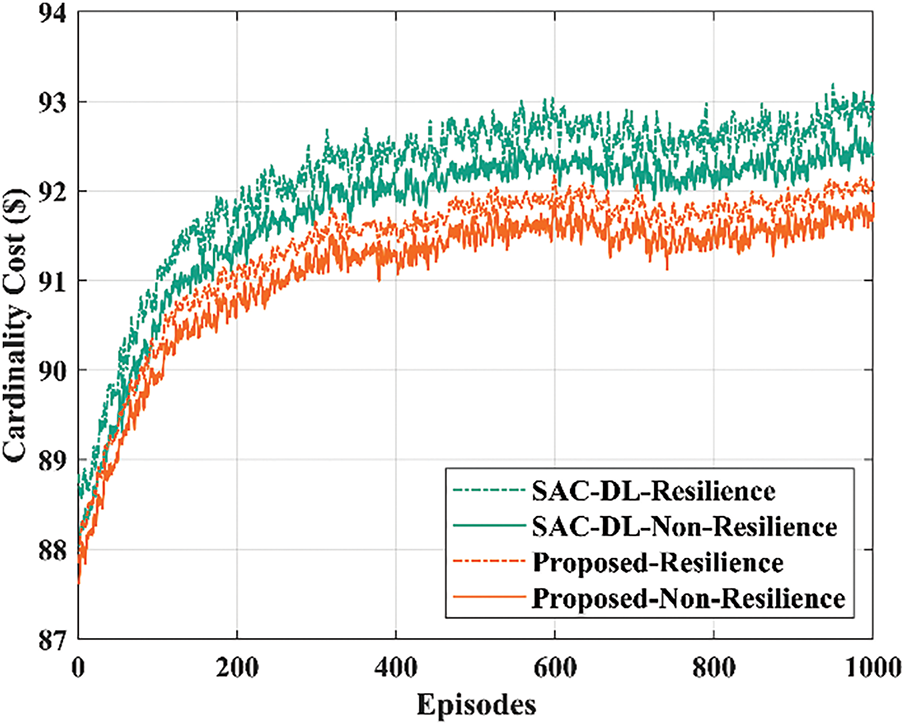
Figure 5: Comparison of cardinality cost imposed for scenarios

Figure 6: Average resilient time analysis over episodes

The graphical representation shows a minimizing trend in the resilience time, resembling that the system becomes more effectual at improving from disruptions since it learns and adapts through the episodes. This enhancement is attributed to the proposed EMR-DRL based method, which optimizes the response of the system to failures and improves its capability to preserve performance. The overall performance underscores the efficiency of EMR-DRL method in attaining proactive resource management and resilience in slice-enabled 6G networks.

4.4 Assessment of Utilization and Cardinality Cost

In this section, the utilization and cardinality cost of the proposed method is assessed. The cost incurred from utilizing network resources, like transmission power, computational capacity and bandwidth is referred to as the utilization cost. On the other hand, the cardinality cost is related to the number of resources or complexity involved in provisioning network slices. In 6G networks, both the cardinality and utilization costs are signification to optimize resource allocated and ensure proactive, resilient and efficient network performance. Fig. 7 deliberates the network topologie’s impact on cardinality and utilization costs of the proposed method. The graphical representation shows that the imposed cost rises as the network size maximizes. This is because the network is more extensive and widely distributed. However, the proposed method accomplished greater performance than the existing method.

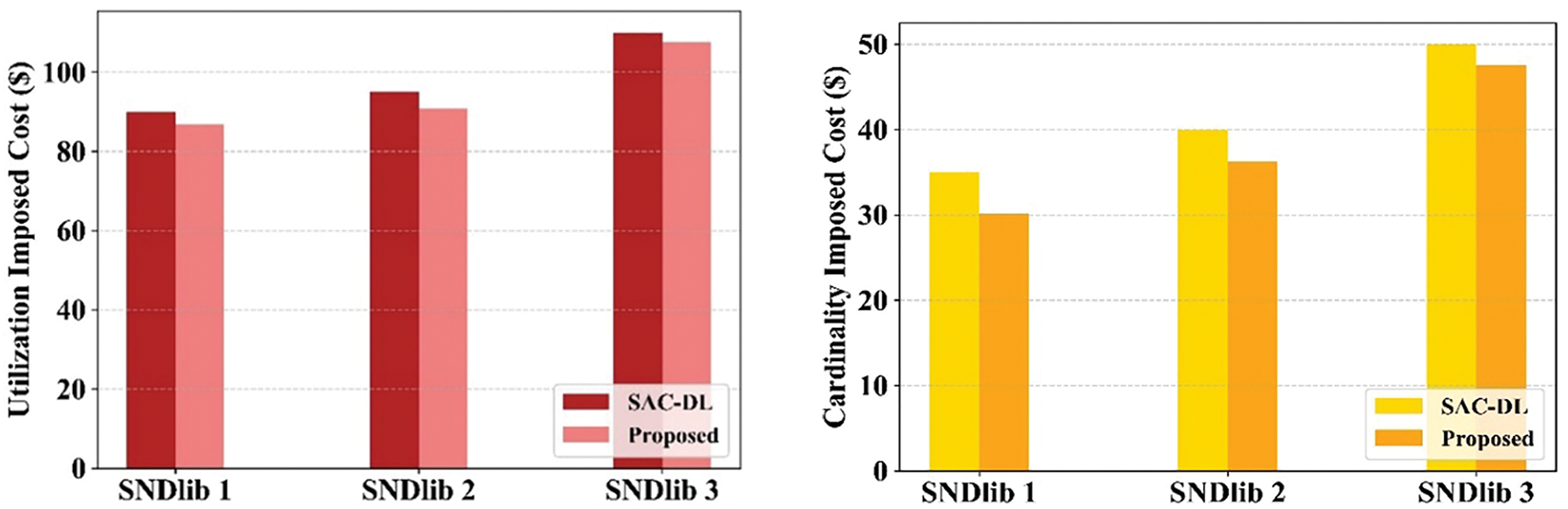
Figure 7: Impact of network architecture on cardinality and utilization costs

4.5 Assessment of Average Arrival Packets and Tolerable Delay

This section examines the impact of the average number of slice arrival packets and maximum allowable slice delay on the PSSPr for the proposed and baseline methods. Fig. 8 presents the comparison of average arrival packets of slices for the proposed and baseline methods. As illustrated in Fig. 8, the PSSPr falls as the number of generated packets rises because of resource limitations. Based on this, the network’s capacity to compensate for its performance is diminished when the quantity of packets increases. The results show that the proposed EMR-DRL-based approach can increase PSSPr by an average of 12% when the number of arrival packets changes. Further, the proposed method inspects how the PSSPr is impacted by the maximum allowable slice delay. Fig. 9 suggests the comparison of the maximum tolerable delay of slice for the proposed and baseline methods. As exposed in Fig. 10, the PSSPr rises as the maximum allowable delay maximizes. The experimental results display that the proposed EMR-DRL method can increase PSSPr by an average of 10% when the maximum allowable delay is varied. A parameter sensitivity learning was performed to evaluate the performance effects of fluctuations in learning rate, discount factor, manta ray population, Chebyshev map order, and Levy index. The findings indicate that a learning rate of 0.005 and a discount factor of 0.95 produced steady training with elevated PSSPr. A population size of 40 and a Chebyshev order of 3 augmented explorations, while a Lévy index of 1.5 refined local search. The comparisons are now included in the discussion to substantiate the robustness of our suggested strategy Fig. 10.

Figure 8: Training and validation accuracy vs. loss

Figure 9: Comparison of average number of arriving packets

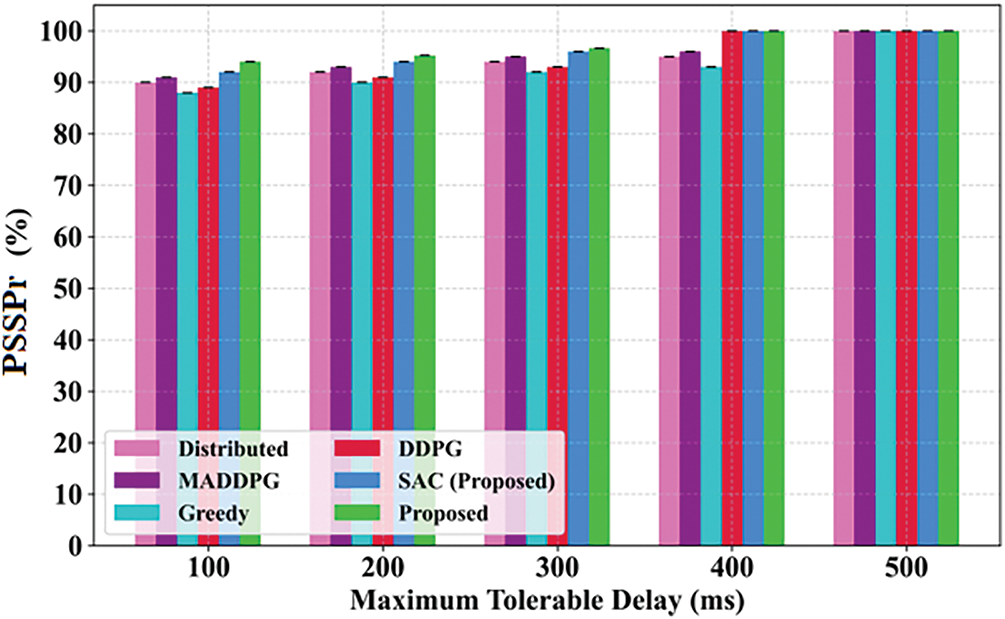
Figure 10: Comparison of maximum tolerable delay on

4.6 Assessment of Coefficient Factors Influence

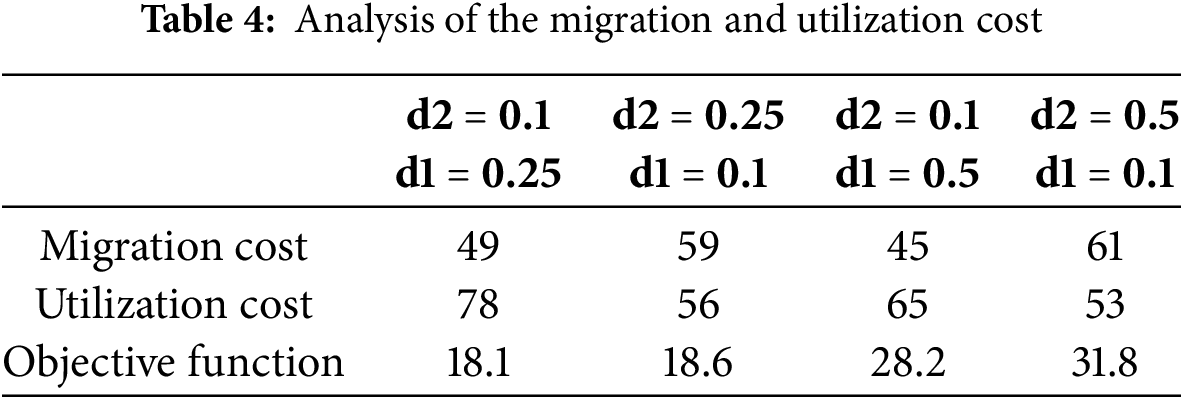
In this sub-section, the coefficients and are altered and scrutinised to assess the coefficient factors in the simulation results. Here, the coefficients and are set to 0.1. Table 4 shows the influence of the coefficients and with varying values, on the objective function. In the tabular representation, it is perceived that each cost’s objective function further declines as its coefficient factor rises.

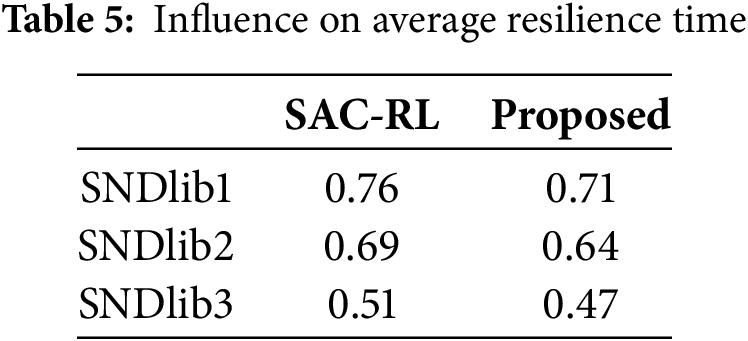
Furthermore, the network topology’s influence on resilience time is offered in Table 5. In the graphical representation, it is perceived that the proposed method has attained low resilience time in contrast to the existing SAC-RL model. This resembles that the proposed system can speedily recover from disruptions as well as return to its desired performance level. Moreover, the lower resilience time replicates better robustness and efficiency to the desired performance level in managing unexpected events or network failures, which is a critical aspect of handling optimal performance in slice-enabled 6G networks.

5  Conclusion

This research proposes a novel approach to ETE resource management in network slicing by deliberating the qualities of resilience and proactivity. The optimization problem that mathematically models resilience and proactivity has been included in this framework. Furthermore, a comprehensive function for the PSSPr is constructed. An effective resource management framework is implemented by the suggested strategy using ImpMRFO and DRL. The incorporation of Chebyshev’s chaotic map and levy flight into ImpMRFO addresses the convergence and local optima issues. When comparing the proposed approach with other approaches, the used ImpMRFO-based method increased the PrSSP by 12% according to an evaluation of the data. Also, the proposed method reduced the costs associated with resource management while guaranteeing a high level of QoS and accomplished a reduction in resiliency time in contrast to non-resilient scenarios. In the future, the proposed method will focus on the incorporation of multi-agent RL methods to boost efficiency and scalability. In addition, the application of federated learning can be investigated to further enhance the robustness and adaptability of network management systems in heterogeneous and highly dynamic network environments. Although current research has examined network slicing using many optimization and learning methodologies, many studies fail to include both proactivity and resilience in dynamic resource management. Previous methodologies often depend on static models or single-layer optimization, limiting flexibility in real-time scenarios. We present an innovative packet-based proactive end-to-end resource management system that integrates advanced deep reinforcement learning with refined manta ray foraging optimization. This hybrid methodology efficiently addresses resource limitations while enhancing slice provisioning efficacy. Our approach exhibits enhanced cost efficiency and reliability relative to conventional, non-resilient models in dynamic network settings.

Acknowledgement: Sincerely thank T-Mobile USA Inc., Axyom.Core, and the Saveetha Institute of Medical and Technical Sciences for providing the necessary support, infrastructure, and collaborative environment that enabled the successful completion of this research.

Funding Statement: Not applicable.

Author Contributions: Conceptualization, Surendran Rajendran; methodology, Raghavendra Kulkarni; software, Binu Sudhakaran Pillai; validation, Venkata Satya Suresh kumar Kondeti; formal analysis, Binu Sudhakaran Pillai; investigation, Venkata Satya Suresh kumar Kondeti; resources, Raghavendra Kulkarni; data curation, Surendran Rajendran; writing—original draft preparation, Surendran Rajendran; writing—review and editing, Venkata Satya Suresh kumar Kondeti; visualization, Binu Sudhakaran Pillai; supervision, Raghavendra Kulkarni; project administration, Raghavendra Kulkarni; funding acquisition, Binu Sudhakaran Pillai. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated and analysed during the current study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Bikkasani D, Yerabolu M. AI-driven 5G network optimization: a comprehensive review of resource allocation, traffic management, and dynamic network slicing. Am J Artif Intell. 2024;8(2):55–62. doi:10.11648/j.ajai.20240802.14. [Google Scholar] [CrossRef]

2. Dangi R, Jadhav A, Choudhary G, Dragoni N, Mishra MK, Lalwani P. ML-based 5G network slicing security: a comprehensive survey. Future Internet. 2022;14(4):116. doi:10.3390/fi14040116. [Google Scholar] [CrossRef]

3. Vidhya P, Subashini K, Sathishkannan R, Gayathri S. Dynamic network slicing based resource management and service aware Virtual Network Function (VNF) migration in 5G networks. Comput Netw. 2025;259(2):111064. doi:10.1016/j.comnet.2025.111064. [Google Scholar] [CrossRef]

4. Rafique W, Rani Barai J, Fapojuwo AO, Krishnamurthy D. A survey on beyond 5G network slicing for smart cities applications. IEEE Commun Surv Tutor. 2025;27(1):595–628. doi:10.1109/comst.2024.3410295. [Google Scholar] [CrossRef]

5. Khan AA, Ali Laghari A, Baqasah AM, Alroobaea R, Reddy Gadekallu T, Avelino Sampedro G, et al. ORAN-B5G: a next-generation open radio access network architecture with machine learning for beyond 5G in industrial 5.0. IEEE Trans Green Commun Netw. 2024;8(3):1026–36. doi:10.1109/TGCN.2024.3396454. [Google Scholar] [CrossRef]

6. Barker R. Advancements in mobile edge computing and open RAN: leveraging artificial intelligence and machine learning for wireless systems. arXiv:2502.02886. 2025. [Google Scholar]

7. Hazarika B, Saikia P, Singh K, Li CP. Enhancing vehicular networks with hierarchical O-RAN slicing and federated DRL. IEEE Trans Green Commun Netw. 2024;8(3):1099–117. doi:10.1109/TGCN.2024.3397459. [Google Scholar] [CrossRef]

8. Dhanashree K, Venkatesan M, Kulkarni AV. Deep learning traffic prediction and resource management for 5G RAN slicing. J Inst Eng. 2024;2(1):1–14. doi:10.1007/s40031-024-01110-2. [Google Scholar] [CrossRef]

9. Mhatre S, Adelantado F, Ramantas K, Verikoukis C. Transfer learning applied to deep reinforcement learning for 6G resource management in intra-and inter-slice RAN-edge domains. IEEE Trans Consum Electron. 2025. doi:10.1109/tce.2025.3553407. [Google Scholar] [CrossRef]

10. Garrido LA, Dalgkitsis A, Ramantas K, Ksentini A, Verikoukis C. Resource demand prediction for network slices in 5G using ML enhanced with network models. IEEE Trans Veh Technol. 2024;73(8):11848–61. doi:10.1109/TVT.2024.3373490. [Google Scholar] [CrossRef]

11. Abba Ari AA, Samafou F, Ndam Njoya A, Djedouboum AC, Aboubakar M, Mohamadou A. IoT-5G and B5G/6G resource allocation and network slicing orchestration using learning algorithms. IET Netw. 2025;14(1):e70002. doi:10.1049/ntw2.70002. [Google Scholar] [CrossRef]

12. Hamza Abdulkadhim A, Saeed Alfoudi A, Hussean Maghool F. End-to-end resource allocation management model in next-generation network: survey. J Al-Qadisiyah Comp Sci Math. 2024;16(3):44. doi:10.29304/jqcsm.2024.16.31642. [Google Scholar] [CrossRef]

13. Sohaib RM, Tariq Shah S, Yadav P. Towards resilient 6G O-RAN: an energy-efficient URLLC resource allocation framework. IEEE Open J Commun Soc. 2024;5:7701–14. doi:10.1109/ojcoms.2024.3510273. [Google Scholar] [CrossRef]

14. Khan MMI, Nencioni G. Resource allocation in networking and computing systems: a security and dependability perspective. IEEE Access. 2023;11:89433–54. doi:10.1109/access.2023.3306534. [Google Scholar] [CrossRef]

15. Wang W, Tang L, Liu T, He X, Liang C, Chen Q. Toward reliability-enhanced, delay-guaranteed dynamic network slicing: a multiagent DQN approach with an action space reduction strategy. IEEE Internet Things J. 2024;11(6):9282–97. doi:10.1109/JIOT.2023.3323817. [Google Scholar] [CrossRef]

16. Sefati SS, Haq AU, Nidhi, Craciunescu R, Halunga S, Mihovska A, et al. A comprehensive survey on resource management in 6G network based on Internet of Things. IEEE Access. 2024;12(1):113741–84. doi:10.1109/access.2024.3444313. [Google Scholar] [CrossRef]

17. Herrera JL, Galán-Jiménez J, Berrocal J, Bellavista P, Foschini L. Energy-efficient QoS-aware application and network configuration for next-gen IoT. In: Proceedings of the 2023 IEEE 28th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD); 2023 Nov 6–8; Edinburgh, UK. doi:10.1109/CAMAD59638.2023.10478393. [Google Scholar] [CrossRef]

18. Cai Y, Cheng P, Chen Z, Ding M, Vucetic B, Li Y. Deep reinforcement learning for online resource allocation in network slicing. IEEE Trans Mob Comput. 2024;23(6):7099–116. doi:10.1109/TMC.2023.3328950. [Google Scholar] [CrossRef]

19. Nawfel Saidi A, Lehsaini M. A deep Q-learning approach for an efficient resource management in vehicle-to-everything slicing environment. Int J Commun. 2025;38(4):e6137. doi:10.1002/dac.6137. [Google Scholar] [CrossRef]

20. Kaytaz U, Sivrikaya F, Albayrak S. Multi-policy lazy RAN slicing with Bayesian optimization for energy-efficient B5G ITS. IEEE Trans Intell Transp Syst. 2025;26(6):9022–36. doi:10.1109/TITS.2025.3539027. [Google Scholar] [CrossRef]

21. Ghafouri N, Vardakas JS, Ramantas K, Verikoukis C. A multi-level deep RL-based network slicing and resource management for O-RAN-based 6G cell-free networks. IEEE Trans Veh Technol. 2024;73(11):17472–84. doi:10.1109/TVT.2024.3415656. [Google Scholar] [CrossRef]

22. Mhatre S, Adelantado F, Ramantas K, Verikoukis C. Enhancing AI transparency: XRL-based resource management and RAN slicing for 6G ORAN architecture. arXiv:2501.10292. 2025. [Google Scholar]

23. Zangooei M, Golkarifard M, Rouili M, Saha N, Boutaba R. Flexible RAN slicing in open RAN with constrained multi-agent reinforcement learning. IEEE J Sel Areas Commun. 2024;42(2):280–94. doi:10.1109/JSAC.2023.3336156. [Google Scholar] [CrossRef]

24. Ros S, Kang S, Song I, Cha G, Tam P, Kim S. Priority/demand-based resource management with intelligent O-RAN for energy-aware industrial Internet of Things. Processes. 2024;12(12):2674. doi:10.3390/pr12122674. [Google Scholar] [CrossRef]

25. Nouruzi A, Mokari N, Azmi P, Jorswieck EA, Erol-Kantarci M. Smart dynamic pricing and cooperative resource management for mobility-aware and multi-tier slice-enabled 5G and beyond networks. IEEE Trans Netw Serv Manag. 2024;21(2):2044–63. doi:10.1109/TNSM.2023.3328016. [Google Scholar] [CrossRef]