 Open Access
Open Access
ARTICLE
Deep Multi-Agent Stochastic Optimization for Traffic Management in IoT-Enabled Transportation Networks
Department of Informatics and Computer Systems, College of Computer Science, King Khalid University, Abha, 61421, Saudi Arabia
* Corresponding Author: Nada Alasbali. Email:
(This article belongs to the Special Issue: Intelligent Vehicles and Emerging Automotive Technologies: Integrating AI, IoT, and Computing in Next-Generation in Electric Vehicles)
Computers, Materials & Continua 2025, 85(3), 4943-4958. https://doi.org/10.32604/cmc.2025.068330
Received 26 May 2025; Accepted 12 September 2025; Issue published 23 October 2025
Abstract
Intelligent Traffic Management (ITM) has progressively developed into a critical component of modern transportation networks, significantly enhancing traffic flow and reducing congestion in urban environments. This research proposes an enhanced framework that leverages Deep Q-Learning (DQL), Game Theory (GT), and Stochastic Optimization (SO) to tackle the complex dynamics in transportation networks. The DQL component utilizes the distribution of traffic conditions for epsilon-greedy policy formulation and action and choice reward calculation, ensuring resilient decision-making. GT models the interaction between vehicles and intersections through probabilistic distributions of various features to enhance performance. Results demonstrate that the proposed framework is a scalable solution for dynamic optimization in transportation networks.Keywords
The Internet of Things (IoT) has emerged as a technological paradigm shift, revolutionizing various sectors, including transportation networks, smart agriculture, healthcare, and sensor networks [1–6]. Intelligent Traffic Management (ITM) enables real-time data monitoring and dynamic decision-making in transportation control systems, ensuring smoother traffic flow, reducing congestion, and mitigating environmental impacts [7,8]. The sustainable development of a smart traffic environment has led to a decrease in traffic accidents, reduced fuel consumption and emissions, and alleviation of vehicular congestion. Additionally, incorporating AI-driven systems and IoT devices with ITM has contributed to a smarter and more responsive transportation network [9].
Machine Learning (ML) and Reinforcement Learning (RL) have emerged as transformative technologies in ITM environments, addressing the complex challenges inherent in smart transportation networks. In particular, the RL Deep Q-Learning (DQL) is gaining importance in ITM environments due to its ability to refine the numerical performance metric and drive systems toward a long-term optimization goal [10,11]. The learning agent in DQL receives feedback or rewards for the predicted favorable actions through constant interaction with the system, enabling the agent to improve decision-making and enhance real-time traffic flow.
Game theory has also emerged as a key tool in the context of ITM, particularly for implementing the Nash Equilibrium concept, enabling decision-making that resolves conflicting objectives among various participants [12–14]. The game-theoretical framework in the context of ITM environments models the intersections as players, where the status of the vehicles is monitored at various intersections, and decisions are made based on the Nash equilibrium using cost functions. This concept helps improve the traffic flow at different intersections and optimizes the entire transportation network. Stochastic optimization has also gained prominence in solving complex traffic situations for sustainable transportation networks [15,16].
The growing challenges, including increased vehicle density, inefficient signal management, and traffic congestion in a modern traffic system, have motivated us to develop this optimized framework. The current system has deficits in handling uncertain real-time traffic and may fail to control traffic congestion effectively. The IoT technologies and innovative approaches are capable of handling an intelligent traffic control system that facilitates efficient traffic flow. The research aims to develop a scalable and effective traffic management system for an efficient intelligent system under uncertain conditions.
This research proposes an enhanced ITM framework using DQL and GT approaches. The novelty of the proposed framework lies in the combined functionality of all these methods within the specified multi-agent reinforcement learning paradigm. This approach models traffic flow as a dynamic, non-cooperative game among agents (vehicles or intersections). Each agent learns optimal strategies based on local observations and global traffic states. The proposal also incorporates stochastic optimization techniques such as uniform and normal distributions to further enhance the system’s performance. A key enhancement lies in the introduction of randomness within the action selection process, enabling the decision-making system to explore a more comprehensive range of potential solutions.
Additionally, the model’s capability is improved as it learns from real-time data collected by IoT devices, resulting in a more adaptive and optimal traffic management system. It is beneficial for urban traffic management systems from a practical point of view, as a hybrid decision-making architecture is introduced that advances the IoT-based traffic management system. This not only enhances the effectiveness of current traffic management systems but also lays the foundation for an innovative and self-optimizing network.
The rest of the paper is structured as follows. Section 2 presents a detailed literature review on the interactions between RL and GT within ITM environments. Section 3 introduces the proposed framework, highlighting its methodology and the implementation of DQL, GT, and stochastic optimization within such a framework. Section 4 details and discusses the obtained results, while Section 5 presents conclusions and recommendations for future work.
Machine Learning (ML), Reinforcement Learning (RL), and Game Theory (GT) are the latest emerging approaches that are being utilized in solving the complex challenges of transportation networks systems, including Intelligent Traffic Management (ITM) and enhancing security and scalability, and reliability features in such dynamic environments [17–19]. Indeed, numerous ML and RL models, particularly Deep Q-Learning (DQL), are implemented in ITM environments to promote smoother traffic flow, improve traffic light control, enable seamless lane changes, and mitigate environmental side effects.
Alruban et al. presented an AI-based optimization algorithm for traffic flow prediction [20]. The Hierarchical Extreme Learning Machine (HELM) was employed in their approach to predict flow levels, and the Artificial Hummingbird Optimization Algorithm (AHOA) was utilized for enhancing hyperparameter selection. The authors in [21] proposed an ML-based approach for traffic flow prediction and monitoring, integrated with cloud data warehousing, to enhance ITM services. The study’s experimental results demonstrated significant improvements in traffic flow prediction, highlighting the crucial role of combining advanced data warehousing techniques with machine learning (ML) algorithms for enhanced accuracy and performance.
Numerous studies have demonstrated that single-agent and multi-agent reinforcement learning (RL) techniques are crucial in enhancing both cybersecurity and road safety within green transportation systems. Furthermore, deep learning-based security solutions in intelligent transportation systems have been introduced to reduce accidents and safeguard against various cyberattacks [22,23].
IoT-assisted traffic signal control systems leveraging deep learning (DL) and real-time modeling have been analyzed to enhance the optimal policy results [24]. Various mathematical models, including the Markov decision process (MDP), policy iteration method, and fuzzy-based Deep Reinforcement Learning, have been utilized for optimal action selection [25,26]. The consideration of normal and emergency vehicle categories enabled the highest priority assignment for smart traffic control. The traffic light control and navigation for different intersections, both between and within sub-zones of the road infrastructure, were also considered in the proposed work.
Some studies have shown that combining the GT approach with RL not only enhances the computational requirements of ITM but also lowers the communication latency. Various GT approaches have been proposed for various ITM applications, including, for instance, GT for vehicular edge computing [27], bi-hierarchical GT [28], deep inverse RL [29], and Bayesian GT combined with a Deep RL framework [30], showing promising results. Additionally, stochastic optimization and 5G/6G-based smart transportation systems have attracted significant attention in recent years [31,32].
Furthermore, several studies have demonstrated that AI-enabled techniques can optimize flow management, traffic signal control, congestion control, and environmental effects within the context of intelligent traffic management [33–36]. These techniques offer comprehensive solutions to a wide range of challenges within transportation networks. In light of the literature above, the ITM capabilities to solve complex traffic problems are extensive. The individual and integrated novel technologies have made the system simpler and more effective. There is a need to utilize the combined properties of GT, RL, and SO optimization to further enhance and improve the system’s performance. This study proposes a novel ITM system that utilizes an integrated approach. In the next section, a comprehensive description of the proposed methodology for ITM has been presented.
This research proposes an innovative, integrated framework that leverages Deep Q-Learning (DQL), Game Theory (GT), IoTs, and Stochastic Optimization (SO) to optimize Intelligent Traffic Management (ITM) in transportation networks. The proposed framework gathers real-time traffic data from a network of IoT devices, including smart sensors, traffic lights, and cameras, which provide the system with a multifaceted view of current traffic scenarios and environmental conditions, capturing crucial metrics such as vehicle speed, traffic flow, traffic light timing, and CO2 emissions. DQL agents process this rich dataset to create a state representation of the traffic scenario at various critical intersections. Indeed, these agents are tasked with selecting the optimal actions, such as adjusting signal durations or proposing lane changes, with the primary objectives of minimizing wait times and optimizing traffic flow. The GT component has been integrated into the framework through the implementation of Nash Equilibrium. This integration ensures that no single intersection can update its conditions in isolation, thus promoting a holistic approach to traffic management. Uniform and normal distributions have been introduced for random action selection to further enhance decision-making. This approach allows the DQL and GT components to explore a broader range of potential strategies. It also improves the framework’s ability to balance exploration and exploitation, optimizing ITM solutions in dynamic environments. The detailed methodology for the proposed framework is presented next.
In our proposed framework, the DQL agent perceives the current state
The DQL agent’s policies undergo continuous refinement to maximize cumulative rewards, focusing on three key objectives: optimizing traffic flow, minimizing delays, and reducing environmental impact. The DQL utilizes deep neural networks for Q-value approximation, enabling the handling of a large state space in complex traffic scenarios. A state represents the current traffic condition at an intersection that includes features such as queue length
The DQL agent employs a set of actions that includes increasing and decreasing the green light duration
The reward function
where
The difference between the current and the new estimate is represented by the temporal difference as,
The optimal Q-value is obtained using the following condition
The Nash Equilibrium GT approach is employed in strategy selection at intersections to enhance intelligent traffic management, leading to improved traffic flow, reduced environmental impact, and minimized congestion. In this framework, each player, such as a vehicle or a traffic controller, shares the action to optimize performance, demonstrating that the intersection cannot improve its performance individually. The set of players is represented by N, and each player follows the strategy
The players’ strategies
Nash Equilibrium guides individual intersections (players) to independently optimize their strategies, resulting in a stable and efficient traffic system. Traffic flow, wait time, conditions, and vehicle speeds are the factors that represent the utility of the player. The utility function
and
where R represents the rewards associated with various factors while
Stochastic Optimization (SO), leveraging uniform and normal distributions, plays a vital role in enhancing intelligent traffic management. In uniform distribution, all possible actions have the same occurrence probability, which supports random exploration, thereby facilitating a balanced exploration of a wide range of solutions and considering all of them without bias. In normal distribution, optimal actions are assigned higher probabilities based on historical data. The traffic control system can be improved further by adjusting probabilities based on current real-time traffic conditions. The probability of each action can be represented as [37],
The Cumulative Distribution Function (CDF) for uniform and normal distributions is given as [38],
and
The mean and variance for both the distributions can be expressed as
The Q-value update rule in Deep Q-Learning (DQL), shown in Eq. (1), is crucial for the agent’s learning process. It enables the agent to revise its estimates of expected future rewards based on current states, actions, and observed outcomes, thereby facilitating improved decision-making in dynamic environments. In this research, the Q-value update rule has been modified to address uncertainty in real-world traffic scenarios. Traffic features, such as vehicle entrance time and green signal interval time, are uniformly distributed within the interval
The DQL algorithm employs an epsilon-greedy policy to balance exploration and exploitation, utilizing uniformly distributed actions. This policy balances the probability of selecting random actions across various traffic scenarios, ensuring diverse exploration, and can be expressed as follows:
The normal distribution is applied in DQL for both action selection and reward calculation, using the mean
The reward function can also be represented using a normal distribution as follows:
The Q-value update using the normally distributed actions and rewards is represented as:
In the proposed framework, we integrate Stochastic Optimization (SO) into Game Theory (GT) for Intelligent Traffic Management (ITM), leveraging both uniform and normal distributions to model the inherent variability in traffic systems. The strategies are applied at the intersection, where players interact and obey probabilistic distributions for various features. The uniformly distributed
where
The proposed framework for Intelligent Traffic Management (ITM) is comprehensively described in Algorithms 1 and 2.


In this section, we present a detailed evaluation of the proposed framework, focusing on assessing its performance across various metrics and comparing results under both uniform and normal distribution scenarios. The proposed model, based on deep game stochastic optimization (DGSO), is designed for a moderate traffic management system. It confirms compatibility with agents and the state space size to minimize memory and computational usage. The CPU and memory operated at a reasonable range of up to 40% and 60%. It demonstrates that the framework is well-supported by the memory and CPU requirements in an intelligent traffic management environment.
To evaluate our proposed intelligent traffic management system, we conducted comprehensive simulations using the Simulation of Urban Mobility (SUMO) simulator, a highly regarded open-source traffic simulator. Key simulation parameters are summarized in Table 1. Inter-agent communication is conducted using a message-passing protocol. The simulated road network comprises seven key intersections, each equipped with IoT-assisted smart traffic lights. In this setup, each intersection is connected to alternative routes, allowing for dynamic detour simulations. The transmission ranges for incoming traffic are 175, 650 m for urban areas, 450 m for suburban areas, between intersections, and 350 m for alternate paths. Each simulation episode involves 8000 vehicles, comprising 10% trucks, 20% buses, and 70% cars, reflecting a realistic traffic scenario. The green and yellow light durations are set at 6 and 3 s, respectively, with traffic light control intervals set to one second. The simulation setup utilizes 35 re-routers and 18 lane area detectors to monitor traffic flow. Each simulation run lasts for 15,000 s, providing a substantial time frame to observe the system’s performance across various traffic conditions and patterns.
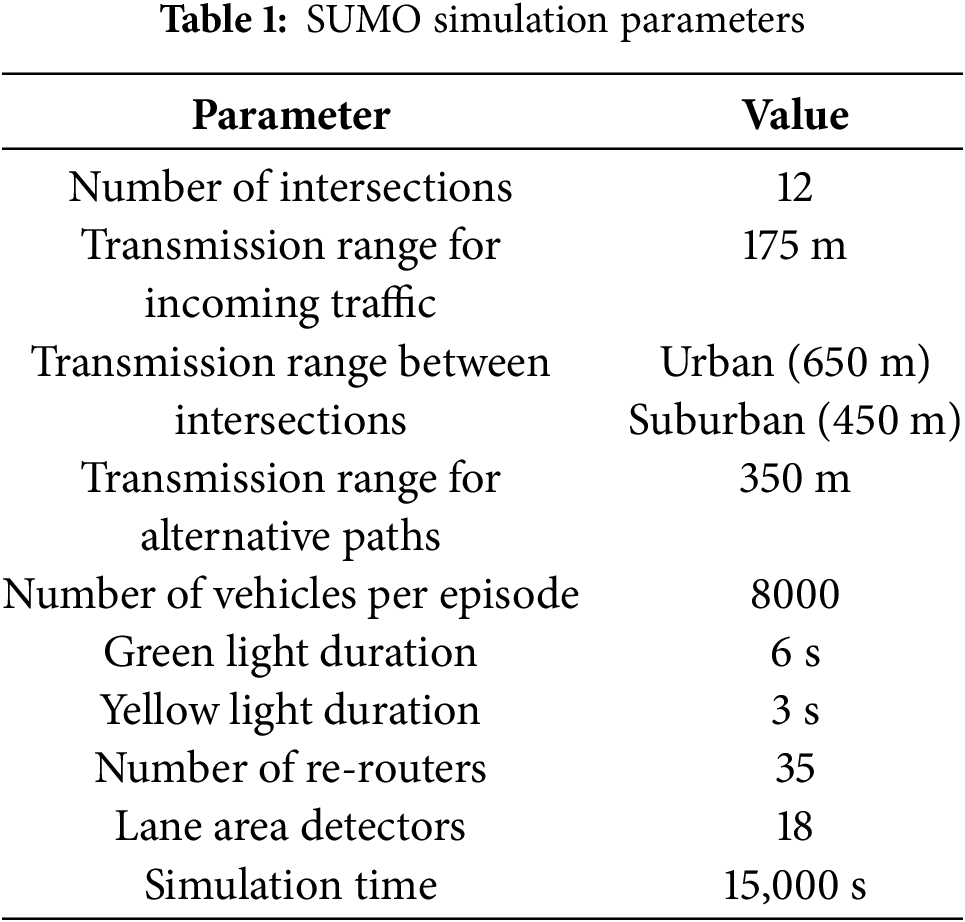
Table 2 shows the simulation parameters for the proposed DGSO framework. The key hyperparameters include learning rate, discount factor, exploration rate, and batch size. Their values were selected using a grid search to explore their broad range. A refined random search was then applied based on average reward and training loss. The parameters were tested with various values, and a final refined value was selected, demonstrating improved performance and efficiency. The complexity of the multi-agent environment was accommodated by maintaining a moderately deep network architecture.

In this subsection, we present the results of our proposed framework under three distinct configurations: 1) Baseline Configuration: without Deep Q-Learning, Game Theory, and Stochastic Optimization (DGSO), 2) DGSO with uniform distribution, and 3) DGSO with normal distribution. Fig. 1 shows the average travel time (ATT) per vehicle for each configuration under various episodes. As can be observed from the figure, the baseline configuration, without DGSO, exhibits ATT values ranging from 240 to 270 s, reflecting inefficient traffic flow, suboptimal travel times, and high congestion. The DGSO under uniform distribution shows improved performance, reducing the ATT to 180–220 s, approximately 18%–25%, across various episodes. This can be attributed to the system’s capacity to introduce a more balanced distribution of traffic across the network, resulting in reduced congestion and smoother flow. Further optimization is achieved with the DGSO using a normal distribution, which exhibits ATT values between 160 and 190 s, enhancing the performance by 11%–22% compared to the uniform distribution. The normal distribution’s superiority can be attributed to its ability to accurately model real-world traffic patterns.
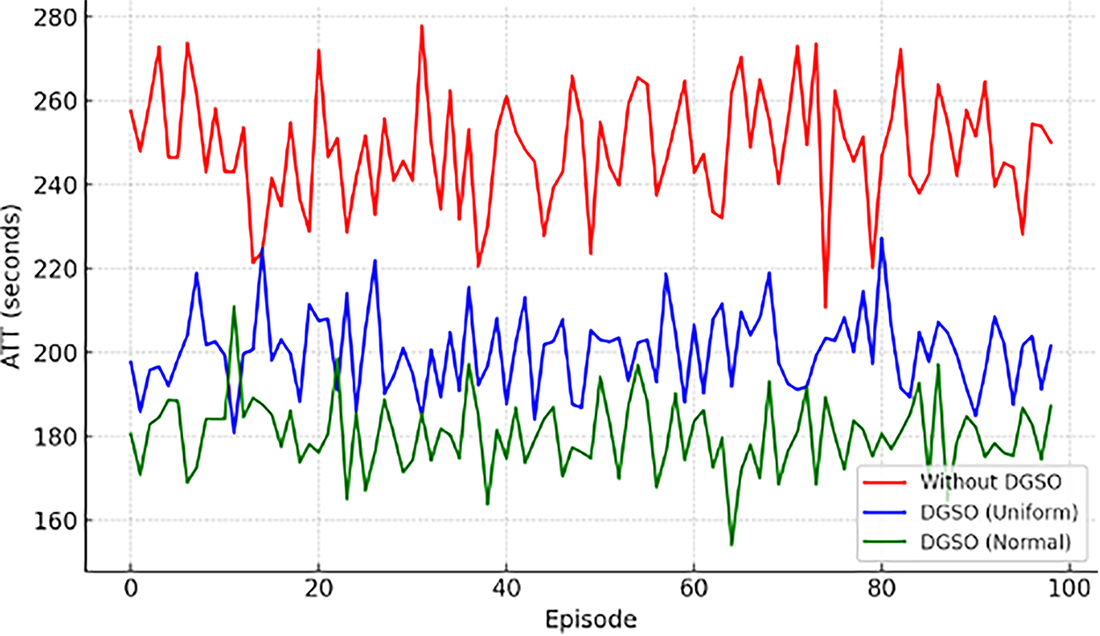
Figure 1: Average travel time per vehicle across episodes
Fig. 2 shows the average waiting time (AWT) at intersections under various episodes for the three simulated configurations. Similarly, the DGSO with a uniform distribution shows a marked improvement, with AWT values ranging from 60 to 80 s, compared to the baseline scenario, which recorded AWT values between 92 and 114 s. This represents a reduction in average waiting time at intersections of approximately 30%–35%, highlighting the enhanced efficiency in traffic management achieved through the application of DGSO under uniform distribution. Further optimization has also been achieved with the DGSO using a normal distribution, which exhibits AWT values between 45–55 s. The AWT for uniform distribution shows noteworthy improvements in wait time at the intersections, whereas the AWT for the normal distribution demonstrates significant enhancement in the model performance.
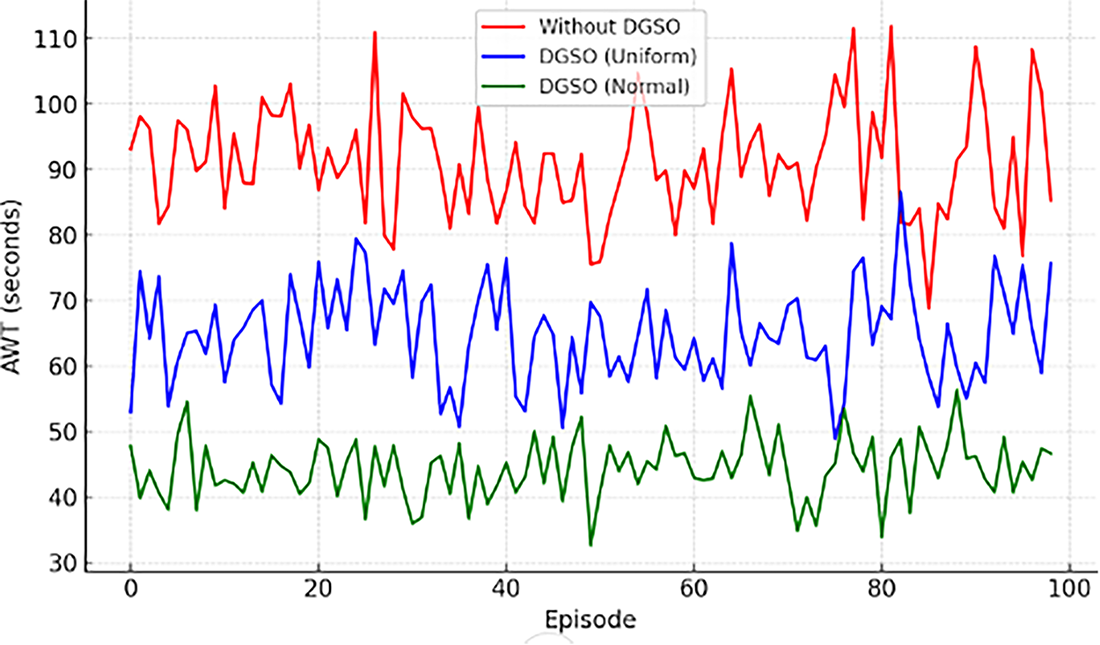
Figure 2: Average waiting time at intersections across episodes
Fig. 3 shows traffic light utilization and congestion levels before and after model implementation. The comparison has been conducted for all three traffic lights (green, yellow, and red). The durations of the green, yellow, and red lights before optimization were 30, 7, and 23 s, respectively. After optimization, the durations were 24, 5, and 18 s, respectively. The reduction in time indicates a traffic flow adjustment aimed at balancing congestion. It is worth mentioning that the congestion time for all the lights has been reduced after the model implementation.
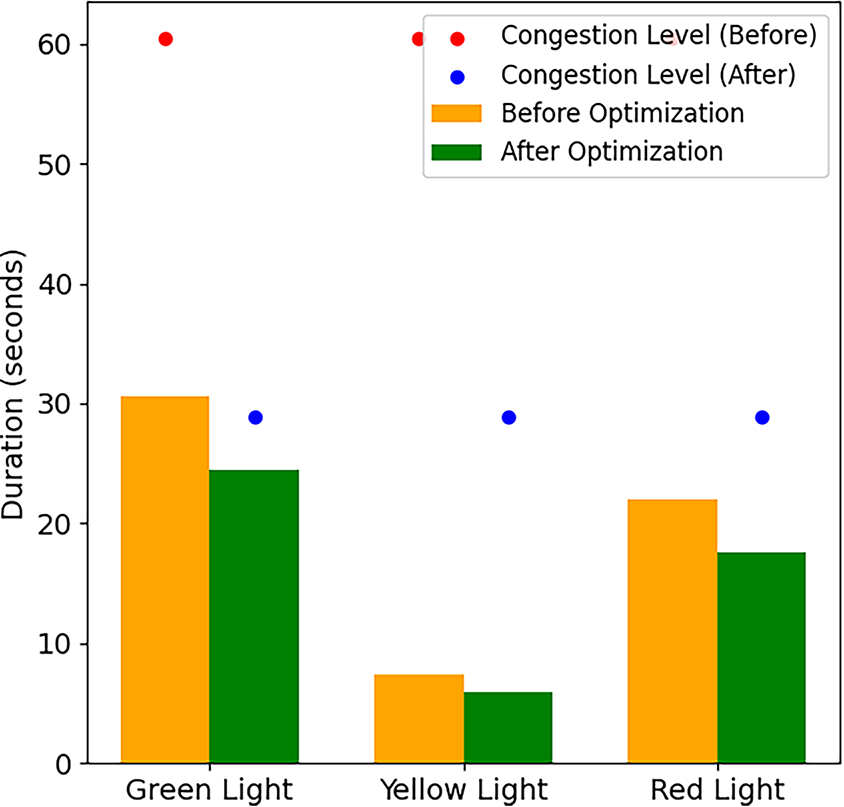
Figure 3: Traffic Light utilization before and after DGSO implementation
The average rewards over various episodes for DGSO with uniform distribution and DGSO with normal distribution are depicted in Fig. 4. The results reveal that the DGSO with normal distribution consistently achieves higher average rewards, reflecting improved performance and greater stability in the learning process compared to the uniform distribution.
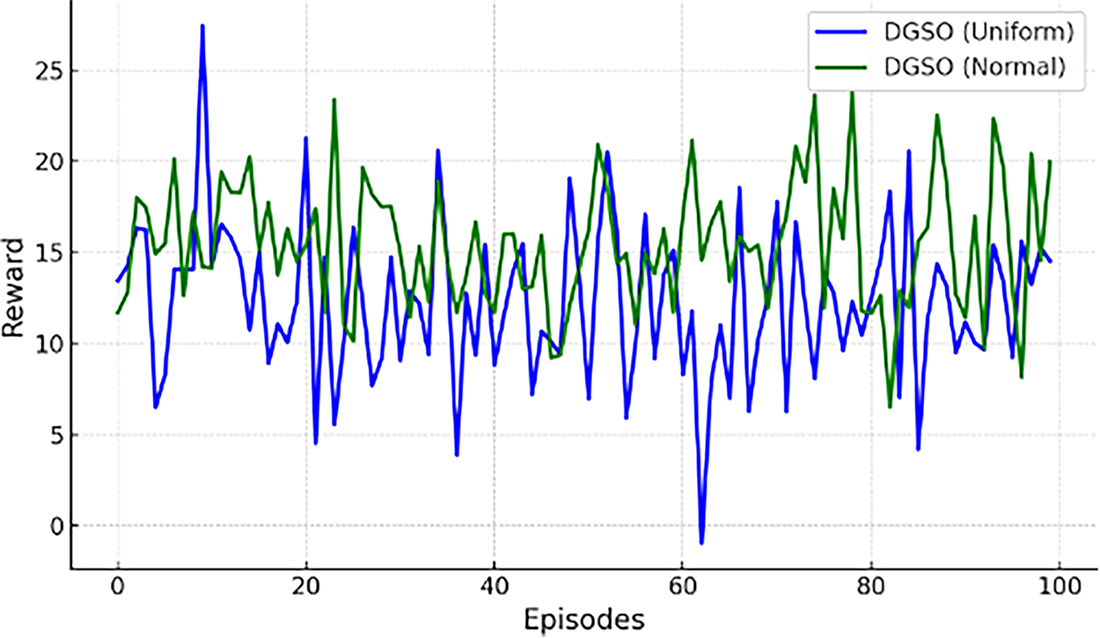
Figure 4: Average reward over episodes for DGSO with uniform and normal distributions
Fig. 5 illustrates the average training loss over various episodes for DGSO with uniform distribution and DGSO with normal distribution. The figure reveals that the uniform distribution has a slightly lower initial loss of 0.051 compared to the normal distribution’s 0.080. However, the final loss value for the uniform distribution is slightly higher, at 0.077, whereas the final loss value for the normal distribution is 0.071. Notably, the uniform distribution demonstrates a faster initial reduction in loss, indicating more aggressive exploration in the early stages of training. In contrast, the normal distribution maintains a consistently lower overall loss curve, suggesting a more optimized and stable learning process throughout.
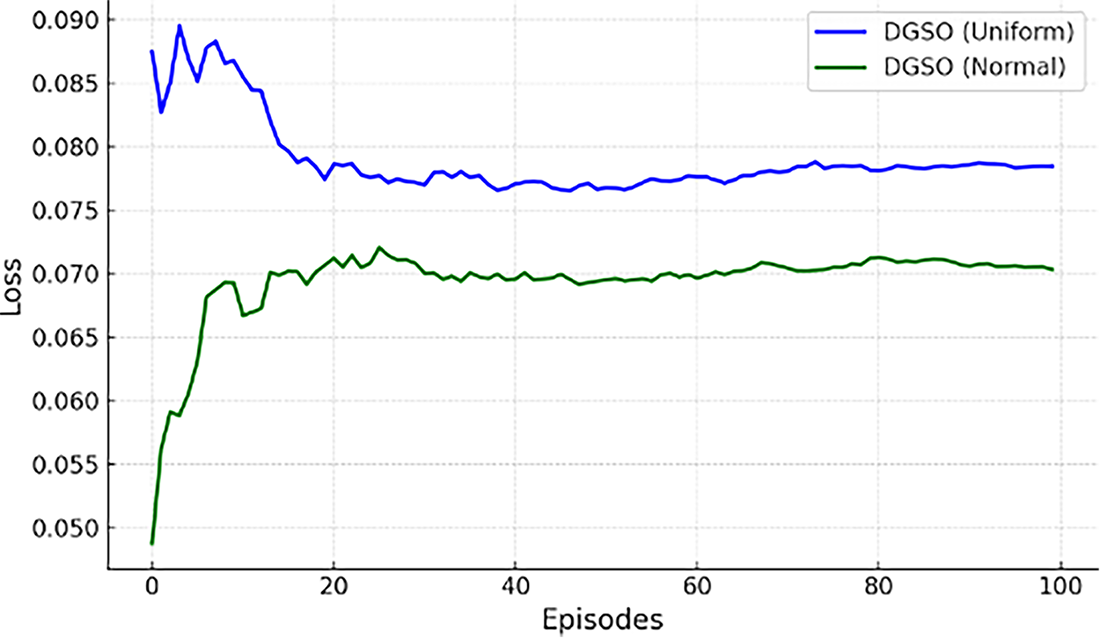
Figure 5: Average training loss over episodes for DGSO with uniform and normal distributions
Table 3 shows the performance summary of the proposed DGSO model for both uniform and normal distributions. The DGSO (normal) configuration presents superior performance, achieving the lowest training loss compared to DGSO (uniform). It indicates more efficient learning and better model convergence. Moreover, DGSO (normal) yields a higher average reward compared to DGSO (uniform), suggesting improved decision-making. Additionally, the standard deviation of the rewards remains constant for both configurations, indicating consistent performance throughout the training episodes. Furthermore, the final epsilon for the DGSO (normal) is lower, indicating that the agent transitions confidently from exploration to exploitation.

In larger and more complex networks, the deployment of the proposed DGSO framework is a critical consideration. The increasing number of agents increases the computational and memory requirements. This system supports decentralized training and execution, allowing agents to learn policies and coordinate in congested regions. The parallel processing feature enhances scalability, thereby reducing the load on centralized computation. The Q-learning component further improves generalization among similar states, handling the dimensionality issues. The multi-agent feature of the proposed DGSO frameworks shows a resilient potential for real-time traffic environments. Reinforcement learning, edge computing, and IoT infrastructure allow the system to operate across a large transportation network. Data collected from various sensors, vehicular communication, and automated traffic signals can be processed at low-edge servers. Real-time decision making can be achieved with minimal computational overhead and reduced delays. The model’s ability to learn optimal policies helps mitigate congestion in random traffic conditions.
The performance improvements of the proposed framework was conducted using statistical testing. The average reward and training losses were compared by employing a two-sample t-test for both the uniform and normal configurations. Results reveal that DGSO (normal) outperforms DGSO (uniform) in terms of average reward and training loss. It demonstrates that the performance enhancement is not due to random variation but rather to the stochastic game optimization model, which further highlights the effectiveness of the proposed framework.
Table 4 presents a detailed comparative analysis between the baseline model and the proposed study. This comparison highlights the various models using stochastic optimization and game theory approaches. Specifically, the proposed DGSO approach outperforms the other approaches in terms of average travel time, average waiting time, congestion control, and average training loss.
This research advances intelligent traffic management (ITM) by proposing an innovative framework that integrates Deep Q-learning, Game Theory, and Stochastic Optimization (DGSO) to address complex traffic scenarios. The framework leverages IoT infrastructure to enable real-time traffic monitoring and dynamic decision-making across multiple intersections. To address the inherent uncertainties in traffic behavior, both uniform and normal distribution techniques are employed, enhancing the model’s adaptability and effectiveness. The DQL agent is trained on uniformly distributed traffic scenarios, utilizing exploration and exploitation rates to implement the epsilon-greedy policy. A normal distribution is employed to guide action selection and reward calculation. The game-theoretic approach is applied at the intersection, modeling them as players following probabilistic distributions for key features. Experimental results validate the effectiveness of our proposed framework, showing significant improvements, including reduced congestion and shorter travel times. This research represents an important step forward in developing more efficient, sustainable, and responsive urban transportation systems. Future work focuses on enhancing the scalability and effectiveness of the framework in complex traffic networks. Real-world sensor data and edge intelligence will improve the practicality and applicability of the model.
Acknowledgement: The author extends her appreciation to the Deanship of Scientific Research at King Khalid University for funding this research through the Large Group Research Project under grant number RGP2/324/46.
Funding Statement: The author extends her appreciation to the Deanship of Scientific Research at King Khalid University for funding this research through the Large Group Research Project under grant number RGP2/324/46.
Availability of Data and Materials: Not applicable. This article does not involve data availability, and this section is not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The author declares no conflicts of interest to report regarding the present study.
References
1. Nallaperuma D, Nawaratne R, Bandaragoda T, Adikari A, Nguyen S, Kempitiya T, et al. Online incremental machine learning platform for big data-driven smart traffic management. IEEE Trans Intell Transp Syst. 2019;20(12):4679–90. doi:10.1109/TITS.2019.2924883. [Google Scholar] [CrossRef]
2. Lee S, Kim Y, Kahng H, Lee SK, Chung S, Cheong T, et al. Intelligent traffic control for autonomous vehicle systems based on machine learning. Expert Syst Appl. 2020;144(1):113074. doi:10.1016/j.eswa.2019.113074. [Google Scholar] [CrossRef]
3. Masood F, Ahmad J, Al Mazroa A, Alasbali N, Alazeb A, Alshehri MS. Multi IRS-aided low-carbon power management for green communication in 6G smart agriculture using deep game theory. Comput Intell. 2025;41(1):e70022. doi:10.1111/coin.70022. [Google Scholar] [CrossRef]
4. Modi Y, Teli R, Mehta A, Shah K, Shah M. A comprehensive review on intelligent traffic management using machine learning algorithms. Innov Infrastruct Solut. 2022;7(1):128. doi:10.1007/s41062-021-00718-3. [Google Scholar] [CrossRef]
5. Nigam N, Singh DP, Choudhary J. A review of different components of the intelligent traffic management system (ITMS). Symmetry. 2023;15(3):583. doi:10.3390/sym15030583. [Google Scholar] [CrossRef]
6. Masood F, Khan WU, Jan SU, Ahmad J. AI-enabled traffic control prioritization in software-defined IoT networks for smart agriculture. Sensors. 2023;23(19):8218. doi:10.3390/s23198218. [Google Scholar] [PubMed] [CrossRef]
7. Djenouri Y, Belhadi A, Srivastava G, Lin JCW. Hybrid graph convolution neural network and branch-and-bound optimization for traffic flow forecasting. Future Generat Comput Syst. 2023;139(9):100–8. doi:10.1016/j.future.2022.09.018. [Google Scholar] [CrossRef]
8. Aouedi O, Piamrat K, Parrein B. Intelligent traffic management in next-generation networks. Fut Inter. 2022;14(2):44. doi:10.3390/fi14020044. [Google Scholar] [CrossRef]
9. Atassi R, Sharma A. Intelligent traffic management using IoT and machine learning. J Intell Syst Inter Things. 2023;8(2):8–19. doi:10.54216/JISIoT.080201. [Google Scholar] [CrossRef]
10. Reza S, Oliveira HS, Machado JJ, Tavares JMR. Urban safety: an image-processing and deep-learning-based intelligent traffic management and control system. Sensors. 2021;21(22):7705. doi:10.3390/s21227705. [Google Scholar] [PubMed] [CrossRef]
11. Saleem M, Abbas S, Ghazal TM, Khan MA, Sahawneh N, Ahmad M. Smart cities: fusion-based intelligent traffic congestion control system for vehicular networks using machine learning techniques. Egypt Inform J. 2022;23(3):417–26. doi:10.1016/j.eij.2022.03.003. [Google Scholar] [CrossRef]
12. Ferdowsi A, Eldosouky A, Saad W. Interdependence-aware game-theoretic framework for secure intelligent transportation systems. IEEE Internet Things J. 2021;8(22):16395–405. doi:10.1109/JIOT.2020.3020899. [Google Scholar] [CrossRef]
13. Chandra R, Manocha D. Gameplan: game-theoretic multi-agent planning with human drivers at intersections, roundabouts, and merging. IEEE Robot Autom Lett. 2022;7(2):2676–83. doi:10.1109/LRA.2022.3144516. [Google Scholar] [CrossRef]
14. Qin Z, Ji A, Sun Z, Wu G, Hao P, Liao X. Game theoretic application to intersection management: a literature review. IEEE Trans Intell Vehicles. 2025;10(4):2589–607. doi:10.1109/tiv.2024.3379986. [Google Scholar] [CrossRef]
15. Park B, Yun I, Ahn K. Stochastic optimization for sustainable traffic signal control. Int J Sustain Transport. 2009;3(4):263–84. doi:10.1080/15568310802091053. [Google Scholar] [CrossRef]
16. Jin J, Ma X, Kosonen I. A stochastic optimization framework for road traffic controls based on evolutionary algorithms and traffic simulation. Adv Eng Softw. 2017;114(5):348–60. doi:10.1016/j.advengsoft.2017.08.005. [Google Scholar] [CrossRef]
17. Nama M, Nath A, Bechra N, Bhatia J, Tanwar S, Chaturvedi M, et al. Machine learning-based traffic scheduling techniques for intelligent transportation system: opportunities and challenges. Int J Commun Syst. 2021;34(9):e4814. doi:10.1002/dac.4814. [Google Scholar] [CrossRef]
18. Gangwani D, Gangwani P. Applications of machine learning and artificial intelligence in intelligent transportation system: a review. In: Applications of Artificial Intelligence and Machine Learning: Select Proceedings of ICAAAIML. Singapore: Springer; 2020. p. 203–16. doi:10.1007/978-981-16-3067-5_16. [Google Scholar] [CrossRef]
19. Zhang R, Mao J, Wang H, Li B, Cheng X, Yang L. A survey on federated learning in intelligent transportation systems. IEEE Trans Intell Vehicles. 2025;10(5):3043–59. doi:10.1109/tiv.2024.3446319. [Google Scholar] [CrossRef]
20. Alruban A, Mengash HA, Eltahir MM, Almalki NS, Mahmud A, Assiri M. Artificial hummingbird optimization algorithm with hierarchical deep learning for traffic management in intelligent transportation systems. IEEE Access. 2024;12:17596–603. doi:10.1109/ACCESS.2023.3349032. [Google Scholar] [CrossRef]
21. Yang P, Chen Z, Su G, Lei H, Wang B. Enhancing traffic flow monitoring with machine learning integration on cloud data warehousing. Appl Computat Eng. 2024;77(1):238–44. doi:10.54254/2755-2721/77/2024MA0058. [Google Scholar] [CrossRef]
22. Li Y, Niu W, Tian Y, Chen T, Xie Z, Wu Y, et al. Multiagent reinforcement learning-based signal planning for resisting congestion attack in green transportation. IEEE Transact Green Communicat Netw. 2022;6(3):1448–58. doi:10.1109/TGCN.2022.3162649. [Google Scholar] [CrossRef]
23. AlEisa HN, Alrowais F, Allafi R, Almalki NS, Faqih R, Marzouk R, et al. Transforming transportation: safe and secure vehicular communication and anomaly detection with intelligent cyber-physical system and deep learning. IEEE Transact Consum Elect. 2023;70(1):1736–46. doi:10.1109/TCE.2023.3325827. [Google Scholar] [CrossRef]
24. Dui H, Zhang S, Liu M, Dong X, Bai G. IoT-enabled real-time traffic monitoring and control management for intelligent transportation systems. IEEE Int Things J. 2024;11(9):15842–54. doi:10.1109/JIOT.2024.3351908. [Google Scholar] [CrossRef]
25. Huang Z, Sheng Z, Ma C, Chen S. Human as AI mentor: enhanced human-in-the-loop reinforcement learning for safe and efficient autonomous driving. Commun Transp Res. 2024;4:100127. doi:10.1016/j.commtr.2024.100127. [Google Scholar] [CrossRef]
26. Trabelsi Z, Ali M, Qayyum T. Fuzzy-based task offloading in internet of vehicles (iov) edge computing for latency-sensitive applications. Internet Things. 2024;28(3):101392. doi:10.1016/j.iot.2024.101392. [Google Scholar] [CrossRef]
27. Zhang H, Liang H, Hong X, Yao Y, Lin B, Zhao D. DRL-based resource allocation game with influence of review information for vehicular edge computing systems. IEEE Trans Veh Technol. 2024 Jul;73(7):9591–603. doi:10.1109/tvt.2024.3367657. [Google Scholar] [CrossRef]
28. Zhu Y, He Z, Li G. A bi-hierarchical game-theoretic approach for network-wide traffic signal control using trip-based data. IEEE Trans on Intell Transp Syst. 2022;23(9):15408–19. doi:10.1109/TITS.2022.3140511. [Google Scholar] [CrossRef]
29. Li W, Qiu F, Li L, Zhang Y, Wang K. Simulation of vehicle interaction behavior in merging scenarios: a deep maximum entropy-inverse reinforcement learning method combined with game theory. IEEE Trans Intell Veh. 2023;9(1):1079–93. doi:10.1109/TIV.2023.3323138. [Google Scholar] [CrossRef]
30. Liang J, Ma M, Tan X. GaDQN-IDS: a novel self-adaptive IDS for VANETs based on Bayesian game theory and deep reinforcement learning. IEEE Trans Intell Transp Syst. 2021;23(8):12724–37. doi:10.1109/TITS.2021.3117028. [Google Scholar] [CrossRef]
31. Wang X, Garg S, Lin H, Kaddoum G, Hu J, Hassan MM. Heterogeneous blockchain and AI-driven hierarchical trust evaluation for 5G-enabled intelligent transportation systems. IEEE Trans Intell Transp Syst. 2021;24(2):2074–83. doi:10.1109/TITS.2021.3129417. [Google Scholar] [CrossRef]
32. Deng X, Wang L, Gui J, Jiang P, Chen X, Zeng F, et al. A review of 6G autonomous intelligent transportation systems: mechanisms, applications and challenges. J Syst Archit. 2023;142(3):102929. doi:10.1016/j.sysarc.2023.102929. [Google Scholar] [CrossRef]
33. Said Y, Alassaf Y, Saidani T, Ghodhbani R, Rhaiem OB, Alalawi AA. Context-aware feature extraction network for high-precision UAV-based vehicle detection in urban environments. Comput Mater Contin. 2024;81:4349–70. doi:10.32604/cmc.2024.058903. [Google Scholar] [CrossRef]
34. Karri C, Machado JJ, Tavares JMR, Jain DK, Dannana S, Gottapu SK, et al. Recent technology advancements in smart city management: a review. Comput Mater Contin. 2024;81(3):3617–63. doi:10.32604/cmc.2024.058461. [Google Scholar] [CrossRef]
35. Sharif A, Sharif I, Saleem MA, Khan MA, Alhaisoni M, Nawaz M, et al. Traffic management in internet of vehicles using improved ant colony optimization. Comput Mater Contin. 2023;75(3):5379–93. doi:10.32604/cmc.2023.034413. [Google Scholar] [CrossRef]
36. Umair MB, Iqbal Z, Bilal M, Nebhen J, Almohamad TA, Mehmood RM. An efficient internet traffic classification system using deep learning for IoT. Comput Mater Contin. 2021;71(1):407–22. doi:10.32604/cmc.2022.020727. [Google Scholar] [CrossRef]
37. Masood F, Khan WU, Ullah K, Khan A, Alghamedy FH, Aljuaid H. A hybrid CNN-LSTM random forest model for dysgraphia classification from hand-written characters with uniform/normal distribution. Appl Sci. 2023;13(7):4275. doi:10.3390/app13074275. [Google Scholar] [CrossRef]
38. Masood F, Khan MA, Alshehri MS, Ghaban W, Saeed F, Albarakati HM, et al. AI-based wireless sensor IoT networks for energy-efficient consumer electronics using stochastic optimization. IEEE Trans Consum Electr. 2024;70(4):6855–62. doi:10.1109/TCE.2024.3416035. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF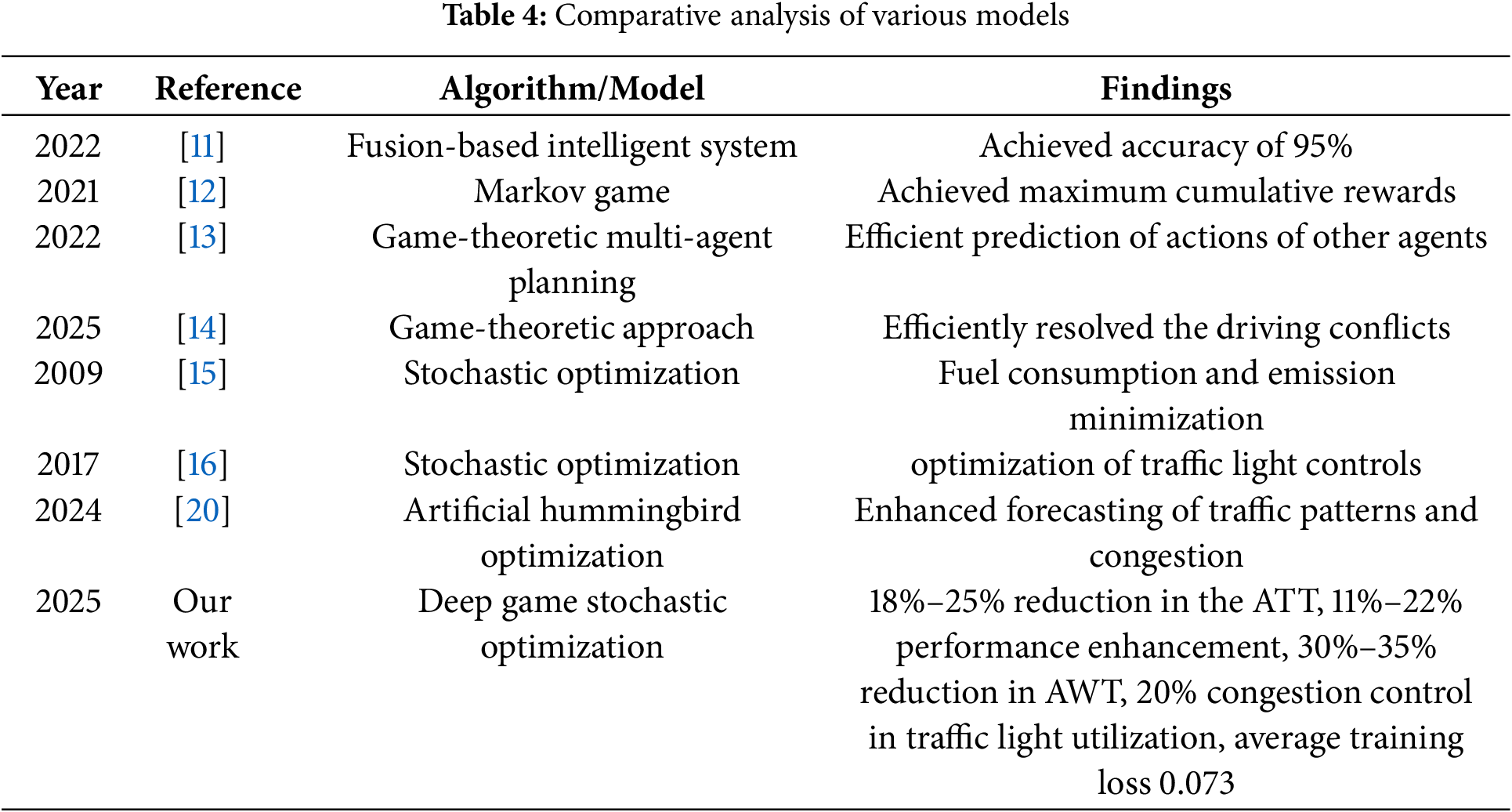
 Downloads
Downloads
 Citation Tools
Citation Tools