ISTIRDA: An Efficient Data Availability Sampling Scheme for Lightweight Nodes in Blockchain

1  Introduction

Blockchain’s decentralization, immutability, transparency, and traceability have driven impact across finance [1–3], supply chains [4–6], healthcare [7–9], and digital identity [10–13], enabling more efficient, secure, and auditable systems [14]. Nevertheless, scalability remains a primary barrier [15]: Ethereum processes about 60 transactions per second [16], whereas conventional payment rails sustain roughly 1700 TPS and peak near 24,000. The proliferation of decentralized applications (dApps) aggravates congestion and confirmation delays [17,18], reinforcing the urgency of scalable designs for broad adoption.

The use of lightweight nodes [19,20] is key to blockchain scalability. By storing only block headers, they cut storage and computation costs, lowering the participation barrier and promoting decentralization [21]. But without full block data, they cannot directly verify transactions and thus rely on a secure data-availability mechanism. We focus on public blockchains, where full and lightweight nodes coexist and decentralization hinges on the participation of resource-constrained clients. We assume an open, adversarial peer-to-peer setting (e.g., Ethereum-like networks), where lightweight nodes cannot trust arbitrary relays and instead depend on cryptographic data-availability guarantees. This defines our threat model and performance goals, and differentiates our work from permissioned or consortium settings.

Data availability sampling (DAS) [22] is a core cryptographic technique used to resolve the security and performance trade-off in blockchain. This technique allows light nodes to efficiently verify the availability of all data by randomly sampling a small amount of data. This enables light nodes to ensure network security while maintaining low resource consumption.

However, existing DAS designs face various deployment and performance limitations. Hall-Andersen et al. proposed two constructions of DAS schemes [23]. One construction uses vector commitments combined with succinct non-interactive arguments of knowledge (SNARKs), which is sound but computationally expensive and relies on strong cryptographic assumptions. Another, adopted by Ethereum, uses two-dimensional Reed–Solomon (RS) codes [24] with Kate–Zaverucha–Goldberg (KZG) polynomial commitment scheme [25], offering good performance at the expense of a heavy trusted setup. More recently, Hall-Andersen et al. introduced a DAS scheme called FRIDA [26], which is built on FRI [27], a Fast Reed–Solomon interactive oracle proof of proximity (IOPP). FRIDA does not require trusted setup, but still incurs high constant factor communication costs and uses a fixed code rate that does not adapt well to different data scales [28].

To overcome these limitations, we turn to improvements at the IOPP layer. In particular, our work is inspired by the Shift-to-Improve-Rate (STIR) protocol [29]. STIR improves efficiency by reducing the polynomial degree and code rate through recursion. However, its fixed folding ratio and code rate can lead to redundancy or premature shrinking of the query domain. We therefore develop ISTIR, an improved RS IOPP with adaptive folding and dynamic code-rate adjustment. Building on ISTIR, we design ISTIRDA, a DAS scheme tailored for high-frequency and large-data settings. The main contributions of this work are summarized as follows:

•   This paper presents a DAS that couples recursive RS degree reduction with dynamic code-rate adjustment, restructuring the IOPP to cut communication and accelerate verification—effects most pronounced at large data scales, easing lightweight-node bandwidth pressure.

•   This paper proposes an adaptive folding method that selects the folding ratio and adjusts the code rate of each round based on the data size and security requirements, thereby maintaining efficiency and avoiding redundant communication. After 16 MB, ISTIRDA is faster than FRIDA in verification speed, and the gap will become larger and larger as the data size increases.

•   This paper provides formal security under standard assumptions and a prototype evaluation: at D = 128 MB, the proof size of ISTIRDA is 60% smaller and the verification time 25% shorter than FRIDA, with the query complexity, the verification time, and proof size reported.

2  Related Work

2.1 Data Availability and Origin of DAS

Data availability refers to the ability of all participants in a blockchain network to access the data needed to verify transactions and blocks. This characteristic is crucial for maintaining the network’s decentralization and trustlessness, enabling nodes to independently verify the blockchain’s history and state. DAS is a method for verifying data availability without downloading the complete dataset, and is particularly suitable for lightweight nodes with limited storage capacity.

The concept of DAS was first introduced by Al-Bassam et al. [22]. In a DAS scheme, a potentially malicious block proposer encodes the block’s contents into a short commitment com and a larger codeword π using an erasure code. The commitment com is placed in the block header. To verify that the block data is available, lightweight nodes randomly sample a few positions in π. If those samples can be obtained successfully, then with high probability the entire block data is available. Early implementations of this idea discussed DAS only informally [30–32], without precise security definitions or formal proofs. Hall-Andersen et al. [23] addressed this gap by formally defining DAS as a cryptographic primitive and introducing erasure-code commitments as a way to guarantee data availability. They proved that a secure DAS scheme can be built from any erasure-code commitment that meets certain binding and availability properties.

2.2 Existing DAS Protocols

To improve the efficiency of DAS in practice, Hall-Andersen et al. developed the FRIDA [26], which applies the FRI protocol to data availability. FRIDA avoids a trusted setup and achieves communication complexity that grows polylogarithmically with the block size. It was among the first schemes to explicitly integrate an IOPP into a DAS design, demonstrating that the FRI protocol can be adapted for checking data availability.

In parallel, Wagner et al. [33] presented PeerDAS, a scheme intended for integration into Ethereum. PeerDAS uses RS codes in combination with KZG polynomial commitments to enable sampling-based data availability checks for light clients. Their work describes optimizations for selecting random sample columns and verifying the corresponding commitments efficiently.

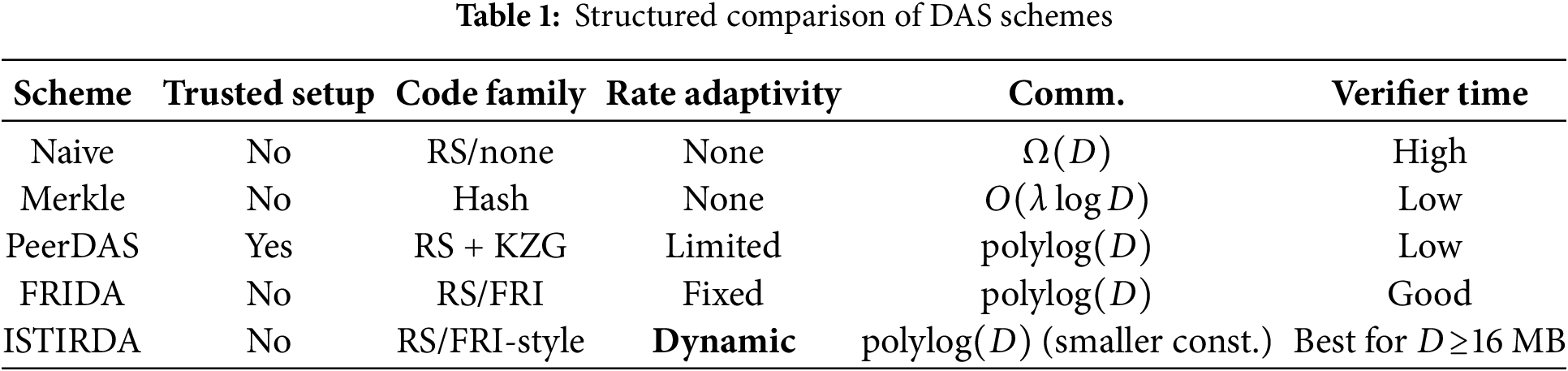
Despite these advances, existing DAS protocols still face scalability challenges. Even schemes with polylogarithmic complexity (such as FRIDA and PeerDAS) incur substantial communication and verification costs when block sizes become very large. Moreover, static choices of code rate or sampling density may be suboptimal under changing network conditions or adaptive adversaries. These limitations motivate ISTIRDA. ISTIRDA introduces adaptive folding and dynamic rate adjustment to tune the coding and sampling process for the data scale and threat model. In effect, ISTIRDA retains the security guarantees of IOPP-based DAS while significantly lowering communication and verification overhead in high-throughput, large-block settings. To highlight the advantages of our proposed scheme, Table 1 presents a comparison of existing schemes.

3  Preliminaries

3.1 Interactive Oracle Proofs of Proximity

Key parameters. Let L⊆Σn be a language over alphabet Σ. For x,y∈Σn, the Hamming distance is d(x,y)=|{i∈[n]:xi≠yi}|. Write d(x,L)=miny∈Ld(x,y) and define the proximity set Lε={x∈Σn: d(x,L)≤εn}.

Completeness. If x∈L, an honest P makes V accept with probability at least 1−δ.

Soundness. If x∉Lε, any P′ convinces V with probability at most γ.

Query complexity. Q=∑i=1rqi≪n.

Fig. 1 depicts the workflow of an IOPP. IOPP is an interactive protocol between a prover P and a verifier V that certifies x∈Lε with sublinear query access to x. The protocol runs for r rounds with per-round query budgets q1,…,qr. In round i, ci=Vi(m1,…,mi−1), mi=Pi(ci,x), Qi⊆[n], |Qi|≤qi, and V reads {xj}j∈Qi and checks consistency with mi. After r rounds V accepts if all checks pass.

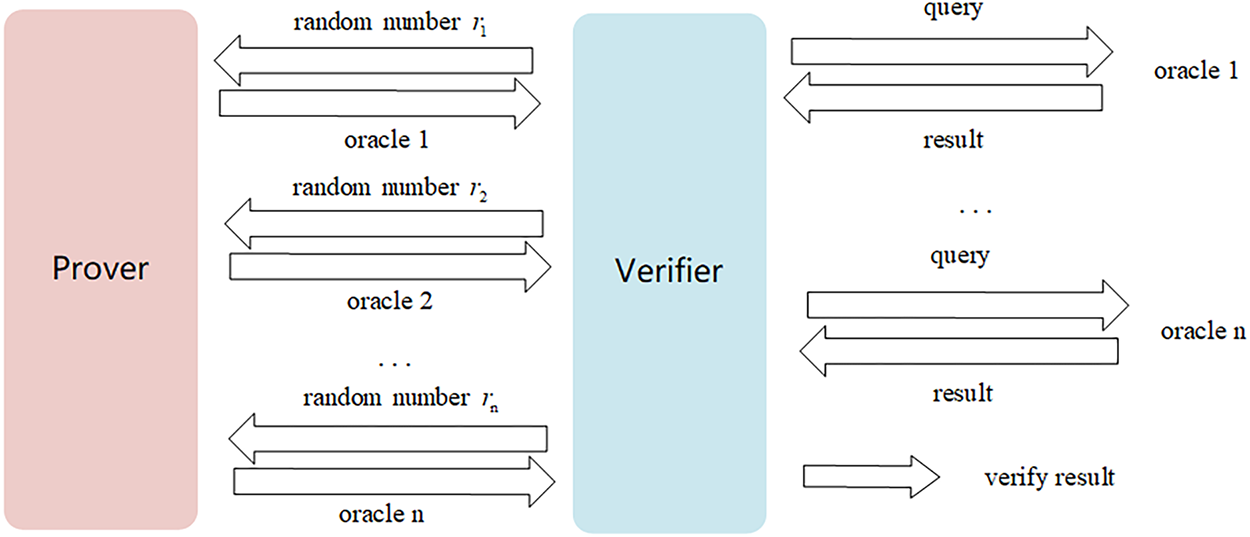
Figure 1: Workflow of an interactive oracle proofs of proximity

In this paper, the sequence {ri} jointly drives adaptive folding and dynamic code-rate adjustment, contracting the evaluation domain over rounds and reducing communication and verification cost so that data availability can be certified with sublinear read access.

3.2 Reed–Solomon Codes

As visualized in Fig. 2, a message polynomial of degree strictly less than k is evaluated at n pairwise distinct field points to produce n coded symbols; because RS codes are maximum distance separable, any k symbols suffice to reconstruct the message.

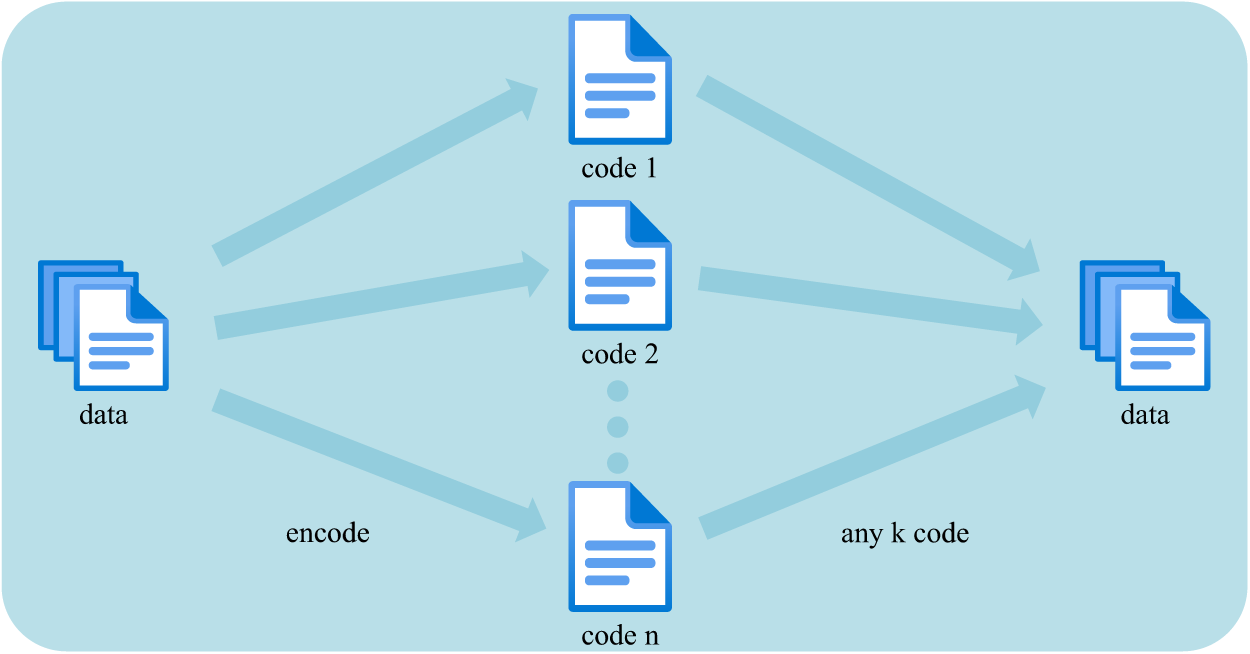
Figure 2: Illustration of RS codes

Let Fq be a finite field and let α1,…,αn∈Fq be pairwise distinct. An (n,k,d) RS code encodes a message polynomial m(x)∈Fq[x] with deg⁡m<k (equivalently, deg⁡m≤k−1) by evaluation: c=(m(α1),…,m(αn)),R=kn. Since RS codes are maximum distance separable, the minimum (Hamming) distance is dmin=n−k+1 and the unique-decoding radius is t=⌊(n−k)/2⌋. Equivalently, encoding admits the cyclic form c(x)=m(x)xn−kmodh(x), for a suitable generator polynomial h(x), where n−k is the number of parity symbols.

For illustration, take n=8 and k=4. Then R=12 and dmin=n−k+1=5, so up to t=⌊(dmin−1)/2⌋=⌊(n−k)/2⌋=2 symbol errors can be uniquely corrected. Increasing redundancy (i.e., decreasing k/n) improves error-correction capability but raises communication and storage costs. In this paper, dynamic code-rate adjustment adapts k/n to balance target robustness against resource budgets, selecting appropriate rates across rounds and data scales.

4  Our Proposed DAS Protocol

4.1 Overview

Fig. 3 illustrates the end-to-end flow of the proposed protocol: The original data is first Reed-Solomon encoded to obtain the codeword π, which is then bound to the block header commitment com. This interaction phase then proceeds, progressing by round i. The prover publicly publishes a queryable view πi (derived from π through folding/state transfer). The verifier, comprised of two submodules, V1→tran→V2, collaborates to initiate sparse queries on πi and perform algebraic and cross-round consistency checks under the constraints of the public commitment com. tran is responsible for transferring/contracting the evaluation domain between rounds. Once all checks pass, the extractor extra combines the commitment with the sampled symbols to recover the original data. If any step fails, the data is deemed unusable.

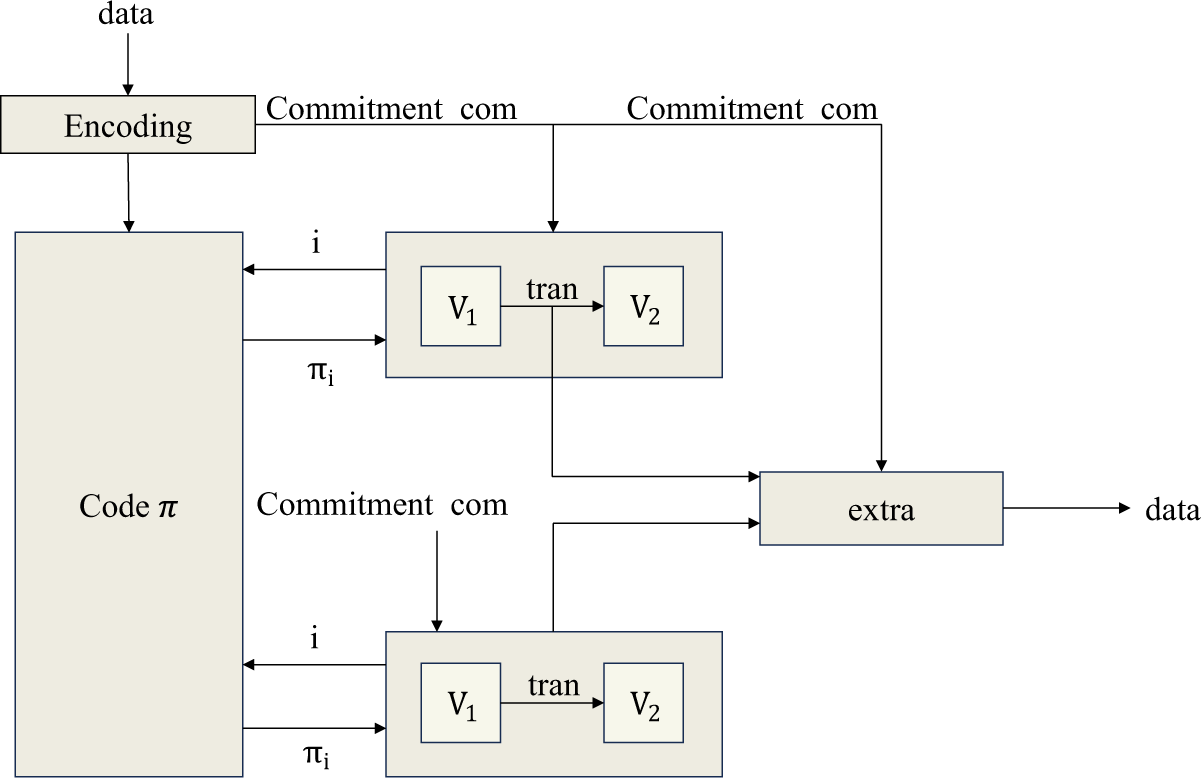
Figure 3: Flow of the data availability scheme

In what follows, we refine STIR [29] by removing redundant steps and introducing two mechanisms: adaptive folding and dynamic code-rate adjustment. Unlike STIR’s fixed folding schedule, ISTIR selects the folding ratio per round based on the remaining evaluation domain, residual polynomial degree, and security/redundancy targets, thereby avoiding late-round over-redundancy and premature domain contraction; this reduces both evaluation points and communication, especially at large data scales. The dynamic code-rate rule re-optimizes the rate at each recursion rather than letting it decay on a fixed schedule, balancing early-round bandwidth savings with stronger late-round soundness. We then analyze the resulting complexity parameters, which serve as performance indicators for ISTIRDA.

We further prove that ISTIR satisfies opening consistency under our model, ensuring transcripts remain well-structured across rounds, either close to a valid codeword or rejected, thus precluding attacks that exploit recursive folding. This security foundation enables the standard transformation from ISTIR to an erasure-code commitment and, following FRIDA’s framework [26], to a complete DAS scheme, which we call ISTIRDA.

4.2 Construction of Our Protocol

Table 2 lists the protocol parameters and definitions. The specific protocol execution steps are as follows.

Initialization. Define function f0:L0→F as a queried oracle. For an honest execution, the condition f0∈RS[F,L0,d0] holds true. Thus, the prover can respond accurately to oracle queries about polynomial f0. This polynomial belongs to the space F<d0[X] and is restricted to domain L0.

Initial Folding Step. The verifier randomly selects a folding scalar r0fold from the field F and transmits it.

Interactive Protocol Rounds. For round index i=1,…,M:

(a)   Prover Polynomial Folding Transmission: The prover computes and submits the folded function hi:Li→F. Under honesty, hi corresponds exactly to the evaluated folding polynomial h^i:=PolyFold(fi−1,ki,ri−1fold) on domain Li.

(b)   The verifier selects random points: ri,1out,…,ri,uout from domain Li outside previously queried positions.

(c)   For these out-of-domain queries: The verifier receives responses βi,1,…,βi,u from the prover. Under honest conditions, each response is computed as βi,j=gi(ri,jout).

(d)   ISTIR-specific Communication: The verifier sends a random scalar riISTIR,comm∈F and points for queries ri,1ISTIR,query,…,ri,tiISTIR,query∈Li−1.

(e)   The prover transmits a prediction message, denoted Filli:{0,1}∗→F, which is defined as a polynomial. In the honest execution, this message is constructed by the prover as Hi={riISTIR,comm,ri,1ISTIR,query,…,ri,tiISTIR,query}, and hi′=PolyQuotient(hi,Hi), and satisfies Filli(ri,jISTIR,query)=hi′(ri,jISTIR,query)(if ri,jISTIR,query∈Li). Additionally, in an honest execution, the prover computes and transmits the polynomial fi′∈F<di[X] whose degree is corrected with respect to the challenge and folding set: fi′=DegCor(di,riISTIR,comm,hi,di−|Hi|). With the current round complete, the protocol transitions into the next phase at index i+1.

Final Round. At this stage, the prover outputs a polynomial ρ∈F<dM[X] consisting of dM coefficients. When acting honestly, the polynomial satisfies ρ^=Fold(fM,kM,rMfold).

Verifier Decision Phase. The verifier executes the following verification steps:

(a)   Iterative Verification Procedure: For i=1,…,M:

i.   For each j∈[ti−1], the verifier evaluates Fold(fi−1,ki−1,ri−1fold)(ri−1,jISTIR,query). To do so, fi−1 must be accessed at all ki−1 evaluation points in Li−1, where the relation xki−1=ri−1,jISTIR,query holds.

ii.   Construct the query set Hi={riISTIR,comm,ri,1ISTIR,query,…,ri,ti−1ISTIR,query}, and define a response mapping Ansi:Hi→F such that Ansi(ri,jISTIR,comm)=βi, and for each j, we have Ansi(ri,jISTIR,query)=Fold(fi−1,ki−1,ri−1fold)(ri−1,jISTIR,query). Based on these assignments, the verifier virtually computes the polynomial hi′=Quotient(hi,Hi,Ansi).

iii.   Define a virtual oracle function fi′: fi′=DegCor(di,riISTIR,comm,hi,di−|Hi|).In practice, any query to fi′ is redirected to hi if the input point is not in Hi, or to Filli otherwise.

(b)   Consistency Check for the Final Folding Step:

i.   Randomly select evaluation points r1final,…,rmfinal∈LM.

ii.   For each j∈[m], verify that ρ(rjfinal)=Fold(fM,kM,rMfold)(rjfinal) holds.

iii.   Cross-validate with Ansi: for all i∈{1,…,M} and x∈Hi∩Li, evaluate hi(x) and ensure hi(x)=Ansi(x).

Algorithm 1 gives the Fiat-Shamir compact form of the interactive protocol described above, where the challenge is derived in the random oracle model via rt=Hash(Tr). Throughout, we define ft≡kt (folding factor/rate), τmin denotes the decoding margin, requiring (1−ρ)/2≥τmin.

Complexity Parameters.

The protocol involves a total of 2M+1 communication rounds. During each round indexed by i∈{1,…,M}, the prover transmits the folded polynomial hi with length |Li|, a set of out-of-domain responses βi,1,…,βi,u, and the oracle function Filli, which contains at most ti−1+u symbols.

In the final stage, the prover additionally sends dM=d/∏j=0Mkj field elements. Hence, the total proof size accumulates to ∑i=1M(|Li|+u+ti−1)+d∏j=0Mkj. On the verifier’s side, it processes t0 queries, each requiring the evaluation of k0 points. Since the same set of k0 points is always accessed as a unit, this allows for treating them as a single composite symbol, and the input query cost in this alphabet is thus t0. For subsequent rounds i∈{1,…,M}, the verifier issues ti queries to the folded polynomial: Fold(fi−1,ki−1,ri−1fold), which necessitates reading ki−1 grouped symbols from the previous function fi−1.

In addition, the verifier may submit up to |Hi|≤ti−1 individual queries to fi. When i=1, these queries directly access terminal data. For i>1, however, fi represents a virtual layer, where each access is rerouted either to a single point evaluation of Filli−1, or to a corresponding position in hi−1, which again involves accessing ki−1 symbols. Because the ki symbols are accessed simultaneously, they can be compressed into a single higher-level symbol. Therefore, the query complexity of the proof string is 2⋅∑i=1Mti.

4.3 Opening Consistency

4.3.1 Defining the Suitable Transcript Set

In an interactive ISTIR protocol, a partial transcript is any prefix of the interaction between the prover and the verifier.

The lucky set consists of partial prover transcripts that satisfy algebraic collision and proximity conditions. In round i the prover sends Hi−1; let Hi∗ be a nearest codeword. If there exists an algebraic hash hρi such that hρi(Hi−1) collides with hρi(Hi∗), and the designated blockwise distance and post-folding proximity conditions hold, then the transcript up to round i is lucky.

Formally, the lucky set contains all partial transcripts for which either hρ(Hi−1)=hρ(Hi−1∗) or the folding step honestly reduces the distance.

Definition 1 (Lucky Set for ISTIR). Define the unique decoding radius as δ∗=(1−ρ)/2. The collection of partial prover transcripts referred to as the lucky set is given by Lucky=LuckyColl∪LuckyDist, with the components defined by the following steps:

A partial transcript of the form (H0,ρ1,…,Hi−1,ρi) is said to belong to LuckyColl if the following two criteria are satisfied simultaneously:

(a)   The symbol vector Hi−1 resides within the decoding radius of the ball around code Ci−1, i.e., δB(Hi−1,Ci−1)≤δ∗, where Hi−1∗∈Ci−1 denotes the nearest codeword.

(b)   There exists some element ui∈Li such that the evaluations of the hash function coincide, i.e., hρi[Hi−1](ui)=hρi[Hi−1∗](ui), while for some ui−1∈Li−1, the deviation is nonzero: q(ui−1)=ui−1⋅(Hi−1(ui−1)−Hi−1∗(ui−1))≠0.

Furthermore, a partial transcript (H0,ρ1,…,Hi−1,ρi,Ci) is classified into LuckyDist if at least one of the following holds: either the previous layer lies exactly on the boundary, i.e., δB(Hi−1,Ci−1)=δ∗, and the hash proximity satisfies δ(hρi[Hi−1],Ci)≤δ∗; or alternatively, the hashed distance is strictly closer, i.e., δ(hρi[Hi−1],Ci)<δB(Hi−1,Ci−1)≤δ∗.

The definition of the bad set is relative to the lucky set. A partial transcript is considered part of the bad set if it is not contained in the lucky set and satisfies certain specific “bad” conditions. These conditions include: the prover’s final oracle message does not match the intended codeword; or in some round, the oracle deviates from its expected codeword; or the oracle is closer to an incorrect codeword and fails to preserve the folding structure.

Definition 2 (Bad Set in ISTIR). The unique decoding radius is given by δ∗=(1−ρ)/2. We define the Bad set of a partial transcription (H0,ρ1,H1,…,ρr,Hr) as the set of all transcripts for which all prover round prefixes are in the Lucky set and which also meet at least one of the following criteria:

(a)   Hr≠Cr.

(b)   there exists some i∈{0,…,r−1} such that δB(Hi,Ci)>δ∗.

(c)   for every i∈{0,…,r−1}, the inequality δB(Hi,Ci)≤δ∗ holds; however, there exists some i∈[r] such that Hi∗≠hρi[Hi−1∗], where Hi∗ denotes the unique nearest codeword of Hi.

4.3.2 Four Fundamental Properties of Opening Consistency

No Luck. We need to show that for every i∈[k] (where k denotes the total number of rounds in ISTIR), and for any subset of 2i−1 elements of partial verifier transcripts T, the probability that their extension reaches the lucky set is bounded.

During every round of interaction, the verifier selects a random challenge, and the prover replies based on that challenge. By analyzing the folding of functions, hash operations, and codeword distances within the ISTIR protocol, we can compute the probability that a transcript is extended into the lucky set under certain conditions. For example, given T=(H0,ρ1,⋯,Hi−1), when the verifier issues a new challenge ρi, we analyze the conditions under which T∘ρi enters the lucky set. This may involve the behavior of function Hi−1 and its nearest codeword under the hash operation, as well as considerations of blockwise and other relevant distance conditions. Ultimately, we derive an upper bound for Prρi[T∘ρi∈Lucky].

Lemma 1 (No Luck). ISTIR satisfies the No Luck property, and ϵ1≤2(F−1)|L0||F|.

Proof. Fix i∈[r], and let T=(H0,ρ1,ρ2…,Hi−1) be a partial verifier transcript. Consider ρi∈F sampled uniformly at random. We aim to upper-bound the probability that T∘ρi∈Lucky. For the LuckyColl case, we claim: Prρi[T∘ρi∈LuckyColl]≤(F−1)|L0||F|. To prove this, we bound the probability over each input ui∈Li causing LuckyCollui. By union bound: Prρi[T∘ρi∈LuckyColl]≤∑ui∈LiPrρi[LuckyCollui].

In what follows, fix an arbitrary ui∈Li and Prρi[LuckyCollui]≤F−1|F|. Since |Li|≤|L0|, this suffices. To define LuckyCollui, as the event that arises precisely when the following two conditions are met: hρi[Hi−1](ui)=hρi[Hi−1∗](ui) and {(ui−1,Hi−1(ui−1))}ui−1∈q−1(ui)≠{(ui−1,Hi−1∗(ui−1))}ui−1∈q−1(ui). This implies two distinct polynomials of degree at most (F−1) agree on a point. Let p,p∗∈FF denote the coefficient vectors of Hi−1 and Hi−1∗ under the hash operation hρi. If we can show p≠p∗, the proof is complete. Let ui−1,1,…,ui−1,F∈Li−1 be the preimage set of ui. Define the associated Vandermonde matrix Vui∈FF×F with j-th row (1,ui−1,j,…,ui−1,jF−1), which is invertible.

Define hui,hui∗∈FF as the evaluation vectors of Hi−1 and Hi−1∗ on ui−1,1,,…,ui−1,F, respectively. If LuckyCollui occurs, then hui≠hui∗, and thus: p=Vui−1hui≠Vui−1hui∗=p∗, so p≠p∗, which contradicts their equality under hρi. Therefore, the probability that this happens for any ui is at most 1/|F| per degree-F collision, and across (F−1) degrees we get the desired bound. This completes the proof. □

Bad is Rejected. Suppose T=(H0,ρ1,⋯,Hk) be a transcript with T∈Bad. Our goal is to show that the probability Prρk+1[VH0,H1,⋯,Hk(ρ1,⋯,Hk,ρk+1)=1] is bounded.

If a transcript T lies in the bad set, then by the definition of Bad, it either contains a final prover message that is inconsistent with the code, or it contains some intermediate round where distance-related conditions or folding operations do not permit switching arguments. We analyze the verifier’s acceptance probability across these cases. For example, if the final prover message does not lie within the code, then according to the ISTIR verification rule, the verifier’s probability of accepting during the final check should be negligibly small. More generally, for the other types of badness, we can analyze the verifier’s decision process and the structure of the code to upper-bound this acceptance probability.

Lemma 2 (Bad is Rejected). ISTIR satisfies the property that any transcript labeled as “Bad” will be rejected by the verifier during the opening consistency process.

Proof. Consider T=(H0,ρ1,H1,…,ρr,Hr) such that T∈Bad, as defined in Definition 2. Let ρr+1=u0←$ℒ0 be a freshly sampled point from the domain ℒ0, and execute the verifier’s procedure on the extended transcript T∘u0. The goal is to establish an upper bound on the probability that the verifier accepts. We proceed by analyzing two scenarios. Firstly, suppose Hr∉𝒞r∘. In this situation, the verifier clearly rejects.

Now consider the case where Hr∈𝒞r∘. According to the definition of Bad, there must exist some index i∈{0,…,r−1} such that the decoding distance exceeds the unique radius, i.e., δB(Hi,Ci)>δ∗, or alternatively, all such distances satisfy δB(Hi,Ci)≤δ∗ for i∈{0,…,r−1}, but there is some i∈[r] for which the decoding of Hi disagrees with the intended image under the hash, i.e., Hi∗≠hρi(Hi−1∗), where Hi∗ is the unique codeword closest to Hi. This completes the proof. □

Suitability is Close. Let T=(H0,ρ1,…,Hk) denote a transcript that satisfies the conditions of both Bad and Lucky sets. We aim to show that H0 (or more generally, the function or codeword involved) is within decoding radius, i.e., δ(C,H0)≤δ∗.

According to the definitions of suitable transcripts, as well as those of Lucky and Bad sets, we analyze how the ISTIR protocol operations in each round affect the distance between functions and codewords. We demonstrate that all the operations composing a suitable transcript induce only limited growth in codeword distance. For example, in a particular round, the folding or hashing operations may only slightly alter the proximity between functions and their corresponding codewords. By combining such structural and distance-preserving properties, and leveraging the metric’s definition, we conclude that the transcript satisfies the “Suitability is Close” property.

Lemma 3 (Suitable is Close). ISTIR satisfies the “suitability is close” of opening consistency.

Proof. Suppose T=(H0,ρ1,…,Hr) is suitable to both the bad set and the lucky set. This suitability implies that T∉Bad, and none of its prefixes belong to Lucky. According to the definitions of Bad and Lucky, we can conclude that δB(Hi,Ci)≤δ∗ holds. Then, by applying Lemma 2 from [26], it follows that δ(Hi,Ci)≤δ∗. In particular, this inequality also holds for H0, which completes the proof. □

Inconsisteny is Rejected. Suppose T=(H0,ρ1,…,Hk) is suitable to both the bad set and the lucky set. Suppose H0∗∈C is the only codeword nearest to H0. If there exists an index j∈Q0(T∘ρk+1) such that H0j≠H0j∗,then it must be shown that the transcript does not satisfy the verifier’s checks: VH0,H1,…,Hk(ρ1,…,Hk,ρk+1)=0. When an inconsistency arises with respect to the unique closest codeword, we analyze the verifier’s decision process and the verification rules of the ISTIR protocol. Since the verifier performs function queries and corresponding checks in each round, we demonstrate—by analyzing these operations and studying the inconsistency detection mechanism—that the verifier is capable of identifying such inconsistencies and rejecting the transcript.

Lemma 4 (Inconsistency is Rejected). ISTIR satisfies the property of inconsistency rejection for opening consistency.

Proof. Recall that suitability implies T∉Bad and none of its prefixes lie in Lucky. Suppose Hi∗∈Ci is the only codeword nearest to Hi. By the definition of Bad, we know Hi∗=hρi[Hi−1∗] for every i∈[r]. Now, consider using ρr+1=u0∈ℒ0 to complete the transcript T. For each i∈[r], let ui be the value queried by the ISTIR verifier, defined by ui=q(ui−1).

Now, there must exist a query location x∈Q0(T∘u0)⊆ℒ0 such that H0∗(x)≠H0(x), and we aim to prove that the completed transcript T∘u0 is rejected by the verifier. Let i0∗ be the smallest index in {0,…,r} such that for a queried location ui′∈ℒi, the verifier’s query yields Hi0(ui0′)≠Hi0∗(ui0′). Notice this index exists since we assumed Hr=Hr∗.

Moreover, since there exists a query x∈Q0(T∘u0)⊆ℒ0 with H0∗(x)≠H0(x), we have i0>0. Such an assumption cannot be reconciled with the fact that T∘u0 is accepted. Then, we get the equality ∀i∈[r],Hi(ui)=Interpolate(ρi,{(ui−1,Hi−1(ui−1))∣ui−1∈q−1(u)}), where Interpolate(z,U) receives z∈F and U⊆F2, putting the unique polynomial P(z) of a degree less than |U| that satisfies P(x)=y for all (x,y)∈U. Therefore, we derive hρi0[Hi0−1](ui0)=Hi0(ui0)=Hi0∗(ui0). Furthermore, we have Hi0∗(ui0)=hρi0[Hi0−1∗(ui0)], because for all i we have Hi0∗=hρi0[Hi0−1∗].Therefore hρi0[Hi0−1](ui0)=hρi0[Hi0−1∗](ui0).

By the definition of the minimal index i0, there must also exist a query location ui0−1′∈ℒi0−1 satisfying q(ui0−1′)=ui0 and Hi0−1(ui0−1′)≠Hi0−1∗(ui0−1′). Therefore, we conclude (H0,ρ1,…,Hi0−1,ρi0)∈LuckyColl⊆Lucky, which contradicts the suitability assumption of transcript T. This completes the proof. □

We formally state the opening consistency property of ISTIR in the next theorem.

Theorem 1 (Opening Consistency of ISTIR). ISTIR satisfies opening consistency relative to the formal definitions of Bad and Lucky provided in Definitions 1 and 2, with error bounds ϵ1 and ϵ2, where ϵ1≤2(F−1)|L0||F| and ϵ2≤1−δ∗.

5  Performance

In this section, we conduct a detailed performance evaluation of ISTIRDA. Our evaluation metrics include communication cost, verification time and Time-to-Confidence (TTC). For communication cost and verification time, the schemes compared include Naive, Merkle, FRIDA, and ISTIRDA. Naive and Merkle are used as baseline schemes. Our experimental environment is built on a single machine, equipped with an Intel Core i7-9750H CPU running at 2.6 GHz, 16 GB of RAM, and a 64-bit Ubuntu 14.04 LTS operating system. We use Python 3.8 for implementation. This setup ensures reliable and accurate results. To illustrate system-level behavior, we measure TTC and compare only FRIDA and ISTIRDA. Because ISTIRDA targets permissionless public blockchains, we evaluate it in a controlled peer-to-peer emulation rather than a live network. One proposer process and 10–460 light-client processes run on a single physical host, and we inject latency and packet loss via Linux tc/netem to approximate wide-area blockchain conditions. This preserves the protocol’s logical one-to-many dissemination while giving us strict control over network parameters. We report TTC, defined as the wall-clock time for a light client to reach the target availability confidence. TTC is measured under fixed protocol and network parameters (block size, sampling rate λ, quorum size k, round-trip latency) while varying only the number of light clients and the packet loss rate. A limitation is that single-host emulation is not a substitute for a geographically distributed deployment or a public testnet; Section 6 outlines ongoing work on multi-host and public Ethereum-compatible testnet evaluation.

5.1 Communication Cost

For different encoded data sizes D=|Data|, we compare the commitment size, encoding size, communication complexity per query, and the total communication complexity of being able to reconstruct the data with probability at least 1−2−40.

Fig. 4 presents a performance comparison among ISTIRDA, FRIDA, and other baseline schemes (Naive, Merkle) under different data sizes (D=1, D=32, D=128 MB), with respect to four evaluation metrics: Commitment size (KB), Encoding (MB), Communication cost per query (KB), and Total communication cost (MB). The communication cost incurred by ISTIRDA exhibits a significant advantage over that of the FRIDA scheme. Specifically, as the data size increases, the communication cost of FRIDA ranges from 1.25 to 2.46 times that of ISTIRDA. This advantage becomes even more pronounced in scenarios with large-scale data.

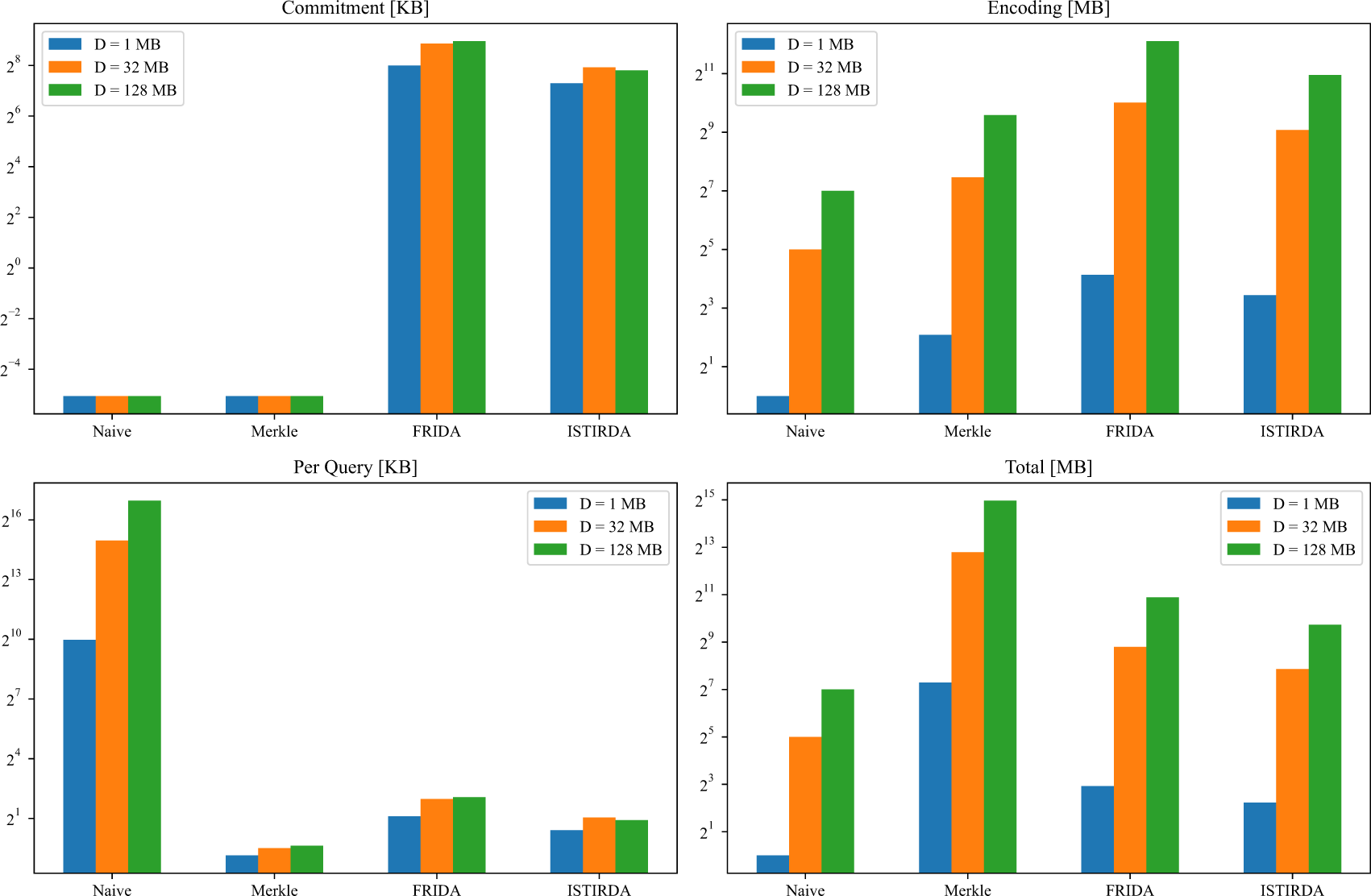
Figure 4: Performance comparison of data availability schemes across multiple metrics and data sizes

5.2 Time Cost

Prover computational time. In our tested dataset, the prover’s computational time for ISTIRDA is slightly longer compared to FRIDA. According to measurements, its slowdown ranges from approximately 0.64 to 0.95 times. As shown in Table 3, when processing data of size |Data|=16 MB, ISTIRDA takes 36.63 s to generate a proof sequentially, whereas FRIDA requires only 29.52 s.

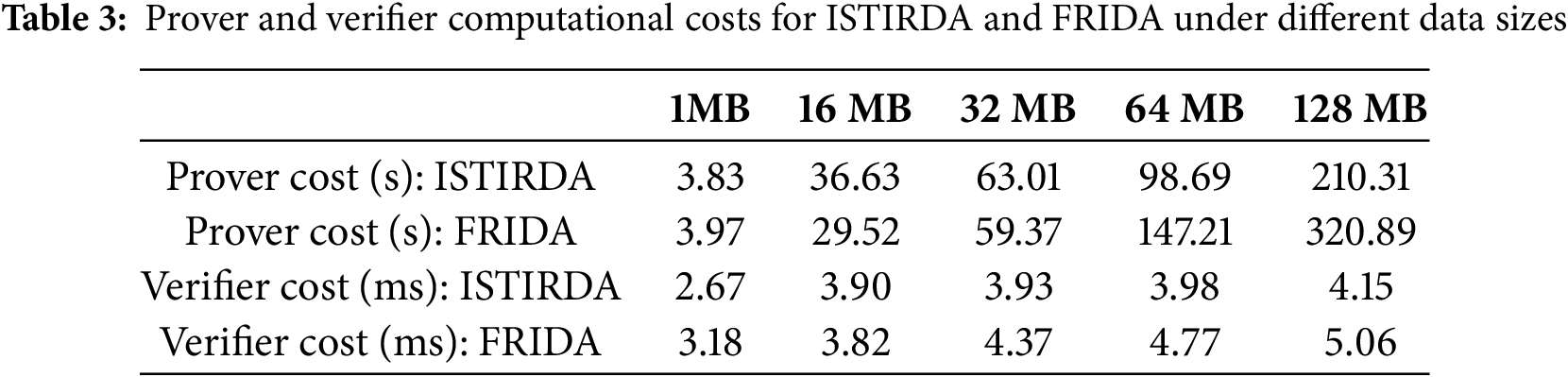
Verifier computational time. The data shows that when the data size D=1 MB, FRIDA’s verification time is shorter than that of ISTIRDA. At D=16 MB, the verification times of both schemes are comparable. However, for data sizes exceeding 16 MB, ISTIRDA’s verification time becomes shorter than FRIDA’s, and the gap continues to widen as the data size increases. The underlying reason for this phenomenon is that when D<16 MB, ISTIRDA’s folding operation introduces computational overhead that outweighs its efficiency advantages. For larger data sizes, the folding operation’s computational overhead increases slowly. Its growth rate is significantly lower than the verifier’s data complexity growth. Therefore, for data sizes exceeding 16 MB, ISTIRDA’s verification time is significantly lower than that of FRIDA.

5.3 Time-to-Confidence

Fig. 5 shows how the time to reach a confident decision varies with node count and packet loss. We observe that as node count and packet loss increase, FRIDA’s TTC rises sharply, indicating that it becomes increasingly sensitive to load concentration. In contrast, ISTIRDA’s TTC curve is much flatter, indicating that its distributed P2P collaborative architecture shares the load and maintains relatively fast convergence to confidence. Thus, under large-scale or degraded network conditions, ISTIRDA exhibits a clear robustness advantage over FRIDA.

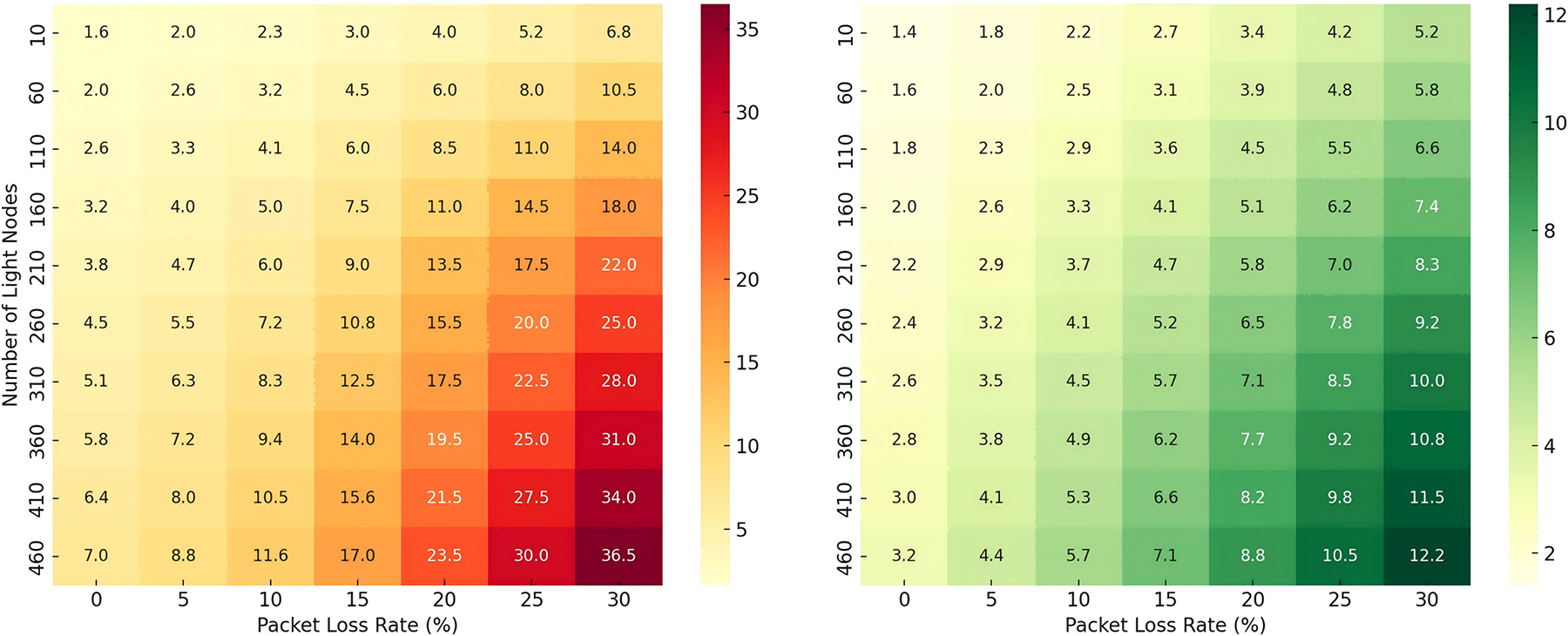
Figure 5: Heatmaps of TTC. The x-axis represents node count, the y-axis represents packet loss rate, and the color gradient indicates the time to reach a confident inference. (a) FRIDA; (b) ISTIRDA

6  Conclusion and Future Work

ISTIRDA improves upon DAS through rate-adaptive RS-IOPP (ISTIR), reducing the evaluation scope without sacrificing reliability. Experiments demonstrate that ISTIRDA significantly reduces communication and verifier time compared to Naive, Merkle, and FRIDA, especially for large data sizes (e.g., >16 MB), while only adding a small amount of prover overhead. TTC results demonstrate that, under matched reliability and typical bandwidth/loss conditions, ISTIRDA reaches the target availability confidence level faster, and its advantage increases with increasing block size or deteriorating network conditions. This makes ISTIRDA a reliable, scalable, and secure choice for lightweight clients.

This work demonstrates both the theoretical soundness and the practical feasibility of ISTIRDA for public blockchains using a controlled peer-to-peer emulation. Future efforts will move beyond single-machine tc/netem simulations toward physical multi-node testbeds and public testnets instrumented for heterogeneous latency, churn, and loss. A prototype light client integrated into an existing blockchain client (e.g., Geth or Nethermind) will enable end-to-end measurements of bandwidth, CPU/memory footprint, TTC, and failure modes under live consensus dynamics. The comparative scope will expand to emerging data availability designs, including 2D erasure-coded DA chains and ML-guided adaptive sampling to dynamically optimize parameters like folding ratio in response to network conditions, thereby maximizing efficiency while preserving soundness. These evaluations will stress-test scalability and robustness across data scales and adversarial conditions. Finally, compatibility with Layer-2 systems will be explored by sampling published batch data and exposing a lightweight API for provers and light clients, with experiments mapping batch size, sampling rate, and security margins to L1/L2 throughput and latency.

Acknowledgement: The authors thank the Key Lab of Education Blockchain and Intelligent Technology, Ministry of Education for supporting this study.

Funding Statement: This work was supported in part by the Research Fund of Key Lab of Education Blockchain and Intelligent Technology, Ministry of Education (EBME25-F-08).

Author Contributions: Conceptualization, Jiaxi Wang; methodology, Jiaxi Wang; validation, Jiaxi Wang; investigation, Wenbo Sun; resources, Ziyuan Zhou; writing—original draft preparation, Jiaxi Wang; writing—review and editing, Shihua Wu; visualization, Jiaxi Wang; supervision, Shan Ji; project administration, Jiang Xu; funding acquisition, Shan Ji. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Chang V, Baudier P, Zhang H, Xu Q, Zhang J, Arami M. How Blockchain can impact financial services—the overview, challenges and recommendations from expert interviewees. Technol Forecast Soc Change. 2020;158(6):120166. doi:10.1016/j.techfore.2020.120166. [Google Scholar] [PubMed] [CrossRef]

2. Patel R, Migliavacca M, Oriani ME. Blockchain in banking and finance: a bibliometric review. Res Int Bus Finance. 2022;62(4–5):101718. doi:10.1016/j.ribaf.2022.101718. [Google Scholar] [CrossRef]

3. Kowalski M, Lee ZWY, Chan TKH. Blockchain technology and trust relationships in trade finance. Technol Forecast Soc Change. 2021;166:120641. doi:10.1016/j.techfore.2021.120641. [Google Scholar] [CrossRef]

4. Han Y, Fang X. Systematic review of adopting blockchain in supply chain management: bibliometric analysis and theme discussion. Intl J Prod Res. 2024;62(3):991–1016. doi:10.1080/00207543.2023.2236241. [Google Scholar] [CrossRef]

5. Surucu-Balci E, Iris Ç, Balci G. Digital information in maritime supply chains with blockchain and cloud platforms: supply chain capabilities, barriers, and research opportunities. Technol Forecast Soc Change. 2024;198(16):122978. doi:10.1016/j.techfore.2023.122978. [Google Scholar] [CrossRef]

6. Ren Y, Leng Y, Qi J, Sharma PK, Wang J, Almakhadmeh Z, et al. Multiple cloud storage mechanism based on blockchain in smart homes. Fut Gener Comput Syst. 2021;115(3):304–13. doi:10.1016/j.future.2020.09.019. [Google Scholar] [CrossRef]

7. Miao J, Wang Z, Wu Z, Ning X, Tiwari P. A blockchain-enabled privacy-preserving authentication management protocol for Internet of Medical Things. Exp Syst Appl. 2024;237(1):121329. doi:10.1016/j.eswa.2023.121329. [Google Scholar] [CrossRef]

8. Samadhiya A, Kumar A, Arturo Garza-Reyes J, Luthra S, del Olmo García F. Unlock the potential: unveiling the untapped possibilities of blockchain technology in revolutionizing Internet of medical things-based environments through systematic review and future research propositions. Inf Sci. 2024;661(14):120140. doi:10.1016/j.ins.2024.120140. [Google Scholar] [CrossRef]

9. Zhou X, Huang W, Liang W, Yan Z, Ma J, Pan Y, et al. Federated distillation and blockchain empowered secure knowledge sharing for Internet of medical Things. Inf Sci. 2024;662(4):120217. doi:10.1016/j.ins.2024.120217. [Google Scholar] [CrossRef]

10. Yan Z, Zhao X, Liu YA, Luo XR. Blockchain-driven decentralized identity management: an interdisciplinary review and research agenda. Inf Manag. 2024;61(7):104026. [Google Scholar]

11. Al Sibahee MA, Abduljabbar ZA, Ngueilbaye A, Luo C, Li J, Huang Y, et al. Blockchain-based authentication schemes in smart environments: a systematic literature review. IEEE Internet Things J. 2024;11(21):34774–96. doi:10.1109/jiot.2024.3422678. [Google Scholar] [CrossRef]

12. Shen H, Wang T, Chen J, Tao Y, Chen F. Blockchain-based batch authentication scheme for internet of vehicles. IEEE Trans Veh Technol. 2024;73(6):7866–79. doi:10.1109/tvt.2024.3355711. [Google Scholar] [CrossRef]

13. Wang C, Wang C, Shen J, Vasilakos AV, Wang B, Wang W. Efficient batch verification and privacy-preserving data aggregation scheme in V2G networks. IEEE Trans Vehicular Technol. 2025;74(8):12029–12041. doi:10.1109/tvt.2025.3552494. [Google Scholar] [CrossRef]

14. Sun L, Wang Y, Ren Y, Xia F. Path signature-based XAI-enabled network time series classification. Sci China Inform Sci. 2024;67(7):170305. doi:10.1007/s11432-023-3978-y. [Google Scholar] [CrossRef]

15. Rebello GAF, Camilo GF, de Souza LAC, Potop-Butucaru M, de Amorim MD, Campista MEM, et al. A survey on blockchain scalability: from hardware to layer-two protocols. IEEE Commun Surv Tutor. 2024;26(4):2411–58. [Google Scholar]

16. Yaish A, Qin K, Zhou L, Zohar A, Gervais A. Speculative denial-of-service attacks in ethereum. In: 33rd USENIX Security Symposium (USENIX Security 24). Philadelphia, PA, USA: USENIX Association; 2024. p. 3531–48. [Google Scholar]

17. Ren Y, Lv Z, Xiong NN, Wang J. HCNCT: a cross-chain interaction scheme for the blockchain-based metaverse. ACM Trans Multimed Comput Commun Appl. 2024;20(7):1–23. doi:10.1145/3594542. [Google Scholar] [CrossRef]

18. Sheng X, Wang C, Shen J, Sattamuthu H, Radhakrishnan N. Verifiable private data access control in consumer electronics for smart cities. IEEE Consumer Electron Magaz. 2025;14(6):100–6. doi:10.1109/mce.2024.3524750. [Google Scholar] [CrossRef]

19. Chatzigiannis P, Baldimtsi F, Chalkias K. SoK: blockchain light clients. In: Eyal I, Garay J, editors. Financial cryptography and data security. Cham, Switzerland: Springer International Publishing; 2022. p. 615–41. doi:10.1007/978-3-031-18283-9_31. [Google Scholar] [CrossRef]

20. Zong J, Wang C, Shen J, Su C, Wang W. ReLAC: revocable and lightweight access control with blockchain for smart consumer electronics. IEEE Trans Consumer Electron. 2024;70(1):3994–4004. doi:10.1109/tce.2023.3279652. [Google Scholar] [CrossRef]

21. Zamyatin A, Avarikioti Z, Perez D, Knottenbelt WJ. TxChain: efficient cryptocurrency light clients via contingent transaction aggregation. In: Garcia-Alfaro J, Navarro-Arribas G, Herrera-Joancomarti J, editors. Data privacy management, cryptocurrencies and blockchain technology. Cham, Switzerland: Springer International Publishing; 2020. p. 269–86. doi:10.1007/978-3-030-66172-4_18. [Google Scholar] [CrossRef]

22. Al-Bassam M, Sonnino A, Buterin V, Khoffi I. Fraud and data availability proofs: detecting invalid blocks in light clients. In: Borisov N, Diaz C, editors. Financial cryptography and data security. Berlin/Heidelberg, Germany: Springer; 2021. p. 279–98. doi:10.1007/978-3-662-64331-0_15. [Google Scholar] [CrossRef]

23. Hall-Andersen M, Simkin M, Wagner B. Foundations of data availability sampling. IACR Commun Cryptol. 2023;1(4):79. doi:10.62056/a09qudhdj. [Google Scholar] [CrossRef]

24. Reed IS, Solomon G. Polynomial codes over certain finite fields. J Soc Ind Appl Math. 1960;8(2):300–4. doi:10.1137/0108018. [Google Scholar] [CrossRef]

25. Kate A, Zaverucha GM, Goldberg I. Constant-size commitments to polynomials and their applications. In: Abe M, editor. ASIACRYPT 2010: Advances in Cryptology. Vol. 6477. Berlin/Heidelberg, Germany: Springer; 2010. p. 177–94. doi: 10.1007/978-3-642-17373-8_11. [Google Scholar] [CrossRef]

26. Hall-Andersen M, Simkin M, Wagner B. FRIDA: data availability sampling from FRI. In: Reyzin L, Stebila D, editors. Advances in Cryptology–CRYPTO 2024. Cham, Switzerland: Springer Nature; 2024. p. 289–324 doi: 10.1007/978-3-031-68391-6_9. [Google Scholar] [CrossRef]

27. Ben-Sasson E, Bentov I, Horesh Y, Riabzev M. Fast reed-solomon interactive oracle proofs of proximity. In: Chatzigiannakis I, Kaklamanis C, Marx D, Sannella D, editors. 45th International Colloquium on Automata, Languages, and Programming (ICALP 2018). Vol. 107. Dagstuhl, Germany: Schloss Dagstuhl-Leibniz-Zentrum für Informatik; 2018. p. 14:1–7. [Google Scholar]

28. Ben-Sasson E, Carmon D, Ishai Y, Kopparty S, Saraf S. Proximity gaps for reed-solomon codes. In: 2020 IEEE 61st Annual Symposium on Foundations of Computer Science (FOCS). Piscataway, NJ, USA: IEEE; 2020. p. 900–9. [Google Scholar]

29. Arnon G, Chiesa A, Fenzi G, Yogev E. STIR: reed-solomon proximity testing with fewer queries. In: Reyzin L, Stebila D, editors. Advances in Cryptology—CRYPTO 2024. Cham, Switzerland: Springer Nature; 2024. p. 380–413. doi: 10.1007/978-3-031-68403-6_12. [Google Scholar] [CrossRef]

30. Yu M, Sahraei S, Li S, Avestimehr S, Kannan S, Viswanath P. Coded merkle tree: solving data availability attacks in blockchains. In: Bonneau J, Heninger N, editors. Financial cryptography and data security. Cham, Switzerland: Springer International Publishing; 2020. p. 114–34. doi:10.1007/978-3-030-51280-4_8. [Google Scholar] [CrossRef]

31. Sheng P, Xue B, Kannan S, Viswanath P. ACeD: scalable data availability oracle. In: Borisov N, Diaz C, editors. Financial cryptography and data security. Berlin/Heidelberg, Germany: Springer; 2021. p. 299–318. doi:10.1007/978-3-662-64331-0_16. [Google Scholar] [CrossRef]

32. Nazirkhanova K, Neu J, Tse D. Information dispersal with provable retrievability for rollups. In: Proceedings of the 4th ACM Conference on Advances in Financial Technologies, AFT ’22. New York, NY, USA: ACM; 2023. p. 180–97. doi:10.1145/3558535.3559778. [Google Scholar] [CrossRef]

33. Wagner B, Zapico A. A documentation of Ethereum’s PeerDAS. Cryptology ePrint Archive. 2024. [Google Scholar]