Optimal Deep Learning Enabled Communication System for Unmanned Aerial Vehicles

1  Introduction

Intelligent communication systems with different simulation and performance evaluations are needed due to the current trend in research opportunities and activities in various fields like beyond 5G (6G) communications, bioinformatics, Internet of Things (IoT), healthcare, social networks, and manufacturing business [1]. Current computation science techniques in intelligent communication systems are giving unexpected solutions and that seems impossible [2,3]. With the use of robots in human intelligence and production, Industry 5.0 presents the concept of collaborative robots (cobots) that is applied for the optimization of reliability and productivity. Industry 5.0 brings a complete structure for automated and linked systems in the independent cars to unmanned aerial vehicles (UAV) with stringent and diverse requirements according to data rate, latency, reliability, and energy efficiency [4]. It is also known as drones perform as a most important part in wide-ranging scenarios that exceed 5G and 6G [5]. Due to the exclusive features of UAVs such as independence, flexibility, and mobility function, they are extensively employed in various applications. For example, some applications of UAVs comprise media production, remote construction, real time surveillance, and package delivery [6].

Some of the specialized UAVs perform several tasks and aimed to develop multi-cluster network. Nevertheless, the UAV transmission system suffers from many complicated crises and issues. The constraint battery is the most important problem in which UAV was utilized for battery recharging or replacement that restrictions the strength of UAV [7]. Energy efficiency (EE) in bits/J is most efficiency metrics from UAV wireless transmission. It can be noted that different from traditional terrestrial system, UAVs needs maximal propulsion power that is crucial for transmission [8]. With the EE, the trajectory technique for UAV transmission is most paramount. Clustering is the most common energy efficient method that is accountable for choosing CH among the nodes. The wide range of tiny-UAV is introduced as set of intelligent swarms. The advancement of Self-organized UAV is an example of current cluster deployment. In event of smart clustering, UAV is pertinent to utilize dynamic connectivity modification.

When the connection is interrupted, UAV self-organizes itself and is re-connected to the network [9]. The newly advanced model is well developed by embedding the camera sensor to provide a chance for UAV fields such as examination, prediction, and observation of active and passive crises at disastrous scenarios such as landslide sites, road collisions, flooding, and fire spots in forest regions. Land cover classification can be determined as a building block of UAV, and it is very challenging to develop the independent process. Furthermore, several researches on UAV succeed to observe certain kinds of objects such as landing transports, areas, landmarks, and users like movement of people. Hence, only some research is included from object prediction as target object prediction has important for large UAV fields [10].

This paper presents a group teaching optimization algorithm with deep learning enabled smart communication system (GTOADL-SCS) technique for UAV networks. The proposed GTOADL-SCS model includes a GTOA based clustering scheme to elect cluster heads (CHs) and organize clusters. Besides, the GTOADL-SCS model develops a fitness function (FF) containing three input parameters as residual energy of UAVs, average neighoring distance, and UAV degree. For classification process, the GTOADL-SCS model applies pre-trained densely connected network (DenseNet201) feature extractor with gated recurrent unit (GRU) classifier. For ensuring the enhanced performance of the GTOADL-SCS model, a widespread simulation analysis is performed.

2  Related Works

Ganesan et al. [11] presented an effective method for the CH selection that heads the other drones in the network. The major goal is to present a powerful solution to select the CHs amongst multiple drones at distinct periods according to the physical constraint of drones. The selected CH performs as decision-maker and allocates task to another drone. Now, a distributed solution is named Bio-Inspired Optimized Leader Election for Multi Drones (BOLD), i.e., depending on two AI-based optimization methods. Pustokhina et al. [12] suggested an energy-effective cluster-based UAV network using deep learning (DL)-based scene classifier model. The presented approach includes a clustering with parameter tuned residual network (C-PTRN) system that works on 2 primary stages i.e., scene classification and cluster formation. At first, the UAV is clustered by T2FL method. Following, the selected CH transmits the captured image to BS. At the next phase, a DL based ResNet50 method using KELM is employed to execute the scene classifier method.

Azevedo et al. [13] presented the power line detection and modelling based LiDAR method. The PL 2 DM, Power Line LiDAR-based Detection and Modelling, is a technique for detecting power lines. It is basis is a scan-by-scan adoptive neighboring minimalist comparison for each point in a point cloud. The presented method can be attained by grouping and matching line segments, with the collinearity property. Pustokhina et al. [14] developed an Energy Effective Neuro-Fuzzy Cluster based Topology Construction using Meta-heuristic Route Planning (EENFC-MRP) approach for UAV. The suggested technique includes EENFC based clustering and MRP based routing process. Additionally, Quantum ALO (QALO) based MRP was employed for selecting an optimum group of paths for inter-cluster UAV transmission.

In [15], suggested an approach incorporating fuzzy inference system (FIS) and fuzzy cc-means (FCM) clustering for the assessment of UAV. The FCM clustering method was employed for determining the cluster, rules are generated for the FIS via expert assessment, and alternate UAV techniques were prioritized. Pedro et al. [16] proposed a safety problem i.e., frequently overlooked because of a lack of solutions and technology to resolve it: collision with non-stationary object. A technique is determined that uses DL technique to resolve the computational problem of real-world collision avoidance with dynamic objects through off-the-shelf commercial vision sensor. Salam et al. [17] projected the localization and clustering of UAVs to the detection of targeted regions in the tomato crops. The localization of UAV is dependent upon the weight of environmental features. The honey bee optimization (HBO) technique was employed to the localization and formation of multi UAV clusters to precisely find the targeted region.

3  The Proposed Model

In this study, a novel GTOADL-SCS approach was established for effective communication and clustering processes for multiple drones. The proposed GTOADL-SCS model encompasses a two stage process namely clustering and classification. Firstly, the GTOA based clustering scheme is performed utilizing a FF containing 3 input parameters like residual energy of UAVs, average neighoring distance, and UAV degree. Next, the GTOADL-SCS model applied DenseNet201 feature extractor with GRU classifier. Fig. 1 illustrates the overall process of GTOADL-SCS model.

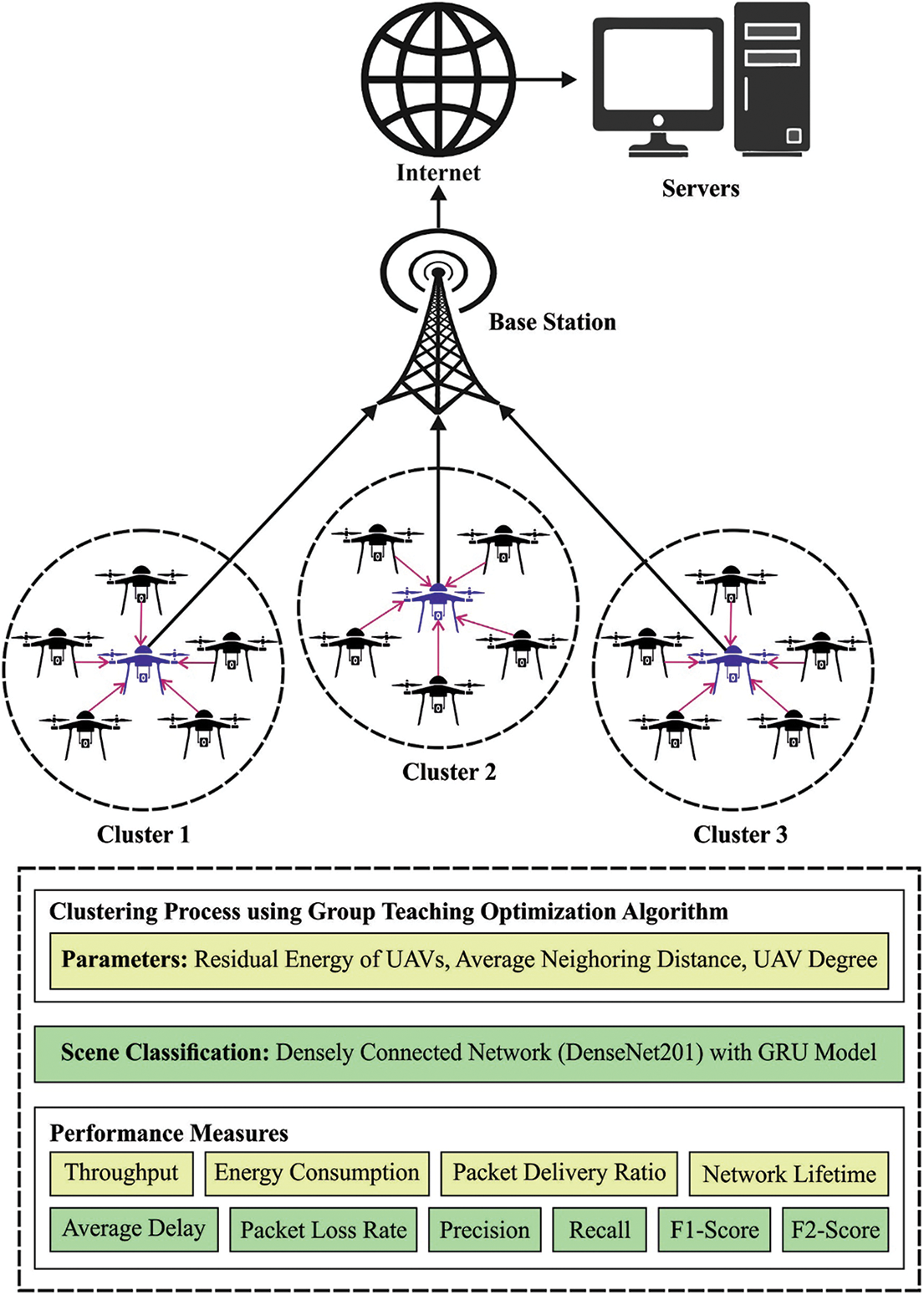
Figure 1: The workflow of GTOADL-SCS model

3.1 Design of GTOA Based Clustering Scheme

Primarily, the GTOADL-SCS technique involves the design of GTOA for clustering the drones or UAVs to effectual communication. GTOA is inspired by a group teaching approach, the acquaintance of class (c) could be improved that is basic model later the proposed algorithm [18].

3.1.1 Ability Grouping

To characterize the knowledge of whole classes, normal distribution function has been applied that is formulated in the following equation.

f(x)=12πδexp(x−μ)2 (1)

whereas χ defines the value where the standard distributing is required. μ signifies the mean and δ implies the SD. In the presented method, every student is classified as to outstanding group and average group, in outstanding group, groups have optimal capability to grasp knowledge, whereas in average group, the group of students having a poor capability to grasp knowledge.

3.1.2 Teacher Phase

Here, students learned in the teacher, i.e., the 2nd rule. In GTOA the teacher makes distinct methods for average and outstanding groups.

3.1.3 Teacher Phase I

The teacher pays more attention to improving the skill of whole classes owing to the better ability of students to accept the knowledge. Students belonging to the outstanding group have higher possibility of improving knowledge as follows.

Xteacher−jt+1=Xjt+a×(Tt−F×(B×Mt+c×Xjt)) (2)

Mt=1N (3)

b+c=1 (4)

Now, N represent the student count, Xj represents the knowledge of students, T shows the teacher knowledge, M stands for the mean group knowledge. F represent Teacher factor, Xteacher−j signifies the knowledge of student j learns in the teacher. b, and c represent arbitrary value within [0, 1].

3.1.4 Teacher Phase II

Due to the weak acceptance knowledge capacity, based on the 2nd rule, the teacher provides great attention to average group. They could attain knowledge by using the following equator

Xieacher,jt+1=Xjt+2×d×(Tt−Xjt) (5)

Here d denotes arbitrary value within [0, 1] . Eq. (6) resolve the problem where a student couldn’t attain knowledge from the teacher phase.

Xieacher,jt+1={Xteacher,j′tf(Xieacher,jt+1)<f(Xjt)Xjt,f(Xteacher,jt+1)≥f(Xjt) (6)

3.1.5 Student Phase

In their free time, student attains knowledge by interacting with classmates, or self-learning. The student phase linked to the 3rd rule by adding student stages I & II.

Xteacher,jt+1={Xteacher,jt+e×(Xteacher,jt+1−Xteacher,kt+1)+g×(Xteacher,jt+1−Xjt), f(Xteacher,jt+1)<f(Xteacher,kt+1)Xieacher,jt−e×(Xieacher,jt+1−Xieacher,kt+1)−g×(Xieacher,jt+1−Xjt), f(Xieacher,jt+1)≥f(Xieacher,kt+1) (7)

Now e & g represent arbitrary value within [0, 1], Xstudent,jt+1 characterizes the knowledge of student i, and Xteacher,jt+1 signifies the knowledge of student j learns in the teacher. Students couldn’t gain knowledge in this phase. He/she can be addressed as follows.

Xjt+1={Xteacher,j′tf(Xieacher,jt+1)<f(Xstudent,jt)Xsiudeni,j′tf(Xteacher,jt+1)≥f(Xsiudeni,jt) (8)

3.1.6 Teacher Allocation Phase

For enhancing knowledge of the student, a decent teacher distribution strategy is significant, and that is described in the 4th rule. Stimulated by the hunting behavior of grey wolves, the top 3 students are elected, as follows.

T={ xfirst′tf(Xfirstt)≤f(Xfirstt+Xsecondt+Xthirdt3)Xfirstt+Xsecondt+Xthirdt3>f(Xfirstt+Xsecondt+Xthirdt3)(9)

Here, Xfirstt,  Xsecond′t and Xthirdt shows the top 3 best students.

In the proposed model, the GTOA uses UAV degree, residual energy (RE), and distance is regarded as in CH selection. The UAV with maximal RE, degree, and minimal distance is selected as CH.

The RE of UAV (x) but interacting k bits to target UAV (y) on a distance d, is described as follows

RE=E−(ET(k,d)+ER(k)) (10)

whereas E signifies the current energy of the UAV and ET indicates the energy used to sense data.

ET(k,d)=kEe+KEad2 (11)

Here Ee represents the energy of electrons and Ea denotes the amplified energy, ER(k) indicates the energy dissipated for receiving information, as follows

ER(k)=kEe (12)

The second parameter for CH selection is average distance (AvgD) to neighboring UAVs. The AvgD represents the average distance value to the UAV to its single hob adjacent UAV, as follows

AvgNBDisti=∑j=1NBi⁡dist(i,nbj)NBi (13)

Here dist(i,nbj) denotes the distance in the UAV to the neighboring jth UAV.

For time sample t, the degree of UAV defines the amount of adjacent nodes that exist in the UAV.

Degx=|N(x)| (14)

Whereas N(x)={ny/dist(x,y)<transrange}x≠y , and dist(x,y) characterizes the distance amongst two UAVs nx and ny , transrange denotes the transmission range of the UAV.

3.2 Process Involved in UAV Image Classification

In order to classify the images captured by UAVs, the GTOADL-SCS technique performs two processes namely DenseNet201 feature extraction and GRU based classification. In transfer learning, the knowledge gained by training on a large dataset with several classes is transported to similar problems via weight sharing [19]. Likewise, the weight is adjusted and trained is shared and utilized with other problems, namely the classification of acral lentiginous melanoma. Transfer learning was widely and successfully employed for distinct applications. The third pretrained module is DenseNet201. DenseNet simplifies the connectivity patterns by guaranteeing data flow among layers than other advanced Deep CNN structures. This uses network potential via feature reuse in place of drawing feature representation ability from deep or wide structures reuse. It needs some parameters when compared to a classical CNN, therefore it is not essential for learning unwanted feature maps. The feature maps in DenseNet are concatenated afterward Dense block that performs as an input for the following dense block. This method comprises four dense blocks and a transition block. The topmost layer containing dense blocks is fine-tuned, and weight is upgraded. Global average pooling layer and four fully connected (FC) layers with ReLU activation are added on top of the pretrained module. At last, a sigmoid layer with two units is utilized as the output layer. DenseNet201 has 201 convolution layers. The finetuning of performed by un-freezing Dense block 4. Global average pooling layer and four fully connected layers with 1024, 512, and 256 units, correspondingly, with ReLU activation, are added on top of the model. Finally, a sigmoid layer with two units is utilized as the output layer.

Once the features are derived by the DenseNet model, they are provided into the GRU approach to classify them into distinct class labels [20]. DNN resolves the limitations of shallow networks and is the robust ability of nonlinear fitting. However, the typical DNN approach does not assume the temporal connections amongst the classification samples are important to loss of data under the classifier. The RNN techniques were established for resolving the problem of time dependency. The RNN makes a feedback link among the hidden layer and thus network is endure the learning data to existing moment and calculate the end outcome of networks with input of current moments. An efficacy of RNN for solving time related problems is estimated from various regions of applications. However, it undergoes in the vanishing gradient procedure resulting from worse convergence of networks and fails for overcoming the effects of long-term dependencies. Many approaches for improving the RNN performance are projected and an extremely utilized network is LSTM [20]. It employs reset as well as update gates to replace the 3 gates from the LSTM method in which the reset gate defines the approach integrates a novel data with present memory and update gate provides the method of storing the current data to existing time step. The basic computational procedure of GRU technique is obtainable in the subsequent.

a) Candidate State

ht=g(Wfhxt+Wrh(ht−1⊙rt)+ϕh) (15)

b) Reset Gate

rt=f(Wfrxt+Wrrht−1+ϕr) (16)

c) Update Gate

zt=f(Wfzxt+Wrzht−1+ϕz) (17)

d) Current State

ht=(1−zt)⊙h~t+zt⊙ht−1 (18)

whereas rt and zt implies the outcome vector of reset as well as update gates at present time step t, but ht and h~t signifies the state and candidate state vector. ϕh∈Rn×1 , ϕr∈Rn×1 , and ϕz∈Rn×1 denotes the bias vector. Wfh∈Rn×m , Wfr∈Rn×m , and Wfz∈Rn×m defines the weighted matrix of feed-forward link. Also, Wrh∈Rn×n , Wrr∈Rn×n , and Wrz∈Rn×n demonstrates the weighted matrix of recurrent link. Mostly, the weighted sharing method was utilized for different time steps t. ⊙ refers the element wise multiplication amongst the vector. g(⋅) and f(⋅) denotes the neuron activation functions, in which g(⋅) and f(⋅) defines the tanh and sigmoid function. Besides, the Adam optimizing was utilized to speed-up the gradient descent from the process of error BP and remove the local optimum problems. Fig. 2 showcases the framework of GRU.

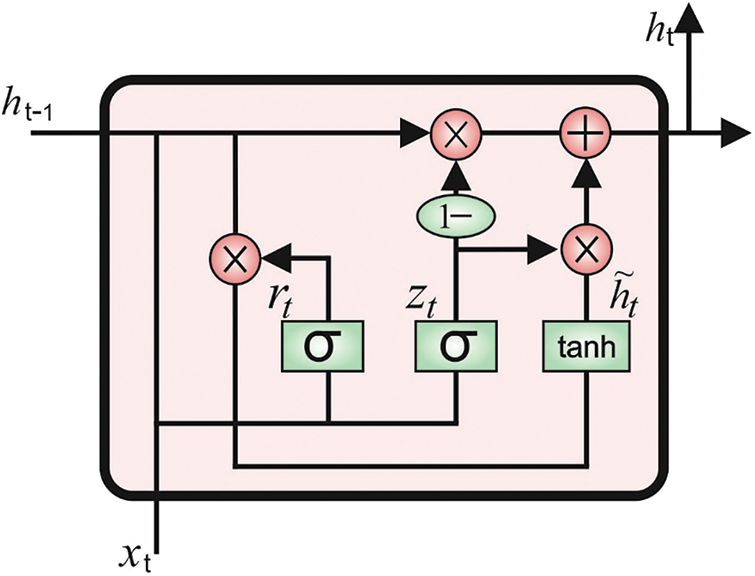
Figure 2: Structure of GRU model

4  Experimental Validation

This section investigates the clustering and classification outcomes of the GTOADL-SCS model. The results are investigated using UCM dataset [21]. The results are examined under distinct number of UAVs. A few sample images are demonstrates in Fig. 3.

Figure 3: Sample UAVs images

Tab. 1 and Fig. 4 assess the throughput (THRP) examination of the GTOADL-SCS model with recent models [22] under several UAVs. The results indicated that the GTOADL-SCS model has showcased maximum THRP over the other models. For instance, with 10 UAVs, the GTOADL-SCS model has provided higher THRP of 96.89 Mbps whereas the EENFC, KHOA, GWOA, and ACOA models have obtained lower THRP of 93.35, 93.79, 93.06, and 87.75 Mbps respectively. Likewise, with 50 UAVs, the GTOADL-SCS model has attained increased THRP of 82.14 Mbps whereas the EENFC, KHOA, GWOA, and ACOA models have offered reduced THRP of 77.72, 69.02, 63.27, and 54.42 Mbps respectively. In addition, with 100 UAVs, the GTOADL-SCS model has reached maximum THRP of 68.43 Mbps whereas the EENFC, KHOA, GWOA, and ACOA models have gained minimal THRP of 65.48, 57.66, 52.35, and 46.45 Mbps respectively.

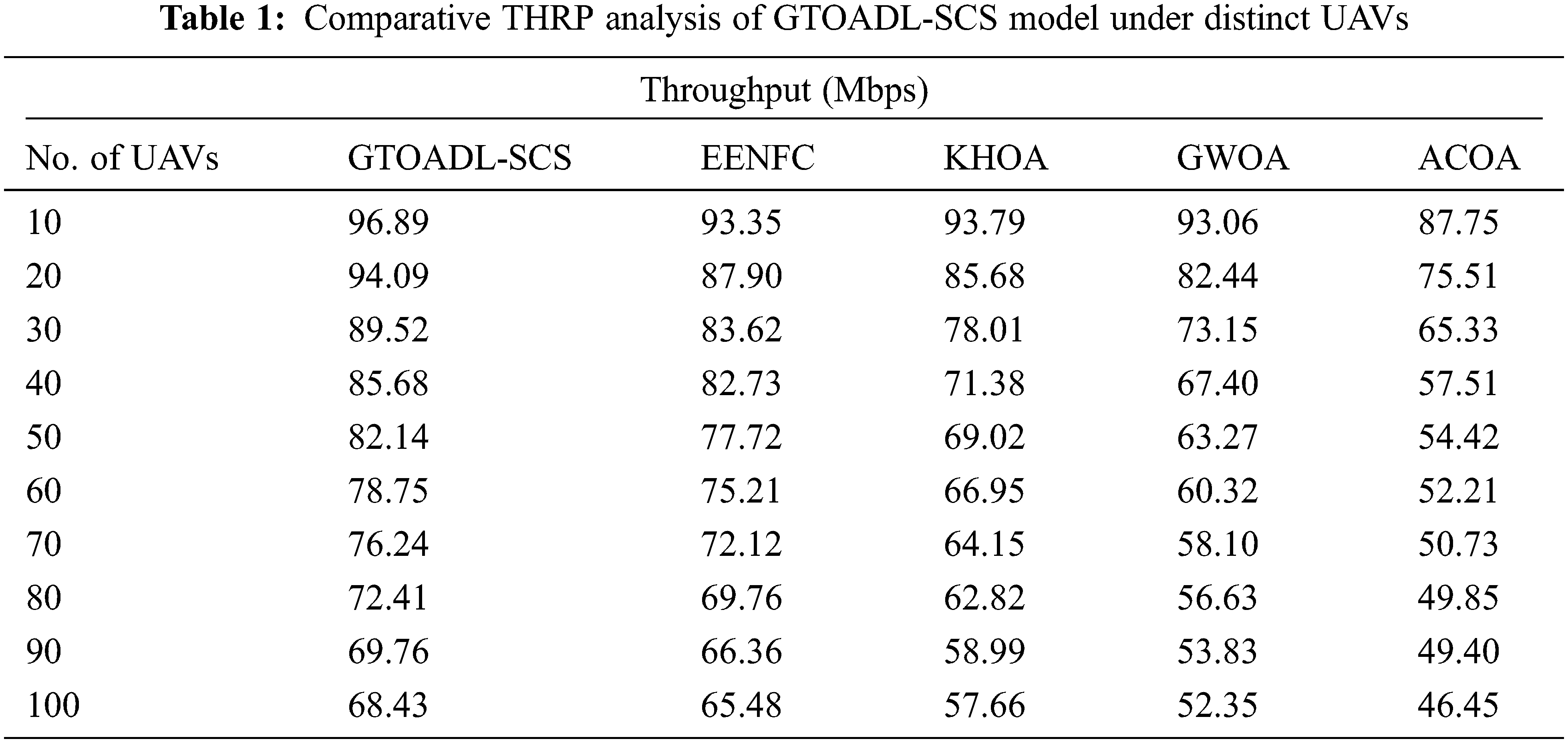
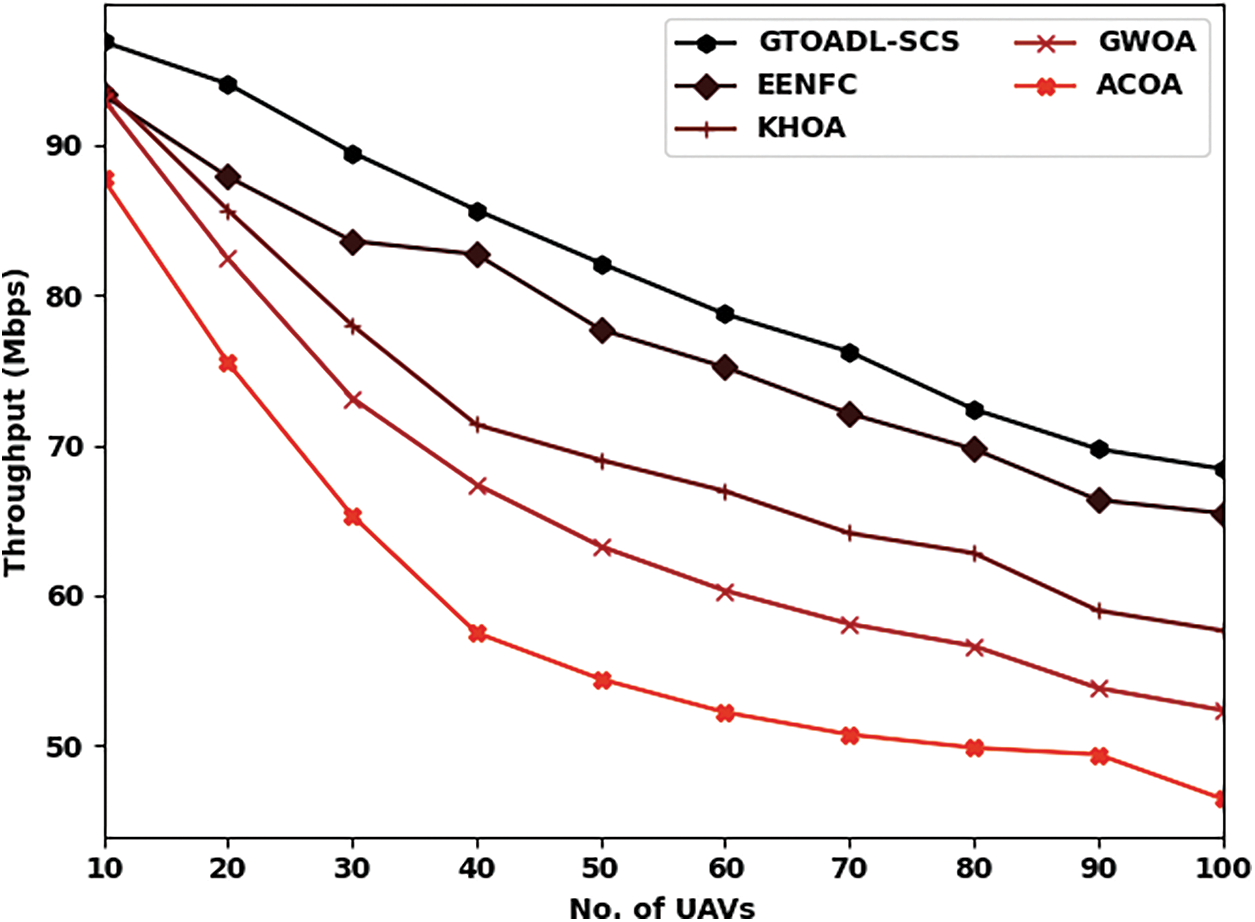
Figure 4: THRP analysis of GTOADL-SCS with recent models

A detailed ECM examination of the GTOADL-SCS model with existing ones are perfomed in Tab. 2 and Fig. 5. The obtained values pointed out the enhanced outcomes of the GTOADL-SCS model with least ECM under all UAVs. For instance, with 10 UAVs, the GTOADL-SCS model has accomplished least ECM of 20.82 mJ whereas the EENFC, KHOA, GWOA, and ACOA models have attained increased ECM of 24.76, 32.06, 41.62, and 48.36 mJ respectively. Along with that, with 50 UAVs, the GTOADL-SCS model has gained reduced ECM of 82.09 mJ whereas the EENFC, KHOA, GWOA, and ACOA models have exhibited improved ECM of 119.18, 157.96, 150.65, and 169.76 mJ respectively. Furthermore, with 100 UAVs, the GTOADL-SCS model has exhibited decreased ECM of 137.73 mJ whereas the EENFC, KHOA, GWOA, and ACOA models have demonstrated enhanced ECM of 187.18, 210.57, 225.40, and 236.64 mJ respectively.

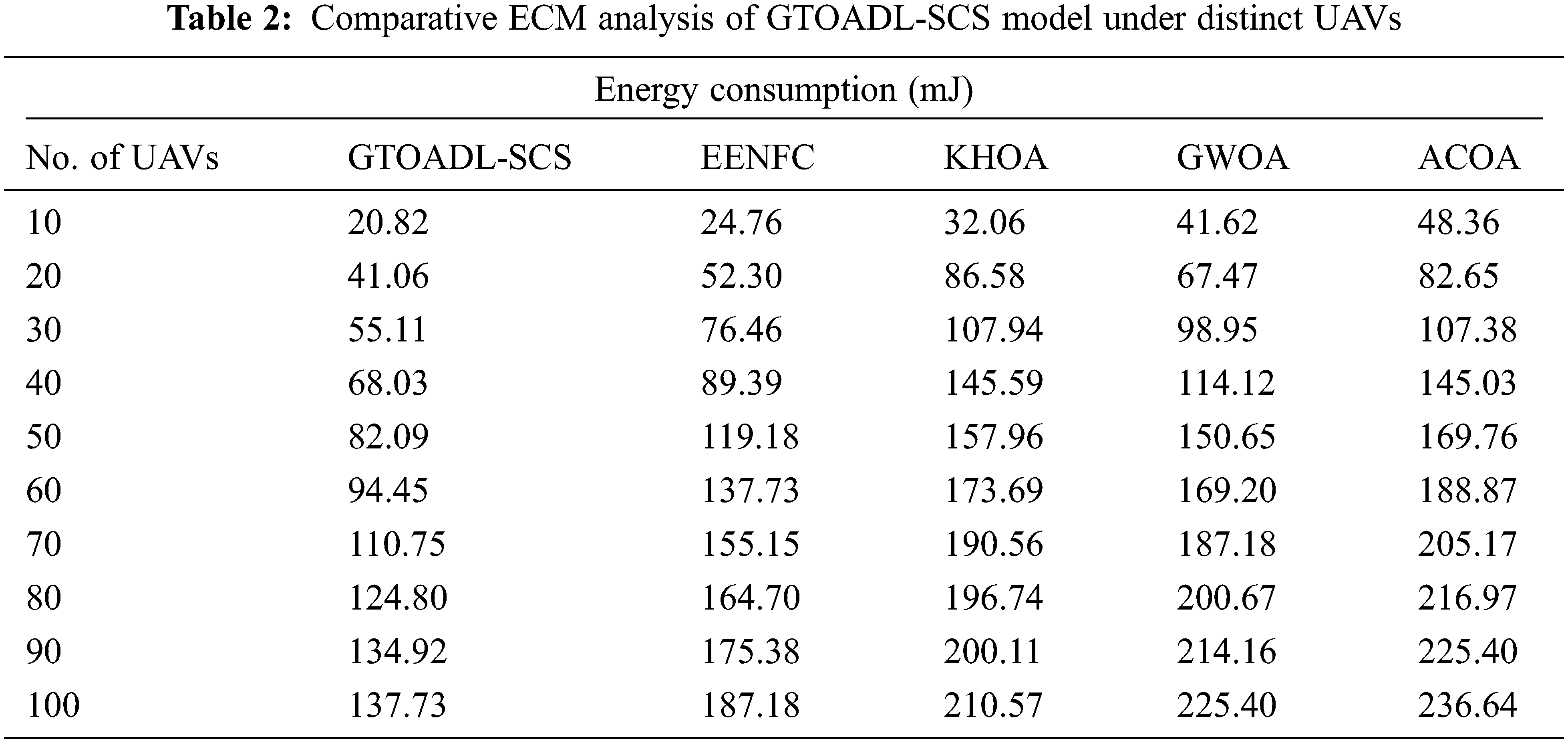
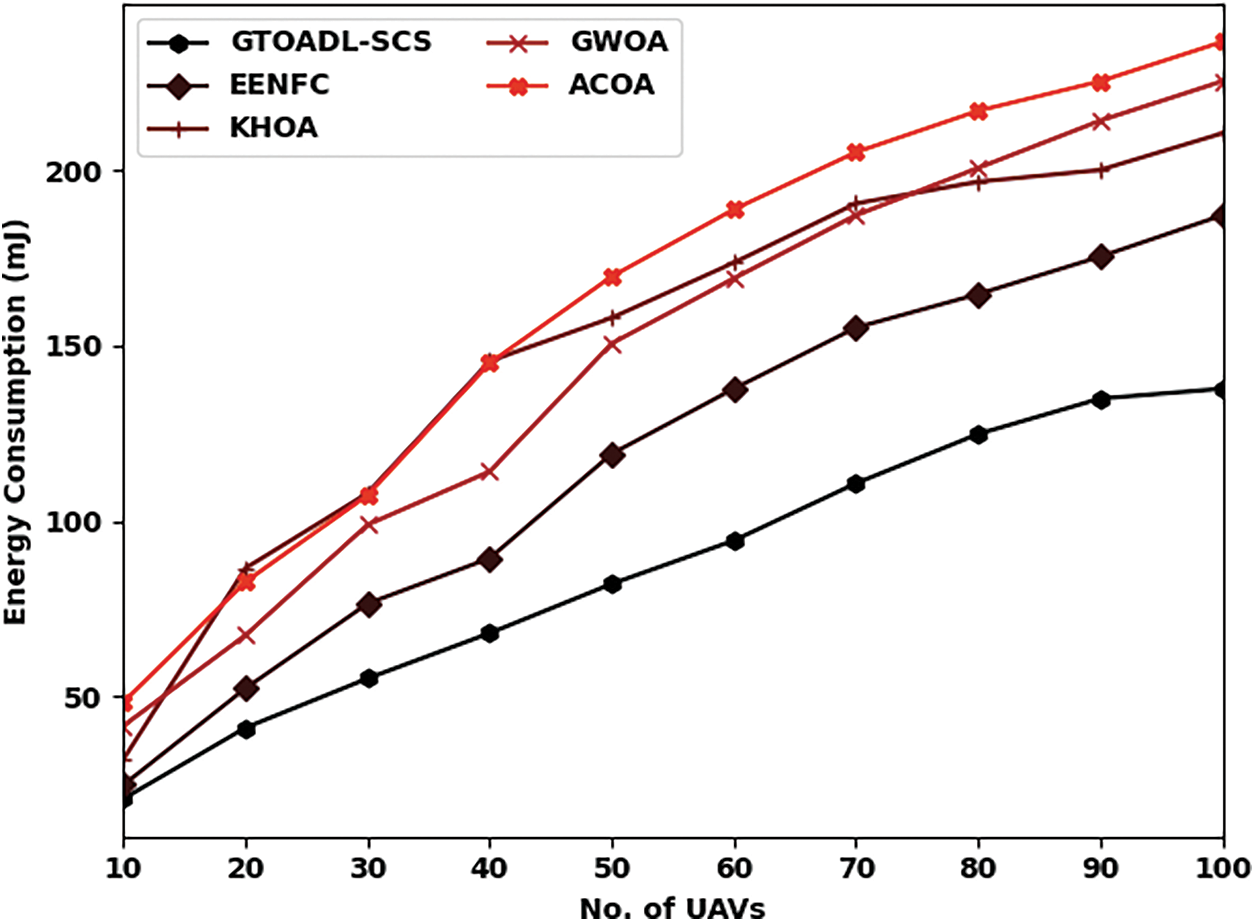
Figure 5: ECM analysis of GTOADL-SCS with recent models

Tab. 3 and Fig. 6 evaluate the network lifetime (NLFT) investigation of the GTOADL-SCS model with recent models under several UAVs. The results designated that the GTOADL-SCS model has showcased supreme NLFT over the other models. For instance, with 10 UAVs, the GTOADL-SCS model has delivered greater NLFT of 5454 rounds whereas the EENFC, KHOA, GWOA, and ACOA models have gained lesser NLFT of 5336, 4905, 4806, and 4505 rounds respectively. Equally, with 50 UAVs, the GTOADL-SCS model has achieved improved NLFT of 4898 rounds whereas the EENFC, KHOA, GWOA, and ACOA models have offered reduced NLFT of 4656, 4407, 4119, and 3701 respectively. In line with, with 100 UAVs, the GTOADL-SCS model has reached maximum NLFT of 3995 rounds whereas the EENFC, KHOA, GWOA, and ACOA models have gained minimal NLFT of 3544, 3282, 3073, and 3027 rounds respectively.

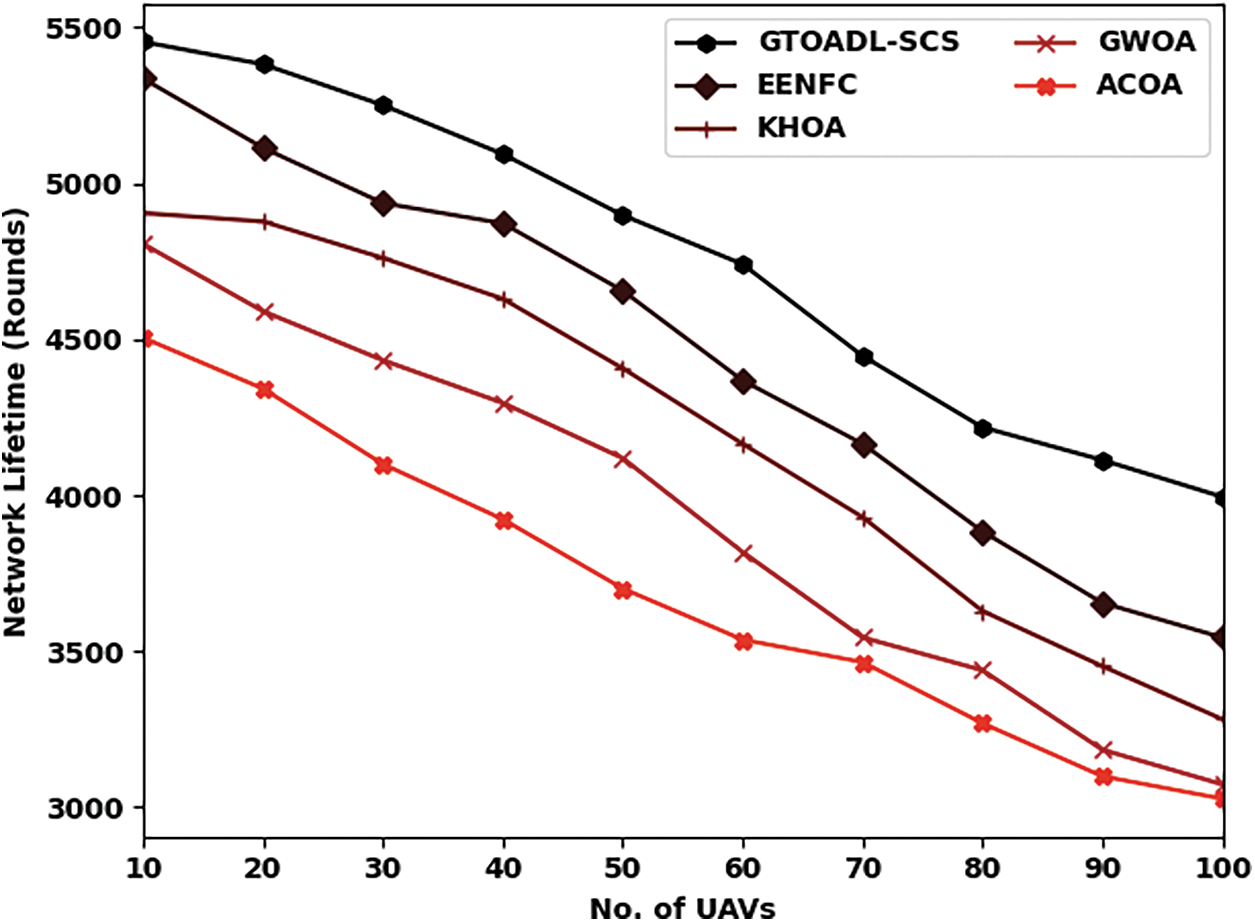
Figure 6: NLFTE analysis of GTOADL-SCS with recent models

Tab. 4 and Fig. 7 measures the comparative packet delivery ratio (PDR) analysis of the GTOADL-SCS model with recent models under numerous UAVs. The results directed that the GTOADL-SCS model has exhibited effective PDR over the other models. For instance, with 10 UAVs, the GTOADL-SCS model has reached improved higher PDR of 92.60% whereas the EENFC, KHOA, GWOA, and ACOA models have resulted to reduced PDR of 87.67%, 86.94%, 86.94%, and 85.46% respectively. Simultaneously, with 50 UAVs, the GTOADL-SCS model has attained increased PDR of 73.64% whereas the EENFC, KHOA, GWOA, and ACOA models have offered recued PDR of 60.60%, 54.20%, 48.54%, and 33.77% respectively. Concurrently, with 100 UAVs, the GTOADL-SCS model has reached improved PDR of 54.69% whereas the EENFC, KHOA, GWOA, and ACOA models have gained reduced PDR of 50.01%, 42.87%, 33.03%, and 23.92% respectively.

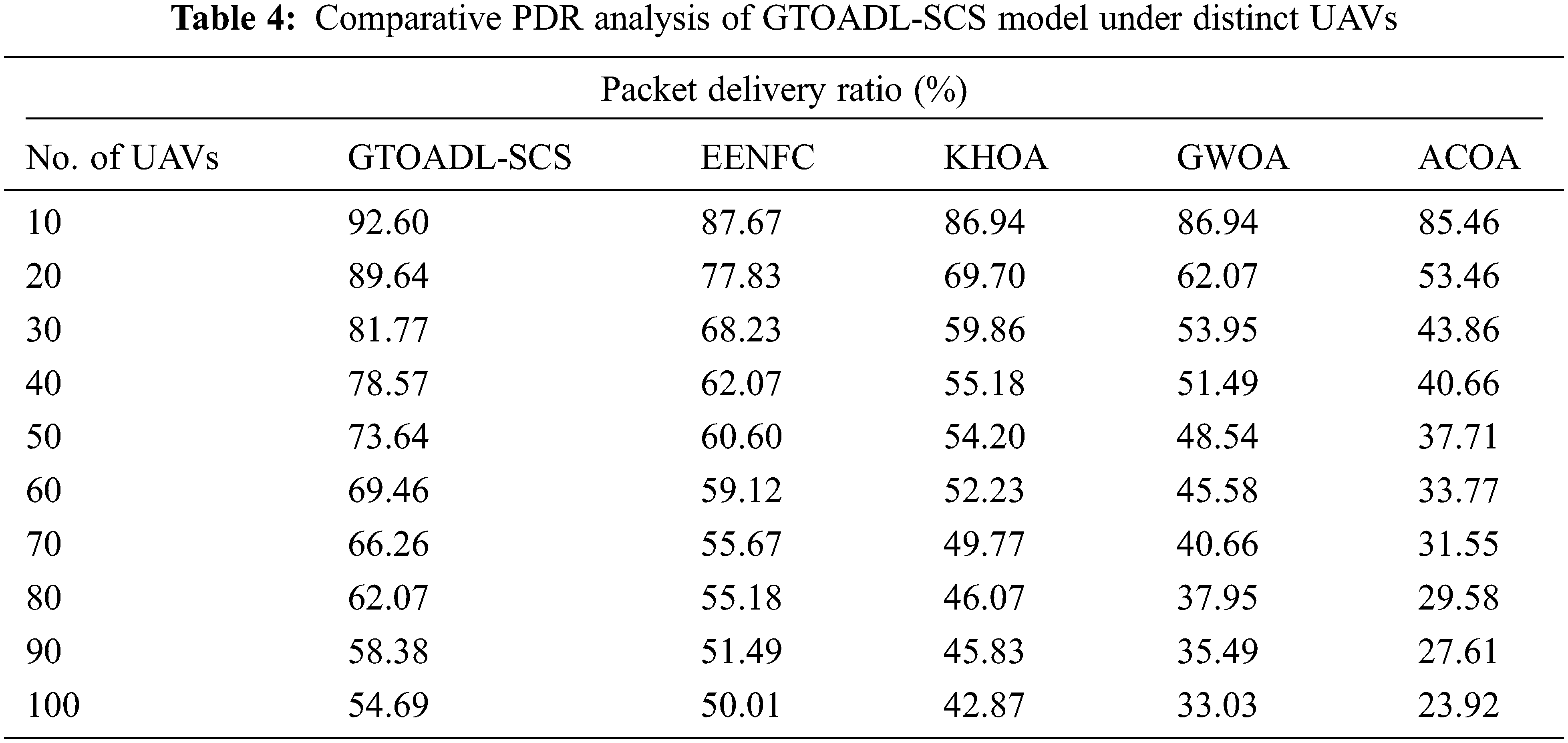
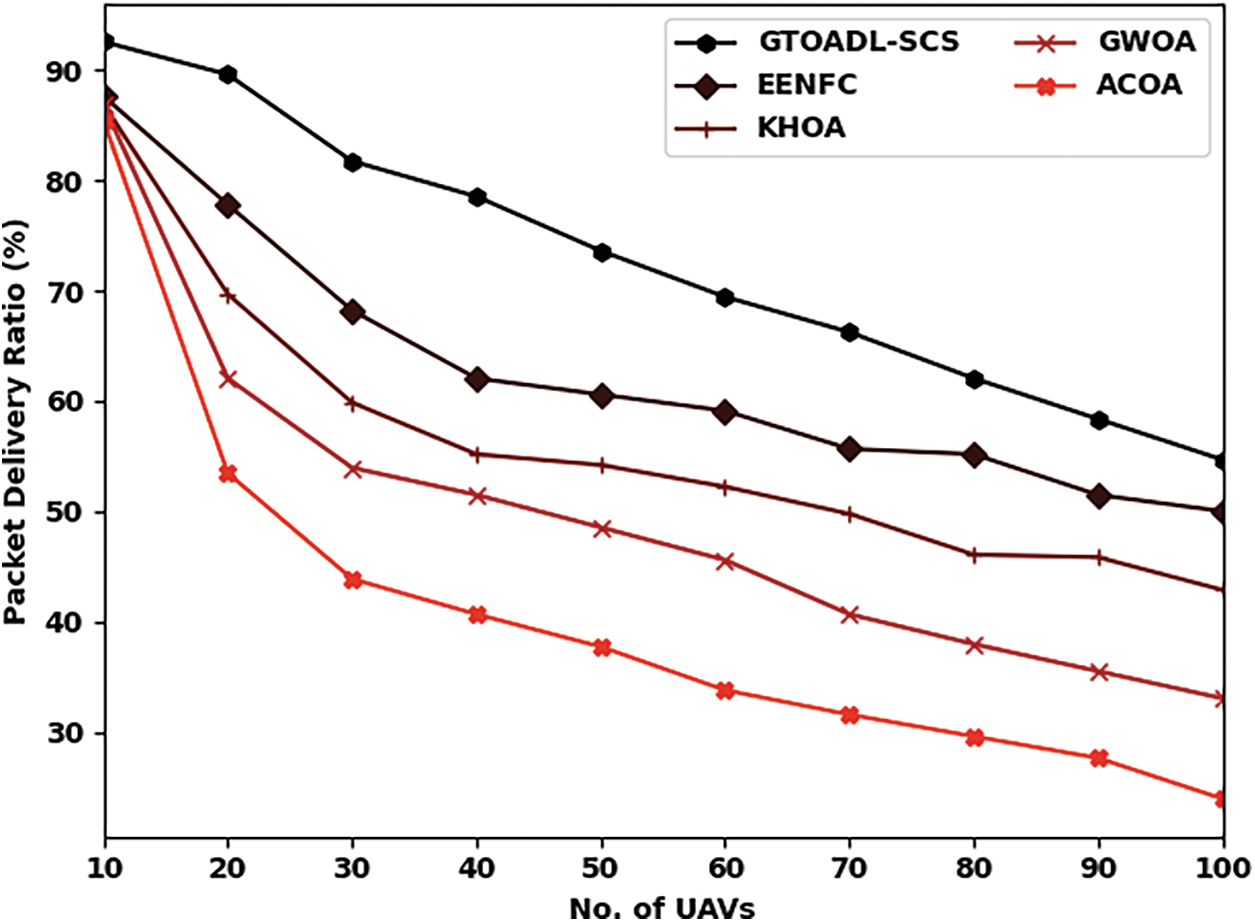
Figure 7: PDR analysis of GTOADL-SCS with recent models

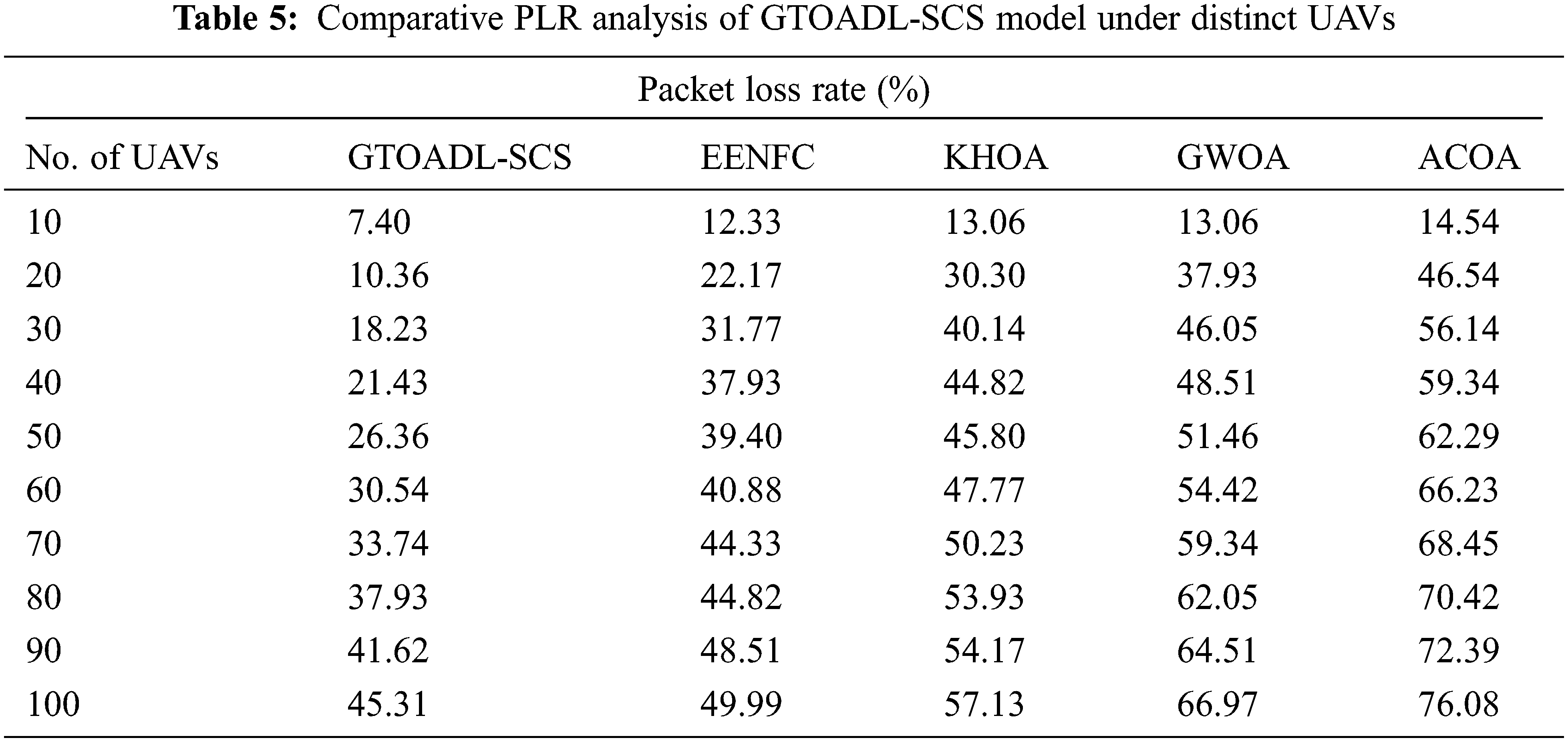
A comprehensive PLR inspection of the GTOADL-SCS model with existing ones are performed in Tab. 5. The gained values pointed out the improved outcomes of the GTOADL-SCS model with least PLR under all UAVs. For instance, with 10 UAVs, the GTOADL-SCS model has presented decreased PLR of 7.40% whereas the EENFC, KHOA, GWOA, and ACOA models have depicted raised PLR of 12.33%, 13.06%, 13.06%, and 14.54% respectively. Eventually, with 50 UAVs, the GTOADL-SCS model has gained reduced PLR of 26.36% whereas the EENFC, KHOA, GWOA, and ACOA models have exhibited improved PLR of 39.40%, 45.80%, 51.46%, and 62.29% respectively. Meanwhile, with 100 UAVs, the GTOADL-SCS model has revealed decreased PLR of 45.31% whereas the EENFC, KHOA, GWOA, and ACOA models have established enhanced PLR of 49.99%, 57.13%, 66.97%, and 76.08%respectively.

5  Conclusion

In this study, a novel GTOADL-SCS approach was established for effective communication and clustering processes for UAV networks. The proposed GTOADL-SCS model encompasses a two stage process namely clustering and classification. Firstly, the GTOA based clustering scheme is performed utilizing a FF containing three input parameters like residual energy of UAVs, average neighoring distance, and UAV degree. Next, the GTOADL-SCS model applied DenseNet201 feature extractor with GRU classifier. For ensuring the enhanced performance of the GTOADL-SCS model, a widespread simulation analysis is performed and the comparative study reported the significant outcomes over the existing approaches. In future, the performance of the GTOADL-SCS approach is extended by utilize of hyperparameter tuning strategies.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP 2/158/43). Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R238), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the ‎Deanship of Scientific Research at Umm Al-Qura University ‎for supporting this work by Grant Code: 22UQU4340237DSR13.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. E. Franklin, “Pixel-and object-based multispectral classification of forest tree species from small unmanned aerial vehicles,” Journal of Unmanned Vehicle Systems, vol. 6, no. 4, pp. 195–211, 2018. [Google Scholar]

 2.  M. Y. Arafat and S. Moh, “A survey on cluster-based routing protocols for unmanned aerial vehicle networks,” IEEE Access, vol. 7, pp. 498–516, 2018. [Google Scholar]

 3.  S. Khan, C. F. Liew, T. Yairi and R. McWilliam, “Unsupervised anomaly detection in unmanned aerial vehicles,” Applied Soft Computing, vol. 83, pp. 105650, 2019. [Google Scholar]

 4.  S. Kunde, E. Palmer and B. Duncan, “Recognizing user proficiency in piloting small unmanned aerial vehicles (sUAV),” IEEE Robotics and Automation Letters, vol. 7, no. 2, pp. 2345–2352, 2022. [Google Scholar]

 5.  M. D. Beyene, “Crop field classification using fusion approach of unmanned aerial vehicle (UAV) and sentinel 2A satellite data: The case of Oda dhawata kebele cluster farmland, Oromia region, Ethiopia,” Doctoral dissertation, Addis Ababa University, 2021. [Google Scholar]

 6.  J. Guo, H. Gao, Z. Liu, F. Huang, J. Zhang et al., “ICRA: An intelligent clustering routing approach for UAV Ad Hoc networks,” IEEE Transactions on Intelligent Transportation System, pp. 1–14, 2022. https://doi.org/10.1109/TITS.2022.3145857. [Google Scholar]

 7.  J. G. E. Flores, S. Sandoval and E. G. Romero, “Unmanned aerial vehicle images in the machine learning for agave detection,” Environmental Science and Pollution Research, 2022. https://doi.org/10.1007/s11356-022-18985-7. [Google Scholar]

 8.  L. Zhang, G. Wang and W. Sun, “Automatic extraction of building geometries based on centroid clustering and contour analysis on oblique images taken by unmanned aerial vehicles,” International Journal of Geographical Information Science, vol. 36, no. 3, pp. 453–475, 2022. [Google Scholar]

 9.  A. Saif, K. Dimyati, K. A. Noordin, G. C. Deepak, N. S. M. Shah et al., “An efficient energy harvesting and optimal clustering technique for sustainable postdisaster emergency communication systems,” IEEE Access, vol. 9, pp. 78188–78202, 2021. [Google Scholar]

10. H. Wu, D. Dai, B. Pang, Z. Wei and X. Wang, “Unmanned aerial vehicle recognition based on clustering by communication with local agents and multiple polarimetric features,” in 2021 IEEE 6th Int. Conf. on Signal and Image Processing (ICSIP), Nanjing, China, pp. 861–865, 2021. [Google Scholar]

11. R. Ganesan, X. M. Raajini, A. Nayyar, P. Sanjeevikumar, E. Hossain et al., “BOLD: Bio-inspired optimized leader election for multiple drones,” Sensors, vol. 20, no. 11, pp. 3134, 2020. [Google Scholar]

12. I. V. Pustokhina, D. A. Pustokhin, P. K. Pareek, D. Gupta, A. Khanna et al., “Energy-efficient cluster-based unmanned aerial vehicle networks with deep learning-based scene classification model,” International Journal of Communication Systems, vol. 34, no. 8, 2021. [Google Scholar]

13. F. Azevedo, A. Dias, J. Almeida, A. Oliveira, A. Ferreira et al., “LiDAR-Based real-time detection and modeling of power lines for unmanned aerial vehicles,” Sensors, vol. 19, no. 8, pp. 1812, 2019. [Google Scholar]

14. I. V. Pustokhina, D. A. Pustokhin, E. L. Lydia, M. Elhoseny and K. Shankar, “Energy efficient neuro-fuzzy cluster based topology construction with metaheuristic route planning algorithm for unmanned aerial vehicles,” Computer Networks, vol. 196, pp. 108214, 2021. [Google Scholar]

15. M. Çolak, İ Kaya, A. Karaşan and M. Erdoğan, “Two-phase multi-expert knowledge approach by using fuzzy clustering and rule-based system for technology evaluation of unmanned aerial vehicles,” Neural Computing and Applications, vol. 34, no. 7, pp. 5479–5495, 2022. [Google Scholar]

16. D. Pedro, J. P. M. Carvalho, J. M. Fonseca and A. Mora, “Collision avoidance on unmanned aerial vehicles using neural network pipelines and flow clustering techniques,” Remote Sensing, vol. 13, no. 13, pp. 2643, 2021. [Google Scholar]

17. A. Salam, Q. Javaid and M. Ahmad, “Bio-inspired cluster–based optimal target identification using multiple unmanned aerial vehicles in smart precision agriculture,” International Journal of Distributed Sensor Networks, vol. 17, no. 7, pp. 155014772110340, 2021. [Google Scholar]

18. Y. Zhang and Z. Jin, “Group teaching optimization algorithm: A novel metaheuristic method for solving global optimization problems,” Expert Systems with Applications, vol. 148, pp. 113246, 2020. [Google Scholar]

19. S. H. Wang and Y. D. Zhang, “DenseNet-201-based deep neural network with composite learning factor and precomputation for multiple sclerosis classification,” ACM Transactions on Multimedia Computing, Communications, and Applications, vol. 16, no. 2s, pp. 1–19, 2020. [Google Scholar]

20. R. Zhao, D. Wang, R. Yan, K. Mao, F. Shen et al., “Machine health monitoring using local feature-based gated recurrent unit networks,” IEEE Transactions on Industrial Electronics, vol. 65, no. 2, pp. 1539–1548, 2018. [Google Scholar]

21. http://weegee.vision.ucmerced.edu/datasets/landuse.html. [Google Scholar]

22. D. K. Jain, Y. Li, M. J. Er, Q. Xin, D. Gupta et al., “Enabling unmanned aerial vehicle borne secure communication with classification framework for industry 5.0,” IEEE Transactions on Industrial Informatics, 2021. https://doi.org/10.1109/TII.2021.3125732. [Google Scholar]