Peak-Average-Power Ratio Techniques for 5G Waveforms Using D-SLM and D-PTS

1  Introduction

Wireless applications play an important role in improving the quality of life in every sector, including education, industry, and healthcare [1]. The demand for high data speed is increasing rapidly, forcing academicians, engineers, and industry people to design more robust, high-quality, and high-speed devices. In the present scenario, Fourth Generation (4G) standards based on OFDM are implemented [2]. Several applications are based on the OFDM waveform. However, OFDM is not suitable for advanced radio due to several disadvantages, such as loss of spectrum due to Cyclic Prefix (CP), high PAPR, high latency, and not suitable for gigantic device connectivity. As a result, it has become critical to look for an alternative to OFDM for 5G and beyond. In recent years, several advanced waveforms such as FBMC, UFMC, UMC, and NOMA have been recommended for the 5G waveform [3]. Among various proposed waveforms, NOMA has been considered as the best choice for 5G and beyond 5G. NOMA has attractive characteristics such as high data rate, low latency, the ability to connect millions of devices and low outage probability. However, the utilisation of Inverse Fast Fourier Transform (IFFT) in NOMA causes high PAPR. High PAPR is seen as a serious drawback of the NOMA waveform, which reduces the efficiency of the power amplifier. PAPR is a common problem in multicarrier waveforms [4]. Presently, there are several PAPR algorithms designed for the OFDM waveform. However, the PAPR algorithms designed for OFDM cannot be used for the 5G waveform due to the difference in waveform structure [5]. Hence, the PAPR algorithm should be specifically designed for 5G waveforms considering their structure and different parameters [6]. In [7], the author has studied the performance of PAPR algorithms on the OFDM waveform. The parameters such as BER and PAPR were analyzed, and it was concluded that the peak insertion algorithm can effectively reduce the PAPAR of the OFDM framework. However, the complexity of the proposed algorithm is not discussed in the work. The authors proposed a peak windowing and clipping algorithm to reduce the PAPR of the OFDM waveform [8]. The outcome of the work demonstrated that the proposed method obtained a gain of 3 dB as compared with the conventional algorithm. PTS and SLM algorithms are implemented for the OFDM waveform [9]. It is concluded that the PTS achieved a 2 dB gain as compared with SLM. The conventional OFDM waveform is implemented by utilising IFFT and FFT. In [10], wavelet transform is utilized, PAPR transform is utilized, and PAPR reduction is achieved by using the clipping computing method. It is observed that the proposed method achieved good performance. The authors introduced a linear predictive algorithm to overcome the PAPR problem in the OFDM waveform. The proposed technique utilises the signal whitening characteristics of linear predictive. The outcome of the work reveals that the presented algorithm effectively reduces the PAPR of the frame work with an improvement in throughput and spectral density [11]. In [12], it is seen that the PAPR of the FBMC system can be effectively reduced by using Active Constellation Technique (ACT). The experimental outcome of the work reveals that the ACT obtained a gain of 2.6 dB as compared with the conventional ACT. In [13], the authors investigated the PAPR problem in a multicarrier waveform. It is seen that the high PAPR problem in the multicarrier waveform .It is seen that the high PAPR degrades the performance of the power amplifier. This work proposed non-linear computing algorithms to reduce the PAPR of the FBMC waveform. The simulation outcome reveals that the proposed method obtained a better result than the conventional Companding methods. The authors introduced a novel P-PTS algorithm to reduce the high PAPR in the FBMC waveform [14]. The projected algorithm achieved an ideal optimization in the double stage. In the initial stage, the FBMC sub-lock is multiplied by the phase vector and the final stage PTS PAPR algorithm is applied. The outcomes of the work reveal that the P-PTS method significantly lowers the PAPR with minimal complexity as compared with the conventional PTS method. The authors introduced a hybrid PAPR method based on PTS and the discrete Fourier transforms [15]. The experimental outcomes show that the proposed method obtained excellent PAAPR BER performance as compared with conventional algorithms. In [16], the authors introduced a PTS method for PAPR reduction in 5G waveforms. The waveform symbol is multiplied by the optimal phase rotation vector to obtain an ideal PAPR value. The outcome of the work demonstrates that the proposed method efficiently enhances the BER, MER, and PAPR performance as compared with the existing PTS algorithm. The author investigated the PAPR reduction algorithms for different transmission waveforms [17]. The main objective of the work was to apply the conventional PAPR algorithms to FDMC waveforms. The experiment reveals that conventional algorithms increase the complexity and degrade the performance. The authors introduced a hybrid algorithm based on a combination of tone reservation and companding methods. The experimental result concludes that the proposed hybrid algorithm outperforms the conventional PAPR algorithms [18]. In [19], the high PAPR in FBMC is reduced by applying the DSLM algorithm. It is concluded that the proposed algorithm efficiently enhances throughput PAPR performance as compared with SLM. NOMA is an advanced waveform technique for 5G radio. High PAPR in NOMA is reduced by integrating the SLM and Walsh-Hadamard method. The experimental outcome shows that the proposed algorithm obtained a gain of 4.3 dB in PAPR and 9.5 dB in BER performance [20]. In multicarrier structures, PAPR occurs due to the IFFT of random signals. The authors [21] implemented the NOMA waveform by replacing IFFT with Wavelet Transform. Furthermore, several WT band PAPR algorithms such as PTS and SLM are applied to the NOMA. The outcomes of the article reveal that the proposed system achieved a significant increase in PAPR and BER performance as compared with the existing IFFFT based SLM P-PTS. The authors in [22] comprehensively studied the conventional PAPR algorithms and implemented a novel hybrid algorithm for the NOMA and FBMC structures. The proposed method was based on a combination of SLM and PTS. In the simulation graph, it is seen that the hybrid method gave much better performance for NOMA as compared to the FBMC. In [23], the author compared the performances of the Discrete Sine Transform (DST) and Walsh Hadamard Transform (WHT) PAPR algorithms for the NOMA waveform. It is concluded that DST outperforms the WHT. In [24], the clipping method is designed for the OFDM-NOMA structure. It is seen that the proposed system improves the SNR requirement and PAPR performance. However, the complexity of the system is not discussed in this article. The regularisation of the 5G network is taking place sooner or later. The present network will be replaced by 5G. In this work, the author has introduced a novel DSLM-CT algorithm which effectively lowers the paper of the advanced waveform. It is concluded that the proposed DSLM-CT effectively reduces the PAPR with low computational complexity [25]. The main objectives of the proposed work are given below.

•   We aim to investigate the PAPR reduction algorithms for the 5G waveform.

•   We proposed a novel hybrid algorithm for the 5G waveform.

2  Multicarrier Waveform Techniques

In MCWT, the data is transmitted by dividing a single carrier into a number of subcarriers. In the last several years, several waveform methods have been studied and concluded that PAPR is one of the big issues in multicarrier waveforms.

2.1 OFDM

The structure of the OFDM waveform is given in Fig. 1. PAPR is the result of IFFT utilisation in the transmitting part of the OFDM structure [26].

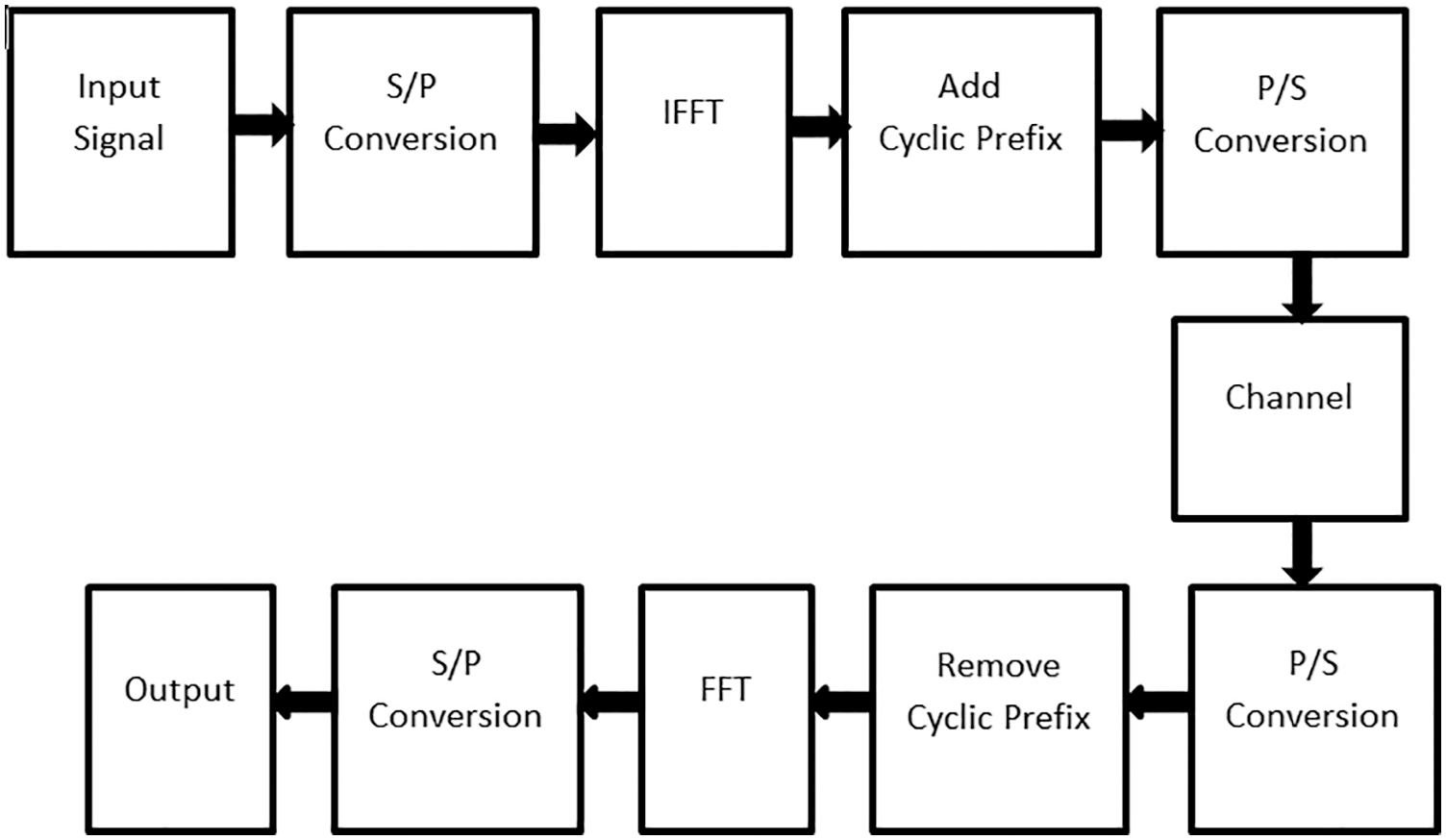
Figure 1: OFDM schematic

The OFDM symbol can be represented as:

Y0={YL,L=0,1,…,N−1} (1)

where Yk is the OFDM symbol transmitted by Lth sub-carrier. The IFFT will convert the frequency domain OFDM signal into the time domain, given by:

y(n)=1N∑l=0N−1⁡YLexpj(i2πLnN) (2)

Eq. (2) denotes the number of transmitted sub-carriers which increases the PAPR of the system. The PAPR of the OFDM signal can be written as:

PAPR(dB)=10log10[Max|yn|2E|yn|2] (3)

Here E is the expected operator.

2.2 FBMC

The structure of FBMC is shown in Fig. 2. A group of filters is used at the transmitting and receiving terminals of the FBMC scheme. A group of sub-carriers is filtered and processed to overcome the interference [27]. The FBMC scheme does not add the Cyclic Prefix (CP). Hence, high PAPR is a common problem in OFDM and FBMC [28].

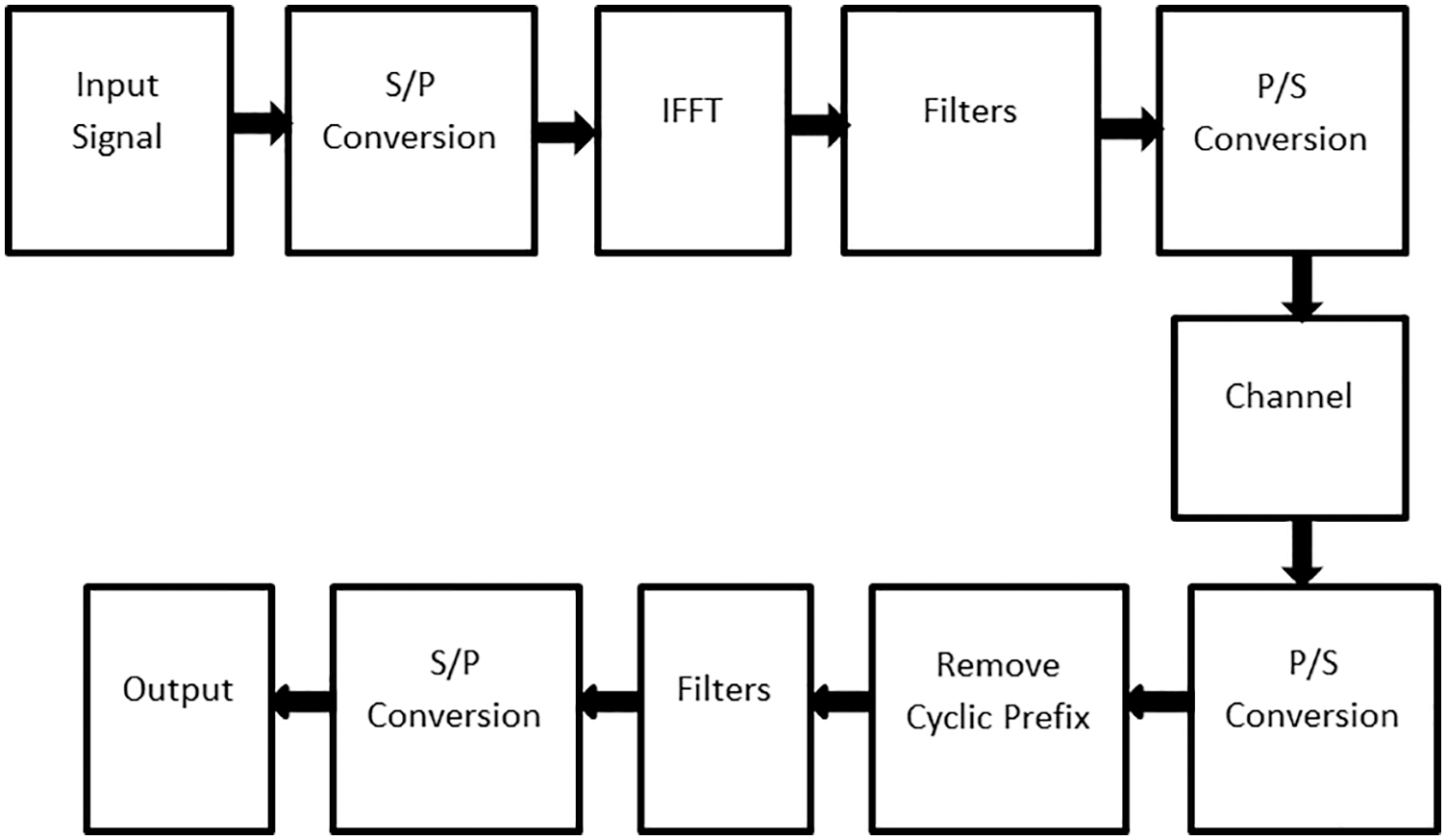
Figure 2: FBMC schematic

The FBMC transmitted signal is given by:

YL=∑n=−∞∞⁡∑m=02N−1⁡Sm,nf(l−nN)exp⁡(iπm(l−d2)N)exp(iθm,n) (4)

In this case yk is the FBMC symbol for L=0,1,…,M−1 . The number of sub-carriers is given by L = 2 N, Sm,n is the FBMC input signal at Lth sub-carrier, M, and n is the sub-carrier and symbol index, f(n) is the filter and d is the delay. In generally, θm,n is written as θm,n=3.142(m+n) and the filter g(n) is represented by:

f(n)=f(l−in)eπM(L−d/2)N (5)

The PAPR of FBMC is given by:

PAPR(dB)=10log10Max|yL|2E|yL|2 (6)

The Complementary Cumulative Distribution Function (CCDF) is used to analyze the efficacy of PAPR algorithms, which is represented as:

CCDF=P(PAPR>Xt) (7)

where Xt is the threshold value.

2.3 NOMA

The schematic of the NOMA structure is given in Fig. 3. NOMA is attracting a lot of attention for 5G radio due to its several characteristics, such as low latency, high speed, and massive device connectivity. The transmitted NOMA signal is given by [29].

Yn=∑l=0N−1⁡Ynej2πnLN (8)

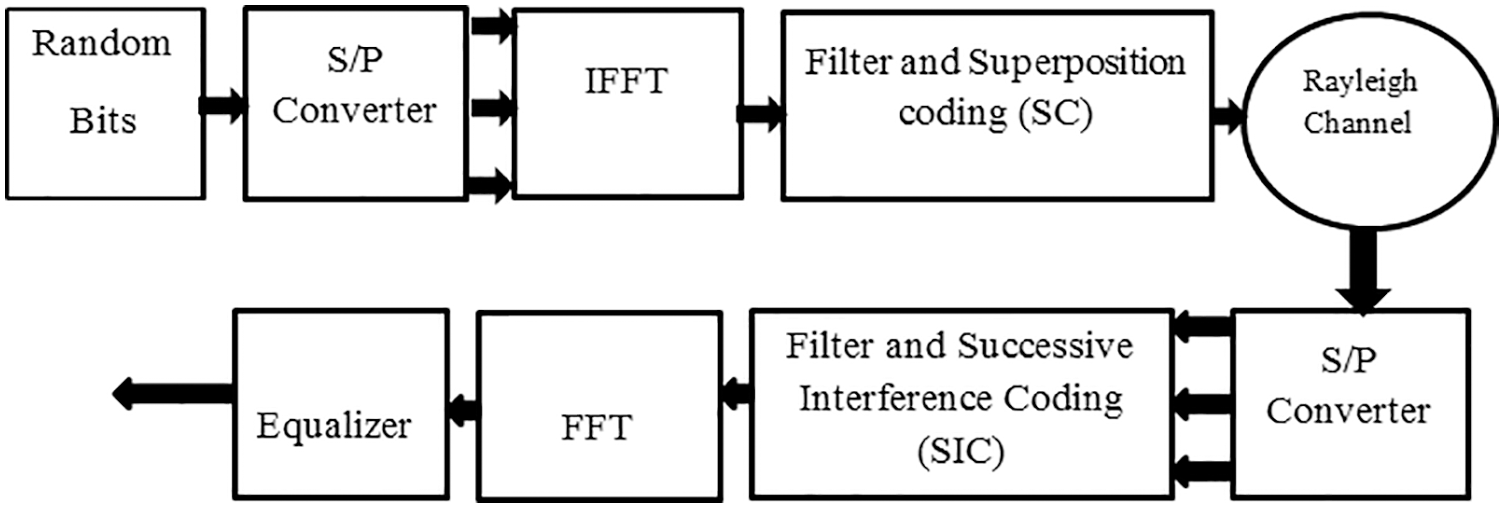
Figure 3: NOMA

Considering Eq. (8), the PAPR is defined as:

PAPR(dB)=10log10[Max|yn|2E|yn|2] (9)

3  System Model

In recent years, there have been several PAPR algorithms investigated for OFDM and 5G waveforms.

3.1 D-SLM

Let us consider symbols mapped into the 64-QAM transmission scheme. Those symbols are loaded into parallel order, given as Sp . The series Sp symbols are divided into R∈Sp(l) real and I∈Sp(l) imaginary parts for l=0,1,…,N−1 . Thereafter, each element of a real and imaginary signal is multiplied with phase elements, pv(l)∀∈(0,1,…,V−1) where v represents the number of blocks and pv(l)∈{−1,1} . The Matrix Multiplication between real and imaginary signals by pv(l) is given by:

Svr=R{Sp}∗pv (10)

Svi=I{Sp}∗pv (11)

An IFFFT is applied to the Eqs. (10) and (11), given as:

yrv=IFFT(Prv) (12)

yiv=IFFT(Piv) (13)

Thereafter, the signal with the minimum PAPR value is transmitted, given by:

PAPR(dB)=10log10[Max|ynu|2E|ynu|2] (14)

where u represents the series of minimum PAPR values. The effectiveness of SLM is analysed by estimating CCDF, given as:

yv¯=yv={arg min0≤v≤v−1⁡(PAPRrvPAPRiv)} (15)

The Eq. (15) can be represented as:

Pr(PAPRv¯>PAPR0)=(1−(1−exp(−PAPR0)αN)v2 (16)

where, α is define as PAPR reduction factor.

3.2 D-PTS

Let us consider a complex multicarrier signal for nth symbol given as:

{Yns,n=0,1,…,Ns−1,s=1,2,…S} (17)

The Yns is divided in to v sub-blocks, given as:

Yvs=[Yv,0s,Yv,1s,…,Yv,sNs−1]T,0≤v≤V−1 (18)

Hence, Yvs can be written as Yv=∑v=0V−1⁡Yvs . An IFFFT is applied at Yvs to estimate the time domain of the signal, given by:

yvs=IFFT(Yvs) (19)

To lower the PAPR, the time domain sequence Yvs is multiplied by phase rotation elements given as:

yv=∑v=0V−1⁡Pvu∗yv (20)

The Pvu is generated by using the Hadamard matrix given by:

Pvu(0≤v≤v−1,0≤u≤u−1) (21)

The ideal Pvu is estimated as:

Pv¯=argminPu∈Pv⁡(max0≤n≤N−1⁡|∑v=0V−1⁡Pvuyv,n|) (22)

4  Results

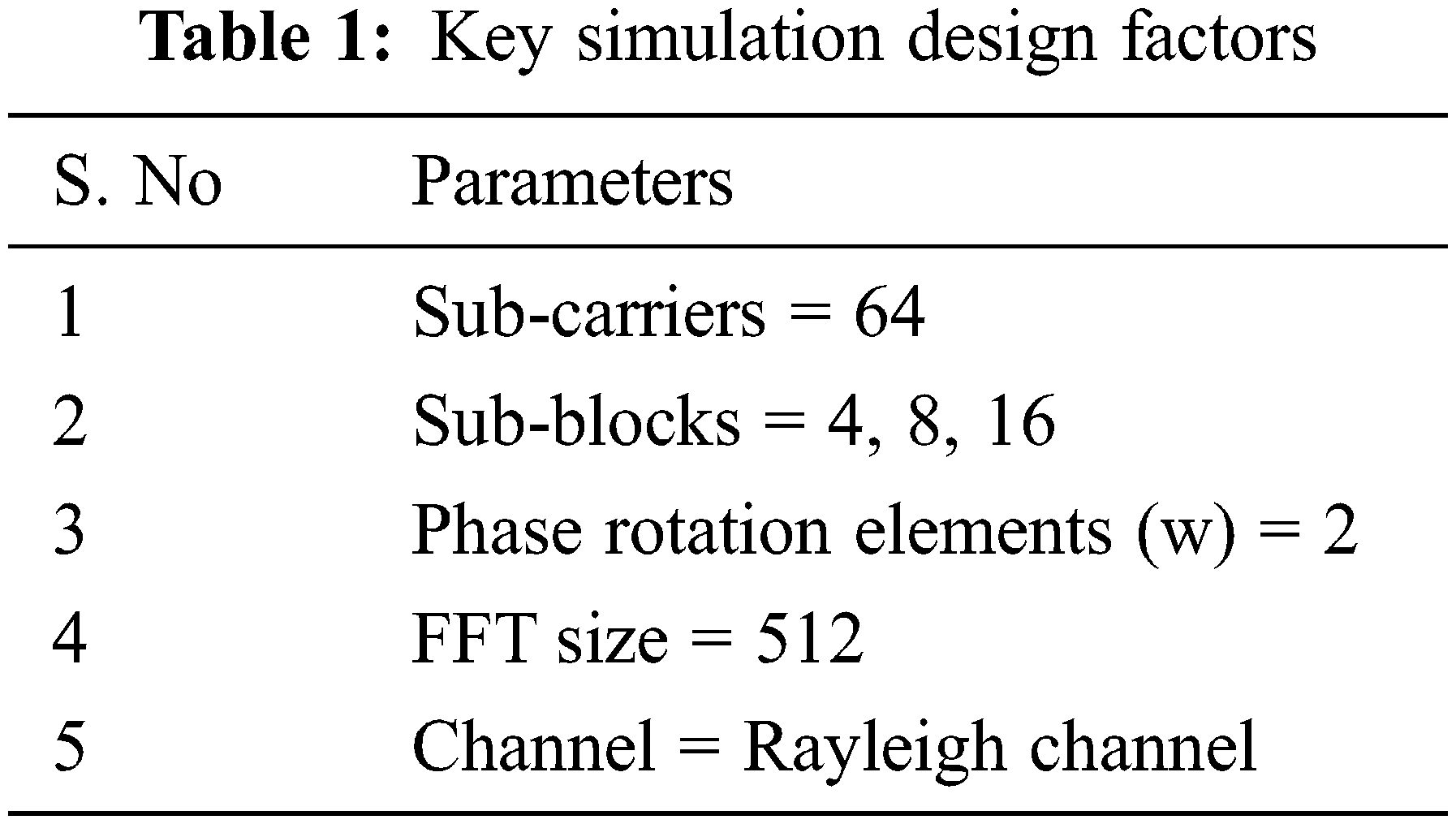
We have used Matlab-2014 to implement the PAPR algorithm techniques for multi-carrier waveforms. The key design factors are given in Tab. 1.

4.1 PAPR Performance

In this section, we have analysed the efficiency of the D-PTS algorithm on NOMA, FBMC, and OFDM waveforms. It is seen that the D-PTS effectively reduces the PAPR of the waveforms and outperforms the conventional PTS method. Further, it is noted that by increasing the number of sub-blocks, the ideal PAPR value is obtained as Figs. 4–10 indicate that the D-PTS v = 16, w = 2 gave the best PAPR performance.

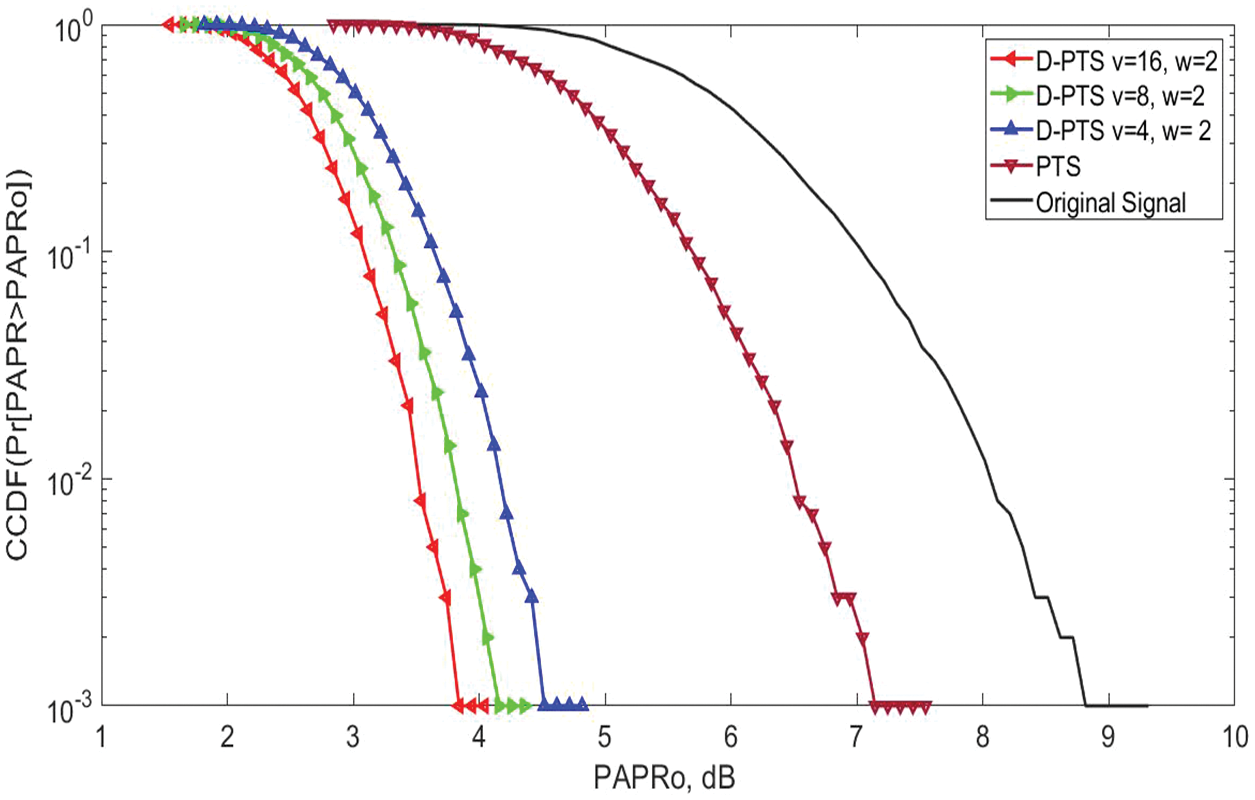
Figure 4: PAPR vs. CCDF performance of the D-PTS and conventional PTS algorithms for the NOMA waveform using sub-blocks (u = 4, 8, and 16) and phase rotation elements (w = 2). The proposed D-PTS obtained a gain of 2.8 dB as compared with the PTS

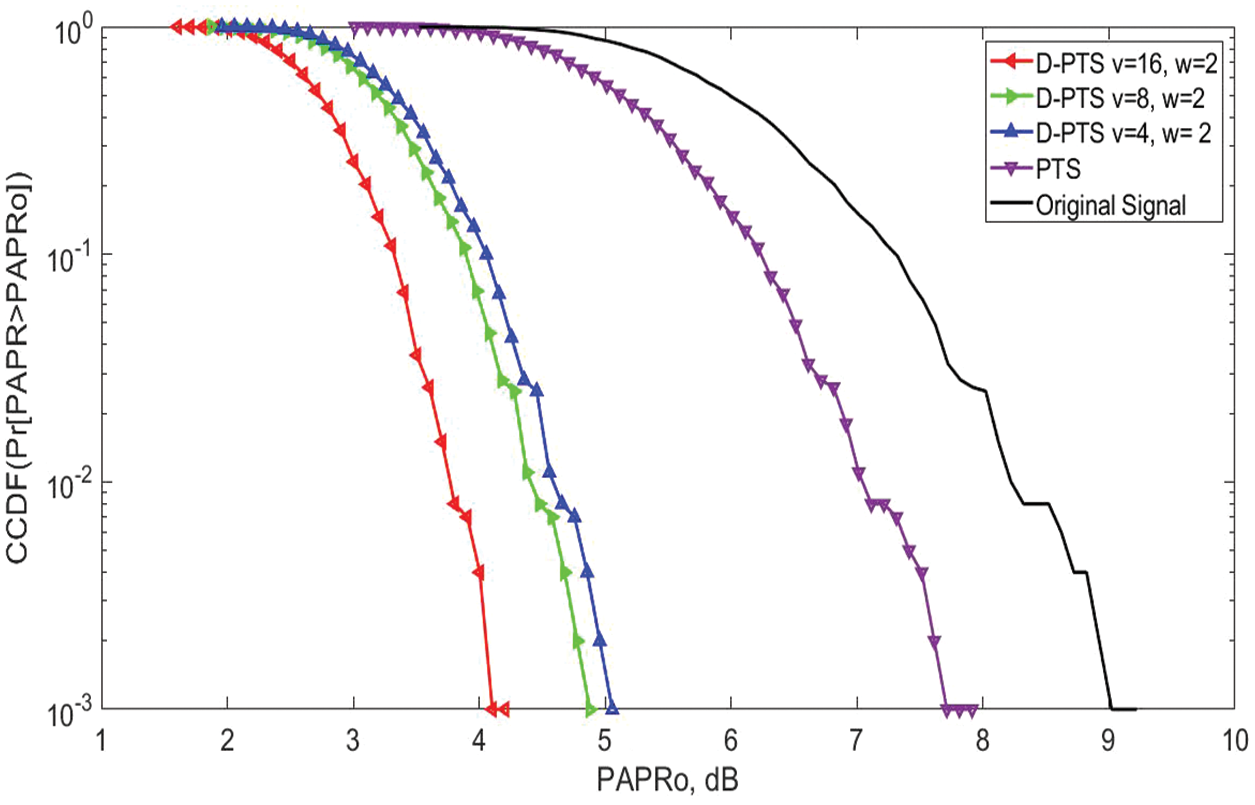
Figure 5: At 10−3 CCDF-PAPR performance of the D-PTS and Conventional PTS algorithm for the FBMC waveform using sub-blocks (u = 4, 8 and 16) and phase rotation elements (w = 2). The proposed D-PTS obtained a gain of 3 dB as compared with the PTS

Figure 6: PAPR vs. CCDF performance of the D-PTS and conventional PTS algorithms for the OFDM waveform using sub-blocks (u = 4, 8, and 16) and phase rotation elements (w = 2). The performance of the D-PTS is poor due to the difference in structural arrangement between the 5G and 4G waveforms

Figure 7: PAPR vs. CCDF performance of the D-SLM and conventional SLM algorithms for the NOMA waveform using sub-blocks (u = 4, 8, and 16) and phase rotation elements (w = 2). The proposed D-SLM obtained a gain of 6.6 dB as compared with the PTS

Figure 8: At 10−3 CCDF-PAPR performance of the D-SLM and conventional PTS algorithm for the FBMC waveform using sub-blocks (u = 4, 8 and 16) and phase rotation elements (w = 2). The proposed D-SLM obtained a gain of 4.8 dB as compared with the PTS

Figure 9: PAPR vs. CCDF performance of the D-SLM and conventional PTS algorithms for the OFDM waveform using sub-blocks (u = 4, 8, and 16) and phase rotation elements (w = 2). The performance of the D-SLM is poor due to the difference in structural arrangement between the 5G and 4G waveforms

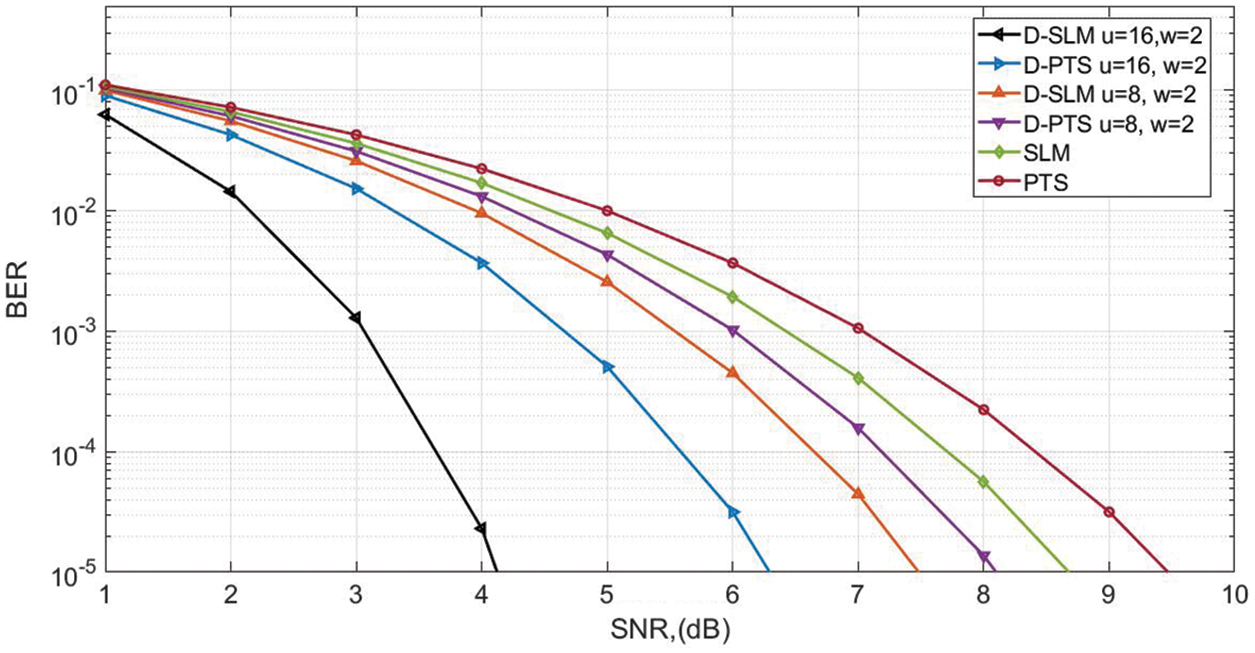
Figure 10: SNR vs. BER

Finally, it is concluded that the proposed D-SLM gave an efficient PAPR performance and outperformed the D-PTS for the given waveforms.

4.2 BER Performance

In this part, we have studied the BER analysis of NOMA waveform after applying the proposed D-PTS and D-SLM algorithms to the Rayleigh channel. The proposed D-SLM, D-PTS (u = 16, 8 and w = 2) and conventional SLM and PTS achieved the BER of 10−5 at the SNRs of 4.2, 6.3, 7.5, 8.1, 8.7, and 9.2 dB as shown in Fig. 10. Hence, it is concluded that the D-SLM outperforms the other algorithms.

5  Conclusion

The work highlighted a combination of multi-data block DPTS and DSLM along with tone reservation. In this, an overlapping factor is used to determine the number of data blocks for every group. Here, considering only those data blocks that have minimum signal power, the use of a phase rotation element (w) is required to eliminate the segment’s peaks. Simulation results reveal that the suggested hybrid PTS-TR technique proves to be better than the conventional PTS scheme. The requirement of side information for each data block results in losses in data rates in selective mapping techniques. A novel D-SLM method has been proposed to reduce the complexity of the waveforms. The evaluation outcome shows that the suggested methods provide better performance in the reduction of PAPR and also promise a better BER.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP 2/46/43). Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R237), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the ‎Deanship of Scientific Research at Umm Al-Qura University ‎for supporting this work by Grant Code: 22UQU4310373DSR11.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Sengupta and B. K. Lande, “An approach to PAPR reduction in OFDM using goppa codes,” Procedia Computer Science, vol. 167, pp. 1268–1280, 2020. [Google Scholar]

 2.  G. Monsalve, J. L. Ros, L. Brossier and J. M. Mestdagh, “An improved green ofdm scheme for papr reduction,” Telecom, vol. 1, pp. 196–210, 2020. [Google Scholar]

 3.  S. Thota, Y. Kamatham and C. S. Paidimarry, “Analysis of hybrid papr reduction methods of ofdm signal for hpa models in wireless communications,” IEEE Access, vol. 8, pp. 22780–22791, 2020. [Google Scholar]

 4.  R. Gopal and S. K. Patra, “Combining tone injection and companding techniques for papr reduction of fbmc-oqam system,” in 2015 Global Conf. on Communication Technologies (GCCT), Thuckalay, India, pp. 709–713, 2020. [Google Scholar]

 5.  F. Zou, Z. Liu, X. Hu and G. Wang, “A novel papr reduction scheme for ofdm systems based on neural networks,” Wireless Communications and Mobile Computing, vol. 2021, pp. 1–8, 2021. https://doi.org/10.1155/2021/5574807. [Google Scholar]

 6.  L. Dai, B. Wang, Z. Ding, Z. Wang, S. Chen et al., “A survey of non-orthogonal multiple access for 5 g,” IEEE Communications Surveys & Tutorials, vol. 20, no. 3, pp. 2294–2323, 2018. [Google Scholar]

 7.  P. P. Ann and R. Jose, “Comparison of papr reduction techniques in ofdm systems,” in 2016 Int. Conf. on Communication and Electronics Systems (ICCES), Coimbtore, INDIA, pp. 1–5, 2016. [Google Scholar]

 8.  R. Musabe, M. B. Lionel, M. Ushindi, M. Atupenda, J. Ntaganda et al., “PAPR reduction in LTE network using both peak windowing and clipping techniques,” Journal of Electrical Systems and Information Technology, vol. 6, no. 3, pp. 1–11, 2019. https://doi.org/10.1186/s43067-019-0004-1. [Google Scholar]

 9.  S. Sengar and P. P. Bhattacharya, “Performance improvement in ofdm system by papr reduction,” Signal & Image Processing: An International Journal (SIPIJ), vol. 3, no. 2, pp. 157–159, 2012. [Google Scholar]

10. S. Sarowa, N. Kumar and S. Agrawal, “Evolution of PAPR reduction techniques: A wavelet based OFDM approach,” Wireless Personal Communications, vol. 115, pp. 1565–1588, 2020. [Google Scholar]

11. M. M. Hasan, “A new papr reduction technique in ofdm systems using linear predictive coding,” Wireless Personal Communications, vol. 75, pp. 707–72, 2014. [Google Scholar]

12. N. V. Neut, B. T. Maharaj, F. H. Lange, G. González, F. Gregorio et al., “Papr reduction in fbmc systems using a smart gradient-project active constellation extension method,” in 2014 21st Int. Conf. on Telecommunications (ICT), Lisbon, Portugal, pp. 134–139, 2014. [Google Scholar]

13. I. A. Shaheena, A. Zekrya, F. Newagya and R. Ibrahimb, “Performance evaluation of papr reduction in fbmc system using nonlinear companding transform,” ICT Express, vol. 5, pp. 41–46, 2018. [Google Scholar]

14. L. Kaiming, H. Jundan, Z. Peng and L. Yuanan. “PAPR reduction for fbmc-oqam systems using p-pts scheme,” The Journal of China Universities of Posts and Telecommunications, vol. 22, no. 6, pp. 78–85, 2015. [Google Scholar]

15. N. A. Harthi, Z. Zhang, D. Kim and S. Choi, “Peak-to-average power ratio reduction method based on partial transmit sequence and discrete Fourier transform spreading,” Electronics, vol. 10, no. 6, pp. 642. 2021. [Google Scholar]

16. A. Kumar, M. Gupta, D. Le and A. A. Aly, “Pts-papr reduction technique for 5G advanced waveforms using BFO algorithm,” Intelligent Automation & Soft Computing, vol. 27, no. 3, pp. 713–722, 2021. [Google Scholar]

17. A. Kumar and H. Rathore, “Reduction of papr in fbmc system using different reduction techniques,” Journal of Optical Communications, vol. 42, no. 2, pp. 303–309, 2021. [Google Scholar]

18. S. Senhadji, Y. M. Bendimerad and F. T. Bendimerad, “Enhancing papr reduction for fbmc-oqam systems by joint both tone reservation and companding methods,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 21, no. 2, pp. 919–926, 2021. [Google Scholar]

19. A. kumar and H. Rathore, “Modified dslm technique for papr reduction in fbmc system,” Radio Electronics and Communications Systems, vol. 62, no. 8, pp. 416–421, 2019. [Google Scholar]

20. M. Kazemian, J. Abouei and A. Anpalagan, “A low complexity enhanced-noma scheme to reduce inter-user interference, ber and papr in 5 g wireless systems,” Physical Communication, vol. 48, pp. 101–412, 2021. [Google Scholar]

21. M. K. Sharma and A. Kumar, “PAPR reduction in noma by using hybrid algorithms,” Computers, Materials & Continua, vol. 69, no. 1, pp. 1391–1406, 2021. [Google Scholar]

22. A. Kumar, “A novel hybrid papr reduction technique for noma and fbmc system and its impact in power amplifiers,” IETE Journal of Research, 2019. https://doi.org/10.1080/03772063.2019.1682692. [Google Scholar]

23. I. Baig, N. Hasan, M. Zghaibeh, I. U. Khan and A. S. Saand, “A dst precoding based uplink noma scheme for papr reduction in 5 g wireless network,” in 2017 7th Int. Conf. on Modeling, Simulation, and Applied Optimization (ICMSAO), Sharjah, United Arab Emirates, pp. 1–4, 2017. [Google Scholar]

24. T. Tao, Y. Mao and G. Hu, “A fair power allocation approach to OFDM-based NOMA with consideration of clipping,” Electronics, vol. 9, no. 10, pp. 1743, 2020. [Google Scholar]

25. A. Kumar and M. Gupta, “A comprehensive study of papr reduction techniques: Design of dslm-ct joint reduction technique for advanced waveform,” Soft Computing, vol. 24, pp. 11893–11907, 2020. [Google Scholar]

26. A. Kumar, M. A. Albreem, M. Gupta, M. H. Alsharif and S. Kim, “Future 5 g network based smart hospitals: Hybrid detection technique for latency improvement,” In IEEE Access, vol. 8, pp. 153240–153249, 2020. [Google Scholar]

27. A. Kumar, “Design and simulation of mimo and massive mimo for 5 g mobile communication system,” Int. Journal of Wireless Mobile Computing, vol. 14, no. 2, pp. 197–207, 2018. [Google Scholar]

28. A. Kumar, “Detection in 5G mobile communication system using hybrid technique,” National Academic Science Letter, vol. 44, pp. 39–42, 2021. [Google Scholar]

29. A. Kumar and M. Gupta, “A review on activities of fifth generation mobile communication system,” Alexandria Engineering Journal, vol. 57, pp. 1125–1135, 2018. [Google Scholar]