Al-Biruni Earth Radius (BER) Metaheuristic Search Optimization Algorithm

1  Introduction

Metaheuristic and evolutionary optimization algorithms are currently used to solve a variety of problems in a variety of fields, including machine learning [1], formulas estimation [2,3], integrated decision making [4], transportation [5], mechanics [6], engineering [7], economics [8], business processes [9], and scheduling [10]. Optimization is the process of selecting the best solution from a large number of options for a given problem. Typically, a multi-dimensional search issue is turned into an optimization problem. In practice, this entails reducing or increasing the quality of candidate solutions, which is often represented as a vector in the search space. The optimization strategy based on metaheuristics yields satisfying results in a reasonable time [11]. These methods are used to solve complicated and complex issues in science and engineering.

The simplicity and flexibility of optimization algorithms based on metaheuristics make these algorithms widespread more than the traditional and accurate optimization algorithms such as Local Search and Greedy Search [12]. The metaheuristic optimization algorithms are easy to understand and use since they are based on simple concepts. These optimization algorithms are versatile in general because they may be employed in various applications and domains without requiring major implementation and design changes. Additionally, their stochastic nature allows them to explore the search space more extensively to avoid stalling at local optima. Unlike gradient-based algorithms, metaheuristic optimization algorithms do not require derivative information from the search space. Since the search space is usually highly intricate, metaheuristics are better suited to tackling real-world problems with expensive or unknown derivative information and many local optima.

2  Literature Review

Metaheuristics are broad techniques for resolving challenging combinatorial problems. In general, computer scientists have complex time-solving metaheuristic algorithms because they require them to consider many possibilities, typically exponential and with competing purposes [13]. Water allocation and crop planning [14], Parkinson’s diagnosis [15], Power load dispatch [16], Image segmentation [17], and Nurse Rostering [18] and are only a few of the real-world challenges for which metaheuristic algorithms have been proposed.

Nature-inspired metaheuristic algorithms have piqued the curiosity of scientists who want to solve complex real-world challenges. Harmony Search (HS) [19], Cuckoo Search (CS) [20], Bat Algorithm (BA) [21], Biogeography-based Optimization (BO) [22], Social Spider Optimization [23], Grey Wolf Optimization (GWO) [24,25], Symbiotic Organisms Search (SOS) [26], Whale Optimization Algorithm (WOA) [27], Firefly Algorithm (FA) [28], Gravitational Search Algorithm (GSA) [29], Bacterial Foraging Optimization (BFO) [30], Sine Cosine Algorithm (SCA) [31], Genetic Algorithm (GA) [32], and Particle Swarm Optimization (PSO) [33] are examples of the metaheuristic optimization algorithms.

Many researchers in the literature have proposed hybrid optimization algorithms. These algorithms combine the benefits of two or more optimization techniques to overcome the limits of a single algorithm. In [34], for example, SCA is merged with PSO algorithm and the levy fly technique to create PSOSCA, a novel hybrid optimizer. In the search space, the levy flight technique introduces random walks. These random walks ensure that there is a lot of investigation and that local optima are avoided. PSO’s exploration and exploitation capabilities are improved by the position update equations in SCA. Standard benchmark functions and real restricted engineering situations validated the novel hybrid PSOSCA. PSOSCA has shown its benefits and efficacy vs. the majority of PSO versions.

The Al-Biruni earth radius (BER) optimization methodology, which is inspired by the computation of the earth radius to estimate the search space surrounding the solutions in the cooperative behavior of swarm members to fulfill their global goals, is presented in this paper. BER tries to compromise between guaranteeing quick convergence and minimizing local optima stagnation. This is accomplished by employing the Al-Biruni technique, which aids in improving exploitation performance, striking a healthy balance between exploration and exploitation, expanding search space exploration, and boosting variety among present population individuals. The introduction of BER as a novel optimization technique with fresh insights into tackling various optimization issues is a significant contribution to this research. According to preliminary results, BER is promising, competitive, and capable of surpassing existing evolutionary algorithms based on swarm optimization. Furthermore, the performance of the proposed algorithm has been tested in terms of seven benchmark optimization functions and one design optimization problem from the engineering domain.

3  The Proposed BER Algorithm

3.1 Inspiration

In the eleventh century, Al-Biruni worked out the radius of the Earth [35]. It was measured the distance between the horizon and the ground from a hilltop. Al-Biruni measured twice. He began by determining the elevation of a mountain. From two different points, he measured the angle to the mountain’s peak twice. He was able to calculate the hill’s height using the following equation, as illustrated in Fig. 1.

h=dtan⁡θ1tan⁡θ2tan⁡θ2−tan⁡θ1 (1)

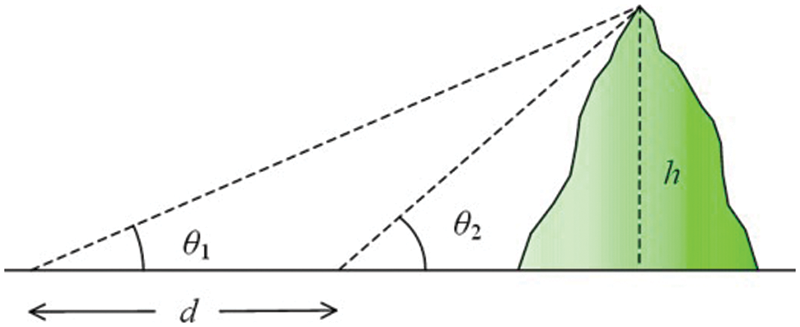
Figure 1: Calculation of hill height based on the Al-Biruni method

Second, Al-Biruni scaled the mountain’s peak and measured the horizon’s dip. He was able to compute the radius of the Earth using the following equation based on his data, as shown in Fig. 2.

R=hcos⁡α1−cos⁡α (2)

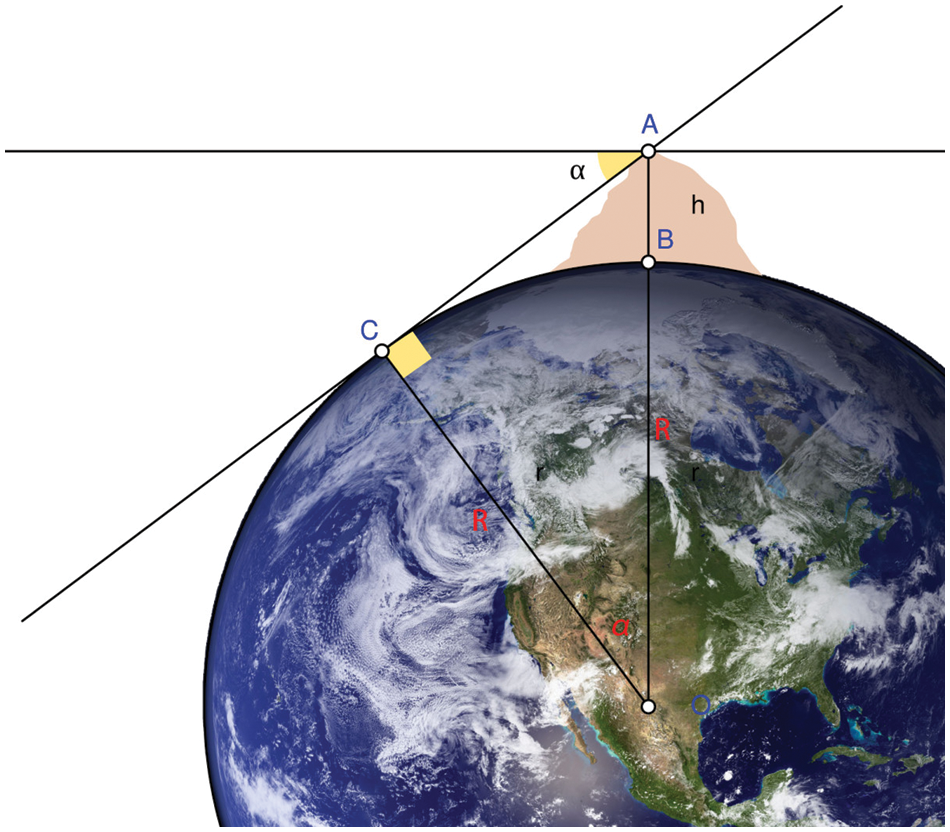
Figure 2: Calculation of earth radius based on the Al-Biruni method

The proposed optimization method used the Al-Biruni technique for the cooperative optimization algorithm’s exploration and exploitation tasks, simulating swarm collaboration to achieve a global optimization goal. In real life, swarm live in groups and communicate together to achieve their goals. They usually work together to acquire food and defend themselves from invaders, exchanging responsibilities as required. They split up into sub-groups, with individuals collaborating both inside their sub-group and with members of other groups to achieve their ultimate goal. Swarm collaboration may be seen in ant and bee colonies, for example. Each member of the swarm makes a distinct contribution to the colony. The colony’s warriors are fed by workers who go out and gather food. The concept of BER was inspired by the fact that members of groups are frequently separated into sub-groups to complete various activities at different times and collaborate to reach their goals. The exploration and exploitation activities are usually performed to find the best solution to an optimization problem. In our case, BER divides individuals into two sub-groups, each accounting for one of the two activities. In BER, the exploitation and exploration activities ensure a deep investigation of the search space to avoid the local optima stagnation. The majority of cooperative optimization approaches need everyone to undertake exploitation after iterations, which might cause local optima to stagnate. BER avoids this case by keeping a collection of search agents that explore more areas in the search space through time. BER also swiftly increases the number of individuals investigating the search space if the algorithm’s performance does not improve after three iterations through solution mutation.

3.2 Basic Concepts and Formulation

Finding the optimal solution to a problem with a set of constraints is the target of optimization algorithms. In BER, an individual from the population can be represented by a vector, S→={S1,S2,…,Sd}∈Rd , where Si is a parameter or feature in the optimization problem, and d is the size of the search space. A fitness function f is used in the proposed method to determine how well an individual performs up to a given point. The optimization procedure uses the following phases to search through populations for a specific optimum vector S* that maximizes the fitness function. The algorithm begins with a group of random individuals (solutions). For the optimization process to begin, BER requires the following parameters: the fitness function, the lower and upper bounds for each solution, the dimension, and the population size.

3.3 Exploration-Exploitation Balance

As the population is divided into subgroups in the proposed algorithm, the number of individuals in each group is modified dynamically to improve the balance between the tasks of exploitation and exploration. The process starts with dividing the population into two groups for exploration and exploitation [36–44]. The size of the exploration group is 70% of the population, whereas the size of the exploitation group is 30% of the population. To improve the fitness values of individuals in each group, the number of individuals in the exploitation task is set initially at 30%, then increased over the optimization iterations to reach 70% of the population count. On the other hand, the number of individuals in the exploration group is decreased to 30% over iterations, where the initial number is set to 70%. This process allows for more remarkable improvement in the global average of the fitness of individuals. In addition, to guarantee the convergence of the optimization process for the population, the elitism strategy is employed by keeping the process’s leading solution if no better solution is found. In the BER optimization algorithm, if the fitness of a solution does not improve significantly for three iterations, this could be a local optimum and consequently, another exploration individual can be generated by applying the mutation operation.

3.4 Exploration Operation

Exploration is in charge of not only locating exciting locations in the search space but also of avoiding local optima stagnation through the movement towards the best solution, as discussed next.

3.4.1 Heading Towards the Best Solution

The individual in the exploration group uses this strategy to seek prospective regions around its current position in the search space. This is accomplished by repeatedly searching among surrounding feasible alternatives for a superior option in terms of fitness value. The following equations are utilized in the BER investigation for this purpose:

r=hcos(x)1−cos(x) (3)

D→=r1→.(S→(t)−1) (4)

S→(t+1)=S→(t)+D→.(2r2→−1) (5)

where 0<x≤180 , h is a number that is randomly selected from the range [0, 2], r1→ and r2→ are coefficient vectors whose values are measured by Eq. (3), S→(t) is the solution vector at iteration t, and D→ is the diameter of the circle in which the search agent will look for promising areas.

3.5 Exploitation Operation

The exploitation team is in charge of improving existing solutions. The BER calculates all individuals’ fitness values at each cycle and distinguishes the best individual. The BER employs two different approaches to achieve exploitation, as detailed in the sections below.

3.5.1 Heading Towards the Best Solution

The following equations are used to move the search agent towards the best solution:

S→(t+1)=r2(S→(t)+D→) (6)

D→=r3→(L→(t)−S→(t)) (7)

where r3→ is a random vector calculated using Eq. (3) that controls the movement steps towards the best solution, S→(t) is the solution vector at iteration t, L→ is the best solution vector, and D→ refers to the distance vector.

3.5.2 Investigating Area Around Best Solution

Most promising is the region surrounding the best solution (leader). As a result, some individuals hunt in the vicinity of the best solution with the potential of finding a better solution. To realize this operation, the BER utilizes the following equation.

S→(t+1)=r(S∗→(t)+k→) (8)

k→=z+2×t2N2 (9)

where S∗→ refers to the best solution, z is a random number in the range [0, 1], t is the iteration number, and N is the total number of iterations. A demonstration of the exploration and exploitation activities is shown in Fig. 3.

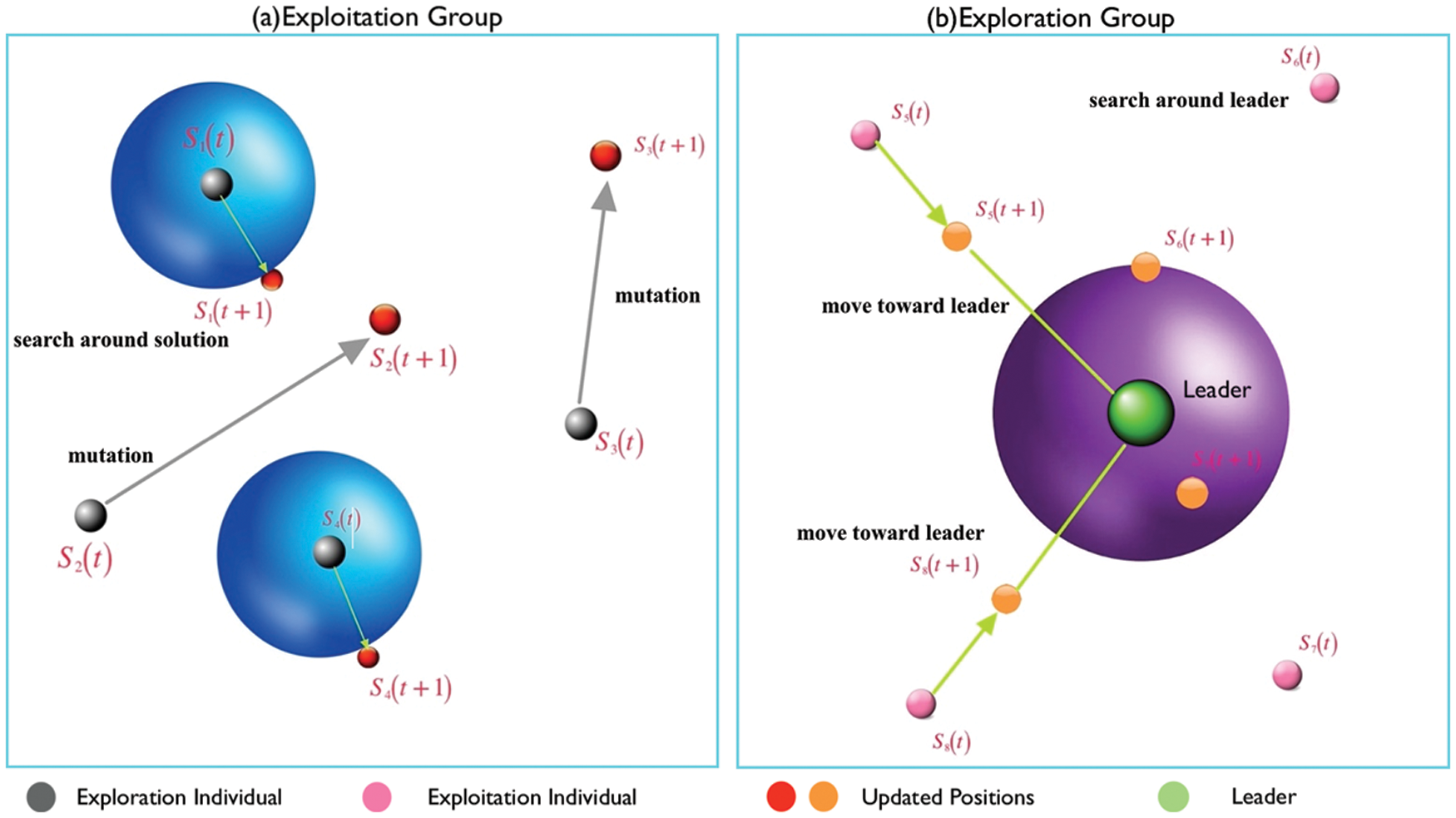
Figure 3: Demonstration of the exploration and exploitation activities

3.6 Mutation Operation

The mutation is another method used by the BER to do research. It is a genetic operator utilized to create and sustain population variety. It may be considered a probabilistic local random disruption of one or more components in individuals. It prevents early convergence by helping to avoid local optima—such a shift in the search field functions as a springboard to another interesting topic. Indeed, the mutation is significant for the BER’s excellent exploration potential.

S→(t+1)=k→∗z2−hcos(x)1−cos⁡(x) (10)

3.7 Selection of the Best Solution

The BER chooses the best solution for the next iteration to ensure the quality of discovered solutions. Although the elitism method enhances algorithm efficiency, it can cause premature convergence in multimodal functions. It is worth noting that the BER offers impressive exploration capabilities by employing a mutation technique and searching around individuals in the exploration group. The BER can avoid early convergence due to its strong exploration capabilities. Algorithm 1 shows the BER pseudo-code. First, we give the BER some input parameters: number of iterations, population size, and mutation rate. The individuals are then separated into two groups by the BER, namely exploration and exploitation groups. The BER algorithm dynamically controls the number of individuals in each group during the search iterations for the best solution. To complete their responsibilities, each group employs two distinct strategies. To ensure diversity and high exploration, the BER randomly orders solutions after each iteration. For example, a solution from the exploration group in one iteration can become a member of the exploitation group in the next. The elitism method used in the BER helps avoid the loss of the leader throughout the iterations.

4  Experimental Results

In this section, the evaluation of the proposed algorithm is performed in terms of two scenarios on experiments. In the first case, seven typical benchmark mathematical functions were utilized to find their minimum values in a specified domain of the search space to evaluate the performance of the proposed optimization technique. These functions are commonly used to benchmark optimization algorithms in the literature. In addition, the second scenario of experiments is based on solving one of the well-known constrained design engineering problems. These two scenarios of experiments are presented and discussed in the following sections.

On the other hand, the literature has several optimization techniques. In this research, the performance of the proposed approach is compared to five well-known optimization algorithms in the literature to show the superiority and effectiveness of the proposed algorithm. These algorithms are GWO, PSO, GA, WOA, and GSA. The selection of these three algorithms is based on their usefulness and popularity. Unique collaboration to attain global goals is a common theme in the proposed BER, WOA, GWO, and PSO. The GA and GSA are chosen as an example of evolutionary algorithms influenced by natural evolution theory.

4.1 Experimental Setup

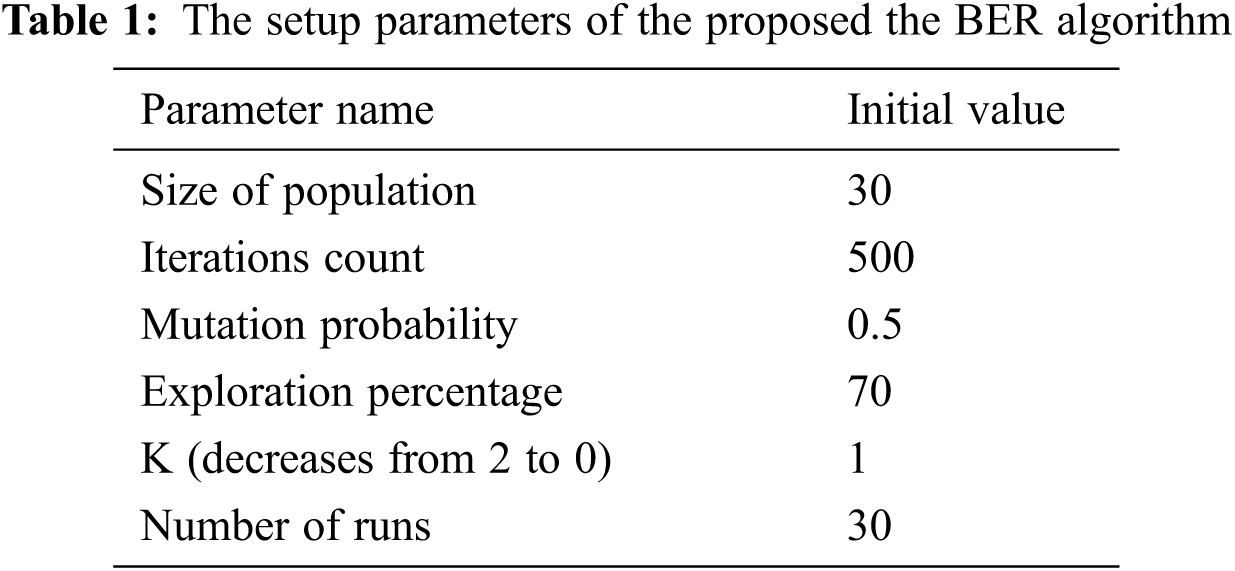
In all scenarios of the conducted experiments, we executed 30 runs of the optimization algorithms for both scenarios due to the random initialization of the individuals in the first population. Each run was composed of 500 iterations. One of the algorithm’s parameters is the population size. In this research, it has been set at 30 individuals. The initial parameters of the proposed algorithm are listed in Tab. 1.

4.2 First Scenario: Unimodal Benchmark Functions

Tab. 2 presents the seven unimodal benchmark functions (F1-F7) employed in the first scenario, where D denotes the function’s dimension and fmin refers to the function’s optimal value. Because these functions have just one global optimum, they are utilized to test how well optimization strategies are exploited.

4.2.1 Performance Analysis

Tab. 3 shows Statistical results of the results achieved by the proposed the BER and other algorithms for the benchmark functions. As shown in the table, the BER was the most efficient optimizer when compared to the other four optimizers, namely, WOA, GWO, PSO, and GA. This is because, in every cycle, the BER employs two separate exploitation strategies. The first method is to go toward the best solution, whereas the second method is to search for the best solution. These strategies assist the BER in achieving exploitation by locating better solutions in the vicinity of the best solution identified thus far. The high exploitation potential of the BER is due in part to integrated exploitation strategies, but it also has to do with the balance between exploration and exploitation. The BER, unlike most optimizers, starts the exploitation process early in the iteration and gradually raises the number of individuals in the exploitation group. This helps explain why the BER beat other optimizers in most unimodal benchmark functions.

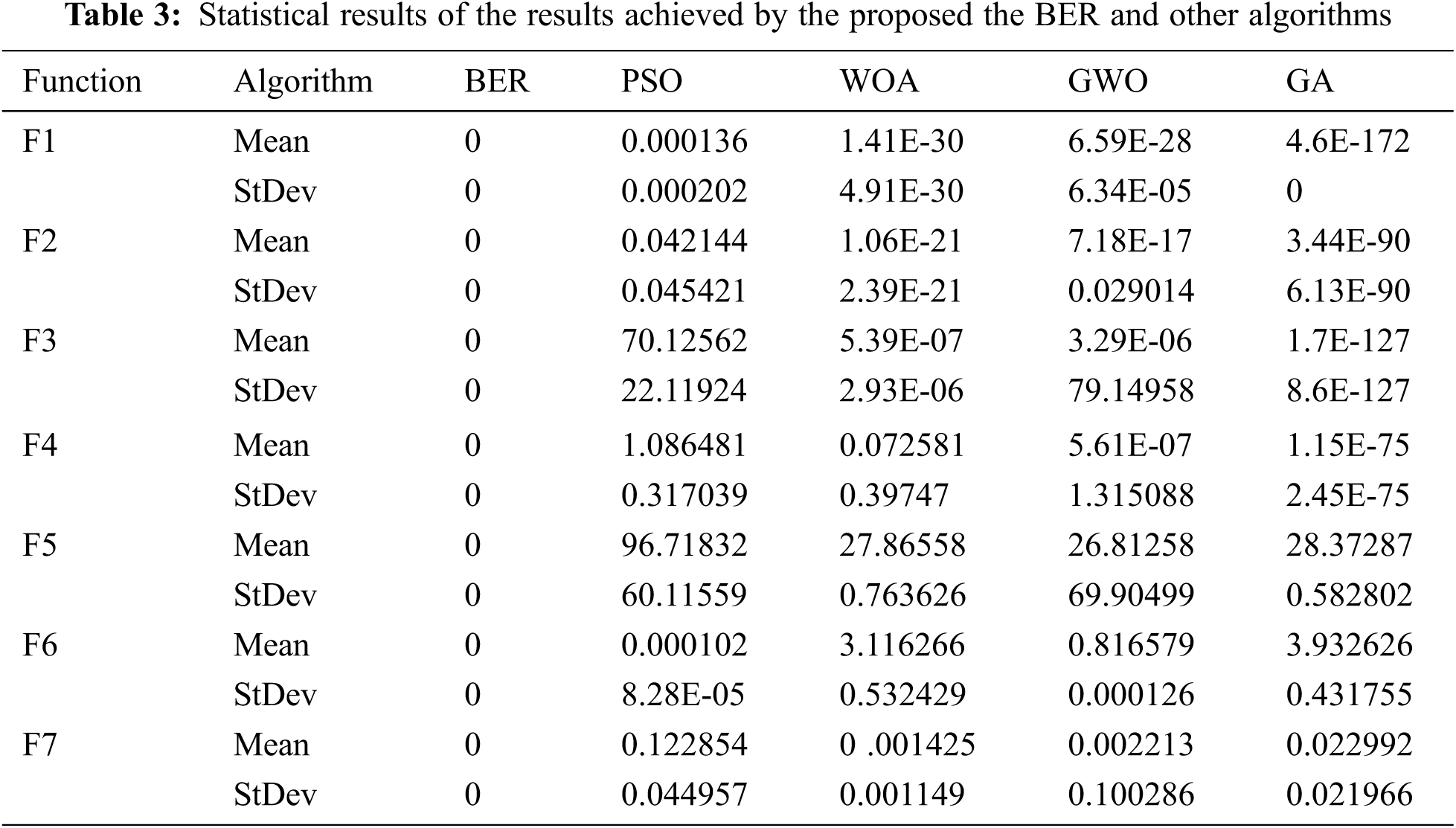
4.2.2 Statistical Significance of the Results

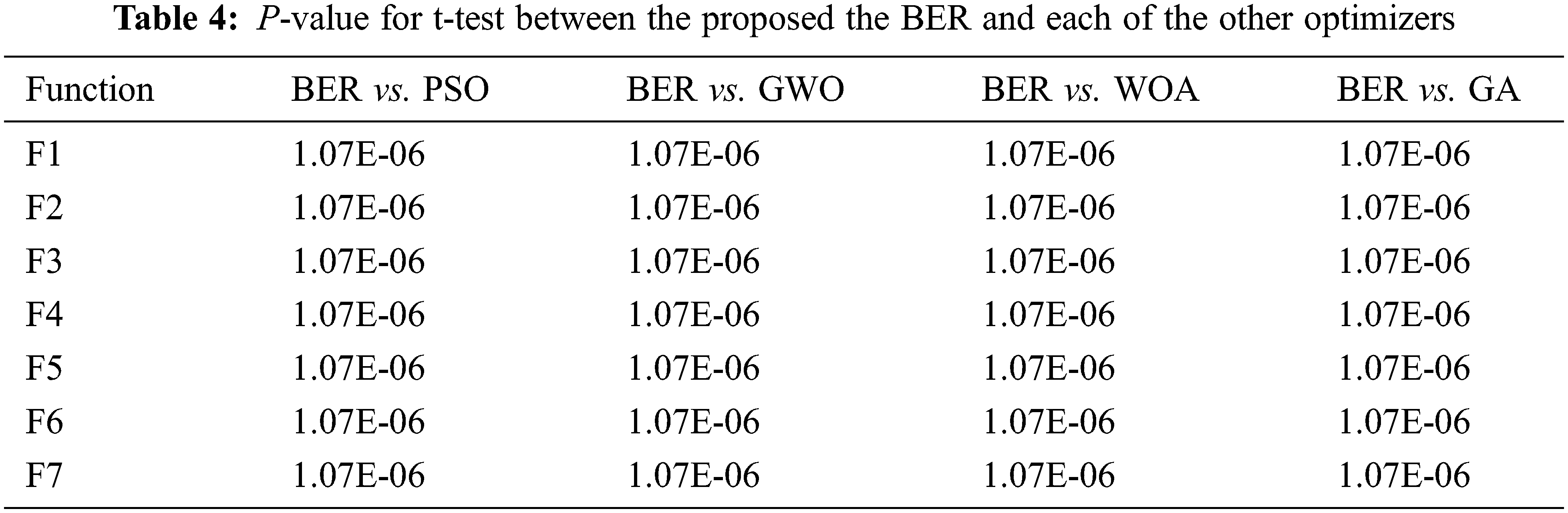
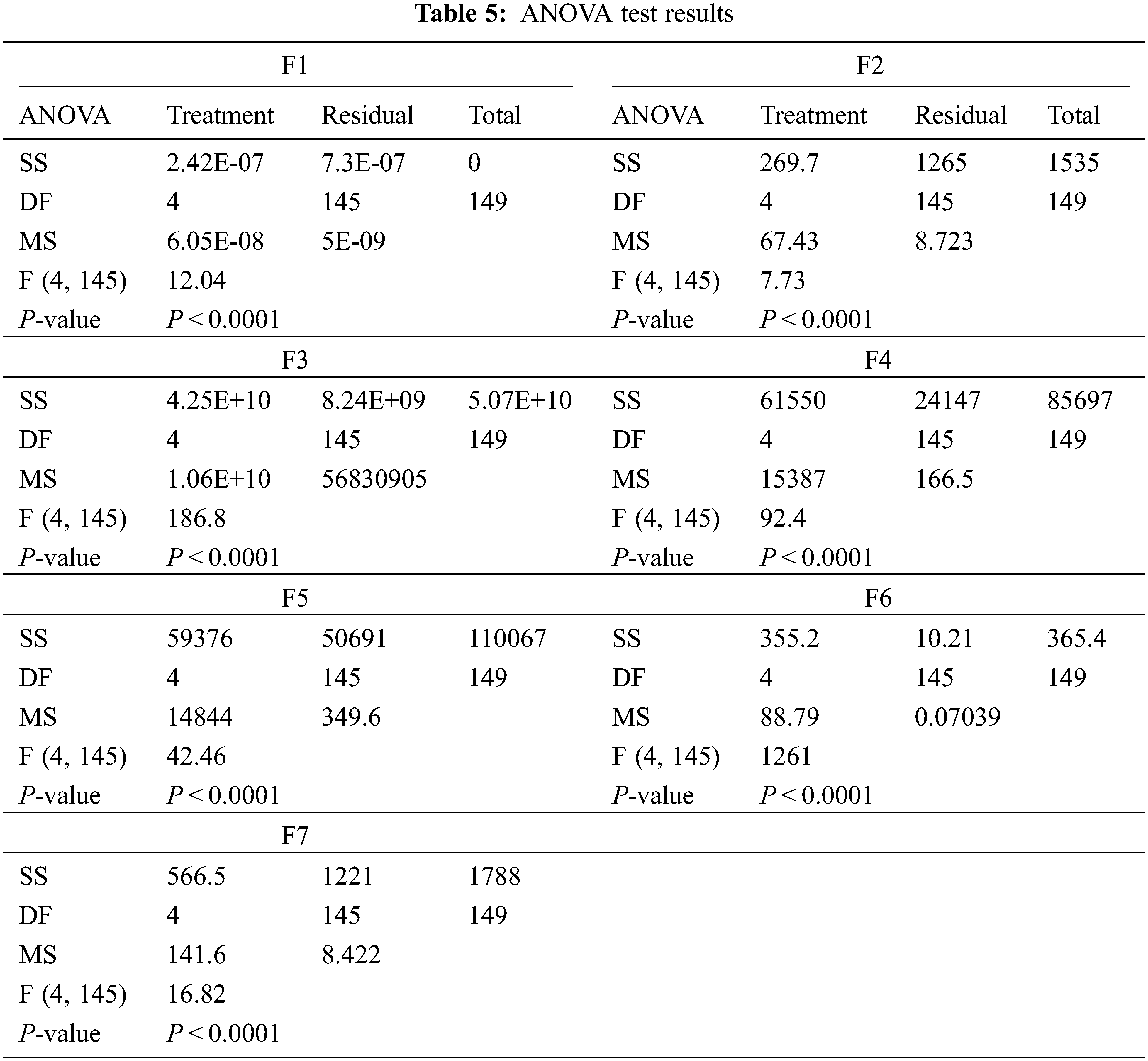
A one-tailed t-test with a significance threshold of 50% is used for each benchmark function to ensure that the findings generated by the BER have statistical significance. The p-values of the t-test results of comparing the BER to other optimizers in determining the minimum of each benchmark function are shown in Tab. 4. According to the findings, the BER outperforms the competing optimization algorithms included in the conducted experiment. It can be noticed that the BER and other optimizers were able to discover the global optima of the seven functions with almost identical averages but different standard deviations. This might explain why no statistical significance has been found. On the other hand, the one-way analysis of variance (ANOVA) test is performed to study the significant difference between the proposed BER algorithm and the four different algorithms. The results of this test are presented in Tab. 5. This test is based on two hypotheses, H0, and H1, where the H0 refers to the equality of means of these optimizers. As shown in the table, the analysis shows no significant difference between the proposed BER and other algorithms.

4.2.3 Visual Analysis of the Results

Fig. 4 shows the boxplots of the results achieved by the proposed the BER algorithm and the other optimization algorithms (BER, PSO, WOA, GWO, and GA). The table shows that the proposed algorithm could achieve the best performance. In addition, the curves of convergence of the benchmark functions based on the optimization algorithms are shown in Fig. 5. As shown in the figure, the proposed algorithm shows a clear superiority when compared to the other algorithms.

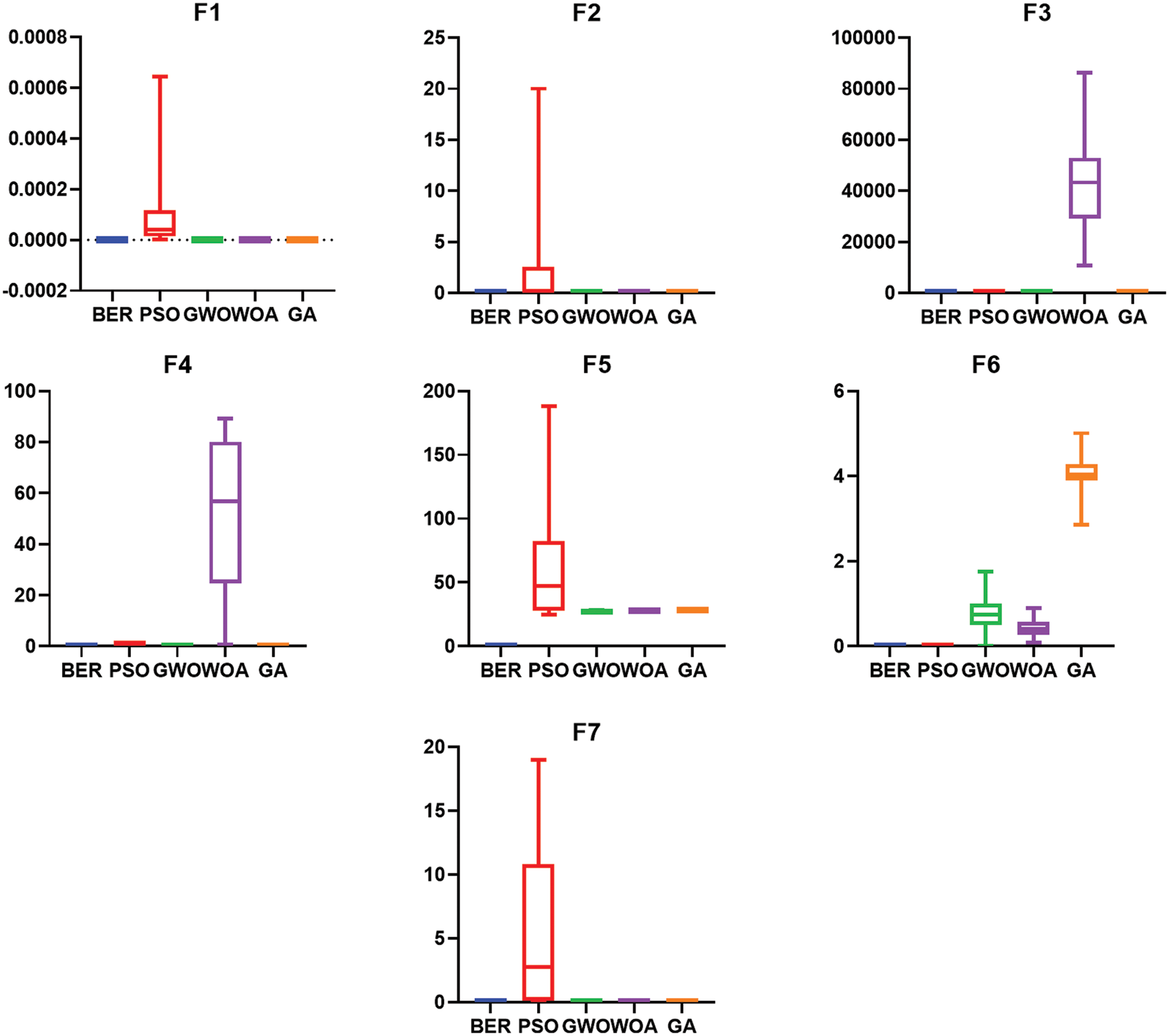
Figure 4: Boxplots of the BER and other competing algorithms for benchmark functions (f1 ... f7)

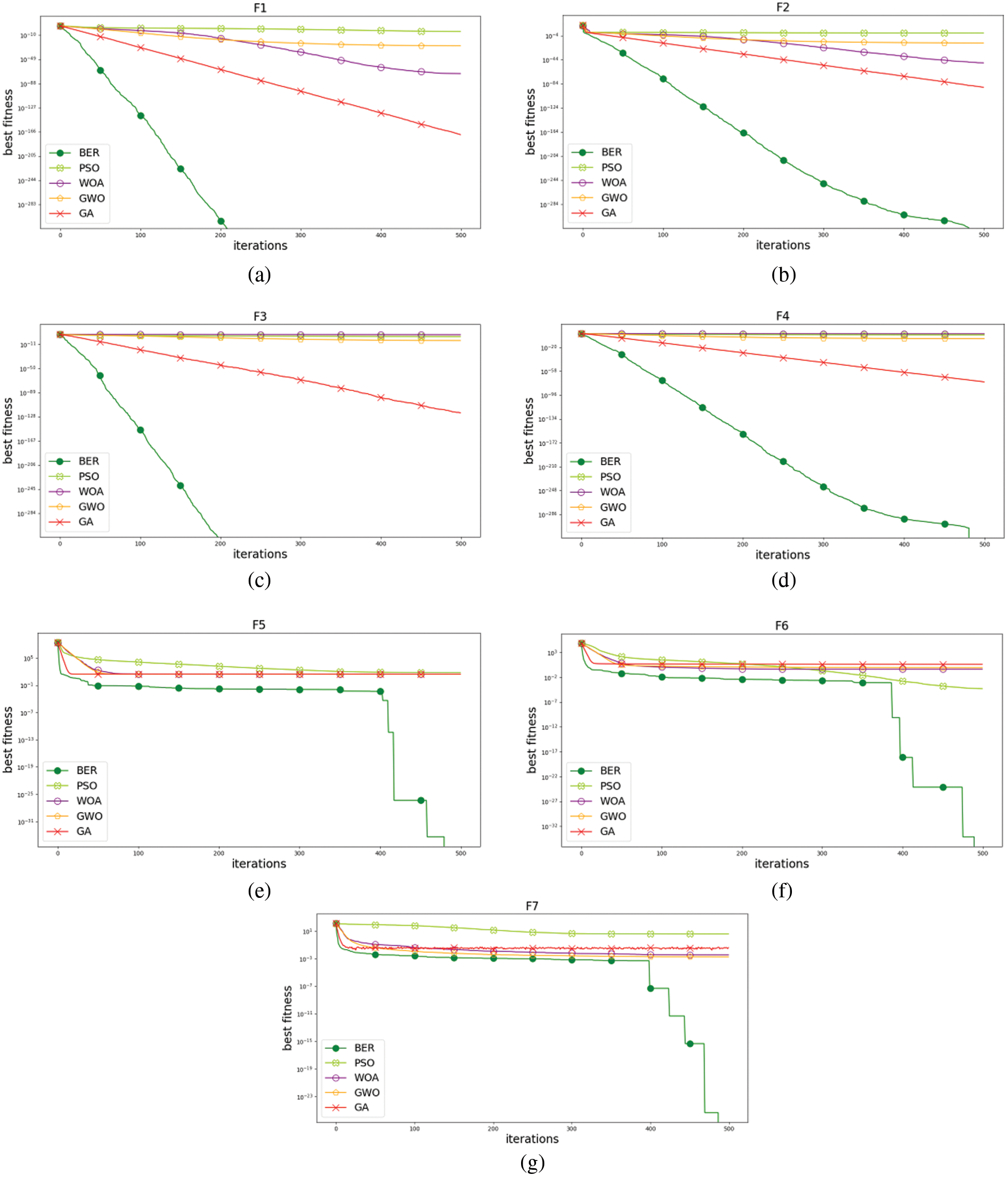
Figure 5: The curves of convergence of BER, PSO, WOA, GWO, and GA for the benchmark functions

4.3 Second Scenario: A Constrained Engineering Problem

The proposed BER optimization algorithm is used to solve one of the well-known design engineering problems, referred to as tension/compression spring design, to prove the effectiveness of the proposed algorithm in real-world handling challenges in engineering constrained problems. Based on the components of optimization problems, such as inequality constraints, equality constraints, and upper and lower limits, the formulation of this engineering problem is expressed by the following equations.

Minimizef(x)

Subject to the constraints:

gi(x)=0,i=1,2,…,p

gj(x)≤0,j=1,2,…,m

lk≤xk≤uk,k=1,2,…,n (11)

where the objective function, equality, and in-equality constraints are denoted by f(x),gi(x), and gj(x) . The constraints of this problem are handled and characterized using scalar penalty functions since these restricted optimization problems include numerous equality and inequality requirements. The constraint optimization problem is obtained from the unconstrained problem through these penalty functions. Consequently, the description of the new objective function is represented by the following equation:

minφk(x)=f(x)+pk∑i∈I⁡g(ci(x)) (12)

In this equation, the new objective function is referred to as φk(x) is, the penalty function is denoted by g(ci(x))=max(0,ci(x))2 , ci(x) refers to the constraints of the problem, f(x) denotes the objective function, and the penalty coefficient is referred to as pk .

4.3.1 The Tension/Compression Spring Engineering Problem

Fig. 6 depicts the structure of the tension/compression spring engineering problem. The main goal of this problem is to reduce the spring’s weight with respect to a set of constraints referred to as geometry, surge frequency, stress, and deflection. Four constraints of type inequalities and nonlinear, in addition to three continuous variables, namely, a number of coils (L), mean coil diameter (d), and wire diameter (w), are the design variables of this problem.

Figure 6: The structure of the engineering design problem of type compression/tension spring

The spring design problem has the following mathematical model:

Minimizeg(L,d,w,d)=(L+2)w2d

Subject to the constraints:

c1=1−d3L71785w4≤0

c2=d(4d−w)12566(dw3−w4)+15108w2−1≤0

c3=1−140.45wd2L≤0

c4=2(w+d)3−1≤0 (13)

where the ranges of design variables are specified as follows:

2.0≤L≤15,

0.25≤d≤1.3,

0.05≤w≤2.0

4.3.2 Performance Analysis

A Comparison between the best solutions discovered by the proposed BER and the other competing algorithms is presented in Tab. 6. In this table, the solution found by the BER is better than the other solutions when compared to the reference solution. In addition, a comparison of statistical results achieved by the BER and different competing algorithms is listed in Tabs. 7 and 8. These results show the effectiveness and superiority of the proposed BER when compared to PSO, GSA, and WOA algorithms.

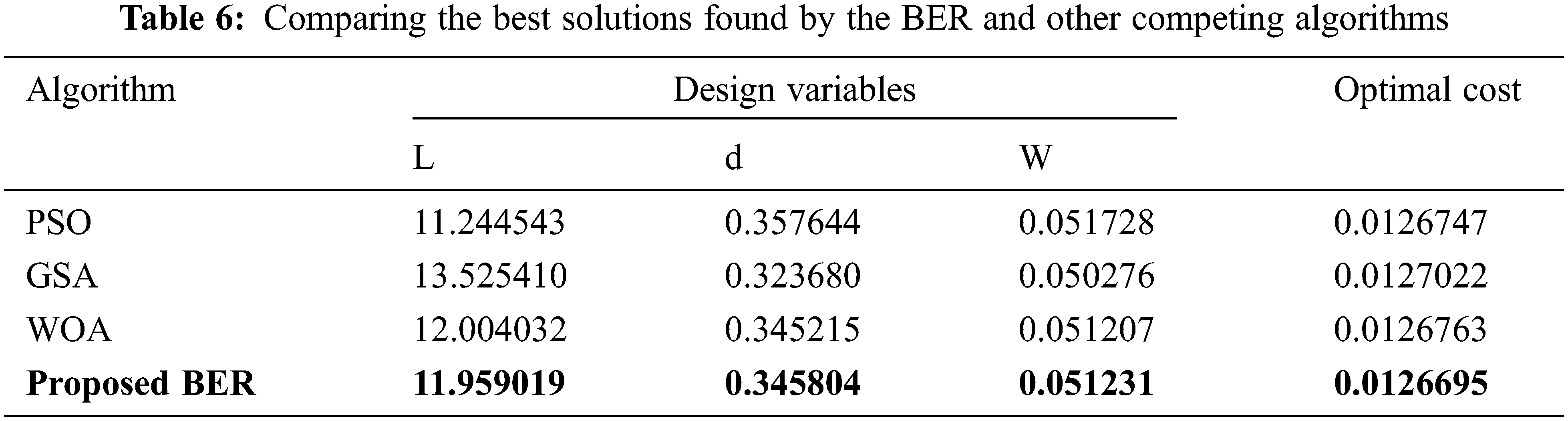
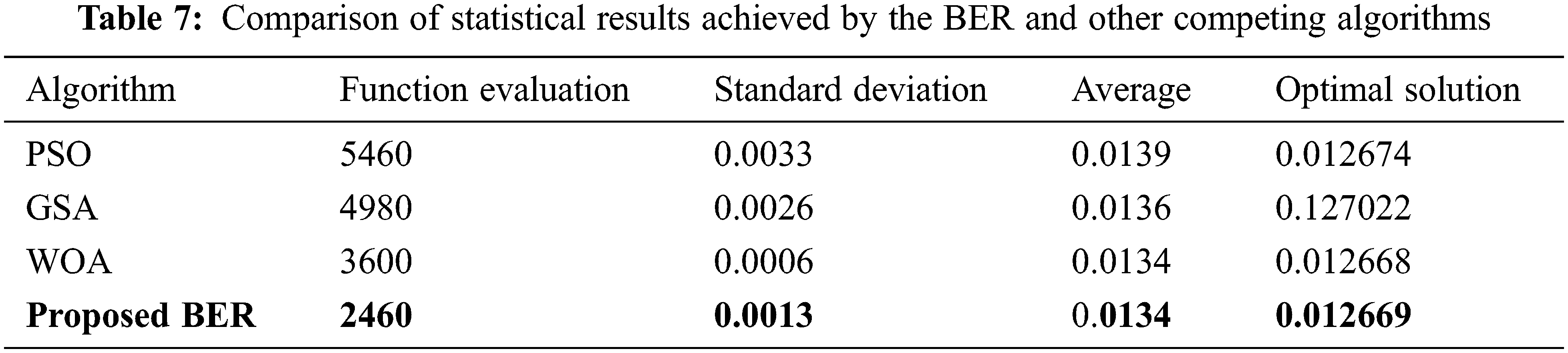
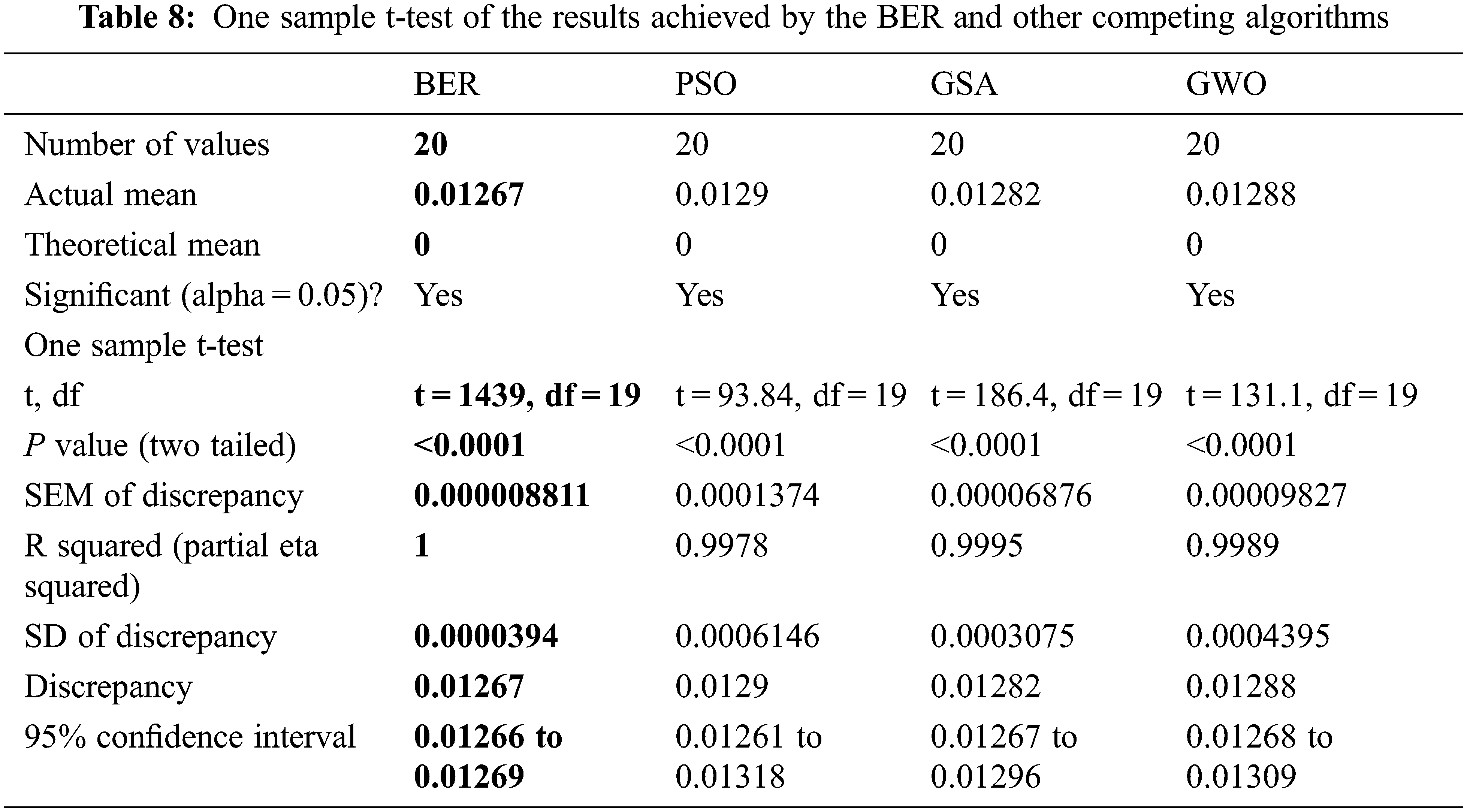
On the other hand, a visual analysis of the results achieved by the optimization algorithms is depicted in the plots shown in Figs. 7 and 8. The histograms of the results achieved by the BER and other competing algorithms shown in Fig. 7 emphasize the superiority of the proposed algorithms. The analysis plots are shown in Fig. 8 depict the proposed algorithm’s effectiveness in solving the adopted optimization problems.

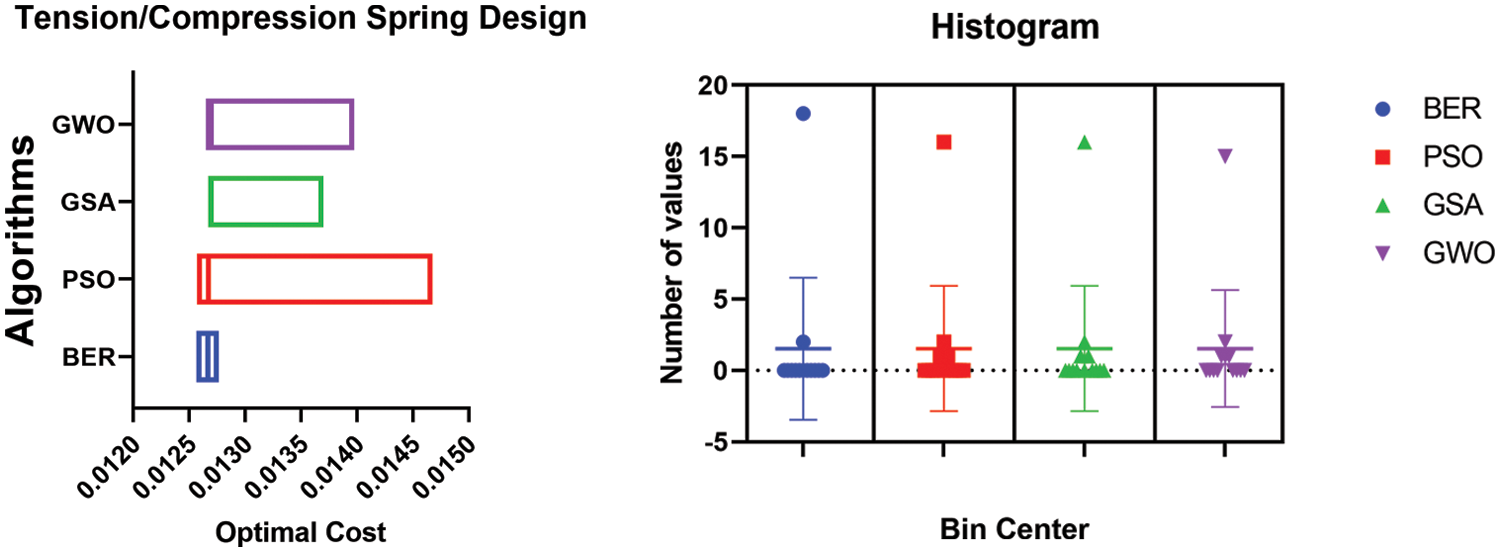
Figure 7: Histograms of the results achieved by the BER and other competing algorithms

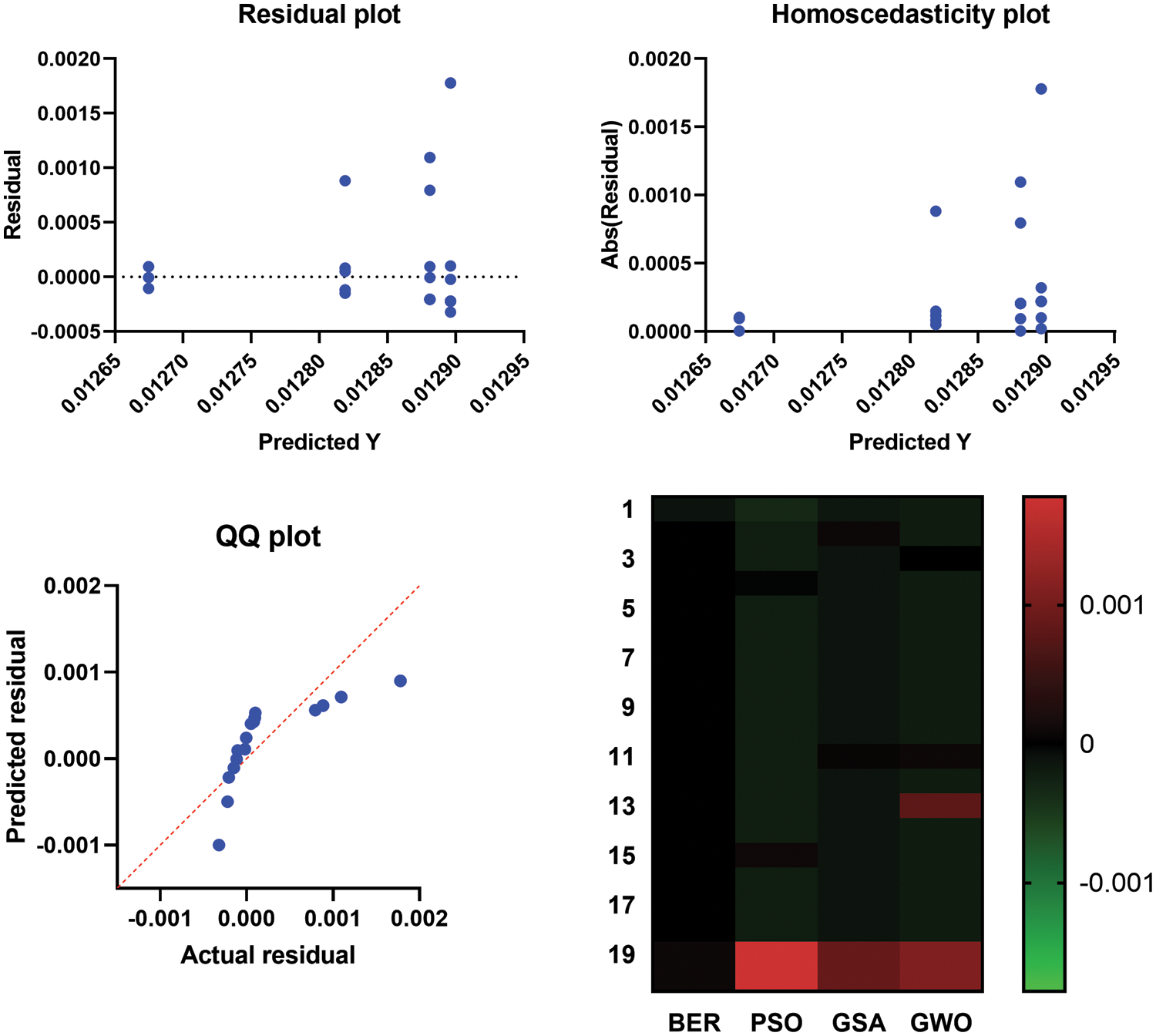
Figure 8: Analysis plots of the results achieved by the BER and other algorithms

5  Conclusions

Al-Biruni Earth Radius (BER) search optimization algorithm is a new optimization algorithm that we proposed in this research. The proposed algorithm is based on exploring the area around the local solutions using the Al-Biruni method, which can help individuals to reach the global solution. Individuals are divided into two groups: exploration and exploitation. The exploration group employs the search strategy to examine the search space for potential solutions thoroughly. On the other hand, the exploitation group uses two approaches to identify better solutions from excellent ones (Move toward the leader and Search around the leader). To ensure finding the best solution, the BER permits mutation of the solutions that do not achieve progress in terms of the fitness function for three iterations. To test the effectiveness of the proposed algorithm in discovering the optimum points of each function and studying its convergence behavior, a comparison was conducted on seven typical benchmark mathematical optimization functions. The findings indicated that the BER is competitive with current metaheuristic and evolutionary optimization algorithms. Due to its promising exploration and exploitation capabilities and its ability to avoid local optima, the proposed BER algorithm has a quick convergence characteristic. In addition, it has been employed to solve a typical engineering design optimization problem referred to as the tension/compression spring design optimization problem. These findings emphasize the effectiveness of the proposed BER algorithm in tackling constraint optimization problems optimally. The future perspective of this research is to include more mathematical optimization functions and engineering problems in the conducted experiments.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R308), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R308), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Ibrahim, H. A. Ali, M. M. Eid and E. -S. M. El-kenawy, “Chaotic harris hawks optimization for unconstrained function optimization,” in Int. Computer Engineering Conf., Cairo, Egypt, pp. 153–158, 2020. [Google Scholar]

 2.  R. Al-Hajj and A. Assi, “Estimating solar irradiance using genetic programming technique and meteorological records,” AIMS Energy, vol. 5, no. 5, pp. 798–813, 2017. [Google Scholar]

 3.  R. Al-Hajj, A. Assi and F. Batch, “An evolutionary computing approach for estimating global solar radiation,” in IEEE Int. Conf. on Renewable Energy Research and Applications, Birmingham, UK, pp. 285–290, 2016. [Google Scholar]

 4.  Y. Li, J. Wang, D. Zhao, G. Li and C. Chen, “A two-stage approach for combined heat and power economic emission dispatch: Combining multi-objective optimization with integrated decision making,” Energy, vol. 162, no. 1, pp. 237–254, 2018. [Google Scholar]

 5.  X. Wang, T. -M. Choi, H. Liu and X. Yue, “A novel hybrid ant colony optimization algorithm for emergency transportation problems during post-disaster scenarios,” IEEE Transactions on Systems, Management, Cybernetic Systems, vol. 48, no. 4, pp. 545–556, 2018. [Google Scholar]

 6.  R. V. Rao and G. G. Waghmare, “A new optimization algorithm for solving complex constrained design optimization problems,” Engineering Optimization, vol. 49, no. 1, pp. 60–83, 2017. [Google Scholar]

 7.  I. E. Grossmann, “Global optimization in engineering design,” in Nonconvex Optimization and Its Applications, 1st ed., US: Springer, vol. 9, pp. 231–289, 2013. [Google Scholar]

 8.  W. -Y. Lin, “A novel 3D fruit fly optimization algorithm and its applications in economics,” Neural Computing Applications, vol. 27, no. 5, pp. 1391–1413, 2016. [Google Scholar]

 9.  Y. Cheng, S. Zhao, B. Cheng, S. Hou, Y. Shi et al., “Modeling and optimization for collaborative business process towards IoT applications,” Mobile Information Systems, vol. 2018, no. 1, pp. 1–17, 2018. [Google Scholar]

10. M. Nouiri, A. Bekrar, A. Jemai, S. Niar and A. C. Ammari, “An effective and distributed particle swarm optimization algorithm for flexible job-shop scheduling problem,” Journal of Intelligent Manufacturing, vol. 29, no. 3, pp. 603–615, 2018. [Google Scholar]

11. M. M. Eid, E. -S. M. El-kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in National Computing Colleges Conf. (NCCC), Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]

12. K. Hussain, M. N. Mohd Salleh, S. Cheng and Y. Shi, “Metaheuristic research: A comprehensive survey,” Artificial Intelligence Review, vol. 52, no. 4, pp. 2191–2233, 2019. [Google Scholar]

13. J. Hao and C. Solnon, “Metaheuristics and artificial intelligence,” In: P. Marquis, O. Papini, H. Prade, (Eds.in A Guided Tour of Artificial Intelligence Research: AI Algorithms, 1st ed., Cham, Denmark: Springer, vol. 2, pp. 27–52, 2020. [Google Scholar]

14. O. Mohammad rezapour, I. Yoosef Doost and M. Ebrahimi, “Cuckoo optimization algorithm in optimal water allocation and crop planning under various weather conditions (case study: Qazvin plain, Iran),” Neural Computing and Applications, vol. 31, no. 1, pp. 1879–1892, 2017. [Google Scholar]

15. D. Gupta, S. Sundaram, A. Khanna, A. Hassanien and V. Albuquerque, “Improved diagnosis of Parkinson’s disease using optimized crow search algorithm,” Computer and Electrical Engineering, vol. 68, no. 1, pp. 412–424, 2018. [Google Scholar]

16. K. B. O. Medani, S. A. Sayah and A. Bekrar, “Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system,” Electric Power Systems Research, vol. 163, no. 1, pp. 696–705, 2018. [Google Scholar]

17. M. Ahmadi, K. Kazemi, A. Aarabi, T. Niknam and M. S. Helfroush, “Image segmentation using multilevel thresholding based on modified bird mating optimization,” Multimedia Tools Applications, vol. 78, no. 1, pp. 23003–23027, 2019. [Google Scholar]

18. M. Hadwan, M. Ayob, N. R. Sabar and R. Qu, “A harmony search algorithm for nurse rostering problems,” Information Sciences, vol. 233, no. 1, pp. 126–140, 2013. [Google Scholar]

19. M. Hadwan, M. Ayob, M. A. Rassam and E. A. Hezam, “Deluge harmony search algorithm for nurse rostering problems,” in 2019 First Int. Conf. of Intelligent Computing and Engineering (ICOICE), Hadhramout, Yemen, pp. 1–5, 2019. [Google Scholar]

20. X. -S. Yang and S. Deb, “Cuckoo search via lévy flights,” in 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, pp. 210–214, 2009. [Google Scholar]

21. X. S. Yang, “A new metaheuristic bat-inspired algorithm,” in Nature Inspired Cooperative Strategies for Optimization (NICSO 2010), 1st ed., Berlin, Heidelberg: Springer, vol. 284, pp. 65–74, 2010. [Google Scholar]

22. D. Simon, “Biogeography-based optimization,” IEEE Transactions on Evolutionary Computation, vol. 12, no. 6, pp. 702–713, 2008. [Google Scholar]

23. E. Cuevas, M. Cienfuegos, D. Zaldí and M. Pérez-Cisneros, “A swarm optimization algorithm inspired in the behavior of the social-spider,” Expert Systems with Applications, vol. 40, no. 16, pp. 6374–6384, 2013. [Google Scholar]

24. E. -S. El-Kenawy and M. Eid, “Hybrid gray wolf and particle swarm optimization for feature selection,” International Journal of Innovative Computing, Information and Control, vol. 16, no. 3, pp. 831–844, 2020. [Google Scholar]

25. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, no. 1, pp. 46–61, 2014. [Google Scholar]

26. C. Min-Yuan and D. Prayogo, “Symbiotic organisms search: A new metaheuristic optimization algorithm,” Computers and Structures, vol. 139, no. 1, pp. 98–112, 2014. [Google Scholar]

27. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, no. 1, pp. 51–67, 2016. [Google Scholar]

28. X. -S. Yang, “Firefly algorithm, stochastic test functions and design optimization,” arXiv preprint, arXiv:1003.1409, 2010. [Google Scholar]

29. E. Rashedi, H. Nezamabadi-Pour and S. Saryazdi, “GSA: A gravitational search algorithm,” Information Sciences, vol. 179, no. 13, pp. 2232–2248, 2009. [Google Scholar]

30. K. M. Passino, “Biomimicry of bacterial foraging for distributed optimization and control,” IEEE Control Systems Magazine, vol. 22, no. 1, pp. 52–67. 2002. [Google Scholar]

31. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, no. 1, pp. 120–133, 2016. [Google Scholar]

32. H. Holland, “Genetic algorithms,” Scientific American, vol. 267, no. 1, pp. 66–73, 1992. [Google Scholar]

33. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of Int. Conf. on Neural Networks, Perth, WA, Australia, vol. 4, no. 6, pp. 1942–1948, 1995. [Google Scholar]

34. S. N. Chegini, A. Bagheri and F. Najafi, “PSOSCALF: A new hybrid PSO based on sine cosine algorithm and levy flight for solving optimization problems,” Applied Soft Computing, vol. 73, no. 1, pp. 697–726, 2018. [Google Scholar]

35. W. Colman, “Measuring the radius of the earth,” The Mathematical Gazette, vol. 95, no. 532, pp. 72–76, 2011. [Google Scholar]

36. E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced metaheuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, no. 1, pp. 36019–36037, 2021. [Google Scholar]

37. E. S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and newton’s laws,” IEEE Access, vol. 9, no. 1, pp. 115750–115765, 2021. [Google Scholar]

38. A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Alharthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, no. 1, pp. 125787–125804, 2021. [Google Scholar]

39. A. A. Salamai, E. -S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4.0,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]

40. N. Khodadadi and S. Mirjalili, “Truss optimization with natural frequency constraints using generalized normal distribution optimization,” Applied Intelligence, vol. 2022, no. 1, pp. 1–14, 2022. [Google Scholar]

41. E. -S. M. El-kenawy, H. F. Abutarboush, A. W. Mohamed and A. Ibrahim, “Advance artificial intelligence technique for designing double T-shaped monopole antenna,” Computers, Materials & Continua, vol. 69, no. 3, pp. 2983–2995, 2021. [Google Scholar]

42. M. M. Fouad, A. I. El-Desouky, R. Al-Hajj and E. -S. M. El-Kenawy, “Dynamic group-based cooperative optimization algorithm,” IEEE Access, vol. 8, no. 1, pp. 148378–148403, 2020. [Google Scholar]

43. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]

44. W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A multi-feature learning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3560, 2021. [Google Scholar]