Double Deep Q-Network Method for Energy Efficiency and Throughput in a UAV-Assisted Terrestrial Network

1  Introduction

In recent years, unmanned aerial vehicle (UAV)-assisted fifth-generation (5G) communication has provided an attractive way to connect users with different devices and improve network capacity. However, data traffic on cellular networks increases exponentially, Thus, resource allocation (RA) is becoming increasingly critical [1]. Industrial spectrum bands experience increased demand for channels, leading to a spectrum scarcity situation. In the context of 5G, mmWave is considered a potential solution to meet this demand [2,3]. Moreover, other techniques, such as beamforming, multi-input multi-output (MIMO), and advanced power control, are introduced as promising solutions in the design of future networks [4]. Despite all these attempts to satisfy this demand, RA remains a priority to accommodate users in terms of Quality of Service (QoS). RA problems are often formulated as nonconvex problems requiring proper management [5,6]. Optimal solutions are obtained by implementing heuristic methods, such as genetic algorithm, particle swarm optimization, and simulated annealing [7,8]. However, such solutions end up with quasioptimal solutions and converge relatively slowly. Therefore, alternative solutions and flexible algorithms that exploit late development in artificial intelligence are desirable to explore. Recently, deep learning (DL) [9] has emerged as an effective tool to increase flexibility and optimize RA in complex wireless communication networks. First, DL-based RA is flexible because the same deep neural network (DNN) can be implemented to achieve different design objectives by modifying the loss function [10]. Second, the computation time required by DL to obtain RA results is lower than that of conventional algorithms [11]. Finally, DL can receive complex high-dimensional information as input and allocate the optimal action for each input statistic in a particular condition [10]. On the basis of the above analysis, DL can be chosen as an accurate method for RA.

1.1 Related Works

As an emerging technology, DL has been used in several research studies to improve RA for terrestrial networks. For instance, the authors in [12] investigated the deep reinforcement learning (DRL)-based time division duplex configuration to allocate radio resources dynamically in an online manner and with high mobility. In [1], Lee et al. proposed deep power control based on a convolutional neural network to maximize spectral efficiency (SE) and energy efficiency (EE). In this study, a comparison between the DL model and a conventional weighted minimum mean square error was realized. In the same context, [13] performed a max-min and max-prod power allocation in downlink massive MIMO. To maximize EE, a deep artificial neural network scheme was applied in [14], where interference and system propagation channels were considered. Deep Q-learning (DQL)-based RA has also attracted much attention in recent literature. In [15], the authors studied the RA problem to enhance EE. The proposed method formulated a combined optimization problem, considering EE and QoS. More recently, a supervised DL approach in 5G multitier networks was adopted in [16] to solve the joint RA and remote–radio–head association. For this model, efficient subchannel and power allocation were used to generate training data. According to the decentralized RA mechanism, the authors in [17] developed a novel decentralized DL for vehicle-to-vehicle communications. The main objective was to determine the optimal sub-band and power level for transmission without requiring or waiting for global information. The authors used a DRL-based power control to investigate the problem of spectrum sharing in a cognitive radio system. The aim of this framework is that the secondary user shares the common spectrum with the primary user. Instead of unsupervised learning, the authors in [18] introduced supervised learning to maximize the throughput of device-to-device with maximum power constraint. The authors in [19] presented a comprehensive approach and considered DRL to maximize the total network throughput. However, this work did not include EE for optimization. Majority of the learning algorithms introduced above do not incorporate constraints directly into the training cost functions. Nowadays, literatures focus on RA in UAV-assisted cellular networks based on artificial intelligence. In reference [20], authors proposed a multiagent reinforcement learning framework to study the dynamic RA of multiple UAVs. The objective of this investigation was to maximize long-term rewards. However, the work did not consider UAV height. In [21], the authors used deep Q-network to solve the RA for UAV-assisted ultradense networks. To maximize system EE, a link selection strategy was proposed to allow users to select the optimal communication links. The authors did not consider the influence of SE on EE. In addition, the authors in [22] studied the RA problem of UAV-assisted wireless-powered Internet of Things systems, aiming to allocate optimal energy resources for wireless power transfer. In [23], the authors thoroughly investigated deep Q-network (DQN), invoking the difference of convex-based optimization method for multicooperative UAV-assisted wireless networks. This work assumed beamforming technique to serve users simultaneously in the same spectrum and maximize the sum user achievable rate. However, the work was not focused on EE. Another DQN work in [24] was presented to study the low utilization rate of resources. A novel DQN-based method was introduced to address the complex problem. The authors in [25] analyzed RA for bandwidth, throughput, and power consumption in different scenarios for multi-UAV-assisted IoT networks. On the basis of machine learning, authors considered DRL to address the joint RA problem. Although the proposed approach remained efficient, it did not consider ground network, EE and total throughput. In the present study, we aim to optimize EE and total throughput in UAV-assisted terrestrial networks subject to the constraints on transmission power and UAV height. Our main efforts are to apply a double deep Q-network (DDQN) that obtains optimal rewards better than DQN [26].

1.2 Contribution

Existing research on RA in UAV-assisted 5G networks focuses on single objective optimization and considers the DQN algorithm to generate data. Following the previous analysis, we investigate the RA problem in UAV-assisted cellular networks that maximize EE and total network throughput. Especially, DDQN is proposed to address intelligent RA. The main contributions of this study are listed below.

(1)   We formulate EE and total throughput in mmWave scenario while ensuring the minimum QoS requirements for all users according to the environment. However, the optimization problem is formulated as a mixed integer nonlinear program. Multiple constraints, such as the path loss model, number of users, channel gains, beamforming, and signal-to-interference-plus-noise ratio (SINR) issues, are used to describe the environment.

(2)   We investigate a multiagent DDQN algorithm to optimize EE and total throughput. We assume that each user equipment (UE) behaves as an agent and performs optimization decisions on environmental information.

(3)   We compare the performance of the proposed algorithm, QL, and the DQN approaches already proposed in terms of RA.

The remainder of this paper is organized as follows: An overview for DRL is presented in Section 2, and the system model is introduced in Section 3. Then, the DDQN algorithm is discussed in Section 4, followed by simulation and results in Section 5. Lastly, conclusions and perspectives are drawn in Section 6.

2  Overview of DRL

DRL is a prominent case of machine learning and thus a class of artificial intelligence. It allows agents to identify the ideal performance based on its own experience, rather than depending on a supervisor [27]. In this approach, a neural network is used as an agent that learns by interacting with the environment and solves the process by determining an optimal action. Compared with the standard ML, namely supervised and unsupervised learning [28], DRL does not depend on data acquisition. Thus, sequential decision making occurs, and the next input is based on the decision of the learner or system. Moreover, in DRL, the Markov decision process (MDP) is formalized as a mathematical approach to modeling and decision-making situations. The reinforcement learning process operates as follows [29]: the agent begins in a specific state within its environment s0∈S by obtaining an initial observation w0∈Ω and takes an action at∈A at each time step t . As illustrated in Fig. 1, the DRL can be categorized into three algorithms, such as value-based, policy gradient, and model-based methods. In value-based DRL, the agent uses the learned value function to evaluate (s,a) pairs and generate a policy [30]. DQL is a much more popular and efficient algorithm in this category. By contrast, a policy-based algorithm is intuitive, where algorithms learn a policy π . Learning a policy to act in an environment is sensible; thus, a policy function π considers a state s as input to generate an action a∼π(s) .

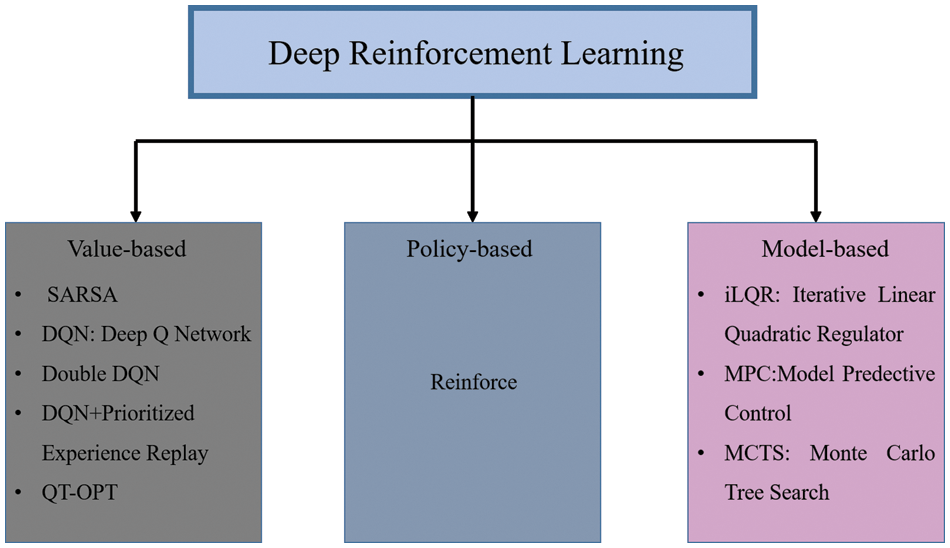
Figure 1: DRL algorithms

2.1 Q-Learning

As a popular branch of machine learning, Q-learning is based on the main concept of the action value function qπ(s,a) for policy π . It uses the Bellman equation to learn and calculate the optimum values of the Q-function in an iterative way [30], which is expressed as

Q(st,at)←Q(st,at)+αt[rt+1+γαt+1maxQ(st+1,αt+1)−Q(st,at)] (1)

where αt is the step-size parameter that defines the extent to which the new data contribute to the existing Q value, γ is the MDP discounter factor, rt+1 is the numerical reward for the agent after the execution of the action, and st+1 indicates that the environment changes to a new state, with transition probability p(s′,r|s,a) , as illustrated in Fig. 2. However, the Q-learning algorithm could be applied only to RA problems with low dimensionality in state and action, resulting in an evolutionary limitation [31]. Moreover, this application is only used when the state and action spaces are discrete (e.g., channel access) [32].

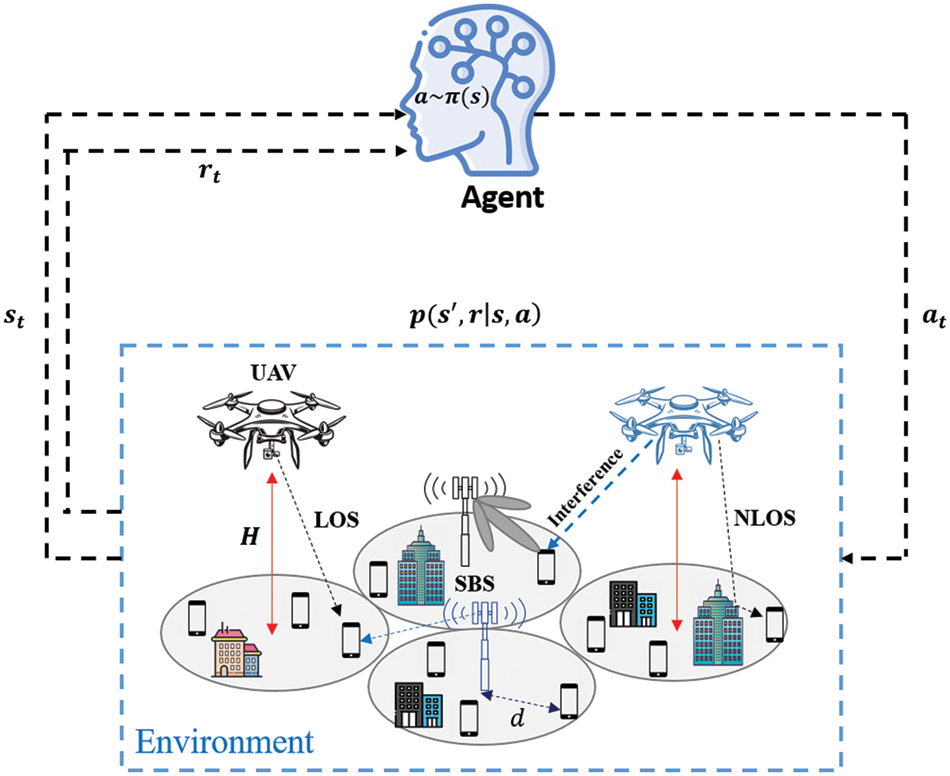
Figure 2: Q-learning algorithm for UAV-assisted SBS

2.2 Deep Q-Network

As stated above, the Q-learning algorithm faces difficulties in obtaining the optimal policy when the action and state spaces become exceptionally large [33]. This constraint is often observed in the RA approaches of cellular networks. To solve this problem, the DQN algorithm, which connects the traditional Q-learning algorithm to a convolutional neural network, was proposed [34]. The main difference with the Q-learning algorithm is the replacement of the table with the function approximator called DNN; this process attempts to approximate the Q values. Approximators have two types: a linear function and a nonlinear function [35]. However, in a nonlinear DNN, the new Q function is defined as Q(st,at|ω)≈Q∗(s,a) , where ω represents the weights of the neural network. At each time t , action at is taken in accordance with the ϵ -greedy policy, and the transition tuple ( st,at,rt,st+1) is stored mainly in a replay memory denoted by D. During the training process, a minibatch is sampled randomly from experience D to optimize the mean squared error. Thus, the target Q-network is used to improve the stability of DQN, whose ω is regularly adjusted to follow those of the principal Q-network. On the basis of the Bellman equation, the optimal state-action function is given by [35]

Q∗(st,at)=Est′[r+γat′maxQ∗(st′,at′)|st,at]. (2)

To train the DQN, iterative updating of the weight ω is used, thus minimizing the mean squared error of the Bellman equation. Mathematically, the loss function at each iteration is given by

L(ωt)=Est,at,rt,st+1∈D[rt(st,at)+γat+1maxQ(st+1,at)|ω′−Q(st,at)|ω]2 (3)

3  System Model and Problem Formulation

In the proposed model, we consider the downlink communication of a UAV-assisted cellular network comprising a set of small base stations (SBSs) denoted as S={SBS1,SBS2,…,SBSM} and a set of UAVs which is defined as U={UAV1,UAV2,…,UAVu} . UAVs are placed at a particular altitude H , and Hmin≤H≤Hmax is assumed to be constant for all UAVs. Each cell contains an mm-wave band and some user N distributed randomly in a dense area. We assume that a particular user is assigned to a single base station that provides the strongest signal. In this work, MBS and UEs are assumed to be equipped with omnidirectional antennas, i.e., antennas with unit gain, and every UAV are equipped with directional antennas [36]. Moreover, each UE associated with UAVs are assigned with orthogonal resource blocks RBs (an RB consists of 12 subcarriers, with a total bandwidth of 180 kHz in the frequency domain and one time slot 0.5 ms in the time domain), whereas UEs associated with SBSs share the remaining RBs [37]. The transmission power allocated by UAVs and SBSs are denoted by PUAV , PSBS respectively. Furthermore, the link between BS = UAVs ∪ SBSs and users can have two conditions, i.e., line-of-sight (LoS) or non-line-of-sight (NLoS) link. As illustrated in Fig. 3, interference powers from adjacent base stations are considered. Table 1 summarizes the notations that were used in this article.

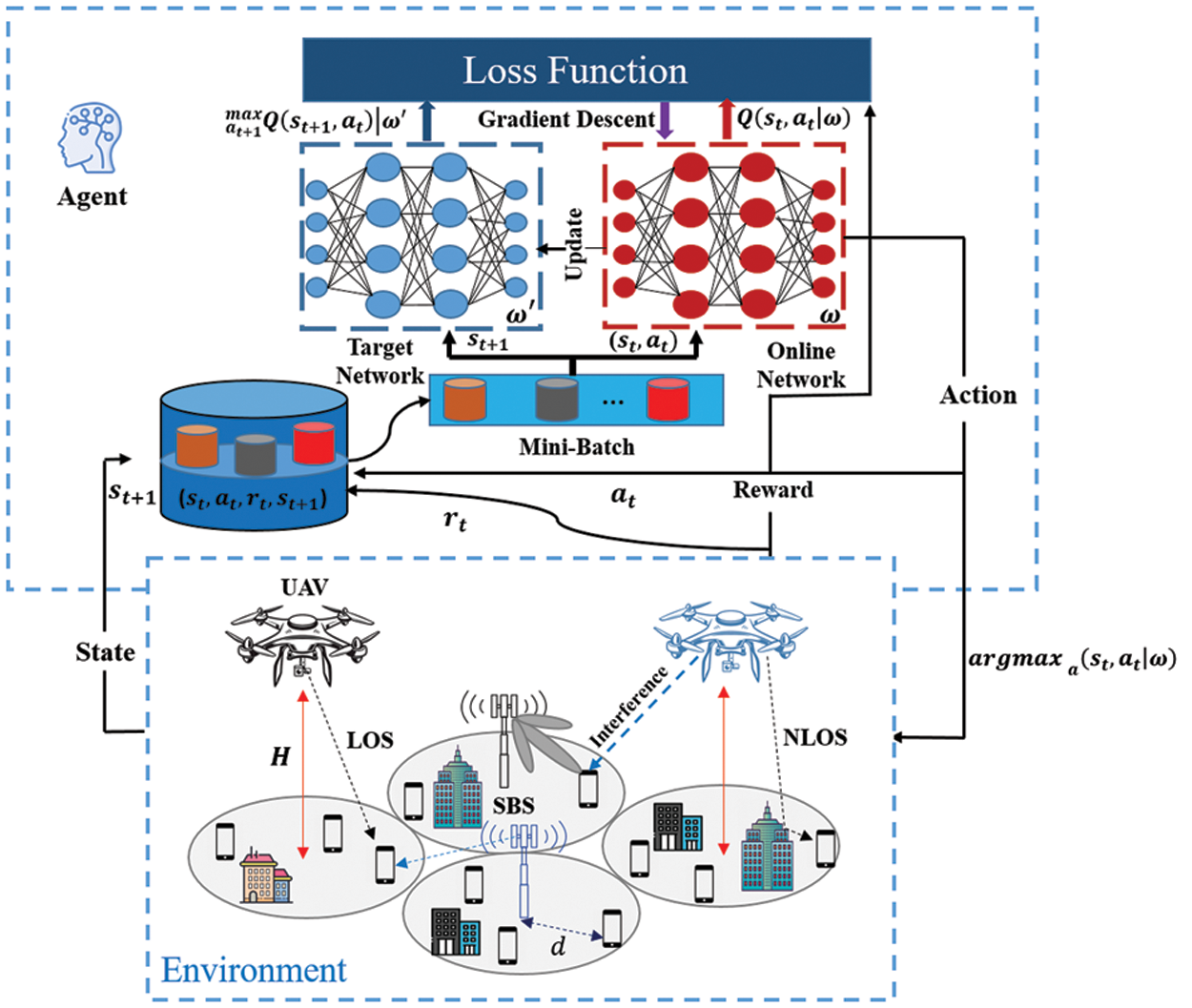
Figure 3: DQN architecture for UAV-assisted SBS

3.1 Fading and Achievable Data Rate

The channel between the base station and UE can be fixed or time varying. Fading is defined as the fluctuation in received signal strength with respect to time, and it occurs due to several factors, including transmitter and receiver movement, propagation environment, and atmospheric condition. Similar to [38], we model the channel in a way that it can capture small-scale and large-scale fading. At each time slot t , the small-scale fading between UAVs, SBSs, and UEs is considered frequency-selective fading, whose objective is to obtain a delay spread greater than the symbol period. By contrast, the channel in every subcarrier is supposed to be flat fading. This combination means that the channel gains can remain unchanged. All UEs periodically transmit their channel quality information to the related BS. In addition, let hBS,k,n designate the channel gain from BS to user k on different subcarriers n . A binary variable φ is introduced to define the association mode. If UE is associated with the UAV/SBS according to LoS link, then φ=0 ; otherwise φ=1 . We apply the following assumption in formulation. The mm-wave signal is affected by various factors, such as buildings in urban areas, making the link susceptible to effect blockage. Thus, the downlink achievable throughput (data rate) of user k on the nth subcarrier can be given by the following equation as

RBS,k,n=Plink,UAVRUAV,k,n+Plink,SBSRSBS,k,n (4)

RBS,k,n=|(φ−PLoS,UAV)|BUAVlog2(1+SINRUAV,k,n)+|(φ−PLoS,SBS)|BSBSlog2(1+SINRSBS,k,n) (5)

where PLoS,UAV , PLoS,SBS are the blockage probabilities when the link between the UAV/SBS and UE is LoS; they are expressed as [39,40]

PLoS,UAV(z)=11+b+exp(−c(180πtan−1(Hz)−b)) (6)

where b and c are constants that depend on the network environment, and z=R2−H2 is the Euclidean distance between the typical UE and UAV (see Fig. 4).

PLoS,SBS=1−eβd (7)

where β is the blockage parameter that defines the average size of obstacles. Here, d corresponds to the distance between SBS and UE.

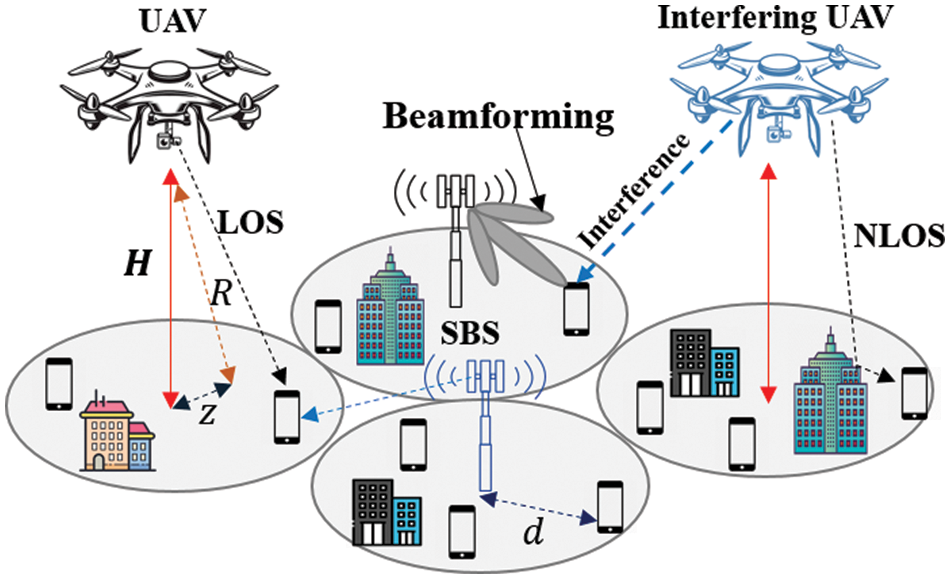
Figure 4: UAV-assisted terrestrial network (SBS)

3.2 SINR and Path Loss Model

Adding additional gain to the system remains necessary due to the propagation losses that occur at mm-wave frequencies. One of the main solutions proposed by several research for future wireless networks is beamforming [41]. The fundamental principle of beamforming is to control the direction of a wavefront toward the UE. According to [42], UAV and SBS serve UE through beamforming technology. In this manner, the SINR of UE from UAV at time slot t can be written as

γUAVt=PUAVthUAV,k,ntGUAVtPLUAVtISBS+IUAV′+σ2 (8)

where GUAVt represents the directional beamforming gain for the desired link, and σ2 refers to additive white Gaussian noise. ISBS and IUAV′ represent the interference from the adjacent SBS and UAV, respectively, and are expressed as

ISBS=PSBSthSBS,k,ntGSBSt (9)

IUAV′=PUAV′thUAV′,k,ntGUAV′t (10)

Without loss of generality, different properties are displayed in terms of propagation. For air-to-ground communication, the path loss of LoS and NLoS links at time slot t can be experienced depending on additional path losses in LoS and NLoS links φLoSt,φNLoSt and path loss exponents αLoSt , αNLoSt as

PLUAVt={φLoSt(R2+H2)αLoSt/2forLoSlinkφNLoSt(R2+H2)αNLoSt/2forNLoSlink (11)

Similarly, we define the SINR when UE is associated with SBS. In this case, we adopt the standard power-law path loss model with the mean δLoSt , δNLoSt for LoS and NLoS, respectively. Hence, the path loss model can be given as

PLSBSt={δLoStd−aLoStforLoSlinkδNLoStd−aNLoStforNLoSlink (12)

The SINR additional loss at the typical UE when it is connected to SBS is given by (13), where IUAV=PUAVthUAV,k,ntGSBSt and ISBS′=PSBS′thSBS′,k,ntGSBS′t are the interferences from UAV and SBS, respectively.

γSBSt=PSBSthSBS,k,ntGSBStPLSBStIUAV+ISBS′+σ2 (13)

3.3 Spectral Efficiency and Energy Efficiency

SE and EE are the key metrics to evaluate any wireless communication system. SE is defined as the efficiency capability of a given channel bandwidth. In other words, it represents the transmission rate per unit of bandwidth and is measured in bits per second per hertz. The EE metric is used to evaluate the total energy consumption for a network. It is defined as a ratio of the total transferred bits to the total power consumption. Nevertheless, EE and SE have a fundamental relationship. Let PC be the power consumed in the circuit of the transmitter; then, EE can be given by

EEi∈{UAV,SBS}=SEi∈{UAV,SBS}Pi+PC (14)

where Pi is the transmit power i∈{UAV,SBS} , which ranges 0<Pi≤Pmax ; the achievable SEi∈{UAV,SBS} of transmitter can be computed as

For UAV

SEUAV=log2(1+PUAVthUAV,k,ntGUAVtPLUAVtISBS+IUAV′+BUAVσ2) (15)

For SBS

SESBS=log2(1+PSBSthSBS,k,ntGSBStPLSBStIUAV+ISBS′+BSBSσ2) (16)

3.4 Objective Formulation

The proper performance of EE approaches is of paramount importance in UAV-assisted terrestrial networks because it is directly related to the choice of objectives and constraints for relevant optimization problems. In this work, we aim to optimize two specific objectives for RA, namely, the maximization of EE and throughput. From the SE perspective, the EE maximization problem can be formulated as

max∑k∈N⁡EEt (17)

s.t. C1 : 0<Pi≤Pmax∀i∈{UAV,SBS};∀UAV∈U;∀SBS∈S

   C2:Hmin≤H≤Hmax∀UAV∈U

   C3:EEUAVt≥EESBSt∀UAV∈U;∀SBS∈S

   C4 : RBS,k,n≥RBS,k,nQos

   C5 : γUAVt≥γUAVth∀UAV∈U

   C6 : γSBSt≥γSBSth∀SBS∈S

   C7 : ξ∈{0,1}∀UAV∈U;∀SBS∈S

Constraint C1 means that the transmit power PUAV and PSBS must be in the interval [0,Pmax] . It specifies the upper limit of the power transmission. Constraint C2 indicates that the UAV should be positioned between a minimum and maximum height. At higher heights, the distance between the UAV and UE increases, resulting in considerable path loss. By contrast, when the UAV is located at a certain minimum height, the NLoS conditions are recorded and may affect EE; hence, this constraint must be studied. The constraint in C3 guarantees that the EE of UAV must be greater than that of SBS. In C4 , RBS,k,n defines the maximum downlink achievable data rate, whereas RBS,k,nQos accounts for the data rate requirement. Constraints C5 and C6 specify that the SINR of the UE should be higher than a certain threshold; the SINR threshold differs from each tier (UAV, SBS). Lastly, the last constraint ensures that the UE is connected with a single BS. In a subsequent section, we will present our second objective, which is to maximize the total network throughput. The overall throughput RBS,k,n is defined as the sum of the data rates that are provided perfectly to all UE. Mathematically, the maximization problem can be computed as

max∑k∈N⁡RBS,k,nt (18)

s.t. C1 : 0<Pi≤Pmax∀i∈{UAV,SBS};∀UAV∈U;∀SBS∈S

   C2 : Hmin≤H≤Hmax∀UAV∈U

   C3 : γUAVt≥γUAVth∀UAV∈U

   C4:RBS,k,n≥RBS,k,nmin∀UAV∈U;∀SBS∈S

   C5 : PLoS,SBS<PLoS,UAV∀UAV∈U;∀SBS∈S

The constraint in C4 indicates the minimum required data rate for QoS. Here, constraint C5 means that the LoS probability of the SBS must be less than that of the UAV.

4  Double Deep Q-Network Algorithm

In this section, we present a DRL algorithm-based EE and throughput RA framework to address the network problems of (17) and (18). The task of the DRL agent is to learn an optimal policy from state to action, thus maximizing the utility function. We formulate the optimization problem as a fully observable Markov decision process. Similar to literature, we consider a tuple ( st,at,rt,st+1) . Based on the transition probability p(st+1|st,at) , the current network state st learns a new state according to the action at selected by the agent at time slot t . A DDQN is applied to achieve an optimal solution. However, we assume that UAV and SBS act as an agent that continuously interacts with the environment to optimize the policy. First, the agent j observes the state stj and decides to take an action atj in accordance with the optimal policy. Then, at each time policy, the agent receives reward rtj conditioned by the action and moves to the next state st+1j . This procedure concerns the DQN algorithm with a single agent. The major inconvenience of this algorithm lies in the confusion of the selection or evaluation of actions, leading to overestimation of action values and unstable training. To solve this overestimation, Hasselt et al. proposed a DDQN architecture, where the max function estimators is decomposed into action selection and evaluation, as illustrated in Fig. 5. The fundamental concept of the algorithm is to change the target network YtDQN=rt+1+γamaxQ(st+1,at|ωt′) as

YtDDQN=rt+1+γQ(st+1,a∗argmaxQ(st+1,a∗|ωt);ωt′) (19)

Figure 5: DDQN architecture

At each time t, the weighted parameters ωt of the online network is used to evaluate the greedy policy, whereas the weighted parameter ωt′ estimates the policy value. For improved performance evaluation, the target network for DDQN can use any parameters from the previous iteration (t−1) . Therefore, a periodic update of the target network settings is applied with copies of the online network.

4.1 State and Observation

The state describes a specific configuration of the environment. At time slot t , UAVs and SBSs act as agents and define the observation space Ojt . The observation of each BS=UAV∪⁡SBS includes the SINR measurement from the UAV and SBS to UE, the height of UAVs H , and spectral efficiency. We define the global state as

stj=(Ot1,Ot2,…OtBS) (20)

where OtBS represents the set of observation and can be expressed as

Otj=(SINRtj,Htj,SEtj) (21)

4.2 Action

In our problem, each agent must choose an appropriate base station (i.e., UAV or SBS), power transmission, UAV height, and LoS/NLoS link probability. At time step t , the action of UAV/SBS can be expressed as

atj=(btjPtj,Htj,Ptj) (22)

where btj∈{0,1,…β} is the selected BS; Ptj={0,1,…Pmax} is the power transmission requirement, which indicates how much power should be assigned to UE; Htj={0,1,…Hmax} is the UAV elevation.

4.3 Reward

Reinforcement learning is based on the reward function, stating that the agent (UAV and SBS) is guided toward an optimal policy. As mentioned above, we model this problem as a fully observable MDP to maximize EE and throughput. Therefore, the reward of j can be computed as

rtj=w1rEE+w2rThroughput (23)

where rEE=∑i=1M+u⁡EEt and rThroughput=∑i=1M+u⁡RBS,k,n . w1 and w2 are the weights for each objective, respectively. The pseudo code for DDQN is outlined in Algorithm 1.

5  Simulation Results

This section discusses the simulation and results for EE and throughput in the downlink UAV-assisted terrestrial network comprising eight SBSs with a radius of 500 m and five UAVs deployed randomly in the area. The cell contains 20 randomly distributed users and uses mm-wave bands. We assume that the maximum power transmission for SBS is Pmax,SBS=23dBm , and different values of maximum Pmax,UAV is shown in simulation. The path loss exponent in the LoS and NLoS links for the UAV and SBS have the values αLoSUAV=3 , αNLoSUAV=3,5 , αLoSSBS=2 , and αNLoSSBS=4 . In addition, the power consumed in the circuit of the transmitter Pc=40dBm . The added white Gaussian noise σ2=−114dBm . In the DDQN algorithm, the DNN of each agent is a four-layer fully connected neural network with two hidden layers of 64 and 32 neurons. Other simulation and DDQN parameters are listed in Table 2. The simulation is realized using MATLAB (R2017a) running on a Dell PC (2.8 Ghz @ Intel Core i7-7600U, 16 GB). In our simulation, we consider w1=0.6 and w2=0.4 .

5.1 Energy Efficiency Analysis

In this subsection, we show some results of EE, which are obtained using DDNQ. For improved performance validation, we compare our proposed algorithm with the DQN and QL architectures. Moreover, the effect of UE demand, number of UAVs, and beamforming on maximum power Pmax,UAV are discussed. In the simulation evaluation, the parameter values in Table 2 are used, unless otherwise specified. First, we evaluate the effect of UE demand on the EE for different algorithms in Fig. 6. A common observation in Fig. 6 is that increasing UE demand can lead to increased EE; however, from 60 Mbps, EE converges less quickly.

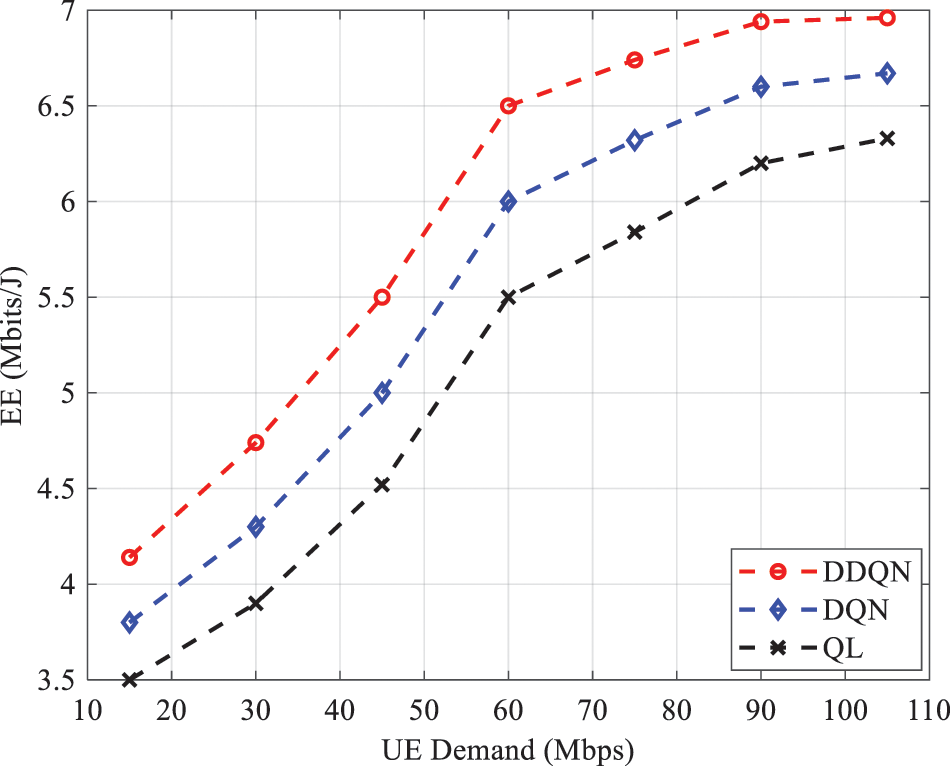
Figure 6: EE as a function of UE demand for different algorithms

This result is obtained because when UE demand increases considerably ( 60Mbps>) , all algorithms (DDQN, DQN, and QL) aim to maximize network throughput, which requires high transmission power, causing reduced EE. Another comment from Fig. 6 is that the DDQN algorithm can outperform DQN and QL. This outcome is achieved because the agent selects a more appropriate Q value to estimate the action. This perfection is mainly due to the two separate estimators applied in DDQN. In other terms, the use of the opposite estimator is cost effective for obtaining unbiased Q-values. A proposed solution to the EE problem when UE demand increases is to add base stations. The increase in the number of UAVs has a remarkable effect on EE, as illustrated in Fig. 7. As the number of UAVs increases, EE improves because the number of users covered in UAV LoS increases.

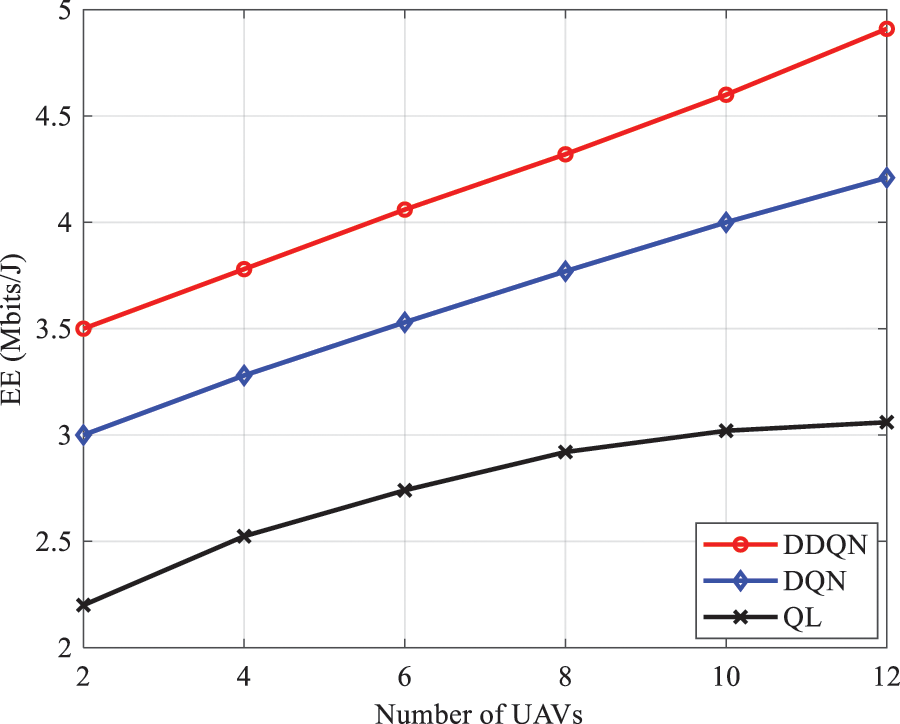
Figure 7: EE as a function of number of UAVs for different algorithms

Moreover, Fig. 7 demonstrates that the DDQN algorithm outperforms DQN and QL by 13.3% on EE because traditional RL algorithms use a one-actor network to train multiple agents; thus, conflicts between agents are recorded. Next, EE is plotted as a function of the number of UE for different UAV height ( Hmax constraint), as shown in Fig. 8. Moreover, an increase in the number of UE results in EE degradation because of the increase in energy consumption. Fig. 8 also shows that UAV height can affect EE. Therefore, EE increases as Hmax increases because the increase in UAV height results in additional UEs in the LoS link condition, leading to an increase in the total number of bits transmitted.

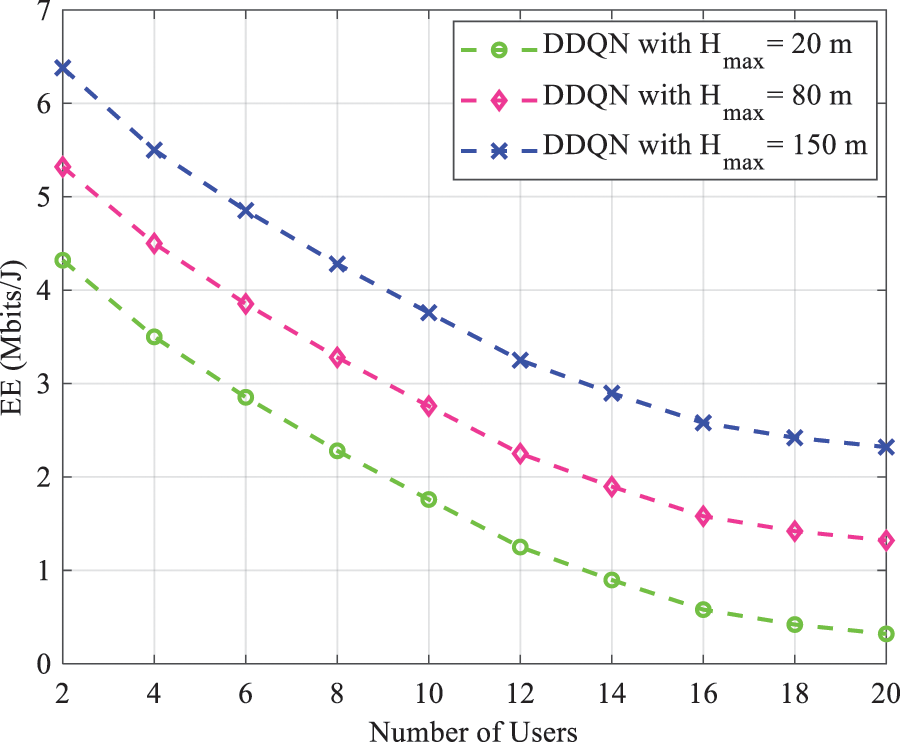
Figure 8: EE as a function of number of users for different Hmax constraints

As the number of UE increases, the power assigned to UE declines. Therefore, the increase in height compensates this shortcoming. Fig. 9 shows EE vs. the maximum power of UAV Pmax,UAV with and without beamforming. A common observation in Fig. 9 is that EE decreases by extending the maximum transmission power of the UAV due to the increased energy consumption by users. In addition, when the power of UAVs increases, the links between UAVs and UEs are in NLoS condition, thus reducing EE. This analysis is conducted with and without beamforming. As illustrated in Fig. 9, applied beamforming improves EE in each algorithm (DDQN and DQN) because beamforming provides additional gains and can overcome mm-wave blockage constraints.

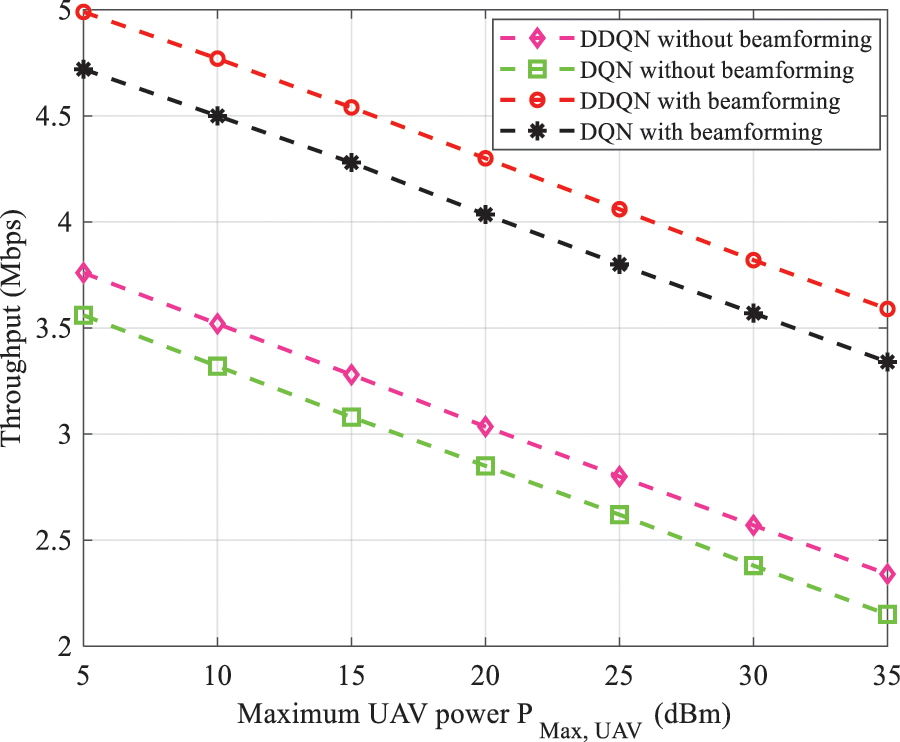
Figure 9: EE vs. maximum UAV power transmission with and without beamforming

5.2 Throughput Analysis

To validate the accuracy of our approach, we analyze the total throughput (second objective) according to the number of UAVs deployed, UAV height HMax , and beamforming. Considering the first scenario, Fig. 10 depicts the total throughput as a function of the number of UAVs. As the number of UAVs increases, the total throughput is enhanced. Thus, DDQN outperforms DQN and QL. However, this effect is mainly due to the increase in LoS links. The same figure also shows that the total throughput reaches a congestion level at a particular number of UAVs due to the rise in interference between UAVs.

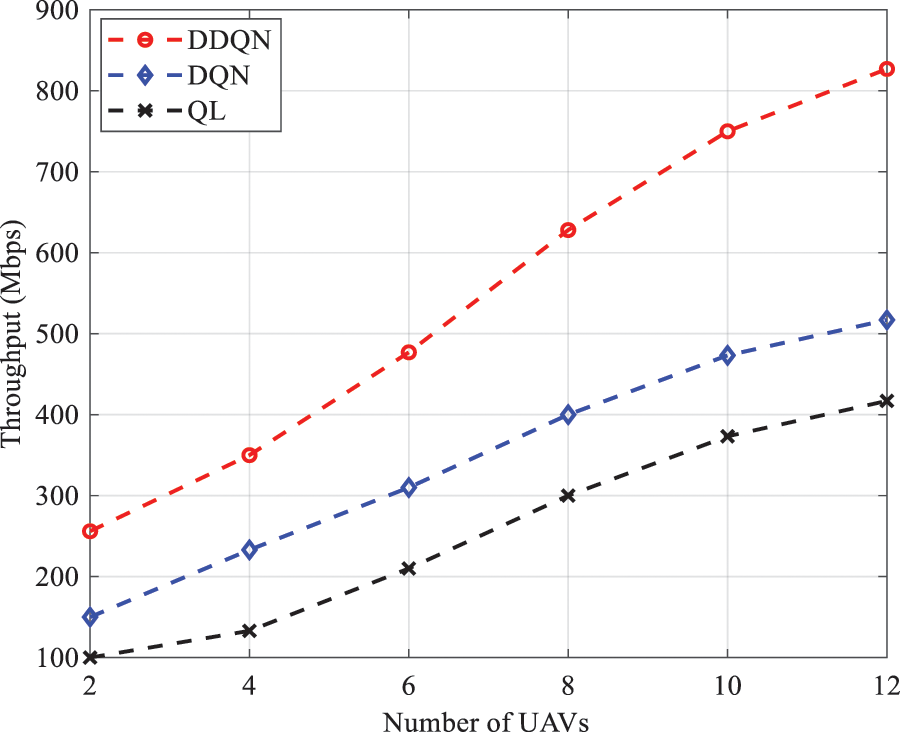
Figure 10: Throughput as a function of number of UAVs with different algorithms

Fig. 11 illustrates the variation of throughput vs. UAV height in different AI algorithms. According to Fig. 11, throughput increases with maximization of altitude HMax because at low altitude, the propagation condition is in NLoS, and interference between tiers is observed. By contrast, when the UAV height increases, the LoS condition occurs, resulting in reduced loss. Moreover, saturation is experienced from an altitude of 130 m because as UAV height increases, the distance between the UAV and UE increases, leading to signal attenuation.

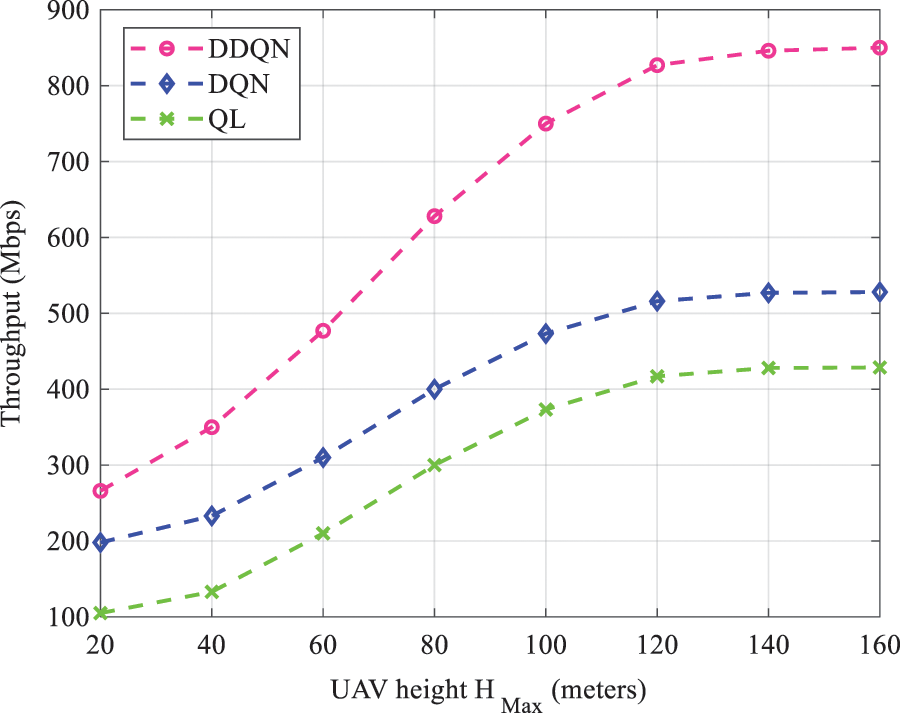
Figure 11: Throughput analysis as a function of UAV height

Fig. 12 shows the variation of the throughput vs. maximum UAV power. As expected, the total throughput increases as PMax,UAV increases. Fig. 12 also reveals that DDQN achieves a maximum throughput of 582.7 Mbps with a maximum power of PMax,UAV=35 dBm. By contrast, DQN achieves a maximum throughput of 269,234 Mbps at the same PMax,UAV . Again, the proposed DDQN algorithm outperforms DQN. Finally, we plot the throughput as a function of blockage parameter β for SBS when UAVs are assumed to be located at HMax=120 m, as shown in Fig. 13. When β increases, the total throughput of the network decreases. Therefore, with the increase in obstacle density, more UEs are served by NLoS conditions. In addition, Fig. 13 shows that the proposed DDQN scheme converges to highly satisfactory solutions compared with the other approaches because it handles interference perfectly.

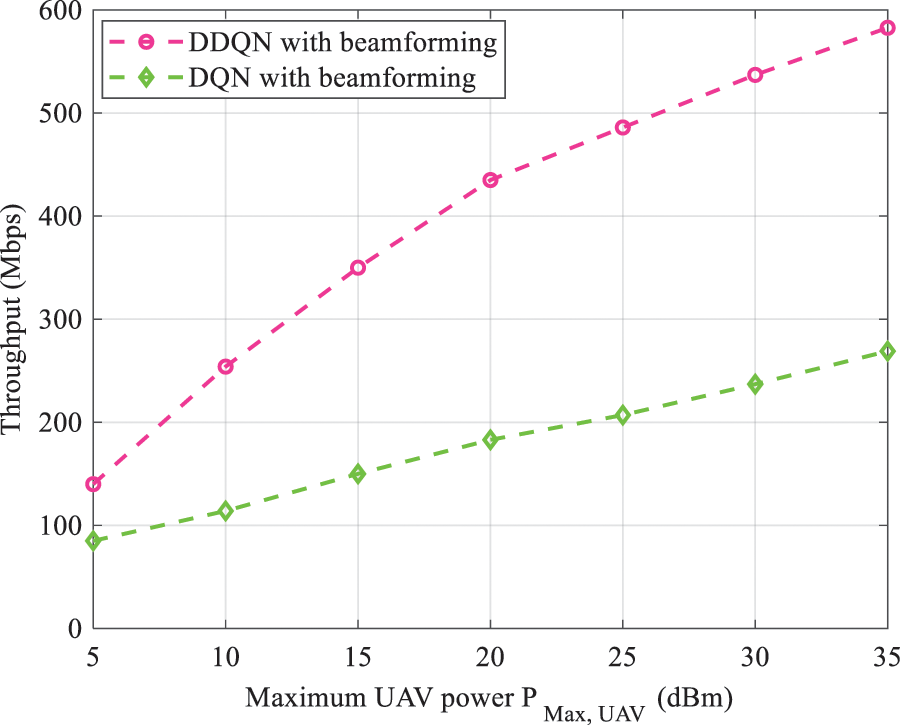
Figure 12: Throughput as a function of UAV power with beamforming

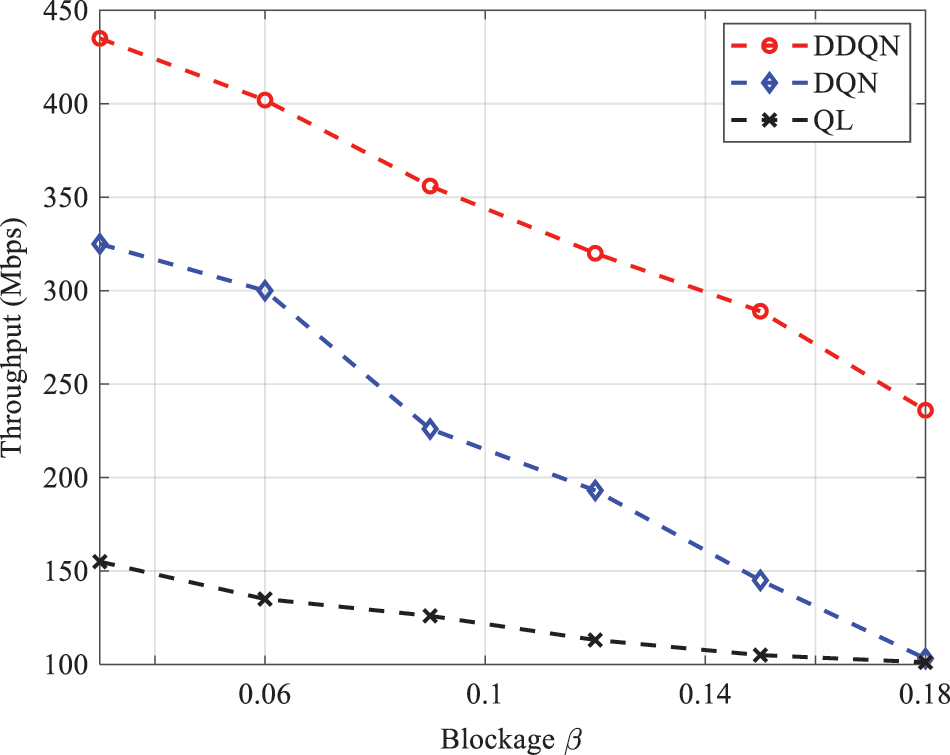
Figure 13: Throughput vs. blockage parameter

6  Conclusion

In this study, we proposed a DDQN scheme for RA optimization in UAV-assisted terrestrial networks. The problem is formulated as EE and throughput maximization. Initially, we provided a general overview of deep reinforcement architectures. Then, we presented the network architecture where the base stations use the beamforming technique during transmission. The proposed EE and throughput were assessed under the number of UAVs, beamforming, maximum UAV power transmission, and blockage parameter. The algorithm accuracy of the obtained EE and throughput was demonstrated by a comparison with deep Q-network and Q-learning. Our results indicate that EE can be affected by the number of UAVs to be deployed in the coverage area, as well as the maximum altitude variation (constraint). Moreover, the use of beamforming can be cost effective in improving EE. Our investigation also revealed other useful conclusions. For throughput analysis, the blockage parameter has a dominant influence on the throughput, and an optimal value can be selected. In terms of convergences, our DDQN consistently outperforms DQN and QL. In future work, other issues can be explored and investigated. For instance, UAV mobility can be considered, and an optimal mobility model can be selected to maximize throughput. Interference coordination may also be introduced between tiers.

Acknowledgement: The authors would like to acknowledge the financial support received from Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R323), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia and Taif University Researchers Supporting Project Number TURSP-2020/34), Taif, Saudi Arabia.

Funding Statement: This work was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R323), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia, and Taif University Researchers Supporting Project Number TURSP-2020/34), Taif, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Z. Sylia, G. Cédric, O. M. Amine and K. Abdelkrim, “Resource allocation in a multi-carrier cell using scheduler algorithms,” in 4th Int. Conf. on Optimization and Applications (ICOA), Mohammedia, Morocco, pp. 1–5, 2018. [Google Scholar]

 2.  T. O. Olwal, K. Djouani and A. M. Kurien, “A survey of resource management toward 5G radio access networks,” IEEE Communications Surveys & Tutorials, vol. 18, no. 3, pp. 1656–1686, 2016. [Google Scholar]

 3.  T. S. Rappaport, “Millimeter wave mobile communications for 5G cellular: It will work!,” IEEE Access, vol. 1, pp. 335–349, 2013. [Google Scholar]

 4.  M. A. Ouamri, M. E. Oteşteanu, A. Isar and M. Azni, “Coverage, handoff and cost optimization for 5G heterogeneous network,” Physical Communication, vol. 39, pp. 1–8, 2020. [Google Scholar]

 5.  C. Sun, C. She, C. Yang, T. Q. S. Quek, Y. Li et al., “Optimizing resource allocation in the short blocklength regime for ultra-reliable and low-latency communications,” IEEE Transactions on Wireless Communications, vol. 18, no. 1, pp. 402–415, Jan. 2019. [Google Scholar]

 6.  Y. Hu, M. Ozmen, M. C. Gursoy and A. Schmeink, “Optimal power allocation for QoS-constrained downlink multi-user networks in the finite blocklength regime,” IEEE Transactions on Wireless Communications, vol. 17, no. 9, pp. 5827–5840, Sept. 2018. [Google Scholar]

 7.  L. Zhu, J. Zhang, Z. Xiao, X. Cao, D. O. Wu et al., “Joint Tx-Rx beamforming and power allocation for 5G millimeter-wave non-orthogonal multiple access networks,” IEEE Transactions on Communications, vol. 67, no. 7, pp. 5114–5125, July 2019. [Google Scholar]

 8.  S. O. Oladejo and O. E. Falowo, “Latency-aware dynamic resource allocation scheme for multi-tier 5G network: A network slicing-multitenancy scenario,” IEEE Access, vol. 8, pp. 74834–74852, 2020. [Google Scholar]

 9.  L. Lei, Y. Yuan, T. X. Vu, S. Chatzinotas and B. Ottersten, “Learning-based resource allocation: Efficient content delivery enabled by convolutional neural network,” in IEEE 20th Int. Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, pp. 1–5, 2019. [Google Scholar]

10. K. I. Ahmed, H. Tabassum and E. Hossain, “Deep learning for radio resource allocation in multi-cell networks,” IEEE Network, vol. 33, no. 6, pp. 188–195, Dec. 2019. [Google Scholar]

11. L. Liang, H. Ye, G. Yu and G. Y. Li, “Deep-learning-based wireless resource allocation with application to vehicular networks,” Proceedings of the IEEE, vol. 108, no. 2, pp. 341–356, Feb. 2020. [Google Scholar]

12. F. Tang, Y. Zhou and N. Kato, “Deep reinforcement learning for dynamic uplink/downlink resource allocation in high mobility 5G HetNet,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 12, pp. 2773–2782, 2020. [Google Scholar]

13. L. Sanguinetti, A. Zappone and M. Debbah, “Deep learning power allocation in massive MIMO,” in 2018 52nd Asilomar Conf. on Signals, Systems, and Computers, USA, pp. 1257–1261, 2018. [Google Scholar]

14. A. Zappone, M. Debbah and Z. Altman, “Online energy-efficient power control in wireless networks by deep neural networks,” in IEEE 19th Int. Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Greece, pp. 1–5, 2018. [Google Scholar]

15. H. Li, H. Gao, T. Lv and Y. Lu, “Deep Q-learning based dynamic resource allocation for self-powered ultra-dense networks, in IEEE Int. Conf. on Communications Workshops (ICC Workshops), USA, pp. 1–6, 2018. [Google Scholar]

16. S. Ali, A. Haider, M. Rahman, M. Sohail and Y. B. Zikria, “Deep learning (DL) based joint resource allocation and RRH association in 5G-multi-tier networks,” IEEE Access, vol. 9, pp. 118357–118366, 2021. [Google Scholar]

17. H. Ye, G. Y. Li and B. F. Juang, “Deep reinforcement learning based resource allocation for V2V communications,” IEEE Transactions on Vehicular Technology, vol. 68, no. 4, pp. 3163–3173, April 2019. [Google Scholar]

18. D. Ron and J. -R. Lee, “DRL-based sum-rate maximization in D2D communication underlaid uplink cellular networks,” IEEE Transactions on Vehicular Technology, vol. 70, no. 10, pp. 11121–11126, Oct. 2021. [Google Scholar]

19. R. Amiri, M. A. Almasi, J. G. Andrews and H. Mehrpouyan, “Reinforcement learning for self organization and power control of two-tier heterogeneous networks,” IEEE Transactions on Wireless Communications, vol. 18, no. 8, pp. 3933–3947, Aug. 2019. [Google Scholar]

20. J. Cui, Y. Liu and A. Nallanathan, “Multi-agent reinforcement learning-based resource allocation for UAV networks,” IEEE Transactions on Wireless Communications, vol. 19, no. 2, pp. 729–743, Feb. 2020. [Google Scholar]

21. X. Chen, X. Liu, Y. Chen, L. Jiao and G. Min, “Deep Q-Network based resource allocation for UAV-assisted Ultra-Dense Networks,” Computer Networks, vol. 196, pp. 1–10, 2021. [Google Scholar]

22. B. Liu, H. Xu and X. Zhou, “Resource allocation in unmanned aerial vehicle (UAV)-assisted wireless-powered internet of things,” Sensors, vol. 19, no. 8, pp. 1908–1928, 2019. [Google Scholar]

23. P. Luong, F. Gagnon, L. -N. Tran and F. Labeau, “Deep reinforcement learning-based resource allocation in cooperative UAV-assisted wireless networks,” IEEE Transactions on Wireless Communications, vol. 20, no. 11, pp. 7610–7625, Nov. 2021. [Google Scholar]

24. W. Min, P. Chen, Z. Cao and Y. Chen, “Reinforcement learning-based UAVs resource allocation for integrated sensing and communication (ISAC) system,” Electronics, vol. 11, no. 3, pp. 441, 2022. [Google Scholar]

25. Y. Y. Munaye, R. -T. Juang, H. -P. Lin and G. B. Tarekegn, “Resource allocation for multi-UAV assisted IoT networks: A deep reinforcement learning approach,” in Int. Conf. on Pervasive Artificial Intelligence (ICPAI), Taiwan, pp. 15–22, 2020. [Google Scholar]

26. H. van Hasselt, A. Guez and D. Silver, “Deep reinforcement learning with double Q-learning,” in Proc. AAAI Conf. Artif. Intell., Phoenix, Arizona, USA, pp. 2094–2100, Sep. 2016. [Google Scholar]

27. H. A. Shah, L. Zhao and I. -M. Kim, “Joint network control and resource allocation for space-terrestrial integrated network through hierarchal deep actor-critic reinforcement learning,” IEEE Transactions on Vehicular Technology, vol. 70, no. 5, pp. 4943–4954, May 2021. [Google Scholar]

28. M. M. Sande, M. C. Hlophe and B. T. Maharaj, “Access and radio resource management for IAB networks using deep reinforcement learning,” IEEE Access, vol. 9, pp. 114218–114234, 2021. [Google Scholar]

29. M. Agiwal, A. Roy and N. Saxena, “Next generation 5G wireless networks: A comprehensive survey,” IEEE Communications Surveys & Tutorials, vol. 18, no. 3, pp. 1617–1655, 2016. [Google Scholar]

30. L. Liang, H. Ye, G. Yu and G. Y. Li, “Deep-learning-based wireless resource allocation with application to vehicular networks,” in Proc. of the IEEE, vol. 108, no. 2, pp. 341–356, Feb. 2020. [Google Scholar]

31. A. Iqbal, M. -L. Tham and Y. C. Chang, “Double deep Q-network-based energy-efficient resource allocation in cloud radio access network,” IEEE Access, vol. 9, pp. 20440–20449, 2021. [Google Scholar]

32. Y. Zhang, X. Wang and Y. Xu, “Energy-efficient resource allocation in uplink NOMA systems with deep reinforcement learning,” in 11th Int. Conf. on Wireless Communications and Signal Processing (WCSP), Xi’an, China, pp. 1–6, 2019. [Google Scholar]

33. X. Lai, Q. Hu, W. Wang, L. Fei and Y. Huang, “Adaptive resource allocation method based on deep Q network for industrial internet of things,” IEEE Access, vol. 8, pp. 27426–27434, 2020. [Google Scholar]

34. F. Hussain, S. A. Hassan, R. Hussain and E. Hossain, “Machine learning for resource management in cellular and IoT networks: Potentials current solutions, and open challenges,” IEEE Communications Surveys & Tutorials, vol. 22, no. 2, pp. 1251–1275, 2021. [Google Scholar]

35. S. Yu, X. Chen, Z. Zhou, X. Gong and D. Wu, “When deep reinforcement learning meets federated learning: Intelligent multitimescale resource management for multiaccess edge computing in 5G ultradense network,” IEEE Internet of Things Journal, vol. 8, no. 4, pp. 2238–2251, 2021. [Google Scholar]

36. J. Zhang, Y. Zeng and R. Zhang, “Multi-antenna UAV data harvesting: Joint trajectory and communication optimization,” Journal of Communications and Information Networks, vol. 5, no. 1, pp. 86–99, March 2020. [Google Scholar]

37. A. Pratap, R. Misra and S. K. Das, “Maximizing fairness for resource allocation in heterogeneous 5G networks,” IEEE Transactions on Mobile Computing, vol. 20, no. 2, pp. 603–619, Feb. 2021. [Google Scholar]

38. Y. Fu, X. Yang, P. Yang, A. K. Y. Wong, Z. Shi, et al.,, “Energy-efficient offloading and resource allocation for mobile edge computing enabled mission-critical internet-of-things systems,” EURASIP Journal on Wireless Communications and Networking, vol. 2021, no. 1, 2021. [Google Scholar]

39. A. Al-Hourani, S. Kandeepan and S. Lardner, “Optimal LAP altitude for maximum coverage,” IEEE Wireless Commun. Lett., vol. 3, no. 6, pp. 569–572, Dec. 2014. [Google Scholar]

40. M. A. Ouamri, M. E. Oteşteanu, G. Barb and C. Gueguen “Coverage analysis and efficient placement of drone-BSs in 5G networks,” Engineering Proceedings, vol. 14, no. 1, pp. 1–8, 2022. [Google Scholar]

41. Md. A. Ouamri “Stochastic geometry modeling and analysis of downlink coverage and rate in small cell network,” Telecommun Syst, vol. 77, no. 4, pp. 767–779, 2021. [Google Scholar]

42. D. Alkama, M. A. Ouamri, M. S. Alzaidi, R. N. Shaw, M. Azni et al., “Downlink performance analysis in MIMO UAV-cellular communication with LoS/NLoS propagation under 3D beamforming,” IEEE Access, vol. 10, pp. 6650–6659, 2022. [Google Scholar]