Remote Sensing Image Encryption Using Optimal Key Generation-Based Chaotic Encryption

1  Introduction

Recently, an important spread of the Internet of Things (IoT) gadgets was noted. Gartner estimates that the IoT will reach 26 billion units by 2020, and research work by Statista states that this number will become 75.44 billion by 2025 [1]. The usage of such gadgets is increasing in numerous applications like mobile health, industrial control, environmental monitoring, Internet of Vehicles, and smart homes spreading the scope of mobile transmissions from interpersonal transmissions to smart interconnection among people and things, and also amongst things and things [2,3]. Remote sensing has emerged with the arrival of the IoT, allowing cheap and fast attainment of data from billions and millions of interconnected gadgets positioned globally. The IoT and the continual data stemming from IoT have altered the conventional interpretation of remote sensing (indulges how capturing and extracting knowledge from this data can be done). IoT Remote Sensing presents the foundation for supporting the growth of Digital Earth Twins, which would make huge chances for addressing significant societal and environmental difficulties in fields like geology, agriculture, and smart cities, amongst others [4].

Grand difficulties posed by brownfield and greenfield IoT remote sensing placements invoke federated learning, big data acquisition, scalability, connectivity, unmanned aerial vehicles (UAVs), security and privacy, spatial data analytics, and mobility [5]. Remote sensing images (RSI) play a significant part in disaster prevention and mitigation, agriculture, minerals, land, weather, national defence, air pollution monitoring, water resources, and much more, presenting a solid technical guarantee of sustainable advancement of a national economy. They were the main source of information procurement, data processing, and analysis [6]. Moreover, sensor systems to acquire RSIs were generally installed on space stations, satellites, spacecraft, etc. So, RSIs were exposed to space radiation atmosphere, and the data presented in images would unavoidably experience serious interference risks and attacks during communication [7]. Thus, the protection of RSIs security slowly highlights its significance.

Since a significant fundamental decision-making information source, RSI plays a vital part in decision making in the domain of military affairs and national security. Nowadays, it is a most potential, secure, and dependable means of surveillance that could perform comprehensive and real-time remote sensing inspection in combat regions. The conventional encoding technique of RSI details generally leverages the prevailing public key for encoding an image [8]. This encryption technique raises encryption security by altering primary circumstances. But, after the initial conditions and public key were altered, the encryption would fail, which was inappropriate for the RSI details encoding. Image encryption has become a key and effective way of protecting the security of image information. Recently, researchers have brought forth many exemplary methods for image encryption [9]; because of its complications and extreme sensitivity to primary parameters and values, chaotic mechanisms tend to be a common encryption technique as a pseudorandom number originator for image encoding. The prevailing enhanced encoding technology depends on chaotic mechanisms invoking deoxyribonucleic acid (DNA) encrypting, mathematical model, S-box replacement, lifting scheme, compressive sensing, and Zigzag scrambling.

This study introduces an Improved Sine Cosine Algorithm with Chaotic Encryption based Remote Sensing Image Encryption (ISCACE-RSI) technique in IoT Environment. The proposed model initially experiences pre-processing to enhance the image. Next, the ISCACE-RSI technique exploits the double layer remote sensing image encryption (DLRSIE) to encrypt the images. The DLRSIE technique incorporates the design of Chaotic Maps and the DNA Strand Displacement (DNASD) approach. For an optimal key generation of the DLRSIE technique, the ISCA is applied with an objective function of the maximization of peak signal to noise ratio (PSNR). A detailed set of simulations were conducted to illustrate the improvised performance of the ISCACE-RSI model.

The rest of the study is planned here. Section 2 explains the related works, Section 3 presents the proposed model, Section 4 offers result analysis, and Section 5 draws a conclusion.

2  Literature Review

Zhang et al. [10] established a new approach of fast and productive measurement matrix and arbitrary stage mask to colour image encrypted, where Kronecker product (KP) was integrated with a chaotic map. The encrypted model depended on 2D compressive sensing (CS) and fraction Fourier transforms (FrFT). During this technique, the KP was utilized to extend the lower dimensional seed matrix to obtain a higher dimensional measurement matrix and arbitrary stage masks. Liu et al. [11] present a new image encrypt approach based on DNA base probabilities and execute it for RSIs for data protection. Primary, the plain image was arbitrarily encoded from DNA rule, and their outcome contributes from DNA and DNA mask created with a 2D logistic map. Second, the cryptosystem applies a 2D logistic map over DNA base probabilities against differential attacks. Tertiary, the pixel-level rearrangement and DNA base-level rearrangement correspondingly executed for chaos sequence to permutation and diffusion.

In [12], an effectual image encryption approach dependent upon the chaotic map and Advanced Encryption Standard (AES) was presented to application on-board Earth observation satellite. The presented approach involves several technical and attraction features for higher security levels and tolerance to Single Event Upsets (SEU). In [13], the authors plan a visually secure encrypt model using the parallel compressive sensing (PCS) counter mode and embedded approach. To achieve a superior security level, the Logistic-Tent model and 3D Cat map are established to construct the measurement matrix and disturb the sequences of embedding data correspondingly. Nan et al. [14] present an RSI compression and encrypt technique dependent upon block compressive sense and several S-boxes, which employs a new hyperchaotic method. Especially to provide which RSIs were large-sized, it can establish a block compression–encrypt technique including a new hyperchaotic model integrated with block compressive sense. The presented hyperchaotic model contains a 2D Logistic coupling Cubic map which couples the Logistic map and Cubic map.

In [15], a new triple-image encrypt and hidden technique was presented by integrating a 2D chaotic system, compressive sensing (CS), and 3D-discrete cosine transform (DCT). Primary, 3 grayscale plain images were sparsely demonstrated by 2D-DWT. The resultant sparse matrix is scrambled twice with index sort scramble and 3D zigzag scramble. Afterwards, the measurement matrix created with a 2D chaotic model was utilized to compress the scrambled matrix. In [16], a 7D hyperchaotic map was utilized to produce the confidential keys to image encrypt. While this hyperchaotic map needs many primary parameters, the manual evaluation has been computationally general. Thus, minimax differential development was employed to provide an optimum parameter to the hyperchaotic map. The fitness of parameters is estimated utilizing correlation coefficient and entropy.

3  The Proposed Model

In this study, a novel ISCACE-RSI algorithm was projected to encrypt remote sensing images in the IoT environment. The presented ISCACE-RSI technique follows a three-stage process: pre-processing, encryption, and optimal key generation. Firstly, the remote sensing images are pre-processed to enhance image quality. After this, the ISCACE-RSI technique uses the DLRSIE technique to encrypt the images. For an optimal key generation of the DLRSIE technique, the ISCA is applied with an objective function of the maximization of PSNR. Fig. 1 depicts the overall process of the ISCACE-RSI technique.

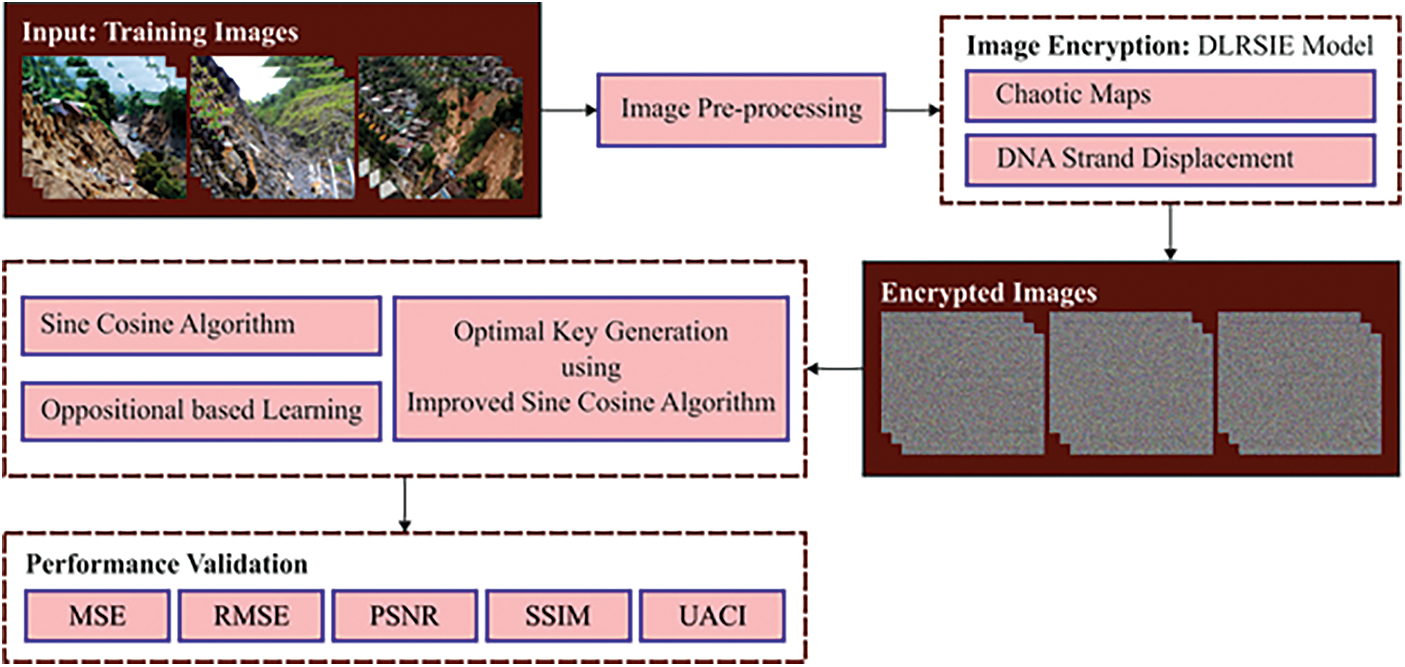
Figure 1: Overall process of ISCACE-RSI technique

3.1 Image Pre-Processing

Firstly, the ISCACE-RSI technique initially encounters pre-processing to enhance image quality. Thin clouds and mist bring a slight blur to RSI. Those blurs have dramatically decreased the resolution of an image. The procedure of local light passes via the thin cloud and mist vapour, viz., the procedure of light waves being blurred by optical channel modulation using fog and cloud, and the modulation was a convolutional operation. Therefore this type of blur is regarded as a smooth convolutional blur. The positive spike function using the negative side lobe was carefully chosen as the filter function. Also, originally blurred images are convolved to acquire good recovery outcomes. This restoration technique can be a type of grayscale edge enhancement technique. Since the operations among frequency domain matrices are of equivalent size, beforehand of the Fourier transform (FT), the filter function was filled with zero to the right and extended to 256 × 256, viz., size of the fuzzy image to be treated, later convolved through original images. The fog and cloud are removed from RSI. Some corrections were made to the Gaussian mechanism for RSI with severe blurring via repeated experiments as follows:

f(x, y)=g(x, y)∗h(x, y)(1)

The FT formulation of the processed image is as follows:

F(u, v)=G(u, v)H(u, v)(2)

Here, u and v represent frequency-domain variables, F(u, v) denotes an f(x, y) FT approaching the original clear image, and G(u, v) indicates the FT of satellite RSI g(x, y) blurred through thin cloud and mist.

3.2 Remote Sensing Image Encryption Technique

To encrypt the remote sensing images, the ISCACE-RSI technique utilized the DLRSIE model, which includes the process of chaotic maps and the DNASD model. The DLRSIE encryption system is classified as follows: encryption at a level of DNASD and chaotic map. At a level of DNASD, a diversity of DNASD is used for performing diverse DNASD-based encryption rules. At the level of chaos, Lorenz chaotic and Lorenz hyperchaotic maps are employed in carrying out XOR diffusion and pixel position scrambling correspondingly [17].

Step 1. A gray image T of size M×N was the plaintext image.

Step 2. A group value of Lorenz hyperchaotic map first value x0,y0,z0,w0 are selected as the key, as well as the hyperchaotic map equation is repeated through the fourth-order Runge-Kutta model for M×N+t times. The outcome of chaos can be improved by eliminating the initial t iteration. Beginning with t+1, afterward 3000 iterations, the chaotic state x0 is perturbed slightly using the following formula, and h refers to the step length; next, we obtain a pseudo-random chaotic sequence S of length M×N. The pseudorandom sequence X is attained by normalizing the S pseudo-random sequences to the integer interval [1, M×N]. The recurrent pseudo-random number in sequence X retains the initial occurrence. In contrast, the number in integer interval [1, M×N] that doesn’t emerge in sequence X is arranged after a sequence X in ascending order from smaller to larger. There is also no duplicate value in sequence X.

x0=x0+h∗sin(y0).(3)

Step 3. The original plain-text image matrixes T(M, N) are scrambled through sequence X and Eq. (4). Also, the resultant matrix is represented by (M, N).

t=T(X(i));T(X(i))=T(X(M∗N−i+1));T(X(M∗N−i+1))=t.(4)

Step 4. A group value of Lorenz chaotic map primary value x0,y0,z0 is selected as the key, as well as the chaotic map equation is repeated through the fourth-order Runge-Kutta algorithm for M×N+t times. Three pseudo-random chaotic sequences, Lx, Ly, and Lz, with lengths of  M×N are attained by removing the preceding t iteration. Lx,Ly, and Lz were mapped into integer intervals [0, 255] as well as the 3 pseudo-random sequences were recreated into the matrixes with M×N size, represented by Lxm, Lym, and Lzm. The matrix A(M, N) in Step 3 is processed by B(M, N) using the XOR operation with the Lxm matrix.

Step 5. The matrix B(M, N) is first converted into the binary matrices and then to DNA matrix C (every position in DNA sequence matrix C was no longer a decimal number but 4 bases). The DNA sequence matrix C can be divided into columns, one block per 4 columns, and we acquire the DNA sequence matrices D1, D2, D3,…, DN/4. The size of the matrix Di(i=1∼(N/4)) is ×(N/4), and it has four bases at every location. Hence every row of matrix Di is a 16 nt DNA sequence. Fix the direction of the DNA sequence from left to right as 5′ to 3′ terminals.

In DNASD based encryption rule, the key of DNASD-rule a and b is made up of 4 bases. Also, the key of DNASD-rule c is comprised of sixteen bases. Owing to the pseudo-random of chaotic sequence, we apply the Lym and Lzm matrixes in Step four for generating the key needed by the DNASD-based encryption rule. The Lym and Lzm matrixes are first converted into the eight-bit binary matrixes and then converted to the DNA sequence Lykey and Lzkey matrices with M×N size. Every position in the Lykey matrix comprises four bases; therefore, there exist M×N keys needed for the DNASD-rule a and b in the Lykey matrix. Also, every position in the Lzkey matrix comprises four bases. Therefore, there exist (M×N/4) keys needed for the DNASD-rule c in the Lzkey matrix. For matrix Di(i=1∼(N/4)), there are 3 forms of DNASD-related encryption rules that it could select. For realizing encryption faster, matrixes D1, D4,…,D1+3n (n represents a natural number, then 1+3n∈[1, (N/4)]) are encrypted using DNASD-rule a, matrixes D2, D5,…, D2+3n (n denotes a natural number, then 2+3n∈[2, (N/4)]) are encrypted using DNASD-rule b, and matrixes D3, D6,…,D3+3n (n refers to natural number, then 3+3n∈[3, (N/4)]) were encrypted using DNASD-rule c.

For matrices D1,D4,…, D1+3n, remove the 1st column of every block matrix based on DNASD-rule a; the original matrix has four columns in a row M transformed into three columns in row M, and 1st n columns of Lykey matrix were inserted to the 4th columns of every block matrix to obtain an encrypted block matrixes E1, E4,…, E1+3n. For matrices D2, D5,…, D2+3n, remove the 4th column of every block matrix based on DNASD-rule b, and the n+1 column to n+3n columns of Lykey matrix were inserted to the 1st column of each block matrix to obtain encrypted block matrixes E2,E5,…,E2+3n. For matrices D3,D6,…,D3+3n, each displaced with the 1st 3n columns of Lzkey matrix based on DNASD-rule c, and the encrypted block matrices E3, E6,…, E3+3n were attained.

Step 6. The encrypted block matrix Ei(i=1∼(N/4)) attained in Step 5 were combined into a DNA sequence matrix E of size M×N.

Step 7. A random DNA coding rule can be carefully chosen for decoding the DNA sequences matrix E, and later it can be converted into the decimal matrix F, and lastly, the encrypted image is attained.

3.3 Optimal Key Generation Process

In this study, the ISCA technique is utilized to generate the keys for the DLRSIE technique optimally. Mirjalili [18] proposed an SCA based on mathematical modelling of the sine and cosine trigonometric functions. The solution position in the population is upgraded according to the sine and cosine function output, that makes them oscillate around the optimal solution. The return value of this function lies between −1 and +1, that keeps the solution fluctuating. An algorithm initiates by producing a set of solution candidates randomly within the boundary of the searching space in the initialized stage. Exploitation and exploration are controlled through the implementation of random adaptive variables.

The solution location update method can be implemented in every iteration, whereby Xit and Xit+1 denote the existing solution location in i-th varibale at t and i+1 iterations, correspondingly, r1−3 indicates the pseudo-randomly produced number, the Pi∗ indicates the destination point location (existing optimal calculation) in the i-th parameter, whereas || signifies the total value. The same notation in the original manuscript where the technique was firstly projected is applied in these manuscripts.

Xit+1=Xit+r1⋅sin(r2)⋅|r3⋅Pi∗t−Xit|(5)

Xit+1=Xit+r1⋅cos(r2)⋅|r3⋅Pi∗t−Xit|(6)

The above formula is applied to control variable r4:

Xit+1={Xit+1=Xit+r1⋅sin(r2)⋅|r3⋅Pi∗t−Xit|,r4<0.5Xit+1=Xit+r1⋅cos(r2)⋅|r3⋅Pi∗t−Xit|,r4≥0.5,(7)

In Eq. (7), r4 refers to a randomly produced value within zero and one.

Note that, for each solution in the population, a novel value for pseudo-random parameter r1−4 is produced [19]. Fig. 2 illustrates the flowchart of SCA.

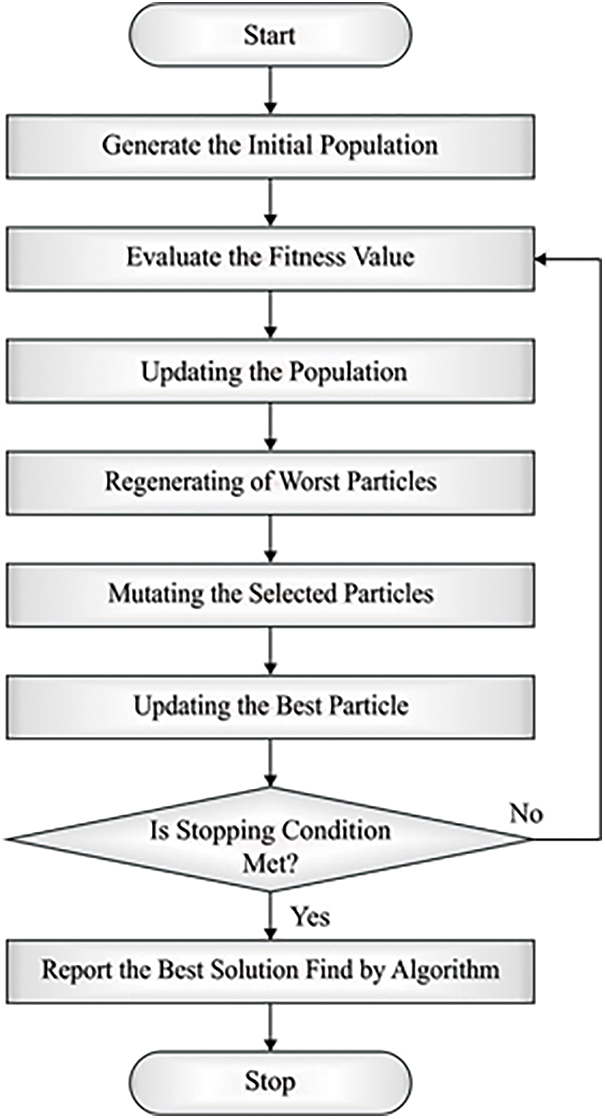
Figure 2: Flowchart of SCA

Four random variables control the algorithm search method, and they affect the present and the optimal solution position. To converge toward the global optimal, a balance between solutions is needed. Exploitation is assured by the fact that sine and cosine function exhibits cyclic pattern that enables for reposition of the solution. Modifications in the range of sine and cosine functions allow searching outside the destination. Moreover, the solution needs location not to overlap with the area of other solutions.

For improved quality of randomness, the value for variable r2 is produced within the range [0,2Π] and assurances exploration. The control of the balance between diversification and exploitation is given below.

r1=a−taT,(8)

In Eq. (8), t denotes the current iteration, T indicates the maximal iterations count, and a represents a constant. In several cases, the population creates individuals from an arbitrary fashion. But, when the technique begins with searching in a place distant from the optimum solutions, particularly during the worst case whereas the primary solutions are placed opposite the optimum solutions, the searching is obtained a considerable count of time. Thus, an optimum approach is searching from every direction, particularly in opposite directions. This article utilizes opposition-based learning (OBL) from the 2 phases of population initialization and algorithm stagnation. OBL mostly completes the subsequent 3 parts.

•   A primary place of individual gorillas are Xi,j, i=1,2,⋯,N, j=1,2,⋯,D. N implies the population size, and D denotes the dimensional of the searching space. The population at this time is termed P1.

•   The population was created based on Eq. (9) and termed P2.

Xi,j′=lb(j)+ub(j)−rand×Xi,j,(9)

Tizhoosh’s technique is utilized and for broadening the searching space. In Eq. (9), lb(j) refers to the lower bound of jth dimensional and ub(j) implies the upper bound of jth dimensional. Rand refers to the arbitrary value from the range zero to one. Xi,j′ denotes the opposite gorilla.

•   During the population P1 and P2, this technique chooses the number N of individuals with optimum fitness for procedure and initializing population.

During the population initialized phase, this process initially creates a primary population and implements OBL [20]. Based on the technique flow, SCA is a slow method, the primary solution to optimum solutions. But, because of the restriction of several factors, this technique was inclined to the premature phenomenon and decreases as local optimum solutions, which leads to evolutionary stagnation. Thus, if the technique stagnates, SCA executes OBL to expand the scope of explorations and escape the present local optimal solution as possible.

Primary, the SCA requires performing stagnant recognition. This article establishes the sliding window approach for designing the technique for efficiently detecting the stagnation of technique. The size of the windows is fixed to 4. If the optimum values computed by the technique are all equivalent to the neighboring 4 iterations, it represents that technique was stagnant. At this time, the original population was upgraded by OBL. In this study, the ISCA is derived using SCA with the OBL concept. The objective function of ISCA is evaluated according to the fitness function. The primary intention was to design a steganography model that must maximize PSNR and minimize the error rate (MSE) and is estimated by the following equation

F={min(MSE), max(PSNR)}(10)

The maximized and minimized values can be acquired by leveraging the CSO system.

4  Experimental Validation

In this section, the experimental validation of the ISCACE-RSI model is carried out using a set of remote-sensing images. Fig. 3 shows the sample results offered by the ISCACE-RSI model. Fig. 3a depicts the original remote-sensing images, and Fig. 3b denotes the encrypted versions of the original images.

Figure 3: (a) Original images (b) Encrypted images

Table 1 provides an overall analysis of the ISCACE-RSI methodology on various test images. The attained values implied that the ISCACE-RSI model had enhanced results under all images. Fig. 4a depicts a detailed MSE inspection of the ISCACE-RSI technique under distinct images. The figure shows that the ISCACE-RSI approach has achieved better results with minimum MSE values. For example, in image 1, the ISCACE-RSI model has offered MSE of 0.4070. Also, in image 3, the ISCACE-RSI approach has provided MSE of 0.2450. Next, in image 5, the ISCACE-RSI technique has shown MSE of 0.4060. Then, in image 6, the ISCACE-RSI approach demonstrated MSE of 0.4210.

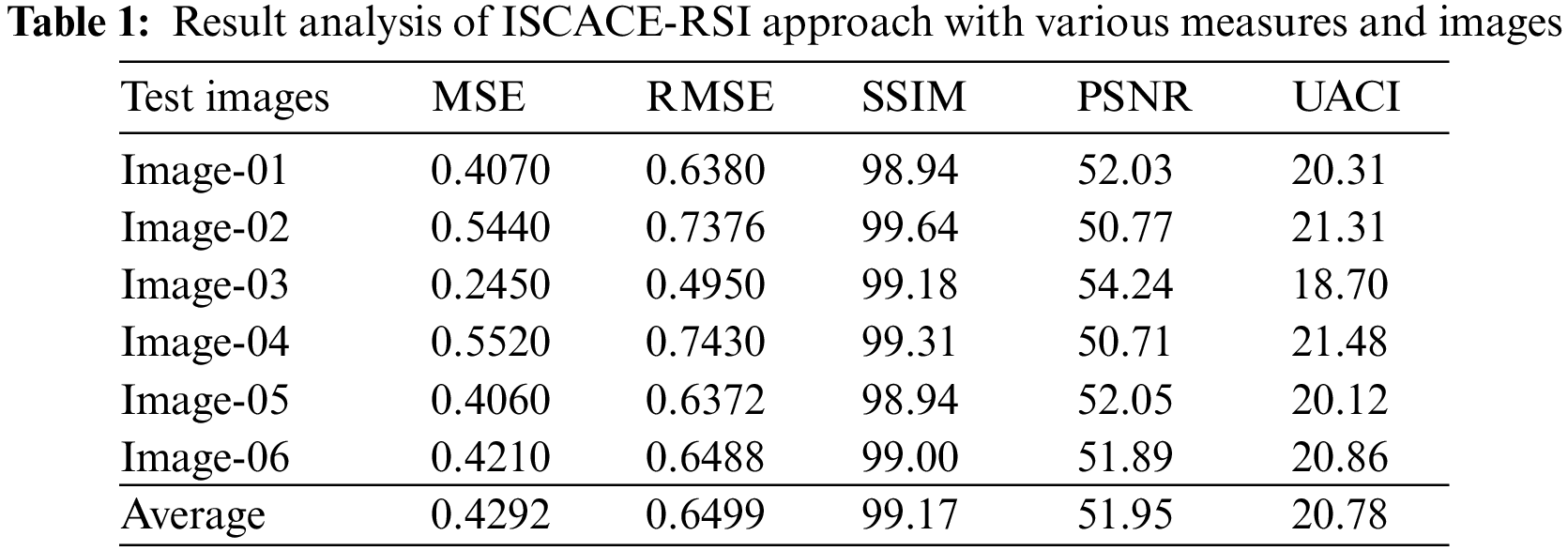
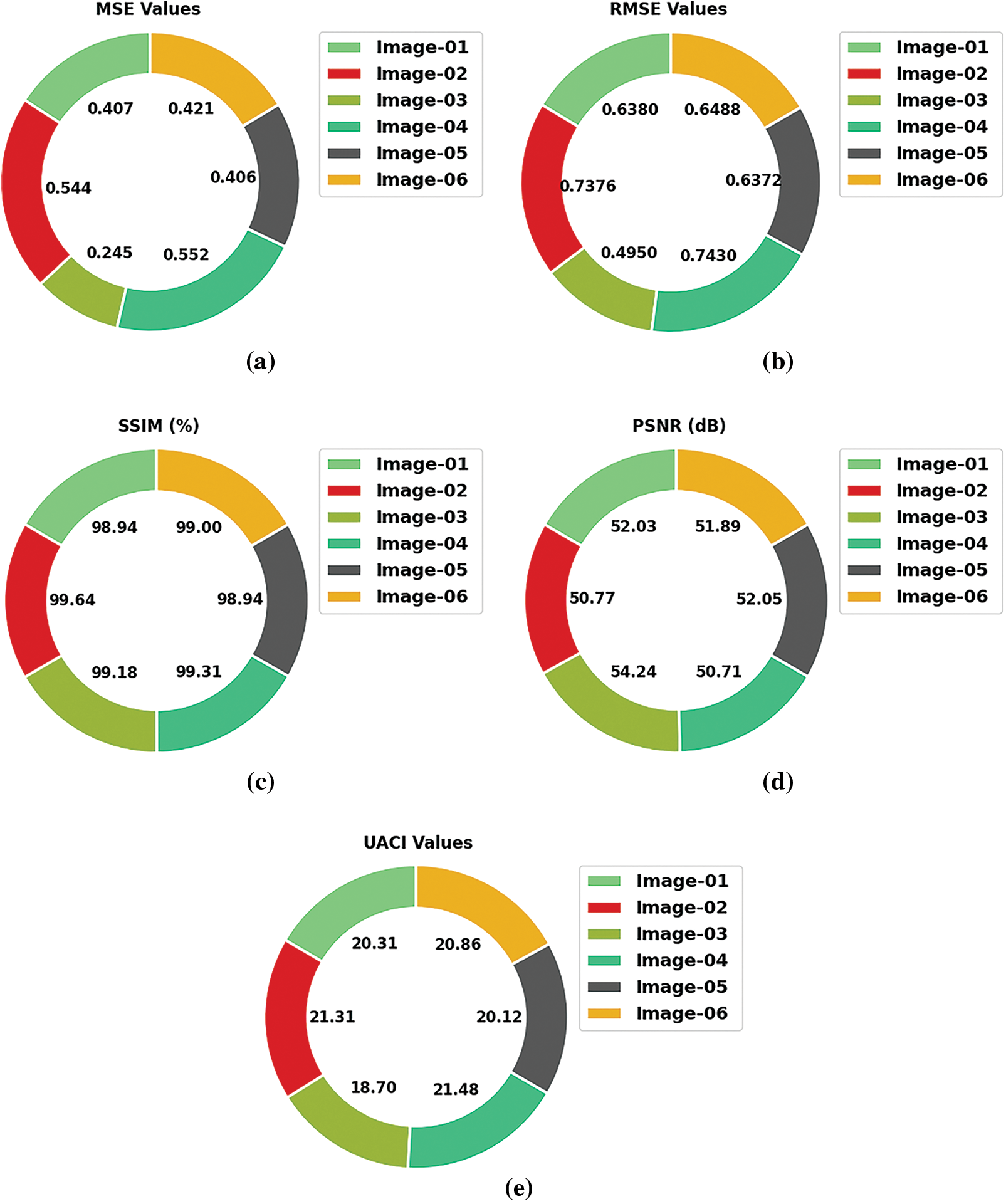
Figure 4: Result analysis of ISCACE-RSI approach (a) MSE, (b) RMSE, (c) SSIM, (d) PSNR, and (e) UACI

Then, Fig. 4b shows a thorough RMSE analysis of the ISCACE-RSI technique under different images. The figure described the ISCACE-RSI method has obtained improved outcomes with the least RMSE values. For example, in image 1, the ISCACE-RSI system has rendered an RMSE of 0.6380. Moreover, in image 3, the ISCACE-RSI algorithm has presented an RMSE of 0.4950. And then, in image 5, the ISCACE-RSI method offered an RMSE of 0.6372. Next, in image 6, the ISCACE-RSI approach has provided an RMSE of 0.6488.

Fig. 4c shows the SSIM assessment of the ISCACE-RSI model under six distinct test images. The figure highlighted that the ISCACE-RSI model has resulted from ineffectual outcomes with increased SSIM values under all images. For instance, in image 1, the ISCACE-RSI model has provided an SSIM of 98.94. Meanwhile, in image 2, the ISCACE-RSI model has offered SSIM of 99.64. Concurrently, in image 3, the ISCACE-RSI methodology has rendered SSIM of 99.18. Afterward, on image 5, the ISCACE-RSI approach presented SSIM of 98.94. At last, in image 6, the ISCACE-RSI methodology has provided SSIM of 99.

Fig. 4d exhibits the PSNR assessment of the ISCACE-RSI algorithm under six distinct test images. The figure emphasized that the ISCACE-RSI methodology has resulted to effectual outcomes with increased PSNR values under all images. For example, on image 1, the ISCACE-RSI method has presented PSNR of 52.03 dB. At the same time, on image 2, the ISCACE-RSI techniques have offered PSNR of 50.77 dB. Simultaneously, on image 3 the ISCACE-RSI model has provided PSNR of 54.24 dB. After, on image 5, the ISCACE-RSI algorithm offered PSNR of 52.05 dB. Finally, on image 6, the ISCACE-RSI methodology has provided PSNR of 51.89 dB.

Fig. 4e depicts a detailed UACI inspection of the ISCACE-RSI method under distinct images. The figure established that the ISCACE-RSI model has accomplished better results with minimal UACI values. For example, on image 1, the ISCACE-RSI approach has rendered UACI of 0.20.31. Besides, on image 3, the ISCACE-RSI technique has offered UACI of 0.18.70. Next, on image 5, the ISCACE-RSI approach has presented UACI of 20.12. Then, on image 6, the ISCACE-RSI model has offered UACI of 20.86.

For illustrating the improvised outcomes of the ISCACE-RSI methodology, a wide range of comparison study with recent models is performed in Table 2. The experimental results implied that the ISCACE-RSI model has gained enhanced results in terms of different measures [21–24].

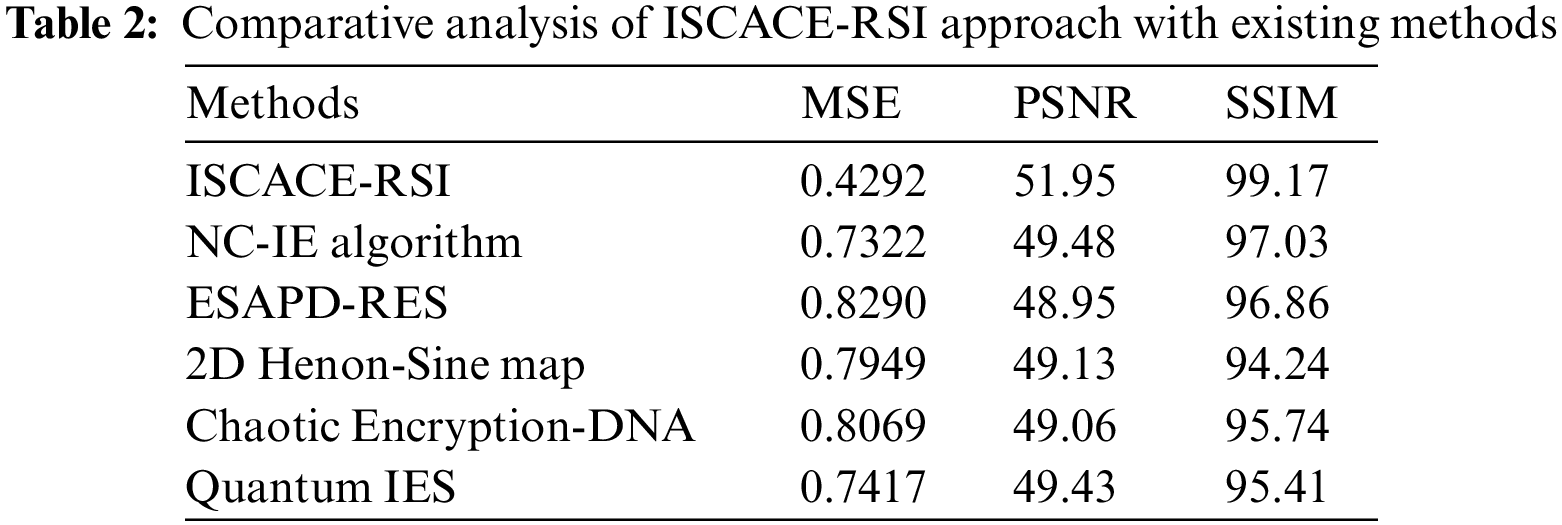
Fig. 5 illustrates a comparative MSE inspection of the ISCACE-RSI model with recent models. The figure implied that the chaotic encryption-DNA and ESAPD-RES models have shown ineffectual outcomes with increased MSE values of 0.8069 and 0.8290 respectively. Followed by, the 2D Henon-Sine map model has attained a slightly reduced MSE of 0.7949. Next to that, the ESAPD-RES and quantum Integrated Encryption Scheme (IES) models reported reasonable MSE of 0.7417. Though the NC-IE technique has showcased considerable MSE of 0.7322, the presented ISCACE-RSI model has shown effectual performance with minimal MSE of 0.4292.

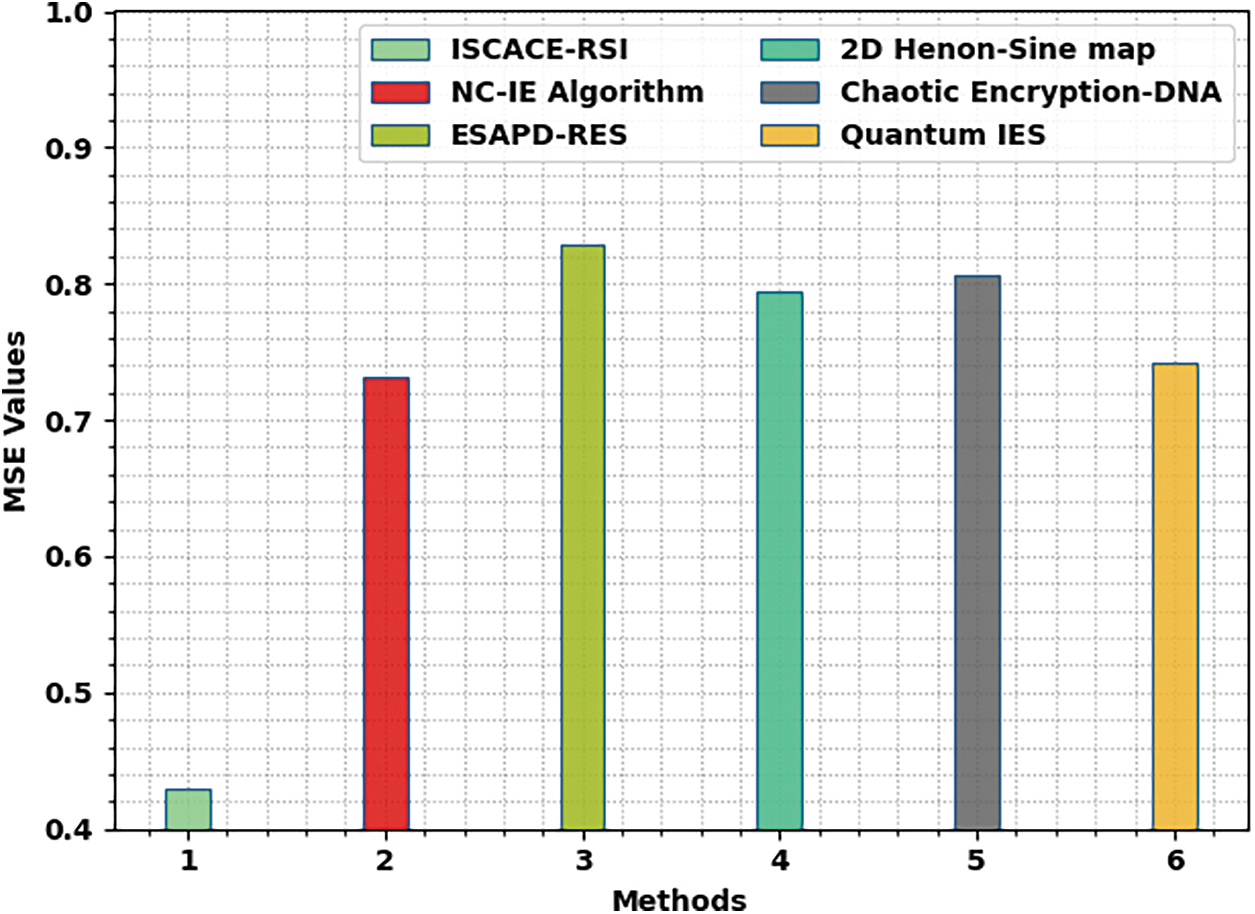
Figure 5: MSE analysis of ISCACE-RSI approach with existing methodologies

A detailed PSNR examination of the ISCACE-RSI model with existing techniques is made in Fig. 6. The results identified that the ESAPD-RES model has demonstrated poor results with minimal PSNR of 48.95 dB. Along with that, the 2D Henon-Sine map and chaotic encryption-DNA techniques have obtained slightly enhanced performance with PSNR of 49.13 and 49.06 dB respectively. Next to that, the NC-IE and quantum IES techniques have reported moderately closer PSNR values of 49.48 and 49.43 dB respectively. However, the ISCACE-RSI model has showcased better performance with higher PSNR of 51.95 dB.

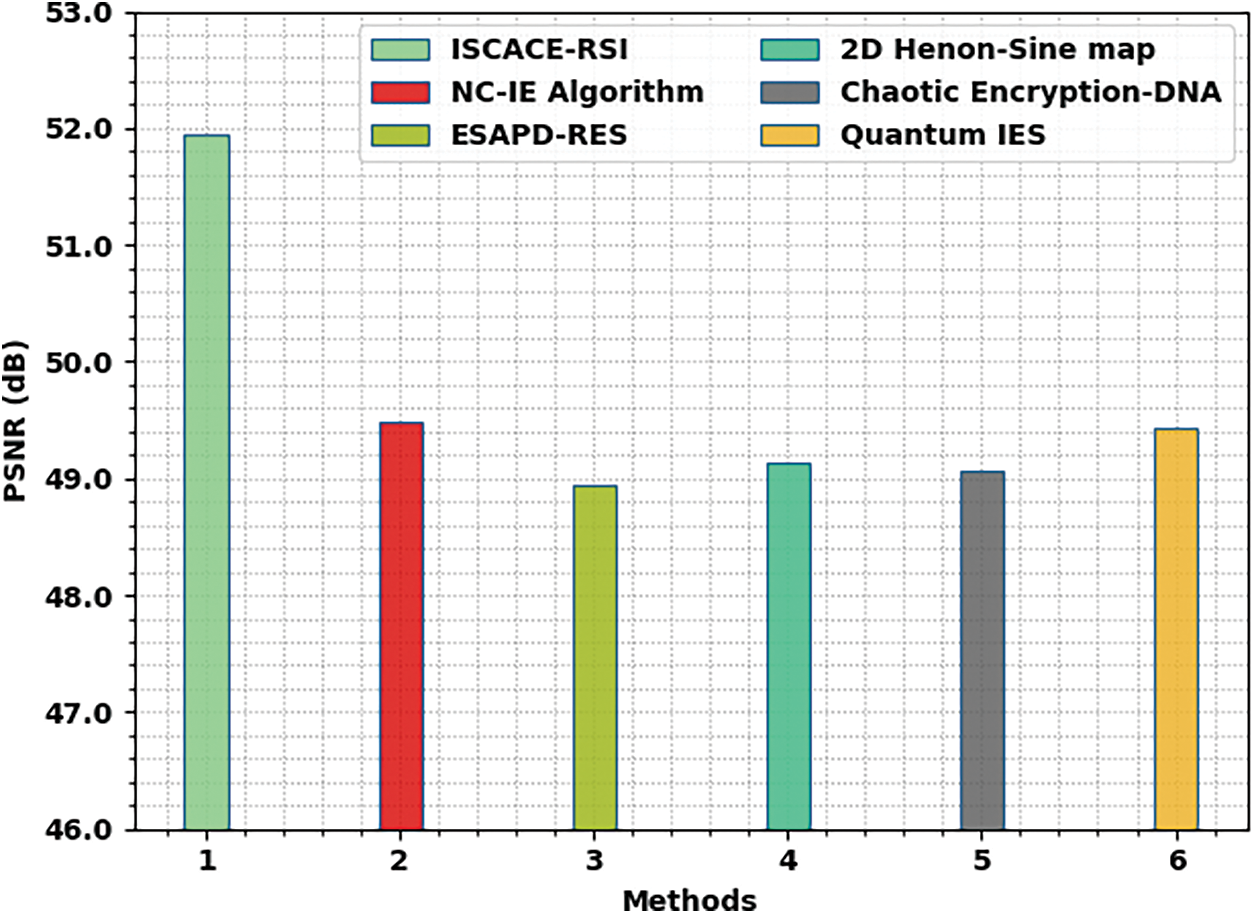
Figure 6: PSNR analysis of ISCACE-RSI approach with existing methodologies

A detailed SSIM check of the ISCACE-RSI method with existing methods is made in Fig. 7. The results identified that the 2D Henon-Sine map model has illustrated poor results with minimal SSIM of 94.24%. Also, the Quantum IES and chaotic encryption-DNA techniques have gained slightly enhanced performance with SSIM of 95.41% and 95.74% correspondingly. Next, the NC-IE and ESAPD-RES approaches have reported moderately closer SSIM values of 97.03% and 96.86% correspondingly. But, the ISCACE-RSI algorithm has showcased better performance with higher SSIM of 99.17%.

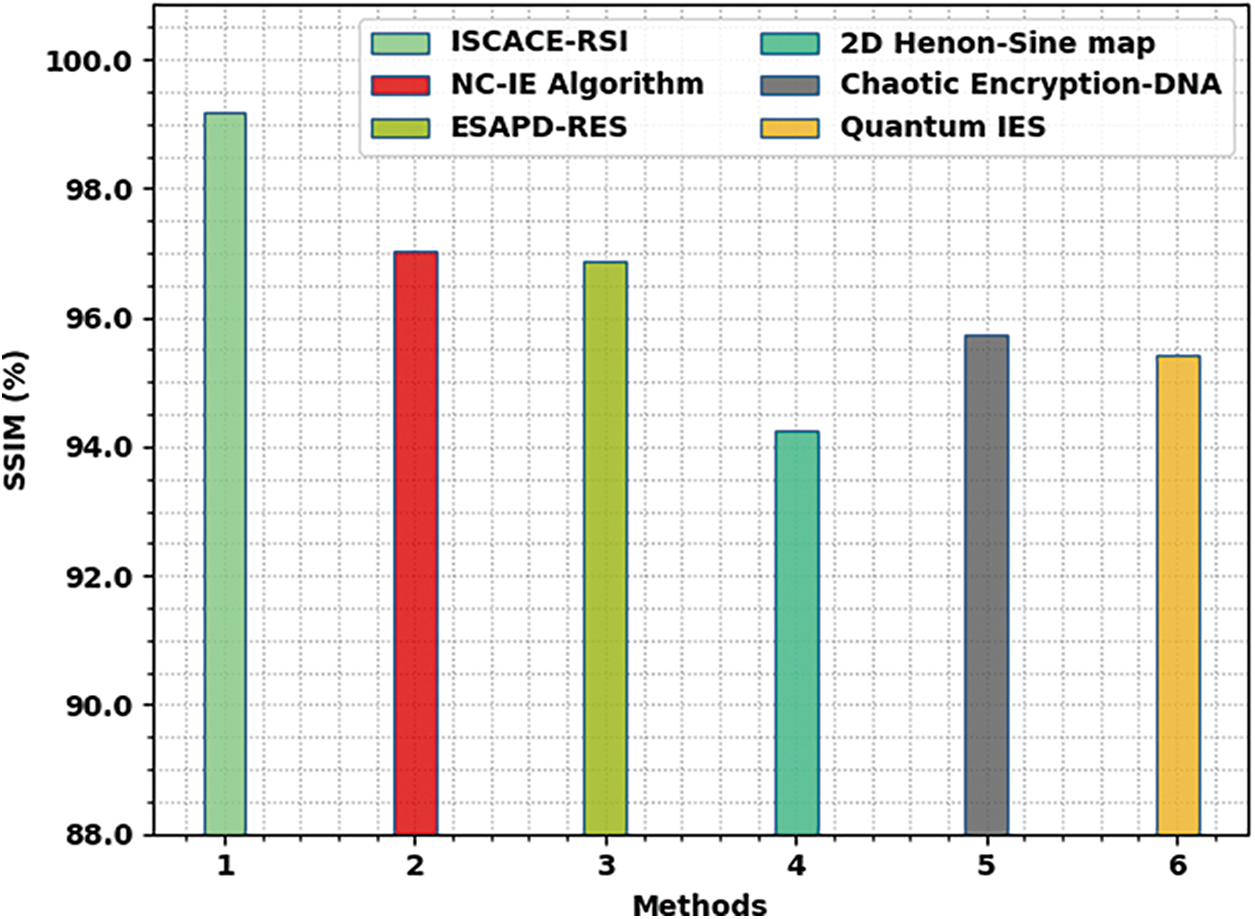
Figure 7: SSIM analysis of ISCACE-RSI approach with existing methodologies

By observing the above mentioned tables and discussion, it is confirmed that the ISCACE-RSI model has shown effectual encryption performance over other models.

5  Conclusion

In this study, a new ISCACE-RSI algorithm has been proposed for remote sensing image encryption in the IoT environment. The presented ISCACE-RSI technique follows a three stage process, namely pre-processing, encryption, and optimal key generation. Firstly, the remote sensing images are pre-processed to enhance image quality. Then, the ISCACE-RSI technique makes use of DLRSIE technique to encrypt the images. For an optimal key generation of the DLRSIE technique, the ISCA is applied with an objective function of the maximization of PSNR. To demonstrate the improvised performance of the ISCACE-RSI model, a detailed set of simulations were conducted. The comparative study reported the better performance of the ISCACE-RSI model over other existing approaches. In the future, image watermarking and steganography techniques can be included to improve the overall security of the ISCACE-RSI technique.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R319), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4210118DSR48).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Kaur and V. Kumar, “A comprehensive review on image encryption techniques,” Archives of Computational Methods in Engineering, vol. 27, no. 1, pp. 15–43, 2020. [Google Scholar]

2. K. N. Singh and A. K. Singh, “Towards integrating image encryption with compression: A survey,” ACM Transactions on Multimedia Computing, Communications, and Applications, vol. 18, no. 3, pp. 1–21, 2022. [Google Scholar]

3. X. Zhang and X. Wang, “Remote-sensing image encryption algorithm using the advanced encryption standard,” Applied Sciences, vol. 8, no. 9, pp. 1540, 2018. [Google Scholar]

4. M. A. Al-Khasawneh, S. M. Shamsuddin, S. Hasan and A. A. Bakar, “An improved chaotic image encryption algorithm,” in 2018 Int. Conf. on Smart Computing and Electronic Enterprise (ICSCEE), Shah Alam, pp. 1–8, 2018. [Google Scholar]

5. Z. Liu, L. Wang, X. Wang, X. Shen and L. Li, “Secure remote sensing image registration based on compressed sensing in cloud setting,” IEEE Access, vol. 7, pp. 36516–36526, 2019. [Google Scholar]

6. Y. Q. Zhang, Y. He, P. Li and X. -Y. Wang, “A new color image encryption scheme based on 2DNLCML system and genetic operations,” Optics and Lasers in Engineering, vol. 128, pp. 106040, 2020. [Google Scholar]

7. X. Xu and S. Chen, “A remote sensing image encryption method combining chaotic neuron and tent map,” Journal of Computers, vol. 32, no. 2, pp. 108–123, 2021. [Google Scholar]

8. B. Vaseghi, S. S. Hashemi, S. Mobayen and A. Fekih, “Finite time chaos synchronization in time-delay channel and its application to satellite image encryption in ofdm communication systems,” IEEE Access, vol. 9, pp. 21332–21344, 2021. [Google Scholar]

9. G. Yuan and Q. Hao, “Digital watermarking secure scheme for remote sensing image protection,” China Communications, vol. 17, no. 4, pp. 88–98, 2020. [Google Scholar]

10. D. Zhang, X. Liao, B. Yang and Y. Zhang, “A fast and efficient approach to color-image encryption based on compressive sensing and fractional Fourier transform,” Multimedia Tools and Applications, vol. 77, no. 2, pp. 2191–2208, 2018. [Google Scholar]

11. H. Liu, B. Zhao and L. Huang, “A remote-sensing image encryption scheme using dna bases probability and two-dimensional logistic map,” IEEE Access, vol. 7, pp. 65450–65459, 2019. [Google Scholar]

12. Y. Bentoutou, E. -H. Bensikaddour, N. Taleb and N. Bounoua, “An improved image encryption algorithm for satellite applications,” Advances in Space Research, vol. 66, no. 1, pp. 176–192, 2020. [Google Scholar]

13. H. Wang, D. Xiao, M. Li, Y. Xiang and X. Li, “A visually secure image encryption scheme based on parallel compressive sensing,” Signal Processing, vol. 155, pp. 218–232, 2019. [Google Scholar]

14. S. Nan, X. Feng, Y. Wu and H. Zhang, “Remote sensing image compression and encryption based on block compressive sensing and 2D-LCCCM,” Nonlinear Dynamics, vol. 108, no. 3, pp. 2705–2729, 2022. [Google Scholar]

15. X. Wang, C. Liu and D. Jiang, “A novel triple-image encryption and hiding algorithm based on chaos, compressive sensing and 3D DCT,” Information Sciences, vol. 574, pp. 505–527, 2021. [Google Scholar]

16. M. Kaur, D. Singh and V. Kumar, “Color image encryption using minimax differential evolution-based 7D hyper-chaotic map,” Applied Physics B, vol. 126, no. 9, pp. 147, 2020. [Google Scholar]

17. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, pp. 120–133, 2016. [Google Scholar]

18. J. Xia, D. Yang, H. Zhou, Y. Chen, H. Zhang et al., “Evolving kernel extreme learning machine for medical diagnosis via a disperse foraging sine cosine algorithm,” Computers in Biology and Medicine, vol. 141, pp. 105137, 2022. [Google Scholar] [PubMed]

19. M. Li, G. Xu, Q. Lai and J. Chen, “A chaotic strategy-based quadratic opposition-based learning adaptive variable-speed whale optimization algorithm,” Mathematics and Computers in Simulation, vol. 193, pp. 71–99, 2022. [Google Scholar]

20. X. Chai, Y. Chen and L. Broyde, “A novel chaos-based image encryption algorithm using DNA sequence operations,” Optics and Lasers in Engineering, vol. 88, pp. 197–213, 2017. [Google Scholar]

21. X. Chai, Z. Gan, Y. Lu, Y. Chen and D. Han, “A novel image encryption algorithm based on the chaotic system and DNA computing,” International Journal of Modern Physics C, vol. 28, no. 5, pp. 1750069, 2017. [Google Scholar]

22. J. Wu, X. Liao and B. Yang, “Image encryption using 2D Hénon-Sine map and DNA approach,” Signal Processing, vol. 153, pp. 11–23, 2018. [Google Scholar]

23. H. Liu, B. Zhao and L. Huang, “Quantum image encryption scheme using arnold transform and s-box scrambling,” Entropy, vol. 21, no. 4, pp. 343, 2019. [Google Scholar] [PubMed]

24. J. Chen, Z. Zhu, L. Zhang, Y. Zhang and B. Yang, “Exploiting self-adaptive permutation–diffusion and DNA random encoding for secure and efficient image encryption,” Signal Processing, vol. 142, pp. 340–353, 2018. [Google Scholar]