 Open Access
Open Access
ARTICLE
Securing Healthcare Data in IoMT Network Using Enhanced Chaos Based Substitution and Diffusion
1 Department of Computer Engineering, Jamia Millia Islamia, New Delhi, 110025, India
2 Department of Information Technology, College of Computer and Information Sciences, Princess Nourah bint Abdulrahman University, P.O. Box 84428, Riyadh, 11671, Saudi Arabia
3 Department of Electronics and Electrical Communications Engineering, Faculty of Electronic Engineering, Menoufia University, Menouf, 32952, Egypt
4 Security Engineering Laboratory, Department of Computer Science, Prince Sultan University, Riyadh, 11586, Saudi Arabia
* Corresponding Author: Reem Ibrahim Alkanhel. Email:
Computer Systems Science and Engineering 2023, 47(2), 2361-2380. https://doi.org/10.32604/csse.2023.038439
Received 13 December 2022; Accepted 24 February 2023; Issue published 28 July 2023
Abstract
Patient privacy and data protection have been crucial concerns in E-healthcare systems for many years. In modern-day applications, patient data usually holds clinical imagery, records, and other medical details. Lately, the Internet of Medical Things (IoMT), equipped with cloud computing, has come out to be a beneficial paradigm in the healthcare field. However, the openness of networks and systems leads to security threats and illegal access. Therefore, reliable, fast, and robust security methods need to be developed to ensure the safe exchange of healthcare data generated from various image sensing and other IoMT-driven devices in the IoMT network. This paper presents an image protection scheme for healthcare applications to protect patients’ medical image data exchanged in IoMT networks. The proposed security scheme depends on an enhanced 2D discrete chaotic map and allows dynamic substitution based on an optimized highly-nonlinear S-box and diffusion to gain an excellent security performance. The optimized S-box has an excellent nonlinearity score of 112. The new image protection scheme is efficient enough to exhibit correlation values less than 0.0022, entropy values higher than 7.999, and NPCR values around 99.6%. To reveal the efficacy of the scheme, several comparison studies are presented. These comparison studies reveal that the novel protection scheme is robust, efficient, and capable of securing healthcare imagery in IoMT systems.Keywords
Privacy and security have always been important issues and requirements for any healthcare organization. Any intrusion should be scrutinized to check the authenticity of the attempt to access the service [1–6]. Patient privacy is violated when sensitive data is shared on the Internet of Medical Things (IoMT) networks. As a result, there is a serious risk to the security of medical data carried across the IoMT network as part of an e-healthcare service [7]. Additionally, for intelligent monitoring, diagnosis, and decision-making processes, many smart devices contribute real-time sensitive healthcare data to IoMT networks [8]. However, a public communication channel is used to exchange the generated healthcare data, creating questions regarding diagnosis security and privacy. Therefore, cryptographic solutions that can be used to securely transmit the image data are tough security requirements for IoMT applications [9]. This is because healthcare data generated by various image-intensive and other IoMT devices must be protected against unauthorized access and alterations. An enormous amount of images is currently exchanged across open channels because of the rapid advancement of technologies like the Internet of Things (IoT), cloud computing, and fifth-generation (5G) communications. Private information about specific individuals is frequently included in the images sent. They may contain a person’s social security number, health information, and, occasionally, secret defense information about a country [10]. Since only approved and intended recipients may access the images, they must be processed before being delivered.
Image encryption is one of the potential techniques to enable the safe transmission of data across networks. This approach conceals real message data by transforming images into meaningless, noise-like data. Images are frequently sent across the network extensively and frequently have significant pixel correlation and redundancy. Additionally, images are frequently multi-dimensional image data. Therefore, considerations like security, speed, computational complexity, and transmission cost must be thought of when building a digital image encryption algorithm [11,12]. Images can be securely communicated over the network and transmitted effectively by taking these parameters into account in the algorithm. Numerous image encryption algorithms have been proposed in the literature, employing various techniques. For instance, techniques based on DNA computing [13], compressive sensing [14,15], cellular automata [16], and chaotic systems [13–17] have been utilized to create cipher images. Due to the unique characteristics of chaotic maps, chaos-based encryption is regarded as an effective solution for image encryption [18]. There are a lot of chaos-based image cryptosystems that depend on confusion and diffusion features to work properly. The confusion property is related to moving pixel positions in an image. The diffusion property is related to altering image pixel values. Both confusion and diffusion can be implemented at either the pixel level [19] or the bit level [20]. Pixel-level operation modifies the location pixels while preserving the image histograms. On the other hand, the operation at the bit level modifies the pixel values. To achieve a high level of encryption efficiency, a good level of confusion needs to be achieved. Many of the existing image ciphering algorithms are depend on the heavy usage of chaotic mechanisms, like multiple chaotic maps and/or high-dimensional chaotic systems. Others rely on computationally intensive approaches to realize good encryption quality. However, these schemes suffer from low throughput and long encryption times, making them unsuitable for real-time applications.
The properties of chaotic dynamical systems include high sensitivity to initial conditions and system parameters, excellent auto-correlation properties, pseudo-random behaviour of produced sequences, large entropy, and mixing, which have made them appropriate for potential applications in cryptography [21]. Therefore, these systems are conducive to developing effective and robust cryptographic algorithms. Chaotic systems have been used to develop cryptographic algorithms for multimedia encryption, S-boxes, information hiding, and hash functions for the past few decades [22]. However, the security of such algorithms largely depends on the dynamics of chaotic maps. Nonetheless, one should be cautious because not all chaotic maps are suitable for obtaining robust chaos-based cryptosystems. One should avoid using a chaotic system with frail performance and considerable non-chaotic regions [23]. For example, many research findings have established that some existing discrete chaotic maps, such as Logistic, Sine, Cubic, and other chaotic maps, provide weak performance [24]. Therefore, there is a need to design chaotic systems with rich dynamical characteristics to qualify for robust cryptographic applications.
1.2 Motivation and Research Contributions
Based on the literature analysis, it is found that there exist limitations in image encryption methods including:
– The conventional discrete chaotic maps have a low Lyapunov exponent, revealing a low degree of chaoticity and sensitivity of the map, low entropy, high computations, and non-uniform coverage of space through phase attractors. The robustness and security of the encryption scheme heavily rely on the features of utilized chaotic maps.
– Numerous computationally-intensive meta-heuristics-based S-box generation algorithms are available in the literature, but very few achieve a nonlinearity of up to 112 for 8 × 8 S-box design. A simple and effective dynamic S-box generation method is desirable to produce highly nonlinear S-boxes. Furthermore, a single S-box usage for image encryption typically reveals some patterns of the plain image. These patterns may be used by attackers to gain some knowledge about the plain image information.
– Almost multimedia ciphering techniques heavy floating-point computations, which cause low throughput and long encryption times and making them unsuitable for real-time applications.
The above limitations and challenges motivate the need to develop cryptographically strongS-boxes, chaotic maps with frail-free performance, and efficient image encryption algorithms that are fast and robust. This paper tackles all these issues and provides three contributions. We present a proposed security scheme to investigate and meet the security need of protecting medical image data exchanged in IoMT networks that are responsible for intelligent, smart operations and decisions. The proposed security framework explores the features of an enhanced model of discrete chaos and adopts dynamic substitution to achieve excellent performance. To validate the efficacy and prestige of the framework, several comparison studies will be examined and analyzed to justify that the novel data transmission framework is robust, efficient, and capable of securing the imagery data. To achieve this goal, this paper is committed to designing an enhanced 2-D discrete chaotic map. The proposed map is applied to generate cryptographic, highly nonlinear S-boxes meant for the dynamical substitution of image pixels. The novel map is also responsible for carrying out required pixel diffusion operations, resulting in a strong image cryptosystem and encryption quality.
The main contributions suggested in this paper are the following:
• A novel and a dynamically rich 2-D discrete chaotic map are designed, which guarantees frail-free performance.
• A strong and highly nonlinear cryptographic S-boxes method is analyzed and investigated.
• A fast and efficient image encryption scheme is proposed to secure healthcare data generated and exchanged in an IoMT environment.
• Analyses have been performed to evaluate the performance of the proposed enhanced chaotic map, generated S-box, and image protection scheme.
The flow of the rest of this work is as follows: The proposed 2D discrete chaotic map is discussed in Section 2, and its dynamical features are analyzed in Section 3. The cryptographic S-box generation procedure using the enhanced 2D chaos map is discussed in Section 4. Next, Section 5 describes a method for securing digital image data generated in IoMT networks. The security evaluation of the proposed image data secure transmission scheme is done, and the comparison of the suggested secure ciphering approach is achieved in Section 6. Lastly, the summary of this work is concluded in Section 7.
2 Proposed Discrete Chaotic Map
The security and robustness of cryptographic schemes are heavily reliant on the dynamic properties of the chaotic maps used. The frail performance of chaotic maps may result in a weak security impact provided by cryptographic systems [24]. However, many of the existing chaotic maps were shown to have one or more drawbacks that limited their use in developing a strong cryptographic scheme. Chaos systems with poor dynamics are week for ciphering process and render them vulnerable to assaults. Such chaotic maps have issues like restricted chaotic range and behavior, and no uniform reportage of chaos attractors [25]. This encourages the development of chaotic maps with richer and better dynamical properties than typical chaotic maps [26]. As a result, an enhanced 2D chaotic map is created, which has many superior properties compared to 2D chaotic maps. The dynamics of the novel 2-D discrete chaotic map have the mathematical form given in Eq. (1).
where, xi, yi are state variables that take bounded values in (0, 1), a and b are control parameters of the chaotic map. Dynamical characteristics of the suggested chaotic map are demonstrated in the below subsections, and the features of the new map are compared with the conventional 2-D Henon chaotic map [27] and the 2-D SLMM chaotic map investigated in [28].
3 Analysis of Proposed Chaotic Map
This section offers the performance and dynamical features analysis of the novel enhanced 2-D discrete chaotic map and its comparison study with the well-known chaotic maps, i.e., the 2-D Henon map and 2-D SLMM map. The simulations are done for the initial conditions for x0 = 0.726 and y0 = 0.238.
3.1 Lyapunov Exponents Analysis
The Lyapunov exponent (LE) is an indicator of the chaotic degree of dynamical maps. Dynamical maps having positive LE specify the existence of chaotic phenomena underlying the map [25]. The higher value of LE specifies the accelerated divergence pace of its trajectory and corresponds to the high degree of chaos exhibited by the map [24]. The behaviour of the LE for the proposed 2-D discrete map is shown in Eq. (1) is studied for different values of control parameters a and b. The new map’s LEs are displayed in Figs. 1c–1f. The exponents for different values of parameter a from 0 to 20 are shown in Fig. 1c when b = 3. The exponents’ behaviour for varying values of b from 0 to 20 is presented in Fig. 1d when a = 7. This range of parameters a and b are only used for experimentation.
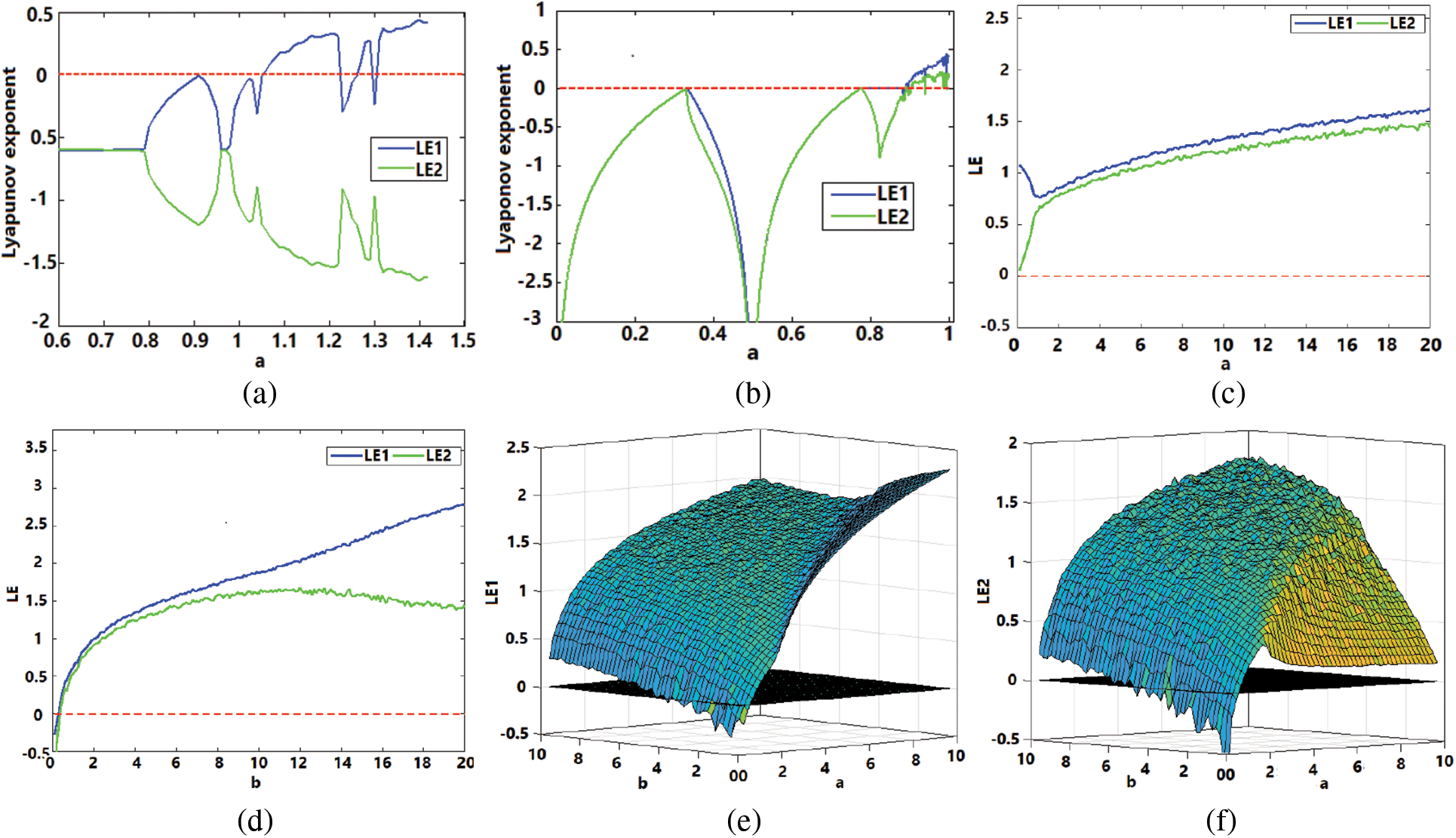
Figure 1: Lyapunov exponents analysis for x0 = 0.726, y0 = 0.238: (a) Henon map, (b) SLMM map, and (c) proposed map: LE vs. a when b = 3, (d) proposed map: LE vs. b when a = 7, (e) proposed map: LE1 vs. a and b, and (f) proposed map: LE2 vs. a and b
The simulation is performed to study the behaviour of both LE for simultaneous variations in parameters a and b, and the obtained behaviours of Lyapunov exponent-1 (LE1) and Lyapunov exponent-2 (LE2) are shown in Figs. 1e and 1f, respectively. According to Fig. 1c, both exponents increase as the parameter increases, reflecting the greater divergence of trajectories and arduous chaotic behaviour in the proposed discrete map. Fig. 1e also demonstrates that the magnitude of LE1 rises with an increase in the values of parameters a and b as well. For higher values of parameters, both LEs come out to be sufficiently greater than zero, which confirms the hyperchaotic nature of the proposed 2-D discrete map. Consequently, the KY dimension of the proposed discrete map comes out to be 2 since both exponents are positive. The LE feature of the novel map is compared with the 2-D Henon map and 2-D SLMM maps. Their LE spectrums are shown in Figs. 1a and 1b, respectively. The LE plots of the maps make it evident that the suggested chaotic map shows better exponent behaviour, i.e., larger LE values and greater chaoticity for a wider range of control parameters compared to the two well-known existing chaotic maps.
The bifurcation diagram assists in gaining knowledge of the long-term state of dynamical maps, which may include stable, unstable, periodic, and chaotic states. The state behaviour of a dynamical map is analyzed for varying values of control parameters, usually referred to as bifurcation parameters [23]. Since the proposed 2-D discrete chaotic map has two parameters, the bifurcation diagrams for one control parameter are simulated, as shown in Fig. 2c (for b = 3). The proposed chaotic map also exhibits similar bifurcation behaviour for parameter b as well. Whereas the bifurcation behaviour of the 2-D Henon chaotic map and the 2-D SLMM chaotic map is simulated, as shown in Figs. 2a and 2b. The bifurcation diagrams show that there exist no periodic or non-chaotic windows in Fig. 2c, unlike in Figs. 2a and 2b. As a result, the proposed chaotic map demonstrates that it has superior bifurcation conduct than the Henon and SLMM maps because it covers the entire control parameter region.
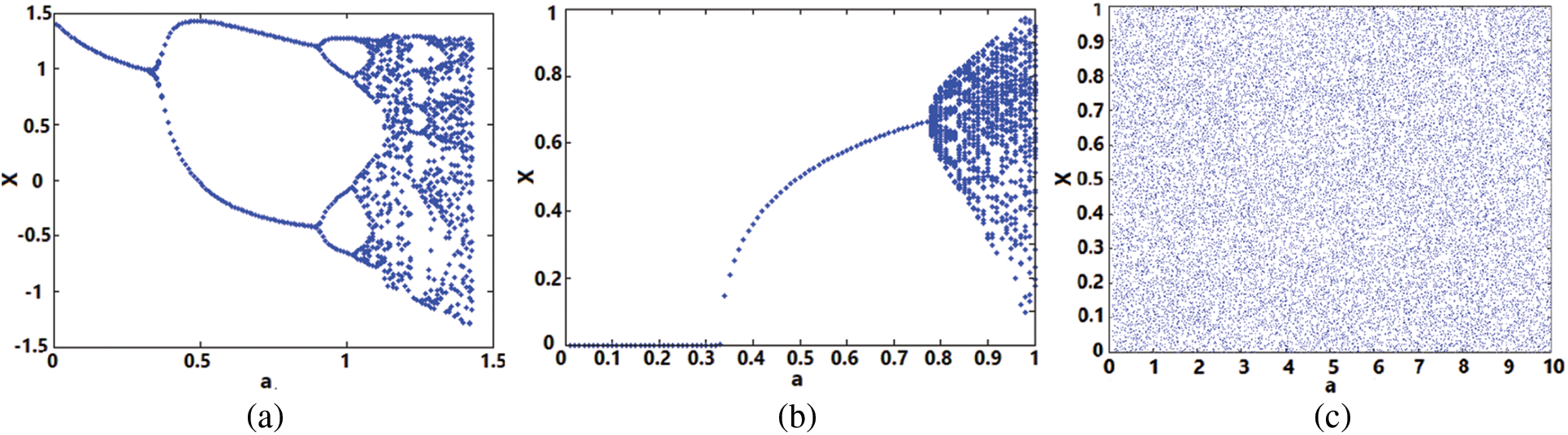
Figure 2: Bifurcation behavior of 2D chaotic maps (a) Henon, (b) SLMM, and (c) proposed
3.3 Approximate Entropy Analysis
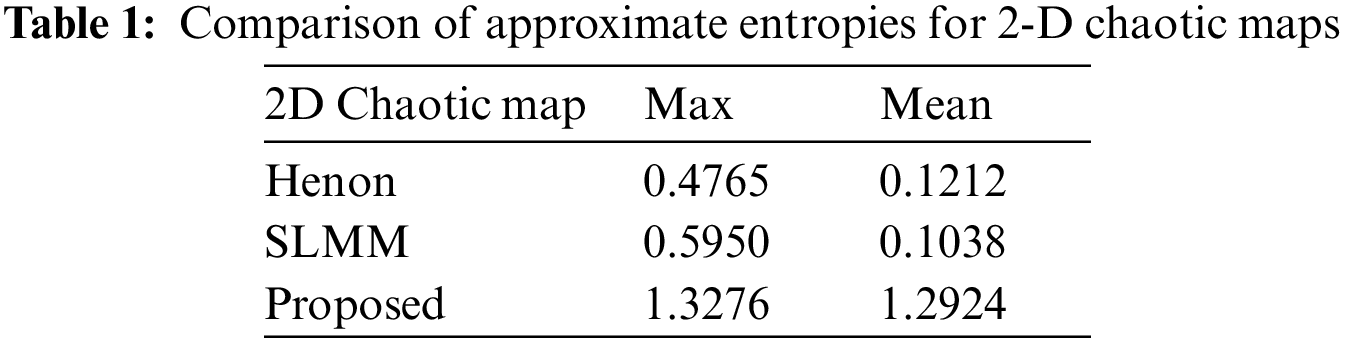
The approximate entropy measure is aimed at assessing the complexity contained in dynamical systems and maps. It quantifies the extent of unpredictability and irregularities within the time series generated by the system. ApEn with a higher magnitude is expected for systems containing greater complexity and randomness [29]. The ApEn measure is computed for the three 2-D chaotic maps with similar initial values. The ApEn for different permissible values of their bifurcation parameter is stored, and the behaviour is shown in Fig. 3. The mean and maximum statistics from the ApEn plots for the three chaotic maps are determined and listed in Table 1. The maximum and mean ApEn scores for the proposed chaotic are 1.3276 and 1.2924, respectively. The comparison in Fig. 3 and Table 1 demonstrates that the proposed chaotic map attains higher values than the 2-D chaotic Henon and SLMM maps, which clearly indicates that our map has higher complexity, unpredictability, or randomness. This analysis demonstrates that the proposed chaotic map is well-suited for cryptographic applications and security primitive designs.
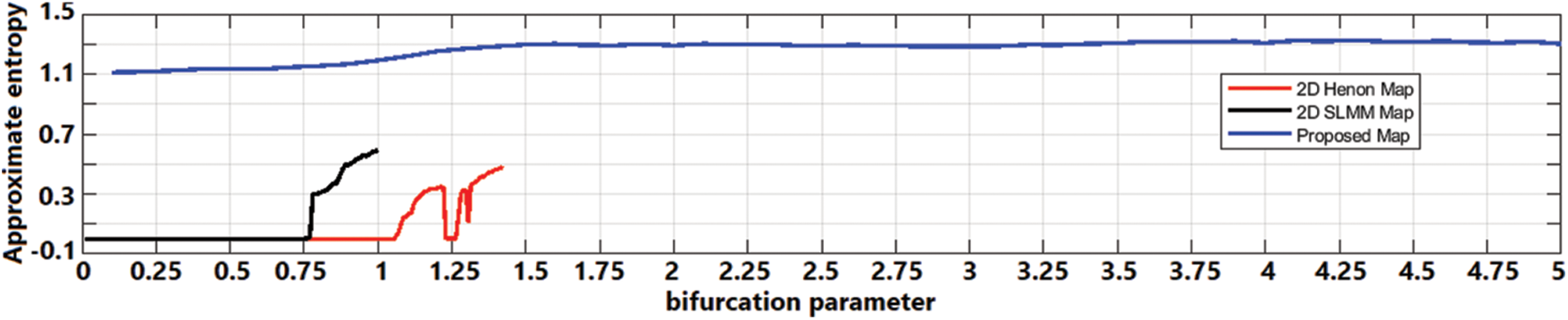
Figure 3: Approximation entropy complexity of 2D chaotic maps: Henon, SLMM, and proposed
A chaotic sequence showing rich randomness performance should be able to cover the entire phase space uniformly and randomly. Hence, the phase coverage of the trajectories of chaotic maps is analyzed, as shown in Fig. 4. A suitable cryptographic chaotic map should have an attractor with a specific shape. It can be seen from Fig. 4 that there is an uneven distribution of chaotic sequences generated from 2-D chaotic Henon and SLMM maps. Moreover, the entire phase space is not covered by the chaotic variables. The chaotic variables never visit many areas of the phase space. In comparison, the proposed chaotic map has a uniform distribution of its generated sequences and covers the entire phase space randomly and uniformly.
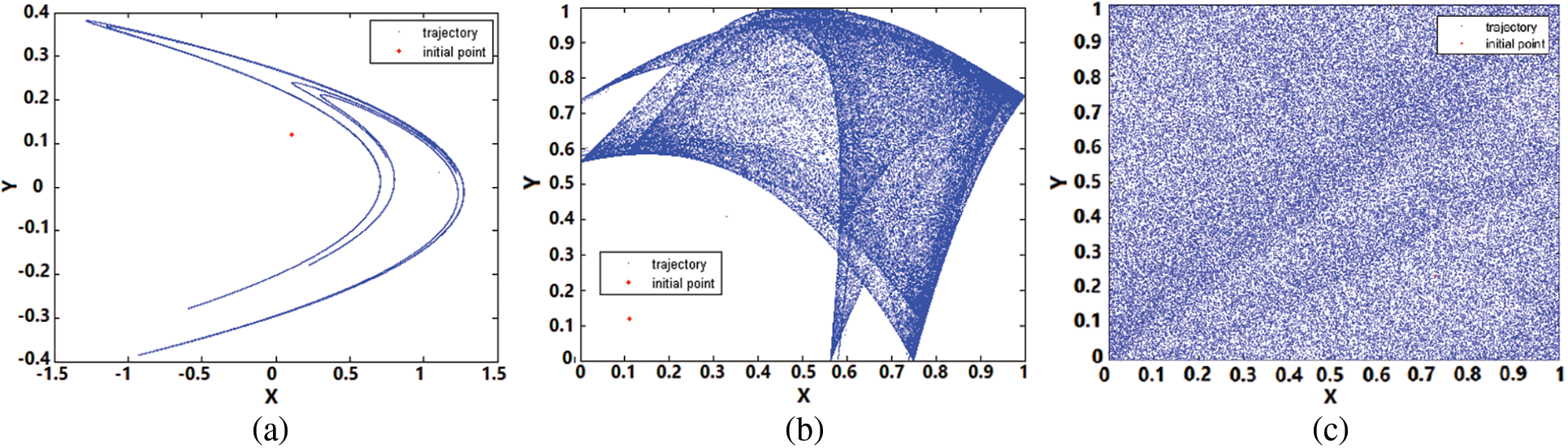
Figure 4: Phase diagrams depicting attractors of 2D chaos maps (a) Henon, (b) SLMM, and (c) proposed
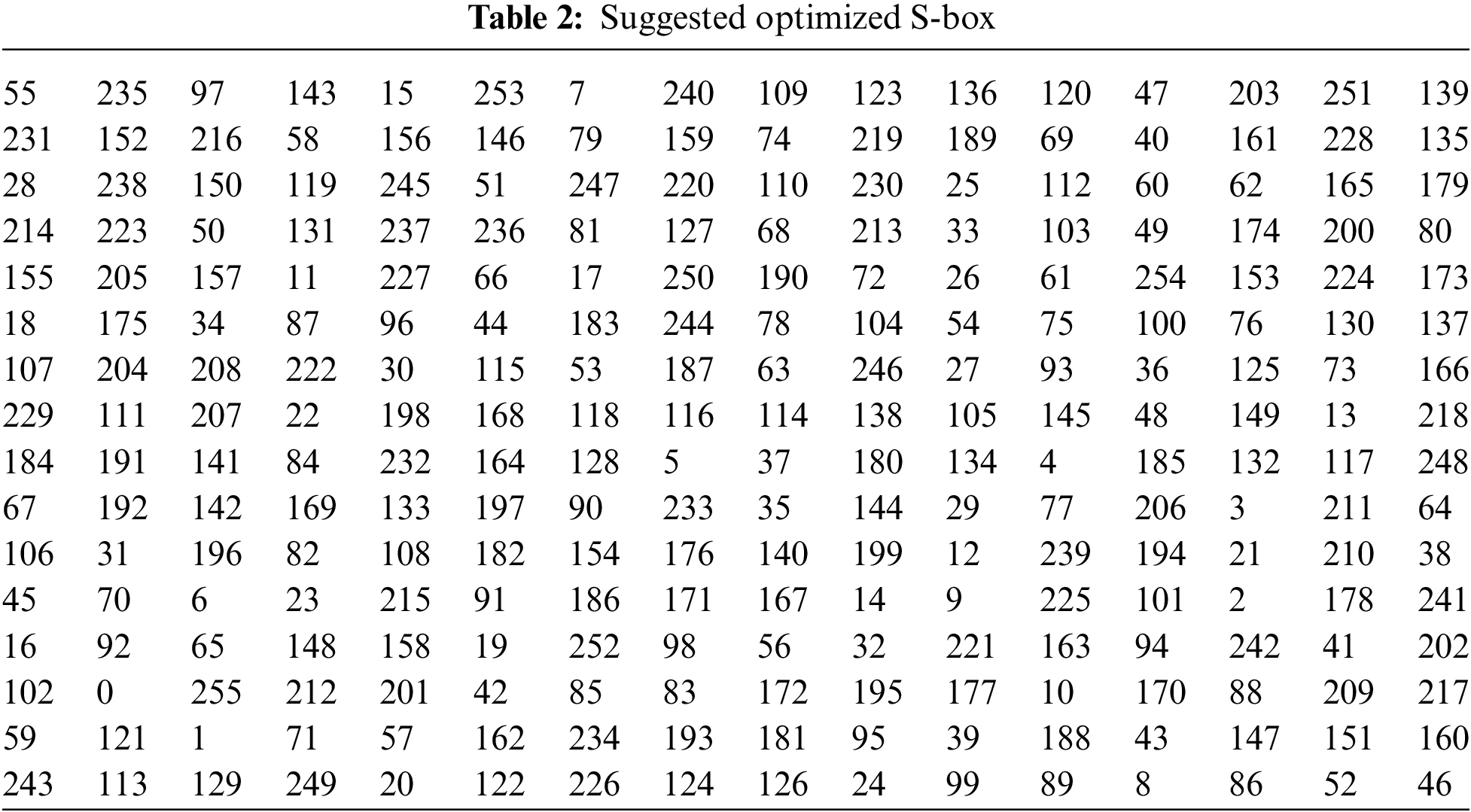
In the proposed security scheme, strong S-boxes are needed during the image encryption phase to perform the dynamic substitution. Highly nonlinear and robust S-boxes are needed, which can bring a strong nonlinear transformation of plain data to make the encryption algorithm resistant to possible attempts. The anticipated S-box generation is based on the effective hill-climbing approach by swapping operations [30]. The S-box procedure explores the dynamics of the proposed chaotic map for preliminary S-box design and the random coordinates needed for swapping the elements of the current S-box. The S-box procedure depicted in Algorithm 1 aims to achieve high nonlinearity. The chaotic map, as shown in Algorithm 2, is used to generate an initial 8 × 8 S-box. Then, two random coordinates in the range of [0,255] are derived from the chaotic map as coord1 ← (floor(xi × 1014))%(28), and coord2 ← (floor(yi × 1014))%(28). The two elements in the current S-box are swapped. The change in the S-box is retained if the new S-box has better or equal nonlinearity. Repeating the operation of swapping for a specified number of counts produces S-boxes with pretty decent nonlinearity. The S-box procedure is executed for x0 = 0.726, y0 = 0.238, a = 7, b = 3, and max_itr = 250000 or until the nonlinearity of 112 is reached. For the mentioned setting, an S-box shown in Table 2 is obtained. However, with a slight variation in the initial conditions x0 and y0, entirely different configurations of S-boxes with a nonlinearity score of 112 can be obtained.


Some well-known standard parameters are used to assess the performance of S-boxes, such as nonlinearity, SAC, BIC, differential uniformity, LAP, etc., [31]. A higher nonlinearity score is responsible for making the transformation of plaintext data into ciphertext data more complex. It mitigates any linear attacks. SAC stands for strict avalanche criterion, which entails that there should be around a 50% change in output if any of the input bits are flipped, thereby indicating the uniform change in the output vectors so as to avoid leaking any information to the attackers. The bits independence criterion states that the possible input vectors are mutually exclusive from each other and that each of the vectors should have high nonlinearity performance. Low differential uniformity values are essential to nullify any possibility of leakage of information to the attackers. This parameter is responsible for offering resistance to differential cryptanalysis. Linear approximation probability is equally significant in mitigating linear cryptanalysis [32]. The good tradeoff of these parameters makes a strong S-box that can do effective substitution while encrypting the plaintext data into ciphertext data. For a detailed description of these S-box parameters, readers are referred to the author’s previous S-box in [24]. Here, the strength of the S-box is improvised with respect to nonlinearity, and we quantified the performance of our S-box. The performance scores are shown in Table 3. It also reports the performance indices of some recently investigated S-box studies. From Table 3, it is apparent that the proposed S-boxes have quite decent and better cryptographic strength compared to some recent S-boxes investigated in [33–40].

5 Secure Image Data Transmission Scheme
In the Internet of Medical Things networks, real-time sensitive healthcare data has been generated by various smart sensing devices for intelligent monitoring, decision-making, and smart diagnosis operations. However, the generated clinical imagery data is exchanged over a public channel, which raises concerns about the security and privacy of patients' data. Therefore, to protect sensitive medical data from various image sensing and other IoMT devices against illegal access by an adversary, a cryptographic solution that can preserve image data privacy is one of the challenging security needs for secure and trustworthy healthcare systems. It is worth noting that traditional data privacy schemes designed for either text or image data have been found to be inadequate for meeting the real-time and fast processing of transmitted multimedia data in IoMT networks. The existing encryption schemes involve high computation, long encryption and decryption times, low robustness to pertinent attacks, etc. Hence, such shortcomings and challenges motivate the need for low-cost, robust, and fast data privacy schemes through which real-time, secure data transmission for IoMT and healthcare systems becomes practical.
The security strength of an S-box-based cryptosystem heavily influences its security. Therefore, strong S-boxes are essential to building secure cryptosystems. We proposed an optimization process to evolve the nonlinear features of the initial S-box and generate highly nonlinear S-boxes for use in robust and fast image data protection. This phase is about the scheme for protecting the image data for the IoMT system. The proposed security scheme involves the encrypting of image data using the action of a strong S-box and enhanced chaotic map. The encryption scheme is simple to have low computation time but with high robustness and security features. The proposed image encryption scheme is presented in Algorithm 3. Take the initial values of x0, y0, a, and b and retrieve the optimized 8 × 8 S-box SB (as demonstrated in Table 1) using the suggested chaotic map through the procedure described in the previous section. Let P be the pending plain image, the SB be the generated optimized S-box (shown in Table 1), M and N be the size of the image P, and 0 ≤ C0 ≤ 255. The presented encryption algorithm is to be followed reversely to perform the decryption of the encrypted image at the receiver side to maintain the integrity of the sensitive image data.
6 Performance Analysis of Encryption Scheme
To implement our encryption scheme, the experimental environment involves Windows 10 Pro with an Intel CoreTM i3 processor running at 3.4 GHz and 8 GB of RAM. The proposed security scheme for image-data protection consists of many prominent performance results. The key features of the performance outcomes include: (a) the proposed encryption scheme is suitable for lightweight applications like IoMTs due to its simplicity, low computation, and lower encryption time, resulting in high throughputs of more than 1450 Kbps; (b) the proposed security scheme has a sufficiently large key space ≥ 2251 and is highly sensitive to slight variations in the pending image, (c) the inclusion of an enhanced chaotic map assisting in the generation of highly nonlinear and dynamic S-boxes in the scheme makes it extremely robust against adversarial cryptanalysis attempts. The recital evaluation of the suggested encryption scheme is presented, and various security analyses have been studied along with the results, which are also compared with a few recent encryption schemes.
To avoid cryptanalysis via the pixels distribution pattern by an attacker in a cipher-only attack, a histogram of a ciphered image must depict a flat or shape of pixel intensities. The first row in Fig. 5 illustrates plain images as our benchmark images considered for analysis. Their corresponding encrypted images using our proposed encryption scheme are shown in the fourth row of Fig. 5. On visually inspecting the figure, it is clear that the encrypted images show no traces or patterns of original data, therefore exhibiting effective encryption. The second and fifth rows of Fig. 5 depict histograms of plain and encrypted images, respectively. The encrypted image’s histogram has a uniform and flat pixel distribution, whereas the plain image’s histogram illustrates peaks, indicating a non-uniform distribution of pixel intensities. Henceforth, the image information will be difficult to discern because the histogram of an encrypted image depicts an undeviating pixel distribution all throughout the plot. The chi-square χ2 can be used to determine how pixels are distributed in an image.
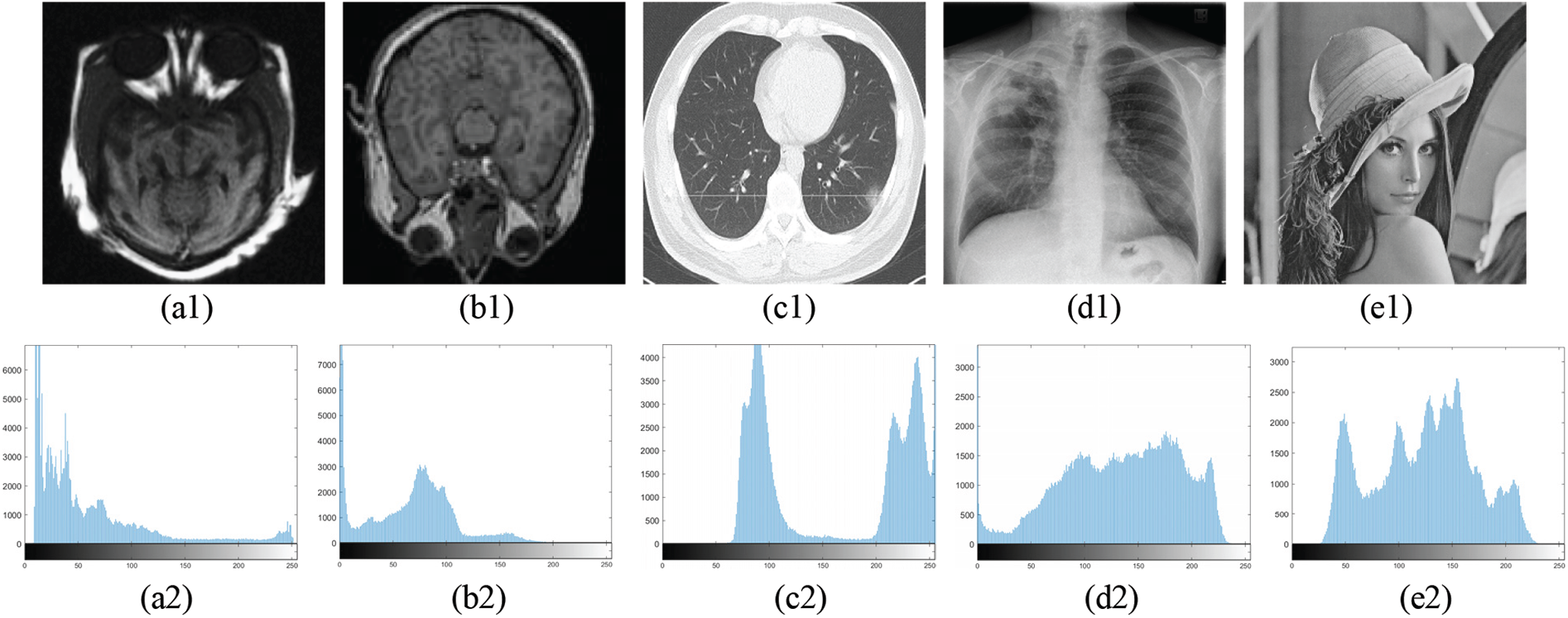
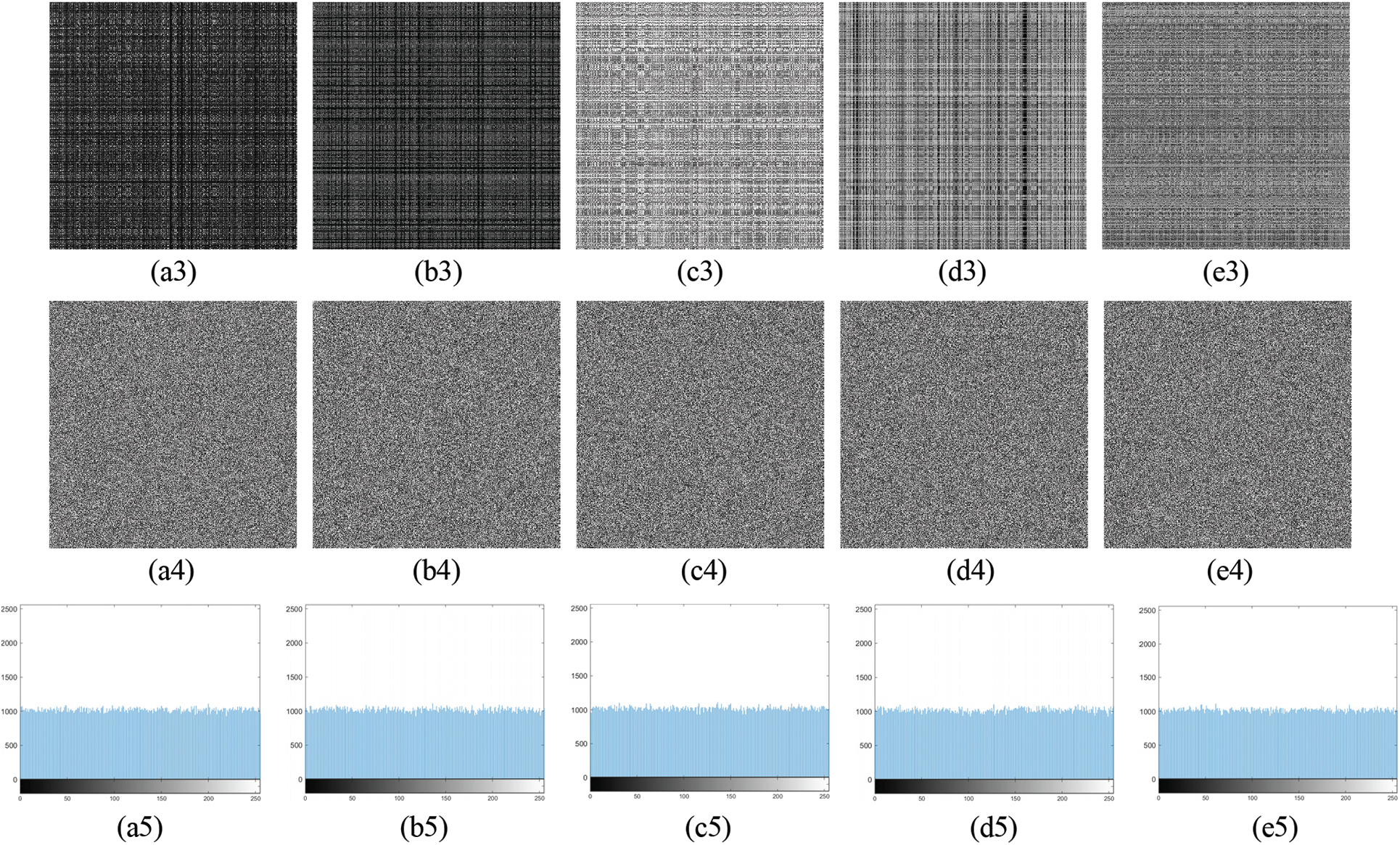
Figure 5: Simulation of proposed encryption scheme: (a1–a5) plain-images P, (b1–b5) histograms of P, (c1–c5) shuffled images S, (d1–d5) encrypted images C, and (e1–e5) histograms of C
where Pi represents the actual occurrence, and Ei denotes the expected pixel frequency of the i-th pixel value. If the chi-square test value of an image is less than 293.2478 (a standard value at a significance level of 0.05 [41]), then the image is likely to have a uniform pixel spread. Table 4 lists the calculated chi-square values of different plain images that mostly have associated pixels and encrypted images that have randomly distributed pixels. The average of the chi-square test value over the plain images is 918258.7. This high score indicates the pixels in the images are highly dispersed in a non-uniform fashion, which can provide some clue about the information content of the attacker. Where the average chi-square test value computed over the listed encrypted images is 249.5. The score of 249.5 is near the expected value presented in [41] and very far from the average obtained for the plain images. The obtained score for the proposed encryption method is found to be comparable to the chi-square reported in [40]. It is inferred from the chi-square test results that the encrypted image pixel intensities are uniformly distributed. This analysis verifies that the proposed encryption method can substantially withstand statistical attacks.
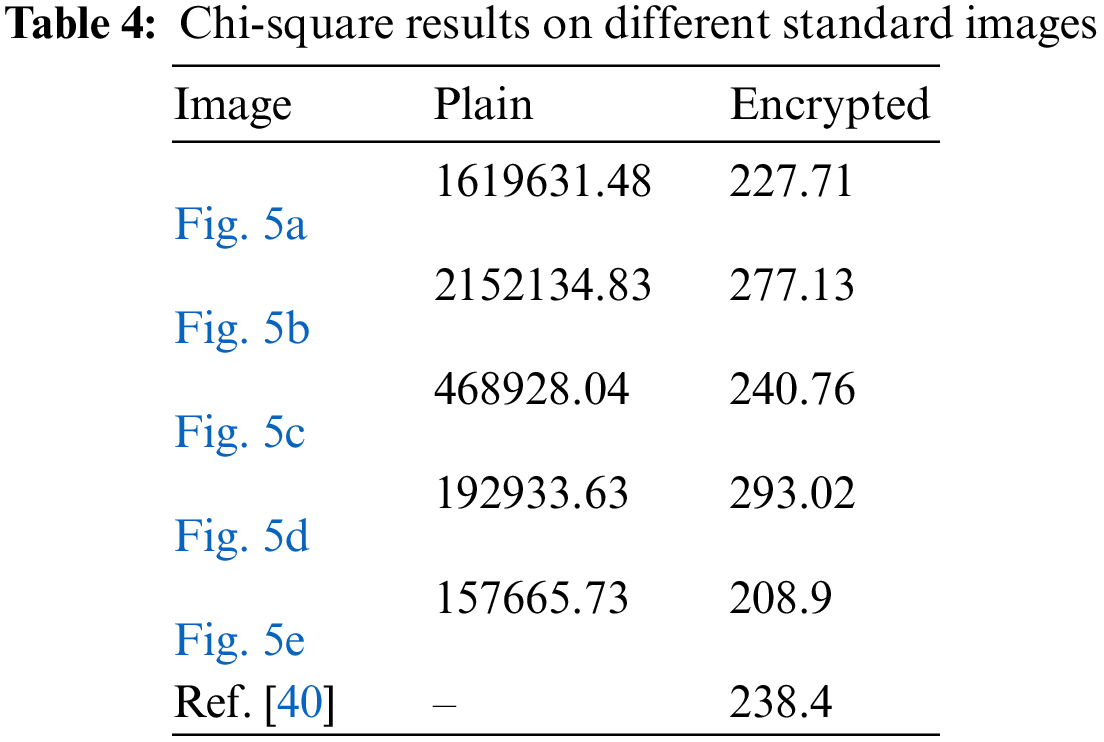
The image pixels usually retain high correspondence with their adjoining pixels. This interdependence of pixels expedites cryptanalysis. Therefore, a good cipher is required to reduce or even remove the correlation between pixels in order to prevent any statistical analysis. The dissimilarity or likeness of image pixels with their adjacent pixels is computed using a correlation coefficient [42]. Very low values of the correlation coefficient (near zero) for an image suggest the least similarity among its pixels. Therefore, the image is considered robust for transmission over an unreliable channel. The correlation coefficient γ is defined as:
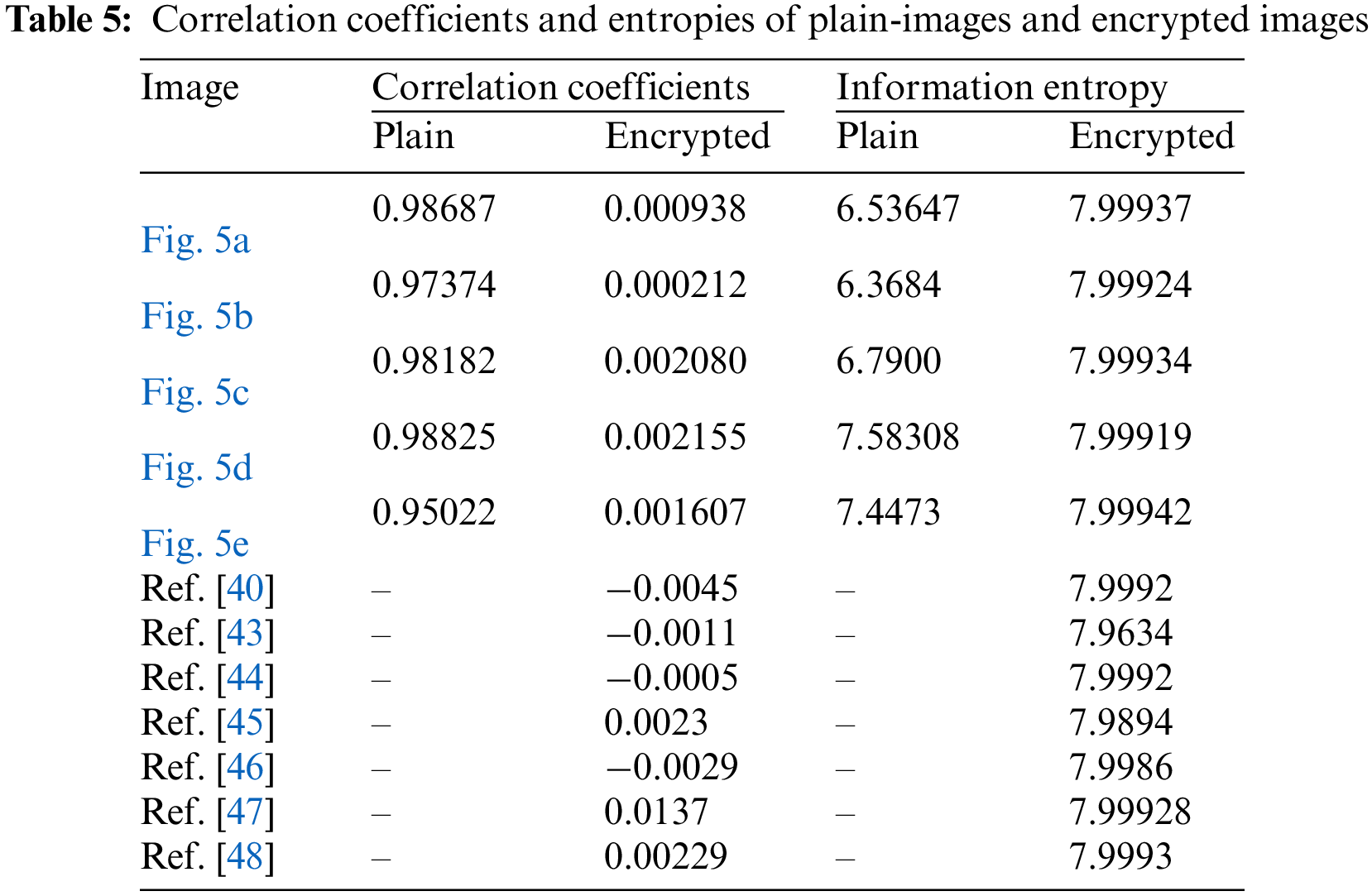
where i and j signify the position of row and column values in an image under observation. The factors μ and σ denote the variance and the standard deviation, respectively. The correlation is computed using Eq. (3) and presented in Table 5. The correlation scores clearly illustrate that the correlation are fairly near 1.0, implying a strong correlation between their neighbouring pixels. However, the ciphertext images exhibit weak correlation, as the correlation coefficients are near zero. The visual analyses of the correlation among adjacent pixels of images have been performed, and the results obtained are shown in Fig. 6. The figure signifies the correlation of pixels in plain images and encrypted images. We can observe that the pixels in plain-images are closely correlated to their neighbouring pixels because the adjacent pixel is confined close to its neighbouring pixels. But, there is no such correlation or confinement visible in the second row of the figure, which is for encrypted images. In encrypted images, the pixel values are uniformly distributed and cover the whole available space. Table 5 shows that the adjacent pixels in encrypted images obtained from the proposed method are more uncorrelated compared to the scores reported in [40,43–48]. It can be inferred that the low correlation of pixels in encrypted images will prevent attackers from obtaining meaningful information via any statistical attacks. So, we can say that the proposed encryption algorithm protects strongly against any statistical analysis.
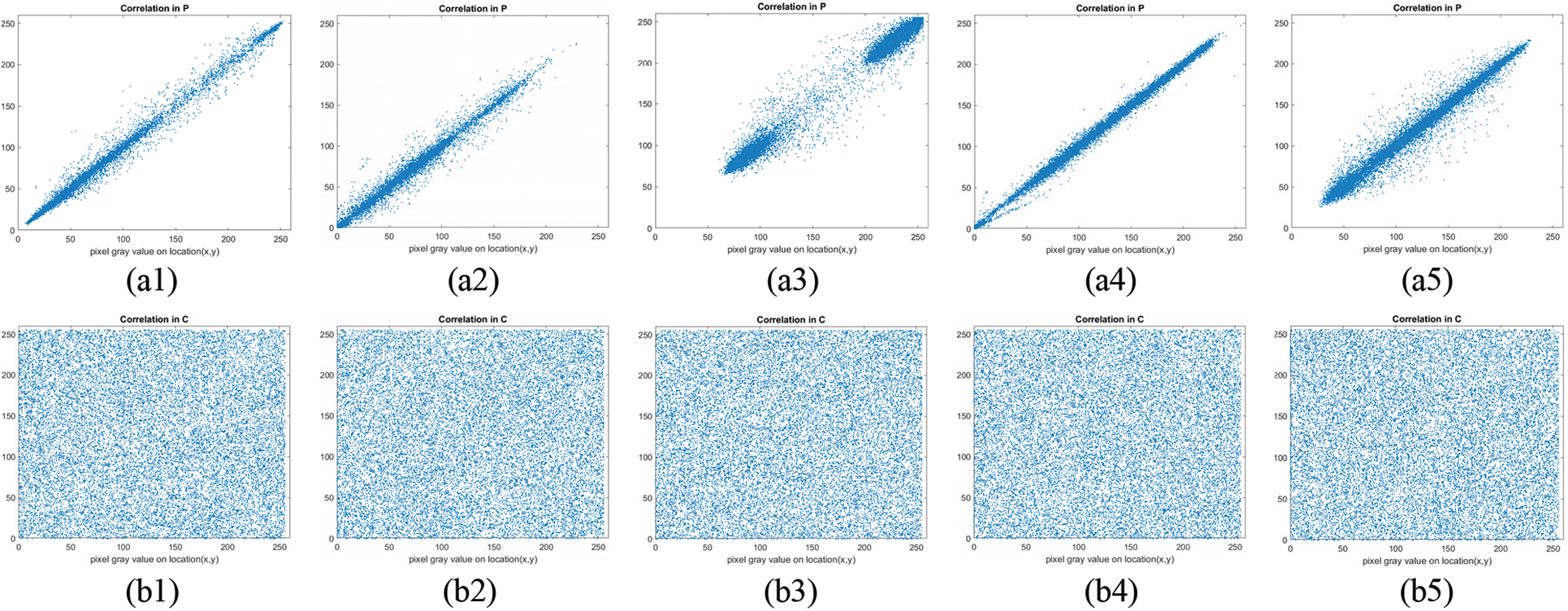
Figure 6: Simulation of correlation among adjacent pixels of (a1–a5) plain-images P, and (b1–b5) encrypted images C
In information theory, the entropy of a variable is the quantity of uncertainty of information [47]. It typically reflects the randomness and unpredictability of test information. It is normally measured in bits and mathematically defined as:
where p(xi) is the probability of the message source xi. If the information entropy value for an encrypted image is high, then it suggests a uniform spread of pixels’ intensities, thereby strengthening image security. In contemporary, if it is lower than 8, then there is a high chance of envisaging the image, hence intimidating the image’s security. The information entropy scores for the selected test images are determined, and the results are offered in Table 5. The entropies of plain images are considerably away from their ideal value. However, the encrypted images have entropy values greater than 7.999. This entails that each pixel’s intensity is equally probable in the encrypted content. Moreover, the obtained entropy score for the proposed scheme is better than a few of the encryption schemes investigated in [43,45,46] and comparable to other schemes mentioned in Table 5. So, the proposed image protection scheme is strong enough to add enough information and randomness to the encrypted content so that it can withstand attempts made to steal sensitive plain-image information that is based on entropy.
6.4 Differential Attack Analysis
The primary goal of the cryptanalyst is to gain partial or full access to the contents of the secret data, which the sender legitimately encrypts for its intended recipient before its transmission over the network [44]. During normal practice, the attacker tries to obtain information about the original unencrypted (plain-image) data by making changes to plain images, encrypting them, and comparing the output with a list of encrypted images. This approach of attackers can be avoided by employing a strategy in which the encryption process is entirely dependent on plain images. This method will ensure that exclusively different encrypted data will be obtained from the encryption process even when a plain image is minutely changed. We have offered an image encryption method that incorporates the method of having high sensitivity to change in plain images so as to thwart differential cryptanalysis attempts. In order to assess these, we selected two performance metrics, namely the number of pixels change rate (NPCR) and the unified average changing intensity (UACI). The NPCR metric quantifies the pace of altered pixels in the encrypted data that get changed when a minor alteration is made in the plain-text data. While the UACI metric measures the average of the difference in intensities between plain-text and encrypted images. The two metrics are computed by following a process. First, we selected two plain images, P1 and P2, which are only different by one pixel. Second, the encrypted images for these images are computed and named C1 and C2. The metrics are then mathematically defined as:
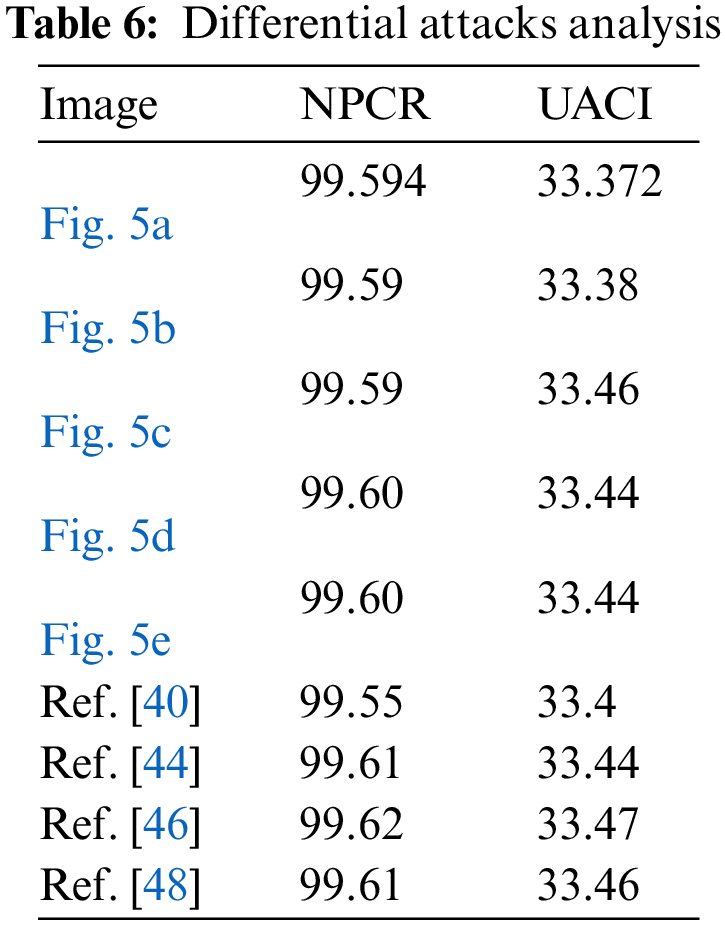
where D(i,j) is 1 if C1(i,j) ≠ C2(i,j) else it is 0, and M × N is the size of the plain-image. The experimental results of this differential attack analysis through the computation of NPCR and UACI parameters for the selected five plain-images are presented in Table 6. It is evident that the minute change in the plain-image has an extreme effect on the encrypted content. The scores of NPCR and UACI provided in Table 6 are about 99.6 and 33.33, respectively. Differential analysis is one of the crucial tests to assess the robustness against differential attacks by attackers. The obtained scores demonstrate that the projected image protection approach is robust enough to resist differential attacks and offers great sensitivity to even small changes in the plain-image data.
To fulfill standards with today’s high-speed communication technologies, an encryption algorithm should spawn encrypted data at a swift pace. Therefore, an efficient image encryption algorithm is considered effective for real-world applications. In the proposed image encryption scheme, we have taken into account the time complexity of the encryption process. The encryption time taken by our scheme is around 1.402 s for encrypting a 512 × 512 image, which offers a throughput of 1495 Kbps. The short encryption time and high throughput indicate that the proposed encryption scheme is suitable for real-time applications to realize security. We make a comparative study by listing the encryption time incurred by some existing encryption schemes in Table 7. The comparison made in Table 7 shows that our encryption has a fairly shorter time, hence faster and greater throughput, compared to some existing encryption schemes investigated in Refs. [47–51] except Ref. [52], wherein selective encryption of only the facial portion within the image is performed.
In contrast, our proposed method performs full encryption of the images. Hence, the proposed encryption scheme can encrypt the images quickly with better throughput compared to many recently investigated schemes.
This paper described a security scheme for the protection and secure transmission of healthcare image data originating in the Internet of Medical Things network. The proposed encryption scheme is simple, effective, robust, and faster, which makes it suitable for securing healthcare data in IoMT environments. The proposed scheme explores the features of the newly developed 2D discrete chaotic map, which has better dynamics than existing 2D Henon and SLMM maps and optimizes highly nonlinear S-boxes that are spawned with the new chaotic map. The optimized S-box also has greater and stronger security strength compared to many recently investigated S-boxes. Several experimental and standard simulation analyses have been conducted to assess the recital of the suggested image protection scheme. The performance and comparative results validate the consistency and better performance of the new encryption scheme. The proposed scheme has been found suitable for encrypting the healthcare imagery generated in IoMT networks. For future work, we intend to use multiple stages for securing medical data in healthcare applications. Also, artificial intelligence tools may be incorporated to secure medical information in big data medical applications.
Acknowledgement: The authors would like to acknowledge the support received from the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University, through the Research Funding Program, Grant No. (FRP-1443-11).
Funding Statement: This research was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University, through the Research Funding Program, Grant No. (FRP-1443-11).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. A. Wani and R. Khaliq, “SDN-based intrusion detection system for IoT using deep learning classifier (IDSIoT-SDL),” CAAI Transactions on Intelligence Technology, vol. 6, no. 3, pp. 281–290, 2021. [Google Scholar]
2. S. Das and S. Namasudra, “MACPABE: Multi-authority-based CP-ABE with efficient attribute revocation for IoT-enabled healthcare infrastructure,” International Journal of Network Management, vol. 2, no. 1, pp. 1–15, 2022. [Google Scholar]
3. A. Gutub, “Boosting image watermarking authenticity spreading secrecy from counting-based secret-sharing,” CAAI Transactions on Intelligence Technology, vol. 4, no. 2, pp. 1–13, 2022. [Google Scholar]
4. Z. Chen, “Research on internet security situation awareness prediction technology based on improved RBF neural network algorithm,” Journal of Computational and Cognitive Engineering, vol. 3, no. 2, pp. 1–16, 2022. [Google Scholar]
5. R. Verma, A. Kumari, A. Anand and V. S. S. Yadavalli, “Revisiting shift cipher technique for amplified data security,” Journal of Computational and Cognitive Engineering, 2022. https://doi.org/10.47852/bonviewJCCE2202261 [Google Scholar] [CrossRef]
6. S. Das and S. Namasudra, “Multi-authority CP-ABE-based access control model for IoT-enabled healthcare infrastructure,” IEEE Transactions on Industrial Informatics, 2022. https://doi.org/10.1109/TII.2022.3167842 [Google Scholar] [CrossRef]
7. A. Alarifi, S. Sankar, T. Altameem, K. Jithin, M. Amoon et al., “A novel hybrid cryptosystem for secure streaming of high efficiency H.265 compressed videos in IoT multimedia applications,” IEEE Access,vol. 8, pp. 128548–128573, 2020. [Google Scholar]
8. W. El-Shafai, M. Aly, A. Algarni, F. Abd El-Samie and N. Soliman, “Secure and robust optical multi-stage medical image cryptosystem,” Computers, Materials & Continua, vol. 70, no. 1, pp. 895–913, 2022. [Google Scholar]
9. R. Hamza, Z. Yan, K. Muhammad, P. Bellavista and F. Titouna, “A privacy-preserving cryptosystem for IoT E-healthcare,” Information Sciences, vol. 52, no. 7, pp. 493–510, 2020. [Google Scholar]
10. J. Sheikh, S. Akhter, S. Parah and G. Bhat, “Blind digital speech watermarking using filter bank multicarrier modulation for 5G and IoT driven networks,” International Journal of Speech Technology, vol. 21, no. 3, pp. 715–722, 2018. [Google Scholar]
11. W. Feng, Y. He, H. Li and C. Li, “A plain-image-related chaotic image encryption algorithm based on DNA sequence operation and discrete logarithm,” IEEE Access, vol. 7, pp. 181589–181609, 2019. [Google Scholar]
12. A. Toktas, U. Erkan, F. Toktas and Z. Yetgin, “Chaotic map optimization for image encryption using triple objective differential evolution algorithm,” IEEE Access, vol. 9, pp. 127814–127832, 2021. [Google Scholar]
13. X. Wu, H. Kan and J. Kurths, “A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps,” Applied Soft Computing, vol. 3, no. 7, pp. 24–39, 2015. [Google Scholar]
14. F. Musanna and S. Kumar, “A novel image encryption algorithm using chaotic compressive sensing and nonlinear exponential function,” Journal of Information Security and Applications, vol. 5, no. 4, pp. 102–125, 2020. [Google Scholar]
15. L. Zhu, D. Jiang, J. Ni, X. Wang, X. Rong et al., “A stable meaningful image encryption scheme using the newly-designed 2D discrete fractional-order chaotic map and Bayesian compressive sensing,” Signal Processing, vol. 19, no. 5, pp. 108–119, 2022. [Google Scholar]
16. P. Naskar, S. Bhattacharyya, D. Nandy and A. Chaudhuri, “A robust image encryption scheme using chaotic tent map and cellular automata,” Nonlinear Dynamics, vol. 100, no. 3, pp. 2877–2898, 2020. [Google Scholar]
17. J. Zheng, Z. Luo and Q. Zeng, “An efficient image encryption algorithm based on multi chaotic system and random DAN coding,” Multimedia Tools and Applications, vol. 79, no. 39, pp. 29901–29921, 2020. [Google Scholar]
18. D. Trujillo-Toledo, O. López-Bonilla, E. García-Guerrero and E. Inzunza-González, “Real-time RGB image encryption for IoT applications using enhanced sequences from chaotic maps,” Chaos, Solitons & Fractals, vol. 15, no. 3, pp. 111–119, 2021. [Google Scholar]
19. C. Pak, K. An, P. Jang, J. Kim and S. Kim, “A novel bit-level color image encryption using improved 1D chaotic map,” Multimedia Tools and Applications, vol. 7, no. 8, pp. 12027–12042, 2019. [Google Scholar]
20. H. Li, Y. Wang and Z. Zuo, “Chaos-based image encryption algorithm with orbit perturbation and dynamic state variable selection mechanisms,” Optical Lasers and Engineering, vol. 11, no. 5, pp. 197–207, 2019. [Google Scholar]
21. J. Teh, M. Alawida and Y. Sii, “Implementation and practical problems of chaos-based cryptography revisited,” Journal of Information Security and Applications, vol. 50, no. 9, pp. 102–124, 2020. [Google Scholar]
22. L. Kocarev and S. Lian, “Chaos-based cryptography: Theory, algorithms and applications,” Science & Business Media, vol. 35, no. 6, pp. 102–117, 2011. [Google Scholar]
23. Z. Hua and Y. Zhou, “Exponential chaotic model for generating robust chaos,” IEEE Transactions on Systems, vol. 51, no. 6, pp. 3713–3724, 2021. [Google Scholar]
24. M. Ahmad, E. Al-Solami, A. Alghamdi and M. Yousaf, “Bijective S-boxes method using improved chaotic map-based heuristic search and algebraic group structures,” IEEE Access, vol. 8, pp. 110397–110411, 2020. [Google Scholar]
25. Z. Hua, B. Zhou and Y. Zhou, “Sine chaotification model for enhancing chaos and its hardware implementation,” IEEE Transactions on Industrial Electronics, vol. 66, no. 2, pp. 1273–1284, 2018. [Google Scholar]
26. M. Alawida, A. Samsudin, J. S. Teh and R. S. Alkhawaldeh, “A new hybrid digital chaotic system with applications in image encryption,” Signal Processing, vol. 160, no. 3, pp. 45–58, 2019. [Google Scholar]
27. J. Gallas, “Structure of the parameter space of the Hénon map,” Physical Review Letters, vol. 70, no. 3, pp. 2714–2717, 1993. [Google Scholar] [PubMed]
28. Z. Hua, Y. Zhou, C. Pun and C. Chen, “2D sine logistic modulation map for image encryption,” Information Sciences, vol. 29, no. 7, pp. 80–94, 2015. [Google Scholar]
29. S. Pincus, “Approximate entropy as a measure of system complexity,” Sciences of the United States of America, vol. 8, no. 18, pp. 2297–2301, 1991. [Google Scholar]
30. Y. Wang, P. Lei and K. Wong, “A method for constructing bijective S-box with high nonlinearity based on chaos and optimization,” International Journal of Bifurcation and Chaos, vol. 25, no. 10, pp. 155–169, 2015. [Google Scholar]
31. M. Ahmad, H. Haleem and P. Khan, “A new chaotic substitution box design for block ciphers,” in Proc. of IEEE Int. Conf. on Signal Processing and Integrated Networks (SPIN), Noida, India, pp. 255–258, 2014. [Google Scholar]
32. M. Ahmad and M. Malik, “Design of chaotic neural network based method for cryptographic substitution box,” in Proc. of IEEE Int. Conf. on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, pp. 864–868, 2016. [Google Scholar]
33. P. Zhou, J. Du, K. Zhou and S. Wei, “2D mixed pseudo-random coupling PS map lattice and its application in S-box generation,” Nonlinear Dynamics, vol. 103, no. 10, pp. 1151–1166, 2021. [Google Scholar]
34. M. Açikkapi and F. Özkaynak, “A method to determine the most suitable initial conditions of chaotic map in statistical randomness applications,” IEEE Access, vol. 9, pp. 1482–1494, 2020. [Google Scholar]
35. U. Çavuşoğlu and A. Kökçam, “A new approach to design S-box generation algorithm based on genetic algorithm,” International Journal of Bio-Inspired Computation, vol. 17, no. 1, pp. 52–62, 2021. [Google Scholar]
36. H. Alhadawi, M. Majid, D. Lambić and M. Ahmad, “A novel method of S-box design based on discrete chaotic maps and cuckoo search algorithm,” Multimedia Tools and Applications, vol. 80, no. 5, pp. 7333–7350, 2021. [Google Scholar]
37. F. Artuğer and F. Özkaynak, “An effective method to improve nonlinearity value of substitution boxes based on random selection,” Information Sciences, vol. 57, no. 6, pp. 577–588, 2021. [Google Scholar]
38. K. Zamli, “Optimizing S-box generation based on the adaptive agent heroes and cowards algorithm,” Expert Systems with Applications, vol. 18, no. 2, pp. 115–209, 2021. [Google Scholar]
39. T. Zhang, C. Chen, L. Chen, X. Xu and B. Hu, “Design of highly nonlinear substitution boxes based on I-Ching operators,” IEEE Transactions on Cybernetics, vol. 48, no. 12, pp. 3349–3358, 2018. [Google Scholar] [PubMed]
40. Y. Zhang, J. Hao and X. Wang, “An efficient image encryption scheme based on S-boxes and fractional-order differential logistic map,” IEEE Access, vol. 8, pp. 54175–54188, 2020. [Google Scholar]
41. X. Wang, P. Li, Y. Zhang, L. Liu and X. Wang, “A novel color image encryption scheme using DNA permutation based on the Lorenz system,” Multimedia Tools and Applications, vol. 77, no. 5, pp. 6243–6265, 2018. [Google Scholar]
42. S. Gao, R. Wu, X. Wang, J. Wang, Q. Li et al., “A 3D model encryption scheme based on a cascaded chaotic system,” Signal Processing, vol. 202, no. 1, pp. 728–745, 2023. [Google Scholar]
43. L. Liu, S. Miao, H. Hu and M. Cheng, “N-phase logistic chaotic sequence and its application for image encryption,” IET Signal Processing, vol. 10, no. 3, pp. 1096–1104, 2016. [Google Scholar]
44. M. Wang, X. Wang, T. Zhao, C. Zhang and N. Yao, “Spatiotemporal chaos in improved cross coupled map lattice and its application in a bit-level image encryption scheme,” Information Sciences, vol. 5, no. 4, pp. 1–24, 2020. [Google Scholar]
45. X. Li, D. Xiao, H. Mou, D. Lu and M. Peng, “Compressive sensing based image encryption and compression algorithm with identity authentication and blind signcryption,” IEEE Access, vol. 8, pp. 211676–211690, 2020. [Google Scholar]
46. Z. Gan, X. Chai, J. Zhang, Y. Zhang and Y. Chen, “An effective image compression-encryption scheme based on compressive sensing (CS) and game of life (GOL),” Neural Computing and Applications, vol. 32, no. 17, pp. 14113–14141, 2020. [Google Scholar]
47. X. Wang and D. Xu, “A novel image encryption scheme based on Brownian motion and PWLCM chaotic system,” Nonlinear Dynamics, vol. 75, no. 1, pp. 345–353, 2021. [Google Scholar]
48. X. Chai, Z. Gan, K. Yuan, Y. Lu and Y. Chen, “An image encryption scheme based on three-dimensional Brownian motion and chaotic system,” China Physics B, vol. 26, no. 2, pp. 99–113, 2017. [Google Scholar]
49. M. Samiullah, W. Aslam, H. Nazir, M. Lali and H. Afzal, “An image encryption scheme based on DNA computing and multiple chaotic systems,” IEEE Access, vol. 8, pp. 25650–25663, 2020. [Google Scholar]
50. Q. Lu, C. Zhu and X. Deng, “An efficient image encryption scheme based on the LSS chaotic map and single S-box,” IEEE Access, vol. 8, pp. 25664–25678, 2020. [Google Scholar]
51. X. Zhang, R. Guo, H. Chen, Z. Zhao and J. Wang, “Efficient image encryption scheme with synchronous substitution and diffusion based on double S-boxes,” China Physics B, vol. 27, no. 8, pp. 111–119, 2018. [Google Scholar]
52. S. Gao, R. Wu, X. Wang, J. Liu, Q. Li et al., “EFR-CSTP: Encryption for face recognition based on the chaos and semi-tensor product theory,” Information Sciences, vol. 621, no. 1, pp. 766–781, 2023. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF

 Downloads
Downloads
 Citation Tools
Citation Tools