Enhancement of Large Renewable Distributed Generation Penetration Levels at the Point of Common Coupling

Nomenclature

1  Introduction

All Loading capability and power reliability are some of the benefits of RDG integration to the power system, thereby permitting easy transferring of power to the grid. It is expected that power quality and voltage regulation should be adequately controlled and properly coordinated in such networks combining RDGs. A weak DN turns to active and smart network, the transformation occurs only by the connection of RDGs, incorporation of an automation system, communication, and information technology systems capable of monitoring power flows from points of generation to points of consumption. However, utility and Power System Operator’s (PSO) concern grow with the transformation of the RDG integration penetration levels and the challenges it brings to the system in respect of planning, safety, and control [1–3]. The power flows with DRGs connection are bidirectional unlike conventional with the unidirectional power flow, DRGs has altered the existing protection schemes, monitoring and method of control. DRGs integration to DN give a new approach to handle voltage rise regulation, distortion, voltage unbalance, and harmonics at the PCC without disconnection. These power quality issues are undeniably harmful to DNs, as evidenced by reduced cable life, deterioration of consumer electronics, and failure of variable speed drives [4]. Introduction of a robust control scheme at PCC, which can be existing in isolation to dampen the effects of voltage rise and distortion even when there are any grid disturbances, so that continuity of power supply would not be altered and would go a longer way. In such a situation, an algorithm-based decision should be considered to where reference signals would have been connected with the variabilities of the power quality criterion as established in the utility standard operation. Utility and Independent Power Producers (IPPs) experience lots of unbearable occurrences because of imbalance current from inductive loads, non-linear loads, unbalanced load and voltage rise at PCC. Overvoltage and reverse power flow at the point of interconnection is caused by the DG system supplying more real power than is required by the load, with the excess supplied back to the grid [5]. Power quality issue such as undervoltage, line losses, power factor correction etc., were being addressed in the past by the usage of capacitor banks [6,7]. Even at that, the occurrence of similar faults cannot be over-emphasised in power system because of the method in-effectiveness and also, some of the methods used cannot solved two or more power qualities problem at a time. For example, capacitor banks are used to solve power factor issue in the past, but it cannot solve voltage rise or distortions at PCC. Using palliative measure such as capacitor bank and passive filters to tackle some of these critical power quality challenges can result to more havoc than the initial condition [8,9]

It could be a bit difficult to compensate for voltage rise, unbalance voltage, harmonic, and power factor correction etc., with local means without the fore understanding of the design and load sequences involving the dynamic fluctuations in power system parameters at the PCC. Meanwhile, usage of active filtering circuitry was previously used [9], not because of the financial implication of the installation, but because of the extensive deployment of converters associated with RDGs integration to DN [10–12]. Power quality issues with renewable RDG systems are primarily caused by power electronic-based generation technologies rather than traditional synchronous generators, as well as the intermittent nature of RESs. The primary power quality concern is voltage and frequency fluctuations caused by uncontrollable inconsistency in renewable energy. The inconsistency of renewable energy behavior as a result of frequently changing weather characteristics causes voltage and frequency fluctuations at the grid of integration [13]. Modular multilevel converters were developed in response to the need for high-power converters with lower Harmonic distortion and higher efficiency. It was recommended to cut switching losses, strengthen output power quality, and distribute voltage evenly across switches [14]. FBMCs have emerged as attractive topologies for voltage applications, they offer scalable to high voltage without the need for series device connection, modular structure with internal fault management during operation and low semiconductor losses. Its modularity and functionality made it extremely adaptable to a wide range of applications. The converters produce a high-quality voltage waveform with a lower switching frequency, making them ideal for a variety of applications including high-power transmission in HVDC and renewable energy high-power motor drives such as railway traction motor drives and high-power accelerators. MMCs are now extensively used in both medium and high voltage transmission networks because they resolve most of those constraints of traditional VSCs, such as scalability to higher voltages through the addition of more levels, the requirement of smooth output voltage waveforms at a lower switching frequency, and the complete removal of low-order harmonics, which typically necessitate large filters [15,16]. The switching device blocking during a disturbance is appropriate to reduce any AC grid involvement in the DC fault current, which is one of the attractive characteristics of the device. Diverse features of the FBMCs have been researched, the basic operational principle, modulation and capacitor voltage balancing are presented in [17–19]. The authors in [20] implemented the application of a single reference per phase for sinusoidal pulse width modulation and staircase with the nearest voltage levels while fundamental switching frequency modulation and capacitor voltage balancing for multilevel converter is presented in [21]. The application of phase-shifted carrier pulse width modulation for multilevel converter, where each cell is controlled independently, including regulation of the cell capacitor voltages is considered in [22]. Hence, the assessment has not been made on the application capability of FBMC to mitigate distortion, unbalanced current and regulation of over voltage at the PCC. The RDGs integration gain attention because of their renewable sources, cleanness, flexibility, compliment to the energy supply by the utility, reduction in transmission losses, reduction in demand of energy from the utility companies and the resources is available and renewable on human time scale, etc. [23,24]. However, the power quality of these consumers needs to be reinforced for voltage rise, distortion, unbalanced current, extra consumption of reactive power and current harmonic at the PCC. This paper presents a method of regulating an over-voltage, unbalanced current and distortion at PCC with RDG Active Power Filter and Full Bridge Multi-Level Converter (FBMC) to safeguard power quality to the grid. The contribution of this research paper is as follows:

•   The development of a techniques to control the potential threat of unbalanced current, and distortion at the PCC.

•   The generation of positive reactive power during a worst-case scenario of a DN with RDG integration to control the phase angle and the reference point with FBMC.

•   The proposed method generates high-quality AC and DC side waveforms with near-zero harmonics and DC ripples, attenuates voltage rise and reverse power flow, regulates active and reactive power, allowing more RDG penetration levels to the grid without disconnection while maintaining the PCC's standard power quality requirement.

2  Conventional Electrical Circuit Analysis

Consider the 3-∅ network carrying three conductors, which are regarded to be unbalanced, non-sinusoidal system and the loads connected are characterized by the vector (j) [25]. The current consumed by the load is given by (jL), which can be defined by the Eq. (1). All the currents defined in Eq. (1) are at right angle to each other hence (orthogonal), the Root Mean Square (RMS) value is defined in Eq. (2). The receiving end power (A2) can be obtained in Eq. (3) by multiplying Eq. (2) with Point of Common Coupling (PCC) voltage (VPcc2). The power factor of the three phase loads at PCC can therefore be defined in Eq. (11). The characteristics of the current and power in the Eqs. (2) and (3) is defined in [26–27]. The RMS of the phase is defined as (X) in Eq. (13), by considering the voltage imbalance, harmonics, current distortion, voltage rise and phase shift between voltage and current at PCC, the power factor can be disintegrated to Eqs. (14) to (16). Merely analysing the Eqs. (12), (14) to (16), Eq. (17) also define PCC power factor. By accessing the impacts of unbalance voltage, current distortion, harmonics and voltage equations in (14) to (17) within the power factor as analysed in [9,27] hence, Eqs. (14) to (16) are identified as a load conformity factor. In a non-sinusoidal and unbalanced system parameter, there is a need to differentiate what actually need to be compensated. Therefore, the outcome should depend on the recognition of the current components and voltage rise that causes the deterioration of the power quality at the PCC or the network as a whole in order to suppress the voltage unbalance, harmonic, voltage rise and distortion current.

The voltage and the current should be regarded as unbalanced/distorted if a compensation is to be designed. Therefore, the connected converter’s reference signal at PCC can be obtained from Eq. (17) and the compensation should be considered for all the components of the current with respect to the load connected as expressed in Eq. (18). Based on the Eq. (18), each of the components or group is associated with the aim of the compensation, which means that the compensation strategy can be drawn. When RDGs are integrated into a distribution network, it is expected that energy is transported into the network, that is the aim. Therefore, there should be a way of generating a reference signal that will give way for power (PRDG) produce by the RDG. The aim can be defined in Eq. (19). The conductance (GRDG) can be obtained as a balanced conductance (Gb) related to research work in [26,27] and for the system to produce a large power factor in the Eq. (20). The Eq. (20) indicates the strength of RDG to produce energy, which can be dimensioned through the conductance as expressed in Eq. (21). The wave produces by the current that injected to the system is usually generated from the reference voltage (Vref) and the waveform can be in difference format. The Eqs. (18) and (19) permit the active power absorb by the network, also give room for the recognition of the current/voltage components and the compensation to suppress power quality issues that may occur. Therefore, the current produces by the converter/inverter to the network can be described in Eq. (22) and the vector produces due to current is expressed in Eq. (23). The Eq. (23) shows that the result of the aim selected may not be the same under certain voltage condition. Hence, the peculiarity of the approach offered can be defined through the conventional electrical circuit analysis to obtain current and power terms. The conventional electrical circuit analysis offers advantages such that all the electrical characteristics linked to the load are dissociated by the orthogonal disintegration of the current, generated power and the power factor in (abc) coordinates in Eqs. (1), (6) and (17).

The primary aim of compensation for power quality challenges at the PCC is to ascertain that the power quality absorbs or generated into the system is within an acceptable range establish by the utility or to international standard. Then the target aim is accomplished if some of the distortions at PCC are suppressed, unbalanced voltage made balanced, voltage rise mitigated, and harmonic reduced by the compensation strategy as compared to the initial state before the compensation. The fundamental rule of compensation can be expressed in Eq. (24), in this Eq. (24), the subscript (x) signified unwanted current components such as unbalance voltage, voltage rise and distortion current while the maximum value for this unwanted current or voltage that can move round the system without going against the set value by the utility or international standard in respect of power quality is represented by the superscript (max). In comparison to factors, (x) denotes unwanted signals that is to say, it is a conformity factor while the superscript (max) denotes the peak range allow for certain power quality requirements. Based on the Eq. (24), the amount of conformity factor generated is the same impact as compensation of the unwanted signals. Hence, the outcome of the compensation should result to waveform improvement and reduce to a minimum the power quality issues at the PCC. The state at which (μxmax) can be calculated is that the compensation current is produced due to the compensation constant to consider the reference signal related to the chaos generated by the connected loads as expressed in Eq. (25). The scaling coefficient that can be traced to the mitigation of the unwanted signal are (kr,kv and ku) therefore, the remaining unwanted signal that attenuated (residual) that are still moving round the network can be expressed in Eq. (26). The Eq. (27) is obtained based on the assumption in Eq. (26), the peak current passing across the network that meet up with the set standard and range of power quality specifications including the power produced by RDGs.

The vector to balance the active current in the network is regarded as (jGab) and it can be obtained in Eq. (30) where the sign (±) shows that RDGs can generate and absorb the active power at PCC. The later probability satisfies battery banks are provided for the converter/inverter connected to PCC. The Eq. (29) shows that the main purpose of the compensation is to ensure that (jGrbres,jures and jGbres) generate values that can do away with possible penalty resulting from unwanted signals. Therefore, by making use of the Eqs. (14) to (16) and (29), the conformity factors of the peak current passing across the network can be calculated in Eqs. (32), (34) and (36). These equations show the important and satisfactory reasons to attain peak value for unwanted signals factors on the grid side such that the absorption of the unwanted signal in Eq. (25) is accessed based on the approximation of (kr,kv and kv). The reason to ascertain that power quality components satisfy the specified limit as stipulated by the utility or international standard is that (μGDmax,μGQmax and μGUmax) are defined as pre-set reference value as yardstick to obtain (kr,kv and kv). Eqs. (17), (32), (34) and (36) show that if values are set for (μGDmax,μGQmax and μGUmax), then the lower power factor in the system can be ensured as expressed in Eq. (37). The Eq. (36) can be rearranged to obtain the scaling factor from Eqs. (38) to (40) while Eqs. (41) to (43) produced conformity factor with respect to the compensation. Kirchhoff’s law can be used to obtain the conformity factors in the Eqs. (41) to (43) depending on the current through the converter and the load connected.

The reference signal signs would be convenient to obtain compensation in Eq. (44) haven got the pre-set values through Eqs. (25), (32), (34), (36), and (41)–(43). The power quality parameters will definitely remain within an acceptable range set by the unity and international standard. The expression in Eq. (45) can be referred to as a scaling factor. It is pertinent to know that if this Eq. (45) is equal to zero, then the maximum compensation can be achieved. However, if the Eq. (45) is equal to unity as expressed in Eq. (46), then it means that there is no application of compensation of the system. In a situation where there is no occurrence of power quality challenges in the network, that is to say that the system power factor is unity, hence, then the conformity factor in the equations in (32), (34) and (36) would be equal to zero.

jL=jLab+jLrb+jLu+jLv(1)

IL2=ILab2+ILrb2+ILu2+ILv2(2)

A2=VPcc2(ILab2+ILrb2+ILu2+ILv2)(3)

A2=VPcc2×ILab2+VPcc2×ILrb2+VPcc2×ILu2+VPcc2×ILv2(4)

=VPcc2ILab2+VPcc2ILrb2+VPcc2ILu2+VPcc2ILv2(5)

=P2+Q2+U2+D2(6)

P=VPccILab(7)

Q=VPccILrb(8)

U=VPccILu(9)

D=VPccILv(10)

μL=PP2+Q2+U2+D2(11)

μL=ILabILab2+ILrb2+ILu2+ILv2(12)

X=Xa2+Xb2+Xc2(13)

μLD=DP2+Q2+U2+D2=ILvILab2+ILrb2+ILu2+ILv2(14)

μLU=UP2+Q2+U2+D2=ILuILab2+ILrb2+ILu2(15)

μLQ=QP2+Q2+U2+D2=ILrbILab2+ILrb2(16)

μL=(1−μLQ2)(1−μLU2)(1−μLD2)(17)

jC=jLrb+jLu+jLv=jL−jLab(18)

jRDG=GRDGVref(19)

GRDG=PRDGVPcc2(20)

GRDG=Gb=PRDG=GbVPcc2=P(21)

jI2G=jRDG+jC(22)

jG=jL−jI2G=jL−(jRDG+jC)(23)

jx=0↔λx=0→jx=jxmax↔μx=μxmax(24)

jC=(jLrb−KrjLrb)+(jLu−KLujLu)+(jLv−KLvjLv)(25)

jGres=jLrb+jLu+jLv−jC(26)

jGres=KrjLrb+KujLu+KvjLv(27)

jGmax=jLab±jRDG+KrjLrb+KujLu+KvjLv(28)

jGmax=jGab+jGrbres+jGures+jGbres(29)

jGab=jLab±jRDG(30)

μGDmax=IGDresIGab2+IGrb(res)2+IGures2+IGvres2(31)

μGDmax=KvILvIGab2+IGrb(res)2+IGures2+(KvILv)2(32)

μGUmax=IGUresIGab2+IGrb(res)2+IGures2(33)

μGUmax=KuILuIGab2+IGrb(res)2+(KuILu)2(34)

μGQmax=IGrb(res)IGab2+IGrb(res)2(35)

μGQmax=KrILrIGab2+(KrILr)2(36)

μGmini=(1−μGQmax2)(1−μGUmax2)(1−μGDmax2)(37)

kv=μGDmaxμD=1−μD2(1−(μGDmax)2≅μGDmax1μD2−1(38)

ku=μGUmaxμU=1−μU2(1−(μGUmax)2≅μGUmax1μU2−1(39)

kr=μGQmaxμD=1−μQ2(1−(μGQmax)2≅λGQmax1μQ2−1(40)

μD=ILvIGab2+IGrb(res)2+IGu(res)2+(ILv)2(41)

μU=ILuIGab2+IGrb(res)2+(ILu)2(42)

μQ=ILrbIGab2+(ILrb)2(43)

jC=(1−Kr)jLrb+(1−Ku)jLv+(1−Kv)jLv(44)

Kr=Kv=Ku=0(45)

Kr=Kv=Ku=1(46)

3  PCC Over-Voltage Concept

The occurrence of over voltage at PCC creates an undue restriction to the integration of a large RDG to the power system. The current flowing across an electrical grid through resistance is directly proportional to the voltage at the PCC (Ohm’s law), such that the voltage increases with current or resistance. For AC system, the impedance is made of inductance, resistance, and capacitance, when these components are altered, the network power quality, voltage and current thereby improves or reduces. However, the reduction in the voltage due to the line impedance, the consumer loads connected to the system, the current that flows across and the sending end voltage determine the amount of receiving end voltage at the far end of the network. The network voltage drop must be greater than the smallest voltage at the peak hour while the highest voltage at the consumption of light load should be lesser than the voltage drops at the transmission lines [11,28]. Because of the over voltage at PCC, regulation of voltage is vital as primary indices to the integration of RDG to the power system. Figs. 1 and 2 show the conventional circuit, RDG connection and voltage drop analysis in a distribution network. The current, which is a function of load, where a distribution system consisting of two buses and RDG is connected. (Va) is the Voltage from the Substation, (Vb) is the Voltage at the load, (Rab) is the Resistance of the Line, (Xab) is Reactance of the Line, (I) is the Current, (Pab) is the Active Power Flowing through the Line, (Qab) is the Reactive Power Flowing through the Line, (Pload) is the Real Power Demand of the Load, (Qload) is the Reactive Power Demand of the Load, and the (S) is the Apparent Power. The apparent power is therefore defined in Eq. (47), while the Eq. (48) defined the load voltage and current in Eq. (49), respectively. The transmission power flowPab and Qab are equal to the load power demand Pload and Qload, when there is no RDG connected to the system. (Pab,Qab) = (Pload, Qload)/unit, when no RDG is connected. The current I in Fig. 1 is the line current, (Va) is the voltage in bus (a) and (Vb) is the voltage in bus (b). Thus, the voltage drops between nodes (a) and (b) is deduced in (51). The reduction in voltage drop across the transmission line can be obtained in Eq. (51), by evaluating Eqs. (49) into (50), Eq. (52) is obtained.

Figure 1: Equivalent circuit of distribution system and the phasor diagram

Figure 2: Flows of power in the distribution grid feeder with RDG

Transmissions are made of inductance (X), resistance (R), capacitance (C) and conductance (G). The construction of the transmission line, cross section area, materials of the conductor and the distance between the conductor and the insulator depend on the value of these parameters. In a distribution network, conductors transmit power at lower voltages. The distance between the wires are narrower than the transmission line. This leads to a lower magnetic energy, thereby its inductance per unit length will be lower [13,29]. Similarly, the distance between the wires are made higher in transmission line and lead to higher magnetic energy storage, thereby the inductance per unit length is higher. Since R/X ratio is high in transmission and lower in distribution while R/X ratio is high in distribution, Relatively high R/X ratios in distribution networks affect also the ability of compensators to regulate voltage at PCC [30], therefore the change in the voltage (Va−Vb) can be approximated. The injection of power into the system by the RDGs will result in Eq. (53). Where (PDG) is the Active power injected by the RDG, (QDG) is the Reactive power injected by the RDG. When RDG’s active power increases, (Pload−PDG) results into negative and (Va) will be less than (Vb), PDG≫Pload then Va<Vb. It can be deduced from the Eq. (56) that the active power of the RDG is directly proportional to the voltage rise while Eq. (57) shows that voltage rise at PCC depends on the resistance R of the distribution line and the power injected by the RDG. If the reactive power supply from the RDG is zero or at unit power factor. Where (R) and (X) are the line resistance and reactance. (PDG), and (QDG) are active and reactive power output from RDG. (ΔVpcc) is the change in voltage at PCC. Therefore, a large amount of RDGs both in capacities and numbers can be integrated into the distribution network if voltage rise challenges can be suppressed or mitigated. If RDG produces more active and reactive powers than the load, P(PRDG−Pload) and P(QRDG−Qload) become positive in (54) then the voltage difference will be positive. From (54), the voltage swell/rise (Va−Vb) produced by the RDG is reconstructed in term of equivalent supply impedance (Z=R2+X2) and R/X ratio to obtained Eq. (58). The expression of Eq. (58) in the term of short circuit fault level in MVA (KVAsc or MVAsc) and grid nominal voltage (VO) by assumption Vb ≈ VO. Substituting the supply impedance with fault level and obtained Eq. (59).

S=Pload−jQload(47)

Vload=Vb=SI=Pload−jQloadI(48)

SVb=Pload−jQloadVb(49)

ΔV=Va−Vb(50)

Va−Vb=I(Rab+jXab)(51)

Va−Vb=(Rab+jXab)Pload−jQloadVb=(RabPload−jRabQload+jXabPload−jXabjQloadVb=(RabPload+XabQload−jRabQload+jXabPloadVb=(RabPload+XabQload)−j(RabQload−XabPload)Vb(52)

Va−Vb=(Pload−PRDG)Rab+(Qload±QRDG)XabVb=(RabPload+XabQload)Vb(53)

Va−Vb=(Pload−PRDG)Rab+(Qload±QRDG)XabVb(54)

Va−Vb=(Pload−PDG)Rab+(Qload±QDG)Xab(55)

PRDG αVb(56)

ΔVpcc=RPDG+XQDG(57)

(PRDGZ1+XR2+QRDGZ1+RX2)∗1Vb(58)

(z=VO2MVAsc)=Va−VbVO=(PRDG1+XR2+QRDG1+RX2)∗1MVAsc(59)

4  Reactive Power Concept in an Electrical Network

Consider a portion between (Va) and (Vb) consist of Resistance (R), inductance (X) of the equivalent circuit for a distribution network in Figs. 1 and 2 carrying a sinusoidal current. The orientation of the resistance is usually horizontal while reactance is vertical in the Impedance (Z) diagram. In the complex quantity orientation, the (Z) can be defined in Eq. (60). The voltage/current vector is depicted in Fig. 3 where voltage leads the current by the angle (Φ) and the system power is obtained in Eq. (61). By analogues, the reactive power can be obtained (63), plotting real and reactive power gives the power angle diagram in Fig. 3c and the vector sum of them when sinusoidal voltage/current are involved which defined the vector power (S) known as apparent power of the system. The apparent power is the product of the impedance as a complex quantity and the square of the current magnitude in the Eq. (65) while the real power is defined in Eq. (66). By following the same analogue thinking, the reactive power can be defined in Eq. (67). For the reactive power (Q) in Eq. (67) to agree with Eq. (67), (ϕ) in the Fig. 3b is taken as positive such that it must be defined as the positive angle by the voltage leads the current as defined in Eq. (68), in terms of Eqs. (66) and (67), the apparent power is redefined in Eq. (69). Therefore, the voltage/current of the vector are defined in Eq. (70) and the conjugate of the current and voltage vector when in parallel circuit by analogue is defined in Eq. (71). By substituting the voltage and the current conjugate in Eq. (69), the apparent power can also be obtained in Eq. (72). Thus, the real part is the real power while the imaginary part is the reactive power [31]. In a normal electrical circuit, inductive reactive power causes a voltage drop in the direction of its flow through an inductive circuit similar to real power that causes a voltage drop in its direction of flow through resistive circuit. With inductive reactive power as positive, positive real power flow and positive reactive power flow both produce voltage drops in the direction of flow in the normal circuit. With the oppositive convention, positive reactive power flow produces a voltage rise in the direction of flow.

Figure 3: (a) Impedance diagram, (b) Voltage/Current (c) Power diagram

Z=R+jX(60)

P=RI2(61)

Q=XI2(62)

S=P+jQ(63)

=RI2+jX2=(R+jX)I2)=ZI2(64)

P=IVCosϕ(65)

=IVCos(α−β)Q=IVSinϕ(66)

=IVSin(α−γ)ϕ=α−β(67)

S=P+jQ=VI(Cosϕ+jSinϕ)=VI[Cos(α−β)+jSin(α−β)]=VIejQ=VejαIe−jβ(68)

V=Vejα(69)

I=Iejβ(70)

I=Ie−jβ and V=Ve−jα(71)

S=P+jQ=VconjI(72)

5  Full Bridge Multi-Level Converter Modelling

The Full-Bridge Multi-Level Converter (FBMC) comprises of multiple series-connected power modules, each unit consists of one half-bridge and one capacitor on the DC side. It uses Insulated Gate Bipolar Transistor (IGBT)/diode pairs, a multilevel Pulse Width Modulation (PWM) generator produces firing pulses 0 or 1, which initiate switching in the device [32,33]. It’s made use of a switching-function model, two voltage sources, two diodes on the AC side, and two current sources on the DC side. It is usually regulated by firing pulses generated by a PWM generator or by firing pulses averaged over a specified period (PWM in averaging signals from 0 through 1) [34,35]. This model type is suitable for real-time simulation. It is modelled with a switching-function model directly controlled by the reference voltage signals. This model provides the fastest simulations as compared to ordinary active power filter circuit; the multilevel converter topologies can achieve a high number of the output voltage levels [36]. Hence, the smaller filter size is needed as the output voltage waveform. The FBMC is divided into three phases, each with an upper and lower arm as shown in Fig. 4.

Figure 4: Grid connected full bridge multi-level converter [37]

Each converter arm contains N cascaded FBSMs, each of which contains a dc capacitor and four insulated gate bipolar transistors. The full bridge cells have each voltage source of which the output voltage ranges between (−V0) and (+kVdc2) where (V0<Vdc2) and (k≥1) while the half bridge possesses each voltage source of the output voltage ranges between (0) and (Vdc2). Each cell in the full bridge can possess a negative output voltage hence, the output voltage of full bridge can be higher than (Vdc2) as depicted in Fig. 5a. Whereas, to achieve the output phase peak voltage (Vac,pk) in the half bridge, the least DC link voltage must have (Vac,pk) with additional required modulation margin such that 10%, (Vdc2) will be equal to 1.1 (Vac,pk) as depicted in Fig. 5b. Full-bridge, half-bridge type and cell module of FBMC are shown in Figs. 5c–5e, where the positive/negative legs are connected to the positive/negative poles. The average voltage of the capacitor cell can be obtained in Eq. (73) with k≥1 and is the boost factor, the rate at which the frequency switched is regarded as infinite and the size of the capacitor is higher to obtain a constant voltage with no ripples. The full bridge is of the bipolar where the carrier signal possesses a frequency (fsw) ranges between (1) and (−1), the voltage/current output for phase 1 of the system can be obtained in Eqs. (74) and (75). Eqs. (74) and (75) can be further solved by the application of Kirchhoff’s law as shown in Eqs. (76) to (80). Eq. (81) established a symmetrical situation in (3−ϕ). The (Ia) in Eq. (85) is the RMS of the current output for phase 1 therefore, the switching function of the cell (I) and (i) can be defined in the Eq. (86) where (k≥1) as mentioned in the Eq. (73). If the required voltage and current are to be obtained in steady state in Eq. (75), the switching function will be part of the Eqs. (87) and (88) where (M1) regulate the system output volta while (M2) regulate (20) current harmonics order and (M0) regulate DC output current in the system. The current (Icap,a.p) flows through the capacitor can be obtained by substituting Eqs. (75), (76), (85) and (87) and to put into consideration the zero-circulating current in Eq. (88). The Eq. (90) must be imposed if the capacitor current of the positive leg cell must be zero to sustain the capacitor voltage while the instantaneous can be obtained in Eq. (91). The average value of the capacitor is equal to the rated value kVdcN. By considering the switching function in (88), the arm voltage can also be obtained. The compensation flow sequence for the device is depicted in Fig. 6, where the device detects the voltage rise or unbalance load, harmonics current at the PCC, it absorbs/generates reactive power to sustain the network voltage level to acceptable limits. But it stays in its steady state when there is no power quality issue on the grid.

Figure 5: (a) AC output (b) (Vdc) (c) Half-bridge type (d) Full-bridge type (e) Cell module [38]

Figure 6: Compensation step flow for FBMC

Vcap=kVdcN(73)

va0=Va0Sin(wt)(74)

ia=IaSin(wt+φ)(75)

ia,p=ia2+ia,in+icirc(76)

ia,n=ia2+ia,in+icirc(77)

Vdc2−va,p−Lddtia,p−vao=0(78)

Vdc2−va,n−Lddtia,n−vao=0(79)

va0=va,n−va,p2−L2ddtiaVdc=va,p+va,n+2Lddt(ia,in+ia,circ)(80)

ia,p+ib,p+ic,p=Idc(81)

ia,in=133VacIaCos(φ)Vdc(82)

Vac=MackVdc232(83)

Vac,pk=MacKVdc2(84)

ia,in=KMac4IaCos(φ)(85)

fsw,i,l=12(K−1+Ml(t))(86)

fsw,a,p=12(K−1+Ma,p(t))fsw,a,p=12K−1+M0−M1Sin(wt−α1)+M2Sin(2wt+α2)(87)

fsw,a,n=12(K−1+Ma,n(t))fsw,a,n=12K−1+M0−M1Sin(wt−α1)+M2Sin(2wt+α2)(88)

icap,a,p=fsw,a,pia,p=Ia8{Mac(kM0+1)Cos(φ)−M1Cos(α1−φ)+2(1k+M0)Sin(wt+φ)+M2Cos(wt+α2−φ)−kM1MacCos(φ)Sin(wt+α1)+kM2MacCos(φ)Sin(2wt+α2)+M1Cos(2wt+α1+φ)−M2Cos(3wt+α1+φ)}(89)

Ia8[−M1Cos(α1−φ)+Mac(1+kM0)Cosφ]=0(90)

vcap,a,p=Vcap¯+1c∫icap,a,pdt=kvdcN+Ia24ckw{2M2sin⁡(3wt2)cos(α2+3wt2+φ)cos⁡(φ)[3k2M1Mac{cos⁡(α1+wt)−cos⁡(α1)}+3k2M2Macsin⁡(wt)sin⁡(α2+wt)+6kM0+6]−6(kM0+1)cos⁡(wt+φ)+k[3M1sin⁡(wt)cos⁡(α1+wt+φ)+6M2Sin(wt2)cos(α2+wt2−φ)−2M2sin⁡(3wt2)cos(α2+3wt2+φ)}(91)

6  Simulation, Result and Discussion

The system is designed in MATLAB/Simulink environment and scenarios are observed such as: the network is designed as balanced AC network such that there is no distortion to the PCC and no active power generated to the grid from the RDG side. The RDG connected to PCC possesses the ability to compensate for partial power quality issues (active power filter). The network is also designed as balanced AC Voltages with RDG Active Power, distorted and symmetrical voltages without RDG’s power to the grid, balanced AC Voltages with RDG Active Power Generation and balanced AC Voltages with FBMC Connection at PCC.

6.1 Scenario 1: Balanced AC Voltages without RDG Producing Active Power

The system is designed in MATLAB/Simulink environment as a balanced AC network such that there is no distortion to the PCC and no active power generated to the grid from the RDG side. The RDG connected to PCC possesses the ability to compensate for partial power quality issues (active power filter). When the mitigation activities is carried out, it is projected on the grid that the following aim can be achieved such that µGD=µGDmax=0.1, µGU=µGUmax=0.1 and µGQ=µGQmax=0.33. The loads connected to the system are balanced linear, unbalanced linear load and non-linear loads, the PCC voltage and current are shown in Fig. 7a. It shows that the system undergone some level of inherent distortions and harmonic current flow across the grid, unbalanced current, deviation in currents phases, and out of phase current as compared to voltage. By considering the Eq. (37), the power factor (µG) of which the network is operating can be obtained. Hence, µG=µGmini=0.9345. The simulation results in Figs. 7b–7c show that the system undergoes distortion from the current side than voltage side before 0.5 s, the harmonics generated at the phases A, B and C are 32%, 45%, 46% while unbalance current is about 52%. The system is not within an acceptable range before 0.5, out of phase current occurs between 0 s to 0.04 s at Cos Cos∅≅(Sin−10.8010)=0.5987. The pre-compensation process is carried out by the grid connected RDG and reached to an anticipated value for µGD≅THDIabc=0.1, µGU=0.1, Cos(Sin−10.3301)=0.9439 and maintain an acceptable range of power factor on the grid side. The level of harmonic content with amplitude variation are minimized. This method controls the active power flow from the renewable energy source to the grid while also performing nonlinear load current harmonic compensation by keeping the grid current nearly sinusoidal which is similar to the research work carried out in [39]. The unbalance current or phase displacement current are diminished in Fig. 8c compared to that of voltage to any substantial point in relation to the pre-determined aim.

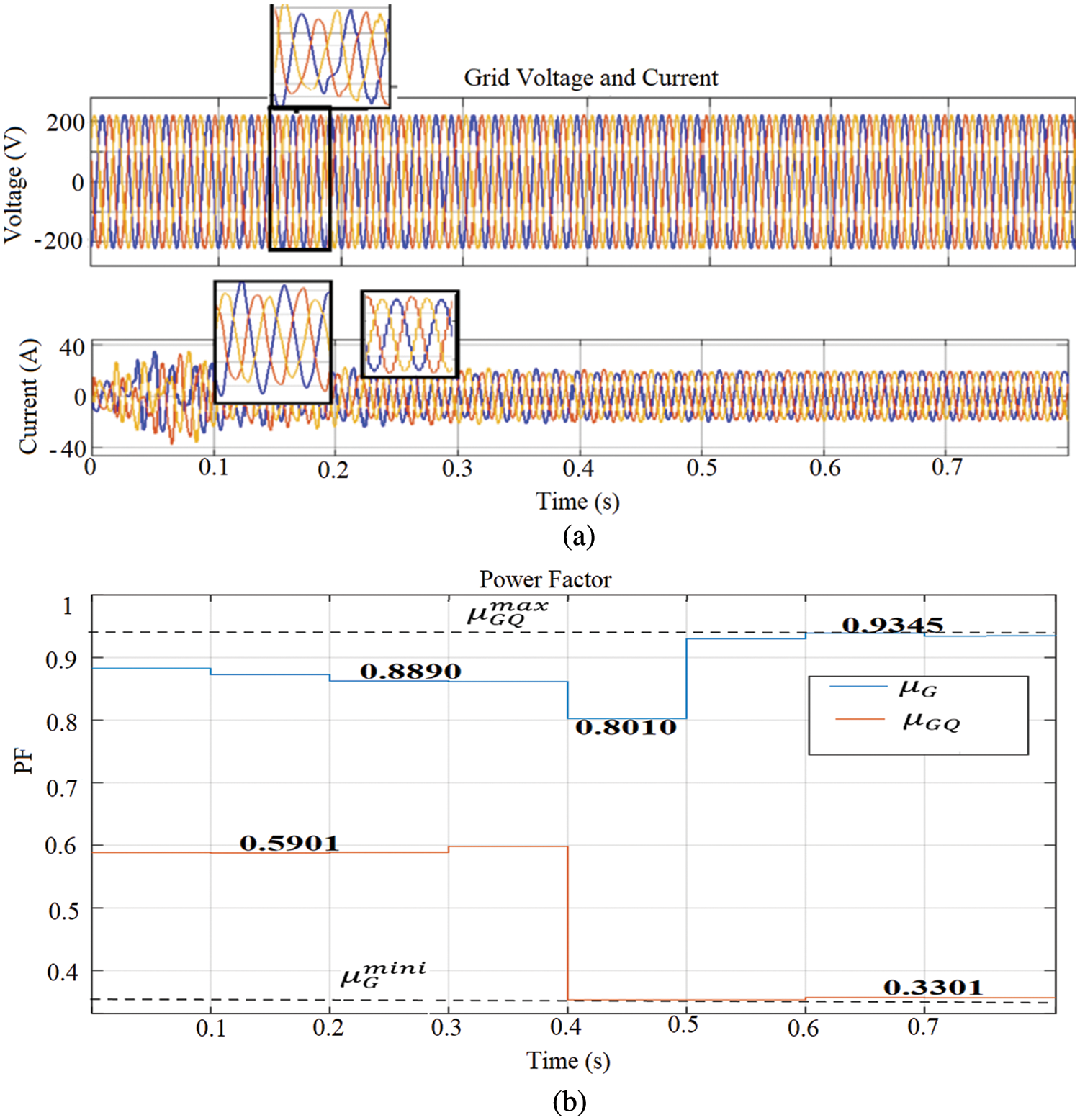
Figure 7: (a) PCC voltage and current (b) Power factor (c) Conformity factors

Figure 8: PCC voltage, grid and RDG current

6.2 Scenario 2: Balanced AC Voltages with RDG Active Power

The voltages are maintained sinusoidal and symmetric similar to scenario 1, RDG does not generate active power to the grid at the PCC while it is allowed to pre-compensate for the grid reactive power. The same condition for scenario 1 is also applied such that that μGD=μGDmax=0.1, μGU=μGUmax=0.1 and μGQ=μGQmax=0.33. The temporary mitigation for reactive power, unbalance currents and generation of harmonic start at 0.3 s (μGQmax=0.33), 0.5 s μGQmax=0.33, μGUmax=0.1) and 0.7 s, μGQmax=0.33, μGUmax=0.1), respectively. The objectives are achieved similar to the result in Fig. 7b. Although, there is a slight reduction in the reactive current causes an increase in harmonic current which could be confirmed with the decrease in the current angle as compared to voltage, the component of positive sequence decreases while the negative sequence remains unchanged because of the partial mitigation of the reactive power. Therefore, the decrease in the fundamental component because of the partial compensation of the reactive current resulted in the increase in the unbalance currents and the harmonics in the system. This method of pre-compensation can be beneficial to any network where RDGs are to be integrated because it reduces the circulation of current in the system, hence, minimizes network losses. Thus, it can be confirmed by the reduction in current amplitude as shown in Fig. 8 at 0.3 s. The ability of RDG integration to reduce current circulation flow and minimize network losses can be attributed to its location within the network, as demonstrated by research work conducted in [40], which confirmed that RDGs can minimize losses to a reasonable percentage in a distribution network. In any network, it is worthy to note that the sequence of pre-compensation will help in minimizing any factor that can harm the component of power quality either the compensation for unbalance current first, follows by the distortions and the reactive current.

6.3 Distorted and Symmetrical Voltages without RDG’s Power to the Grid

This section discusses the outcome of the simulation when additional industrial or commercial loads are added to the network and observe if the proposed method is adequate and firm under such operation. The order of pre-compensation as scenario 1 is followed such that µGD=µGDmax=0.1, µGU=µGUmax=0.1 and µGQ=µGQmax=0.33. With the additional loads added to the network, there is more distortion of the grid and asymmetrical voltage flows. It was observed that there was 6% more increase in the negative sequence grid voltage and harmonic distortion of 6% increase when the pre-compensation has not started. These increases in the distortion and the negative sequence voltage are not because of unbalanced non-linear loads connected to the network only, but also the contribution of distorted signal generated from the voltage source. The result obtained after the active power filter compensation is similar to that of the result obtained in scenario 1, the shifting in phase of the current, the distortion and the imbalance as compared to voltage are reduced, which means that even under the distorted and asymmetrical voltage, RDG with active power filter can be used to mitigate power quality issues that is related to current imbalance, current phase shift and harmonics to some certain extent.

6.4 Balanced AC Voltages with RDG Active Power Generation

This section discusses the simulation outcome when RDG generates active power to the network and the voltages are kept sinusoidal and symmetrical. The measured voltages in various buses are shown Table 1 and its graphical representation in Fig. 9. The system voltage profiles improved significantly with increase in the RDG penetration level. The voltage at the bus 9 (PCC) is slightly more than other buses voltage because of the active power generated by the RDG. The influence of the RDGs is obvious at the PCC’s voltage and the nearest buses. The network voltage profiles are within an acceptable limit as indicated by IEEE 1547 and the South Africa grid code act. The research work carried out in this paper showed that with the increase in RDG penetration level, there is an improved in the system voltage profiles in Fig. 9a which is also established in the research work carried out in [41]. Consequently, the weak network becomes an active system while incorporating an automation system, capable of monitoring power flows from points of generation to points of consumption. The measured values across the system buses at 69% penetration level causes an over-voltage as shown in Fig. 9b while the simulation result at t = 0.6 s around the PCC and in the grid are shown in Fig.10. At 1 s, the rise in voltage is higher on phases A and C while phase B voltage is within an acceptable range when the RDG’s penetration is 40% as observed in the grid. It is also observed that the voltages of all the phases are distorted, unbalanced, and the over-voltage is higher between 1 to 1.5 s, at 69% penetration at PCC which can be observed in Fig. 10. Morealso, the distortion increases when the connected loads drawn more current, phase shifted and unbalanced, then, harmonics current increases progressively. When the order of compensation is carried out with active power filter strategy only, such that µGD=µGDmax=0.1, µGU=µGUmax=0.1 and µGQ=µGQmax=0.33. There is slight improvement in the system as compared to when RDG is not supplying active power to the network, which means that the RDG plus active power filter is more efficient when it is not supplying power to the grid but act as a compensator as compared to when perform both operation such that it generates active power to the grid and also act as a compensator. The reason why it could not perform well during both operations may be attributed to the fact that it has to mitigate distortions on the RDG side and also on the grid sides. It could be more beneficial if external compensation can be employed when RDG with active filter is used to perform multirole in power system, i.e., when it is used for reactive current/distortion control and also to generate active power. Furthermore, the increase in the RDG penetration levels causes the occurrence of the voltage rises at PCC. This voltage rise issue of the PCC is a great limitation to RDG penetration levels if it cannot be controlled as it is specified in the IEEE-1547, otherwise it must be disconnected. It is necessary to provide an external compensator at PCC to mitigate the voltage rise such that the RDG penetration levels of the power system can be limitless. If such an action strategy is not provided at PCC, apart from the fact that a voltage rise/overvoltage issue limits the amount of RDG penetration levels that can be integrated into a network, it is also a threat to the sensitive and expensive equipment connected at PCC because of damage it can cause and to the power consumers connected to the network.

Figure 9: (a) Improved voltage profile with RDG (b) Voltage rise

Figure 10: Grid and PCC voltage rise

6.5 Balanced AC Voltages with FBMC Connection at PCC

This section presents the dynamic operation and performance analysis for reactive power generation/absorption and voltage control of proposed FBMC at PCC. Its act as a compensator to manage power quality challenges at PCC with RDG integration. The key purpose of employing the compensator is to improve the voltage rise, unbalanced current, minimize distortion and reactive power control at the PCC without RDG disconnection, to increase power flow capacity, release thermal capacity, reduce unbalance voltage/current, minimize harmonic and losses. Power transfer ability and grid strengthening should be enhanced with RDG integration to the power system without negative impacts. Usually, power quality problem arises in power system network due to the reactive power loss [42]. To achieve this aim, the dynamic performance analysis of the (FBMC) is investigated at PCC without RDG connection to the network and the simulation is carried out in the MATLAB/Simulink environment. The simulation analysis is depicted in Fig. 11, the proposed model has the capability to cope with voltage drops, unbalanced current/voltage originating from switching electrical loads and when the power supply is reduced due to intermittent of RDG. It possesses the ability to generate and absorb reactive power with fast response, which is performed through its phase reactance. The device behaves like inductance when the PCC voltage increases than the device voltage, it absorbs reactive power. But when PCC voltage is lower than the voltage of the device, it behaves like a capacitor thereby generating reactive power and it can also be regulated individualistically of the AC system voltage. Fig. 11a depicts the steady state operation strategy control of FBMC when the simulation run for at 0.1 s, where it produces in-phase voltage waveform with the PCC voltage such that the voltage generated is equal in magnitude to network voltage where there is no voltage rise issues and with zero current output, it does not absorb nor provide reactive power to the network. It is observed between 0 to 0.02 s, flow of switch-on surge current occurs, the FBMC quickly generates reactive power immediately to reduce the switching losses, its voltage is slightly increased than the PCC voltage which shows a fast response attribute of the device and quickly maintain the network voltage when the current goes off at t = 0.02 s. FBMC generates reactive power that is capacitive with leading output current flows across the grid and maintains zero after 0.02 s, showing that there is no exchange of power across the grid and there is no voltage rise occurrence at PCC above 0.02 s. The simulation results in Figs. 11b–11d depict the reactive power capability of the device when operating as purely inductive, capacitive, and as both such that, it generates a voltage waveform lower in magnitude than the network, enable the FBMC to perform as an inductive device and absorbing reactive power from the PCC. Likewise, it generates a voltage waveform higher in magnitude than the network, enable the FBSMC act as a capacitive device and generating reactive power to the grid.

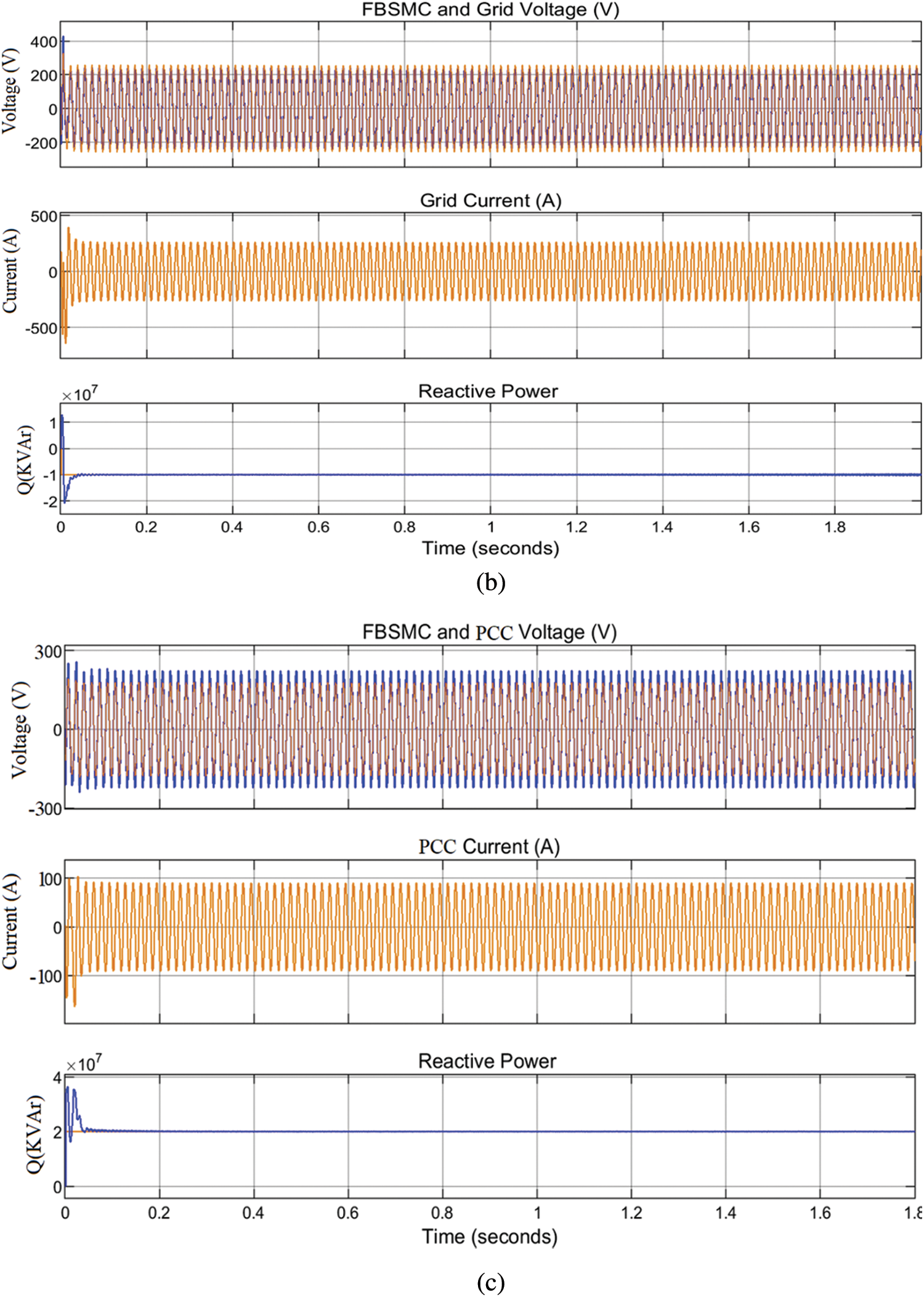
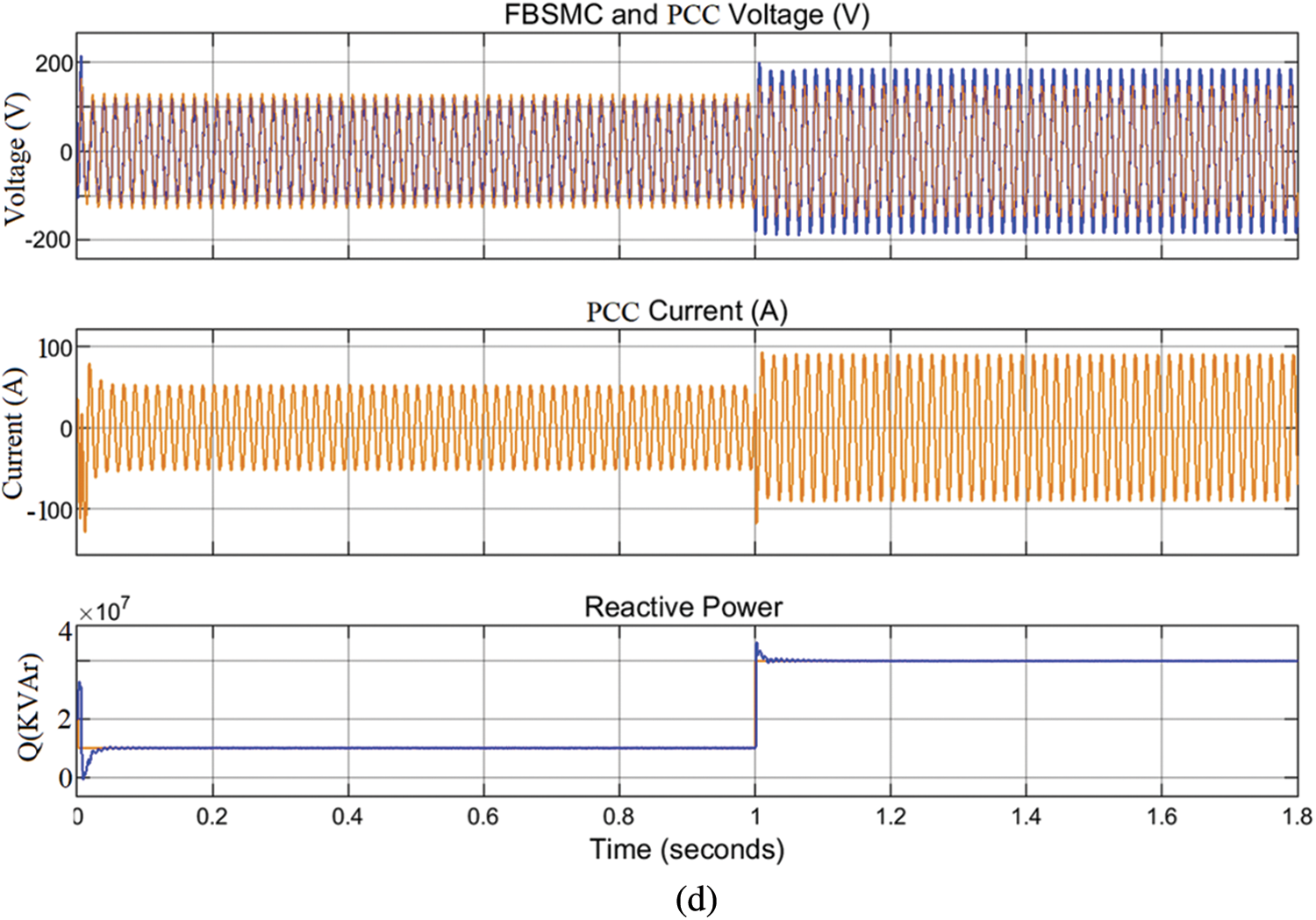
Figure 11: (a) FBMC in-phase voltage with PCC voltage, grid current and reactive power (b) FBSMC acts as inductive (c) FBMC acts at capacitive (d) FBMC acts as both

6.6 Reactive Power/Voltage Control at PCC

This section presents the impact of reactive power generation/absorption capability of FBMC at PCC when unbalanced and voltage rise occurs. For the coordination of the voltage control techniques at the PCC, online communication strategy is established between RDG units for the compensator to sense and communicate in case there is any voltage discrepancies or grid fault. The performance evaluation is carried out in the entire simulation 1.8 s at the PCC under normal operation condition. Integration of RGD to the network improves the network voltage profile while active power in Fig. 12a is being delivered to the grid, but when the penetration levels reach 69%, voltage rise occurs at the PCC as shown in Tables 1 and 2 of the voltage (per unit) measured across the buses of the network. IEEE-1547-2013 recommends disconnecting RDG at PCC whenever a voltage rise occurs to avoid distraction and damage to power equipment, whereas IEEE-1547-2018 recommends voltage rises regulation criteria at PCC, allowing RDG to ride through and remain connected [43,44]. At the 120% penetration levels of RDG into the network, the PCC voltage increases above 10% percent of its nominal value rating and the voltage rise in Figs. 12b–12e is not acceptable by the IEEE-1547-2013 specification, it is either the device is disconnected, or the voltage is regulated to an acceptable limit as specified by IEEE-1547-2018/2020. To compensate for the rise in voltage at PCC, FBMC is connected at PCC and the simulation procedures are repeated for 1.8 s. The simulation results are depicted in Figs. 12f–12i for 69% and 120% RDG penetration, respectively. The FBMC compensates for the voltage increase at PCC by absorbing reactive power from the PCC, such that the value of the reactive power absorbed by the device is equal to +0.18 Mvar at 1 s. The more RDG penetration at PCC, the more voltage rise overshoot increases the more FBMC compensate for this voltage increase by absorbing reactive power of +0.18 Mvar at 0.4 s in Figs. 12j–12m. The dynamic performance of the device is demonstrated at t = 1, when the device increases the reactive power for compensation from +0.18 Mvar to 0.2 Mvar. The calculated load current unbalance ratio is estimated to be 20%, the source current is quickly corrected to nearly balanced, and the source current unbalance ratio is improved to 2%. The converter produces the respective low-order harmonics with almost the same magnitude, hence, avoids them to appear in the output voltage. It shows that the highest low order harmonics having 12% with respect to the fundamental, while the harmonics lower than the 13% are successfully eliminated by the proposed method. FBMC produces high-quality AC and DC side waveforms, as well as a large number of output voltage levels per phase, the total voltage across the half bridge and full bridge chain-links of each arm are tightly controlled around the desired set-points. The total obstructing voltage of each half bridge chain-link in the FBMC arm is the full pole-to-pole dc link voltage, while the total obstructing voltage of each full bridge chain in the FBMC arm is half of the half bridge cell capacitor voltage. As a result, the total semiconductor loss associated with the addition of these extra full bridge chain-links is reduced. The full bridge chain-links function as active power filters, generating anti-phase voltage harmonics to cancel out the inherent harmonics in the arm voltages generated by the half bridge chain-links. The implementation of the proposed FBMC is exceedingly excellent considering the rapid reference tracking, fast response and convergence as shown in Fig. 12n. The assessment of THD during the voltage rise at PCC is depicted in Table 3. It is evidence that the voltage THD of the proposed FBMC at PCC during the occurrence of voltage rise is 0. 21% as compared to the inbuilt active power filter of the RDG which agrees with the IEEE requirements. Fig. 12m depicts the PCC and the grid voltage after the compensation activities. It shows that the over voltage, current ripples and the THD in the grid drop substantially faster while power quality remains within acceptable limit which agrees to the IEEE standard. The THDs analysis during the voltage rise, the compensating activities and the system measure voltages are shown in Tables 1–3, respectively. The FBMC continuously damps the PCC voltage rise, distortion, unbalanced current and harmonics during the PCC and grid disturbance. It supports the grid power quality parameters and maintains the network voltage throughout the simulation activities. Fig. 13 shows the sequence workflow of the simulations.

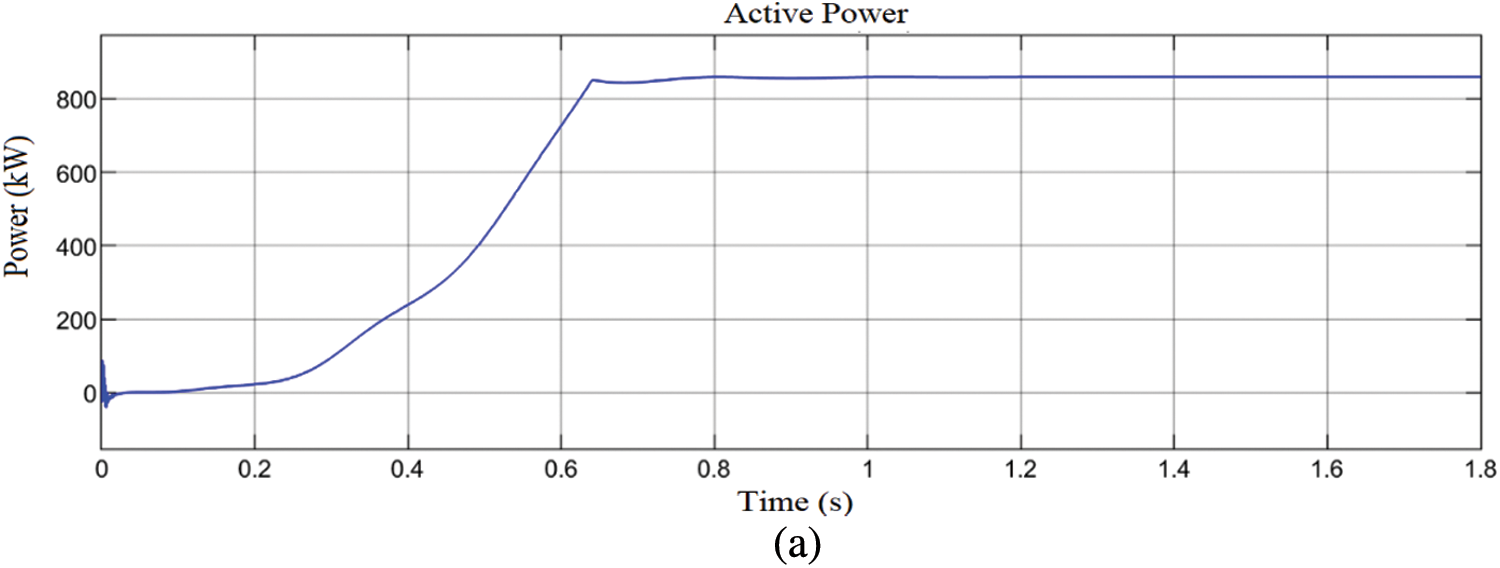
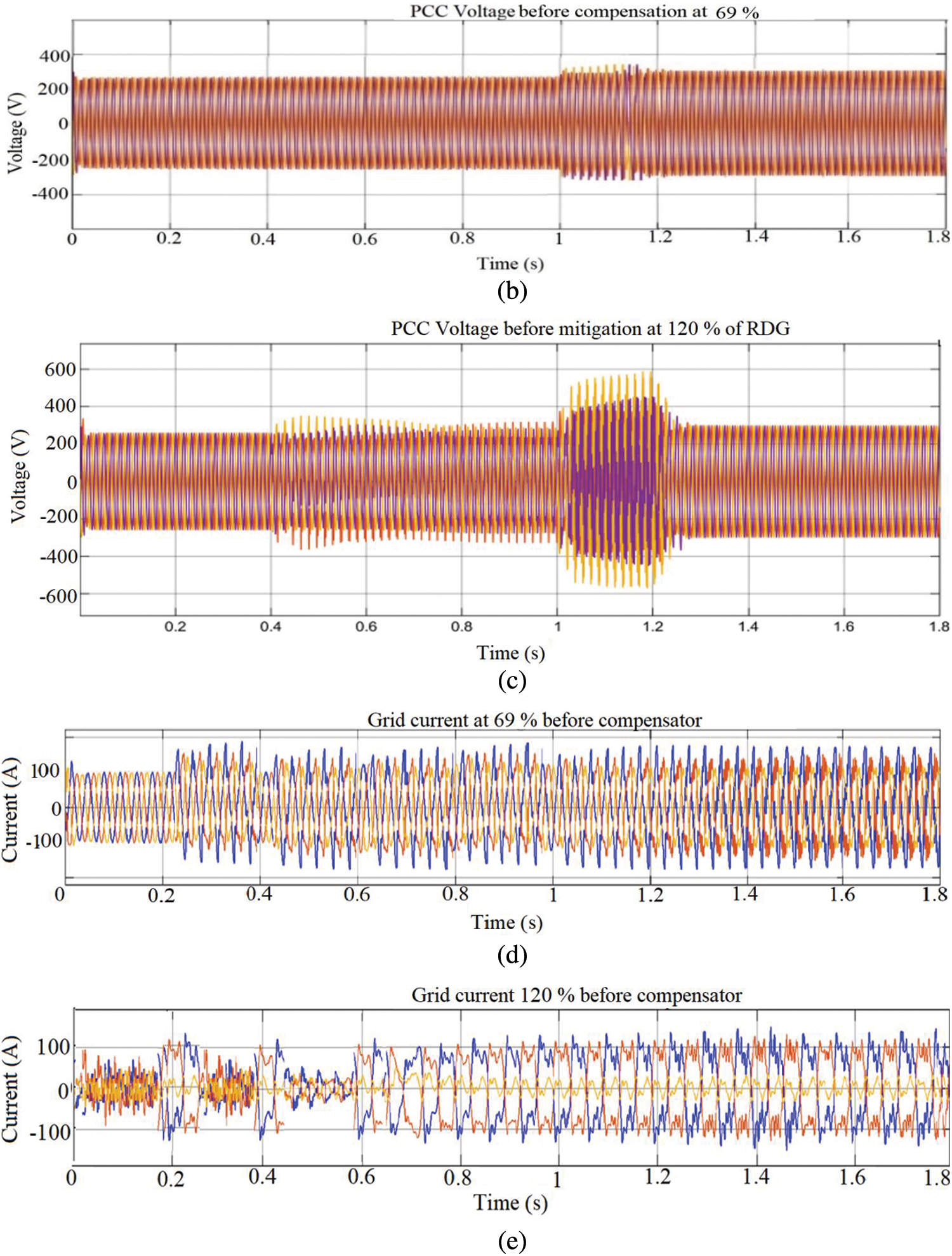
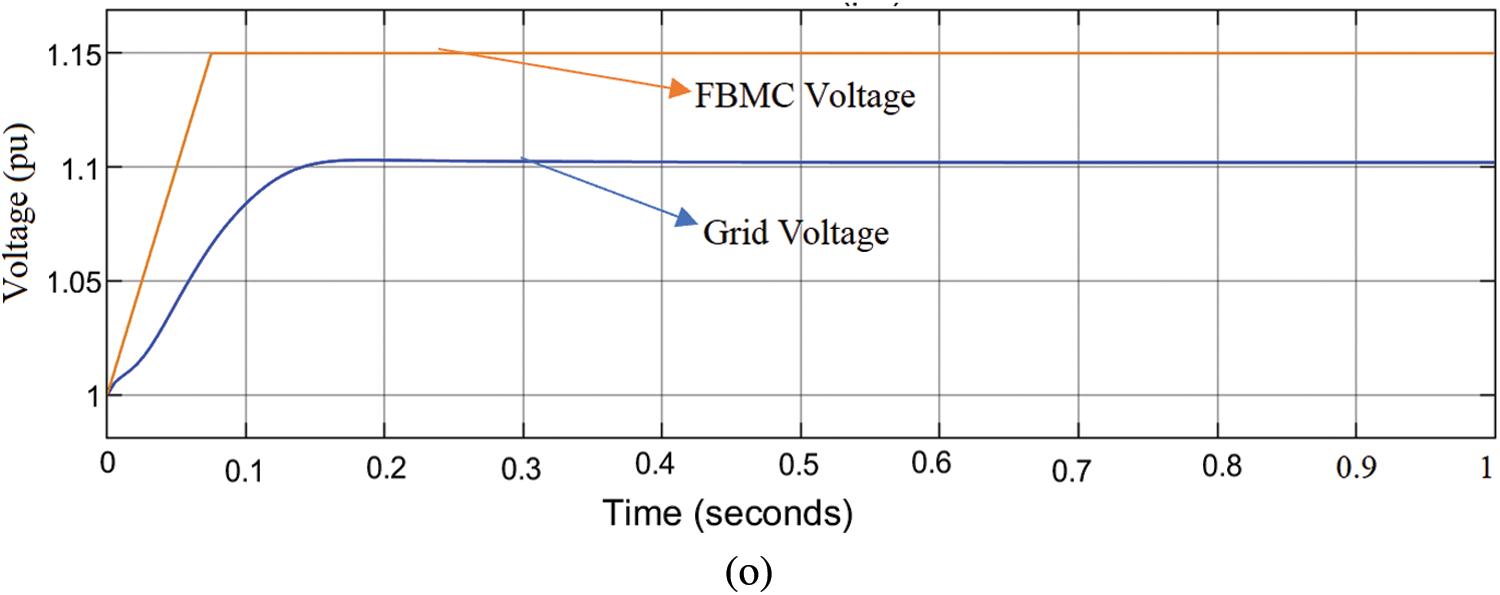
Figure 12: (a) Active power supplied to the grid (b) PCC voltage at 69% RDG before compensation (c) PCC voltage at 120% RDG before compensation (d) Grid current at 69% RDG before compensation (e) Grid current at 120% before compensation (f) PCC voltage at 69% RDG after compensation (g) PCC voltage at 120% RDG after compensation (h) Grid current at 69% RDG after compensation (i) Grid current at 120% after compensation Integration (j) FBMC current during compensation at 69% RDG (k) FBMC current during compensation at 120% (l) FBMC reactive power compensation at 69% RDG (m) FBMC reactive power compensation at 120% RDG (n) PCC voltage and FBMC voltage during compensation (o) Grid voltage and PCC voltage after compensation

Figure 13: Workflow chart

6.7 FBMC Sensitivity Analysis

Sensitivity analysis of the FBMC is the study of how uncertainty in the output of a model can be apportioned to different sources of uncertainty in the model input [45], it is the measure of the effect of a given input on a given output. i.e., how sensitive the output is to a perturbation of the input. Each phase of FBMC is made up of two arms, each with three power cells (sub-module). A single power cell, as shown in Fig. 4, is made up of a DC capacitor, arm inductance, and four semiconductor switches that form a bidirectional chopper-cell. In addition to the main parameters, the power cell includes a dc-link capacitor, insulated gate bipolar transistor (IGBT) stray inductances, and busbar inductance. When the output is chosen to be the peak voltage across semiconductor devices of each sub-module, sensitivity analysis is performed at three different levels of sub-module, arm, and phase to predict the maximum voltage stress across semiconductor devices in the FBMC. The first order index of a power cell's dc-link capacitor, busbar stray inductance, IGBT stray inductance, and fall time is approximately 0.39, 0.119, 0.079, and 0.519, respectively, while the other switch parameters are less than 0.03. This indicates that, excluding the dc capacitance, busbar and IGBT stray inductances, and IGBT fall time, the relative merits of all parameters of a single power cell is negligible in establishing the power cell's peak voltage. Although the FBMC has nonlinear and time variant behavior as long as we are far away from the converter's resonant point. This paper's analysis is limited to only one switch in each sub-module. Switch 2 produces the same result. However, the busbar stray inductance for switches 3 and 4 would be different. This difference could be attributed to the different current commutation loops that each switch has when turned off.

7  Conclusion

The proposed strategy employed in this research paper successfully managed the PCC’s power quality to an acceptable range in relation to IEEE and South Africa grid voltage requirement. It limits the unbalanced current, distortion and voltage rise regulation at the PCC. It regulates the grid reactive power flow and minimizes the unbalanced current and distortion generated from the non-linear load. In steady state, the FBMC voltage and current at PCC has very low THD <0.4% and negative or zero sequence 0.0048 pu even with high penetration of RDG without any passive filter. The active power filter and FBMC utilized was able to compensate for the power quality challenge under grid disturbances such as voltage rise, unbalance load conditions. The FBMC's dynamic performance in terms of reactive power generation/absorption is adequate, with a fast response. The network accepts high concentration of RDG penetration power at PCC without disconnecting, while FBSMC regulates the voltage rise, harmonics distortion, unbalanced current and reverse power flow to be within an acceptable limit. The simulation analysis and experiment tests are presented over the whole power range and various operating modes. The results show that the proposed FBMC successfully mitigates the circulating fault current level, over-voltage, unbalance current and distortion. The FBMC enables more RDG penetrations into the network without overvoltage at the PCC, unbalanced current, or harmonic distortions to the system. The FBMC possesses a very high response time, higher accuracy, and harmonic mitigation capability as compared to active power filter. The application of voltage rise, revers power flow and distortion in different situations would have different impacts on the power flow at PCC and the grid if not for the variety of reactive power regulation and voltage rise control strategies at PCC for RDG integration to the power system. According to the findings of the paper, if the regulation capability of the active filter and FBMC are taken into account when determining the most practical and efficient method of regulating PCC voltage rise and distortion, the latter may be preferred. It has been demonstrated that the FBMC has the potential to reduce power circuit complexity, which is critical for condition monitoring and the protection of high-value assets such as high voltage direct current devices.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Rezkallah, M., Chandra, A., Singh, B., Singh, S. (2019). Microgrid: Configurations, control and applications. IEEE Transaction on Smart Grid, 10(2), 1290–1302. DOI 10.1109/TSG.2017.2762349. [Google Scholar] [CrossRef]

 2.  Mohammad, S. G., David, J. H., Mehdi, B. (2021). A secondary control method for voltage unbalance compensation and accurate load sharing in networked microgrids. IEEE Transaction on Smart Grid, 12(4), 2822–2833. DOI 10.1109/TSG.2021.3062404. [Google Scholar] [CrossRef]

 3.  Ndamulelo, T., Ali, N. H., Thokozani, S. (2021). A fault level-based system to control voltage and enhance power factor through an on-load tap changer and distributed generators. IEEE Access, 9, 34023–34039. DOI 10.1109/ACCESS.2021.3061622. [Google Scholar] [CrossRef]

 4.  Bajaj, M., Singh, A. K. (2022). Optimal design of passive power filter for enhancing the harmonic-constrained hosting capacity of renewable DG systems. Computers and Electrical Engineering, 97, 107646. DOI 10.1016/j.compeleceng.2021.107646. [Google Scholar] [CrossRef]

 5.  Bajaj, M., Singh, A. K. (2022). Performance assessment of hybrid active filtering technique to enhance the hosting capacity of distorted grids for renewable energy systems. International Journal of Energy Research, 46(3), 2783–2809. DOI 10.1002/er.7345. [Google Scholar] [CrossRef]

 6.  IEEE (2019). IEEE approved draft guide for the application of shunt power capacitors. IEEE P1036/D9, 1–98. [Google Scholar]

 7.  Kalair, A., Abas, N., Kalair, A. R., Saleem, Z., Khan, N. (2017). Review of harmonic analysis, modeling and mitigation techniques. Renewable and Sustainable Energy Review, 78, 1152–1187. DOI 10.1016/j.rser.2017.04.121. [Google Scholar] [CrossRef]

 8.  Velásquez, M. A., Lara, V. M. (2019). Explosion of power capacitors in a change of transformers with reactive power compensation. Engineering Failure Analysis, 106, 104181. [Google Scholar]

 9.  Moreira, A. C., Paredes, H. K., Souza, W. A., Marafão, F. P., Silva, C. P. (2018). Intelligent expert system for power quality improvement under distorted and unbalanced conditions in three-phase AC micro-grids. IEEE Transaction on Smart Grid, 6(6), 6951–6960. [Google Scholar]

10. Moreira, A. C., Souza, W. A., Conrado, B. R., Morales-Paredes, H. K. (2022). Disturbing load classification based on the grey relational analysis method and load performance index. Journal of Control Automation and Electrical System, 31(1), 141–152. DOI 10.1007/s40313-019-00511-9. [Google Scholar] [CrossRef]

11. Arbab-Zavar, B., Palacios-Garcia, E., Vasquez, J., Guerrero, J. (2019). Smart inverters for microgrid applications: A review. Energies, 12(5), 840. DOI 10.3390/en12050840. [Google Scholar] [CrossRef]

12. Wang, L., Lam, C. S., Wong, M. C. (2018). Analysis, control, and design of a hybrid grid-connected inverter for renewable energy generation with power quality conditioning. IEEE Transaction on Power Electronics, 33(8), 6755–6768. DOI 10.1109/TPEL.2017.2753838. [Google Scholar] [CrossRef]

13. Mohamed, H. H., Salah, K., Mahmoud, A., Tahir, K., José, L. D. et al. (2021). Optimal reactive power dispatch with time-varying demand and renewable energy uncertainty using Rao-3 algorithm. IEEE Access, 9, 23264–23283. DOI 10.1109/ACCESS.2021.3056423. [Google Scholar] [CrossRef]

14. Sakib, M. N., Azad, S. P., Kazerani, M. (2022). A critical review of modular multilevel converter configurations and submodule topologies from DC fault blocking and ride-through capabilities viewpoints for HVDC applications. Energies, 15(11), 4176. DOI 10.3390/en15114176. [Google Scholar] [CrossRef]

15. Wang, K., Song, Q., Xu, S. (2022). Analysis and design of the energy storage requirement of hybrid modular multilevel converters using numerical integration and iterative solution. Energies, 15(3), 1225. DOI 10.3390/en15031225. [Google Scholar] [CrossRef]

16. Bajaj, M., Kumar, A. (2020). Singh grid integrated renewable DG systems: A review of power quality challenges and state-of-the-art mitigation techniques. International Journal of Energy Research, 44(1), 26–69. DOI 10.1002/er.4847. [Google Scholar] [CrossRef]

17. Zabihinejad, A., Viarouge, P. (2018). Global optimization of high-power modular multilevel active-front-end converter using analytical model. Electrical Engineering, 100(2), 509–518. DOI 10.1007/s00202-017-0523-5. [Google Scholar] [CrossRef]

18. Zhang, Y., Adam, G. P., Lim, T. C., Finney, S. J., William, B. W. (2012). Analysis of modular multilevel converter capacitor voltage balancing based on phase voltage redundant states. IET Power Electronics, 5(6), 726–738. DOI 10.1049/iet-pel.2010.0305. [Google Scholar] [CrossRef]

19. Adam, G. P., Anaya-Lara, O., Burt, G. M., Telford, B. W., Williams, D. et al. (2010). Modular multilevel inverter: Pulse width modulation and capacitor balancing technique. IET Power Electronics, 3(5), 702–715. DOI 10.1049/iet-pel.2009.0184. [Google Scholar] [CrossRef]

20. Giddani, O. A., Adam, G. P., Anaya-Lara, O., Burt, G., Lo, K. L. (2010). Control strategies of VSC-HVDC transmission system for wind power integration to meet GB grid code requirements. International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), pp. 385–390. Pisa, Italy. DOI 10.1109/SPEEDAM.2010.5542237. [Google Scholar] [CrossRef]

21. Du, S., Liu, J., Liu, T. (2014). Modulation and close-loop based DC capacitor voltage control for MMC with fundamental switching frequency. Power Electronics, IEEE Transactions, 30(1), 327–338. [Google Scholar]

22. Hagiwara, M., Akagi, H. (2009). Control and experiment of pulse width-modulated modular multilevel converters. Power Electronics, IEEE Transactions, 24(7), 1737–1746. DOI 10.1109/TPEL.2009.2014236. [Google Scholar] [CrossRef]

23. Parvin, K., Hossain-Lipu, M. S., Hannan, M. A., Abdullah, M. A., Jern, K. P. et al. (2021). Intelligent controllers and optimization algorithms for building energy management towards achieving sustainable development: Challenges and prospects. IEEE Access, 9, 41577–41602. DOI 10.1109/ACCESS.2021.3065087. [Google Scholar] [CrossRef]

24. Sajjad, H., Milad, Z. M., Behrooz, B. (2021). Optimal allocation and sizing of synchronous condensers in weak grids with increased penetration of wind and solar farms. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 11(1), 199–209. DOI 10.1109/JETCAS.2021.3053554. [Google Scholar] [CrossRef]

25. Tenti, P., Paredes, H. K., Mattavelli, P. (2011). Conservative power theory, a framework to approach control and accountability issues in smart microgrids. IEEE Transaction on Power Electronics, 26(3), 664–673. DOI 10.1109/TPEL.2010.2093153. [Google Scholar] [CrossRef]

26. Tenti, P., Mattavelli, P., Morales-Paredes, H. K. (2010). Conservative power theory, sequence components and accountability in smart grids. International School on Non-Sinusoidal Currents and Compensation, Lagow, Poland. [Google Scholar]

27. Souza, W. A., Liberado, E. V., Silva, L. C., Marafão, F. P., Morales-Paredes, H. K. (2013). Load analyzer using conservative power theory. International School on Non-Sinusoidal Currents and Compensation, Zielona, Gora. [Google Scholar]

28. Liu, J., Zhao, C. C., Xie, Z. H. (2021). Power and current limiting control of wind turbines based on PMSG under unbalanced grid voltage. IEEE Access, 9, 9873–9883. DOI 10.1109/ACCESS.2021.3049839. [Google Scholar] [CrossRef]

29. Oscar, C. Z., Jose, B. D., Fernando, M. D., Francisco, A. S., Rafael, C. N. (2021). Control of photovoltaic inverters for transient and voltage stability enhancement. IEEE Access, 9, 44363–44373. DOI 10.1109/ACCESS.2021.3066147. [Google Scholar] [CrossRef]

30. Gyu, S. L., Pyeong-Ik, H., Seung, M. (2021). Reactive power control of hybrid multi-terminal HVDC systems considering the interaction between the AC network and multiple LCCs. IEEE Transactions on Power Systems, 36(5), 4562–4574. DOI 10.1109/TPWRS.2021.3056565. [Google Scholar] [CrossRef]

31. Peng, L., Grain, P. A., Derrick, H., Barry, W. (2021). Controlled transition full-bridge hybrid multilevel converter with chain-links of full-bridge cells. IEEE Transactions on Power Electronics, 36(1), 23–38. [Google Scholar]

32. Hamasaki, S., Hadano, K., Eguchi, S., Tsuji, M. (2016). Control of full bridge type modular multilevel converter for single phase AC/AC conversion. International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan. [Google Scholar]

33. Miodrag, B., Dražen, D. (2021). Hybrid modular multilevel converter for variable DC link voltage operation. CPSS Transactions on Power Electronics and Applications, 6(2), 178–190. DOI 10.24295/CPSSTPEA.2021.00016. [Google Scholar] [CrossRef]

34. Zhang, Y., Zhang, J., Deng, F., Xu, Z., Zhao, J. (2021). Hybrid modular multilevel converter with self-balancing structure. IEEE Transactions on Industry Applications, 57(5), 5039–5051. DOI 10.1109/TIA.2021.3087669. [Google Scholar] [CrossRef]

35. Chen, Y., Pan, S., Huang, M., Zhu, Z., Liu, Y. et al. (2021). MMC-MTDC transmission system with partially hybrid branches. CES Transactions on Electrical Machines and Systems, 5(2), 124–132. DOI 10.30941/CESTEMS.2021.00016. [Google Scholar] [CrossRef]

36. Mohamed, A., Yousef, N., Fahad, A., Khaled, H., Ayman, S. et al. (2021). A new hybrid dual active bridge modular multilevel based DC-DC converter for HVDC networks. IEEE Access, 9, 62055–62073. DOI 10.1109/ACCESS.2021.3074543. [Google Scholar] [CrossRef]

37. IEEE (2020). IEEE standard for interconnection and interoperability of distributed energy resources with associated electric power systems interfaces—Amendment 1: To provide more flexibility for adoption of abnormal operating performance category III. IEEE. [Google Scholar]

38. Thakur, S. S., Odavic, M., Allu, A., Zhu, Z. Q., Atallah, K. (2022). Analytical modelling and optimization of output voltage harmonic spectra of full-bridge modular multilevel converters in boost mode. IEEE Transactions on Power Electronics, 3(37), 3403–3420. DOI 10.1109/TPEL.2021.3108877. [Google Scholar] [CrossRef]

39. Bojoi, R. I., Limongi, L. R., Roiu, D., Tenconi, A. (2011). Enhanced power quality control strategy for single-phase inverters in distributed generation systems. IEEE Transactions on Power Electronics, 26(3), 798–806. DOI 10.1109/TPEL.2010.2103572. [Google Scholar] [CrossRef]

40. Sakulphaisan, G., Junhuathon, N., Chayakulkheeree, K. (2022). Minimizing power loss in a DC distribution system through an analysis of the loss sensitivity factor and distributed generator loss characteristics. International Electrical Engineering Congress (IEECON), Khon Kaen, Thailand. [Google Scholar]

41. Akinyemi, A. S., Musasa, K., Davidson, I. E. (2022). Analysis of voltage rise phenomena in electrical power network with high concentration of renewable distributed generations. Scientific Reports, 12(1), 7815. DOI 10.1038/s41598-022-11765-w. [Google Scholar] [CrossRef]

42. Sultana, W., Jebaseelan, S. D. (2022). Improved grid power transmission using solar panel (PV-Statcom) in day and night. International Conference on Advances in Computing, Communication and Applied Informatics (ACCAI), Chennai, India. [Google Scholar]

43. IEEE (2020). IEEE approved draft standard for interconnection and interoperability of distributed energy resources with associated electric power systems interfaces-Amendment 1 to IEEE Std 1547-2018 to provide more flexibility for adoption of abnormal operating perf. IEEE. [Google Scholar]

44. IEEE (2022). IEEE draft application guide for IEEE Std 1547(TMIEEE standard for interconnecting distributed resources with electric power systems. IEEE. [Google Scholar]

45. Stefano, S. A., Campolongo, T. F., Ratto, M. (2004). Sensitivity analysis in practice: A guide to assessing scientific models. Ispra, Italy: John Wiley & Sons. [Google Scholar]