Optimization of Chiller Loading Problem Using Improved Golden Jackal Optimization Algorithm Leads to Reduction in Energy Consumption

1  Introduction

Energy is the basis of society’s progress and development, and the sustainability of operations in the production, service, and improvement of people’s living conditions is contingent on adequate energy supplies [1]. On the one hand, investment in fossil fuels has decreased, and on the other hand, the lack of opportunities for a comprehensive transition to renewable and clean energy has led to a less prosperous world, while energy prices are also rising [2–5]. The constantly rising energy prices remind people that despite efforts to shift the world towards clean and sustainable electricity, the world still inevitably relies on fossil fuels [6–8].

Due to the increasing demand for energy and the dwindling fossil fuel supply, it is more important to save energy than ever before. It should be emphasized that, in addition to switching to sustainable energy resources like solar energy, energy-consuming systems’ optimization can play a significant role in the reduction of energy consumption [9].

Energy has gotten little attention around the world, and government subsidies, both overt and covert, have always kept people from paying attention to the importance of energy. In recent years, paying enough attention to both energy use and energy savings has become an inevitable necessity [10,11]. More than one-third of global energy is used in buildings, estimated to be worth $6 billion a year at current global prices.

Due to the fact that most modern human life occurs within buildings, it is crucial to create suitable environmental conditions within buildings, with the most important being the provision of air conditioning for residents, as this is an activity [12,13]. Air conditioning improves life and makes it easier to work. This includes temperature and relative humidity control in the range of 22 to 28 degrees Celsius and 40–60 percent, respectively.

Weather conditions, heat load, and building design all influence the effectiveness of an air conditioning system. Chillers are the biggest energy users in terms of energy consumption [14]. As a result, selecting and operating the appropriate chiller is critical for reducing energy use [15]. Selecting the incorrect air conditioning system might result in higher costs while also failing to deliver adequate cooling and comfort to inhabitants [16,17].

According to studies, cooling and heating consume approximately half of the energy used in the construction industry. Due to a deficiency in energy sources and price volatility, experts have changed the applications and structure of air conditioning systems.

HVAC, accounts for a significant proportion of the total energy consumption of a building, from 25% to 30% in residential buildings to over 50% in commercial buildings. Between 40% and 60% of this need is met by chillers, which account for the majority of overall use of energy.

Records indicate that the efficiency of HVAC systems is closely related to the efficiency of cooling units [18]. Due to the fact that multiple coolers typically use various devices, there are usually multiple cooling combinations that can be provided by the coolers to meet refrigeration needs. The challenge for OCL is to identify the required capacity fraction for each cooler to reduce system power consumption.

Researchers have considered the necessity for highly efficient cold production cycles because of the growing importance of energy preservation internationally and the requirement for cold production in diverse industries [19]. As a result, researchers have developed various cold-producing cycles.

The process of employing these systems can be economized by minimizing energy usage in the chiller cycle. Because testing such systems is so expensive, the necessity for computer models to optimize them is obvious [20]. Due to the increase in energy consumption, the air conditioning industry is increasingly focusing on coolers as efficient systems. Optimizing the performance of these systems through computer techniques and metaheuristic algorithms is one of the major challenges.

Air-conditioning systems make up the bulk of the energy use in buildings, and their chillers are the main source of energy consumption. Accordingly, energy conservation is critical for chiller systems. The OCL (Optimal Chiller Load) is investigated using a variety of optimization approaches. Optimization devices have been developed in recent years for various uses. Several of them have been successful in resolving the OCL issue.

Chen et al. [21] implemented smart models to save energy while optimizing chiller loading. Neural Networks (NNs) were used to create chiller energy consumption models, and the PSO approach (which stands for Particle Swarm Optimization) was used to OCL for minimal energy use. After evaluation with ELD (Equal Load Distribution) and LR (Linear Regression) approaches, they achieved 17.63% and 12.68% energy savings at seventy and fifty-five percent PLR (chiller load rate), respectively. As a result, the NNPSO approach resolved the velocity convergence problem on the OCL and provided very precise findings in a small chunk of time. The suggested strategies could be used to optimize air conditioning units and associated challenges.

Gheydi et al. [22] utilized ANN techniques and optimization programming to optimize load in a multiple-chiller system. The variety of research on central air conditioning optimization models concentrates on a single chiller or numerous ones with identical types and capacities. Based on ANN, an energy consumption model is built which considers the operational constraints of each type of chiller. The current technique can conserve power usage up to 16.68 percent more than the MM method, according to simulated data assessment over a one-year operation interval.

Sohrabi et al. [23] suggested optimal chiller loading to save energy. This research uses 3 case studies to analyze the performance of the EMA (Exchange Market Algorithm) and make a comparison between it and former optimization approaches used to tackle the OCL issue. The EMA is an effective way of resolving the OCL problem, and it may also be utilized in air-conditioning units, according to the findings. In electrical energy consumption and fast convergence terms, it is more power-saving and quicker than earlier optimization approaches used for this problem.

Lee et al. [24] assessed the implementation of a PSO algorithm for OCL to improve energy efficiency. The particle swarm approach has been presented for chiller system continuous parameter optimization problems. The optimum parameters are PLR, and the target function is energy consumption. In this paper, the results of the optimal model constructed by GA and the Lagrangian method are compared with each other. In both cases, the PSO is superior to the evolutionary algorithm in overcoming the divergence of the Lagrange method.

Ardakani et al. [25] suggested a novel method to optimize chiller loading utilizing PSO. Two novel procedures are utilized in this work to solve the OCL problem. PSO and continuous GA successfully weather shortages in other conventional optimization procedures because the nature of variables in the OCL problem is continuous. The proposed program has significant advantages such as simple execution, fast convergence, avoiding falling into local optima, and independent solutions. The results show that the proposed method can be well applied to air conditioning systems.

In this paper, we propose a new IGJO algorithm to solve OCL problems. An important drawback of the GJO (golden jackal optimization) algorithm is its unavailability in the search. Here, an improved version is proposed to modify this issue and provide an efficient optimal chiller loading with lower energy consumption.

2  Problem Formulation

A chiller is a device that uses absorption refrigeration or a vapor-compression cycle to lessen the temperature of a particular fluid by removing heat from it. After that, the fluid is sent to a heat exchanger to chill the atmosphere. The wasted heat produced during refrigeration must be either released into the air or collected for heating [26]. In some air-conditioned buildings, there is a central cooling system, which uses a number of parallel/serial chillers to meet different cooling requirements. As a result, one of the most vital aspects of HVAC in big publicly-used constructions is numerous chiller systems.

Fig. 1 shows the topology of the coupled system and the topology of multiple chillers. All chillers in Fig. 1 have various load values for energy consumption [27–29]. For the multiple chiller systems based on the chillers’ general energy consumption, the total energy consumption is obtained by Eq. (1) as follows:

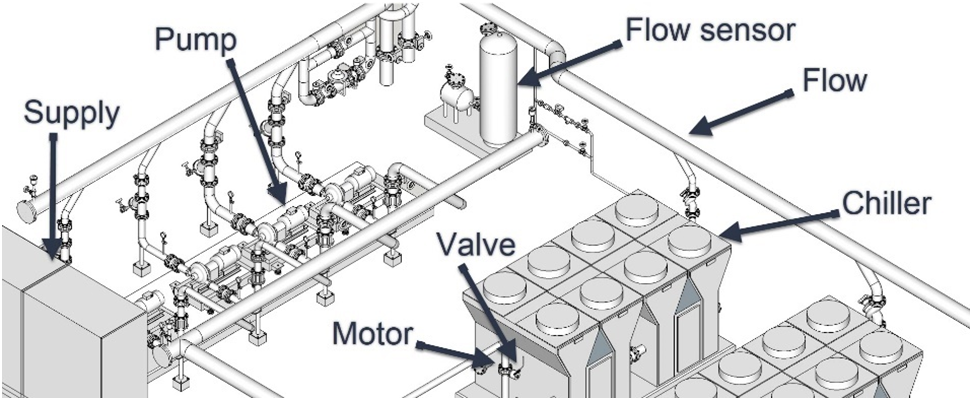
Figure 1: A decoupled system accompanied by the multi-chiller one

ET=∑l=1LPl(1)

In this equation, Pi is the energy consumption of the chiller number i, and M is the total number of chillers.

Different targets can be utilized for designing a good configuration for the chiller system. This research considers minimizing the temperature of the wet bulb as an objective function (Cwb), that is,

Cwb=minl(∑l=1LPl)(2)

where, Pl signifies the on/off state for the complex number i:

Pl={1on0off(3)

Another important statistic, that describes the chiller cooling load ratio and design capacity, is PLR. l is considered the chillers’ number, Consequently, the PLRl is zero if the chiller number l is shut down (Pl=0), and it takes a random value between 0.3 and 1, if the chiller number i is on (Pl=1):

PLRl={rand (0.3,1) if on0if shut down(4)

The centrifugal chiller power consumption is described by considering three different cases is:

Pl={αl+βl×PLRl+γl×PLRl2ifPl=1(case 1)αl+βl×PLRl+γl×PLRl2+δl×PLRl3ifPl=1(case 2 and 3)0ifPl=0(5)

where, αl, βl, γl, and δl describe pa redefined set of values of the KW/Part Load Ratio curve of the ith chiller.

The Pl is not negative in the preceding equation because of the positive value of the chiller’s energy usage. To provide promising cooling in the system that fulfills the load requirement, the correct choice for multiple chiller systems must be made, moreover, the cooling load for each chiller and the system should be equal. The mathematical formula for system cooling load (Lc) is as follows:

Lcool=∑l=1LCl×PLRl(6)

where, Cl represents the capacity of the chiller with number i (ith) [30].

3  Improved Version of Golden Jackal Optimization (IGJO) Algorithm

3.1 IGJO Algorithm

The inspiration for the offered procedure and the mathematical model are stated respectively in this part.

3.1.1 Motivation

The vertical height of golden jackals is about 41 cm and the size of their tails is about 26 cm [31]. In general, their body length is between 71 and 86 cm. Their fur color varies depending on where they live and the season. This color difference can be yellow, rough brown, or pale gold. Golden jackals dash vast distances to catch prey, and this is due to their physical characteristics, including their extended legs and small bodies. Golden jackals have a very varied diet [32]. They are both vegetarian and carnivorous. Their diet includes land birds, youthful gazelles, reptiles, rodents, insects, fish, frogs, rabbits, and fruits.

Golden jackals live in pairs with their mates, both parents are responsible for protecting and providing food. Hence, the family is provided by helpers in many aspects. Adults use “rumble growl” and “predator bark” to warn the cubs of their hiding place, and one adult can effectively avoid large predators. The helpers also provide food for a nursing mother, hence more time is spent hunting by parents. Golden jackals discover each other’s position using a wide range of howls.

Golden jackals usually hunt and relax with their mates. There is harmony in all their behavior. The number of individuals reported in one group is up to 5 or 10 individuals. They use their urine to keep intruders out of the area. Golden jackals need to work together to forage and hunt more extensive prey in the accessible areas. Pairs that hunt together can get more prey than those that hunt alone. In duo or collective hunting, they move parallel to the target while crossing it. Similarly, they move along narrow streams or rivers to catch aquatic rodents and birds and impel their prey between each other.

The following steps are original steps for hunting by a golden jackal couple:

1.    Exploring, and advancing in the direction of the target.

2.    Surrounding, and annoying the target up to it no longer moves.

3.    Invasion toward the target.

3.1.2 Algorithm and Mathematical Model

GJO is also a metaheuristic approach based on population. Thus, the primary answer as the first test is uniformly distributed in the solution space:

X0=Xmin+rand(Xmax−Xmin)(7)

where rand indicates a uniform random vector between [0, 1] and the lower and higher range for parameters are represented by Xmin and Xmax.

The matrix is below the Prey matrix, which is obtained by initialization. The first and second best of this matrix is the jackal’s couple.

Prey=[X1,1X2,1⋮Xn,1X1,2X2,2⋮Xn,2⋯⋯⋮⋯X1,dX2,d⋮Xn,d](8)

where Xij indicates the ith prey of jth dimension. In general, the quantity of parameters and existing prey are d and n, respectively. Certain solution variables are defined by the location of the prey. The cost function is introduced into the optimal algorithm to obtain the fitness of predators. The following matrix summarizes the degree of adaptation of each animal:

FOA=[f(X1,1;X1,2;⋯;X1,d)f(X2,1;X2,2;⋯;X2,d)⋮f(Xn,1;Xn,2;⋯;Xn,d)](9)

where the cost function is indicated by f. The first and second fittest define male and female jackals.

3.1.3 Seeking the Prey, or Exploration Phase

In this section, the exploration strategy in the considered algorithm is presented. Jackals can instinctively find prey and pursue it. In some cases, the prey getaways and is not easily obtained. Therefore, the jackals stay and explore for another target.

X1(t)=XM(t)−E.|XM(t)−rl.Prey(t)|(10)

X2(t)=XFM(t)−E.|XFM(t)−rl.Prey(t)|(11)

where Prey(t) represents the location vector of the target, t is the present iteration, and the location of the female and male jackel are described by XFM(t) and XM(t). The updated location of female and male jackel associated with the target is defined by X1(t) and X2(t).

E is Escaping Energy related to prey. It is defined as followed:

E=E0∗E1(12)

whereby, E0 and E1 denote the initial and reducing energy of the target, respectively.

E0=(r−1)∗2(13)

In Eq. (13), r is a random amount in the intervals 0 and 1.

E1=c1∗(1−(tT))(14)

Adding or subtracting this distance to the present location depends on the escape energy of the prey. “rl” indicates the arbitrary numbers’ vector on L'evy distribution basis, which describes the L'evy walk. The motion of prey in L'evy procedure is simulated by the multiplication of prey and “rl”.

rl=0.05∗LF(x)(15)

where the levy flight function is represented by LF, which is obtained as follows:

LF(x)=0.01×(μ×σ)|v(1β)|;σ=(Γ(1+β)×sin⁡(πβ2)Γ(1+β2)×β×(2β−12))1/β(16)

where v, u are arbitrary amounts in the interval 0, 1, β is equal to 1.5. Ultimately, by averaging Eqs. (4) and (5).

X(t+1)=X1(t)+X2(t)2(17)

3.1.4 Surrounding or Abducting Prey or Exploitation Stage

The energy that the prey can expend to escape is reduced by annoying the jackal, afterward, the prey is surrounded by the jackal pair. Attacking and swallowing prey takes place after encirclement. The mathematical expression of hunting manners related to male and female jackals is presented below:

X1(t)=XM(t)−E.|rl.XM(t)−Prey(t)|(18)

X2(t)=XFM(t)−E.|rl.XFM(t)−Prey(t)|(19)

where location is indicated by X1(t) and X2(t) which is related to the target, the energy of Prey’s Escaping is composed of Eq. (6).

Jackals may encounter natural problems during the chase, which prevents them from moving quickly and properly on the way to the prey. The main aim of “rl” is to consider these obstacles’ aftermath [33].

3.1.5 Alteration from One Exploration to Another

Attacking and applying force to the victim is done in the algorithm |E|<1. Briefly, the search in the proposed algorithm starts by generating a population of victims that are candidates to solve the problem. The location of potential prey was estimated by male-female hunting pairs over the ages [34]. Each opponent’s pair-to-pair distance has been updated. To emphasize search and exploitation, the variable E1 was reduced from 1.5 to 0, and when hunting, a pair of Golden Buckthorns moved closer to the victim if E was less than one, and away from the victim if E was greater than one. In the last step, the algorithm ends by providing the final model.

3.2 IGJO Algorithm

This section discusses two enhancements to the IGJO algorithm. The GOA is changed in this context by combining its original structure with the OBL mechanism to present the capability of fully exploration of the solution area and quickly achievement of the ideal value. The chaotic mechanism was enhanced to boost GJO’s exploration ability and solve the GJO’s premature convergence.

By advocating the candidates’ values and their opposing values, the OBL technique delivers a proper candidate selection. The following equation is used to get the opposite values of a candidate:

Y(t+1)=Y¯(t)+Y_(t)+−Y(t)(20)

where, Y¯(t) and Y_(t) denote the solution’s maximum and minimum values After completing the GJO’s exploration phase, the OBL technique is used to keep 40 percent of the domain space determined by the GJO. This phase enables the original domain space to swiftly approach the ideal values and fix out-of-range values.

The second improvement to the IGJO Algorithm here is to utilize a chaotic system as much as possible [35]. All random values, according to the chaotic mechanism, may be characterized as some regular numbers that are related to one another. For the algorithm to give faster convergence, this method generates pseudo-random values rather than random values. The present study uses scale factor as a chaos operator for updating r term of the algorithm from a random term between 0 and 1 into a self-learn parameter. The mathematical model of the scale factor is given below:

α=α_+(α¯−α_)×(1−arccos⁡((−2×init+1)π))(21)

where, in and it represent the iteration number, and the maximum iteration value, respectively, and α¯ and α_ are the topmost and the lowest values of α.

Therefore, by applying this mechanism to the algorithm, the constant value (c1) is achieved as follows:

c1∗=2×α−1(22)

3.3 Validation of Algorithm

The efficiency validation of the suggested IGJO on Algorithm is implemented by carrying out several tests on the first ten benchmark functions from the “CEC-BC-2020 test suite” [36], that have been frequently applied in earlier works [37]. These functions are classified as multimodal, unimodal, hybrid, and composite functions [38]. They are created via combining 15 elementary test functions, namely, Bent Cigar, Discus, High Conditioned Elliptic, Expanded Griewank plus Ackley, Rosenbrock, Griewank, Weierstrass, Expanded Schaf, Rosenbrock, Modified Schwefel, Katsuura, Happy Cat, HGBat, Lunacek bi-Rastrigin, and Rastrigin [39]. The description of the above functions is shown in Fig. 2.

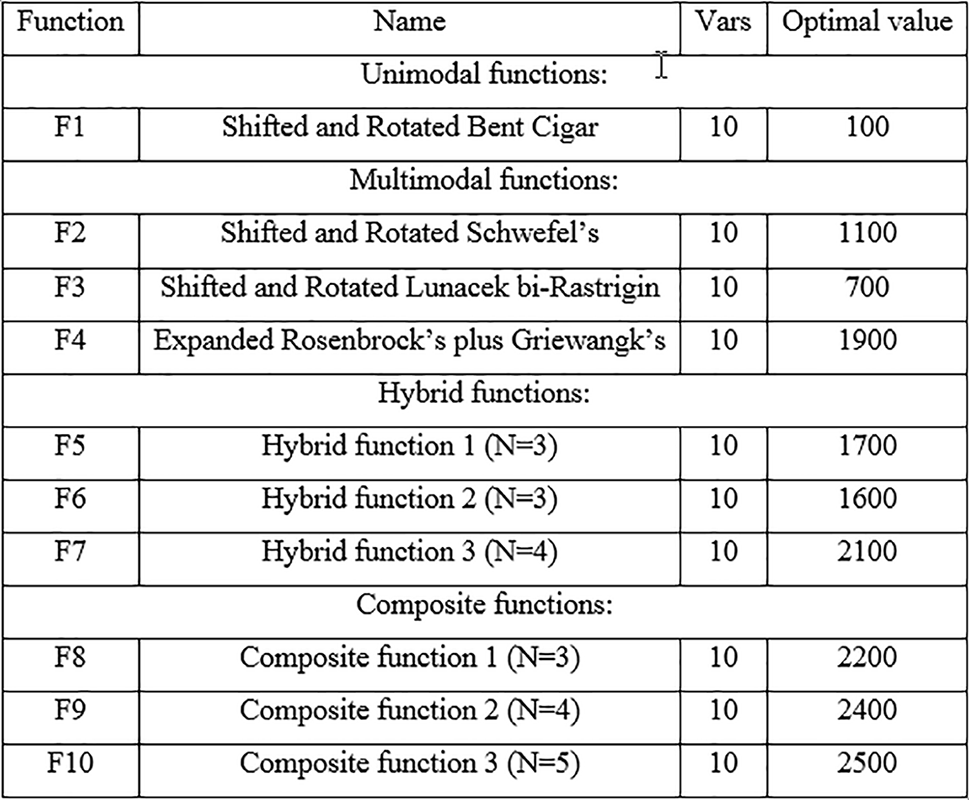
Figure 2: Mathematical definition of the utilized functions from “CEC-BC-2020 test suite” [40], where Vars defines the dimension of the functions

The simulation process was programmed with Matlab R2020a (64 bit) installed on Microsoft WIN10 operating system configuration: Intel core i7-9090H, CPU frequency of 2.60 GHz, 16.0 G memory, RTX 2070 for 8 G. In all algorithms, the maximum population size is set to 60 and the maximum blocking algorithm is set to 200. A total of 4000 performance tests were performed by running each algorithm 20 times on each task. Each function is bounded between −100 and 100. Table 1 shows the parameters and values of the algorithms in the text used in the validation process.

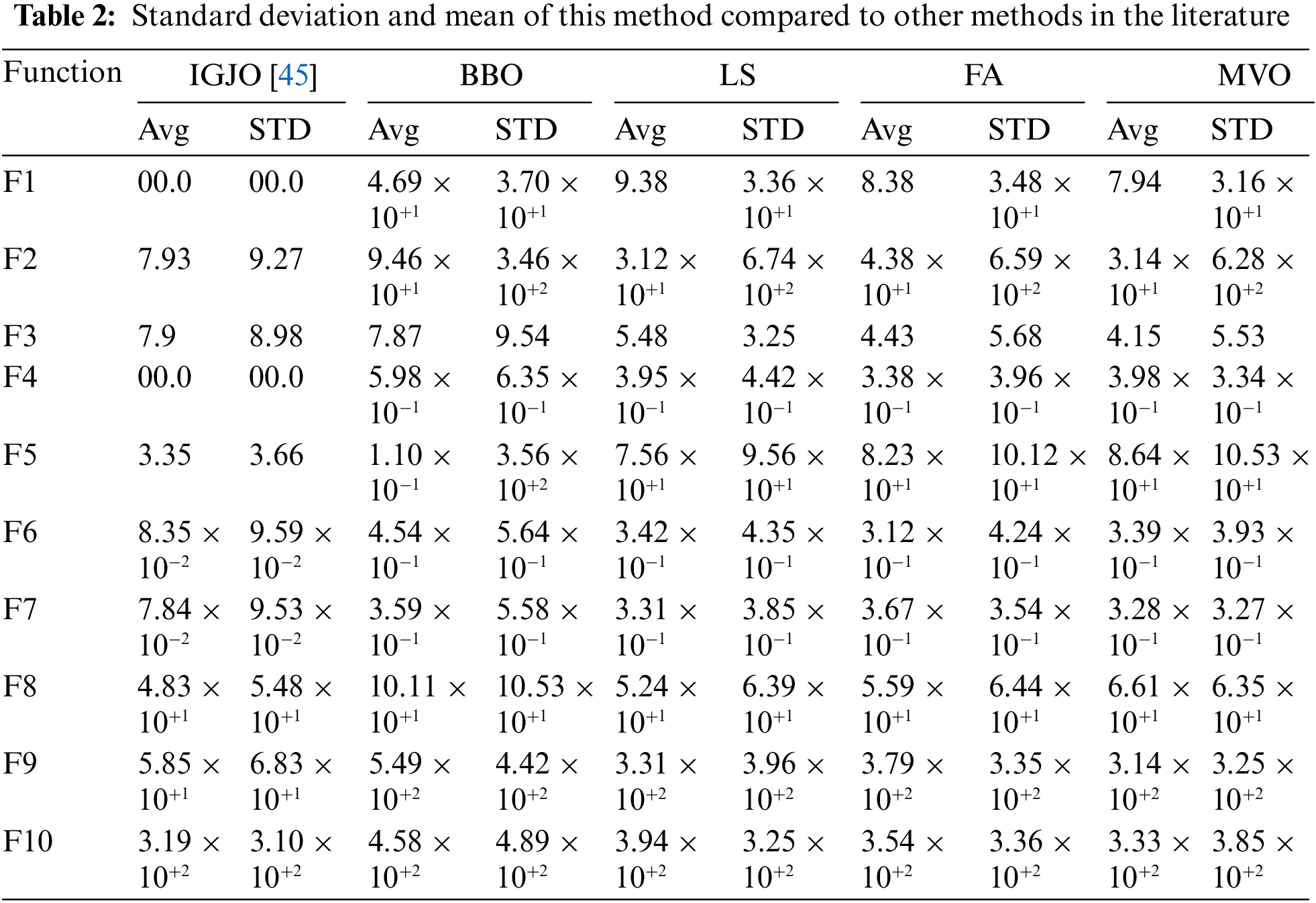
Table 2 shows the standard deviation (STD) and mean (Avg) values of the proposed procedure compared to the 4 methods described above.

Regarding Table 2, it is obvious that the suggested IGJO Algorithm outperforms the MVO, FA, LS, BBO, and the GJO (GJO) on all 10 benchmark functions of the CEC 2020. The suggested IGJO’s better findings demonstrate its increased accuracy in determining the global optimal value. In addition to the accuracy value, utilizing the suggested IGJO algorithm with a lower StD value demonstrates that this technique with a lower standard deviation value produces consistent results across 20 independent runs. This demonstrates that the suggested technique is more precise than the current algorithms in the literature. This motivates us to use the algorithm for optimal chiller loading applications to provide better results.

4  Improved Golden Jackal Optimization Algorithm for Solving OCL Problem

Using the suggested IGJO Algorithm is able to increase the optimization procedure’s efficiency in addressing the optimal chiller loading, as previously proposed and confirmed. As a result, in this section, the approach for using the suggested Golden Jackal Optimization Algorithm to optimize the OCL as a continuous optimization problem has been provided. PLR of the chillers is utilized here as the optimization algorithm’s decision variables. When there are n coolers working in parallel in multiple cooler systems, the actual values of the coolers are used to describe their partial load ratio. After opening up the chiller, the PLR is set from 0.3 to one. When the chiller is turned off, the PLR is 0. The method of directing the limitation to the jackal candidates is formulated below:

PLRl=a+(b−a)×rand,l=1,2⋯n(23)

where, a=0.3, b=0.7, and rand defines a random value from zero to one.

As mentioned before, the main purpose is to minimize the OCL problem (Cwb) subject to the limitations by considering the power consumption of the chiller number i. The following equation shall be taken into account to determine the fitness of each jackal candidate during the OCL:

Fj={1fl+h,ifGj<01fl,ifGj≥0(24)

Gj=∑l=0nPLRl×RTl−CL(25)

If Gj<0, a big penalty value has been provided to the candidate number j to satisfy the cooling load.

5  The Results of the Simulation

In this part, 3 separate case studies are presented, and then they are evaluated to evaluate the suggested IGJOA performance in addressing OCL issues. The data for the first example is taken from [46], whereas, the 2nd and 3rd cases’ data are taken from [47]. Table 3 shows the chiller settings used in the different tests.

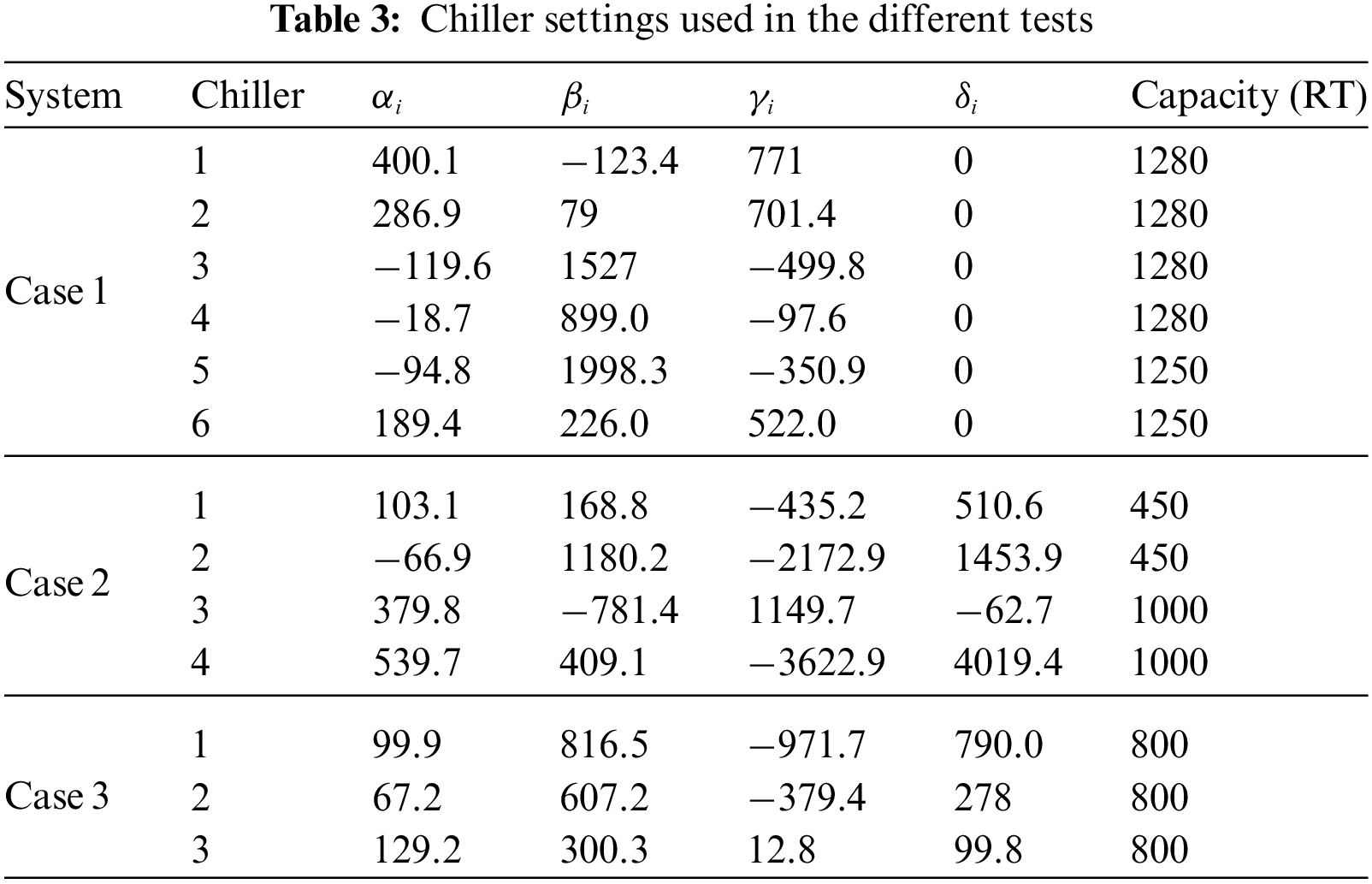
The method uses various simulations with their set parameters to deliver an optimal selection of the decision variables and to get efficient optimal chiller loading. The efficiency assessment has been performed by applying the proposed improved Golden Jackal Optimization Algorithm to the three introduced OCL case studies and comparing it with some related works based on metaheuristic algorithms, including AFS (Artificial Fish Swarm) [48], IWO (Invasive Weed Optimization) [49], BMO (Barnacles Mating Optimizer), and the original GJO (Golden Jackal Optimization) algorithms [50].

The optimization procedure bases the outcomes on an ordinary value of 30 separate runs to create a fair analysis. The algorithm is carried out on the Matlab R2020a environment. Table 4 shows the simulation findings for Case-Study 1.

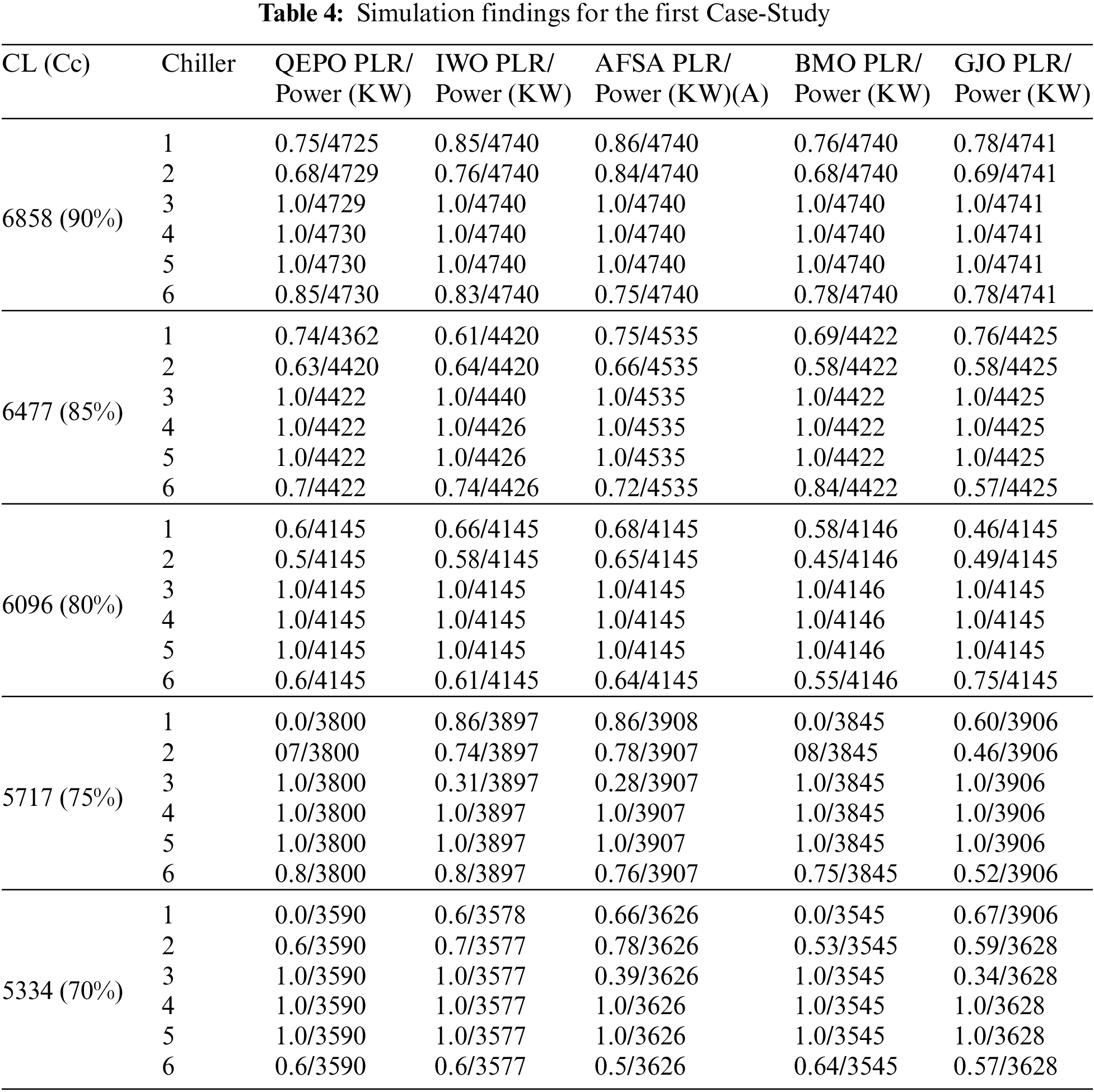
According to the data presented above, the suggested improved golden jackal optimization algorithm provides the greatest performance and the minimum energy consumption for all PLRs. The improved golden jackal optimization algorithm results are displayed in Fig. 3.

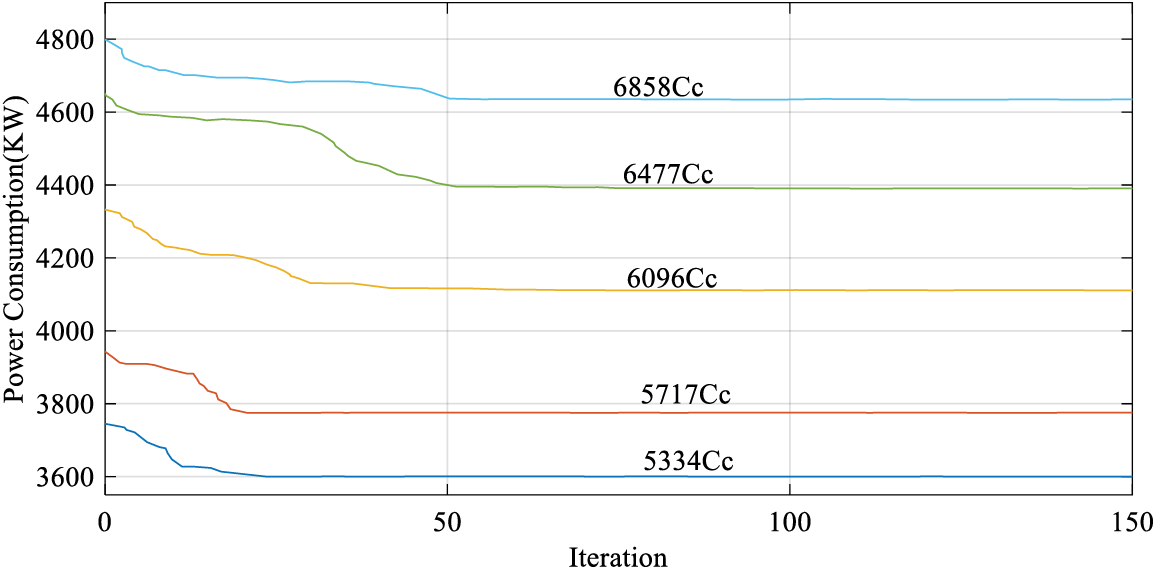
Figure 3: Optimal chiller loading of Case-Study 1 by the proposed improved golden jackal optimization

Table 5 shows the simulation findings for Case-Study 2.

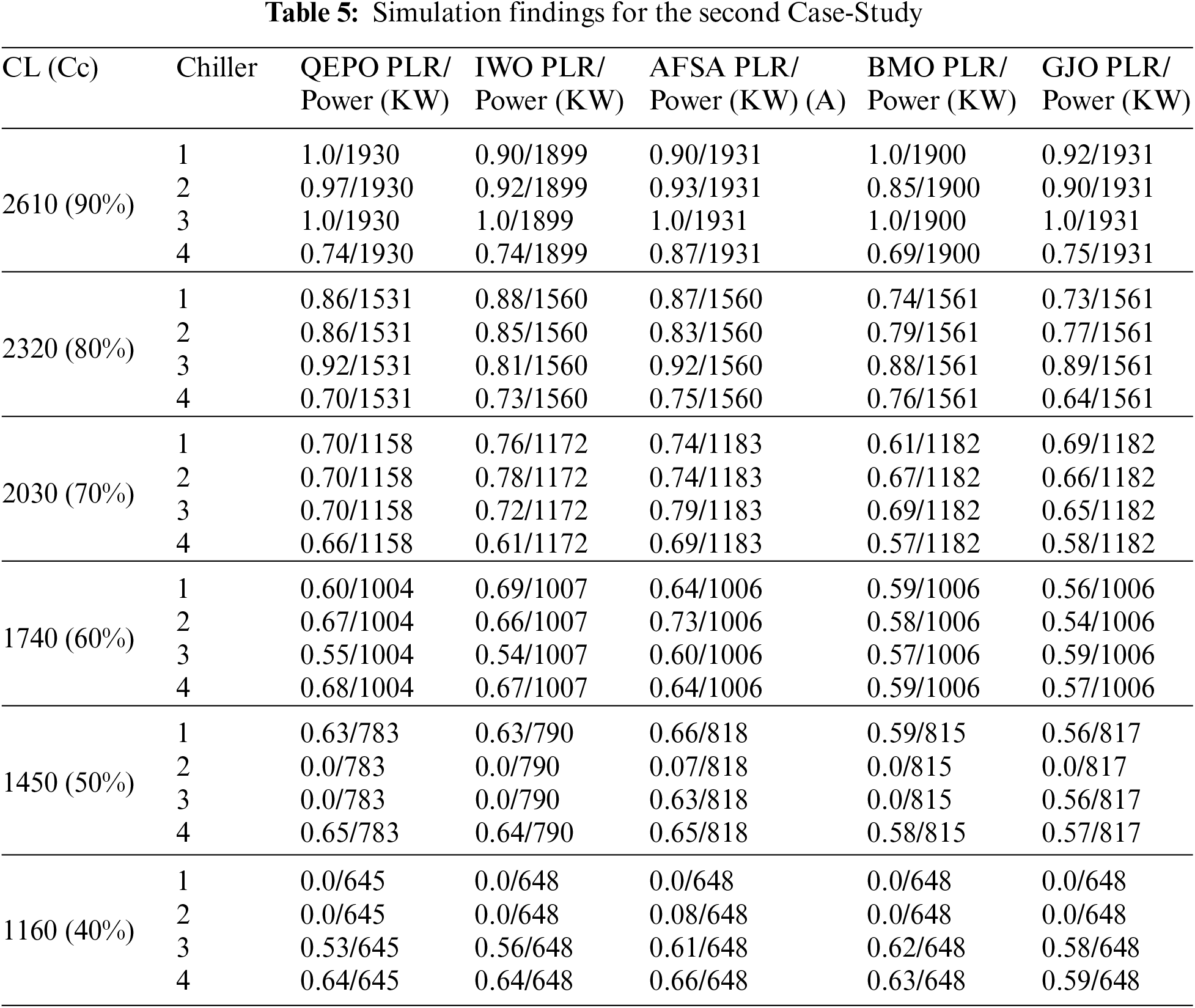
As can be observed in this research study, the suggested improved golden jackal optimization algorithm provides the highest efficiency while consuming the least amount of power for the system [51]. The graphical concept of the diagram, as well as the outcomes of optimization for the improved golden jackal optimization algorithm, is illustrated in Fig. 4.

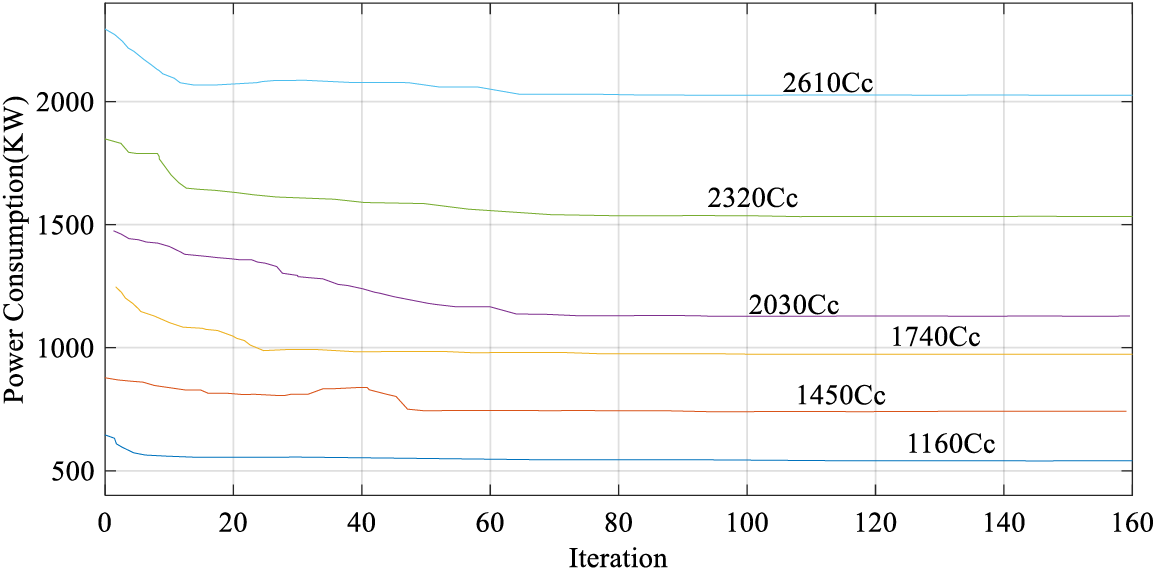
Figure 4: Optimal chiller loading of Case-Study 2 by the proposed improved golden jackal optimization

Table 6 compares the simulation results of the suggested improved golden jackal optimization toward the IWO, AFS, BMO, and the original GJO algorithms for Case-Study 3 [52]. It can be observed that, as shown in the first two case studies, the proposed improved GJO algorithm outperforms other algorithms.

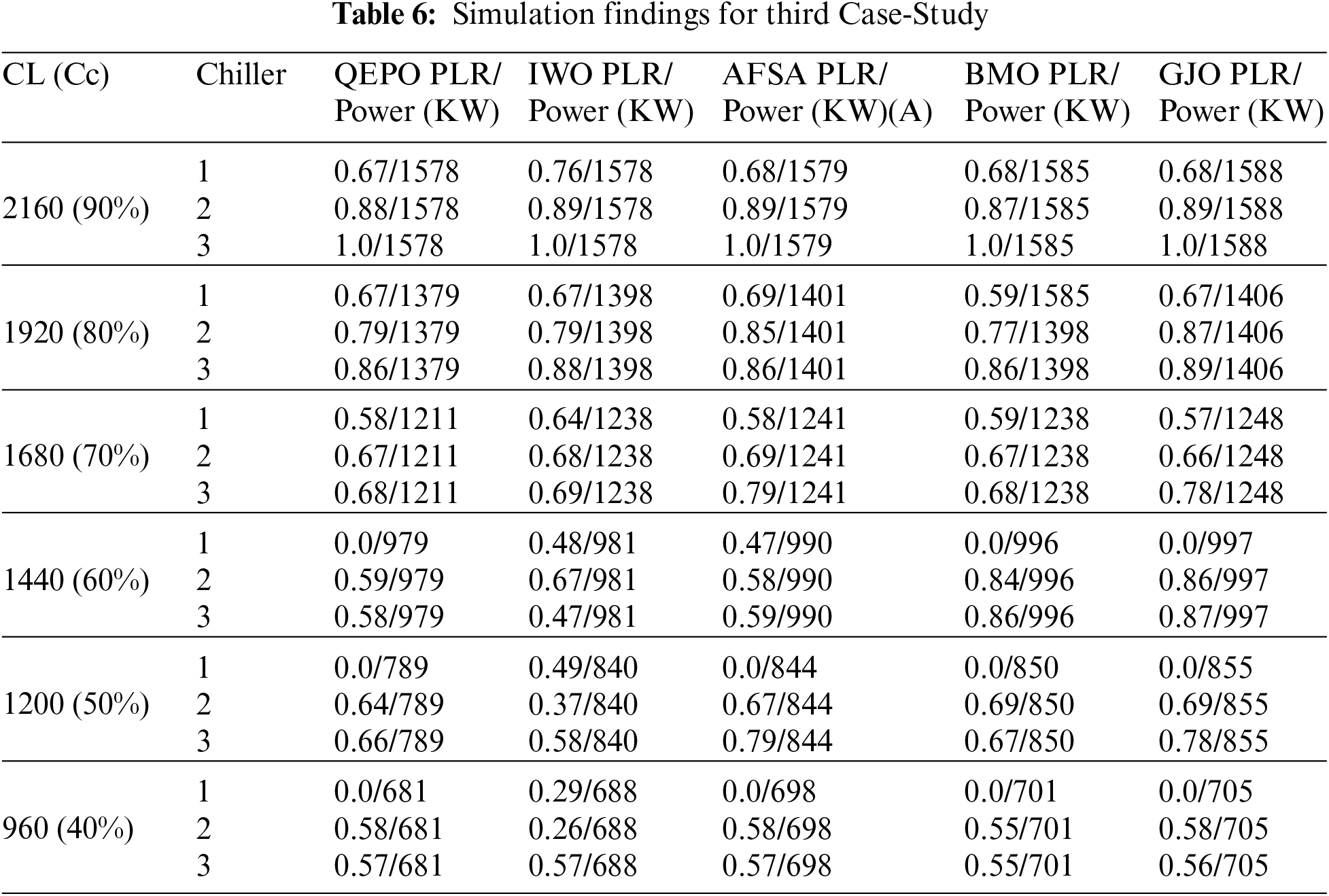
Fig. 5 depicts the optimal chiller loading for the suggested improved golden jackal optimization algorithm in Case-Study 3.

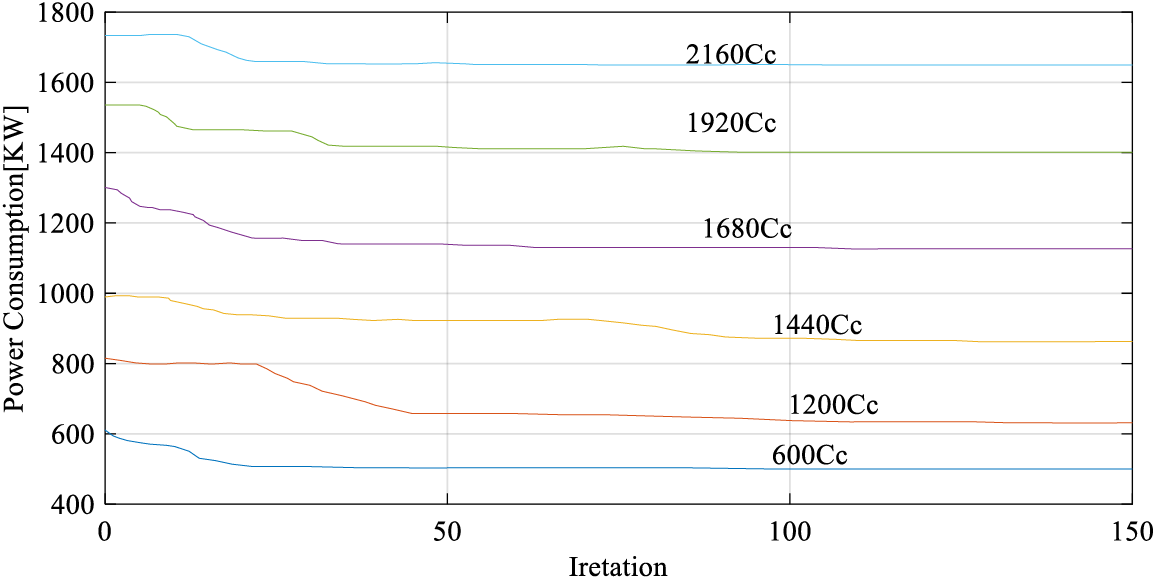
Figure 5: Optimal chiller loading ofCase-Study 3 by the proposed improved golden jackal optimization

The findings of three case studies show that applying the proposed strategy produces quick convergence outcomes. The primary reason for this rapid convergence is the use of the OBL technique and self-learner mechanisms which also provide better global optimal results.

6  Conclusions

In this paper, an IGJO algorithm is suggested to handle the OCL problem. The basic goal of minimizing the energy use of refrigerators is to minimize the LR (load ratio) of each component, which is considered the optimal parameter. To implement the validation, three case studies are authenticated, then a comparison is made between the results and several diverse meta-heuristics, including AFS (Artificial Fish Swarm), IWO (Invasive Weed Optimization), BMO (Barnacles Mating Optimizer), and the original GJO (Golden Jackal Optimization) Algorithms to show the system efficiency. Regarding the results, compared to other current optimal algorithms, the proposed IGJO algorithm can find better or equivalent optimal answers. In addition, the provided program has good convergence ability. The computer test results achieved by setting various parameters demonstrate the elasticity and stability of the IGJO algorithm. In summary, the IGJO algorithm can become an effective and appropriate technique for optimizing cooler load problems, which can be applied to other optimization problems.

Acknowledgement: We would like to express our gratitude to all those who contributed to the completion of this research paper. We are also grateful to the participants who took part in the study and provided valuable data and insights. We would like to thank our colleagues and friends who provided encouragement and constructive feedback during the writing process.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Na Dong; data collection, analysis and interpretation of results: Xiao Yang; draft manuscript preparation: Nasser Yousefi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Aghajani, G., Ghadimi, N. (2018). Multi-objective energy management in a micro-grid. Energy Reports, 4, 218–225. [Google Scholar]

2. Zheng, Z. X., Li, J. Q. (2018). Optimal chiller loading by improved invasive weed optimization algorithm for reducing energy consumption-sciencedirect. Energy & Buildings, 161, 80–88. [Google Scholar]

3. Lin, C. M., Tseng, K. Y., Lin, S. F. (2020). Optimal chiller loading using modified artificial bee colony algorithm. Sensors and Materials, 32(7), 2387. [Google Scholar]

4. Hamian, M., Darvishan, A., Hosseinzadeh, M., Lariche, M. J., Ghadimi, N. et al. (2018). A framework to expedite joint energy-reserve payment cost minimization using a custom-designed method based on mixed integer genetic algorithm. Engineering Applications of Artificial Intelligence, 72, 203–212. [Google Scholar]

5. Bagheri, M., Nurmanova, V., Abedinia, O., Naderi, M. S., Naderi, M. S. et al. (2018). A novel wind power forecasting based feature selection and hybrid forecast engine bundled with honey bee mating optimization. 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe, pp. 1–6. Palermo, Italy. [Google Scholar]

6. Bahmanyar, D., Razmjooy, N., Mirjalili, S. (2022). Multi-objective scheduling of IoT-enabled smart homes for energy management based on Arithmetic Optimization Algorithm: A Node-RED and NodeMCU module-based technique. Knowledge-Based Systems, 247, 108762. [Google Scholar]

7. Bolufé-Röhler, A., Chen, S. (2020). A multi-population exploration-only exploitation-only hybrid on cec-2020 single objective bound constrained problems. 2020 IEEE Congress on Evolutionary Computation (CEC), pp. 1–8. Glasgow, UK. [Google Scholar]

8. Cai, W., Mohammaditab, R., Fathi, G., Wakil, K., Ebadi, A. G. et al. (2019). Optimal bidding and offering strategies of compressed air energy storage: A hybrid robust-stochastic approach. Renewable Energy, 143, 1–8. [Google Scholar]

9. Cao, Y., Li, Y., Zhang, G., Jermsittiparsert, K., Razmjooy, N. (2019). Experimental modeling of PEM fuel cells using a new improved seagull optimization algorithm. Energy Reports, 5, 1616–1625. [Google Scholar]

10. Cao, Y., Wu, Y., Fu, L., Jermsittiparsert, K., Razmjooy, N. (2019). Multi-objective optimization of a PEMFC based CCHP system by meta-heuristics. Energy Reports, 5, 1551–1559. [Google Scholar]

11. Gollou, A. R., Ghadimi, N. (2017). A new feature selection and hybrid forecast engine for day-ahead price forecasting of electricity markets. Journal of Intelligent Fuzzy Systems, 32(6), 4031–4045. [Google Scholar]

12. Chang, Y. C., Chan, T. S., Lee, W. S. (2010). Economic dispatch of chiller plant by gradient method for saving energy. Applied Energy, 87(4), 1096–1101. [Google Scholar]

13. Ghadimi, N. (2015). An adaptive neuro-fuzzy inference system for islanding detection in wind turbine as distributed generation. Complexity, 21(1), 10–20. [Google Scholar]

14. Chopra, N., Ansari, M. M. (2022). Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Systems with Applications, 198, 116924. [Google Scholar]

15. Cuevas, E., Fausto, F., González, A. (2020). New advancements in swarm algorithms: Operators and applications. In: Intelligent systems reference library, pp. 139–159. [Google Scholar]

16. Dehghani, M., Ghiasi, M., Niknam, T., Kavousi-Fard, A., Shasadeghi, M. et al. (2020). Blockchain-based securing of data exchange in a power transmission system considering congestion management and social welfare. Sustainability, 13(1), 1. [Google Scholar]

17. Eslami, M., Moghadam, H. A., Zayandehroodi, H., Ghadimi, N. (2018). A new formulation to reduce the number of variables and constraints to expedite SCUC in bulky power systems. Proceedings of the National Academy of Sciences, India Section A: Physical Sciences, 89, 311–321. [Google Scholar]

18. Fei, X., Xuejun, R., Razmjooy, N. (2019). Optimal configuration and energy management for combined solar chimney, solid oxide electrolysis, and fuel cell: A case study in Iran. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 45, 1–21. [Google Scholar]

19. Firouz, M. H., Ghadimi, N. (2016). Concordant controllers based on FACTS and FPSS for solving wide-area in multi-machine power system. Journal of Intelligent Fuzzy Systems, 30(2), 845–859. [Google Scholar]

20. Geem, Z. W. (2011). Solution quality improvement in chiller loading optimization. Applied Thermal Engineering, 31(10), 1848–1851. [Google Scholar]

21. Chen, C. L., Chang, Y. C., Chan, T. S. (2014). Applying smart models for energy saving in optimal chiller loading. Energy and Buildings, 68, 364–371. [Google Scholar]

22. Gheydi, M., Nouri, A., Ghadimi, N. (2016). Planning in microgrids with conservation of voltage reduction. IEEE Systems Journal, 12(3), 2782–2790. [Google Scholar]

23. Sohrabi, F., Nazari-Heris, M., Mohammadi-Ivatloo, B., Asadi, S. (2018). Optimal chiller loading for saving energy by exchange market algorithm. Energy and Buildings, 169, 245–253. [Google Scholar]

24. Lee, W. S., Lin, L. C. (2009). Optimal chiller loading by particle swarm algorithm for reducing energy consumption. Applied Thermal Engineering, 29(8–9), 1730–1734. [Google Scholar]

25. Ardakani, A. J., Ardakani, F. F., Hosseinian, S. (2008). A novel approach for optimal chiller loading using particle swarm optimization. Energy and Buildings, 40(12), 2177–2187. [Google Scholar]

26. Lee, W. S., Chen, Y. T., Kao, Y. (2011). Optimal chiller loading by differential evolution algorithm for reducing energy consumption. Energy and Buildings, 43(2–3), 599–604. [Google Scholar]

27. Guo, Y., Dai, X., Jermsittiparsert, K., Razmjooy, N. (2020). An optimal configuration for a battery and PEM fuel cell-based hybrid energy system using developed Krill herd optimization algorithm for locomotive application. Energy Reports, 6, 885–894. [Google Scholar]

28. Liu, J., Chen, C., Liu, Z., Jermsittiparsert, K., Ghadimi, N. (2020). An IGDT-based risk-involved optimal bidding strategy for hydrogen storage-based intelligent parking lot of electric vehicles. Journal of Energy Storage, 27, 101057. [Google Scholar]

29. Meng, Q., Liu, T., Su, C., Niu, H., Hou, Z. et al. (2020). A single-phase transformer-less grid-tied inverter based on switched capacitor for PV application. Journal of Control, Automation and Electrical Systems, 31(1), 257–270. [Google Scholar]

30. Mirjalili, S., Mirjalili, S. M., Hatamlou, A. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Computing and Applications, 27(2), 495–513. [Google Scholar]

31. Mohamed, A. K., Hadi, A. A., Mohamed, A. W. (2020). Generalized adaptive differential evolution algorithm for solving CEC, 2020 benchmark problems. 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), pp. 391–396. Giza, Egypt. [Google Scholar]

32. Mohamed, A. W., Hadi, A. A., Mohamed, A. K., Awad, N. H. (2020). Evaluating the performance of adaptive gainingsharing knowledge based algorithm on CEC 2020 benchmark problems. 2020 IEEE Congress on Evolutionary Computation (CEC), pp. 1–8. Glasgow, UK. [Google Scholar]

33. Ramezani, M., Bahmanyar, D., Razmjooy, N. (2021). A new improved model of marine predator algorithm for optimization problems. Arabian Journal for Science and Engineering, pp. 1–24. Glasgow, UK. [Google Scholar]

34. Salgotra, R., Singh, U., Saha, S., Gandomi, A. H. (2020). Improving cuckoo search: Incorporating changes for CEC, 2017 and CEC, 2020 benchmark problems. 2020 IEEE Congress on Evolutionary Computation (CEC), pp. 1–7. Glasgow, UK. [Google Scholar]

35. Simon, D. (2008). Biogeography-based optimization. IEEE Transactions on Evolutionary Computation, 12(6), 702–713. [Google Scholar]

36. Chan, T. S., Chang, Y. C., Huang, J. H. (2017). Application of artificial neural network and genetic algorithm to the optimization of load distribution for a multiple-type-chiller plant. Building Simulation, 10(2), 711–722. [Google Scholar]

37. Sulaiman, M. H., Ibrahim, H., Daniyal, H., Mohamed, M. R. (2014). A new swarm intelligence approach for optimal chiller loading for energy conservation. Procedia-Social and Behavioral Sciences, 129, 483–488. [Google Scholar]

38. Sulaiman, M. H., Mustaffa, Z. (2022). Optimal chiller loading solution for energy conservation using Barnacles Mating Optimizer algorithm. Results in Control and Optimization, 7, 100109. [Google Scholar]

39. Sun, L., Han, X. F., Xu, Y. P., Razmjooy, N. (2021). Exergy analysis of a fuel cell power system and optimizing it with Fractional-order Coyote Optimization Algorithm. Energy Reports, 7, 7424–7433. [Google Scholar]

40. Tian, M. W., Yan, S. R., Han, S. Z., Nojavan, S., Jermsittiparsert, K. et al. (2020). New optimal design for a hybrid solar chimney, solid oxide electrolysis and fuel cell based on improved deer hunting optimization algorithm. Journal of Cleaner Production, 249, 119414. [Google Scholar]

41. Viktorin, A., Senkerik, R., Pluhacek, M., Kadavy, T., Zamuda, A. (2020). DISH-XX solving CEC2020 single objective bound constrained numerical optimization benchmark. 2020 IEEE Congress on Evolutionary Computation (CEC), pp. 1–8. Glasgow, UK. [Google Scholar]

42. Wang, Z., Wang, Q., Zhang, Z., Razmjooy, N. (2021). A new configuration of autonomous CHP system based on improved version of marine predators algorithm: A case study. International Transactions on Electrical Energy Systems, 31(4), e12806. [Google Scholar]

43. Mohammadbeigi, A., Maroosi, A., Hemmati, M. (2022). Optimal chiller loading for energy conservation using a hybrid whale optimization algorithm based on population membrane systems. International Journal of Modelling & Simulation, 48(1), 101–116. [Google Scholar]

44. Yang, Z., Liu, Q., Zhang, L., Dai, J., Razmjooy, N. (2020). Model parameter estimation of the PEMFCs using improved barnacles mating optimization algorithm. Energy, 212, 118738. [Google Scholar]

45. Yu, D., Ghadimi, N. (2019). Reliability constraint stochastic UC by considering the correlation of random variables with Copula theory. IET Renewable Power Generation, 13(14), 2587–2593. [Google Scholar]

46. Yu, D., Wang, Y., Liu, H., Jermsittiparsert, K., Razmjooy, N. (2019). System identification of PEM fuel cells using an improved Elman neural network and a new hybrid optimization algorithm. Energy Reports, 5, 1365–1374. [Google Scholar]

47. Yuan, Z., Wang, W., Wang, H., Ghadimi, N. (2020). Probabilistic decomposition-based security constrained transmission expansion planning incorporating distributed series reactor. IET Generation, Transmission Distribution, 14(17), 3478–3487. [Google Scholar]

48. Zhang, G., Xiao, C., Razmjooy, N. (2020). Optimal parameter extraction of PEM fuel cells by meta-heuristics. International Journal of Ambient Energy, 43, 1–10. [Google Scholar]

49. Zheng, Z. X., Li, J. Q. (2018). Optimal chiller loading by improved invasive weed optimization algorithm for reducing energy consumption. Energy and Buildings, 161, 80–88. [Google Scholar]

50. Zheng, Z. X., Li, J. Q., Duan, P. Y. (2019). Optimal chiller loading by improved artificial fish swarm algorithm for energy saving. Mathematics and Computers in Simulation, 155, 227–243. [Google Scholar]

51. Yuan, Z., Wang, W., Wang, Q., Y., H., Navid, R. (2021). New approaches for regulation of solid oxide fuel cell using dynamic condition approximation and STATCOM. International Transactions on Electrical Energy Systems, 31(2), e12756. [Google Scholar]

52. Yuan, Z., Wang, W. Q., Cheng, J., Navid, R. (2021). Interval linear quadratic regulator and its application for speed control of DC motor in the presence of uncertainties. ISA Transactions, 125, 252–259. [Google Scholar]