Reactive Power Flow Convergence Adjustment Based on Deep Reinforcement Learning

1  Introduction

The power flow calculation is essential to solve the nonlinear equation system according to the known system variables and obtain the state variables in the operation mode. The calculation results have two cases: convergence and non-convergence. With the multi-energy grid connection of modern power grids, the interconnection of transmission and distribution networks in the form of AC and DC, the power electronics reform of the core equipment of the source-network-load, and the high proportion of new energy connected to the system, the initial operation mode of the power system is often difficult to converge. The reasons for the non-convergence can be divided into two categories: one is that the power flow calculation has a solution, but the numerical solution cannot be obtained due to the algorithm defects, and the algorithm needs to be improved; the other is that the demand for power supply and load cannot be balanced due to the control variables improperly arranged in the system, which is called the problem of unsolvable power flow [1]. This paper mainly studies the second type of non-convergence problem.

At present, power grid analysts mainly rely on manual processes to adjust the initial operating conditions of the operation mode to solve the power flow non-convergence. Obviously, due to the expansion of the power grid scale, trial and error adjustment is difficult, inefficient, and labor-consuming. With the gradual application of intelligent algorithms in all aspects of the power system, it is increasingly advantageous to replace human labor with intelligent analysis methods. The convergence adjustment work of the power flow urgently needs to be combined with intelligent algorithms to provide operators with feasible strategies, thereby liberating the labor force.

Many scholars have researched power flow convergence. The intermediate variation law in the iterative process is studied and an index for judging the power flow convergence calculation was established in literature [2]. Literature [3] converted all the PQ nodes of high voltage levels in the system into PV nodes and makes corresponding reactive power compensation according to the power shortage at the original PQ nodes after the conversion. Literature [4,5] reasonably used the rotating reserve of units in the system to balance between load and generator. Literature [6] adopted a new method of system’s concept to achieve safe and economic hourly generation scheduling. Literature [7] studied the power flow convergence adjustment method based on a nonlinear programming model, introduces a set of slack variables into the power flow equation and transforms it into a nonlinear programming model with the smallest sum of squares, and constructs a reactive power flow based on the electrical distance between nodes. Literature [8–10] upgraded the Newton method to improve the convergence and convergence speed of the algorithm. It is a pity that none of the above-mentioned literature can realize automatic adjustment of power flow convergence. Literature [11,12] established an ill-conditioned power flow automatic adjustment model based on the interior point method according to the ill-conditioned characteristics of power flow and transforms the power flow convergence problem into an optimal power flow problem to minimize the system load shedding. The point method takes many constraints into account and it is difficult to set the initial value. The shear load in the calculation result cannot be generally guaranteed to be 0. Literature [13,14] proposed a two-stage optimization method to divide a complex power system into several regions to achieve reliable, safe, and optimal generator scheduling. The non-convergence problem of power flow caused by the unreasonable distribution of reactive power based on the power flow minimization was studied in literature [15]. Literature [16] proposed an improved method for active power flow adjustment in safety-constrained economic dispatch. Literature [17] used the mixed integer nonlinear programming optimization method to realize the optimal supply of electricity and heat load. Literature [18] defined the calculation rules of reactive power flow. The reactive power imbalance of the nodes after the power flow calculation of the power system is connected to the surrounding reactive power sources according to the distribution factor. However, once the power flow calculation in the actual system does not converge, it will reach the upper limit of the number of calculations, and the power flow results at this time have diverged. Literature [19] decoupled AC and DC power flow from active and reactive power flow respectively and designs a transmission line and transformer model with a virtual midpoint. Based on this model, the convergence adjustment of power flow is realized.

In recent years, artificial intelligence algorithms have been widely used in many fields of power systems and studies on power flow adjustment have begun to combine with intelligent algorithms. Based on the improved DC power flow algorithm, the quantitative index of active and reactive power is set and the convergence is adjusted through an intelligent algorithm in literature [20]. Literature [21] developed an intelligent grid operation mode layout and decision support system. Literature [22] used deep reinforcement learning to search for the optimal switch for power flow change in the distribution network, which improves the reliability of power flow in the distribution network. Literature [23] proposed a method for adjusting the cross-section flow based on reinforcement learning. Literature [24] proposed an automatic power flow adjustment method relying on knowledge and experience derived from the experience playback function of deep reinforcement learning. Literature [25,26] used transfer reinforcement learning and swarm reinforcement learning and realizes real-time generation scheduling and reactive power optimization.

Aiming at the non-convergence problem of reactive power flow, this paper establishes a reactive power flow convergence adjustment model based on deep reinforcement learning. First, the provincial network is taken as the research object through network simplification and equivalence. The 500 kV PQ nodes with parallel compensation in the low-voltage side of the system are converted to PV nodes, to get the index of reactive power non-convergence. By reasonably designing the reward value and tuning the network parameters in the model, the power flow convergence adjustment strategy is required. Finally, the effectiveness of the algorithm is verified by an actual large-scale system.

The main sections are organized as follows: Section 1 gives a literature review and background introduction. Section 2 describes influencing factors and adjustment measures of power flow convergence. Section 3 introduces deep reinforcement learning and Section 4 provides a reactive power flow adjustment model. The simulation results and discussions are presented in Section 5. Finally, Section 6 summarizes the paper.

2  Influencing Factors and Adjustment Measures of Power Flow Convergence

2.1 Factors for Non-Convergence of Power Flow Calculation

The essence of power flow convergence is that the power system balances the active power and reactive power. All load nodes can obtain the corresponding power from the power source through the network topology. Currently, the Newton-Raphson method is often used in power flow calculation in the power industry. Taking the polar coordinate form of the New Pull method as an example, the balance equations of active power and reactive power of each node in the system are shown in Eqs. (1) and (2).

Pi.gen−Pi.load=Ui∑j=1nUj(Gijcos⁡θij+Bijsin⁡θij)(1)

Qi.gen−Qi.load=Ui∑j=1nUj(Gijsin⁡θij−Bijcos⁡θij)(2)

where Pi.gen and Qi.gen are the active and reactive power output at node i; Pi.load and Qi.load are the active and reactive load at node i; Ui and Uj are the voltage amplitude at node i and node j of the current system; Gij and Bij are the branch admittance value between node i and node j; and θij is the phase angle difference between node i and node j.

In practical engineering, the factors that affect the results of power flow calculation are as follows:

1) Unreasonable data

For power flow calculation of a large power grid, the simulation software needs to write a lot of data and it is easy to cause data mis-input or omission. In actual operation, the transformation ratio of the transformer, parameters of the transmission line, and small switch branch are prone to such problems, resulting in non-convergence of power flow calculations.

2) Excessive node voltage offset

The Newton-Raphson method takes the offset of the node state quantity as the convergence criterion. Generally, the voltage at the node in the convergent power flow section will not have a large offset from the reference value. When there are too many nodes with too high or too low voltage in the system, the convergence is poor. Adjusting the power flow at this time is likely to cause non-convergence.

3) Balance unit output

When calculating the power flow of any power system, it is necessary to arrange a unit to balance the power in the system. In the actual system, the generator output is limited. When its active or reactive power output exceeds the allowable range, the power flow calculation does not converge.

4) Reactive power distribution

The long-distance transmission of reactive power will cause an increase in network loss, which is not conducive to the economy and makes it difficult to balance the system power. Reactive power needs to be balanced on-site according to zoning conditions and voltage levels. Reactive power shortages are prone to occur in DC transmission converter stations, regional substations, new energy access nodes, and tie lines between different regions, resulting in power flow non-convergence.

2.2 Power Flow Adjustment Measures

In the simulation platform, operators divide the transmission network into two voltage levels: 500 and 220 kV. The 220 kV part is the provincial transfer area, obtaining the power from the 500 kV grid through substations. For the convergence adjustment of the actual power grid system, the active power is usually adjusted before the reactive power. Since the active power of PV and PQ nodes are known quantities and the active power loss of the transmission network is small, the active power is easily balanced. The active load and unit output of the 220 kV subarea can be counted, and the active power output of the generator can be adjusted according to the exchange relationship between the active power flow in the 500 kV area and each subarea. When the output of the balance unit is within the allowable range, the active power adjustment ends.

The adjustment of reactive power is more flexible. The load can not only obtain reactive power from the generator but also obtain the compensation amount from components, such as capacitors, condensers, and flexible AC transmission devices. In addition, by adjusting the transformer ratio in the system, the switching series reactance can change the reactive power distribution. This paper mainly switches the reactive power compensation device to maintain the reactive power flow convergence. The actual reactive power compensation of the transmission network is placed at the node of 500 kV area. For the problem of power flow non-convergence caused by reactive power, generally, the node voltage with a large reactive power deviation in power flow calculation can be kept constant, so that the power flow calculation is converged. Then, the reactive power compensation device is switched according to the reactive power size of the node needing compensation.

3  Deep Reinforcement Learning

3.1 Reinforcement Learning

In Reinforcement Learning, the agent takes different behaviors, interacts with the environment in multiple iterations to obtain corresponding numerical rewards, and finally determines the strategy according to the reward value in the model after training. The elements of reinforcement learning mainly include agent, environment, actions, states, and reward values [27,28], which belong to the typical Markov Decision Process. The algorithmic decision process is shown in Fig. 1.

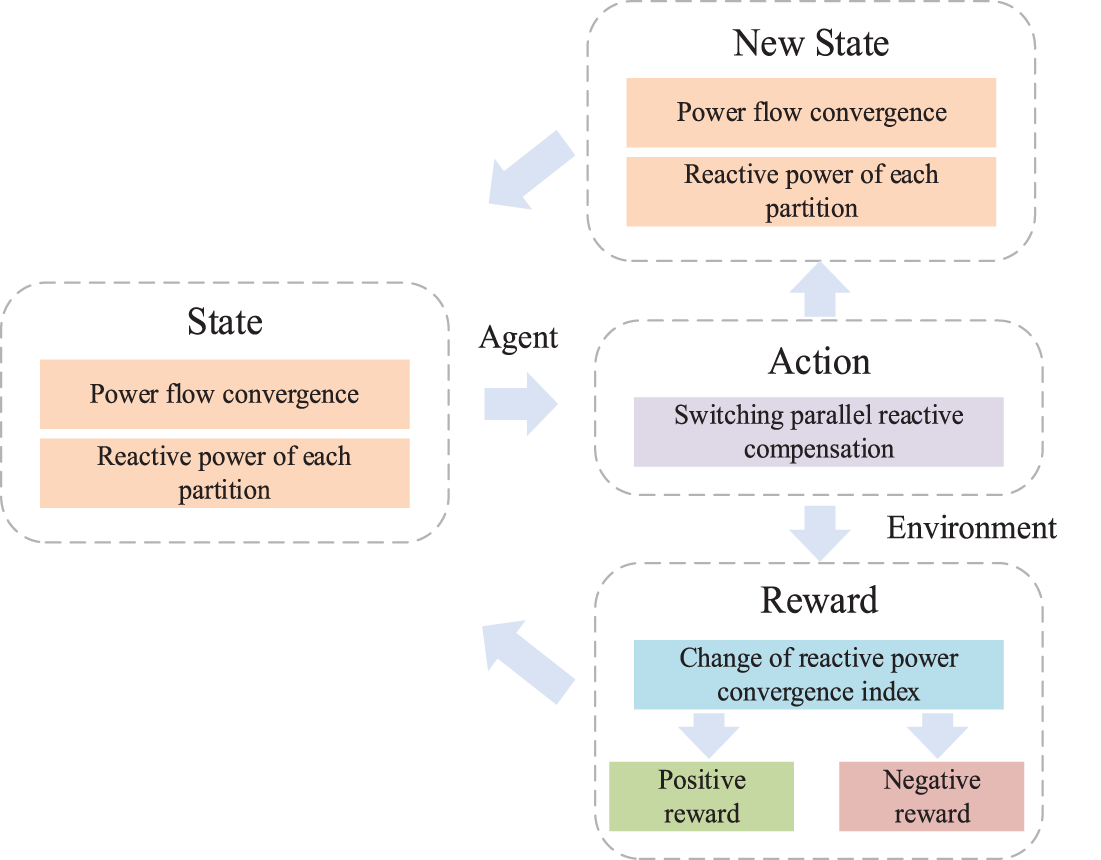
Figure 1: Decision process of reinforcement learning algorithm

In the decision-making process, the agent will enter a new state after an action and obtain the reward value of the action. The future state of the Markov Decision Process only depends on the current system state. Assuming that S={S1,S2,S3,…,Si} is progressively changing, the probability function of the Markov Decision Process is shown in Eq. (3).

P(Si|Si−1)=P(Si|S1,S2,…,Si−1)(3)

where P(Si|Si−1) is the probability from state Si−1 to state Si; and P(Si|S1,S2,…,Si−1) is the probability from state S to state Si.

In the Markov decision-making process, the goal of the agent’s action is to reach the desired state and obtain the maximum total benefit. The learning process of the agent is carried out in the interaction with the environment and the total benefit is shown in Eq. (4).

Gi=ri+1+μri+2+μ2ri+3+⋅⋅⋅=∑j=0nμjri+j+1(4)

where Gi is the benefit of the current action; ri+j+1 is the reward value at the state i+j+1; and μ is the discount factor of the reward value.

In the initial state, the selection of any action is a probabilistic event. When the action reward value is determined, a value function is defined to describe the expected value of the future action reward under a certain strategy. The value function can usually be expressed by mathematical expectations, as shown in Eq. (5).

ν(s)=E(Gi|Si=s)=∑i=1nGiP(Si|Si−1)(5)

where ν(s) is the value of the strategy.

In this paper, Q-Learning is used as the reinforcement learning algorithm. The Q-Learning algorithm determines the value of the state-action function based on the temporal difference principle. The core equation of the algorithm is shown in Eq. (6).

qi+1(s,a)=(1−α)qi(s,a)+α[ r(s,a)+μmaxa′(qis′,a′) ](6)

where qi+1(s,a) is the updated state-action function value; qi(s,a) is the state-action function value in the current state; r(s,a) is the reward value obtained by the current action; maxa′qi(s′,a′) is the maximum state function value that can be obtained from future actions after taking the current action; and α is the learning rate.

3.2 Deep Q Network

The reinforcement learning algorithm needs to generate a corresponding state-action function table and guide the agent action according to the values in it. In the power flow adjustment of large power grids, the number of state variables and control variables in the system is large. Reinforcement learning will generate a high-dimensional state-behavior function table, which makes computation difficult. Deep Q Network is a deep reinforcement learning algorithm. Based on reinforcement learning, a deep neural network is introduced to fit the state-action function through the deep neural network, as shown in Fig. 2.

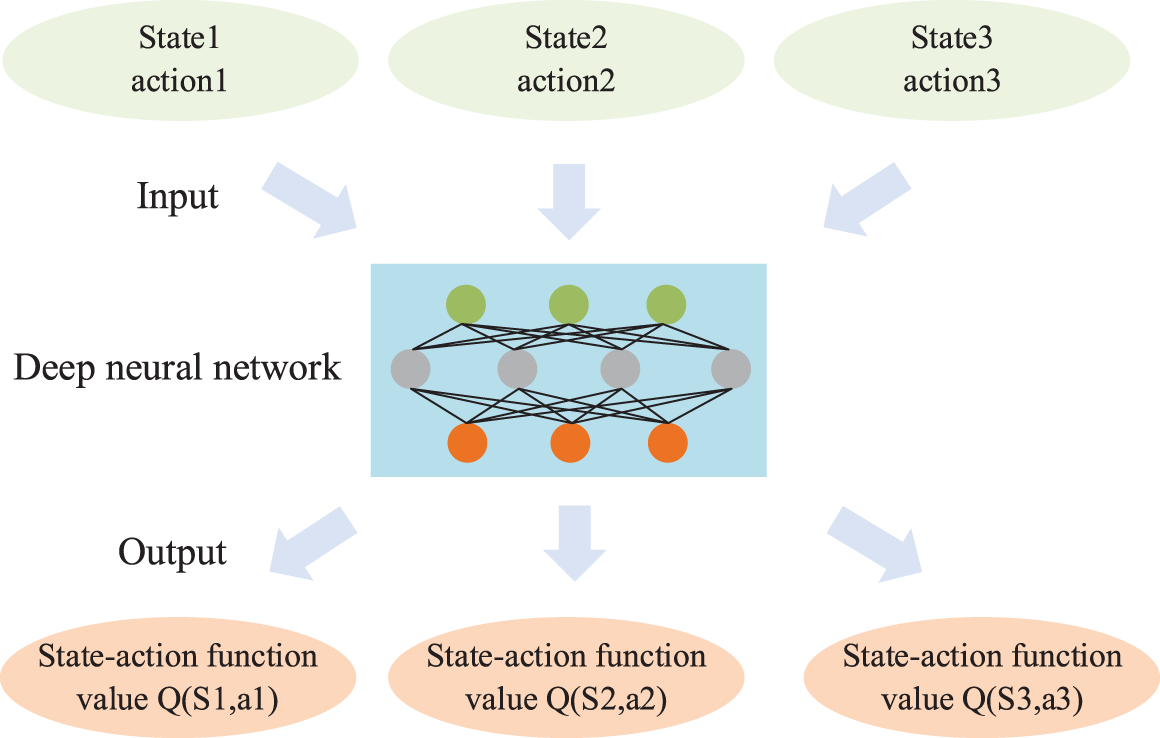
Figure 2: Deep network of DQN algorithm

The deep neural network can solve the dimension disaster problem of reinforcement learning and the expression to obtain the state-behavior function value is shown in Eq. (7).

q(s,a)=ω1s+ω2a+b(7)

where ω1, ω2 and b are the parameters and biases of the deep neural network.

It can be seen from Eq. (7) that when the state and action are determined, the network parameters determine the accuracy of the prediction network. After using the deep neural network to approximate the state-behavior function value, the loss function is used to compare with the actual value to determine the rationality of the network parameters. The loss function of deep reinforcement learning is shown in Eq. (8).

Loss=[ r(s,a)+μmaxa′qi(s′,a′;θ)−qi(s,a;θ) ]2(8)

where Loss is the loss function value; and θ is the network parameter set.

The smaller the loss function is, the more reasonable the network parameters and the better the training effect of the deep neural network is. The samples trained in the deep reinforcement learning algorithm are collected by Eq. (6).

4  Reactive Power Flow Adjustment Model Based on Improved DQN

4.1 Network Simplified Equivalent

1) Network simplified equivalent

In the modern power system, there are tie lines between power grids in different provinces. Therefore, using the complete power grid structure as a deep reinforcement learning environment will lower the algorithm’s efficiency. The existing network structure should be treated equivalently and only the provincial power grid to be studied should be retained. This composition adopts the equivalent value of zero-line transmission power. The method is to obtain the power and line loss on the tie line through power flow calculation and set the virtual generator and load equivalent to the transmission line power at both ends according to the power direction, to separate the provincial power grid. Finally, it sets a balance node in the provincial power grid for study. Using this method not only ensures that the structure of the original large power grid does not change, but also makes the provincial power grid data independent in form, simplifying the state space and action space of deep reinforcement learning. The zero-line transmission power equivalent is shown in Fig. 3.

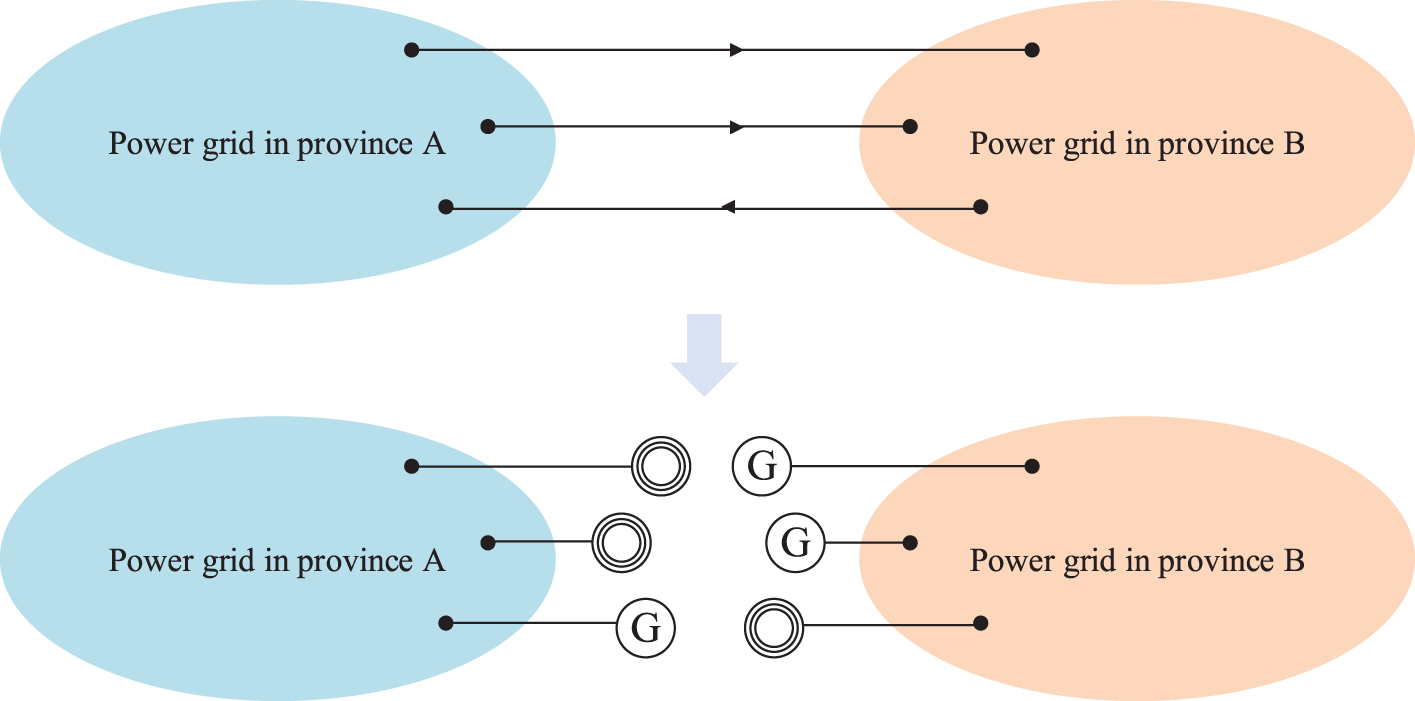
Figure 3: Zero-line transmission power equivalent

2) Reactive power non-convergence index

The reactive power in the system is the main reason for the power flow non-convergence when arranging the operation mode. Compared with active power, the reactive power adjustment is more difficult because only the reactive load demand of the system can be obtained in the initial power flow condition. Once the power flow does not converge, the algorithm will iterate to the set upper limit times. The power flow has diverged and has no reference significance for convergence adjustment. In addition, insufficient or excessive input of the compensation amount will raise the reactive power loss significantly and affect the voltage level of other partitions. Therefore, an index that can reflect the reactive power flow non-convergence is required as the reactive power adjustment direction. In this paper, the reactive power index is obtained based on the node type switching. The 500 kV substation nodes with compensation devices on the low-voltage side in each sub-region and other access points with compensation devices on the main grid frame are converted from PQ to PV nodes, then the capacitors and reactors are switched according to the reactive power situation not arranged in the system.

Unscheduled reactive power refers to the difference between the reactive power required to keep the node constant and the actual reactive power of the node. The unarranged reactive power expression is shown in Eq. (9).

Qi.unsc=Qi.in−Qi.gen+Qi.load(9)

where Qi.unsc is the unarranged reactive power at node i and Qi.in is the reactive power injected by the switching type node i to maintain a constant voltage.

After the size of the node’s unarranged reactive power is determined, the total amount of unarranged reactive power in the whole system is shown in Eq. (10).

ΔQ=∑i=1mQi.unsc=Qtotal.ind−Qtotal.cap(10)

where ΔQ is the total amount of unscheduled reactive power; Qtotal.ind is the inductive reactive power not arranged by the system; and Qtotal.cap is the capacitive reactive power not arranged by the system.

In this composition, the node voltage amplitude of the transition type in the initial power flow condition is set as 1. Since the nodes of conversion type are the nodes with the highest voltage level in each sub-region, when their voltage is constant, the voltage of other nodes will not deviate too much, which makes the power flow converge. However, it is not a real convergence and the reactive power compensation device in the system needs to be adjusted. At this time, the total unarranged reactive power of the system is generally large and it is difficult to balance only by the node’s compensation device. It should be coordinated with other nodes with reactive power compensation devices. The goal of deep reinforcement learning is to obtain a small unscheduled reactive power by adjusting capacitors and reactors to make the reactive power flow converge.

4.2 Deep Reinforcement Learning Model

1) Algorithm state space

This paper relies on node-type switching to obtain reactive power indicators, converting the substation nodes connected to the 500 kV grid in each partition and all access points with compensation devices on the main grid to PV nodes, making the power flow converge. Then, the capacitors and reactors are adjusted according to the amount of reactive power compensation not arranged in the system. The state space is used to reflect the system operation state. For the non-convergence of power flow caused by reactive power, the reactive load is used to describe the reactive power situation of each partition and the convergence of the system is reflected by the reactive power not being arranged. The state space of reactive power flow adjustment is shown in Eq. (11).

s(k)=[Qzone.1,Qzone.2,…,Qzone.i,Qtotal.ind,Qtotal.cap]T(11)

where Qzone.i is the total reactive load demand of the partition i.

2) Algorithm action space

For the non-convergence adjustment of reactive power flow, the action space of the DQN algorithm is shown in Eq. (12).

a(k)=[λR1,λR2,…,λRn]T(12)

where λRn is the amount of compensation that the node n with reactive power compensation puts into the system.

3) Algorithm reward value

The reward value setting of deep reinforcement learning is very important for the accuracy of the final result. A good reward value distribution can allow the agent to fully consider the impact of the actions of all adjustment objects on the system and select an appropriate adjustment strategy. For the non-convergence adjustment of reactive power flow, the reward value is mainly divided into two categories: the immediate reward for compensation and the final reward for power flow convergence.

4.2.1 Reward Setting for Reactive Power Compensation

Parallel reactive power compensation is used to improve the reactive power situation in the system, which belongs to discrete regulation. The nodes with compensation in the actual system are generally equipped with inductive and capacitive compensation of varied compensation amounts. According to the switching effect of capacitors and reactors, the reward value is set as in Eq. (13).

{rQ=1.2ΔQi−ΔQi+11+ΔQiΔQi+1<ΔQirQ=−5else(13)

where rQ is the reward value of reactive power compensation ΔQi and ΔQi+1 are the total amount of reactive power not arranged in the system before and after capacitor or reactor switching.

Under this reward value setting, the smaller the amount of reactive power compensation not arranged in the system, the higher the total reward value obtained by the agent is. When the compensation amount adopted by the node is valid, the agent gets a positive reward value; when the compensation has a negative effect, it gets a negative reward value.

4.2.2 Reward Setting for Power Flow Convergence

When the power flow converges during the adjustment process, it indicates that the agent has reached the target state and obtained a larger reward value. Since the adjustment cannot reach the convergence state by one-step action, to avoid affecting the subsequent adjustment process and the overall reward value, the reward value for non-convergence is set as 0. The convergent reward is shown in Eq. (14).

{r1=100   if converger1=0      else(14)

Considering that the power flow is convergent after the node type switching, the non-arranged reactive power compensation amount is used to replace the power flow calculation result to obtain the convergence reward value. Usually, the value to restore the node type after the total unscheduled reactive power of the actual system is lower than that to make the reactive power flow converge. In this paper, it is assumed that when the total unscheduled reactive power is lower than 100 MVar, the remaining nodes will be restored. If the power flow converges, the agent obtains the adjusted final reward value.

4.3 Power Flow Adjustment Strategies

1) Reactive power adjustment path

In this paper, the DQN algorithm is used for step-by-step adjustment. The nodes of the switching type are restored in order. And the reactive power compensation device is switched by the DQN algorithm. The unscheduled reactive power in the system is reduced during the node recovery process and the power flow calculation can still maintain convergent. However, in most cases, the unscheduled reactive power value is still very large when there is only one PV node of switching type in the system. The calculation does not converge. The unscheduled reactive power of a single node is only inductive or capacitive, so it can be reduced by adjusting the reactive power compensation device on the low-voltage side of the substation and by relying on the reactive power compensation close to the node for reactive power support.

To improve the power flow convergence probability during the training process, this section will use the Q-Learning algorithm to determine the reactive power compensation points close to each 500 kV node of the main grid. Since the node admittance array in the power flow calculation process reflects the connection relationship of the power grid, it can be used as the state space of Q-Learning to search the reactive path. The state space and reward value of the path search setting are shown in Eqs. (15) and (16), respectively.

s(k1)=[node1,node2,…,nodei]T(15)

{r2=10     sele=1r2=−1    else(16)

where nodei is the state of the ith node of the main grid, which is initially set as 0. If the agent passes through this node in the searching process for the compensation, it is set as 1; and sele is the state of the node with reactive power compensation.

According to the reward value setting, to obtain the shortest possible reactive power adjustment path, the agent will get a negative reward value every time it searches.

A positive reward value is achieved when reactive power compensation is found.

2) Reactive power flow adjustment process based on improved DQN

In this composition, the reactive power convergence is adjusted by changing the capacity of the compensation device input by the node. The entire reactive power flow convergence adjustment process based on the improved DQN algorithm is shown in Fig. 4.

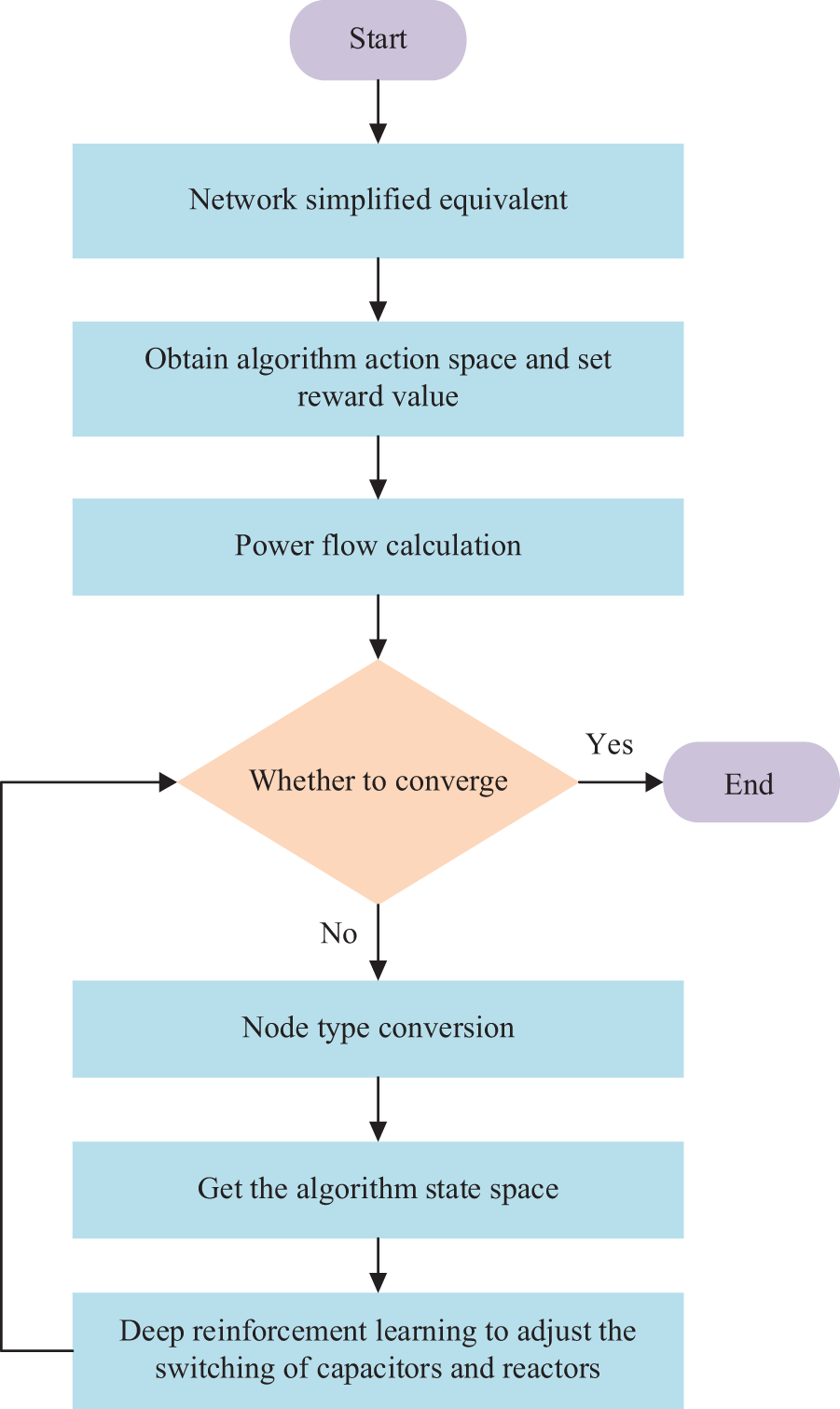
Figure 4: Flow chart of power flow adjustment based on improved DQN

5  Case Study

In this paper, the actual transmission network in a certain province is used for the case study. It has a total of 29 subarea divisions and more than 2400 nodes, of which 164 are parallel reactive power compensation nodes. Based on the typical operation mode of the summer peak in 2021, the reactive load demand of each node is randomly modified to obtain reactive power flow samples. Some non-convergent samples are used as the algorithm adjustment objects. The power flow calculation is carried out by the Newton-Raphson method through the PSD-BPA simulation platform and the upper limit of iteration is set as 25 times. First, taking a scenario with a large deviation from the initial reactive power demand as an example, the reactive power load of each partition before and after sample generation is shown in Fig. 5.

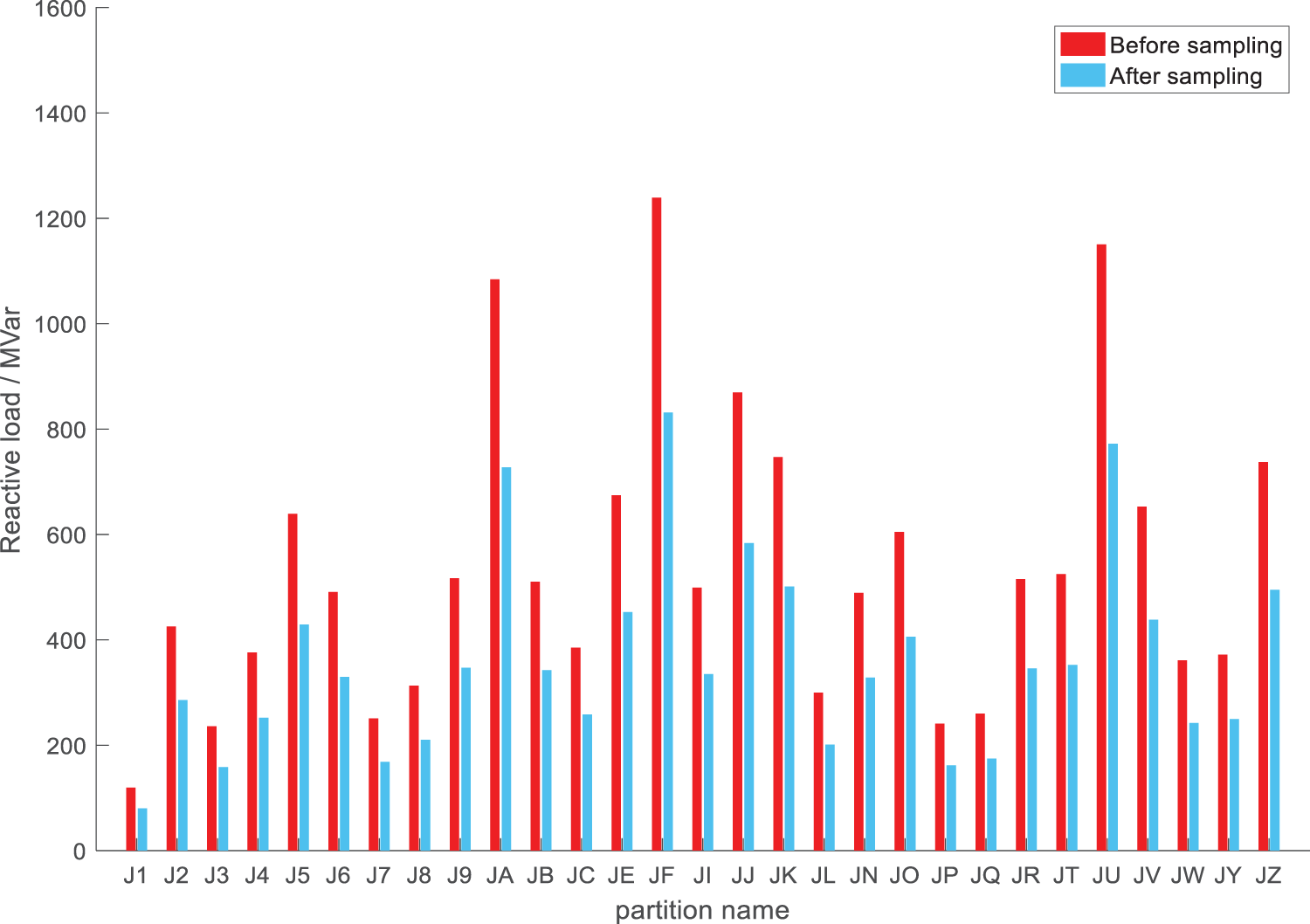
Figure 5: Variation of reactive load in each partition before and after sampling

It can be seen from Fig. 5 that the reactive power load of each partition of the current system is greatly reduced and the result does not converge when the power flow calculation is performed according to the compensation capacity of the original operation mode. The DQN algorithm is used to adjust the non-convergent power flow. The average cumulative reward value curve of the algorithm adjustment process and the changing trend of the unarranged reactive power compensation amount in the final adjustment strategy are shown in Figs. 6 and 7, respectively.

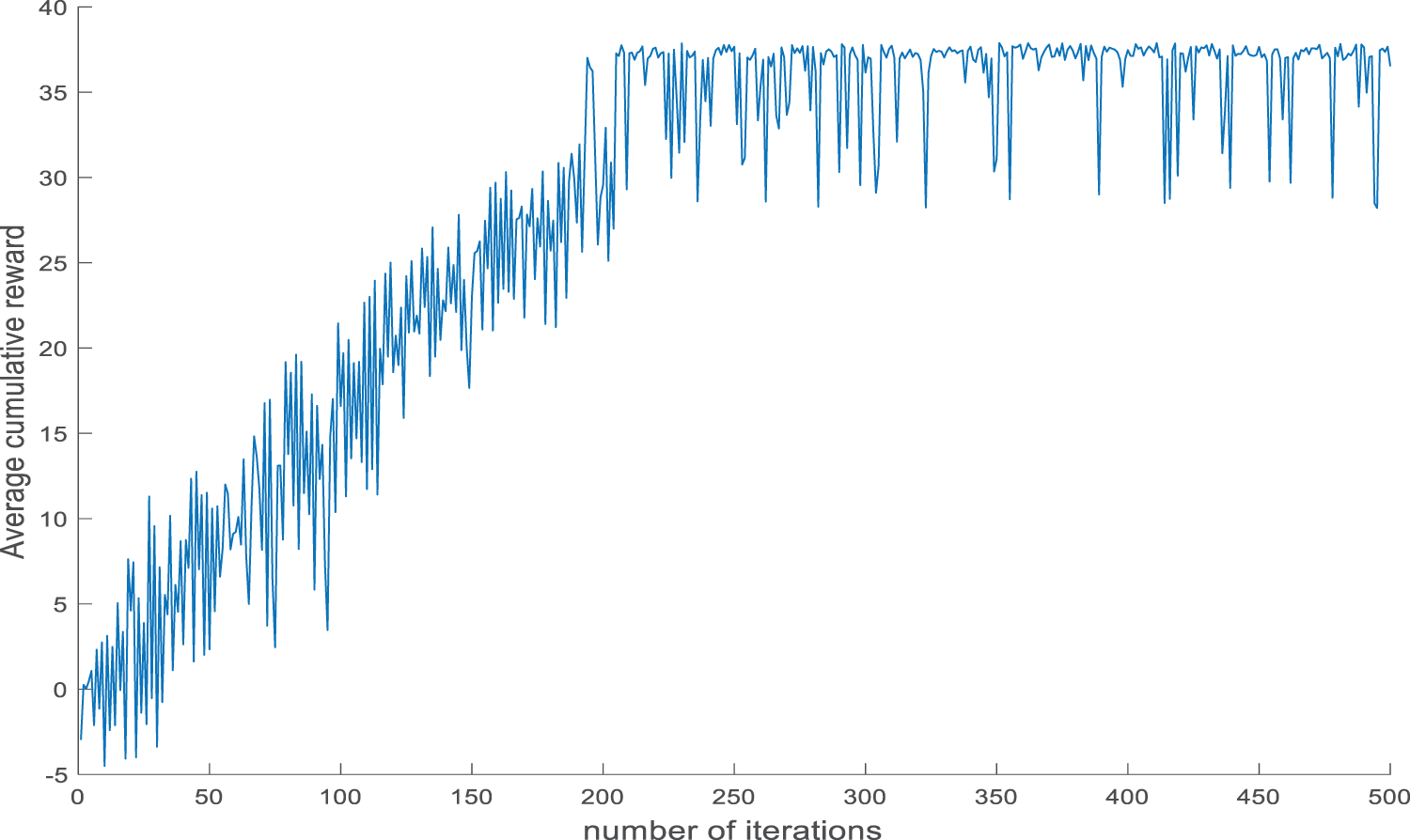
Figure 6: Average cumulative reward of reactive power adjustment

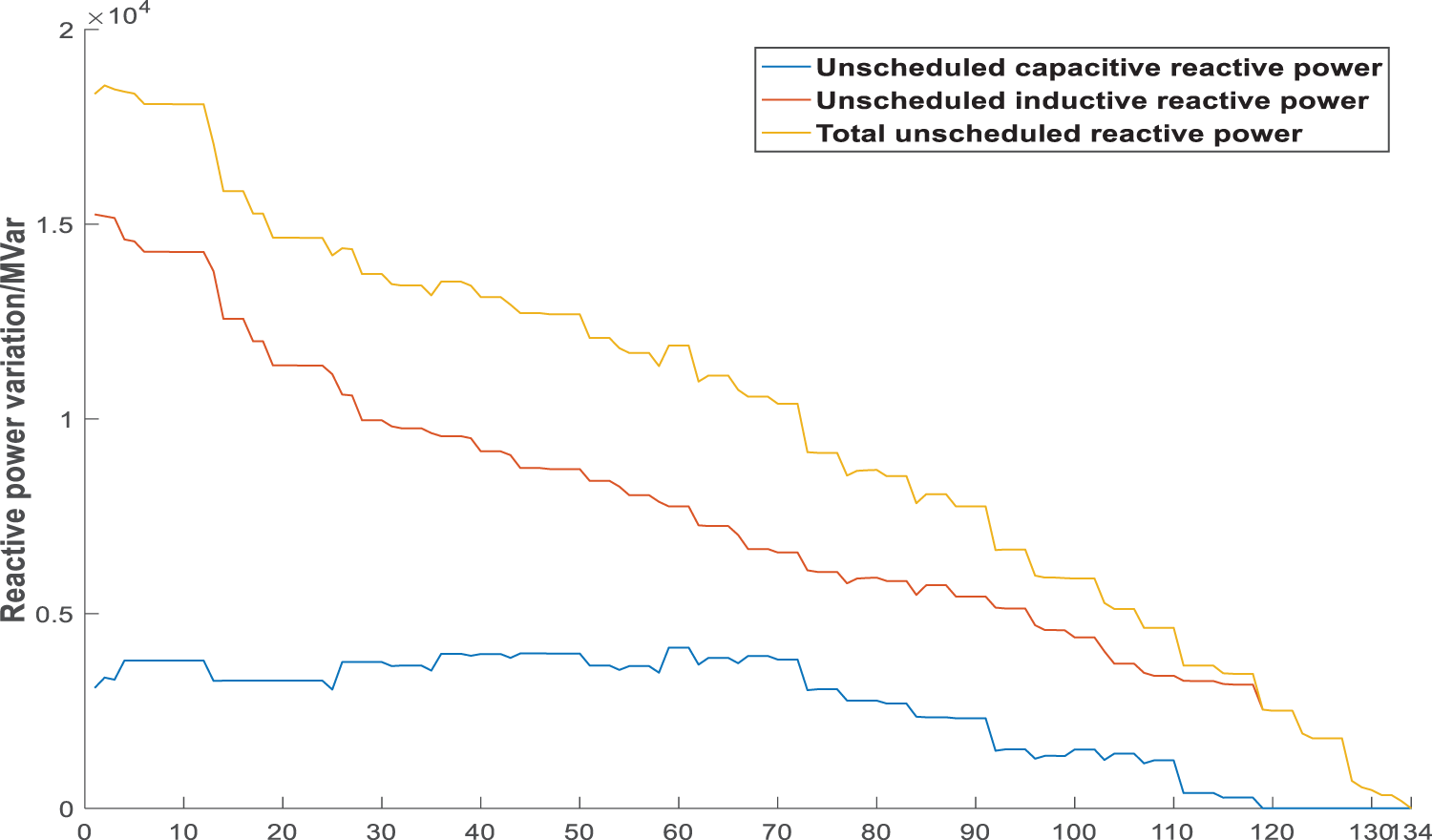
Figure 7: Trend graph of unscheduled reactive power compensation changes

As is seen from Fig. 7, for the actual large-scale power grid, when some high-voltage substations are set as PV nodes, the inductive reactive power and capacitive reactive power that are not arranged in the system exist at the same time. Since the algorithm switches on and off the reactive power compensation devices of the 500 kV substations in each partition during the PV node restoration, the total amount of unscheduled reactive power during the adjustment process is continuously reduced and the system can maintain convergent. The algorithm reduces the unscheduled capacitive reactive power to 0 in the 118th round, and the PV node of the last switching type can rely on its reactive power device and the reactive power compensation point determined by the optimal path to improve the capacitive reactive power level of the system. In the 134th round, the unscheduled reactive power is reduced to the allowable range, the node type is restored and the power flow is successfully converged, which verifies the feasibility of the algorithm in the power flow analysis of large power grids. The compensation amount of each reactive power compensation node before and after adjustment changes is shown in Fig. 8.

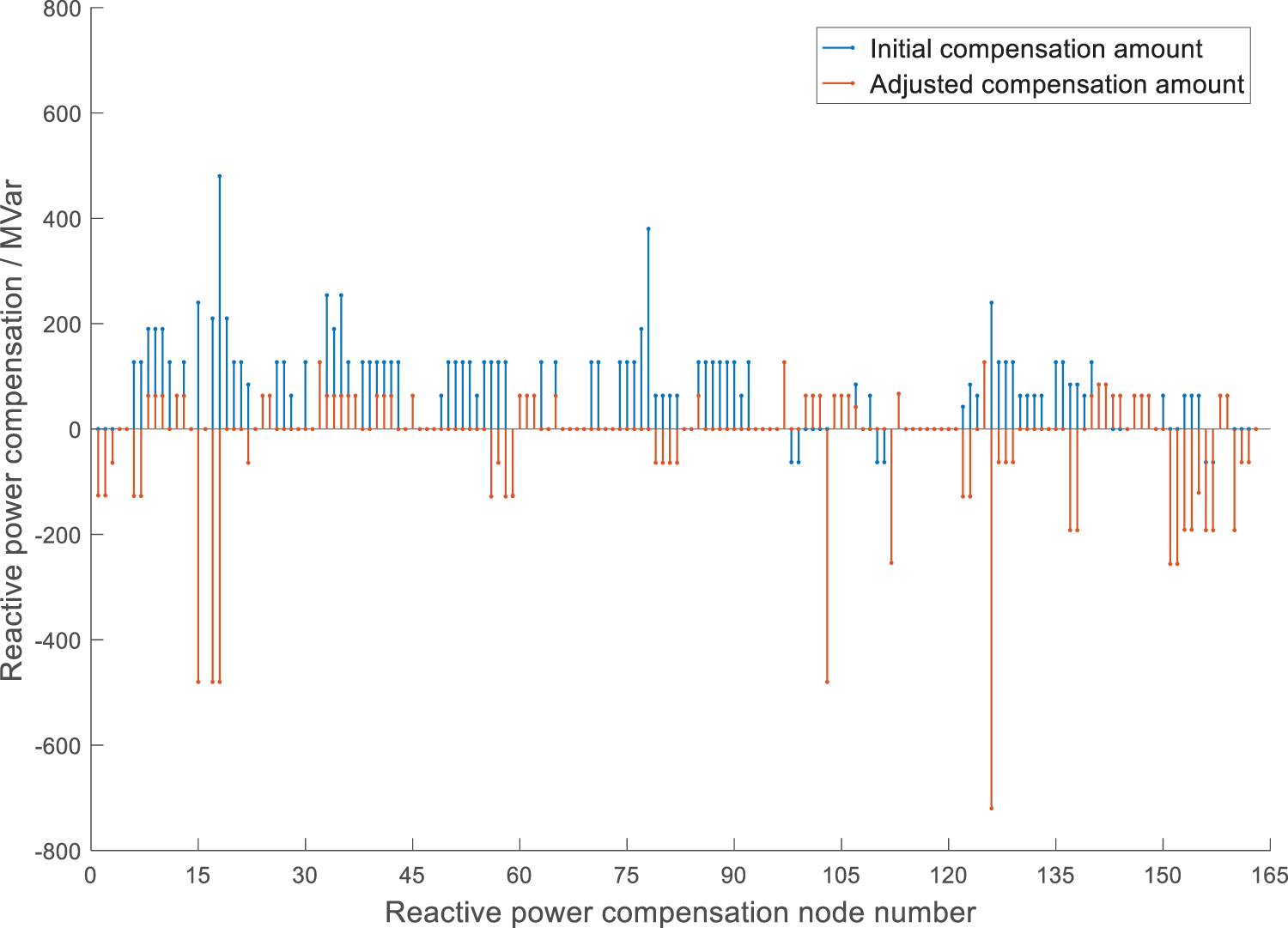
Figure 8: Variation of nodes’ reactive power compensation

The DQN algorithm has adjusted the 164 main grid nodes with reactive power compensation devices in the system. Since the reactive load of this sample is greatly reduced compared with the initial situation, the system mainly removes the capacitor’s input in the original operation mode and adds reactors for compensation. The DQN algorithm only needs to obtain results through the trained neural network, so the adjustment speed is fast and the average running time of each step is 0.72 s. After that, the DQN algorithm is used to adjust all the collected non-convergent samples, and the interior point method of optimal power flow is used as the comparison algorithm. The adjustment success rate of different algorithms is shown in Table 1.

According to the test results of the example, the interior point method works poorly on the reactive power convergence adjustment of large systems, mainly because the actual system takes into account many constraints and it is difficult to set the initial value of the algorithm. In addition, the objective function of the interior point method is to minimize the load cut-off amount. For large-scale power grids, it is difficult to ensure that the amount of load cut-off is close to 0 when the system’s reactive load changes greatly. The power flow adjustment algorithm based on DQN can adjust and converge most of the cross-sections with reactive power non-convergence, which verifies the effectiveness of the algorithm. The system is mainly adjusted by switching capacitors and reactors. Although the quantitative index of reactive power non-convergence can be obtained by the node type switching, which provides directionality for the agent action and reduces the action space, the adjustment method of reactive power flow is discrete. The compensation reactive power can only be corrected to several specific values according to the compensation device capacity. It is necessary to adjust the nodes searched by the path to fully cooperate with different nodes with compensation devices to achieve the balance of reactive power. Once the compensation equipment is not well matched, the reactive power of the partition needs to be obtained from a distant power supply. The long-distance reactive power flow will cause greater losses in the system and more difficulty in power balance. Therefore, there are a few samples that do not converge after adjustment.

6  Conclusion

Combining the actual working conditions of the power system, this paper proposes an improved deep reinforcement learning algorithm for the reactive power flow convergence in the transmission network. To make the reactive power flow adjustment directional, the quantitative index of reactive power non-convergence is obtained based on the node type switching. Then, the Q-Learning algorithm is used to determine the reactive power adjustment path of the main grid, so that the power flow in the training process has a higher convergence probability. Finally, the reward value is reasonably designed and the DQN algorithm is used to adjust the reactive power compensation device switching by taking the system’s unarranged reactive power as the state space. Through practical examples of reactive power non-convergence, it is shown that the improved deep reinforcement learning algorithm can make the non-convergence operation mode converge and has a stronger ability to restore power flow convergence than the traditional method.

Funding Statement: This work was partly supported by the Technology Project of State Grid Jiangsu Electric Power Co., Ltd., China, under Grant No. J2022095.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Zhao, M. L., Lai, Y. N. (2009). Quantitative analysis and online recovering control of power flow unsolvability. Journal of Nanjing Institute of Technology(Natural Science Edition), 7(4), 27–30. [Google Scholar]

2. An, J., Song, J., Ge, W. (2020). Convergence identification and adjustment method of power flow calculation for large-scale power system. Electric Power Automation Equipment, 40(2), 103–108. [Google Scholar]

3. Li, Z., Han, Y., Su, Y., Sun, X., Huang, H. et al. (2015). A convergence adjustment method of power flow based on node type switching. Automation of Electric Power Systems, 39(7), 188–193. [Google Scholar]

4. Ansari, J., Malekshah, S. (2019). A joint energy and reserve scheduling framework based on network reliability using smart grids applications. International Transactions on Electrical Energy Systems, 29(11), 12096. [Google Scholar]

5. Malekshah, S., Alhelou, H. H., Siano, P. (2021). An optimal probabilistic spinning reserve quantification scheme considering frequency dynamic response in smart power environment. International Transactions on Electrical Energy Systems, 31(11), 13052. [Google Scholar]

6. Malekshah, S., Ansari, J. (2020). A novel decentralized method based on the system engineering concept for reliability-security constraint unit commitment in restructured power environment. International Journal of Energy Research, 45(1), 703–726. [Google Scholar]

7. Lin, Y., Sun, H., Wu, W., Yu, J., Zhang, B. (2012). A schedule power flow auto generating technology in day-ahead security validation. Automation of Electric Power Systems, 36(20), 68–73. [Google Scholar]

8. Tostado, M., Kamel, S., Jurado, F. (2019). Developed Newton-Raphson based predictor-corrector load flow approach with high convergence rate. International Journal of Electrical Power and Energy Systems, 105(9), 785–792. [Google Scholar]

9. Chu, Z., Yu, Q. Y., Li, X. W. (2016). Newton method for solving power flow of distribution network with small impedance branch. Proceedings of the CSU-EPSA, 28(9), 36–41. [Google Scholar]

10. Hu, W. B., Chen, X. W., Wang, Z. (2018). Application of Weighted Newton Raphson method in power system. Smart Power, 46(3), 68–73. [Google Scholar]

11. Peng, H., Li, F., Yuan, H., Bao, Y. (2018). Power flow calculation and condition diagnosis for operation mode adjustment of large-scale power systems. Automation of Electric Power Systems, 42(3), 136–142. [Google Scholar]

12. Tao, X., Bo, G., Wang, H., Bao, W., Guo, R. (2014). An optimization method based on weighted least absolute value to restore power flow solvability of bulk power system. Automation of Electric Power Systems, 38(23), 60–64. [Google Scholar]

13. Malekshah, S., Malekshah, Y., Malekshah, A. (2021). A novel two-stage optimization method for the reliability based security constraints unit commitment in presence of wind units. Computers and Electrical Engineering, 4(5), 100237. [Google Scholar]

14. Malekshah, S., Banihashemi, F., Daryabad, H., Yavarishad, N., Cuzner, R. (2022). A zonal optimization solution to reliability security constraint unit commitment with wind uncertainty. Computers and Electrical Engineering, 99(10), 107750. [Google Scholar]

15. Chen, H., Hua, Z., Hui, L., Wang, Z., Wang, J. (2018). Research on adjustment method of power flow convergence based on planning model. IOP Conference Series: Materials Science and Engineering, 439(3), 32–38. [Google Scholar]

16. Huang, G., Cui, H., Xu, D., Ding, Q., Zhai, X. (2016). A method of active power flow adjustment in security constrained economic dispatch. Power System Protection and Control, 44(4), 91–96. [Google Scholar]

17. Malekshah, S., Hovanessian, A., Gharehpetian, G. B. (2016). Combined heat and power sizing in residential building using mixed integer nonlinear programming optimization method. Iranian Conference on Electrical Engineering, 7, 1208–1213. [Google Scholar]

18. Feng, H., Construction, D. O. (2017). Adjustment method of power flow non-convergence calculation. Journal of Electric Power Science and Technology, 32(3), 57–62. [Google Scholar]

19. Wang, H., Tao, X., Li, B., Mu, S., Wang, Y. (2018). An approximate power flow model based on virtual midpoint power. Proceedings of the Chinese Society of Electrical Engineering, 38(21), 6305–6313. [Google Scholar]

20. Zhang, S., Zhang, D., Huang, Y., Li, W., Chen, X. et al. (2021). Research on automatic power flow convergence adjustment method based on modified DC power flow algorithm. Power System Technology, 45(1), 86–97. [Google Scholar]

21. Zhang, H. S., Song, W., Xue, T. (2006). Implementing operation modes of electric power grids based on artificial intelligence. Electric Power, 39(7), 61–64. [Google Scholar]

22. Malekshah, S., Rasouli, A., Malekshah, Y., Ramezani, A., Malekshah, A. (2022). Reliability-driven distribution power network dynamic reconfiguration in presence of distributed generation by the deep reinforcement learning method. Alexandria Engineering Journal, 61(8), 6541–6556. [Google Scholar]

23. Xu, H. T., Yu, Z. H., Zheng, Q. P., Hou, J. X., Wei, Y. W. et al. (2019). Deep reinforcement learning-based tie-line power adjustment method for power system operation state calculation. IEEE Access, 33(7), 156160–156174. [Google Scholar]

24. Wang, T., Tang, Y., Guo, Q., Huang, Y., Chen, X. et al. (2020). Automatic adjustment method of power flow calculation convergence for large-scale power grid based on knowledge experience and deep reinforcement learning. Proceedings of the Chinese Society of Electrical Engineering, 40(8), 2396–2405. [Google Scholar]

25. Zhang, X. S., Yu, T., Yang, B., Cheng, L. F. (2017). Accelerating bio-inspired optimizer with transfer reinforcement learning for reactive power optimization. Knowledge-Based Systems, 116(2), 26–38. [Google Scholar]

26. Zhang, X. S., Li, C. Z., Yin, X. Q., Yang, B., Gan, L. X. et al. (2021). Optimal mileage-based PV array reconfiguration using swarm reinforcement learning. Energy Conversion and Management, 232(2), 113892. [Google Scholar]

27. Chen, S., Wei, Z. N., Sun, G. Q., Cheung, K. W., Wang, D. et al. (2019). Adaptive robust day-ahead dispatch for urban energy systems. IEEE Transactions on Industrial Electronics, 66(2), 1379–1390. [Google Scholar]

28. Li, J., Yu, T., Pan, Z. (2020). Real-time stochastic dispatch method for incremental distribution network based on reinforcement learning. Power System Technology, 44(9), 3321–3332. [Google Scholar]