Stackelberg Game-Based Optimal Dispatch for PEDF Park and Power Grid Interaction under Multiple Incentive Mechanisms

Nomenclature

1  Introduction

On a global scale, renewable energy has become a key factor in promoting energy transformation and achieving sustainable development. With the continuous development of new energy technologies, more and more renewable energy sources such as solar and wind energy are being introduced into the power grid system. This change not only poses challenges to traditional energy supply, but also brings new opportunities and challenges to the operation and management of the power grid. As one of the important fields of global energy consumption, the architecture sector accounts for a significant proportion of global carbon emissions. Therefore, the energy transformation in the construction sector is of great significance for energy conservation and carbon reduction.

The photovoltaic, energy storage, direct current, and flexible load (PEDF) building system is a new type of building distribution system that can effectively solve two key issues in the zero-carbonization transformation of the power system: increasing the installed capacity of distributed renewable energy generation and effectively absorbing fluctuations in renewable energy generation [1]. The building energy systems that implement PEDF technologies are also called PEDF parks. The system integrates technologies such as photovoltaic (PV) power generation, energy storage, direct current (DC) power distribution, and flexible energy consumption to form a whole to achieve friendly interaction between buildings and the power grid.

Specifically, the four key components of a PEDF system are described as follows:

•   PV Power Generation: Distributed solar PV power generation facilities in buildings, which can be fixed in the surrounding area, on the exterior surface, or directly become components of the building.

•   Energy Storage: Use energy storage devices to store excess electricity for emergency use while also suppressing fluctuations in renewable energy generation.

•   DC Power Distribution: Compared to alternating current (AC) distribution, DC distribution can reduce losses in the process of energy transmission and improve energy utilization efficiency by using direct current for distribution [2].

•   Flexible Energy Consumption: By exploiting the flexibility of energy consumption in the system, it can achieve efficient utilization and optimized configuration of building energy through smart control and management.

The application of the PEDF system can bring various advantages. First, it can improve the efficiency of renewable energy utilization and reduce dependence on traditional energy. Second, it conducts real-time monitoring, control, and optimization of building energy systems to improve energy efficiency. In addition, it can also provide auxiliary services for the power grid, such as peak shaving and frequency regulation, to improve the stability of the power system.

The friendly interaction with the power grid can achieve efficient utilization and optimized configuration of renewable energy, improve the stability and reliability of the power system, and promote energy transformation and sustainable development [3]. Grid-friendly interaction technologies covers the areas of demand response (DR), smart power consumption, energy internet, microgrid, electricity market trading, and so on. These technologies can be organically integrated in a PEDF building park to promote friendly interaction and cooperation between power users and the power grid. Under this setting, how to effectively manage and dispatch of energy supply, as well as how to motivate users to better participate and cooperate with the power grid, has become an urgent problem to be solved. In order to better understand the interactive relationship between PEDF users and the power grid, this paper mainly explores the optimal dispatch problem under various incentive mechanisms, in order to achieve the goal of reducing power supply pressure, reducing electricity costs, and improving the time matching of power supply and consumption. In our study, a Stackelberg game model (also called leader-follower game model) [4] is constructed to analyze user behavior choices under various incentive mechanisms.

1.1 Literature Review

At present, scholars have achieved a series of important achievements in PEDF technologies, incentive mechanisms, and Stackelberg game.

a) PEDF Technologies: Recent research on PEDF technologies focuses on the optimization of system dispatch, operation, and simulation. Reference [5] designs an optimal operation strategy for PEDF systems that minimizes the operation and maintenance cost and uses improved chip optimization algorithm to solve the optimization model. In [6], an optimal dispatch method of PEDF microgrids is proposed to minimizing carbon emission and maximizing carbon trading benefit based on the carbon emission flow theory. Reference [7] builds a simulation model for residential PEDF building systems and tests the stability of the simulated system. However, the friendly interaction between the PEDF system and the power grid is seldom considered in these works.

b) Incentive Mechanisms: In related research, incentive mechanisms mainly include incentive-compatible pricing mechanism, incentive-based DR mechanism, and the combination of both mechanisms. The authors of [8] provide an incentive-compatible pricing mechanism for energy storage markets which minimizes grid operation cost by integrating the storage capability of electric vehicles. In [9], a real-time electricity pricing strategy is studied to reduce electricity consumption cost and increase social welfare of end users. In [10], the authors design an incremental incentive mechanism for DR where the incentives can vary according to different consumers’ marginal cost. Apart from economic incentive mechanisms, the potential of noneconomic incentive methods, such as green certification [11], social responsibility [12], or reputation system [13], cannot be ignored in encourage the friendly interaction between PEDF users and the grid.

c) Stackelberg Game: The Stackelberg game model can provide a deep understanding of the strategic behavior of different stakeholders and help design effective market mechanisms and pricing strategies to achieve expected goals including efficiency, reliability, and sustainability of energy systems. For example, reference [14] designs a market trading mechanism for energy retailers and consumers to increase the overall profit of retailers, modeled by a multi-leader and multi-follower Stackelberg game. In [15], a three-level Stackelberg game is formulated to reach a balance between the gird, retailers, and end users in implementing the real-time pricing and real-time incentive for a hybrid DR mechanism. Similarly, the Stackelberg game can also be utilized to describe the interaction between the PEDF park and the grid.

1.2 Contributions of This Paper

In this paper, we study the day-ahead optimal dispatch problem in a PEDF park system. The grid will purchase electricity from generation entities, and is responsible for power transmission and distribution. The PEDF park is a prosumer that relies on its own PV power generation to meet daily energy consumption needs. When PV generation cannot meet its own energy consumption needs, electricity will be purchased from the grid; When there is a surplus in PV generation, electricity can also be sold to the grid. We will explore the interaction between the PEDF park and the grid by designing multiple incentive mechanisms, including hybrid DR mechanism and reputation mechanism. The grid makes a decision on TOU prices and incentive price, while the PEDF park adjusts its participation in load, energy storage, and demand response based on the price information given by the grid. The reputation mechanism, on the other hand, will affect the willingness of the PEDF park to fulfil DR tasks and further provide more discounts for the PEDF park with good reputation. The goal of the incentive mechanisms is to relieve the pressure of the grid by guiding the behavior of the PEDF park.

The contributions of this paper are as follows:

1.    This paper studies the optimization of the day-ahead dispatch of a PEDF system. The dispatch considers the hybrid DR model that combines the price-based DR and the incentive-based DR. In the price-based DR, electricity selling and purchasing prices varies as time. In the incentive-based DR, the PEDF park can acquire subsidies by reducing its electricity consumption. The novelty of the DR model is that the incentive price also varies as time. In other words, the PEDF park will receive a higher incentive price when reducing its consumption during peak hours than flat or valley hours.

2.    In this paper, multiple incentive mechanisms are designed to encourage the friendly interaction of the PEDF park with the grid. In addition to economic incentives that are commonly studied in existing works, this paper also includes the impact of noneconomic incentive. To be more specific, the noneconomic incentive mechanisms studied in this paper mainly refers to reputation-based discount mechanism [16]. In our settings, the PEDF park that maintains a good reputation score can receive discount during the trading with the grid. The reputation score can also influence the willingness of the PEDF park to fulfil DR tasks. Although this incentive mechanism is converted economic approaches during the dispatch, we still regard it as noneconomic ones because its implementation largely depends on the promotion of reputation-related policies and regulations.

3.    We model the interaction between the PEDF park and the grid by a Stackelberg game. The grid is modeled as the leader that maximizes its revenue from electricity trading and providing incentive subsidies, while also alleviating grid pressure through the objective of peak shaving. The PEDF park is modeled as the follower that minimizes its dispatch cost, enhances load utility, and promotes PV penetration rate based on the prices offered by the grid. Since the model of the PEDF park is nonconvex and nonlinear, it can be rather difficult to solve the Stackelberg game model through traditional methods. As a result, we use particle swarm optimization (PSO) algorithm to find the optimal strategies.

The rest of this paper is arranged as follows: Section 2 introduces the PEDF park system and incentive mechanisms studied in this paper; Section 3 constructs the Stackelberg game model that describes the interaction between the PEDF park and the grid; Section 4 provides case analysis based on real data; Section 5 concludes this paper.

2  System Model and Incentive Mechanisms

This section introduces the PEDF park system and incentive mechanisms studied in this paper.

2.1 PEDF Park System

The architecture of the PEDF park system is shown in Fig. 1. The system collects solar energy through PV panels installed on the roof or facade of the building. These PV panels not only provide clean electricity for buildings, but also reduce reliance on traditional energy sources (e.g., the power grid). The battery energy storage system (BESS) is integrated to store excess electricity generated by PVs. During peak electricity demand, these energy storage devices can release electrical energy and provide continuous and stable power supply to buildings. Various DC loads are equipped, including flexible loads and other nonflexible loads. When there is a change in electricity demand, the system can adjust flexible loads’ electricity consumption, achieving a balance between electricity demand and supply. The main function of the DC distribution system is to achieve the transmission and distribution of electrical energy, ensuring that the DC energy from PV and BESS can effectively supply the DC loads inside the building.

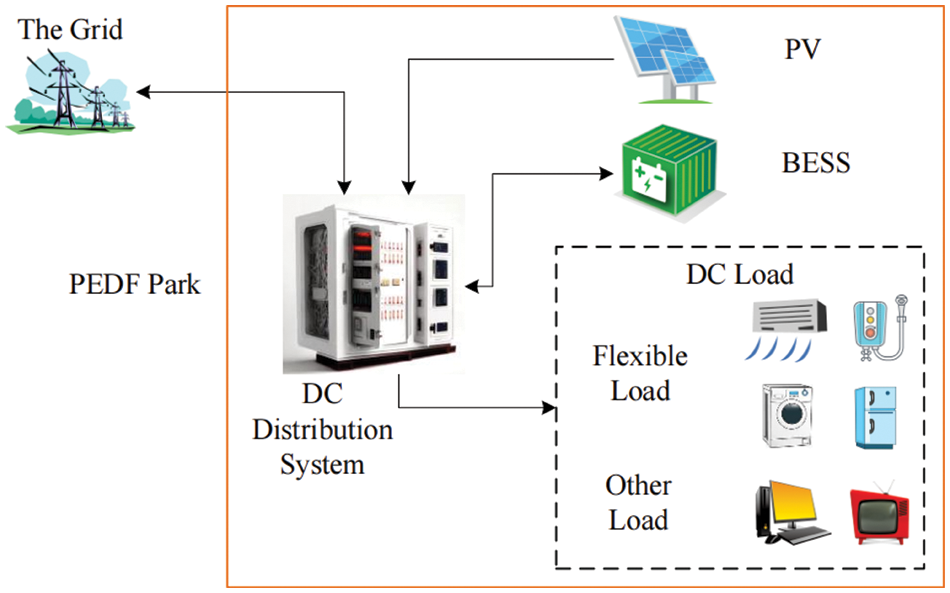
Figure 1: Architecture of the PEDF park system

This paper studies the day-ahead dispatch problem of the PEDF park. We divide the day into T time slots of equal length (for example, an hour). In this case, the tth hour can be represented by time slot t (=1,2,…,T). According to the forecast data of PV output and load power consumption on the dispatching day, the day ahead dispatching decides the plans for energy storage charging and discharging, load power consumption, and electricity trading in advance for each future time slot t.

2.1.1 Battery Energy Storage System Model

The BESS is implemented to store surplus energy and discharge when the energy supply is insufficient. The dynamics of the BESS is usually modeled as follows:

SoC(t)=SoC(t−1)+[ηchEch(t)−Edch(t)ηdch]1Ebess(1)

where SoC(t) is the state of charge (SoC) of the BESS at time t, Ech(t) and Edch(t) are the charging and discharging energy of the BESS at time t, ηch and ηdch are the charging and discharging rates, and Ebess is the capacity of the BESS.

SoC is a percentage value between 0 and 1 that represents the ratio of the current amount of electricity that a battery can provide to the amount of electricity it can provide when fully charged. In the BESS, SoC is a very important parameter as it directly reflects the system’s energy storage capacity, discharge capacity, and operational efficiency. When the SoC value is high, it indicates that the BESS has more available power and can support longer discharge times or higher discharge power. When the SoC value is low, it is necessary to consider charging the battery to ensure the normal operation and energy storage capacity of the system.

The energy charged and discharged at time t cannot exceeds its charging and discharging capability:

0≤Ech(t)≤Echmax(2)

0≤Edch(t)≤Edchmax(3)

where Echmax and Edchmax are the maximum amount of energy can be charged and discharged. We require that the BESS cannot charge and discharge at the same time:

Edch(t)Edch(t)=0(4)

To protect the BESS, the state of charge of the BESS is recommended to fall within a proper range:

SoCmin≤SoC(t)≤SoCmax(5)

where SoCmin and SoCmax are the recommended SoC lower and upper bounds for the BESS.

2.1.2 Load Model

In general, a PEDF system only involves DC distribution and DC load devices. The DC loads in our system include flexible loads and other nonflexible loads. Flexible loads can interact with the power grid by participating in DR. Suppose L0(t) is the load consumption at time t before participating in DR. Then after participating in DR, the load consumption L(t) is calculated by:

L(t)=[1−ρL(t)s(r,L(t−1))]L0(t)(6)

where ρL(t) is the predicted reduction rate of load consumption during DR, and s(r,L(t−1)) is the willingness for the PEDF park to fulfil its DR task, which is related to the load consumption of the previous time slot and r∈[0,1], the reputation score of the PEDF park [16].

The willingness of DR is generally related to various factors such as energy consumption experience, price, and participation frequency. To simplify the model, we calculate s(r,L(t−1)) as follows:

s(r,L(t−1))={16b3a2ru(L(t−1)),u(L(t−1))<3a216b1,u(L(t−1))≥3a216b(7)

where u(⋅) is a load utility function, and a and b are constant coefficients. The load utility function is defined to describe the satisfaction of electricity consumption [17]:

u(L(t))={aL(t)−b(L(t))2,L(t)<a2ba24b,otherwise(8)

To simplify the model, we assume that r remains unchanged during the day-ahead dispatch and only changes after one-day dispatch is completed. We can see from (7) that the willingness of fulfilling DR tasks increases with the increase of previous load utility (energy consumption satisfaction) and the reputation of the PEDF park.

Since nonflexible loads are also included, we have:

0≤ρL(t)≤ρLmax(9)

where ρLmax∈[0,1) is the maximum load reduction rate.

2.1.3 Electricity Trading Model

The power grid plays a supporting role in the system, providing energy to the PEDF system when the park is low on power, while interacting with flexible load devices in the PEDF park. The following energy balance should be satisfied at all time:

Ebuy(t)+Epv(t)+Edch(t)=L(t)+Ech(t)+Esell(t)(10)

where Epv(t) is the amount of energy generated by PV at time t, Ebuy(t) is the energy purchased from the grid, and Esell(t) is the energy sold to the grid.

When PV generation is sufficient, then the PEDF park can sell surplus energy Esell(t) to the grid. If PV generation is insufficient, the PEDF park can choose to purchase extra energy Ebuy(t) from the grid. We require that the PEDF park cannot sell and buy electricity at the same time:

Ebuy(t)Esell(t)=0(11)

Considering the possibility of transaction congestion, we require that the amount of energy traded between the PEDF park and the grid has an upper bound:

0≤Ebuy(t)≤Etxmax(12)

0≤Esell(t)≤Etxmax(13)

where Etxmax is the maximum amount of energy allowed to be traded.

2.2 Incentive Mechanisms

In this paper, we combine two incentive mechanisms, including hybrid DR mechanism and reputation-based discount mechanism.

2.2.1 Hybrid Demand Response

In this paper, we consider the hybrid DR model, where price-based DR model and incentive-based DR model are both included [18].

In price-based DR model, electricity trading prices are decided by the grid dynamically based on the time of day. It is also called time-of-use (TOU) pricing mechanism. It can encourage the PEDF park to reduce peak load consumption to improve grid stability. Suppose λsell(t) and λbuy(t) are the electricity selling and purchasing prices at time t. To avoid price inflation and cashing out, the following constraint should be satisfied:

0<λsell(t)<λbuy(t)<Λ(14)

where Λ is the upper bound of electricity trading prices.

Then the electricity purchasing cost of the PEDF park during one day, denoted by Cbuy, is calculated by:

Cbuy=∑t=1Tλbuy(t)Ebuy(t)(15)

Similarly, the revenue of the PEDF park acquired from selling electricity during one day, denoted by Rsell, is calculated by:

Rsell=∑t=1Tλsell(t)Esell(t)(16)

In incentive-based DR model, the PEDF park can receive subsidies for reducing its load consumption. Suppose μ(t) is the incentive price at time t, which is also decided by the grid based on the time of day. Then the revenue of participating incentive-based DR, denoted by Rincentive, is calculated by:

Rincentive=∑t=1Tμ(t)[L0(t)−L(t)](17)

Moreover, the incentive price is also bounded:

0<μ(t)<M (18)

where M  is the upper bound of the incentive price.

2.2.2 Reputation-Based Discount Mechanism

Reputation mechanisms are typically used to establish trust relationships between entities in an open environment. In the setting of interaction between PEDF park and the power grid, the reputation of PEDF park can be seen as its previous contribution to system dispatch. The reputation also has an influence on the willingness of fulfilling DR tasks. If the grid can bring more benefits to PEDF park with higher reputations, PEDF park will be more inclined to maintain a good reputation. PEDF park can enhance its reputation in many different ways, such as actively participating in grid scheduling and DR, which can be defined and implemented by the grid in practice. Therefore, reputation mechanisms can motivate PEDF parks to take actions that are beneficial to the power grid.

The idea of reputation-based discount mechanism in this paper derives from the discount priority mechanism proposed by [18] that changes the electricity charging price according to users’ reputation scores. This paper applies the discount in both electricity selling prices and electricity purchasing prices. Different from the discount priority mechanism that applies to all users, the reputation-based discount mechanism only applies when the reputation score of the PEDF park is sufficiently high.

Denote the discounts for electricity purchasing and selling by dbuy(r) and dsell(r), respectively. Then we require that the PEDF park cannot get the discount unless its reputation score r reaches 0.8, i.e.,

dbuy(r)={0,0≤r<0.8r−ϵ1,0.8≤r≤1(19)

dsell(r)={0,0≤r<0.8r−ϵ2,0.8≤r≤1(20)

where ϵ1,ϵ2∈(0,0.8) are constants.

As a result, the electricity purchasing cost Cbuy and the electricity selling revenue Rsell are changed into:

Cbuy′=∑t=1T(1−dbuy(r))λbuy(t)Ebuy(t)(21)

Rsell′=∑t=1T(1+dsell(r))λsell(t)Esell(t)(22)

where Cbuy′ and Rsell′ are the electricity purchasing cost and the electricity selling revenue after the discounts are applied.

2.2.3 Intermediate Carbon Emission Penalty

The intermediate carbon emission penalty cost Ccarbon is related to the amount of electricity purchased from the grid:

Ccarbon=ccarbonεcarbon∑t=1TEbuy(t)(23)

where ccarbon is the carbon emission penalty cost, and εcarbon is the coefficient of intermediate carbon emission.

3  Stackelberg Game between the Grid and the PEDF Park

Stackelberg game model is a noncooperative game model where followers will change their strategies according to the strategy of the leader. In this paper, we model the interaction between the grid and the PEDF park as a Stackelberg game model. The Stackelberg game model is a two-stage fully informative dynamic game, in which the power grid acts as the leader to make decisions first, and the PEDF park acts as a follower to react based on the leader’s decision. This structure allows the model to consider the decision-making order of participants and reflect the leading advantages that the power grid may have in reality.

The grid acts as the leader who tries to maximize the revenue of selling electricity to the park, while minimizing the cost of purchasing electricity from the park, providing DR subsidies, and the peak load of the PEDF park. The optimization goal of the grid can be represented by:

maxxF=maxx{Cbuy′−Rsell′−Rincentive−wpeakLpeak}(24)

where

x=[λbuy(t)λsell(t)μ(t)]t=1T(25)

is the strategy (decision variable) of the grid.

Peak load Lpeak is calculated as the maximum load consumption during the dispatch time interval:

Lpeak=max1≤t≤TL(t)(26)

and wpeak is the amplification factor of Lpeak to increase the influence of Lpeak in F.

On the contrary, the PEDF park acts as the follower who tries to minimize the cost of purchasing electricity from the grid, and intermediate carbon emission, while maximizing the utility of electricity consumption, the revenue of selling electricity to the grid, the DR incentive subsidy, and the penetration rate of renewable energy. The optimization goal of the PEDF park can be written as:

minyG=miny{Cbuy′+Ccarbon−U−Rsell′−Rincentive−wpenerationθ}(27)

where

y=[ρL(t)Ech(t)Edch(t)Ebuy(t)Esell(t)]t=1T(28)

is the strategy (decision variable) of the PEDF park.

The total utility of electricity consumption for the PEDF park, denoted by U, is calculated by:

U=∑t=1Tu(L(t))(29)

The penetration rate of renewable energy (PV) in the PEDF park, denoted by θ, can be calculated by:

θ=∑t=1TEpv(t)∑t=1T[Epv(t)+Ebuy(t)]×100%(30)

and wpeneration is the amplification factor to increase the influence of θ in G.

Seeing the fact that u(L(t)) is nonlinear and nonconvex, and therefore the optimization problems of the leader and the follower are also nonlinear and nonconvex. It could be rather difficult to find the solution to the optimization problem via traditional solvers. For one thing, the nonlinearity makes the search space for the global optimal solution huge and complex, and traditional optimization methods are difficult to find satisfactory solutions within limited resources. For another, the nonconvexity may lead to the algorithm falling into multiple local optima, affecting global search and slowing down convergence speed.

Consequently, we use PSO, one of the commonly used heuristic algorithms for solving complicated optimization problems, to find the optimal strategies for the leader and the follower in the Stackelberg game. PSO is an optimization algorithm based on swarm intelligence, which seeks the optimal solution by simulating the foraging behavior of bird flocks [19]. The PSO algorithm can search for potential solutions globally through information sharing and collaboration among particles, avoiding local optimal traps. Its speed and position update formula can be adaptively adjusted to adapt to different nonlinear and nonconvex functions, and particles can be calculated in parallel to improve computational efficiency, thereby finding better solutions within limited resources. PSO has the advantages of simplicity, ease of implementation, fewer parameters, and fast convergence speed, making it and its improved versions widely used in various optimization problems [20–22].

In this paper, we use the PySwarms Python library to implement the solvers for the leader and the follower [23]. The PySwarms library provides a concise and intuitive API, allowing users to easily integrate it into Stackelberg game models. Compared to other complex optimization libraries, the code of PySwams is more concise and easier to understand, reducing the threshold for learning and using. PySwarms allows users to flexibly adjust various parameters of the PSO algorithm, such as particle count, inertia weight, learning factor, etc. This helps to customize and optimize the specific characteristics of the Stackelberg game model, therefore improving solution efficiency.

The steps for solving the Stackelberg game model are as follows:

1.    Read load and PV data from files, set parameters, and initialize the leader’s optimal strategy x∗;

2.    Based on the leader’s strategy x∗, solve the follower’s strategy y∗ via PSO;

3.    If the maximum iteration number is reached, then output x∗ and y∗ as the final solution; otherwise, solve the leader’s strategy x via PSO with respect to the current follower’s strategy y, and go back to Step 2.

4  Case Study

In this section, we demonstrate a case study to show the effectiveness of the proposed incentive mechanisms by comparison. To simulate the PEDF park system, we use the hourly PV and load data during a certain day tailored based on [24,25]. The PV generation Epv(t) and the original load L0(t) are depicted in Fig. 2. Parameters are tested by repeated experiments and the configuration is shown in Table 1. Note that we set SoC(0)=SoC(T)=0.5 in our simulation. Through this setting, the stability of SoC can be maintained throughout the dispatch cycle, enabling the BESS to maintain high charging and discharging efficiency and a longer service life throughout the entire dispatch cycle [26].

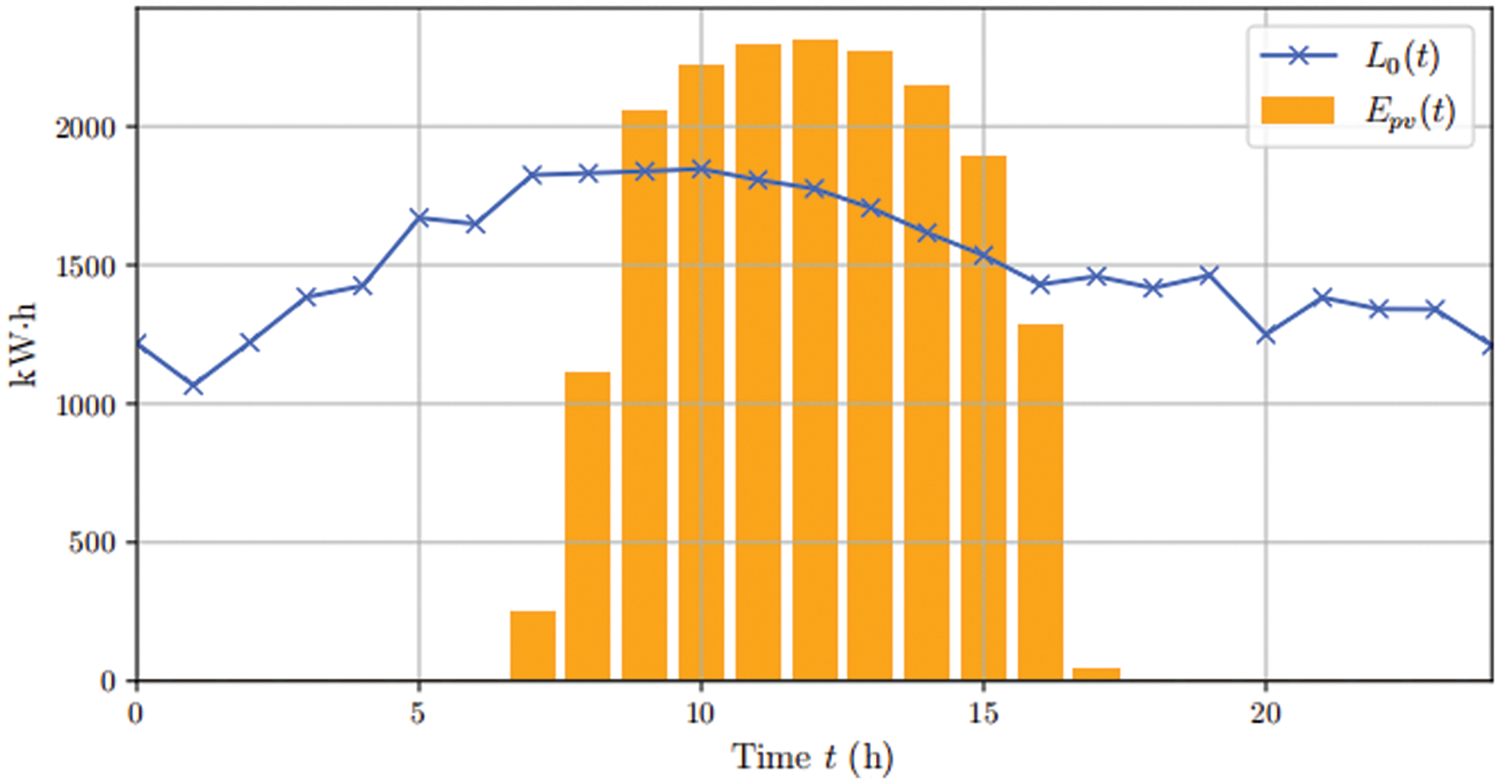
Figure 2: The PV generation Epv(t) and the original load L0(t)

Due to the nonconvexity and nonlinearity of the optimization problem, we use PSO to solve the Stackelberg game model. Fig. 3 shows the objective changes of the leader and the follower during the solving process. We can see that the objectives of the leader and the follower fluctuate a lot at the beginning, and eventually converges after the 31th iteration. This also provides evidence for the fast and strong convergence of PSO.

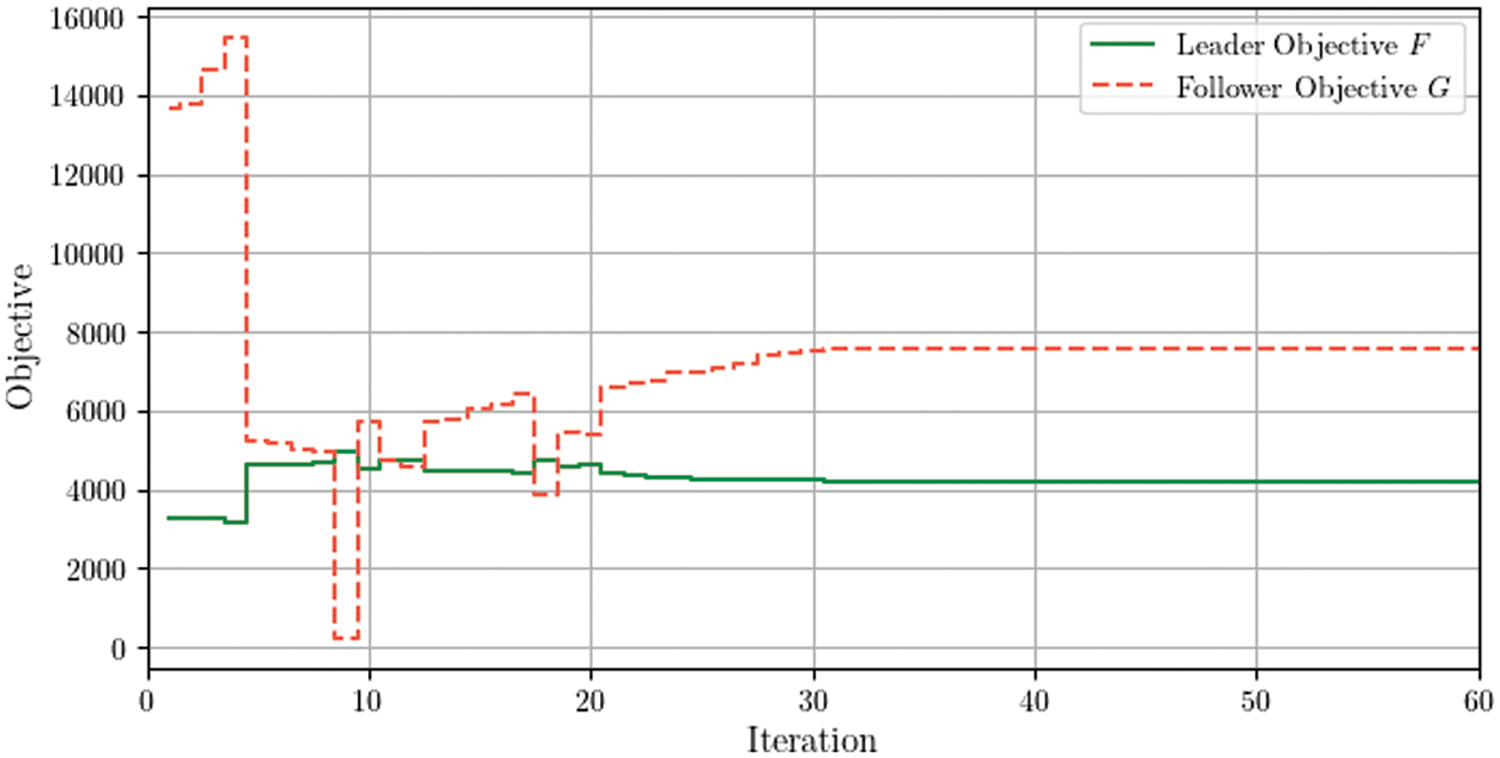
Figure 3: Objective changes of the leader and the follower

In the next, we will compare the dispatch results of four different cases. The incentive mechanism settings of different cases are shown in Table 2. Among them, Case 1 with both incentive mechanisms configured represents the dispatch strategy proposed in this paper, Cases 2 and 3 choose only one from the two mechanisms, and Case 4 is the default case without incentive mechanism.

4.1 Effect on Load Consumption

First, we compared the load curves of the PEDF park in different cases. The results in Fig. 4 show that under the guidance of the hybrid DR, the PEDF park in Cases 1 and 2 exhibits more flexible energy consumption adjustment ability compared to that in Cases 3 and 4. Correspondingly, Fig. 5 demonstrates the load utility change during the dispatch day. It can be seen that the load utility of Case 1 from 3:00 am to 7:00 pm has an obvious decrease due to load reduction. It indicates that although multiple incentive mechanisms help optimize the overall objective of the PEDF park, its electricity consumption satisfaction is compromised to some extent. In addition, the peak loads and average loads in the four cases are shown in Table 3. We observe that the hybrid DR reduces the peak load, thereby helping relieve the pressure of the power grid. Note that the load curves of Cases 3 and 4 overlap because the load of the PEDF park remains unchanged at a constant electricity purchasing price in both cases.

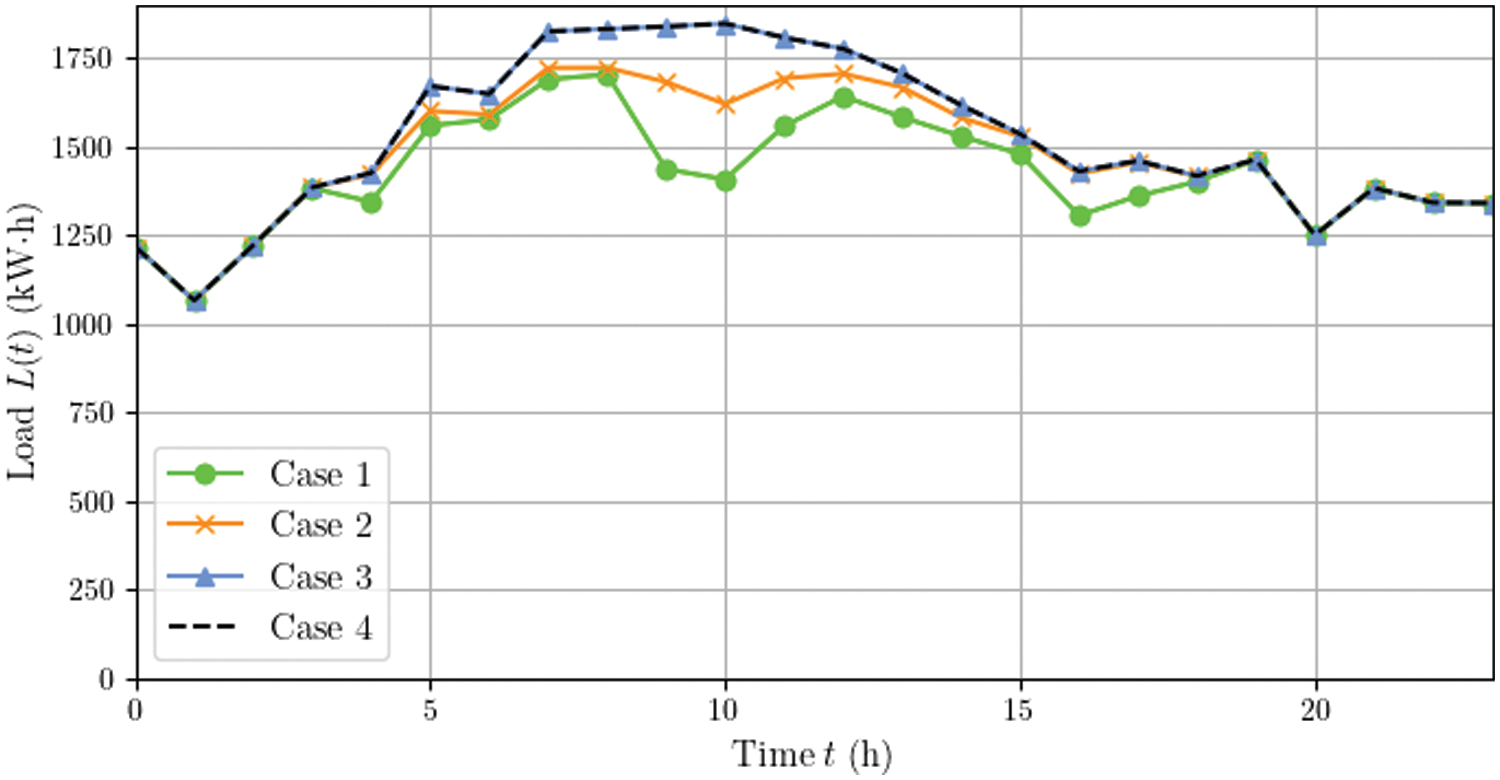
Figure 4: Load curves of different cases

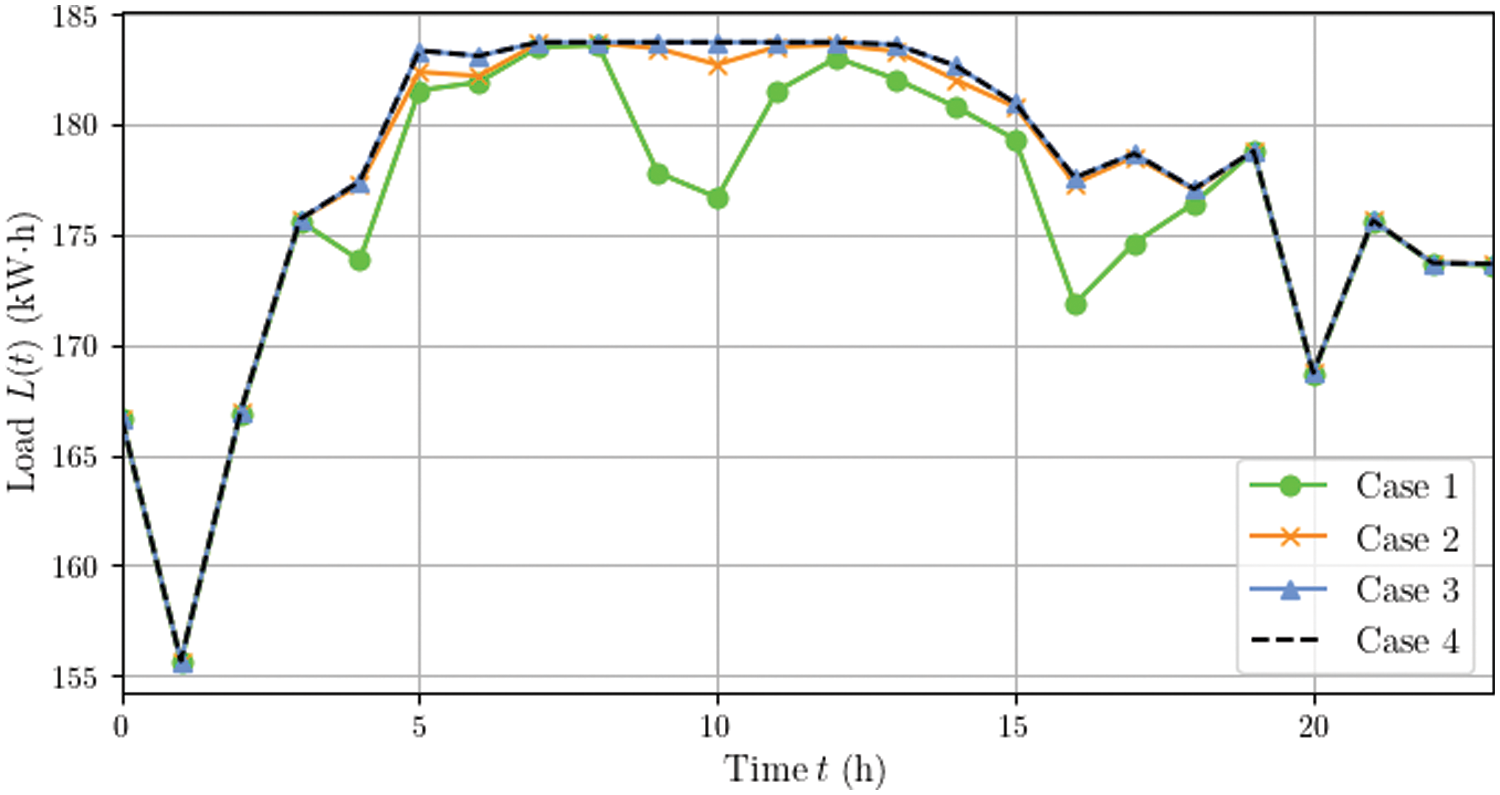
Figure 5: Load utility of different cases

Intuitively, the reputation-based discount mechanism offers lower electricity purchasing prices for the PEDF park, the load reduction rate of Case 1 could have been less than that of Case 2 in Fig. 4. However, from Eq. (6), we know that the PEDF park with a higher reputation score is more willing to achieve the predicted load reduction rate, which explains the slightly lower load curve of Case 1 compared to the load curve of Case 2.

4.2 Effect on Profit and Cost

Table 4 shows the profit and cost of the grid and the PEDF park, and Fig. 6 shows the TOU and incentive prices of different cases. As we can see from Table 4, the PEDF park in Case 1 with our multiple incentive mechanisms achieves the greatest cost reduction rate, followed by Cases 2 and 3 with one of the two incentive mechanisms implemented. Among them, the electricity selling revenue of Case 1 is apparently higher than that of other cases. It is because that Case 1 has the highest load reduction rate, and the PEDF park will have more surplus PV generated electricity. Moreover, the reputation-based discount also helps raise the electricity selling revenue, which is supported by the revenue rise in Case 3 as well. On the other hand, the electricity purchasing costs in both Cases 1 and 2 increase compared to that of Case 4 due to the application of TOU prices. As we can see from Fig. 6a, the TOU prices are higher than the fixed electricity purchasing price in Cases 3 and 4, and the TOU prices of Case 1 is even higher than that of Case 2. This is because that under the reputation-based discount mechanism, the grid needs to set up higher prices to increase its profit.

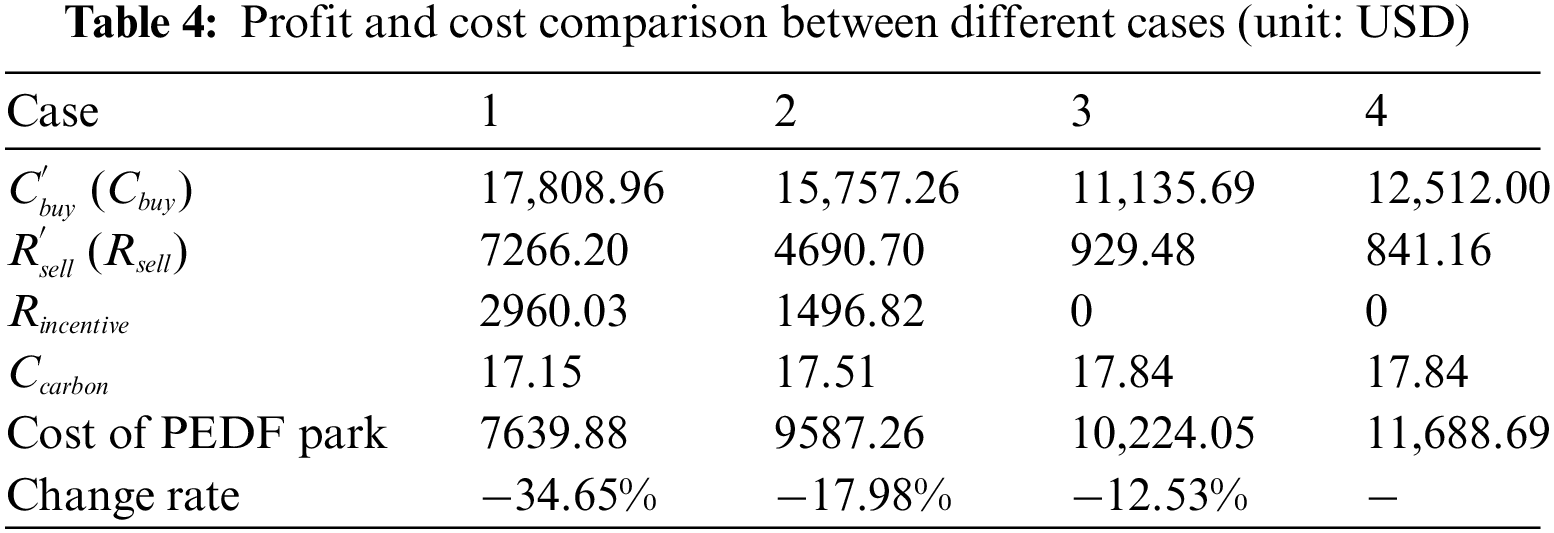
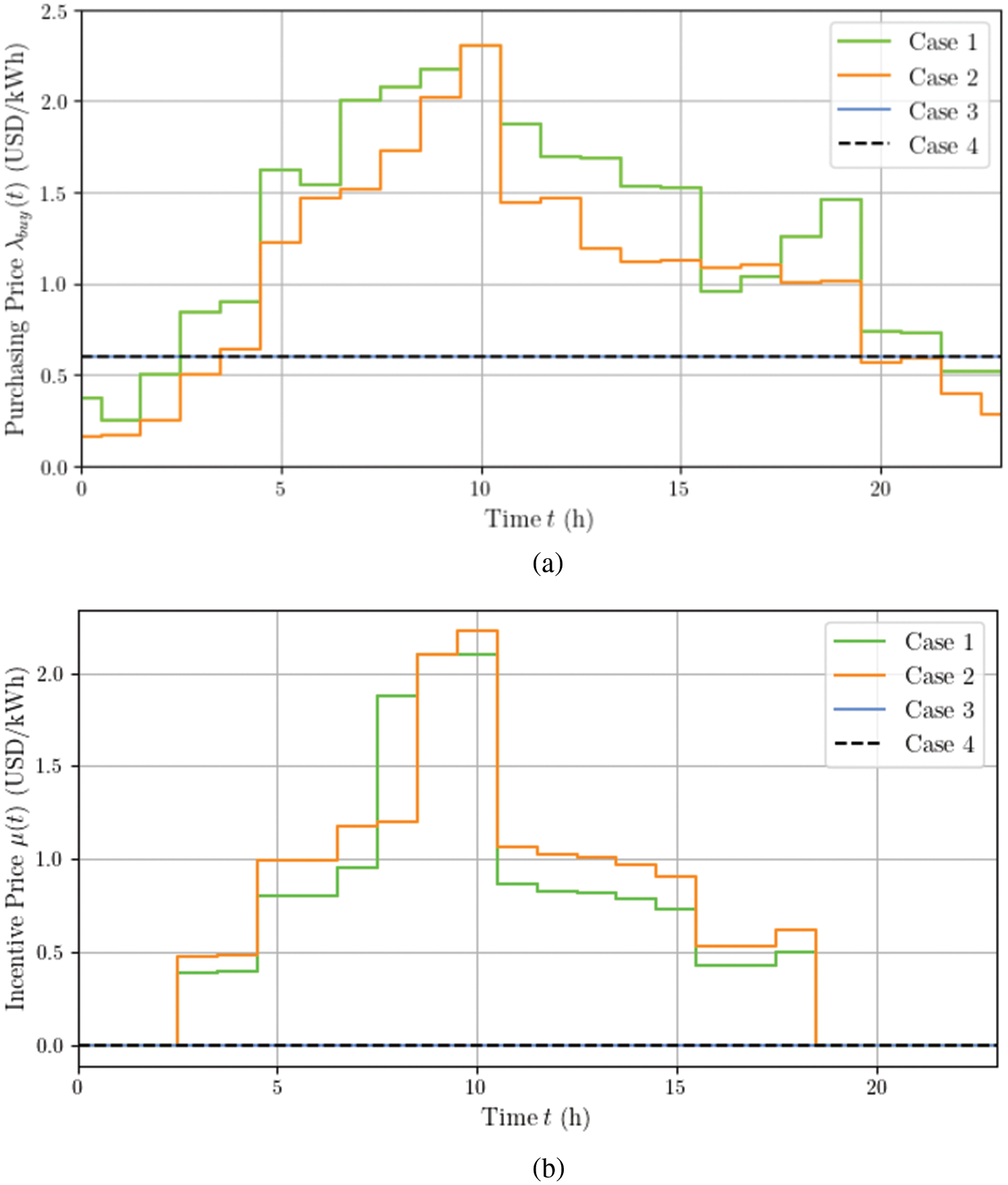
Figure 6: TOU and incentive prices of different cases. (a) TOU prices. (b) Incentive prices

4.3 Effect on Sustainability

From Table 4, we can see a slight reduction on the carbon emission penalty cost in Case 1 and Case 2, by 3.87% and 1.85%, respectively. Eq. (23) indicates that the Ccarbon is proportional to Ebuy(t). Therefore, the reduction in the carbon emission amount and the corresponding penalty cost is caused by the reduction of the amount of electricity purchased from the grid.

Moreover, Table 5 compares the penetration rates of renewable energy generation in different cases. We can see that the penetration rate of renewable energy of both Cases 1 and 2 increases compared to that of Cases 3 and 4. This indicates that our multiple incentive mechanism is also helpful in enhancing the degree of renewable energy utilization and energy structure optimization.

5  Conclusion

In this study, we propose multiple incentive mechanisms aimed at promoting a friendly relationship between building power systems integrated with PEDF and the power grid. Our focus is to develop economic and noneconomic methods tailored to the unique characteristics of PEDF parks, taking into account economic, environmental, and operational considerations. Through our modeling and simulation, we demonstrate the feasibility and effectiveness of these mechanisms in optimizing energy consumption, minimizing grid pressure, and promoting a more resilient and responsive power system.

We argue that encouraging cooperation between building PEDF parks and the power grid can help improve the resilience of the power grid. It can also promote the intelligence of dispatch decisions, thereby bringing more efficient energy consumption and cost savings to both PEDF building parks and grid operators. However, the integration of multiple incentive mechanisms may pose challenges to PEDF parks, power supply companies, and even the government, because they require careful consideration of technological compatibility and regulatory frameworks. The adaptation of PEDF parks to these incentive mechanisms may also involve initial costs, which may also pose obstacles to widespread implementation.

In the future, we will continue our research into the improvement in energy storage, control system, and DC distribution network of PEDF systems. Further study can also focus on exploring of regulatory frameworks and policy incentives that contribute to creating a friendly environment for promoting PEDF technologies.

Acknowledgement: None.

Funding Statement: This work was supported by Guangxi Power Grid Science and Technology Project (GXKJXM20222069). This project was established by Guangxi Power Grid Co., Ltd. (https://www.gx.csg.cn/, accessed on 10 May 2024), and the grant was received by Yun Zhao.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Weidong Chen, Yuxin Lu; data collection: Min Guo; analysis and interpretation of results: Yun Zhao, Xiaorui Wu; draft manuscript preparation: Ziwen Cai. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The raw data supporting the conclusion of this article will be made available by the authors with reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Liu et al., “Energy management and capacity optimization of photovoltaic, energy storage system, flexible building power system considering combined benefit,” Energy Eng., vol. 120, no. 2, pp. 541–559, 2023. doi: 10.32604/ee.2022.022610. [Google Scholar] [CrossRef]

2. F. Molina-Martin, O. D. Montoya, L. F. Grisales-Noreña, and J. C. Hernández, “A mixed-integer conic formulation for optimal placement and dimensioning of DGs in DC distribution networks,” Electronics, vol. 10, no. 2, pp. 176, 2021. doi: 10.3390/electronics10020176. [Google Scholar] [CrossRef]

3. Y. Liu, Y. Zhang, G. Cheng, K. Lv, J. Zhu and Y. Che, “Grid-friendly energy prosumers based on the energy router with load switching functionality,” Int. J. Electr. Power Energy Syst., vol. 144, no. 4, 2023, Art. no. 108496. doi: 10.1016/j.ijepes.2022.108496. [Google Scholar] [CrossRef]

4. C. Tang, M. Liu, M. Xie, P. Dong, J. Zhu and S. Lin, “A single-leader and multiple-follower Stackelberg model for the look-ahead dispatch of plug-in electric buses in multiple microgrids,” Energy, vol. 214, no. 2, 2021, Art. no. 118929. doi: 10.1016/j.energy.2020.118929. [Google Scholar] [CrossRef]

5. W. Tang, Z. Wang, Y. Zhao, J. Wang, Y. Qin and G. Liao, “Research on optimal operation of PEDF system based on improved ChOA,” in 2023 5th Int. Conf. Electron. Eng. Inform. (EEI), Wuhan, China, 2023, pp. 322–327. [Google Scholar]

6. T. Xiong et al., “A method for low-carbon dispatch of PEDF (photovoltaic, energy storage, direct current and flexibility) microgrid considering indirect carbon emissions,” in 2022 Asian Conf. Front. Power Energy (ACFPE), Chengdu, China, 2022, pp. 578–584. [Google Scholar]

7. C. Liu, J. Dai, C. Duan, and X. Xue, “Simulation and analysis of fault characteristics of PEDF building energy systems,” in 2023 6th Asia Conf. Energy Electr. Eng. (ACEEE), Chengdu, China, 2023, pp. 354–358. [Google Scholar]

8. B. Satchidanandan and M. A. Dahleh, “An efficient and incentive-compatible mechanism for energy storage markets,” IEEE Trans. Smart Grid, vol. 13, no. 3, pp. 2245–2258, 2022. doi: 10.1109/TSG.2022.3145689. [Google Scholar] [CrossRef]

9. T. Alquthami, A. H. Milyani, M. Awais, and M. B. Rasheed, “An incentive based dynamic pricing in smart grid: A customer’s perspective,” Sustainability, vol. 13, no. 11, 2021, Art. no. 6066. doi: 10.3390/su13116066. [Google Scholar] [CrossRef]

10. D. Liu, Z. Qin, H. Hua, Y. Ding, and J. Cao, “Incremental incentive mechanism design for diversified consumers in demand response,” Appl. Energy, vol. 329, no. 2, 2023, Art. no. 120240. doi: 10.1016/j.apenergy.2022.120240. [Google Scholar] [CrossRef]

11. D. Erten and B. Kılkış, “How can green building certification systems cope with the era of climate emergency and pandemics?,” Energy Build., vol. 256, 2022, Art. no. 111750. doi: 10.1016/j.enbuild.2021.111750. [Google Scholar] [CrossRef]

12. K. Leng, Z. Li, and Z. Tong, “How will tradable green certificates affect electricity trading markets under renewable portfolio standards? A China perspective,” Clean Energy, vol. 4, no. 4, pp. 585–598, 2022. [Google Scholar]

13. T. Wang, J. Guo, S. Ai, and J. Cao, “RBT: A distributed reputation system for blockchain-based peer-to-peer energy trading with fairness consideration,” Appl. Energy, vol. 295, 2021, Art. no. 117056. doi: 10.1016/j.apenergy.2021.117056. [Google Scholar] [CrossRef]

14. X. Liu, Q. Wang, and C. Wu, “A Stackelberg game approach for heterogeneous energy market in integrated energy system,” Int. J. Energy Res., vol. 45, no. 1, pp. 1038–1054, 2020. [Google Scholar]

15. B. Xu, J. Wang, M. Guo, J. Lu, and L. Han, “A hybrid demand response mechanism based on real-time incentive and real-time pricing,” Energy, vol. 231, no. 1, 2021, Art. no. 120940. doi: 10.1016/j.energy.2021.120940. [Google Scholar] [CrossRef]

16. T. Wang, J. Wang, Y. Zhao, J. Shu, and J. Chen, “Multi-objective residential load dispatch based on comprehensive demand response potential and multi-dimensional user comfort,” Elect. Power Syst. Res., vol. 220, 2023, Art. no. 109331. doi: 10.1016/j.epsr.2023.109331. [Google Scholar] [CrossRef]

17. H. Pourbabak, J. Luo, T. Chen, and W. Su, “A novel consensus-based distributed algorithms for economic dispatch based on local estimation of power mismatch,” IEEE Trans. Smart Grid, vol. 9, no. 6, pp. 5930–5942, 2018. doi: 10.1109/TSG.2017.2699084. [Google Scholar] [CrossRef]

18. X. Guo, S. Han, L. Sun, T. Wang, and J. Shu, “A novel hybrid demand response model under a distributed reputation framework,” in 2022 5th Int. Conf. Power Energy Appl. (ICPEA), Guangzhou, China, 2022, pp. 577–584. [Google Scholar]

19. Z. Meng, Y. Zhong, G. Mao, and Y. Liang, “PSO-sono: A novel PSO variant for single-objective numerical optimization,” Inf. Sci., vol. 586, no. 1, pp. 176–191, 2022. doi: 10.1016/j.ins.2021.11.076. [Google Scholar] [CrossRef]

20. C. Nagarajan, K. Umadevi, S. Saravanan, and M. Muruganandam, “Performace analysis of PSO DFFP based DC-DC converter with non isolated CI using PV panel,” Int. J. Robot. Control Syst., vol. 2, no. 2, pp. 408–423, 2022. [Google Scholar]

21. G. Singh Chawda, O. Prakash Mahela, N. Gupta, M. Khosravy, and T. Senjyu, “Incremental conductance based particle swarm optimization algorithm for global maximum power tracking of solar-PV under nonuniform operating conditions,” Appl. Sci., vol. 10, no. 13, 2020, Art. no. 4575. doi: 10.3390/app10134575. [Google Scholar] [CrossRef]

22. N. Pragallapati, T. Sen, and V. Agarwal, “Adaptive velocity PSO for global maximum power control of a PV array under nonuniform irradiation conditions,” IEEE J. Photovolt., vol. 7, no. 2, pp. 624–639, 2017. doi: 10.1109/JPHOTOV.2016.2629844. [Google Scholar] [CrossRef]

23. L. J. V. Miranda, “PySwarms: A research toolkit for particle swarm optimization in Python,” J. Open Source Softw., vol. 3, no. 21, 2018, Art. no. 433. doi: 10.21105/joss.00433. [Google Scholar] [CrossRef]

24. Meteonorm Software, Accessed: Apr. 25, 2024. [Online]. Available: https://meteonorm.com/en/ [Google Scholar]

25. National Renewable Energy Laboratory (NRELEnd-Use Load Profiles for the U.S. Building Stock, NREL, Apr. 25, 2024. doi: 10.25984/1876417. [Google Scholar] [CrossRef]

26. T. Wang, H. Hua, T. Shi, R. Wang, Y. Sun and P. Naidoo, “A bi-level dispatch optimization of multi-microgrid considering green electricity consumption willingness under renewable portfolio standard policy,” Appl. Energy, vol. 356, no. 6, 2024, Art. no. 122428. doi: 10.1016/j.apenergy.2023.122428. [Google Scholar] [CrossRef]