Research on Regulation Method of Energy Storage System Based on Multi-Stage Robust Optimization

1  Introduction

The vigorous development of renewable energy sources such as new energy has gradually weakened the status of traditional energy. Mbungu et al. [1] discussed an optimal load management control method for economic load shedding problems. The control scheme is based on the coordination of a diesel generator (DG) system with a separate MG system comprising PER (Potential Energy Recovery) wind and photovoltaic (PV), two biomass power generation systems and an energy storage system (ESS). The control model minimizes the fuel cost of the DG unit, where the mill is part of the load. The optimal control scheme is adopted to minimize the operating cost of DG, maximize the energy of rrs, and ultimately increase the profit of MG in the load shedding operation. Only a qualified power dispatching system can ensure the stability, safety, and economy of the operation of the power grid [2]. In the face of renewable energy with an increasing proportion year by year, due to its strong randomness and high volatility in power output, it is necessary to adopt a conservative power generation strategy in the dispatching process. In this way, a large amount of spare capacity is reserved to cope with the impact of power output fluctuations, resulting in problems such as insufficient load rate of thermal power units and uneven consumption of renewable energy. Moreover, the above contradictions are intensifying with the development of renewable energy, and there is an urgent need for new dispatching systems to deal with the above uncertainties in a timely manner.

The new integrated energy system covers multiple energy sources. The development of energy sources including natural gas and heat energy has become an important development direction for the current national response to the energy crisis [3]. Due to its extensive coverage of energy storage and transducer equipment, it possesses the capability to effectively manage the uncertainties associated with renewable energy. However, it also greatly increases the complexity of the operation of the scheduling system. For problems of uncertainty optimization, the problem is effectively solved by an algorithm. Khodaya et al. [4] suggested a two-stage stochastic optimization model that has been experimentally verified to be suitable for optimizing the power dispatch of wind power and pumped energy storage systems. Dispatch of the power system [5] is arranged in stages, so as to effectively obtain the unit regulation and dispatch situation in the case of wind output. Zhang et al. [6] put forward a robust chance-constrained optimization model based on wind power uncertainty analysis and generalized energy storage reserve. The uncertainty of wind power output was analyzed using Latin hypercube sampling and fuzzy C-means clustering algorithm. To tackle this uncertainty, a generalized energy storage optimization rotating reserve capacity was introduced. Furthermore, a robust chance-constrained optimization model, which combines stochastic programming and robust optimization, was developed to minimize operating costs in an integrated energy system. This approach aims to enhance system robustness and efficiency. However, it is important to consider that this method may require a longer computation time. Si et al. [7] conducted an analysis of the source-load characteristics of active distribution networks. They took into account the uncertain impact of renewable energy and energy storage systems on these networks and established a foundational model for renewable energy and energy storage systems. Through the linear dual theory and Lagrange transformation method, the constraints with uncertain variables were transformed into constraints with only certain variables, and then the multi-objective robust optimal scheduling scheme under the fluctuation of renewable energy was obtained. This approach is advantageous in mitigating the fluctuations in the distribution network and enhancing the stability and flexibility of the system. However, this method is prone to data redundancy in the calculation process. Samy et al. [8] proposed a method to determine the size of photovoltaic grid-connected systems with different cell technologies. In this method, the technical and economic performance of PV energy systems under five different battery technologies, namely lead-acid battery, Li-ion battery, vanadium REDOX battery and nickel-iron battery, is compared. Depending on the frequency of grid outages, this survey conducts 0 to 500 outages per year. The main comparative indicators considered are the cost of investment, the proportion of renewable energy and surplus electricity. Grid-connected PV/nickel-iron battery systems are most efficient at high failure frequencies in the main grid. However, it is worth noting that this method may experience delays.

Robustness optimization is an optimization method that makes use of interval disturbance information to make the best decision under the worst disturbance condition. Recently, it has been applied to the dispatching decision of power systems because of its advantages such as easily available basic data, high computational efficiency, and suitability for solving large-scale systems. Based on this, this paper studies the regulation method of energy storage systems based on multi-stage robust optimization. Aiming at robust optimization parameters, wind power uncertainty, photovoltaic power generation uncertainty parameters, renewable energy output uncertainty model, and load uncertainty model, multi-stage robust optimization of energy storage is carried out. By constructing a multilevel robust optimal allocation model, the upper optimization model and the lower optimization model are refined. By applying decision constraints, the performance of the energy storage power station system is improved, resulting in enhanced system efficiency and reduced computation time. The use of generalized Benders Decomposition facilitates coordinated operation and eliminates unnecessary power data. Taking into account the coordinated operation among different systems, the power dispatch plan should be developed to enhance the visibility of renewable energy contribution and avoid operational delays. Experimental results demonstrate that this method can adjust the uncertain set boundaries by introducing various constraint parameters. It effectively addresses the conservativeness issue commonly encountered in other robust optimization approaches, enabling a more reasonable reduction in energy storage capacity within the power system. Consequently, it enhances the responsive capabilities of large-scale renewable energy integration into the grid.

2  Optimal Allocation Model Design for Energy Storage in Power Systems

2.1 Setting Robust Optimization Parameters

The primary objective of power system dispatch is to ensure a balance between the total energy generated and the total energy consumed by the load. With the presence of renewable energy, the static balance of the power system evolves into a dynamic equilibrium over time. That is, in the process of power dispatching, it is necessary to maintain the energy regulation capacity of the system is greater than the fluctuation range of the energy consumption load.

Robust optimization is an optimization method for uncertainties. In the process of system operation, assuming that the value range of uncertainties is fixed, the purpose of the optimal solution is to make the values of any uncertainties meet the constraint requirements of the system [9,10]. And even if the uncertainty is the worst in all cases, it will still make the system cost the lowest.

The establishment of a good set of uncertainties is the key to solving the problem of inconsistencies. In the power dispatching problem, renewable energy is the main source of system uncertainty. Various factors, including seasonal changes and environmental conditions, can impact wind energy. Therefore, it is important to enhance the accuracy of wind power output prediction. Similarly, the output of photovoltaic systems is influenced by factors such as day-night cycles, solar intensity, and cloud conditions. These factors contribute to more intense fluctuations in the short-term output of photovoltaic systems.

2.2 Model of Wind Power Generation Uncertainty

The main influencing factor of the fan output is the size of the wind speed. In the case of a certain air quality, the power generated by the fan P can be expressed as:

P=12CπρR2v3(1)

where, ρ is the density of the air in the case of fan output [11]. R is the size of the radius of the fan blade. v is the wind speed situation at the corresponding time. C is the probability of its contribution.

The fan’s specific output is influenced by factors such as wind speed, wind direction, air pressure, and temperature. The uncertainty associated with these factors leads to fluctuations in the actual output of the fan around its theoretical value. Additionally, due to the non-linear relationship between wind speed and wind output power, the distribution of wind power output power varies under different wind speed conditions.

2.3 Model of Photovoltaic Generation Uncertainty

The situation of solar power generation is mainly determined by the intensity of light at the time of power output [12]. According to statistical laws, under normal circumstances, the light intensity of solar light over a period of time has a certain regularity. It can be approximated as a beta distribution, which can be expressed as:

f(I)=Γ(α+β)Γ(α)Γ(β)(I(t)α−1Imax)(1−I(t)Imax)β−1(2)

where, I(t) is the light intensity of the corresponding system at the moment t. Imax is the maximum light intensity on a photovoltaic power generation system during a statistical time period. α and β are the shape distribution coefficients in the system.

In addition to the impact of light intensity, factors such as air temperature, cloud cover, and atmospheric conditions also affect the output power of photovoltaic power generation systems. Therefore, it has obvious output uncertainty.

2.4 Models of Uncertainty in Renewable Energy Output

With the development of multi-energy systems, the share of renewable energy sources in the electricity mix is steadily rising. However, the unpredictable, fluctuating, and sporadic nature of renewable energy output presents considerable challenges to the power system. These factors can significantly impact the stability and safety of the power system.

The uncertainty related to renewable energy sources like wind and photovoltaics can be characterized by the disparity between forecasts and actual output. Thus the model Gk of renewable energy output can be expressed as:

Gk=Gk¯+ΔGk(3)

where, Gk¯ is the predicted value of the output of uncertain energy sources such as wind and photovoltaics. ΔGk is the deviation between the actual output and the predicted result.

By establishing an uncertain regulation model, the multi-energy composite system is represented as:

pkD=pr{GkD−Giv2<Gk<GkD+Giv2}(4)

where, GkD represents the anticipated renewable energy output within the system. The probability of unit output prediction deviation ΔGkD in the system is pkD. The probability that Pr’s contribution to renewable energy meets the conditions for occurrence, At this time, the system has an output prediction bias, and the output difference can be calculated by the event probability. Giv is the maximum power capacity that the unit can regulate.

For renewable energy, the ability to regulate its output also has certain uncertainties. Its uncertainty can be expressed in the model as:

Gk(z,t)=∑k=1skpk(t)zGkD(t)(5)

where, sk is the state of the load coordination process in renewable energy [13,14]. z is the formula transformation of the energy system.

2.5 Model of Load Uncertainty

In a diverse energy system, uncertainties exist not only in the output of renewable energy sources but also in the load. The load variation in such systems is influenced by uncertain factors like weather conditions, energy prices, and behavioral patterns, resulting in load uncertainty [15]. The matching problem between the uncertainty of unit output and load demand is the main problem of multi-energy systems.

In the operation of multi-energy systems, the presence of various uncertain disturbances can significantly impact system stability. Evaluating the compatibility between energy load demand and system stability in uncertain conditions is of utmost importance. Furthermore, developing an uncertain load model is critical for ensuring the safety and reliability of the system during its operation. The model for constructing the load level L(t) is:

L(t)=Pa(t)Pb(t)Pc(t)Lm+N(0,σ2)(6)

where, Lm is the maximum annual load in the system. Pc(t) is the ratio of the peak load at the time of t. Similarly, Pb(t) is the ratio of daily peak load. Pa(t) is the annual peak load ratio. N(0,σ2) is the standard normal distribution.

3  Robust Control Design of Power System with Load

3.1 Multi-Stage Robust Optimization Problem

Given the inherent unpredictability of renewable energy sources, the integration of energy storage systems plays a vital role in enhancing the flexibility of power systems during power dispatch. By storing surplus energy generated from renewables during high production periods and releasing it during low production periods, energy storage systems help mitigate fluctuations and ensure a stable and dependable power supply [16]. Energy storage capacity allocation optimization is a scheme to seek the optimal capacity allocation for the purpose of improving the reliability, safety, and economy of the system, taking into account various factors such as energy storage technology itself, equipment response characteristics, and installation cost. Optimizing the configuration of equipment energy storage capacity helps avoid idle energy storage capacity, leading to improved operational economy and meeting reliability and security requirements. Optimizing the allocation of energy storage system capacity can improve system coordination and flexibility, while meeting the economic requirements of the power grid and ensuring cost-effective power operation. Hence, it is crucial to consider the economic scheduling of different types of energy storage, such as pumped energy storage and battery energy storage, in the daily production process planning. The inclusion of uncertainty absorption mechanisms within the energy storage system effectively enhances the power system’s capability to handle extreme events.

When dealing with short-term and ultra-short-term economic scheduling problems, it is important to consider the calculation method used. A typical approach is to employ a forward-looking economic scheduling model with a rolling time scale. To ensure accurate solutions, the time scale for this method typically falls between half an hour and two hours. This does not meet the requirements of economy and effectiveness for economic dispatch that needs to cover the whole day. Therefore, a multi-stage scheduling model is required to ensure system accuracy.

The multi-stage robust optimization model for the daily scheduling model can optimize the energy storage resources for a relatively long time. It can provide the system with extreme situations, making the decision-maker’s decision-making more forward-looking [17].

3.2 Multi-Stage Robust Optimization Configuration Model

Given the uncertain parameters and influences within the system, historical data does not need to be taken into account during system operation [18]. In the configuration of the energy storage system’s dispatch, both economic and robustness factors are considered comprehensively. Once the system input is determined, the model can be represented as:

{minF(s,i)s.t. G(s,i)≤0H(s,i)=0(7)

where, F(s,i) is the power system dispatching the decision target, s is the decision variable in the system, and i is the model input parameter. G(s,i), H(s,i) are the inequality constraints and the equation constraints in this model, respectively.

Decision objective F(s,i) can be expressed as:

F(s,i)=min(D1+D2)(8)

where, D1 represents the construction cost of the energy storage system, D2 represents the operational cost of the energy storage system.

3.3 Upper-Level Optimization Model

In order to effectively cope with the robustness of increasing loads, and fully consider the role of uncertain output and uncertain loads. The setting of the objective function is the maximum fluctuation of the indeterminant. The objective function after optimization of the configuration is:

f=max(Gk,L)(9)

For a multi-objective optimization process, the influence of different factors needs to be considered comprehensively. Consider the conflict between the various uncertainties and weigh the objectives according to their importance. You can optimize a multi-objective problem as a single-objective problem, expressed as:

{f=λ1Gk+λ2Lmin(D1+D2)≤Dbud(10)

where, λ1, λ2 are the weight coefficients for different optimization goals. Dbud is an uncertainty factor.

3.4 Lower-Level Optimization Model

Another optimization goal of the model is to ensure the economics of the distribution system. Thus the optimized objective function is the lowest power purchase cost for the distribution network, expressed as:

minf=min max∑t=1T(Ci(t)Pi(t)−Co(t)Po(t))(11)

where, Ci is the unit price of electricity purchase, Co is the unit price of electricity sold, and Pi and Po are respectively the amount of electricity purchased and sold. For daily running costs, its optimization function can be expressed as:

{min max(dTY)s.t. G(x,y)≤0 H(x,y)=0 α∈U(12)

where, dT represents the coefficient vector of y variable in the objective function. x denotes the system decision variable, primarily the capacity of the energy storage power station. y is a continuous variable in the power dispatching system, encompassing node voltage, load, renewable energy output, and branch power flow. X is a set of column vectors composed of x variables. The x variable typically represents the target variable, such as the system’s capacity and power. Y is the set of column vectors that constitute the y variable.

3.5 Decision Constraints of Power Station Operation

1.   Uncertain output constraint of photovoltaic power generation system, expressed as:

{0≤Pv(t)≤Pvm0≤Pw(t)≤Pwm(13)

where, Pv is the output of the photovoltaic power generation system. Pvm is the maximum capacity value for a photovoltaic system. Pw is the output of wind power systems. Pwm is the maximum capacity value for a wind power system.

2.   Operation limit of power station, expressed as:

In an equalized circuit system, it is assumed that the state of charge changes in each battery are consistent. This means that the output characteristics of the battery pack are equivalent to the output of a single battery. As a result, the battery pack can be simplified using the Thevenan model [19]. Assuming that the AC power value between the power station and the distribution network is constant, the model can be expressed as:

S(t+Δt)=S(t)(1−σ)+ηcPch(t)Δt−Pdis(t)Δt/ηd(14)

where, S represents the battery capacity within the energy storage power station, σ as the battery discharge efficiency, ηc is the system power conversion efficiency, Pch is the power station absorption power efficiency, Δt is the calculation time interval, Pdis is the power station discharge power efficiency, ηd is the inverter conversion efficiency.

3.   Energy balance constraint, expressed as:

{Pi+1(t)=Pi(t)−Pi,L(t)+Pi,G(t)Qi+1(t)=Qi(t)−Qi,L(t)(15)

where, Pi and Qi are the active power and reactive power of the popular i node, respectively. Pi,L and Qi,L are the active loads and the reactive loads on the corresponding node i, respectively. Pi,G is the sum of distributed power generation and energy storage power stations on node i.

4.   Thermal power unit operation constraints, expressed as:

Generally, the fuel cost characteristics of thermal power units are approximated by a smooth quadratic function, and a pulse is superimposed on the unit energy consumption curve considering the threshold effect. The output constraint is shown in Eq. (16). See Eq. (17) for the climbing constraint. The minimum start-stop time constraint is shown in Eq. (18). See Eq. (19) for the logical relationship between the running and start-stop state variables.

Ri,tPi,min≤Pi,t≤Ri,tPi,max,∀i,t(16)

Pi,t−Pi,(t−1)≤Ri,tGRi+(1−Pi,(t−1))Pi,min+Pi,min(Pi,t−Pi,(t−1)),∀i,t(17)

Pi,(t−1)−Pi,t+Pi,k≤1,∀i,t  t≤k≤Toff,i+t−1(18)

Pi,(t−1)−Pi,t+Pi,toff≤0,∀i,t(19)

where, Ri,t is the whole life cycle of the energy storage system; Pi,t is the output of generator i in t period; Pi,min is the lower limit of unit output; Pi,max is the output limit of the unit; The output of Pi,(t−1) generator i in t−1 period; GRi is the number of thermal power units in the system; Is the output of Pi,k generator i in the corresponding wind farm group; Toff,i is the minimum stop time of the unit; Pi,toff is a Boolean variable.

5.   Energy storage system operation constraints, expressed as:

In energy storage systems, the state of charge in each period is affected by both the previous state of charge and the current charge and discharge amounts. To ensure the sustainable operation of the energy storage system, it is essential for the total charge and discharge power to balance out over the entire scheduling period:

∑t−1TPtESS=0(20)

where, PtESS is the frequency modulation power of stored energy at time t. This ensures that the energy storage system maintains a balance between charging and discharging, allowing for efficient and continuous cycling of energy.

6.   Uncertain delay constraint, expressed as:

The uncertain delay is treated by delay dependence, and the margin of preset delay is constrained to minimize to evaluate the robustness of closed-loop systems with different delays. The delay meets the following conditions:

τmin≤d≤τmax(21)

where, τmin delay margin calculated minimum constant; τmax delay margin calculated maximum constant calculated by delay margin. The marginal effect of delay can be optimized by effective delay constraint. The delay margin is the key factor that affects the frequency modulation index in load frequency control. Hence, Eq. (21) can effectively account for the cumulative communication delay during power system energy storage and frequency modulation operations. By addressing the challenges arising from the fluctuations in uncertain energy and load throughout the day, it enables the coordination of load frequency in regional power grids.

3.6 Solution of Optimal Allocation Model Based on Generalized Bending Decomposition

For multi-stage robust optimization problems, the model needs to be solved by generalized Benders Decomposition. This decomposes the problems in the model into sub-problems [20].

A flowchart of the decomposition method is shown in Fig. 1.

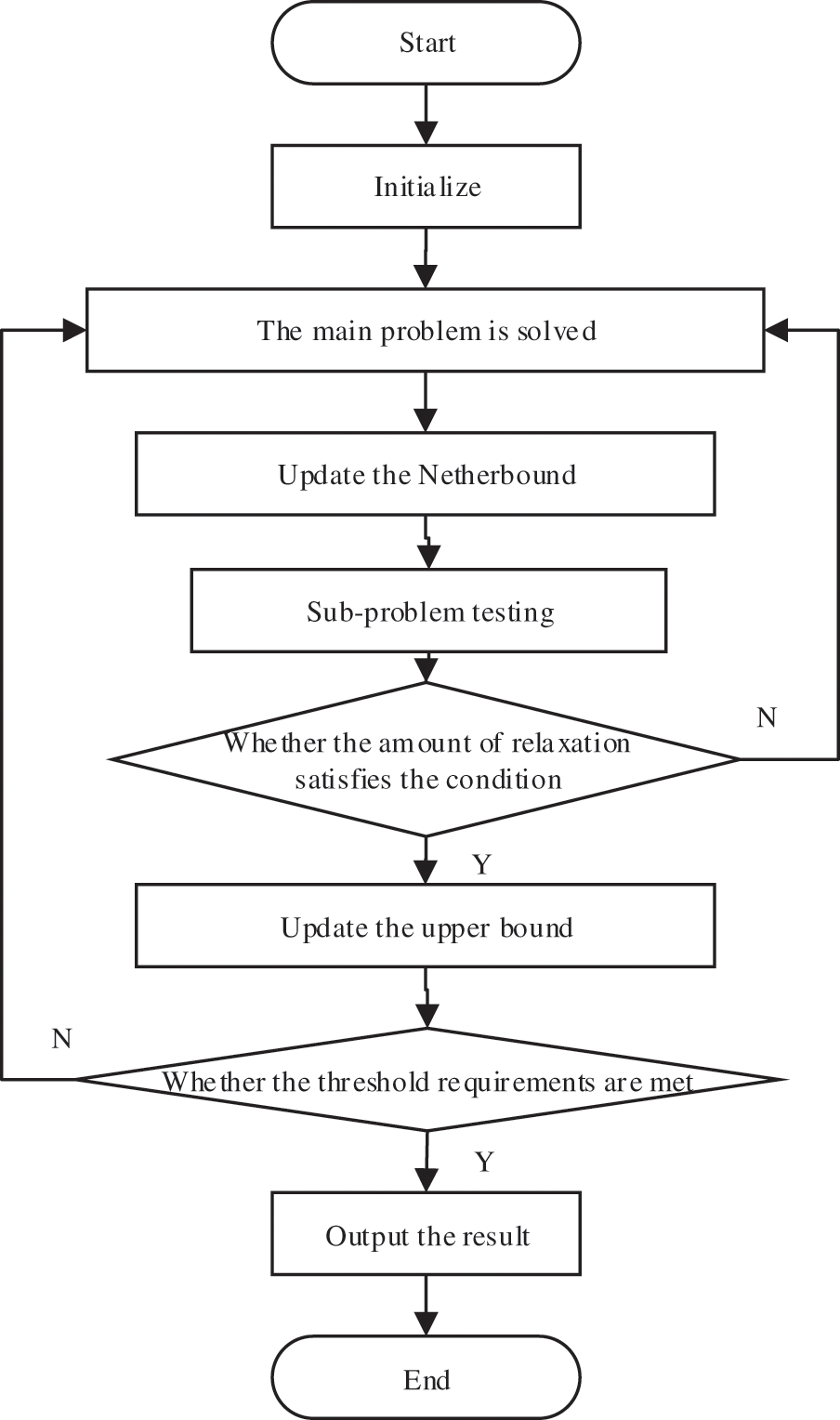
Figure 1: Flowchart of generalized Benders Decomposition

After the decomposition of the model, the main requirements to solve the problems include economic optimization problems, feasibility problems and planning optimization problems.

4  Experimental Results and Data Analysis

4.1 Experimental Node Test System

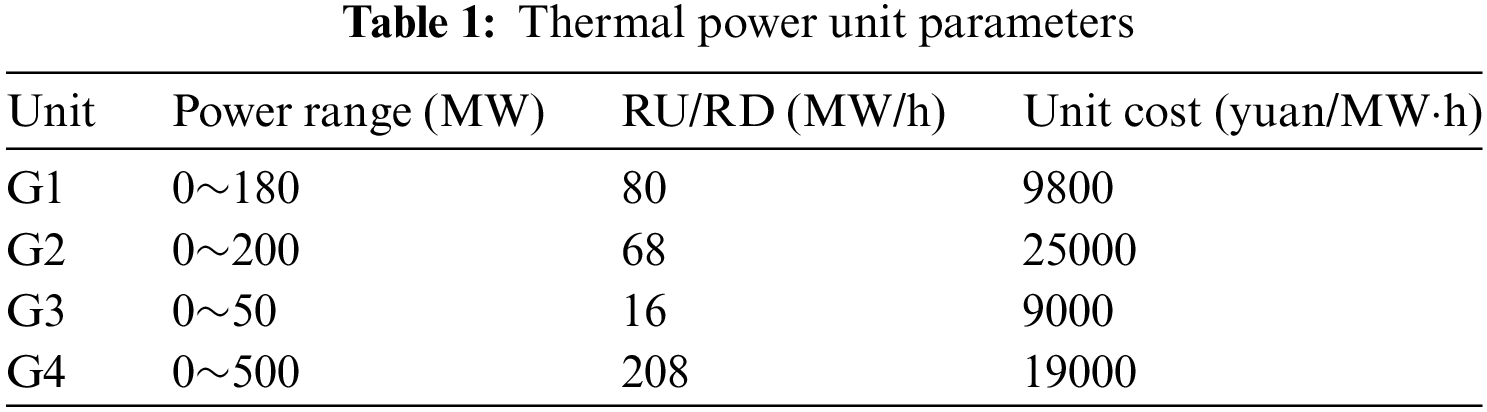
The test system was obtained after modification of the PJM 5-bus system. The system consists of four thermal power units, one wind farm, one photovoltaic power station and one energy storage system. The specific parameters of the test system are as follows: the rated voltage is 10.60 kV, the maximum allowable voltage of a single node is 1.97 pu, the maximum allowable current of the corresponding branch is 1.20 kA, and the minimum required voltage value of the standby is 0.25 pu, the minimum allowable current of the corresponding branch is the minimum. The value is 0.15 kA. Among them, the rated capacity of traditional units is 1000 MW, the proportion of new energy photovoltaic power generation is 20%, the rated power of energy storage power station is 20 MW, and the total power is set at 20 MW·h. The parameters of the generator set are shown in Table 1.

For thermal power sets, the cost function is considered to be a linear change. The penalty cost per unit cut load is 120 yuan/kW·h. The penalty cost of not meeting the standard for uncertain energy consumption is 30 yuan/kW·h.

Set the battery energy storage device of the energy storage power station as a lithium iron phosphate material battery. The unit capacity cost of the battery is 2100 yuan/kW·h, the power cost is set to 1600 yuan/kW·h, and the operation and maintenance cost accounts for 1% of the total investment. Set the fluctuation deviation of renewable energy storage to 10%.

4.2 Experimental Results

1.   Schedule the analysis results

The method of this paper, the method of reference [7] and the method of reference [8] are used to calculate the economic operation cost, and the worst-case impact on the energy storage system is considered. The lower the cost, the better the application effect of the method, and the determination of the calculation results is shown in Fig. 2.

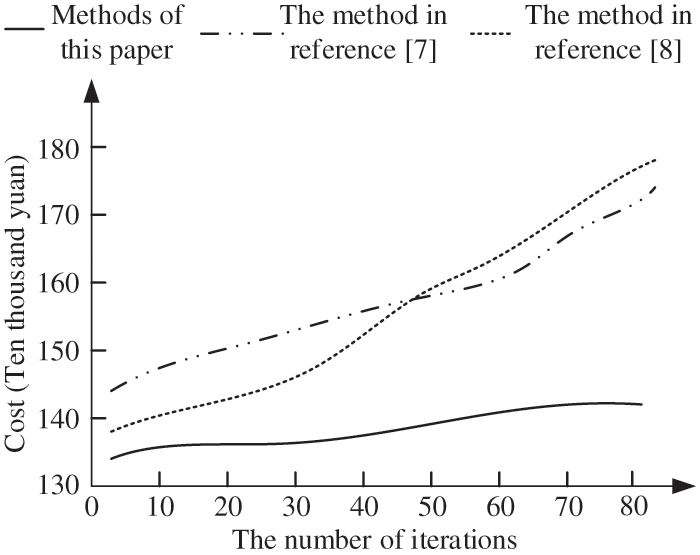
Figure 2: Iteration case

As shown in Fig. 2, when the number of iterations approaches 80, the method in this paper has converged, the cost is low, and the calculation time of the whole model is only 25 s. It is proved that this method has certain applicability. This is because the proposed method constructs constraint strategies in various modes, and optimizes the operation efficiency of power system from all directions and angles.

Considering the worst-case scenario in which the power output in the system is uncertain, the system scheduling scenario is shown in Fig. 3. Since Vitality Generator 3 has the lowest operating cost, it is always under maximum load. Unit 2 has the highest cost and is therefore basically out of service. The load variation of other units changes with the change of net load.

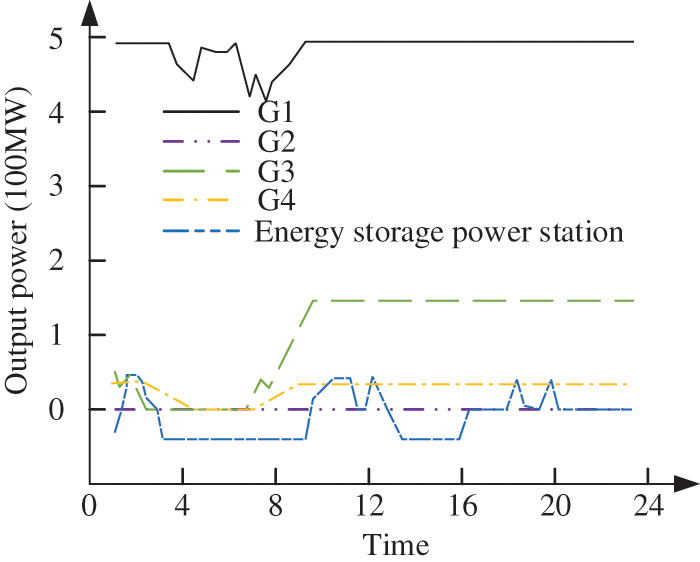
Figure 3: System scheduling schedules

As can also be seen in Fig. 3, the energy storage system is charged during the time period of 3:00 to 9:30 to absorb more fan discharge. Charge from 14:00 to 16:00 to absorb solar and wind loads. Other times are mainly discharged to reduce the operating costs of thermal power.

2.   Algorithm comparison

In order to prove the superiority of this model, it is compared with the methods of reference [7] and the methods of reference [8]. The results are shown in Table 2.

It can be seen from the results in Table 2 that the total cost of the multi-stage robust optimization model in this paper is the lowest among all algorithm models. The cost of this method is slightly lower than that of reference [7] by 4.2% and lower than that of reference [8] by 25.4%. This is because the method proposed in this paper establishes both the upper-level planning objective function and the lower-level planning objective function. By doing so, it effectively calculates the overall life cycle cost of the power system, which includes the fixed investment cost and the operation and maintenance cost. This approach ensures the sustainable operation of the energy storage system and maintains consistent energy storage capacity throughout each dispatching cycle.

3.   Uncertainty analysis

To verify the influence of uncertain source loads on power system dispatching. According to the different deviations of renewable energy fluctuations, the robust dispatching model is analyzed to ensure that the deviation of load fluctuations is less than 10%. Set the fluctuation deviation of renewable energy to 0%–30%. In this scenario, compare the operating cost fluctuation range of the methods in this paper [7,8]. The more stable the change of operating cost, the better the effect of the method. The calculation results are shown in Fig. 4.

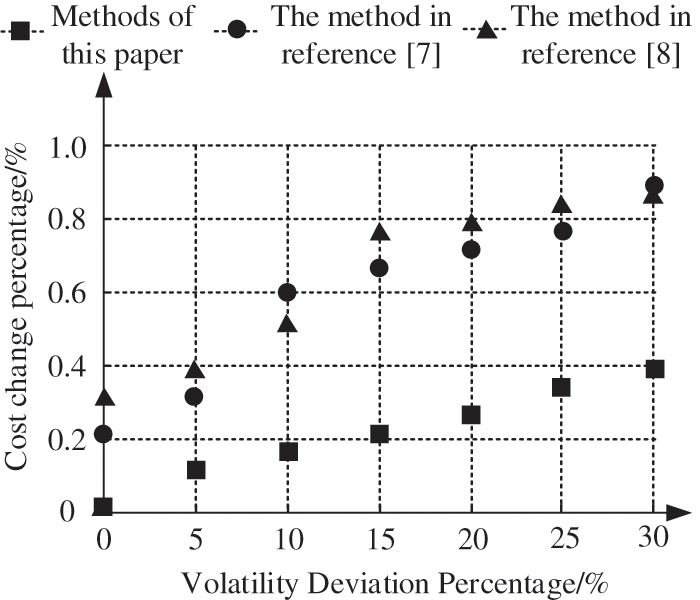
Figure 4: Changes in operating costs

It can be seen from Fig. 4 that the operating costs of the system under the three methods all increase with the fluctuation deviation of renewable energy. When the fluctuation deviation of renewable energy is 0, the three methods have no fluctuation, so the prediction of uncertain energy is more accurate. This makes the system the lowest solution of running cost and the lowest robustness of the system. With the fluctuation of renewable energy gradually increasing and realizing, the prediction error of the system appears, but the error of this method is always smaller than that of the methods in references [7,8]. This is because, in this method, the generalized bending decomposition is adopted to solve the optimal allocation model, and complex variables are introduced to complete the linear programming problem, which effectively ensures the robustness of power system scheduling.

When the fluctuation of uncertain energy sources is small, the system can effectively ensure its economy on the basis of ensuring robustness. In actual scheduling, the staff needs to ensure the economy of the scheduling system according to the fluctuation deviation.

5  Conclusion

To address the scheduling challenges related to energy storage systems and uncertain energy sources, this research proposes a regulation method based on multi-stage robust optimization. The study constructs an optimal allocation model for energy storage in power systems and employs the multi-stage robust optimization approach to address the limitations of traditional methods in terms of time scale. By doing so, it aims to tackle system issues arising from the fluctuations of uncertain environmental energy and unpredictable load variations. The generalized bending decomposition method is utilized to optimize the parameters of the target solution model, reducing the system size and ensuring algorithm convergence. Comparative analysis demonstrates that the proposed model exhibits favorable economic performance when compared to other models. Additionally, the study highlights the significant impact of fluctuation deviations on the system’s operating cost and robustness. This model can effectively enhance the economic efficiency of power systems containing uncertain energy and energy storage systems, making it suitable for guiding the regulation and control of related power systems. Future research can further explore the uncertainty on the power side and investigate the coordinated configuration of energy storage and reactive power compensation equipment with 100% renewable energy supply and support for new energy stations.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design, data collection: Zaihe Yang, Shuling Wang; analysis and interpretation of results: Runhang Zhu, Jiao Cui, Ji Su; draft manuscript preparation: Zaihe Yang, Liling Chen. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Mbungu, N. T., Madiba, T., Bansal, R. C., Bettayeb, M., Naidoo, R. M. et al. (2022). Economic optimal load management control of microgrid system using energy storage system. Journal of Energy Storage, 46, 103843. [Google Scholar]

2. Hosseini, S. A., Toulabi, M., Ashouri-Zadeh, A., Ranjbar, A. M. (2022). Battery energy storage systems and demand response applied to power system frequency control. International Journal of Electrical Power & Energy Systems, 136, 107680. [Google Scholar]

3. Nagpal, H., Avramidis, I. I., Capitanescu, F., Madureira, A. G. (2022). Local energy communities in service of sustainability and grid flexibility provision: Hierarchical management of shared energy storage. IEEE Transactions on Sustainable Energy, 13(3), 1523–1535. [Google Scholar]

4. Khodaya, M. E., Shahidehpour, M., Wu, L. (2013). Enhancing the dispatchability of variable wind generation by coordination with pumped-storage hydro units in stochastic power systems. IEEE Transactions on Power Systems, 28(3), 2808–2818. [Google Scholar]

5. Lorca, Á., Member, S., Sun, X. A. (2014). Adaptive robust optimization with dynamic uncertainty sets for multi-period economic dispatch under significant wind. IEEE Transactions on Power Systems, 30(4), 1702–1713. [Google Scholar]

6. Zhang, Y., Dong, R. N., Wei, Z. H., Gao, X. T. (2022). Robust chance-constrained optimization of integrated energy system considering wind power uncertainty and spinning reserve capacity allocation. Thermal Power Generation, 51(6), 25–33 (In Chinese). [Google Scholar]

7. Si, W., Liu, H. F., Fu, W. J., Zhou, M. (2022). Research on optimization scheduling of active distribution network considering uncertainty of wind and photovoltai. Journal of Huazhong University of Science and Technology. Nature Science Edition, 50(5), 73–77+101 (In Chinese). [Google Scholar]

8. Samy, M. M., Emam, A., Tag-Eldin, E., Barakat, S. (2022). Exploring energy storage methods for grid-connected clean power plants in case of repetitive outages. Journal of Energy Storage, 54, 105307. [Google Scholar]

9. Kim, H. J., Kim, M. K., Lee, J. W. (2021). A two-stage stochastic p-robust optimal energy trading management in microgrid operation considering uncertainty with hybrid demand response. International Journal of Electrical Power & Energy Systems, 124(1), 106422. [Google Scholar]

10. Jani, A., Karimi, H., Jadid, S. (2022). Multi-time scale energy management of multi-microgrid systems considering energy storage systems: A multi-objective two-stage optimization framework. Journal of Energy Storage, 51, 104554. [Google Scholar]

11. Thien, T., Axelsen, H., Merten, M., Sauer, D. U. (2022). Energy management of stationary hybrid battery energy storage systems using the example of a real-world 5 MW hybrid battery storage project in Germany. Journal of Energy Storage, 51, 104257. [Google Scholar]

12. Siti, M. W., Mbungu, N. T., Tungadio, D. H., Banza, B. B., Ngoma, L. (2022). Application of load frequency control method to a multi-microgrid with energy storage system. Journal of Energy Storage, 52, 104629. [Google Scholar]

13. Ishraque, M. F., Shezan, S. A., Ali, M. M., Rashid, M. M. (2021). Optimization of load dispatch strategies for an islanded microgrid connected with renewable energy sources. Applied Energy, 292(1), 116879. [Google Scholar]

14. Coban, H. H., Rehman, A., Mousa, M. (2022). Load frequency control of microgrid system by battery and pumped-hydro energy storage. Water, 14(11), 1818. [Google Scholar]

15. Eshiemogie, S. O., Ighalo, J. O., Banji, T. I. (2022). Knowledge, perception and awareness of renewable energy by engineering students in Nigeria: A need for the undergraduate engineering program adjustment. Cleaner Engineering and Technology, 6, 100388. [Google Scholar]

16. Oskouei, M. Z., Şeker, A. A., Tunçel, S., Demirbaş, E., Gözel, T. (2022). A critical review on the impacts of energy storage systems and demand-side management strategies in the economic operation of renewable-based distribution network. Sustainability, 14(4), 2110. [Google Scholar]

17. Saini, P., Gidwani, L. (2022). An investigation for battery energy storage system installation with renewable energy resources in distribution system by considering residential, commercial and industrial load models. Journal of Energy Storage, 45, 103493. [Google Scholar]

18. Ferahtia, S., Djerioui, A., Rezk, H., Chouder, A., Houari, A. et al. (2022). Adaptive droop based control strategy for DC microgrid including multiple batteries energy storage systems. Journal of Energy Storage, 48, 103983. [Google Scholar]

19. Rezaei, H., Abdollahi, S. E., Abdollahi, S., Filizadeh, S. (2022). Energy management strategies of battery-ultracapacitor hybrid storage systems for electric vehicles: Review, challenges, and future trends. Journal of Energy Storage, 53, 105045. [Google Scholar]

20. Rana, M. M., Uddin, M., Sarkar, M. R., Shafiullah, G. M., Mo, H. et al. (2022). A review on hybrid photovoltaic—Battery energy storage system: Current status, challenges, and future directions. Journal of Energy Storage, 51, 104597. [Google Scholar]