Dynamic Economic Scheduling with Self-Adaptive Uncertainty in Distribution Network Based on Deep Reinforcement Learning

Nomenclature

1  Introduction

Power system economic dispatch is generally modeled as a classical optimization problem. Under the trend of large-scale renewable energy integration, the uncertainty of WT and PV, and other intermittent power outputs brings challenges to grid scheduling and operation [1]. For example, the traditional model-based optimal scheduling problem for distribution networks is a large-scale mixed-integer non-convex nonlinear stochastic or robust optimization problem. In addition, the solution complexity increases exponentially with the increase of the distribution network topology scale and the number of dispatchable devices, which is a non-deterministic polynomial (NP) optimization problem with multiple objectives and constraints [2]. According to whether economic scheduling considers the connection between different time sections, it can be categorized into static economic scheduling [3] and dynamic economic scheduling [4]. Static economic scheduling does not consider the relationship between scheduling periods, while dynamic economic scheduling needs to take into account the relationship between scheduling periods, and can realize flexible scheduling in the case of unpredictable disturbance in the scheduling environment and tasks.

Dynamic economic dispatch takes into account the uncertainty of load and renewable energy output in different scheduling time periods before and after. For the dynamic economic dispatch existing WT, PV, and other renewable energy output uncertainty modeling problems, reference [5] establishes a chance-constrained optimization scheduling model taking into account the output uncertainty of renewable energy based on the output characteristics of renewable energy and transforms the random constraint function into deterministic equivalent constraints by using uncertainty theory. Reference [6] considers that solar illumination intensity and wind speed are random variables subject to Beta distribution and Weibull distribution. Random variables are used to describe the uncertainty of PV and WT output, this fixed form of mathematical analysis limits the prediction accuracy of the model. Reference [7] uses trapezoidal fuzzy numbers to represent PV and WT output, transforms the uncertainty of intermittent power output into the uncertainty of prediction error, and performs probabilistic modeling of prediction error. Reference [8,9] uses Beta distribution and truncated generalized distribution to describe the stochasticity of individual PV and wind farms, respectively. On this basis, reference [10,11] selects appropriate Copula functions to obtain the distribution of total power of distributed PV or multi-wind farms. In addition, the load is also uncertain, and it is difficult to accurately model the whole distribution network system which contains complex uncertain factors.

For the dynamic economic dispatch problem of a distribution network containing intermittent WT and PV, reference [12] introduces the rotating reserve capacity to balance the system power deviation caused by the fluctuation of renewable energy output, and sets a certain positive and negative rotating reserve capacity in advance to cope with the uncertainty of source load and make up for the shortage or excess power generation of units in the scheduling. To ensure the economy of rescheduling when power deviation occurs in the system, the over-scheduling and under-scheduling costs caused by the uncertainty of WT are included in the economic objective function in reference [13]. However, although the above literature can solve the source load uncertainty by reserving rotating in the deterministic model, this will indirectly increase the dispatch cost and violate the idea of economic dispatch. In this regard, the scenario analysis method [14,15] and the chance-constrained programming method [16,17] in the stochastic optimization modeling method further consider the impact of uncertainty on scheduling, and make up for the shortcomings in the above research without sacrificing economy. However, the optimization results of stochastic optimization methods depend on the degree of coincidence between the assumed probability distribution and the actual random variables. Therefore, the robust optimization method does not need to fit the probability distribution of random variables and reduces the computation. Reference [18] constructs a two-stage robust optimization model that takes into account the uncertainty of source load and then solves the unit scheduling scheme with the lowest system operation cost under the worst scenario. However, robust optimization methods tend to ignore the economy to satisfy security in the worst scenario.

Considering that the above methods rely on accurate prediction models, however, due to the rapid increase of system variables and the prediction deviation of source load, it is difficult to obtain an accurate solution model for many practical distribution systems. In addition, it is difficult for these methods to achieve the overall economy of the system considering the coupling between different scheduling times. RL has been widely used in the field of power systems. It does not need accurate physical modeling, but only realizes the maximum cumulative reward through the interactive training between the agent and the environment, and obtains the optimal strategy [19]. Aiming at the economic scheduling problem with WT-PV-BES and considering the continuous decision variables of conventional generator unit output, reference [20] models the generator unit combination and economic scheduling problem as a problem, and solves it with the distributed Q learning algorithm. The output of a continuous unit is regarded as the action object, and the action space satisfies the constraints such as unit start and stop, but Q learning still has limitations in the continuous action space. In this regard, reference [21] uses an approximant-based DDPG algorithm to meet operational constraints and achieve the optimal cost of the interior point method, but the DDPG algorithm cannot realize asynchronous sampling, so reference [22] uses the PPO algorithm to determine the reactive power output of BESS and WT. The PPO algorithm is an improved algorithm of DDPG and can be updated online. The proposed model can realize real-time control, but the scheduling plan of MT units is not considered in the scenario. However, the above studies rarely involve the uncertainty scenario of coordinated optimization of distributed WT, PV, MT, and BESS at the same time, and the PPO algorithm in the above studies does not consider the coupling of MT and BESS output in time and lacks the dynamic economic scheduling considering long-term economic problems.

In response to the above problems, the research contributions of this paper are as follows:

(1) A dynamic economic scheduling method of distribution network considering adaptive uncertainty based on DRL is proposed, and the time-coupling characteristics of MT and BESS are taken into account. This method can deal with the uncertainty of WT, PV, and load, to reduce the overall operating cost of the distribution network system and obtain the optimal scheduling strategy, and improve the economic efficiency of the source-load interaction.

(2) To adjust parameters easily, the PPO algorithm is used for optimization, and the suitable DNN is constructed to fit complex functional relationships and assist the algorithm implementation. The algorithm framework can adapt to the continuous action space to deal with the time-coupled characteristics of MT and BESS effectively and also can realize the dynamic economic scheduling of the distribution network, which has more long-term economic benefits than static economic scheduling. At the same time, a replay buffer containing complete training sample data is established, and the agent can learn from the unrelated sample data from the replay buffer. This interacted mode can shorten the scheduling decision time and improve the quality of scheduling decisions, to realize efficient online decision scheduling.

(3) Based on MDP theory, appropriate state space, action space, and reward function are defined. By setting corresponding input and output variables and corresponding objective functions, complex mathematical modeling is avoided and higher-quality decisions are achieved. The constructed MDP can transform the day-ahead multi-cycle optimal scheduling of the power system into a single-time step optimization decision problem, thus improving the efficiency of the DRL algorithm.

2  Dynamic Economic Dispatching Optimization Problem of Distribution Network with High Proportion of Renewable Energy

2.1 Model Building

The purpose of dynamic economic dispatching is to minimize the economic cost of distribution network operation, while simultaneously adhering to power balance constraints, generator unit output upper and lower limit constraints, and the adjacent time of unit climbing constraints. In this paper, the objective function is constructed using the power purchase cost of the main network, the operation scheduling cost of the MT, and the operational cost of the BESS as shown in Eq. (1):

minE(∑t=1TCt)=E[∑t=1T(Cgrid(t)+CMT(t)+CBA(t))](1)

where, E(⋅) represents the expected value of the random variable; T is the scheduling period; Cgrid(t) main online electricity cost; and CMT(t) is the operating cost of the MT in the scheduling period t; CBA(t) is the operating cost of the BESS during the scheduling period t.

The electricity purchase cost of the main network is shown in Eq. (2):

Cgrid(t)={λbuy(t)Pgrid(t)Pgrid(t)>00Pgrid(t)<0(2)

where, λbuy(t) is the price of power purchased by the distribution network from the main network during the period t; Pgrid(t) refers to the power purchased by the distribution network from the main network. Here, we only consider the power purchased by the distribution network from the main network, that is, when Pgrid(t)<0, the cost is set to 0.

In general, MT is a controllable distributed power supply, and its adjustment cost in power system scheduling has a linear relationship with the generation power, as shown in Eq. (3):

CMT(t)=∑k=1KakPMT,tk(3)

where, K is the number of MT units in the system; PMT,tk are the output of MT unit k in the scheduling period t; ak is the operating cost factor of MT unit k.

For the battery energy storage system, its operating cost is considered, and its cost coefficient is defined as ρ. Then the operating cost of the battery energy storage system is shown in Eq. (4):

CBA(t)=∑k=1K(ρ|PBA,tk|)(4)

where, ρ is the operating cost factor of the battery energy storage system; PBA,tk is the charge and discharge power of the battery energy storage system. When PBA,tk>0, it indicates the discharge of the battery energy storage system. When PBA,tk<0, the battery energy storage system is charged.

2.2 Constraint Condition

Dynamic economic scheduling needs to meet the active power balance of power generation and consumption in each scheduling period t, regardless of the network loss of the system. Therefore, the power balance constraint is shown in Eq. (5):

Pgrid,t+∑k=1K(PPV,t,k+PWT,t,k+PMT,t,k+PBA,t,k)=Pload,t(5)

where, PPV,t,k is the actual active power of PV generator set k in the scheduling period t; PWT,t,k is the actual active power of wind turbine k in the scheduling period t; Pload,t indicates the load output in the scheduling period t.

In addition, in order to ensure the safe operation of the power system and fully reflect the feasibility and effectiveness of the dispatching scheme, it is necessary to set the corresponding safety constraints. The system node voltage constraint is shown in Eq. (6):

Vmin≤Vi≤Vmax(6)

where, Vi is the voltage amplitude of node i; Vmin is the minimum voltage allowed by the system.Vmax indicates the maximum voltage allowed by the system.

The line transmission power of the system should meet the transmission capacity limit constraint, as shown in Eq. (7):

Pj,t2+Qj,t2≤Sj,max(7)

where, Pj,t is the active power transmitted by branch j in the scheduling period t; Qj,t is the reactive power transmitted by branch j in the scheduling period t; Sj,max indicates the upper limit of the apparent power of branch j.

Active power output constraints of distributed PV, distributed WT and MT are as follows:

PPV,min,k≤PPV,t,k≤PPV,max,k(8)

PWT,min,k≤PWT,t,k≤PWT,min,k(9)

PMT,min,k≤PMT,t,k≤PMT,max,k(10)

where, PPV,min,k and PPV,max,k are respectively the minimum and maximum output values of the k-th distributed PV set; PWT,min,k and PPV,max,k are the minimum and maximum output values of the k-th distributed WT, respectively. PMT,min,k and PMT,max,k are respectively the minimum and maximum output values of the k-th MT unit.

The controllable MT output in adjacent periods should also meet the hill climbing constraint, which is the main difference between dynamic economic dispatch and static economic dispatch, as shown in Eq. (11):

{PMT,t,k−PMT,t−1,k≤PMT,up,kPMT,t−1,k−PMT,t,k≤PMT,down,k(11)

where, PMT,up,k and PMT,down,k are respectively the maximum uphill power and the maximum downhill power of the k-th controllable MT.

The active power output constraint of the distributed BESS is shown in Eq. (12):

PBA,min,k≤PBA,t,k≤PBA,max,k(12)

where, PBA,min,k and PBA,min,k respectively represent the maximum and minimum values of the active power output of the k-th distributed BESS.

The state of charge constraint of the distributed BESS is shown in Eq. (13):

SOCmin,k≤SOCt,k≤SOCmax,k(13)

where, SOCmin,k and SOCmax,k respectively represent the lower and upper limits of the charged state of the k-th distributed BESS; SOCt,k is the state of charge of the k-th distributed BESS in the scheduling period t.

The temporal coupling operation constraints of distributed BESS are shown in Eq. (14):

SOCk,t+1=SOCk,t−[ech,t,kPBA,t,kηc,kEBA,k+edis,t,kPBA,t,kEBA,kηd,k]Δt(14)

where, ech,t,k and edis,t,k respectively represent the distributed charge and discharge state variables of the k-th distributed BESS in the scheduling period t, and both values are 0 or 1. ech,t,k=1 when the BESS is charged, ediis,t,k=1 when the BESS is discharged, and ech,t,k=1 when the BESS is discharged. The charging and discharging of the BESS should not be carried out at the same time, that is, ech,t,k⋅edis,t,k=0. ηc,k and ηd,k represent the charging efficiency and discharge efficiency of the k-th distributed BESS, respectively. EBA,k is the rated capacity of the k-th distributed BESS; Δt indicates the scheduling interval.

The dynamic economic dispatch of the distribution network is periodic. This paper specifies that the state of charge of BESS is consistent in the initial period of scheduling and the end period of the dispatch, as shown in Eq. (15):

SOCk(T)=SOCk(0)(15)

where, SOCk(0) represents the initial state of charge of the k-th distributed BESS; SOCk(T) represents the state of charge of the k-th distributed BESS at the end of the entire distribution network dispatching cycle.

The proposed optimization problem is a long-time series decision problem and a nonlinear problem with multiple constraints. In the process of solving the problem, it is necessary to avoid modeling complex random variables. Rational scheduling of controllable equipment in the power system to respond to load demand and economic operation without the need to utilize WT and PV forecast information is the next research focus.

3  An Adaptive Uncertain Dynamic Economic Scheduling Model Based on Deep Reinforcement Learning

3.1 Markov Decision Process

In order to efficiently solve the above optimization problems, RL method is used, and its mathematical basis is MDP. MDP can be represented by the elements <S,A,P,R,γ>. S represents a finite set of states, which are the state observations of the environment. A represents the finite set of actions and is the decision made by the agent. P represents the transition probability of a state, which is the probability of performing an action in a state and then moving to a new state. γ is the discount factor, γ∈[0,1], indicating how much attention the system pays to the current reward. MDP is a cyclic process in which the agent changes state through actions, receives a reward, and interacts with the environment. Adaptability is reflected in the adoption of model-free RL, which does not need to know the specific nature of a certain distribution of random variables but only needs to learn from historical data, and constantly iterate until the final scheduling decision results are consistent with the statistical distribution characteristics of the uncertain environment.

In this paper, under the framework of RL, the MDP of the dynamic economic scheduling model with adaptive uncertainty is established as follows:

(1) State space S

Select the MT active power output PMT,t,k′, PV output predicted value PPV,t,k′, WT power output predicted value PWT,t,k′, load predicted value Pload,t, and power purchase price buy λbuy(t) of the distribution network as state variables, from which the state space can be established as follows:

S={PMT,t,k′,PPV,t,k′,PWT,t,k′,Pload,t,λbuy(t)}(16)

(2) Action space A

Considering that the output of each unit presents sequential coupling characteristics at different time periods, the planned output of the MT unit at the current time t is set as the decision variable PMT,t,k as shown below. In order to determine the optimal output plan of the new energy station, the actual output of the PV power station and WT power generation is set as the decision variables PPV,t,k and PWT,t,k. At the same time, in order to fully respond to the change in TOU price to improve the absorption rate of new energy, the charge and discharge power of the BESS is set as the decision variable PBA,t,k. Thus, the action space of the agent is obtained as follows:

A={PMT,t,k,PPV,t,k,PWT,t,k,PBA,t,k}(17)

(3) Reward function R

rt∈Rt is defined as the reward of the agent in each short time step t. The dispatching decision center applies the dispatching decision scheme to the distribution network system, and the system gives back the reward according to the current state, so as to reflect the quality of the dispatching decision scheme and guide the update of the dispatching decision. In this paper, the objective function and constraint conditions in the dynamic economic scheduling model are converted into corresponding reward functions and penalty reward functions respectively, as shown in Eq. (18):

rt=−∑t=1T(Cgrid(t)+CMT(t)+CBA(t))−FV,t(18)

where, rt represents the instant reward that the agent can get after selecting the action at at the state st. FV,t is the penalty for the system node voltage exceeding the limit, as shown in Eq. (19):

FV,t=−eV,t∑i[max(Vi,t−1.05,0)+max(0.95−Vi,t,0)](19)

where, −eV,t is the penalty coefficient.

The cumulative reward function of the whole scheduling cycle T is shown in Eq. (20):

Rt=∑t=1Tγt−1rt(20)

where, Rt represents the cumulative reward obtained by the agent during the period [t,T].

3.2 Proximal Policy Optimization

According to the state space and action space are continuous spaces, this paper chooses an algorithm based on the Actor-Critic framework. In the Actor-Critic framework algorithm, PPO is an off-line learning algorithm that integrates dynamic step mechanism and importance sampling technology under the Actor-Critic framework. With its characteristics of fast convergence speed, low parameter setting difficulty, and adaptability to complex environments, PPO has achieved good application results in the field of optimal scheduling of power systems [22]. The PPO algorithm is modified by the trust region policy optimization (TRPO) algorithm, and its objective function is shown in Eq. (21):

maximizeφ^Et[min(rt(φ)At∧,clip(rt(φ),1−ε,1+ε)At∧)](21)

where, φ is the parameter of the actor-network; rt(φ) is the relative probability of the old and new strategies; A^t is the dominant function. ε is a hyperparameter between 0 and 1. The Clip function limits the ratio between new and old policies to a small [1−ε,1+ε] range, thus limiting the magnitude of policy updates.

PPO agents interact with the environment to temporarily store interactive data collection in the sample replay buffer. Since the PPO algorithm is an on-policy algorithm, the sample data collected last time needs to be released after a policy update. The sample data is input into the actor-network and the critic network, and the actor-network parameters are updated and the critic network parameters are updated, respectively. Through the above interactive updates, the actor-network and the critic network are finally more accurate, and the PPO agent training is gradually stable until convergence. Therefore, for the update of the critic network, its loss function is first constructed, as shown in Eq. (22):

L(θ)=E(Vθtarg⁡et(st)−Vθ(st))2(22)

where, E(⋅) is the expectation function, and Vθ(st) is the current value function, that is, the output of the critic network. Vθtarg⁡et(st) is expressed as a goal value function that evaluates the accuracy of the output of the critic network. Based on the temporal difference algorithm, the calculation equation of Vθtarg⁡et(st) can be obtained as shown in Eq. (23):

Vθtarg⁡et(st)=rt+γVθ(st+1)(23)

According to the loss function of the critic network, the critic network is updated gradient, as shown in Eq. (24):

θ=θ−ηθ∇L(θ)(24)

where, ηθ is the learning rate of critic network; L(θ) represents the gradient of the critic network loss function with respect to the parameter θ.

In order to further evaluate the advantages and disadvantages of samples and improve the convergence performance of PPO, the advantage function A^t is introduced into the training of policy network, which represents the advantage of taking action at under the current state st over the average performance of the following strategy π, as shown in Eq. (25):

At∧(st,at)=Qθ(st,at)−Vθ(st)(25)

Vθ(st)=E(Rt|st=s;π)(26)

where, Qθ(st,at) represents the action value function, that is, the reward expectation of the action at executed according to strategy π under a given state st, and the influence of changes in wind-light-load and scheduling plan on operation economy can be quantified. In Eq. (26), Vθ(st) represents the expected value of the objective function obtained by executing all scheduling schemes in accordance with policy π under the current state st.

At the same time, in the process of parameter updating of the actor network, the advantage function is also used as the loss function of the actor network, which is used to guide the actor network to gradually improve the network performance in the interactive training between the agent and the environment. Thus, the parameter updating of the actor-network is obtained as shown in Eq. (27):

φ=φ−ηφ∇A∧(27)

In addition, the PPO reinforcement learning algorithm based on strategy gradient incorporates the ratio of sampling probabilities of the new and old strategies into the step size setting, and selecting the appropriate step size can get a better training effect without training divergence. The dynamic learning rate ηφ of the actor network is shown in Eq. (28):

ηφ=ηφ,basemin(Pφ(at,st)Pφ′(at,st),CLIP(Pφ(at,st)Pφ′(at,st),1−ε,1+ε))(28)

where, ηφ,base represents the benchmark learning rate of the actor-network; Pφ(st,at) and Pφ′(st,at) respectively for the new and old strategy of πθ(at,st) and πθold(at,st) sampling probability.

The process of adaptive uncertainty dynamic economic scheduling based on the PPO algorithm is shown in Table 1. PPO agent generates batch sample data by interacting with the power system environment, and uses a gradient descent mechanism to conduct batch network training until the maximum training period is reached and the reward function converges. At this time, the trained actor-network can be applied online. Driven by WT,PV, and load data, MT units and strategic schemes of new energy stations can be output in real-time to meet the dynamic economic scheduling of the distribution network to better achieve the expected target setting.

3.3 Dynamic Economic Scheduling Method of New Energy Distribution Network System Based on Deep Reinforcement Learning

In this paper, based on the PPO algorithm, a dynamic economic scheduling framework for offline training and online application of distribution network is established, as shown in Fig. 1.

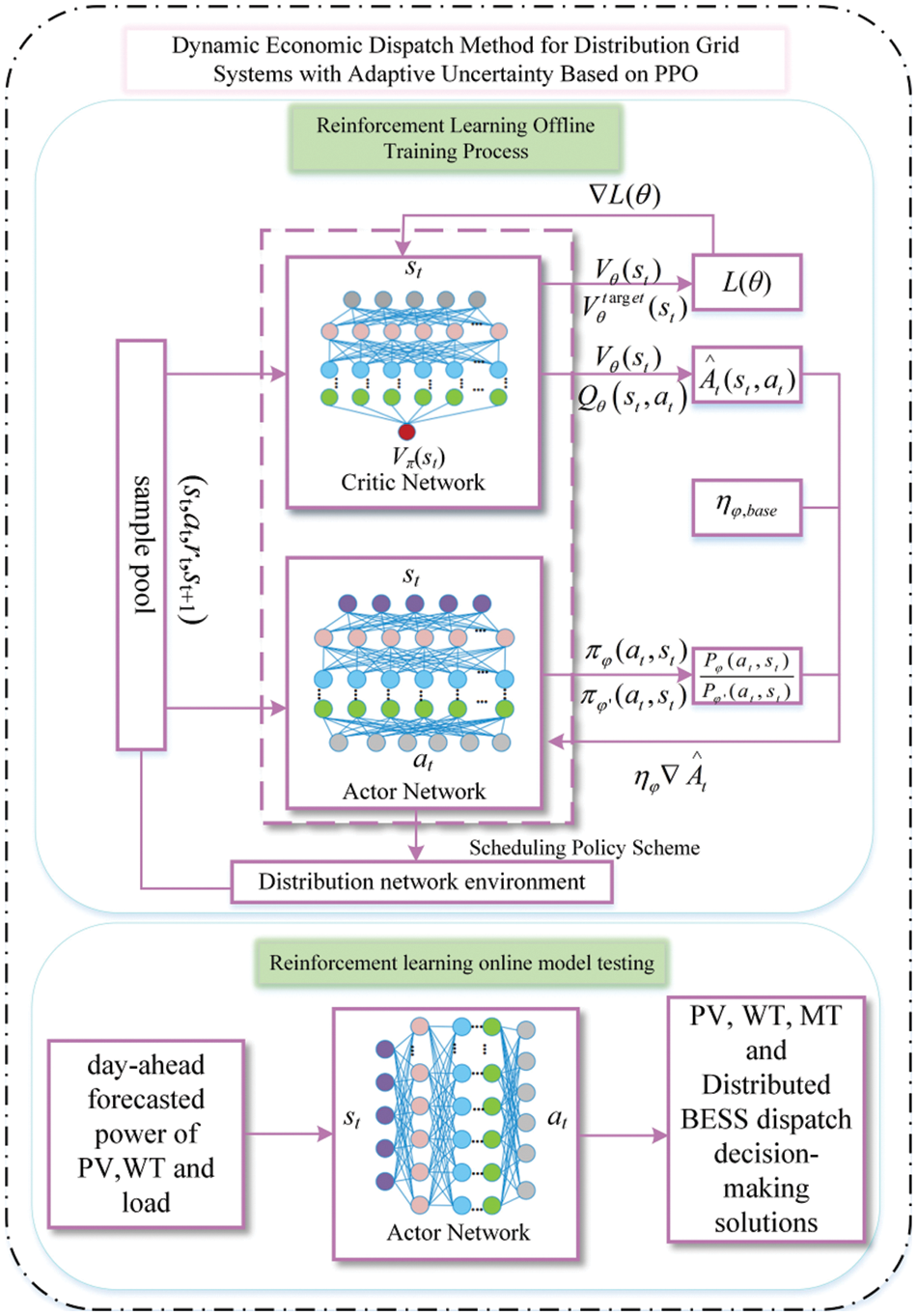
Figure 1: The structure of dynamic economic dispatch method based on PPO

As shown in Fig. 1, the PPO algorithm can complete the algorithm goal only with the actor-network and the critic network. The input of the actor-network and the critic network is the observed state st of the power system. The actor-network is used to generate scheduling decision scheme. At the input layer, normalization is used to extract different features from input data, scale and adjust them, eliminating the dimension and difference of features, and thus speeding up the learning of strategy. The neurons in the output layer correspond to the mean and standard deviation of the probability distribution respectively, which can be used to form the corresponding action output distribution, and the action at can be determined according to the probability distribution. The standard deviation in the probability distribution can reflect the agent’s exploration ability. A large standard difference at the initial stage of training can increase the space of action exploration and avoid falling into local optimality during training. As the training process gradually stabilizes, the standard deviation also gradually stabilizes at a smaller value. The actions of the agent after exploration are limited to the range [−1,1], which can be mapped to the actual output value based on the rated capacity and parameters of the dispatchable device.

The critic network is used to evaluate the advantages and disadvantages of the scheduling scheme. During the scheduling cycle, the current observed state st of the power system is taken as the input, the decision center constantly interacts with the environment of the power system, and each sample data is collected into the replay buffer, and the observed state value in the replay buffer is input into the critic network, and the value function Vθ(st) of the observed state can be output. At the same time, through this dynamic data feedback, the network parameters are updated. In Fig. 1, φ and θ are parameters of the actor network and the critic network, respectively.

The dynamic economic scheduling method based on DRL can be divided into two stages: the off-line training process and the online testing process. In the off-line training process, the actor network and the power grid environment constantly interact to generate a batch of training samples that can cover the whole given WT, PV, and load output interval and put them into the replay buffer for the actor network and the critic network to learn and train. In the online model testing process, only the actor network is used to observe the environmental state and the optimal dynamic economic scheduling scheme is given.

4  Example Analysis

4.1 Experimental Scene Setup

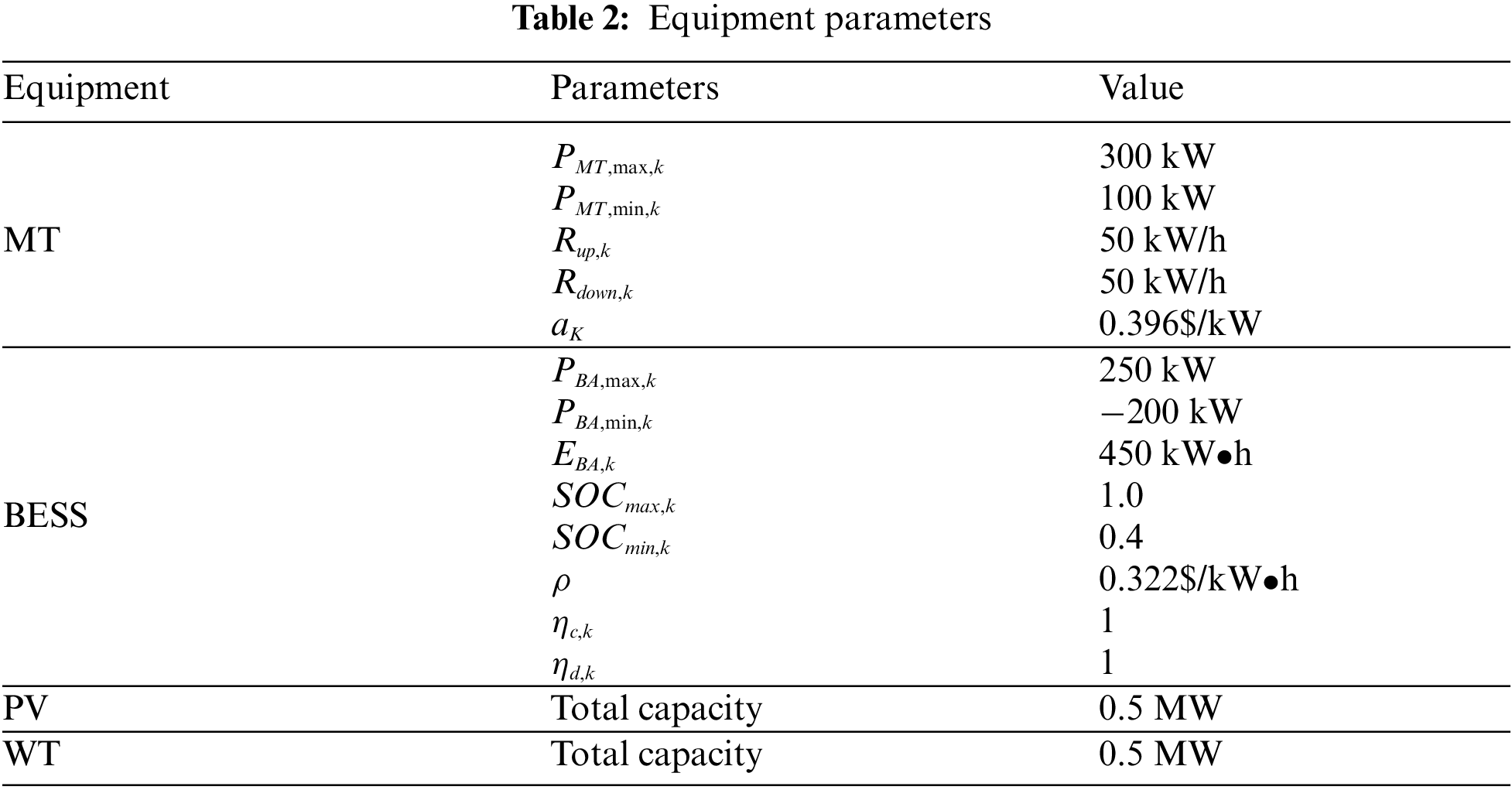
An improved IEEE 33 node system is used to verify the validity and applicability of the proposed method. According to the equipment parameters provided in the references [20–23], the network topology of the distribution network system is shown in Fig. 2, and the equipment parameters are shown in Table 2. The IEEE 33 node system connects MT on nodes 3, 9, 24 and 28, distributed PV on nodes 7 and 20, distributed WT on nodes 16 and 29, and distributed BESS on nodes 12 and 32.

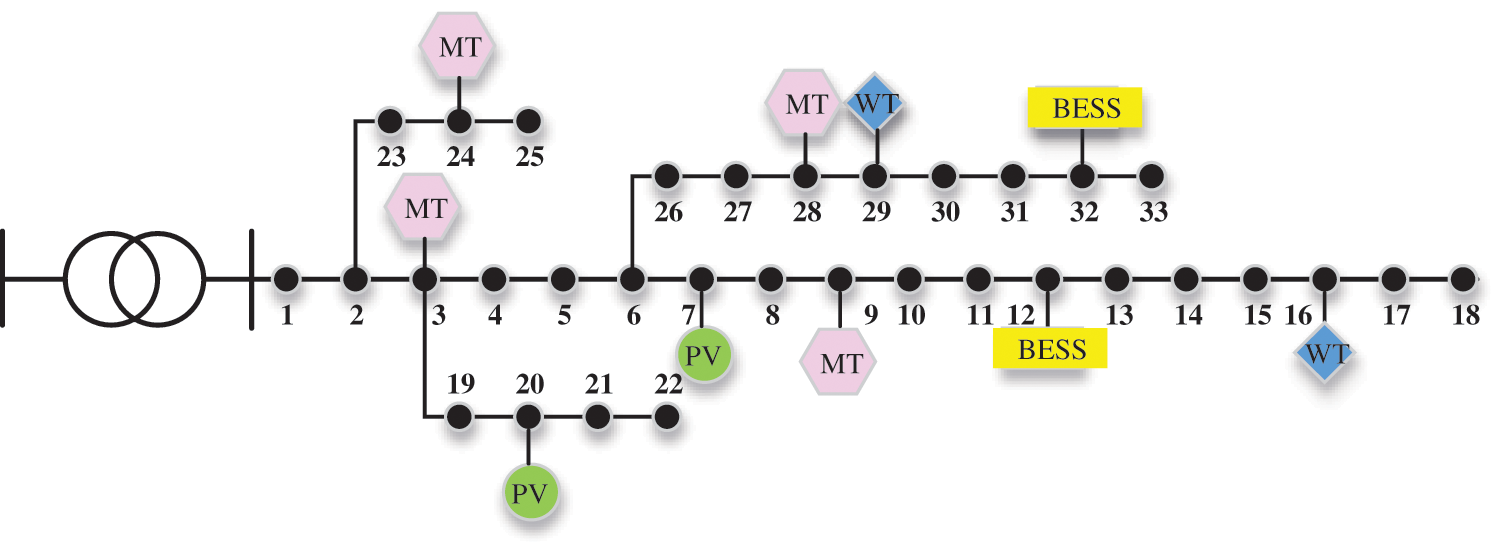
Figure 2: The improved IEEE 33-Node simulation system

Hyperparameters setting according to references [22,24], the state observations of the PPO agent are represented as 9-dimensional array vectors, and the actions are represented as 8-dimensional array vectors. In the AC framework, the policy network has 3 hidden layers, each with 128 ReLU neurons, and the output layer has 8 linear neurons. Critic networks and actor networks have the same network structure. The learning rates of the critic network and the actor-network were set as ηθ=0.001 and ηφ=0.001, respectively. The parameter settings in the training process are shown in Table 3.

4.2 The Results of Model Training

The simulation is based on the hardware platform Intel(R) Core (TM) i7-10510U CPU. The single-agent model of dynamic economic dispatching of the distribution network is built on the MATLAB/SIMULINK platform. The model was trained 3000 times, that is, 3000 episodes, which took 10569 seconds, and achieved excellent training results. The change in reward function during training is shown in Fig. 3.

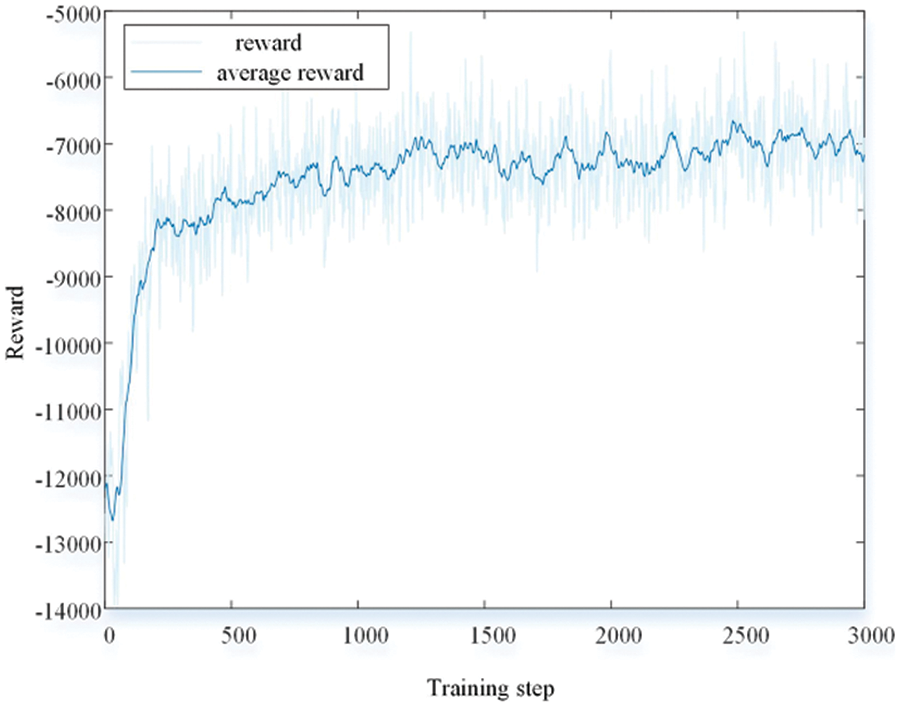
Figure 3: The reward of agent

In the process of agent training, the PPO algorithm undergoes a process of exploration followed by gradual convergence during the training process of the agent. In the early stage of interactive training between the agent and environment, the actions explored by the agent often violated the system constraints because of the agent’s little understanding of the environment, and the noise interference introduced by the outside world leads to the unstable situation of agent training. However, the early learning and training speed of the agent is also fast. With the increase of the interaction between the agent and the environment, the agent gradually explores a better scheduling decision scheme, the parameters of the neural network are constantly updated, and the reward function gradually converges. At this time, the actions explored by the agent are constantly meeting the goal of economic optimization in dynamic economic scheduling problems. As training progresses, the agent gradually learns more effective strategies and behaviors, and the convergence rate may gradually accelerate. By the late stage of training, the agent has learned the optimal scheduling strategy and can provide a suitable scheduling scheme for different scheduling scenarios for online applications. At the same time, there are error fluctuations in the value of the reward function, which is due to the different fluctuations of renewable energy output and load in different scenarios, which causes the difference of the economic cost at different moments, so the reward function will undergo a certain degree of oscillation, which is a normal phenomenon. On the whole, the reward function in the training process shows a trend of growth and convergence, which means that the training effect of the agent is gradually getting better.

4.3 The Results of Dynamic Economic Scheduling

In order to verify the effectiveness of the proposed method, typical forecast data of WT, PV and typical load changes of a certain day in the data set according to references [20–23] were selected for testing, as shown in Figs. 4 and 5, and the trained model was used for dynamic economic scheduling before the day. After online testing, the scheduling results of active power obtained are shown in Fig. 6.

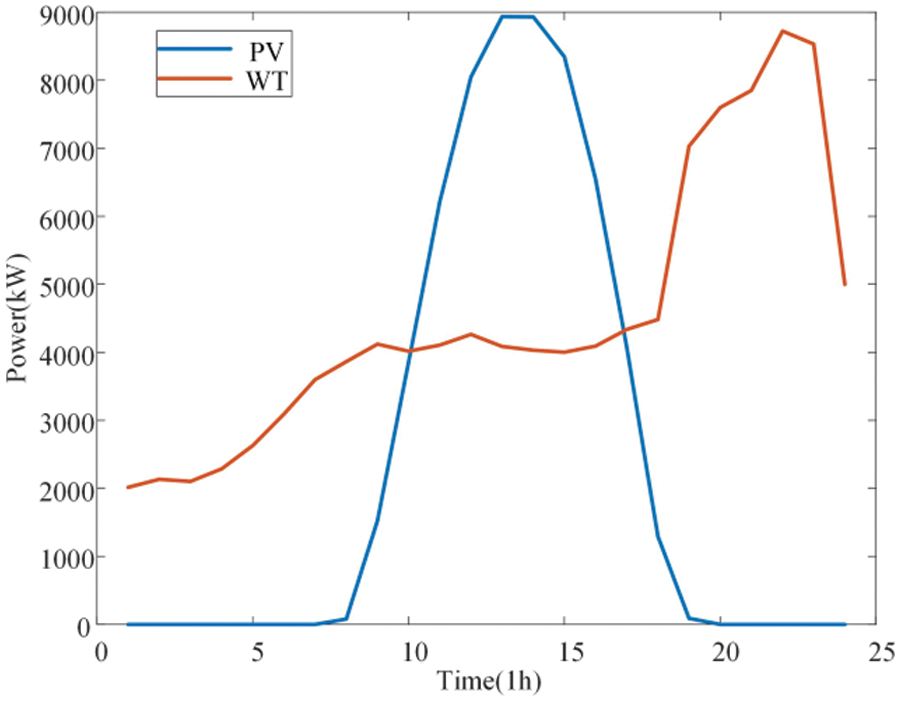
Figure 4: 24-hour PV and WT output profile

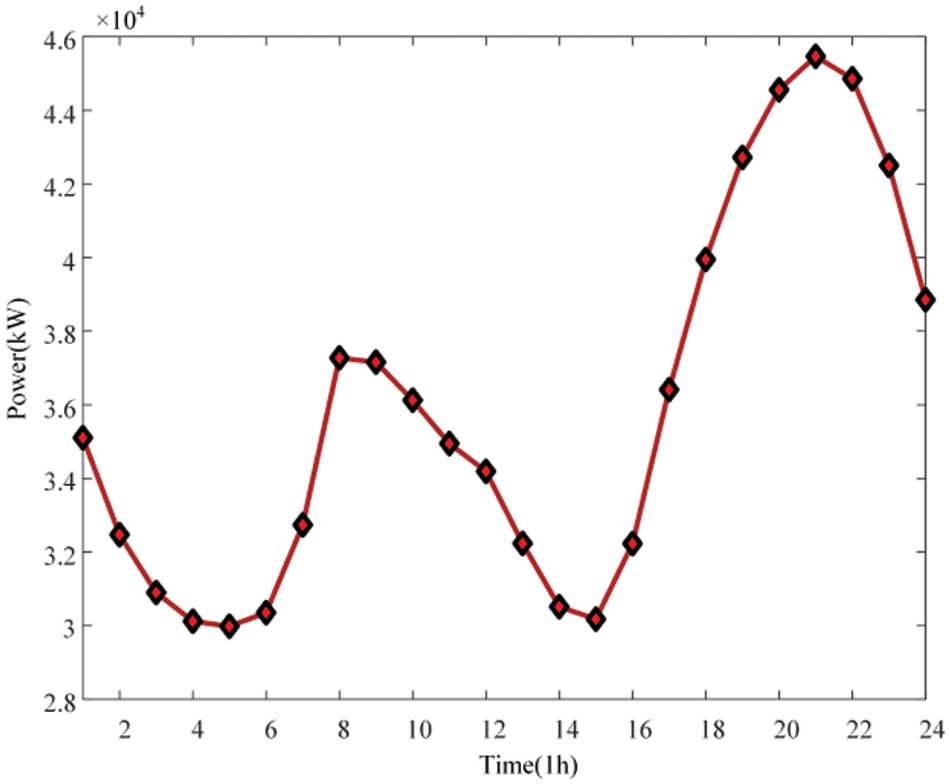
Figure 5: 24-hour load demand profile

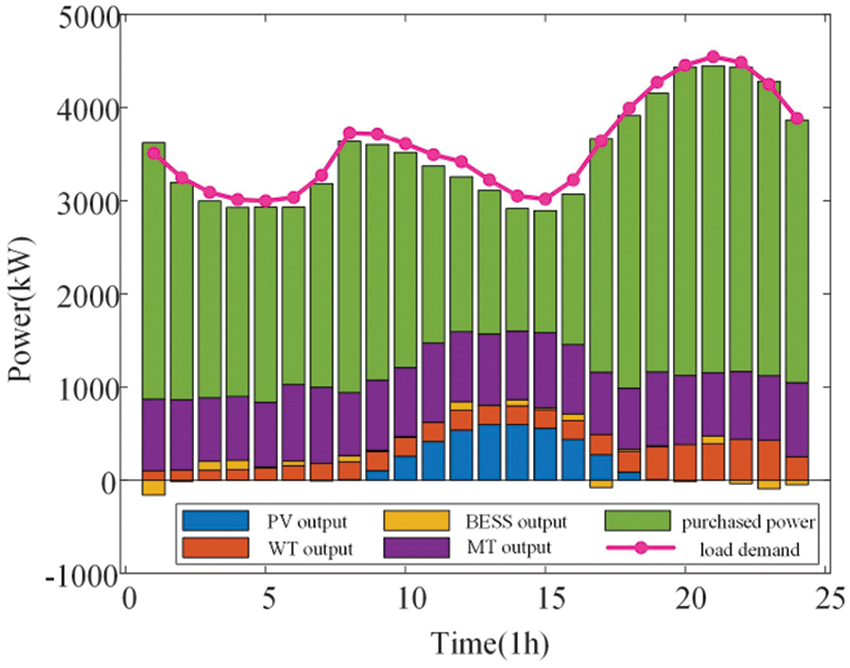
Figure 6: The result of dynamic economic dispatch

In this paper, the dispatch cost of renewable energy generation is assumed to be 0, and only the purchase of power from the main network is considered. As can be seen from the figure, the low price periods of 0:00–8:00 and 12:00–14:00 are also the low load periods. At this time, the power purchase cost of the main network of the distribution network is lower than the joint supply cost of MT and distributed battery energy storage system. Therefore, in order to reduce the total economic cost, the distribution network will give priority to reducing the total economic cost under the condition that the relevant inequality constraints are not violated. Purchase power according to the maximum power that can be transmitted by the transmission line, and then reduce the generation power of the MT and BESS; Thus, reducing the total economic cost; In the hours of 9:00–11:00 and 15:00–23:00, the peak load is also the peak period of the main network power purchase price. In order to focus on reducing the main network power purchase cost of the distribution network, the MT and BESS respectively output active power with the maximum transmission capacity of 300 and 250 kW to ensure the balance of supply and demand.

The output of the MT within 1 day is shown in Fig. 7. The MT can complement the BESS, PV, and WT. The system preferentially meets the load through the output of PV and WT and then meets the load through the MT and BESS when the output of PV is insufficient. During the 9:00–18:00 period, PV and WT can meet the load with the maximum generation power and reduce the operation and scheduling costs of MT and BESS under the safety constraints of the power system. At the same time, the BESS can store the excess scenery to promote the absorption of the scenery. In the hours of 0:00–9:00 and 18:00–24:00, the load level is greater than the output level of the wind, so the MT will operate at 5:30 and 18:00, considering that this paper assumes that the operation scheduling cost of the BESS is higher than that of the MT, the MT will discharge efficiently with the maximum climbing power of 50 kW/h to meet the load demand and complement with the BESS, and reduce the operation scheduling cost of the BESS.

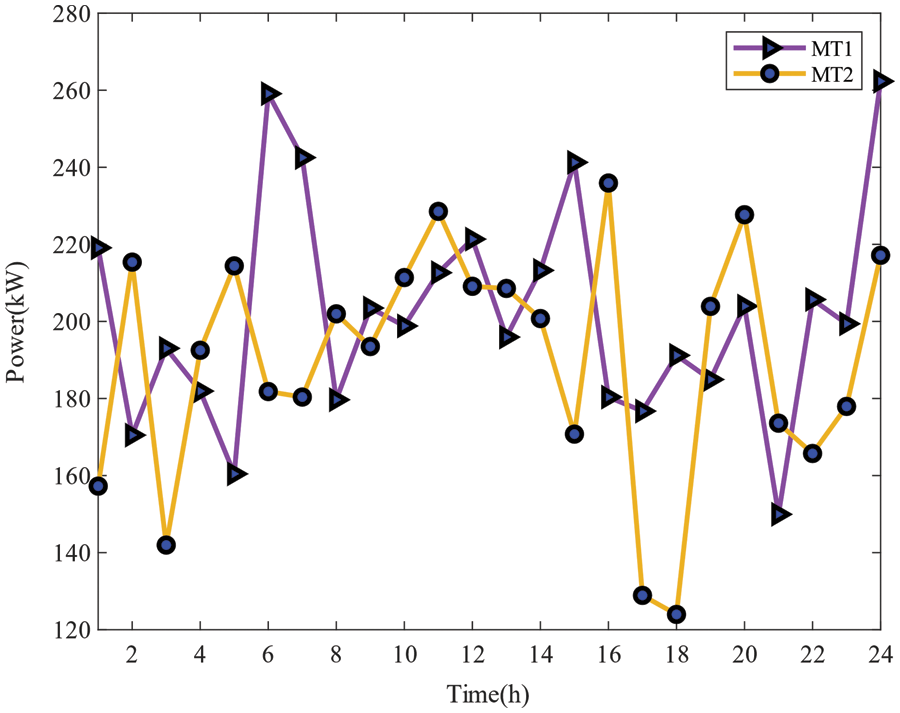
Figure 7: One-day power output curve of MT

The change of charge and discharge power of the battery energy storage system within 1 day is shown in Fig. 8. When the power is set as positive, the battery energy storage system will discharge; conversely, when it is negative, it will charge. Under the control of the agent, the BESS needs to store energy as much as possible before the load peak and release energy during the peak demand period to reduce the dispatching cost of the distribution network system. However, considering that the operating cost of the BESS itself is higher than that of the MT, the output of the BESS will be limited to a certain extent in order to meet the overall economy of the system.

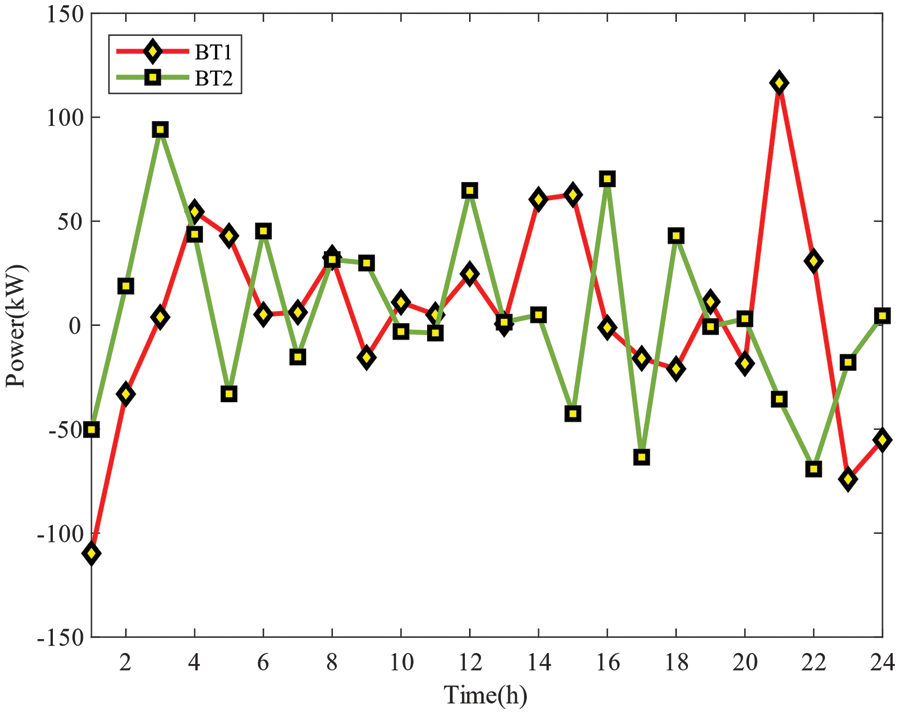
Figure 8: One-day power exchange curve of BESS

The actual optimal scheduling results for each PV and WT are shown in Fig. 9, and the actual output changes of PV and WT are consistent with the probability distribution of the predicted output.

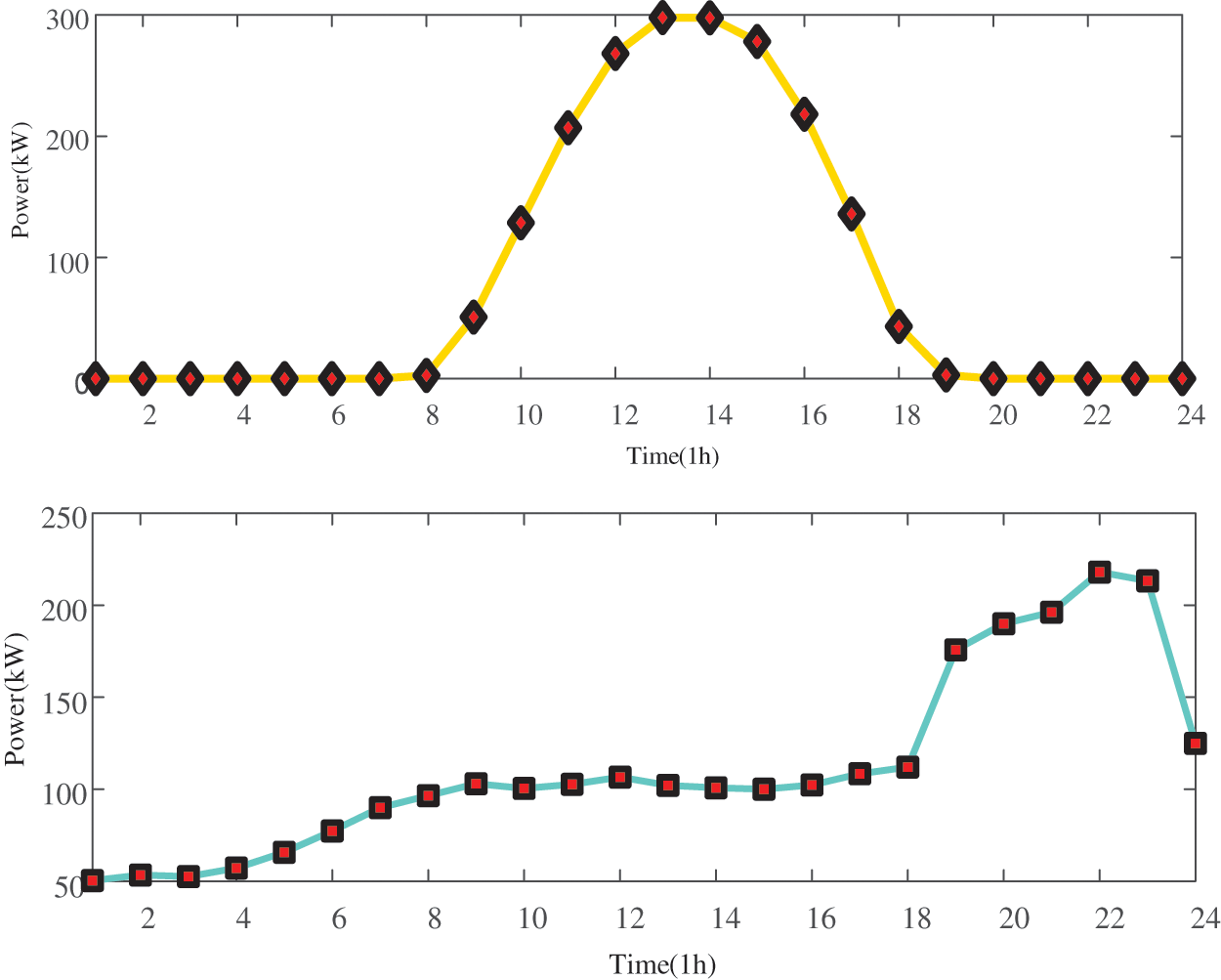
Figure 9: The actual output of PV and WT

Comparing the actual output power with the predicted power, during the period from 12:00 to 16:00, in order to meet the constraint that the node voltage does not exceed the limit, a part of the active power needs to be reduced, so there will be a part of the phenomenon of PV power abandonment. Similarly, for wind farms, during 19:00 to 23:00 at night, due to the large wind power at night, more power is emitted, but due to the security constraints in the power grid and the load requirements of users, there will also be some WT power curtailment phenomenon.

Combined with the scheduling decision results of the above-mentioned controllable devices, when the lowest operating cost of the distribution network is taken as the objective function, due to the different emphasis on the three sub-items of cost that the agent pays attention to in different periods, and in order to take into account the overall economic cost of the system, the uncertainty of the source load and the coupling relationship between the output of the MT unit in different periods, etc. Through 3000 episodes of interactive training learning, the agent can basically give the decision results satisfying the economic scheduling.

4.4 Economic Evaluation

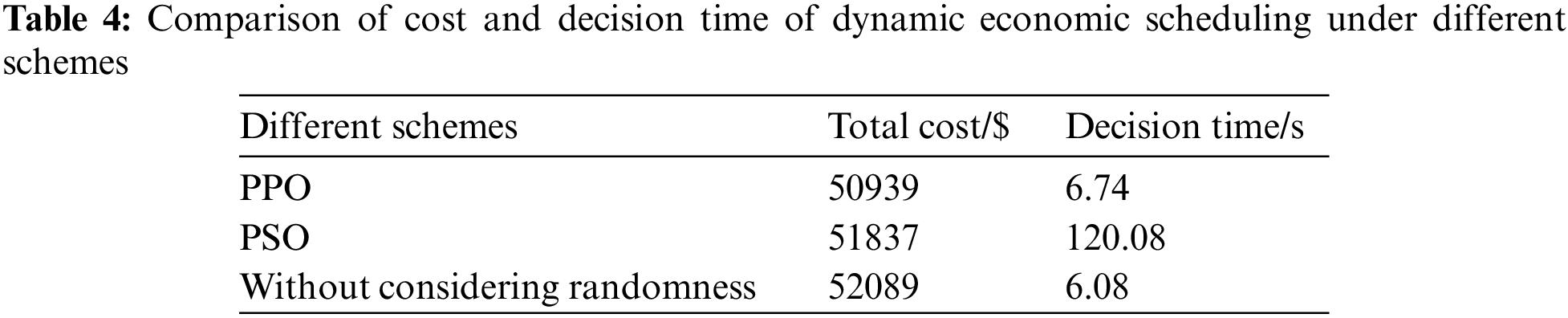
In the training process of the PPO agent, the total economic cost of the distribution network is shown in Fig. 10. It can be seen that the total economic cost converges and decreases with the gradual convergence of the agent reward function. In order to measure the effectiveness and economy of the model established in this paper, the economic scheduling based on the PSO algorithm and dynamic economic scheduling without considering randomness is taken as the control group, and the economic cost and scheduling decision time of the three schemes are calculated and compared, as shown in Table 4.

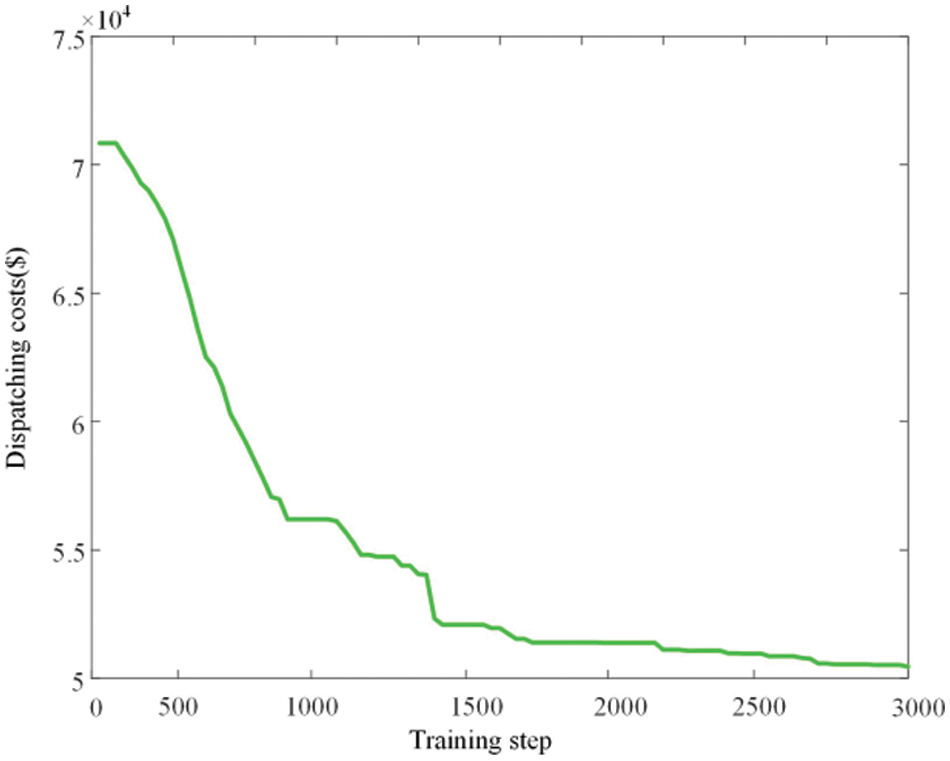
Figure 10: Distributed network dispatching costs

The comparison results show that the proposed method has the following advantages:

1) In terms of the total optimization cost of the distribution network, the optimized scheduling cost of the proposed method is reduced by 1.73% compared with the traditional PSO algorithm, and by 2.21% compared with the economic scheduling without considering randomness. It can be seen that the proposed algorithm can adapt to the uncertainty of source load in the power system, and can effectively reduce the total optimization cost.

2) In terms of decision time, although the PPO method based on deep reinforcement learning takes 10,596 s in the offline training process, the online decision time only takes 6.74 s when the uncertainty of source load is taken into account, which is significantly improved compared with the traditional PSO algorithm. In the proposed method, the optimization time is borne by the offline training process, and the online decision process is directly mapped from the input to the output based on the trained actor-network. It can be seen that after PPO agent model training is completed, its scheduling and decision-making efficiency has been significantly improved.

4.5 The Comparison of Different DRL Algorithms

In order to fully demonstrate the applicability and superiority of the PPO algorithm in this paper, we compare the performance of several different DRL algorithms. Therefore, choosing the DDQN [20] algorithm, which is a DRL algorithm based on deep learning and Q-learning, and an improved version of the classic DQN algorithm. DDQN is based on replay buffer learning. At the same time, this paper also chooses the classical DDPG [21] algorithm, which belongs to the off-line DRL algorithm, which is based on the replay buffer feedback and is also applicable to the continuous state-action space learning method. The PPO algorithm in this paper is an improved algorithm of the DDPG algorithm. In this paper, the performance of different DRL algorithms is compared and analyzed.

As shown in Fig. 11, it is obvious that compared with the three DRL algorithms, the PPO algorithm applied in this paper has the fastest convergence speed, a very stable training process, and the maximum convergence reward value, thus showing superior scheduling decisions. Secondly, the training effect of the DDPG algorithm is relatively stable, and it is extremely sensitive to the setting of hyperparameters, and it is an off-line learning mode, so that it does not show good performance in terms of convergence speed, stationarity, and convergence degree. Because the DDQN algorithm is not suitable for continuous action space, and is relatively sensitive to hyperparameters, the training process is very unstable, so the DDQN algorithm has the worst performance among the three reinforcement learning algorithms. The PPO used is superior to other reinforcement learning algorithms in terms of average reward, strategy stability, and convergence speed.

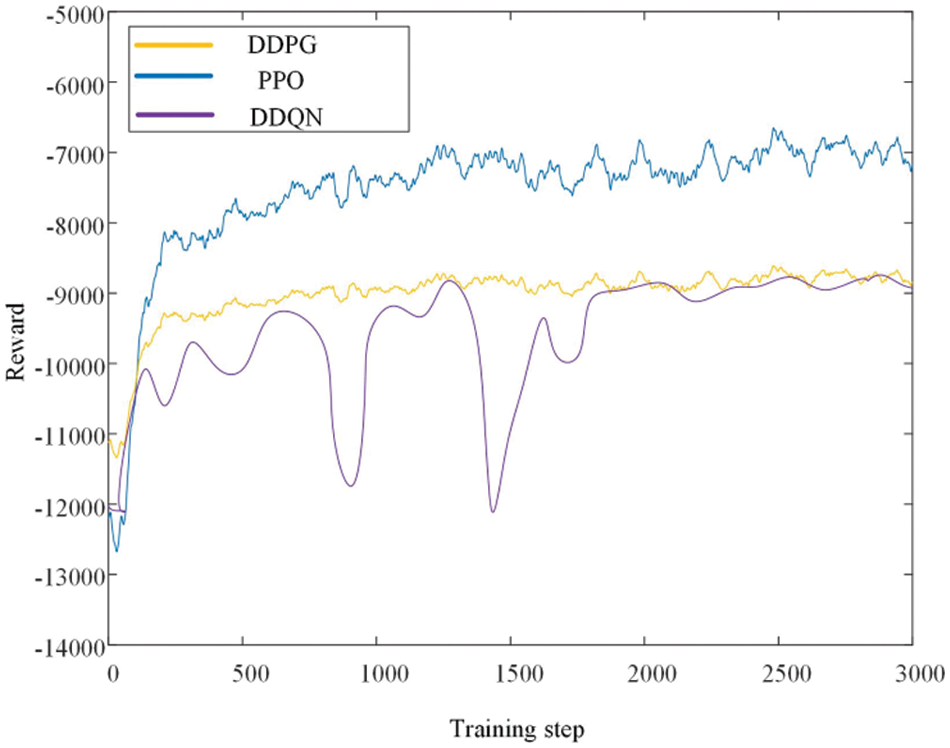
Figure 11: Comparison of convergence of different DRL algorithms

Compared with DDPG and DDQN, PPO convergence speed and convergence process are stable, because PPO is a method based on policy gradient, which directly optimizes policies and PPO has higher sampling efficiency, while DDPG is a DRL algorithm based on value function and needs to constantly perform experience feedback and update the target Q network. At the same time, the PPO algorithm will cut the strategy gradient to reduce the size of batch update data to avoid instability. Therefore, for the distribution network system with large-scale access to distributed power supply, reinforcement learning can first learn the optimal scheduling policy through offline training, so as to adapt to more distribution network scenarios, and then apply the trained agent online to adapt to the dynamic changes of the model and parameters.

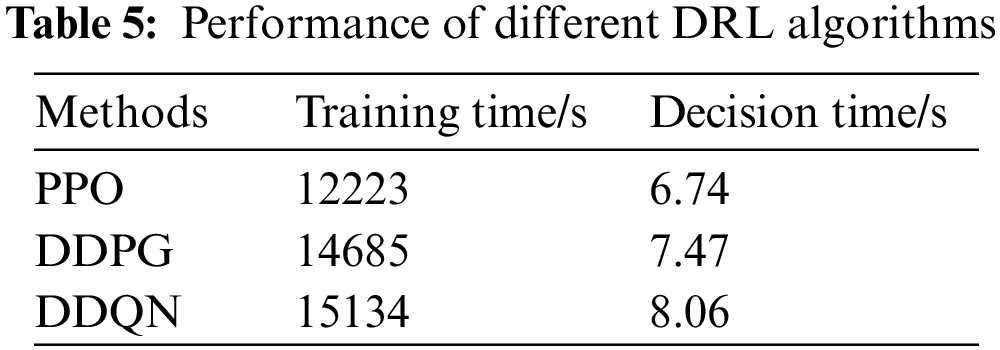
As shown in Table 5, comparing the training and execution time of several coordination strategies. The PPO algorithm applied is superior to other reinforcement learning algorithms in terms of training time and execution time. Despite the complex power system, all three reinforcement learning algorithms can complete scheduling decisions and execute them in a few seconds, which indicates that real-time control is feasible compared with model-based methods.

4.6 The Influence of Hyperparameters on PPO Algorithm

In order to find the optimal PPO algorithm hyperparameter, different hyperparameters are set in the analysis of simulation example analysis, and obtains the PPO algorithm hyperparameters suitable for this research scenario are through the references [22,24] and simulation examples. In the simulation experiment, when analyzing the influence of learning rate on the reward value of the agent, it is necessary to keep the value of batch size unchanged. Similarly, when analyzing the influence of batch size on the reward value, it is necessary to keep the learning rate unchanged.

As shown in Figs. 12 and 13, with the increase of the value of the hyperparameter, the reward fluctuation within a certain range, but they have little impact on the final experimental results. Besides, since hyperparameter is not the focus of this paper, if the subsequent research involves the study of the influence of hyperparameters on optimal scheduling decision-making, the author will also follow up on the relevant research at any time.

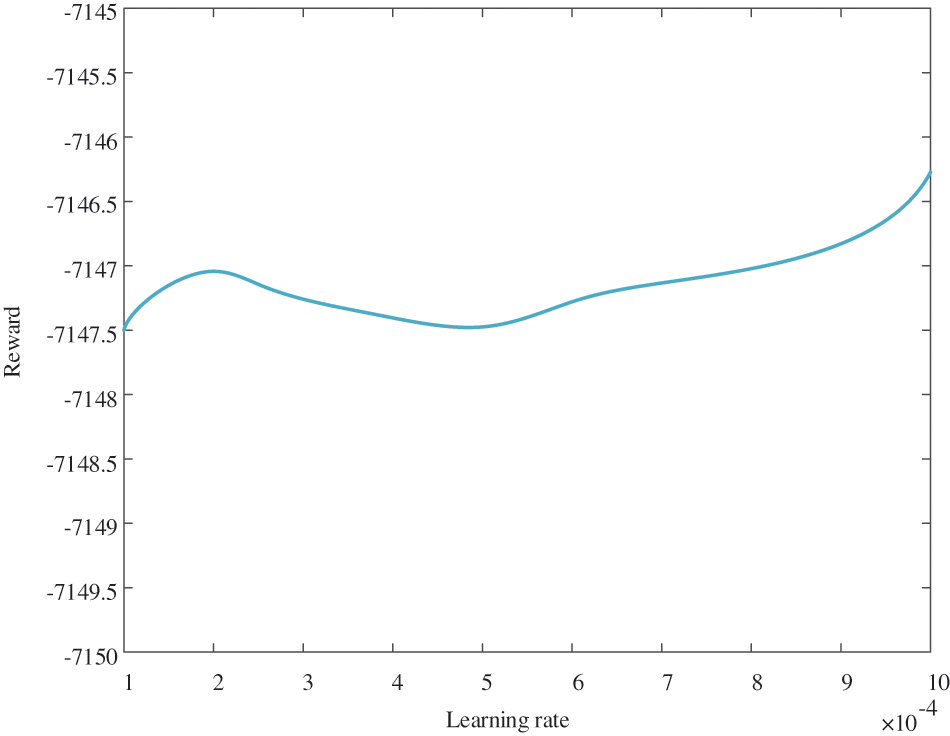
Figure 12: Reward change with different learning rates

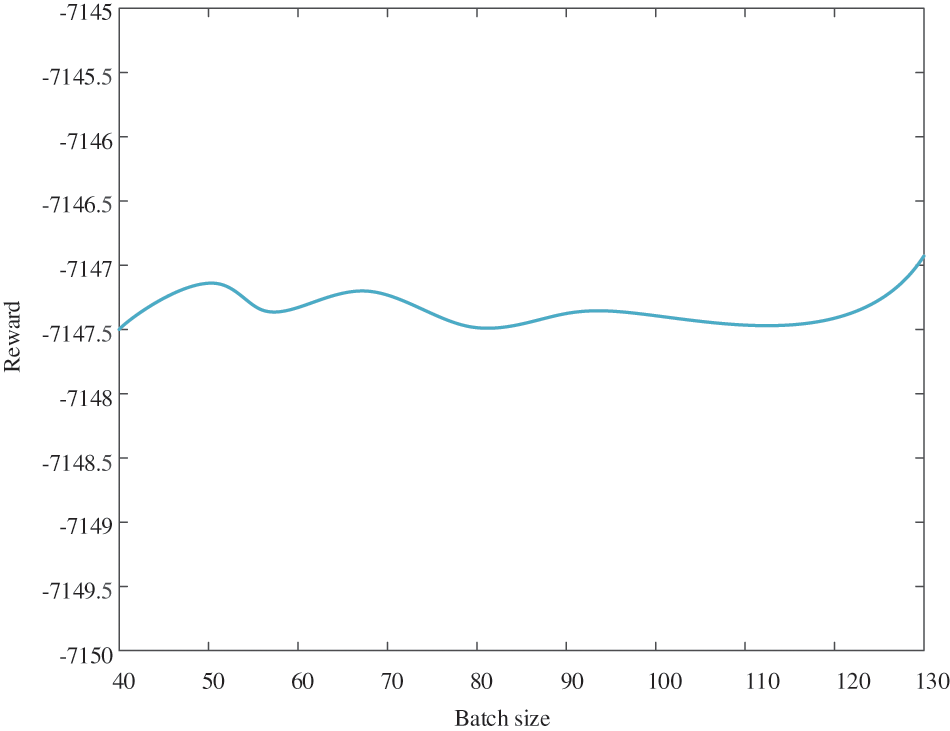
Figure 13: Reward change with different batch size

5  Conclusion

In this paper, a multi-stage dynamic economic dispatch decision-making method based on DRL is proposed for the dynamic economic dispatch problem of the power system with a high proportion of renewable energy. Considering the uncertainty of WT and PV output and load changes, a multi-stage dynamic economic scheduling decision-making method based on deep reinforcement learning is proposed, which has the following advantages:

1) Taking into account the internal relationship of time points, a sequential decision model of dynamic economic scheduling based on MDP is constructed for the distribution network, and then DNN is built to realize the optimal scheduling decision based on the PPO algorithm. Compared with the optimization method based on a physical model, the proposed method can adapt to the uncertainty of source load, and effectively solve the modeling problem of highly nonlinear and complex large-scale systems by using a data-driven approach. Moreover, the PPO algorithm has a strong adaptability to the changes in the power grid, ensuring the efficiency and economy of scheduling decision schemes.

2) Applying the DRL framework of offline training-online execution for distributed power supply cooperative optimization, the intelligent body avoids the local optimum by finding the approximate optimal solution through offline learning to achieve the global optimality and stability of the scheduling decision. In the online execution process, the trained agent quickly outputs the scheduling decision result only by the observed state, which effectively reduces the decision-making time, improves the control efficiency, and realizes the real-time dynamic economic scheduling of the distribution network.

3) Finally, the results of the numerical analysis show that the proposed multi-stage dynamic economic scheduling decision-making method based on DRL is suitable for the dynamic economic scheduling problem of power systems considering the uncertainty of renewable energy. Compared with the traditional methods, the most important feature of this method is that it can learn the probability distribution of WT and load from the historical data, so as to give the optimal dynamic economic scheduling strategy from the perspective of expectation. The proposed method only takes 6.74 s to formulate the dynamic economic dispatch scheme for 24 time periods, which is 94.39% faster than the 120.08 s of the traditional PSO algorithm, which is fully feasible in practice.

Acknowledgement: None.

Funding Statement: This research was funded by the State Grid Liaoning Electric Power Supply Co., Ltd. (Research on Scheduling Decision Technology Based on Interactive Reinforcement Learning for Adapting High Proportion of New Energy, No. 2023YF-49).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Guanfu Wang and Yudie Sun; data collection: Jiang Yu and Chunhui Li; analysis and interpretation of results: Guanfu Wang, Jinling Li, Jiang Yu and Chunhui Li; draft manuscript preparation: Guanfu Wang, Jinling Li, Huanan Yu, He Wang and Shiqiang Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article. And the additional data that support the findings of this study are available on request from the corresponding author, upon reasonable request.

Conflicts of Interest: The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Guerrero, J., Gebbran, D., Mhanna, S., Chapman, A. C., Verbi, G. et al. (2020). Towards a transactive energy system for integration of distributed energy resources: Home energy management, distributed optimal power flow, and peer-to-peer energy trading. Renewable and Sustainable Energy Reviews, 132, 110000. https://doi.org/10.1016/j.rser.2020.110000 [Google Scholar] [CrossRef]

2. Chen, X., Qu, G., Tang, Y., Low, S., Li, N. (2022). Reinforcement learning for selective key applications in power systems: Recent advances and future challenges. IEEE Transactions on Smart Grid, 13(4), 2935–2958. https://doi.org/10.1109/TSG.2022.3154718 [Google Scholar] [CrossRef]

3. Zhang, X. H. (2015). Research on dynamic economic dispatching of power system including wind power (Master Thesis). Yanshan University, China. [Google Scholar]

4. Bechert, T. E., Kwatny, H. G. (1972). On the optimal dynamic dispatch of real power. IEEE Transactions on Power Apparatus and Systems, PAS-91(3), 889–898. https://doi.org/10.1109/TPAS.1972.293422 [Google Scholar] [CrossRef]

5. Karagiannopoulos, S., Aristidou, P., Hug, G. (2019). Data-driven local control design for active distribution grids using off-line optimal power flow and machine learning techniques. IEEE Transactions on Smart Grid, 10(6), 6461–6471. https://doi.org/10.1109/TSG.5165411 [Google Scholar] [CrossRef]

6. Li, J., Zhou, J., Chen, B. (2020). Review of wind power scenario generation methods for optimal operation of renewable energy systems. Applied Energy, 280, 115992. https://doi.org/10.1016/j.apenergy.2020.115992 [Google Scholar] [CrossRef]

7. Liang, R. H., Liao, J. H. (2007). A fuzzy-optimization approach for generation scheduling with wind and solar energy systems. IEEE Transactions on Power Systems, 22(4), 1665– 1674. https://doi.org/10.1109/TPWRS.2007.907527 [Google Scholar] [CrossRef]

8. Qiu, H., Gu, W., Liu, P., Sun, Q., Wu, Z. et al. (2022). Application of two-stage robust optimization theory in power system scheduling under uncertainties: A review and perspective. Energy, 251, 123942. https://doi.org/10.1016/j.energy.2022.123942 [Google Scholar] [CrossRef]

9. Tang, C., Xu, J., Sun, Y., Liu, J., Li, X. et al. (2018). Look ahead economic dispatch with adjustable confidence interval based on a truncated versatile distribution model for wind power. IEEE Transactions on Power Systems, 33(2), 1755– 1767. https://doi.org/10.1109/TPWRS.2017.2715852 [Google Scholar] [CrossRef]

Becker, R. (2018). Generation of time-coupled wind power infeed scenarios using pair-copula construction. IEEE Transactions on Sustainable Energy, 9(3), 1298–1306. https://doi.org/10.1109/TSTE.2017.2782089 [Google Scholar] [CrossRef]

11. Liu, J., Xu, J., Sun, Y. Z., Zhou, G. H., Wang, J. et al. (2019). Dynamic economic dispatch of power system considering temporal correlation of wing power sequence. Automation of Electric Power Systems, 43(3), 43–45 (In Chinese). [Google Scholar]

12. Chen, G. G., Chen, J. F. (2013). Environmental/economic dynamic dispatch modeling and method for power systems integrating wind farms. Proceedings of the CSEE, 33(10), 27–35 (In Chinese). [Google Scholar]

13. Ma, H., Liu, Z., Li, M., Wang, B., Si, Y. et al. (2021). A two-stage optimal scheduling method for active distribution networks considering uncertainty risk. Energy Reports, 7, 4633–4641. https://doi.org/10.1016/j.egyr.2021.07.023 [Google Scholar] [CrossRef]

14. Xu, Y., Dong, Z. Y., Zhang, R., Hill, D. J. (2017). Multi-timescale coordinated voltage/var control of high renewable-penetrated distribution systems. IEEE Transactions on Power Systems, 32(6), 4398–4408. https://doi.org/10.1109/TPWRS.2017.2669343 [Google Scholar] [CrossRef]

15. Niknam, T., Zare, M., Aghaei, J. (2012). Scenario-based multi-objective volt/var control in distribution networks including renewable energy sources. IEEE Transactions on Power Delivery, 27(4), 2004–2019. https://doi.org/10.1109/TPWRD.2012.2209900 [Google Scholar] [CrossRef]

16. Liu, D. W., Guo, J. B., Huang, Y. H., Wang, W. S. (2013). Dynamic economic dispatch of wind integrated power system based on wind power probabilistic forecasting and operation risk constraints. Proceedings of the CSEE, 33(16), 9–15+24 (In Chinese). [Google Scholar]

17. Cao, D., Zhao, J., Hu, W., Ding, F., Huang, Q., et al. (2021). Data-driven multi-agent deep reinforcement learning for distribution system decentralized voltage control with high penetration of PVs. IEEE Transactions on Smart Grid, 12(5), 4137–4150. https://doi.org/10.1109/TSG.2021.3072251 [Google Scholar] [CrossRef]

18. Li, X., Zeng, Y., Lu, Z. (2022). Decomposition and coordination calculation of economic dispatch for active distribution network with multi-microgrids. International Journal of Electrical Power & Energy Systems, 135, 107617. https://doi.org/10.1016/j.ijepes.2021.107617 [Google Scholar] [CrossRef]

19. Zhang, Y., Wang, X., Wang, J., Zhang, Y. (2021). Deep reinforcement learning based volt-VAR optimization in smart distribution systems. IEEE Transactions on Smart Grid, 12(1), 361–371. https://doi.org/10.1109/TSG.5165411 [Google Scholar] [CrossRef]

20. Li, F. Y., Qin, J. H., Zheng, W. X. (2020). Distributed Q-learning-based online optimization algorithm for unit commitment and dispatch in smart grid. IEEE Transactions on Cybernetics, 50(9), 4146–4156. https://doi.org/10.1109/TCYB.6221036 [Google Scholar] [CrossRef]

21. Yan, Z. M., Xu, Y. (2020). Real-time optimal power flow: A lagrangian based deep reinforcement learning approach. IEEE Transactions on Power Systems, 35(4), 3270–3273. https://doi.org/10.1109/TPWRS.59 [Google Scholar] [CrossRef]

22. Cao, D., Hu, W., Xu, X., Wu, Q., Huang, Q. et al. (2021). Deep reinforcement learning based approach for optimal power flow of distribution networks embedded with renewable energy and storage devices. Journal of Modern Power Systems and Clean Energy, 9(5), 1101–1110. https://doi.org/10.35833/MPCE.2020.000557 [Google Scholar] [CrossRef]

23. Zhang, C., Xu, Y. (2020). Hierarchically-coordinated voltage/VAR control of distribution networks using PV inverters. IEEE Transactions on Smart Grid, 11(4), 2942–2953. https://doi.org/10.1109/TSG.5165411 [Google Scholar] [CrossRef]

24. El Helou, R., Kalathil, D., Xie, L. (2021). Fully decentralized reinforcement learning-based control of photovoltaics in distribution grids for joint provision of real and reactive power. IEEE Open Access Journal of Power and Energy, 8, 175–185. https://doi.org/10.1109/OAJPE.2021.3077218 [Google Scholar] [CrossRef]