 Open Access
Open Access
ARTICLE
Thermodynamic Performance Analysis of Geothermal Power Plant Based on Organic Rankine Cycle (ORC) Using Mixture of Pure Working Fluids
1 Department of Mechanical Engineering, Mehran University of Engineering and Technology, Jamshoro, 76062, Pakistan
2 Department of Mechanical and Industrial Engineering, College of Engineering, Qatar University, Doha, 00000, Qatar
3 Sustainable & Renewable Energy Engineering Department, University of Sharjah, Sharjah , 00000, United Arab Emirates
* Corresponding Author: Laveet Kumar. Email:
Energy Engineering 2024, 121(8), 2023-2038. https://doi.org/10.32604/ee.2024.051082
Received 27 February 2024; Accepted 22 May 2024; Issue published 19 July 2024
Abstract
The selection of working fluid significantly impacts the geothermal ORC’s Efficiency. Using a mixture as a working fluid is a strategy to improve the output of geothermal ORC. In the current study, modelling and thermodynamic analysis of ORC, using geothermal as a heat source, is carried out at fixed operating conditions. The model is simulated in the Engineering Equation Solver (EES). An environment-friendly mixture of fluids, i.e., R245fa/R600a, with a suitable mole fraction, is used as the operating fluid. The mixture provided the most convenient results compared to the pure working fluid under fixed operating conditions. The impact of varying the evaporator pressure on the performance parameters, including energy efficiency, exergy efficiency and net power output is investigated. The system provided the optimal performance once the evaporator pressure reached the maximum value. The efficiencies: Energy and Exergy, and Net Power output of the system are 16.62%, 64.08% and 2199 kW for the basic cycle and 20.72%, 67.76% and 2326 kW respectively for the regenerative cycle.Keywords
Nomenclature
| E | Flow exergy (J) |
| EnE | Energy efficiency (%) |
| ExE | Exergy efficiency (%) |
| h | Specific enthalpy (J/kg) |
| Mass flow rate (kg/s) | |
| P | Pressure (kPa) |
| Q | Heat transfer rate (kW) |
| s | Entropy (kJ/kgK) |
| T | Temperature (°C) |
| Work (kW) | |
| Xd | Exergy destruction (kW) |
| Subscript | |
| con | Condenser |
| d | Exergy destruction |
| Eva | Evaporator |
| Geo | Geothermal brine |
| p | Pump |
| t | Turbine |
| wf | Working fluid |
| Greek Symbols | |
| ε | Exergy |
| η | Efficiency |
| Abbreviations | |
| B-ORC | Basic Organic Rankine Cycle |
| IHX | Internal Heat Exchanger |
| R-ORC | Regenerative Organic Rankine Cycle |
Geothermal energy is the cleanest form of heat energy that resides beneath the surface of the earth and is considered a renewable energy resource. Notably, geothermal energy, with a storage capacity of 43,000,000 EJ, may be found at a depth of up to 3 km with a temperature range of 50°C to 350°C. 70% of these enormous resources are low-enthalpy and water dominated resources below 150°C [1]. Owing to the usage of fossil fuels and the challenges of producing electricity without harming the environment besides the depletion of these fuels, the need for clean and alternative energy sources has increased. It has received more interest than other renewable energy forms, such as wind and solar energy because of its consistency, strength, predictability, steadiness, etc. [2,3]. Compared to geothermal energy, other renewable energy resources are expensive, unreliable, and require sophisticated control systems to produce grid-ready electricity [4]. Furthermore, to increase the stability and flexibility of the power grid, geothermal power facilities must relate to energy storage technologies [3]. Organic Rankine Cycles (ORCs) are efficient for extracting geothermal heat [5]. Ceglia et al. studied the potential for using ORC technology to generate power from geothermal sources at low to medium temperatures [4]. Ahmadi et al. focused on using geothermal resources as a substitute for fossil fuels in ORC power plants [6]. Dezfouli et al. investigated eight parameter optimizations, proposing a nascent method combining three geothermal cycles to generate electricity [3]. Yağlı et al. assessed the R245fa-based subcritical and supercritical ORCs’ thermal and energetic performance in recovering exhaust heat from the biogas-fuelled combined engine [7]. Kerme et al. examined the organic Rankine cycle’s exergetic and energetic performance by generating solar with the great impact of parabolic solar collectors [8]. Akkaya investigated a power production system based on the ORC that harnesses the thermal Energy from the waste gases of an industrial facility [9]. Almutairi et al. investigated the effectiveness of combining an electrolyzer and an ORC in a geothermal flash-binary cycle that generates Power and hydrogen [10]. Zare went into a deep sight of the ORC and Kalina Cycle, which uses geothermal energy based on trigeneration systems [11]. Wang et al. examined a geothermal system that blends a trans-critical CO2 recovery cycle with a single flash geothermal cycle using an internal heat exchanger to overcome heat losses [2]. Kaynakli et al. examined ORC thermodynamically under specific operating circumstances without requiring additional heat exchangers [12]. Jafary et al. carried out an extensive energy and exergy study of a multigeneration system using solar power and two novel ORC designs [13]. Chen et al. developed a theoretical model of energy efficiency at lower temperatures for subcritical ORC. According to the total energy efficiency, they discovered that the ideal working fluids operating at different temperatures were R365mfc, R245fa, R245ca and R36ea [14]. Assareh et al. examined the novel design of a hybrid power plant that uses a transitional geothermal fluid to provide heat from a biomass source to produce clean energy [15]. Bademlioglu et al. used statistical analysis techniques, including the Taguchi and ANOVA methodologies to examine the influence of weights and parameter importance on the Efficiency of the ORC [16]. Song et al. investigated geothermal power plant thermo-economic optimization by contrasting the effectiveness of various cycle configurations by using a functional fluid parametric analysis [17]. Moloney et al. compared recuperative supercritical ORC with the existing binary cycle. They discovered pentane, isopentane, neopentane, butane, and R1233zd(E) were optimum working fluids [18]. Zhang et al. executed a selection and assessment study on isentropic and dry working fluids and found R123 the most convenient [19]. Fan et al. evaluated the ORC’s performance using the working fluid’s characteristics as a basis and developed a criterion for the distinct features of the working fluid [20]. Zhou et al. evaluated the thermodynamic performance of the mixture R245fa/R227ea for the partly evaporating ORC. They discovered that by utilizing R227ea as the refrigerant, this cycle generated around 25% more Power than the subcritical cycle [21]. Deethayat et al. examined the operation of 50 kW ORC with IHX while utilizing the R245fa/R152a refrigerant combination [22]. Efficiency is heavily influenced by the choice of working fluid [23]. Many authors investigated the choice of pure fluids that are clean and have an ORC cycle operating temperature under 100°C. The efficiency rises with increasing fluid critical pressure and varies between 0.3%–13% according to the working fluid used. Using a mixture of working fluids is an intriguing strategy to improve the efficiency and output of the plant [24].
As the aforementioned literature shows, there is little or no agreement on the use of a mixture of organic working fluids in basic and modified ORC configurations integrated with high-temperature geothermal brine as a heat source.
The main objectives and novelties of this study follow are as follows:
• Develop a thermodynamic simulation of two arrangements of an ORC system.
• Utilizing exergy analysis as an effective tool to determine exergy destruction and efficiency.
• Comparative analysis for both systems with mixture working fluids (R245fa/R600a) based on energy and exergy analysis.
• Parametric analysis determines the effect of evaporator pressure, turbine and pump efficiency on the ORC system.
The remainder of this paper is organized as follows: Section 2 illustrates a detailed description of the investigated cycles and working fluid. Section 3 gives the mathematical modeling. Section 4 validates the model and demonstrates the impact of input parameters on the system, and the results of energy, and exergy analysis. Finally, conclusions are drawn in Section 5.
2 Model Architecture and Selection of Working Fluid
The working principle of the geothermal ORC is like the traditional Rankine Cycle, with the only difference being the operating fluid. The schematic of the basic ORC (B-ORC) is shown in Fig. 1. Brine, extracted from the geothermal source and sent to the evaporator, is used in the cycle. Heat is transferred from the brine to the mixture of organic fluids used in the cycle in the evaporator. Where the organic fluid reaches the maximum temperature and is sent to the turbine to get the mechanical work out of it. In the turbine, the fluid is expanded. The working fluid, exiting from the turbine, enters the condenser for condensation. The condensed working fluid enters the pump and is pressurized to enter the evaporator. Fig. 2 demonstrates the regenerative ORC (R-ORC), which has the additional component: the internal heat exchanger used for preheating the fluid, and heat is recovered from the vapor leaving the turbine. The working fluid is headed to the condenser, where it cools down using air. The pump used raises the pressure of the operating fluid, then is directed to the evaporator, and the cycle continues.
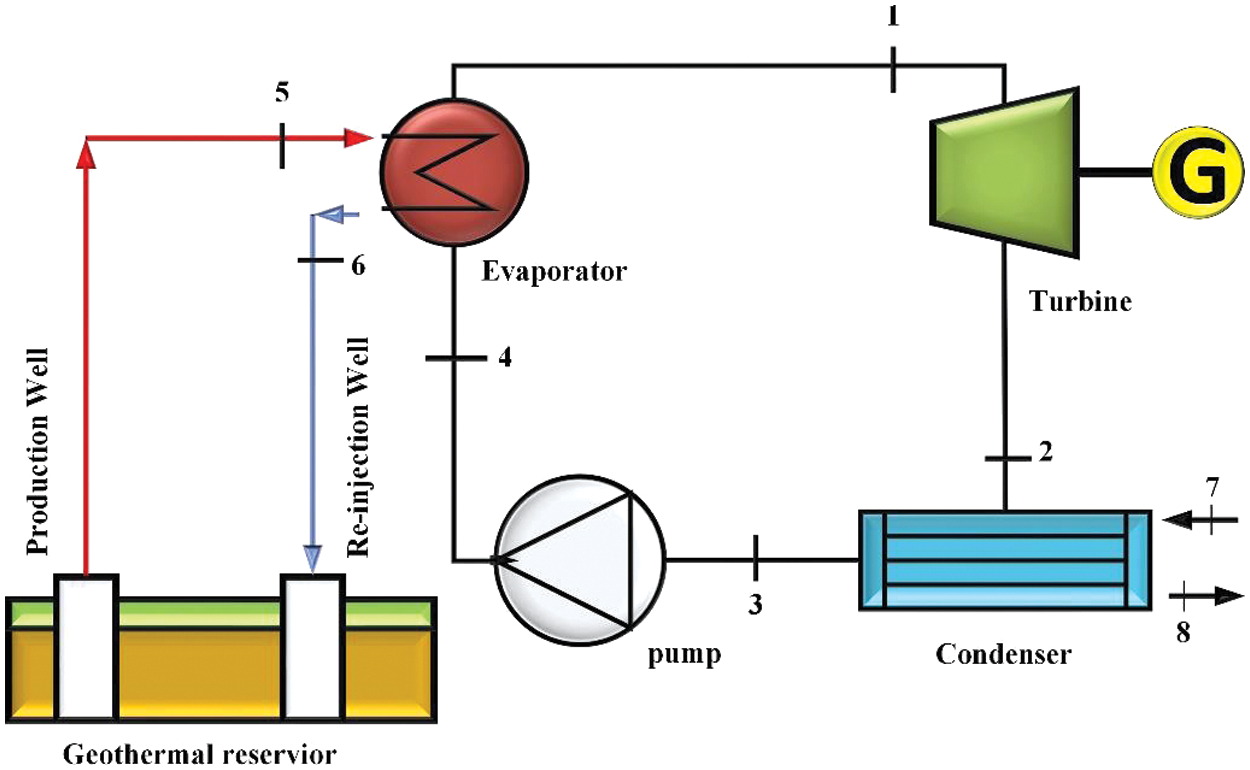
Figure 1: Schematic of basic ORC (B-ORC)
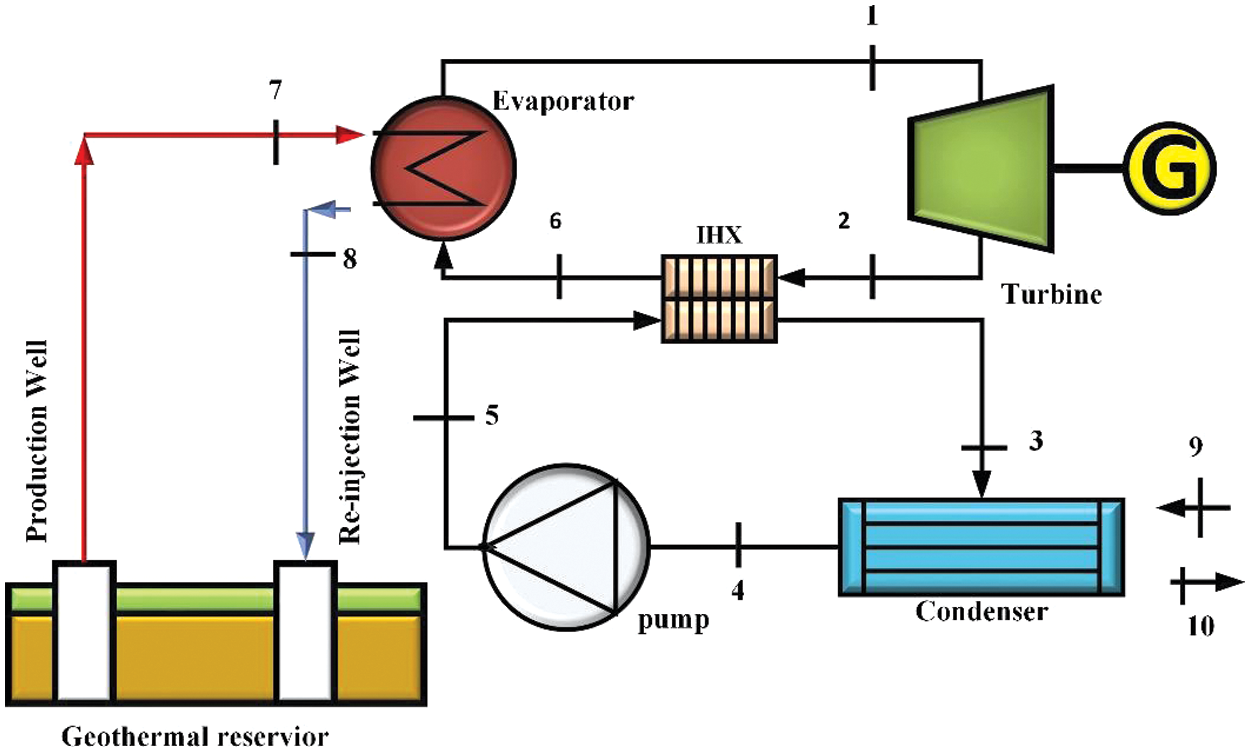
Figure 2: Schematic of regenerative ORC (R-ORC)
2.2 Selection of Working Fluid
The design of ORC heavily depends on the fluid selection process. It can be challenging because of temperature variations, cycle performance, safety and environmental concerns, different types of heat sources and operation changes. Based on the challenges, an environment-friendly fluid mixture, i.e., R245fa/R600a is used as the operating fluid. Using the proper mole fraction, i.e., 0.6/0.4 of operating fluid results in maximum output at the fixed input parameters. Parametric optimisation is conducted for the working fluid mixture.
3.1 Assumption for Thermodynamic Modelling of Geothermal ORC
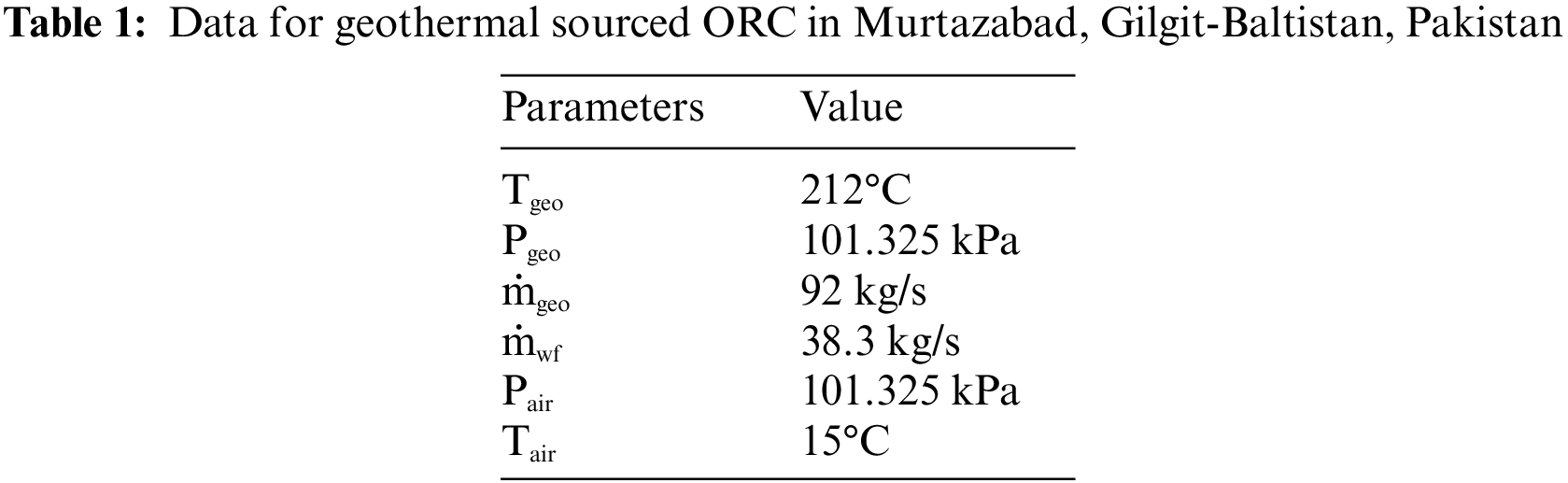
Geothermal brine is used to heat the working fluid The input parameters used in the model and simulation are mentioned in the Table 1 [25]. The ORCs were simulated using EES (Engineering Equation Solver). The following assumptions were considered [26,27]:
• The cycle operates in steady-state flow conditions.
• The assumed isentropic efficiencies of the turbine and pump are 85% and 80%, respectively.
• The kinetic and potential energy changes are negligible.
• Pressure and friction losses are neglected.
• The Dead state conditions are taken as: T0; 15°C and P0; 101.325 kPa.
3.2 Thermodynamic Modelling of Geothermal ORC
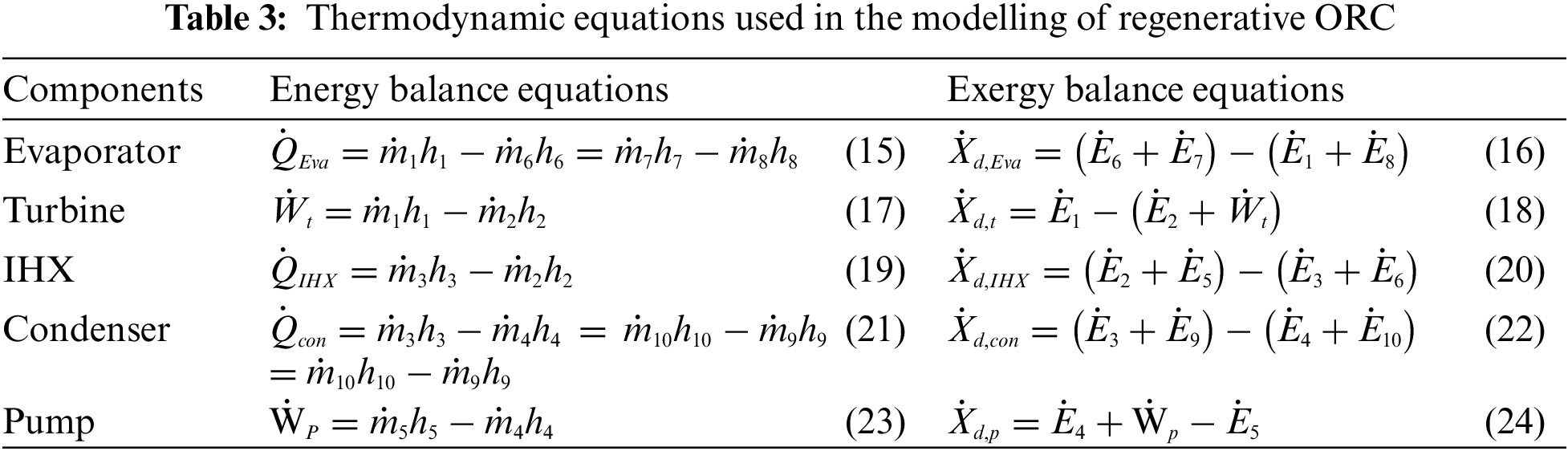
The thermodynamic performance of the geothermal ORC is analysed by employing the laws of thermodynamics. To implement these laws, thermodynamic analysis is offered mathematically over mass, Exergy, and energy balances by Eqs. (1)–(3), respectively. The laws of thermodynamics (both First and Second) have direct connection to the Energy and Exergy in which Exergy is the overall maximum work done by the system when it is balanced against the environment [15]. Tables 2 and 3 represent thermodynamic equations for basic and regenerative ORCs, respectively.

Here,
Heat transfer rate is symbolised to
On owing to achieve exergy analysis of the different components of the cycle and to calculate the exergy efficiency on behalf of exergy destruction, thermodynamics’ second law would be more reliable. The chemical exergy is neglected because of no chemical reaction taking place. However, the physical exergy is considered and represented by Eq. (4).
where h0, s0 and T0 are the dead-state enthalpy, entropy and temperature respectively and
The energy efficiency (EnE) of each cycle is calculated by Eq. (5):
The exergy efficiency (ExE) of each cycle is calculated by Eq. (6):
Here, the thermodynamic model, used in the geothermal ORC, is simulated and results are described. Then, the performance parameters, i.e., energy efficiency, exergy efficiency, net power output and exergy destruction are enhanced through parametric optimisation.
The proposed system in this study is novel in terms of mixture of organic working fluids used in the system. The model of the studied systems is validated by taking the input parameters reported by [28]. The regenerative ORC (R-ORC), energy efficiency, and exergy efficiency (ExE) were selected for comparison. The results from the simulated study and literature are presented in Table 4. The results show little difference, and it can be concluded that the model is accurate.

The impact of varying the evaporator pressure on the performance parameters, which include energy efficiency and, exergy efficiency, and net power output is investigated. Furthermore, the effect of varying the pump and turbine efficiencies on the performance parameters, including energy efficiency, exergy efficiency and net power output, is also investigated. The evaporator pressure is increased up to 3000 kPa due to subcritical operating conditions of the systems. The turbine and pump efficiencies are also varied between 70%–90% and 65%–85%, respectively.
4.2.1 Effect of Evaporator Pressure on System Performance
The outcome of varying the evaporator pressure on the Net Power output of ORC operating with R245fa/R600a with a mole fraction of 0.6/0.4 is shown in Fig. 3. It is observed that increasing the evaporator pressure increases the Net Power output for both the cycles, i.e., the basic cycle and the cycle operating with an internal heat exchanger. Maximum Net Power output yielded for both cycles is 2199 and 2326 kW, respectively, at the most appropriate evaporator pressure. The power output increases with the rise in pressure due to higher average temperatures at which the heat is added.
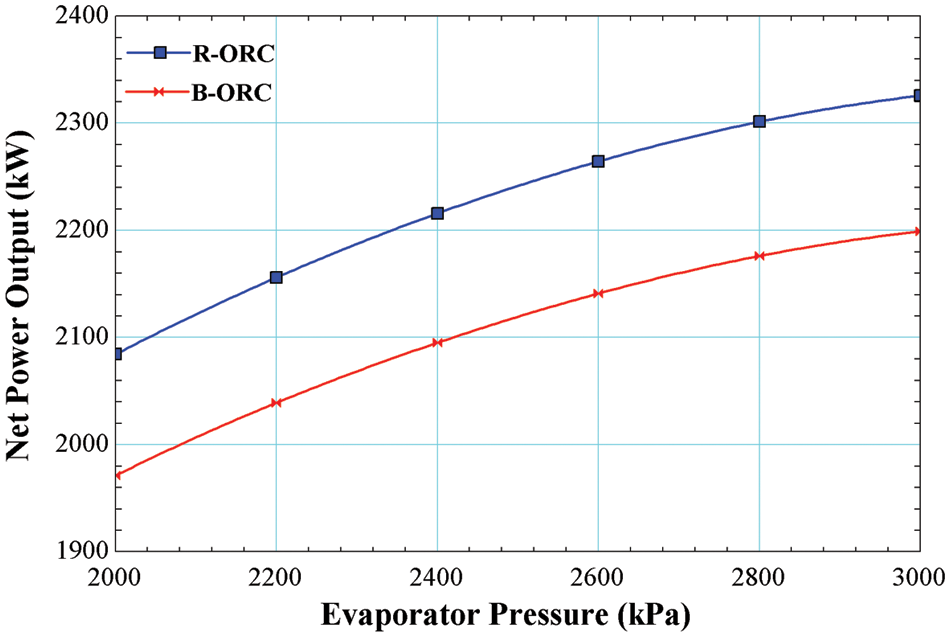
Figure 3: Impact of evaporator pressure on net power output
Fig. 4 reveals the impact of varying the evaporator pressure on the energy efficiency of the system operated by R245fa/R600a with the mole fraction of 0.6/0.4. Energy efficiency is increased with the increase in evaporator pressure which is a maximum of 16.62% for the basic cycle and 20.72% for the cycle using an internal heat exchanger. The energy increases with the rise in pressure due to reduction in heat load at evaporator due to higher temperatures.
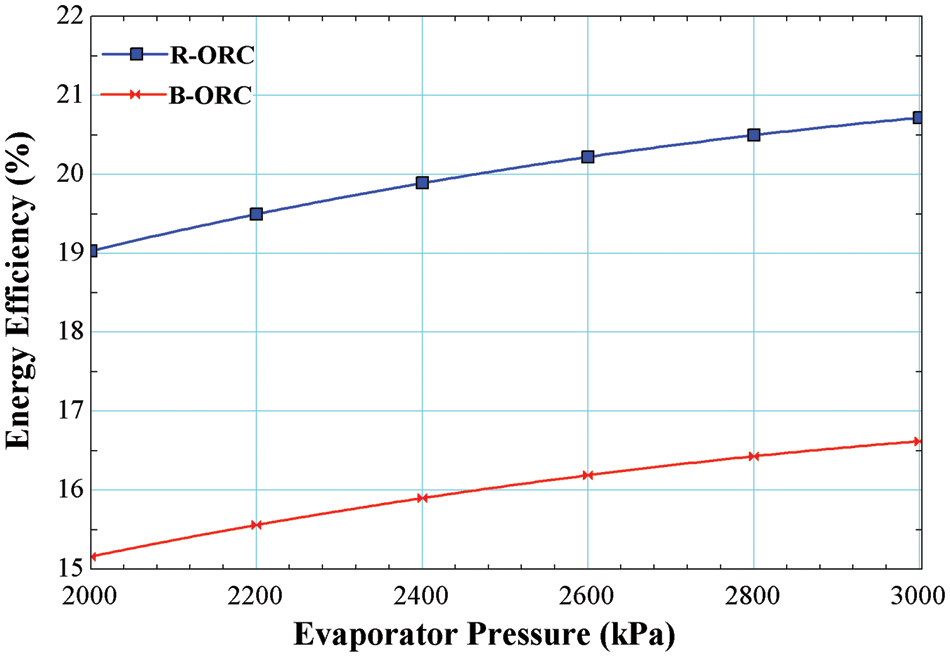
Figure 4: Effect of evaporator pressure on energy efficiency
Fig. 5 shows the deviation in the exergy efficiencies of R245fa/R600a with the mole fraction of 0.6/0.4 for both the cycles, i.e., the basic cycle and the cycle operating with an internal heat exchanger. It is evident from the Fig. 6, exergy efficiency is increased by increasing in the evaporator pressure. It is a maximum of 64.04% for the basic cycle and 67.76% for the cycle using an internal heat exchanger. The Exergy increases with the rise in pressure due to reduction in exergy destruction at the evaporator due to higher temperatures.
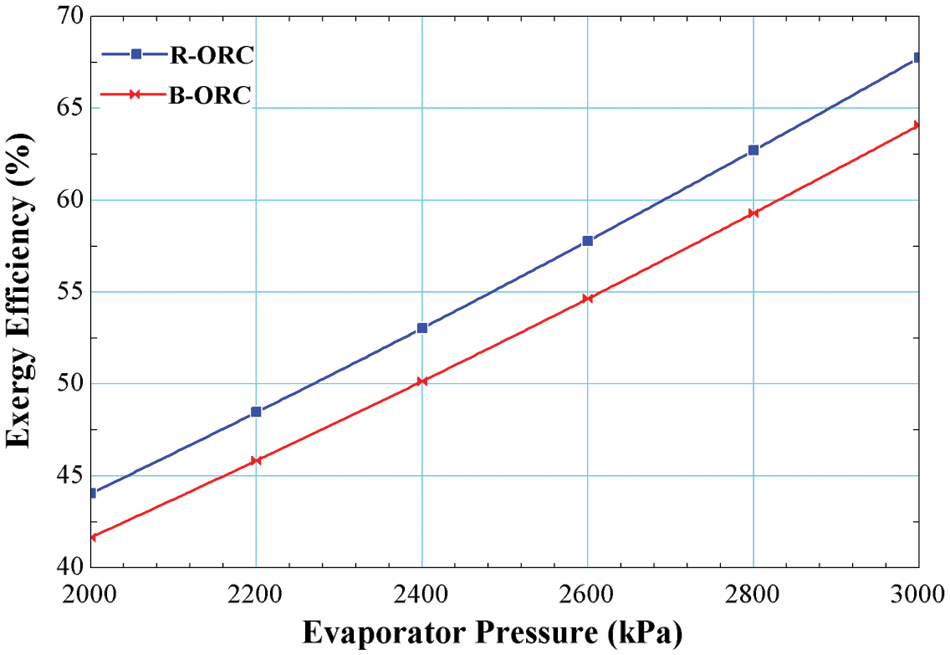
Figure 5: Effect of evaporator pressure on exergy efficiency
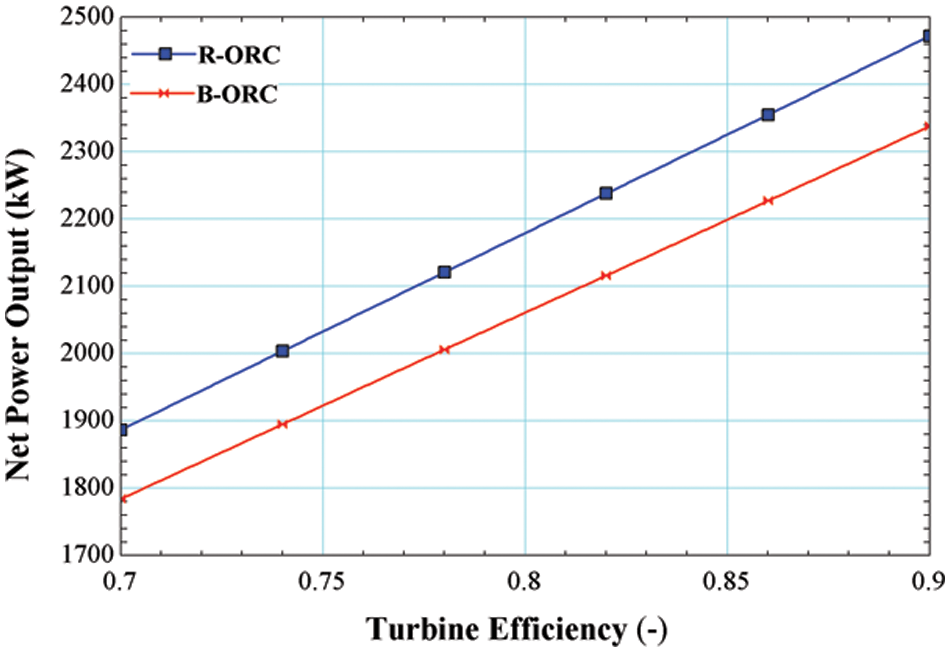
Figure 6: Impact of turbine efficiency on net power output
4.2.2 Effect of Turbine Efficiency on System Performance
The outcome of varying the turbine efficiency on the Net Power output of ORC operating with R245fa/R600a with a mole fraction of 0.6/0.4 is shown in Fig. 6. It is observed that increasing the turbine efficiency increases the Net Power output for both the cycles, i.e., the basic cycle and regenerative cycle, maximum Net Power output yielded maximum turbine efficiency, i.e., 0.9 for both cycles is 2338 and 2472 kW, respectively. Increasing the turbine efficiency results greater power output from the turbine at the fixed heat input.
Fig. 7 demonstrates the impact of turbine efficiency pressure on the energy efficiency of the system operated by R245fa/R600a with the mole fraction of 0.6/0.4. Energy efficiency is increased with the increase in turbine efficiency which is a maximum of 17.67% for the basic cycle and 22.02% for the cycle using an internal heat exchanger. Increasing the turbine efficiency results greater power output from the turbine at the same heat input resulting higher energy efficiency.
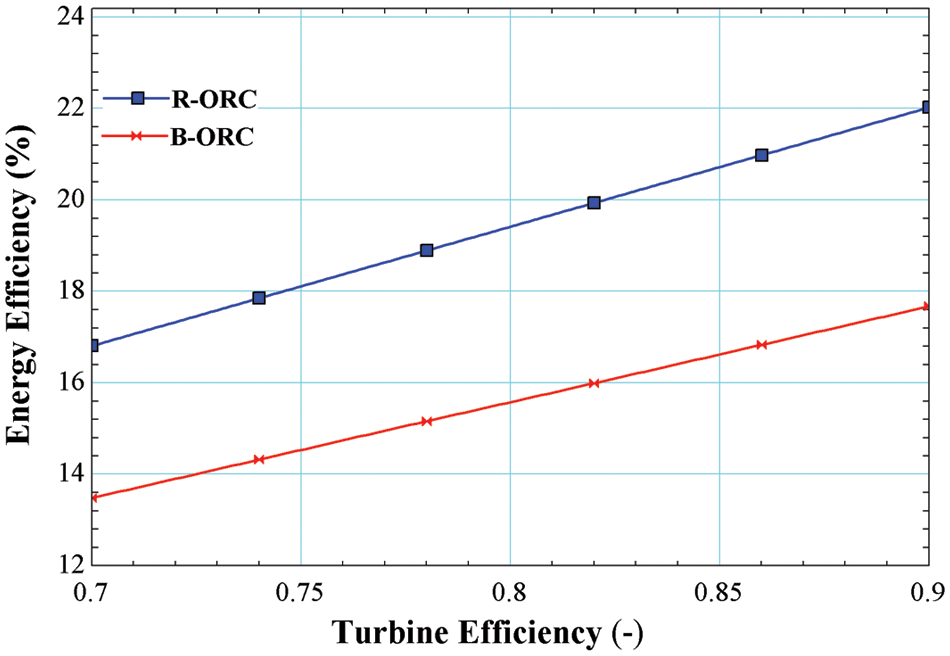
Figure 7: Impact of turbine efficiency on energy efficiency
Fig. 8 shows the deviation in the exergy efficiencies of R245fa/R600a with the mole fraction of 0.6/0.4 for both the cycles, i.e., the basic cycle and the cycle operating with an internal heat exchanger. It is evident from the Fig. 8; exergy efficiency is increased by increasing in the turbine efficiency. It is a maximum of 68.11% for the basic cycle and 72.02% for the cycle using an internal heat exchanger. Increasing the turbine efficiency results greater power output from the turbine at the same heat input resulting higher exergy efficiency.
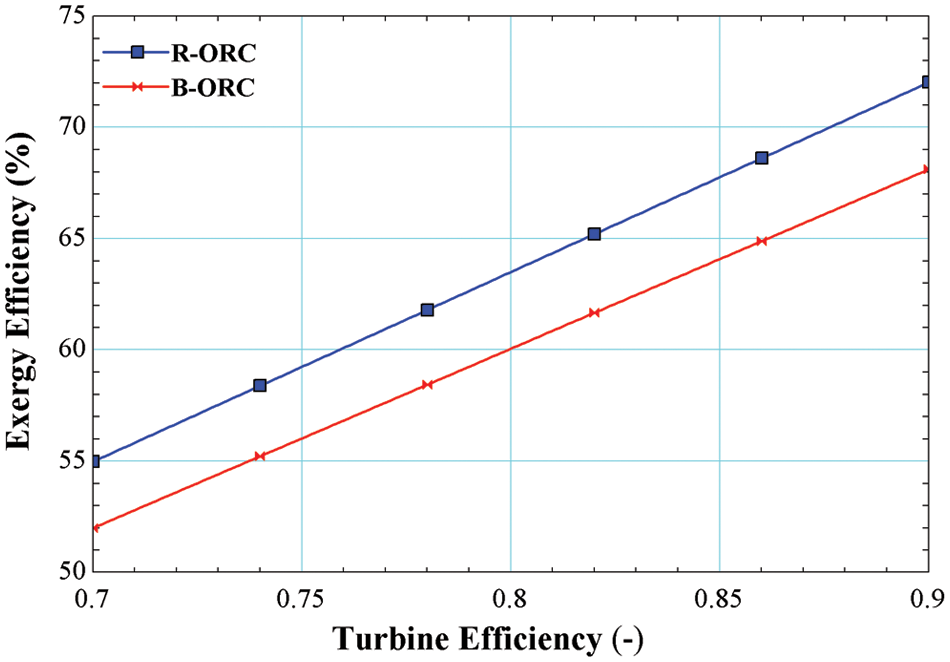
Figure 8: Impact of turbine efficiency on exergy efficiency
4.2.3 Effect of Pump Efficiency on Performance
The outcome of varying the pump efficiency on the Net Power output of ORC operating with R245fa/R600a with a mole fraction of 0.6/0.4 is shown in Fig. 9. It is observed that by increasing the pump efficiency increases the Net Power output for both the cycles, i.e., the basic cycle and regenerative cycle, maximum Net Power output yielded maximum turbine efficiency, i.e., 0.85 for both cycles is 2208 and 2335 kW, respectively. Increasing the pump efficiency results in lower power input requirements and greater power supply from the turbine.
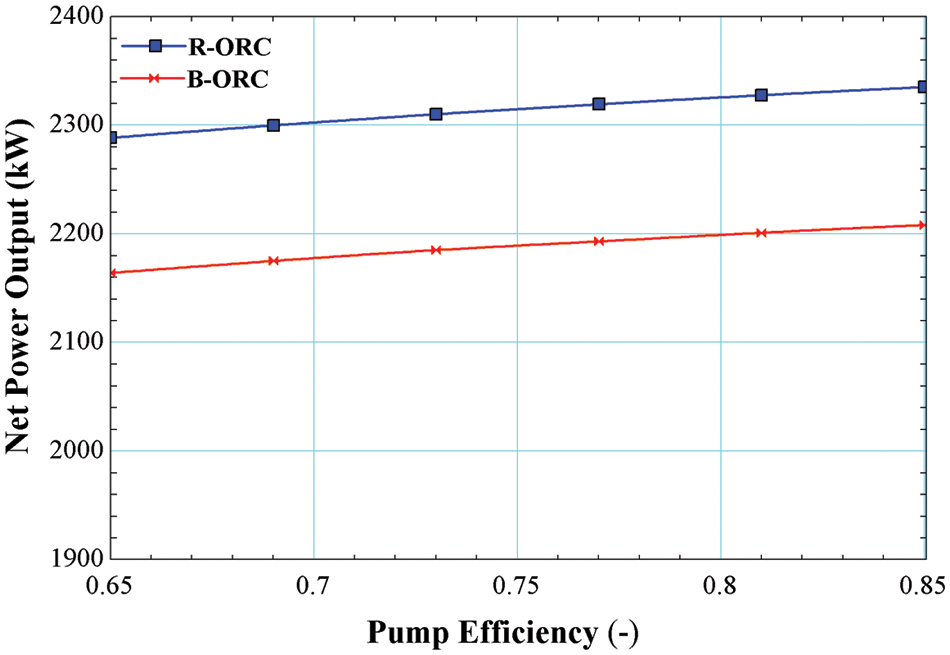
Figure 9: Impact of pump efficiency on net power
Fig. 10 illustrates the impact of pumpefficiency pressure on the energy efficiency of the system operated by R245fa/R600a with a mole fraction of 0.6/0.4. Energy efficiency is increased with the increase in pump efficiency, which is a maximum of 16.69% for the basic cycle and 20.8% for the cycle using an internal heat exchanger. Increasing the pump efficiency results in lower power input requirements, resulting in greater power supply from the turbine, thus enhancing the energy efficiency of the system.
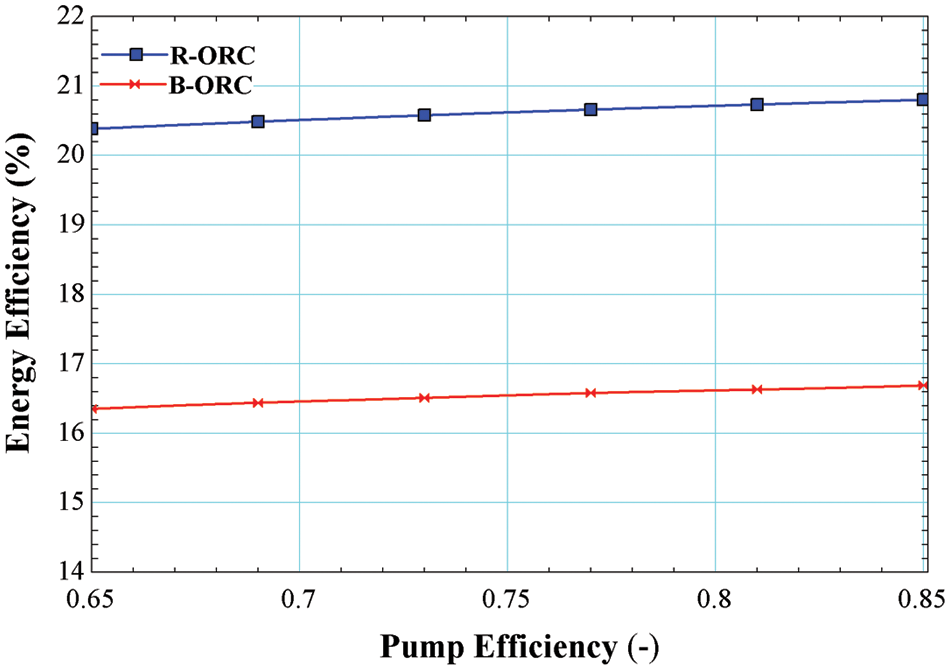
Figure 10: Impact of pump efficiency on energy efficiency
Fig. 11 reveals the deviation in the exergy efficiencies of R245fa/R600a with the mole fraction of 0.6/0.4 for both the cycles, i.e., the basic cycle and the cycle operating with an internal heat exchanger. It is evident from the Fig. 11; exergy efficiency is increased by increasing in the pump efficiency. It is a maximum of 64.39% for the basic cycle and 68.04% for the cycle using an internal heat exchanger. Increasing the pump efficiency results lower power input requirements resulting lower back work ratio thus enhancing the exergy efficiency of the system.
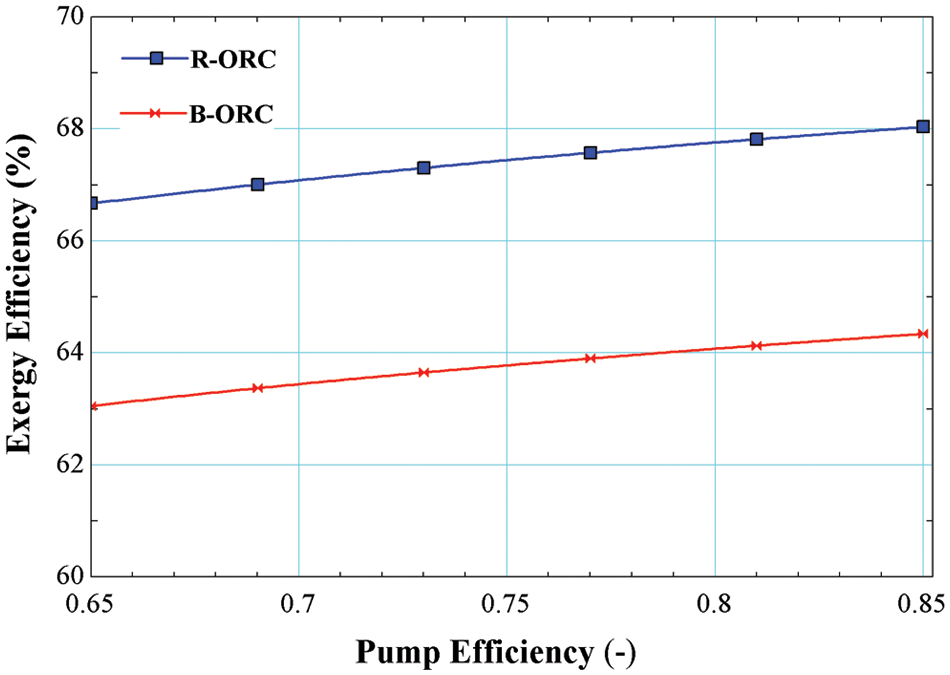
Figure 11: Effect of pump efficiency on exergy efficiency
It is observed from the parametric study that the system performance is optimal at evaporator pressure Peva; 3000 kPa and condenser pressure Pcon; 200 kPa. The flow parameters obtained under these conditions are specified in Tables 5 and 6. Whereas, Fig. 12 illustrates the exergy destruction rate in components of basic and regenerative ORC at optimal operating conditions.
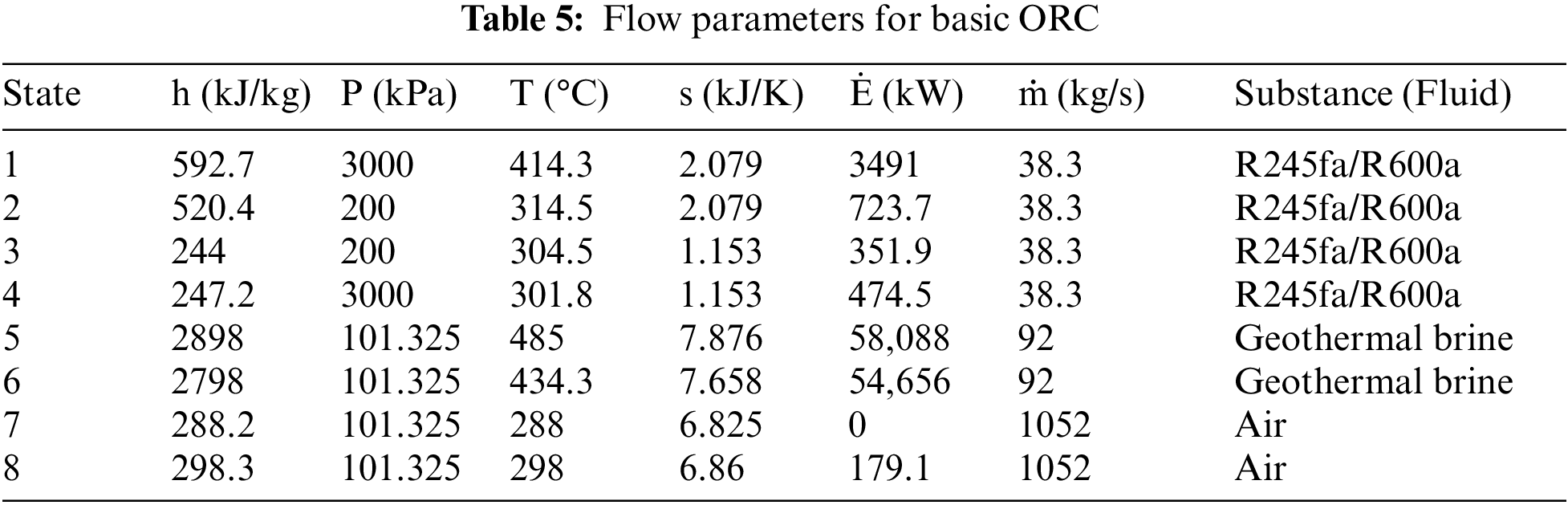
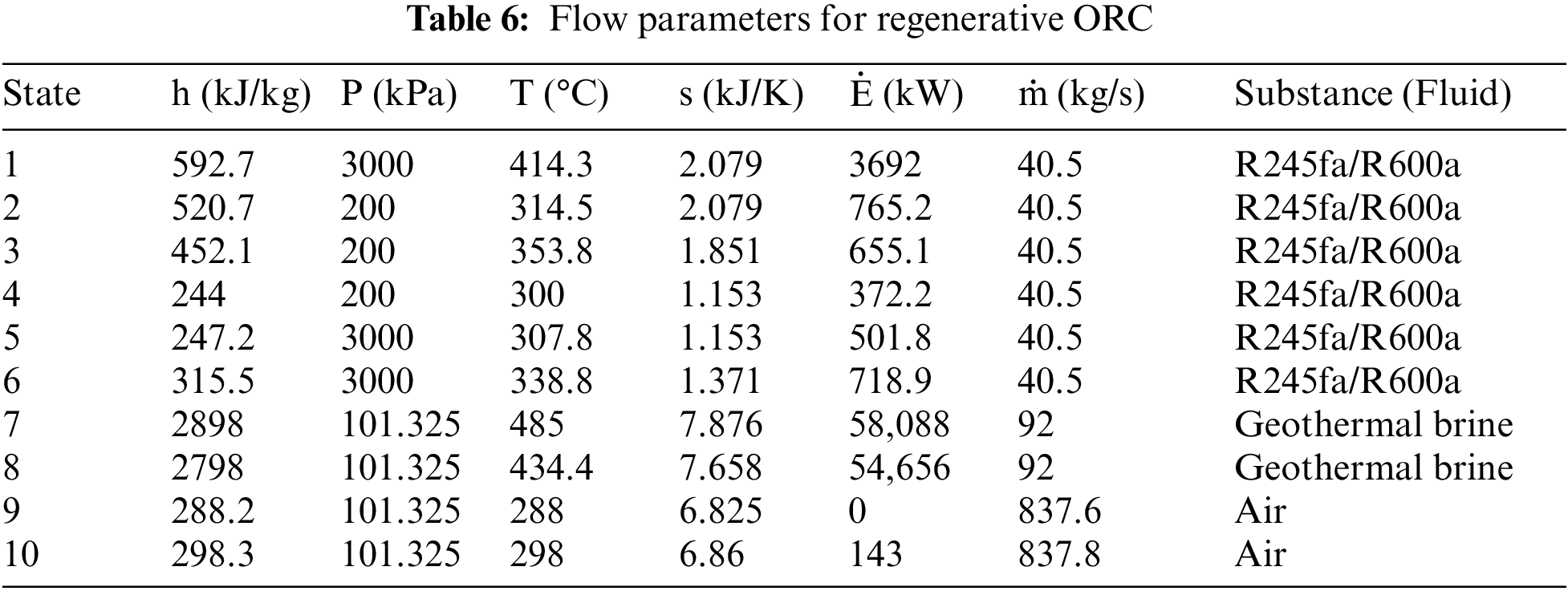
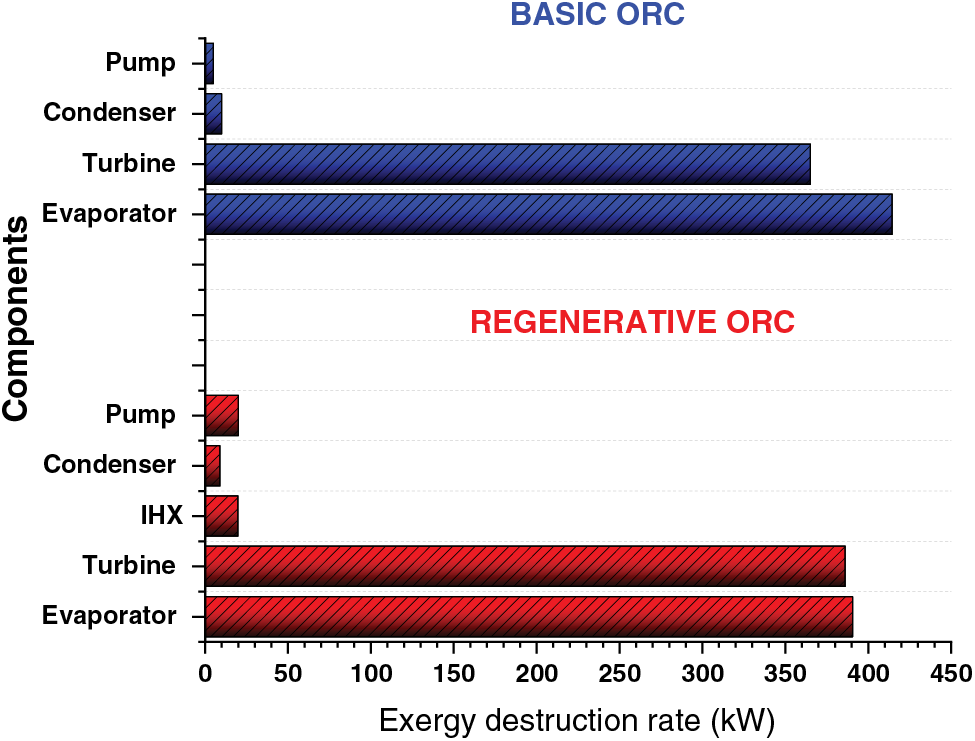
Figure 12: Exergy destruction rate in components of basic and regenerative ORC at optimal operating conditions
Table 7 represents the optimal performance parameters calculated from the flow parameters presented in Tables 5 and 6. Fig. 12 shows the exergy destruction rate of the most convenient fluid, such as R245fa/R600a, at each component of the working cycle. The turbine and the evaporator have the maximum exergy destruction rates of 386.2 and 390.6 kW.
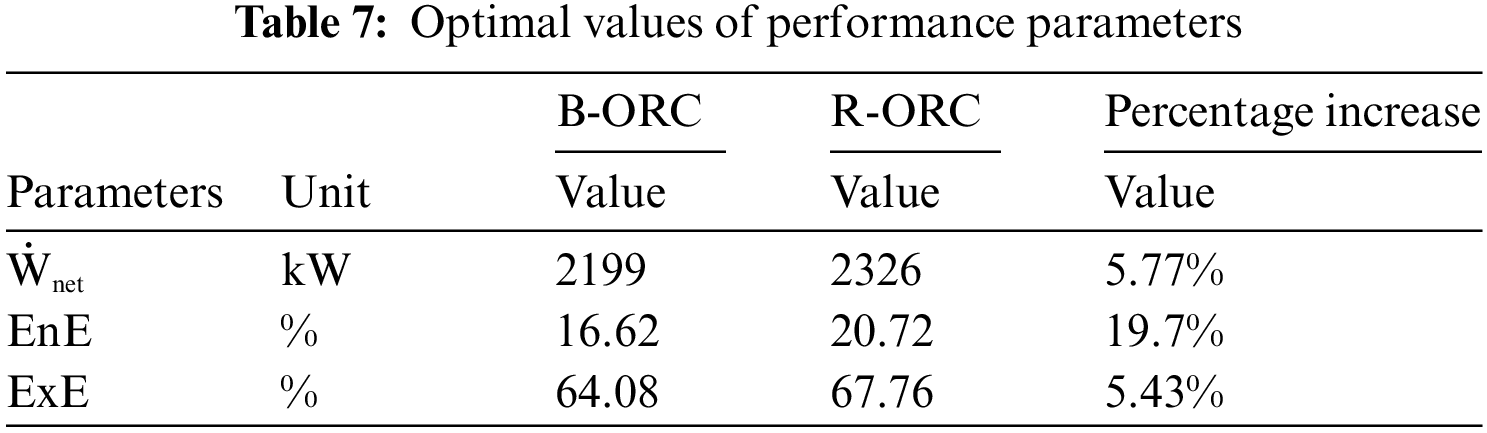
In the current study, the modeling and thermodynamic analysis of the geothermal ORC operating with the mixture of working fluids, i.e., R245fa/R600a with the mole fraction 0.6/0.4, are performed. The parametric optimization is conducted over the working fluid mixture, i.e., R245fa/R600a with a mole fraction of 0.6/0.4. Furthermore, energy and exergy analysis were executed by using the mixture of the operating fluid and the fluid with a mole fraction of 0.6/0.4, yielding optimal results. The maximum performance of the cycle is attained once it is at the peak of evaporator pressure, which yielded 16.62%, 64.08% and 2199-kW energy cum exergy efficiencies and net power output for the basic cycle and the same parameters for the regenerative cycle are 20.72%, 67.76% and 2326 kW, respectively. The regenerative ORC, as compared to Basic ORC, shows a 5.77%, 5.23%, and 5.43% rise in net power output, Energy efficiency and Exergy efficiency, respectively.
Acknowledgement: The authors acknowledge the support from Department of Mechanical Engineering, Mehran University of Engineering and Technology, Jamshoro, Pakistan.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Abdul Sattar Laghari, Mohammad Waqas Chandio, Laveet Kumar, Mamdouh EL Haj Assad; data collection: Abdul Sattar Laghari; analysis and interpretation of results: Abdul Sattar Laghari, Mohammad Waqas Chandio; draft manuscript preparation: Abdul Sattar Laghari, Mohammad Waqas Chandio, Laveet Kumar, Mamdouh EL Haj Assad. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data is available within the article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. M. Marefati, M. Mehrpooya, and S. A. Mousavi, “Introducing an integrated SOFC, linear fresnel solar field, stirling engine and steam turbine combined cooling, heating and power process,” Int. J. Hydrogen Energy, vol. 44, no. 57, pp. 30256–30279, 2019. [Google Scholar]
2. H. Wang et al., “Thermodynamic investigation of a single flash geothermal power plant powered by carbon dioxide transcritical recovery cycle,” Alex. Eng. J., vol. 64, pp. 441–450, 2023. [Google Scholar]
3. A. H. M. Dezfouli, N. Niroozadeh, and A. Jahangiri, “Energy, exergy, and exergoeconomic analysis and multi-objective optimization of a novel geothermal driven power generation system of combined transcritical CO2 and C5H12 ORCs coupled with LNG stream injection,” Energy, vol. 262, p. 125316, 2023. [Google Scholar]
4. F. Ceglia, E. Marrasso, C. Roselli, and M. Sasso, “Effect of layout and working fluid on heat transfer of polymeric shell and tube heat exchangers for small size geothermal ORC via 1-D numerical analysis,” Geothermics, vol. 95, p. 102118, 2021. [Google Scholar]
5. A. Haghighi, M. R. Pakatchian, M. E. H. Assad, V. N. Duy, and M. A Nazari, “A review on geothermal organic rankine cycles: Modeling and optimization,” J. Therm. Anal. Calorim., vol. 144, pp. 1799–1814, 2021. [Google Scholar]
6. A. Ahmadi et al., “Applications of geothermal organic rankine cycle for electricity production,” J. Clean. Prod., vol. 274, no. 4, pp. 122950, 2020. doi: 10.1016/j.jclepro.2020.122950. [Google Scholar] [CrossRef]
7. H. Yağlı, Y. Koç, A. Koç, A. Görgülü, and A. Tandiroğlu, “Parametric optimization and exergetic analysis comparison of subcritical and supercritical organic rankine cycle (ORC) for biogas fuelled combined heat and power (CHP) engine exhaust gas waste heat,” Energy, vol. 111, no. 5, pp. 923–932, 2016. doi: 10.1016/j.energy.2016.05.119. [Google Scholar] [CrossRef]
8. E. Kerme and O. Jamel, “Exergy-based thermodynamic analysis of solar driven organic rankine cycle,” J. Therm. Eng., vol. 1, no. 5, pp. 192–202, 2015. doi: 10.18186/jte.25809. [Google Scholar] [CrossRef]
9. A. V. Akkaya, “Performance analyzing of an organic rankine cycle under different ambient conditions,” J. Therm. Eng., vol. 3, no. 5, pp. 1498–1504, 2017. doi: 10.18186/journal-of-thermal-engineering.338897. [Google Scholar] [CrossRef]
10. K. Almutairi, S. S. H. Dehshiri, A. Mostafaeipour, A. Issakhov, K. Techato and J. A. Dhanraj, “Performance optimization of a new flash-binary geothermal cycle for power/hydrogen production with zeotropic fluid,” J. Therm. Anal. Calorim., vol. 145, no. 3, pp. 1633–1650, 2021. doi: 10.1007/s10973-021-10868-2. [Google Scholar] [CrossRef]
11. V. Zare, “A comparative thermodynamic analysis of two tri-generation systems utilizing low-grade geothermal energy,” Energy Convers. Manag., vol. 118, pp. 264–274, 2016. doi: 10.1016/j.enconman.2016.04.011. [Google Scholar] [CrossRef]
12. O. Kaynakli, A. H. Bademlioglu, N. Yamankaradeniz, and R. Yamankaradeniz, “Thermodynamic analysis of the organic rankine cycle and the effect of refrigerant selection on cycle performance,” International Journal of Energy Applications and Technologies, vol. 4, no. 3, pp. 101–108, 2017. [Google Scholar]
13. S. Jafary, S. Khalilarya, A. Shawabkeh, M. Wae-hayee, and M. Hashemian, “A complete energetic and exergetic analysis of a solar powered trigeneration system with two novel organic rankine cycle (ORC) configurations,” J. Clean. Prod., vol. 281, no. 15, pp. 124552, 2021. doi: 10.1016/j.jclepro.2020.124552. [Google Scholar] [CrossRef]
14. G. Chen, Q. An, Y. Wang, J. Zhao, N. Chang and J. Alvi, “Performance prediction and working fluids selection for organic rankine cycle under reduced temperature,” Appl. Therm. Eng., vol. 153, no. 25, pp. 95–103, 2019. doi: 10.1016/j.applthermaleng.2019.02.011. [Google Scholar] [CrossRef]
15. E. Assareh, M. Delpisheh, A. Baldinelli, G. Cinti, H. Emami and M. Lee, “Integration of geothermal-driven organic rankine cycle with a proton exchange membrane electrolyzer for the production of green hydrogen and electricity,” Environ. Sci. Pollut. Res., vol. 30, no. 19, pp. 54723–54741, 2023. doi: 10.1007/s11356-023-26174-3. [Google Scholar] [PubMed] [CrossRef]
16. A. Bademlioglu, A. Canbolat, N. Yamankaradeniz, and O. Kaynakli, “Investigation of parameters affecting organic rankine cycle efficiency by using Taguchi and ANOVA methods,” Appl. Therm. Eng., vol. 145, pp. 221–228, 2018. doi: 10.1016/j.applthermaleng.2018.09.032. [Google Scholar] [CrossRef]
17. J. Song, P. Loo, J. Teo, and C. N. Markides, “Thermo-economic optimization of organic rankine cycle (ORC) systems for geothermal power generation: A comparative study of system configurations,” Front. Energy Res., vol. 8, pp. 6, 2020. doi: 10.3389/fenrg.2020.00006. [Google Scholar] [CrossRef]
18. F. Moloney, E. Almatrafi, and D. Goswami, “Working fluid parametric analysis for recuperative supercritical organic rankine cycles for medium geothermal reservoir temperatures,” Renew. Energy, vol. 147, pp. 2874–2881, 2020. doi: 10.1016/j.renene.2018.09.003. [Google Scholar] [CrossRef]
19. X. Zhang, C. Zhang, M. He, and J. Wang, “Selection and evaluation of dry and isentropic organic working fluids used in organic rankine cycle based on the turning point on their saturated vapor curves,” J. Therm. Sci., vol. 28, no. 4, pp. 643–658, 2019. doi: 10.1007/s11630-019-1149-x. [Google Scholar] [CrossRef]
20. W. Fan, Z. Han, P. Li, and Y. Jia, “Analysis of the thermodynamic performance of the organic rankine cycle (ORC) based on the characteristic parameters of the working fluid and criterion for working fluid selection,” Energy Convers. Manag., vol. 211, no. 7, pp. 112746, 2020. doi: 10.1016/j.enconman.2020.112746. [Google Scholar] [CrossRef]
21. Y. Zhou, F. Zhang, and L. Yu, “Performance analysis of the partial evaporating organic rankine cycle (PEORC) using zeotropic mixtures,” Energy Convers. Manag., vol. 129, pp. 89–99, 2016. doi: 10.1016/j.enconman.2016.10.009. [Google Scholar] [CrossRef]
22. T. Deethayat, T. Kiatsiriroat, and C. Thawonngamyingsakul, “Performance analysis of an organic rankine cycle with internal heat exchanger having zeotropic working fluid,” Case Stud. Therm. Eng., vol. 6, pp. 155–161, 2015. doi: 10.1016/j.csite.2015.09.003. [Google Scholar] [CrossRef]
23. Q. Liu, A. Shen, and Y. Duan, “Parametric optimization and performance analyses of geothermal organic rankine cycles using R600a/R601a mixtures as working fluids,” Appl. Energy, vol. 148, no. 1, pp. 410–420, 2015. doi: 10.1016/j.apenergy.2015.03.093. [Google Scholar] [CrossRef]
24. F. Heberle, M. Preißinger, and D. Brüggemann, “Zeotropic mixtures as working fluids in organic rankine cycles for low-enthalpy geothermal resources,” Renew. Energy, vol. 37, no. 1, pp. 364–370, 2012. doi: 10.1016/j.renene.2011.06.044. [Google Scholar] [CrossRef]
25. U. Younas et al., “Pakistan geothermal renewable energy potential for electric power generation: A survey,” Renew. Sustain. Energ. Rev., vol. 63, no. 9, pp. 398–413, 2016. doi: 10.1016/j.rser.2016.04.038. [Google Scholar] [CrossRef]
26. L. Colak and T. Bahadir, “Modeling thermodynamic analysis and simulation of organic rankine cycle using geothermal energy as heat source,” presented in the 12th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Costa de Sol, Spain, 2016. [Google Scholar]
27. V. Zare, “A comparative exergoeconomic analysis of different ORC configurations for binary geothermal power plants,” Energy Convers. Manag., vol. 105, pp. 127–138, 2015. doi: 10.1016/j.enconman.2015.07.073. [Google Scholar] [CrossRef]
28. R. S. El-Emam and I. Dincer, “Exergy and exergoeconomic analyses and optimization of geothermal organic rankine cycle,” Appl. Therm. Eng., vol. 59, no. 1–2, pp. 435–444, 2013. doi: 10.1016/j.applthermaleng.2013.06.005. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools