Performance and Degradation Assessment of PV Modules Exposed to Short-Term Outdoor Conditions in Two Distinct US Climatic Zones

1  Introduction

The exploitation and use of fossil fuels have a significant environmental impact due to the production of carbon dioxide (CO2), a major greenhouse gas contributing to climate change. To achieve a stable level of atmospheric CO2 stability, it is imperative to transition to a decarbonized world as soon as possible [1]. Relying on renewable energy represents the primary alternative to facilitate this transition.

Solar energy has become a promising source in the field of renewable energy technologies worldwide, particularly in hot and sunny regions of the Middle East (ME) and Africa, where solar irradiation is abundant [2]. As a result, these regions are increasingly adopting PV module power plants at both residential and commercial scales. For example, Dubai (ME) has launched a clean energy strategy aiming to produce 75% of its energy needs from clean energy sources by 2050 [2]. Similarly, Morocco (Africa) has initiated an energy strategy aiming to cover 52% of its energy needs by 2030 [1]. PV systems exhibit the fastest growth rate among competing renewable energy sources and have now reached grid parity in some regions [3]. With the continuation of current investments, PV energy is expected to play a key economic role. Economic incentives are driving research into the reliability and long-term performance of PV modules.

The lifespan of solar panels and their energy production over time are influenced by several factors, including climate and module type [3–7]. The gradual decrease in solar panel performance over time is known as degradation. Numerous studies have examined the causes of PV module degradation and have identified several contributing factors, including discoloration of Ethylene-Vinyl Acetate (EVA), accumulation of dust and pollutants, delamination of modules, cell cracks, and moisture that can condense inside the module, thereby increasing corrosion rates. This corrosion damages the metal connections of PV cells, reducing their performance, increasing leakage currents, and weakening the bond between the cells and the metal frame [1,5,8–10]. Degradation can be assessed by determining the DR using several methods, including linear least squares fitting, the temporal evolution of effective maximum power (power at STC), the temporal evolution of performance ratio (PR).

Numerous studies have employed the method of temporal evolution of effective maximum power [5,11–15]. This approach involves converting the maximum power under real conditions into effective maximum power, followed by linear adjustment to determine the slope and intercept, thus allowing the calculation of the DR. This represents the percentage decrease in effective maximum power over a year. However, due to limitations of the maximum power model for low irradiance levels, authors focus solely on experimental data corresponding to high irradiances GPOA≥700W/m2. Regarding the PR method, which compares array yield to reference yield, linear adjustment of its temporal evolution enables evaluation of the DR [16–20].

This document provides an analysis of DR for various PV modules, including m-Si, p-Si, HIT, CIGS, CdTe, and a-Si/μc-Si. These modules were subjected to outdoor conditions in two distinct climates in the US (Cocoa and Eugene) over a period of three years. The data used were provided by NREL, and the analysis relies on the method of linear least squares fitting of effective maximum power. A new approach has been employed to describe the temporal evolution of key points of the I-V characteristic, such as short-circuit current (ISC), maximum power current (IMPP), maximum power voltage (VMPP), open-circuit voltage (VOC), and fill factor (FF), under specific meteorological conditions (GPOA∗=1000W/m2;TSTC=25∘C). By considering these temporal evolutions, it is possible to estimate the DR of different key points of the I-V characteristic.

Given that the PV metrics can be represented by a SDM electronic circuit characterized by five physical parameters: photocurrent (IPh), saturation current (IS), ideality factor (η), shunt resistance (RSh), and series resistance (RS), the evolution of these physical parameters over time allows for a better understanding of the performance variations of PV modules and the long-term behavior of their output power. This requires monitoring the evolution of the key points of the I-V characteristic mentioned earlier. Additionally, the relationship between photocurrent IPh and short-circuit current ISC, as well as the use of the transcendental equation describing current as a function of voltage at different key points of the I-V characteristic, leads to a system of equations to determine the various physical parameters and their evolution over time. By introducing these physical parameters into the transcendental equation I (V), it is possible to generate the I-V and P-V characteristics of different PV module technologies. These characteristics will then be compared to experimental data recorded by NREL.

The remainder of this article is organized as follows: following an introduction, Section 2 outlines the methodology and explicit models. Section 3 presents the various results obtained, beginning with the temporal evolution of effective maximum power, followed by key points of the I-V characteristic and the fill factor, as well as physical parameters. Subsequently, the comparison between the I-V characteristics generated under real operating conditions and in STC and those obtained experimentally under real operating conditions and translated into STC. Finally, the generated and experimental I-V and P-V characteristics under STC are discussed. The conclusion is presented in Section 4.

2  Methodology

2.1 Specifications of PV Modules and Experimental Data

In this study, short-term meteorological and PV data collected by NREL researchers on PV modules representing various flat plate manufacturing technologies are employed [21,22]. Data were collected over a 3-year period at two different climatic sites in the US (Cocoa and Eugene). PV module technologies tested by NREL include monocrystalline Silicon (m-Si), polycrystalline Silicon (p-Si), Cadmium Telluride (CdTe), Copper Indium Gallium Selenium (CIGS), heterojunction with intrinsic thin-layer (HIT) and amorphous Silicon/microcrystalline silicon (a-Si/μc-Si).

NREL provided the PV modules measurements equipment at both sites, the first in Cocoa, and the second in Eugene. The duration of the outdoor exhibition is segmented into two sub-periods: the initial period started on 21 January 2011, and ended on 04 March 2012, in Cocoa, while the subsequent sub-period started on 20 December 2012, and ended on 20 January 2014, in Eugene.

Cocoa, situated in Brevard County, Florida, is a port city that fronts the North Atlantic Ocean, the measurement site’s geographic coordinates are as follows: longitude 80.46°, latitude 28.39°, and altitude 12 m, Cocoa experiences a humid subtropical climate. Eugene is a city located in the north western region of the US, specifically within Lane County, Oregon. Positioned with a view towards the North Pacific Ocean, Eugene displays a west coast marine climate. The measurement site is defined by geographic coordinates of longitude 123.07°, latitude 44.05°, and an altitude of 145 m.

The measurement platform includes weather and electrical sensors, connected to a central data recording system. Meteorological data include ambient temperature, atmospheric pressure, relative humidity, precipitation, solar irradiances such as direct normal, diffuse horizontal, global horizontal and global for a fixed inclined plane (plane-of-array irradiance). PV data include module temperature, key points of I-V curve, maximum power, fill factor and I-V curves. All quantities were measured with a fixed time step equal to five minutes [21,22].

The main parameters of six different types of PV modules used in this study at STC: GPOA∗=1000W/m2;TSTC=25∘C; AM1.5, are given in Table 1.

2.2 PV Performance Metrics and Degradation Analysis

When choosing solar panels, it is crucial to take into account the efficiency of solar cells, which measures their ability to convert sunlight into electricity. This electrical efficiency is directly affected by various climatic factors such as solar irradiance, wind speed, pollution, and geographical location. A careful evaluation of the efficiency of PV modules is essential to ensure the sustainable operation and growth of solar power plants [23]. In addition, a thorough analysis of the DR of PV modules is essential to correctly size the components and determine the operational costs of the installation. To carry out an evaluation of degradation, the effective performance of the PV system is taken into account. Weather variations affect the voltage, current and power of the PV device. Due to the effect of temperature and solar irradiance, the choice of these weather conditions is therefore necessary to adjust the PV measurements [23].

2.2.1 Filtering Conditions

The analysis of DR requires the temporal monitoring of PV modules under real-world conditions. NREL provided us with experimental data measured outdoors in two different climates. Among this data, we find PV metrics such as ISC, IMPP, VMPP, VOC and PMPP, measured under various irradiance and temperature conditions, which are also provided. To evaluate the DR of different PV modules, this study defines a specific condition based on module temperature and solar irradiance. The filtering condition for selecting experimental data under well-defined meteorological conditions is described below:

•   Solar irradiance values ranges from 999.5 W/m2 to 1000.5 W/m2 (999.5≤GPOA∗≤1000.5).

•   For the module temperature (TM), the values used correspond to the selected solar irradiance conditions.

2.2.2 Translation of Maximum Power to STC

The DR of PV modules can be estimated by examining the evolution of the effective maximum power values (PMPP,STC∗) of the PV modules throughout the monitoring period. The solar irradiance is fixed at GPOA∗=(1000±0.5)W/m2, but the temperature TM is different, therefore it is necessary to translate TM into TSTC to obtain STC ((GPOA∗,TSTC). Since power varies linearly with temperature, the effective maximum power of a PV module is given by the following equation [15,24–26]:

PMPP,STC∗(GPOA∗,TSTC)=PMPP(GPOA∗,TM)1+α(TM−25)(1)

where α is the temperature coefficient of maximum power.

2.2.3 Translation of I-V Curve Key Points to STC

In the same way as the effective maximum power, we can translate the four key points (IMPP, VMPP, ISC, VOC) of the I-V characteristic currant-voltage to STC:

–   The effective short-circuit current ISC,STC∗;

ISC,STC∗(GPOA∗,TSTC)=ISC(GPOA∗,TM)1+β(TM−25)(2)

–   The effective open-circuit voltage VOC,STC∗;

VOC,STC∗(GPOA∗,TSTC)=VOC(GPOA∗,TM)1+γ(TM−25)(3)

–   The effective maximum power current IMPP,STC∗;

IMPP,STC∗(GPOA∗,TSTC)=IMPP(GPOA∗,TM)1+δ(TM−25)(4)

–   The effective maximum power voltage VMPP,STC∗;

VMPP,STC∗(GPOA∗,TSTC)=VMPP(GPOA∗,TM)1+χ(TM−25)(5)

where β, γ, δ and χ are the temperature coefficients.

2.2.4 Fill Factor Expression at STC

The fill factor is a measure of the squareness of the I-V characteristic curve and indicates the quality of the solar cell. The fill factor ((FFSTC∗) of a PV module is given by the following equation [11]:

FFSTC∗(GPOA∗,TSTC)=PMPP,STC∗ISC,STC∗VOC,STC∗(6)

2.2.5 Annual Degradation Rate (DR)

In order to evaluate the DR, a linear adjustment method is applied to the effective values of the PV measurements (PMPP,STC∗,ISC,STC∗,VOC,STC∗,VMPP,STC∗ and IMPP,STC∗) under STC. Using the trend lines, the DR can be estimated as follows [13,27]:

DR(%/year)=365⋅pc⋅100,(7)

where p (/day) is the slope of the line and c is the y-intercept:

y=p⋅t+c.(8)

2.2.6 PV Module Modelling: Equivalent Circuit and Fundamental Equations of Single Diode Model

The PV generator is modeled by a single diode electronic circuit, frequently used and characterized by five physical parameters (see Fig. 1). The five physical parameters include the photocurrent (IPh) generated by the PV solar cell when exposed to sunlight, the saturation current (IS), and the diode ideality factor (η), which represents the PN junction. The series resistance (RS) takes into consideration the ohmic losses due to the resistivity of the metal contacts, while the parallel resistance (RSh) takes into account the leakage currents occurring in the PV cell [28–31].

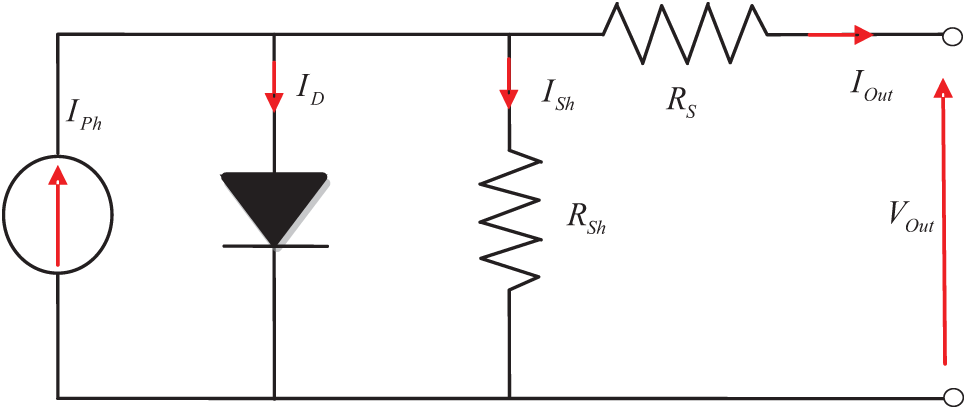
Figure 1: Single-diode equivalent circuit describing PV module [30]

Utilize Kirchhoff’s current law to deduce the equation representing the cell/module output current in the following manner [28].

IOut=IPh−ID−ISh(9)

ID=IS(exp⁡(IOutRS+VOutηNSVTh)−1)(10)

ISh=IOutRS+VOutRSh(11)

By substituting Eqs. (10) and (11) into Eq. (9), the transcendental equation establishes a relationship between the output current, the output voltage, and the five physical parameters of a PV module which NS is the number of PV cells connected in series, as expressed in the following equation [30–33]:

IOut=IPh−IS(exp⁡(IOutRS+VOutηNSVTh)−1)−IOutRS+VOutRSh(12)

The characteristic equations at key points of the current-voltage curve (the open-circuit voltage point (VOC,0), short-circuit current point (0,ISC), and the maximum power point (IMPP,VMPP) are provided by the following equations, respectively.

0=IPh−IS(exp⁡(VOCηNSVTh)−1)−VOCRSh(13)

ISC=IPh−IS(exp⁡(ISCRSηNSVTh)−1)−ISCRSRSh(14)

IMPP=IPh−IS(exp⁡(IMPPRS+VMPPηNSVTh)−1)−IMPPRS+VMPPRSh(15)

At the point of maximum power, the slope of the power-voltage curve is equal to zero while the slope of the current-voltage curve is equal to the opposite of the optimal conductance GMPP (GMPP=IMPP/VMPP).

−IMPPVMPP=−ISηNSVTh(1−IMPPVMPPRS)exp⁡(VMPP+IMPPRSηNSVTh)−1RSh(1−IMPPVMPPRS)(16)

2.2.7 Translation I-V and P-V Curves to STC

The PV metric data provided under real conditions are accompanied by the I-V characteristic, also provided in real-time and under real operating conditions. Since we have selected only I-V characteristics corresponding to condition GPOA∗, but the module temperature TM can also influence this characteristic, in order to assess the modifications that may result from material aging on the I-V curve over time, it is necessary to compare characteristics measured under the same conditions (GPOA∗,TSTC).

After translating the two key points of the I-V curve (ISC,STC∗,VOC,STC∗), the current-voltage characteristics under conditions (GPOA∗,TM) can be translated into STC (GPOA∗,TSTC) using the following equations [34]:

IOut,STC∗(GPOA∗,TSTC)=IOut(GPOA∗,TM)(ISC,STC∗ISC(GPOA∗,TM))(17)

VOut,STC∗(GPOA∗,TSTC)=VOut(GPOA∗,TM)(VOC,STC∗VOC(GPOA∗,TM))(18)

The output power at STC can be calculated using following equation:

POut,STC∗(GPOA∗,TSTC)=VOut,STC∗(GPOA∗,TSTC)IOut,STC∗(GPOA∗,TSTC)(19)

2.2.8 Numerical Method to Extract Physical Parameters

In this subsection, our objective is to evaluate the changes in the five physical parameters of the model throughout the period of operation of the PV modules. The parameter extraction method used in this investigation is in accordance with the approach used by [35]. To obtain the remaining five model physical parameters (IPh,STC∗(t), IS,STC∗(t), RS,STC∗(t), RSh,STC∗(t), and ηSTC∗(t)), the translated values of the four key points of the I-V curve at STC are employed throughout the operational period of PV modules.

–   The effective photocurrent at STC is given by the following equation:

IPh,STC∗(t)=IPh,STC(t0)IES,STC∗(t)GPOA∗(20)

where IES,STC∗ is the effective solar irradiance at STC:

IES,STC∗(t)=GPOA∗ISC,STC∗(t)ISC,STC(t0)(21)

–   The effective saturation current deduced from Eq. (13):

IS,STC∗(t)=IPh,STC∗(t)−VOC,STC∗(t)/RSh,STC∗(t)e(VOC,STC∗(t)/ηSTC∗(t)NSVTh(TSTC))−1(22)

In determining the values of the three remaining physical parameters (RS,STC∗(t), RSh,STC∗(t) and ηSTC∗(t)), a system of three equations with three unknowns was established by replacing Eq. (22) in Eqs. (14)–(16).

ISC,STC∗(t)−IPh,STC∗(t)+(IPh,STC∗(t)−VOC,STC∗(t)/RSh,STC∗(t)e(VOC,STC∗(t)/ηSTC∗(t)NSVTh(TSTC))−1)(e(RS,STC∗(t)ISC,STC∗(t)VOC,STC∗(t)/ηSTC∗(t)NSVTh(TSTC))−1)+RS,STC∗(t)ISC,STC∗(t)RSh,STC∗(t)=0(23)

IMPP,STC∗(t)−IPh,STC∗(t)+IPh,STC∗(t)−VOC,STC∗(t)/RSh,STC∗(t)e(VOC,STC∗(t)/ηSTC∗(t)NSVTh(TSTC))−1(e(VMPP,STC∗(t)+RS,STC∗(t)IMPP,STC∗(t)ηSTC∗(t)NSVTh(TSTC))−1)+RS,STC∗(t)IMPP,STC∗(t)+VMPP,STC∗(t)RSh,STC∗(t)=0(24)

IMPP,STC∗(t)VMPP,STC∗(t)−IPh,STC∗(t)−VOC,STC∗(t)/RSh,STC∗(t)ηSTC∗(t)NSVTh(TSTC)e(VOC,STC∗(t)/ηSTC∗(t)NSVTh(TSTC))−1(1−RS,STC∗(t)IMPP,STC∗(t)VMPP,STC∗(t))e(VMPP,STC∗(t)+IMPP,STC∗(t)RS,STC∗(t)ηSTC∗(t)NSVTh(TSTC))−VMPP,STC∗(t)−RS,STC∗(t)IMPP,STC∗(t)RSh,STC∗(t)VMPP,STC∗(t)=0(25)

The Eqs. (23)–(25) found the system of nonlinear equations which allows the values of RS,STC∗(t), RSh,STC∗(t), and ηSTC∗(t) to be calculated using the translated values of the key points of the I-V curve (ISC,STC∗(t), IMPP,STC∗(t), ;VOC,STC∗(t), and VMPP,STC∗(t)) at STC for all days. IPh,STC∗(t) provided by Eq. (20), the value of IS,STC∗(t) is deduced from Eq. (22) according to the diagram presented in Fig. 2. Incorporating these physical parameters determined at STC into the following equation (the solution of transcendental equation Eq. (12), we can generate the I-V and P-V characteristics at STC. By reversing the Eqs. (17) and (18), we can then plot the I-V and P-V characteristics generated under real conditions.

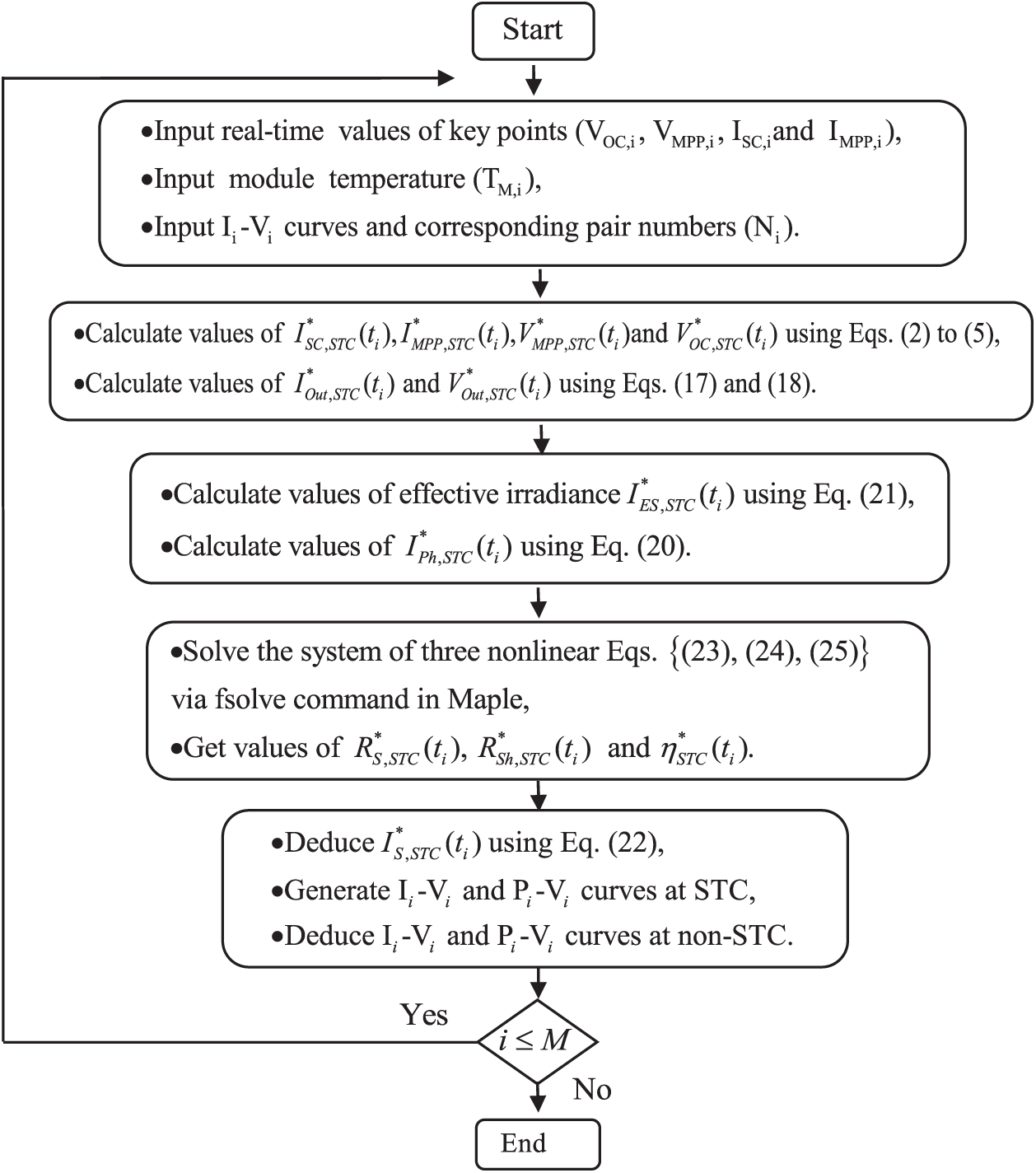
Figure 2: Flowchart for calculating model parameters values of a PV module operating outdoors throughout the operational period

IOut,STC∗(t)=−NSηSTC∗(t)VTh(TSTC)RS,STC∗(t)W0(LA)+IPh,STC∗(t)+IS,STC∗(t)−VOut,STC∗(t)RSh,STC∗(t)1+RS,STC∗(t)RSh,STC∗(t)(26)

where LA is the argument of LambertW function (W0).

LA=RS,STC∗(t)IS,STC∗(t)NSηSTC∗(t)VTh(TSTC)(1+RS,STC∗(t)RSh,STC∗(t))exp⁡(RS,STC∗(t)(IPh,STC∗(t)+IS,STC∗(t))+VOut,STC∗(t)NSηSTC∗(t)VTh(TSTC)(1+RS,STC∗(t)RSh,STC∗(t)))

To assess the reliability of the physical parameters and PV metrics found to generate features, namely I(V) and P(V) curves as close as possible to experimental curves under real conditions and translated into STC, we rely on a widely used statistical indicator to calculate the discrepancies between measured and generated values: the normalized root mean square error (NRMSE) [31,33].

NRMSE=1N∑i=1N(XGeneratedi−XMeasuredi)2/1N∑i=1NXMeasuredi(27)

3  Results and Discussion

3.1 Analysis of PV Module Degradation

In this subsection, we depicted the progression of PV metrics (ISC,STC∗, IMPP,STC∗, VOC,STC∗, VMPP,STC∗, PMPP,STC∗) and the fill factor FFSTC∗ over time (days), and we derived the DR of each parameter based on this dataset.

3.1.1 Effective Maximum Power

Fig. 3 illustrates the temporal evolution of PMPP,STC∗ obtained for the six PV modules. The daily calculated values of PMPP,STC∗ after the filtering process described above reveal a significant degradation of the PV modules based on thin films compared to the crystalline silicon-based modules. As indicated in Table 2, the most substantial reduction in PMPP,STC∗ was observed for the a-Si/µc-Si module, with a power decrease of 3.26% per year. The power reduction observed in the CIGS module is 2.45% per year, while the CdTe module shows a power reduction of approximately 2.03% per year, and the HIT module of 1.75% per year. Moreover, the p-Si and m-Si modules exhibit a DR of 1% per year and 0.87% per year, respectively. The result obtained is in agreement with that presented in the literature (see Table 3). The DR of a PV system is influenced by various factors, including the type of PV cell, climate, system size, tilt, and orientation of the PV module, as well as the duration of outdoor exposure [9]. The obtained DR values are accompanied by 95% confidence intervals and the corresponding p-values. All technologies exhibit statistically significant degradation trends, as evidenced by p-values well below the 0.05 threshold, indicating that the observed effects are unlikely to be due to random fluctuations. Moreover, the narrow confidence intervals confirm the reliability and precision of the estimates. Overall, these results highlight clear, technology-dependent degradation behaviors, with strong statistical support for all devices under study (see Table 2). The observed effect is thus real, precisely estimated, and leaves no ambiguity regarding its existence and it is not the result of random variation.

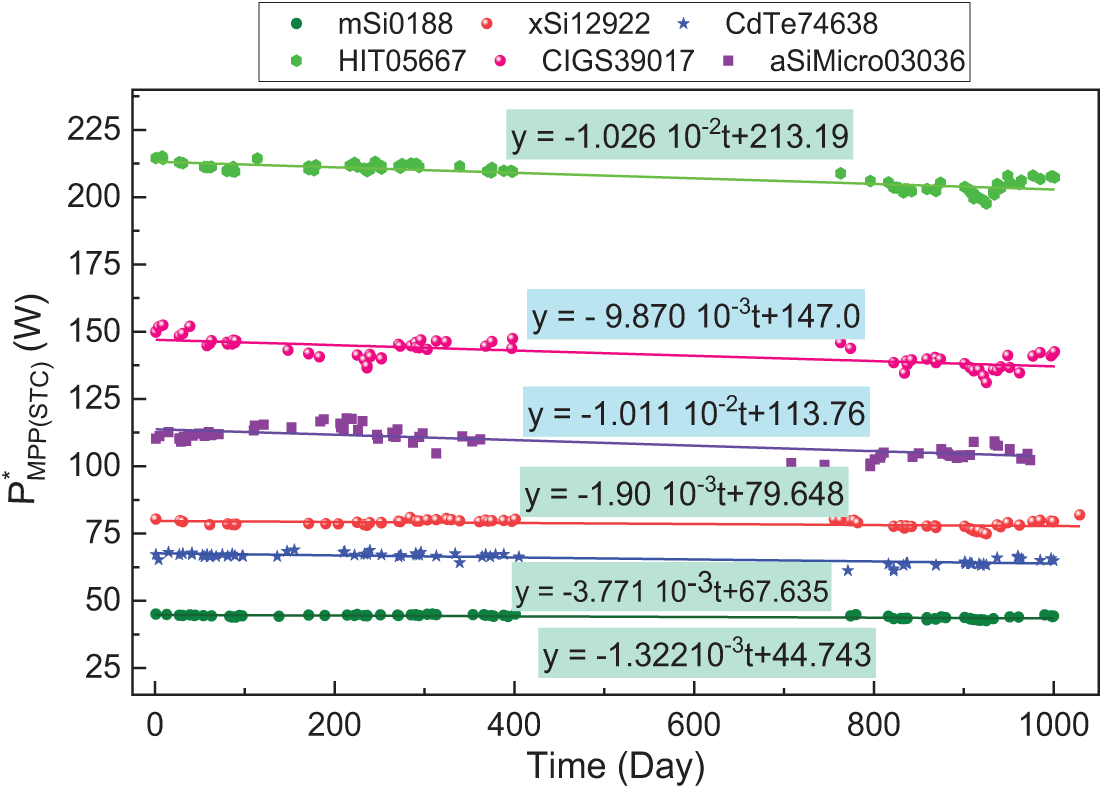
Figure 3: Temporal evolution of effective maximum power for various PV module technologies

3.1.2 Four Key Points of I-V Curve

The effective maximum power PMPP,STC∗ of PV modules depends on the electrical performance parameters (ISC,STC∗, IMPP,STC∗, VMPP,STC∗, and VOC,STC∗). The higher the electrical performance parameters, the higher the power output. Thus, the degradation of one of these parameters contributes to the degradation of the effective maximum power of the PV modules [12]. The following graphs (Fig. 4) illustrate the variation of currents and voltages over time for various PV modules. Based on these results, the DR of key points on the I-V curve has been calculated and presented in Table 4.

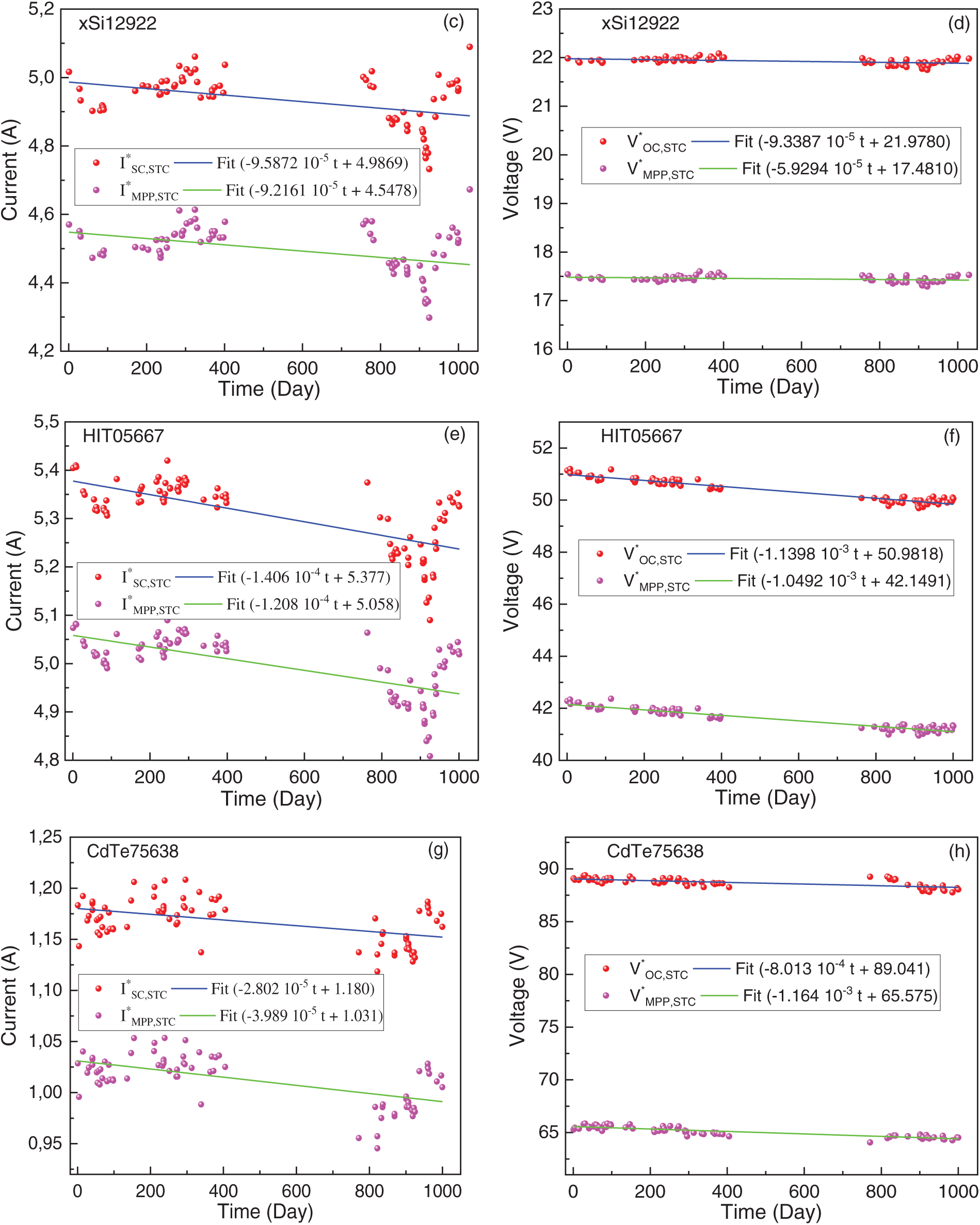
Figure 4: Evolution of the four key points of I-V curve at STC for various PV module technologies. (a, c, e, g, i, k) show the evolution of current vs. time, (b, d, f, h, j, l) show the evolution of voltage vs. time

For the crystalline silicon modules (m-Si and p-Si), the currents ISC,STC∗ (0.70%/year; 0.83%/year, respectively) and IMPP,STC∗ (0.74%/year; 0.81%/year, respectively) decrease slightly, while the voltages VOC,STC∗ (0.15%/year; 0.25%/year, respectively) and VMPP,STC∗ (0.12%/year; 0.27%/year, respectively) experience minimal decline, even though the voltages for p-Si decrease almost twice as much as those for m-Si. As for the HIT module, it exhibits a reduction in key points on the I-V curve at an almost similar rate (ISC,STC∗: 0.95%/year; IMPP,STC∗: 0.85%/year; VMPP,STC∗: 0.91%/year; VOC,STC∗: 0.82%/year). The CdTe, ISC,STC∗ decreases slightly (0.87%/year), while IMPP,STC∗ decreases significantly (1.41%/year). Regarding voltages, VMPP,STC∗ (0.65%/year) decreases almost twice as much as VOC,STC∗ (0.33%/year). Concerning the CIGS module, both currents, ISC,STC∗ (1.76%/year) and IMPP,STC∗ (1.72%/year), decrease markedly and almost in the same manner, while the voltages VOC,STC∗ (0.76%/year) and VMPP,STC∗ (0.76%/year) have decreased slightly and similarly. Finally the a-Si/µc-Si module, both ISC,STC∗ (1.31%/year) and IMPP,STC∗ (2.05%/year) decrease significantly, and the voltages VMPP,STC∗ exhibit a substantial decline (1.36%/year), while VOC,STC∗ decreases slightly (0.86%/year), resulting in a significant decrease in maximum power. These values are accompanied by 95% confidence intervals, which provide an estimate of the precision, and p-values that indicate whether the observed degradation is statistically significant. The p-values are almost all well below the 0.05 threshold, often on the order of 10−9 or even smaller. This indicates that the observed degradations are highly statistically significant, and it is therefore very unlikely that these results are due to random variation. Moreover, the confidence intervals are narrow, reflecting a high level of precision in the estimation of the degradation rates. This further strengthens the credibility of the results (see Table 4).

There are several factors that influence the decrease in current in PV modules, depending on the type of module and technology used. Among these factors are dirt, discoloration of the EVA, or the reduction in the transmission of shortwave photons [46]. The aging of electronic components in the PV module, such as connections and cables, is also a determining factor [12,47,48]. Since the PV modules were cleaned daily during their exposure to the outdoors [22], dirt does not contribute to the degradation of the modules. However, we have no information on the visual defects presented by the various PV modules, such as discoloration of the encapsulant, which could significantly contribute to the degradation of module current [12]. Most often, it is the discoloration of the encapsulant that reduces the light transmitted to the PV cells and degrades the current, leading to maximum power degradation. Similarly, a slight degradation of the module voltage was also attributed to the relatively exposure (3 years) of the modules to outdoor conditions [12].

Environmental conditions, such as the thermal cycle, also influence the material quality due to expansion during the day under heat and contraction at night. These variations lead to the appearance of cracks and fractures in the material over time, resulting in its degradation. Consequently, this deterioration contributes to the decrease in voltage and current, impacting the overall power of PV modules.

3.1.3 Fill Factor

The effective fill factor (FFSTC∗) value is also affected by the degradation phenomena. Fig. 5 illustrates the evolution of the daily effective fill factor (FFSTC∗) values achieved for the studied PV systems during the monitoring campaign. As clearly shown in Fig. 6, there is no significant variation (decrease) in FFSTC∗ was observed for m-Si (0.02%/year), p-Si (0.01%/year), HIT (0.01%/year), and CIGS (increase) (0.04%/year) modules. However, a remarkable decrease in FFSTC∗ is noted for CdTe (1.13%/year), and a-Si/µc-Si (1.21%/year), which could lead to the long-term distortion of the I-V characteristic.

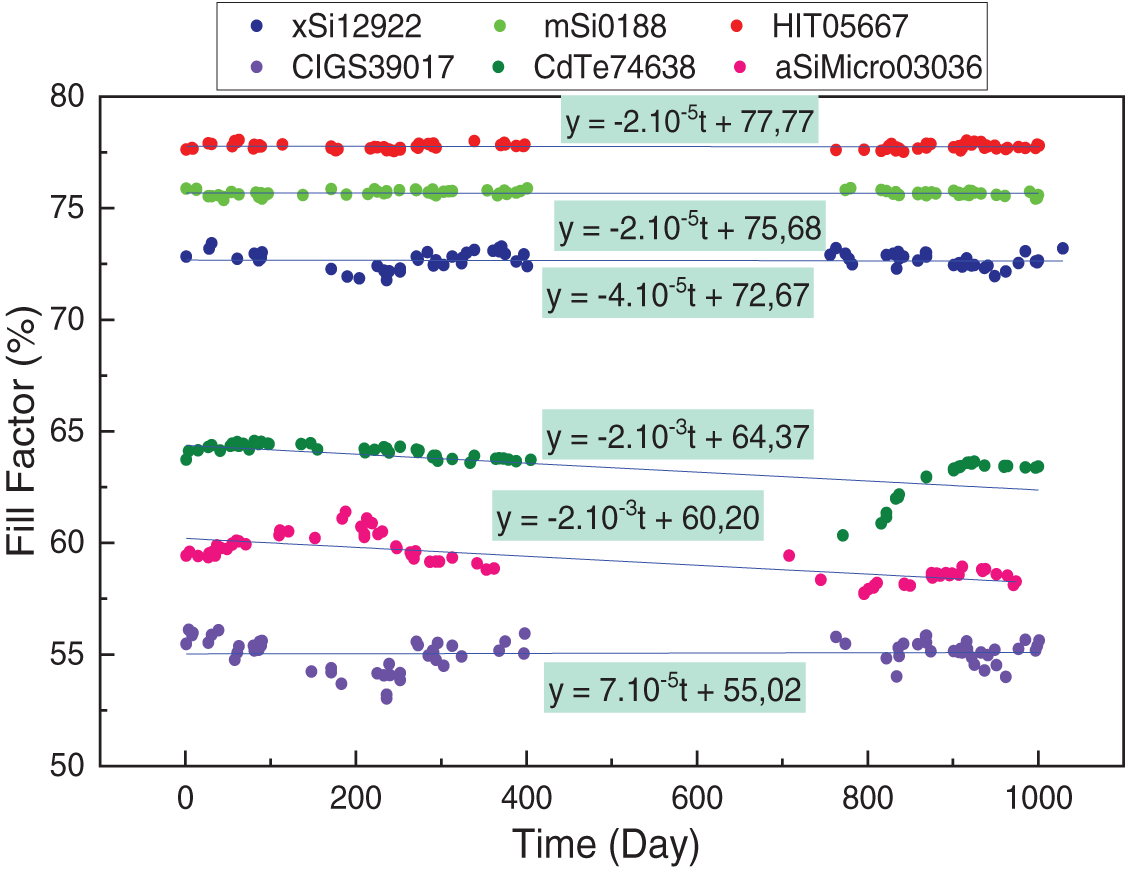
Figure 5: Evolution of effective fill factor values for different PV module technologies

Figure 6: Evolution of effective values of series resistance (RS,STC∗) for various PV modules

3.2 Effective Values of SDM Model Parameters

To investigate the causes of degradation, changes in the series resistance (RS,STC∗), shunt resistance (RSh,STC∗), photocurrent (IPh,STC∗), saturation current (IS,STC∗), and ideality factor (ηSTC∗) of the modules are monitored daily throughout the experiment. Figs. 6–10 depict the temporal evolution of the physical parameters obtained using the numerical method described earlier. In Fig. 6, the RS,STC∗ exhibits a decreasing trend over time for m-Si, CdTe, and a-Si/µc-Si modules, while p-Si, HIT, and CIGS modules show an increase in series resistance. Fig. 7 presents the daily variations in RSh,STC∗, with m-Si, CdTe, and a-Si/µc-Si modules showing a downward trend over time, whereas p-Si, HIT, and CIGS modules display an increase in shunt resistance. In Fig. 8, the daily variations in IPh,STC∗ reveal a decrease across all PV modules. Additionally, Fig. 9 illustrates the daily variations in IS,STC∗, where p-Si, HIT, and CIGS modules demonstrate a decrease over time, while m-Si, CdTe, and a-Si/µc-Si modules show an increase. The last figure (Fig. 10) displays the daily variations in ηSTC∗, with p-Si, HIT, and CIGS modules exhibiting a decreasing trend, while m-Si, CdTe, and a-Si/µc-Si modules show an increase. These findings provide insights into the dynamic behavior of various parameters of PV modules over time, which are crucial for understanding their performance and degradation characteristics.

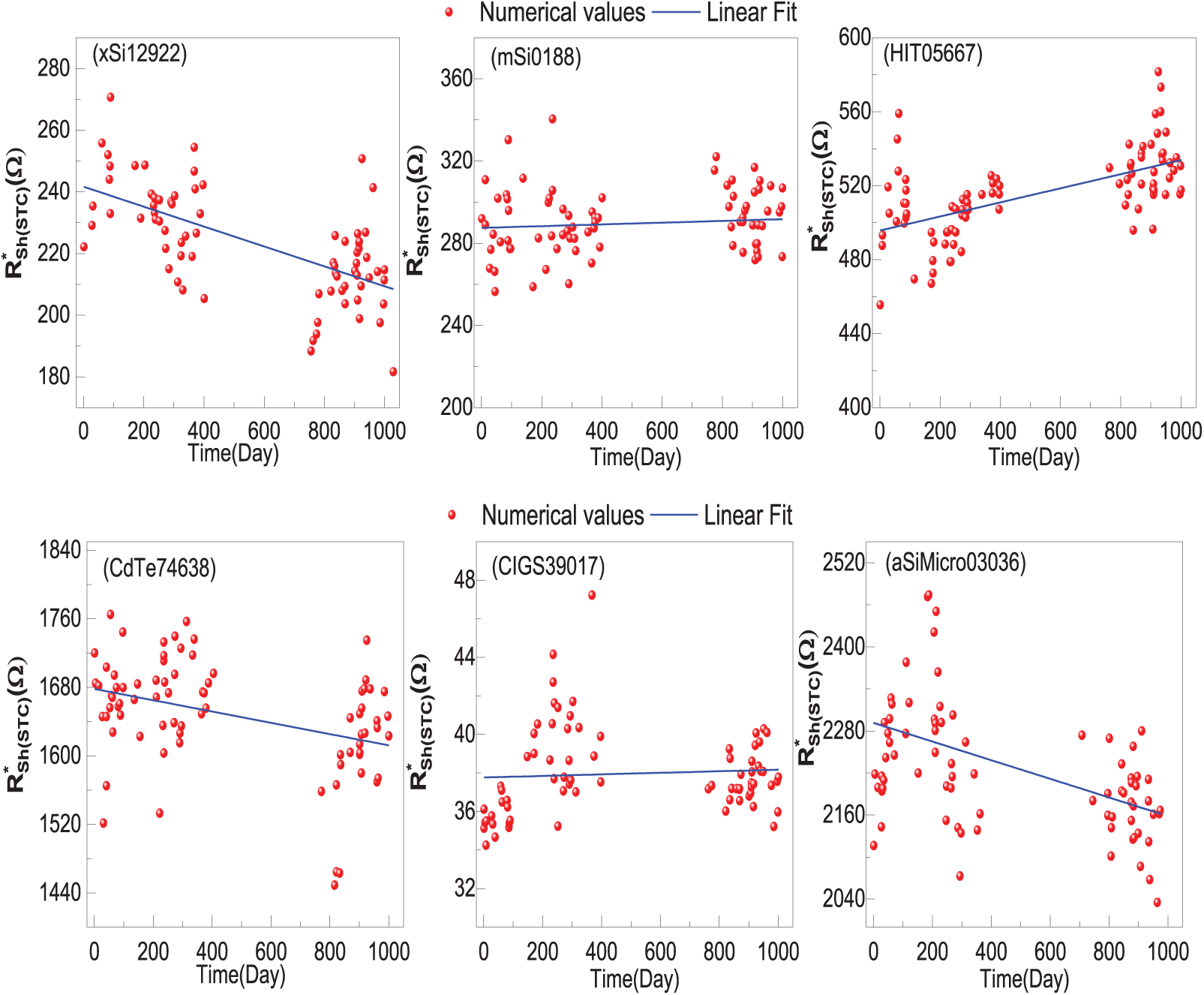
Figure 7: Evolution of effective values of shunt resistance (RSh,STC∗) for various PV modules

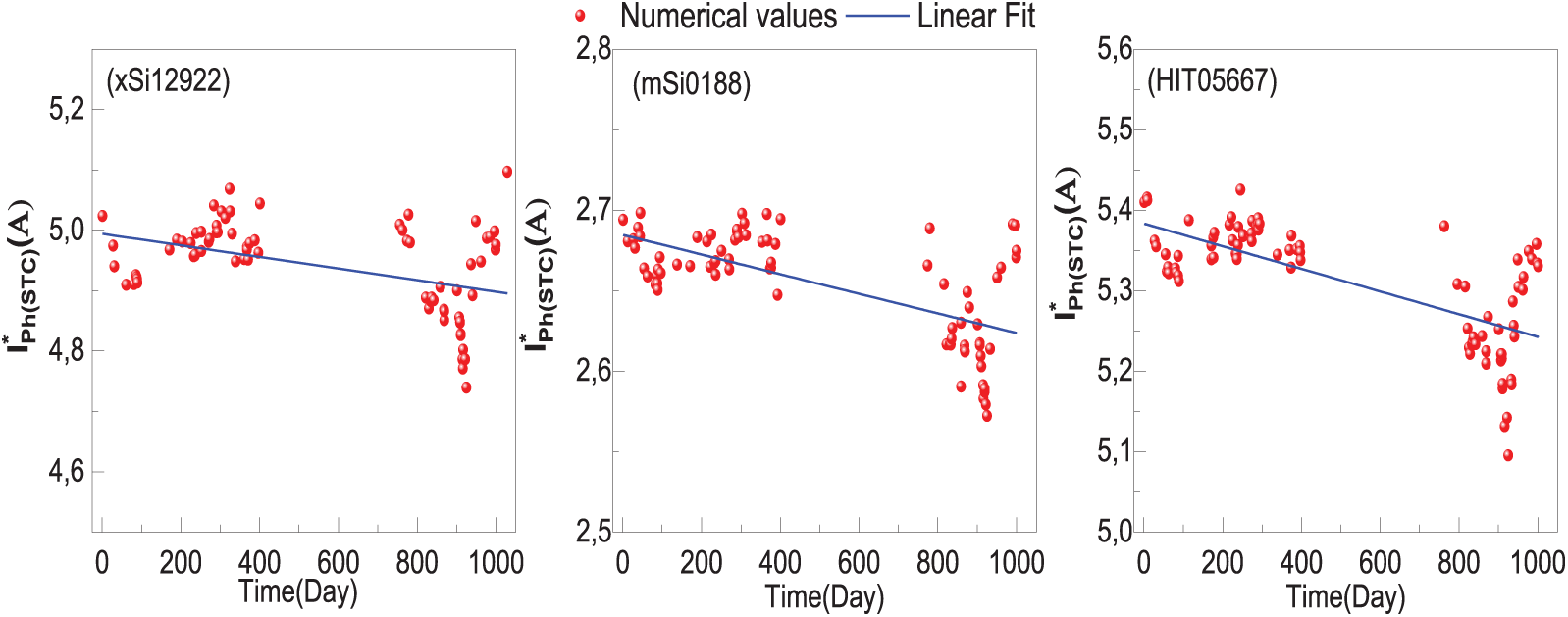
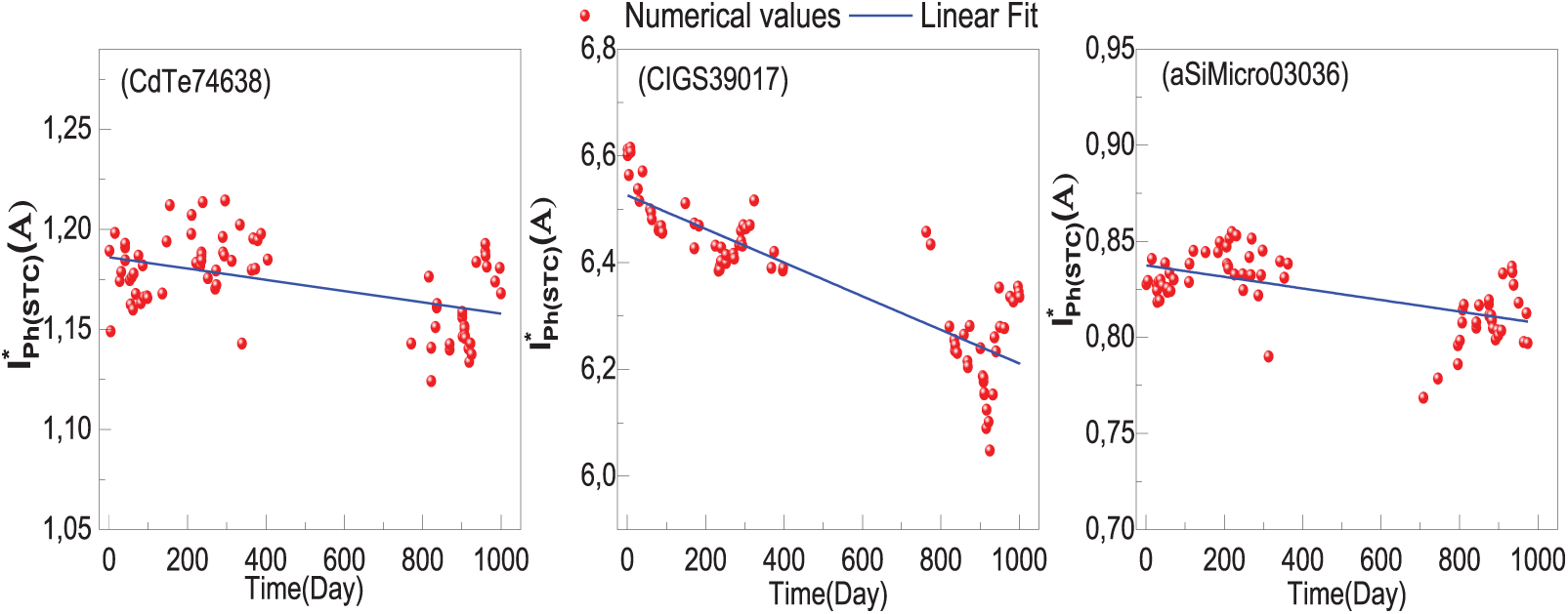
Figure 8: Evolution of effective values of photocurrent (IPh,STC∗) for various PV modules

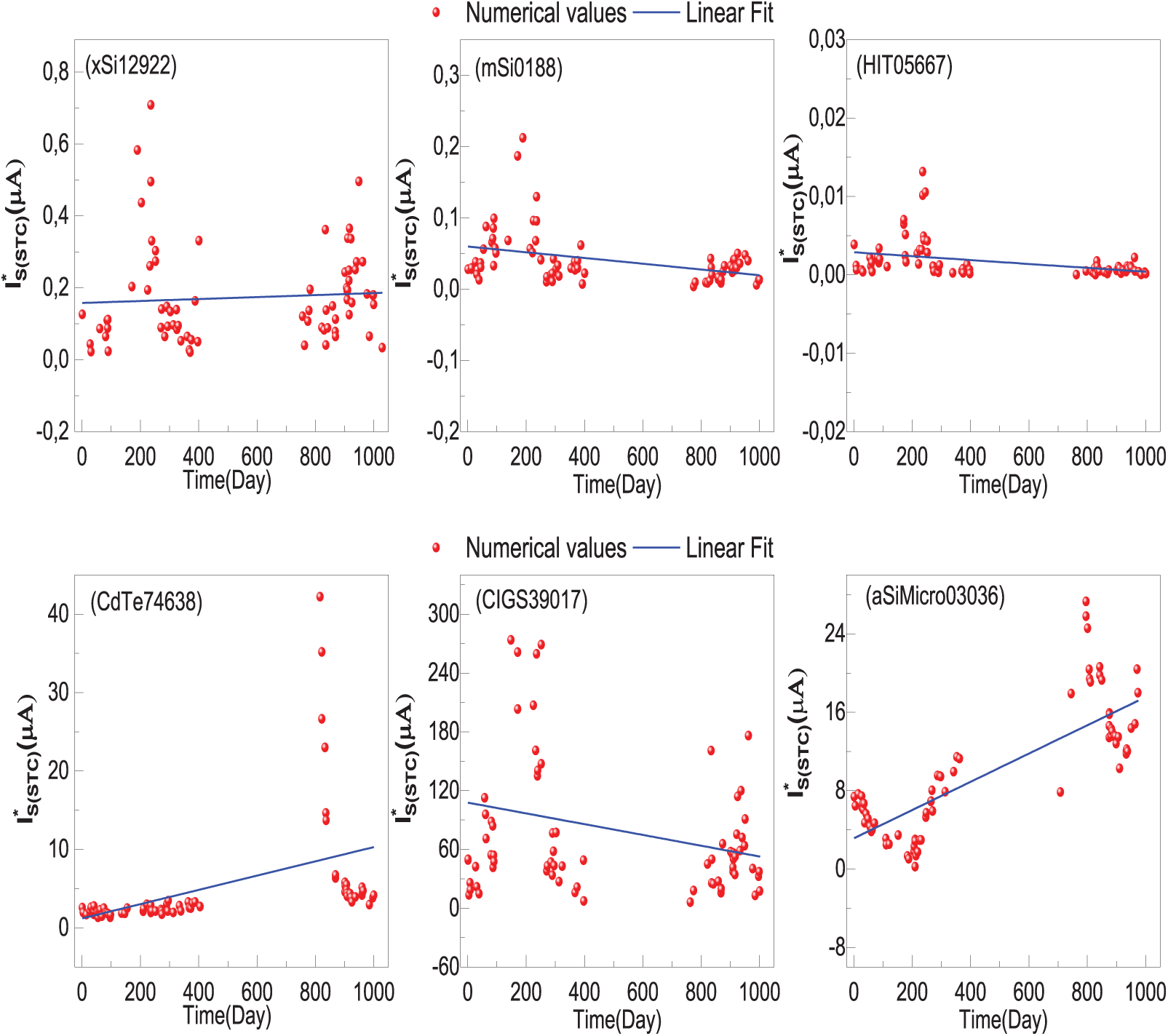
Figure 9: Evolution of effective values of saturation current (IS,STC∗) for various PV modules

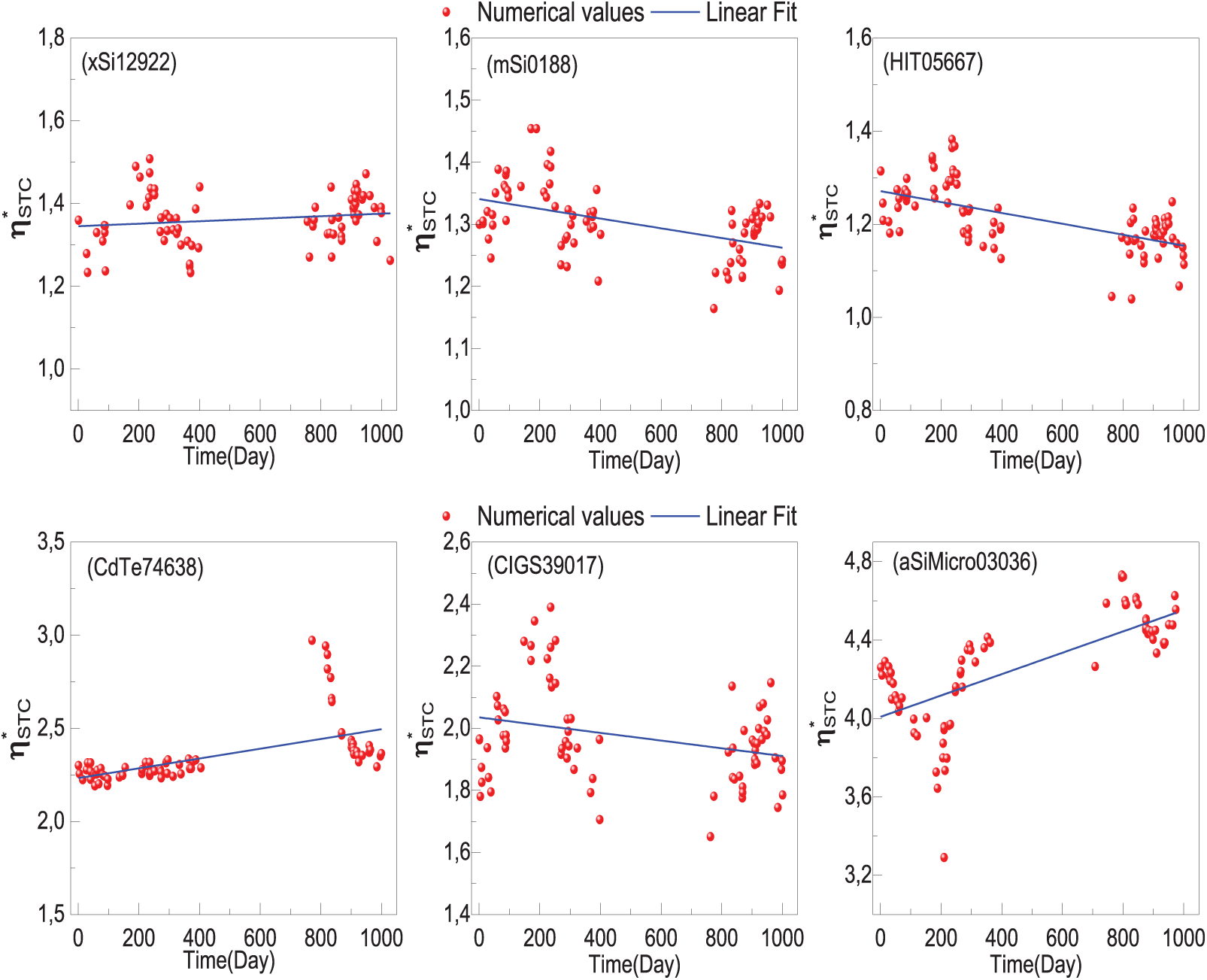
Figure 10: Evolution of effective values of ideality factor (ηSTC∗) for various PV modules

The monotony of physical parameters over time, except for the photocurrent IPh,STC∗, strongly depends on the slope of decay of key points of I-V characteristic such as ISC,STC∗, IMPP,STC∗, VMPP,STC∗, and VOC,STC∗. The difference in the evolution (increase or decrease) of the same physical parameter over time, observed from one module to another, is primarily due to the fact that key points do not maintain the same slopes from one module to another. Despite the random evolution of each physical parameter with respect to the different PV modules, with the exception of the photocurrent which decreases for all PV modules, they present I-V characteristics generated that are identical to those given experimentally under real operating conditions, as well as under STC, which we will discuss later. Moreover, during the tracking period, the physical parameters, except the photocurrent, have a slight influence on the characteristic, leading to a translation without changing the shape of the curve over time, as we will see later.

3.3 Adjustment of I-V Characteristics to STC

The aim of this paragraph is to demonstrate that the previously determined physical parameters provide an I-V characteristic that is consistent with the experimental characteristic, whether under real conditions or at STC.

STC translation equations used in this study allow for the translation of all experimental data from the instantaneous I-V curve under real conditions (red curve, points) to STC (blue curve, points). Additionally, the characteristics generated under STC (orange curve, line) and under real conditions (green curve, line), based on previously determined physical parameters, are also presented and compared to the translated and real experimental characteristics. Fig. 11 summarizes all experimental and generated I-V curves under real and STC conditions for various PV modules. The subfigures (a)–(f) are similar and differ only by the type of technology, which is already indicated on the figure itself. Therefore, no additional explanation is needed in the caption.

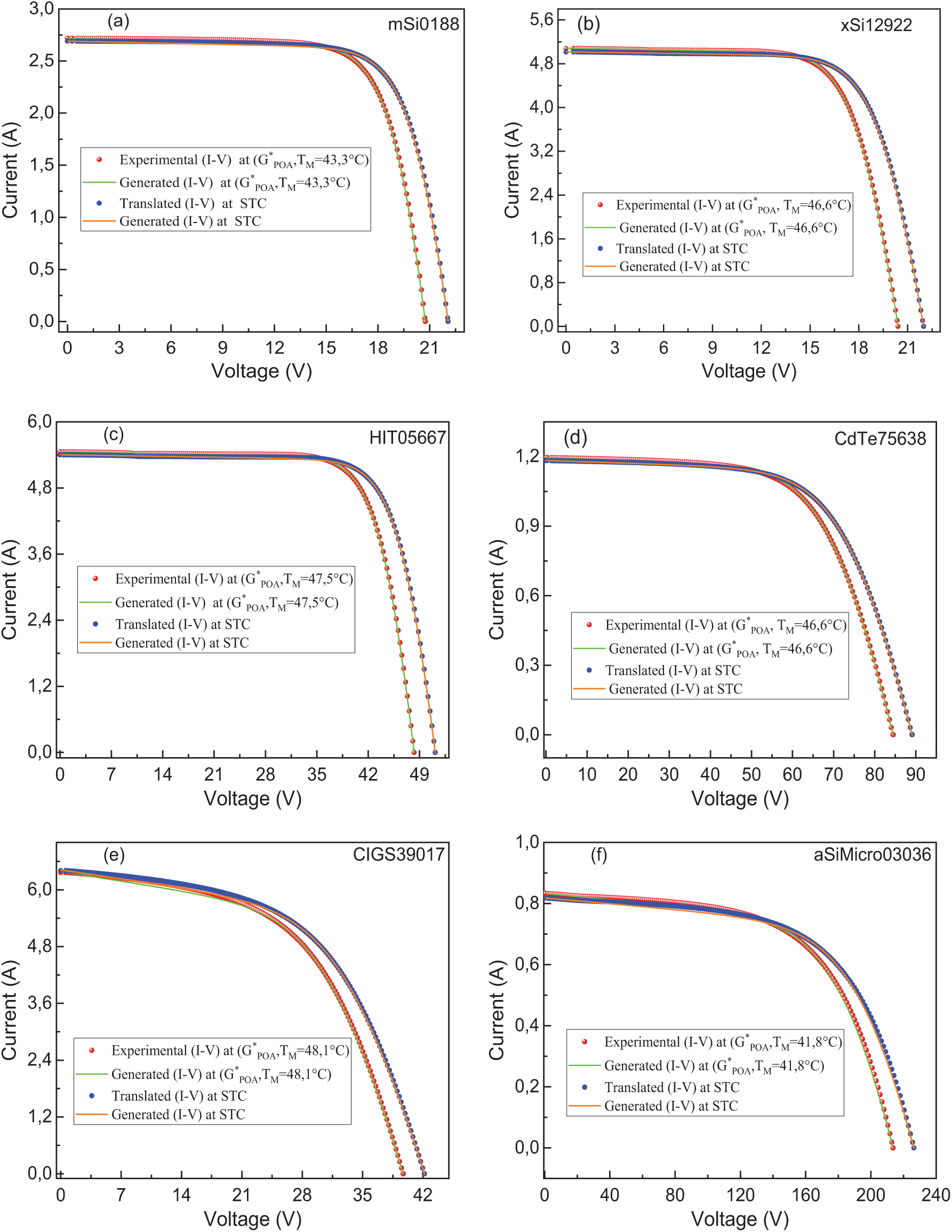
Figure 11: Experimental and generated I-V curves obtained under non-standard test conditions (GPOA∗,TM), along with translated generated I-V curves plots under STC for various PV modules

Based on the obtained results, it is evident that the experimental and generated characteristics agree well. However, to assess the accuracy between the different curves, a commonly used measure is the NRMSE. For this purpose, the NRMSE is calculated between the experimental and generated I-V curves. The NRMSE values obtained are depicted over time (Fig. 12). It is observed that all NRMSE are below 2% between the experimental and generated curves, thus justifying the reliability of the translation equations used in this study and the previously determined physical parameters. The red circles represent the NRMSE between the points of the experimental I-V curve and the one generated under real conditions (the red points and the green curve), while the blue points represent the NRMSE between the points of the I-V curve translated into STC and the one generated under STC (the blue points and the orange curve).

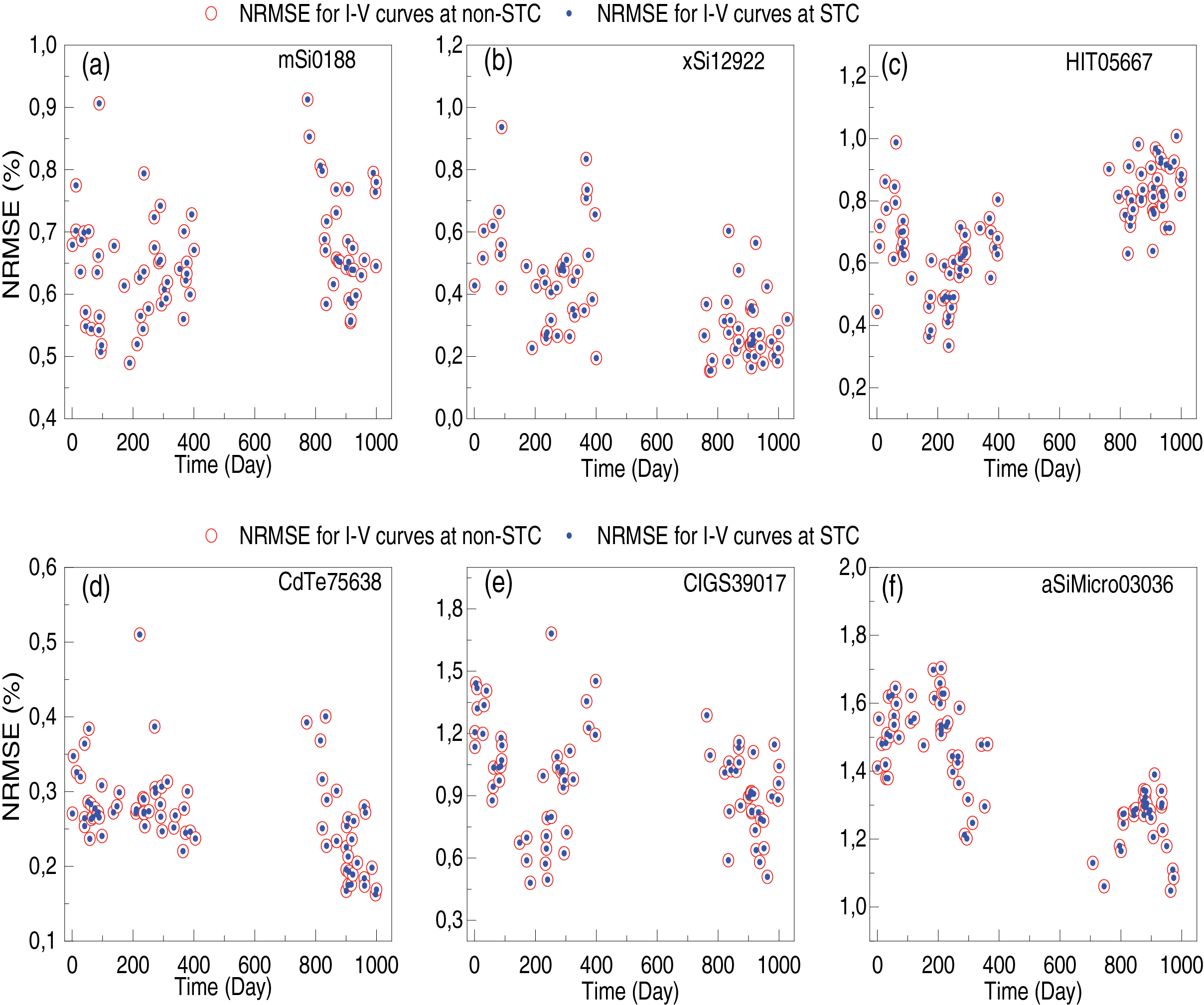
Figure 12: NRMSE values for generated I-V curves under non-STC (GPOA∗,TM), along with those under STC for various PV modules.

3.4 The Degradation Effects on the Shapes of the I-V and P-V Characteristics

This paragraph discusses the effects of aging on the I-V and P-V characteristics of various PV modules. It examines the temporal evolution of key characteristics and the impact of physical parameters on these features. To provide a visual representation of degradation, we compare the I-V and P-V curves measured under the same conditions (STC) on two different days for the same module. Fig. 13 shows the I-V (experimental and generated) and P-V (experimental and generated) curves under STC for six different modules. The degradation effects on the shapes of the I-V and P-V characteristics are clearly visible in the following curves. Consequently, the PV metrics also deteriorate [49].

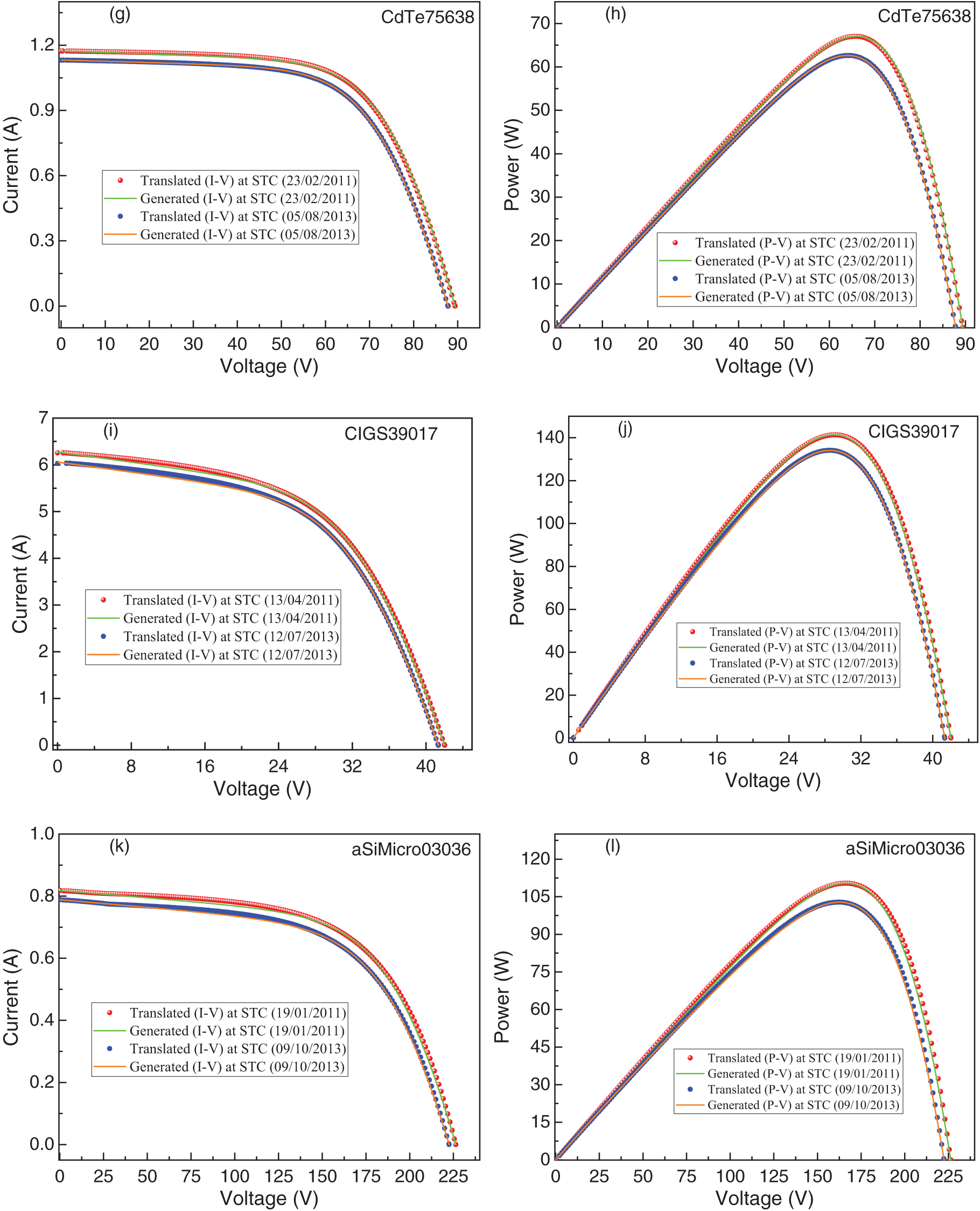
Figure 13: Translated and generated I-V and P-V curves under STC at different times for various PV modules. (a, c, e, g, i, k) represent the evolution of current as a function of voltage, (b, d, f, h, j, l) represent the evolution of power as a function of voltage

Since the I-V and P-V curves were measured under the same conditions, it is reasonable to assume that the differences observed in these curves for the same module result from module degradation rather than differences in measurement conditions. For all six modules, there is a decrease in PV metrics (ISC,STC∗, IMPP,STC∗, VMPP,STC∗, VOC,STC∗, and PMPP,STC∗) over time. In addition, during the two observed days for the same module, there is no distortion in the shape of the I-V characteristic. It is merely a homothetic transformation of one relative to the other, allowing us to conclude that the variation in physical parameters over the monitoring period has no significant influence.

4  Conclusion

This study aims to assess the performance of various PV modules, including crystalline silicon types (m-Si and p-Si) and thin-film types (HIT, CdTe, CIGS, and a-Si/µc-Si), in two different regions of the US. PV modules were sequentially installed in Cocoa and Eugene, then monitored over a period of approximately three years, from January 2011 to March 2012 in Cocoa and from December 2012 to January 2014 in Eugene. The findings from this study reveal several significant aspects. Firstly, the reduction in peak power for crystalline silicon modules was approximately 1% per year during the study period. In contrast, for thin-film modules such as HIT, CdTe, CIGS, and a-Si/µc-Si, the power reduction rates were 1.75%, 2.03%, 2.45%, and 3.26% per year, respectively. These results suggest that thin-film modules exhibit higher degradation rates compared to those based on crystalline silicon, aligning with available literature data. The degradation of power output appears to be linked to the loss of PV metrics such as ISC,STC∗, IMPP,STC∗, VMPP,STC∗, VOC,STC∗, and FFSTC∗. The analysis reveals a consistent decrease in all PV metrics over time for all modules except FFSTC∗ remains constant for m-Si, p-Si, HIT, and CIGS, and slightly decreases for CdTe and a-Si/µc-Si modules. The observed variations in PV metrics affect physical parameters such as RS,STC∗, RSh,STC∗, ηSTC∗, IPh,STC∗, and IS,STC∗. IPh,STC∗ decreases over time for all modules, while other physical parameters vary randomly from one module to another. Consequently, the shape of I-V characteristics and P-V curves evolves over time, resulting in a reduction in the area under these curves. It is crucial to note that PV modules were cleaned daily, excluding the potential influence of dust and dirt on module degradation. Therefore, the results of this study genuinely reflect the aging of materials due to irradiance and temperature cycles as well as other meteorological effects (humidity, rain, ...).

Acknowledgement: The authors would like to thank Chouaïb Doukkali University (UCD) for its support of this work. They also extend their thanks to the National Renewable Energy Laboratory (NREL) for providing the meteorological and photovoltaic data used in this study.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Bouasria Youssef: Conceptualization, Methodology, Software, Writing, Original draft, Review and editing. Zaimi Mhammed: Conceptualization, Methodology, Software, Writing, Original draft, Review and editing. El Ainaoui Khadija: Methodology, Writing, Formal analysis, Original draft, Review and editing. Assaid El Mahdi: Conceptualization, Methodology, Software, Writing, Original draft, Review and editing, Supervision. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Given the nature of this research, the participants did not authorize the public release of their data; therefore, the supporting data are not available.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Glossary

References

1. Abdelouahed A, Elmamoun S, Berrada A, Ameur A. Photovoltaic modules degradation assessment using different statistical techniques. Intl J Energy Res. 2022 10;46(12):16593–607. doi:10.1002/er.8320. [Google Scholar] [CrossRef]

2. Adothu B, Kumar S, Jaeckel B, Muttumthala NL, Shekason Z, Daßler D, et al. Identification and investigation of materials degradation in photovoltaic modules from Middle East hot desert. In: Proceedings of the 40th European Photovoltaic Solar Energy Conference and Exhibition; 2023 Sep 18–22; Lisbon, Portugal. doi:10.4229/EUPVSEC2023/3AV.2.29. [Google Scholar] [CrossRef]

3. Salah FEA, Maouhoub N, Tifidat K, Nam Y, Abouhawwash M. An efficient analytical approach for forecasting the peak power of PV panels working in outdoor conditions based on explicit model. Energy Convers Manag X. 2023;20(3):100423. doi:10.1016/j.ecmx.2023.100423. [Google Scholar] [CrossRef]

4. Abraim M, El Ydrissi M, Ghennioui H, Ghennioui A, Hanrieder N, Wilbert S, et al. PVSMS: a system for quantifying soiling effects and optimizing cleaning schedule in PV solar plants. Energy Convers Manag. 2023;284:116978. doi:10.1016/j.enconman.2023.116978. [Google Scholar] [CrossRef]

5. Chekal Affari B, Kahoul N, Haouam A, Cheghib H, Necaibia A, Younes M, et al. Power losses in PV arrays of field-aged modules. Microelectron Reliab. 2023;147:115052. doi:10.1016/j.microrel.2023.115052. [Google Scholar] [CrossRef]

6. Li B, Karin T, Meyers BE, Chen X, Jordan DC, Hansen CW, et al. Determining circuit model parameters from operation data for PV system degradation analysis: PVPRO. Sol Energy. 2023;254:168–81. doi:10.1016/j.solener.2023.03.011. [Google Scholar] [CrossRef]

7. Oum’bark F, Lotfi H, Bennouna A, Ouacha EH. Degradation assessment of two silicon photovoltaic technologies under subtropical desert climate. IJEECS. 2023;29(3):1233. doi:10.11591/ijeecs.v29.i3.pp1233-1246. [Google Scholar] [CrossRef]

8. Atia DM, Hassan AA, El-Madany HT, Eliwa AY, Zahran MB. Degradation and energy performance evaluation of mono-crystalline photovoltaic modules in Egypt. Sci Rep. 2023;13(1):13066. doi:10.1038/s41598-023-40168-8. [Google Scholar] [PubMed] [CrossRef]

9. Bansal N, Jaiswal SP, Singh G. Comparative investigation of performance evaluation, degradation causes, impact and corrective measures for ground mount and rooftop solar PV plants—a review. Sustain Energy Technol Assess. 2021;47(7):101526. doi:10.1016/j.seta.2021.101526. [Google Scholar] [CrossRef]

10. Okorieimoh CC, Norton B, Conlon M. Disaggregating longer-term trends from seasonal variations in measured PV system performance. Electricity. 2024;5(1):1–23. doi:10.3390/electricity5010001. [Google Scholar] [CrossRef]

11. Dag HI, Buker MS. Performance evaluation and degradation assessment of crystalline silicon based photovoltaic rooftop technologies under outdoor conditions. Renew Energy. 2020;156(4):1292–300. doi:10.1016/j.renene.2019.11.141. [Google Scholar] [CrossRef]

12. Gyamfi S, Aboagye B, Peprah F, Obeng M. Degradation analysis of polycrystalline silicon modules from different manufacturers under the same climatic conditions. Energy Convers Manag X. 2023;20(1):100403. doi:10.1016/j.ecmx.2023.100403. [Google Scholar] [CrossRef]

13. Kichou S, Wolf P, Silvestre S, Chouder A. Analysis of the behaviour of cadmium telluride and crystalline silicon photovoltaic modules deployed outdoor under humid continental climate conditions. Sol Energy. 2018;171:681–91. doi:10.1016/j.solener.2018.07.028. [Google Scholar] [CrossRef]

14. Kichou S, Silvestre S, Nofuentes G, Torres-Ramírez M, Chouder A, Guasch D. Behavioral data of thin-film single junction amorphous silicon (a-Si) photovoltaic modules under outdoor long term exposure. Data Brief. 2016;7:366–71. doi:10.1016/j.dib.2016.02.055. [Google Scholar] [PubMed] [CrossRef]

15. Silvestre S, Kichou S, Guglielminotti L, Nofuentes G, Alonso-Abella M. Degradation analysis of thin film photovoltaic modules under outdoor long term exposure in Spanish continental climate conditions. Sol Energy. 2016;139(1):599–607. doi:10.1016/j.solener.2016.10.030. [Google Scholar] [CrossRef]

16. Livera A, Tziolis G, Theristis M, Stein JS, Georghiou GE. Estimating the performance loss rate of photovoltaic systems using time series change point analysis. Energies. 2023;16(9):3724. doi:10.3390/en16093724. [Google Scholar] [CrossRef]

17. Mannino G, Tina GM, Cacciato M, Todaro L, Bizzarri F, Canino A. A photovoltaic degradation evaluation method applied to bifacial modules. Sol Energy. 2023;251(23):39–50. doi:10.1016/j.solener.2022.12.048. [Google Scholar] [CrossRef]

18. Pascual J, Martinez-Moreno F, García M, Marcos J, Marroyo L, Lorenzo E. Long-term degradation rate of crystalline silicon PV modules at commercial PV plants: an 82-MWp assessment over 10 years. Prog Photovolt. 2021;29(12):1294–302. doi:10.1002/pip.3456. [Google Scholar] [CrossRef]

19. Yaichi M, Tayebi A, Boutadara A, Bekraoui A, Mammeri A. Monitoring of PV systems installed in an extremely hostile climate in southern Algeria: performance evaluation extended to degradation assessment of various PV panel of single-crystalline technologies. Energy Convers Manag. 2023;279(6):116777. doi:10.1016/j.enconman.2023.116777. [Google Scholar] [CrossRef]

20. Elhamaoui S, Benazzouz A, Elamim A, Abdelmoula IA, Tijani K, Ghennioui A, et al. Long-term outdoor performance and degradation evaluation of CIS PV plant under the semi-arid climate of Benguerir Morocco. Energy Rep. 2023;9(1):322–39. doi:10.1016/j.egyr.2023.05.272. [Google Scholar] [CrossRef]

21. Marion B, Deceglie MG, Silverman TJ. Analysis of measured photovoltaic module performance for Florida, Oregon, and Colorado locations. Sol Energy. 2014;110:736–44. doi:10.1016/j.solener.2014.10.017. [Google Scholar] [CrossRef]

22. Marion W, Anderberg A, Deline C, Glick S, Muller M, Perrin G, et al. User’s Manual for Data for Validating Models for PV Module. Performance/Report No. NREL/TP-5200-61610, 1130632 [Internet]. 2014 Apr [cited 2024 Jan 25]. Available from: http://www.osti.gov/servlets/purl/1130632/. [Google Scholar]

23. Goswami A, Sadhu PK. Degradation analysis and the impacts on feasibility study of floating solar photovoltaic systems. Sustain Energy Grids Netw. 2021;26(11):100425. doi:10.1016/j.segan.2020.100425. [Google Scholar] [CrossRef]

24. Martínez-Moreno F, Lorenzo E, Muñoz J, Moretón R. On the testing of large PV arrays. Prog Photovolt. 2012;20(1):100–5. doi:10.1002/pip.1102. [Google Scholar] [CrossRef]

25. Silvestre S, Tahri A, Tahri F, Benlebna S, Chouder A. Evaluation of the performance and degradation of crystalline silicon-based photovoltaic modules in the Saharan environment. Energy. 2018;152(6):57–63. doi:10.1016/j.energy.2018.03.135. [Google Scholar] [CrossRef]

26. Tahri A, Silvestre S, Tahri F, Benlebna S, Chouder A. Analysis of thin film photovoltaic modules under outdoor long term exposure in semi-arid climate conditions. Sol Energy. 2017;157(1):587–95. doi:10.1016/j.solener.2017.08.048. [Google Scholar] [CrossRef]

27. Sharma V, Sastry OS, Kumar A, Bora B, Chandel SS. Degradation analysis of a-Si, (HIT) hetro-junction intrinsic thin layer silicon and m-C-Si solar photovoltaic technologies under outdoor conditions. Energy. 2014;72:536–46. doi:10.1016/j.energy.2014.05.078. [Google Scholar] [CrossRef]

28. Premkumar M, Jangir P, Ramakrishnan C, Kumar C, Sowmya R, Deb S, et al. An enhanced Gradient-based Optimizer for parameter estimation of various solar photovoltaic models. Energy Rep. 2022;8(6):15249–85. doi:10.1016/j.egyr.2022.11.092. [Google Scholar] [CrossRef]

29. Tifidat K, Maouhoub N, Askar SS, Abouhawwash M. Numerical procedure for accurate simulation of photovoltaic modules performance based on the identification of the single-diode model parameters. Energy Rep. 2023;9(4):5532–44. doi:10.1016/j.egyr.2023.04.378. [Google Scholar] [CrossRef]

30. Zaimi M, Ainaoui KE, Assaid EM. New analytical expressions of output current for multi-exponential model of PV solar cells and modules based on Taylor series expansion. Sol Energy. 2024;282(8):112953. doi:10.1016/j.solener.2024.112953. [Google Scholar] [CrossRef]

31. El Ainaoui K, Zaimi M, Flouchi I, Elhamaoui S, El Mrabet Y, Ibaararen K, et al. Novel optimized models to enhance performance forecasting of grid-connected PERC PV string operating under semi-arid climate conditions. Sol Energy. 2024;282:112976. doi:10.1016/j.solener.2024.112976. [Google Scholar] [CrossRef]

32. Premkumar M, Kumar C, Sowmya R. Mathematical modelling of solar photovoltaic cell/panel/array based on the physical parameters from the manufacturer’s datasheet. Int J Renew Energy Dev. 2020;9(1):7–22. doi:10.14710/ijred.9.1.7-22. [Google Scholar] [CrossRef]

33. Zaimi M, Ainaoui KE, Mahdi Assaid E. Mathematical models to forecast temporal variations of power law shape parameters of a PV module working in real weather conditions: prediction of maximum power and comparison with single-diode model. Sol Energy. 2023;266:112197. doi:10.1016/j.solener.2023.112197. [Google Scholar] [CrossRef]

34. Hali A, Khlifi Y. New translation method to STC of photovoltaic module characteristics: a comparison of conventional approaches and proposal of a novel method. Microelectron Reliab. 2024;154(1):115324. doi:10.1016/j.microrel.2024.115324. [Google Scholar] [CrossRef]

35. Zaimi M, El Achouby H, Zegoudi O, Ibral A, Assaid EM. Numerical method and new analytical models for determining temporal changes of model-parameters to predict maximum power and efficiency of PV module operating outdoor under arbitrary conditions. Energy Convers Manag. 2020;220:113071. doi:10.1016/j.enconman.2020.113071. [Google Scholar] [CrossRef]

36. Ye JY, Reindl T, Aberle AG, Walsh TM. Performance degradation of various pv module technologies in Tropical Singapore. IEEE J Photovolt. 2014;4(5):1288–94. doi:10.1109/JPHOTOV.2014.2338051. [Google Scholar] [CrossRef]

37. Phinikarides A, Kindyni N, Makrides G, Georghiou GE. Review of photovoltaic degradation rate methodologies. Renew Sustain Energy Rev. 2014;40:143–52. doi:10.1016/j.rser.2014.07.155. [Google Scholar] [CrossRef]

38. Malvoni M, De Giorgi MG, Congedo PM. Forecasting of PV Power Generation using weather input data-preprocessing techniques. Energy Proc. 2017;126(3):651–8. doi:10.1016/j.egypro.2017.08.293. [Google Scholar] [CrossRef]

39. Jordan DC, Kurtz SR. Photovoltaic degradation rates—an analytical review. Prog Photovolt. 2013;21(1):12–29. doi:10.1002/pip.1182. [Google Scholar] [CrossRef]

40. Bouasria Y, Zaimi M, Ainaoui KE, Assaid EM. Analysis of degradation and aging effects on polycrystalline silicon and thin-film PV modules operating outdoors under two US climates. In: Proceedings of the 2024 International Conference on Circuit, Systems and Communication (ICCSC); 2024 Jun 28–29; Fes, Morocco. doi:10.1109/ICCSC62074.2024.10616487. [Google Scholar] [CrossRef]

41. Santhakumari M, Sagar N. A review of the environmental factors degrading the performance of silicon wafer-based photovoltaic modules: failure detection methods and essential mitigation techniques. Renew Sustain Energy Rev. 2019;110:83–100. doi:10.1016/j.rser.2019.04.024. [Google Scholar] [CrossRef]

42. Ozden T, Akinoglu BG, Turan R. Long term outdoor performances of three different on-grid PV arrays in central Anatolia—an extended analysis. Renew Energy. 2017;101:182–95. doi:10.1016/j.renene.2016.08.045. [Google Scholar] [CrossRef]

43. Kichou S, Silvestre S, Nofuentes G, Torres-Ramírez M, Chouder A, Guasch D. Characterization of degradation and evaluation of model parameters of amorphous silicon photovoltaic modules under outdoor long term exposure. Energy. 2016;96(4):231–41. doi:10.1016/j.energy.2015.12.054. [Google Scholar] [CrossRef]

44. Bouaichi A, Merrouni AA, Hajjaj C, Zitouni H, Ghennioui A, Amrani AE, et al. In-situ inspection and measurement of degradation mechanisms for crystalline and thin film PV systems under harsh climatic conditions. Energy Proc. 2019;157(9):1210–9. doi:10.1016/j.egypro.2018.11.287. [Google Scholar] [CrossRef]

45. Chandel M, Agrawal GD, Mathur S, Mathur A. Techno-economic analysis of solar photovoltaic power plant for garment zone of Jaipur city. Case Stud Therm Eng. 2014;2:1–7. doi:10.1016/j.csite.2013.10.002. [Google Scholar] [CrossRef]

46. Bansal N, Jaiswal SP, Singh G. Prolonged degradation and reliability assessment of installed modules operational for 10 years in 5 MW PV plant in hot semi-arid climate. Energy Sustain Dev. 2022;68(39):373–89. doi:10.1016/j.esd.2022.04.008. [Google Scholar] [CrossRef]

47. King DL, Quintana MA, Kratochvil JA, Ellibee DE, Hansen BR. Photovoltaic module performance and durability following long-term field exposure. Prog Photovolt—Res Appl. 2000;8(2):241–56. doi:10.1002/(SICI)1099-159X(200003/04)8:2<241::AID-PIP290>3.0.CO;2-D. [Google Scholar] [CrossRef]

48. Sánchez-Friera P, Piliougine M, Peláez J, Carretero J, Sidrach De Cardona M. Analysis of degradation mechanisms of crystalline silicon PV modules after 12 years of operation in Southern Europe. Prog Photovolt. 2011;19(6):658–66. doi:10.1002/pip.1083. [Google Scholar] [CrossRef]

49. Cárdenas-Bravo C. Computation of Faulty IV curves based on a distributed solar cell algorithm. In: Proceedings of the 8th World Conference on Photovoltaic Energy Conversion; 2022 Sep 30; Milan, Italy. doi:10.4229/WCPEC-82022-3BV.3.32. [Google Scholar] [CrossRef]