Robust Load Frequency Control in Hybrid Power Systems Using QOSCA-Tuned PID with EV Loads

1  Introduction

Bulk power systems are frequently operated by viewing them as composed of control regions connected to one another [1]. Load frequency control, or LFC, is the process of regulating the real power output of producing units within predetermined bounds in response to variations in system frequency and tie-line power interchange [2]. The power pool is significantly impacted by the automated load frequency control component of automatic generating control, which maintains scheduled system frequency and scheduled tie line power during regular operation and minor disturbances [3,4]. Every control area needs to supply the exchange power that is scheduled for it, as well as its own needs. By keeping an eye on frequency deviation, we can identify any discrepancy between the load and the generation [5]. The use of Automatic Generation Control (AGC) can accomplish this balance between generation and load.

Several forms of generation, including hydro, thermal, gas, solar, and so forth, may be present in each control area. A model in this study has been investigated that can be quite like real-world circumstances. Through the findings in [6], an attempt has been made to investigate the performance of AGC in a two-area system with thermal, hydro, and gas generators. Thus, we have thought about a load scenario that changes arbitrarily. Most past studies in the field of AGC only looked at utilising AI approaches to optimise additional control parameters. Few people look to the governor speed regulation parameter, or principal control loop parameter R, selection [7]. Reading literature makes it clear that significant control variables, such as B and R, have an effect on system performance. Sensitivity analysis is conducted by altering the loading situation and two system parameters, R (Governor Speed regulation) and B (Frequency Bias parameter), in order to test the stability and robustness of the suggested controller.

Most of the previous study is limited to hydrothermal systems; gas generation is not included, whereas in this work it has been considered. This study investigates the robustness of controllers for deviation in R and B parameters as well as modifying PID controller parameters for each thermal, hydro, and gas generation due to random changes in the load. The aim of this study is to investigate the AGC of power systems with thermal-hydro-gas generation in each region in an effective manner compared with the existing literature.

1.1 Background Perspective

A critical overview of the literature on power systems’ AGC is reported in [8]. Research on improving power systems operation with novel optimization techniques is a popular research field [9–13].

In [14,15], various optimization techniques and controllers are followed (genetic algorithms, particle swarm optimization, grey wolf optimization techniques TLBO-TS and TLBO-EDO optimization techniques, and whale optimization algorithm (WOA)) for a load frequency control study. The WOA-optimized 2DOFTIDF controller produced improved dynamic performances when compared to DE-TIDF, LSTM + GA-PID, hGSA-PS-PIDF/PI, DAPI/PID/2DOFPID, WOA-2DOFSFC, WOA-DMPI, and WOA-TIDF controllers [16]. But the intricacy of these intricate processes and the need for users to be knowledgeable about these methods restricts their applicability. Power system engineers still choose to utilize the conventional Proportional Integral Derivative (PID) controller due to its dependable design, favorable performance to cost ratio, and simplicity of usage. Additionally, it offers cheap development effort, simpler dynamic models, and lowered user skill requirements, all of which are major issues in engineering practice. Recently, methods utilizing artificial intelligence have been put forth to enhance the AGC system’s PI/PID controller settings. Using a variety of conventional controller topologies, such as Integral (I), Proportional Integral (PI), Integral Derivative (ID), PID, and Integral Double Derivative (IDD), the performance of the AGC system was investigated in [17]. A review of the literature reveals that AC-DC parallel tie lines receive less attention than AC tie lines when it comes to connecting multi-area power networks in order to stabilise frequency oscillation. In [18], on a multi-source generation that included thermal-hydro-gas systems, they considered an HVDC connection connected in parallel with the current AC link and an ideal output feedback controller. In comparison with the updated literature in the relevant field, it reveals that LFC multi-source coordination (such as thermal, hydro, gas, solar, wind, and battery) is not considered in a hybrid power system network with EV loads in terms of robustness and sensitivity.

1.2 Motivation of This Work

Till now, the proposed optimization method, known as the Quasi Oppositional Sine Cosine Algorithm (QOSCA) has not yet been used to adjust the controller in AGC analysis. The present study has employed the optimization approach to optimise the controller for load frequency regulation in the presence of several real power sources. In paper [19], detailed information on SCA, along with its application in order to ensure completeness and a better understanding of the study, has been discussed. Numerous researchers have solved a wide range of challenging engineering and non-engineering problems using the Sine Cosine method (SCA), a simple and efficient swarm intelligence-based optimization technique established by [19]. When it comes to the outcomes, the SCA algorithm performs better than a lot of other algorithms [20]. However, SCA, like other swarm intelligence algorithms, has poor optimization precision and a slow convergence pace when it comes to tackling complex problems with large-scale electrical power networks. Therefore, a quasi-opposition-based learning (QOBL) approach is used to improve its performance in [21]. When compared to the algorithms’ basic form and the form infused with the OBL idea, improvements in terms of outcomes have been observed. Numerous researchers have employed algorithms infused with the QOBL concept in the past to handle various real-world challenges [22,23]. This drives the current work to attempt applying the QOBL idea for the first time to the fundamental SCA to speed up the process of locating the global optimal solution. When the concept of QOBL is blended with the fundamental sine cosine algorithm, a new hybrid algorithm known as the quasi-opposition-based sine cosine algorithm (QOSCA) is produced. The capability of the suggested QOSCA is successfully utilized in the current work to solve the LFC problem [23,24]. The application of QOBL in addition to other algorithms for LFC analysis has been discussed in [25–27]. The dynamic outcomes of the proposed QOSCA have been compared with the traditional SCA in this work, which has not been shown in any other work till now.

In the next ten years, EVs will surely overtake combustion engines fueled by fossil fuels as the primary mode of transportation due to the devastation caused by these engines’ chemically charged emissions, which have also poisoned the ecology. As a result, the integration of EVs into power networks is currently receiving a lot of scholarly interest [28]. An additional source of spinning reserves and effective control over a large number of EVs (charging/discharging) can be achieved with additional equipment such as energy converters, bi-directional communication interfaces, power electronics interfaces, and meter devices to connect with the aggregator entity. Grid-connected EVs can replace energy storage devices. Incorporating EVs can also absorb excess electricity and lower the cost of building and maintaining peak plants [29]. An enormous power plant can be created by connecting thousands of EVs to the grid for charging and discharging [30]. Consequently, it is generally anticipated that EVs will meet the future need for electricity [31]. When coordinating the power system’s LFC problem with EVs, distributed functional observers are employed to account for high voltage direct current (HVDC) connections and open communication infrastructure. However, this technique needs information about the states of the system, which might not be available in an emergency or might be very challenging to implement in real-world situations. First, ISO needs to make sure that EV aggregators can locate EVs in order for them to take part in wholesale electric markets [31]. Subsequently, the aggregator will engage in the day-ahead market to buy the electricity. According to the contract, EV owners are only allowed to charge their batteries during off-peak hours, which are from 10 p.m. to 8 a.m. [31,32]. EV aggregators have to maximize the battery’s state of charge (SOC) during this period as well. The owner of the PEV will receive a set retail price for a regular non-PEV (plug-in hybrid electric vehicle) load that is less than the nominal retail price and even less than the off-peak (time-of-use) pricing. As a result, the aggregator will make the most money when the cost of purchased energy is extremely low. The aggregator’s job is to gather and deliver the control operator’s request for EV status data. Electric vehicles (EVs) instantaneously update their data and information upon receiving the control signal from the operator. Examples of such data include SOC, EV capacity, and the number of EVs plugged into charging stations. The discussion reveals that there is a dearth of debate regarding the effects of EVs on LFC in a deregulated environment. Here in this work, the EV system is only treated as the electrical load variation regarding its charging and discharging operation in our proposed interconnected system.

Because of its potential to improve system stability and certain financial advantages, HVDC transmission is also utilized. A fleet of thousands of EVs can be used as controllable energy storage devices to participate in power system operation thanks to V2G technology, which is noteworthy because EVs have their own batteries [33,34]. A fleet of EVs making use of a huge BESS works incredibly well to stabilize load and frequency variation [35,36], owing to the quick reaction features of EV batteries [37]. When parking at a station or at home, the majority of EVs are connected to the grid, making this scenario possible [38,39]. Consequently, EVs might take part in the LFC to help power units quickly reduce load variations [40]. The idea of an aggregator was created in order to organize a fleet of thousands of EVs [41]. Here, an aggregator’s job is to collect data on the EVs’ condition, transmit it to the control center, and then redistribute the control command to distribute the EVs. An open communication infrastructure, such as a network control system or wide-area communication, is required to create a smart power grid that can incorporate EVs. EVs get control signals and real-time data updates, including their level of charge, power capacity, and the number of EVs connected to the grid, owing to this communication infrastructure [39]. Power line communication, general packet radio service, an Internet connection, wireless protocol with ZigBee technology, and Bluetooth [17,34] make up the communication infrastructure for EVs. In this work, we examine that the majority of EVs are parked at stations in each locality. Which are shut together, and the conversation takes place at an extremely high speed in comparison to the closed-loop’s speed system. As a result, we disregard any communication delay that might be caused by the network on the channel. We propose a new LFC scheme in this investigation that incorporates EVs into load fluctuation stabilization.

1.3 Contribution of the Present Work

The main accomplishments of this study are as follows:

1.   This study leverages the suggested QOSCA optimization technique outperforms the SCA technique in terms of system dynamic operations. The novelty of the proposed QOSCA, as an optimization tool for the Load Frequency Control analysis of the proposed IHPS model, is explored.

2.   A critical study is analyzed where only one PID controller instead of three PID controllers is enough for maintaining contemporary stability consideration without losing any physical circuitry condition.

3.   In order to assess the resilience and stability of the suggested controller, sensitivity analysis is conducted by altering the loading condition and the system parameters, namely the frequency bias parameter (B) and the governor speed regulation (R).

1.4 Layout of the Paper

The rest of the paper is arranged as follows. Section 2 demonstrates the modeling of several IHPS components. In Section Control Scheme of the System under Study, the details of IHPS and its parameters have been discussed. Mathematical problem formulation of the proposed work is carried out in Section 3. Section 4 gives the overview of traditional SCA and foundational concepts of QOBL. In Section 4.2, QOSCA is discussed. The works of this paper have been discussed one by one in Section 5. The scenario-wise simulation results obtained from the different case studies are presented and discussed in Section 5.1. Finally, the research findings and future scope of the present work are concluded in Section 6.

2  System Configuration

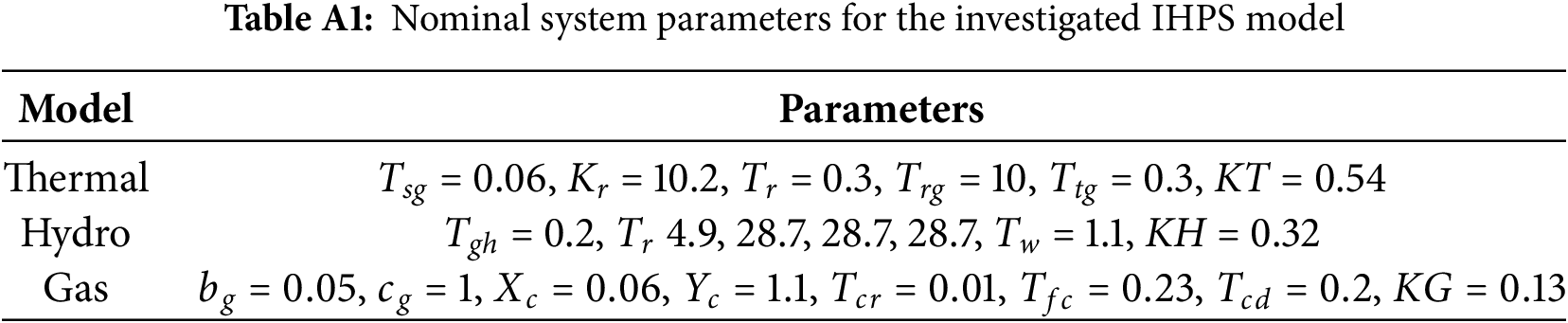
The thermal, hydro, gas power generating station & EV are the four components of the examined IHPS in this paper. Fig. 1 depicts the IHPS system under investigation. The system parameters of the studied IHPS are given in Appendix A. Eq. (1) gives the total power balance equation in the IHPS model.

ΔPIHPS=ΔPHD+ΔPGD+ΔPTPPD−ΔPD+ΔPtie+ΔPdc±ΔPEVD(1)

where, ΔPHD is the variation in the power output of the hydro power plant, ΔPTPPD is the variation in the power output of the TPP, ΔPGD is the variation in the power output of the Gas power plant (GPP), ΔPEVD is the variation in the power output of the EV. ΔPtie is the tie line power variation. ΔPIHPS is the total output variation of the IHPS model and ΔPD is the variation of the load disturbance.

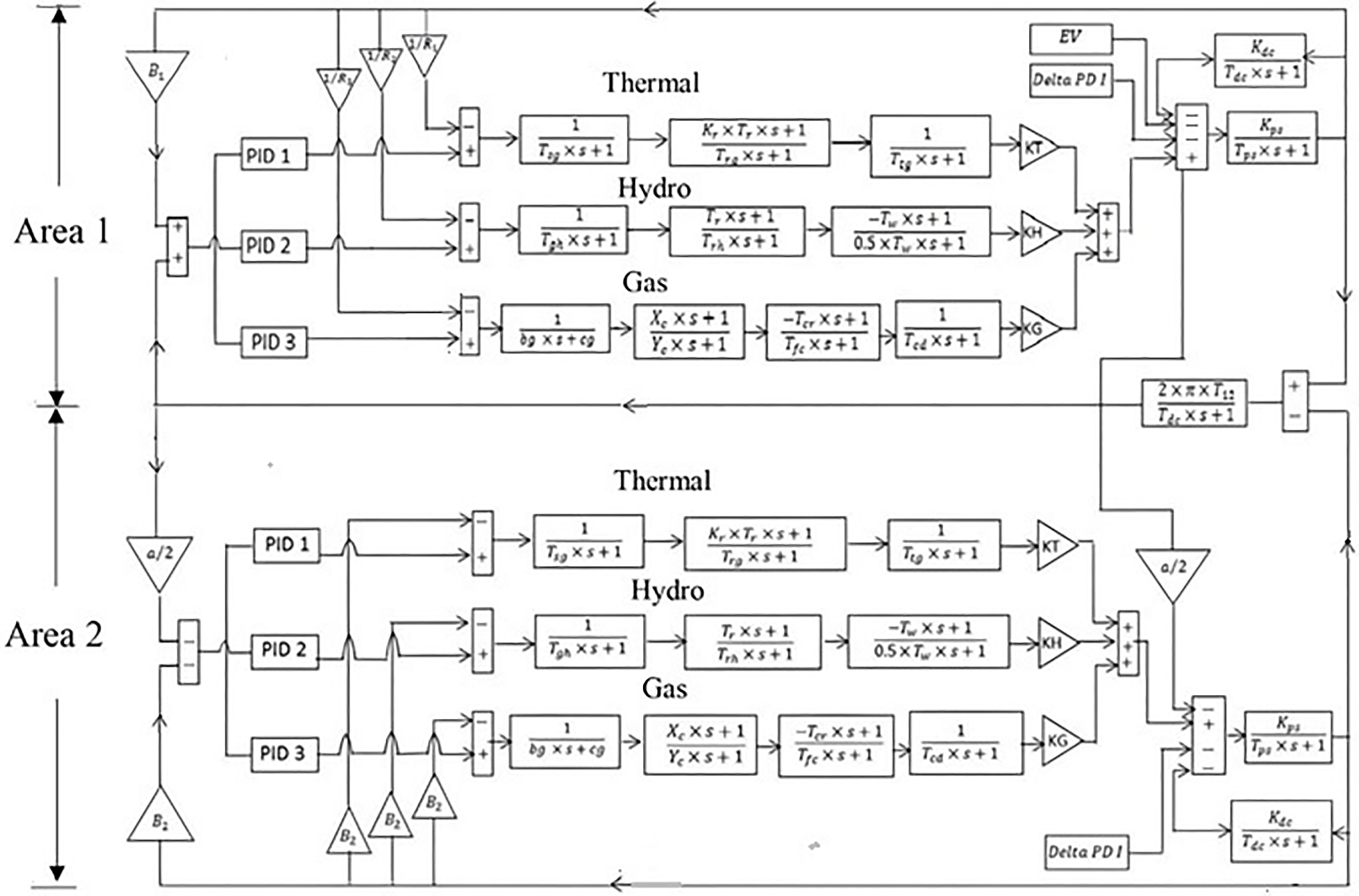
Figure 1: Transfer function model of an interconnected hybrid power system (with 3 PID controllers in each area)

Control Scheme of the System under Study

A single area system with hydro, thermal with reheat turbine, and gas units is taken into consideration initially while developing the controller for the system. As shown in Fig. 1, the linearized models of governors—gas turbines, hydro turbines, and reheat turbines—are used in the power system’s LFC analysis and simulation. Each unit provides a certain amount of the nominal loads, which is determined by its regulatory parameter and participation factor. Every control’s participation factor added should equal 1. The regulating parameters of each unit of the proposed IHPS model are, represented by the letters R1, R2, and R3 in Fig. 1. The control outputs for each unit of the proposed IHPS model are, respectively, UT, UH and UG. The participation factors of each unit of the proposed IHPS model are, respectively, KT, KH, and KG. TSG is the expression for a TPP’s speed governor time constant. The TPP’s time constant is expressed as TT. TW is the nominal starting time of water in penstock. The TPP’s reheat time constant is expressed as Kr. whereas Tr is TPP’s reheat time constant in seconds. The HPP’s speed governor reset time is measured in seconds TRS, the GPP’s speed governor lead time constant is measured in secondsTGS. Xc is the HPP’s speed governor main servo time constant and measured in seconds, cg is the GPP’s valve positioner, bg is the GPP’s constant of valve positioner, and Yc is the lag time constant of GPP’s speed governor in seconds. TPS is the power system time constant in seconds, ΔPD is the gradual shift in load variation, ΔF is the gradual shift in frequency variation, and KPS is the power system gain in Hz/puMW. The system’s nominal parameters are listed in reference.

3  Problem Formation

The current challenge is formulated in a deregulated domain with an AGC perspective. To ensure the validity of the results, it is necessary to examine the effects of PID controllers. In light of this, the following three subsections have been discussed in this paper.

All participating generators’ participation factors add up to unity. The market operator establishes that the following expression [42] must be met by the participation factor:

∑i=1niβni=1(2)

For secondary frequency regulation, the participation factor’s value ranges from 0≤βni≤1. ΔPD,i and ΔPEVD,i denote load disturbance and change in EV’s behavior that must be compensated by the AGC loop, respectively.

The ith unit regulation parameter is denoted by Ri and the equivalent regulation parameter of that ith area, Req,i is necessary to express the frequency bias parameter, Bi using the following equation [43]:

Bi=Di+1Req(3)

where, Di is the load damping factor of ith area and can be found by the following equation

1Req=∑i=1ni1Ri(4)

The area control error (ACE) is computed from the linear combination of the tie line power flow deviations and frequency deviations and it’s given as:

ACEi=BiΔωi+∑jεNiTij1S(Δωi−ai)(5)

ΔPtie,i,j=∑jεNiTij1S(Δωi−ai)(6)

where, Tij = Synchronizing torque coefficients

ai = Area interface signal

From the above equation it can be easily mentioned that if ACEi is minimized to zero, then the tie line power flow and frequency deviation are regulated.

Thus, the frequency deviation dynamics in the kth region of the interconnected power system depicted in Fig. 2 accept the following expression:

Δfk=12HkS+Dk(ΔPth,k+ΔPhd,k+ΔPg,k−ΔPD(Load),k+ΔPtie,k±ΔPevd,k)(7)

where,

ΔPth,k=11+STtg,k(ΔPth,k)(7a)

ΔPhd,k=−Tw,kS+11+S0.5Tw,k(ΔPhd,k)(7b)

ΔPg,k=11+STcd,k(ΔPg,k)(7c)

where, Hk is the inertia constant and is the damping constant in the k-th area. ΔPth,k, ΔPhd,k and ΔPg,k are the thermal, hydro and gas’s incremental power in k-th area, respectively. Ttg, Tw, and Tcd are the different time constants of thermal, hydro and gas power plants in k-th area. ΔPevd,k is representing the charging and discharging of EV system. In contrast to conventional power generation, which modifies its output in response to frequency fluctuations, electric vehicle (EV) systems exchange electricity with the grid based on fluctuating system frequencies.

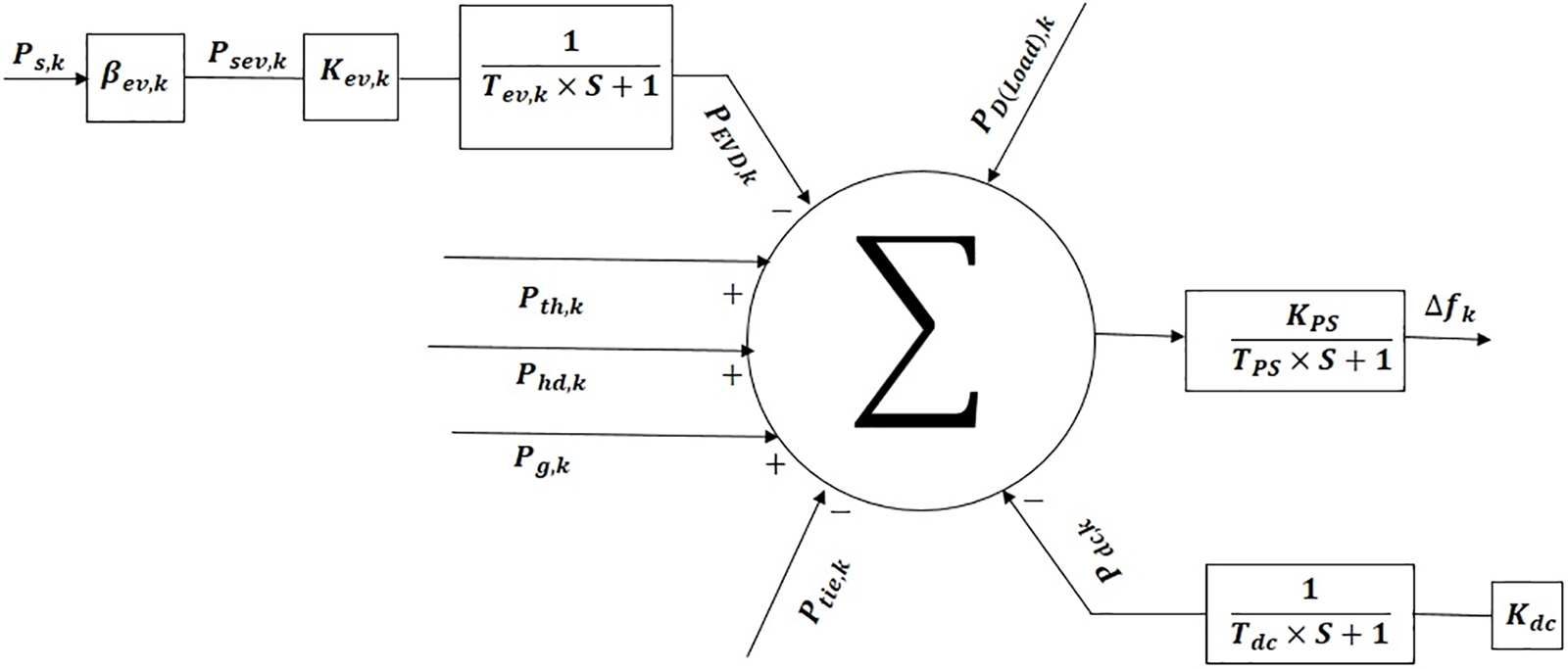
Figure 2: Transfer function model of EV & HVDC line

The steady state error, which is provided by the following equation, is decreased in order to adjust the PID controller parameters.

J=∫0t(|ACE1|+|ACE2|+|ACE3|)dt(8)

Thus, the proposed controller receives the reference value of ACEi, the area control error ACEi, and the load perturbation ΔPD1 as inputs in order to generate the control signal output. All of the ACEi reference values need to be set to zero. In order to minimize the quantity of performance matrices, such as overshoot, undershoot, and settling time for various signals, the objective function is built. The objective function for minimizing frequency deviation by optional PID parameter adjustment is as follows [43]:

minJ=∫ACE(ΔF1,ΔF2,ΔPtie−i)(9)

Fig. 2 shows kth area HVDC links, represented in the model by Pdc,k from the main transfer function block diagram of Fig. 1

The control center sends an incremental change in power set-point, Ps,k, to maintain system frequency and power tie-line at the scheduled values. Through participation factor βev,k, control signal Psev,k is sent to regulate the power output of the generating units and EVs, respectively. EVs can contribute to the LFC control as a power plant by using their power capacity, and the bidirectional power electronic devices enable them to pump energy into the grid. All EV data is gathered by the aggregator and sent to the control center. Furthermore, the control center sends the power set-point to the aggregator, which distributes it among the scattered EVs. An EV fleet is represented using a first-order model with time constant Tev,k and gain Kev,k [44,45]. According to Fig. 2, the output power deviation of EVs is

PEVD,k(S)=Kev,kTev,k×S+1Psev,k(S)(10)

Using the supplemental HVDC PID controller, HVDC lines can be integrated into LFC. With a time constant Tdc,k, the HVDC control signal Kdc,k determines the HVDC power interchange, Pdc,k, of k-th area [46]. The difference between frequency deviations of k-th area and l-th is used to calculate the Kdc. l=1,2,……,N,l≠k with a HVDC gain Kdc. So, Pdc,k can be expressed as follows.

Pdc,k(S)=Kdc,k(S)Tdc×S+1(11)

where,

Kdc,k(S)=∑l=1,l≠kNKkl(fk(s)−fl(s))(11a)

Kkl=0 wthen there is no HVDC link between areas k and l.

3.1 Assessment of Performance

To maximize the advantages of the controller architecture, the values of four performance indicators are analyzed in this section. So, the program’s final calculations determine the (a) integrated absolute error (IAE), (b) integrated squared error (ISE), (c) integrated time weight absolute error (ITAE), and (d) integrated time weight square error (ITSE) in this work. According to the order given in (12)–(15), the mathematical equation for the performance indices under consideration of [27] and shown in following equations

IAE=∫0ts(Δf1+Δf2+ΔPtie)dt(12)

ISE=∫0ts(Δf12+Δf22+ΔPtie2)dt(13)

ITAE=∫0ts(Δf1+Δf2+ΔPtie)tdt(14)

ITSE=∫0ts(Δf12+Δf22+ΔPtie2)tdt(15)

where, t is the simulation time. The optimization program that was built determines the values of the aforementioned indices.

3.2 Structure of the Objective Function

In this optimization method, the ITAE is regarded as an objective (J) out of the four indices listed in (2)–(5). Compared to its counterparts in ISE and ITSE, ITAE tuning allows for faster Δf, settling. Because the ITAE criterion takes absolute error into account, the maximum percentage of overshoot is thus minimized. When compared to other integral-based performance indices, the ITAE yields better result. The study’s mathematical conundrum can be stated as shown in [27] and Eq. (16)

MinimizeJ=MinimizeITAE(16)

3.3 Restraints of the Optimization Problem

The current optimization technique restricts the tunable parameters of the controller included in the studied IHPS model to a particular range throughout the optimum process. The limitations concerning the gains of the PID controller, whose values have to be as Eq. (17) according to [23].

Kpjmin≤Kpj≤Kpjmax,j=1,2Kijmin≤Kij≤Kijmax,j=1,2Kdjmin≤Kdj≤Kdjmax,j=1,2}(17)

where, the superscripts min and max stand for the minimum and maximum values of the relevant variable.

4  Formulation of Quasi Oppositional Sine Cosine Algorithm

Using the mathematical functions for sine and cosine, which are described in detail in [8], SCA is a chaotic population-based optimization technique that produces fresh, updated solutions. Based on the sine and cosine functions, it uses a mathematical model. In the beginning, potential solutions are thrown into the solution space at random. Additionally, candidate solutions are updated frequently. Updated individuals move in the direction of the global optimal solution or away from it. Once the algorithm has determined the optimal answer, it is preserved and never lost. With an increase in iterations, the sine and function range are updated. Exploitation is guaranteed in this instance. When the uttermost number of iterations allowed by the method is reached, the optimizations process ends. The SCA optimization procedure consists of two phases. There are two steps in the SCA optimizations process. High reconnaissance and avoiding the local optimum are guaranteed by SCA. Additionally, the fastest time to the result is found.

The position updating equations listed below are suggested for both stages in this work by Eq. (18) according to [19]

xit+1=xit+r1xsin⁡(r2)x|r3Pit−xit|r4<0.5xit+1=xit+r1xcos⁡(r2)x|r3Pit−xit|r4≤0.5}(18)

where, i is the size and t is the present iteration number. xit is the ith size value of the agent at the tth iteration and Pit is the ith size value of the uttermost individual at the tth iteration. The arbitrary integers r1, r2, r3 and r4 have values in the interval [0, 1]. To strike a balance between exploration and exploitation, r1 is determined using the Eq. (19) as per [19]

r1=α−t∝T(19)

where, T is the uttermost number of iterations and ∝ is constant values (taken as 2).

4.1 Foundational Concepts of QOBL

Making use of arbitrary integers and their opposites, the OBL can accelerate the pace of convergence when creating initial estimates in an optimization process. To boost performance, add variety to the solution and accelerate the optimization method’s rate of convergence. In [14], it was suggested to use QOBL, or arbitrary integer population with its quasi-opposition number. The definitions of the opposite point and opposite integer in OBL are as follows.

(i) Opposite integer:

It can be thought of as the mirror image of the solution from the middle of the search space. Assume, in an interval [a,b], the real number is x (i.e., x∈[a,b]); if Ox0 is the opposite of x, then it can be expressed as (20) as proposed in [24,25].

Ox0=a+b−x(20)

(ii) Opposite point: Yilmaz Assume, in D-dimensional space, P(x1,x2,…,xD) is a point.

where, x1,x2,…,xD are real numbers, xi∈|ai,bi| and i=1,2,…,D.

The contrary point of P is expressed by P(Ox1,Ox2,…,OxD) and calculated by (21) according to [25,26]

Oxi=ai+bi−xi(21)

(iii) Quasi-opposite number:

The number that is between the opposite number and the search space’s center, [a,b], is known as the quasi-opposite integer. Quasi-opposite integer can be mathematically expressed in [25] and given in Eq. (22):

QOx0=rand(a+b2,a+b−x)(22)

(iv) Quasi-opposite point:

The quasi-opposite point QOxi(QOx1,QOx2,…,QOxd) can be described by Eq. (13) for a d-dimensional search space as shown in [25]

QOxi=rand(ai+bi2,ai+bi−xi)(23)

where, i=1,2,…,d.

4.2 Proposed Algorithm: QOSCA

The flowchart of the QOSCA proposed in this work is given in Fig. 3. It follows the QOBL technique in the parent SCA algorithm. Quasi oppositional generation Jumping is employed in the QOBL concept to accelerate the convergence profile and increase solution accuracy. Here is how QOSCA is being implemented:

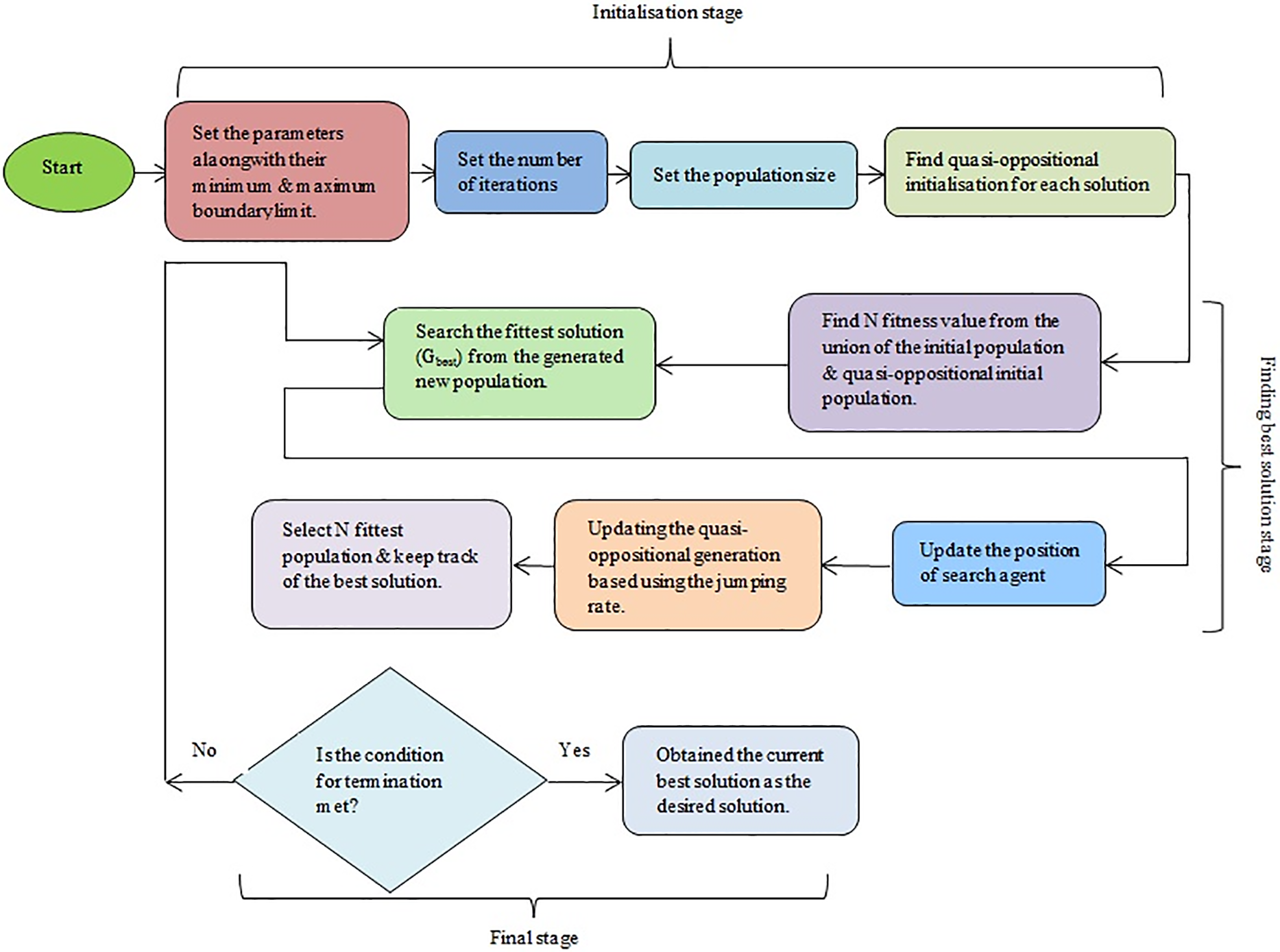
Figure 3: Flow chart of the proposed QOSCA

Step 1 Using random function Initial population needs to be generated (look up agent integer = 10, no. of iterations = 100, minimum and maximum bounds = 0.01 and 2, respectively).

Step 2 Setting the initial values against the quasi-opposition parameters (using Eqs. (21) and (22) and jumping rate = 0.8).

Step 3 Analyze the proposed IHPS model (Fig. 1) and assemble the objective function and load disturbance.

Step 4 Keep initially a zero in the iteration count.

Step 5 Determine which search agent is the best by calculating each one’s fitness.

Step 6 Utilizing Eq. (4), change the location to the most effective search agent and continue to look for the finest answer.

The idea behind quasi-opposition based population generation is to make them more diverse from one another so that the evolutionary process can move on to a new, more suitable candidate solution. The existing population is subjected to an idea akin to the quasi-opposition based initial population creation inside the iterative loop while the method is running. The jumping rate/jumping probability (jr) is used to generate a new quasi-opposite population. Hence, instead of using the preset minimum and maximum border limitations, the algorithm uses the smallest and largest quantities of each variable in the present population, the detail of the proposed system is given in Fig. 2.

4.3 Specification of Transient Parameter

The primary goal of this work is to optimize the controller gain by modifying the required parameters to ensure that the power system’s dynamic response is neither excessively rapid nor slow. The dynamic response of the system is quantified in relation to settling time (ts(s)), peak overshoot (Hz/V/pu) and peak undershoot (Hz/V/pu). The values of all the performance indices and transient responses previously discussed have also been computed in this work.

5  Outcomes and Discussions of Results

This section describes the application of the innovative QOSCA to adjust the various gains of the PID controller, which have been employed one at a time in the studies of the IHPS model, shown in Fig. 1. Here in this work, controller I connects to the governor of the thermal unit, while controller II regulates the pitch angle of the hydro unit and controller III connects to the Gas unit.

PID Model IHPS of Fig. 1: In this model, the dynamic performances of the studied IHPS model have been considered by controllers I, II, and III, which are regarded as PID controllers. Dynamic performance (settling time (ts(s)), maximum overshoot (Hz/V/pu) and maximum undershoot (Hz/V/pu)) comparison is done in different scenarios in this paper, which are explained below.

In this work, three cases have been studied, and they are as follows: In Case 1, the applications of the PID controllers are considered for performance assessments and their comparison which results in the two situations that are outlined as Scenario 1 (With SCA optimization technique) and Scenario 2 (With proposed QOSCA optimization technique). In Case 2, effects of the PID controllers have been checked for simplifying the IHPS system. Finally, in Case 3, the system’s robustness has been checked along with proposed optimization algorithm.

Assessment of Performance

This section analyses the dynamic performance of the IHPS controller models in the time domain. Next, two scenarios of change of tuning process of required parameters have been examined for the three PID controller-based models. The optimization techniques have been compared under various conditions in order to improve performance in the IHPS model under consideration. The innovative SCA and QOSCA have been employed for controller parameter tuning and optimization with the aim of suppressing the frequency deviation of the investigated IHPS model. Requirement of PID controllers have been checked. In accordance with all of this the system’s robustness has been checked by varying the load at area 1.

Case 1

Here, the necessary parameters have been tuned using SCA & QOSCA optimization techniques to examine the dynamic behavior of the suggested IHPS model: TPP, HPP, GPP, and EV (area 1) and TPP, HPP, and GPP (area 2). The comparison of the dynamic characteristics of the suggested IHPS model followed by two scenarios has been shown in Fig. 4. Further, Table 1 displays comparison in two scenarios with respect to settling time (ts(s)), maximum overshoot (Hz/V/pu) and maximum undershoot (Hz/V/pu)of the proposed models under study.

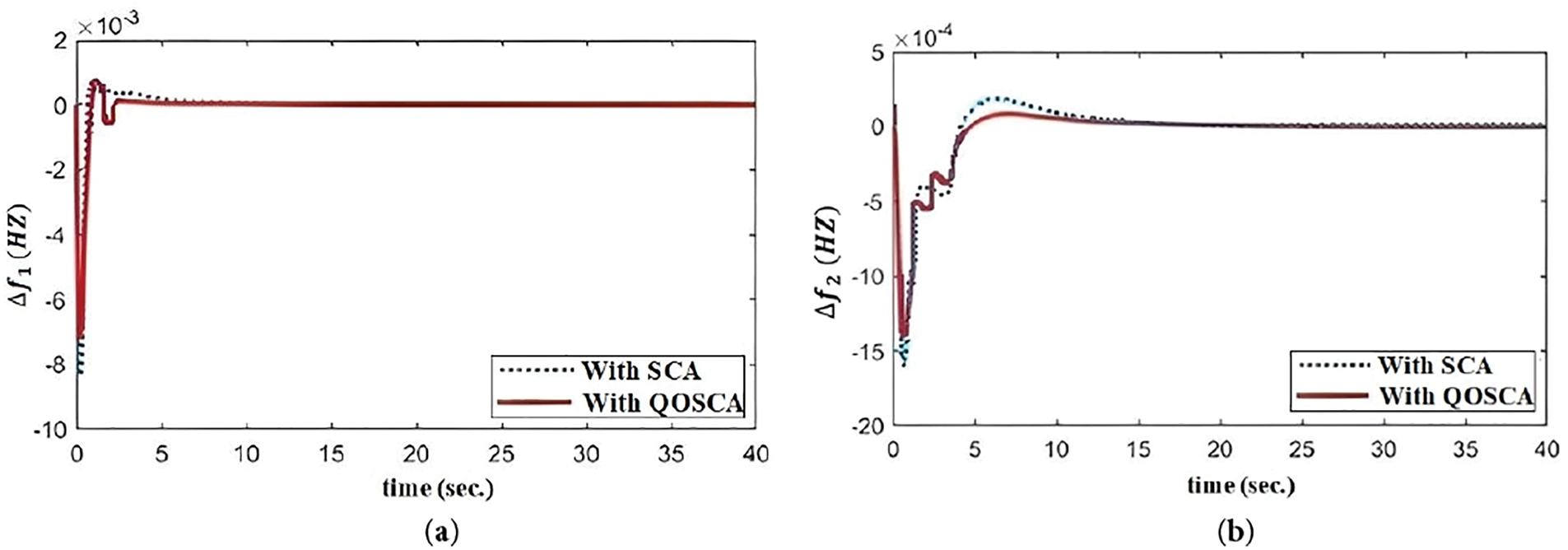
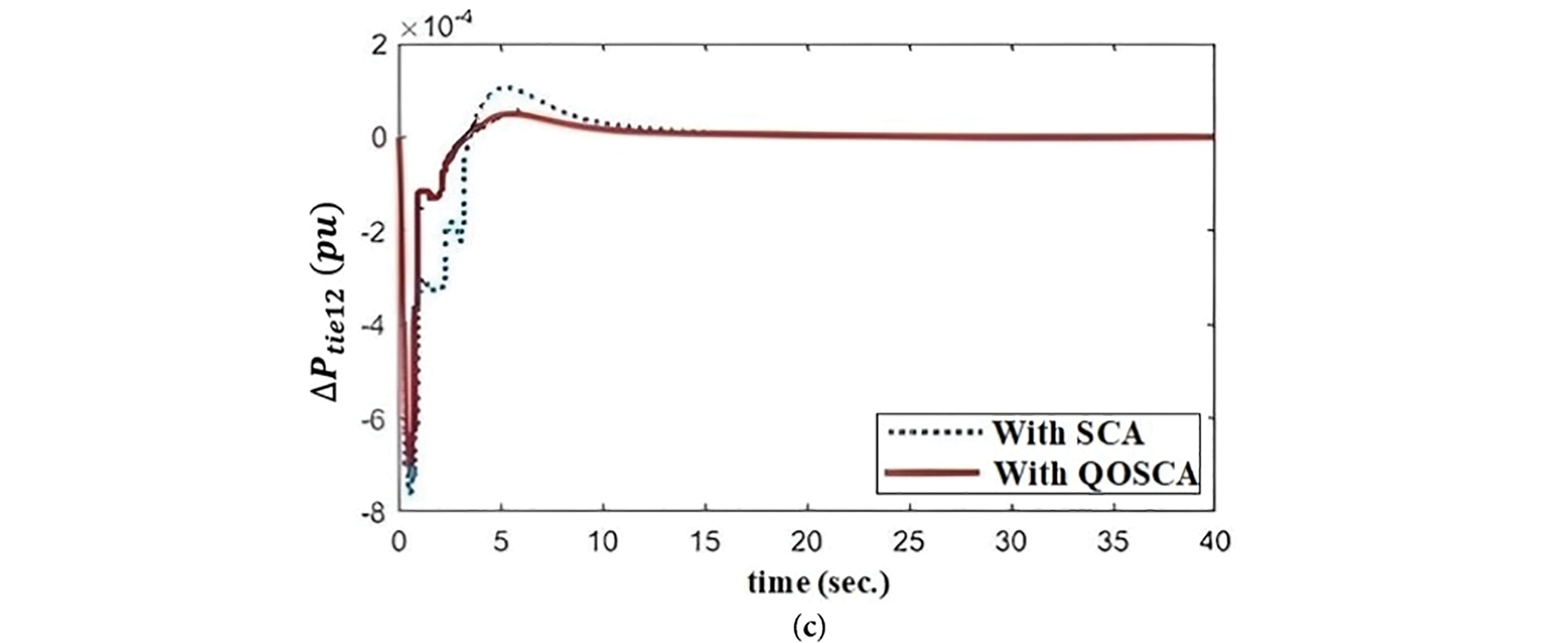
Figure 4: (a) Frequency deviation of Area 1, (b) Frequency deviation of Area 2 and (c) Tie line power variation vs. time in sec

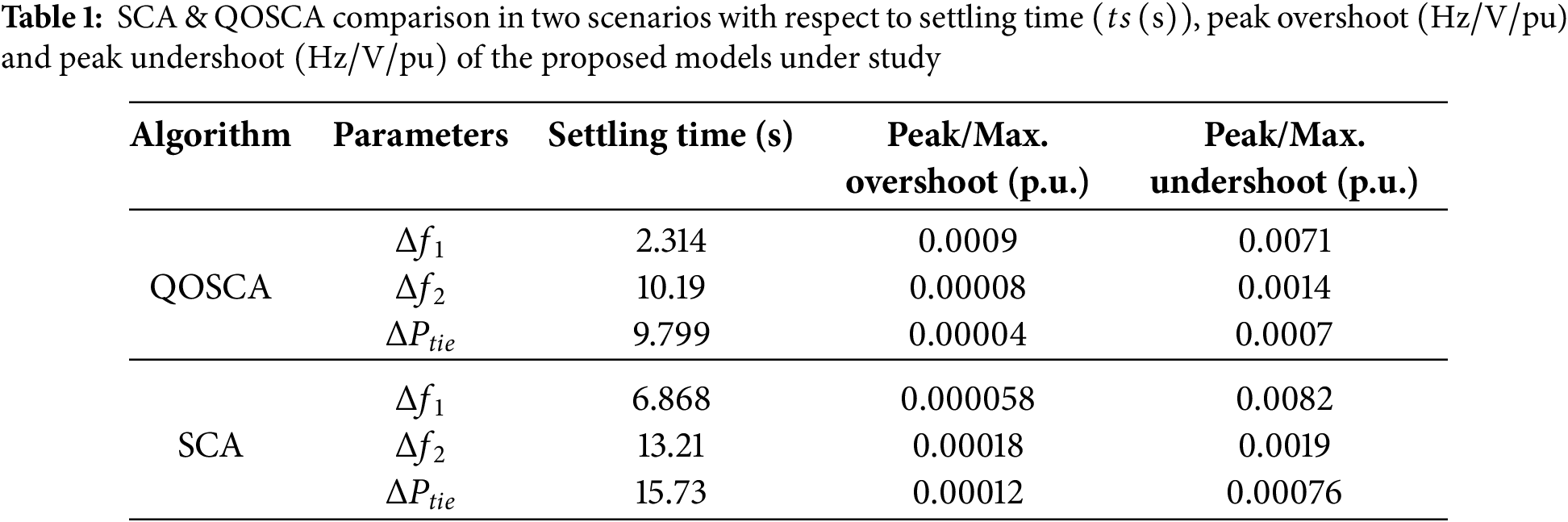
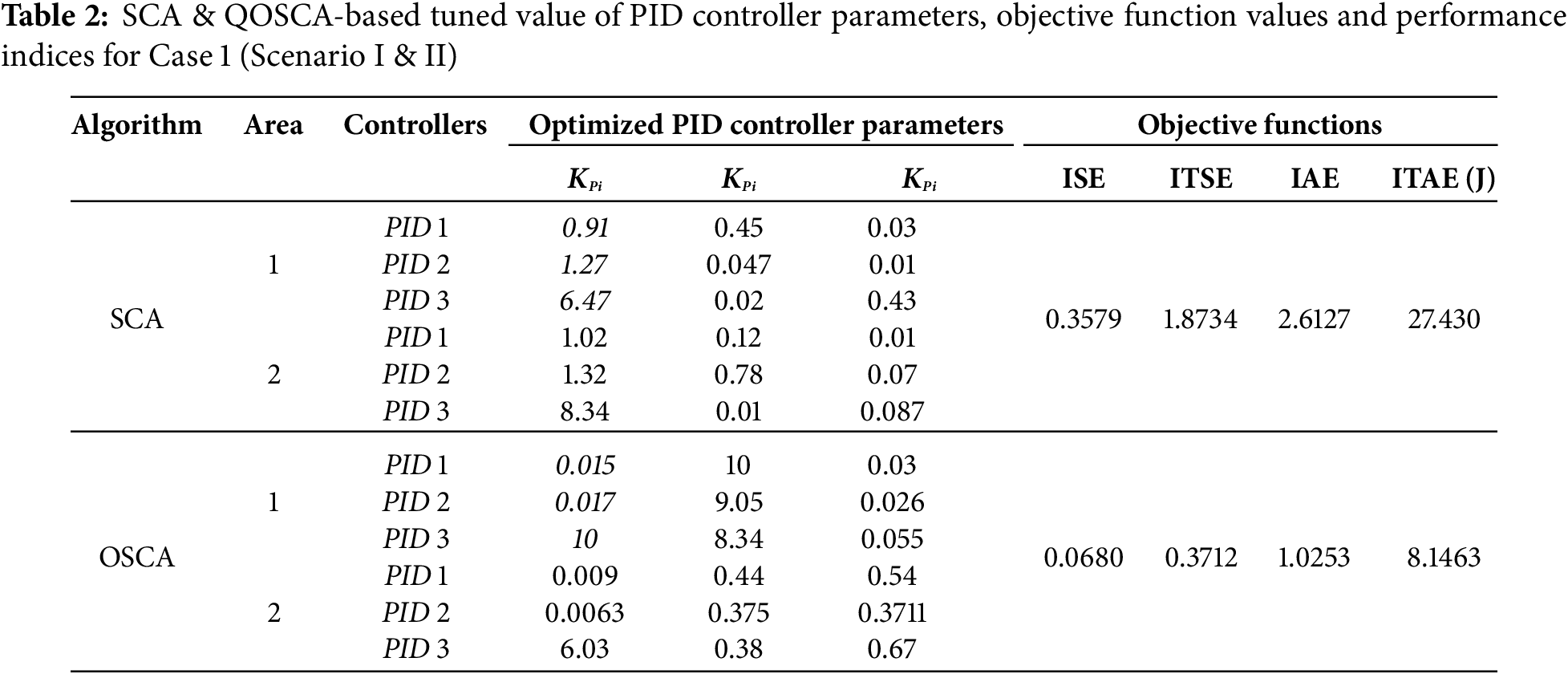
From Fig. 4a and Table 1, it is clear that, in the case of the frequency vs. time deviation analysis, the suggested QOSCA strategy is outperforming the SCA approach in terms of settling time, peak overshoot, and peak undershoot findings. Same thing is going on in case of Δf2 vs. time and ΔPtie vs. time. So, from Fig. 4a–c and Table 1, it can easily be seen that the result of proposed QOSCA optimization techniques provide better dynamic responses than the studied optimization techniques (SCA technique) as mentioned in literature survey [14]. In case of controllers with different types of optimization techniques, this work is also proving the better settling time, peak overshoot and peak undershoot rather than the work mentioned in literature survey [16]. The objective functions and other dynamic responses are also better than that of other QOBL based optimization techniques as mentioned in literature survey [23–26]. Table 2 depicts the QOSCA based optimization technique better controller gains, objective function values and performance indices than the SCA based approach. So, it may infer that using the suggested QOSCA method consistently produces a superior dynamic behavior than the SCA approach.

After seeing Fig. 5, it is very easy to say that the application of proposed QOSCA algorithm gives always the faster result than the traditional SCA optimization technique. From this convergence curve it also can be noticed that the QOSCA gives the better result of objective function rather than the SCA approach.

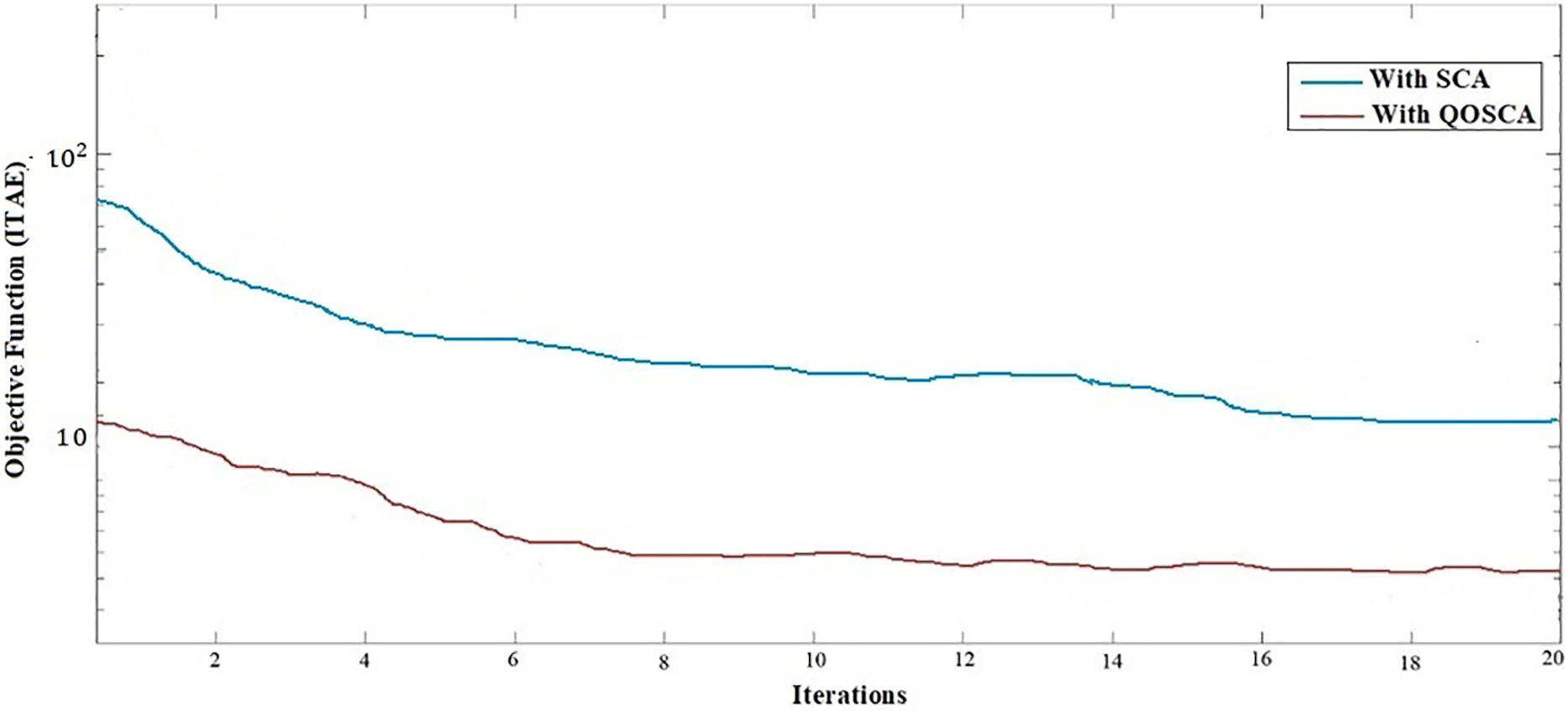
Figure 5: Convergence of iterations with respect to objective function (IATE)

Case 2

As demonstrated by the analysis of case 1, the QOSCA technique outperforms the SCA technique in our suggested system when it comes to adjusting the controllers’ necessary parameters to obtain improved dynamic performance.

Now under case 2, the IHPS model needs to be simplified in such a manner that no such great change will be introduced in the system; thus, the physical behavior of the system will not be hugely distorted. Table 2 shows the modified values of the different PID controller parameters when three PID controllers are used in a region with the QOSCA technique (a metaheuristic optimization tactic). On the other hand, Table 3 displays the adjusted values of the PID controller gains, objective function values and performance indices for the two area systems using the same optimization method when there is only one PID controller is used against an area. Table 4 shows settling time (ts(s)), peak overshoot (Hz/V/pu) and peak undershoot (Hz/V/pu) of the proposed models under study in Case 2.

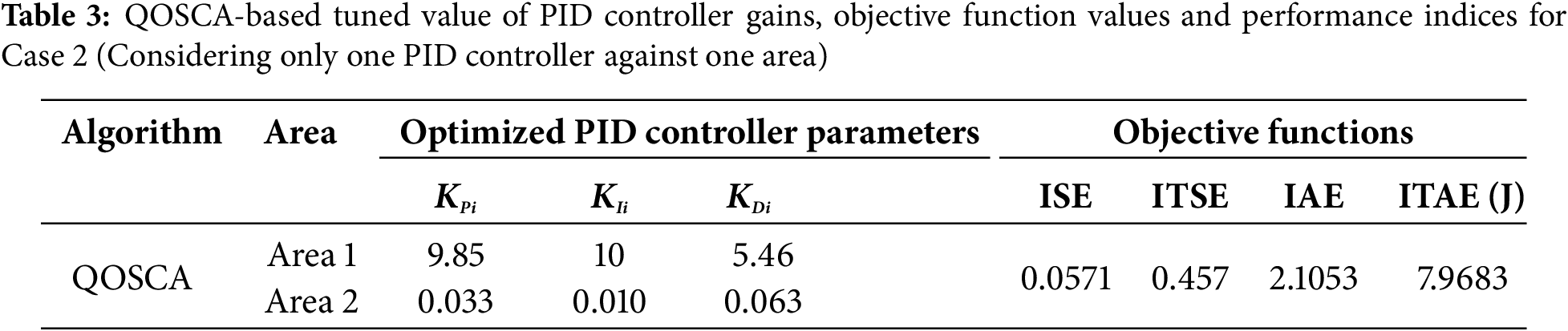
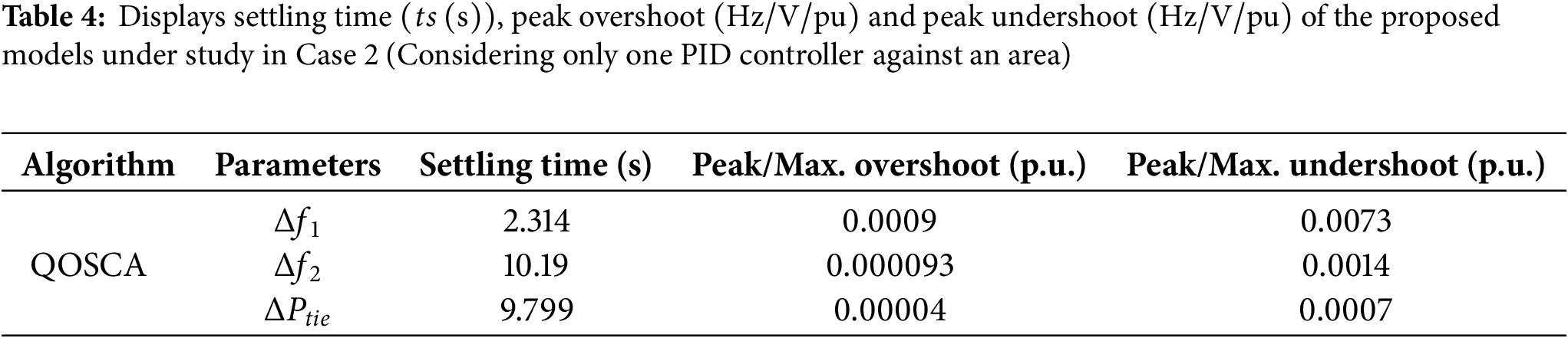
Based on Tables 2 and 3, three outputs of QOSCA have been shown in Fig. 6a–c as follows:

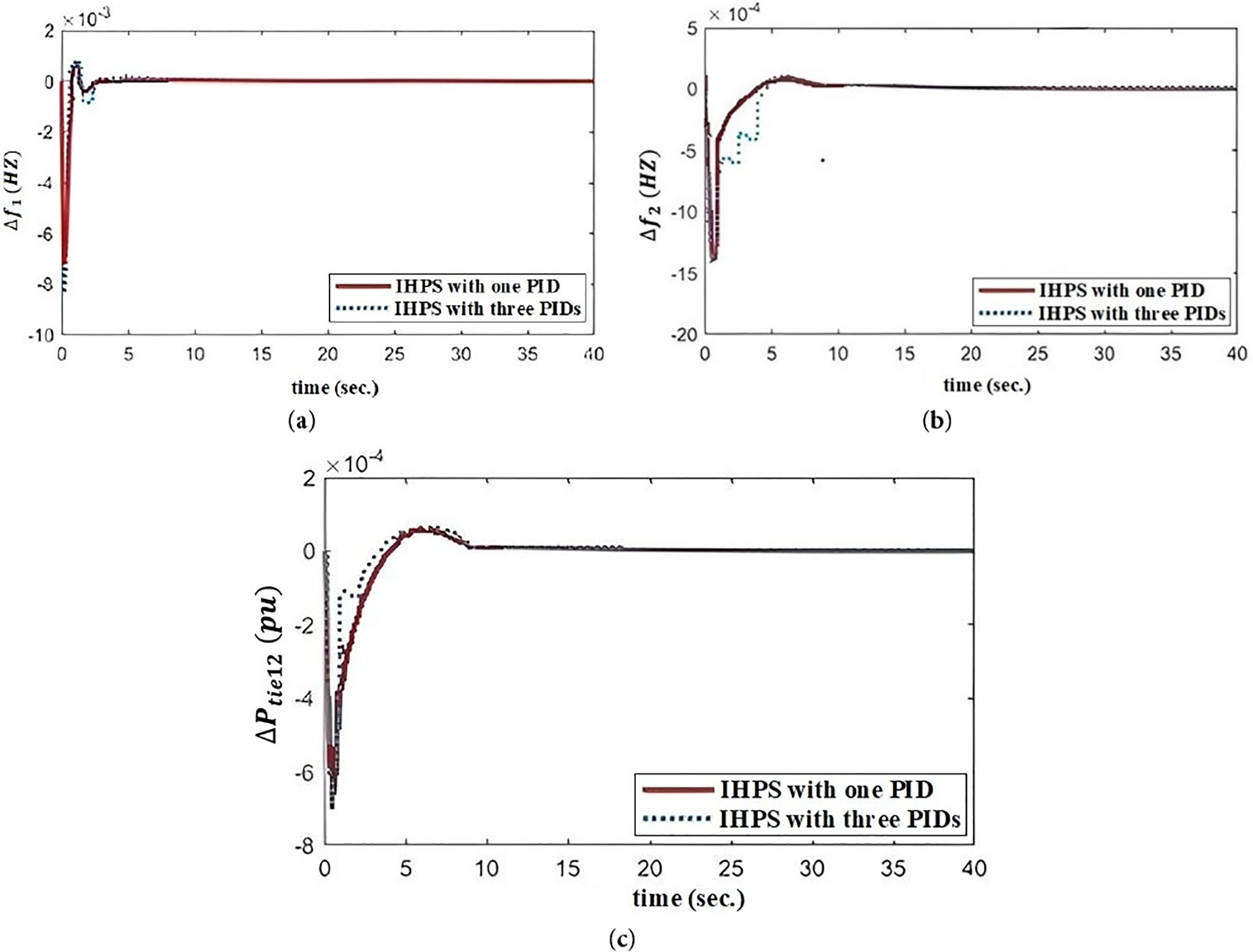
Figure 6: (a) Frequency deviation of Area 1, (b) Frequency deviation of Area 2 and (c) Tie line power variation vs. time in sec. using QOSCA optimization technique

In this instance the QOSCA optimization technique has only been followed for checking the dynamic response of our proposed IHPS system by considering area wise one PID controller as well as three PID controllers. Fig. 6a–c shows the significant dynamic characteristic curves; the bold line indicates how one PID controller responds to each area, while the dashed line indicates how three PID controllers respond to each area. In case of study of each case, the characteristic curves look similar. Comparing Tables 1 and 4, it can be easily justified that the dynamic responses of the proposed system (settling time (ts(s)), peak overshoot (Hz/V/pu) and peak undershoot (Hz/V/pu)) under study in both of two cases are just similar to each other. Within this range of time limits of dynamic response of the system, rather than using three PID controllers we can use one PID controller only against each area safely. The QOSCA optimization method improves the dynamic response of the system effectively in such a manner that helps to simplify the interconnected system by reducing the number of PID controllers. Consequently, our interconnected model will become simpler than the last proposed model (as shown in Fig. 1) and the proposed model shown in Fig. 7 can be considered. This kind of approach of reduction of number of controllers is rarely discussed by researchers.

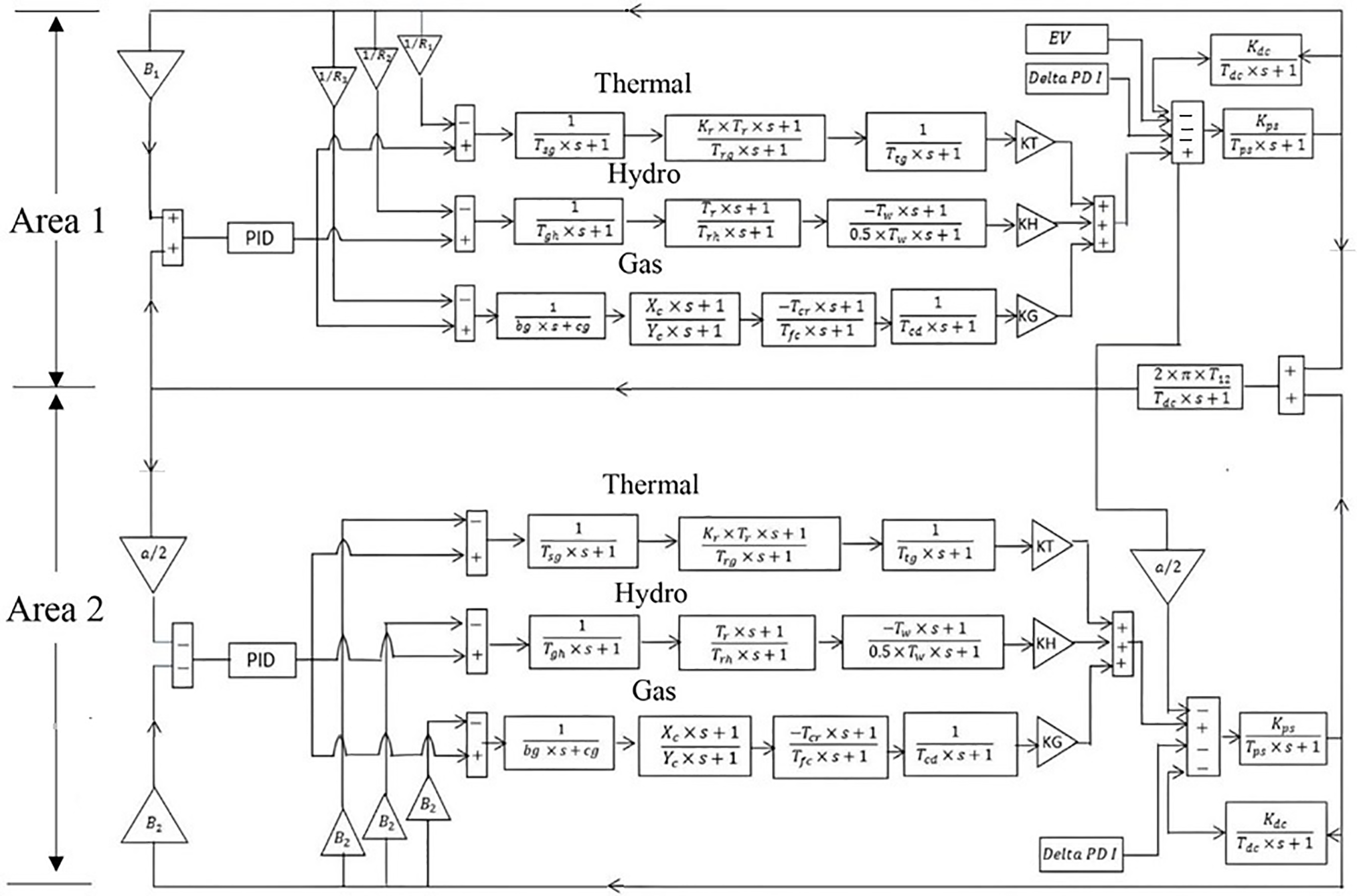
Figure 7: Transfer function model of an interconnected hybrid power system (with only one PID controller against an area)

Case 3

The system dynamic responses of the sensitivity analysis carried out on the system model by altering operating load circumstances and the system parameters, R (governor speed regulation) and B (frequency bias parameter), as shown in Fig. 8. Results are shown in Figs. 9–12. To show how resilient the suggested QOSCA-optimized PID controller is to parameter uncertainties, parametric variations were added to the system model. The system reactions caused by the suggested control method in the system model were then examined. The robustness of the power system to large changes in the system parameters was examined by simultaneously varying the frequency bias parameter, B, and the governor speed regulation parameter, R, of both control areas in steps of 10%, one at a time, from their nominal values in the range of +25% to −25%. The dynamic system performance or behavior with the QOSCA optimized PID controller for 1% step load perturbations in area 1 for variation in the aforementioned parameters is shown in Figs. 9–12. The findings of sensitivity analysis make it clear that changing the operational load situation and system parameters little affects the system’s dynamic performances. The suggested optimized PID controller provides a satisfactory degree of robustness and stability at nominal parameters, as demonstrated by Figs. 9–12. These ideal controller parameter values do not need to be reset for notable changes in the system parameters or system loads. The suggested controller has effectively shown its efficacy and resilience to parametric uncertainty since changes in several system parameters have no discernible impact on control performance.

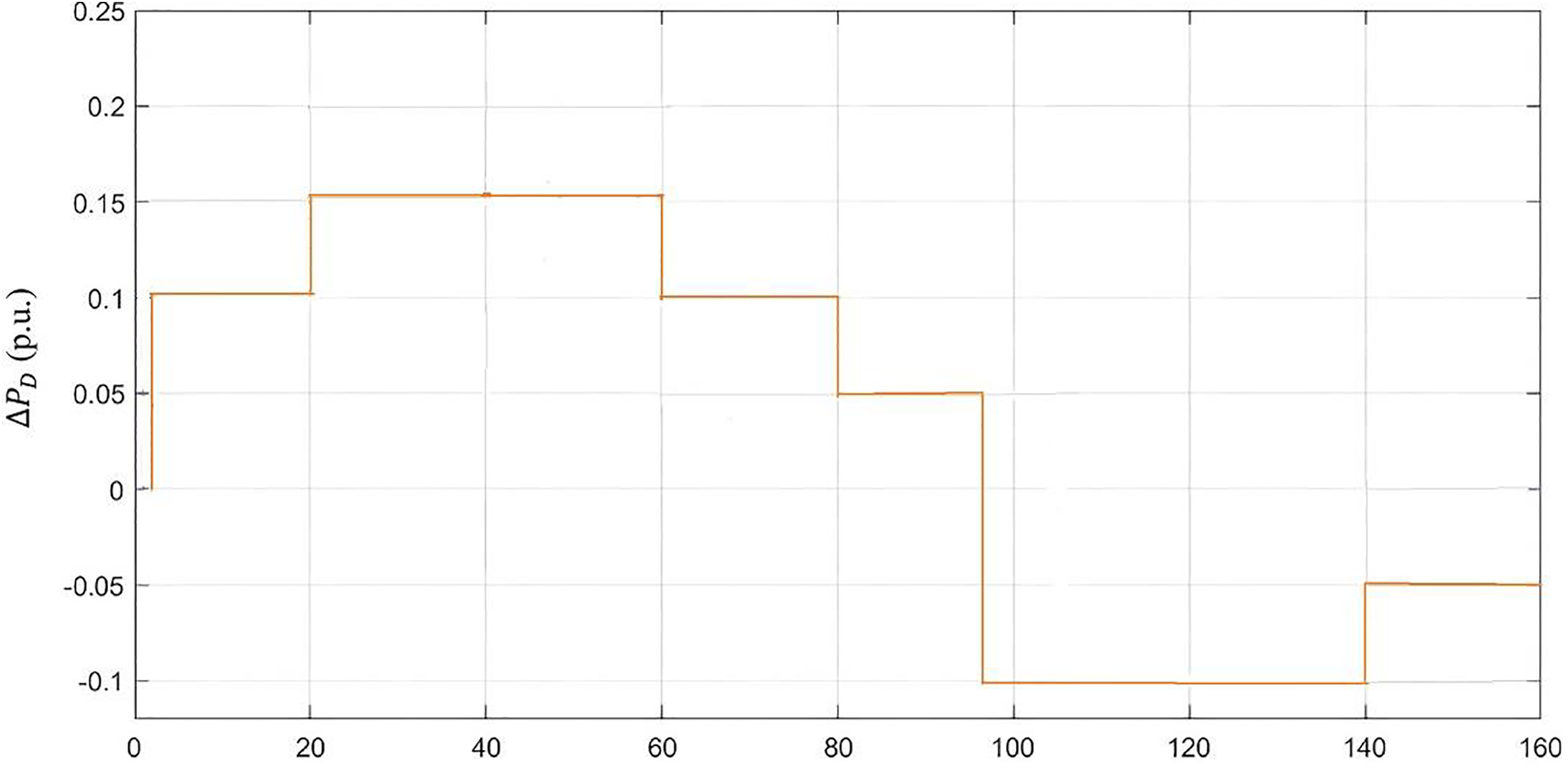
Figure 8: It shows the random SLP (ΔPD) in per unit (p.u.) vs. time in seconds

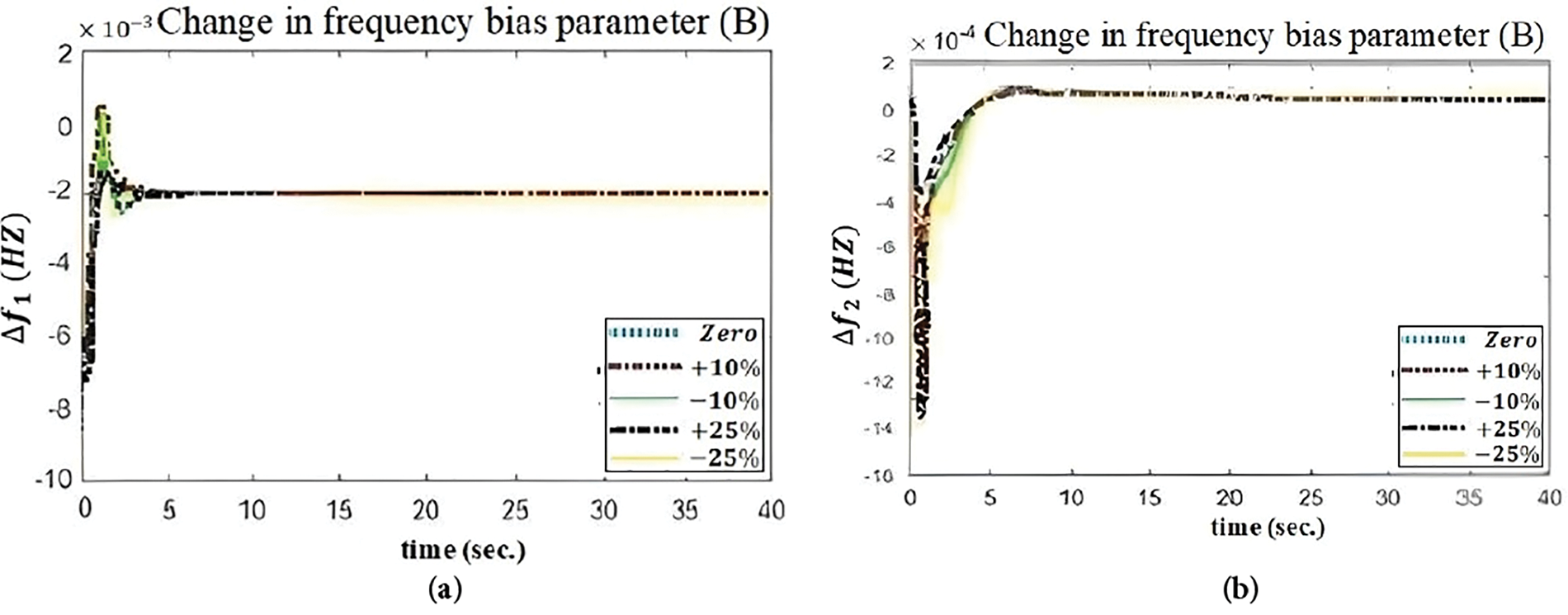
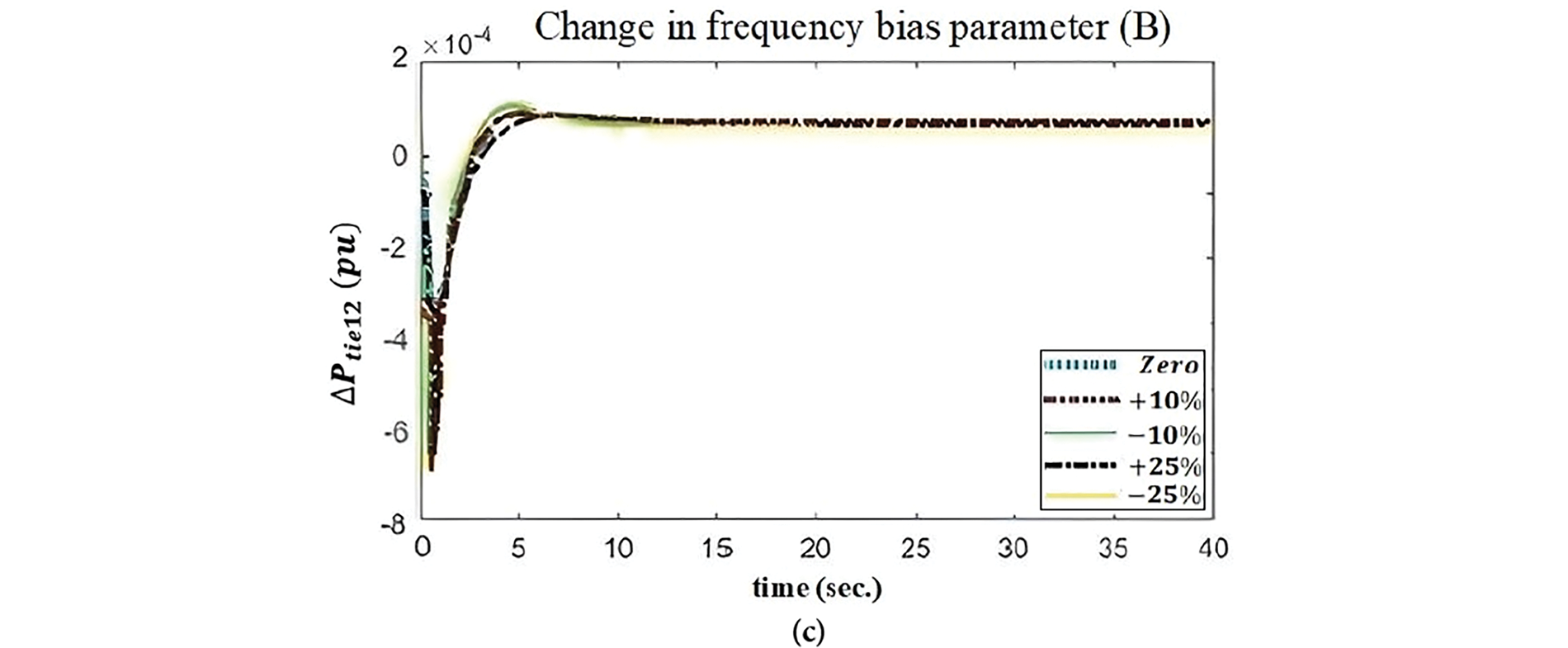
Figure 9: Change in frequency bias parameter (B) considering (a) Δf1 vs. time(s), (b) Δf2 vs. time(s), (c) ΔPtie vs. time(s)

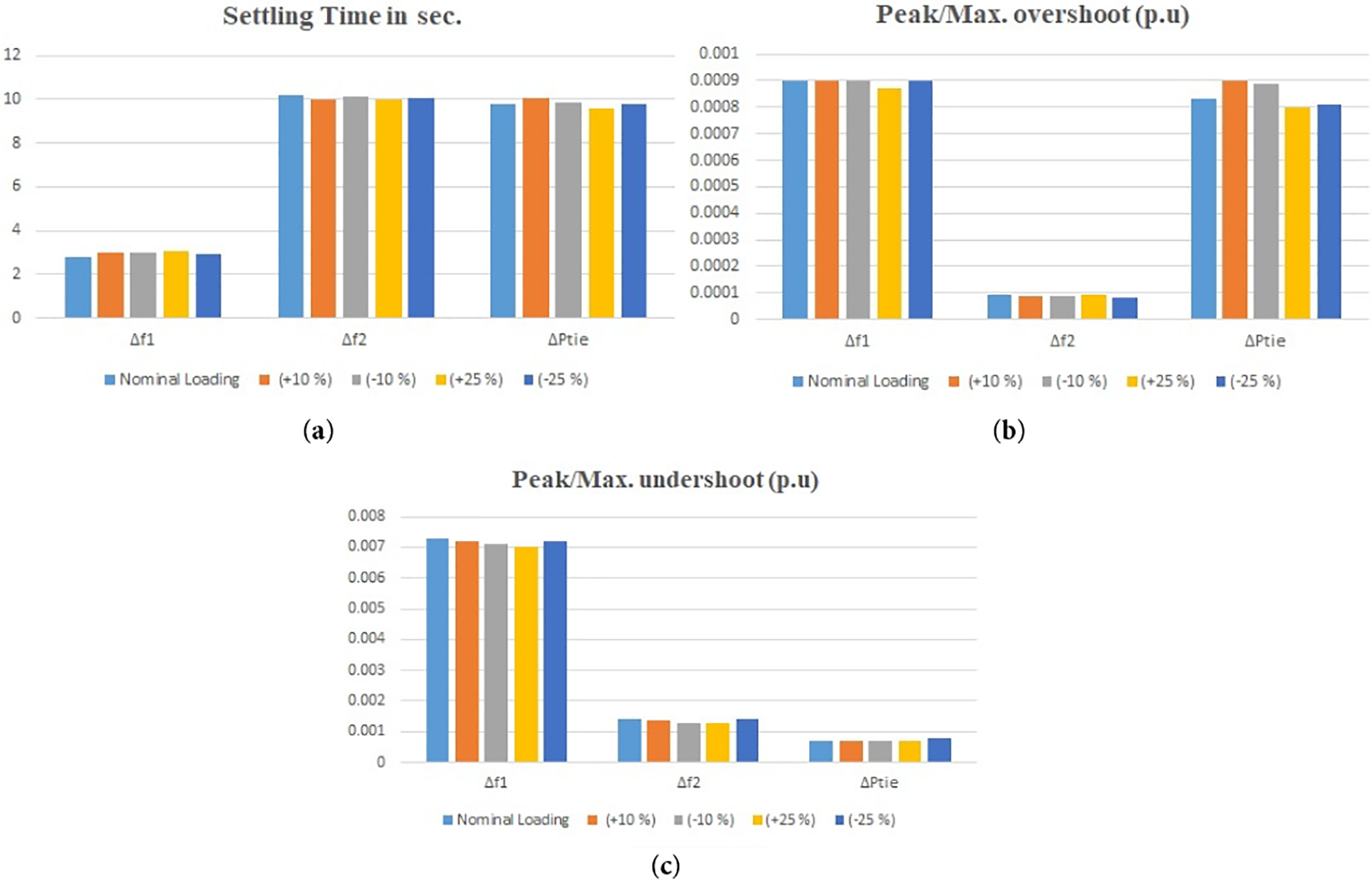
Figure 10: It displays robustness of the proposed model under study by varying the load ±10% and ±25% considering frequency bias parameter B with respect to (a) settling time (ts(s)), (b) peak overshoot (Hz/V/pu) and (c) peak undershoot (Hz/V/pu) of the proposed models under study

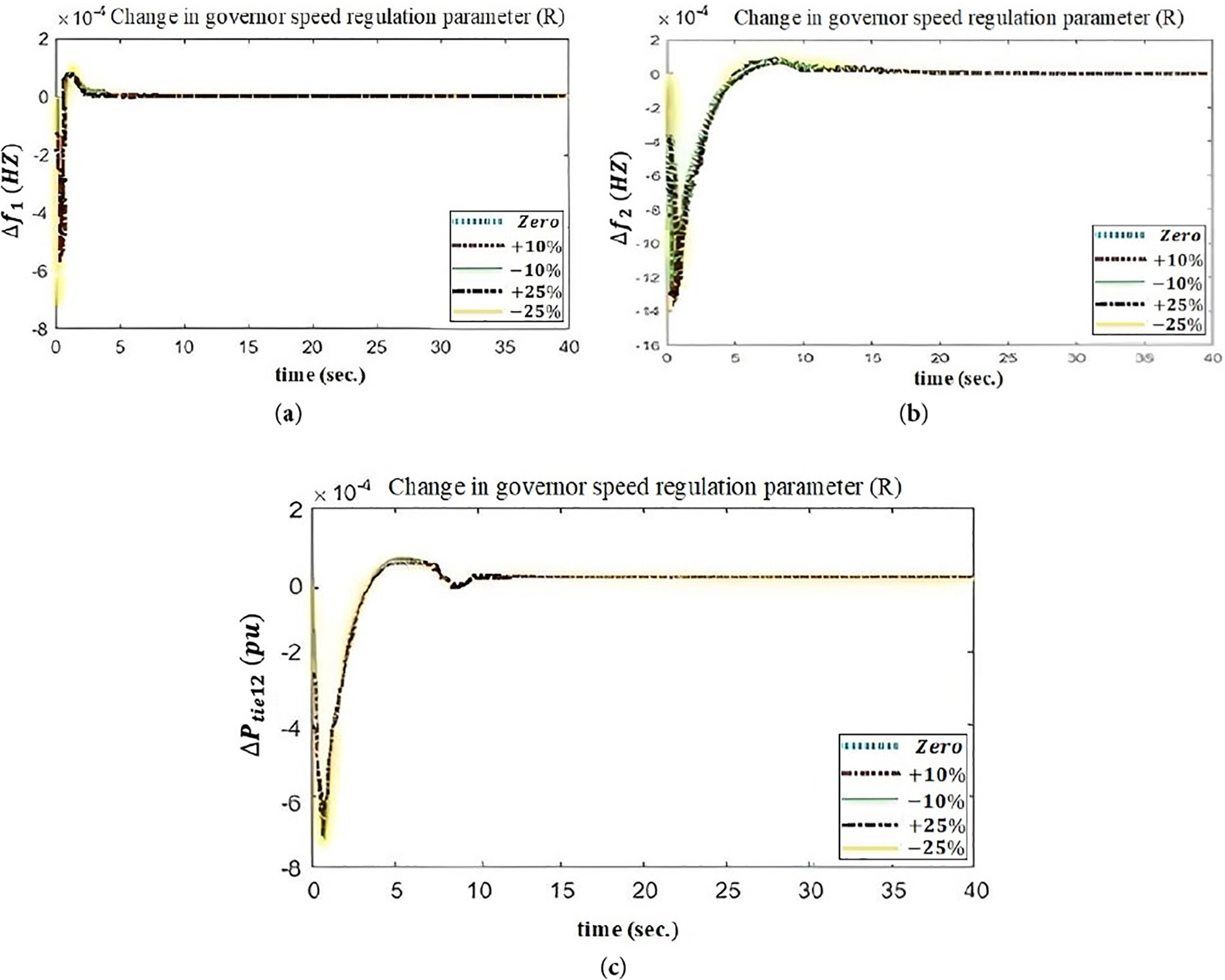
Figure 11: Change in governor speed regulation parameter (R) considering (a) Δf1 vs. time(s), (b) Δf2 vs. time(s), (c) ΔPtie vs. time(s)

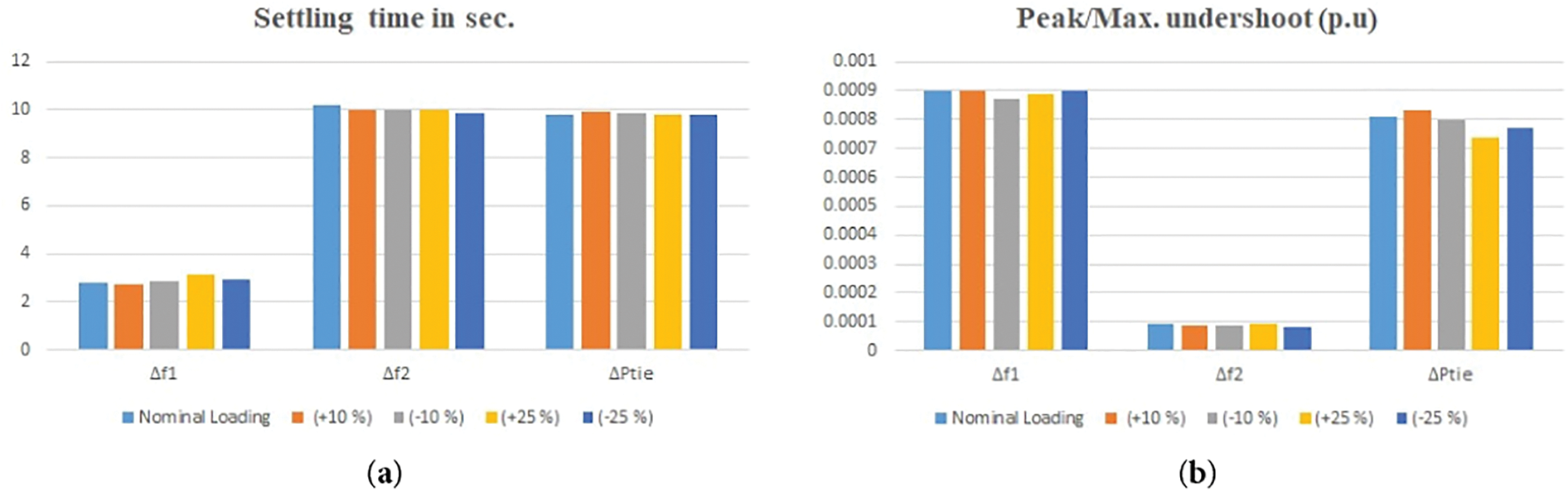
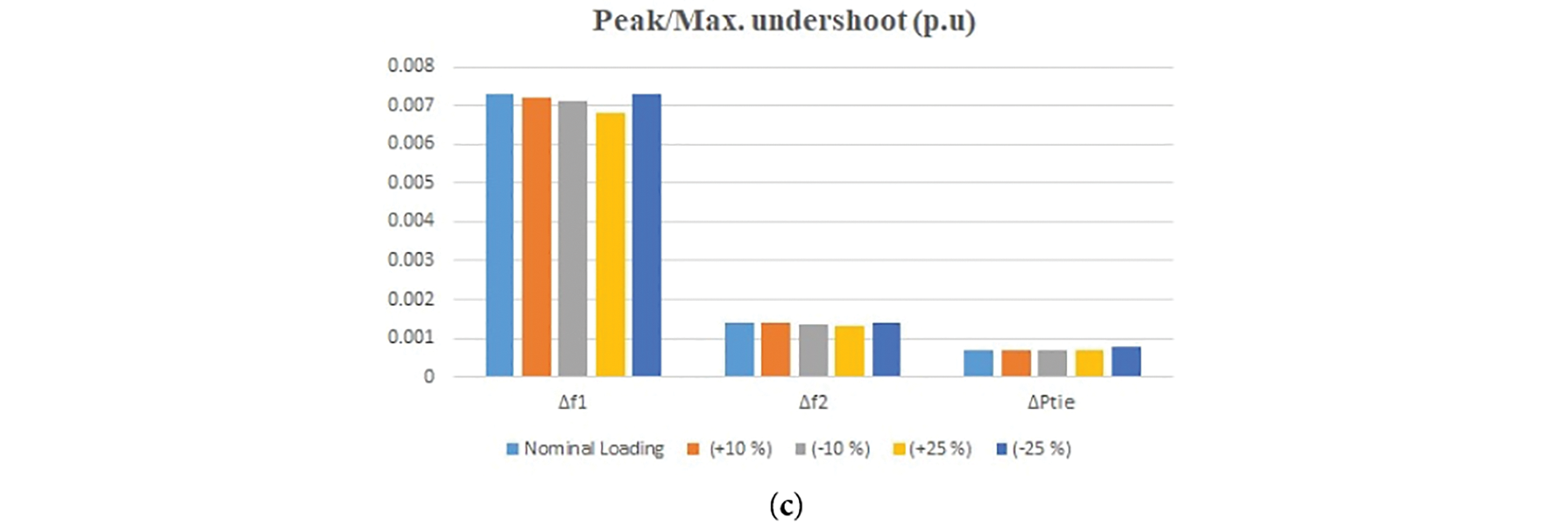
Figure 12: It displays robustness of the proposed model under study by varying the load ±10% and ±25% considering speed regulation parameter R with respect to (a) settling time (ts(s)), (b) peak overshoot (Hz/V/pu) and (c) peak undershoot (Hz/V/pu) of the proposed models under study

Fig. 8 shows the random SLP (ΔPD) in per unit (p.u.) vs. time in seconds. The SLP changes from 0 to 0.1 p.u. at 1-s intervals from 1.2 to 20 s, then remains at 0.15 p.u. from 20 to 60 s. Subsequently, it drops to 0.1 p.u. at 60 s and remains same up to 80 s. At 80 s again it drops to 0.05 p.u. and remains there until 98 s. Further, it decreases to −0.1 p.u. at 98 s and remains constant until 140 s. Finally, it returns to −0.05 p.u. at 140 s and remains there until 160 s.

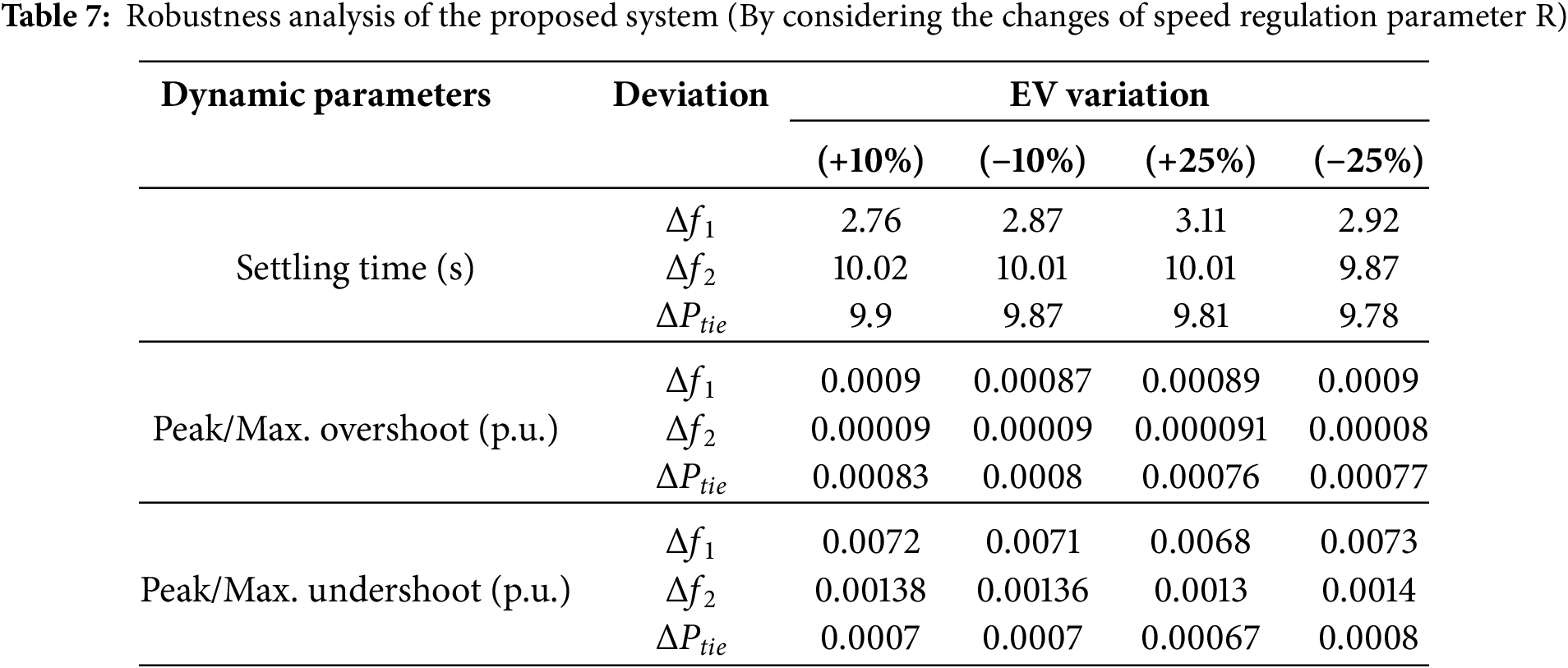
Tables 5–7 display settling time (ts(s)), peak overshoot (Hz/V/pu) and peak undershoot (Hz/V/pu) of the proposed models under study in Case 3. It can be seen from the different dynamic results of Figs. 9–12 (as shown in Tables 5 and 6) that the values are quite similar to the values shown in Table 4, despite a wide range of EV operating conditions. There is no significant change in the responses when compared to the nominal values. The system’s resilience is thus highlighted since it is not necessary to reset the parameters that were established at the nominal condition to a wide range of system loading fluctuations.

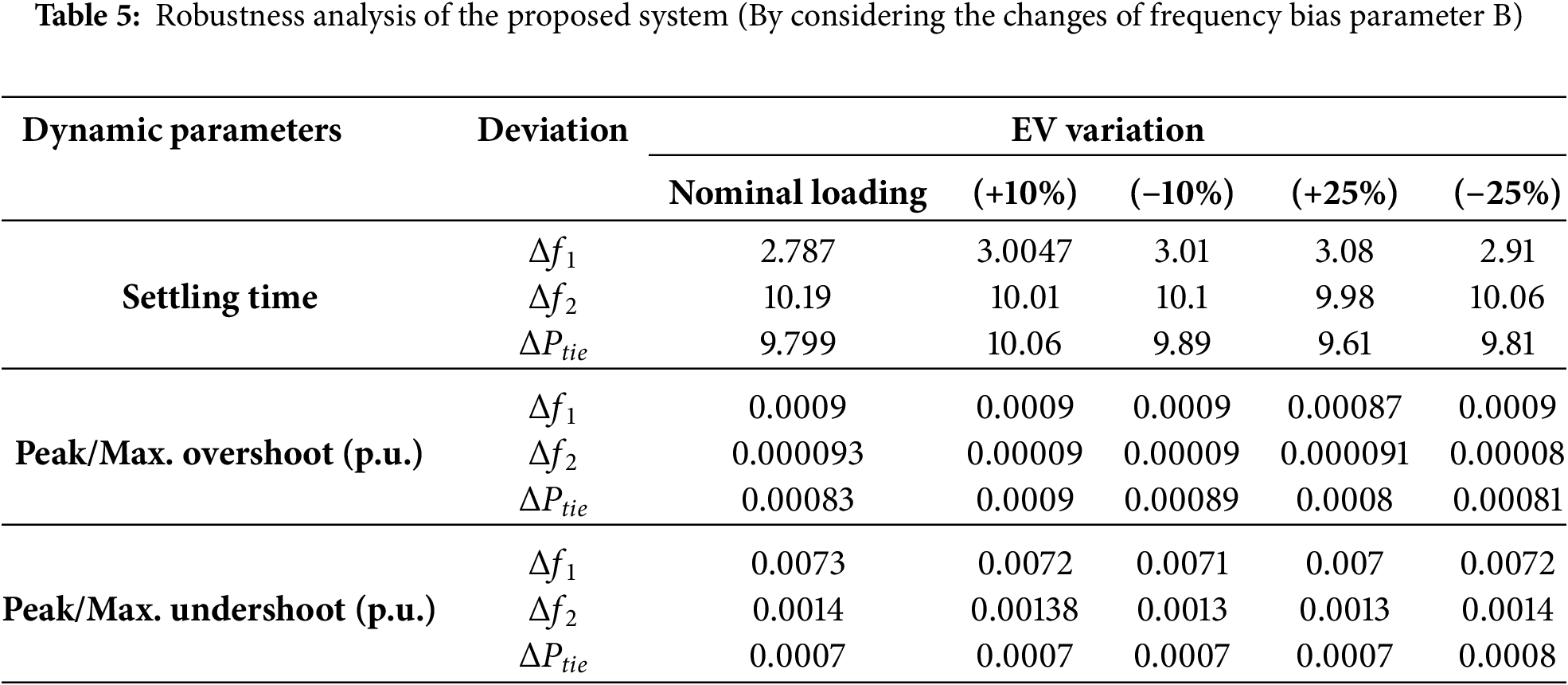
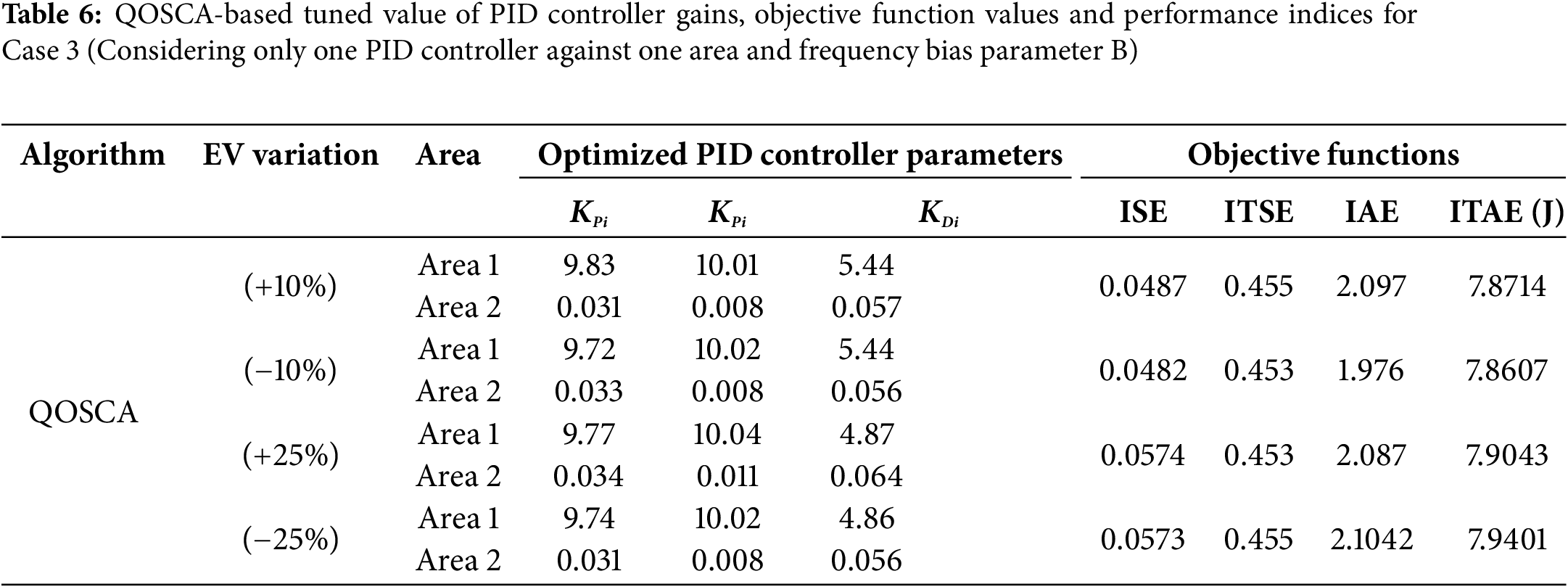
From Fig. 10, the three charts are clearlly shown the robustness of the system with proposed optimisation technique under different loading conditions. In Table 6, the optimised PID controller parameters, objective function values and and performance indices with respect to frequency bias parameter B has been shown under different loading condition. These results are quit similar to Table 3. Therefore, it can be said that QOSCA optimisation technique finally gives the robustness of the system in such a large scale variation of load.

Similarly from Fig. 9, the three charts are clearlly shown the robustness of the system with proposed optimisation technique under different loading conditions. The results, which has been shown in Table 8 by considering speed regulation parameter R, are quite similar to Table 3. So, through this approach it can be shown clearlly the effectiveness of QOSCA algorithm on this model model.

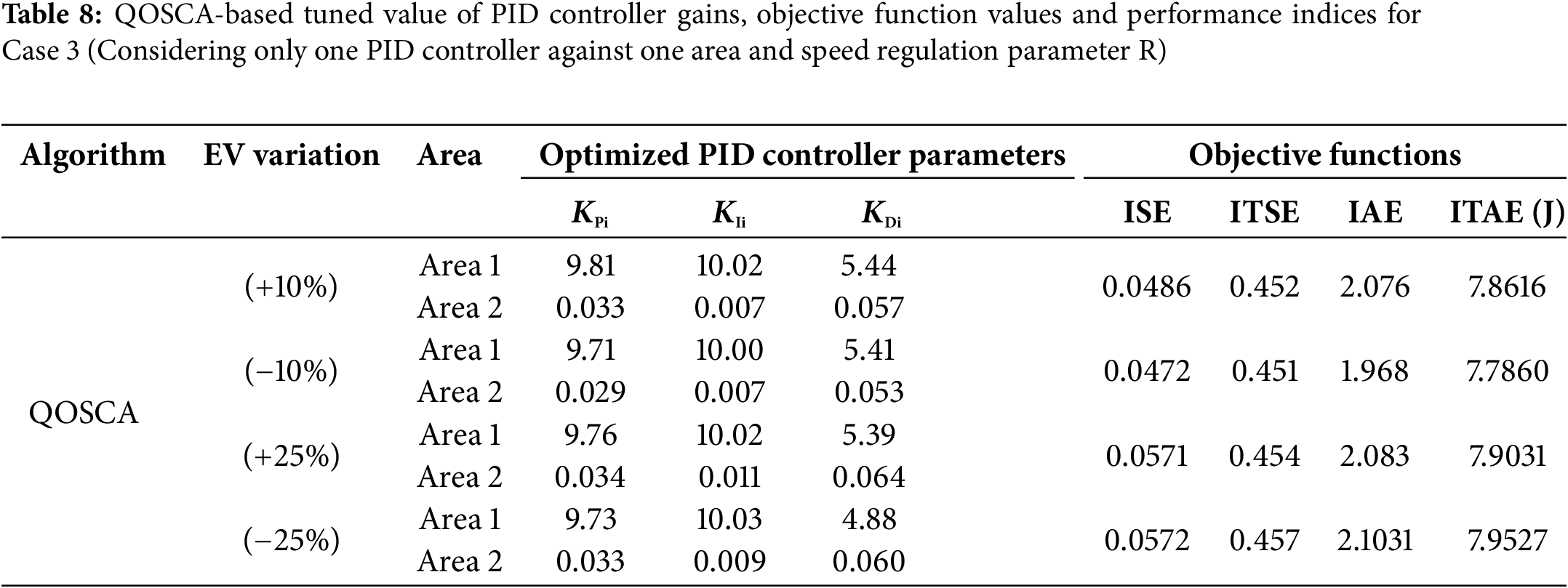
To verify the stability and robustness of the proposed controller, sensitivity analysis is carried out by varying the loading scenario and two system parameters, R (Governor Speed regulation) and B (Frequency Bias parameter). This approach rarely has been addressed in other works. The robustness of the system along with the proposed QOSCA optimization technique has been checked successfully in this work.

6  Conclusions and Scope of Future Work

In this study, we propose the load frequency control analysis of a multi-unit source power system with several power generation sources, such as hydro, thermal, and gas power plants. PID controllers have been employed to regulate both the power and the frequency changes in this two-area interconnected system. In order to improve the dynamic response of our suggested system in a short amount of time, the necessary controller parameters have been adjusted using the metaheuristic hybrid optimization technique QOSCA and traditional SCA. In the case of QOSCA, the main performance indices (i.e., ITAE) are 8.1463, whereas the SCA-based approach gives the result of ITAE 27.430. Based on the results, it is evident that, for our analysis, the suggested QOSCA technique performs better than the standard SCA technique. This paper is unique because it applies to the QOSCA optimization technique, which has only been demonstrated in this work in the context of an LFC investigation so far.

An attempt has been made to simplify the circuit by reducing the number of PID controllers without hampering any dynamic response or other circuitry properties of the main circuit. It has been observed that the ITAE is 7.9683 when we are applying one PID controller only against one area, which is just the same as the IATE value (81,463) along with three PID controllers against one area. In addition to this, the dynamic responses (i.e., settling times, peak overshoots, and peak undershoots) of frequency variations and tie line power variations are similar. So, the application of one PID controller against one area can be an alternative to the application of three PID controllers against that particular area. Thus, it is possible to simplify the proposed system by using one PID controller in place of three PID controllers. This type of approach, which is considered to simplify the circuit configuration, is one more unique approach of this paper. After the reduction of the circuit by applying the QOSCA optimization technique and varying the load, the sensitivity of the proposed system has been checked. The redesigned interconnected model’s dynamic characteristic has been verified. The robustness of the system demonstrates that the controller is stable for a wide range of load changes. The EV system (Electrical Load) variation is followed by ±10% and ±25%. The ITAE values are 7.8714, 7.8607, 7.9043 and 7.9401 against the +10%, −10%, +25% and −25% load variation respectively which are quite similar to IATE of the zero load variation (i.e., 7.9683). The result analysis also shows that the dynamic responses are similar both under zero-load variation and under several cases of load variation. Thus, the robustness of the system has been checked in this work for a large range of load variations.

In future studies, more work can be done by enhancing and modifying the interconnected area, as well as including more detailed functions of the EV system, and with grid interconnection.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, Investigation, Writing—Original Draft, Writing—Review and Editing: Pralay Roy, Pabitra Kumar Biswas, Chiranjit Sain and Taha Selim Ustun. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data and materials are available from the corresponding authors upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A

Nominal system parameters for the IHPS model investigated are given in Table A1.

Nomenclature

References

1. Kundur P. Power system stability and control. New York, NY, USA: Mc-Grall Hill; 1994. [Google Scholar]

2. Elgerd OI. Electric energy systems theory an introduction. New Delhi, India: Tata McGraw-Hill; 1983. [Google Scholar]

3. Hassan B. Robust power system frequency control. New York, NY, USA: Springer; 2009. [Google Scholar]

4. Farooq Z, Rahman A, Suhail Hussain SM, Ustun TS. Power generation control of renewable energy based hybrid deregulated power system. Energies. 2022;15(2):517. doi:10.3390/en15020517. [Google Scholar] [CrossRef]

5. Latif A, Suhail Hussain SM, Das DC, Ustun TS. Optimization of two-stage IPD-(1+I) controllers for frequency regulation of sustainable energy based hybrid microgrid network. Electronics. 2021;10(8):919. doi:10.3390/electronics10080919. [Google Scholar] [CrossRef]

6. Barisal AK. Comparative performance analysis of teaching learning based optimization for automatic load frequency control of multi-source power systems. Int J Electr Power Energy Syst. 2015;66(4):67–77. doi:10.1016/j.ijepes.2014.10.019. [Google Scholar] [CrossRef]

7. Nnada J, Parida M, Kalam A. Automatic generation control of a multi-area power system with conventional integral controllers. Int J Eng Trends Technol. 2017;50(2):75–84. doi:10.1016/j.jestch.2015.07.011. [Google Scholar] [CrossRef]

8. Ibraheem, Kumar P, Kothari DP. Recent philosophies of automatic generation control strategies in power systems. IEEE Trans Power Syst. 2005;20(1):346–57. doi:10.1109/TPWRS.2004.840438. [Google Scholar] [CrossRef]

9. El Mallahi A, Mharzi H. An maximum power point tracking algorithm for photovoltaic power systems using the particle swarm optimization technique. In: 2025 5th International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET); 2025 May 15–16; Fez, Morocco. p. 1–8. doi:10.1109/IRASET64571.2025.11008184. [Google Scholar] [CrossRef]

10. Hussain I, Das DC, Sinha N, Latif A, Suhail Hussain SM, Ustun TS. Performance assessment of an islanded hybrid power system with different storage combinations using an FPA-tuned two-degree-of-freedom (2DOF) controller. Energies. 2020;13(21):5610. doi:10.3390/en13215610. [Google Scholar] [CrossRef]

11. Das A, Dawn S, Gope S. A strategy for system risk mitigation using FACTS devices in a wind incorporated competitive power system. Sustainability. 2022;14(13):8069. doi:10.3390/su14138069. [Google Scholar] [CrossRef]

12. Abdolrasol MGM, Ayob A, Mutlag AH, Ustun TS. Optimal fuzzy logic controller based PSO for photovoltaic system. Energy Rep. 2023;9(14):427–34. doi:10.1016/j.egyr.2022.11.039. [Google Scholar] [CrossRef]

13. Khan MA, Singh A. Maximum power point tracking using particle swarm optimization for photovoltaic systems. In: 2025 International Conference on Sustainable Energy Technologies and Computational Intelligence (SETCOM); 2025 Feb 21–23; Gandhinagar, India. p. 1–6. doi:10.1109/SETCOM64758.2025.10932479. [Google Scholar] [CrossRef]

14. Saakshi S, Kapil P, Raunak J. Whale optimization algorithm based PID controller design of two area load frequency control with nonlinearities. Int J Res Eng Sci Manag. 2020;3(2):101–6. doi:10.1007/978-981-15-5077-5_35. [Google Scholar] [CrossRef]

15. Ashraf H, Shimaa M, Mountasser M. Load frequency control using optimized control techniques. J Eng Sci Assiut Univ. 2020;48(6):1119–36. doi:10.21608/jesaun.2020.42349.1011. [Google Scholar] [CrossRef]

16. Sahu PR, Simhadri K, Mohanty B, Hota PK, Abdelaziz AY, Albalawi F, et al. Effective load frequency control of power system with two-degree freedom tilt-integral-derivative based on whale optimization algorithm. Sustainability. 2023;15(2):1515. doi:10.3390/su15021515. [Google Scholar] [CrossRef]

17. Saikia LC, Nanda J, Mishra S. Performance comparison of several classical controllers in AGC for multi-area interconnected thermal system. Int J Electr Power Energy Syst. 2011;33(3):394–401. doi:10.1016/j.ijepes.2010.08.036. [Google Scholar] [CrossRef]

18. Parmar KPS, Majhi S, Kothari DP. Improvement of dynamic performance of LFC of the two area power system: an analysis using MATLAB. Int J Comp Appl. 2012;40:28–32. [Google Scholar]

19. Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems. Knowl Based Syst. 2016;96(63):120–33. doi:10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

20. Priyanka SS, Kumar AK, Shivani P, Swetha S. Investigations on analog circuits using optimization algorithms. In: 2025 3rd International Conference on Advancements in Electrical, Electronics, Communication, Computing and Automation (ICAECA); 2025 Apr 4–5; Coimbatore, India. p. 1–5. doi:10.1109/ICAECA63854.2025.11012413. [Google Scholar] [CrossRef]

21. Rahnamayan S, Tizhoosh HR, Salama MMA. Quasi-oppositional differential evolution. In: 2007 IEEE Congress on Evolutionary Computation; 2007 Sep 25–28; Singapore. p. 2229–36. doi:10.1109/CEC.2007.4424748. [Google Scholar] [CrossRef]

22. Roy PK, Sarkar R. Solution of unit commitment problem using quasi-oppositional teaching learning based algorithm. Int J Electr Power Energy Syst. 2014;60(2):96–106. doi:10.1016/j.ijepes.2014.02.008. [Google Scholar] [CrossRef]

23. Shiva CK, Shankar G, Mukherjee V. Automatic generation control of power system using a novel quasi-oppositional harmony search algorithm. Int J Electr Power Energy Syst. 2015;73(1):787–804. doi:10.1016/j.ijepes.2015.05.048. [Google Scholar] [CrossRef]

24. Shiva CK, Vedik B, Mahapatra S, Nandi M, Raj S, Mukherjee V. Load frequency stabilization of stand-alone hybrid distributed generation system using QOHS algorithm. Int J Numer Model Electron Netw Devices Fields. 2022;35(4):e2998. doi:10.1002/jnm.2998. [Google Scholar] [CrossRef]

25. Paul C, Roy PK, Mukhaerjee V. Optimal solution for hydro-thermal–wind-solar scheduling using opposition-based whale optimization algorithm. Soft Comput. 2024;28(7):6003–37. doi:10.1007/s00500-023-09315-1. [Google Scholar] [CrossRef]

26. Mudi J, Shiva CK, Mukherjee V. Quasi-oppositional whale optimization optimized load frequency stabilization of hybrid power systems integrated with electric vehicle. Adv Theory Simul. 2022;5(4):2100510. doi:10.1002/adts.202100510. [Google Scholar] [CrossRef]

27. Debbarma S, Dutta A. Utilizing electric vehicles for LFC in restructured power systems using fractional order controller. IEEE Trans Smart Grid. 2017;8(6):2554–64. doi:10.1109/TSG.2016.2527821. [Google Scholar] [CrossRef]

28. Singh J, Singh J, Kumar R, Bansal R. Load frequency control of two-area power with electrical vehicles using soft computing technique. Int J Electron Eng. 2017;9(2):1–8. [cited 2025 Jan 1]. Available from: https://www.researchgate.net/publication/318787069_Load_Frequency_Control_of_Two_-_Area_Power_With_Electrical_Vehicles_Using_Soft_Computing_Technique. [Google Scholar]

29. Arya Y. Effect of electric vehicles on load frequency control in interconnected thermal and hydrothermal power systems utilising CFFOIDF controller. IET J Gener Transm Distrib. 2020;14(14):2666–75. doi:10.1049/iet-gtd.2019.1217. [Google Scholar] [CrossRef]

30. Aftab MA, Hussain SS, Ali I, Ustun TS. IEC 61850 and XMPP communication based energy management in microgrids considering electric vehicles. IEEE Access. 2018;6:35657–68. doi:10.1109/ACCESS.2018.2848591. [Google Scholar] [CrossRef]

31. Wu D, Cai C, Aliprantis DC. Potential impacts of aggregator controlled plug-in electric vehicles on distribution systems. In: 2011 4th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP); 2011 Dec 13–16; San Juan, PR, USA. p. 105–8. doi:10.1109/CAMSAP.2011.6135898. [Google Scholar] [CrossRef]

32. Tappeta VSR, Appasani B, Patnaik S, Ustun TS. A review on emerging communication and computational technologies for increased use of plug-In electric vehicles. Energies. 2022;15(18):6580. doi:10.3390/en15186580. [Google Scholar] [CrossRef]

33. Yilmaz M, Krein PT. Review of battery charger topologies, charging power levels, and infrastructure for plug-in electric and hybrid vehicles. IEEE Trans Power Electron. 2013;28(5):2151–69. doi:10.1109/tpel.2012.2212917. [Google Scholar] [CrossRef]

34. Guille C, Gross G. A conceptual framework for the vehicle-to-grid (V2G) implementation. Energy Policy. 2009;37(11):4379–90. doi:10.1016/j.enpol.2009.05.053. [Google Scholar] [CrossRef]

35. Liu H, Hu Z, Song Y, Lin J. Decentralized vehicle-to-grid control for primary frequency regulation considering charging demands. IEEE Trans Power Syst. 2013;28(3):3480–9. doi:10.1109/tpwrs.2013.2252029. [Google Scholar] [CrossRef]

36. Takagi M, Yamaji K, Yamamoto H. Power system stabilization by charging power management of plug-in hybrid electric vehicles with LFC signal. In: 2009 IEEE Vehicle Power and Propulsion Conference; 2009 Sep 7–10; Dearborn, MI, USA. p. 822–6. Available from: https://ieeexplore.ieee.org/document/5289763/ [Google Scholar]

37. Mishra D, Maharana MK, Kar MK, Nayak A, Islam MM, Ustun TS. A metaheuristic algorithm for regulating virtual inertia of a standalone microgrid incorporating electric vehicles. J Eng. 2024;2024(5):e12383. doi:10.1049/tje2.12383. [Google Scholar] [CrossRef]

38. Babina Babu M, Shereef RM. Optimal scheduling of electric vehicles for peak clipping services. In: 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020); 2020 Jan 2–4; Cochin, India. p. 1–6. doi:10.1109/pesgre45664.2020.9070736. [Google Scholar] [CrossRef]

39. Masuta T, Yokoyama A. Supplementary load frequency control by use of a number of both electric vehicles and heat pump water heaters. IEEE Trans Smart Grid. 2012;3(3):1253–62. doi:10.1109/tsg.2012.2194746. [Google Scholar] [CrossRef]

40. Almeida PR, Lopes JP, Soares FJ, Vasconcelos MH. Automatic generation control operation with electric vehicles. In: 2010 IREP Symposium Bulk Power System Dynamics and Control-VIII (IREP); 2010 Aug 1–6; Rio de Janeiro, Brazil. p. 1–7. doi:10.1109/VPPC.2009.5289763. [Google Scholar] [CrossRef]

41. Wu D, Aliprantis DC, Ying L. Load scheduling and dispatch for aggregators of plug-in electric vehicles. IEEE Trans Smart Grid. 2011;3(1):368–76. doi:10.1109/tsg.2011.2163174. [Google Scholar] [CrossRef]

42. Singh NK, Koley C, Gope S, Dawn S, Ustun TS. An economic risk analysis in wind and pumped hydro energy storage integrated power system using meta-heuristic algorithm. Sustainability. 2021;13(24):13542. doi:10.3390/su132413542. [Google Scholar] [CrossRef]

43. Gbadega PA, Sun Y. Primal-dual interior-point algorithm for electricity cost minimization in a prosumer-based smart grid environment: a convex optimization approach. Energy Rep. 2022;8(4):681–95. doi:10.1016/j.egyr.2022.10.144. [Google Scholar] [CrossRef]

44. SeyedShenava SJ, Asefi S. Tuning controller parameters for AGC of multi-source power system using SCA algorithm. In: 6th International Conference on Electrical, Computer, Mechanical and Mechatronics Engineering (ICE2017); 2017 Feb 9–10; Dubai, United Arab Emirates. [cited 2025 Jan 1]. Available from: https://www.researchgate.net/publication/323557181_Tuning_Controller_Parameters_for_AGC_of_Multisource_Power_System_using_SCA_Algorithm [Google Scholar]

45. Pappachen A, Fathima AP. Load frequency control in deregulated power system integrated with SMES-TCPS combination using ANFIS controller. Int J Electr Power Energy Syst. 2016;82(2):519–34. doi:10.1016/j.ijepes.2016.04.032. [Google Scholar] [CrossRef]

46. Al-Majidi SD, AL-Nussairi Kh, Mohammed M, Dakhil AJ, Abbod AM, Al-Raweshidy MF, et al. Design of a load frequency controller based on an optimal neural network. Energies. 2022;15(17):6223. doi:10.3390/en15176223. [Google Scholar] [CrossRef]