Artificial Neural Networks and Taguchi Methods for Energy Systems Optimization: A Comprehensive Review

1  Introduction

1.1 Background and Significance of Energy System Optimization

The Industrial Revolution in the 18th century marked a significant turning point, initiating a dramatic increase in energy consumption and its applications. This period witnessed a remarkable surge in global energy demand, resulting in substantial growth in manufacturing output, population, and economic development [1]. Consequently, energy and its uses garnered considerable attention.

According to the IEO 2016 projection shown in Fig. 1a, global consumption of marketed energy from all fuel sources is expected to increase through 2040. Renewable energy sources are projected to be the fastest-expanding energy source globally over this period, with consumption increasing by an average of 2.6% annually between 2012 and 2040. Following renewables, nuclear power is identified as the world’s second-fastest-growing energy source, with its consumption anticipated to increase by 2.3% per year during the same timeframe. Fig. 1b illustrates the total global net electricity generation by different fuel types through 2040. Renewables are also expected to be the fastest-expanding energy source for electricity generation, experiencing an average annual growth of 2.9% from 2012 to 2040. After renewables, natural gas and nuclear power are projected to be the fastest-growing sources of electricity generation. From 2012 to 2040, electricity generation from natural gas is estimated to increase by 2.7% annually, while nuclear power generation is expected to rise by approximately 2.4% per year.

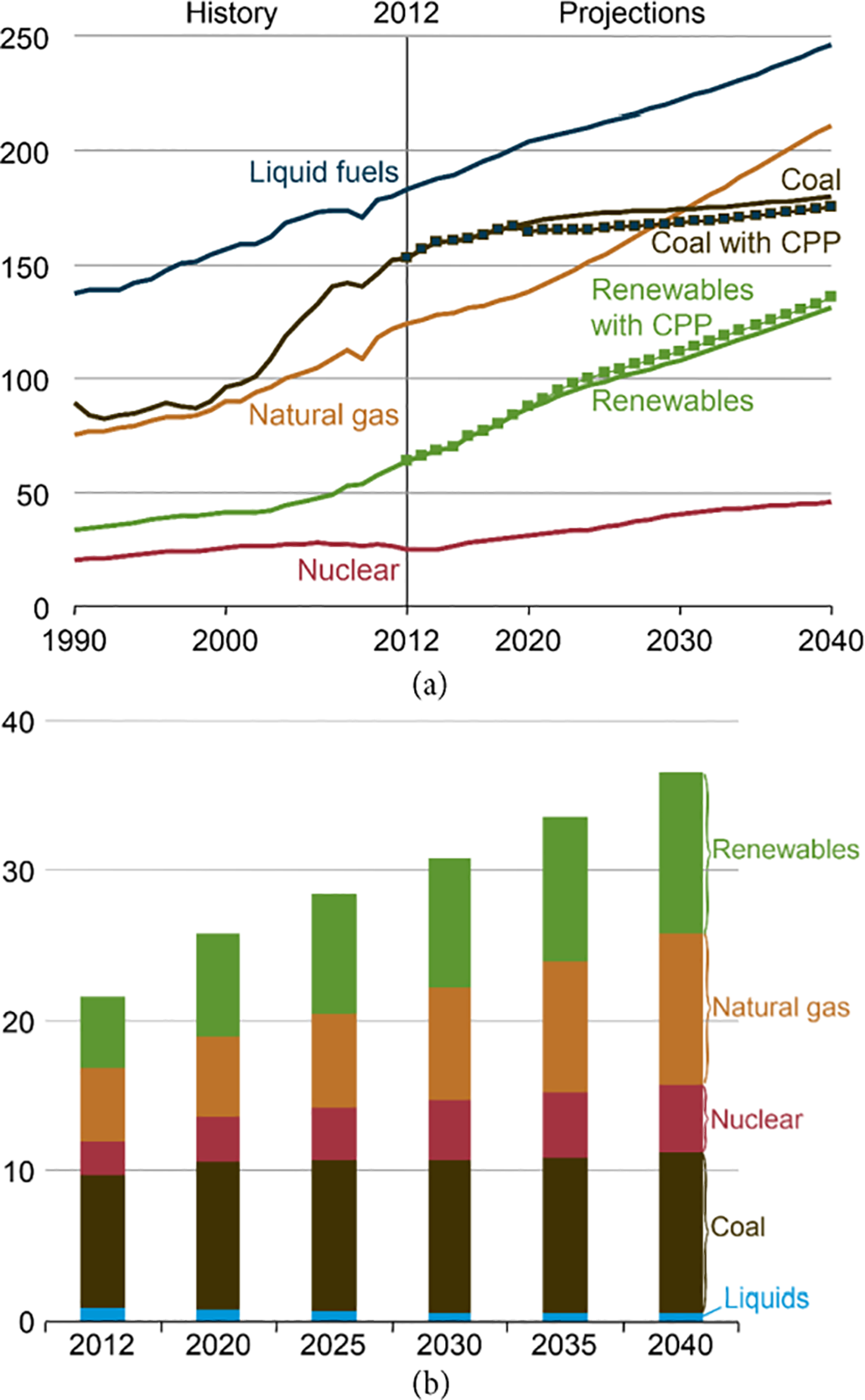
Figure 1: (a) Total world energy consumption by energy source, 1990–2040 (Quadrillion Btu). Dotted lines for coal and renewables show the projected effects of the U.S. Clean Power Plan (CPP). (b) World net electricity generation by fuel, 2012–40 (trillion kilowatt-hours) [2]

Energy systems encompass all components involved in the production, conversion, distribution, and utilization of energy. They can vary in scope, ranging from local to global, depending on the specific case under study [3]. Properly designed energy systems aim to optimize energy consumption, enhance process efficiency, and recover waste energy [4,5]. Developing countries often face the challenge of reducing their heavy reliance on conventional energy systems, which predominantly use non-renewable fossil fuels. These traditional systems are inefficient and contribute to environmental problems, including global warming.

A long-term goal for global society is the transition to completely sustainable and clean energy systems [6–8]. In the short term, improving the performance of existing energy systems is a crucial solution. This pursuit fosters economic, environmental, technical, and social development, alongside promoting efficient energy use.

Optimizing energy systems requires substantial data and a range of tools. To minimize energy losses, a thorough analysis of diverse subjects is essential [9–11]. In energy systems, objective functions such as quality, performance, and cost can be optimized to achieve optimal results. This involves determining the optimal combination of input variables that influence the objective function and quality characteristics. Furthermore, it is necessary to statistically calculate the impact weight and sensitivity analysis of output parameters relative to input variables.

1.2 Overview of Optimization Techniques: Taguchi and ANN

1.2.1 Taguchi Method

The Taguchi optimization approach is an increasingly vital and widely used technique for solving various energy system problems [12–14]. Taguchi-based methods offer robust and resource-efficient experimental designs, effectively managing variations in input parameters. These methods excel at systematically identifying influential factors, thereby facilitating multivariate optimization across diverse applications. However, their assumption of linearity and sensitivity to initial estimates can limit their effectiveness with continuous variables. Furthermore, their capacity to explore interaction effects is limited, making them more suitable for specific contexts, such as manufacturing or engineering design. Optimal application requires careful consideration of these strengths and limitations to ensure their appropriateness for the problem domain. Consequently, numerous scholars have employed Taguchi-based methodologies in energy conversion applications to optimize the performance of both single and multi-response objective problems, including turbine [15], PV [16], hydrogen generation [17], desalination [18], thermoelectric generator [19], fuel cell [20], Diesel engine [21], wave energy [22], PVT [23], integrated energy system [24], etc.

1.2.2 Artificial Neural Networks (ANNs)

Artificial Neural Networks (ANNs), inspired by the human brain, are computational models adept at modelling complex, nonlinear relationships between input and output variables. This makes them powerful tools for optimization, simulation, and prediction across various applications. ANNs consist of interconnected neurons organized into layers, where each neuron processes input and transmits results to subsequent layers. Training involves adjusting connection weights to minimize prediction errors, enabling the network to learn from data [25,26]. Over the past decade, ANNs have been extensively employed for optimization in a broad spectrum of energy applications, such as refrigeration [27], PV [28], fuel cell [29], Diesel engine [30], building [31], electrolyzer [32], heat pump [33], hybrid energy system [34], heat exchanger and thermal storage [35], PTC-driven power plant [36], etc. Moreover, ANN techniques have received favorable reviews in diverse engineering and other domains, such as building electrical energy [37], nanofluid applications [38], pharmaceutical [39], solar collectors [40], and HVAC systems [41].

While ANNs offer unparalleled flexibility and accuracy, they do have limitations. Their “black-box” nature makes it challenging to interpret the underlying relationships between variables. Additionally, ANNs require large datasets for training, which may not always be available in energy system applications. Despite these challenges, ANNs have proven invaluable in addressing the complexities of modern energy systems.

1.3 Rationale for Focusing on Taguchi and ANN Methods

While numerous optimization techniques exist, this review explicitly examines the integration of the Taguchi method and Artificial Neural Networks (ANNs) for optimization, given their distinct advantages. The Taguchi method is more than just a DOE technique; it’s a robust design philosophy aimed at minimizing the impact of uncontrollable “noise” factors, which are common in real-world energy systems with fluctuating conditions. Unlike full factorial designs, which are impractical for numerous parameters, Taguchi’s orthogonal arrays provide a resource-efficient method for identifying key factors. While methods like Central Composite Design (CCD) are effective for response surface modelling and precise optimization, the Taguchi method excels in achieving robustness during the initial design and optimization phases, making it highly suitable for engineering applications.

ANNs are chosen for their superior ability to model the complex, non-linear relationships prevalent in most energy systems, a limitation for statistically linear models like Taguchi. Although more advanced deep learning models such as Convolutional Neural Networks (CNNs) and ensemble methods like Random Forests exist, foundational architectures like the Multi-Layer Perceptron (MLP) are most frequently combined with Taguchi-based DOE in the literature. Therefore, this review focuses on this established pairing to understand its combined strengths and limitations before exploring more complex hybrid models.

1.4 Research Gap and Novelty

Although the Taguchi method and ANNs have been extensively studied in isolation, a significant research gap persists in the literature: a comprehensive review that explores their synergistic and integrated application in energy system optimization. Previous reviews tend to focus on one method or a single energy application, failing to analyze the complementary nature of these two powerful but philosophically distinct approaches. The Taguchi method provides a structured, robust framework for experimentation, while ANNs offer unparalleled capability in modelling the resulting nonlinear system behaviors. This review aims to fill this gap by:

1.    Few studies have comprehensively compared the effectiveness of different statistical optimization methods.

2.    Providing a systematic analysis of the combined application of Taguchi and ANN methods across diverse energy systems.

3.    Highlighting their complementary strengths and limitations.

4.    Offering a framework for their implementation in multi-objective optimization problems.

By addressing these gaps, this review aims to enhance the understanding of optimization techniques in energy systems and offer practical insights for researchers and practitioners. Moreover, the primary objectives of this review are to: 1-Analyze the principles and methodologies of the Taguchi method and ANNs. 2-Evaluate their application in various energy systems, including internal combustion engines, thermal energy storage, solar energy, wind turbines, and hybrid systems. 3-Compare their effectiveness in addressing single-objective and multi-objective optimization problems. 4-Identify challenges, limitations, and future research directions for their combined application.

1.5 Paper Structure

The remainder of this paper is organized as follows:

•   Section 2: Provides an in-depth analysis of the Taguchi method, including its key concepts, applications, and limitations.

•   Section 3: Discusses the principles and applications of ANNs in energy system optimization.

•   Section 4: Explores the combined application of Taguchi and ANN methods across various energy systems.

•   Section 5: Compares the performance of these methods and discusses their complementary strengths.

•   Section 6: Summarizes the key findings and concludes the review.

2  Taguchi Technique

2.1 Single-Objective Optimization

Dr. Genichi Taguchi has developed a strategy based on orthogonal array (OA) experiments which presents much more decreased variance for the issues with optimum control variable settings. Accordingly, the combination of the design of experiments (DoE) by optimization of control variables in order to receive the best outcomes is acquired by using this strategy. As yet, there are numerous literatures have published on the detailed methodology, principles, and fundamentals of the Taguchi optimization approach. Nevertheless, this section characterizes an introduction to the notion of this method for single-objective problems. This optimization approach presents a simple and well-organized procedure to optimize the objective function [42]. It is also known as a prevalent utilized statistical technique to acquire importance ranking for various input parameters against the corresponding output responses [43]. The method is employed in various types of study, such as numerical, theoretical, and experimental [44–47]. Generally, the Taguchi OA design and signal-to-noise (S/N) ratio are the two main tools utilized in this strategy. By applying the S/N ratio and OA, this technique allows for determining the optimum combination of design variables with fewer experiments [48].

2.1.1 Signal-to-Noise Ratio (S/N)

The deviation between the experimental results and desired values can be determined by using the Taguchi quality loss function, which is also known as the S/N ratio. This parameter is employed as a criterion of the ability regarding a process, system or product to perform adequately against the noises. In other words, S/N ratio characterizes how close system’s performance is to the ideal situation. The signal factors describe the desired quantity and could be arranged to meet a particular output value. The undesirable design parameters which are uncontrollable through the process, are called noise factors. The main objective of the Taguchi optimization method is cutting down the noises’ effects on the output [49]. The mentioned concept is illustrated in Fig. 2 called Parameter Diagram (P-Diagram).

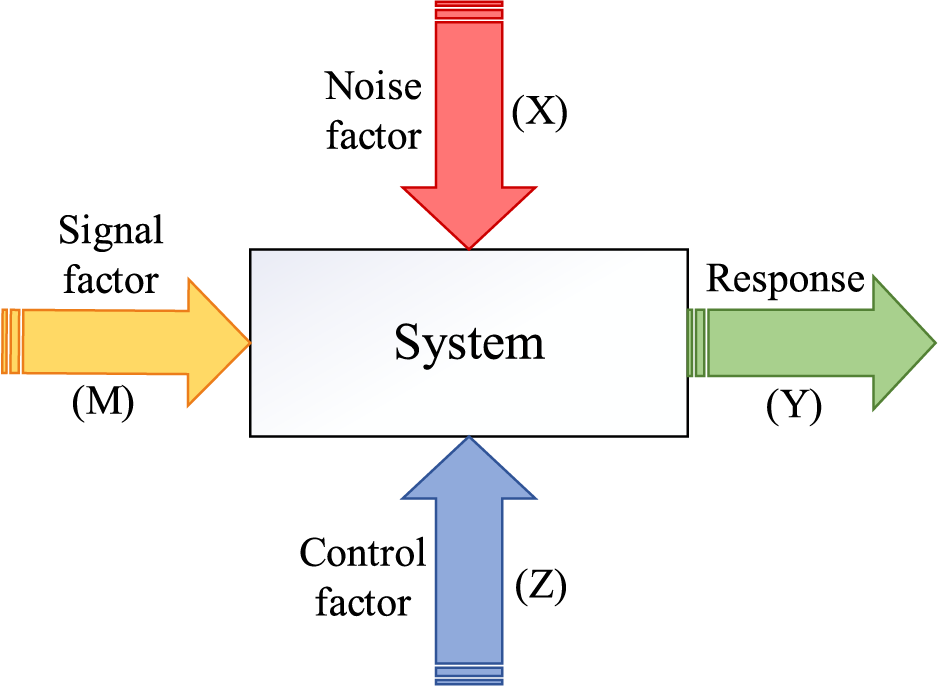
Figure 2: The P-Diagram showing the Taguchi method concept

More than 40 different types of S/N ratios have introduced by Taguchi. Three types of the most crucial being is defined by following responses [50,51]:

Smaller the better: A smaller the better (lower the better) response is one that does not take on negative values, and has the target value of zero. The S/N ratio for those characteristics in which the main objective is set to be minimized, is represented by Eq. (2):

SN=−10log[1n∑i=1nyi2](1)

Larger the better: This type of response in which the most favorable value is infinity is named the larger-the-better (higher the better). It also does not bear negative values, and there is no pre-arranged objective value. Thus, the larger the characteristic’s value, the better it is. The S/N ratio for this response is as follows, here number of experiments, and experimental response are defined by n, and y, respectively:

SN=−10log[1n∑i=1n1yi2](2)

Nominal the best: When a particular value is the most desirable, a nominal-the-best response is employed. In other words, either a lower or a higher value for this output response kind is undesirable. It is demonstrated by Eq. (3):

SN=10log[y¯2s2](3)

here y¯ denotes mean, y¯=∑i=1nyi/n, and s representing standard deviation, which is s=∑i=1n(yi−y¯)/n−1.

To illustrate, consider a simple experiment to optimize a solar PV system’s power output. If four experimental runs with different parameter settings yield power outputs (yi) of 150, 155, 148, and 160 W, the S/N ratio for this ‘Larger the better’ characteristic is calculated as:

SN=−10log[1n∑i=1n1yi2]=−10log[14(11502+11552+11482+11602)]≈43.78 dB

This dB value provides a robust measure of performance that can be compared across different experimental settings to identify the optimal combination of factors.

2.1.2 Orthogonal Array (OA)

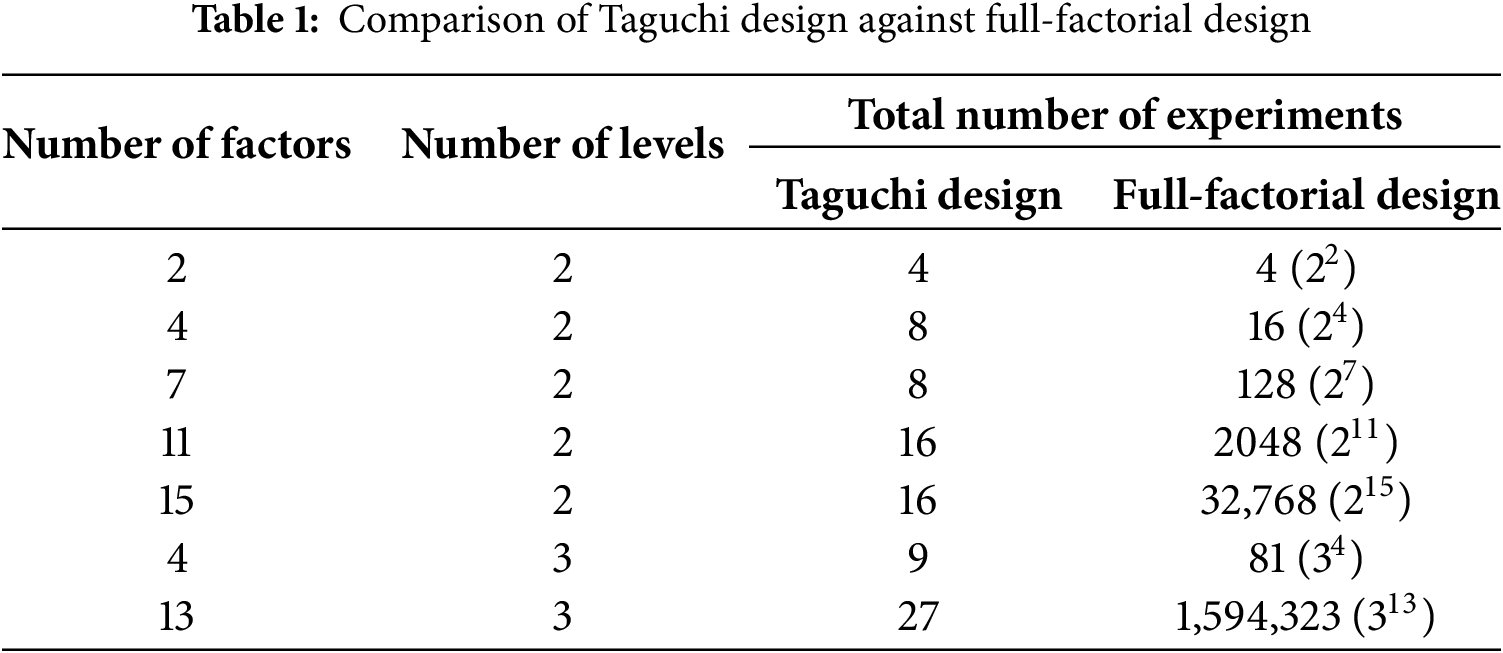
The Taguchi orthogonal array (OA) is defined as a set of matrices for performing the design of experiments that require the least of the full experimental combinations. In order to specify the optimum setting of the control parameters influencing the response, employing the orthogonal array leads to improving the measurement of output response and reducing its variability [52]. The OA trials carry the pairwise balancing feature. This feature makes variables possible to be explored simultaneously so that the effect of none of the variables is neglected. Thus, involving the OA design effectively downsizes the number of experiments [53]. Accordingly, the Taguchi design against the full-factorial design is compared in Table 1. In this table, the total experiments available for various numbers of factors with levels of 2 and 3 proposed by Taguchi’s design and full-factorial design is given. The total number of experiments suggested by Taguchi design is significantly fewer than the full-factorial design. Hence, the advantage of the Taguchi design is well evident in order to the DoE for high-number factor studies.

In DoE process, it is significant to consider the proper OA type. The OA table determination depends on computing the overall degree of freedom (DOF). It is an important parameter for analysis and is acquired via the summation of each factor’s DOF. Generally, the OA is specified by following equation:

La(bc)(4)

where L is Latin square, a is the number of experiments (rows), b is the number of levels, and c is the number of factors (columns). Additionally, to determine the OA and DOF of the process, the following relations are considered:

Factordegreeoffreedom=b−1(5)

Thetotaldegreeoffreedom=∑Factordegreeoffreedom(6)

Thetotaldegreeoffreedom≤Orthogonalarray(7)

For instance, L8(27), which demonstrates a Taguchi OA including eight experiments for 7 factors with 2-levels, is provided in Table 2.

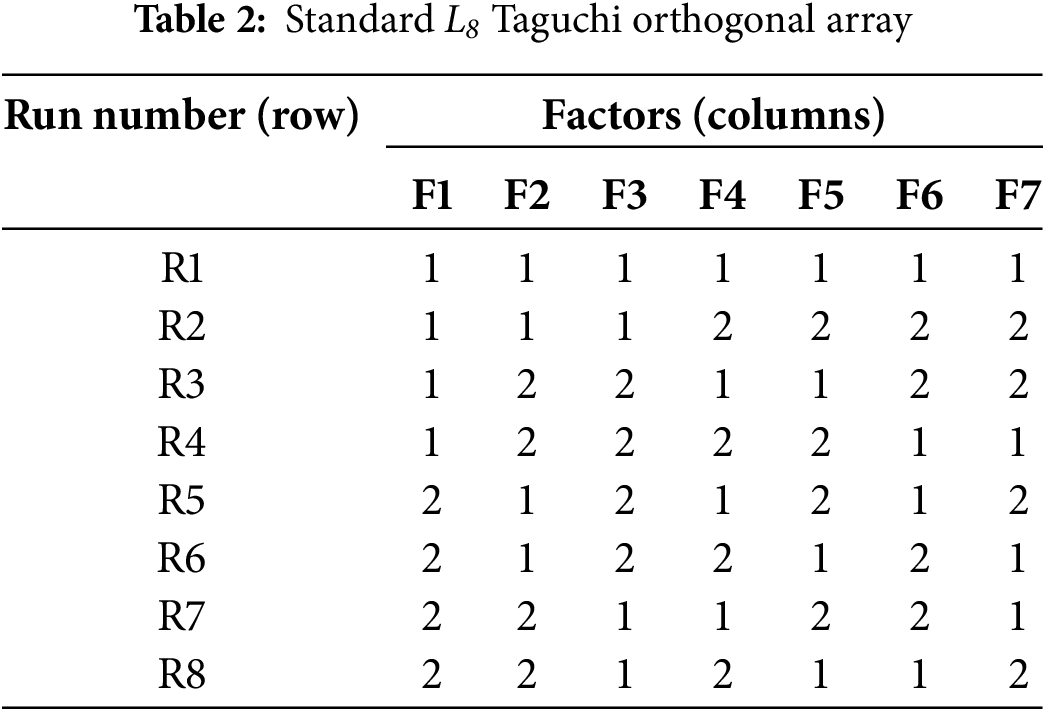
In Table 2, there are eight experimental runs from R1 to R8. The low and high level of each factor is indicated by the 1s and 2s in the matrix, respectively. Each column contains a same number of 1s and 2s. In addition, only four combinations (2, 2), (2, 1), (1, 2), and (1, 1) are employed in each pair of columns, presenting the orthogonal array concept.

2.1.3 Analysis of Variance (ANOVA)

Analysis of variance (ANOVA) is an examination tool used in statistics that helps to find an observed aggregate variability inside a data set. In the Taguchi optimization approach, the insignificant and significant input factors affecting the performance characteristics of the system are determined by using the ANOVA. The main items which are employed in an ANOVA table are as follows [54,55]:

1)   Degree of freedom (DOF): The DOF is defined as the amount of information your data provides that you can spend to estimate the values of unknown population parameters, as well as calculate the variability of these estimates. It is calculated as the level of each input factor minus one. The total DOF is specified as the sum of the singular DOF of factors.

2)   Sum of squares (SS): The sum of squares denotes a measurement of deviation or variation from the mean. It is computed as a summation of the squares of the differences from the mean. In the ANOVA table, the total sum of squares enables the presentation of the total variation attributed to different factors. It includes the treatment sum of squares (SST) plus the sum of squares of the residual error (SSE).

3)   Experimental error: The various experimental results under a similar set of conditions are defined as the experimental error. To increase the precision of the experimental design, the experimental error should be minimized.

4)   Contribution: The contribution percentage represents the proportion of the SS for each input factor. Besides, the ratio of total quality loss generated by the deviation of the factor is defined by contribution.

5)   F-value (F): The F-value is defined as the mean square divided by the mean square error. It is employed to specify whether the impact of the factor on the experimental results is significant. It means that the larger the F-value of the factor, the more significant the impact of the factor regarding the objective function.

The framework of the Taguchi optimization approach is illustrated in Fig. 3.

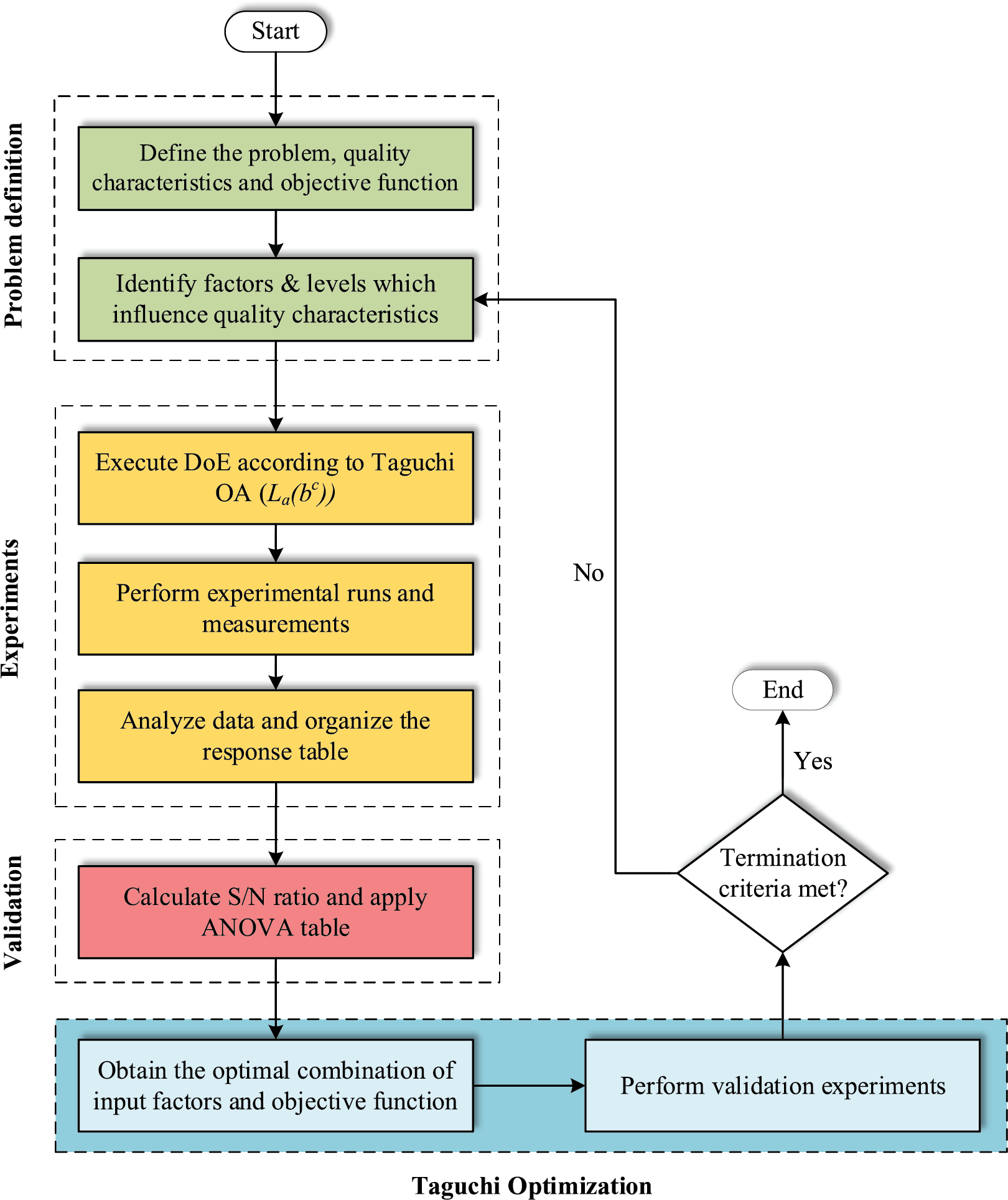
Figure 3: The framework for the Taguchi optimization method

2.2 Multi-Objective Optimization

Using the Taguchi technique solitary is not sufficient for describing the effect of input parameters for multi-objective problems. Hence, the Taguchi coupled with Grey relational analysis (GRA), and technique of preference by similarity to ideal solution (TOPSIS) could be employed in optimization of multi-response problems. The Taguchi-based TOPSIS and Taguchi-based GRA are easy to perform, adaptable, and uncomplicated methods compared to the other multi-objective optimization techniques. Accordingly, these techniques are the most widespread optimization methods combined with Taguchi that have been scrutinized in this study.

2.2.1 Grey Relational Analysis (GRA)

The grey relational analysis (GRA) was first proposed by Deng [56]. If we display the utterly known and clear information of a given system in white color and the entirely unknown information of a system in black color, then the information related to most of the systems in the world is not white (entirely known), or black (entirely unknown) information. Rather, they are a combination of the two, i.e., grey. Such systems are called gray systems, whose main characteristics are the incompleteness of information related to that system. According to the GRA, when the data distribution and variation in a sequence are large, the measurement unit of the sequences is not the same. So, data pre-processing is needed. Data pre-processing is a method of converting original numeric sequences into comparable numeric sequences. Hence, the data should be normalized and scaled so that there would be a comparison between sequences. Accordingly, each output response specified by the experimentations is normalized through the 0 to 1 range. It is known as the grey relational generation.

Generally, the normalization can be conducted in three kinds of approaches, and the original sequence could be normalized by following Equations [57]:

I.   The smaller the better:

yi(k)=maxxi0(k)−xi0(k)maxxi0(k)−minxi0(k)(8)

II.   The larger the better:

yi(k)=xi0(k)−minxi0(k)maxxi0(k)−minxi0(k)(9)

III.   The nominal the best:

yi(k)=1−|xi0(k)−x0|maxxi0(k)−x0(10)

where the normalization value for grey relational generation is provided by yi(k), x0 indicates the optimum value, and minxi0(k) and maxxi0(k) are specified as the minimum and maximum definitions for xi0(k). Moreover, the grey relational coefficient is introduced by ξi(k), defining a relationship between the actual and ideal normalized values. It is determined by the following Equations [58]:

ξi(k)=Δmin+∅ΔmaxΔ0i(k)+∅Δmax(11)

Δ0i(k)=|y0(k)−yi(k)|(12)

Δmax=max∀j∈imax∀ky0(k)−yi(k)(13)

Δmin=min∀j∈imin∀ky0(k)−yi(k)(14)

where Δ0i(k) expresses the deviation between values of yi(k) and y0(k). The distinguishing coefficient is defined by ∅ and is bounded in the range of 0 < ∅ < 1. Generally, it is considered equal to 0.50 in investigations [59–62]. Further, the minimum and maximum values of the Δ0i are defined by Δmin and Δmax. The evaluation of the correlation between the comparative and original sequences is specified by the grey relational grade. So that these sequences are identical, the grade is the highest and means the best results are obtained. The grey relational grade (γi) is calculated by:

γi=1n∑k=1nwkξi(k)(15)

which, n denotes the number of tests and wk introducing weighting factor. In order to compute the weighting factor, firstly, the delta value must be calculated. The delta is the difference between the largest and smallest values of each output response S/N ratio, for each input factor. Then, the overall delta value should be obtained through summation of the individual delta values. Ultimately, the ratio of the cumulative delta values calculated for each factor to the total delta value of all output responses is indicated. The weighting factor (wi) is determined by the following relation:

wi=∑j=1pDeltai,j∑i=1m∑j=1pDeltai,j(16)

Here, delta means S/N ratio range, p is the number of input parameters, and m is the number of output responses. The framework of the Taguchi-based GRA optimization method is represented in Fig. 4.

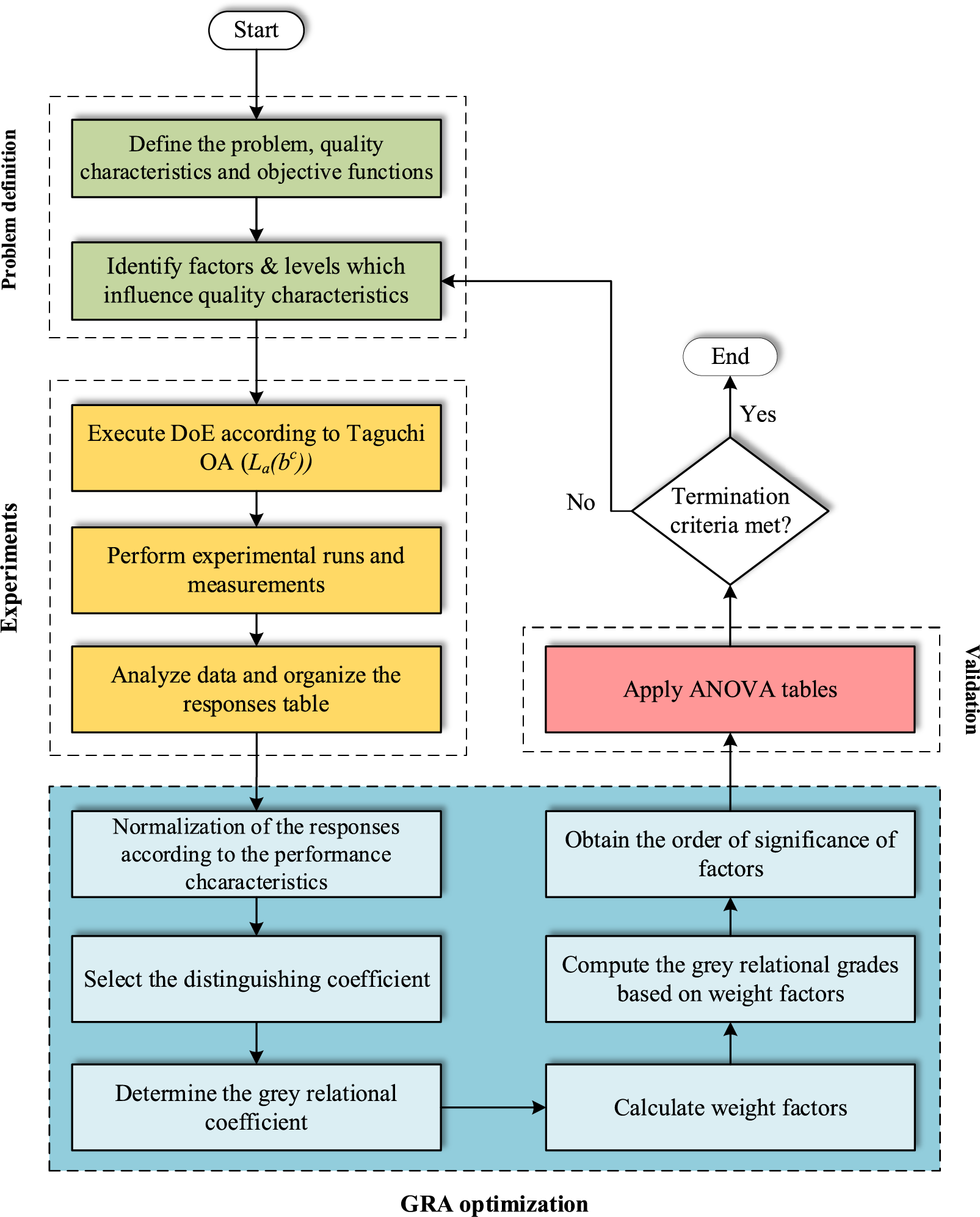
Figure 4: The framework of the Taguchi-based GRA optimization method

2.2.2 Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)

Same as the GRA, this technique is employed to convert a multi-objective optimization problem into a single-objective one. Generally speaking, this technique is applied to incorporate all performance attributes of the system into a single attribute. The Taguchi-based TOPSIS method contains the concept of a multi-objective robust design technique to work out the given multi-objective optimization problem. The robust design indicates an efficient method to specify the optimum combination of the control parameters such it stands robust to the noise factors, and also arises a high performance. The concept of quality loss is practical to the investigation when the performance characteristics are transformed into the (S/N) ratios [63]. As mentioned before, the S/N ratio (η) is a beneficial strategy to specify important parameters by assessing the minimum variance, and it is employed to calculate the performance of a system. To convert the multi-objective problem into a single-objective one by using the Taguchi-based TOPSIS method, the following steps are introduced [64]:

1)   Creating the decision matrix by using the number of experimentations and determined S/N ratios for each response as presented in Eq. (17):

D=[η11η21η12η22…η1n…η2n…………ηm1ηm2…ηmn](17)

where η denotes S/N ratio, and the number of experiments (m) are represented by i, and j defining the number of responses (n).

2)   Calculation of normalized ratings via the vector normalization:

rij=−ηij∑i=1mηij2;i=1,2,…,m;j=1,2,…,n(18)

3)   Calculation of weighted normalized decision matrix (V):

V=⌊vij⌋m×n;i=1,2,…,m;j=1,2,…,n(19)

vij=wjvij;i=1,2,…,m;j=1,2,…,n(20)

∑j=1nwj=1(21)

wj indicates the weight of response j.

4)   Exploration of positive ideal solution (Ai∗;i=1,2,...,m), and negative ideal solution (Ai−;i=1,2,…,m). The Ai∗ is generated from all the best values (maximum S/N ratio), and the Ai− is generated from all the worst values (minimum S/N ratio) in the weighted normalized decision matrix (V):

Ai∗={υ1∗,υ2∗,…,υj∗,…,υn∗}={(maxiυij|jϵJ1),(miniυij|jϵJ2)}(22)

Ai−={υ1−,υ2−,…,υj−,…,υn−}={(miniυij|jϵJ1),(maxiυij|jϵJ2)}(23)

Here, J1 is defined as a set of benefit attributes, and J2 is defined as a set of cost attributes.

5)   Determination of separation measures: The distance from each alternative (experimental number) to the positive ideal solution, Ai∗, is represented by Si∗:

Si∗=∑j=1n(υij−υij∗)2;i=1,2,…,m(24)

and the distance from the negative ideal solution, Ai−, is represented by Si−:

Si−=∑j=1n(υij−υj−)2;i=1,2,…,m(25)

6)   Determine similarities to the ideal solution by calculation of ranking score (Ci∗) via Eq. (26):

Ci∗=Si−Si−+Si∗;i=1,2,…,m(26)

It should be noted 0≤Ci∗≤1, where Ci∗=0 when Ai=A−, and Ci∗=1 when Ai=A∗.

7)   Rank preference order: Choose experimentation with maximum Ci∗ or rank experimentations according to Ci∗ in descending order.

The framework of the Taguchi-based TOPSIS optimization method is provided in Fig. 5.

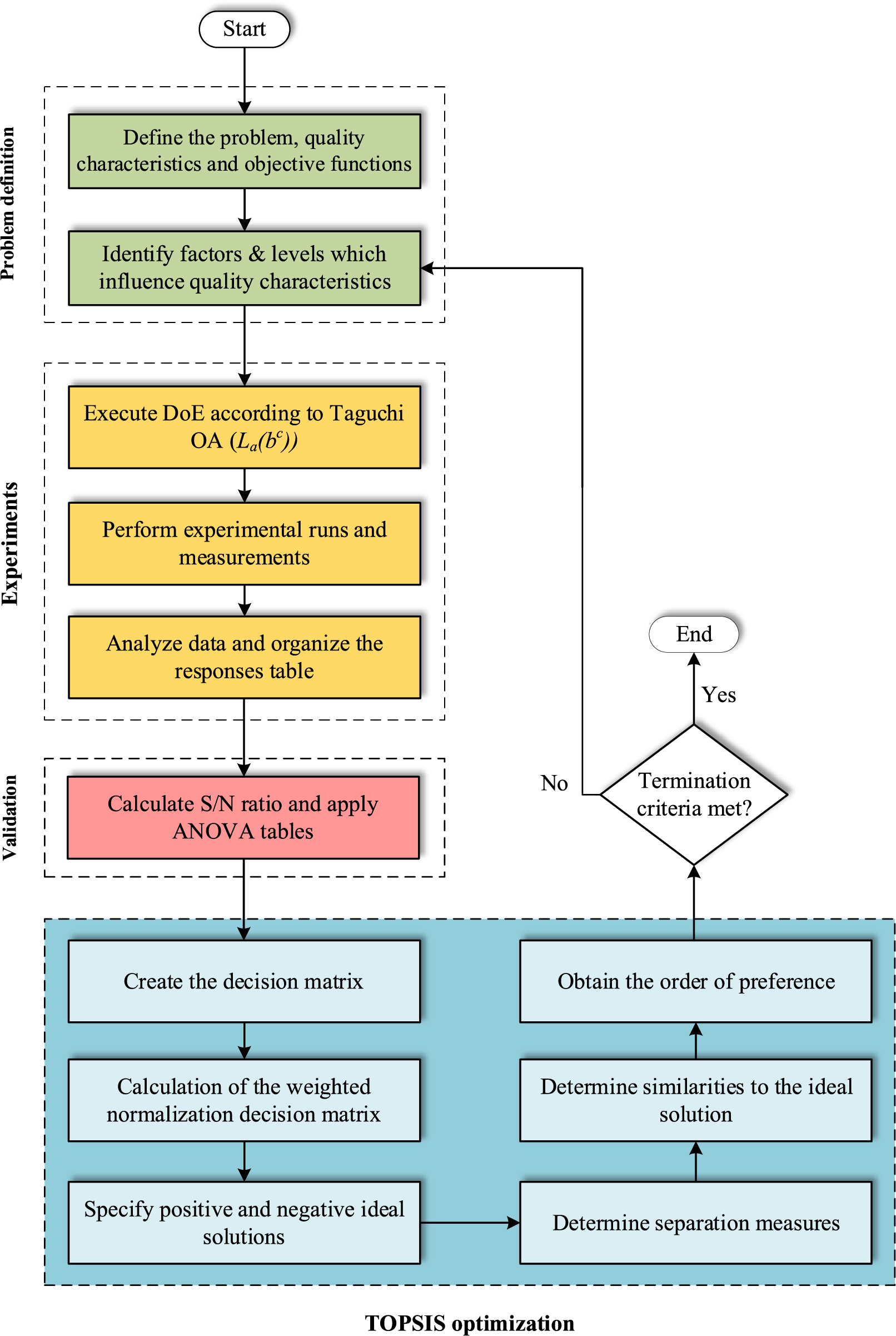
Figure 5: The framework of the Taguchi-based TOPSIS optimization method

3  Artificial Neural Network (ANN)

3.1 Concept

The utilization of ANN techniques extends to modeling, optimization, simulation, and performance prediction of systems. Over the past two decades, its popularity has surged due to its enhanced processing speed and heightened accuracy. Functioning akin to the data processing systems of the human brain, artificial neural networks are composed of neurons, analogous to the fundamental elements regarding biological networks. These neurons comprise components like dendrites (which receive input signals), the cell body or soma (which functions as a processor), synapses (serving as links), and axons (providing exiting signals toward neighboring neurons and executing nonlinear processes) [65]. Fig. 6 illustrates a typical biological human brain’s neuron. The ANN model consists of numerous operating components known as neurons, operating akin to the human brain, it learns and stores knowledge through interconnected links known as weights. Influenced by connection weights, every neuron gains different input signals from neighboring neurons, employs a non-linear activation function, and produces a singular output-signal. This output may then proceed to other neurons, with the neurons collectively processing and forwarding input data to subsequent layers within the network.

Figure 6: Biological neuron of human brain

Evaluation of the comprehensive applications of ANNs is feasible by considering factors such as fault tolerance, processing performance, latency, speed, scalability, and convergence accuracy [66]. The substantial potential of ANNs, particularly their fast-speed operating in a massively parallel execution, underscores the necessity for further exploration in this realm. ANN models have demonstrated significant adaptability, nonlinearity, and self-learning capabilities advancements in input-to-output mapping, leading to their widespread use in various functions. Presently, owing to these attributes, ANNs are prominently employed for global method approximation across various numerical paradigms, indicating their effectiveness, efficiency, and success in addressing both simple and complex issues across diverse real-life challenges [67]. ANN can consist of numerous layers, broadly categorized into the input layer, hidden layer, and output layer. The input layer encompasses all input parameters, followed by data computation in the hidden layer, and at the end, the computation of the output vector in the output layer. The implementation of an ANN involves three primary stages: (1) the inputs and outputs selection, (2) the training, and (3) testing. Typically, input and output data are normalized within a specific range, although some studies utilize the data in its raw form without scaling. Subsequently, the data is randomly divided for training, testing, and validation purposes. Essential pre-analysis parameters for ANN include the activation function, input and output selection, the number of neurons in hidden layers, the count of hidden layers, and the training algorithms [68]. Notably, ANN is classified as supervised learning, undergoing training based on input variables and outputs. The learning algorithm’s primary role is to adjust network variables, namely biases and weights, to ensure accurate predictions within acceptable error limits. Commonly known as the cost function, signifies the error signal, which is propagated backward until reaching the minimum signal over numerous training iterations (or epochs). After the training phase concludes, the testing and validation stage assesses the performance of advanced ANN prediction models. Accuracy is gauged using correlation coefficients (R) and coefficients of determination (R2) for training, validation, and testing. Validation involves presenting the new set of inputs to the network, and additional statistical analyses may be conducted to assess the efficiency of predicted responses. The algorithm of ANN method is provided in Fig. 7.

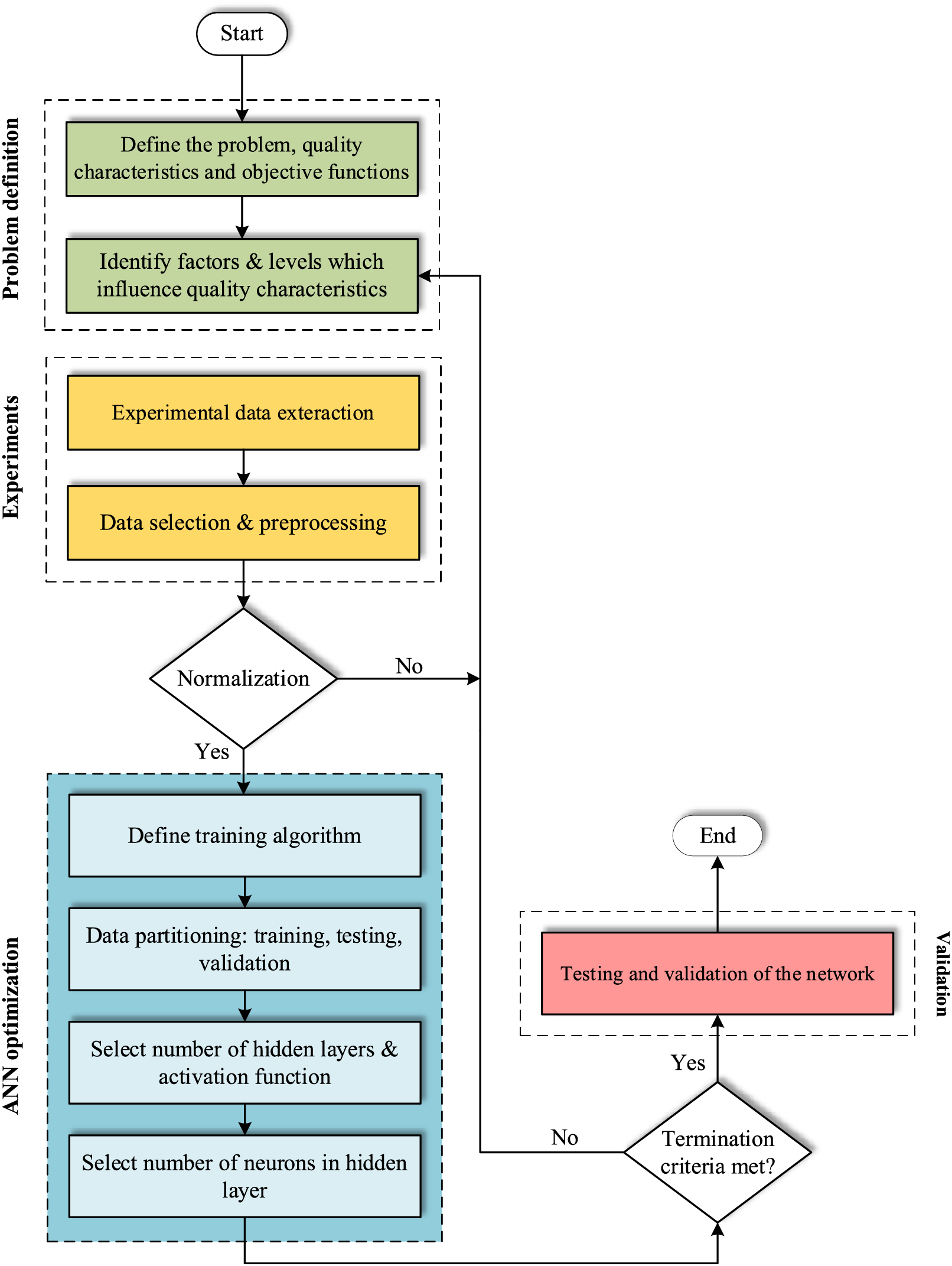
Figure 7: The framework of the ANN method

3.2 Classification

ANNs constitute a potent category of machine-learning models inspired by the neural architecture of the human brain. In the realm of classification, ANNs demonstrate exceptional proficiency in capturing intricate patterns and relationships present in data, enabling them to learn and generalize from examples. ANNs are broadly categorized into feedforward and recurrent architectures. Feedforward networks, with their layered structure, process information sequentially from input to output layers. They are commonly employed in tasks where data exhibits a clear input-output mapping. Recurrent Neural Networks (RNNs), on the other hand, incorporate feedback loops, allowing them to capture temporal dependencies in sequential data. This makes RNNs well-suited for tasks that involve natural language processing and time-series analysis. Hybrid models, such as Convolutional Neural Networks (CNNs) for image classification, showcase the versatility of ANNs by integrating specialized layers for extracting hierarchical features [69,70]. As ANNs continue to evolve, their adaptability across diverse domains positions them as a key player in advancing the capabilities of automated classification systems. In Fig. 8, the classification of ANNs is illustrated, focusing on the feedforward neural network (FFNN) as a prominent machine learning classification algorithm. The FFNN structure is characterized by organized layers resembling neuron processing units in the human brain. Each unit within the layers is interconnected, and the strength or weight of these connections varies. The network’s knowledge capacity is determined by the weights of these connections. In a typical FFNN operation, information processing occurs unidirectionally from input units through hidden layers to output units, establishing the network as a classifier. Unlike recurrent networks, FFNNs lack feedback connections between layers. In FFNNs, the information flow is unidirectional, highlighting the progression from input through hidden nodes and ultimately to output nodes [71]. Single-layer and multilayer perceptions are exemplary FFNNs, as depicted in Fig. 8 (right), showcasing a 2-layered FFNN with 3 units in input layer, 4 units in hidden layer, and 5 units in output layer. Notably, input units are determined as the virtual layer with 0 layers, while the hidden layer is distinct from both input and output layers. FFNN applications are categorized into two groups, encompassing conventional machine learning methods and dynamical systems’ control. Networks with at least two hidden layers are acknowledged as deep networks, signifying increased complexity [72].

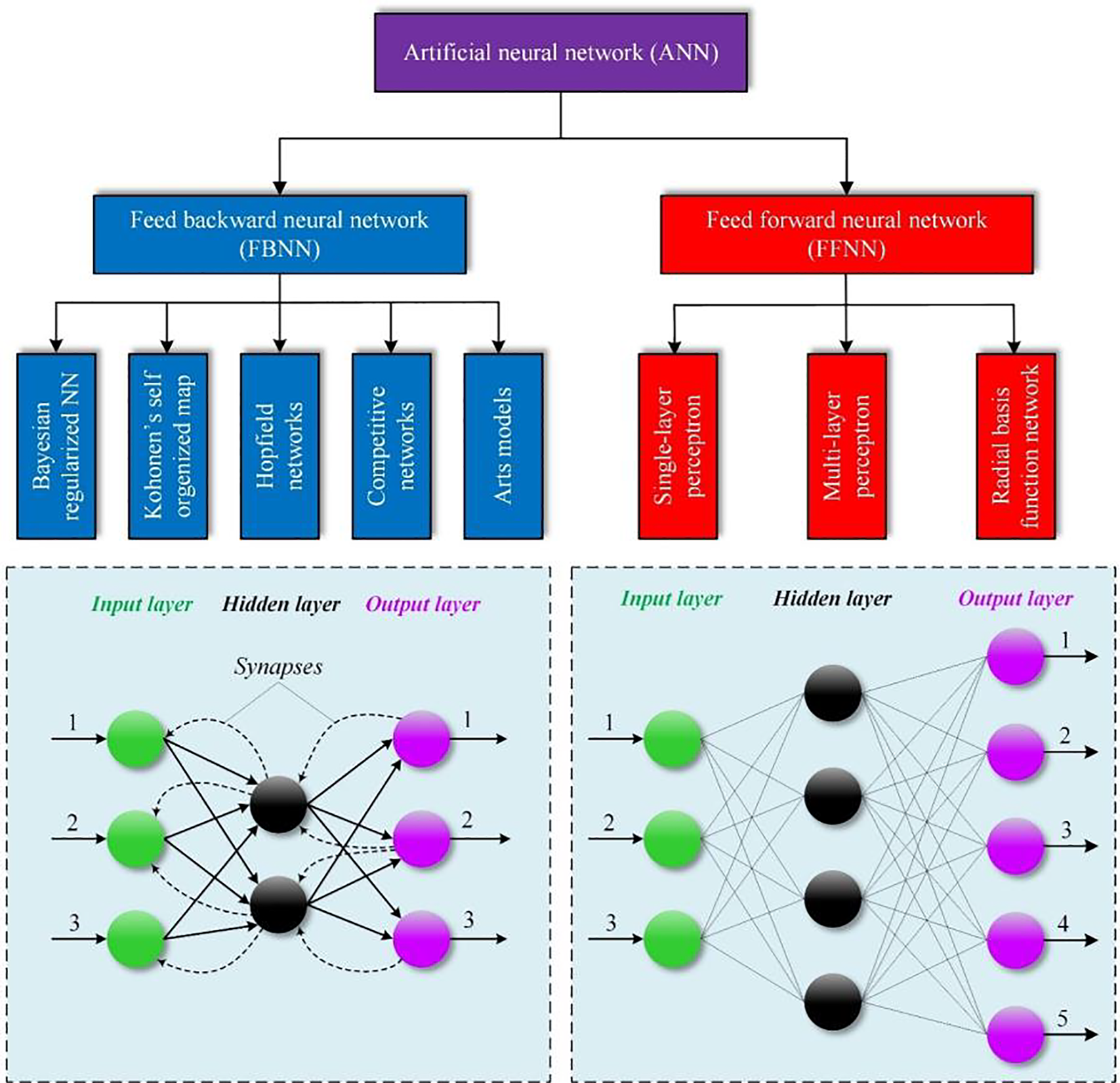
Figure 8: ANN classification

A single-layer FFNN comprises only input and output layers, with the input layer not involved in computations and therefore not considered. In this setup, the relationship between the output layer and input nodes is strictly one-way. The key feature of a multi-layer FFNN, as opposed to its single-layer counterpart, is the inclusion of at least two hidden neuron layers. In multi-layer FFNNs containing computational neurons, input signals undergo processing within the initial hidden layer. The weighted output parameters in the first layer serve as inputs for the subsequent layer of neurons. Particularly, studies have shown that increasing the quantity of hidden layers improves the network’s capacity to capture non-linear relationships between inputs and outputs, particularly when the quantity of input units of the network is great [73].

Feed backward Neural Networks (FBNN) represent a crucial class of artificial neural networks designed for efficient information processing in a unidirectional manner. These networks find extensive applications in diverse fields because of their capacity to apprehend intricate relationships within data. The architecture involves layers of interconnected neurons, with data flowing from the input layer through hidden layers to the output layer, lacking feedback loops. This unidirectional flow makes FBNNs adept at tasks like pattern recognition, classification, and regression [74]. In this extended discussion, we delve into the classification of FBNNs, including variations like Bayesian Regularized NN, Kohonen’s Self-Organized Map, Hopfield Networks, competitive networks, and ART models. Bayesian Regularized Neural Networks integrate Bayesian principles into the network’s architecture, providing a probabilistic framework for handling uncertainties in the data. This enables more robust decision-making and enhanced generalization capabilities, making them suitable for scenarios with limited data or noisy inputs. Kohonen’s SOM, also known as a self-organizing map or Kohonen map, is an unsupervised learning algorithm within the FBNN category. It is particularly adept at clustering and visualizing high-dimensional data, offering a topological representation of input patterns, making it valuable in tasks such as data mining and dimensionality reduction. Hopfield Networks are a type of recurrent FBNN that serve as content-addressable memory systems. They are well-suited for pattern recognition and associative memory tasks. Hopfield Networks exhibit stable states where specific patterns can be retrieved even when presented with incomplete or noisy input. Competitive networks, also known as winner-take-all networks, involve neurons competing for activation based on input patterns. These networks are often employed in clustering and pattern recognition tasks, where the strongest neuron (winner) represents the recognized pattern. Adaptive Resonance Theory (ART) models, a family of FBNNs, are designed to self-organize in response to varying input patterns [75]. These models exhibit dynamic learning and stability, making them suitable pattern recognition and classification in changing environments.

While FBNNs and FFNNs share the fundamental structure of layered neural networks, their operational distinctions are noteworthy. FBNNs, with their unidirectional flow, are well-suited for tasks requiring the processing of static input data, such as image recognition and classification. In contrast, FFNNs, with their feedforward and feedback connections, excel in capturing temporal dependencies and sequential patterns, making them ideal for tasks like natural language processing and time-series analysis. The choice between FBNNs and FFNNs relays on the particular conditions of the given task, emphasizing the importance of understanding their respective strengths and limitations in the context of the application (see Fig. 8). It’s important to note that overfitting poses a significant challenge in ANN training, where the system may accurately predict outcomes using known datasets but may fail to perform well when presented with new data [76].

In the realm of energy systems, the predominant ANN models employed are as follows:

(1)   Multi-layer perceptron (MLP) FFNN

(2)   Radial basis function (RBF) FFNN

The details of these architectural structures are outlined below.

3.2.1 Multi-Layer Perceptron (MLP) FFNN

The MLP architecture is composed of three fundamental layers: the input layer, several hidden layers, and the output layer. Within this architecture, neurons receive input information from neighboring neurons, pass within hidden layers, and eventually reach the output layer. Neurons, serving as interconnected processing nodes, collectively form the ANN. Each neuron’s output is determined by a weighted set of inputs. The basic configuration of MLP is provided in Fig. 9.

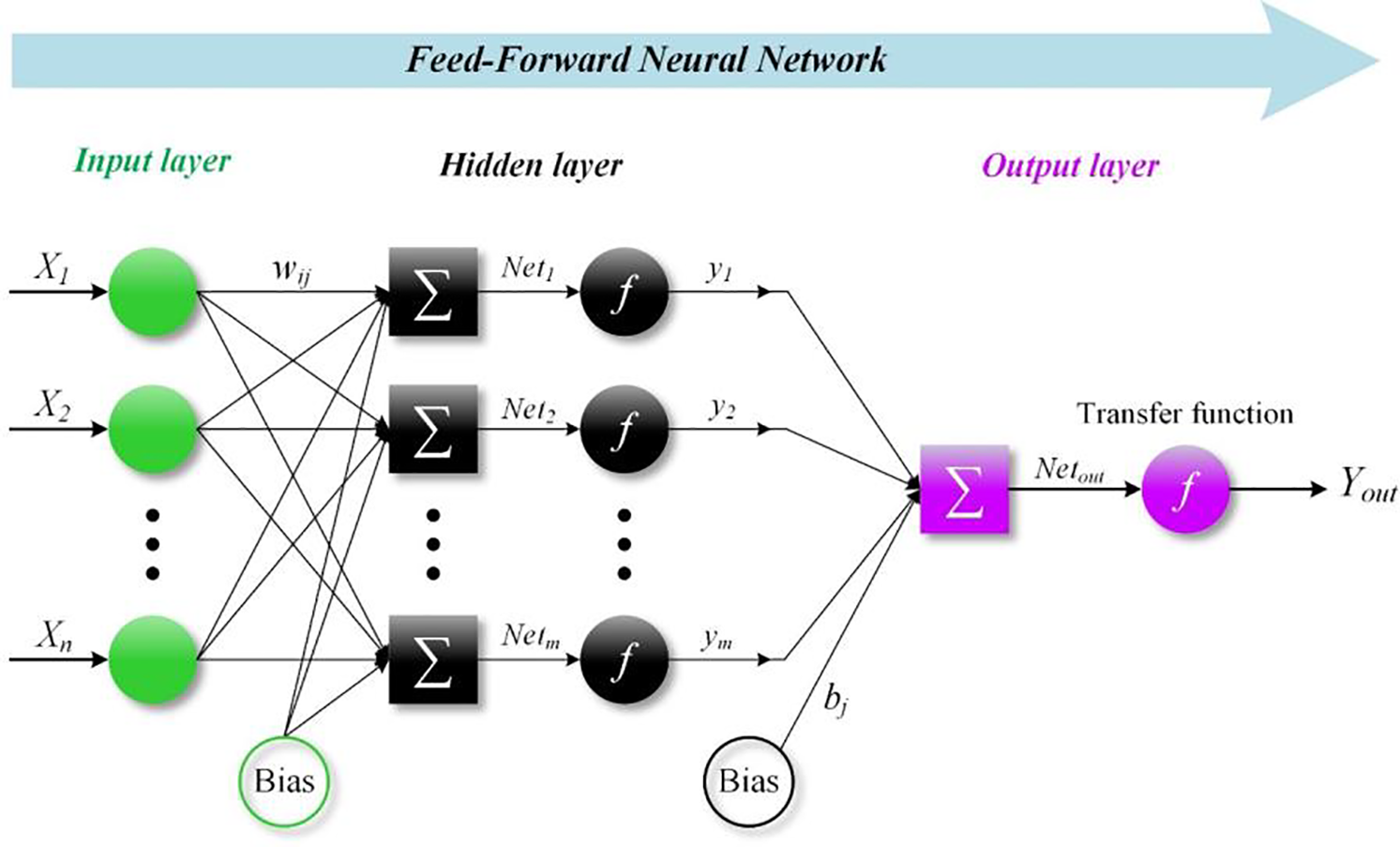
Figure 9: Basic structure of multi-layer perceptron FFNN

Based on the MLP modeling, the collective sum of weighted input units, formed by neurons, is expressed as follows:

X=∑i=1n(wijxi+bj)(27)

In this context, i represents the index of input data (i = 0, 1, 2, ..., n), while wij refers to the weights connecting to the input data ai. Moreover, bj denotes the bias related to the neuron. The configuration of connection weights and biases encodes the information. A transfer function F is utilized to handle the sum of weighted input units in combination with the bias. The output is determined by Eq. (28):

Y=F(X)=F[∑i=1n(wijxi+bj)](28)

Typically, both output and hidden layers feature an activation function. It can be either non-linear or linear. Various learning algorithms are accessible for establishing connections between inputs and outputs, with the FF back-propagation learning algorithm being the most prevalent. The sigmoid function, is a commonly employed non-linear activation function, characterized by an outcome range spanning from 0 to 1:

F(X)=11+ex(29)

If negative values are encountered in the output or input layer, a transfer function called tansig is employed:

F(X)=1−e−2x1+e−2x(30)

The model undergoes training with a specified number of neurons in the hidden layer, transfer function, learning rate, and momentum factor. The MLP stands out as the most prevalent neural model to forecast the efficiency of multiple types of energy systems.

3.2.2 Radial Basis Function (RBF) FFNN

The model shares a 3-layer structure with the MLP model, including the input layer, the hidden layer, and the output layer. Both models operate as feedforward neural networks. Considering the RBF, inputs gathered at the input layer and then transmitted to the second layer, known as the hidden layer. As demonstrated in Fig. 10, after processing in the hidden layer, the signals proceed to the output layer, where the final output data is generated. In the RBF hidden layer, a radial basis activation function is utilized, whereas a linear function is employed at the output layer.

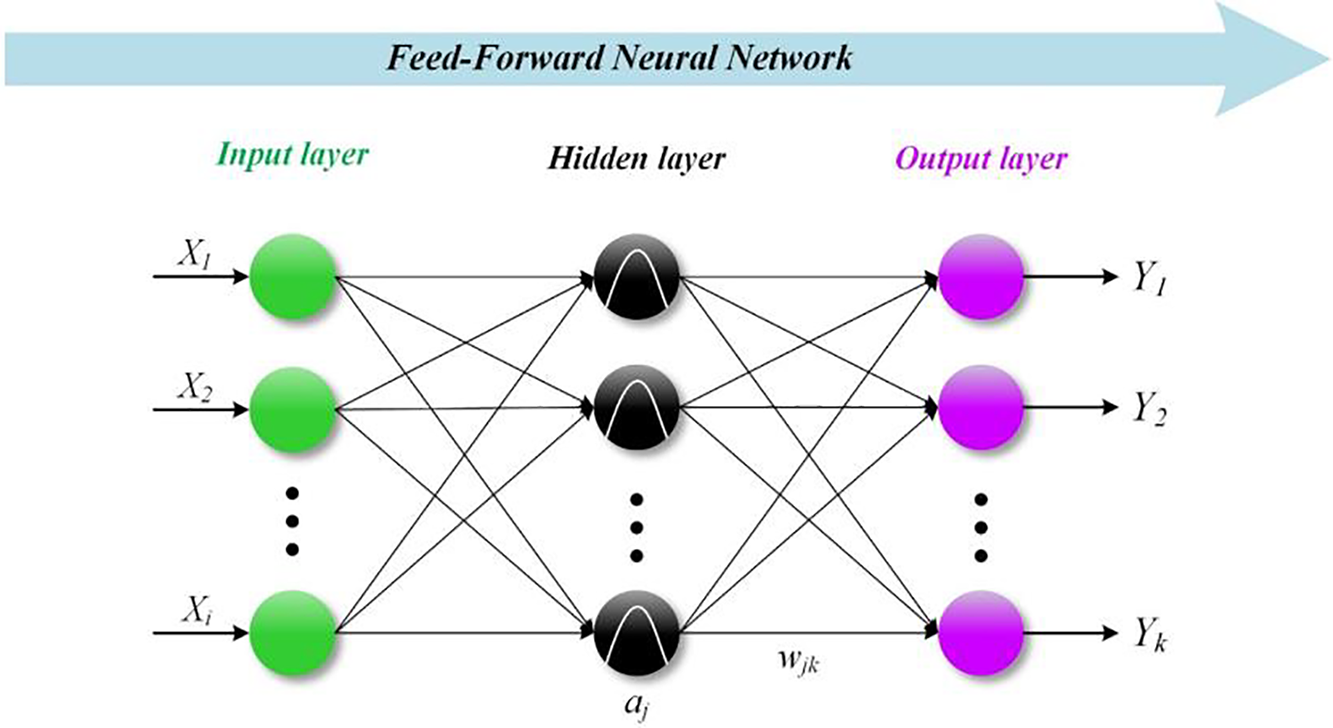
Figure 10: Basic structure of radial basis function FFNN

Typically, the transfer function in the RBF hidden layer is the Gaussian function:

aj(x)=exp(−‖xi−cj‖22σj2)(31)

Here, σj represents width of the neuron, while the RBF unit’s input and center values are represented by xi and cj, respectively. In addition, aj represents the output of the jth RBF unit. The output layer’s operation is linear, as expressed in Eq. (32).

yk(x)=∑j=1n(wjkaj(x)+bk)(32)

In this notation, yk denotes the kth output unit corresponding to the input vector x, bk signifies the bias, and the weight of the connection linking the kth output unit to the jth hidden layer unit is defined by wjk.

4  Application of Taguchi and ANN in Energy Systems

4.1 Taguchi

Over the past years, most studies in energy applications have highlighted the benefits of the Taguchi optimization method as an examination tool to achieve the maximum amount of information for a given experimental dataset. By utilizing Taguchi-based optimization techniques, factors influencing energy production, transmission, and consumption can be fine-tuned to achieve optimal performance levels regarding both the single-objective and multi-objective problems. This section extensively examines the utilization of Taguchi-based methodologies across a broad range of energy systems, encompassing internal combustion engines (ICEs), thermal energy storage systems (TESs), solar energy installations, thermodynamic cycles, heat exchangers (HXs), as well as wind and tidal turbines.

4.1.1 Internal Combustion Engines (ICEs)

Subramani and Govindasamy [77] optimized the design and fuel factors of a direct injection compression ignition engine in order to lower the NOx and emissions as well as enhance the engine brake thermal efficiency (BTE). The effects of eight input factors, including percentage of biodiesel/diesel blend, butanol, pentanol and propanol, together with injection timing, EGR percentage, piston geometry, and injection pressure, were investigated. The best combination of input factor levels against the objective responses was obtained by using Taguchi OA and the S/N ratio. It was concluded that the effects of the percentage of biodiesel in the diesel/biodiesel blend and the percentage of EGR were negligible. Additionally, compared to other alcohols, propanol has the lowest effect on output responses. Simsek et al. [78] examined the performance and emission characteristics of diesel engine in terms of effects of several proportions of biodiesel fuel mixtures and 2-Ethylhexyl nitrate (EHN) at various engine loads. The percentage blend of EHN, the engine load, and percentage blend of biodiesel fuel mixtures by three levels of each, were considered as control factors (Fig. 11). Hence, the experimental runs were arranged by using L27 OA. The optimization was accomplished to achieve the optimum combination of input control factors and output responses, namely BTE, carbon monoxide (CO), nitrogen oxides (NOx), hydrocarbons (HC), BSFC, and smoke emission. Optimization results showed that a load of 2300 W, and a biodiesel/EHN ratio of around 99/1%, were defined as the optimum combination of control factors. The suggested Taguchi design had the ability to map engine output paradigms with excellent accuracy.

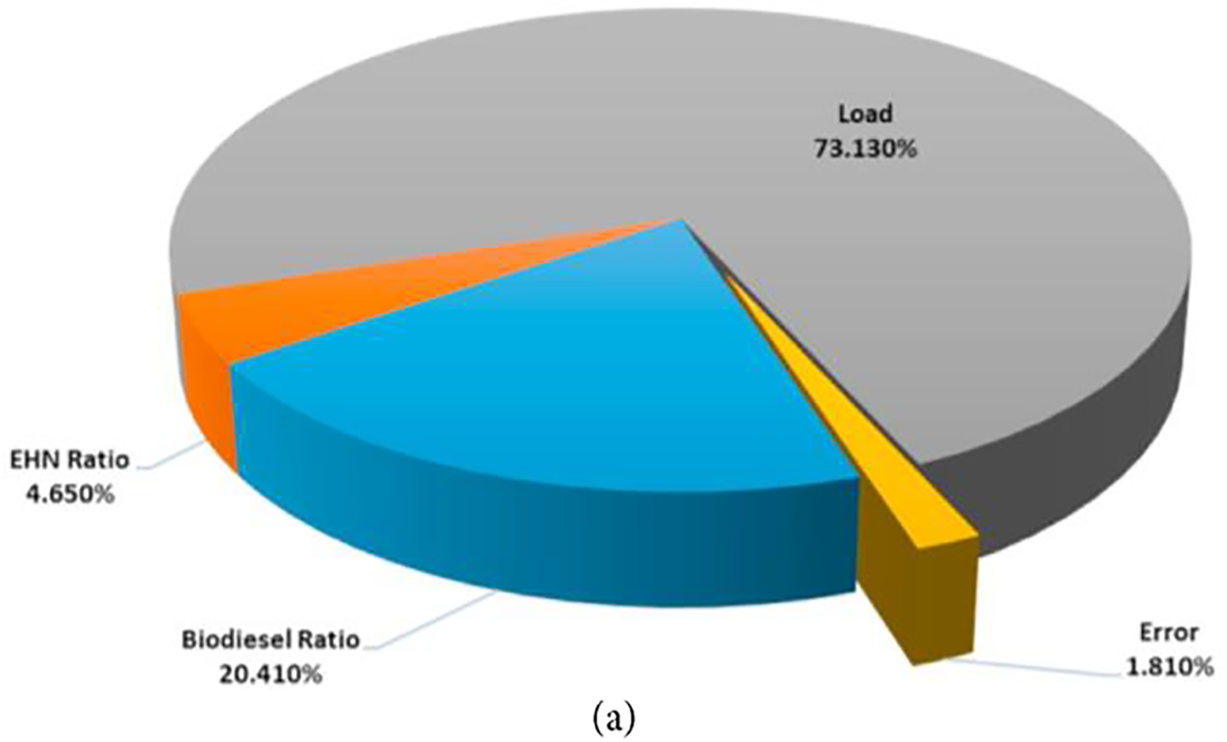
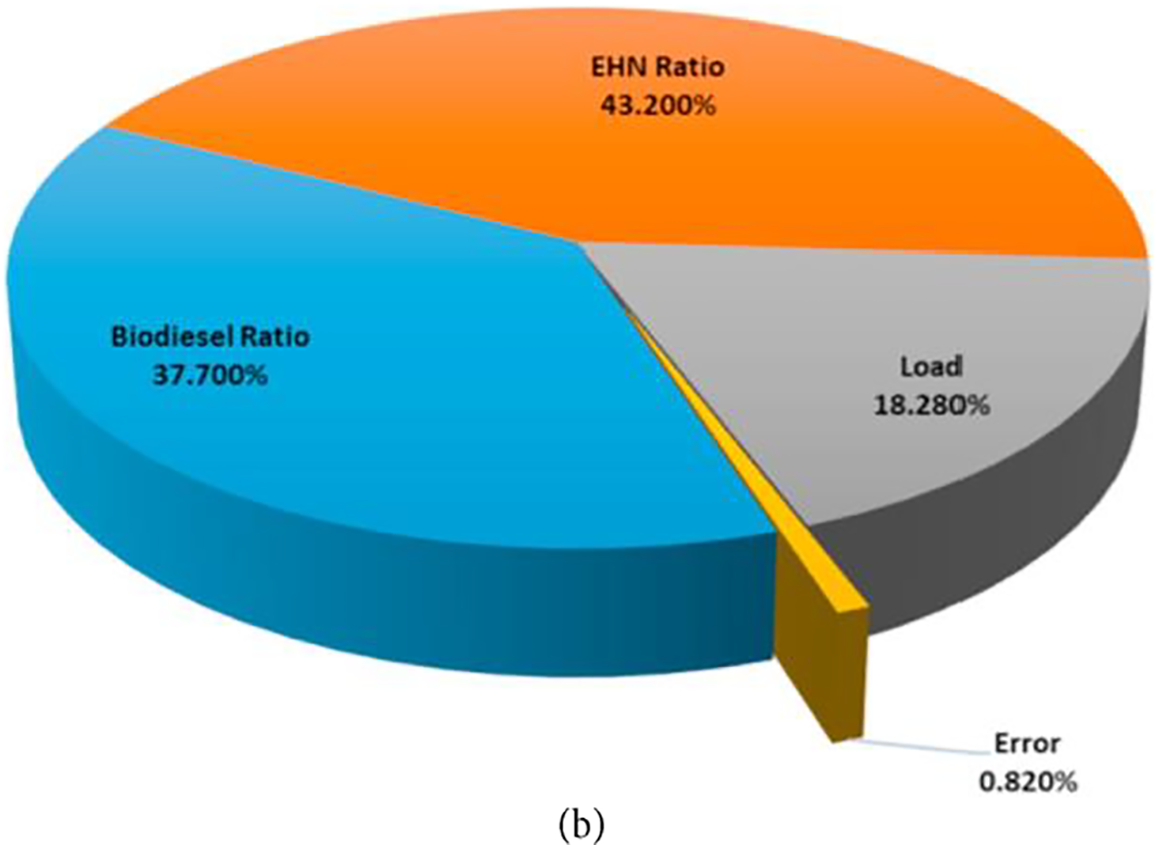
Figure 11: Effect of engine variables on (a) BTE and (b) BSFC [78]

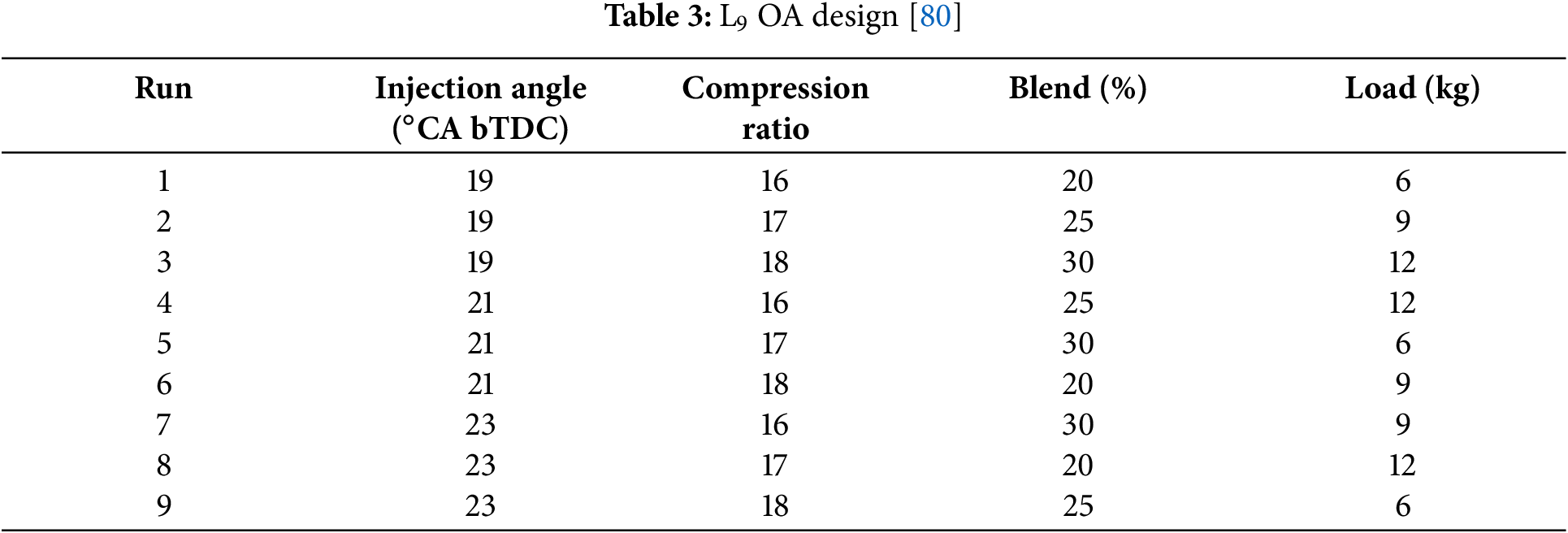
The impacts of engine load, compression ratio (CR), engine speed and, EGR as the control parameters of a port fuel injection SI engine modified from a CI engine fueled by methanol were investigated by Zhou et al. [79]. The thermal efficiency, NOx emissions, and BSFC were as target responses. By employing the Taguchi method and ANOVA, it was revealed that higher amounts of EGR rate and lower CR leads to lower NOx emissions. On the other hand, higher CR was suitable for reducing the BSFC. Additionally, 17:1 was found to be the optimal CR for the investigated engine. Moreover, it was concluded that with an increase in the rate of EGR, flame propagation was decreased, as well as the pressure rise rate and the heat release rate were reduced. The influences of biodiesel, ethanol, and diesel blending on engine performance, combustion, and emissions were explored by Shrivastava et al. [80]. Experimental observations were performed on a CI engine at a constant speed of 1500 rpm and the injection pressure of 210 bar. The four input parameters—injection angle, compression ratio (CR), fuel blend percentage, and engine load—are adjusted to achieve optimal objective responses such as BTE, BSFC, CO2, CO, NOx, HC emissions, and exhaust gas temperature. In order to obtain the optimal combination of the input factors and objective responses, Taguchi L9 OA was applied (Table 3). Furthermore, the ANOVA was operated to specify the contribution of input factor. Injection angle of 19°CA bTDC, CR of 18, fuel blend of 30%, and 50% of the load was calculated as the optimum combination of inputs. By applying the optimum combination, the responses displayed a marginal decrease of BTE by around 2%, BSFC increased by 3%, exhaust gases temperature increased by 3%, CO2 raised by 0.86%, HC reduced by 12 PPM, CO and NOx decreased by up to around 0.029% and 8%, respectively.

Performance characteristics examination and optimization of a CI engine running dual biodiesel fuel using the Taguchi method were conducted by Pandey et al. [81]. The impacts of several input factors, including CR, percentage of biodiesel blend, and fuel injection pressure against the operating variables such as BTE, BSFC, and emissions, were characterized. According to the experimental design of Taguchi L16 OA, the trials were accomplished for the single-cylinder CI engine operating by the dual biodiesel blends of Soyabean and Karana. To achieve a better performance and exhaust emission features, the best combination of input factors and output responses was calculated. Hence, the Taguchi optimization results indicated that the best combination of input factors to meet the maximum values of BTE had been observed as a biodiesel blend of 20%, CR of 16:1, and fuel injection pressure of 230 bar. A small number of studies have operated the Taguchi-GRA in order to perform multi-response optimization of coconut oil-diesel fuel blends by using different input variables. Hence, Heng Teoh et al. [82] experimentally (Fig. 12) focused on discovering the best combination of biodiesel blend ratio, engine load, and speed under various conditions using the Taguchi-GRA method. The Taguchi method with an L16 OA was employed for DOE. For calculating the optimal variables, the S/N ratio and GRA grade were applied. Moreover, the ANOVA table was utilized to examine the importance of the three engine inputs against the objective responses. The outcomes revealed that considering the combustion features, exhaust emissions, and performance of the CI engine, the following factors were the optimum combination of inputs: a 30% blend ratio, an engine speed of 3850 RPM, and an engine load of 25%. As a comparison to traditional diesel fuel, employing the optimal engine conditions increases TC boost air pressure, CO emissions, O2 levels, and smoke emissions by approximately 0.44%, 12.9%, 1.15%, and 14.97%, respectively.

Figure 12: The arrangement for the experimental setup; (1) test engine, (2) eddy current dynamometer, (3) engine coolant heat exchanger, (4) turbocharger, and (5) fuel supply tank [82]

The emission characteristics and combustion performance of a 4-stroke 1-cylinder engine operating canola oil combined diesel with Al2O3 NPs through single and multi-objective optimization techniques were improved by Ramesh et al. [83]. To maximize BTE, and minimize NOx emission along with the fuel cost, the Taguchi S/N ratio, GRA, as well as RSM techniques were utilized. Percentage of the canola oil blend, NPs concentration, injection timing and pressure were considered as the practical input variables. Accordingly, considering Taguchi-GRA integrated with RSM, the optimum combination of inputs was determined as follows: canola oil blend percentage of around 19%, 30 ppm for the concentration of NPs, 220 bar for injection pressure, and fuel injection timing of 21° bTDC. The mentioned combination improves the BTE by up to 16%, together with a reduction of NOx by about 3% in comparison to diesel fuel. By using Taguchi-based GRA, a multi-factor optimization mechanism for combustion efficiency of a hydrogen-fueled micro-cylindrical combustor was explored by Zuo et al. [84]. Taguchi L25 OA was provided according to six input factors, namely inlet velocity, hydrogen/air equivalence ratio, convective heat transfer coefficient (h), inlet temperature, wall emissivity, and wall thermal conductivity. Further, GRA and ANOVA were utilized to assess the impact of these input variables on combustion efficiency, ranking them from highest to lowest effectiveness. Hence, inlet temperature, inlet velocity, and hydrogen/air equivalence ratio were specified as the most influential factors in the combustion efficiency, respectively. To discover the best engine running variables against the optimum engine responses, the Taguchi optimization method was applied by Uslu et al. [85]. They scrutinized the influences of diethyl ether ratio, palm oil ratio, engine load, and injection advance on the performance and emission of the diesel engine. Examinations were configured according to Taguchi L27 OA, considering factors and responses such as BTE, BSFC, exhaust gases temperature, HC, CO, NOx, and smoke. The influential engine input variables on output responses were specified by using ANOVA. The results showed that the largest S/N ratios for BSFC, BTE, and exhaust gas temperature were detected by the lower diethyl ether ratio ratios, lower advance in injection variables, and intermediate engine load values. Moreover, the largest S/N ratio for smoke and CO were observed when using a 20% palm oil blend. Conversely, the maximum S/N ratio for other outputs were attained when using a 0% palm oil blend. Sharma et al. [86] conducted research to investigate and optimize the input variables of a diesel engine operating at full load, fueled with a blend of Pongamia biodiesel. To find the optimum results, a hybrid utility theory-Taguchi optimization method was employed. Experimentation was conducted concerning the combination of utility theory and Taguchi optimization methods. Hence, for multiple input variables, namely fuel injection timing, blends of Pongamia biodiesel, fuel injection pressure, and responses such as NOx, BTE, and smoke, the optimization was carried out (Fig. 13). It was concluded that the 10% of blending for Pongamia biodiesel with injection timing of 23° bTDC, and injection pressure of 22 MPa was discovered as the best engine factors vs. output responses.

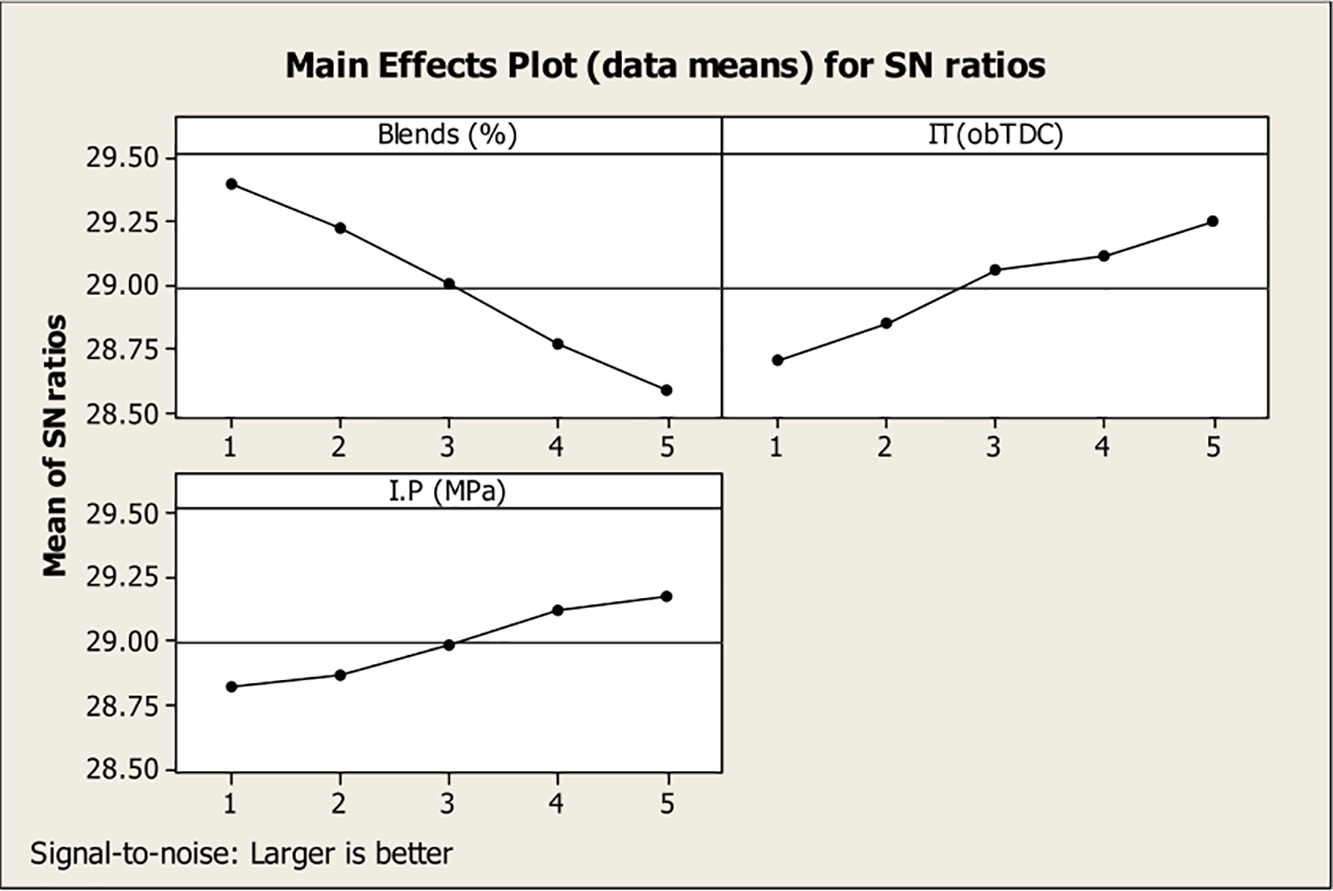
Figure 13: Main effect plot of the S/N ratio for BTE [86]

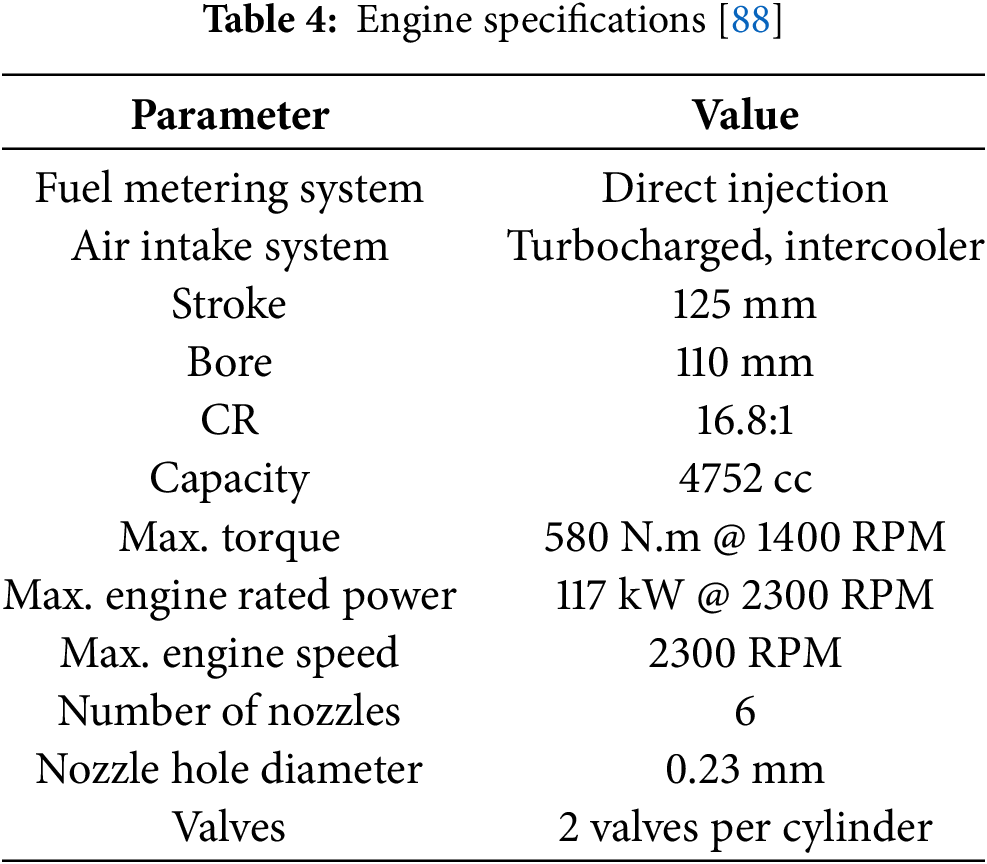
Multi-response optimization of an engine operating by various fuel types, including additives, by using the Taguchi-based GRA technique was conducted by Çelik et al. [87]. Two types of biodiesel fuel called rapeseed oil biodiesel and cottonseed oil biodiesel were considered for this single-cylinder diesel engine. Additionally, n-hexane and n-hexadecane were utilized as additives. Based on input factors and levels, the Taguchi L18 OA was considered, and three levels of 4%, 8%, and 12% were allocated to the additives. Comparing between rapeseed and cottonseed, the outcomes exhibited that rapeseed oil depicted the optimum system responses. Moreover, utilizing the hexadecane offered a better result compared to the hexane additive. ANOVA also indicated that blend and type of fuel were selected as the predominant operating factor influencing the GRA grade in terms of optimization of engine emissions and performance. The optimization outcomes also demonstrated that the best condition of the diesel engine arises by operating rapeseed oil biodiesel including 12% hexadecane as the additive. Taguchi-based GRA and ANN-based optimization to achieve the best performance by low-emission diesel engine fueled with biodiesel was investigated by Gul et al. [88]. The engine’s operational characteristics are indicated in Table 4. The Taguchi L9 OA was applied to acquire the best combination of practical input factors, including the fuel nature, as well as the DI-diesel engine speed and load. The diesel engine was alternatively fueled by waste cooking oil based on pure biodiesel and the 20% blend of biodiesel with regular diesel. The main objective functions were defined to decrease NOx and smoke emissions as well as to enhance in-cylinder pressure, heat release rate, the BSFC, and brake power at different loads. The GRA result determined the best input factors as follows: full engine load, pure biodiesel as the fuel, 2300 RPM for engine speed. Further, the ANOVA revealed that the fuel type was considered the main prominent variable with around 44% influence on the output responses.

Fuzzy logic-based Taguchi method optimization of two input factors called CR and fuel injection timing of a constant-speed diesel engine fueled with oxygenated blends, was studied by Kumar Chidambaram et al. [89]. The examinations involved three types of blends labeled as DEE6 (6% diethyl ether with 94% diesel), DEE8 (8% diethyl ether with 92% diesel), and DEE10 (10% diethyl ether with 90% diesel). The findings revealed an improvement in engine performance when utilizing a compression ratio (CR) of 19:1 for the blends. Among the emissions, NOx emission was noted to be the highest, while CO, unburned HC, and smoke emissions were minimized. The engine performance operating DEE8 with CR of 19:1 and 21°bTDC leads to a 6% improvement in BTE, and a reduction in smoke, HC, and CO up to around 14%, 25%, and 21%, respectively. The fuzzy logic-based Taguchi approach outcomes depicted that the optimum combination of considered input factors was 21°bTDC for fuel injection timing and a 19:1 CR.

Jain et al. [90] focused on producing biodiesel from Water Hyacinth and testing it in a diesel engine to address the twin challenges of the fossil fuel crisis and increasing pollution. A 3.5 kW single-cylinder research engine was used with varied injection timings and engine loads. Results showed the maximum BTE at 80% load, 20° bTDC injection timing, and a compression ratio of 17.5. The L16 OA, S/N ratios, and ANOVA were employed for efficient testing and data analysis. RSM-based desirability optimization yielded reliable predictive models, indicating engine load’s significant impact on brake thermal efficiency and emissions. The optimized output of 24.44% BTE, 51.2 bar PCP, 29.6 ppm CO, 1.51 vol% CO2, 176 ppm NOx, and 23.66 ppm HC was achieved at 78% load and 20° injection advance. The modeling residuals were below 6% in the validation test, affirming the accuracy of the developed correlations. In a similar investigation, the influence of the design and control parameters on the performance and emissions features of a single-cylinder boosted GDI SI engine, was investigated experimentally using the Taguchi method by Atis et al. [91]. The Taguchi L18 OA design has been applied to examine the input factors: intake valve closing (IVC), EGR rate, fuel injection timing, CR, intake port tumble design, piston bowl design, injector spray pattern, and fuel injection pressure. It was concluded that computation of the S/N ratios caused an understanding of the +/− effects of each input factor at three speed-load conditions of the engine. Furthermore, in terms of specified factors, IVC timing, CR, intake port design, EGR rate, and fuel injection timing were determined as more effective factors for the responses.

Taguchi-based optimization strategy and investigation for combined effects of EGR rate, supercharging pressure, biodiesel blends, and ethanol injection through the intake manifold of a DI diesel was accomplished by Ayhan et al. [92]. Experimental runs were performed according to the Taguchi L16 OA design. The appropriate engine operational parameters were specified through the Taguchi optimization method in terms of responses such as engine brake-specific heat consumption, NO, HC, smoke, CO2, and CO emissions. The results revealed that the optimum smoke, HC and CO emissions were achieved in 40% of engine load, biodiesel fuel blend of 50%, without ethanol injection, without EGR, at an engine speed of 1600 RPM, and supercharging pressure of 2.1 bar. Further, the optimized NO emission was observed at engine load of 40%, pure diesel fuel, without ethanol, EGR rate of 20%, the engine speed of 2400 RPM, and supercharging pressure of 2.1 bar.

Manigandan et al. [93] employed the Taguchi technique to examine the influence of blends of multiwall carbon nanotubes (MCNs) and hydrogen on the efficiency and emissions of the diesel engine. The Taguchi L16 OA was employed to investigate the effects of the following input parameters: MCNs of 30, 50, and 80 ppm by various fuel blend features, as well as hydrogen of 10%, 20%, and 30%, at various engine loads of 25%–100%. Additionally, the ignition pressure and timing were evaluated at four levels of 180–240 bar and 210–310 CA bTDC, respectively. Results indicated that in a comparison to pure diesel, the hydrogen and MCNs additions reduce the emission accompanied by an increase in the BTE value. The importance of the optimal input parameters was also dissected using the ANOVA table. Hence, it was noticeable that the addition of hydrogen and MCNs led to an improvement in the performance and emission features. Furthermore, results revealed that at the full engine load conditions, brake power was enhanced by up to 13%, and BSFC was decreased by up to 8%. Zhang et al. [94] studied optimizing control parameters for an ICCI type engine, which incorporates an additional DI system (Fig. 14). Taguchi design of experiment, utilizing an L18 orthogonal array, simplified the optimization process. The impacts of factors such as excess air ratio, engine speed and load, premixed strategies, and the fuel energy ratio of E85 (comprising 15% gasoline and 85% ethanol) were examined by using the S/N ratio and the ANOVA regarding their influence on particle number (PN), indicated thermal efficiency (ITE), and gaseous emissions. The Taguchi method provided optimized control rules for ICCI across various operating conditions. Engine load and speed were found to have significant influences on ITE, whereas E85 energy ratio, premixed strategies, and excess air ratio exhibited contrasting degrees of impact on emission characteristics. The optimized strategy achieved an 80% E85 substitution ratio led to a reduction in CO2 emissions to below 500 g/kWh in most conditions, with the ICCI combustion load reaching 75% of the original diesel engine load.

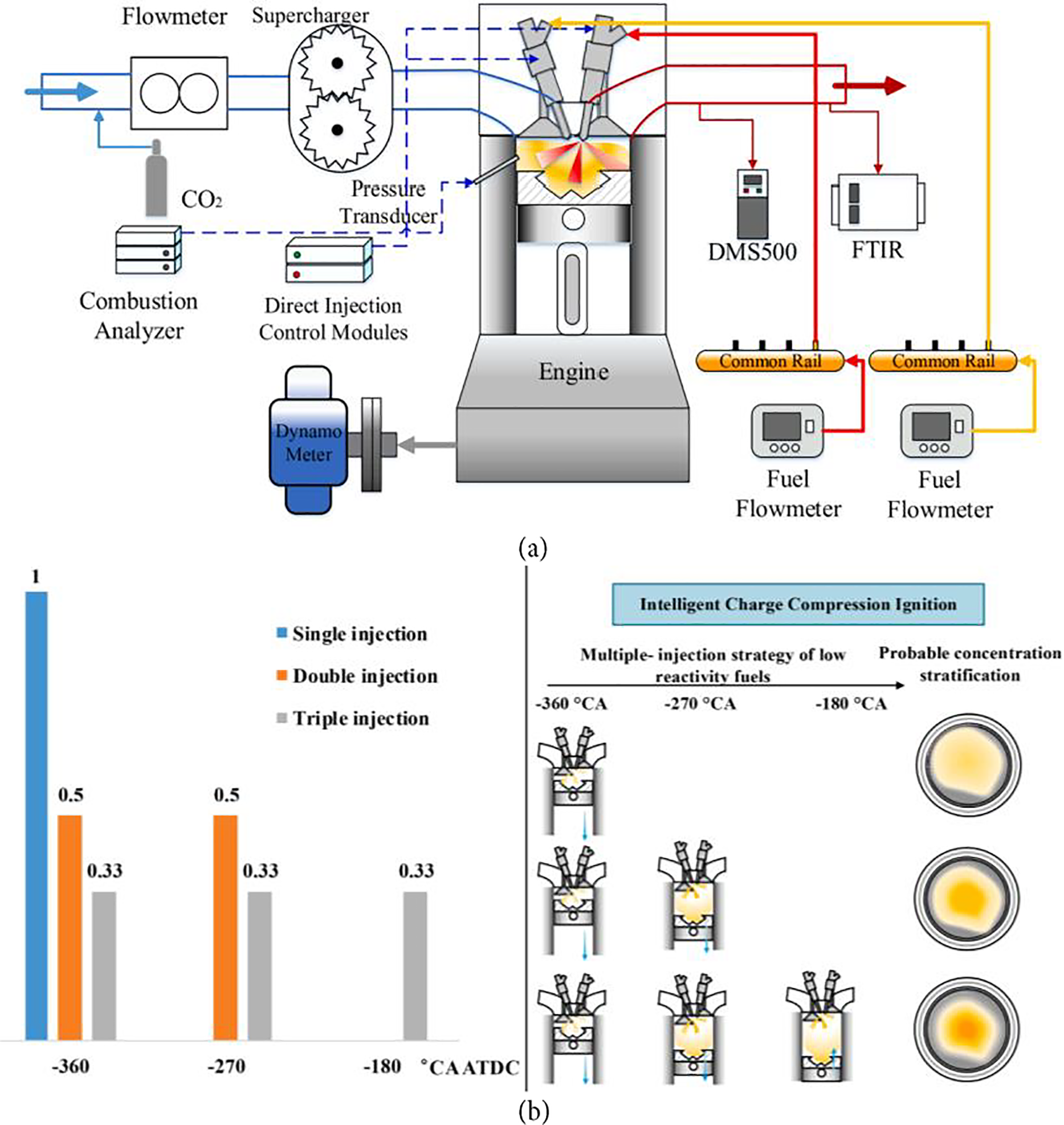
Figure 14: (a) Schematic of the experimental setup system (b) Multiple-injection strategy description [94]

4.1.2 Thermal Energy Storages (TESs)

The experimental investigation and Taguchi-based optimization of phase change material (PCM) layer as insulation wall for TES system were conducted by Kurnia et al. [95]. The impacts of main geometric and operating variables such as inlet volumetric flow rate and temperature of the HTF and the ratio of PCM volume to HTF volume were assessed against the efficiency characteristics of the hybrid TES. The results indicated that the hybrid TES system with a PCM wall layer presents a better insulation performance. This arises a higher retained temperature within the storage compared to conventional TES. The capacity of TES heat storing was improved by employing the PCM wall. Moreover, among the input variables, HTF inlet temperature was found to be the most influential parameter on the performance of the Hybrid TES system. By using the Taguchi-based GRA, Çinici et al. [96] experimentally examined the optimum factors affecting the melting time of solar TES unit, including a spring-type heat transfer enhancer of thermal energy storage unit (Fig. 15). Considering the Taguchi L9 OA, the impacts of various input factors including spring diameter, spring pitch, and wire diameter vs. the characteristics of time-dependent enhancement ratio and melting time of latent heat TES unit were scrutinized. The ANOVA tables were utilized to find out the most significant input parameter against the melting time and time-dependent enhancement ratio. Performing the GRA simplifies the optimization process into a single-objective problem rather than a multi-objective one. As a result, the optimal levels were determined to be the highest levels of spring pitch and wire diameter, along with the minimum level of spring diameter.

Figure 15: Experimental arrangement of different copper springs in the PCM storage [96]

The solidification behavior of nano-enhanced PCMs in triplex-tube and shell-and-tube TES units was investigated through the Taguchi optimization approach by Khatibi et al. [97]. The solidification process, as well as thermophysical features of PCM incorporating various metal oxide NPs such as ZnO, SiO2, Al2O3, and CuO inside a triplex tube, was evaluated. To specify the best performance of the system, a comparative study for various HTF temperatures and tube diameters among three typical TES units was conducted. Therefore, triplex-tube plus shell-and-tube with inner and outer cooling by the similar volume for the storage unit were determined. According to the Taguchi analysis, compared to the other NP-PCMs, the Al2O3-PCM indicates a higher rate of solidification at the volume fraction of 2%. In addition, dispersing nanoparticles in PCM is found to be the less effective parameter. As a comparison to other units, the triplex tube presents a better solidification time at any level of input parameters.

The characteristics of the petal-shaped pipes in a shell-and-tube TES unit, were numerically investigated and optimized using the Taguchi method by Ghalambaz et al. [98]. The effects of applying two types of NPs-additives called copper (Cu) and graphene oxide (GO) for heat transfer enhancement, together with the geometrical characteristics of the petal pipe vs. the thermal performance of the TES unit were analyzed. The Taguchi optimization results revealed that compared to a typical design, the optimized tube design could enhance the energy storage capacity for Cu and GO by up to around 23% and 22%, respectively. In comparison to a circular tube without using NP, the optimal design in which Cu operates as NP enhances the heat transfer by around 45%. According to the ANOVA table results, the operating range of petal shaped-tube could impact the energy storage by a contribution ratio of almost 41%, while the NPs share was calculated at about 6%.

The Taguchi-based optimization of melting heat transfer rate in terms of using capric acid PCM in a channel shape TES unit was numerically explored by Mehryan et al. [99]. A mixture of Cu NPs and copper foam was applied to improve the melting heat transfer rate and to enhance the thermal conductivity further. Considering the Taguchi optimization approach, input parameters, including the shape and the porosity of the copper foam layer, plus the volume fraction of NPs, were optimized in order to attain minimum charging time. The outcomes showed that the higher the porosity and volume fraction of NPs leads to the lower charging time of TES. Additionally, simultaneous utilizing the mixture of copper-foam and Cu NPs together with the optimum design of the porous layer decreased the melting time by up to 300%. Besides, it was found that the foam layer porosity was the most effective variable in the heat transfer.

Taguchi optimization and evaluation of the transient thermal performance of PCM outfitted walls were conducted by Zhang and Deng [100]. The effective input parameters considered are as follows: the phase change temperature deviation of PCMs from ambient ones, total latent heat and location of PCMs, along with the thermal conductivity of the wall. Considering the importance of input parameters, the criteria for high thermal performance were acquired. Additionally, a comparison table including three values of synthesis score, thermal index value, and thermal performance level was considered to classify the walls’ performance. Multi-objective optimization, together with experimental research of a TES using PCMs for solar air systems were introduced by Lin et al. [101]. Two conflicting objective functions called effective PCM charging time along with the average heat transfer effectiveness were considered as output responses. The Taguchi L9 OA was proposed for effective input parameters, namely inlet air temperature of the TES unit, charging air flow rate, number of PCM bricks along the TES unit, and number of air channels. Besides, the experimental exploration revealed the impacts of critical parameters on the performance of the air-based PCM-TES system. It was concluded that the system’s average heat transfer effectiveness could be enhanced by up to 15%. At the same time, the effective PCM charging time is raised by up to about 1.5 h.

The experimental study and Taguchi optimization of various control parameters, including plate inclination angle, HTF velocity, and HTF temperature for a plate-type TES unit using PCMs, were accomplished by Sun et al. [102]. The energy charging rate was determined as the objective function of the optimization. According to the optimization results, 55°C for the HTF temperature, the plate inclination of 75°, and the HTF velocity of 5 m/s were defined as the optimum values for input parameters. Applying the mentioned optimum values for input parameters, the optimal energy charging rate was determined to be 760 W, resulting in a 23% improvement. Furthermore, it was observed that the most significant parameters were the HTF temperature followed by the HTF velocity for the melting process. Optimizing the plate inclination angle proved to be an effective method for enhancing the melting process without requiring additional energy or materials.

A 3-dimensional CFD numerical modeling and evaluation of dual medium thermocline TES was conducted by Nandi et al. [103]. The thermal performance and characteristics of the proposed system were explored under various working conditions to evaluate the charging and discharging processes of a 50 MWh fixed-size TES (Fig. 16) The 3-dimensional CFD model was developed according to a macroscopic version of the k–epsilon equation for turbulent flow conditions. Besides, the Taguchi optimization approach was employed to optimize design factors related to the thermocline TES system. Hence, the influence of the design factors, namely the inlet fluid Re number, aspect ratio, porosity, and filler size, on the TES performance was assessed. The research outcomes demonstrated that the porosity and aspect ratio were the most significant design factors for thermocline TES, respectively.

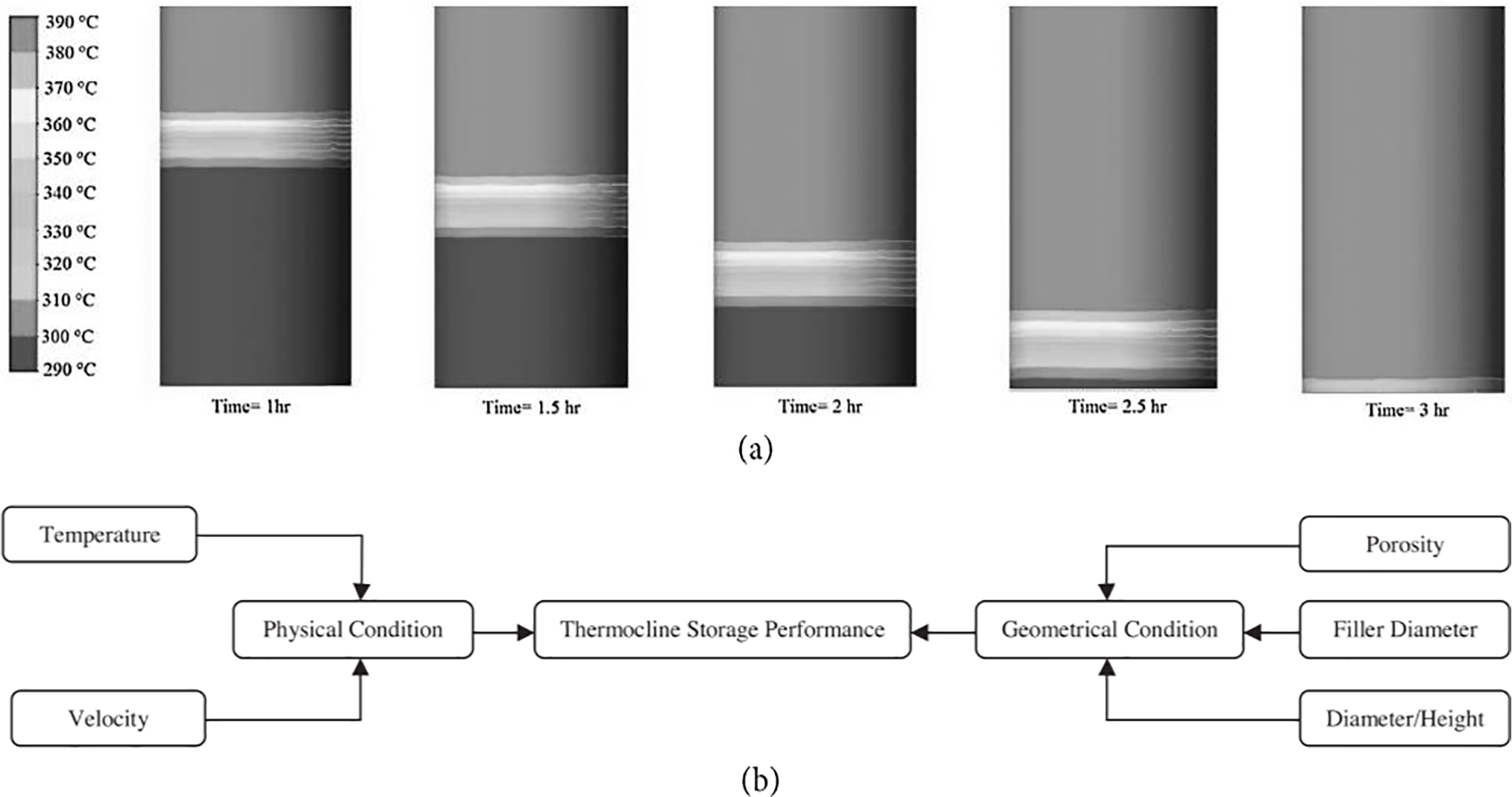
Figure 16: (a) Thermocline thermal storage tank temperature distributions at a different charging time (b) Parameters influence thermocline thermal storage performance [103]

4.1.3 Heat Exchangers (HXs)

The efficiency of the coaxial HX with semicircular striped turbulators was examined by Turgut and Yardımcı [104], considering Taguchi-based GRA (Fig. 17). Control factors were Re number, thickness, pitch, arrangement style, and diameter. As well, the Nu number, thermal performance factor, and friction factor were considered as responses. The Taguchi OA design was considered to find the optimum control parameter levels for maximum heat transfer and minimum friction factor. Considering the GRA, the multi-objective optimization of performance features was calculated, and the impacts of input variables on the pressure loss and the heat transfer were assessed. Based on the ANOVA outcomes, the most influential variable against the Nu number was the Re number with 31% of the contribution. In contrast, the least effective factor was the pitch with about 2%. In addition, results indicated that the Re number was specified as the most critical factor in respect of the total performance characteristics of the HX. Moein Darbari et al. [105] conducted a study to evaluate the performance of a HX by performing a sensitivity evaluation of nanofluid flow through various flat tubes confined between two parallel plates. by utilizing the Taguchi method and ANOVA. The nanofluid, including NPs of AlO by various flat tubes with axial ratios of 1.5–2.5, volume fractions of 0%–8%, and square sections tubes in comparison with circular were employed as input factors. The Taguchi L25 OA design and ANOVA were considered to analyze the sensitivity of pressure drop and heat transfer features of the HX. The conclusion drawn was that by adjusting the further flattening and cross-section, the pressure drop and heat transfer were reduced together. On the other hand, by raising the NPs volume fraction, the heat transfer and flow pressure drop were incremented.

Figure 17: (a) schematic view and (b) photo of turbulators [104]

A parametric optimization study of a wavy fin and tube air HX by using the Taguchi-based GRA was accomplished by Kumar and Sahoo [106] (Fig. 18). The HX parametric study for the air-side was considered in terms of heat transfer and friction factor characteristics. Thus, experimental runs were performed for the Taguchi L27 OA design. Examination results exposed the highest contribution ratio against outputs by 47% for fin pitch, followed by 25% for air velocity, and 24% for fin thickness. The output responses were friction factor, heat transfer coefficient, and Colburn factor. The optimum input factors determined by GRA were as follows: air velocity of 5 m/s, 1.8 mm for the waffle height, 6 mm for the tube of fin pitch, 0.12 mm for fin thickness, and 6 for the tube row number. In a comprehensive study conducted by Razak Kaladgi et al. [107], the impacts of various input variables on the thermal characteristics of a car radiator were analyzed and optimized by employing the integrated Taguchi-GRA along with the response surface methodology (RSM). Additionally, the artificial neural network (ANN) modeling was applied to find a more acceptable projection of the non-linear formation of critical data. The Re number, air velocity, and nanofluid concentration were considered as inputs, and polyethylene glycol (PEG) nanofluids comprising NPs of ZnO by different volume concentrations (0.2%–0.6%) were operated. Considering the Taguchi OA and calculating the weighted GRA grade, the following thermal characteristics were optimized: Nusselt number, convection heat transfer coefficient, pressure drop, and the pumping power. The main finding of the study was that heat transfer improvement arises in radiators working with nanofluids at the expense of the pressure drop as well as pumping power.

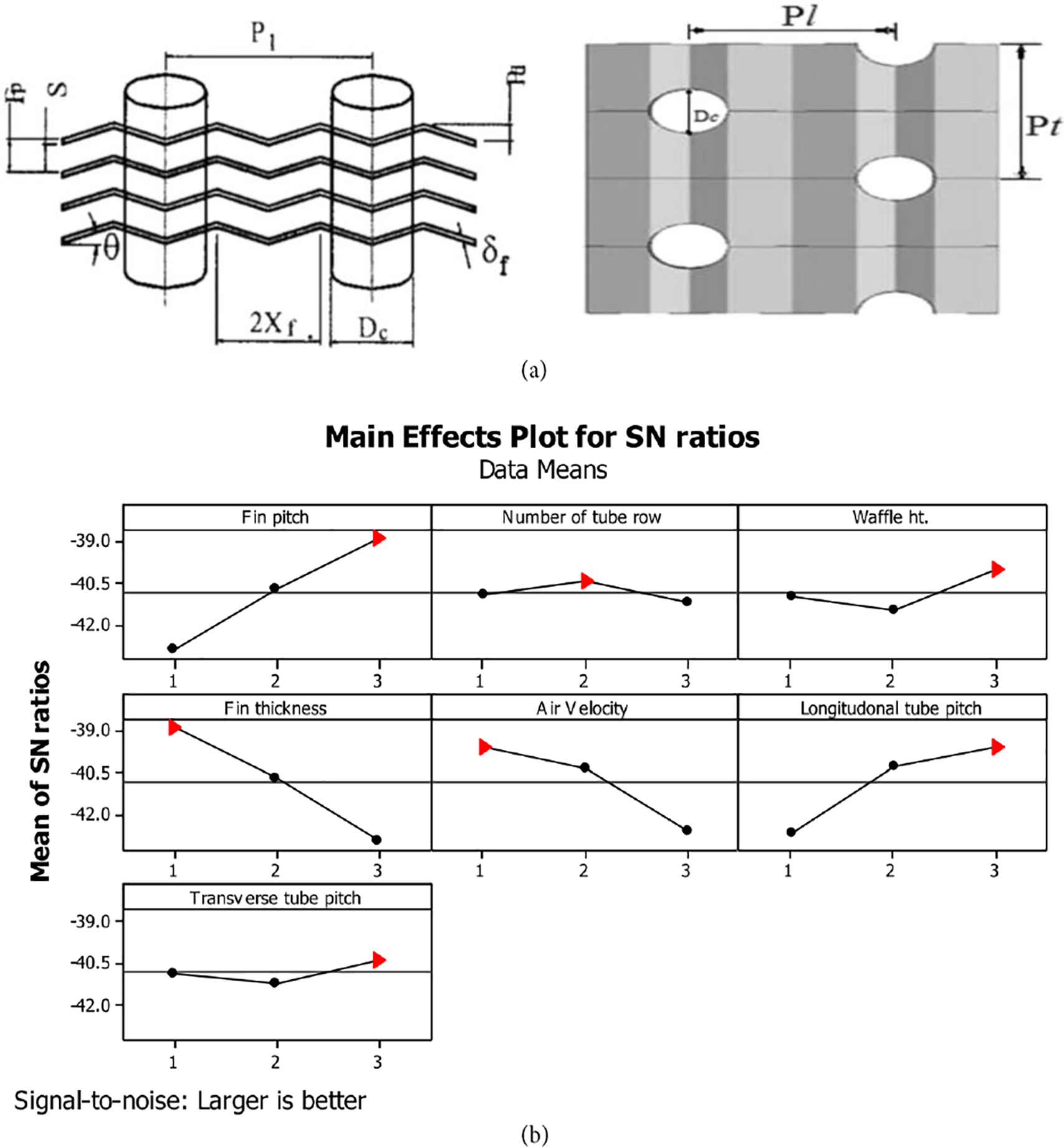
Figure 18: (a) The geometrical design of a wavy fin and tube radiator of staggered arrangement and (b) effect of design parameters on Colburn factor [106]

Multi-response optimization and numerical investigation for dimples variables affecting the thermal and hydraulic features of a dimpled HX tube employing the Taguchi-based GRA and the RSM were performed by Dagdevir [108]. Dimple diameter of 3–7 mm, dimple pitch length of 10–30 mm, and dimple height of 1.0–1.4 mm were defined as the geometrical input parameters. Accordingly, the maximum value of, h, and the lowest pressure drop were established as the objective functions (Fig. 19). Experimental trials were conducted considering the Taguchi L25 OA design. Hence, the Taguchi analysis and GRA were operated for the single-response and multi-response optimization, respectively. It was found that the dimple pitch length has a higher impact on the pressure drop and convective heat transfer coefficient concurrently. It is followed by the other variables, dimple height and dimple diameter. Additionally, the results demonstrated that the optimum configuration for dimple with a diameter of 7 mm, pitch length of 30 mm, and height of 1.0 mm leads to the maximum h and minimum pressure drop. Taguchi optimization and numerical investigation of the heat transfer characteristics of a spirally corrugated tube was executed by Yang et al. [109]. A 3-dimensional numerical model was developed employing ANSYS FLUENT commercial software. The geometric parameters such as corrugation depth and corrugation spacing were analyzed vs. the heat transfer features. The results represented that heat transfer was improved by generating the secondary flow around the spirally corrugated tube wall. The ANOVA tables exhibited that the contributions of the corrugation spacing and depth against to heat transfer coefficient were around 90%. Increasing the corrugation spacing leads to a reduction of the mean heat transfer coefficient by up to 5%. It was enhanced almost by up to 36% when corrugation depth was augmented from 1–3 mm. Moreover, the optimal combination of inputs, including 3 mm for corrugation depth and 9 mm for corrugation spacing with Re of 30,000, improved the heat transfer by up to 15.0%. Mallik et al. [110] investigated the CFD modeling and optimization of utilizing the Taguchi approach, a cylindrical reactor was created with longitudinal finned cooling tubes that bifurcate, intended to function as a HX for an large-scale metal hydride reactor system. The optimization process was conducted for seven different control parameters using the Taguchi L18 OA design. The 3-dimensional modeling was executed by COMSOL Multiphysics, and the absorption features were examined by considering the variation of pressure and HTF temperature. The results revealed that number of fins, the number of cooling tubes, and the fin length were found to be the most significant variables in optimizing absorption time. Additionally, at an inlet pressure of 20 bar, a cooling fluid temperature of 20°C in a 50 kg system with eight bifurcating finned cooling tubes, a hydrogen storage capacity of 1.21% was acquired in 700 s.

Figure 19: (a) a view of the grid structure for the dimpled tube and (b) effect of dimple diameter on the ℎ and the ΔP [108]

Optimization and sensitivity investigation of an experimental vertical earth-to-air HX system combining the annular PCM using the Taguchi approach were conducted by Liu et al. [111] (Fig. 20). The examination of thermophysical parameters of PCM was executed corresponded to cooling capacity and outlet air temperature fluctuation. Results revealed that fusion temperature of PCM, as well as latent heat of PCM were the most critical parameters corresponding to the cooling capacity, with contribution ratios of almost 38% and 29%, respectively. Whereas melting temperature and thickness of PCM were specified as the most influential parameters corresponding to the temperature fluctuation with contribution ratios of about 26% and 31%, respectively. The energy and exergy study of the heat transfer and pressure drop characteristics of helically corrugated coiled tube HX using the Taguchi approach, was executed by Heydari et al. [112]. To dissect the hydrothermal features of HX, various control factors called inlet fluid flow rate, corrugation pitch, corrugation depth, and the number of rounds were considered. The results demonstrated that when the corrugation depth, inlet fluid flow rate on the coil side, and the number of rounds were increased, the pressure drop and heat transfer were raised concurrently. Furthermore, the most significant variables related to the thermal efficiency of the HX were determined to be the fluid flow rate on the coil side and corrugation depth, respectively. As well, considering the HX hydrodynamic characteristics, the fluid flow rate on the coil side and corrugation pitch were calculated as the most critical parameters, respectively.

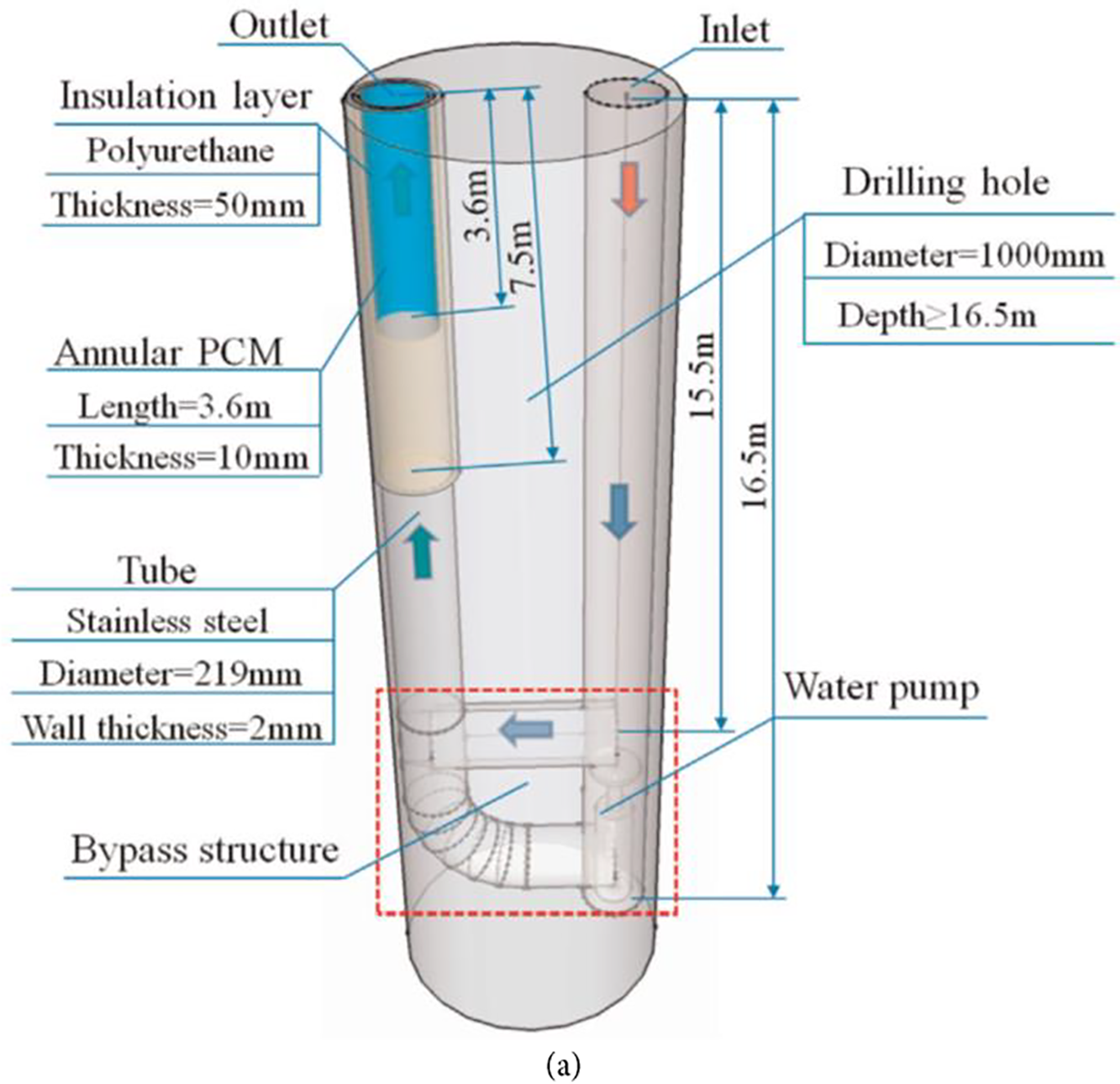
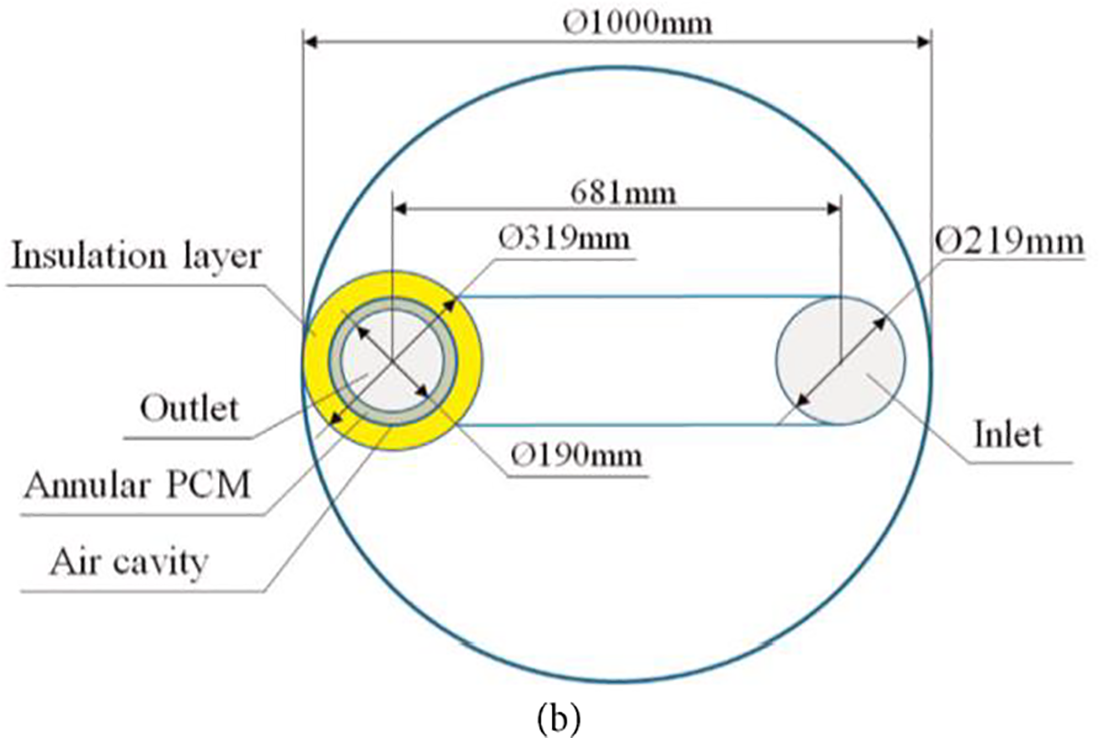
Figure 20: (a) The system configuration and (b) its detailed dimensions [111]

To enhance the performance of the helically grooved shell and tube HX, the energy, and exergy investigation of the HX by utilizing the Taguchi optimization method was conducted by Miansari et al. [113]. Considering the Taguchi design, various levels for control parameters called cold fluid rate, groove height, and cold inlet temperature were considered in the survey. According to their findings, the groove boosts the heat transfer rate by up to 5% and was approximately ineffective in the pressure drop. Further, it was revealed that the thermal efficiency of HX varies from 23%–49% in terms of different conditions. The flow rate, together with the inlet temperature had the same influence on the exergy losses. Moreover, the optimum value of groove height was 10 mm. The Taguchi optimization approach was applied by Biçer et al. [114] regarding a shell-and-tube HX operating by a novel three-zonal baffle. CFD analysis was employed to visualize the 3D turbulent flow domain (Fig. 21). The Taguchi technique was operated to define optimum design configurations. The Taguchi L16 OA was applied for different control factors, namely distance between baffles, the ratio of outer diameter to the inner diameter, the rotation angle of the baffle, the ratio of openness to closure, and angle of openness to center. In comparison to the standard baffled shell-and-tube HX, the thermal characteristics of the HX with three-zonal baffles were enhanced moderately. Additionally, the shell-side pressure drop was decreased dramatically. The pressure drop of the shell side was reduced by up to 49% together with a raise in the shell side ΔT by up to around 7%. Furthermore, the three-zonal baffles enhanced the shell-and-tube HX total performance regarding heat transfer rate and pressure drop.

Figure 21: Pressure distributions in the heat exchanger at a mass flow rate of 0.5 kg/s [114]

4.1.4 Solar Energy Systems

Considering the Taguchi optimization strategy, Raina et al. [115] investigated the optimum orientation of the bifacial photovoltaic (PV) module in India. The main control parameters affecting the power generation and performance characteristics of the PV were: the elevation of the module above the ground, tilt angle, azimuth angle, and the albedo of the location. According to the Taguchi optimization results, an elevation of 0.8 m, an azimuth angle of 22.5°, and a tilt angle of 40° were determined as the best mixtures of control factors to maximize the output response. Further, the adequacy of the Taguchi analysis was calculated via ANOVA tables. Moreover, it was concluded that for modules installed at optimum orientation, boosting the value of albedo leads to improving the performance. In a similar investigation, a bifacial photovoltaic thermal (PVT) system design, as well as parameter optimization, was explored by Kuo et al. [116] (Fig. 22). The input variables, namely the number of collectors, collector material, diameter, mass flow rate (MFR), the ratio of storage tank volume to the surface area, azimuth angle, and cycle temperature, were considered effective control parameters of the design. The electrical and energy efficiencies of the system were defined as the quality characteristics of the study. The outcomes represented that according to the 20-year warranty of the PV module, the bifacial PVT system economic benefit was enhanced by up to 18% and 460% compared to the PVT and PV systems, respectively. Additionally, the overall energy output per unit of area for the bifacial PVT system was higher by up to 20% and 210% compared to the PVT and PV systems, respectively.

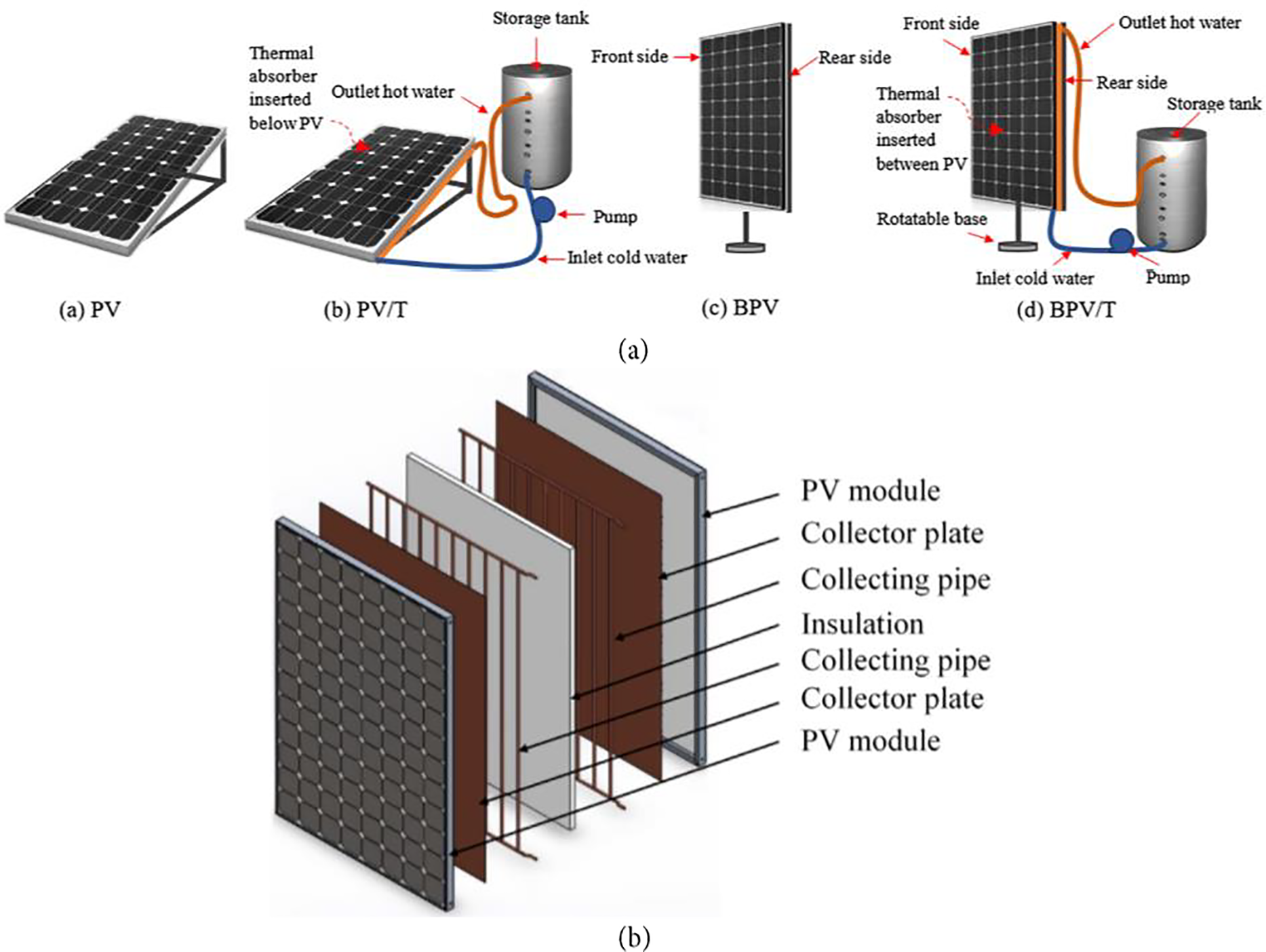
Figure 22: (a) Illustrations of PV, PV/T, BPV, BPV/T and (b) Anatomy of the BPV/T module [116]

Jafari [117] optimized the energy of a geothermal HX in order to cooling of a PV panel by using the Taguchi optimization approach (Fig. 23). The considered coolant was a combination of ethylene glycol and water, which circulated between two HXs. The mini channel HX was bounded to the PV cells, and the geothermal HX was utilized to remove the PV cells’ heat to the ground. The Taguchi L27 OA design was considered for six control factors, including pipe thickness, pipe length, pipe’s inner diameter, coolant flow rate, soil thermal conductivity, and adjacent coil distance. The results indicated that compared to the conventional PV panel, the mean net electricity generation of the PV panel with a cooling system was improved up to about 10%. Further, the optimal setting of the geothermal cooling system had the potential to improve the net electricity generation of the twin cooled panels by around 12%. For the case study of a 30 kW PV solar plant, the levelized cost of energy (LCOE) of the optimized system was determined as 0.089 €/kWh against the ordinary panel of 0.102 €/kWh. An innovative combined system designed by associating a PVT module with a solar thermal (ST) collector in series was investigated through the Taguchi-based GRA multi-objective optimization approach [118]. Considering the Taguchi L25 OA design, the impacts of various control factors such as MFR, coolant inlet temperature, ambient temperature, wind speed, and absorbed solar radiation vs. performance of the system were examined. Thermal efficiency, as well as electrical efficiency of the PVT-ST system, were considered as the output responses of the system. The optimization results showed that solar radiation was found to be the most dominant parameter, with a contribution ratio of about 55% to the proposed system. Whereas an almost contribution ratio of 9% for MFR indicated that approximately this parameter was the most ineffective one. Furthermore, exploiting the optimum combination of the control factors based on the Taguchi-based GRA method enhanced the thermal and electrical efficiencies of the system by up to about 36% and 24%, respectively.

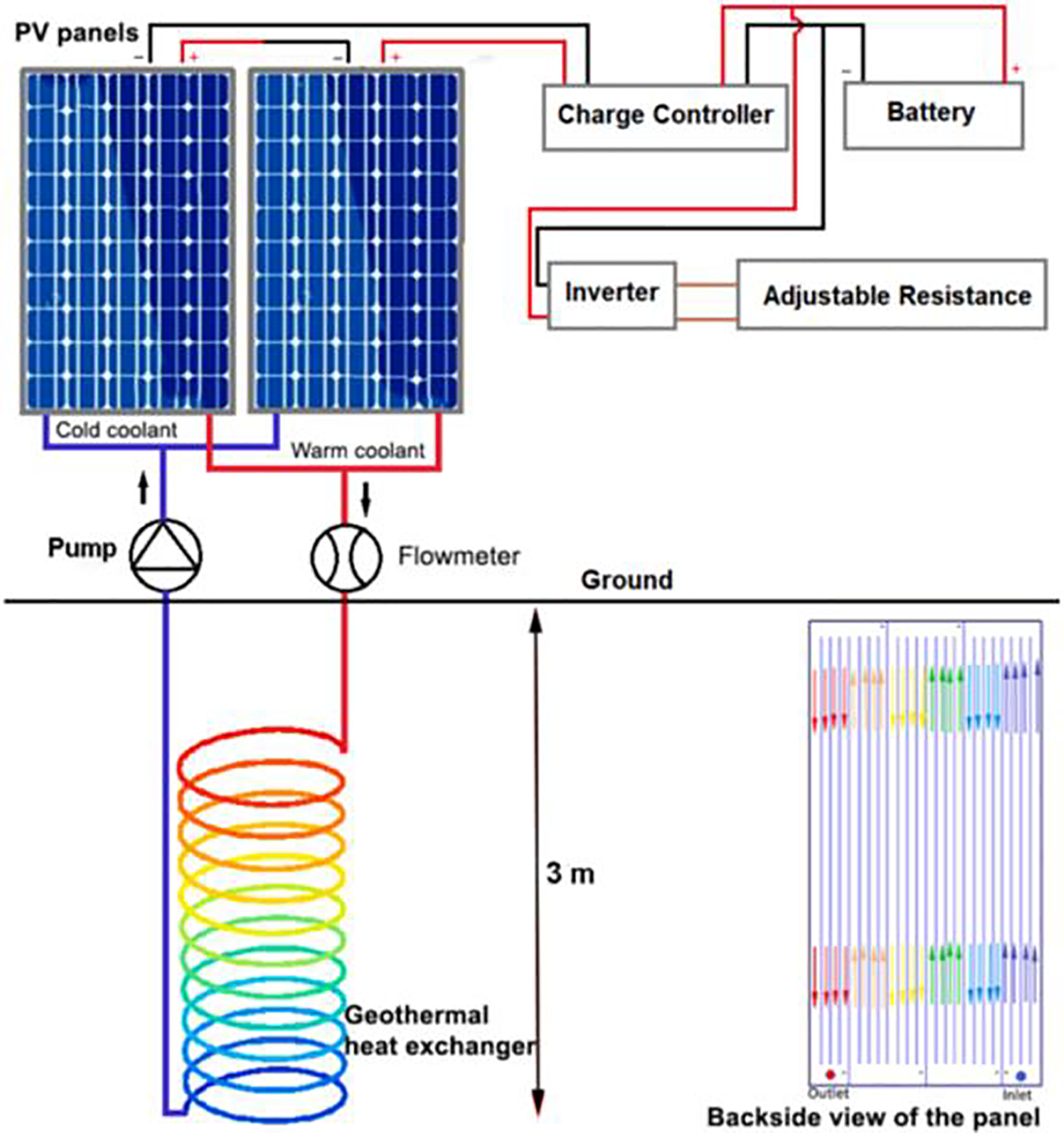
Figure 23: Schematic connections of the designed PV panel with cooling system [117]

Through the Taguchi optimization method, a solar thermoelectric generator (STEG) under different operating conditions was carried out for geometry optimization by Ji et al. [119]. The study focused on the solar concentration ratio plus height, the fill-ratio, and ratio of the cross-sectional area of n-type material to p-type material in the thermoelectric module as control variables. In order to achieve maximum power generation, the Taguchi L27 OA design was utilized. The interaction between input parameters, together with identifying the importance of variables, was obtained through ANOVA tables. The results showed that employing the Taguchi optimum combination improves the output power of the system by up to around 3.5 W. By an experimentally examination, thermodynamic features of a PVT module using various materials and configurations of fins were optimized by Özakın and Kaya [120]. Experimentations were accomplished based on multiple fins configurations and materials such as copper, brass, and aluminum with polycrystal and, monocrystal panels (Fig. 24). The Taguchi optimization approach, together with the ANOVA tables, were employed to optimize effective input parameters such as air velocity, panel temperature, and fins material. Hence, the Taguchi L9 OA was applied for DoE. The energy, exergy, and electrical efficiencies of the PVT system were considered as the output responses of the system, and the S/N ratios were scrutinized. According to the ANOVA results, it was found the fin material was the most significant variable against both the energy and exergy efficiencies of the system. It is followed by the airflow rate and panel temperature.

Figure 24: (a) Mobile PVT system and measuring devices for outdoor tests (left: Polycrystal, right: Monocrystal) and Exergy efficiency of polycrystal panel for (b) Copper (c) Aluminum (d) Brass [120]

Multi-response optimization of a small-sized solar PVT water collector employing Taguchi and NSGA-II coupled with TOPSIS was performed by Podder et al. [121]. Considering the Taguchi L16 OA for three input variables called MFR, inclination angle, and inlet temperature, the DoE was conducted. As well, ANOVA tables were employed to acquire the critical control parameters affecting both the electrical and thermal efficiencies of the collector. The multi-response optimization process was proposed by a variant of NSGA-II, and the most optimal solution was found through the TOPSIS method. The maximum thermal and electrical efficiencies were found to be around 83%, and 10% were achieved under an optimal condition of MFR equal to 0.02 kg/s, inlet temperature of 32°C, and inclination angle of about 39°. Multi-response optimization of a nanofluid cooled hybrid PVT system by employing the Taguchi, and fuzzy triangular numbers coupled with TOPSIS was investigated by Qeays et al. [122]. The Taguchi L16 OA was applied for experimental study of control parameters such as MFR, ambient temperature, irradiance, and concentration of the nanofluid on outputs. The output responses were as follows: entropy generation, overall efficiency, surface temperature, exergy loss, and electrical efficiency. Weighting factors were determined by the fuzzy methodology, and the best combination of the control parameters was defined by using the TOPSIS method. The performance of a portable evacuated tube solar cooker in terms of the design and weather parameters was numerically explored by Hosseinzadeh et al. [123]. The Taguchi optimization technique was considered to obtain the optimized thermal power and efficiency of the solar cooker. The effective input parameters were the absorber coating absorptivity and emissivity, the absolute pressure of the vacuum envelope, and solar radiation. The results revealed that 0.01–100 Pa increment of the absolute pressure of the vacuum envelope diminishes the efficiency of the solar cooker by up to about 23%. Further, when a material with an absorptivity of 0.95 was employed in the absorber coating, the thermal power improved by up to around 34 W compared to that of absorptivity equal to 0.75. Taguchi optimization results also indicated that solar radiation was the most significant variable against the thermal power of the cooker (Fig. 25).

Figure 25: (a) A view of the solar cooker experimental setup and (b) S/N ratio value for different levels of solar radiation [123]

A multi-response Taguchi-based TOPSIS optimization approach for a hybrid PVT-solar air heater (SAH) system in order to maximize the beneficial thermal energy production as well as net electricity gains was explored by Fan et al. [124]. The L16 Taguchi OA was used for various input factors, including materials, channel depth, fin number, absorber thickness, air gap, PV covering factor, MFR, the thickness of back insulation, PV reference efficiency, the thickness of fin, the thickness of glass cover, and thermal emissivity of absorber plate (see Fig. 26). The ANOVA tables were used to identify the significant design parameters. TOPSIS was applied to specify the best design from the generated set of Pareto fronts. Based on the results, it was found that the optimized parameters design could improve useful thermal efficiency and net electricity gains by up to around 22% and 20%, respectively. Taguchi optimization and numerical investigation of solar thermal and heat pump combined system under five cities’ climatic conditions were accomplished by Li et al. [125]. TRNSYS software was employed to simulate the solar collector and heat pump combi system. The Taguchi optimization approach was applied to introduce the best combination of parameters based on two system modes (single- and dual-tank) through calculating the higher-the-better objective function of the S/N ratio. It was concluded that the dominant factor influencing performance differed for the two hydraulic configurations but was similar between the five metropolitan areas. In addition, the flow rate of the heat pump was the most significant parameter in the single-tank system. As well, the solar collector flow rate was the most effective one considering the dual-tank system. parametric study and Taguchi optimization of a nanofluid-based PVT were performed by Hosseinzadeh et al. [126]. The impacts of the main operating factors vs. the PVT system’s energy and electrical efficiencies utilizing the water/ZnO nanofluid were investigated. The practical input factors were: coolant inlet temperature, ambient temperature, coolant MFR, mass fraction of NP in nanofluid of ZnO/water, wind speed, and absorbed solar irradiation. According to the research results, decreasing the inlet temperature of coolant by 20°C causes an improvement in the energy efficiency of the PVT system operating with nanofluid (about 16%). Furthermore, it was concluded that the studied factors were approximately ineffective to the electrical efficiency of the proposed system. Whereas the inlet temperature of coolant was discovered as the most significant variable in the PVT system.

Figure 26: (a) Overview of the hybrid PVT-SAH system with fins and (b) section view of the hybrid system [124]

4.1.5 Thermodynamic Cycles

Advanced exergy analysis of a vapor compression refrigeration cycle using the Taguchi optimization method and refrigerant selection considering TOPSIS were carried out by Ustaoglu et al. [127]. The output responses such as exergy efficiency, COP, total exergy destruction rate, together with avoidable and unavoidable exergy destruction rates, were determined vs. design parameters (Fig. 27). According to the optimum performance of the system, R513a, R134a, and R448 were selected as the best refrigerants for the system, respectively. Based on the best combination of factors, the system operating by R134a showed the best COP of 2.65, exergy efficiency of 10% and a minimum rate of 0.34 kW for total exergy destruction. The evaporator temperature was selected as the most significant variable against the performance with about 43% of the contribution rate. It is followed by the condenser and refrigerant with an almost share of 32% and 14%, respectively. Additionally, compressor efficiency was discovered as the most influential parameter against the avoidable destruction rate. A combined heat and power (CHP) system based on gasification of municipal solid waste was optimized through the Taguchi optimization approach by Khalilarya et al. [128]. The control parameters of the system were selected as gasification temperature, the flow rate of solid waste, the inlet temperature of the turbine, and pressure ratio. Further, the power output, as well as the hot water flow rate of the system, were assessed as the performance features of the system. Taguchi optimization method was applied to find the best power generation in various medium cases such as air, steam, and oxygen. It was concluded that regarding the various system-based air, steam, and oxygen gasifying mechanisms, the best output power of the system was about 278, 280, and 267 kW, respectively.

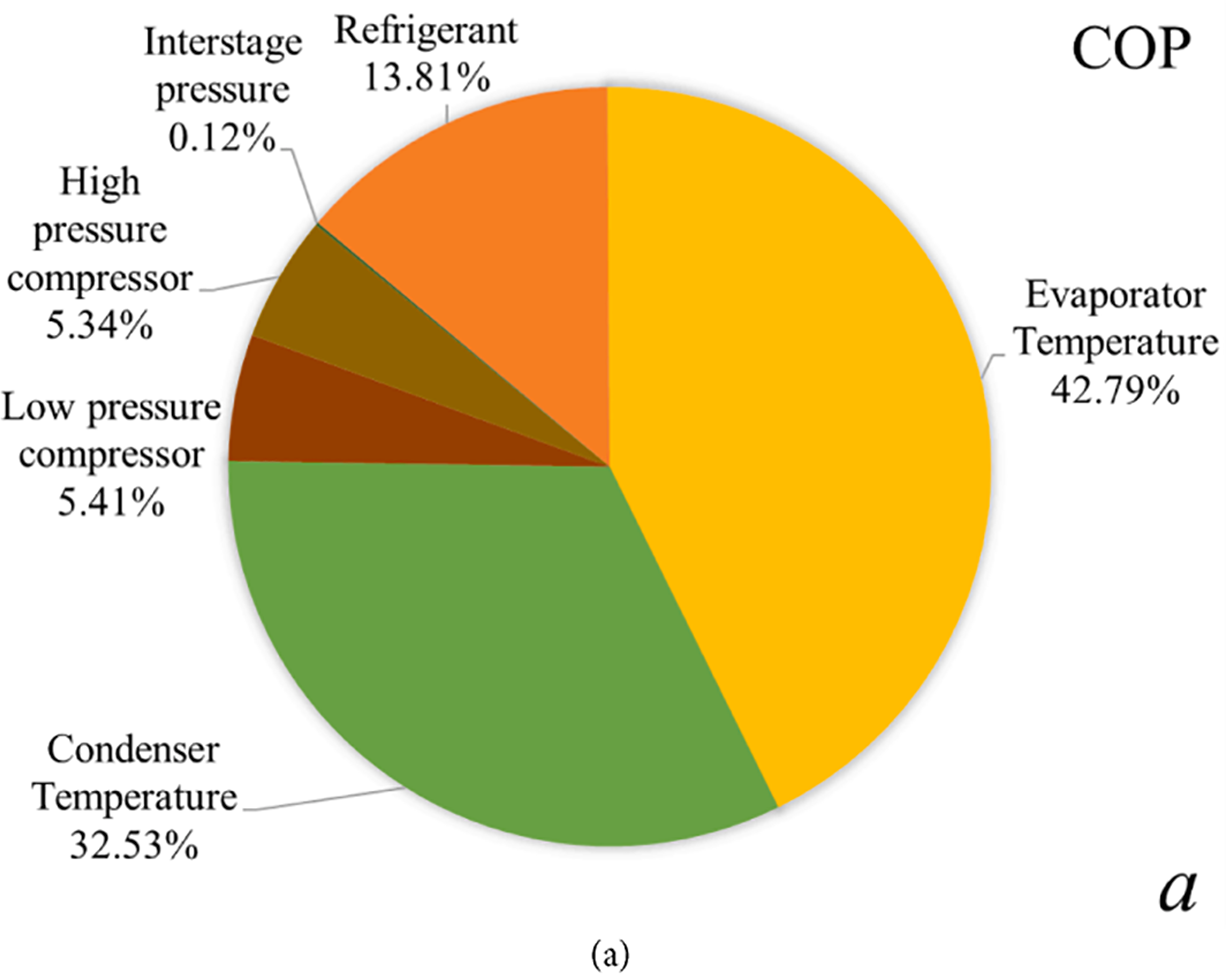
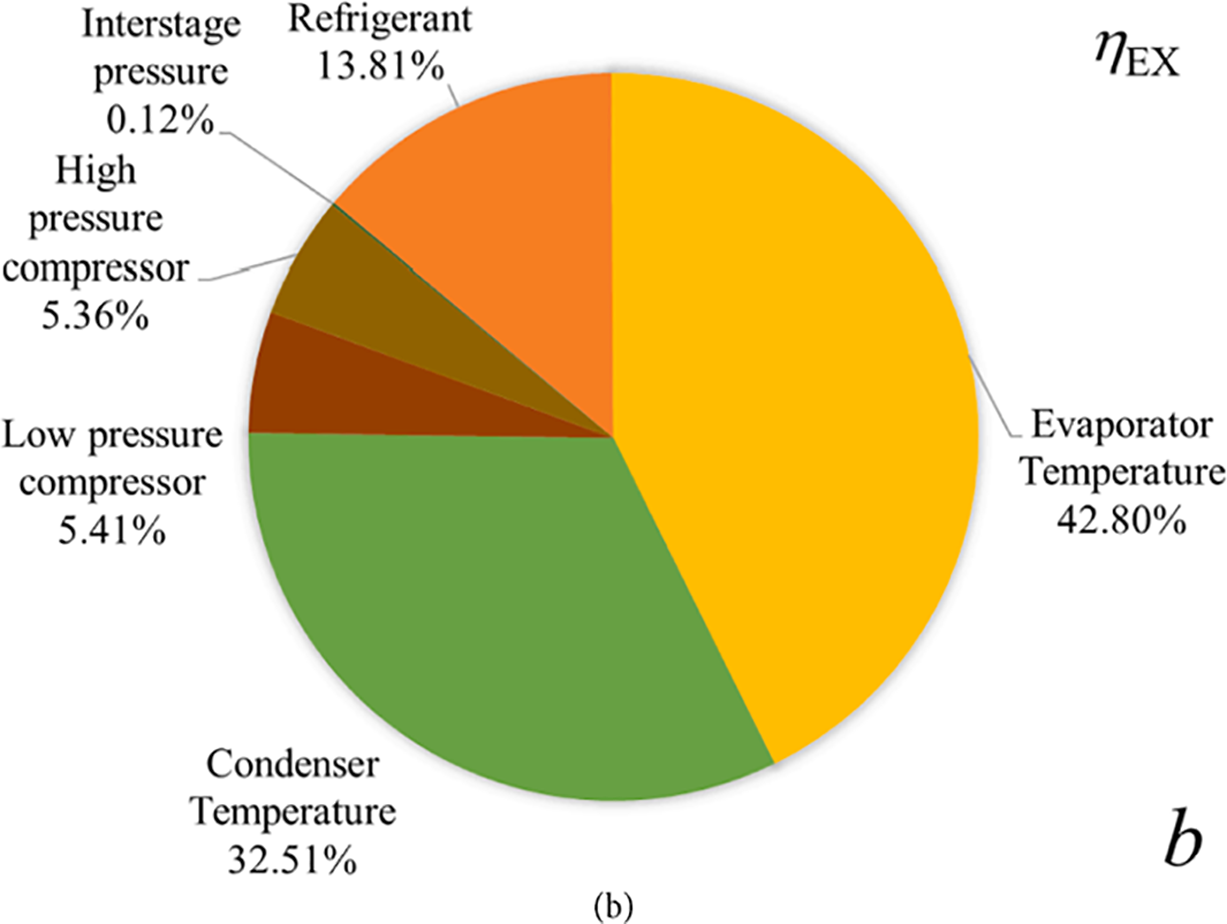
Figure 27: (a) Contribution ratio of operating parameters on COP and (b) exergy performance of vapor compression refrigeration-system [127]

Multi-objective optimization of a CHP system with the prime mover of SOFC by utilizing the Taguchi-based TOPSIS method coupled with analytical hierarchy process (AHP) was conducted by Mojaver et al. [129] (Fig. 28). The Taguchi L25 OA design was operated for 5-levels input parameters called current density, SOFC outlet temperature, and fuel utilization factor (Table 5). To find the importance of parameters, ANOVA tables were introduced. The S/N ratio was applied to minimize or maximize the eight output responses separately. The exergy destruction rate, power generation, cell voltage, fuel MFR, electrical, energy and exergy, efficiencies of the SOFC, and CO2 emission were defined as the output responses of the study. The ANOVA outcomes demonstrated the current density was discovered as the most crucial factor concerning the output power, fuel MFR, and exergy destruction rate. The optimization output revealed that 950°C for SOFC outlet temperature, a 5500 A/m2 for the current density, and 0.8 for the fuel utilization factor were determined as the optimum combination of input parameters. Multi-objective optimization of the control variables of an organic Rankine cycle (ORC) efficiency specifications using Taguchi-based GRA was explored by Bademlioglu et al. [58]. The Taguchi L27 OA design was utilized for nine different process parameters such as the effectiveness of the HX, pump efficiency, turbine efficiency, evaporator temperature, and condenser temperature, and pinch point temperature differences within the evaporator as well as condenser. ANOVA strategy was operated to acquire the importance of the parameters vs. objective functions, namely energy and exergy efficiencies. It was revealed that evaporator temperature, condenser temperature, and turbine efficiency were discovered as the most significant parameters (total contribution ratio of about 83%) against the energy efficiency of the ORC. Moreover, results indicated that under the optimum combination of process parameters, the energy and exergy efficiencies of the system were determined to be around 18% and 65%, respectively.

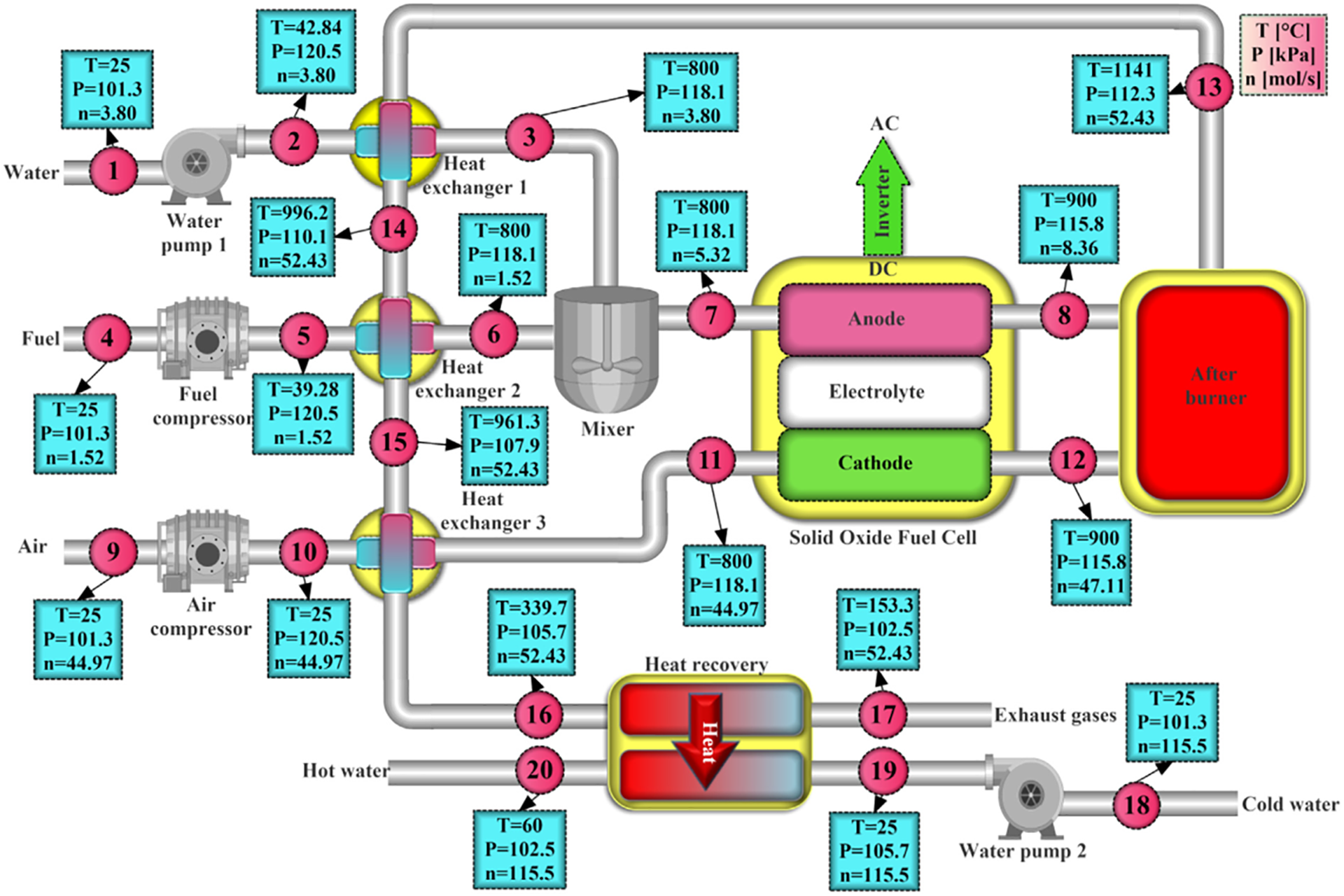
Figure 28: System configuration proposed by [129]

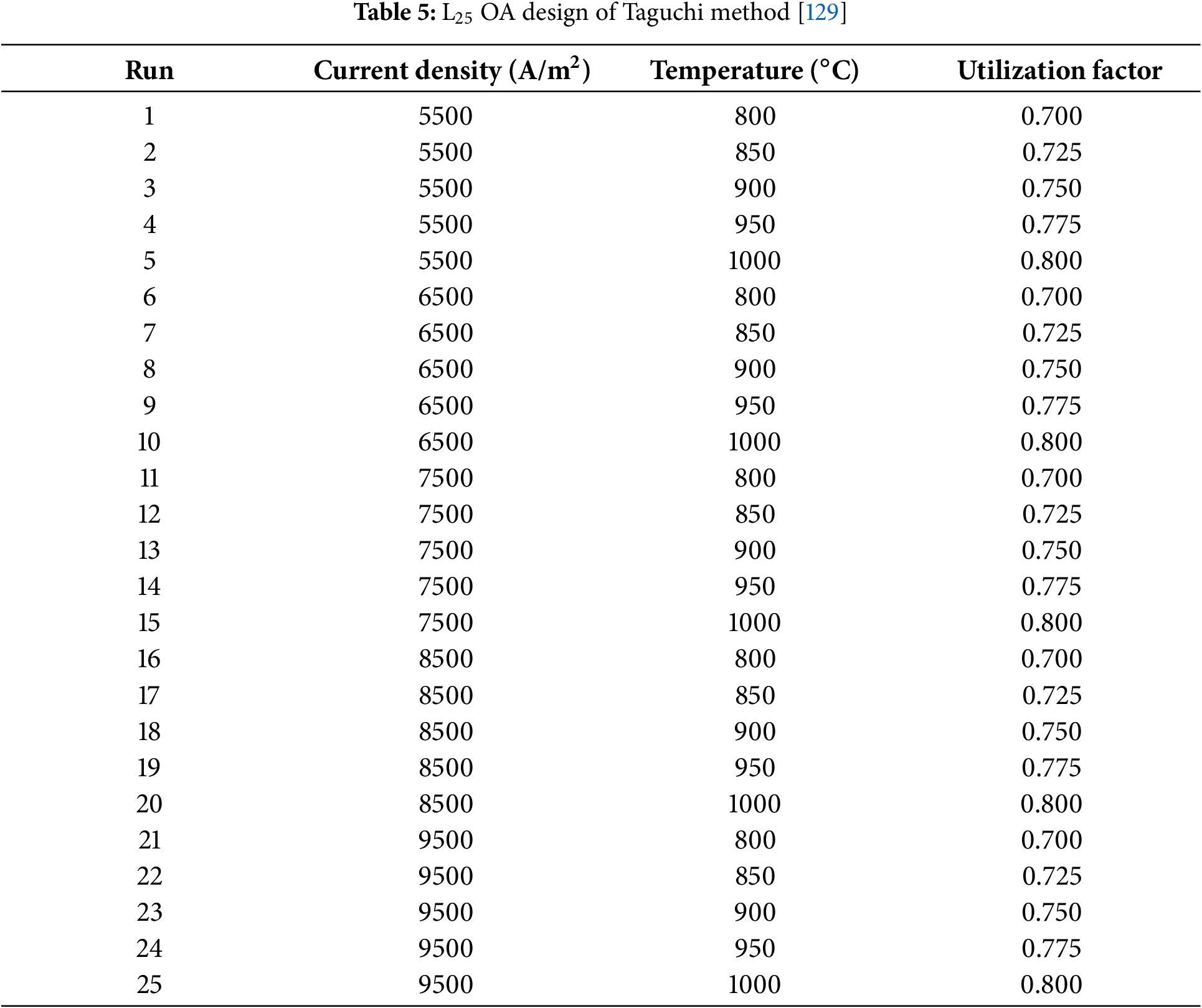
Performance characteristics optimization of an absorption refrigeration cycle via Taguchi-based GRA was accomplished by Canbolat et al. [130] (Fig. 29). The Taguchi L27 OA design was established for eight parameters with 3-levels of each. The main process parameters considered for optimization were evaporator temperature, absorber temperature, pump efficiency, etc. The impact ranking concerning the input variables was defined by the ANOVA tables. The optimum operating conditions were specified to attain the maximum values of COP (0.62) and exergy efficiency (0.28) of the proposed system. It was concluded that the temperatures of the absorber and evaporator were calculated as the most critical variables for the system’s performance by a contribution ratio of around 30% and 26%, respectively. Whereas the most ineffective factor was discovered to be the pump efficiency with a share of 0.48%. Omrani et al. [131] employed an integrated Taguchi-neural network-fuzzy-TOPSIS approach to discover the optimal level of five power plants containing steam, wind, gas, combined cycle, and hydroelectric. The Taguchi technique was applied for designing the input and output combinations, and determining S/N ratios. Afterward, the neural network was used to estimate the remaining S/N ratios. Then, the TOPSIS method was operated to select the optimum mixtures of input variables and output responses. It was concluded that medium-large size power plants for renewable resources are preferable. In contrast, small size power plants for fossil resources are more desirable. Examination of influential input variables on performance characteristics of the ORC by considering the Taguchi method and ANOVA was carried out by Bademlioglu et al. [132]. The system’s numerical model was provided, and the effects of several input factors with corresponding levels were studied against the system’s energy efficiency. The outcomes indicated that the evaporator temperature was determined as the most significant variable in terms of obtaining the system’s maximum energy efficiency. In contrast, the pinch point temperature differences of evaporator and condenser were specified as the least effective parameters for the system’s performance. As well, the most optimized and the least optimized combination of parameters were defined. Accordingly, operating under the best and worst conditions leads to a system thermal efficiency of around 18% and 9%, respectively.

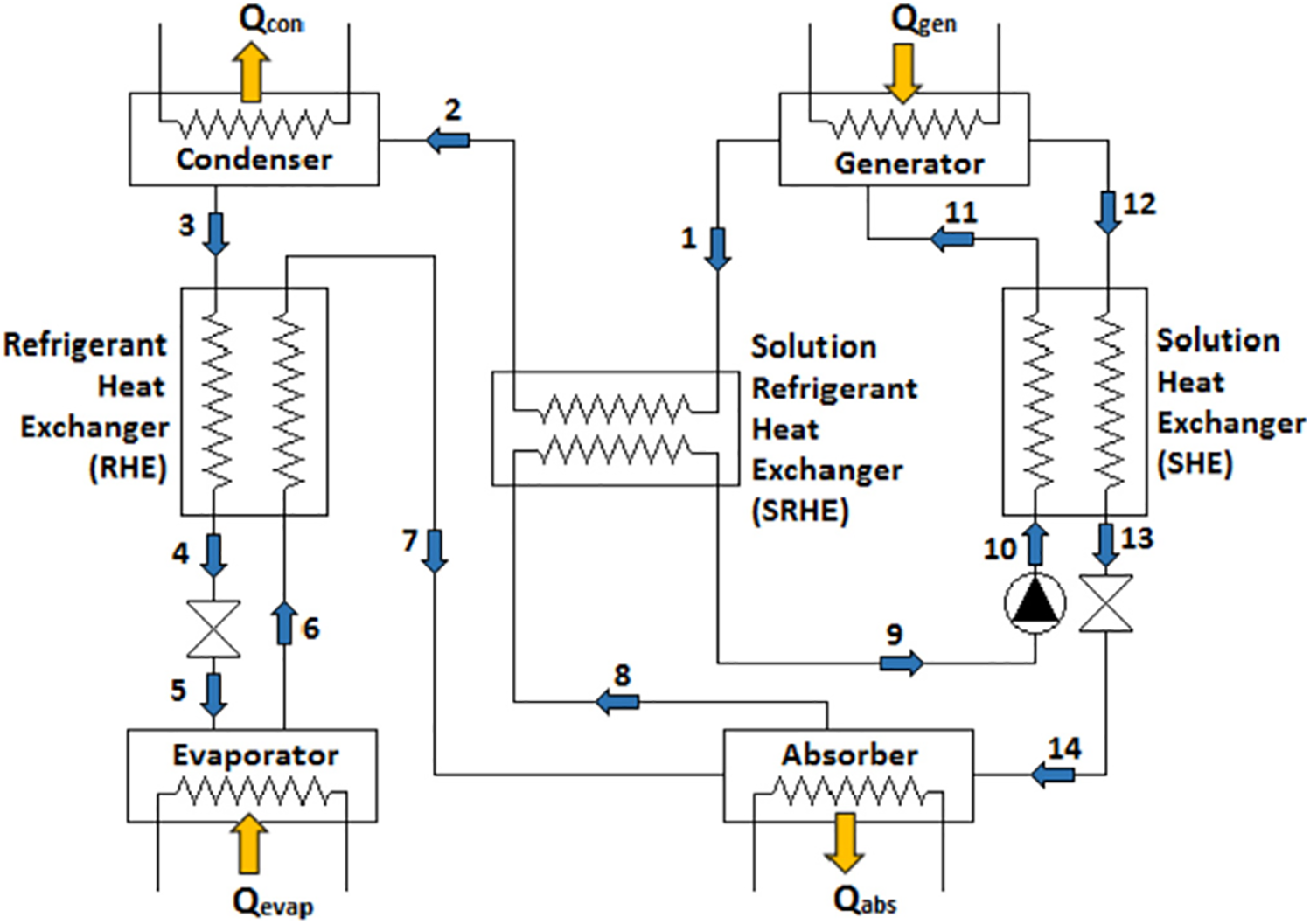
Figure 29: The schematic of single-stage absorption refrigeration system [130]

4.1.6 Wind and Tidal Turbines

The study of twin vertical axis wind turbines (VAWTs) via large eddy simulations and the Taguchi optimization method was accomplished by Peng et al. [133]. A Taguchi L16 OA design for five control parameters containing aspect ratio, turbine spacing, rotational direction, pitch angle, and solidity ratio was established. The results indicated that the pitch angle was discovered as the most influential parameter on power characteristics, followed by turbine spacing, and aspect ratio (Fig. 30). In addition, the rotational direction was discovered to be the least influential one. The optimum and worst combination of control parameters were determined and under these operating conditions, the power generation of twin array units was increased by up to around 14% and 7%, respectively. The hydrodynamic characteristics of a vertical axis hydrokinetic turbine (VAHT) were optimized using the Taguchi optimization approach by Ma et al. [134]. In order to maximize the power coefficient (Cp), the Taguchi L16 OA was employed to optimize the five input variables of the VAHT, including small shaft position, enwinding ratio, pitch angle, airfoil, and solidity ratio. An S/N ratio investigation of the CFD analysis outcomes was performed, and the optimized VAHT was evaluated in terms of hydrodynamic characteristics. According to the outcomes, the impact strength ranking of input factors on the Cp was specified by the following: airfoil > solidity ratio > small shaft position. Considering the S/N ratio, the best combination of control parameters was defined as an airfoil equal to 0020, the pitch angle of 0°, an enwinding ratio of 1.25, a solidity ratio of 0.382, and a small shaft position of 0.5. Furthermore, it was concluded that the Cp of the optimized VAHT was around 0.195, which was almost 17% larger than the preliminary design.

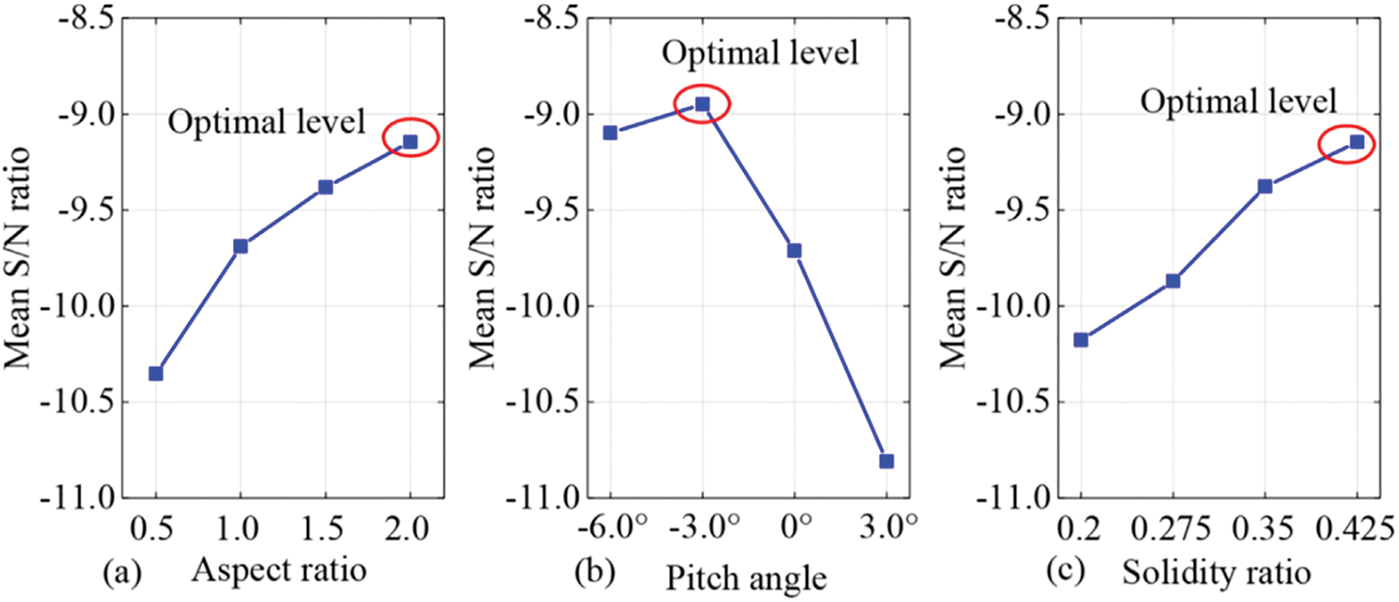
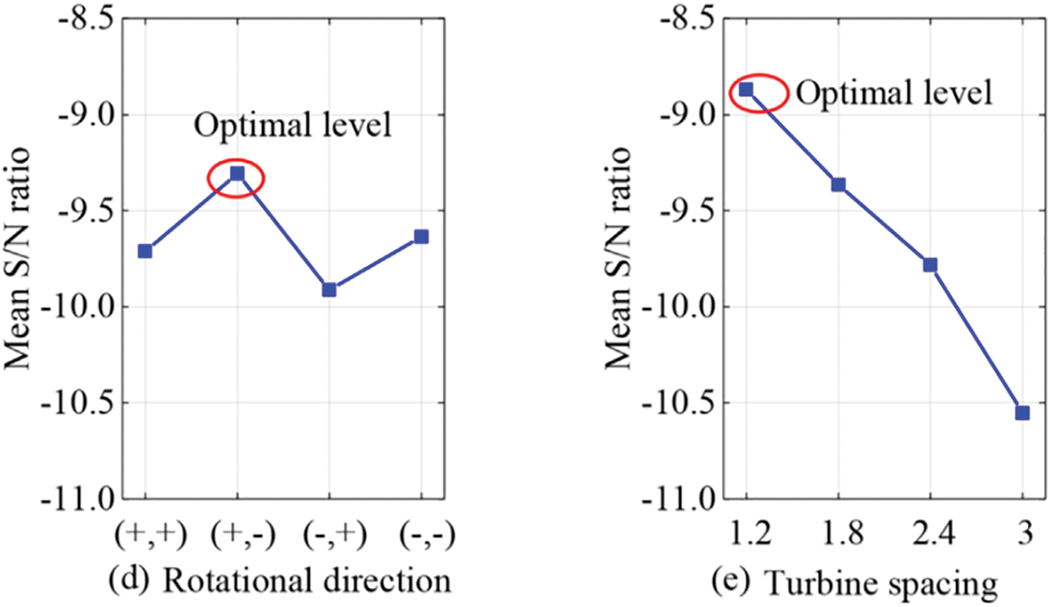
Figure 30: Mean S/N ratios of design factors at different levels: (a) aspect ratio, (b) pitch angle, (c) solidity ratio, (d) rotational direction, and (e) turbine spacing [133]

The blade design and optimization of dual Darrieus wind turbines (DDWTs) by using the Taguchi technique was conducted by Cheng et al. [135]. The Taguchi L9 OA design was provided in order to consider the interaction effects of three control parameters, chord ratio, radius difference, and offset angle (Table 6). To figure out the maximum Cp, CFD analyses were executed under various tip speed ratios (TSRs). It was concluded that the best configuration of double-layer blades, including the optimum factors combination of chord ratio of 3 and radius difference of 0.25 m, can improve the power production by about 8%.

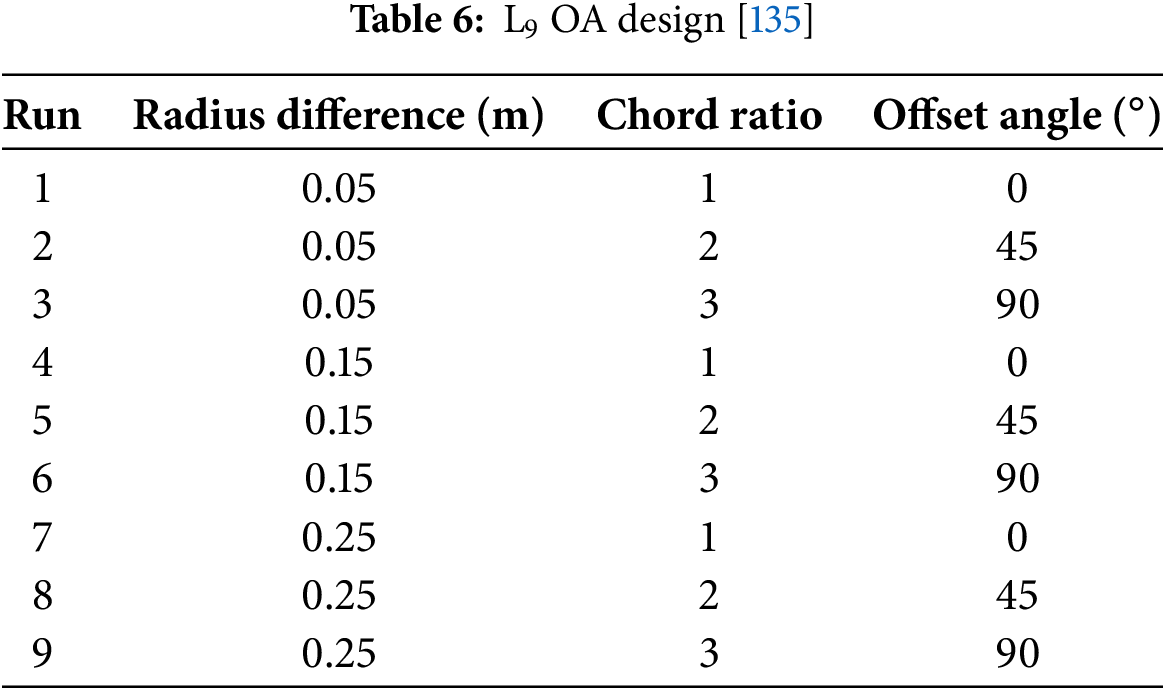
Hassanpour and Azadani [136] optimized the configuration of a pair of Darrieus VAWT using the CFD analysis and the Taguchi optimization method. The Taguchi OA design was established for three control factors containing the vertical distance between the mid-heights of two turbines, the horizontal distance between the axes of turbines, and the orientation of turbines. The mean S/N for these parameters at each level is provided in Fig. 31. Based on the findings, the ranking of the most significant control factors in terms of the maximum power generation was determined in this order: the vertical distance, the orientation, and the horizontal distance between paired turbines. Furthermore, when paired turbines were located side-by-side, by a similar height, and with a minimum horizontal distance, the power production was the largest. It was concluded that for the optimum configuration, the power production of paired wind turbines was increased by up to about 27% compared to a single one.

Figure 31: The mean S/N ratio for each parameter at each level [136]

The CFD modeling and optimization of the hydrodynamic characteristics of a vertical axis tidal (VAT) turbine by utilizing the Taguchi approach was studied by Khanjanpour and Javadi [137] (Fig. 32). The interaction of four input variables, including twist angle, camber position, maximum camber, and chord/radius ratio, was examined by ANOVA. The Taguchi optimization approach results indicated that the twist angle was the most critical variable influencing the hydrodynamic features of the turbine, while the chord/radius ratio was found to be the most insignificant factor. In comparison to the basic design, it was exhibited that the Cp of the optimized VAT turbine was enhanced by up to 24%. Further, considering the pressure coefficient response, the hydrodynamic characteristics of the VAT turbine were found sensitive to the cambered blades.

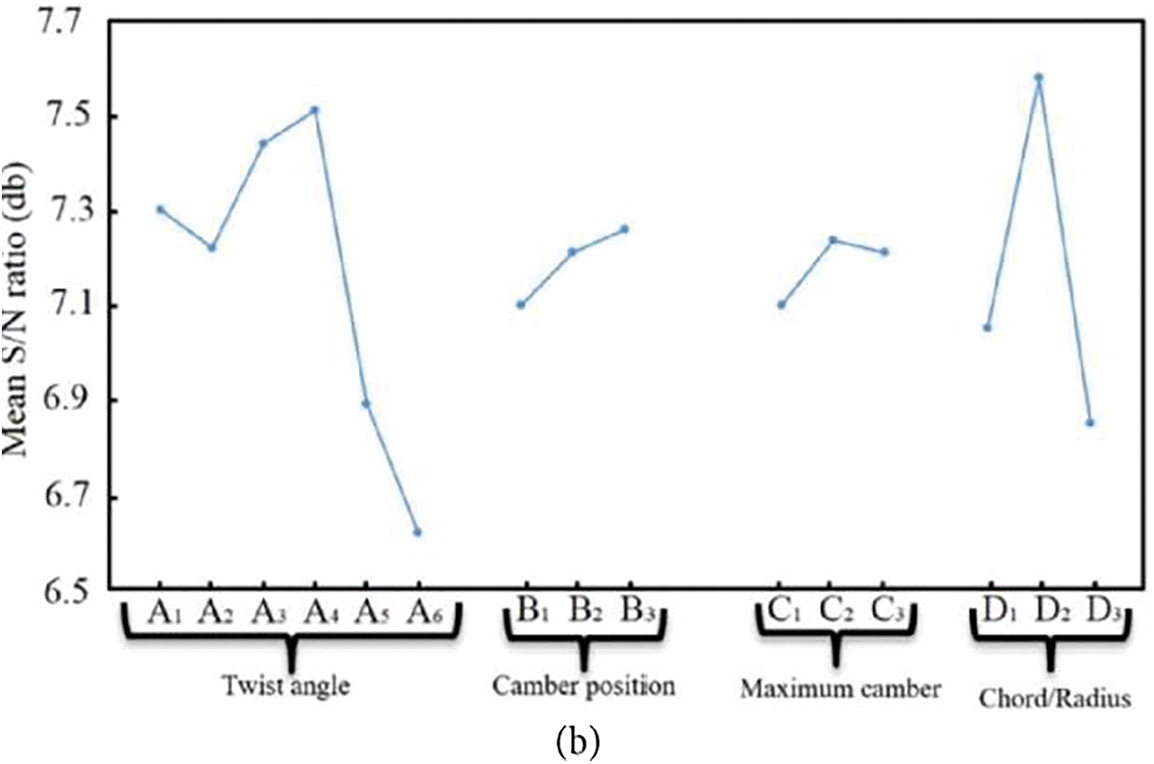
Figure 32: (a) Intensive mesh around the blades and (b) the mean S/N ratio for parametric design [137]

A 3-dimensional simulation and the Taguchi-based optimization of the power generation for a VAWT combined with a flat plate deflector were executed by Qasemi and Azadani [138]. In order to find out the best values of position, orientation, and dimensions of the deflector, the Taguchi L16 OA was utilized for DoE. Effects of the following five design parameters on the power generation of turbine were examined: the width of the deflector, the horizontal distance of the top edge of the deflector from the axis of rotation of the turbine, the angle of the deflector concerning the axis of rotation of the turbine, the vertical distance of the top edge of the deflector from the bottom of the blades, and the length of the deflector. According to the results, the angle of the deflector concerning the axis of rotation of the turbine was found to be the most significant on the output power of VAWT (Fig. 33). In contrast, the length of the deflector ranked as the least effective one. Moreover, operating the deflector with an optimum combination of variables boosted the wind turbine’s efficiency by up to around 16% compared to the preliminary turbine. Chen et al. [139] examined the performance advancement of a VAWT using a deflector through the Taguchi optimization technique combined with the modified additive method (MAM). The ANOVA tables were utilized to assess the impacts of control variables on the efficiency of the VAWT. An upper deflector and a lower deflector were separately evaluated to explore the aerodynamic performance characteristics of the VAWT. It was concluded that the average Cp of VAWT with the upper deflector configuration was improved by up to 20%. At the same time, the average Cp of VAWT with the lower deflector configuration was increased by up to around 17% concerning the non-deflector VAWT design.

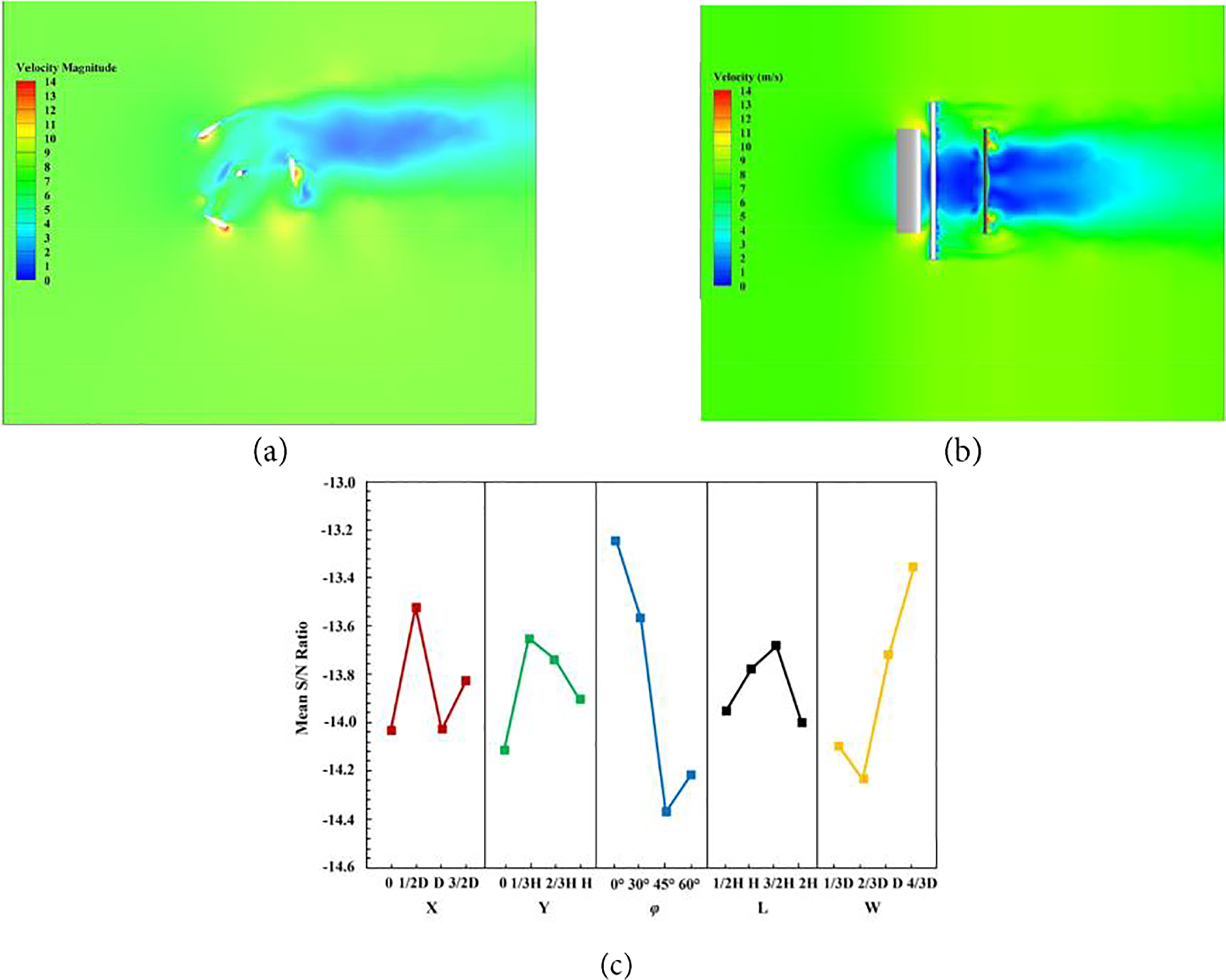
Figure 33: Velocity contours for the bare turbine at 30° azimuth angle (a) top view, (b) side view, and (c) mean S/N ratio for deflector physical parameters at each level [138]

4.1.7 Summary

Considering Table 7, a summary of essential outcomes and the main issues that have been stated regarding the Taguchi-based optimization of energy systems are provided in this division.

When Taguchi-based optimization techniques are implemented, some advantages and disadvantages need to be acknowledged, as provided in Tables 8–10. Single-objective Taguchi optimization method offers valuable advantages in terms of robustness, efficiency, and identifying key factors, particularly in manufacturing and process optimization. However, its applicability is relying on the assumptions of linearity and the suitability of the experimental design to the specific problem. Understanding these advantages and limitations is crucial for making informed decisions when applying Taguchi methods to optimization challenges. In multi-objective optimization problems both Taguchi-GRA and Taguchi-TOPSIS have their strengths and limitations. The choice between them should be based on the specific characteristics of the optimization problem, considering factors such as linearity, multicriteria nature, and the level of complexity involved.

4.2 ANN

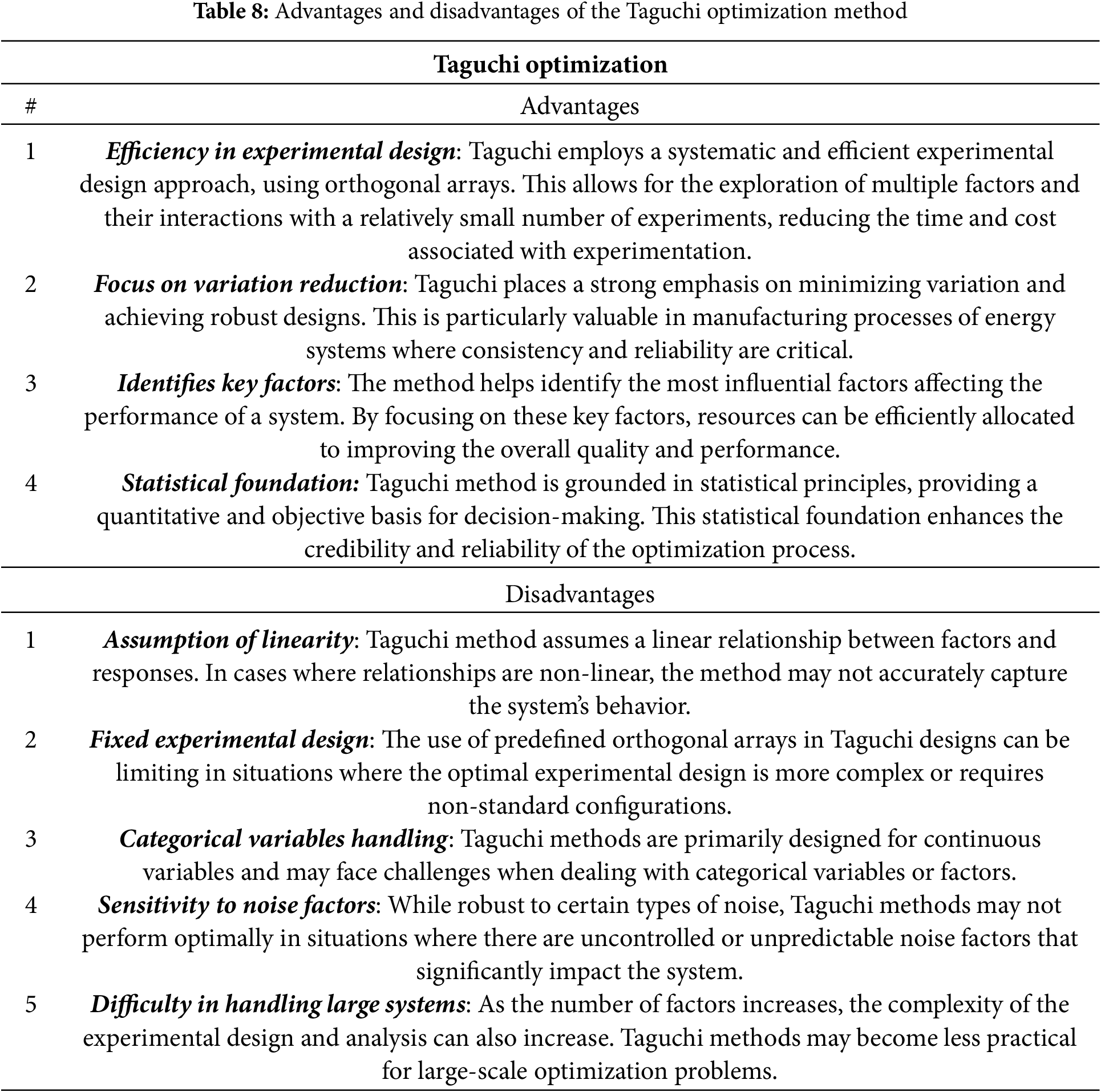
ANNs represent one of the most extensively employed techniques in energy systems and applications. The capacity of ANNs to conduct non-linear analyses emerges as a notable advantage in managing these systems. Accordingly, this section provides an overview of ANNs’ applications across diverse disciplines of energy systems, including ICEs, TESs, HXs, solar energy systems, thermodynamic cycles, wind turbines, as well as hybrid energy systems.

4.2.1 Internal Combustion Engines (ICEs)

The combustion procedure in HCCI represents an effective approach within futuristic combustion technologies. Given the absence of a direct control mechanism for start of the combustion (SOC) in these engines, the characteristics of the air-fuel mixture upon entry into the combustion chamber determine the ignition timing. To regulate SOC, the development of a precise predictive model relying on the properties of the entering air-fuel mixture is essential. The utilization of ANN emerges as a viable solution, offering reduced computational expenses compared to conventional physics-based modeling. Taghavi et al. [140] investigated a multi-input single-output model for predicting HCCI engine’s SOC across diverse operations employed the Nonlinear Autoregressive Network with Exogenous Inputs (NARX), MLP and RBF architectures (Fig. 34). Trained on data from a one-cylinder Ricardo engine, the models were optimized using Genetic Algorithm (GA). The optimized networks exhibited superior structures, enhanced predictive behaviors, and reduced simulation costs. Post-optimization, MLP’s regression ratio increased from 0.8965 to 0.96166, and RBF’s from 0.7623 to 0.83991. GA significantly reduced the training time for NARX from 3.12 s to 0.46 s.

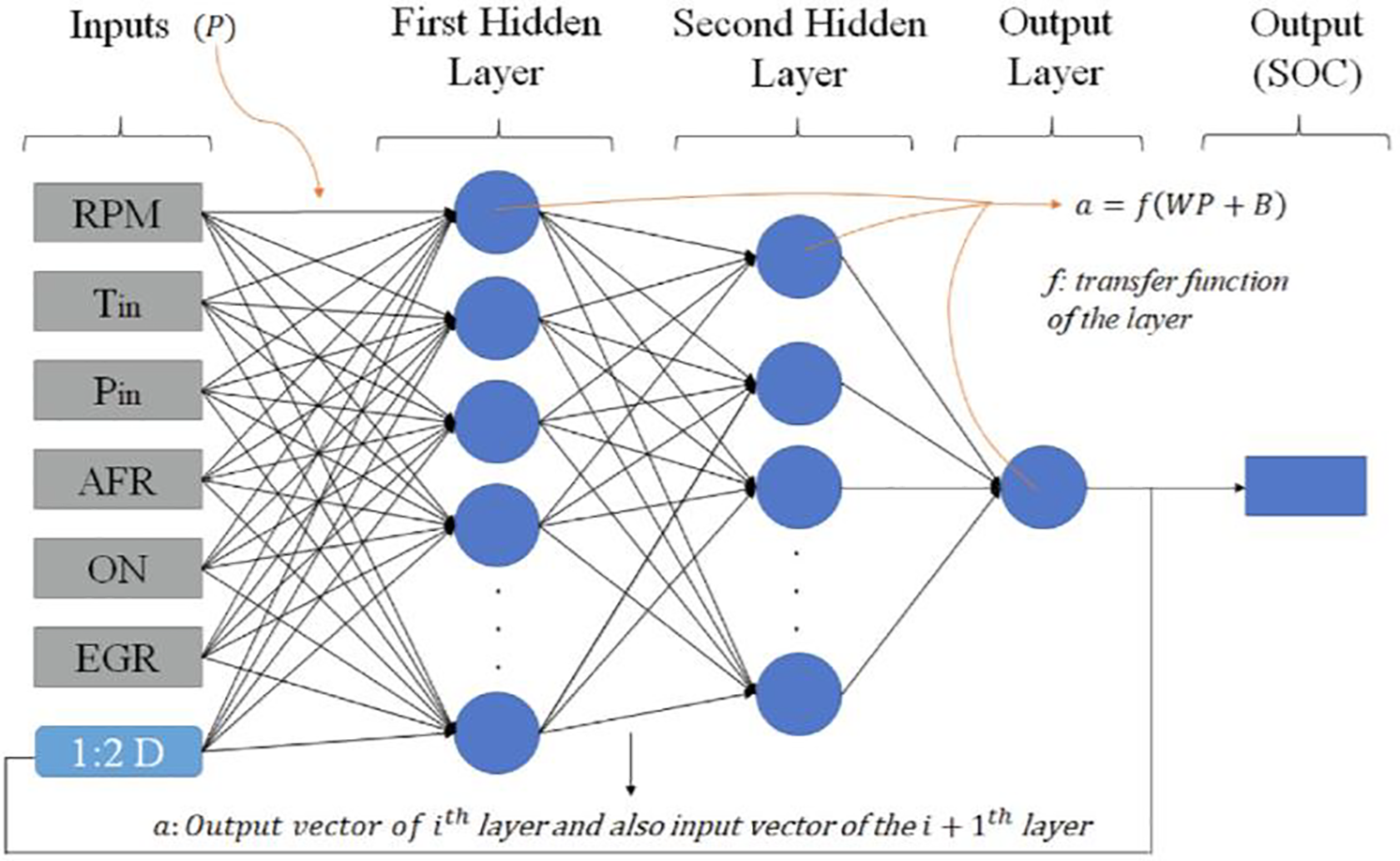
Figure 34: The MLP network architecture employed for modeling of the Ricardo HCCI engine [140]

Dey et al. [141] explored the utilization of an ANN model to estimate emissions (NOx, UHC, CO2) and BSEC in a 1-cylinder engine running on various diesel-palm biodiesel-ethanol blends. Employing the Levenberg-Marquardt backpropagation algorithm with logistic-sigmoid activation function, the ANN demonstrates excellent prediction accuracy with high overall correlation coefficients (R) ranging from 0.99329 to 0.99875 and minimal mean square error (MSE) between 0.0001 and 0.0004. Comparative analysis using fuzzy interface system (FIS) reveals optimal engine operating parameters, underscoring the robustness and reliability of ANN and fuzzy logic for prediction and optimization in engine parameters. Ammonia has a high potential in the world’s fuel sector application. Accordingly, Böyükdipi et al. [142] through an experimental study explored the impact of ammonia as a fuel additive on engine vibrations, blending NH3 into sunflower biodiesel at ratios of 5%, 10%, and 15% (Fig. 35). Conducted on a diesel engine under no-load conditions at varying speeds (1200–2400 rpm), vibration data were recorded and an ANN model accurately predicted the results. Results indicate that increasing NH3 additives led to higher vibration levels, negatively affecting engine vibration. Vibration changes were evident across all NH3 ratios, with the highest and lowest recorded as 12.96 and 9.12 m/s2 for 15% and 5% NH3, respectively. ANN models demonstrated high accuracy rates ranging from 99.206% to 99.675%.

Figure 35: ANNs model R error values for the fuel mixture of 95% sunflower biodiesel and 5% NH3 as the additive [142]

Marine Diesel engine ANN modelling with multiple output for complete engine performance map was investigated by Castresana et al. [143]. ANN has shown effectiveness in predicting parameters. After defining the optimum network structure and training the ANN with 1000 samples, the model demonstrated robust generalization capability, achieving MAPE below 8.5%, except for CO and NO2 emissions. The ANN’s high accuracy and swift calculation times (0.109 s) affirm its potential for predicting multiple outputs throughout the entire engine performance map. While engine spray models relying on phase equilibrium have advanced in simulating trans/supercritical engine spray processes, drawbacks exist in the conventional phase equilibrium algorithm. These limitations stem from its iterative schemes for solving intricate nonlinear equations, resulting in compromised efficiency and stability. As a consequence, Yue et al. [144] studied a method based on ANN as a potential alternative to the conventional algorithm applied in the engine spray models to achieve fast and robust phase equilibrium calculations. The results demonstrate that the ANN method significantly improves efficiency while maintaining accuracy compared to the conventional algorithm. In a high-fidelity n-dodecane spray simulation, the conventional phase equilibrium calculation consumes up to 70% of total computational time, while the proposed ANN approach reduces this to negligible levels, showcasing its potential for fast and robust phase equilibrium calculations in engine spray models.

4.2.2 Thermal Energy Storages (TESs)

Maleki et al. [145] optimized a finned latent heat thermal energy storage unit using a hybrid approach involving CFD, grouped method of data handling (GMDH) ANN, NSGA-II, and multi-criteria decision-making (MCDM). The design variables, comprising fin geometrical parameters (number, length, and volume fraction), were optimized to minimize phase change time and maximize total stored energy. CFD simulations analyze the effects of design variables on objective functions, and GMDH-type ANN models predict objective function values. The NSGA-II algorithm identifies Pareto optimal points, and MCDM methods propose design points per weight. Results indicate that a significant portion of pareto optimal points exhibits high dimensionless fin length and low volume fraction, providing insights into the optimal design of the finned LHTES unit. Sorption technology holds promise for creating thermal storage units with high energy density and minimal losses. However, realizing the full potential of this storage technology requires significant progress in both experimental and computational aspects to accurately model its performance on a system scale. Scapino et al. [146] introduced and investigated the application of artificial neural network (ANN) models to forecast the performance of a sorption thermal energy storage system. They highlighted their potential benefits, including decreased computational expenses compared to conventional physics-based models and smooth integration into larger energy system models. Two neural network structures were devised to dynamically anticipate the outlet temperature, thermal power output, and state of charge of a sorption storage reactor. (Fig. 36). Through systematic training and evaluation, optimal configurations for each modeling and operating mode were identified. Test cases demonstrated the model’s capability to precisely replicate the storage system’s dynamic behavior, indicating the promising potential of ANN for precise and computationally efficient sorption heat storage modeling.

Figure 36: (a) Conceptual scheme of the two ANN architectures. Left: NARX architecture layout the state of charge estimation. Right: FFNN architecture layout for the outlet temperature estimation (b) Conceptual layout of the sorption reactor neural networks model [146]

Motahar [147] examined the heat transfer characteristics during the melting phase of n-octadecane, which is a PCM, using experimental analysis. (Fig. 37). Following the experiments, an ANN model was employed to forecast the melting behavior of the PCM. Results revealed that natural convection predominantly influences heat transfer during the melting process. A MLP FFNN, trained with the Levenberg-Marquardt algorithm, predicts the melted volume fraction and Nu number using Rayleigh, Stefan, and Fourier numbers as input factors. The optimized ANN structure demonstrates high accuracy, with mean square error and correlation coefficient of 4.42 × 10−6 and 0.999, respectively. The proposed ANN yields predictions within around ±6.5% and ±6.2% for the melted volume fraction and Nu number, respectively.

Figure 37: (a) Schematic diagram of the experimental setup for PCM melting (b) Optimal ANN configuration for predicting Nusselt number [147]

Olimat et al. [148] employed ANN as an efficient tool for solving the thermal energy storage transient non-linear heat equations. The research combined a computational approach and experimental validation to predict the solidification and melting phenomena of eutectic molten salt in a heat storage system. A MLP FFNN through an optimized 2–2-16–2 modeling, trained by the Levenberg-Marquardt algorithm, was developed. The temperature related to stabilization during melting and solidification modes aligns with experimental results, ranging from (174–191)°C and (184–188)°C, respectively. Predicted energy rates during melting/solidification at 220°C and 250°C were around 1.4/0.77 and 1.9/0.97 kW·h, respectively. Pearson’s correlation coefficient for predicted datasets was 0.9999, and the MSE was approximately 0.00028. The artificial neural network model more accurately approximated melting and solidification times compared to traditional regression methods. Monitoring the state of PCM is vital for efficient thermal management systems. Hence, Anooj et al. [149] proposed a machine learning-based diagnostic technique, utilizing RNN, to predict the liquid fraction of PCM based on surface temperature history. RNNs were chosen for their non-linear and time-dependent nature. The training data set, generated through numerical simulations, includes various heat input types. The RNN model, trained with 345 samples, demonstrates high correlation (up to 0.99) and low RMSE (less than 0.015) for predicting temporal liquid fractions. The RNN model achieves accurate predictions with reduced computational time and power, making it applicable in real-life scenarios. Additionally, the study highlighted the efficacy of machine learning in addressing complex heat transfer problems.

4.2.3 Heat Exchangers (HXs)

In the context of the escalating energy demand driven by population growth, energy integration stands out as a promising solution to address shortages. This involves recirculating heat within a system through heat exchange between the coolant and the heat source. Traditional coolants, constrains by low thermal conductivity, are enhanced using nanofluids—mixtures of conventional coolants with nanoparticles, characterized by higher thermal conductivity. Experimentation for nanofluid heat transfer is resource-intensive, leading to the acceptance of ANN as efficient models to correlate complex relationships between inputs and outputs. Therefore, Kamsuwan et al. [150] analyzed a combined modeling of ANN and conventional process for heat transfer in a nanofluid-based heat exchanger, exploring parameter sensitivity (see Fig. 38). Developed with 2723 datasets, the ANN nanofluid predictive model exhibits superior accuracy (maximum error of only 4.1%) compared to other numerical methods. The study concludes by demonstrating the effectiveness of combining ANN and conventional simulation methods to analyze nanofluid-enhanced heat exchanger performance, featuring a parameter sensitivity test on a plate heat exchanger with improved heat transfer coefficient, maintained pressure drop, and performance efficiency coefficient.

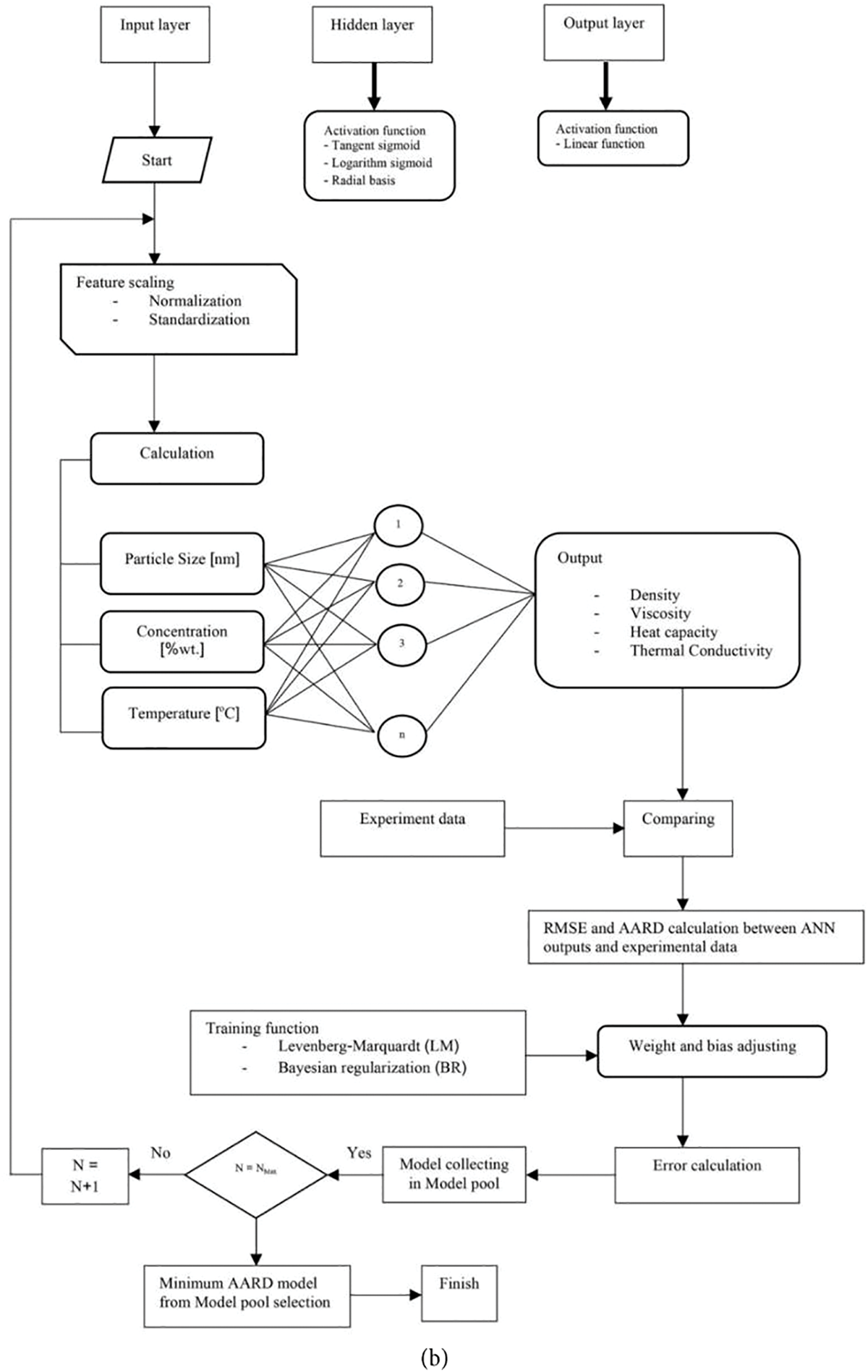
Figure 38: (a) preliminary test and parameter sensitivity for each property (b) Flow chart of ANN model [150]

Moya-Rico et al. [151] introduced an ANN model designed to predict pressure drops and heat transfer rates in a triple concentric-tube HX using both non-corrugated and corrugated inner tubes. The fluid involved was commonly utilized in the food industry, with variations in depth and pitch for corrugated tubes. Utilizing a vast dataset of 181 experimental cases, the ANN model was trained and validated, employing the Bayesian regulation as the most effective training algorithm. The optimal configuration of the ANN comprises two hidden layers, with the first layer consisting of 15 nodes and the second layer consisting of 21 nodes. The outcomes exhibited excellent conformity with experimental findings, indicating an absolute average relative deviation of less than around 3.8% for the pressure drop, and less than around 1.9% for the h. This underscores the model’s simplicity and accuracy when applied to a wide range of experimental data. Giannetti et al. [152] predicting the complex phenomenon of two-phase flow distribution in heat exchangers by employing methods with enhanced mathematical flexibility. The focus of investigation was on constructing and training an ANN to accurately identify the intricate interactions of various physical phenomena occurring at different scales. Experimental data from a full-scale air-conditioning system’s heat exchanger are utilized to train and test the ANN. The optimized ANN structure, achieved through Bayesian regularization, comprises 4 inputs, 3 hidden layers, and 3 neurons per layer. Deviations on the single output were mostly below ±10%, and the correlation index surpasses 98% when the entire dataset was used for training. Increasing the number of training data enhanced accuracy without apparent overfitting, highlighting the effectiveness of the approach.

Hojjat [153] developed an ANN model to forecast the hydrodynamic and thermal efficiencies of two varieties of Newtonian nanofluids employed as coolants in a shell and tube HX. The ANN model incorporated Reynolds number, nanoparticle volume concentration, Prandtl number, and nanoparticle thermal conductivity as input variables. Findings revealed that the ANN model effectively forecasts experimental observations, with Nu number values having at most a 9% difference and pressure drop showing a 9.6% variation. Multi-objective optimization, using the NSGA-II algorithm, aimed to minimize total pressure drop and maximize nanofluid Nusselt number in the HX. Decision parameters included nanofluid concentration and Reynolds number. The Pareto front was obtained, and optimal solutions, selected using decision-making methods LINMAP and TOPSIS, demonstrated a 30% enhance in Nu number and a 10% reduce in pressure drop compared to the base fluid. Çolak et al. [154] focused on shell and helically coiled tube HXs, compact designs with increased heat transfer area. Two ANN structures were developed to predict outputs such as heat transfer coefficient, pressure drop, Nusselt number, and performance evaluation criteria (Fig. 39). Inputs include tubing and coil diameters, Reynolds and Dean numbers, curvature ratio, and mass flow rate. With 105 data points, 70% for training, 15% for validation, and 15% for testing, the Levenberg-Marquardt algorithm in multi-layer perceptron network models achieved a coefficient of determination exceeding 0.99 and a mean deviation below 0.01%. Results demonstrate the accuracy of the ANN in estimating the desired outputs.

Figure 39: Configuration of the designed MLP network model [154]

4.2.4 Solar Energy Systems

Solar energy is an environmentally friendly and sustainable energy source, with its accessibility at a specific location contingent upon the local meteorological variables. Hence, to train an ANN model, Rao K et al. [155] examined various meteorological parameters including daily minimum and maximum temperatures, daily global solar radiation, temperature range, theoretical sunshine hours, sunshine hours, and extraterrestrial radiation. They trained six different ANN models (denoted as ANN-1 to ANN-6) using 32 potential input combinations. Based on outcomes, the Relative Root Mean Square Error (RRMSE) highlights the efficiency of the ANN-2 model with a minimum value of 3.96%. The ANN models outperform empirical models, showcasing excellent estimation with fewer inputs, which requires no measured meteorological parameters. Sadeghi et al. [156] focused on enhancing the thermal characteristics of an evacuated tube solar collector through experiments with copper oxide/water (Cu2O/W) nanofluid and a parabolic concentrator at varying fluid flow rates. Different volume fractions of the nanofluid are tested to analyze their impact on energy and exergy efficiencies, convective heat transfer coefficient, Nusselt number, and useful heat gain. ANN, specifically MLP and RBF models (see Fig. 40), were employed to validate experimental accuracy. The results indicated that MLP provides more precise predictions than RBF, with lower error rates. Additionally, it was observed that increasing both flow rate and nanofluid concentration enhances the solar collector’s thermal performance.

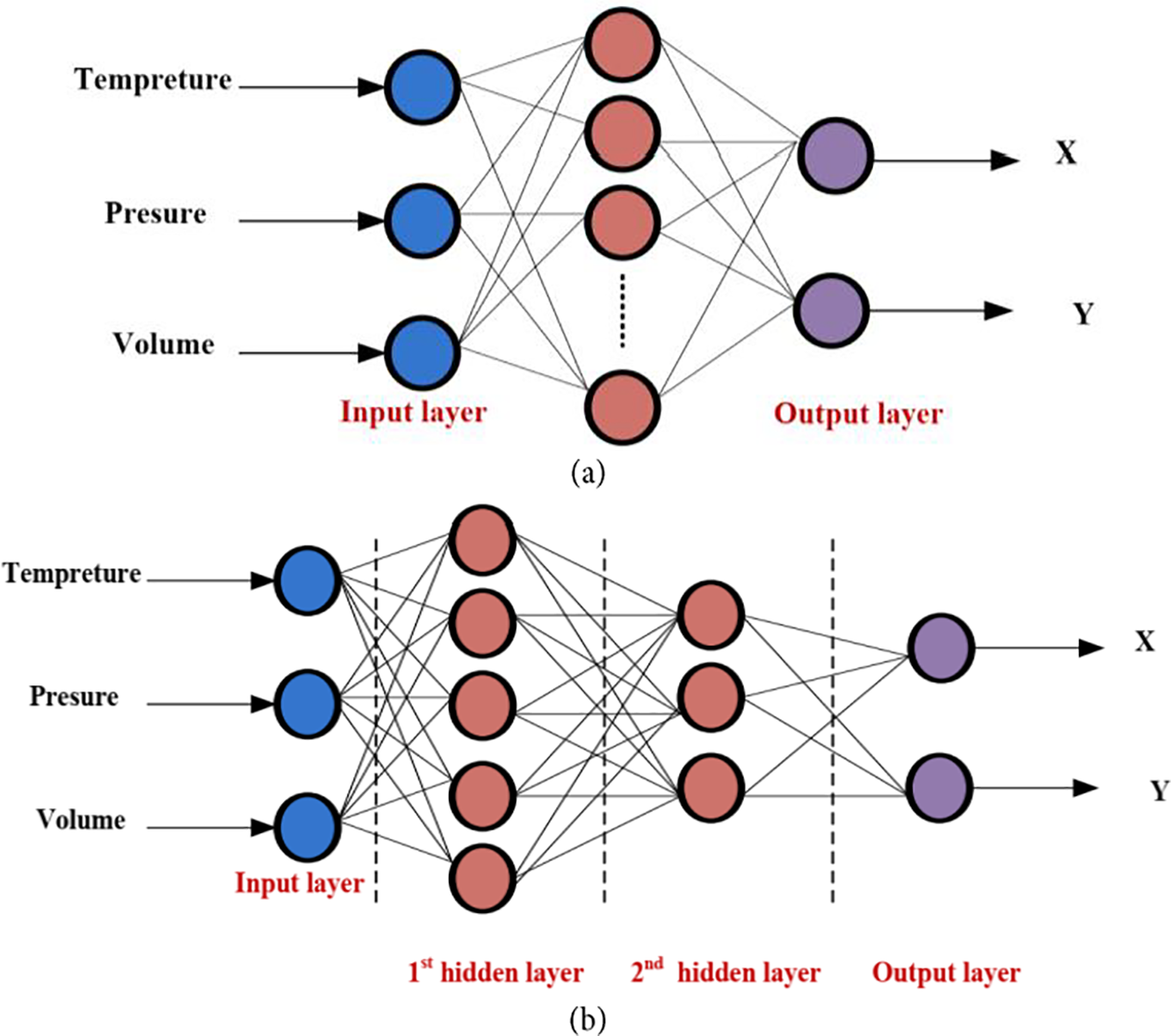
Figure 40: Architecture of the designed (a) RBF and (b) MLP networks [156]

A PV/T system integrates photovoltaic and thermal collectors, presenting a promising technology, particularly for building-integrated PV/T systems. Al-Waeli et al. [157] investigated PV/T systems utilizing nanofluid/nano-PCM, water-PCM, and water cooling systems flowing within cooling pipes. (Fig. 41). The study evaluated various PV/T systems—conventional PV, water-based PVT, water-nanofluid PVT, and nanofluid/nano-PCM—under identical conditions using an ANN based MLP system. The developed ANN model demonstrated that incorporating nanofluid/nano-PCM substantially enhances electrical efficiency (8.07% to 13.32%) and achieves a remarkable thermal efficiency of 72%. Validation using multiple metrics, including MAE and MSE, confirms the accuracy of the ANN model, which aligns with experimental and published results. Wang et al. [158] developed forecasting configurations for tubular solar still productivity, specifically hourly production, using machine learning techniques. Various models, including classical ANN with/without Bayesian optimization, random forest with/without Bayesian optimization, and traditional multilinear regression, are compared. Prior to Bayesian optimization method, both ANN and random forest forecast hourly generation, with random forest demonstrating superior performance and negligible error. The determination coefficients for random forest, ANN, and multilinear regression are 0.9758, 0.9614, and 0.9267, respectively, and MAPE were computed around 5.21%, 7.697%, and 10.911%, respectively. Bayesian optimization significantly improves the performance of ANN by around 35%, and optimization results indicated random forest is less sensitive to hyperparameters compared to ANN. A model was developed by Bahiraei et al. [159] to predict the thermal efficiency of a single-slope solar still provided by thermoelectric modules, employing ANFIS and PSO-enhanced ANN. Cu2O nanoparticles in the solar still basin are modeled for energy efficiency based on various parameters. Experimental observations were employed for training, and the best prediction was obtained with ANFIS with nine clusters and ANN featuring three hidden neurons. The inclusion of PSO significantly enhances prediction performance. Comparison of PSO-based ensemble models indicates the superiority of PSO-ANFIS over PSO-ANN, achieving R2 values of around 0.988 and 0.99 for the training and test sets, respectively.

Figure 41: Schematic diagram of the designed system, (a) experimental setup; (b) schematic diagram [157]

4.2.5 Thermodynamic Cycles

Feng et al. [160] explored performance prediction and multi-objective optimization for an ORC using a backpropagation (BP) neural network. They established a BP-ORC configuration through training process, utilizing a 3-kW ORC experimental platform and collecting data from 950 sets of experimental runs (Fig. 42). The model’s prediction accuracy was assessed based on errors in test and training samples. The influence of six operational parameters on thermal efficiency and net output work was studied, and the Pareto optimal frontier for maximizing both net output work and thermal efficiency was analyzed. Findings showed a minimal prediction error for the BP-ORC model, and experimental system performance improvement could be achieved by adjusting parameters based on model predictions. This revealed a tradeoff relationship between the outputs.

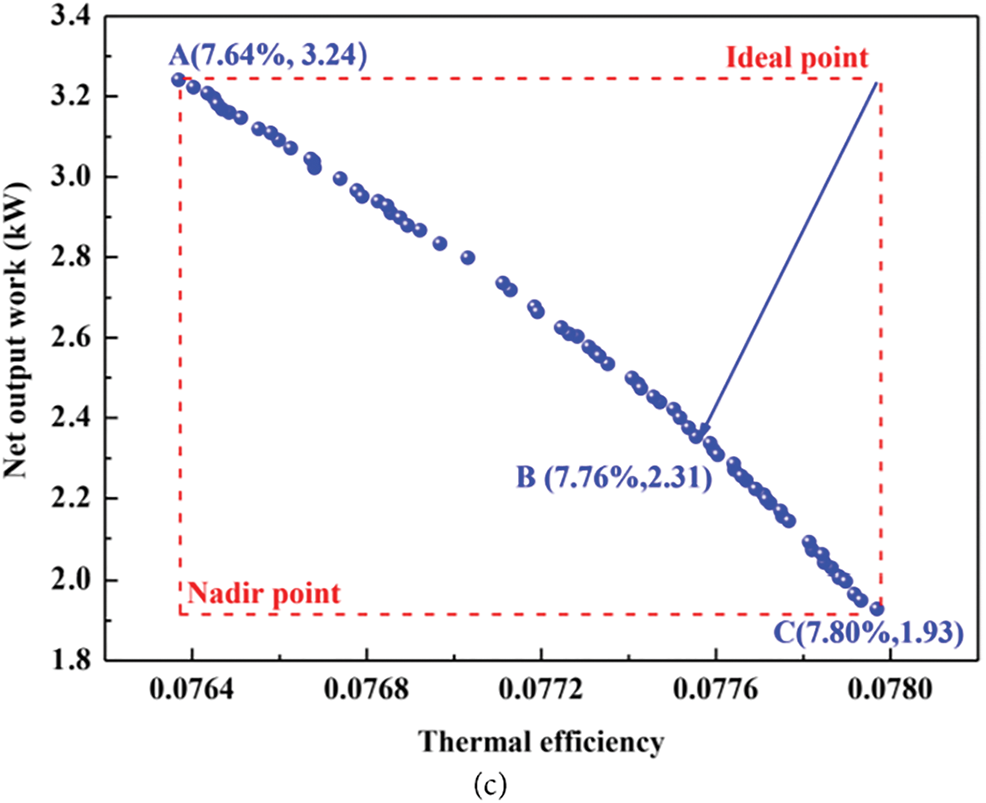
Figure 42: (a) The schematic diagram of a 3 kW ORC waste heat generation system (b) BP-ORC neural network with a single hidden layer (c) The Pareto optimal frontier between net output work and thermal efficiency [160]

The supercritical CO2 (sCO2) Brayton cycle is a promising technology for efficient and compact coal-fired power generation. To maximize performance, a combined sCO2 Brayton cycle-ORC design was developed for coal-fired power plants by Chen et al. [161]. A novel ANN model, considering specific designs for sCO2 boiler, recuperators, coolers, and turbomachinery, was formulated for optimization. An accurate ANN model estimated system pressure drops, reducing model complexity. Applied to three different combined cycles’ design problems, the proposed combined cycle achieves a thermal efficiency of 45.73%, a 2.75 percentage point improvement over standalone design. Senturk Acar [162] optimized the geothermal energy powered Kalina cycle employing a multi-stage ANN analysis. The ANN model comprised two stages, with one network in the first stage and three networks in the second stage. Analyzing 365 designs for four variable parameters through thermodynamic and economic analysis, the data were used to model the multi-stage ANN structure aiming to maximize net present value (NPV). Input parameters included turbine inlet pressure, geothermal water outlet temperature at evaporator, condenser pressure, and ammonia mass fraction, while energy efficiency and exergy efficiency were outputs of the first stage, and NPV was the output of the third network of the second stage. The optimized multi-stage ANN achieved high accuracy with NPV values, with cov, MPE, RMSE, and R2 values calculated as 2.558308, 1.077997189, 1.777658128, and 0.994693, respectively, for NPV. The analytical findings for the optimum system model demonstrated NPV, energy efficiency, and exergy efficiency of 113.0732 M$, 6.7285%, and 46.8701%, respectively, aligning closely with the ANN results.

Surrogate models play a crucial role in replacing computationally-intensive physics-based simulation models for various applications, including energy system optimization. Accordingly, in the study of Zhang et al. [163], five ANN-based surrogate models were developed to replace the physics-based model of a novel regenerative trans-critical power cycle with methanol as the working fluid, integrated with a small modular reactor. The surrogate models, featuring seven design parameters as input, accurately predict 1st-law efficiency, levelized cost of energy, and penalty. Evaluation results revealed high R2 scores, low relative absolute errors, and low L1 losses, with the MLP FFNN model demonstrating superior performance. Soltani et al. [164] conducted a study to reduce costs and enhance exergy efficiency in an innovative system utilizing municipal solid waste (MSW), wood, and paper as biomass fuels. The system integrates power, heating, cooling, fresh water, and hydrogen fuel production (Fig. 43a). A parametric study evaluates its performance from a thermodynamic and thermo-economic perspective. The system employs a gasifier to produce gas for an externally fired gas turbine, with waste heat utilized for S-CO2 and ORC power generation, absorption chiller, humidification-dehumidification desalination, and proton exchange membrane electrolyzer. Multi-objective optimization, facilitated by a genetic algorithm and ANN, determines optimal operating conditions. Results indicate that, under optimal conditions, the system achieves exergy efficiencies of 41.21%, 40.25%, and 39.33% with MSW, wood, and paper, respectively, along with corresponding LCOE values. The proposed MSW-based system demonstrates favorable thermodynamic and cost-effective performance. Liu et al. [165] investigated a method to enhance the performance of the CO2 trans-critical two-phase ejector in refrigeration systems. CFD technology was employed to analyze the influence of geometric parameters on ejector efficiency, generating a database. Subsequently, a time-efficient ANN surrogate model was developed to predict ejector performance, replacing the complex CFD model. Finally, a GA method optimized the ejector to maximize efficiency, resulting in an optimized ejector with 35.39% efficiency. The optimization increased secondary flow velocity, eliminated vortex formation, and improved efficiency by over 8% on average compared to the initial ejector under various primary and secondary flow conditions.

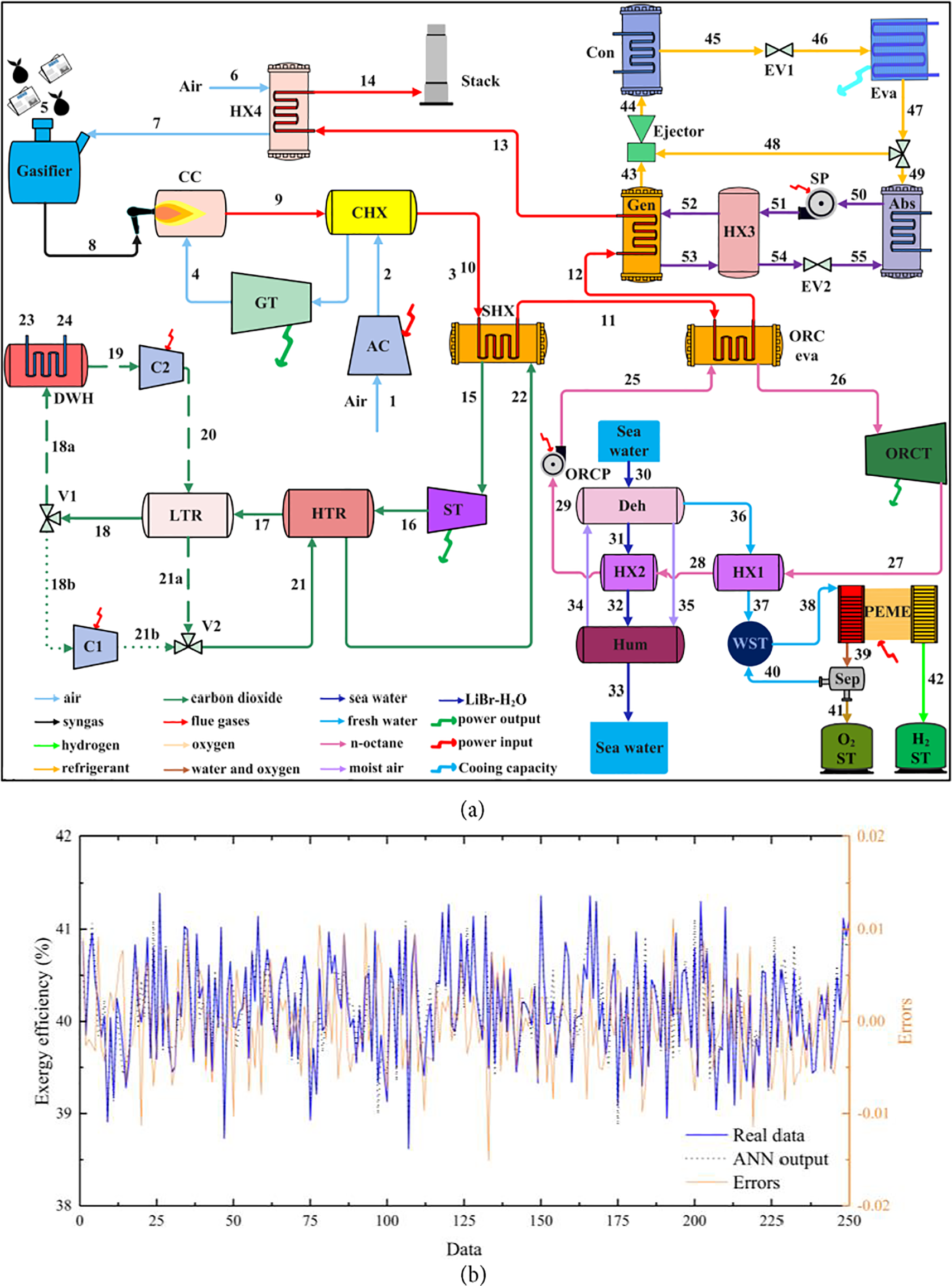
Figure 43: (a) The configuration of the proposed system (b) comparison of ANN performance against real data and the maximum error rate per data for 250 random data

4.2.6 Wind Turbines

Wind power, a prominent renewable energy source, faces limitations within the Betz-Joukowsky limit, capped at 0.593. The cubic relationship between wind speed and generated power underscores the significance of incremental wind speed for substantial power growth. To surpass the Betz limit, shrouding wind turbines is a common practice, accelerating wind flow through the rotor plane. The Siavash et al. [166] introduced a controllable duct that varies the shrouding angle, influencing performance at each opening angle. Due to the time and cost constraints of wind tunnel experiments, four duct opening angles were assessed. The study employed multiple linear regression and ANN to predict turbine performance across a broad range of opening angles. The ANN model outperformed the regression model in estimating turbine power and rotor speed. The findings highlighted the significant impact of shrouding angle on turbine performance at higher wind velocities. A robust machine learning approach, employing ANN with the FFBP algorithm, was implemented by Nielson et al. [167] to create a site-specific power curve for a full-scale wind turbine operating in an atmospheric boundary layer. The methodology significantly enhances power predictions and, consequently, monthly energy production estimates, crucial for evaluating the financial feasibility of wind farms. The study considered atmospheric stability and air density in turbine power predictions, incorporating input parameters such as wind speed, density, Richardson number, turbulence intensity, and wind shear into the ANN model. Comparison with other correction techniques reveals a 40% improvement in MAE compared to density correction. The 4-layer FFBP ANN model achieved an average energy production error of 0.4% over nine months, outperforming air density correction methods. Additionally, the study assessed the FFBP ANN model’s performance across different atmospheric stability regimes, revealing varying MAE with the largest occurring in strongly stable conditions.

Luna et al. [168] studied an advanced Nonlinear Model Predictive Control (NMPC) strategy to minimize fatigue of the wind turbine tower while ensuring maximum energy generation from the wind. Various ANN architectures were trained and evaluated to assess tower fatigue as an alternative to the conventional Rainflow Counting (RFC) technique. Using data from previous fatigue states and tower top oscillation velocity, ANNs directly predict fatigue progression. The selected ANN was then integrated into an economic-tracking NMPC (etNMPC) solution for real-time tower fatigue reduction. Comparative analysis with baseline controllers demonstrated the effectiveness of the proposed strategy, and discussions cover computational cost, real-time deployment capabilities, and potential future research directions. The design of offshore wind turbine (OWT) support structures necessitates dynamic characterization of the entire structural system, including the soil-foundation subsystem. Achieving distinct structural natural frequencies is crucial to prevent resonance phenomena. However, obtaining these frequencies, especially with dynamic soil-structure interaction (SSI), can be computationally expensive. Quevedo-Reina et al. [169] proposed an ANN-based surrogate model to estimate the fundamental frequency of the wind turbine assembly, including the jacket support structure and pile foundation. The surrogate model, trained using a finite element sub structuring approach with dynamic SSI, accurately reproduced the fundamental frequency’s sensitivity to multiple wind turbine, site and jacket structure variables key variables (Fig. 44). This high accuracy, coupled with substantial computational cost reduction, justified the ANN surrogate model’s use in applications requiring numerous evaluations.

Figure 44: (a) An offshore wind turbine supported on an jacket with pile foundation (b) ANN model with 22 neurons in the input layer, 10 neurons in each of the two hidden layers, and 1 neuron in the output layer [169]

The Savonius rotor, a member of VAWTs, possesses advantageous features like direction independency, simplicity, suitability for low wind speeds, and standalone system capability. Rathod et al. [170] explored the utilization of ANN and genetic expression programming (GEP) to predict the performance of Savonius wind rotors based on different independent design variables (Fig. 45). Experimental data on Savonius rotors was employed to train ANN and GEP. Input variables was included design shape factors, number of blades, gap and overlap lengths, rotor height and diameter, freestream velocity, end plate diameter, and tip speed ratio. Trained ANN and GEP models effectively estimate rotor performance with R² ≈ 0.97 and R² ≈ 0.65, respectively, correlating well with reported experimental data. Wind turbines are increasingly being deployed in cold regions for better wind resources, but this comes with the challenge of ice accumulation on blades, affecting natural frequency. Experiments with a 2-kW wind turbine involving ice accumulation at different locations (tip, middle, root, or whole blade), and relationships between iced blade natural frequencies and icing mass were established by Li et al. [171]. Two ANNs was utilized to predict ice location and mass based on these relationships. Training with 335 data sets, the back propagation and RBF neural networks indicated promising prediction results. Relative percentage errors for local region icing decrease with increased ice accumulation, while mean errors for whole blade icing were below 7.5%, with BP network outperforming RBF. Application on a 2 MW wind turbine blade using finite element method yields a mean error of 13.21% with BP neural network.

Figure 45: The normalized/standardized design representation: (a) depiction of three- and two-staged rotors, (b) depiction of three- and two-bladed rotors, and (c) cross section of twobladed rotor

4.2.7 Hybrid Energy Systems

Integrating diverse energy systems into a unified, combined system represents a strategic approach to leverage the strengths of individual systems while mitigating their weaknesses. This synergy allows for a more resilient and efficient energy infrastructure. By seamlessly combining different energy sources, such as wind, solar, and traditional power generation, a hybrid system can harness the benefits of each, providing continuous and reliable energy even when specific sources face fluctuations or downtime. Energy storage technologies, such as batteries and thermal storage, play a crucial role in balancing the intermittent nature in renewable resources, ensuring a consistent power supply. Additionally, coupling these systems with smart grid technologies and advanced control systems enhances overall stability and responsiveness. The integration of various energy systems contributes not only to improved energy reliability but also to enhanced sustainability by reducing environmental impact. This comprehensive approach aligns with the broader goal of creating resilient and adaptive energy networks capable of meeting the demands of a dynamic and evolving energy landscape. Asadabadi and Moghimi [172] explored a combined model to harness waste heat from a SOFC, which integrates a two-bed adsorption chiller, a Kalina cycle, reverse osmosis, thermoelectric generator, and PEM electrolyzer. A parametric examination assessed the productivity of the system using environmental, economic, exergy, and, energy metrics. Optimization using ANN results in optimal values for total cost rate, exergy efficiency, cooling load, and freshwater production. Waste heat recovery from SOFC was found to decrease carbon dioxide emissions by 36.41 kg per megawatt of output. Operating at around 0.074 kg/s for the fuel consumption rate, the system achieved a maximum power generation, cooling load, freshwater production, and hydrogen generation with energy and exergy efficiencies of around 64% and 51%, respectively. Moustafa et al. [173] concentrated on increasing the energy efficiency and water yield of the tubular solar still, a lightweight desalination unit (Fig. 46). An electrical heater derived by a PV was employed as the absorber plate, significantly improving the water yield and overall performance. The modified solar still exhibited an average water yield of about 3.4 L/m2/day, representing a significant enhancement of around 32% compared to the standard design. The daytime thermal efficiency of the modified system reached 38.6%, surpassing the conventional system’s efficiency of 30.6%. Additionally, a tuned ANN model, optimized by the humpback whale optimizer, was developed to predict thermal efficiency and water yield. This model outperformed standalone ANN and PSO models, displaying the highest correlation coefficients between 0.983 and 0.999. The results highlighted the significance of the electrical heater in improving energy productivity and the proficiency of the ANN-humpback whale optimizer in increasing forecasting precision of conventional ANN architectures.

Figure 46: A schematic diagram of the tubular solar still experimental setup [173]

Abubaker et al. [174] studied gas turbine drawbacks by combining a cascaded system into a hybrid cycle. PTC preheat the air at the inlet of the combustion chamber and run an absorption inlet-air cooling cycle to control the temperature of ambient-air at the inlet of the compressor. Utilizing the 2nd law efficiency of the thermodynamics, the maximum available electric exergy efficiency, energy, and maximum irreversible exergy destruction were estimated. ANN and multi-objective optimization were employed to analyze system performance. Design improvements for the combustion chamber and parabolic trough collectors’ field were suggested to reduce irreversibility. The integration of ANN into optimization process enhanced electric exergy efficiency up to around 46% while minimizing the exergy destruction to about 489 MW, surpassing values from the simple design point. Akkouche et al. [175] developed a model for the Micro-CHP system functioning in dual-fuel mode, drawing on experimental findings obtained from a 3.5 kW AVL engine. The engine utilized synthetic biogas as the primary fuel and diesel as a pilot fuel. ANN modeling was employed for engine operation, with three models for pilot fuel flow, airflow, and exhaust gas temperature (Fig. 47). Furthermore, the ANN models underwent training and validation with experimental data. Simulations were conducted to assess the effect of varying the number of digesters operating in parallel mode over a 50-day digestion period. The results unveiled optimal conditions characterized by the utilization of five digesters and a 70% load, requiring less than 10% energy from diesel. For a 1 kWe micro-CHP unit, a dual fuel generator, five digesters, and a daily effluent availability of 171 kg/day were necessary, enabling the generation of up to 2.45 kW of thermal power from the exhaust. Steam ejectors, widely used in industries for energy-saving purposes. While existing models offer reasonably accurate predictions for steam ejectors, discrepancies with experiments can be as high as 20%.

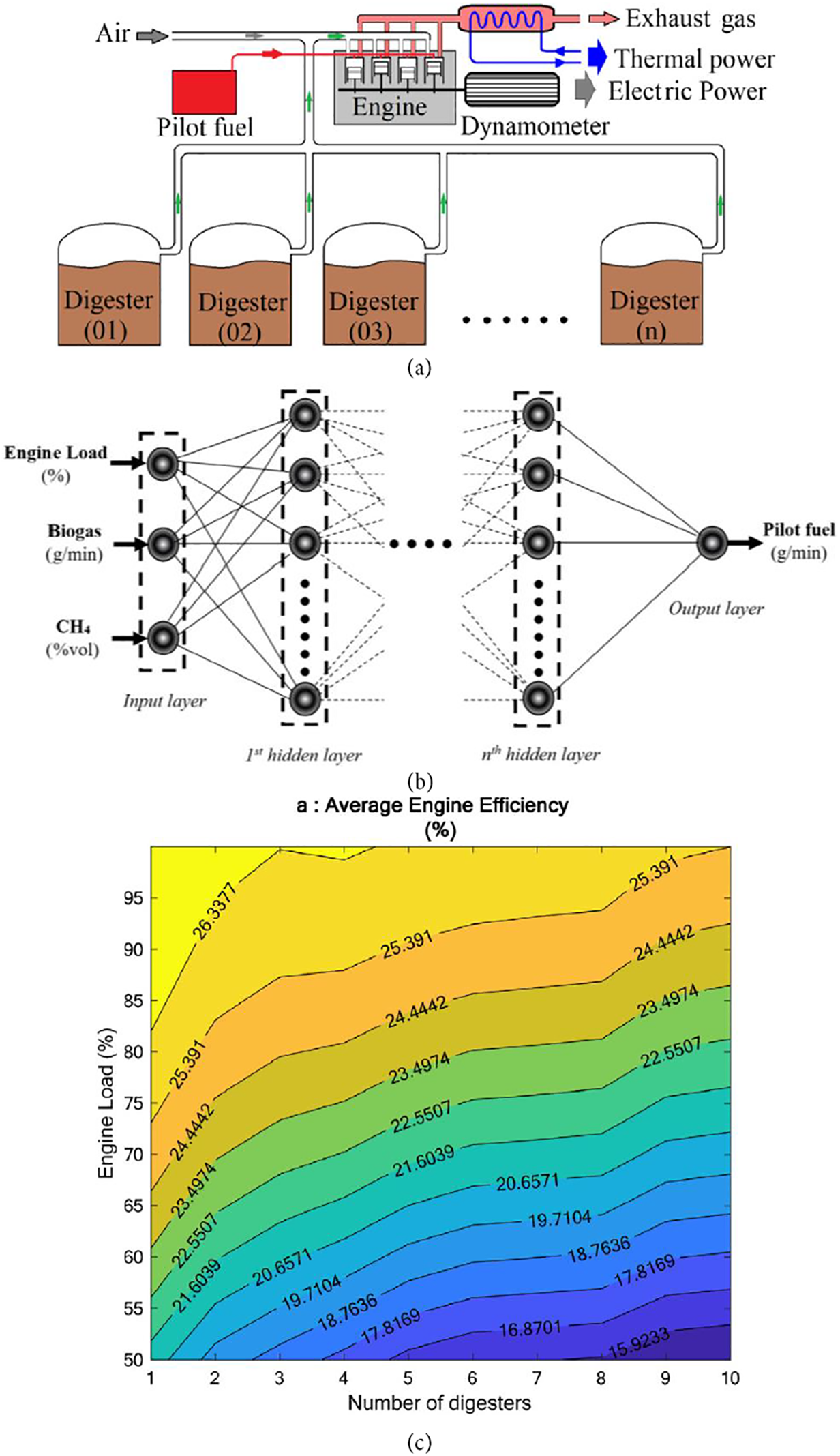
Figure 47: (a) Schematic of the CHP plant operating with biogas from n digesters (b) configuration of MLP estimating pilot fuel flow rate and (c) engine efficiency vs. engine load and number of digesters [175]

Traditional CFD simulations are computationally expensive, requiring careful selection of parameters. As a consequence, Ahmed and Chen [176] introduced an ANN model for a steam ejector, leveraging data-driven techniques. The ANN model was trained using various geometrical and operational conditions, employing four input factors and predicting two output parameters: COP and Pressure Reduction Ratio (PRR). Among tested optimizers, the ANN model trained with the ADAM optimizer performs the best. The model, with a hidden layer of 102 neurons and a split ratio of 0.2, exhibits an average error of ±1.8% for COP and ±2.4% for PRR predictions. This ANN model proved valuable for enhancing steam ejector system configuration and operation.

Du et al. [177] proposed an energy system which involved an ammonia-water fueled SOFC-GT-KC cascade, aiming for a zero-carbon, high-efficiency, and cost-effective solution. Key operational parameters, especially fuel ammonia mass fraction, significantly impacted total energy efficiency and LCOE. Using ANN-multi-objective Harris hawks optimizer, rapid prediction and multi-objective optimization showcased a 12.92% increase in total energy efficiency and an 8.91% decrease in LCOE compared to the traditional SOFC system. Parametric analysis emphasized the impact of fuel ammonia mass fraction on system performance, and multi-objective optimization highlighted the sensitivity of LCOE to ammonia price. A robust nonlinear relationship characterizes the Atkinson cycle engine, and leveraging ANN, has gained prominence for accurate modeling.

4.2.8 Summary

In this section, a condensed overview of key findings and primary concerns related to the application of ANN in diverse energy systems is presented, drawing insights from Table 11.

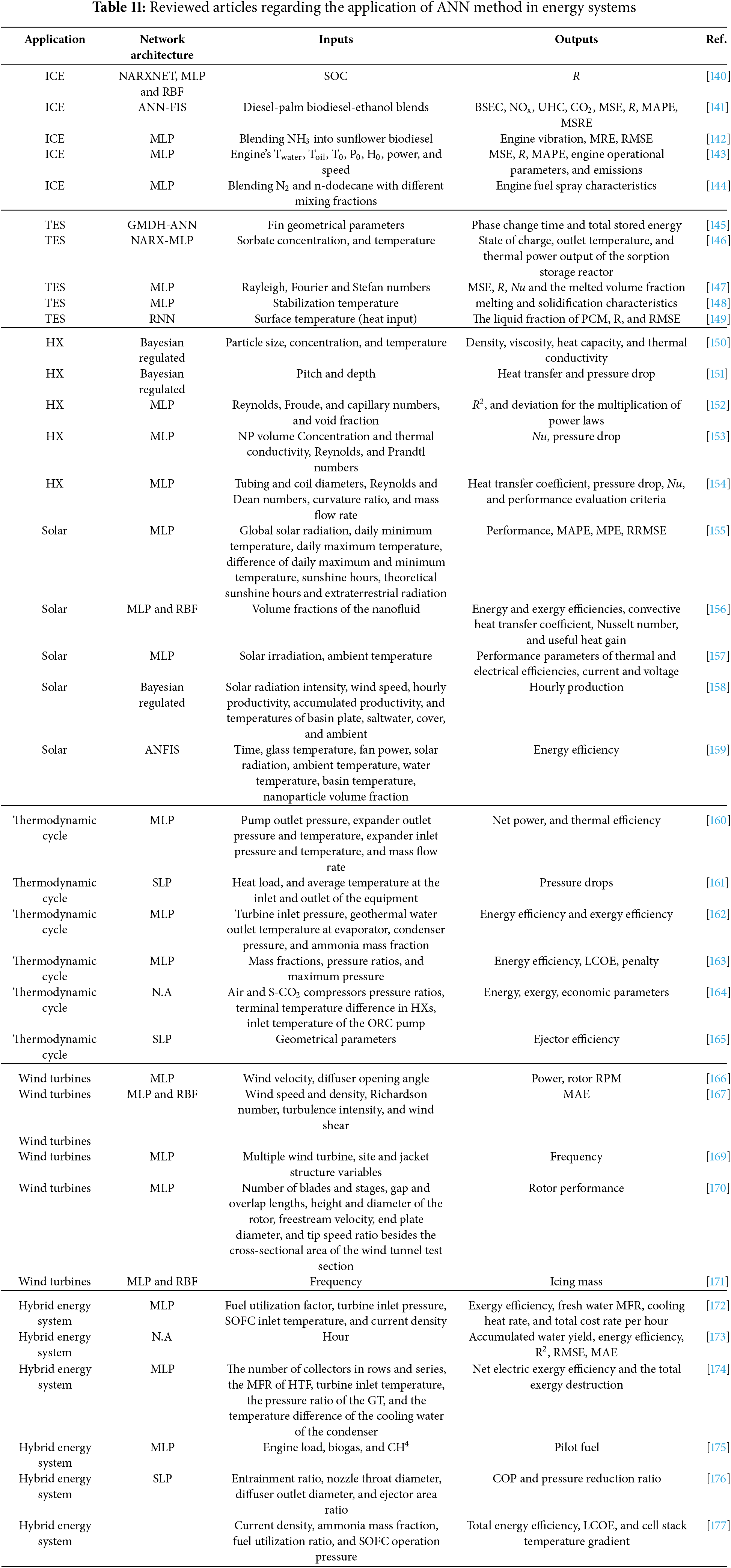
It is crucial to recognize both the merits and disadvantages associated with the utilization of ANN in energy systems and applications, detailed in Table 12. Given the complicated nature of energy systems, characterized by various influencing factors, the capacity of ANNs to conduct non-linear analyses emerges as a notable advantage in managing these systems.

5  Recommendations and Future Directions

Leveraging Taguchi methodologies such as the S/N ratio, Taguchi-GRA, and Taguchi-TOPSIS holds promise for optimizing energy system performance while mitigating environmental impacts. Firstly, the application of Taguchi S/N ratio offers a systematic approach to identify optimal parameter settings that minimize noise and maximize system efficiency. Utilizing the S/N ratios and analysis of variance (ANOVA) enables the optimization of factors contributing to defects in single-objective energy system problems, while also identifying the influence of each factor. Taguchi orthogonal arrays are commonly utilized as alternatives to traditional full-factorial experimental designs for conducting experiments. This substitution is motivated by the efficiency gained through the implementation of Taguchi orthogonal arrays, which reduces the need for a large number of experiments. Consequently, this approach significantly reduces both the time and overall costs associated with conducting experiments. Future research could explore the integration of advanced computational techniques to enhance the efficiency and accuracy of S/N ratio calculations, thereby providing more robust insights into energy system optimization. Moreover, incorporating sensitivity and uncertainty analyses alongside the S/N ratio can further enhance the reliability of optimization outcomes, ensuring robust performance under real-world operating conditions. Additionally, the fusion of Taguchi methodologies with multi-criteria decision-making techniques like GRA and TOPSIS presents a comprehensive framework for addressing complex trade-offs in energy system optimization. Taguchi-GRA enables the assessment of the relationship between input factors and system performance, facilitating informed decision-making for enhancing energy efficiency and reducing environmental impacts. Future recommendations may involve refining GRA methodologies to accommodate dynamic system interactions and non-linear relationships, thereby improving the accuracy of optimization outcomes. Furthermore, integrating Taguchi-TOPSIS methods offers a structured approach to prioritize alternative energy system designs based on multiple performance criteria. Future research could focus on developing hybrid optimization algorithms that leverage the strengths of both Taguchi-TOPSIS and machine learning techniques, enabling more efficient and accurate decision-making in energy system design and operation. By embracing these recommendations and advancing research in Taguchi methodologies, the optimization of energy systems performance and environmental impacts can be achieved with greater efficacy and sustainability.

Throughout this review, there is a widespread agreement on the pivotal role of employing AI approaches in forecasting the environmental impacts and performance of energy systems. Regardless of its considerable potential, the utilization of the AI methods encounters numerous research challenges and a current scarcity of suitable techniques, particularly concerning optimization algorithms. These limitations manifest in issues such as noisy experimental conditions, model resilience, and the imprecise and time-varying nature of approximate models. ANN stand out as a superior technique compared to traditional computing software due to their rapid processing speed and short computation times. However, significant challenges persist in implementing ANN models in forecasting energy systems outcomes. Achieving an excellent precision to predict energy systems performance and environmental impacts with ANN methods necessitates extensive information. It could be difficult to acquire due to the high costs associated with experimental setups and the requirements for appropriate operating conditions and precise measuring mechanisms & devices. Additionally, the choice of input factors represents a second challenge for ANN modeling, as this selection is deemed to significantly influence the model’s accuracy and performance. Certainly, the importance and independence of input variables are recognized as crucial factors influencing the selection of inputs. Thus, techniques such as filtering and dimensionality reduction may be employed to choose input data that aligns well with the outcomes. Moreover, subsets of data such as validation, testing, and training, are typically utilized in ANN models. Consequently, complex issues arise in the training process in determining connection weights, during testing process in optimizing ANN structure, and during validation process in assessing generalization ability. These difficulties highlight the necessity for efficient algorithms to oversee the data. Alternatively, data normalization is necessary due to variable differences. Nevertheless, considering the proliferation of ANN methods and their utilization, it is foreseeable that these optimization approaches will become increasingly relevant in estimating the performance of energy systems, owing to the model’s robust reliability. According to the presented literature review, it has been found that the subsequent points remain unexplored and may serve as potential areas for future research in the domain of energy applications. (1) The performance prediction of energy systems can be conducted using various ANN models like RBF, MLP, GRNN, NARX, etc. with the aim of comparing their performance. Furthermore, this process seeks to identify the most optimal neural model that yields precises outcomes. (2) A comparative study of various ANN learning algorithms to evaluate their efficiency in predicting energy systems outcomes. The objective could be determining the optimal learning algorithm that produces the most accurate outputs. (3) To determine the quantity of neurons in the hidden layer of an ANN setup utilizing multiple relationships documented by multiple investigators, with the ultimate goal of achieving accurate predictions. (4) The comparison of results obtained from ANN models with those derived from other soft computing techniques, including PSO, GA, SVM, ANFIS, etc., could be conducted to assess their respective performances and determine the most effective approach. (5) Employing SA and PSO techniques to optimize the architecture of ANN for predicting the performance of diverse energy systems.

6  Conclusions

This paper provides a comprehensive discussion on the application of Taguchi and ANN approaches for optimizing single and multi-objective energy systems. These methods offer significant advantages in this field. Both techniques are widely used for forecasting and optimization, with continuous efforts to identify the most precise approach. Furthermore, combining these two methodologies has the potential to further enhance accuracy. The key conclusions of this review paper, along with the merits and disadvantages of utilizing these methods, are presented below:

•   Taguchi’s method offers a systematic and efficient approach to experimental design through the use of orthogonal arrays. This allows for the investigation of multiple factors and their interactions with fewer experiments, thereby reducing the time and cost involved. Rooted in statistical principles, the Taguchi method utilizes ANOVA tables to provide a quantitative and objective foundation for decision-making. This statistical basis enhances the credibility and reliability of the optimization process in energy systems. The method also helps in identifying the most influential factors impacting system performance, enabling efficient resource allocation to improve overall quality and performance.

•   The Taguchi S/N ratio method has several limitations. It assumes a linear relationship between factors and responses, which may not accurately reflect system behavior in non-linear scenarios. The reliance on predefined orthogonal arrays can also be restrictive when more complex or non-standard experimental designs are required. Furthermore, this method is primarily designed for continuous variables, posing challenges when dealing with categorical variables. As the number of factors increases, the complexity of experimental design and analysis grows, potentially making Taguchi methods less practical for large-scale optimization. Finally, while robust to certain types of noise, the Taguchi S/N ratio may not perform optimally when uncontrolled or unpredictable noise factors significantly impact the system.

•   Taguchi-based optimization methods, such as GRA and TOPSIS, are designed to deliver stable and reliable results, even with data variability or noise. GRA is particularly accessible due to its relative simplicity, making it suitable for practitioners without extensive optimization expertise. This method facilitates efficient decision-making in energy systems (e.g., ICEs, HXs) where relationships between factors may be ill-defined. One of GRA’s key strengths is its ability to handle multiple objectives simultaneously, which is advantageous when several criteria are involved in the optimization process. Furthermore, GRA helps reduce data dimensionality by converting data into a grey relational grade, thereby simplifying decision-making by prioritizing the most relevant factors.

•   The Taguchi-GRA method has limitations, particularly in energy applications. It presumes a linear relationship between factors, which may not always be accurate, potentially failing to capture non-linear relationships effectively. The method’s effectiveness is also susceptible to the precise selection of parameters, such as weighting factors, where inappropriate choices can introduce bias. Furthermore, despite its robustness, Taguchi-GRA may struggle with uncertainties or variations not explicitly addressed during the optimization process.

•   Taguchi-TOPSIS is a flexible method for multicriteria decision-making in energy systems, capable of handling both quantitative and qualitative criteria. It’s well-suited for engineers who need to simultaneously consider multiple factors and situations with trade-offs between different criteria. The method provides a systematic approach to finding the best compromise, and its results are easy to interpret, presented as a ranking that indicates the preference order of alternatives. This makes it applicable in various real-world energy contexts.

•   The Taguchi-TOPSIS method has also several limitations. It is sensitive to how criteria are normalized, as it assumes all criteria hold equal importance, and the normalization process can influence the outcomes. The assignment of weights to criteria can be subjective, and varying weight allocations may yield different results, underscoring the importance of accurate weight assignment for drawing meaningful conclusions. Furthermore, Taguchi-TOPSIS performs best with a clearly defined set of alternatives and may encounter difficulties when managing a large number of alternatives or when new options are introduced.

•   ANN are highly effective in energy applications due to their ability to model complex, non-linear relationships that traditional linear models often miss. Their adaptive nature allows them to learn from experience and adjust to dynamic and unpredictable environments, making them suitable for evolving datasets and changing conditions. ANNs also offer inherent parallelism, processing multiple pieces of information simultaneously, which enhances efficiency when handling large datasets. Furthermore, this technique streamlines data processing by automatically identifying relevant features from input data, eliminating the need for manual feature engineering.

•   The Artificial Neural Network (ANN) method presents several challenges. Its internal workings can be complex and difficult to interpret, creating a “black box” problem where the decision-making process is not easily explainable. This method typically requires large amounts of data for practical training, and its performance may suffer with limited data, which can be a significant limitation when acquiring extensive datasets is challenging. Training complex neural networks can also demand substantial computational resources and time, especially for deep learning architectures, due to their computational intensity. Furthermore, the ANN technique is prone to overfitting, meaning it may learn noise or irrelevant patterns from the training data, leading to poor generalization on new data. Therefore, regularization techniques are often necessary to mitigate overfitting.

According to the studies and the presented review, the ANN models demonstrated a notably high determination coefficient when comparing predicted outcomes to experimental data, indicating their strong predictive capability regarding energy systems behaviors with an accuracy surpassing approximately 90%. Likewise, the evaluation also concludes that the Taguchi-GRA and Taguchi-TOPSIS optimization techniques are significantly effective in analyzing and optimizing energy-related problems in terms of performance and environmental impacts.

Acknowledgement: The authors acknowledge that during the preparation of this work, the authors used AI tools for language editing, grammar correction, and improving the clarity of our phrasing. After utilizing this tool, the authors thoroughly reviewed and edited the content as necessary and take full responsibility for the final content of the published article.

Funding Statement: This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author Contributions: Mir Majid Etghani: Writing—review & editing, Supervision, Conceptualization, Resources, Project administration. Homayoun Boodaghi: Writing—review & editing, Writing—original draft, Visualization, Validation, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available on request.

Ethics Approval: This article does not contain any studies with human participants or animals performed by any of the authors.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

A*	Positive ideal solution
A-	Negative ideal solution
b	Number of levels
c	Number of factors
C*	Ranking score
Cp	Power coefficient
F	Factor
H0	Relative humidity
h	Convection heat transfer coefficient
J	Set of attributes
L	Latin square
n	Number of experiments
Nu	Nusselt number
P0	Ambient pressure
R	Response, correlation coefficient
Re	Reynolds number
s	Standard deviation
S*	Distance of each alternative to the positive ideal solution
S-	Distance of each alternative to the negative ideal solution
T0	Ambient temperature
V	Weighted normalized decision matrix
w	Weighting factor
y	Experimental response
η	S/N ratio
Abbreviations
AI	Artificial intelligence
ANFIS	Adaptive neuro fuzzy inference system
ANN	Artificial neural network
ANOVA	Analysis of variance
ATDC	After top dead center
BTDC	Before top dead center
BSFC	Brake specific fuel consumption
BTE	Brake thermal efficiency
CA	Crank angle
CFD	Computational fluid dynamic
CHP	Combined heat and power
CI	Compression ignition
CO	Carbon monoxide
CPP	Clean power plan
CR	Compression ratio
DDWT	Dual Darrius wind turbines
DEE	Diethyl ether
DI	Direct injection
DoE	Design of experiments
DOF	Degree of freedom
EGR	Exhaust gas recirculation
FIS	Fuzzy interface system
GA	Genetic algorithm
GRA	Grey relational analysis
GT	Gas turbine
HC	Hydrocarbon
HCCI	Homogenous charge compression ignition engine
HTF	Heat transfer fluid
HX	Heat exchanger
KC	Kalina cycle
ICCI	Intelligent charge compression ignition
ICE	Internal combustion engine
LCOE	Levelized cost of energy
LCOH	Levelized cost of heat
MAE	Mean absolute error
MAPE	Mean absolute percentage errors
MFR	Mass flow rate
MOO	Multi-objective optimization
MRE	Mean root error
MMSE	Minimum mean square error
MSRE	Mean square relative error
NARX	Nonlinear autoregressive network with exogenous inputs
NSGA	Non-dominated sorting genetic algorithm
NOx	Nitrogen oxides
NP	Nanoparticle
ORC	Organic Rankine cycle
OA	Orthogonal array
PCM	Phase change material
PTC	Parabolic through collector
PV	Photovoltaic
PVT	Photovoltaic thermal
RMSE	Root mean square error
RSM	Response surface methodology
SA	Sensitivity analysis
SI	Spark ignition
S/N	Signal-to-noise ratio
SOI	Start of injection
SS	Sum of squares
SSE	Sum of squares of the residual error
SST	Treatment sum of squares
ST	Solar thermal
TC	Turbocharger
TES	Thermal energy storage
TSR	Tip speed ratio
UHC	Unburnt hydrocarbon
VAHT	Vertical axis hydrokinetic turbine
VAT	Vertical axis tidal
VAWT	Vertical axis wind turbine
WHR	Waste heat recovery

References

1. Özokcu S, Özdemir Ö. Economic growth, energy, and environmental Kuznets curve. Renew Sustain Energy Rev. 2017;72(12):639–47. doi:10.1016/j.rser.2017.01.059. [Google Scholar] [CrossRef]

2. Conti J, Holtberg P, Diefenderfer J, LaRose A, Turnure JT, Westfall L. International energy outlook 2016 with projections to 2040. Washington, DC, USA: USDOE Energy Information Administration (EIA); 2016. Technical Report. No.: DOE/EIA–0484(2016). doi:10.2172/1296780. [Google Scholar] [CrossRef]

3. IPCC. IPCC fifth assessment report—synthesis report. Rome, Italy: iPPC; 2014. [Google Scholar]

4. Klemm C, Wiese F. Indicators for the optimization of sustainable urban energy systems based on energy system modeling. Energy Sustain Soc. 2022;12(1):3. doi:10.1186/s13705-021-00323-3. [Google Scholar] [CrossRef]

5. Boodaghi H, Etghani MM, Sedighi K. Performance analysis of a dual-loop bottoming organic Rankine cycle (ORC) for waste heat recovery of a heavy-duty diesel engine, part I: thermodynamic analysis. Energy Convers Manag. 2021;241(10):113830. doi:10.1016/j.enconman.2021.113830. [Google Scholar] [CrossRef]

6. Bogdanov D, Gulagi A, Fasihi M, Breyer C. Full energy sector transition towards 100% renewable energy supply: integrating power, heat, transport and industry sectors including desalination. Appl Energy. 2021;283(1):116273. doi:10.1016/j.apenergy.2020.116273. [Google Scholar] [CrossRef]

7. Al-Ghussain L, Abubaker AM, Darwish Ahmad A. Superposition of renewable-energy supply from multiple sites maximizes demand-matching: towards 100% renewable grids in 2050. Appl Energy. 2021;284(14):116402. doi:10.1016/j.apenergy.2020.116402. [Google Scholar] [CrossRef]

8. Singer S, Denruyter JP, Yener D. The energy report: 100% renewable energy by 2050. In: Towards 100% renewable energy. Cham, Switzerland: Springer International Publishing; 2017. p. 379–83. doi:10.1007/978-3-319-45659-1_40. [Google Scholar] [CrossRef]

9. Sorrell S, O’Malley E. The economics of energy efficiency. Cheltenham, UK: Edward Elgar Publishing; 2004. [Google Scholar]

10. Iris Ç, Lam JSL. A review of energy efficiency in ports: operational strategies, technologies and energy management systems. Renew Sustain Energy Rev. 2019;112(5):170–82. doi:10.1016/j.rser.2019.04.069. [Google Scholar] [CrossRef]

11. Zakari A, Khan I, Tan D, Alvarado R, Dagar V. Energy efficiency and sustainable development goals (SDGs). Energy. 2022;239(4):122365. doi:10.1016/j.energy.2021.122365. [Google Scholar] [CrossRef]

12. Gong T, Wu Y, Li J, Lin W, Gao L, Shen L, et al. A system level optimization of on-chip thermoelectric cooling via Taguchi-Grey method. Appl Therm Eng. 2022;214(5):118845. doi:10.1016/j.applthermaleng.2022.118845. [Google Scholar] [CrossRef]

13. Lin Y, Feng H, Yang W, Hao X, Tian L, Yuan X. Thermal performance optimization of a semi-nested building coupled with an earth-to-air heat exchanger using iterative Taguchi method. Renew Energy. 2022;195(6):1275–90. doi:10.1016/j.renene.2022.06.116. [Google Scholar] [CrossRef]

14. Cheng SWY, Kurnia JC, Ali Ghoreishi-Madiseh S, Sasmito AP. Optimization of geothermal energy extraction from abandoned oil well with a novel well bottom curvature design utilizing Taguchi method. Energy. 2019;188:116098. doi:10.1016/j.energy.2019.116098. [Google Scholar] [CrossRef]

15. Wang Z, Su Z, Goyal V, Kumar NB, Dahari M, Abdulwahab A, et al. Optimization and evaluation of a municipal solid waste-to-energy system using taguchi technique in a tri-generation system based on gas turbine with air and steam agents. Process Saf Environ Prot. 2023;173(15):461–71. doi:10.1016/j.psep.2023.03.037. [Google Scholar] [CrossRef]

16. Pan JS, Tian AQ, Snášel V, Kong L, Chu SC. Maximum power point tracking and parameter estimation for multiple-photovoltaic arrays based on enhanced pigeon-inspired optimization with Taguchi method. Energy. 2022;251:123863. doi:10.1016/j.energy.2022.123863. [Google Scholar] [CrossRef]

17. Karaoglu S, Yolcular S. Optimization of hydrogen generation process from the hydrolysis of activated Al-NaCl–SiC composites using Taguchi method. Int J Hydrog Energy. 2022;47(66):28289–302. doi:10.1016/j.ijhydene.2022.06.171. [Google Scholar] [CrossRef]

18. Khanjanpour MH, Javadi AA. Optimization of a Horizontal Axis Tidal (HAT) turbine for powering a Reverse Osmosis (RO) desalination system using Computational Fluid Dynamics (CFD) and Taguchi method. Energy Convers Manag. 2021;231(1):113833. doi:10.1016/j.enconman.2021.113833. [Google Scholar] [CrossRef]

19. Seo JH, Garud KS, Lee MY. Grey relational based Taguchi analysis on thermal and electrical performances of thermoelectric generator system with inclined fins hot heat exchanger. Appl Therm Eng. 2021;184(1):116279. doi:10.1016/j.applthermaleng.2020.116279. [Google Scholar] [CrossRef]

20. Amadane Y, Mounir H. Performance improvement of a PEMFC with dead-end anode by using CFD-Taguchi approach. J Electroanal Chem. 2022;904(26):115909. doi:10.1016/j.jelechem.2021.115909. [Google Scholar] [CrossRef]

21. Özel S, Vural E, Binici M. Optimization of the effect of thermal barrier coating (TBC) on diesel engine performance by Taguchi method. Fuel. 2020;263(4):116537. doi:10.1016/j.fuel.2019.116537. [Google Scholar] [CrossRef]

22. Al Shami E, Wang X, Zhang R, Zuo L. A parameter study and optimization of two body wave energy converters. Renew Energy. 2019;131(1):1–13. doi:10.1016/j.renene.2018.06.117. [Google Scholar] [CrossRef]

23. Ben Seddik Z, Ben Taher MA, Laknizi A, Ahachad M, Bahraoui F, Mahdaoui M. Hybridization of Taguchi method and genetic algorithm to optimize a PVT in different Moroccan climatic zones. Energy. 2022;250:123802. doi:10.1016/j.energy.2022.123802. [Google Scholar] [CrossRef]

24. Aquila G, de Queiroz AR, Rotela PJr, Rocha LCS, de Oliveira Pamplona E, Balestrassi PP. Contribution for bidding of wind-photovoltaic on grid farms based on NBI-EFA-SNR method. Sustain Energy Technol Assess. 2020;40:100754. doi:10.1016/j.seta.2020.100754. [Google Scholar] [CrossRef]

25. Abiodun OI, Jantan A, Omolara AE, Dada KV, Mohamed NA, Arshad H. State-of-the-art in artificial neural network applications: a survey. Heliyon. 2018;4(11):e00938. doi:10.1016/j.heliyon.2018.e00938. [Google Scholar] [PubMed] [CrossRef]

26. Djebali R, Ferhi M, Khemiri K, Mechighel F, Pateyron B, Ouerhani M, et al. Integration of artificial neural networks and process simulation for optimizing direct current atmospheric plasma spraying of enhanced zirconia coatings. In: 2025 15th International Renewable Energy Congress (IREC); 2025 Feb 2–4; Hammamet, Tunisia. p. 1–6. doi:10.1109/IREC64614.2025.10926821. [Google Scholar] [CrossRef]

27. Tugcu A, Arslan O. Optimization of geothermal energy aided absorption refrigeration system—GAARS: a novel ANN-based approach. Geothermics. 2017;65(4):210–21. doi:10.1016/j.geothermics.2016.10.004. [Google Scholar] [CrossRef]

28. Kulaksız AA, Akkaya R. A genetic algorithm optimized ANN-based MPPT algorithm for a stand-alone PV system with induction motor drive. Sol Energy. 2012;86(9):2366–75. doi:10.1016/j.solener.2012.05.006. [Google Scholar] [CrossRef]

29. Szabłowski Ł, Milewski J, Badyda K, Kupecki J. ANN-supported control strategy for a solid oxide fuel cell working on demand for a public utility building. Int J Hydrog Energy. 2018;43(6):3555–65. doi:10.1016/j.ijhydene.2017.10.171. [Google Scholar] [CrossRef]

30. Thodda G, Madhavan VR, Thangavelu L. Predictive modelling and optimization of performance and emissions of acetylene fuelled CI engine using ANN and RSM. Energy Sources Part A Recovery Util Environ Eff. 2023;45(2):3544–62. doi:10.1080/15567036.2020.1829191. [Google Scholar] [CrossRef]

31. Li A, Xiao F, Fan C, Hu M. Development of an ANN-based building energy model for information-poor buildings using transfer learning. Build Simul. 2021;14(1):89–101. doi:10.1007/s12273-020-0711-5. [Google Scholar] [CrossRef]

32. Zahadat P, Milewski J. Modeling electrical behavior of solid oxide electrolyzer cells by using artificial neural network. Int J Hydrog Energy. 2015;40(23):7246–51. doi:10.1016/j.ijhydene.2015.04.042. [Google Scholar] [CrossRef]

33. Gang W, Wang J, Wang S. Performance analysis of hybrid ground source heat pump systems based on ANN predictive control. Appl Energy. 2014;136(1):1138–44. doi:10.1016/j.apenergy.2014.04.005. [Google Scholar] [CrossRef]

34. Ayoub N, Musharavati F, Pokharel S, Gabbar HA. ANN model for energy demand and supply forecasting in a hybrid energy supply system. In: 2018 IEEE International Conference on Smart Energy Grid Engineering (SEGE); 2018 Aug 12–15; Oshawa, ON, Canada. p. 25–30. doi:10.1109/SEGE.2018.8499514. [Google Scholar] [CrossRef]

35. Vaferi K, Farajollahi A, Gholizadeh T, Rostami M. Enhancing charging and discharging performance in a novel latent heat storage via design optimization and artificial neural network modeling. J Energy Storage. 2025;114(1):115757. doi:10.1016/j.est.2025.115757. [Google Scholar] [CrossRef]

36. Boukelia TE, Arslan O, Mecibah MS. ANN-based optimization of a parabolic trough solar thermal power plant. Appl Therm Eng. 2016;107(4):1210–8. doi:10.1016/j.applthermaleng.2016.07.084. [Google Scholar] [CrossRef]

37. Ahmad AS, Hassan MY, Abdullah MP, Rahman HA, Hussin F, Abdullah H, et al. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew Sustain Energy Rev. 2014;33(10):102–9. doi:10.1016/j.rser.2014.01.069. [Google Scholar] [CrossRef]

38. Djebali R, Ferhi M, Mechighel F, Khemiri K, Bjaoui M, Ouerhani M, et al. Deep learning analysis and numerical simulation of exergy and nanofluid heat transfer efficiency in a two-compartment heat exchanger with internal heat generation and baffles. In: 2025 15th International Renewable Energy Congress (IREC); 2025 Feb 2–4; Hammamet, Tunisia. p. 1–6. doi:10.1109/IREC64614.2025.10926804. [Google Scholar] [CrossRef]

39. Agatonovic-Kustrin S, Beresford R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J Pharm Biomed Anal. 2000;22(5):717–27. doi:10.1016/s0731-7085(99)00272-1. [Google Scholar] [PubMed] [CrossRef]

40. Ghritlahre HK, Prasad RK. Application of ANN technique to predict the performance of solar collector systems—a review. Renew Sustain Energy Rev. 2018;84(6):75–88. doi:10.1016/j.rser.2018.01.001. [Google Scholar] [CrossRef]

41. Afram A, Janabi-Sharifi F, Fung AS, Raahemifar K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: a state of the art review and case study of a residential HVAC system. Energy Build. 2017;141(1):96–113. doi:10.1016/j.enbuild.2017.02.012. [Google Scholar] [CrossRef]

42. Taguchi G, Jugulum R. The Mahalanobis-Taguchi strategy. Hoboken, NJ, USA: John Wiley & Sons, Inc.; 2002. doi:10.1002/9780470172247. [Google Scholar] [CrossRef]

43. Bement TR, Ross PJ. Taguchi techniques for quality engineering. Technometrics. 1989;31(2):254. doi:10.2307/1268823. [Google Scholar] [CrossRef]

44. Załuski D, Stolarski MJ, Krzyżaniak M. Validation of the Taguchi method on the example of evaluation of willow biomass production factors under environmental stress. Ind Crops Prod. 2022;185:115170. doi:10.1016/j.indcrop.2022.115170. [Google Scholar] [CrossRef]

45. Lagzian M, Ehsan Razavi S, Goharimanesh M. Investigation on tumor cells growth by Taguchi method. Biomed Signal Process Control. 2022;77(10):103734. doi:10.1016/j.bspc.2022.103734. [Google Scholar] [CrossRef]

46. Jiang SJ, Chu SC, Zou FM, Shan J, Zheng SG, Pan JS. A parallel Archimedes optimization algorithm based on Taguchi method for application in the control of variable pitch wind turbine. Math Comput Simul. 2023;203(2):306–27. doi:10.1016/j.matcom.2022.06.027. [Google Scholar] [CrossRef]

47. Aliha MRM, Imani DM, Salehi SM, Shojaee M, Abedi M. Mixture optimization of epoxy base concrete for achieving highest fracture toughness and fracture energy values using Taguchi method. Compos Commun. 2022;32:101150. doi:10.1016/j.coco.2022.101150. [Google Scholar] [CrossRef]

48. Phadke MS. Quality engineering using robust design. Hoboken, NJ, USA: Prentice Hall PTR; 1995. [Google Scholar]

49. Fowlkes WY, Creveling CM. Engineering methods for robust product design: using Taguchi methods in technology and product development. 1st ed. London, UK: Addison-Wesley Publishing Company; 1995. [Google Scholar]

50. Lin PK, Sullivan LP, Taguchi G. Using Taguchi methods in quality engineering. Quality Progress. 1990;23(9):55–9. [Google Scholar]

51. Parr WC, Taguchi G. Introduction to quality engineering: designing quality into products and processes. Technometrics. 1989;31(2):255. doi:10.2307/1268824. [Google Scholar] [CrossRef]

52. Roy RK. A primer on the Taguchi method. Southfield, MI, USA: Society of Manufacturing Engineers; 2010. [Google Scholar]

53. Kackar RN. Off-line quality control, parameter design, and the taguchi method. J Qual Technol. 1985;17(4):176–88. doi:10.1080/00224065.1985.11978964. [Google Scholar] [CrossRef]

54. Montgomery DC. Design and analysis of experiments. 9th ed. Hoboken, NJ, USA: John Wiley & Sons; 2017. [Google Scholar]

55. Wang HK, Wang ZH, Wang MC. Using the Taguchi method for optimization of the powder metallurgy forming process for Industry 3.5. Comput Ind Eng. 2020;148(4):106635. doi:10.1016/j.cie.2020.106635. [Google Scholar] [CrossRef]

56. Deng JL. Introduction to grey system theory. J Grey Syst. 1989;1(1):1–24. doi:10.5555/90757.90758. [Google Scholar] [CrossRef]

57. Acır A, Canlı ME, Ata İ, Çakıroğlu R. Parametric optimization of energy and exergy analyses of a novel solar air heater with grey relational analysis. Appl Therm Eng. 2017;122(6):330–8. doi:10.1016/j.applthermaleng.2017.05.018. [Google Scholar] [CrossRef]

58. Bademlioglu AH, Canbolat AS, Kaynakli O. Multi-objective optimization of parameters affecting Organic Rankine Cycle performance characteristics with Taguchi-Grey Relational Analysis. Renew Sustain Energy Rev. 2020;117:109483. doi:10.1016/j.rser.2019.109483. [Google Scholar] [CrossRef]

59. Chamoli S, Yu P, Kumar A. Multi-response optimization of geometric and flow parameters in a heat exchanger tube with perforated disk inserts by Taguchi grey relational analysis. Appl Therm Eng. 2016;103:1339–50. doi:10.1016/j.applthermaleng.2016.04.166. [Google Scholar] [CrossRef]

60. Naqiuddin NH, Saw LH, Yew MC, Yusof F, Poon HM, Cai Z, et al. Numerical investigation for optimizing segmented micro-channel heat sink by Taguchi-Grey method. Appl Energy. 2018;222:437–50. doi:10.1016/j.apenergy.2018.03.186. [Google Scholar] [CrossRef]

61. Kumar Rai R, Rekha Sahoo R. Taguchi-Grey method optimization of VCR engine performance and heat losses by using Shorea robusta biodiesel fuel. Fuel. 2020;281:118399. doi:10.1016/j.fuel.2020.118399. [Google Scholar] [CrossRef]

62. Jeffrey Kuo CF, Su TL, Jhang PR, Huang CY, Chiu CH. Using the Taguchi method and grey relational analysis to optimize the flat-plate collector process with multiple quality characteristics in solar energy collector manufacturing. Energy. 2011;36(5):3554–62. doi:10.1016/j.energy.2011.03.065. [Google Scholar] [CrossRef]

63. Yang T, Chou P. Solving a multiresponse simulation-optimization problem with discrete variables using a multiple-attribute decision-making method. Math Comput Simul. 2005;68(1):9–21. doi:10.1016/j.matcom.2004.09.004. [Google Scholar] [CrossRef]

64. Şimşek B, İç YT, Şimşek EH. A TOPSIS-based Taguchi optimization to determine optimal mixture proportions of the high strength self-compacting concrete. Chemom Intell Lab Syst. 2013;125(2):18–32. doi:10.1016/j.chemolab.2013.03.012. [Google Scholar] [CrossRef]

65. Imran MMH, Jamaludin S, Mohamad Ayob AF. A critical review of machine learning algorithms in maritime, offshore, and oil & gas corrosion research: a comprehensive analysis of ANN and RF models. Ocean Eng. 2024;295:116796. doi:10.1016/j.oceaneng.2024.116796. [Google Scholar] [CrossRef]

66. Qiu Y, Vo T, Garg D, Lee H, Kharangate CR. A systematic approach to optimization of ANN model parameters to predict flow boiling heat transfer coefficient in mini/micro-channel heatsinks. Int J Heat Mass Transf. 2023;202:123728. doi:10.1016/j.ijheatmasstransfer.2022.123728. [Google Scholar] [CrossRef]

67. Mo L, Lou S, Wang Y, Liu Z, Ren P. Studying the evolutions, differences, and water security impacts of water demands under shared socioeconomic pathways: a SEMs-bootstrap-ANN approach applied to Sichuan Province. J Environ Manage. 2024;349(2):119455. doi:10.1016/j.jenvman.2023.119455. [Google Scholar] [PubMed] [CrossRef]

68. Zhang Z, Wei S, Zhang S, Ni S. Study of RP-3/n-butanol fuel spray characteristics and ANN prediction of spray tip penetration. Energy. 2024;292(3):130515. doi:10.1016/j.energy.2024.130515. [Google Scholar] [CrossRef]

69. Kumar A, Gaur N, Chakravarty S, Alsharif MH, Uthansakul P, Uthansakul M. Analysis of spectrum sensing using deep learning algorithms: CNNs and RNNs. Ain Shams Eng J. 2024;15(3):102505. doi:10.1016/j.asej.2023.102505. [Google Scholar] [CrossRef]

70. Siddique MNI, Shafiullah M, Mekhilef S, Pota H, Abido MA. Fault classification and location of a PMU-equipped active distribution network using deep convolution neural network (CNN). Electr Power Syst Res. 2024;229(8):110178. doi:10.1016/j.epsr.2024.110178. [Google Scholar] [CrossRef]

71. Xie Y, Chen Y, Wei Q, Yin H. A hybrid deep learning approach to improve real-time effluent quality prediction in wastewater treatment plant. Water Res. 2024;250:121092. doi:10.1016/j.watres.2023.121092. [Google Scholar] [PubMed] [CrossRef]

72. Alharthi MA, Almohammadi BA, Sharafeldin MA, Abdelghany MT, Bendoukha S, Refaey HA. Heat transfer and pressure drop of Al2O3/water nanofluid in conically coiled tubes: experimental and artificial neural network prediction. Case Stud Therm Eng. 2024;54(1):104043. doi:10.1016/j.csite.2024.104043. [Google Scholar] [CrossRef]

73. Dar AA, Chen Z, Rodríguez-Rodríguez S, Haghighat F, González-Rosales B. Assessing greenhouse gas emissions in Cuban agricultural soils: implications for climate change and rice (Oryza sativa L.) production. J Environ Manag. 2024;353(3):120088. doi:10.1016/j.jenvman.2024.120088. [Google Scholar] [PubMed] [CrossRef]

74. Chinatamby P, Jewaratnam J. A performance comparison study on PM2.5 prediction at industrial areas using different training algorithms of feedforward-backpropagation neural network (FBNN). Chemosphere. 2023;317:137788. doi:10.1016/j.chemosphere.2023.137788. [Google Scholar] [PubMed] [CrossRef]

75. Rizeakos V, Bachoumis A, Andriopoulos N, Birbas M, Birbas A. Deep learning-based application for fault location identification and type classification in active distribution grids. Appl Energy. 2023;338(14):120932. doi:10.1016/j.apenergy.2023.120932. [Google Scholar] [CrossRef]

76. Park HJ, Kim JS, Nam BW, Kim JS. ANN-based prediction models for green water events around a FPSO in irregular waves. Ocean Eng. 2024;291(8):116408. doi:10.1016/j.oceaneng.2023.116408. [Google Scholar] [CrossRef]

77. Subramani S, Govindasamy R. Application of MRSN ratio and Taguchi parametric design in optimization of parameters of DI CI engine fuelled with diesel-biodiesel-higher alcohol blends. Fuel. 2021;285(8):119116. doi:10.1016/j.fuel.2020.119116. [Google Scholar] [CrossRef]

78. Simsek S, Uslu S, Simsek H, Uslu G. Multi-objective-optimization of process parameters of diesel engine fueled with biodiesel/2-ethylhexyl nitrate by using Taguchi method. Energy. 2021;231:120866. doi:10.1016/j.energy.2021.120866. [Google Scholar] [CrossRef]

79. Zhou Y, Hong W, Xie F, Li X, Su Y, Hu Y, et al. Potential of compression ratio and exhaust gas dilution on improving combustion and nitrogen oxides emission performance on a PFI engine fueled with methanol. Fuel. 2022;323(14):124197. doi:10.1016/j.fuel.2022.124197. [Google Scholar] [CrossRef]

80. Shrivastava K, Thipse SS, Patil ID. Optimization of diesel engine performance and emission parameters of Karanja biodiesel-ethanol-diesel blends at optimized operating conditions. Fuel. 2021;293(7):120451. doi:10.1016/j.fuel.2021.120451. [Google Scholar] [CrossRef]

81. Pandey AK, Mishra VB, Verma V. Performance characteristics analysis of CI engine using dual biodiesel. Int J Engine Res. 2023;24(5):1804–12. doi:10.1177/14680874221098845. [Google Scholar] [CrossRef]

82. Heng Teoh Y, Geok How H, WenLee S, Lin Loo D, Danh Le T, Tho Nguyen H, et al. Optimization of engine out responses with different biodiesel fuel blends for energy transition. Fuel. 2022;318:123706. doi:10.1016/j.fuel.2022.123706. [Google Scholar] [CrossRef]

83. Ramesh P, Vivekanandan S, Sivaramakrishnan, Prakash D. Performance optimization of an engine for canola oil blended diesel with Al2O3 nanoparticles through single and multi-objective optimization techniques. Fuel. 2021;288(1):119617. doi:10.1016/j.fuel.2020.119617. [Google Scholar] [CrossRef]

84. Zuo W, Li J, Zhang Y, Li Q, Jia S, He Z. Multi-factor impact mechanism on combustion efficiency of a hydrogen-fueled micro-cylindrical combustor. Int J Hydrog Energy. 2020;45(3):2319–30. doi:10.1016/j.ijhydene.2019.11.012. [Google Scholar] [CrossRef]

85. Uslu S, Aydın M. Effect of operating parameters on performance and emissions of a diesel engine fueled with ternary blends of palm oil biodiesel/diethyl ether/diesel by Taguchi method. Fuel. 2020;275(5):117978. doi:10.1016/j.fuel.2020.117978. [Google Scholar] [CrossRef]

86. Sharma A, Maurya NK, Singh Y, Singh NK, Gupta SK. Effect of design parameters on performance and emissions of DI diesel engine running on biodiesel-diesel blends: taguchi and utility theory. Fuel. 2020;281(2):118765. doi:10.1016/j.fuel.2020.118765. [Google Scholar] [CrossRef]

87. Çelik M, Bayındırlı C, Mehregan M. Multi-objective optimization of a diesel engine fueled with different fuel types containing additives using grey-based Taguchi approach. Environ Sci Pollut Res Int. 2022;29(20):30277–84. doi:10.1007/s11356-021-18012-1. [Google Scholar] [PubMed] [CrossRef]

88. Gul M, Shah AN, Aziz U, Husnain N, Mujtaba MA, Kousar T, et al. Grey-Taguchi and ANN based optimization of a better performing low-emission diesel engine fueled with biodiesel. Energy Sources Part A Recovery Util Environ Eff. 2022;44(1):1019–32. doi:10.1080/15567036.2019.1638995. [Google Scholar] [CrossRef]

89. Kumar Chidambaram R, Sonthalia A, Poornananadan G, Varuvel EG, Subramanian T. Optimization of compression ratio and injection timing of a diesel engine Fueled with oxygenated blends using fuzzy logic-based Taguchi method. Energy Sources Part A Recovery Util Environ Eff. 2025;47(1):4482–502. doi:10.1080/15567036.2020.1871123. [Google Scholar] [CrossRef]

90. Jain A, Bora BJ, Kumar R, Sharma P, Deepanraj B, Irshad K, et al. Application of hybrid Taguchi L16 and desirability for model prediction and optimization in assessment of the performance of a novel Water Hyacinth biodiesel Run diesel engine. Fuel. 2023;339(2):127377. doi:10.1016/j.fuel.2022.127377. [Google Scholar] [CrossRef]

91. Atis C, Huisjen A, Hardman K, Schock H. Experimental investigation on the effects of design and control factors on the performance and emissions characteristics of a boosted GDI engine using taguchi method. SAE Tech Pap Ser. 2021:2021-1-0466. doi:10.4271/2021-01-0466. [Google Scholar] [CrossRef]

92. Ayhan V, Çangal Ç, Cesur İ, Safa A. Combined influence of supercharging, EGR, biodiesel and ethanol on emissions of a diesel engine: proposal of an optimization strategy. Energy. 2020;207(2):118298. doi:10.1016/j.energy.2020.118298. [Google Scholar] [CrossRef]

93. Manigandan S, Atabani AE, Ponnusamy VK, Pugazhendhi A, Gunasekar P, Prakash S. Effect of hydrogen and multiwall carbon nanotubes blends on combustion performance and emission of diesel engine using Taguchi approach. Fuel. 2020;276(270):118120. doi:10.1016/j.fuel.2020.118120. [Google Scholar] [CrossRef]

94. Zhang Y, Wu H, Mi S, Zhao W, He Z, Qian Y, et al. Comprehensive optimization of a diesel-E85 engine over the full operating range using the Taguchi method in intelligent charge compression ignition (ICCI) mode. Fuel. 2023;332(4):126042. doi:10.1016/j.fuel.2022.126042. [Google Scholar] [CrossRef]

95. Kurnia JC, Haryoko LAF, Taufiqurrahman I, Chen L, Jiang L, Sasmito AP. Optimization of an innovative hybrid thermal energy storage with phase change material (PCM) wall insulator utilizing Taguchi method. J Energy Storage. 2022;49:104067. doi:10.1016/j.est.2022.104067. [Google Scholar] [CrossRef]

96. Çinici OK, Canlı ME, Çakıroğlu R, Acır A. Optimization of melting time of solar thermal energy storage unit containing spring type heat transfer enhancer by Taguchi based grey relational analysis. J Energy Storage. 2022;47(1):103671. doi:10.1016/j.est.2021.103671. [Google Scholar] [CrossRef]

97. Khatibi M, Nemati-Farouji R, Taheri A, Kazemian A, Ma T, Niazmand H. Optimization and performance investigation of the solidification behavior of nano-enhanced phase change materials in triplex-tube and shell-and-tube energy storage units. J Energy Storage. 2021;33:102055. doi:10.1016/j.est.2020.102055. [Google Scholar] [CrossRef]

98. Ghalambaz M, Mehryan SAM, Veismoradi A, Mahdavi M, Zahmatkesh I, Kazemi Z, et al. Melting process of the nano-enhanced phase change material (NePCM) in an optimized design of shell and tube thermal energy storage (TEStaguchi optimization approach. Appl Therm Eng. 2021;193:116945. doi:10.1016/j.applthermaleng.2021.116945. [Google Scholar] [CrossRef]

99. Mehryan SAM, Ayoubloo KA, Mahdavi M, Younis O, Kazemi Z, Ghodrat M, et al. Optimum configuration of a metal foam layer for a fast thermal charging energy storage unit: a numerical study. J Energy Storage. 2022;48(2):103950. doi:10.1016/j.est.2021.103950. [Google Scholar] [CrossRef]

100. Zhang Y, Deng M. Taguchi optimization and a fast evaluation method on the transient thermal performance of phase change material outfitted walls. J Energy Storage. 2021;43(3):103120. doi:10.1016/j.est.2021.103120. [Google Scholar] [CrossRef]

101. Lin W, Ma Z, Ren H, Gschwander S, Wang S. Multi-objective optimisation of thermal energy storage using phase change materials for solar air systems. Renew Energy. 2019;130(7187):1116–29. doi:10.1016/j.renene.2018.08.071. [Google Scholar] [CrossRef]

102. Sun X, Mo Y, Li J, Chu Y, Liu L, Liao S. Study on the energy charging process of a plate-type latent heat thermal energy storage unit and optimization using Taguchi method. Appl Therm Eng. 2020;164:114528. doi:10.1016/j.applthermaleng.2019.114528. [Google Scholar] [CrossRef]

103. Nandi BR, Bandyopadhyay S, Banerjee R. Numerical modeling and analysis of dual medium thermocline thermal energy storage. J Energy Storage. 2018;16:218–30. doi:10.1016/j.est.2018.01.020. [Google Scholar] [CrossRef]

104. Turgut E, Yardımcı U. Comprehensive analysis of the performance of the coaxial heat exchanger with turbulators. Int J Therm Sci. 2022;176:107502. doi:10.1016/j.ijthermalsci.2022.107502. [Google Scholar] [CrossRef]

105. Moein Darbari A, Alavi MA, Saleh SR, Nejati V. Sensitivity analysis of nanofluid flow over different flat tubes confined between two parallel plates using Taguchi method and statistical analysis of variance. Int J Therm Sci. 2022;173:107428. doi:10.1016/j.ijthermalsci.2021.107428. [Google Scholar] [CrossRef]

106. Kumar V, Sahoo RR. Parametric and design optimization investigation of a wavy fin and tube air heat exchanger using the T-G technique. Heat Transf. 2022;51(5):4641–66. doi:10.1002/htj.22516. [Google Scholar] [CrossRef]

107. Razak Kaladgi A, Afzal A, Manokar AM, Thakur D, Agbulut U, Alshahrani S, et al. Integrated Taguchi-GRA-RSM optimization and ANN modelling of thermal performance of zinc oxide nanofluids in an automobile radiator. Case Stud Therm Eng. 2021;26:101068. doi:10.1016/j.csite.2021.101068. [Google Scholar] [CrossRef]

108. Dagdevir T. Multi-objective optimization of geometrical parameters of dimples on a dimpled heat exchanger tube by Taguchi based Grey relation analysis and response surface method. Int J Therm Sci. 2022;173(3):107365. doi:10.1016/j.ijthermalsci.2021.107365. [Google Scholar] [CrossRef]

109. Yang P, Zhang H, Zheng Y, Fang Z, Shi X, Liu Y. Investigation and optimization of heat transfer performance of a spirally corrugated tube using the Taguchi method. Int Commun Heat Mass Transf. 2021;127(6):105577. doi:10.1016/j.icheatmasstransfer.2021.105577. [Google Scholar] [CrossRef]

110. Mallik A, Sharma P. Modeling and numerical simulation of an industrial scale metal hydride reactor based on CFD-Taguchi combined method. Energy Storage. 2021;3(3):e227. doi:10.1002/est2.227. [Google Scholar] [CrossRef]

111. Liu Z, Sun P, Xie M, Zhou Y, He Y, Zhang G, et al. Multivariant optimization and sensitivity analysis of an experimental vertical earth-to-air heat exchanger system integrating phase change material with Taguchi method. Renew Energy. 2021;173:401–14. doi:10.1016/j.renene.2021.03.106. [Google Scholar] [CrossRef]

112. Heydari O, Miansari M, Arasteh H, Toghraie D. Optimizing the hydrothermal performance of helically corrugated coiled tube heat exchangers using Taguchi’s empirical method: energy and exergy analysis. J Therm Anal Calorim. 2021;145(5):2741–52. doi:10.1007/s10973-020-09808-3. [Google Scholar] [CrossRef]

113. Miansari M, Ali Valipour M, Arasteh H, Toghraie D. Energy and exergy analysis and optimization of helically grooved shell and tube heat exchangers by using Taguchi experimental design. J Therm Anal Calorim. 2020;139(5):3151–64. doi:10.1007/s10973-019-08653-3. [Google Scholar] [CrossRef]

114. Biçer N, Engin T, Yaşar H, Büyükkaya E, Aydın A, Topuz A. Design optimization of a shell-and-tube heat exchanger with novel three-zonal baffle by using CFD and taguchi method. Int J Therm Sci. 2020;155:106417. doi:10.1016/j.ijthermalsci.2020.106417. [Google Scholar] [CrossRef]

115. Raina G, Vijay R, Sinha S. Study on the optimum orientation of bifacial photovoltaic module. Int J Energy Res. 2022;46(4):4247–66. doi:10.1002/er.7423. [Google Scholar] [CrossRef]

116. Kuo CJ, Yang PC, Umar ML, Lan WL. A bifacial photovoltaic thermal system design with parameter optimization and performance beneficial validation. Appl Energy. 2019;247(5):335–49. doi:10.1016/j.apenergy.2019.04.038. [Google Scholar] [CrossRef]

117. Jafari R. Optimization and energy analysis of a novel geothermal heat exchanger for photovoltaic panel cooling. Sol Energy. 2021;226(1):122–33. doi:10.1016/j.solener.2021.08.046. [Google Scholar] [CrossRef]

118. Kazemian A, Parcheforosh A, Salari A, Ma T. Optimization of a novel photovoltaic thermal module in series with a solar collector using Taguchi based grey relational analysis. Sol Energy. 2021;215(2):492–507. doi:10.1016/j.solener.2021.01.006. [Google Scholar] [CrossRef]

119. Ji D, Hu S, Feng Y, Qin J, Yin Z, Romagnoli A, et al. Geometry optimization of solar thermoelectric generator under different operating conditions via Taguchi method. Energy Convers Manag. 2021;238(4):114158. doi:10.1016/j.enconman.2021.114158. [Google Scholar] [CrossRef]

120. Özakın AN, Kaya F. Experimental thermodynamic analysis of air-based PVT system using fins in different materials: optimization of control parameters by Taguchi method and ANOVA. Sol Energy. 2020;197(2):199–211. doi:10.1016/j.solener.2019.12.077. [Google Scholar] [CrossRef]

121. Podder B, Biswas A, Saha S. Multi-objective optimization of a small sized solar PV-T water collector using controlled elitist NSGA-II coupled with TOPSIS. Sol Energy. 2021;230(2-3):688–702. doi:10.1016/j.solener.2021.10.078. [Google Scholar] [PubMed] [CrossRef]

122. Qeays IA, Yahya SM, Asjad M, Khan ZA. Multi-performance optimization of nanofluid cooled hybrid photovoltaic thermal system using fuzzy integrated methodology. J Clean Prod. 2020;256(6):120451. doi:10.1016/j.jclepro.2020.120451. [Google Scholar] [CrossRef]

123. Hosseinzadeh M, Faezian A, Mirzababaee SM, Zamani H. Parametric analysis and optimization of a portable evacuated tube solar cooker. Energy. 2020;194(6):116816. doi:10.1016/j.energy.2019.116816. [Google Scholar] [CrossRef]

124. Fan W, Kokogiannakis G, Ma Z. A multi-objective design optimisation strategy for hybrid photovoltaic thermal collector (PVT)-solar air heater (SAH) systems with fins. Sol Energy. 2018;163(11):315–28. doi:10.1016/j.solener.2018.02.014. [Google Scholar] [CrossRef]

125. Li YH, Kao WC. Taguchi optimization of solar thermal and heat pump combisystems under five distinct climatic conditions. Appl Therm Eng. 2018;133(7):283–97. doi:10.1016/j.applthermaleng.2018.01.002. [Google Scholar] [CrossRef]

126. Hosseinzadeh M, Salari A, Sardarabadi M, Passandideh-Fard M. Optimization and parametric analysis of a nanofluid based photovoltaic thermal system: 3D numerical model with experimental validation. Energy Convers Manag. 2018;160:93–108. doi:10.1016/j.enconman.2018.01.006. [Google Scholar] [CrossRef]

127. Ustaoglu A, Kursuncu B, Metin Kaya A, Caliskan H. Analysis of vapor compression refrigeration cycle using advanced exergetic approach with Taguchi and ANOVA optimization and refrigerant selection with enviroeconomic concerns by TOPSIS analysis. Sustain Energy Technol Assess. 2022;52(2):102182. doi:10.1016/j.seta.2022.102182. [Google Scholar] [CrossRef]

128. Khalilarya S, Chitsaz A, Mojaver P. Optimization of a combined heat and power system based gasification of municipal solid waste of Urmia University student dormitories via ANOVA and taguchi approaches. Int J Hydrog Energy. 2021;46(2):1815–27. doi:10.1016/j.ijhydene.2020.10.020. [Google Scholar] [CrossRef]

129. Mojaver P, Khalilarya S, Chitsaz A, Assadi M. Multi-objective optimization of a power generation system based SOFC using Taguchi/AHP/TOPSIS triple method. Sustain Energy Technol Assess. 2020;38(25):100674. doi:10.1016/j.seta.2020.100674. [Google Scholar] [CrossRef]

130. Canbolat AS, Bademlioglu AH, Arslanoglu N, Kaynakli O. Performance optimization of absorption refrigeration systems using Taguchi, ANOVA and Grey Relational Analysis methods. J Clean Prod. 2019;229:874–85. doi:10.1016/j.jclepro.2019.05.020. [Google Scholar] [CrossRef]

131. Omrani H, Alizadeh A, Emrouznejad A. Finding the optimal combination of power plants alternatives: a multi response Taguchi-neural network using TOPSIS and fuzzy best-worst method. J Clean Prod. 2018;203(24):210–23. doi:10.1016/j.jclepro.2018.08.238. [Google Scholar] [CrossRef]

132. Bademlioglu AH, Canbolat AS, Yamankaradeniz N, Kaynakli O. Investigation of parameters affecting Organic Rankine Cycle efficiency by using Taguchi and ANOVA methods. Appl Therm Eng. 2018;145:221–8. doi:10.1016/j.applthermaleng.2018.09.032. [Google Scholar] [CrossRef]

133. Peng HY, Liu MN, Liu HJ, Lin K. Optimization of twin vertical axis wind turbines through large eddy simulations and Taguchi method. Energy. 2022;240:122560. doi:10.1016/j.energy.2021.122560. [Google Scholar] [CrossRef]

134. Ma Y, Zhu Y, Zhang A, Hu C, Liu S, Li Z. Hydrodynamic performance of vertical axis hydrokinetic turbine based on Taguchi method. Renew Energy. 2022;186:573–84. doi:10.1016/j.renene.2022.01.037. [Google Scholar] [CrossRef]

135. Cheng B, Du J, Yao Y. Power prediction formula for blade design and optimization of Dual Darrieus Wind Turbines based on Taguchi Method and Genetic Expression Programming model. Renew Energy. 2022;192(10):583–605. doi:10.1016/j.renene.2022.04.111. [Google Scholar] [CrossRef]

136. Hassanpour M, Azadani LN. Aerodynamic optimization of the configuration of a pair of vertical axis wind turbines. Energy Convers Manag. 2021;238(8):114069. doi:10.1016/j.enconman.2021.114069. [Google Scholar] [CrossRef]

137. Khanjanpour MH, Javadi AA. Optimization of the hydrodynamic performance of a vertical Axis tidal (VAT) turbine using CFD-Taguchi approach. Energy Convers Manag. 2020;222(2):113235. doi:10.1016/j.enconman.2020.113235. [Google Scholar] [CrossRef]

138. Qasemi K, Azadani LN. Optimization of the power output of a vertical axis wind turbine augmented with a flat plate deflector. Energy. 2020;202(5):117745. doi:10.1016/j.energy.2020.117745. [Google Scholar] [CrossRef]

139. Chen WH, Wang JS, Chang MH, Mutuku JK, Hoang AT. Efficiency improvement of a vertical-axis wind turbine using a deflector optimized by Taguchi approach with modified additive method. Energy Convers Manag. 2021;245:114609. doi:10.1016/j.enconman.2021.114609. [Google Scholar] [CrossRef]

140. Taghavi M, Gharehghani A, Nejad FB, Mirsalim M. Developing a model to predict the start of combustion in HCCI engine using ANN-GA approach. Energy Convers Manag. 2019;195(11):57–69. doi:10.1016/j.enconman.2019.05.015. [Google Scholar] [CrossRef]

141. Dey S, Reang NM, Majumder A, Deb M, Das PK. A hybrid ANN-Fuzzy approach for optimization of engine operating parameters of a CI engine fueled with diesel-palm biodiesel-ethanol blend. Energy. 2020;202:117813. doi:10.1016/j.energy.2020.117813. [Google Scholar] [CrossRef]

142. Böyükdipi Ö, Tüccar G, Soyhan HS. Experimental investigation and artificial neural networks (ANNs) based prediction of engine vibration of a diesel engine fueled with sunflower biodiesel-NH3 mixtures. Fuel. 2021;304(2):121462. doi:10.1016/j.fuel.2021.121462. [Google Scholar] [CrossRef]

143. Castresana J, Gabiña G, Martin L, Basterretxea A, Uriondo Z. Marine diesel engine ANN modelling with multiple output for complete engine performance map. Fuel. 2022;319(4):123873. doi:10.1016/j.fuel.2022.123873. [Google Scholar] [CrossRef]

144. Yue Z, Zhu H, Wang C, Li Z, Wang H, Yao M, et al. Artificial neural network models for phase equilibrium predictions under engine trans/supercritical spray conditions. Fuel. 2023;339(12):127425. doi:10.1016/j.fuel.2023.127425. [Google Scholar] [CrossRef]

145. Maleki H, Ashrafi M, Ilghani NZ, Goodarzi M, Muhammad T. Pareto optimal design of a finned latent heat thermal energy storage unit using a novel hybrid technique. J Energy Storage. 2021;44(10):103310. doi:10.1016/j.est.2021.103310. [Google Scholar] [CrossRef]

146. Scapino L, Zondag HA, Diriken J, Rindt CCM, Van Bael J, Sciacovelli A. Modeling the performance of a sorption thermal energy storage reactor using artificial neural networks. Appl Energy. 2019;253:113525. doi:10.1016/j.apenergy.2019.113525. [Google Scholar] [CrossRef]

147. Motahar S. Experimental study and ANN-based prediction of melting heat transfer in a uniform heat flux PCM enclosure. J Energy Storage. 2020;30(2):101535. doi:10.1016/j.est.2020.101535. [Google Scholar] [CrossRef]

148. Olimat AN, Al-Shawabkeh AF, Al-Qadi ZA, Al-Najdawi NA, Al-Salaymeh A. Experimental study and computational approach prediction on thermal performance of eutectic salt inside a latent heat storage prototype. Therm Sci Eng Prog. 2023;37(3):101606. doi:10.1016/j.tsep.2022.101606. [Google Scholar] [CrossRef]

149. Anooj GVS, Marri GK, Balaji C. A machine learning methodology for the diagnosis of phase change material-based thermal management systems. Appl Therm Eng. 2023;222:119864. doi:10.1016/j.applthermaleng.2022.119864. [Google Scholar] [CrossRef]

150. Kamsuwan C, Wang X, Piumsomboon P, Pratumwal Y, Otarawanna S, Chalermsinsuwan B. Artificial neural network prediction models for nanofluid properties and their applications with heat exchanger design and rating simulation. Int J Therm Sci. 2023;184(12):107995. doi:10.1016/j.ijthermalsci.2022.107995. [Google Scholar] [CrossRef]

151. Moya-Rico JD, Molina AE, Belmonte JF, Córcoles Tendero JI, Almendros-Ibáñez JA. Characterization of a triple concentric-tube heat exchanger with corrugated tubes using Artificial Neural Networks (ANN). Appl Therm Eng. 2019;147:1036–46. doi:10.1016/j.applthermaleng.2018.10.136. [Google Scholar] [CrossRef]

152. Giannetti N, Redo MA, Sholahudin, Jeong J, Yamaguchi S, Saito K, et al. Prediction of two-phase flow distribution in microchannel heat exchangers using artificial neural network. Int J Refrig. 2020;111(1–2):53–62. doi:10.1016/j.ijrefrig.2019.11.028. [Google Scholar] [CrossRef]

153. Hojjat M. Nanofluids as coolant in a shell and tube heat exchanger: ANN modeling and multi-objective optimization. Appl Math Comput. 2020;365(3):124710. doi:10.1016/j.amc.2019.124710. [Google Scholar] [CrossRef]

154. Çolak AB, Akgul D, Mercan H, Dalkılıç AS, Wongwises S. Estimation of heat transfer parameters of shell and helically coiled tube heat exchangers by machine learning. Case Stud Therm Eng. 2023;42(3):102713. doi:10.1016/j.csite.2023.102713. [Google Scholar] [CrossRef]

155. Rao KDVSK, Premalatha M, Naveen C. Analysis of different combinations of meteorological parameters in predicting the horizontal global solar radiation with ANN approach: a case study. Renew Sustain Energy Rev. 2018;91:248–58. doi:10.1016/j.rser.2018.03.096. [Google Scholar] [CrossRef]

156. Sadeghi G, Nazari S, Ameri M, Shama F. Energy and exergy evaluation of the evacuated tube solar collector using Cu2O/water nanofluid utilizing ANN methods. Sustain Energy Technol Assess. 2020;37(11):100578. doi:10.1016/j.seta.2019.100578. [Google Scholar] [CrossRef]

157. Al-Waeli AHA, Sopian K, Yousif JH, Kazem HA, Boland J, Chaichan MT. Artificial neural network modeling and analysis of photovoltaic/thermal system based on the experimental study. Energy Convers Manag. 2019;186(23):368–79. doi:10.1016/j.enconman.2019.02.066. [Google Scholar] [CrossRef]

158. Wang Y, Kandeal AW, Swidan A, Sharshir SW, Abdelaziz GB, Halim MA, et al. Prediction of tubular solar still performance by machine learning integrated with Bayesian optimization algorithm. Appl Therm Eng. 2021;184:116233. doi:10.1016/j.applthermaleng.2020.116233. [Google Scholar] [CrossRef]

159. Bahiraei M, Nazari S, Safarzadeh H. Modeling of energy efficiency for a solar still fitted with thermoelectric modules by ANFIS and PSO-enhanced neural network: a nanofluid application. Powder Technol. 2021;385(3):185–98. doi:10.1016/j.powtec.2021.03.001. [Google Scholar] [CrossRef]

160. Feng YQ, Liu YZ, Wang X, He ZX, Hung TC, Wang Q, et al. Performance prediction and optimization of an organic Rankine cycle (ORC) for waste heat recovery using back propagation neural network. Energy Convers Manag. 2020;226(1):113552. doi:10.1016/j.enconman.2020.113552. [Google Scholar] [CrossRef]

161. Chen W, Liang Y, Luo X, Chen J, Yang Z, Chen Y. Artificial neural network grey-box model for design and optimization of 50 MWe-scale combined supercritical CO2 Brayton cycle-ORC coal-fired power plant. Energy Convers Manag. 2021;249(6):114821. doi:10.1016/j.enconman.2021.114821. [Google Scholar] [CrossRef]

162. Senturk Acar M. Multi-stage artificial neural network structure-based optimization of geothermal energy powered Kalina cycle. J Therm Anal Calorim. 2021;145(3):829–49. doi:10.1007/s10973-020-10125-y. [Google Scholar] [CrossRef]

163. Zhang Y, Bryan J, Richards G, Wang H. Development and comparative selection of surrogate models using artificial neural network for an integrated regenerative transcritical cycle. Appl Energy. 2022;317:119146. doi:10.1016/j.apenergy.2022.119146. [Google Scholar] [CrossRef]

164. Soltani MM, Ahmadi P, Ashjaee M. Techno-economic optimization of a biomass gasification energy system with Supercritical CO2 cycle for hydrogen fuel and electricity production. Fuel. 2023;333(24):126264. doi:10.1016/j.fuel.2022.126264. [Google Scholar] [CrossRef]

165. Liu G, Zhao H, Deng J, Wang L, Zhang H. Performance improvement of CO2 two-phase ejector by combining CFD modeling, artificial neural network and genetic algorithm. Int J Refrig. 2023;154:151–67. doi:10.1016/j.ijrefrig.2023.07.005. [Google Scholar] [CrossRef]

166. Siavash NK, Ghobadian B, Najafi G, Rohani A, Tavakoli T, Mahmoodi E, et al. Prediction of power generation and rotor angular speed of a small wind turbine equipped to a controllable duct using artificial neural network and multiple linear regression. Environ Res. 2021;196(8):110434. doi:10.1016/j.envres.2020.110434. [Google Scholar] [PubMed] [CrossRef]

167. Nielson J, Bhaganagar K, Meka R, Alaeddini A. Using atmospheric inputs for Artificial Neural Networks to improve wind turbine power prediction. Energy. 2020;190:116273. doi:10.1016/j.energy.2019.116273. [Google Scholar] [CrossRef]

168. Luna J, Falkenberg O, Gros S, Schild A. Wind turbine fatigue reduction based on economic-tracking NMPC with direct ANN fatigue estimation. Renew Energy. 2020;147(1):1632–41. doi:10.1016/j.renene.2019.09.092. [Google Scholar] [CrossRef]

169. Quevedo-Reina R, Álamo GM, Padrón LA, Aznárez JJ. Surrogate model based on ANN for the evaluation of the fundamental frequency of offshore wind turbines supported on jackets. Comput Struct. 2023;274(12):106917. doi:10.1016/j.compstruc.2022.106917. [Google Scholar] [CrossRef]

170. Rathod UH, Kulkarni V, Saha UK. On the application of machine learning in savonius wind turbine technology: an estimation of turbine performance using artificial neural network and genetic expression programming. J Energy Resour Technol. 2022;144(6):061301. doi:10.1115/1.4051736. [Google Scholar] [CrossRef]

171. Li F, Cui H, Su H, Iderchuluun, Ma Z, Zhu Y, et al. Icing condition prediction of wind turbine blade by using artificial neural network based on modal frequency. Cold Reg Sci Technol. 2022;194(1):103467. doi:10.1016/j.coldregions.2021.103467. [Google Scholar] [CrossRef]

172. Asadabadi MJR, Moghimi M. Direct waste heat recovery from a solid oxide fuel cell through Kalina cycle, two-bed adsorption chiller, thermoelectric generator, reverse osmosis, and PEM electrolyzer: 4E analysis and ANN-assisted optimization. Appl Therm Eng. 2024;236(2013):121307. doi:10.1016/j.applthermaleng.2023.121307. [Google Scholar] [CrossRef]

173. Moustafa EB, Hammad AH, Elsheikh AH. A new optimized artificial neural network model to predict thermal efficiency and water yield of tubular solar still. Case Stud Therm Eng. 2022;30(1):101750. doi:10.1016/j.csite.2021.101750. [Google Scholar] [CrossRef]

174. Abubaker AM, Darwish Ahmad A, Salaimeh AA, Akafuah NK, Saito K. A novel solar combined cycle integration: an exergy-based optimization using artificial neural network. Renew Energy. 2022;181(2):914–32. doi:10.1016/j.renene.2021.09.087. [Google Scholar] [CrossRef]

175. Akkouche N, Loubar K, Nepveu F, El Amine Kadi M, Tazerout M. Micro-combined heat and power using dual fuel engine and biogas from discontinuous anaerobic digestion. Energy Convers Manag. 2020;205:112407. doi:10.1016/j.enconman.2019.112407. [Google Scholar] [CrossRef]

176. Ahmed F, Chen W. Investigation of steam ejector parameters under three optimization algorithm using ANN. Appl Therm Eng. 2023;225(4):120205. doi:10.1016/j.applthermaleng.2023.120205. [Google Scholar] [CrossRef]

177. Du Y, Zhang Y, Lou J, Wang J, Zhao P. Conception and thermo-economic performance investigation of a novel solid oxide fuel cell/gas turbine/Kalina cycle cascade system using ammonia-water as fuel. Appl Therm Eng. 2024;239(1):122118. doi:10.1016/j.applthermaleng.2023.122118. [Google Scholar] [CrossRef]