Enhancement of Frequency Regulation in AC-Excited Adjustable-Speed Pumped Storage Units during Pumping Operations

1  Introduction

The scale of grid-connected operation of wind, light and other renewable clean energy sources is gradually expanding. However, these renewable energy sources are characterized by randomness, volatility and intermittency, which will lead to deterioration of the frequency characteristics of the power grid. Pumped storage is one of the most important means to solve the grid frequency problem. Conventional pumped storage units do not participate in grid frequency regulation because the power cannot be continuously adjusted under pumping condition [1].

The novel pumped storage power station, founded upon the double-fed pumped storage unit (DFPSU), boasts the capability to operate at variable speeds within a designated range. This advancement not only surmounts the limitations of conventional pumped storage units, such as the suboptimal efficiency stemming from the fixed motor speed and the incapacity to modulate power during pumping, but also endows the station with augmented power regulation flexibility. It has been demonstrated that through variable-speed operation, the DFPSU possesses augmented frequency regulation capacity and a measure of frequency regulation potential, thereby offering a viable solution to address the mounting challenges posed by grid frequency regulation. Nevertheless, the conventional control strategy employed in DFPSU results in the decoupling of unit speed from grid frequency, thereby hindering the unit’s capacity to autonomously contribute to grid frequency adjustment. Reference [2] introduces an improved virtual inertia control strategy, addressing the negative damping effects in later frequency regulation stages by replacing the df/dt loop with dΔf/dt loop. Consequently, the utilization of DFPSU for frequency control tasks, the investigation of the DFPSU frequency control strategy to adapt to varying power generation and pumping conditions, and the exploration of the unit’s frequency control potential are of significant research and practical value in enhancing grid frequency characteristics and system stability.

Recent research on DFPSU has primarily focused on modeling and power decoupling control. Study [3] has developed models for the electrical and hydraulic components of DFPSUs, analysing both steady-state and transient behaviours. Additionally, reference [4] proposes rapid power response strategies based on unit operating characteristics. Given the similarities between doubly-fed induction generators and DFPSUs during power generation, much of the current frequency regulation research for DFPSUs follows approaches from doubly-fed wind turbines, such as droop control and virtual inertia control to quickly convert frequency deviations into power adjustments.

While simulation-based validations in prior research confirm the feasibility of DFPSUs’ autonomous participation in grid frequency regulation across both generating and pumping modes, these investigations uniformly assume a generation-dominant control paradigm. Research on the integrated electromechanical control between reversible pump-turbine units and AC excitation machines (ACEM) remains relatively scarce. Existing studies predominantly focus on the stand-alone control of the ACEM itself, with most applications centered in the wind power generation field. For instance, Reference [5] proposed a vector control method based on rotor flux orientation to investigate power decoupling control within the machine. Reference [6] examined the steady-state characteristics and starting performance of the machine under various converter topologies. Notably, they omit critical analysis of the dynamic hydraulic-mechanical coupling effects inherent to reversible pump-turbine operations. The literature [7] has established a DFPSU participation in the frequency control in the pumping condition that accounts for the characteristics of the water pump turbine. Nevertheless, due to the variability in DFPSU operation, the application of fixed frequency parameters is inadequate for ensuring the stability of the hydroelectric turbine under varying conditions. Moreover, it hinders the recovery of the frequency during the frequency adjustment phase. In the domain of Doubly fed Induction Generator, literature [8] explores methodologies for enhancing the adaptability of frequency control strategies in the presence of variable wind speeds and disturbances. This research leads to the development of a variable-parameter frequency control strategy. Recent work by Gulzar et al. [9] proposes an adaptive tilt fractional-order PID (ATFOPID) controller optimized via tunicate search algorithm to enhance transient stability in renewable-integrated hybrid power systems. However, it is noteworthy that this particular research area is seldom addressed in the context of DFPSU.

This paper first develops a mathematical model for the DFPSU, including the pump-turbine, along with a corresponding control strategy for pumping mode. Subsequently, a frequency control strategy is proposed that converts frequency deviations into additional speed and active power commands under pumping conditions. This strategy leverages the coordination between the inverter and the pump-turbine to enhance the DFPSU’s flexible power regulation capabilities. Furthermore, an analysis is conducted on the impact of DFPSU operating states and frequency control parameters. With the goal of maximizing rotor kinetic energy release while imposing constraints on speed and power, an adaptive parameter optimization method based on Deep Reinforcement Learning (DRL) is introduced. This method aims to reduce the maximum frequency deviation and shorten the frequency recovery time, thereby improving the overall system frequency stability. Finally, the effectiveness of the proposed frequency control strategy is validated through a comparative analysis of the frequency dynamic response in a four-machine, two-area system model, in which DFPSU is integrated, and compared with traditional frequency control methods.

2  Math Model DFPSU and Control Strategies

As is shown in Fig. 1, the DFPSU system is predominantly constituted by a reversible pump/turbine and its regulating system, the DFIM, a back-to-back converter, and the associated control modules. The coordination of the hydraulic, mechanical, and electrical components under varying operational conditions facilitates the regulation of speed and the decoupling of active and reactive power.

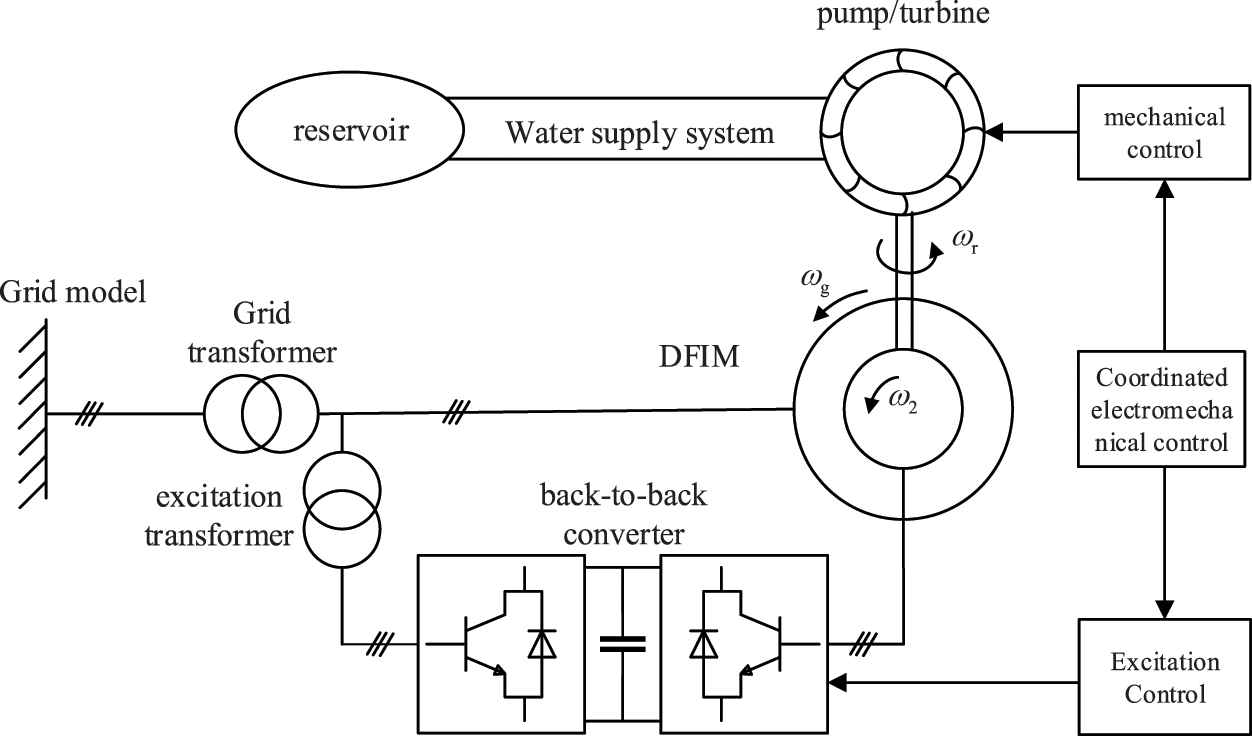
Figure 1: Structure of DFPSU unit

2.1 DFIG Mathematical Model

DFPSU employs a dual-feedback configuration, enabling the selection of an appropriate magnetic control strategy to achieve rapid and precise regulation of various physical quantities. In circumstances where the stator and rotor are both equipped with permanent magnet synchronous motors, the dual-feedback electrical machine’s mathematical model is expressed as follows:

Te=32np(ψsdisq−ψsqisd)=32np(ψrqird−ψrdirq)(1)

{Ps=32(usdisd+usqisq)Qs=32(usqisd−usdisq)(2)

where subscripts s and r denote stator/rotor-side affiliation of parameters. Subscripts d and q specify dq-axis components in synchronous rotating coordinates. Fundamental variables are defined as: u (voltage), i (current), ψ (flux linkage), and np (pole count), maintaining consistency with IEEE Std 115-2019 rotating machinery nomenclature.

2.2 Mathematical Model of Water Supply System

The water supply system consists of a water cave, a pressure regulating chamber and a pressure pipe. As the water flow through the pipe will cause a series of energy losses including friction loss in the pipe and friction loss in the valves and accessories, the required head of the device not only includes the static head determined by the difference in water level between the upper and lower tanks, but also the additional head required to compensate for this loss [7]. The characteristics of the pipe can be obtained as shown in Eq. (3).

{Hneed=Hst+HlossHloss=KfQ2Kf=fp+1Z(3)

where Hneed is the head required by the device; Hst is the static head; Hloss is the head loss; Q is the flow rate; Kf is the loss coefficient, which includes the friction coefficient of the pressure pipe fp and the friction coefficient of the guide vane.

Mathematical models of water delivery systems can be divided into rigid and elastic models, depending on whether the elasticity of water hammer is taken into account. When the elasticity of the water flow and the pipe wall is taken into account, an elastic dynamic model of the water delivery system is obtained as shown in Eq. (4). Further expansion of the hyperbolic function in the equation according to an infinite series allows the dynamic model to be selected according to the requirements of the application. In general, expansion of the second term is sufficient to meet the requirements of most power system stability studies.

{Q=1Zhptanh⁡(sTep)(Hst−H−Hloss)tanh⁡(sTep)=∑n=1∞22n(22n−1)B2n(sTep)2n−1(2n)!(4)

where s is the differential operator; H is the effective head; Zhp is the normalized hydraulic resistance of the pressure pipe; Tep is the elastic time constant of the pressure pipe; n is the expansion order; and B is the Bernoulli number.

The theory of rigid water hammer posits that, for a relatively short water supply pipeline (<800 m), the water hammer pressure can be instantaneously transmitted to the entire water supply pipeline, i.e., Tep≈0. Retaining the expansion of Eq. (4) to the first term enables the rigid model to be obtained. It is also noted that the inertial time constant of the water flow in the pressure pipe, Tω=ZhpTep, and Eq. (5) is obtained. Combining the pipe characteristics given in Eq. (3) results in the rigid dynamic model of the water delivery system, as shown in Fig. 2.

Q=1Tωs(Hst−H−Hloss)(5)

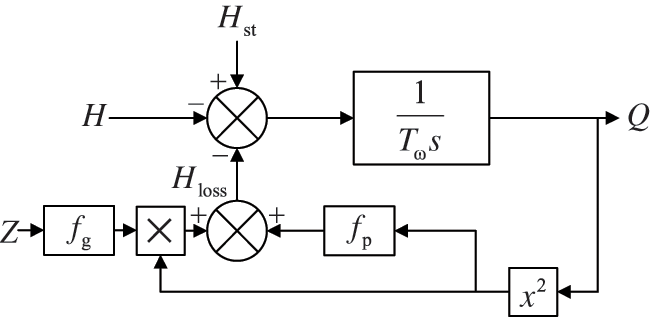
Figure 2: Rigid dynamic model of water delivery system

When the pump-turbine is switched to pump mode, the unit is near rated operation, the guide vane opening is large, and there is serious crossing of the full characteristic curve in the corresponding area. At this time, the unit’s flow rate is basically not affected by the guide vane opening, and its mechanical power and efficiency are closely related to the speed. The adjustment of the input active power is mainly achieved by controlling the speed rather than the guide vane opening.

In this mode, the pump’s operating characteristics are characterized by fitting the full characteristic curve of the pump turbine. In this section, the head-flow (H−Q) curve, power-flow (P−Q) curve, and efficiency-flow (η−Q) curve of the pump at varying speeds are fitted. The corresponding expressions are shown in Eqs. (6)–(8). The fitted curves are presented in Fig. 3.

H=a0ω2+a1ωQ+a2Q2(6)

P=b0ω3+b1ω2Q+b2ωQ2+b3Q3(7)

η=c0+c1ωQ+c2ω2Q2+c3ω3Q3(8)

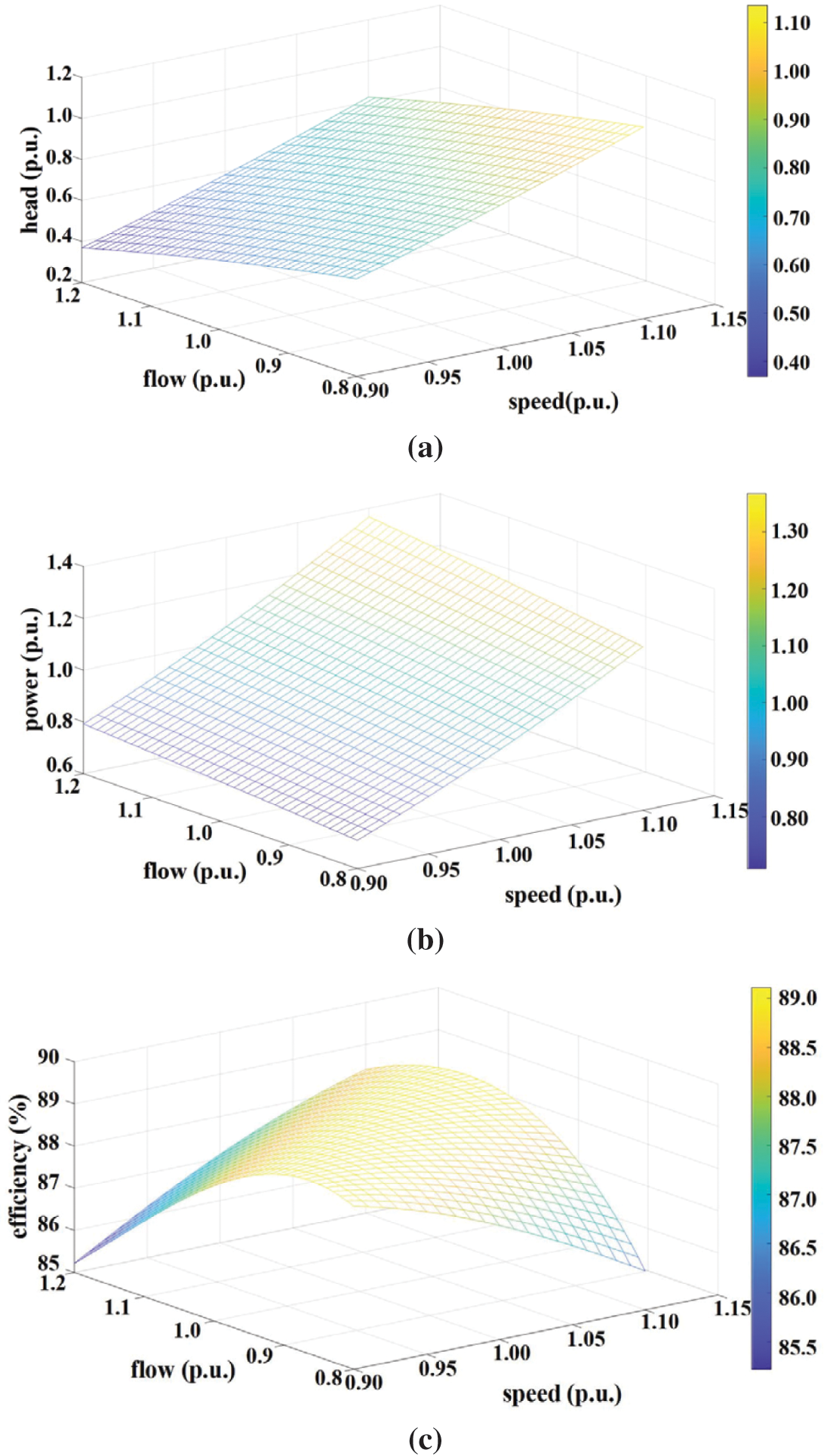
Figure 3: Operating characteristic curves of pump: (a) H−Q curve; (b) P−Q curve; (c) η−Q curve

In consideration of the aforementioned points, this section synthesizes the rigid water hammer model of the water supply system with the power and head expressions, respectively, to derive the pump-turbine model in the state of the pump (see Fig. 4).

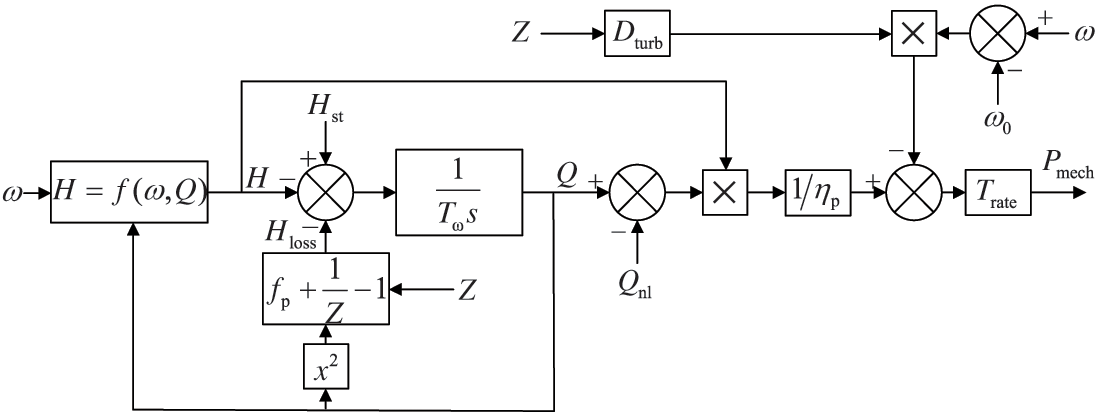
Figure 4: Model of reversible pump/turbine in pump mode

2.3 Speed Priority Control Strategy

When the DFPSU is in pumping operation, active power control can be achieved by adjusting the speed of the unit, and the primary objective is to require the speed to accurately and quickly track the optimal value. To this end, the speed priority control strategy shown in Fig. 5 is selected under pumping conditions. First, the active power command Pref of the unit and the current head are passed to the efficiency optimization module to obtain the corresponding optimal speed ωref and optimal guide vane opening Zref. Second, ωref and the reactive power command Qref are passed to the converter for fast control. As the speed tracking command changes, the input active power of the unit is also adjusted accordingly. At the same time, Pref and Zref are passed to the regulator at the pump-turbine unit, ensuring that the pump-turbine unit operates efficiently while keeping the active power reliably and stably near the reference value.

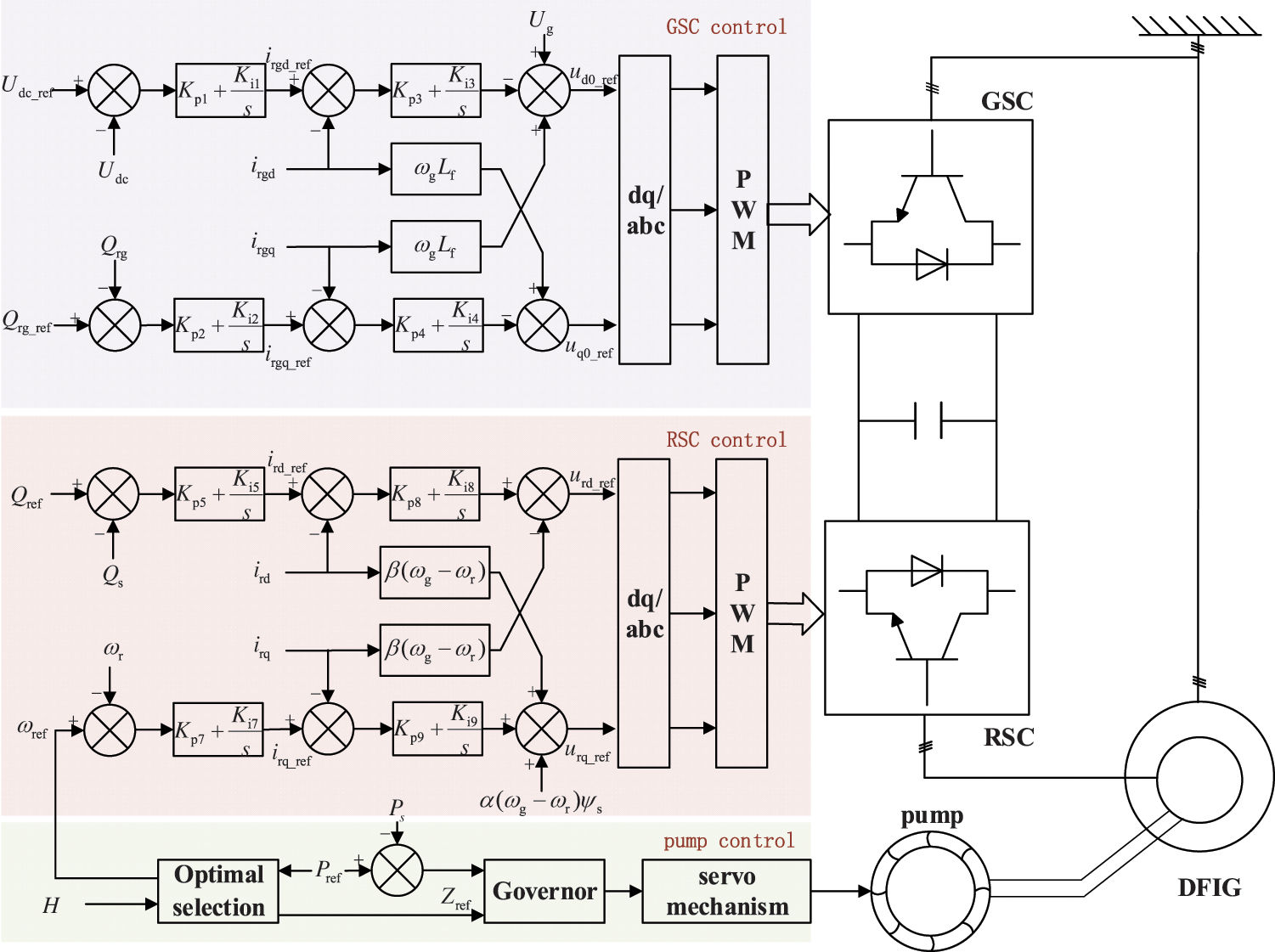
Figure 5: Control structure of speed priority control strategy

3  DFPSU Frequency Control Strategy

3.1 Additional Frequency Control Module

In the event that the DFPSU is engaged in pumping mode, the unit employs a speed priority control strategy, whereby the response speed of the active power is directly modified by adjusting the opening of the pump guide vane. However, the response is characterized by its relatively slow nature. Concurrently, the time scale of primary frequency regulation is relatively brief, thereby classifying this process as a transient phenomenon within electromechanical systems. During this process, the action of the pump efficiency optimization module is not taken into account, and the corresponding control cannot be automatically completed. Consequently, if the traditional strategy consistent with the power generation operating condition is employed at this time, it becomes challenging to ensure the speed and effectiveness of the frequency regulation response [10]. To address these challenges, this paper proposes a novel frequency control method, as illustrated in Fig. 6. This method converts the frequency deviation (Δf) into an additional speed command, thereby enhancing the converter’s rapid regulatory capabilities and ensuring a swift frequency regulation response. The proportional and differential coefficients of the frequency control module, designated as Kωp and Kωd, respectively, are of paramount importance.

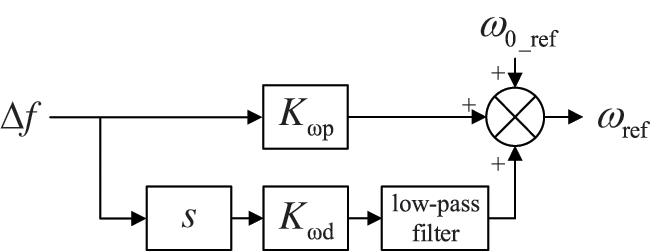
Figure 6: Frequency response model of DFPSU

3.2 Low-Order System Frequency Response Model

The system frequency response (SFR) model is a significant method for analyzing the dynamic response of a power system to frequency fluctuations [11]. The primary focus of this model is the study of frequency fluctuations in the context of electrical processes, while simplifying other time-scale processes. This approach enables the effective reduction of other time-scale processes, while maintaining the key capabilities of the power system. The frequency response model is a significant method for analyzing the dynamic response of an electrical system to frequency changes. It focuses on the dynamic changes in the electrical system itself, while simplifying other time-scale processes. This approach can effectively reduce the dynamic response of an electrical system, while preserving its key characteristics.

The frequency response model consists of various frequency control models and the model of constant load power generation. The frequency control model in this paper is a model of frequency control and load-flow, which is used to describe the dynamic changes in power generation caused by frequency deviations.

3.2.1 Frequency Control Model

In order to reduce the order of the DFPSU unit frequency control model, the unit’s change process on a time scale other than the electromechanical transient is simplified, focusing on the rapid regulation of the converter on the unit’s active power. The following assumptions are made: the change process of the internal magnetic flux of the motor is ignored, and it is considered to remain unchanged during frequency regulation; the minute-level regulation process at the pump-turbine is ignored, that is, it is considered that the efficiency optimization module does not operate during frequency regulation, and the influence of the pump-turbine on the unit’s power regulation is not counted.

The rotor-side converter constitutes the core component of the inverter, serving to achieve precise and expeditious tracking of the command value. Within the double-loop control structure of the inverter, the current inner loop reflects the change of the rotor current, and its response time is in the millisecond range. It can be regarded as instantaneous in the time scale of the electromechanical transient of frequency regulation [12], thereby simplifying the inverter to Gc(s).

Gc(s)=irqirq∗=1τcs+1(9)

Assuming that the dynamic change in the magnetic flux of the motor stator is negligible, it can be deduced that the active power and electromagnetic torque of the generator are proportional to the q-axis component of the rotor current during frequency control. Consequently, a relationship can be established between the change in the converter control command ΔTcmd and the actual control quantity change ΔT, as depicted in Eq. (10):

ΔT=Gc(s)ΔTcmd(10)

As demonstrated above, the model of a water pump in pumping mode consists of H−Q and P−Q curves at varying speeds. The specific operating point of the pump is determined by the intersection of the H−Q and Hneed−Q curve. Consequently, when the operating point of the water pump undergoes a change in response to a modification in speed, the corresponding head and flow rate undergo corresponding alterations. The input power of the water pump undergoes adjustment in accordance with these changes, as illustrated in Fig. 7.

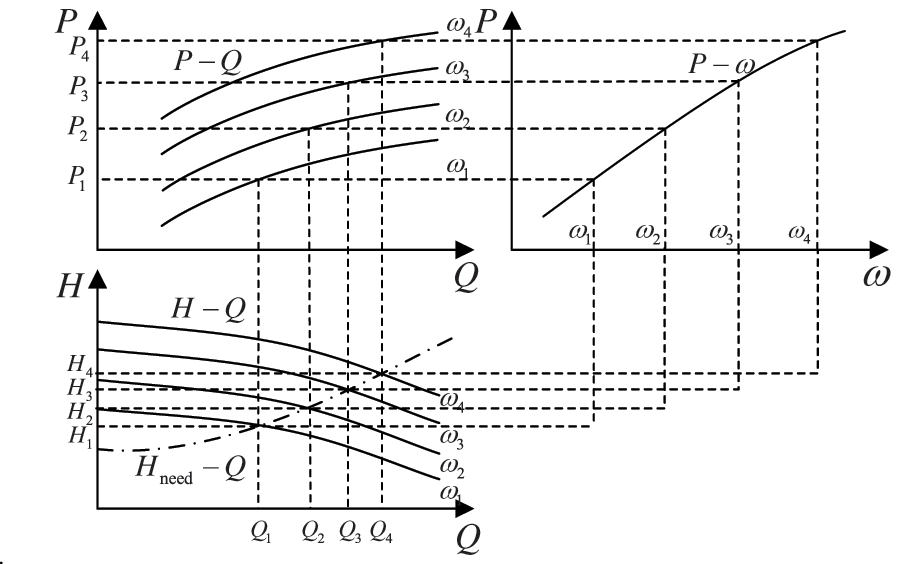
Figure 7: Schematic of operating characteristics of pump

The DFPSU employs a speed regulation mode that utilizes a constant vane opening near the rated operating point under pumping conditions. Consequently, the P – Q curve can be mapped to a power-speed (P−ω) curve, as depicted in Eq. (7). The relationship between the active power Pin absorbed by the DFPSU and ω can be further obtained by utilizing the energy flow relationship.

Pin=1ηm(k0ω3+k1ω2+k2ω+k3)(11)

where ki is the fitting coefficient, i = 0, 1, 2, 3.

The linearization of Eq. (11) at the steady state with rotational speed ω0 yields the following relationship between the change in active power input ΔP of the DFPSU corresponding to the change in rotational speed Δω, where p is a coefficient:

ΔP=f(Δω)=3k0ω02Δω=pΔω(12)

In conjunction with the previously mentioned frequency control module, the frequency control model of the DFPSU is illustrated in Fig. 8. The figure elucidates the time constants T1 and T2 of the frequency detection module and low-pass filter, respectively. ΔPmot signifies the primary frequency control output of the DFPSU under pumping conditions. In pumping mode, the DFPSU converts Δf into an additional speed command Δωf. The converter is then used to rapidly track the provided speed, after which the frequency control output due to the speed change must be derived using Eq. (12).

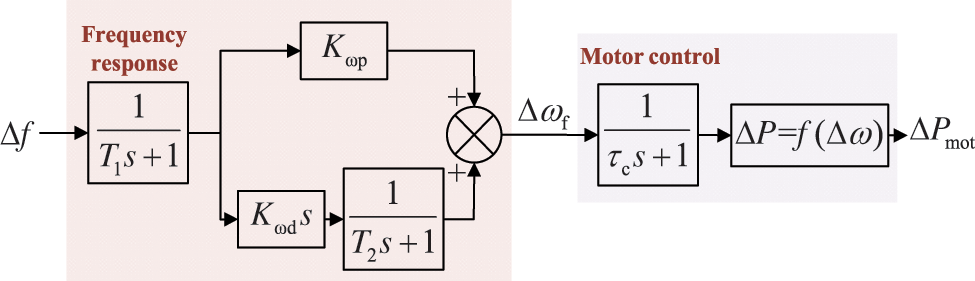
Figure 8: Frequency control models of DFPSU [11]

3.2.2 Generator-Load Model

As asserted by literature [13], the generator-load model of the power system is determined by the sum of the outputs of various types of frequency regulation units, designated here as ΔPm, and the load disturbance, denoted as ΔPL. To elaborate, the imbalance between ΔPm and ΔPL gives rise to a frequency deviation, whilst the inertia response characteristics of the generator and the frequency regulation characteristics of the load affect the specific frequency change.

Δf=12Hs+D(ΔPm−ΔPL)(13)

where H is the inertia time constant of the system; D is the frequency regulation effect coefficient of the load.

In the SFR model, H is the equivalent inertia time constant obtained by combining each power source and treating it as equivalent, calculated according to Eq. (14). Due to the original control of the DFPSU, its speed is decoupled from the grid frequency, and its contribution to the grid inertia is negligible. At this time, only the inertia provided by the traditional unit is considered, and the virtual inertia of the DFPSU due to additional frequency control will be analyzed in detail in next section.

H=∑i=0xSTNiHTiSN(14)

3.2.3 General System Frequency Response Model

Based on the above analysis, the unit is connected to a four-machine, two-zone model, and an improved SFR model containing a doubly-fed induction generator unit is proposed as shown in Fig. 9. In order to depict the dynamic process of frequency control of thermal power units and hydroelectric power units, typical parameters are taken for thermal units, and the classical small-signal model is used for hydraulic turbines. In the case of hydro units, the governor is appropriately compensated for inadequate gain and phase margin of the system.

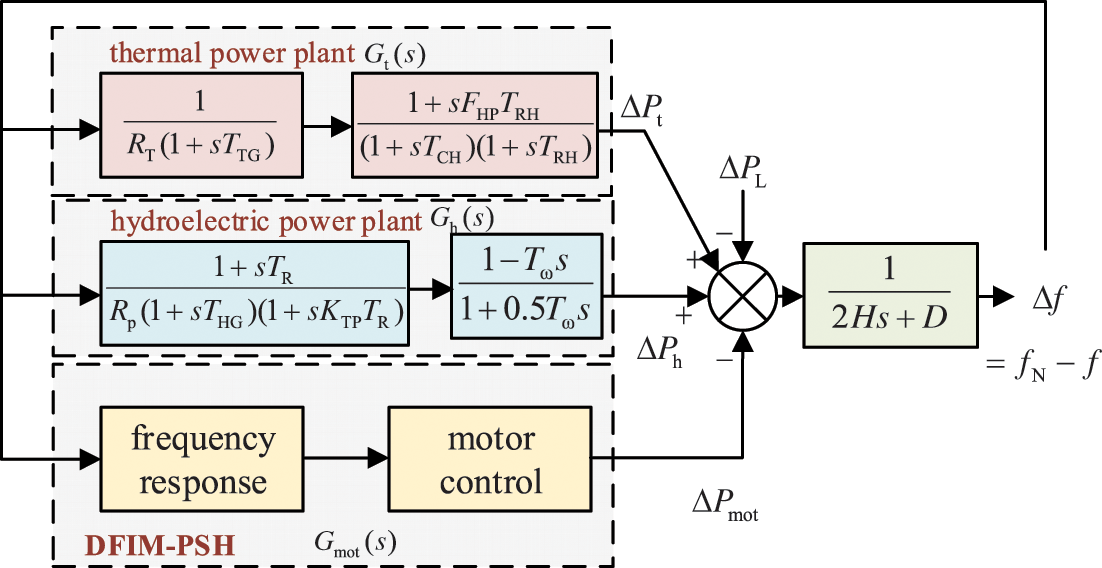
Figure 9: SFR model of system with DFPSU

Based on Fig. 9, we can derive the expression for the calculation of the grid Δf during a load disturbance.

Δf−ΔPL=12(∑i=1mStNiSNHti+∑i=1nShNiSNHhi)s+D+(∑i=1mStNiSNGti(s)+∑i=1nShNiSNGhi(s)−Gmot(s))(15)

where subscript i denotes the ith unit; SN is the sum of the rated capacities of all power sources in the grid, including thermal power units, hydropower units; StN and ShN are the rated power rates of thermal power units and hydropower units, respectively. Ht and Hh are the equivalent inertia time constants of thermal power units and hydropower units, respectively; m and n are the numbers of thermal power units and hydropower units in the grid, respectively.

4  Adaptive Control Strategies

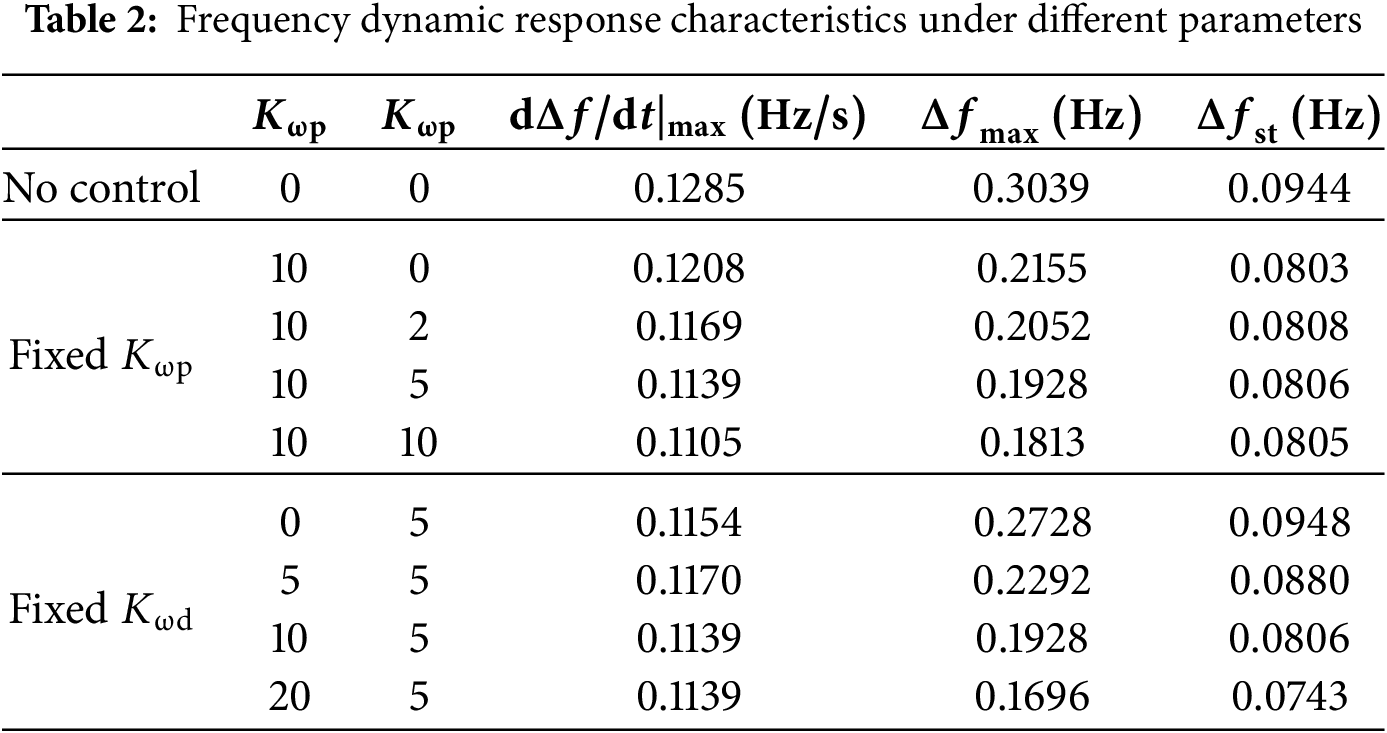
4.1 Influence of Kωp and Kωd on Frequency Response

The frequency dynamic response index, which is a measurement of the effect of frequency control, principally includes frequency deviation, the rate of change (dΔf/dt), maximum frequency deviation (Δfmax), and steady-state frequency deviation (Δfst). As demonstrated in Fig. 10 below:

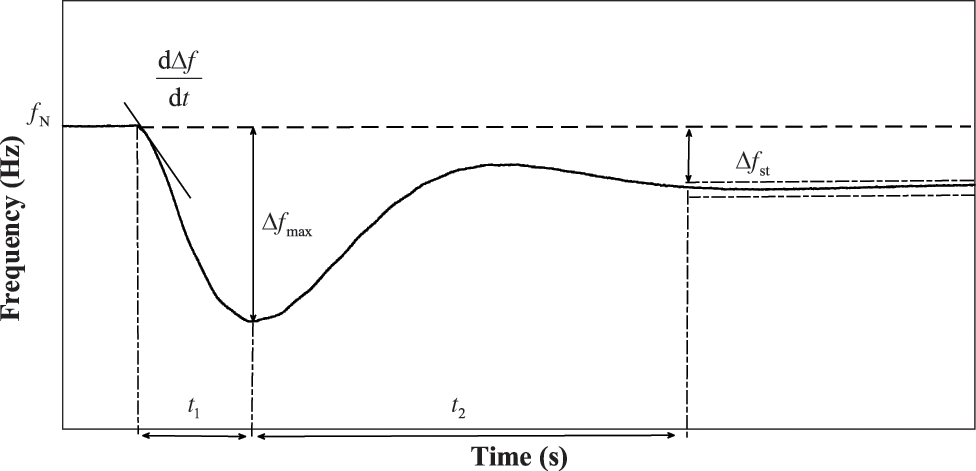
Figure 10: Response curve of primary frequency regulation

The rate of frequency change, or dΔf/dt, is a crucial metric in the analysis of system behavior. It is primarily influenced by the power imbalance within the system and the inertia time constant. At the onset of frequency control, dΔf/dt attains a maximum value, denoted as dΔf/dt|max. This maximum value exerts a direct influence on the operation of the system’s protective devices. The magnitude of Δfmax is a critical indicator of the system’s frequency stability, with its specific value being influenced by the preceding dΔf/dt conditions. During the intermediate and late stages of frequency control, dΔf/dt becomes negative, impeding the restoration of the frequency. Eventually, the action of each frequency control unit leads to the attainment of a steady-state value, designated as Δfst.

Based on Fig. 8, ignoring the time constants of the frequency detection module and the low-pass filter in the DFPSU unit, the primary frequency control output under different operating conditions can be obtained as follows:

ΔPmot=p(Kωp+Kωds)τcs+1Δf(16)

Considering that only DFPSU units are involved in frequency control in the system and ignoring their millisecond converter response time, the frequency response model shown in Fig. 9 can be rewritten as follows:

ΔPL=(2H+Kωd)sΔf+(D+Kωp)Δf(17)

It is hypothesized that the system is subjected to a disturbance of amplitude ΔPstep, whose transfer function is ΔPL(s)=ΔPstep(s)/s. Under these conditions, Δf and dΔf/dt are given by Eqs. (18) and (19), respectively.

Δf(s)=ΔPsteps2(2H+Kωd)+s(D+Kωp)(18)

dΔf(s)dt=ΔPsteps(2H+Kωd)+D+Kωp(19)

Pursuant to the initial value theorem, calculate the derivative of the function dΔf/dt at the initial moment, that is to say, dΔf/dt|max:

dΔfdt|max=lims→∞sdΔf(s)dt=ΔPstep2H+Kωd(20)

In accordance with the final value theorem, the steady-state frequency deviation, designated as Δfst, can be calculated:

Δfst=lims→0sΔf(s)=ΔPstepD+Kωp(21)

As demonstrated in Eqs. (20) and (21), the differential control channel of the constructed frequency control module is equivalent to increasing the equivalent inertia of the system. This can rapidly suppress frequency changes, i.e., reduce dΔf/dt|max, and thereby significantly reduce Δfmax. In contrast, the proportional control channel has the same effect as the frequency control of a conventional unit. It increases the damping of the system and provides the corresponding power support with frequency changes, thereby helping to reduce Δfst.

In order to verify the rationality of the aforementioned inference, this study will substitute different values of Kωp and Kωd into the system transfer function described by Eq. (15). The typical parameters in the function are shown in Table 1. The resulting function curve is shown in Fig. 11. The specific simulation verification results will be described in detail in the following sections.

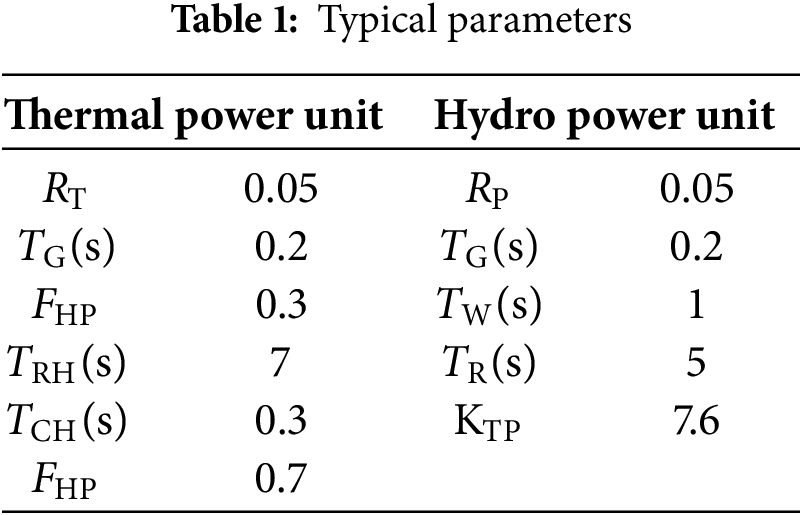
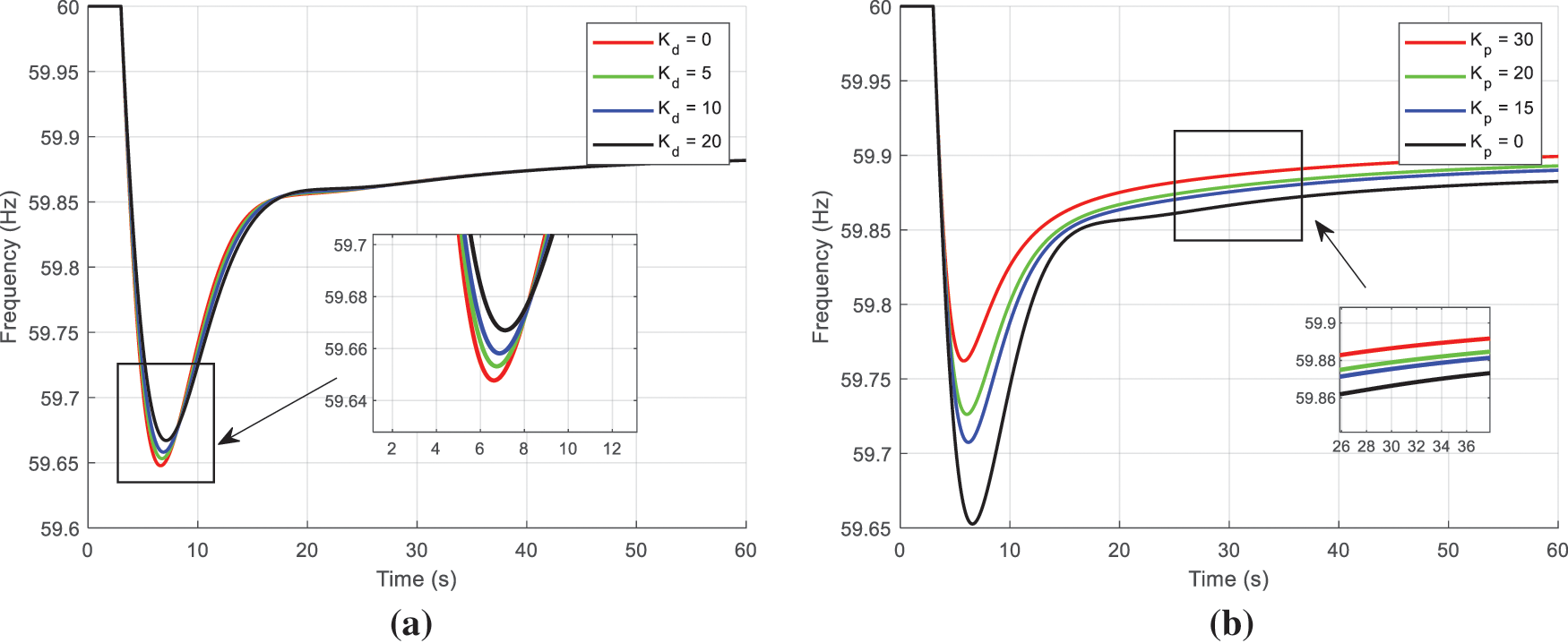
Figure 11: Comparison of response curves under different parameters: (a) response curves under different Kωd (Kωp=0); (b) response curves under different Kωp (Kωd=0)

4.2 Extremum Determination for Parameters

The root locus of each frequency control parameter is plotted according to Eq. (15). In the figure, the damping ratio is denoted by ξ, the overshoot is indicated by Mp and the natural oscillation angular frequency is represented by ωn.

As illustrated in Fig. 12a, when the fixed Kωp is a typical value and Kωd varies from [0,∞], stability is achieved due to the placement of all system poles and zeros in the left-hand side of the complex s-plane. When 0 < Kωd < 34.4, the system is in an underdamped state, and the magnitude of the zero pole, designated as ξ, is substantial, corresponding to an index (Mp) less than 5%. This ensures that the system’s response to frequency control can be reliably guaranteed to a certain extent. Conversely, when Kωp ranges from [0,∞], the system’s stability is contingent on the condition Kωp < 308. It is noteworthy that the magnitude of Kωp directly correlates with the system’s Mp generation, with higher values of Kωp resulting in greater Mp generation. To ensure that the resulting control Δf is minimal, the region where |ξ| > 0.707 is selected, i.e., 0 < Kωp< 23.8. Consequently, the corresponding Mp is less than 4.16%, and the value of ωn is substantial, thereby effectively reducing the frequency fluctuation time.

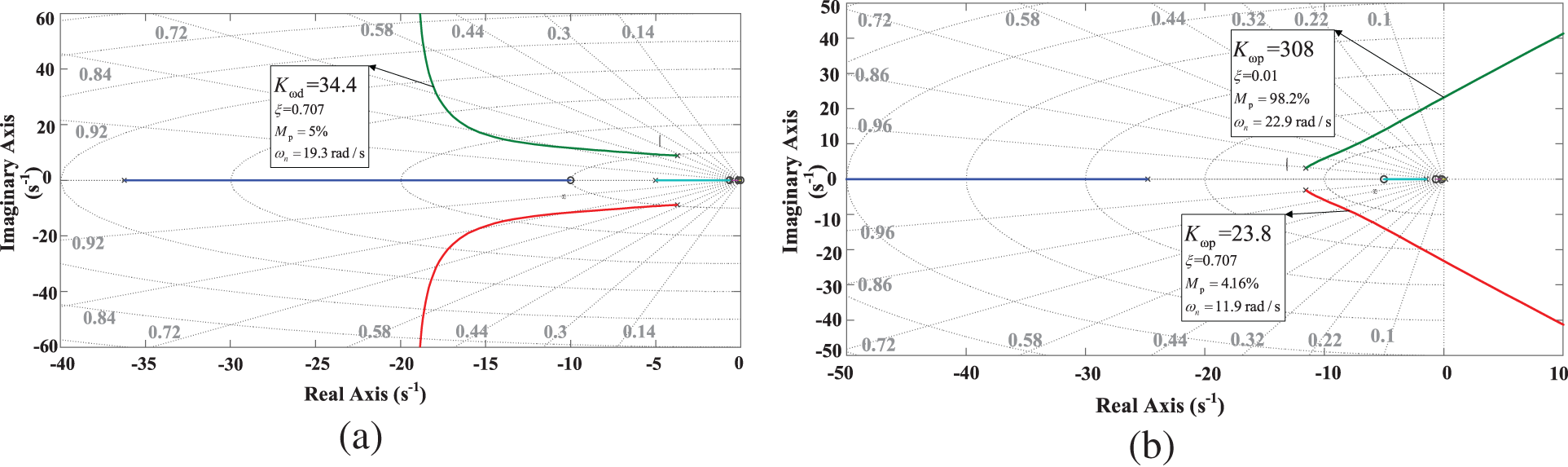
Figure 12: Zero-pole trajectory of frequency deviation transfer function: (a) Kωd varies from [0,∞] (Kωp is fixed at 10); (b) Kωp varies from [0,∞] (Kωd is fixed at 5)

4.3 DRL-Based Adaptive Parameter Optimization

4.3.1 Introduction to Algorithms

Deep reinforcement learning (DRL) is a type of learning based on the state of the environment. The agent engages with the environment to acquire state information and perpetually refines its strategy to optimize the anticipated reward [14]. This approach to learning from past experiences has proven effective in circumventing the issue of overparameterization and the subsequent challenge of ascertaining the present control method. In this paper, the current well-performing twin delayed deep deterministic policy gradient (TD3) algorithm [15] is employed to address the issue of energy storage participation in primary frequency regulation. TD3 employs the Actor-Critic framework, which facilitates the generation of continuous actions and represents an enhancement over the deep deterministic policy gradient (DDPG) algorithm [16].

4.3.2 Design of Frequency Control Agents

The issue of integrating DFPSU into primary frequency control of the power grid is represented by a Markov decision process (MDP), which necessitates the delineation of a quintuple {O,A,R,P,γ}. Specifically, O denotes the system observation space, A represents the agent’s action space, R signifies the reward function, P is the state transition probability, which is unknown in this problem and is learned by the agent during training, and γ is the discount factor, which represents the agent’s attention to future rewards and is set to 0.96. The specific solution and interaction process is illustrated in Fig. 13.

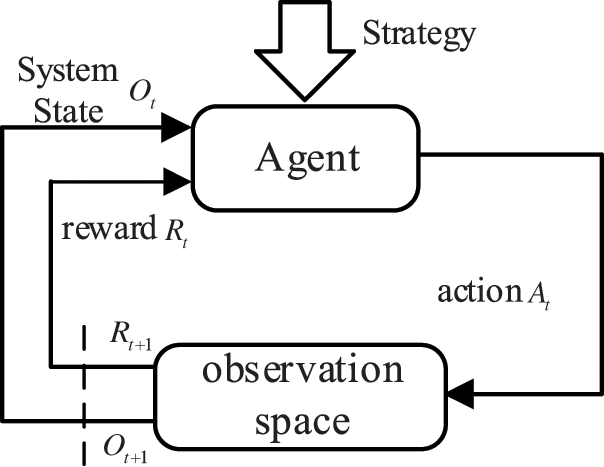
Figure 13: The process of solving problem and interaction in DRL algorithm

The state space of an agent is the agent’s observational information about the current state of the environment. This paper includes three parts in the observation: the current frequency deviation of the power grid, the change in frequency deviation, and the current speed state of the generator.

O={Δf(t),Δf(t)−Δf(t−1),Δω(t)}(22)

The control quantities are defined as the Frequency Control parameters Kωp and Kωd. The values are numerically continuous.

A={Kωp(t),Kωd(t)}(23)

The reward function is the sole criterion by which the agent assesses the quality of an action, and its design is intimately associated with the evaluation index. To this end, the reward function in this paper is composed of two constituent parts: an evaluation index and a punishment index.

The evaluation index is composed of the weighted frequency control effect evaluation index and the unit release kinetic energy index. The traditional frequency evaluation index is the difference between the current frequency f(t) and fN.

ΔfP=1N∑ι=0T(f(t)−fN)2(24)

The alteration in the unit’s kinetic energy is associated with the initial and current rotational speeds of the unit during frequency control.

ΔEP=12Pd2J(ω02−ω(t)2)(25)

where the quantity of poles of the generator set is denoted by Pd; the generator set’s natural inertia is denoted by J; the initial rotor speed during the frequency control phase is denoted by ω0; and the current generator set speed is denoted by ω(t).

In summary, the formula for the evaluation index in the reward function is as follows:

r1=x1Δfp+x2ΔEp(26)

where x1 and x2 are the weight coefficients.

This method penalizes the agent for frequently changing its action direction in commands, with the objective of guiding the agent to issue smoother commands. Specifically, a penalty is imposed when the agent has changed direction twice in the last three commands. This penalty significantly exceeds the reward received from this mode of operation.

r2={b,if Pb(t)Pb(t−1)<0and Pb(t−1)Pb(t−2)<00,otherwise(27)

where b is a constant.

In summary, the agent’s reward function is

R=r1−r2(28)

In order to ensure the safe operation of the unit, the following restrictions on unit power and speed are hereby proposed, based on actual operating conditions:

s.t.{ωmin≤ωr≤ωmaxPmin≤Ps≤Pmax(29)

The proposed control strategy robustly accommodates parametric variations—such as seasonal load-response shifts and renewable generation fluctuations—through real-time state feedback mechanisms. However, when confronting structural changes including grid topology reconfigurations or unit outages, which fundamentally alter the system frequency response (SFR) transfer function and inertia constant H, a transfer learning-based rapid retraining protocol is employed: Pretrained networks are adaptively fine-tuned using topology-specific operational data, achieving convergence within 50 training episodes.

4.4 Analysis of Optimization Results

After optimizing the unit under several typical operating conditions, the optimal frequency control parameters can be obtained for each scenario. In this example, a 10% load increase is considered. Initially, the Support Vector Regression (SVR) method is employed to model the data, thereby addressing issues such as noise or outliers. The Support Vector Regression (SVR) method has emerged as a prominent machine learning fitting technique in recent years, adeptly capturing the nonlinear characteristics of data and yielding more precise fitting outcomes. The objective of the fitting process is to approximate the overall trend of the data through the SVR model to obtain a more accurate fitting curve. Subsequently, the data is smoothed using cubic spline interpolation to further optimize the smoothness and continuity of the curve. The efficacy of cubic spline interpolation in generating a smooth curve with continuous first and second derivatives between data points is well-documented. This approach effectively reduces oscillation during the fitting process, thereby maintaining the overall trend of the data.

The specific training process is illustrated in Fig. 14. Agent achieved substantial convergence after approximately 50 training episodes, attaining a final real-time reward value of −23.6822. This demonstrates strong online learning capability, indicating favorable convergence characteristics of the agent system. Consequently, it enables reliable simulation of frequency stabilization under disturbance scenarios across diverse DFPSU operating conditions.

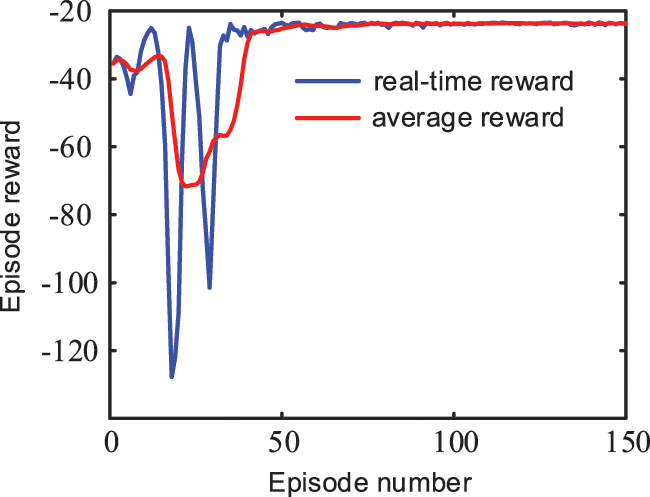
Figure 14: Training process

Taking the frequency drop scenario as an optimization example, the resulting curve is shown in Fig. 15. Combining the frequency control characteristics of the generator set during a frequency drop, i.e., the generator set will reduce the speed to release the rotor kinetic energy, and increase the active power output or reduce the active power input to provide stable power support, it is not difficult to summarize the law of change of the final frequency control parameters: when the generator set is in the low speed stage, the value of the frequency control parameters is relatively small, so as to avoid the generator set from causing a serious speed drop due to excessive release of the rotor kinetic energy. As the speed increases, the frequency control parameter gradually increases to make full use of the rotor kinetic energy contained in the unit. However, when the speed increases to a certain value, the input/output active power of the corresponding unit will also increase to a higher level. At this time, in order to ensure that the unit does not overreact and the power exceeds the allowable range, the frequency control parameter is reduced accordingly. Since the principle of changing the limit frequency control parameter for the frequency increase scenario is the same as that for the frequency decrease scenario, it will not be presented here.

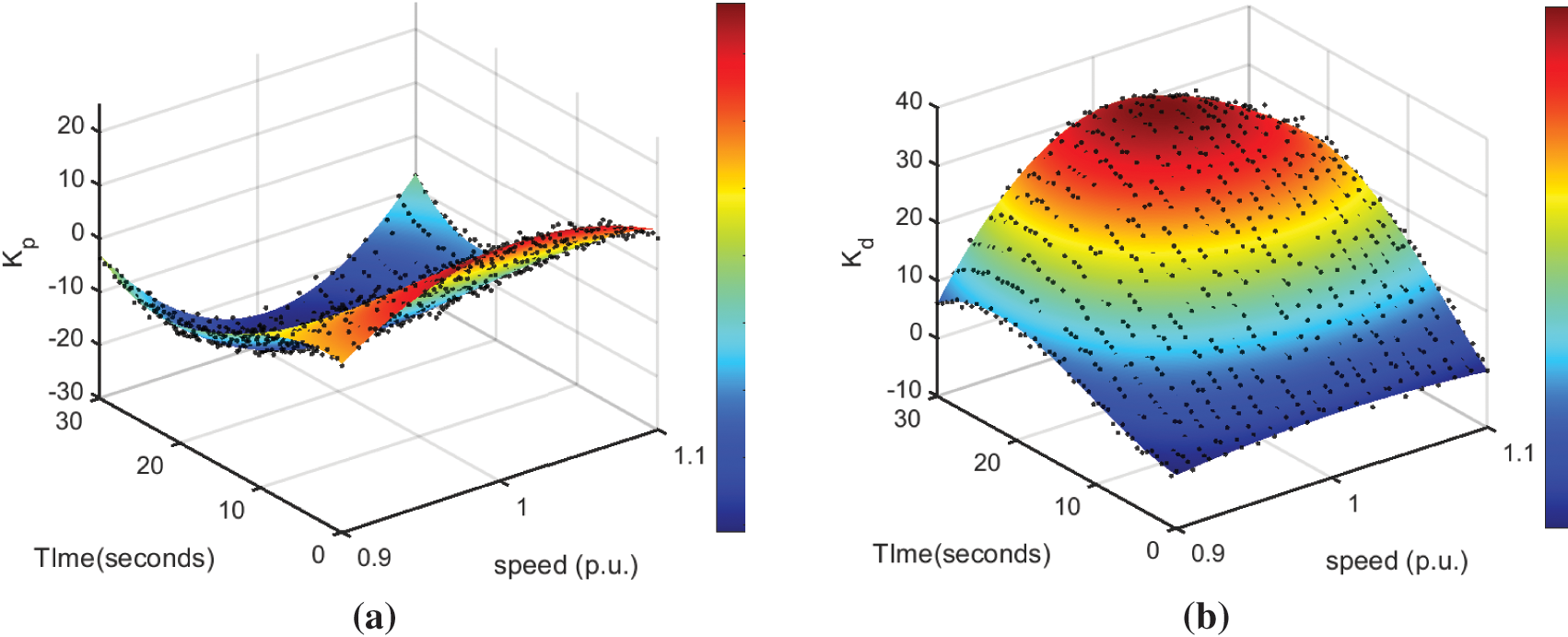
Figure 15: Optimal frequency control parameter curve: (a) Optimal Kωp curve; (b) Optimal Kωd curve

The differential control coefficient Kωd is selected to a larger value when the dΔf/dt value is large at the beginning of frequency control. This ensures that the rotor kinetic energy of the generator set is fully released to suppress the frequency change. Conversely, as dΔf/dt diminishes, Kωd undergoes a gradual reduction to decelerate the release of the rotor kinetic energy of the generator set, thereby averting an excessive decline in speed. Furthermore, when the sign of dΔf/dt undergoes a transition from positive to negative, Kωd undergoes an adjustment to a negative value, thereby facilitating frequency recovery and reducing the continuous deviation of the speed. The proportional control coefficient Kωp can be adjusted to a smaller value at the beginning of frequency control, while a larger value can be selected in the middle and late stages to complement the response and support time of the differential control.

5  Simulation Results

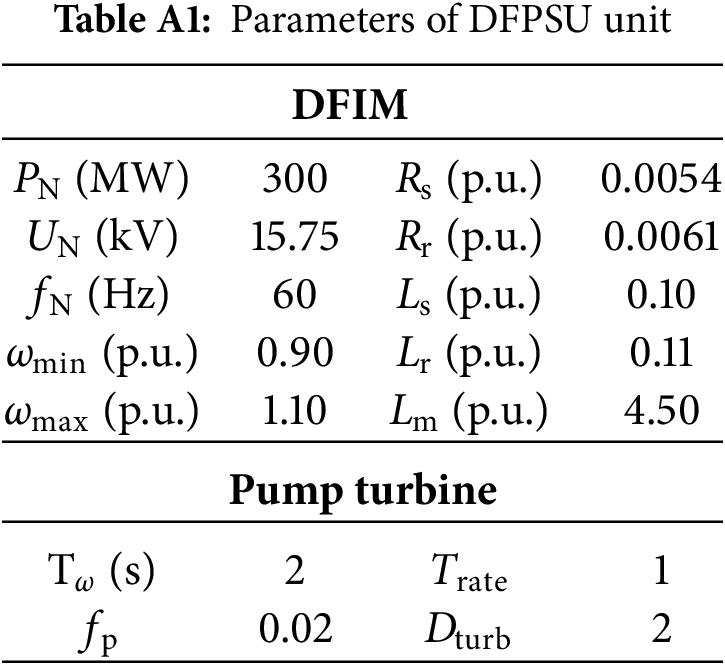
To evaluate the performance of the DFPSU frequency control module developed in this paper and to demonstrate the superiority of the proposed adaptive variable-parameter frequency control strategy, this section presents a simulation of the DFPSU model integrated into a four-machine two-area system, as depicted in Fig. A1 and Table A1, using the PSCAD/EMTDC simulation platform. The frequency dynamics of the system are analyzed under a sudden step load increase, with comparisons drawn between different control methods and parameter settings. The corresponding dynamic response characteristics are then assessed and compared to validate the effectiveness of the proposed control approach.

5.1 Simulation Verification of Additional Frequency Control Module

The initial active power command of the DFPSU is set to −0.8 p.u., and the corresponding optimal speed command is 0.987 p.u. After the unit has been operating stably for 20 s, the load suddenly increases by 10%. The response of the system frequency, active power, and speed of the generator under the control mentioned in this paper, including traditional control, proportional control channel only, differential control channel only, and both channels acting, is shown in Fig. 16. In the context of DFPSU in pumping mode, the speed is identified as the primary control target of the converter. Consequently, the active power of the system is contingent upon the adjustment of the guide vane opening at the pump. Conversely, if the traditional control method, which converts Δf into a power command, is employed, the frequency regulation response speed will be considerably decelerated due to the restriction of the guide vane opening adjustment speed. Conversely, the converter maintains its original optimal speed control, which is faster, thereby ensuring the unit’s speed remains consistent and the rotor kinetic energy cannot be released to provide inertia support. In contrast, the control method outlined in this paper, which converts Δf into a speed command, utilizes the converter’s rapid response capability to ensure the speed of the frequency response. The rapid adjustment of speed enables a corresponding adjustment of input power, thereby effectively mitigating frequency fluctuations.

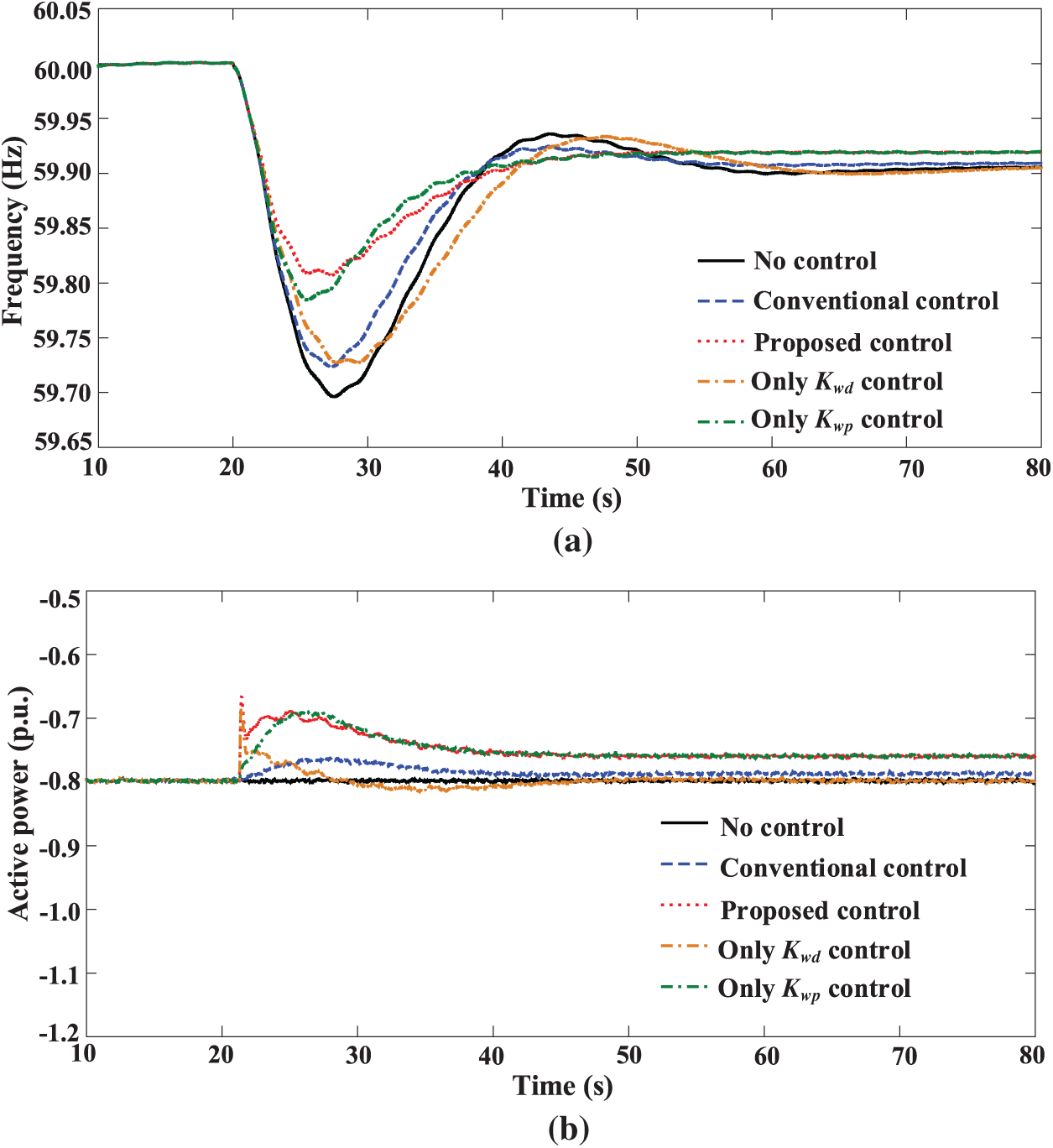
Figure 16: Response results of system when DFPSU adopts different frequency control strategies in pumping mode: (a) frequency; (b) active power of DFPSU; (c) speed of DFPSU

A subsequent examination of the system’s response during the proposed control with solely proportional and differential control reveals the efficacy of differential control during the initial phase of frequency control, characterized by a substantial value of dΔf/dt. It has been demonstrated that differential control facilitates the release of rotor kinetic energy by adjusting the speed to achieve instantaneous support of the active power. This, in turn, effectively reduces dΔf/dt. However, its efficacy gradually diminishes during the middle and late stages of frequency control. As the speed reverts to its original value, the active power of the unit gradually recovers, indicating that this control channel is incapable of providing continuous power support. In contrast, the proportional control channel maintains its effectiveness throughout the entire frequency control process. Subsequent to a change in speed, it can be utilized to regulate the active power of the generator unit stably by leveraging the characteristics of the pump-turbine. The effectiveness of this control channel directly corresponds to the magnitude of Δfst. The combination of these two channels has been shown to enhance their respective benefits, thereby effectively mitigating frequency fluctuations, reducing dΔf/dt, and significantly diminishing both Δfmax and Δfst.

As demonstrated in the preceding analysis, the differential control channel is analogous to virtual inertia control, a strategy that has been proven to effectively suppress frequency changes and, by extension, reduce dΔf/dt during the initial stage of frequency control. In comparison with the conventional approach of setting dΔf/dt as a power correction quantity to release rotor kinetic energy, the method proposed in this paper directly controls the speed to achieve adjustment of the rotor kinetic energy, and the inertia support effect is more rapid and obvious. The proportional control channel is analogous to droop control, which facilitates continuous power support throughout the entire frequency control process in response to changes in Δf. This approach offers significant advantages in terms of reducing Δfst. However, due to the inherent characteristics of the water pump under pumping conditions, the input active power of the DFPSU is proportional to the cube of the speed. While the proportional control method outlined in this paper may not be as intuitive as the conventional method of converting Δf into a power command, the control response speed and effectiveness are comparable to those of the traditional control method. In addition to the parameters determined using the conventional method for frequency control parameters, Fig. 17 presents the frequency response curves of the system under various frequency control parameters. It also compares their frequency dynamic response indicators as shown in Table 2, which further substantiates the impact of each control channel and parameter. It is evident that as the magnitude of Kωd increases, the initial dΔf/dt values decrease, thereby enhancing the suppression of frequency change. It is important to note that Δfmax is directly influenced by dΔf/dt; therefore, a larger Kωd will result in a smaller Δfmax. However, the differential control channel exerts a negative damping effect on frequency recovery during the later stages of frequency control, thereby slowing the rate of Δf reduction. Conversely, Kωp signifies the extent to which the timing group reliably provides a response to Δf. Consequently, an augmentation in Kωp is more advantageous in diminishing Δf, resulting in a substantial reduction in both Δfmax and Δfst.

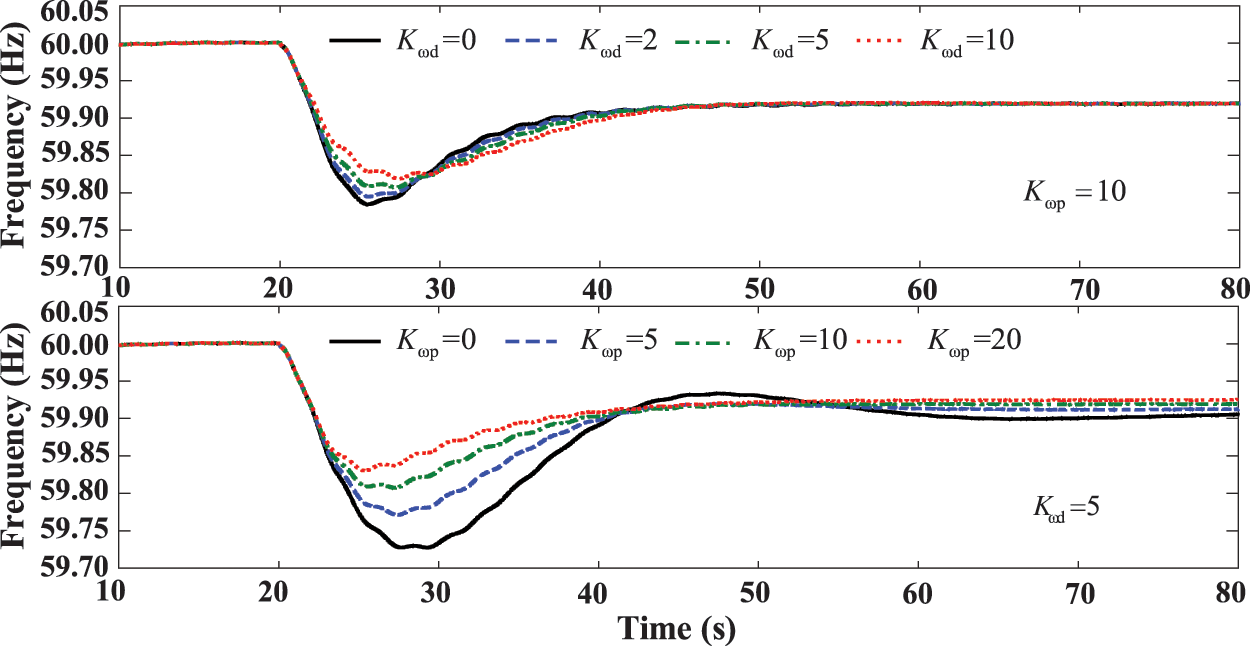
Figure 17: Response results of system under different parameters

5.2 Simulation Verification of Adaptive Variable-Parameter Frequency Control Strategy

In the event that the DFIM-PSH is operating in pumping mode, the dynamic response curves of the system at unit input powers of −0.7 and −0.9 p.u. are demonstrated in Figs. 18 and 19, respectively. Concurrently, a variable-parameter frequency control strategy can attain optimal frequency control outcomes. The DFIM-PSH adjusts the input active power by altering the speed, thereby providing stable power support to reduce Δfst. Concurrently, the inherent characteristics of differential control induce fluctuations in the speed of the generator set, thereby leading to increased frequency fluctuations. However, this does not compromise the overall effectiveness of the control strategy.

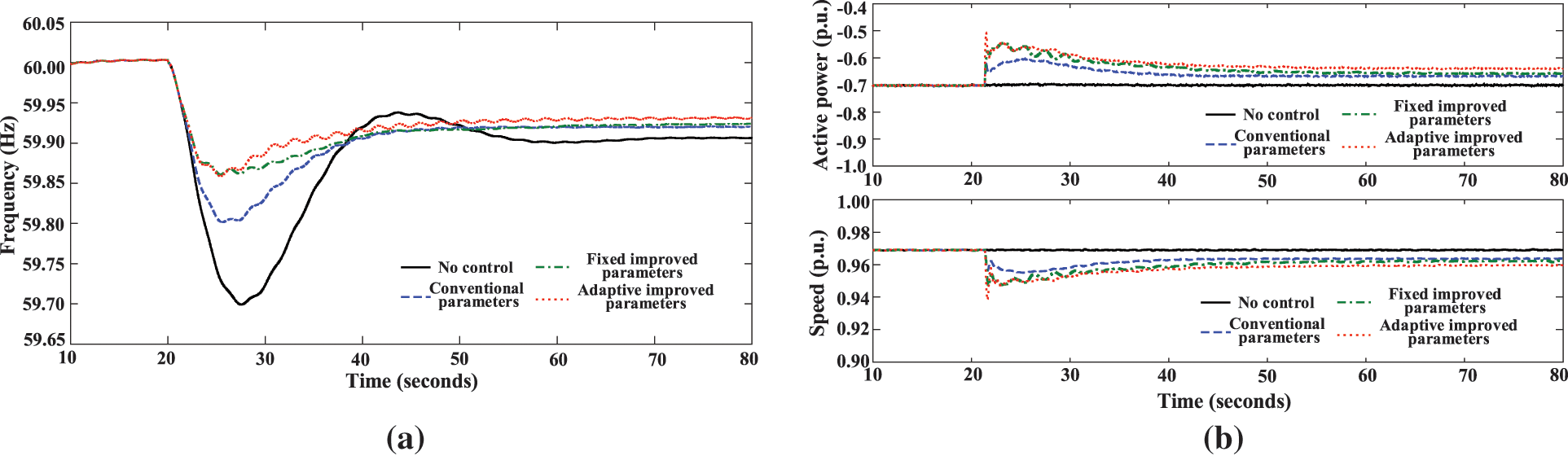
Figure 18: Response results of the system when DFPSU in sub-synchronous pumping mode: (a) system frequency; (b) active power and speed of DFPSU

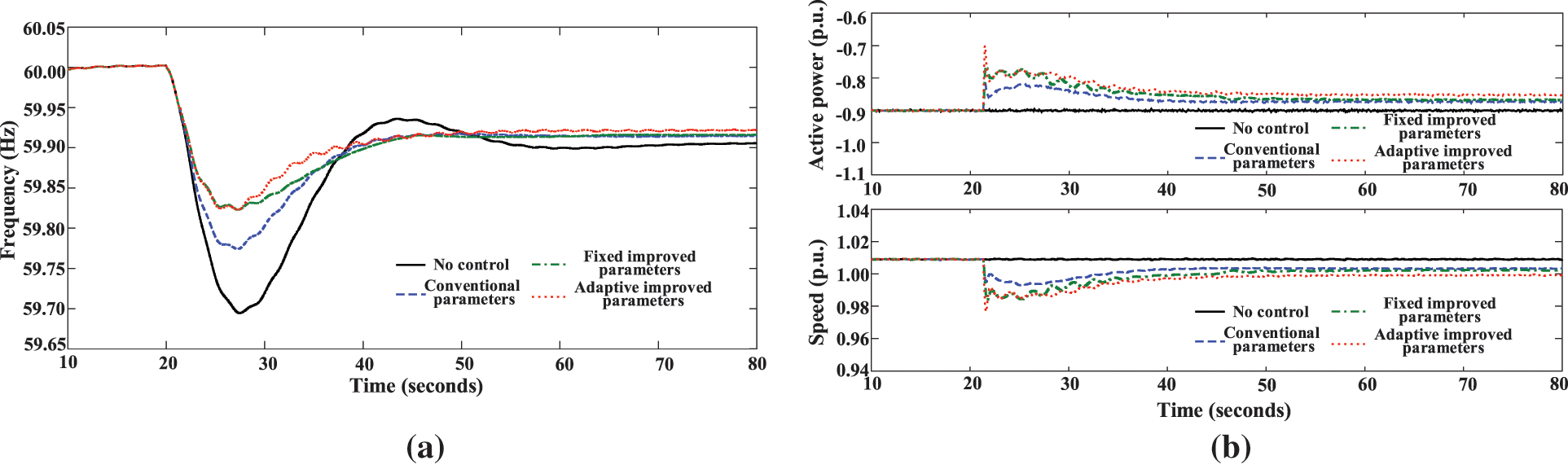
Figure 19: Response results of the system when DFPSU in super-synchronous pumping mode: (a) system frequency; (b) Active power and speed of DFPSU

In comparison with conventional parameters, the improved parameter–adaptive control facilitates the unit in altering the speed significantly more rapidly at the commencement of frequency control. Consequently, this reduces Δfmax from 0.1985 to 0.1412 Hz in the sub-synchronous state and from 0.2261 to 0.1772 Hz in the super-synchronous state, representing a reduction of more than 20% in both instances. In the middle and late stages of frequency control, the modified parameter variable parameter control has been shown to be capable of reliably reducing the input active power with changes in speed, thereby promoting rapid frequency recovery. The resulting control Δfst reduction in both operating conditions has been shown to exceed 10%.

Fig. 20 shows the system’s frequency dynamic response index when DFPSU is in different operating conditions and states. As we can see from this analysis, the adaptive variable parameters determined using the method described in this paper can make the most of the rotor kinetic energy and frequency control capacity of the generator set when it is operating in different conditions. At the same time, they can also make sure that the generator set speed and power stay within the limits. In other words, the improved parameters are strong when the generator set is in different operating conditions. At the same time, since the variable parameters also adapt to changes in frequency, each frequency control channel can have a positive effect on restoring the correct frequency throughout the entire process. As well as reducing df/dt, Δfmax and Δfst, it also has a significant effect on reducing tst.

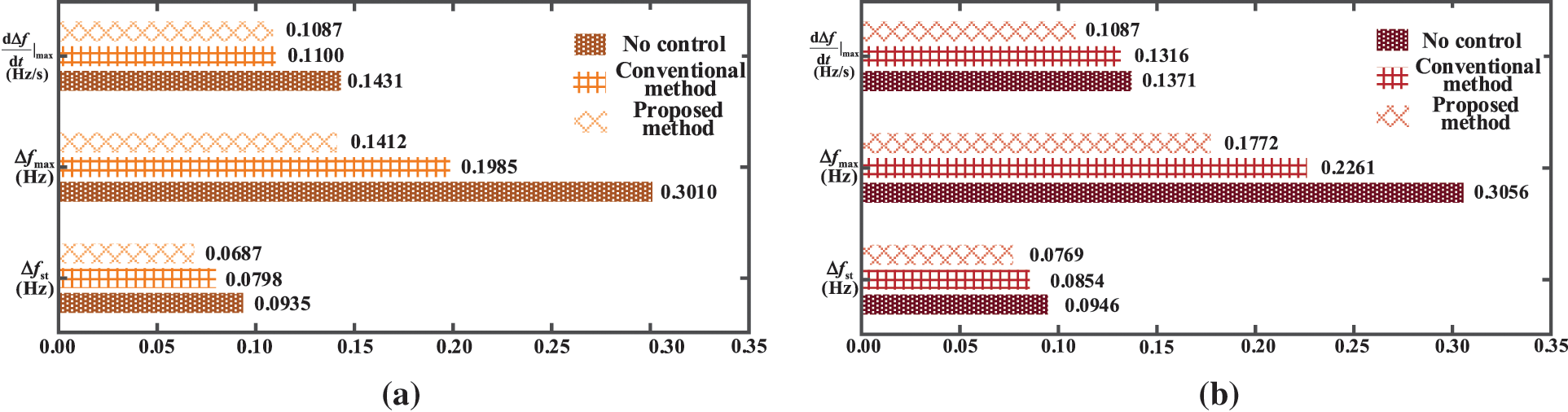
Figure 20: Frequency dynamic response indexes under different frequency control parameters: (a) sub-synchronous state; (b) super-synchronous state

6  Conclusion

This paper designs a frequency control module for the DFPSU under pumping conditions, and constructs a low-order frequency response model to analyze its inertia response and Primary Frequency Control characteristics and related influencing factors. It is on this basis that an adaptive variable-parameter frequency control strategy is proposed. This strategy is designed to take into account the safe and stable operation of the unit and the characteristics of frequency variation. The innovation lies in the real-time adjustment of the amplitude and sign of specific parameters with frequency variation, which ensures that each frequency control channel can effectively promote frequency restoration throughout the entire frequency control process, and that the frequency control capability can be maximized on the premise of maintaining safe and stable operation. The validity of the proposed approach is substantiated by simulation verification, which demonstrates that the frequency control module constructed in this paper, which converts Δf into an additional speed command under pumping conditions, can fully realize the fast response capability of the converter in the DFPSU. The module enables a substantial and rapid adjustment of the input power by expeditious adjustment of the speed, thereby effectively suppressing frequency changes. This approach boasts significant advantages over conventional frequency control methods.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Shuxin Tan and Wei Yan; methodology, Shuxin Tan and Wei Yan; software, Lei Zhao and Ziqiang Man; validation, Yu Lu, Wei Yan and Teng Liu; formal analysis, Lei Zhao, Yu Lu and Ziqiang Man; investigation, Yu Lu, Wei Yan and Teng Liu; resources, Gaoyue Zhong and Weiqun Liu; data curation, Gaoyue Zhong and Weiqun Liu; writing—original draft preparation, Xianglin Zhang and Yu Lu; writing—review and editing, Shuxin Tan, Wei Yan and Linjun Shi; visualization, Shuxin Tan, Xianglin Zhang and Wei Yan; supervision, Lei Zhao; project administration, Lei Zhao and Linjun Shi; funding acquisition, Ziqiang Man. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Xianglin Zhang, Hohai University, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Abbreviations

Appendix A

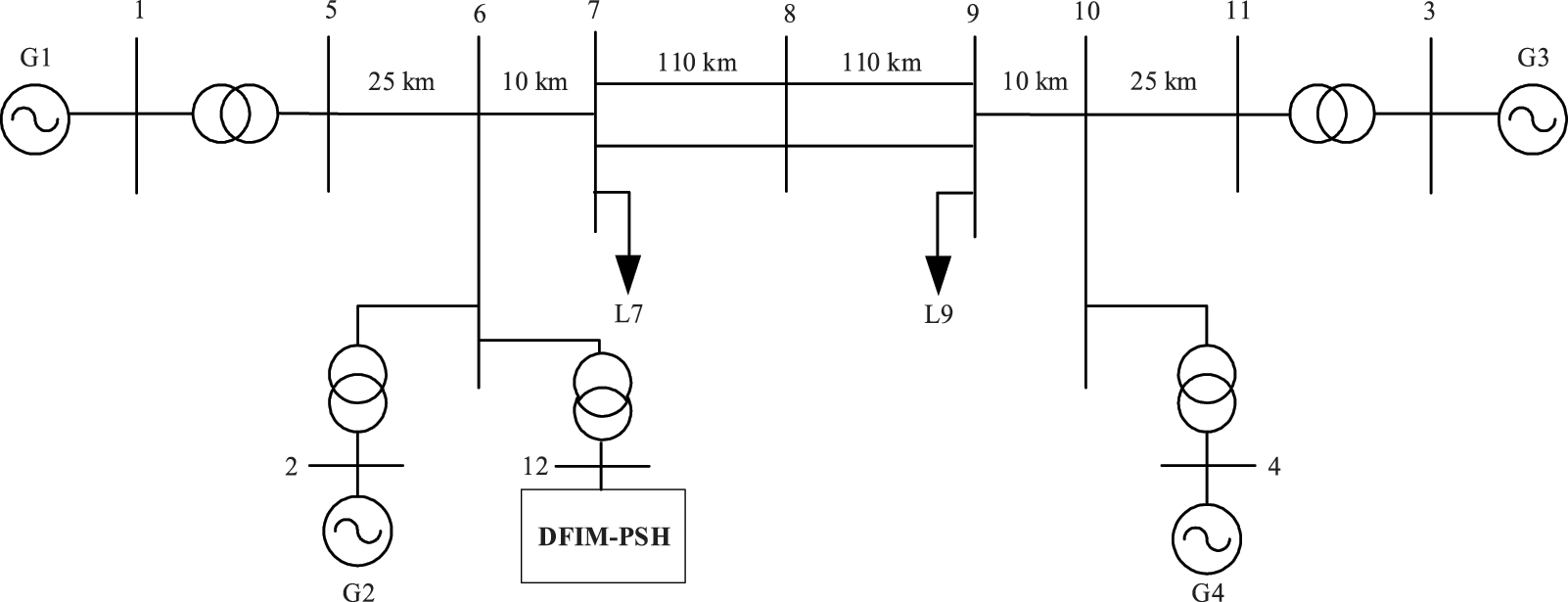
Figure A1: Schematic diagram of DFIM-PSH connecting to a four-machine two-zone system

References

1. Donalek PJ. Pumped storage hydro: then and now. IEEE Power Energy Mag. 2020;18(5):49–57. doi:10.1109/mpe.2020.3001418. [Google Scholar] [CrossRef]

2. Li H, Liu H, Song E, Xiao HW, Luo L, Huang ZX. Improved virtual inertia control strategy of doubly fed pumped storage unit for power network frequency modulation. Autom Electr Power Syst. 2017;41(10):58–65. doi:10.7500/AEPS20160706008. [Google Scholar] [CrossRef]

3. Yu CY, Zhu Y, Gao GY. Control strategies for rapid power responses of doubly-fed hydro generators. J Hydroelectr Eng. 2019;38(5):89–96. doi:10.11660/slfdxb.20190510. [Google Scholar] [CrossRef]

4. Li H, Huang Z, Liu H, Song E, Xiao H, Luo L, et al. Control strategy of rapid power response for AC excited pump storage unit. Electr Power Autom Equip. 2017;37(11):156–61. doi:10.16081/j.issn.1006-6047.2017.11.025. [Google Scholar] [CrossRef]

5. Lung JK, Lu Y, Hung WL, Kao WS. Modeling and dynamic simulations of doubly fed adjustable-speed pumped storage units. IEEE Trans Energy Convers. 2007;22(2):250–8. doi:10.1109/TEC.2006.875481. [Google Scholar] [CrossRef]

6. Kruger K, Koutnik J. Dynamic simulation of pump-storage power plants with different variable speed configurations using the simsen tool. Int J Fluid Mach Syst. 2009;2(4):334–45. doi:10.5293/ijfms.2009.2.4.334. [Google Scholar] [CrossRef]

7. Chen Y, Xu W, Liu Y, Bao Z, Mao Z, Rashad EM. Modeling and transient response analysis of doubly-fed variable speed pumped storage unit in pumping mode. IEEE Trans Ind Electron. 2023;70(10):9935–47. doi:10.1109/TIE.2022.3224154. [Google Scholar] [CrossRef]

8. Huang W, Chen W, Wu J. Auxiliary frequency modulation method of DFIG-based wind turbine based on principle of power balance control. Electr Power Autom Equip. 2019;39(1):66–72. doi:10.16081/j.issn.1006-6047.2019.01.010. [Google Scholar] [CrossRef]

9. Gulzar MM, Sibtain D, Khalid M. Innovative design for enhancing transient stability with an ATFOPID controller in hybrid power systems. J Energy Storage. 2024;99:113364. doi:10.1016/j.est.2024.113364. [Google Scholar] [CrossRef]

10. Zhu Z, Pan W, Liu T, Li Y, Liu M. Dynamic modeling and eigen analysis of adjustable-speed pumped storage unit in pumping mode under power regulation. IEEE Access. 2021;9:155035–47. doi:10.1109/access.2021.3128627. [Google Scholar] [CrossRef]

11. Chen Y, Xu W, Liu Y, Rashad EM, Bao Z, Jiang J, et al. Reduced-order system frequency response modeling for the power grid integrated with the type-II doubly-fed variable speed pumped storage units. IEEE Trans Power Electron. 2022;37(9):10994–06. doi:10.1109/TPEL.2022.3166567. [Google Scholar] [CrossRef]

12. Shi L, Lao W, Wu F, Zheng T, Lee KY. Frequency regulation control and parameter optimization of doubly-fed induction machine pumped storage hydro unit. IEEE Access. 2022;10:102586–98. doi:10.1109/access.2022.3208960. [Google Scholar] [CrossRef]

13. Fan P, Ke S, Yang J, Li R, Li Y, Yang S, et al. A load frequency coordinated control strategy for multimicrogrids with V2G based on improved MA-DDPG. Int J Electr Power Energy Syst. 2023;146:108765. doi:10.1016/j.ijepes.2022.108765. [Google Scholar] [CrossRef]

14. Hu J, Niu H, Carrasco J, Lennox B, Arvin F. Voronoi-based multi-robot autonomous exploration in unknown environments via deep reinforcement learning. IEEE Trans Veh Technol. 2020;69(12):14413–23. doi:10.1109/tvt.2020.3034800. [Google Scholar] [CrossRef]

15. Fujimoto S, Hoof H, Meger D. Addressing function approximation error in actor-critic methods. In: Proceedings of the 35th International Conference on Machine Learning; 2018 Jul 10–15; Stockholm, Sweden. p. 1587–96. [Google Scholar]

16. Lillicrap TP, Hunt JJ, Pritzel A, Heess N, Erez T, Tassa Y. Continuous control with deep reinforcement learning. arXiv:1509.02971. 2015. doi:10.48550/arXiv.1509.02971. [Google Scholar] [CrossRef]