 Open Access
Open Access
ARTICLE
Optimizing Efficiency and Performance in a Rankine Cycle Power Plant Analysis
1 Department of Interdisciplinary Courses in Engineering, Chitkara University Institute of Engineering & Technology, Chitkara University, Rajpura, 140401, India
2 Jadara University Research Center, Jadara University, Irbid, 21110, Jordan
3 School of Automation, Banasthali Vidyapith, Banasthali, 304022, India
4 Applied Science Research Center, Applied Science Private University, Amman, 11931, Jordan
5 Science Engineer Laboratory for Energy, National School of Applied Sciences, Chouaib Doukkali University of EI Jadida, EI Jadida, 24000, Morocco
6 Department of Electronics and Communication Engineering, Indira Gandhi Institute of Technology, Sarang, Dhenkanal, 759146, Odisha, India
* Corresponding Author: Manish Kumar Singla. Email:
Energy Engineering 2025, 122(4), 1373-1386. https://doi.org/10.32604/ee.2025.058058
Received 03 September 2024; Accepted 06 December 2024; Issue published 31 March 2025
Abstract
Enhancing the efficiency of Rankine cycles is crucial for improving the performance of thermal power plants, as it directly impacts operational costs and emissions in light of energy transition goals. This study sets itself apart from existing research by applying a novel optimization technique to a basic ideal Rankine cycle, focusing on a specific power plant that has not been previously analyzed. Currently, this cycle operates at 41% efficiency and a steam quality of 76%, constrained by fixed operational parameters. The primary objectives are to increase thermal efficiency beyond 46% and raise steam quality above 85%, while adhering to operational limits: a boiler pressure not exceeding 15 MPa, condenser pressure not dropping below 10 kPa, and turbine temperature not surpassing 500°C. This study utilizes numerical simulations to model the effects of varying boiler pressure (Pb) and condenser pressure (Pc) within the ranges of 12 MPa < Pb < 15 MPa and 5 kPa < Pc < 10 kPa. By systematically adjusting these parameters, the proposed aim to identify optimal conditions that maximize efficiency and performance within specified constraints. The findings will provide valuable insights for power plant operators seeking to optimize performance under real-world conditions, contributing to more efficient and sustainable power generation.Keywords
The Rankine cycle, a fundamental thermodynamic process for converting heat into mechanical work, has been a cornerstone of steam power plant design since the mid-19th century [1]. While significant advancements have been made in improving the cycle’s efficiency through innovations in materials, turbine design, and operating parameters, there remains a persistent need for further optimization to meet the ever-increasing demands for energy efficiency and sustainability. The Rankine cycle, named after William John Macquorn Rankine, has been a cornerstone in the design and operation of steam power plants since the mid-19th century [1]. This thermodynamic cycle describes the process by which heat energy is converted into mechanical work, forming the basis for electricity generation in many power plants. Despite significant advancements over the years, modern power plants continue to seek further improvements in efficiency to meet growing energy demands and environmental standards [2]. However, current technologies and methods still face limitations that hinder optimal performance. For instance, many existing studies have not adequately addressed the operational constraints or explored the full potential of pressure optimizations within the Rankine cycle. This study aims to fill this research gap by focusing on these specific challenges, proposing innovative solutions to enhance the cycle’s efficiency [3].
The essential focuses on analyzing the overall performance of a strength plant operating on a primary perfect Rankine cycle. The Rankine cycle is a fundamental thermodynamic cycle utilized in steam power generation, generally achieving a maximum efficiency of round 41% below standard conditions [2]. However, advancements in era and optimization techniques provide the ability to significantly improve this efficiency. The primary objective to enhance the strength plant’s performance to over 46% while simultaneously growing steam first-rate from 76% to above 85%. These improvements to be achieved within the constraints of boiler and condenser pressures, and without exceeding a turbine temperature of 500°C [3–6]. This takes a look at delve into the overall performance analysis of a power plant working on an idealized Rankine cycle. The Rankine cycle is a fundamental thermodynamic cycle hired in steam energy generation, usually attaining a most performance of about 41% underneath standard operating situations [2]. Nevertheless, improvements in technology and optimization strategies present opportunities for improvements in this performance.
The primary objective of this task is to enhance the strength plant’s performance to surpass 46%, whilst concurrently increasing steam best from 46% to over 85%. These enhancements ought to be attained at the same time as adhering to constraints on boiler and condenser pressures, and making sure that the turbine temperature does not surpass 500°C [3–6]. The objective of this research is to enhance the cycle performance addressing the restrictions of previous optimizations. By analyzing the advancements and analysis out the chronic inefficiencies, this examine justifies the need for further research and development. The transition from past achievements to current objectives highlights the continuous evolution of the Rankine cycle and underscores the necessity for ongoing enhancements. This have a look at now not best targets to enhance the efficiency of the Rankine cycle however additionally to provide a comprehensive analysis of the operational constraints and capability optimizations that have been overlooked in earlier studies. This approach ensures a greater cohesive expertise of the cycle’s capabilities and paves the manner for destiny improvements in steam electricity plant technology.
The main contributions of this work lie in its systematic approach to optimizing steam power cycles through innovative enhancements in both efficiency and steam quality, particularly by maintaining a minimum dryness fraction of 85%. Initially focused on steam quality, the introduction of a reheating mechanism and fixed first regeneration pressures only yielded a modest efficiency of approximately 46%. To address this, a second regeneration stage was implemented, alongside a MATLAB (Matrix Laboratory) function designed to analyze and identify optimal second regeneration pressures, leading to improved cycle efficiency. Furthermore, the exploration of boiler and condenser pressures, with the same steam quality constraint, allowed for a comprehensive evaluation of their impact on overall system performance. By employing iterative computational analysis to visualize the relationships between various pressures, efficiency, and work output, this work demonstrates a significant advancement in the design and optimization of steam power cycles, combining theoretical principles with practical computational tools for enhanced energy performance.
This paper aims to investigate the enhancement of power plant efficiency operating on an ideal Rankine cycle. The project’s objective is enhancing the efficiency from 41% to over 46% and to increase steam quality from 76% to above 85%, while maintaining constraints on boiler pressure (15 MPa), condenser pressure (10 kPa), and turbine temperature (500°C). The study will also explore the impact of varying boiler and condenser pressures within specified ranges to understand their effects on overall system performance. This investigation builds on existing research and seeks to implement practical solutions to enhance power plant efficiency and performance.
Several research have explored methods to improve Rankine cycle overall performance and plant performance. To optimize the efficiency of a Rankine cycle, this consists of enhancing circuit parameters and improving components [6], also show in Table 1. His studies specialize in the results of boiler pressurization and warmth trade system enhancements on general performance. The Rankine cycle stays the cornerstone of thermal energy era. And many research goal to improve common overall performance and efficiency. This assessment synthesizes current studies exploring diverse techniques. From optimizing circuit parameters to optimizing the performance of the components [7,8].
Cycle parameter optimization analyzing a comprehensive approach aimed toward optimizing the Rankine cycle, their research highlights the importance of changing important cycle parameters consisting of boiler pressure and exchange strategies. The authors located a substantial development in thermal performance because of better steam temperature and stress. This consequences in accelerated strength production in line with cycle [8,9]. Additionally, their study well-known shows advances in heat exchange era that facilitate extra efficient heat conduction. These findings highlight the importance of operational and technological enhancements to optimize the Rankin cycle [9,10].
The role of superheating and reheating extended the optimization strategy by exploring the role of superheating and reheating in the Rankine cycle [8]. Their work showed that improvements Steam quality through superheating not only increases thermal efficiency. but also increases the efficiency of the overall circuit. This indicates a direct relationship, which is important in preventing turbine blade erosion. Their results suggest that the adjustment of cycle parameters is systematic. This is especially true with respect to superheating and reheating steps. It can provide significant benefits in terms of thermal efficiency and operational reliability [11–13].
Effects of Condenser and Boiler Pressures Rankine focused on the important role of condenser and boiler pressures in determining circuit performance [13]. Their research revealed that fine-tuning these pressures over a specific operating range It can obviously improve the efficiency and stability of the circuit. deserved because these things cause Imbalance in the chakras Their work in identifying the most appropriate pressure settings generated valuable insights into operational strategies that can increase the efficiency and longevity of power plant components [14,15]. The results suggest that careful management of these parameters is essential to achieve a stable and efficient Rankin cycle [16]. The body of literature shows clear approaches to improving the efficiency of the Rankin cycle through various methods [11]. These studies contribute to a deeper understanding of how to increase the efficiency of thermal power plants to the maximum. As the demand for efficient energy production increases from optimizing circuit parameters to improving component technology to fine adjustment of operating pressure, it may be useful to consider the interaction of various factors affects the efficiency of the circuit. As a result, the power generation system will be more robust and efficient [17,18].
The Rankine cycle is a fundamental thermodynamic process widely employed in various vapor power plants, including coal-fired and nuclear power plants. This ideal cycle comprises four critical intermediate steps, each occurring in a distinct component: the pump, boiler, turbine, and condenser, such as shown in Fig. 1. Water, the working fluid in this cycle, undergoes multiple phase changes as it progresses through these stages [19].
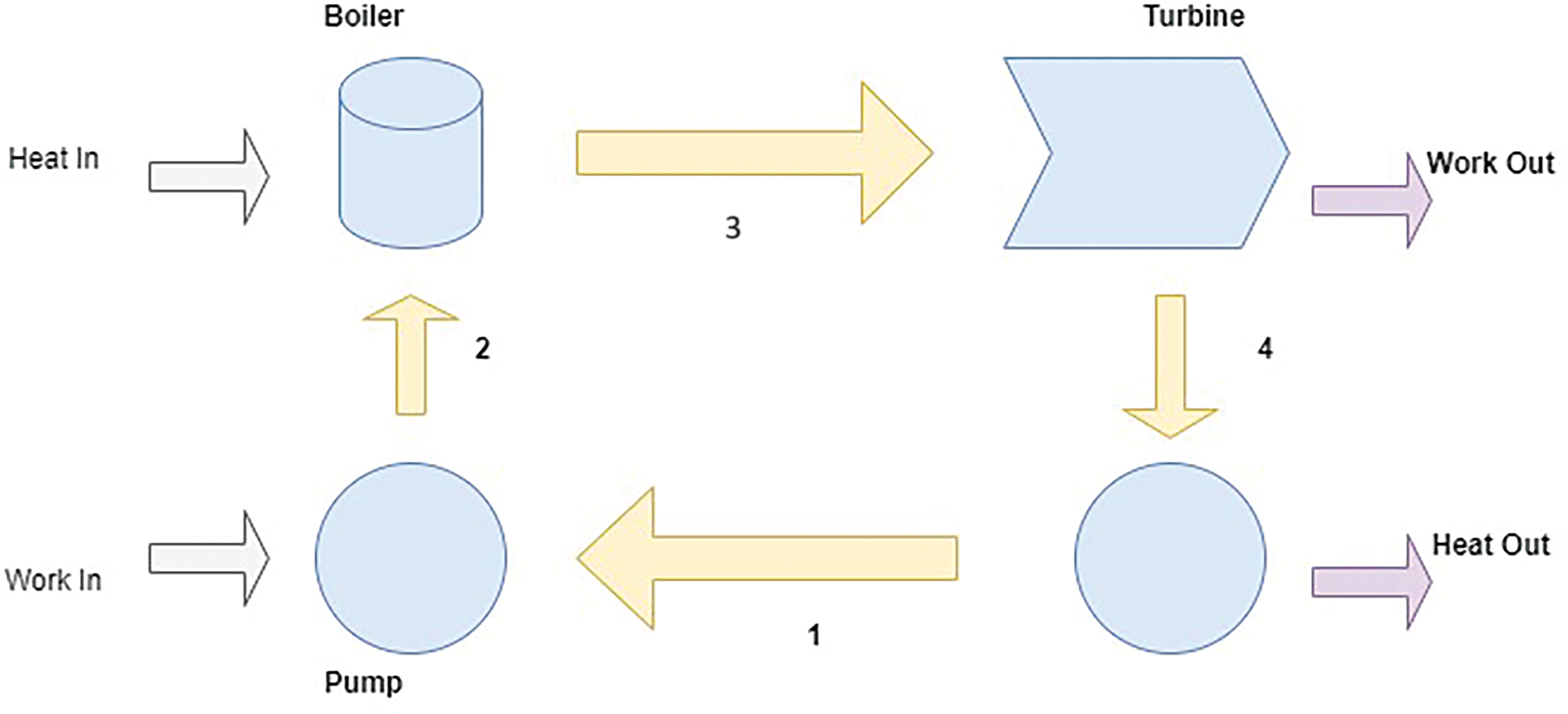
Figure 1: Ideal Rankine cycle block diagram
The process begins with. In this initial step, water in its saturated liquid state is compressed is entropically isentropic compression in the pump, meaning it is compressed in such a way that entropy remains constant. This compression increases the pressure of the water until it reaches the operational pressure of the boiler. As the water is compressed, its specific volume decreases, which consequently raises its temperature [20].
Following compression, the water enters the boiler, where it undergoes constant-pressure heat addition. Here, the water is heated at a constant pressure, turning it into superheated vapor. The heat required for this transformation is typically sourced from the combustion of coal in coal power plants or from nuclear reactions in nuclear reactors [21]. This stage is crucial as it supplies the thermal energy necessary for the subsequent work-producing phase.
The superheated vapor then moves to the turbine, where it undergoes isentropic expansion. In the turbine, the vapor expands is entropically, which means that the process occurs without any change in entropy. During this expansion, the vapor does work on the turbine blades, which translates into mechanical energy output. As the vapor expands, both its pressure and temperature drop, and it transitions into a liquid-vapor mixture with high steam quality [21,22].
Finally, the liquid-vapor mixture flows into the condenser, where constant-pressure heat rejection takes place. In the condenser, the mixture is cooled and condensed at constant pressure by rejecting heat to an external reservoir, such as a lake, river, or the atmosphere. As a result of this heat rejection, the mixture transforms into a saturated liquid, ready to be pumped back to the boiler. This completed cycle of phase changes and energy transfers ensures that the Rankine cycle remains continuous and efficient in power generation [22–24]. The Rankine cycle, a thermodynamic cycle used in steam power plants, is often depicted using a temperature-entropy (T-s) diagram, such as shown in Fig. 2. This diagram visually illustrates the four main processes involved. Firstly, a liquid is compressed from low to high pressure, represented by a vertical line. Secondly, the liquid is heated at constant pressure in a boiler, transforming it into a superheated vapor. Thirdly, the superheated vapor expands in a turbine, producing work. Finally, the vapor is condensed at constant pressure in a condenser, returning to a liquid state, shown as a horizontal line [25].
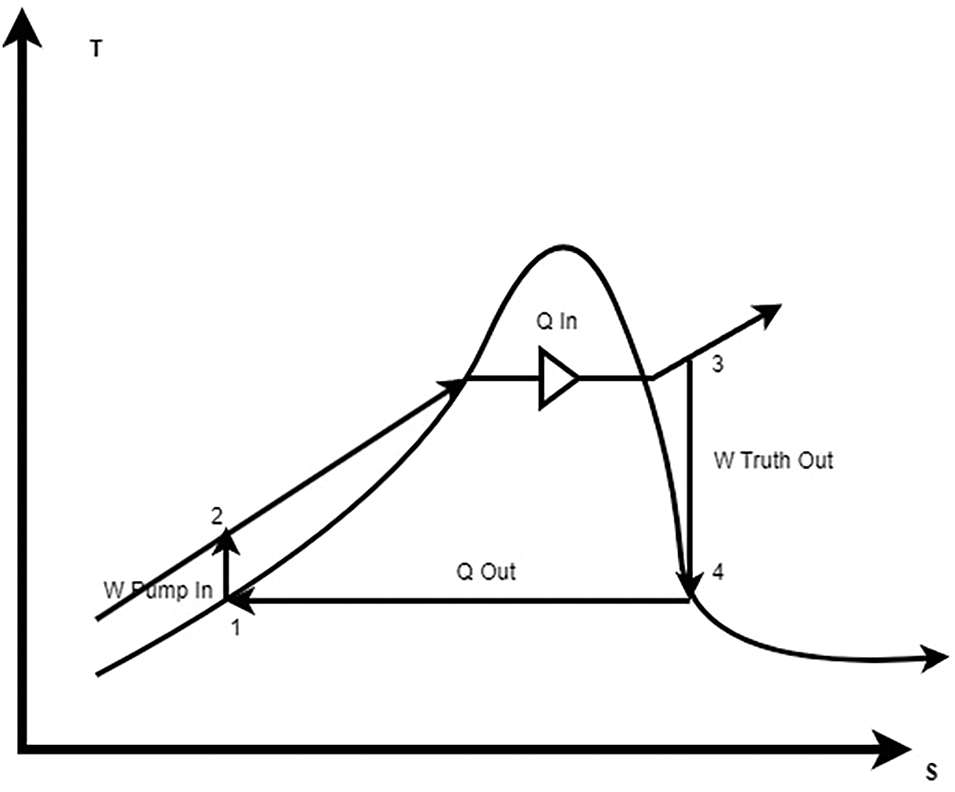
Figure 2: Graphical representation of the Rankine cycle
Reheating in a Rankine cycle is a technique used to improve the overall efficiency of a steam power plant. In a traditional Rankine cycle, steam generated in the boiler expands through the turbine, producing work, and is then condensed in the condenser before being pumped back to the boiler [23]. Reheating involves taking the steam at an intermediate pressure, after it has partially expanded through the turbine, and then raising its temperature back to a high level before allowing it to expand further through a second turbine stage. The steps of a Rankine cycle with reheating are the same as that of a traditional Rankine cycle, except that of the intermediate step of reheating the purpose of reheating is to avoid the high moisture content that can occur at the exit of a high-pressure turbine. Moisture in the steam can lead to erosion and damage to the turbine blades. Reheating allows the steam to be returned to a high-temperature, high-pressure state before it expands further, reducing the moisture content and improving the overall efficiency of the cycle [26,27].
In a Rankine cycle, a closed feedwater heater is a type of heat exchanger used to preheat the feedwater before it enters the boiler. The feedwater is the water that is supplied to the boiler to be converted into steam. The purpose of preheating the feedwater is to improve the overall efficiency of the power plant by reducing the amount of heat that needs to be added in the boiler [28].
In a closed feedwater heater, the extracted steam from the turbine is passed through one side of the heat exchanger, while the cold feedwater is passed through the other side. The heat from the steam is transferred to the feedwater, raising its temperature before it enters the boiler, reducing the amount of heat that needs to be added in the boiler to achieve the desired steam conditions, thereby improving the efficiency of the Rankine cycle. The term “closed” refers to the fact that the water and steam sides of the heat exchanger are physically separated, and there is no direct mixing of the two fluids, come to the second part of the question, which involves changing the Boiler and Condenser pressures [28,29].
To first fixed the steam quality once again at 85%. This fixed the pressure for reheating and first regeneration. For the second regeneration pressure, to fix the value of the optimum pressure obtained from the first part. The created another function in MATLAB which took the boiler and condenser pressures as inputs and returned efficiency and work output of the cycle as outputs. This was done using loops and updating the values of boiler and condenser pressures and inputting them to the function we created and stored the data in arrays and plotted graphs for the same to visualize the variation in the required quantities [30,31].
3.3 Energy Balance Equations for the Rankine Cycle
The Rankine cycle, a fundamental thermodynamic cycle for power generation, involves four primary components: the pump, boiler, turbine, and condenser. Applying the steady-flow energy equation to each component, we can derive the following energy balance equations:
In the pump, the liquid water is compressed is entropically from Eqs. (1) to (2). Assuming negligible kinetic and potential energy changes and neglecting any heat transfer, the energy balance equation for the pump is:
where,
In the boiler, heat is added to the water, converting it into high-pressure steam. The energy balance equation for the boiler, neglecting kinetic and potential energy changes and assuming no work input, is:
where,
In the turbine, the high-pressure steam expands isentropically, generating work. The energy balance equation for the turbine, neglecting kinetic and potential energy changes and assuming no heat transfer, is:
where,
In the condenser, the steam is condensed into liquid water. The energy balance equation for the condenser, neglecting kinetic and potential energy changes and assuming no work input, is:
where,
By combining these equations and considering the net work output (
The main goal is to improve a steam power cycle in two ways: increase efficiency and ensure high-quality steam (at least 85% dryness fraction). We also wanted to understand how boiler and condenser pressures affect performance. First, we focused on steam quality. We implemented reheating, setting a minimum quality threshold of 85%. Additionally, we fixed the first regeneration pressure to match the reheat pressure. Unfortunately, this approach only achieved an efficiency of around 46%.
Seeking further improvement, we introduced a second regeneration stage. To optimize this, we developed a function in MATLAB that calculated cycle efficiency for various second regeneration pressures. Running this function for different pressures allowed us to identify the configuration with the highest efficiency (optimal pressure). We also visualized this relationship by plotting efficiency against the second regeneration pressure.
Next, we explored the impact of boiler and condenser pressures. Again, we maintained a minimum steam quality of 85%, which determined the reheat and first regeneration pressures. We used the optimal second regeneration pressure we found earlier. Another function was created in MATLAB, this time taking boiler and condenser pressures as inputs and calculating both efficiency and work output. By utilizing loops, we iterated through various pressure combinations, feeding them into the function. Efficiency and work output data were stored for each combination. Finally, we plotted these results to visualize how efficiency and work output change with varying boiler and condenser pressures. This process demonstrates a systematic approach to optimizing a steam power cycle using computational tools. By combining reheating, multi-stage regeneration, and software-driven analysis, we achieved significant improvements in both efficiency and steam quality.
From the graph provided in below figures, it becomes evident that identifying the optimal pressure for the second regeneration stage is crucial for enhancing the efficiency of the Rankine cycle. Our project involved two primary objectives: first, to increase the overall efficiency of the cycle while simultaneously improving steam quality; and second, to investigate how varying the boiler and condenser pressures affects the efficiency and work output of the system. To address the first objective, we focused on improving steam quality through the implementation of reheating. We established that the steam quality needed to be maintained at a minimum threshold of 85%. This required us to set the pressure for the first regeneration stage equal to the pressure used during reheating. Despite these adjustments, our results showed that achieving an efficiency greater than 46% remained elusive.
To further enhance efficiency, decided to introduce a further regeneration cycle. This caused our next step of task is determining out the superior pressure for this 2nd regeneration stage to maximize cycle performance. To accomplish this, the applied MATLAB with Cantera for our calculations. And to develop a characteristic in MATLAB that computed the performance of the Rankine cycle for numerous values of 2d regeneration pressure. This statistic was systematically stored in an array, which allowed us to analyze and pick out the most efficiency workable and the corresponding foremost stress. Additionally, we created a graph plotting efficiency in opposition to 2d regeneration pressure in Fig. 3. This visible illustration enabled us to have a look at and analyze how efficiency varied with one-of-a-kind stress settings, offering precious insights into the connection among pressure and overall performance in the second regeneration stage. Through this system, we were capable of pinpoint the choicest strain that offered the best efficiency, thereby substantially enhancing the overall performance of the Rankine cycle.
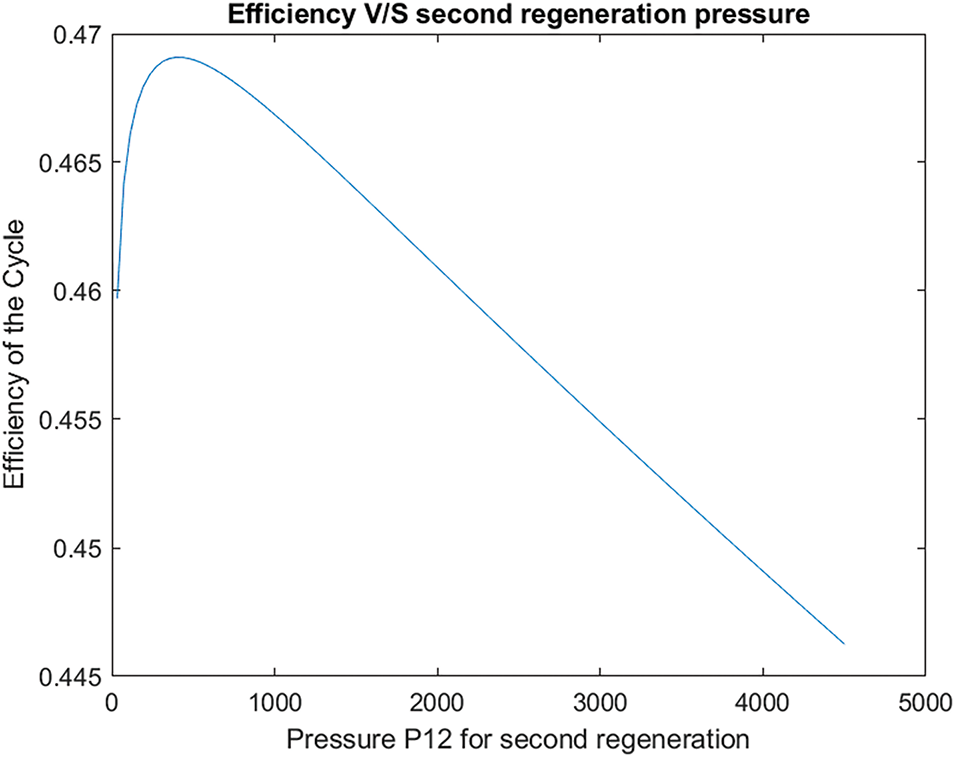
Figure 3: The plotting efficiency against second regeneration pressure
From the graph presented, it is evident that the efficiency of the Rankine cycle exhibits a decline as the condenser pressure increases, shown in Fig. 4. To generate this graph, we maintained the boiler pressure at a constant 12 MPa while varying only the condenser pressure. The results demonstrate that the modified cycle achieves its maximum efficiency of approximately 48.7% when the condenser pressure is set to 5 kPa.
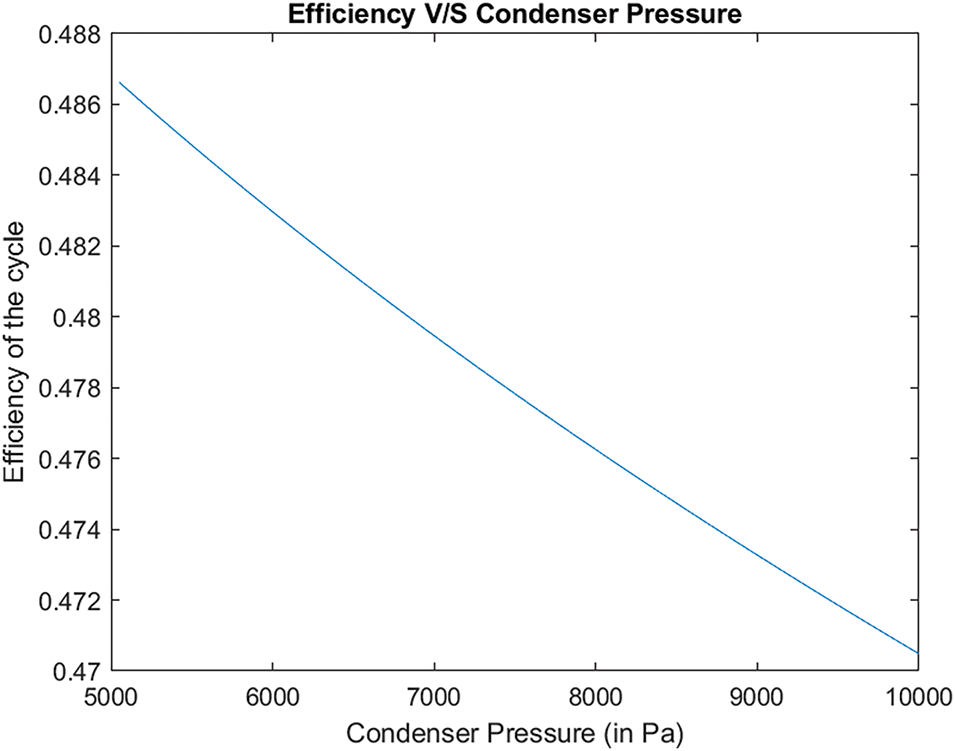
Figure 4: The efficiency against condenser pressure
In addition to efficiency, the work output of the cycle also shows in Fig. 5 of a similar trend in response to changes in condenser pressure. The graph reveals that the maximum work output occurs at a condenser pressure of 5 kPa and a boiler pressure of 15 MPa. Under these conditions, the maximum work output reaches around 1.33 MW.
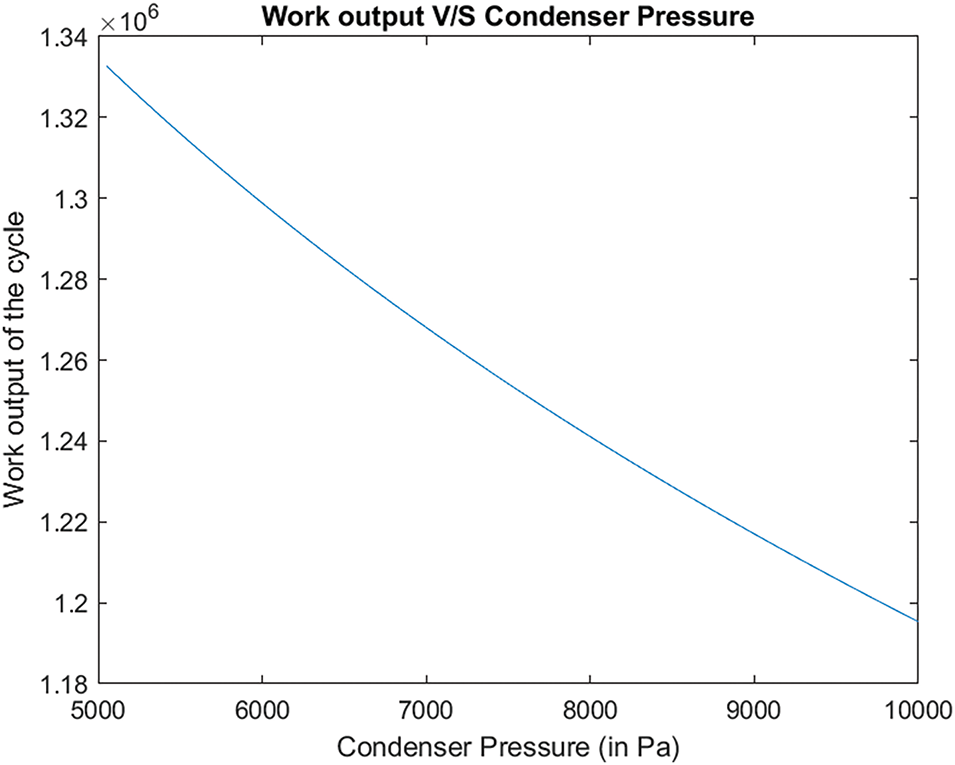
Figure 5: Work output vs. condenser pressure
The observed decrease in efficiency with increasing condenser pressure can be attributed to the increased thermal resistance in the condenser, which hampers the effective rejection of heat and thus reduces the cycle’s overall performance. Conversely, the work output is optimized at lower condenser pressures, as the lower pressure facilitates a greater expansion of steam, thereby generating more work. These findings underline the critical balance required in optimizing condenser pressure to achieve both high efficiency and substantial work output in the Rankine cycle.
Looking at the graph below, we observe how work output changes with variations in boiler pressure, such as shown in Fig. 6. The data clearly shows that as boiler pressure increases, the work output also rises. This trend is similarly observed in the efficiency of the cycle, such as shown in Fig. 7 of efficiency with respect to boiler pressure. Specifically, at a constant condenser pressure of 10 kPa, the cycle achieves its peak work output of approximately 1.195 MW when the boiler pressure reaches 15 MPa. Additionally, the cycle’s maximum efficiency reaches 47.1% under these conditions.
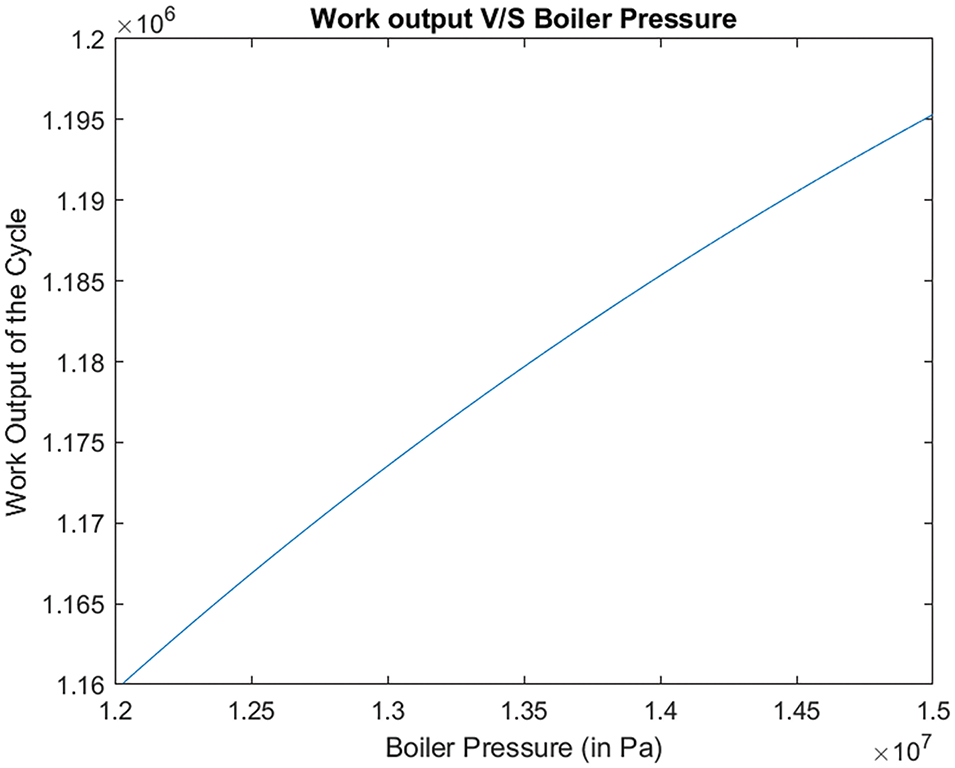
Figure 6: The work output changes in boiler pressure
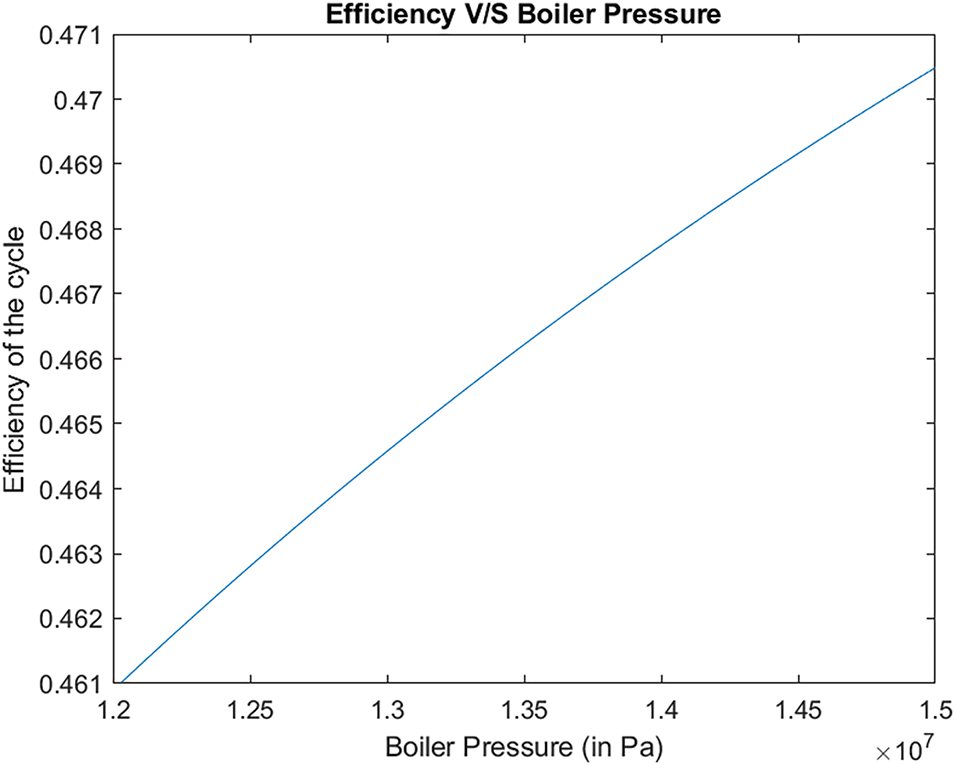
Figure 7: The efficiency changes in boiler pressure
The results indicate that the optimal pressure for the second regeneration stage, maximizing efficiency, is 3.9129 × 106 Pa, with the initial maximum efficiency recorded at 46.91% while maintaining a low-pressure turbine outlet quality of 85%. Analysis of the cycle’s performance reveals that efficiency decreases with increasing condenser pressure. Specifically, when the boiler pressure is held constant at 12 MPa and the condenser pressure is varied, the modified cycle achieves a maximum efficiency of approximately 48.7% at a condenser pressure of 5 kPa. This trend is mirrored in the work output, with maximum output occurring at a condenser pressure of 85 kPa and a boiler pressure of 15 MPa, yielding around 1.33 MW.
Further examination of the relationship between work output and boiler pressure shows a clear increasing trend; at a constant condenser pressure of 10 kPa, the cycle reaches a maximum work output of 1.195 MW at a boiler pressure of 15 MPa, corresponding to a maximum efficiency of 47.1%. This behavior can be attributed to the interplay between boiler and condenser pressures: as boiler pressure rises, the working fluid’s temperature and specific enthalpy also increase, enhancing turbine performance and, consequently, the overall efficiency of the cycle. The findings underscore the critical balance between maximizing boiler pressure and minimizing condenser pressure to optimize steam cycle performance effectively.
Several factors contribute to the observed behavior of the cycle. Optimal performance is achieved with the highest possible boiler pressure and the lowest possible condenser pressure. As the boiler pressure rises, the temperature of the working fluid also increases, leading to a higher specific enthalpy. This increase in specific enthalpy translates to greater work output from the turbine, which, in turn, enhances the cycle’s efficiency. Therefore, maximizing the boiler pressure while minimizing the condenser pressure results in the most efficient and effective cycle performance. The analyse and connect the results regarding the impact of condenser and boiler pressure on the Rankine cycle’s efficiency and work output shown in Table 2.

This study has demonstrated that significant improvements in Rankine cycle efficiency can be achieved through careful optimization of operating parameters. By setting the boiler pressure at 15 MPa and the condenser pressure at 10 kPa, while maintaining the turbine temperature below 500°C, the cycle’s efficiency can be increased from 41% to 47.1%, and steam quality can be elevated from 76% to 85%. The findings of this study have important implications for the design and operation of steam power plants. An efficiency of 47.1% represents a substantial improvement over traditional Rankine cycle performance, leading to increased energy output, reduced fuel consumption, and lower operational costs. This achievement establishes a new benchmark for the industry and offers a valuable optimization strategy for existing power plants. The graph clearly demonstrates that increasing the boiler pressure leads to enhanced work output and improved efficiency. At a boiler pressure of 15 MPa and a constant condenser pressure of 10 kPa, the cycle achieves its maximum work output of approximately 1.195 MW and an efficiency of 47.1%. These results highlight the importance of optimizing both boiler and condenser pressures to improve overall cycle performance. Higher boiler pressures increase the working fluid’s temperature and specific enthalpy, leading to greater turbine work output and enhanced efficiency.
Furthermore, these results contribute to addressing broader energy challenges. By improving the efficiency of steam power generation, this study helps to reduce greenhouse gas emissions and enhance energy security. The insights gained from this research can inform the development of future power plant designs that incorporate more efficient Rankine cycle configurations and potentially explore advanced technologies such as supercritical or ultra-supercritical cycles.
To further enhance the cycle’s efficiency past 46% and improve steam exceptional to over 85%, future research has to discover several key areas. Investigating the consequences of extending the boiler pressure beyond 15 MPa and reducing the condenser strain under 5 kPa should provide additional performance upgrades. Additionally, advancing substances and technology to withstand better temperatures and pressures may be essential for properly accomplishing those goals. Exploring alternative working fluids with advanced thermodynamic homes, optimizing heat recuperation systems, and growing dynamic manipulate strategies may even make a contribution to maximizing efficiency. Comprehensive monetary and environmental impact assessments will ensure that performance profits are balanced with price and sustainability. Enhanced simulation and modeling strategies will similarly help these advancements through presenting more accurate predictions and insights materials.
Acknowledgement: The authors would like to thanks the Department DICE, CUIET, Chitkara University, Punjab for providing useful infrastructure and support to carry out various studies related to this paper.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Ramesh Kumar, Manish Kumar Singla; data collection: Abdullah Bin Queyam; Mohamed Louzazni, Dipak Kumar Mishra drafted manuscript preparation. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Nomenclature
| Pa | Pressure unit |
| Pb | Boiler pressure |
| Pc | Condenser pressure |
| °C | Temperature unit |
| x | Steam quality |
References
1. Rankine WJM. On the thermo-dynamic theory of steam-engines with dry saturated steam, and its application to practice. Philos Trans R Soc Lond. 1859;149:177–92. doi:10.1098/rstl.1859.0010. [Google Scholar] [CrossRef]
2. Chen H, Goswami DY, Stefanakos EK. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew Sustain Energy Rev. 2010;14(9):3059–67. doi:10.1016/j.rser.2010.07.006. [Google Scholar] [CrossRef]
3. Desai NB, Bandyopadhyay S. Process integration of organic Rankine cycle. Energy. 2009;34(10):1674–86. doi:10.1016/j.energy.2009.04.037. [Google Scholar] [CrossRef]
4. Bao J, Zhao L. A review of working fluid and expander selections for organic Rankine cycle. Renew Sustain Energy Rev. 2013;24(8):325–42. doi:10.1016/j.rser.2013.03.040. [Google Scholar] [CrossRef]
5. Macchi E, Astolfi M. Organic rankine cycle (ORC) power systems: technologies and applications. Cambridge, UK: Woodhead Publishing; 2016. [Google Scholar]
6. Alrbai M, Al-Dahidi S, Alahmer H, Al-Ghussain L, Al-Rbaihat R, Hayajneh H, et al. Integration and optimization of a waste heat driven organic Rankine cycle for power generation in wastewater treatment plants. Energy. 2024;308:132829. doi:10.1016/j.energy.2024.132829. [Google Scholar] [CrossRef]
7. Hu S, Yang Z, Li J, Duan Y. A review of multi-objective optimization in organic Rankine cycle (ORC) system design. Energies. 2021;14(20):6492. [Google Scholar]
8. Wang J, Tian H, Wang X, Li L, Sun R, Bian X, et al. Process design methodology for Rankine cycle based on heat matching. Renew Sustain Energy Rev. 2024;193:114295. doi:10.1016/j.rser.2024.114295. [Google Scholar] [CrossRef]
9. Nie X, Xue J, Zhao L, Deng S, Xiong H. New insight of thermodynamic cycle in thermoelectric power generation analyses: literature review and perspectives. Energy. 2024;292(20):130553. doi:10.1016/j.energy.2024.130553. [Google Scholar] [CrossRef]
10. Zhang Y, Tsai YC, Ren X, Tuo Z, Wang W, Gong L, et al. Experimental study of the external load characteristics on a micro-scale organic Rankine cycle system. Energy. 2024;306:132453. doi:10.1016/j.energy.2024.132453. [Google Scholar] [CrossRef]
11. Sprouse CE III. Review of organic Rankine cycles for internal combustion engine waste heat recovery: latest decade in review. Sustainability. 2024;16(5):1924. doi:10.3390/su16051924. [Google Scholar] [CrossRef]
12. Corigliano O, Algieri A, Fragiacomo P. Turning data center waste heat into energy: a guide to organic Rankine cycle system design and performance evaluation. Appl Sci. 2024;14(14):6046. doi:10.3390/app14146046. [Google Scholar] [CrossRef]
13. Moradi R, Cioccolanti L. Modelling approaches of micro and small-scale organic Rankine cycle systems: a critical review. Appl Therm Eng. 2023;236(21):121505. doi:10.1016/j.applthermaleng.2023.121505. [Google Scholar] [CrossRef]
14. Elwardany M. Enhancing steam boiler efficiency through comprehensive energy and exergy analysis: a review. Process Saf Environ Prot. 2024;184(1):1222–50. doi:10.1016/j.psep.2024.01.102. [Google Scholar] [CrossRef]
15. Elwardany M, Abdelrazik AS, Fathi H, Omar AMA, Abdelkawy N. Practicality and economic assessment on using the solar organic Rankine cycle as a power source for a specific membrane-based desalination system. Water Conserv Sci Eng. 2024;9(2):46. doi:10.1007/s41101-024-00273-9. [Google Scholar] [CrossRef]
16. Chu S, Majumdar A. Opportunities and challenges for a sustainable energy future. Nature. 2022;488(7411):294–303. doi:10.1038/nature11475. [Google Scholar] [PubMed] [CrossRef]
17. Gruber S, Rola K, Urbancl D. Recent advances in ejector-enhanced vapor compression heat pump and refrigeration systems—a review. Energies. 2024;17(16):4043. doi:10.3390/en17164043. [Google Scholar] [CrossRef]
18. Dahham RY, Wei H, Pan J. Improving thermal efficiency of internal combustion engines: recent progress and remaining challenges. Energies. 2022;15(17):6222. doi:10.3390/en15176222. [Google Scholar] [CrossRef]
19. Xu W, Li H, Mao SS, Deng S. Towards novel low temperature thermodynamic cycle: a critical review originated from organic Rankine cycle. Appl Energy. 2020;270(9):115186. doi:10.1016/j.apenergy.2020.115186. [Google Scholar] [CrossRef]
20. Xu W, Zhao R, Deng S, Zhao L, Mao SS. Is zeotropic working fluid a promising option for organic Rankine cycle: a quantitative evaluation based on literature data. Renew Sustain Energy Rev. 2021;148:111267. doi:10.1016/j.rser.2021.111267. [Google Scholar] [CrossRef]
21. Schilling J, Entrup M, Hopp M, Gross J, Bardow A. Towards optimal mixtures of working fluids: integrated design of processes and mixtures for Organic Rankine Cycles. Renew Sustain Energy Rev. 2021;135(10):110179. doi:10.1016/j.rser.2020.110179. [Google Scholar] [CrossRef]
22. Giménez-Prades P, Navarro-Esbrí J, Arpagaus C, Fernández-Moreno A, Mota-Babiloni A. Novel molecules as working fluids for refrigeration, heat pump and organic Rankine cycle systems. Renew Sustain Energy Rev. 2022;167(12):112549. doi:10.1016/j.rser.2022.112549. [Google Scholar] [CrossRef]
23. Al-Sayyab AKS, Mota-Babiloni A, Navarro-Esbrí J. Renewable and waste heat applications for heating, cooling, and power generation based on advanced configurations. Energy Convers Manag. 2023;291:117253. doi:10.1016/j.enconman.2023.117253. [Google Scholar] [CrossRef]
24. Tian H, Liu P, Shu G. Challenges and opportunities of Rankine cycle for waste heat recovery from internal combustion engine. Prog Energy Combust Sci. 2021;84(5):100906. doi:10.1016/j.pecs.2021.100906. [Google Scholar] [CrossRef]
25. Ma X, Zhao X, Zhang Y, Liu K, Yang H, Li J, et al. Combined Rankine cycle and dew point cooler for energy efficient power generation of the power plants: a review and perspective study. Energy. 2022;238:121688. doi:10.1016/j.energy.2021.121688. [Google Scholar] [CrossRef]
26. Ohji A, Haraguchi M. Steam turbine cycles and cycle design optimization: the Rankine cycle, thermal power cycles, and IGCC power plants. In: Tadashi T, editor. Advances in steam turbines for modern power plants. Cambridge, UK: Woodhead Publishing; 2017. p. 11–40. doi:10.1016/B978-0-08-100314-5.00002-6. [Google Scholar] [CrossRef]
27. Anastasovski A, Rasković P, Guzović Z. A review of heat integration approaches for organic Rankine cycle with waste heat in production processes. Energy Convers Manag. 2020;221:113175. doi:10.1016/j.enconman.2020.113175. [Google Scholar] [CrossRef]
28. Tariq MU, Ali R, Haris SM, Ali S. Performance analysis of advanced nuclear power plant with variation of sea water temperature. Mater Proc. 2024;17(1):21. doi:10.3390/materproc2024017021. [Google Scholar] [CrossRef]
29. VSaxena VK, Kumar R, Kumar S. Energy, exergy, sustainability and environmental emission analysis of coal-fired thermal power plant. Ain Shams Eng J. 2024;15(2):102416. doi:10.1016/j.asej.2023.102416. [Google Scholar] [CrossRef]
30. Zhou J, Huang D, Zhou L. Modeling and thermal economy analysis of the coupled system of compressed steam energy storage and Rankine cycle in thermal power plant. Energy. 2024;291(1):130309. doi:10.1016/j.energy.2024.130309. [Google Scholar] [CrossRef]
31. Choudhary NK, Karmakar S. Thermoeconomic analysis of organic Rankine cycle with different working fluids for waste heat recovery from a coal-based thermal power plant. J Therm Anal Calorim. 2024;149(16):8873–84. doi:10.1007/s10973-024-13142-3. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools