An Equivalent Fuel Consumption Minimizing Strategy for Fuel Cell Ships Considering Power Degradation

1  Introduction

Fuel cell ships are seen as a key innovation in future maritime transportation due to their environmentally friendly attributes, including zero emissions, quiet operation, and high efficiency [1]. However, fuel cells suffer from limitations like slow response times and weak dynamic performance, which can impair the vessel’s capabilities, particularly during startup and acceleration. As a result, their real-time responsiveness and dynamic behavior are significantly less effective compared to traditional propulsion systems [2]. To address this issue, researchers are increasingly exploring the integration of auxiliary energy storage systems, such as supercapacitors and batteries, to enhance the dynamic effectiveness and productivity of fuel cell systems [3].

In fuel cell and battery hybrid power ships, hydrogen fuel is converted to electricity through the onboard fuel cells system to meet most of the ship’s energy requirements. The onboard batteries are used to store renewable energy and meet peak power demands. This is because the large fluctuations in fuel cell output power and high-current output power can accelerate the catalyst detachment of the proton exchange membrane, leading to performance degradation and shortened lifespan of the fuel cells. Batteries, on the other hand, can operate under high currents, compensating for the weaknesses of fuel cells [4]. Unlike pure electric ships, the energy system of hybrid fuel cell-powered ships can be downsized, thereby reducing the overall weight and cost of the ship, saving ship space.

In hybrid power systems, batteries often experience frequent power fluctuations, which can lead to unexpected degradation [5]. However, supercapacitors rely on the principle of electric double-layer capacitance and the charge separation mechanism rather than chemical reactions, which results in minimal performance degradation. To mitigate battery degradation, supercapacitors are combined with batteries to form a hybrid energy storage system (HESS) [6]. In a HESS, supercapacitors manage power demand fluctuations, thereby reducing battery wear and allowing batteries to provide stable power output. This integration of batteries and supercapacitors is regarded as an effective ESS topology [7].

Integrating a HESS into fuel cell hybrid power systems effectively extends the lifespan of fuel cells and reduces the frequency of battery charging and discharging, thereby enhancing overall system efficiency and reliability. The FC-HESS system comprises three power sources: fuel cells, batteries, and supercapacitors, each with distinct dynamic characteristics that collectively meet diverse power demands across different time scales. However, the key challenge lies in developing an efficient energy control strategy to regulate power distribution between the energy sources and the DC bus, ensuring optimal dynamic response, maximizing energy utilization, and prolonging the system’s operational lifespan.

There has been considerable research on energy control strategies for hybrid power systems. Among them, ECMS has been widely studied due to its small computational burden, simple structure, effective control, and real-time optimization [8]. ECMS is a real-time optimization approach that does not depend on prior information about the complete driving cycle of the ship. This approach primarily transforms the energy of batteries and supercapacitors into equivalent hydrogen consumption (EHC), optimizing the EHC per cycle to achieve the best fuel efficiency for the system. The conventional equivalent consumption minimization strategy is the simplest and earliest optimization method for reducing EHC. It includes only a penalty factor for the battery state of charge (SOC), with upper (SOCH) and lower (SOCL) limits. For instance, Wang et al. [9] used the SOC to guide the values of equivalent factors, which is relatively easy to implement with simple control logic. However, its functionality is relatively limited. To improve the dynamic response performance of hybrid energy storage systems, Ge et al. [10] proposed the design of a fuzzy logic controller. This controller enhances the ECMS by adaptively adjusting the equivalent factors in real-time, optimizing the fuel cell system’s operating point, and improving overall system efficiency. However, the degradation effects of fuel cells and batteries on the system were not considered. Of course, there are many other research results on the application of ECMS in hybrid power systems. For example, Li et al. [11] considered a fuel cell hybrid vehicle composed of fuel cells, batteries, and supercapacitors. They proposed an ECMS based on sequential quadratic programming, defined as SECMS. Compared to rule-based control strategies, the EHC was reduced by 2.16%, but the impact of fuel cells and batteries degradation on the system was not taken into account. Li et al. [12] studied a hybrid power vehicle with fuel cells, batteries, and supercapacitors, and developed an ECMS strategy that considers fuel cells degradation. However, their work only considered fuel cells degradation without considering batteries degradation. As the batteries degrade over time, the battery capacity decreases and internal resistance increases, resulting in a reduction in the battery’s output voltage. Therefore, the formulation of the EHC minimization strategy should involve multi-objective optimization. While considering minimizing EHC for fuel cells, it should also aim to reduce the EHC for batteries and supercapacitors.

To address the above issue, considering the superior power density of supercapacitors and the substantial energy density of fuel cells and batteries, a control strategy is developed to reduce equivalent fuel consumption, taking into consideration the degradation factors of both fuel cells and batteries.

The method proposed in this paper primarily contributes to:

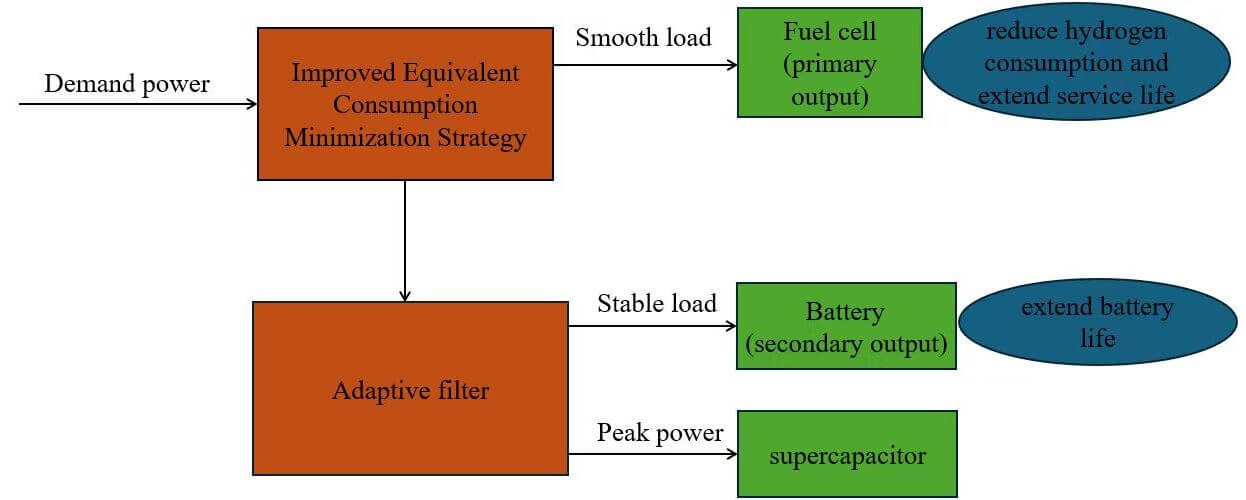
1.    Introducing a hierarchical energy control strategy that fully exploits the potential of fuel cells, batteries, and supercapacitors. In this strategy, fuel cells provide stable energy and seek maximum efficiency in their efficient operating range, batteries serve as the main energy buffer, maintaining their charge at the end of the driving cycle, and supercapacitors provide peak power.

2.    Designing a low-level strategy based on an adaptive low-pass filtering method to allocate peak power and regenerative energy to supercapacitors. This strategy adjusts the time constant of the low-pass filter based on the error between the supercapacitor’s SOC and a given reference value, fully exploiting the characteristics of supercapacitors.

3.    Improving the ECMS by incorporating adaptive algorithms to account for power source degradation. Depending on different power requirements, when the load power demand has a significant impact on fuel cells degradation, the strategy adopts a power allocation function considering degradation; when the load power demand has a minor impact on fuel cells degradation, it employs a power allocation function that minimizes EHC.

The remaining layout of the paper is organized into five main parts: Section 2 introduces the specifications and load requirements for the ship, providing the foundation for the study. Section 3 focuses on developing models for the hybrid power system of fuel cell ships, while Section 4 presents the proposed energy control strategy to optimize power and energy management. Section 5 analyzes the simulation results to evaluate system performance, and Section 6 concludes the paper by summarizing key findings and contributions.

2  Problem Description

This paper aims to develop an energy control system for fuel cell hybrid power ships that reduces fuel consumption while considering power degradation. The hybrid energy sources proposed in this paper include fuel cells, batteries, and supercapacitors. These energy sources supply the power required by the ship, including engine power and other power consumptions such as lighting, pumps, and air conditioning. In this section, the system architecture of the ship and its load requirements will be introduced.

2.1 System Structure of Hybrid Power Ships

In this study, HESS composed of batteries and supercapacitors. Fuel cells serve as the main power source, connected to the DC bus via a unidirectional DC/DC converter, while the HESS acts as a secondary power source connected through two bidirectional DC/DC converters. The energy control strategy regulates the flow of energy, managing dynamic load requirements efficiently for various ship systems, including propulsion motors, pumps, air conditioning, and lighting, ensuring optimal energy distribution and system performance. The hybrid power system for the ship is shown in Fig. 1 [13].

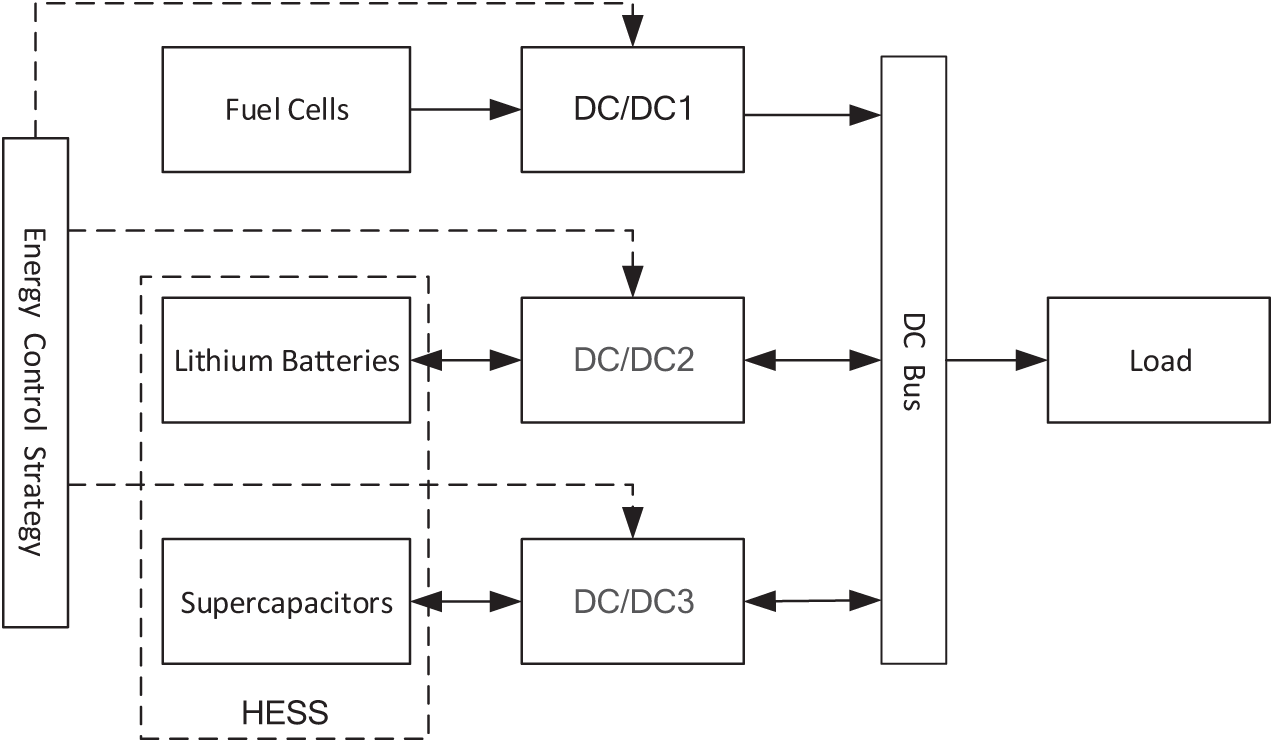
Figure 1: Diagram of hybrid power system for ships

2.2 Load Requirements

The experimental data obtained from the test platform is used to simulate the load demand of the ship. The load power curve at a given ship speed is shown in Fig. 2, which represents the test platform’s operational conditions. In this simulation, the ship sails according to a series of operating procedures based on a predetermined destination. The ship first goes through the startup and acceleration phases, gradually increasing its speed until it reaches a stable cruising speed. When approaching the destination with a short distance remaining, the ship undergoes four gradual deceleration stages, progressively reducing its speed, until it reaches the destination. To ensure the accuracy of the simulation, the test platform is designed to replicate the key operating conditions of real ships, such as the load changes due to speed variations and the energy demands during different stages of the voyage. By aligning the simulation with actual ship behavior, this test platform allows us to assess the power requirements under realistic operational scenarios.

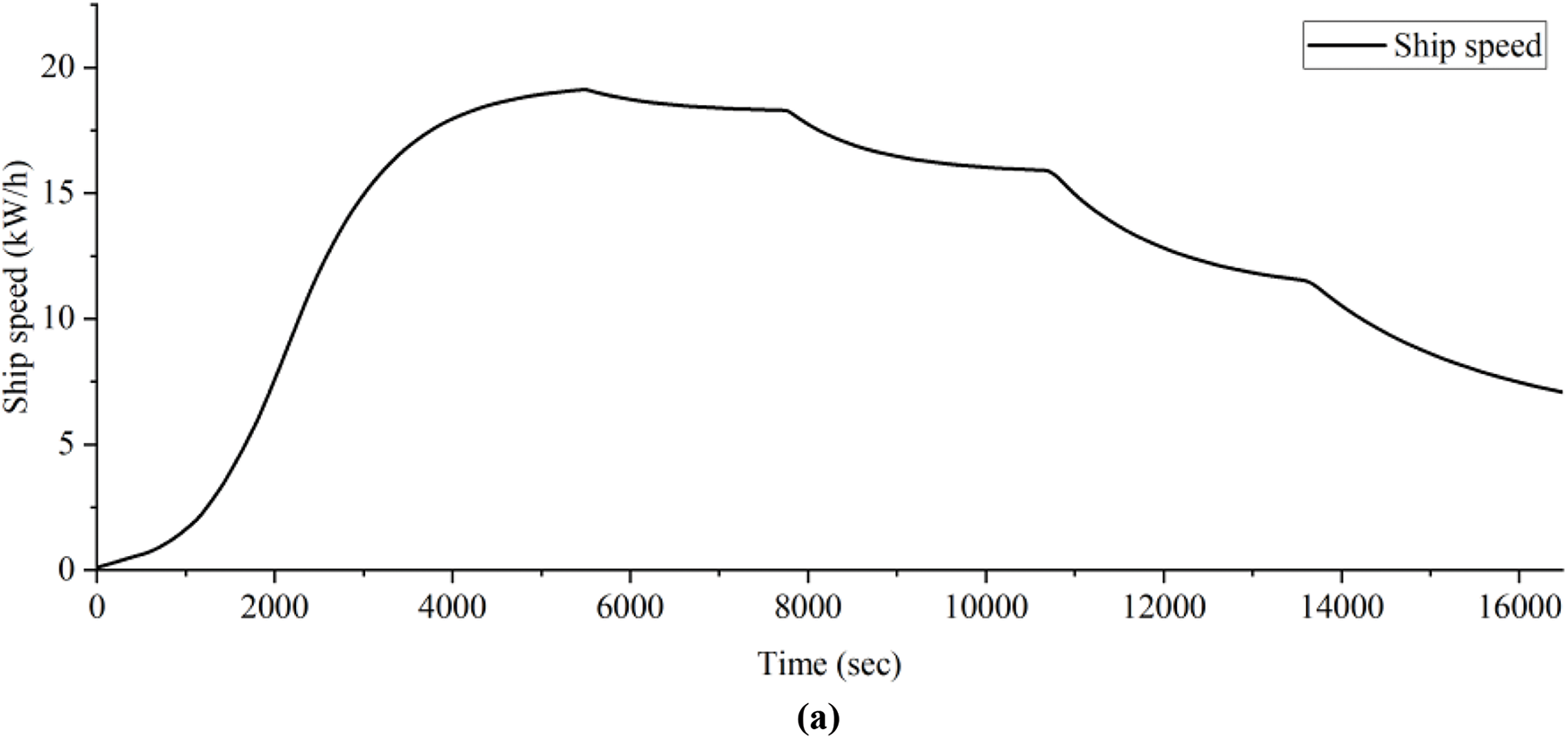
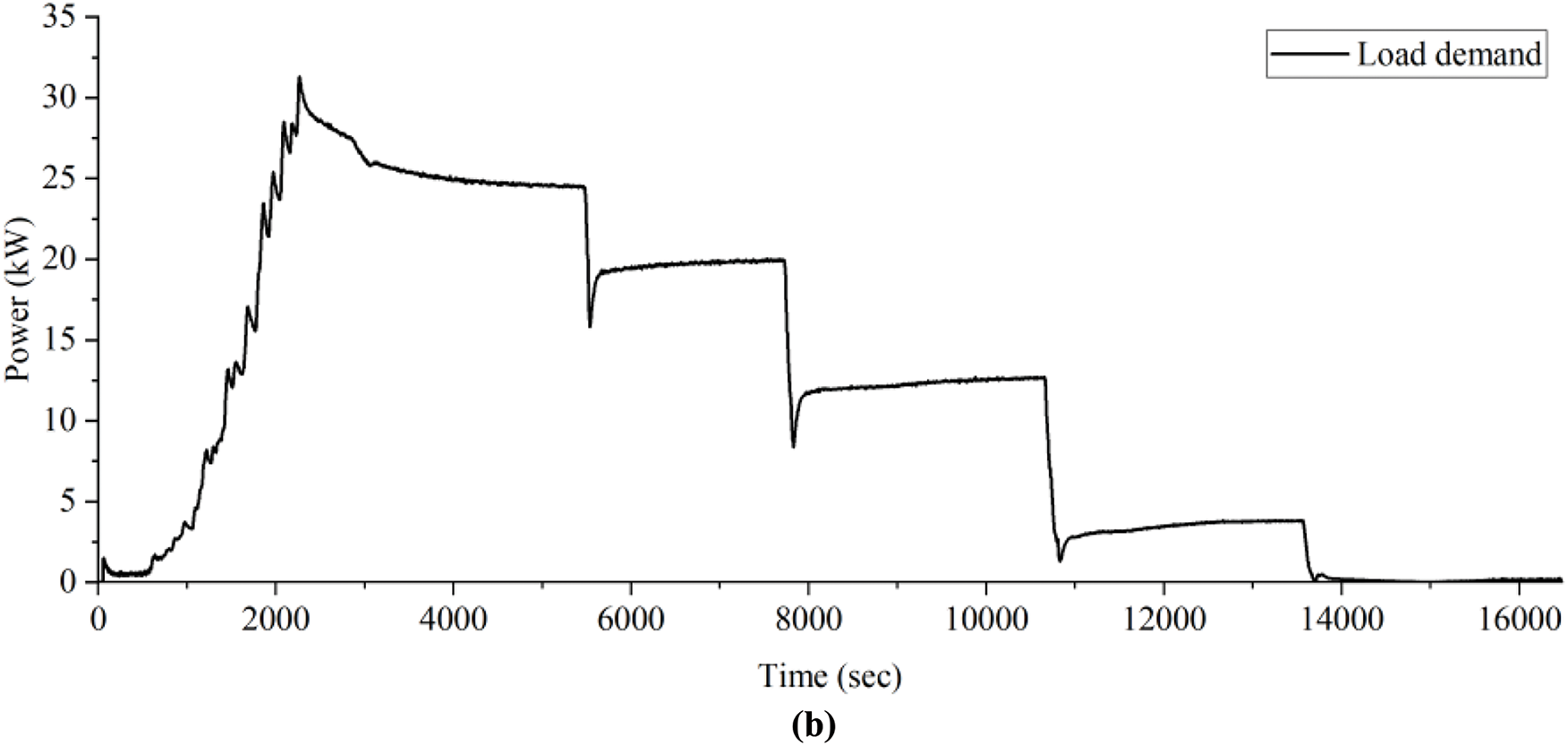
Figure 2: Ship speed and load demand. (a) Ship speed; (b) Load demand

3  Model of the Hybrid Power System

In order to maintain the stable and efficient functioning of a fuel cell hybrid power system, besides selecting key components and parameters that meet actual operational requirements, it is essential to design a real-time energy control strategy. This process involves establishing models for various key components. This section focuses on establishing models for the key components of the fuel cell hybrid power systems and based on reference [14], designing the system architecture for the hybrid power ship to support subsequent energy control strategy design. The models mainly include the fuel cells voltage model, lithium batteries model, supercapacitor model, and DC/DC converter model. The establishment of the models and the analysis and simulation of the fuel cell hybrid power system were both completed in the MATLAB R2022b environment.

3.1 Fuel Cell Voltage Model

In this study, a simplified fuel cells model was employed [15]. The fuel cells voltage Vfc is calculated as follows:

Vfc=E−(Vohm+Vact+Vconc)(1)

where, Vfc denotes the voltage of the fuel cells, E stands for the open circuit voltage, while Vohm, Vact, and Vconc correspond to the Ohmic, activation, and concentration voltage losses, respectively.

3.2 Lithium Battery Model

Batteries serve as buffer energy sources to improve the efficiency of the fuel cell system and ensure the normal operation of supercapacitors. The energy stored in the batteries should be maintained within a safe range. SOC is defined as the state of charge of the batteries, indicating the available state of remaining charge in the batteries. It is described as follows:

SOCb(t)=SOCb0−α⋅∫0tIb(t)dtEbmax(2)

wherein, SOCb(t) represents the batteries SOC at time t, and SOCb0 is the initial SOC of the batteries. Ebmax is the maximum capacity of the batteries, Ib is the batteries current, and α is the charge/discharge efficiency.

3.3 Supercapacitor Model

Supercapacitors are recognized for their high power density and rapid charge and discharge rates. These attributes make them ideal for managing power fluctuations or providing support during ship startup, reducing the load on both fuel cells and batteries. The SOC of a supercapacitor can be calculated as follows:

SOCsc=EscEsc_nor=0.5⋅CVsc20.5⋅CVsc_max2=Vsc2Vsc_max2(3)

wherein, SOCsc denotes the charge level of the supercapacitor, Esc represents the energy stored in the supercapacitor, Esc_nor is the nominal energy stored, C is the ideal capacitance value, Vsc is the supercapacitor’s voltage, and Vsc_max refers to the maximum voltage of the supercapacitor.

3.4 DC/DC Converter

The power system incorporates two kinds of DC-DC converters. The first, a unidirectional converter, controls energy flow in only one direction. It is typically used for managing power in systems such as fuel cells, motors, or solar panels. In this research, a unidirectional DC-DC converter is used to control the output power of the fuel cell system, as shown in Fig. 3a. The second type is a bidirectional converter, which allows energy flow to be controlled in both directions. This is commonly applied to batteries and energy storage systems, such as supercapacitors. Fig. 3b demonstrates the use of this converter to manage the power of both batteries and supercapacitors.

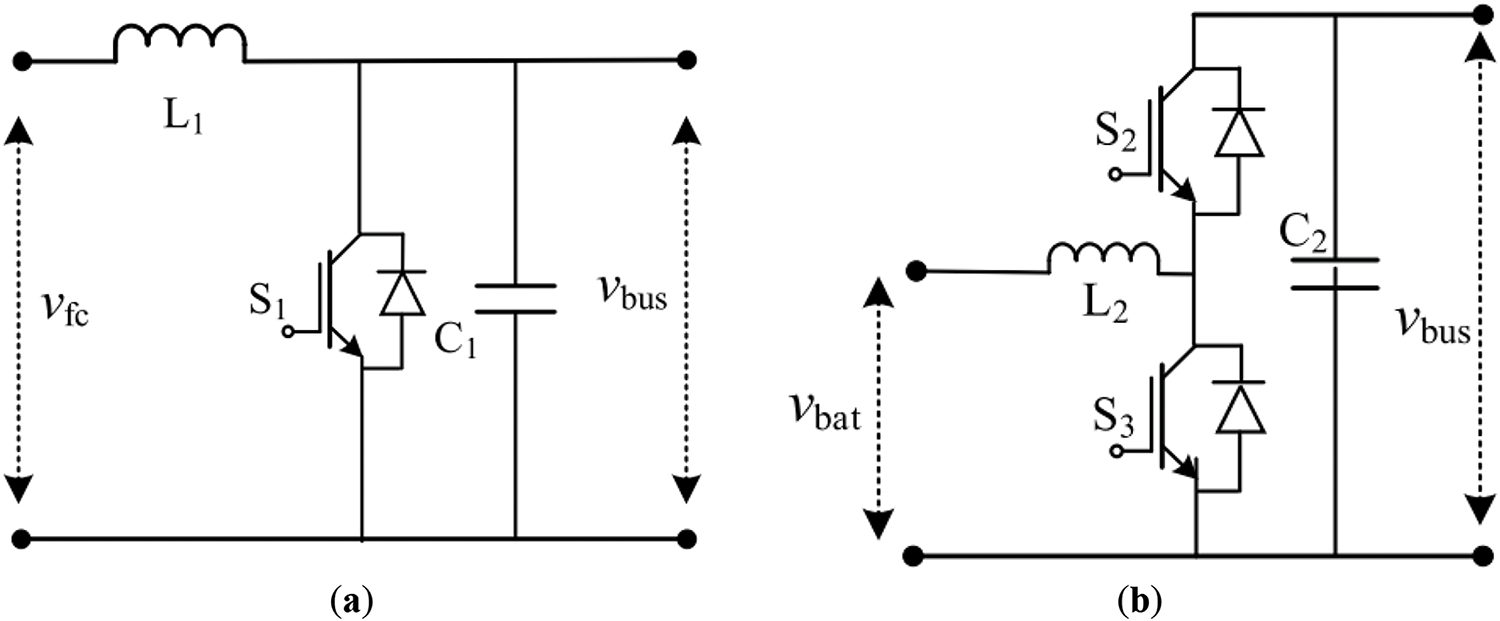
Figure 3: DC/DC converters in ship hybrid power systems. (a) Fuel cell DC/DC converter; (b) Lithium battery/supercapacitor DC/DC converter

4  Energy Control Strategy

To develop effective energy control systems, it is essential to analyze key elements of the power system, including fuel cell efficiency, fuel consumption, battery and supercapacitor charging/discharging power, and the SOC of each energy storage unit. Tailored energy management strategies must be adapted to the unique characteristics of each energy storage device to optimize performance. The energy control system serves as a central component of the ship’s electrical system, ensuring reliable and stable operation of the ship’s grid while optimizing power distribution.

As shown in Fig. 4, the proposed two-layer energy control strategy consists of two levels of management. In the high-level strategy, energy distribution between the fuel cells and HESS is considered, with adaptive adjustment using the minimum equivalent degradation strategy and the minimum EHC strategy to ensure that the fuel cells operate within the high-efficiency region. In the low-level strategy, taking into account the high power density of supercapacitors, the adaptive low-pass filtering method is proposed to regulate the SOC of the supercapacitors, enabling them to provide peak power and recover energy during braking. The power balance can be expressed as:

Pload(t)=Pfc(t)+PHESS(t)=Pfc(t)+Pbat(t)+Psc(t)(4)

where, Pload(t) represents the load power demand, PHESS(t) represents the output power of the energy storage system, Pfc(t) represents the output power of the fuel cells, Pbat(t) represents the output power of the batteries, and Psc(t) represents the output power of supercapacitor. In Fig. 4, “*” represents multiplication.

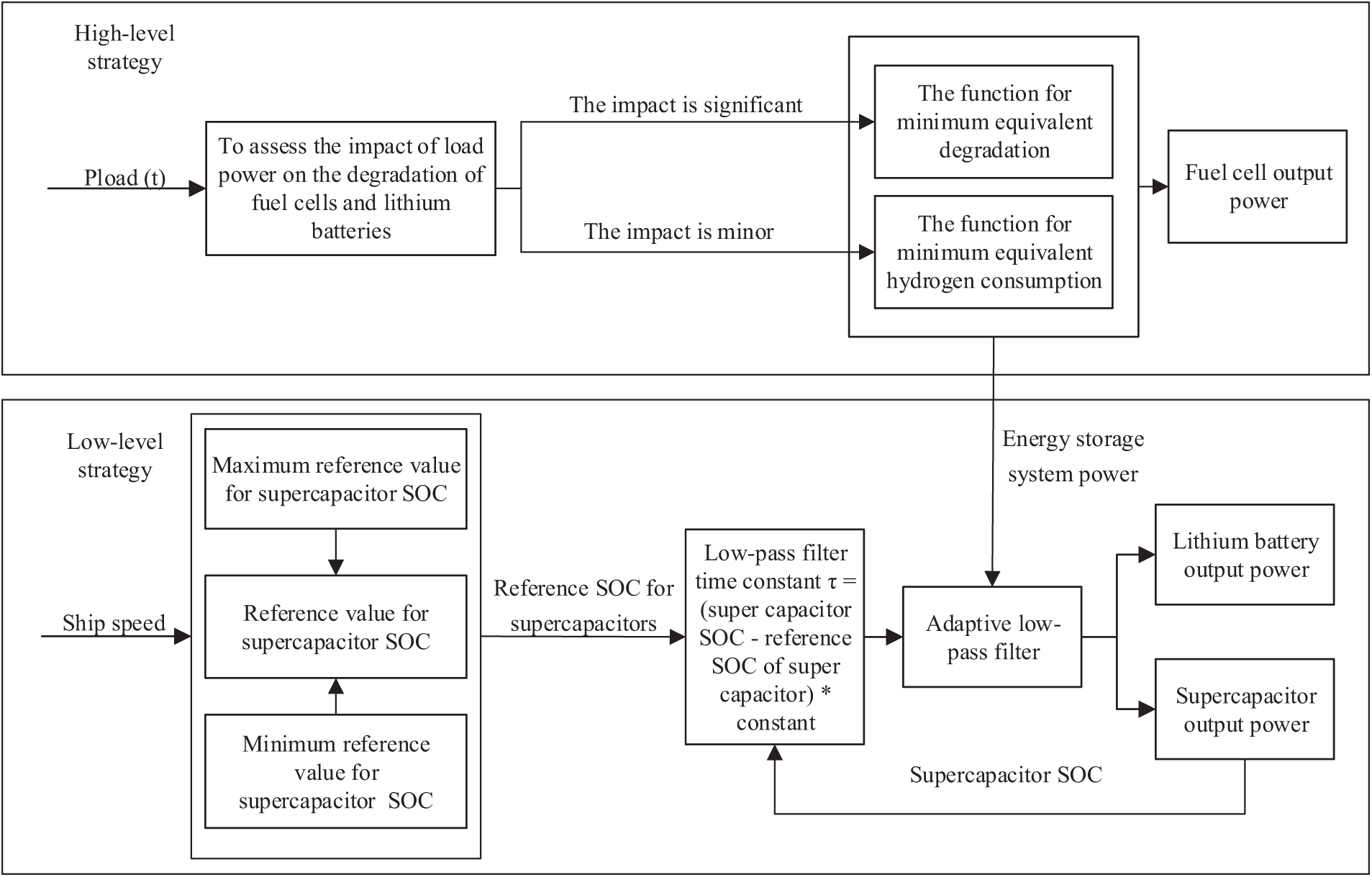
Figure 4: Energy control strategy

4.1 High-Level Strategy

The high-level strategy improves upon the minimum equivalent fuel consumption strategy considering degradation, mainly allocating output power for fuel cells and batteries, enhancing fuel economy while also increasing the lifespan of fuel cells. For the hybrid power ship described in this article, the energy stored in batteries and supercapacitors is provided by the fuel cells, and supercapacitors can also recover braking energy.

The focus of this strategy is to determine different power allocation strategies under various load demand conditions. When there are significant fluctuations in load power demand or during startup, a power allocation function considering degradation is employed. When the load power demand fluctuates less, indicating less damage to the fuel cells, a power allocation function considering minimum EHC is utilized. In contrast, traditional strategies considering degradation assign separate weight coefficients to degradation and minimum equivalent consumption models, and these coefficients are used simultaneously at all times. This approach does not achieve the best results in terms of both protecting the fuel cells and reducing fuel consumption.

4.1.1 Decision Model

The decision model is as follows:

F=std(Plt−4,Plt−3,Plt−2,Plt−1,Plt)(5)

wherein, std represents the standard deviation function, Plt represents the ship’s load power demand at time t. The magnitude of F determines whether to adopt the degradation strategy or the minimum EHC strategy, and the value of F will be used in the next module.

4.1.2 Optimization Model

To develop more scientific and reasonable energy utilization strategies for multi-energy systems, the global optimization problem is reformulated as a local optimization problem by minimizing the equivalent fuel consumption. This involves converting the energy consumption of batteries and supercapacitors into hydrogen consumption, as well as equivalently considering the degradation of fuel cells and lithium batteries as hydrogen consumption. This strategy aims to determine the most efficient power allocation to achieve minimal EHC C in the hybrid power system. The calculation method is as follows: when the fluctuation of load power demand is small (F<h), the power distribution function that minimizes EHC is used to decrease the total EHC in the fuel cell hybrid power system. When the fluctuation of load power demand is large (F≥h), the power allocation function that converts the degradation of fuel cells and batteries into EHC is utilized. In this context, Cfc, Cbat, and Csc represent the EHC of fuel cells, batteries, and supercapacitors, respectively. CDfc and CDbat represent the degradation-related EHC of fuel cells and batteries. The optimization model is as follows [16]:

Pfc,Phess=min{Cfc+k1Cbat+k2CscF<hCDfc+CDbatF≥h(6)

wherein k1 and k2 are penalty coefficients for batteries and supercapacitors, respectively, and h is the adjustment parameter (In this study, k1 = 0.95, k2 = 0.95 and h = 1).

4.1.3 Fuel Cell Hydrogen Consumption Model

The power output of the fuel cell (Pfc) and its EHC (Cfc) are related as follows [9]:

Cfc=a⋅Pfc2+b⋅Pfc+c(7)

wherein a, b, and c are fitting parameters, and Pfc represents the fuel cells power (In this study, a = 0.0001, b = 0.99 and c = 0).

4.1.4 Equivalent Hydrogen Consumption of Batteries

Under normal circumstances, it is difficult to determine the operating states of fuel cells, batteries, and supercapacitors. Therefore, this paper adopts an average operating state. The EHC for the batteries (Cbat) can be determined as:

Cbat=σ⋅Pbat⋅CFC_avgPFC_avg(8)

In this equation, CFC_avg denotes the average EHC of the fuel cells, PFC_avg represents the average power output of the fuel cells, and σ can be calculated as:

σ={1ηbat_chgavg⋅ηbat_dis,Pbat≥0ηbat_chg⋅ηbat_disavg,Pbat<0(9)

In this context, ηbat_chgavg denotes the average charging efficiency of the batteries, ηbat_disavg denotes the average discharging efficiency of the batteries, ηbat_chg refers to the charging efficiency of the batteries, and ηbat_dis refers to the discharging efficiency of the batteries. These parameters can be computed as follows:

ηbat_dis=12(1+1−4Rbat_disPbatVbat2)(10)

ηbat_chg=21+1+4Rbat_chgPbatVbat2(11)

4.1.5 Equivalent Hydrogen Consumption of Supercapacitors

Similar to the EHC model for batteries, the EHC Csc of supercapacitors can be calculated as:

Csc=σ⋅Psc⋅CFC_avgPFC_avg(12)

wherein, CFC_avg represents the average consumption of the fuel cells, PFC_avg represents the average power of the fuel cells, and σ can be calculated as:

σ={1ηsc_chgavg⋅ηsc_dis,Psc≥0ηsc_chg⋅ηsc_disavg,Psc<0(13)

wherein, ηsc_chgavg represents the average charging efficiency of the supercapacitor; ηsc_disavg represents the average discharging efficiency of the supercapacitor; ηsc_chg represents the charging efficiency of the supercapacitor, and ηsc_dis represents the discharging efficiency of the supercapacitor. They can be calculated as:

ηsc_dis=12(1+1−4Rsc_disPscVsc2)(14)

ηsc_chg=21+1+4Rsc_chgPscVsc2(15)

wherein, Vsc represents the voltage of the supercapacitor, Rsc_dis and Rsc_chg respectively represent the discharging resistance and charging resistance of the supercapacitor.

4.1.6 Fuel Cell Degradation Model

The primary factor influencing the performance degradation of fuel cells is the extent of variation in operating conditions. In this study, the fuel cell degradation model [17] is utilized, which is expressed as follows:

∂Vdecay∂t=13600(kfuel⋅std(Pft−4,Pft−3,Pft−2,Pft−1,Pft)+10)(16)

In this equation, ∂Vdecay∂t represents the rate of voltage degradation of the fuel cells; std denotes the standard deviation function, and Pft represents the fuel cells’ output power at time t.

Due to the disparity between the decay rate of ∂ and hydrogen consumption, designing a cost function for the real-time optimization of the Energy Management System proves to be quite difficult. As a result, ∂Vdecay∂t is translated into EHC based on the costs of fuel cell devices and hydrogen fuel:

CDfc=∂Vdecay⋅MFC10⋅CH2(17)

where, MFC represents the price of the fuel cell device, CH2 denotes the price of hydrogen fuel, and a 10% reduction in fuel cell system performance is considered the maximum allowable limit.

4.1.7 Lithium Battery Degradation Model

The primary factors leading to the degradation of lithium batteries are the extent of current fluctuations and high current levels. As outlined in Reference [18], to prevent the impact of high currents, this study uses a battery degradation model, which is expressed as follows:

CDbat=ibat⋅tEMS⋅MbatQbat⋅Bcycle⋅CH2(18)

In this equation, tEMS represents the sampling interval, Mbat denotes the cost of the battery device, Bcycle is the batteries cycle time, and Qbat is the nominal charge capacity of the batteries.

4.2 Low-Level Strategy

The low-level objective of the energy control strategy proposed in this paper is to utilize supercapacitors to provide peak power through a low-pass filter and recover braking energy, thereby ensuring the propulsion performance of hybrid power ships, alleviating pressure on fuel cells and batteries, and protecting fuel cells and lithium batteries. The time constant τ of the low-pass filter is determined by the difference between the given reference value and the SOC of the supercapacitor. When the difference between the supercapacitor’s SOC and its reference value is significant, the τ decreases, reducing the filter’s ability to smooth fluctuations, and thereby limiting the charging and discharging capacity of fuel cells and batteries for supercapacitors. The low-pass filter used in this study is defined as follows:

G(s)=1τs+1(19)

The τ is a function of the supercapacitor SOC and its corresponding reference value, and can be expressed as:

τ=(SOCsc−SOCscref)⋅fs(20)

where, SOCscref represents the reference SOC of the supercapacitor, and fs denotes the adjustment factor.

For the selected low-pass filter, it is essential to maintain the supercapacitor’s reference SOC within an optimal range to satisfy acceleration or deceleration demands. Specifically, the supercapacitors must store adequate energy to supply peak power, thereby reducing the load on the fuel cells and batteries during acceleration. Conversely, during deceleration, the supercapacitors can recover braking energy. The power delivered by the supercapacitors is determined by the discrepancy between the power supplied by the fuel cells and batteries and the required power. The reference SOC for the supercapacitor at the subsequent time step can be calculated based on its current SOC, as illustrated in the equation.

SOCscref(t+Ts)=SOCsc(t)−∫0Ts(Pload−Pbat−Pfc)dtCsc(21)

where, Ts denotes the sampling interval, and Csc is the maximum capacity.

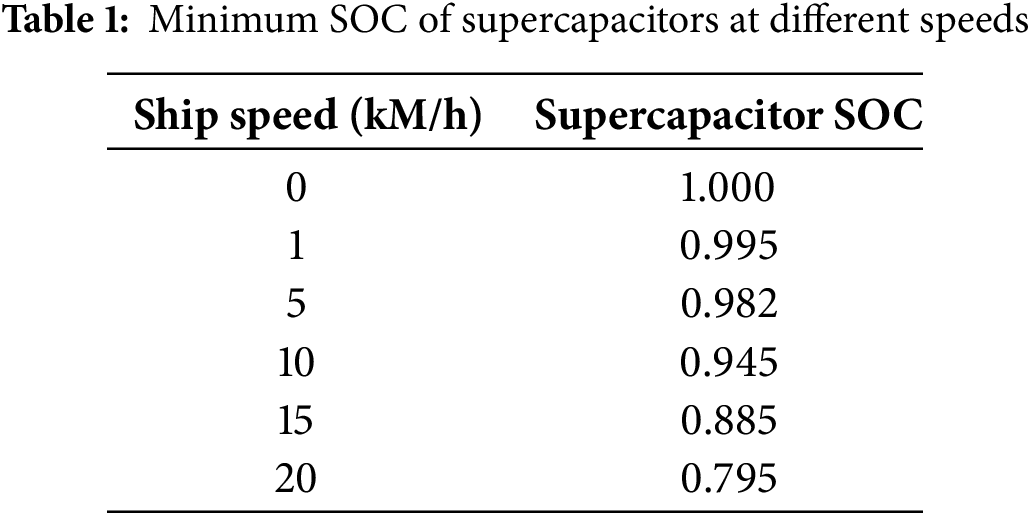
Furthermore, to reduce the pressure on the fuel cells and batteries, the energy stored in the supercapacitors must exceed the amount required to accelerate from the current speed to the maximum speed. Therefore, within the MATLAB/Simulink environment, assuming optimal performance of the fuel cells and batteries, the minimum energy required for acceleration from the current speed to the maximum speed can be calculated. The corresponding minimum energy required for acceleration from 5, 10, 15, and 20 to 30 km/h is presented in Table 1 in the MATLAB/Simulink model. The relationship between speed and minimum SOC, based on a polynomial fit of the data in Table 1, can be expressed by the following polynomial:

SOCscl=−6.63×10−6⋅v3−0.0002819⋅v2−0.001884⋅v+0.9988(22)

where, SOCscl represents the lower bound of the supercapacitor’s SOC, and v represents the speed of the ship.

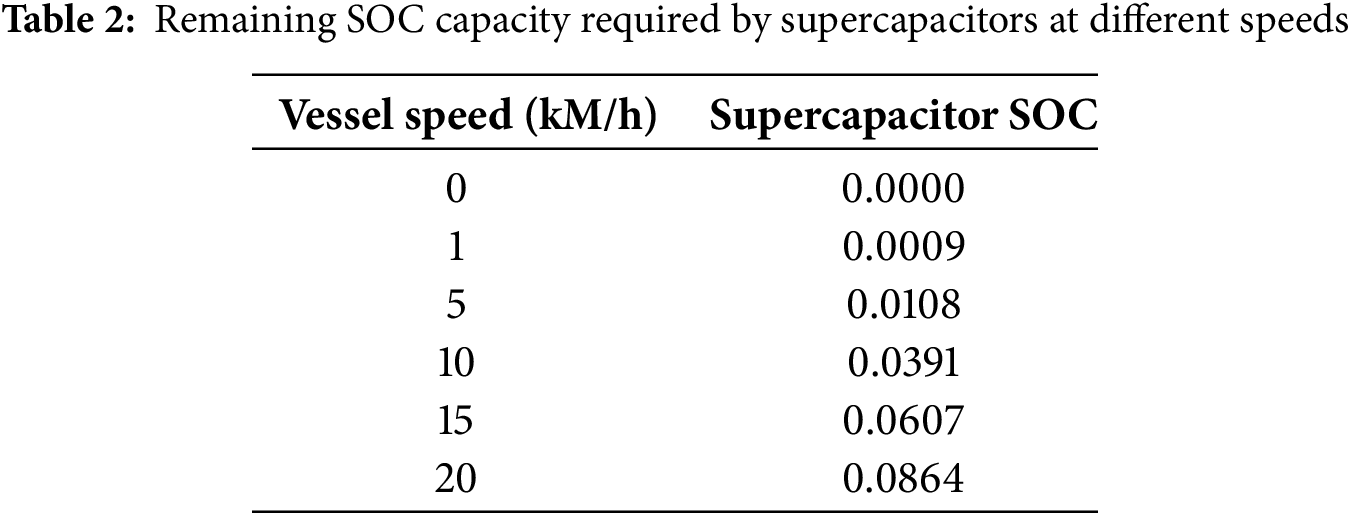
Similarly, the supercapacitor can recover braking energy, thereby enhancing energy efficiency and mitigating the potential reduction in battery lifespan caused by high current output. In the MATLAB/Simulink environment, the energy recoverable by the supercapacitor during deceleration from speeds of 5, 10, 15, and 20 to 0 km/h is computed, as detailed in Table 2. The functional relationship between speed and the residual SOC capacity required by the supercapacitor, obtained through polynomial fitting of the data presented in the table, is given by the following polynomial expression:

SOCscr=−1.611×10−6⋅v3+0.0001288⋅v2+0.002559⋅v−0.001405(23)

wherein, SOCscr represents the remaining SOC capacity required by the supercapacitor.

Therefore, by integrating the values of SOCscl and SOCscr, the reference SOC of the supercapacitor can be determined as follow.

SOCscl≤SOCscref≤1−SOCscr(24)

In the low-level strategy, the fluctuating part of the power demand is allocated to the supercapacitor through a low-pass filter, improving the power performance of the ship and alleviating the pressure on the fuel cells and batteries.

5  Experimental and Analysis

This section presents the simulation results for the improved minimum equivalent consumption strategy proposed in this paper. To verify the effectiveness of the strategy improvement and the protective effect on the power supply when considering degradation, a comparison with the conventional ECMS [9] and conventional ECMS considering degradation [12] is provided. The proposed hybrid power system has been evaluated in the MATLAB/Simulink environment. The power demand of the fuel cell hybrid ship in Fig. 2 is taken into account. The main parameters of the power system model are shown in Table 3 [17].

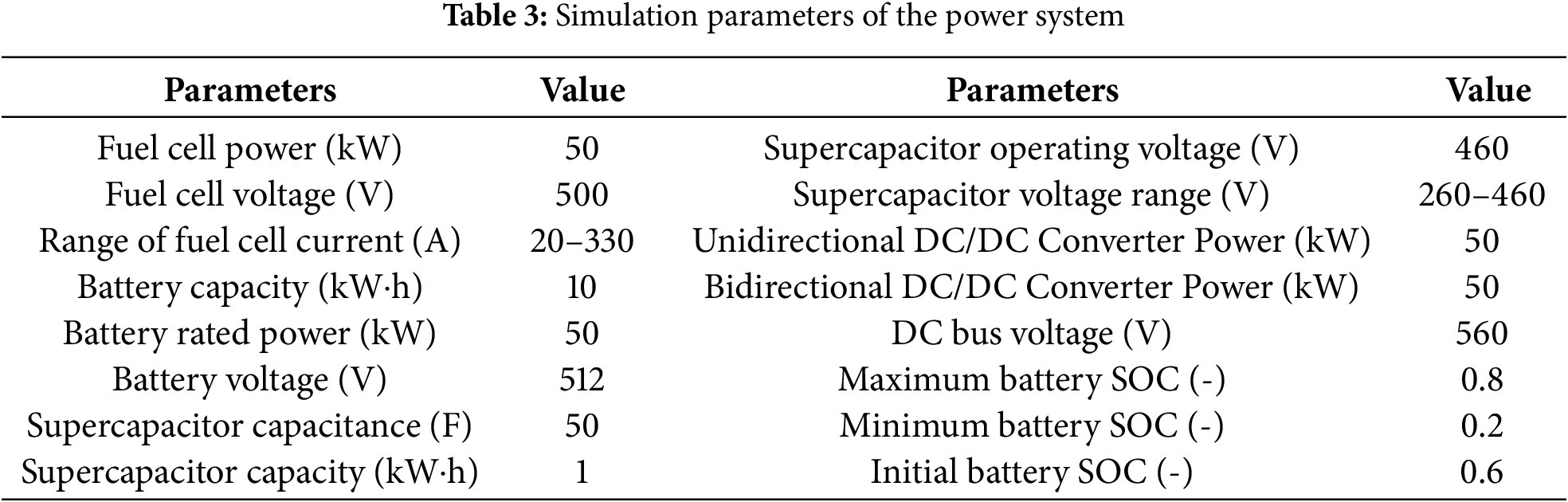
The proposed control strategy is compared with conventional ECMS [9] and degradation-aware ECMS [12]. The curves are shown in black, red, and blue, respectively. Fig. 5 displays the fuel cell output power for different strategies. It can be observed that during the startup process, the conventional ECMS control leads to a sharp increase in fuel cells power. Additionally, a magnified view of the local details from 7000 to 7800 s reveals that conventional ECMS control results in significant fluctuations in fuel cells power. According to reference [19], such large fluctuations in fuel cells output power will accelerate catalyst degradation in the proton exchange membrane, leading to a decrease fuel cells performance and a shorter lifespan, which is highly detrimental to fuel cells protection. Although conventional ECMS considering degradation reduces the fluctuations, the proposed strategy completely eliminates them. This implies that the proposed strategy can prolong the fuel cells lifespan and reduce costs.

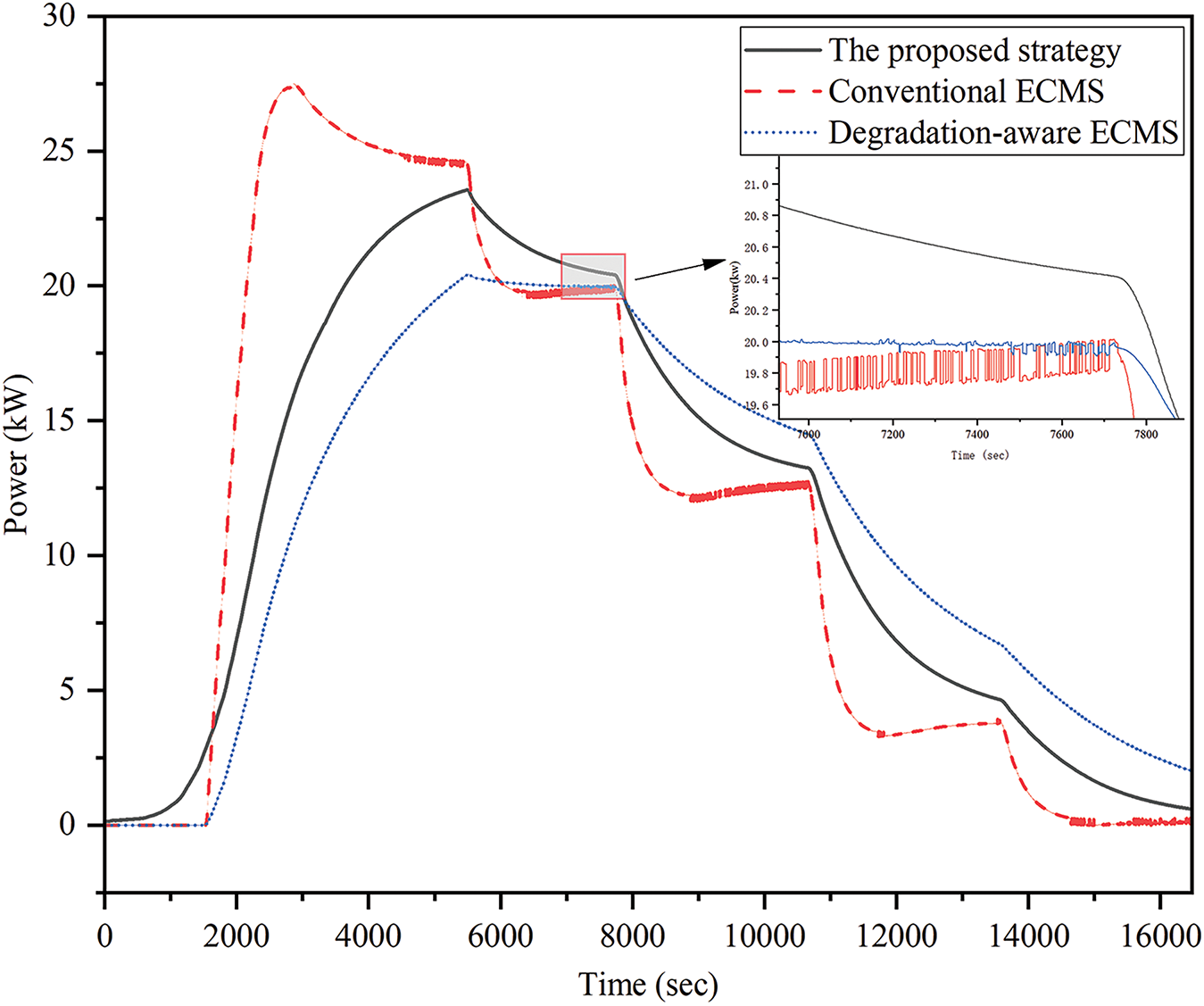
Figure 5: The power output of the fuel cells under different strategies

As shown in Figs. 6 and 7, the battery power under the previous strategy and the hierarchical strategy is illustrated. As previously mentioned, the batteries and supercapacitor provide the low-frequency and high-frequency components of the HESS power, respectively. The use of the HESS improves the efficiency of the fuel cells. Compared to the battery power in the previous strategy, the fluctuations in battery power have decreased, indicating that the hierarchical strategy provides good protection for the batteries. Furthermore, compared to the conventional degradation-aware ECMS, the maximum batteries power has decreased by 20%. This indicates that the proposed hierarchical strategy can extend the lifespan of the lithium batteries and reduce costs compared to conventional degradation-aware ECMS.

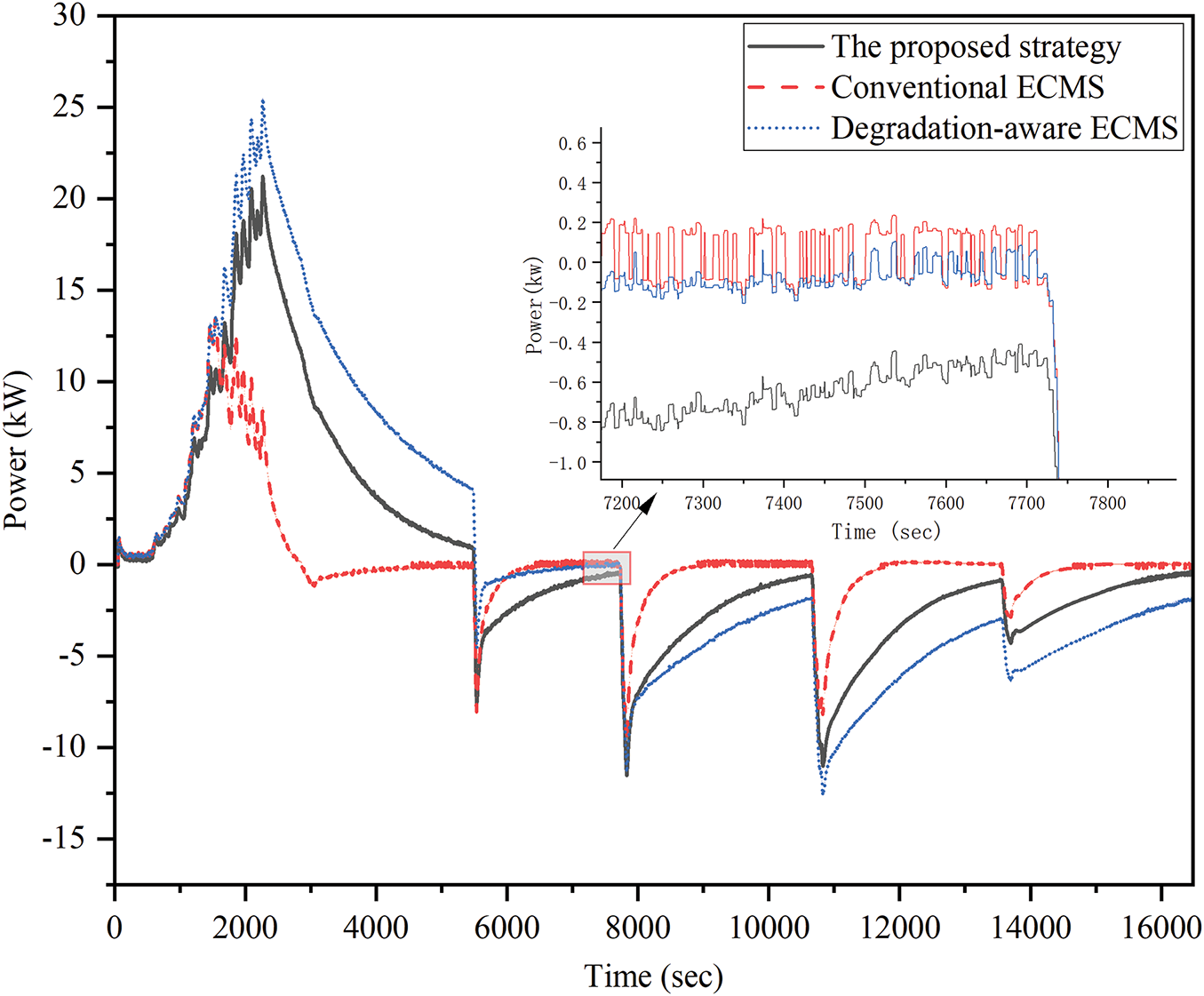
Figure 6: Battery power without the hierarchical strategy

Figure 7: Battery power under the hierarchical strategy

The total energy consumption results of the different strategies are presented in Fig. 8. The total energy consumption includes fuel cells energy consumption (Efc), batteries energy consumption (Ebat), and supercapacitor energy consumption (Esc). The specific parameters for total energy consumption and individual power sources are provided in Table 4. It can be seen that, compared to the conventional degradation-aware ECMS, the proposed control strategy has reduced energy consumption by 1.6%. Although the energy efficiency is reduced compared to conventional ECMS, this is because conventional ECMS does not consider fuel cells degradation.

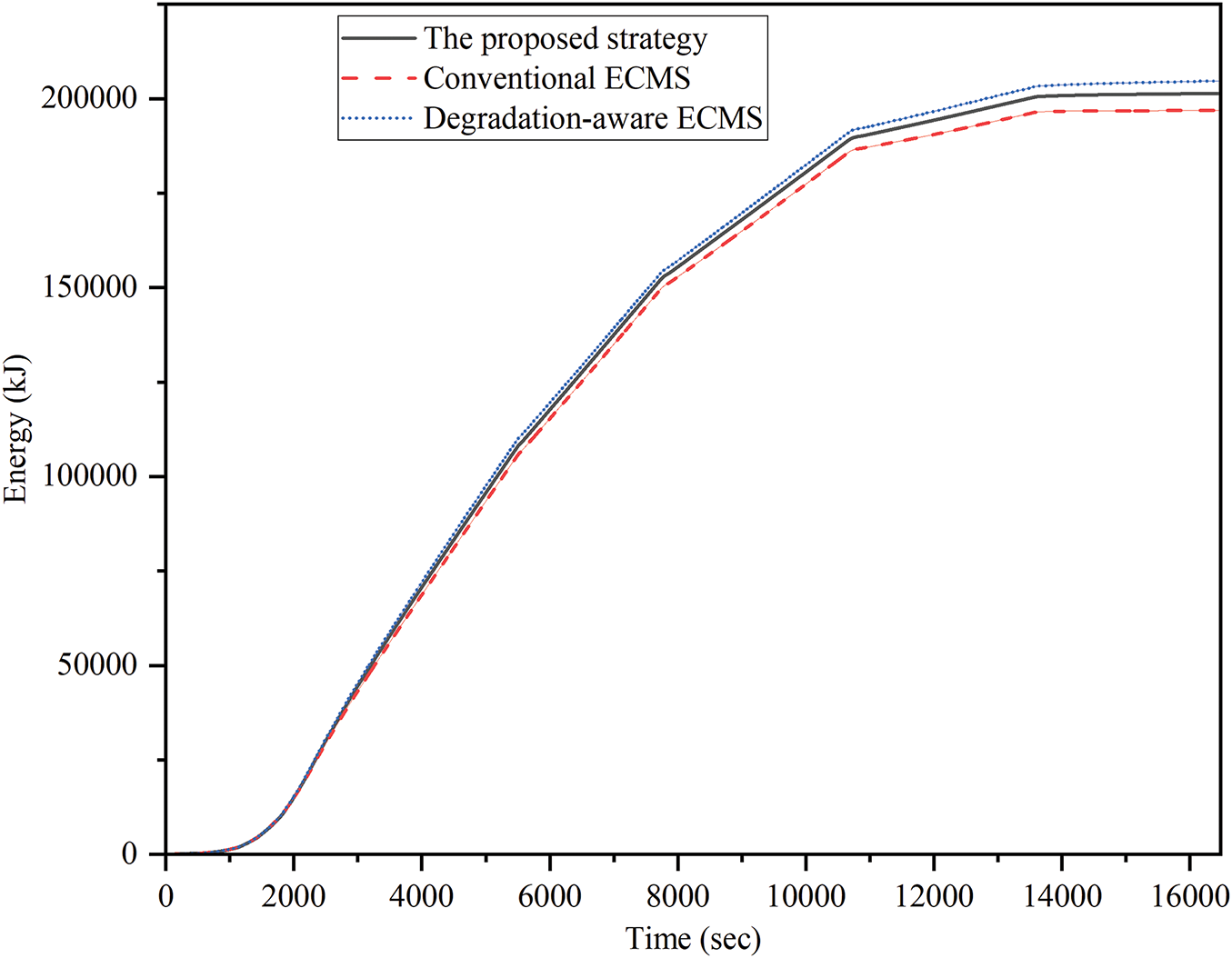
Figure 8: Total energy consumption under different strategies

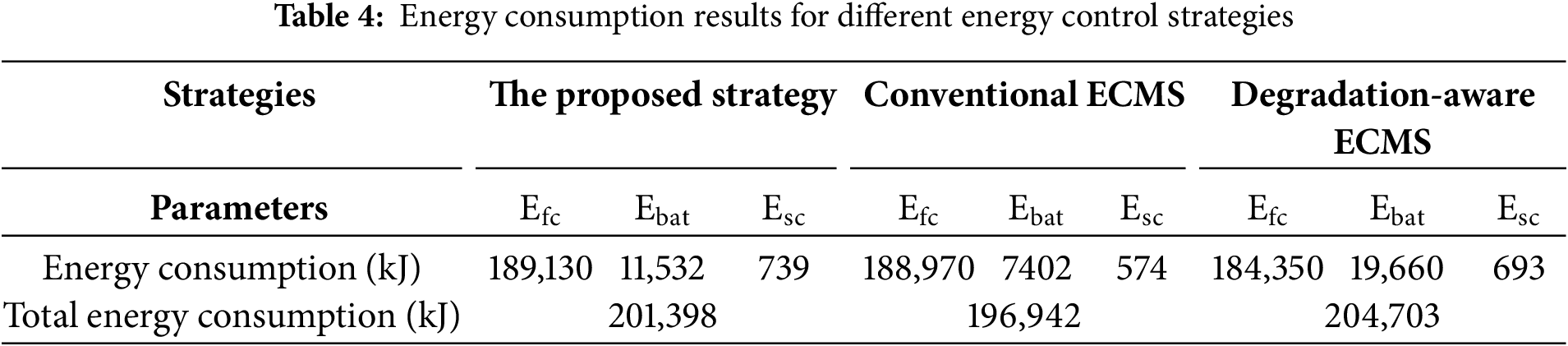
The power of the supercapacitor and the speed of the ship as proposed by the strategy in this study are shown in Fig. 9. When the ship accelerates, the supercapacitor can rapidly provide peak power, while during deceleration, it recovers braking energy, reducing the pressure on the fuel cells and lithium batteries. The energy stored in the supercapacitor is shown in Fig. 10. From the strategy curves proposed in this paper, it can be seen that when the ship speed is low, the supercapacitor SOC is high, providing acceleration energy to ensure the subsequent dynamic performance of the ship. When the ship speed is high, sufficient supercapacitor capacity is reserved for regenerative braking. In contrast, the other two strategies maintain a relatively high supercapacitor SOC even at high speeds, which is disadvantageous for braking energy recovery.

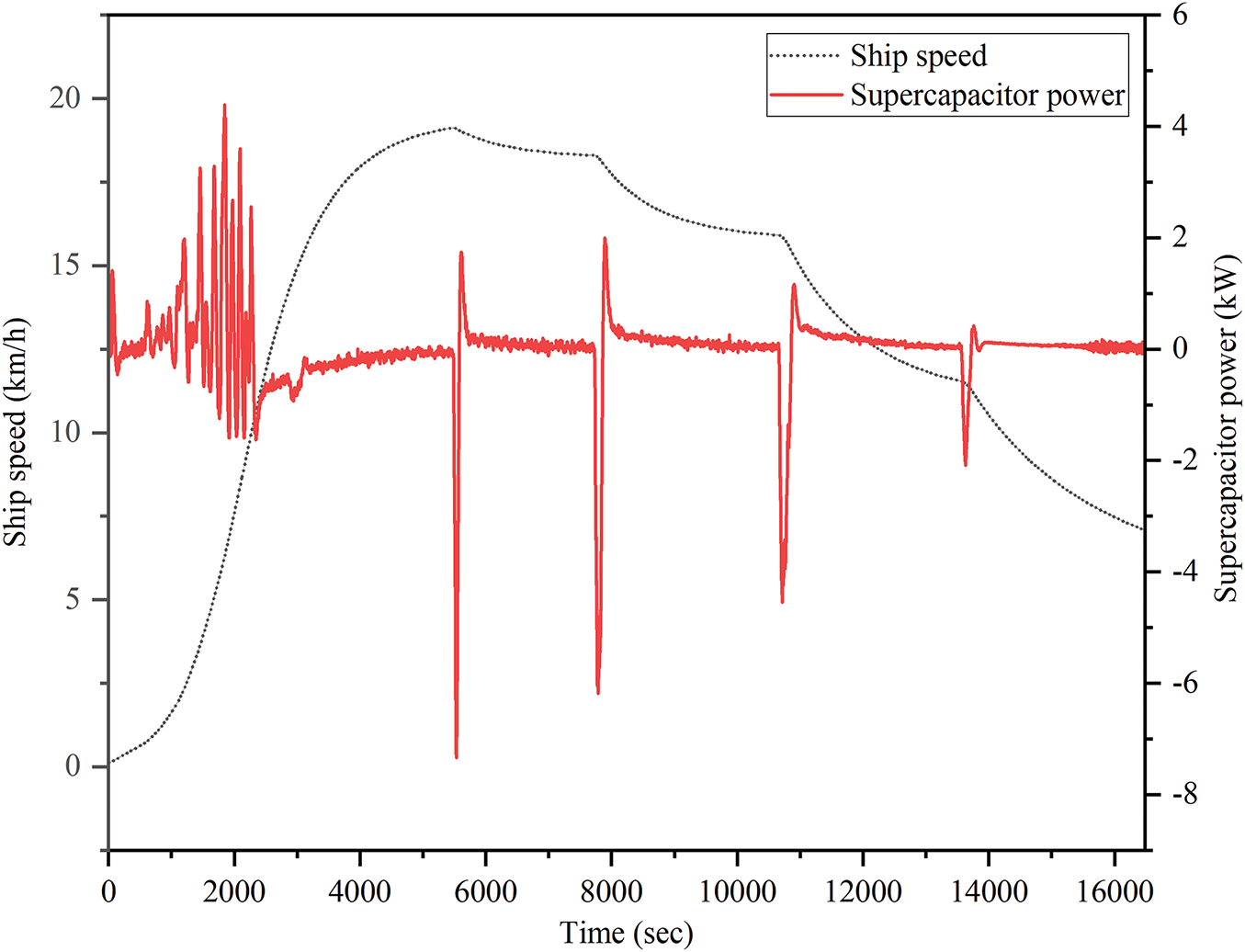
Figure 9: Power of the supercapacitor and the speed graph proposed by the strategy

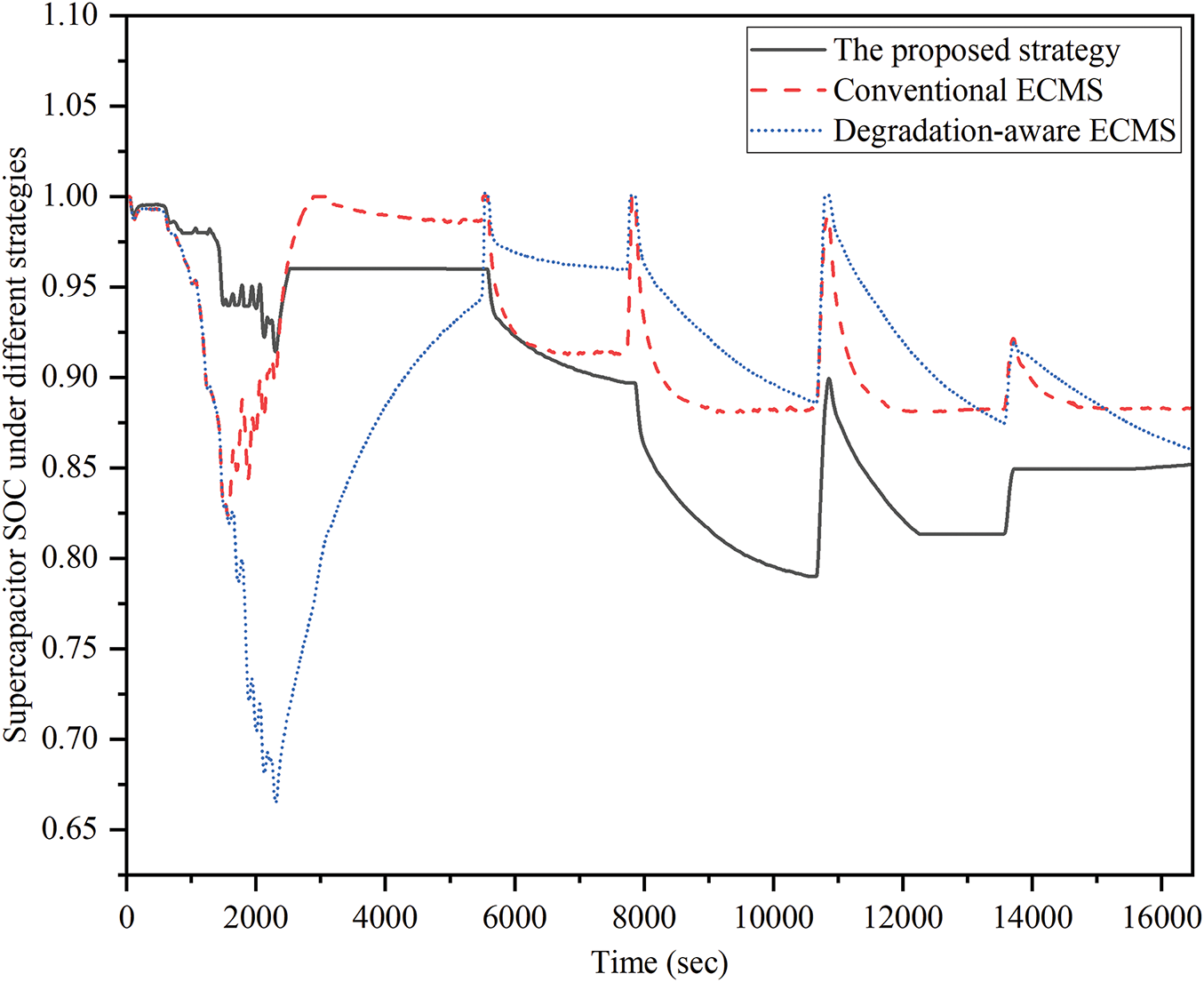
Figure 10: SOC of the supercapacitor under different strategies

6  Conclusion

This study presents a hierarchical energy management strategy for fuel cells, battery, and supercapacitor hybrid power ships, aiming to significantly enhance propulsion performance, fuel economy, and the lifespan of the energy system. The proposed strategy effectively reduces the power fluctuation coefficient of the fuel cell and decreases the peak power output of the battery by 20%, substantially extending the service life of both the battery and the fuel cell. Additionally, compared to the conventional degradation-aware ECMS, the improved ECMS achieves a further 1.6% reduction in energy consumption. By incorporating a low-pass filter, the supercapacitor is ensured to efficiently handle peak power demands and recover braking energy while maintaining its SOC within an appropriate range. This enhances the propulsion performance and energy utilization efficiency of the ship. Simulation and experimental results demonstrate that the proposed hierarchical energy management strategy significantly improves fuel economy, extends the lifespan of the energy system, and optimizes dynamic performance, offering valuable guidance for efficient energy management in hybrid fuel cell-powered ships.

This paper only considers adaptive algorithms for power source degradation. In future work, real-time driving conditions and vehicle state can be incorporated into the adaptive control algorithm, allowing the ECMS to dynamically adjust the control strategy based on real-time driving conditions and vehicle state, thereby enhancing adaptability.

Acknowledgement: The authors would like to thank the anonymous reviewers for their constructive and insightful comments for further improving the quality of this note.

Funding Statement: The study was founded by the National Key R&D Program of China (2022YFB4301403).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Diju Gao, Shuai Li; data collection: Diju Gao; analysis and interpretation of results: Diju Gao, Shuai Li; draft manuscript preparation: Shuai Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the corresponding author, Shuai Li, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

List of Acronyms

References

1. Stark C, Xu Y, Zhang M, Yuan Z, Tao L, Shi W. Study on applicability of energy-saving devices to hydrogen fuel cell-powered ships. J Mar Sci Eng. 2022;10(3):388. doi:10.3390/jmse10030388. [Google Scholar] [CrossRef]

2. Zhao J, Cai S, Luo X, Tu Z. Dynamic characteristics and economic analysis of PEMFC-based CCHP systems with different dehumidification solutions. Int J Hydrog Energy. 2022;47(22):11644–57. doi:10.1016/j.ijhydene.2022.01.182. [Google Scholar] [CrossRef]

3. Mohammed AS, Atnaw SM, Salau AO, Eneh JN. Review of optimal sizing and power management strategies for fuel cell/battery/super capacitor hybrid electric vehicles. Energy Rep. 2023;9(2):2213–28. doi:10.1016/j.egyr.2023.01.042. [Google Scholar] [CrossRef]

4. De Wolf D, Smeers Y. Comparison of battery electric vehicles and fuel cell vehicles. World Electr Veh J. 2023;14(9):262. doi:10.3390/wevj14090262. [Google Scholar] [CrossRef]

5. Lu H, Tao F, Fu Z, Sun H. Battery-degradation-involved energy management strategy based on deep reinforcement learning for fuel cell/battery/ultracapacitor hybrid electric vehicle. Electr Power Syst Res. 2023;220:109235. doi:10.1016/j.epsr.2023.109235. [Google Scholar] [CrossRef]

6. Sahoo BB, Pandey VS, Dogonchi AS, Mohapatra PK, Thatoi DN, Nayak N, et al. A state-of-art review on 2D material-boosted metal oxide nanoparticle electrodes: supercapacitor applications. J Energy Storage. 2023;65(10):107335. doi:10.1016/j.est.2023.107335. [Google Scholar] [CrossRef]

7. Wang Z, Li J, Hu C, Li X, Zhu Y. Hybrid energy storage system and management strategy for motor drive with high torque overload. J Energy Storage. 2024;75(5):109432. doi:10.1016/j.est.2023.109432. [Google Scholar] [CrossRef]

8. Vignesh R, Ashok B. Intelligent energy management through neuro-fuzzy based adaptive ECMS approach for an optimal battery utilization in plugin parallel hybrid electric vehicle. Energy Convers Manag. 2023;280(2):116792. doi:10.1016/j.enconman.2023.116792. [Google Scholar] [CrossRef]

9. Wang T, Li Q, Wang X, Qiu Y, Liu M, Meng X, et al. An optimized energy management strategy for fuel cell hybrid power system based on maximum efficiency range identification. J Power Sources. 2020;445(0):227333. doi:10.1016/j.jpowsour.2019.227333. [Google Scholar] [CrossRef]

10. Ge Y, Zhang J, Zhou K, Zhu J, Wang Y. Research on energy management for ship hybrid power system based on adaptive equivalent consumption minimization strategy. J Mar Sci Eng. 2023;11(7):1271. doi:10.3390/jmse11071271. [Google Scholar] [CrossRef]

11. Li H, Ravey A, N’Diaye A, Djerdir A. A novel equivalent consumption minimization strategy for hybrid electric vehicle powered by fuel cell, battery and supercapacitor. J Power Sources. 2018;395(6):262–70. doi:10.1016/j.jpowsour.2018.05.078. [Google Scholar] [CrossRef]

12. Li H, Ravey A, N’Diaye A, Djerdir A. Equivalent consumption minimization strategy for fuel cell hybrid electric vehicle considering fuel cell degradation. In: 2017 IEEE Transportation Electrification Conference and Expo (ITEC); 2017 Jun 22; Chicago, IL, USA. p. 540–4. doi:10.1109/ITEC.2017.7993328. [Google Scholar] [CrossRef]

13. Rezk H, Nassef AM, Ali Abdelkareem M, Alami AH, Fathy A. Comparison among various energy management strategies for reducing hydrogen consumption in a hybrid fuel cell/supercapacitor/battery system. Int J Hydrogen Energy. 2021;46(8):6110–26. doi:10.1016/j.ijhydene.2019.11.195. [Google Scholar] [CrossRef]

14. Yang R, Li K, Du K, Shen B. An ameliorative whale optimization algorithm (AWOA) for HES energy management strategy optimization. Reg Stud Mar Sci. 2021;48(1):102033. doi:10.1016/j.rsma.2021.102033. [Google Scholar] [CrossRef]

15. Motapon SN, Tremblay O, Dessaint LA. A generic fuel cell model for the simulation of fuel cell vehicles. In: 2009 IEEE Vehicle Power and Propulsion Conference; 2009 Sep 7–10; Dearborn, MI, USA. p. 1722–9. doi:10.1109/VPPC.2009.5289692. [Google Scholar] [CrossRef]

16. Zhang H, Li Q, Wang H, Li Q, Qin G, Wu Q. A review of energy management optimization based on the equivalent consumption minimization strategy for fuel cell hybrid power systems. Fuel Cells. 2022;22(4):116–30. doi:10.1002/fuce.202200089. [Google Scholar] [CrossRef]

17. Lin X, Li X, Shen Y, Li H. Charge depleting range dynamic strategy with power feedback considering fuel-cell degradation. Appl Math Model. 2020;80:345–65. doi:10.1016/j.apm.2019.11.019. [Google Scholar] [CrossRef]

18. Zia MF, Elbouchikhi E, Benbouzid M. Optimal operational planning of scalable DC microgrid with demand response, islanding, and battery degradation cost considerations. Appl Energy. 2019;237(2):695–707. doi:10.1016/j.apenergy.2019.01.040. [Google Scholar] [CrossRef]

19. Duong PA, Ryu B, Jung J, Kang H. Design, modelling, and thermodynamic analysis of a novel marine power system based on methanol solid oxide fuel cells, integrated proton exchange membrane fuel cells, and combined heat and power production. Sustainability. 2022;14(19):12496. doi:10.3390/su141912496. [Google Scholar] [CrossRef]