Environmental and Economic Optimization of Multi-Source Power Real-Time Dispatch Based on DGADE-HDJ

1  Introduction

The power system is not only one of the key areas for the continuous and stable development of artificial intelligence but also one of the more complex systems in contemporary society. The optimization of power systems has always been a critical research topic in this field. Electric energy is the most commonly used resource in people’s daily lives and work processes; it is ubiquitous and closely related to individuals. If the energy structure of large-scale power systems can be optimized and adjusted, it will not only quickly improve their operational efficiency but also significantly reduce economic costs [1]. Additionally, it has practical significance for the development of green energy. In power system optimization, the Economic Dispatch (ED) problem is of paramount importance. Its essence is to achieve optimal economic cost by using an appropriate dispatch method, under the premise of ensuring the safe and stable operation of the power system and meeting the constraints and load demands of the system [2]. Optimizing the ED problem is crucial for ensuring the safe and economic operation of the power system. Dynamic Environment Economic Dispatch (DEED) is characterized by high dimensionality, nonlinearity, non-convexity, and complex constraints [3]. Currently, research on DEED primarily focuses on solving the model. Some studies use Price Penalty Factors (PPFs) to transform multi-objective DEED into single-objective DEED, and employ gravitational search algorithms to solve the transformed single-objective DEED [4]. Other research applies weighted sum and semidefinite programming strategies to convert the multi-objective problem, and then solves it by adjusting the weights of the various objectives [5]. Although these solution methods are efficient and fast, they impose high requirements on the objective function. If the objective function is a non-differentiable non-convex form, they cannot be solved effectively. Additionally, these methods are highly sensitive to the selection of initial values, often falling into local optima and making it difficult to achieve a true Pareto-optimal front (PF). As a result, many researchers address DEED as a direct multi-objective optimization problem [6].

To address the issues of energy shortages and environmental pollution, it is crucial to coordinate environmental protection with socio-economic sustainable development, accelerate the formation of green development and lifestyle, and resolve the energy and pollution problems in the power industry. Currently, related technological measures include: desulfurization treatment of coal to reduce the emission of sulfur compounds and other pollutant gases; installing catalytic devices on thermal power plants to absorb and treat pollutant gases; or treating pollution emissions as optimization objectives in the economic dispatch problem to achieve environmental protection goals [7]. However, this requires power plants to upgrade their generation technologies and equipment, resulting in relatively high generation costs. Under the background of large-scale integration of diverse renewable energy sources, it is inevitable to build a new power system that substitutes fossil fuels with renewable energy [8].

To align with the energy transition trend, accelerating the development of new energy industries such as wind power and photovoltaics, promoting clean, low-carbon, and efficient energy utilization, and enhancing the capacity for renewable energy consumption and storage have become key measures. However, wind and solar power, being part of nature, are highly unpredictable, leading to the uneven distribution and instability of power generation, which creates difficulties for their production and grid integration [9]. While clean energy is rapidly developing, the problem of energy consumption remains severe, with issues like wind and solar power curtailment being common [10]. As one of the core components of the power system, power system dispatch plays a significant role in the rational distribution of unit output and in improving the capacity for consuming heterogeneous renewable energy [11]. However, after the large-scale integration of various heterogeneous renewable energies, their unpredictability makes the power system dispatch model more complex [12]. In response, this study considers a power system dispatch model involving multiple heterogeneous renewable energy sources and designs intelligent optimization methods for solving the model effectively, which has significant implications for sustainable development [13].

This study focuses on the theory and application of Dynamic Environmental Economic Dispatch (DEED), covering multiple aspects from fundamental model construction to the improvement of multi-objective optimization algorithms and the evaluation of practical applications. In Section 1, the development of environmental economic dispatch in power systems is systematically reviewed. The principles and characteristics of classical optimization methods (Section 1.1.2) and modern intelligent optimization algorithms (Section 1.1.3) are elaborated upon. Furthermore, the integration of optimization algorithms in the context of current dynamic environmental dispatch systems is discussed (Section 1.1.4). A review of environmental economic dispatch methods for wind power integration and their existing shortcomings is provided (Sections 1.2 and 1.3), leading to the introduction of this study’s improvements and innovative conributions to the DEED optimization problem (Section 1.4). Section 2 focuses on the improvement of the DEED model for conventional thermal power systems. It details the construction process and constraint conditions of the thermal power environmental economic model (Section 2.1). Based on preprocessing and adaptive parameter adjustment of parallel multi-objective algorithms (Section 2.2), a dual-population pseudo-parallel GA-DE multi-objective algorithm with multiple strategies and applications is proposed (Sections 2.3 and 2.4). Section 3 extends the discussion to the economic dispatch model for wind power integration. It introduces the modeling methods, key constraints, and solution processes for wind power grid dispatch (Section 3.1). Building on this foundation, an HDJ hybrid optimization algorithm based on greedy selection (Section 3.2) is proposed, along with subsequent solution process optimizations (Section 3.3). These are ultimately integrated effectively with the DEED model (Section 3.4). Section 4 centers on experimental validation and results analysis. First, the performance of the proposed algorithms is tested and evaluated on benchmark functions such as CEC2022 and CEC2005 (Section 4.1). Next, power dispatch problems considering line losses and their simulation results are analyzed (Sections 4.2 and 4.3). Systematic experiments and evaluations are conducted under various scenarios, including cases with and without wind and solar integration, and different configurations of thermal power units across various scales and regions (Sections 4.4–4.6). In Section 5, the study summarizes the advantages and limitations of the proposed methods (Sections 5.1 and 5.2) and provides an outlook on potential future technological advancements (Section 5.3). Finally, Section 6 presents relevant research statements, followed by a list of references, offering readers a more comprehensive technical background and information support.

Through the progressive development of these sections, this study provides new perspectives and improvements for DEED optimization problems in both theoretical and practical dimensions. It offers feasible and efficient solutions for integrated power system dispatch and renewable energy integration.

1.1 Overview of Environmental Economic Dispatch Methods for Power Systems

In today’s era of rapid socio-economic and industrial development, global issues such as climate change and the depletion of fossil fuels have become increasingly severe. The development and utilization of renewable energy, characterized as low-carbon, clean, safe, and inexhaustible, have garnered growing attention worldwide. An international consensus has emerged, emphasizing the need to promote renewable energy development [14]. For the sustainable development of the power industry, this presents both significant opportunities and formidable challenges. Traditional economic operation of power systems, primarily relying on conventional thermal power generation, has focused solely on minimizing generation costs while neglecting the environmental impact of emissions from fossil fuel combustion [15]. This approach no longer meets the requirements of constructing a modern power system. As societies aim for higher living standards, environmental protection has become a priority. To achieve carbon peak and carbon neutrality goals, transitioning to a renewable energy-centered power system is imperative. Renewable energy sources such as wind, photovoltaic (PV), and small hydropower are green and clean, generating no emissions during operation [16]. Additionally, their generation costs are often lower than those of conventional thermal power units. These features are pivotal for restructuring the energy mix, driving energy production and consumption transformations, and promoting ecological civilization. However, these heterogeneous renewable energy sources are inherently intermittent, variable, and unpredictable [17]. Large-scale grid integration of such energy sources increases the complexity of power systems, posing significant challenges to maintaining system stability and ensuring energy security.

1.1.1 Power Dynamic Environment Dispatch

The power system, as one of the most complex industrial production systems, comprises five main components: generation, transmission, transformation, distribution, and consumption. Electricity, the primary product of this system, cannot be stored in large quantities, necessitating a balance between production and consumption at all times [18]. The total electricity generated must equal the total electricity consumed by the system at any given moment, a value that fluctuates continuously [19]. To maintain this balance while minimizing generation costs, Economic Dispatch (ED) has become a critical research focus. The ED problem typically involves determining an optimal generation plan for power units at a given time, subject to constraints such as power balance, spinning reserves, ramping capabilities, and generation limits, to achieve the lowest generation cost. A well-designed ED plan ensures the supply-demand balance of electricity, supports economical operation of generation units, and reduces energy consumption [20]. Consequently, ED remains a core problem in power system optimization, and years of research have yielded significant advances in ED modeling and solution algorithms [21]. Power system environmental and economic dispatch can be categorized into Static Environment and Economic Dispatch (SEED) and Dynamic Environmental and Economic Dispatch (DEED) models [22]. The SEED model focuses on optimizing generation cost and pollutant emissions within a single dispatch period while ensuring stable system operation and meeting load demand under relevant constraints [23]. The DEED model, on the other hand, extends the SEED framework by considering load variations across multiple dispatch intervals. By rationally distributing loads across all intervals, the DEED model aims to simultaneously optimize generation costs and pollutant emissions over the entire dispatch horizon, balancing environmental protection with economic efficiency. Compared to SEED, the DEED model is more complex but better suited to the practical operational requirements of power systems [24].

The SEED model starts with input variables Ui and achieves a single mapping from input to output through mechanism constraint conditions, i.e., U1→P1,U2→P2,…,UN→PN. This model reflects the characteristics of a simple linear mapping under constraint conditions, making it suitable for scenarios where the relationship between inputs and outputs is one-to-one. In contrast, the system structure of the DEED model establishes a more complex mapping relationship. After being constrained by mechanism conditions, input variables Ui can be mapped to multiple outputs Pi,j, forming a one-to-many mapping relationship: U1→ P1,1,P1,2,…,P1,n,U2→P2,1,P2,2,…,P2,n,…,UN→PN,1,PN,2,…,PN,n. This structure significantly enhances the expressive capability of the model, enabling it to capture more complex and diverse relationships between inputs and outputs. The SEED model is suitable for relatively simple one-to-one systems, whereas the DEED model, by introducing one-to-many mappings, is better suited for systems requiring higher complexity and greater descriptive power in their modeling [25].

The reasonable planning and implementation of the environmental economic dispatch (EED) scheme in power systems are of great significance for achieving the “carbon peak, carbon neutrality” goals, energy conservation, loss reduction, and maintaining the safe operation of the system [26]. The mathematical model of EED is characterized by high dimensionality, non-linearity, non-convexity, and complex constraints. Among them, the Dynamic Environmental Economic Dispatch (DEED) model is more complex than the Static Environmental Economic Dispatch (SEED) model due to its multi-period coupling features. Therefore, the DEED model becomes significantly more complicated. In the entire process of power system environmental economic dispatch, the system determines the generation plans of the units based on load demand and operational constraints during the dispatch period, while minimizing pollution emissions and reducing generation costs to the greatest extent. Given the substantial research achievements in economic dispatch, many effective solution methods for economic dispatch models have been applied to environmental economic dispatch problems. Moreover, with the continuous advancement of computer technology in recent years, new solution algorithms have emerged to address environmental economic dispatch problems [27]. Currently, the solution methods for EED problems can be roughly classified into classical optimization methods and modern intelligent optimization algorithms [28].

1.1.2 Classical Optimization Methods

Dynamic programming is an important branch of operations research, primarily used to solve optimization problems in multi-stage decision processes of mathematical models. In dynamic programming, the problem is typically decomposed into several stages where decisions in each stage are interdependent, allowing the resolution of complex mathematical models [29]. Due to its strong adaptability to various complex mathematical models, dynamic programming has been widely used in dynamic environmental economic dispatch problems [30]. However, as the number of variables in the DEED model increases, the “curse of dimensionality” becomes a key constraint on its application. Nonlinear programming, proposed by foreign scholars in 1951, is widely used to solve optimization problems involving nonlinear functions in mathematical models [31]. Therefore, the DEED model is theoretically suitable for solving using nonlinear programming methods. However, due to its non-convex nature, nonlinear programming may often fall into local optima during the direct solution process [32]. To avoid this issue, scholars typically use piecewise linear approximations for nonlinear functions, leading to an approximate linearized model to obtain precise computational results [33]. The environmental economic dispatch problem belongs to nonlinear programming problems. Since the objective function in the EED model is a quadratic real function and the equality constraints are linear functions, the EED problem is a special form of nonlinear programming known as quadratic programming [34]. Quadratic programming is relatively simpler, and various solution methods are available, such as the null space method, value space method/Lagrange multiplier method, and active set method [35]. Some studies have considered wind/solar power penalty factors, unit reserve penalty factors, and wind power forecasting errors in constructing the EED model and solved it using quadratic programming [36]. The EED model contains numerous inequality constraints, making it an inequality-constrained optimization problem. The interior-point method is effective in solving such problems with high computational accuracy. This method ensures that the iteration points remain within the feasible region by setting “barriers” at the boundaries of the feasible domain, thereby maintaining calculation precision [37]. Modern interior-point methods have been applied to solve environmental economic dispatch models with mixed logical constraints, achieving both computational accuracy and efficiency. These four classical mathematical programming algorithms are widely used to solve environmental economic dispatch problems due to their strong model adaptability, simple iterative processes, and high solution efficiency. In addition, methods such as Lagrange’s method and gradient-based methods have also shown promising results in solving environmental economic dispatch problems [38].

1.1.3 Modern Intelligent Optimization Algorithms

The environmental economic dispatch problem in power systems is characterized by non-linearity, multiple constraints, and high dimensionality. Classical optimization methods often struggle with local optima and low solution accuracy when solving such problems. With the rapid development of artificial intelligence and artificial life sciences in recent years, new bio-inspired algorithms, such as Particle Swarm Optimization (PSO), Moth Flame Optimization (MFO), and Firefly Algorithm (FA), have shown promising results in solving environmental economic dispatch problems [39]. Additionally, optimization algorithms based on simulating and revealing natural phenomena and processes, such as Genetic Algorithm (GA), Differential Evolution (DE), and Simulated Annealing (SA), have been widely applied to environmental economic dispatch [40]. In environmental economic dispatch, improvements to traditional FA have helped address issues such as optimization oscillation during the search process. The Genetic Algorithm (GA) is based on the theory of evolution and genetics, mimicking natural selection, mutation, and crossover in biological systems [41]. GA updates the population to improve its adaptability. Various studies have successfully applied GA to solve environmental economic dispatch models. Differential Evolution (DE), proposed by Storn and Price in 1995, is a random parallel search algorithm [42]. DE simplifies the evolution process through real-number encoding, mutation, and relative competitive survival strategies, demonstrating strong model adaptability. Studies have proposed Adaptive Differential Evolution Algorithm (ADEA) and Chaotic Local Search Differential Evolution (CLSDE) to improve DE’s efficiency in solving environmental economic dispatch problems.

Although intelligent optimization algorithms surpass traditional methods in both theoretical principles and practical applications, they also reveal certain limitations when applied to increasingly complex engineering problems that demand higher computational precision. For instance, these algorithms tend to fall into local optima when dealing with high-dimensional complex functions or problems [43]. Moreover, the excessive number of hyperparameters requires meticulous fine-tuning, which becomes even more challenging as different problems necessitate frequent parameter adjustments. Therefore, improving intelligent optimization algorithms is essential for enhancing their performance and broadening their application scope, making it a critical research direction in the field.

Improvement methods for optimization algorithms generally fall into two categories. The first involves enhancing specific aspects of the algorithm’s iterative process by incorporating specialized mechanisms, such as initialization strategies, parameter selection, or update formulas. They dynamically adjusted the search strategy and introduced a survival mechanism to prevent local optima, thereby improving algorithm performance. Tang et al. developed an enhanced whale optimization algorithm (WOA) by incorporating an adaptive strategy and a differential mutation strategy [44]. Additionally, they introduced a controllable variable to address path planning problems, resulting in greater stability and faster convergence compared to other algorithms. Abaci et al. proposed an improved moth-flame optimization (MFO) algorithm, integrating chaotic stochastic adversarial learning and a Cauchy mutation operator to enhance both global and local search capabilities, leading to faster convergence and better feasible solutions [45]. Gharehchopogh et al. introduced a quantum multi-verse optimization algorithm, embedding quantum theory into the multi-verse optimization framework [46]. By leveraging quantum interference and symbolic integration, they enhanced the search space and achieved an optimal balance between global and local search.

The second approach involves hybridizing optimization algorithms by combining the advantages of two or more methods for targeted improvements. Zhu et al. developed a Genetic algorithm ant colony optimization (GA-ACO) algorithm, enhancing ant colony optimization (ACO) with adaptive operators and incorporating a deletion operator into the genetic algorithm (GA) [47]. The suboptimal solutions obtained from the improved ACO were then fed into the modified GA, yielding an optimized algorithm that demonstrated strong performance in vehicle routing problems. Wang et al. proposed a hybrid optimization algorithm combining the bat algorithm with the grasshopper optimization algorithm [48]. They used variable-coefficient Lévy flight to enhance the global search capability of the grasshopper optimization algorithm while leveraging the bat algorithm’s balancing ability to improve overall coordination. Sahoo et al. introduced a hybrid algorithm that combined MFO with the butterfly optimization algorithm (BOA) [49]. The rapid convergence of BOA compensated for MFO’s slower convergence while preserving MFO’s strong local search capability and high search precision. This hybrid algorithm exhibited outstanding performance in extensive function tests. By utilizing the distinct optimization features of these three methods in a cross-search approach, experimental results demonstrated its effectiveness in solving three real-world engineering problems.

1.1.4 The Optimization Algorithm Is Combined with the Dynamic Environment Scheduling System

Renewable energy generation is currently the most ideal form of power generation. However, unlike traditional power generation, renewable energy is integrated into the grid through power electronic converters with relatively weak disturbance resistance [50]. This makes it less adaptable to power fluctuations, leading to significant negative impacts on grid stability. These issues primarily manifest in increased challenges in peak load and frequency regulation, power quality degradation, reactive power compensation and voltage instability, and increased grid interference [51]. In severe cases, they can directly cause major power system failures and economic losses for users. To address these challenges, numerous researchers have made significant efforts from various perspectives. Liu Hongli et al. conducted an in-depth analysis of renewable energy consumption capacity and space constraints using a time-series production simulation method, performing simulations and empirical studies based on renewable energy production in Shanxi Province [52]. Wang considers how to operate energy storage to overcome the problem of solar photovoltaic (PV) in low-voltage (LV) distribution networks, which can be solved by running energy storage systems in a LV distribution network with a large number of PV generators installed [53]. The results demonstrated that this system significantly enhanced control performance and stability. Chen et al. addressed the peak regulation and scheduling problem by considering the advantages and disadvantages of different power generation units [54]. He optimized the scheduling of power systems with integrated renewable energy by incorporating economic and environmental benefits as well as load characteristics during specific time periods. Developing more advanced power dispatch models is the most direct way to mitigate the impact of renewable energy grid integration. A well-designed model and scheduling strategy can ensure the stable performance and efficient utilization of renewable energy generation. Zhang et al. conducted a comprehensive analysis of stability issues associated with large-scale renewable energy grid integration and proposed a novel impedance model for renewable energy systems [55]. He optimized the dispatch scheme by using the short-circuit ratio as a constraint. Yang et al. introduced fuzzy theory and game theory into energy dispatch problems, considering distribution network conditions, wind-solar power consumption [56], and load-side demands. He established a bilevel game model for power systems with source-load uncertainties, and experimental results demonstrated that this model provides an improved dispatch strategy. Alshammari et al. transformed the stochastic nature of wind power into a chance-constrained optimization problem, representing system stability through fuzzy membership functions and proposing a novel power economic-emission dispatch model [57]. Pothireddy et al. developed a multi-objective optimization-based day-ahead scheduling model for thermal, wind, and solar power generation [58]. This model used expected unutilized energy and load loss probability as key indicators to assess the reliability and stability of renewable energy integration. Pijarski proposed a two-stage adaptive robust optimization model for wind, solar, and thermal power integration [59]. They first used an artificial neural network to rapidly generate suboptimal unit commitment decisions and then applied a genetic algorithm with a priority list to fine-tune parameters, ultimately determining the optimal scheduling period and number of generating units. Shi et al. proposed a multi-timescale coordinated scheduling model based on the complementary operation characteristics of wind, solar, thermal, pumped hydro storage, and battery storage systems [60]. This model optimized power output at different timescales—24 h ahead, 1 h ahead, and 15 min ahead—to mitigate fluctuations in grid-integrated power generation. Currently, most power dispatch models have certain limitations and are effective within specific environments, but their scalability still requires further validation.

Recent studies have been conducted on the optimization configuration and scheduling strategies of hybrid energy systems. For hybrid energy systems, fully considering their economic efficiency and reliability while achieving reasonable and effective scheduling optimization holds significant practical importance. Ifaei et al. reviewed the optimization of hybrid energy systems based on evolutionary algorithms, focusing on different optimization objectives, constraint conditions, algorithm performance, and evaluation metrics [61]. They pointed out that the main challenges in hybrid energy system optimization lie in handling uncertainty, dynamics, and complexity, as well as selecting appropriate algorithms and parameter settings. Zhao et al. established a 1 MW geothermal organic Rankine cycle model, using the system’s net power generation per ton of water as the analysis target to study the variation patterns of thermodynamic performance parameters, thereby achieving efficient utilization of geothermal fluids [62]. Bailey et al. investigated the Guide Basin’s hot dry rock reservoir, employing the non-dominated sorting genetic algorithm II (NSGA-II) to optimize the optimal parameter combinations of enhanced geothermal systems, assessing the development potential, as well as economic and environmental benefits of hot dry rock resources [63]. Yuan et al. proposed a model predictive control-based scheduling method to regulate system complementarity and control costs [64]. Wang Ting et al. integrated renewable energy with hydrogen production processes to construct a hybrid energy system [65]. They used a bi-level optimization model to simultaneously optimize construction and operational costs, reducing load losses and achieving favorable economic and environmental benefits. Sohani et al. determined the optimal operating conditions of a solar-geothermal hybrid energy system through a dynamic multi-objective optimization approach [66], improving the system’s economic feasibility and safety. Yang and Li applied a multi-objective optimization method based on genetic algorithms and fuzzy decision-making to optimize system design and operation while analyzing the system from economic, environmental, and social perspectives [67]. Yip et al. proposed a sustainable performance evaluation model based on text mining and grey relational analysis, which identifies key factors affecting sustainable development by calculating keyword weights. This approach can be used in the field of energy modeling to more objectively assess the sustainability of energy systems [68]. Yan et al. emphasize the importance of economic and environmental sustainability in processing, This study proposes a scientific framework for evaluating the processing field, which can provide a new perspective for the evaluation of power dispatch systems in a way that evaluates their economic and environmental sustainability [69].

In various fields such as production scheduling, intelligent control, and path planning, multiple objectives must be optimized simultaneously. However, these objectives often conflict, making it impossible to achieve optimal states for all of them at once. Such problems are collectively referred to as multi-objective optimization problems (MOPs). Unlike traditional single-objective problems, MOPs cannot be solved using linear methods and do not have a unique solution, posing significant challenges for their resolution. Therefore, research on solving MOPs holds substantial practical value. The fundamental idea of solving MOPs is to identify a set of solutions through an optimization process, ensuring that multiple objectives reach the best possible state within given constraints [70]. This set of trade-off solutions is known as the Pareto optimal set. Initially, traditional methods for solving MOPs decomposed complex MOPs into single-objective problems, using approaches such as goal programming, weighted sum methods, and distance function methods. However, these traditional optimization methods rely on prior knowledge and require multiple iterations to approximate the Pareto optimal set (PS), often failing to obtain a satisfactory trade-off solution set. Moreover, as problems become more complex, high-dimensional, dynamic, multimodal, or constrained, it becomes increasingly difficult to find an ideal solution set. Therefore, exploring new approaches for solving high-dimensional and complex MOPs is of great significance. Ye et al. combined multi-objective control technology (CMCT) with particle swarm optimization (PSO), proposing the MOPSO-CDAS algorithm, which optimizes the update mechanism of the non-dominated archive, thereby improving both the convergence and diversity of the solution set [71]. Zapotecas et al. integrated Pareto dominance and decomposition methods into the solution mechanism, introducing a novel integrated PSO algorithm [72]. To further enhance convergence speed, Gu et al. later proposed a new leader particle selection and external archive maintenance mechanism [73].

1.2 Overview of Wind Power Grid Connected Environmental Economic Dispatch Methods

Compared to renewable energy generation, thermal power generation developed earlier, is easier to manage, simpler in program control, and is more widely applied in actual production and daily life. The generation output of thermal power units is controlled by the combustion of fossil fuels such as coal and oil, and is less influenced by environmental factors, climate, and other variables. It operates stably, reliably, with extremely high controllability and accurate load forecasting ability, which can effectively ensure the country’s power supply. In contrast, the output of renewable energy sources such as wind power and photovoltaics is constantly influenced by geographical factors such as wind speed and solar radiation, making it difficult to predict output [74]. These energy sources exhibit randomness, intermittency, and variability. In response to this issue, researchers have conducted extensive studies on renewable energy output forecasting, achieving many substantial results. However, there are still certain errors in predicting natural resources such as wind speed, solar radiation, and water flow, making it challenging to ensure the stable operation and safety of the actual power system [75]. Nevertheless, wind power, photovoltaic, and small hydropower are green and clean renewable energy sources that play an important role in the renewable energy mix for power supply [76]. Once connected to the grid, their uncertainties inevitably affect the safe operation of the power system, but they also bring direct environmental and economic benefits, playing a crucial role in promoting efficient, green, and low-carbon sustainable development, thus holding significant strategic importance. Moreover, in most regions, the areas of electricity consumption and renewable energy generation are widely dispersed and not concentrated. The uncertainty of renewable energy can significantly affect the reliability, power quality, and economics of the power system. Therefore, after the integration of heterogeneous renewable energy sources such as wind, solar, and small hydropower into the grid, numerous uncertainties are introduced into the power system’s dispatch process.

Wind power is intermittent and random. The average absolute percentage error in actual wind power forecasting ranges from 25% to 40% [77]. This can cause power system imbalances during wind power grid integration, leading to phenomena like wind curtailment and even “reverse peak shaving.” To ensure reliable power supply, spinning reserves are required [78]. The dispatch problem of power systems containing wind farms should comprehensively consider multiple factors, such as resource consumption, economic benefits, and environmental benefits [79]. On the generation side, it should focus on fuel costs for thermal power units, the costs of spinning reserve capacity, and the pollutant emissions resulting from fossil fuel combustion [80]. On the residential consumption side, to reduce residents’ electricity purchase costs (the combined costs of power procurement by the grid and transmission and distribution costs), the cost of electricity purchase should also be considered [81]. Furthermore, the random fluctuation characteristics of wind power output and the constant changes in the grid load demand require real-time adjustment of thermal power unit output to maintain the power system’s balance [82]. Therefore, the dynamic output scheduling of thermal power units should be considered over 24 h periods.

To address the challenge of integrating wind power into the energy system, researchers developed a strategy that relies on acceptable forecasting errors and probabilistic models to effectively balance supply and demand [83]. This approach enables more reliable integration of wind power by accounting for its inherent variability. In another effort, a cost-environmental dispatch model was created to optimize both economic and environmental outcomes when dealing with large-scale wind power generation [84]. By transforming the piecewise representation of wind power output into a probabilistic model, the complexities of multi-constraint, multi-objective optimization problems were better managed [85]. Building on these ideas, analysts derived an analytical formula to represent the probability distribution of wind farm output, assuming that wind speeds follow a Rayleigh probability density function [86]. This formula was then translated into a practical mathematical model for turbine output connected to the power grid, providing the foundation for stochastic economic dispatch in power systems. Further advancements included methods to construct wind farm output probability distribution models, coupled with error analysis techniques. These tools offered a more detailed depiction of the probabilistic nature of wind power, improving the accuracy of power system planning [87]. To enhance wind power modeling and dispatchability, a novel method was introduced to establish time-varying probability distributions for wind power clusters. By using virtual units tailored to different periods, this approach significantly improved the precision and flexibility of wind power integration into the grid [88].

1.3 Current Technical Defects and the Improvement Method of This Paper

High-dimensional optimization problems, such as DEED, suffer from the “curse of dimensionality,” which manifests in several ways: (1) the exponential growth of the search space volume leads to a sparsity of feasible solutions, making global optima increasingly difficult to locate [89]; (2) traditional gradient-based solvers struggle with computational intractability as the number of decision variables increases, particularly in the presence of complex operational constraints in power systems [90]; (3) heuristic and metaheuristic methods experience reduced search efficiency due to the increased number of local optima, requiring adaptive strategies for robust exploration-exploitation balancing [91]. Although multi-objective evolutionary algorithms such as NSGA-II and MOEA/D have been applied to DEED, their performance in high-dimensional spaces is not well understood. The loss of selection pressure due to Pareto dominance weakening and the increasing difficulty of maintaining a diverse and well-distributed solution set necessitate specialized modifications.

The DEED problem exhibits strong coupling between generation units due to (1) power balance constraints, (2) network constraints, and (3) interdependencies between environmental and economic objectives. Unlike simple dispatch problems where units can be optimized independently, strong coupling requires considering the joint feasibility of multiple generators across the entire scheduling horizon. From a mathematical perspective, strong coupling manifests as dense constraint Jacobians and Hessians in numerical optimization formulations, increasing the computational burden of Newton-type solvers [92]. In heuristic methods, it leads to difficulty in designing effective crossover and mutation operators, as modifying one decision variable affects the feasibility of others. Existing research on multi-objective particle swarm optimization (MOPSO) and differential evolution (DE) in DEED often fails to rigorously address constraint-handling strategies under strong coupling. Constraint-domination principles, adaptive penalty methods, or co-evolutionary approaches could be explored to improve performance.

The DEED problem is inherently nonlinear due to Quadratic or higher-order cost functions in generator fuel consumption and emissions modeling; Power flow equations (e.g., AC power flow), which introduce transcendental nonlinearity; Renewable energy uncertainty, leading to non-smooth probabilistic constraints. Gradient-based solvers such as interior-point methods require careful handling of nonlinearity, often resorting to second-order approximations that may not be globally valid [93]. In contrast, population-based heuristics tend to approximate Pareto-optimal solutions without explicit gradient calculations, yet they struggle with fine-tuning solutions near highly nonlinear feasibility boundaries. A critical gap in the literature is the lack of rigorous theoretical analysis on how different nonlinearity sources influence algorithmic efficiency and convergence properties.

Non-convexity arises in DEED from unit commitment constraints, valve-point effects, and discrete decision variables in on/off scheduling. Traditional convex relaxation techniques (e.g., semidefinite programming) fail in highly non-convex settings, leading to suboptimal solutions. Multi-modal landscapes with numerous local minima make global optimization particularly challenging. Methods such as DE-PSO attempt to address this by integrating differential evolution’s global search capability with PSO’s fast convergence, but the theoretical guarantees for escaping local optima remain weak. Furthermore, Pareto-optimal front (PF) estimation in non-convex multi-objective spaces is non-trivial. While dominance-based methods (e.g., NSGA-II) rely on empirical PF approximation, decomposition-based methods (e.g., MOEA/D) assume quasi-convexity in subproblems, which may not hold [94]. Addressing non-convexity requires adaptive restart mechanisms, landscape-aware mutation strategies, or hybrid approaches combining metaheuristics with machine learning-based function approximation.

Nowadays, with the rapid development of renewable energy sources, such as wind and solar energy, power systems are facing more and more complex scheduling problems. Especially in the dynamic environment of Power Economic Dispatch (DEED), due to the multi-objective optimization, complex constraints and uncertainty of wind and photovoltaic power generation, traditional optimization methods are difficult to effectively deal with these challenges. The existing power dispatching optimization methods mostly focus on single objective optimization or simple constraint processing, ignoring the complex relationship between multiple objectives, the processing of dynamic constraints and the impact of renewable energy uncertainty on dispatching optimization [95]. The volatility and uncertainty of wind power generation mainly come from the time-varying wind speed, which is greatly affected by meteorological changes and difficult to predict accurately. This uncertainty brings great difficulty to the dispatch of power system, especially in the short-term or long-term dispatch, the power generation of wind power cannot be accurately predicted, which leads to the reduction of the execution efficiency and reliability of the dispatch plan [95]. Most of the existing scheduling methods still rely on traditional static or simple constraint-based scheduling models, and are weak in handling renewable energy uncertainties, which cannot meet the increasingly complex demands in modern power systems. Therefore, finding an efficient and multi-objective optimization method that can effectively solve the dynamic economic dispatch problem in power systems and adapt to the needs of the complexity of modern power systems has become the main motivation of this research.

This paper proposes a dual-population pseudo-parallel GA-DE (genetic algorithm-differential evolution) multi-objective algorithm (referred to as DGADE) to solve the DEED model. Compared with the existing literature, the DGADE algorithm improves the search efficiency and solution quality in multi-objective optimization through the concepts of external elite retention and Pareto dominance. The algorithm combines the average entropy and cubic chaotic map initialization strategy to ensure the generation of high-quality initial population, thereby improving the effectiveness of the whole optimization process. By utilizing differential evolution and genetic algorithms, a dual-population collaborative evolution model is established. Through communication and optimal value sharing strategies between different populations in the evolutionary model, cooperative searching within the population is achieved. Through the communication between different populations and the optimal solution sharing strategy, the model realizes the cooperative search within the population, and effectively avoids the phenomenon of local optimum and premature convergence. Compared with the traditional single algorithm optimization method, this innovation improves the global search ability of the algorithm in solving complex problems. To prevent the algorithm from encountering premature convergence and local optima in later stages, an adaptive strategy for controlling parameters and a tabu search strategy are introduced into the differential evolution algorithm. This method can effectively deal with the local optimum problem that the algorithm may encounter in the later stage, so as to improve the accuracy of the solution and the stability of the search. Additionally, an improved Pareto solution set pruning method is used to trim the external elite archive. A dynamic relaxation constraint mechanism is employed to handle the complex constraints of the DEED model. By adjusting the processing method of constraints flexibly, the model can better adapt to the constraints of the actual power system in the solving process. This innovation effectively improves the adaptability and practicability of the model. The algorithm then obtains a Pareto optimal solution based on the best compromise derived from fuzzy theory. This paper considers the trade-offs between fuel consumption, pollution emissions, and losses, and uses constraints such as generator capacity, power balance, and generator ramping to establish a three-objective DEED model. Finally, the feasibility of the proposed algorithm is verified using a system with 10 units. Taking into account factors such as spinning reserves and network losses, the model addresses the uncertainty of wind and solar output by applying positive and negative spinning reserve capacity constraints. The dual-objective function of generation cost and pollution emissions is transformed into a single-objective function through the use of a normalization factor. This paper develops a DEED dispatch model for wind and solar grid integration. Considering that DE algorithm and JAYA algorithm have complementary characteristics, a hybrid optimization algorithm combining DE and JAYA (referred to as HDJ) is proposed.

1.4 Contribution of the Solution in This Paper to the DEED Optimization Problem

The paper addresses the limitations of current DEED optimization techniques in handling high dimensionality, strong coupling, nonlinearity, and non-convexity, and it introduces the dual-population pseudo-parallel GA-DE multi-objective algorithm (DGADE) as a novel solution.

High-dimensional optimization problems pose significant challenges due to the exponential growth of the search space, leading to an increased risk of slow convergence and suboptimal solutions. Traditional algorithms such as NSGA-II and MOEA/D struggle to maintain diversity and selection pressure in high-dimensional Pareto front approximations. The proposed DGADE algorithm mitigates this issue in several ways, The combination of average entropy and cubic chaotic mapping ensures a diverse initial population, reducing the likelihood of early stagnation in high-dimensional search spaces. Entropy-based initialization distributes solutions more uniformly, while chaotic mapping prevents clustering around local optima. Unlike single-population evolutionary approaches, DGADE utilizes a dual-population framework where genetic algorithms (GA) and differential evolution (DE) evolve in parallel. This structure allows specialized subpopulations to explore different regions of the high-dimensional search space, enhancing global exploration.

In the DEED problem, strong coupling arises due to interdependencies between generation units, power balance constraints, and environmental objectives. Traditional optimization methods often fail to handle this complexity effectively, leading to suboptimal dispatch strategies. By sharing best solutions across GA and DE populations, the algorithm preserves important search knowledge while maintaining diversity. This prevents premature convergence to local optima, which is particularly problematic in highly coupled systems. Unlike static constraint-handling techniques that struggle with tightly coupled constraints, the dynamic relaxation mechanism adjusts constraint processing dynamically, allowing more flexible convergence toward feasible solutions. This is particularly important when dealing with power system constraints, such as ramp rate limits and spinning reserves.

The DEED model includes nonlinear relationships due to factors such as generator fuel cost curves, emission models, and power flow constraints. These nonlinearities lead to complex optimization landscapes with irregular, non-differentiable regions, making classical methods like convex relaxation ineffective. Traditional evolutionary algorithms suffer from convergence stagnation in highly nonlinear spaces. The introduction of tabu search and adaptive parameter control allows the algorithm to adjust search strategies dynamically, preventing stagnation in regions with non-differentiable or highly irregular objective functions. The combination of differential evolution’s mutation operators and genetic algorithm’s crossover strategies allows DGADE to navigate complex, nonlinear objective landscapes more effectively than single-algorithm approaches. By incorporating spinning reserve constraints and network losses, the model dynamically adjusts constraint handling, making it better suited for real-world.

Non-convexity in DEED arises due to valve-point loading effects, discrete operational constraints, and multimodal cost functions. Conventional approaches such as weighted-sum methods fail to capture the full Pareto front in non-convex search spaces. Pareto Dominance-Based External Archive: The elite retention mechanism ensures that Pareto-optimal solutions are maintained and refined throughout the search process, preventing premature convergence to convex subsets of the solution space.

By systematically addressing the fundamental challenges of high dimensionality, strong coupling, nonlinearity, and non-convexity, the DGADE algorithm presents a well-justified and robust solution for DEED optimization. The dual-population evolution framework, adaptive constraint handling, hybrid optimization strategies, and Pareto-based solution refinement collectively enhance the algorithm’s ability to solve complex multi-objective power dispatch problems more effectively than existing methods. The model proposed in this paper can effectively cope with the fluctuation of wind power generation and the uncertainty of solar energy, and improve the robustness of the power system. This study provides a new scheduling optimization method for large-scale access of renewable energy sources such as wind power and photovoltaic, which helps to achieve more efficient and environmentally friendly energy utilization. By using modern optimization algorithms and dynamic scheduling strategies, this study provides new ideas for intelligent scheduling of power systems, and promotes the development of power systems to be more flexible, efficient and green.

2  DEED Model Improvement of Thermal Power System

Firstly, we model the power system, use the double group pseudo-parallel algorithm to coordinate the parallel processing of GA and DE algorithm, and improve the coordination strategy, using the average entropy initialization, cubic chaotic map initialization, parameter adaptive adjustment of these three methods to coordinate GA and DE algorithm. The overall parallel strategy is improved by improving the diversity maintenance strategy based on crowding entropy and the dominant selection operator.

2.1 Construction of Thermal Power Environmental Economic Model

2.1.1 Functions and Model Building

Considering the domain point effects, the fuel cost is expressed as:

Q(PG)=∑t=1T∑i=1N{ai+biPGi,t+ciPGi,t2+|disin[ei(PGimin−PGi,t)]|}(1)

where T is the scheduling period, N is the total number of generators in the system, ai,bi,ci,di,ei are the fuel consumption characteristic coefficients of the i-th generator, PGi,t is the active power output of the i-th generator at time t, PGimin is the minimum active power output of the i-th generator. Without loss of generality, this paper considers all pollutants emitted during the power generation process. The relationship between the pollution emissions and the active power output of the generator is:

E(PG)=∑t=1T∑i=1N(αi+βiPGi,t+γiPGi,t2)+ξiexp⁡(λiPGi,t)(2)

where E(PG) is the pollution emissions during power generation, αi,βi,γi,ξi,λi are the pollution characteristic coefficients of the i-th generator.

The function relationship between the transmission line losses in the power system network and the active power output of the generators is given by:

PL,t(PG)=∑j=1N∑i=1NPGi,tBijPGj,t+∑i=1NBi0PGi,t+B00,t=1,2,…,T(3)

where PL,t(PG) represents the transmission line losses in the power system network, Bij,Bi0,B00 are the transmission loss coefficients.

2.1.2 Model Constraints

To ensure stable operation, the active power output of each generator must be constrained between its minimum and maximum values, i.e.,

PGimin≤PGi,t≤PGimax,i=1,2,…,N(4)

where PGimin and PGimax are the minimum and maximum active power outputs of the i-th generator, respectively. The total generation must meet the total demand PD,t and the network’s active power loss PL,t, i.e., ∑i=1NPGi,t−PD,t−PL,t=0,t=1,2,…,T.

Since the model established is a dynamic scheduling model, the rate of change in the output power of each generator at adjacent time periods must not exceed the generator’s ramp-up or ramp-down limits, i.e.,

DRi≤PGi,t−PGi,t−1≤URi(5)

where DRi and URi are the maximum ramp-up and ramp-down rates, respectively, for the i-th generator’s output power within one time period (1 h).

2.2 Parallel Multi-Objective Algorithm Preprocessing

2.2.1 Cooperative Strategy

The DGADE algorithm proposed in this paper involves one population using an improved Differential Evolution (DE) algorithm, while the other uses a Genetic Algorithm (GA). During the evolution process, the populations exchange information at appropriate times, accelerating the evolution by promoting diversity [96]. DE is easy to operate, with strong global search capability and robustness. To balance the algorithm’s convergence speed with population diversity, the DE/best/2 mutation strategy is chosen. The next generation individual after mutation is given by:

Vi=xrbg+F(xr1g+xr2g−xr3g−xr4g)(6)

where g is the current iteration number, xrbg is the current best individual, xr1g,xr2g,xr3g,xr4g are four randomly selected individuals from the population, F is the mutation operator. The DE/best/2 strategy converges quickly but can easily get trapped in local optima. To address this, a “local search” Tabu Search (TS) strategy is introduced. The advantage of TS is that it allows the acceptance of suboptimal solutions in the search space, but its drawback is that it has a strong dependency on the initial solution. To mitigate the shortcomings of traditional DE and TS, this paper adopts a two-phase hybrid algorithm. In the first phase, DE is used for global search; once convergence reaches a certain level and stagnation occurs, the second phase executes the TS local search. The results obtained from DE are used as the initial solution for TS, helping overcome the problem of poor initial solutions that slow down TS convergence [97]. To increase the diversity of the initial population, the paper uses the average entropy and cubic chaotic mapping strategies for initialization. Control parameters are included in the individual encoding of the population, allowing these parameters to be adaptively adjusted based on the characteristics of the multi-objective optimization.

By using the average entropy initialization strategy, a sufficiently diverse and evenly distributed initial solution across the search space is obtained. Let the initial population consist of NP individuals with a dimension D. According to information theory, the entropy H of the population is expressed as:

H=1D∑j=1DHj(7)

Hj=1m+1∑i=1m(−Piklog2⁡Pik),j=1,2,…,D(8)

where m is the number of known individuals in the initial population, k is the number of new solutions generated during the initialization process, Pik is the similarity between the i-th individual’s two-dimensional variables, expressed as:

Pik=1−|xi(i)−xk(i)|Bi−Ai(9)

Here, Bi and Ai are the upper and lower bounds for the i-th variable, respectively. This strategy ensures that the population’s diversity is sufficiently high, providing a solid foundation for further optimization. Where Ai represents the upper limit of the i-th dimensional variable, and Bi represents the lower limit of the i-th dimensional variable. The average entropy initialization steps are as follows, Randomly generate three known individuals. Randomly generate a new individual. Calculate the average entropy of the new population. If the threshold of the new individual exceeds the set value, it is added to the initialized population. Repeat this process until NP individuals are obtained.

2.2.2 Cubic Chaos Map Initialization

Research shows that the cubic chaos map has better ergodicity and a more uniform distribution compared to the logistic chaos map [98]. Therefore, the cubic chaos map is used to initialize the population of the Differential Evolution (DE) algorithm. The cubic chaos map is defined as:

y(n+1)=4y(n)3−3y(n),−1<y(n)<1,y(n)≠0,n=0,1,2,⋯(10)

Assuming the initial population consists of NP individuals with a dimensionality of D.First, a D-dimensional variable within the interval [−1,1] is randomly generated as the first individual. Assuming the initial population consists of NP individuals with a dimensionality of D, First, a D-dimensional variable within the interval [−1,1] is randomly generated as the first individual. Next, each dimension of the first individual is iteratively computed NP−1 times, producing an NP×D variable matrix. Finally, the variables generated by the cubic chaos map within [−1,1] are mapped to the solution range [xfmin,xfmax] using the following equation:

xij=xfmin+(xfmax−xfmin)yij+12(11)

where yij is the chaotic variable generated, and xij is the mapped chaotic variable. Incorporating Control Parameters CR and F into Individual Encoding.

2.2.3 Adaptive Adjustment of Mutation Factor F

In the mutation operation, three randomly selected individuals are sorted from worst to best, denoted as xb,xm,xw, with corresponding fitness values fb,fm,fw, respectively. The optimized mutation operation is then formulated as:

mi=xb+F⋅(xm+xw)(12)

Additionally, the mutation factor F is adaptively adjusted based on the fitness differences among individuals to balance global and local search capabilities:

Fi=Fl+(Fu−Fl)(fm−fb)(fw−fb)(13)

where Fl=0.1 and Fu=0.9. In each iteration i, a certain number of individuals are selected from the population using the mutation strategy to generate mutant individuals:

mi(t)=pr1(t)+F⋅(pr2(t)−pr3(t)),r1≠r2≠r3(14)

mi=xb+F⋅(xm+xw)(15)

Compared to traditional mutation strategies, the improved differential evolution (DE) algorithm ranks individuals based on fitness values, addressing the issue of slow convergence in the early search stage while maintaining population diversity to prevent local optima. Moreover, in traditional mutation operations, the mutation factor F is fixed, making it impossible to adaptively adjust based on the difference vector of selected individuals.

To overcome this limitation, the fitness values of three randomly selected individuals are ranked, and F is iteratively updated using the fitness differences:

Fi=Fl+(Fu−Fl)(fpr2−fpr1)(fpr3−fpr1)(16)

where fpr1,fpr2, and fpr3 denote the fitness values of individuals in the population, satisfying fpr1 < fpr2 < fpr3. The upper and lower limits of F are set as Fu=0.9 and Fl=0.1, respectively. Although F theoretically ranges between (0,1), its performance is suboptimal when approaching 0 or 1, thus the chosen range ensures a balance between exploration and exploitation. The effect of different mutation factors on the algorithm is shown in Table 1.

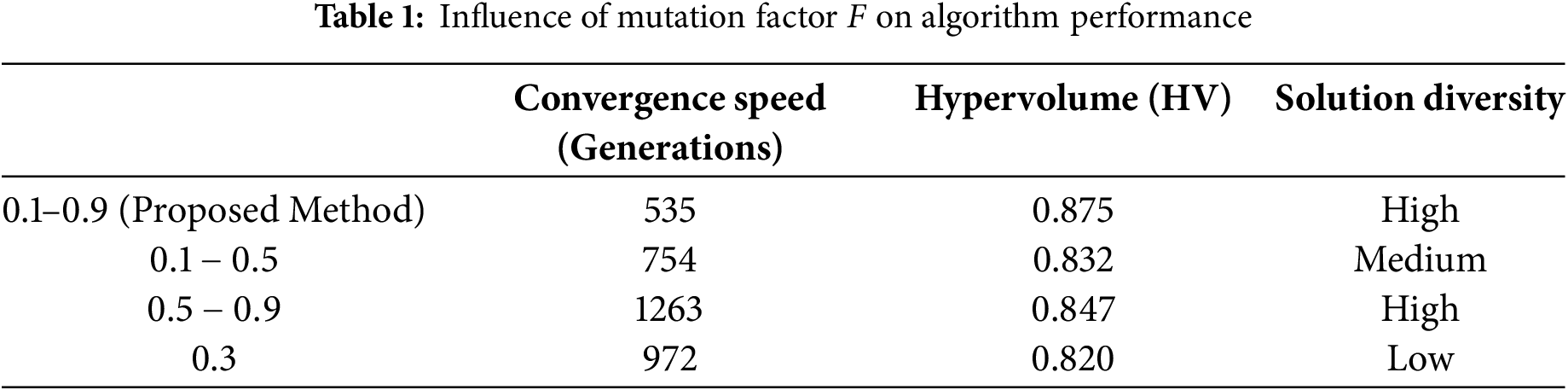
Experimental results indicate that the proposed method (F range: 0.1−0.9) achieves the fastest convergence and the best Pareto front quality. A lower F value (e.g., 0.1) facilitates fine-tuning in later stages, improving the final solution’s accuracy, whereas a higher F value (e.g., 0.9) enhances early-stage exploration to avoid local optima. A large mutation step size in the early search phase improves global search capability, while reducing the step size in later iterations enhances precision. The experiments demonstrate that a moderate F value effectively balances exploration and exploitation.

2.2.4 Adaptive Adjustment of Crossover Probability CR

The crossover probability CR is adaptively selected based on fitness values. When a solution with high fitness is found, a smaller CR is chosen to increase its probability of being passed to the next generation. Conversely, when a solution has low fitness, a larger CR is used to accelerate structural changes and eliminate suboptimal individuals more quickly.

CRi={CRl+(CRu−CRl)(fi−fmin)(fmax−fmin),if fi>f¯CRl,if fi<f¯(17)

where fi is the fitness of individual xi,fmax and fmin represent the best and worst fitness values in the current population, respectively, and f¯ is the average fitness of the population. The upper and lower bounds of CR are set as CRu=0.5 and CRl=0.1, respectively.

To enhance population diversity, a crossover population (trial population) is introduced:

ui(t)={mi(t),ifrand (0,1)≤CRpi(t),otherwise(18)

where CR is the crossover probability, and rand(0,1) is a randomly generated value within (0,1). To ensure that at least one individual from the mutant population m(t) is inherited into the crossover population, the first crossover operation randomly selects the i-th mutant individual mi(t) as the i-th crossover individual. Subsequent crossover operations then use CR to determine whether to select pi(t) or mi(t) to generate the trial individual ui(t). The adaptive adjustment strategy of CR is similar to that of the mutation factor F, as it is also updated based on fitness differences. When an individual’s fitness is above the population average, a larger crossover probability is applied to prevent premature convergence to a local optimum and to enhance solution diversity. Conversely, when the fitness is below average, a smaller CR is used to increase the likelihood of preserving better solutions from the previous generation. The effect of different CR on the algorithm is shown in Table 2.

The proposed method (CR range: 0.0–0.5) balances search stability and global exploration. A lower CR (0.0) helps retain high-quality individuals, enhancing late-stage convergence stability, while a higher CR(0.5) promotes diversity and improves global search ability. In early search stages, maintaining a lower CR strengthens mutation-based exploration, while increasing CR in later stages helps convergence. In multi-objective optimization problems, an excessively high CR may destabilize the Pareto front. The proposed adaptive strategy ensures a good trade-off between exploration and exploitation, leading to better optimization performance.

2.3 Dual-Population Pseudo-Parallel GA-DE Multi-Objective Algorithm

Multi-objective optimization involves achieving the minimum or maximum of multiple objectives simultaneously under their respective constraints, with the goal of obtaining a set of optimal solutions that exhibit sufficient diversity and are uniformly distributed across the entire Pareto front [99]. The DGADE algorithm maintains the diversity of the optimal solution set by using a crowding entropy strategy to trim the external elite archive. Compared to the commonly used crowding distance, crowding entropy provides a more accurate measure of the crowding degree between solutions.

2.3.1 Diversity Preservation Strategy Based on Crowding Entropy

Crowding entropy combines crowding distance and distribution entropy. In the objective space, the expression for distribution entropy is Eij=−[plijlog2⁡plij+puijlog2⁡puij],where plij=dijcij,puij=duijcij,cij=dlij+duij;dlij and duij are the distances of the i-th solution to its two adjacent solutions in the j-th objective function. The expression for crowding entropy is:

CEi=∑j=1kcijEijfjmax−fimin=−∑j=1kdlijlog2plij+duijlog2puijfjmax−fimin(19)

where fjmax and fjmin represent the maximum and minimum values of the j-th objective function, respectively, and k denotes the number of objective functions.

2.3.2 Dominance Selection Operator

To apply the DGADE algorithm to multi-objective optimization, a key modification is required in the selection operator. Based on Pareto theory, the dominance relationship between the target individual xig and the trial individual uig+1 can be categorized into the following three cases: xig dominates uig+1(xig > uig+1). uig+1 dominates xig(uig+1 > xig). Neither dominates the other (uig+1⊀xig∧xig⊀uig+1). The selection operator in the Differential Evolution (DE) algorithm is modified as follows:

xig+1={xig,xig<uig+1,uig+1,xig≻uig+1,LC(uig+1,xig),uig+1≺¯xig∧uig+1≻¯xig,(20)

where g represents the current iteration number, and LC(uig+1,xig) denotes the individual with the smaller crowding entropy between xig and uig+1.

2.4 Application of the DGADE Algorithm to the DEED Model

During the optimization process, the degree of equality constraint violation (constraints violation, CV) of infeasible solutions in the population is first calculated. Then, the average value of constraint violations is determined, and the minimum average value is used as the value of xrbg. This ensures that the DGADE algorithm evolves toward satisfying the constraints [100]. When trimming individuals in the external elite archive, pretrimming is performed first, followed by a secondary trimming based on the diversity preserving strategy of crowding entropy. The specific steps for handling constraints are as follows:

Step 1: Calculate the infeasible solutions, expressed as:

P=[PG1,1PG2,1⋯PGG,1PG1,2PG2,2⋯PGN,2⋮⋮⋮PG1,TPG2,T⋯PGN,T].(21)

Step 2: Determine whether the vector Pt=[PG1,t,PG2,t,…,PGN,t] at each time t satisfies the equality constraint. If the constraint is not satisfied, dynamically adjust the variables in each dimension through relaxation.

Step 3: Set the maximum and minimum values for PGi,t at the initial time step as PGimax and PGimin, respectively.

Step 4: Use the following equation to check whether the power balance constraint is satisfied:

|∑i=1NPGi,t−PD,t−PL,t|≤ε(g)(22)

where:

ε(g)={ε(0)(1−GENG),0<GEN<G0,GEN≥G(23)

and ε(0)=10−6. If Equation is not satisfied, proceed to Step 5; otherwise, proceed to Step 6.

Step 5: For infeasible solutions, calculate the degree of equality constraint violation using:

Dt=∑i=1NPGi,t−PD,t−PL,t(24)

Determine the difference between Pt and its bounds Ptmax and Ptmin using:

Pi¯=Ptmax−Pi(25)

Pi_=Pi−Ptmin(26)

Based on the relaxation magnitude of each variable dimension, distribute Dt, and calculate the floating value as follows:

ΔPijt={Pij¯∑j=1NPij¯|Di|,Di<0,P_ij∑j=1NP_ijDi,Di>0.(27)

By adjusting the infeasible solutions, the updated power allocation Pt′ can be expressed as:

Pt′={Pt+ΔPt,Dt<0,Pt−ΔPt,Dt>0.(28)

The updated Pt′ is then treated as the solution for the current time step.

Step 6: Increment the time step by setting t=t+1, and update the maximum and minimum values of PGi,t for the next time step as follows:

Ptmax=min[Pt−1max,(Pt−1+URt−1)](29)

Ptmin=max[Pt−1min,(Pt−1−DRt−1)](30)

Step 7: Repeat Steps 2.2 to 2.4 until t=T.

Step 8: Return the matrix P.

3  Wind Power Grid Economic Model Calculation Processing

The dynamic environmental economic scheduling of a power system incorporating heterogeneous renewable energy sources such as wind and solar is designed to optimally allocate the output of system generators in conjunction with the output of these renewable energy sources under specific load demands, time periods, and intervals [101]. This scheduling ensures that all system equality and inequality constraints are satisfied, guaranteeing the safe and stable operation of the system. The goal is to achieve an optimal balance between minimizing generation costs and pollution emissions, thereby maximizing both economic and environmental benefits [102]. This approach plays a crucial role in accelerating the transition of the energy and power sectors from high-carbon to low-carbon systems, shifting from a fossil-fuel-based to a clean energy-dominated structure [103]. It contributes to the development of a diversified clean energy supply system on the supply side and the construction of a new type of power system centered on renewable energy, which speeds up the energy structure transformation towards clean and low-carbon energy.

3.1 Power Grid Dispatching Model

3.1.1 Computation and Processing of Grid-Connected Models

The fuel cost, or generation cost, of thermal power units during power generation must account for the valve-point effect [104]. The system’s total generation cost objective function, can be expressed as:

C=∑t=1T∑i=1N(ai+biPi,t+ciPi,t2+|eisin⁡(fi(Pimin−Pi,t))|)(31)

where C is the total fuel cost of the thermal power units. T is the total scheduling period. ai,bi,ci are the fuel cost coefficients for the i-th thermal power unit. ei,fi are the valve-point effect coefficients for the i-th thermal power unit. Pimin is the lower limit of the active output for the i-th thermal power unit. Pi,t is the active output of the i-th thermal power unit at time t. N is the number of thermal power units in the system.

The total pollutant emission objective function can be expressed as:

E=∑t=1T∑i=1N(αi+βiPi,t+γi(Pi,t)2+ζiexp⁡(ψiPi,t))(32)

The active power ramp rate constraints are as follows:

Pi,t−Pi,t−1 ≤ Δt⋅Ru,i,Pi,t−1−Pi,t ≤ Δt⋅Rd,i(33)

where Δt is the scheduling time interval. Ru,i and Rd,i represent the upward and downward ramp rates, respectively, for the i-th thermal power unit.

For positive spinning reserve, the constraint is:

Pw,tuw+Ppv,tupv⩽∑i=1NUi,t(34)

Ui,t=min(Pimax−Pi,t,Ru,iT10)(35)

where uw and upv are the demand coefficients for positive spinning reserve from the wind farm and photovoltaic station at time t, respectively. Ui,t is the positive spinning reserve capacity provided by the i-th thermal power unit at time t. T10 is the chosen response time for reserve activation.

(Pwmax−Pw,t)dw+(Ppvmax−Ppv,t)dpv⩽∑i=1NDi,t(36)

Di,t=min(Pi,t−Pimin,Rd,iT10)(37)

where dw and dpv are the demand coefficients for negative spinning reserve from the wind farm and photovoltaic station at time t, respectively. Di,t is the negative spinning reserve capacity provided by the i-th thermal power unit at time t.

3.1.2 Constraints on Electrical Dispatching

The active and reactive power of the generator must be within its lower and upper limits:

PGi,min≤PGi≤PGi,max,i=1,2,…,NP(38)

QGi,min≤QGi≤QGi,max,i=1,2,…,NG(39)

The bus voltage must be limited within its upper and lower bounds, while the generator bus voltage must be maintained at the rated voltage:

Vi,min≤Vi≤Vi,max,i=1,2,…,NB(40)

The apparent power flowing through each transmission line should be less than its maximum transmission capacity to avoid overload:

max(|LFij|,|LFji|)≤LFk,max,k=1,2,…,NL(41)

The load flow problem involves nonlinear constraints ensuring the active and reactive power balance at each bus, given as follows:

PGi−PDi−Vi∑j=1NBVj[Gijcos⁡(δi−δj)+Bijsin⁡(δi−δj)]=0(42)

QGi−QDi−Vi∑j=1NBVj[Gijsin⁡(δi−δj)+Bijcos⁡(δi−δj)]=0(43)

The transformer tap setting should be restricted within its minimum and maximum range:

Ti,min≤Ti≤Ti,max,i=1,2,…,NT(44)

The reactive power generated by the capacitor should also be within its lower and upper limits:

QCi,min≤QCi≤QCi,max,i=1,2,…,NC(45)

3.1.3 Dynamic Frequency Security Constraints

This section first quantitatively calculates the power imbalance that occurs when a microgrid is established and subsequently constructs a microgrid frequency response model along with dynamic frequency stability constraints.

It is assumed that distribution lines are equipped with remote-controlled switches, enabling rapid fault location and isolation when an upstream line fault occurs. By controlling the switching and closing states of downstream switches, an islanded microgrid can be formed. In distribution networks, the current in inductors is continuous, and when a line is disconnected, sudden changes in power flow can lead to system power imbalances. The power imbalance in an islanded microgrid at the moment of formation is the algebraic difference between the pre-fault injected power and the output power, which can be equivalently expressed as the algebraic sum of the power flow changes in the faulted lines directly connected to the microgrid.

When a disconnection fault occurs in the distribution network, the impact of the sudden change in power flow on line (i,j) on microgrid k is given by:

χij,sk=(vj,sk−vi.sk)pij,T11(46)

Thus, the power imbalance λk in microgrid k at the moment of its formation is:

λsk=∑(i,j)∈Bχij,sk(47)

Furthermore, by establishing the first-order rotor motion equation and discretizing it, the frequency response of the microgrid during formation can be expressed as:

Δf(n+1,s)k=Δf(n,s)k+Δτ2Hsk(−λskSN+∑g∈Gv(g,s)kΔP(g,n,s)G.ld−DskΔf(n,s)k)(48)

Δf(n,s)k represents the frequency deviation of microgrid k at time step n under scenario s, Δτ is the time step size of the frequency response model, ΔP(g,n,s)G.ld denotes the power output response of distributed generation (DG) g at time step n, subject to reserve capacity constraints under scenario s, Hsk and Dsk represent the inertia and damping of microgrid k under scenario s, respectively. Unlike traditional frequency response models where inertia H and damping D are known constants, this work considers island partitioning and introduces the partition state variable vik, making Hsk and Dsk variables.

To prevent generator tripping protection and microgrid frequency collapse, the following dynamic frequency stability constraints are established:

Δfmin≤Δf(n,s)k≤Δfmax(49)

Cmin≤Δfn,sk−Δfn−2,sk2Δτ≤Cmax(50)

2HskCmin≤λskSN≤2HskCmax(51)

Δfmin and Δfmax denote the minimum and maximum allowable frequency deviations. Cmin and Cmax represent the minimum and maximum allowable frequency change rates.

The power regulation of distributed generation g during frequency response can be expressed as:

{ΔP(g,n+1,s)G=ΔP(g,n,s)G+ΔτTg(−∑k∈Kv(g,s)kΔf(n,s)kRg−ΔP(g,n,s)G)ΔP(g,n,s)G.ld=ΔP(g,n,s)G−M(g,n,s)++M(g,n,s)−(52)

ΔP(g,n,s)G represents the output response of generator g at time step n under scenario s, without reserve capacity constraints, Tg is the control time constant of generator g, Rg is the droop coefficient of generator g.

During frequency regulation, the power adjustment of the generator must satisfy PR,gG.d≤ΔPg.n.sG.ltd≤PR,gG.u, This Equation indicates that the magnitude of the power output response is limited by the frequency modulation reserve PRR,gG.min≤(ΔPg.n+1.sG.Id−ΔPg.n.sG.ld)/(Δτ)≤PRR,gG.max. This formula limits the amount of variation in the output response of the DG at adjacent time steps in the frequency modulation process. This equation limits the variation in DG output response between adjacent time steps during frequency regulation. PRR,gG.min and PRR,gG.max denote the minimum and maximum allowable output response variation rates of generator g.

3.1.4 Solution Model

Considering the conflicting nature of the generation cost objective function and the pollution emission objective function, this paper uses the weighted sum method to convert the multi-objective optimization problem into a single-objective optimization problem for solving [105].

CE=(1−w)C+λwE(53)

where w is the weight factor. The coefficient λ is determined by the formula:

λ=C(Pmax)E(Pmax)(54)

This represents the ratio of the maximum generation cost to the maximum emissions. The overall optimization problem can be expressed as:

{minCE(x)s.t.gi(x),i=1,2,⋯,qhj(x),j=1,2,⋯,p(55)

where q is the number of equality constraints. p is the number of inequality constraints. This formulation aims to optimize the generation cost and pollution emissions simultaneously, using a weighted approach to balance the trade-off between the two objectives [106].

3.1.5 Selection of the Optimal Compromise Solution

In order to assist operators in selecting the optimal compromise solution, this paper uses fuzzy mathematics to calculate the satisfaction degree of the Pareto optimal solutions [107].

The satisfaction degree of a single Pareto solution ξi,m for a specific objective function fi,m is defined as:

ξi,m={1,fi,m⩽fm,minfm,max−fi,mfm,max−fm,min,fm,min < fi,m < fm,max0,fi,m⩾fm,max(56)

where fm,max and fm,min represent the maximum and minimum values of the m-th objective function for the i-th solution. The overall satisfaction degree for the i-th Pareto optimal solution is:

ξi=∑m=1Nobjξi,m∑i=1Nc∑m=1Nobjξi,m(57)

where Nc is the number of solutions on the Pareto Optimal Front (POF). Nobj is the number of objective functions.

3.2 HDJ Hybrid Optimization Algorithm Based on Greedy Selection

The DE (Differential Evolution) and JAYA algorithms have simple structures, few control parameters, and are easy to understand and implement [108]. However, when applied to high-dimensional, highly constrained optimization problems, they are prone to local optima, leading to low solution accuracy. To overcome this limitation and achieve better optimization solutions, this chapter proposes a hybrid optimization algorithm combining DE and JAYA, called DE/JAYA Hybrid Algorithm (HDJ), which is based on a greedy selection approach [109].

In the HDJ algorithm, the process is as follows: DE Algorithm is first used to optimize the population and generate a trial solution. If the new solution generated by the DE algorithm is better than the previous trial solution, the DE algorithm will continue to optimize the population. If the new DE solution is worse than the previous solution, the JAYA algorithm will replace DE and be used for further optimization of the population. The pseudo-code for the HDJ algorithm is shown in Table 3. The power structure used is shown in the Fig. 1 below.

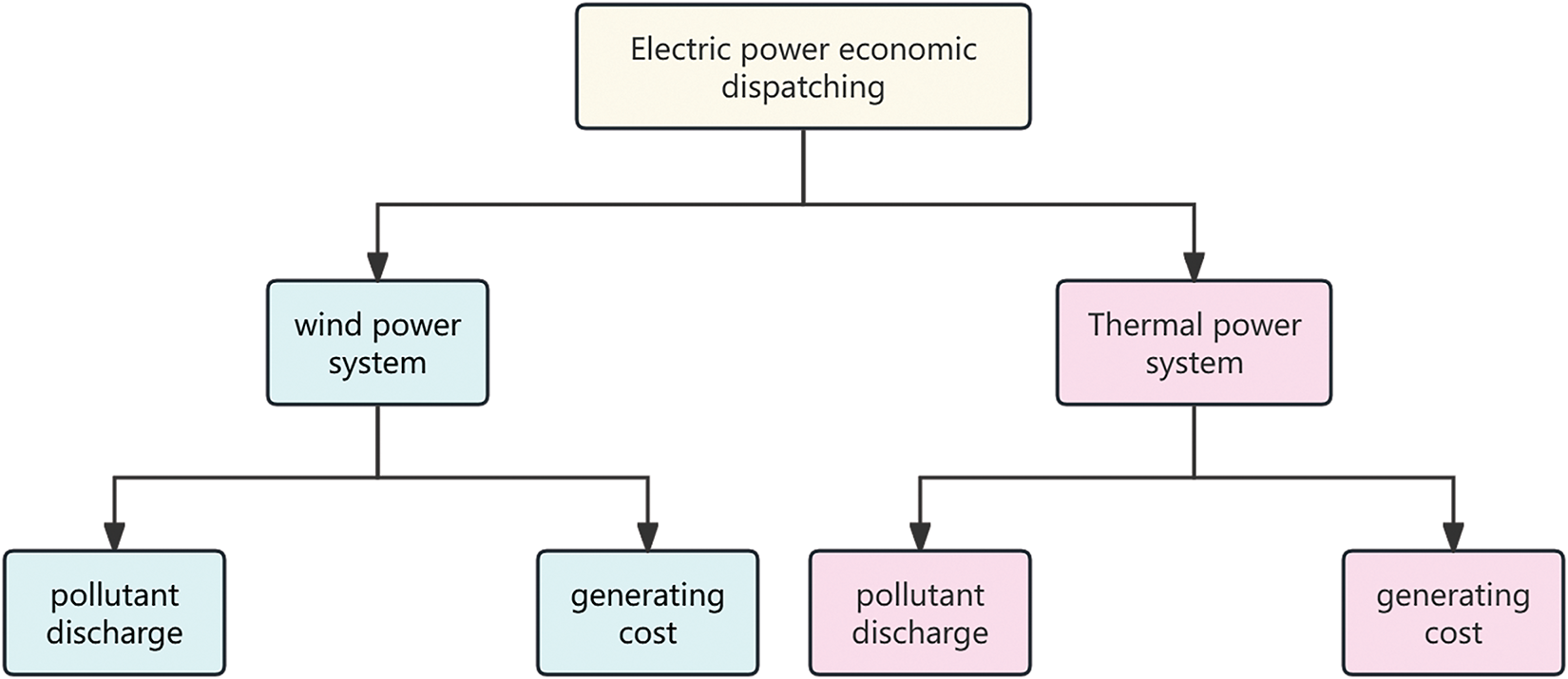
Figure 1: Schematic diagram of the grid-connected power structure of wind power

3.3 Solving Process Optimization

In the solving process, in addition to the core algorithm, the initialization of the algorithm population, the processing of constraints and the termination criterion of the algorithm are very important, which directly affect the efficiency, accuracy and stability of the algorithm.

If the initialization strategy is not appropriate, the initial solution may be too concentrated in a local area, which affects the exploration ability of the algorithm, and then leads to poor convergence in the early stage, and the entire solution space cannot be effectively explored. When the population is initialized, each individual is randomly generated within the allowed range, which can effectively ensure the diversity of the initial population, so as to improve the comprehensiveness of the algorithm in searching the solution space. The diverse population helps the algorithm to jump out of local optimum and increase the ability of global search.

Constraints are an important part of the optimization problem, usually involving such as generator capacity, power balance, start-stop constraints and so on. These constraints play a decisive role in the feasibility of the solution. By setting upper and lower bounds for each generator and adjusting them according to constraints such as ramp-up and ramp-down limits, it is ensured that the solution is always within reasonable limits. This method effectively avoids invalid solutions that do not conform to the physical constraints and ensures the feasibility of the optimization process. When dealing with the constraints, the individuals that do not satisfy the constraints are corrected by means of residual adjustment to ensure that the solution of each individual satisfies the balance as much as possible under the constraints. This method can effectively solve the conflict problem under multiple constraints and ensure the validity of the solution.

The termination criterion determines when the algorithm stops the search process, which affects the quality of the final solution and the computational efficiency. In this paper, by setting the maximum number of evaluations, the invalid calculation after convergence of the algorithm is avoided and the computational efficiency is improved. It avoids premature stopping or excessive iteration of the algorithm and ensures that a good enough solution is found in a reasonable time.

3.3.1 Population Initialization

In the HDJ algorithm, the population consists of multiple individuals, each representing a potential solution to the optimization problem. The population evolves over multiple generations, with each individual being defined by a matrix of decision variables corresponding to different time steps and generator outputs. Specifically, the x-th individual in the g-th generation is represented as:

Pxg=[P1,1gP2,1g⋯PN,1gP1,2gP2,2g⋯PN,2g⋮⋮⋱⋮P1,TgP2,Tg⋯PN,Tg](58)

t=1,2,3,…,T represents the time step, i=1,2,3,…,N corresponds to the generator index, g=1,2,3,…,gmax denotes the generation number, with gmax being the maximum number of iterations. Each element Pi,tg in the matrix denotes the output of generator i at time t in the g-th generation. For instance, P1,1g represents the output of the first generator at the first time step during generation g.

During the population initialization phase of the HDJ algorithm, the initial individuals are generated randomly within predefined boundaries to ensure diversity in the search space. This initialization process plays a crucial role in maintaining solution diversity and avoiding premature convergence to local optima. The initial values of the decision variables are assigned using the following equation:

Pi,tg=Pi,min+rand (0,1)⋅(Pi,max−Pi,min)(59)

Pi,max and Pi,min represent the upper and lower limits of the output for generator i, respectively, rand (0,1) is a randomly generated number within the range [0,1]. This initialization strategy ensures that each generator’s output values are randomly distributed within their respective feasible ranges, promoting solution diversity in the initial population. The use of a uniform random distribution helps to prevent bias in the initial sampling of the solution space, allowing the algorithm to explore a wide range of potential solutions from the beginning. Furthermore, by setting appropriate upper and lower bounds, the algorithm respects physical and operational constraints of the generators, ensuring feasibility in power generation scheduling or other optimization problems related to HDJ. This approach enhances the robustness of the algorithm, providing a solid foundation for subsequent evolutionary operations such as selection, crossover, and mutation.

3.3.2 Constraint Handling

To efficiently handle equality and inequality constraints in dynamic environmental economic dispatch problems, this paper employs a penalty-free constraint handling method. The specific steps are as follows:

Step 1: In the g-th generation (g=1,2,3,…,gmax ), set the scheduling period t=1.

Step 2: For generator i, update the feasible range of its output in scheduling period t using the following formula ( t=1,2,3,…,T,i=1,2,3,…,N) :

{Pi,tup={Pimax,ift=1min{Pimin,Pi,t−1−URi},otherwisePi,tdown={Pimin,ift=1max{Pimax,Pi,t−1+DRi},otherwise(60)

Here, Pi,tdown and Pi,tup represent the lower and upper bounds of Pi,t, while URi and DRi are the ramp-up and ramp-down limits of generator i.

Step 3: After determining the bounds, truncate Pi,tg using the following rule:

Pi,tg={Pi,tup,if Pi,tg > Pi,tupPi,tdown,if Pi,tg < Pi,tdownPi,tg,otherwise(61)

Step 4: Assume there are NP individuals in the population. Each individual x ( x= 1,2,3,…,NP ) consists of N generators ( i=1,2,3,…,N ). Construct a set M to store the generator indices.

Step 5: Calculate the network loss PLoss,x,t for individual x in period t:

PLoss,x,t=∑i=1N∑j=1NPi,tgBijPj,tg(62)

Step 6: Compute the residual Pres,x,t:

Pres,x,t=∑i=1NPi,tg−PLoss,x,t−PLoad,t(63)

Step 7: If Pres,x,t≤δ (where δ is the predefined precision threshold), end the constraint handling for individual x in period t and go to Step 9. Check if M is empty. If not, randomly select generator r from M to eliminate the residual using:

Pr,x,tg={Pr,x,tg−max{Pres.x,t,Pr,x,tg−Pr,xtdown},if Pres,x,t > 0Pr,x,tg+min{Pres,x,t,Pr,x,tup−Pr,x,tg},otherwise(64)

Then proceed to Step 8. If M is empty, set t=t−1 and return to Step 2 to reprocess the constraints for the previous time period.

Step 8: Remove r from M, update M, and return to Step 5 to recalculate the network loss.

Step 9: Set t=t+1. If t < T, go to Step 2 to process the constraints for the next scheduling period t+1. Otherwise, proceed to Step 10.

Step 10: Set x=x+1. If x < NP, go to Step 2 to handle constraints for the next individual x+1. Otherwise, proceed to Step 11.

Step 11: All constraints for all individuals and time periods are completed, ending the constraint handling process.

3.3.3 Termination Criterion

The termination criterion for the HDJ algorithm is based on the maximum number of function evaluations, CEmax. When the number of function evaluations during the algorithm’s execution reaches CEmax, the solution process is terminated. The optimal solution and the optimal value of the objective function are then output.

3.4 DEED Model Based on HDJ Algorithm

In this paper, a hybrid optimization method, HDJ, is designed by combining the DE and JAYA algorithms. The specific steps of this method are illustrated in Fig. 2. The pseudo-code of the DGADE-HDJ algorithm is shown in Table 4. DE Algorithm is first used to optimize the population and obtain a trial solution. If the new solution generated by the DE algorithm is better than the previous trial solution, the DE algorithm continues to optimize the population. If the new solution is worse, the JAYA algorithm replaces DE and is used to optimize the population instead. Before calculating the objective function values, the system constraints must be processed to ensure that they are satisfied. This paper employs the penalty-free constraint handling method proposed to manage the constraints. This method combines the global search capability of DE and the local search capability of JAYA, enhancing the ability to avoid local optima and improving the solution quality for constrained optimization problems.

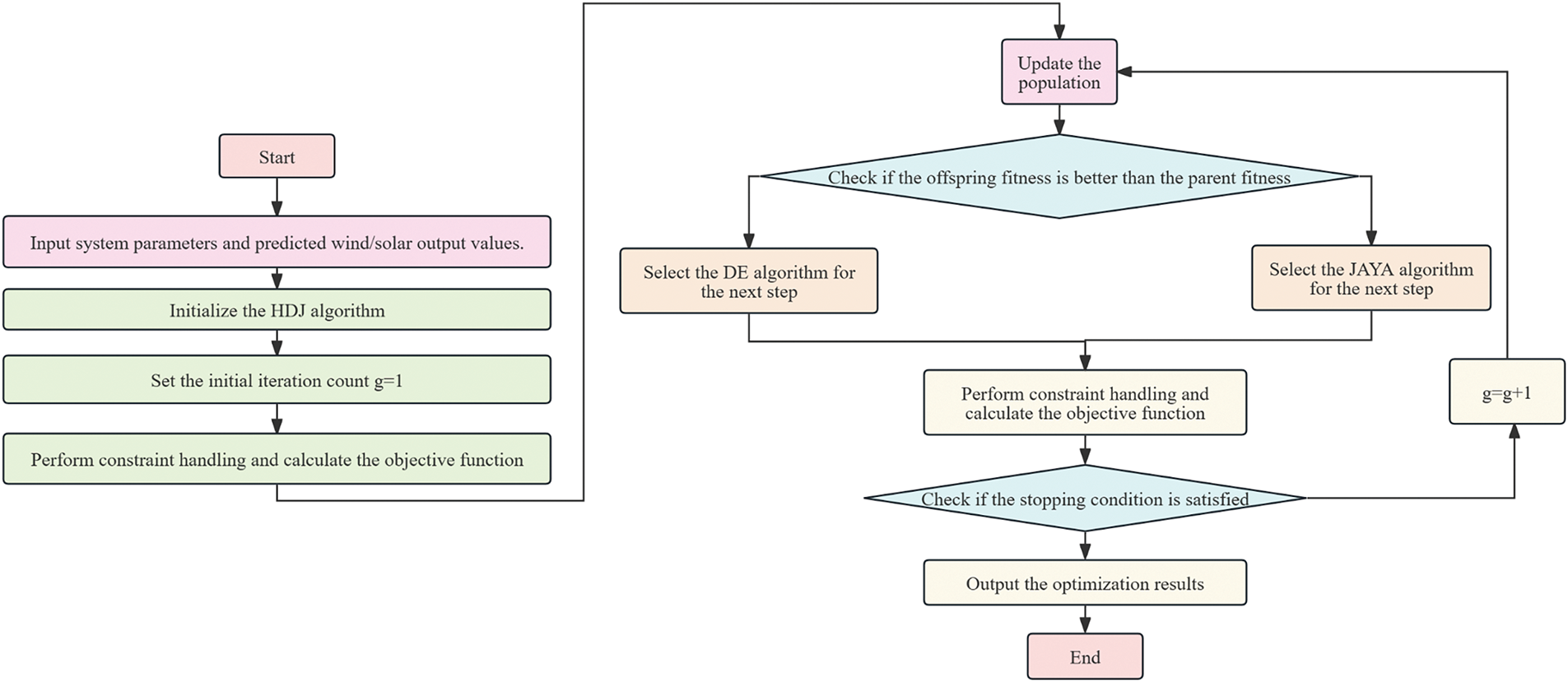
Figure 2: Solution process of HDJ for DEED problem

4  Evaluation of Results

4.1 Performance Analysis of Algorithms on Benchmark Functions

This section conducts experiments by selecting benchmark functions from the internationally recognized test function sets CEC2022 and CEC2005 to verify the effectiveness of the improved method.

The CEC benchmark function is selected for experimental testing because it is not only a common benchmark for testing the performance of algorithms, but also contains functions whose forms are similar to the mathematical expressions of UC models of power systems. Therefore, the CEC benchmark function is used as a test of algorithms. The unimodular function is used to test the exploitation ability of the algorithm because it has no local optimal value in the search space. The multi-mode function is used to test the exploration ability of the algorithm because it has many local optimal values. Since the function contains both unimodal and multimodal functions, the hybrid function is used to simultaneously test the exploration and exploitation capabilities of the algorithm.

4.1.1 CEC2022 Function Experiment

The CEC2022 test set includes 12 standard test functions designed to evaluate the performance of optimization algorithms [110]. These functions exhibit diverse characteristics and levels of difficulty, enabling a comprehensive assessment of algorithmic performance in solving optimization problems [111].

The CEC2022 benchmark function is a standard test function used to evaluate the performance of optimization algorithms, which is usually applied to various optimization fields. These benchmark function designs have different levels of difficulty and cover a variety of optimization problems such as linear and nonlinear, multimodal and unimodal, continuous and discrete. These functions are widely used in the field of optimization and can be used to examine the efficiency, accuracy and robustness of different algorithms in solving optimization problems. Some benchmark functions in CEC2022, such as “Rastrigin function” and “Griewank function”, have multimodal and complex local optimal solution characteristics, which can imitate complex nonlinear constraints and multiple local optimal solutions in power system dispatch. Test functions like the “Constraint Handling” category, while often used to check the performance of algorithms under constraints, can also reflect constraint handling in power system scheduling problems, such as constraints on power loads, generator capacities, and transmission capabilities. Some multi-objective test functions in CEC2022 are able to model the complexity of optimizing multiple objectives simultaneously in a power system, which is similar to the multiple optimization objectives that may be faced simultaneously in power system dispatch.

Among these, F1 is a unimodal function with a single global optimum, primarily used to test the development capability of algorithms. Functions F2 to F5 are multimodal, containing multiple local optima, and are employed to evaluate the ability of algorithms to escape local optima. Functions F6 to F8 are hybrid functions formed by combining three or more benchmark functions after rotation and shifting operations, which increase the complexity of the optimization process [112] (Fig. 3). Lastly, functions F9 to F12 are composition functions that integrate three or more hybrid or benchmark functions through rotation and shifting operations, further elevating the challenge of optimization. The images of these experimental functions are shown in Fig. 1. The function information is in Table 5.

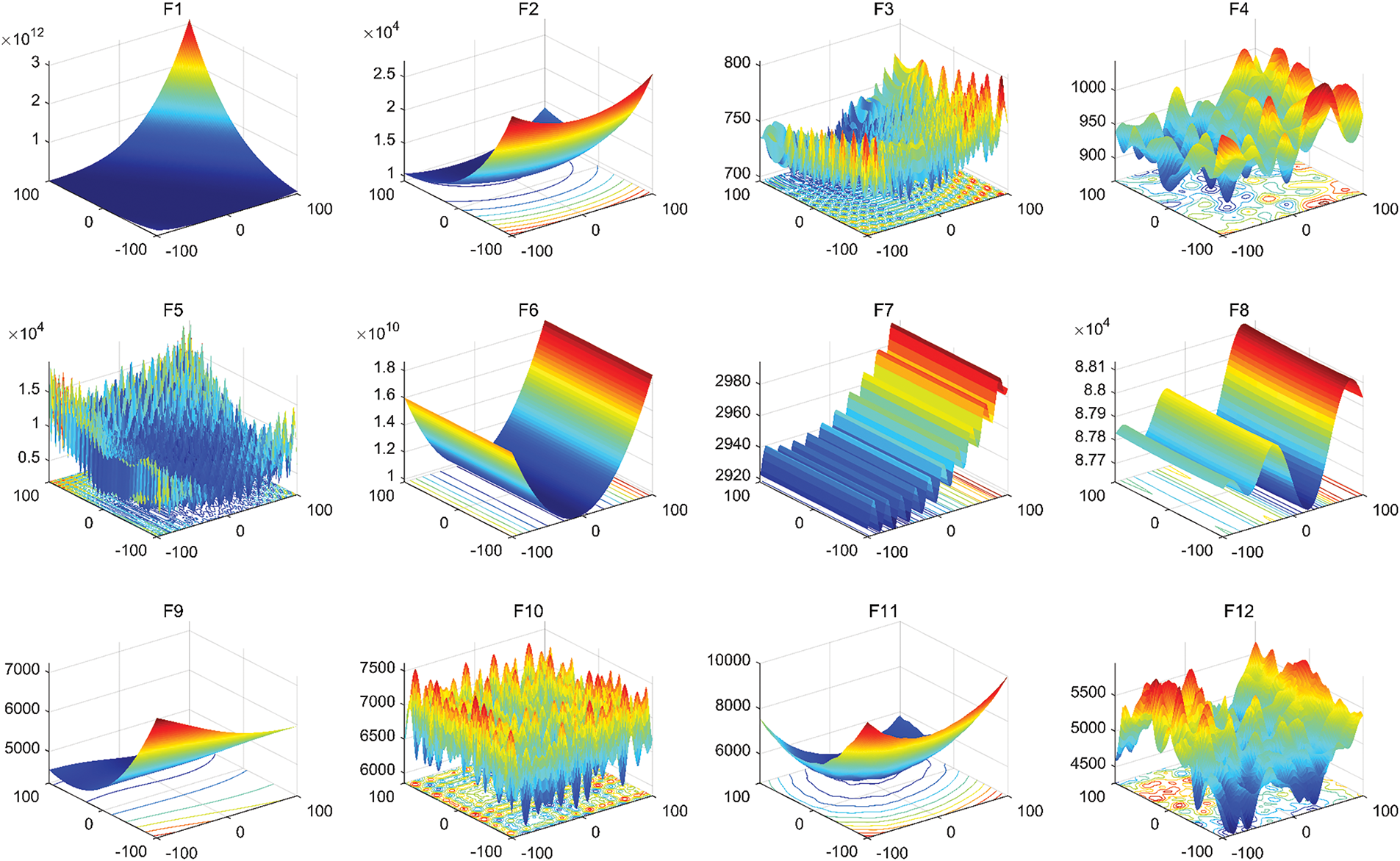
Figure 3: Graph of CEC2022 function

To ensure a fair comparison and validate the effectiveness of the proposed improvement strategy, all test functions were assigned the same evaluation budget. All algorithms were implemented using MATLAB R2024a, and the experiments were conducted on a personal computer equipped with the Windows 11 operating system, an i9-14900K processor, and 96 GB of memory.

The optimization method is compared with DBO, PSO, GWO, and SSA algorithms in operation, and the box plots are made as shown in Fig. 4.

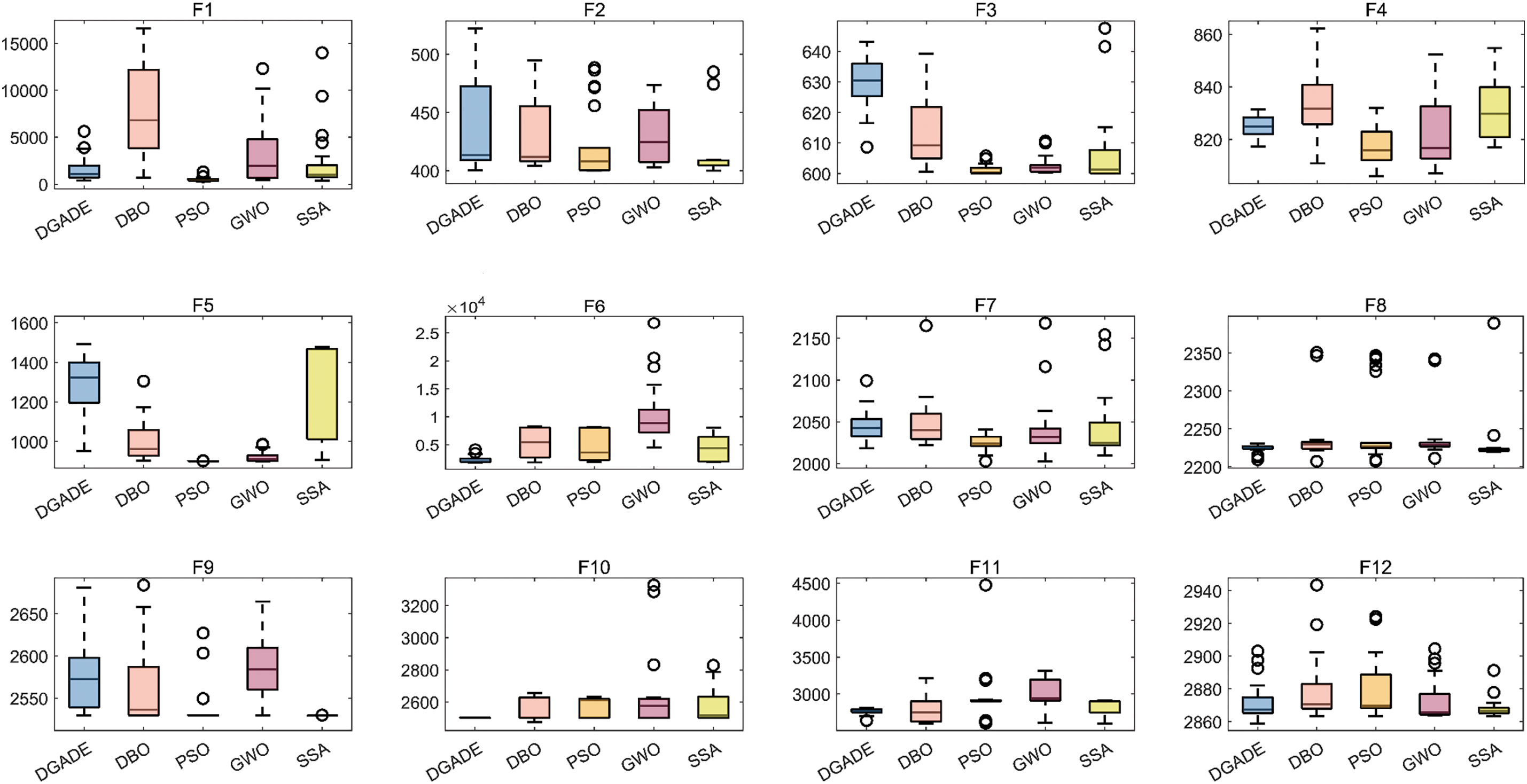
Figure 4: CEC2022 function test box plot F1–F12

Box plots provide a visual representation of the distribution of function values, making it possible to effectively study the stability of algorithms. As shown in Figs. 4 and 5, for functions F6, F7, F10, and F11, the median of DGADE is significantly lower, with both Q1 (25th percentile) and Q3 (75th percentile) also lower than those of other algorithms. Moreover, for functions F2, F5, F9, and F10, DGADE exhibits fewer outliers, indicating greater stability. Additionally, for functions F4, F6, F8, F10, and F11, the box plots of DGADE are flatter, signifying a more uniform and concentrated distribution of function values within the population when employing the GODE algorithm. This demonstrates that the GODE algorithm has superior stability. In conclusion, DGADE outperforms other algorithms in terms of performance across the evaluated functions.

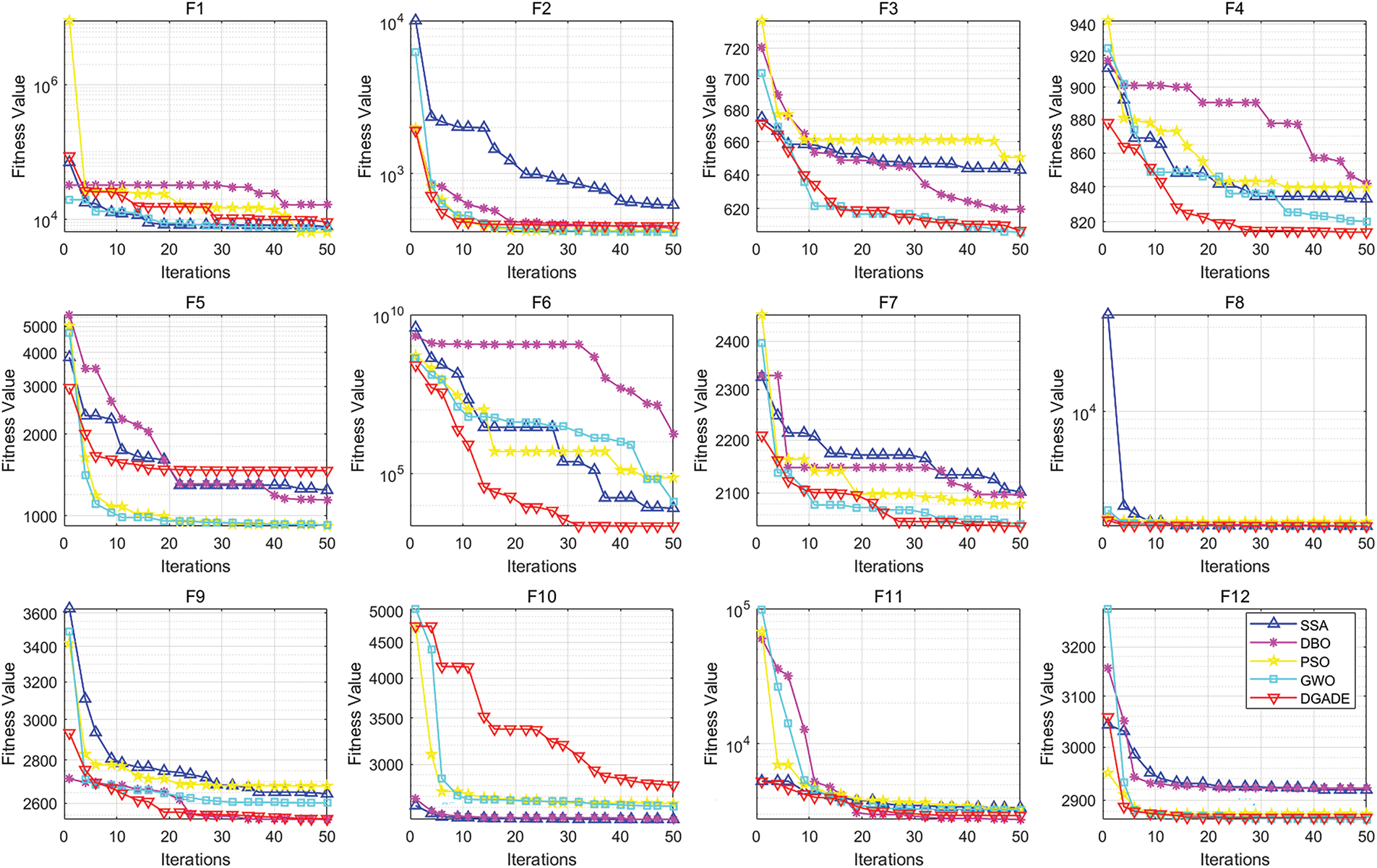
Figure 5: Plot of CEC2022 function convergence

By considering the uncertainty introduced by wind and photovoltaic power in power system scheduling, the DGADE-HDJ algorithm can adapt to dynamic environmental conditions. This ability to incorporate uncertainty is reflected in its robustness when tested against dynamic and multimodal functions, simulating real-world power system variability.

In functions F6, F7, F10, and F11, DGADE-HDJ shows significantly lower medians for these functions compared to other algorithms, with both Q1 and Q3 also lower. This indicates that the algorithm excels in finding solutions closer to the global optimum across multiple runs, demonstrating its ability to balance exploration and exploitation. The low median values also suggest that the population diversity promoted by the hybrid DE-GA approach plays a key role in avoiding local optima, especially in multimodal functions like these. These functions often feature complex local optima that require robust algorithms capable of global search, which is where the dual-population mechanism and Pareto dominance concept help DGADE-HDJ perform better than other algorithms.

In functions F2, F5, F9, and F10, DGADE-HDJ exhibits fewer outliers in the box plots for these functions, indicating greater stability. This is likely a result of the dynamic relaxation constraints and elite archiving, which help prevent the algorithm from diverging or becoming stuck in poor solutions. Fewer outliers suggest that the algorithm consistently produces high-quality solutions across multiple runs, reflecting its reliability and robustness in handling complex optimization problems.

In functions F4, F6, F8, F10, and F11, the box plots for these functions show that DGADE-HDJ produces flatter distributions, meaning that the population’s solutions are more evenly spread within a concentrated region. This could be attributed to the enhanced diversity fostered by chaotic mapping and entropy strategies, preventing the population from becoming too clustered around suboptimal regions. The uniform distribution suggests that the algorithm is well-balanced in exploring the search space and finding a range of high-quality solutions.

The observed stability and low outliers in DGADE-HDJ’s performance can be linked to its population diversity strategies and the Pareto dominance mechanism. These features help the algorithm maintain a broad search while ensuring that the best solutions are preserved. The uniform distribution of solutions in box plots for certain functions suggests that the algorithm’s hybrid approach is effective in maintaining a good balance between exploration and exploitation. The cubic chaotic mapping initialization plays a significant role in achieving this uniform distribution by introducing a high degree of diversity in the initial population, helping the algorithm avoid local optima. The dynamic relaxation mechanism helps the algorithm adjust to changing system conditions (e.g., uncertainty due to renewable energy), ensuring robustness in dynamic environments.

As shown in Fig. 5, for functions F2, F4, F6, F8, F9, F10, and F11, the convergence speed of DGADE is consistently faster than that of other algorithms throughout the entire evolutionary process. For the remaining functions, DGADE also demonstrates relatively faster convergence. By comparing the convergence curves of these five algorithms across different dimensions, it is evident that DGADE achieves significantly faster convergence on most functions. This improvement is attributed to the balance between the global search and local search capabilities of the DGADE algorithm, achieved through its enhancements. During the later stages of population evolution, DGADE effectively avoids getting trapped in local optima and converges rapidly to the global optimum.

The faster convergence of the DGADE algorithm across a wide range of functions in the CEC2022 benchmark, particularly on functions F2, F4, F6, F8, F9, F10, and F11, can be attributed to the distinctive features and enhancements that it integrates. These improvements address the inherent challenges in optimization problems, especially those involving high-dimensionality, nonlinearity, multimodality, and complex constraints. One of the most significant contributors to DGADE’s rapid convergence is the balance between global search and local search. In the context of evolutionary algorithms, global search allows for exploration of the solution space, while local search enhances the precision of the solutions. DGADE achieves this balance through its hybridization of Differential Evolution (DE) and Genetic Algorithm (GA), which complements the strengths of each method:

Differential Evolution (DE) excels at global exploration, making it highly effective in finding diverse candidate solutions, especially in complex landscapes with multiple local optima. The mutation and recombination steps in DE enable it to escape local minima and explore a broad range of the search space. Genetic Algorithm (GA) enhances local search capabilities through crossover and selection mechanisms, which fine-tune the solutions by exploiting the most promising regions found during the global search phase. By combining these two paradigms, DGADE is able to avoid premature convergence to suboptimal solutions, a common pitfall in many evolutionary algorithms, especially in complex multimodal landscapes like those found in CEC2022 functions. The ability to perform efficient local refinement after global exploration is a key reason for the algorithm’s faster convergence.

DGADE uses external elite archiving, which preserves the best-found solutions throughout the evolutionary process. This ensures that no optimal solutions are lost due to the randomness of the evolutionary process. The Pareto dominance concept further strengthens the algorithm’s convergence, especially for multi-objective problems, by focusing the search on improving solutions that dominate others with respect to the optimization goals.

4.1.2 CEC2005 Function Experiment

The CEC2005 benchmark is a widely recognized performance evaluation tool in the industry, which is mainly used to measure the performance of algorithms and computing systems on specific tasks [113]. It simulates real-world computational challenges through a series of carefully designed test cases, ensuring the practicality and accuracy of the evaluation results. The function images of the benchmark functions are shown in Fig. 6.

Figure 6: 3D diagram of CEC2005 function model

Power system dispatch problems usually involve nonlinear and multi-constrained optimization, especially when considering factors such as renewable energy access and load forecasting errors, the optimization problem may have multiple local optimal solutions. Multimodal functions in the CEC2005 test functions such as F6-F12 can simulate this property to test the ability of the algorithm to jump out of local optima. Power dispatch optimization involves the output dispatch of multiple generators, and the number of decision variables is large, which is a high-dimensional optimization problem. CEC2005 test functions provide high-dimensional problems (such as separable functions of F1-F5 and complex hybrid functions of F13-F25), which can be used to verify the convergence ability of optimization algorithms in high-dimensional search space. Some power dispatching problems, such as economic dispatching, involve power balance constraints, unit carrying capacity constraints, etc., and have complex constraints.

The optimization method is compared with DBO, PSO, GWO, and SSA algorithms in operation, and the box plots are made as shown in Fig. 7 and Fig. 8.

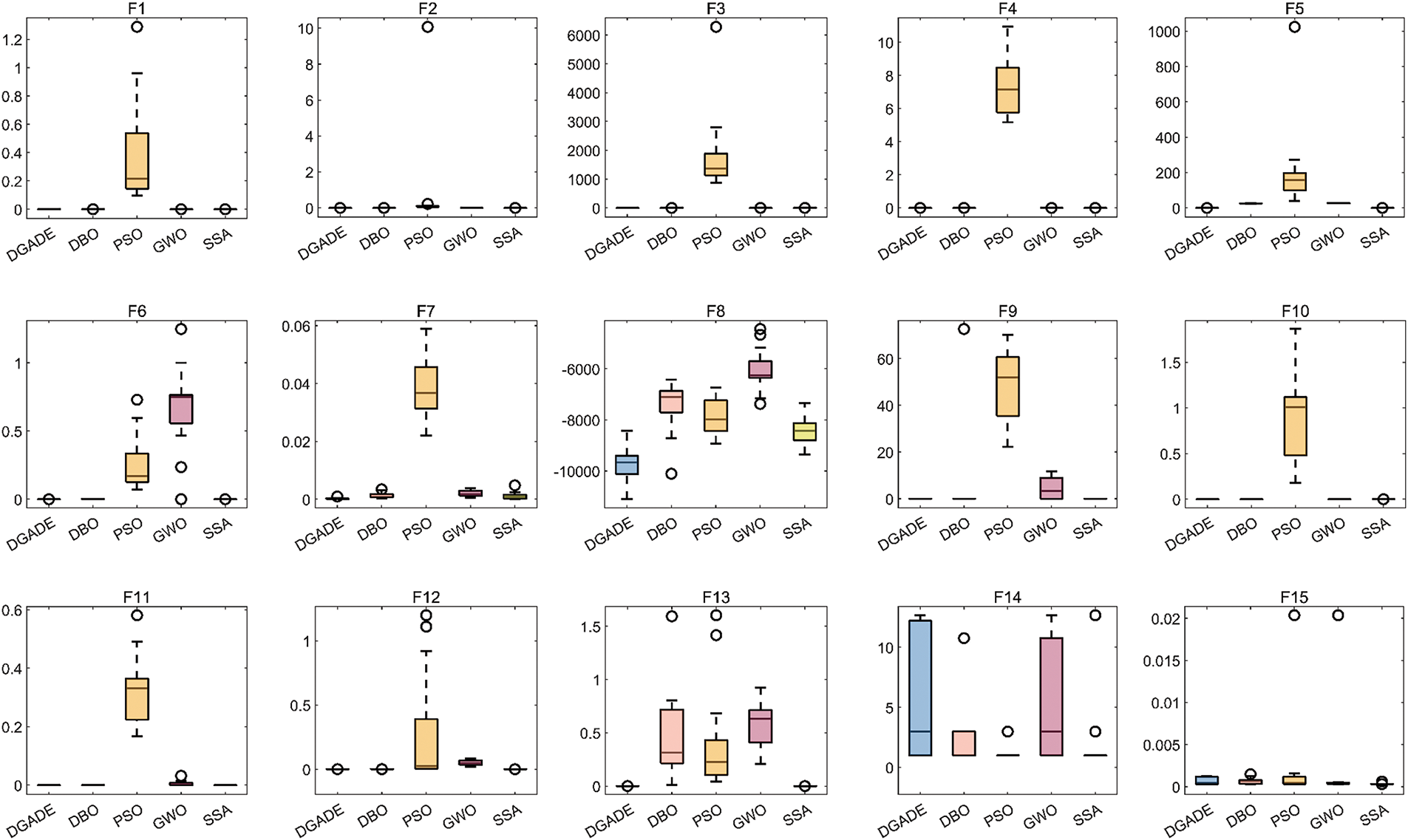
Figure 7: CEC2022 function test box plot F1–F15

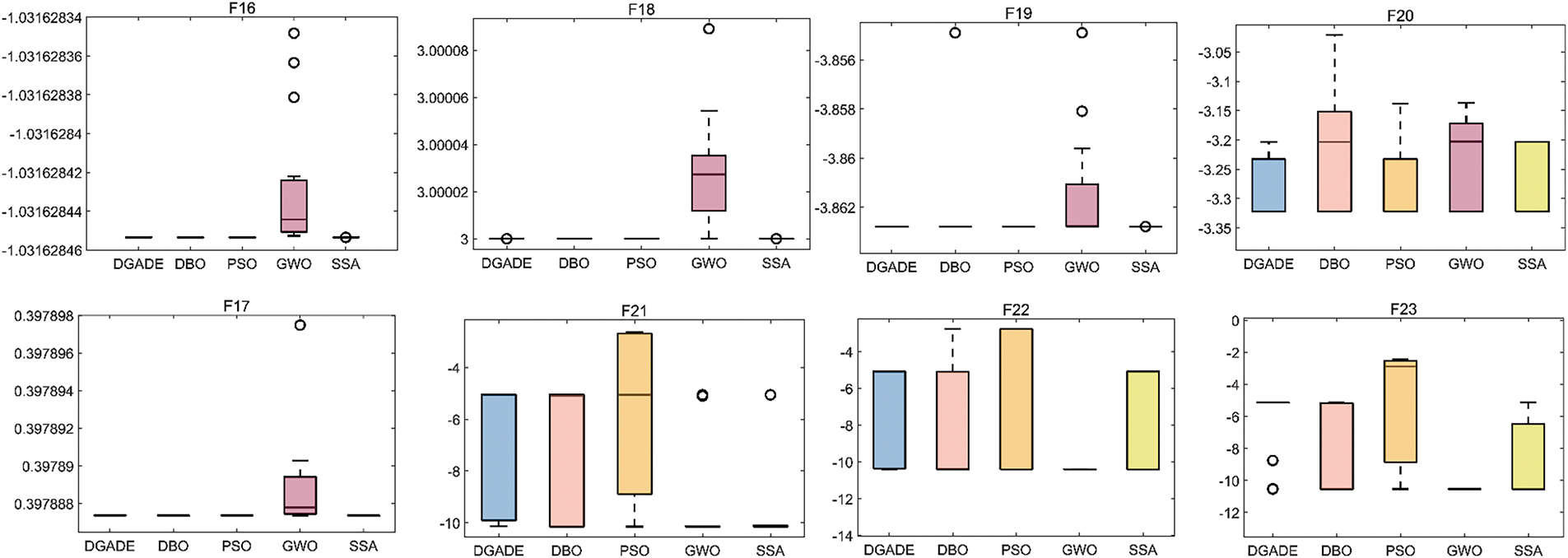
Figure 8: CEC2022 function test box plot F16–F23

Using box plots, the distribution of function values can be visually analyzed, providing a clear perspective on the stability of the algorithms. As shown in Figs. 3 and 4, for functions F1, F3, F5, F7, F8, F13, and F20, the median of DGADE is significantly lower, and both Q1 (25th percentile) and Q3 (75th percentile) are lower than those of other algorithms. Additionally, for functions F1, F3, F9, F10, F11, F14, F15, and F19, DGADE has fewer outliers, indicating more stable performance. Furthermore, for functions F8, F13, F20, and F22, the box plots of DGADE are flatter, indicating a more uniform and concentrated distribution of function values within the population when using the GODE algorithm. This suggests that the GODE algorithm exhibits better stability. In conclusion, DGADE demonstrates superior performance compared to other algorithms for the evaluated functions.

Cubic chaotic mapping ensures that the initial population is spread across the solution space in a non-repetitive, diverse manner. Chaotic sequences have desirable properties, including their ability to cover a wide area without falling into repetitive cycles. This wide exploration capability is crucial in the early stages of the search, where the algorithm is trying to avoid converging too early to suboptimal solutions. Average entropy-based initialization: This method ensures that the population is not only diverse but also well-distributed, preventing the algorithm from getting stuck in regions with low solution quality. The entropy-based approach helps the algorithm maintain diversity throughout the search process, ensuring that different regions of the search space are explored evenly. The improved population diversity provided by these strategies is evident in the box plots for functions F8, F13, F20, and F22, which show a flatter distribution of function values, indicating that the algorithm’s population is well-distributed and concentrated around better solutions. This uniformity reduces the likelihood of the algorithm converging prematurely to suboptimal regions and ensures that the population maintains a broad range of viable solutions.

Dynamic relaxation helps the algorithm explore the search space more freely in the early stages of evolution by loosening constraints. As the optimization process progresses, the algorithm gradually tightens the constraints, ensuring that the solutions not only optimize the objectives but also respect all system constraints. This mechanism enables faster convergence while still ensuring feasible solutions, as the algorithm is able to explore more of the search space initially and then focus on the most promising solutions that satisfy the constraints. This approach helps DGADE converge to solutions more quickly and effectively, particularly when dealing with complex constraints that would otherwise slow down traditional optimization algorithms. The superior performance in high-dimensional functions like F1-F5 (which involve separable functions) and F13-F25 (complex hybrid functions) highlights the efficiency of the relaxation mechanism in dealing with these real-world optimization challenges.

As shown in Fig. 9, for functions F1, F2, F3, F4, F7, F8, F9, F10, F11, F14, F19, and F20, the convergence speed of DGADE is consistently faster than that of other algorithms throughout the entire evolutionary process. For the remaining functions, DGADE also demonstrates relatively faster convergence. By comparing the convergence curves of these five algorithms across different dimensions, it is evident that DGADE achieves significantly faster convergence on most functions. This is due to the improvements that balance the global search and local search capabilities of the DGADE algorithm. During the later stages of population evolution, DGADE effectively avoids becoming trapped in local optima and converges rapidly to the global optimum solution.

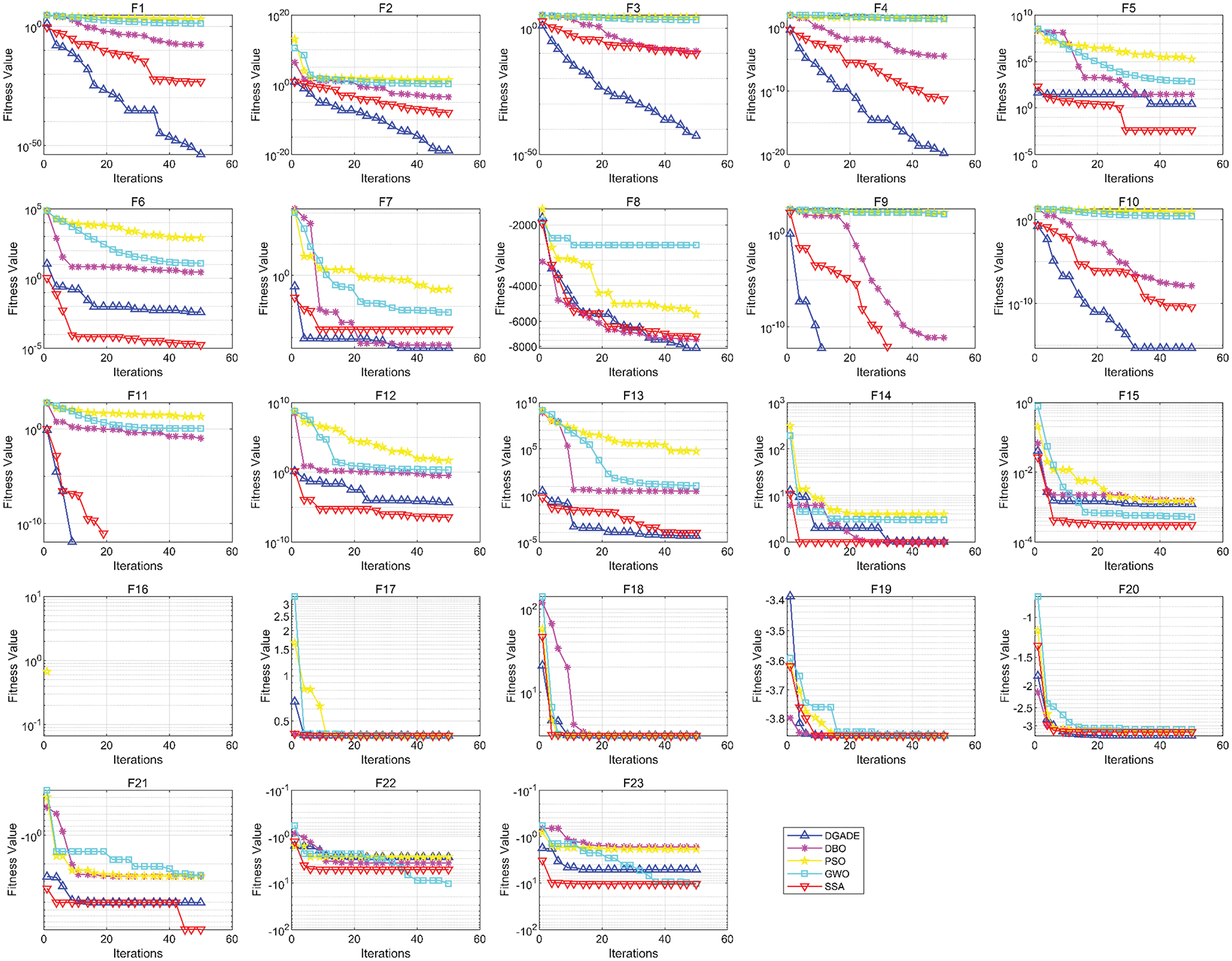
Figure 9: Plot of CEC2005 function convergence

4.2 Power Model Dispatch Analysis

A 10-unit system was used to verify the feasibility of the DGADE algorithm on the Dynamic Economic and Environmental Dispatch (DEED) model [114]. To demonstrate the algorithm’s feasibility, simulations were conducted using a dynamic economic and environmental dispatch model (Model 1) that incorporates two optimization objectives: fuel cost and pollutant emissions. Table 6 presents the optimal trade-off solutions obtained by DGADE for Model 1. DGADE effectively optimizes both fuel cost and emissions simultaneously and efficiently handles power balance constraints during the dispatch process. The visual representation of the unit power is in Fig. 10.

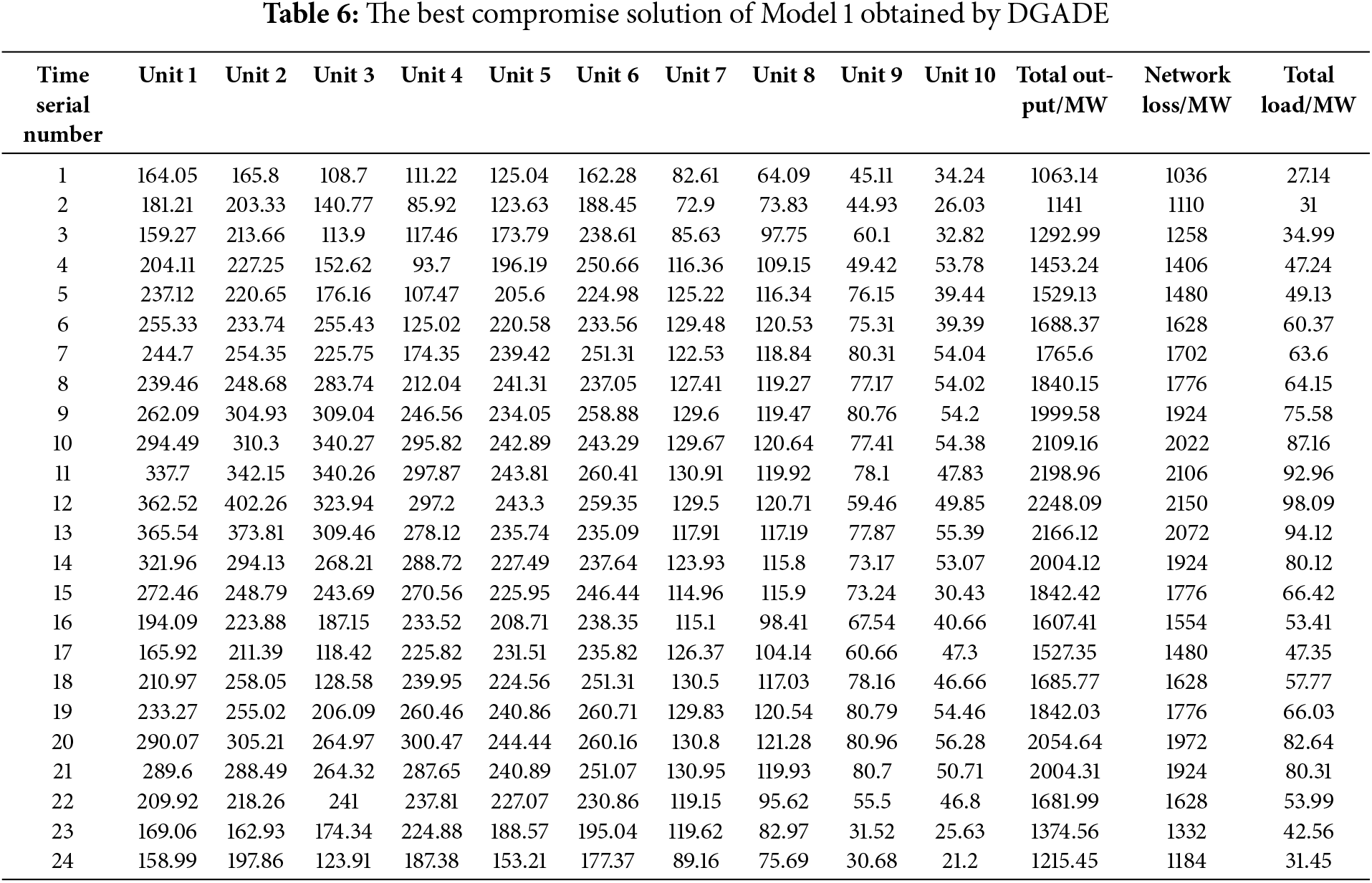
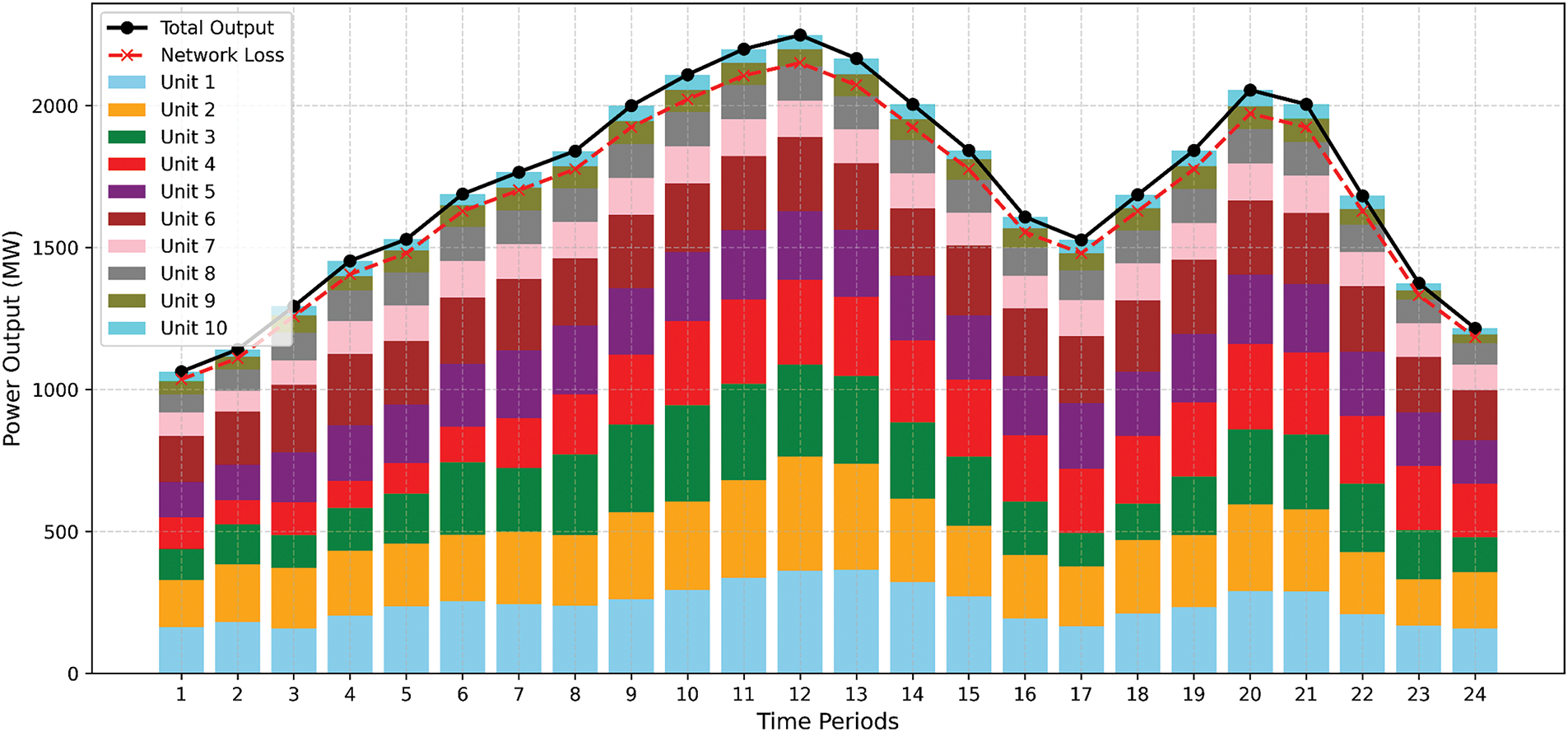
Figure 10: Unit power diagram

To verify the feasibility of DGADE, the results obtained using the DGADE algorithm were compared with those of NSGA-II, the enhanced multi-objective differential evolutionary algorithm with dynamic constraints handling (EMODEDCH), PSO, and MOEA/D [115]. Table 7 provides a comparison of the optimal trade-off solutions obtained by these algorithms in terms of fuel cost and pollutant emissions. The comparison highlights how DGADE performs in balancing these two objectives, offering insights into its competitiveness and effectiveness relative to other state-of-the-art optimization algorithms. This analysis further underscores DGADE’s ability to simultaneously optimize fuel cost and emissions while managing complex constraints, reinforcing its viability for use in the dynamic economic and environmental dispatch (DEED) model.

4.3 Analysis of Power Dispatch Considering Line Loss

In the following analysis, line losses are incorporated as an additional optimization objective into the dispatch model, resulting in a dynamic economic and environmental dispatch model with three objectives (Model 2): fuel cost, pollutant emissions, and line losses. Table 8 presents the optimal trade-off solutions obtained by DGADE for Model 2. The results demonstrate that DGADE effectively optimizes all three objectives—dispatch cost, pollutant emissions, and line losses—while ensuring power balance throughout the scheduling process. This underscores the algorithm’s robustness and adaptability in handling multi-objective optimization problems within dynamic scheduling environments. The unit power of Model 2 is shown in Fig. 11.

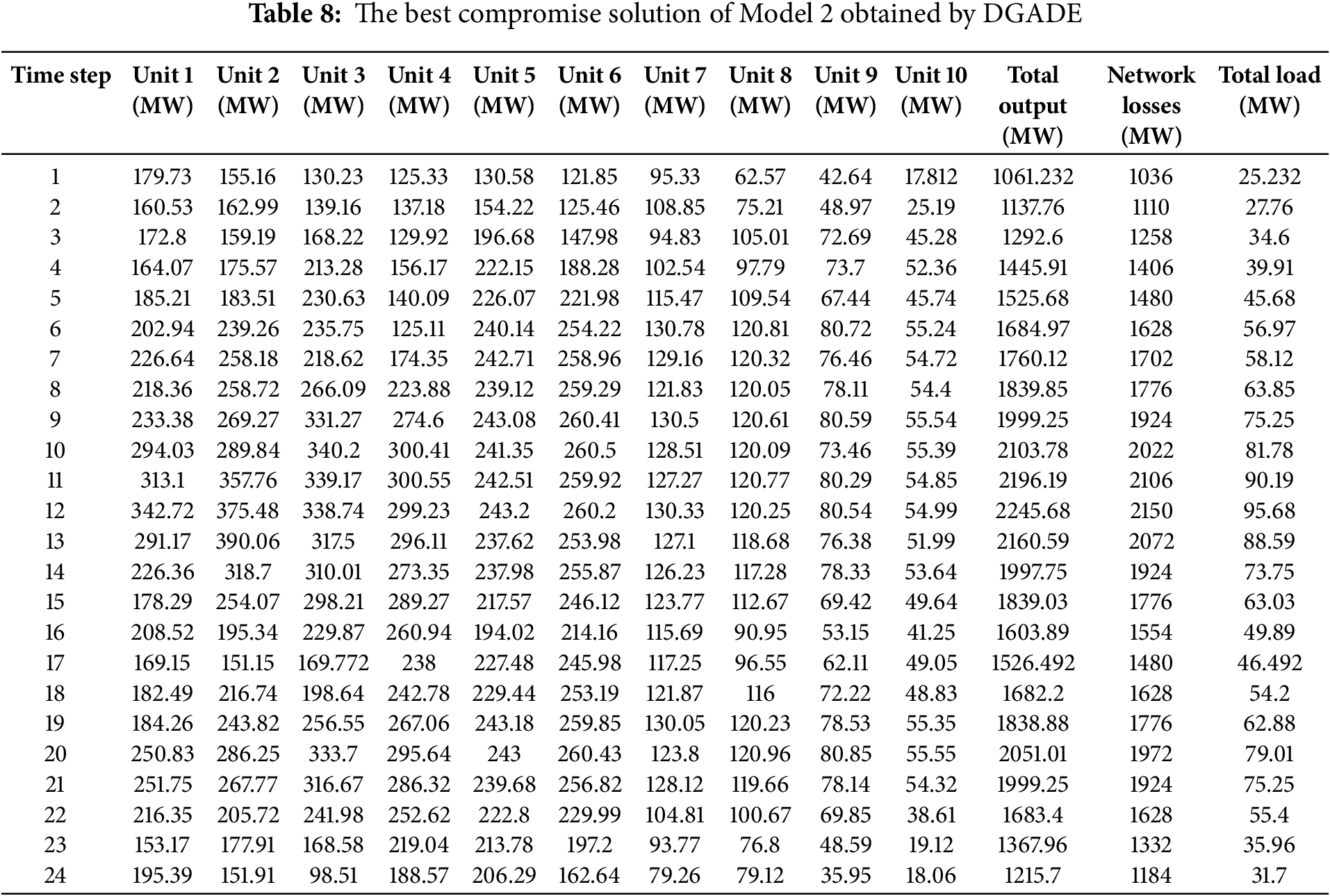
Figure 11: Power diagram of the unit for Model 2

Table 6 compares the fuel cost, pollution emissions, and network losses associated with the optimal trade-off solutions of Models 1 and 2. As shown in Table 9, the pollution emissions of Model 2 increased by only 0.78% compared to Model 1, while the fuel cost and network losses decreased by 2.12% and 1.17%, respectively. This demonstrates that Model 2 achieves a more satisfactory trade-off solution. Therefore, incorporating network losses as an optimization objective into the DEED model and establishing a tri-objective DEED multi-objective optimization model that includes economic, environmental, and network loss considerations has notable economic value.

4.4 Experimental Design of Grid-Connected Power System Model without Wind and PV Generation

The wind power scheduling optimization mentioned in this paper is integrated into the process of power system, which is also applicable to photovoltaic power generation. In this paper, wind power and photovoltaic power generation are connected to the grid at the same time to carry out scheduling simulation, which can better verify the generalization and universality of the model in this paper.

A 10-unit system is employed as a case study to validate the feasibility of the proposed scheduling model and assess the performance of the HDJ algorithm. The system operates on a 24-h scheduling cycle, with each time step spanning 1 h. To evaluate the optimization capabilities of the HDJ algorithm, it is benchmarked against DE, JAYA, and CHDJ algorithms [116]. Each algorithm executes 30 independent runs. For all methods, the population size is fixed at 100, and the maximum number of objective function evaluations is capped at 1000. Additional parameter settings are presented in Table 10. The system integrates a wind farm and a photovoltaic power station, each with a rated capacity of 100 MW, and their respective 24-h power output forecasts are provided in Table 11. To mitigate uncertainties arising from the inclusion of wind and solar energy, both positive and negative spinning reserves are implemented. The positive spinning reserve coefficient is set at 0.2, while the negative reserve coefficient is fixed at 0.3.

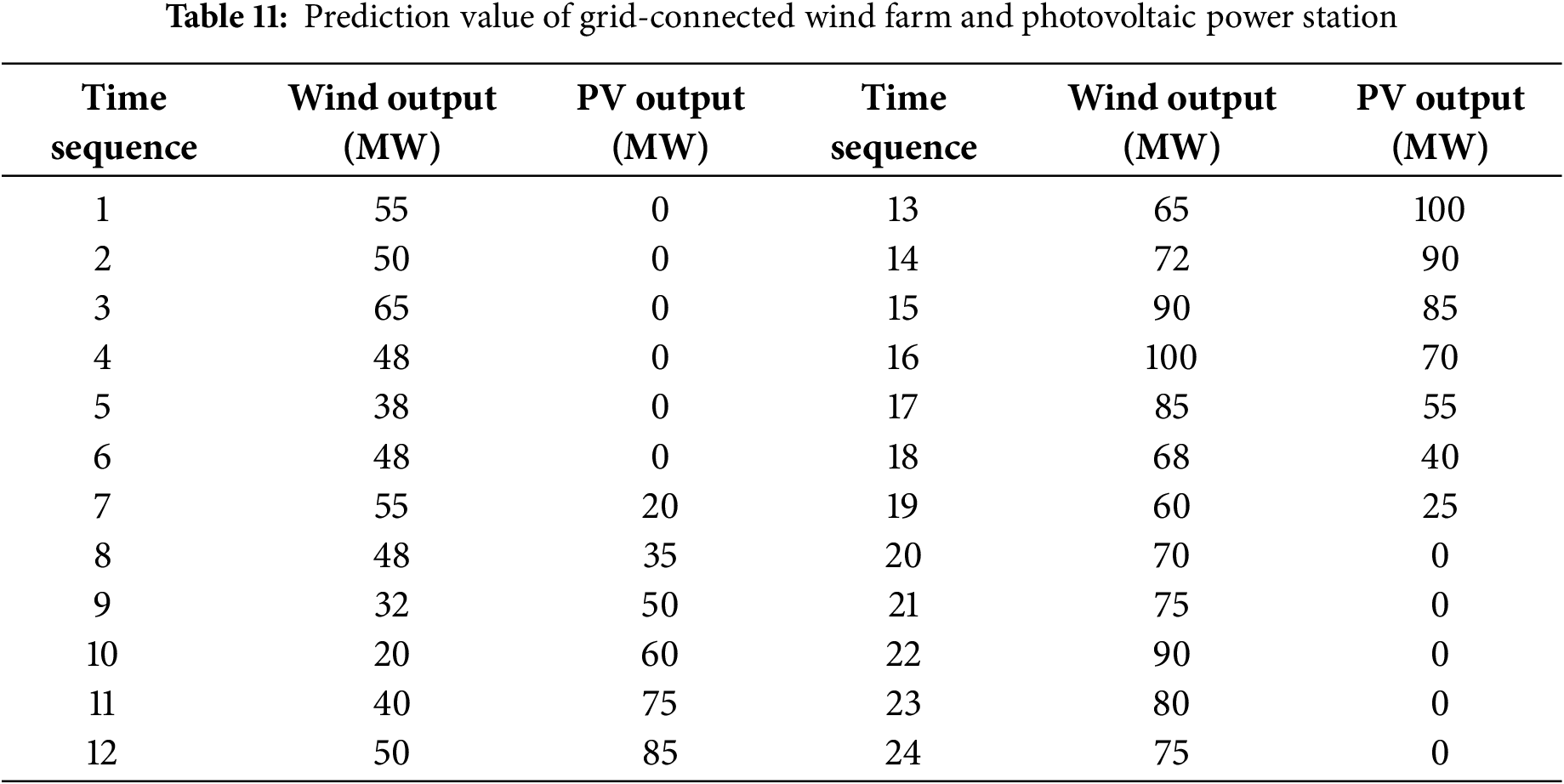
In order to verify the feasibility and effectiveness of the HDJ algorithm proposed in this paper, simulation tests are first carried out on a 10-unit system without considering wind power and PV, and the results are shown in Table 12.

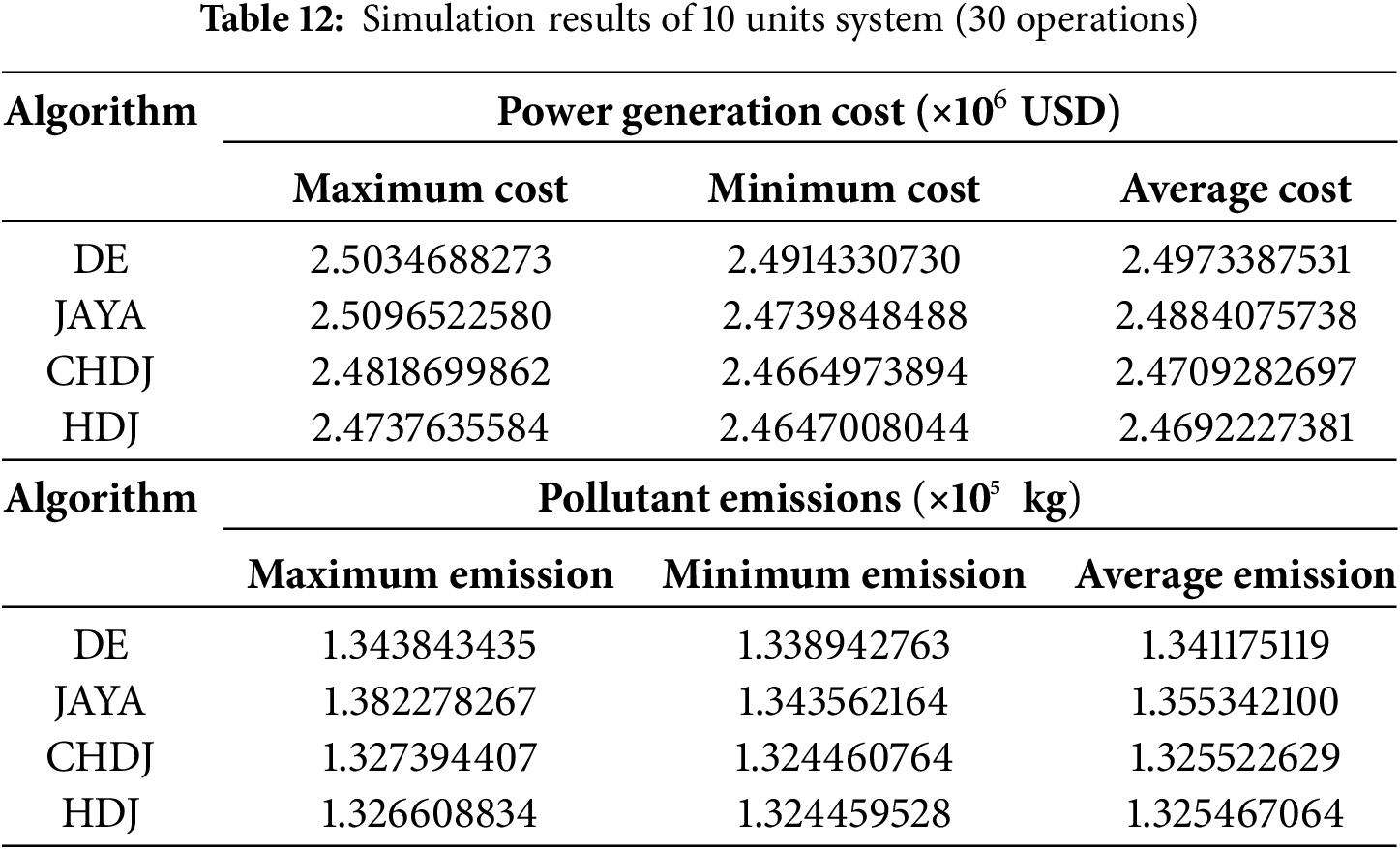
As shown in the data from Table 12, the proposed HDJ algorithm achieves the lowest generation cost and pollution emissions compared to the DE, JAYA, and CHDJ algorithms. The extreme solutions and optimal trade-off solutions are listed in Table 13, it is evident that the solutions obtained by the HDJ algorithm are the best.

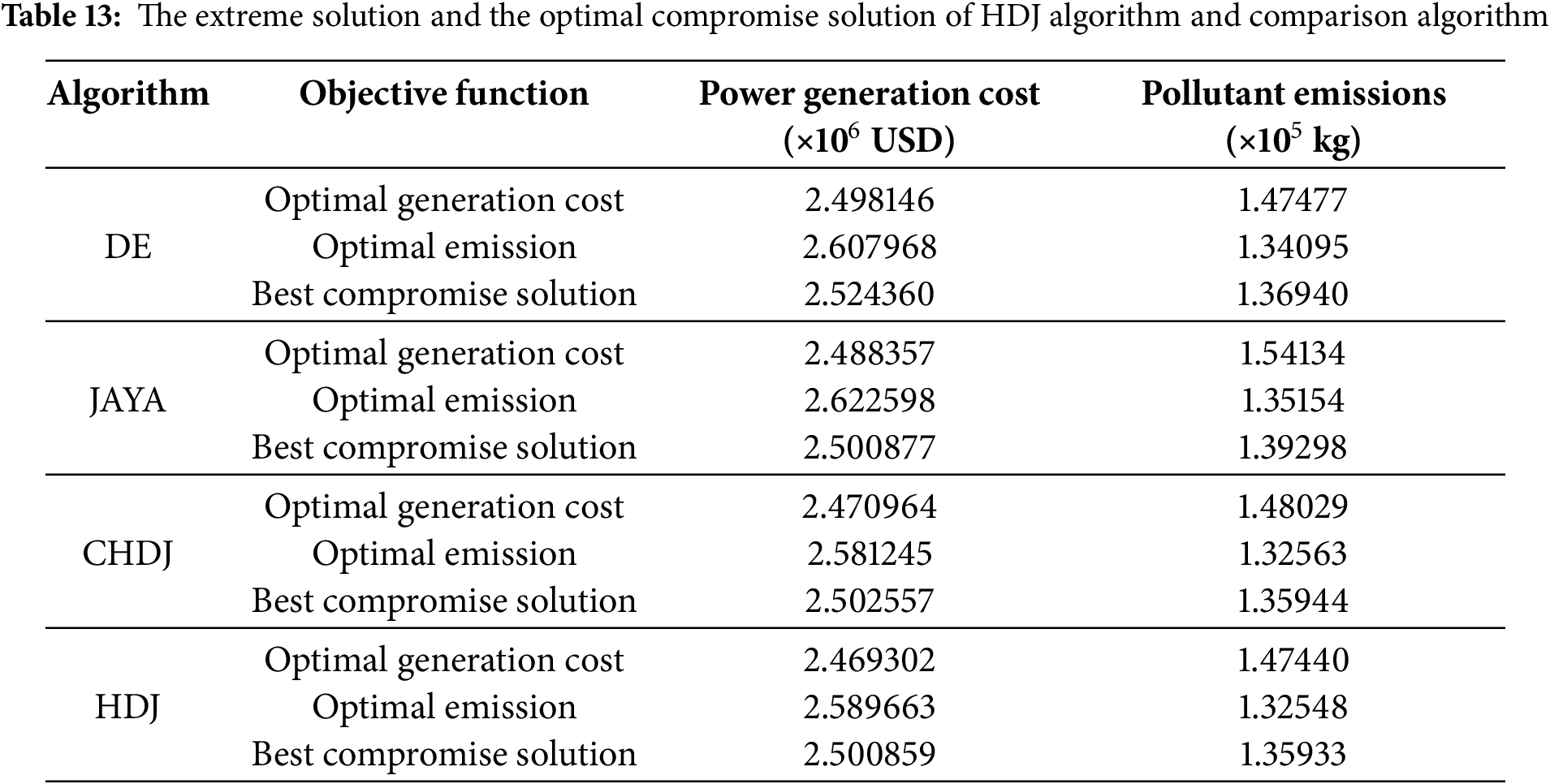
The comparison of the Pareto optimal fronts (POFs) obtained by the HDJ algorithm and the DE, JAYA, and CHDJ algorithms is shown in Table 14. The POF of the HDJ algorithm is closer to the coordinate intersection point, indicating its superior optimization performance.

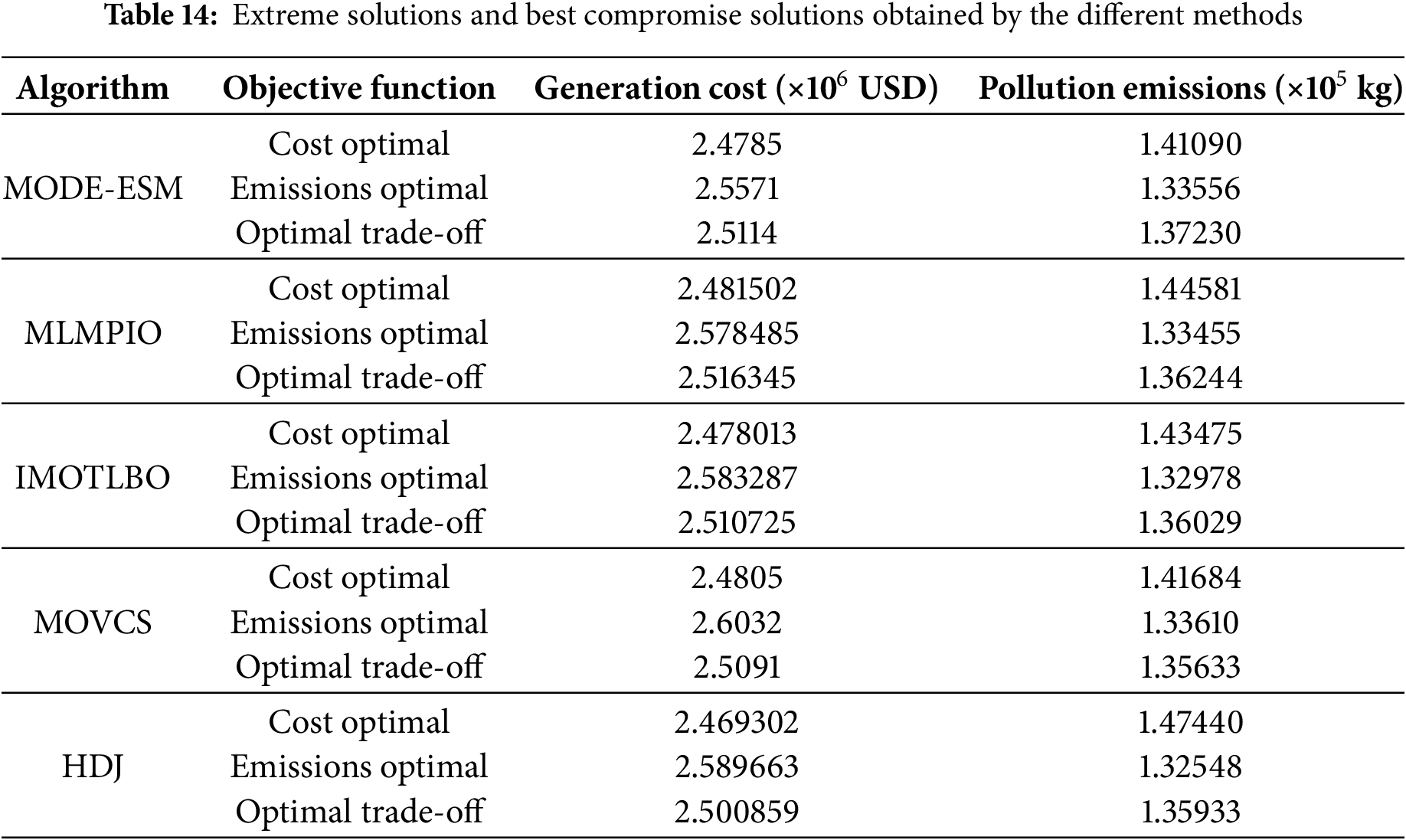
The solution results of the same unit system are horizontally compared between the HDJ algorithm and other solving algorithms, and the comparison results are shown in Table 14.

As shown in Table 11, the HDJ algorithm achieves the optimal generation cost and pollution emissions of 2.469302×106 USD and 1.32548×105 kg, respectively, both of which are the best results. Compared to the MOVCS algorithm, although the HDJ algorithm produces 300 kg more pollution emissions, it reduces generation cost by 8241 USD. Overall, considering its superior global search capability and solution accuracy compared to other algorithms, the HDJ algorithm delivers better economic and environmental benefits.

4.5 Experiments to Integrate Wind and PV Power into the Power System

After the grid connection of scenery, the simulation results of DE, JAYA, CHDJ and HDJ algorithms are shown in Table 15 for 30 operations each.

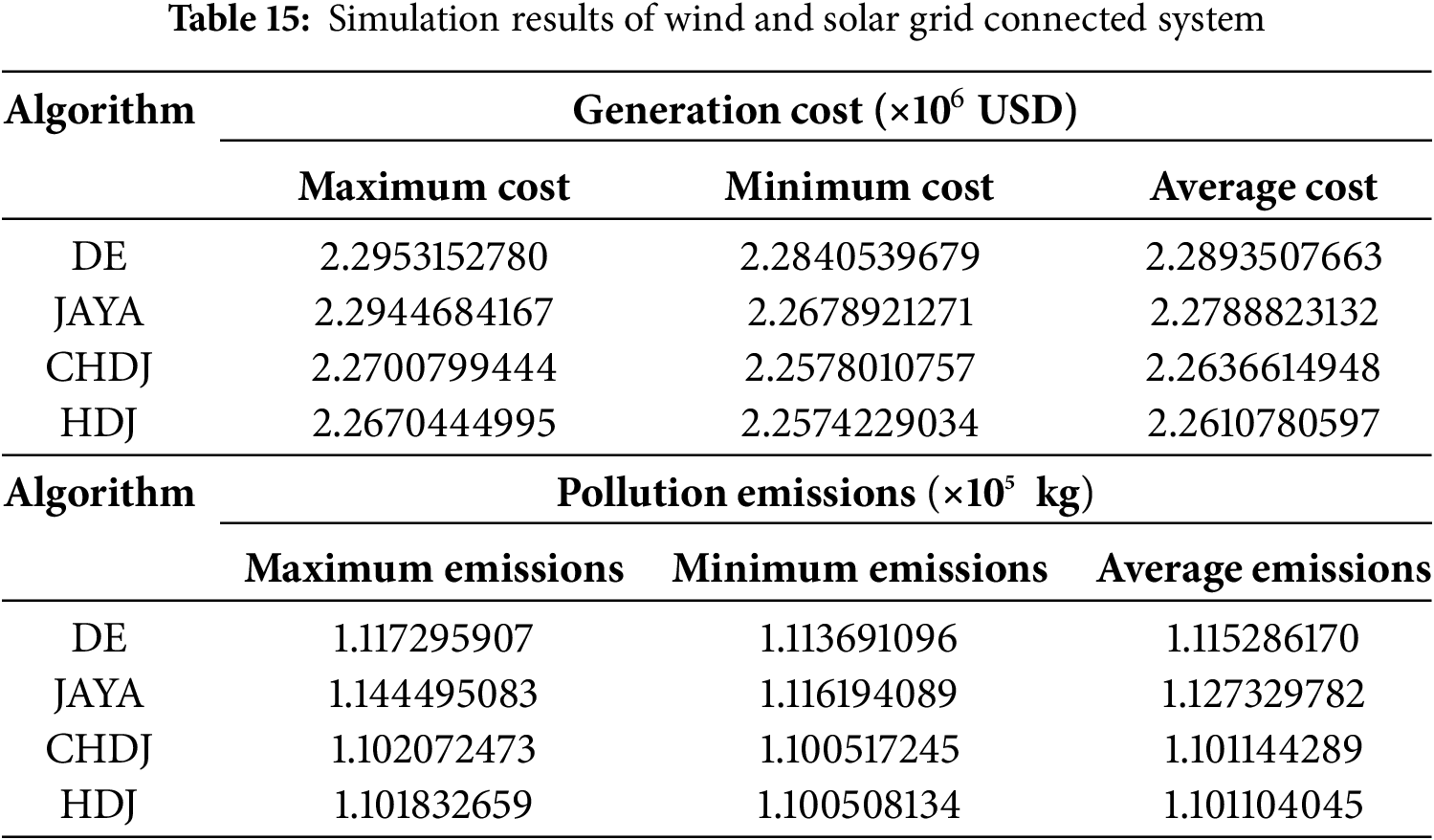
As shown in Table 15 under the condition of uncertain load and wind-solar power integration, the generation cost and pollution emissions obtained by solving the scheduling model using the proposed HDJ algorithm remain the lowest. After wind-solar power integration, the extreme solutions and optimal trade-off solutions of each algorithm are listed in Table 13, and the comparison of the POFs obtained by the algorithms is illustrated in Fig. 12.

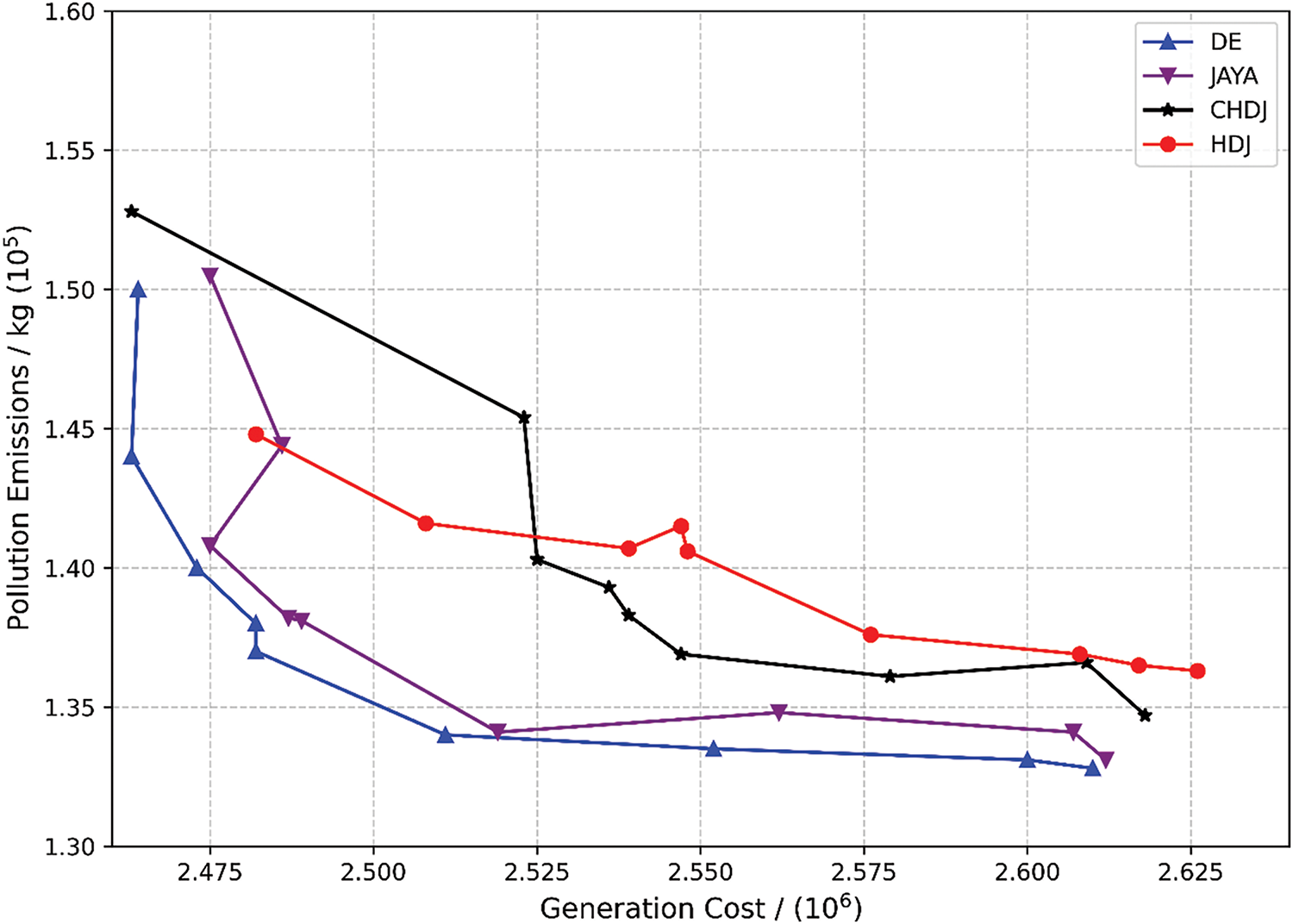
Figure 12: POF obtained by DE/JAYA and its combination

As shown in Table 16 and Fig. 13, the distance between the POF of the HDJ algorithm and that of the CHDJ algorithm becomes larger. This indicates that the optimization performance of the HDJ algorithm is superior to other algorithms when considering wind and solar power uncertainties.

Figure 13: POF for wind grid connection obtained by DE/JAYA and its combination

It can be seen that after the wind and solar grid connection, not only the power generation cost and pollution emissions are reduced, but also the network loss is reduced.

4.6 Evaluation of Multi-Region Power Generation System Applications

To verify the economic dispatch across multiple regions, we conducted simulations for more regions. We will further evaluate the application of the DGADE-HDJ algorithm in two typical multi-region power generation systems. One system is a 3-region, 10-unit system considering multi-fuel selection and valve-point effects, while the other is a 4-region, 40-unit system with significant valve-point effects. Table 17 details the characteristics of these two systems, providing a clear comparison benchmark.

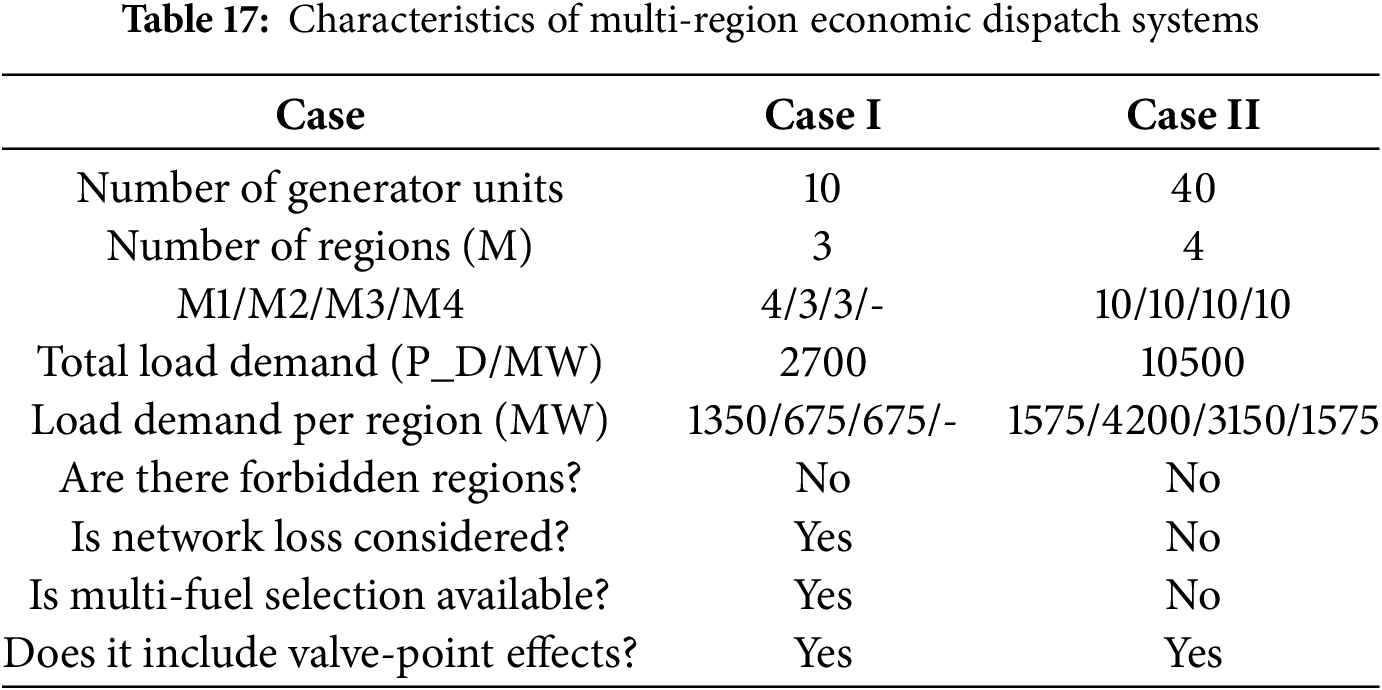
4.6.1 3-Region 10-Unit System with Valve-Point Effects and Multi-Fuel Selection

This system is a classic multi-region power dispatch system, comprising 3 regions and 10 power generation units, with complex features such as multi-fuel selection, valve-point effects, and network losses. According to the data in Table 17, the total load demand for the system is 2700 MW, with regions 1, 2, and 3 accounting for 50%, 25%, and 25% of the total load, respectively. Region 1 includes 4 generator units, while regions 2 and 3 each have 3 generator units. The interconnection between the 3 regions is achieved via 3 tie-lines, each with a power exchange limit of 100 MW. The corresponding simulation results are presented in Table 18.

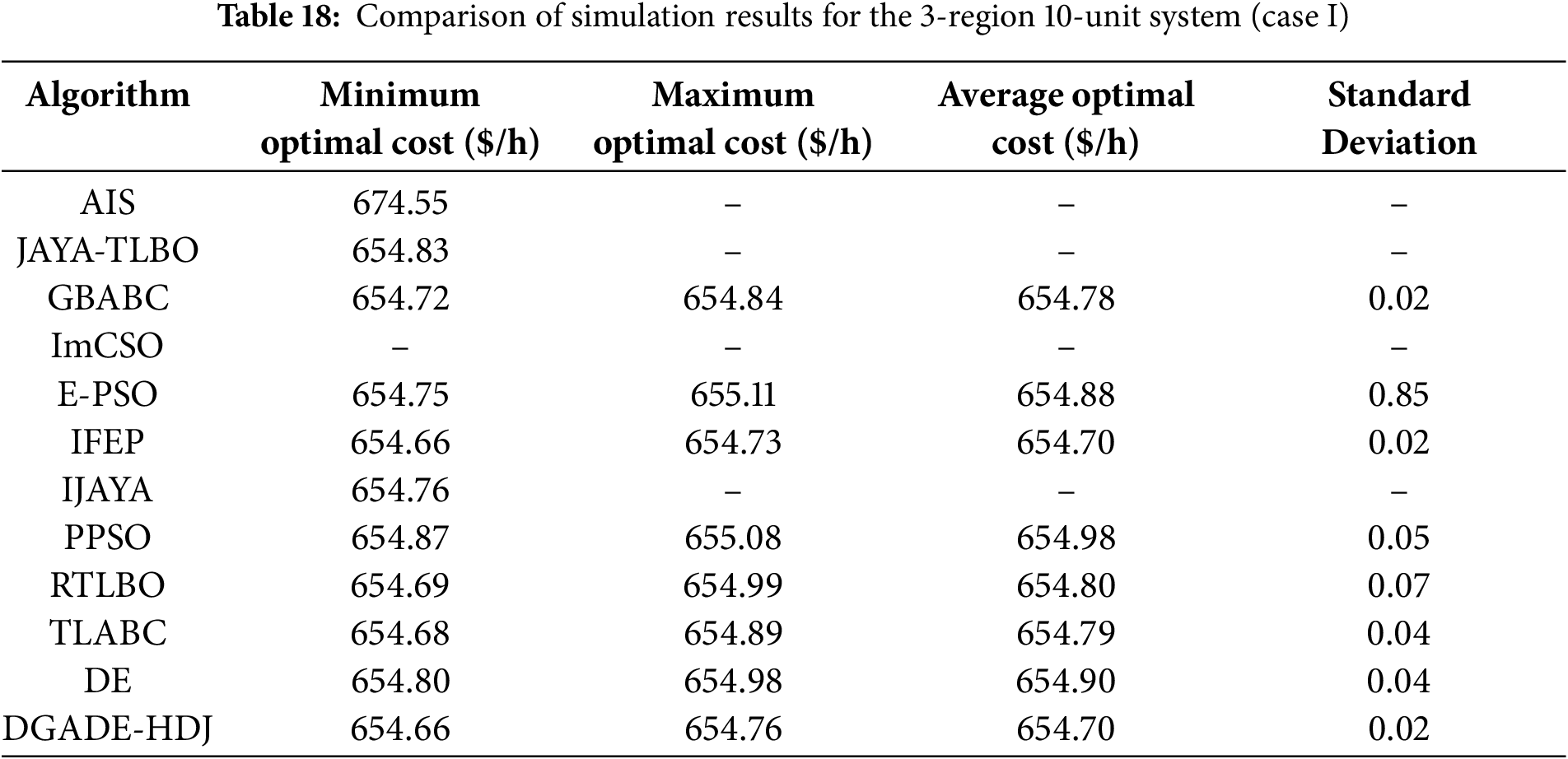
4.6.2 4-Region 40-Unit System with Valve-Point Effects

This study also provides a detailed evaluation of a large 4-region, 40-unit system. According to the data in Table 17, each of the four regions contains 10 generator units, with load demands of 1575, 4200, 3150, and 1575 MW for regions 1 through 4, respectively. The total load demand is 10,500 MW. The interconnection between the 4 regions is achieved via 6 tie-lines. The power exchange limits between tie-lines 1-2, 1-3, and 2-3 (T_12 max, T_13 max, and T_23 max) are all 200 MW, while the limits between tie-lines 1–4, 2–4, and 3–4 (T_14 max, T_24 max, and T_34 max) are 100 MW each. This system exhibits significant valve-point effects, which substantially enhance the non-convexity, non-linearity, and non-smoothness of the multi-region economic dispatch problem, greatly increasing the difficulty of solving the problem. Table 19 presents the simulation results of the system, further validating the superior performance of the proposed algorithm in solving complex non-convex optimization problems.

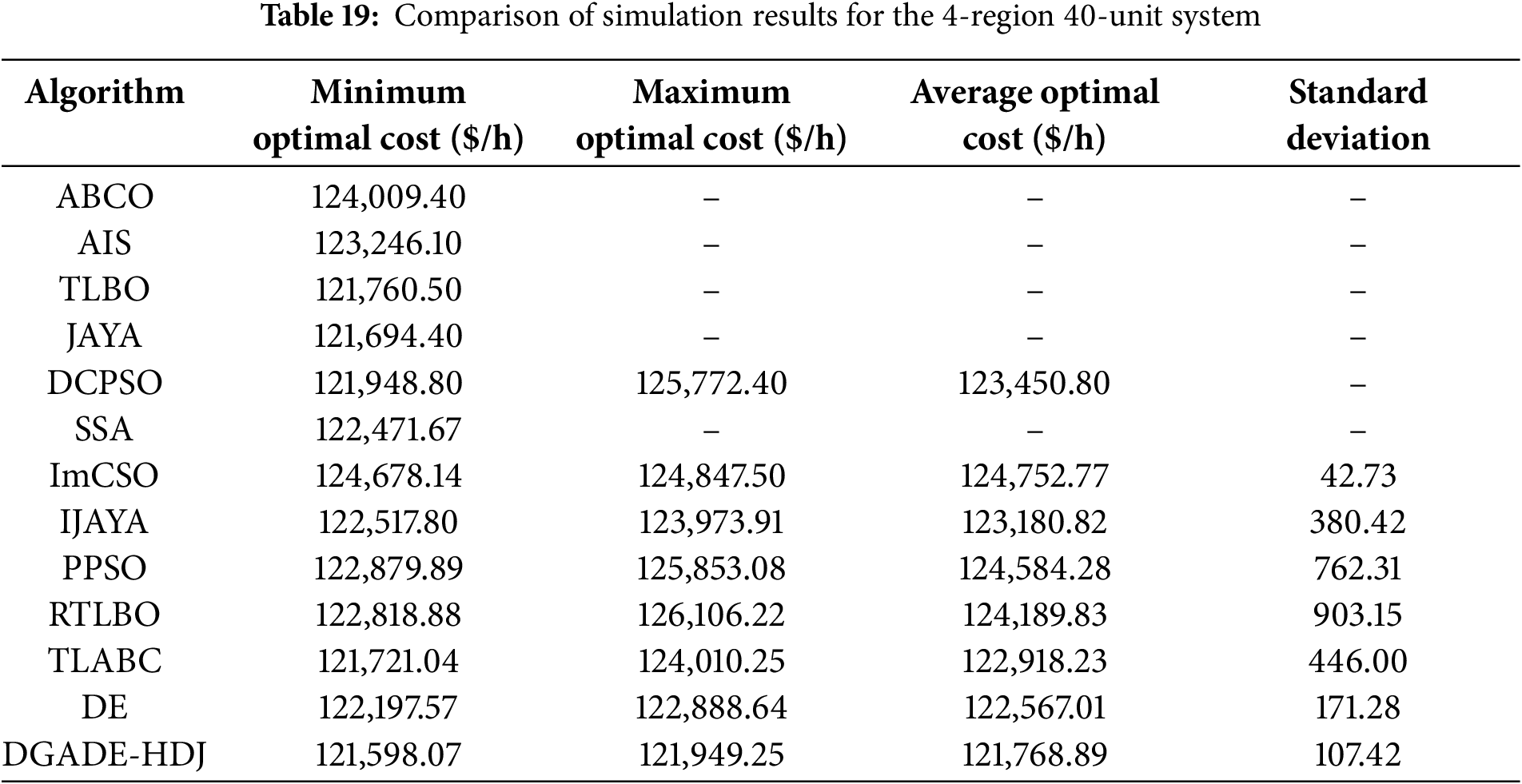
Tables 18 and 19 provide detailed comparisons of the minimum, maximum, and average optimal costs of the DGADE-HDJ algorithm. The results demonstrate that DGADE-HDJ outperforms the other five simulation algorithms and also shows strong competitiveness compared to recent literature results, highlighting its advantages among various simulation algorithms. The experimental results in Table 18 show that in 30 independent runs, the FV-ICLPSO algorithm achieved a very stable optimal cost, with maximum, average, and minimum values of 654.76, 654.70, and 654.66 $/h, respectively. It performed best among the six algorithms listed in this study and showed significant competitiveness when compared to the EPSO algorithm reported in the literature. This outcome demonstrates the exceptional optimization capability of the DGADE-HDJ algorithm when handling complex problems involving multi-fuel selection and valve-point effects. The data in Table 19 further validates the excellence of the DGADE-HDJ algorithm. After 30 independent trials, the maximum, average, and minimum optimal costs were 121,949.25, 121,768.89, and 121,598.07 $/h, respectively. The algorithm achieved a clear advantage over the other algorithms in this study and showed significant competitiveness and application potential when compared to recent research results in the literature.

During the initialization phase, the DGADE-HDJ algorithm initializes the population by incorporating chaotic mapping and an average entropy strategy. The computational complexity of this step is O(N), where N is the population size. In the worst case, evaluating each individual has a complexity of O(D), where D represents the number of decision variables. Assuming that the algorithm runs for T iterations, the complexity of this part is O(N⋅D⋅T). An external elite archive mechanism is employed to preserve the optimal solution set, ensuring that the best solutions are not discarded. Additionally, the Pareto solution set pruning method analyzes the distribution of neighboring solutions to eliminate redundant solutions, thereby improving search efficiency. The complexity of the pruning process is typically O(N), but in certain cases, it may require comparisons across all archived solutions, leading to a worst-case complexity of O(N2). Since the relaxation constraint requires evaluating the current solution and adjusting its feasibility based on the degree of relaxation, its computational complexity is generally O(D). During each iteration, the constraint mechanism may influence multiple solutions, thereby increasing the overall computational load of the algorithm. Consequently, the computational complexity of the DGADE-HDJ algorithm can be expressed as O(N⋅D⋅T+N2), where N is the population size, D is the number of decision variables, and T is the number of iterations.

Assuming that the objective function f(x) is a complex nonlinear function with multiple local optima, the chaotic mapping and Pareto optimization strategies employed in DGADE-HDJ ensure global search capability. The population distribution entropy in generation t is defined as Ht=−∑i=1Npilog⁡pi, where pi represents the distribution probability of individuals in the search space. To maintain algorithmic diversity, the entropy Ht should be maintained at an optimal level Hopt, such Ht≈Hopt,∀t≥0, Due to the chaotic mapping initialization, the initial population covers the search space extensively, ensuring H0≫Hopt, As DGADE-HDJ progresses, the population entropy gradually converges to limt→∞Ht=Hopt, This process guarantees the effectiveness of the global search and enhances the algorithm’s adaptability to large-scale optimization problems.

The scalability of the DGADE-HDJ algorithm lies in its ability to adapt to problems of varying scales and effectively handle complex optimization problems with high dimensionality. As the problem size increases, the algorithm can maintain solution quality by adjusting the population size (N) and the number of iterations (T). While computational costs increase with larger N and T, the use of external elite archiving and Pareto pruning methods helps reduce redundant solution storage and comparisons, effectively alleviating the computational burden introduced by scaling. For high-dimensional problems, the DGADE-HDJ algorithm can handle large decision spaces. Although the computational complexity increases with the dimensionality (D), the chaotic mapping and average entropy initialization strategies help guide the search process in highdimensional spaces, preventing the algorithm from getting trapped in local optima and improving the efficiency of high-dimensional problem-solving. As the problem size and dimensionality grow, the algorithm requires more computational resources, such as memory and processing time. However, by appropriately selecting the population size and iteration count, and leveraging parallel computing techniques, the algorithm maintains strong scalability and competitive performance.

5  Conclusion

5.1 The Results of This Study

This paper presents a DGAGE multi-objective algorithm, and the validation results on a 10-unit demonstration system further substantiate its feasibility. By integrating network losses as an optimization objective in the DEED model—alongside fuel cost and pollution emissions—the proposed approach achieves more satisfactory trade-off solutions compared to traditional models. During the analysis of multi-objective optimization problems, it was discovered that existing multi-objective optimization algorithms struggle with maintaining solution diversity in high-dimensional optimization. Addressing this limitation will be a key focus of future research. To tackle the dynamic environmental economic dispatch (DEED) problem in power systems with integrated wind and solar energy, this study introduces a hybrid HDJ optimization algorithm by combining the DE algorithm with the JAYA algorithm. While the DE algorithm has advantages such as requiring fewer control parameters, exhibiting strong global search capabilities, and achieving fast convergence, it often falls into local optima and lacks solution precision when handling complex DEED models involving uncertain and large-scale heterogeneous renewable energy sources like wind and solar power. To overcome these challenges, the HDJ hybrid optimization algorithm leverages the strengths of both DE and JAYA algorithms to effectively address the DEED problem. In case study analyses, the HDJ algorithm was compared with DE, JAYA, and CHDJ algorithms across various criteria, including cost-optimal, emissions-optimal, and optimal trade-off solutions. The results confirm the feasibility and superiority of the HDJ algorithm in solving DEED problems for power systems that incorporate diverse renewable energy sources.

5.2 Applicability of the Algorithm

The proposed dual-population pseudo-parallel genetic algorithm-differential evolution (GA-DE) multi-objective optimization algorithm exhibits strong applicability in real-world power systems, addressing critical challenges such as high dimensionality, strong coupling, nonlinearity, and non-convexity in dynamic economic dispatch. Its performance in handling uncertainties from renewable energy integration, optimizing system scheduling, and balancing multiple conflicting objectives demonstrates its value for practical deployment.

Power systems operate in dynamic and uncertain environments where multiple conflicting objectives, such as economic efficiency, environmental sustainability, and system reliability, must be considered. Traditional optimization models often struggle to achieve a balance among these objectives. The proposed algorithm effectively transforms a multi-objective problem into a single-objective problem using a normalization coefficient, allowing efficient optimization of generation cost and pollutant emissions. This approach is highly applicable to real-world power dispatch systems, where operators must make trade-offs between cost and environmental impact. Moreover, the incorporation of transmission losses as an explicit optimization objective is a significant enhancement over conventional models. Transmission losses are a major concern in large-scale power grids, affecting overall efficiency and cost. By integrating them into the optimization framework, the model ensures a more realistic and practical solution for power dispatch.

The effectiveness of the proposed model has been rigorously validated using CEC2022 and cec2005 benchmark test functions, which are widely used in optimization research. These tests confirm the algorithm’s superior optimization performance compared to traditional approaches. Furthermore, validation on a classical 10-unit power system demonstrates the model’s feasibility in practical power system scheduling. By effectively managing multiple generating units, optimizing power generation costs, and reducing emissions, the algorithm proves its real-world applicability in industrial-scale power grids.

As power grids become increasingly smart and decentralized, the need for scalable and adaptable optimization models grows. The proposed model is highly scalable, capable of handling large-scale power networks with multiple energy sources. Its adaptability allows it to be applied in various real-world scenarios, including microgrids with distributed energy resources; Smart grids with demand-response mechanisms; Hybrid power systems integrating thermal, wind, and solar energy. With the ability to handle complex constraints and real-time scheduling, the proposed model represents a next-generation optimization approach for power system management.

The proposed GA-DE multi-objective optimization algorithm provides a novel, efficient, and practical solution for dynamic power dispatch in modern power systems. Its ability to optimize multiple conflicting objectives (cost, emissions, and transmission losses); Handle renewable energy uncertainties effectively; Avoid local optima and achieve global convergence; Demonstrate superior performance on benchmark and real-world power systems; Scale to future smart grid applications; makes it a highly applicable and reliable model for real-world power system operations. As energy systems continue to evolve, this approach can play a crucial role in ensuring efficient, stable, and sustainable power distribution.

5.3 Prospect of Technology Improvement

This study proposes an optimization algorithm-based approach for solving economic dispatch problems. However, several aspects warrant further exploration and refinement. The current study considers only the integration of wind power, photovoltaic (PV) power, and small hydropower in assessing the safe and stable operation of the power system, thereby limiting the scope of energy sources included. In practical applications, other renewable energy sources—such as nuclear energy, biomass energy, geothermal energy, and ocean energy—also play crucial roles. Depending on geographical location and energy demand, scenarios involving the simultaneous integration of three or more renewable energy sources may emerge. Future research should extend the scope of energy types considered and examine their impact on power system operations to enhance the comprehensiveness and applicability of the proposed method. Additionally, the case study presented in this research is based on a relatively small-scale unit system. To ensure greater alignment with real-world engineering applications, future studies should incorporate empirical power system data or conduct simulations on larger-scale power system models. While the proposed optimization algorithm demonstrates satisfactory performance within the scope of this study, its effectiveness in large-scale unit systems remains uncertain and necessitates further empirical validation. Furthermore, the power grid dispatch optimization model in this study primarily focuses on economic costs and environmental governance costs. However, real-world power system operations must also consider additional factors, such as grid operational efficiency and power quality. Moreover, in constructing the environmental economic dispatch model for power systems with wind farms, this study does not account for system voltage, monsoon effects, or transmission losses. The omission of these factors introduces potential discrepancies between the optimization results and actual operating conditions. To enhance the realism and applicability of the model, future research should incorporate these factors into the development of dispatch optimization frameworks, thereby improving the model’s ability to reflect real-world power system dynamics.

This study proposes a solution method for Dynamic Environmental Economic Dispatch (DEED) based on optimization algorithms and verifies its feasibility in multi-objective optimization problems. Current optimization algorithms, when solving the DEED problem, are constrained by high-dimensional search spaces, non-convex objective functions, and complex constraints, leaving room for improvement in computational efficiency. Future research can be improved in the following aspects: integrating High-Performance Computing (HPC) architectures and utilizing Graphics Processing Unit (GPU) parallel computing or cloud computing platforms to achieve accelerated computation of the algorithm. Meanwhile, exploring an optimization framework based on distributed computing, where multiple computing nodes collaborate in optimization, can enhance convergence speed. For high-dimensional optimization problems, a Decomposition-Coordination approach can be employed to divide large-scale optimization problems into multiple subproblems, solve them separately, and then perform global coordination. Additionally, dimensionality reduction methods, such as Principal Component Analysis (PCA) or Manifold Learning, can be incorporated to reduce redundant variables and improve computational efficiency. Deep Reinforcement Learning (DRL) techniques, such as Proximal Policy Optimization (PPO) based on policy gradients or Deep Q-Network (DQN) based on value iteration, can be utilized to construct intelligent scheduling decision models, enabling autonomous learning of optimal scheduling strategies under different operating environments. The introduction of a Meta-Learning framework can allow the optimization algorithm to quickly adapt to new problems based on historical solving experiences, improving generalization ability and enhancing applicability to different power system scenarios.

The current study primarily focuses on the impact of wind power, photovoltaic, and small hydropower on grid dispatching, without fully considering multi-energy complementary systems and the complex operational characteristics of the power grid. Future research can be expanded in the following areas: On the basis of existing economic costs and environmental governance costs, key performance indicators such as Power Quality, Load Reliability, and Grid Resilience can be introduced to make the optimization model more aligned with practical power dispatching needs. Further consideration of power flow, reactive power regulation, voltage stability, line losses, meteorological factors (such as the impact of monsoons on wind farms), and uncertainties in the electricity market can enhance the practical adaptability of dispatching schemes. Large-scale simulation tests on actual datasets from the State Grid or regional grids can be conducted to verify the engineering feasibility and scheduling effectiveness of the optimization algorithm. In the electricity market environment, the optimization model needs to balance market bidding mechanisms, transaction costs, and scheduling flexibility. Future research can explore multi-agent game optimization strategies to achieve optimal scheduling decisions driven by market mechanisms.

Acknowledgement: This research gratefully acknowledges the support of the Zhejiang Provincial Department of Education and the Higher Education Division of the Ministry of Education for the project research.

Funding Statement: This research was funded by the Major Humanities and Social Sciences Research Projects in Zhejiang Higher Education Institutions, grant number 2023QN131; National Innovation Training Program Project in China, grant number 202410451009.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Bin Jiang; data collection: Houbin Wang; analysis and interpretation of results: Bin Jiang; draft manuscript preparation: Houbin Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

References

1. Marzbani F, Abdelfatah A. Economic dispatch optimization strategies and problem formulation: a comprehensive review. Energies. 2024;17(3):550. doi:10.3390/en17030550. [Google Scholar] [CrossRef]

2. Shezan SA, Ishraque MF, Muyeen S, Abu-Siada A, Saidur R, Ali M, et al. Selection of the best dispatch strategy considering techno-economic and system stability analysis with optimal sizing. Energy Strategy Rev. 2022;43(2):100923. doi:10.1016/j.esr.2022.100923. [Google Scholar] [CrossRef]

3. Ahmed I, Rehan M, Basit A, Hong K-S. Greenhouse gases emission reduction for electric power generation sector by efficient dispatching of thermal plants integrated with renewable systems. Sci Rep. 2022;12(1):12380. doi:10.1038/s41598-022-15983-0. [Google Scholar] [PubMed] [CrossRef]

4. Ríos A, Hernández EE, Valdez SI. A two-stage mono-and multi-objective method for the optimization of general UPS parallel manipulators. Mathematics. 2021;9(5):543. doi:10.3390/math9050543. [Google Scholar] [CrossRef]

5. Alli KS, Latchman HA. A semidefinite programming method weighted sum based for solving a multi-area emission (Environmental) economic dispatch problem. West Indian J Eng. 2024;46(2):21–33. doi:10.47412/KABN8939. [Google Scholar] [CrossRef]

6. Hassan MH, Kamel S, Domínguez-García JL, El-Naggar MF. MSSA-DEED: a multi-objective salp swarm algorithm for solving dynamic economic emission dispatch problems. Sustainability. 2022;14(15):9785. doi:10.3390/su14159785. [Google Scholar] [CrossRef]

7. Li X, Han J, Liu Y, Dou Z, Zhang T-A. Summary of research progress on industrial flue gas desulfurization technology. Sep Purif Technol. 2022;281(6):119849. doi:10.1016/j.seppur.2021.119849. [Google Scholar] [CrossRef]

8. Sinsel SR, Riemke RL, Hoffmann VH. Challenges and solution technologies for the integration of variable renewable energy sources—a review. Renew Energy. 2020;145:2271–85. doi:10.1016/j.renene.2019.06.147. [Google Scholar] [CrossRef]

9. Li J, Chen S, Wu Y, Wang Q, Liu X, Qi L, et al. How to make better use of intermittent and variable energy? A review of wind and photovoltaic power consumption in China. Renew Sustain Energ Rev. 2021;137:110626. doi:10.1016/j.rser.2020.110626. [Google Scholar] [CrossRef]

10. Hassan Q, Algburi S, Sameen AZ, Salman HM, Jaszczur M. A review of hybrid renewable energy systems: solar and wind-powered solutions: challenges, opportunities, and policy implications. Results Eng. 2023;20(18):101621. doi:10.1016/j.rineng.2023.101621. [Google Scholar] [CrossRef]

11. Zang T, Wang S, Wang Z, Li C, Liu Y, Xiao Y, et al. Integrated planning and operation dispatching of source-grid–load-storage in a new power system: a coupled socio-cyber–physical perspective. Energies. 2024;17(12):3013. doi:10.3390/en17123013. [Google Scholar] [CrossRef]

12. Khalid M. Smart grids and renewable energy systems: perspectives and grid integration challenges. Energy Strategy Rev. 2024;51(13):101299. doi:10.1016/j.esr.2024.101299. [Google Scholar] [CrossRef]

13. Ishraque MF, Shezan SA, Ali M, Rashid M. Optimization of load dispatch strategies for an islanded microgrid connected with renewable energy sources. Appl Energy. 2021;292(4):116879. doi:10.1016/j.apenergy.2021.116879. [Google Scholar] [CrossRef]

14. Hassan Q, Viktor P, Al-Musawi TJ, Ali BM, Algburi S, Alzoubi HM, et al. The renewable energy role in the global energy Transformations. Renew Energy Focus. 2024;48(12):100545. doi:10.1016/j.ref.2024.100545. [Google Scholar] [CrossRef]

15. Yap J, McLellan B. Exploring transitions to a hydrogen economy: quantitative insights from an expert survey. Int J Hydrogen Energy. 2024;66:371–86. doi:10.1016/j.ijhydene.2024.03.213. [Google Scholar] [CrossRef]

16. Rahman A, Farrok O, Haque MM. Environmental impact of renewable energy source based electrical power plants: solar, wind, hydroelectric, biomass, geothermal, tidal, ocean, and osmotic. Renew Sustain Energ Rev. 2022;161(3):112279. doi:10.1016/j.rser.2022.112279. [Google Scholar] [CrossRef]

17. Williams R. The microeconomic challenge with renewable energy. SSRN. 2024. doi:10.2139/ssrn.4718822. [Google Scholar] [CrossRef]

18. He W, King M, Luo X, Dooner M, Li D, Wang J. Technologies and economics of electric energy storages in power systems: review and perspective. Adv Appl Energy. 2021;4(4):100060. doi:10.1016/j.adapen.2021.100060. [Google Scholar] [CrossRef]

19. Ranjan M, Shankar R. A literature survey on load frequency control considering renewable energy integration in power system: recent trends and future prospects. J Energy Storage. 2022;45:103717. doi:10.1016/j.est.2021.103717. [Google Scholar] [CrossRef]

20. Nebey AH. Recent advancement in demand side energy management system for optimal energy utilization. Energy Rep. 2024;11:5422–35. doi:10.1016/j.egyr.2024.05.028. [Google Scholar] [CrossRef]

21. Ozcanli AK, Yaprakdal F, Baysal M. Deep learning methods and applications for electrical power systems: a comprehensive review. Int J Energy Res. 2020;44(9):7136–57. doi:10.1002/er.5331. [Google Scholar] [CrossRef]

22. Kalakova A, Nunna HK, Jamwal PK, Doolla S. A novel genetic algorithm based dynamic economic dispatch with short-term load forecasting. IEEE Trans Indust Appl. 2021;57(3):2972–82. doi:10.1109/TIA.2021.3065895. [Google Scholar] [CrossRef]

23. Xue L, Wang J, Zhang Y, Yong W, Qi J, Li H. Model-data-event based community integrated energy system low-carbon economic scheduling. Renew Sustain Energ Rev. 2023;182(1):113379. doi:10.1016/j.rser.2023.113379. [Google Scholar] [CrossRef]

24. Fu X, Wu X, Zhang C, Fan S, Liu N. Planning of distributed renewable energy systems under uncertainty based on statistical machine learning. Prot Contr Mod Power Syst. 2022;7(4):1–27. doi:10.1186/s41601-022-00262-x. [Google Scholar] [CrossRef]

25. Khan MA, Khan SUR, Haider SZQ, Khan SA, Bilal O. Evolving knowledge representation learning with the dynamic asymmetric embedding model. Evol Syst. 2024;15(6):2323–38. doi:10.1007/s12530-024-09616-2. [Google Scholar] [CrossRef]

26. Wang Y, Guo C-H, Chen X-J, Jia L-Q, Guo X-N, Chen R-S, et al. Carbon peak and carbon neutrality in China: goals, implementation path and prospects. Chin Geol. 2021;4(4):720–46. doi:10.31035/cg2021083. [Google Scholar] [CrossRef]

27. Zhu S, Yu T, Xu T, Chen H, Dustdar S, Gigan S, et al. Intelligent computing: the latest advances, challenges, and future. Intell Comput. 2023;2(7):0006. doi:10.34133/icomputing.0006. [Google Scholar] [CrossRef]

28. Abualigah L, Elaziz MA, Khasawneh AM, Alshinwan M, Ibrahim RA, Al-Qaness MA, et al. Meta-heuristic optimization algorithms for solving real-world mechanical engineering design problems: a comprehensive survey, applications, comparative analysis, and results. Neural Comput Appl. 2022;34(6):1–30. doi:10.1007/s00521-021-06747-4. [Google Scholar] [CrossRef]

29. Gil Y, Garijo D, Khider D, Knoblock CA, Ratnakar V, Osorio M, et al. Artificial intelligence for modeling complex systems: taming the complexity of expert models to improve decision making. ACM Trans Interact Intell Syst. 2021;11(2):1–49. doi:10.1145/3453172. [Google Scholar] [CrossRef]

30. Liu Z-F, Li L-L, Liu Y-W, Liu J-Q, Li H-Y, Shen Q. Dynamic economic emission dispatch considering renewable energy generation: a novel multi-objective optimization approach. Energy. 2021;235(3):121407. doi:10.1016/j.energy.2021.121407. [Google Scholar] [CrossRef]

31. Sinuany-Stern Z. Foundations of operations research: from linear programming to data envelopment analysis. Eur J Oper Res. 2023;306(3):1069–80. doi:10.1016/j.ejor.2022.10.046. [Google Scholar] [CrossRef]

32. Danilova M, Dvurechensky P, Gasnikov A, Gorbunov E, Guminov S, Kamzolov D, et al. Recent theoretical advances in non-convex optimization. In: High-dimensional optimization and probability: with a view towards data. Cham:Springer; 2022. p. 79–163. [Google Scholar]

33. Beirami A, Vahidinasab V, Shafie-khah M, Catalão JP. Multiobjective ray optimization algorithm as a solution strategy for solving non-convex problems: a power generation scheduling case study. Int J Electr Power Energy Syst. 2020;119:105967. doi:10.1016/j.ijepes.2020.105967. [Google Scholar] [CrossRef]

34. Avriel M. Nonlinear programming. In: Mathematical programming for operations researchers and computer scientists.BocaRaton:CRC Press; 2020. p. 271–367. [Google Scholar]

35. Feppon F, Allaire G, Dapogny C. Null space gradient flows for constrained optimization with applications to shape optimization. ESAIM: Control, Optim Calc Var. 2020;26:90. doi:10.1051/cocv/2020015. [Google Scholar] [CrossRef]

36. Fahim KE, Silva LCD, Hussain F, Yassin H. A state-of-the-art review on optimization methods and techniques for economic load dispatch with photovoltaic systems: progress, challenges, and recommendations. Sustainability. 2023;15(15):11837. doi:10.3390/su151511837. [Google Scholar] [CrossRef]

37. Liu Y, Wu L, Chen Y, Li J. Integrating high DER-penetrated distribution systems into ISO energy market clearing: a feasible region projection approach. IEEE Trans Power Syst. 2020;36(3):2262–72. doi:10.1109/TPWRS.2020.3028859. [Google Scholar] [CrossRef]

38. Wu K, Li Q, Lin J, Yi Y, Chen Z, Chen M. Fast distributed Lagrange dual method based on accelerated gradients for economic dispatch of microgrids. Energy Rep. 2020;6(6):640–8. doi:10.1016/j.egyr.2020.11.163. [Google Scholar] [CrossRef]

39. Huang Y. Research status and applications of nature-inspired algorithms for agri-food production. Int J Agric Biol Eng. 2020;13(4):1–9. doi:10.25165/j.ijabe.20201304.5501. [Google Scholar] [CrossRef]

40. Ghannadi P, Kourehli SS, Mirjalili S. A review of the application of the simulated annealing algorithm in structural health monitoring (1995–2021). Frattura Ed Integrità Strutturale. 2023;17(64):51–76. doi:10.3221/IGF-ESIS.64.04. [Google Scholar] [CrossRef]

41. Albadr MA, Tiun S, Ayob M, Al-Dhief F. Genetic algorithm based on natural selection theory for optimization problems. Symmetry. 2020;12(11):1758. doi:10.3390/sym12111758. [Google Scholar] [CrossRef]

42. Georgioudakis M, Plevris V. A comparative study of differential evolution variants in constrained structural optimization. Front Built Environ. 2020;6:102. doi:10.3389/fbuil.2020.00102. [Google Scholar] [CrossRef]

43. Zhou M, Cui M, Xu D, Zhu S, Zhao Z, Abusorrah A. Evolutionary optimization methods for high-dimensional expensive problems: a survey. IEEE/CAA J Autom Sin. 2024;11(5):1092–105. doi:10.1109/JAS.2024.124320. [Google Scholar] [CrossRef]

44. Tang R, Tang X, Zhao H. Enhancing whale optimization algorithm with differential evolution and Lévy flight for robot path planning. Int J Adv Comput Sci Appl. 2024;15(5):401. doi:10.14569/IJACSA.2024.0150540. [Google Scholar] [CrossRef]

45. Abaci K, Yetgin Z, Yamacli V, Isiker H. Modified effective butterfly optimizer for solving optimal power flow problem. Heliyon. 2024;10(12):e32862. doi:10.1016/j.heliyon.2024.e32862. [Google Scholar] [PubMed] [CrossRef]

46. Gharehchopogh FS. Quantum-inspired metaheuristic algorithms: comprehensive survey and classification. Artif Intell Rev. 2023;56(6):5479–543. doi:10.1007/s10462-022-10280-8. [Google Scholar] [CrossRef]

47. Zhu X, Zou F, Li S. Enhancing air quality prediction with an adaptive PSO-optimized CNN-Bi-LSTM model. Appl Sci. 2024;14(13):5787. doi:10.3390/app14135787. [Google Scholar] [CrossRef]

48. Wang X. An intensified northern goshawk optimization algorithm for solving optimization problems. Eng Res Express. 2024;6(4):045267. doi:10.1088/2631-8695/ada222. [Google Scholar] [CrossRef]

49. Sahoo SK, Saha AK. A hybrid moth flame optimization algorithm for global optimization. J Bionic Eng. 2022;19(5):1522–43. doi:10.1007/s42235-022-00207-y. [Google Scholar] [CrossRef]

50. Ang T-Z, Salem M, Kamarol M, Das HS, Nazari MA, Prabaharan N. A comprehensive study of renewable energy sources: classifications, challenges and suggestions. Energy Strategy Rev. 2022;43(4):100939. doi:10.1016/j.esr.2022.100939. [Google Scholar] [CrossRef]

51. Ali ZM, Ćalasan M, Jurado F, Aleem SHA. Complexities of power quality and harmonic-induced overheating in modern power grids studies: challenges and solutions. IEEE Access. 2024;12:151554–151597. doi:10.1109/ACCESS.2024.3477729. [Google Scholar] [CrossRef]

52. Liang Y, Liu H, Zhou H, Meng Z, Liu J, Zhou M. Multi-stage coordinated planning for transmission and energy storage considering large-scale renewable energy integration. Appl Sci. 2024;14(15):6486. doi:10.3390/app14156486. [Google Scholar] [CrossRef]

53. Wang L. Coordinated and non-coordinated control of energy storage for voltage support in low voltage distribution networks.Newcastle:Newcastle University; 2016. [Google Scholar]

54. Chen K, Shao Q, Zhou B, Yang Q, Pan H, Jin T, et al. Optimization of multi-temporal generation scheduling in power system under elevated renewable penetrations: a review. Front Energy Res. 2023;10:1054597. doi:10.3389/fenrg.2022.1054597. [Google Scholar] [CrossRef]

55. Zhang R, Wang W, Liu Z, Li W, Hu Y. Simulation analysis of large-scale centralized access to power grid of new energy based on PSASP. In: 2024 IEEE 2nd International Conference on Image Processing and Computer Applications (ICIPCA); 2024; IEEE. [Google Scholar]

56. Yang B, Zhou Y, Yan Y, Su S, Li J, Yao W, et al. A critical and comprehensive handbook for game theory applications on new power systems: structure, methodology, and challenges. Prot Control Mod Power Syst. 2025; 1–27. doi:10.23919/PCMP.2024.000297. [Google Scholar] [CrossRef]

57. Alshammari ME, Ramli MA, Mehedi IM. A new chaotic artificial bee colony for the risk-constrained economic emission dispatch problem incorporating wind power. Energies. 2021;14(13):4014. doi:10.3390/en14134014. [Google Scholar] [CrossRef]

58. Pothireddy KMR, Vuddanti S, Salkuti SR. Optimal assortment of methods to mitigate the imbalance power in the day-ahead market. Elect Eng. 2025;9(2):1040. doi:10.1007/s00202-025-02950-x. [Google Scholar] [CrossRef]

59. Pijarski P, Belowski A. Application of methods based on artificial intelligence and optimisation in power engineering—introduction to the special issue. Energies. 2024;17(2):516. doi:10.3390/en17020516. [Google Scholar] [CrossRef]

60. Shi L, Duanmu C, Wu F, He S, Lee KY. Optimal allocation of energy storage capacity for hydro-wind-solar multi-energy renewable energy system with nested multiple time scales. J Clean Prod. 2024;446(6):141357. doi:10.1016/j.jclepro.2024.141357. [Google Scholar] [CrossRef]

61. Ifaei P, Esfehankalateh AT, Ghobadi F, Mohammadi-Ivatloo B, Yoo C. Systematic review and cutting-edge applications of prominent heuristic optimizers in sustainable energies. J Clean Prod. 2023;414:137632. doi:10.1016/j.jclepro.2023.137632. [Google Scholar] [CrossRef]

62. Zhao Y, Gao J, Zheng Y, Zhu B, Luo G, Tang Y, et al. Thermodynamic and economic analysis of organic Rankine cycle combined with flash cycle and ejector. Int J Low-Carbon Technol. 2024;19:24–32. doi:10.1093/ijlct/ctad097. [Google Scholar] [CrossRef]

63. Bailey ET, Caldas L. Operative generative design using non-dominated sorting genetic algorithm II (NSGA-II). Autom Constr. 2023;155(3):105026. doi:10.1016/j.autcon.2023.105026. [Google Scholar] [CrossRef]

64. Yuan M, Lin X, Zhong W editors. Model predictive control of distributed adjustable jet pump in district heating system considering renewable energy access. In: 2023 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia); 2023; IEEE. [Google Scholar]

65. Wang T, Han H, Wang Y. A two-stage distributionally robust optimization model for geothermal-hydrogen integrated energy system operation considering multiple uncertainties. Environ, Dev Sustain. 2024;26(6):16223–47. doi:10.1007/s10668-023-03294-x. [Google Scholar] [CrossRef]

66. Sohani A, Delfani F, Hosseini M, Sayyaadi H, Karimi N, Li LK, et al. Dynamic multi-objective optimization applied to a solar-geothermal multi-generation system for hydrogen production, desalination, and energy storage. Int J Hydrog Energy. 2022;47(74):31730–41. doi:10.1016/j.ijhydene.2022.03.253. [Google Scholar] [CrossRef]

67. Yang W, Li Y, Wang H, Jiang M, Cao M, Liu C. Multi-objective optimization of high-power microwave sources based on multi-criteria decision-making and multi-objective micro-genetic algorithm. IEEE Trans Electron Dev. 2023;70(7):3892–8. doi:10.1109/TED.2023.3280151. [Google Scholar] [CrossRef]

68. Yip WS, Yan HE, Zhang B, To S. The state-of-art review of ultra-precision machining using text mining: identification of main themes and recommendations for the future direction. WIREs Data Mining Knowl Discov. 2024;14(1):e1517. doi:10.1002/widm.1517. [Google Scholar] [CrossRef]

69. Yan HE, Guo F, Zhang B, Chan YK, Zhou HT, Sun L, et al. Sustainability assessment during machining processes: evidence from the econ-environmental modelling. J Clean Prod. 2024;448(3):141612. doi:10.1016/j.jclepro.2024.141612. [Google Scholar] [CrossRef]

70. Hao Y, Zhao C, Zhang Y, Cao Y, Li Z. Constrained multi-objective optimization problems: methodologies, algorithms and applications. Knowl Based Syst. 2024;299(1):111998. doi:10.1016/j.knosys.2024.111998. [Google Scholar] [CrossRef]

71. Ye Q, Wang Z, Zhao Y, Dai R, Wu F, Yu M. A clustering-based competitive particle swarm optimization with grid ranking for multi-objective optimization problems. Sci Rep. 2023;13(1):11754. doi:10.1038/s41598-023-38529-4. [Google Scholar] [PubMed] [CrossRef]

72. Zapotecas-Martínez S, García-Nájera A, Menchaca-Méndez A. Improved lebesgue indicator-based evolutionary algorithm: reducing hypervolume computations. Mathematics. 2021;10(1):19. doi:10.3390/math10010019. [Google Scholar] [CrossRef]

73. Gu Q, Liu Y, Chen L, Xiong N. An improved competitive particle swarm optimization for many-objective optimization problems. Expert Syst Appl. 2022;189(9):116118. doi:10.1016/j.eswa.2021.116118. [Google Scholar] [CrossRef]

74. Rouhandeh M, Ahmadi A, Mirhosseini M, Alirezaei R. Economic energy supply using renewable sources such as solar and wind in hard-to-reach areas of Iran with two different geographical locations. Energy Strategy Rev. 2024;55(1):101494. doi:10.1016/j.esr.2024.101494. [Google Scholar] [CrossRef]

75. Tawn R, Browell J. A review of very short-term wind and solar power forecasting. Renew Sustain Energ Rev. 2022;153(10):111758. doi:10.1016/j.rser.2021.111758. [Google Scholar] [CrossRef]

76. Strielkowski W, Civín L, Tarkhanova E, Tvaronavičienė M, Petrenko Y. Renewable energy in the sustainable development of electrical power sector: a review. Energies. 2021;14(24):8240. doi:10.3390/en14248240. [Google Scholar] [CrossRef]

77. Niu D, Sun L, Yu M, Wang K. Point and interval forecasting of ultra-short-term wind power based on a data-driven method and hybrid deep learning model. Energy. 2022;254(11):124384. doi:10.1016/j.energy.2022.124384. [Google Scholar] [CrossRef]

78. Ahmed SD, Al-Ismail FS, Shafiullah M, Al-Sulaiman FA, El-Amin IM. Grid integration challenges of wind energy: a review. IEEE Access. 2020;8:10857–78. doi:10.1109/ACCESS.2020.2964896. [Google Scholar] [CrossRef]

79. Song J, Zhang Z, Mu Y, Wang X, Chen H, Pan Q, et al. Enhancing envrionmental sustainability via interval optimization for low-carbon economic dispatch in renewable energy power systems: leveraging the flexible cooperation of wind energy and carbon capture power plants. J Clean Prod. 2024;442(5):140937. doi:10.1016/j.jclepro.2024.140937. [Google Scholar] [CrossRef]

80. He L, Lu Z, Zhang J, Geng L, Cai Y, Li X. Economic dispatch of multi-area integrated electricity and natural gas systems considering emission and hourly spinning reserve constraints. Int J Electr Power & Energy Syst. 2021;132(2):107177. doi:10.1016/j.ijepes.2021.107177. [Google Scholar] [CrossRef]

81. Li Z, Ma T. Peer-to-peer electricity trading in grid-connected residential communities with household distributed photovoltaic. Appl Energy. 2020;278:115670. doi:10.1016/j.apenergy.2020.115670. [Google Scholar] [CrossRef]

82. Fernández-Guillamón A, Martínez-Lucas G, Molina-García Á, Sarasua JI. An adaptive control scheme for variable speed wind turbines providing frequency regulation in isolated power systems with thermal generation. Energies. 2020;13(13):3369. doi:10.3390/en13133369. [Google Scholar] [CrossRef]

83. Zhu J, Dong H, Zheng W, Li S, Huang Y, Xi L. Review and prospect of data-driven techniques for load forecasting in integrated energy systems. Appl Energy. 2022;321(3):119269. doi:10.1016/j.apenergy.2022.119269. [Google Scholar] [CrossRef]

84. Thirunavukkarasu M, Sawle Y, Lala H. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renew Sustain Energ Rev. 2023;176(26):113192. doi:10.1016/j.rser.2023.113192. [Google Scholar] [CrossRef]

85. Ma Y, Xie K, Zhao Y, Yang H, Zhang D. Bi-objective layout optimization for multiple wind farms considering sequential fluctuation of wind power using uniform design. CSEE J Power Energy Syst. 2021;8(6):1623–35. doi:10.31035/cg2021083. [Google Scholar] [CrossRef]

86. Filom S, Radfar S, Panahi R, Amini E, Neshat M. Exploring wind energy potential as a driver of sustainable development in the southern coasts of iran: the importance of wind speed statistical distribution model. Sustainability. 2021;13(14):7702. doi:10.3390/su13147702. [Google Scholar] [CrossRef]

87. Piotrowski P, Rutyna I, Baczyński D, Kopyt M. Evaluation metrics for wind power forecasts: a comprehensive review and statistical analysis of errors. Energies. 2022;15(24):9657. doi:10.3390/en15249657. [Google Scholar] [CrossRef]

88. Li J, Zhou J, Chen B. Review of wind power scenario generation methods for optimal operation of renewable energy systems. Appl Energy. 2020;280(1):115992. doi:10.1016/j.apenergy.2020.115992. [Google Scholar] [CrossRef]

89. Kropp I, Nejadhashemi AP, Deb K. Benefits of sparse population sampling in multi-objective evolutionary computing for large-scale sparse optimization problems. Swarm Evol Comput. 2022;69(3):101025. doi:10.1016/j.swevo.2021.101025. [Google Scholar] [CrossRef]

90. Mandi J. Towards scalable decision-focused learning for combinatorial optimization problems.Brussel: Vrije Universiteit Brussel; 2023. [Google Scholar]

91. SS VC, A HS. Nature inspired meta heuristic algorithms for optimization problems. Computing. 2022;104(2):251–69. doi:10.1007/s00607-021-00955-5. [Google Scholar] [CrossRef]

92. Qu Z. Advancing discretization methods for fluid simulation.Philadelphia:University of Pennsylvania; 2024. [Google Scholar]

93. Bernal Neira D. Modern computational approaches to nonlinear discrete optimization and applications in process systems engineering. Pittsburgh:Carnegie Mellon University; 2021. [Google Scholar]

94. Verma S, Pant M, Snasel V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access. 2021;9:57757–91. doi:10.1109/ACCESS.2021.3070634. [Google Scholar] [CrossRef]

95. Khalil MIK, Rahman IU, Zakarya M, Zia A, Khan AA, Qazani MRC, et al. A multi-objective optimisation approach with improved pareto-optimal solutions to enhance economic and environmental dispatch in power systems. Sci Rep. 2024;14(1):13418. doi:10.1038/s41598-024-62904-4. [Google Scholar] [PubMed] [CrossRef]

96. Mohamed AK, Hadi AA, Mohamed AWeditors. Generalized adaptive differential evolution algorithm for solving CEC, 2020 benchmark problems. In: 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES); 2020;Piscataway: IEEE. [Google Scholar]

97. Juan AA, Keenan P, Martí R, McGarraghy S, Panadero J, Carroll P, et al. A review of the role of heuristics in stochastic optimisation: from metaheuristics to learnheuristics. Ann Oper Res. 2023;320(2):831–61. doi:10.1007/s10479-021-04142-9. [Google Scholar] [CrossRef]

98. Khan MA, Khan J, Alghamdi AA, Saidan SMAB. Image encryption enabling chaotic ergodicity with logistic and sine map. Int J Adv Comput Sci Appl. 2021;12(7). doi:10.14569/issn.2156-5570. [Google Scholar] [CrossRef]

99. Pereira JLJ, Oliver GA, Francisco MB, Cunha SSJr, Gomes GF. A review of multi-objective optimization: methods and algorithms in mechanical engineering problems. Arch Comput Methods Eng. 2022;29(4):2285–308. doi:10.1007/s11831-021-09663-x. [Google Scholar] [CrossRef]

100. Yang Z, Qiu H, Gao L, Chen L, Cai X. Constraint boundary pursuing-based surrogate-assisted differential evolution for expensive optimization problems with mixed constraints. Struct Multidiscipl Optim. 2023;66(2):40. doi:10.1007/s00158-022-03473-w. [Google Scholar] [CrossRef]

101. Zhang X, Huang W, Chen S, Xie D, Liu D, Ma G. Grid-source coordinated dispatching based on heterogeneous energy hybrid power generation. Energy. 2020;205:117908. doi:10.1016/j.energy.2020.117908. [Google Scholar] [CrossRef]

102. Anvari S, Mahian O, Solomin E, Wongwises S, Desideri U. Multi-objective optimization of a proposed multi-generation cycle based on Pareto diagrams: performance improvement, cost reduction, and CO2 emissions. Sustain Energy Technol Assess. 2021;45(4):101197. doi:10.1016/j.seta.2021.101197. [Google Scholar] [CrossRef]

103. Olujobi OJ, Okorie UE, Olarinde ES, Aina-Pelemo AD. Legal responses to energy security and sustainability in Nigeria’s power sector amidst fossil fuel disruptions and low carbon energy transition. Heliyon. 2023;9(7):e17912. doi:10.1016/j.heliyon.2023.e17912. [Google Scholar] [PubMed] [CrossRef]

104. Al-Bahrani L, Seyedmahmoudian M, Horan B, Stojcevski A. Solving the real power limitations in the dynamic economic dispatch of large-scale thermal power units under the effects of valve-point loading and ramp-rate limitations. Sustainability. 2021;13(3):1274. doi:10.3390/su13031274. [Google Scholar] [CrossRef]

105. Xu W, Hu Y, Luo W, Wang L, Wu R. A multi-objective scheduling method for distributed and flexible job shop based on hybrid genetic algorithm and tabu search considering operation outsourcing and carbon emission. Comput Indust Eng. 2021;157(4):107318. doi:10.1016/j.cie.2021.107318. [Google Scholar] [CrossRef]

106. Zou Y, Zhao J, Ding D, Miao F, Sobhani B. Solving dynamic economic and emission dispatch in power system integrated electric vehicle and wind turbine using multi-objective virus colony search algorithm. Sustain Cities Soc. 2021;67(2):102722. doi:10.1016/j.scs.2021.102722. [Google Scholar] [CrossRef]

107. Biswas S, Belamkar P, Sarma D, Tirkolaee EB, Bera UK. A multi-objective optimization approach for resource allocation and transportation planning in institutional quarantine centres. Ann Oper Res. 2024;4(4):1–45. doi:10.1007/s10479-024-06072-8. [Google Scholar] [CrossRef]

108. Çoşut M, Bekdaş G, Nigdeli SM. Optimization of reinforced concrete beam using hybrid algorithms with multi-objective function as CO2 emission and cost. Challenge J Concr Res Lett. 2023;14(4):96. doi:10.20528/cjcrl.2023.04.001. [Google Scholar] [CrossRef]

109. Bairooz JJ, Mardukhi F. An innovative enhanced JAYA algorithm for the optimization of continuous and discrete problems. Algorithms. 2024;17(11):472. doi:10.3390/a17110472. [Google Scholar] [CrossRef]

110. Sun B, Li W, Huang Yeditors. Performance of composite PPSO on single objective bound constrained numerical optimization problems of CEC 2022. In: 2022 IEEE Congress on Evolutionary Computation (CEC); 2022; Piscataway:IEEE. [Google Scholar]

111. Fu Y, Liu D, Chen J, He L. Secretary bird optimization algorithm: a new metaheuristic for solving global optimization problems. Artif Intell Rev. 2024;57(5):1–102. doi:10.1007/s10462-024-10729-y. [Google Scholar] [CrossRef]

112. Hashim FA, Mostafa RR, Khurma RA, Qaddoura R, Castillo PA. A new approach for solving global optimization and engineering problems based on modified sea horse optimizer. J Comput Des Eng. 2024;11(1):73–98. doi:10.1093/jcde/qwae001. [Google Scholar] [CrossRef]

113. Suganthan PN, Hansen N, Liang JJ, Deb K, Chen Y-P, Auger A, et al. Problem definitions and evaluation criteria for the CEC, 2005 special session on real-parameter optimization. In: KanGAL report; 2005. [Google Scholar]

114. Arsali MH. Power system modeling and optimization methods vis-a-vis integrated resource planning (IRP). Boca Raton: Florida Atlantic University; 1998. [Google Scholar]

115. L X, Wang Weditors. Research on large-scale multi-objective optimization algorithm with irregular frontier for operation dispatching of new generation energy system integration. In: 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2); 2020;Piscataway: IEEE. [Google Scholar]

116. Xiong G, Zhang J, Shi D, Zhu L, Yuan X. Optimal identification of solid oxide fuel cell parameters using a competitive hybrid differential evolution and Jaya algorithm. Int J Hydrogen Energy. 2021;46(9):6720–33. doi:10.1016/j.ijhydene.2020.11.119. [Google Scholar] [CrossRef]