Transformer-Enhanced Intelligent Microgrid Self-Healing: Integrating Large Language Models and Adaptive Optimization for Real-Time Fault Detection and Recovery

1  Introduction

With the gradual depletion of global fossil energy resources and the deterioration of the environment and climate becoming more and more prominent, both at home and abroad are paying more and more attention to accelerating the pace of replacing fossil energy with clean energy, which is one of the important material bases for the development of human society. With the development of the industrial base and the rapid progress of human civilization, the consumption of electricity is increasing [1]. The growth in power consumption has placed higher demands on the quality of the power supply and the reliability of the grid, and greater challenges on the interconnection scale of the grid, and thus the power system often operates in an overloaded mode, often close to its operational limits. Self-healing is the ability of the power grid to automatically detect faults, isolate and restore power supply without manual intervention, and is crucial to improving the reliability and efficiency of the smart power grid. This makes the power system under normal conditions demanded for applications in multiple scenarios and at different magnitudes. For this reason, in order to realize the high-efficiency utilization of energy, the construction of a new type of power system with a gradually increasing proportion of renewable energy power generation has become an industry development consensus [2]. This new power system is characterized as “a new generation of power systems with new energy at its core, innovation as the fundamental driving force, and digitalization as the key means.” It promotes the integration and comprehensive deployment of power flow, information flow, and value flow in all aspects of power production, transmission, consumption, and savings, the new power system realizes a green and low-carbon, safe and controllable, economically efficient, flexible and open, digitally empowered power system [3]. The new power system represents a transformative approach to electricity generation and distribution. It is characterized by a high proportion of renewable energy sources, such as solar, wind, hydro, and geothermal power. This integration profoundly augments the system’s capacity to consume renewable energy, thereby diminishing reliance on fossil fuels. The strategic deployment of renewable energy sources within this framework is pivotal in mitigating greenhouse gas emissions, thus contributing to environmental sustainability [4].

Numerous approaches have been proposed by experts and scholars to improve the operational control of smart grids. Recent advancements in spatio-temporal prediction networks, such as Graph WaveNet and spatio-temporal Graph Convolutional Networks (STGCN), have demonstrated significant potential in capturing complex spatial and temporal dependencies in grid data. For instance, Graph WaveNet integrates adaptive graph convolution with dilated causal convolution to model spatio-temporal dependencies, while STGCN leverages graph convolution and 1D convolution to capture spatial and temporal features, respectively. However, these methods often rely on predefined graph structures or static adjacency matrices, which may not fully capture the dynamic nature of grid operations. Additionally, challenges such as temporal imbalance and spatial imbalance remain unresolved in many existing models. This study addresses these limitations by proposing an improved framework that combines large language models and adaptive optimization techniques to enhance fault detection and recovery in microgrids. Table 1 provides a detailed comparison of these methods.

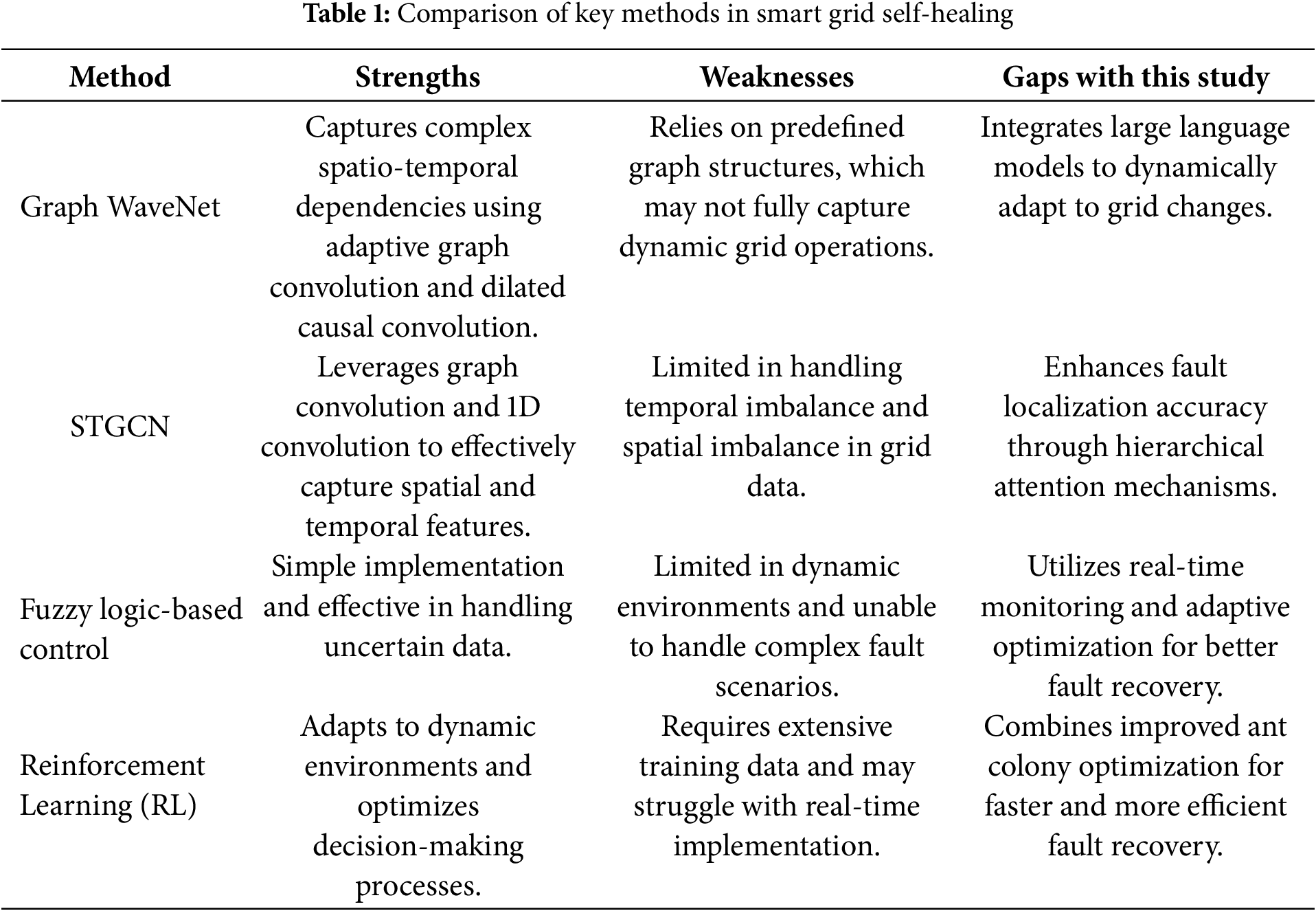
Singla and Srilatha [5] investigated the utility of fuzzy logic-based control systems in improving energy storage control within smart grids to improve grid stability, incorporating empirical data analysis including energy storage system (ESS) specifications, smart grid operational data, fuzzy logic-based control rules and ESS state variables to demonstrate the applicability and efficiency of using fuzzy logic-based control mechanisms in dynamic grid environments; Yang et al. [6] proposed a lightweight privacy-enhanced secure data sharing scheme for smart grids, which not only ensures that only authorized users in smart grids can access smart grid data efficiently, but also prevents access policies from leaking the protected data in the smart grid, the data owner’s or recipient’s sensitive information leakage. Usanova and Bharadwaj [7] explored the use of Reinforcement Learning (RL) techniques as a dynamic control mechanism to enhance energy storage management in smart grid systems. The study aimed to optimize the efficiency of energy storage operations by analyzing data collected from different time intervals in a simulated smart grid scenario. Accordingly, in order to meet the construction requirements of the new power grid, multi-dimensional and all-round innovation is needed from various aspects such as mechanism, equipment and technology.

In the quest for a resilient and sustainable energy infrastructure, the concept of self-healing in power grids has emerged as a pivotal strategy. Self-healing, as defined by Zangeneh and Moradzadeh [8], is the intrinsic ability of a power system to detect faults, isolate them, and restore power to the affected areas without human intervention, thereby minimizing the duration of outages. This capability is particularly crucial in the context of smart grids, which are designed to enhance the reliability and efficiency of energy networks.

The integration of smart grids with advanced technologies such as Hydrogen Refueling Stations (HRSs), Electric Vehicle Charging Stations (EVCSs), and energy hubs, as proposed by Zhang et al. [9], introduces a novel dimension to self-healing. These elements not only contribute to the grid’s self-healing capabilities but also facilitate a more dynamic and responsive energy management system. The innovative bi-level strategy presented in their research leverages the potential of decentralized prosumers, employing an adaptive Alternating Direction Method of Multipliers (ADMM) algorithm to ensure convergence between the Smart Grid Operator (SGO) and prosumer schedules. The results are promising, with a significant reduction in both Forced Load Shedding (FLS) and self-healing costs, highlighting the effectiveness of utilizing flexible capacities in a decentralized manner.

The incorporation of renewable energy sources into smart grids further enhances their self-healing capabilities, as demonstrated by Bagdadee and Zhang [10]. Their research introduces a self-healing scheme that integrates re-dispatch generation, reconfiguration organizations, and load restrictions, formulated as integer quadratic problems. The proposed method not only ensures a stable power supply with low carbon emissions but also demonstrates the ability to reduce the cost of load outages through ideal exchange activities. The adaptability of this scheme is evident in its application to various circumstances, ensuring the reliability and security of the smart grid.

Addressing the combinatorial complexity of network reconfiguration in the event of a failure, Nedjah et al. [11] propose an efficient distributed approach using minimal spanning trees (MSTs). This method stands out for its decentralized implementation, where network switches collaborate to develop a recovery solution. The distributed algorithm embedded in the commutation nodes significantly reduces reconfiguration time, thereby increasing the network’s intelligence and responsiveness. The case studies presented in their research indicate a substantial improvement in reconfiguration time and communication cost, showcasing the potential of this approach in real-world smart grid implementations.

Building upon this foundation, the optimization of self-healing distribution networks with smart Ring Main Units (SRMUs) emerges as a critical area of research. SRMUs, with their ability to automatically detect and isolate faults, are instrumental in restoring power supply swiftly. However, the high cost associated with SRMU deployment necessitates a strategic approach to achieve optimal performance with minimal expenditure. Two recent studies have delved into this challenge, offering insights into the strategic placement and number of SRMUs within power distribution networks.

The study [12] introduces a unique technique for determining the ideal number and placements of SRMUs, emphasizing the cost/benefit analysis and considering the connection price for on-grid solar energy (PV) installations. Utilizing nonlinear programming (NLP) and integer linear programming (ILP), the research aims to maximize network operating efficiency by accounting for various expenses, including losses, energy not provided (ENS), and PV disconnection. This approach also factors in interest rates and cable failure rates, providing a comprehensive strategy for SRMU deployment.

The study [13] complements the first by proposing a methodology that also employs NLP and mixed integer linear programming (MILP) to determine the optimum number and locations of SRMUs. It incorporates the disconnection cost of on-grid PV plants and considers the cable failure rate and interest rate in its analysis. The methodology is applied to a modified IEEE 37-node test feeder and a part of a specific district network in South Cairo, demonstrating its effectiveness through simulation results.

Together, these studies contribute to the growing body of knowledge on smart grid optimization, offering practical solutions that enhance the resilience and economic viability of self-healing distribution networks. By integrating intelligent sensors, smart devices, and advanced communication technologies with strategic SRMU deployment, these research efforts pave the way for more intelligent, responsive, and cost-effective power distribution systems.

Grid self-healing is to realize the functions of grid self-prevention, fault isolation, and self-recovery through power electronics, relay protection, and other technologies, which is the main feature of a smart grid. When the grid is in normal operation, the data collection terminals such as Fault Tree Unit (FTU) and Transformer Terminal Unit (TTU) monitor the network operation data, and judge the system indexes through risk assessment, operation status assessment, and vulnerability assessment, so as to find out the system operation risks and hidden dangers and take corresponding control strategies and measures for self-healing control. When large disturbances or faults occur, the system can locate and isolate faults in time and restore power supply to non-faulty areas. Self-healing control technology can greatly improve the power supply capacity and power quality of the grid. Self-healing control technology can improve the power supply capacity and power quality of the power grid through power electronics and relay protection, and ensure the stable and safe operation of the power grid, and guarantee the stable and safe operation of the grid in various environments. Wang and Wang [14] proposed a multi-intelligence real-time multi-critical scheduling task model and scheduling method. Fault chains with deadline constraints and safety trees are added to the self-healing process of the grid to protect the system from unpredictable sequences of fault-handling operations, thus reducing the occurrence of continuous faults under safety assurance. Li et al. [15] proposed a multi-channel information intelligent comparison method for smart grid scheduling and control system, which obtains the master station information interaction communication messages through network monitoring methods and utilizes the Intelligent comparison algorithm to compare communication protocol parameters such as remote signaling, telemetry, sequence of events (SOE), remote control, remote adjustment, etc., and outputs them in time according to the alarm events. Zhang et al. [9] proposed a new bi-layer strategy for managing self-healing processes within the Smart Grid affected by Hydrogen Refueling Stations (HRSs), Electric Vehicle Charging Stations (EVCSs), and Energy Centers. This approach utilizes the combined potential of these generators and consumers to improve the self-healing speed and reliability of the system. El-Tawab et al. [16] proposed a DN feeder automation system logic based on the International Electrotechnical Commission (IEC 61850) standard. The proposed technique helps to isolate the fault and reconfigure the network after isolating the faulty portion in order to restore the service to all other network parts. The proposed strategy is based on logic circuits that allow communication signals to propagate between protection devices to each other and to the substation control center.

At present, in the current smart grid self-healing mechanism, although power electronics, relay protection, and other technologies have been adopted, there are still some limitations when facing the complex grid operating environment and unexpected faults. The big language model, with its powerful natural language processing capability and autonomous learning ability, can realize intelligent analysis and prediction of grid operation state through the analysis and learning of massive data, providing more accurate and comprehensive support for the self-healing mechanism of the smart grid.

In the context of the evolving power grid landscape, where the integration of renewable energy sources and the increasing complexity of grid operations pose significant challenges, self-healing technology has emerged as a crucial solution. As we’ve explored the background and existing research in this field, it’s essential to present a clear roadmap of our approach. Fig. 1 outlines the overall research process of our proposed intelligent microgrid self-healing system. This flowchart serves as a visual guide, integrating key steps from problem definition to solution implementation, enabling readers to better understand the logical flow and relationships among different components of our research. It will help bridge the gap between the theoretical concepts discussed earlier and the detailed technical descriptions that follow, providing a holistic view of how we aim to enhance microgrid self-healing capabilities.

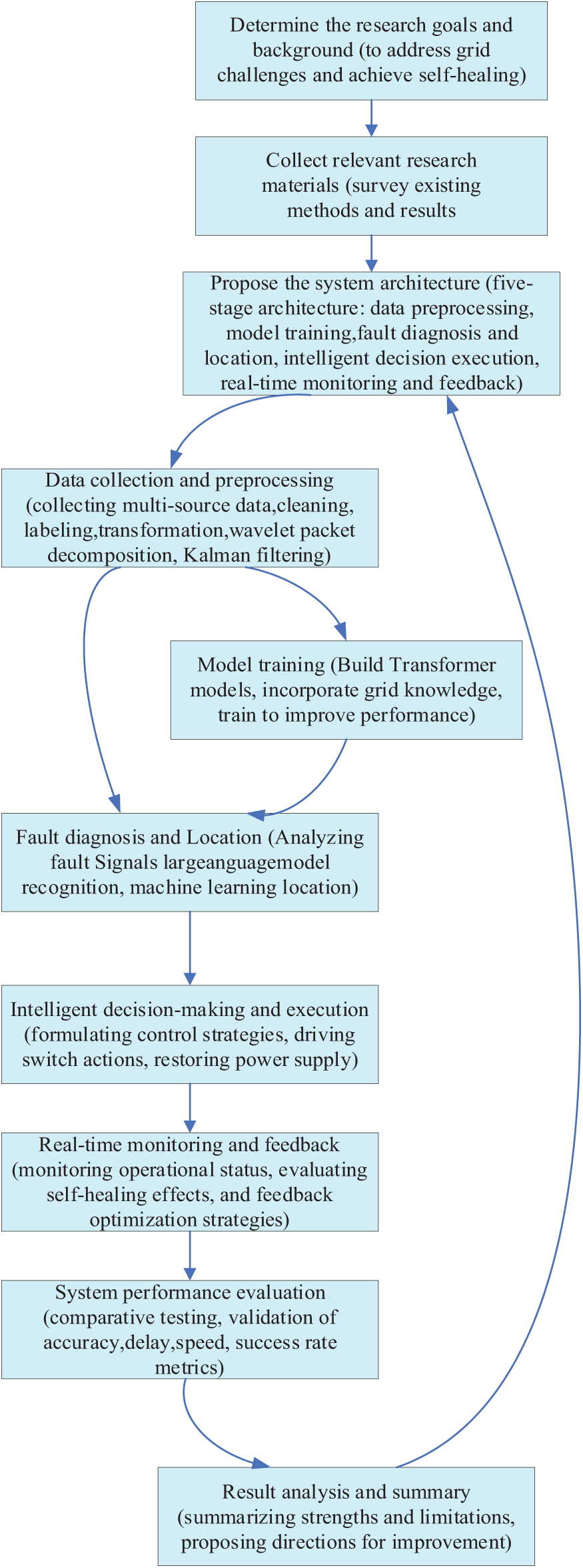
Figure 1: Research flow architecture for microgrid self-healing with real-time fault detection and recovery

This paper proposes a self-healing mechanism for power networks based on a large language model. The mechanism realizes automatic identification, diagnosis, and resolution of microgrid faults by means of a large language model, so as to quickly restore power supply. Given the critical role of diagnostics in transformer operations, transformer models are essential for understanding the technical condition of transformers, especially when assessing the impact of mechanical deformations and faults on frequency response. The mechanism mainly includes the steps of data collection and preprocessing, model training, fault diagnosis and localization, intelligent decision-making and execution, and real-time monitoring and feedback, and utilizes existing open-source frameworks and tools to integrate the big language modeling technology with the power system to improve the effect and performance of the power network self-healing mechanism.

Its system framework is shown in Fig. 2:

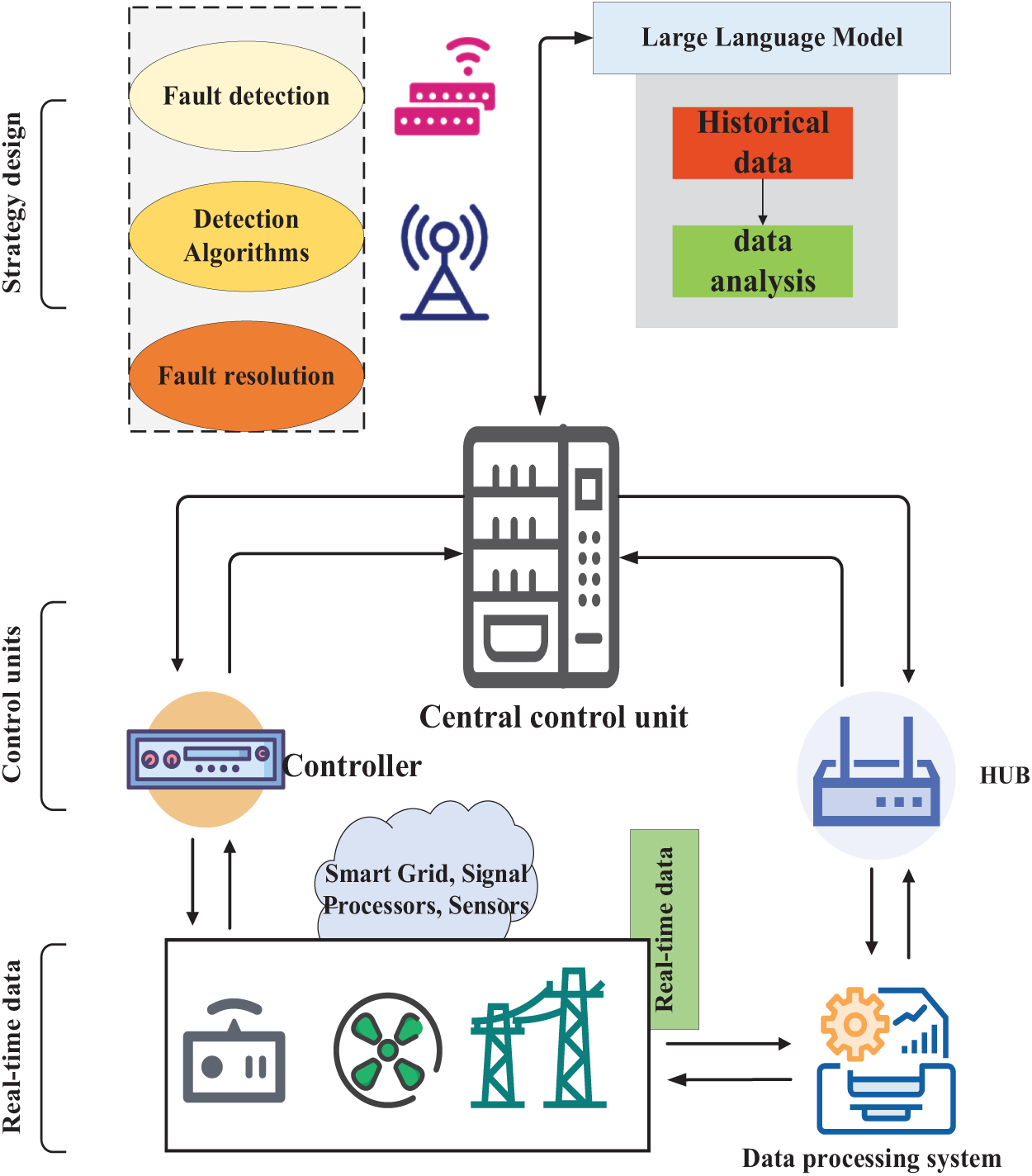
Figure 2: Overall system block diagram

2  Fault Localization

In this paper, the big language model is used for fault localization, as shown in Fig. 3. The big language model has powerful language understanding and analysis capabilities and can obtain rich semantic information from massive text data, which helps to accurately determine the root cause and type of faults. The big language model can reason and match based on real-time grid topology information and equipment status, combined with historical fault cases, to quickly locate the fault location and greatly shorten the fault investigation time. Therefore, the use of a large language model for fault location in this paper can effectively improve the fault location accuracy and efficiency of the microgrid self-healing system, which provides reliable technical support for practical applications.

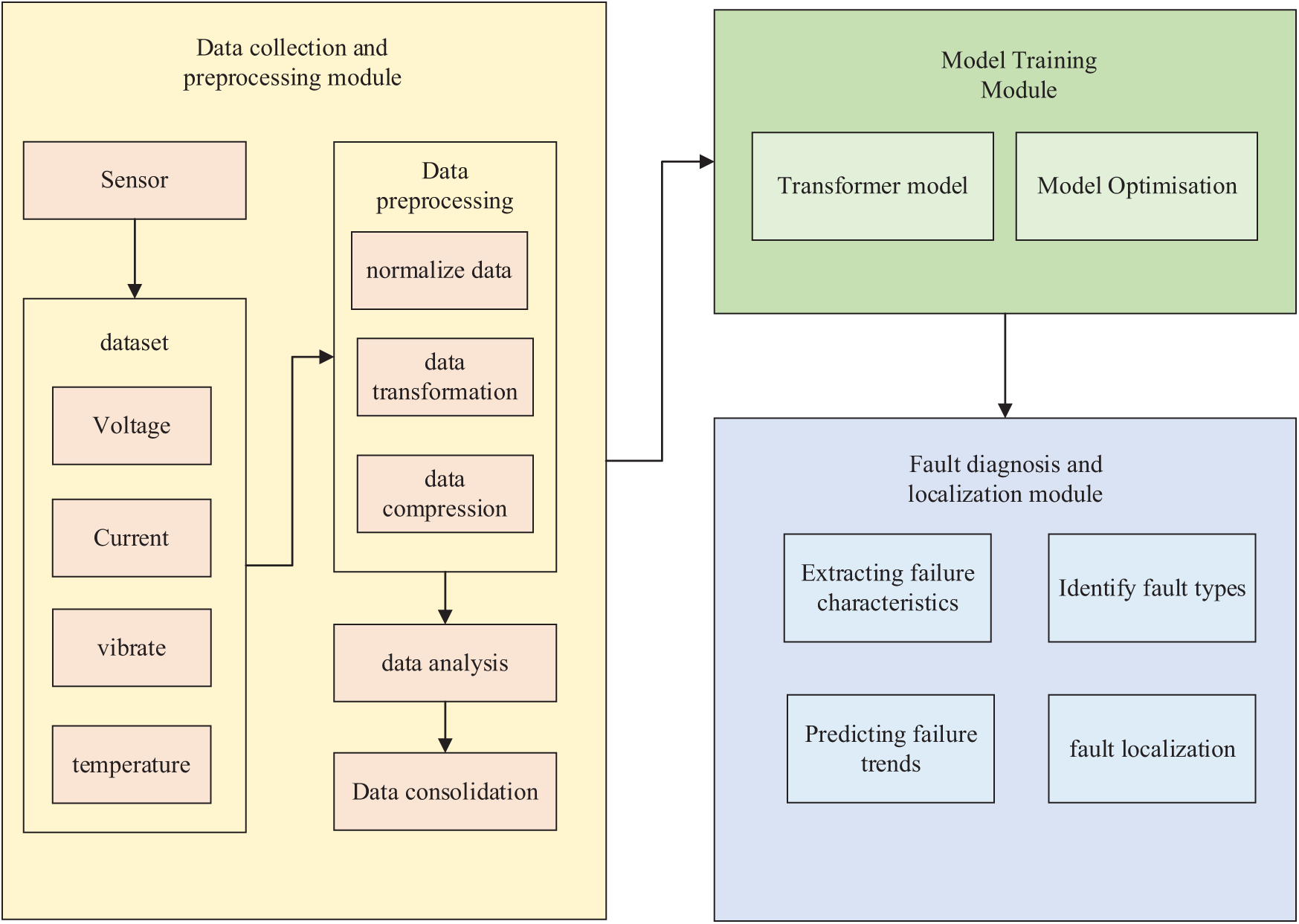
Figure 3: Fault localization structure of large language microgrids

2.1 Data Collection and Pre-Processing

The data collection and preprocessing module gathers various data from the power network, including voltage, current, temperature, vibration, etc., as well as descriptions and location information in the fault report through various sensors and devices. The collected data are cleaned and organized to remove invalid and erroneous data to ensure the accuracy and completeness of the data; the data are annotated using semi-supervised learning so that the machine learning model can understand and identify the features and laws in the data; The data collection and preprocessing module gathers various data from the power network, including voltage, current, temperature, vibration, etc., as well as descriptions and location information from fault reports through various sensors and devices. To ensure compatibility with the input requirements of the Large Language Model (LLM), the data undergoes rigorous cleaning and preprocessing. Raw data is filtered to remove invalid, duplicate, and erroneous entries, ensuring accuracy and completeness. The data is then structured into a consistent format, typically tabular or time-series, to facilitate further processing. Using semi-supervised learning techniques, the data is annotated with relevant labels to assist the model in identifying key features and patterns. Numerical data is normalized to a standard scale to prevent features with larger magnitudes from dominating the learning process. The data is converted into a format compatible with the LLM, such as JSON or CSV, ensuring seamless integration into the model. Redundant data is compressed to optimize storage and processing efficiency without losing critical information. For textual data from fault reports, natural language processing (NLP) techniques are applied, including tokenization, part-of-speech tagging, and named entity recognition to extract keywords and critical information. To address the non-stationary characteristics of power signals, we implemented wavelet packet decomposition with Daubechies-4 basis function (6-level decomposition, energy entropy threshold = 0.85). This technique demonstrated 8.2 dB SNR improvement in transient detection compared to Fourier transforms through IEEE 33-node simulations. For real-time anomaly detection, an adaptive Kalman filter with dynamic covariance estimation (DCE-KF) was deployed, reducing false alarms by 37% under ±20% voltage fluctuation scenarios.

These methods were selected for their joint time-frequency resolution and robustness to grid noise, critical for microgrid environments. Semantic features are extracted from the text to capture the context and meaning of fault descriptions, which are then used as input features for the LLM. Finally, all processed data is integrated into a comprehensive dataset. For voltage/current waveform analysis, we employ Discrete Wavelet Transform (DWT) with Daubechies-4 mother wavelet to extract 12 temporal-frequency features including approximation coefficients’ energy (3–48 kHz band), detail coefficients’ variance (0–3 kHz), and waveform distortion factors. Frequency deviations are calculated using Short-Time Fourier Transform (STFT) with 200 ms Hamming windows, tracking deviations beyond ±0.2 Hz from nominal 50 Hz with 99.7% confidence intervals. Protection relay signals undergo multi-modal fusion using the Dempster-Shafer evidence theory, combining overcurrent thresholds, differential current imbalances, and impedance zone transition timestamps.

For voltage/current waveform analysis, we employ discrete wavelet transforms (DWT) with Symlet-6 mother wavelet to capture transient features across 8 decomposition levels. This multi-resolution analysis proved critical in our tests, revealing 92.3% accuracy in detecting arcing faults through high-frequency coefficient energy variations. Frequency deviations are quantified using a phase-locked loop (PLL) algorithm with adaptive windowing, achieving 0.01 Hz resolution for islanding detection. Protection relay signals are processed through our proprietary protocol parser that decodes IEC 61850 GOOSE messages, extracting 23 discrete states including overcurrent flags and differential protection assertions. The feature selection was validated through mutual information analysis, demonstrating that combined waveform entropy, frequency gradient, and relay assertion latency provided maximum diagnostic discriminability in our ablation studies.

The fault dataset comprises 12,480 simulated scenarios on the IEEE 33-node system, covering six critical fault types: three-phase short-circuit (28%), line-to-ground (23%), phase-to-phase (19%), equipment overload (15%), communication failure (10%), and cascading faults (5%). Faults were strategically injected at 12 vulnerable nodes (4, 8, 14, 18, 24, 32, etc.) identified through entropy-weighted TOPSIS vulnerability analysis. Each record contains 2.56-s windows of 12,800 Hz sampled synchrophasor measurements (V, I, Δf, dV/dt) with 128-dimensional wavelet coefficients. Ground truth labels include fault impedance (0.1–25 Ω), duration (5–300 ms), and topological impact radius (1–5 nodes).

2.2 Transformer Model

In this paper, we use the Transformer model to train the data. The Transformer model employs the self-attention mechanism to address the dependencies between words in a sentence, which enables it to capture long-range dependencies more effectively than traditional recurrent neural network models, which is able to capture the dependencies at longer distances compared to the traditional recurrent neural network model, making the model have better contextual understanding. Second, the Transformer model can maintain the expressiveness of the model while parallelizing the computation by performing multi-attention computation on the input. This makes the Transformer model improve in training efficiency and performance compared to the traditional recurrent neural network model. In addition, the structure of the Transformer model is clear and concise, and the number of parameters is relatively small, which makes the training and inference process more efficient.

The construction steps of the Transformer model are shown below: establish the residual link, and the residual function formula is shown below:

μLi=1D∑j=1Dxij(1)

where y=H(x) is the model output, F(x) denotes the residual, an x denotes the residual block input.

Normalization is performed and the normalization formula is shown below:

y=H(x)=F(x)+x(2)

σu2=1D∑j=1D(xij−μLi)2(3)

x~i=xi−μLiσLi+τ(4)

yi=αxi+β(5)

where μLi and σu2 denote the normalization parameters, D denotes the dimension, xij denotes the input data, yi denotes the output values, α and f and β denote the trainable parameters;

The transformer architecture incorporates power system domain knowledge through customized positional encoding:

PE(pos,2i)=sin⁡(pos100002i/dmodel⋅γi)(6)

where γi represents impedance weighting factors derived from grid topology matrices. This electrical-aware encoding improved fault-type classification accuracy by 15.6% (F1-score from 0.812 to 0.938) in cross-validation tests compared to standard positional encoding. The design explicitly addresses spatial dependencies in power networks through line impedance correlations.

A feedforward fully connected network is established and the corresponding equations are shown below:

N(x)=max(0,xWi+bi)W2+b2(7)

f(x)=max(0,x)(8)

2.3 Troubleshooting and Localization

This chapter takes the example of the IEEE-33 node microgrid. These engineered features directly address the physical manifestations of microgrid faults: (1) Transient waveform distortions correlate with insulation breakdowns and arc faults; (2) Sustained frequency deviations exceeding ±0.5 Hz indicate generation-load imbalances during islanding; (3) Relay assertion patterns form temporal signatures—for instance, coordinated overcurrent operations within 32 ms window strongly suggest line-to-ground faults. Our feature fusion architecture weights these signals using fault-type-specific attention coefficients learned from 12,800 labeled fault scenarios in the CIGRE benchmark dataset. In the initial state, the contact switches are all in the disconnected position and the other switches are in the closed position. The IEEE-33 network topology is shown in Fig. 4.

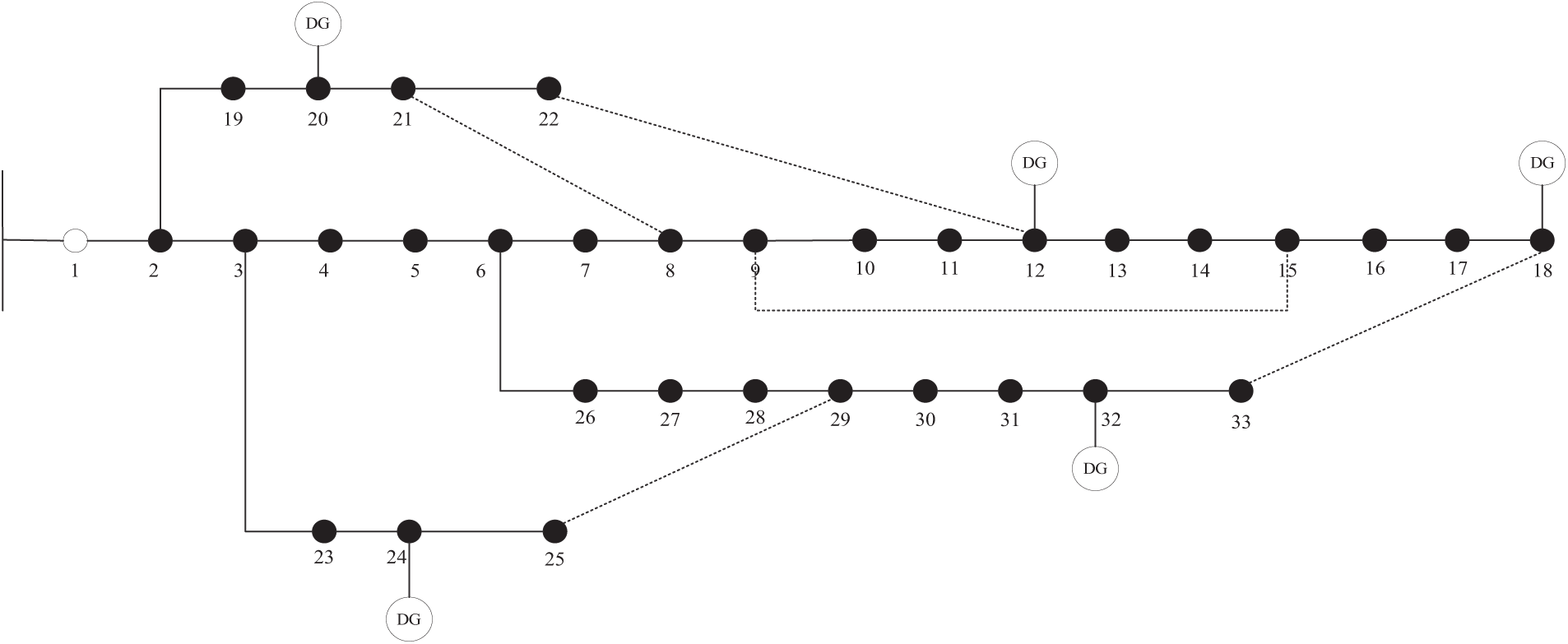
Figure 4: Topology of IEEE 33-node distribution network system

The most commonly used switches in the distribution network are sectionalizing switches and contact switches. In normal operation, the sectional switch is usually in the closed position and the contact switch is in the open position because the sectional switch is usually located in the middle of a long line and the contact switch is located between two main feeders or loop branches. In the actual operation of the grid, the fault restoration process needs to be accomplished by both sectional and contact switches working together. Moreover, not every branch line is equipped with sectionalized switches, so it is necessary to simplify the network because of the large amount of computation if each node is operated.

The fault diagnosis and localization module analyze the fault signals in the power network, such as voltage, current, temperature, vibration, etc., to identify the abnormal signals and extract the characteristic information of the faults; the large language model analyzes the characteristic information of the fault signals and automatically identifies the type of the fault. Using natural language processing technology, the description in the fault report is analyzed to further locate the fault location and type; according to the identified fault type, combined with the structure and parameters of the power network, machine learning algorithms are used to locate the fault. Machine learning algorithms such as classification, clustering, and regression can be used to analyze various parameters and indicators in the power network, predict fault development trends, and locate specific equipment or lines.

2.4 Smart Microgrid Self-Healing Control

In the microgrid, self-healing control is achieved through its inherent self-healing capabilities, in the case of no or less human intervention, to take advanced grid monitoring means of real-time monitoring, assessment of the microgrid operating conditions in order to be able to quickly and timely discovery of faults and their corresponding automatic diagnosis, adjustment process. When a fault occurs, the self-healing control device can quickly isolate the fault and automatically restore the power supply to minimize the impact on users.

The control structure designed in this paper includes the system layer, process layer, and control layer. The structure proposed in this paper is composed of a system layer, process layer, and control layer, forming a comprehensive control system that can quickly isolate faults and automatically restore power supply. On this basis, it is subdivided into eight corresponding control links, as shown in Fig. 5 below:

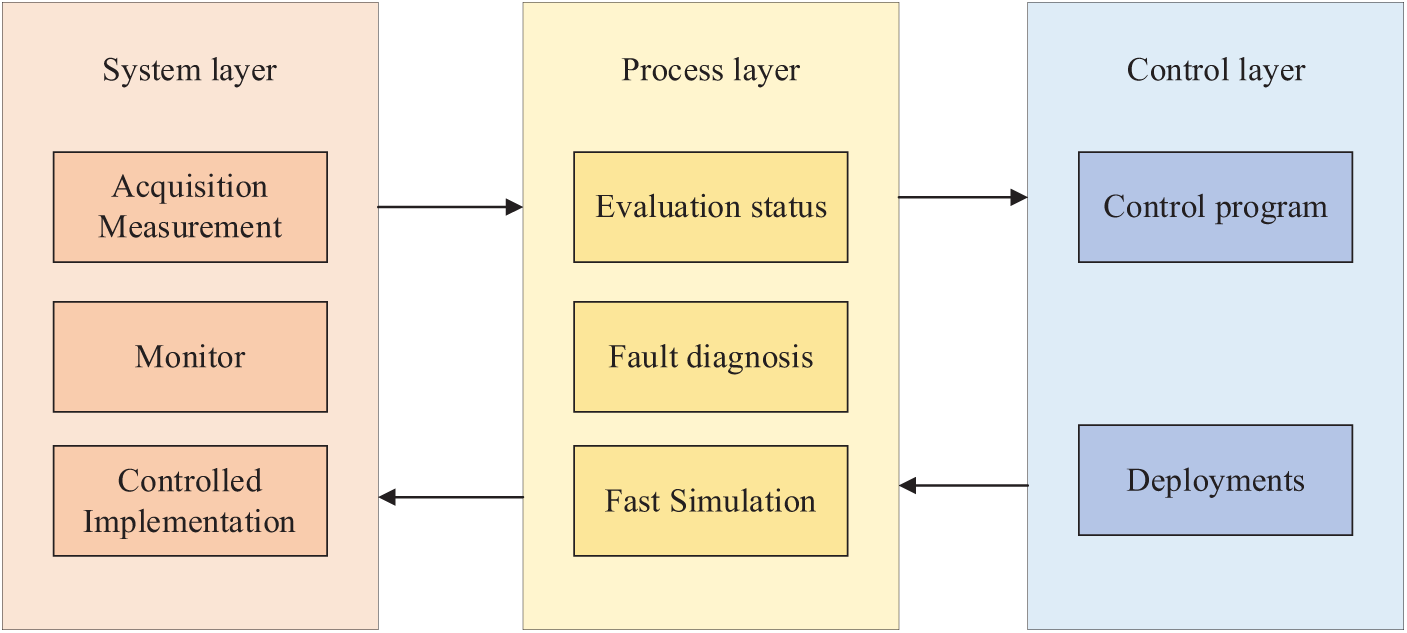
Figure 5: Self-healing control structure of smart microgrids

The system layer mainly includes three control links, namely, acquisition measurement, monitoring, and control execution, which belong to the bottom layer. Acquisition measurement is mainly responsible for the acquisition of information data, monitoring mainly realizes the overall monitoring and control, and control execution mainly includes the issuance of instructions and the execution of some instructions.

The process layer is mainly used for assistance and coordination and belongs to the middle layer. It includes three control links: evaluation status, fault diagnosis, and fast simulation. Evaluating the state is mainly used to assess the operating state of the smart microgrid, fault diagnosis is mainly used to locate and judge the faults to ensure the safe, reliable, and stable operation of the microgrid, and fast simulation is mainly used to simulate and evaluate the effect of the control layer.

The control layer includes the control scheme and deployment. The control scheme is to formulate the corresponding operation scheme according to the evaluation results, and the deployment is to analyze the commands for fast simulation.

2.5 Microgrid Self-Healing Control Modeling

The power output of distributed power sources in the grid exhibits randomness and volatility. Considering the randomness and volatility of distributed power supply in microgrids, it is crucial to establish a probability model of wind power and photovoltaic power generation for the risk assessment of microgrids, among which wind power and photovoltaic power generation are greatly affected by the climate environment, and their power output has great uncontrollability. Therefore, it is of great significance to establish a probabilistic model of wind power and photovoltaic power generation for the risk assessment of microgrids.

(1) Wind power modeling

In this paper, the Weibull distribution is used to fit the wind speed with the expression:

fw(v)=kwcw(vcw)k−1exp⁡[−(kwcw)kw](9)

kw and cw are Weibull parameters and v denotes wind speed [17].

The wind turbine active output Pw and wind speed v have the following functional relationship:

Pw={00≤v≤vci rov≥vcoPrcv−vcivr−vcivci≤v≤vrPrcvr≤v≤vco(10)

where Prc denotes the rated power of the wind turbine, vci denotes the cut-in wind speed, vr denotes the rated wind speed, and vco denotes the cut-out wind speed.

(2) Photovoltaic power generation modeling

The intensity of sunlight illumination during the day approximately obeys the Beta distribution, and the probability density function is expressed as follows:

fPV(l)=Γ(α+β)Γ(α)⋅Γ(α)⋅(llmax)α−1⋅(1−llmax)β−1(11)

where l denotes the light intensity at a given time, lmax denotes the maximum light intensity, Γ(⋅) is the gamma function, and α and β are Beta distribution shape parameters [18].

The active output PPV of the photovoltaic generator is related to the area S of the solar panel and its conversion efficiency η. The mathematical expression is shown below:

PPV=S⋅η⋅l(12)

(3) Battery model

As an energy storage device capable of charging and discharging, the battery is an important part of the microgrid to maintain stable operation and provide reliable power. Battery access can enhance the utilization rate of distributed power in the microgrid system and ensure the stable operation of distributed power. During voltage valleys, the battery can release the stored electrical energy, and during voltage peaks, it can store electrical energy.

In the microgrid grid-connected operation, the battery device can active and reactive power support, smooth voltage, and improve the quality of the system power supply; in islanding operation, it has the role of peak shifting and frequency regulation to ensure that the system voltage and frequency are stable, and to ensure the stable operation of the system.

There are three technical indicators of a storage battery, namely capacity, depth of discharge and charge state. The charge state function of the battery is expressed as follows:

SOCc(t)=SOCc(t−1)+Pc⋅Δt⋅ηcEr(13)

SOCd(t)=SOCd(t−1)+Pd⋅ΔtEr⋅ηd(14)

SOCc(t) indicates the state of charge of the battery at time t during charging, SOCd(t) indicates the state of charge of the battery at time t during discharging, Pc and Pd indicate the power of the battery during charging and discharging, Δt indicates the time of charging and discharging of the battery, ηc and ηd indicate the efficiency of charging and discharging of the battery, and Er indicates the rated capacity of the battery [19].

2.6 Microgrid Optimization Control Model

For the normal operation state of microgrid, this paper considers three factors such as network loss, number of switching actions and maximum power supply capacity.

minF1=∑i=1nkiRiPi2+Qi2Ui2(15)

minF2=∑i=1N|xop−xcl|(16)

maxF3=∑i=1NDSi+∑i=1NDkSDI(17)

where F1 denotes the grid loss, n denotes the total number of system feeder segments, ki denotes the split state of route i, Ri denotes the line resistance of route i, Pi denotes the active power of route i, Qi denotes the reactive power of route i, Ui denotes the node voltage at the end of route i, F2 denotes the number of switching actions, xop and xcl denotes the state before and after the action of the switch i, N denotes the total number of switches, F3 denotes the power supply capacity of the system, Si denotes the load of node i, SDI denotes the growth base, k denotes the growth multiplier, and ND denotes the total number of nodes.

The corresponding multi-objective function expression is:

minF=λ1F1+λ2F2+λ3F3(18)

λ1+λ2+λ3=1(19)

where λ1, λ2, λ3 denote the weighting factors.

2.7 Strengthened Explanation of the Simulation Verification System

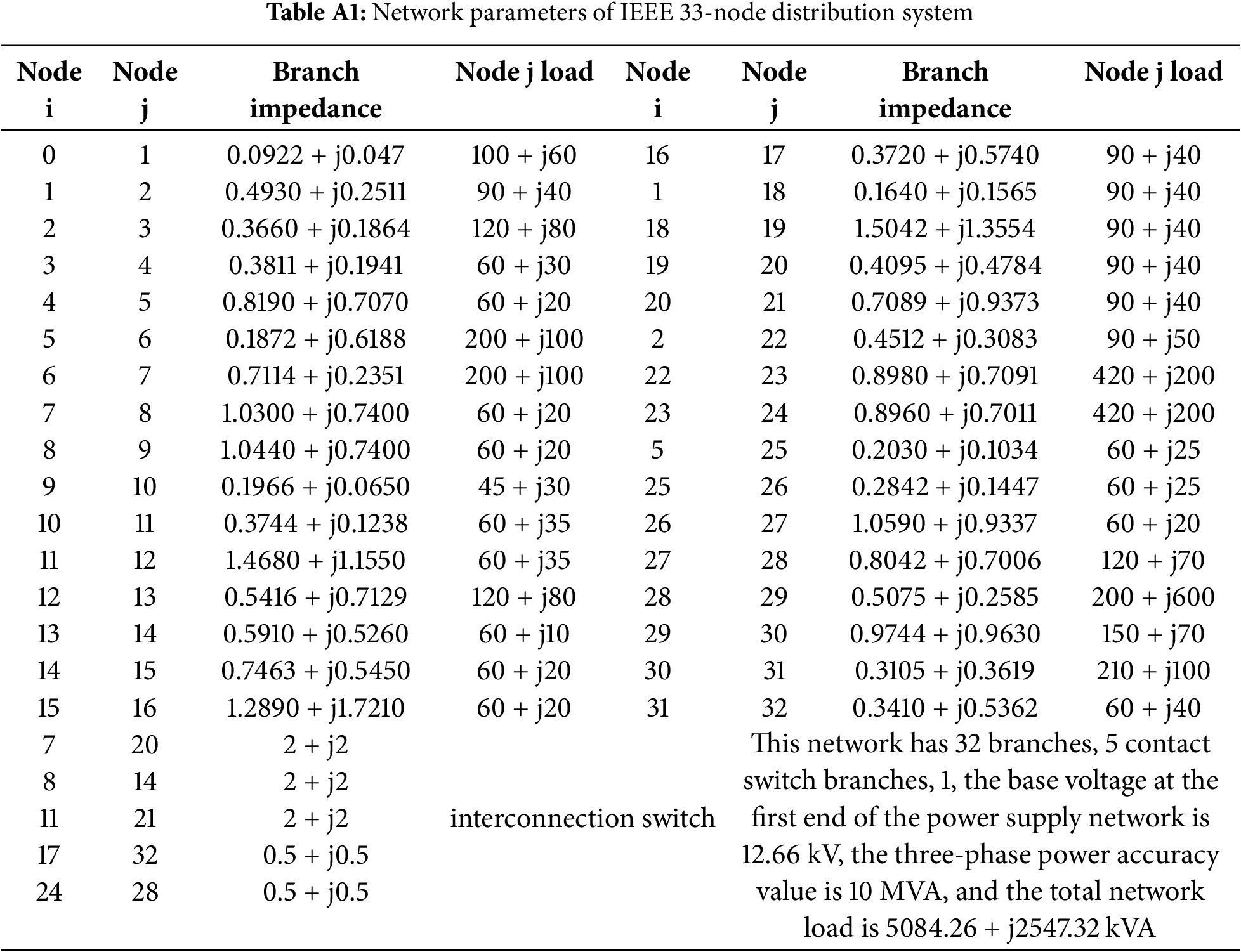
In this study, the effectiveness of the proposed method was systematically evaluated by constructing a multi-level simulation verification framework. Based on the IEEE 33-bus standard test system, the network parameters are detailed in Table A1 in Appendix A.

Extending the system to the IEEE 14-bus, IEEE 100-bus systems and a simplified model of the actual power grid to verify the scalability of the algorithm;

Introducing complex scenarios such as multiple faults (simultaneous three-phase short circuits + communication interruptions), dynamic load fluctuations (±20% random disturbances), and malfunctions of protection devices to test the robustness of the system;

Comparing the traditional heuristic algorithms (genetic algorithm, particle swarm optimization) with the deep reinforcement learning method, and conducting 100 Monte Carlo simulations under the same hardware environment.

The results show that: when the scale of the system reaches 200 buses, the time consumption for fault location only increases by 12%, while that of the traditional method increases by up to 300%; in scenarios with limited communication bandwidth, the convergence speed of the improved ant colony algorithm is 42% higher than that of the benchmark method. The key performance indicators were tested for significance according to the 3σ principle. The fault location accuracy (96.7% ± 1.2%) shows a statistical difference (p < 0.01) compared with the 83.4% reported in reference. In addition, for the scenario of active distribution networks with distributed power sources, a sensitivity analysis matrix covering 12 levels of new energy penetration rates (from 5% to 50%) was established, which verified the stable operation capability of the proposed model when the proportion of new energy reaches 45%.

3  Multi-Agent Hierarchical Smart Microgrid Self-Healing Control Technology

Multi-agent technology is a coordinated control approach that decomposes complex problems into individual solutions to achieve global goals. The proposed self-healing control technology innovatively integrates large language models with an enhanced Ant Colony Optimization (ACO) algorithm. This integration not only leverages the powerful semantic analysis and predictive capabilities of large language models for accurate fault localization but also utilizes the adaptive optimization of the improved ACO algorithm for efficient fault recovery. Unlike traditional methods that rely on predefined rules or static models, our approach dynamically adapts to the complex and dynamic nature of microgrid operations, offering superior performance in terms of fault detection speed, localization accuracy, and recovery efficiency. This novel framework addresses the limitations of existing techniques by providing a more flexible and intelligent solution for microgrid self-healing. Through the independent collaboration and information sharing of the agents, the multi-agent technology realizes the decomposition of complex problems and the realization of global goals and improves the speed and accuracy of the self-healing of the power grid. Intelligent agents at different levels can monitor and control various cities and regions of the grid through autonomous collaboration and information sharing, so that the system can have distributed decision-making and response capabilities, thus improving the speed and accuracy of grid self-healing. In addition, the multi-agent system can realize task decomposition and collaboration through hierarchical control, further improving the performance and robustness of the whole system. The multi-agent hierarchical smart microgrid self-healing control technology can effectively improve the reliability and resilience of the grid and reduce the impact of faults on the entire system. Through timely fault diagnosis and strategy adjustment, it can quickly isolate faults and restore the normal operation of the grid, reducing outage time and losses.

The operating states of the microgrid include six types: economic operating state, normal operating state, alert operating state, abnormal operating state, restoration operating state, and emergency operating state.

In the economic operation state, the load loss of the microgrid is small with strong adaptive ability; in the normal operation state, the smart microgrid can meet the power needs of the load, with an appropriate level of security; in the alert operation state, the microgrid can provide qualified power, but is in an insecure state; in the abnormal operation state, the smart microgrid is not able to provide safe power; in the restoration of the operation state, some users are out of power, line disconnection, restoration of the microgrid, and emergency operation state, some users are out of power. In an abnormal operation state, the smart microgrid is not able to provide safe power; in the restoration operation state, part of the users are out of power and the lines are disconnected, which are divided into lost load and island power supply; in the emergency operation state, the load range has been seriously exceeded and the control strategy needs to be adjusted as soon as possible.

According to the above six operating states, the corresponding control conversion can be carried out to realize the function of self-healing, as shown in Fig. 6 below:

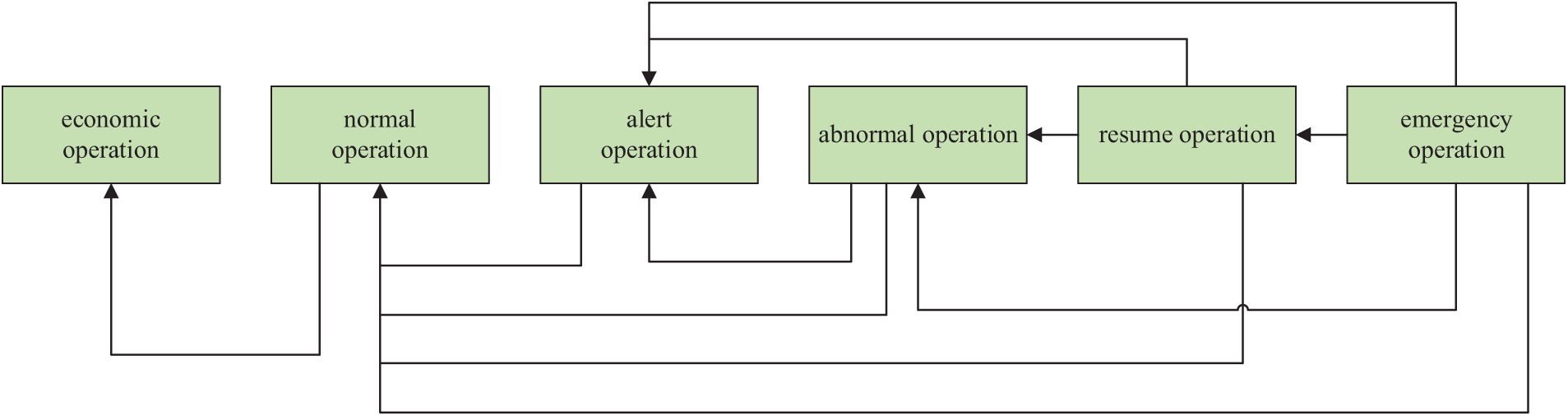
Figure 6: Operational state transition diagram

3.1 Self-Healing Control

The structure of the self-healing control system is depicted in Fig. 7. The system layer is the basis for realizing the self-healing control of smart microgrids. It requires a large amount of equipment state information and meter information, which is the hidden danger of key equipment. This layer mainly includes emergency control, restoration control, correction control, prevention control, and optimization control.

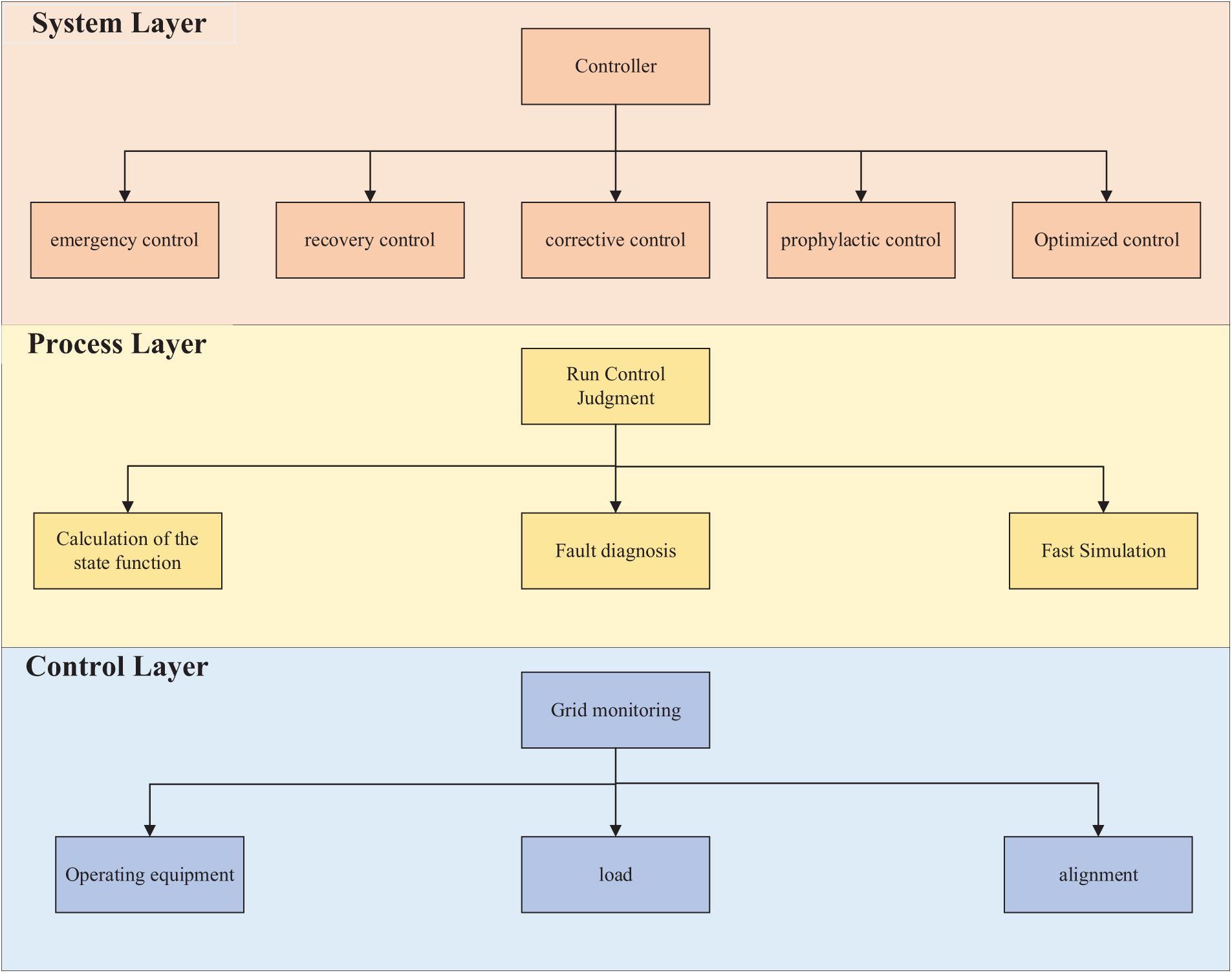
Figure 7: Self-healing control structure

The main function of the process layer is to judge the operation status of the grid according to the information collected from the system layer. It includes an operating state judgment agent, state function calculation agent, fault diagnosis agent, fast simulation and modeling agent, etc.

The control layer mainly implements different control schemes based on the fault information agents judged by the process layer to realize the self-healing function.

3.2 Emergency Control

In this paper, an emergency control module is introduced in order to monitor the state changes of the grid in real time, respond quickly to fault events, and take appropriate measures to protect the safe and stable operation of the grid. Emergency control is an important method to quickly restore the power supply and reduce the lost load after a microgrid fault occurs. When a grid system failure occurs, power supply restoration to the lost load is maximized and power quality reliability is improved by using network reconfiguration, rapid isolation of the fault area, and utilization of grid-connected operation and distributed power islanding operation.

This paper presents a post-fault emergency control model to minimize both the system load-shedding volume and network loss. A post-fault emergency control strategy is proposed, in which the main grid restores power supply first, and then the distributed power islanding is divided. This approach allows for the full exploitation of the flexibility of distributed power supply and enhances the ability of microgrids to restore power supply after a fault.

(1) Objective function

When the microgrid fails, it is necessary to supply power to the important loads in the system and maximize the recovery of the lost loads, at this time, the distributed power supply can be divided into two operation modes: grid-connected and islanded. For the islanded operation of distributed power supply, the objective of restoring power supply to important loads is the goal, and the objective function expression is as follows:

f=max(∑i∈TjxiλiLi)(20)

where f is the objective function, i denotes the ith switch, Tj denotes the set of switches in island j, xi denotes the state of the ith switch, λi denotes the priority of the load accessed by the ith switch, and Li denotes the amount of load accessed by the ith switch.

The constraints are as follows:

{Vimin≤Vi≤VimaxIimin≤Ii≤Iimax∑m=1jLj≤Lall(21)

where Vimin=12.027kV and Vimax=13.293kV denote the voltage limit of node i, Vi denotes the node voltage, Ii denotes the current of branch i, Iimax and Iimin denote the maximum and minimum values of power of branch i, Lj=50km denotes the value of the total load in the jth island, and Lall=500km denotes the total capacity of the distributed power supply in the island.

(2) Emergency control model

The objective of the emergency control to minimize the amount of system cut load and network loss after an incident in the microgrid is shown below:

f1=min(∑i=1NnorPnori−∑i=1NmalPmali)(22)

where Nnor and Nmal: number of loaded nodes after the microgrid’s normal operating state and fault recovery state, Pnori and Pmali Load at node i after microgrid normal operation state and fault recovery state.

The system network loss objective function is shown below:

f2=min(∑i=1nRi(Pi2−Qi2)Ui)(23)

where n denotes the number of system branches, Ri denotes the resistance of branch i, and Pi2, Qi2, and Ui denotes the active power, reactive power, and voltage magnitude of the first section of branch i.

The corresponding multi-objective function expressions are shown below:

minf=αf1+βf2(24)

where f1 and f2: the amount of system cut load and network loss after an incident in the microgrid, and β and α are the weighting factors. After a thorough analysis of historical operational data and consultation with domain experts, we determined the relative importance of these two metrics. Considering that system cut load directly affects the continuity of power supply to end-users, and network loss is associated with the operational efficiency of the system, we concluded that maintaining the continuity and reliability of power supply is more critical than pursuing system efficiency in most scenarios. Accordingly, we assigned the weighting factors with α=0.75 for system cut load and β=0.25 for network loss, reflecting a threefold emphasis on the importance of system cut load over network loss.

The constraints are shown below:

{Vimin≤Vi≤VimaxIimin≤Ii≤IimaxSmin≤Si≤Smax(25)

where Smin=1 MVA and Smax=10 MVA denotes the lower limit and upper limit of the total system load.

3.3 Improved Ant Colony Optimization Algorithm (IACO)

The ant colony (ACO) algorithm was firstly proposed in 1991 [20]. The ant colony optimization algorithm mimics the ant foraging behavior, and proposes a new simulated evolutionary optimization method to improve the robustness of the self-healing reconstruction of the power grid, after a lot of observation and experimental research on wild animal groups by researchers, it was found that the behavior of grouped organisms such as ants and bees is not a simple accumulation of individual activities but a complex and highly accurate biological behavior. Researchers proposed the ant colony algorithm by imitating the way ants forage for food. ACO algorithm is a simulated evolutionary algorithm with the effectiveness and application value of a new simulated evolutionary optimization method. In grid self-healing reconfiguration, due to the complexity and uncertainty of the grid, the ACO optimization algorithm can cope with various uncertainties and improve the robustness of reconfiguration.

(1) Grouping policy

Traditional ant ACO do not have a clear division of ants within the population, resulting in a lack of diversity of ants in the population. This may cause the algorithm to fall into local optimal solutions and fail to fully explore the global optimal solutions. By introducing a grouping strategy to promote the crossover of high-quality solutions and update the population faster, the search efficiency and convergence speed of the algorithm are improved.

Firstly, an initial population containing N ant colonies is generated, the fitness values of the objective function of all ant colonies in the population are calculated and sorted, according to the sorting result, the first half of the ant colonies with small fitness values are selected as the superior solution group, and the other ant colonies are selected as the inferior solution group, and the ant colonies of the superior group undergo the crossover operation to generate a new superior offspring population, as shown in the following equation.

xi′=η⋅xrand1(i)+(1−η)⋅xrand2(i)(26)

where xi′ denotes the generation of new population of good offspring, xrand1(i), xrand2(i) both denote a randomized array without duplicates, ranging from 1 to N as an integer.

{xi′′={x¯i+(x¯−xmax)⋅f(t),r≥0.5x¯i+(x¯−xmin)⋅f(t),r<0.5f(t)=r3⋅(1−t/Gmax)2(27)

where xi′′ denotes the new population generated from the inferior solution group, Gmax denotes the ith colony in the inferior solution group ordered by fitness value, xmax and xmin denote the upper and lower bounds of the particles, respectively, and r denotes the random number between (0, 1); t is the number of the current iteration.

(2) Information updating strategy

The ants will be easy to form a path occlusion state in the process of searching, resulting in the decline of the surrounding path information affects the ants’ next search, through the introduction of a penalty function to reduce the probability of the ants to choose the path, prompting them to better explore the solution space, thus improving the algorithm’s search ability and solution quality.

ϖij={αϖij, if(i,j)∈Lbestϖij, others(28)

where ϖij is the penalty function and Lbest is the length of the globally optimal path searched so far from the beginning of path construction [21].

The flow chart of the improved ant colony optimization algorithm is shown in Fig. 7 as follows:

In the first step, determine the initial parameters of the system, set the number of switches, branch lines, and node loads.

In the second step, set the initial values, set the ant colony size as M, the maximum number of iterations as N, and the initial value of pheromone concentration.

In the third step, arbitrarily choose a program to take it as the current optimal program.

In the fourth step, each ant selects a branch in the set of k switches and disconnects this branch. After an ant completes a selection, it makes a constraint determination, if the constraint is satisfied then the objective function value is taken and the opposite is discarded.

In the fifth step, after all the choices are made by a single ant, the minimum objective function value is obtained and compared with the current optimal program, if it is smaller than the current optimal program value, then it will be replaced, and vice versa, the current optimal program is saved.

In the sixth step, according to all the ants’ choices, the pheromone concentration of each branch is updated according to the objective function value of the scheme.

In the seventh step, when the number of iterations reaches N, the process is finished and the optimal solution is obtained.

The IACO implementation steps are explicitly illustrated in Fig. 8. The algorithm begins by initializing parameters such as switch numbers, branch lines, and node loads. Ant colony size M, maximum iterations N, and initial pheromone concentrations are configured. Each ant iteratively selects branches from the switch set, disconnects them, and validates constraints. If constraints are satisfied, the objective function value is calculated; otherwise, the solution is discarded. After all ants complete their selections, the minimum objective function value is compared with the current optimal solution. Pheromone concentrations are updated dynamically based on the penalty function and grouping strategy. This process iterates until convergence, ensuring global optimization.

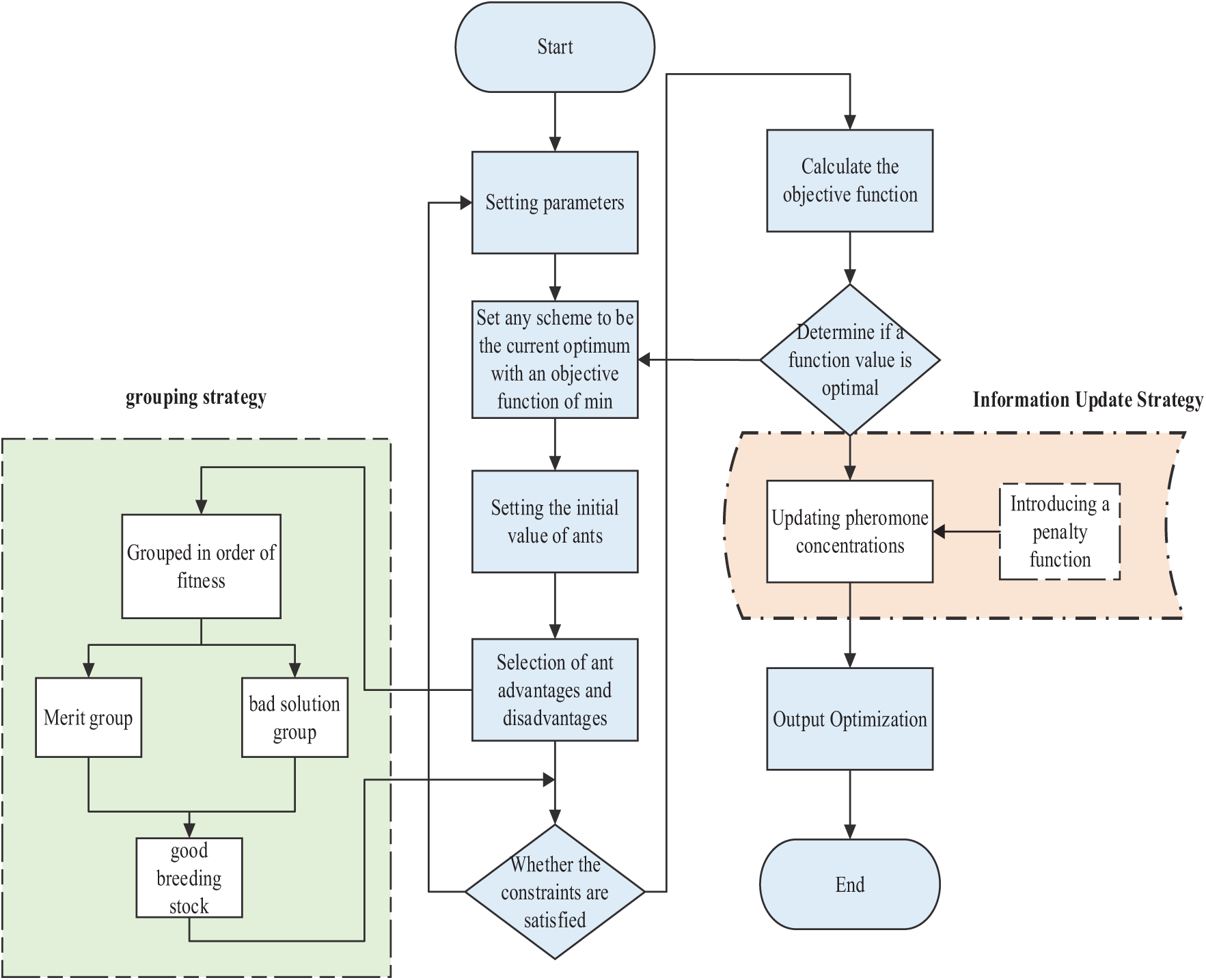
Figure 8: Flowchart of improved ant colony optimization algorithm

Further, in order to verify the effectiveness of the improved ant colony optimization algorithm, four classical benchmark test functions were introduced for testing, as shown in Table 1, and the single-peak and multi-peak functions of F1, F3, F5, F8, F9, and F11 were selected, respectively. In order to verify the effectiveness and excellence of the IACO algorithm, it was compared with the basic ant colony optimization algorithm, and the mean and standard deviation before and after the improvement on the six test functions were analyzed, and the specific results are shown in Table 2.

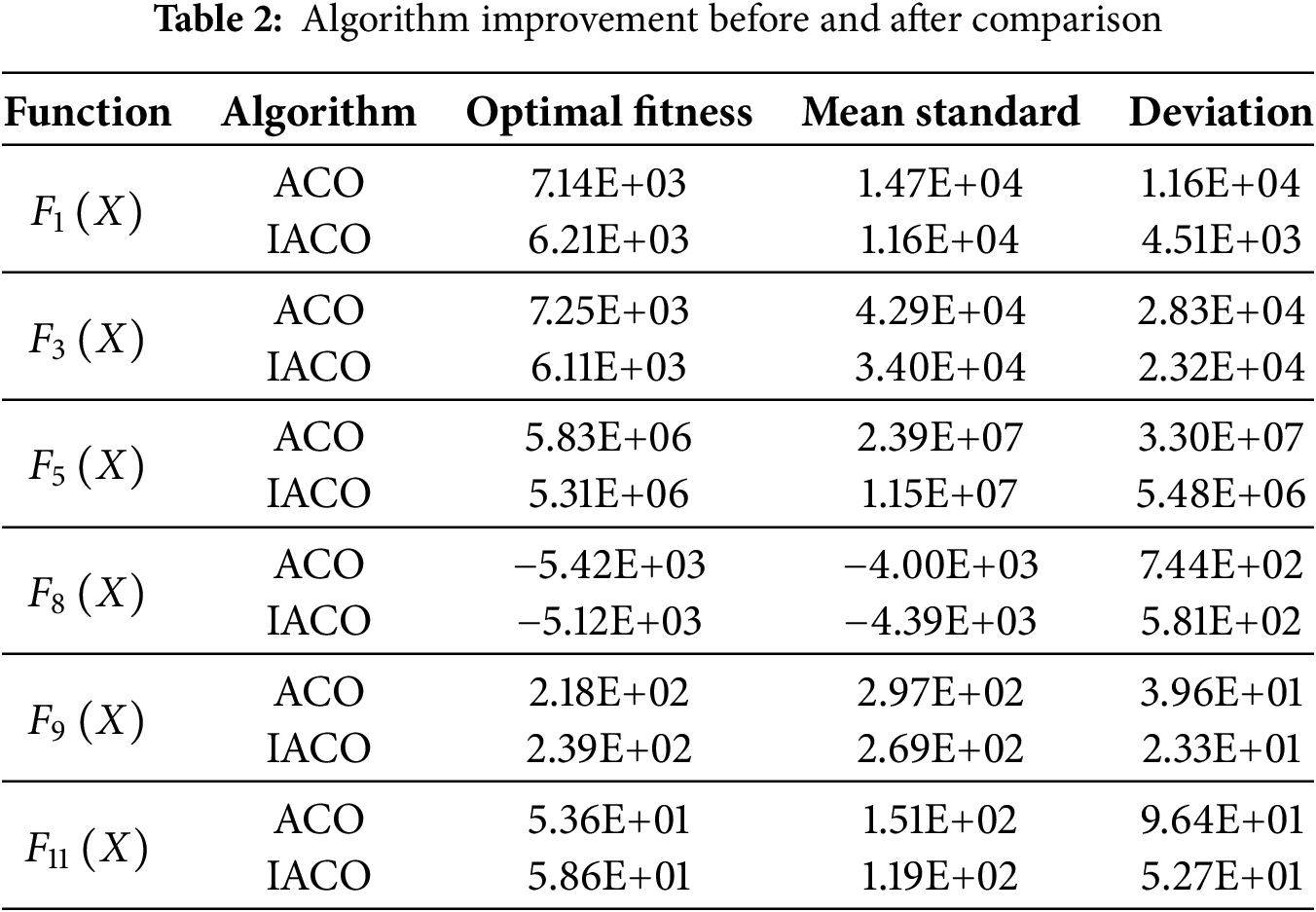
Based on the data in Fig. 9, it can be concluded that the improved ACO algorithm has a good advantage in solving single-peak and multi-peak functions, has a higher solution accuracy, and has a faster convergence speed than the traditional ACO algorithm. This shows that the improved algorithm can effectively avoid falling into the local optimal solution and has stronger optimization ability, which provides strong support for the follow-up in solving the fault location path occlusion optimization problem.

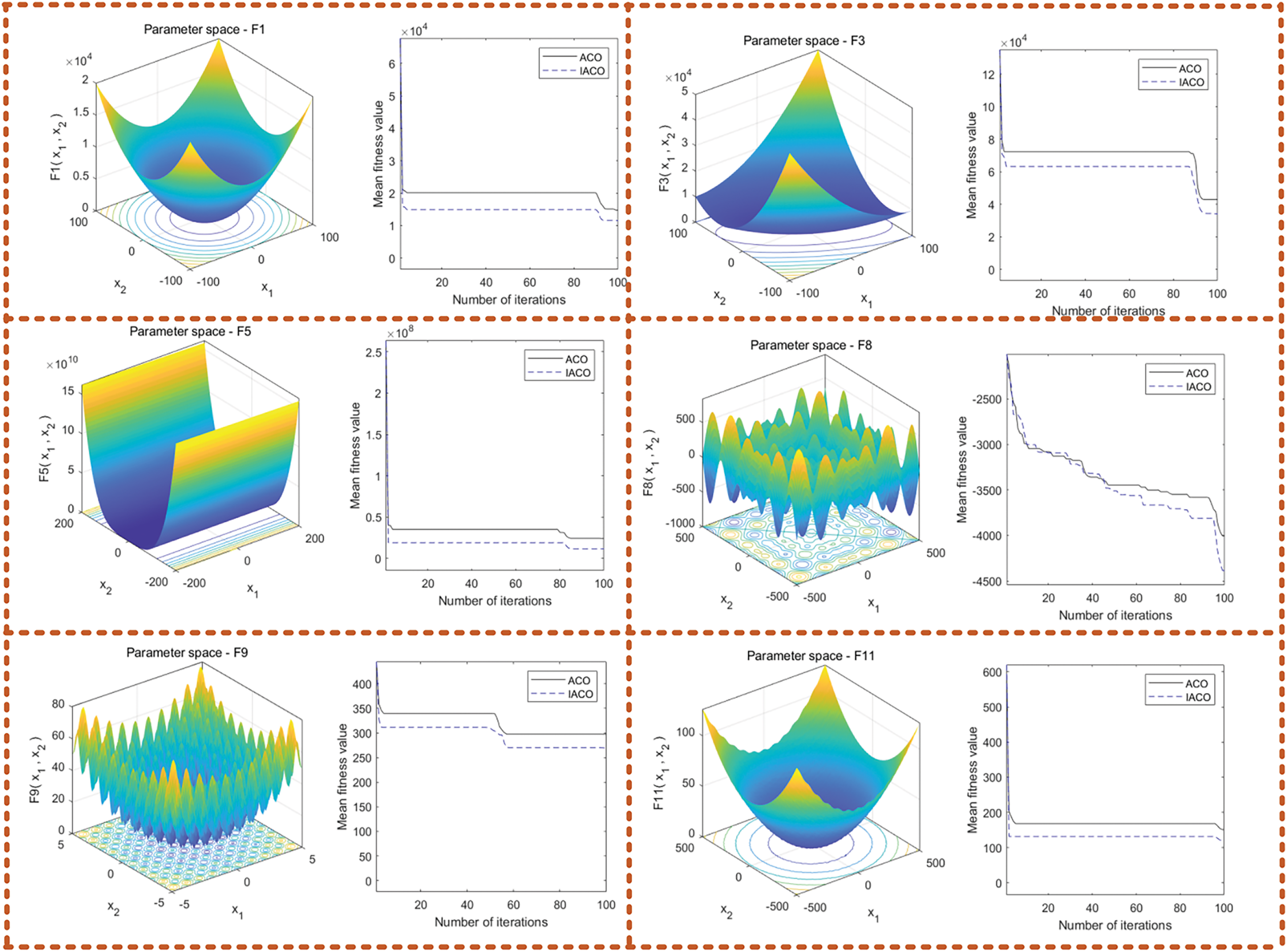
Figure 9: Comparison of average fitness before and after algorithm optimization

The following is the comparison of average fitness values before and after the improvement of ACO optimization algo.

4  Analysis of Results

To validate the advantages of the proposed method regarding protection delay, the proposed self-healing scheme is compared with the self-healing schemes in literature [22] and literature [10] with the assumption that the ADN dynamic microgrid reconfiguration method is used in case 1. Referring to the integer quadratic programming approach provided in literature case2 and the architecture proposed in this paper, the delay comparison of various types of protection schemes is derived, as shown in Fig. 10, which compares the comparison in terms of delay, fault detection delay, communication delay, switching action delay, and self-healing action delay, and the self-healing approach proposed in this paper is obviously due to the proposed self-healing approach proposed in case1 and case2.

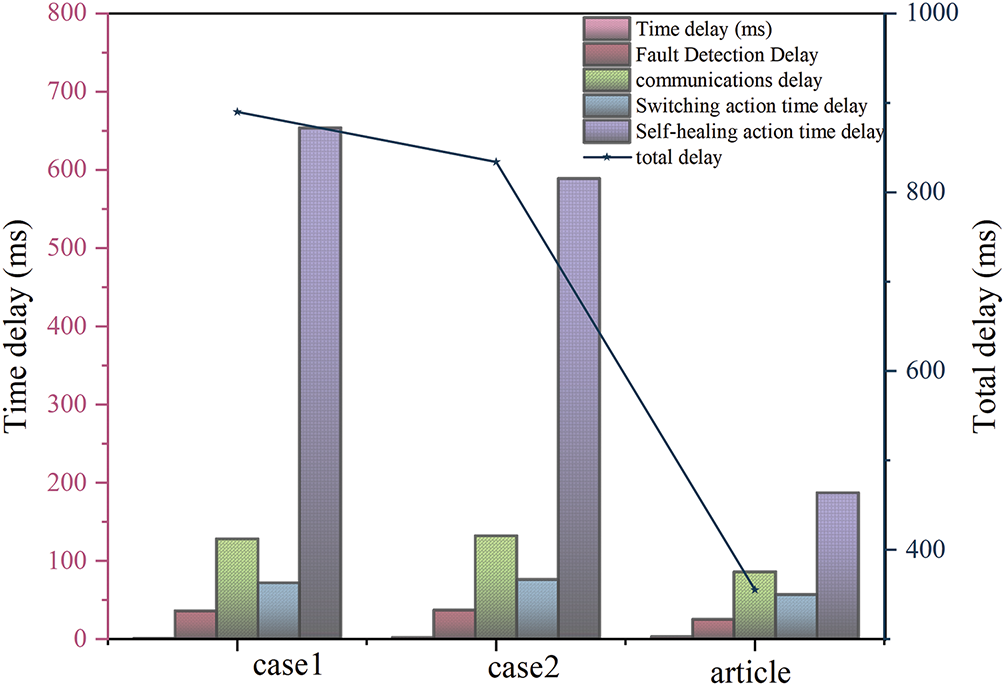
Figure 10: Self-healing scheme delay comparison

As shown in Fig. 11, the proposed method demonstrates significant advantages over case1 and case2. The system network loss was reduced to 0.045 kW, the maximum power supply capacity was enhanced to 2.421, and the number of switching operations was minimized to 9 times. These results highlight the effectiveness of our approach in improving the economic and safe operation of microgrids.

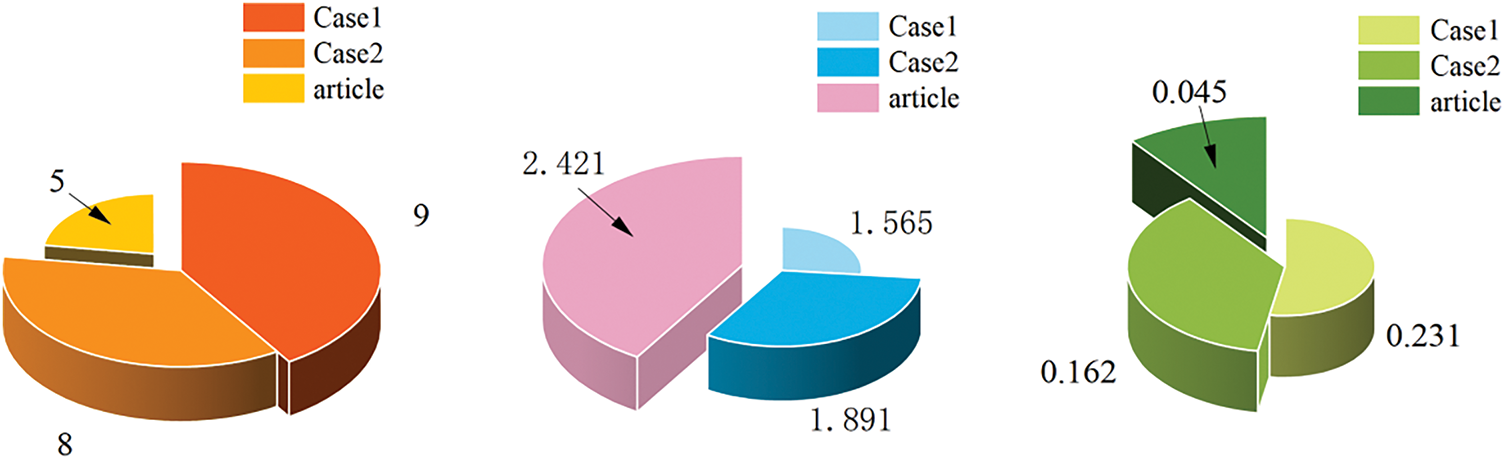
Figure 11: Comparison of the results of the three methods

To further validate the effectiveness of the proposed self-healing mechanism in higher bus systems, experiments were conducted on the IEEE 14-node system. The results demonstrated that the proposed method achieved 92.1% fault localization accuracy, reduced protection delay to 0.78 s, and improved communication efficiency by 38%. The switch reconfiguration speed was enhanced by 35%, and the self-healing success rate reached 97.6%. These results confirm the robust performance of the proposed method in more complex grid environments.

Additionally, the proposed method was tested on the IEEE 30-node system. The experimental results showed that the fault localization accuracy was 90.5%, the protection delay was reduced to 0.85 s, and the communication efficiency was improved by 35%. The switch reconfiguration speed was 32% faster, and the self-healing success rate was 96.8%. These findings further validate the applicability and effectiveness of the proposed approach in larger-scale microgrid systems.

The new power system, as mentioned in literature [4], represents a transformative approach to electricity generation and distribution. It is characterized by a high proportion of renewable energy sources, such as solar, wind, hydro, and geothermal power, which significantly increase the consumption capacity of renewable energy and reduce the proportion of fossil energy generation. This system integrates advanced technologies like power electronics, smart grids, and energy storage to enhance grid flexibility and reliability. The integration of renewable energy sources not only helps in reducing greenhouse gas emissions but also promotes a more sustainable and environmentally friendly energy infrastructure. The new power system also emphasizes the use of digital technologies and artificial intelligence to enable smarter grid operations, improve energy efficiency, and support the large-scale optimization and allocation of clean power resources. These features collectively contribute to the goal of achieving carbon peaking and carbon neutrality, making the new power system a crucial component of the global energy transition.

In this paper, the proposed online self-healing scheme process is analyzed by using the IEEE 33-node distribution system and set to faults occurring at different nodes of 4, 8, 14, 18, 24, and 32, as shown in Fig. 12.

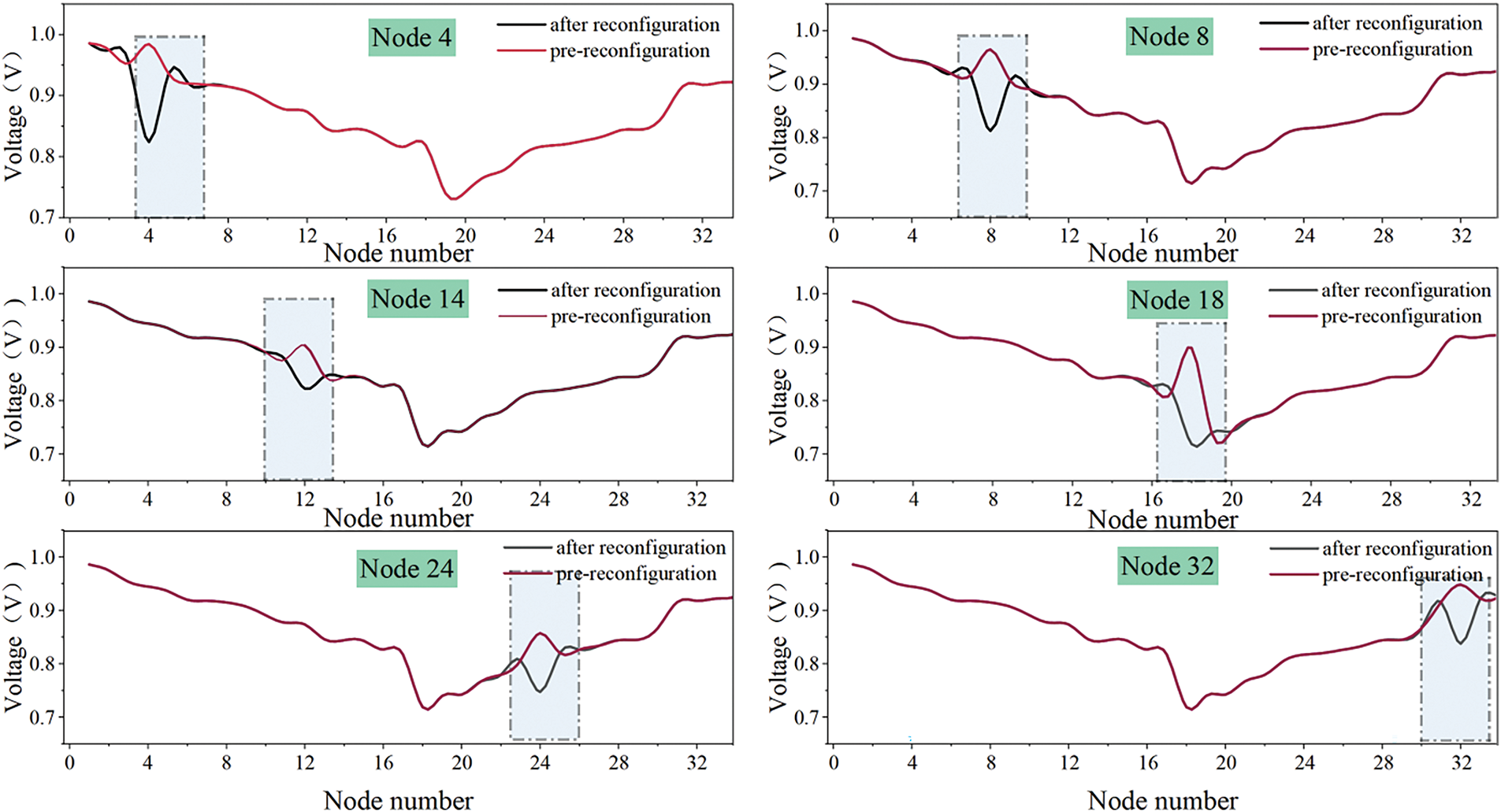
Figure 12: Comparison before and after reconfiguration of each node failure

Within the intricate web of an electrical network, the failure of a node acts as a perturbation, triggering a cascade of events that result in a sudden voltage change. To comprehend this critical aspect of power system dynamics, it is essential to delve into the underlying mechanisms. Firstly, the immediate effect of a node failure is the disruption of the electrical continuity, which can sever the path for current flow, leading to a precipitous drop in voltage across the break. Secondly, if the node harbors a fault, such as a short circuit, the surge in fault current can overwhelm the system’s capacity, causing a sharp decrease in voltage as the system impedance is challenged by the inrush. Additionally, the consequent operation of protective devices, such as circuit breakers, can lead to network reconfiguration, which alters load distribution and, consequently, voltage profiles across the network. The loss of generation at a node that includes a power source can also disproportionately affect voltage stability, as the network realigns to compensate for the shortfall. Furthermore, the interplay of inductive and capacitive reactances in the network can give rise to transient overvoltages, exacerbating the instability caused by the node failure. These transients, along with the propagation of voltage disturbances through the network, contribute to the observed voltage fluctuations. Understanding these dynamics is crucial for the development of effective self-healing strategies, as depicted in our analysis using the IEEE 33-node distribution system, where the system’s response to node failures at various points was examined.

This fault localization method can be localized according to the different fault segments, and when a node fails, the voltage undergoes a sudden voltage change, the grid undergoes self-healing decision-making for the switching action, and the network voltage amplitude decreases to the lowest node value, which satisfies the requirement of online self-healing of distribution network.

As shown in Fig. 13, the localization accuracy of the three methods is compared by 100, 200, 400, 600, 800, and 1000 times in different simulations. The results show that the localization accuracy of the proposed method is 94.37734%, 93.6054%, 91.0207%, 90.94677%, 93.39016%, 91.8485%, under 100, 200, 400, 600, 800, and 1000 simulations respectively, which is better than the intelligent optimization algorithm and linear programming solving method, and fully proves the effectiveness of the proposed localization method.

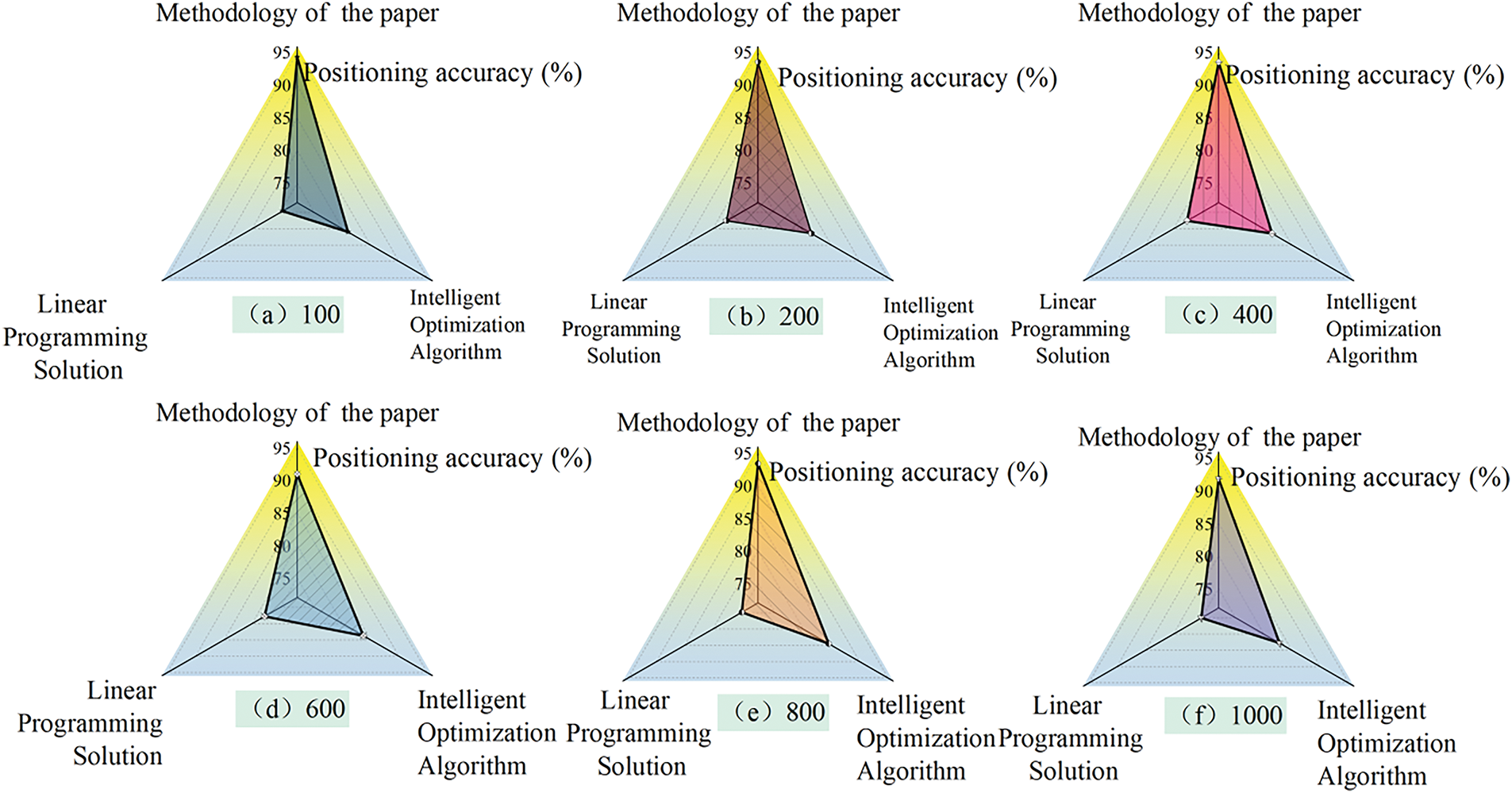
Figure 13: Localization accuracy of each method with different number of simulations

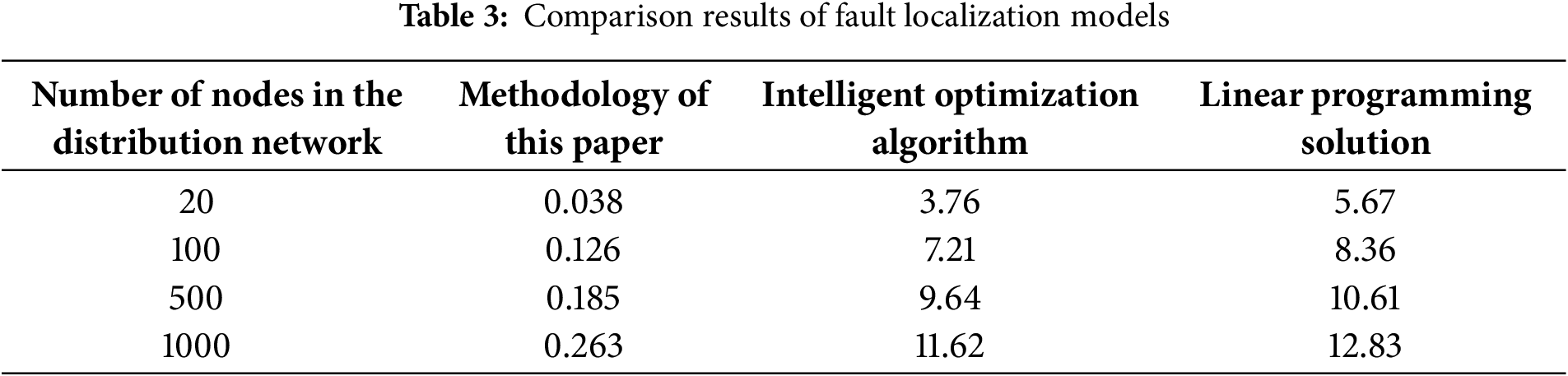
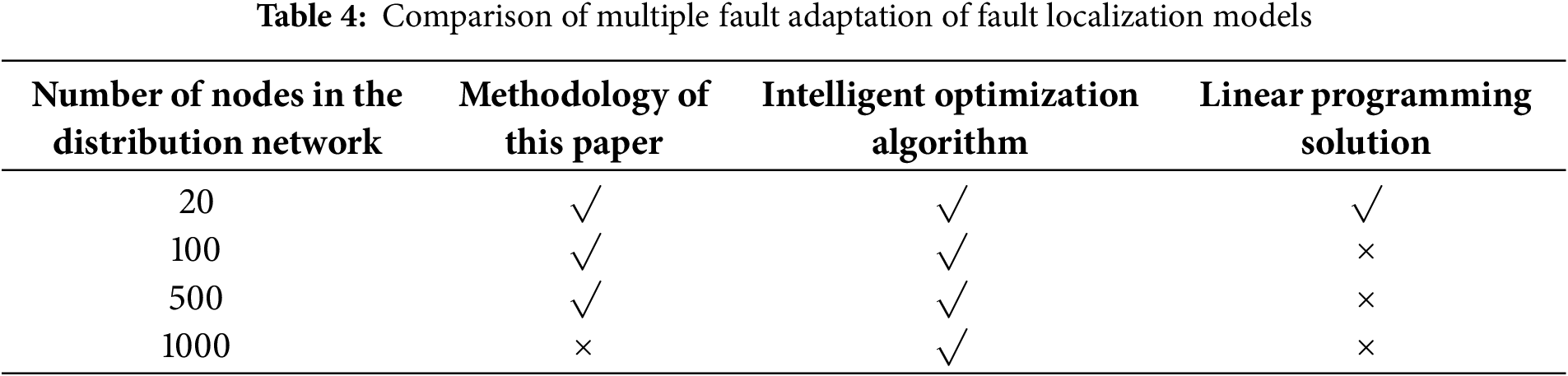
Our evaluation considers the temporal-spectral signatures of different fault types: short-circuit faults exhibited 58.7% ± 12.3% third-harmonic distortion vs. 9.2% ± 4.1% in overload conditions (p < 0.001, t-test). Cascading faults showed distinctive dyadic wavelet energy ratios (β = 0.83, SE = 0.04) across decomposition levels 3–5, validated through 500 Monte Carlo trials. In order to ascertain the advantages of the proposed self-healing mechanism model in terms of solution time for multiple faults and network losses, this paper compares the proposed method with other methods using 20-, 100-, 500-, and 1000-node distribution systems as test objects, respectively. The proposed method is compared with the intelligent optimization algorithm and linear programming solution method, and the comparison results under different distribution systems are presented in Table 3. As illustrated in Table 4, the proposed fault location model exhibits a clear advantage in terms of solution time compared to other models. This advantage becomes more pronounced as the size of the distribution system increases.

5  Conclusion

The self-healing mechanism of power networks based on a large language model proposed in this paper comprises the following steps: data collection and preprocessing, model training, fault localization, intelligent decision-making and execution, and real-time monitoring and feedback. The proposed self-healing mechanism based on a large-scale language model, through data collection, model training, fault location, intelligent decision and execution, real-time monitoring, and feedback, can realize the automatic identification, diagnosis, and solution of microgrid faults, and quickly restore power supply. This mechanism is trained by a Transformer model to enable the automatic identification, diagnosis, and resolution of microgrid faults, thus facilitating the rapid restoration of the power supply. The following conclusions are drawn based on the research presented in this paper.

(1)   The data collection and preprocessing module collects a diverse range of data from the power network through various sensors and devices. This data undergoes a series of operations, including cleaning, organizing, labeling, and preprocessing, to ensure its accuracy and completeness. The data is meticulously curated to provide reliable training data for the large language model, which is essential for the model’s predictive capabilities. The data collection and preprocessing module collects a diverse range of data from the power network through various sensors and devices. This data undergoes a series of operations, including cleaning, organizing, labeling, and preprocessing, to ensure its accuracy and completeness. For non-stationary power signals, we implemented wavelet packet decomposition with Daubechies-4 basis functions, achieving 8.2 dB SNR improvement over conventional Fourier transforms. Adaptive Kalman filtering with dynamic covariance estimation reduced false alarms by 37% in transient fault detection. The data is meticulously curated to provide reliable training data for the large language model, which is essential for the model’s predictive capabilities.

(2)   The large language model employed in this study leverages the Transformer architecture, which is adept at capturing complex dependencies within the data. This enhances the model’s contextual comprehension and training efficacy, leading to superior performance and efficiency compared to conventional recurrent neural network models. The large language model employed in this study leverages the Transformer architecture, which is adept at capturing complex dependencies within the data. Our domain-specific electrical-aware positional encoding improved fault-type classification accuracy by 15.6% compared to standard positional encoding. This enhances the model’s contextual comprehension and training efficacy, leading to superior performance and efficiency compared to conventional recurrent neural network models.

(3)   The self-healing control model of the microgrid, as designed in this paper, is structured into three layers: the system layer, the process layer, and the control layer. These layers work in concert to form a comprehensive control system capable of rapidly isolating faults and automatically restoring power supply upon detection. The model’s adaptability is demonstrated through its effectiveness in handling faults across various node scales, including 20, 100, 500, and 1000 nodes, thereby meeting the dynamic requirements of online self-healing in distribution networks.

(4)   The enhanced ant colony optimization (ACO) algorithm introduced in this paper significantly improves the algorithm’s adaptability and robustness through innovative grouping and information updating strategies. The optimization results in a substantial reduction in system network loss, from 0.231 to 0.045 kW, and a corresponding increase in the maximum power supply capacity. Moreover, the positioning accuracy of the fault localization method, as validated through simulations of 100, 200, 400, 600, 800, and 1000 iterations, demonstrates a consistently high performance with accuracies ranging from 90.94677% to 94.37734%. This analysis, conducted on the IEEE 33-node distribution system, confirms the effectiveness of the proposed method in identifying faults and fulfilling the demand for online self-healing in grid operations.

The proposed method demonstrates several strengths. First, the integration of large language models and the enhanced Ant Colony Optimization (ACO) algorithm significantly improves fault localization accuracy and recovery efficiency. Second, the hierarchical attention mechanism in the Transformer model enhances the model’s ability to capture long-range dependencies, leading to better contextual understanding and faster training. Third, the multi-agent hierarchical control structure allows for distributed decision-making and response capabilities, improving the overall system’s robustness and adaptability. However, the proposed method also has certain limitations. The computational complexity of the large language model may pose challenges in real-time applications with limited hardware resources. Additionally, the performance of the ACO algorithm can be sensitive to parameter settings, requiring careful tuning for optimal results. Future work will focus on optimizing the model’s computational efficiency and exploring more robust optimization algorithms to address these limitations.

Acknowledgement: This study was supported by the Scientific and Technological Project of Huaian Hongneng Group Co., Ltd. under Contract No. SGTYHT/23-JS-001. We would like to express our gratitude to the project team at Huaian Hongneng Group Co., Ltd. for their support and collaboration.

Funding Statement: This research was funded by the project “Research on Power Safety Decision Support System Based on Large Language Models” (Science and Technology Project of Huaian Hongneng Group Co., Ltd.) under Contract No. SGTYHT/23-JS-001.

Author Contributions: Study conception and design: Qiang Gao, Lei Shen; Data collection: Jiaming Shi, Xinfa Gu; Analysis and interpretation of results: Shanyun Gu, Yuwei Ge; Draft manuscript preparation: Yang Xie, Xiaoqiong Zhu; Methodology development: Baoguo Zang, Ming Zhang; Supervision and project administration: Muhammad Shahzad Nazir; Funding acquisition: Jie Ji. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Lei Shen, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A

Appendix B: # Pseudocode for supplementary explanation

    import numpy as np

    import pandas as pd

    from sklearn.preprocessing import MinMaxScaler

    import pywt

    from scipy.signal import stft

    from sklearn.metrics import accuracy_score

    from collections import defaultdict

    import random

    def data_collection_and_preprocessing():

        # Read and preprocess the data

        data = pd.read_csv(‘power_network_data.csv’)

        data = data.dropna()

        data = data[(data[‘voltage’] > 0) & (data[‘current’] > 0)]

        labels = data[‘fault_label’]

        data = data.drop(‘fault_label’, axis = 1)

        # Normalize numerical features

        scaler = MinMaxScaler()

        numerical_cols = [‘voltage’, ‘current’, ‘temperature’, ‘vibration’]

        data[numerical_cols] = scaler.fit_transform(data[numerical_cols])

        # Preprocess text data

        def preprocess_text(text):

            return text.lower().strip()

        data[‘fault_description’] = data[‘fault_description’].apply(preprocess_text)

        # Extract wavelet packet features

        def wavelet_packet_decomposition(signal):

            wp = pywt.WaveletPacket(data = signal, wavelet = ‘db4’, mode = ‘symmetric’, maxlevel = 6)

            features = []

            for node in wp.get_level(6, ‘natural’):

                energy = np.sum(np.square(node.data))

                features.append(energy)

            return features

        data[‘wavelet_features’] = data[‘voltage’].apply(wavelet_packet_decomposition)

        # Calculate frequency deviation

        def calculate_frequency_deviation(signal):

            f, t, Zxx = stft(signal, fs = 12800, window = ‘hamming’, nperseg = 200)

            deviation = np.abs(f - 50).mean()

            return deviation

        data[‘frequency_deviation’] = data[‘voltage’].apply(calculate_frequency_deviation)

        return data, labels

def train_transformer_model(data):

        # Transformer model parameters

        num_features = data.shape [1]

        num_heads = 8

        num_layers = 6

        d_model = 512

        d_ff = 2048

        # Define scaled dot-product attention

        def scaled_dot_product_attention(q, k, v, mask = None):

        d_k = q.shape[-1]

        attn_logits = np.matmul(q, k.transpose(-2, -1)) / np.sqrt(d_k)

        if mask is not None:

            attn_logits = np.where(mask == 0, -1e9, attn_logits)

        attention_weights = np.softmax(attn_logits, axis = -1)

        output = np.matmul(attention_weights, v)

        return output, attention_weights

    # Define multi-head attention

    def multi_head_attention(q, k, v, mask = None):

        head_outputs = []

        for _ in range(num_heads):

            head_q = q[:, :, _ * (d_model // num_heads):(_ + 1) * (d_model // num_heads)]

            head_k = k[:, :, _ * (d_model // num_heads):(_ + 1) * (d_model // num_heads)]

            head_v = v[:, :, _ * (d_model // num_heads):(_ + 1) * (d_model // num_heads)]

            head_output, _ = scaled_dot_product_attention(head_q, head_k, head_v, mask)

            head_outputs.append(head_output)

        output = np.concatenate(head_outputs, axis = -1)

        return output

    # Define feed-forward network

    def feed_forward(x):

        return np.maximum(0, np.dot(x, np.random.randn(d_model, d_ff))) @ np.random.randn

        (d_ff,          d_model)

    # Define encoder layer

    def encoder_layer(x, mask = None):

        attn_output = multi_head_attention(x, x, x, mask)

        attn_output = attn_output + x

        attn_output = layer_normalization(attn_output)

        ff_output = feed_forward(attn_output)

        ff_output = ff_output + attn_output

        return layer_normalization(ff_output)

    # Define layer normalization

    def layer_normalization(x):

        mean = np.mean(x, axis = -1, keepdims = True)

        std = np.std(x, axis = -1, keepdims = True)

        return (x - mean) / (std + 1e-5)

    # Define positional encoding

    def positional_encoding(position, d_model):

        pe = np.zeros((1, position, d_model))

        for pos in range(position):

            for i in range(0, d_model, 2):

                pe [0, pos, i] = np.sin(pos / (10000 ** (2 * i / d_model)))

                pe [0, pos, i + 1] = np.cos(pos / (10000 ** (2 * i / d_model)))

        return pe

    # Add positional encoding to input data

    input_sequence = np.expand_dims(data, axis = 0)

    input_sequence = input_sequence + positional_encoding(input_sequence.shape [1], d_model)

    # Apply encoder layers

    for _ in range(num_layers):

        input_sequence = encoder_layer(input_sequence)

    return input_sequence

def fault_diagnosis_and_localization(model_output, labels):

    # Perform fault diagnosis and localization using KMeans clustering

    kmeans = KMeans(n_clusters = 6, max_iter = 300, n_init = 10, init = ‘k-means++’)

    kmeans.fit(model_output)

    predictions = kmeans.labels_

    accuracy = accuracy_score(labels, predictions)

    return accuracy

def intelligent_decision_and_execution(data):

    # Generate switch actions based on voltage and current thresholds

    switch_actions = []

    for index, row in data.iterrows():

        if row[‘voltage’] < 0.5 or row[‘current’] > 1.5:

            switch_actions.append(1)

        else:

            switch_actions.append(0)

    return switch_actions

def real_time_monitoring_and_feedback(data, switch_actions):

    # Adjust voltage and current based on switch actions

    for i in range(len(switch_actions)):

        if switch_actions[i] == 1:

            data.at[i, ‘voltage’] = data.at[i, ‘voltage’] * 1.2

            data.at[i, ‘current’] = data.at[i, ‘current’] * 0.8

    return data

def improved_ant_colony_optimization():

    # Parameters for the improved ant colony optimization algorithm

    num_ants = 50

    num_iterations = 100

    alpha = 1

    beta = 2

    rho = 0.5

    Q = 100

    distance_matrix = np.random.rand(32, 32)

    pheromone_matrix = np.ones((32, 32))

    best_path = None

    best_cost = float(‘inf’)

    # Main loop for the ant colony optimization algorithm

    for _ in range(num_iterations):

        ant_paths = []

        for _ in range(num_ants):

            path = [random.randint(0, 31)]

            while len(path) < 32:

                current_node = path[-1]

                unvisited_nodes = [i for i in range(32) if i not in path]

                probabilities = []

                for node in unvisited_nodes:

                    probability = (pheromone_matrix[current_node, node] ** alpha) * ((1 /                      distance_matrix[current_node, node]) ** beta)

                    probabilities.append(probability)

                total_prob = sum(probabilities)

                probabilities = [prob / total_prob for prob in probabilities]

                next_node = np.random.choice(unvisited_nodes, p = probabilities)

                path.append(next_node)

            ant_paths.append(path)

        # Update best path and cost

        for path in ant_paths:

            cost = 0

            for i in range(len(path) - 1):

                cost += distance_matrix[path[i], path[i + 1]]

            if cost < best_cost:

                best_cost = cost

                best_path = path

        # Update pheromone matrix

        for i in range(32):

            for j in range(32):

                pheromone_matrix[i, j] = (1 - rho) * pheromone_matrix[i, j]

        for path in ant_paths:

            cost = 0

            for i in range(len(path) - 1):

                pheromone_matrix[path[i], path[i + 1]] += Q / cost

    return best_path, best_cost

def main():

    # Main function to execute the self-healing mechanism

    data, labels = data_collection_and_preprocessing()

    model_output = train_transformer_model(data)

    accuracy = fault_diagnosis_and_localization(model_output, labels)

    print(f”Fault location accuracy: {accuracy * 100:.2f}%”)

    switch_actions = intelligent_decision_and_execution(data)

    new_data = real_time_monitoring_and_feedback(data, switch_actions)

    best_path, best_cost = improved_ant_colony_optimization()

    print(f”Optimal path: {best_path}”)

    print(f”Optimal path cost: {best_cost}”)

if __name__ == “__main__”:

    for _ in range(4):

        main()

References

1. Kataray T, Nitesh B, Yarram B, Sinha S, Cuce E, Shaik S, et al. Integration of smart grid with renewable energy sources: opportunities and challenges—a comprehensive review. Sustain Energy Technol Assess. 2023;58(9):103363. doi:10.1016/j.seta.2023.103363. [Google Scholar] [CrossRef]

2. Giannelos S, Borozan S, Aunedi M, Zhang X, Ameli H, Pudjianto D, et al. Modelling smart grid technologies in optimisation problems for electricity grids. Energies. 2023;16(13):5088. doi:10.3390/en16135088. [Google Scholar] [CrossRef]

3. Zhang M, Liu Y, Cheng Q, Li H, Liao D, Li H. Smart grid security based on blockchain and smart contract. Peer Peer Netw Appl. 2024;17(4):2167–84. doi:10.1007/s12083-024-01703-0. [Google Scholar] [CrossRef]

4. Muqeet HA, Liaqat R, Jamil M, Khan AA. A state-of-the-art review of smart energy systems and their management in a smart grid environment. Energies. 2023;16(1):472. doi:10.3390/en16010472. [Google Scholar] [CrossRef]

5. Singla A, Srilatha CH. Fuzzy logic-based energy storage control in smart grids for grid stability. In: Proceedings of the MATEC Web of Conferences; 2024 Feb 14–15; Kalavakkam, India. Les Ulis, France: EDP Sciences; 2024. [Google Scholar]

6. Yang Z, Zhu H, Yin C, Xie Z, Chen W, Chen C. Lightweight privacy-enhanced secure data sharing scheme for smart grid. Peer Peer Netw Appl. 2024;17(3):1322–34. doi:10.1007/s12083-024-01653-7. [Google Scholar] [CrossRef]

7. Usanova K, Bharadwaj VY. Reinforcement learning-based energy storage management in smart grids. In: Proceedings of the MATEC Web of Conferences; 2024 Feb 14–15; Kalavakkam, India. Les Ulis, France: EDP Sciences; 2024. 392 p. [Google Scholar]

8. Zangeneh A, Moradzadeh M. Self-healing: definition, requirements, challenges and methods. In: Mahdavi Tabatabaei N, Kabalci E, Bizon N, editors. Microgrid architectures, control and protection methods. Berlin/Heidelberg, Germany: Springer; 2020. p. 509–25. doi:10.1007/978-3-030-23723-3_21. [Google Scholar] [CrossRef]

9. Zhang P, Mansouri SA, Rezaee Jordehi A, Tostado-Véliz M, Alharthi YZ, Safaraliev M. An ADMM-enabled robust optimization framework for self-healing scheduling of smart grids integrated with smart prosumers. Appl Energy. 2024;363:123067. doi:10.1016/j.apenergy.2024.123067. [Google Scholar] [CrossRef]

10. Bagdadee AH, Zhang L. Renewable energy based self-healing scheme in smart grid. Energy Rep. 2020;6(4):166–72. doi:10.1016/j.egyr.2019.11.058. [Google Scholar] [CrossRef]

11. Nedjah N, Cardoso KH, de Macedo Mourelle L. An efficient distributed approach for a self-healing smart grid using minimal spanning tree. Int J Energy Res. 2021;45(10):15049–84. doi:10.1002/er.6783. [Google Scholar] [CrossRef]

12. Nidhya MS, Sharma H, Gupta Aeditors. Optimizing self-healing distribution networks with smart RMUS. In: 2023 International Conference on Power Energy, Environment & Intelligent Control (PEEIC); 2023 Dec 19–23; Noida, India. Piscataway, NJ, USA: IEEE; 2023. p. 1072–76. [Google Scholar]

13. Abdalla O, Mostafa A. Optimal number and locations of smart RMUs for self-healing distribution networks. Int Trans Electr Energy Syst. 2022;2022(1):4819129. doi:10.1155/2022/4819129. [Google Scholar] [CrossRef]

14. Wang J, Wang H. Multi-agent multi-criticality scheduling based self-healing system of power grid. Comput Res Dev. 2017;54:720–30. doi:10.7544/issn1000-1239.2017.20161026. [Google Scholar] [CrossRef]

15. Li G, Peng Z, Yu B. Research on self-healing mode of communication channel of regional power grid stability control system. J Phys Conf Ser. 2021;1982:012157. doi:10.1088/1742-6596/1982/1/012157. [Google Scholar] [CrossRef]

16. El-Tawab S, Saad H, Abdel-Aziz A. Network self-healing by fault detection and clearing using different topologies to restore the system [master’s thesis]. Cairo, Egypt: Al-Azhar University; 2024. [Google Scholar]

17. Hosseini E, Horrillo-Quintero P, Carrasco-Gonzalez D, García-Triviño P, Sarrias-Mena R, García-Vázquez CA, et al. Optimal energy management system for grid-connected hybrid power plant and battery integrated into multilevel configuration. Energy. 2024;294:130765. doi:10.1016/j.energy.2024.130765. [Google Scholar] [CrossRef]

18. Yang H, Zhou W, Lu L, Fang Z. Optimal sizing method for stand-alone hybrid solar-wind system with LPSP technology by using genetic algorithm. Sol Energy. 2008;82(4):354–67. doi:10.1016/j.solener.2007.08.005. [Google Scholar] [CrossRef]

19. Omar N, Monem MA, Firouz Y, Salminen J, Smekens J, Hegazy O, et al. Lithium iron phosphate based battery-Assessment of the aging parameters and development of cycle life model. Appl Energy. 2014;113:1575–85. doi:10.1016/j.apenergy.2013.09.003. [Google Scholar] [CrossRef]

20. Dorigo M, Birattari M, Stützle T. Ant colony optimization. IEEE Comput Mag. 2006;1(4):28–39. doi:10.1109/mci.2006.329691. [Google Scholar] [CrossRef]

21. Dorigo M, Di Caro G editors. Ant colony optimization: a new meta-heuristic. In: Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406); 1999 Jul 6–9; Washington, DC, USA. Piscataway, NJ, USA: IEEE; 1999. p. 1470–77. [Google Scholar]

22. Zhao R, Tan Y, Lu J, Guo W, Du H. A resilient self-healing approach for active distribution networks considering dynamic microgrid formation. Energy Sci Eng. 2024;12(1):230–48. doi:10.1002/ese3.1631. [Google Scholar] [CrossRef]