A Partitioned Yaw Control Algorithm for Wind Farms Using Dynamic Wake Modeling

1  Introduction

Approximately 3% of global energy consumption is supplied by wind energy, and it is predicted that wind energy will supply up to 34% of total electricity demand by 2050 [1,2]. However, wake effects present considerable challenges to the performance and lifespan of wind turbines within wind farms [3,4]. These effects typically cause a 10%–20% reduction in annual energy production and can significantly increase turbine fatigue loads [5,6]. When wind passes through an upstream turbine, it creates a wake characterized by reduced wind speed and increased turbulence intensity downstream. The reduced wind speed lowers the power output of downstream turbines, and increased turbulence subjects turbine blades to complex aerodynamic forces, increasing structural loads and accelerating fatigue [7]. Therefore, effective wake control is critical for optimizing energy capture and ensuring the structural integrity of turbines throughout the wind farm’s operational life.

Wake models are essential for managing wake effects. While Computational Fluid Dynamics (CFD) models offer high accuracy, their computational cost makes them unsuitable for real-time optimization control [8]. Analytical models are thus preferred for control applications. The Jensen model [9], the first analytical wake model, is based on mass conservation. It assumes that the axial wind speed in the wake increases with downstream distance, while the radial wind speed remains uniform. Despite its simplicity and foundational importance, the Jensen model’s uniform velocity deficit assumption is inconsistent with observed wake profiles [10].

The Gaussian wake model [11] addresses these limitations by using a Gaussian distribution for radial wind speed, better representing actual wake patterns. Building on these steady-state analytical models, dynamic wake models have emerged to capture the transient behavior of wakes, which is important for control design under changing wind conditions [12]. The FLORIS model [13] and the dynamic FLORIDyn model [14] (FLOw Redirection and Induction Dynamics) integrate wake models with yaw turbine deflection models based on high-fidelity CFD simulations. FLORIS [15] and FLORIDyn [16] offer improved wake modeling capabilities. FLORIDyn provides dynamic representations of wind farm wake development and distribution, enabling more accurate simulations.

As wind farms become larger and control strategies more advanced, optimization challenges increase. Recent research explores sophisticated techniques like coordinated pitch and yaw control using deep reinforcement learning [17] and yaw optimization strategies considering fatigue load constraints [18]. While these advanced methods show promise, their computational demands can be significant, especially for large farms. Combined yaw and pitch control strategies [19,20] also add complexity. To mitigate complexity, a wind farm partitioning approach allows for independent optimization of smaller sections. Existing partitioning methods often rely on simplified wake models, which may not accurately capture the complex wake interactions in large wind farms, leading to suboptimal control strategies [21–24]. For example, some methods [21] use the simplified Park wake model, a 2D model that cannot account for non-uniform velocity distribution, turbulence intensity, or vertical height differences. Others [22,23] use the Jensen model, neglecting turbulence intensity effects. While the Gaussian model is used [24], significant simplifications to the velocity decay formula are introduced, overlooking vertical height effects. These simplifications can result in inaccurate assessments of wake interactions and limit the effectiveness of the partitioning and control strategies.

These limitations highlight a critical need for wake interaction algorithms that accurately capture the impacts of turbulence intensity and vertical height, which are crucial for accurate wake interaction modeling and optimizing wind farm partitioning and control.

To address these challenges, this paper proposes a partitioned yaw control optimization algorithm based on the 3D dynamic FLORIDyn model. By incorporating turbulence intensity and vertical height effects, the FLORIDyn model enhances the accuracy of wake interaction calculations and improves overall wind farm power generation. The main contributions of this study are as follows: (1) The dynamic simulation process of the FLORIDyn wake model is refined, detailing the calculation of effective wind speed and the quantitative assessment of wake influence relationships among turbines. (2) A wind farm partitioning method is proposed, dividing the farm into decoupled partitions to simplify control problem complexity. (3) A heuristic control algorithm tailored to the FLORIDyn model is developed and demonstrated to enhance total wind farm power generation.

The remainder of this paper is structured as follows: Section 2 analyzes the FLORIDyn wake model, detailing the calculation of effective wind speed and the quantitative assessment of wake influence relationships among turbines. Section 3 presents a wind farm partitioning algorithm based on these relationships. Section 4 designs a heuristic control algorithm for partitioned yaw optimization. Section 5 evaluates the algorithm’s effectiveness through simulations. Finally, Section 6 concludes the paper, summarizing key findings and outlining directions for future research.

2  FLORIDyn Wake Model

The FLORIDyn wake model [16] is a three-dimensional dynamic simulation framework used to calculate wind turbine power output considering wake evolution and propagation (see Fig. 1 for a visualization). It extends steady-state engineering models like FLORIS by incorporating dynamic effects such as the time delay for wake advection and dynamic wake meandering. This study utilizes the core components of the FLORIDyn framework, including the Gaussian wake model for velocity deficits, the Jimenez model for yaw-induced wake deflection, and the sum-of-squares method for combining multiple wake effects. FLORIDyn simulates 3D wake characteristics, accounting for turbulence intensity and vertical wind shear (via the power law, Eq. (1)), which is crucial for the accurate assessment of wake interactions needed for the partitioning algorithm proposed herein. The model operates by dynamically evolving the state of wake structures downstream from each turbine. While suitable for transient simulations, this study uses the FLORIDyn framework to compute the quasi-steady-state wake interactions corresponding to specific inflow conditions and yaw settings, which then inform the partitioning and optimization. The FLORIDyn framework has been validated against high-fidelity CFD simulations and field measurements, demonstrating good agreement in predicting wake behavior under various operating conditions. The specific parameters configuring the atmospheric conditions and turbine characteristics for the simulations in this paper (e.g., turbulence intensity, shear exponent) are detailed in the Case Study (Section 5). For the fundamental model equations and implementation details, readers are referred to the original FLORIDyn literature 16.

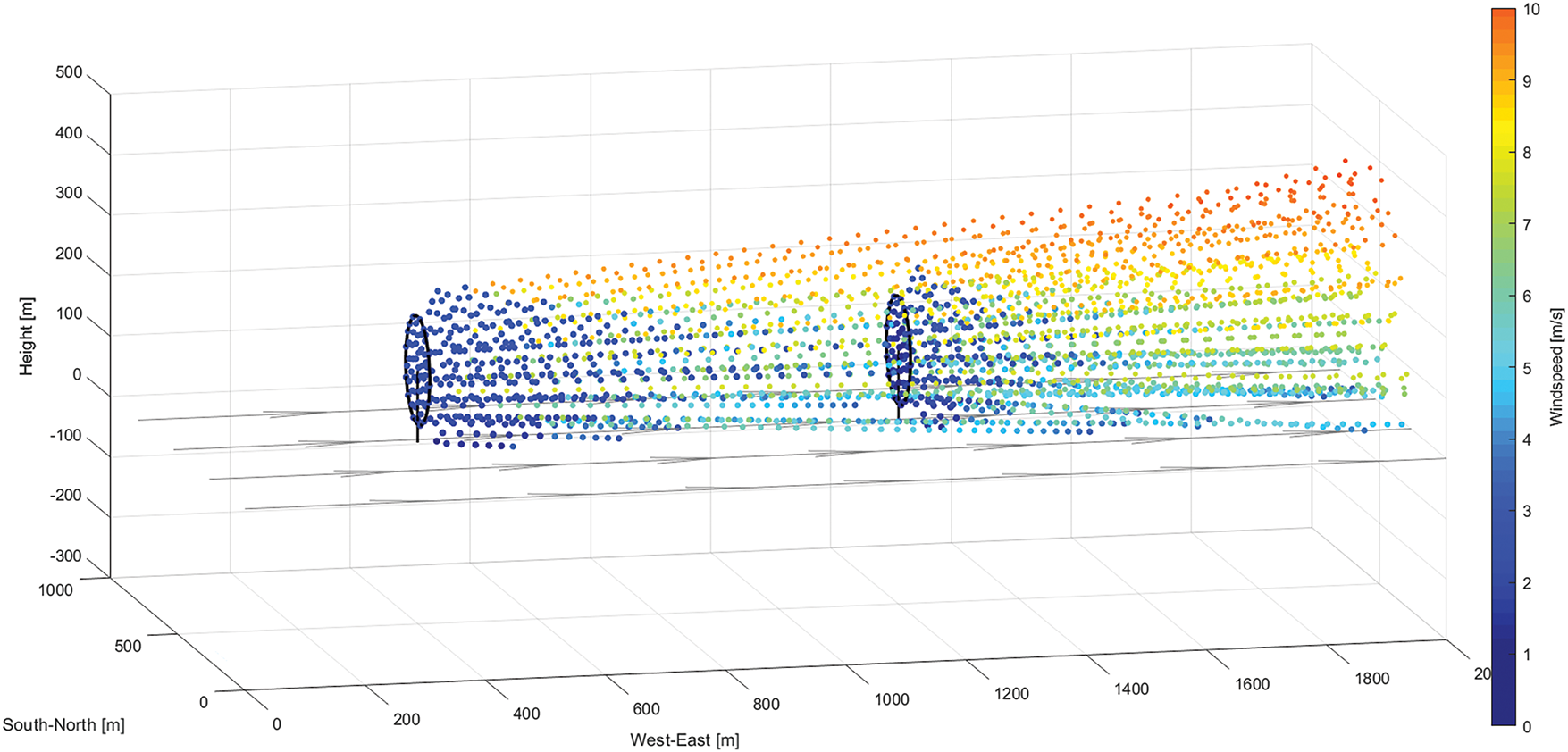
Figure 1: FLORIDyn model

The FLORIDyn model builds upon the Gaussian wake model [11] and dynamically generates Observation Points (OPs) on the wind turbine’s surface during each simulation step. These OPs characterize the local Gaussian FLORIS wake properties at their respective positions. Each observation point inherits state parameters from its associated wind turbine, such as yaw angle, turbulence intensity, and thrust coefficient. These parameters are then used to calculate the wind speed deficit and deflection within the FLORIDyn framework’s wake calculation routines.

The effective wind speed at an observation point is calculated using the following Eq. (1):

ueff,OP=ufree,OP(zOPz0)α(1−rown)∏i=1nT(1−ri)(1)

where

•   ufree,OP is the free-stream wind speed at the observation point [m/s]. A typical value would be the measured or estimated wind speed at the turbine location without considering wake effects.

•   zOP is the height of the observation point above the ground [m], and is the roughness length of the terrain [m], which accounts for surface irregularities. The roughness length typically ranges from 0.0001 m (for smooth surfaces like ice) to 0.1 m or higher (for rough terrain with vegetation or obstacles).

•   α is the wind shear exponent, describing the variation of wind speed with height (dimensionless). It usually ranges from 0.1 to 0.3, depending on atmospheric stability.

•   rown denotes the reduction in wind speed at the observation point caused by the wake generated by the turbine itself (dimensionless). This value depends on the turbine’s thrust coefficient and the wake’s characteristics.

•   nT is the number of turbines, and represents the wake influence of the i-th upstream turbine (dimensionless).

The effective wind speed for a wind turbine is then determined by summing the weighted effective wind speeds of all observation points on its surface [16]:

ueff,T=∑i=1nopwiueff,OP,i(2)

where denotes the total number of observation points, and represents the corresponding weight.

While FLORIDyn offers improved accuracy compared to simpler wake models, it also has a higher computational cost. This trade-off between accuracy and computational efficiency should be considered when applying FLORIDyn in real-time control scenarios or for very large wind farms. Understanding the strengths and limitations of FLORIDyn, Section 3 will build upon its accuracy to develop a method for quantifying the wake influence relationships between turbines, which is critical for effective partitioning.

To provide a clear overview of the proposed approach, Fig. 2 presents a master flowchart illustrating the entire workflow. This flowchart details the process starting from the input parameters (wind farm layout, wind conditions), proceeding through wake influence analysis using FLORIDyn, partitioning the farm based on these influences, performing heuristic yaw optimization within each partition, and finally synthesizing the optimized yaw angles for the entire wind farm. Subsequent sections will elaborate on each key stage depicted in the flowchart.

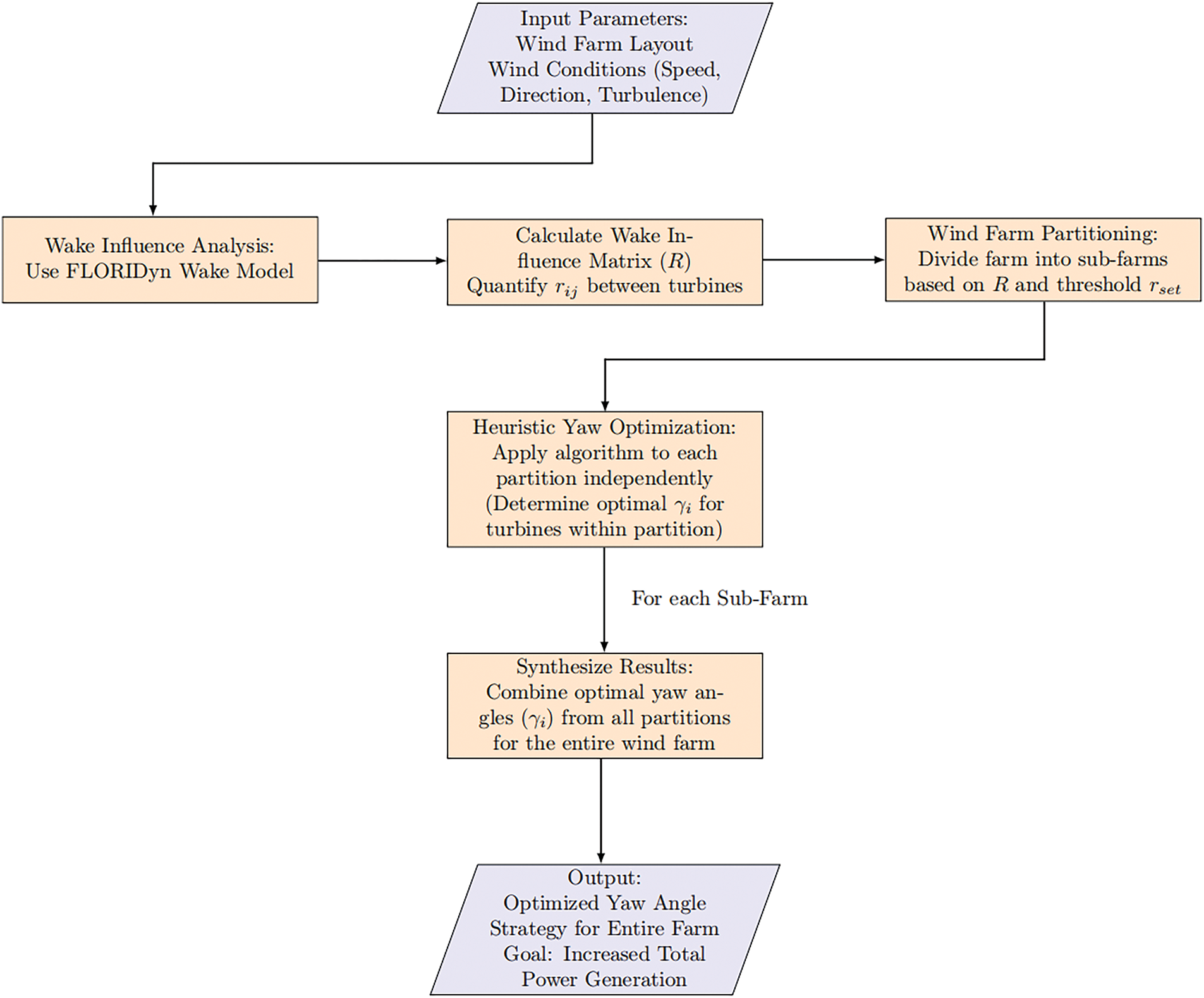
Figure 2: Overall methodology of the proposed partitioning-based yaw control algorithm

3  Analysis of Wind Turbine Wake Influence Relationship

The wake effect in wind farms creates coupling between the effective wind speeds of different wind turbines. This coupling results from the influence of the wake generated by an upstream turbine on downstream turbines. This study quantifies this influence using the FLORIDyn dynamic wake model. Let denote the FLORIDyn-calculated fractional wind speed reduction that turbine experiences due to the wake of turbine i. The relationship matrix R, representing the influence among all turbines in the wind farm, can be expressed as:

R=[r11⋯r1nT⋮⋱⋮rnT1⋯rnTnT](3)

where is the number of turbines, indicates that turbine has a non-zero wake influence on turbine j, and confirms the unidirectional nature of the wake influence, where the upstream turbine affects the downstream turbine but not vice versa. The calculation of inherently accounts for the relative spatial positions (distances and angles) between turbines, as FLORIDyn simulates wake propagation within the 3D farm layout defined by the input turbine coordinates.

By treating(the transpose of R) as the adjacency matrix of a directed graph DR, the wind turbines in the wind farm can be represented as nodes, and the directed edges between nodes represent the wake influence relationships. To simplify analysis and control, the directed edges in can be converted into undirected edges, resulting in an undirected graph GR. The connected components of can then be used to partition the wind farm into sub-wind farms. Each connected component corresponds to a sub-wind farm where turbines are mutually influenced by wakes, but no wake influence exists between turbines in different sub-wind farms. This partitioning facilitates independent optimization and control of each sub-wind farm. Note that turbines can have an in-degree and out-degree of zero. If a turbine has both zero in-degree and out-degree, it forms a sub-wind farm by itself, as it neither influences nor is influenced by any other turbines. In other cases, a grouping of turbines could have a zero in-degree and out-degree. These turbines can also be defined as micro-wind farms.

From Eq. (1), the effective wind speed ueff,T of a turbine can be expressed as:

ueff,T=∑i=1n∞[wiufree,OP,i(zOP,iz0)α(1−rown,i)∏j=1nT(1−rj,OP,i)](4)

where:

•   ueff,T is the effective wind speed of the turbine.

•   n∞ is the number of observation points (OPs) on the turbine’s surface.

•   ufree,OP,i is the free-stream wind speed at the i-th OP.

•   zOP,i is the height of the i-th OP.

•   rown,i accounts for the reduction in wind speed due to the turbine’s own wake.

•   rj,OP,i represents the wake influence of the j-th turbine on the i-th OP.

The degree of wake influence between two turbines can then be determined using:

rij=∑k=1nOP,j[wk(zOP,kz0)α(1−rown,k)ri,OP,k](5)

where denotes the number of observation points on turbine j, and captures the wake influence of turbine on the k-th observation point of turbine j, is the weighting factor for the k-th OP, accounts for the wind shear effect at the OP’s height, represents the reduction due to turbine j’s own wake at that OP, and is the specific wake deficit factor (0 to 1) at the k-th OP of turbine caused by the wake from turbine i, as computed by the FLORIDyn simulation. This computation within FLORIDyn uses the provided turbine locations and wind direction to determine the interaction strength.

To simplify the turbine influence relationship, a threshold is introduced, where edges with are ignored. The simulations in Section 5 are used, meaning that wake influences below 1% are considered negligible. The sensitivity of the results to this parameter is analyzed in Section 5. Figs. 3 and 4 illustrate the influence relationships between turbines and the resulting wind farm partitioning.

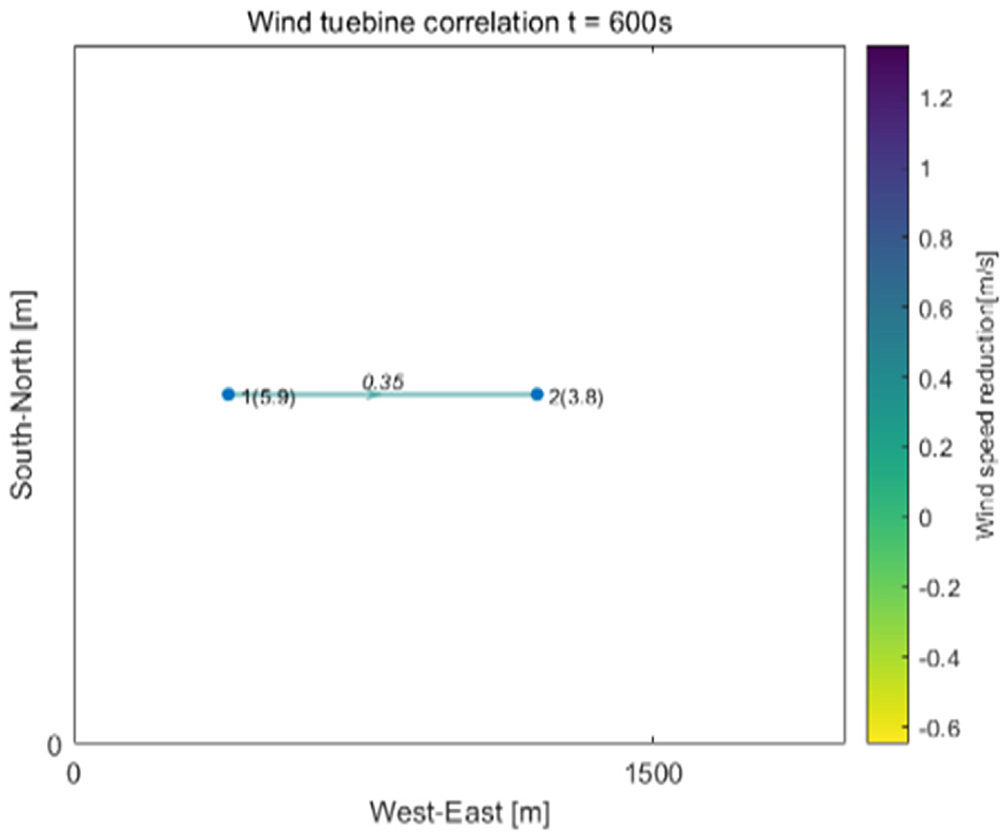
Figure 3: The influence relationship between turbines

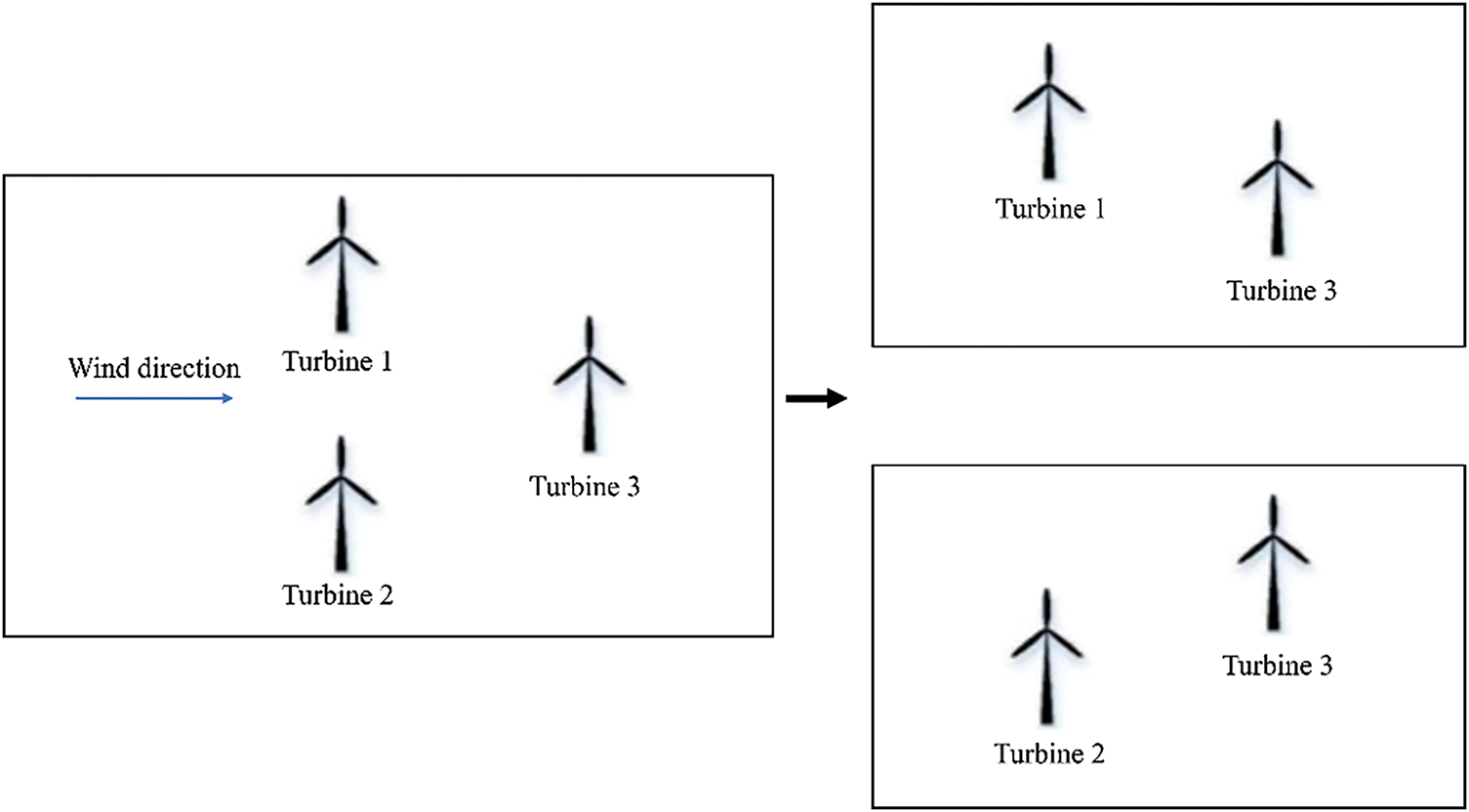
Figure 4: Wind farm partitioning diagram

This approach promotes efficient wind farm modeling and control by reducing computational demands and facilitating modular optimization strategies. Having established a method for analyzing wake influence, the subsequent section will detail the wind farm partitioning algorithm based on these relationships, enabling a more structured approach to control optimization.

4  Multi-Turbine Wind Farm Partitioning Algorithm

In this paper, a wind turbine that does not produce a wake influence on other turbines in the wind farm is defined as the most downstream turbine. These turbines play a critical role in the proposed wind farm partitioning method. The partitioning strategy involves dividing the wind farm based on the most downstream turbines, ensuring that each sub-wind farm includes at least one downstream turbine. This ensures that the optimization and control strategies applied to each sub-wind farm can be seamlessly aggregated to generate an overall yaw strategy for the original wind farm.

4.1 Partitioning Multi-Turbine Yaw Control Framework

For the most downstream turbines, their optimal yaw strategy follows a greedy control approach, where the yaw angle is always set to 0∘. This ensures that the turbine captures the maximum wind energy without disrupting upstream turbines, thereby avoiding conflicts when the yaw strategies for all turbines in the original wind farm are synthesized.

The steps for generating sub-wind farms using this partitioning algorithm are as follows:

1.    Identify the Most Downstream Nodes: Using the directed graph DR, the turbines corresponding to nodes with an out-degree of zero are identified. These turbines are classified as the most downstream turbines. If a node has both zero out-degree and in-degree, it forms a sub-wind farm by itself, as it neither influences nor is influenced by any other turbines. For other nodes with zero out-degree, they are added to the set Vds, which represents the collection of most downstream turbines.

2.    Construct the Undirected Graph: The undirected graph is obtained by converting all directed edges in into undirected edges. Nodes inand their associated edges are removed from to form a reduced graph GR′. The connected components in are then identified using a union-find data structure, which efficiently determines groups of turbines that are mutually influenced by wake effects.

3.    Form Sub-Wind Farms: For each connected component in GR′, the turbines within the component are grouped to form a sub-wind farm. Additionally, any turbines in that are connected to the component in the original graph are added to the same sub-wind farm. This ensures that all wake influence relationships are preserved within each sub-wind farm.

4.    Output the Sub-Wind Farms: The sub-wind farms obtained in the previous steps 1 and 3 represent the final partition of the wind farm. Each sub-wind farm can be independently optimized and controlled, and the yaw strategies of the turbines in all sub-wind farms are combined to generate the overall yaw strategy for the original wind farm.

The steps for generating sub-wind farms using this partitioning algorithm are detailed in Algorithm 1.

This algorithm simplifies the optimization problem by dividing it into smaller, independent sub-problems while ensuring that the control strategies for all turbines remain consistent and coherent. The partitioning method leverages the structural properties of the directed graph and its undirected counter part to efficiently identify groups of turbines that can be optimized separately. This is particularly beneficial for large-scale wind farms, where complex wake interactions make direct optimization computationally infeasible. By introducing the set to account for most downstream turbines and employing graph-based techniques to detect connected components, the proposed method ensures both scalability and accuracy. This partitioning method provides a foundation for the heuristic control algorithm detailed in the next subsection.

4.2 Heuristic Control Algorithm Design

Within the multi-agent system control framework, a heuristic control algorithm is developed to optimize the yaw strategy of the wind farm. This algorithm reduces the computational complexity of yaw optimization by decomposing the problem into smaller, manageable sub-problems. The key idea is to represent the wake influence relationship between turbines as a directed graph and then use depth-first search (DFS) to guide the sequential optimization of turbines. The process is as follows:

First, the wind farm or each sub-wind farm (after partitioning) is represented as a directed graph DR=(V,E), where the nodes V correspond to turbines, and the directed edges represent wake influence relationships between turbines. The depth of each node, denoted as Depv, is initialized to zero for all nodes:

Depv←0,∀v∈V(6)

Next, nodes in with an in-degree of zero are identified. These nodes represent turbines that are not affected by the wake of any other turbines. Their depth is updated to 1:

Depv←1,∀in(v)=0(7)

where denotes the in-degree of node v. Starting from these nodes, a depth-first search (DFS) is performed to update the depth of other nodes. For a directed edge (u,v)∈E, the depth of node is updated to the maximum of its current depth and the depth of node plus 1:

Depv←max(Depu+1,Depv),∀(u,v)∈E(8)

Once the depth of all nodes is determined, the turbines are optimized sequentially in ascending order of their depth. For turbines at the same depth, the optimization order is determined randomly. During the optimization process, the yaw angles of turbines that have not yet been optimized are initialized to 0∘, and the yaw angles of turbines already optimized are kept unchanged.

The optimization objective for each turbine is designed to align with the overall goal of the wind farm. If the overall goal is to maximize the power output of the wind farm, the objective for each turbine is to maximize the combined power of itself and the turbines affected by its wake:

maxyawu(Pu+∑(u,v)∈EPv)(9)

where represents the power output of turbine u, and accounts for the power outputs of downstream turbines affected by the wake of turbine u. If the overall optimization goal differs, the objective for each turbine agent can be modified accordingly.

The choice of Depth-First Search (DFS) for determining the optimization order is motivated by its simplicity and efficiency in traversing directed graphs. DFS allows for a straightforward identification of the topological order of turbines based on wake influence, ensuring that upstream turbines are optimized before downstream turbines.

A tailored heuristic approach, rather than a standard meta heuristic like Genetic Algorithms (GA) or Particle Swarm Optimization (PSO), is employed for the yaw optimization step within each partition. This decision is primarily driven by the need for extreme computational efficiency and seamless integration with the partitioning framework. Standard meta heuristics, while powerful, typically involve iterative population updates and numerous objective function evaluations (requiring repeated FLORIDyn simulations), which can still be computationally demanding, even within partitions. The proposed heuristic, detailed below, leverages the calculated depths directly, optimizing each turbine sequentially in a single pass. It is specifically designed for speed and simplicity, directly utilizing the graph structure derived from the wake analysis. While heuristics do not guarantee global optimality, this approach provides a practical trade-off between computational cost and solution quality, aiming for significant power improvements with minimal overhead, making it suitable for potential real-time or frequent optimization cycles. Empirical results in Section 5 demonstrate its effectiveness. Although other optimization techniques could be adapted, the proposed method prioritizes scalability and efficient integration within the partitioning context.

This heuristic control algorithm can be summarized as follows:

(1)   Graph Construction: Represent the wind farm as a directed graph based on the wake influence relationships between turbines. Initialize the depth of all nodes in the graph to zero.

(2)   Depth Calculation: Identify nodes with zero in-degree and set their depth to 1. Perform a DFS to calculate the depth of remaining nodes, ensuring that the depth of each node reflects the longest path from a zero in-degree node.

(3)   Yaw Angle Optimization: Optimize turbines sequentially in ascending order of their depth. For turbines at the same depth, determine the optimization order randomly. Design the optimization objective for each turbine to align with the overall goal of the wind farm.

The algorithm flow diagram is presented in Fig. 5, which outlines the steps involved in determining the optimal yaw angle for each turbine. This diagram illustrates how environmental wind conditions, upstream turbine yaw angles, and downstream turbine power outputs are integrated into the decision-making process.

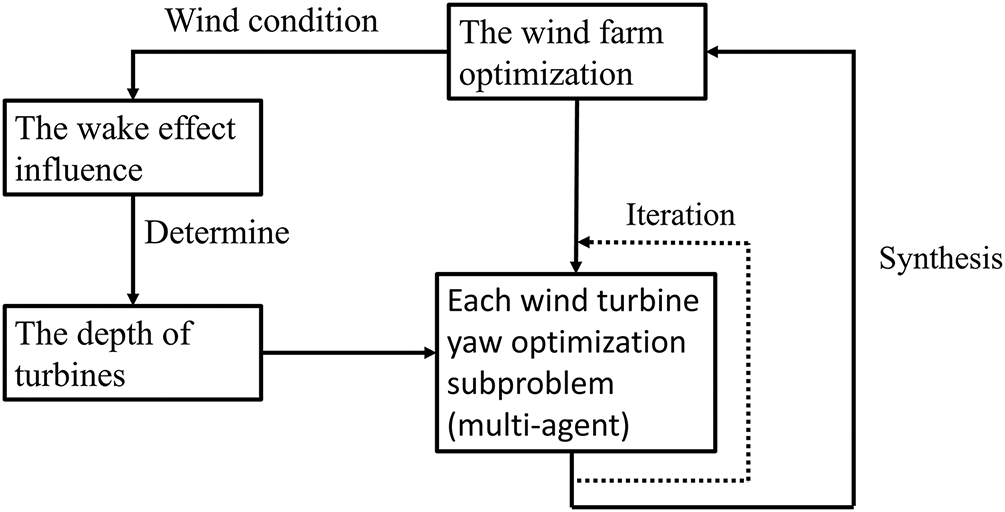
Figure 5: Yaw control algorithm flow diagram

This approach reduces the computational complexity of yaw optimization by dividing the problem into smaller sub-problems. In each sub-problem, only turbines with wake influence relationships are considered, simplifying the computation. The solutions to these sub-problems are then aggregated to form the yaw optimization strategy for the entire wind farm. The performance of the algorithm depends on how well the individual turbine objectives are aligned with the overall wind farm optimization goal and the accuracy of the wake model in predicting wake interactions. With the partitioning and heuristic control algorithm established, Section 5 will present a case study to evaluate the effectiveness of this approach in enhancing overall power output.

5  Case Study

This section presents an evaluation of the partition control algorithm’s optimization effect on both an 11-turbine and a 28-turbine wind farm. The primary objective is to demonstrate the algorithm’s effectiveness in enhancing overall power output through yaw angle optimization without iterative processes.

The FLORIDyn model is used to analyze wake effects and calculate individual turbine power outputs based on specified environmental conditions. This study utilizes specific, representative wind condition scenarios rather than time-series data to clearly demonstrate the algorithm’s effectiveness under defined states. For the main case studies, the model is configured with a turbulence intensity (TI) of 0.06 and a wind shear exponent of 0.2, which are typical values for onshore wind farms. Standard air density is assumed. The specific wind speeds and directions for each case are detailed in Table 1.

The optimization process involves decision-making at each turbine agent level based on several factors: the prevailing environmental wind conditions, the yaw angles of upstream turbines whose wakes impact the current turbine, and the power generated by downstream turbines. The optimal yaw angle for each turbine is determined in a single step, reducing the computational time required for optimization.

5.1 11-Turbine Wind Farm

Table 1 outlines the specific, constant environmental parameters used for the 11-turbine simulation scenario, including the inflow wind speed, wind direction, and turbulence intensity. The wind shear exponent was set to 0.2 (as mentioned above) With these settings, the wake influence relationships among all turbines are computed, resulting in a matrix representing the degree of interaction between turbines. Edges with weights less than 0.01 in this matrix are disregarded to simplify the network and focus on significant interactions. This threshold, rset=0.01, was chosen as a starting point based on initial testing. Values significantly lower led to complex, highly interconnected networks that were computationally expensive to solve, while higher values risked neglecting potentially important wake interactions. A more detailed sensitivity analysis is presented later in this section.

Subsequently, the depth of each turbine node is calculated following the methodology in Section 3. Depth refers to the number of intermediate nodes (turbines) between a given turbine and the farthest downstream turbine it influences. This calculation allows for the partitioning of the turbines into groups, as summarized in Table 2. Each partition is treated as a subsystem, improving the efficiency of the optimization process.

The methodical approach results in a more efficient algorithm and a clearer understanding of the dynamics within the wind farm. Each zone, as defined in Table 2, represents a cluster of turbines that share similar wake interaction characteristics. This segmentation facilitates a focused optimization strategy that considers the unique operational conditions of each turbine group.

Fig. 6 illustrates the wake influence relationship diagram for the 11-turbine wind farm. This diagram visualizes the interactions between turbines, particularly in terms of wake effects.

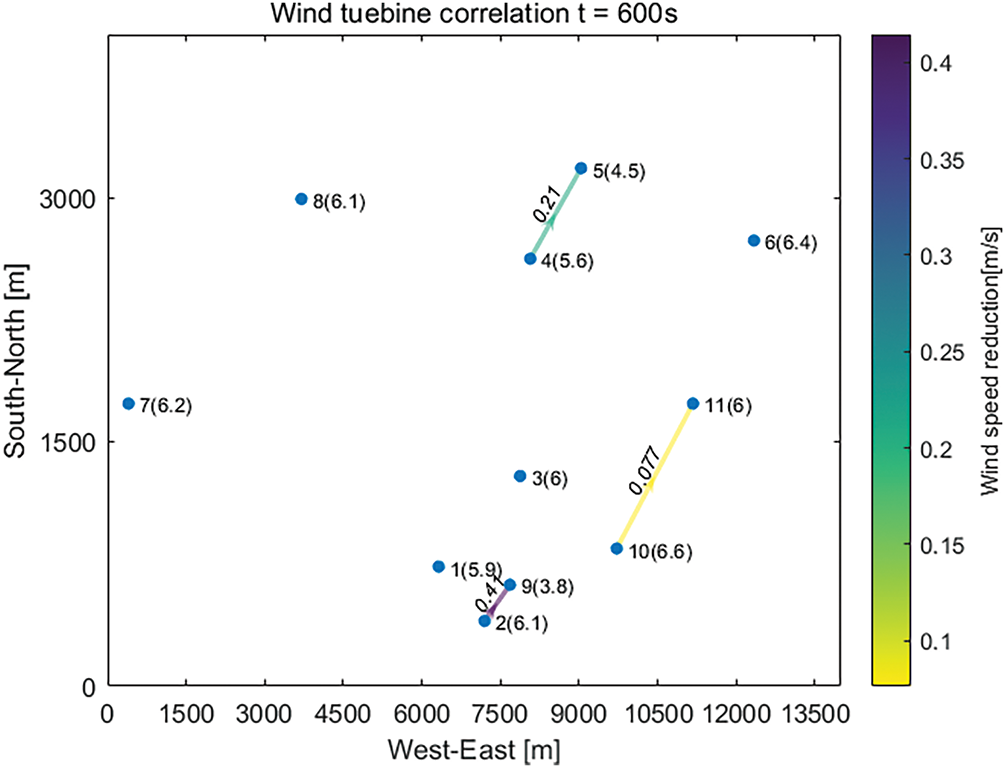
Figure 6: Wake influence relationships in the 11-turbine wind farm

The search algorithm employed to find the optimal yaw angle for each turbine considers the depth size, which indicates the number of intermediate turbines between a given turbine and the farthest downstream turbine it influences. For example, turbines 2, 4, and 5 are optimized to yaw at 40.8°, −30.6°, and −15.6°, respectively. These adjustments are made to redirect wakes away from downstream turbines in zones 1 and 2, thereby increasing their effective wind speeds and power output. Consequently, the total power output of the 11-turbine farm increased from 1033.074 kW under a “direct wind strategy” to 1128.936 kW after yaw optimization, representing an increase of 9.78%. The “direct wind strategy” refers to a baseline scenario where all turbines are aligned with the incoming wind direction (i.e., zero yaw angle), without any active wake control. This is a common practice baseline for evaluating the performance of wake steering algorithms.

5.2 28-Turbine Wind Farm

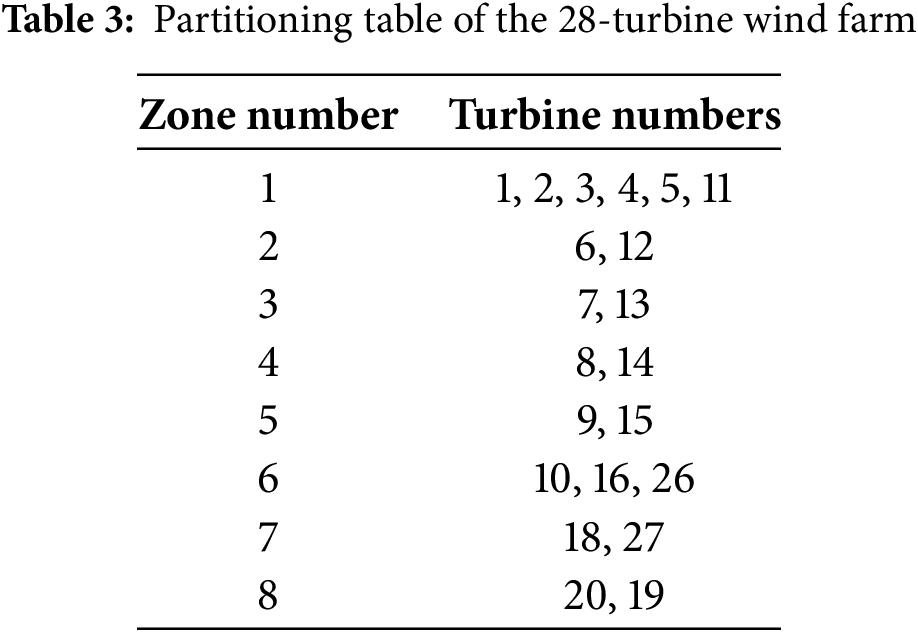
Next, the same algorithmic approach is applied to a larger wind farm comprising 28 turbines. The simulation environment parameters for this larger farm remain consistent with those used for the 11-turbine farm; however, the wind direction is set at −45°. The wake influence relationships among turbines in the 28-turbine wind farm are calculated as depicted in Fig. 7. Using the method outlined in Section 4, the distance-weighted relationship matrix is obtained, where edges with weights less than 0.01 are ignored to simplify the network analysis. Subsequently, the depth of each turbine node is calculated, leading to the partitioning of turbines as detailed in Table 3.

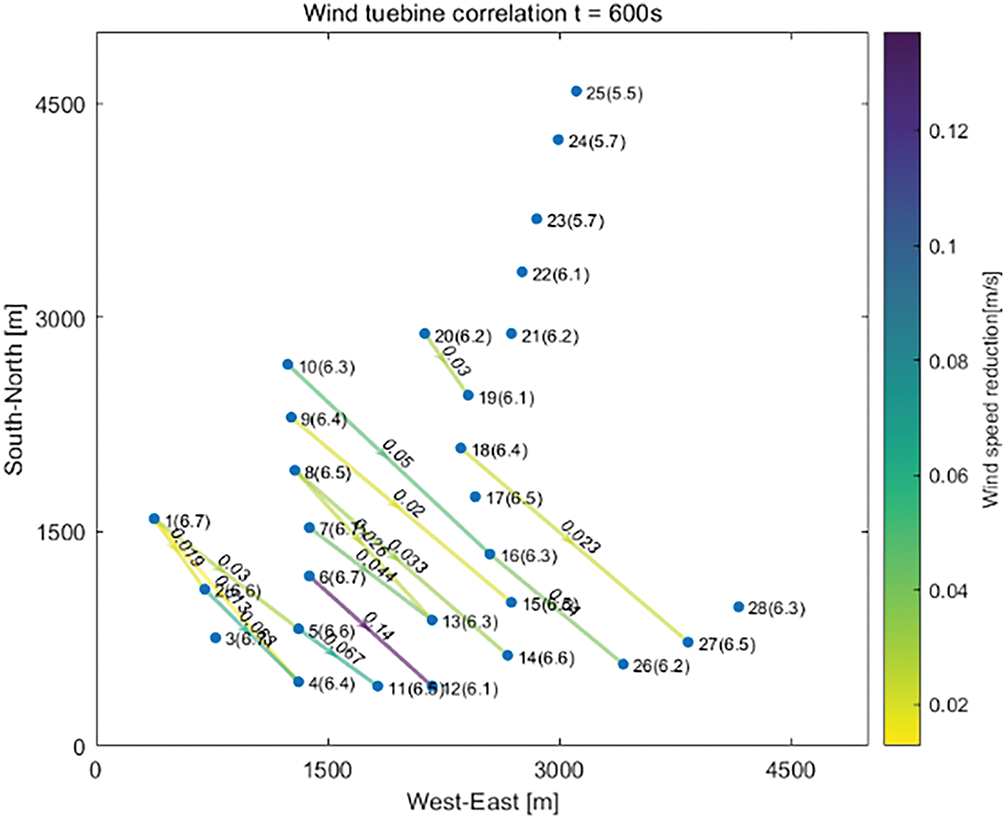
Figure 7: Wake influence relationships in the 28-turbine wind farm

The optimal yaw angles that maximize the power output are obtained using the search algorithm based on the calculated depth sizes. These results are summarized in Table 4, and the corresponding wake distribution after yaw optimization is shown in Fig. 8.

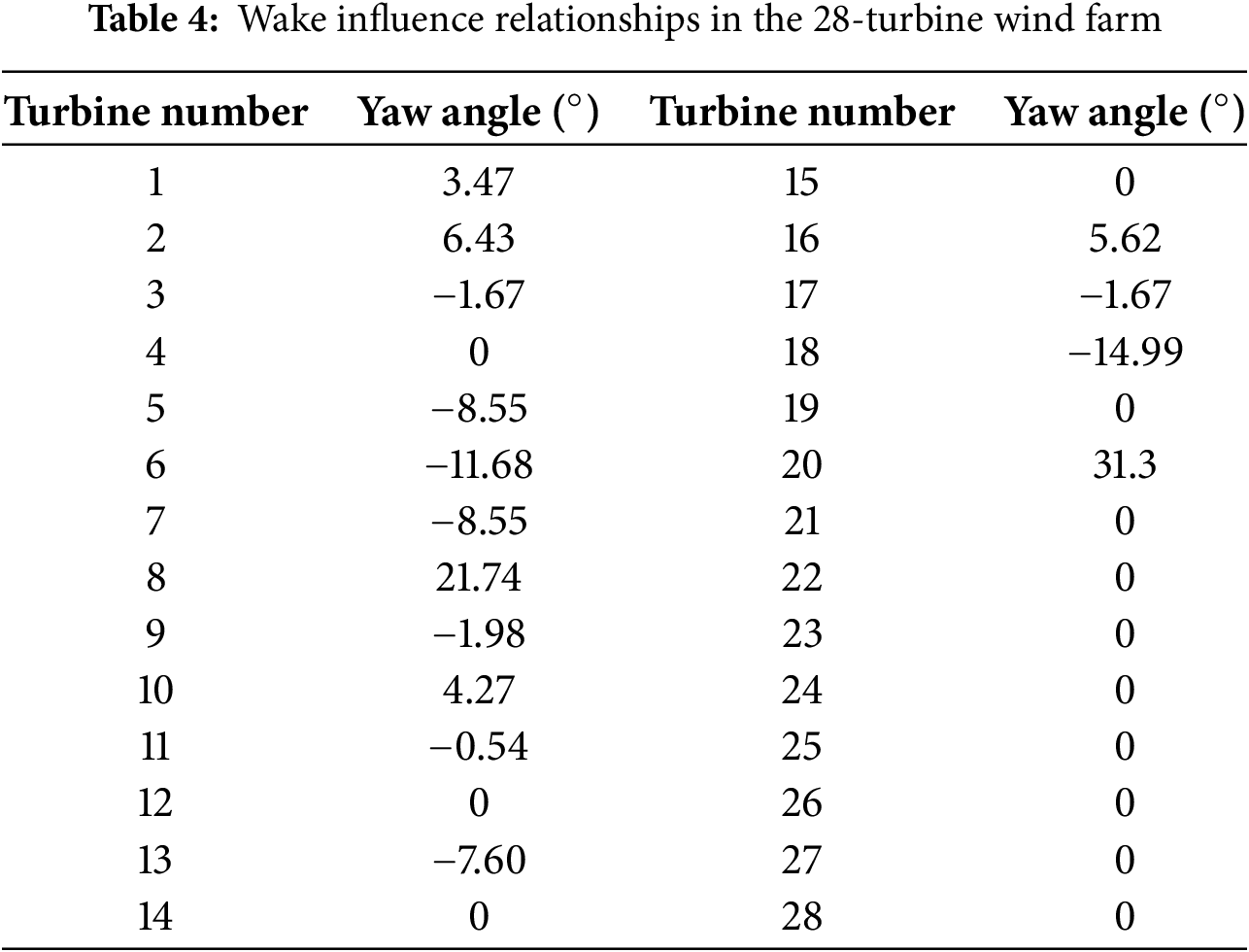
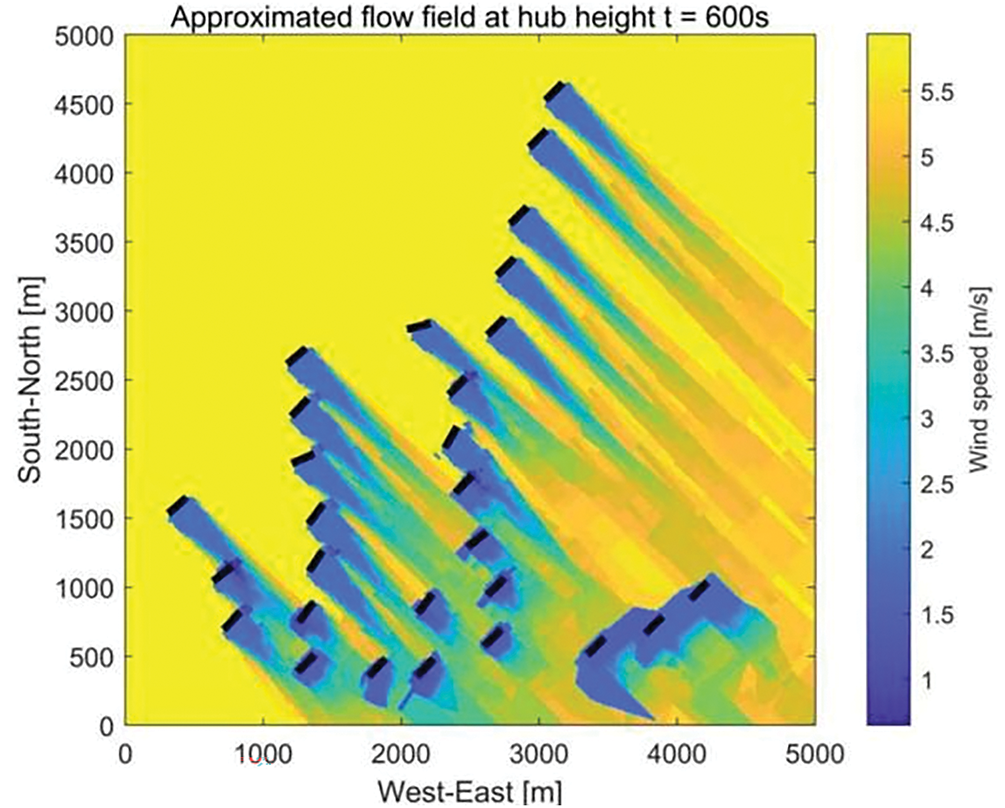
Figure 8: Wake distribution after yaw optimization in the 28-turbine wind farm

As a result of these optimizations, the total power output of the 28-turbine farm improved from 46,219.822 kW under a direct wind strategy to 47,044.185 kW post-yaw optimization, marking an increase of 1.78%. While this percentage increase may seem modest, it is important to consider the already optimized baseline power output achieved with the direct wind strategy. The yaw adjustments, particularly for turbines in zones 1, 2, and 4, contribute to this increase by mitigating wake effects on downstream turbines. For instance, the yaw angle of turbine 20 is significantly adjusted to 31.3 degrees. This adjustment can potentially redirect its wake away from turbine 19, thereby improving the latter’s power capture. It is important to note that the 1.78% increase, although seemingly small, could represent a significant absolute power gain for a large wind farm, translating to substantial economic benefits over time.

The relatively small power increase in the 28-turbine case compared to the 11-turbine case may be attributed to the higher turbine density and more complex wake interactions in the larger wind farm. In denser wind farms, the wake from one turbine can be affected by multiple upstream turbines, creating a cascading effect that makes it more difficult to optimize individual turbine yaw angles. One potential reason for the limited improvement in the 28-turbine case is the heuristic nature of the control algorithm. The algorithm’s performance is also influenced by the choice of rset, which determines the threshold for considering wake interactions.

5.3 Sensitivity Analysis

To further validate the algorithm’s effectiveness and assess the impact of the parameter, a sensitivity analysis and yaw optimizations were conducted across 100 different environmental wind conditions, characterized by wind speeds ranging from 4 to 12 m/s and a fixed wind direction of 180°. For the sensitivity analysis, three different values, specifically, 0.005, 0.01, and 0.015, were used to evaluate the performance of the proposed method under different conditions. Under these varied conditions, the average power increase was 1.12%, 1.27% and 1.18%, respectively, demonstrating the robustness and reliability of the proposed method in improving wind farm output power. The size of the sub wind farms vary with values, for values of 0.005, 0.01, and 0.015, the average number of turbines in each sub wind farm is 4.2, 3.8 and 3.1, respectively. The computational time for partitioning and optimization of the 28-turbine wind farm was approximately 15 min on a standard desktop computer with an Intel Core i7 processor and 16 GB of RAM.

The sensitivity analysis indicates that the algorithm’s performance is relatively stable across different values. The optimal value appears to be around 0.01, which balances the need to capture significant wake interactions with the desire to simplify the optimization problem.

5.4 Result

In summary, despite several assumptions made in the development and evaluation phases, the FLORIDyn wake model demonstrated superior accuracy when compared to simpler models. The precision of this model is closely tied to the quality of input data and the validity of its underlying physical assumptions. For the simulations, typical values for onshore wind farms were adopted, such as turbulence intensity and wind shear exponent, ensuring practical relevance.

This study advances previous research by integrating a dynamic wake model and partitioning strategy within a heuristic optimization framework, specifically focusing on wind farm control. Prior studies have already highlighted yaw control’s effectiveness in reducing wake effects and boosting power output. The proposed algorithm takes this a step further by offering a scalable and computationally efficient method for managing wind farms.

One notable advantage of this approach is its distributed nature, facilitating parallel processing which minimizes communication overhead—a stark contrast to more centralized control methods. Additionally, the heuristic yaw control algorithm, chosen for its simplicity and speed over more complex meta heuristics, is straightforward to implement and demands minimal computational resources, making the overall approach highly accessible and scalable.

The efficacy of applying the partition control algorithm to both 11-turbine and 28-turbine wind farms has been confirmed, showing significant improvements in power generation efficiency through strategic adjustments of yaw angles. This methodology not only enhances power output but also presents a scalable solution that can adapt to different wind farm sizes and varying environmental conditions, thereby setting a new benchmark for wind farm optimization strategies.

6  Conclusion

This study developed and evaluated a wind farm partitioning control algorithm utilizing the FLORIDyn dynamic wake model. By quantifying wake interactions using FLORIDyn, the algorithm partitions the farm into computationally manageable zones based on influence relationships exceeding a defined threshold. A heuristic yaw control optimization, guided by turbine depth within the partitioned structure, is then applied sequentially.

Testing on 11-turbine and 28-turbine wind farm case studies demonstrated the algorithm’s effectiveness, yielding power generation increases of 9.78% and 1.78%, respectively, compared to baseline operation without yaw control. These results highlight the algorithm’s ability to enhance power output while significantly reducing the computational complexity associated with optimizing large farms. The sensitivity analysis also indicated robustness across various wind conditions, with an optimal rset value around 0.01 providing a good balance between capturing relevant interactions and simplifying the problem.

Compared to traditional methods relying on simplified wake models or computationally intensive centralized control, the proposed approach offers a scalable balance between accuracy (leveraging FLORIDyn) and efficiency (through partitioning and heuristic optimization). The modular nature of the partitioning strategy facilitates adaptation to varying wind conditions and farm layouts. While demonstrating promise, future work should focus on validation with real-world data, comparison with other advanced control strategies, and extension to offshore applications.

Acknowledgement: The authors would like to express their sincere gratitude to China South Power Grid Co., Ltd. for the generous support and funding provided for this research.

Funding Statement: This paper is supported by the Science and Technology Project of China South Power Grid Co., Ltd. under Grant No. 036000KK52222044 (GDKJXM20222430).

Author Contributions: Yinguo Yang: Data analysis, experimental validation. Lifu Ding: Algorithm design, manuscript writing. Yang Liu: Technical discussions, experimental validation. Bingchen Wang: Code development, experimental testing. Weihua Wang: Data analysis, experimental validation. Ying Chen: Conceptual framework, project supervision. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Liu B, He Z, Jin H. Wind power generation status and development trend. J Northeast Dianli Univ. 2016;36(2):7–13. [Google Scholar]

2. China Renewable Energy Society Wind Energy Professional Committee. China Wind power hoisting capacity statistics Briefing in 2022. Wind Energy, 2023(4):40–56. [Google Scholar]

3. Zhao R. Research on power optimization Method of wind farm based on Active Wake control [PhD thesis]. Xi’an, China: Xi’an University of Technology; 2021. [Google Scholar]

4. Vølund P. Loads on a horizontal axis wind turbine operating in wake. J Wind Eng Ind Aerodyn. 1992;39(1–3):317–28. doi:10.1016/0167-6105(92)90556-P. [Google Scholar] [CrossRef]

5. Barthelmie RJ, Jensen LE. Evaluation of wind farm efficiency and wind turbine wakes at the Nysted offshore wind farm. Wind Energy. 2010;13(6):573–86. doi:10.1002/we.408. [Google Scholar] [CrossRef]

6. Hansen KS, Barthelmie RJ, Jensen LE, Sommer A. The impact of turbulence intensity and atmospheric stability on power deficits due to wind turbine wakes at Horns Rev wind farm. Wind Energy. 2012;15(1):183–96. doi:10.1002/we.512. [Google Scholar] [CrossRef]

7. Sun J, Chen Z, Yu H, Gao S, Wang B, Ying Y, et al. Quantitative evaluation of yaw-misalignment and aerodynamic wake induced fatigue loads of offshore Wind turbines. Renew Energy. 2022;199(1):71–86. doi:10.1016/j.renene.2022.08.137. [Google Scholar] [CrossRef]

8. Mehta D, van Zuijlen AH, Koren B, Holierhoek JG, Bijl H. Large Eddy Simulation of wind farm aerodynamics: a review. J Wind Eng Ind Aerodyn. 2014;133(3):1–17. doi:10.1016/j.jweia.2014.07.002. [Google Scholar] [CrossRef]

9. Jensen N. A note on wind turbine interaction. Tech. Rep. Ris-M-2411. Roskilde, Denmark: Risø National Laboratory; 1983. [Google Scholar]

10. Lopes AMG, Vicente AHSN, Sánchez OH, Daus R, Koch H. Operation assessment of analytical wind turbine wake models. J Wind Eng Ind Aerodyn. 2022;220(8):104840. doi:10.1016/j.jweia.2021.104840. [Google Scholar] [CrossRef]

11. Bastankhah M, Porté-Agel F. A new analytical model for wind-turbine wakes. Renew Energy. 2014;70(1):116–23. doi:10.1016/j.renene.2014.01.002. [Google Scholar] [CrossRef]

12. Pao LY, Johnson KE. A tutorial on the dynamics and control of wind turbines and wind farms. In: 2009 American Control Conference; 2009 Jun 10–12; St. Louis, MO, USA. p. 2076–89. [Google Scholar]

13. Gebraad PMO, Teeuwisse FW, van Wingerden JW, Fleming PA, Ruben SD, Marden JR, et al. A data-driven model for wind plant power optimization by yaw control. In: 2014 American Control Conference; 2014 Jun 4–6; Portland, OR, USA. p. 3128–34. [Google Scholar]

14. Gebraad PMO, van Wingerden JW. A control-oriented dynamic model for wakes in wind plants. J Phys: Conf Ser. 2014;524:012186. doi:10.1088/1742-6596/524/1/012186. [Google Scholar] [CrossRef]

15. NREL. FLORIS; 2023 [Internet]. [cited 2025 Apr 29]. Available from: https://github.com/WISDEM/FLORIS. [Google Scholar]

16. Becker M, Ritter B, Doekemeijer B, van der Hoek D, Konigorski U, Allaerts D, et al. The revised FLORIDyn model: implementation of heterogeneous flow and the Gaussian wake. Wind Energ Sci. 2022;7(6):2163–79. doi:10.5194/wes-7-2163-2022. [Google Scholar] [CrossRef]

17. Nakhchi ME, Win Naung S, Rahmati M. A novel hybrid control strategy of wind turbine wakes in tandem configuration to improve power production. Energy Convers Manag. 2022;260(6):115575. doi:10.1016/j.enconman.2022.115575. [Google Scholar] [CrossRef]

18. Nakhchi ME, Win Naung S, Rahmati M. Wake and power prediction of horizontal-axis wind farm under yaw-controlled conditions with machine learning. Energy Convers Manag. 2023;296:117708. doi:10.1016/j.enconman.2023.117708. [Google Scholar] [CrossRef]

19. van Dijk MT, van Wingerden JW, Ashuri T, Li Y. Wind farm multi-objective wake redirection for optimizing power production and loads. Energy. 2017;121(5):561–9. doi:10.1016/j.energy.2017.01.051. [Google Scholar] [CrossRef]

20. Zhao H, Wu Q, Guo Q, Sun H, Xue Y. Distributed model predictive control of a wind farm for optimal active power ControlPart I: clustering-based wind turbine model linearization. IEEE Trans Sustain Energy. 2015;6(3):831–9. doi:10.1109/TSTE.2015.2418282. [Google Scholar] [CrossRef]

21. Siniscalchi-Minna S, Bianchi FD, Ocampo-Martinez C, Domínguez-García JL, De Schutter B. A non-centralized predictive control strategy for wind farm active power control: a wake-based partitioning approach. Renew Energy. 2020;150(3):656–69. doi:10.1016/j.renene.2019.12.139. [Google Scholar] [CrossRef]

22. Dhoot A, Antonini EGA, Romero DA, Amon CH. Optimizing wind farms layouts for maximum energy production using probabilistic inference: benchmarking reveals superior computational efficiency and scalability. Energy. 2021;223:120035. doi:10.1016/j.energy.2021.120035. [Google Scholar] [CrossRef]

23. Chen Y, Joo YH, Song D. Multi-objective optimisation for large-scale offshore wind farm based on decoupled groups operation. Energies. 2022;15(7):2336. doi:10.3390/en15072336. [Google Scholar] [CrossRef]

24. Cai W, Hu Y, Fang F, Yao L, Liu J. Wind farm power production and fatigue load optimization based on dynamic partitioning and wake redirection of wind turbines. Appl Energy. 2023;339(3):121000. doi:10.1016/j.apenergy.2023.121000. [Google Scholar] [CrossRef]