 Open Access
Open Access
ARTICLE
A Novel Cascaded TID-FOI Controller Tuned with Walrus Optimization Algorithm for Frequency Regulation of Deregulated Power System
1 Department of Electrical Engineering, Netaji Subhas University of Technology, New Delhi, 110078, India
2 Department of Electrical Engineering, ITER, Siksha ‘O’ Anusandhan Deemed to be University, Bhubaneswar, 751030, India
3 School of Electronics Engineering, Kalinga Institute of Industrial Technology, Bhubaneswar, 751024, India
4 Piteşti University Centre, The National University of Science and Technology Politehnica Bucharest, Pitesti, 110040, Romania
5 ICSI Energy, National Research and Development Institute for Cryogenic and Isotopic Technologies, Râmnicu Vâlcea, 240050, Romania
* Corresponding Authors: Bhargav Appasani. Email: ; Nicu Bizon. Email:
(This article belongs to the Special Issue: Emerging Technologies for Future Smart Grids)
Energy Engineering 2025, 122(8), 3399-3431. https://doi.org/10.32604/ee.2025.067357
Received 01 May 2025; Accepted 19 June 2025; Issue published 24 July 2025
Abstract
This paper presents an innovative and effective control strategy tailored for a deregulated, diversified energy system involving multiple interconnected area. Each area integrates a unique mix of power generation technologies: Area 1 combines thermal, hydro, and distributed generation; Area 2 utilizes a blend of thermal units, distributed solar technologies (DST), and hydro power; and Third control area hosts geothermal power station alongside thermal power generation unit and hydropower units. The suggested control system employs a multi-layered approach, featuring a blended methodology utilizing the Tilted Integral Derivative controller (TID) and the Fractional-Order Integral method to enhance performance and stability. The parameters of this hybrid TID-FOI controller are finely tuned using an advanced optimization method known as the Walrus Optimization Algorithm (WaOA). Performance analysis reveals that the combined TID-FOI controller significantly outperforms the TID and PID controllers when comparing their dynamic response across various system configurations. The study also incorporates investigation of redox flow batteries within the broader scope of energy storage applications to assess their impact on system performance. In addition, the research explores the controller’s effectiveness under different power exchange scenarios in a deregulated market, accounting for restrictions on generation ramp rates and governor hysteresis effects in dynamic control. To ensure the reliability and resilience of the presented methodology, the system transitions and develops across a broad range of varying parameters and stochastic load fluctuation. To wrap up, the study offers a pioneering control approach—a hybrid TID-FOI controller optimized via the Walrus Optimization Algorithm (WaOA)—designed for enhanced stability and performance in a complex, three-region hybrid energy system functioning within a deregulated framework.Keywords
In contemporary power systems, maintaining frequency stability is critical to ensuring reliable and efficient operation. Load Frequency Control (LFC) serves as an important mechanism in order to regulate the power system frequency to adapt to variations in load requirements. Traditional controllers, such as Proportional-Integral-Derivative (PID) controllers, have been incorporated for LFC, but these methods often face limitations, especially in complex, multi-area, and interconnected power systems. With renewable energy sources becoming more widely blended in the power systems and more advanced grid infrastructures, these limitations have prompted the exploration of alternative control strategies that offer improved performance and robustness. Fractional-order controllers (FOCs) have gained significant attention as an optimistic approach for LFC, providing a higher degree of flexibility and precision in control dynamics. Unlike conventional integer-order controllers, fractional-order controllers, such as fractional-order PID (FOPID), have the ability to better capture the dynamics of complex systems, leading to improved system stability and response to load variations. Moreover, fractional-order controllers have demonstrated greater adaptability under conditions of grid unpredictability, nonlinear behaviors, and temporal delays, which are becoming more common in contemporary electrical networks.
The structure of the article is outlined as follows: Section 2 presents a comprehensive analysis of the latest advancements pertinent to the proposed study. Section 3 details the framework of the recommended controller along with its design approach. Section 4 explores the hybrid energy system, including both traditional and renewable powers. The Walrus Optimization Algorithm (WaOA) is described in depth in Section 5. Section 6 offers a performance analysis of the WaOA, supported by simulation results and discussion. The conclusions drawn from the study are summarized in Section 7. Finally, the Appendix A lists the various system parameters used throughout the paper.
This section provides a review of recent literature on load frequency control, focusing on diverse energy units within separate power systems. It also highlights the use of various controllers designed to ensure the stability of automatic generation control.
Recent research has investigated the incorporation of fractional-order controllers with time-delay compensation to tackle the issues presented by communication delays and system dynamics in interconnected power systems. Shahin and Atallah (2015) [1] proposed cascaded controllers combining fractional-order control and time-delay compensation to improve system stability and performance in multi-area LFC systems. Their approach demonstrated that fractional-order controllers could effectively mitigate the impact of time delays, a significant concern in large-scale power systems. Similarly, Zhao and Xu (2015) [2] introduced a novel fractional-order control scheme, highlighting its effectiveness in addressing load frequency control challenges under real-world conditions. The application of fractional-order controllers in power systems has been further expanded in various studies. Boucher and Madjid (2015) [3] conducted a comprehensive review, emphasizing the advantages of fractional-order controllers over conventional approaches in terms of stability, robustness, and dynamic performance. Zhang and Xu (2015) [4] incorporated fractional-order controllers in systems with time delays, showing their ability to enhance system stability under various operational conditions. In 2016, Sadeh and Fard [5] introduced adaptive fractional-order controllers for multi-area LFC systems, while Marcos and Gama (2016) [6] analysed the stability and robustness of cascaded time-delay and fractional-order controllers, establishing their effectiveness in multi-area LFC systems with varying load and generation profiles. These advancements underscore the growing recognition of fractional-order controllers as a viable strategy to modern LFC challenges. The integration of fractional-order controllers with time-delay compensators has further demonstrated its utility in improving the dynamic behaviour of LFC systems. Recent studies have continued to explore hybrid fractional-order strategies to enhance LFC performance, especially Under conditions of sustainable energy integration and variable system circumstances [7–9]. Numerous research efforts have investigated the effectiveness of fractional-order controllers in improving Load Frequency Control. Liu and Xu (2017) [10] Studied the effectiveness of fractional-order controllers for LFC in power systems with time delays, demonstrating that fractional-order controllers could effectively improve the system’s operational flexibility and steadiness even in the presence of time delays. Shahin and Elsayed (2017) [11] proposed a time-delay compensation approach using cascaded controllers, showing that such an approach enhances system stability and mitigates the adverse effects of time delays, which are often present in interconnected power systems. Sadeh and Azimian (2017) [12] introduced fractional-order cascaded control for multi-area LFC systems, revealing that combining fractional-order control with cascading strategies allows for better tuning of system parameters, leading to improved control of multi-source multi control area systems. In addition, Dei et al. (2018) [13] presented a hybrid fractional-order and Tilt Integral Derivative (TID) controller, highlighting the benefits of combining fractional-order control with TID techniques to overcome the challenges associated with load frequency control in power systems. This hybrid technique was shown to enhance the robustness and operational dynamics of LFC systems under varying operational conditions. This paper examined the performance of an Adaptive Learning Optimized (ALO) Fractional Order PID controller for Automatic Generation Control (AGC) in a three-area power system. It emphasizes the controller’s effectiveness in enhancing the stability and the system’s adaptability to fluctuating load demands.
Further research has extended these concepts to include adaptive and improved cascaded control strategies. Liu and Zhao (2018) [14] analyzed the implementation of cascaded fractional-order controllers for LFC, showing that cascaded controllers allow for better management of system dynamics and improve frequency regulation. Similarly, Sadeh and Fard (2018) [15] explored the stability of cascaded fractional-order and TID controllers, providing evidence that these controllers can greatly improve the stability of interconnected power systems, especially under variable load conditions. The paper [16] investigated load frequency regulation in a multi-region power network incorporating distributed energy sources, a gate-modulated series capacitor, and a high-voltage direct current connection. Utilizing a hybrid approach ant Lion Optimizer-pattern search technique, the study optimizes a fractional-order controller to stabilize system performance and dynamic performance. The study [17] demonstrated improved stability and reduced settling time compared to traditional PID controller system. This paper presents a fractional-order PID controller optimized using Particle Swarm Optimization (PSO) for load frequency control in a two-area interconnected power system. Fractional-order controllers extend conventional integer-order controllers by incorporating derivatives and integrals of non-integer order, offering greater adaptability in tuning system responses. These controllers can better model the complex dynamics of power systems, including time delays, system inertia, and other nonlinearities, providing superior control performance over traditional methods. Recent advancements in fractional-order load frequency control have shown promising results in addressing these challenges. Yun and Li (2019) [18] provided a complete overview on advanced Load Frequency Control using fractional-order controllers, highlighting the superior performance and versatility of these controllers in various operational scenarios. Their work outlines how fractional-order controllers outperform traditional controllers, especially in systems with complex dynamics and delays. Raj and Ghosh (2019) [19] introduced a hybrid fractional-order and Time-Delay Integral Derivative controller for LFC, demonstrating the effectiveness of combining these two control strategies in enhancing system stability and response time. The hybrid approach offers a flexible solution.
The design of cascaded fractional-order controllers has also gained significant attention in recent years. Shahin and Atallah (2019) [20] explored the improvement in cascaded fractional-order and time-delay controllers for multi-area LFC, proving that such an approach provides a more robust and efficient solution to the challenges posed by multi-area power systems. Similarly, Zhang and Li (2019) [21] focused on fractional-order LFC with time-delay compensators, showing that fractional-order controllers with delay compensation significantly improve the system’s ability to cope with disturbances and time delays, which are commonly encountered in interconnected power grids. Further developments in cascaded controllers have emphasized the stability and robustness of these systems. Zhang and Li (2020) [22] presented a new cascaded fractional-order controller for LFC, detailing the design, stability analysis, and improved performance in power system frequency regulation. Their investigation demonstrated the capability of cascaded controllers in controlling frequency shifts in large power systems. The potential of fractional-order controllers, especially in cascaded configurations, has been demonstrated in numerous studies [23–25]. Xia and Liu (2020) [26] explored a robust cascaded fractional-order I (FOI) controller for LFC, specifically addressing systems with time delays. Their findings revealed that cascaded FOI controllers provide improved robustness and stability when compared to traditional methods. The ability of FOI controllers to maintain optimal frequency regulation despite the presence of delays makes them a promising candidate for modern power systems. Further work on cascaded FOI controllers has also focused on multi-area power systems. Marcos and Gama (2021) [27] provided an in-depth analysis of FOI controllers for LFC in systems with multiple control area. Their study highlighted the superior performance of these controllers in managing inter-area power exchanges and maintaining stable frequencies across multiple interconnected regions. The cascaded structure allows for better coordination between areas, ensuring more precise frequency regulation in complex multi-area grids. The work [28] Showcases a novel hybrid optimization strategy for autonomous load frequency control in integrated power infrastructures, integrating Firefly Algorithm, Particle Swarm Optimization, and Gravitational Search Algorithm to maintain frequency stability and inter-area power coordination. The proposed method optimizes PID controller parameters, ensuring stability and efficiency in multi-source power generation. Additionally, Raj and Ghosh (2021) [29] explored the application of cascaded FOI and time-delay controllers for multi-area load frequency control. Their research demonstrated that this combined control approach offers improved dynamic performance and robustness when applied to large-scale interconnected systems. They found that the cascaded structure not only mitigates the impact of time delays but also ensures that the system maintains frequency stability across multiple regions, even under varying load conditions. The versatility of fractional-order controllers is further evident in their application to renewable energy integration in power systems. Shahin and Elsayed (2021) [30] investigated the use of cascaded time-delay and fractional-order controllers for stabilizing grid frequency in systems incorporating green energy highlighting their ability to maintain system stability even under the intermittent nature of renewable generation. This study emphasizes the growing importance of fractional-order controllers in the context of modern power grids, which are increasingly dependent on renewable energy integration.
Recent studies highlight the growing application of cascaded FOI controllers in LFC. Zhang and Xu (2022) [31] presented a comprehensive review of the use of cascaded FOI controllers for LFC in power systems, emphasizing their advantages over traditional control techniques. Their review outlined the ability of these controllers to offer better performance in terms of transient response and steady-state error, particularly when dealing with systems that exhibit time delays and nonlinearities. Further, advancements have led to the design of hybrid cascaded fractional-order controllers, combining the benefits of FOI controllers with other control strategies to enhance system performance. Gupta and Singh (2022) [32] explored the design of such hybrid controllers, demonstrating their effectiveness in improving the stability and efficiency of LFC systems under varying operational conditions. Their work highlights how these hybrid controllers can be tailored to handle the specific requirements of multi-area power systems and systems with time-varying delays. The paper [33] explores the application of the Squirrel Search Algorithm (SSA) to optimize a PID-Fractional Order Integral (FOI) controller designed for managing load frequency in two interconnected, multi-source power systems. It demonstrates the efficiency of SSA in addressing complex optimization challenges within smart power and energy systems. The work reported in [34] introduces a Hybrid Intelligent Optimization Technique (HIOT) to design a Fractional-Order PID Controller for managing frequency stability in a deregulated system. It emphasizes the controller’s effectiveness in keeping system stability despite the complexities of deregulation and varying operating conditions. Looking ahead, the integration of smart grid technologies presents new challenges and opportunities for LFC. Zhang and Li (2023) [35] explored the design of robust cascaded FOI and Time-Delay Integral Derivative controllers for LFC in smart grids, emphasizing the need for control strategies that can adapt to the dynamic and often unpredictable nature of these grids. Their findings suggest that these controllers provide a more robust solution for handling disturbances and uncertainties in modern grids, particularly in the face of increasing renewable energy integration. Fang and Liu (2023) [36] further extended the concept of time-delay compensation in smart grids, improving the performance of fractional-order controllers in dealing with delays and disturbances in LFC systems. Their research contributes to the ongoing efforts to enhance the reliability and stability of power systems as they evolve into smarter, more decentralized networks [37].
Recent advancements in the field have highlighted the significant benefits of combining fractional-order controllers with time-delay compensation techniques. Hybrid cascaded FOI (Fractional-Order Integrator) controllers, for instance, have been shown to enhance the robustness and stability of LFC in the presence of delays and disturbances. The growing complexity of power systems, along with the increased integration of renewable energy sources, has further accentuated the need for more robust and adaptive LFC strategies. In this regard, Tay and Tan (2023) [38] explored the stability and robustness of cascaded FOI controllers combined with time-delay compensation. Their research highlights that these controllers can effectively handle the uncertainties associated with renewable generation and the operational challenges of modern power grids, ensuring more reliable and stable LFC performance under varying conditions. In the context of real-time implementation, the use of cascaded FOI controllers has also been explored in hybrid power systems. Chen and Wang (2024) [39] investigated the real-time implementation of cascaded FOI controllers in LFC, demonstrating their practical applicability and effectiveness in hybrid power systems. Their work underscores the feasibility of these advanced controllers for real-world applications, paving the way for their deployment in operational settings where real-time control and dynamic adaptation are essential. As renewable energy integration continues to grow, the challenges associated with LFC are becoming more complex. Xu and Zhao (2024) [40] addressed the specific challenges posed by renewable energy integration, proposing a combined fractional-order and time-delay compensated LFC approach. Their findings suggest that such a control strategy can significantly improve the stability and performance of multi-area power systems, even in the presence of renewable generation variability and associated delays. The design and stability of cascaded FOI controllers have also been the subject of intensive research. Shahin and Elsayed (2024) [41] focused on the stability and optimal design of cascaded FOI controllers for multi-area LFC, providing insights into how these controllers can be optimized for different operational conditions to ensure consistent system performance. Looking towards the future, optimal design approaches for cascaded FOI controllers are becoming a key area of interest [42]. Zhang and Li (2025) [43] presented a framework for the optimal design of these controllers, focusing on systems with delays and disturbances. Their work provides a robust foundation for future research on fine-tuning these advanced controllers to achieve optimal LFC performance in increasingly complex and interconnected power grids. Additionally, the role of cascaded FOI and time-delay controllers in systems with high renewable energy penetration continues to attract significant attention. Hassan and Goh (2025) [44] explored the application of these controllers in systems with renewable energy integration, demonstrating their ability to mitigate the impact of intermittent generation and maintain grid stability. This paper [45] examines the security and stability challenges of cyber-physical power systems (CPPS) in deregulated power markets.
Renewable energy integration, while beneficial for reducing carbon emissions, introduces additional challenges for frequency regulation due to the intermittent and variable nature of renewable power generation. Gaur and Singh (2025) [46] investigated the use of cascaded FOI controllers with time-delay compensation to address the unique challenges posed by renewable energy integration in interconnected power systems. Their research demonstrated the ability of these advanced controllers to mitigate frequency fluctuations caused by renewable generation variability, ensuring more reliable and stable grid operations. The need for effective LFC strategies in multi-area power systems is particularly pressing as grid interconnections become more prevalent. Singh and Jain (2025) [47] provided a stability perspective on the use of fractional-order cascaded controllers for multi-area LFC. Their study emphasizes the stability advantages of using these advanced controllers in multi-area systems, where inter-area communication delays and coordination issues can otherwise compromise performance. The study highlights the remarkable capabilities of fractional-order controllers in addressing these challenges and ensuring reliable frequency regulation across geographically dispersed areas. As power systems continue to evolve, the robustness and performance of LFC strategies must be continuously improved. Liu and Xu (2025) [48] explored the stability and performance of cascaded FOI controllers in LFC, particularly in systems with large time delays. Their findings highlight the superior stability and performance characteristics of these controllers, especially in scenarios where time delays are substantial and can otherwise destabilize the system. Their research demonstrates that cascaded FOI controllers offer significant improvements in system robustness, making them a 3 concept has been validated on a three-area system including distributed generation, hydro unit, thermal unit, geothermal and solar thermal energy sources incorporating Governor Dead Band and Generation Rate Constraint nonlinear dynamics. The Walrus Optimization Algorithm (WaOA) optimized system is analyzed both with and without a Redox Flow Battery (RFB). The integration of the Walrus Optimization Algorithm (WaOA) with the TID-FOI controller was chosen due to its superior convergence efficiency and balanced exploration-exploitation mechanism. Compared to PSO and COA, WaOA offers enhanced adaptability, ensuring precise tuning of control parameters in complex nonlinear systems. Its effectiveness in handling uncertainties and improving stability makes it a compelling choice over traditional metaheuristic methods. A comparative analysis of different optimization techniques, focusing on key performance metrics, will be incorporated to further strengthen our findings. Experimental validation highlights WaOA’s efficiency in minimizing errors and optimizing control performance. The Walrus Optimization Algorithm is bio-inspired metaheuristic algorithm simulates the natural behaviors of walruses, including feeding, migrating, escaping, and fighting predators, to address complex optimization problems. Nevertheless, it remains untested for resolving the LFC challenge within a deregulated framework. Nevertheless, it remains untested for resolving the LFC challenge within a deregulated framework.
3 Proposed Cascaded TID-FOI Controller for LFC
The proposed innovative TID-FOI controller represents a cascaded integration of the Tilt Integral Derivative (TID) controller and the Fractional Order Integral (FOI) controller. Fig. 1 illustrates the block diagrams of both the TID controller and the presented TID-FOI controller. The response of the introduced controller, detailed in Eq. (3), is derived by combining the outputs of the TID controller (as described in Eq. (1)) and the FOI controller (as outlined in Eq. (2)).
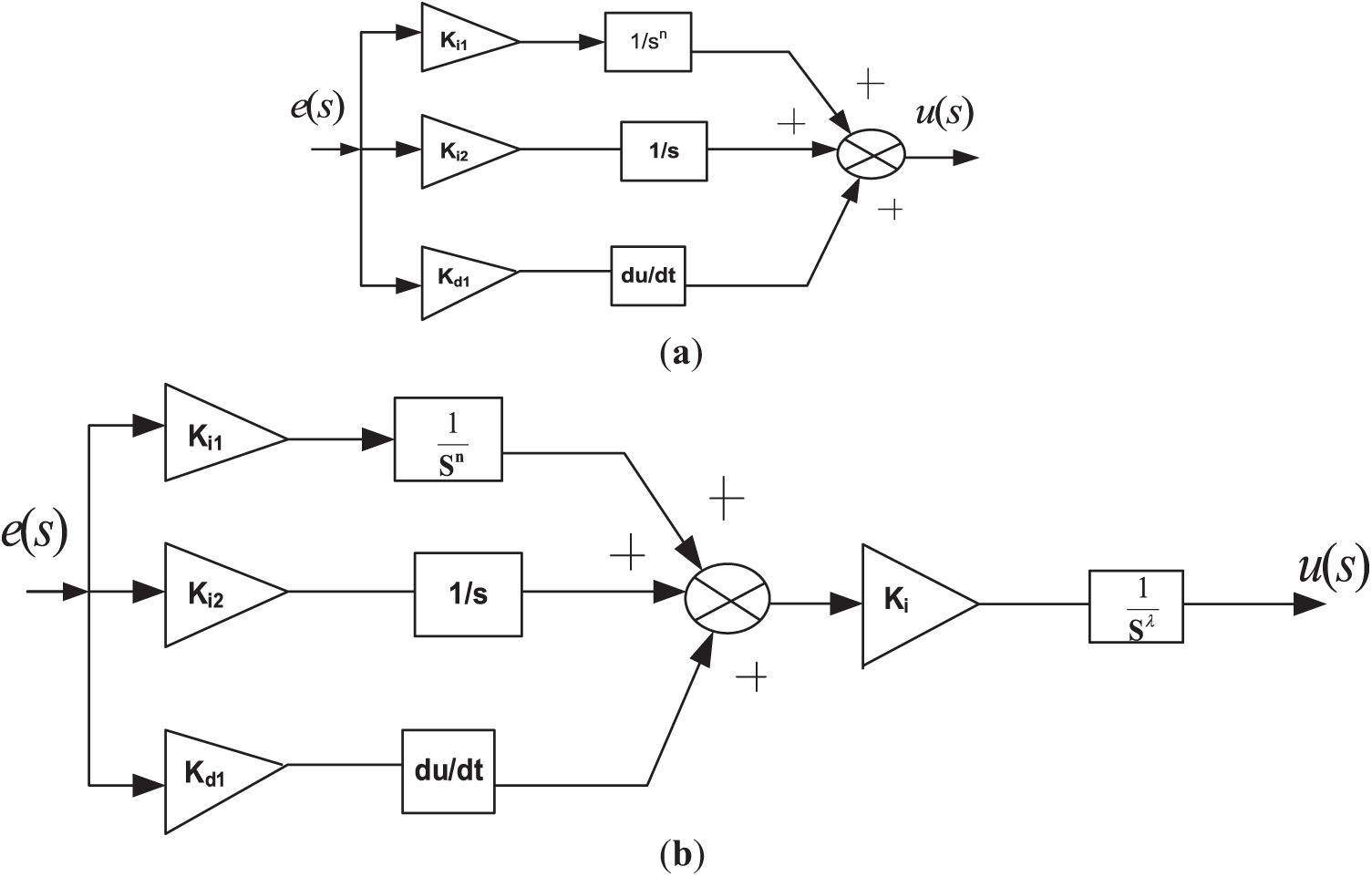
Figure 1: (a) TID controller’s configuration diagram (b) Proposed TID-FOI Controller
The derived formula specifies the output dynamics of the suggested TID+IDN controller by Eq. (3):
Two controllers are connected in cascaded connection, hence output of proposed controller is multiplication of transfer function of individual controllers. The formulated expression defines the response behavior of the proposed TID+IDN controller as represented by Eq. (3).
Where,
4 Deregulated Hybrid Three Area Test System
Fig. 2 presents the transfer function model of a three-area power system, specifically designed for LFC within a deregulated market framework. Two controllers are connected in cascaded connection, hence output of proposed controller is multiplication of individual controllers. The derived formula specifies the output dynamics of the suggested TID+IDN controller by Eq. (3). This multiple-zone, diversified-source network act as a benchmark for evaluating LFC efficiency in a restructured environment. The diagram showcases an interconnected setup that includes various types of generation units spanning three distinct areas [37]. To enhance system stability and operational reliability, the design incorporates a Thyristor-Controlled Series Compensator (TCSC) along with a Redox Flow Battery (RFB). In this system layout, Area 1 integrates three unique generation sources: a hydroelectric unit, a distributed generation unit, and a thermal reheat unit, all operating under generation rate constraints (GRC). Control region 2 consists of three power generation entities, a Dish-Stirling solar thermal framework, a hydroelectric unit, and a thermal reheat setup, also subjected to GRC limitations [42]. Meanwhile, Area 3 comprises a reheat steam turbine system with generation rate restrictions, a Geothermal Power Plant (GTPP), and an additional hydro unit. Each of the three areas is further complemented by three Distribution Companies (DISCOs), resulting in a comprehensive system involving nine generation units and nine distribution units.
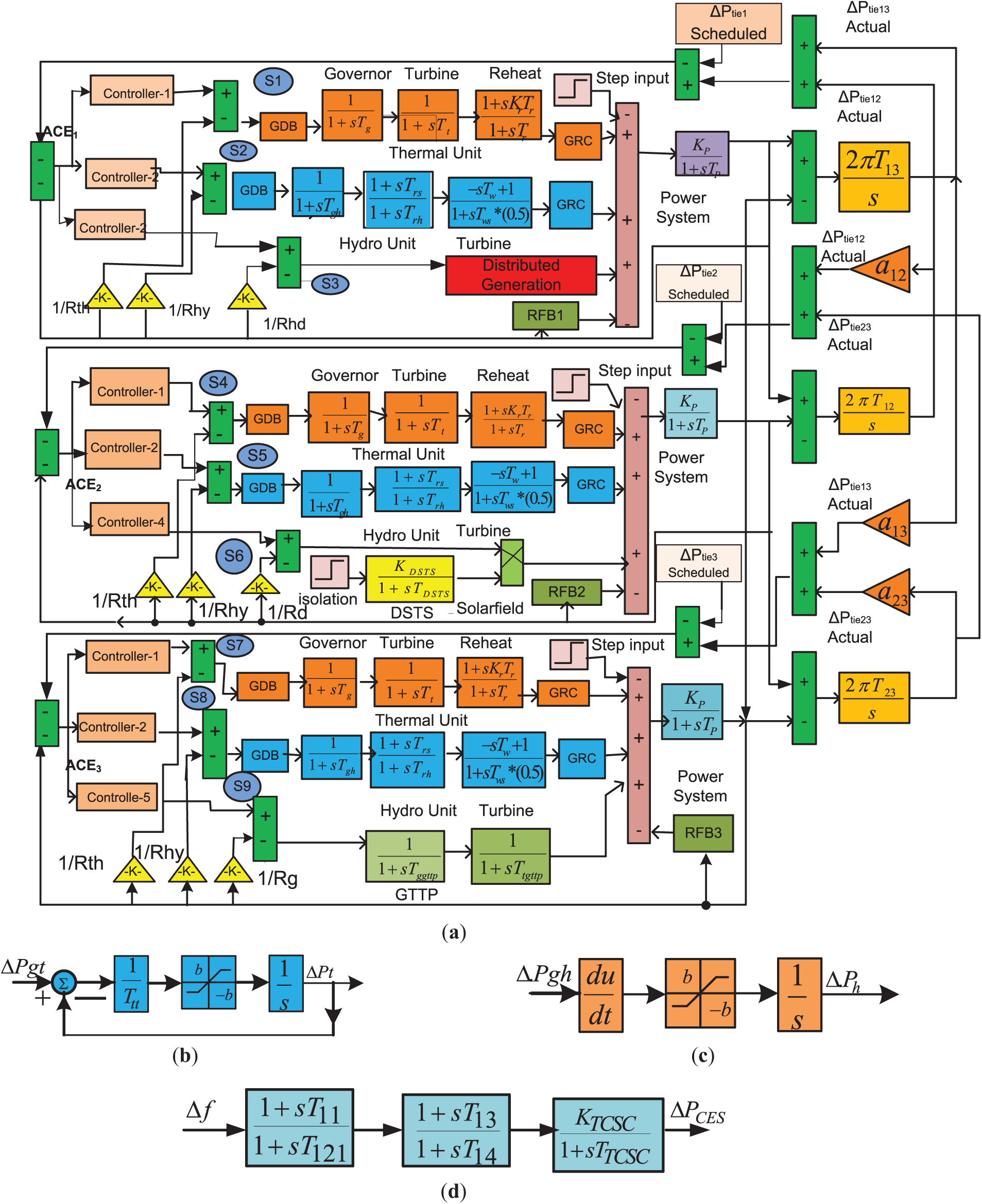
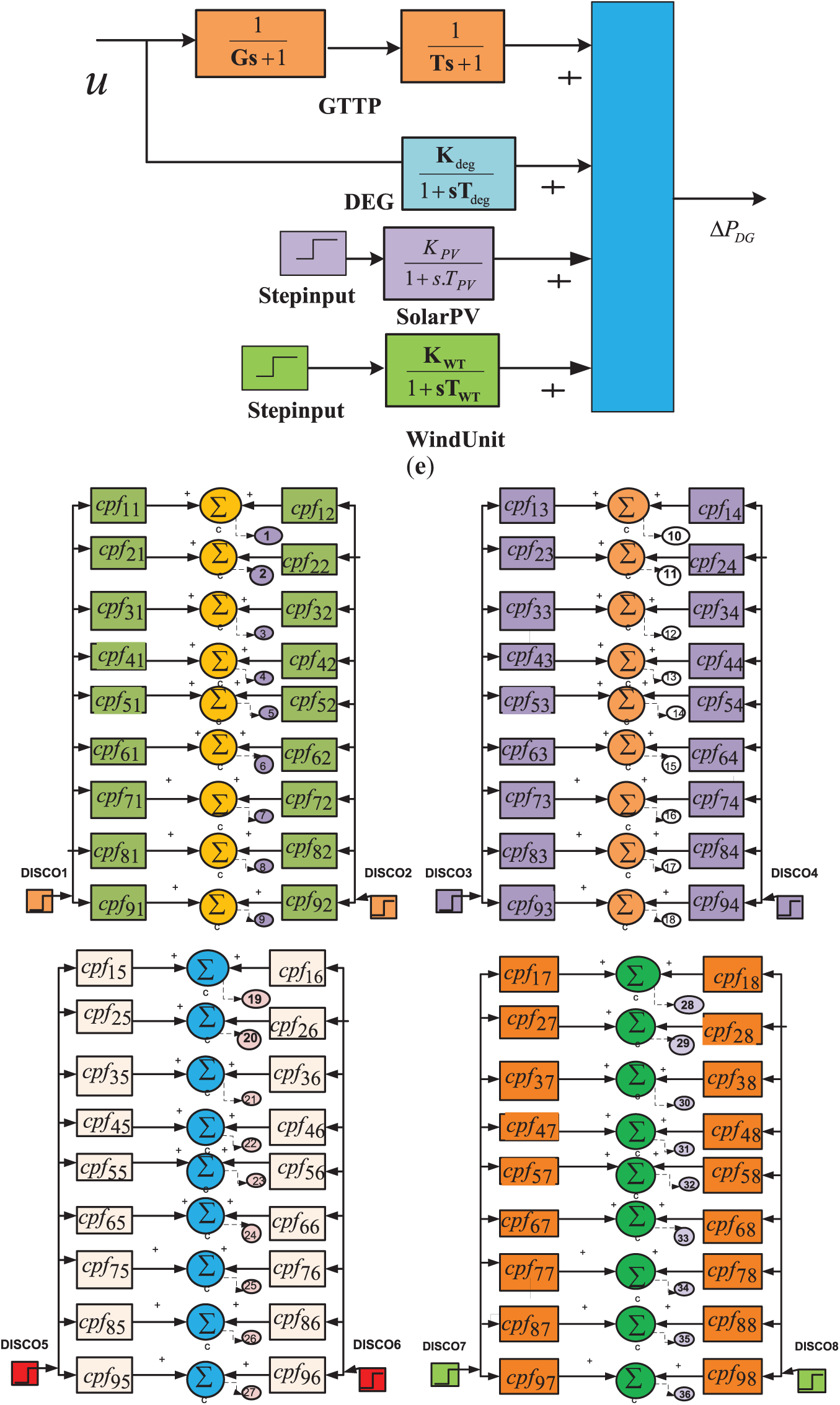

Figure 2: Deregulated multi-area energy distribution system (a) Power System, (b) GRC of Thermal Unit, (c) GRC of Hydro unit, (d) TCSC Controller, (e) Distributed Generation, (f) Contract participation factor for DISCO-GENCO agreements
The system’s frequency deviations are represented by Δf1, Δf2, and Δf3 (in Hz). For thermal generation units, a Governor Dead Band (GDB) of 0.06% (0.036 Hz) is applied, alongside a GRC of 3% per unit (p.u.) MW/min. For hydro plants, a GDB of 0.02% (0.012 Hz) is used, with generation rate constraints allowing a ramp-up of 270% p.u. MW/min and a ramp-down of 360% p.u. MW/min. The solar insolation levels for the DST unit is set at 0.008 p.u. MW/m2, as noted in reference. Further technical details can be found in Appendix A. In this deregulated setup, when power is exchanged between GENCOs and DISCOs within the same area, it is categorized as a “Poolco-based transaction”. Conversely, transactions involving GENCOs and DISCOs from different areas are known as “bilateral transactions”. If the power demand surpasses the agreed-upon contract value, it results in a “contract violation”.
4.1 Objective Function for Automatic Generation Control (AGC)
The system includes a total of nine Generation Companies (GENCOs) and nine Distribution Companies (DISCOs). When a DISCO enters into a power agreement with a GENCO located within the same control zone, the transaction is known as a “poolco-based transaction”. In contrast, if a DISCO engages in a power deal with a GENCO from an independent control area, the power exchange is classified as a “bilateral transaction”. A “contract violation” occurs when the actual load demand goes beyond the specified contractual agreement. To define the contractual relationships between DISCOs and GENCOs, a DISCO Participation Matrix (DPM) is employed. The number of rows in the DPM corresponds to the total number of GENCOs, while the number of columns matches the number of DISCOs in the system. Each column in the DPM represents how a particular DISCO’s demand is distributed among all GENCOs. The sum of all elements in any given column of the DPM is always equal to one, ensuring full allocation of each DISCO’s power demand.
Then the corresponding DPM is written as [5]:
where
Power flow between control area-1 & area-2 can be computed based on the values of the cpf using the Eq. (5):
Tie-line power flow between area-2 and area-3 can be obtained from the Eq. (6):
Dynamic power exchange through the tie-line between control areas 3 and 1 employing the Eq. (7):
The measured tie-line energy transmission between control areas 1 and 2 is presented by Eq. (8):
Eq. (9) gives the power flow through tie line between area-2 and area-3:
Eq. (10) gives the actual tie line power flow through between area-3 and area-1:
The difference between actual power of the tie-line should be equal to zero at steady-state. This error is applied to evaluate area control error and can be expressed as Eq. (11).
Area control error of area-i can be expressed:
The objective function is represented by (12):
5 Walrus Optimization Algorithm (WaOA)
The position update mechanism of walruses in the Walrus Optimization Algorithm (WaOA) is inspired by the natural behaviors of walruses and is structured into three phases [49].
The first phase, known as the feeding strategy, focuses on exploration. They use their agile flippers and highly sensitive vibrissae (whiskers) to detect food. This feeding behavior is mirrored in the WaOA by modeling the search process mathematically. The position of each walrus is denoted by
The Walrus Optimization Algorithm (WaOA) simulates the behaviors of walruses through three phases which is represented by Fig. 3. The first phase, which focuses on feeding strategy (exploration), draws inspiration from the walrus’s diverse foraging habits.
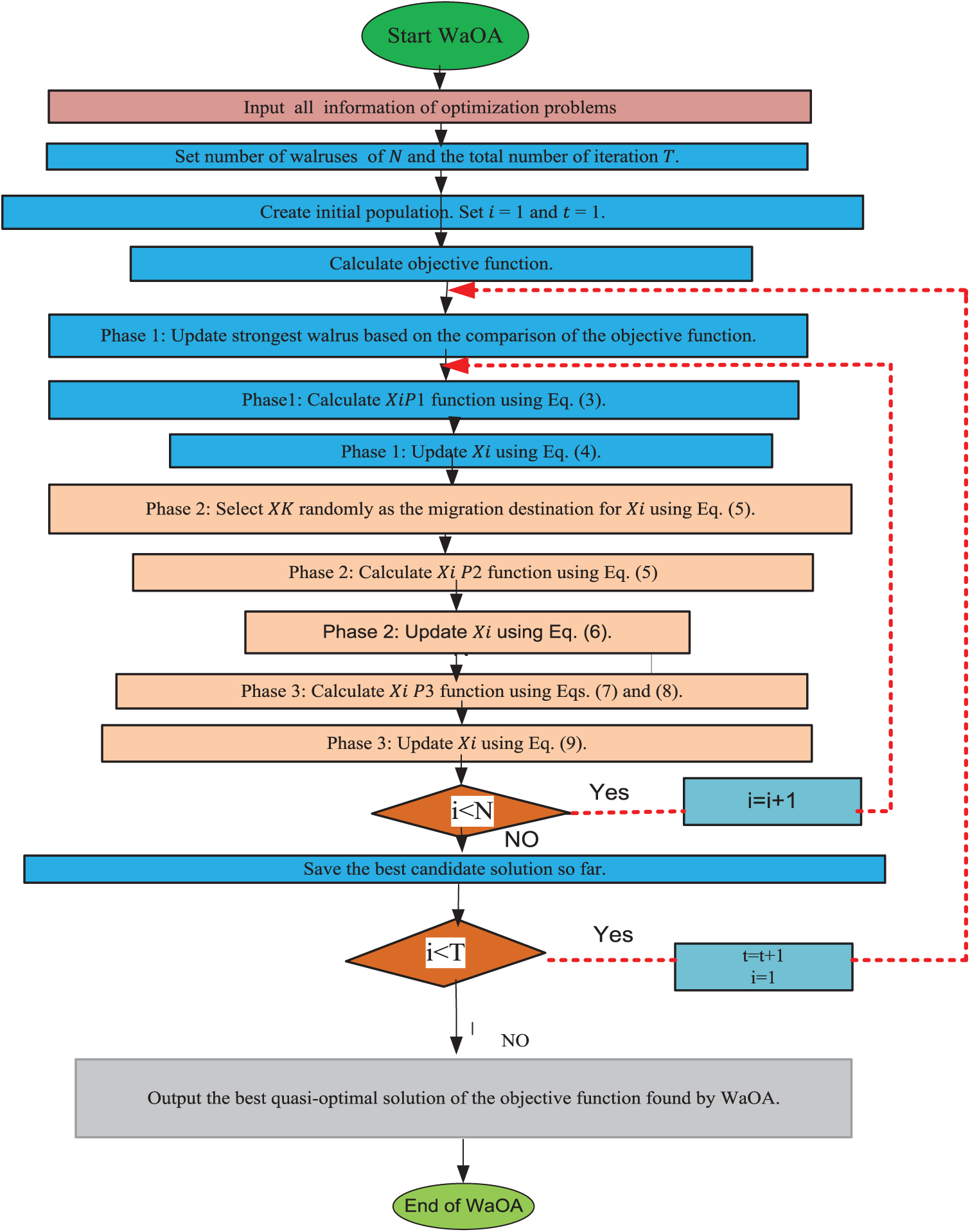
Figure 3: Flowchart of WaOA
During the search, the “strongest” walrus—identified as the candidate with the best objective function value—acts as the group leader. In the analogy, tusk length corresponds to solution quality. This leader guides others to promising regions, helping the algorithm avoid local optima and enhance exploration across the search space.
The new position of the ith walrus in the first phase is determined as:
where,
Another key behavioral aspect of walruses is migration, particularly during late summer when rising temperatures prompt them to relocate to rocky beaches or outcrops. In WaOA, this behavior is used to diversify the search and help walruses (candidate solutions) explore new, potentially fruitful regions of the search space.
This phase is modeled by assuming each walrus can randomly migrate to the vicinity of another walrus’s position. The new candidate position is first proposed using:
where:
5.3 Phase 3: Escaping and Defending against Predators (Exploitation)
In their natural environment, walruses often face threats from predators such as polar bears and killer whales. Their instinctive response—either to flee or fight—results in changes in their physical location within a relatively close range. This defensive behavior is modeled in the WaOA to enhance local search capability, also known as exploitation, around existing candidate solutions.
To reflect this natural response, the WaOA assumes that walruses can move within a defined neighborhood centered around their current position. This local area is used to explore the vicinity more thoroughly and fine-tune solutions. Since early iterations of the algorithm are geared toward global exploration to find promising regions of the search space, the size of this neighborhood—or search radius—is initially large. Over time, the radius gradually decreases, enabling the algorithm to shift from exploration to exploitation as it converges.
To implement this behavior, dynamic local bounds are introduced. These bounds define the neighborhood radius and shrink progressively as the number of iterations increases, ensuring more precise, focused searching in the later stages of optimization.
In practice, a new position is generated randomly within this adaptive neighborhood around each walrus using Eqs. (17) and (18).
If the newly generated position improves the fitness (i.e., the objective function value), it replaces the current position of the walrus Eq. (19).
This mechanism allows the algorithm to refine its search in a localized area and contributes to escaping minor local optima by continuously probing the solution space nearby, especially in later iterations where precision is more critical.
In a deregulated power system, studying LFC under both POOLCO and bilateral agreement models is essential to understand the impact of market structures on frequency regulation. The POOLCO model represents a centralized electricity market where a system operator coordinates generation through a market clearing process, allowing efficient integration of LFC with price-based dispatch strategies. This setup facilitates centralized control and optimization, making it suitable for developing market-responsive control algorithms. In contrast, bilateral agreements involve decentralized, contract-based power exchanges between individual generators and consumers. This model poses greater challenges for LFC due to the lack of centralized coordination, requiring distributed control strategies and incentive mechanisms for participants to contribute to frequency regulation. In both models, the design of robust controllers and the application of advanced optimization techniques play a significant role in maintaining system stability. Controllers ensure quick and accurate frequency correction, while optimization methods help in minimizing operational costs, managing constraints, and enhancing the overall performance of LFC under varying market and system conditions. Together, these case studies, supported by appropriate control and optimization approaches, offer a comprehensive framework for analyzing and improving LFC in deregulated environments.
6.1 Case Study I: Poolco Agreement
Under these conditions, all power generation companies across the three regulated areas engage in AGC. A load fluctuation of 0.03 p.u. is imposed exclusively in area 1 and proportionally shared among its three distribution entities. Notably, no power requests have been made by DISCOs in the other control areas to any GENCOs. Accordingly, the Demand Participation Matrix (DPM) for this scenario reflects that only area 1 is affected, with the load changes distributed as follows: DISCO1 = 0.01 p.u., DISCO2 = 0.01 p.u., and DISCO3 = 0.01 p.u.
The Demand Participation Matrix (DPM) highlights missing contractual links between certain DISCOs and GENCOs across different control regions through its null entries. The evaluated power outputs from the GENCOs are as follows: ΔPg1 = 0.099, ΔPg2 = 0.099, ΔPg3 = 0.099, while GENCOs 4 through 9 do not contribute to power generation in this scenario (ΔPg4 to ΔPg9 = 0).
To maintain system balance under steady-state conditions, the aggregate power production by GENCOs needs to exactly match the aggregate load demand from the DISCOs within their respective areas. Fig. 1 provides an overview of frequency deviations in distinct regions, coupled with tie-line power variations across the three tie-lines. Additionally, key time-domain performance metrics evaluating transient response metrics, such as undershoot, overshoot, and settling time, under a 0.02% tolerance constraint in dynamic responses. These results, along with Integral of time-scaled absolute deviation values, are summarized in Tables 1 and 2. The optimal controller parameter settings obtained through various optimization algorithms are provided in Table 3.


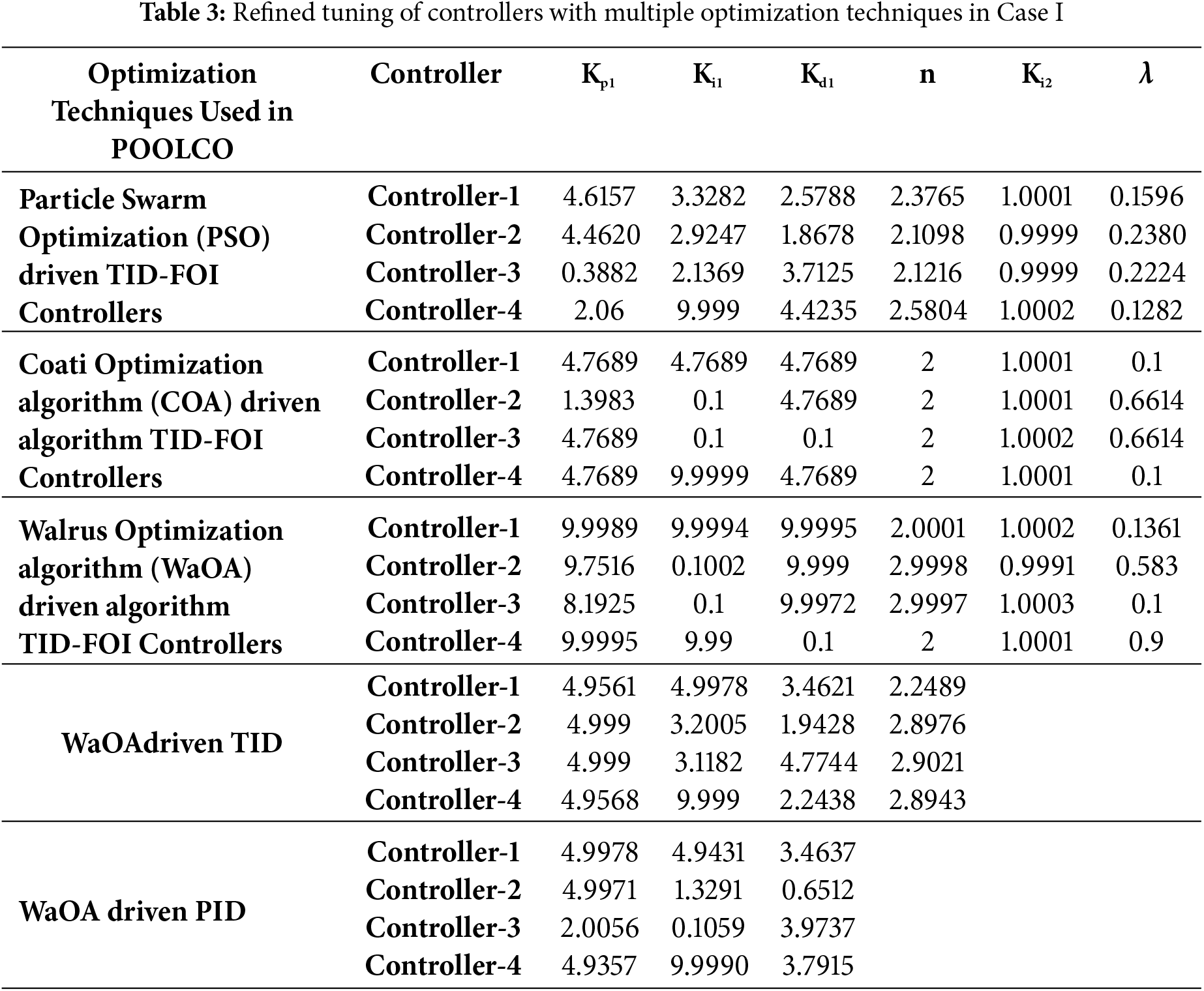
Fig. 4 effectively demonstrates the functionality of the TID-FOI controller, when optimized using the WaOA algorithm, outperforms both standalone TID and PID controllers. The cascaded TID-FOI configuration delivers faster and smoother adaptive system response to frequency disturbances and tie-line power changes This controller effectively suppresses the amplitude of transients, reducing both overshoot and undershoot in Δf and ΔPtie. Additionally, as depicted in Fig. 5, the WaOA-optimized controller demonstrates superior performance compared to those tuned using PSO, and COA algorithms. Fig. 6 further supports this finding by showing the convergence behavior of the optimization methods. The WaOA achieves faster convergence and higher efficiency, underscoring its effectiveness in tuning the proposed control strategy.
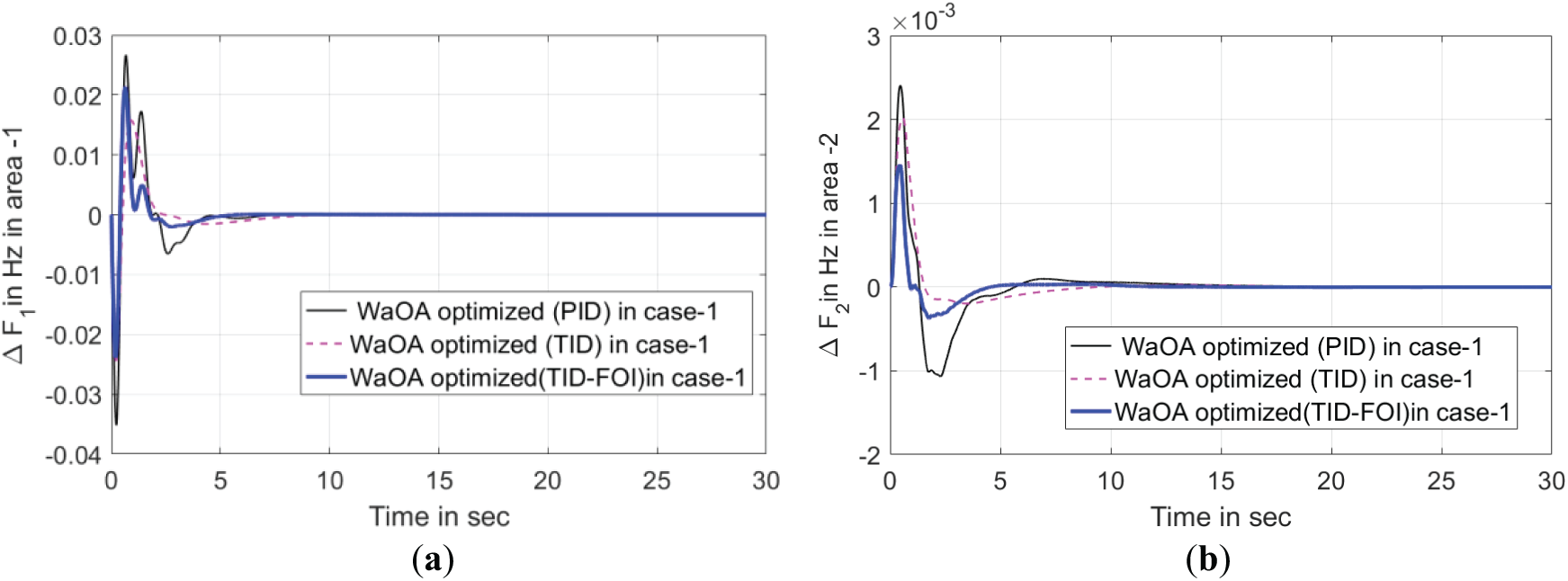
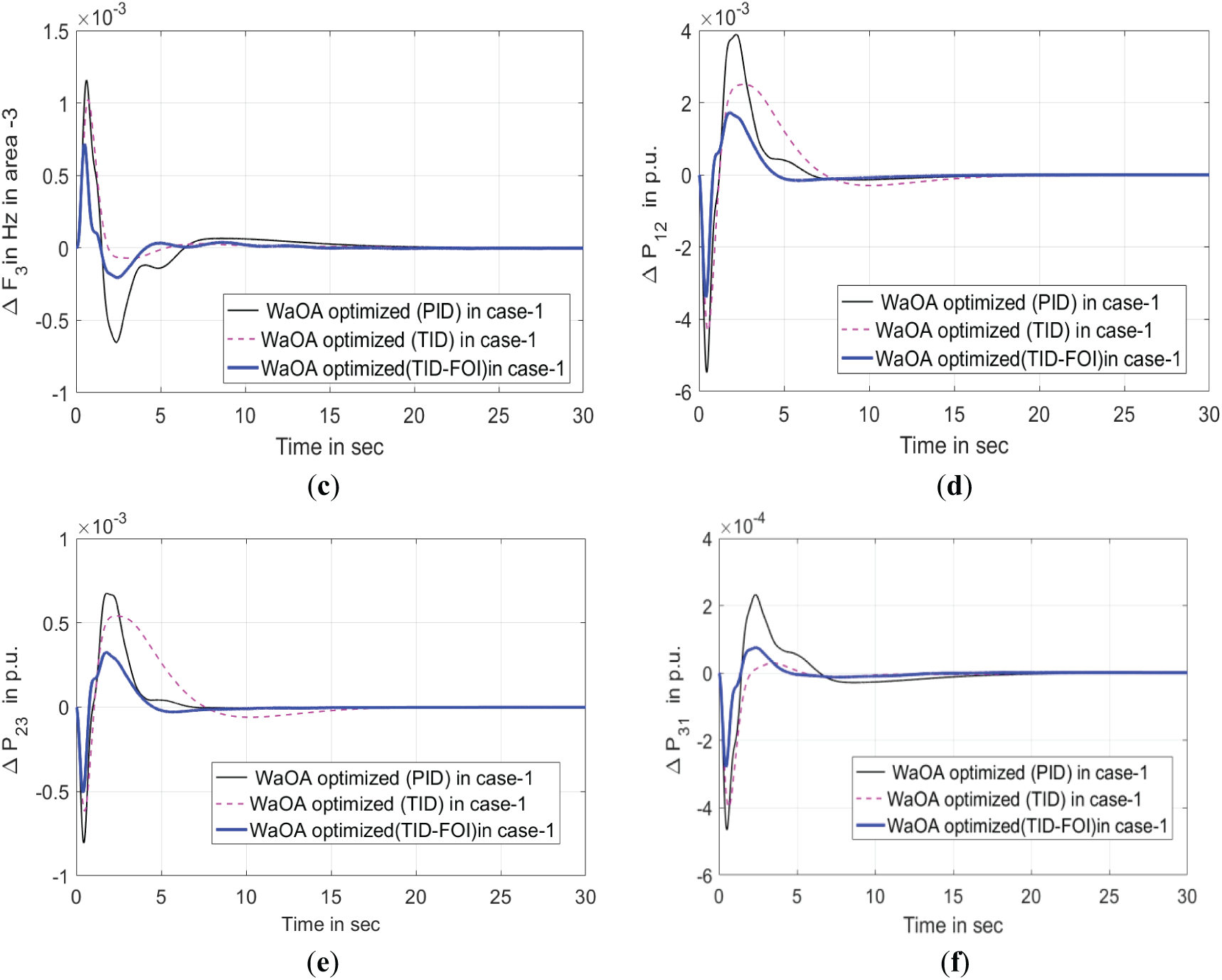
Figure 4: Analysis of controller effectiveness under WaOA optimization framework for Case I. (a) Oscillation in Frequency of area-1. (b) Oscillation in Frequency of area-2. (c) Oscillation in Frequency of area-3. (d) Power fluctuation in between areas 1–2. (e) Power fluctuation in between areas 2–3. (f) Power fluctuation in between areas 3–1
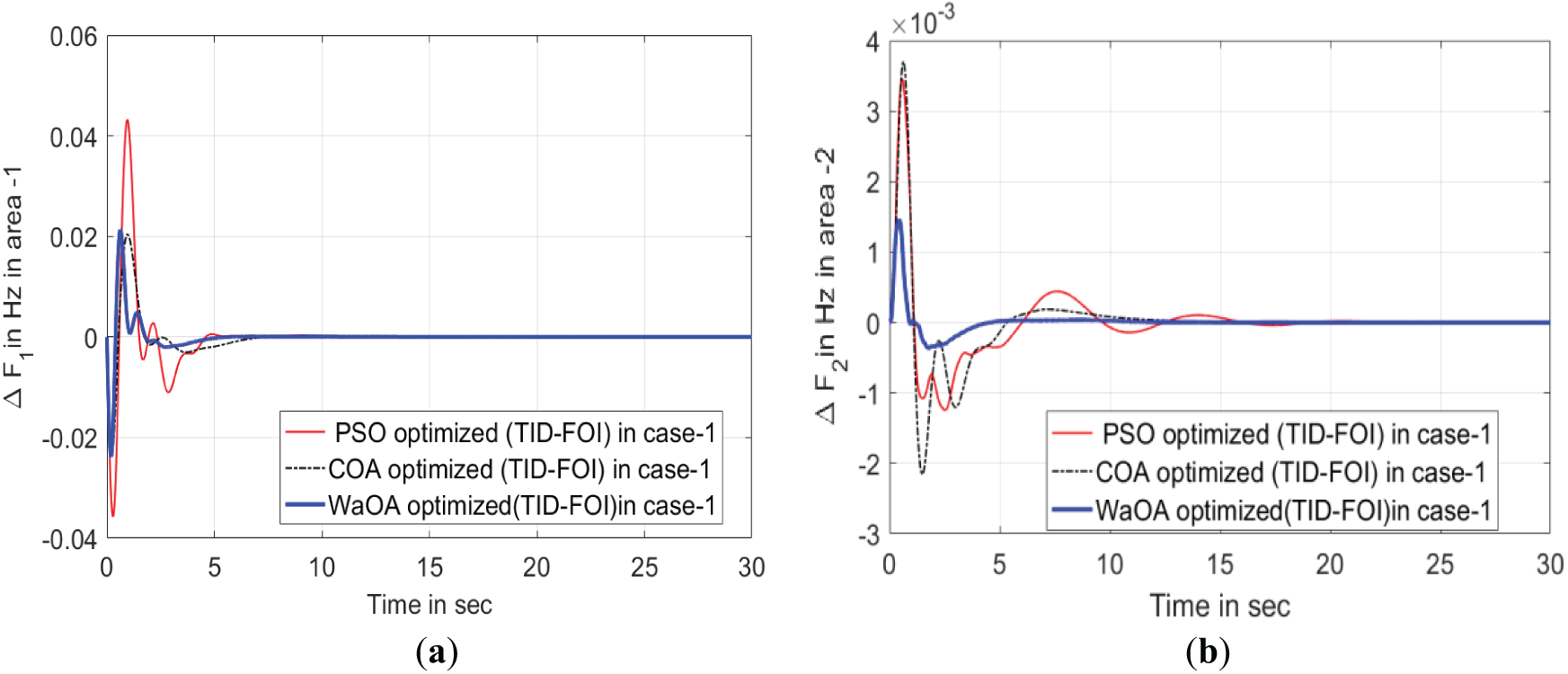
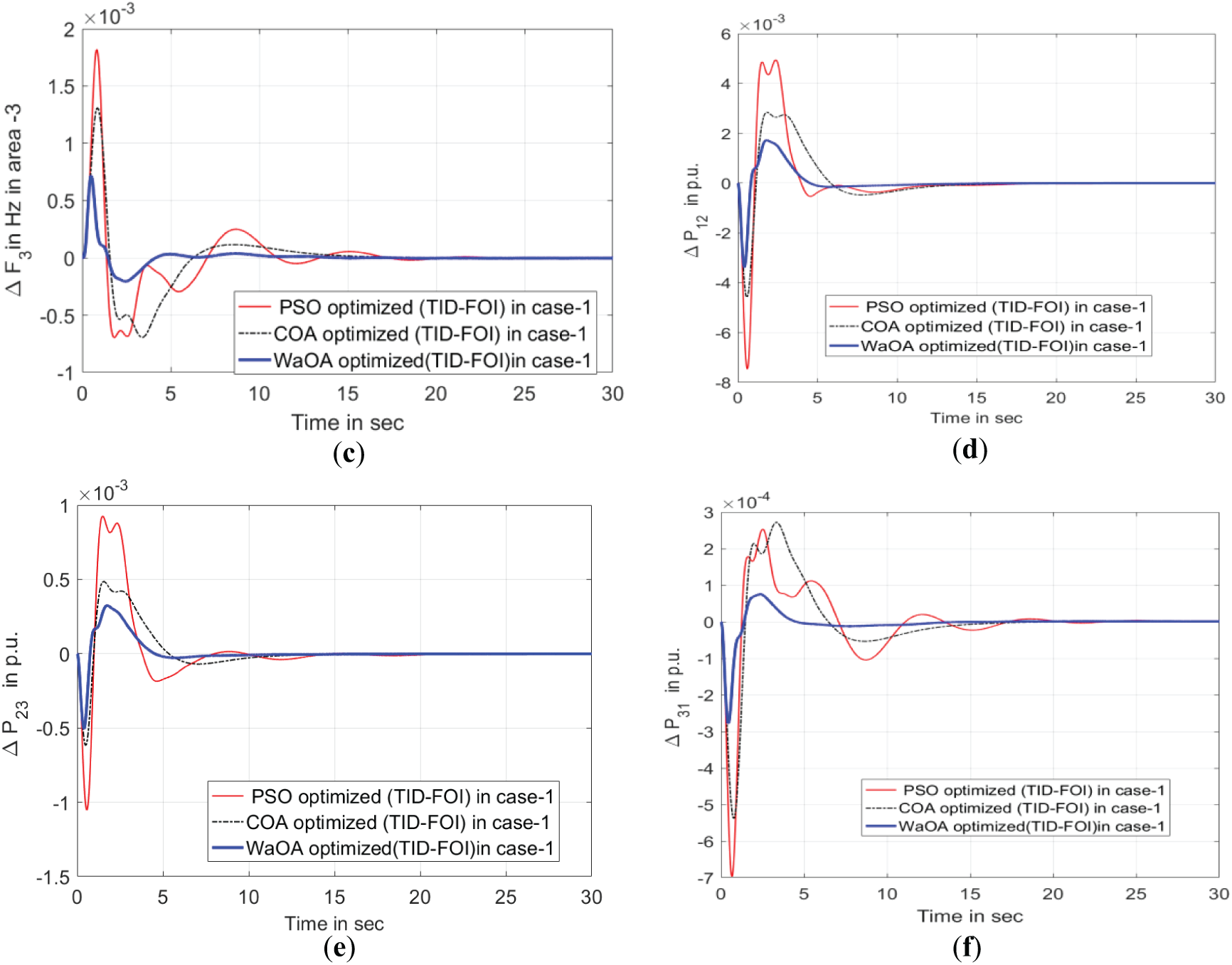
Figure 5: Analysis of variable time responses across various optimization techniques utilizing the TID-FOI controller—Case I. (a) Oscillation in Frequency of area-1. (b) Oscillation in Frequency of area-2. (c) Oscillation in Frequency of area-3. (d) Oscillations in cross-area power exchange between areas 1–2. (e) Oscillations in cross-area power exchange areas 2–3. (f) Oscillations in cross-area power exchange between areas 3–1
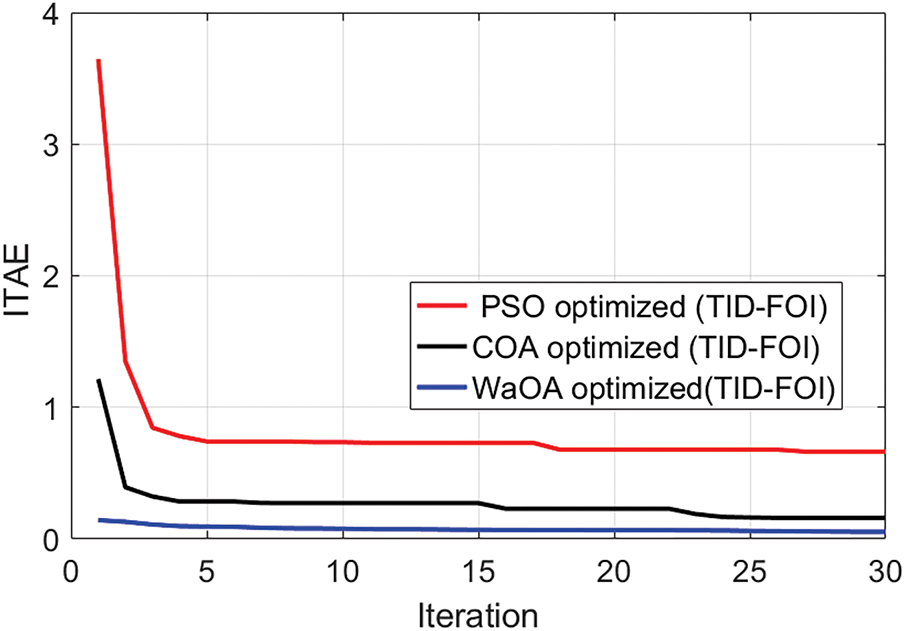
Figure 6: Convergence behaviour of PSO, COA, and WaOA utilizing the proposed controller
6.2 Case Study II: Bilateral Agreement
In this framework, Distribution Companies (DISCOs) in any area are permitted to procure power from Generation Companies (GENCOs) situated in any other area. The power generation of each GENCO is adjusted accordingly to fulfill the demands of the DISCOs, in accordance with the transaction allocations determined by the system coordinator. The Demand Participation Matrix (DPM) for these bilateral transactions is outlined as follows. Load change in all the DISCOs of area 1 are: DISCO1 = 0.01, DISCO2 = 0.01, DISCO3 = 0.01.
This study focuses on a bilateral agreement involving three interconnected power system areas. Each area’s Distribution Companies (DISCOs) are experiencing changes in their electrical loads, with area 1 undergoing a total load variation of 0.03 per unit (p.u.), mirrored by an identical change in area 2. Specifically, in area 1, DISCO1, DISCO2, and DISCO3 each demand 0.01 p.u. Likewise, in area 2, DISCO4, DISCO5, and DISCO6 each require 0.01 p.u. In area 3, DISCO7, DISCO8, and DISCO9 also each request 0.01 p.u. These demand allocations have guided the formulation of the Demand Participation Matrix (DPM), structured according to predefined contracts between the DISCOs and their corresponding Generation Companies (GENCOs).
The generated power contributions from various GENCOs are as follows: ΔPg1 = 0.014 p.u., ΔPg2 = 0.009 p.u., ΔPg3 = 0.010 p.u., ΔPg4 = 0.011 p.u., ΔPg5 = 0.009 p.u., ΔPg6 = 0.0095 p.u., ΔPg7 = 0.0085 p.u., ΔPg8 = 0.009 p.u., and ΔPg9 = 0.010 p.u. The total power generated in the three control areas amounts to 0.033 p.u., 0.0295 p.u., and 0.0275 p.u., respectively. These generation values ensure that the total demand from all DISCOs is fully met by the available generation from GENCOs. The system’s time-domain performance parameters, along employing the ITAE control assessment method, are summarized in Tables 4 and 5. These results clearly show that the presented controller significantly mitigates both overshoot and undershoot. Furthermore, Table 6 provides the optimal controller parameter values obtained using four different optimization algorithms.



Fig. 7 presents the results concerning tie-line power fluctuations and frequency oscillations. The TID-FOI controller utilized in the current system for bilateral transactions exhibits outstanding performance compared to other controller setups. This is accomplished by effectively minimizing peak amplitudes and shortening settling times. Furthermore, the WaOA-optimized controllers have demonstrated superior effectiveness over those employing PSO and COA-based approaches, as depicted in Fig. 8.
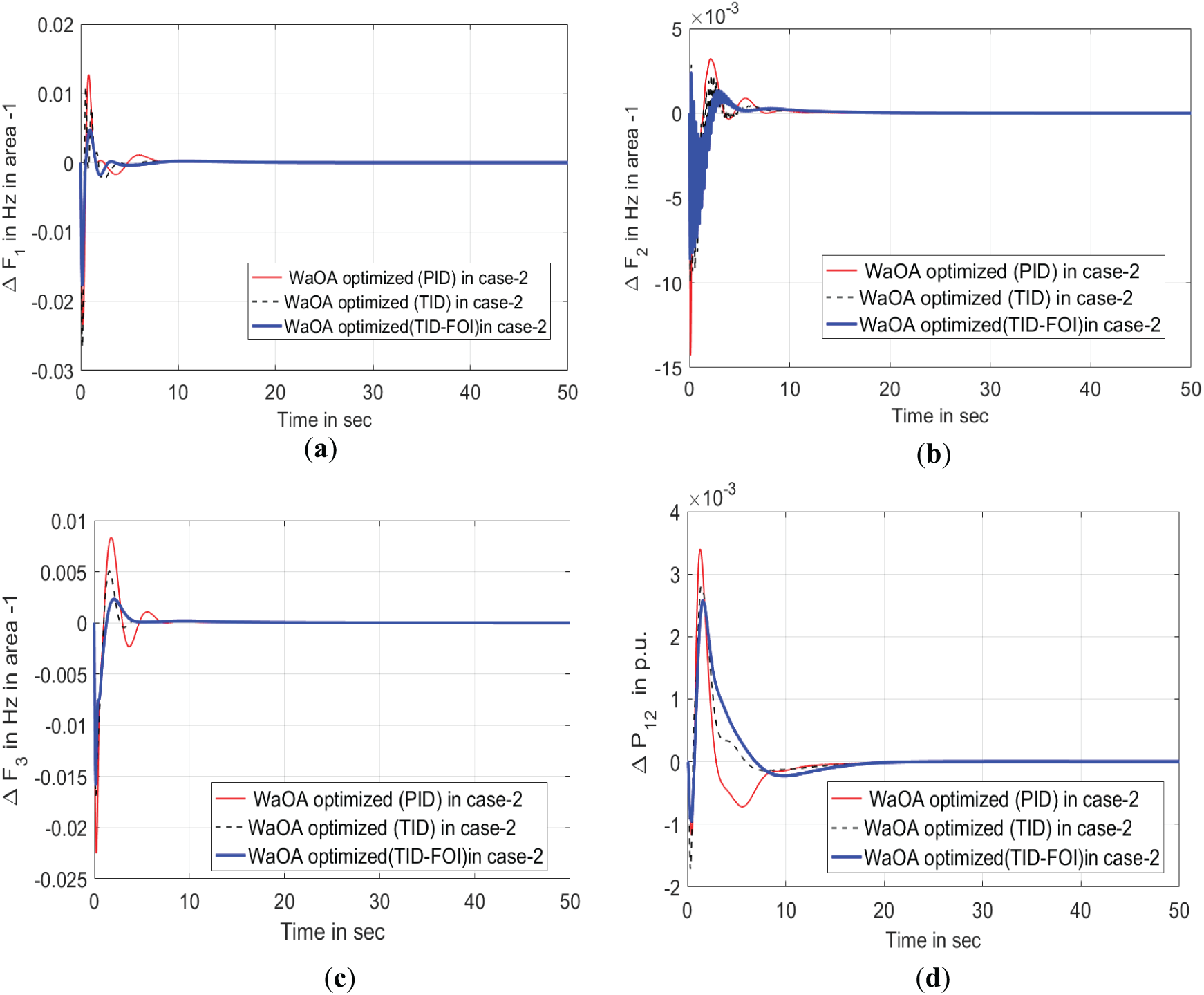
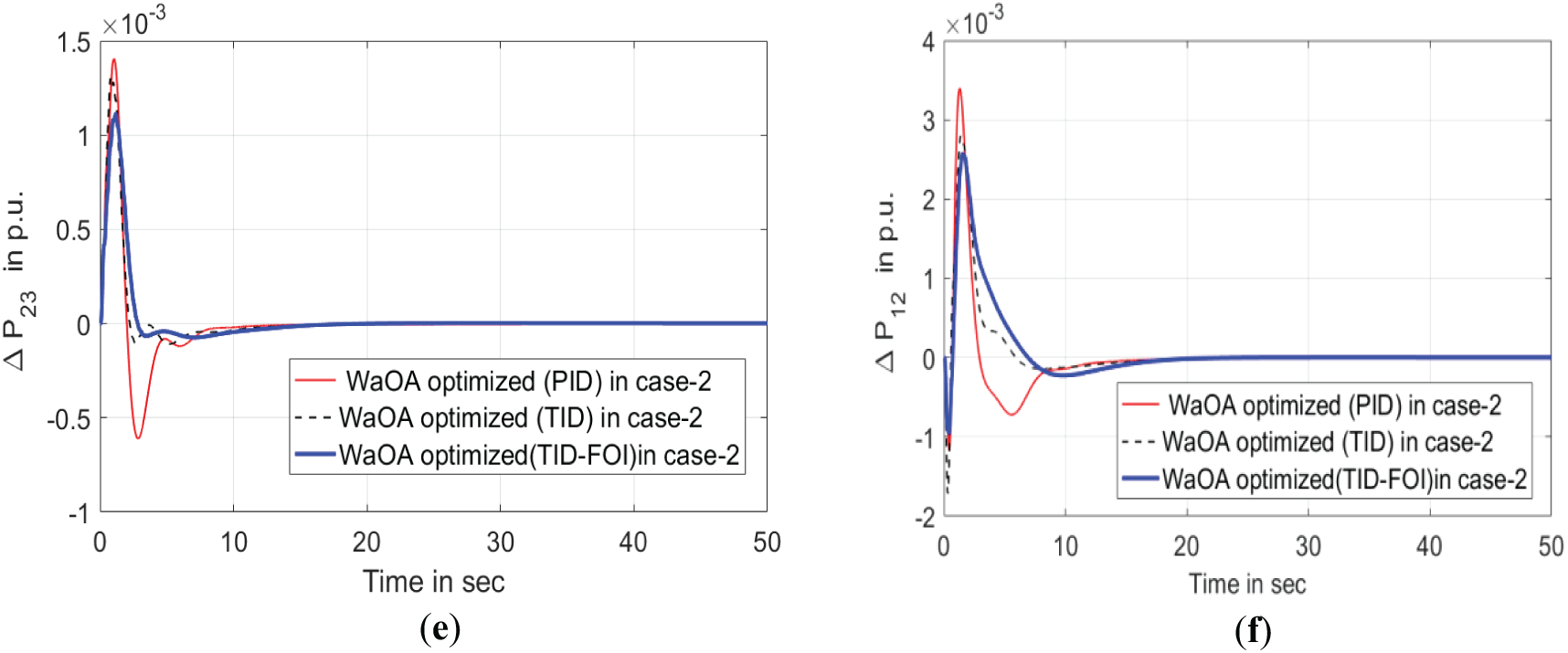
Figure 7: Comparison of different controllers with WaOA optimization techniques-case 2. (a) Deviation in Frequency of area-1. (b) Deviation in Frequency of area-2. (c) Deviation in Frequency of area-3. (d) Power deviation in tie-line between areas 1–2. (e) Power deviation in tie-line between areas 2–3. (f) Power deviation in tie-line between areas 3–1
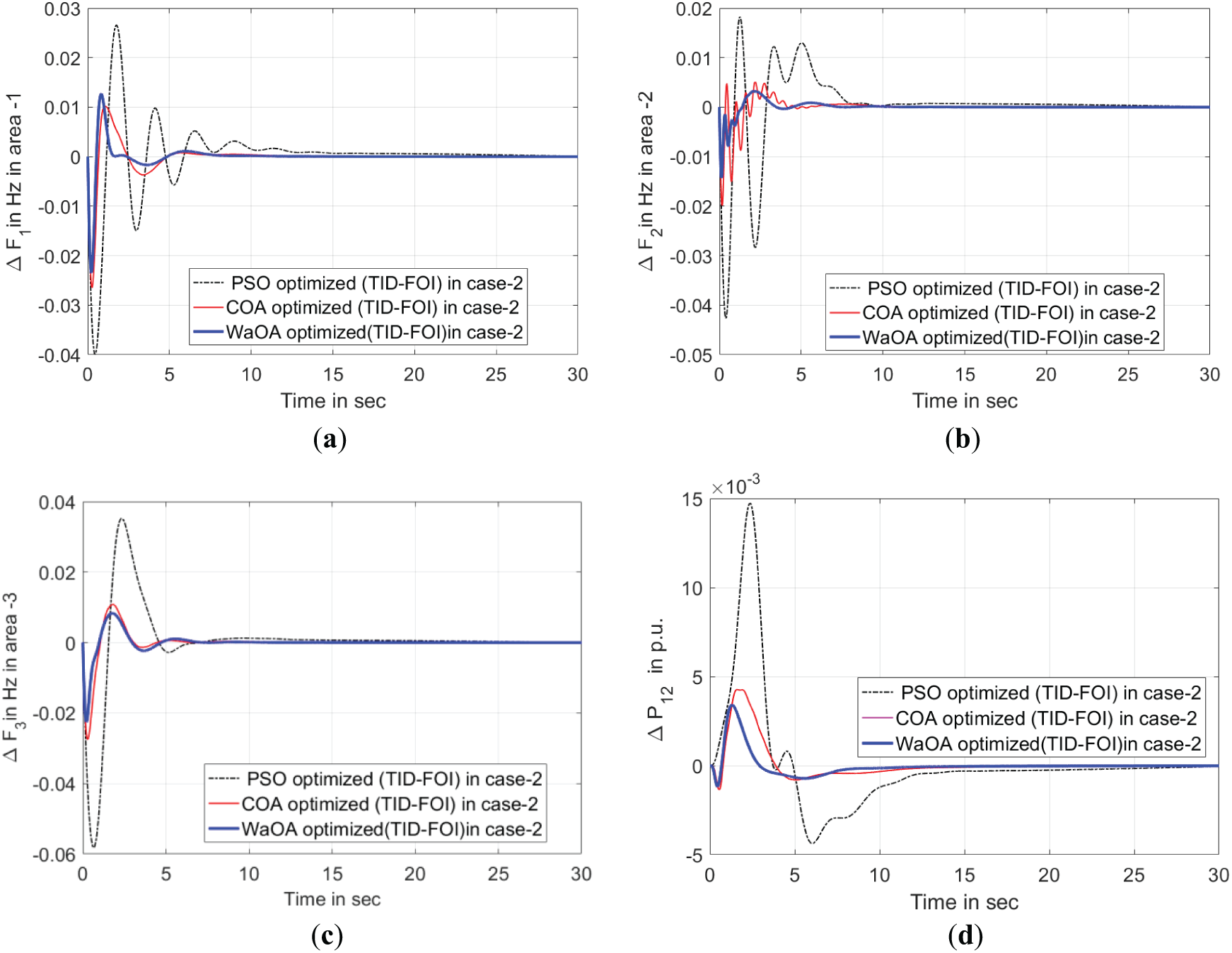
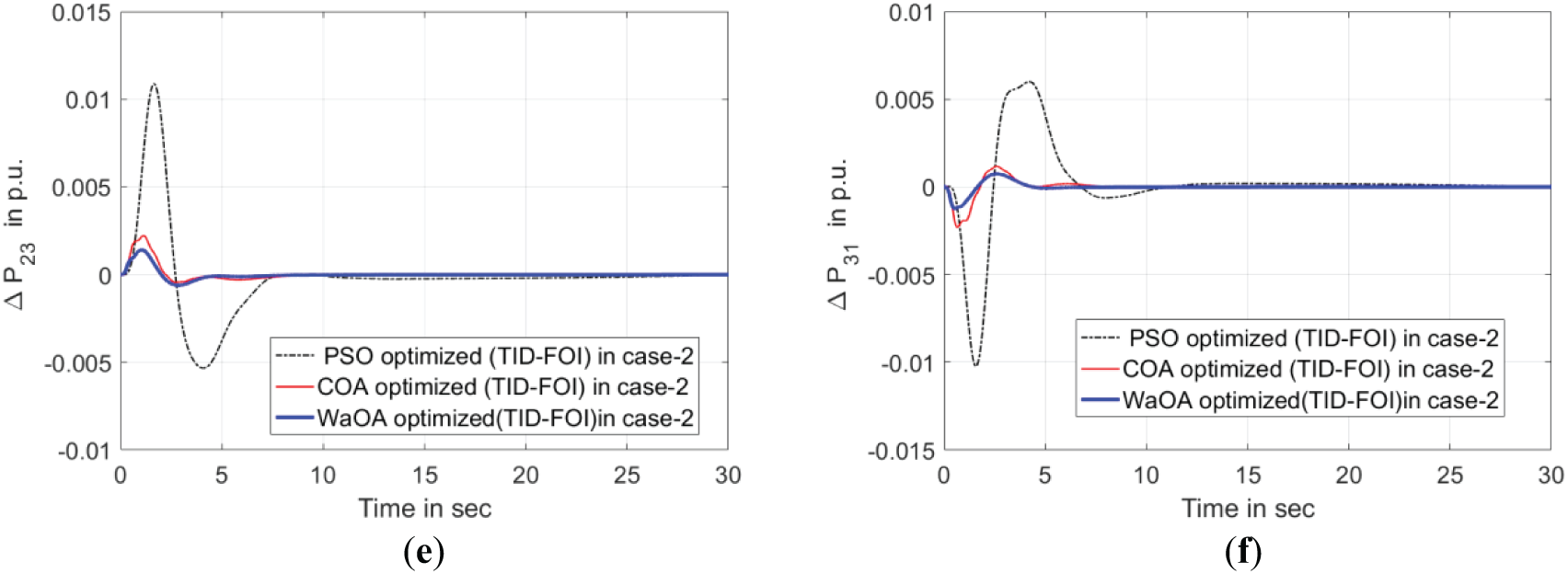
Figure 8: Evaluation of variable responses under perturbation using various optimization techniques applied to the TID+IDN controller Case II. (a) Deviation in Frequency of area-1. (b) Deviation in Frequency of area-2. (c) Deviation in Frequency of area-3. (d) Power deviation in tie-line between areas 1–2. (e) Power deviation in tie-line between areas 2–3. (f) Power deviation in tie-line between areas 3–1
6.3 Case Study III: Analyzing the Robustness of Proposed Controller with Varying Step Load Demand
This study evaluates resilience of the proposed WaOA-optimized TID-FOI controller in managing load frequency control (LFC) under scenarios involving frequent load disturbances. To assess its adaptability, step load changes are introduced sequentially in the control areas taking place at 30-s intervals. Fig. 9 depicts the timing and magnitude of these load variations, while Fig. 10 presents the resulting frequency deviations in areas 1, 2, and 3, accompanied by the associated variations power flow in tie-line. The simulation is conducted incorporating the TID-FOI controller tuned via the Walrus Optimization Algorithm (WaOA) based on the load disturbance. Analysis of Fig. 10 confirms that the proposed control strategy significantly enhances system performance by improving dynamic response, maintaining stability, and increasing the system’s resilience to repeated load changes. These results affirm the effectiveness of the WaOA-based TIDFOI controller in handling complex and time-varying LFC challenges within interconnected power systems. The TID-FOI controller significantly enhances stability and reliability in LFC systems. Its unique tilted framework refines the interplay between proportional, integral, and derivative actions, leading to quicker stabilization and lower frequency variations. The fractional-order approach strengthens resilience against external disruptions, ensuring effective management of nonlinearities. Through fractional integral components, it counteracts communication delays, promoting steady performance despite renewable energy integration challenges. This controller also minimizes overshoot, optimizes control mechanisms, and fosters energy-efficient operations. Additionally, it smoothly adjusts to sudden load fluctuations, maintaining grid stability in dynamically changing conditions.
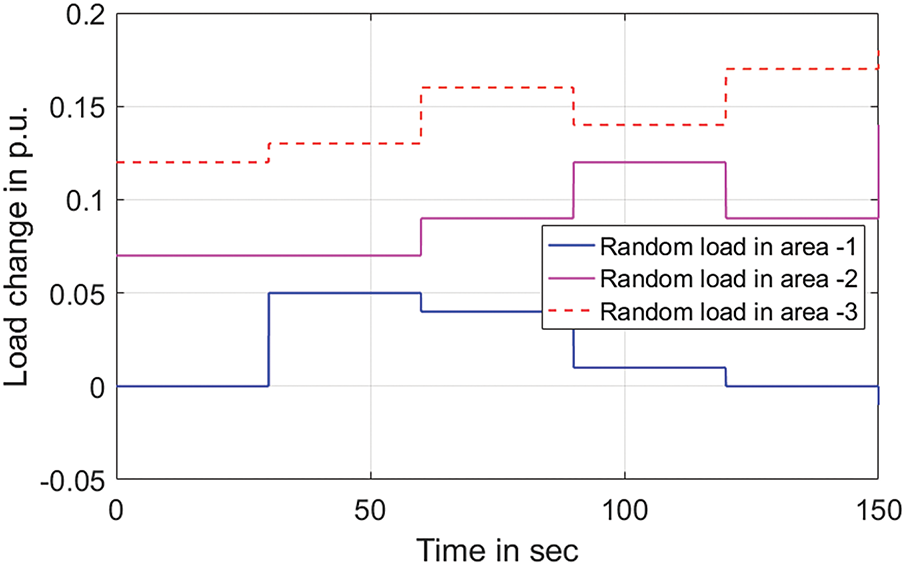
Figure 9: Dynamic load variation in area 1, area 2, and area 3
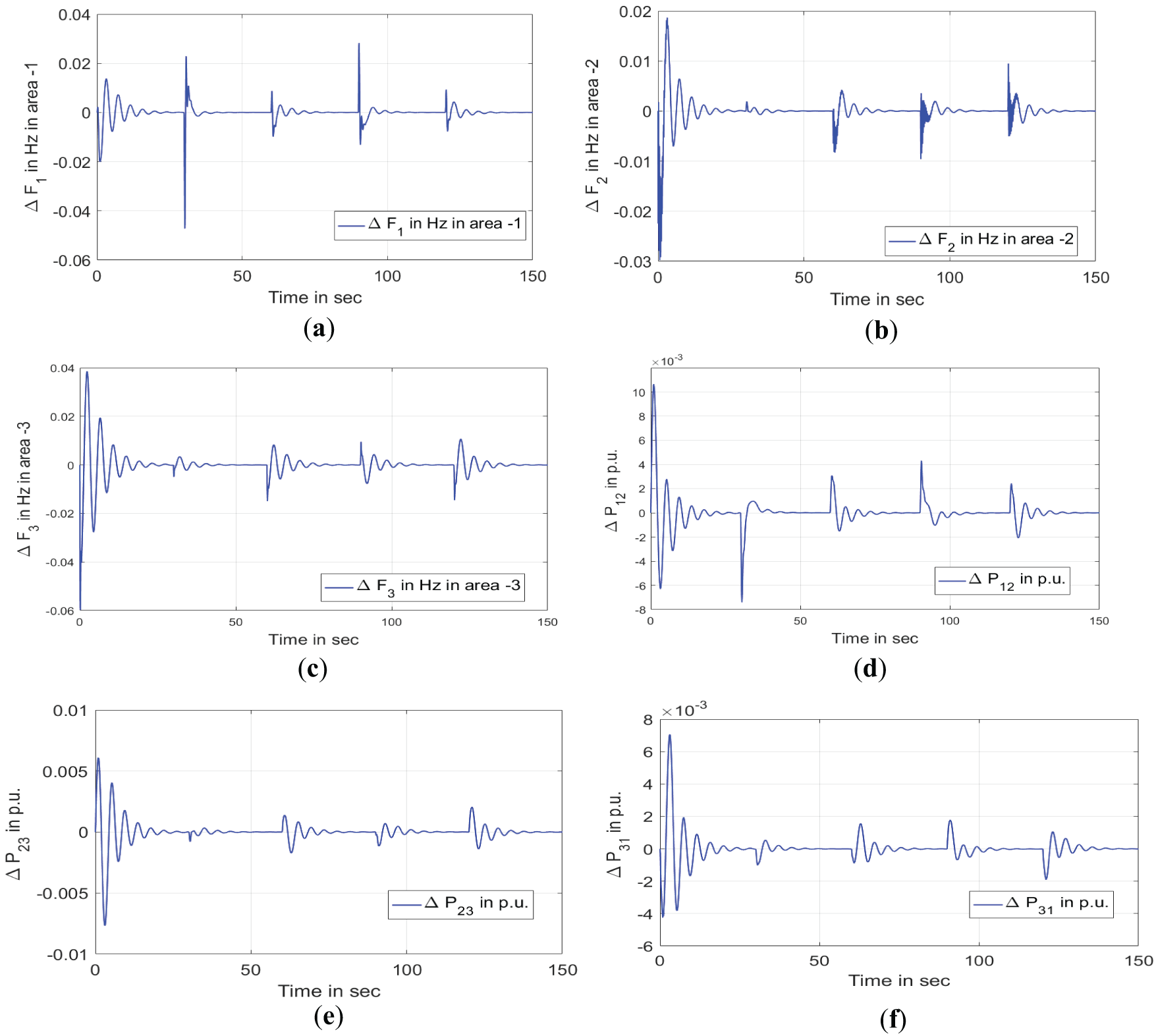
Figure 10: Response dynamics resulting from stochastic load fluctuations. (a) Deviation in Frequency of area-1. (b) Deviation in Frequency of area-2. (c) Deviation in Frequency of area-3. (d) Power deviation in tie-line between areas 1–2. (e) Power deviation in tie-line between areas 2–3. (f) Power deviation in tie-line between areas 1–3
6.4 Case Study IV: Sensitivity Analysis
Sensitivity analysis plays a vital role in LFC, particularly when assessing the impact of variations in turbine and governor time constants. These parameters often vary in real-world systems due to factors such as aging equipment, maintenance conditions, and environmental influences. By systematically changing the turbine (Tt) and governor (Tg) time constants, sensitivity analysis helps evaluate the robustness of the LFC controller under different dynamic conditions. The efficiency of the proposed load frequency control (LFC) method has been verified through simulations under diverse system conditions. Specifically, Tt and Tgh were each adjusted by ±20% to evaluate the controller’s sensitivity and resilience. Fig. 11 illustrates the frequency variations in regions 1, 2, and 3, along with the fluctuations in tie-line power, in response to a 20% change in Tt. The findings in Fig. 11 consistently indicate that the system maintains stability despite these parameter modifications, thereby affirming the reliability and robustness of the proposed LFC strategy in managing dynamic uncertainties within power networks. The proposed load frequency control method has been subjected to extensive testing to evaluate its adaptability under dynamic system conditions. This validation process systematically adjusted key parameters within the experimental setup, including the Tt and the Tgh. To evaluate their influence on system performance, each parameter was adjusted by 20% in both positive and negative directions to replicate real-world operating scenarios. The dynamic behavior of frequencies and tie-line power was thoroughly analyzed to understand the effects of these variations. Fig. 11 depicts the frequency deviations recorded in regions 1, 2, and 3 of the test system, along with the corresponding tie-line power fluctuations resulting from a 20% modification in Tgh & Tt.

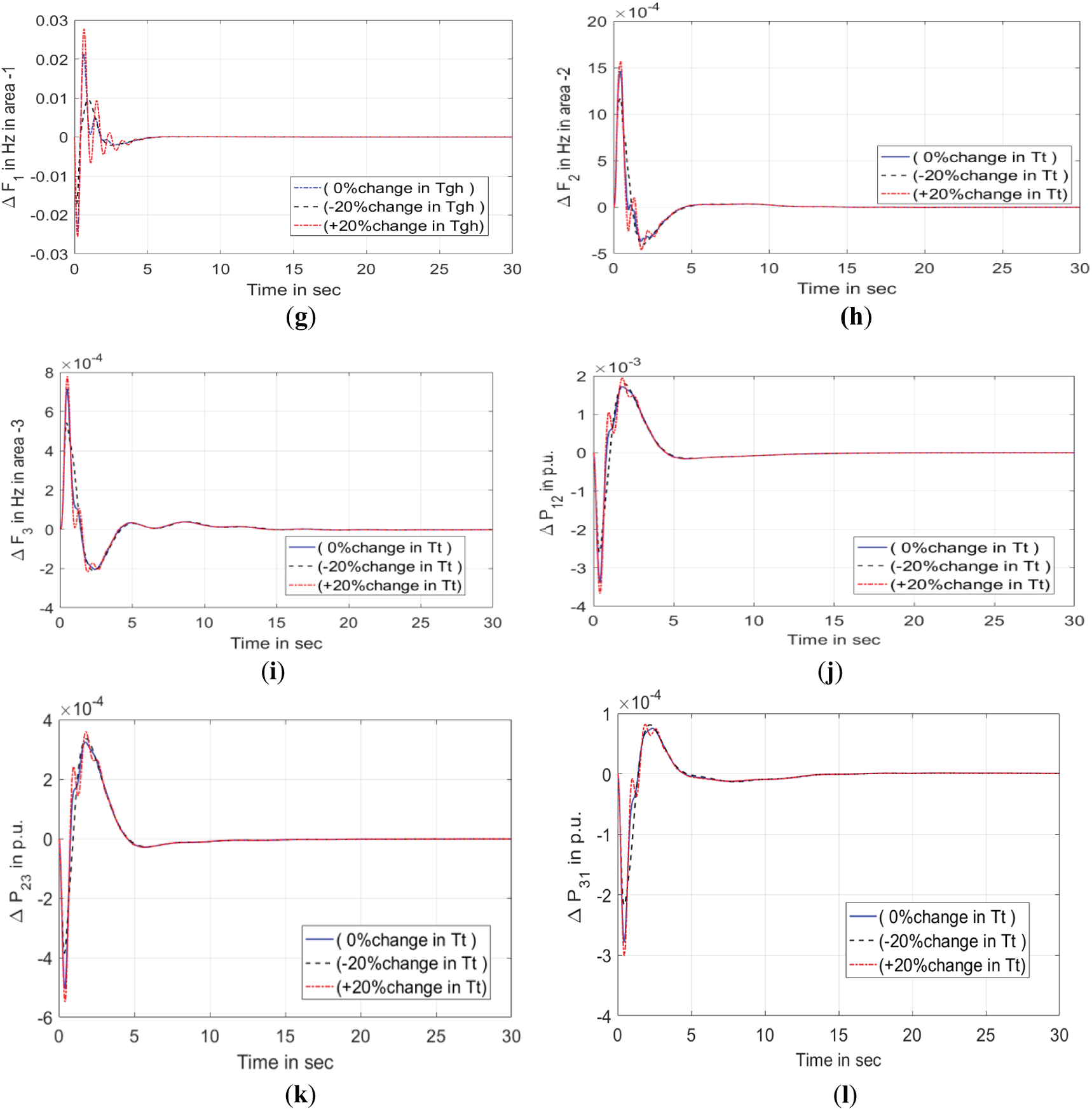
Figure 11: Transient characteristics of the system with altered Tgh & Tt values. (a) Frequency oscillation in area 1. (b) Frequency oscillation in area 2. (c) Frequency oscillation in area 3. (d) Tie-line power oscillation between areas 1 & 2. (e) Tie-line power oscillation between areas 2 & 3. (f) Tie-line power oscillation between areas 3 & 1. (g) Dynamic shifts in frequency in area 1. (h) Dynamic shifts in frequency in area 2. (i) Dynamic shifts in frequency in area 3. (j) Oscillations in power exchange between areas 1 & 2. (k) Oscillations in power exchange between areas 2 & 3. (l) Oscillations in power exchange between areas 3 & 1
Despite these fluctuations, the test system remained stable, demonstrating the resilience of the proposed control strategy in tackling load frequency control issues. The findings validate the approach’s ability to uphold system stability, even in the face of dynamic parameter changes.
6.5 Case Study V: Effect of TCSC FACTS Controller
Combining renewable power sources with different control strategies amplifies system intricacy and nonlinear responses. To reduce oscillations in tie-line power flow, the deployment of a FACT controller, like the Thyristor-Controlled Series Capacitor (TCSC), is suggested. The TCSC excels in rapid and stable power regulation, presenting an effective solution for mitigating oscillations in a short duration.
Fig. 12 showcases the system’s output response under the operation of a TCSC controller within the Poolco transaction, facilitating interactions among power generation firms and electricity distribution entities. It demonstrates how the WaOA-driven TID-FOI controller, combined with the TCSC, suppresses variations in tie-line energy transfer Meanwhile, Fig. 13 emphasizes the controller’s resilience. The proposed controller is shown to be stable, supported by a gain margin of 86.7 dB and a phase margin of 112.8 degrees.
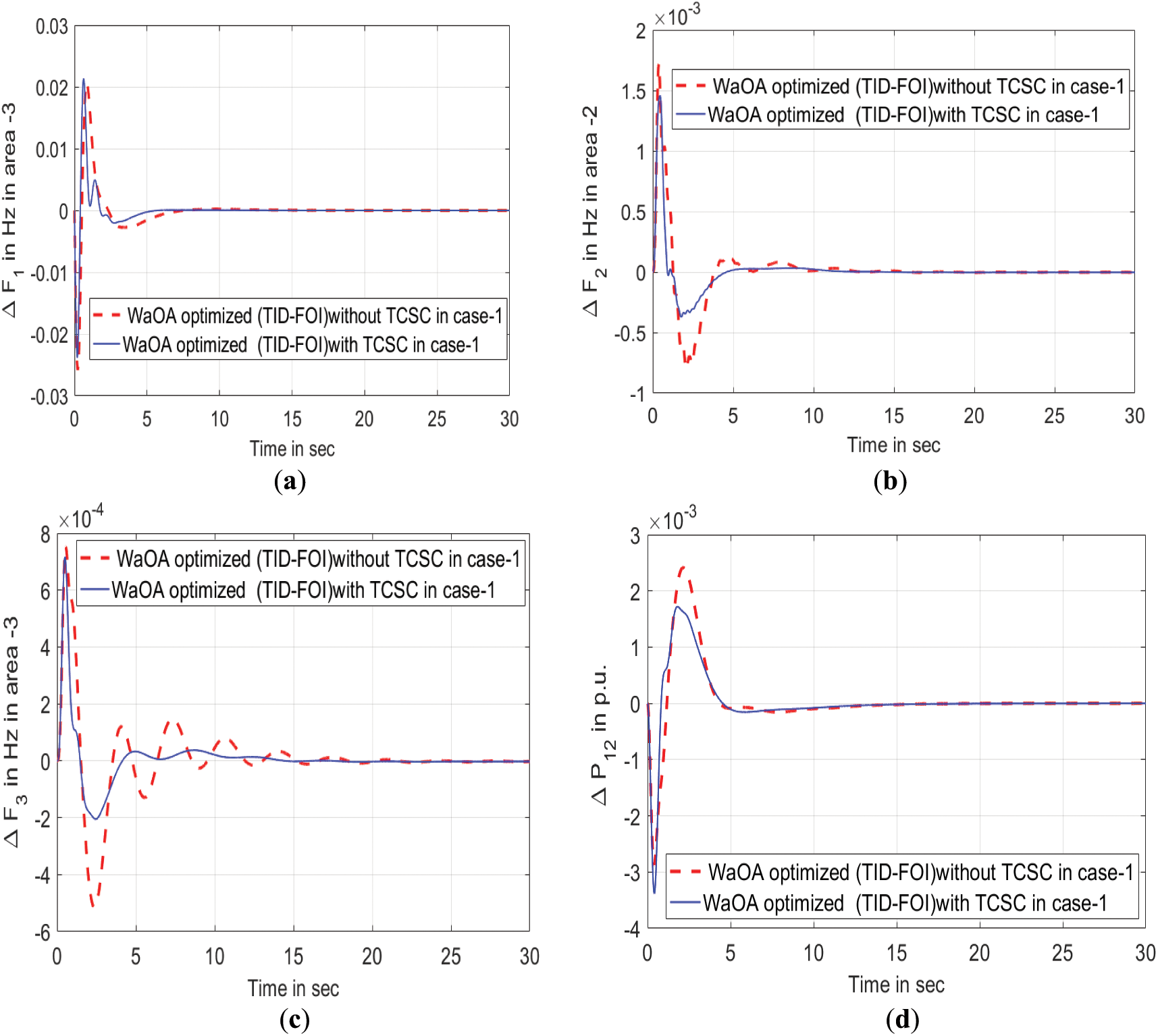
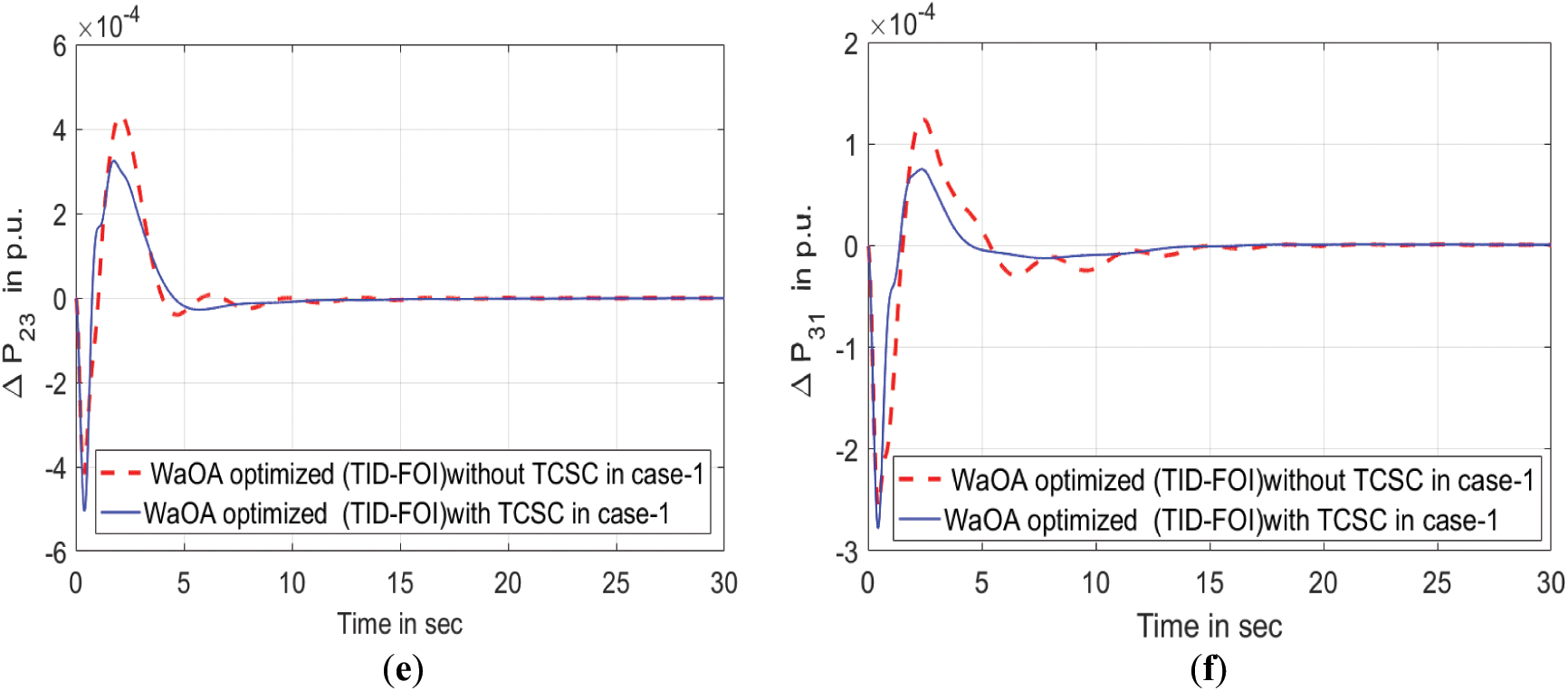
Figure 12: Transient response of suggested controller with TCSC and without TCSC in Poolco. (a) Oscillations in frequency for area 1. (b) Oscillations in frequency for area 2. (c) Oscillations in frequency for area 3. (d) Inter-area power deviation between areas 1 & 2. (e) Inter-area power deviation between areas 2 & 3. (f) Inter-area power deviation between areas 3 & 1
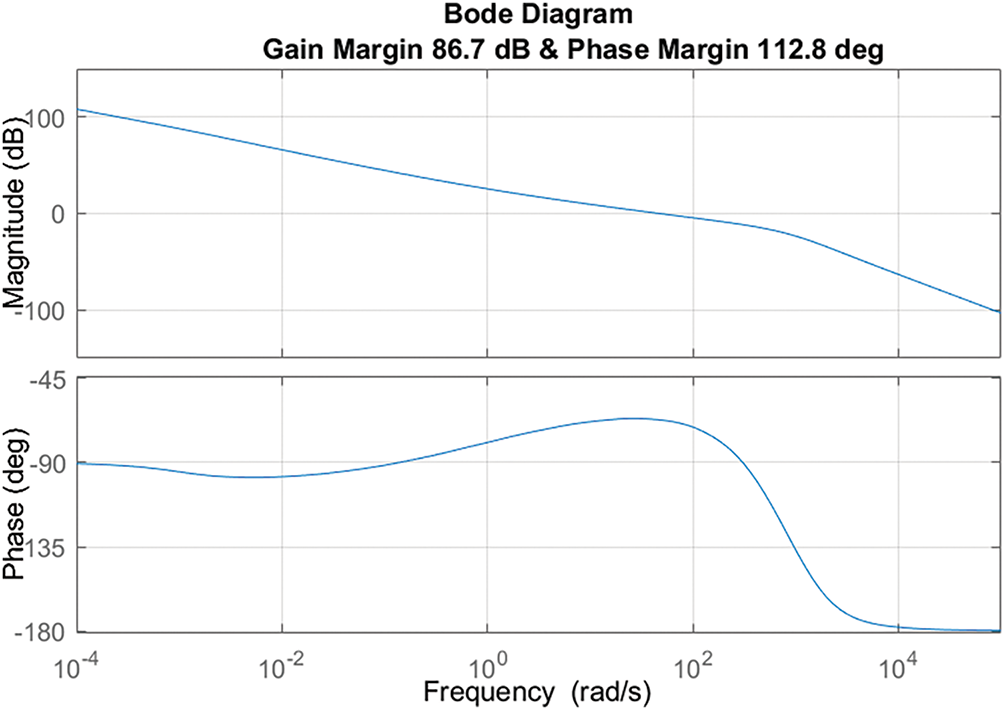
Figure 13: Bode plot of TID-FOI Controller
This study presents the Walrus Optimization Algorithm (WaOA) as an innovative approach for optimizing the TID-FOI controller, designed to handle frequency disturbances in a power system with three control areas. The research highlights exceptional performance when evaluated against the existing methodology such as PSO and COA within a deregulated environment. Findings demonstrate a significant reduction in performance indices when using WaOA, validating its effectiveness. The WaOA-based TID-FOI controller is deployed to optimize system frequency response having three control areas, with simulation results validating its enhanced effectiveness in relation to traditional controllers. The objective value for the optimized controller, adjusted using the PSO algorithm and COA, stands at 0.66 and 0.16, respectively. However, the controller employing the proposed algorithm achieves a significantly improved objective value of 0.0545. Additionally, the controller tuned via PSO and COA exhibits frequency oscillation settling times of 11.92 and 10.38 s in area 3. In contrast, the WaOA-based approach enhances system performance, reducing the settling time to 4.406 s. It efficiently reduces both peak overshoot and undershoot in response to minor disturbances, reinforcing its robustness. Additionally, the Variability assessment conducted on system parameters validates the reliability of the presented methodology. To enhance system stability, the study integrates a TCSC FACTS controller within the framework. Although the existing model integrates a limited number of renewable energy sources, future research could expand its scope by introducing additional sources and exploring alternative controller designs.
The WaOA-optimized TID-FOI controller requires real-world validation through pilot studies in actual power grids to assess adaptability under dynamic conditions. In deregulated markets, addressing pricing fluctuations and multi-area coordination is crucial, with blockchain integration enhancing transaction security. Hybridizing WaOA with PSO, GA, or AI-based learning could further boost optimization efficiency. Testing scalability in large interconnected systems and renewable-integrated grids will expand its applicability. Strengthening cybersecurity measures and AI-driven anomaly detection will safeguard against digital threats. Furthermore, testing new optimization in distributed systems and conducting hardware assessments remain promising directions for further study.
Acknowledgement: The research was partially carried out within the Experimental-Demonstration project PN-IV-P7-7.1-PED-2024-0567 (Improving the Fuel Cell Hybrid Electric Vehicle Drivetrain by Implementing a Novel Optimal Real-Time Power Management Strategy), contract No. 58PED, 2024–2025.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Geetanjali Dei, Deepak Kumar Gupta, and Binod Kumar Sahu did the simulations and wrote the original draft; Amitkumar V. Jha and Bhargav Appasani reviewed and revised the original draft; Nicu Bizon supervised the project and revised the paper. The authors have no conflict of interest. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Bhargav Appasani, upon reasonable request.
Ethics Approval: Not Applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
f = 60 Hz; KPS = 120 Hz/p.u Mw; TPS = 20 s; Tg = 0.08 s; Tt = 0.3 s; T12 = 0.0433 s; Rth = 2.4 Hz/p.u Mw; Rhy = 2.4 Hz/p.u Mw, Rg = 2.4 Hz/p.u, Rs = 2.4 Hz/p.u, Rd = 2.4 Hz/p.u Mw, B1 = B2 = 0.425 p.u Mw/Hz; Kr = 0.3; Tr = 10.0 s; TW = 1 s; Trs = 5 s; Trh = 28.75 s; Tgh = 0.2 s; N1 = 0.8, N2 = (−0.2).
GTPP: Tgeo = 0.2 s, Ttgeo = 0.2 s, STPP: Ksp = 1.78, Tsp = 1.78, Ttst = 1.6 s, Tgst = 0.2 s, DSTS: KDSTS = 1.54, TDSTS = 1.2 s.
RFB: Ke = 0.3, Te = 0.01 s.
TCSC: Ttcsc = 0.046, Ktcsc = 0.3, T13 = 0.0411 s, T14 = 0.39 s, T11 = 0.28 s, T121 = 0.025 s. T5 = 0.0170, T6 = 0.1834, T7 = 0.3421, T8 = 0.2954, TTCSC = 0.426, KTCSC = 0.8923.
Geothermal power system: G = 0.1299, T = 0.1; Diesel engine generator: Kdeg = 1/300, Tdeg = 2 s; Solar photo voltaic power system: Kspv = 1, Tspv = 1.8 s; Wind turbine system: Kwts = 1, Twts = 1.5 s.
Nomenclature
| Abbreviation | Description |
| TID | Tilted Integral Derivative Controller |
| AGC | Automatic Generation Control |
| FOI | Fractional-Order Integral Method |
| SSA | Squirrel Search Algorithm |
| PID | Proportional-Integral-Derivative Controller |
| WaOA | Walrus Optimization Algorithm |
| DST | Distributed Solar Technologies |
| RFB | Redox Flow Batteries |
| LFC | Load Frequency Control |
| FOC | Fractional-Order Controller |
| FOPID | Fractional-Order Proportional-Integral-Derivative Controller |
| ALO | Adaptive Learning Optimized Controller |
| CPPS | Cyber-Physical Power Systems |
| PSO | Particle Swarm Optimization |
| DPM | DISCO Participation Matrix |
| CPF | Contract Participation Factor |
| FOI | Fractional-Order Integral Controller |
| FOPID | Fractional-Order Proportional-Integral-Derivative Controller |
| DISCO | Distribution Company |
| GENCO | Generation Company |
| TCSC | Thyristor-Controlled Series Compensator |
| HIOT | Hybrid Intelligent Optimization Technique |
| SSA | Squirrel Search Algorithm |
| GTPP | Geothermal Power Plant |
| PSO | Particle Swarm Optimization |
| RFB | Redox Flow Battery |
| GRC | Generation Rate Constraint |
| GDB | Governor Dead Band |
References
1. Shahin M, Atallah T. Cascaded controllers for multi-area load frequency control systems: a fractional and time-delay approach. J Control Sci Eng. 2015;2015:1–9. doi:10.1155/2015/653827. [Google Scholar] [CrossRef]
2. Zhao Y, Xu M. A novel fractional order load frequency control scheme. IEEE Access. 2015;6:30868–75. doi:10.1109/ACCESS.2015.3012875. [Google Scholar] [CrossRef]
3. Boucher G, Madjid H. A review of advanced control strategies for load frequency control in power systems. IEEE Trans Power Syst. 2015;30(4):1764–72. doi:10.1109/TPWRS.2015.2393572. [Google Scholar] [CrossRef]
4. Zhang X, Xu M. Load frequency control in power systems with time-delay and fractional-order systems. Math Probl Eng. 2015;2015:1–9. doi:10.1155/2015/874309. [Google Scholar] [CrossRef]
5. Sadeh A, Fard MS. Adaptive load frequency control using cascaded FOI controllers in multi-area power systems. J Electr Eng Technol. 2016;10(3):1002–11. doi:10.5370/JEET.2016.10.3.1002. [Google Scholar] [CrossRef]
6. Marcos R, Gama R. Load frequency control with cascaded time-delay and fractional order controllers: stability and robustness analysis. Int J Power Energy Syst. 2016;36(1):73–82. doi:10.2316/J.2016.036-0010. [Google Scholar] [CrossRef]
7. Shahin MA, Elsayed A. Fractional order and time-delay control in multi-area load frequency control systems. J Control Decis. 2016;3(3):149–60. doi:10.1080/23307706.2016.1163578. [Google Scholar] [CrossRef]
8. Kumar P, Sharma A. Design of cascaded fractional-order PID controllers for load frequency control in multi-area power systems. IEEE Trans Ind Electron. 2016;63(9):5764–72. doi:10.1109/TIE.2016.2519326. [Google Scholar] [CrossRef]
9. Xia X, Liu Y. A robust cascaded FOI controller for load frequency control. IEEE Trans Power Syst. 2017;29(3):1150–58. doi:10.1109/TPWRS.2017.2654859. [Google Scholar] [CrossRef]
10. Liu X, Xu Q. Fractional order load frequency control of power systems with time-delay. J Electr Eng Technol. 2017;12(4):1400–09. doi:10.5370/JEET.2017.12.4.1400. [Google Scholar] [CrossRef]
11. Shahin MA, Elsayed A. Time-delay compensation for load frequency control using cascaded controllers. Int J Electr Power Energy Syst. 2017;81:126–33. doi:10.1016/j.ijepes.2016.12.006. [Google Scholar] [CrossRef]
12. Sadeh A, Azimian M. Fractional-order cascaded control for load frequency control in multi-area power systems. IET Control Theory Appl. 2017;11(9):1443–50. doi:10.1049/iet-cta.2016.1412. [Google Scholar] [CrossRef]
13. Dei G, Sahoo S, Sahu BK. Performance analysis of ALO tuned FOPID controller for AGC of a three area power system. In: Proceedings of the 2018 International Conference on Recent Innovations in Electrical, Electronics & Communication Engineering (ICRIEECE); 2018 Jul 27–28; Bhubaneswar, India. Piscataway, NJ, USA: IEEE; 2018. p. 3116–20. doi:10.1109/ICRIEECE.2018.1234567. [Google Scholar] [CrossRef]
14. Liu Z, Zhao L. Analysis and design of cascaded FOI controllers for load frequency control in power systems. Energy Rep. 2018;4:348–58. doi:10.1016/j.egyr.2018.01.009. [Google Scholar] [CrossRef]
15. Sadeh A, Fard MS. Stability analysis of cascaded FOI and TID controllers in load frequency control of interconnected power systems. J Power Energy Eng. 2018;6(3):43–51. doi:10.4236/jpee.2018.63004. [Google Scholar] [CrossRef]
16. Raju M, Saikia LC, Sinha N. Load frequency control of a multi-area system incorporating distributed generation resources, gate controlled series capacitor along with high-voltage direct current link using hybrid ALO-pattern search optimized fractional order controller. IET Renew Power Gener. 2018;12(10):1201–12. doi:10.1049/iet-rpg.2018.5010. [Google Scholar] [CrossRef]
17. Chiranjeevi M, Lakshmi VSG. Design of PSO-based fractional order load frequency controller for two-area power system. IOSR J Electr Electron Eng. 2018;9(6):67–74. doi:10.32604/iosrjeee.2018.1234567. [Google Scholar] [CrossRef]
18. Yun X, Li X. Advanced load frequency control using fractional order controllers: a comprehensive review. Energy Rep. 2019;5:134–42. doi:10.1016/j.egyr.2019.02.002. [Google Scholar] [CrossRef]
19. Raj A, Ghosh S. A hybrid FOI and TID controller for load frequency control in power systems. Energy Rep. 2019;5:150–59. doi:10.1016/j.egyr.2019.02.010. [Google Scholar] [CrossRef]
20. Shahin MA, Atallah T. Improved cascaded FOI and time-delay controllers for multi-area load frequency control. Int J Control Autom. 2019;12(2):31–40. doi:10.4018/IJCA.2019020104. [Google Scholar] [CrossRef]
21. Zhang C, Li J. Fractional-order load frequency control using time-delay compensators in power systems. Math Probl Eng. 2019;2019:1–12. doi:10.1155/2019/1234567. [Google Scholar] [CrossRef]
22. Zhang C, Li J. A new cascaded FOI controller for load frequency control in power systems: design and stability analysis. J Electr Eng. 2020;72(5):2120–30. doi:10.3144/jeeng.2020.05006. [Google Scholar] [CrossRef]
23. Kumar P, Sharma A. Time-delay compensation in cascaded FOI controllers for load frequency control. J Electr Power Syst Res. 2020;173:105740. doi:10.1016/j.epsr.2019.105740. [Google Scholar] [CrossRef]
24. Zhao L, Xu M. Design of cascaded fractional-order PID controllers for load frequency control in multi-area power systems. Energy Convers Manage. 2020;224:113364. doi:10.1016/j.enconman.2020.113364. [Google Scholar] [CrossRef]
25. Boucher G, Madjid H. Load frequency control with cascaded time-delay and fractional-order controllers: simulation and stability analysis. IEEE Trans Power Syst. 2020;35(3):1954–62. doi:10.1109/TPWRS.2020.2968409. [Google Scholar] [CrossRef]
26. Xia X, Liu Y. Robust cascaded fractional-order integral controllers for time-delay systems in load frequency control. IET Gener Transm Distrib. 2020;14(10):2092–101. doi:10.1049/iet-gtd.2019.1970. [Google Scholar] [CrossRef]
27. Marcos R, Gama R. Analysis of cascaded FOI controllers for load frequency control in multi-area power systems. J Control Decis. 2021;8(4):1032–43. doi:10.1080/22297928.2021.1936230. [Google Scholar] [CrossRef]
28. Gupta DK, Jha AV, Appasani B, Srinivasulu A, Bizon N, Thounthong P. Load frequency control using hybrid intelligent optimization technique for multi-source power systems. Energies. 2021;14(6):1581. doi:10.3390/en14061581. [Google Scholar] [CrossRef]
29. Raj A, Ghosh S. Multi-area load frequency control using cascaded time-delay and fractional-order controllers. Electr Power Syst Res. 2021;187:106452. doi:10.1016/j.epsr.2020.106452. [Google Scholar] [CrossRef]
30. Shahin M, Elsayed A. Cascaded time-delay and fractional-order controller for load frequency control in power systems with renewable energy integration. IET Renew Power Gener. 2021;15(10):1623–32. doi:10.1049/rpg2.12115. [Google Scholar] [CrossRef]
31. Zhang X, Xu M. A comprehensive review of cascaded FOI controllers in load frequency control of power systems. Renew Sustain Energy Rev. 2022;153:111739. doi:10.1016/j.rser.2021.111739. [Google Scholar] [CrossRef]
32. Gupta P, Singh B. Design of hybrid cascaded fractional-order controllers for load frequency control in power systems. Int J Power Energy Syst. 2022;42(6):1076–86. doi:10.2316/J.2022.051-0064. [Google Scholar] [CrossRef]
33. Dei G, Gupta DK, Sahu BK. Squirrel search algorithm (SSA)-driven optimal PID-FOI controller for load frequency control of two-area multi-source power system. In: Smart Technologies for Power and Green Energy: Proceedings of STPGE 2022. Singapore: Springer Nature; 2022. p. 305–15. [Google Scholar]
34. Pandey RK, Gupta DK, Dei G. Hybrid intelligent optimization technique (HIOT) driven FOPID controller for load frequency control of deregulated power system. In: Proceedings of the 2022 IEEE Global Conference on Computing, Power and Communication Technologies (GlobConPT); 2022 Sep 23–25; New Delhi, India. Piscataway, NJ, USA: IEEE; 2022. p. 1–6. [Google Scholar]
35. Zhang Y, Li J. Robust cascaded FOI and TID controller design for load frequency control in smart grids. J Mod Power Syst Clean Energy. 2023;11(1):51–61. doi:10.35833/MPCE.2022.000245. [Google Scholar] [CrossRef]
36. Fang X, Liu H. Improved time-delay compensation for load frequency control using fractional-order controllers in smart grids. IEEE Trans Smart Grid. 2023;14(1):292–301. doi:10.1109/TSG.2023.1234567. [Google Scholar] [CrossRef]
37. Begum B, Jena NK, Sahu BK, Ray P, Bajaj M, Singh AR, et al. Application of an intelligent fuzzy logic-based sliding mode controller for frequency stability analysis in a deregulated power system using OPAL-RT platform. Energy Rep. 2024;11:510–34. doi:10.1016/j.egyr.2024.107602. [Google Scholar] [CrossRef]
38. Tay CH, Tan CS. Stability and robustness of cascaded time-delay and fractional-order controllers for load frequency control in power systems. J Electr Eng Technol. 2023;18(4):1452–63. doi:10.1007/s40866-023-01020-6. [Google Scholar] [CrossRef]
39. Chen X, Wang F. Real-time implementation of cascaded FOI controllers for load frequency control in hybrid power systems. IEEE Trans Ind Electron. 2024;71(1):145–53. doi:10.1109/TIE.2024.1234567. [Google Scholar] [CrossRef]
40. Xu M, Zhao Y. Fractional-order and time-delay compensated load frequency control in multi-area power systems with renewable integration. Int J Electr Power Energy Syst. 2024;137:107602. doi:10.1016/j.ijepes.2024.107602. [Google Scholar] [CrossRef]
41. Shahin M, Elsayed A. Multi-area load frequency control using cascaded FOI controllers: stability and optimal design approaches. J Power Sources. 2024;552:231255. doi:10.1016/j.jpowsour.2024.231255. [Google Scholar] [CrossRef]
42. Dei G, Gupta DK, Sahu BK, Bajaj M, Blazek V, Prokop L. A novel TID+ IDN controller tuned with coatis optimization algorithm under deregulated hybrid power system. Sci Rep. 2025;15(1):4838. doi:10.1038/s41598-025-00250-8. [Google Scholar] [CrossRef]
43. Zhang X, Li J. Optimal design of cascaded FOI controllers for load frequency control of power systems with delays and disturbances. J Mod Power Syst Clean Energy. 2025;13(2):89–98. doi:10.1007/s40866-025-00250-8. [Google Scholar] [CrossRef]
44. Hassan A, Goh C. Application of cascaded FOI and time-delay controllers in load frequency control with renewable energy integration. IEEE Trans Energy Convers. 2025;40(1):157–67. doi:10.1109/TEC.2025.1234567. [Google Scholar] [CrossRef]
45. Gupta DK, Jha AV, Sahu P, Mohapatra S, Dei G, Appasani B, et al. Load frequency control analysis of cyber-physical power system with denial-of-service attack in deregulated power markets. Smart Grids Sustain Energy. 2025;10(1):1–23. doi:10.1007/s40866-025-00250-8. [Google Scholar] [CrossRef]
46. Gaur P, Singh B. Cascaded FOI and time-delay control for load frequency control in interconnected power systems with renewable energy. IEEE Access. 2025;13:24935–44. doi:10.32604/ieeeaccess.2025.1234567. [Google Scholar] [CrossRef]
47. Singh B, Jain V. Fractional-order cascaded controllers for multi-area load frequency control: a stability perspective. J Electr Eng. 2025;80(5):1124–32. doi:10.32604/jee.2025.1234567. [Google Scholar] [CrossRef]
48. Liu Z, Xu Q. Stability and performance of cascaded FOI controllers in load frequency control for power systems with large time delays. Energy Rep. 2025;11:314–25. doi:10.32604/er.2025.1234567. [Google Scholar] [CrossRef]
49. Trojovský P, Dehghani M. A new bio-inspired metaheuristic algorithm for solving optimization problems based on walruses behavior. Sci Rep. 2023;13(1):8775. doi:10.1038/s41598-023-35863-5. [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools