 Open Access
Open Access
ARTICLE
Optimal Dispatch of Urban Distribution Networks Considering Virtual Power Plant Coordination under Extreme Scenarios
State Grid Sichuan Electric Power Company, Tianfu New Area Power Supply Branch, Chengdu, 610200, China
* Corresponding Author: Yuxuan Chen. Email:
(This article belongs to the Special Issue: Construction and Control Technologies of Renewable Power Systems Based on Grid-Forming Energy Storage)
Energy Engineering 2026, 123(1), 9 https://doi.org/10.32604/ee.2025.069257
Received 18 June 2025; Accepted 19 August 2025; Issue published 27 December 2025
Abstract
Ensuring reliable power supply in urban distribution networks is a complex and critical task. To address the increased demand during extreme scenarios, this paper proposes an optimal dispatch strategy that considers the coordination with virtual power plants (VPPs). The proposed strategy improves system flexibility and responsiveness by optimizing the power adjustment of flexible resources. In the proposed strategy, the Gaussian Process Regression (GPR) is firstly employed to determine the adjustable range of aggregated power within the VPP, facilitating an assessment of its potential contribution to power supply support. Then, an optimal dispatch model based on a leader-follower game is developed to maximize the benefits of the VPP and flexible resources while guaranteeing the power balance at the same time. To solve the proposed optimal dispatch model efficiently, the constraints of the problem are reformulated and resolved using the Karush-Kuhn-Tucker (KKT) optimality conditions and linear programming duality theorem. The effectiveness of the strategy is illustrated through a detailed case study.Graphic Abstract
Keywords
Power supply support refers to the ability of the distribution system to maintain or restore critical electricity supply to essential loads during extreme scenarios. The concept encompasses both real-time power delivery and flexible demand-side management to ensure system resilience. As the critical link between transmission systems and end-users, urban distribution grids directly determine supply reliability, voltage stability, and outage resilience for high-density load centers. Improving the power supply security and integrated capacity of urban distribution networks is crucial to support the development of a modern energy system and a reformed power grid structure.
However, the high penetration of renewable energy sources has brought significant uncertainty and instability to the operation and control of urban distribution networks [1–4]. Frequent extreme events further exacerbate the challenges of ensuring power supply in urban distribution networks [5–8]. To ensure a reliable power supply of urban distribution networks, the authors in [9] established a supply support framework incorporating multidimensional factors, providing novel solutions to short supply support cycles and limited resource diversity. In [10], a load restoration strategy based on multi-energy coordination is proposed to improve the resilience of UIES, with the goal of restoring important loads as much as possible. The authors in [11] analyzed the Sichuan high-temperature drought power rationing event, identifying the power supply support challenges of modern power systems in planning, operation, trading, and policy, and proposing corresponding control strategies.
Building on these efforts, several studies have explored the utilization of distributed resources for resilient service restoration. The authors in [12] proposed a novel operational strategy for distribution systems based on real-time formation of multiple microgrids powered by distributed generation (DG). This approach enhances system resilience under extreme scenarios by enabling autonomous operation of localized energy systems, thereby isolating affected areas and maintaining power supply to essential loads. In [13], a resilient feeder restoration method is proposed for power distribution networks that utilizes distributed energy resources (DERs) to restore critical loads following extreme weather events. A two-stage optimization method is proposed in [14] for critical load restoration in distribution systems following extreme events, leveraging microgrids, distributed generators, and other local resources. The first stage determines the optimal post-event network topology, while the second stage identifies the set of critical loads to be restored and the corresponding output of available distributed resources.
Additionally, virtual power plants (VPPs) have emerged as a crucial technology for aggregating and optimizing flexible resources such as photovoltaic (PV) systems, energy storage, and interruptible loads, thereby to providing flexibility and controllability for power system operation. The authors in [15] proposed an equivalent aggregation models for the VPP to participate in contingency reserve services. The authors in [16] proposed a reduced-order dynamic model of the VPP, enabling transmission system operators to effectively assess the impact of VPPs on grid stability and facilitating their integration into modern power systems. In [17], an optimal coordinated scheduling of electric vehicles for a VPP is proposed to coordinate charging/discharging strategies of massive and dispersed EVs. Given their ability to efficiently aggregate diverse flexible resources, VPPs are well-suited to play a pivotal role in enhancing the power supply support capabilities of urban distribution networks under extreme scenarios.
Although there have been several strategies proposed in literature to guarantee the power supply for urban distribution network under extreme scenarios [18,19]. However, these works do not fully leverage the potential of VPPs in coordinating heterogeneous flexible resources under extreme conditions. Moreover, they often overlook the need to balance power supply support with economic performance, particularly when faced with high levels of renewable uncertainty. These gaps motivate this study, which proposes an optimal dispatch strategy for urban distribution networks during extreme scenarios, integrating VPPs to coordinate flexible resources while accounting for both reliability and economic efficiency. Firstly, Gaussian process regression is employed to estimate the power output scenarios or power adjustment ranges of photovoltaic systems and adjustable loads within each VPP, enabling the distribution of power supply support responsibilities among individual VPPs. Then, a leader-follower game model is employed to dispatch the coordination of flexible resources within each VPP, ensuring the power output of flexible resources meet the demands of power supply. In this framework, VPP pricing is used as a key decision variable to coordinate the dispatch objectives between the distribution system operator and the VPPs, balancing economic incentives with operational reliability. The effectiveness of the proposed strategy is verified through simulation analysis under extreme scenarios. This strategy ensures efficient resource coordination while enhancing the reliability of urban distribution networks. In the considered urban distribution network, various flexible resources are included, such as solar PV systems and adjustable loads. These resources are aggregated and managed through the VPP, enabling them to play a more significant role in grid operation and dispatch. The VPP not only integrates different types of resources but also coordinates their interactions to optimize their outputs according to the grid’s demand variations.
Additionally, the urban distribution network incorporates smart meters for real-time monitoring and adjustment of user-side consumption behaviors, supporting the effective implementation of demand response programs. This comprehensive framework provides a solid foundation for enhancing the flexibility, reliability, and efficiency of the grid. Against this backdrop, the proposed optimal dispatch strategy not only enhances system flexibility and responsiveness but also provide robust support for power supply support.
While the proposed strategy primarily focuses on optimizing the dispatch of flexible resources aggregated by VPPs, other operational strategies such as network reconfiguration, sectionalizing switch control, and feeder reorganization also play important roles in enhancing the resilience and efficiency of distribution networks. These strategies can be integrated into the proposed framework in future extensions, potentially leading to a more comprehensive and robust dispatch methodology.
The main contributions of this paper are summarized as follows:
• An optimal dispatch strategy incorporating VPPs is proposed to enhance the reliability of urban distribution networks during extreme scenarios by optimizing the power adjustment of flexible resources.
• Gaussian process regression is applied to evaluate the adjustable power range of VPPs, providing a robust and probabilistic method to quantify their potential contribution to power supply support.
• An optimal dispatch model based on leader-follower game theory is developed to coordinate system operators and VPPs, aiming to optimize both system resilience and resource utilization during extreme events. And the model incorporating VPP pricing as an incentive mechanism to align the dispatch decisions of system operators and VPPs, promoting both reliability and economic efficiency.
• The Karush-Kuhn-Tucker conditions and the duality principle of linear programming are utilized to reformulate and solve the optimization problem efficiently, transforming it into a tractable mathematical formulation.
Organization: Section 2 analyses the operating characteristics of photovoltaic systems and temperature-sensitive loads in extreme scenarios. In Section 3, we introduce the optimal dispatch strategy. In Section 4, case studies are conducted and the simulation results are discussed. We conclude the paper in in Section 5.
2 Analysis of Operating Characteristics of Photovoltaic Systems and Temperature-Sensitive Loads in Extreme Scenarios
In this study, extreme scenarios refer to severe weather-induced disruptions, such as high-temperature droughts, heavy storms, and sandstorms, which significantly impact the power generation of renewable energy sources and increase the demand for electricity. These scenarios are simulated by introducing uncertainty sets and probabilistic scenarios for photovoltaic output and adjustable load demand, based on historical weather and load data.
This section presents a detailed analysis of the operational characteristics of PV systems and temperature-sensitive loads under extreme weather conditions. The operational characteristics of PV systems are introduced in Section 2.1, detailing how environmental factors such as temperature, solar irradiance, dust, and snow affect PV outputs. Section 2.2 then elaborates on the operating characteristics of temperature-sensitive loads, explaining how varying ambient temperatures impact energy consumption for devices like air conditioners and electric heaters.
2.1 Operational Characteristics of Photovoltaic Systems
The performance of PV systems is affected by environmental temperature, solar irradiance, dusty conditions [20], and snow accumulation. As shown in Fig. 1, the PV output curves vary under different weather scenarios. Here is the summary of different environmental factors on PV outputs. Solar irradiance directly determines PV output and higher radiation levels result in increased power generation. Extreme temperatures can change the conductivity of PV panels, i.e., high temperatures decrease energy conversion efficiency, while low temperatures can slightly enhance efficiency, though excessively low temperatures may result in component or inverter failures. Dust accumulation during dusty weather blocks sunlight, therefore reducing PV outputs. And in snowy conditions, full snow coverage prevents PV panels from receiving radiation until the snow is removed or melts.
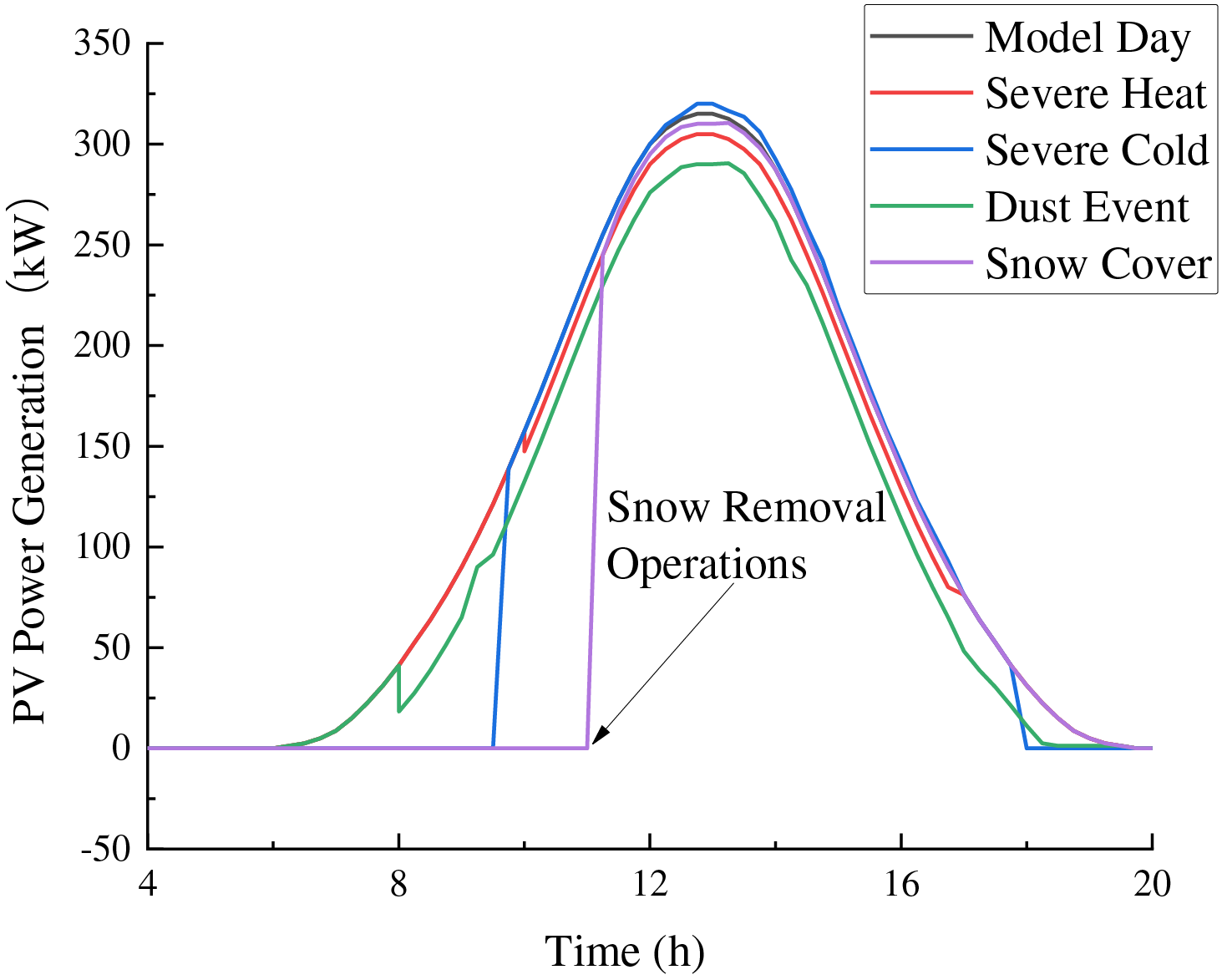
Figure 1: Photovoltaic output across various weather scenarios
2.2 Operating Characteristics of Temperature-Sensitive Loads
Temperature-sensitive loads refer to electrical devices whose energy consumption is highly dependent on ambient temperature, such as air conditioning systems and electric heaters. In high-temperature environments, air conditioning systems must increase the frequency and duration of cooling cycles to maintain indoor comfort, resulting in a significant increase in electricity consumption. Conversely, in low-temperature conditions, the heating function of air conditioners (such as heat pumps or auxiliary electric heaters) operates continuously to counteract cold external air, similarly increasing energy demand. Electric heaters exhibit similar behavior under extreme cold. They often operate for extended periods and may reach their maximum output to maintain indoor thermal comfort.
3 Two-Stage Virtual Power Plant Dispatch Strategy for Power Supply Support
Building upon the operational characteristics discussed in Section 2, a two-stage optimal dispatch strategy is proposed for VPPs to provide reliable power supply for urban distribution networks under extreme scenarios, with its framework illustrated in Fig. 2. In the first stage, Gaussian process regression is applied to assess the adjustable power ranges of each VPP, enabling the distribution network operator to assign power supply support demands to individual VPPs. In the second stage, a leader-follower game is established: the upper level maximizes the revenue of VPPs, while the lower level maximizes the revenue of distributed resource aggregators. The solution of the model provides power supply support strategies for various time periods.

Figure 2: Framework of the power supply support dispatch strategy for urban distribution networks with VPP interactions
The Stackelberg game framework is adopted to model the hierarchical decision-making process between the VPP and its internal flexible resources. In this framework, the VPP acts as the leader, responsible for setting subsidy prices to coordinate the dispatch of flexible resources. Each flexible resource acts as a follower, optimizing its own dispatch strategy in response to the received price signal.
Specifically, the VPP assumes the role of a price-maker, leveraging its global information and system-level optimization objective to design incentive-compatible subsidy prices. This reflects the real-world operation of VPPs, where the aggregator has the authority to influence resource behavior through economic signals. About the follower side, responsive loads are modeled as rational agents who adjust their consumption based on the trade-off between utility and cost.
Compared to non-cooperative game models such as the Nash equilibrium, where all players make decisions simultaneously and symmetrically, the Stackelberg framework better captures the asymmetric information structure and hierarchical control inherent in VPP systems. This enables more effective coordination under extreme conditions, especially when rapid response and centralized control are required.
3.1 Allocation of Power Supply Support Based on Adjustable Aggregation Power Ranges
Based on the evaluation produced by the Gaussian Process Regression (GPR) model for the adjustable aggregated power ranges of flexible resources, our objective is to achieve an optimal dispatch of VPPs in the distribution network. This allows each VPP to make rapid local decisions based on their own adjustable power ranges while ensuring overall power balance.
(1) Evaluation of Adjustable Aggregated Power Ranges for Flexible Resources: Flexible resources are aggregated effectively and efficiently through VPPs to provide reliable power support for urban distribution networks under extreme weather. Here, the GPR method developed in [21] is utilized to evaluate the adjustable ranges of the aggregated power for VPPs involved in power supply support, enabling the determination of the adjustable power ranges of each VPP at various time instants.
Historical data on the output of flexible resources in the VPP, along with environmental factors such as temperature and solar irradiance, are gathered as training data for the GPR model. An appropriate kernel function is chosen to estimate the adjustable power ranges of the m-th VPP’s flexible loads at time instant t, denoted as
Considering
where
The posterior distribution of the predicted value
The mean and covariance are determined by the following expressions:
The combination of the RBF Kernel and LIN Kernel covariance functions yields the total covariance function of the GPR model.
where
The adjustable aggregated power ranges for the m-th virtual power plant (VPP) at different time instants is expressed as
(2) Allocation of Power Supply Support Quantities among VPPs: At time instant t, each VPP submits its assessed adjustable aggregated power ranges to the distribution network system operator (DNSO). Utilizing the information and the power supply support demand at time instant t, the DNSO allocates the required power supply support quantities to each VPP and announces the corresponding incentive price. The power supply support quantity assigned to the m-th VPP at time instant t is expressed as:
where M is the number of VPPs in the distribution network capable of participating in power supply support;
3.2 Bi-Level Optimization Model for VPP Dispatch: Revenue Maximization with Distributed Resource Coordination under Extreme Scenarios
To enhance clarity, the key parameters and decision variables in the proposed optimization model are summarized as follows (Table 1):
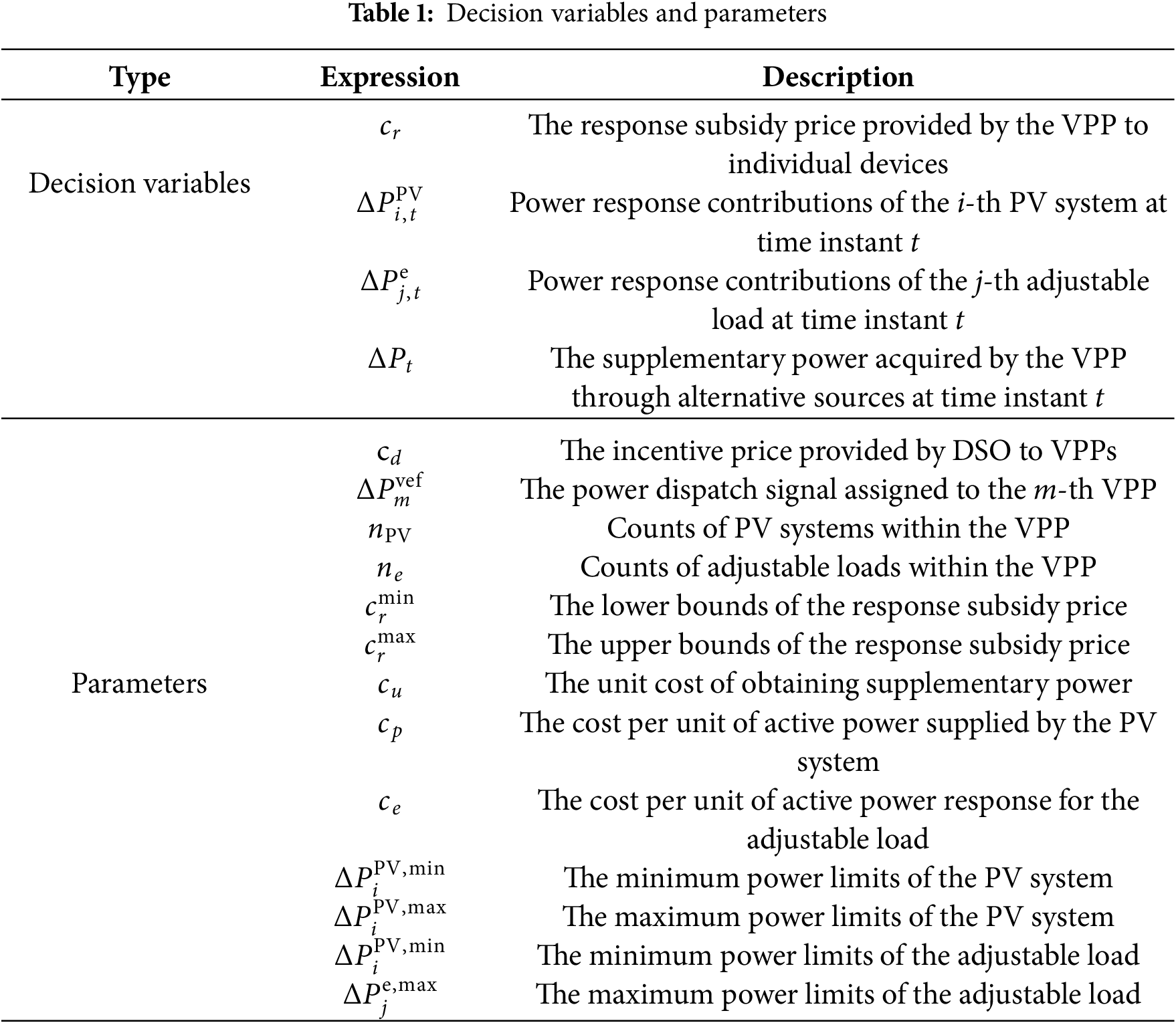
A bi-level leader-follower optimization model is proposed for the DNSO to obtain the optimal dispatch signals for VPPs in the system. In this hierarchical framework, the upper-level problem represents the decision-making process of the DNSO, which aims to maximize the overall revenue of the VPPs while ensuring reliable power supply across different time instant. The lower-level problem corresponds to the response of distributed resource aggregators, who coordinate their adjustable loads and controllable photovoltaic resources to follow the dispatch signals issued by the VPPs, with the objective of maximizing their own revenues. Each VPP acts as an intermediary that coordinates the operation of its internal distributed energy resources to execute the dispatch signal. The response subsidy price
where
The function (8a) is designed to maximize the revenue of the VPP. The constraint (8b) guarantees the response subsidy price within limit. The constraint (8c) is set to ensure the balance of supply power and load demand. The constraint (8d) guarantees the supplementary power to be non-negative.
Given the dispatch signal by the VPP, each distributed resource such as PV systems and adjustable loads—then independently responds based on its own operational constraints and incentive preferences. Specifically, the optimization problem for the i-th PV system is described as follows:
where
The function (9a) is designed to maximize the revenue of the PV system. The constraint (9b) guarantees the power output of the PV system within limit during the power supply support period. The constraint (9c) is set to ensure the power output of the PV system to be zero beyond the period of the power supply support
And the optimization problem for the j-th adjustable load is formulated as follows:
where
The function (10a) is designed to maximize the revenue of the adjustable load. The constraint (10b) guarantees the power output of the adjustable load within limit during the power supply support period. The constraint (10c) is set to ensure the power output of the adjustable load to be zero beyond the period of the power supply support.
To solve the above optimization model, the lower-level problem is first transformed into an equivalent nonlinear programming formulation using KKT conditions. Boolean variables are then introduced to recast these conditions as linear inequality constraints. Subsequently, duality theory is applied to linearize the objective function. Finally, the entire bi-level leader-follower game model is reformulated as a mixed-integer linear programming (MILP) model.
The detailed mathematical derivations, including the KKT conditions for the lower-level optimization problems of photovoltaic systems and adjustable loads, as well as the linearization steps, are provided in Appendix A.
To further simplify the bi-level optimization model, duality theory is applied to linearize the objective function. Duality theory indicates that when both the primal and dual problems achieve their optimal solutions, their objective functions are equal. From Eqs. (9a) and (10a), the following equality can be derived:
By integrating the reformulated constraints from the lower-level problems and the linearized objective function, the entire bi-level leader-follower game model is ultimately transformed into a MILP problem. The proposed optimization model aims to maximize the total economic benefit of VPPs while ensuring reliable power supply under extreme scenarios. The objective function is defined as:
s.t. (8b)–(8d), (A1a), (A1d), (A2a), (A2d) and (A3a)–(A6b).
The proposed model incorporates distribution network constraints through a linearized power flow formulation, ensuring that voltage and line flow limits are respected during dispatch. These constraints are specifically listed in Appendix B.
4 Experiment and Result Analysis
This section presents a specific case study designed to confirm the efficacy of the bi-level leader-follower game model for VPP pricing and the associated solution approach introduced in Section 2. Additionally, while ensuring compliance with power supply support demands, the influence of the minimum pricing threshold of VPPs on their revenue and that of adjustable devices is explored. A case study diagram of an urban distribution network incorporating VPPs is shown in Fig. 3, where the abbreviation AL denotes adjustable load, and VPP represents the smart control platform that aggregates various flexibility resources.

Figure 3: Diagram of an urban distribution network incorporating VPPs
4.1 Evaluation of Adjustable Power Ranges
Historical data, including PV output, serves as training samples for the GPR model to generate daily output curves for PV systems, as depicted in Fig. 4. The generated profile mirrors the overall trend of historical generation curves. By extension, assessments of the adjustable ranges for flexible resources within various VPPs can be achieved.
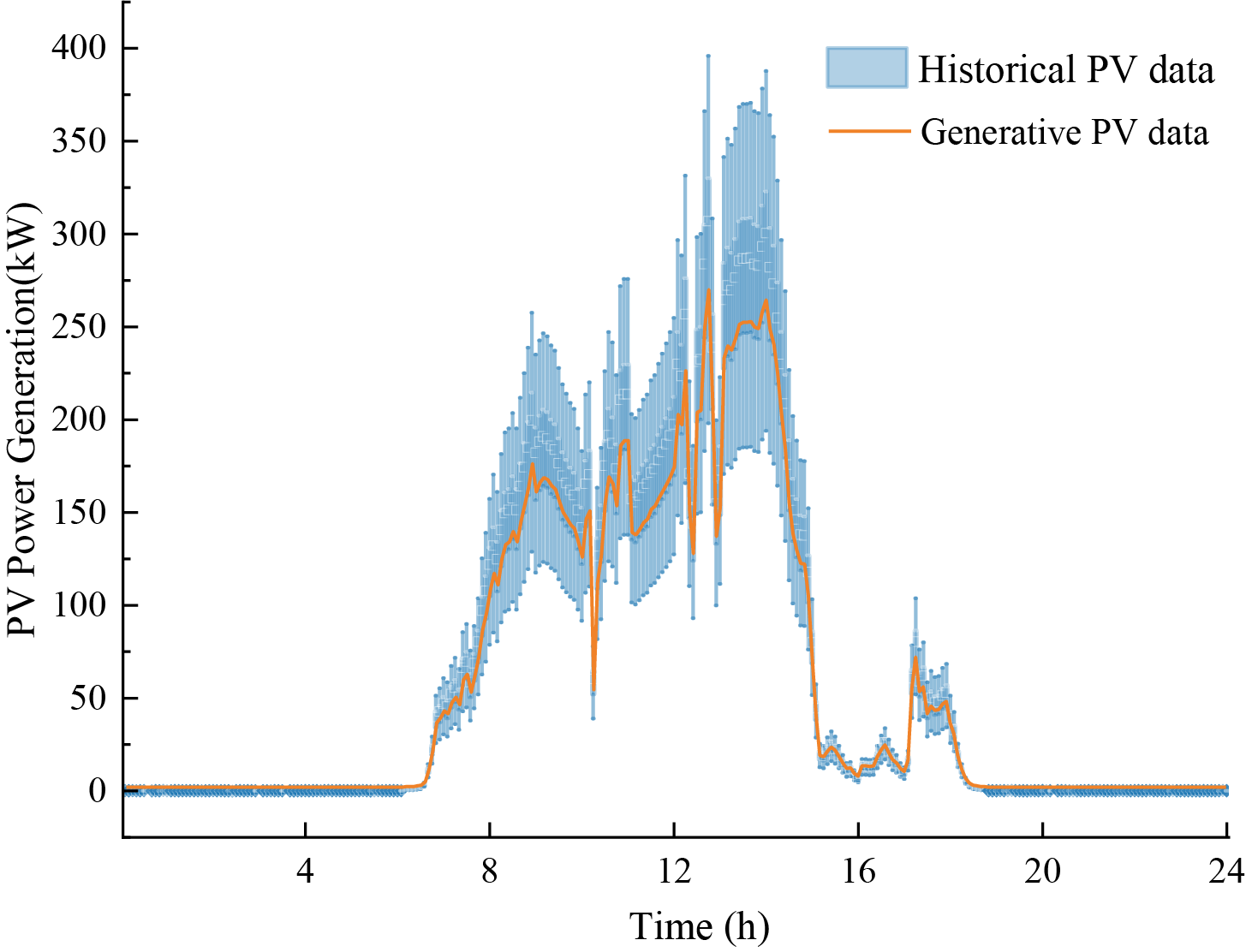
Figure 4: Comparative curves of historical and simulated PV output
The dataset used for training and validating the GPR model was collected from historical response data of DERs. A total of 1200 samples were generated by simulating various subsidy price signals across different time periods and weather conditions. The input features include subsidy prices, time periods, temperature, solar irradiance (applicable to photovoltaic systems), and load demand (applicable to adjustable loads). The output features include the actual response power of each flexible resource. All features were normalized to the range [0, 1] to improve model convergence and performance.
To justify the use of GPR for forecasting the adjustable power output of PV systems, we conduct a comparative analysis with two widely used forecasting methods: Long Short-Term Memory (LSTM) networks and Autoregressive Integrated Moving Average (ARIMA). The comparison is based on a 24-h-ahead forecasting task, where the goal is to predict the PV output under varying weather conditions using historical power generation data and meteorological features (e.g., temperature, irradiance).
The dataset is partitioned into a 70% training set and a 30% test set. All models are trained on the same input features and evaluated using the Mean Absolute Error (MAE), the results show that GPR achieves the lowest MAE of 5.2 kW, outperforming LSTM (5.8 kW) and ARIMA (8.1 kW). Furthermore, GPR provides uncertainty bounds for its predictions, which is crucial for risk-aware dispatch decisions in extreme weather scenarios. Given its superior accuracy and interpretability, GPR is well-suited for the short-term forecasting needs of VPPs in this study.
To simulate the impacts of extreme weather events, the proposed model incorporates uncertainty sets for photovoltaic output based on historical irradiance data under extreme conditions, as well as load demand scenarios generated using Gaussian process regression to capture load surges that occur during such events.
Upon completing information exchange with the DNSO, each VPP regulates its flexible resources based on the power dispatch signal from the DNSO.
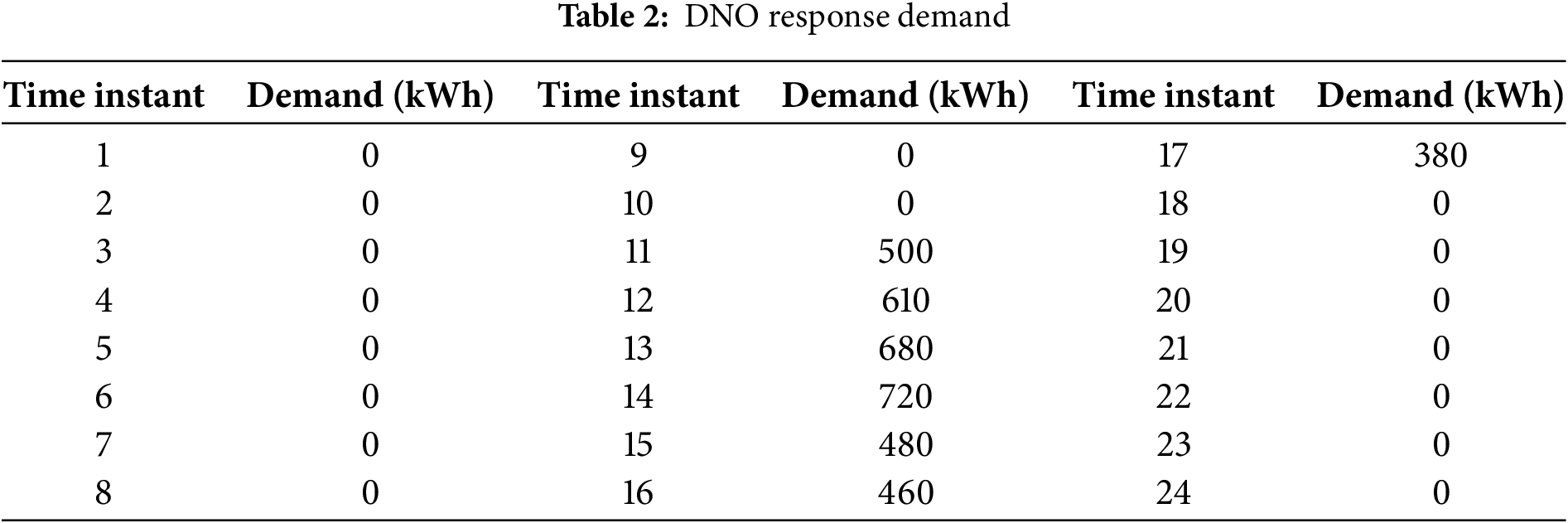
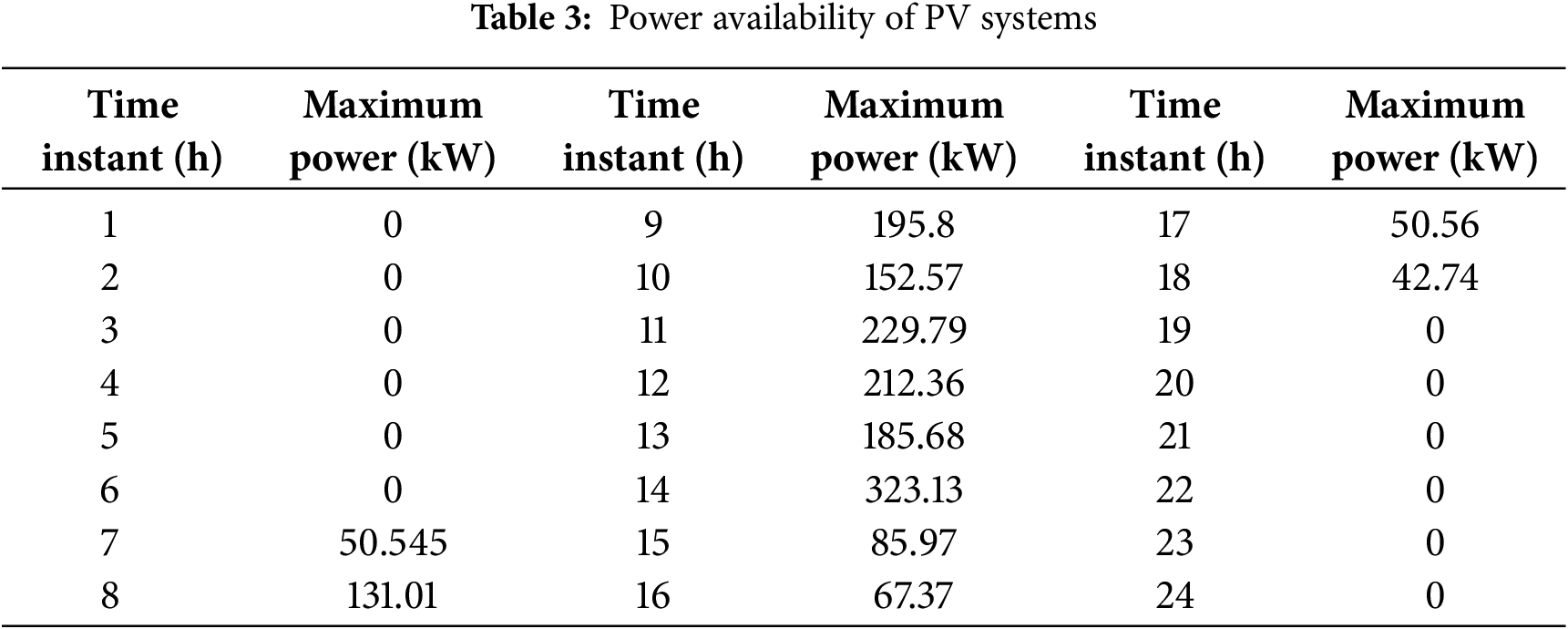
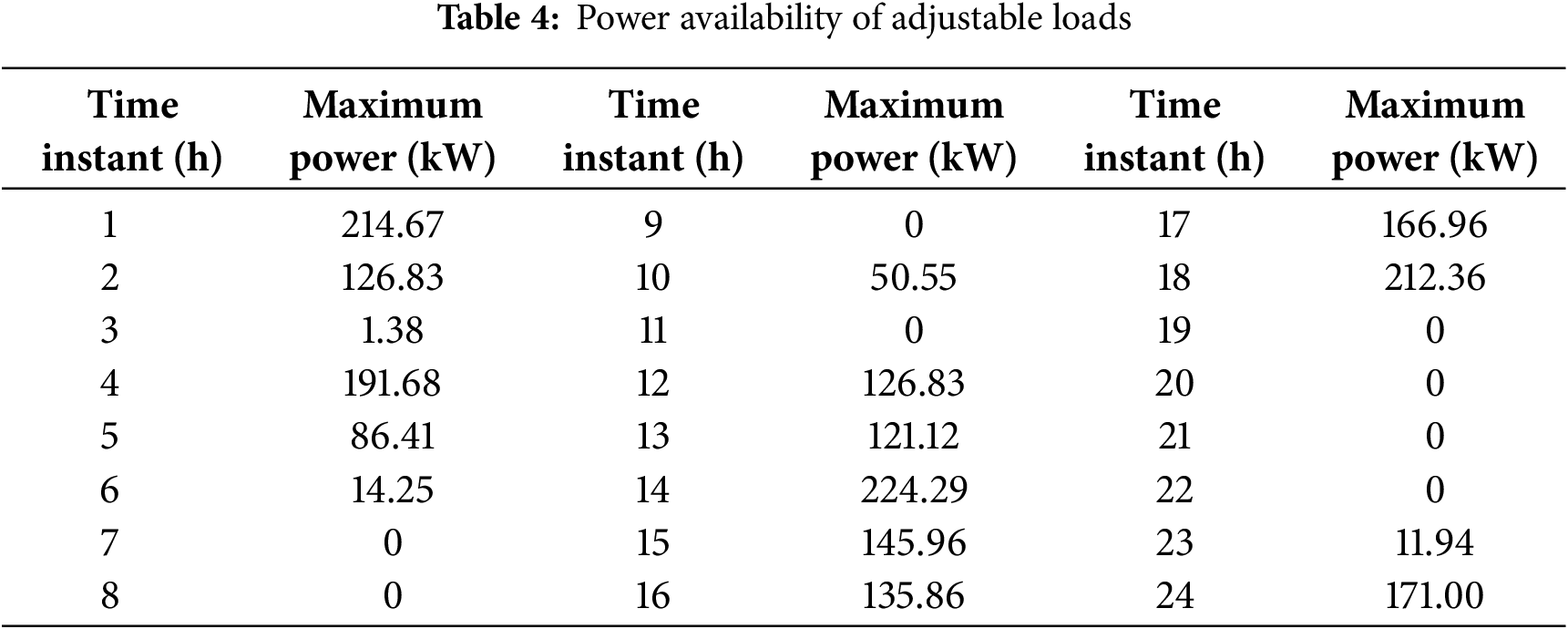
The response demand specified by the DNO for a particular VPP during extreme weather conditions is listed in Table 2. The total demand specified for the day amounts to 3830 kWh. The response reward price provided by the DNO to the VPP is 2.5 CNY/kWh. The response subsidy prices offered by the VPP to individual devices fall within the range [1.0, 2.3] CNY/kWh. The power supply costs for PV systems and adjustable loads are 1.26 CNY/kWh and 1.53 CNY/kWh, respectively. Their aggregated power contributions are presented in Tables 3 and 4, and the cost of supplementary power is 2.4 CNY/kWh.
The optimal solution to the equivalent MILP model, based on the data from Section 3.2, yields the subsidy pricing strategy for the virtual power plant (VPP) and the dispatch strategies for the flexible resources, as detailed in Fig. 5. The supplementary power during period 12 is calculated to be 121.58 kW. The results indicate that flexible resources remain inactive during periods without power supply support demands. During power supply support periods, the subsidy prices and dispatch strategies are determined based on factors such as the required response volume, the maximum output capacity of each flexible resource, and their associated costs. These calculations aim to maximize benefits for the VPP, PV aggregators, and adjustable load aggregators. In this scenario, the subsidy prices are mainly affected by the maximum active power output and cost limitations of the flexible resources.
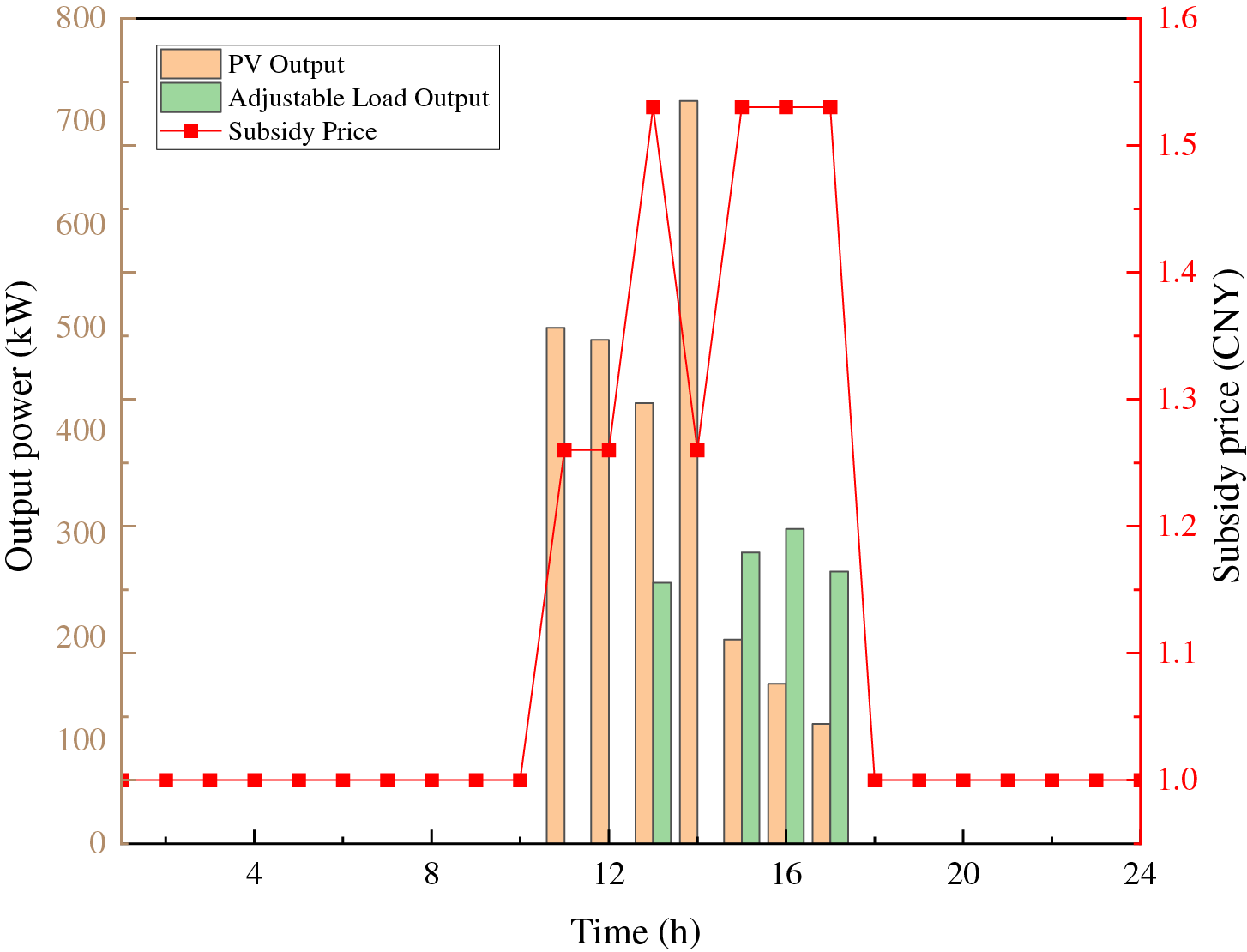
Figure 5: Optimal subsidy pricing and flexibility resource dispatch strategy
Under the VPP coordination, the DNO pays a total cost of 9575 CNY to support the 3830 kWh power demand. At the same time, the objective function yields a profit of 4332.51 CNY for the VPP, demonstrating the economic viability of the proposed coordination mechanism.
While the main optimization model focuses on economic dispatch and pricing strategies, the feasibility of the solution in terms of network constraints (e.g., voltage limits, line flow limits, and radial structure) is verified using a post-processing AC power flow simulation. The results confirm that all voltage magnitudes remain within [0.95 p.u., 1.05 p.u.], and no line flow exceeds its thermal limit.
4.4 Impact of Supplemental Power Cost Pricing on Optimal Solutions
During power supply support periods, if the PV and adjustable load capacities within a VPP fall short of the targeted supply, the VPP can secure additional supplemental power either by purchasing from other VPPs or by tapping into alternative resources. The approach taken to obtain supplemental power affects its corresponding cost price. Fig. 6 depicts the trends in VPP profitability and the average subsidy prices for PV and adjustable loads under varying supplemental power costs. It demonstrates that as the cost of supplemental power increases, the VPP must adjust its subsidy prices upwards to maintain power supply stability, leading to reduced profit margins. Once the supplemental power cost hits 2.7 CNY/kWh, the VPP’s profitability plateaus, implying that further increases in supplemental power costs will not significantly alter the VPP’s ultimate profits. This underscores the necessity of evaluating the cost-effectiveness of supplemental power when crafting VPP operational strategies to harmonize economic gains with supply support duties.
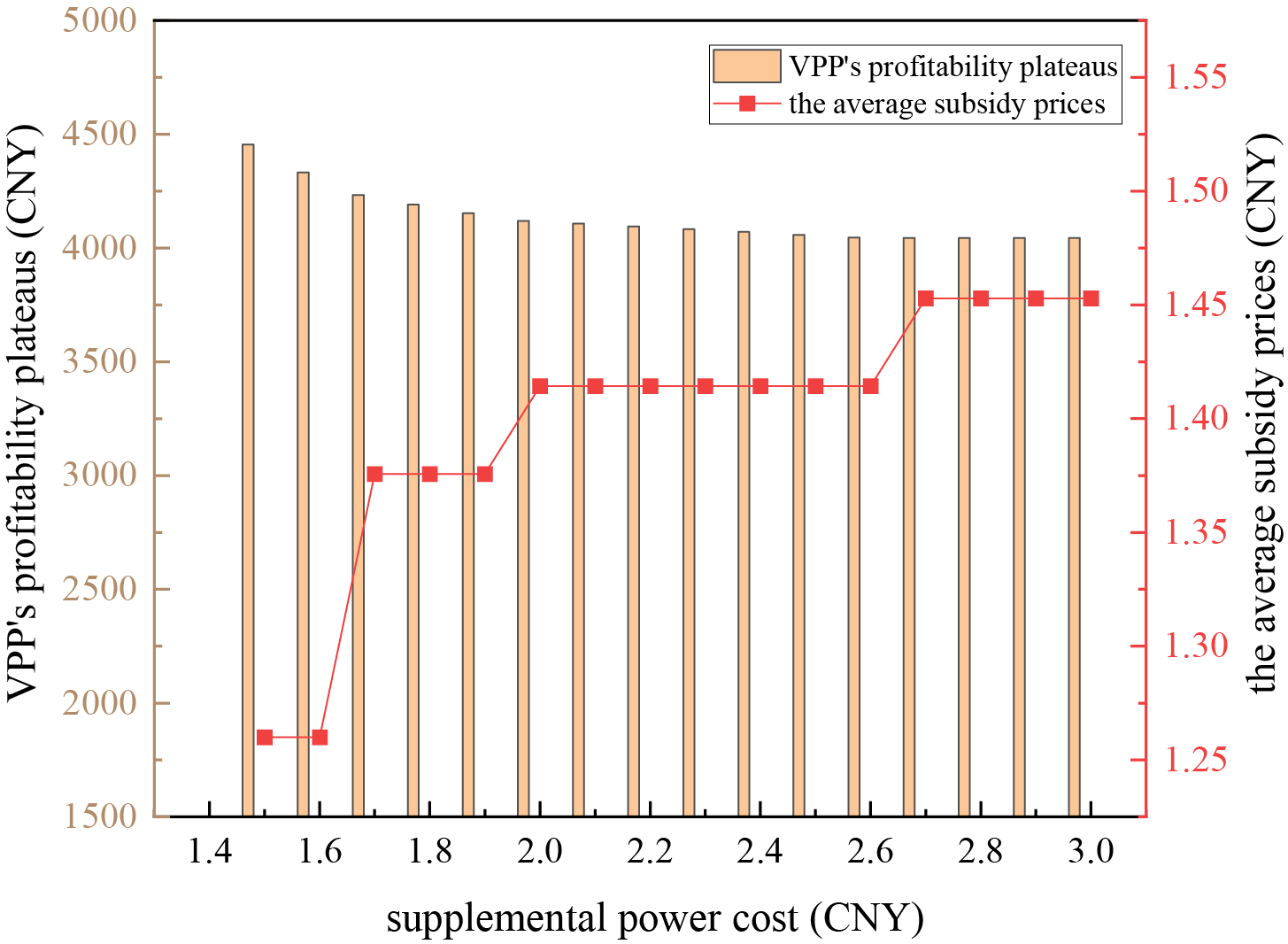
Figure 6: Comparative analysis of VPP profitability and average subsidies across different supplemental power costs
4.5 Comparison with the Scenario without VPP Coordination
To fully evaluate the effectiveness of the VPP coordination mechanism, we introduce a baseline scenario in which the DSO meets the power demand without VPP support. This section describes and analyzes that baseline scenario and compares it with the VPP-coordinated case.
In the baseline scenario without VPP coordination, the DSO must rely solely on market purchases or self-generation to supply power support. Assuming a power shortage of 3830 kWh needs to be covered, the DSO can fulfill this demand by purchasing electricity from the market. In certain regions, peak-time electricity prices can reach as high as 2–4 CNY/kWh. For illustrative purposes, we adopt a moderate market price of 3.0 CNY/kWh. Under this assumption, the total cost for the DSO to cover the 3830 kWh shortfall would be 11,490 CNY. If the DSO were to use self-generation instead, the marginal generation cost would likely be even higher than the market purchase cost, especially during peak hours.
In contrast, under the Stackelberg-based VPP coordination framework, the DSO pays a total cost of 9575 CNY to fully support the same 3830 kWh demand. This means that the cost in the coordinated scenario is approximately 83% of the cost in the non-coordinated baseline scenario. This comparison highlights the economic benefits of VPP coordination. Not only does the VPP enable the DSO to significantly reduce its operational expenditure, but it also facilitates the efficient utilization of distributed energy resources. Moreover, in this coordinated framework, the VPP aggregator earns a profit of 4332.51 CNY. The VPP acts as an effective intermediary that enhances system flexibility, improves supply reliability, and supports the integration of renewable energy sources.
In summary, the VPP coordination mechanism provides a more cost-effective and resource-efficient solution compared to the scenario without VPP support. It not only reduces the financial burden on the DSO but also promotes the sustainable development of the power system.
To address the power supply support challenges of urban distribution networks in extreme scenarios, an optimal dispatch strategy is proposed based on the evaluation and interaction of aggregated power from VPPs. By establishing a bi-level leader-follower game model and reformulating it as a MILP model through KKT conditions, the strategy significantly improves the flexibility and responsiveness of power supply support in such scenarios.
Numerical case studies validate that the proposed strategy can rapidly respond to the power supply support requirements of urban distribution networks, efficiently coordinate PV and adjustable load resources within VPPs, and maintain the flexibility and stability of power supply support by incorporating supplementary power to account for the diversity of VPP power sources. Future research will focus on incorporating energy storage systems and market-based mechanisms into power supply support strategies to further optimize VPP operations. Additionally, we will continue to delve into the effectiveness of the proposed methods under various extreme scenarios and evaluate system flexibility, responsiveness, and the robustness of power supply support with metrics.
Acknowledgement: Not applicable.
Funding Statement: This work was supported by the Science and Technology Project of Sichuan Electric Power Company “Power Supply Guarantee Strategy for Urban Distribution Networks Considering Coordination with Virtual Power Plant during Extreme Weather Event” (No. 521920230003).
Author Contributions: Formal analysis, Guowei He; Methodology, Yong Li; Resources, Chenxi Dai; Software, Yuxuan Chen; Validation, Jiahui He; Writing—original draft, Yong Li and Yuxuan Chen; Writing—review & editing, Jingjing Tong and Wenting Lei. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Abbreviations
| VPPs | Virtual power plants |
| GPR | Gaussian Process Regression |
| KKT | Karush-Kuhn-Tucker |
| UIES | User Integrated Energy System |
| PV | Photovoltaic |
| EVs | Electric Vehicles |
| MILP | Mixed-integer linear programming |
| DNSO | Distribution network system operator |
| LSTM | Long Short-Term Memory |
| ARIMA | Autoregressive Integrated Moving Average |
| MAE | Mean Absolute Error |
This appendix presents the full derivation of the solution methodology for the bi-level optimization model described in Section 3.2. It includes the KKT conditions for the lower-level optimization problems, the linearization of complementary slackness conditions, and the final reformulation as a mixed-integer linear programming (MILP) model.
A.1Conversion to Equivalent Nonlinear Programming: For the bi-level leader-follower game model of VPP pricing, the linear programming constraints (9b), (9c), (10b), and (10c) are replaced with their corresponding KKT conditions [22]. This transformation allows the lower-level optimization problems to be expressed as constraints for the upper-level VPP optimization model.
A.1.1KKT Conditions for the i-th PV System: Let the dual variables be denoted as
where
KKT Conditions for the k-th Adjustable Load: Similarly, for the k-th adjustable load, let the dual variables as
Linearization of Complementary Slackness Conditions: To linearize the complementary slackness conditions, boolean variables are introduced to convert Eqs. (A1b), (A1c), (A2b), and (A2c) into linear inequality constraints:
where M represents a sufficiently large positive constant; and
To ensure the operational feasibility of the distribution network, the following network constraints are considered in the implementation of the proposed dispatch strategy:
1. Power Flow Equations
The power flow between nodes is governed by the AC power flow equations:
where
2. Voltage Magnitude Limits
where
3. Line Flow Limits
To prevent thermal overloading and ensure safe operation, the apparent power flow on each branch must not exceed its thermal capacity:
where
Although these constraints are not explicitly integrated into the leader-follower game model for simplicity, they are considered during the implementation phase to ensure that the final dispatch strategy complies with physical and operational limits of the distribution network.
References
1. Baviskar A, Das K, Koivisto M, Hansen AD. Multi-voltage level active distribution network with large share of weather-dependent generation. IEEE Trans Power Syst. 2022;37(6):4874–84. doi:10.1109/TPWRS.2022.3154613. [Google Scholar] [CrossRef]
2. Balaban G, Dumbrava V, Lazaroiu AC, Kalogirou S. Analysis of urban network operation in presence of renewable sources for decarbonization of energy system. Renew Energy. 2024;230:120870. doi:10.1016/j.renene.2024.120870. [Google Scholar] [CrossRef]
3. Cutore E, Volpe R, Sgroi R, Fichera A. Energy management and sustainability assessment of renewable energy communities: the Italian context. Energy Convers Manag. 2023;278(15):116713. doi:10.1016/j.enconman.2023.116713. [Google Scholar] [CrossRef]
4. Varathan G. A review of uncertainty management approaches for active distribution system planning. Renew Sustain Energy Rev. 2024;205(4):114808. doi:10.1016/j.rser.2024.114808. [Google Scholar] [CrossRef]
5. Jing R, Wang X, Zhao Y, Zhou Y, Wu J, Lin J. Planning urban energy systems adapting to extreme weather. Adv Appl Energy. 2021;3:100053. doi:10.1016/j.adapen.2021.100053. [Google Scholar] [CrossRef]
6. Potts J, Tiedmann HR, Stephens KK, Faust KM, Castellanos S. Enhancing power system resilience to extreme weather events: a qualitative assessment of winter storm Uri. Int J Disaster Risk Reduct. 2024;103(12):104309. doi:10.1016/j.ijdrr.2024.104309. [Google Scholar] [CrossRef]
7. Mujjuni F, Betts TR, Blanchard RE. Evaluation of power systems resilience to extreme weather events: a review of methods and assumptions. IEEE Access. 2023;11:87279–96. doi:10.1109/ACCESS.2023.3304643. [Google Scholar] [CrossRef]
8. Vedullapalli DT, Hadidi R, Bozeman LS. Distribution system restoration using graph theory after multiple faults. IET Energy Syst Integr. 2020;2(3):235–42. doi:10.1049/iet-esi.2019.0118. [Google Scholar] [CrossRef]
9. Wen X, Zhou Q, Sun T, Yang Y, Mao R, Wen SA. Construction of power trading supply guarantee system of high proportion of hydropower in the southwest power grid under extreme climate scenarios. Power Syst Technol. 2025;49(1):113–23. (In Chinese). doi:10.13335/j.1000-3673.pst.2023.2258. [Google Scholar] [CrossRef]
10. Li X, Du X, Jiang T, Zhang R, Chen H. Coordinating multi-energy to improve urban integrated energy system resilience against extreme weather events. Appl Energy. 2022;309(3):118455. doi:10.1016/j.apenergy.2021.118455. [Google Scholar] [CrossRef]
11. Gao HJ, Guo MH, Liu JY, Liu TJ, He SJ. Power supply challenges and prospects in new power system from Sichuan electricity curtailment events caused by high-temperature drought weather. Proc CSEE. 2023;43(12):4517–38. (In Chinese). doi:10.13334/j.0258-8013.pcsee.222971. [Google Scholar] [CrossRef]
12. Chen C, Wang J, Qiu F, Zhao D. Resilient distribution system by microgrids formation after natural disasters. IEEE Trans Smart Grid. 2016;7(2):958–66. doi:10.1109/TSG.2015.2429653. [Google Scholar] [CrossRef]
13. Poudel S, Dubey A. Critical load restoration using distributed energy resources for resilient power distribution system. IEEE Trans Power Syst. 2019;34(1):52–63. doi:10.1109/TPWRS.2018.2860256. [Google Scholar] [CrossRef]
14. Wang Y, Xu Y, He J, Liu CC, Schneider KP, Hong M, et al. Coordinating multiple sources for service restoration to enhance resilience of distribution systems. IEEE Trans Smart Grid. 2019;10(5):5781–93. doi:10.1109/TSG.2019.2891515. [Google Scholar] [CrossRef]
15. Feng C, Chen Q, Wang Y, Kong PY, Gao H, Chen S. Provision of contingency frequency services for virtual power plants with aggregated models. IEEE Trans Smart Grid. 2023;14(4):2798–811. doi:10.1109/TSG.2022.3229273. [Google Scholar] [CrossRef]
16. Chen J, Liu M, Milano F. Aggregated model of virtual power plants for transient frequency and voltage stability analysis. IEEE Trans Power Syst. 2021;36(5):4366–75. doi:10.1109/TPWRS.2021.3063280. [Google Scholar] [CrossRef]
17. Zhou B, Zhang K, Chan KW, Li C, Lu X, Bu S, et al. Optimal coordination of electric vehicles for virtual power plants with dynamic communication spectrum allocation. IEEE Trans Ind Inform. 2021;17(1):450–62. doi:10.1109/TII.2020.2986883. [Google Scholar] [CrossRef]
18. Tao R, Zhao D, Xu C, Wang H, Xia X. Resilience enhancement of integrated electricity-gas-heat urban energy system with data centres considering waste heat reuse. IEEE Trans Smart Grid. 2023;14(1):183–98. doi:10.1109/TSG.2022.3197626. [Google Scholar] [CrossRef]
19. Zhou Y. Low-carbon urban-rural modern energy systems with energy resilience under climate change and extreme events in China—a state-of-the-art review. Energy Build. 2024;321(1):114661. doi:10.1016/j.enbuild.2024.114661. [Google Scholar] [CrossRef]
20. Kaldellis JK, Kapsali M. Simulating the dust effect on the energy performance of photovoltaic generators based on experimental measurements. Energy. 2011;36(8):5154–61. doi:10.1016/j.energy.2011.06.018. [Google Scholar] [CrossRef]
21. Mihoub R, Chabour N, Guermoui M. Modeling soil temperature based on Gaussian process regression in a semi-arid-climate, case study Ghardaia, Algeria. Geomech Geophys Geo-Energy Geo-Resour. 2016;2(4):397–403. doi:10.1007/s40948-016-0033-3. [Google Scholar] [CrossRef]
22. Wu HC. The Karush–Kuhn–Tucker optimality conditions in multiobjective programming problems with interval-valued objective functions. Eur J Oper Res. 2009;196(1):49–60. doi:10.1016/j.ejor.2008.03.012. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2026 The Author(s). Published by Tech Science Press.
Copyright © 2026 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools