Analysis of Heat Transport in a Powell-Eyring Fluid with Radiation and Joule Heating Effects via a Similarity Transformation

Nomenclature

1  Introduction

Eyring-Powell fluids are a significant type of non-Newtonian fluid. Additionally, these fluids are classified as differential types, integral models, and shear rate models. The Eyring-Powell fluid has a particular advantage over the power-law model because it is based on liquid kinetic theory. For low and high shear rates, this fluid’s Newtonian behaviour decreases. These fluids are extremely valuable since they can be used in a variety of engineering, manufacturing, and industrial applications, including pulp, plasma, and other biological technology. Additionally, these fluids play a critical role in fermentation, boiling, bubble formation, column processing, and the processing of plastic foam, with substances such as mud, colours, toothpaste, blood, corn starch, custard, and honey serving as insignificant examples of non-Newtonian fluids [1].

Recent technological and engineering advancements have resulted in the development of a diverse range of non-Newtonian fluids with a number of major differences from viscous fluids. Ziegenhagen [2] explored the slow flow of a Powell-Eying type fluid and used variational techniques to obtain results. He studied the behaviour of Oldroyd and Powell Eyring fluids and discovered that both fluids behave identically in situations involving extremely slow fluid flow. Sirohi et al. [3] studied it by observing the flow of Powell-Eyring fluid around the accelerating plate. They compared three distinct techniques. Yoon et al. [4] pioneered the concept of a stretched sheet by providing a precise solution to the resulting differential system. Recent academics have investigated this topic from a variety of perspectives [5–13]. Bahia et al. [14] investigated the Powell-Eyring fluid flow and heat transport past a stretched sheet exponentially. They discovered that increasing the velocity ratio parameter results in a thinned boundary layer. Malik et al. [15] examined the Powell-Eyring fluid flow and heat transport with varying viscosity over a stretching cylinder by examining the steady condition. They concluded that as Prandtl and Reynolds numbers increase, the boundary layer shrinks. Akbar et al. [16] studied the effect of magnetic factors on Eyring-Powell fluid flow past a stretched surface. They investigated flow resistance as the magnetic and hydrodynamic properties of the fluid under study increased.

Kumar et al. [17] investigated the Powell-Eyring nanofluid passing via an inclined permeable sheet. They demonstrated that temperature increases as thermophoresis parameter values increase. While the contrary is true for nanoparticle concentration due to higher chemical reactions and Brownian parameters, increasing thermophoresis parameter values results in an increase in concentration. Pal et al. [18] demonstrated magneto-bioconvection of Powell-Eyring nanofluid via a vertical stretched sheet that is convectively heated and also contains motile gyrotactic microorganisms. They discovered that as the Schmidt number and chemical reaction parameters increase, the concentration of nanoparticles drops. Thermal relaxation time is the time required for a fluid to return to its original temperature after being heated. It is a frequently used parameter for determining the time required for heat to leave a fluid. Hayat et al. [19] investigated the effects of mass flux models on Eyring Powell fluid flow in three dimensions. They discovered that temperature and thermal-relaxation time have an inverse relationship. Reddy et al. [20] studied the effect of chemical reaction on the activation energy of Eyring Powell nanofluid flow via a stretching cylinder. They concluded that as the relaxation parameter increases, the temperature curves lose their shape. It takes a long time for an increase in the relaxation parameter assessment to transfer heat to neighbouring material particles. Additionally, the Nusselt number improves behaviour when non-dimensional thermal relaxation calculations are performed.

Mustafa [21] researched the Maxwell fluid with a generalised heat flux model for rotating flow and heat transfer. They also discovered that the thermal relaxation period is inversely proportional to temperature and thermal boundary thickness. On an unstable porous stretching sheet, Ishaq et al. [22] demonstrated the entropy production of Eyring Powell fluid flow with nanofluid thin film flow by considering the heat radiation and MHD impact. They discovered that when the Brinkmann, Hartmann, and Reynolds numbers grow, so does the entropy profile. For increasing values of the Eyring Powell and radiation parameters, the entropy profile reduces. The Eyring Powell nanofluid flow with non-linear mixed convection and entropy generation was explored by Alsaedi et al. [23]. They arrived at the conclusion that entropy generation showed a falling tendency for some fluid parameter values while increasing for others. Through a permeable stretching surface, Bhatti et al. [24] studied the irreversibility of MHD Eyring Powell nanofluid.

Ali et al. [25] used both perturbation and computational methods to examine the steady non-isothermal flow of an Eyring–Powell fluid in a conduit. The findings are provided for two viscosity models, the Reynolds and the Vogel models, which were solved using the shooting and perturbation methods, respectively. It was determined that the shooting approach outperformed the perturbation method. Nazeer et al. [26] investigated the effects of constant and space-dependent viscosity on a circular conduit filled with Eyring–Powell fluid. Additionally, heat transmission analysis is considered. The finite difference scheme is compared to the perturbation method. Numerous researchers discussed the Eyring-Powell model under a variety of scenarios and solved it analytically and numerically using a variety of numerical schemes such as the RK method, the shooting technique, and the perturbation method [27–34].

According to the existing literature, no attempt has been made to investigate the electrically conducting Eyring-Powel fluid with radiation, thermal relaxation time, and joule heating effects beyond an exponentially stretched sheet. This research fills a void in the literature and lays the groundwork for future researchers to contribute their perspectives to the open literature. This is structured as follows: Section 1 contains the literature review, Section 2 the mathematical formulation, Section 3 the methodology, Section 4 the results, and Section 5 the conclusion.

2  The Problem’s Formulation

Consider an incompressible Powell Eyring fluid flowing across an exponentially stretched surface subjected to magnetic, joule heating, thermal radiation, and thermal relaxation periods, as illustrated in Fig. 1. The sheet is put on the x -and y -axes, respectively, and the flow is restricted to y≥0. Let Uw(x)=ae(xl) represent the sheet velocity, U∞=be(xl) representing the external fluid velocity, and Tw(x)=T∞+ce(x2l) representing the surface temperature, with T∞ being the ambient temperature.

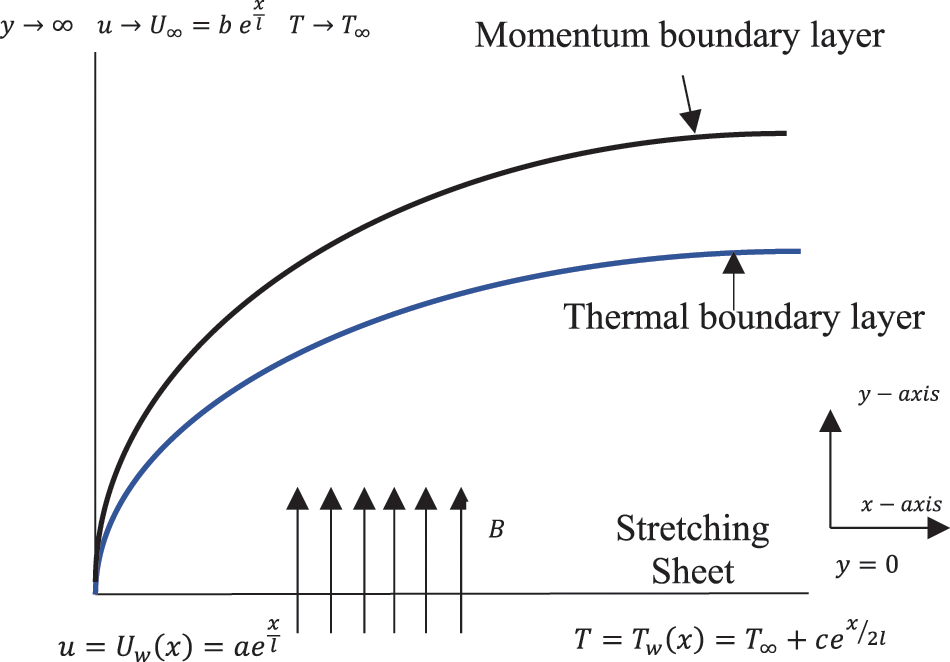
Figure 1: Configuration of the flow over a stretching sheet and geometrical coordinates

The governing equations so obtained are given as [35]

∂u∂x+∂v∂y=0, (1)

u∂u∂x+v∂u∂y=U∞dU∞dx+(v+1ρβC)∂2u∂y2−12ρβC3(∂u∂y)2∂2u∂y2−σρB02(U∞−u), (2)

u∂T∂x+v∂T∂y=kρCp(−∇.q)+σB02ρCp(U∞−u)2−1ρCp∂qrad∂y, (3)

where ν,ρ,u(x,y),v(x,y),β,C,T,k,qrad,Cp,B0,andq are kinematic viscosity, fluid density, the velocities, fluid parameters, the temperature, the thermal-conductivity, thermal radiation, the specific-heat at constant pressure, the strength of magnetic field, and heat flux, respectively, which satisfy the relation [36] q+δt(∂q∂t+V.∇q−q.∇V+(∇.V)q).

Furthermore, by means of Rosseland approximation for radiation, we get qrad=−4σ∗3k∗∂T4∂y,k∗ and σ∗ as absorption coefficient and the Stefan Boltzmann constant. By expanding T4 in a Taylor’s series around T∞ and neglecting higher order terms, we have the relation T4=4T∞3T−3T∞4 . The appropriate boundary conditions are

u=Uw(x)=aexl,v=0,T=Tw(x)=T∞+cex2l,aty=0,u→U∞(x)=bexl,T→T∞,asy→∞.}, (4)

Taking the similarity transformations as

η=a2νLex/2Ly,u=aexLf′(η),v=−νa2Lex2L[f(η)+ηf′(η)],θ(η)=T−T∞Tw−T∞. (5)

With the above transformation the continuity equation is satisfied identically and Eqs. (2)–(4) is converted into the following form:

(1+K)f′′′+ff′′−2f′2−KΓf′′2f′′′+2λ2−M(λ−f′)=0, (6)

(1+Rd)θ′′+Pr((fθ′−θf′)−γ(3f′2θ−θff′′+f2θ′′−3ff′θ′))+MEc(λ−f′)2=0, (7)

f(0)=0,f′(0)=1,θ(0)=1,f′(∞)→λ,θ(∞)→0,

where (8)

λ=ba,K=1μβC,Γ=Uw34νLC2,Pr=μCpk,M=δρ(2LB02Uw),Rd=16T∞3σ∗3k∗Cpμ,

Ec=Uw2Cpcex2l,γ=δtaexL2L. (9)

Here λ and Pr denote velocity ratio and Prandtl-number respectively. Where, K and Γ are the dimensionless fluid parameters. Since Γ is a function of x, therefore, we use a local similarity solution of (6)–(8) that allows us to analyze parameter behaviour. For K=0 , we have the case of Newtonian fluid. The Cf and the local Nu are mathematically describe as

Cf=τwρUw2,Nu=xqw(1+Rd)k(Tw−T∞), (10)

here, τw and qw are mathematically describe as

τw=(μ+1βC)|y=0−16βC3(∂u∂y)3|y=0,qw=−k(∂T∂y)|y=0. (11)

The mathematical form of local Nusselt number and skin friction coefficient are given as under

2Re.Cf=(1+K)/f′′(0)−KΓ3.(f′′(0))3,2LxNuRex12=−θ′(0)(1+Rd), (12)

where local Reynolds numbers are Re=UwLv,andRex=Uwxv .

3  Solution Methodology

Rahimi et al. [37] solved a non-Newtonian model known as the Powell Eyring fluid model using the collocation approach. Agrawal et al. [38] solved the Eyring Powell fluid model using a fourth-order precision methodology and the homotopy analysis method (H.A.M). Jafari Moghaddam [39] studied the Eyring Powell model and described fluid flow and heat transfer over a stretching sheet. The Eyring-Powell model is also solved by using different techniques as mentioned in [40–42]. He then solved the governing PDEs by using homotopy perturbation and homotopy analysis methods to convert them to ODEs. The flow chart of the numerical scheme is presented in Fig. 2 below. The third order nonlinear ordinary differential Eq. (6) and the second order nonlinear ordinary differential Eq. (7) are expressed as difference equations and solved using BVP4C and MATLAB in this article.

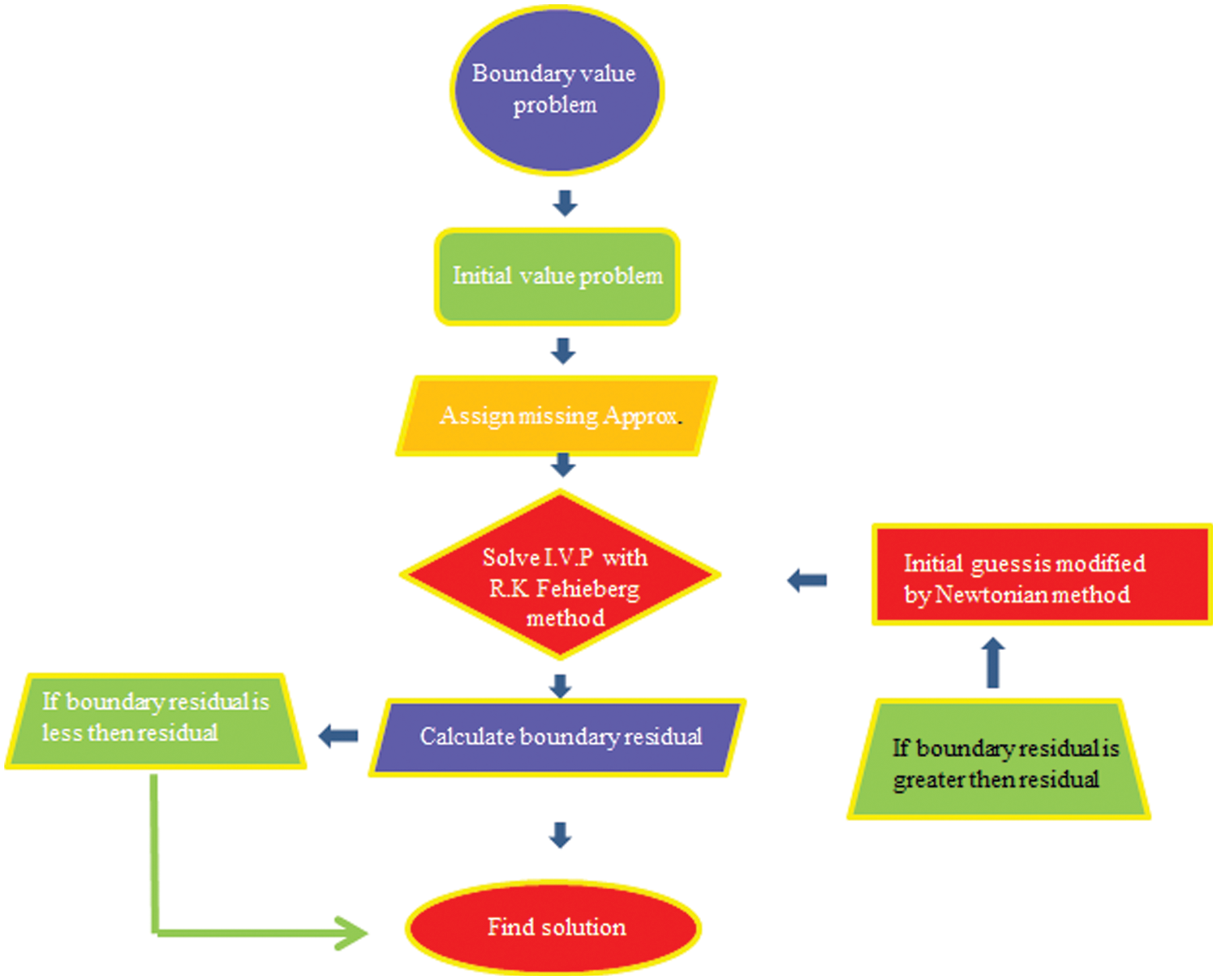
Figure 2: Flow chart related to numerical scheme

f=y1,f′=y2,f′′=y3,f′′′=yy1,yy1=1(1+K−ΓKy32)(M(λ−y2)−y1y3+2y22−2λ2),} (13)

θ=y4,θ′=y5,θ′′=yy2,yy2=1(1+Rd−Prγy12)(Pr((y2y4−y1y5)+γ(3y22y4−y1y3y4−3y1y2y5))−MEc(λ−y2)2),} (14)

y1(0)=0,y2(0)=1,y5(0)=1,y2(∞)→λ,y5(∞)→0, (15)

The iterative approach will conclude with the required precision.

4  Result and Discussion

The velocity ratio parameter, the fluid parameter K , the magnetic parameter M, the non-dimensional fluid parameter, and the velocity profile are all monitored for variation. Additionally, this section discusses the influence of the Prandtl number Pr , the velocity ratio parameter, the fluid parameter K, the Eckert number Ec , the radiation parameter Rd , the thermal relaxation time T, and the magnetic parameter M on the dimensionless temperature θ(η) . Tables and graphs of heat energy and velocity fields vs. physical parameters are included below.

4.1 Visualization of a Velocity Field

Two types of boundary layers near the sheet have evolved in a flow with exponentially changing free stream velocity over an exponentially stretched sheet. Which means that they are depending on the velocity ratio parameter b/a , for values of b/a greater than or equal to one. Additionally, it is worth to note that when b/a=1 , no velocity boundary layer arises near the sheet. The velocity profiles for various values of λ are depicted in Fig. 3. According to Fig. 4, increasing K results in a drop in fluid viscosity, which results in an increase in velocity. Additionally, as K increases, the viscosity of the fluid becomes lower due to the increase in the velocity of the fluid. The velocity profile declines as Γ grows, but changes toward the border, indicating that the boundary layer’s thickness has decreased, which is depicted in Fig. 5. As the magnetic field intensity increases, the velocity profile in Fig. 6 drops. This is because an increase in the Lorentz force creates resistance to fluid flow, resulting in a drop in the velocity profile.

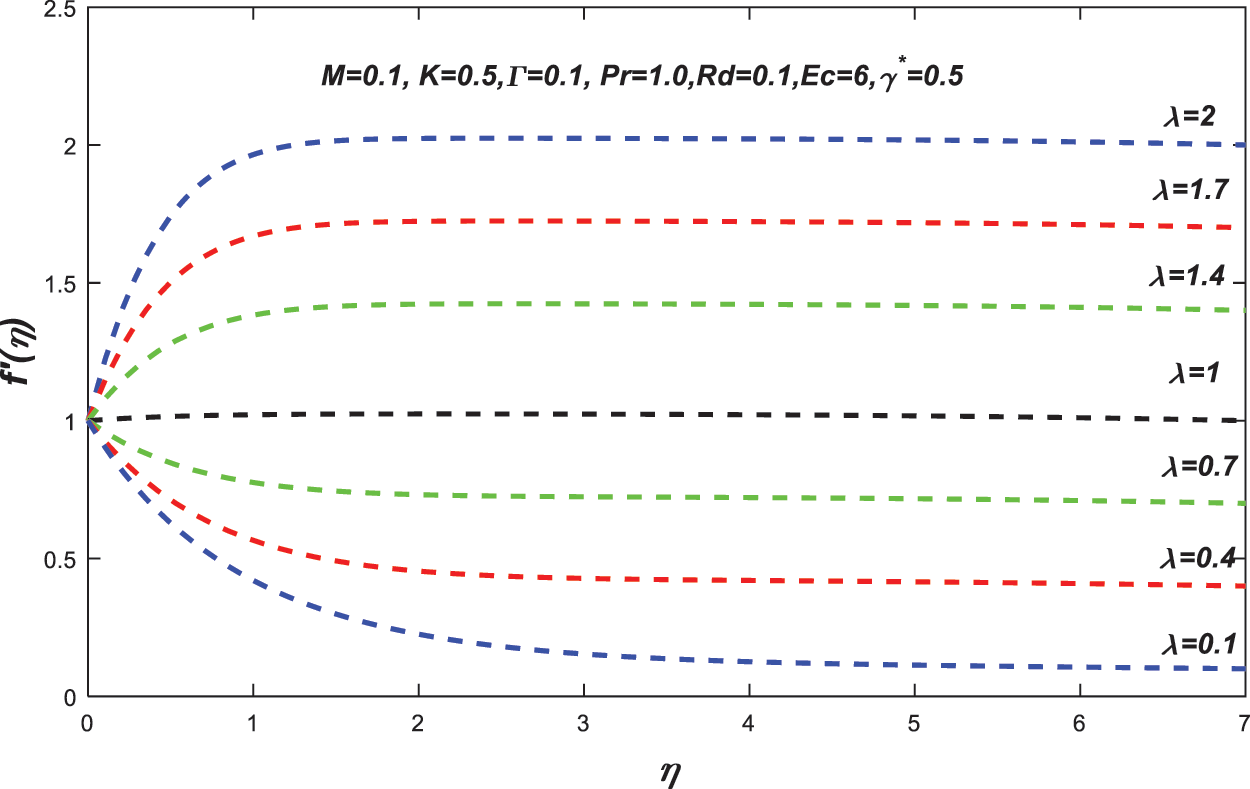
Figure 3: Change in the value of f′(η) for different values of λ

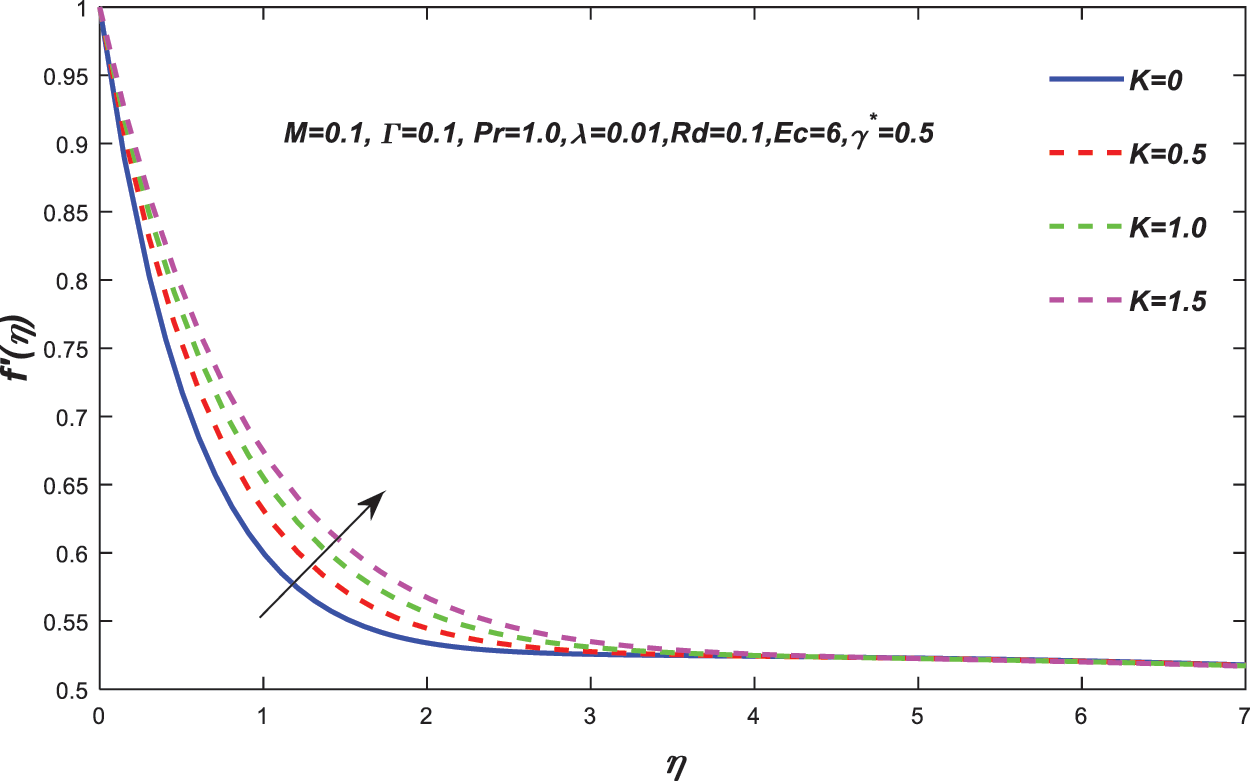
Figure 4: Change in the value of f′(η) for different values of K

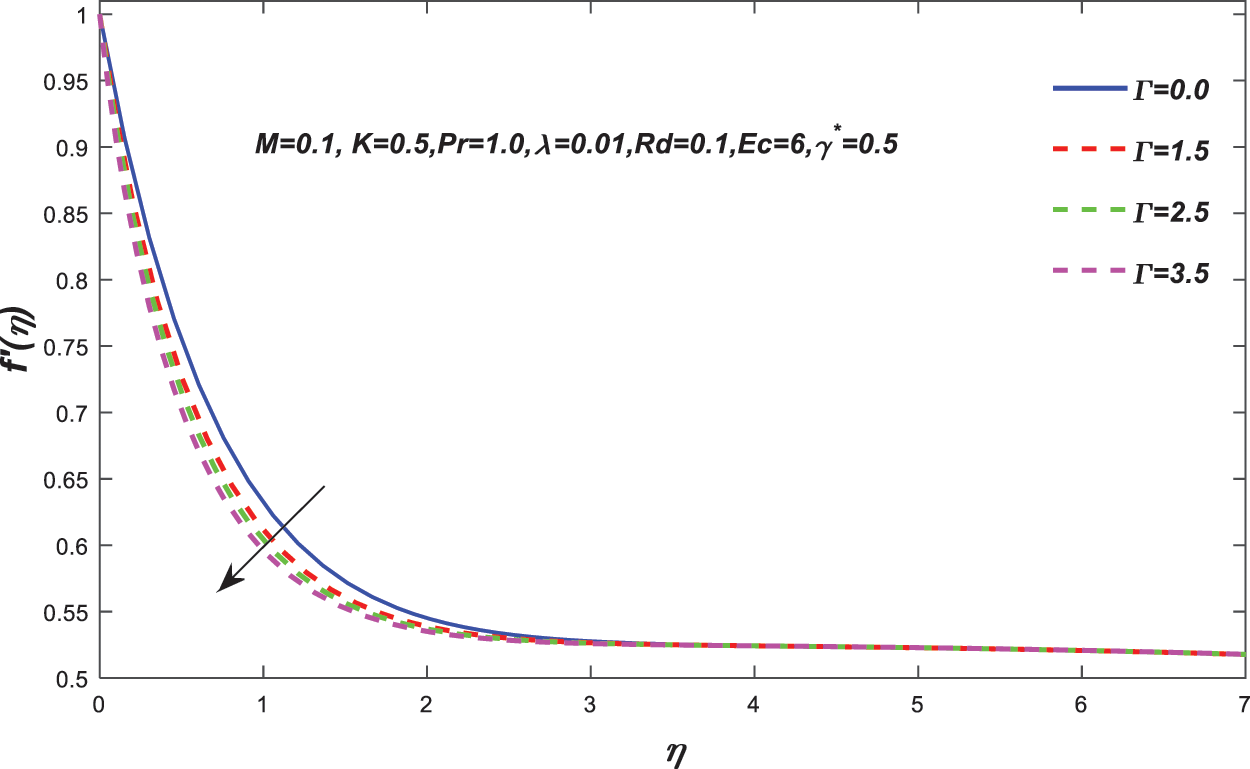
Figure 5: Change in the value of f′(η) for different values of Γ

Figure 6: Change in the value of f′(η) for different values of M

4.2 Visualization of a Temperature Field

The fluctuation of the velocity ratio parameter on the temperature profile is depicted in Fig. 7. Temperature has been discovered to be a decreasing function of λ . This data may imply that greater sheet velocity results in a thicker thermal boundary layer. As K increases, there is a slight reduction in temperature, as illustrated in Fig. 8. Due to the lack of viscous dissipation effects, the fluid parameter K is not explicitly included in the energy calculation and hence has a reduced effect on the thermal boundary layer. Fig. 9 illustrates the effect of Pr on temperature θ(η) . The temperature profile falls as Pr=μCpk increases. Additionally, rising values of Pr decrease the thickness of the thermal boundary layer. As a result, heat travels rapidly, leading to a decrease in fluid temperature.

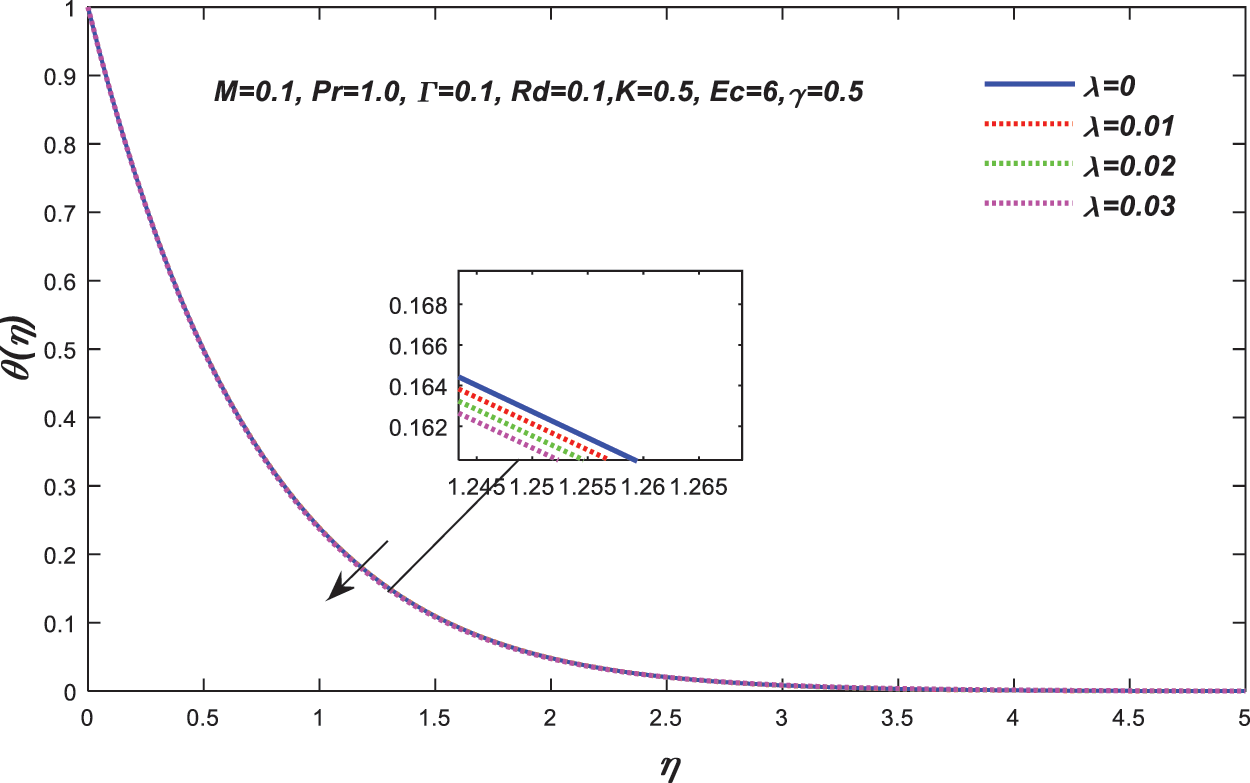
Figure 7: Change in the value of θ(η) for different values of λ

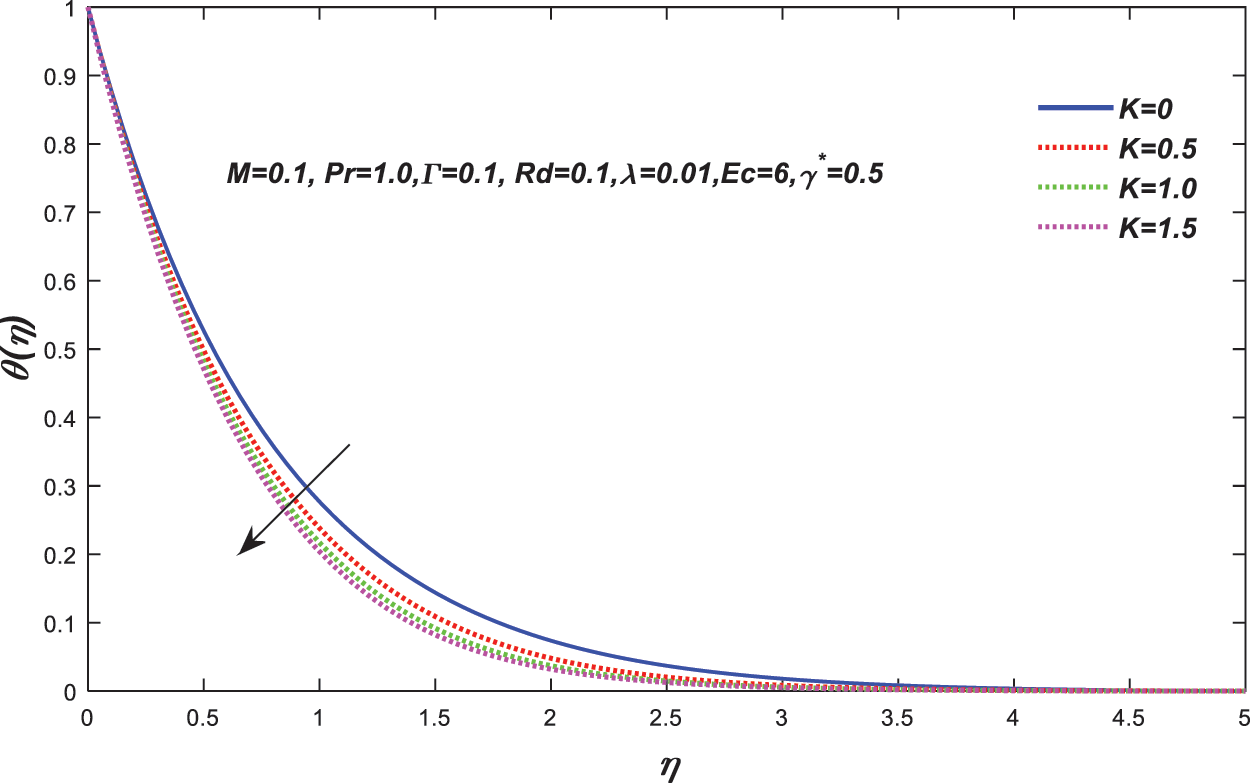
Figure 8: Change in the value of θ(η) for different values of K

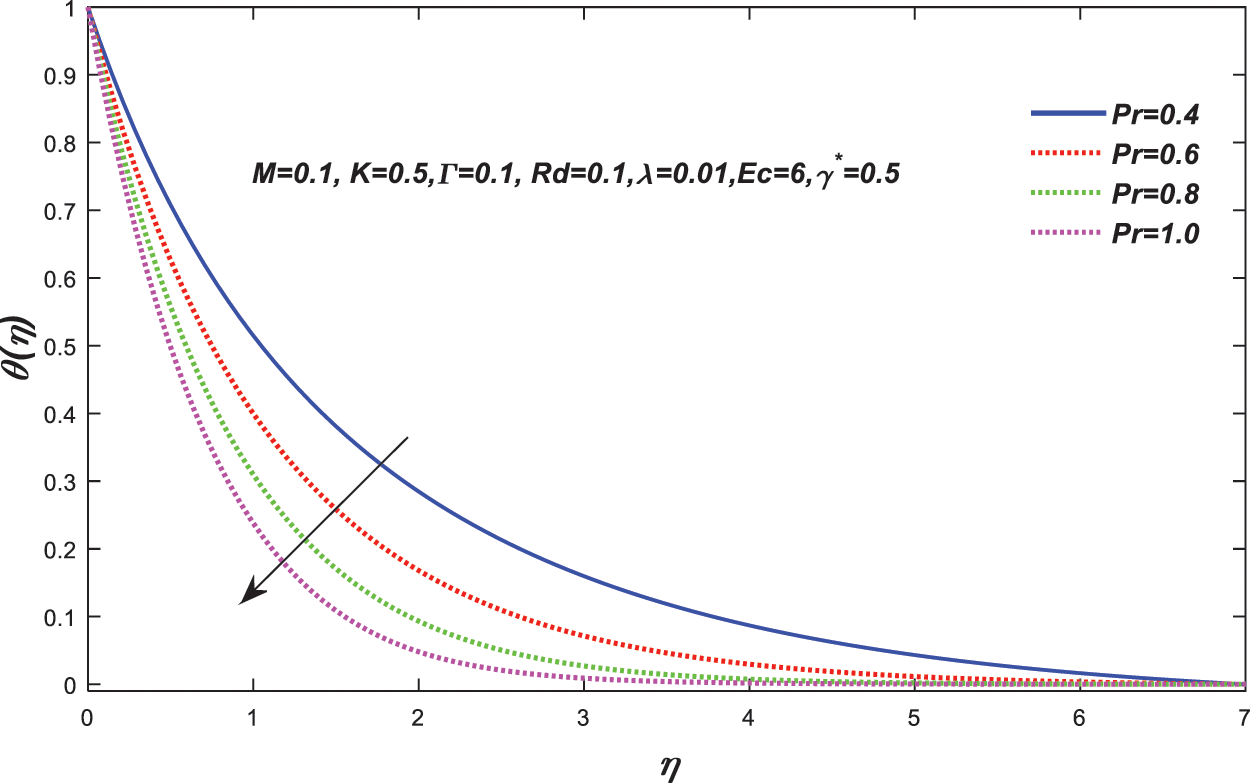
Figure 9: Change in the value of θ(η) for different values of Pr

The influence of radiation on temperature distributions can be seen in Fig. 10. Increases in Rd result in an increase in heat fluxes from the sheet, which results in a rise in temperature. Ec’s effect on the temperature profile θ(η) is depicted in Fig. 11. As the Ec value grows, the sheet’s wall temperature increases. Due to the fact that when Ec is high, the rate of heat transfer at the surface is low, the thickness of the thermal boundary layer increases. Frictional heating happens at the surface, raising the fluid’s temperature. The effect of thermal relaxation time γ on the temperature profile is illustrated in Fig. 12. Temperature and thermal relaxation time have been found to have an inverse connection. Physically, when we increase, the fluid elements have to work harder to transfer heat to their neighbouring components, resulting in a temperature drop. When γ=0 , heat rapidly spreads throughout the fluid. Fig. 13 illustrates the effects of the magnetic parameter M on the temperature profile.

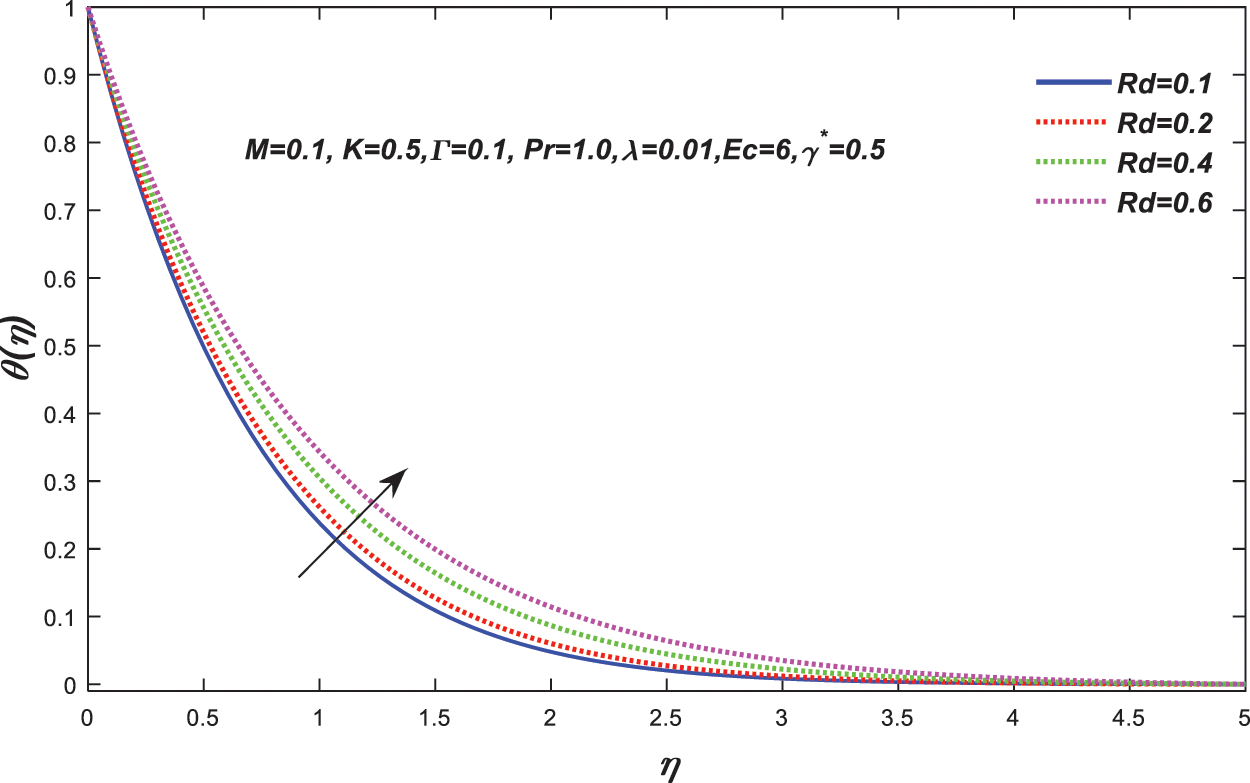
Figure 10: Change in the value of θ(η) for different values of Rd

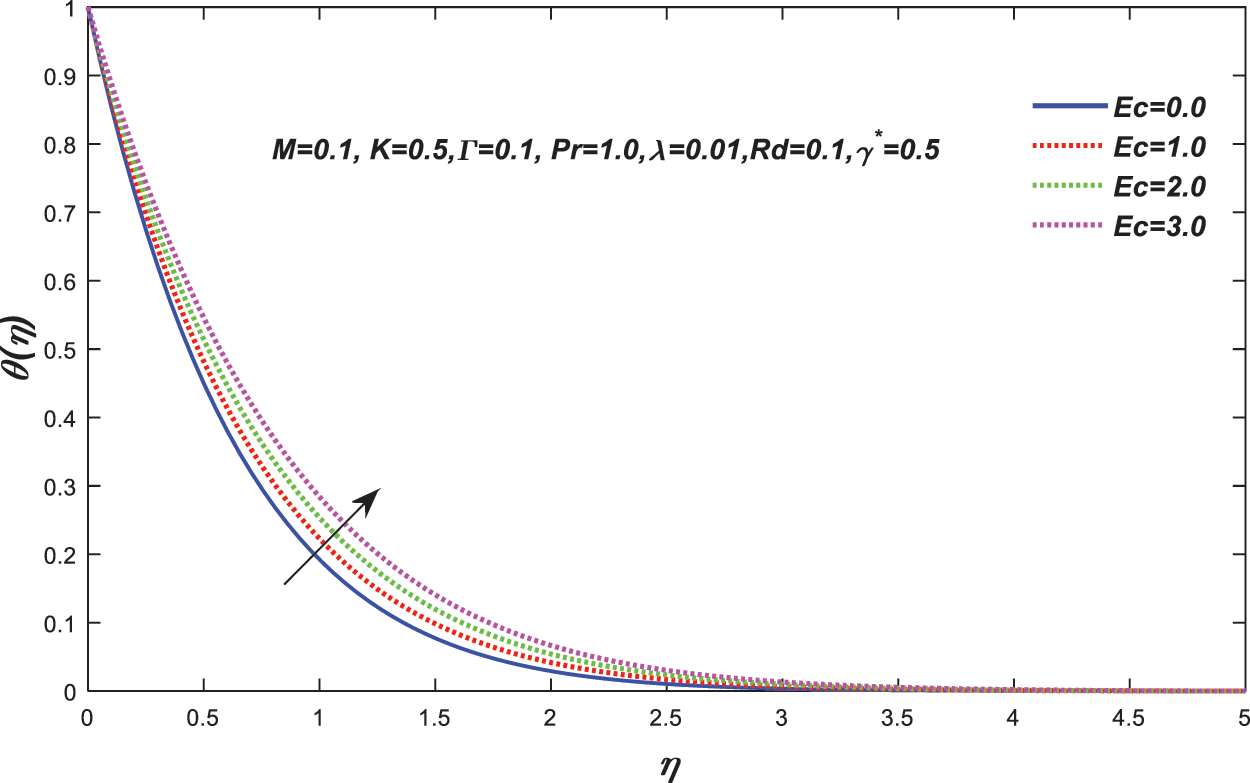
Figure 11: Change in the value of θ(η) for different values of Ec

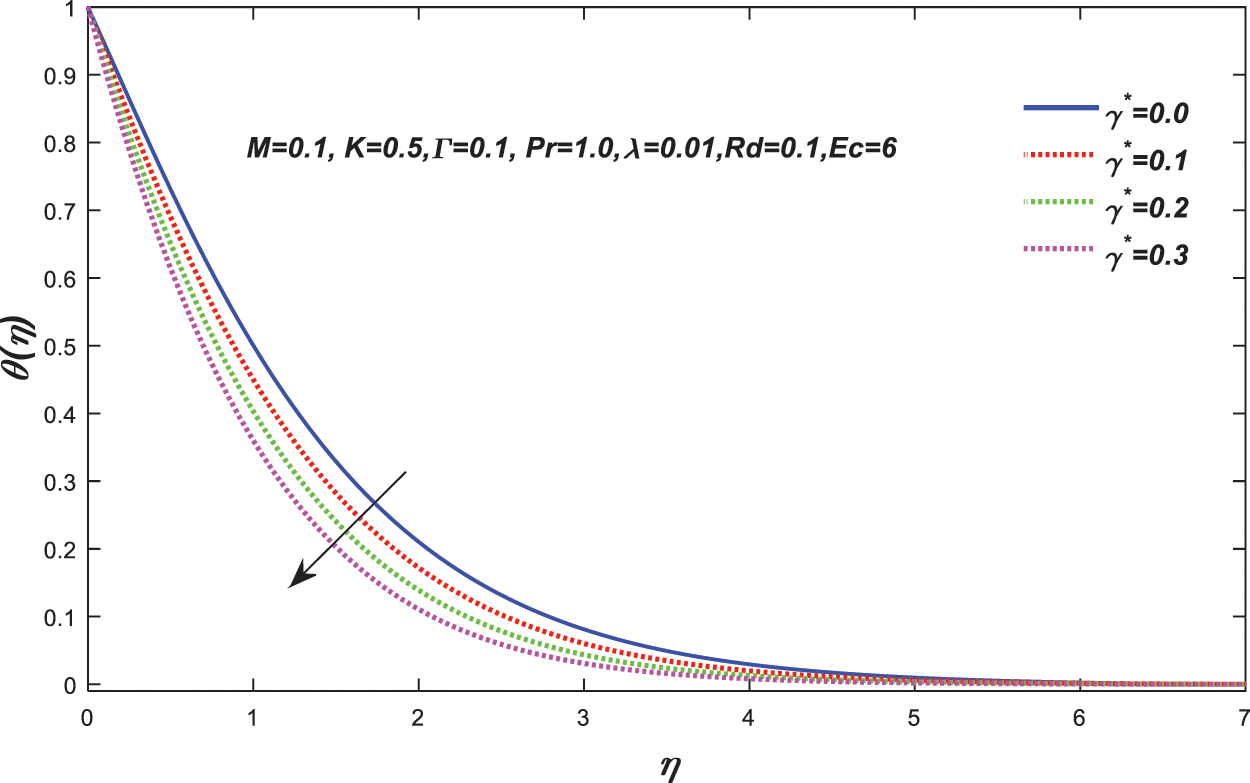
Figure 12: Change in the value of θ(η) for different values of γ

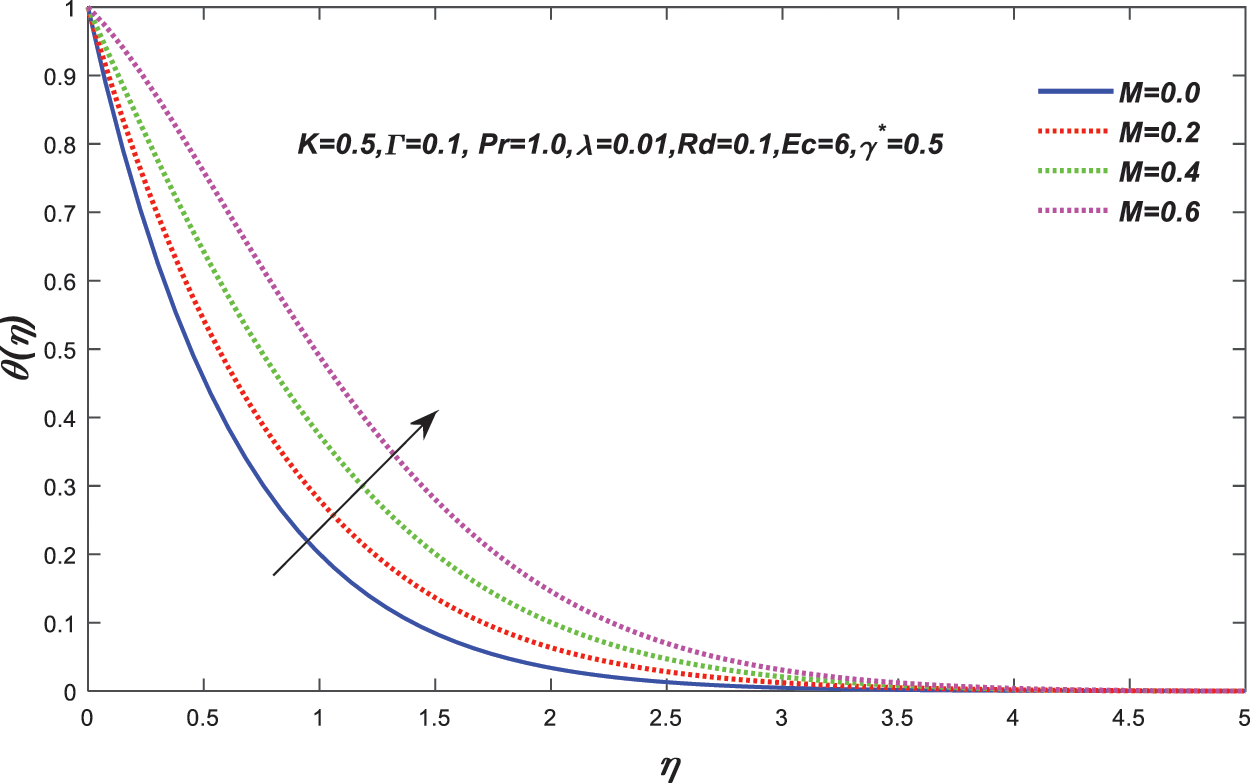
Figure 13: Change in the value of θ(η) for different values of M

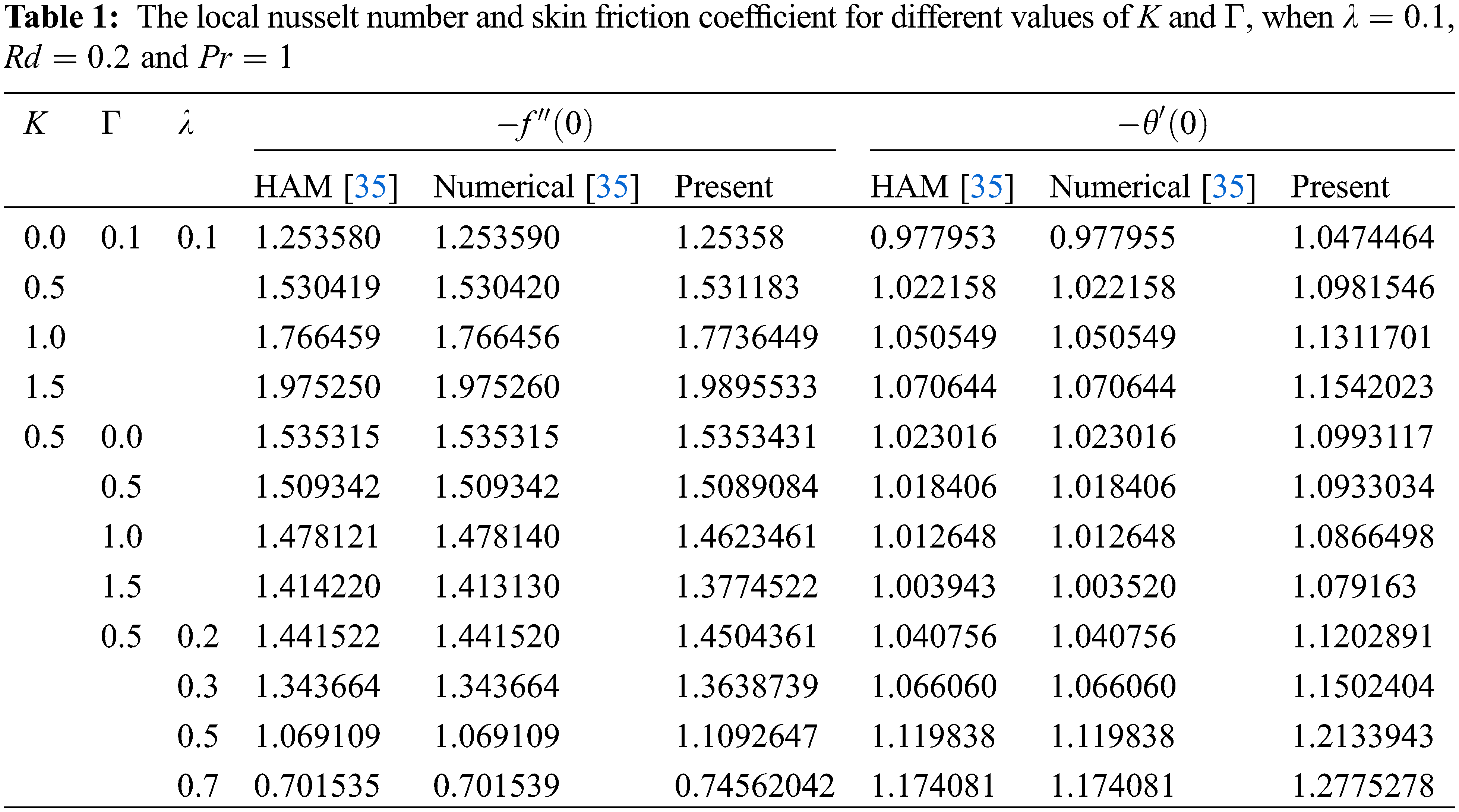
4.3 Matching Results to Published Work

The local Nusselt number and skin friction are listed in Table 1, and were estimated using a MATLAB method with fourth-order precision (BVP4C). The skin friction coefficient increases as K increases. As a result, as Γ increases, the coefficient of friction on the skin lowers. According to Mushtaq et al. [13], on an exponentially stretched surface, the magnitude of the skin friction coefficient decreases significantly as the velocity ratio grows. It has already been noted that when K grows, the thermal boundary layer’s thickness decreases. As a result, the heat transfer rate at the stretching sheet is increased. Additionally, as Γ grows, the size of the local Nusselt population decreases dramatically. Additionally, it increases as the values of K and λ increase.

5  Concluding Remarks

Thermal transport in the Powell-Eyring model via generalised heat flux over an exponentially stretching sheet is examined. The impact of Powell-Eyring fluid parameter, magnetic parameter M, Eckert number Ec, radiation parameter Rd , and thermal relaxation time γ was investigated. The study’s most important features are listed below:

•   The velocity profile increases as the fluid parameter K increases, but reverse behaviour is noticed for the temperature profile.

•   For increasing values of the magnetic parameter M, the velocity profile falls while the temperature rises. In addition, the resistance to flow increases as the magnetic field intensity and K increase.

•   The temperature and thickness of the thermal boundary layer are inversely related to the thermal relaxation time γ , whereas the Eckert number Ec has the opposite trend. With an increase in Ec , the temperature rises.

•   Increasing values of Rd (radiation parameter) increase the heat fluxes from the surface, which causes the increase in the fluid’s temperature and velocity.

Simulations of local Nusselt number and skin friction/co-efficient are used to validate the published work.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Riaz, N. (2019). Thermal radiation effect on an MHD eyring–Powell fluid flow (Doctoral Dissertation). Capital University. [Google Scholar]

 2.  Ziegenhagen, A. (1965). The very slow flow of a Powell–Eyring fluid around a sphere. Applied Scientific Research, Section A, 14(1), 43–56. [Google Scholar]

 3.  Sirohi, V., Timol, M. G., Kalthia, N. L. (1987). Powell–Eyring model flow near an accelerated plate. Fluid Dynamics Research, 2(3), 193. DOI 10.1016/0169-5983(87)90029-3. [Google Scholar] [CrossRef]

 4.  Yoon, H. K., Ghajar, A. J. (1987). A note on the Powell–Eyring fluid model. International Communications in Heat and Mass Transfer, 14(4), 381–390. DOI 10.1016/0735-1933(87)90059-5. [Google Scholar] [CrossRef]

 5.  Sohail, M., Ali, U., Al–Mdallal, Q., Thounthong, P., Sherif, E. S. M. et al. (2020). Theoretical and numerical investigation of entropy for the variable thermophysical characteristics of couple stress material: Applications to optimization. Alexandria Engineering Journal, 59(6), 4365–4375. DOI 10.1016/j.aej.2020.07.042. [Google Scholar] [CrossRef]

 6.  Rajagopal, K. R., Na, T. Y., Gupta, A. S. (1984). Flow of a viscoelastic fluid over a stretching sheet. Rheologica Acta, 23(2), 213–215. DOI 10.1007/BF01332078. [Google Scholar] [CrossRef]

 7.  Naz, R., Sohail, M., Hayat, T. (2020). Numerical exploration of heat and mass transport for the flow of nanofluid subject to hall and ion slip effects. Multidiscipline Modeling in Materials and Structures, 16(5), 951–965. DOI 10.1108/MMMS-07-2019-0125. [Google Scholar] [CrossRef]

 8.  Imran, N., Javed, M., Sohail, M., Farooq, S., Qayyum, M. (2020). Outcome of slip features on the peristaltic flow of a rabinowitsch nanofluid in an asymmetric flexible channel. Multidiscipline Modeling in Materials and Structures, 17(1), 181–197. DOI 10.1108/MMMS-02-2020-0039. [Google Scholar] [CrossRef]

 9.  Bachok, N., Ishak, A., Pop, I. (2010). Melting heat transfer in boundary layer stagnation–point flow towards a stretching/shrinking sheet. Physics Letters A, 374(40), 4075–4079. DOI 10.1016/j.physleta.2010.08.032. [Google Scholar] [CrossRef]

10. Imran, N., Javed, M., Sohail, M., Gokul, K. C., Roy, P. (2020). Exploration of thermal transport for Sisko fluid model under peristaltic phenomenon. Journal of Physics Communications, 4(6), 065003. DOI 10.1088/2399-6528/ab9557. [Google Scholar] [CrossRef]

11. Naseem, T., Nazir, U., El-Zahar, E. R., Algelany, A. M., Sohail, M. (2021). Numerical computation of Dufour and Soret effects on radiated material on a porous stretching surface with temperature–Dependent thermal conductivity. Fluids, 6(6), 196. DOI 10.3390/fluids6060196. [Google Scholar] [CrossRef]

12. Naseem, T., Nazir, U., Sohail, M. (2021). Contribution of Dufour and Soret effects on hydromagnetized material comprising temperature-dependent thermal conductivity. Heat Transfer, 50(7), 7157–7175. DOI 10.1002/htj.22222. [Google Scholar] [CrossRef]

13. Adjal, S., Aklouche-Benouaguef, S., Zeghmati, B. (2022). Numerical study of natural convection in an inclined porous cavity. Fluid Dynamic & Material Process,M- 18(5), 1389–1397. DOI 10.32604/fdmp.2022.021619. [Google Scholar] [CrossRef]

14. Bahia, G., Ouannas, A., Batiha, I. M., Odibat, Z. (2021). The optimal homotopy analysis method applied on nonlinear time-fractional hyperbolic partial differential equations. Numerical Methods for Partial Differential Equations, 37(3), 2008–2022. DOI 10.1002/num.22639. [Google Scholar] [CrossRef]

15. Malik, M. Y., Hussain, A., Nadeem, S. (2013). Boundary layer flow of an Eyring–Powell model fluid due to a stretching cylinder with variable viscosity. Scientia Iranica, 20(2), 313–321. [Google Scholar]

16. Akbar, N. S., Ebaid, A., Khan, Z. H. (2015). Numerical analysis of magnetic field effects on Eyring–Powell fluid flow towards a stretching sheet. Journal of Magnetism and Magnetic Materials, 382, 355–358. DOI 10.1016/j.jmmm.2015.01.088. [Google Scholar] [CrossRef]

17. Kumar, B., Srinivas, S. (2020). Unsteady hydromagnetic flow of Eyring–Powell nanofluid over an inclined permeable stretching sheet with joule heating and thermal radiation. Journal of Applied and Computational Mechanics, 6(2), 259–270. [Google Scholar]

18. Pal, D., Mondal, S. K. (2022). Magneto–bioconvection of Powell Eyring nanofluid over a permeable vertical stretching sheet due to gyrotactic microorganisms in the presence of nonlinear thermal radiation and joule heating. International Journal of Ambient Energy, 43(1), 924–935. [Google Scholar]

19. Hayat, T., Nadeem, S. (2017). Aspects of developed heat and mass flux models on 3D flow of Eyring–Powell fluid. Results in Physics, 7, 3910–3917. DOI 10.1016/j.rinp.2017.09.048. [Google Scholar] [CrossRef]

20. Reddy, S. R. R., Bala Anki Reddy, P., Rashad, A. M. (2020). Activation energy impact on chemically reacting Eyring–Powell nanofluid flow over a stretching cylinder.M- Arabian Journal for Science and Engineering, 45(7), 5227–5242. [Google Scholar]

21. Mustafa, M. (2015). Cattaneo–Christov heat flux model for rotating flow and heat transfer of upper–convected Maxwell fluid. AIP Advances, 5(4), 047109. DOI 10.1063/1.4917306. [Google Scholar] [CrossRef]

22. Ishaq, M., Ali, G., Shah, Z., Islam, S., Muhammad, S. (2018). Entropy generation on nanofluid thin film flow of Eyring–Powell fluid with thermal radiation and MHD effect on an unsteady porous stretching sheet. Entropy, 20(6), 412. DOI 10.3390/e20060412. [Google Scholar] [CrossRef]

23. Alsaedi, A., Hayat, T., Qayyum, S., Yaqoob, R. (2020). Eyring–Powell nanofluid flow with nonlinear mixed convection: Entropy generation minimization. Computer Methods and Programs in Biomedicine, 186, 105183. DOI 10.1016/j.cmpb.2019.105183. [Google Scholar] [CrossRef]

24. Bhatti, M. M., Abbas, T., Rashidi, M. M., Ali, M. E. S., Yang, Z. (2016). Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy, 18(6), 224. DOI 10.3390/e18060224. [Google Scholar] [CrossRef]

25. Ali, N., Nazeer, F., Nazeer, M. (2018). Flow and heat transfer analysis of an Eyring–Powell fluid in a pipe. Zeitschrift für Naturforschung A, 73(3), 265–274. DOI 10.1515/zna-2017-0435. [Google Scholar] [CrossRef]

26. Nazeer, M., Ahmad, F., Saleem, A., Saeed, M., Naveed, S. et al. (2019). Effects of constant and space–dependent viscosity on Eyring–Powell fluid in a pipe: Comparison of the perturbation and explicit finite difference methods. Zeitschrift für Naturforschung A, 74(11), 961–969. DOI 10.1515/zna-2019-0095. [Google Scholar] [CrossRef]

27. Hajamalala, A. M., Noarijaona, R., Belkacem, Z.(2022). Modeling the unsteady flow of a newtonian fluid originating from the hole of an open cylindrical reservoir. Fluid Dynamic & Material Process, 18(6), 1737–1748. DOI 10.32604/fdmp.2022.022047. [Google Scholar] [CrossRef]

28. Ahmad, F., Nazeer, M., Saeed, M., Saleem, A., Ali, W. (2020). Heat and mass transfer of temperature–dependent viscosity models in a pipe: Effects of thermal radiation and heat generation. Zeitschrift Für Naturforschung A, 75(3), 225–239. DOI 10.1515/zna-2019-0332. [Google Scholar] [CrossRef]

29. Nazeer, M., Ahmad, F., Ali, W., Ijaz Khan, M., Saleem, A. (2022). Perturbation and numerical solutions of non-Newtonian fluid bounded within in a porous channel: Applications of pseudo-spectral collocation method. Numerical Methods for Partial Differential Equations, 38(3), 278–292. [Google Scholar]

30. Nazeer, M., Khan, M. I., Rafiq, M. U., Khan, N. B. (2020). Numerical and scale analysis of Eyring–Powell nanofluid towards a magnetized stretched Riga surface with entropy generation and internal resistance. International Communications in Heat and Mass Transfer, 119, 104968. DOI 10.1016/j.icheatmasstransfer.2020.104968. [Google Scholar] [CrossRef]

31. M Ijaz, K., Yu-Ming, C. (2021). Regular perturbation solution of Couette flow (non–Newtonian) between two parallel porous plates: A numerical analysis with irreversibility. Applied Mathematics and Mechanics, 42(1), 127–142. DOI 10.1007/s10483-021-2677-9. [Google Scholar] [CrossRef]

32. Chu, Y. M., Ahmad, F., Khan, M. I., Nazeer, M., Hussain, F. et al. (2021). Numerical and scale analysis of non–Newtonian fluid (Eyring–Powell) through pseudo–spectral collocation method (PSCM) towards a magnetized stretchable Riga surface. Alexandria Engineering Journal, 60(2), 2127–2137. DOI 10.1016/j.aej.2020.12.017. [Google Scholar] [CrossRef]

33. Nazeer, M. (2021). Numerical and perturbation solutions of cross flow of an Eyring–Powell fluid. SN Applied Sciences, 3(2), 1–11. DOI 10.1007/s42452-021-04173-8. [Google Scholar] [CrossRef]

34. Hussain, F., Subia, G.S., Nazeer, M., Ghafar, M.M., Ali, Z. (2021). Simultaneous effects of Brownian motion and thermophoretic force on Eyring–Powell fluid through porous geometry. Zeitschrift für Naturforschung A, 76(7), 569–580. [Google Scholar]

35. Mushtaq, A., Mustafa, M., Hayat, T., Rahi, M., Alsaedi, A. (2013). Exponentially stretching sheet in a Powell–Eyring fluid: Numerical and series solutions. Zeitschrift für Naturforschung A, 68(12), 791–798. DOI 10.5560/zna.2013-0063. [Google Scholar] [CrossRef]

36. Dong, Y., Cao, B. Y., Guo, Z. Y. (2011). Generalized heat conduction laws based on thermomass theory and phonon hydrodynamics. Journal of Applied Physics, 110(6), 063504. DOI 10.1063/1.3634113. [Google Scholar] [CrossRef]

37. Rahimi, J., Ganji, D. D., Khaki, M., Hosseinzadeh, K. (2017). Solution of the boundary layer flow of an Eyring–Powell non–Newtonian fluid over a linear stretching sheet by collocation method. Alexandria Engineering Journal, 56(4), 621–627. DOI 10.1016/j.aej.2016.11.006. [Google Scholar] [CrossRef]

38. Agrawal, R., Kaswan, P. (2021). MHD Eyring–Powell nanofluid past over an unsteady exponentially stretching surface with entropy generation and thermal radiation. Heat Transfer, 50(5), 4669–4693. [Google Scholar]

39. Jafarimoghaddam, A. (2019). On the homotopy analysis method (HAM) and homotopy perturbation method (HPM) for a nonlinearly stretching sheet flow of Eyring–Powell fluids. Engineering Science and Technology, an International Journal, 22(2), 439–451. DOI 10.1016/j.jestch.2018.11.001. [Google Scholar] [CrossRef]

40. Avramenko, A. A., Kovetskaya, M. M., Shevchuk, I. V. (2022). Self–similar analysis of Eyring–Powell fluid in boundary layer without simplification. Chinese Journal of Physics, 75, 28–37. DOI 10.1016/j.cjph.2021.10.025. [Google Scholar] [CrossRef]

41. Avramenko, A. A., Kobzar, S. G., Shevchuk, I. V., Kuznetsov, A. V., Iwanisov, L. T. (2001). Symmetry of turbulent boundary–layer flows: Investigation of different eddy viscosity models. Acta Mechanica, 151(1), 1–14. DOI 10.1007/BF01272521. [Google Scholar] [CrossRef]

42. Avramenko, A. A., Shevchuk, I. V. (2019). Lie group analysis and general forms of self–similar parabolic equations for fluid flow, heat and mass transfer of nanofluids. Journal of Thermal Analysis and Calorimetry, 135(1), 223–235. DOI 10.1007/s10973-018-7053-x. [Google Scholar] [CrossRef]