Impact of Radiation and Slip on Newtonian Liquid Flow Past a Porous Stretching/Shrinking Sheet in the Presence of Carbon Nanotubes

Nomenclature

1  Introduction

The fluid flow with carbon nanotubes (CNTs) through porous media considering the mass transpiration is an important concept in the field of industry and medicine, especially in nano-medicine. The porous media approach is useful in the treatment of cancer tumors as the tumor growth is represented by the mathematical model where the mass transfer represents the process of growth and death. The model of tumor growth represented by the porous media approach studied in detail by Shelton [1]. In 2014, Sunil et al. [2] solved the system of fractional differential equation by using the homotopy analysis method and Laplace transform method and obtain the convergence series. Bhattacharya [3] studied the first order homogeneous chemical reaction with the impact of mass transfer by using shooting method. The influence of viscous dissipation and chemical reaction on the stagnation point flow of NF over the stretching/shrinking plate was studied by Murthy et al. [4]. Talay et al. [5] investigated the chemical reaction of non-Newtonian fluid through porous medium to obtain exact solution and some interesting properties that leads to further study on chemically reactive species.

Fazle et al. [6] studied the unsteady flow with velocity, thermal and solutal slips further obtain the numerical solution. The Newtonian fluid flow due to superlinear stretching sheet is investigated by Siddheshwar et al. [7]. Mahabaleshwar et al. [8–11] studied the impact of slip and radiation on the flow of Walters’ B liquid over linearly stretching plate embedded in porous media and got the analytical solution for different fluids with the presence of different parameters. Siddheshwar et al. [12] approached the new analytical solution procedure for both Newtonian and non-Newtonian fluid flow due to linear stretching sheet using the technique of perturbation and obtain the analytical solution for velocity and stream function. Mahabaleshwar et al. [13] modeled the problem of axisymmetric flow over stretching sheet in the presence slip which does not have exact analytical solution leads to obtain solution by suing differential transform method and Pade approximation. Some authors use Laplace transformation (LT) to get the analytical solution for the flow and heat transfer of CNTs and nanofluids with the presence of different parameters. Abdelhalim et al. [14] studied in the presence of magnetic field and obtain new analytical solution. Hoda et al. [15] investigated on the medical application, mainly on cancer tumor treatment of it with convective condition and gives some numerical results. Malkeet et al. [16] gave the detailed applications and properties of Laplace transformation. Mahabaleshwar et al. [17] made the contribution on the inclined MHD flow, mass and heat transfer with radiation effect. Mahabaleshwar et al. [18] investigated the MHD flow with carbon nanotubes by considering the effect of mass transpiration and radiation on it. Anusha et al. [19,20] examined the unsteady inclined MHD flow for Casson fluid with hybrid nanoparticles and due to porous media, respectively. Sneha et al. [21] investigated the flow and heat transfer of dusty fluid for its analytical solution.

Hamad [22] studied on natural convection flow and found the analytical solution for the MHD flow by adding NF. Andersson et al. [23] investigated the incompressible flow with the consequence of transverse MHD due to stretching sheet by using the power law model. Andersson et al. [24] first time gave the work on concentration distribution with the impact of higher order chemical reaction for the linearly stretching sheet and found numerical solution for momentum and concentration. Paul et al. [25] considered the hydrodynamic flow and a body is located in it from which a chemically reactive species is emitted and he consider the two reaction types viz, reactant is destroyed in one reaction type and it is generated in another.

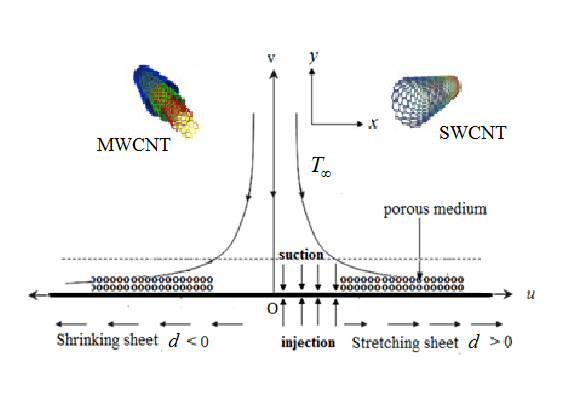
The intend of the current examination is to analyze the influences of radiation and mass transpiration with porous media on the flow of CNTs due to stretching/shrinking plate with the existence of Navier’s slip and physical model is as shown in Fig. 1. Further to obtain the analytic solution for velocity profile and temperature field.

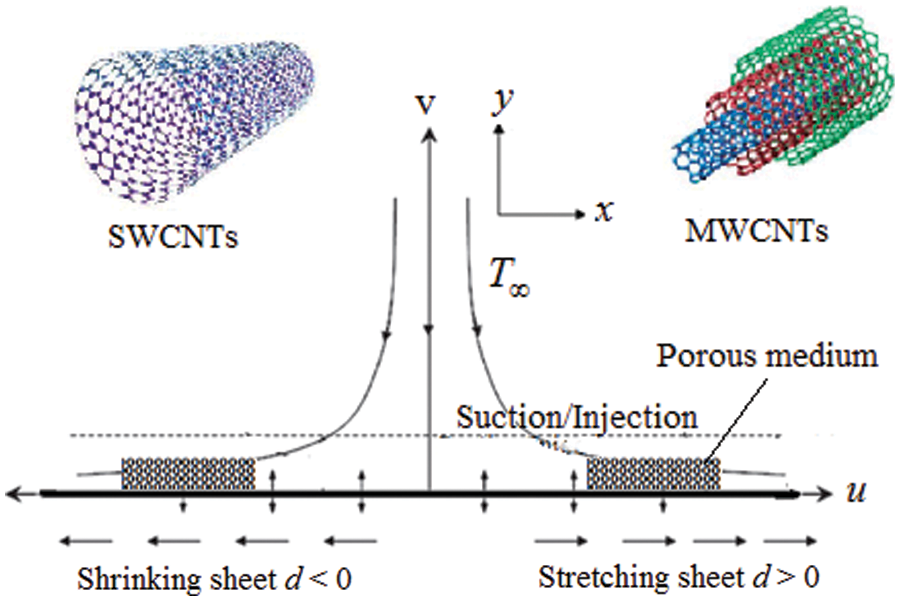
Figure 1: Schematic diagram of the flow problem

2  Equations and Mathematical Expressions

The steady 2-D flow and heat transfer of electrically conducting fluid due to stretching/shrinking sheet in porous media with permeability K is considered in the presence of mass transpiration and radiation. The flow is along x-axis and y is perpendicular to it. The wall temperature is maintained constant at Tw and T∞ is the ambient temperature. The fluids considered are base liquids like water, ethylene glycol and engine oil with single and multi-walled carbon nanotubes. The governing equations for described momentum and energy conservations are as follows:

∂u∂x+∂v∂y=0, (1)

u∂u∂x+v∂u∂y=νnf∂2u∂y2−νnfKu, (2)

u∂T∂x+v∂T∂y=knf(ρCP)nf∂2T∂y2−1(ρCP)nf∂qr∂y, (3)

with B.Cs as

u=dax+A∂u∂y+B∂2u∂y2,v=vw,−kf∂T∂y=h(Tw−T)aty=0,

u→0,T→T∞asy→∞, (4)

where, qr=−16σ∗T∞33κ∗∂2T∂y2 is the radiative heat flux and all parameters are as mentioned in nomenclature. On considering the suitable similarity transformation giving velocity component,

u=cx∂F∂η,v=−cνfF(η),θ(η)=T−T∞Tw−T∞withη=cνfy, (5)

and

1β1=μhnfμf=1(1−ϕ1)2.5, (6a)

β2=ρhnfρf=(1−ϕ)+ϕ(ρCNTρf), (6b)

this gives, νnf=νfβ1β2 ,

β3=(ρCP)nf(ρCP)f=(1−ϕ)+ϕ(ρCp)CNT(ρCP)f, (6c)

β4=knfkf=kCNT+2kf+2ϕ(kCNT−kf)kCNT+2kf−ϕ(kCNT−kf), (6d)

On applying (5) and (6a) to (6d) in (2) and (3) gives,

1β1β2∂3F∂η3+F∂2F∂η2−(∂F∂η)2−1β2Da−1∂F∂η=0, (7a)

β4β3(1+43Rd)∂2θ∂η2+PrF(η)∂θ∂η=0, (7b)

and B.Cs reduces to,

F(0)=S,(∂F∂η)η=0=d+γ1(∂2F∂η2)η=0+γ2(∂3F∂η3)η=0,(∂F∂η)η→∞=0,

(∂θ∂η)η=0=−Bi[1−θ(0)],θ(∞)=0. (7c)

Here, Da−1=νfKc is the inverse Darcy number,

Rd=4σ∗T∞3κ∗knf is the radiation parameter,

γ1=Acνfandγ2=Bcνf are first and second order slips respectively (see Mahantesh et al. [26], Lin [27]),

Bi=hkfνfc is the Biot number.

Take β = β1β2 and use the function transformation as, F(η)=1βf(ξ),θ(η)=ϕ(ξ),ξ=βη ,

∂3f∂η3+f∂2f∂η2−(∂f∂η)2−KP∂f∂η=0, (8a)

(1+43Rd)∂2ϕ∂ξ2+Pr∗f(ξ)∂ϕ∂ξ=0, (8b)

here,

KP=Da−1β2and Pr∗=Prβ3cβ4.

By taking the substitutions γ1β=χ1,γ2β=χ2,Sβ=f0,Biβ=K1 , the reduced B.Cs are,

f(0)=f0,,(∂F∂η)η=0=d+χ1(∂2f∂ξ2)ξ=0+χ2(∂3f∂ξ3)ξ=0,(∂f∂ξ)ξ→∞=0, (8c)

(∂ϕ∂ξ)ξ=0=−K1[1−ϕ(0)],ϕ(∞)=0. (8d)

2.1 Solution of Momentum Problem

The exact analytical solution of Eq. (8a) as in Turkyilmazoglu [28] is as,

f(ξ)=f0+d(1−exp[−αξ])α(1+χ1α−χ2α2), (9)

This gives the velocity as,

∂f∂ξ=dexp[−αξ]1+χ1α−χ2α2, (10)

Using this in (8a) gives the relation,

χ2α4−(χ1+f0χ2)α3−(1−f0χ1+KPχ2)α2+(f0+KPχ1)α+(d+KP)=0, (11)

From this equation the exponent α can be obtained.

2.2 Solution of Energy Problem

The exact solution of Eq. (8b) can be found by using the new variable t=Pr∗α2exp[−αξ] and gives,

Rt∂2ϕ∂t2+(R−ε2+ε1t)∂ϕ∂t=0 (12)

here

R=1+43Rd,ε1=d1+χ1α−χ2α2,ε2=Pr∗[d+f0α(1+χ1α−χ2α2)]α2(1+χ1α−χ2α2) are dummy variables.

The solution of Eq. (12) using the B.Cs (8d) is in the form of incomplete gamma function is as below:

ϕ(t)=K1exp(ε1Pr∗Rα2){Γ[ε2R,0]−Γ[ε2R,ε1Rt]}α(Pr∗α2)ε2/R(ε1R)ε2/R+K1exp(ε1Pr∗Rα2){Γ[ε2R,0]−Γ[ε2R,ε1Pr∗Rα2]}, (13a)

ϕ in terms of ξ becomes,

ϕ(ξ)=K1exp(ε1Pr∗Rα2){Γ[ε2R,0]−Γ[ε2R,ε1RPr∗α2e−αξ]}α(Pr∗α2)ε2/R(ε1R)ε2/R+K1exp(ε1Pr∗Rα2){Γ[ε2R,0]−Γ[ε2R,ε1Pr∗Rα2]}, (13b)

Then the temperature distribution will becomes,

θ(η)=K1exp(ε1Pr∗Rα2){Γ[ε2R,0]−Γ[ε2R,ε1RPr∗α2exp[−αβη]]}α(Pr∗α2)ε2/R(ε1R)ε2/R+K1exp(ε1Pr∗Rα2){Γ[ε2R,0]−Γ[ε2R,ε1Pr∗Rα2]}, (14)

The scaled Nusselt number is given by, Nu=−(∂θ∂η)η=0.

3  Figures and Discussions

The influence of mass transpiration, Navier’s slip and thermal slips on the flow of incompressible viscous MWCNT/SWCNT is investigated. The system of PDEs is changed to system of nonlinear ODEs with constant coefficients by using the suitable similarity transformations for velocity and temperature. Then the analytical solution for velocity profile is obtained in exponential form and that for the temperature field was obtained in terms of incomplete gamma function. The concerned effects are analyzed by the help of different graphs for MWCNT/SWCNT. The model is shown for the flow over porous medium and the advantages of using porous medium for its applications in industry and medicine field. To study the effects of different base fluids for MWCNT and SWCNT, the different graphs are shown here.

In Fig. 2 the effect of solid volume fraction on β is plotted for all mentioned base fluids shown that SWCNT is more effected by ϕ than MWCNT. Among the base fluids engine oil is more effected and ethylene glycol has less effected by ϕ. Figs. 3 and 4 demonstrate the behaviour of skin friction verses mass transpiration for different values of permeability parameter by taking different roots. Fig. 5 is the plot for skin friction verses mass transpiration for different values of first order slip. Further in Fig. 6 the effect of ϕ on Pr as in Eq. (15) is studied for mentioned base fluids. And shown that water has less Pr value and engine oil has highest Pr value. Pr value of SWCNTs is more than that of MWCNTs.

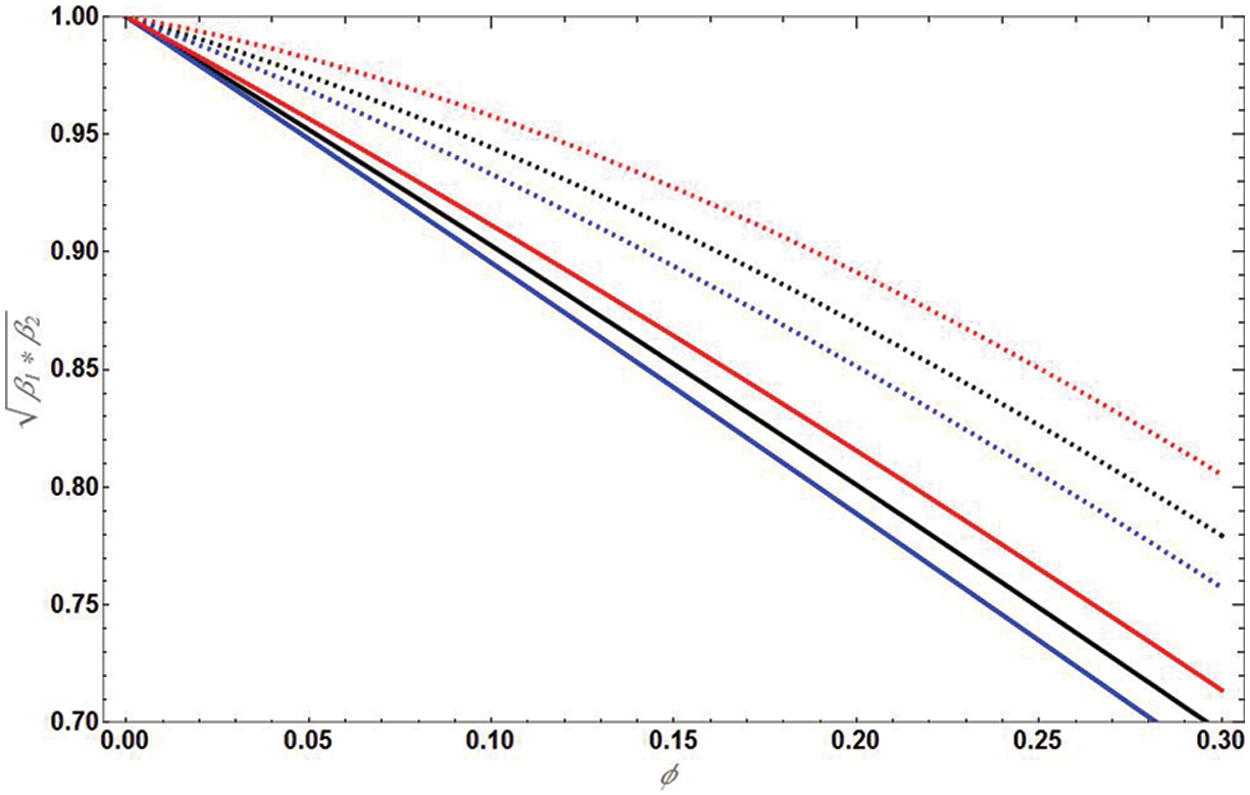
Figure 2: The plot showing the values β against the solid volume fraction ϕ, where dotted lines for SWCNT and solid lines are for MWCNT, black curves are for water base fluid, blue curves are for ethylene glycol base fluid and red curves are for engine oil base fluid

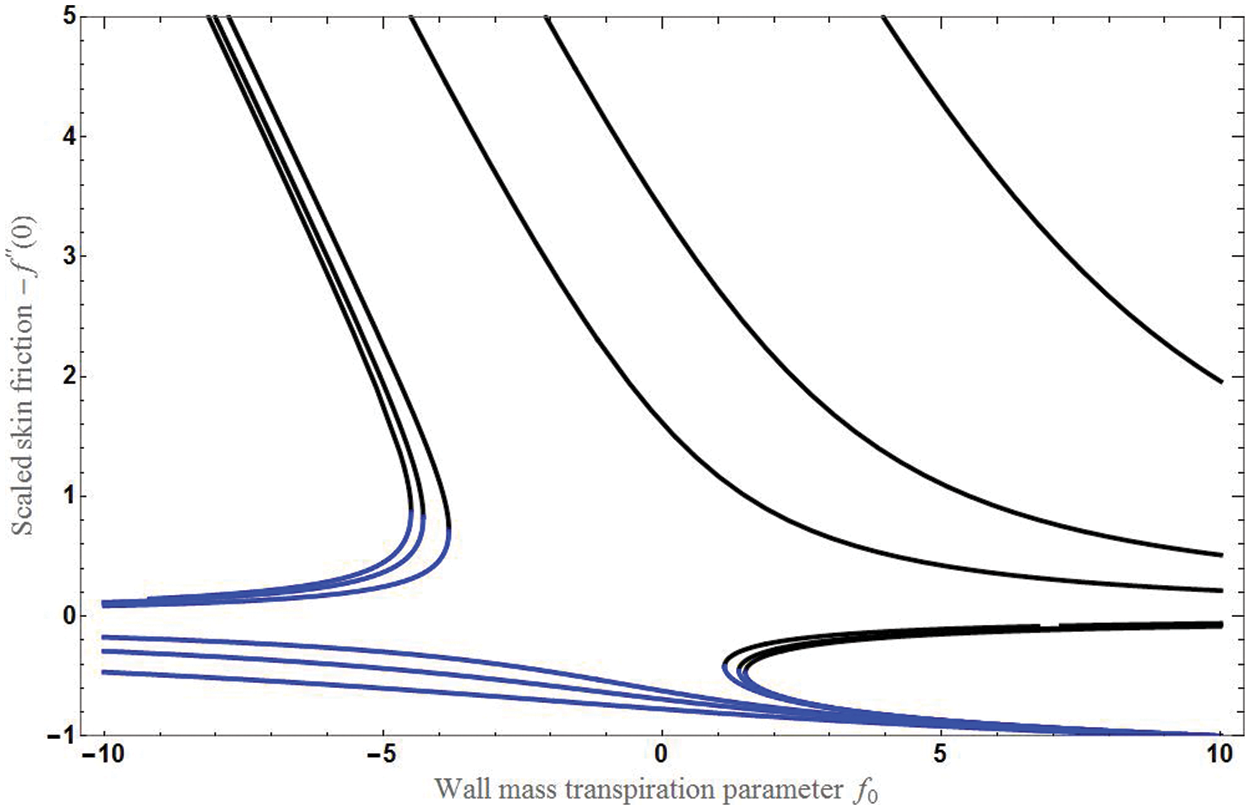
Figure 3: The graph of skin friction verses mass transpiration for various values of permeability parameter (KP = 0, 0.1, 0.3, 3, 5, 10) for 2nd and 3rd roots of Eq. (11) with χ1 = 1, χ2 = 0.01 in case of shrinking sheet (d=−1)

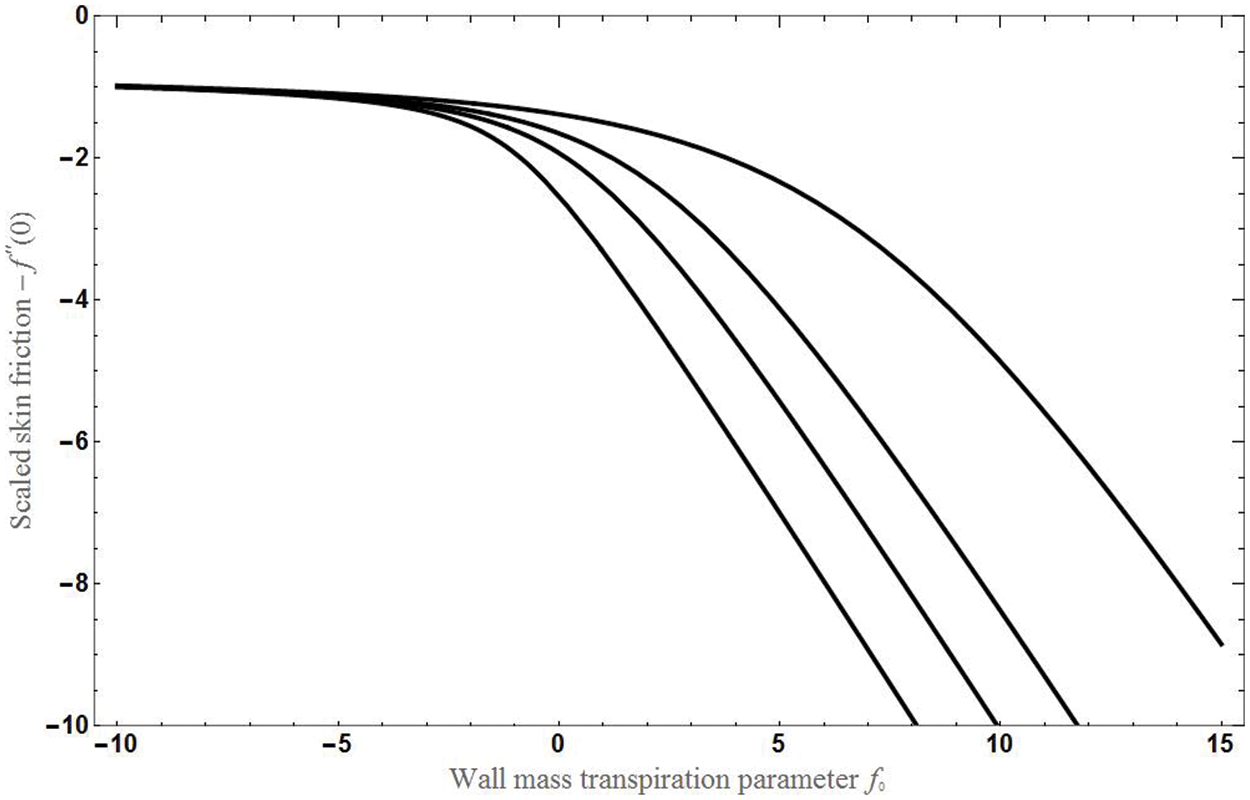
Figure 4: The graph of skin friction verses mass transpiration for various values of permeability parameter (KP = 1, 3, 5, 10) for 1st root of Eq. (11) with χ1 = 1, χ2 = 0.01 in case of shrinking sheet (d=−1)

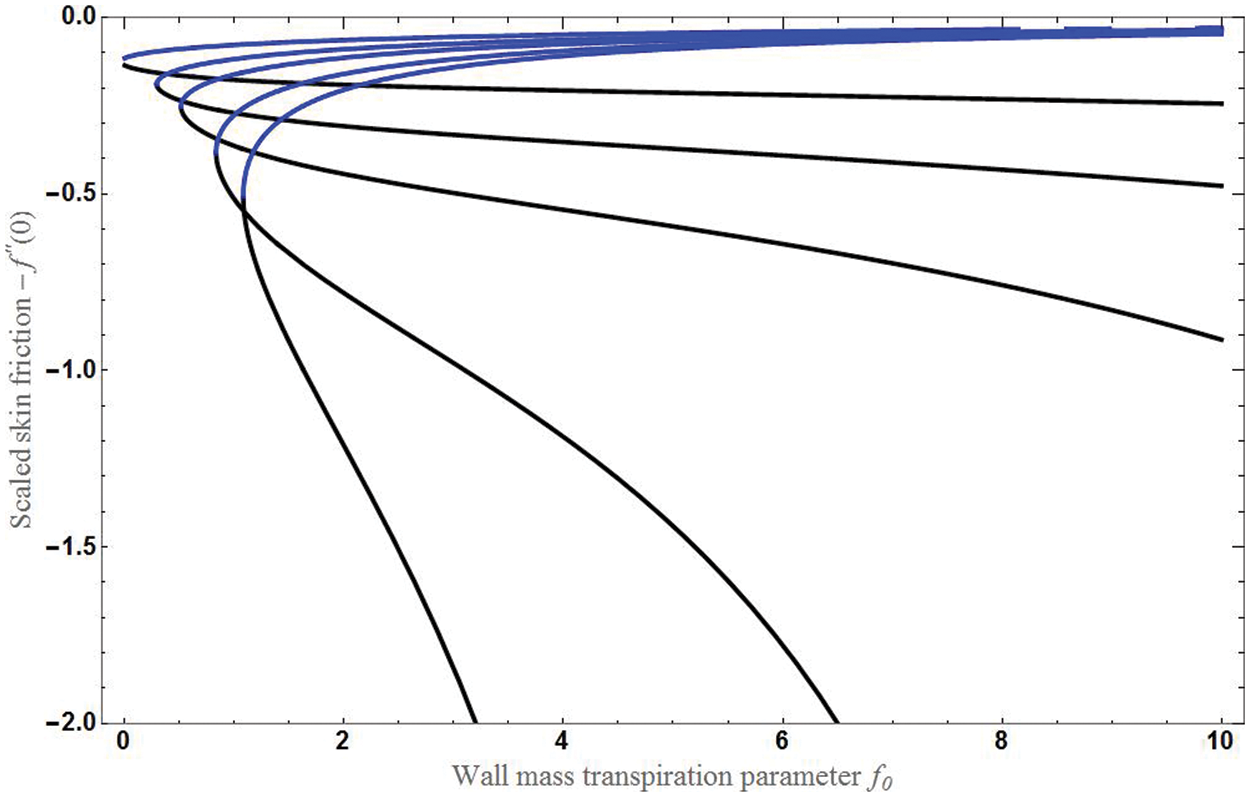
Figure 5: The graph of skin friction verses mass transpiration for various values of (χ1 = 0.5, 1, 2, 3, 5) for 2nd and 3rd roots of Eq. (11) with KP = 0.5, χ2 = 0.1 in case of shrinking sheet (d=−1)

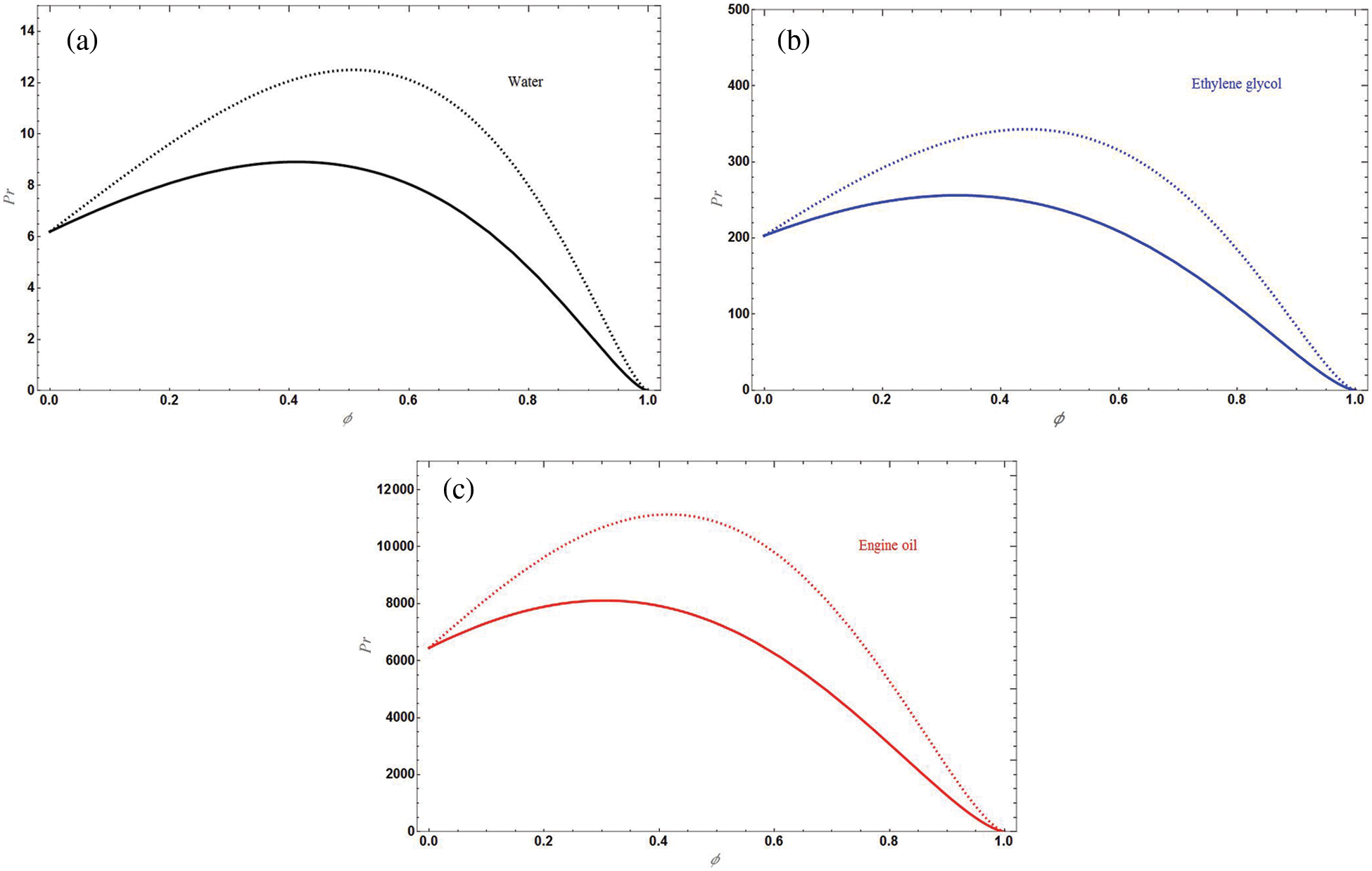
Figure 6: The plot showing the values Pr against the solid volume fraction ϕ, where dotted lines for SWCNT and solid lines are for MWCNT

To study the variation of skin friction with mass transpiration f0 is studied for different conditions and for different roots values of Eq. (11).

Variation of Pr with ϕ for MWCNT and SWCNTs is given by,

Pr=(1−ϕ)5/2[1−ϕ+ϕ(ρCNTρf)](1−ϕ)+ϕ(ρCp)CNT(ρCP)f[kCNT+2kf+2ϕ(kCNT−kf)kCNT+2kf−ϕ(kCNT−kf)]Pr∗, (15)

4  Concluding Remarks

The influence of mass transpiration and Navier’s slip on the flow of incompressible viscous MWCNT/SWCNT for different base fluids is studied. The concerned effects are analyzed by the help of different graphs for MWCNT/SWCNT. The effects observed are,

•   Analytical solution is obtained for velocity and temperature field.

•   Prandtl number is lower for water and highest for engine oil.

•   Prandtl number for SWCNT is more than that of MWCNT.

•    β decreases as the solid volume fraction increases.

•    β more for SWCNT than for MWCNT.

Acknowledgement: The author T. Anusha is thankful to Council of Scientific and Industrial Research (CSIR), New Delhi, India, for financial support in the form of Junior Research Fellowship: File No. 09/1207(0003)/2020-EMR-I.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Sarah, E. S. (2011). Mechanistic modeling of cancer tumor growth using a porous media approach. DOI 10.17615/3x7g-e498. [Google Scholar] [CrossRef]

 2.  Sunil, K., Devendra, K., Mahabaleshwar, U. S. (2014). A new adjustment of laplace transform for fractional Bloch equation in NMR flow. Applications and Applied Mathematics, 9(1), 201–216. [Google Scholar]

 3.  Bhattacharyya, K. (2011). Dual solutions in boundary layer stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet. International Communications in Heat and Mass Transfer, 38, 917–922. DOI 10.1016/j.icheatmasstransfer.2011.04.020. [Google Scholar] [CrossRef]

 4.  Murthy, P. V. S. N., Ramreddy, C., Chamkha, A. J., Rashad, A. M. (2015). Significance of viscous dissipation and chemical reaction on convective transport in boundary layer stagnation point flow past a stretching/shrinking sheet in a nanofluid. Journal of Nanofluids, 4, 214–222. DOI 10.1166/jon.2015.1136. [Google Scholar] [CrossRef]

 5.  Talay, A. F., Hamid, B., Vajravelu, K. (2006). Diffusion of chemically reactive species in a porous medium over a stretching sheet. Journal of Mathematical Analysis and Applications, 320, 322–339. DOI 10.1016/j.jmaa.2005.06.095. [Google Scholar] [CrossRef]

 6.  Fazle, M., Stanford, S. (2019). Multiple slip effects on MHD unsteady flow heat and mass transfer impinging on permeable stretching sheet with radiation. Modelling and Simulation in Engineering, 2019, 1–11. DOI 10.1155/2019/3052790. [Google Scholar] [CrossRef]

 7.  Siddheshwar, P. G., Mahabaleshwar, U. S. (2018). Flow and heat transfer to a newtonian fluid over non-linear extrusion stretching sheet. International Journal of Applied and Computational Mathematics, 4(1), 35. DOI 10.1007/s40819-017-0466-6. [Google Scholar] [CrossRef]

 8.  Mahabaleshwar, U. S., Ioannis, E. S., Giulio, L. (2018). Effect of radiation and navier slip boundary of walters’ liquid B flow over a stretching sheet in a porous media. International Journal of Heat and Mass Transfer, 127, 1327–1337. DOI 10.1016/j.ijheatmasstransfer.2018.02.084. [Google Scholar] [CrossRef]

 9.  Mahabaleshwar, U. S., Sarris, I. E., Hill, A. A. (2017). An MHD couple stress fluid due to a perforated sheet undergoing linear stretching with heat transfer. International Journal of Heat and Mass Transfer, 105, 157–167. DOI 10.1016/j.ijheatmasstransfer.2016.09.040. [Google Scholar] [CrossRef]

10. Mahabaleshwar, U. S., Vinay, K., Mikhail, S. P. N. (2016). Magnetohydrodynamics flow of a nanofluid driven by a stretching/shrinking sheet with suction. SpringerPlus, 5, 1901. DOI 10.1186/s40064-016-3588-0. [Google Scholar] [CrossRef]

11. Mahabaleshwar, U. S., Nagaraju, K. R., Sheremet, M. A., Vinay Kumar, P. N., Lorenzini, G. (2019). Effect of mass transfer and MHD induced navier’s slip flow due to a non linear stretching sheet. Journal of Thermophysics, 28(4), 578–590. DOI 10.1134/S1810232819040131. [Google Scholar] [CrossRef]

12. Siddheshwar, P. G., Mahabaleshwar, U. S., Andersson, H. I. (2013). A new analytical procedure for solving the non-linear differential equation arising the stretching sheet problem. International Journal of Applied Mechanics and Engineering, 18(3), 955–964. DOI 10.2478/ijame-2013-0059. [Google Scholar] [CrossRef]

13. Mahabaleshwar, U. S., Nagaraju, K. R., Vinay, K. (2018). An MHD navier’s slip flow over axisymmetric linear stretching sheet using differential transform method. International Journal of Applied and Computational Mathematics, 4, 30. DOI 10.1007/s40819-017-0446-x. [Google Scholar] [CrossRef]

14. Abdelhalim, E., Mohammed, A., Al, S. (2015). Application of laplace transform for the exact effect of a magnetic field on heat transfer of carbon nanotubes- suspended nanofluids. Zeitschrift für Naturforschung A, 70(6), 471–475. DOI 10.1515/zna-2015-0125. [Google Scholar] [CrossRef]

15. Hoda, S., Elham, A., Abdelhalim, E. (2017). Medical applications for the flow of carbon-nanotubes suspended nanofluids in the presence of convective condition using laplace transform. Journal of the Association of Arab Universities for Basic and Applied Sciences, 24(1), 206–212. DOI 10.1016/j.jaubas.2016.12.001. [Google Scholar] [CrossRef]

16. Malkeet, S. B. (2018). Study on properties and applications of laplace transformation: A review. Pramana Research Scholar Journal, 8, 4. [Google Scholar]

17. Mahabaleshwar, U. S., Anusha, T., Sakanaka, P. H., Suvanjan Bhattacharyya. (2021). Impact of inclined lorentz force and schmidt number on chemically reactive newtonian fluid flow on a stretchable surface when stefan blowing and thermal radiation are significant. Arabian Journal of Science and Engineering, 46(12), 12427–12443. DOI 10.1007/s13369-021-05976-y. [Google Scholar] [CrossRef]

18. Mahabaleshwar, U. S., Sneha, K. N., Huang, N. H. (2021). An effect of MHD and radiation on CNTS-water based nanofluid due to a stretching sheet in a newtonian fluid. Case Studies in Thermal Engineering, 28, 101462. DOI 10.1016/j.csite.2021.101462. [Google Scholar] [CrossRef]

19. Anusha, T., Huang, N. H., Mahabaleshwar, U. S. (2021). Two dimensional unsteady stagnation point flow of casson hybrid nanofluid over a permeable flat surface and heat transfer analysis with radiation. Journal of the Taiwan Institute of Chemical Engineers, 127, 79–91. DOI 10.1016/j.jtice.2021.08.014. [Google Scholar] [CrossRef]

20. Anusha, T., Mahabaleshwar, U. S., Yahya, S. (2021). An MHD of nanofluid flow over a porous stretching/shrinking plate with mass transpiration and brinkman ratio. Transport in Porous Media, 159, 1–20. DOI 10.1007/s11242-021-01695-y. [Google Scholar] [CrossRef]

21. Sneha, K. N., Mahabaleshwar, U. S., Bennacer, R., Ganaoui, M. E. (2021). Darcy brinkman equations for hybrid dusty nanofluid flow with heat transfer and mass transpiration. Computation, 9, 118. DOI 10.3390/computation9110118. [Google Scholar] [CrossRef]

22. Hamad, M. A. A. (2011). Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. International Communications in Heat and Mass Transfer, 38, 487–492. DOI 10.1016/j.icheatmasstransfer.2010.12.042. [Google Scholar] [CrossRef]

23. Andersson, H. I., Bech, K. H. (1992). Magnetohydrodynamic flow of a power-law fluid over a stretching sheet. International Journal of Non-Linear Mechanics, 27(6), 929–936. DOI 10.1016/0020-7462(92)90045-9. [Google Scholar] [CrossRef]

24. Andersson, H. I., Olav, R., Hansen, O. R., Holmedal, B. (1994). Diffusion of a chemically reactive species from a stretching sheet. International Journal of Heat and Mass Transfer, 37(4), 659–664. DOI 10.1016/0017-9310(94)90137-6. [Google Scholar] [CrossRef]

25. Chambré, P. L., Young, J. D. (1958). On the diffusion of a chemically reactive species in a laminar boundary layer flow. Physics of Fluids, 1, 48. DOI 10.1063/1.1724336. [Google Scholar] [CrossRef]

26. Mahantesh, M., Nandeppanavar, Vajravelu, K., Subhas, M., Abel Siddalingappa, M. N. (2012). Second order slip flow and heat transfer over a stretching sheet with non-linear navier boundary condition. International Journal of Thermal Science, 58, 143–150. DOI 10.1016/j.ijthermalsci.2012.02.019. [Google Scholar] [CrossRef]

27. Lin, W. (2008). A slip model for rarefied gas flows at arbitrary knudsen number. Applied Physics Letters, 93, 253103. DOI 10.1063/1.3052923. [Google Scholar] [CrossRef]

28. Turkyilmazoglu, M. (2012). Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids. Chemical Engineering Science, 84, 182–187. DOI 10.1016/j.ces.2012.08.029. [Google Scholar] [CrossRef]