Unsteady Heat Transfer in Bilayer, and Three-Layer Materials

Nomenclature

1  Introduction

The heat equation, describing heat transfer by conduction, is a partial differential equation, established by J. Fourier in the end of the 19th century after certain experiments. It has a great interest in mathematics and physics. This transfer can be studied either in a single body or through several systems with different thermo-physical properties. In the literature, there are several interesting works, based on certain original references [1]. The research is varied according to the interests of the authors, such as the fractional order heat equation in higher space-Time dimensions [2], its numerical resolution [3], and application for heat spreading of electronic components [4]. For numerical resolution of heat equation in various conditions, Local least–squares element differential method is used to solve heat conduction problems in composite structures [5]. Recently, regarding the problems of realization on the site related to the use of heat sources as well as the optimization of energy consumption, a one-dimensional model is used by Tlili et al. [6] to research the belongings of different functional and geometrical parameters on energy consumption of flat distance direct contact membrane distillation (DCMD) for solar desalination tasks. Furthermore, to reduce the energy consumption in the fresh water production, using the solar energy, the same model is utilized to examine the effect of dissimilar operational and geometrical parameters on energy consumption of flat sheet DCMD for solar desalination purposes [7].

In our paper, the transfer problem by conduction across bilayer and three-layer materials is investigated, adopting the same notations, as used in [8], with some small modifications. Firstly, the separation of variables method (SVM) is used to solve the two heat equations in the two slabs with the associated boundary and initial conditions. The total procedure is well detailed in [9,10], showing how to obtain the so-called Eigen-problem whose dimensionless solutions called roots, are used to give the explicit form of the heat transfer. Then, using orthogonal properties between the two space solutions, we get the integral constants, and thus, the final form of the solutions. Subsequently, according to the material’s thermo-physical properties [11], the transfer heat change is explained. The influence of these properties on the heat transfer between the two layers materials is described. In the three-layer case, a new coupling function Ω governing the transfer, is introduced which is a very rich subject. In the case of two layers, this function is not defined. Finally, the correspondence between the two cases is mentioned. For simplicity, in all our calculus, dimensionless parameters are used.

2  Bilayer Material

We consider a material composed of two different regions S1 , and S2 , as shown in Fig. 1, with a perfect thermal contact [12,13]. The thermo-physical properties of both layers are the Conductivity ki , diffusivity αi , specific heat Cpi , density ρi , and thickness ai . The convection coefficients, in both sides, are hi , where i refers the region. Both layers are maintained, respectively, at the two initial temperatures T01 , and T02 . For simplicity, this change of variable is used

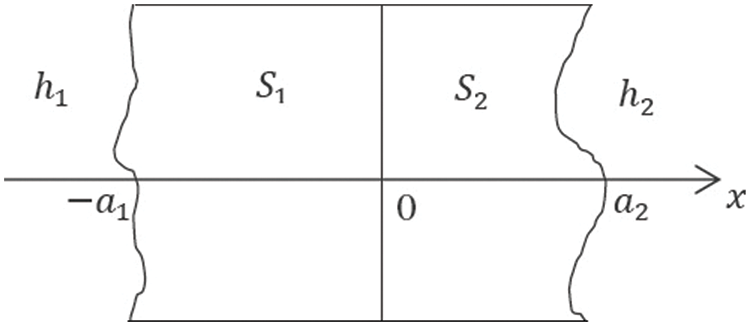
Figure 1: Representation of bilayer material

θi(x,t)=Tamb−Ti(x,t) (1)

where, Tamb is the ambient temperature, assumed to be constant and uniform, and Ti is the space-time depending temperature of i layer. We will omit the dependence (x,t) below and it will be automatic.

The one-dimensional heat conduction without thermal source for the two slabs, is given by [1]

∂2θi∂x2=1αi∂θi∂t (2)

with the set of boundary conditions (BCs) [8] at the edges

−k1∂θ1∂x|x=−a1+h1θ1|x=−a1=0 (3)

k2∂θ2∂x|x=a2+h2θ2|x=a2=0, (4)

and on the contact surface, we have

θ2|x=0=θ1|x=0 (5)

k1∂θ1∂x|x=0=k2∂θ2∂x|x=0 (6)

The initial conditions (ICs), for each layer, are supposed constants

θ0i=Tamb−T0i (7)

We have now, a full solvable system constructed by Eqs. (2)–(7). The analytic solutions are

θi(x,t)=Xi(x).Gi(t) (8)

For each layer, the solutions are obtained easily by SVM, where

Xi(x)=Aicos⁡(λix)+Bisin⁡(λix) (9)

Gi(t)=exp⁡(−αiλi2t) (10)

αi is kept for the time part. We have chosen negative constants −λi2 by the convergence stress in Gi(t) . Ai and Bi are integration constants. We have t≥0 , and −a1≤x≤0 for the first layer ( i=1 ), and 0≤x≤a2 for the second one ( i=2 ).

Dimensionless calculus has been used for several reasons and purposes. We are talking about: The simplicity of the calculations, the reduction of the parameters, the permanent verification of the homogeneity of the equations, the writing of the formulas will be more compact and more significant as well as the ease of reading the curves because the intervals of variations of the solution temperatures are reduced to acute and positive intervals. Then, the dimensionless group is defined by [10].

ω=α1α2 (11)

κ=k2/k1 (12)

γ=a2/a1 (13)

and the Biot numbers

Bioti=hia1k1 (14)

Then, after some manipulations (see [12] for full detail), we can reduce our problem to the determination of the constants

βn=a1λ1,n,n>0, (15)

called Eigen values, representing the non-vanishing dimensionless roots of the function

E(β)=P1(β)+P2(β)κω (16)

With

Pi(β)=(κω)i−1β + Biotitg((ωγ)i−1β)Bioti−(κω)i−1βtg((ωγ)i−1β) (17)

We reconstruct our solutions under the dimensionless form, as

X1,n(ξ)=P1(βn)cos⁡(βnξ)+sin⁡(βnξ)

X2,n(ξ)=P1(βn)cos⁡(ωβnξ)+1κωsin⁡(ωβnξ)

G1,n(τ)=G2,n(τ)=exp⁡(−βn2τ) (18)

where, we introduce the space-time dimensionless coordinates: ξ=xa1 , and τ=α1a12t , with τ≥0 , and −1≤ξ≤0 for the first layer, and 0≤ξ≤γ for the second one. The final dimensionless solution is then a linear combination with respect to n of the space-time solutions of Eq. (18)

Θi(ξ,τ)=∑n=1∞CnXi,n(ξ)Gi,n(τ) (19)

The determination of Cn can be done by using initial conditions Eq. (7) and the orthogonal property of Xi,n [8]. The first 20 Eigen-values of the function E(β) for ω=0.5,κ=1.5,γ=1.5,Biot1=1.5 , and Biot2=2.5 are calculated by implementation Newton method in Maple software. They are collected in Table 1.

An order higher than 20 roots can be reached, having a small influence on the result (see Section 4.1). We note that initially, there is an unsteady equilibrium temperature between the two slabs. It is analytically given by [12]

Teq1,2=k1ρ1Cp1T01+k2ρ2Cp2T02k1ρ1Cp1+k2ρ2Cp2 (20)

where, Cpi and ρi ( i=1,2 ) are, respectively, the specific heat and density material. Since the thermal diffusivity is related on these properties and ki by the relation αi=ki/ρiCpi , we obtain by simple calculus the dimensionless unsteady equilibrium temperature as

Feq1,2=Tamb−TeqTamb−T01=κωF2+1κω+1 (21)

where, the dimensionless initial temperatures Fi=θ0i/θ01 is defined. After sufficient time, all temperatures go to Tamb (the thermal equilibrium), and Θi goes to 0. We can regroup the temperatures in the two layers in a single expression, describing the whole material as

Θ(ξ,τ)={Θ1(ξ,τ)if−1≤ξ≤0Θ2(ξ,τ)if0≤ξ≤γ (22)

The error is defined as the relative difference, at zero time, between calculated temperature, obtained by Eq. (22), and our initial conditions ( F1=1 for the first layer and F2 for the second one) are

ϵ(ξ)={1−Θ1(ξ,0) if −1≤ξ≤01F2(F2−Θ2(ξ,0)) if 0≤ξ≤γ (23)

As can be seen, ϵ becomes negligible as soon as we exceed the 20th root, the reason why, we stopped in the sum (Eq. (19)) at order 20.

3  Three-Layer Material

The same reasoning can be used, for the case of three-layer material. We consider a material composed of three different regions S1 , S2 and S3 , as shown in Fig. 2, with perfect contact between any two adjacent regions. The three layers are, respectively, maintained at the initial constant temperatures T01 , T02 and T03 . So we generalize the first case by adding the index i=3 of the third region. The dimensionless group is extended to {ωi,κi,γi,Biot1,Biot3,Fi} for i=2,3 . Therefore, we have

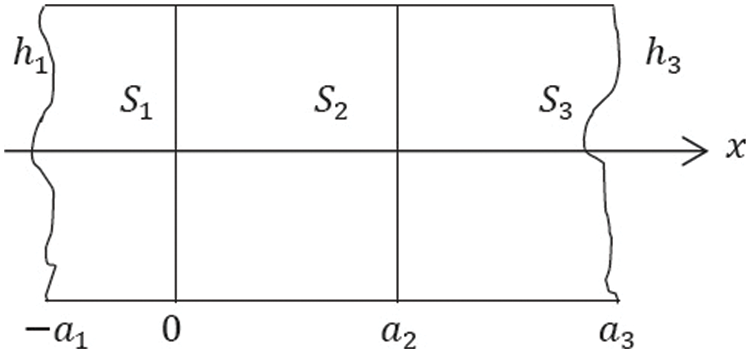
Figure 2: Representation of three-layer material

ωi=α1αi, (24)

κi=kik1, (25)

γi=aia1 (26)

with τ≥0 for all layers, −1≤ξ≤0 , 0≤ξ≤γ1 , and γ1≤ξ≤γ2 for the first, second, and third layers, respectively. In that notation, our problem becomes greatly simplified as an Eigen problem

E(β)=cos⁡(ω2γ2β)−κ2ω2P1(β)sin⁡(ω2γ2β)sin⁡(ω2γ2β)+κ2ω2P1(β)cos⁡(ω2γ2β)−κ3ω3cos⁡(ω3γ2β)+P3(β)sin⁡(ω3γ2β)κ2ω2sin⁡(ω3γ2β)−P3(β)cos⁡(ω3γ2β)=0 (27)

where, P3(β) is expressed by

P3(β)=κ3ω3β+Biot3tg(γ3ω3β)Biot3−κ3ω3βtg(γ3ω3β) (28)

Thus, the temporal and space solutions take, according to the Eigen values set {βn} , the forms

G1,n(τ)=G2,n(τ)=G3,n(τ)=exp⁡(−βn2τ) ,

X1,n(ξ)=P1(βn)cos⁡(βnξ)+sin⁡(βnξ) ,

X2,n(ξ)=P1(βn)cos⁡(ω2βnξ)+1κ2ω2sin⁡(ω2βnξ) , and

X3,n(ξ)=Ω(βn){−P3(βn)cos⁡(ω3βnξ)+sin⁡(ω3βnξ)} (29)

Ω(βn) is a coupling function, defined as

Ω(βn)=κ2ω2P1(βn)cos⁡(ω2γ2βn)+sin⁡(ω2γ2βn)κ2ω2(sin⁡(ω3γ2βn)−P3(βn)cos⁡(ω3γ2βn)) (30)

The final dimensionless solution is expanded as a linear combination of products of the temporal and space parts

Θi(ξ,τ)=∑n=1∞CnXi,n(ξ)Gi,n(τ) (31)

We can regroup, similarly as Eq. (22), the three temperatures in a single expression, describing the whole material as

Θ(ξ,τ)={Θ1(ξ,τ)if−1≤ξ≤0Θ2(ξ,τ)if0≤ξ≤γ2Θ3(ξ,τ)ifγ2≤ξ≤γ3 (32)

Note that the unsteady equilibrium temperature, between any two adjacent slabs i, i+1 ( i=1,2 ), is given by

Teqi,i+1=kiρiCpiT0i+ki+1ρi+1Cpi+1T0,i+1kiρiCpi+ki+1ρi+1Cpi+1 (33)

The final dimensionless solution is expanded as a linear combination of products of the temporal and space parts. Therefore, the dimensionless unsteady equilibrium temperature is

Feqi,i+1=Tamb−Teqi,i+1Tamb−T01=κωFi+1+1κω+1 (34)

The error is defined by

ϵ(ξ)={1−Θ1(ξ,0)   if−1≤ξ≤01F2(F2−Θ2(ξ,0))   if0≤ξ≤γ21F3(F3−Θ3(ξ,0))   ifγ2≤ξ≤γ3 (35)

4  Results and Discussions

4.1 Bilayer Material

By taking the instance, presented in Table 1, and for Tamb=300K,T01=400K,T02=500K , we find F2=2 and the unsteady equilibrium (Eq. (21)) of Feq1,2≈1.43 is obtained. The values of the dimensionless ratios are chosen so that the calculation by the method of does not ascert in order that one can choose close or distant between them. Fig. 3 is a 3D representation of temperature evolution. Fig. 4 shows the temperature evolution and its error with respect to dimensionless position. For different times, as shown in Fig. 4a, the unsteady equilibrium between the two slabs around the point (0,1.4) is observed, which is in excellent agreement with Feq1,2 , mentioned above. The thermal equilibrium is the cooling of both layers until reaching ambient temperature, approximately achieved after a dimensionless time τ=2 . If a1 is in the order of millimeters, the real time t will be in that of τ since in general α is in the order of 10−6 order.

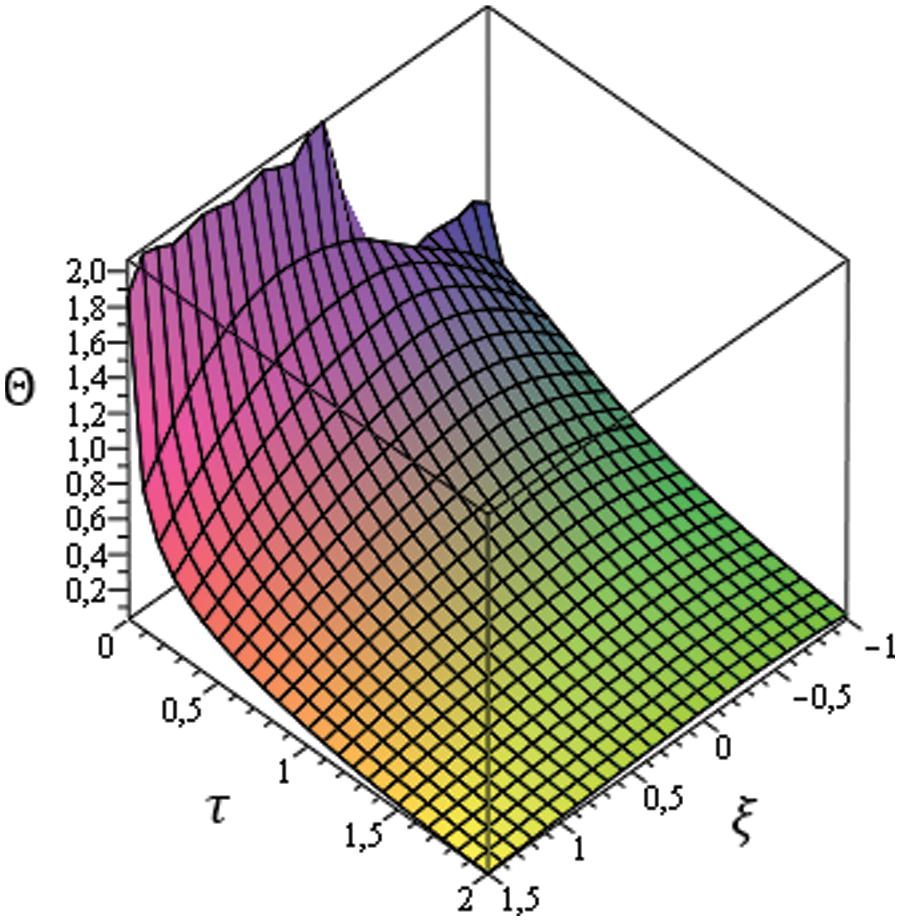
Figure 3: 3D representation of temperature evolution in bilayer material

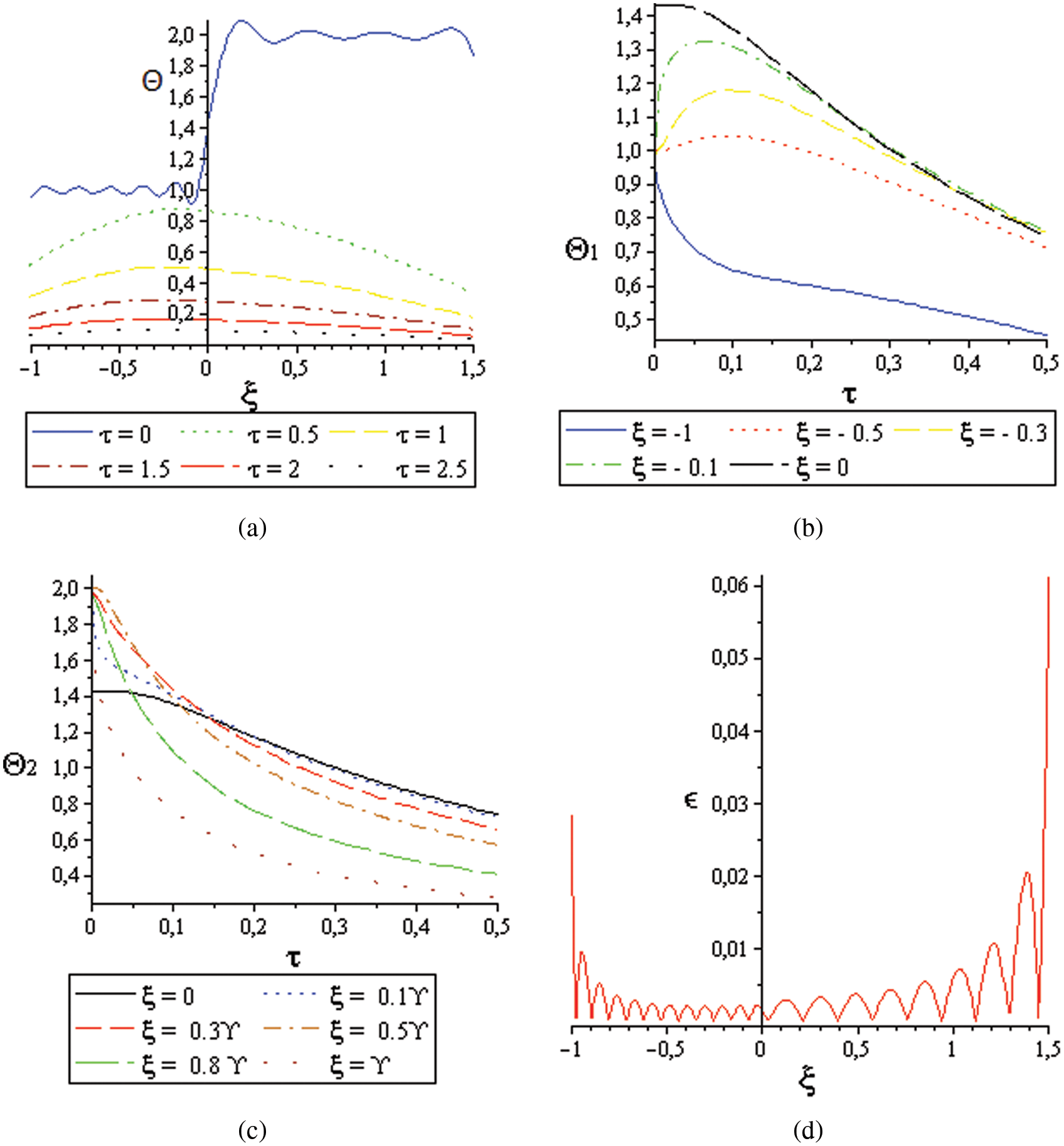
Figure 4: Temperature curves; (a): With respect to the position in different times, (b): For S1, in different positions in the first moments, (c): For S2, in different positions in the first moments, (d): The error with respect to the position for equal ICs

Figs. 4b and 4c represent the temperature in term of time at selected points, in both layers. From Fig. 4b, the unsteady equilibrium can clearly be seen.

To reach that, in the first layer, the temperature increases, proportionally to the distance from the contact surface, with small values, called temperature jumps, while the taken time is inversely proportional to this distance. Hence, the final thermal equilibrium is achieved. For the second layer, the temperature converges to the equilibrium one, with a much slower pace, due to its thickness that is greater than that of the first layer.

We also emphasize that the unsteady equilibrium is clear, for ξ=0 , as illustrated in the two figures (Figs. 4b and 4c), whereas it does not appear, for the point ξ=−1 , because it is far away from the contact surface. In addition, Fig. 4d shows the error on the temperature, for T01=T02=400K . Its value in the open interval [−1,1.5] is less than 0.5%, and this explains why 20 roots are sufficient in the sum Eq. (19).

The heat transfer, in bilayer material, is well described according to thermo-physical properties (Eqs. (11)–(14)) of the two layers (cf. Section 2). For equal ICs, (from full Maple procedure) its behavior is presented according to the number of roots in the solution, and parameter, keeping the others constants (Fig. 5). This parametric study consists in fixing a thermo-physical property such as the conductivity, and diffusivity, of the first layer with changing that of the other [12,13].

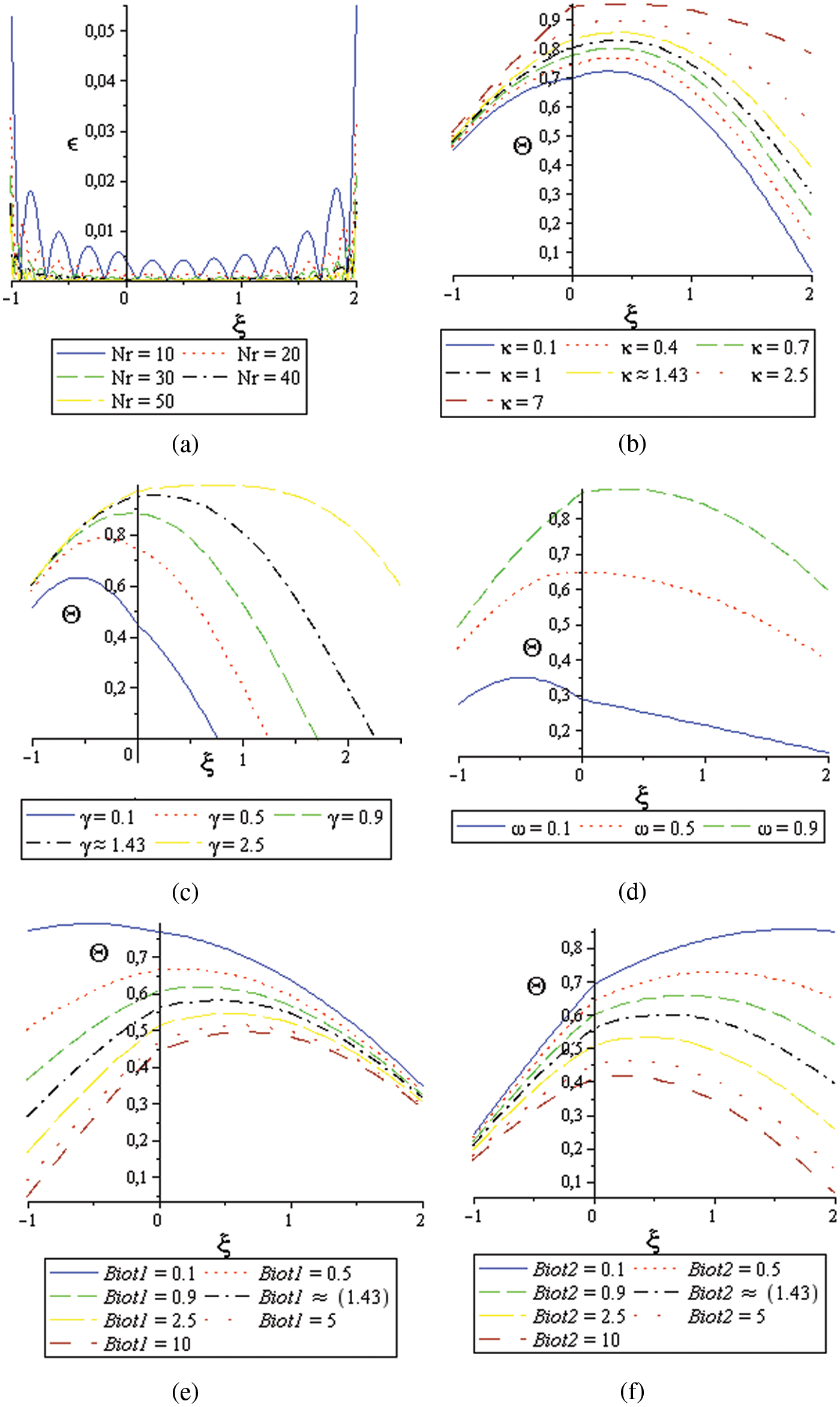
Figure 5: Parametric study; (a): Error according to the number of the roots Nr , (b): Θ(ξ,0.67) with respect to dimensionless conductivity, (c): Θ(ξ,0.29) with respect to dimensionless thickness, (d): Θ(ξ,0.70) with respect to dimensionless diffusivity. (e): Θ(ξ,1.67) with respect to Biot1 , (f): Θ(ξ,1.67) with respect to Biot2

The error with respect to the number of roots Nr is illustrated in Fig. 5a, with determined thermo-physical property, taken by de Monte in [8]: κ=2,γ=2,ω=1,Biot1=1 , and Biot2=2 . According to these curves, we conclude, as we have previously reported, that 20 roots is sufficient to have a good description of the phenomenon. In Fig. 5b, we describe how the heat flux reacts as a function of κ . We notice that if we increase the κ values for chosen time ( τ=0.67 ), cooling process of both layers becomes slow, specially in the second layer.

Similarly, one can observe the same reaction of heat transfer vs. the thickness report γ by means of Fig. 5c, since the thin layer cools faster than the thick one. In Fig. 5d, only three curves, for diffusely values of 0.1, 0.5, and 0.9 at τ=0.70 are represented, due to the heat transfer divergence for the other values in Newton method. We remark that the cooling speed of composite material is inversely proportional to the diffusivity report. The last two graphs Fig. 5e and Fig. 5f demonstrate the effect of Biot numbers. Since they depend on convection coefficients, an increasing one of the two will leads to a faster cooling, especially in the same layer.

4.2 Three-Layer Material

In this case, we consider the example where κ2=2,γ2=2,ω2=1,Biot1=1,κ3=1.5,γ3=3,ω3=1 and Biot3=2 . For ICs: Tamb=300K,T01=400K,T02=450K , and T03=500K , we obtain F2=1.5 and F3=2 . We can represent in Fig. 6 the temperature evolution in 3D. Fig. 7 shows the temperature’s behavior over the three slabs.

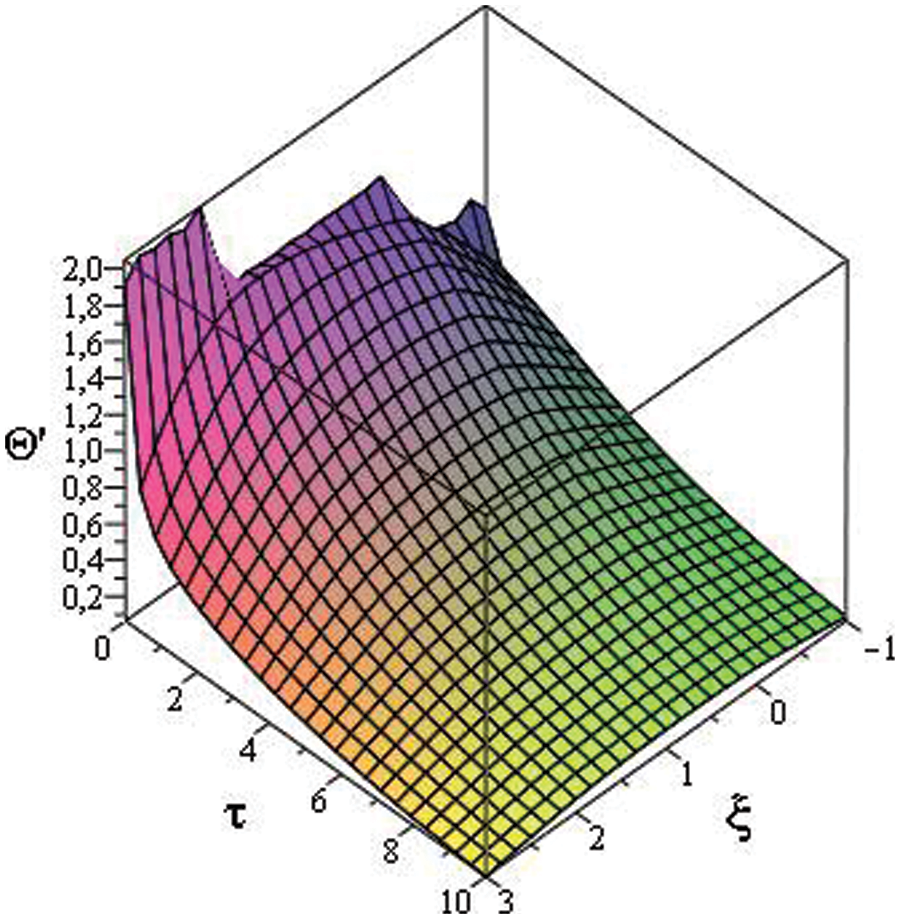
Figure 6: 3D representation of temperature evolution in three-layer material

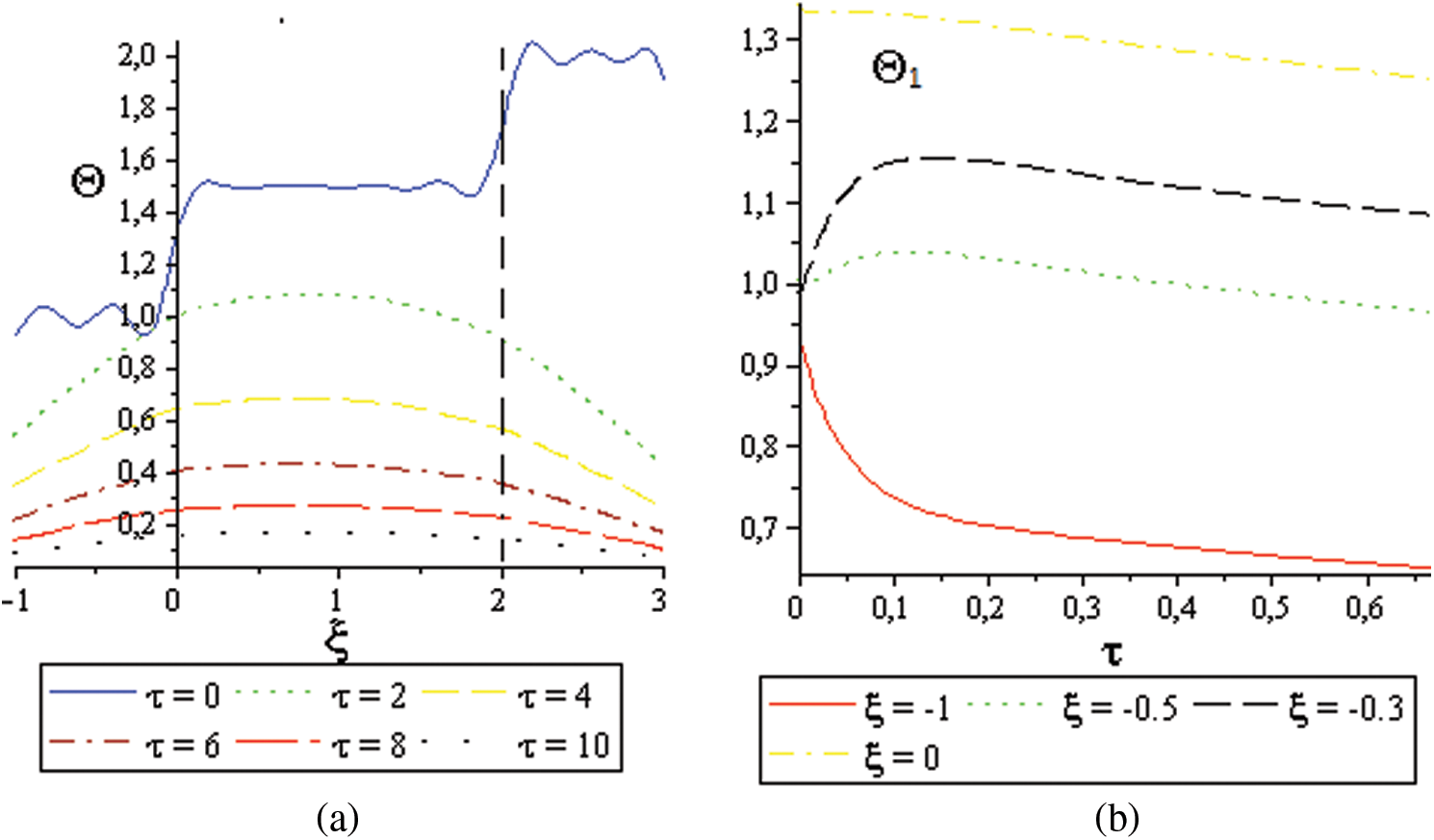
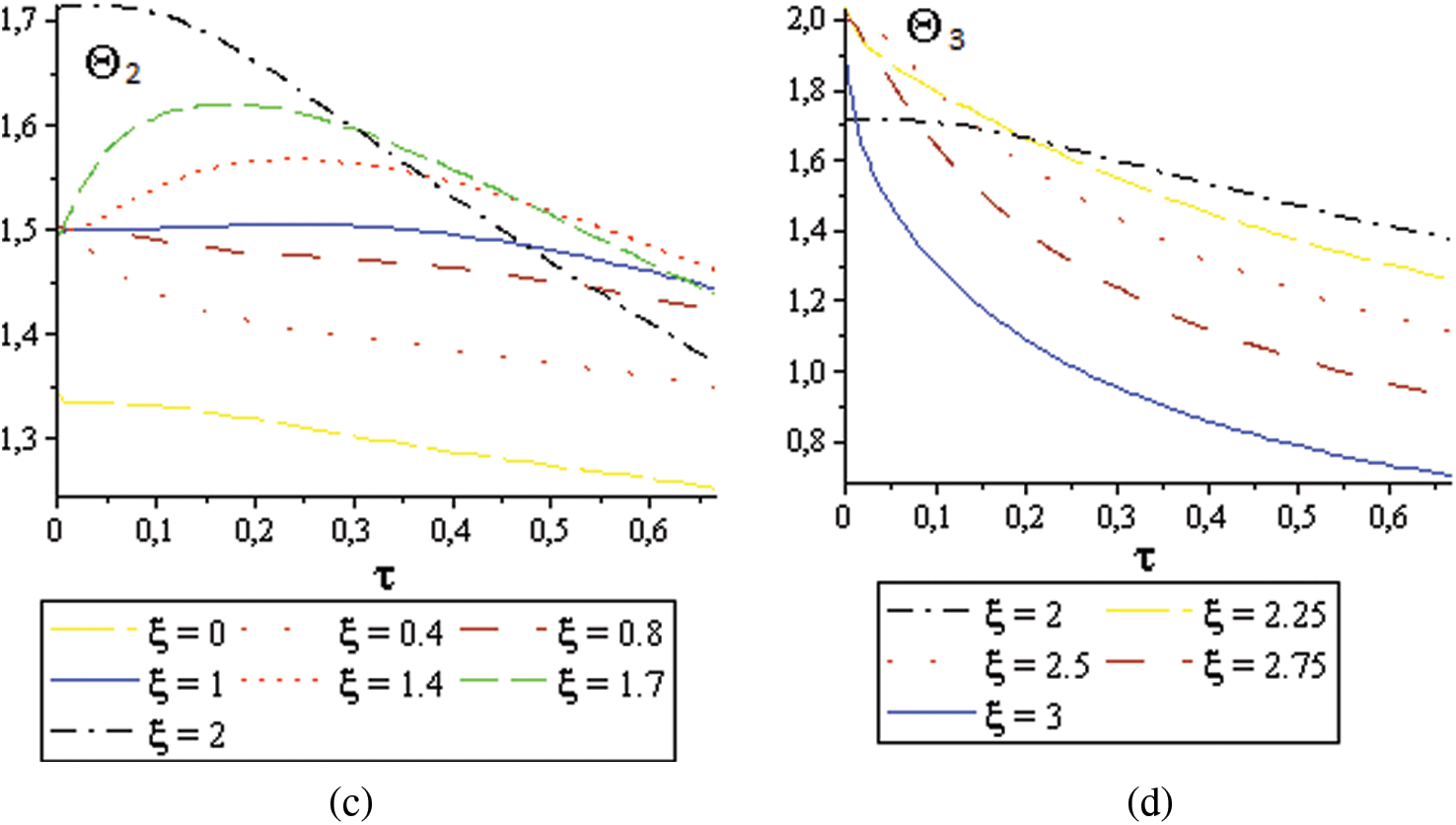
Figure 7: Temperature’s behavior in three-layer material: (a) Heat transient in different times, (b) Heat behavior in the first layer at the first moments in different points, (c) Heat behavior in the second layer in different points at the first moments, (d) Heat behavior in the third layer in different points at the first moments

Fig. 7a shows, in the first moments, the heat transit at ξ positions (Eq. (32)) in the material, where we can observe the thermal equilibrium, approximately started from τ=10 . However, the unsteady equilibrium is clear, as reflected in the curve τ=0 . At the first contact surface (between the two adjacent layers S1 and S2), it takes place at Feq12≈1.3 while at the second one (between S2 and S3), it takes Feq23≈1.7 . This is in excellent agreement with Eq. (34) giving the two values of 1.33 and 1.71 , for the first and second contact surfaces, respectively. In Figs. 7b–7d, the temperature in term of the time at selected points, in the three layers, is presented. As shown in Figs. 7b and 7c, the unsteady equilibrium in the form of temperature jumps are observed which becomes clearer when the point is close to the contact surface ( ξ=−0.3 and ξ=1.7 ). After some dimensionless seconds, thermal equilibrium (steady equilibrium) occurs. Since the third layer is warmer initially, temperature jumps are not observed in Fig. 7d.

The continuity of Θ between layers (at contact surfaces) can also be observed for ξ=0 and ξ=2 . The cooling speed of points, near the outer surface, can also be observed compared to the internal points. Finally, note that we can pass from three-layer case to bilayer case by setting γ2=γ3 .To clarify the accuracy of our results, the error behavior (defined by Eq. (35)), as illustrated in Fig. 8, for equal ICs (400 K), is smaller than 0.5% .

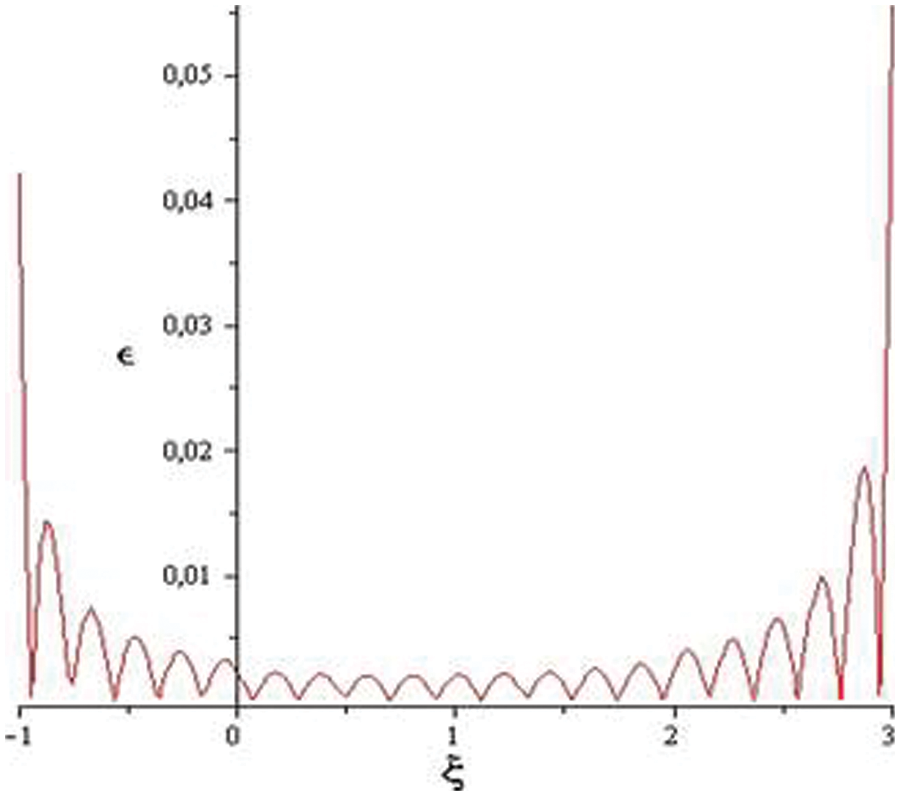
Figure 8: Error with respect to the position for a three-layer material

The divergence of the graphs in the boundaries ( ξ=−1 , and ξ=3 ) comes from the fact that the solutions of the heat equation are valid only in the open interval of the variation of ξ .

5  Conclusion

This analytical study shows that there is a similarity in the evolution of heat transfer between two layers as well as between three layers. In both cases, we note that an unsteady thermal equilibrium occurs moments before the final thermal equilibrium. Mathematically, we notice that we get the same form for the solutions, except for the coupling function Ω , which appears in the case of three layers. We can also ascertain the equivalence of: the value of the unsteady equilibrium between two adjacent layers with the value observed over the curves. We can then predict the general behavior of heat transfer through more than three layers, and that there will be an unsteady equilibrium between every two adjacent layers, and that calculating the first 20 eigenvalues is sufficient to describe the evolution of heat diffusion in the studied medium. In the case of a two layers system, the cooling was studied in term of the dimensionless thermo-physical properties of the material. The results show that it develops proportionally with each of the conductivities, diffusivities, and thicknesses, and inversely with Biot numbers. The study of three-layer material gave us a natural confirmation of the first case in term of existing unsteady equilibrium.

Concerning the accuracy of the results, this is based on two points having almost significant equivalence: The first is the exact analytical calculation by SVM and using the Maple Program, which brings us back to the similar results detailed in the literature. The second point is the concordance with the experimental prediction, which explains the existence of two kinds of equilibrium: Unsteady, and permanent similar to the damped movement in the mechanical vibration of solids or fluids (Transitional and permanent diverge).

Acknowledgement: T. Sahabi would like to thank Prof. F. de Monte for his assistance in this research in terms of providing references and answering questions, and Prof. Mohamed El Ganaoui for his encouragement and providing references.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Carslaw, H. S., Jaeger, J. C. (1959). Conduction of heat in solids. England: Oxford University Press. [Google Scholar]

 2.  Singh, D., Tiwari, B. N., Yadav, N. (2017). Fractional order heat equation in higher space-time dimensions. https://arxiv.org/abs/1704.04101#. [Google Scholar]

 3.  Filipov, S., Faragó, I. (2018). Implicit Euler time discretization and FDM with Newton method in non-linear heat transfer modeling. International Scientific Journal, Mathematical Modeling, 2, 94–98. DOI 10.48550/arXiv.1811.06337. [Google Scholar] [CrossRef]

 4.  Samia, S., Dmitri, K., Alexander, A. B. (2009). Graphene heat spreaders for thermal management of nano-electronic circuits. DOI 10.48550/arXiv.0910.1883. [Google Scholar] [CrossRef]

 5.  Gao, X. W., Zheng, Y. T., Fantuzzi, N. (2020). Local least-squares element differential method for solving heat conduction problems in composite structures. Numerical Heat Transfer, Part B: Fundamentals, 77(6), 441–460. DOI 10.1080/10407790.2020.1746584. [Google Scholar] [CrossRef]

 6.  Tlili, I., Sajadi, S. M., Baleanu, D., Ghaemi, F. (2022). Flat sheet direct contact membrane distillation study to decrease the energy demand for solar desalination purposes. Sustainable Energy Technologies and Assessments, 52, 102100. DOI 10.1016/j.seta.2022.102100. [Google Scholar] [CrossRef]

 7.  Zhang, J., Sajadi, S. M., Chen, Y., Tlili, I., Fagiry, M. A. (2022). Effects of Al2O3 and TiO2 nanoparticles in order to reduce the energy demand in the conventional buildings by integrating the solar collectors and phase change materials. Sustainable Energy Technologies and Assessments, 52, 102114. DOI 10.1016/j.seta.2022.102114. [Google Scholar] [CrossRef]

 8.  de Monte, F. (2000). Transient heat conduction in one-dimensional composite slab. A ‘natural’ analytic approach. International Journal of Heat and Mass Transfer, 43(19), 3607–3619. DOI 10.1016/S0017-9310(00)00008-9. [Google Scholar] [CrossRef]

 9.  de Monte, F. (2002). An analytic approach to the unsteady heat conduction processes in one-dimensional composite media. International Journal of Heat and Mass Transfer, 45(6), 1333–1343. DOI 10.1016/S0017-9310(01)00226-5. [Google Scholar] [CrossRef]

10. de Monte, F. (2003). Unsteady heat conduction in two-dimensional two slab-shaped regions. Exact closed-form solution and results. International Journal of Heat and Mass Transfer, 46(8), 1455–1469. DOI 10.1016/S0017-9310(02)00417-9. [Google Scholar] [CrossRef]

11. Grimvall, G. (1999). Thermo-physical properties of materials. North Holland: Elsevier. [Google Scholar]

12. Belghazi, H. (2008). Modélisation analytique du transfert instationnaire de la chaleur dans un matériau bicouche en contact imparfait et soumis à une source de chaleur en mouvement (Ph.D. Thesis). France: University of Limoges. [Google Scholar]

13. Belghazi, H., El Ganaoui, M., Labbe, J. C. (2010). Analytical solution of unsteady heat conduction in a two-layered material in imperfect contact subjected to a moving heat source. International Journal of Thermal Sciences, 49(2), 311–318. DOI 10.1016/j.ijthermalsci.2009.06.006. [Google Scholar] [CrossRef]