Libration-Generated Average Convection in a Rotating Flat Layer with Horizontal Axis

Nomenclature

1  Introduction

The study of heat and mass transfer in rotating hydrodynamic systems [1] is of great interest and importance from both fundamental and applied perspectives. A significant amount of research has been dedicated to the study of convective flows in rotating containers [2]. A considerable number of laboratory studies concentrated on the analysis of Rayleigh-Benard convection [3,4]. When a fluid is heated from below and cooled from above within a rotating container, the resulting heat transfer is attributed to the effect of gravity [5]. In numerous hydrodynamic systems, the influence of gravity is augmented by the background rotation of the container, which can result in modifications in the flow pattern [6–9]. These studies focused on the impact of time-periodic rotation, which is commonly referred to as libration. The study of the flows resulting from libration is of critical importance for the investigation and modeling of astrophysical, geophysical, and oceanographic processes, as well as for the development of technical, medical, and industrial applications.

The effect of periodic change of rotation rate is most clearly represented in astrophysical problems, where the gravitational interaction of a planet with its satellites leads to the generation of large-scale vortices on its surface or inside it [10–12]. The article [13] examines the impact of libration on flow structures in rotating convective systems and presents a summary of the results of laboratory studies on the dynamics of the planetary core. In the isothermal case [14], it has been found that libration produces time-averaged effects, such as zonal flow and retrograde differential rotation of the core. These effects are combined with those caused by gravity.

In the field of geophysics, the adaptation of the liquid column to changes in its rotation is a crucial process in oceanography, particularly in the study of currents in the upper layers of the oceans [15,16] and their impact on large-scale processes within the fluid volume. The underwater obstacles create special conditions for the existence of wave attractors, a phenomenon in which waves of certain frequencies and wavelengths converge or intersect at certain locations in the ocean. These wave attractors facilitate an increase in the fluid flow. As demonstrated in [17], the phenomenon of a wave attractor can be reproduced by the libration of a cylindrical cavity with symmetrically inclined end walls. It has been demonstrated in numerous experimental studies that oscillations of a rotating fluid may result in the generation of waves [18,19]. These waves are often referred to as inertial waves [20]. The development of these waves in a rotating fluid requires a specific dispersion relation to be satisfied [20]. The effect of the Coriolis force can substantively enhance the mass transfer in fluid due to the generation of inertial waves.

Fluid dynamics under libration can be modeled numerically using either the finite element method or the spectral element method (SEM) [21]. SEM is of interest due to its high accuracy in modeling flows in the case of periodically varying flow parameters. A numerical study of the dynamics of nanofluids is of significant importance for the development of new technologies and materials [22].

As previously stated, numerous studies have analyzed the mass transfer under the combined effect of libration and gravity [23,24]. When the effect of gravity is weak or negligible, the excitation of the time-averaged flow [25] is possible due to vibrations [26]. The distinction between the vibrational convection and the gravitational convection is that the fluid motion is caused by an external oscillating force rather than the buoyancy force [27]. For instance, the gravitational influence of a planet’s massive satellite gives rise to tidal fluctuations in its atmosphere, oceans, and liquid core. Therefore, the oscillating force can generate thermal vibrational convection [26]. A theoretical description of the thermal vibrational convection in rotating cavities can be found in [28]. Experimental studies in this field are limited to the case in which the force field remains constant in a rotating system (rotation frequency is equal to the frequency of the force action N=1 ) [29,30]. Nevertheless, the frequency of the force oscillations can be modified by varying the rotation rate. The effect of libration on the threshold of the onset of the thermal vibrational convection was studied in [31]. It was demonstrated that modulation of the rotation rate results in the development of a system of toroidal vortices with a spatial period comparable to the thickness of the fluid layer. Further investigation is required to identify the effect of libration on thermal vibrational convection induced by an oscillating force at a given rotation rate of the cavity. The results of experiments are crucial for understanding the influence of libration on convective flows and mass transfer in liquid under conditions of reduced gravity action.

The phenomenon of libration may prove to be a valuable tool for crystal growth in conditions of reduced gravity [32]. Libration can facilitate the even distribution of solutes and prevent the formation of defects in the crystal. The reduced gravity can decelerate or even eliminate thermal convection and sedimentation, thus resulting in a cleaner and more homogeneous crystal. The objective of this study is to identify effective means of optimizing such processes by examining the various flow regimes.

The previously used thermochromic visualization technique [33] permitted the identification of vortical flow yet did not permit the revelation of the flow pattern. In the present study, the fluid flow is investigated for the first time using the PIV technique. The proposed technique allows the study of the instantaneous velocity field in a diametral or azimuthal cross-section. The analysis of the obtained velocity field permits the determination of the oscillation velocity of the fluid and the observation of its change over the libration cycle. The ability to measure the threshold for the onset of average convection enables the determination of the stability curve in the plane of dimensionless oscillation frequency and pulsation Reynolds number in a wide range of experimental parameters.

In particular, this study examines the time-averaged flows in a flat layer with boundaries of different temperatures under non-uniform rotation about a horizontal axis (Fig. 1). The present study investigates flow patterns employing the PIV technique across a broad range of dimensionless oscillation frequencies, with the objective of identifying regions where inertial modes may occur.

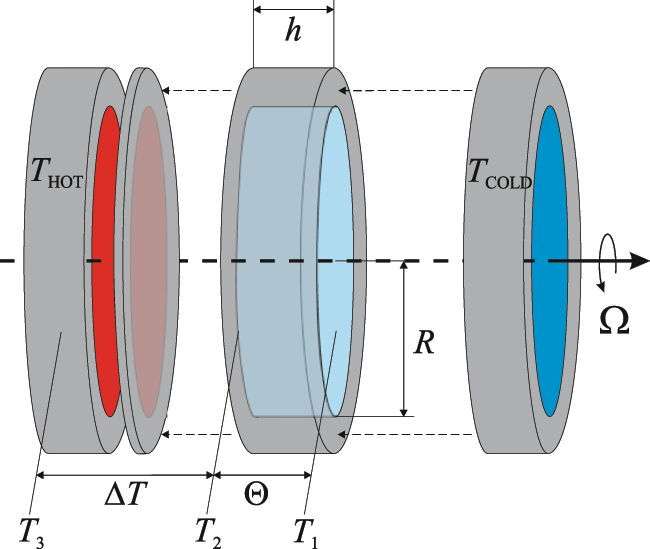
Figure 1: Scheme of the fluid layer

2  Experimental Technique

The study examines the time-averaged flow in a non-uniformly rotating (librating) flat layer of distilled water. The cylindrical layer with a radius of R=7.0 cm and a thickness of h=1.0; 2.0 cm and is placed between two heat exchangers (the cylindrical wall of the layer is thermally insulated). The cavity rotates about a horizontal axis with Ω velocity, T1, T2 of the boundaries are homogeneous due to the circulation of water at a specific temperature Thot, Tcold through the heat exchangers. Θ and the heat flux ΔT is measured in the course of the experiment. The flow regimes are recorded by digital camera through the transparent heat exchanger.

Fig. 2 shows the scheme of the experimental setup. The uneven rotation of the cavity is provided by a stepper motor FL86STH156 1, controlled by an SMD-78 driver 2 and a digital generator ZET-210 3. The rotation velocity varies within the range frot=0.01−3.00 rps. The rotation velocity follows the law Ω=Ωrot[1+εsin(Ωlibt)] , where Ωrot is the average angular velocity of cavity rotation, Ωlib is the cyclic frequency of angular oscillations, and ε is the amplitude of angular velocity modulation. The couplings 4 facilitate the transmission of rotation from the motor to all elements of the experimental setup.

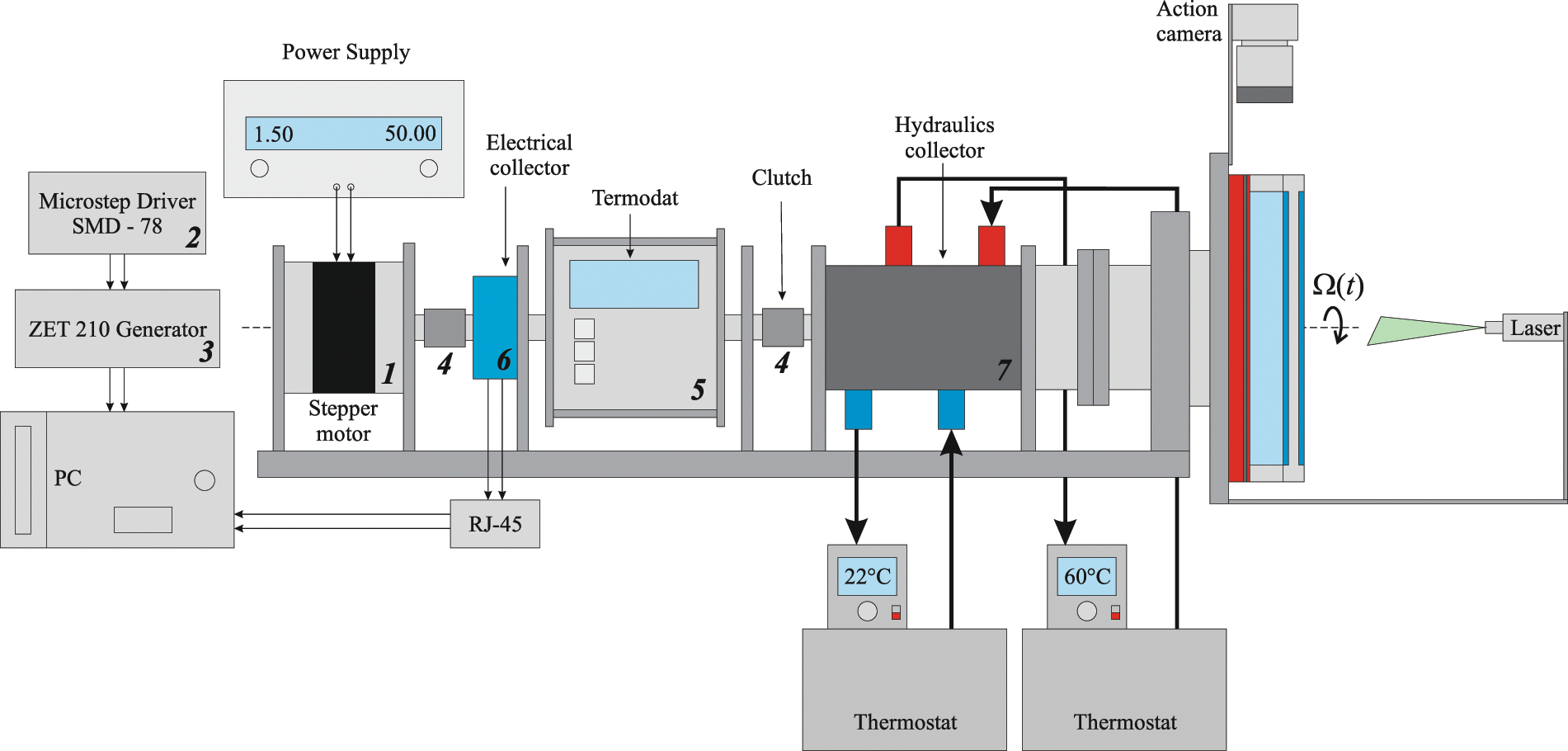
Figure 2: Schematic of experimental setup

The temperature of the layer boundaries is monitored in real time via the use of temperature sensors positioned within the cavity. The temperature data are transmitted to the measuring module Thermodat-13IC 5. Electrical collector 6 with sliding contacts is used to transmit the temperature data to the computer. Module 5 is connected to the stepper motor 1 and electric manifold 6 on one side, and the hydraulic manifold 7 on the other. The hydraulic manifold 7 provides the circulation of hot water and cold water between rotating heat exchangers and thermostats. The hydraulic manifold has two pairs of openings for supplying and draining the fluid to the heat exchangers. The high flow rate (5 liters per min) ensures a homogeneous temperature distribution across the entire surface of the heat exchanger. The temperature of the circulating fluid can be set between 18°C and 70°C. The thermostat exhibits an accuracy of temperature maintenance of 0.1°C.

The PIV method is used to investigate the convective fluid flow. The liquid is seeded neutrally buoyant high-reflective 50 μm diameter polystyrene particles. The camera is positioned opposite the polished layer wall and rotated together with the cavity. The frame rate is set to 50 fps, allowing for the investigation of the instantaneous velocity field within the laser light sheet (Fig. 3).

Figure 3: Convective flow regimes visualized by aluminum powder particles ( h=1.0 cm)

3  Experimental Results

3.1 Uniform Rotation of a Flat Liquid Layer around a Horizontal Axis

The rotation of the cavity affects fluid dynamics through the action of a rotating gravitational force [28–30]. The oscillations of a non-isothermal fluid relative to the cavity, induced by an oscillating force field, result in the generation of a flow of vibrating nature (Fig. 3) and the emergence of time-averaged effects.

In a rapidly rotating cavity, we observe toroidal vortices near the cylindrical wall of the cavity (Figs. 3a and 3b). These vortices are generated by inertial waves [19]. The intensity of vortical flow increases as the cavity rotation rate decreases. When the rotation rate reaches the critical value of frot=0.40 rps, the thermal vibrational convection manifests in the form of convective cells with hexagonal order (Fig. 3c). In the supercritical region, the convective cells rearrange into a large-scale vortical pattern (Fig. 3d).

The results of the study of the time-averaged fluid flow in the diametral section by the PIV technique are presented in Fig. 4. For the sake of simplicity, the images have been rotated 90 degrees counterclockwise. Then, the lower boundary of the image corresponds to the side adjacent to the hot heat exchanger, while the upper boundary is next to the cold heat exchanger. The average velocity field is obtained by averaging the instantaneous velocity fields over one rotation period of the cavity. Here, blue indicates negative vorticity (the clockwise rotation of the fluid), and red indicates positive vorticity (the counterclockwise rotation of the fluid).

Figure 4: Averaged velocity field in the layer with thickness h=1.0 cm at Θ=8.4 °C

At high rotation rates, the low-intensity flow is localized to the flat boundaries of the layer (Fig. 4a), and heat transfer is driven by molecular diffusion (Fig. 5a, curve 1). As the rotational velocity decreases, the vorticity increases, resulting in a system of concentric vortices (Figs. 3b and 4b). The vortices that emerge prior to the onset of thermal vibrational convection influence the dimensions of the vibration cells. At the threshold of thermal vibrational convection, regular pairs of opposing vortices are observed (see Fig. 4c). The interaction between vertically arranged vortices can be described in a limited manner. It is assumed that a pair of large vertical vortices (Fig. 4d) intertwines with a pair of smaller vortices, thereby forming a paired spiral. Two adjacent vertical pairs of vortices create a convective cell of vibrational nature. At low rotation rates, large convective patterns emerge, significantly enhancing heat transfer (Fig. 4e). The dimensions of these patterns are considerably larger than the layer thickness.

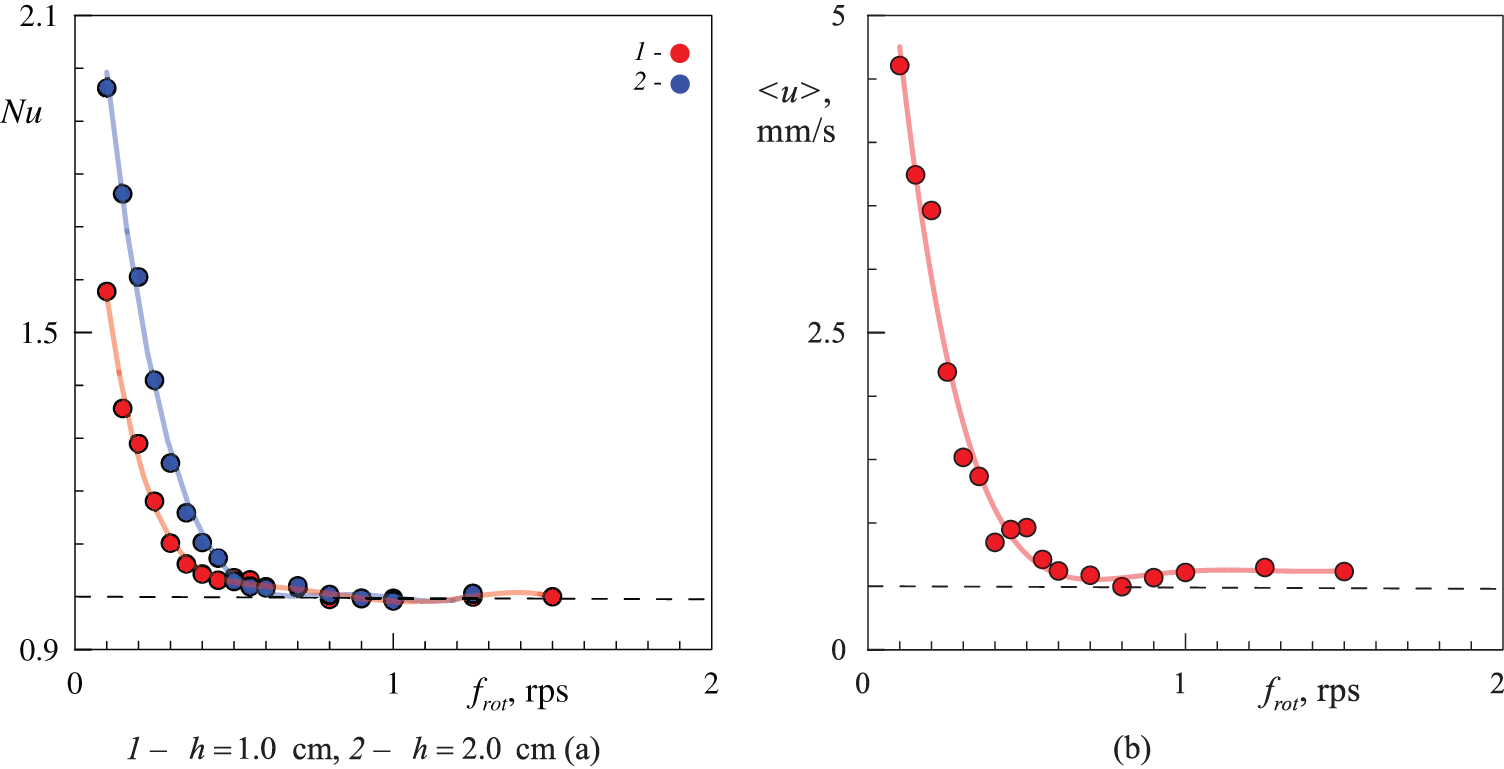
Figure 5: Heat transfer (a) and average velocity of fluid oscillations (b) depending on the frot

The average over diametral cross-section instantaneous velocity is defined as u=1S∫suh2+ur2ds –where uh and ur are axial and radial velocity components, S is the area of the cross-section. Then, the time-averaged velocity can be calculated by the formula <u>=1Trot∫Trotudt . At least ten rotation periods Trot are taken into account when calculating the time average velocity. Fig. 5b illustrates the dependence of the time-averaged fluid velocity <u> on the rotation velocity.

A comparison of the excitation thresholds of thermal vibrational convection in the planes is proposed frot, Nu and frot, <u> . Here, the Nusselt number Nu=ΔT/\DeltaTΔT0ΔT0 corresponds to the quasi-equilibrium regime Nu=1 . The threshold for thermal vibrational convection is determined by oscillation velocity and temperature measurements. The threshold values of rotation rate are comparable in both cases and equal to frot=0.40 rps.

As the layer thickness increases to the value h=2.0 cm, the number of vortices decreases. The average velocity field at a rotation rate of frot=0.50 rps is shown in Fig. 6. The threshold of vibrational convection shifts to the region of higher rotation rates (Fig. 5a, curve 2).

Figure 6: Averaged velocity field in the layer with thickness h=2.0 cm

A comparison of the dependences of heat transfer and the average velocity of fluid oscillations on the rotation velocity at even cavity rotation about the horizontal axis indicates that the PIV technique is able to accurately determine the threshold of convection.

3.2 Modulated Rotation of a Flat Liquid Layer around a Horizontal Axis

Experiments were conducted to investigate the effect of modulated rotation (libration) on the development of thermal vibrational convection in the subcritical domain [29]. This allowed us to exclude the influence of the vibration mechanism [27] on the average fluid flow. It is assumed that libration can increase the effect of inertial waves on the fluid flow in the subcritical region.

Let’s discuss the heat transfer in a fluid layer under libration (Figs. 7 and 8). The experimental results ε,Nu show that libration with small amplitude does not affect heat transfer. When the amplitude reaches a critical value, convection is initiated, resulting in an enhancement of heat transfer within the layer.

Figure 7: Nusselt number vs. libration amplitude at different temperature differences (a) and at different layer thicknesses (b)

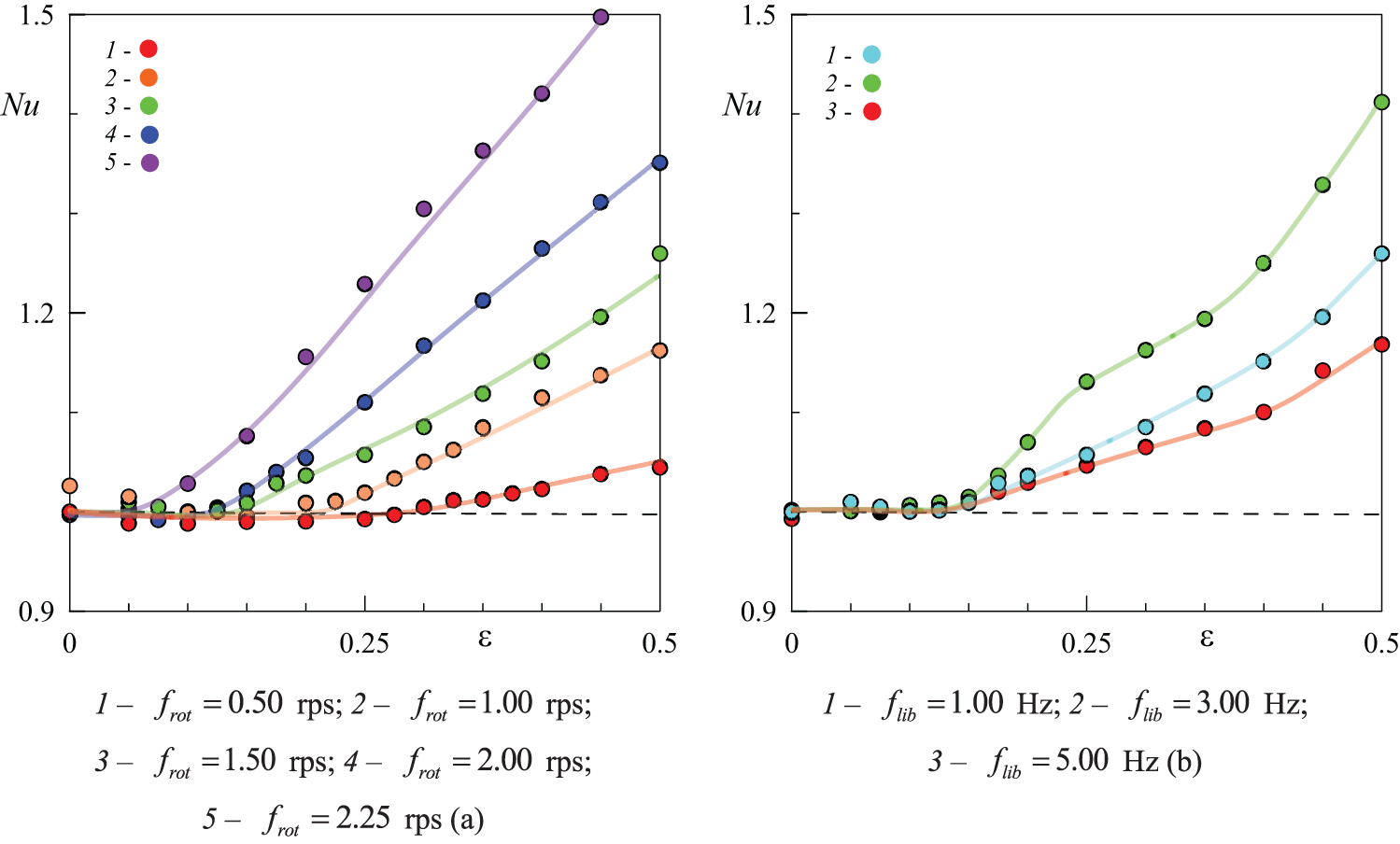
Figure 8: Nusselt number vs. amplitude of modulation at different rotation rates (a) and libration frequencies (b)

The experiments in Fig. 7a were conducted at a libration frequency of flib=1.00 Hz and a rotation velocity of frot=2.00 rps with different temperature differences. One can find that changes in temperature at the layer boundaries do not affect the threshold of the average convection. This implies that the formation of the time-averaged flow is not a consequence of the interaction between the fluid and the temperature field. Instead, convection merely indicates the emergence of the fluid motion.

The effect of modifying the cavity geometry (layer thickness) on heat transfer is illustrated in Fig. 7b. Here, experiments were performed at a rotation rate of frot=1.00 rps and a libration frequency of flib=1.80 Hz. When a thicker layer is used, the heat transfer curve shifts to higher values of the Nusselt number. The threshold of averaged convection is observed to shift to smaller cavity libration amplitudes.

The experiments were carried out at different rotation velocities (Fig. 8a). Heat transfer curves were obtained for rotation velocities frot=2.25, 2.00, 1.50, 1.00, 0.50 rps at Θ=10.6 °C. It was demonstrated that an increase in the rotation velocity resulted in a shift of the threshold towards smaller libration amplitudes. Additionally, an increase in the rotation rate results in an intensification of heat transfer, accompanied by an increase in the slope of the heat transfer curves. For a fixed value of ε=0.50 , the value of the Nusselt number increases with increasing cavity rotation.

Here, we examine the effect of libration amplitude on heat transfer at a fixed rotation rate and temperature difference between the cavity boundaries. The investigation is conducted at different libration frequencies (Fig. 8b). The slope angles of the curves change non-monotonically as the libration frequency increases. Section 3.4 presents a study on heat transfer across a wide range of frequencies and amplitudes of cavity libration at varying rotational velocities.

The study of heat transfer was conducted in dependence on a variety of experimental parameters in order to identify general laws and determine specific domains of heat transfer enhancement.

3.3 Fluid Flow Under Modulated Rotation

The velocity field in an unevenly rotating cavity was investigated using the particle image velocimetry technique. Fig. 9 illustrates the instantaneous velocity field at different values of libration amplitude at fixed phase of the cavity libration ( h=1.0 cm, Θ=8.4 °C, frot=1.00 rps, flib=1.80 Hz). The frames were selected at a fixed phase of the libration cycle and were taken at a time interval that was a multiple of the libration period according to the formula (1+(1N~+1)+(2N~+1)+...+(MN~+1))/(1+(1N~+1)+(2N~+1)+...+(MN~+1))(M+1)(M+1) . Here, N~ is the number of frames fitting into the libration period, and the number of libration periods M is chosen to be at least ten.

Figure 9: Instantaneous velocity field as a function of libration amplitude

It has been demonstrated that as the amplitude of cavity libration increases, so does the vorticity. A flow pattern consisting of two counter-rotating vortices is formed at ε=0.10 (Fig. 9b). As the amplitude of libration increases, so do the vorticity and radial size of the vortices. At the maximum libration amplitude, a vortex system of considerable intensity is observed to occupy the entire cavity.

A pair of counter-rotating vortices is observed on both sides of the rotation axis. The sign of vorticity changes during a libration cycle (Fig. 10).

Figure 10: Change in vorticity sign occurs once per libration period at ε=0.20

The dependence of the fluid oscillation velocity u on time can be determined by analyzing the instantaneous velocity fields obtained during a libration cycle at a constant value of ε (Fig. 11a).

Figure 11: Instantaneous fluid velocity vs. time during the libration cycle (a) and average velocity of fluid oscillations as a function of cavity libration amplitude (b)

It is evident that the liquid velocity reaches its maximum and minimum values twice during one cycle of libration which is associated with a periodic change in the vorticity sign (Fig. 10). This phenomenon has been observed in all experiments conducted within the range of libration frequencies studied. An increase in the libration amplitude results in a wider range of variation of the instantaneous velocity and an increase in its mean value.

In order to calculate the space-averaged velocity, it is necessary to apply the averaging process over the libration period. This can be achieved by applying the formula <u>=1Tlib∫Tlibudt . The dependence of the average velocity on the libration amplitude is illustrated in Fig. 11b. It can be observed that even minor libration amplitudes result in a notable enhancement in the fluid velocity, while the heat transfer remains unchanged (Fig. 7a). It is suggested that the observed reduction in velocity can be attributed to the disruption of the vortical flow that emerges at even rotation and contributes to a marginal enhancement in the intensity of fluid oscillations. When the libration amplitude exceeds a value of ε=0.10 , the curve exhibits a kink, which indicates the development of the time-averaged fluid flow. This conclusion is also supported by temperature measurements indicating additional heat transfer through the layer (Fig. 7b, curve 1). An increase in the libration amplitude results in a non-monotonic increase in the average velocity of fluid oscillations.

In the initial phase of the experiments [33], a thermochromic film was utilized for the flow study. A thermochromic film applied to the surface of a heated heat exchanger recorded the temperature distribution at a flat boundary of the layer. The temperature field allowed us to detect a vortex, which was close to the cylindrical wall. As the libration amplitude increased, the radial size of the vortex exhibited a corresponding increase, eventually reaching the center of the cavity. The results obtained with the use of PIV and thermochromic film are in qualitative agreement with each other: Both methods indicate vortices in the fluid. It is suggested that the flow pattern at large libration amplitudes is similar to the radial motion of the fluid, resulting in the axial motion of the fluid (so-called Ekman pumping).

3.4 The Effect of Dimensionless Oscillation Frequency on Heat Transfer and Oscillation Velocity

The investigation of heat transfer and fluid oscillation velocity at different rotation rates, amplitudes, and libration frequencies enables the mapping of the modes of averaged convection. Fig. 12a allows for the comparison of heat transfer curves as a function of dimensionless oscillation frequency at different libration amplitudes at a fixed rotation rate frot=1.00 rps. One can observe multiple resonance zones of heat transfer enhancement at different dimensionless libration frequencies. An increase in the libration amplitude results in a monotonic increase in heat transfer at nearly the same values of the resonant frequencies. The Nusselt number exhibits a pronounced increase at flib=0.20,1.00,2.00 Hz at different libration amplitudes.

Figure 12: Nusselt number vs. dimensionless frequency

Furthermore, experiments conducted at varying rotational velocities also revealed the existence of resonance zones. The dependence of the heat transfer intensity on the dimensionless frequency at a fixed modulation amplitude for different rotational rates is illustrated on the N, Nu plane (Fig. 12b). The heat transfer curves obtained at different rotational velocities converge. These results indicate that an increase in rotation rate is associated with an increase in both fluid flow intensity and heat transfer intensity (Fig. 8a). The intensity of the fluid flow and heat transfer can be estimated by measuring the oscillation velocity of the fluid in the diametral cross section using the PIV technique previously described in Section 3.3. Fig. 13 illustrates the averaged oscillation velocity for a fixed rotation rate of frot=1.00 rps at different amplitudes and frequencies.

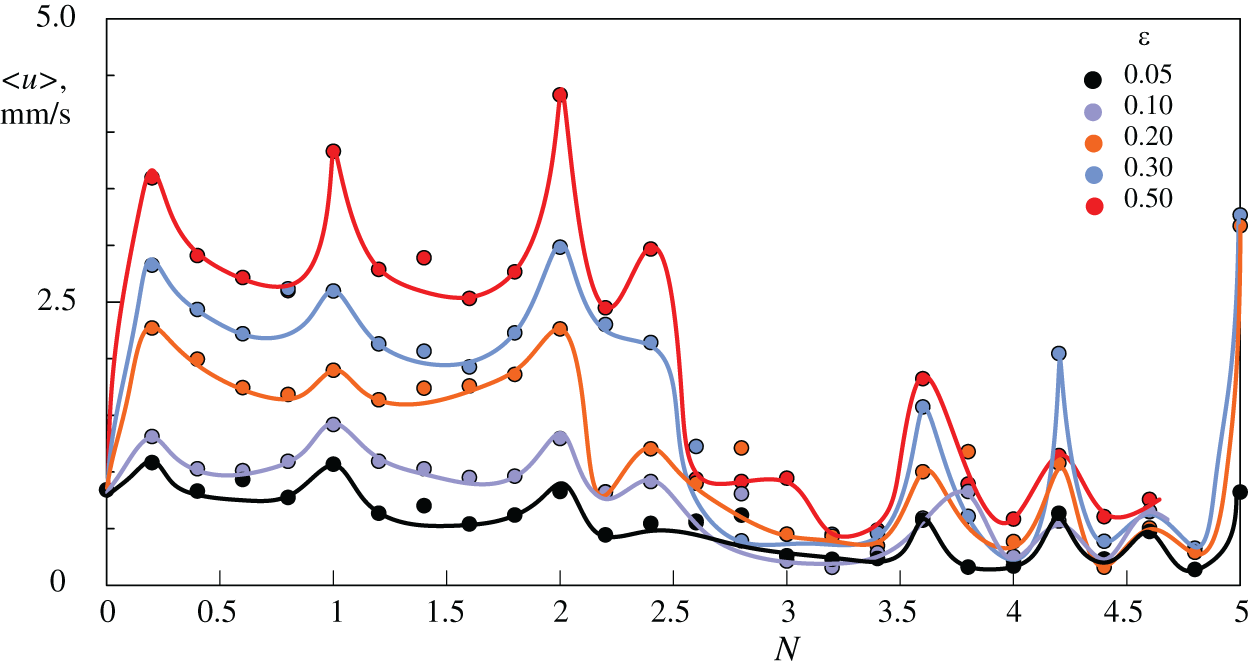
Figure 13: The averaged velocity of fluid oscillations vs. dimensionless libration frequency

A comparison of the results of heat transfer measurement (Fig. 12) and average fluid oscillation velocity measurement (Fig. 13) indicates the presence of domains in which the values of these parameters exhibit an increase. It is possible that these regions indicate the existence of resonant phenomena. A more detailed examination of the phenomena occurring within these areas necessitates the investigation of the average azimuthal velocity. The proposed study will reveal flow features in resonant regions, including vortex formation and changes in fluid direction. This will enable us to understand how the dimensionless oscillation velocity affects the fluid flow and heat transfer.

When comparing the heat transfer curves (Fig. 12) with the curves of the mean oscillation velocity of the liquid (Fig. 13), it is evident that there are certain regions where these parameters increase. These regions may indicate the possible presence of resonance phenomena in the system. To conduct a more in-depth analysis of these zones, it is necessary to study the azimuthal velocity field of the averaged flow from the flat side of the working layer. This study aims to investigate the flow features in resonance regions, including vortex formation and changes in fluid motion direction. The analysis of this field will provide insights into how changes in dimensionless oscillation velocity affect flow structure and heat transfer in the system.

4  Discussion

The principal dimensionless parameters of the problem are the pulsation Reynolds number, the dimensionless frequency of oscillation, and the Nusselt number. The intensity of the time-averaged flows is described by the pulsation Reynolds number Rep=φ02R2Ωlib/φ02R2Ωlibνν [34]. The ratio of Coriolis force to viscous forces is determined by the dimensionless rotation velocity ωrot=Ωroth2/Ωroth2νν . The Nusselt number is a dimensionless quantity that characterizes the average motion of a fluid resulting from the modulation of the rotation rate of a cavity. Fig. 14a illustrates the dependence of heat transfer on angular amplitude. Heat transfer curves at a fixed libration frequency and different rotation rates exhibit similar dynamics. As the libration frequency increases, the threshold for the onset of averaged convection shifts to the domain of smaller angular amplitudes.

Figure 14: Nusselt number vs. angular amplitude (a) and pulsation Reynolds number vs. dimensionless rotational velocity (b)

Heat transfer is a secondary indicator of the onset of fluid motion and the threshold for the development of the averaged convection. The threshold for the onset of the convection is determined by the appearance of the time-averaged flow in the form of a vortex, which leads to an increase in heat transfer in the fluid. The threshold value of the Reynolds number in dependence on the dimensionless rotation velocity is shown in Fig. 14b. As the rotation velocity of the cavity increases, the threshold value of the Reynolds number linearly grows at a fixed value of flib . As flib decreases, the threshold curve shifts to the region of larger values of the pulsation Reynolds number. As flib decreases, the fluid is permitted a longer period of time to interact with the temperature field, resulting in an augmented flow intensity.

The dimensionless parameters N−1, Rep can be used to analyze the modes of fluid motion in dependence on the cavity geometry, flow velocity, and frequency of fluid oscillations (Fig. 15). The threshold curve indicates the point at which the convective motion of the fluid becomes intense, resulting in the occurrence of convection.

Figure 15: Stability curve in the plane of control parameters

An increase in the intensity of motion is observed with an increase in the pulsation component of velocity, which is associated with a decrease in viscosity. Additionally, an increase in the libration frequency leads to a decrease in the threshold value of the pulsation Reynolds number.

5  Conclusion

The present study investigates the flow in a flat liquid layer with isothermal boundaries of different temperatures under cavity libration. The study has revealed that the libration-induced time-averaged flow can significantly enhance heat and mass transfer. When the cavity rotation rate is modulated, the average flow in the form of two counter-rotating vortices is observed. During a libration cycle, the direction of these vortices undergoes a change. The observed flow exhibits similarities to Ekman pumping.

The analysis of experimental data obtained at different dimensionless oscillation frequencies has revealed the existence of domains in which there is a sharp increase in heat transfer and average velocity of fluid oscillations. The results demonstrate that the fluid flow intensity depends on the rotation velocity and amplitude of the cavity libration. The threshold curve of averaged convection is identified in the plane of control parameters.

The study revealed the development of inertial modes within the h=2.0 cm thick layer. Further investigation is necessary to gain a deeper understanding of the fluid flow and heat transfer dynamics within the cavity, particularly in the context of developing inertial effects. It is of great importance to direct attention to the study of azimuthal velocity using the PIV technique. This will clarify the flow pattern and explain the reasons for the significant increase in fluid oscillation velocity.

Acknowledgement: The author thanks Professor Victor Kozlov for his interest in the task and fruitful discussions of the results and the team of the Laboratory of Vibrational Hydromechanics of PSHPU.

Funding Statement: This work was financially supported by the Russian Science Foundation (Grant No. 22-71-00086).

Availability of Data and Materials: All data are included in this published article.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. Lappa M. Thermal convection: patterns, evolution and stability. Chichester, England: Wiley; 2009. [Google Scholar]

2. Lappa M. Rotating thermal flows in natural and industrial processes. Chichester, England: Wiley; 2012. [Google Scholar]

3. Chandrasekhar S. Hydrodynamic and hydromagnetic stability. New York: Oxford University Press; 1961. [Google Scholar]

4. Rossby HT. A study of Benard convection with and without rotation. J Fluid Mech. 1969;36(2):309–35. [Google Scholar]

5. Madonia M, Guzmán AJ, Clercx JH, Kunnen PJ. Velocimetry in rapidly rotating convection: spatial correlations, flow structures and length scales. Europhys Lett. 2021;135(5):54002. [Google Scholar]

6. Le Bars M, Cébron D, Le Gal P. Flows driven by libration, precession, and tides. Annu Rev Fluid Mech. 2015;47:163–93. [Google Scholar]

7. Grannan AM, Bars MLE, Cébron D, Aurnou JM. Experimental study of global-scale turbulence in a librating ellipsoid. Phys Fluids. 2014;26(12):126601. [Google Scholar]

8. Sauret A, Dizès SL. Libration-induced mean flow in a spherical shell. J Fluid Mech. 2013;718:181–209. [Google Scholar]

9. Wu K, Welfert BD, Lopez JM. Librational forcing of a rapidly rotating fluid-filled cube. J Fluid Mech. 2018;842:469–94. doi:10.1017/jfm.2018.157. [Google Scholar] [CrossRef]

10. Noir J, Calkins MA, Lasbleis M, Cantwell J, Aurnou JM. Experimental study of libration-driven zonal flows in a straight cylinder. Phys Earth Planet Inter. 2010;182(1–2):98–106. doi:10.1016/j.pepi.2010.06.012. [Google Scholar] [CrossRef]

11. Calkins MA, Noir J, Eldredge JD, Aurnou JM. Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys Fluids. 2010;22(8):086602. doi:10.1063/1.3475817. [Google Scholar] [CrossRef]

12. Seuren F, Triana SA, Rekier J, Barik A, Hoolst VA. Effects of the librationally induced flow in Mercury’s fluid core with an outer stably stratified layer. Planet Sci J. 2023;4(9):161. doi:10.3847/PSJ/acee77. [Google Scholar] [CrossRef]

13. Olson P. Experimental dynamos and the dynamics of planetary cores. Annu Rev Earth Planet Sci. 2013;41(1):153–81. doi:10.1146/annurev-earth-050212-124033. [Google Scholar] [CrossRef]

14. Kozlov VG, Subbotin SV. Librations induced zonal flow and differential rotation of free inner core in rotating spherical cavity. Phys Fluids. 2017;29(9):096601. doi:10.1063/1.5000864. [Google Scholar] [CrossRef]

15. Anderson LT, Killworth PD. Spin-up of a stratified ocean, with topography. Deep Sea Res. 1977;24(8):709–32. doi:10.1016/0146-6291(77)90495-7. [Google Scholar] [CrossRef]

16. Smeed DA. A laboratory model of benthic fronts. Deep Sea Res A. Oceanogr Res Pap. 1987;34(8):1431–59. doi:10.1016/0198-0149(87)90136-1. [Google Scholar] [CrossRef]

17. Subbotin S, Shiryaeva M. Inertial wave beam path in a Non-uniformly rotating cylinder with sloping ends. Microgravity Sci Technol. 2023;35(3):35–2. doi:10.1007/s12217-023-10054-z. [Google Scholar] [CrossRef]

18. Lopez JM, Marques F. Inertial waves in rapidly rotating flows: a dynamical systems perspective. Phys Scr. 2016;91(12):124001. doi:10.1088/0031-8949/91/12/124001. [Google Scholar] [CrossRef]

19. We K, Welfert BD, Lopez JM. Inertial wave attractors in librating cuboids. J Fluid Mech. 2023;973:A20. [Google Scholar]

20. Greenspan HP. The theory of rotating fluids. Cambridge: University Press; 1968. [Google Scholar]

21. Mahariq I, Kurt H. Strong field enhancement of resonance modes in dielectric microcylinders. J Opt Soc Am. 2016;656–662:B33. [Google Scholar]

22. Gangadhar K, Shashidhar RK, Prameela M, Wakif A. Generation of entropy on blood conveying silver nanoparticles embedded in curved surfaces. P I Mech Eng E-J Pro, 2024. doi:10.1177/09544089231224523. [Google Scholar] [CrossRef]

23. Sterl S, Li HM, Zhong JQ. Dynamical and statistical phenomena of circulation and heat transfer in periodically forced rotating turbulent Rayleigh-Bénard convection. Phys Rev Fluids. 2016;1(8):084401. [Google Scholar]

24. Gutierrez-Castillo P, Lopez JM. Differentially rotating split-cylinder flow: responses to weak harmonic forcing in the rapid rotation regime. Phys Rev Fluids. 2017;2:084802. [Google Scholar]

25. Balagopal S, Lappa M. On the relationship between solid particle attractors and thermal inhomogeneities in vibrationally-driven fluid-particle systems. Phys Fluids. 2023;35(10):103316. doi:10.1063/5.0170162. [Google Scholar] [CrossRef]

26. Gershuni GZ, Lyubimov DV. Thermal vibrational convection. New York: Wiley; 1998. [Google Scholar]

27. Wu XL, Guo JZ, Zhao WF, Wang BF, Chong KL, Zhou Q. Flow structure transition in thermal vibrational convection. J Fluid Mech. 2023;974:A29. [Google Scholar]

28. Kozlov VG. Thermal vibrational convection in rotating cavities. Fluid Dyn. 2004;39(1):3–11. doi:10.1023/B:FLUI.0000024806.35710.e7. [Google Scholar] [CrossRef]

29. Vjatkin AA, Ivanova AA, Kozlov VG, Rysin KY. Effect of the tangential component of a force field on convection in a rotating plane layer. Izv Atmos Ocean Phys. 2017;53(2):187–94. doi:10.1134/S000143381702013X. [Google Scholar] [CrossRef]

30. Vjatkin AA, Siraev RR, Kozlov VG. Theoretical and experimental study of thermal convection in rotating horizontal annulus. Microgravity Sci Technol. 2020;32(6):1133–45. doi:10.1007/s12217-020-09827-7. [Google Scholar] [CrossRef]

31. Vjatkin AA, Kozlov VG, Sabirov RR. Experimental study of thermal convection in a cylindrical layer with a longitudinal partition at modulated rotation. J Phys: Conf Ser. 2021;1945(1):012061. doi:10.1088/1742-6596/1945/1/012061. [Google Scholar] [CrossRef]

32. Nguyen TP, Chen JC. Effect of crucible and crystal rotations on the solute distribution in large size sapphire crystals during Czochralski growth. Int J Heat Mass Transf. 2019;130(1):1307–21. doi:10.1016/j.ijheatmasstransfer.2018.11.042. [Google Scholar] [CrossRef]

33. Rysin KY. Averaged convection in a flat layer at modulated rotation around a horizontal axis. In: Proceedings of the 10th International Conference on Fluid Flow, Heat and Mass Transfer (FFHMT’23); 2023 Jun. 7–9; Ottawa, Canada. doi:10.11159/ffhmt23.163. [Google Scholar] [CrossRef]

34. Ivanova AA, Kozlov VG. Vibrational convection in nontranslationally oscillating cavity (isothermal case). Fluid Dyn. 2003;38(2):186–92. doi:10.1023/A:1024260716608. [Google Scholar] [CrossRef]