Impact of a Magnetic Dipole on Heat Transfer in Non-Conducting Magnetic Fluid Flow over a Stretching Cylinder

Nomenclature

1  Introduction

Ferrofluids are synthetically developed and comprise magnetic nanoparticles, non-conducting carrier liquids, and surfactants. The role of surfactants is to prevent the nanoparticles from accumulating. In the dearth of a magnetic field, the behavior of ferrofluid is like a normal fluid. Nevertheless, when exposed to a magnetic field, the fluid magnetizes and the magnetization changes the thermal characteristics of ferrofluid. Based on the thermomagnetic behavior of ferrofluid and magnetization force, the researchers have shown different types of practical applications of ferrofluid in the field of engineering and medical science [1–5].

In this section, different physical aspects investigated by researchers for the flow over an elongated cylinder are presented. Wang [6] presented a theoretical model for the passing of viscous material outside a stretched cylinder. To calculate the fluid velocity and pressure fields, he devised an analytical solution and derived equations. In addition, he provided numerical evidence to support his solution. Usman et al. [7] evaluated the effects of thermal and velocity slippage on Casson nanofluid stream over an inclined permeable stretched cylinder using a collocation method. This includes looking into how slip parameters, the Prandtl number, and the Casson parameter affect flow characteristics. They also presented numerical results to validate their solutions. Tlili et al. [8] investigated the effects of various slip parameters on MHD non-Newtonian nanofluids passing over a stretched cylinder in a porous medium with radiation and chemical reaction. This included studying the effects of radiation, chemical reaction, and slip parameters on the temperature, concentration, and velocity fields of nanofluids. Fang et al. [9] concluded that a similarity transformation framework can be used to describe unsteady viscous flux over an expanding elongated cylinder. They demonstrated that the Reynolds and Weber numbers influence the shapes of velocity distributions near the stretching surface. Munawar et al. [10] investigated the thermal behavior of an oscillatory stretching cylinder. They developed a numerical scheme based on boundary layer theory and investigated how to flow parameters such as Reynolds number and oscillation frequency affect system heat transfer Replace Munawar By Ishak et al. [11] constructed the model for magnetohydrodynamic glide and heat transmission caused by stretching cylinder. Wang et al. [12] researched the slipstream over a stretching cylinder and obtained the asymptotic solution large radius of the cylinder. Ishak et al. [13] considered the impact of suction and injection on the flow due to a stretched cylinder and solved similarity equations numerically using the finite difference method. Similar flow with different fluid and physical properties was investigated by researchers [14–16]. Chu et al. [17] used Roseland approximation for the thermal behavior of hybrid ferrofluid and implemented the control volume finite element method (CVFEM) to obtain the solution. Kumar et al. [18] investigated the influence of single-wall and multi-wall carbon nanotubes on the Maxwell nanofluid flow in the presence of magnetic dipole. Hashmi et al. [19] studied the Oldroyd-B fluid flow over a stretchable disk and measured the influence of Joule heating and chemical reaction. Khan et al. [20] used the concept of fractional derivative to investigate the convective flow and heat transfer between two parallel plates.

This section presents the description of different techniques used by researchers to obtain the solution of similarity equations. Malik et al. [21] implemented the RKF algorithm to solve similarity equations of the Sisko glide of fluid due to stretching cylinder. Kumar et al. [22] employed the RKF fourth-fifth order algorithm to find the numerical solution of ferromagnetic nanofluid flux over a stretched cylinder. Bilal et al. [23] solved the similarity equations through the shooting iteration method for the glide of Williamson nanofluid fluid due to the stretching cylinder. Bhandari [24] has used the finite element methodology to measure the consequences of radiation and chemical reaction for the magnetohydrodynamic flux of nanofluid over a stretched sheet. Some of the numerical techniques have been used by researchers to procure the solution of nonlinear related differential equations for the flow over a stretching cylinder [25–28]. Salahuddin et al. [29] investigated the flow of hybrid nano liquid over a highly magnetized heated cylinder. Salahuddin et al. [30] looked into the heat and mass transfer characteristics of viscoelastic fluid flow in the vicinity of forward and infrequent stagnation spots in two dimensions. Ullah et al. [31] studied oscillatory mixed convection stratified fluid and heat transfer properties at various stations of a non-conducting horizontally circular cylinder in the presence of a thermally stratified medium. Song et al. [32] analyzed the bioconvective flow over a stretching cylinder and measured the role of microorganisms parameters in the flow. Kumar et al. [33] studied the boundary layer flow of Prandtl fluid due to stretching surface and used similarity transformation to obtain a set of nonlinear ordinary differential equations from the governing equations. On magnetic fluid flow across vertically stretched porous material, Kalaivanan et al. [34] looked into the effects of buoyancy force and activation energy. To research the impact of radiation and Joule heating, Naseem et al. [35] explored Eyring-Powel fluid flow across an exponentially stretched sheet.

The ferrohydrodynamic flow over a stretched cylinder is significant because it allows for a better understanding of how different magnetized fluids behave upon the existence of a magnetic field. This understanding can be used to develop more efficient methods of controlling and manipulating fluids in a variety of applications, such as energy conservation, drug delivery, and waste management. Furthermore, modeling ferrofluid flow provides insight into the consequences of a variety of parameters such as temperature, viscosity, and magnetism on the motion of ferrofluids, which is important for a variety of applications. The above-stated literature assessment shows that almost all of the research papers were communicated on the flow of ordinary viscous fluid and conducting magnetic fluid over a stretched cylinder. In this paper, the model for the flow of ferrofluid over a stretching cylinder is developed in the emergence of a bipolar magnet. The governing equations of the flow are converted into non-dimensional forms using similarity variables. The transformed nonlinear equations are solved numerically by finite element techniques in COMSOL Multiphysics and the model is validated with the previous numerical models.

2  Mathematical Formulation of the Theoretical Model

Fig. 1 graphically shows the diagram of ferrofluid movement attributable to a stretching cylinder in the axial direction. In this flow, altitudinal axis z is assumed along the line of the cylinder, and radial axis r is assumed a radial path. The magnetic dipole is kept at a distance a from the center. The elongation cylinder is maintained at a constant temperature Tw lower than the Curie temperature Tc . The fluid atoms away from the cylinder are considered to be at a temperature T=Tc . The fluid element at T=Tc is Unmagnetizable until this layer begins to cool due to the adjacent integument layer in the flow. The governing equations of the assumed flow are as follows [6,11,36]:

∂(rw)∂z+∂(ru)∂r=0 (1)

w∂w∂z+u∂w∂r=μ0ρMd∂H∂z+ν(∂2w∂r2+1r∂w∂r) (2)

w∂T∂z+u∂T∂r=kρ cρ(∂2T∂r2+1r∂T∂r)−μ0ρ cρT∂Md∂T(w∂H∂z+ur∂H∂r) (3)

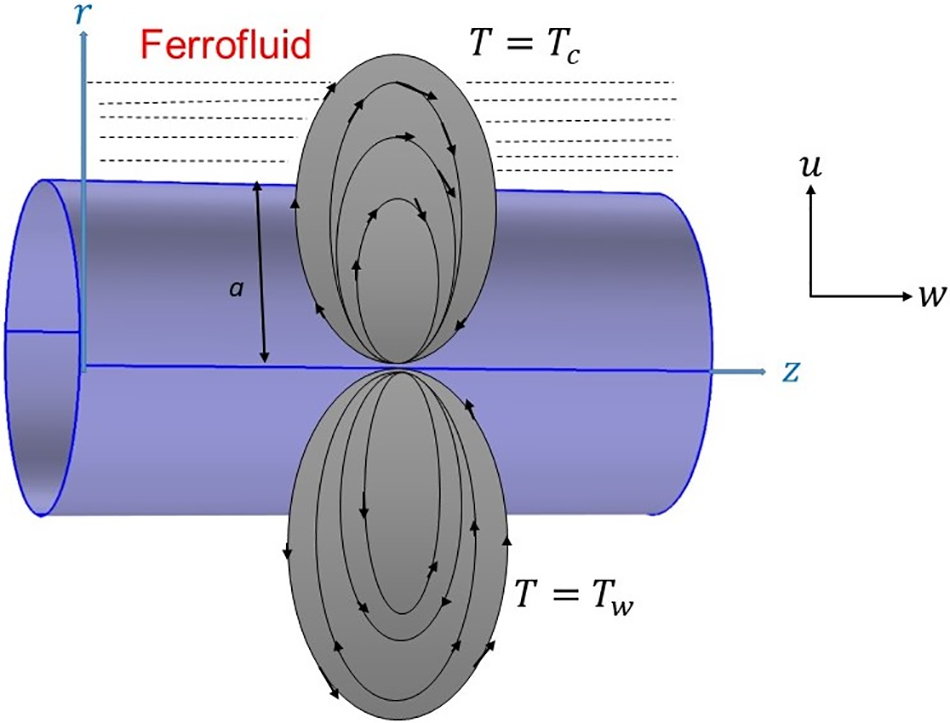
Figure 1: Ferrofluid flow layout over a stretched cylinder upon the existence of a permanent dipole

Boundary conditions for considered flow:

u=0, w=ww, T=Twatr=a; w→0, T→T∞asr→∞ (4)

Magnetic dipole potential can be calculated as [37–39]:

Θ=γ2π{zz2+(r+a)2} (5)

The Magnetic Flux Intensity ( Hz , Hr ) along z and r lines can be stated as:

Hz=−∂Θ∂z=γ2π[z2−(r+a)2{z2+(r+a)2}2] (6)

Hr=−∂Θ∂y=γ2π[2z(r+a){z2+(r+a)2}2] (7)

The total strength of the magnetic field is:

H=[(∂Θ∂z)2+(∂Θ∂r)2]12 (8)

The magnitude of the magnetic charge strength change alongside the  z and r lines is:

∂H∂z=γ2π{2z(r+a)4} (9)

∂H∂r=γ2π{−2(r+a)3+4z2(r+a)5} (10)

We consider magnetization as a linear function of temperature. It can be expressed as:

Md=Ka(Tc−T) (11)

To obtain the non-dimensional equations, we use the following similarity transformation [6,11]:

η=(ra)2, u=−caf(η)η, w=2cdfdηz, θ(η)=Tc−TTc−Tw (12)

Using Eq. (12), the governing equations of the flow take the following form:

ηd3fdη3+d2fdη2−Re{(dfdη)2−fd2fdη2}−116βRe1(η+1)4θ=0 (13)

ηd2θdη2+(1+RePrf)dθdη−βλ(ε+θ)1(η+1)4dfdη−βλ[−121(η+1)3+1(η+1)5]f(ε+θ)=0 (14)

The boundary conditions in Eq. (4) become:

f(1)=0, (dfdη)η=1=1, θ(1)=1; (dfdη)η→∞=0, θ(∞)=0 (15)

The non-dimensional quantities are as follows:

Re=ca22ν, β=γμ0Ka(Tc−Tw)ρ2πμ2, λ=cμ2ρk(Tc−Tw), ε=TcTc−Tw, Pr=νρCpk (16)

The coefficient of viscous friction and the Nusselt coefficient can be defined as:

Cf=2τwρww2, Nu=aqwk(Tc−Tw) (17)

The measurement of viscous friction and heat propagation rate can be obtained from:

τw=μ(∂w∂r)r=a, qw=−k(∂T∂r)r=a (18)

Using Eq. (12), the non-dimensional form of these quantities for the present study is as follows:

CfRe za=f′′(1), Nu=−2θ′(1) (19)

3  Problem Solution and Its Validation

The Finite Element Method (FEM) is a numerical procedure for addressing differential equations associated with physical phenomena in the COMSOL Multiphysics software. The FEM divides the entire domain into elements and then approximates the equation solutions. Using variational calculus, linear algebra, and numerical integration techniques, a system of linear equations is derived from the differential equations, leading to an approximate solution at the element nodes. COMSOL Multiphysics finite element procedure is exercised to simulate an extensive range of physical phenomena by utilizing advanced features such as adaptive meshing, visualization tools, and parametric studies. To implement the confined element approach in COMSOL Multiphysics, we reduce the order of the differential equations.

Eqs. (13)–(15) are reduced using the transformation f=L , dfdη=M . The reduced equations are as follows:

dLdη−M=0 (20)

ηd2Mdη2+dMdη−β16 Re(η+1)4θ−Re M2+Re GdMdη=0 (21)

ηd2θdη2+dθdη−βλε(η+1)4M+βλε2(η+1)3L+RePrL dθdη−βλ(η+1)4θM−βλ(η+1)5Lθ=0 (22)

L(1)=0, M(1)=1, θ(1)=1; M(∞)=0, θ(∞)=0 (23)

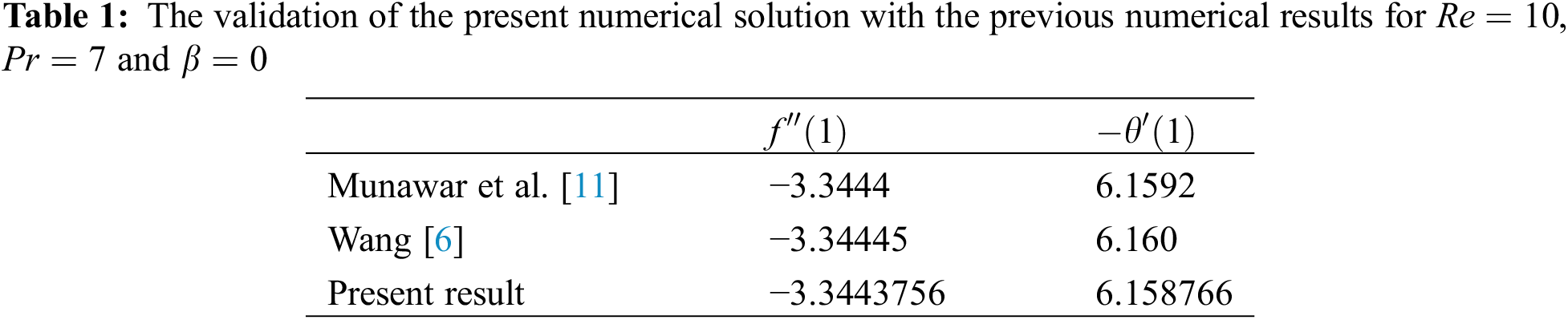
Fig. 2 demostrates the convergence plot for the present numerical solution. During solution, we considered the element size as 0.0001. The present numerical solution is correct up to six decimal places. Table 1 represents the authentication of the present conceptual model with the available theoretical model in the literature. If we consider the values of the parameters Re=10 , Pr=7 and β=0 , the values of the f′′(1) and θ′(1) has a match that is sympathetic to the former results [6,11].

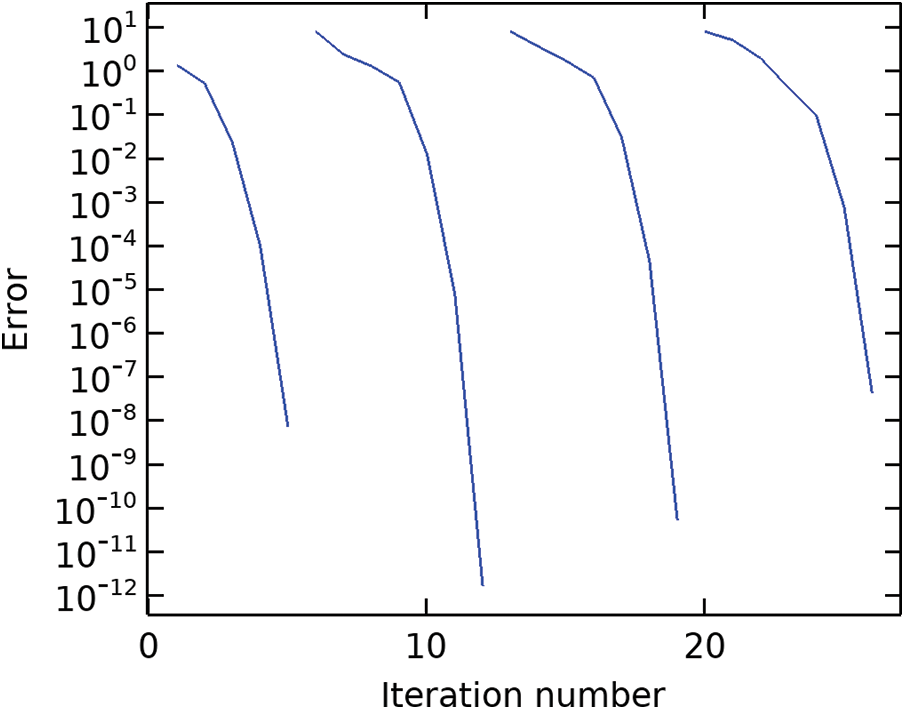
Figure 2: Convergence plot of numerical solution

4  Findings and Analysis

Present numerical results are obtained after the numerical solution of non-dimensional similarity equations using the Confined Element program in COMSOL Multiphysics Software. The Velocity and temperature distribution profiles are obtained here with the existence of ferromagnetic response number (β) , Prandtl number (Pr) , Reynolds number (Re) and viscous dissipation parameter (λ) . The ferromagnetic interaction number has an impact on the momentum and energy equations. It is mainly contingent on the intensity of the magnetic charge. The viscous dissipation parameter represents the role of viscous forces in heat conveyance in the flow.

Fig. 3 represents the behavior of temperature distribution with the variation of Prandtl number (Pr) . The range of Prandtl numbers for varied types of ferrofluids is available in the literature [3]. In ferrofluids, heat transfer occurs due to fluid momentum rather than fluid conduction. Enhancement in the Prandtl number diminishes the temperature field since this enhancement in Pr reduces the thermal boundary layer. This type of behavior of the Prandtl number is also available in the literature [11]. Figs. 4 and 5 demonstrate the control of the Reynolds number (Re) on the velocity (f′) and temperature (θ) . As we boost the value of the Reynolds number in the flow, it indicates that inertial forces dominant over viscous forces. The Reynolds number is also useful to differentiate the nature of the passage that whether it is orderly or chaotic. However, the present range keeps the flow laminar but heightening the values of Re reduces the velocity and temperature in stream. In case of ordinary viscous fluid, the velocity and temperature decreases for increasing Reynolds number and this pattern [6,11]. This pattern of reduction in the velocity and temperature is also for ferrofluids.

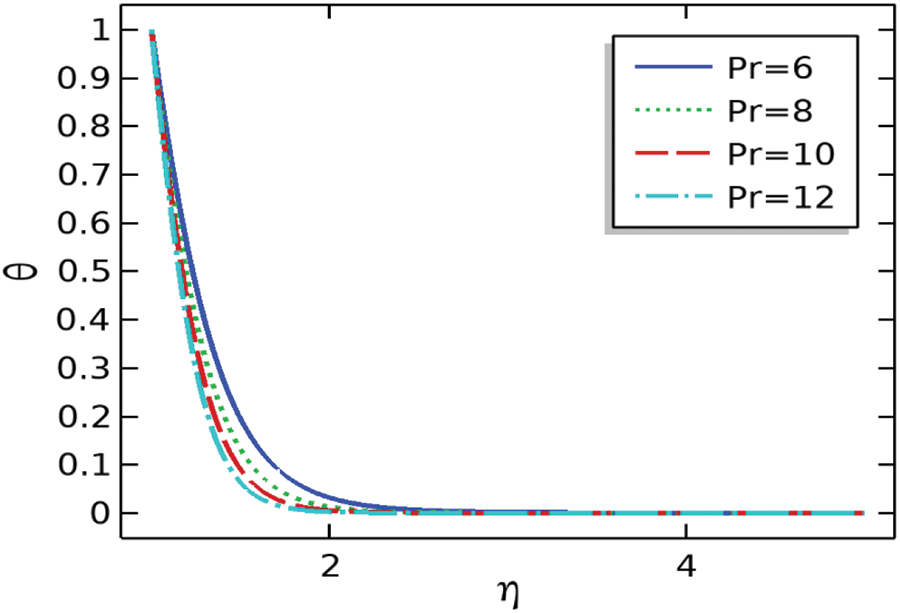
Figure 3: The repercussion of Pr on the temperature profile (θ) for given Re=2 , β=5 , λ=0.01 , and ε=2

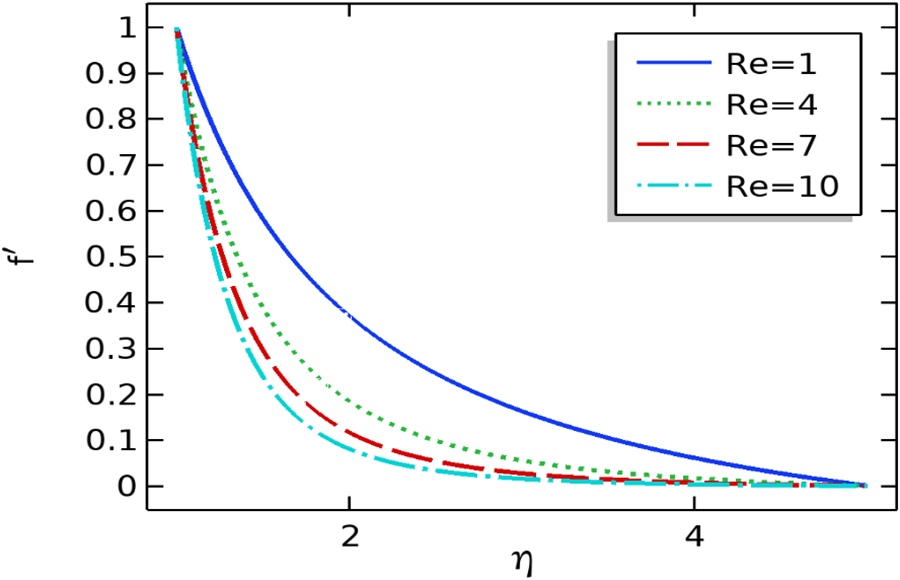
Figure 4: The repercussion of Re on the velocity profile (f′) for given Pr=10 , β=5 , λ=0.01 , and ε=2

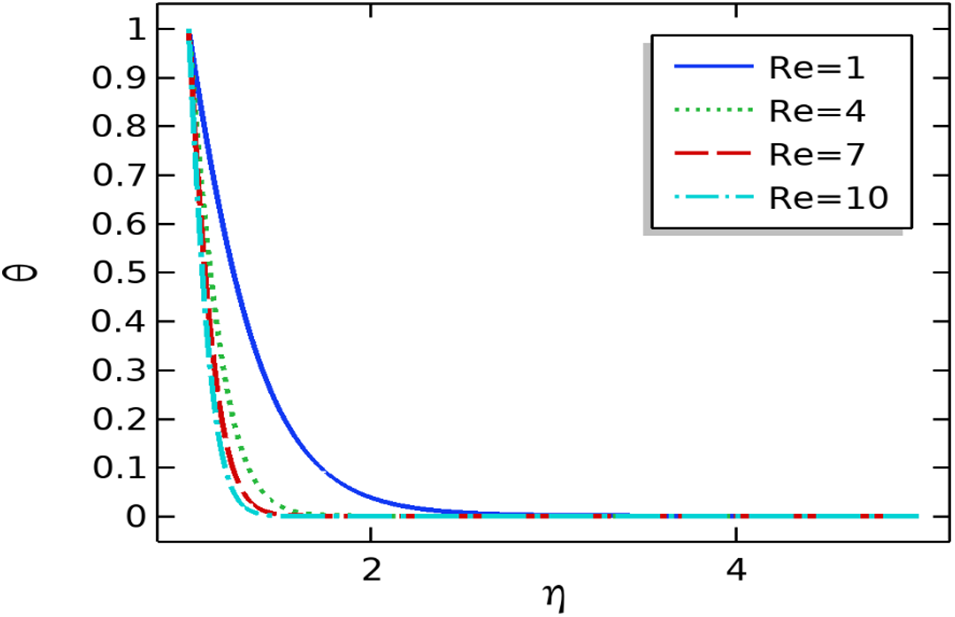
Figure 5: The repercussion of Re on the temperature profile (θ) for given Pr=10 , β=5 , λ=0.01 , and ε=2

Figs. 6 and 7 describe the persuasion of ferromagnetic response numbers on the velocity and temperature profiles (β) . The parameter β exhibits the interaction of magnetization and thermal forces. A case β=0 shows that there is no impact of magneto-thermomechanical interaction. This case can be achieved in the absence of a magnetic flux. The magnetic dipole reduces the ferrofluid velocity and enhances the temperature of the fluid. The parameter β has a crucial role in the heat transfer enhancement in ferrhydrodynamic flow. Fig. 8 represents the role of the viscous dissipation parameter (λ) in temperature distribution. The parameter shows the impact of shear forces on heat transfer. The parameter λ does not affect the temperature distribution when shear forces are small. Despite that, for higher range of λ is useful to heat transfer enhancement.

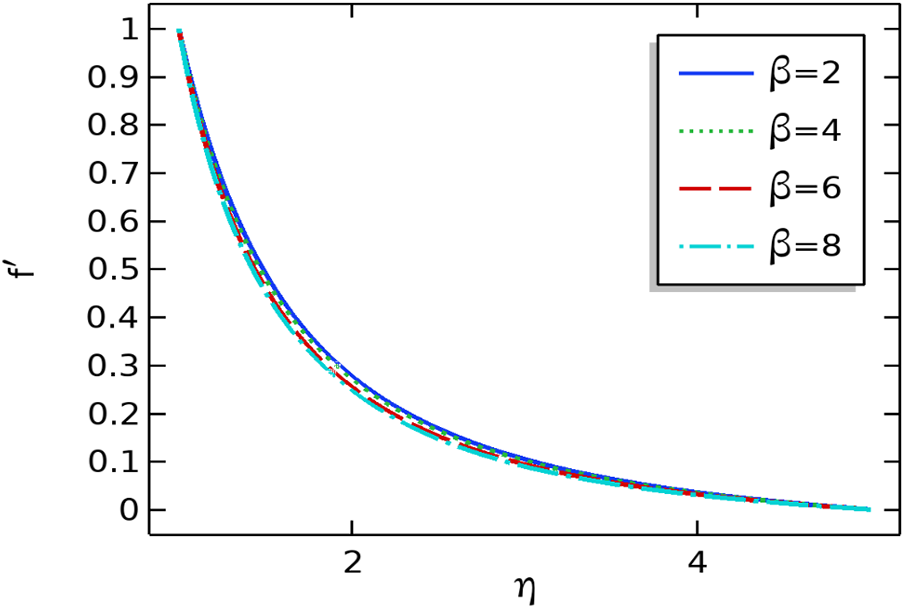
Figure 6: The repercussion of β on the velocity profile (f′) for given Pr=10 , Re=2 , λ=0.01 , and ε=2

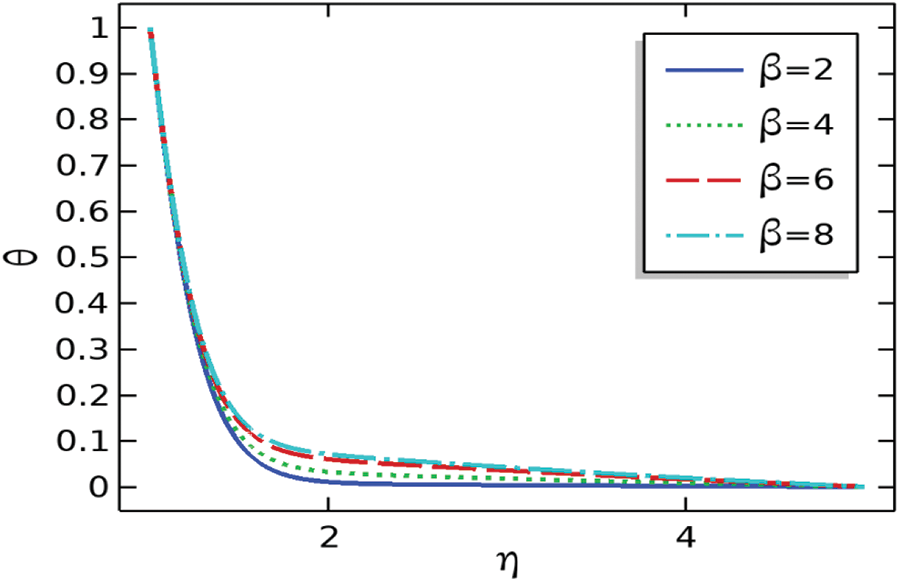
Figure 7: The repercussion of β on the temperature profile (θ) for given Pr=10 , Re=2 , λ=0.01 , and ε=2

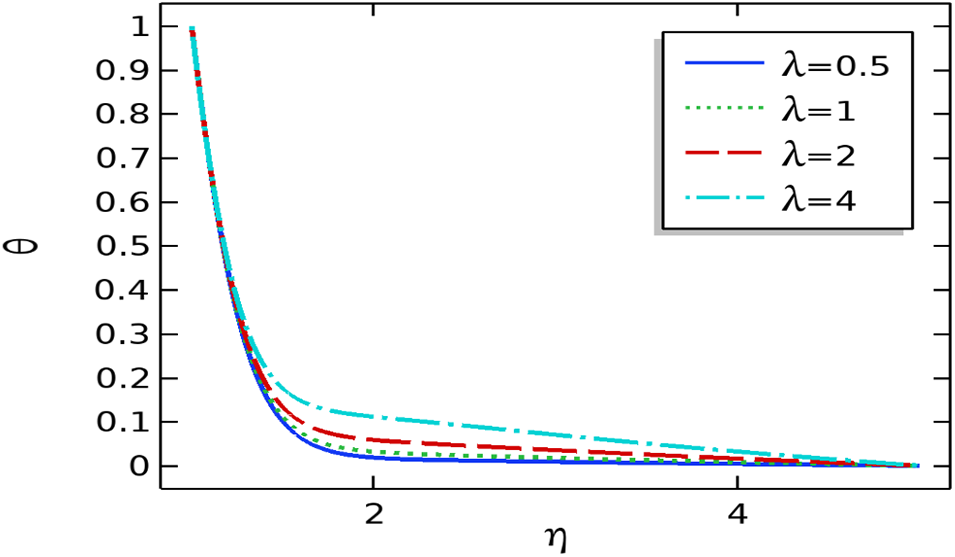
Figure 8: The repercussion of λ on the temperature profile (θ) for given Pr=10 , Re=2 , β=5 , and ε=2

Table 2 represents variation in friction coefficient and surface Nusselt number for different ranges of physical characteristics. The friction and the thermal flow rate are higher in the present study as compared to ordinary viscous fluid reported in the previous investigations [6,11]. Enhancing the values of Re intensifies the friction on the surface of the cylinder and favors the local heat transfer. This range of heat transfer in ordinary viscous fluid is attained for Re=100 where the Prandtl number is taken seven [11]. In the present model, magnetization force and Prandtl number influence the range of local heat transfer.

5  Conclusions

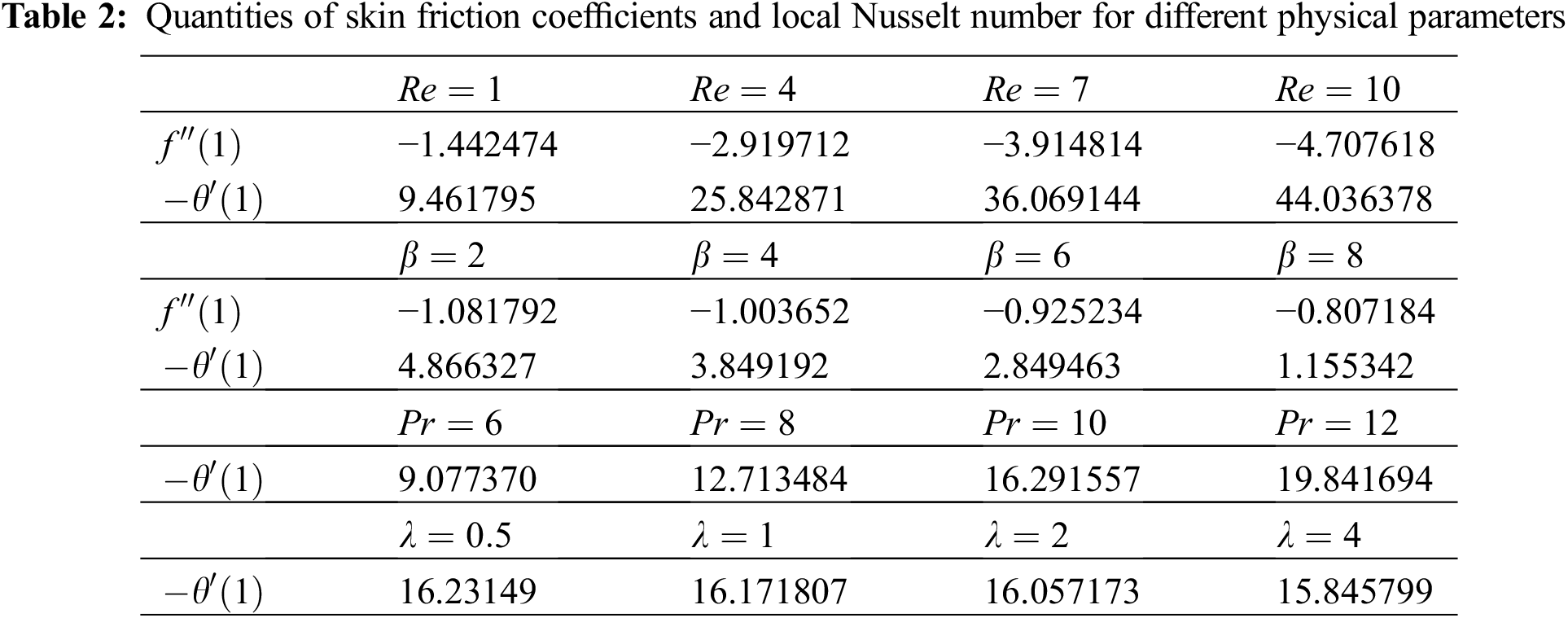
The present study demonstrates the influence of the parameters Pr , Re , β and λ on the velocity and temperature in the flow of ferrofluid due to the stretching cylinder. The Prandtl number for ferrofluid keeps higher heat transfer on the surface of the cylinder as compared to ordinary viscous fluid. At the lower span of Reynolds numbers from 1 to 10, the magnetic dipole intensifies the heat transfer in the magnetic fluid. However, for ordinary viscous fluid, this amount of heat transfer can be obtained, if the Reynold number is greater than 100 [6,11]. When inertial forces dominate over viscous forces, the velocity, and temperature in the flow decrease. Boosting the amounts of ferromagnetic response number enhances the magnetism-thermomechanical linkage in the course of flow and this interaction reduces the velocity and enhances the temperature.

Acknowledgement: None.

Funding Statement: The author received no specific funding for this study.

Author Contributions: All the work done by corresponding author.

Availability of Data and Materials: The data that support the findings of this study are available on request from the corresponding author.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. Odenbach, S., Thurm, S. (2002). Magnetoviscous effects in ferrofluids. Berlin, Heidelberg: Springer Berlin Heidelberg. https://doi.org/10.1007/3-540-45646-5_10 [Google Scholar] [CrossRef]

2. Bailey, R. L. (1983). Lesser known applications of ferrofluids. Journal of Magnetism and Magnetic Materials, 39(1–2), 178–182. https://doi.org/10.1016/0304-8853(83)90428-6 [Google Scholar] [CrossRef]

3. Rosensweig, R. E. (1985). Ferrohydrodynamics. Cambridge, New York, USA: Cambridge University Press. [Google Scholar]

4. Blums, E., Cebers, A., Maiorov, M. M. (2010). Magnetic fluids. Berlin: Walter de Gruyter. [Google Scholar]

5. Berkovsky, B. M., Medvedev, V. F., Krakov, M. S. (1993). Magnetic fluids: Engineering applications. New York: Oxford University Press. [Google Scholar]

6. Wang, C. Y. (1988). Fluid flow due to a stretching cylinder. The Physics of Fluids, 31(3), 466–468. https://doi.org/10.1063/1.866827 [Google Scholar] [CrossRef]

7. Usman, M., Soomro, F. A., Haq, R. U., Wang, W., Defterli, O. (2018). Thermal and velocity slip effects on casson nanofluid flow over an inclined permeable stretching cylinder via collocation method. International Journal of Heat and Mass Transfer, 122, 1255–1263. https://doi.org/10.1016/j.ijheatmasstransfer.2018.02.045 [Google Scholar] [CrossRef]

8. Tlili, I., Khan, W. A., Khan, I. (2018). Multiple slips effects on MHD SA-Al2O3 and SA-Cu non-newtonian nanofluids flow over a stretching cylinder in porous medium with radiation and chemical reaction. Results in Physics, 8, 213–222. https://doi.org/10.1016/j.rinp.2017.12.013 [Google Scholar] [CrossRef]

9. Fang, T. G., Zhang, J., Zhong, Y. F., Tao, H. (2011). Unsteady viscous flow over an expanding stretching cylinder. Chinese Physics Letters, 28(12), 124707. https://doi.org/10.1088/0256-307X/28/12/124707 [Google Scholar] [CrossRef]

10. Munawar, S., Ali, A., Mehmood, A. (2012). Thermal analysis of the flow over an oscillatory stretching cylinder. Physica Scripta, 86(6), 065401. https://doi.org/10.1088/0031-8949/86/06/065401 [Google Scholar] [CrossRef]

11. Ishak, A., Nazar, R., Pop, I. (2008). Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Energy Conversion and Management, 49(11), 3265–3269. https://doi.org/10.1016/j.enconman.2007.11.013 [Google Scholar] [CrossRef]

12. Wang, C. Y., Ng, C. O. (2011). Slip flow due to a stretching cylinder. International Journal of Non-Linear Mechanics, 46(9), 1191–1194. https://doi.org/10.1016/j.ijnonlinmec.2011.05.014 [Google Scholar] [CrossRef]

13. Ishak, A., Nazar, R., Pop, I. (2008). Uniform suction/blowing effect on flow and heat transfer due to a stretching cylinder. Applied Mathematical Modelling, 32(10), 2059–2066. https://doi.org/10.1016/j.apm.2007.06.036 [Google Scholar] [CrossRef]

14. Mukhopadhyay, S. (2013). MHD boundary layer slip flow along a stretching cylinder. Ain Shams Engineering Journal, 4(2), 317–324. https://doi.org/10.1016/j.asej.2012.07.003 [Google Scholar] [CrossRef]

15. Khan, M., Ahmed, A., Irfan, M., Ahmed, J. (2021). Analysis of Cattaneo–Christov theory for unsteady flow of Maxwell fluid over stretching cylinder. Journal of Thermal Analysis and Calorimetry, 144, 145–154. https://doi.org/10.1007/s10973-020-09343-1 [Google Scholar] [CrossRef]

16. Maskeen, M. M., Zeeshan, A., Mehmood, O. U., Hassan, M. (2019). Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. Journal of Thermal Analysis and Calorimetry, 138, 1127–1136. https://doi.org/10.1007/s10973-019-08304-7 [Google Scholar] [CrossRef]

17. Chu, Y. M., Bilal, S., Hajizadeh, M. R. (2020). Hybrid ferrofluid along with MWCNT for augmentation of thermal behavior of fluid during natural convection in a cavity. Mathematical Methods in the Applied Sciences. https://doi.org/10.1002/mma.6937 [Google Scholar] [CrossRef]

18. Kumar, V., Madhukesh, J. K., Jyothi, A. M., Prasannakumara, B. C., Khan, M. I. et al. (2021). Analysis of single and multi-wall carbon nanotubes (SWCNT/MWCNT) in the flow of Maxwell nanofluid with the impact of magnetic dipole. Computational and Theoretical Chemistry, 1200, 113223. https://doi.org/10.1016/j.comptc.2021.113223 [Google Scholar] [CrossRef]

19. Hashmi, M. S., Khan, N., Khan, S. U., Khan, M. I., Khan, N. B. et al. (2021). Dynamics of coupled reacted flow of Oldroyd-B material induced by isothermal/exothermal stretched disks with Joule heating, viscous dissipation and magnetic dipoles. Alexandria Engineering Journal, 60(1), 767–783. https://doi.org/10.1016/j.aej.2020.10.007 [Google Scholar] [CrossRef]

20. Khan, D., Ali, G., Khan, A., Khan, I., Chu, Y. M. et al. (2020). A new idea of fractal-fractional derivative with power law kernel for free convection heat transfer in a channel flow between two static upright parallel plates. Computers, Materials & Continua, 65(2), 1237–1251. https://doi.org/10.32604/cmc.2020.011492 [Google Scholar] [CrossRef]

21. Malik, M. Y., Hussain, A., Salahuddin, T., Awais, M. (2016). Numerical solution of MHD Sisko fluid over a stretching cylinder and heat transfer analysis. International Journal of Numerical Methods for Heat & Fluid Flow, 26(6), 1787–1801. https://doi.org/10.1108/HFF-06-2015-0211 [Google Scholar] [CrossRef]

22. Kumar, R. N., Gowda, R. P., Abusorrah, A. M., Mahrous, Y. M., Abu-Hamdeh, N. H. et al. (2021). Impact of magnetic dipole on ferromagnetic hybrid nanofluid flow over a stretching cylinder. Physica Scripta, 96(4), 045215. https://doi.org/10.1088/1402-4896/abe324 [Google Scholar] [CrossRef]

23. Bilal, M., Sagheer, M., Hussain, S. (2018). Numerical study of magnetohydrodynamics and thermal radiation on Williamson nanofluid flow over a stretching cylinder with variable thermal conductivity. Alexandria Engineering Journal, 57(4), 3281–3289. https://doi.org/10.1016/j.aej.2017.12.006 [Google Scholar] [CrossRef]

24. Bhandari, A. (2019). Radiation and chemical reaction effects on nanofluid flow over a stretching sheet. Fluid Dynamics & Materials Processing, 15(4), 557–582. https://doi.org/10.32604/fdmp.2019.04108 [Google Scholar] [CrossRef]

25. Reddy, S. R. R., Bala Anki Reddy, P., Rashad, A. M. (2020). Activation energy impact on chemically reacting Eyring–Powell nanofluid flow over a stretching cylinder. Arabian Journal for Science and Engineering, 45, 5227–5242. https://doi.org/10.1007/s13369-020-04379-9 [Google Scholar] [CrossRef]

26. Ferdows, M., Murtaza, M. G., Tzirtzilakis, E. E., Alzahrani, F. (2020). Numerical study of blood flow and heat transfer through stretching cylinder in the presence of a magnetic dipole. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 100(7), e201900278. https://doi.org/10.1002/zamm.201900278 [Google Scholar] [CrossRef]

27. Nobari, M. R. H., Naderan, H. (2006). A numerical study of flow past a cylinder with cross flow and inline oscillation. Computers & Fluids, 35(4), 393–415. https://doi.org/10.1016/j.compfluid.2005.02.004 [Google Scholar] [CrossRef]

28. Rehman, K. U., Khan, A. A., Malik, M. Y., Hussain, A. (2017). Numerical study of a thermally stratified flow of a tangent hyperbolic fluid induced by a stretching cylindrical surface. The European Physical Journal Plus, 132(9), 389. https://doi.org/10.1140/epjp/i2017-11677-3 [Google Scholar] [CrossRef]

29. Salahuddin, T., Siddique, N., Khan, M., Chu, Y. M. (2022). A hybrid nanofluid flow near a highly magnetized heated wavy cylinder. Alexandria Engineering Journal, 61(2), 1297–1308. https://doi.org/10.1016/j.aej.2021.06.014 [Google Scholar] [CrossRef]

30. Salahuddin, T., Khan, M., Chu, Y. M. (2021). Zero velocity regions near forward and rare points of circular cylinder: A heat and mass transfer study. Ain Shams Engineering Journal, 12(2), 2255–2261. https://doi.org/10.1016/j.asej.2020.12.011 [Google Scholar] [CrossRef]

31. Ullah, Z., Ashraf, M., Zia, S., Chu, Y., Khan, I. et al. (2020). Computational analysis of the oscillatory mixed convection flow along a horizontal circular cylinder in thermally stratified medium. Computers, Materials & Continua, 65(1), 109–123. https://doi.org/10.32604/cmc.2020.011468 [Google Scholar] [CrossRef]

32. Song, Y. Q., Waqas, H., Al-Khaled, K., Farooq, U., Khan, S. U. et al. (2021). Bioconvection analysis for Sutterby nanofluid over an axially stretched cylinder with melting heat transfer and variable thermal features: A Marangoni and solutal model. Alexandria Engineering Journal, 60(5), 4663–4675. https://doi.org/10.1016/j.aej.2021.03.056 [Google Scholar] [CrossRef]

33. Kumar, K. G., Manjunatha, S., Rudraswamy, N. G. (2020). MHD flow and nonlinear thermal radiative heat transfer of dusty Prandtl fluid over a stretching sheet. Fluid Dynamics & Materials Processing, 16(2), 131–146. https://doi.org/10.32604/fdmp.2020.0152 [Google Scholar] [CrossRef]

34. Kalaivanan, R., Ganesh, N. V., Al-Mdallal, Q. M. (2021). Buoyancy driven flow of a second-grade nanofluid flow taking into account the Arrhenius activation energy and elastic deformation: Models and numerical results. Fluid Dynamics & Materials Processing, 17(2), 319–332. https://doi.org/10.32604/fdmp.2021.012789 [Google Scholar] [CrossRef]

35. Naseem, T., Bibi, I., Shahzad, A., Munir, M. (2023). Analysis of heat transport in a Powell-Eyring fluid with radiation and Joule heating effects via a similarity transformation. Fluid Dynamics & Materials Processing, 19(3), 663–677. https://doi.org/10.32604/fdmp.2022.021136 [Google Scholar] [CrossRef]

36. Nadeem, S., Ullah, N., Khan, A. U., Akbar, T. (2017). Effect of homogeneous-heterogeneous reactions on ferrofluid in the presence of magnetic dipole along a stretching cylinder. Results in Physics, 7, 3574–3582. https://doi.org/10.1016/j.rinp.2017.09.006 [Google Scholar] [CrossRef]

37. Neuringer, J. L. (1966). Some viscous flows of a saturated ferro-fluid under the combined influence of thermal and magnetic field gradients. International Journal of Non-Linear Mechanics, 1(2), 123–137. https://doi.org/10.1016/0020-7462(66)90025-4 [Google Scholar] [CrossRef]

38. Bhandari, A. (2021). Entropy generation and heat transfer analysis for ferrofluid flow between two rotating disks with variable conductivity. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 235(21), 5877–5891. https://doi.org/10.1177/0954406221991184 [Google Scholar] [CrossRef]

39. Bhandari, A., Husain, A. (2021). Optimization of heat transfer properties on ferrofluid flow over a stretching sheet in the presence of static magnetic field. Journal of Thermal Analysis and Calorimetry, 144, 1253–1270. https://doi.org/10.1007/s10973-020-09636-5 [Google Scholar] [CrossRef]