 Open Access
Open Access
ARTICLE
Numerical Simulation of Microscopic Seepage Mechanisms in Gas Reservoir Storage Systems
1 National Key Laboratory of Oil & Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, 610500, China
2 Chongqing Gas Mine, Southwest Oil & Gas Field Company, Petroleum China, Chongqing, 400000, China
3 Research Institute of Petroleum Exploration & Development, Southwest Oil and Gas Field Company, PetroChina, Chengdu, 610041, China
* Corresponding Author: Yang Luo. Email:
(This article belongs to the Special Issue: Fluid and Thermal Dynamics in the Development of Unconventional Resources III)
Fluid Dynamics & Materials Processing 2025, 21(12), 3073-3090. https://doi.org/10.32604/fdmp.2025.070685
Received 21 July 2025; Accepted 15 December 2025; Issue published 31 December 2025
Abstract
The development of underground gas storage (UGS) systems is vital for maintaining stability between energy supply and demand. This study explores the dynamic response mechanisms of carbonate reservoirs subjected to intense injection–production cycling during UGS operations. By integrating three-dimensional digital core technology with a coupled poro-mechanical model, we simulate the pore-scale behavior of a representative Huangcaoxia UGS carbonate core. The results demonstrate that fluid–solid coupling effects markedly amplify permeability reduction, far exceeding the influence of porosity variations alone. More significantly, gas production leads to a pronounced decline in permeability driven by rising effective stress, arising from localized stress concentration at pore throats and reorganization of the internal flow field. The provided insights are intended as a theoretical basis for refining operational strategies and enhancing the long-term performance and reliability of underground gas storage facilities.Keywords
The importance of UGS is universally acknowledged in regions with evolving energy structures and growing reliance on natural gas. The efficient construction and safe operation of UGS facilities are critically dependent on dynamic simulation monitoring during the injection and production processes [1]. Such monitoring is indispensable for optimizing storage strategies, ensuring operational safety, and mitigating risks associated with rapid cycling and fluctuating reservoir pressures.
The efficacy and safety of UGS operations are fundamentally governed by the multiphysical processes occurring at the pore scale, where the microstructure of the rock dictates fluid flow and geomechanical response [2,3]. In this context, “microscopic seepage” refers specifically to the complex flow dynamics of natural gas within the intricate network of pores and throats (typically at micron to nanometer scales), driven by pressure gradients during injection and production cycles [4]. It is critical to distinguish this pore-scale physics from microseepage, a term used in near-surface geochemistry to describe the vertical migration of light hydrocarbon gases to the surface [5,6]. Recent advances, particularly leveraging modern sensing and interpretation frameworks, highlight the growing application of microseepage detection for integrity surveillance of geological gas storage sites [6]. Understanding microscopic seepage is paramount because it directly controls the macroscopic properties of the reservoir, such as absolute permeability and storativity [7]. Dynamic alterations in pore geometry, which are induced by the effective stress changes from cyclic pressure loading, can significantly modify these properties. This process ultimately determines the injectivity, deliverability, and long-term integrity of the storage facility [8].
Accurately modeling this pore-scale coupling is therefore critical for predicting reservoir integrity and optimizing storage operations, yet it remains a formidable challenge. Macroscopic field-scale models, which are currently predominant in UGS simulation studies [9], often inadequately represent the fluid-solid coupling effects that dynamically alter key seepage parameters, including porosity, permeability, and volumetric strain, at the microscale during cyclic injection and production [10]. These alterations are driven by effective stress variations induced by pore pressure fluctuations [11,12,13]. The theoretical underpinnings for fluid-solid coupling (FSC) in deformable porous media were established by Terzaghi’s principle of effective stress [14] and subsequently generalized into a three-dimensional continuum theory by Biot [15]. The ensuing decades saw the development of robust computational frameworks to solve these coupled equations numerically. Foundational work by Lewis, Schrefler, Zienkiewicz, and others [16,17] was instrumental in formalizing the Finite Element Method (FEM) for poroelasticity, while other numerical strategies like the Finite Difference Method (FDM) and Finite Volume Method (FVM) were advanced for efficient solution on structured grids [18,19]. For explicitly modeling discontinuities, the Discrete Element Method (DEM) introduced a transformative approach [20]. While these matured theoretical and numerical frameworks have been successfully applied to predict macroscopic field-scale behavior in problems ranging from hydraulic fracturing [21,22,23] to salt cavern integrity [24], a significant gap persists. The majority of these applications, including recent investigations into hydrogen storage [25] and repurposed mines [26], operate at the macroscopic scale. They often rely on constitutive models that cannot resolve the critical pore-throat deformation mechanisms and the consequent dynamic evolution of flow pathways, which are the fundamental origins of the macroscopic behaviors they seek to predict. Furthermore, while multiscale modeling frameworks [27,28] have been proposed to bridge this scale disparity, their application in predicting the evolution of microscopic seepage parameters in UGS contexts remains limited.
This critical gap impedes a mechanistic understanding of how pore-throat deformation and seepage field evolution interact, ultimately limiting the predictive accuracy of macroscopic models for UGS performance. To address this fundamental limitation, this study investigates a typical carbonate reservoir from the Huangcaoxia Gas Storage facility. We construct a true digital core model derived from high-resolution 3D X-ray computed tomography (CT) scanning data. Moving beyond conventional macroscopic approaches or simplified pore-network models, we develop a novel microscale finite-element fluid-solid coupling model. This model uniquely integrates the Navier-Stokes equations for fluid flow with a linear elastic constitutive model for the solid matrix [29,30], enabling the simulation of fully coupled hydro-mechanical processes at the pore scale. The primary objective is to systematically simulate the impact of stress-pressure cyclic loading during intense injection-production operations on reservoir multi-physical field parameters. This framework allows us to quantitatively elucidate the dynamic deformation characteristics of pore-throat structures [23], the stress-dependent evolution of flow channel efficiency, and the energy transfer mechanisms between the matrix and fluid phases [31], thereby providing pore-scale insights that are critical for predicting the long-term behavior of UGS reservoirs. Furthermore, while this study focuses on the internal pore-scale mechanisms governing storage performance, it is recognized that ensuring the long-term security of UGS operations also relies on monitoring external signals. Techniques such as geochemical microseepage detection provide an independent and critical means to verify containment security by detecting potential gas leakage to the surface, thereby complementing the predictive models developed from fundamental pore-scale studies [5].
2 Microscopic Fluid-Solid Coupling Theory and Model Solving Steps
The simulation methods for solving fluid-solid coupling (FSC) problems are constantly evolving, with each technique offering distinct advantages for specific scenarios. The commonly used numerical methods include the finite volume method (FVM), renowned for its inherent conservation properties making it a predominant choice for computational fluid dynamics problems [18]; the finite difference method (FDM), which is straightforward to implement for structured grids but can become complex for irregular geometries [19]; and the discrete element method (DEM), which excels in simulating discontinuous media, such as the mechanical behavior of fractured rock masses [20].
However, for modeling the complex, heterogeneous geometries of real pore-fracture systems and solving the coupled system of partial differential equations governing fluid flow and solid deformation, the finite element method (FEM) presents superior advantages. The FEM provides exceptional flexibility in handling intricate boundaries and a strong theoretical foundation for modeling multiphysics phenomena [29,30], which are critical requirements for this study.
Consequently, this study employs an innovative numerical simulation approach based on FEM to achieve precise modeling of microscale seepage behavior in realistic pore-fracture systems, with full consideration of fluid-solid coupling effects. The methodology bridges the gap in conventional single-physics modeling by establishing mutual coupling between hydrodynamic and geomechanical fields. Specifically, the mathematical framework consists of three core equation systems: the fluid flow governing equations, the solid deformation governing equations, and the bidirectional fluid-solid coupling equations. The model is solved using the finite element method, with adaptive mesh refinement technology implemented to ensure micron-level computational accuracy at pore-fracture interfaces.
The governing equations for fluid flow adopt an incompressible formulation with gravitational effects neglected. This simplification is justified for the following reasons: (1) At the pore scale and for the pressure gradients investigated in this study, the Bond number is significantly less than 1, indicating that capillary forces dominate over gravitational forces. (2) For the single-phase methane flow under the operational pressures of the target gas storage facility, the pressure changes are insufficient to induce significant density variations, justifying the incompressible flow assumption. This approach maintains computational efficiency while capturing the essential flow physics dominated by viscous and capillary forces at the pore scale. The momentum equation is written according to the conservation of momentum.
It is acknowledged that these assumptions limit the direct applicability of the results to scenarios with stronger buoyancy drives (e.g., CO2 storage) or significantly higher pressure differentials.
The seepage process is described by the Navier-Stokes equation that reflects the velocity field
The solid mechanics governing equation characterizes the solid volume strain by the effect of stress [34]. The solid mechanics governing equation applicable to micro-deformation is as follows:
The fluid-solid coupling equation reflects the fluid load on the structure [35]:
And the effect of velocity transfer to the fluid [35]:
This study employs the finite element method to numerically solve the established fluid-solid coupling governing equations [36], with Fig. 1 illustrating the complete solution workflow. The implementation procedure consists of the following key steps:
- (1)Model Discretization & Initialization: The computational domain is spatially discretized using high-order tetrahedral elements (quadratic shape functions) based on imported mesh files, dividing the region into characteristic elements. Initial material parameters (including porosity, permeability, elastic modulus, etc.) are assigned to each representative element, with triaxial stress and pore pressure boundary conditions applied according to operational scenarios.
- (2)Nonlinear System Solution: The coupled nonlinear PDE system is solved via Newton-Raphson iteration, where the fluid field adopts incremental Navier-Stokes equations and the solid field employs updated Lagrangian formulation for finite deformation. Interface data transfer ensures field coupling at each iteration.
- (3)Multiphysics Data Extraction: Key physical quantities are extracted from representative elements post-calculation, including: Von Mises stress (matrix strength), logarithmic strain (finite deformation), volumetric flow rate (seepage capacity), and displacement vector fields (structural deformation), with 3D field distributions exported.
- (4)Parametric Sensitivity Analysis: Systematic variation of triaxial confining pressure and pore pressure investigates effective stress effects on the coupled system. Comparative analysis with uncoupled models (single-field only) quantifies fluid-solid interaction mechanisms.
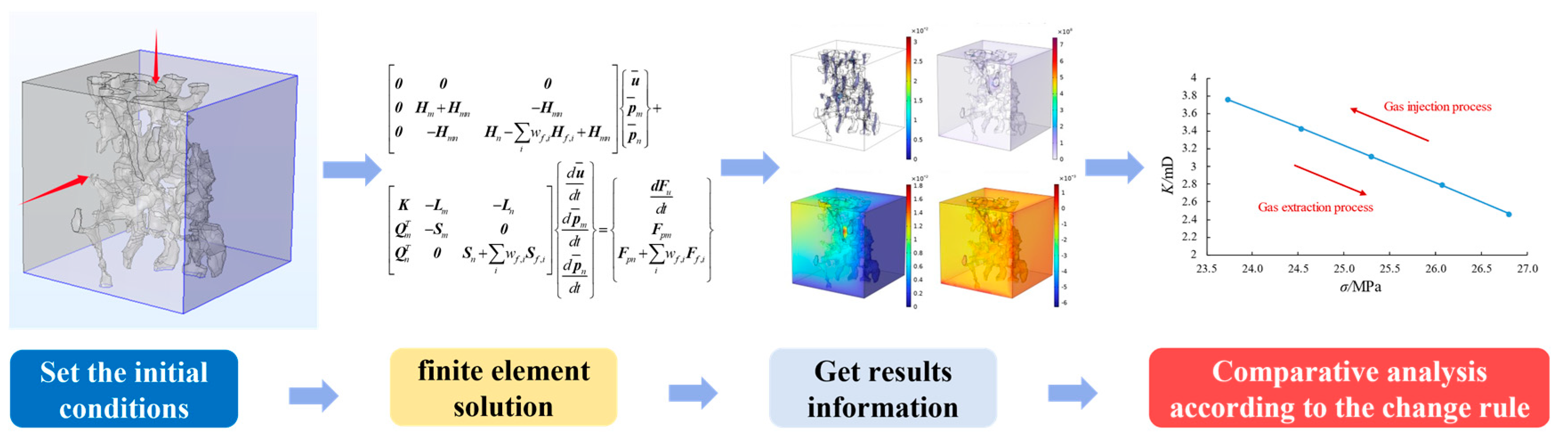
Figure 1: Numerical simulation solution process.
3 Fluid-Solid Coupling Model Based on 3D Digital Core
The Huangcaoxia reservoir, as a typical porous carbonate formation, has its complex spatial characteristics accurately characterized through 3D digital core technology. As shown in Fig. 2, the research team first conducted high-resolution CT scanning (0.15 μm resolution) of core samples, followed by threshold segmentation using an improved Otsu algorithm and 3D connectivity analysis to eliminate noise interference. The characteristic Representative Elementary Volume (REV) scale was determined by analyzing the convergence of the porosity [37]. To ensure statistical robustness and avoid contingency, the mean porosity was calculated from sub-volumes extracted from three independent locations (top, center, and bottom) of the digital core for each volume size. As shown in Fig. 3, the mean porosity stabilizes (variation < 1%) when the cube edge length exceeds ~130 voxels. Considering pore-throat network integrity and computational efficiency, a cube of 150 × 150 × 150 voxels was selected for digital core reconstruction. This REV scale is characteristic of the complex pore structure and heterogeneity of the studied carbonate sample.
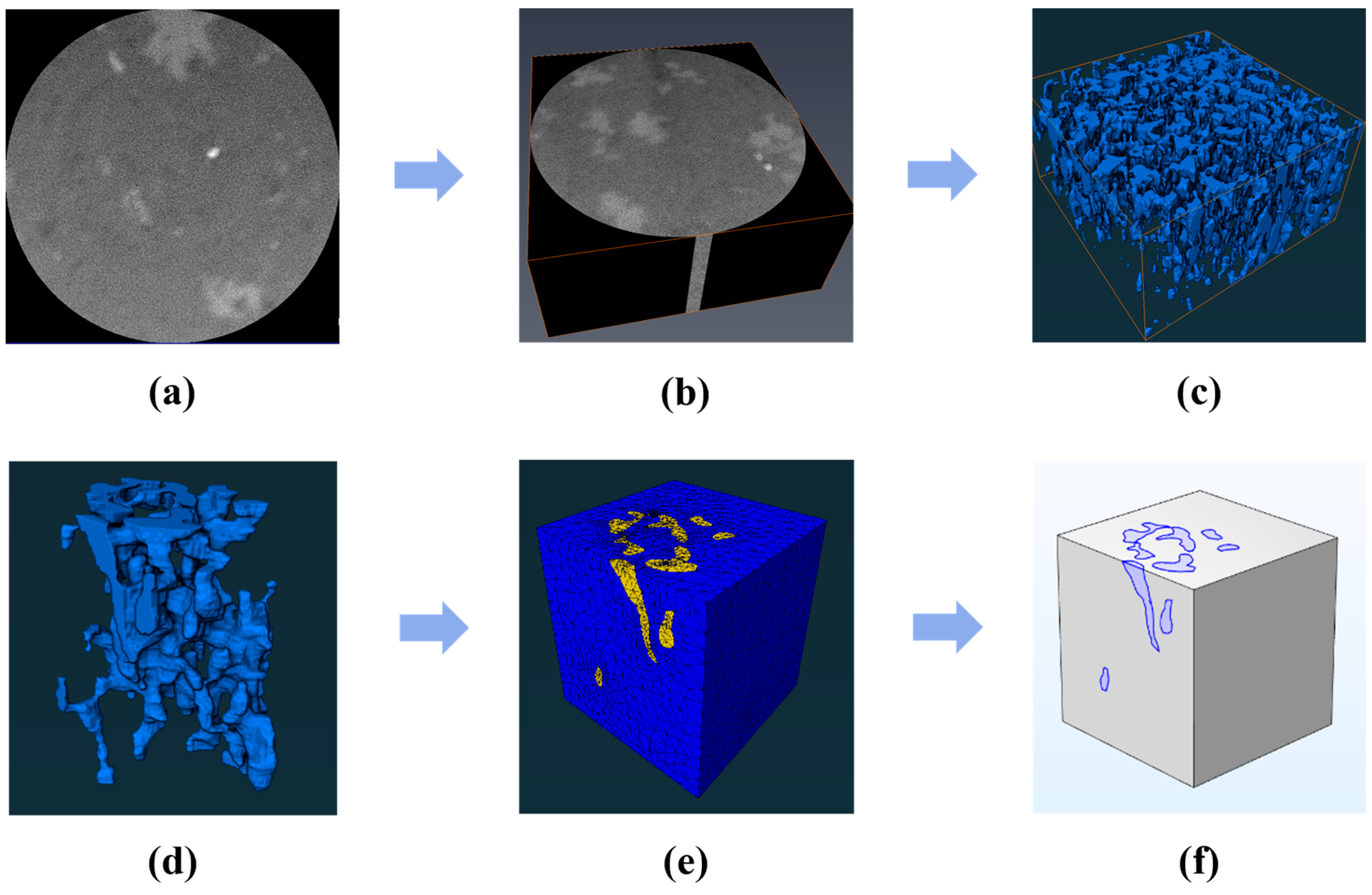
Figure 2: Fluid-solid coupling model establishment: (a) CT image; (b) 3D reconstruction; (c) Digital core; (d) Cropped pore model; (e) Matrix-pore model; (f) Domain (purple: pores, gray: matrix).
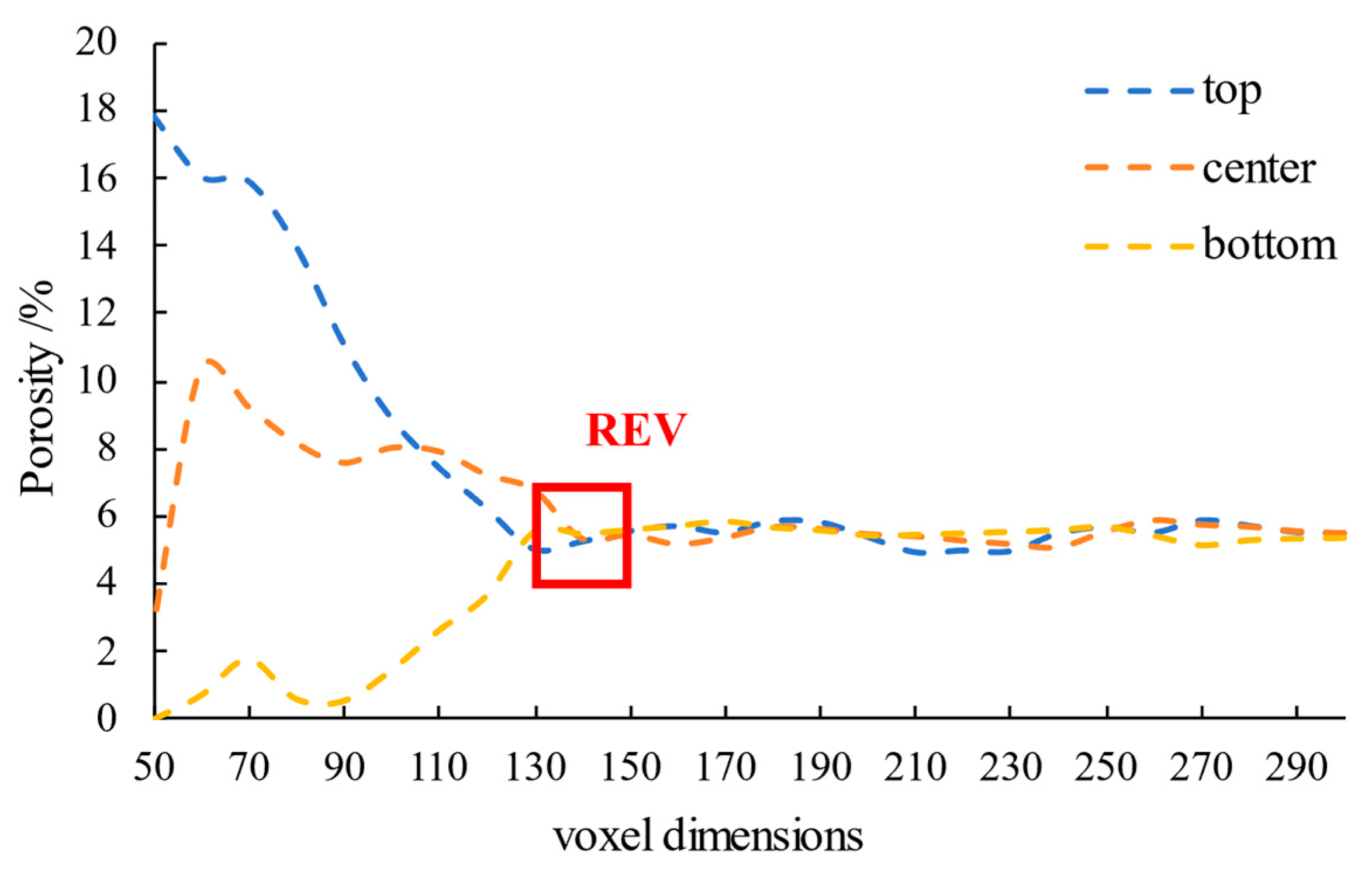
Figure 3: REV verification results.
Based on the grid independence verification (Fig. 4) and considering both grid quality and computational stability, the optimal mesh size was determined to be 84,816 cells [38]. The corresponding mesh structure was illustrated in Fig. 2e. To accurately capture the physical behavior of methane (CH4) under reservoir conditions (8.2~12.6 MPa), its density and dynamic viscosity were defined as functions of local pressure, implemented via user-defined functions based on the Peng-Robinson equation of state and the Lucas method, respectively. By coupling solid mechanics with laminar flow and dynamic meshing, a high-fidelity fluid-solid coupled FEM model was established.
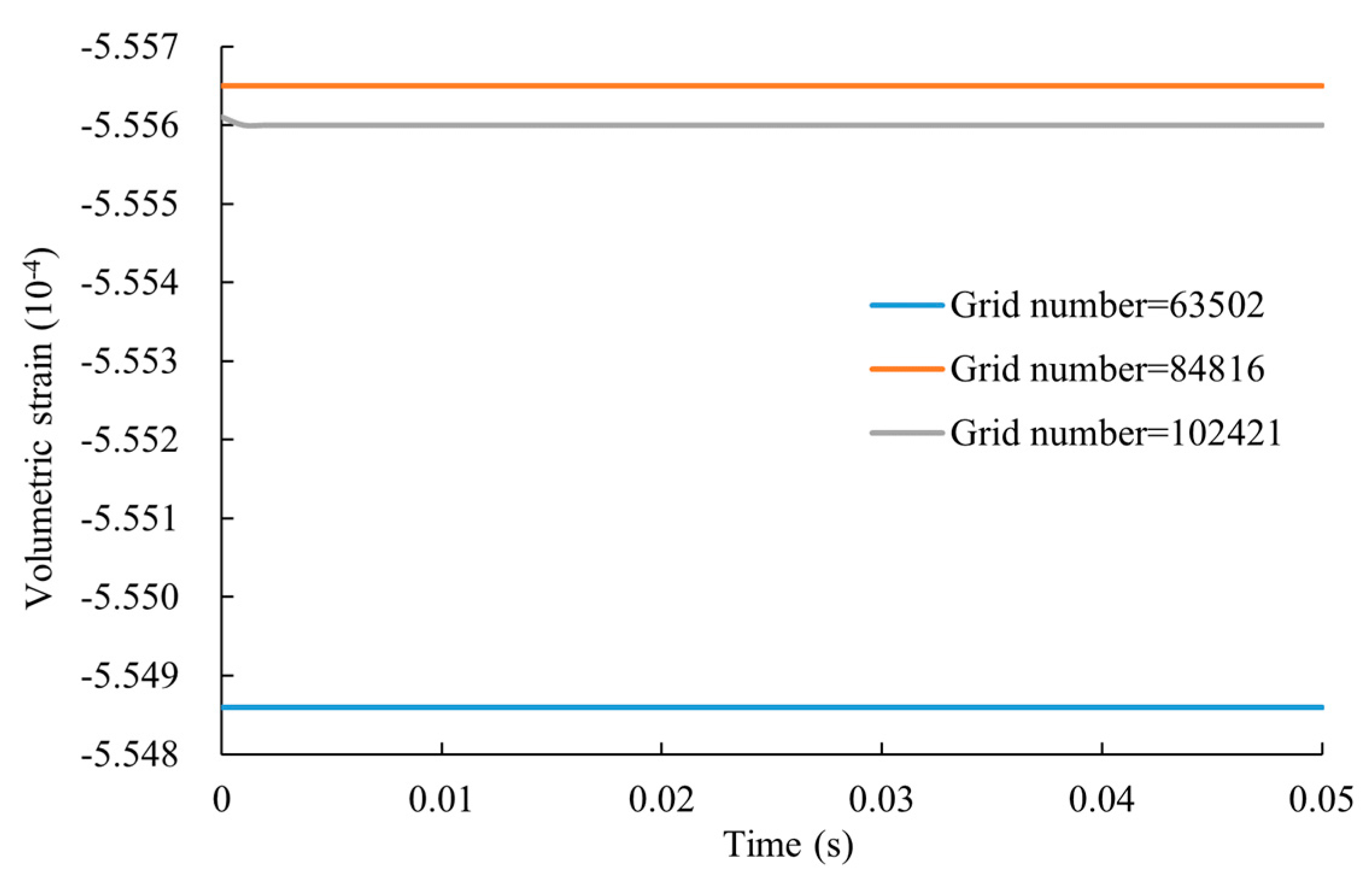
Figure 4: Grid independence verification.
To accurately characterize rock mechanical behavior in fluid-solid coupling simulations, mechanical parameters must be calibrated against experimental data. Triaxial tests from Well #1 of Huangcaoxia Gas Storage (Table 1) reveal significant heterogeneity: under 30 MPa confining pressure, core samples from 1040.37–1040.53 m depth show Young’s modulus of 49.5 GPa, Poisson’s ratio 0.29, and compressive strength 171.2 MPa; whereas samples from 1072.13–1072.25 m exhibit higher stiffness (68.79 GPa) and strength (527.1 MPa) at 20 MPa.
Table 1: Partial results of triaxial compression experiment of Caochu 1 well.
| Sample | Depth (m) | Confining Pressure (MPa) | Young’s Modulus (GPa) | Poisson’s Ratio | Compressive Strength (MPa) |
|---|---|---|---|---|---|
| 1 | 1040.37~1040.53 | 30 | 49.50 | 0.29 | 171.2 |
| 2 | 1072.13~1072.25 | 20 | 68.79 | 0.36 | 527.1 |
| 3 | 1169.97~1170.18 | 30 | 52.61 | 0.27 | 385.4 |
For the purpose of this pore-scale study, which focuses on the universal response of pore structures to effective stress changes rather than modeling a specific depth interval, a representative set of mechanical parameters is adopted. The matrix material parameters in the coupling model are set as: density 2700 kg/m3, Young’s modulus 5 × 1010 Pa (i.e., 50 GPa), and Poisson’s ratio 0.3. These values were obtained through a weighted averaging of the experimental data (<3% error) to represent the general mechanical behavior of the carbonate formation. We acknowledge that this approach homogenizes the inherent heterogeneity of the rock. However, given that the digital core model itself captures the geometric heterogeneity of pore spaces, and considering that the primary objective of this study is to investigate fundamental mechanisms and relative comparisons of stress-dependent permeability evolution at the pore scale, the use of representative averaged mechanical properties provides a consistent and well-defined baseline for such mechanistic exploration, an approach that is well-established in pore-scale numerical studies [13,25]. Future work will incorporate spatially varying mechanical properties to explore the effects of mineralogical heterogeneity on the coupled processes.
Fig. 5 provides a schematic representation of the boundary conditions implemented in the fluid-solid coupling model. For the matrix domain, a triaxial stress model was established: fixed constraints were applied to the bottom surface along three axial directions, overburden pressure was imposed on the top surface, while maximum and minimum horizontal principal stresses were applied to the other two side surfaces to simulate confining pressure conditions. For the pore domain, an initial pore pressure value was set to simulate the pore pressure environment.
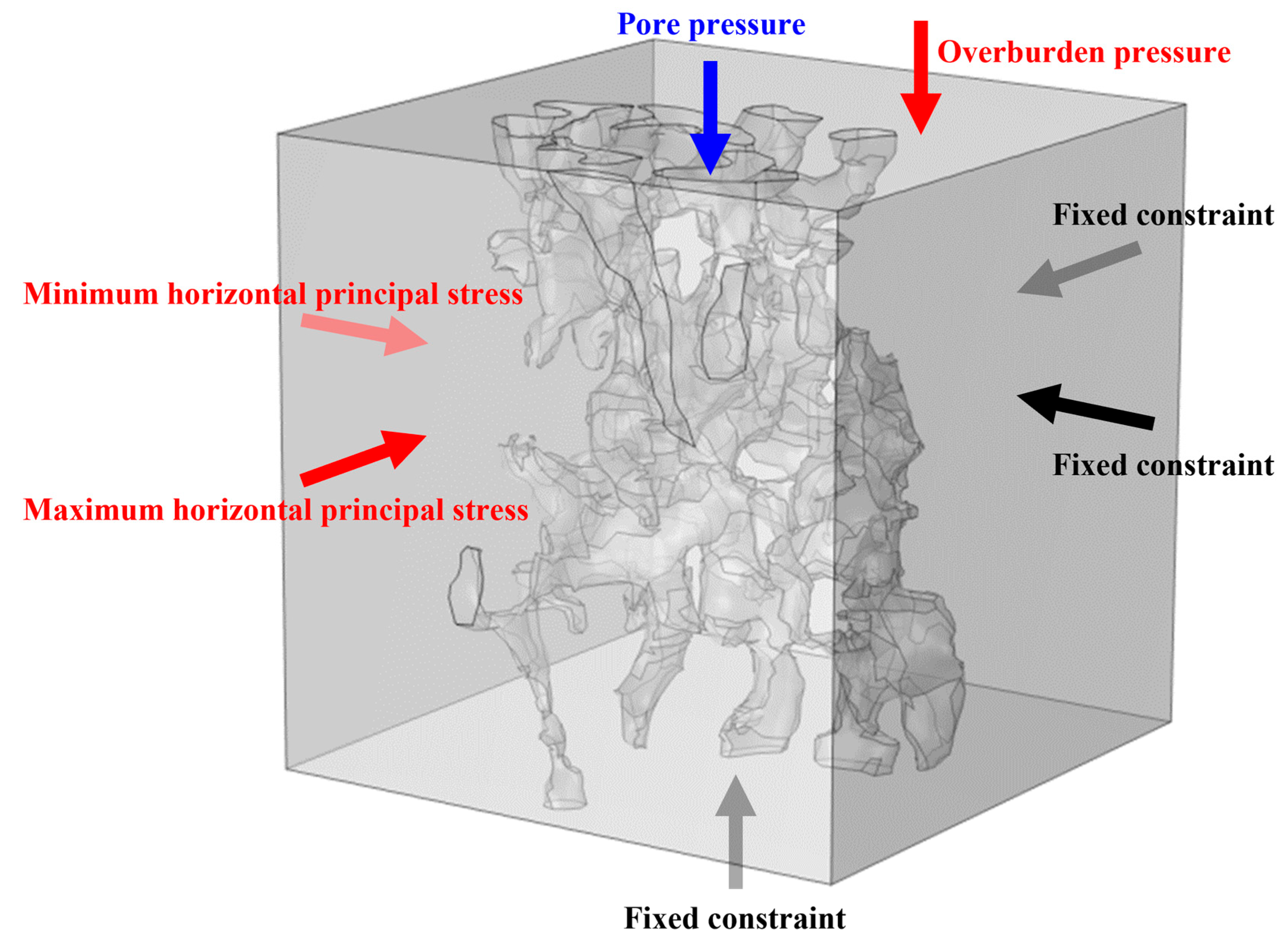
Figure 5: Schematic diagram of boundary conditions.
4 Numerical Simulation Results and Analysis
4.1 Stress Response Characteristics under Multi-Stage Confining Pressure Loading
An integrated coupled hydro-mechanical model was developed to examine stress-dependent behavior variations across varying confinement scenarios, with simulations conducted under a consistent pore fluid pressure of 1 MPa. The confinement pressure was systematically elevated from an initial 5 MPa to a final 40 MPa, employing 5 MPa stepwise increments throughout the pressure range (5, 10, 15, 20, 25, 30, 35, and 40 MPa). Fig. 6 clearly demonstrates the Von Mises stress distribution within the rock matrix at four representative confining pressure levels (10, 20, 30, and 40 MPa). Numerical results exhibit a pronounced positive dependence of rock matrix stress magnitude on the applied confinement pressure. Specifically, when the confining pressure was set at 10 MPa, the corresponding matrix stress reached approximately 2.53 MPa. This value exhibited a substantial increase to 21 MPa when the confining pressure was elevated to 40 MPa, indicating a strong stress sensitivity response. Furthermore, distinct stress concentration phenomena were consistently observed at the interfaces between the matrix and pores, particularly noticeable at higher confining pressure conditions. These interfacial stress concentrations were most pronounced in regions surrounding pore throats and irregular pore geometries. The interfacial stress concentrations highlight the importance of microstructural heterogeneity in stress distribution characteristics.
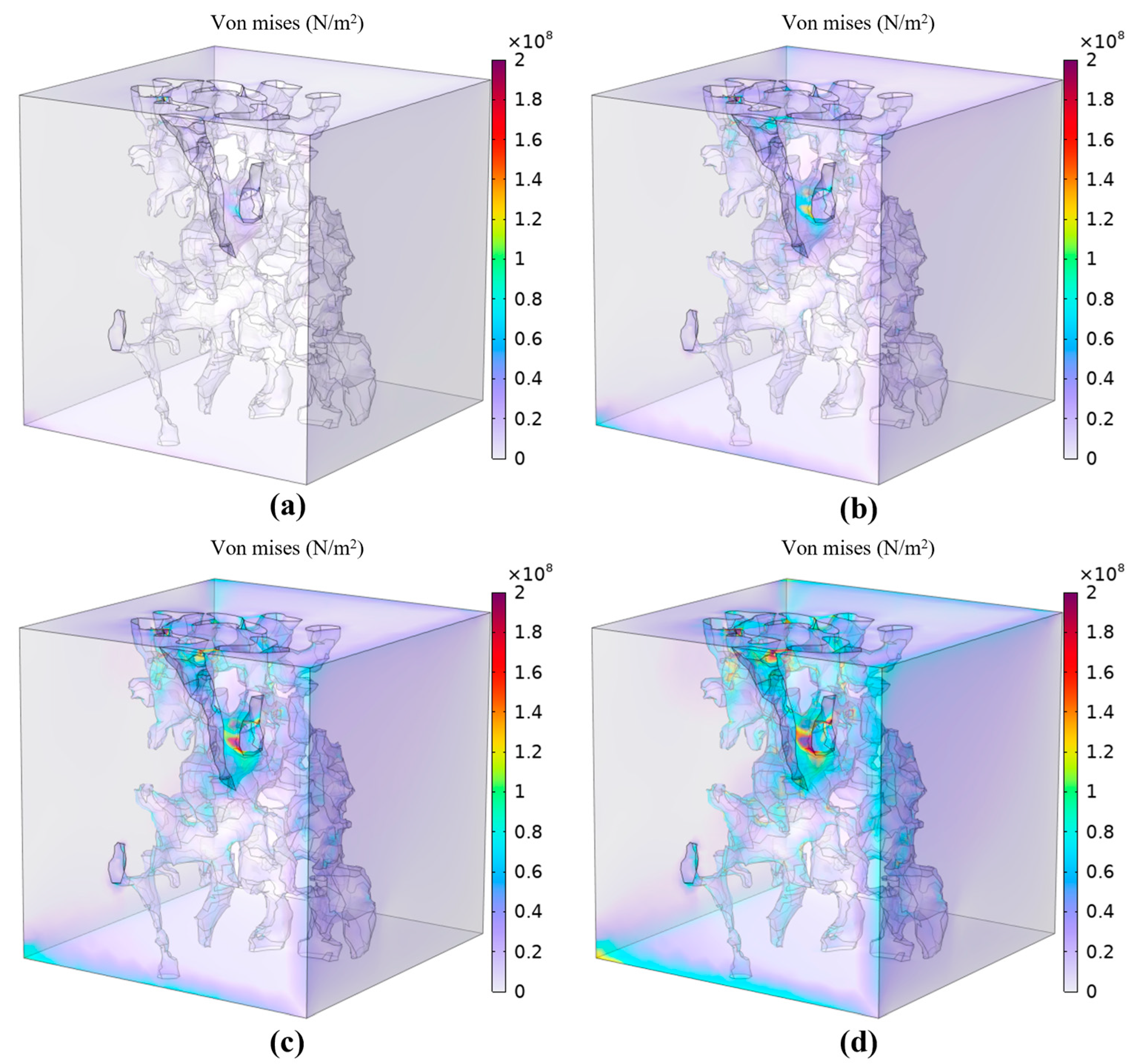
Figure 6: Von Mises stress distribution under different confining pressures: (a) 10 MPa, (b) 20 MPa, (c) 30 MPa, (d) 40 MPa.
Fig. 7 displays the spatial patterns of displacement fields within the rock matrix across four confinement levels (10, 20, 30, and 40 MPa). The computational outcomes indicate a marked progressive escalation in displacement amplitudes corresponding with increasing confinement intensity. Specifically, the matrix displacement reaches approximately 5.48 × 10−4 μm at 5 MPa confining pressure, and rises to 4.43 × 10−3 μm at 40 MPa (representing an 8.1-fold increase). The displacement field displays remarkable anisotropy: a pronounced displacement gradient develops along the loading direction, with maximum displacements occurring at the pressure-applied surfaces. Of particular note is the distinct displacement concentration effect observed at matrix-pore interfaces.
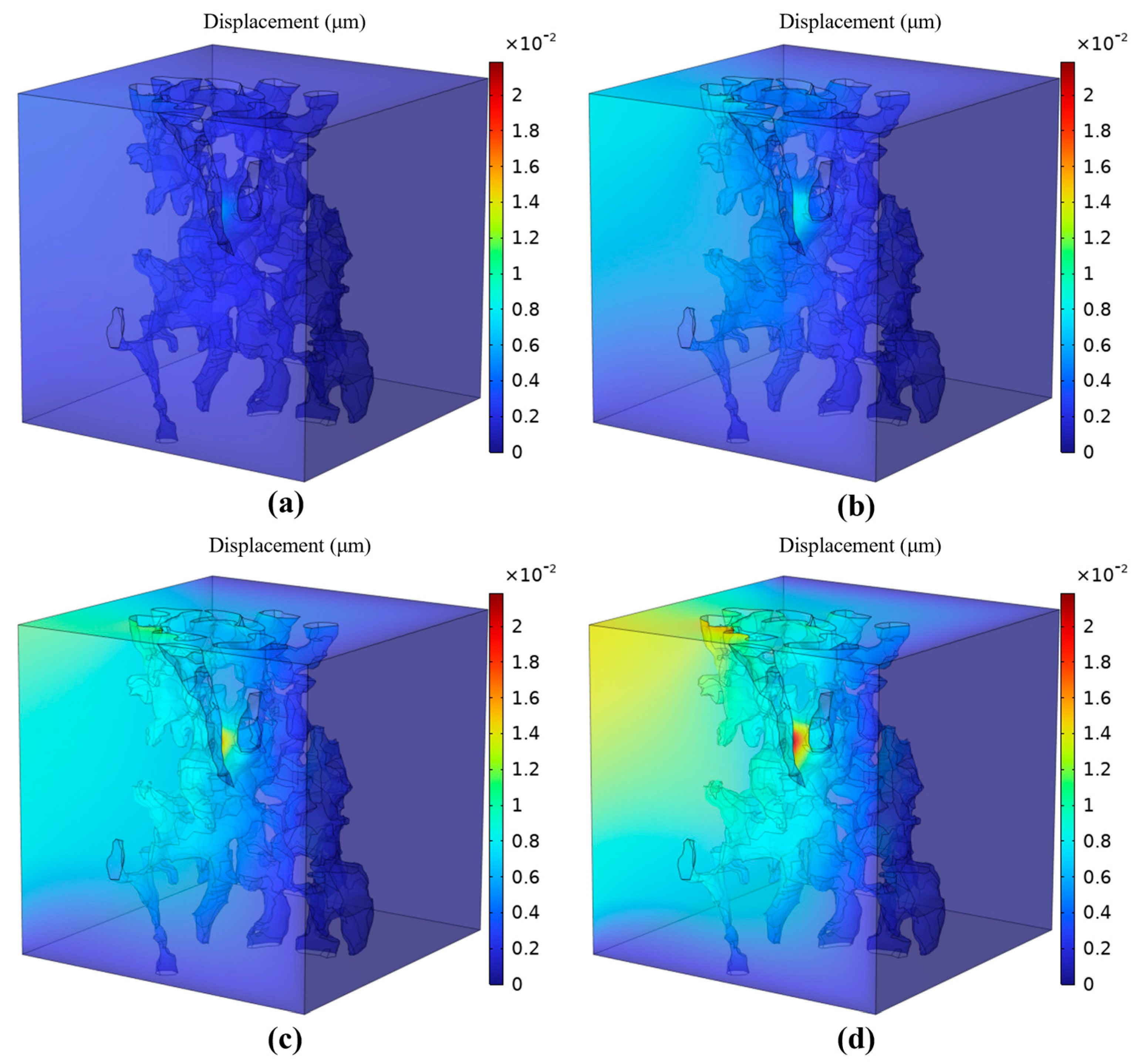
Figure 7: Displacement distributions under different confining pressures: (a) 10 MPa, (b) 20 MPa, (c) 30 MPa, (d) 40 MPa.
The porosity of the model is defined as the ratio of the volume of the current pore space to the volume of the pore matrix. Therefore, the porosity of the model considering the influence of matrix deformation on the spatial volume of the seepage channel is:
Fig. 8 demonstrates the porosity evolution under varying confining pressures. As the confining pressure increases from 5 MPa to 40 MPa, the porosity decreases by 0.13%. Theoretical analysis reveals that the pore volume exhibits higher sensitivity to confining pressure variations compared to the matrix volume, resulting in a monotonic decreasing trend of porosity with increasing pressure. However, constrained by the high stiffness characteristics of carbonate rocks (elastic modulus = 50 GPa), the volumetric strain induced by confining pressure changes remains below 0.15%, leading to limited stress sensitivity effects on porosity.
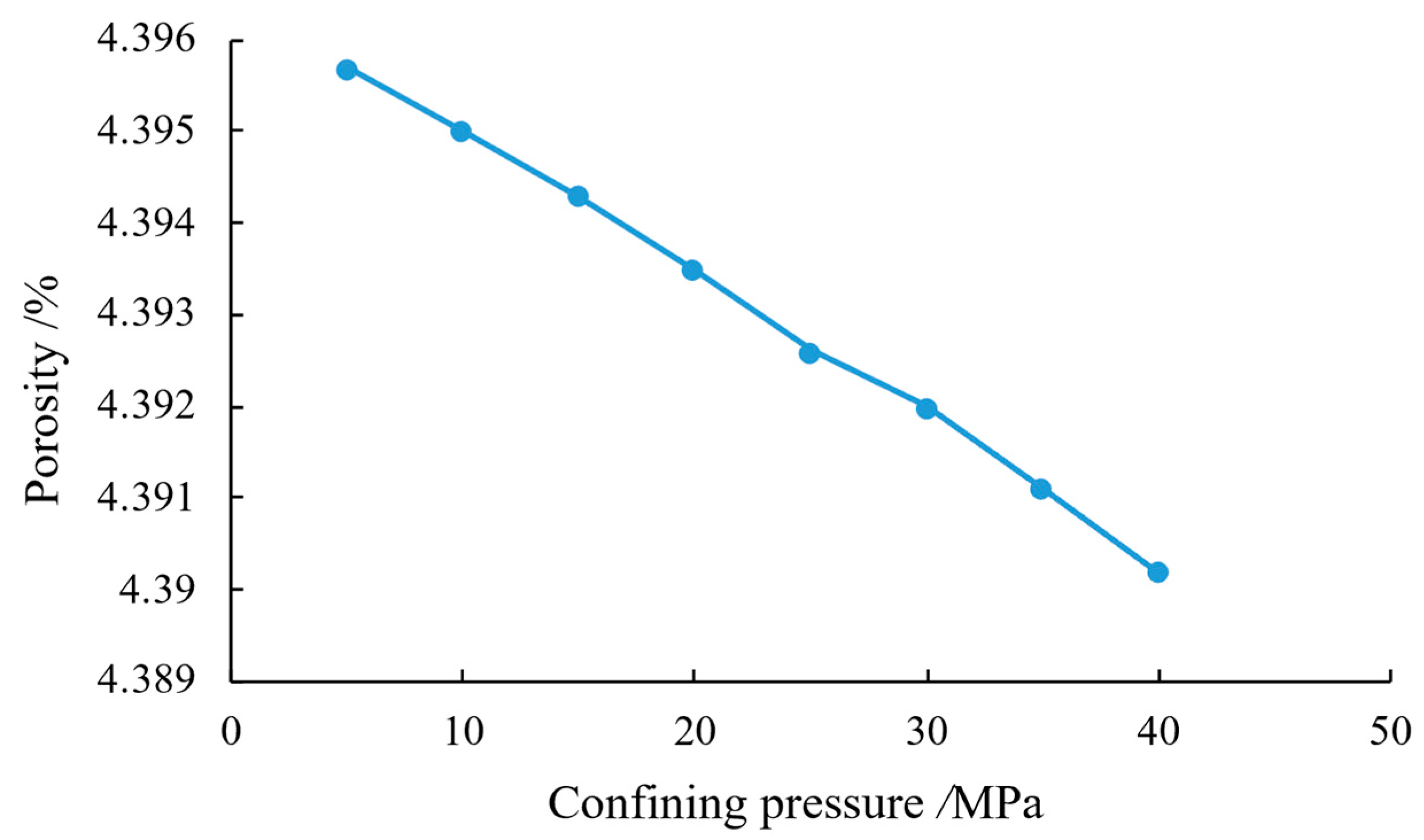
Figure 8: Variation of porosity with confining pressure.
4.2 Analysis of Fluid-Solid Coupling Effect
To simulate the fluid-solid coupling effects during the gas injection phase in underground gas storage operations, the initial geomechanical boundary conditions were meticulously defined. The in-situ stress field was characterized through a robust numerical-experimental methodology. Core samples from the target interval of the Huangcaoxia Jialingjiang Formation (at approximately 1100 m depth, carbonate rock) underwent triaxial compression testing to determine the fundamental rock mechanical parameters (as listed in Table 1, Section 3). A one-dimensional stress profile was subsequently calculated and calibrated against field data. This calibrated model provided the definitive in-situ stress state at the wellbore: a vertical stress of 36.5 MPa, a maximum horizontal principal stress of 38.2 MPa, and a minimum horizontal principal stress of 30.3 MPa. The initial pore pressure was set to 8.2 MPa, and a production pressure differential of 100 Pa (equivalent to a pressure gradient of 4.44 MPa/m) was applied to drive the injection process. This approach ensures that the simulated stress regime is physically consistent and directly constrained by experimental measurements from the specific storage formation.
To assess the representativeness of the digital core model itself, the macroscopic permeability and porosity were upscaled from the simulation results, yielding values of approximately 2.4 mD and 4.4%, respectively. These values align well with the characteristic range of properties measured from core samples within the target depth interval of the Huangcaoxia formation, providing a primary validation of the model’s geometric accuracy. While this pore-scale study provides fundamental mechanistic insights, it is acknowledged that a full field-scale validation, such as history matching the model’s predictions against long-term injection/production data from the entire storage facility, remains beyond its scope. This represents a necessary future step to translate these microscopic findings into operational forecasts.
The finite element simulation results presented in Fig. 9 reveal two key interrelated phenomena: localized strain zones develop within the reservoir matrix, and these mechanically deformed regions exhibit significant perturbations in flow velocity fields. This demonstrates the bidirectional coupling mechanism under fluid-solid interaction, where matrix deformation first alters pore geometry, subsequently modifying flow fields, and ultimately generating fluid pressure feedback that affects solid stress fields.
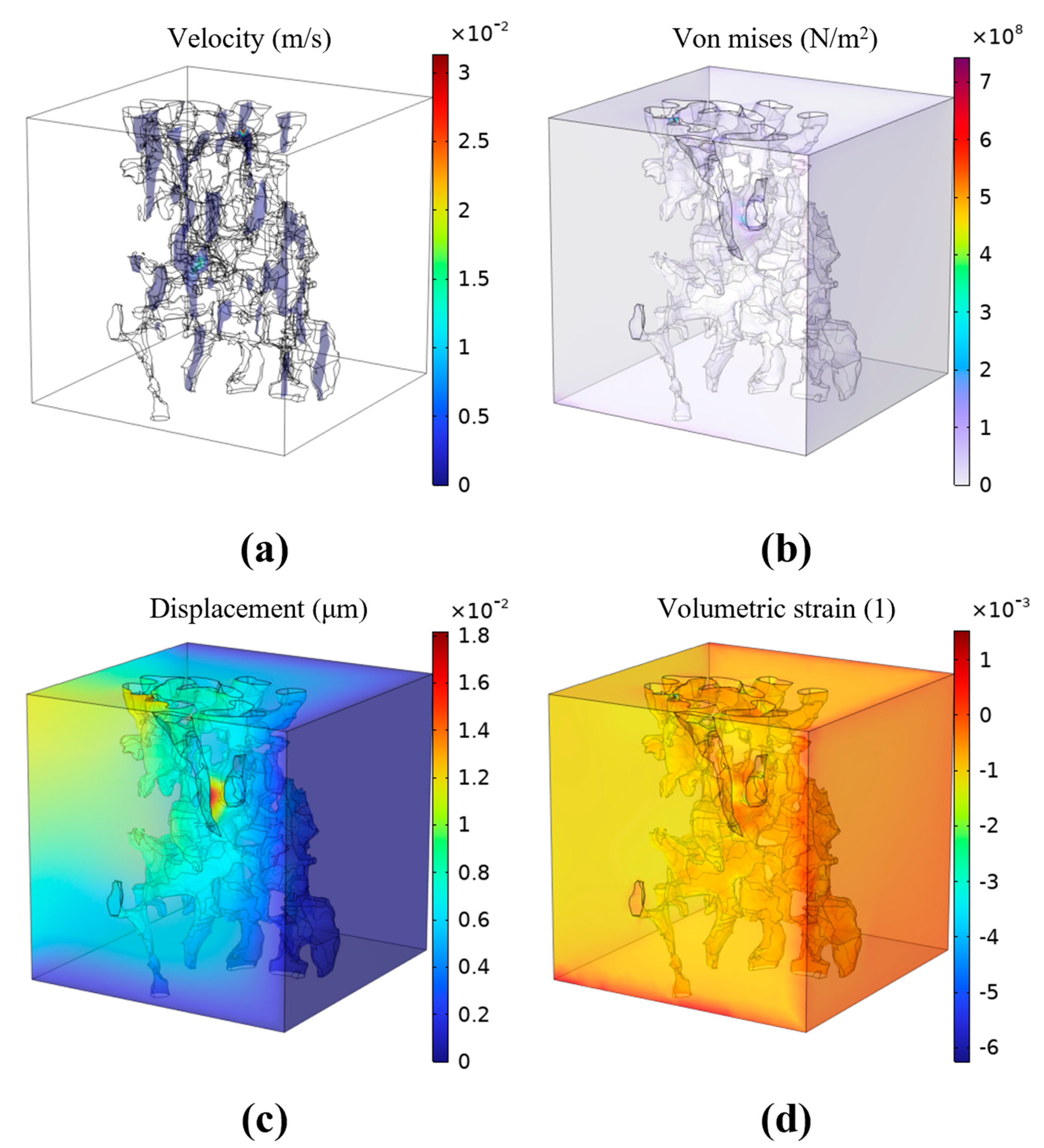
Figure 9: Fluid-solid coupling results: (a) Velocity; (b) Stress; (c) Displacement; (d) Volumetric strain.
Building upon the modeling results, a systematic investigation was conducted on the coupling mechanisms between pore fluid transport and matrix deformation. As demonstrated by the volumetric strain cross-section in Fig. 10, both fluid flow behavior and solid deformation characteristics are significantly governed by effective stress, with enhanced sensitivity observed in narrow throat regions.
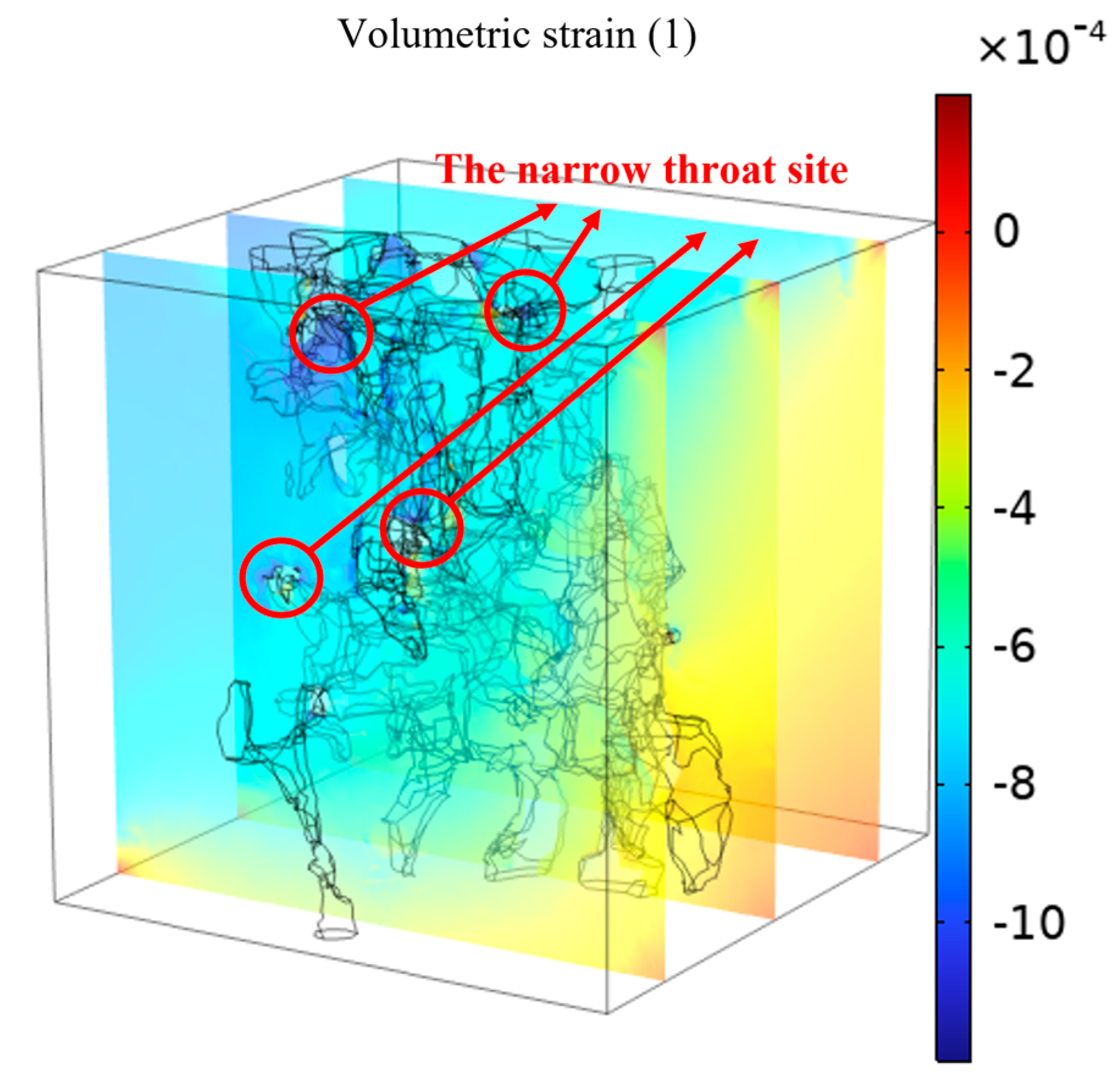
Figure 10: Volume strain section results.
To move beyond qualitative description and quantitatively unveil the heterogeneity of deformation induced by pore-throat structures, the statistical distribution of volumetric strain is meticulously analyzed and presented in Fig. 11. The histogram, constructed from 2077 data points, provides profound insights into the micromechanical behavior of the rock matrix under stress.
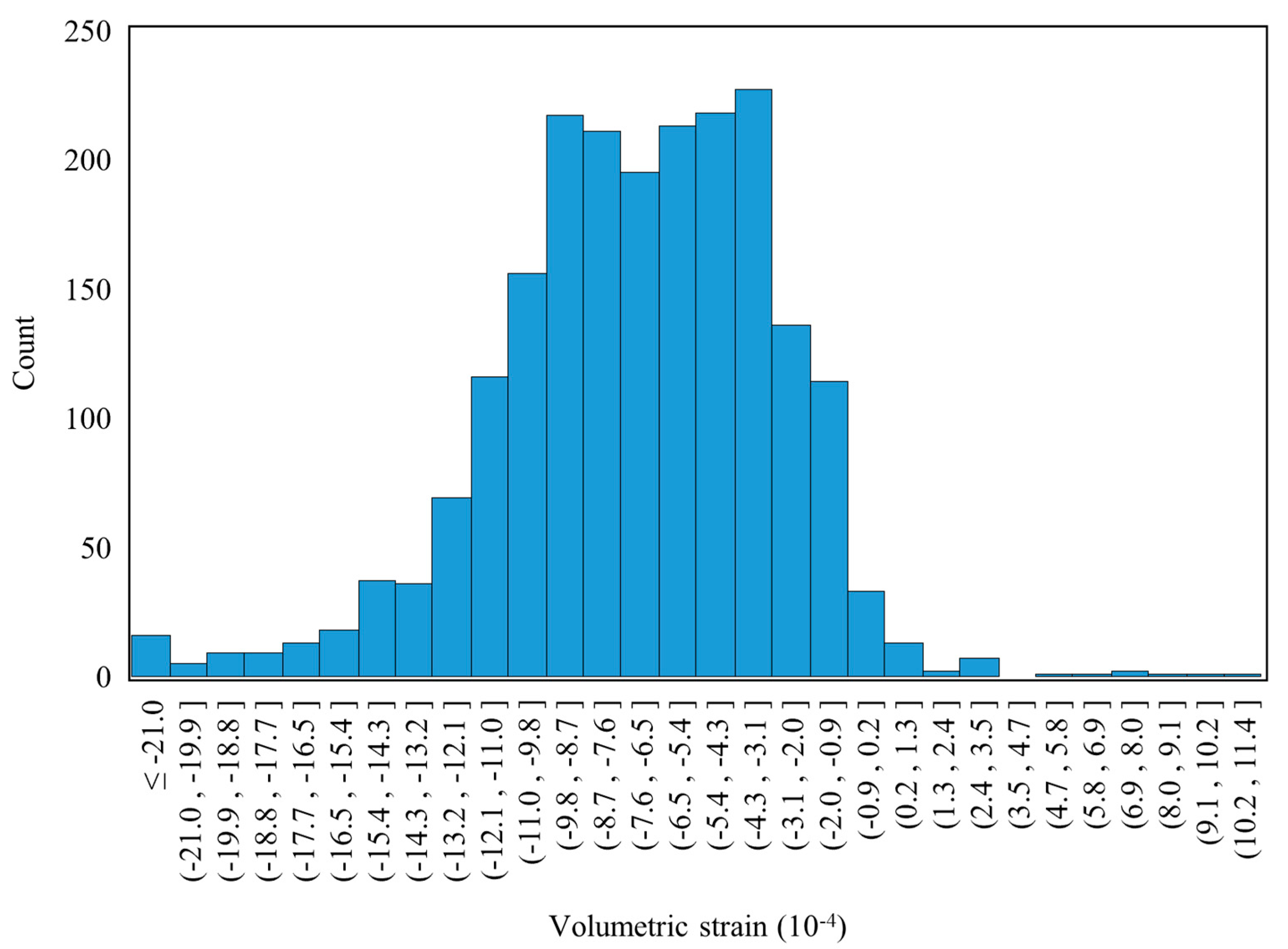
Figure 11: Histogram of volume strain distribution.
The distribution is characterized by a strong negative skewness, with the vast majority of data points (over 99%) exhibiting negative volumetric strain, confirming the dominance of compaction throughout the modeled domain. The mean volumetric strain is calculated to be −8.29 × 10−4, which aligns with the overall compaction trend. However, the key novelty lies in the significant standard deviation of 4.07 × 10−4 and the extreme values revealed by the distribution.
Notably, the strain values range from severe compaction of −70.07 × 10−4 to slight dilation of +11.36 × 10−4. This range of nearly 81.43 × 10−4 underscores the intense deformation heterogeneity at the pore scale. Critically, the distribution features a long tail towards the negative end, indicating the presence of localized “strain hotspots” where deformation is dramatically intensified. Approximately 6% of the elements experience compaction exceeding −15.00 × 10−4, with the most extreme 1% of values falling below −22.50 × 10−4. These hotspots are unequivocally associated with the geometric complexities of pore throats and grain contacts, where stress concentration is maximal. This quantitative analysis directly links specific microscopic features to the mechanical response, providing a predictive framework for understanding stress-sensitive permeability evolution.
Under effective stress, the volumetric strain of the matrix leads to the progressive expansion of its irregular protrusions, which subsequently encroach upon the pore space. This deformation results in the narrowing of fluid flow channels, causing concurrent reductions in both porosity and permeability. The fluid-solid coupling effect manifests through dual mechanisms: firstly, the matrix volume changes directly alter the pore structure morphology; secondly, the pressure-driven directional flow exerts continuous hydraulic impingement on the protrusions, inducing dynamic deformation responses in the matrix. These two mechanisms interact synergistically, collectively influencing the seepage characteristics of the reservoir.
Using the aforementioned fluid-solid coupling simulation results as the benchmark, two uncoupled control models were established under identical stress boundary conditions: a mechanical model considering only the stress field and a fluid model considering only the seepage field. Through systematic numerical simulations, comparative data of key parameters (including porosity, permeability, and volumetric strain) were obtained between the coupled and uncoupled models.
The model permeability was calculated using a modified Darcy’s law formulation, with the assumptions of incompressible fluid, steady-state single-phase flow, and no chemical reactions between the fluid and rock matrix. Thus, the permeability calculation formula for the model is expressed as [39]:
Statistical analysis of porosity, permeability, and volumetric strain results from the fluid-solid coupling model, compared with uncoupled models (Table 2), reveals that incorporating coupling effects leads to a 0.07% reduction in porosity, 5.6% decrease in permeability, and 1.27% increase in volumetric strain. The results demonstrate that coupling effects exert more pronounced impacts on permeability than on porosity or strain. This is attributed to microstructural alterations in pore-throat geometry under effective stress, which interact with fluid flow to significantly modify seepage velocity. For the dense carbonate rocks from Huangcaoxia Gas Storage (elastic modulus = 50 GPa), minimal matrix deformation results in negligible changes in porosity and strain.
Table 2: Statistical comparison of fluid structure coupling and uncoupled models.
| Model | Porosity (%) | Permeability (mD) | Volumetric Strain |
|---|---|---|---|
| Coupling model | 4.390 | 2.328 | −5.56E−4 |
| Uncoupled model | 4.393 | 2.466 | −5.49E−4 |
| Ratio of change (%) | 0.07 | 5.6 | 1.27 |
4.3 Fluid-Solid Coupling Mechanisms under Dynamic Effective Stress Evolution
To investigate the mechanical response during gas storage injection-production cycles, this study conducted a series of fluid-solid coupling simulations under different effective stress conditions. These conditions were designed to represent key stages of an operational cycle (e.g., initial state, peak injection, production), with the confining and pore pressures for each scenario prescribed as constant values, informed by pressure evolution data from 4D geomechanical simulations as presented in Table 3. Although the pressures were held constant within each simulation, this multi-scenario approach allows for the analysis of how deformation induced by different effective stress levels fundamentally alters the pore structure and consequently impacts the seepage field. The effective stress for each scenario was computed as a constant using the classical relationship governed by the preset pore fluid pressure and three-dimensional confinement stresses:
Table 3: Four dimensional stress simulation results of Caochu 1 well.
| Vertical Stress (MPa) | Maximum Horizontal Principal Stress (MPa) | Minimum Horizontal Principal Stress (MPa) | Pore Pressure (MPa) | Effective Stress (MPa) |
|---|---|---|---|---|
| 36.5 | 38.2 | 30.3 | 8.2 | 26.8 |
| 36.7 | 38.5 | 30.9 | 9.3 | 26.1 |
| 36.9 | 38.7 | 31.5 | 10.4 | 25.3 |
| 37 | 38.9 | 32.2 | 11.5 | 24.5 |
| 37.1 | 39.3 | 32.6 | 12.6 | 23.7 |
Fig. 12 presents a magnified view of the volumetric strain distribution, where distinct stress concentration phenomena are observed at pore-matrix interfaces under effective stress. These localized loading zones induce micrometer-scale matrix deformation and adaptive pore structure reorganization, though the overall volumetric strain and porosity variations remain constrained due to the high stiffness of carbonate matrix. Correspondingly, Fig. 13 reveals that effective stress variations significantly alter hydrodynamic characteristics in flow channels, particularly generating abrupt velocity gradients at narrow pore throats—a microscopic mechanism accounting for the sensitive macroscopic permeability response. Comparative analysis of both figures demonstrates the spatial heterogeneity of mechanical deformation and flow response in tight reservoirs.
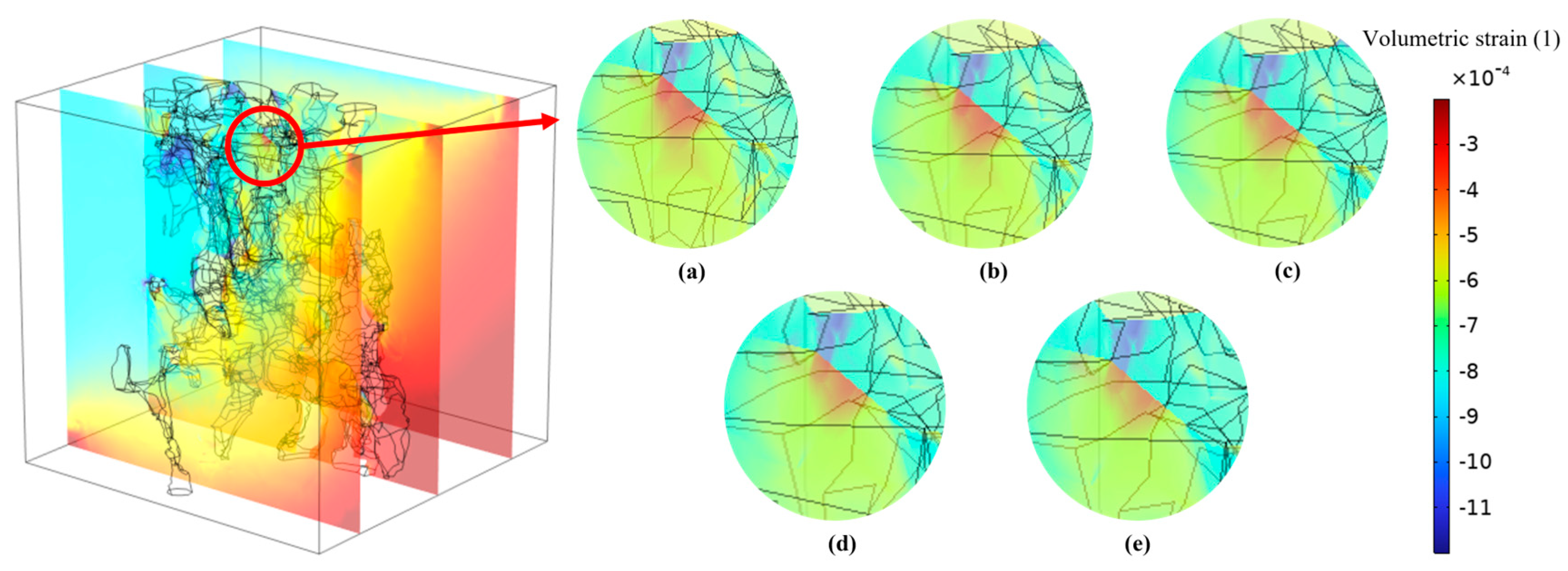
Figure 12: Volumetric strain distribution under progressively decreasing effective stress: (a) 26.8 MPa, (b) 26.1 MPa, (c) 25.3 MPa, (d) 24.5 MPa, (e) 23.7 MPa.
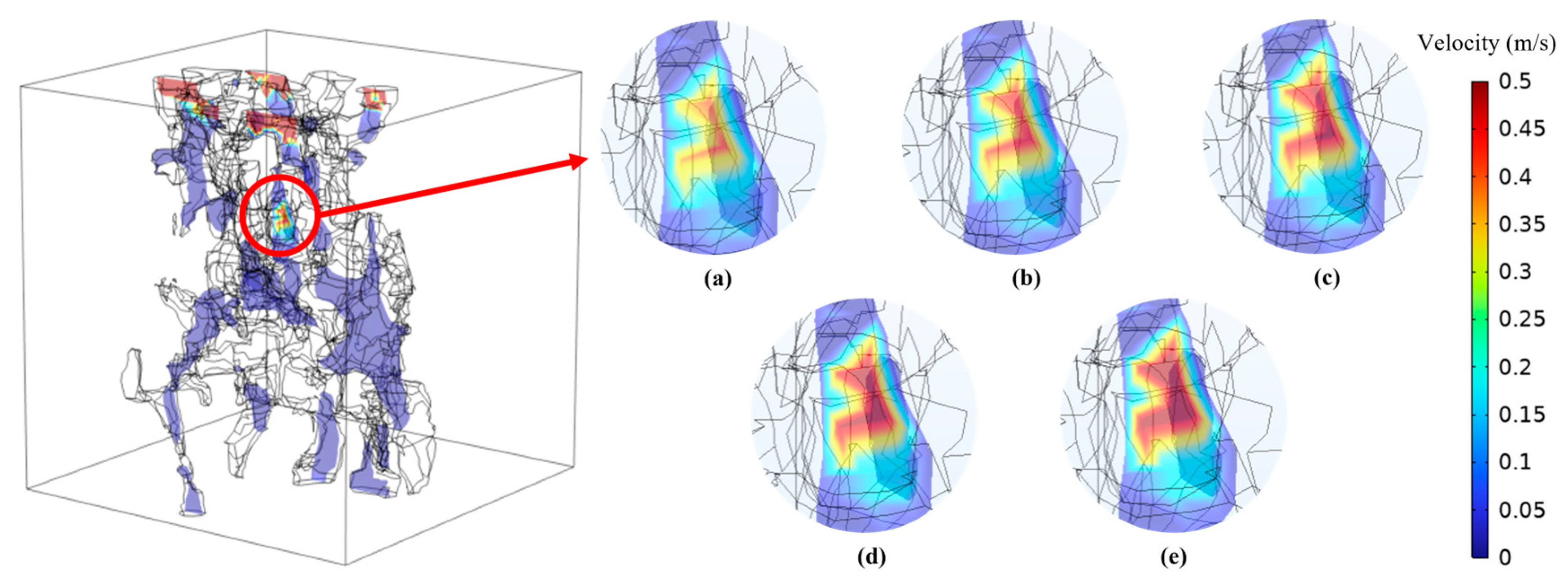
Figure 13: Fluid velocity results under progressively decreasing effective stress: (a) 26.8 MPa, (b) 26.1 MPa, (c) 25.3 MPa, (d) 24.5 MPa, (e) 23.7 MPa.
Numerical simulations elucidate the evolution of petrophysical properties and matrix deformation under varying effective stress (Fig. 14). During gas production phases (increasing effective stress), the model exhibits distinct stress-sensitivity responses: permeability decreases by 34.4%, whereas porosity and volumetric strain decrease merely by 0.02% and 4.3% respectively. To validate the model’s predictive capability, the magnitude of permeability reduction (from 3.8 mD to 2.5 mD as effective stress increases from 23.7 MPa to 26.8 MPa) was compared against experimental stress-sensitivity curves for carbonates reported in the literature [40]. The observed 34.4% reduction falls within the reported range of 0.7% to 37.5% for various carbonate pore structures under similar effective stress changes, thereby corroborating the reliability of our numerical results. This divergence in property evolution stems from the dual characteristics of tight reservoirs—while fluid velocity shows high sensitivity to effective stress (drastically reducing flow channel efficiency), the high-stiffness matrix (elastic modulus = 50 GPa) effectively resists bulk deformation.
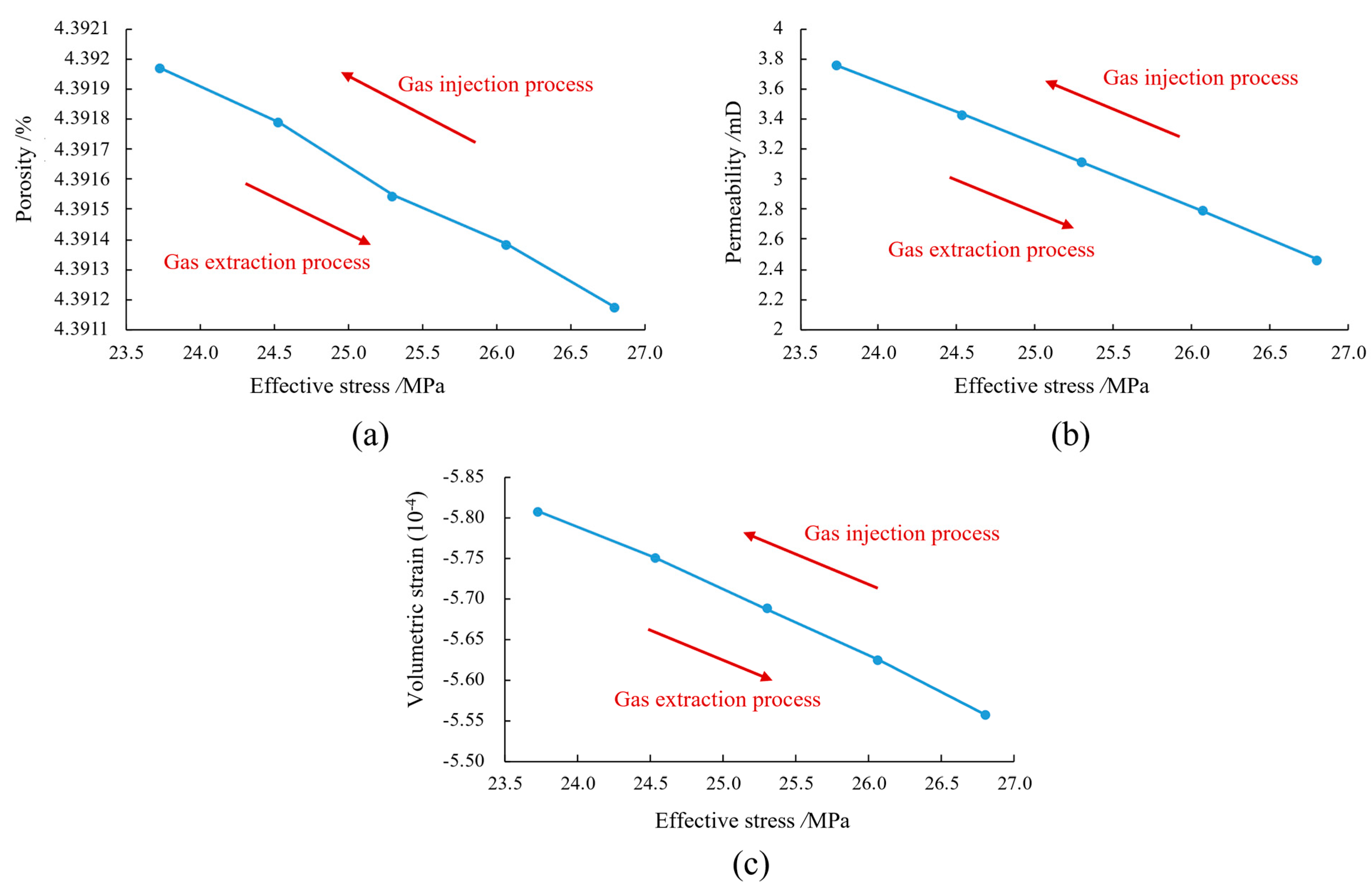
Figure 14: Stress-dependent characteristics: (a) porosity; (b) permeability; (c) matrix deformation under varying effective stress.
These findings strongly advocate for implementing a cyclic pressure management strategy during intense injection-production operations. This strategy is defined as the active regulation of pore pressure within a predefined optimal window. Based on our quantitative analysis of permeability evolution, this window can be defined with greater operational specificity:
The upper limit remains bounded by the caprock fracture pressure to ensure geomechanical stability.
The lower limit should be strategically set to maintain the in-situ effective stress below a critical threshold of approximately 26 MPa, corresponding to the onset of significant permeability damage in our model.
Our simulations reveal that allowing the effective stress to escalate into a “high-risk” band (26–27 MPa) would induce a substantial permeability reduction of 20–34%, directly compromising well deliverability. Therefore, the paramount objective of this strategy is to maintain the effective stress within a “safe operating band” (below 26 MPa), thereby mitigating the stress-induced permeability damage identified in this study and preserving the reservoir’s long-term flow capacity.
This study established a microscale fluid-solid coupling model for Huangcaoxia Gas Storage carbonate reservoirs by integrating high-resolution 3D digital core technology with finite element simulations. The investigation yields the following key insights with significant engineering implications:
- (a)Pore-throat scale mechanics control macroscale response: The model reveals that stress concentrations at microscopic pore throats are the primary driver of macroscopic deformation and permeability reduction. This multiscale interaction explains how localized deformation propagates through heterogeneous microstructures to govern overall reservoir performance during injection-production cycles.
- (b)Permeability is the most stress-sensitive parameter: Comparative analysis demonstrates that the fluid-solid coupling effect induces a significantly more pronounced reduction in permeability compared to changes in porosity or volumetric strain. This differential response underscores that permeability is the critical, limiting factor for gas storage performance.
- (c)Effective stress management is paramount for storage integrity: The rapid elevation of effective stress during gas production is identified as the fundamental cause of irreversible permeability damage. Consequently, the core operational strategy must focus on maintaining a relatively low effective stress environment.
These findings directly advocate for the implementation of a cyclic pressure management strategy during intense injection-production operations. This strategy involves actively regulating reservoir pressure within a predefined optimal window bounded by an upper limit to ensure caprock and geomechanical stability and a lower limit to prevent severe stress-induced permeability damage that compromises well deliverability. By prioritizing the mitigation of effective stress, operators can preserve the long-term flow capacity and ensure the injectivity/productivity sustainability of underground gas storage facilities.
Acknowledgement:
Funding Statement: This research was funded by the Science and Technology Cooperation Project of the CNPC-SWPU Innovation Alliance (No. 2020CX010403).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yulong Zhao; data collection: Yuming Luo; model construction and calculation: Yulai Pang; analysis and interpretation of results: Ruihan Zhang; draft manuscript preparation: Yang Luo; manuscript revision: Zihan Zhao. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data supporting the findings of this study are available from the corresponding author upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Fan Y , Gao XP , Ning F , Peng JL , Li LM , Peng H , et al. Seepage law of gas-reservoir UGSs during multi-cycle injection and production. Nat Gas Ind. 2023; 43( 10): 103– 11. (In Chinese). [Google Scholar]
2. Afagwu C , Alafnan S , Mahmoud M , Akkutlu IY . Modeling of natural gas self-diffusion in the micro-pores of organic-rich shales coupling sorption and geomechanical effects. J Nat Gas Sci Eng. 2022; 106: 104757. doi:10.1016/j.jngse.2022.104757. [Google Scholar] [CrossRef]
3. Deglint HJ , Clarkson CR , Ghanizadeh A , DeBuhr C , Wood JM . Comparison of micro- and macro-wettability measurements and evaluation of micro-scale imbibition rates for unconventional reservoirs: implications for modeling multi-phase flow at the micro-scale. J Nat Gas Sci Eng. 2019; 62: 38– 67. doi:10.1016/j.jngse.2018.11.026. [Google Scholar] [CrossRef]
4. Sun Z , Wang J . Analysis of reservoir damage and microscopic seepage simulation in low permeability oil and gas reservoirs based on pore topology structure. J Eng Res. 2025; 13( 3): 2730– 8. doi:10.1016/j.jer.2024.05.032. [Google Scholar] [CrossRef]
5. Klusman RW . Comparison of surface and near-surface geochemical methods for detection of gas microseepage from carbon dioxide sequestration. Int J Greenh Gas Control. 2011; 5( 6): 1369– 92. doi:10.1016/j.ijggc.2011.07.014. [Google Scholar] [CrossRef]
6. Atwah I , AlSaif M , Yeadon A , Srinivasan P . Depth dimension in seepage detection: insights for exploration and geological gas storage surveillance. Geoenergy Sci Eng. 2024; 243: 213242. doi:10.1016/j.geoen.2024.213242. [Google Scholar] [CrossRef]
7. Hu J , Yang S , Wang B , Deng H , Wang M , Li J , et al. Effect of pore structure characteristics on gas-water seepage behaviour in deep carbonate gas reservoirs. Geoenergy Sci Eng. 2024; 238: 212881. doi:10.1016/j.geoen.2024.212881. [Google Scholar] [CrossRef]
8. Wang M , Chen B , Xu J , Gong YA , Gao X , Li X , et al. Permeability evolution of the rock–concrete interface in underground high-pressure gas storage. J Rock Mech Geotech Eng. 2025; 17( 7): 4539– 58. doi:10.1016/j.jrmge.2024.09.036. [Google Scholar] [CrossRef]
9. Ye W , Liu J , Gan L , Wang H , Qin L , Zang Q , et al. Fluid-structure coupling analysis in liquid-filled containers using scaled boundary finite element method. Comput Struct. 2024; 303: 107494. doi:10.1016/j.compstruc.2024.107494. [Google Scholar] [CrossRef]
10. Zheng X , Zhao YC , Zhao ZH , Tang HY , Zhao YL . Mechanism investigation on in situ stress characteristics and mechanical integrity of fracture-cavity carbonate underground gas storage reservoir. Petrol Reserv Eval Dev. 2024; 14( 5): 814– 24. (In Chinese). doi:10.13809/j.cnki.cn32-1825/te.2024.05.018. [Google Scholar] [CrossRef]
11. Zhang J , Zhou X , Liu X , Fang L , Liu Y , Wang Y . Deformation and permeability of fractured rocks using fluid-solid coupling under loading-unloading conditions. J Rock Mech Geotech Eng. 2025; 17( 8): 4889– 907. doi:10.1016/j.jrmge.2024.09.048. [Google Scholar] [CrossRef]
12. Liu R , Wang M , Xu J , Li X , Wu W , Gao X , et al. Seepage characteristics of porous media under stress-gas pressure coupling. J Energy Storage. 2025; 109: 115119. doi:10.1016/j.est.2024.115119. [Google Scholar] [CrossRef]
13. Yang HJ , Cai ZZ , Zhang H , Sun C , Li J , Meng XY , et al. Study on the fluid-solid coupling seepage of the deep tight reservoir based on 3D digital core modeling. Energy Eng. 2025; 122( 2): 537. doi:10.32604/ee.2024.058747. [Google Scholar] [CrossRef]
14. Terzaghi K . Theoretical soil mechanics. Hoboken, NJ, USA: John Wiley & Sons, Inc.; 1943. doi:10.1002/9780470172766. [Google Scholar] [CrossRef]
15. Biot MA . General theory of three-dimensional consolidation. J Appl Phys. 1941; 12( 2): 155– 64. doi:10.1063/1.1712886. [Google Scholar] [CrossRef]
16. Pao WKS , Lewis RW . Three-dimensional finite element simulation of three-phase flow in a deforming fissured reservoir. Comput Meth Appl Mech Eng. 2002; 191( 23–24): 2631– 59. doi:10.1016/s0045-7825(01)00420-0. [Google Scholar] [CrossRef]
17. Khanghahi-Bala B , Habibagahi G , Ghabezloo S , Ghahramani A , Schrefler BA . Heat generation by ultrasound wave propagation in porous media with low permeability: theoretical framework and coupled numerical modeling. Comput Geotech. 2020; 124: 103607. doi:10.1016/j.compgeo.2020.103607. [Google Scholar] [CrossRef]
18. Yang X , Li B , Li Y , Yang B , Zhou K . A finite volume–based thermo-fluid-mechanical model of the LPBF process. Int J Mech Sci. 2024; 284: 109759. doi:10.1016/j.ijmecsci.2024.109759. [Google Scholar] [CrossRef]
19. Gharibi F , Ali Hosseini S , Thévenin D . A hybrid lattice Boltzmann/immersed boundary method/finite-difference model for thermal fluid-solid interactions. Int Commun Heat Mass Transf. 2024; 155: 107525. doi:10.1016/j.icheatmasstransfer.2024.107525. [Google Scholar] [CrossRef]
20. Huang L , Zhan W , Zhao H , Sheng G . A novel fluid-solid coupling method for fractured reservoirs: 3d DDM-EDFM integration with proppant mechanics. Comput Geotech. 2025; 181: 107127. doi:10.1016/j.compgeo.2025.107127. [Google Scholar] [CrossRef]
21. Burman E , Fernández MA , Frei S , Gerosa FM . 3D-2D stokes-darcy coupling for the modelling of seepage with an application to fluid-structure interaction with contact. In: Numerical Mathematics and Advanced Applications ENUMATH 2019. Cham, Switzerland: Springer International Publishing; 2020. p. 215– 23. doi:10.1007/978-3-030-55874-1_20. [Google Scholar] [CrossRef]
22. Hagemann B , Wegner J , Ganzer L . Investigation of hydraulic fracture re-orientation effects in tight gas reservoirs. In: Proceedings of the European COMSOL Conference 2012; 2012 Oct 10; Milan, Italy. [Google Scholar]
23. Zhu Y , Liu C , Zhang H , Zhao C , Wang B , Mao M , et al. Micro mechanism investigation of hydraulic fracturing process based a fluid-solid coupling discrete element model. Comput Geotech. 2024; 174: 106640. doi:10.1016/j.compgeo.2024.106640. [Google Scholar] [CrossRef]
24. Chen X , Li Y , Shi Y , Yu Y , Jiang Y , Liu Y , et al. Tightness and stability evaluation of salt cavern underground storage with a new fluid–solid coupling seepage model. J Petrol Sci Eng. 2021; 202: 108475. doi:10.1016/j.petrol.2021.108475. [Google Scholar] [CrossRef]
25. Mahmoodpour S , Singh M , Omrani S , Sass I , Drews M . Thermo-hydro-mechanical simulation considering cushion gases, reservoir heterogeneity and sensitivity analysis of hydrogen storage in saline aquifers. J Energy Storage. 2025; 130: 117302. doi:10.1016/j.est.2025.117302. [Google Scholar] [CrossRef]
26. Deng X , Shi X , Wu Z , An Y , Wang J , Li S , et al. Evolution of rock mass stress, movement, and deformation during injection-production processes in coal mines that have been converted into natural gas storage facilities. Geomech Energy Environ. 2025; 43: 100703. doi:10.1016/j.gete.2025.100703. [Google Scholar] [CrossRef]
27. Saeedmonir S , Khoei AR . Multiscale modeling of coupled thermo-hydro-mechanical analysis of heterogeneous porous media. Comput Meth Appl Mech Eng. 2022; 391: 114518. doi:10.1016/j.cma.2021.114518. [Google Scholar] [CrossRef]
28. Berndt E , Sevostianov I . Multiscale modeling of fluid permeability of a non-homogeneous porous media. Int J Eng Sci. 2012; 56: 99– 110. doi:10.1016/j.ijengsci.2012.03.036. [Google Scholar] [CrossRef]
29. Kou H , Zhang X , Huang J . Fluid-solid coupling large deformation failure analysis of bucket foundations in saturated clay. Eng Fail Anal. 2025; 179: 109807. doi:10.1016/j.engfailanal.2025.109807. [Google Scholar] [CrossRef]
30. Lazareff M , Moretti R , Errera MP . Coupling methodology for thermal fluid-solid simulations through a full transient flight cycle. Int J Heat Mass Transf. 2023; 202: 123691. doi:10.1016/j.ijheatmasstransfer.2022.123691. [Google Scholar] [CrossRef]
31. Zhu Y , Liu C , Liu H , Kou YD , Shi B . A multi-field and fluid–solid coupling method for porous media based on DEM-PNM. Comput Geotech. 2023; 154: 105118. doi:10.1016/j.compgeo.2022.105118. [Google Scholar] [CrossRef]
32. Khoei AR , Ahmadi E , Tabatabaei MH . Modeling fluid flow in fractured porous media with a combined Phase-Field and Navier-Stokes technique. Adv Water Resour. 2025; 205: 105082. doi:10.1016/j.advwatres.2025.105082. [Google Scholar] [CrossRef]
33. Narsilio GA , Buzzi O , Fityus S , Yun TS , Smith DW . Upscaling of Navier–Stokes equations in porous media: theoretical, numerical and experimental approach. Comput Geotech. 2009; 36( 7): 1200– 6. doi:10.1016/j.compgeo.2009.05.006. [Google Scholar] [CrossRef]
34. Yao WJ , Deng CB , Fan N , Shen WM , Zhang LF , Zhang PL . Numerical simulation of fluid-solid-thermal coupling for CO2 injection enhanced mining in deep coal seams. Saf Coal Mines. 2024; 55( 7): 31– 8. (In Chinese). doi:10.13347/j.cnki.mkaq.20230293. [Google Scholar] [CrossRef]
35. Liu LJ . Numerical Simulation of coupled flow and geomechanical process in fractured karst carbonate reservoirs [ dissertation]. Qingdao, China: China University of Petroleum; 2021. [Google Scholar]
36. de F Meirelles PH , Fernandes JWD , Sanches RAK , Wutzow WW . A modular finite element approach to saturated poroelasticity dynamics: fluid–solid coupling with Neo-Hookean material and incompressible flow. Finite Elem Anal Des. 2024; 242: 104256. doi:10.1016/j.finel.2024.104256. [Google Scholar] [CrossRef]
37. Guo JJ , Wang DH , Wang PR , Xiong RF , Wang HT , Wang SB . Pore structure of low-permeability reservoir and distribution characteristics of remaining oil after water flooding based on digital core. Spec Oil Gas Reserv. 2023; 30( 2): 101– 8. (In Chinese). [Google Scholar]
38. Mokaddes Ali M , Akhter R , Alim MA . Hydromagnetic natural convection in a wavy-walled enclosure equipped with hybrid nanofluid and heat generating cylinder. Alex Eng J. 2021; 60( 6): 5245– 64. doi:10.1016/j.aej.2021.04.059. [Google Scholar] [CrossRef]
39. Wiedemann D , Peter MA . A Darcy law with memory by homogenisation for evolving microstructure. J Math Anal Appl. 2025; 546( 2): 129222. doi:10.1016/j.jmaa.2025.129222. [Google Scholar] [CrossRef]
40. Sun K , Liu H , Leung JY , Wang J , Feng Y , Liu R , et al. Impact of effective stress on permeability for carbonate fractured-vuggy rocks. J Rock Mech Geotech Eng. 2024; 16( 3): 942– 60. doi:10.1016/j.jrmge.2023.04.007. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools