Diffusive Transfer between a Droplet and an Immiscible Oscillating Liquid in a Radial Hele-Shaw Cell

1  Introduction

Molecular diffusion is a fundamental process that enables the transfer of substances in various technological and biological systems. This transfer occurs in multiple media, including gases, liquids, and solids. The following examples illustrate the aforementioned diffusion: drying, adsorption, dissolution, impregnation, desorption, distillation, and reactions involving chemical changes [1–3]. Diffusion plays an important role in a number of practical applications, including fluid extraction and mass transfer in porous materials, semiconductor manufacturing, and the food industry [4–6]. Moreover, diffusion affects the metabolic processes occurring between the organism and the environment as well as between different cellular and tissue components within the organism [7–9]. It is, therefore, essential to study diffusion and develop methods of mass transfer intensification, both in relation to practical applications and from a fundamental perspective.

Droplet inclusions are a widely employed technique for the study of diffusion exchange within multicomponent media. The review [10] presents a discussion of the results of theoretical and experimental studies of droplets and multicomponent systems that have gradients in concentration. The study includes both the ‘seated’ droplets (maintaining their mean position) on a surface and the dynamics of droplet movement within the liquid. The diffusion rate depends on numerous conditions, both external and intrinsic to the diffusion system itself. A number of factors, including the physical and chemical properties of the interface, the presence of surfactant or nanoparticles at the interface, thermal effects, external oscillations, and the physical and chemical characteristics of the solvent (liquid droplet) or the solute, affect the diffusion rate. The oscillatory dynamics of systems with an interface in a Hele-Shaw cell are carried out for both low-viscosity fluids and fluids with high-viscosity contrast. The dynamics of the interface in a rectangular Hele-Shaw cell between miscible and immiscible fluids are studied in [11] and [12], respectively. It is revealed that fluid oscillations affect the interface stability and the mass transfer rate. The excitation of fluid oscillations in flat channels of different geometry by means of a hydraulic pump and a shaker is demonstrated to be an effective tool for external influence on various fluid systems. Fluid oscillations in a thin layer can cause the interface to become unstable [11,13]. For example, when a droplet is in an oscillating fluid, the droplet surface oscillates while the droplet drifts due to the inhomogeneity of the oscillatory motion of the ambient fluid [14]. The oscillatory flow gives rise to interface oscillations, which in turn give rise to intense time-averaged flow within the droplet. The effect of wall oscillations in an elastic sphere (deformable container) on the fluid velocity field within the sphere is examined in [15]. Here, the sphere plays the role of a droplet model. It is revealed that the intense time-averaged flow can significantly intensify mass transfer inside a drop in an oscillating flow.

The study aims to develop and validate an experimental setup and experimental technique for determining the mass transfer rate at the interface between two fluids. In [16], the authors previously described and tested a method for determining the diffusion mass transfer rate under conditions of a rectangular Hele-Shaw cell filled with water using the laser-induced fluorescence method, in other words, the spectroscopic method. The method is based on the determination of the concentration of fluorescent Rhodamine B in water by measuring the intensity of fluorescence emission and the rate of its diffusion in the liquid with time (on the rate of change of diffusion zone width). In the present study, diffusive mass transfer in a more complex system between a phase inclusion and the surrounding fluid in a radial Hele-Shaw cell is considered. A droplet of chlorobenzene or octanol is used as the phase inclusion, while distilled water plays the role of the surrounding fluid. The Rhodamine B dissolved in the droplet is used as a tracer dye to determine the mass transfer rate. In the absence of oscillations, the dye penetrates through the interface and then spreads in the radial and azimuthal directions due to molecular diffusion. When the surrounding liquid oscillates, the diffusion rate of the dye is determined by the amplitude of these oscillations.

2  Experimental Technique

The experimental setup (Fig. 1a) consists of several principal elements: an experimental cell, a linear motor with a power supply and control system, a hydraulic system, and a phase inclusion injection device. The linear motor 1 generates fluid oscillations within the cell. The motor rod undergoes linear translational oscillations in the horizontal plane. The rod is directly coaxially connected with the rod of a hydraulic pump 2, which consists of two volumes separated by a rubber membrane and operates on the ‘pull-push’ principle. The motor rod oscillations are transmitted to the separating membranes 3 by displacement of the pump membrane. The oscillatory motion of the liquid within the cell 4 is a consequence of the stretching and compression of the separating membranes. The cell is a circular layer confined between two glass plates of thickness 10 mm and radius R=75.0 mm. The glass elements are mounted within metallic frames that establish an expansion volume surrounding the fluid layer, thereby providing uniform pressure at the outer boundary. The observation is made through a “window” with a radial size of r=55.0 mm. The thickness of the fluid layer is h=0.99±0.05 mm.

Figure 1: Scheme of the experimental setup (side view, a): 1—linear motor; 2—pump; 3—separation membranes; 4—radial axisymmetric Hele-Shaw cell; 5—linear motor driver and power supply; 6—computer; 7—droplet inclusion injection device; 8—laser; 9—digital camera. Schematic of a radial Hele-Shaw cell filled with a working fluid with droplet inclusion (top view, b)

The linear motor is managed by a driver, a power supply unit 5, and a computer 6. The frequency of the fluid oscillations fvib=Ωvib/2π is maintained at a constant value of 4.0 Hz while the amplitude of radial oscillations b varies within the range of 0–1.2 mm in experiments. Fig. 1b demonstrates the schematic of a radial Hele-Shaw cell. The liquid in the experimental cuvette layer oscillates according to the law ∼cos⁡Ωvibt. The arrows on Fig. 1b demonstrate the direction of fluid oscillations generated by a linear pump and a hydraulic circuit with zero mean flow rate at a given frequency. In the main part of the cuvette, the flow is radial; however, in the vicinity of the droplet inclusion, its inhomogeneous flow is observed. The experiments are carried out with low-viscosity fluids. The cell is filled with water that has been preliminarily degassed to prevent the formation of air bubbles during the fluid oscillations.

The droplet is made of chlorobenzene or octanol (1-octane). These liquids are immiscible with water and have different densities with respect to the latter. In particular, chlorobenzene has a higher density than water, whereas octanol has a lower density. The physical properties of the fluids are presented in Table 1.

A droplet is injected into the fluid layer volume by means of the injection device 7. Due to the specific feature of the droplet inclusion injection, its shape is elongated along the radius of the layer. In this case, the diametral size of the drop along the azimuthal direction is dDa=4.5±0.5 mm, and along the radial direction—dDr=9.5±0.5 mm. The size of the droplet inclusion is smaller than the characteristic size of the flat layer. The volume of the droplet is equal to approximately 1.5 mL in all experiments. The solute within the droplet is the fluorescent dye Rhodamine B, which is soluble in water, chlorobenzene and octanol. The diffusion of Rhodamine B from the droplet into the surrounding water is found. This dye absorbs light from 460 to 590 nm, with a maximum at 540 nm. It fluoresces in the green light with a wavelength of 520 nm. The green laser has a Powell lens, which makes a narrow laser beam appear as a straight line. The mass transfer of Rhodamine B is documented using a Fujifilm X-E4 camera with a Tamron SP AF 90 mm f/2.8 Di Macro 1:1 macro lens. The orange filter is used to block green laser light from the observation area of the camera. The images are processed using the ImageJ software in order to calculate the intensity of the fluorescent illumination as a function of the coordinates.

3  Experimental Results and Discussion

3.1 Molecular Diffusion of Rhodamine B

The mass transfer rate of Rhodamine B from the droplet to the surrounding fluid in the absence of oscillations is determined by molecular diffusion. The droplet and the surrounding liquid are illuminated with a laser sheet, which allows for the observation of the fluorescence emission of both liquids and the control of the concentration of Rhodamine B within them. The liquid droplet undergoes radial stretching within the liquid layer as a consequence of the injection process. The elongated shape of the droplet along the radial direction of the radial Hele-Shaw cell leads to noticeable differences in its azimuthal and diametral dimensions dD. The laser sheet could be oriented in both azimuthal (horizontal line in Fig. 2a,b) and radial (vertical line in Fig. 2b) directions. In the absence of fluid oscillations, Rhodamine B diffuses through the interface in radial and azimuthal directions irrespective of the initial shape of the drop (Fig. 2).

Figure 2: Photos of an octanol droplet containing Rhodamine B illuminated by the laser sheet: (a) azimuthal and (b) both azimuthal and radial directions

The primary objective of the experiments is to investigate the azimuthal propagation of solute under fluid oscillations. Fig. 3 illustrates the diffusion of Rhodamine B from chlorobenzene and octanol droplets into the surrounding water over time. A grayscale filter is applied to the photos for further image processing in order to obtain quantitative data. Each pixel in the grayscale image is identified by a color, with a numerical value ranging from 0 to 255 (from black and white, respectively). The maximum concentration of solute is associated with a white color while a zero concentration is associated with a black color. The study of diffusion is carried along the x-axis, which coincides with the direction of the laser beam, with the origin located at the interface (Fig. 3). Rhodamine B diffuses from the droplet into the surrounding liquid. Accordingly, the solute concentration and the width of the diffusion zone, along with their temporal evolution, can be determined from the measurement of the intensity of the fluorescent radiation.

Figure 3: Photos of a droplet of chlorobenzene (a, c) and octanol (b, d) illuminated with a laser sheet oriented in the azimuthal direction at (a) 900 s; (b) 300 s; (c) 10,800 s; (d) 7200 s

The gray value is measured in dependence on the x-coordinate along the selected direction (Fig. 3). Fig. 4 demonstrates the dependence of the gray value on the x-coordinate for chlorobenzene and octanol droplets in water after t=5400 s from the start of the observation. The maximum gray value, and thus concentration, of Rhodamine B is observed at the interface between the droplet and water. As the solute diffuses into water, the gray value decreases to almost zero, indicating the absence of Rhodamine B. The width Δx of the diffusion zone and the change in concentration ΔC can be calculated from the distribution of gray value along the x-axis.

Figure 4: Dependence of the gray number on the x-coordinate at time t=5400 s after the start of the observation: (a) chlorobenzene droplet and (b) octanol droplet

If it is assumed that the Rhodamine B diffuses only in the chosen direction, as it was described in [17], the second Fick’s law may be written in the following form:

dCdt=Dd2Cdx2,(1)

where C is the concentration of dissolved fluorescent dye, x is the coordinate along which the diffusion of dye in water is considered and D is the diffusion coefficient. The corresponding boundary conditions are C=1 at x=0 and C=0 at x→∞, assuming that the solute concentration is constant at the boundaries of the diffusion zone.

The solution of Eq. (1) and the expression for calculating the concentration gradient of the solute are provided in [17,18]. Bushueva et al. [16] used the findings of [17,18] to develop an experimental technique for determining the molecular diffusion coefficient of Rhodamine B in water in a vertical rectangular cell. The basic principle of the technique is to determine the width of the diffusion zone Δx in accordance with a corresponding change in concentration ΔC. The dependence of the square of the diffusion zone width Δx2 on the parameter 4πt is determined. The dependence is linear and therefore, the tangent of the slope of the line is equal to the molecular diffusion coefficient of Rhodamine B in water:

Dm=Δx2/4πt.(2)

The technique described is applied to the liquids under investigation in this study. The square of the diffusion zone width as a function of time is determined for Rhodamine B diffusing from octanol and chlorobenzene droplets into the surrounding water. The size of the droplets is considerably smaller than the characteristic size of the liquid layer, and the diffusion of Rhodamine B can be considered uniform in all directions. Fig. 5 illustrates the dependence of Δx2 on 4πt obtained in the experiments with chlorobenzene and octanol droplets shown in Fig. 3. These dependencies are linear and allow the determination of the value of the molecular diffusion coefficient of Rhodamine B in water.

Figure 5: Dependence of the square of the diffusion zone width on time (parameter 4πt) in water surrounding octanol (a) and chlorobenzene (b) droplets saturated with Rhodamine B

Table 2 presents values of the molecular diffusion coefficient of Rhodamine B in water. The diffusion coefficients calculated using expression (2) are in good agreement with the known values of the coefficient Dm, confirming the applicability of the proposed technique for measuring the diffusion coefficient of Rhodamine B in the droplet experiments.

3.2 Effective Diffusion of Rhodamine B

When water oscillates, the droplet remains in a fixed position and does not drift due to the formation of a more effective wetting layer on the glass walls of the cell than water. Simultaneously, the interface between the droplet and the surrounding water oscillates in the direction of water flow. The dynamics of fluid flow within a droplet with an oscillating surface is modelled in the experiments of Kozlov et al. [15]. It is demonstrated that the surface oscillations result in the generation of time-averaged flows, the structure and intensity of which are dependent on the parameters of surrounding liquid oscillations. The present study demonstrates that the oscillation of the ambient liquid enhances the mass transport of solute at the interface and increases the solute diffusion rate in the ambient liquid. This study examines the oscillatory dynamics of a droplet and mass transfer of Rhodamine B in the case of a droplet of octanol (Fig. 6). Once the surrounding water begins to oscillate, the droplet inclusion deforms while maintaining elongation along the cell radius. The experiments are conducted with a single droplet at a fixed frequency and a varying amplitude b of oscillation.

Figure 6: Photos of the aqueous solution of Rhodamine B near the octanol droplet at a frequency fvib=4.0 Hz and amplitude b=0.56 mm at t=0 s (a) and t=1800 s (b)

It can be assumed that the amplitude of radial oscillations is dependent on the radial coordinate within the cell, but not on the azimuthal one. Consequently, when the laser sheet is azimuthally oriented, the amplitude of water oscillations is approximately unchanged in the area of Rhodamine B concentration measurements. The diffusion of the dye is examined over time for given values of fvib and b. It is important to note that in the radial direction, which coincides with the direction of the oscillations, there is no evidence of growth in the diffusion zone of Rhodamine B (Fig. 6). However, the dye is transported in the azimuthal direction to a distance that is significantly larger than the initial droplet size.

The experiments show that the width xmax of the zone in which Rhodamine B is present is significantly larger than the width of the molecular diffusion zone in the absence of the fluid oscillations (Fig. 7). The maximum gray value (equivalent to the solute concentration) is observed at the interface between octanol and water while the minimum gray value is observed at a considerable distance from the droplet. The dependence of the gray value on the coordinate x exhibits a breakpoint. It seems reasonable to suggest that in the region preceding the breakpoint, the time-averaged flow is responsible for mixing the dye within the water. This zone has a considerable width of xmax−Δx in Fig. 7. The domain of width Δx between the dashed lines in Fig. 7 illustrates the diffusion zone of Rhodamine B in water against the background of radial oscillations of the liquid. The width of the diffusion zone increases with time. Rhodamine B has not been detected in the water outside the xmax zone. The averaged flows are generated only in the region Δx because of the presence of a seated droplet in the flow path.

Figure 7: Dependence of the gray value on the coordinate x at t=0 s (a) and t=1800 s (b). The data are obtained from the photos shown in Fig. 6

Thus, oscillating fluids provide additional solute transport to molecular diffusion. The combined effect of molecular diffusion and mass transport caused by fluid oscillations is quantified by the effective diffusion coefficient Deff. It is important to note that the domain of diffusive mass transport is confined to the region outside the mixing zone. The effective diffusion coefficient is evaluated in a manner identical to that employed for the measurement of the molecular diffusion coefficient. When liquids oscillate at a frequency of fvib=4.0 Hz and an amplitude of b=0.56 mm the coefficient Deff=5.2⋅10−6 cm2/s is greater than the molecular diffusion coefficient Dm=3.4⋅10−6 cm2/s. It can thus be concluded that oscillatory flow near the droplet results in an intensification of solute transport from the droplet to the surrounding liquid occurring beyond the mixing zone.

Fig. 8 illustrates the temporal evolution of the width of the diffusion zone at different amplitudes of the fluid oscillations. The experiment is carried out in the three distinct phases. In the initial phase of the experiment, the oscillation amplitude is set to 0.39 mm, and the width xmax of the zone in which Rhodamine B is present is measured for approximately 2000 s. Then, the oscillations are switched off in order to set a new oscillation amplitude b=0.59 mm. Once the oscillations have been initiated, the measurement of the distance xmax is continued for a further 2000 s. Finally, the amplitude is increased to 1.1 mm. At the start of each experimental phase, the distance xmax increases rapidly. Then, the expansion of the zone containing Rhodamine B decelerates, and the distance xmax tends towards a constant value. The greater the amplitude b, the faster the initial growth of the width of the zone containing Rhodamine B.

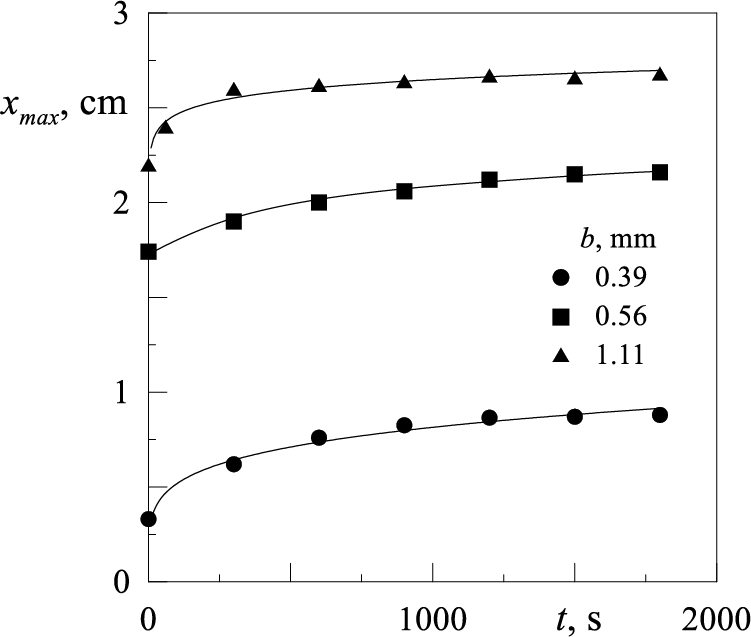
Figure 8: Temporal evolution of the zone in which Rhodamine B is present at different amplitudes of fluid oscillations at a fixed frequency fvib=4.0 Hz

The effective diffusion coefficients Deff obtained in the three phases of the experiment are given in Table 3. As the oscillation amplitude increases, the width of the zone in which Rhodamine B is present also increases, as does the effective diffusion rate.

Finally, it is demonstrated that the oscillations of the liquid near the droplet enhance the solute mass transfer due to the azimuthal time-averaged flow. In the future, the objective is to conduct a detailed study of mass transfer in relation to a number of key parameters, including oscillation frequency and amplitude, fluid viscosities, surface tension, and the intensity of the time-averaged flows.

4  Conclusion

The effect of the oscillatory flow on the mass transfer of a dye between a droplet and a surrounding liquid in a radial Hele-Shaw cell is studied experimentally. An experimental setup comprising a linear motor and a flat radial cell which permits the direct injection of a droplet inclusion into the fluid layer, has been designed and assembled. The experimental technique for determining the diffusion rate of Rhodamine B in water by measuring the width of the diffusion zone is validated. The experimental results demonstrate the intensification of solute mass transfer which is caused by intensive time-averaged flow in the liquid near the droplet. It is revealed that the solute mass transfer and the growth of the mixing zone increase with the oscillation amplitude. The experimental technique employed for the determination of the effective diffusion coefficient is examined in the context of the diffusion zone peripheral to the mixing zone. It is demonstrated that an increase in the amplitude of the fluid oscillations leads to a considerable widening of the diffusion zone and a marked enhancement in the rate of the solute mass transfer.

Acknowledgement: The authors would like to express their gratitude to Professor Victor Kozlov for invaluable assistance in the preparation of this article.

Funding Statement: This work was financially supported by the Russian Science Foundation (Grant No. 23-11-00242).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Ivan Karpunin; data collection: Ivan Karpunin; analysis and interpretation of results: Ivan Karpunin; draft manuscript preparation: Ivan Karpunin and Denis Polezhaev; interpretation of results in the process of preparing responses to reviewers: Denis Polezhaev. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data are included in this published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

References

1. Bennamoun L, Belhamri A, Mohamed AA. Application of a diffusion model to predict drying kinetics changes under variable conditions: experimental and simulation study. Fluid Dyn Mater Process. 2009;5(2):177–92. doi:10.3970/fdmp.2009.005.193. [Google Scholar] [CrossRef]

2. Rudobashta SP, Kartashov EM. Chemical technology: diffusion processes. Moscow: Yurait Publishing House; 2024 (In Russian). [Google Scholar]

3. Abdeljabar R. On the behavior of an interface under molecular diffusion: a theoretical prediction and experimental study. Fluid Dyn Mater Process. 2009;5(2):193–210. doi:10.3970/fdmp.2009.005.193. [Google Scholar] [CrossRef]

4. Bokhary A, Leitch M, Liao BQ. Liquid-liquid extraction technology for resource recovery: applications, potential, and perspectives. J Water Process Eng. 2021;40:101762. doi:10.1016/j.jwpe.2020.101762. [Google Scholar] [CrossRef]

5. Dentz M, Hidalgo JJ, Lester D. Mixing in porous media: concepts and approaches across scales. Transport Porous Med. 2023;146(1):5–53. doi:10.1007/s11242-022-01852-x. [Google Scholar] [CrossRef]

6. Cussler EL. Diffusion: mass transfer in fluid systems. Cambridge, UK: Cambridge University Press; 2009. [Google Scholar]

7. Stein W. Transport and diffusion across cell membranes. Amsterdam, The Netherlands: Elsevier; 2012. [Google Scholar]

8. Kapellos GE, Alexiou TS, Payatakes AC. A multiscale theoretical model for diffusive mass transfer in cellular biological media. Math Biosc. 2007;210(1):177–237. doi:10.1016/j.mbs.2007.04.008. [Google Scholar] [PubMed] [CrossRef]

9. Mogre SS, Brown AI, Koslover EF. Getting around the cell: physical transport in the intracellular world. Phys Biol. 2020;17(6):061003. doi:10.1088/1478-3975/aba5e5. [Google Scholar] [PubMed] [CrossRef]

10. Lohse D, Zhang X. Physicochemical hydrodynamics of droplets out of equilibrium. Nat Rev Phys. 2020;2(8):426–43. doi:10.1038/s42254-020-0199-z. [Google Scholar] [CrossRef]

11. Bushueva A, Vlasova O, Polezhaev D. Averaged dynamics of fluids near the oscillating interface in a Hele-Shaw cell. Fluid Dyn Mater Process. 2024;20(4). doi:10.32604/fdmp.2024.048271. [Google Scholar] [CrossRef]

12. Kozlov VG, Vlasova OA, Dyakova VV. Stability of the interface of liquids oscillating in a vertical flat channel. Interfacial Phenom Heat Transf. 2024;12(1). doi:10.1615/InterfacPhenomHeatTransfer.v12.i1. [Google Scholar] [CrossRef]

13. Kozlov V, Karpunin I, Kozlov N. Finger instability of oscillating liquid-liquid interface in radial Hele-Shaw cell. Phys Fluids. 2020;32(10):102102. doi:10.1063/5.0018541. [Google Scholar] [CrossRef]

14. Karpunin IE, Kozlov VG, Kozlov NV. Influence of high-frequency fluid oscillations on viscous droplet inclusion in a Hele-Shaw cell. Convective Flows. 2019;9:36–51 (In Russian). [Google Scholar]

15. Kozlov VG, Sabirov RR, Subbotin SV. Steady flows in an oscillating spheroidal cavity with elastic wall. Fluid Dyn. 2018;53(2):189–99. doi:10.1134/S0015462818020118. [Google Scholar] [CrossRef]

16. Bushueva A, Polezhaev D. Mass transfer of solute in an oscillating flow in a two-dimensional channel. Phys Fluids. 2024;36(4):045150. doi:10.1063/5.0204206. [Google Scholar] [CrossRef]

17. Rashidnia N, Balasubramaniam R, Kuang J, Petitjeans P, Maxworthy T. Measurement of the diffusion coefficient of miscible fluids using both interferometry and Wiener’s method. Int J Thermophys. 2001;22:547–55. doi:10.1023/A:1010735117408. [Google Scholar] [CrossRef]

18. Ray E, Bunton P, Pojman JA. Determination of the diffusion coefficient between corn syrup and distilled water using a digital camera. Am J Phys. 2007;75(10):903–6. doi:10.1119/1.2752819. [Google Scholar] [CrossRef]

19. Rani SA, Pitts B, Stewart PS. Rapid diffusion of fluorescent tracers into Staphylococcus epidermidis biofilms visualized by time lapse microscopy. Antimicrob Agents Chemother. 2005;49(2):728–32. doi:10.1128/AAC.49.2.728-732.2005. [Google Scholar] [PubMed] [CrossRef]

20. Fang X, Xuan Y, Li Q. Experimental investigation on enhanced mass transfer in nanofluids. Appl Phys Lett. 2009;95(20). doi:10.1063/1.3263731. [Google Scholar] [CrossRef]