Relevant Fluid Dynamics Aspects of the Internal Ballistics in a Small-Scale Hybrid Thruster

1  Introduction

The space sector has undergone significant transformations since the beginning of its history, largely due to the continuous advancement of technology and scientific knowledge. In the past two decades, small satellites and nanosatellites have gained an increasingly significant role in this domain, with market shares rising to an estimated 2.1 billion $ by 2021 [1]. A considerable percentage of these spacecraft is constituted by CubeSat platforms, a standard that was developed in 1999 by researchers at California Polytechnic State University and Stanford [2]. The basic element is the CubeSat unit (namely 1U), which is defined as a 10 cm square cube [3]. These platforms may comprise a single unit or a combination of standard units, resulting in different form factors (3U, 6U, 12U, for instance). CubeSats were initially conceived by academic institutions for educational purposes, with the potential for scientific and commercial applications being quite limited at that stage [4]. However, the subsequent development of miniaturized payloads, coupled with significant technical advances, has resulted in a considerable expansion of their scope [5]. In this context, the mission scope has significantly enlarged, modifying the mission requirements at both system and subsystem levels. The development of innovative technologies to meet these renewed needs has been prompted, requiring notable modifications such as the introduction of propulsion systems. Until May 2024, more than 200 nanosatellites have been equipped with thrusters to enable maneuvering capabilities [5]. This share, which to date represents about 10% of the total 2604 nanosat launch attempts, marks an emerging trend in the space community.

Among numerous available technologies, the research group in Aerothermochemistry, Microgravity and Space Propulsion at the University of Naples Federico II has focused its work on the development, design, and testing of monopropellant and hybrid propellant thrusters of different scales. These classes of chemical engines were selected for nanosatellite applications because they combine the main advantages of solid and liquid propulsion systems [6]. They are able to provide thrust in the order of tens of Newtons with low power consumption, enabling orbital maneuvering, formation reconfiguration, and de-orbit capabilities. Limited geometrical envelope and low system complexity ensure that the stringent mass and volumetric requirements typical of CubeSat platforms are met. Moreover, hybrid propellant thrusters are characterized by re-ignition and thrust regulation capabilities. These features, typical of liquid propellant rocket engines [7], are crucial to broaden the range of mission profiles that may be achieved through hybrid rocket engines. Another main advantage is represented by the intrinsic safety guaranteed by this technology since the liquid (or gaseous) oxidizer cannot accidentally encounter the solid fuel grain. Moreover, hybrid rocket thrusters enable the employment of environmentally friendly and non-toxic propellants such as hydrogen peroxide, standing as a viable alternative to hydrazine-based systems, currently in phase-out for future space missions. A major disadvantage lies in their low technology level, with a Technology Readiness Level (TRL) of 6 for small-scale systems [8]. Furthermore, system scalability is typically complex, and an accurate performance prediction is more challenging compared to solid and liquid thrusters, for which a broader literature is available. The lower specific impulse values with respect to electric or chemical liquid propellant systems require a careful selection of propellant pairs to be used. In addition, lower average regression rates with respect to comparable solid rocket motors [9,10] imply reduced thrust levels.

This work aims to address some of the aforementioned issues by investigating typical aspects of small-scale hybrid propulsion to improve understanding and facilitate future operational use. The present study complements various previously published works. Rampazzo and Barato [11] have addressed numerical methodologies for the simulation of the regression rate under varying heat fluxes. An in-depth analysis of the CFD assessment of HDPE firing test performed with a 1 kN-class hybrid rocket is performed by Bianchi et al. in [12]. Tian et al. [13] have presented an extensive discussion of injection pattern effects in hybrid engines [13]. Meng et al. [14] have discussed a three-dimensional numerical model based on dynamic mesh techniques. In all cited cases, the discussions and analyses concern larger-scale engines than the one of interest, with thrusts from 1 kN upwards. The present work aims to supplement the pre-existing literature with information on a smaller scale, which is necessary given the difficulties of scalability for hybrid rocket thrusters. Numerous studies carried out by the authors have demonstrated a higher regression rate in comparison with larger engines using comparable propellant pairs [15,16] and a greater impact of the thermal characteristics on the fluid-dynamic behavior of the thruster [17]. These analyses are crucial for a complete understanding of small-scale hybrid thruster internal ballistics since scarce data are currently available for this class of engine. The limited information available in the literature, coupled with the difficulties of scaling down the inferred relations and phenomena analyzed for larger thrusters, requires a dedicated study for smaller hybrid rocket engines. Specifically, the present study proposes an experimental characterization and numerical assessment of a hydrogen peroxide-based hybrid micro-thruster employing a polymeric fuel grain. This work is focused on the numerical investigation of two peculiar behaviors recorded during an experimental campaign. Exploiting transient Computational Fluid Dynamics (CFD) simulations, the objective is to properly reproduce these experimental findings through the numerical model employed. A proper matching between empirical and numerical data could enhance the reliability of the results deduced from CFD analyses, increasing reconstruction capabilities. Furthermore, a solid numerical method could be exploited to thoroughly investigate fluid dynamic phenomena determining thruster performance. Section 1 has described the general context in which the engine was developed, summarizing the state of the art and the challenges to be faced. Section 2 will discuss the experimental setup, the engine configuration, and its design process. An overview of the experimental data post-processing technique and the numerical models employed will be reported in Section 3. In addition to this, computational grid information and convergence analysis will be provided. In Section 4, experimental results of the HDPE and ABS-like firing test will be discussed, in combination with a brief assessment of the thrust chamber thermal behavior. Section 5 will present the main results of the extensive numerical analyses performed, while conclusions of the work will be presented in Section 6.

2  Laboratory Setup, Engine Design and Configuration

2.1 Firing Test Facility

The experimental data used for the present study were collected during a firing test campaign conducted exploiting dedicated experimental facilities equipped with an instrumented test bench. The empirical investigation of small-scale monopropellant and hybrid thrusters employs a dedicated hydrogen peroxide feed line, shown in Fig. 1. The 87.5% concentrated H2O2 (namely High-Test Peroxide, HTP) is stored in a 2 L stainless steel tank and pressurised with nitrogen gas. N2 pressure is controlled through a regulator to attain the required values. A manual shut-off valve is placed on the oxidizer feed line for safety. Downstream, a Bronkhorst Cori-Flow M45 flow meter is used to perform both mass flow-regulated and pressure-regulated tests. For this work, the instrument is employed exclusively to measure the mass flow rate of hydrogen peroxide, with an accuracy of 0.2% on the estimated values, as per catalogue [18]. The last element on the feed line is a Parker Miniature Calibrant Valve Series 9 solenoid valve, which controls the oxidizer flow to the thruster injector. It is electronically controlled, and it can be used to operate the engine in pulsed or continuous mode, as studied in [19]. Hybrid and monopropellant thrusters are tested on an instrumented test bench, which allows temperature, pressure and thrust measurements to be recorded by means of dedicated sensors installed on the engine. Table 1 summarises the sensors used during the experimental campaign. Their location will be specified in the following section, where the thruster design is discussed. The signals are routed via a National Instruments PXI 1082e acquisition system to the control computer, where they are managed and stored.

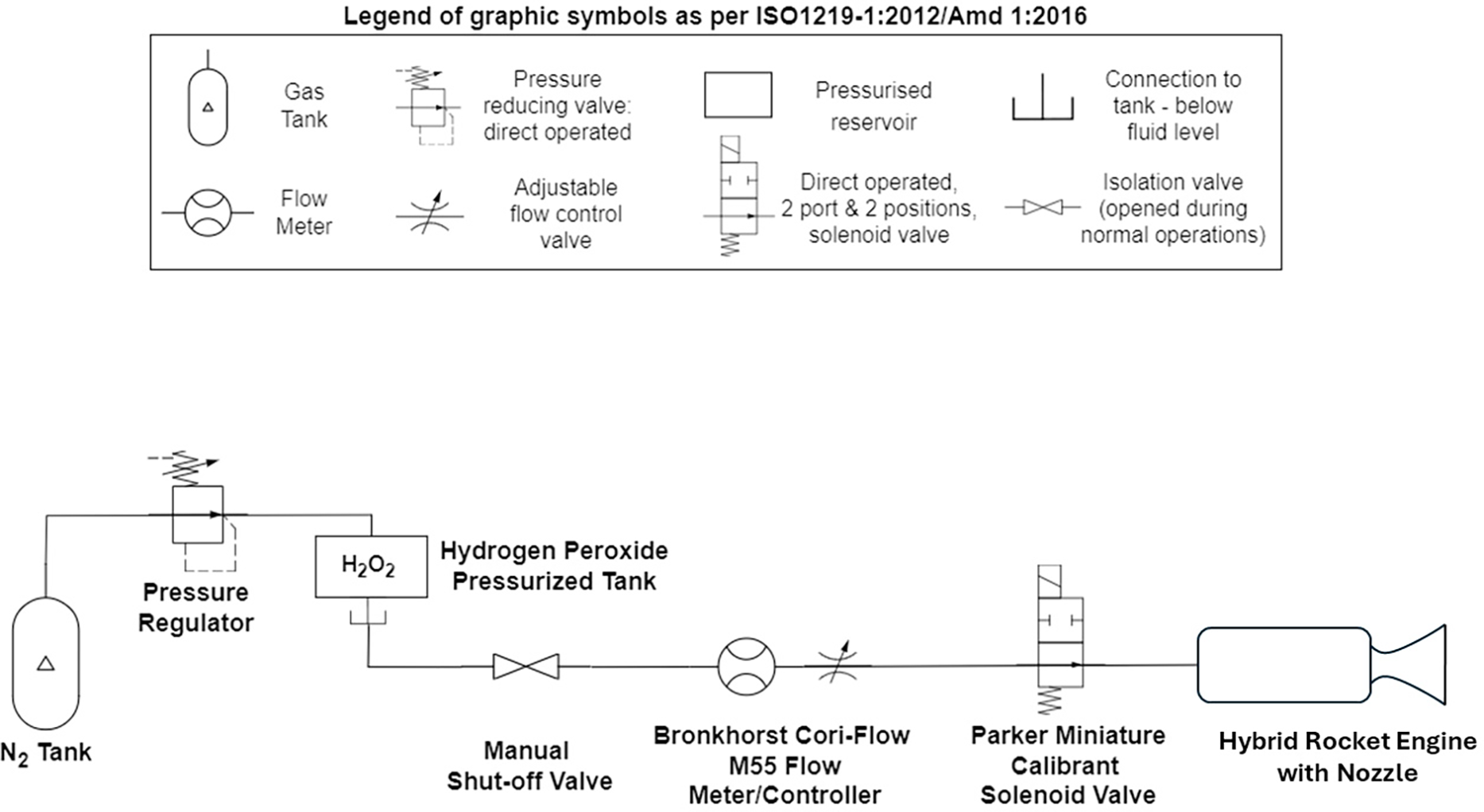
Figure 1: Hydrogen peroxide feed line. The graphic symbols adopted are in accordance with International Standard Organisation ISO 1219-1:2012/Amd 1:2016 [20]

2.2 Engine Configuration

The hybrid propellant rocket engine studied in this work is schematically represented in Fig. 2. Detailed technical drawings are reported in the Supplementary Materials to provide precise information regarding the technical specifications and geometrical dimensions of the elements constituting the tested assembly. The thruster is connected to the hydrogen peroxide feed line through a dedicated channel of the support flange, which also acts as the mechanical interface with the test bench (Fig. S1). The liquid injection plate (Fig. S2) delivers the oxidiser through three 0.3 mm diameter holes into the decomposition chamber. It consists of a 44 mm long cylinder, with an inner diameter of 20 mm. All the relevant dimensions are reported in Fig. S3. The inner volume is filled with inert alumina pellets mixed with a disposable catalyst. It consists of a MnOx-based powder that is interposed between two layers of porous pellets, which mainly serve a structural function by holding the compound in place. The decomposition process is monitored through a pressure sensor and a thermocouple situated at a distance of 13 mm from the inlet in the axial direction. The thermocouple is placed at a radial distance of 2 mm from the periphery of the internal wall. The technical specifications of the sensors, as well as the instruments in the combustion chamber, can be found in Table 1. A drilled retaining plate (Fig. S4) serves as a physical barrier to avoid accidental occlusion of the 2 mm throat convergent nozzle. Hydrogen peroxide decomposition follows the reaction scheme reported in Eq. (1). It is triggered by the combined action of two mechanisms: chemical interaction with catalysts and to a minor degree thermal decomposition due to the high temperatures reached in the chamber [21]. Using disposable MnOx-based powder drastically increases the reactivity of the system and ensures high decomposition efficiency, as detailed below. This allowed hybrid tests to be carried out without requiring pre-heating stages, reducing the fuel grain heating prior to ignition [16]. To assess decomposition performance, a monopropellant version of the thruster under investigation (i.e., a configuration of the same engine without the combustion chamber) was tested before the hybrid rocket experimental campaign. Fig. 3 displays pressure and temperature measurements acquired in the catalytic chamber during a 14 s long monopropellant firing test. The oxidizer mass flow rate was set to 5 g/s. The temperature profile over time shows that the catalytic system employed was able to guarantee the satisfying decomposition of hydrogen peroxide in a short amount of time. The maximum recorded temperature of approximately 945 K corresponds almost exactly with the 959.65 K value, which is representative of the adiabatic decomposition temperature for 87.5 wt% H2O2 [22]. In addition to this, an estimation of the decomposition efficiency was derived from the pressure data by comparing the theoretical characteristic velocity with the experimental one, obtaining a value of around 92%. The decomposition performance reported above were also found to be representative of the subsequent hybrid tests studied in this work.

H2O2(l)→H2O(g)+12O2(g)+Heat(1)

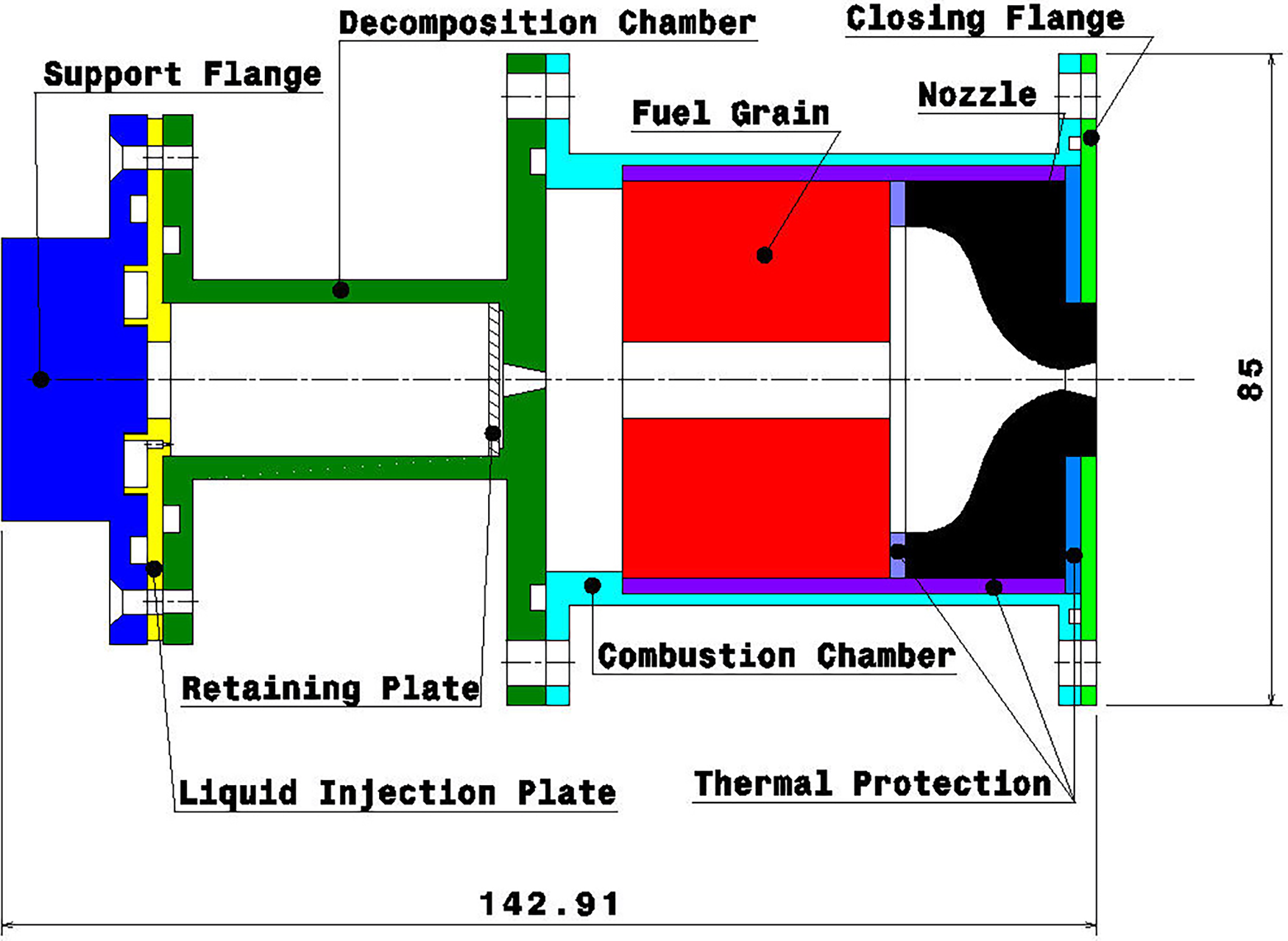
Figure 2: Cross section of the small-scale hybrid propellants rocket engine. Overall dimensions are reported in [mm]

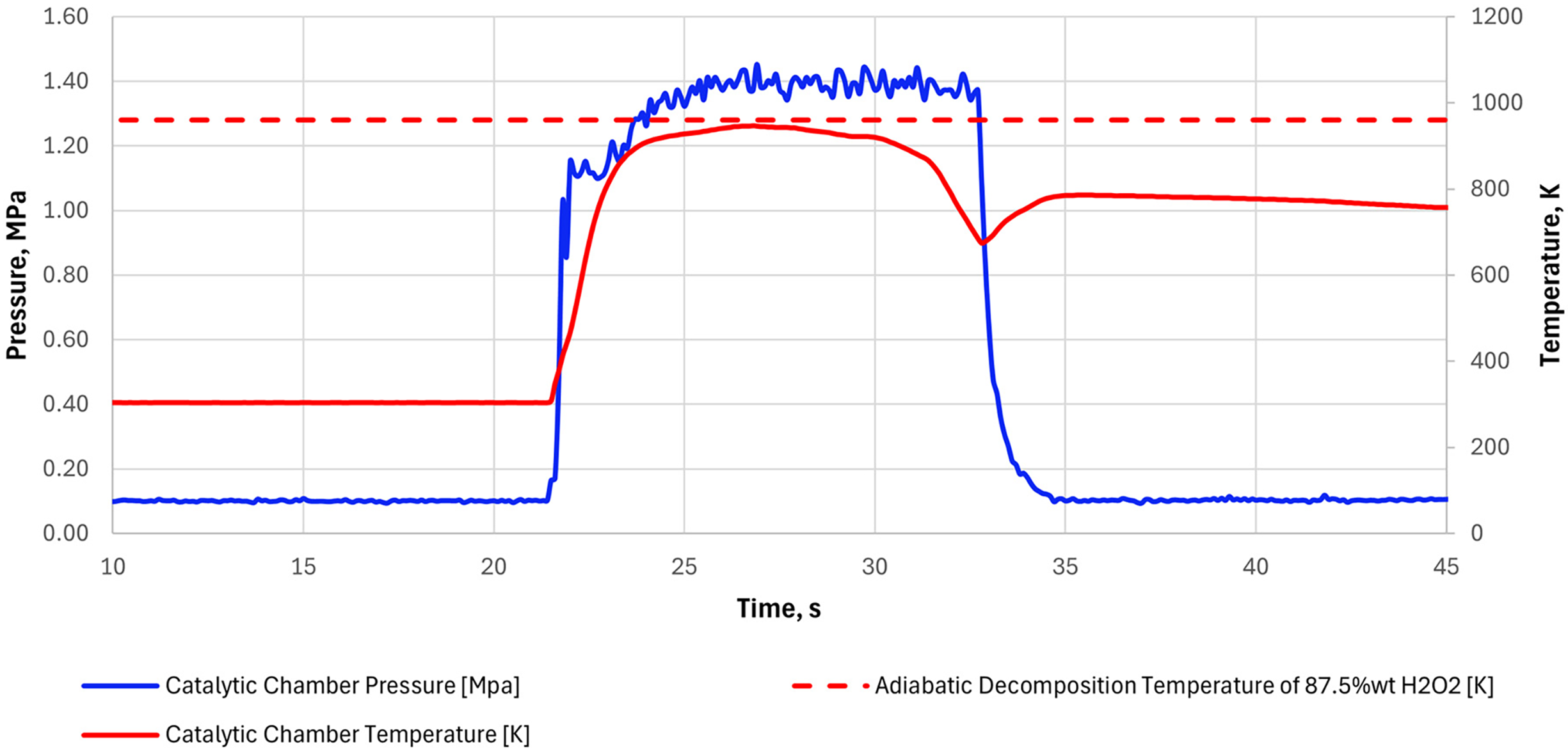
Figure 3: Pressure and temperature signals acquired in the catalytic chamber during a 14 s long monopropellant test, performed to assess decomposition performance

The decomposition products are injected into the combustion chamber, detailed in Fig. S5, which comprises a 10 mm long pre-chamber to facilitate the generation of a recirculation zone. The goal is to enhance the mixing process between the oxidizer and the fuel, increasing the engine’s combustion efficiency. An HDPE (High-Density Polyethylene) and an ABS (Acrylonitrile Butadiene Styrene)-like cylinder with an external diameter of 56 mm and a cylindrical port of 10 mm are employed as fuel for the combustion reaction. The fuel grain is thermally insulated from the combustion chamber wall and the nozzle thanks to thermal protections interposed between the elements. This decreases the conductive heat flow to the grain and avoids excessive temperature increase, thus preventing unwanted melting phenomena. The graphite converging-diverging nozzle (Fig. S6) incorporates a 10 mm long post-chamber conceived to increase the residence time of the combustion products. The nozzle is characterized by a throat diameter of 2.6 mm and an expansion ratio of 3.4, which is relatively low considering its employment for ground tests. A closing flange (Fig. S7) is mounted to allow the full assembly of the thruster and its proper sealing. An additional thermal protection is inserted between the closing flange and the nozzle to prevent overheating of the external case. The combustion chamber assembly is equipped with a pressure transducer and a thermocouple in the pre-chamber to monitor the combustion process. Three further thermocouples are mounted on grooves on its outer wall to acquire data of the case heating during the firing test, at respectively 8, 33.96, and 61.41 mm from the combustion chamber inlet section.

2.3 Engine Design

The engine configuration presented in the previous section is derived directly from a redesign process of the hybrid mini-thruster shown in Fig. 4, which has been extensively investigated in previous experimental campaigns [15].

Figure 4: Old configuration (a) and new configuration (b) of the H2O2-based hybrid rocket engine. Labels display the position and designation of the thermocouples on the combustion chamber

The new setup was designed to meet the requirements of a space-based remote sensing mission in which the research group was involved. The objective was the development of a hybrid propulsion system for in-orbit demonstration of the technology. During phase 0/A (as defined by the European Space Agency ESA [23]), initial requirements for the mission were established in terms of thrust and chamber pressure ranges, ΔV and maximum length. Starting from the list of values reported in Table 2, an iterative process was developed to determine the optimized configuration. An estimation of the performance of different setups was carried out by varying 3 control parameters:

•   Oxidizer mass flow rate m˙ox, with values of 3, 3.5, and 4 g/s;

•   Nozzle expansion ratio Ae/At, between 9 and 20;

•   Different fuel compositions and corresponding regression laws.

To account for the effect of different fuels during the preliminary design phase, two regression laws were considered. Specifically, two experimental r˙ vs. Gox relations obtained for a hydrogen peroxide-based hybrid rocket engine of comparable scale were used, employing either PolyVinyl Chloride (PVC) or HDPE as fuels. Since PVC exhibits problems related to outgassing in vacuum, its use for space applications is questionable. For this reason, starting from the regression law defined experimentally in [15], a 30% margin was applied obtaining two additional r˙ relations, as shown in Fig. 5.

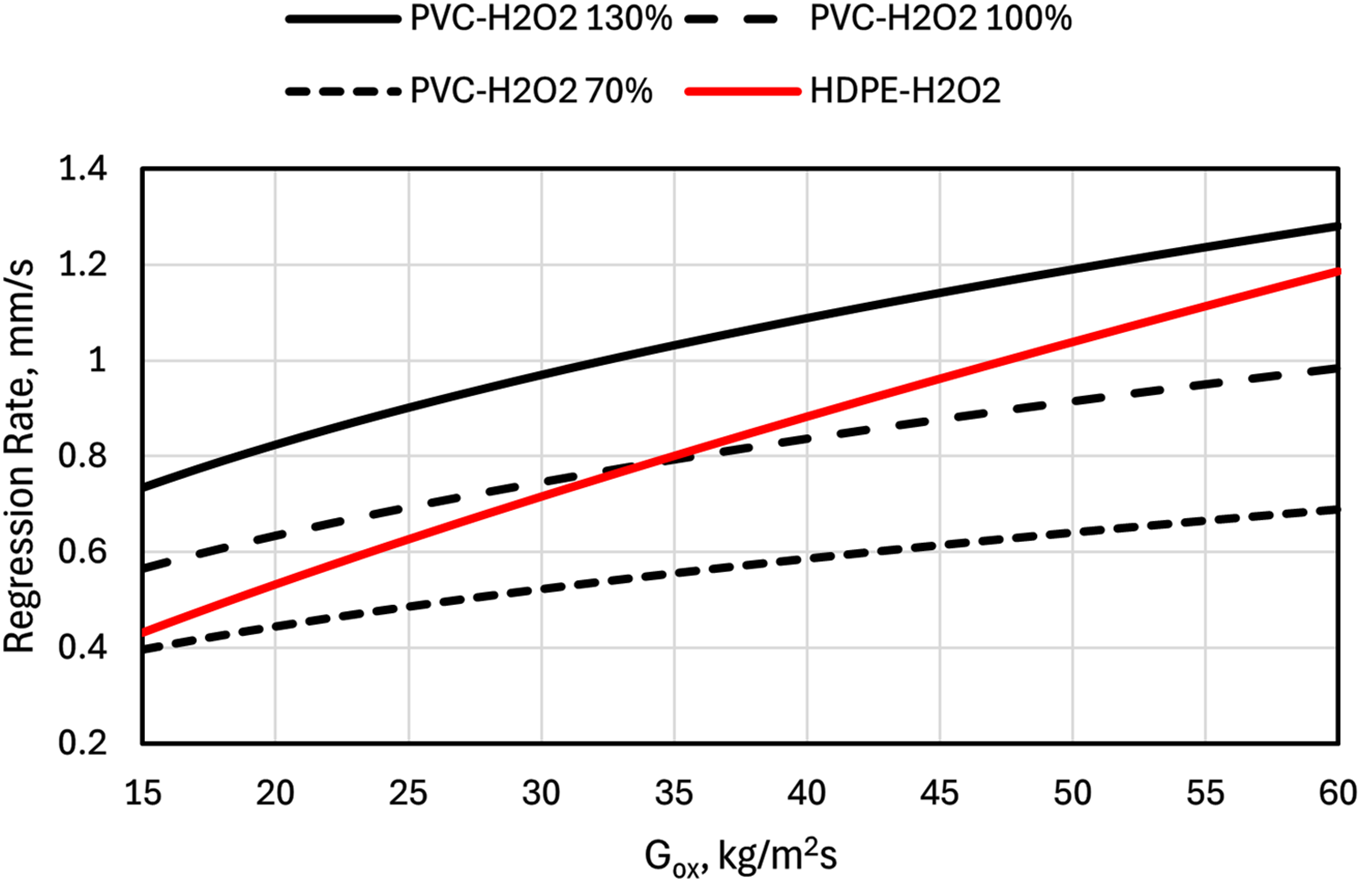
Figure 5: Regression laws used for the iterative design process

A performance analysis was carried out for each combination of variables, using the desired total impulse value as the target parameter (as represented in Fig. 6). Numerous designs varying in grain length, diameter and composition were collected and compared. Among the several alternatives, the setup characterised by the maximum diameter was chosen for simulation, production and testing. Indeed, it constitutes the worst-case scenario both from the point of view of the geometrical envelope, since the thruster shall be contained entirely within a volume of 1.5 CubeSat Units (comprising fluidic feed lines and tanks), and from the fluid-dynamic point of view since a lower length-to-diameter ratio could affect sensibly the internal ballistic with respect to what is already known in the case of the previous setup. Moreover, this configuration attained three objectives. First, a larger diameter for the combustion chamber could enable an extension of the burning time, typically limited to less than 10 s for the previous configuration. Furthermore, adopting a larger fuel grain allowed for the study of a wider oxidizer mass flow rate (Gox) range, thus enabling the assessment of any effect that the progressive widening of the burning area might have on the fluid dynamic field and propulsive performance. The third objective was to evaluate the impact of thermal behavior on the regression rate. As observed in [15,17], this class of engine exhibits a higher r˙ in comparison with larger-scale thrusters using the same propellant pairs [24]. Since one of the possible causes of this peculiar characteristic could be the greater sensitivity to the heating of the fuel grain, a larger diameter allowed it to be thermally insulated from the combustion chamber case, aiding the study of this phenomenon. The longer firing times could also be used to further analyse the impact of the incoming heat flux on the HDPE cylinder during the test.

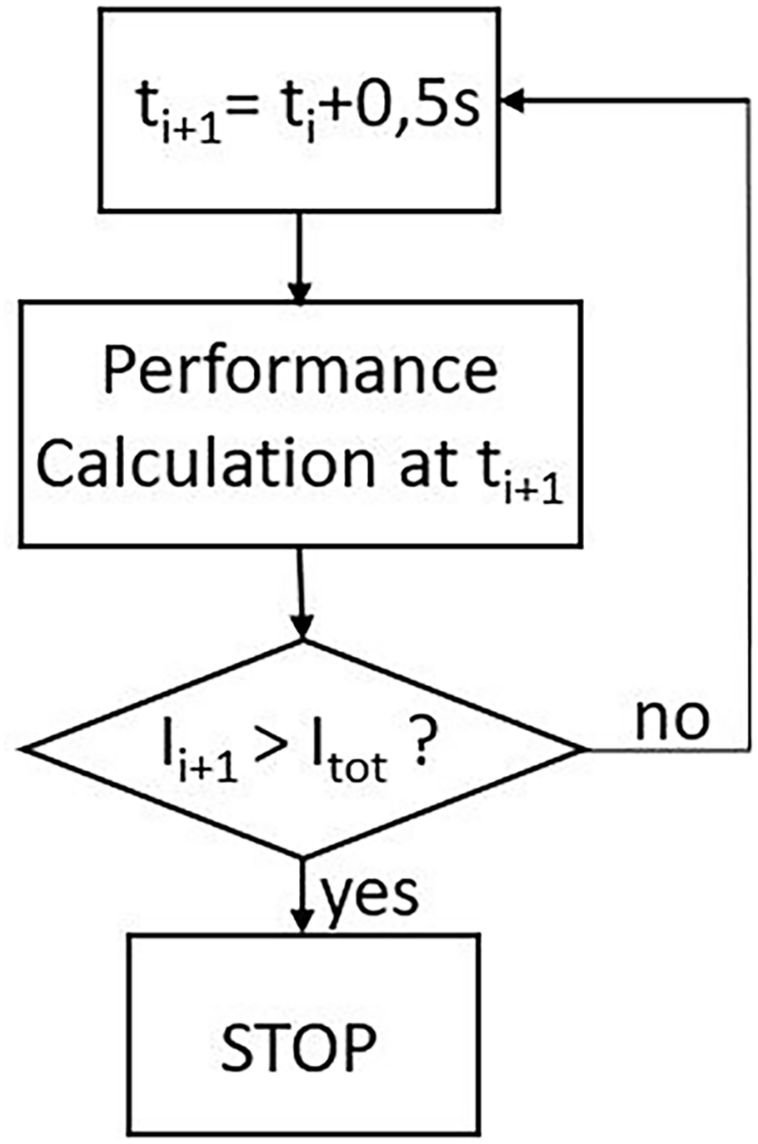
Figure 6: Conceptual scheme of the iteration logic employed for the design process

Once the new combustion chamber diameter was determined, preliminary analyses were carried out to obtain a theoretical and approximate estimate of the expected engine performance. This allowed to evaluate the updated configuration during the design phase before the procurement of the required elements. The preliminary assessment was performed through an in-house MATLAB code for the experimental data prediction, implementing simplified analytical equations based on the Rocket Propulsion Analysis (RPA) open software to model the thermo-fluid-dynamic condition of the combustion mixture, as described in [16]. The initial assumptions underlying this internal ballistic model include:

•   Ideal gas;

•   Homogeneous mixture;

•   Complete and adiabatic combustion;

•   Steady-state flow in the combustion chamber;

•   One-dimensional and iso-entropic flow in the nozzle;

•   Chemical Equilibrium in the nozzle;

•   Null temperature and velocity gradients between gaseous and condensed chemical species.

Considering 87.5 wt% hydrogen peroxide and HDPE as propellant pair and employing preliminarily the experimental regression law obtained with the previous configuration of the thruster, it is possible to estimate the propulsive performance from the initial data presented in Table 3. tb is the burning time, m˙ox is the oxidizer mass flow rate, a and n represent the parameters of the Marxman Law. Lg is the grain length, Di is the initial port diameter, Dt is the nozzle throat diameter, ρf is the density of the fuel grain, while Ae/At is the ratio between the nozzle exit area and its throat area.

The results of a 25-s firing test simulation are reported in Table 4. The simulation predicts a large grain consumption due to the relatively high burning time, with the port diameter increasing up to 27 mm. Consequently, a sensible oxidizer-to-fuel ratio (O/F) shift is expected during the test. The oxidizer mass flux Gox=m˙ox/Ab has an average value of 11.16 kg/m2s, varying strongly throughout the experiment owing to the significant variation of the burning area. The thrust obtained is slightly more than 7 N at sea level and the specific impulse Isp is lower than 200 s. This information was used to validate the design, for example, by checking that the grain consumption was below the imposed dimensional limits, with enough margin to avoid direct contact between the flame and the combustion chamber wall. It also forms the baseline for evaluating the actual performance of the thruster, which will be discussed in the following sections.

3  Data Post-Processing Technique and Numerical Modelling

3.1 Measured Data Reduction Technique

Each firing test allows the acquisition of experimental data sets obtained through sensor measurements (as shown in Table 1) and post-test grain evaluation. These direct measurements can be either instantaneous values recorded over time or time-averaged data and comprise important parameters such as oxidizer mass flow rate m˙ox, combustion chamber pressure pc, engine thrust T, fuel grain mass consumption ΔM, and test duration tb. It is possible to estimate numerous derived quantities from the measured data [17], which will prove useful in the subsequent analyses. Firstly, the quality of the combustion process can be assessed through the evaluation of the characteristic velocity c∗, defined as:

c∗=pcAtm˙¯ox+m˙¯f(2)

where At is the nozzle throat area, m˙¯ox is the time-averaged oxidizer mass flow rate (estimated as in Eq. (3)), and m˙¯f is the time-averaged fuel mass flow rate (computed as in Eq. (4)).

m˙¯ox=m˙ox,tottb(3)

m˙¯f=ΔMtb(4)

The space-averaged final port diameter D~p,f is evaluated as:

D~p,f=Dp,i2+4πΔMρfL(5)

where ρf is the fuel density as defined by the polymeric fuel material properties, and L is the grain length. From D~p,f, Eq. (6) is used to derive the space- and time-averaged grain port diameter D¯p.

D¯p=Dp,i+D~p,f2(6)

The time-averaged oxidiser mass flux Gox is defined as:

G¯ox=4πm˙¯oxD¯p2(7)

Eq. (8) describes the time-averaged oxidiser-to-fuel ratio O/F during the test:

OF=m˙¯oxm˙¯f(8)

Once the measured and estimated quantities have been collected, a comprehensive characterization of the thruster behavior during the test may be performed. The analysis of error propagation for quantities estimated as products or ratios of other quantities was carried out based on the measurement instrument errors listed in Table 1, following the formulas provided in [25]. The estimated error values have been reported in Tables 6 and 9.

3.2 Numerical Modeling

Computational Fluid Dynamics simulations were performed as a support tool for experimental results. The use of models that reproduce realistically the rocket engine’s internal ballistics allows an in-depth study of the physical phenomena at play. To properly capture the relevant fluid-dynamic features, a commercially available software employing a pressure-based algorithm and a control volume approach is used to solve the Raynolds-Averaged Navier-Stokes (RANS) equations, specified for the case of turbulent single-phase multicomponent flows [26]. The Shear Stress Transport (SST) k–ω model is applied for turbulence closure [27]. Since the chemical kinetics is considerably faster than the characteristic diffusion time of the system for hybrid rocket engines, a methodology based on chemical equilibrium coupled to the Probability Density Function (PDF) is used. This method reproduces the combustion reaction through a pure mixing problem, circumventing the difficulties typically associated with closing nonlinear mean reaction rates. The interactions between turbulence and chemical reactions are described in terms of the average mixture fraction, denoted by f, and its variance, f′2. The β-function of these two quantities describes the derived PDF. Calculating the f and f′2 values on the entire flow field, the probability density function obtained is used to estimate the time-averaged values of individual species temperature, density and mole fractions. These results are realized through the execution of thermochemical calculations founded upon the minimization of Gibbs free energy [28]. The local regression rate is implemented through an in-house model reproducing the gas-surface interaction solving mass and energy balance equations, with an Arrhenius-like equation to account for the effect connected to the wall temperature. Even though the products of solid fuel pyrolysis are numerous, and their composition is dependent on both the wall temperature and heating rate, the most common practice in the existing literature is to consider only the gaseous monomers. Consequently, in this study, gaseous ethylene (C2H4) has been employed as the fuel injected from the grain surface when considering firing tests conducted with HDPE polymeric grains, while butadiene (C4H6) is used to reproduce the ABS combustion process.

3.3 Computational Domain and Boundary Conditions

The numerical calculations are performed employing two-dimensional structured grids, which represent the internal volume of the pre-chamber, the fuel grain port, the post-chamber and the nozzle. In Fig. 7, a typical computational grid is represented.

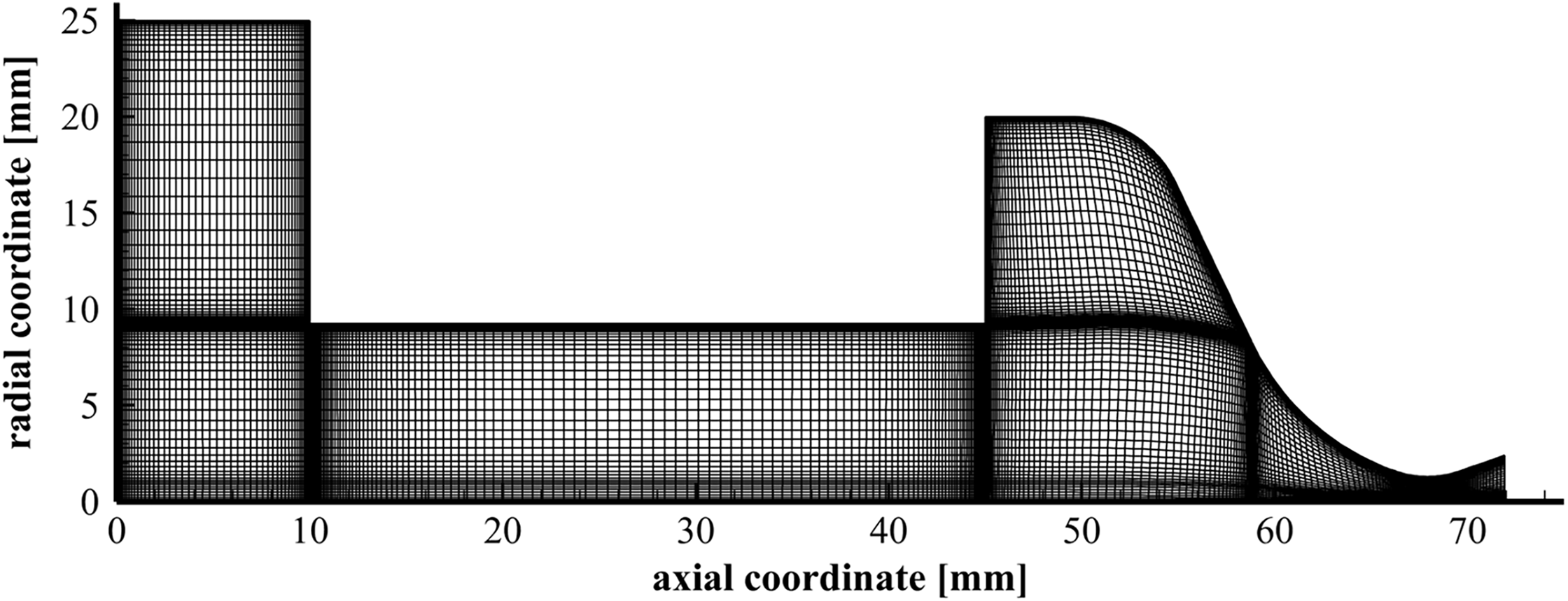
Figure 7: Representative axisymmetric two-dimensional computational grid for numerical simulation of the hybrid mini-thruster internal ballistics

It should be noted that this is an illustrative example, as the grain length and port diameter vary in accordance with the different cases under analysis. As shown in Fig. 7, cells are clustered in proximity to the grain wall, ensuring that the y+ maximum value is approximately between 2 and 3 in the cells adjacent to the wall along the entire grain length for all test cases considered. Furthermore, additional mesh refinement is performed in the regions proximate to the inlet and outlet sections of the grain and for the inner surfaces of the pre-chamber, post-chamber, and nozzle. Following the naming scheme reported in Fig. 8, boundary conditions are applied for each inner surface of the thruster. No-slip and adiabatic conditions are imposed on the surface of both the pre-and post-chamber, as well as on the nozzle wall. A mass flow inlet condition is prescribed for the injector, assigning appropriate values for the injection temperature (900 K), oxidizer mass fraction and turbulent quantities. The pressure outlet boundary condition is set to the nozzle exit.

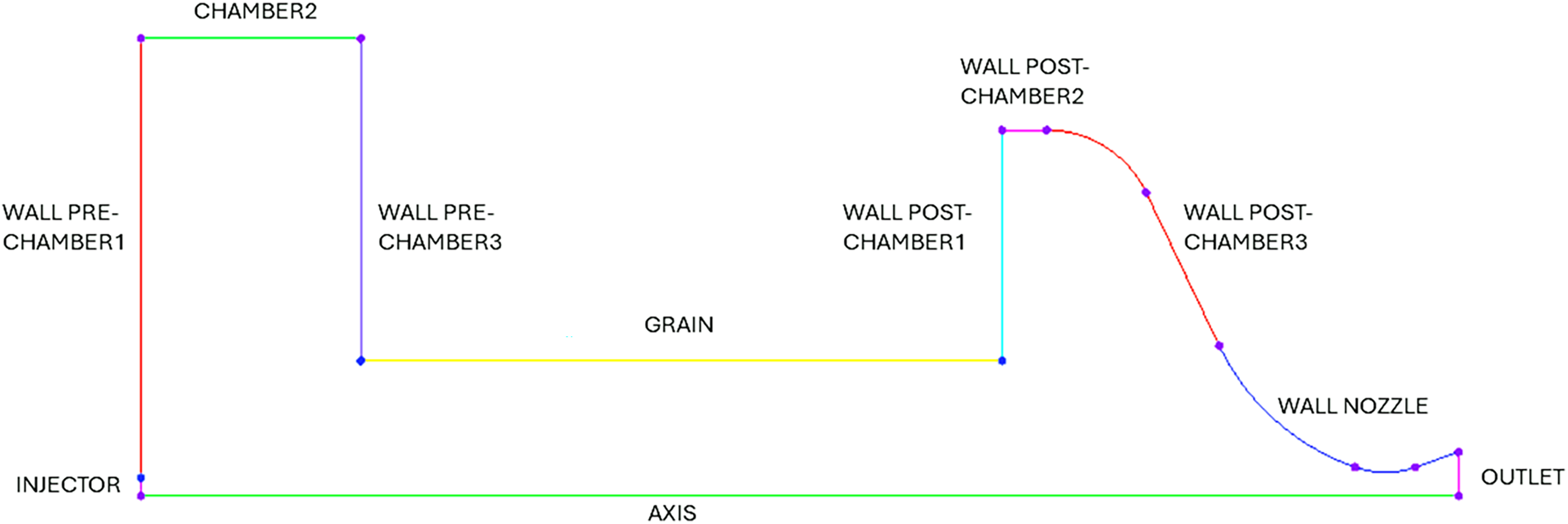
Figure 8: Naming scheme applied for the computational grid boundary conditions

3.4 Grid Sensitivity Analysis

To evaluate the numerical results presented in the subsequent sections, a grid sensitivity analysis is conducted using three levels of mesh refinement. The coarser mesh is created by doubling the cell size in both the axial and radial directions compared to the reference mesh, while the finer mesh is produced by halving the cell size in both directions. Fig. 9 displays the axial profiles of the regression rate computed with the different meshes.

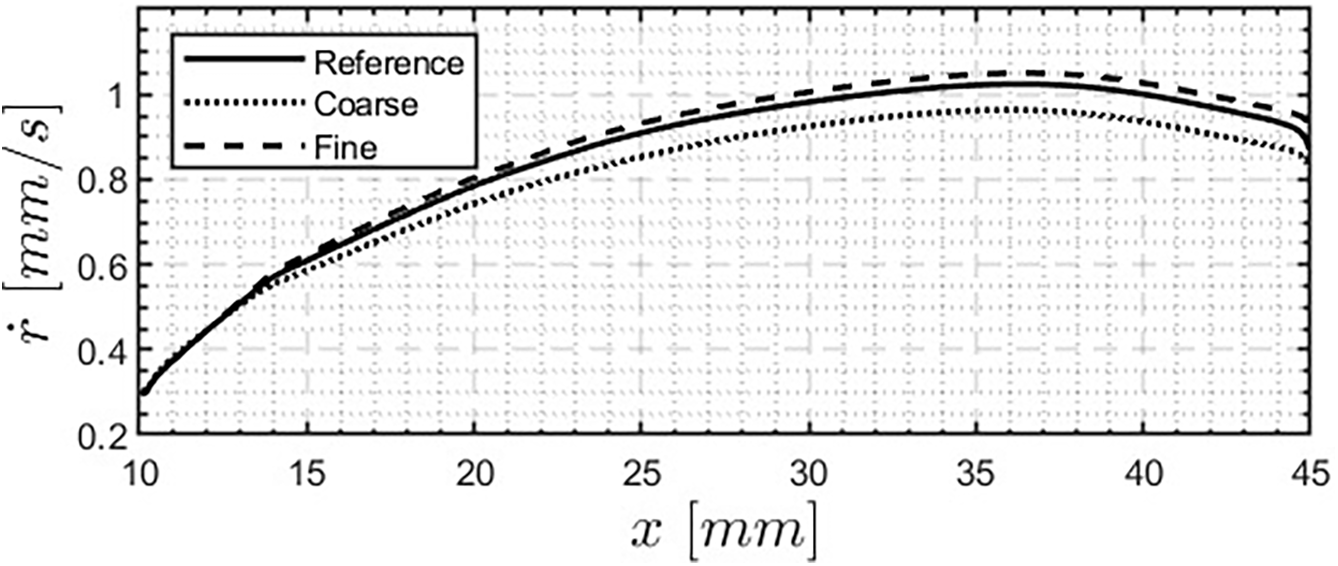
Figure 9: Numerical regression rate profiles calculated with different refined computational grids

Table 5 presents the averaged regression rates calculated using the different meshes, along with the associated numerical errors. These errors are determined using the methods outlined in [29], where the exact value of the asymptotic value pas is estimated through the appropriate Richardson extrapolation:

pas=pfine+(pfine−pref)2g−1(9)

where g is the order given by:

g=log⁡pcoarse−prefpref−pfinelog⁡2(10)

and pcoarse, pref and pfine are the values of the considered quantity computed with the coarse, medium and fine grids, respectively. The numerical error is then defined as the relative difference between the computed value and the exact value estimated with Eq. (10). It can be seen that the numerical error gathered with the reference mesh is around 5% and, therefore, it can be stated that a satisfying convergence of the numerical results is obtained.

3.5 Grain Geometry Update Technique

Numerical analyses of hybrid rocket engines are typically performed by conducting a single CFD simulation based on an appropriate geometry capable of properly reproducing the fluid dynamics phenomena involved. As shown in [30], an estimation of the r˙¯ obtained through numerical simulations that account for the grain geometry variations over time exhibits negligible deviation from that derived from a single CFD analysis performed on a geometry with a diameter equal to the mean grain diameter, as defined in Eq. (6). This method simplifies the evaluation of the most important propulsive parameter by lowering the computational cost required, and it is therefore frequently used. Even when analyses have been conducted at various stages of engine firing, the internal diameter has been consistently regarded as uniform along the grain. Consequently, uneven radial distributions have been typically disregarded. On the contrary, the present study employs a grain update geometry technique (as in [25]) to properly reproduce a variable regression rate along the thruster longitudinal axis. This method emulates a variable node displacement over the entire inner grain surface, thus achieving a greater degree of accuracy in the replication of experimental findings [31].

An iterative process based on a sequence of stationary CFD simulations with a forward integration scheme is employed to update the grain geometry during the firing test simulation. Starting from the prior knowledge of the local regression rate rn˙(xi) for point xi at time instant tn, the objective is to compute the coordinates of the same grid node at the following time instant tn+1. The local displacement Δin is evaluated as:

Δin=rn˙(xi)Δt(11)

where Δt is the time step defined as Δt=tn+1−tn. Given that the regression rate is defined perpendicularly to the grain surface, the displacement of a generic point could occur not only along the radial direction but also along the axial direction. If ϑi is the fuel surface local inclination with respect to the radial direction, as shown in Fig. 10, the coordinates of the i-th node at the time instant tn+1 can be computed as shown in Eqs. (12) and (13).

xin+1=xin−Δincos⁡ϑi(12)

yin+1=yin−Δinsin⁡ϑi(13)

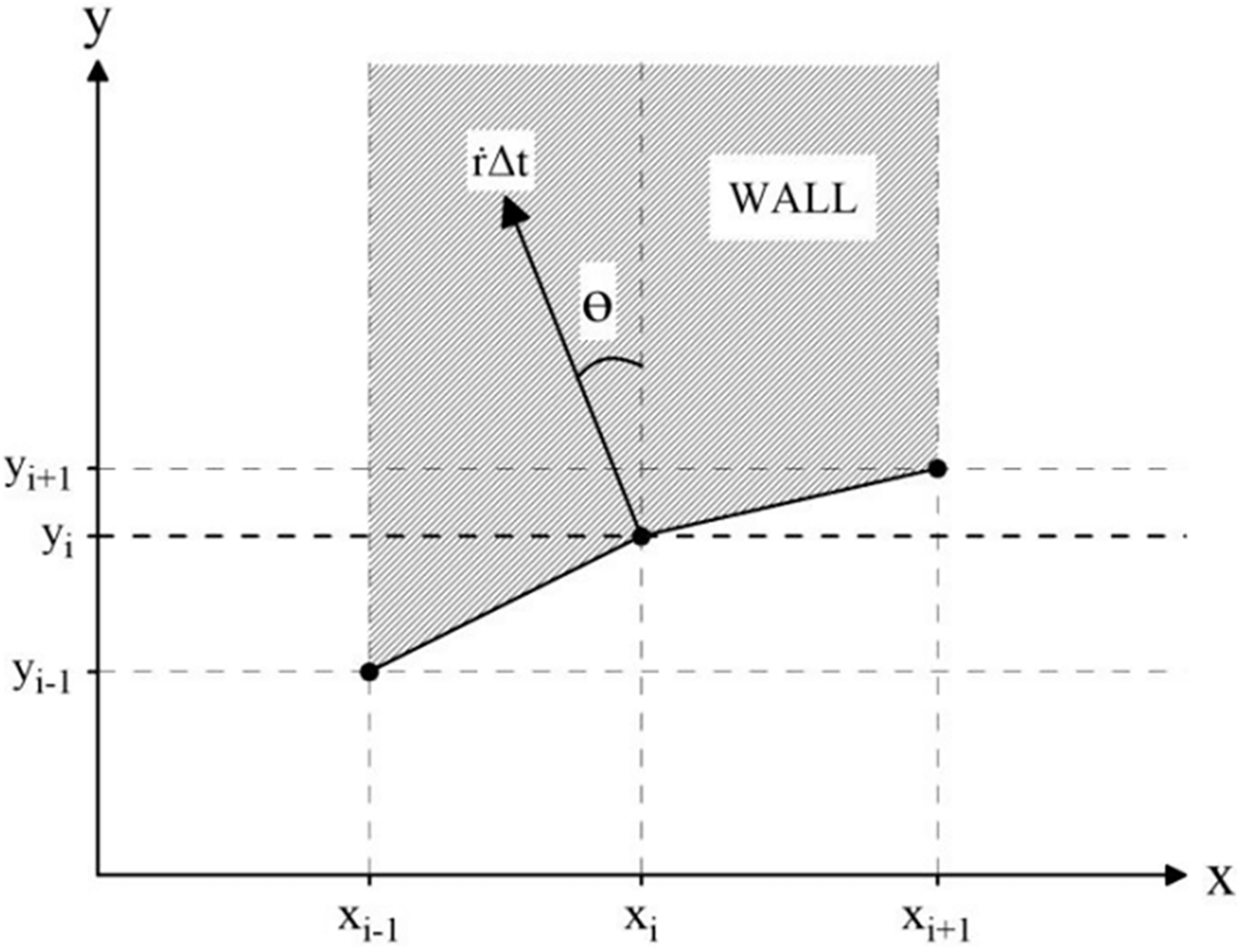
Figure 10: Schematic of node displacement for the i-th node. Reprinted from Reference [32]. 2023, The Combustion Institute

Once the nodes position at time instant tn+1 is obtained, the subsequent grain geometry is univocally defined, and a new stationary CFD simulation related to the new configuration is performed to calculate the updated regression rate distribution [32]. This provides the set of local regression rates r˙n+1(xi) along the grain, and by propagating this scheme over time, the axial and radial nodes coordinates are computed step-by-step and the evolution of the grain port diameter during the firing test is modeled. The final geometry established for t=tb can be used to numerically estimate the grain volumetric mass loss. Under the assumption that the radial mass consumption could be approximated as the volume of a truncated cone, the volume lost during the burning time can be estimated as represented in Fig. 11 and reported in Eq. (14).

V≈∑i=1N13πΔh(Ri2+ri2+Riri)(14)

where N represents the number of stations considered, Δh is the truncated cone height, while Ri and ri are the major and minor base radii, respectively. The volume of a cylinder whose height is the grain length of the grain, and whose radius is the initial port radius has to be subtracted from the resulting volume in order to estimate the actual radial volumetric loss. Knowing the material density of the fuel grain, it is then possible to estimate the mass loss obtained from CFD simulations, which can be compared with the experimental value and can contribute to the performance analysis.

Figure 11: Volumetric loss calculation scheme

4  Experimental Results

This section will present the experimental results of two test cases performed with the thruster configuration described in Section 2.2. Since the main objective of the present work is the numerical simulation of the engine internal ballistics on the basis of experimental firing tests, two different materials were employed as fuels for the combustion reaction. This approach allowed to assess the fidelity of the CFD model under investigation while considering variable material properties and fluid dynamics behaviours. Specifically, Section 4.1 will consider a firing test carried out with a HDPE fuel grain coupled with 87.5% concentrated High Test Peroxide (HTP), with an average oxidizer flow rate of 7.2 g/s and a burning time of approximately 6.5 s. Section 4.2 will show the results of an experimental test employing ABS-like and 87.5 wt% HTP as propellant pair, with a time-averaged m˙ox of 5.15 g/s and a similar target duration. For both test cases, the hydrogen peroxide feed pressure is the same, as is the thruster setup and the sensors used (as described in Table 1). The difference in oxidizer flow rate is due to the different combustion processes, related to the properties of the materials used, as well as other factors such as decomposition efficiency. This does not affect the validity of the work, as the primary objective of the study does not involve a direct comparison of the performance of the two fuels, but their analysis using the available numerical models. Furthermore, the tests performed allowed the new thruster configuration to be tested and its fluid-dynamic and propulsive behavior to be compared with the preliminary assessments made in the pre-design phase.

4.1 Performance Analysis and Experimental Findings for the HDPE Test Case

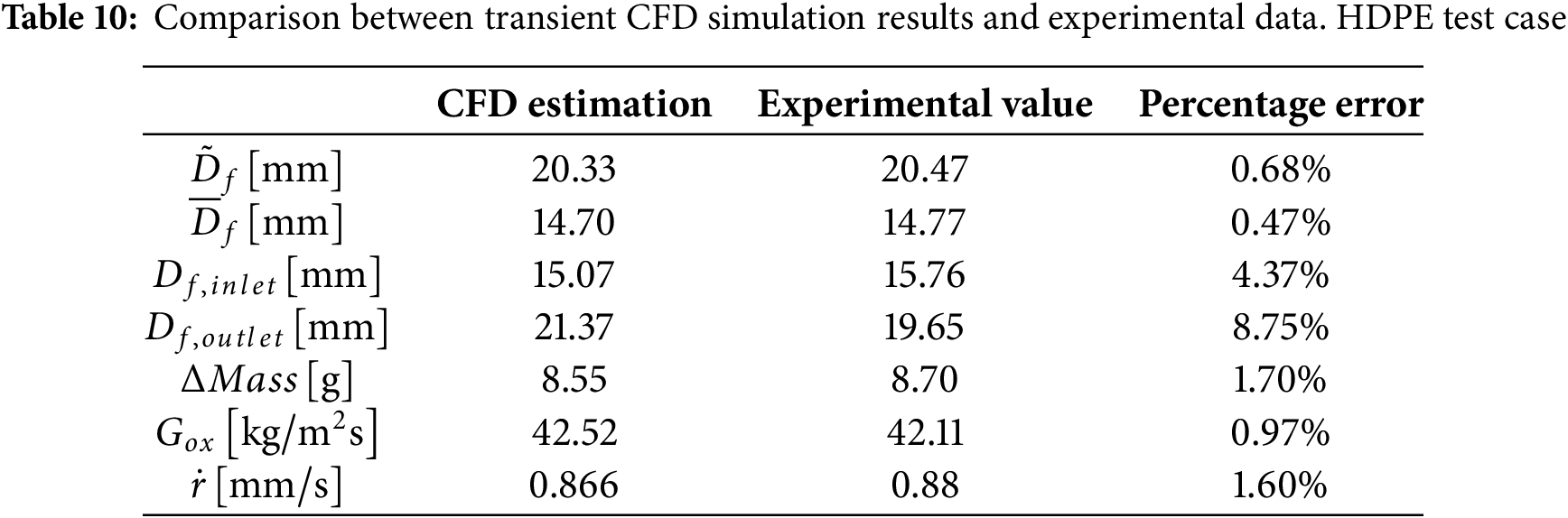
The experimental results and the main performance parameters for the firing test conducted with an HDPE fuel grain are reported in Table 6, where both measured and estimated quantities are shown. The latter were obtained following the procedure described in Section 3.1. Two different regression rate estimates are shown in Table 6. The first one is calculated using the mass loss method, as detailed in Section 3.5, while the second is derived from the inner port diameters measured at the end of the test. Among them, the value of 0.88 mm/s is considered more reliable, as it is obtained from a global measurement that takes into account the mass consumption of the entire grain. It is also based on a measurement that is less affected by errors and uncertainties, providing a more effective evaluation. For these reasons, in the following analyses, the reference value for the HDPE test will be the one calculated using the mass loss technique.

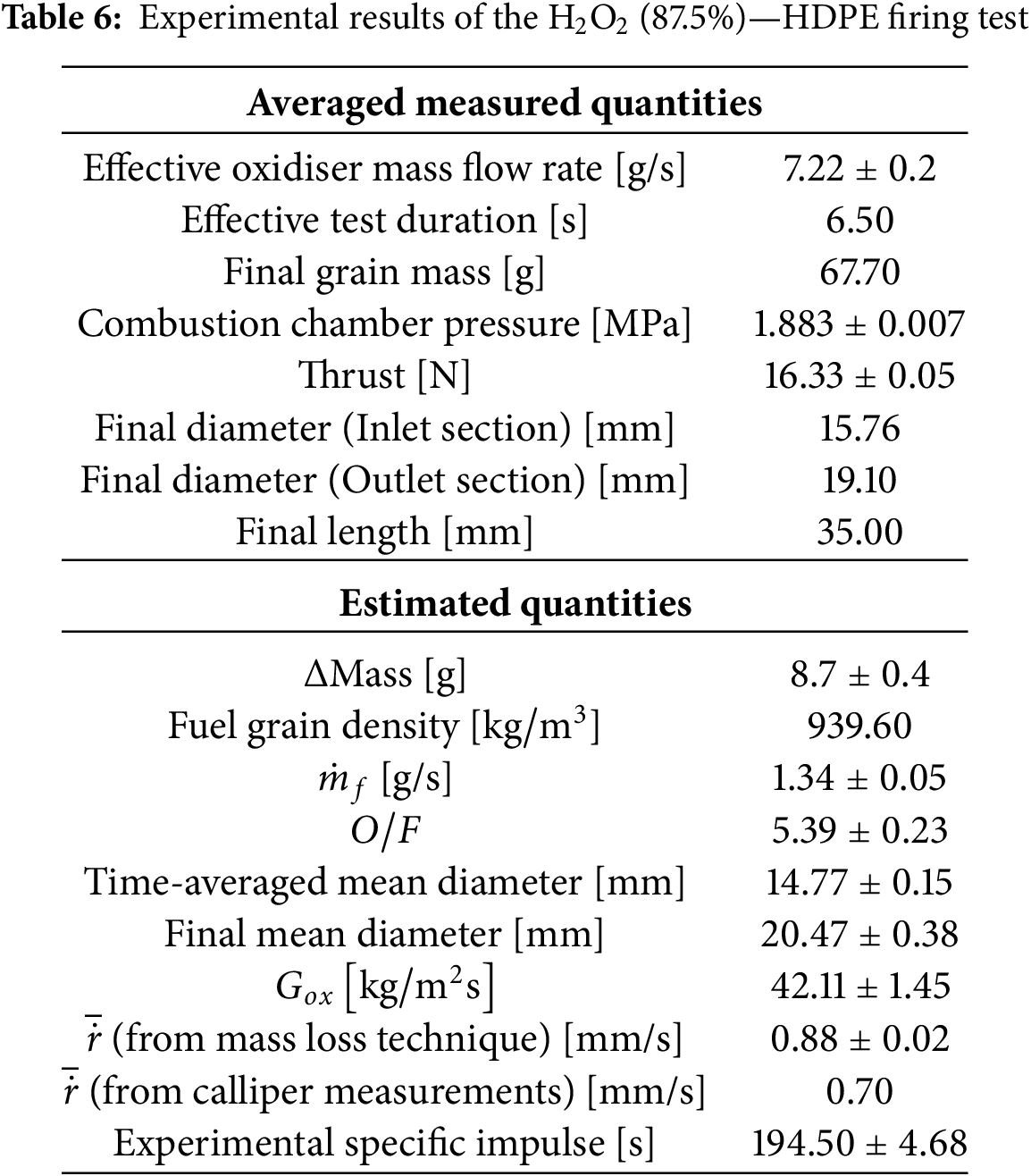
By analysing these data, the thruster performance can be assessed by considering important propulsion parameters such as thrust, chamber pressure, specific impulse, average regression rate and oxidiser-to-fuel ratio O/F. Starting from the experimental data, an additional analysis can be carried out by comparing the actual performance against that obtained using a one-dimensional code that estimates the operating conditions in the combustion chamber using data from NASA’s Chemical Equilibrium with Applications (CEA) software, as detailed in [16]. Using as input parameters a burning time and an oxidiser mass flow rate equal to the average experimental values, results listed in Table 7 were obtained. Burning time and oxidiser mass flow rate were selected to be to the average experimental values, and a regression law derived empirically with the same propellants pair and similar thruster configuration was used. Table 7 summarise the main results.

Combining experimental data with mono-dimensional simulation results, some similarities and some differences can be noted. The estimated average regression rate was very similar for both cases, if considering the experimental value computed through the mass loss technique. This implies comparable m˙f and oxidiser-to-fuel ratio. On the other hand, combustion chamber pressure during the test differed sensibly from the numerical evaluation. The discrepancy may be justified considering that the value obtained with the in-house code is theoretical and does not account for inefficiencies in the combustion and decomposition processes. Similarly, the different thrust levels can be attributed to the low efficiency of the non-optimized nozzle used for ground tests, which causes a non-negligible decrease in the thrust coefficient cf. Together with the lower value of characteristic velocity c∗ with respect to the ideal case, the experimental value resulted lower. A further consideration should be reserved for the final port diameter. Although the time-averaged diameter is comparable, the grain post-test measurements showed a significant difference in diameter between the inlet and outlet sections, as reported in Table 6. This phenomenon could not be reproduced by the simulation since the 1D approach to the problem is used to study the radial evolution of the grain, but it is not able to account for different behaviors along the grain length. Consequently, the estimated final diameter closely approximates the experimental value measured at the outlet section but exhibits a non-negligible difference to the inlet. The recorded discrepancy between these two quantities was unexpected and caught the authors’ attention. Therefore, the fuel grain was cut longitudinally during the postprocessing phase to further investigate the phenomenon. As displayed in Fig. 12, an uneven distribution of port diameters was observed along the entire grain, showing that this feature did not exclusively affect the areas near the inlet and outlet. Measurements were executed with a 5 mm step, as indicated by the black marks in Fig. 12b. To reduce the sensitivity to measurement errors, each station was characterized through four independent values. An average diameter and an error estimate were thus obtained for each location of interest. The collection of the acquired data is reported in Table 8. It is possible to notice that the average diameter increased steadily, moving away from the inlet section, reaching a maximum at around 2/3 of the grain length, decreasing slightly toward the outlet. The investigation of the physical phenomenology generating this distribution of port diameters (and consequently of local regression rates) will be carried out employing appropriate numerical simulations, whose discussion and results are reported in Section 5.

Figure 12: Front view (a) and cross-section (b) of the HDPE grain after the firing test. Red arrow: flow direction

4.2 Performance Analysis and Experimental Findings for the ABS-Like Test Case

As anticipated, an additional test was carried out with an ABS-like grain to complement the experimental and numerical analyses performed with HDPE. The fuel cylinder has the same geometrical characteristics as the previous one. However, it was produced employing the stereolithography additive manufacturing technique, using an ABS-like commercial resin polymerized with 405 nm UV light. The test results, conducted with the same setup, test duration and feed pressure as in the HDPE case study, are summarised in Table 9. Fig. 13 shows the set of signals acquired through the measuring equipment described in Section 2.1 during the 8.8 s firing test. The test duration is estimated considering the time interval between half the rise of the combustion chamber pressure signal and half the descent at the end of the experiment. A time lag can be observed between the pressure signal recorded in the catalytic chamber and the one in the combustion chamber, due to the ignition delay of the fuel grain. The thrust and pressure transducer measurements were fairly constant throughout the test. The oxidiser Mass Flow Rate (MFR) undergoes an initial decrease, then stabilises at a value corresponding to the experimental mean value in Table 9.

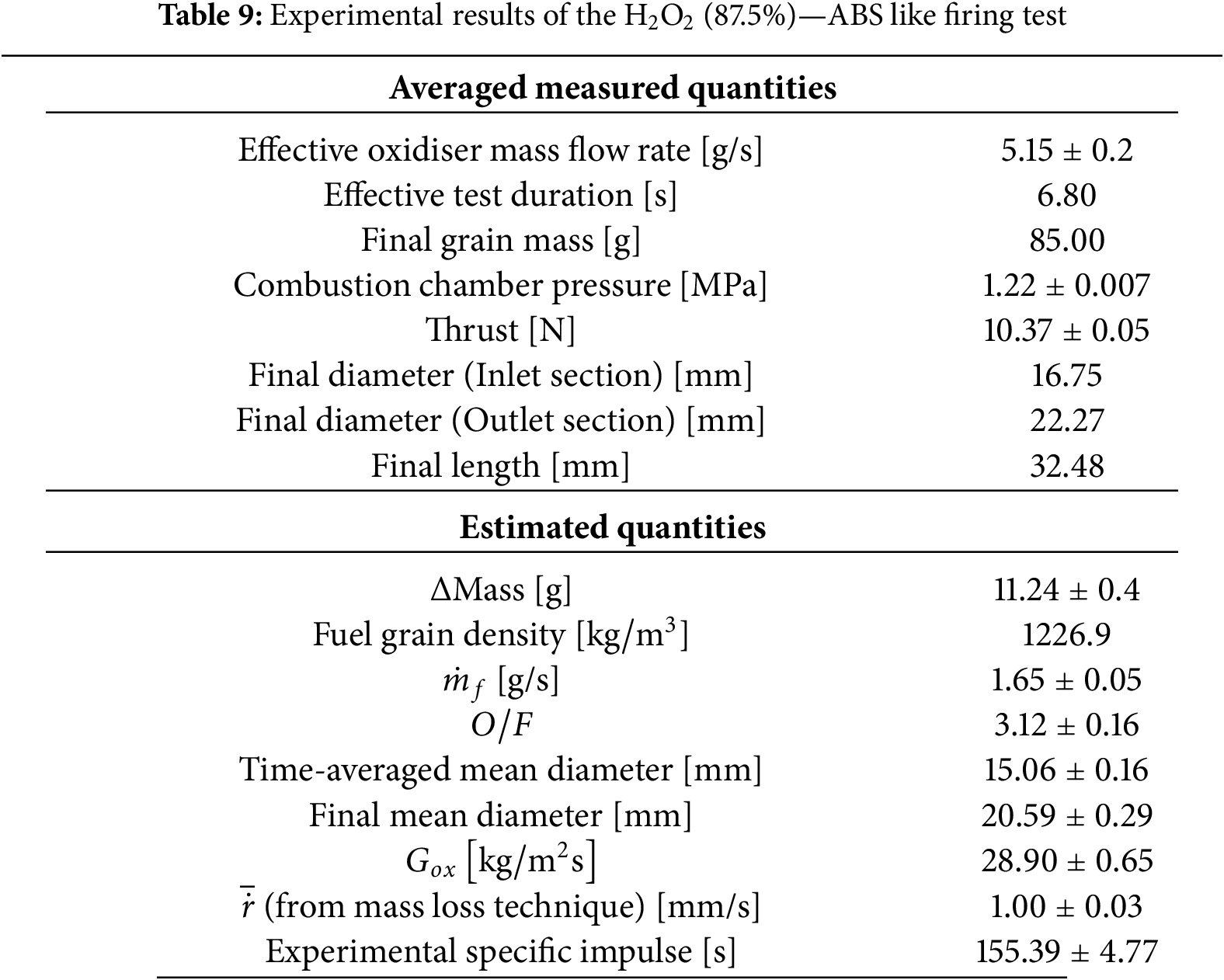
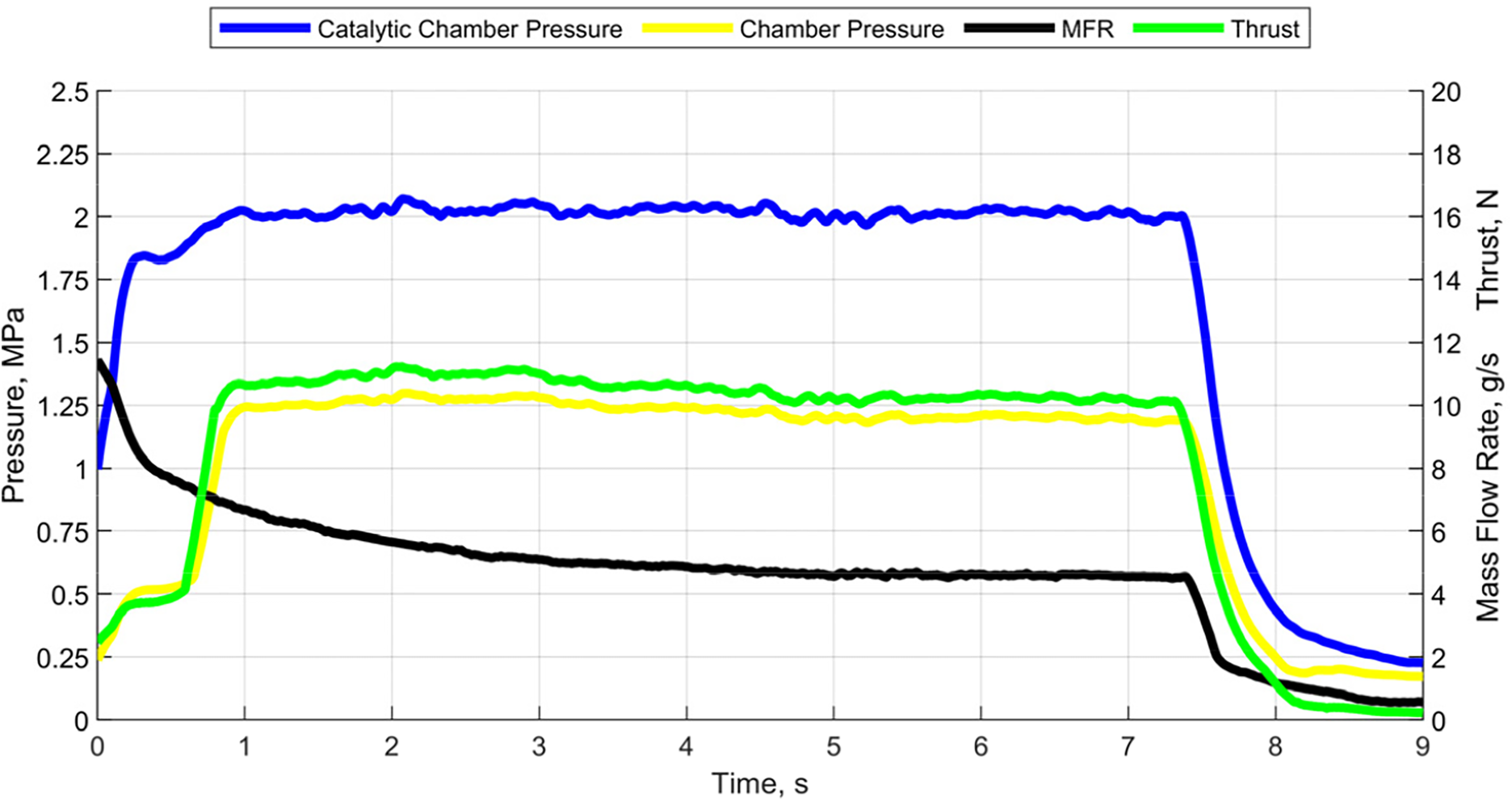
Figure 13: Mass Flow Rate (MFR), chamber pressures and thrust signals acquired during the ABS-like firing test

From the comparison of data reported in Tables 6 and 9, some differences might be noticed. The ABS-like average regression rate is sensibly higher than the previous experiment, reflecting the different combustion characteristics of the two materials. The numerical value is slightly overestimated for reasons that will be shown shortly, but the result is in line with what was already found for tests carried out with the same propellants and with the propeller in its previous configuration. The higher m˙f in combination with a lower m˙ox determined a lower O/F ratio. Averaged combustion chamber pressure and thrust resulted lower in comparison with the HDPE test. Differences between port diameters for inlet and outlet sections are even more evident, showing that the issue is significant for the thruster under investigation regardless of the fuel employed. For this reason, additional numerical simulations will be executed considering the characteristics of the present polymeric material, trying to reproduce the experimental results and simultaneously investigating the fluid-dynamic causes of the phenomenon. Another noteworthy feature that ought to be mentioned is the presence of axial regression, as demonstrated by the final grain length reported in Table 9. This peculiar characteristic will be assessed through numerical simulations in the following section, pairing its effect to the radial regression to properly reproduce the grain evolution over time. The axial consumption results to be a key fluid-dynamic feature since it affects the evaluation of the overall regression rate characterizing the material. The ability to replicate this phenomenon within the numerical model facilitates a more precise estimation of the true value, which, as previously indicated, may be overestimated when measured experimentally through mass loss. Consequently, its analysis will be included in the numerical simulation of the ABS-like test case.

4.3 Thermal Behaviour Experimental Assessment

As discussed in Section 2.3, one of the primary objectives of the redesign process that led to the definition of the upgraded thruster under investigation was the improvement of the engine thermal management during extended firing tests. This section will address the rationale behind this requirement and the evaluation of the thruster’s thermal behavior. As discussed in [17], the previous configuration (Fig. 4a) suffered a discrepancy in terms of regression rate when comparing experimental and numerical r˙ laws. Fig. 14 represents the four experimental points and the related power-law trendline (in red), obtained through a dedicated firing test campaign performed using the HDPE-HTP (87.5%) propellant pair. The blue line displays the CFD simulation results, which appear to systematically underestimate the empirical trend. After extensive analyses, the numerical downshift was attributed to an unexpected heating of the fuel grain during firing tests [17]. This was caused by the heat transfer from the graphite nozzle through the stainless-steel case, combined with the pulsed mode technique employed to facilitate H2O2 decomposition. The combined action of the two mechanisms led to an increase in the temperature of the HDPE cylinder, resulting in a decreased accuracy of numerical simulations with a grain wall temperature of 300 K. By increasing the wall temperature applied to the numerical model, it was possible to ensure matching with the experimental data, but the value to be imposed remains challenging to quantify. In order to enhance the reliability of the model’s predictions, the updated thruster configuration was fitted with thermal protection between the grain and the graphite nozzle, as well as at the interface with the combustion chamber. Furthermore, the use of a disposable catalyst has improved decomposition performance, making pulsed preheating unnecessary. This approach enables the simulation of grain combustion starting from a wall temperature of 300 K, without the necessity for additional assumptions regarding the Twall to employ.

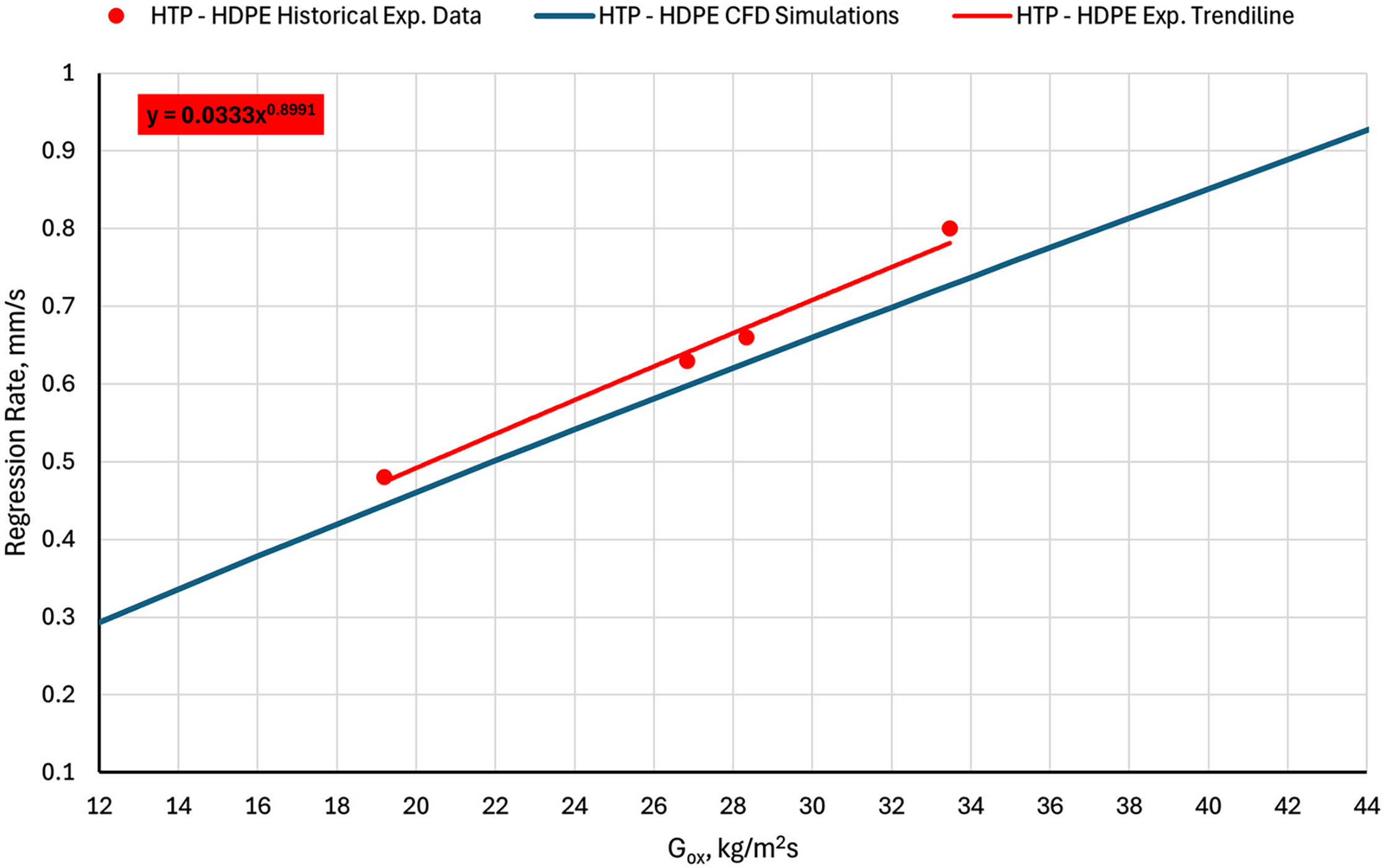
Figure 14: Numerical and experimental regression rates as a function of oxidizer mass flux for the previous engine configuration [17]. Reprinted from Reference [17]. 2024, the International Astronautical Federation (IAF)

The thermal behavior of the upgraded configuration was assessed by collecting temperature measurements via the three thermocouples mounted on the combustion chamber case. As an example, Fig. 15 plots the signals acquired during the experimental test with HDPE grain. The results obtained are fully comparable with those recorded in the ABS-like case, which will therefore not be shown for brevity’s sake. Temperatures were measured at three different locations on the stainless-steel case: the first thermocouple was placed near the pre-chamber, the second was located about halfway along the grain length, and the last was positioned in correspondence with the post-chamber. They are respectively named Twall,1,Twall,2,and Twall,3. Fig. 15 shows that the grain temperature throughout the entire test was unchanged. The remaining signals exhibited a marginal increase, with a more pronounced rise observed in the case of Twall,1, attributable to the proximity to the injector from which the hot gases are released. In all instances, the increase is negligible, with a maximum temperature of 317.35 K attained after a 6.5 s test. For tests of similar duration, the previous configuration recorded much higher temperature increases due to preheating phase and conduction heat flow from the nozzle, with values up to 523 K. This shows that the thermal insulation in the thruster under investigation is effective and allows the grain to be maintained at a constant temperature, enhancing the accuracy of the numerical modeling. Furthermore, the new configuration enables the execution of longer firing tests preventing potential structural damages caused by overheating of metal components. A side effect of the lower initial temperature is the realization of slightly lower regression rates, which allows for lower axial consumption and smaller bulkiness requirements in terms of diameter.

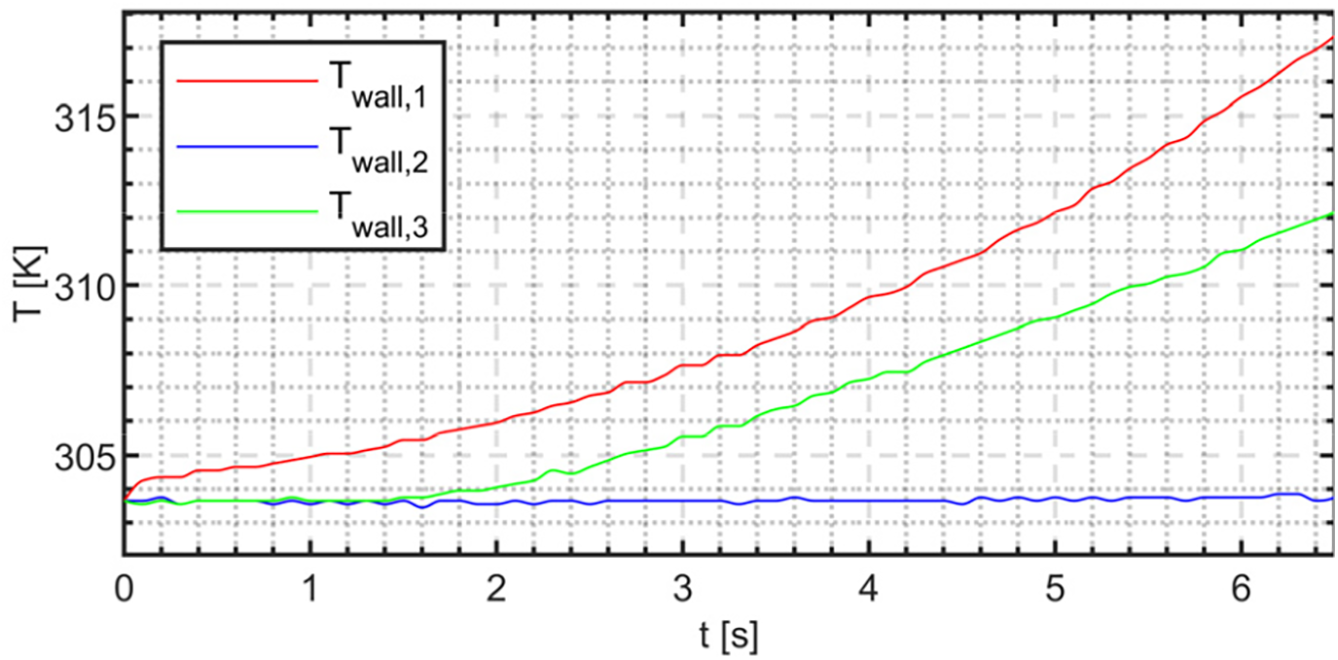
Figure 15: Temperature distribution recorded at three different locations during the HDPE-HTP (87.5%) firing test

5  CFD Analyses of Experimental Findings

The two experimental firing tests described in Section 4 provided important insights into peculiar behaviors exhibited during the combustion process. The objective is now to employ CFD simulations to achieve a dual purpose. Firstly, these simulations enable a comprehensive investigation into the internal ballistics of the thruster, thus aiding the analysis of the physical phenomena underlying off-nominal characteristics such as uneven regression rate distribution and axial grain consumption. Furthermore, the development of models capable of reproducing these behaviors could contribute to mitigating their impact during the design of future small-scale hybrid thrusters with similar configurations. Some limitations arise from the use of numerical analyses. The CFD model applied for the simulation of ABS test cases involves the exclusive use of butadiene, which is only one of the three monomers constituting the entire molecule. This is clearly an approximation, and consequently, the chemical characteristics are slightly different from the experimental case. With regard to the oxidizer, a complete decomposition of the hydrogen peroxide is assumed, which may not always be verified in practical tests. Another aspect to consider is the lack of coupling in the numerical model between axial and radial regression. Moreover, transient CFD simulations do not manage to reproduce unsteady phenomena, which may play a significant role in the ignition phase. The grain heating before ignition and the consequent softening of the material are other features that are not faithfully reproduced and can have a non-negligible impact on performance. All these aspects were taken into account when analyzing the results of the numerical simulations. Despite the inherent limitations of the model, this chapter will show that the results obtained are an effective approximation of the real case, providing important insights into the physical processes at work during the firing tests and their consequences.

5.1 Comparison between Experimental Data and CFD Simulation Results

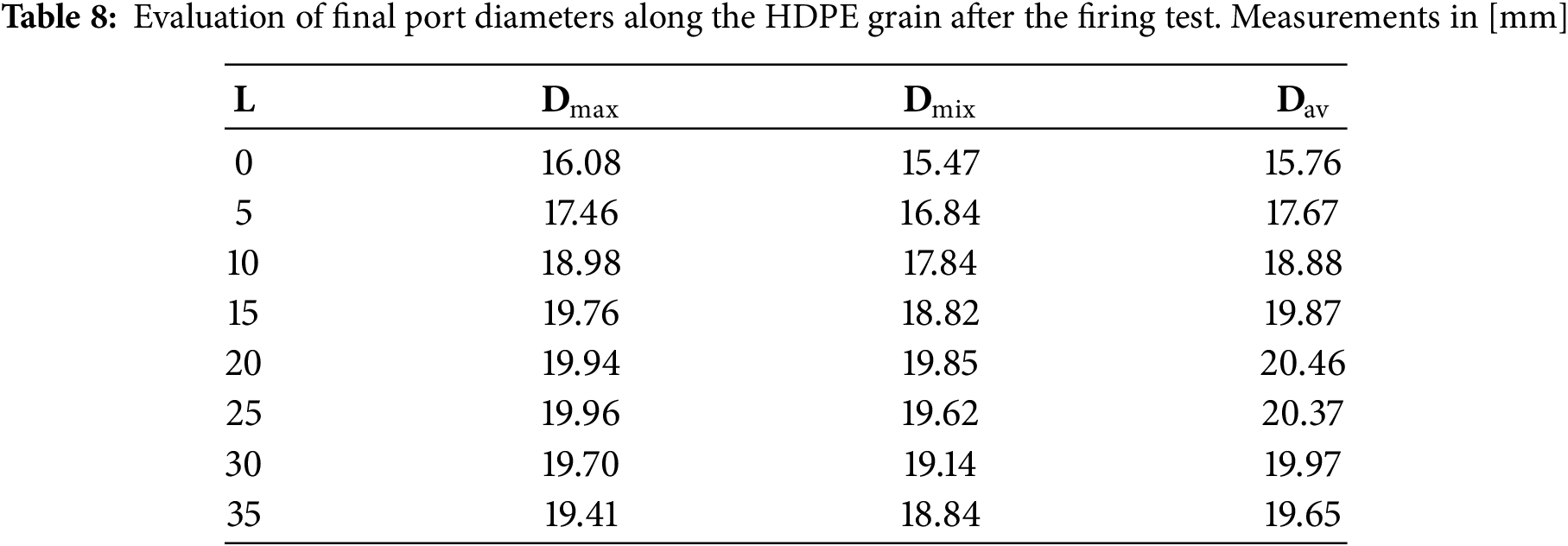
The first step of the numerical investigation was performed through transient CFD simulations. Following the methodology shown in Section 3.5, an assessment of the thruster internal ballistic was realized at different time instants, with a timestep of 1 s. The results are presented in Sections 5.1 and 5.2, where they will be discussed in detail. To assess the ability of reproducing numerically the experimental distribution of port diameters along the grain, a direct comparison of the two quantities of interest is given in Fig. 16, where results of the HDPE firing test and the corresponding numerical analyses are reported.

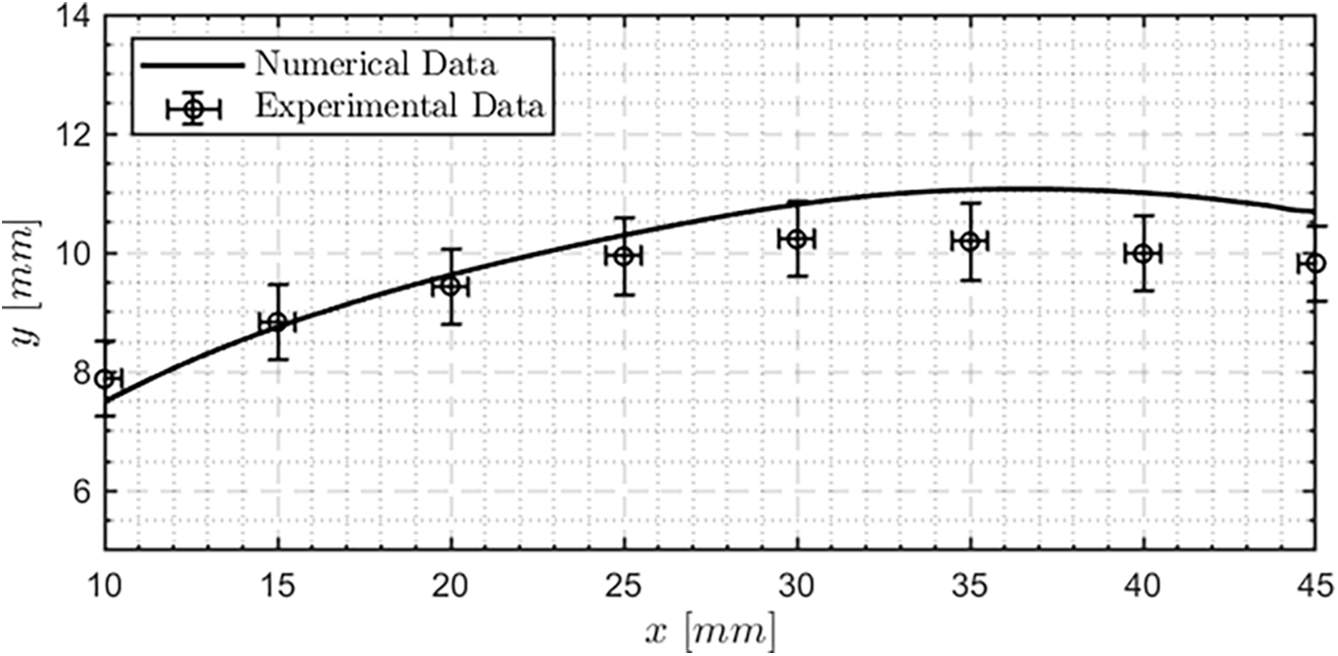
Figure 16: Comparison of port radius distribution along the grain between CFD simulations and experimental results for the HDPE test case. The x-coordinate represents the distance from the injector, which is separated from the grain by a 10 mm long pre-chamber

The black line represents the predicted grain configuration at the end of a 6.5 s firing test, as computed by transient CFD analyses. Experimental data are reported as points whose position depended on the average experimental value measured at each station, as listed in Table 8. Each point is provided with error bars for both x- and y-coordinates. Uncertainties in the x-direction are due to potential inaccuracies in the positioning of measurement stations, estimated as ±0.5 mm of the nominal value. Error bars on the y-axis account for measurement errors and potential eccentricity in the grain port as a consequence of the burning process. Their value was determined by estimating the deviation between the average diameter and min/max values at each measuring station, as reported in Table 8. Following the identification of the maximum deviation, which was approximately ±5% of the radius, it was applied uniformly to all experimental measurements. This process was undertaken in order to obtain a conservative estimate of the radial distributions resulting in the trend shown in Fig. 16. Although a stationary CFD simulation performed employing the experimental mean diameter can be used to obtain a regression rate value close to the experimental one, it is evident that, for this specific case, it cannot satisfactorily approximate the trend of the port diameters along the grain. On the contrary, from Fig. 16 it is possible to state that the transient CFD technique is capable of providing a consistent estimation of the port diameter distribution along the longitudinal axis. Despite experimental and numerical points do not perfectly overlap, the reconstructed trend provides a reliable approximation of the HDPE firing test result. In the first half of the grain, experimental and CFD trends correspond significantly. Moving towards the outlet, the numerical value is overestimated compared to the measured values. The relative error is always limited, with a maximum value of less than 9% near the outlet section. The results of a methodical comparison of the estimated quantities can be found in Table 10. Transient CFD simulations proved to properly reproduce all the main parameters, including space- and time-averaged diameters, grain mass consumption, and average regression rate within a 5% margin from the experimental value.

5.2 Numerical Analysis of the HDPE Firing Test

So far, transient CFD models have shown a reasonable degree of reliability when employed as numerical simulation tools for reproducing peculiar experimental findings. Once their effectiveness was established, they could be exploited to investigate in detail the physical phenomena that cause unexpected behaviors, such as uneven regression rate distribution and axial grain consumption. The HDPE test case was studied through a sequence of stationary numerical simulations employing the grain geometry update technique reported in Section 3.5. The results obtained for each 1-s timestep are summarised in Fig. 17, where temperature contours in the thruster combustion chamber and flow streamlines are shown. Additional information regarding the temporal evolution of grain port diameter and r˙ during the 6.5 s firing test are reported in Fig. 18a,b.

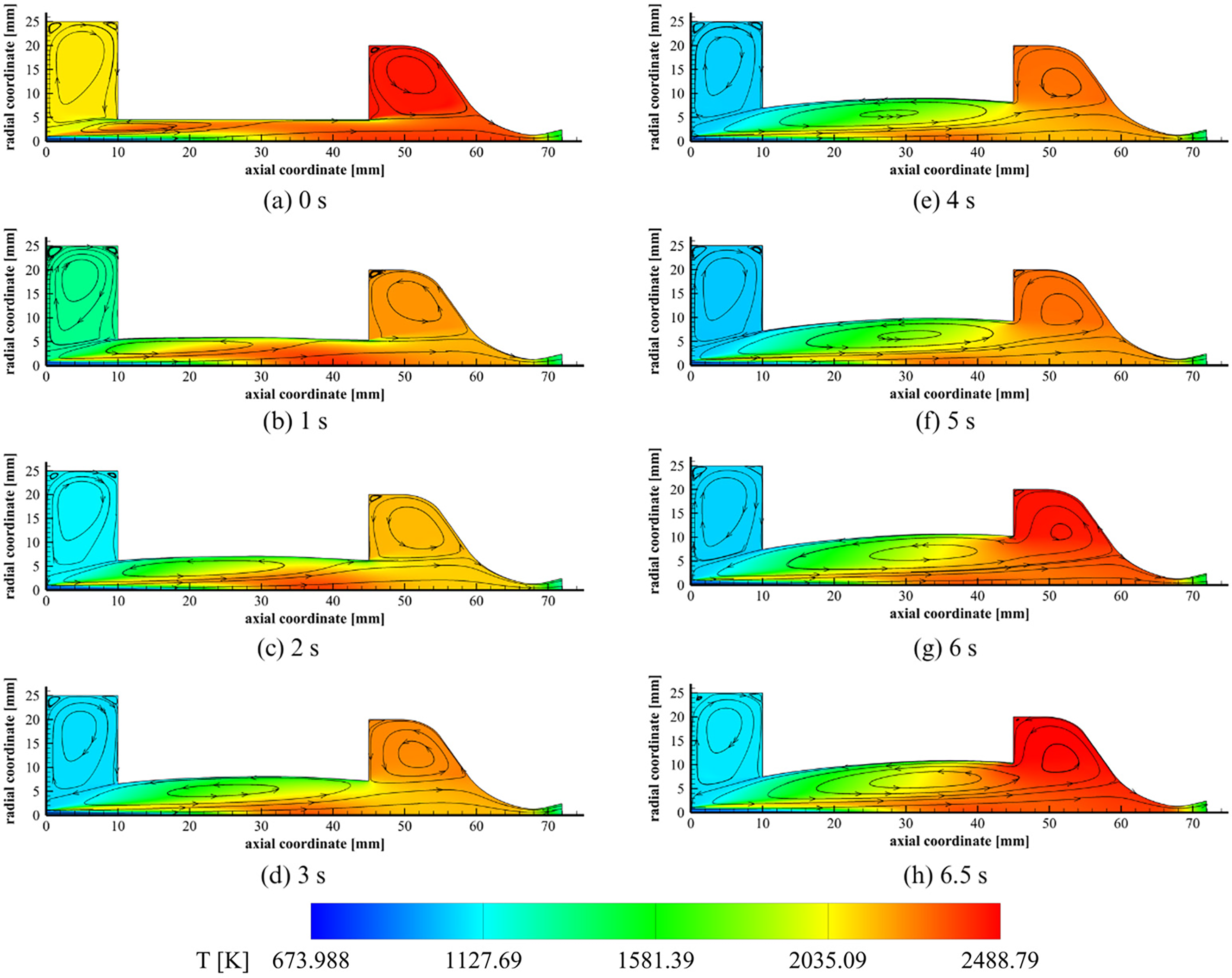
Figure 17: Evolution in time of temperature contours and streamlines of the HDPE firing test exploiting transient CFD simulations

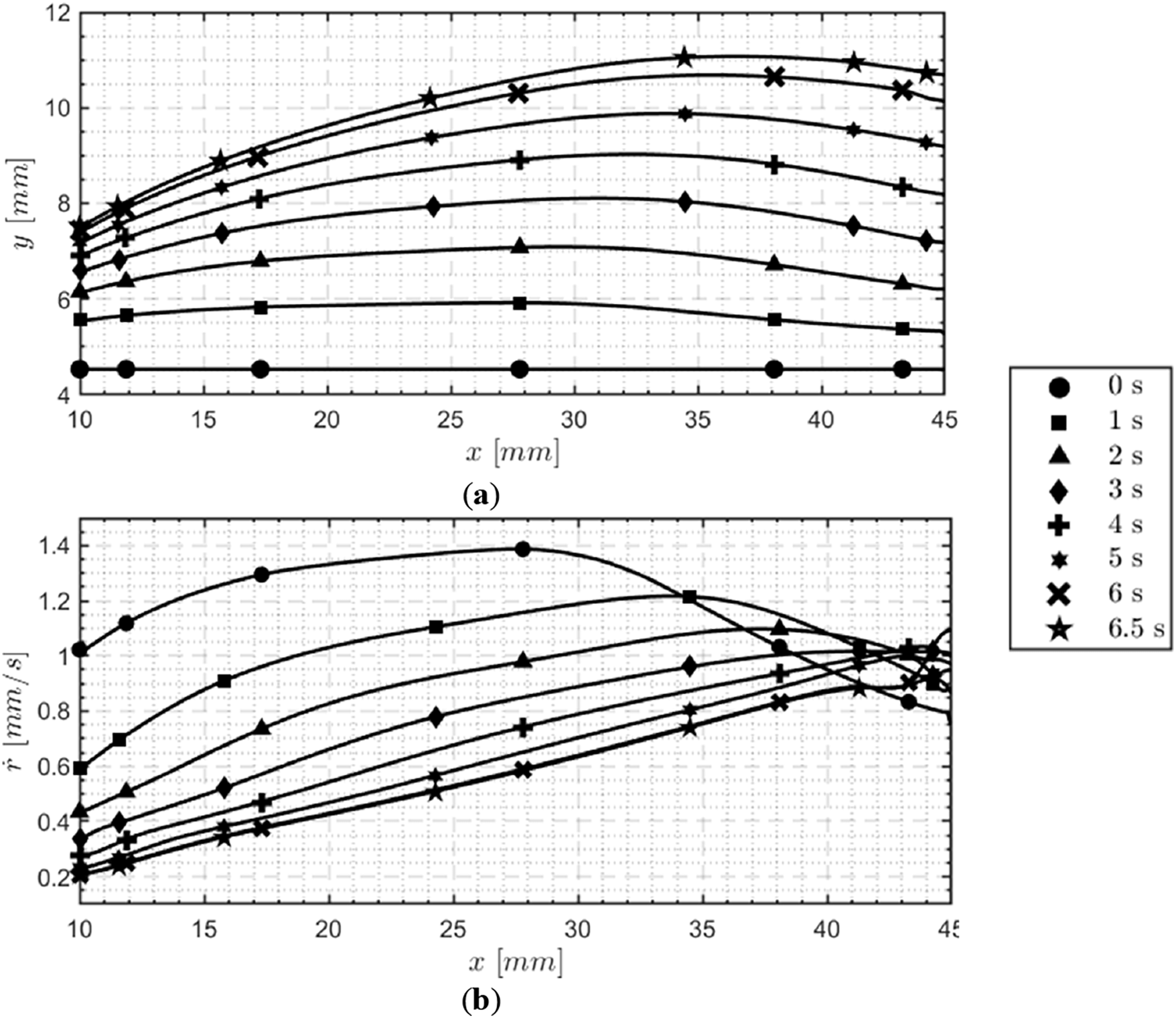
Figure 18: Simulation of the temporal evolution of grain port diameters (a) and local regression rates (b) during the HDPE firing test

From the combined analysis of the simulation data collected, some interesting fluid-dynamic aspects could be examined. At t=0s, corresponding to Fig. 17a, three recirculation zones can be recognized: the first is located in the pre-chamber, another one is established in the post-chamber, and a third is formed next to the injector, as a result of the interaction between the incoming gaseous oxidizer and the grain wall. As time progresses, some changes are noted. The recirculation zone, which is initially located in proximity to the inlet section, increases in size and moves gradually toward the outlet. Comparing the simulations carried out at 0 and 5 s (Fig. 17a,f), it can be seen that the recirculation zone is at first limited to an area approximately 10 mm long, while, in the final part of the test, it affects almost the entire grain length. This is caused by the peculiar configuration of the engine, which is characterized by a relatively low length-to-diameter ratio L/D. Indeed, the large port diameter coupled with the limited length of the thruster has an impact on the internal fluid dynamics of the combustion chamber, generating the shift of the recirculation zone towards the nozzle. The phenomenon has already been studied for other hybrid thruster configurations available in the literature. However, its impact on the internal ballistics and performance is significantly greater for the combustion chamber under investigation due to its small scale. The downstream displacement of the recirculation zone causes an area of amplified wall turbulence towards the outlet, which in turn results in an increased radial consumption. This is shown by the temporal evolution of the local regression rates, which exhibit a maximum that steadily moves towards the nozzle during the firing test following the behavior of the recirculation area, as reported in Fig. 18b. Consequently, the grain geometry is affected by an enhanced mass loss in the area next to the outlet section, as displayed in Fig. 18a. This result explains the uneven distribution of grain port diameters and is in accordance with the discussion reported in Section 5.1. The downstream shift of the recirculation zone leads to an interaction with the one located in the post-chamber, eventually generating merging, as shown in Fig. 17e–h.

Fig. 17 exhibits another interesting fluid dynamics feature of the thruster. The temperature distribution within the combustion chamber evolves significantly during the burning time. At the beginning of the simulated firing test, a high-temperature zone develops not only along the grain surface but also in the post-chamber. This phenomenon can be explained by the elevated regression rate observed for t = 0 s, as illustrated in Fig. 18, which is caused by the high instantaneous value of Gox at the engine start. The relatively large amount of fuel injected implies that the combustion process affects the entire engine length, and it is completed inside the post-chamber, which is conceived precisely to increase the residence time and promote the full development of the reaction. During the following time instants (Fig. 17b–h), the pre-chamber undergoes progressive cooling as a consequence of the combined action of the convective heat flux, due to the fresh oxidizer injected at a temperature of 900 K, and the progressive displacement of the recirculation zone along the grain, which consequently displaces the zone with the greatest radial fuel injection. The flame is stably localised in the zone between 20 and 35 mm of grain length. The post-chamber exhibits an initial decrease in temperature (Fig. 17b,c), followed by a subsequent gradual re-heating related to the increasingly advanced position of the recirculation zone (Fig. 17e,f). During the last 1.5 s, the combined action of the recirculation zone spreading along the entire grain length coupled with the fact that the maximum regression rate occurs in increasingly downstream sections, results in a combustion process that is completed just in the post-chamber.

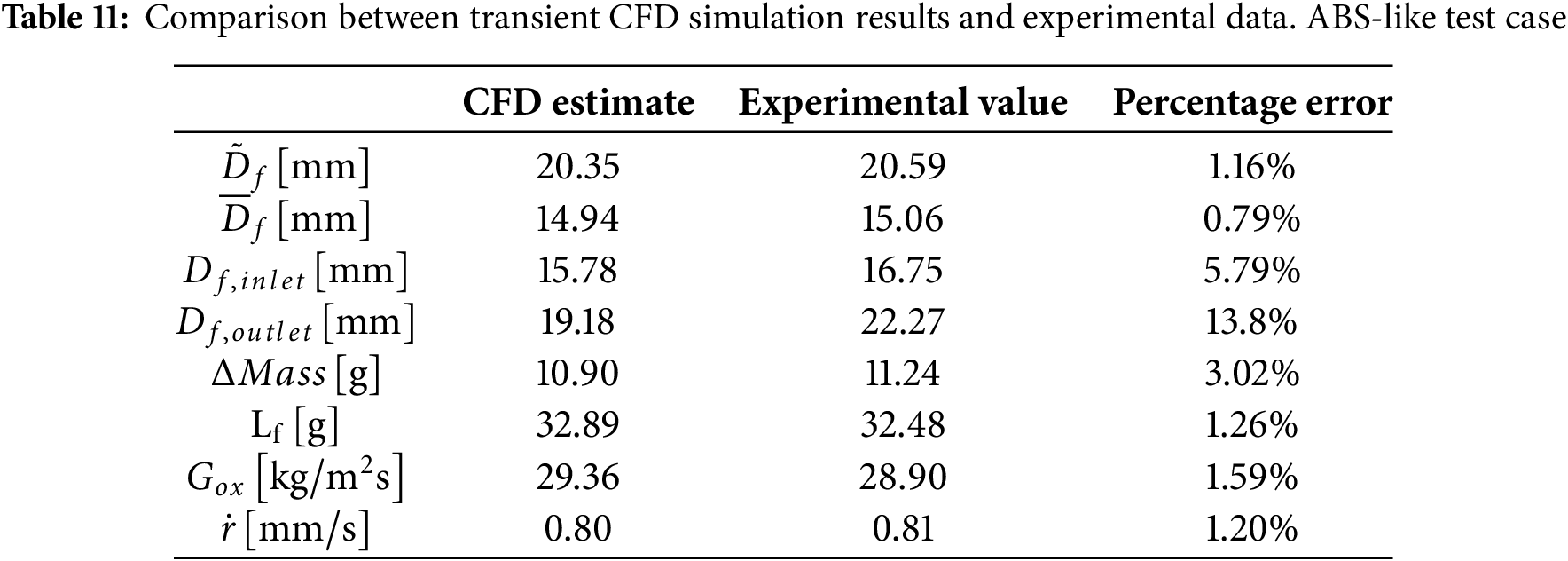
To complement these analyses, Fig. 19 reports the oxidizer-to-fuel ratio computed through CFD transient simulations at different time steps during the burning time. Starting from a value of 6.4, the space-averaged numerical O/F decreases rapidly in the first 2 s as an effect of the relatively high regression rates. The progressive r˙ decrease (shown in Fig. 18) is balanced by increased turbulence induced by the recirculation zone, which globally ensures a quite steady fuel mass flow rate along the grain. Since the m˙ox is kept constant during the simulated firing test, the corresponding O/F results rather stable, with a slight increase during the last 1.5 s. Computing the time- and space-averaged oxidizer-to-fuel ratio from transient CFD simulations a value of 5.52 is obtained. It appears to be in line with the experimental value of 5.153 reported in Table 6, with a percentage error of 7.12% on the empirical measurement. This shows that despite the non-uniform combustion and the action of the physical phenomena involved, the CFD methodology employed is able to return overall average values consistent with those recorded experimentally.

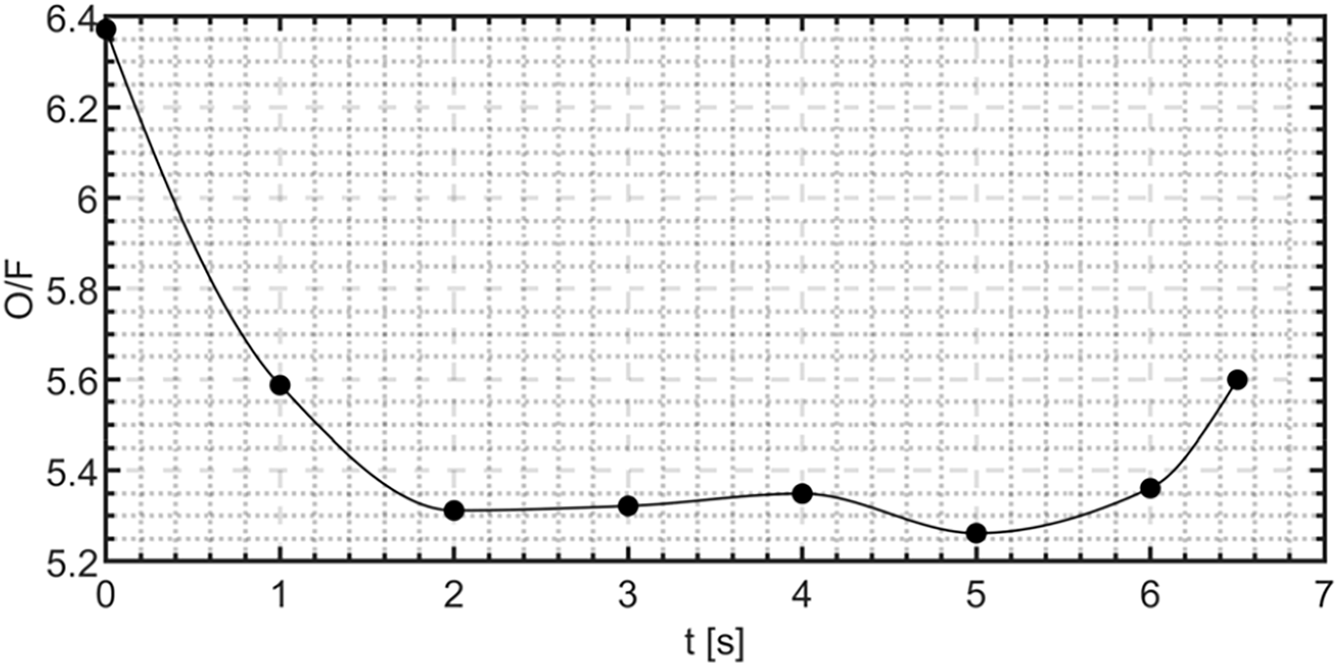
Figure 19: Average oxidizer-to-fuel ratio computed through numerical simulations as a function of time. HDPE test case

The thruster internal ballistic, detailed in Fig. 17, can also be interpreted in light of two further propulsive parameters: the characteristic velocity c∗ and the combustion efficiency ηc∗. Their numerical estimations are displayed respectively in Figs. 20 and 21. c∗ was computed starting from its definition, as presented in Eq. (15). For each simulation, the average chamber pressure Pc and the numerical fuel mass flow rate m˙f were evaluated together with the known parameters of critical area Acr and oxidiser flow rate m˙ox to calculate the corresponding characteristic velocity.

c∗=PcAcrm˙ox+m˙f(15)

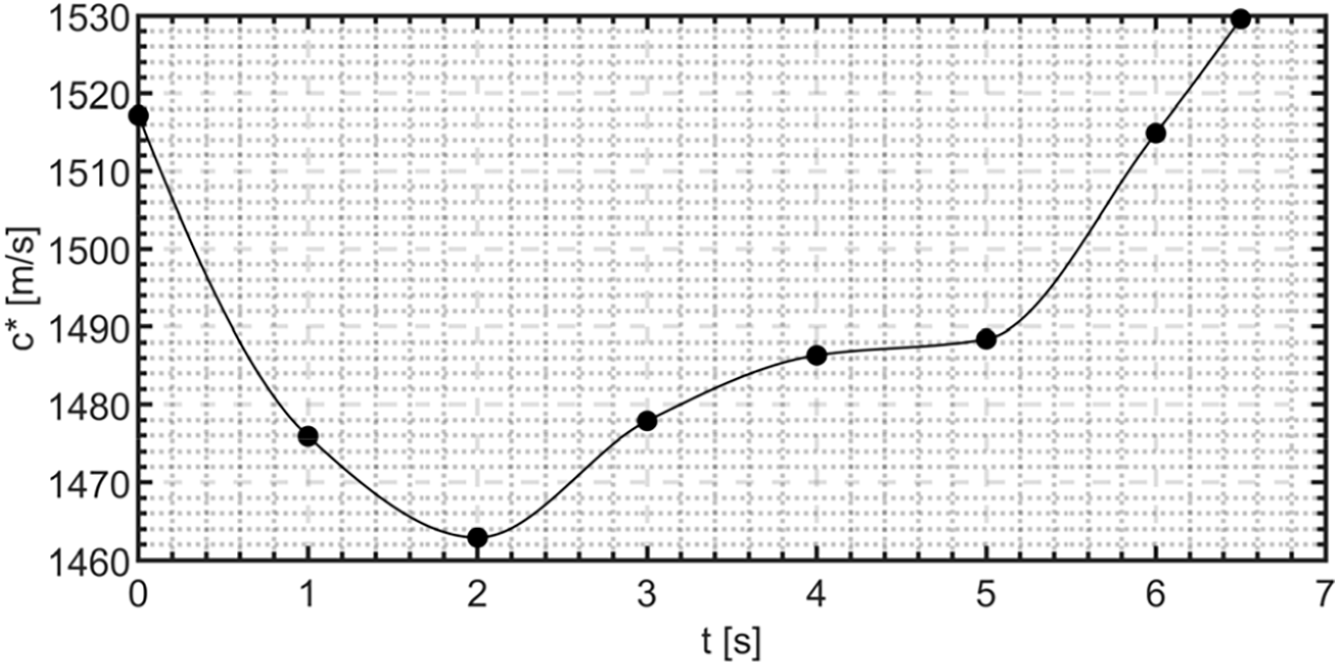
Figure 20: Characteristic velocity as a function of time, as estimated through transient CFD simulations. HDPE test case

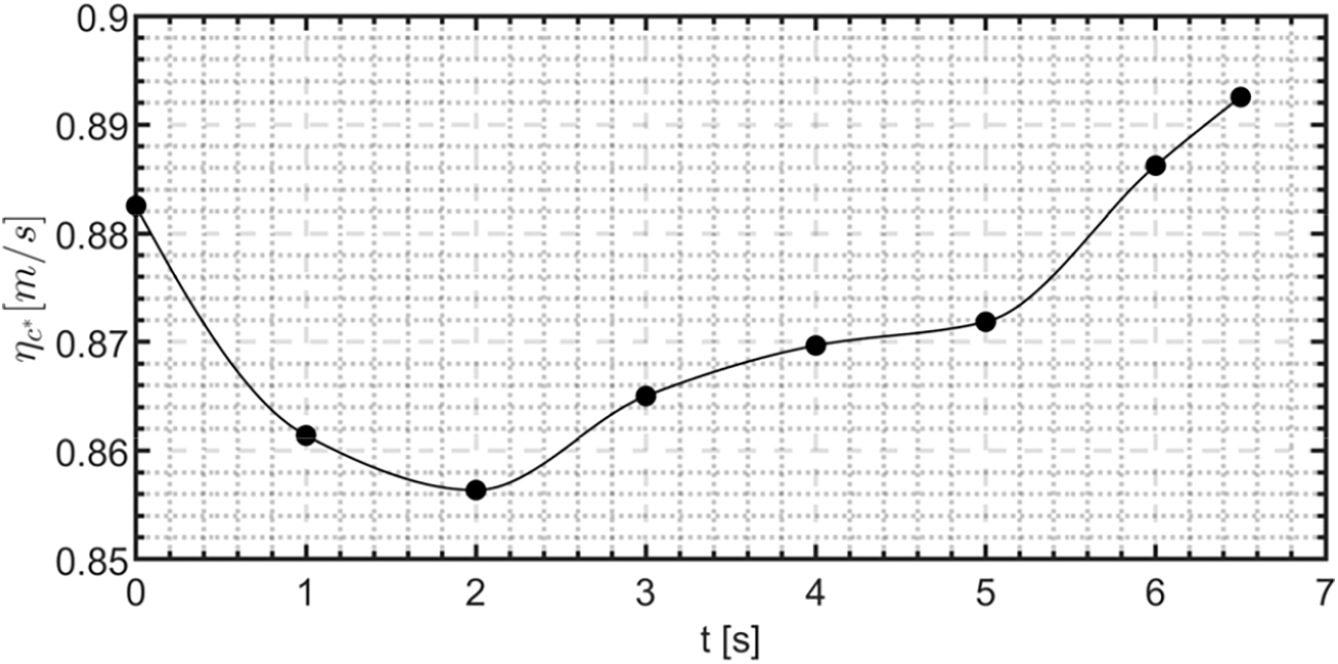
Figure 21: Numerical estimation of the engine combustion efficiency for the HDPE test case

The c∗ evolution over time, depicted in Fig. 20, was evaluated through a comprehensive analysis, finding a dependency on both O/F behavior and the structure of the fluid dynamic field inside the engine. In order to investigate the latter, Fig. 22 was created with the aim of achieving a proper understanding of the mixing phenomena in action. At different time instants (0, 2, and 6.5 s), the mean mixture fraction f¯ was numerically estimated [33] on the computational grid as the Favre density-averaged value of the mixture fraction f, determined as in Eq. (16) [34]. This quantity represents the distribution of the fuel-to-oxidizer ratio inside the combustion chamber. Consequently, it was used to assess the mixing process inside the thruster combustion chamber. Fig. 22 displays the f¯ contours accompanied by isolines to enhance the visualisation of ox-rich and fuel rich-areas. Gray areas in Fig. 22b,c are associated with zones with a mean mixture fraction > 0.2, which are of no interest at this stage of the discussion and are consequently not represented.

f=Zi−Zi,oxZi,fuel−Zi,ox(16)

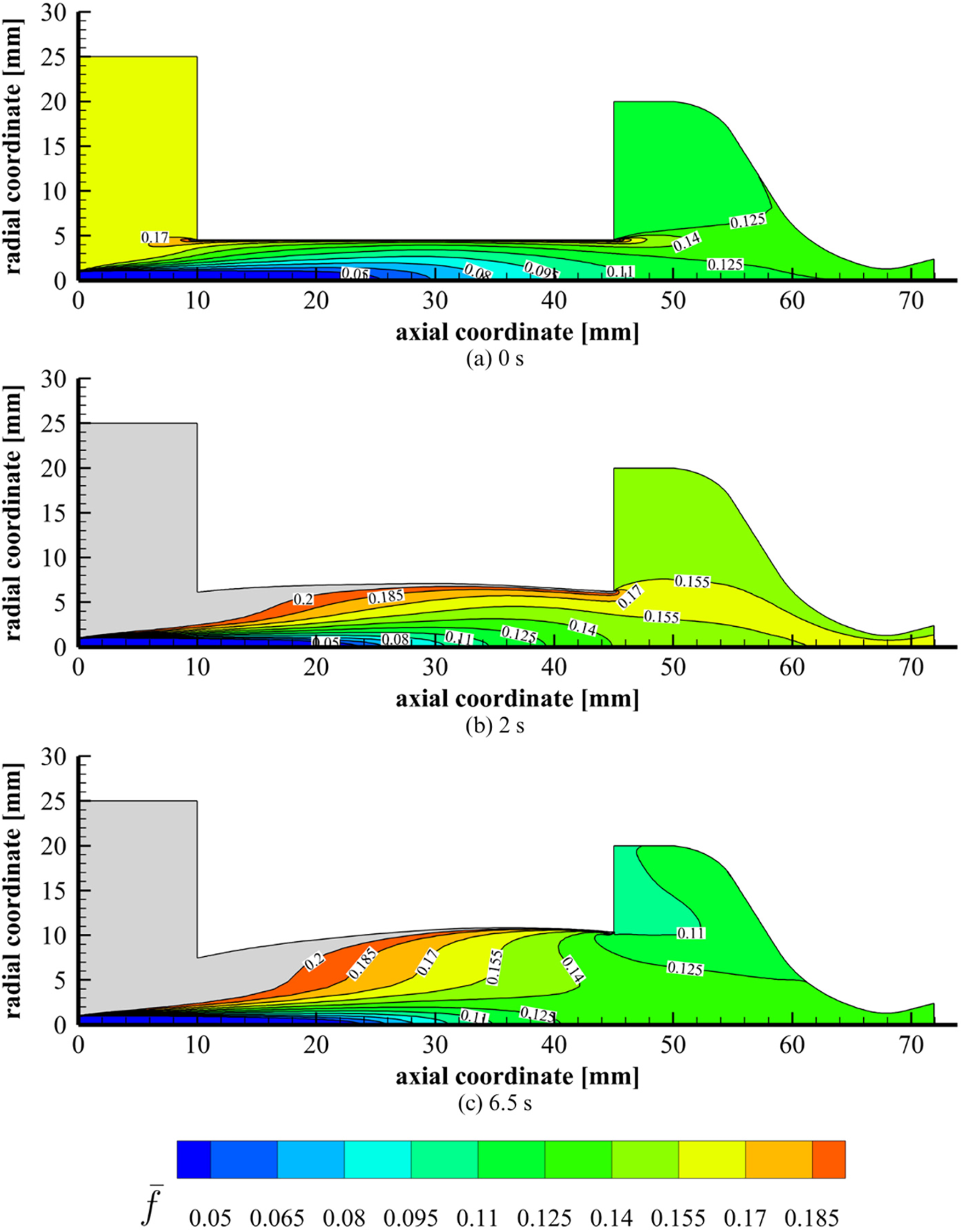
Figure 22: Mean mixture fraction contours in the hybrid rocket thrust chamber at t = 0 s (a), t = 2 s (b) and t = 6.5 s (c). Isolines are labelled with their numerical values. HDPE test case

Coupling oxidiser-to-fuel ratios and f¯, it is possible to properly understand the characteristic velocity behavior. At t=0 s, the average O/F is 6.4, slightly lower than the stoichiometric value of 7, as estimated for the HDPE-HTP (87.5wt%) pair through the NASA’s CEA software. As shown in Fig. 22a, this is coupled with a rather uniform distribution along the grain of the optimal f¯ zone, corresponding to a value around 0.125 (denoted by green tones). Consequently, combustion develops efficiently in large areas of the thrust chamber, generating a high c∗ value and justifying the temperature contour shown in Fig. 17a. In the following two seconds, the mixing process is worsened by the translation of the recirculation zone. As illustrated in Fig. 22b, a significantly larger fuel-rich zone (indicated by yellow and red coloring) is established, implying a decrease in the combustion efficiency. Its effect, paired with a global lowering of the O/F and a shift away from the stoichiometric conditions, results in a decrease in characteristic velocity. Once the recirculation area on the grain merges the post-chamber one, there is a new improvement in oxidiser-fuel mixing, as observed in Fig. 22c. The fuel-rich zone is still present but limited to the central part of the grain, with optimal f¯ value areas towards the outlet and in the post-chamber. The mixture is therefore able to react effectively, leading to a new increase in c∗ for the remaining duration of the simulated firing test. This analysis also allowed to account for post-chamber temperature increases recorded in Fig. 17d–h, and particularly evident in the interval between 5 and 6.5 s. A further improvement in terms of c∗ is noted during the last 1.5 s due to an increase in the global O/F, which in presence of an almost stable mixing improves performance.

As anticipated, the last step of the present analyses involved the study of combustion efficiency, defined as in Eq. (17). In order to compute that, the theoretical characteristic velocity was evaluated through NASA’s CEA software, using as input the CFD chamber pressure at the given time instant, the O/F estimation and the propellant pair properties, considering HDPE and 87.5% HTP. The result is presented in Fig. 21.

ηc∗=c∗cth∗(17)

From a comparison between Figs. 20 and 21, it is possible to state that the behavior of the combustion efficiency is dominated by the variations in terms of c∗, implying that the temporal trend of ηc∗ largely mirrors that of the characteristic velocity. From a physical point of view, this is determined by the fact that the HDPE test case was characterized by O/F values close to stoichiometric. Consequently, the theoretical characteristic velocity undergoes minimal variations due to changes in the mixing ratio during the simulated firing test. Since cth∗ constitutes the denominator of Eq. (17), the ηc∗ value is determined almost exclusively by the characteristic velocity calculated from the simulations, obtaining values ranging from 0.85 to 0.89.

The set of data described in this section is helpful in obtaining a complete fluid-dynamic characterization of the engine, which can support the design of future propulsion systems belonging to this category. The numerical CFD modeling employed enables the estimation of important performance parameters (such as O/F, c∗, and ηc∗), supporting the investigation of fluid dynamic phenomena that would be otherwise hidden in the outcome of experimental firing test campaigns. In addition, knowledge of the spatial and temporal distribution of temperatures is useful for defining the thermal loads of the engine and for an analysis of the related heat fluxes.

5.3 Numerical Analysis of the ABS-Like Firing Test

Transient CFD simulations were employed to investigate the evolution of the thruster internal ballistic during the ABS-like firing test, following the approach adopted for the HDPE test case described in Section 5.2. To properly model the axial regression mechanism whose effects were detected experimentally, the boundary condition applied to the surface adjacent to the post-chamber (namely Wall Post-Chamber 1, as in Fig. 8) was modified, enabling an axial fuel consumption typically neglected. Results are summarized in Figs. 23 and 24.

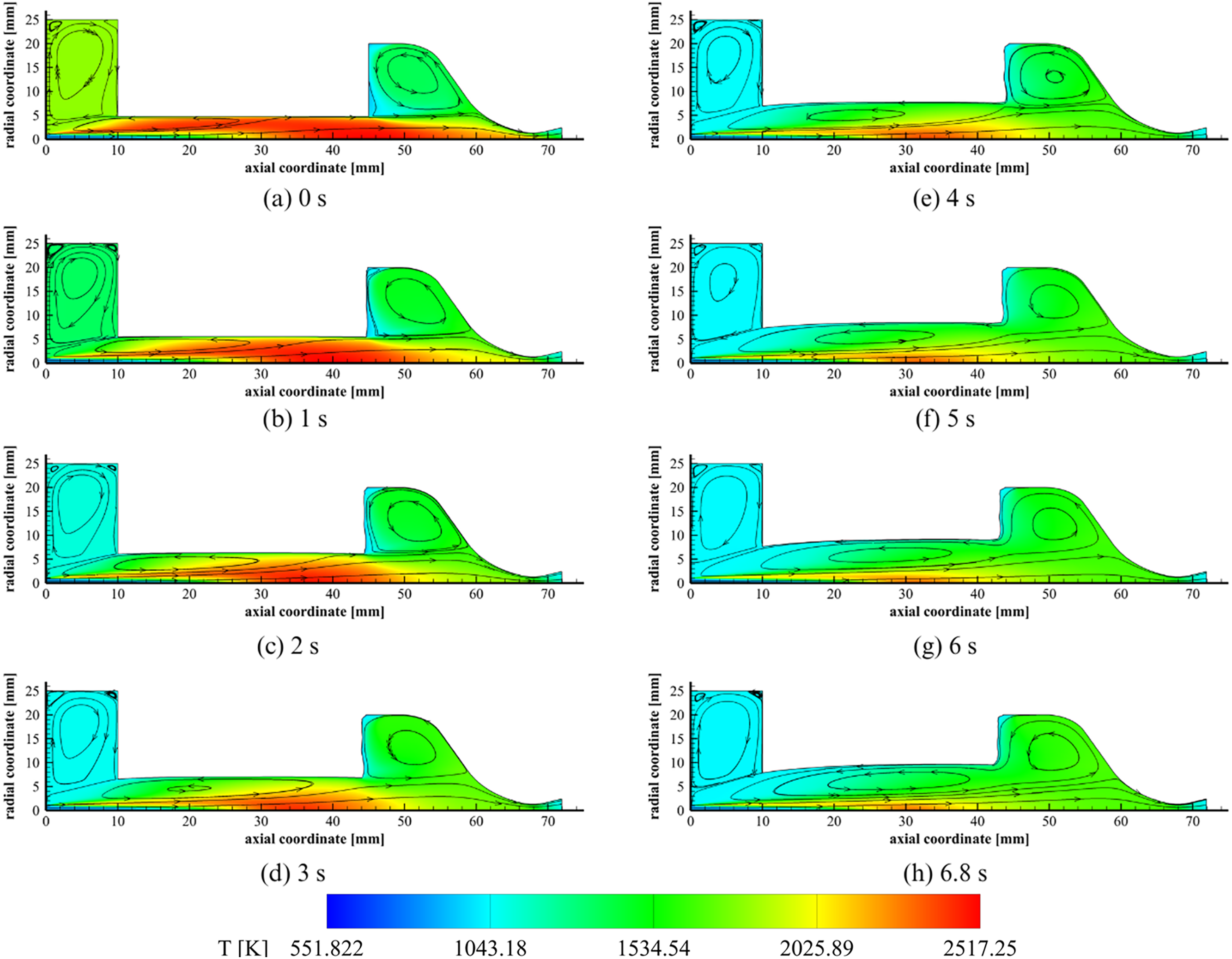
Figure 23: Evolution in time of temperature contours and streamlines of the ABS-like firing test exploiting transient CFD simulations

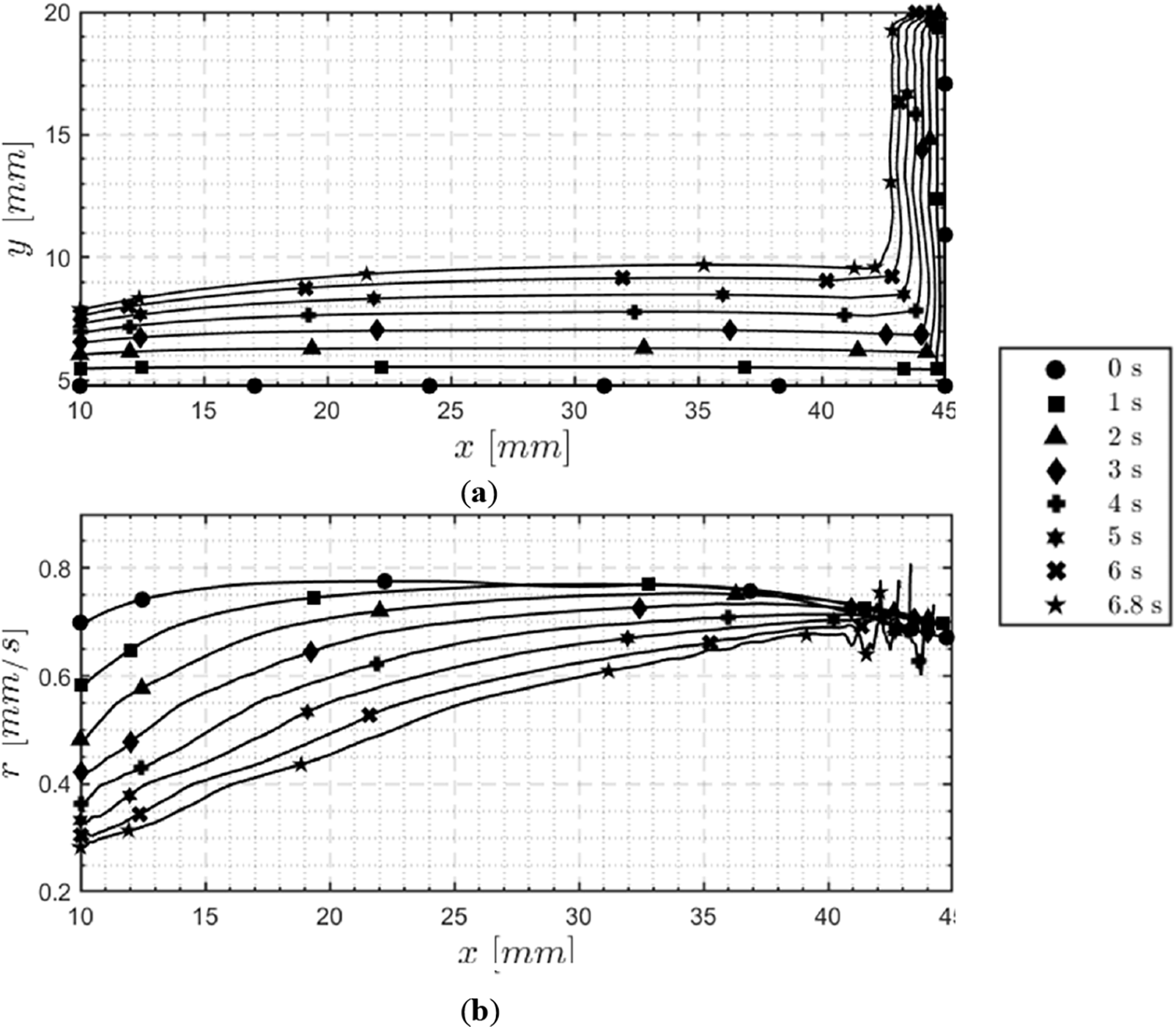
Figure 24: Simulation of the temporal evolution of grain port diameters (a) and local regression rates (b) during the ABS-like firing test

The temporal evolution of the thruster’s internal ballistic for the ABS-like test case mainly overlaps with the HDPE numerical investigations described in Section 5.2. The grain recirculation zone, which is initially established next to the inlet section (Fig. 23a), develops over time increasing in size and moving towards the outlet (Fig. 23b–d). After 4 s, it merges with the recirculation zone in the post-chamber, strongly altering the combustion chamber fluid dynamics field. The regression rate along the grain shows a decreasing trend during the simulated firing test, with its maximum shifting towards the outlet as time increases. The additional turbulence acting in sections close to the nozzle implies a local increase in radial consumption. In addition to this, the fuel grain undergoes progressive axial regression, with a longitudinal grain consumption of 2.52 mm. As reported in Table 11, the final length estimated by CFD transient simulations matches the experimental measurement with an error of 1.26%. The estimates in terms of mass consumption, regression rate, Gox and average final diameters are also in line with the experimental results, demonstrating that the numerical methodology employed is able to faithfully reproduce the experimental findings even in the presence of off-nominal phenomena such as uneven regression and axial burning. A larger error is found for the outlet diameter due to a higher measurement error in the experimental data. Indeed, owing to the complex geometry resulting from the interaction between radial and axial regression, the uncertainty associated with the experimental evaluation was increased, affecting the accuracy of the empirical estimation. Given that the higher error pertaining to Df,outlet is limited to an acceptable value and in consideration of the consistency exhibited by all the remaining data, the discrepancy in terms of final outlet diameter does not affect the overall validity of the numerical reconstruction of the test.

An additional insight attained through CFD transient simulation for the ABS-like test case concerns the temperature distributions within the mini-thruster combustion chamber. As shown in Fig. 23a, the high-temperature zone is initially extended over the entire grain length of the grain. In the final phase of the firing test, the regions exhibiting temperatures close to 2500 K become almost absent, with a prevalence of values around 2000 K near the longitudinal axis (Fig. 23f–h). The temporal evolution of the temperature distribution results as rather different in the firing test with ABS-like when compared to what has already been discussed for HDPE. To properly understand the physical phenomena causing these different behaviors, an analysis of O/F, c∗ and ηc∗ at various simulated time instants was performed. Fig. 25 displays the space-averaged oxidiser-to-fuel ratio evaluated through numerical simulations, exhibiting a decreasing trend throughout the firing test. The O/F estimated values result steadily lower than the stoichiometric value of 5.65 for the ABS-HTP (87.5 wt%) propellant pair, with an increasingly fuel-rich fluid dynamic field as time passes. This observation is consistent with the numerical findings reported in Fig. 23, where the rise in m˙f leads to a combustion process occurring under conditions that deviate significantly from stoichiometric values. Therefore, progressively lower temperatures are numerically estimated in the combustion chamber.

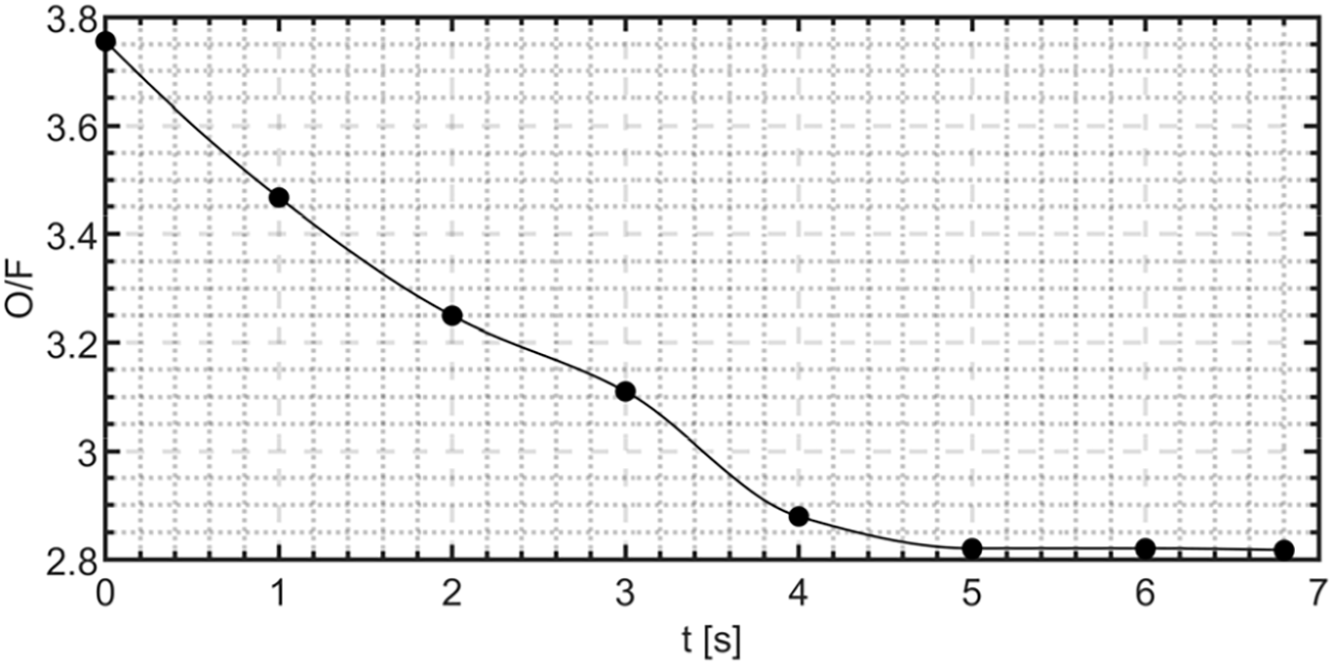
Figure 25: Average oxidizer-to-fuel ratio computed through numerical simulations as a function of time. ABS-like test case

As an effect of the progressive O/F shift towards reducing values, the less effective combustion causes a decreasing trend of the characteristic velocity with small fluctuations, as represented in Fig. 26. In contrast to the observations made in Section 5.2, the merging of the recirculation zones does not result in a substantial alteration of the mixing process. A mean mixture fraction analysis was conducted at different time instants to investigate this behavior. Fig. 27 represents the f¯ contours at the test start, after 2 s and at the end of the firing experiment. The area characterised by a f¯ close to the stoichiometric value of 0.15 for ABS-HTP (87.5%) is initially extended over the entire grain and part of the post-chamber. Due to the O/F shift, this zone (shown in light green) becomes smaller and smaller while the fuel-rich zones (characterized by red coloring) increase in size. Enhanced mixing in the area close to the after-chamber has a detrimental effect, as it promotes the chemical diffusion of the fuel and favors the extension of the fuel-rich zone, worsening the combustion reaction.

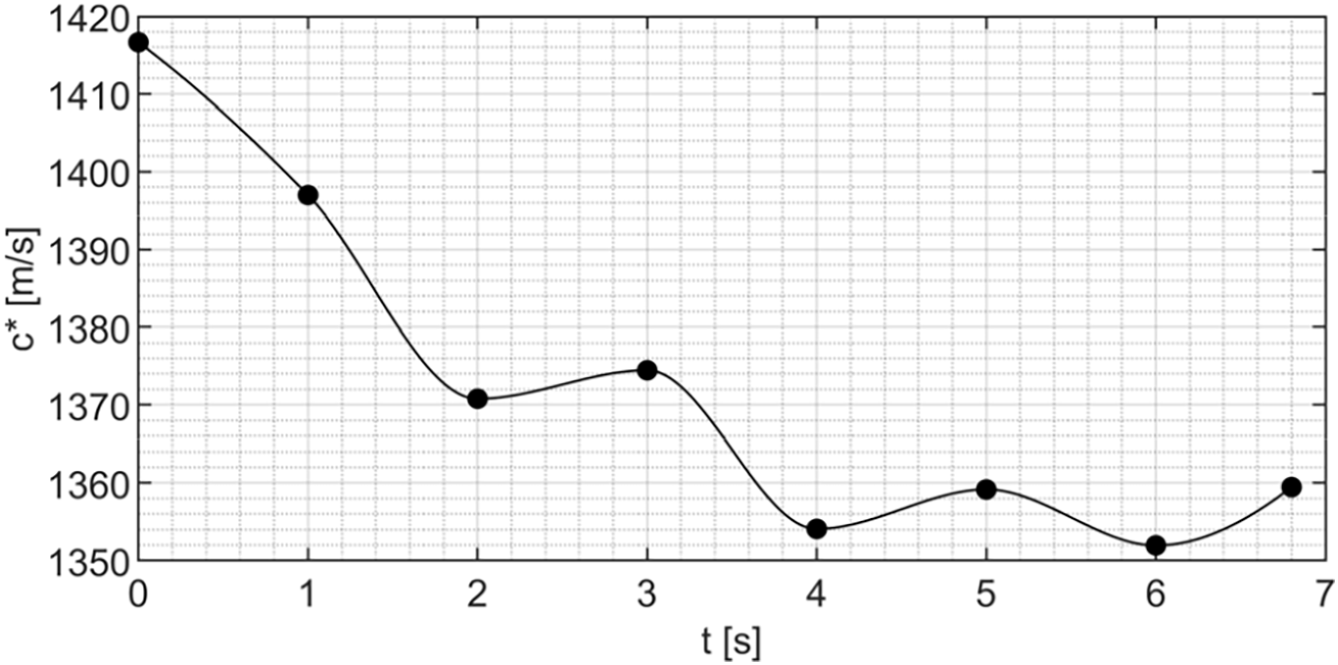
Figure 26: Characteristic velocity as a function of time, as estimated through transient CFD simulations. ABS-like test case

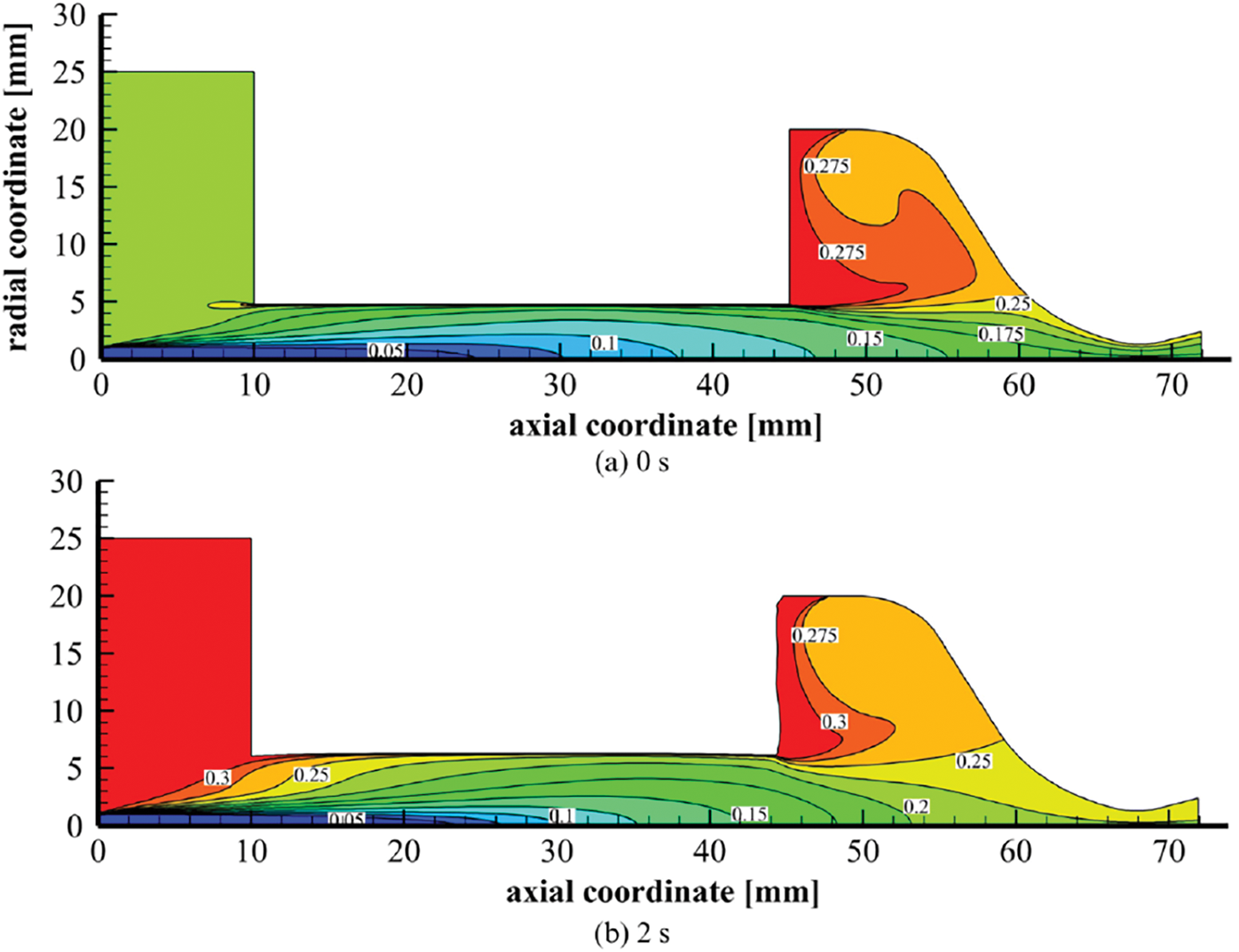
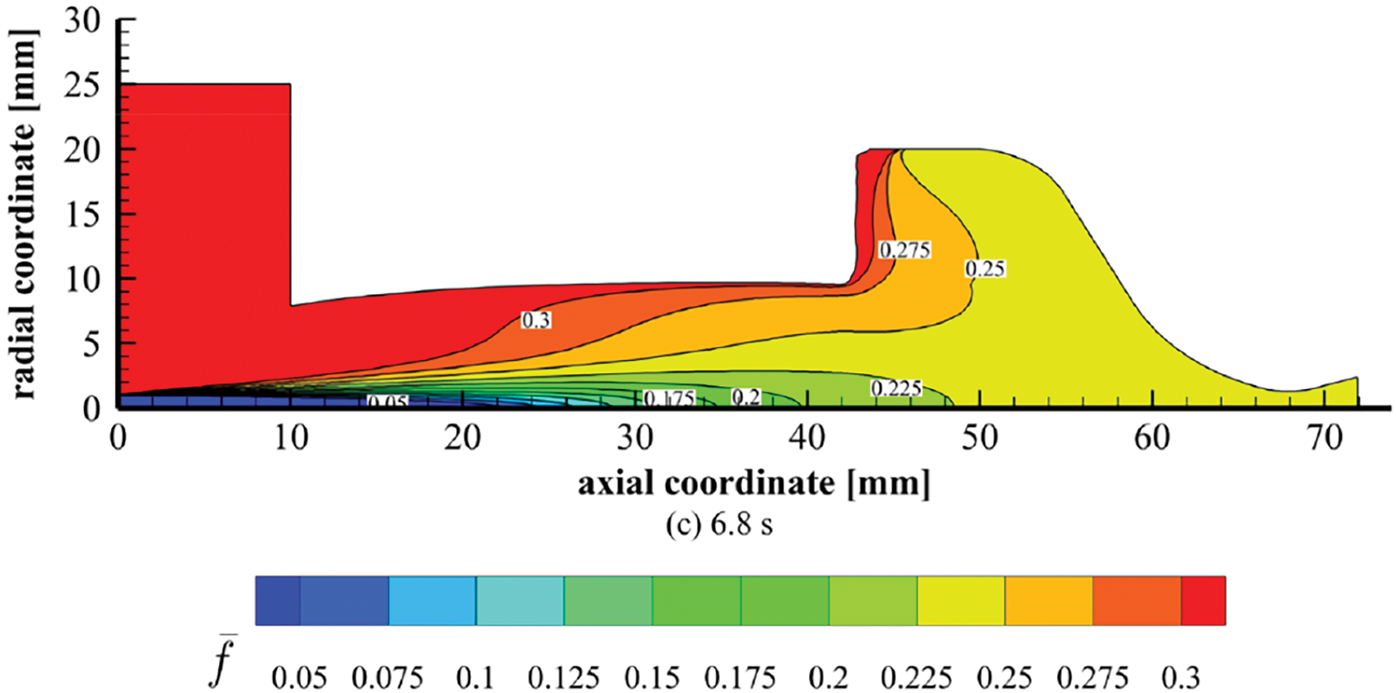
Figure 27: Mean mixture fraction contours in the hybrid rocket thrust chamber at t = 0 s (a), t = 2 s (b) and t = 6.8 s (c). Isolines are labelled with their numerical values. ABS-like test case

Despite the decreasing trend of c∗ over time, the combustion efficiency ηc∗ exhibits an oscillating behavior in a range between 0.82 and 0.84. In this case, indeed, combustion happens far from stoichiometric conditions. Therefore, a variation in O/F leads to relevant deviations in terms of both characteristic velocity and theoretical characteristic velocity. Consequently, ηc∗ depends on a combination of factors, resulting in the trend displayed in Fig. 28. In this case, more limited variations are observed with respect to the HDPE firing test simulations.

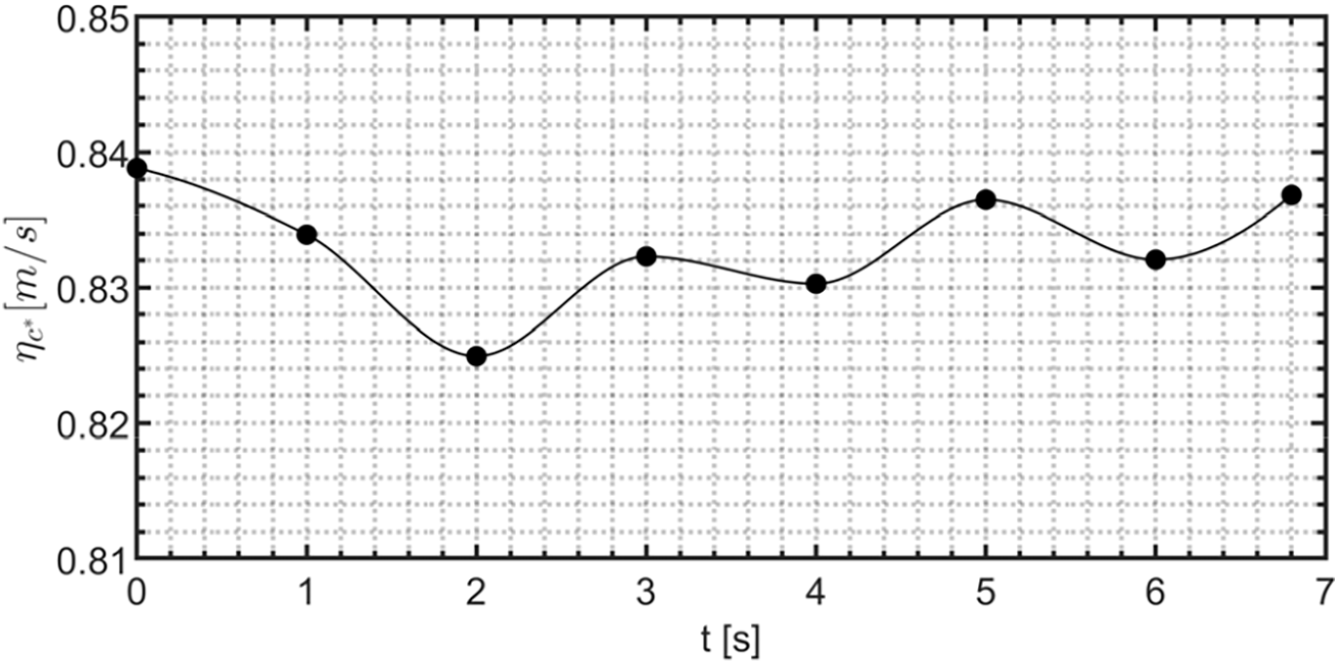
Figure 28: Numerical estimation of the engine combustion efficiency for the ABS-like test case

6  Conclusions

This work presented the results of a numerical and experimental investigation of a 10 N-class hydrogen peroxide-based hybrid thruster. The upgraded configuration proved satisfying propulsive capabilities, in line with theoretical predictions. Moreover, the additional thermal insulation layers showed better performance in terms of reduction of conductive heat transfer, which conveys thermal energy from the graphite nozzle to the polymeric fuel grain. Temperature monitoring on the combustion chamber case confirmed that the heat flux was mitigated, keeping the grain temperature practically unchanged. This will allow longer tests to be carried out, preventing the detrimental effects of heating that have been proven crucial in hybrid rocket engines of this scale. In addition, proper thermal insulation of the fuel cylinder will enable the evaluation of re-ignition capabilities, preventing the melting phenomena of the polymeric material. The implementation of enhanced control mechanisms pertaining to the thruster’s internal thermal processes was demonstrated to effectively mitigate a significant source of variability that is commonly encountered in numerical simulation methodologies. This enhancement facilitates the execution of numerical CFD analyses, ensuring more reliable results and a higher degree of fidelity with experimental results.

The comprehensive analysis of experimental results pointed out two unexpected features of the fuel grain at the end of the firing tests. An uneven port diameter distribution along the grain length was recorded for both HDPE and ABS-like materials, while a non-negligible axial burning was noted for the ABS-like fuel grain. An extensive numerical investigation was performed to investigate the physical phenomena underlying these off-nominal behaviors. Transient CFD simulations performed with a 1-s timestep revealed that the geometrical configuration of the engine caused the establishment of a larger recirculation zone. During the firing test, this zone shifted towards the outlet section and was progressively enlarged until it merged with the recirculation zone located in the thruster post-chamber. The resulting fluid dynamics field generated an increased wall turbulence toward the nozzle, enhancing the regression rate in the sections close to the outlet. A comparison between port grain distribution resulting from CFD simulations and experimental measurements was performed, proving a satisfying capability of reconstructing empirical behaviors. The effect of the O/F shift and the mixing was investigated in relation to propulsive performances. The numerical modeling technique employed provided reliable results in simulating the axial regression for the ABS-like test case, with mass loss estimation, grain length variation, and regression rate in accordance with experimental findings.

In conclusion, the transient CFD simulations proved to be a valuable tool for identifying complex physical phenomena beyond the reach of classical CFD or purely experimental methods. Their ability to reproduce experimental results and explain underlying mechanisms was demonstrated, highlighting key design challenges. These insights can guide both the analysis of existing thrusters and the early-stage design of future configurations, helping to mitigate unwanted fluid-dynamic effects.

Acknowledgement: This study was carried out within the Space It Up project funded by the Italian Space Agency, ASI, and the Ministry of University and Research, MUR, under contract no. 2024-5-E.0-CUP no. I53D24000060005.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Sergio Cassese; Methodology, Sergio Cassese and Stefano Mungiguerra; Software, Sergio Cassese, Riccardo Guida, and Daniele Trincone; Validation, Sergio Cassese, Riccardo Guida, and Stefano Mungiguerra; Formal analysis, Sergio Cassese, Riccardo Guida, and Daniele Trincone; Investigation, Sergio Cassese and Riccardo Guida; Resources, Raffaele Savino; Data curation, Sergio Cassese, Riccardo Guida, and Daniele Trincone; Writing—original draft preparation, Sergio Cassese and Riccardo Guida; Writing—review and editing, Sergio Cassese, Riccardo Guida, and Stefano Mungiguerra; Visualization, Sergio Cassese, Riccardo Guida, and Daniele Trincone; Supervision, Stefano Mungiguerra and Raffaele Savino; Project administration, Raffaele Savino; Funding acquisition, Raffaele Savino. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Riccardo Guida, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Supplementary Materials: The supplementary material is available online at https://www.techscience.com/doi/10.32604/fdmp.2025.065605/s1.

Glossary

References

1. Leccese G. Propulsion systems trends in Italian Space Agency ALCOR program. [cited 2024 Jul 24]. Available from: https://www.asi.it/wp-content/uploads/2024/07/Leccese_Workshop_CubeSat_2024.pdf. [Google Scholar]

2. Puig-Suari J, Schoos J, Turner C, Wagner T, Connolly R, Block RP. CubeSat developments at Cal Poly: the standard deployer and PolySat. Small Payloads Space. 2000;4136:72–8. doi:10.1109/aero.2001.931726. [Google Scholar] [CrossRef]

3. Lan W. CubeSat design specification Rev. 13. San Luis Obispo, CA, USA: California Polytechnic State University; 2014. [Google Scholar]

4. Poghosyan A, Golkar A. CubeSat evolution: analyzing CubeSat capabilities for conducting science missions. Prog Aerosp Sci. 2017;88:59–83. doi:10.1016/j.paerosci.2016.11.002. [Google Scholar] [CrossRef]

5. Total nanosatellites and CubeSats launched [Internet]. [cited 2024 Sep 24]. Available from: https://www.nanosats.eu/img/fig/Nanosats_total_2024-05-31_large.png. [Google Scholar]

6. Sutton GP, Biblarz O. Rocket propulsion elements. 9th ed. Hoboken, NJ, USA: John Wiley & Sons; 2017. [Google Scholar]

7. Casiano MJ, Hulka JR, Yang V. Liquid-propellant rocket engine throttling: a comprehensive review. J Propuls Power. 2010;26(5):897–923. doi:10.2514/1.49791. [Google Scholar] [CrossRef]

8. ESA—technology readiness levels (TRL) [Internet]. [cited 2024 Aug 23]. Available from: https://www.esa.int/Enabling_Support/Space_Engineering_Technology/Shaping_the_Future/Technology_Readiness_Levels_TRL. [Google Scholar]

9. Lysien K, Stolarczyk A, Jarosz T. Solid propellant formulations: a review of recent progress and utilized components. Materials. 2021;14(21):6657. doi:10.3390/ma14216657. [Google Scholar] [PubMed] [CrossRef]

10. Yilmaz N, Donaldson B, Gill W, Erikson W. Solid propellant burning rate from strand burner pressure measurement. Propellants Explos Pyrotech. 2008;33(2):109–17. doi:10.1002/prep.200800216. [Google Scholar] [CrossRef]

11. Rampazzo A, Barato F. Modeling and CFD simulation of regression rate in hybrid rocket motors. Fire. 2023;6(3):100. doi:10.3390/fire6030100. [Google Scholar] [CrossRef]

12. Bianchi D, Leccese G, Nasuti F, Onofri M, Carmicino C. Modeling of high density polyethylene regression rate in the simulation of hybrid rocket flowfields. Aerospace. 2019;6(8):88. doi:10.3390/aerospace6080088. [Google Scholar] [CrossRef]

13. Tian H, Jiang X, Yu R, Zhu H, Zhang Y, Cai G. Numerical analysis of the hybrid rocket motor with axial injection based on oxidizer flow distribution. Acta Astronaut. 2022;192:245–57. doi:10.1016/j.actaastro.2021.12.025. [Google Scholar] [CrossRef]

14. Meng X, Tian H, Yu R, Lu Y, Gu X, Tan G, et al. Three-dimensional numerical simulation of hybrid rocket motor based on dynamic mesh technology. Aerosp Sci Technol. 2023;141:108573. doi:10.1016/j.ast.2023.108573. [Google Scholar] [CrossRef]

15. Cassese S, Mungiguerra S, Guida R, Cecere A, Savino R. Regression rate and performance analysis via ballistic reconstruction of a small-scale H2O2-based hybrid rocket fuelled by Polyvinyl Chloride. Aerosp Sci Technol. 2024;146(4):108911. doi:10.1016/j.ast.2024.108911. [Google Scholar] [CrossRef]

16. Cassese S, Capone VM, Guida R, Mungiguerra S, Savino R. Properties and behavior of 3D-printed ABS fuel in a 10 N hybrid rocket: experimental and numerical insights. Aerospace. 2025;12(4):291. doi:10.3390/aerospace12040291. [Google Scholar] [CrossRef]

17. Cassese S, Guida R, Mungiguerra S, Savino R. Fuel characterization, performance assessment and thermal analysis of a hydrogen peroxide-based hybrid thruster for CubeSats. In: 75th International Astronautical Congress (IAC); 2024 Oct 14–18; Milan, Italy. [Google Scholar]

18. Datasheet M54 CORI-FLOWTM M54 low flow coriolis mass flow meter/controller. [cited 2024 Mar 25]. Available from: https://www.wagner-msr.de/files/wagner-mess-regeltechnik/Downloads/Datenblaetter/Cori-Flow/m54%20cori-flow_reva.pdf. [Google Scholar]

19. Cassese S, Mungiguerra S, Capone VM, Guida R, Cecere A, Savino R. Fuel ignition in HTP hybrid rockets at very low mass fluxes: challenges and pulsed preheating techniques using palladium-coated catalysts. Aerospace. 2024;11(11):884. doi:10.3390/aerospace11110884. [Google Scholar] [CrossRef]

20. ISO 1219-1:2012/Amd 1:2016. Fluid power systems and components—graphical symbols and circuit diagrams—part 1: graphical symbols for conventional use and data-processing applications. 3rd ed. Geneva, Switzerland: International Organization for Standardization (ISO); 2016. [Google Scholar]

21. Mezyk L, Gut Z, Mohan K, Kindracki J, Rarata G. Initial research on thermal decomposition of 98% concentrated hydrogen peroxide in thruster-like conditions. Eng Sci Technol. 2022;31(1):101054. doi:10.1016/j.jestch.2021.08.011. [Google Scholar] [CrossRef]

22. Williams GC, Satterfield CN, Isbin HS. Calculation of adiabatic decomposition temperatures of aqueous hydrogen peroxide solutions. J Am Rocket Soc. 1952;22(2):70–7. doi:10.2514/8.4427. [Google Scholar] [CrossRef]

23. Wertz JR, Everett DF, Puschell JJ. Space mission engineering: the new space mission analysis and design. 3rd ed. Vol. 28. Portland, OR, USA: Microcosm Press, Space Technology Library; 2011. [Google Scholar]

24. Paravan C, Hashish A, Santolini V. Test activities on hybrid rocket engines: combustion analyses and green storable oxidizers—a short review. Aerospace. 2023;10(7):572. doi:10.3390/aerospace10070572. [Google Scholar] [CrossRef]

25. Ku HH. Notes on the use of propagation of error formulas. J Res Natl Bur Stand Sect C Eng Instrum. 1966;70C(4):263. [cited 2024 Apr 25]. Available from: https://nistdigitalarchives.contentdm.oclc.org/digital/collection/p16009coll6/id/99848. [Google Scholar]

26. Chorin AJ. Numerical solution of the navier-stokes equations. Math Comput. 1968;22(104):745–62. doi:10.1090/s0025-5718-1968-0242392-2. [Google Scholar] [CrossRef]

27. Menter FR. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994;32(8):1598–605. doi:10.2514/3.12149. [Google Scholar] [CrossRef]

28. Gordon S, Cleveland A, Mcbride BJ. Computer program for calculation of complex chemical equilibrium compositions and applications. Part 1: analysis. In: NASA Reference Publication 1311. Cleveland, OH, USA: Office of Management, NASA Scientific and Technical Information Program; 1994. [Google Scholar]

29. Roache PJ. Verification of codes and calculations. AIAA J. 1998;36(5):696–702. doi:10.2514/2.457. [Google Scholar] [CrossRef]

30. Bianchi D, Betti B, Nasuti F, Carmicino C. Simulation of gaseous oxygen/hydroxyl-terminated polybutadiene hybrid rocket flowfields and comparison with experiments. J Propuls Power. 2015;2015(3):919–29. doi:10.2514/1.B35587. [Google Scholar] [CrossRef]

31. Di Martino GD, Carmicino C, Savino R. Transient computational thermofluid-dynamic simulation of hybrid rocket internal ballistics. J Propuls Power. 2017;33(6):1395–409. doi:10.2514/1.b36425. [Google Scholar] [CrossRef]

32. Gallo G, Kamps L, Hirai S, Carmicino C, Harunori N. Prediction of the fuel regression-rate in a HDPE single port hybrid rocket fed by liquid nitrous oxide. Combust Flame. 2024;259(1):113160. doi:10.1016/j.combustflame.2023.113160. [Google Scholar] [CrossRef]

33. Ansys Inc. Ansys fluent theory guide. Canonsburg, PA, USA: Ansys Inc.; 2013. p. 724–46. [Google Scholar]

34. Sivathanu YR, Faeth GM. Generalized state relationships for scalar properties in nonpremixed hydrocarbon/air flames. Combust Flame. 1990;82(2):211–30. doi:10.1016/0010-2180(90)90099-d. [Google Scholar] [CrossRef]