 Open Access
Open Access
REVIEW
Grouting Flow in Deep Fractured Rock: A State-of-the-Art Review of Theory and Practice
1 State Key Laboratory of Geomechanics and Geotechnical Engineering Safety, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan, 430071, China
2 University of Chinese Academy of Sciences, Beijing, 100049, China
3 School of Civil Engineering, Henan Polytechnic University, Jiaozuo, 454003, China
4 The Key Laboratory of Safety for Geotechnical and Structural Engineering of Hubei Province, School of Civil Engineering, Wuhan University, Wuhan, 430072, China
* Corresponding Author: Bin Liu. Email:
Fluid Dynamics & Materials Processing 2025, 21(8), 2047-2073. https://doi.org/10.32604/fdmp.2025.068268
Received 24 May 2025; Accepted 18 August 2025; Issue published 12 September 2025
Abstract
Grouting is a widely applied technique for reinforcing fractured zones in deep soft rock tunnels. By infiltrating rock fissures, slurry materials enhance structural integrity and improve the overall stability of the surrounding rock. The performance of grouting is primarily governed by the flow behavior and diffusion extent of the slurry. This review considers recent advances in the theory and methodology of slurry flow and diffusion in fractured rock. It examines commonly used grout materials, including cement-based, chemical, and composite formulations, each offering distinct advantages for specific geological conditions. The mechanisms of reinforcement vary significantly across materials, requiring tailored application strategies. The rheological properties of grouting slurries, particularly cement-based types, have been widely modeled using classical constitutive approaches. However, the influence of time- and space-dependent viscosity evolution on slurry behavior remains underexplored. Experimental studies have provided valuable insights into slurry diffusion, yet further research is needed to capture real-time behavior under multi-scale and multi-physics coupling conditions. Similarly, current numerical simulations are largely limited to two- and three-dimensional models of single-fracture flow. These models often neglect the complexity of fracture networks and geological heterogeneity, highlighting a need for more realistic and integrated simulation frameworks. Future research should focus on: (1) fine-scale modeling of slurry hydration and mechanical reinforcement processes; (2) cross-scale analysis of slurry flow under coupled thermal, hydraulic, and mechanical fields; and (3) development of real-time, three-dimensional dynamic simulation tools to capture the full grouting process. These efforts will strengthen the theoretical foundation and practical effectiveness of grouting in complex underground environments.Keywords
The 21st century has seen the large-scale development and use of underground space. However, geotechnical engineering projects are susceptible to instability and damage due to complex geological conditions [1,2]. As mining operations extend to greater depths, engineers encounter increasingly challenging tunnel conditions, characterized by soft rock formations and strong rheological deformation, leading to ground pressure impacts, large-scale rock instability, and other dynamic hazards [3,4]. Deep bedrock strata present complicated hydrogeological conditions, where the risk of high-pressure water inflow from microfissures and porous water-bearing formations increases with depth, potentially causing serious accidents and construction delays.
Among various ground reinforcement techniques, grouting offers unique advantages over conventional methods. Unlike rigid surface treatments such as steel arch supports and shotcrete, which provide only external reinforcement, grouting penetrates cracks and voids to strengthen the rock mass from within while maintaining its original structural integrity. This penetrative capability gives grouting a significant advantage over localized solutions like rock anchors, which provide effective support in intact rock but perform poorly in fractured or water-saturated areas, where grouting excels. Additionally, grouting requires minimal heavy equipment and causes little disturbance, making it ideal for confined or environmentally sensitive areas.
These advantages have led to the widespread use of grouting technology in mining, hydraulic engineering, and civil infrastructure projects [5,6]. Its adaptability to complex geometries, cost-effectiveness, and multifunctional properties, including enhanced strength, watertightness, and long-term durability, make grouting particularly well-suited to contemporary underground engineering challenges.
Grouting involves the injection of gelatinous materials into rock strata and fractures under pressure or through electro-osmosis to reinforce formations, repair cracks, and prevent water infiltration [7]. The selection of appropriate grouting materials is critical to process efficiency, equipment requirements, and cost control, with material performance determining the effectiveness of grouting [8,9]. Grouting materials should ideally meet the following requirements: (1) Maintain stable properties under normal temperature and atmospheric pressure conditions to ensure long-term performance. (2) Exhibit strong permeability, low viscosity, and high fluidity, allowing easy injection into small cracks under applied pressure. (3) Provide adjustable setting times without significant shrinkage during curing. (4) Achieve high compressive and flexural strength upon hardening, with excellent impermeability and corrosion resistance. (5) Be convenient to prepare, economical, non-toxic, and non-polluting.
Grouting materials are diverse and generally classified into inorganic, organic, and composite types. In the past decade, they have been modified to eliminate their shortcomings or enhance their performance. Additionally, green grouting materials have been developed, which are non-toxic and non-polluting and have low carbon dioxide emissions. This article introduces the current research status of the main grouting materials and the experimental and simulation processes involved in grouting in the context of deep rock mechanics.
2 Classification of Slurry Material
2.1 Inorganic Grouting Material
Ordinary silicate cement is widely used in engineering grouting due to its low cost, durability, and high strength. However, its limitations—including poor stability, particle size restrictions (difficulty penetrating fractures <0.2 mm), and long setting times—have prompted the development of advanced cementitious composites [10]. Lower initial cost but limited to larger fractures (>0.2 mm) and requires higher grouting volumes for comparable reinforcement. Recent innovations can be broadly categorized into five groups, each addressing specific performance gaps (Table 1).
Ultrafine cementitious grouting materials have the advantages of small particle size and high reactivity, effectively improving the injectability, permeability, and bond strength of the slurry and enhancing its durability and resistance to environmental erosion [11]. Yu et al. [12] demonstrated that increasing the mesh size of ultrafine cement can reduce the water-cement (W/C) ratio and enhance the stability of slurry, thereby increasing its injectability and mechanical strength compared with ordinary cement. Zhao et al. [13] explored the effect of nano-MgO content on the properties of ultrafine cementitious sealing materials and elucidated the mechanism by which nano-MgO improves the properties of modified materials. Although its production cost is approximately 20%–30% higher than that of traditional cement due to the use of advanced grinding technology, it offers superior injectability into finer fractures (<0.2 mm) and a 3%–5% strength gain, reducing long-term maintenance costs.
Fly ash is a fine, powdery by-product generated during the combustion of coal in thermal power plants. It can replace cement in concrete and other construction applications, enhancing durability and workability while reducing permeability. Moreover, its internal spherical particles can increase a material’s compatibility and damping effect [14]. Zhang et al. [15] investigated the impact of the fly ash content, W/C ratio, and mass ratio of sodium silicate to slurry on key grouting properties, including splitting rate, coagulation rate, and uniaxial compressive strength. They demonstrated that an increase in the fly ash admixture reduced the slurry’s strength and elastic modulus but enhanced its ductile deformation behavior (Fig. 1).
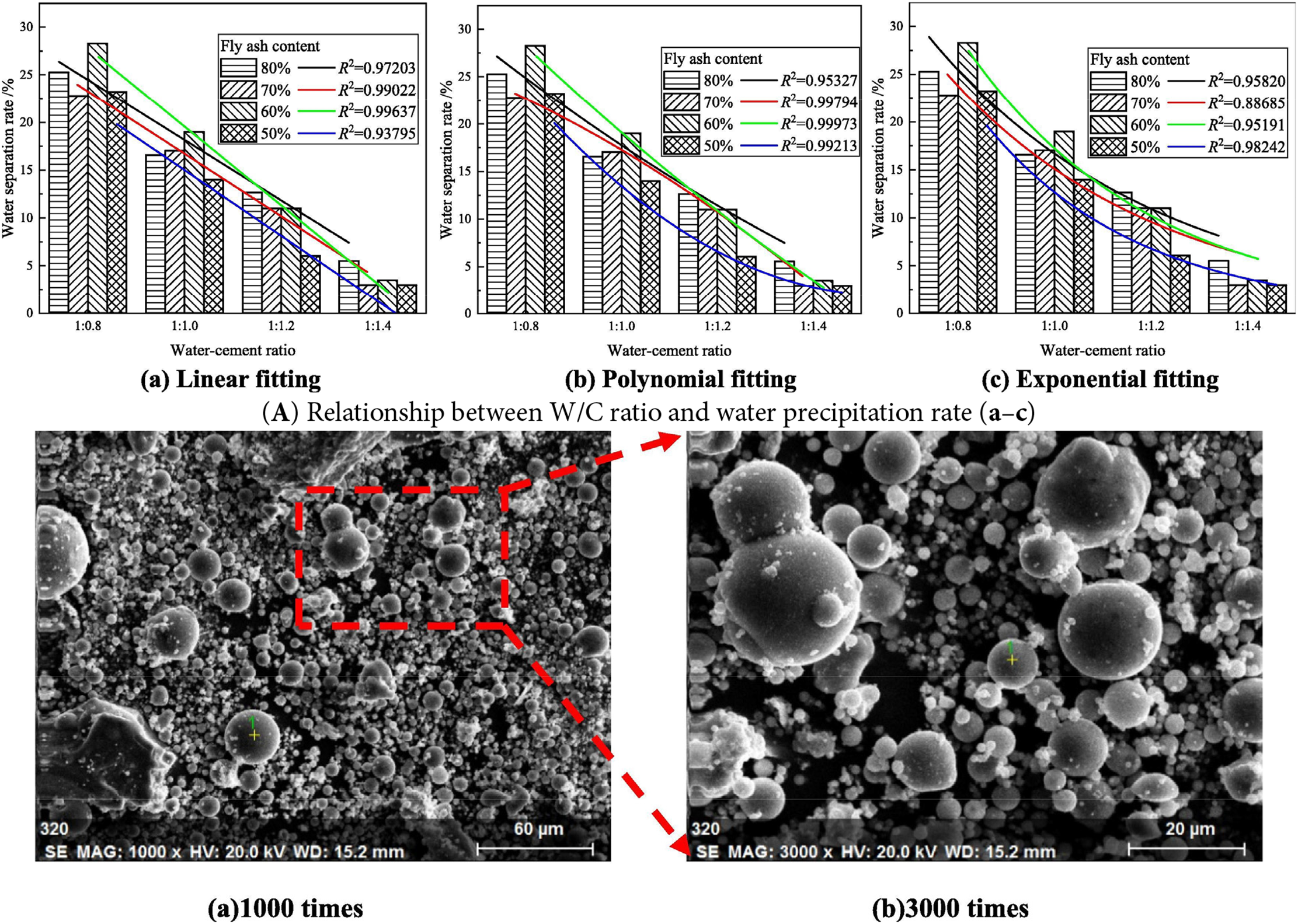
Figure 1: Macroscopic and microscopic properties and SEM images of ultrafine fly ash-cement grouting material. Adapted with permission from Ref. [15]. Copyright © 2021, Elsevier Ltd.
Magnesium phosphate cement is a ceramic-like binder that exhibits superior strength development at an early stage compared with other cementitious materials. It can be used to develop slurry materials with high early strength. Gao et al. [16] found that magnesium phosphate cements can be enhanced with silica fume to develop high-early-strength slurry materials. Qin et al. [17] discovered that a high magnesium-phosphate (M/P) ratio (e.g., 3.5), a very low W/C ratio (e.g., 0.12), and an appropriate amount of retarder can result in lower shrinkage and higher early strengths than conventional cements. Adding 2 vol% steel fibers increased 6-h and 28-day strengths from 87.8 and 105.4 MPa to 112.2 and 141.9 MPa, respectively. He et al. [18] developed a new magnesium phosphate cementitious material (MPC-UHPC) reinforced with 2 vol% steel fibers with comparable strength.
Nanomaterials have been used in concrete engineering and grouting materials due to their excellent chemical activity, nucleation effect, and filling effect [21]. Literature found that adding 1%–2% nano-SiO2 and 1%–5% silica powder significantly improved the compressive strength of hardened cement paste by adding nano-SiO2, silica sol, and nano-CaCO3 [22].
Lin et al. [23] used gangue, steel slag powder, and a polycarboxylic acid water-reducing agent as admixtures to optimize the ratio and obtain a new type of modified silicate cement grouting material. They confirmed that after activation treatment, gangue and steel slag can be used as mixing materials to optimize the performance of cement grouting materials. The compressive strength increased with increasing gangue content and decreased with increasing steel slag powder content.
Lazorenko et al. [24] created a soil model to study the effects of reinforcement mechanisms (i.e., skeleton and compaction mechanisms). They found that compaction dominated reinforcement. Grouting pressure, grout modulus, and soil modulus affected the compressive modulus of the soil, and an optimal pressure exists, with higher pressures not necessarily being better.
Recently developed graphene/graphene oxide (GO) materials have also been explored as potential grouting materials. Ling et al. [25] found that adding GO to cementitious composite grouting materials effectively improved bleeding and setting times. Liu et al. [19] analyzed the mechanical properties of mortars with GO contents of 0%, 0.01%, 0.03%, 0.05%, and 0.07%. After 28 days, the mortar with 0.05% GO had the highest flexural strength (10.8 MPa) and the highest impermeability (80% greater than the control). Zhang et al. [20] found that adding GO to cement slurry reduced fluidity but increased tensile, compressive, and flexural strengths. Erosion and permeability resistance were also improved. Upon adding 0.05% GO, compressive and flexural strengths rose by 6.8% and 8.3%, respectively, and the microstructure became denser.
Cementitious grouting materials are extensively used in the domain of coal mine grouting technology owing to their numerous advantages, including their low cost, broad spectrum of raw materials, ease of preparation, and convenient construction. Current research has focused on the impact of a single admixture on the engineering application of cement-based grouting materials. To explore the influence of multiple admixture materials on the performance, mechanical strength, and diffusion mechanism of cement slurry, various approaches should be combined, including numerical simulation, experimental research, micro-analysis, and engineering trials.
Ultrafine cementitious grouting materials have recently attracted significant attention in the grouting industry. The development of an ultrafine grinding process, coupled with enhanced grinding efficiency, has led to predictions of significant expansion in the mining applications of these materials in the future. Mixing with fly ash can effectively improve the stability and fluidity of cement slurry, but remaining challenges include developing durable hardened grout, improving the stability of structures, and obtaining the key proportioning parameters suitable for actual construction environments. Although new cement-based composite grouting materials, including magnesium phosphate cement composite slurries, nanomaterial-cement slurries, activated gangue/slag-cement slurries, and GO-cement slurries, have shown promising application prospects, field implementation has progressed relatively slowly, and in-depth research is needed.
2.2 Chemical Grouting Material
Chemical grouting materials are used in foundation treatment and in repairing cracks in concrete buildings. This technology involves the formulation of an inorganic or organic chemical material into a true solution, which is then pressed into the ground layer or crevice through the application of pressure. This results in the diffusion, gelation, or solidification of the material, thereby increasing the strength of the ground layer, reducing its permeability, and preventing deformation. At present, chemical grouting agents used for coating or consolidation include synthetic organic polymers, such as water glass, polyurethane materials [26], epoxy resins [27], urea-formaldehyde resins [28], polyacrylamides [29], and lignosulfonates [30] (Fig. 2).
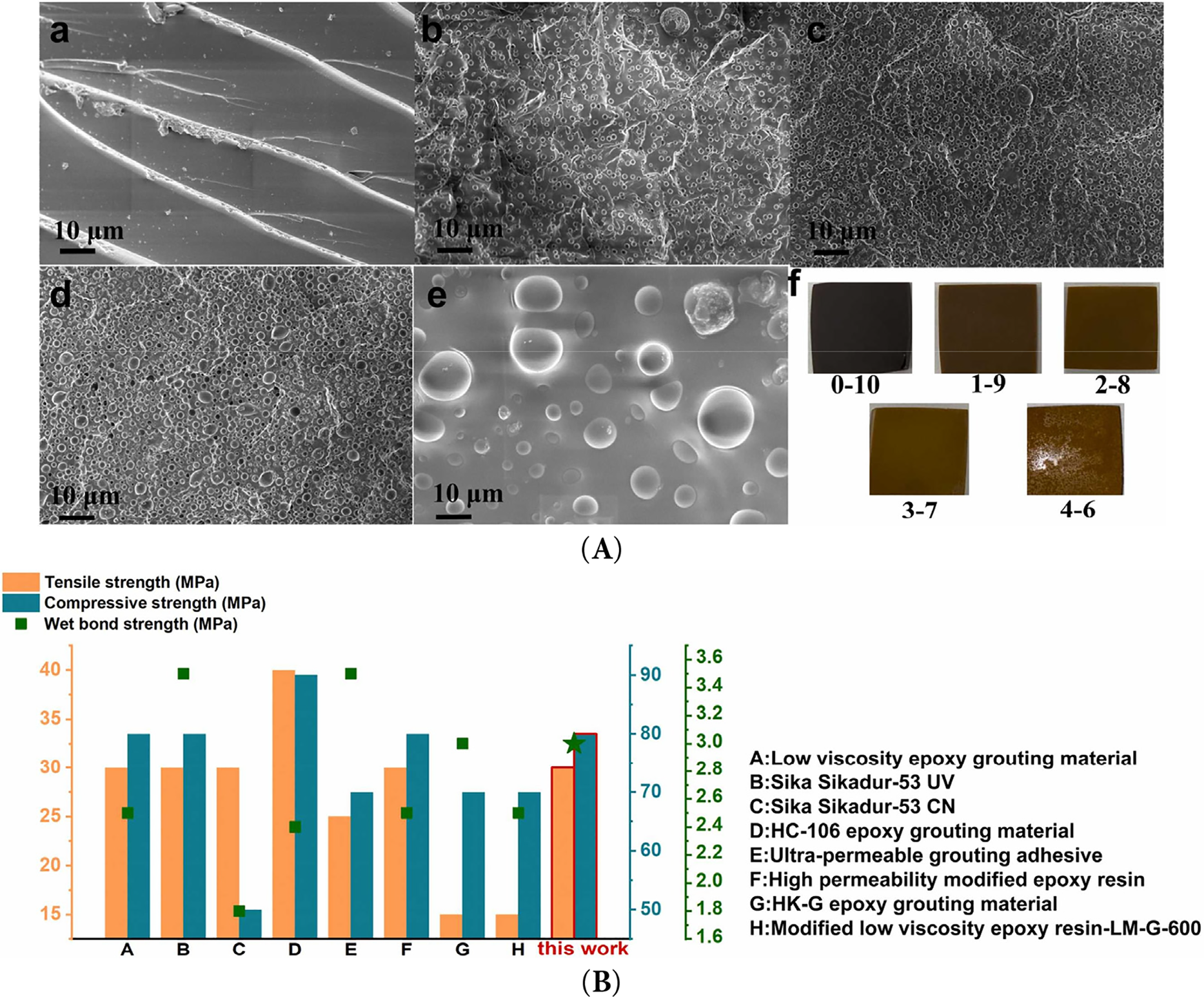
Figure 2: Structured polyurethane/epoxy grouting materials with interpenetrating polymer network. Adapted with permission from Ref. [27]. Copyright © 2024, Elsevier Ltd. (A) SEM images of composite material with different mass ratio of PU to EP: (a) 0:10, (b) 1:9, (c) 2:8, (d) 3:7 (e) 4:6 (f) Specimens with different mix ratios. (B) Comparison of polyurethane/epoxy and other grouting materials
Water glass is a grouting material widely used in tunnel grouting reinforcement and hydraulic control. However, its disadvantages include a low-intensity solid body, short setting time, poor durability, and high cost. Thus, it requires modification to enhance its range of grouting applications. To address these limitations, Guan [31] explored the use of water glass as a grouting material in fine sand formations. They found that acidic water glass was effective for grouting in fine sand formations, and the gelation time could be controlled by controlling the water glass-sulfuric acid ratio. Liu et al. [32] studied a composite of polyurethane and water glass and synthesized a flame-retardant composite slurry with low toxicity, easy installation, and high compressive strength by a one-step method.
Polyurethane concrete grouting materials are mainly used due to their adaptable properties, substantial permeability, elevated compressive strength, and ease of fabrication [33]. Ma et al. [34] incorporated flexible polyurethane and nano-silica into cement. The compressive strength of the resulting experimental material was compared with that of a control sample containing no nano-silica at 3 and 28 days. They found that the experimental material demonstrated superior compressive strength to conventional cement paste. Moreover, X-ray diffraction spectroscopy revealed that the polyether constituent in the material contributed to the hydration process during curing. However, the use of polyurethane composite grouts in substantial quantities has the potential to compromise the quality of work and result in personnel safety concerns due to their high heat release and low thermal conductivity during curing. This can lead to critical thermal damage and asphyxiation in enclosed environments. Moreover, the elevated viscosity of polyurethane slurry, in conjunction with the additives themselves, could influence the transfer and reaction of the material. This may create difficulties in inserting the material into microcracks or micropores during construction.
Chemical slurries, such as urea-formaldehyde resin and acrylamide, have significant potential in containing elevated permeability seepage and interstitial fluid flow in fractured reservoirs. This is due to their stability, pumpability, high sealant strength, low abrasive viscosity, and capacity for tightly bonding with surfaces to which they are applied. The use of chemical slurries in seepage and leakage prevention has been extensively documented, particularly in the context of tunnels, underground engineering, and dam construction. Here, the pH level of the soil is also important, given that compounds exhibit divergent properties at different pH levels. For example, polyurethane requires an alkaline pH level for its use as a grouting material. However, the toxicity of grouting materials may result in groundwater contamination. In some localities, the use of specific chemicals has been proscribed owing to their deleterious effect on the environment. Huo et al. [35] successfully synthesized Poly-UF and Poly-UF-m by a conventional alkaline-acid-alkaline process through secondary condensation, incorporating functional enhancers including flow-correcting agents, curing accelerators, and volumetric expanders. These enhancers were used to increase the resistance of the materials to temperature and shear, as well as salt, water, and coal. These materials were demonstrated to exhibit resistance to shear, water, paraffin, and acid/alkali materials, in addition to exhibiting satisfactory sealing strength. Zhu et al. [36] investigated the impact of polyacrylamide (PAM) on the setting time of cement paste. They found that PAM addition delayed the setting process. Furthermore, the incorporation of an appropriate amount of PAM enhanced the flexural strength of the overall structure.
Polyurethane slurry is usually used to control seepage and plug leaks. Epoxy resin slurry is commonly applied as reinforcement. A comparison of the viscosity of inorganic and organic grouting materials reveals that the former have lower viscosity and the latter have superior penetrative capacity. However, they have low strength, poor durability, and toxic slurry, increasing the risk of casualties in the construction process and pollution of the surrounding environment, including the groundwater [37].
Chemical grouting materials have significant impact in foundation treatment and concrete fracture repair. Water glass slurry has a low cost and an adjustable gel time, making it suitable for fine sand strata with low strength and poor durability. Polyurethane has excellent permeability and high early strength (up to 30 MPa after 3 days), but it reacts exothermically and has toxicity problems. Epoxy resin has high bonding strength (>3 MPa) and chemical stability, but it is expensive and brittle. Urea-formaldehyde resin has low viscosity and is injectable. However, it releases formaldehyde and contaminates the environment. Polyacrylamide extends the working performance of cement paste and improves the flexural strength but has the problem of environmental persistence. Current research has focused on developing low-toxicity, high-performance composite pastes and bio-based materials with low environmental impact to balance engineering performance and environmental safety. The selection of these materials necessitates comprehensive consideration of factors such as strength requirements, construction conditions, and environmental constraints.
2.3 Composite Grouting Materials
The incorporation of polymers markedly affects the flow characteristics of cementitious grouting materials. Polymers typically function by reducing water, aerating the mixture, and retaining water, thereby enhancing the performance of cementitious materials. Nevertheless, the impact of each polymer on the viscoelastic properties of the grouting material varies [38,39]. A comparison of polymer organic grouting materials (such as acrylamide, epoxy resin, methacrylate, and polyurethane) with inorganic grouting materials reveals several advantages of the former. These include low viscosity of the slurry and good injectability into fine fissures due to the small particle size. However, they tend to be toxic, flammable, expensive, and complicated to prepare. Moreover, the strength of the hardened body is low [40]. To address these problems, small quantities of organic materials have been added to cementitious materials to obtain low-toxicity and efficient organic-inorganic composite grouting materials used in mining applications. A typical chemical slurry material is polyurethane, usually containing polyisocyanate and polyether resin, which is mixed with various additives.
In situ polymerized polymers demonstrate superior dispersibility in cementitious materials compared with directly added polymers [41]. An additional advantage of in situ polymerization is cost-effectiveness. Moreover, it can enhance the bonding between the cement product and the PAM [42]. Liu et al. [43] used an in situ polymerized cement-toughening material, prepared using acrylic acid, to enhance ductility by 100%. Yin et al. [44] used in situ polymerized acrylamide to enhance the bending strength of pozzolanic materials by 130%.
Yan et al. and Liu et al. [45,46] enhanced the tensile strength and brittleness of cement by incorporating polyurethane polymers while simultaneously increasing its resistance to water erosion. Zhang and Yan, and Jiang et al. [47,48] found that adding epoxy resin to cement promoted crystallization and improved the structural integrity of the composite. They also found that although the cement retained its strength up to an epoxy content of 80%, the compressive strength was reduced. Fang et al. [49] incorporated environmentally friendly polyurethane into concrete and comprehensively investigated its mechanical properties and cross-sectional morphology. They demonstrated that incorporating polyurethane into cement grouting materials enhanced their strength, toughness, and stability (Fig. 3).
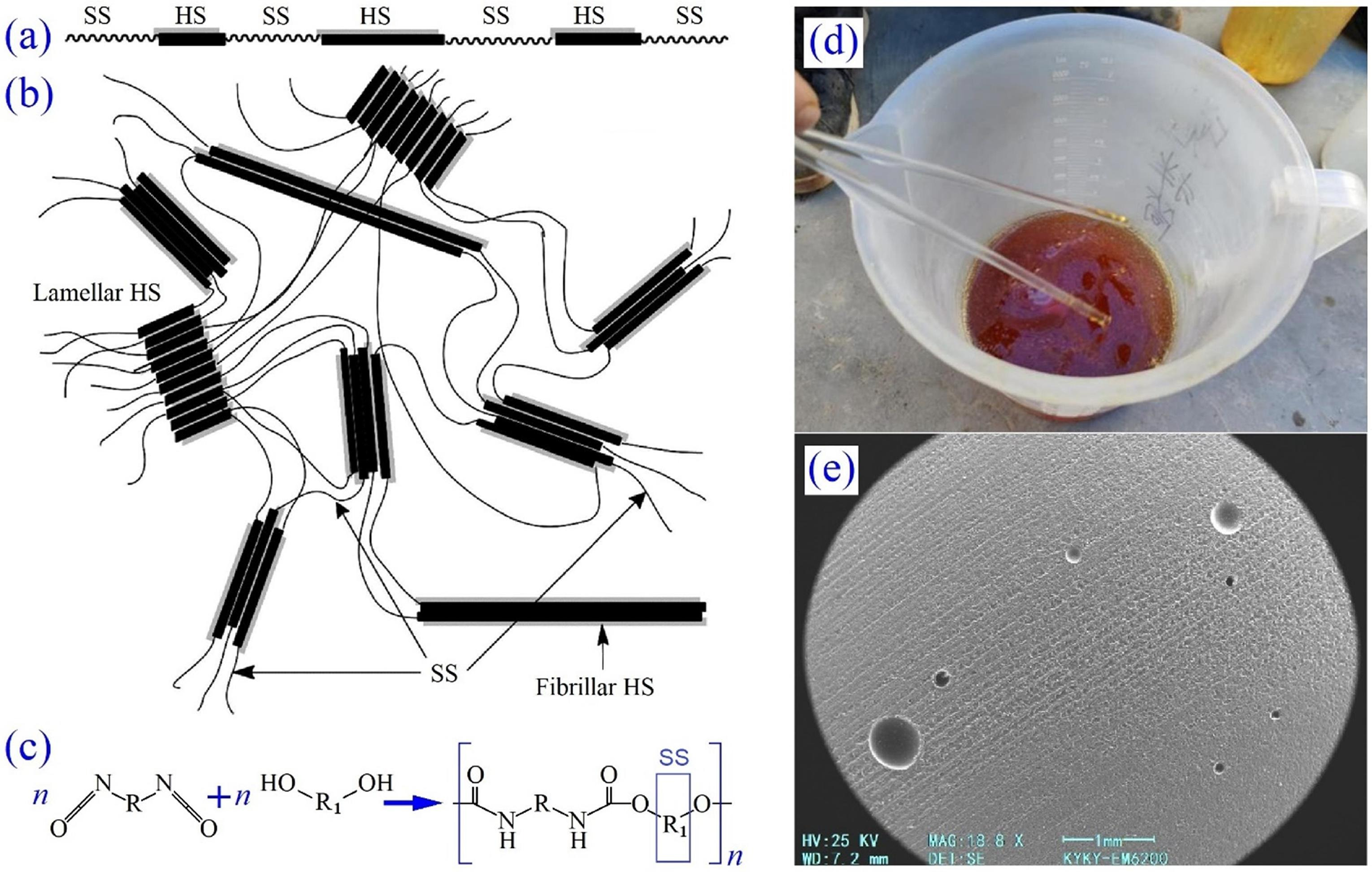
Figure 3: Polyurethane elastomer chain: (a) periodic soft (PS) and hard (HS) segments; (b) segmented copolymer [30]; (c) curing reaction equation; (d, e) before/after grouting material. Adapted with permission from Ref. [49]. Copyright © 2022, Elsevier Ltd.
Huang et al. [50] modified cement mortar with water-based epoxy resin, which prolonged the hydration time of the cement. Although the compressive strength of the cement mortar was slightly reduced when the polymer-ash ratio was less than 2%, its flexural strength was improved.
Guan et al. [51] developed inorganic-organic composite grouting and reinforcement materials for soft rock in deep wells. Materials suitable for reinforcing low-permeability roadway perimeter rock were obtained by mixing a clinker of sulfoaluminate cement, gypsum, and lime with lithium-aluminum hydrotalcite and an organic adjusting agent, supplemented with additives such as water-reducing and retarding agents.
Shang [52] found that the cement-water glass slurry grouting effect was remarkable, and the mechanical properties and permeability of the fractured rock body were greatly improved. The stress and strain in the non-fissure region of the grouted rock body were less than those in the fissure rock body, and the seepage rate was less than that of the fissure rock body in the fissure region.
Industrial solid waste materials occupy large areas of land and cause environmental pollution. The utilization of solid waste can be effectively improved by compounding it with organic materials or cementitious systems. Zhang et al. [53] developed an eco-friendly alkali-activated lithium slag composite material with calcium carbide slag as a key component. The material demonstrated outstanding performance, with a compressive strength of 17.64 MPa and flowability of 243 mm. This innovative material is a sustainable alternative to traditional cement in underground backfill applications, offering cost efficiency and enhanced use of industrial by-products.
Liu et al. [54] predicted the properties of slurries modified with mineral waste, including fly ash and mineral powder, using a mechanistic approach. They found that incorporating mineral powder and fly ash into slurry solutions enhanced their fluidity. It also increased the early strength and the growth rate of the slurry aggregates. The HGC of 4050 mPa·s was found to be significantly higher than that of silicate cement (297 mPa·s) and sulfoaluminate cement (245 mPa·s).
Zhao et al. [55] prepared a gangue-steel slag-cement composite cementitious material with gangue substituting for cement. They demonstrated that the compressive strength and flexural strength of the specimens increased by 15.21% and 15.78%, respectively. They established that the combination of gangue and steel slag resulted in the greater production of hydration products while reducing the internal porosity of the material.
Solid waste-based composites have the potential to surpass the mechanical properties of conventional materials, thereby enhancing fluidity and accelerating the development of early strength. Conventional cement production is energy-intensive and carbon-intensive. Waste-organic composites can partially substitute for cement, enabling the development of green materials.
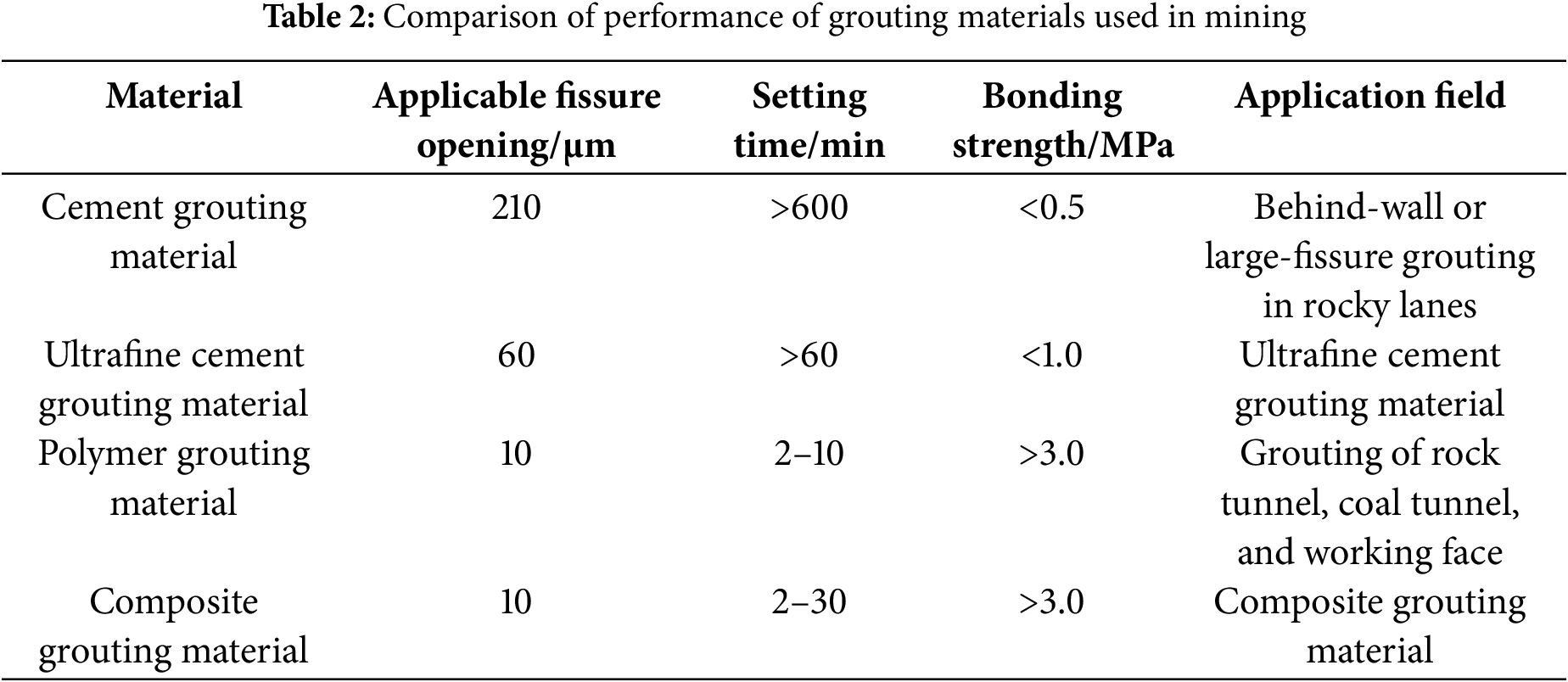
At present, the high price of polymers, the dosage in cement is on the high side, and part of the polymer has toxicity, modified cement-based grouting materials with low compressive strength in the early stage, limiting the development of polymer cement. Composite materials reduce the cost of grouting materials while retaining the advantages of a single grouting material. They also optimize the reinforcing effect, adapt to the low-pressure grouting process, and have potential use in the fields of coal rock reinforcement and seepage and leakage control, which are currently active areas of research. However, they have some limitations. Polymers are relatively expensive, and some polymers are toxic. Additionally, the compressive strength of polymer cementitious composite materials is relatively low. It is also necessary to adjust the slurry formulation for different engineering applications (Table 2).
3 Rheological Characterization of Slurry
Cementitious composites constitute a dispersion of solid particulates within a cement matrix, resulting in a viscous and non-uniform fluid. The rheological behavior of these suspensions in their original state is characterized by one of two primary categories: shear flow or tensile flow. In the context of fluid mechanics, the movement of fluid elements can be categorized into two primary flow types: shear flow and tensile flow. Shear flow occurs when fluid elements move toward each other or pass through each other. In contrast, tensile flow is characterized by the movement of fluid elements in close proximity to, or away from, each other.
A non-Newtonian fluid is typically distinguished by a nonlinear relationship between shear stress and strain. The viscosity of such a fluid varies with the applied shear rate. A non-Newtonian flow is exhibited by liquids and suspensions containing molecules and particles that vary in shape and size. This is because the magnitude, configuration, and cohesion of the constituent elements govern the magnitude of force necessary for each component to traverse during the flow process. Varying the applied shear rate changes the arrangement of the particles, thereby changing the force required to maintain the fluid flow [56,57].
The flow model provides a concise overview of the flow characteristics of grouting in rock fractures, thereby establishing the theoretical foundation for subsequent studies of grouting. To study the flow characteristics, it is necessary to consider both the characteristics of grouting and the geometrical characteristics of cracks. In the context of grouting flows in cracks, the conventional approach entails a force analysis of grouting microunits in flat cracks, in conjunction with the intrinsic model of grouting, to establish the flow model. Two-dimensional (2D) single-crack grout flow is usually modeled using differential equations of motion and grout structural equations (Fig. 4 and Table 3).
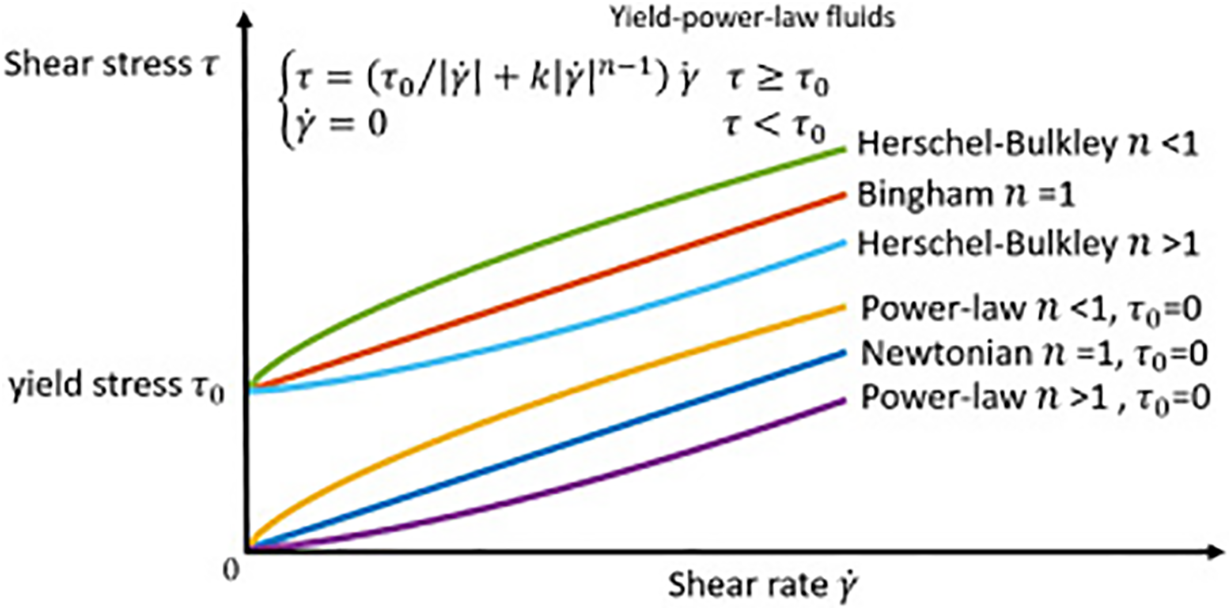
Figure 4: Grouting fluids models
In previous studies, grout was considered to be a single-phase flow of a Newtonian fluid with time-varying viscosity [63,64]. However, engineered grouts are non-Newtonian fluids characterized by yield stress [65] and exhibit flow behavior exclusively under conditions of shear stress that exceed the initial yield stress (Table 3).
The Bingham model and modified Bingham model were used to derive mathematical approximations of the grout mixtures using linear and second-order responses with yield stresses, respectively. Ding et al. [66] and Zou et al. [67] developed a model to simulate the flow of two kinds of grouts within a circular plate that contains a single crack. Ding et al. [68] also calculated the roughness correction factor. Wang et al. [69] used the Bingham model to characterize the time-varying viscosity of cementitious grout and determined the effect of basic factors on the spreading of the grout. The Bingham model yielded the optimum fit to the data concerning the shear stress and shear rate. Gao et al. [70] used a modified time-varying viscosity grouting model for the flow model of Newtonian fluid in a circular plate, improved Bingham model for time-varying viscosity grouting to investigate the effect of key parameters on the sealing efficiency of cement slurry by orthogonal methods. The results showed that increasing the diameter of the grouting holes promoted the distribution of the slurry and improved the sealing efficiency of the cracks. Zou et al. [71] explicitly models dual-phase flow in fractures using the Reynolds equation, highlighting the critical role of viscosity ratios and water phase effects.
Cement-based grouts (e.g., ultrafine cement, fly ash composites) are typically modeled using the Bingham or Herschel-Bulkley (HB) constitutive equations due to their yield stress and shear-thinning/thickening behaviors.
Composite materials exhibit distinct rheological traits due to organic additives. Lower viscosity, enhanced Injectability and many existing types show non-Newtonian behavior. The rheology is dominated by particle size distribution and hydration kinetics, leading to time-dependent viscosity evolution. Composite materials exhibit distinct rheological traits due to organic additives, with lower viscosity and enhanced injectability. Polymers like polyacrylamide (PAM) or epoxy resins reduce initial viscosity, enabling penetration into finer fractures (<10 μm).
These materials often follow the power law or modified Bingham models, with shear-thinning tendencies (n < 1) due to polymer chain alignment under shear. For example, in-situ polymerized acrylamide increases flexural strength by 130% while maintaining low viscous resistance. Besides, chemical reactions introduce rapid viscosity growth post-injection, contrasting with gradual hydration.
Existing rheological models exhibit trade-offs between accuracy and practicality (Table 2). The Bingham model, while simple, fails to capture shear-thickening effects. In contrast, the Herschel-Bulkley (HB) model reduces MSE to 4.8 Pa for shear-thinning slurries but overestimates yield stress by 18%–22% at low shear rates. The Casson model performs poorly for graphene-modified slurries, highlighting the need for material-specific model selection (Fig. 5).
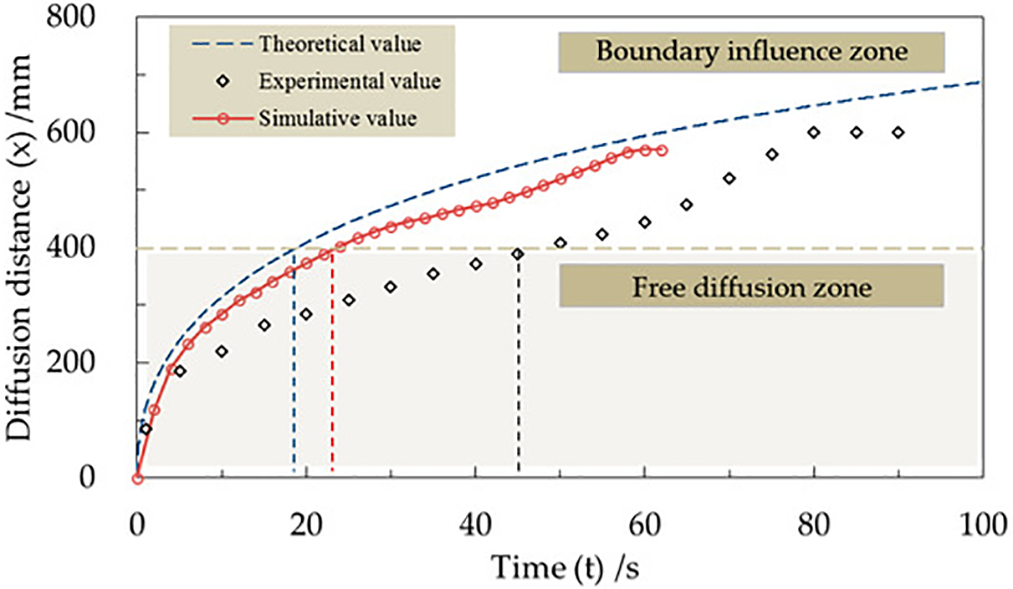
Figure 5: Comparison of theoretical, experimental, and simulated values in a study of slurry flow and diffusion in deep soft rock grouting reinforcement. Adapted with permission from Ref. [67]. Copyright © 2020, CSRME Publishing
The HB model combines power and yield stress equations to account for the rheological properties of Bingham fluids [72]. It demonstrates how power is expressed and how a material changes when subjected to pressure. The simplified HB model can be used for cement slurries (n = 1). Güllü [73] found that the HB model describes rheology data more accurately than the Bingham model. Zhang et al. [74] studied how the red mud (RM) particle size affected the performance of RM-modified cement slurry. They found that larger particles increased both the setting time and the fluidity, and that the time-varying viscosity could be described by the HB model. Although this model is superior to the Bingham model for cement slurries, it overestimates yield stress owing to mathematical limitations at low shear rates.
The Casson model is based on the assumption of specific interaction forces among disseminated particles in a suspended state, establishing a sequence of assumptions. Rehman et al. [75] showed that, compared with the Bingham, modified Bingham, and HB models, the Casson model provided the worst fit for graphene-based cement composites and the highest mean standard error, a conclusion also obtained by Reches [76]. Güllü [73] demonstrated that the Casson model was incapable of predicting shear stresses observed in concrete systems incorporating stabilizers.
Rheological models are also used to study the viscosity of cement-based systems. Some of these models are simple and easy to analyze, such as the Bingham model, whereas other models require complex calculations. The above-mentioned rheological models can be used with varying degrees of success to describe the flow of cementitious composites. Accurate measurement depends on calibrating the nonlinear segment of the curve at low rates.
Existing flow models are based on viscous grouting flows and do not consider inertia, unlike conditions in actual projects. The use of non-directional flow theory may result in discrepancies among radial flow, experimental, and simulation outcomes.
4 Slurry Flow Diffusion Behavior Testing
Visualizing flow dynamics in fractured rock grouting poses significant challenges. Simulating grout diffusion is an important approach in research for understanding diffusion mechanics. Factors such as diffusion range, pressure, flow rate, grouting channels, and viscosity affect grout propagation in fractured rock.
In field model tests, fissures are generally simplified to smooth flat plates to facilitate research. Li et al. [77] developed a large-scale quasi-3D flat slab fissure grouting simulation test system, carried out fissure dynamic water grouting sealing simulation tests, and obtained a dynamic water grouting diffusion law for quick-setting slurry and cement slurry. Lu et al. [78] and Wang et al. [79] simulated a flat slab fissure by using a smooth steel channel. They created two different types of fissure openings in the channel and studied the pressure change before and after the position of the local contraction of the grout to indirectly assess the position of the sudden change of the fissure opening through the local contraction. The pressure changes before and after the slurry passes through the local contraction position were investigated to indirectly assess the percolation effect before and after the sudden change of the fracture opening, and the time evolution law of the filter cake thickness before and after the slurry passes through the local contraction position was analyzed. Wang [80] conducted a grouting feasibility study using a self-developed grouting simulation system to assess the tensile and shear resistance of rough fissures. They measured the effects of fracture opening, fracture roughness, and the roughness difference between the upper and lower fracture surfaces on the grouting pressure, pressure distribution, and local pressure drop. Zhai and Bai [81] conducted dynamic water grouting tests on flat plate fissures with different inclination angles. They then analyzed the mechanism by which the fissure inclination angle influences grouting sealing (Fig. 6).
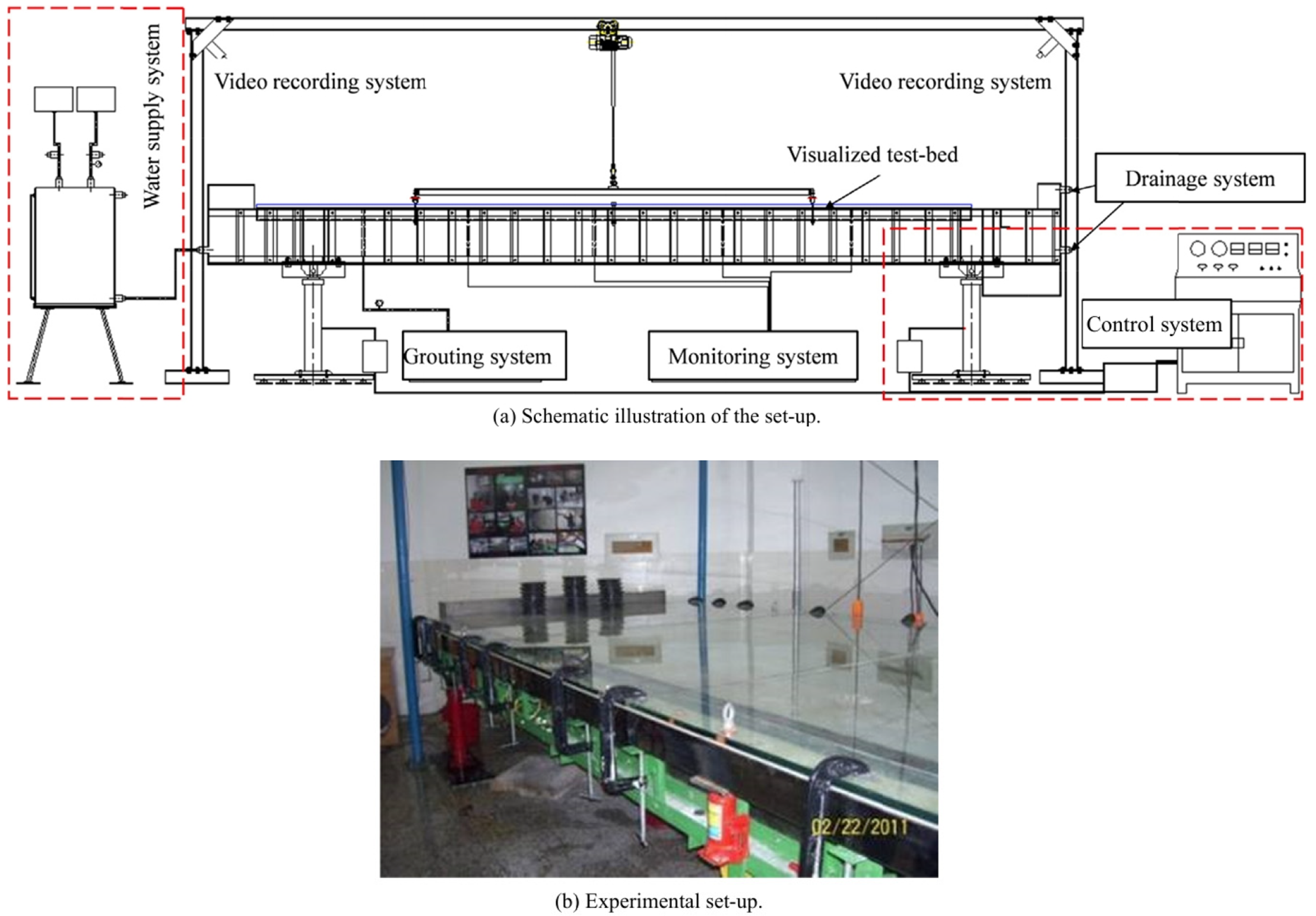
Figure 6: Model of dynamic water grouting and the experimental setup used (a, b). Adapted with permission from Ref. [77]. Copyright © 2016, CSRME Publishing
Xu et al. [82] developed a full-scale simulation apparatus to investigate the grouting of high-pressure cracks in deep subterranean rocks. They quantitatively and qualitatively assessed the factors influencing grouting, including the crack surface roughness, the grouting fluid flow velocity, and the initial viscosity of the grout. Ding et al. [83] and Zhao et al. [84] conducted a reduced-scale experiment to assess the feasibility of simultaneous grouting in large shield tunnels, where they replaced steel tube sheets with transparent Plexiglas tube sheets to observe the flow. The diffusion pattern and pressure dissipation of the slurry were observed throughout the synchronous process, and the diffusion range and slurry distribution were also investigated (Fig. 7).
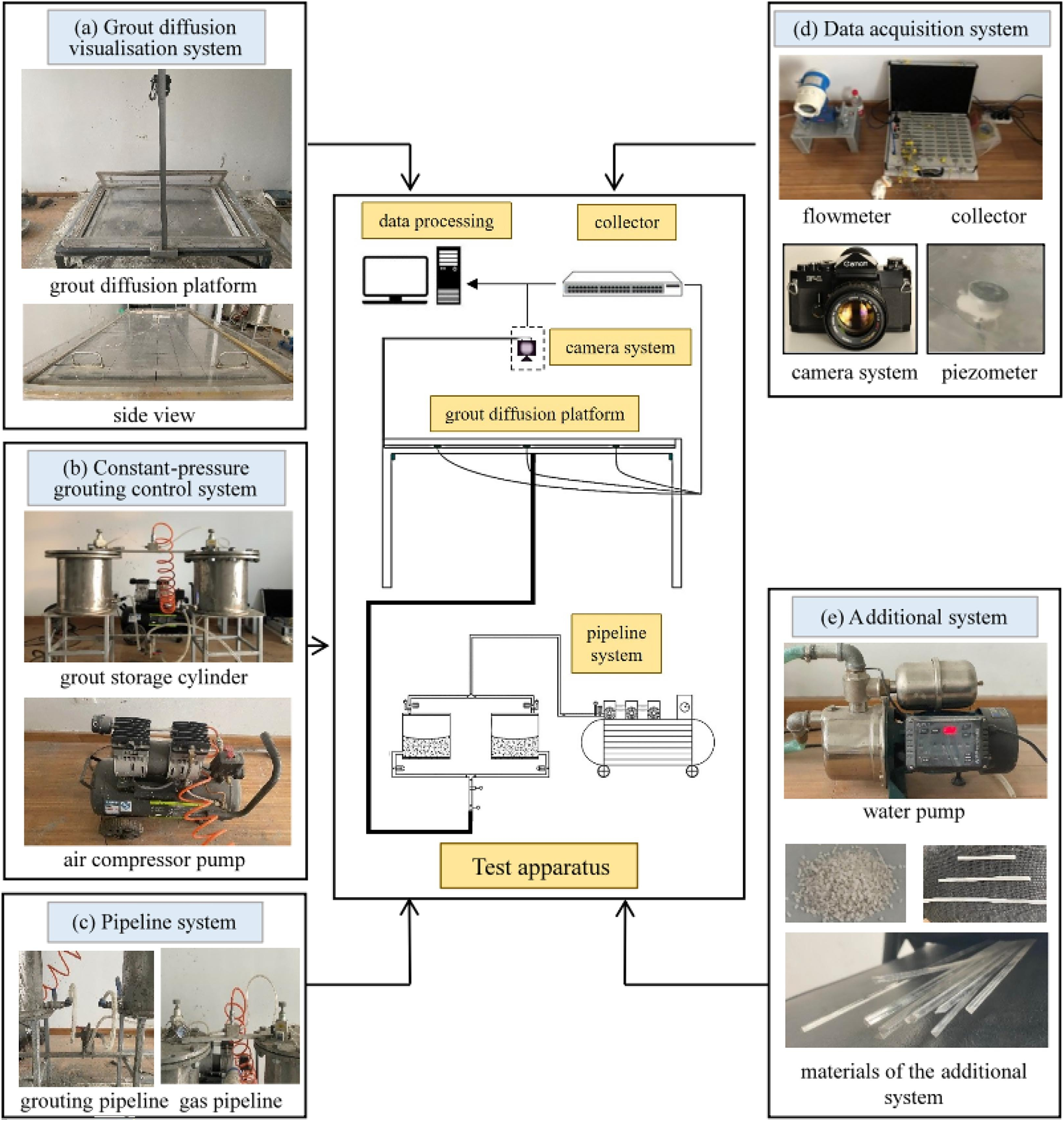
Figure 7: Equipment for studying grout diffusion and visualization (a–e). Adapted with permission from Ref. [85]. Copyright © 2025 Elsevier Ltd.
The existing experimental prototypes are assumed to comprise a solitary fracture, with a uniform surface separating two parallel plates and the ultimate grouting pressure of the developed models rarely exceeding 5 MPa. Furthermore, the role of groundwater in physical modeling has historically been underestimated. In the context of surface pre-grouting in deep coal mining, the development of test models with high sealing capacity is imperative. The impact of groundwater must be thoroughly considered.
Wang et al. [86] designed a constant-pressure indoor infiltration grouting device to study the diffusion mechanism of infiltrating polymers in a sand layer under infiltration grouting conditions. Li et al. [87] carried out constant-pressure infiltration grouting experiments in sandy soils, which revealed the reinforcing mechanism and the transport law of the cement slurry under seepage conditions.
Jin et al. [88] designed and developed an independent simulation test device for grouting in rough cracks, which they used to investigate the effects of the water-to-cement ratio and normal pressure on the nonlinear seepage characteristics of an ultrafine cement slurry. Yang et al. [89] conducted simulation experiments on carbon fiber cement composite slurry grouting in rough cracks under dynamic water conditions; they investigated the effects of crack aperture and roughness on slurry diffusion. Hu et al. and Liu et al. [90,91] proposed the important role of discrete fracture network (DFN) medium theory in describing the fracture properties of rock bodies. They posited that the essence of reinforcement grouting is to enhance the cementation and mechanical properties of structural surfaces to improve the shear capacity of the reinforcement. Zhang et al. [92] and others built a visual simulation test system to analyze the infiltration and diffusion law of a sand layer under different grouting conditions. They obtained the functional relationship between the permeability coefficient of the grouting material, the slurry ratio of W/C, and the specimen under maintenance.
Simulation tests of slurry injection in a fissure enable the visual study of the migration and diffusion process of the slurry and reveal the seepage phenomenon and deposition law of slurry intuitively. Additionally, sensors installed around the test equipment can describe transient changes in the pressure field, velocity field, and seepage field, as well as the dynamic response of stress–seepage coupling in the slurry flow. Such setups are effective for in-depth investigation of grouting theory, providing a foundation for optimal design of the grouting parameters in actual projects.
Nevertheless, the existing grouting simulation experiments also have some limitations that require addressing. First, grouting models can withstand relatively low grouting pressure, except for a few experimental models that can simulate the spreading of slurry under higher grouting pressure. In practical engineering applications, high-pressure grouting is common, resulting in limitations to current experiments to simulate the grout diffusion process of fissured rock under high stress. Second, with the continuous refinement of grouting theory research, to obtain more accurate information more in line with actual engineering grouting test results, the simulation test system in the simulation of engineering geological conditions, the model boundary processing, and so on, there is still a large space for improvement.
Based on the characteristics and shortcomings of many existing grouting simulation experiments, future research should focus on the following aspects. First, in the development of grouting test models, experimental devices with high pressure resistance and effective sealing should be prioritized to enable simulation of the grout diffusion process in a fractured rock body under high stress. Secondly, research involving simulation tests should focus on key issues such as the direction of grout diffusion and cementation in the 3D fracture network. Additionally, the influence of various parameters in the flow process, such as fracture opening, inclination, roughness, and groundwater, should be considered comprehensively to further improve the accuracy and practicality of simulation tests and better serve geotechnical engineering applications.
5 Numerical Simulation of Slurry Reinforcement Process
Numerical simulation has become an important method of studying grouting in fissured rock bodies. As grouting occurs within the rock, it is difficult to investigate slurry diffusion and the morphology of the rock body and to evaluate the effectiveness of grouting. Moreover, the slurry is a fluid with non-uniform and time-varying viscosity, making its diffusion considerably different from that of general fluids. Quantitative computation must account for these various nonlinear factors. Numerical simulation software is used to guide grouting projects and evaluate their effectiveness in their later stages. The diffusion of slurry through fissures or pores can also be explored by numerical simulation. In this section, we summarize the current use of simulation methods, including the finite element method (FEM), finite difference method (FDM), discrete element method (DEM), continuum-discontinuous methods (finite-discrete element method (FDEM) and numerical manifold method (NMM)), and 3D fracture network modeling.
FEM is widely used to analyze continuous media problems. A continuous solution region is discretized by dividing it into a set of unit assemblies. Within each unit, the unknown field functions to be solved on the solution domain are represented piecewise with an assumed approximation function. Liang et al. [93] examined the propagation of chemical grout in water and sediment flow using a transparent inclined crack grouting test apparatus, incorporating the crack inclination. They showed that the crack aperture increased with fluid pressure, thus extending the penetration distance. In their seminal contributions, Zhang et al. [94,95] advanced the discourse on the impact of predominant factors on grout flow behavior. The penetration distance is influenced by the water conditions and crack inclination. More consideration should be given to temperature when evaluating the grouting effect to ascertain viscosity (Figs. 8 and 9).
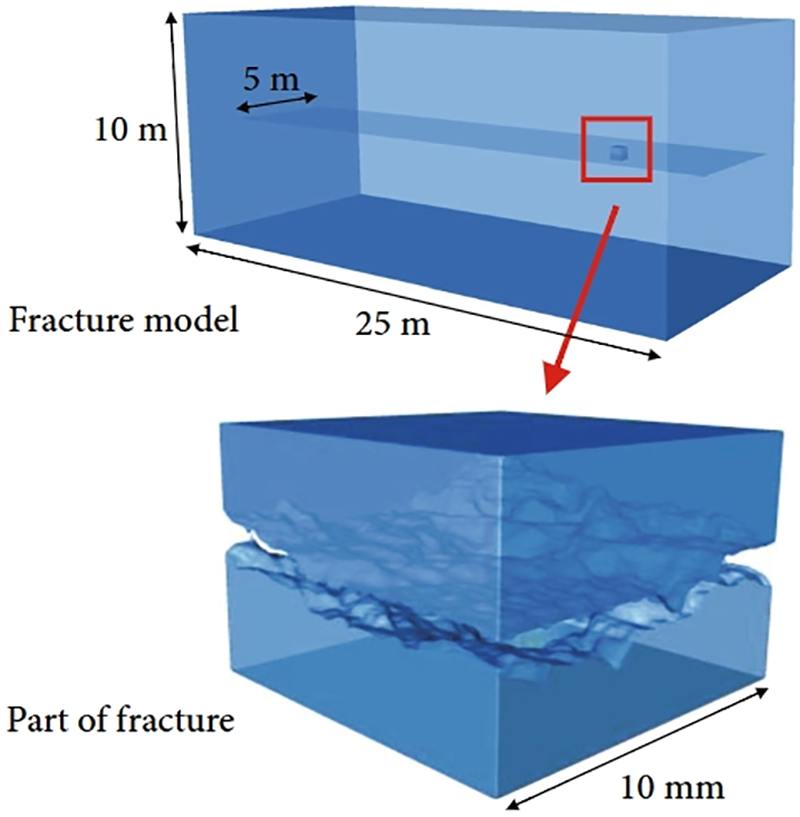
Figure 8: Sandstone model with a single fracture. Adapted with permission from Ref. [95]. Copyright © 2022 Zhang et al.
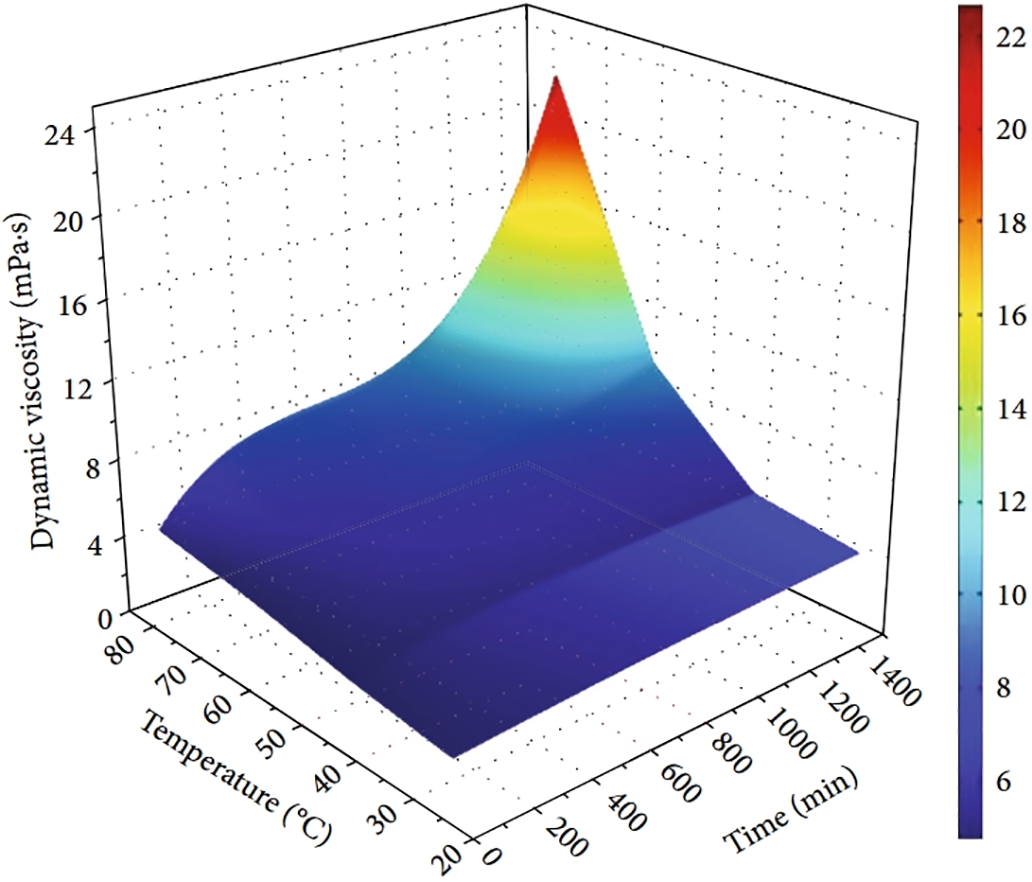
Figure 9: Viscosity-temperature-time of grout. Adapted with permission from Ref. [95]. Copyright © 2022 Zhang et al.
FDM divides the whole computational area into regular lattices and represents the differential terms in partial differential equations as difference terms between adjacent lattice nodes, thus obtaining a solution by replacing partial differential equations with finite difference equations. Cheng [96] utilized FLAC3D software to formulate a numerical model, which they used to simulate the effect of grouting at various distances in front of a work face on the control of encompassing rock. By comparing the simulation results for different grouting schemes, they concluded that grouting 50 m in front of the work face minimized the deformation of the surrounding rock of the tunnel. Zheng et al. [97] employed FLAC3D to construct a numerical model, which they used to simulate the control effect of grouting on the surrounding rock. They also developed a numerical model using FLAC3D to verify that an innovative real-time capsule [97].
FEM demonstrates strong predictive accuracy for continuous media problems, particularly when simulating grouting processes in single fractures. For example, Liang et al. [93] used FEM to analyze hydrodynamic coupling effects, showing that the expansion of the crack aperture under fluid pressure aligns with theoretical expectations.
Zhang et al. [94,95] further validated FEM’s capability to incorporate dominant factors such as dynamic water conditions and temperature, achieving close agreement between simulated and experimental results.
DEM involves dividing the whole computational area into discrete units, determining the lifting relationship between the units, obtaining the interaction force between the units from the ontological relationship of the contact, updating each physical field based on Newton’s equations of motion, and then using the updated physical quantities of the units to proceed to the next stage of the calculation. Xiao et al. [98] used discontinuous deformation analysis to reveal that the grout flow in a network of cracks is influenced by the crack size and connectivity. Al-Aghbari and Mohamedzein [99] investigated the effect of cement kiln dust content on grouting characteristics using custom-made equipment to conduct grouting tests in a sand layer. Similarly, Zou et al. [100] examined how silt is consolidated using different grouting materials. Xu et al.’s extended DFN model [101] directly supports our analysis of aperture heterogeneity and fracture length correlations. Their statistical evaluation of 50 DFN realizations demonstrated how uncorrelated apertures delay propagation, while length-correlated apertures enhance it (Fig. 10).
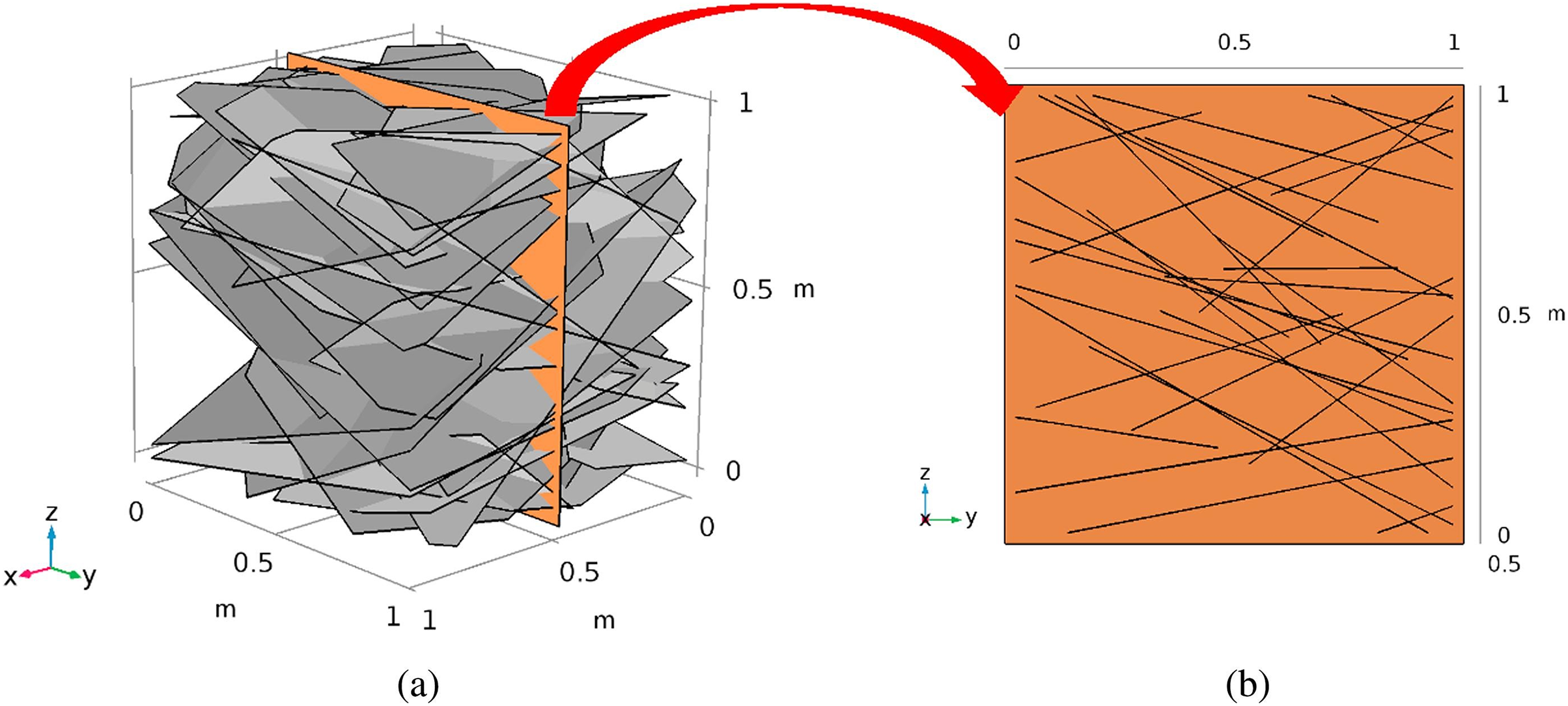
Figure 10: Diagram of fracture networks: (a) 3D; (b) 2D. Adapted with permission from Ref. [98]. Copyright © 2019 Elsevier Ltd.
Furthermore, Zhu et al. [102] developed a numerical model for fluid–solid coupling using DEM that can account for the effect of time-varying grout viscosity. Using this model, the grout diffusion behavior in various fracture networks was simulated and analyzed, demonstrating that time-varying viscosity markedly influences penetration length (Fig. 11). The predicted penetration lengths were within 10% of the experimental data, demonstrating the excellent performance of DEM in modeling discontinuous fracture networks.
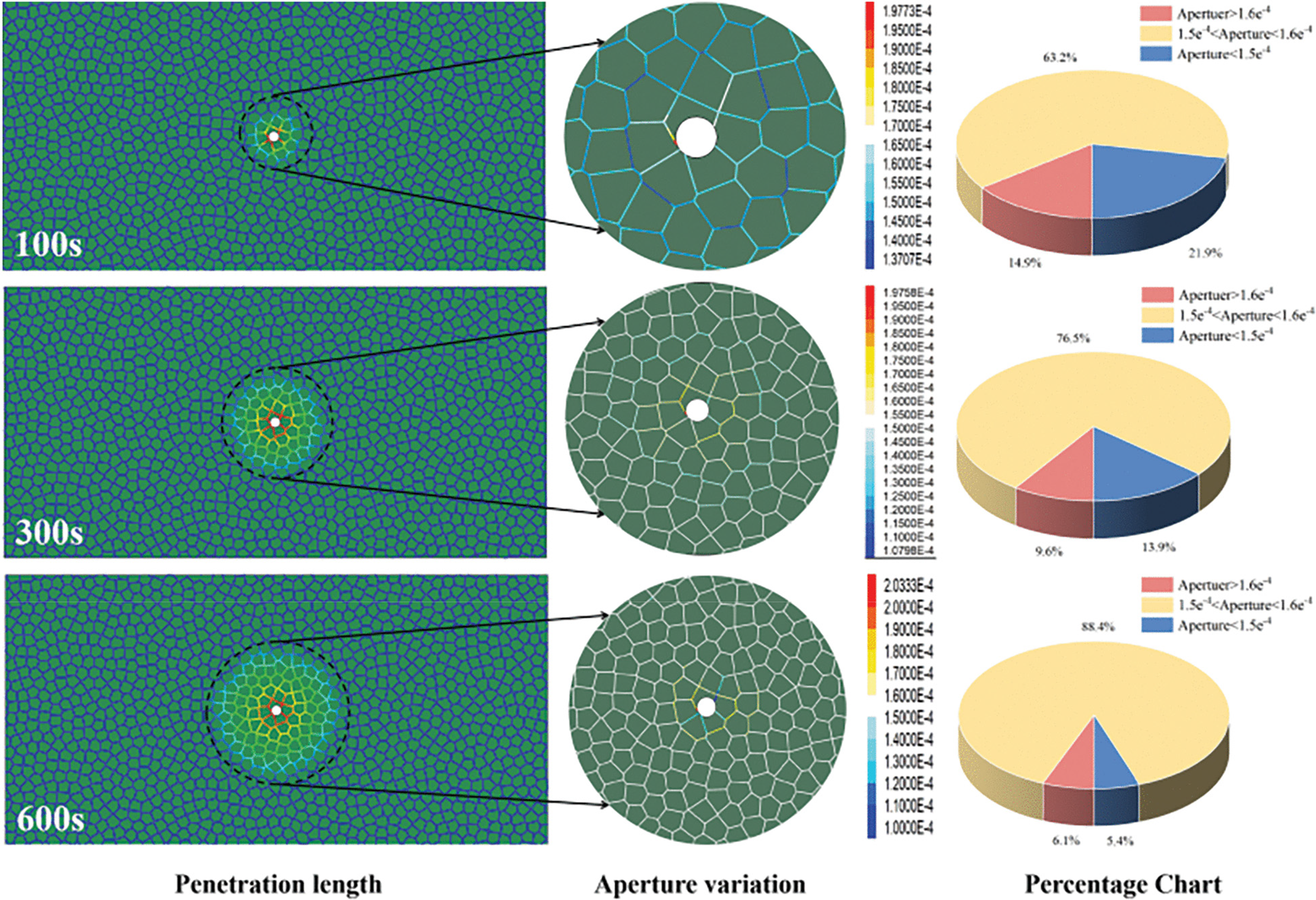
Figure 11: Variation of crack width and penetration length. Adapted with permission from Ref. [102] Copyright © 2024 Zhu et al. Published by Tech Science Press
5.3 Continuous-Discontinuous Methods
FDEM integrates the strengths of FEM in delineating plastic strains and the ability of DEM to handle discontinuities in modeling the behavior of fractured rock. It can also be used to simulate hydraulic fracture in conjunction with a fluid flow solver. Sun et al. [103,104] proposed a coupled hydro-mechanical model to study the grouting process, which they used to investigate the effect of in situ stress conditions on anisotropic grout touchdown, as well as grouting pressure. Yan et al. [105] proposed a 2D grouting model that took into account fracturing in fractured rock.
FDEM combines deformation analysis with discontinuity handling of FEM. Sun et al. [104] achieved a 15% improvement in predicting grout penetration under hydro-mechanical coupling compared to traditional FEM, as FDEM captures fracture interactions more realistically.
Yan et al. [105] demonstrated the robustness of FDEM in modeling fracture-induced flow paths, with yield stress and injection pressure errors below 12% (Fig. 12).
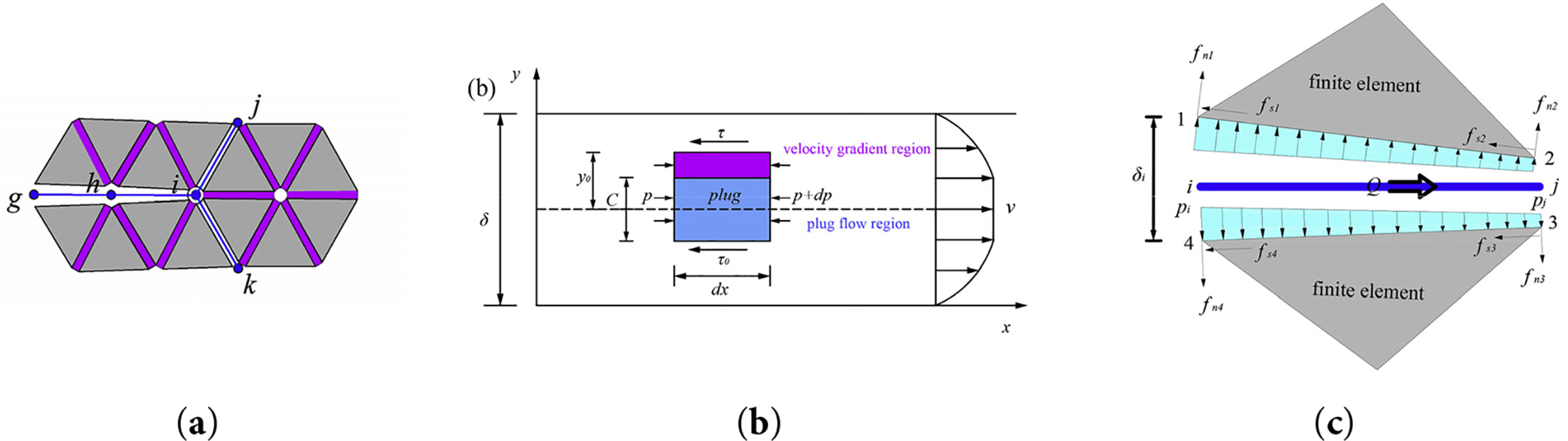
Figure 12: (a) Two sets of Y-grouting grids. (b) Bingham grout flow. (c) Grout force. Adapted with permission from Ref. [104] ©2019. Elsevier Ltd.
The NMM is also a continuous-discontinuous method used widely in rock engineering [106]. Liu et al. [107–110] derived a load calculation formula for nodes on a fracture-surface-based DFN model and investigated the variation of fracture width under grout pressure. They also proposed an NMM to simulate fracture expansion under seepage and stress coupling. Additionally, they developed a numerical manifold discretization scheme for the cement grout rheological equation and a grout diffusion simulation algorithm that accounts for time-varying viscosity and temperature effects. This methodology facilitates the analysis of the grout flow in the rock damage network, the flow path, and the resulting rock deformation characteristics, showing superior accuracy in modeling complex geometries. The integration of time-varying viscosity and temperature effects in this method reduced simulation errors by 20% compared with DEM (Fig. 13).
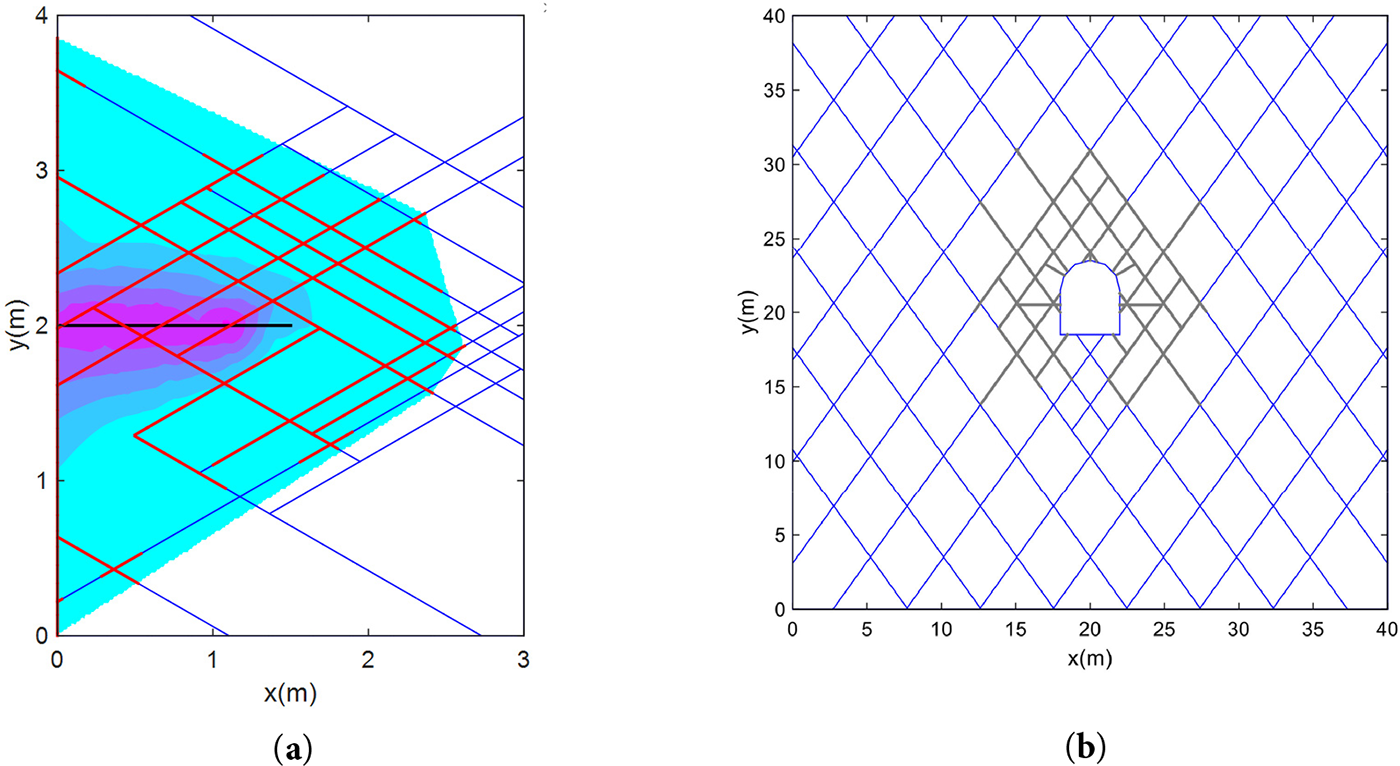
Figure 13: NMM simulation results of grouting: (a) grouting in DFN model; (b) grouting in a roadway. Adapted with permission from Ref. [110] © 2021 Elsevier Ltd.
Current simulations are mainly based on a 2D or simplified 3D single-fracture model, which cannot easily truly reflect the slurry diffusion behavior in complex fracture networks. In engineering applications, the rock fracture system has multiscale characteristics and a non-uniform distribution, and many existing models have portrayed changes in fracture crossings, connectivity, roughness, and openings with insufficient accuracy, resulting in the deviation of simulation results from the actual situation. Although the diffusion of slurry in fractures is affected by multiple factors, such as ground stress, temperature, and groundwater seepage, many existing simulations do not fully take them into consideration. Most studies assume that the slurry is a Newtonian fluid, but grouting materials often have non-Newtonian fluid properties. In addition, modeling of the settling and leaching effects of solid-phase particles in slurries and two-phase flows (slurry-gas/water) is still immature (Table 4).

While current simulations rely on simplified 2D or single-fracture models [93,94], significant advances have been made in 3D fracture network modeling. Wang et al. [111] developed a stochastic 3D fracture network model for dam bedrock grouting, revealing that not only aperture size but also spatial connectivity governs slurry penetration distance. Huang et al. [112] combined 3D printing with numerical modeling to quantify flow resistance in rough 3D fractures, demonstrating that roughness can reduce permeability by 18%–25% compared with idealized smooth fractures. However, these advances remain constrained by three critical limitations. (1) Neglect of time-varying slurry properties. Many 3D models [111,112] assume constant viscosity, ignoring hydration-driven changes that alter flow paths [70]. (2) Omission of multifield coupling. No 3D model fully integrates ground stress-seepage-temperature effects, despite proof-of-concept 2D FDEM work [105]. (3) Validation deficits. Models rely on synthetic networks; no models replicate in situ fracture topology.
Future research can develop modeling methods based on DFNs or equivalent continuous media, combined with CT scanning, 3D printing, and other technologies, to construct a fracture system model that is closer to actual rock conditions. A multifield coupling model that considers the effects of stress, slurry solidification, and temperature on slurry viscosity and fissure opening could also be developed. Transparent fissure grouting experiments combined with particle image velocimetry could also be used to observe slurry flow patterns, and in situ monitoring technologies should be developed to obtain on-site grouting data to calibrate numerical models. In the future, the theoretical study of slurry injection in fissure rock is predicted to develop in the direction of greater refinement, multiscale approaches, and intelligent systems, focusing on the following three aspects.
(1) Microscopic evolution and mechanical model of slurry hydration and reinforcement: In-depth study of the chemical-mechanical coupling mechanism of the slurry-rock interface, combined with micro-CT, digital image correlation, and other technologies, to establish a microscopic mechanical model that considers the hydration reaction, pore evolution, and strength growth and to reveal the microscopic mechanism of grouting and reinforcement.
(2) Cross-scale flow characteristics of slurry under multifield coupling conditions: Develop theory for multifield coupling of flow-solidification-chemistry-heat, study the flow-permeability-solidification laws of slurry under different scales, and construct a cross-scale numerical model applicable to complex geological conditions.
(3) Three-dimensional real-time dynamic simulation method for the entire grouting process: Integrate high-performance computing and artificial intelligence technology, develop a 3D dynamic simulation system based on a real fissure network, and combine it with real-time monitoring for visual prediction and intelligent regulation of grouting diffusion, pressure evolution, and the reinforcement effect.
Such research will promote the development of grouting theory from empirical to precise and intelligent approaches and will provide more reliable scientific support for grouting projects under complex geological conditions.
(1) Cement-based grouting materials are low-cost, widely available, and easy to prepare. Although they are cost-effective for large fissures (>60 μm) in stable rock masses, their injectability is limited in fine fractures. Chemical-based slurries are suitable for fine fractures (<10 μm) and dynamic water conditions, offering rapid setting (2–10 min) and high bonding strength (>3 MPa). However, their toxicity restricts their use in environmentally sensitive areas. Therefore, a key direction for future research will be to add organic materials to cement-based materials to obtain low-toxicity and efficient organic-inorganic composite grouting materials for use in mining.
(2) FEM is ideal for analyzing single fractures in continuous media and accurately simulating hydrodynamic coupling effects. DEM excels in studying discontinuous fracture networks with irregular apertures, particularly when accounting for time-varying viscosity. FDEM is superior for examining complex fracture networks under multifield coupling. Flow models use unidirectional flow theory, which may lead to discrepancies with radial flow theory. The effect of two-phase flow and the propagation mechanism of grouting materials in water-saturated rock fractures are still unknown, indicating the need for further study of how viscosity changes over time and space.
(3) In the study of key problems of grouting in fractured rock, 2D fracture networks have mainly been established, while grouting is carried out in a 3D fracture network in the field. This leads to differences between research results and actual engineering effects, making the extension of the fracture network to 3D fissures the key to the future study of grouting problems. The roughness of 3D fissures, fissure openings, and the effect of groundwater and other parameters on the grouting are also key factors that require consideration in future studies.
Acknowledgement: Not applicable.
Funding Statement: This research was funded by the National Natural Science Foundation of China [U22A20234], Hubei Province key research and development project [2023BCB121], and Wuhan innovation supporting projects [2023020201010079].
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Xuewei Liu, Bin Liu, Quansheng Liu and Jinze Sun; validation, Jinze Sun, Bin Liu, Yongshui Kang and Yongchao Tian; formal analysis, Jinze Sun and Xuewei Liu; data curation, Jinze Sun and Yuan Zhou; writing—original draft preparation, Jinze Sun; writing—review and editing, Jinze Sun and Xuewei Liu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Zhang Q, Huang C, Liu J, Zhang L, Wang X, Pei Y. Diffusion mechanism of quick-setting slurry in water-rich fractured rock mass based on circle-outburst diffusion model. Int J Rock Mech Min Sci. 2024;181:105856. doi:10.1016/j.ijrmms.2024.105856. [Google Scholar] [CrossRef]
2. Wang X, Mu W, Li L, Yang T, An J, Lu J. Durability and permeability characteristics of consolidated bodies after grouting in freeze-thaw rock in cold regions. Rock Mech Rock Eng. 2024;57(12):11117–37. doi:10.1007/s00603-024-04140-w. [Google Scholar] [CrossRef]
3. Zheng Z, Li S, Liu R. Analysis on structural characteristics of grout and rock distribution in complex geological mixtures after grouting reinforcement and its mechanical strength. Rock Mech Rock Eng. 2021;54(8):3757–82. doi:10.1007/s00603-021-02461-8. [Google Scholar] [CrossRef]
4. Cao Z, Xiong Y, Xue Y, Du F, Li Z, Huang C, et al. Diffusion evolution rules of grouting slurry in mining-induced cracks in overlying strata. Rock Mech Rock Eng. 2025;58(6):6493–512. doi:10.1007/s00603-025-04445-4. [Google Scholar] [CrossRef]
5. Mathur GK, Jha AK, Tiwari G, Singh TN. Experimental study on effect of grouting and high temperature on the anisotropic compressive strength behaviour of soft jointed rocks with an impersistent flaw. J Rock Mech Geotech Eng. 2025;17(4):2374–95. doi:10.1016/j.jrmge.2024.05.046. [Google Scholar] [CrossRef]
6. Cheng S, Chen T, Xue Z, Zhu K, Li J. Reinforcement of clay soils through fracture grouting. Fluid Dyn Mater Process. 2022;18(6):1649–65. doi:10.32604/fdmp.2022.018789. [Google Scholar] [CrossRef]
7. Liu X, Chen H, Liu B, Deng W, Liu Q, Zhang Z. Experimental and numerical study on failure characteristics and mechanism of coal under different quasi-static loading rates. Theor Appl Fract Mech. 2022;121:103478. doi:10.1016/j.tafmec.2022.103478. [Google Scholar] [CrossRef]
8. Guo Y, Zhao P, Zhang Q, Liu R, Zhang L, Liu Y. Investigation of the mechanism of grout penetration in intersected fractures. Fluid Dyn Mater Process. 2019;15(4):321–42. doi:10.32604/fdmp.2019.07844. [Google Scholar] [CrossRef]
9. Burnwal RK, Singh A. True-triaxial characterisation of the cement-based grout for application in underground space construction. Constr Build Mater. 2025;487:141887. doi:10.1016/j.conbuildmat.2025.141887. [Google Scholar] [CrossRef]
10. Zuo J, Hong Z, Yu M, Liu H, Wang Z. Research on gradient support model and classification control of broken surrounding rock. J China Univ Min Technol. 2022;51(2):221–31. (In Chinese). doi:10.3876/j.issn.1000-1980.2023.01.019. [Google Scholar] [CrossRef]
11. Jia L, Jia W, Guo J, Sun Y. Nano-silica-enhanced high-performance magnesium phosphate cement repair mortars: optimization of interfacial bonding. Constr Build Mater. 2025;490:142447. doi:10.1016/j.conbuildmat.2025.142447. [Google Scholar] [CrossRef]
12. Yu W, Zhou M, Wan X, Guan Q. Experimental study on physical properties of superfine cement grouting material. Front Mater. 2022;9:1056135. doi:10.3389/fmats.2022.1056135. [Google Scholar] [CrossRef]
13. Zhao J, Tian S, Chen C, Zhang X, Ma T, Ran Q, et al. Research on the performance and application of nano-MgO modified ultrafine cement-based sealing materials. Case Stud Constr Mater. 2025;22:e04694. doi:10.1016/j.cscm.2025.e04694. [Google Scholar] [CrossRef]
14. Wang K, Guo S, Yuan H, Ren J, Chen P, Zhang Q. Influence of cement particle size, ultra-fine fly ash, and ultra-fine silica fume on the physical and microscopic properties of slurry. Case Stud Constr Mater. 2025;22:e04337. doi:10.1016/j.cscm.2025.e04337. [Google Scholar] [CrossRef]
15. Zhang C, Fu J, Song W, Du C, Fu H. High-volume ultrafine fly ash-cement slurry mechanical properties and strength development model establishment. Constr Build Mater. 2021;277:122350. doi:10.1016/j.conbuildmat.2021.122350. [Google Scholar] [CrossRef]
16. Gao M, Chen B, Lang L, Ahmad Muhammad R. Influence of silica fume on mechanical properties and water resistance of magnesium-ammonium phosphate cement. J Mater Civ Eng. 2020;32(3):04019368. doi:10.1061/(asce)mt.1943-5533.0003035. [Google Scholar] [CrossRef]
17. Qin J, Dai F, Ma H, Dai X, Li Z, Jia X, et al. Development and characterization of magnesium phosphate cement based ultra-high performance concrete. Compos Part B Eng. 2022;234:109694. doi:10.1016/j.compositesb.2022.109694. [Google Scholar] [CrossRef]
18. He ZH, Jiang YY, Shi JY, Qin J, Liu DE, Yalçınkaya Ç, et al. Effect of silica fume on the performance of high-early-strength UHPC prepared with magnesium ammonium phosphate cement. Case Stud Constr Mater. 2024;20:e03351. doi:10.1016/j.cscm.2024.e03351. [Google Scholar] [CrossRef]
19. Liu C, Huang X, Wu YY, Deng X, Zheng Z. The effect of graphene oxide on the mechanical properties, impermeability and corrosion resistance of cement mortar containing mineral admixtures. Constr Build Mater. 2021;288:123059. doi:10.1016/j.conbuildmat.2021.123059. [Google Scholar] [CrossRef]
20. Zhang P, Sun Y, Wei J, Zhang T. Research progress on properties of cement-based composites incorporating graphene oxide. Rev Adv Mater Sci. 2023;62:20220329. doi:10.1515/rams-2022-0329. [Google Scholar] [CrossRef]
21. Zhang X, Zhu J, Zhang X, Tang L, Chen X, Wu H, et al. Performance study of Portland cement grouting materials enhanced with nanobubbles. Dev Built Environ. 2025;22:100647. doi:10.1016/j.dibe.2025.100647. [Google Scholar] [CrossRef]
22. Zhang J, Peng H, Sun Y. Experimental investigation of nanomaterial regulating the mechanical properties of grouting concrete. Iran J Sci Technol Trans Civ Eng. 2022;46(3):2085–97. doi:10.1007/s40996-021-00658-z. [Google Scholar] [CrossRef]
23. Lin Y, Wang Q, Wu C, Wang C. Performance analysis of steel slag powder-coal gangue grouting material. IOP Conf Ser Earth Environ Sci. 2021;787(1):012046. doi:10.1088/1755-1315/787/1/012046. [Google Scholar] [CrossRef]
24. Lazorenko G, Kasprzhitskii A, Yatsenko EA, Li W, Chaudhary S. Towards coal mining waste valorization: gangue as resource for the production of geopolymer and related alkali-activated materials. Green Technol Sustain. 2025;3(3):100205. doi:10.1016/j.grets.2025.100205. [Google Scholar] [CrossRef]
25. Ling X, Guo X, Zhong J, Ma J, Tang L, Xing D, et al. Investigation of the effect of graphene oxide on the properties and microstructure of clay-cement composite grouting materials. Materials. 2022;15(5):1623. doi:10.3390/ma15051623. [Google Scholar] [PubMed] [CrossRef]
26. Yu X, Wang Y, Sun G. Comparative analysis of mechanical properties and fracture characteristics between sodium silicate modified polyurethane and polyurethane materials. Constr Build Mater. 2024;444:137917. doi:10.1016/j.conbuildmat.2024.137917. [Google Scholar] [CrossRef]
27. Li X, Wang F, Cai X, Meng S, Hu X, Tang L. A porous IPN-structured polyurethane/epoxy grouting material with low viscosity, high strength and low volume shrinkage. Constr Build Mater. 2024;449:138312. doi:10.1016/j.conbuildmat.2024.138312. [Google Scholar] [CrossRef]
28. Gao Y, Sui WH. Modelling of chemical grout column permeated by water in transparent soil. Int J Environ Pollut. 2016;59(2–4):142–55. doi:10.1504/ijep.2016.079906. [Google Scholar] [CrossRef]
29. Chhun KT, Lee SH, Keo SA, Yune CY. Effect of acrylate-cement grout on the unconfined compressive strength of silty sand. KSCE J Civ Eng. 2019;23(6):2495–502. doi:10.1007/s12205-019-1968-z. [Google Scholar] [CrossRef]
30. Zhang Y, Pang H, Wei D, Li J, Li S, Lin X, et al. Preparation and characterization of chemical grouting derived from lignin epoxy resin. Eur Polym J. 2019;118:290–305. doi:10.1016/j.eurpolymj.2019.05.003. [Google Scholar] [CrossRef]
31. Guan ZW. Study on gelation time of acidic sodium silicate in silty-fine sand stratum grouting construction. China Water Power Electrif. 2019;(11):13–6. (In Chinese). doi:10.16617/j.cnki.11-5543/TK.2019.11.04. [Google Scholar] [CrossRef]
32. Liu X, Yang Z, Guan X, Zhang C. Preparation and property of the polyurethane/silicate gel based on polyether glycol. New Chem Mater. 2015;43(7):224–6,233. (In Chinese). [Google Scholar]
33. Mahmood W, Mohammed A, Ghafor K. Viscosity, yield stress and compressive strength of cement-based grout modified with polymers. Results Mater. 2019;4:100043. doi:10.1016/j.rinma.2019.100043. [Google Scholar] [CrossRef]
34. Ma J, Shu X, Zheng S, Qi S, Ran Q. Effects of polyurethane-silica nanohybrids as additives on the mechanical performance enhancement of ordinary Portland cement paste. Constr Build Mater. 2022;338:127666. doi:10.1016/j.conbuildmat.2022.127666. [Google Scholar] [CrossRef]
35. Huo J, Liu X, Zhao J, Zhang X, Zhang S, Wei C. Urea formaldehyde resin used as plugging agent in fractured and caved reservoirs: preparation, optimization and modification. Polymer. 2025;317:127901. doi:10.1016/j.polymer.2024.127901. [Google Scholar] [CrossRef]
36. Zhu XJ, Zhu XT, Zhu YJ, Liu NJ, Zhu XB, Zhang XJ, et al. Experimental study on the effect of polyacrylamide on the properties of sulphoaluminate cement. J Build Mater Technol Appl. 2018;3:4–7. (In Chinese). [Google Scholar]
37. Huang Q, Yuan C, Li S, Feng X, Zhou H, Han Y, et al. Influence of raw material temperature on the properties of silicate-modified polyurethane grouting materials. Case Stud Constr Mater. 2024;21:e03479. doi:10.1016/j.cscm.2024.e03479. [Google Scholar] [CrossRef]
38. Yu X. Preparation and structure analysis of aluminum oxide/water glass/polyurethane composite grouting material for mining. J Build Eng. 2023;76:107170. doi:10.1016/j.jobe.2023.107170. [Google Scholar] [CrossRef]
39. Pan D, Zhang N, Xiang Z, Xie Z. Performance improvement of nanocolloidal silica-aluminate cement composite grouting materials with organic acids. Case Stud Constr Mater. 2024;20:e03166. doi:10.1016/j.cscm.2024.e03166. [Google Scholar] [CrossRef]
40. Shu X, Zhao Y, Liu Z, Zhao C. A study on the mix proportion of fiber-polymer composite reinforced cement-based grouting material. Constr Build Mater. 2022;328:127025. doi:10.1016/j.conbuildmat.2022.127025. [Google Scholar] [CrossRef]
41. Hirai T, Yagi K, Nakai K, Okamoto K, Murai D, Okamoto H. High-entropy polymer blends utilizing in situ exchange reaction. Polymer. 2022;240:124483. doi:10.1016/j.polymer.2021.124483. [Google Scholar] [CrossRef]
42. Liang R, Liu Q, Hou D, Li Z, Sun G. Flexural strength enhancement of cement paste through monomer incorporation and in situ bond formation. Cem Concr Res. 2022;152:106675. doi:10.1016/j.cemconres.2021.106675. [Google Scholar] [CrossRef]
43. Liu Q, Lu Z, Hu X, Chen B, Li Z, Liang R, et al. A mechanical strong polymer-cement composite fabricated by in situ polymerization within the cement matrix. J Build Eng. 2021;42:103048. doi:10.1016/j.jobe.2021.103048. [Google Scholar] [CrossRef]
44. Yin B, Hua X, Qi D, Wang P, Qiao G, Fan F, et al. Performance cement-based composite obtained by in situ growth of organic-inorganic frameworks during the cement hydration. Constr Build Mater. 2022;336:127533. doi:10.1016/j.conbuildmat.2022.127533. [Google Scholar] [CrossRef]
45. Yan G, Bai L, Zhang Z, Yang T, Liu J. Test and application of PU modified sulphoaluminate cement. J China Coal Soc. 2020;S2:747–54. (In Chinese). [Google Scholar]
46. Liu YT, Sun DW, Wan Y, Zhou X, Li B, Yin H. Preparation and property study of water swelling polyurethane cement composite grouting material. China Build Waterproofing. 2015;22:1–5. (In Chinese). doi:10.15901/j.cnki.1007-497x.2015.22.001. [Google Scholar] [CrossRef]
47. Zhang Z, Yan P. Hydration kinetics of the epoxy resin-modified cement at different temperatures. Constr Build Mater. 2017;150:287–94. doi:10.1016/j.conbuildmat.2017.05.225. [Google Scholar] [CrossRef]
48. Jiang J, Lu Z, Niu Y, Li J. Investigation of the properties of high-porosity cement foams containing epoxy resin. Constr Build Mater. 2017;154:115–22. doi:10.1016/j.conbuildmat.2017.06.178. [Google Scholar] [CrossRef]
49. Fang H, Zhao P, Zhang C, Pan W, Yu Z, Cai K, et al. A cleaner polyurethane elastomer grouting material with high hardening strain for the fundamental rehabilitation: the comprehensive mechanical properties study. Constr Build Mater. 2022;318:125951. doi:10.1016/j.conbuildmat.2021.125951. [Google Scholar] [CrossRef]
50. Huang Z, Chen W, Li Q, Wang M, Fan J. Mechanical properties and microstructure of waterborne epoxy resin modified cement mortar. Bull Chin Ceram Soc. 2017;36(8):2530–5. (In Chinese). [Google Scholar]
51. Guan X, Li X, Zhang H, Yang Z, Li H, Di H, et al. Research and application of inorganic and organic composite grouting reinforcement materials in deep weak rock. Coal Sci Technol. 2023;51(8):1–11. (In Chinese). doi:10.13199/j.cnki.cst.2023-0216. [Google Scholar] [CrossRef]
52. Shang H. Study on deformation and permeability characteristics of fractured rock mass grouting stone [master’s thesis]. Wuhan, China: Wuhan University of Light Industry; 2017. (In Chinese). [Google Scholar]
53. Zhang X, Zhang X, Liu J, Zhu K, Zheng Z, Dong Y. Study on properties and hydration mechanism of green alkali-activation lithium slag composite cementitious materials. Constr Build Mater. 2025;473:140966. doi:10.1016/j.conbuildmat.2025.140966. [Google Scholar] [CrossRef]
54. Liu X, Wang S, Liu B, Liu Q, Zhou Y, Chen J, et al. Cement-based grouting material development and prediction of material properties using PSO-RBF machine learning. Constr Build Mater. 2024;417:135328. doi:10.1016/j.conbuildmat.2024.135328. [Google Scholar] [CrossRef]
55. Zhao X, Wang L, Wang C, Xu J, Hu W, Li Q, et al. Study on hydration and hardening performance of coal gangue-steel slag-cement composite cementitious material. KSCE J Civ Eng. 2024;28(5):1992–2004. doi:10.1007/s12205-024-1956-9. [Google Scholar] [CrossRef]
56. Zou L, Håkansson U, Cvetkovic V. Yield-power-law fluid propagation in water-saturated fracture networks with application to rock grouting. Tunn Undergr Space Technol. 2020;95:103170. doi:10.1016/j.tust.2019.103170. [Google Scholar] [CrossRef]
57. Neffah Z, Kahalerras H, Fersadou B. Heat and mass transfer of a non-Newtonian fluid flow in an anisotropic porous channel with chemical surface reaction. Fluid Dyn Mater Process. 2018;14(1):39–56. doi:10.1615/ichmt.2008.cht.1120. [Google Scholar] [CrossRef]
58. Chhabra RP. Non-Newtonian fluids: an introduction. In: Rheology of complex fluids. Berlin/Heidelberg, Germany: Springer; 2010. p. 3–34. doi:10.1007/978-1-4419-6494-6_1. [Google Scholar] [CrossRef]
59. Tattersall GH, Banfill PFG. The rheology of fresh concrete. London, UK: Pitman Books Limited; 1983. 356 p. [Google Scholar]
60. Atzeni C, Massidda L, Sanna U. Comparison between rheological models for Portland cement pastes. Cem Concr Res. 1985;15(3):511–9. doi:10.1016/0008-8846(85)90125-5. [Google Scholar] [CrossRef]
61. Yahia A, Khayat KH. Analytical models for estimating yield stress of high-performance pseudoplastic grout. Cem Concr Res. 2001;31(5):731–8. doi:10.1016/S0008-8846(01)00476-8. [Google Scholar] [CrossRef]
62. Nehdi M, Rahman MA. Estimating rheological properties of cement pastes using various rheological models for different test geometry, gap and surface friction. Cem Concr Res. 2004;34(11):1993–2007. doi:10.1016/j.cemconres.2004.02.020. [Google Scholar] [CrossRef]
63. Chen YF, Fang S, Wu DS, Hu R. Visualizing and quantifying the crossover from capillary fingering to viscous fingering in a rough fracture. Water Resour Res. 2017;53(9):7756–72. doi:10.1002/2017WR021051. [Google Scholar] [CrossRef]
64. Zhang QS, Zhang LZ, Liu RT, Li SC, Zhang QQ. Grouting mechanism of quick setting slurry in rock fissure with consideration of viscosity variation with space. Tunn Undergr Space Technol. 2017;70:262–73. doi:10.1016/j.tust.2017.08.016. [Google Scholar] [CrossRef]
65. Lavrov A. Flow of non-Newtonian fluids in single fractures and fracture networks: current status, challenges, and knowledge gaps. Eng Geol. 2023;321:107166. doi:10.1016/j.enggeo.2023.107166. [Google Scholar] [CrossRef]
66. Ding W, Duan C, Zhang Q. Experimental and numerical study on a grouting diffusion model of a single rough fracture in rock mass. Appl Sci. 2020;10(20):7041. doi:10.3390/app10207041. [Google Scholar] [CrossRef]
67. Zou L, Håkansson U, Cvetkovic V. Analysis of Bingham fluid radial flow in smooth fractures. J Rock Mech Geotech Eng. 2020;12(5):1112–8. doi:10.1016/j.jrmge.2019.12.021. [Google Scholar] [CrossRef]
68. Ding Y, Yang ZQ, Yang Y, Zhu YY, Guo YF, Zhang J, et al. Study on penetration grouting mechanism based on Newton fluid of time-dependent behavior of rheological parameters. Shock Vib. 2020;2020:8811028. doi:10.1155/2020/8811028. [Google Scholar] [CrossRef]
69. Wang YH, Yang P, Li ZT, Wu SJ, Zhao ZX. Experimental-numerical investigation on grout diffusion and washout in rough rock fractures under flowing water. Comput Geotech. 2020;126:103717. doi:10.1016/j.compgeo.2020.103717. [Google Scholar] [CrossRef]
70. Gao H, Qing L, Ma G, Zhang D. Numerical investigation on grout spread and grouting parameter analysis in fracture with flowing water. Geoenergy Sci Eng. 2023;221:211401. doi:10.1016/j.geoen.2022.211401. [Google Scholar] [CrossRef]
71. Zou L, Håkansson U, Cvetkovic V. Two-phase cement grout propagation in homogeneous water-saturated rock fractures. Int J Rock Mech Min Sci. 2018;106:243–9. doi:10.1016/j.ijrmms.2018.04.017. [Google Scholar] [CrossRef]
72. Mohammed AS. Effect of temperature on the rheological properties with shear stress limit of iron oxide nanoparticle modified bentonite drilling muds. Egypt J Petrol. 2017;26(3):791–802. doi:10.1016/j.ejpe.2016.10.018. [Google Scholar] [CrossRef]
73. Güllü H. Comparison of rheological models for jet grout cement mixtures with various stabilizers. Constr Build Mater. 2016;127:220–36. doi:10.1016/j.conbuildmat.2016.09.129. [Google Scholar] [CrossRef]
74. Zhang J, Li S, Li Z, Gao Y, Liu C, Qi Y. Workability and microstructural properties of red-mud-based geopolymer with different particle sizes. Adv Cem Res. 2021;33(5):210–23. doi:10.1680/jadcr.19.00085. [Google Scholar] [CrossRef]
75. Rehman SKU, Ibrahim Z, Jameel M, Ali Memon S, Javed MF, Aslam M, et al. Assessment of rheological and piezoresistive properties of graphene based cement composites. Int J Concr Struct Mater. 2018;12(1):64. doi:10.1186/s40069-018-0293-0. [Google Scholar] [CrossRef]
76. Reches Y. Nanoparticles as concrete additives: review and perspectives. Constr Build Mater. 2018;175:483–95. doi:10.1016/j.conbuildmat.2018.04.214. [Google Scholar] [CrossRef]
77. Li S, Liu R, Zhang Q, Zhang X. Protection against water or mud inrush in tunnels by grouting: a review. J Rock Mech Geotech Eng. 2016;8(5):753–66. doi:10.1016/j.jrmge.2016.05.002. [Google Scholar] [CrossRef]
78. Lu Y, He M, Wang L, Ren B, Sun X, Zhang K. In-situ visualization experiments on the microscopic process of particle filtration of cement grouts within a rock fracture. Tunn Undergr Space Technol. 2020;95:103157. doi:10.1016/j.tust.2019.103157. [Google Scholar] [CrossRef]
79. Wang K, Wang LG, Lu YL, Sun XK, Zhang KW. Visual experimental study on the infiltration effect of cement slurry in micro-fractures. J China Coal Soc. 2020;45(3):990–7. (In Chinese). doi:10.13225/j.cnki.jccs.sj19.1806. [Google Scholar] [CrossRef]
80. Wang XC. Mechanism of diffusion and reinforcement of rock fracture based on the bleeding effect of cement slurry [dissertation]. Jinan, China: Shandong University; 2021. (In Chinese). [Google Scholar]
81. Zhai M, Bai H. Research on the mechanism of fracture grouting diffusion and its application based on slurry-rock mass coupling effect. Coal Sci Technol. 2024;52(7):158–67. (In Chinese). doi:10.1016/j.conbuildmat.2023.134584. [Google Scholar] [CrossRef]
82. Xu Z, Liu C, Zhou X, Gao G, Feng X. Full-scale physical modelling of fissure grouting in deep underground rocks. Tunn Undergr Space Technol. 2019;89:249–61. doi:10.1016/j.tust.2019.04.008. [Google Scholar] [CrossRef]
83. Ding W, Duan C, Zhu Y, Zhao T, Huang D, Li P. The behavior of synchronous grouting in a quasi-rectangular shield tunnel based on a large visualized model test. Tunn Undergr Space Technol. 2019;83:409–24. doi:10.1016/j.tust.2018.10.006. [Google Scholar] [CrossRef]
84. Zhao T, Ding W, Qiao Y, Duan C. A large-scale synchronous grouting test for a quasi-rectangular shield tunnel: observation, analysis and interpretation. Tunn Undergr Space Technol. 2019;91:103018. doi:10.1016/j.tust.2019.103018. [Google Scholar] [CrossRef]
85. Ding W, Lei B, Duan C, Zhang Q. Grout diffusion model for single fractures in rock considering influences of grouting pressure and filling rate. Tunn Undergr Space Technol. 2025;158:106392. doi:10.1016/j.tust.2025.106392. [Google Scholar] [CrossRef]
86. Wang Y, Yu B, Wan Y, Yu X. Experimental investigation and numerical verification on diffusion of permeable polymers in sandy soils with considering grouting parameters. Int J Civ Eng. 2023;21(4):617–32. doi:10.1007/s40999-022-00780-7. [Google Scholar] [CrossRef]
87. Li S, Feng X, Liu R, Zhang L, Han W, Zhang Z. Study on diffusion law of grouting in sand medium considering percolation effect. Rock Soil Mech. 2017;38(4):925–33. (In Chinese). [Google Scholar]
88. Jin Y, Han L, Xu C, Meng Q, Liu Z, Zong Y. Experimental investigation of grout nonlinear flow behavior through rough fractures. Processes. 2019;7(10):736. doi:10.3390/pr7100736. [Google Scholar] [CrossRef]
89. Yang P, Liu YH, Gao SW, Xue S. Experimental investigation on the diffusion of carbon fibre composite grouts in rough fractures with flowing water. Tunn Undergr Space Technol. 2020;95:103146. doi:10.1016/j.tust.2019.103146. [Google Scholar] [CrossRef]
90. Hu S, Liu Q, Li S, Sang H, Kang Y. Advance and review on grouting critical problems in fractured rock mass. Coal Sci Technol. 2022;50(1):112–26. (In Chinese). doi:10.4028/www.scientific.net. [Google Scholar] [CrossRef]
91. Liu B, Sang HM, Kang YS, Liu QS, Luo CY, Zhao C. Development of grouting simulation test system for rock mass fracture network and its application. Chin J Rock Mech Eng. 2020;39(3):540–9. (In Chinese). doi:10.13722/j.cnki.jrme.2019.0998. [Google Scholar] [CrossRef]
92. Zhang L, Huang C, Li Z, Han X, Zhang Q, Gao Y. Characteristics of slurry-water mixing region in fractured rock mass grouting process: experimental study. Constr Build Mater. 2024;427:136244. doi:10.1016/j.conbuildmat.2024.136244. [Google Scholar] [CrossRef]
93. Liang Y, Sui W, Qi J. Experimental investigation on chemical grouting of inclined fracture to control sand and water flow. Tunn Undergr Space Technol. 2019;83:82–90. doi:10.1016/j.tust.2018.09.038. [Google Scholar] [CrossRef]
94. Zhang JF, Chen XX, Liu Y, Zhang HM, Wang CL, Fang G. Investigation on grouting diffusion in inclined fracture with flowing water conditions. Arab J Geosci. 2022;15(7):629. doi:10.1007/s12517-022-09852-3. [Google Scholar] [CrossRef]
95. Zhang Q, Zhang C, Lin Y, Li Y, He L. Numerical study on seepage of chemical grout flow in rock fracture under temperature field. Geofluids. 2022;2022:7123416–15. doi:10.1155/2022/7123416. [Google Scholar] [CrossRef]
96. Cheng J. Study on Timing of grouting in gob-side entry retaining of fully-mechanized caving face. Coal Mine Mod. 2019;28(6):168–70. (In Chinese). doi:10.13606/j.cnki.37-1205/td.2019.06.058. [Google Scholar] [CrossRef]
97. Zheng G, Su Y, Diao Y, Zhao Y, Chen H, Huang J. Field measurements and analysis of real-time capsule grouting to protect existing tunnel adjacent to excavation. Tunn Undergr Space Technol. 2022;122:104350. doi:10.1016/j.tust.2021.104350. [Google Scholar] [CrossRef]
98. Xiao F, Shang J, Zhao Z. DDA based grouting prediction and linkage between fracture aperture distribution and grouting characteristics. Comput Geotech. 2019;112:350–69. doi:10.1016/j.compgeo.2019.04.028. [Google Scholar] [CrossRef]
99. Al-Aghbari MY, Mohamedzein YEA. Use of cement kiln dust and cement for grouting of granular soils. KSCE J Civ Eng. 2023;27(6):2455–62. doi:10.1007/s12205-023-0508-z. [Google Scholar] [CrossRef]
100. Zou L, Håkansson U, Cvetkovic V. Cement grout propagation in two-dimensional fracture networks: impact of structure and hydraulic variability. Int J Rock Mech Min Sci. 2019;115:1–10. doi:10.1016/j.ijrmms.2019.01.004. [Google Scholar] [CrossRef]
101. Xu C, Han L. Formation mechanism of slurry consolidated body in different grouting media under dynamic water conditions by the test-simulation method. KSCE J Civ Eng. 2023;27(1):169–80. doi:10.1007/s12205-022-0709-x. [Google Scholar] [CrossRef]
102. Zhu L, Liu B, Liu X, Deng W, Yao W, Fan Y. Numerical simulation of slurry diffusion in fractured rocks considering a time-varying viscosity. Fluid Dyn Mater Process. 2024;20(2):401–27. doi:10.32604/fdmp.2023.041444. [Google Scholar] [CrossRef]
103. Sun L, Grasselli G, Liu Q, Aboayanah KR, Huang S, Tang X. Investigating the frost cracking mechanism and the related shallow alpine rockfall initiation process using three-dimensional FDEM. Eng Geol. 2025;348:107960. doi:10.1016/j.enggeo.2025.107960. [Google Scholar] [CrossRef]
104. Sun L, Grasselli G, Liu Q, Tang X. Coupled hydro-mechanical analysis for grout penetration in fractured rocks using the finite-discrete element method. Int J Rock Mech Min Sci. 2019;124:104138. doi:10.1016/j.ijrmms.2019.104138. [Google Scholar] [CrossRef]
105. Yan C, Tong Y, Luo Z, Ke W, Wang G. A two-dimensional grouting model considering hydromechanical coupling and fracturing for fractured rock mass. Eng Anal Bound Elem. 2021;133:385–97. doi:10.1016/j.enganabound.2021.09.013. [Google Scholar] [CrossRef]
106. Liu X, Liu Q, Liu B, Kang Y, He J. Numerical manifold method for thermal-hydraulic coupling in fractured enhance geothermal system. Eng Anal Bound Elem. 2019;101:67–75. doi:10.1016/j.enganabound.2018.12.014. [Google Scholar] [CrossRef]
107. Liu X, Liu Q, He J, Yu F. Numerical simulation of cracking process in rock mass under the coupled thermo-mechanical condition. Int J Comput Methods. 2020;17(9):1950065. doi:10.1142/s0219876219500658. [Google Scholar] [CrossRef]
108. Liu X, Hu C, Liu Q, He J. Grout penetration process simulation and grouting parameters analysis in fractured rock mass using numerical manifold method. Eng Anal Bound Elem. 2021;123:93–106. doi:10.1016/j.enganabound.2020.11.008. [Google Scholar] [CrossRef]
109. Liu X, Deng W, Liu B, Liu Q, Zhu Y, Fan Y. Influence analysis on the shear behaviour and failure mode of grout-filled jointed rock using 3D DEM coupled with the cohesive zone model. Comput Geotech. 2023;155:105165. doi:10.1016/j.compgeo.2022.105165. [Google Scholar] [CrossRef]
110. Liu X, Chen H, Liu Q, Liu B, He J. Modelling slurry flowing and analyzing grouting efficiency under hydro-mechanical coupling using numerical manifold method. Eng Anal Bound Elem. 2022;134:66–78. doi:10.1016/j.enganabound.2021.09.030. [Google Scholar] [CrossRef]
111. Wang XL, Li RJ, Ao XF, Deng SH. Three-dimensional numerical simulation of grouting in stochastic fracture network of dam bedrock in hydropower engineering. Eng Mech. 2018;35(1):148–59. (In Chinese). [Google Scholar]
112. Huang N, Jiang Y, Cheng Y, Liu R. Experimental and numerical study of hydraulic properties of three-dimensional rough fracture networks based on 3D printing technology. Rock Soil Mech. 2021;42(6):1659–68. doi:10.1016/j.csite.2024.105555. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF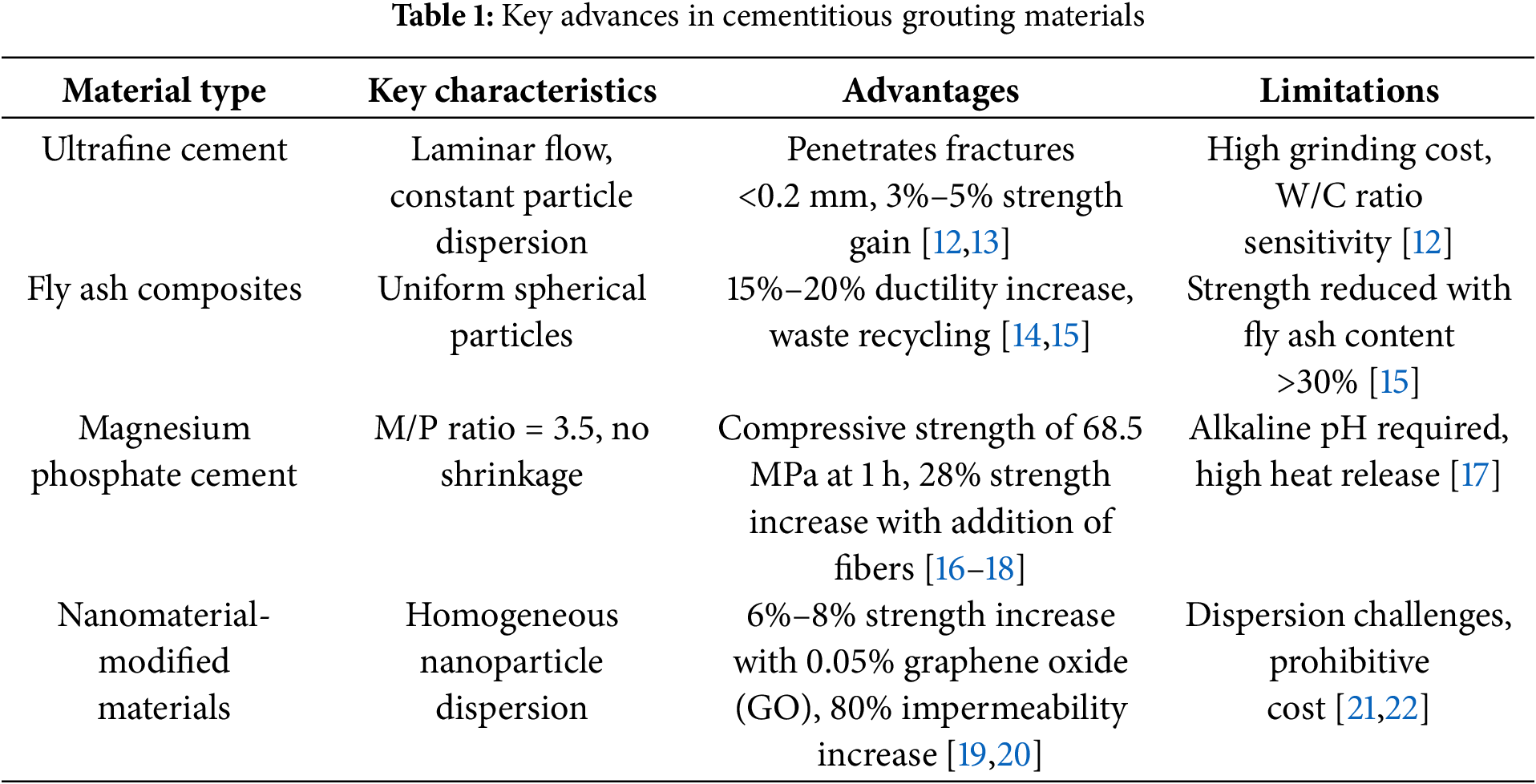

 Downloads
Downloads
 Citation Tools
Citation Tools