Mathematical Study of MHD Micropolar Fluid Flow with Radiation and Dissipative Impacts over a Permeable Stretching Sheet: Slip Effects Phenomena

Nomenclature

1  Introduction

It is highly significant to investigate 2-D boundary layer flow, heat, and mass transport across a nonlinear stretching surface since this kind of research has various practical applications in a wide variety of fields. Molding of a polymer sheet from a dye is one of the industrial uses of viscous flow over a stretched sheet. Other applications include the aerodynamic extrusion of plastic sheets and the condensation operation of metallic surfaces in cooling baths. The molten substance emerges through a slit during the process of fabricating these sheets, and it is later stretched to attain the necessary thickness. Using a similar solution technique, Gupta et al. [1] studied heat and mass transmission in the boundary layer over a stretched sheet when subjected to suction or blowing. The topic of flow and heat transmission of a viscoelastic fluid across a stretched sheet was explored by Cortell [2]. The radiation impact on MHD boundary layer flow caused by an exponentially stretched sheet was described by Goud et al. [3]. Using a numerical technique, Ganesh et al. [4] studied the heat and mass transport of an MHD Casson fluid under radiation via an exponentially porous stretched sheet including a chemical reaction and a hall impact. In a thermal diffusive flow across a stretched sheet of varying thickness, Subhashini et al. [5] analyzed the Dual solutions. Heat and mass transmission of a radiative MHD Casson fluid across an exponentially permeable stretched sheet with a chemical reaction were analyzed by Ibrahim et al. [6]. Over the last several decades, combined mass and heat transport via mixed convection in a micropolar fluid-saturated porous media owing to a stretched surface has attracted significant interest as a solution to a wide variety of geophysical and power engineering challenges. Such thinning and stretching happen in a variety of contexts, including aerodynamic recovery systems, thermal energy storage and continuous filament extrusion, petroleum reservoirs from a dye, and the cooling of an endless metallic plate in a cooling bath, where the thickness and breadth of the plate are reduced and the plate is stretched. Distribution of heat, thickness, and narrowing of breadth are all functions of draw ratio & stretching distance. The efficiency of heat and mass transmission at the surface of the stretch determines the ultimate product quality in all of these methods. Eringen [7] proposed a theory that describes the physical characteristics of micropolar fluids, and that hypothesis is found here. In later years, this theory was expanded to include certain fundamental viscous micropolar fluid flows, such as micropolar fluid flows that heat transfer was studied by Kazakia et al. [8]. Turkyilmazoglu [9] Transfer of heat drives the movement of a micropolar fluid through a porous stretched sheet. Hydromagnetic flow and heat transfer were studied by Yacob et al. [10] in the vicinity of a vertically extending sheet in a micropolar fluid. In a porous medium, Singh et al. [11] investigated melting and other impacts in micropolar fluid stagnation point flow across stretchy porous media. In none of the earlier experiments was it ever determined how the effects of radiation on flow and heat transfer were going to play out. Radiative heat transfer flow is particularly significant in industrial sectors for the construction of dependable equipment, gas turbines, nuclear power plants, and a variety of other propulsion systems for missiles, satellites, airplanes, and space vehicles. In the context of space technology and activities requiring high temperatures, the influence of thermal radiation on the forced and free convection flows is also quite relevant. Joule heating is used in a wide variety of appliances, including electric stoves, electric heaters, soldering irons, and cartridge heaters. Joule heating, in which electricity is passed through food (which acts as an electrical resistor) to generate heat, is used by several types of food processing machinery. Abbas et al. [12] explored the numerical solution for numerous factors affecting non-Newtonian MHD fluid flow and heat mass transfer owing to a nonuniform stretched sheet. The impact of radiation on MHD heat transfer in micropolar fluid flow through a vertical moving porous plate was studied by Goud et al. [13]. Goud [14] investigated how heat production and absorption on a steady extended porous surface affects the motion of a micropolar liquid via a porous media with varying suction/injection. Varied fluid characteristics affected MHD flow and heat transmission across a stretched sheet with varied thickness, according to Prasad et al. [15]. The impact of radiation on the unsteady MHD flow of a micropolar fluid with mass and heat transport was investigated by Hayat et al. [16]. The impact of radiation and heat absorption/generation on the MHD heat transport flow of a micropolar fluid via a wedge with ion slip and Hall currents was studied by Uddin et al. [17]. Study of the generated magnetic field on the 3-grade micropolar flow of fluid over an infinitely extended sheet by Awan et al. [18]. Micropolar fluid in a vertical porous channel under third-order MHD boundary conditions was studied by Prakash et al. [19]. Patil et al. [20] investigated the impact of MHD mixed convection over an exponentially stretched sheet, taking into account the presence of a non-uniform heat source/sink and cross-diffusion. Abdal et al. [21] examined the multi-slip impact on MHD combined convection and unsteady flow of micropolar nanofluid across a shrinking/stretching sheet with radiation and heat source. With heat source/sink impacts the boundary layer movement of micropolar nanoparticles past a stretching surface was studied by Dulal Pal et al. [22]. The impact of ohmic heating and chemical reaction on the MHD motion of a micropolar liquid across a stretched surface was investigated by Goud et al. [23]. Singh et al. [24] investigated Micropolar Fluid Slip Movement via a Permeable Wedge Due to Hall and Ion-Slip Currents. Fatunmbi et al. [25] looked into the flow of MHD micropolar fluids through a porous medium under varying slip conditions. The Numerical investigation of chemical reaction influence on MHD micropolar flow of fluid past via a vertical riga plate was investigated by Goud et al. [26]. Hasnain et al. [27] conducted research on the entropy generation study of 2-phase micropolar nanofluids flowing in an inclined channel while experiencing convective heat transform.

This study uses the micropolar method to examine how the presence of a magnetic field modifies the heat and mass transport properties of a moving flat surface immersed in a non-conducting electrical fluid to address this more complex challenge. The goal of this experiment is to investigate the effect of radiation on heat and mass transfer in a Micropolar MHD free convective fluid flow over a stretched porous sheet by injection and suction fluid through the sheet. According to reports, viscous dissipation also plays a contribution to the energy equation. To convert the controlling boundary layer equations into ordinary differential equations, similarity transformations are used. Afterward, the in-built solver in MATLAB is used to provide a numerical explanation of the equations. Several major influences on flow characteristics have been studied. When compared to other published papers, the findings demonstrate a significant level of coherence. Work in the fields of solar energy collecting, recovery of petroleum products, and the dynamics of fires in insulation may all benefit from this kind of study.

2  Mathematical Analysis

In this scenario, consider a stretching sheet that has a specified surface thermal gradient that is accountable for driving a continuous 2-D laminar movement of a non-compressible micropolar fluid at the ambient temperature T∞. It is thought that the movement is along the axis of x, which carried the plate ahead along the accelerative direction; the y-axis, on the other hand, is thought to be vertical to the x-axis. The direction of flow that has a changing magnetic field is connected in a traditional way to the y-axis via a connection that is formed in that axis.

An external electric field is not implicated. The flow geometry associated with this problem is shown in Fig. 1 under the further assumptions that the magnetic Reynolds amount is relatively small and that the magnetic field generated by the moving fluid has a negligible influence on the magnetic field around the liquid and the equations for the boundary layer that explain constant flow across a stretching sheet are as follows [28].

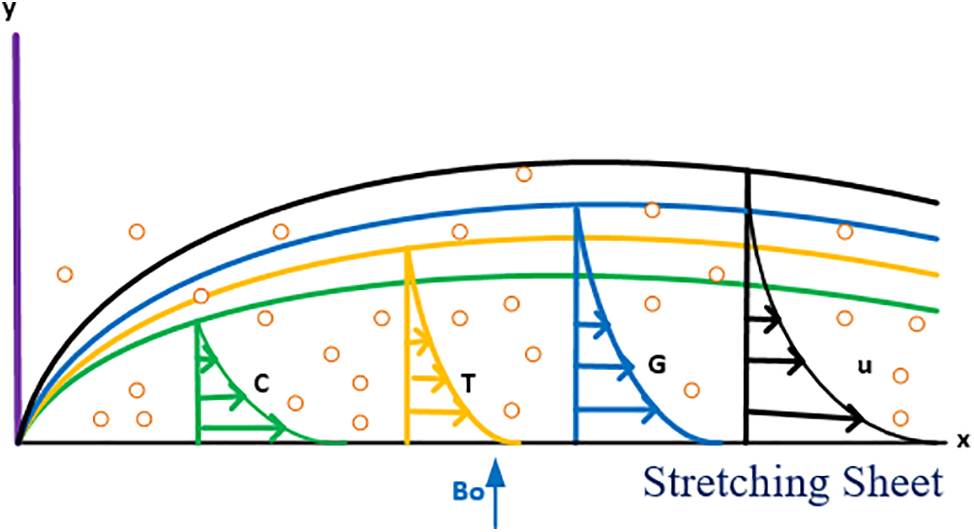
Figure 1: Flow geometry

Continuity:

∂u∂x+∂υ∂y=0(1)

Momentum:

u∂u∂x+υ∂u∂y=(v+kρ)∂2u∂y2+kρ∂N∂y−σB02ρu+vkp∗u(2)

Angular momentum:

u∂N∂x+υ∂N∂y=γjρ∂2N∂y2−kjρ(2N+∂N∂y)(3)

Energy:

u∂T∂x+υ∂T∂y=kfρCp∂2T∂y2+(μ+k)ρCp(∂u∂y)2+σB02ρu2+16σ∗T∞33k∗ρCp∂2T∂y2(4)

Concentration:

u∂C∂x+υ∂C∂y=D∂2C∂y2−Kr(C−C∞)(5)

The appropriate boundary measures to use for physical limits are the following:

u=uw=bx+α∂u∂y, υ=0, N=−s∂u∂y, T=Tw+α∂T∂y, C=cw+β∂C∂yat y=0u=0,N=0,T=T∞,C=C∞asy→∞}(6)

In this case, the right-hand side of Eq. (4) shows terms for the impact of the Ohmic heating and viscous dissipation expressions.

Here γ=(μ+k2)j is presumed to be velocity spin gradient and is given by [28], here j=vb is referred to be the length of reference.

The predicted flow of heat flux, based on the Rosseland estimate [29] is

qr=−4σ∗3α∗∂T4∂y(7)

In this hypothesize the thermal difference exclusive to the flow is insignificant and adequate for T4 to be stated as a linear arrangement of the temperatures. Expand T4 in the Taylor sequence extension approximately T∞ obtains

T4≈4T∞3T−3T∞3(8)

Hence,

∂qr∂y=−16σ∗T∞33α∗∂2T∂y2(9)

In the process of converting Eqs. (2)–(5) together with Eqs. (7) and (9) together into a set of ODEs, we make use of the similar translations and dimensional factors that are outlined in the following paragraphs, specifically:

ζ=(bv)y, u=bxf′(ζ),υ=−bvf(ζ)N=b3vxG(ζ), θ(ζ)=T−T∞Tw−T∞,ϕ(ζ)=C−C∞Cw−C∞}(10)

The changed equations are

(1+K)f‴+ff″−(f′)2+Kg′−(M+Kp)f′=0(11)

(1+K2)G″+fG′−Gf′−K(2G+f″)=0(12)

(1+4R3)θ″+Prfθ′+(1+K)PrEc(f″)2+PrEc(f′)2=0(13)

ϕ″+Scfϕ′−ScKrϕ=0(14)

The newly reshaped boundary circumstances are as follows:

f′(ζ)=1+Af″(ζ);f(ζ)=0;G(ζ)=−sf″(ζ);θ(ζ)=1+Bθ′(ζ);ϕ(ζ)=1+Cϕ′(ζ);}ζ=0;f′(ζ)=0;G(ζ)=0;θ(ζ)=0,ϕ(ζ)=0}ζ→∞(15)

Here “ ′ ”signifies the dif. w.r. to “ ζ ” & the dimensionless quantities are

K=kμ,M=σB02ρb,Pr=ρvcpkf,Kp=bKp∗v,Ec=uw2Cp(Tw−T∞)Sc=vD,Kr=Kr′bα=Abv,β=Bbv,γ=Cbv}(16)

It is possible to determine the shear stress by applying the formula located at the surface.

τw=[(μ+k)(∂u∂ζ)+kN]ζ=0=(μ+k)bxbvf″(0)

By employing uw=bx is called characteristic velocity, the quantity of skin friction, designated by Cf, is to be specified as Cf=τwρuw2=(1+K)f″(0)Rew.

Here local Reynolds number: Rew=uwxv.

The apparent, couple stress is precise as Mw=(γ∂N∂ζ)ζ=0=μuw(1+k2)g′(0).

It is possible to describe the local surface temperature flow according to Fourier’s law, which may be summarized as follows:

qw(x)=−kf(∂N∂ζ)ζ=0=−kf(Tw−T∞)bvθ′(0)

The following expression may be used to calculate the component of the surface heat flux transfer: h(x)=qw(x)(Tw−T∞)=−kfbvθ′(0).

In addition, the Nusselt number can be expressed using the formula as follows: Nux=xh(x)kf=−bvxθ′(0) also we can be written as NuxRew=−θ′(0).

Likewise, local mass flux indicated as Jw=−D(∂C∂ζ)ζ=0.

Also, a quantity of Sherwood number stated Shx=Jw(x)D(Cw−C∞)=−bvxϕ′(0) and it changes to

−ϕ′(0)=ShxRew.

3  Method of Solution

One may find an answer by recasting the system of coupled nonlinear ODEs (11)–(14) and with constraints (15) as an initial value problem. We set

y1=f,y2=f′,y3=f″,y4=g,y5=g′,y6=θ,y7=θ′,y8=ϕ,y9=ϕ′, now the set of ODEs is transformed into the following arrangement:

y′3=−(y1 ∗ y2−(y2)2−((M+Kp) ∗ y2)+(K ∗ y5))/(1+K)

y′5=−((y1 ∗ y5)−(y2 ∗ y4)−(K ∗(2 ∗ y4+y3)))/(1+K2)

y′7=−((Pr(y1 ∗ y7)+(1+K)PrEc(y3)2+PrEc(y2)2))/(1+4R3)

y′9=−(sc(y1 ∗ y9)−ScKry8)

The boundary constraints are

y1(0)=fw,y2(0)=1+A ∗ fa(3),y4(0)−sy3(0),y6(0)=1+B ∗ fa(7),y8(0)=1+C ∗ fa(9)} and y2(∞)=0,y4(∞)=0y6(∞)=0,y8(∞)=0}

The technique used in MATLAB’s built-in algorithm may be utilized to assimilate the preceding differential equations. This technique is carried performed repeatedly until the results achieve the 10−6 the desired degree of accuracy.

4  Results and Discussion

The exploration into the study of micropolar fluid movement with slip conditions, and thermal radiation is now being performed as a component of the examination. Through the use of numerical techniques, flow fields were examined, together with friction factor & quantity of Nusselt number, spanning a range of possible estimates for the characterizing parameters.

This section decides to investigate the diverse range of physical qualities that different embedding configurations have on flow region characteristics. These flow regional profiles are depicted in the pictures. Typical trends of the nondimensional flow fields are shown in Figs. 2a–2d, respectively, over a wide range of values of the magnetic field component. The values of f′(ζ) and G(ζ) diminish when the magnetic field component M is enriched, whereas the values of θ(ζ) and ϕ(ζ) continue to rise. When M increases, the opposite force, which is known as the Lorenz force, also increases. This causes the flow to become even more slow. Subsequently, particle velocity and microrotation are decelerated by a huge M, this makes perfect sense from a physics perspective. As a direct result of this, the parameter M was responsible for controlling both the velocity & the temperature.

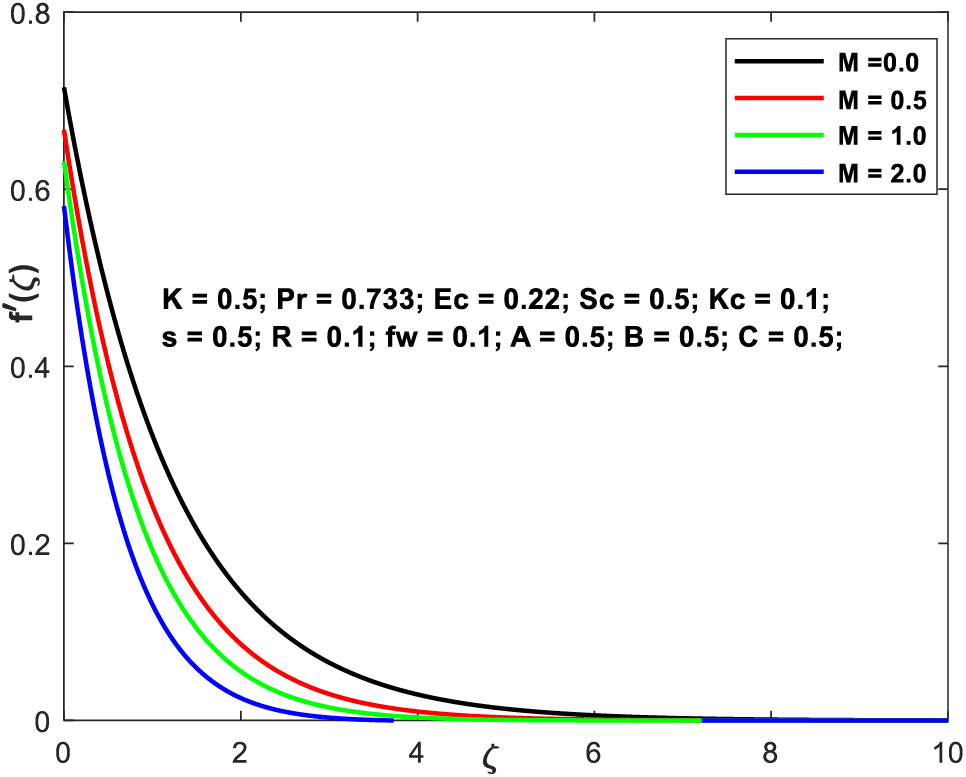
Figure 2a: f′(ζ) vs. M

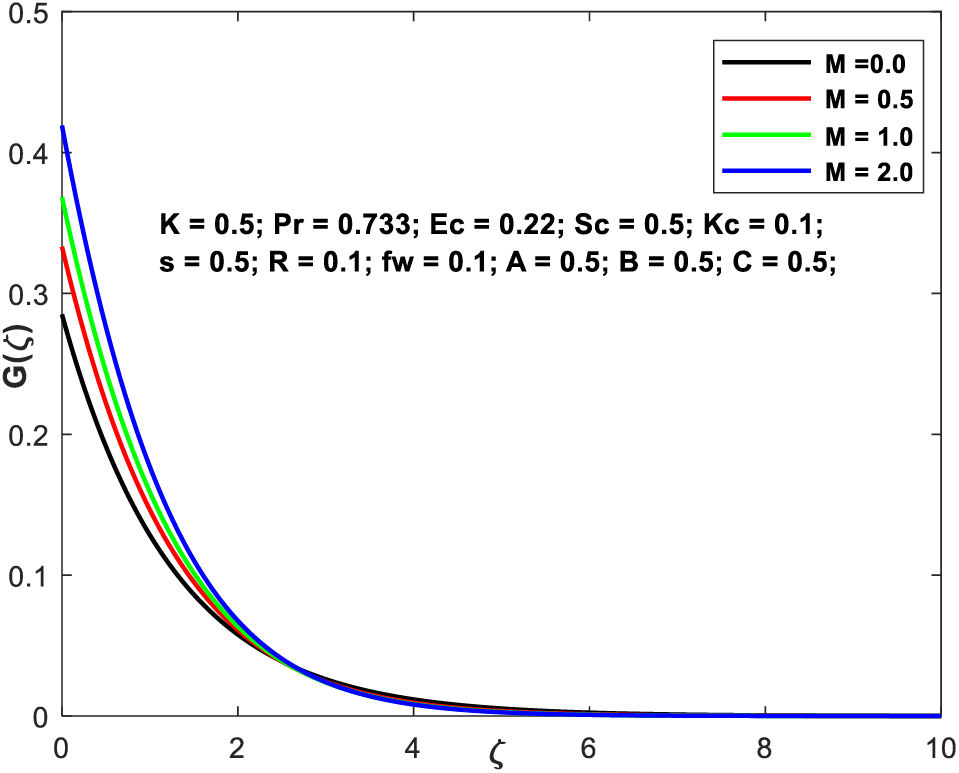
Figure 2b: G(ζ) vs. M

Figure 2c: θ(ζ) vs. M

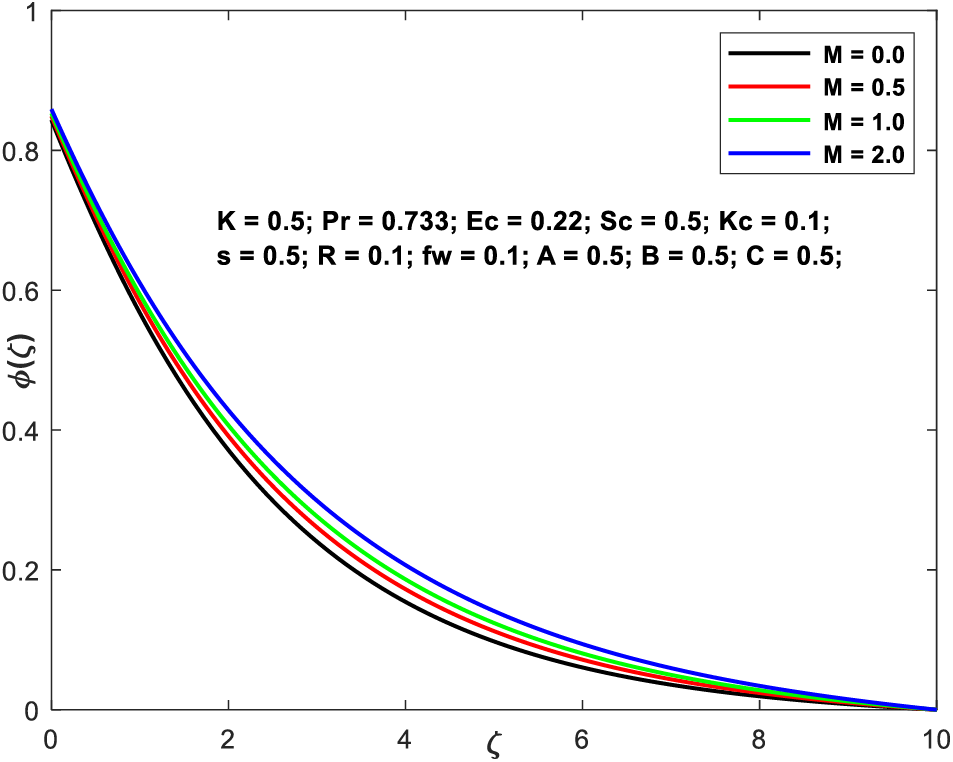
Figure 2d: θ(ζ) vs. M

Figs. 3a–3d demonstrate the f′(ζ), G(ζ),θ(ζ) & ϕ(ζ) outlines fluctuating values of the material factor K. The graph illustrates unmistakably that rising K boosts velocity. As a micro concentration substance enhances, with diverse values of K. Because of this, micro concentration influences the flow pattern. Since K has a positive impact on the width of the boundary level. The graph demonstrates that when the K upsurges and angular rotation at the boundary reduces. Hence, an increase in particle concentration causes a reduction in microrotation near the boundary. An increase in the worth of material property is seen to be accompanied by a drop in temperature. Immediately before the boundary, the temperature spikes and remains high for some time before commencing a slow drop. As the value of the material factor grows, concentration declines. The concentration profile is rather insensitive to this variable’s adjustment.

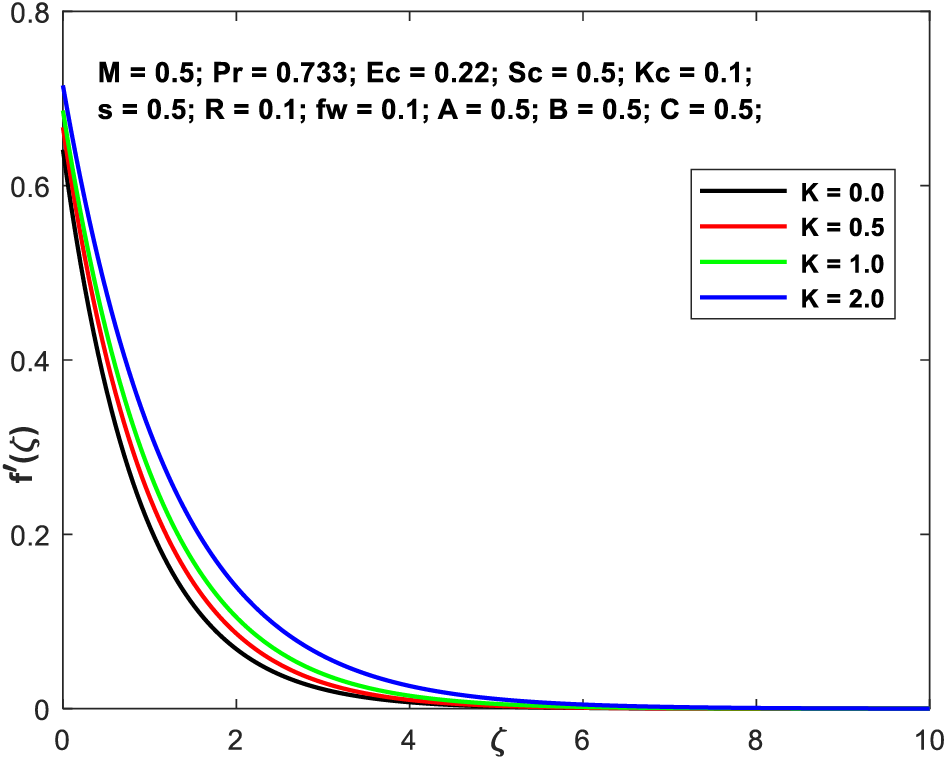
Figure 3a: f′(ζ) vs. M

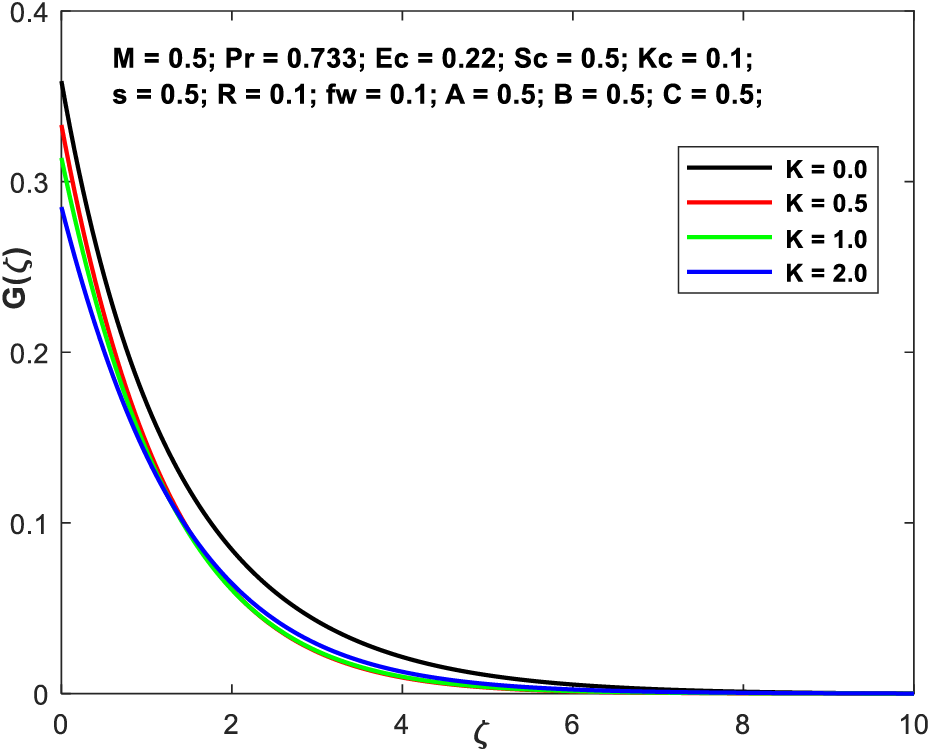
Figure 3b: G(ζ) vs. K

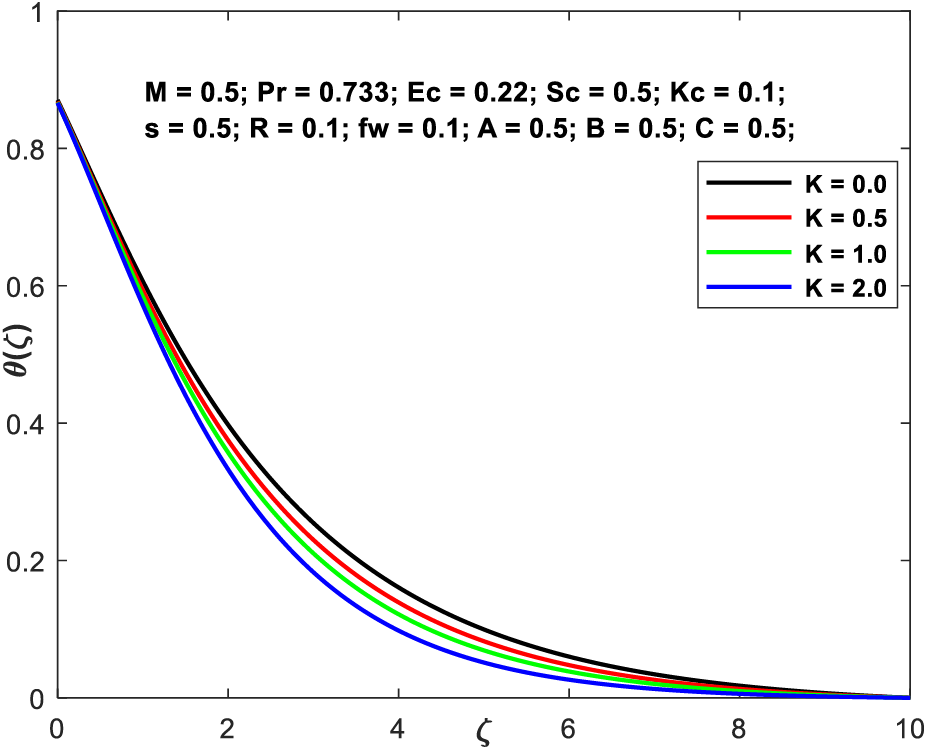
Figure 3c: θ(ζ) vs. K

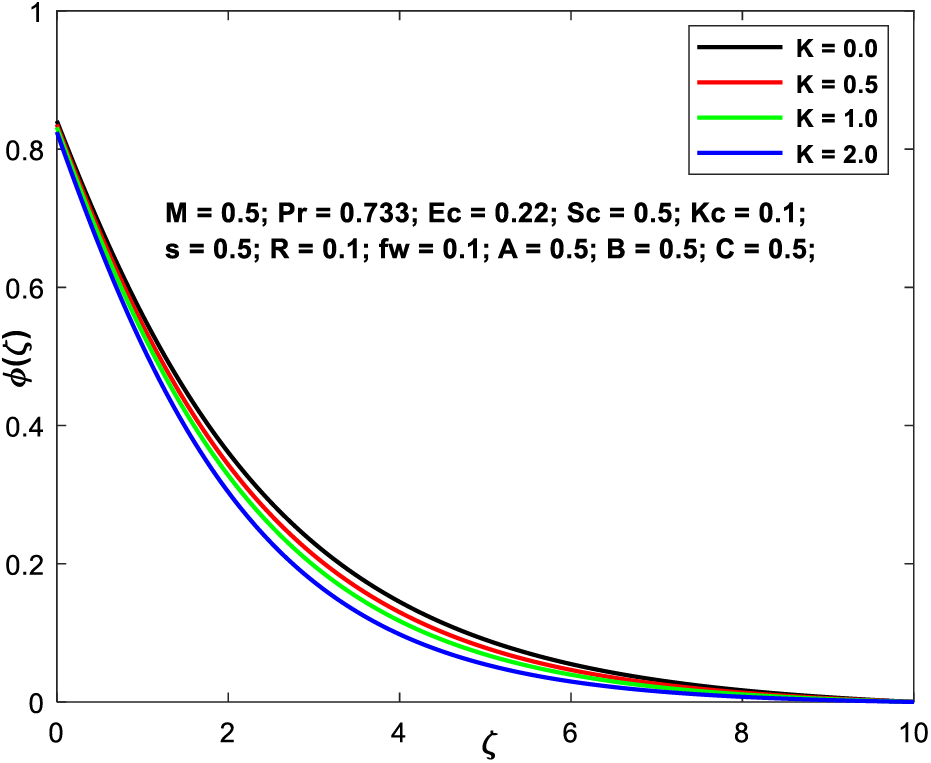
Figure 3d: ϕ(ζ) vs. K

Figs. 4a and 4b exhibit the velocity and microrotation patterns, respectively, as a consequence of the factor (s). It is clear that changing the parameters will result in a reduction in the velocity. The comparable velocity is indeed greater when there is no turn relative to other cases. As s becomes greater, the growth rate accelerates exponentially.

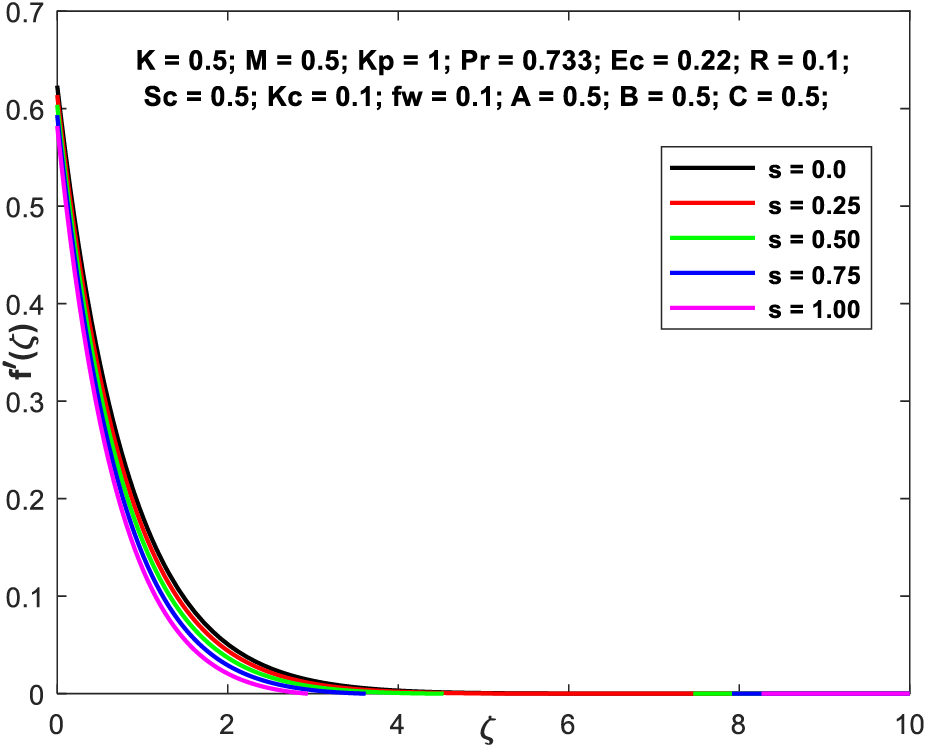
Figure 4a: f′(ζ) vs. s

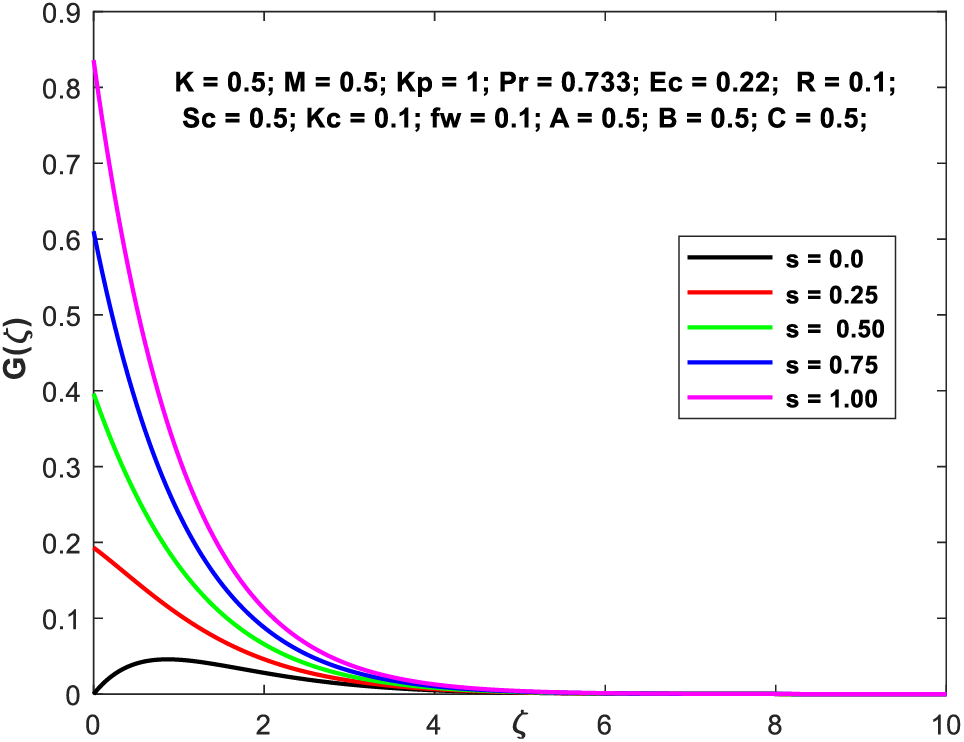
Figure 4b: G(ζ) vs. s

Fig. 5 portrays the contribution of the Schmidt number (Sc) on the concentration profile. Based on this graph, we can see that as Sc enhances, ϕ(ζ) declines.

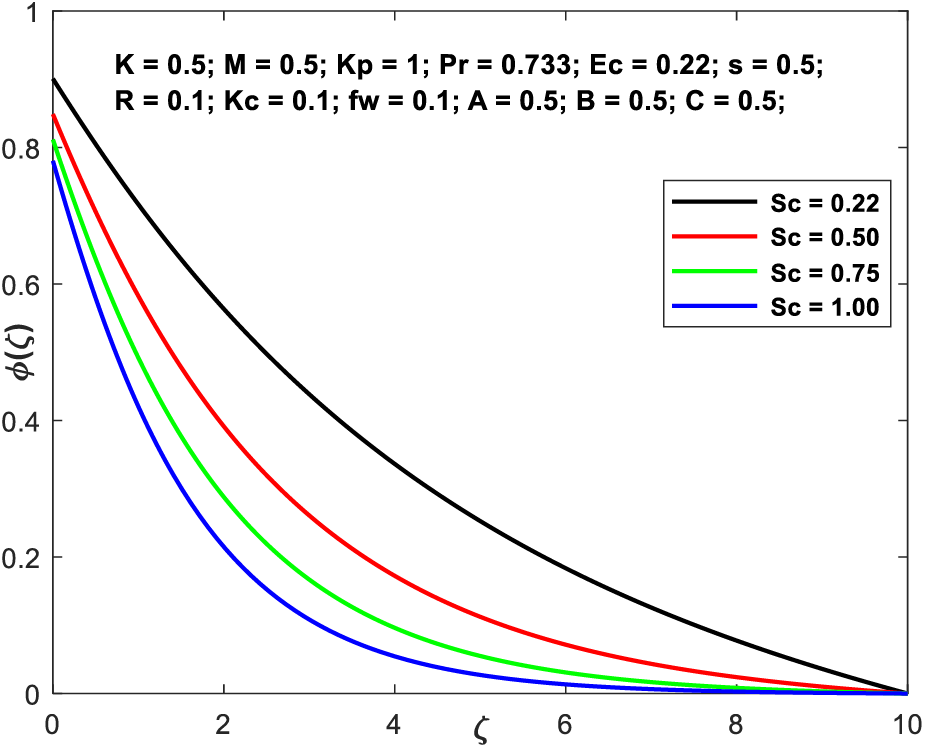
Figure 5: ϕ(ζ) vs. Sc

Fig. 6 illustrates how the Eckert number plays a role in the thermal gradients of the system. It has been found that when the Eckert number increases, there is an accompanying rise in the temperature of the fluid located above the sheet. Even when Ec increases, the liquid region becomes much more effective at loading energy that has been lost due to dissipation as a result of viscosity and elastic properties. This is the case even while Ec is growing.

Figure 6: θ(ζ) vs. Ec

Fig. 7 depicts the variations that take place in the concentration profile as a consequence of the various reaction factors. The saturation curve is demonstrated to have a declining slope the greater “Kr” is made to be.

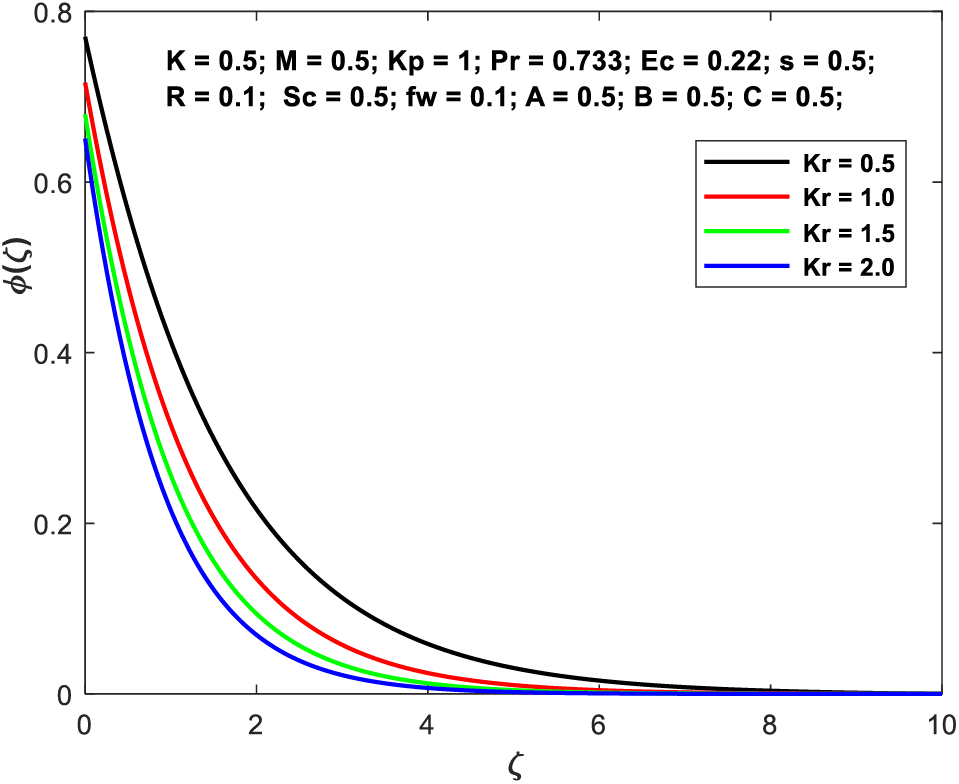
Figure 7: ϕ(ζ) vs. Kr

Fig. 8 is an illustration of temperature gradients for a variety of different radiation input variables (R). It has been shown that R, which stands for R, makes the thermal field more intense. This is due to an elevation in R leading to an intensification in the size of the temperature boundary layer, which brings about the aforementioned effect.

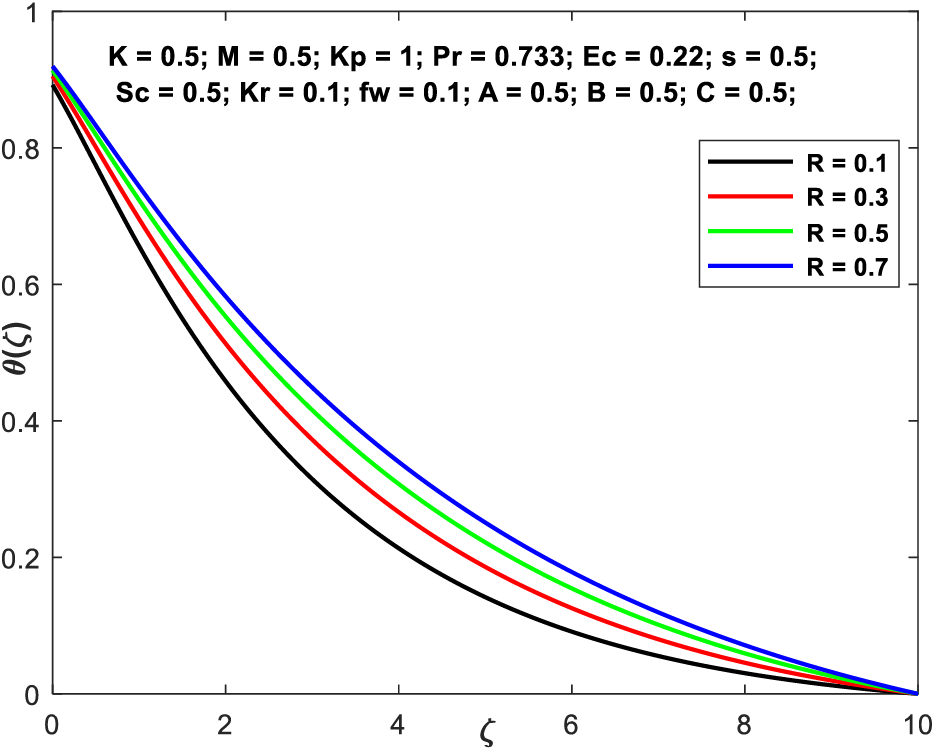
Figure 8: θ(ζ) vs. R

Figs. 9a–9d exhibit how the suction/injection component has a consequence on the geometries of the flow fields (d). Increasing the value of the suction parameter causes a general smoothing out of the profiles. These profiles become narrower as fw gets higher because the heating forces the fluid closer to the sheet’s surface, which leads to a smaller quantity of flow underneath the surface. This is why the profiles get narrower as fw gets higher.

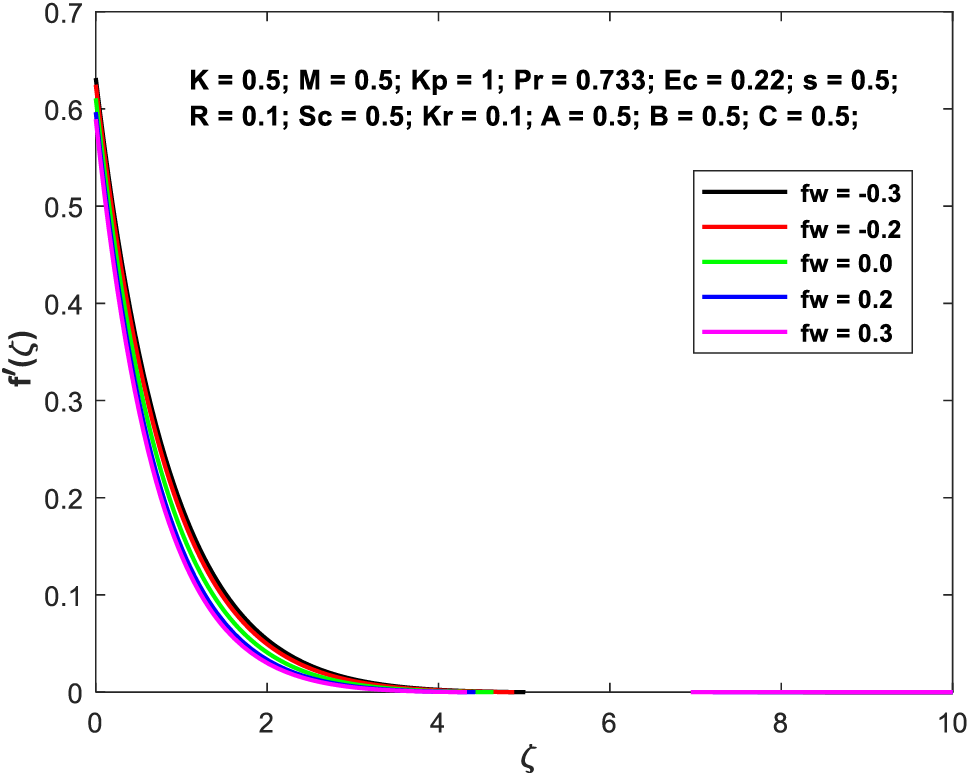
Figure 9a: f′(ζ) vs. fw

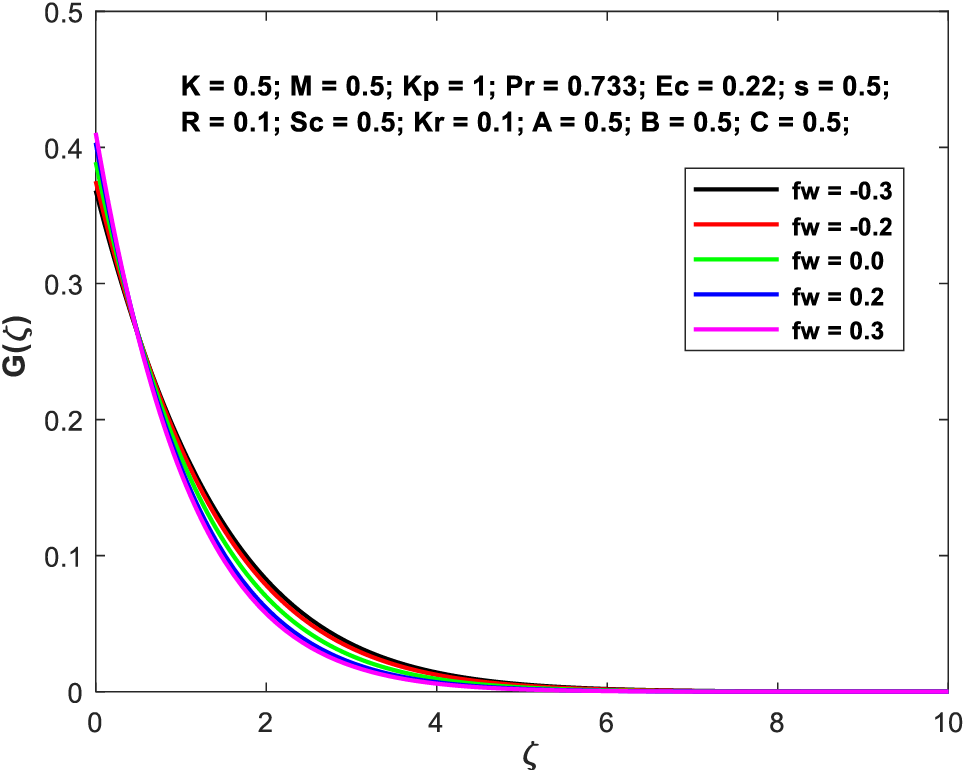
Figure 9b: G(ζ) vs. fw

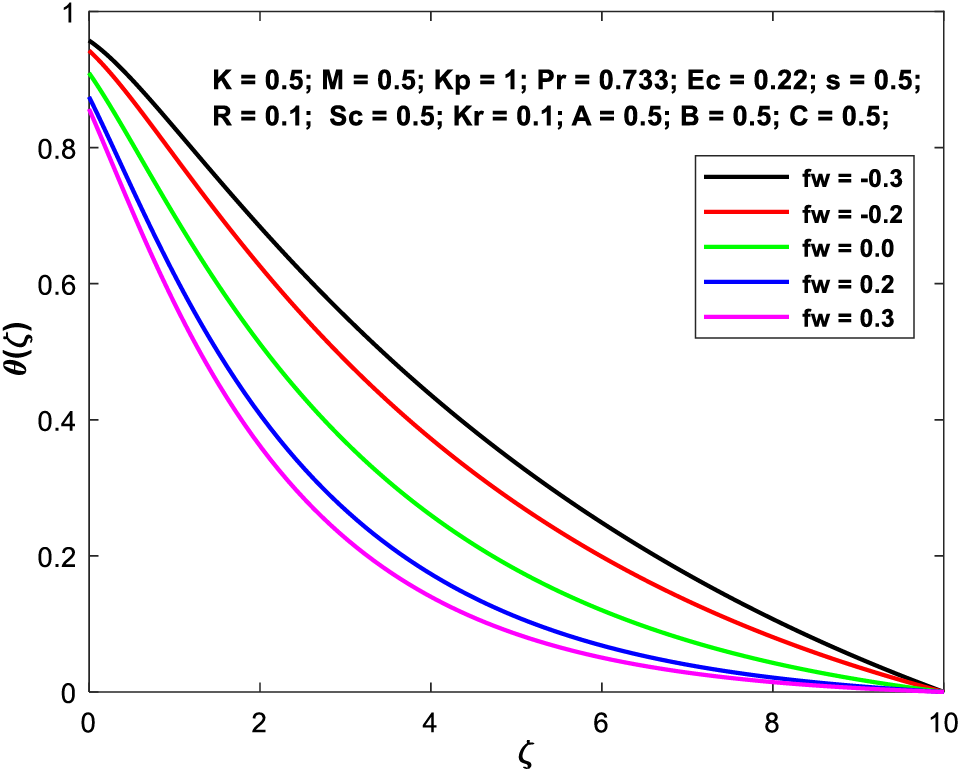
Figure 9c: θ(ζ) vs. fw

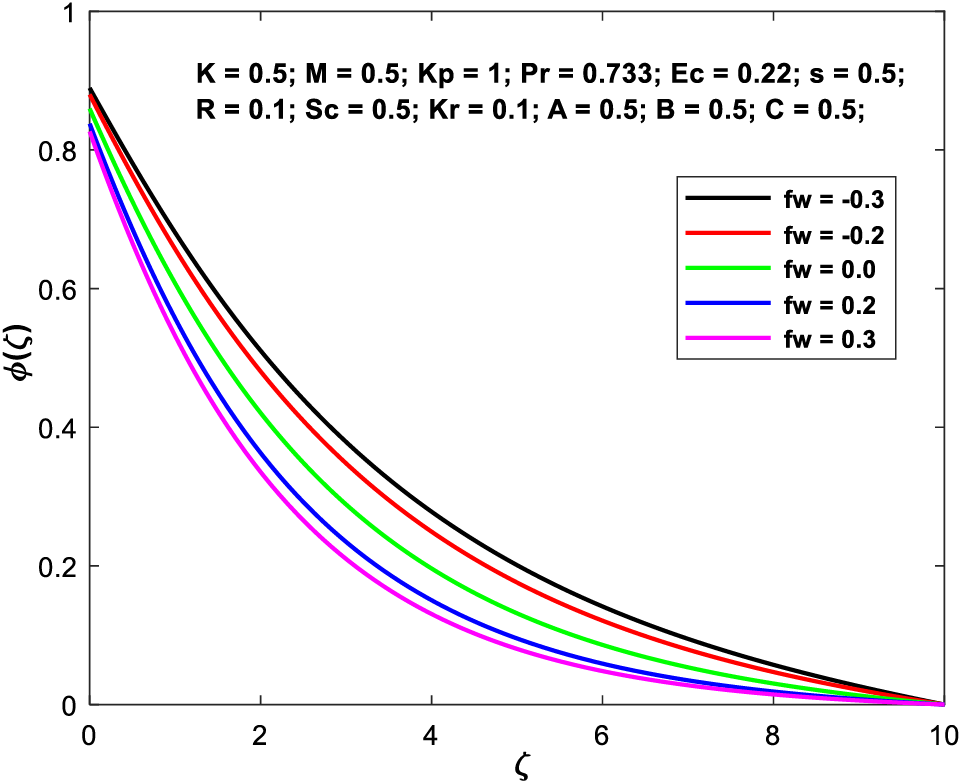
Figure 9d: ϕ(ζ) vs. fw

Due to the reduction in thermal conductivity of the fluid caused by an enhancement in Pr, the heat transfer rate increases as Pr is increased. The energy profile has been deemed unreliable for this same reason and has thus been deprecated. This phenomenon is shown in Fig. 10.

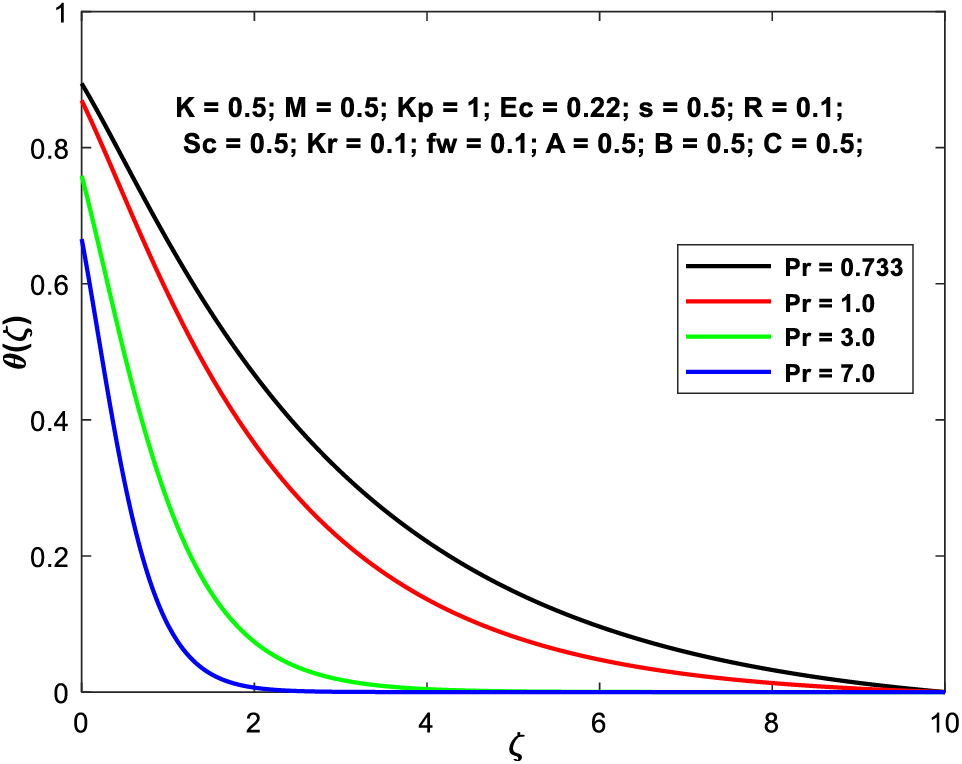
Figure 10: θ(ζ) vs. Pr

Figs. 11a–11d depict the flow profiles vs. varying the velocity slip factor A. Here, the velocity and microrotation of the fluid are lower in the presence of velocity slip than in the absence of slip (A=0), and these decrease as the slip parameter grows whereas A. Meanwhile, As thermal and concentration profiles increase with the enhancement of A. A consequence of imposing the velocity slip condition, the hydrodynamic boundary layer is seen to thin. Nonlinear stretch sheets provide a source of momentum, which is then transmitted to a micropolar fluid. However, as one moves farther from the sheet, the profiles overlap and the slip’s influence diminishes.

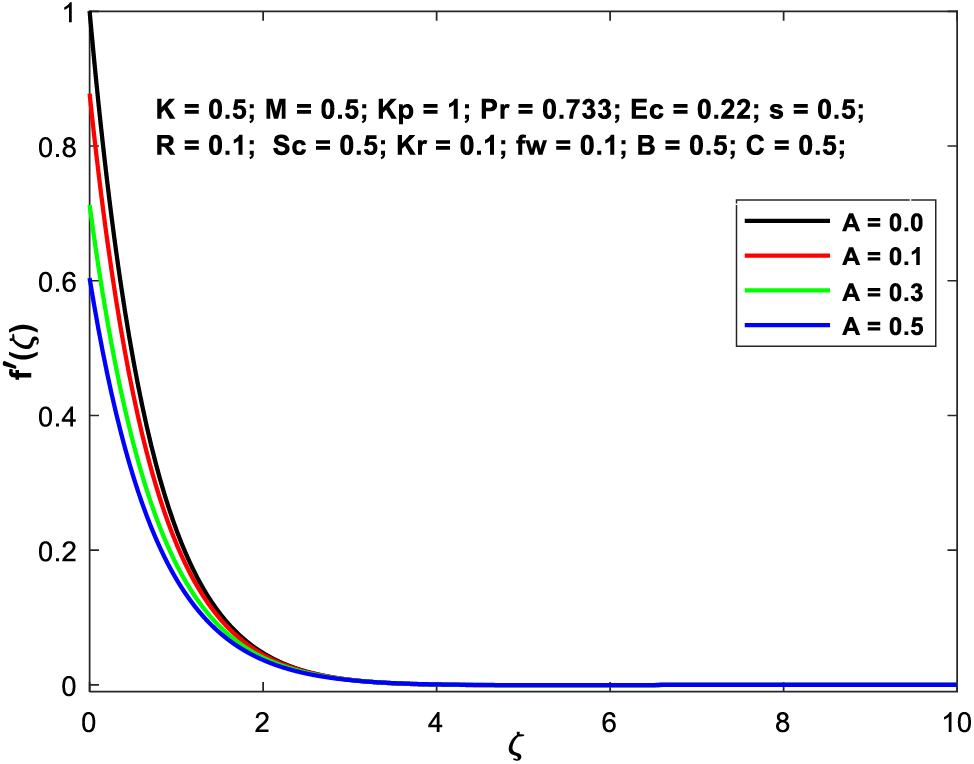
Figure 11a: f′(ζ) vs. A

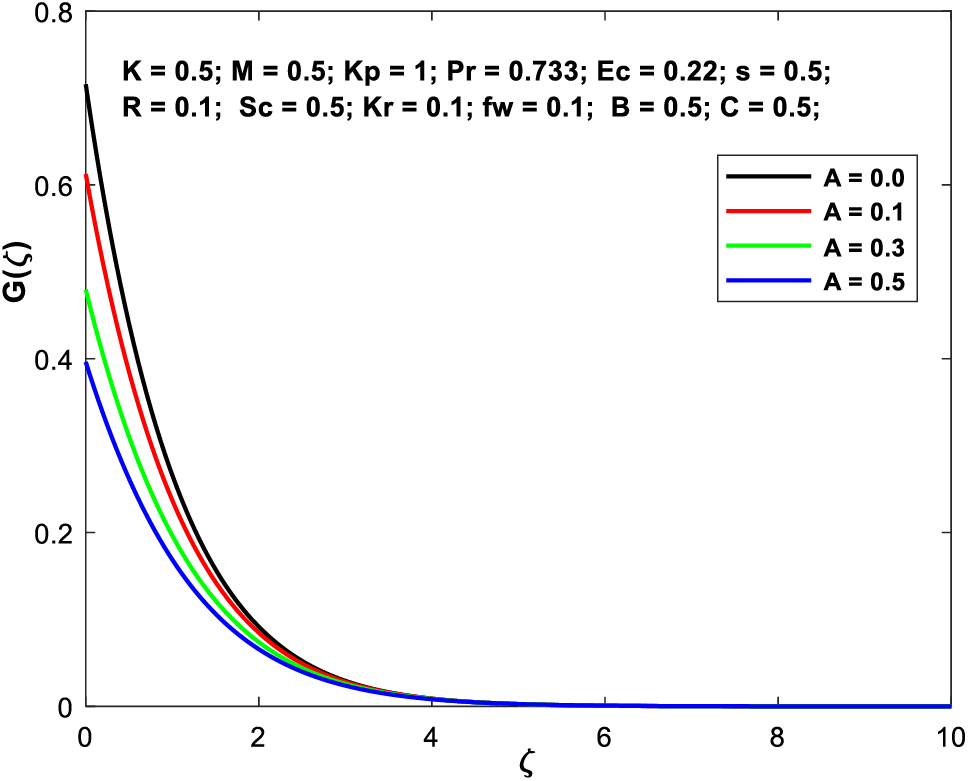
Figure 11b: G(ζ) vs. A

Figure 11c: θ(ζ)vs. A

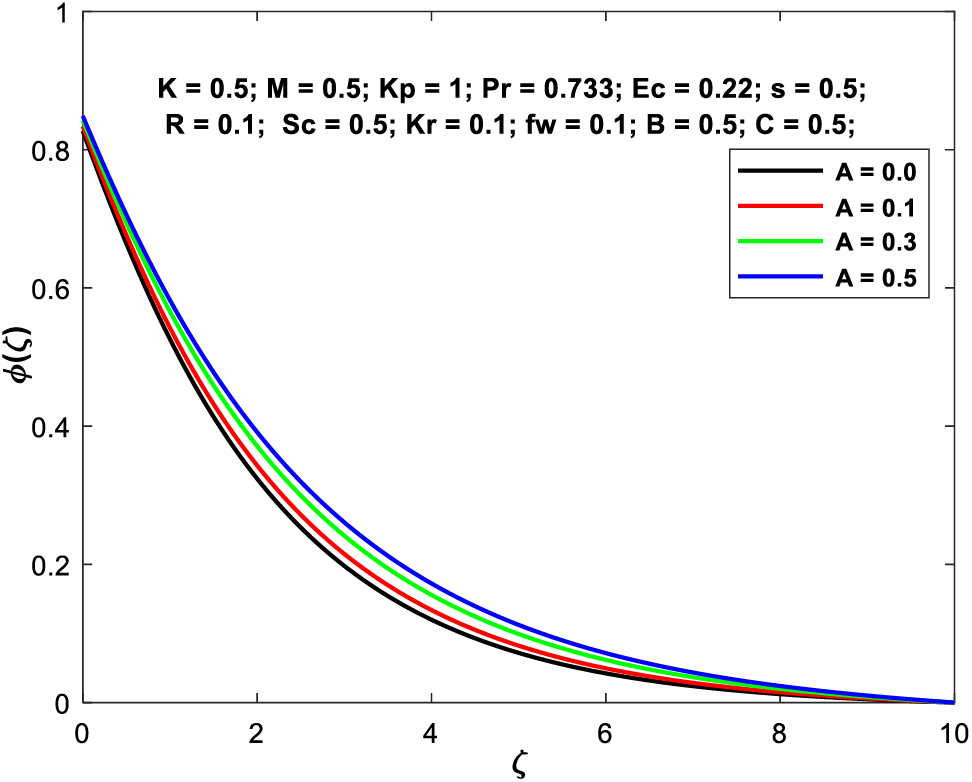
Figure 11d: ϕ(ζ)vs. A

Fig. 12 displays the effect of changing the thermal slip factor on the temperature field in the boundary layer. When B rises, so does the size of the thermal boundary surface enhances. Because of this, the temperature profile becomes more uniform and heat transmission from the sheet to the fluid slows down. When the concentration slip factor C is large, the concentration curves exhibit the same behavior as shown in Fig. 13. As a matter of fact, slip tends to lessen the fluid flow, which in turn serves to decrease the net molecular movement, which in turn lessens the temperature and concentration gradients.

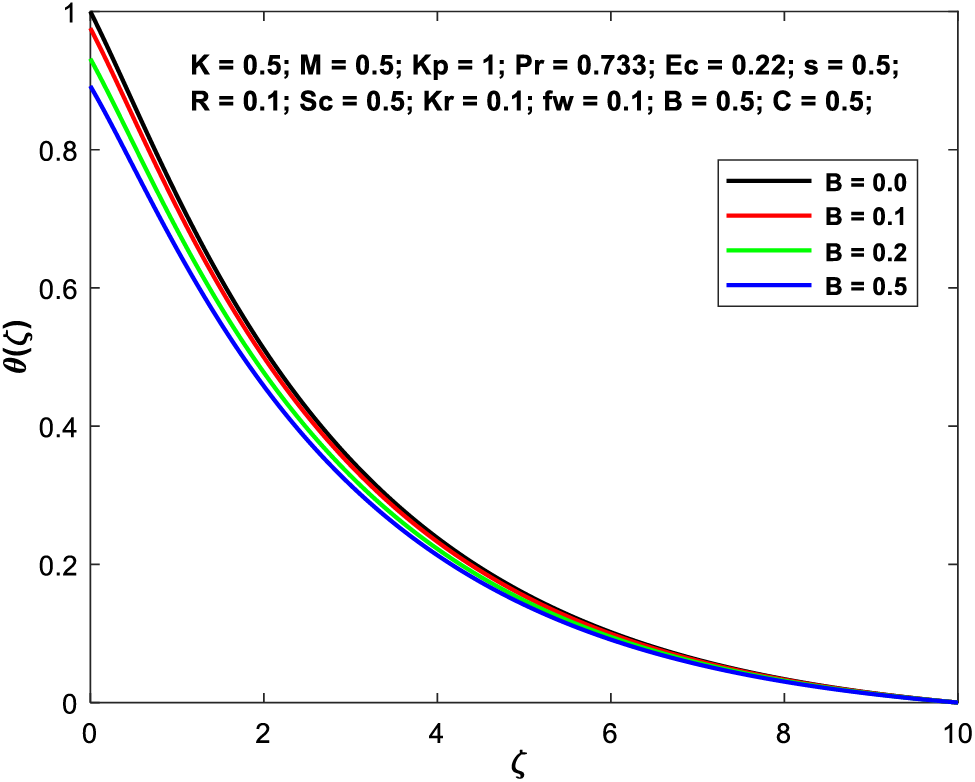
Figure 12: θ(ζ) vs. B

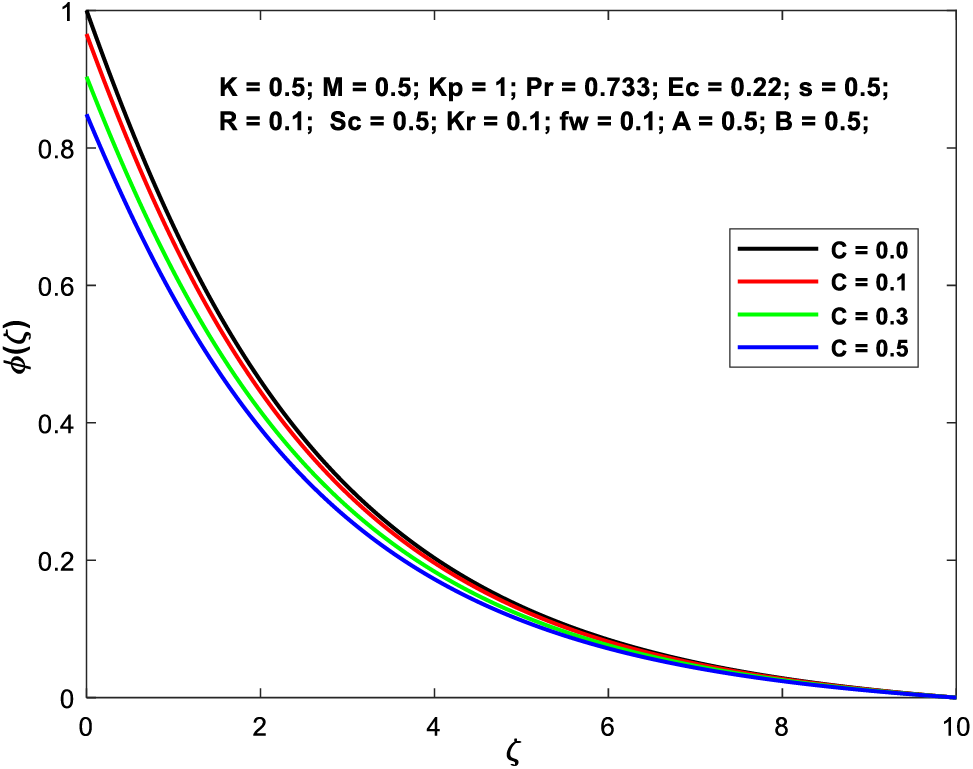
Figure 13: ϕ(ζ) vs. C

Figs. 14a–14d depict the impact of the permeability factor on the flow characteristics across the boundary layer. When Kp increases, the velocity of the fluid declines, and the microrotation temperature and concentration curves increase.

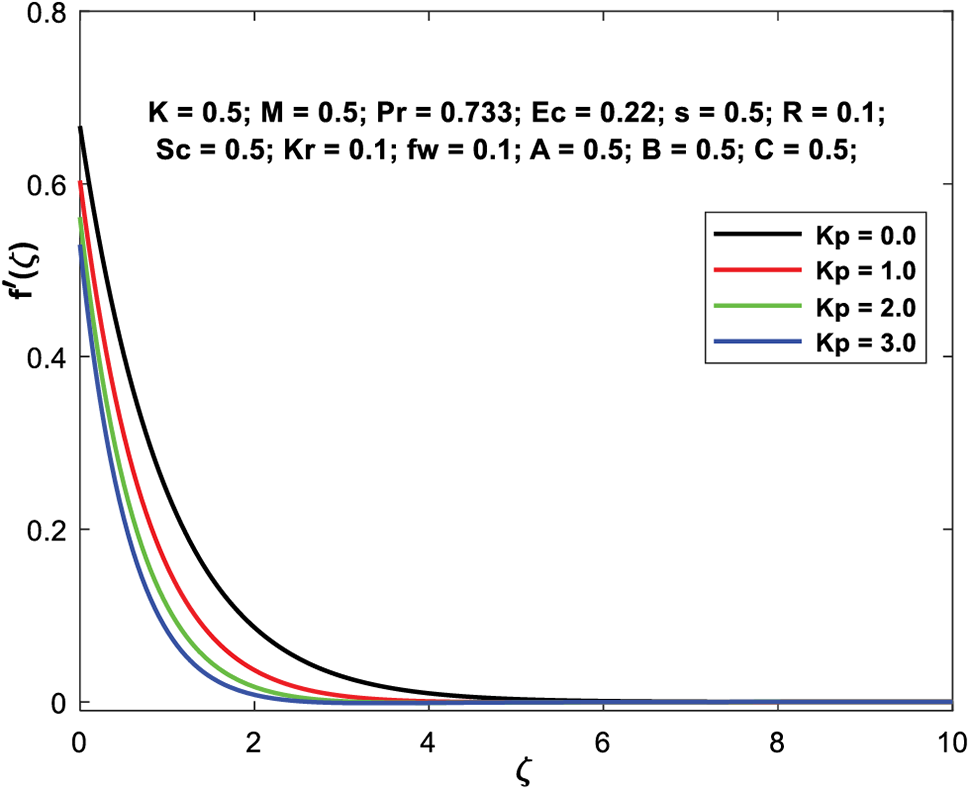
Figure 14a: f′(ζ) vs. Kp

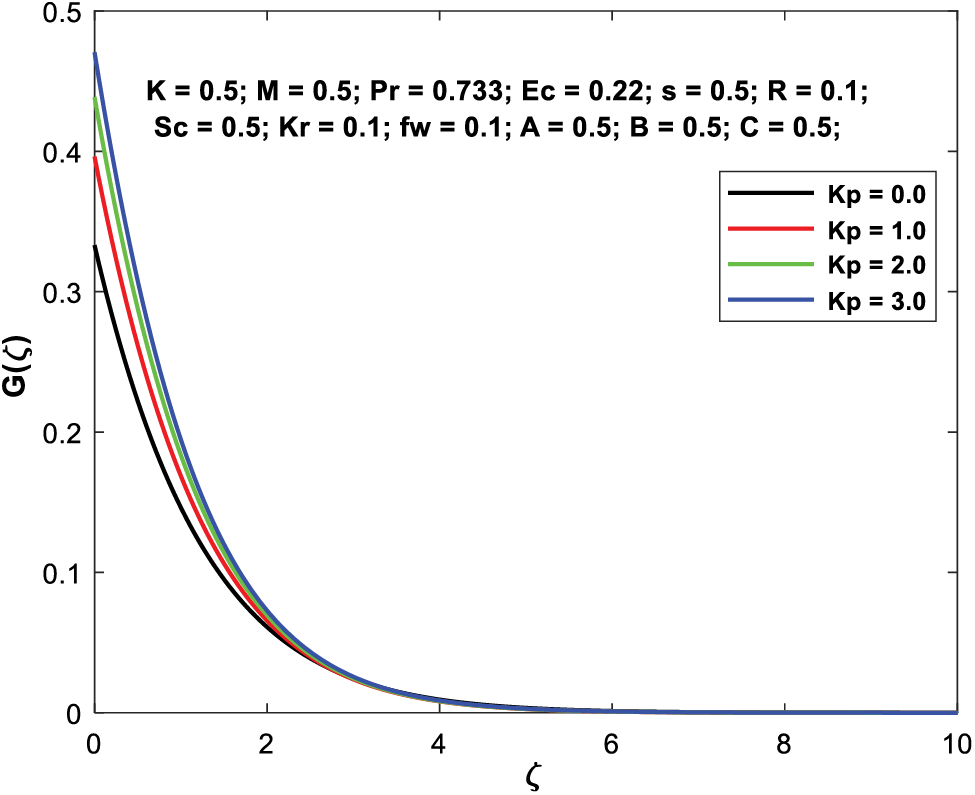
Figure 14b: G(ζ) vs. Kp

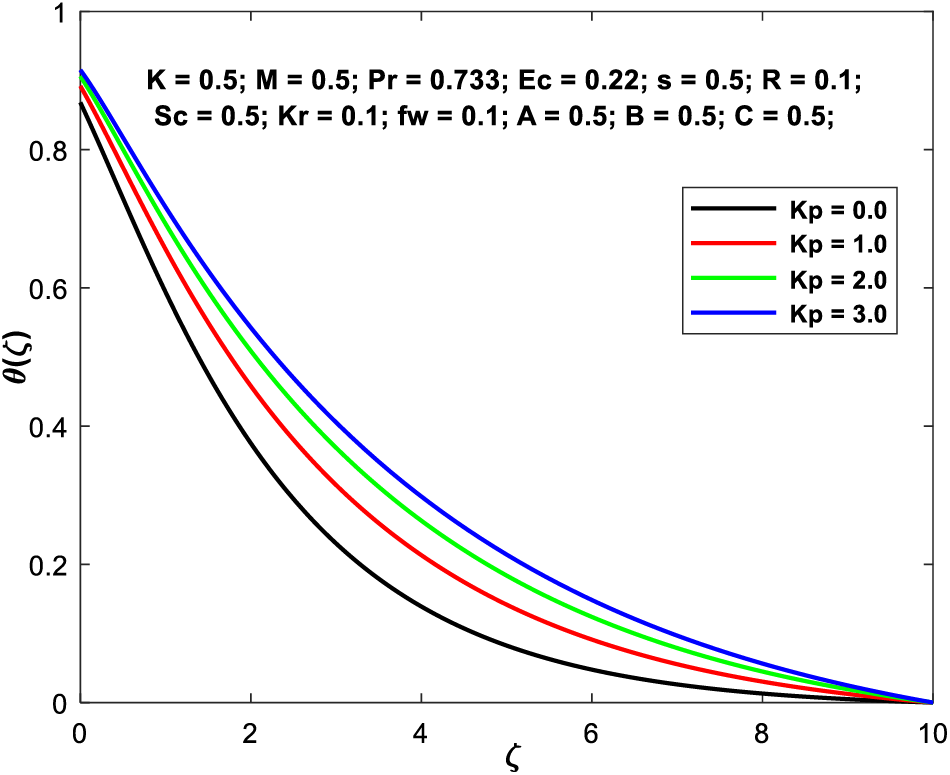
Figure 14c: θ(ζ) vs. Kp

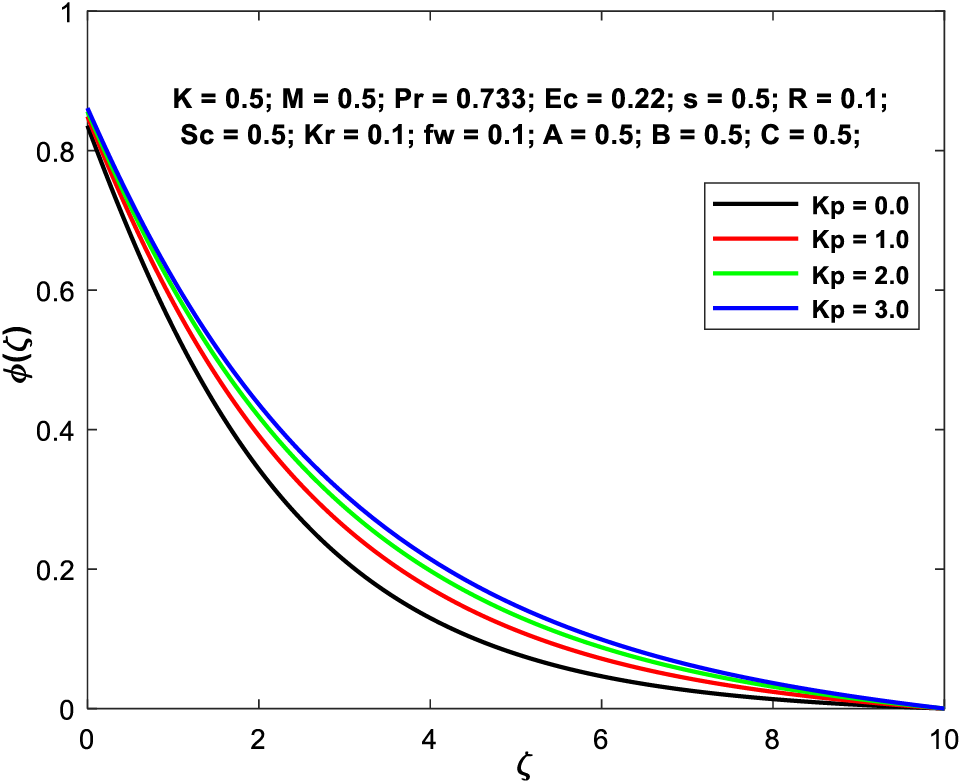
Figure 14d: ϕ(ζ) vs. Kp

Under such precise circumstances for varying values of the Pr, we have assessed by matching our numerical answer to the earlier study of [30–32]. The comparison demonstrates that there is an astounding level of consistency, as can be shown in Table 1.

Table 2 elucidates the friction upsurges with enriched values of M,K,s Kp fw,and A and the contradictory consequence is established in the couple stress. Nusselt number boosts with an increase of fw & A, and the opposite effect is found with a rise of M, K, s Kp & B. Sharewood number enhances with K, fw and reverses a trend observed M, s, Kp, A, C. The results shown in Table 3 illustrate that a rise in Pr results in a higher Nusselt number, but an opposite pattern is seen with Ec and R. The findings presented in Table 4 indicate that an increase in Sc and Kr causes a boost in the Sharewood quantity.

5  Conclusions

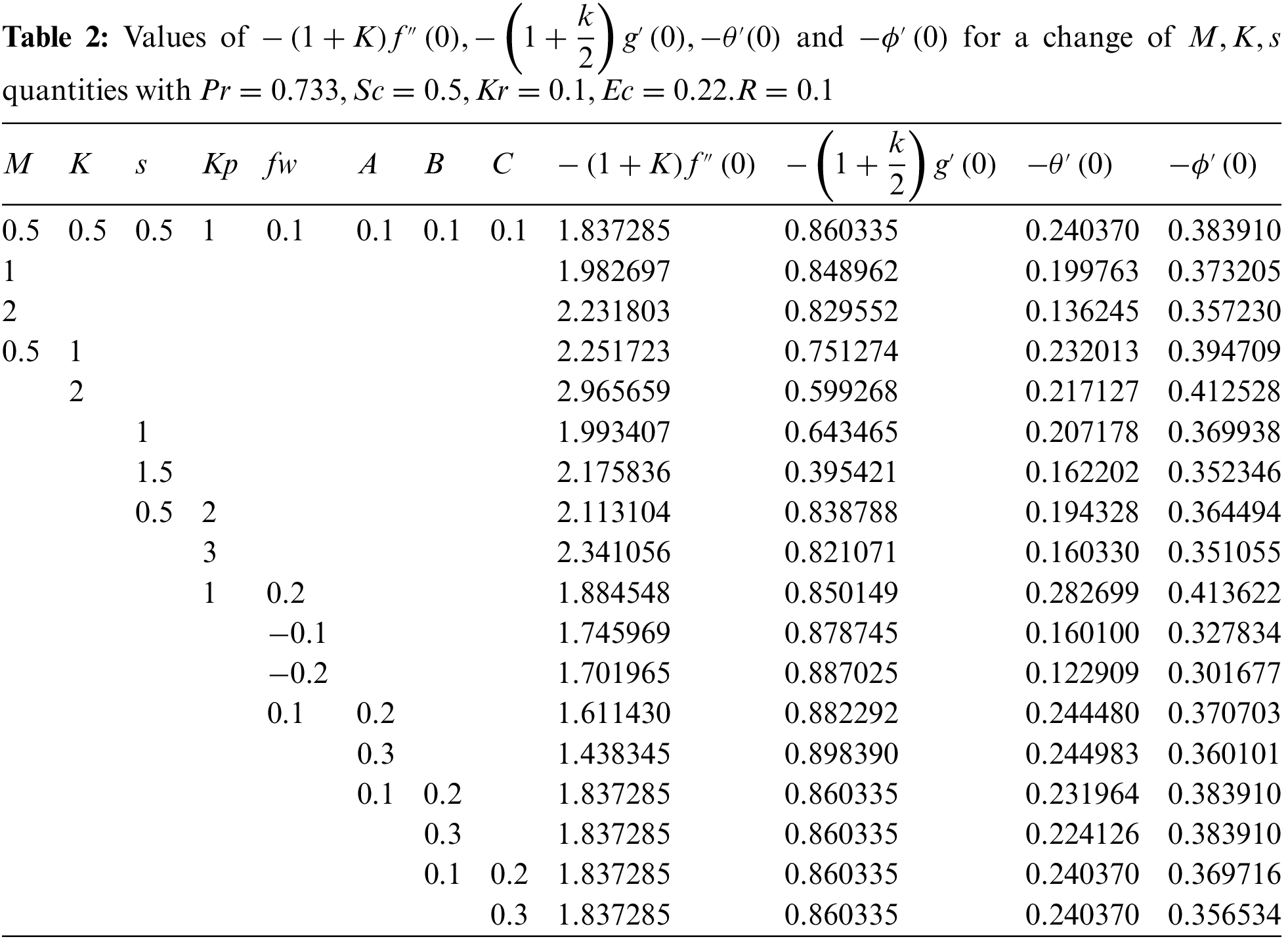
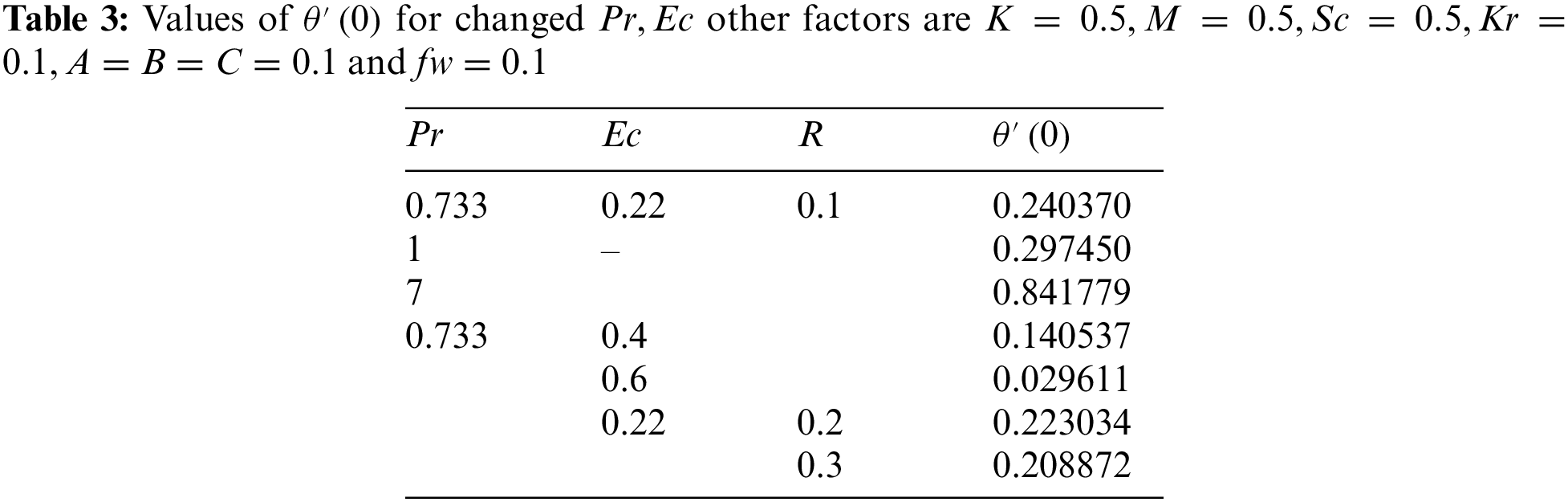
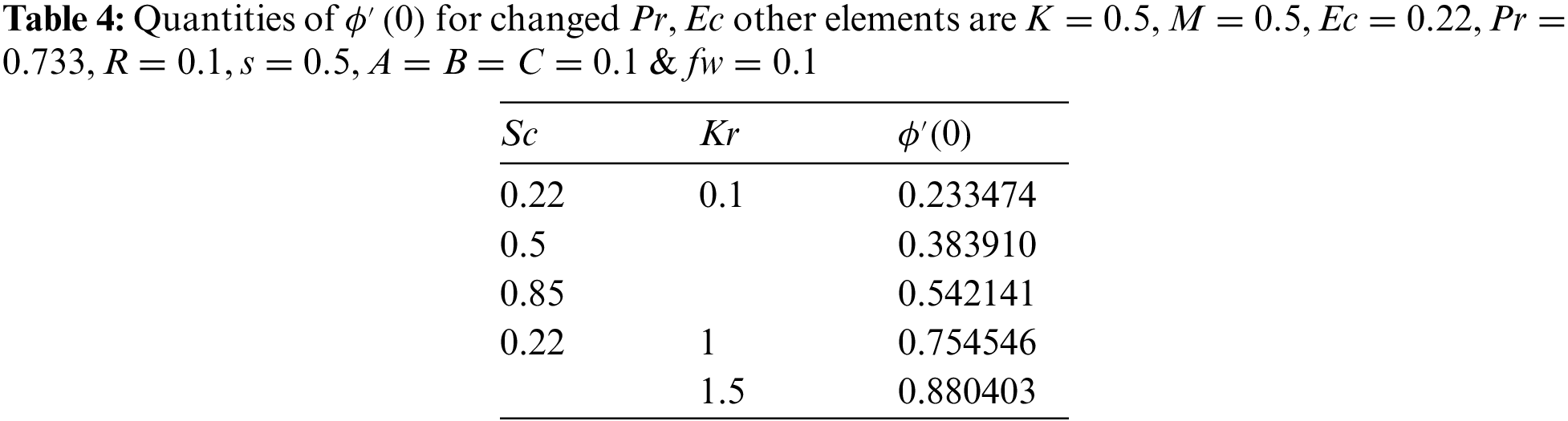
This work examines the impact that a slip impact has on the rate of mass transport along a radially expanding surface. The relevance of a changing magnetic field is also included in the analysis. The governing flow problem might be simplified with the use of a similar conversion model. Combining the shooting method with the bvp4c solver allows for the numerical solution of the resulting nonlinear ODEs. When compared to other published papers, the findings demonstrate a significant level of coherence. Work in the fields of solar energy collecting, recovery of petroleum products, and the dynamics of fires in insulation may all benefit from this kind of study. Key inferences may be made from the numerical data and the visual representation, including the following:

•   Velocity enhances when K values are raised, but declines as M and s quantities rise.

•   Microrotation rises with both M and s factor but declines with a larger K.

•   Raising the M, K, and Ec values raises the temperatures. Thus, by modifying these variables, a higher temperature may be attained.

•   The concentration upsurges as M enhances, but the concentration diminutions as K and Sc enhance.

•   Increases in M & K, the rise in the outcome of the friction and couple stress nevertheless lower −θ′(0) & −ϕ′(0).

•   Couple stress and −θ′(0) enhance with enhancement of sand the opposite effect is found in friction factor and −ϕ′(0).

•   As fw increases the result in friction & −ϕ′(0), −θ′(0).

•   With a rise in R, the result in −θ′(0) rises whereas a fall in Pr diminishes the result. The value of −ϕ′(0) rises when Sc and Kr increase.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: B.S. Goud and P. Srilatha; data collection: B.S. Goud and P. Srilatha; analysis and interpretation of results: E.R. Kumar and P. Srilatha; draft manuscript preparation: B.S. Goud and A.M. Hassan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No data was used for the research described in the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Gupta, P. S., Gupta, A. S. (1977). Heat and mass transfer on a stretching sheet with suction or blowing. The Canadian Journal of Chemical Engineering, 55(6), 744–746. [Google Scholar]

2. Cortell, R. (2006). A note on flow and heat transfer of a viscoelastic fluid over a stretching sheet. International Journal of Nonlinear Mechanics, 41(1), 78–85. [Google Scholar]

3. Goud, B. S., Srilatha, P., Bindu, P., Krishna, Y. H. (2020). Radiation effect on MHD boundary layer flow due to an exponentially stretching sheet. Advances in Mathematics: Scientific Journal, 9(12), 10755–10761. [Google Scholar]

4. Ganesh, G., Sridhar, W. (2021). Numerical approach of heat and mass transfer of MHD Casson fluid under radiation over an exponentially permeable stretching sheet with chemical reaction and hall effect. Frontiers in Heat and Mass Transfer, 16(5), 1–11. https://doi.org/10.5098/hmt.16.5 [Google Scholar] [CrossRef]

5. Subhashini, S. V., Sumathi, R., Pop, I. (2013). Dual solutions in a thermal diffusive flow over a stretching sheet with variable thickness. International Communications in Heat and Mass Transfer, 48, 61–66. [Google Scholar]

6. Ibrahim, S. M., Kumar, P. V., Lorenzini, G. (2020). Analytical modeling of heat and mass transfer of radiative MHD Casson fluid over an exponentially permeable stretching sheet with chemical reaction. Journal of Engineering Thermophysics, 29, 136–155. [Google Scholar]

7. Eringen, A. C. (1966). Theory of micropolar fluids. Journal of Mathematics and Mechanics, 16, 1–18. [Google Scholar]

8. Kazakia, Y., Ariman, T. (1971). Heat-conducting micropolar fluids. Rheologica Acta, 10(3), 319–325. [Google Scholar]

9. Turkyilmazoglu, M. (2016). Flow of a micropolar fluid due to a porous stretching sheet and heat transfer. International Journal of Nonlinear Mechanics, 83, 59–64. [Google Scholar]

10. Yacob, N. A., Ishak, A., Pop, I. (2013). Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet in a micropolar fluid. Thermal Science, 17(2), 525–532. [Google Scholar]

11. Singh, K., Kumar, M., Pandey, A. K. (2020). Melting and chemical reaction effects in stagnation point flow of micropolar fluid over a stretchable porous medium in the presence of nonuniform heat source/sink. Journal of Porous Media, 23(8), 767–781. [Google Scholar]

12. Abbas, W., Megahed, A. M. (2021). Numerical solution for chemical reaction and viscous dissipation phenomena on non-Newtonian MHD fluid flow and heat mass transfer due to a nonuniform stretching sheet with thermal radiation. International Journal of Modern Physics C, 32(9), 2150124. [Google Scholar]

13. Goud, B. S. and Nandeppanavar, M. M. (2023). Effect of thermal radiation on magnetohydrodynamics heat transfer micropolar fluid flow over a vertical moving porous plate. Experimental and Computational Multiphase Flow, 5(2), 149–158. [Google Scholar]

14. Goud, B. S. (2020). Heat generation/absorption influence on steady stretched permeable surface on MHD flow of a micropolar fluid through a porous medium in the presence of variable suction/injection. International Journal of Thermofluids, 7, 100044. [Google Scholar]

15. Prasad, K. V., Vaidya, H., Vajravelu, K., Rashidi, M. M. (2017). Effects of variable fluid properties on MHD flow and heat transfer over a stretching sheet with variable thickness. Journal of Mechanics, 33(4), 501–512. [Google Scholar]

16. Hayat, T., Qasim, M. (2010). Effects of thermal radiation on unsteady magnetohydrodynamic flow of a micropolar fluid with heat and mass transfer. Zeitschrift für Naturforschung A, 65(11), 950–960. [Google Scholar]

17. Uddin, Z., Kumar, M., Harmand, S. (2014). Influence of thermal radiation and heat generation/absorption on MHD heat transfer flow of a micropolar fluid past a wedge considering hall and ion slip currents. Thermal Science, 18(suppl. 2), 489–502. [Google Scholar]

18. Awan, A. U., Akbar, A. A., Hamam, H., Gamaoun, F., Tag-ElDin, E. M. et al. (2022). Characterization of the induced magnetic field on third-grade micropolar fluid flow across an exponentially stretched sheet. Frontiers in Physics, 10, 964653. [Google Scholar]

19. Prakash, D., Muthtamilselvan, M. (2014). Effect of radiation on transient MHD flow of micropolar fluid between porous vertical channel with boundary conditions of the third kind. Ain Shams Engineering Journal, 5(4), 1277–1286. [Google Scholar]

20. Patil, P. M., Kumbarwadi, N. (2018). Effects of MHD mixed convection with non-uniform heat source/sink and cross-diffusion over exponentially stretching sheet. International Journal of Numerical Methods for Heat & Fluid Flow, 28(6), 1238–1255. [Google Scholar]

21. Abdal, S., Ali, B., Younas, S., Ali, L., Mariam, A. (2019). Thermo-diffusion and multislip effects on MHD mixed convection unsteady flow of micropolar nanofluid over a shrinking/stretching sheet with radiation in the presence of heat source. Symmetry, 12(1), 49. [Google Scholar]

22. Pal, D., Mandal, G. (2017). Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. International Journal of Mechanical Sciences, 126, 308–318. [Google Scholar]

23. Goud, B. S., Nandeppanavar, M. M. (2021). Ohmic heating and chemical reaction effect on MHD flow of micropolar fluid past a stretching surface. Partial Differential Equations in Applied Mathematics, 4, 100104. [Google Scholar]

24. Singh, K., Pandey, A. K., Kumar, M. (2020). Slip flow of micropolar fluid through a permeable wedge due to the effects of chemical reaction and heat source/sink with hall and ion-slip currents: An analytic approach. Propulsion and Power Research, 9(3), 289–303. [Google Scholar]

25. Fatunmbi, E. O., Ogunseye, H. A., Sibanda, P. (2020). Magnetohydrodynamic micropolar fluid flow in a porous medium with multiple slip conditions. International Communications in Heat and Mass Transfer, 115, 104577. [Google Scholar]

26. Goud, B. S., Reddy, Y. D., Alshehri, N. A., Jamshed, W., Safdar, R. et al. (2022). Numerical case study of chemical reaction impact on MHD micropolar fluid flow past over a vertical riga plate. Materials, 15(12), 4060. [Google Scholar] [PubMed]

27. Hasnain, J., Abbas, Z. (2019). Entropy generation analysis on two-phase micropolar nanofluids flow in an inclined channel with convective heat transfer. Thermal Science, 23(3), 1765–1777. [Google Scholar]

28. Kumar, L. (2009). Finite element analysis of combined heat and mass transfer in hydromagnetic micropolar flow along a stretching sheet. Computational Materials Science, 46(4), 841–848. [Google Scholar]

29. Brewster, M. Q. (1992). Thermal radiative transfer and properties. John Wiley & Sons, New York. [Google Scholar]

30. Chen, C. H. (1998). Laminar mixed convection adjacent to vertical, continuously stretching sheets. Heat and Mass transfer, 33, 471–476. https://doi.org/10.1007/s002310050217 [Google Scholar] [CrossRef]

31. Fatunmbi, E. O., Adeniyan, A. (2018). Heat and mass transfer in MHD micropolar fluid flow over a stretching sheet with velocity and thermal slip conditions. Open Journal of Fluid Dynamics, 8, 195–215. [Google Scholar]

32. Grubka, L. J., Bobba, K. M. (1985). Heat transfer characteristics of a continuous stretching surface with variable temperature. Journal of Heat Transfer, 107(1), 248–250. https://doi.org/10.1115/1.3247387 [Google Scholar] [CrossRef]