The Numerical Simulation of Nanofluid Flow in Complex Channels with Flexible Wall

Nomenclature

1  Introduction

The topic of improving heat transport in intricate geometries is crucial. This advantage results from its use in a wide variety of heat exchangers, chemical treatment, electrical stations, and electronic device applications in industry and engineering [1]. Nanoparticles, cavities, and fluid structure interaction can be used to improve heat transmission in heat exchangers (FSI) [2].

Fluid structure interaction (FSI) is used in a wide range of cutting-edge systems, including power plants, chemical therapies, the food industry, the paint industry, mixing devices, micro-scale biological investigations, cooling of electronic components and heat exchangers [3], clinical evaluation and medical devices [4]. Electronic component cooling is one of the most critical barriers to system development in terms of being faster, smaller, and more reliable [5].

The focus of this research is FSI installed in flexible walls. Multiple researchers looked into this kind, such as [6]: studied numerically the behavior of convection inside a cavity containing a nanofluid, where the left wall of the cavity moves vertically towards the top and has a cold temperature, while the right wall has a high temperature, and the rest of the cavity wall is isolated. The following parameters were used in a study to study their effect on heat transfer: internal Ra (between 103 and 106), (Ri) between 0.01 and 100, (Ha) between 0 and 50, magnetic field inclination angle (between 0° and 90°), (E of a flexible wall between 5 × 102 and 106) and the effects of nanoparticle volume fractions ranging from 0 to 0.05. The average heat transfer falls when the Richardson number lowers and the Hartmann number and internal Rayleigh number increase. and also conducted another study [7], a numerical representation of the mixed convection that occurs in a square hollow that is filled with SiO2 nanofluid and volumetric heat production with a flexible wall an inner spinning cylinder and. The hollow walls and the surface of the cylinder are considered to be adiabatic, and the top wall is kept cold and the bottom wall hot. For different solid nanoparticle shapes, the effects of external Rayleigh number (103–5 × 105), internal Ra 104–106, E = 5 × 102–106, nanoparticle volume fraction (0–0.03) in fluid flow, the angular rotational speed of the cylinder (from −2000 to 2000) and heat transfer are numerically studied (spherical, cylindrical, brick, and blade). The elastic modulus of the flexible wall and internal Rayleigh number decrease while the outward Rayleigh number enhances local and averaged heat transmission. Cylinder rotation improves heat transmission for all nanoparticle kinds. Cylindrical nanoparticles promote heat transmission better than spherical ones, and also [8] studied numerically explored nanofluid mixed convection, elastic-wall, 3D, inner cylinder and trapezoidal chamber. The impacts of the Ri from (0.05–50), side surface elastic modulus (103–105), side wall inclination angle (0°–20°), and volume friction percentage (0–0.04) on heat transfer of fluid flow in a 3D lid-driven trapezoidal hollow were studied numerically. The relevant factors affect these traits. Flexible side surfaces influence on the rate of transmission of heat. The angles of wall inclination between 0° and 10°, flexible side walls increase and decrease space, respectively, affecting heat transmission. For side wall inclination angles of θ = 0°, increasing the elastic modulus from 1000 to 105 raises Nuavg about 9.80%. At the maximum volume friction percent increases heat transmission linearly by 25.30%, there is another study for [9] about flexible wall, where MHD with nanofluid in a flow square chamber with a lid-driven flexible side wall was quantitatively examined. The cavity’s top wall travels at a steady speed and is cooler than the bottom wall. Insulation covers other cavity walls. For the following parameters: the effect of the flexible wall’s Young’s modulus (104 N/m2–2.5 × 105 N/m2), with Ri = 0.01–5, a Ha = 0–5, and φ = 0–0.04, on flow and heat transmission is quantitatively studied. The average of transmission of heat decreases with Ha and Ri values. As the flexible wall’s Young’s modulus drops for E = 104 N/m2, the mean heat transmission increases by 66.5% compared to E = 2.5 × 105 N/m2. Reference [10] employed a square cavity to probe the effect of natural convection. The cavity was divided into halves by the flexible wall into two triangles. For the purpose of eliciting the movement of the flexibale wall, an arbitrary Lagrangian-Eulerian (ALE) is employed. A number of factors, including fluid characteristics and wall stiffness, were investigated for their effects and also [1] FSI was utilized in order to investigate the process of heat transmission in a compartment with an elastic bottom wall, a lid-driven by mixed convection, and laminar flow. The findings revealed that the flexible bottom wall improves heat transmission. Reference [11] utilized a square elastic-walled chamber with variable Hartmann from (0–200) and Rayleigh numbers from (105–108) and an adjustable magnetic field direction (0–180 degrees). Reference [12] investigated the transport of heat by mixed convection in a cavity that has a wall that is flexible. The impact of heat transfer in a heat exchanger was investigated by using many parameters, such as the ratio of the height of the channel to the height of the cavity, H/D = 0.5–1.1, the radius of the cavity, Ri = 0.1–100, and the length of the heat source = 0.5–1.5. As can be seen from the data, H/D influences the Nusselt number by around 5%. Reference [13] investigated the numerical of the wall FSI for a backward-facing step in nanofluid forced convection. The bottom wall of the step was flexible. The ranges of these parameters were employed in this investigation: Re = 25–250, E = 104–106, and the volume percentage of solid particles = 0–0.035. Heat transmission rates were found to be enhanced when the elastic bottom wall was utilized. At Re = 250 and E = 104, heat transmission is at its maximum. For all Reynolds numbers, the flexible bottom wall has an average increase in Nusselt number of roughly 6.1% compared to a rigid bottom wall at E = 104. Reference [14] used the FSI technique to study its effect on heat transfer, and a cavity in the shape of an “L” with a flexible wall and an inclined wall was used. The study was completed with a magnetic field, whose angle of inclination ranged between 0 and 90 degrees. In addition to that, the following parameters were used: Ha = 0–50, Ra = 104–106, φ = 0–0.04, Ri = 0.03–30, and E = 104–108. The results obtained showed that the flexible wall affected the heat transfer significantly. Nu increases when the size of the nanoparticles used increases. Reference [15] studied wall FSI, utilizing elastic wall cavities. Conventional mixing of a nanofluid consisting of CuO and water was induced in a cavity by the use of an angled magnetic field. Simulations numerically are obtained by utilizing the Arbitrary-Lagrangian-Eulerian method. The numerical effects of changing parameters such as the Reynolds number (from 100 to 500), the magnetic inclination angle (from 0 degrees to 90 degrees), the Hartmann number (from 0 to 40), the elastic modulus of the flexible wall (from 104 to 108), and the nanoparticle volume fraction (from 0 percent to 3 percent), were studied. It was found that the average Nusselt number went up by between 9 and 9.5 percent when the maximum amount of nanoparticles was added, both with and without a magnetic field. Ismael [16] created vortex using a flexible wall with upstream and downstream baffles. According to the findings, heat transport is improved by 94% in channels that are equipped with baffles as opposed to channels that do not have baffles at Re = 250 and [17] analyzing the performance of a right-wall FSI in a square cavity with natural convection and a solid cylinder within. Since the solid cylinder affected the passing solution and altered the interaction between the structure and the flow, the results show that the flexible wall of the hollow maintained its S form. Increased wall flexibility can lead to a 2 percent rise in the average Nusselt number. Reference [18] employed a cavity to study fluid–structure interaction (FSI) by vertically dividing it with a thin flexible wall. The left vertical wall was heated in a sinusoidal way that changed over time, whereas the isothermal cooling method was used to chill the right vertical wall. To tackle this problem, a Lagrangian–Eulerian technique was used. The following characteristics were used to describe impact heat transfer: elasticity modulus (5 × 1012–1016), Prandtl number (0.7–200), and Rayleigh number (104–107). The outcomes reveal frequency of temperature changes has no significant effected on (Nu) and flexible membrane distortion. When the Prandtl number of a fluid goes up, convective heat transfer and membrane stretching go up and Al-Amir et al. [19] employed a hexagonal cavity to investigate the effects of magneto hydrodynamic forced convection on a CNT-water nanofluid. Parameters like the Hartmann number (Ha) = 0–60, the Re = 100–1000, φ = 0–0.1 were used, along with the modulus of elasticity of wall that used in the left and bottom walls between 104–107. Recently, it has come to light that the bottom enclosure wall is very sensitive to the elastic wall.

Also, there are many previous studies that focus on their studies on corrugated channel, such as [20]: studied corrugated channel entry convective heat transfer. Water was tested with two-channel spacing at 20° corrugation. I50 ≤ Re ≤ 4000 flows were tested. Low Reynolds-number flow visualization revealed longitudinal vortices, whereas higher Reynolds numbers exhibited spanwise vortices. Corrugated channels showed 130% and 280% greater friction factors than parallel-plate channels for Re > 1500. Corrugated channels outperformed parallel-plate channels in heat transfer at similar mass flow rate, pumping power, and pressure drop per unit length. Reference [21] studied what happens to heat transfer and pressure drop in a corrugated channel experimentally and explained the effect of each change in phase shaft and channel spacing on heat transfer and pressure drop. parameters were used in his study: Re = 3220–9420, a constant corrugation rate, and a constant wall temperature. According to the findings, the average heat transfer coefficient increased by 2.6 to 3.2 and the pressure decreased by 1.9 to 2.6. Reference [22] studied numerically and experimentally the heat transfer in three channels of different shapes (straight, sinusoidal, and trapezoidal). In channels, SiO2-water was used as the working fluid with volumetric friction of 0%–1%. Whereas the results of his study revealed that the average Nu increases and pressure drop decreases as the volumetric friction of the nanoparticles increases, The corrugated trapezoidal channel promotes more heat transfer than the straight or sinusoidal channel. Reference [23] studied to evaluate the thermal and flow implications that a magnetic source has on mixed convection conditions within an unique arc-shaped lid-driven cavity issue. Ferrofluid made of Fe3O4, and water is what fills it up. Several parameters were applied, including Richardson numbers (about 0.04 to 40), magnetic numbers (about 0 to 100), and solid volume fractions (about 0 to 0.05). According to the findings, an increase in the rate of heat transmission of up to 338.35% is possible when Ri is equal to 0.04, thanks to the activities of the magnetic field, arc-shaped walls, and magnetite nanoparticles suspended in suspension. Reference [24] studied Numerically, the thermal properties of nanofluids inside a semicircular zigzag channel. Water was used as a basic liquid with four types of nanoparticles (CUO, SiO2, ZnO, and Al2O3) with volume frictions between 2 and 8 percent and a diameter between 20 and 80 nanometers. The results obtained in his study explained that the thermal performance effects of a semicircular zigzag channel are greater than those of a flat channel. The results also revealed that increasing the diameter of the nanoparticles resulted in a decrease in Nu, but it increased as volume friction and Re increased. Reference [25] employed silicon dioxide (SiO2)-water nanofluid as a working fluid in two different forms of corrugated channels, including the straight channel (SC) and the new form of a trapezoidal-corrugated channel (TCC). It was done using nanofluids with SiO2 volume fractions from 0.0% to 2.0% with Reynolds numbers (10,000–30,000). When compared to straight channel, the utilization of corrugated channel (TCC) resulted in an increase of heat transfer rates of up to 63.59%, a drop in pressure of up to 1.37 times, and an increase in thermal performance of up to 2.22 times. There are many previous studies that used particles of Al2O3 in working fluid, such as: Naphon [26] investigated heat transport in a wavy channel with variable phase angles (20–60) with a range of Re =400–1600. Where it was found that the wavy surface affects pressure drop and heat transmission. Reference [27] looked at the convection currents in a V-shaped channel at phase angles between 0 and 180 degrees. These findings demonstrated the significant impact the channel’s distinctive V shape had on thermal conduction. Reference [28] examined nanofluid thermal characteristics in a trapezoidal channel using water as the base fluid and four nanotypes (SiO2, ZnO, Al2O3, and CuO) with concentrations of 2%, 4%, 6%, and 8%. SiO2 is the best heat-transfer liquid. Reference [29] investigated Al2O3 performance flow with concentrations (0%–4%) in triangular, trapezoidal, and sinusoidal channels with Re = 6000–22000. Trapezoid shapes had high nusselt numbers also [5] focus in his study at Al2O3 where investigated the behaviour of a 90° elbow-shaped nanofluid of Al2O3 and water. A multiphase mixture model was used to numerically apply it to the forced convection and 3D model. Several Reynolds numbers (between 10,000 and 100,000), nanoparticle volume fractions (between 0.02 and 0.06), and nanoparticle sizes make up the simulation settings (10 to 40). The findings demonstrated that the Reynolds number with a reduced DP and an increase in the volume of the nanoparticle fraction prevented the formation of vortices in the flow. The volume percentage and diameter of the nanoparticles both decrease as the pressure drop rises. Towards the exterior wall, significant heat transfer rates are seen. Reference [30] looked into the relationship between the Reynolds and Nusselt numbers by employing a wavy channel with a phase angle of =0–180 and a Reynolds number (Re) of 1000 to 10000. Nu increased when Re increased, as predicted by the data.

In recent years, there has been an uptick in interest in the study of heat transport in a broad variety of engineering geometries. The majority of studies only considered one-sided, regular-shaped flexible walls (square, rectangle, triangle, etc.). Here, we model fluid flow in a complex channel comprised of six elastic walls. The effort aims to improve heat transmission in cases when cooling is impossible due to the formation of vortices as a result of the structure’s complexity. The vortices were released by the elastic wall's vibration and replaced by additional vortices. This motion is continuous with the movement of the wall, resulting in heat exchange between the wall and the fluid. In this research, heat transfer and fluid flow fields in a heat exchanger with a complex channel were analyzed to examine how the Reynolds number, Cauchy number (modulus of elasticity), and elastic wall location in a heat exchanger with a complex channel shape impact the flow field and heat transfer.

2  Theoretical Formulations

2.1 Model Description

A description of the geometry that is applied throughout this investigation is found in Fig. 1. The geometry is represented by a channel that extends over two dimensions, with the length marked by the letter L1 and the height signified by the letter H1 as shown in Table 1. The intricate channel has a flexible wall that is attached to the wall of the channel in six different locations along the channel wall. The temperature of the wall of the complex channel is kept at a relatively high level TH at all times. The temperature of the Al2O3–water nanofluid that is moving through the complex channel has a uniform temperature Tc and velocity u0. The findings of this research are applied to a number of different geometric shapes that have ratios of L2/H2 that range from 0 to 6, as well as flows that are unstable, incompressible, laminar, and two-dimensional that are forced convective fluxes. The subjects of the parameter assessments were the Reynolds number, which varied from 60 to 160; the Cauchy number of the baffle, which ranged from 10−4 to 10−8; and lastly, the volume percentage of the nanoparticles, which went from 0 to 0.06.

Figure 1: A diagrammatic depiction of the situation of a complicated channel that includes Flexible wall

2.2 Governing Equations

In dimensional vector form, the governing equations of the unstable fluid and the elastic-dynamic structure are written as:

Continuity Equation ∇⋅u∗=0(1)

Momentum Equation∂u∗∂t∗+(u∗−w∗)⋅∇u∗=−1ρf∇p∗+υf∇2u(2)

Thermal energy ∂T∗∂t∗+(u∗−w∗)⋅∇T∗=αf∇2T∗(3)

Thermal energy in solid∂T∗∂t∗=αf∇2T∗(4)

For elastic structure domain, it is possible to write the equations that describe the nonlinear elastic displacement, and the energy of the wall as follows [18]:

ρsd2ds∗dt∗2+∇σ∗=Fv∗(5)

dT∗dt∗=αs∇2T∗(6)

Fv∗ in Eq. (5) is representing the gravitational forces per unit volume and written as [12]:

Fv∗=ρsgy(7)

where (u*) is the velocity vector, (w*) identify the speed of the moving coordinates, (p*) identify the fluid pressure, (T*) identify the fluid/solid temperature, (Fv∗) identify the gravitational force exerted on the heated wall measured in terms of unit volume. However, (Fv∗) is ignored in the current work as the wall elasticity is fastened at one end and unrestrained at the other and (σ*) identify the Cauchy stress tensor. ρf and ρs represent the densities of fluid and solid respectively. αf and αs represent thermal diffusivities of the fluid and the solid, respectively, gy is the gravitational forces, vf identify the kinematic viscosity of the fluid and β is volumetric thermal expansion coefficient.

This stress may be described using the following form of equations. The elastic wall is subjected to a stress tensor as a result of the fluid flow pressure taking the nonlinear geometry variation [12]:

Where F=(I+∇ds∗), (I: unity matrix), J = det. (F) and S is the second Piola-Kirchhoff stress tensor that relevant to the strains in the hot wall [12] as:

S=C,ε=12(∇ds∗+∇ds∗T+∇ds∗T∇ds∗)(8)

where C is a function of dimensional modulus of elasticity and possin’s ratio as shown below and the colon is the double-dot tensor product.

C=C(C⋅υ)(9)

where E is the modulus of elasticity of the wall or and v is the Poisson's ratio.

2.3 Dimensional Boundary Conditions

a)   On the elastic wall, the boundary conditions are continuity of dynamic movement and kinematic forces [18]

∂ds∗∂t∗=u∗(10)

σ∗⋅n=−p∗+Mf∇u∗(11)

where (u*) is the velocity vector, (p*) identify the fluid pressure, el (σ*) identify the Cauchy stress tensor, (n) identify is the normal vector and (μf) identify is the viscosity of fluid.

b)   The energy balance may be defined at the boundary between the fluid and the solid as [18]:

Kf∂T∗∂n|f=Ks∂T∗∂n|s(12)

where Ks and Kf are the thermal conductivities of solid and fluid, respectively, and n is a normal vector.

c)   The elastic wall in the present work with different positions and free displacement fixed with ∂ds∗∂t∗=0 at all corner this mean end and starting of piece of elastic line. The condition of the pressure constraint is applied at the exit hole at the right wall, i.e., p* = 0 [18].

d)   The fluid inlet velocity is u∗=uin

e)   T∗=Th at y = lower and upper wall. 0<y≤L.

f)   T∗=Tc at x=0.0<y≤H.

The following non-dimensional parameter definitions were utilized in order to non-dimensionalize the governing equations [2]:

θ∗=T∗−TcTpn−Tc,X=xL,Y=yL,U∗=u∗uo,Ug∗=uguo,V∗=v∗uo,Vg∗=vgvo,P=pρfuo2,vT=vnfvf,ρT=ρnfρf,Reρf.u0.Lμf,δ=σnfσfKr=knfkf,(ρCp)T=(ρCp)nf(ρCp)f,αT=αnfαf,σ=σ∗E∗,E=E∗.L2ρnf.αnf,Fv=(ρnf−ρs)LEv,ds=ds∗L,τ=u0.tL,Ca=ρf.uo2E

By substituting the non-dimensional parameters from before, the dimensional governing Eqs. (5)–(8) may be expressed in the non-dimensional form as [19]:

∂U∗∂X+∂V∗∂Y=0(13)

∂U∗∂τ+(U∗−Ug∗)∂U∗∂X+(V∗−Vg∗)∂U∗∂Y=−1ρT.∂P∂X+vTRe(∂2U∗∂X2+∂2U∗∂Y2)(14)

∂U∗∂τ+(U∗−Ug∗)∂V∗∂X+(V∗−Vg∗)∂V∗∂Y=−1ρT.∂P∂Y+vTRe(∂2V∗∂X2+∂2V∗∂Y2)(15)

∂θ∗∂τ+(U∗−Ug∗)∂θ∗∂X+(V∗−Vg∗)∂θ∗∂Y=−αTRePr(∂2θ∗∂X2+∂2θ∗∂Y2)(16)

For the elastic Baffle [16]:

CaPrd2dsdt2−∇σ=0(17)

∂θ∂t=αr∇2θ(18)

These equations have been transformed from the dimensional system to the non-dimensional system using the helpful definitions given above and also the dimensionless numbers as shown below:

Pr=υfαf is the Prandtl number, Re=uin(2H)vf is the Reynolds number, Caρfuin2E is the Cauchy number which is defined as the ratio of inertia to elastic forces Fυ=CaHgyρruin2 is the dimensionless body force ρr=ρfρs is density ratio, αr=αsαf is thermal diffusivity ratio.

The value of the body force is assumed to be zero in this calculation. (Fʋ = 0) to ease the problem as mentioned. And Ks = 10 knf.

2.4 Dimensionless Boundary Conditions

Now the previous boundary conditions for the fluid and the solid may be rewritten in a form of dimensionless as follows:

a)   θ=1atY=0,andH,0<X≤L, is dimensionless of hot temperature at upper and lower wall.

b)   θ=0atX=0,0<Y≤H is dimensionless of cold temperature at inlet channel.

c)   ∂θf∂n=Kr∂θs∂n

u=∂ds∂t(19)

1Caσ⋅n=−p+1Re∇u(20)

The inlet velocity becomes U = 1, also assuming a dimensionless shape, the starting temperatures of the wall and the fluid inside the channel are both zero. In addition, the dimensionless pressure is equal to zero (P = 0).

As a result of employing the dimensionless definitions, the previous equation results in [18]:

Nut=−KnfKf∂θ∂n|wall(21)

Nui¯(τ)=−1li∫0LiKnfKf∂θ∂n|wallds(22)

at the point where the wall and the fluid meet one another. In addition, instantaneously integrate the instantaneous local temperature gradient to obtain the average Nusselt number is calculated by Eq. (22) over the distance of interest at the hot wall of the channel as:

where (Nu(t))av is the average Nusselt number, Li is the length of hot wall.

The preceding expression is then averaged throughout a cyclic of time (τ) using the following formula in order to get the time-averaged Nusselt number:

Nuav=1τ∫0τNu(t)avdt(23)

The skin friction coefficient interest with physical quantities of this problem which are defined as [2]:

Cf=τwρUin2(24)

where τw is the shear stress.

It is vital to compute a comprehensive criterion to assess the performance of the heat transfer in the current situation. This criteria is a phrase that does not have any dimensions, and it takes into consideration the process of heat transmission as well as the pressure drop that is created all the way down the channel. Utilizing this criteria, it is feasible to investigate the influence that geometrical factors have under a variety of flow situations [2]:

TEC=(NuavNu0)(ff0)13(25)

The subscript “o” refers to the channel that is not bewildered. The performance of mechanical may be measured in terms of the flow resistance factor, denoted by the letter “f,” which is defined as the ratio of wall shear stress to the kinetic energy of the flow. Following is an equation that was used to derive an estimate for the friction factor depending on the pressure drop readings [2]:

f=2ΔP∗Dhρuin2L(26)

where ρ is density of fluid, L = 30 cm is the length of the channel, ∆p is the dimensional of pressure drop ΔP=ΔP∗ρUin2, Dh is the hydraulic diameter (Dh = H).

ΔP=Pout−Pin(27)

f=23ΔP(28)

The performance evaluation criteria (TEC) was obtained by Eq. (28). Noticeably, TEC > 1 means that improvement of heat transfer larger than pressure drop.

2.5 Effective Thermal Properties of Al2O3-Water Nano Fluid

The use of Nano fluids needs to define the effective properties that are considered experimental such as heat capacity, density, viscosity, thermal conductivity and specific heat [13].

Thermal Conductivity of nanofluid:knfkbf=kp+2kbf+2(kpf−kp)φkp+2kbf −(kbf−kp)φ(29)

Specific Heat of nanofluid:cpnf=φ(cp)P+(1−φ)(cp)bf(30)

Effective Viscosity of nanofluid:μnf=μbf(1+2.5φ)(31)

Effective Density of nanofluid:ρnf=(1−φ)ρbf+φρP(32)

These properties are considered among the most important factors in convective properties for Al203 as nanoparticle and water as base fluid as shown in Table 2 [29].

3  Mesh Independences

As a direct result of the deformation of domains, specific focus should be concentrated on finding numerical solutions to FSI issues. A strategy known as the ALE method emerges as a viable option after reviewing the relevant literature. This method combines elements of both the Eulerian and the Lagrangian approaches.

The FEM was used to solve the Eqs. (13)–(20). Using a weak formulation method, the Galerkin technique is employed to solve the governing equations of the finite element methods. As can be seen in Fig. 2, the cells have been subdivided into non-structural mesh distribution components. The entirety of the computational domain makes use of finite elements Lagrange triangular of varying for the variables of pressure, temperature and velocity. The governing equations are be near to in order to derive the residuals conservation equations. To make the nonlinear momentum equations easier to solve, the Newton-Raphson technique was applied. Solution convergence is predicted if the following prerequisites are met [2].

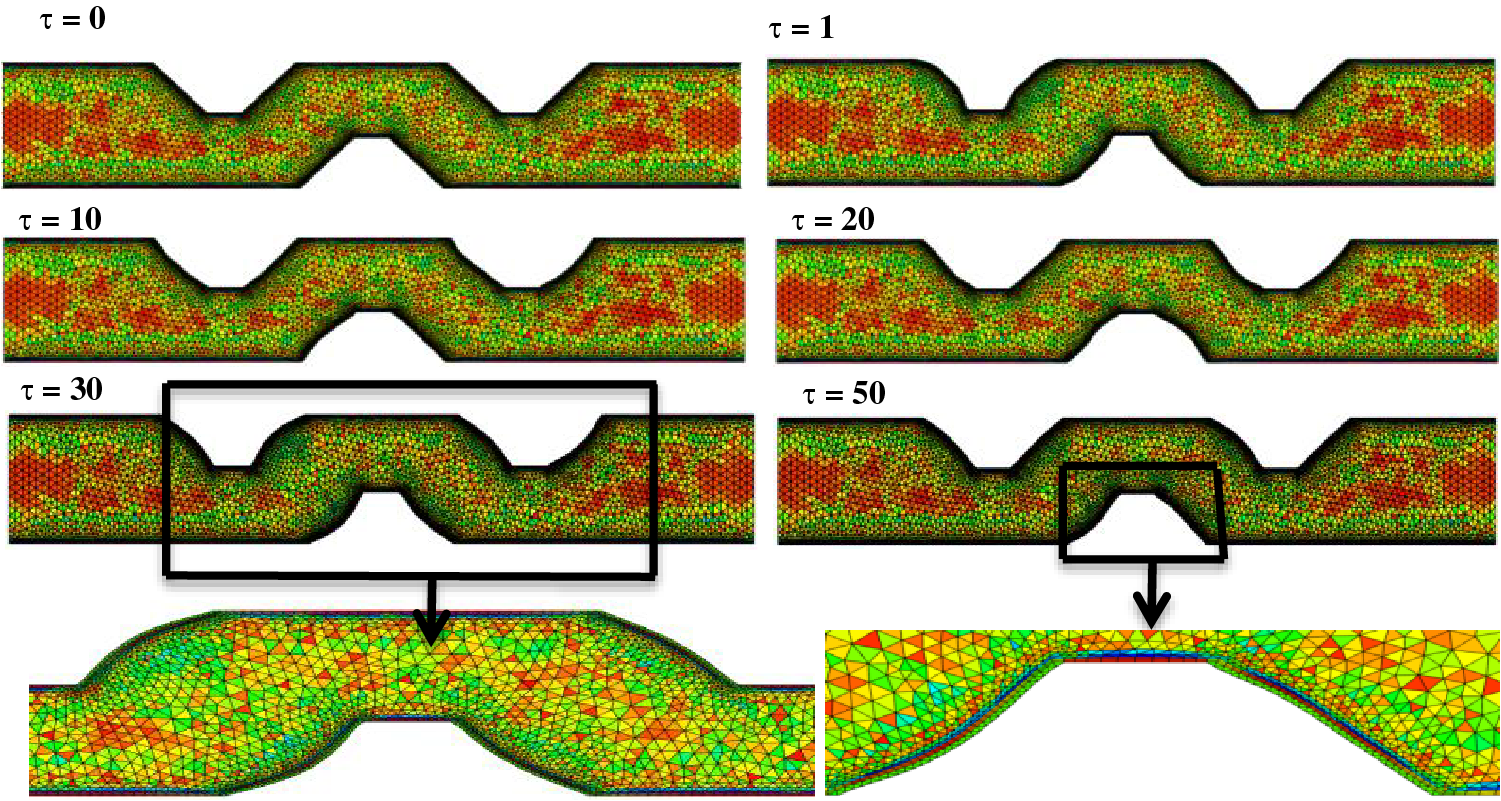
Figure 2: Mesh deformation changes over time for Re = 60, H2/L2 = 3, Ca = 10−4, φ = 0.02 and Pr = 6.9

|ξm+1−ξmξm+1|≤10−6

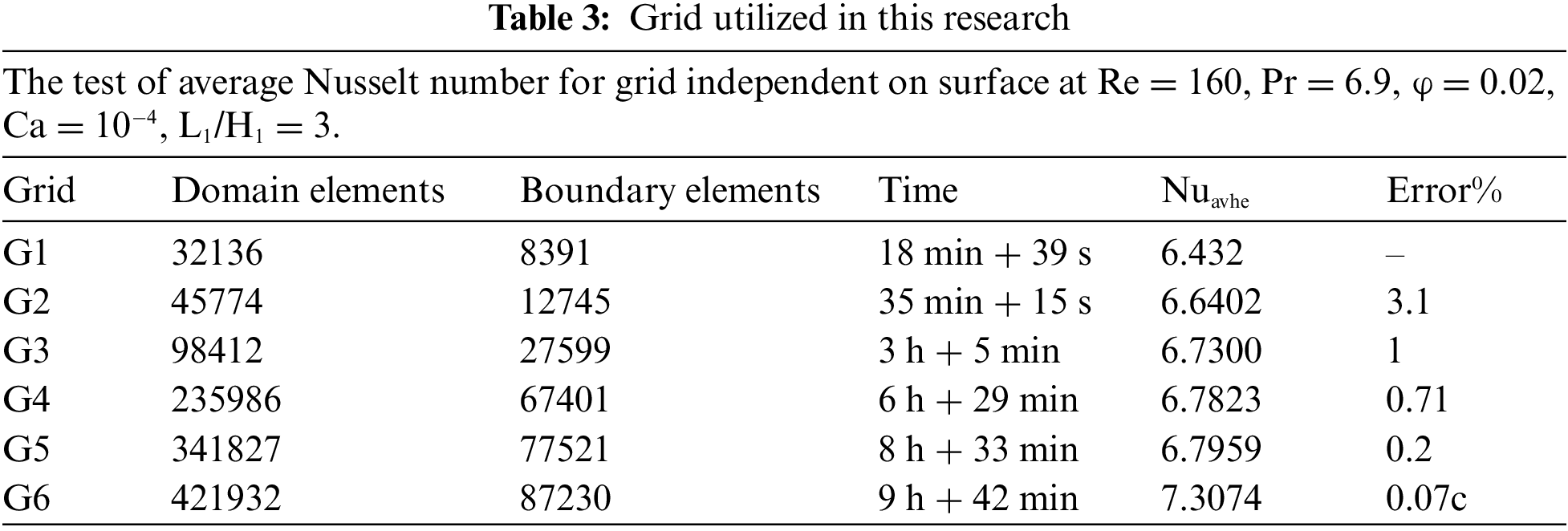
Any independent variables, where m denotes the number of iterations (velocity, temperature or pressure). To validate the correctness of the calculated findings, a grid-independent test is now required. Six grid resolutions were used to accomplish this, as shown in Table 3. The average Nusselt number on the hot surface at Ca = 1e-4, Re = 160, φ = 0.02, Pr = 6.9 was studied during this test. However, the numerical findings must be checked, and Fig. 2 shows that the grid size G5 with domain elements (341827) and boundary elements of (77521) was effective enough to be integrated into the numerical solution, with an error of around 0.2%.

4  Validation

This paper solved the transmission of heat for a forced convection flow problem in a complicated channel with elastic wall. The details of validated geometry Sabbar et al. [12] are displayed in Figs. 3 and 4, at Re = 150, H/D = 0.7 where H is the height of the channel and D is the height of cavity, LH = 0.9 is the length of heat source and Ri = 10. This explains the excellent concordance between the outcomes of our study and those of Sabbar et al.

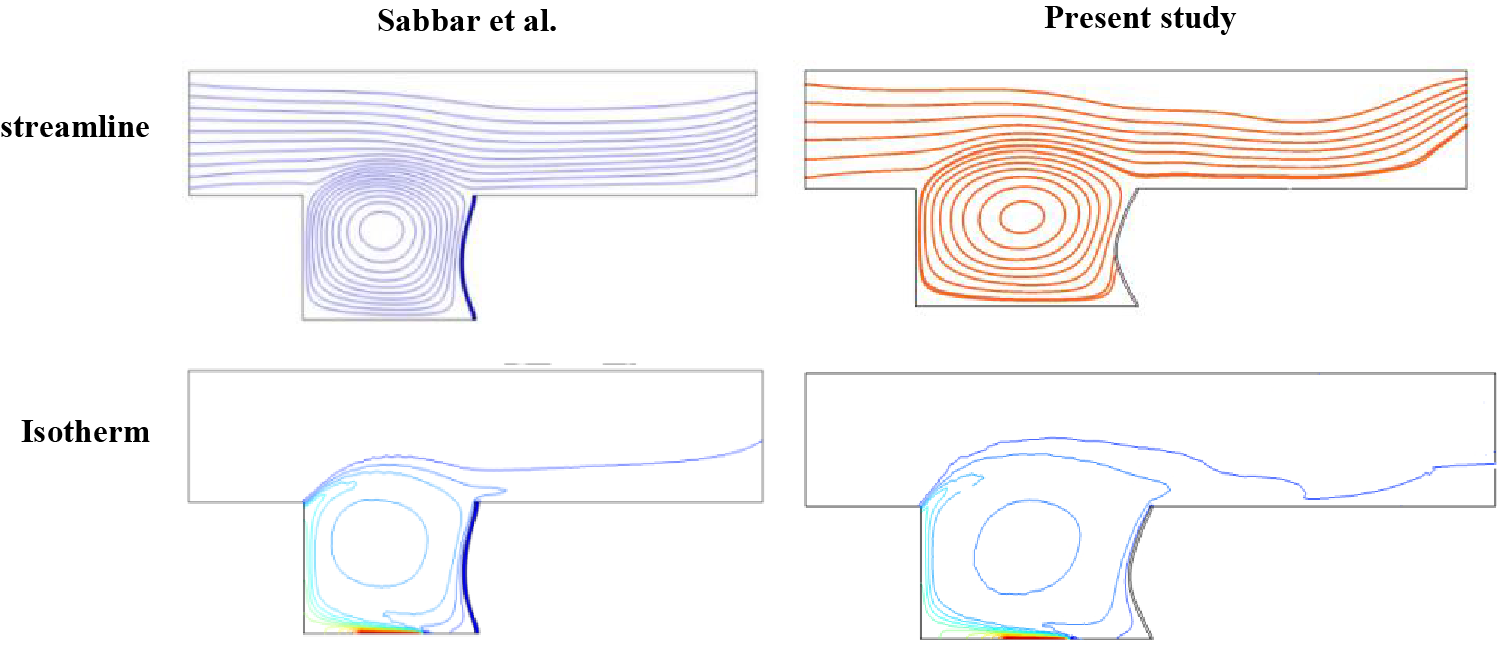
Figure 3: Constriction between several contour map of present work with Sabbar et al. [12] at Re = 150, H/D = 0.7 and Ri = 10

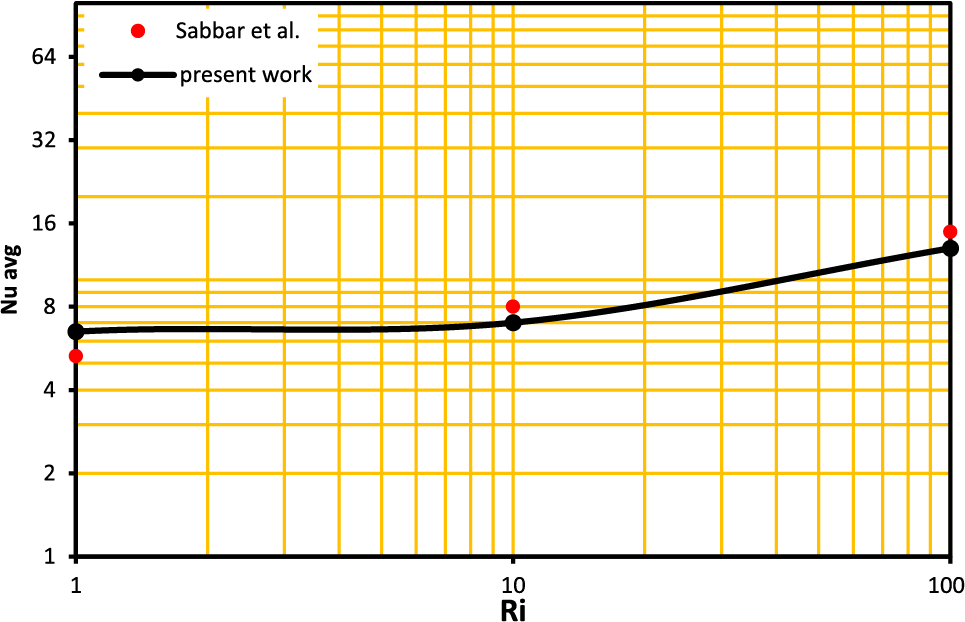
Figure 4: Constriction of Nusselt number of present work with Sabbar et al. [12] at Re = 150, H/D = 0.7 and Ri = 10

5  Result

Results for streamlines, isotherms, average Nusselt numbers, fraction factors, TCE and pressure drop for Ca = 10−4 to 10−8, Re = 60 to 160, and Pr = 6.9 are shown in this section.

5.1 Steady State Time

The investigation of the unsteady state seeks to locate the point in time at which the findings reach the steady state. In order to achieve this goal, the performance of the Nusselt number and wall deformation have been invested with time dimensionless, as can be seen in Figs. 5 and 6. A time step of 0.01 is used, and the computational work was carried on all the way up to t = 50 s. The development of the Nusselt number is seen through time in Fig. 5. In this case, considerable changes in the Nusselt number are caused by the movement of heat energy from the wall into the liquid at the beginning of time. As time passes, the layers that are closest to the wall become hotter than their initial state. As a result, the temperature difference becomes smaller, which causes the Nusselt Number to decrease until it reaches a stable state at time equal to 14 s. To demonstrate the most deformation portion of the channel at Ca = 10−4 and Re = 160, many images of the streamline flow patterns and channel behavior are collected. Fig. 6 depicts how the streamline and elastic wall behave. Due to the liquid pressure being zero on the elastic wall at time τ = 0.01 s, it can be seen that the form of the wall and the streamline are both straight and parallel. The elastic wall’s shape changes over time, becoming an arc blown to the outside of the channel at τ = 2 and τ = 3 s, before returning to contract to the inside of the channel at τ = 5 s with secondary vortex formation inside the cavity. It then continues to grow over time, reaching its largest size at τ = 10 s. The elastic wall again swells and secondary vortex is formation at τ = 14 s. When comparing τ = 14 and τ = 50 s, there are no major variations in streamline patterns. Considering these facts, it's safe to assume that the steady-state time occurs after τ = 14 s, hence all of the data in this study was collected after that point.

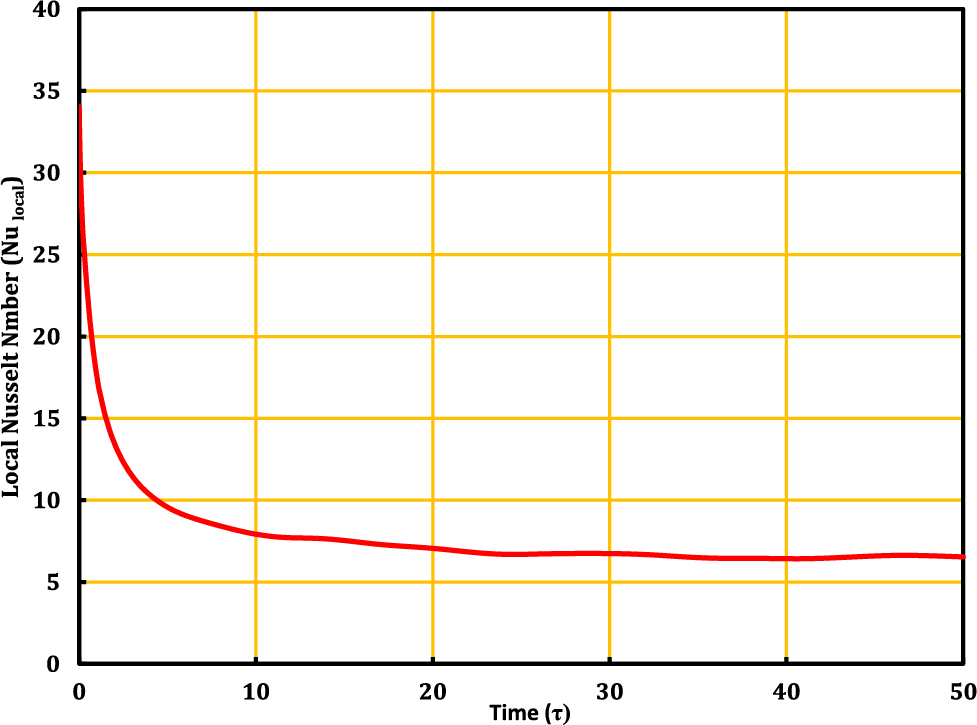
Figure 5: Average Nusselt vs. time for Re = 160, Ca = 10−4, φ = 0.02

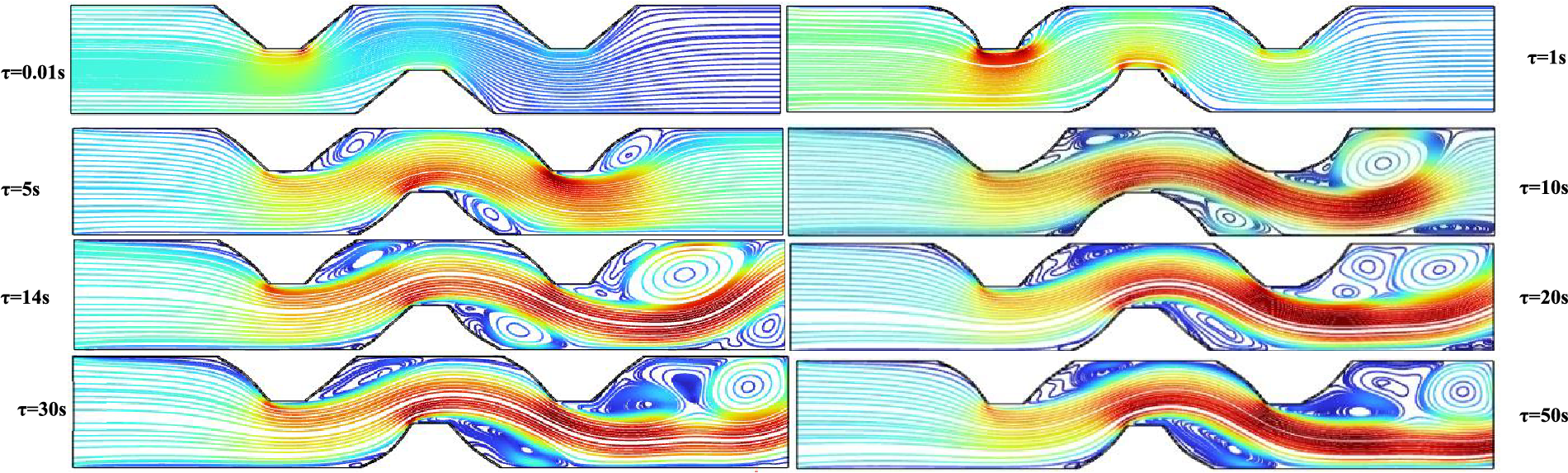
Figure 6: Wall deformation, streamlines for different values of τ at Re = 160, Ca = 10−4

5.2 Effect of Flexible Wall Position

At the parameters Pr = 6.9, Ca = 10−4, φ = 0.02, τ = 20 s, and Re = 60, the positional effect of the elastic wall is given. As shown in Fig. 7 in case A, there is no elastic wall, in cases B and C there are three elastic walls in various positions, and in case D there are six elastic walls. In Fig. 8, the relationship between the average Nusselt number and the Reynolds number, three cases with an elastic wall and a comparison without an elastic wall are depicted. Fig. 7 illustrates that the region of interest is between the recirculation area (3.85 × 10−4) and the acceleration area (3.06). At the channel’s entrance, the velocity gradient is almost zero along the wall due to the friction of the surface wall and one in the channel’s middle. Following the first trapezoidal penetration in the flow, the velocity starts to increase until it reaches a maximum of 3.06 and the flow layers start to separate. The recirculation region is formed by the trapezoid’s corners. As the flow advances within the channel and is exposed to such breaches of the channel’s trapezoid, the speed rises and greater vortices form at the corners of its trapezoid, as in case A. As in cases B, C, and D, a flexible wall was employed to eliminate these eddies and replace by new eddies as a result of the continuous flow. The greatest Nusselt reading is obtained in case C, with a percentage of (34.5%) compared to case A without the elastic wall, as illustrated in Fig. 8 where the vortices are released by the elastic wall's vibration and replaced by additional vortices. This motion is continuous with the movement of the wall, resulting in heat exchange between the wall and the fluid. Due to the lack of vortices at this point, the elastic wall in instance B provides little benefit in terms of heat transmission about (31.4%). Heat transmission is improved in case D (21.5%) as compared to the channel without a flexible wall in example A. We infer from the preceding discussion that energy transmission can be enhanced by utilizing three elastic barriers, as in case C, rather than six, as in case D.

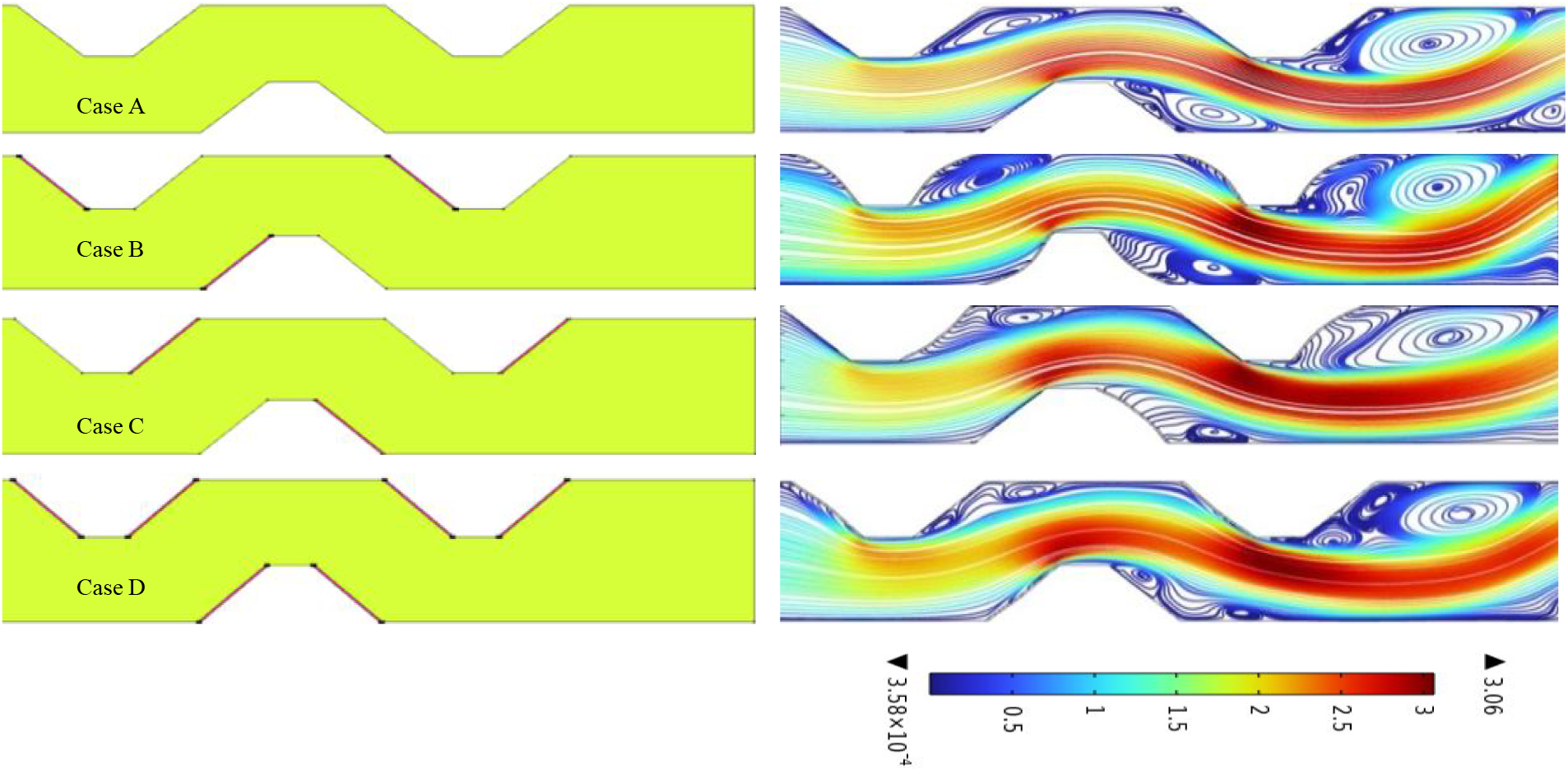
Figure 7: The streamline for the complex channel at different location of the elastic wall at Pr = 6.9, Ca = 1e-4, φ = 0.02, τ = 20 s, and Re = 60

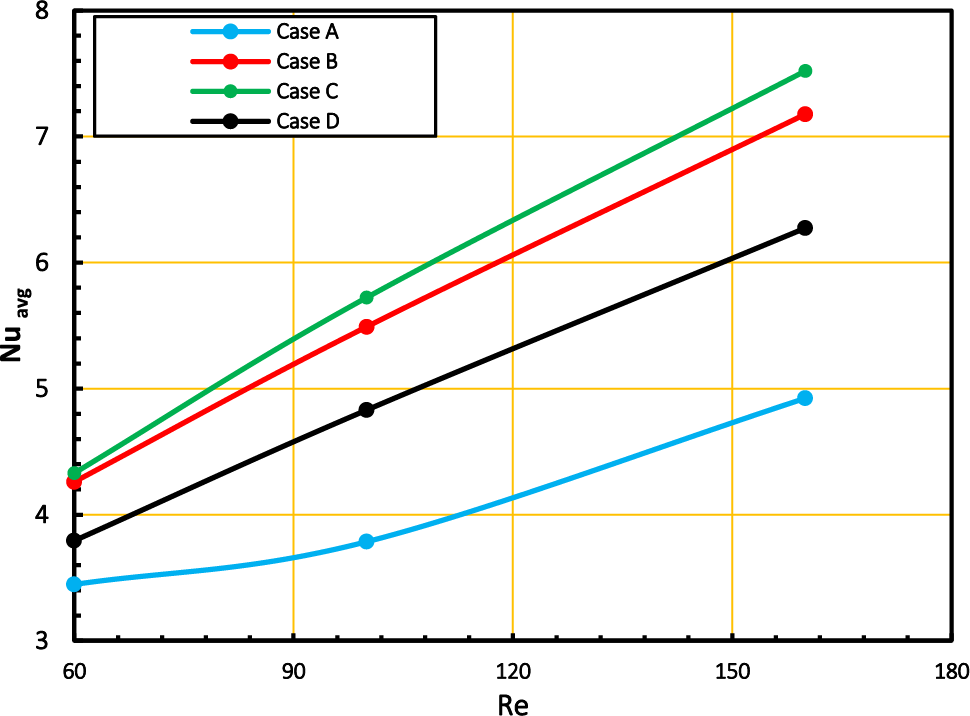
Figure 8: The relation of average Nusselt number with Reynolds number at three cases have elastic wall and comparison without elastic wall

5.3 Heat Transfer at Various Geometry

The geometries of a complicated channel with varying L2/H2 and B/H2 ratios are depicted in Fig. 9, which pertains to case C. The average of Nusselt number is investigated for each of the three possible geometries. The parameters for the L2/H2 configurations are 0, 3, and 6, with Re = 160, Pr = 6.9, and φ = 0.02. The outcomes are contrasted between the geometry B/H2 = 0 and L2/H2 = 0, which lacks an elastic wall, and the geometry B/H2 = 0.8 and L2/H2 = 3, which contains an elastic wall. The results showed that the best case with an elastic wall is reached for B/H2 = 0.8 and L2/H2 = 3, as shown in Fig. 9. The difference between L2/H2 = 3 with an elastic wall and L2/H2 = 0 is 53%. This denotes an increase in the greatest incursion into the channel by a trapezoid. The trapezoid’s interference in the channel amplifies the energy mixture behind it. The momentum and velocity rise across the whole trapezoidal. As momentum increased, so did the mixing and growing vortices. The production of vortices as a result of the structure’s intricacy makes cooling challenging. The reciprocating movement of the wall helps to throw the vortices away from the wall, which leads to their replacement with other vortices. This action occurs continuously with the wall movement, which leads to the exchange of heat between the wall and the fluid. The worst case is when B/H2 = 0 and L2/H2 = 0, which means no trapezoidal in the flow channel and no flexible wall.

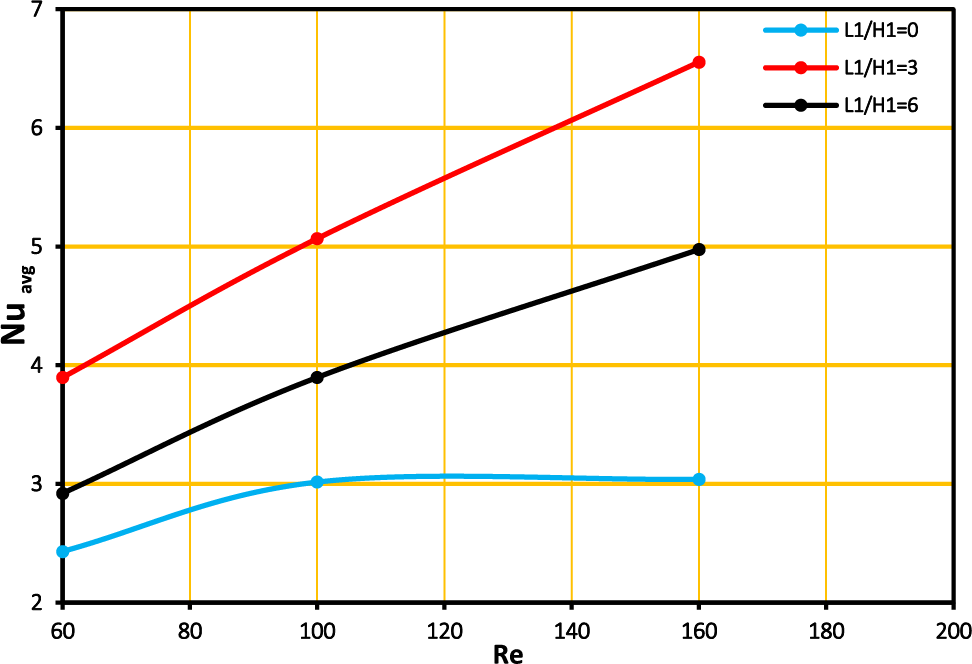
Figure 9: Nusselt number with Reynolds number at different geometry with Pr = 6.9 and φ = 0.02 Ca = 10−4

5.4 The Effect of Cauchy Number (Ca)

Calculating the Cauchy number, as illustrated in Figs. 10 and 11, is important in order to research the influence of the elastic modulus of the elastic wall on the rate of heat transfer. The streamline and isotherm maps are depicted in Fig. 10 for the following sets of parameter values: Re = 160, Pr = 6.9, Ca = 10−4 to 10−8, φ = 0.02, and τ = 50 s. It has been seen that the penetrating of isosceles trapezoid in the flow path causes vortices to form at trapezoidal angles. At Ca = 10−4, the wall has material that is elastic. So, the force of the fluid flow and the recirculation zone pull the elastic wall out of the channel. This is because the elastic wall lets the eddying expand to the outside of the channel. While, at Ca = 10−5 the elastic wall is bended slightly and it is fixed at Ca = 10−8, It indicates that the wall is solid and that the fluid circulating is not enough to force it to bend. Regarding for isotherm in general, the thermal boundary layer extends along the channel wall with a characteristic thermal gradient inside the channel where the maximum temperature indicates a good momentum exchange between the fluid and the source. In general, heat transfer can be summarized by calculating Nusselt number as shown in Fig. 11. It is recorded as the highest reading for the Nusselt number at Ca = 10−4 and Re = 160 about 6.4 because of the large area resulting from the bending of the elastic wall to the outside of the channel, and therefore the available rotation area increases the Nusselt number.

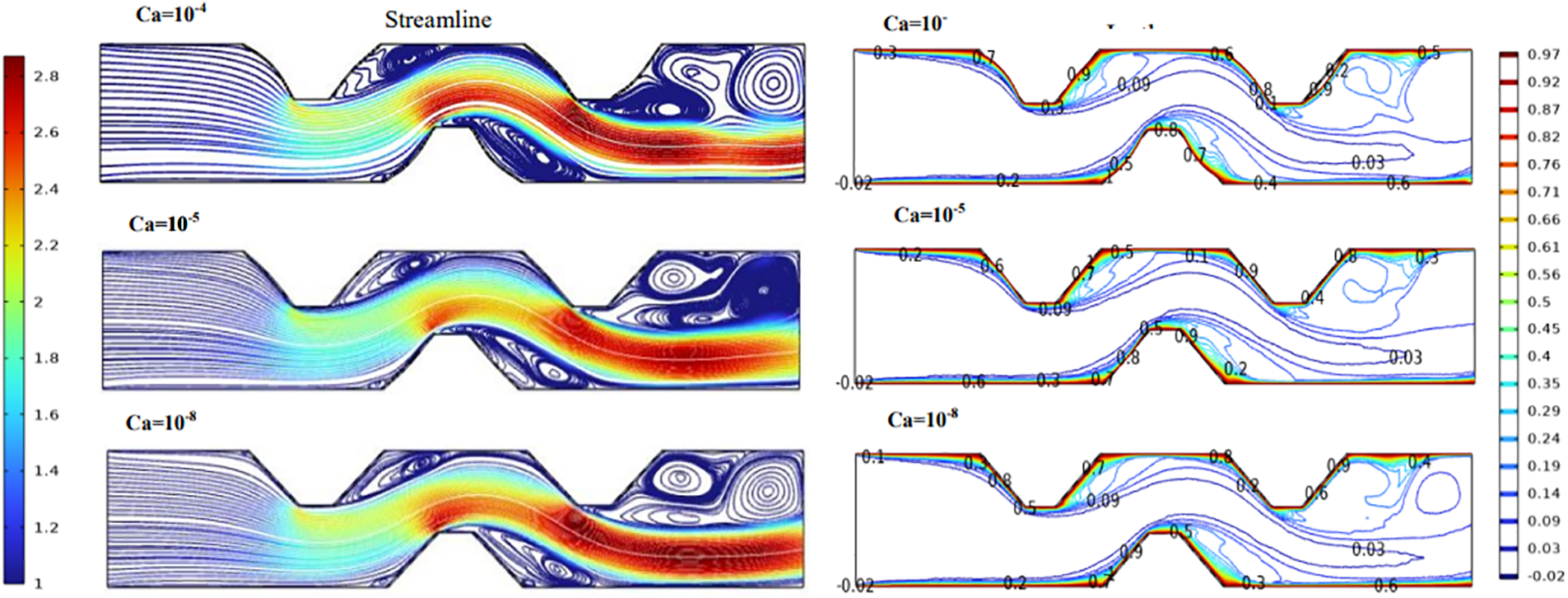
Figure 10: Stream line and isotherm for case D at Re = 160, Ca = 1e-4, φ = 0.02

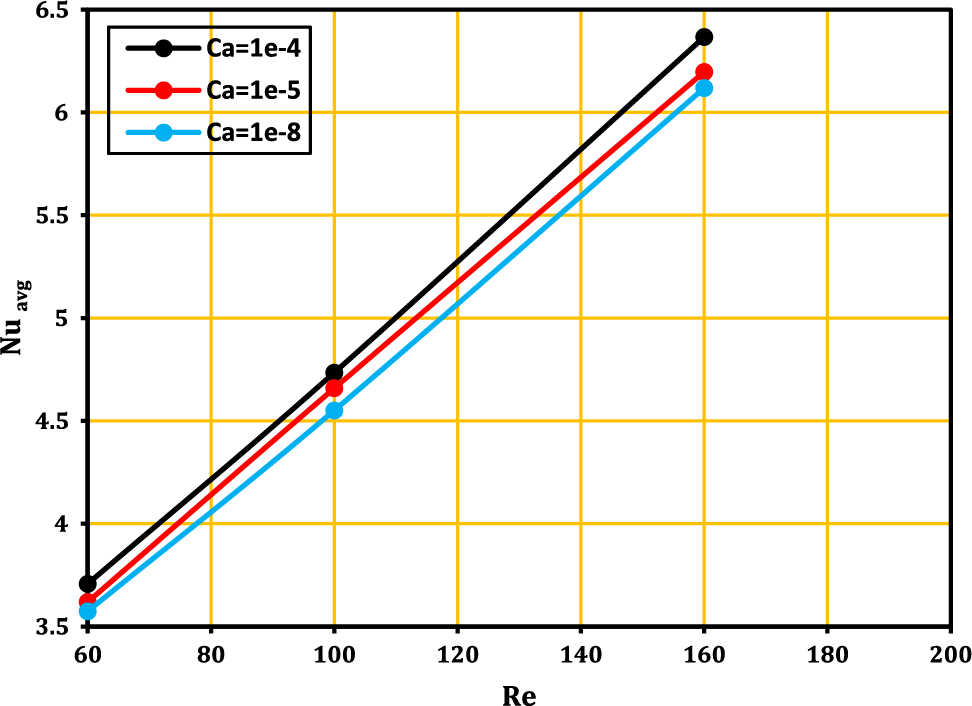
Figure 11: The relation between Reynolds number and average Nusselt number for various Cauchy number at case D at Re = 160, φ = 0.02

5.5 The Effect of Heat Transfer for Hot Wall

The main objective in this section is to find out the sensitivity of the behavior of the elastic wall at Reynolds. The Fig. 12 shows the local Nusselt number of the FSI model along the lower wall of the channel that is indicated by the symbol(s) for different values of Reynolds numbers, where the Nusselt number suffers at the beginning of the inlet channel between (S = 0 to 2) from significant fluctuations due to the transfer of thermal energy from the wall to the liquid.

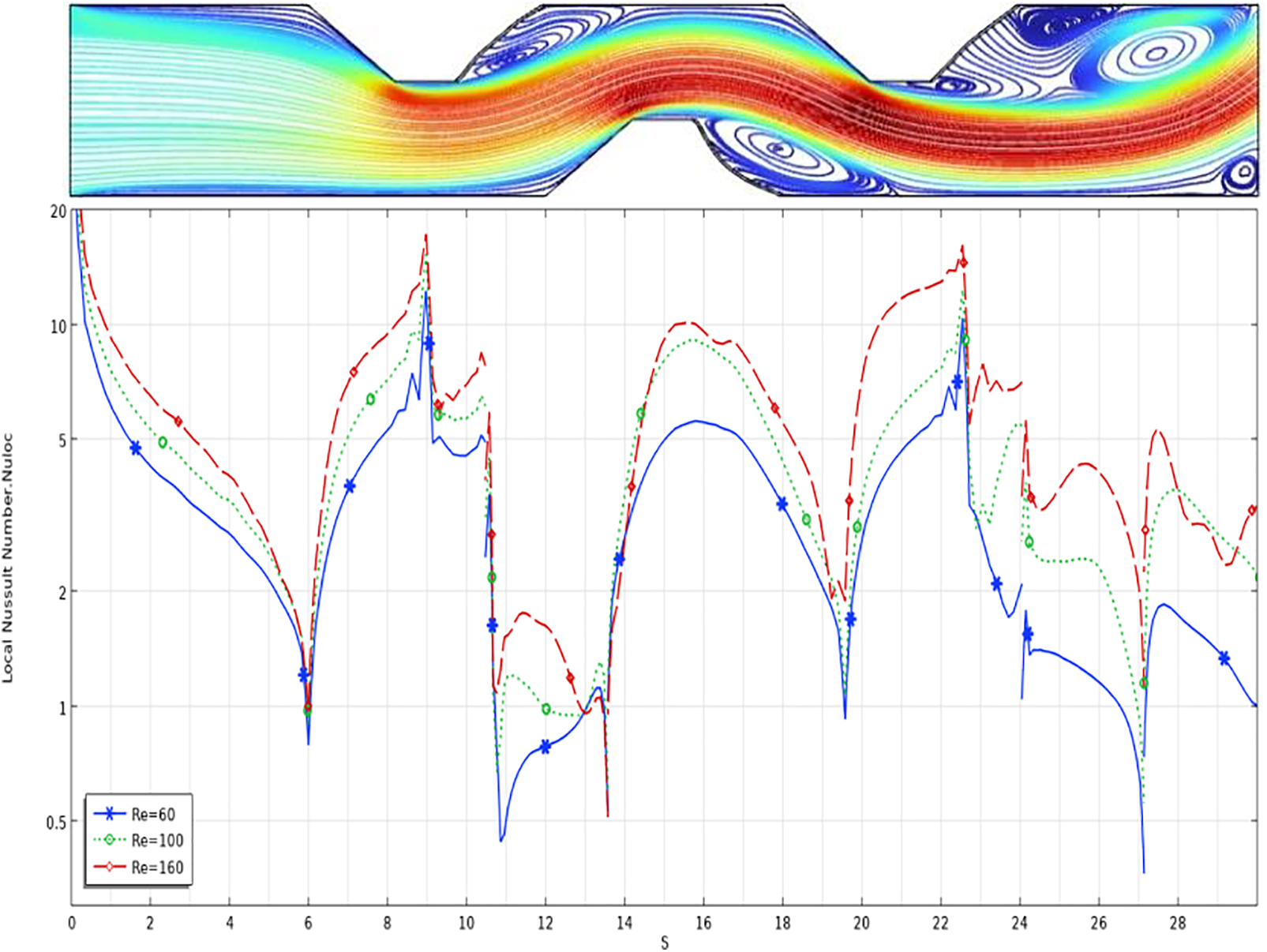
Figure 12: Local Nusselt number along the hot wall at case D with Re = 60, 100, 160, Pr = 6.9 and φ = 0.02

Over time, the layers near the wall become hotter than the initial state, and thus the temperature difference becomes smaller, so that the Nusselt number decreases until it reaches 0.8 at S = 6. The Nusselt number returns to increasing until it reaches its maximum of 18 at S = 9 due to increased velocity at the first trapezoidal penetration in the flow. Between S = 10 and 14, the Nusselt number decreases until it reaches its minimum value of about 0.4 due to the formation of eddies at the corner of the trapezoidal. The Nusselt number is back to increase after S = 14 until reach to high value about 10 at Re = 160 and S = 16, due to acceleration flow at this location and then its drops to value 0.9 at S = 20 due to formation eddy at the bottom wall of channel. once again, the Nusselt number is growth to 27 at S = 23 for Re = 160. After S = 23, the Nusselt number is oscillated between 0.4 for Re = 60 and 5 for Re = 160 due to form main and secondary vortices at the outlet part of channel.

5.6 Impact of the Pressure Drop

It is necessary to study the pressure drop and friction factor to get the best performance because they require high pumping forces. The Fig. 13 shows the relationship of each pressure drop and friction factor with the Reynolds number for a channel containing an elastic wall, as in cases B, C, and D, and compares it with a channel without an elastic wall, as in case A. Cases B, C, and D had lower pressure drops and friction factors than case A because the elastic wall’s reciprocating motion works to renew the formation of vortices constantly, lowering the friction factor and pressure drop. The Fig. 13 also shows that as the Reynolds number increases, the pressure drop increases due to an increase in the friction factor generated by the formation of vortices, as in case A, but the opposite happens in cases B and C, where the pressure drop decreases as the Reynolds number increases due to the reciprocating movement of the elastic wall that drives out the vortices and thus a lower friction factor and pressure drop. As for case D, we notice that with a higher Reynolds number, the pressure drop is higher. This suggests that the use of merging in the elastic wall does not provide a significant benefit in terms of heat transfer.

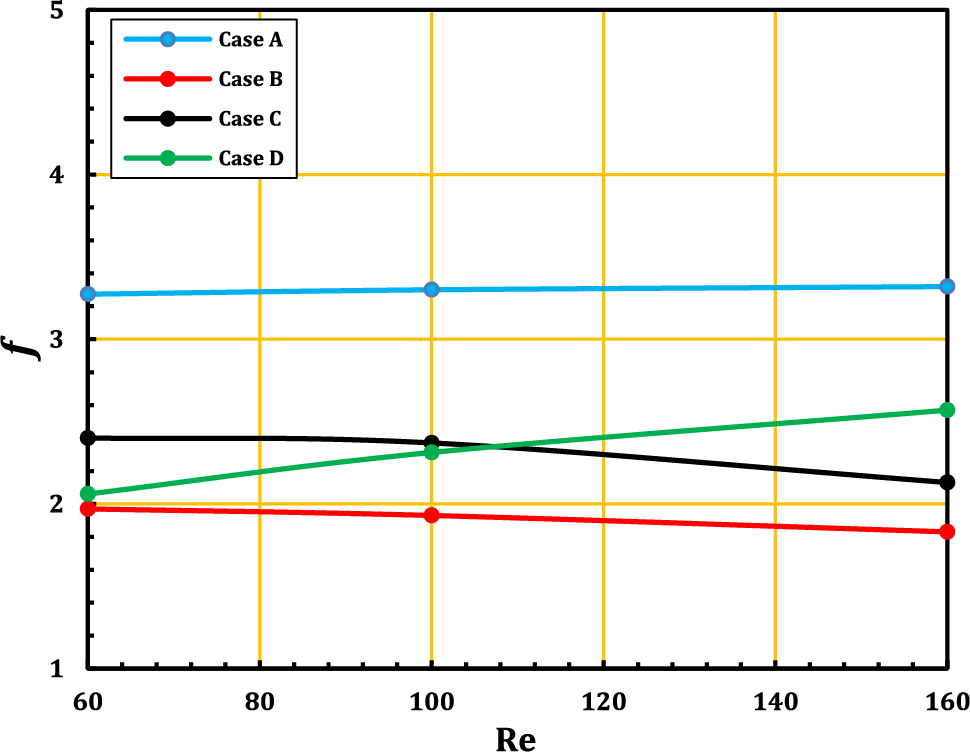
Figure 13: The relation of pressure drop and friction factor with Reynolds number at Ca = 10−4, Pr = 6.9 and φ = 0.02

5.7 Effect of Working Fluid

Earlier findings indicated that case C, including three elastic walls at Re = 160 and Ca = 10−4, had the optimum heat transmission performance. Because of this, in Fig. 14 the Nusselt number is attained with nanoparticles of Al2O3 at concentrations of 0 (no concentration), 0.01, 0.02, and 0.04. where the bigger the nanoparticles, the higher the Nusselt number becomes because of the increased surface area available for heat transmission as seen in the Fig. 14.

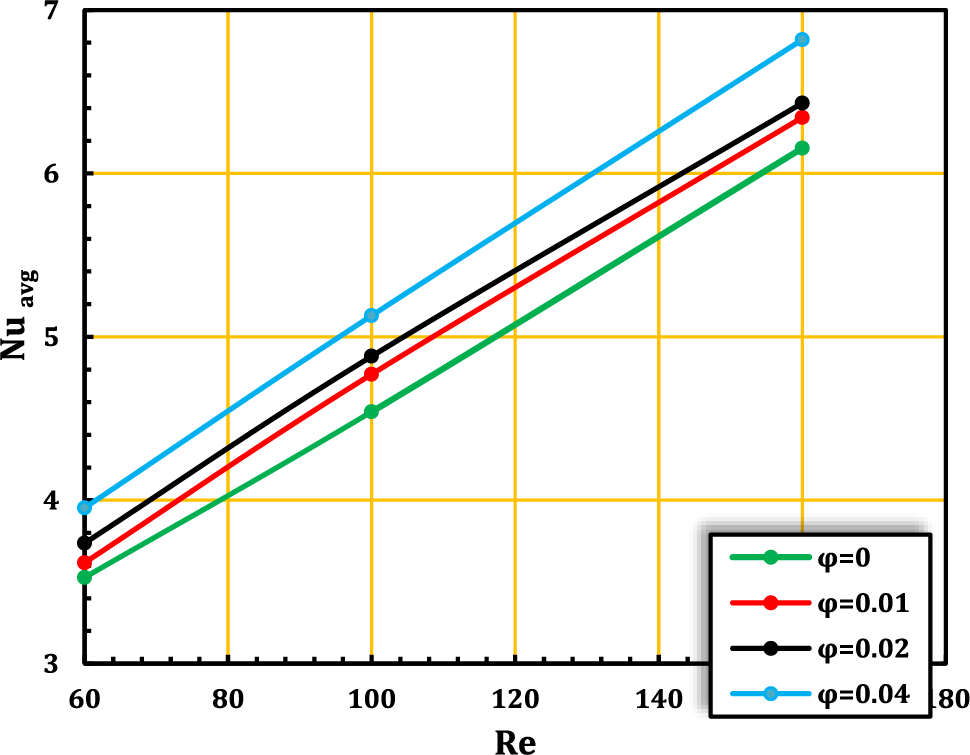
Figure 14: Average Nusselt number with nanoparticle concentration at Ca = 1e-4 and Pr = 6.9

5.8 Thermal Performance

To achieve the best performance, the friction factor and pressure drop must be calculated due to the need for high pumping power. The thermal enhancement criterion (TEC) stated in Eq. (28) can solve this problem. The best thermal enhancement criterion (TEC) can be obtained when the elastic wall is fixed after the trapezoid block of the complex channel, as shown in Fig. 15.

Figure 15: Variations of thermal-hydraulic performance criterion with baffles location and Reynolds numbers at Ca = 1e-4, φ = 0.02

This means that the increase in the average Nusselt number overcomes the losses that result from the pressure drop along the channel. The high thermal enhancement criterion (TEC) is recorded at 1.68 at case C for Re = 160 and at its lowest value of 0.93 at case D for Re = 60.

6  Conclusions

This paper looks at a numerical study of how fluids and structures interact in a complex channel with a trapezoid shape hanging in it. Here, different shap of complex channel (L2/H2 and B/H2) were looked at with Reynolds numbers from 60 to 160, volume fractions from 0.02 to 0.04, a Prandtl number Pr = 6.9, and Cauchy numbers from 10−4 to 10−8. Flow can go over a hot wall, and the following conclusions were drawn:

1.    The greatest Nusselt reading is obtained in case C, with a percentage of (34.5%) compared to case A without the elastic wall, but heat transmission in case B (31.4%) and D (21.5%) as compared to the channel without a flexible wall in case A.

2.    Corrugated channels with B/H2 = 0.8 and L2/H2 = 3 had the best thermal performance under the current thermal conditions. This made the heat exchanger work better.

3.    When Ca = 10−4 is used, the average Nusselt number is higher than when Ca = 10−5 or Ca = 10−8 is used.

4.    The average Nusselt number goes up when the nanoparticles get bigger because there is more surface area for heat to move across.

5.    Cases B, C, and D had lower pressure drops and friction factors than case A.

6.    As the Reynolds number increases, the pressure drop increases, as in case A, but the opposite happens in cases B and C, where the pressure drop decreases as the Reynolds number increases. As for case D, the pressure drop is higher with an increase in Reynolds number. This suggests that the use of merging in the elastic wall does not provide a significant benefit in terms of heat transfer.

Acknowledgement: First of all, I would like to praise and thank GOD for helping me to complete this work. I wish to express my gratefulness to my supervisors, Prof. Dr. Hameed Kadhem Hamzah and Prof. Dr. Hatem Hadi Obied Said for their continuous supervision, positive discussions and important ideas through this research work. Also, very extraordinary deepest thanks to Dr. Farooq H. Ali for his special contribution and help in completing this work. My deepest thanks, love and gratitude for all of My family. This work would not have been completed without their love and continuous support.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Data collection, analysis and interpretation of results: Amal A. Harbood, study conception and design: Hameed K. Hamzah, draft manuscript preparation: Hatem H. Obied.

Availability of Data and Materials: Data are available upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Al-Amiri, A., Khanafer, K. (2011). Fluid-structure interaction analysis of mixed convection heat transfer in a lid-driven cavity with a flexible bottom wall. International Journal of Heat and Mass Transfer, 54(17–18), 3826–3836. [Google Scholar]

2. Yaseen, D. T., Ismael, M. A. (2020). Effect of deformable baffle on the mixed convection of non-Newtonian fluids in a channel-cavity. Basrah Journal for Engineering Science, 20(2), 18–26. [Google Scholar]

3. Xu, H., Liao, S. J. (2009). Laminar flow and heat transfer in the boundary-layer of non-Newtonian fluids over a stretching flat sheet. Computers & Mathematics with Applications, 57(9), 1425–1431. [Google Scholar]

4. Hessenthaler, A., Gaddum, N. R., Holub, O., Sinkus, R., Röhrle, O. et al. (2017). Experiment for validation of fluid-structure interaction models and algorithms. International Journal for Numerical Methods in Biomedical Engineering, 33(9), e2848. [Google Scholar] [PubMed]

5. Korei, Z., Benissaad, S., Chamkha, A., Berrahil, F., Filali, A. (2022). Thermohydraulic and second law analyses during the cooling of an electronic device mounted in an open cavity equipped with magnetic nanofluid, magnetic field inducer, and porous media: A two-phase numerical investigation. International Communications in Heat and Mass Transfer, 139(318), 106497. [Google Scholar]

6. Selimefendigil, F., Öztop, H. F. (2016). Analysis of MHD mixed convection in a flexible walled and nanofluids filled lid-driven cavity with volumetric heat generation. International Journal of Mechanical Sciences, 118, 113–124. [Google Scholar]

7. Selimefendigil, F., Öztop, H. F., Abu-Hamdeh, N. (2016). Mixed convection due to rotating cylinder in an internally heated and flexible walled cavity filled with SiO2-water nanofluids: Effect of nanoparticle shape. International Communications in Heat and Mass Transfer, 71, 9–19. [Google Scholar]

8. Selimefendigil, F., Öztop, H. F., Chamkha, A. J. (2017). Analysis of mixed convection of nanofluid in a 3D lid-driven trapezoidal cavity with flexible side surfaces and inner cylinder. International Communications in Heat and Mass Transfer, 87, 40–51. [Google Scholar]

9. Selimefendigil, F., Öztop, H. F., Chamkha, A. J. (2017). Fluid-structure-magnetic field interaction in a nanofluid filled lid-driven cavity with flexible side wall. European Journal of Mechanics-B/Fluids, 61, 77–85. [Google Scholar]

10. Jamesahar, E., Ghalambaz, M., Chamkha, A. J. (2016). Fluid-solid interaction in natural convection heat transfer in a square cavity with a perfectly thermal-conductive flexible diagonal partition. International Journal of Heat and Mass Transfer, 100(1), 303–319. [Google Scholar]

11. Mehryan, S., Ghalambaz, M., Ismael, M. A., Chamkha, A. J. (2017). Analysis of fluid-solid interaction in MHD natural convection in a square cavity equally partitioned by a vertical flexible membrane. Journal of Magnetism and Magnetic Materials, 424(14), 161–173. [Google Scholar]

12. Sabbar, W. A., Ismael, M. A., Almudhaffar, M. (2018). Fluid-structure interaction of mixed convection in a cavity-channel assembly of flexible wall. International Journal of Mechanical Sciences, 149, 73–83. [Google Scholar]

13. Selimefendigil, F., Öztop, H. F. (2018). Laminar convective nanofluid flow over a backward-facing step with an elastic bottom wall. Journal of Thermal Science and Engineering Applications, 10(4), 041003. [Google Scholar]

14. Selimefendigil, F., Öztop, H. F. (2019). MHD mixed convection of nanofluid in a flexible walled inclined lid-driven L-shaped cavity under the effect of internal heat generation. Physica A: Statistical Mechanics and its Applications, 534, 122144. [Google Scholar]

15. Selimefendigil, F., Öztop, H. F. (2019). Fluid-solid interaction of elastic-step type corrugation effects on the mixed convection of nanofluid in a vented cavity with magnetic field. International Journal of Mechanical Sciences, 152, 185–197. [Google Scholar]

16. Ismael, M. A. (2019). Forced convection in partially compliant channel with two alternated baffles. International Journal of Heat and Mass Transfer, 142, 118455. [Google Scholar]

17. Alsabery, A. I., Saleh, H., Ghalambaz, M., Chamkha, A. J., Hashim, I. (2019). Fluid-structure interaction analysis of transient convection heat transfer in a cavity containing inner solid cylinder and flexible right wall. International Journal of Numerical Methods for Heat & Fluid Flow, 29(10), 3756–3780. [Google Scholar]

18. Ghalambaz, M., Mehryan, S. A. M., Ismael, M. A., Chamkha, A., Wen, D. (2019). Fluid-structure interaction of free convection in a square cavity divided by a flexible membrane and subjected to sinusoidal temperature heating. International Journal of Numerical Methods for Heat & Fluid Flow, 30(6), 2883–2911. [Google Scholar]

19. Al-Amir, Q. R., Hamzah, H. K., Abdulkadhim, A., Ahmed, S. Y., Ali, F. H. et al. (2022). Numerical study of fluid structure interaction of four flexible fins inside nanofliud-filled square enclosure containing hot circular cylinder. Journal of Thermal Analysis and Calorimetry, 147(23), 1–19. [Google Scholar]

20. Burgmann, S., Große, S., Schröder, W., Roggenkamp, J., Jansen, S. et al. (2009). A refractive index-matched facility for fluid-structure interaction studies of pulsatile and oscillating flow in elastic vessels of adjustable compliance. Experiments in Fluids, 47(4–5), 865–881. [Google Scholar]

21. Elshafei, E. A. M., Awad, M. M., El-Negiry, E., Ali, A. G. (2010). Heat transfer and pressure drop in corrugated channels. Energy, 35(1), 101–110. [Google Scholar]

22. Ahmed, M. A., Yusoff, M. Z., Ng, K. C., Shuaibl, N. H. (2015). Numerical and experimental investigations on the heat transfer enhancement in corrugated channels using SiO2-water nanofluid. Case Studies in Thermal Engineering, 6, 77–92. [Google Scholar]

23. Korei, Z., Berrahil, F., Filali, A., Benissaad, S., Boulmerka, A. (2023). Thermo-magnetic convection analysis of magnetite ferrofluid in an arc-shaped lid-driven electronic chamber with partial heating. Journal of Thermal Analysis and Calorimetry, 148(6), 1–20. [Google Scholar]

24. Ajeel, R. K., Salim, W. S., Hasnan, K. (2018). Numerical investigations of flow and heat transfer enhancement in a semicircle zigzag corrugated channel using nanofluids. International Journal of Heat and Technology, 36(4), 1292–1303. [Google Scholar]

25. Ajeel, R. K., Salim, W. I., Hasnan, K. (2019). An experimental investigation of thermal-hydraulic performance of silica nanofluid in corrugated channels. Advanced Powder Technology, 30(10), 2262–2275. [Google Scholar]

26. Naphon, P. (2008). Effect of corrugated plates in an in-phase arrangement on the heat transfer and flow developments. International Journal of Heat and Mass Transfer, 51(15–16), 3963–3971. [Google Scholar]

27. Sakr, M. (2015). Convective heat transfer and pressure drop in V-corrugated channel with different phase shifts. Heat and Mass Transfer, 51(1), 129–141. [Google Scholar]

28. Ajeel, R. K., Saiful-Islam, W., Sopian, K., Yusoff, M. Z. (2020). Analysis of thermal-hydraulic performance and flow structures of nanofluids across various corrugated channels: An experimental and numerical study. Thermal Science and Engineering Progress, 19(133), 100604. [Google Scholar]

29. Salami, M., Khoshvaght-Aliabadi, M., Feizabadi, A. (2019). Investigation of corrugated channel performance with different wave shapes: Nanofluid as working media. Journal of Thermal Analysis and Calorimetry, 138(5), 3159–3174. [Google Scholar]

30. Al-Zurfi, N., Alhusseny, A., Nasser, A. (2020). Effect of rotation on forced convection in wavy wall channels. International Journal of Heat and Mass Transfer, 149(11–12), 119177. [Google Scholar]