Casson Nanofluid Flow with Cattaneo-Christov Heat Flux and Chemical Reaction Past a Stretching Sheet in the Presence of Porous Medium

Nomenclature

1  Introduction

Colloidal suspension of nanoparticles into base fluid has introduced a new class of fluids called nanofluids. Nanofluid passes remarkable properties that the technology was unlikely to attain through conventional fluids. When the nano-meter-sized nanoparticles are dispersed in the convectional fluid, the formed mixture exhibit enhanced chemical reactivity, electrical conductivity characteristics and in particular heat transfer and thermal conductivity. Applications of nanofluids in sectors like aeronautics, medicine, and pharmaceutics have produced numerous innovative products. These products include brake fluids, nuclear reactions, improvements in cooling transformer oil, power plants, and space technologies. Choi et al. [1] is the person who introduced the term nanofluids through his experimental work. This invention opened doors for other researchers and provided humanity with a platform to extract more out of it. The earliest works done on nanofluids were by Wang et al. [2] and Jahani et al. [3]. Buongiorno [4] introduced the nanofluid model. Later, Hussain et al. [5] extended the model for exponentially expanding surfaces.

Khan et al. [6] were able to generate the first-ever paperwork on the laminar flow of nanofluids over a stretching surface emphasizing that behavior can also be well observed in nanofluids. Noghrebatadi et al. [7] and Hady et al. [8] performed similar experiments depicting the behavior of nanofluids. Wang [9] discovered theoretically and experimentally the flow towards a shrinking sheet. Out of many significant characteristics, the most advanced to grasp interest are MHD and thermal radiation effects. Nadeem et al. [10] used the Homotopy method to investigate the two-dimensional flow of heat transfer considering Williamson nanofluids. His work was followed by Prasannakumara et al. [11] analysing chemical activity over a porous medium. Danish et al. [12] provided a thorough extension to this phenomenon. More work on Williamson nanofluids was presented by Srinivasulu et al. [13] who studied MHD and the thermal effects of Williamson flow. The presentation of heat transfer on a hybrid nanofluid model with effects of MHD and thermal radiation was made in its earliest form by Zainal et al. [14]. Reddy et al. [15] investigated thermal radiation improvement on stagnation point flow. Mondal et al. [16] who performed comparative studies keeping in view heat transfer under thermal radiation impact. Further, many researchers have investigated the thermal radiation regimes under the effect of distinct external forces [17–20].

Multiple slips influence on MHD with chemical reaction with heat flux was studied by Gul et al. [21]. Moreover, Pramanik [22] explored heat transfer in the Casson nanofluid flow with thermal radiation. Mahanthesh et al.'s [23] analysis of the flow through an elongating surface was motivated by many physical factors. The difficult problem was reduced to a simpler one by utilizing the boundary layer approach before being resolved using the shooting method. In their analysis, they established a comparative study. Mohyud-Din et al. [24] studied the compressed flow of gas using Non-Newtonian fluid. A thorough explanation of the MHD Casson fluid including the properties of Hall and Dufour was conducted by Vijayaragavan et al. [25]. Yousef et al. [26] examined the dissipative Casson-Williamson fluid under the influence of the chemical reaction. Mukhopadhyay [27] investigated the Casson fluid with heat transfer over a nonlinear stretching surface. Dero et al. [28] explored the impact of viscous dissipation on the Casson fluid over the nonlinear stretching and shrinking surface. Recent research [29–31] has described various elements of these flows utilizing the Casson fluid.

Khan et al. [32] discussed heat transfer in nanotechnology with Casson fluid flow. Mabood et al. [33] investigated boundary layer flow over a nonlinear stretching sheet. Zhang et al. [34] performed a similar investigation of events but using a porous medium, whereas Krishna et al. [35] performed Newtonian heating on MHD hybrid nanofluid, and Nadeem et al.'s [36] work targeted a porous stretching sheet. Bhatti et al. [37] critically evaluated Reynolds number in relation to magnetic field. Manvi et al. [38] studied MHD Casson fluid with boundary layer and Brownian motion, heat production, and thermal profile which were later validated by Popey et al. [39] under the effects of MHD. Chamkha et al. [40] successfully described MHD boundary layer flow with convective slip flow under the effects of heat. Malik et al. [41] unlike others chose a non-Newtonian fluid for instant Casson nanofluid to discuss velocity changes under MHD effects. Ganga et al. [42] and Waheed et al. [43] also contributed significantly by considering unsteady MHD in the fluid flow problems. As discussed by Biswal et al. [44], most chemical reaction processes are determined by the presence of species. Chamkha et al. [45] analyzed heat produced or absorbed by a uniform vertical permeable surface with MHD effects.

In the present work, we discuss the steady 2D MHD flow of Casson nanofluid past a stretching sheet with the boundary conditions by using the thermal radiation. The impact of the inclined magnetic field, Cattaneo-Christov heat flux, and chemical reaction field have also been discussed. For the proposed problem, we utilized the well-known shooting technique, the shooting method is implemented in MATLAB to obtain the solution of a reduced system of nonlinear ODEs with the boundary conditions. The current model’s significant uses include heat energy enhancement, petroleum recovery, energy devices, food manufacturing processes, and cooling device adjustment, among others. The numerical solution for various parameters is discussed for the dimensionless velocity, temperature, and concentration. Investigation of achieved numerical outcomes is given through tables and graphs.

2  Modeling of Problem

2.1 Statement of Problem

Consider steady 2D non-Newtonian MHD Casson nanofluid flow in a porous medium past a stretching sheet with y=0. The flow is considered along the y-axis with y>0. Magnetic field of strength B is applied in the horizontal axis. Energy transport analysis is also carried out in the presence of thermal radiation and Cattaneo-Christov heat flux. Moreover, the concentration of flow is discussed in the presence of a first-order chemical reaction. The sheet is stretched with a velocity of Uw(x)=ax, where Tw is surface temperature and a fluid concentration of Cw.

2.2 Problem Governing Equations

In this section, a mathematical model has been developed using the constitutive relation. Casson fluid constitutive relations have been used for formulation and Cattaneo-Christov model has been used to formulate the energy equation. The modified Buongiorno nanofluid model has been implemented in the present formulation. Fig. 1 illustrates the coordinate system and problem schematic. Flow governing PDE’s are given as follows:

∂u∂x+∂v∂y=0,(1)

u∂u∂x+v∂u∂y=υ(1+1β)∂2u∂y2−σBo2sin2⁡(γ)ρu−μku,(2)

u∂T∂x+v∂T∂y+λ[u∂u∂x∂T∂x+v∂v∂y∂T∂y+u∂v∂x∂T∂y+v∂u∂y∂T∂x+2uv∂2T∂x∂y+u2∂2T∂x2+v2∂2T∂y2]=α∂2T∂y2+τ[DB∂C∂y∂T∂y+DTT∞(∂T∂y)2]−1ρCp(∂qr∂y),(3)

u∂C∂x+v∂C∂y=DB∂2C∂y2+DTT∞∂2T∂y2−KR(C−C∞).(4)

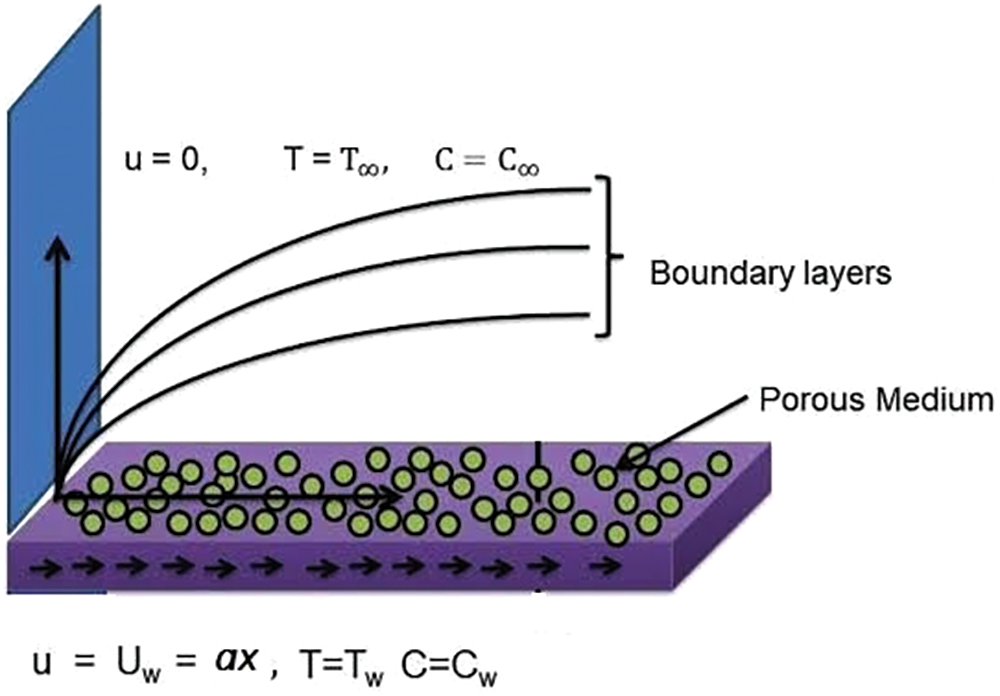
Figure 1: Geometry of presents model

Associated boundary conditions have been taken as

u=uw(x)=ax,v=0,T=Tw,C=Cw at y=0u→0,T→T∞,C→C∞ as y→∞}.(5)

In the above model, qr denotes radiative heat flux and q represents heat generation, respectively. The radiative heat flux is specified by qr=−4σ∗3k∗∂T4∂y, with a negligible temperature differential, then the temperature T4 can be linearize using the Taylor series omitting the more complex expressions, we have T4=4T∞3T−T∞4. Following similarity transformation [45] has been used to convert PDEs Eqs. (1)–(4) into system of ODEs.

u=ax=axf′(ζ),v=−(av)12f(ζ),ζ=y(av)12θ(ζ)=T−T∞Tw−T∞,ϕ(ζ)=C−C∞Cw−C∞}.(6)

where ζ(x,y) is similarity variable. Eqs. (2)–(4) can be construed as the succeeding ODEs by applying the transformation.

(1+ββ)f′′′(ζ)+f(ζ)f′′(ζ)−f′2(ζ)+(K+Msin2(γ))f(ζ)=0,(7)

1Pr(1+4R3)θ′′(ζ)+f(ζ)θ′(ζ)−γ1(f(ζ)f′(ζ)θ′(ζ)+f′2(ζ)θ′′(ζ))+Nbθ′(ζ)ϕ′(ζ)+Ntθ′2(ζ)=0,(8)

ϕ′′(ζ)+Scf(ζ)ϕ′(ζ)+NtNbθ′′(ζ)−Scγ2ϕ(ζ)=0.(9)

The modified BC’ss are as follows:

f(0)=0,f′(0)=1,θ(0)=1,ϕ(0)=1f′(∞)→0,θ(∞)→0,ϕ(∞)→0}.(10)

Different dimensionless variables are formulated as

M=σB02ρa,R=4σ∗T03kk∗,Pr=vα,γ1=λa,γ2=KraSc=νDB,K=νk1a,Nb=τDB(Cw−C∞)v,Nt=Nb=τDT(Tw−T∞)vT∞}.

2.3 Skin Friction, Nusselt and Sherwood Numbers

The important parameters of interest include skin friction coefficient, local Nusselt number, and local Sherwood number, which are formulated as follows:

Cf=τwρUw2, Nux=xqwk(Tw−T∞), shx=xqwDB(Cw−C∞).(11)

Here, the skin friction or shear stress is represented by τw, Here, qw stands for the surface wall heat flux. and concentration flow flux from the surface, denoted as qm and are specified by

τw=μ(∂u∂y)y=0, qw=−k(∂T∂y)y=0, qm=μ(∂C∂y)y=0.(12)

Dimensionless formations of friction, Nusselt & Sherwood numbers are

Rex1/2Cf=f′′(0), Rex−1/2Nux=θ′(0), Rex−1/2Shx=−ϕ′(0).(13)

3  Numerical Solution

To numerically solve ODEs ((7)–(9)) subject to the boundary circumstances ((10)), the shooting technique has been used in MATLAB. The notations listed below have been taken into consideration.

f=Y1,f′=Y1′=Y2,f′′=Y1′′=Y2′=Y3.

Transformed first ODEs is created by converting the momentum (Eqs. (7)–(9)).

Y1′=Y2,Y1(0)=0,(14)

Y2′=Y3,Y2(0)=0,(15)

Y3′=(β1+β)(−Y1Y3+Y22+(K+Msin2(γ))Y2),Y3(0)=s(16)

The RK-4 method will be used to numerically solve the above mentioned initial value problem. The bounded domain [0,ζ∞] has been used in place of the unbounded domain [0,∞) for the numerical results with the thought that it produces solutions that approach convergence asymptotically. The omitted condition ‘s’ is selected so that the subsequent relation is met.

Y2(ζ∞,s)=0.

Newton’s system updates the missing condition m, and the procedure is repeated until the following requirements are satisfied.

|Y2(ζ∞,sn)|<ϵ.

where ϵ is a small positive integer. In this article, Every numerical value is stated in terms of 10−10. After that, the shooting procedure is used to numerically solve Eqs. (8) and (9) while assuming that f is a known function. The following notations are used for this.

θ=Z1,θ′=Z1′=Z2,ϕ=Z3,ϕ′=Z3′=Z4,A1=(1+43R),A2=(A1−Prγ1f2).

The following set of first order coupled ODE’s may be used to represent the system of Eqs. (9) and (10):

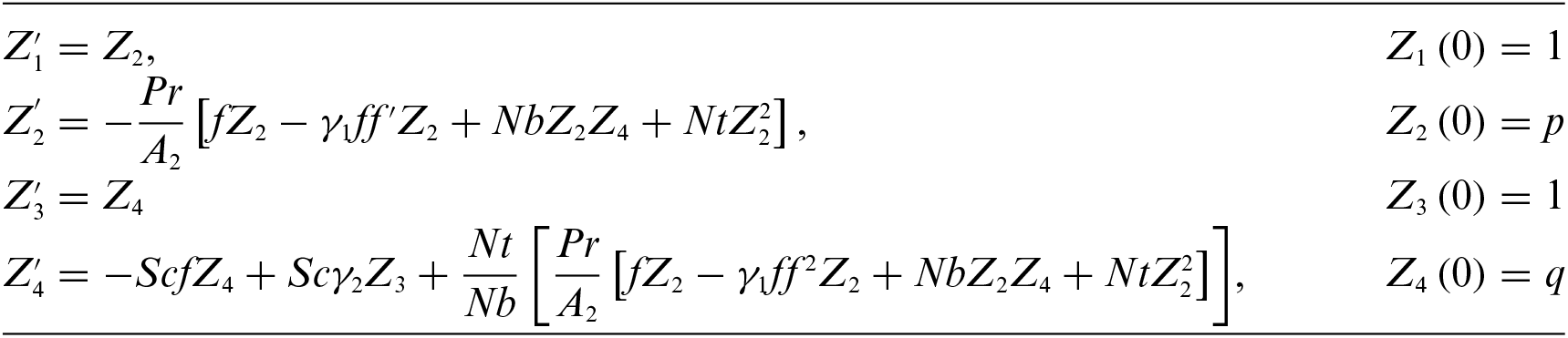
The RK-4 technique will be used to numerically solve the initial value problem mentioned above. The missing conditions p and q in the above system of equations must be selected in such a way that the following condition is satisfied:

Z1(ζ∞,p,q)=0,Z3(ζ∞,p,q)=0.

Fig. 2 illustrates the computational approach for solving our problem. Using Newton’s technique and the following stopping criteria, the two equations above are resolved:

max{|Z1(ζ∞,pn,qn)|,|Z3(ζ∞,pn,qn)|}<ϵ.

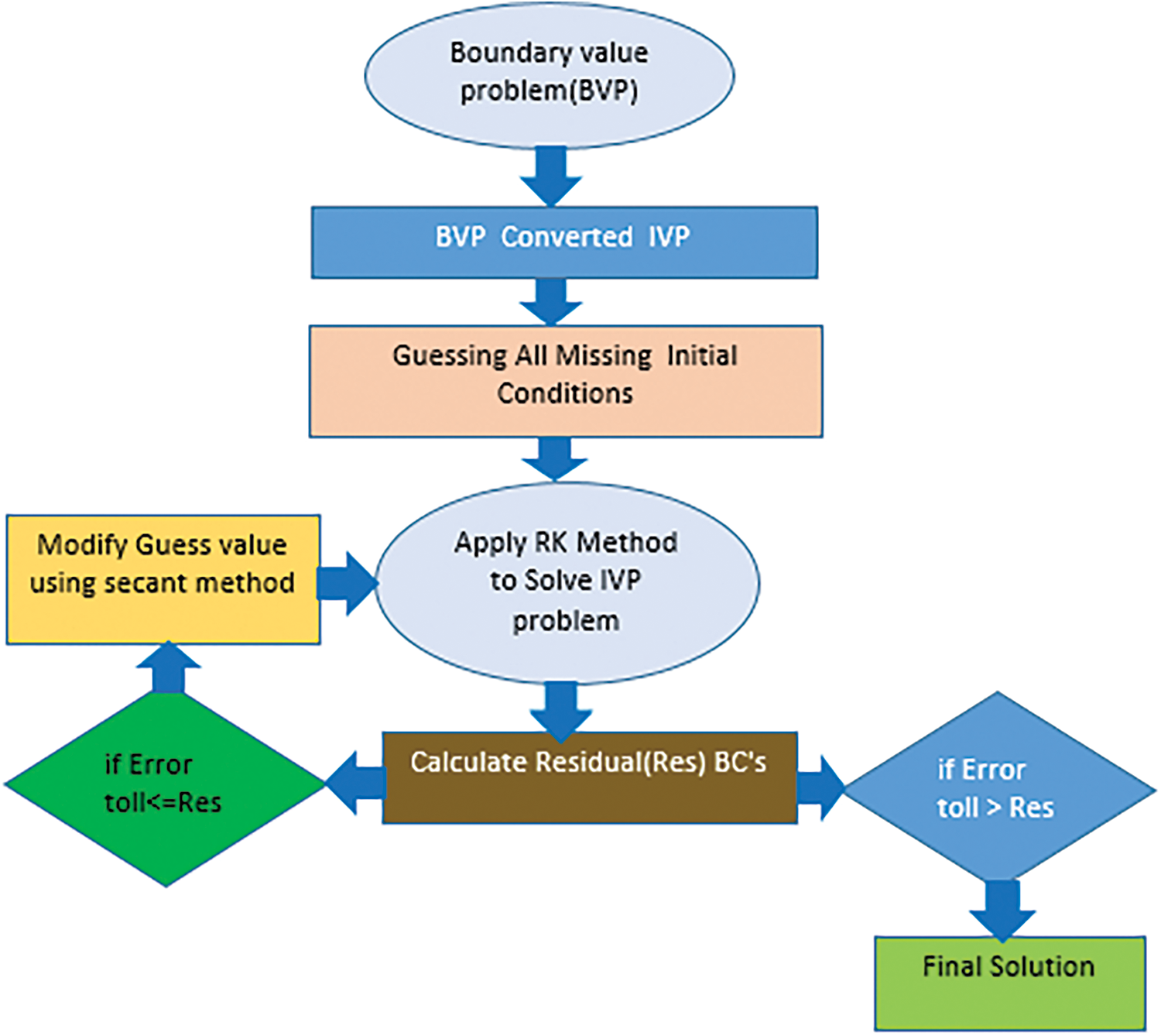
Figure 2: Solution flow chart

4  Results and Discussion

In this section, physical interpretations are provided for the influence of flow parameters such as Casson fluid parameter 0.5<β<2, inclined magnetization 2<M<8, and porosity parameter 0<K<4 on the velocity f′(ζ) and temperature θ(ζ) profiles of the flow. Additionally, thermal radiation 1<Rd<7 and thermal relaxation 0.1<γ1<0.4 influence is also demonstrated on temperature profile θ(ζ). Further, Brownian motion 0.2<Nb<0.6, chemical reaction 0.2<γ2<0.5 and Schmidt number 3<Sc<9 impact has been presented on concentration profile. Skin friction and Nusselt number coefficients have been presented in the tabulated data set.

4.1 Code Validation and Analysis of Results

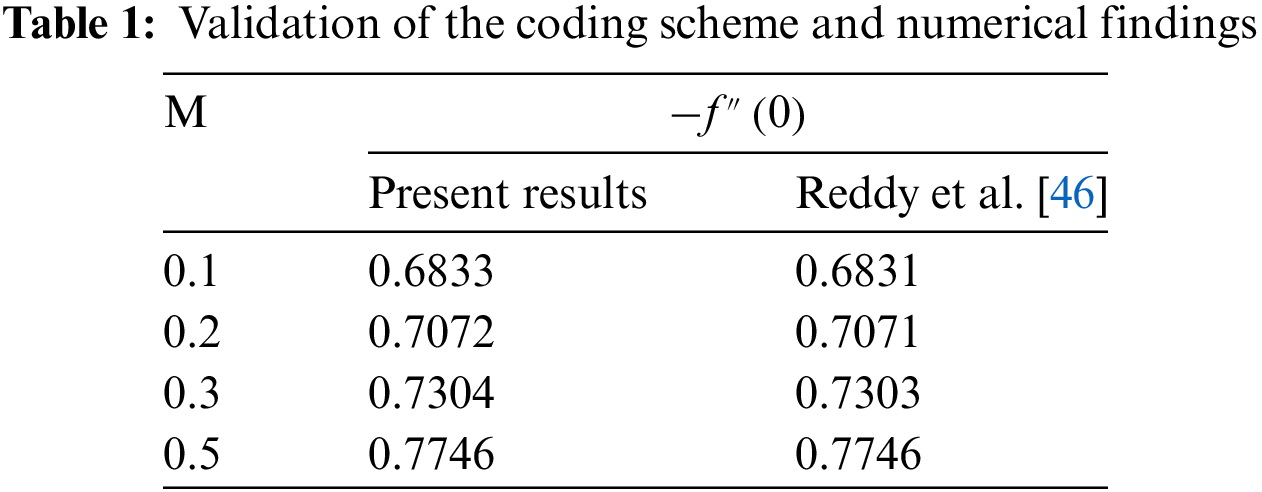
In this subsection, the validation of the presented outcomes has been presented and analyzed in comparison with Reddy et al. [46]. Reddy et al. [46] employed Buongiorno nanofluid model with heat generation/absorption effect in the presence of chemical reaction over the porous medium for non-Newtonian Casson fluid. Additionally, they ignored the Cattaneo-Christov heat flux while modeling the problem. Whereas, in this work, we have addressed the Cattaneo-Christov heat flux with in the presence of thermal radiation, chemical reaction, and Buongiorno nanofluid model. The outcomes in the present study have been obtained using MATLAB using the shooting method. We reproduce Reddy et al.'s [46] skin friction coefficient to ensure the accuracy of our findings. The comparison presented in Table 1 for this comparison we have chosen K=0.3 and β = 0.5. Moreover, Table 1 illustrates good agreement between our results and those obtained by Reddy et al. [46].

4.2 Velocity, Temperature, and Concentration Profiles

In this section, the outcomes of the present study have been presented and discussed under varying influence of the different study parameters such as Casson fluid parameter 0.5<β<2, inclined magnetization 2<M<8, and porosity parameter 0<K<4 on the velocity f′(ζ) and temperature θ(ζ) profiles of the flow. Additionally, thermal radiation 1<Rd<7 and thermal relaxation 0.1<γ1<0.4 influence is also demonstrated on temperature profile θ(ζ). Further, Brownian motion 0.2<Nb<0.6, chemical reaction 0.2<γ2<0.5 and Schmidt number 3<Sc<9. The main goal of the current research is to investigate the effects of various factors on the velocity f′(ζ), temperature θ(ζ) and concentration distribution φ(ζ).

Fig. 3a,b represents the impact of Casson parameter β on the velocity profile f′(ζ) and temperature profile θ(ζ), respectively. By enhancing the value of β, the velocity of fluid decreases and temperature of fluid increases. When Casson fluid parameter β, values are increased, the yield stress is decreased and Casson acts like Newtonian fluid. Furthermore, it is inferred that the velocity of Casson fluid exceeds that of Newtonian fluid. Fig. 3c,d shows the influence of magnetic parameter M on the velocity distribution f′(ζ) and the temperature profile θ(ζ). As the magnetic parameter increases, the velocity profiles decrease. This is due to the Lorentz force increasing along with M, which causes it to resist the fluid motion simultaneously. Consequently, an increase in the magnetic parameter M causes an increase in temperature. Furthermore, the improvement is rather noticeable close to the sheet, while the improvement is hardly noticeable farther away.

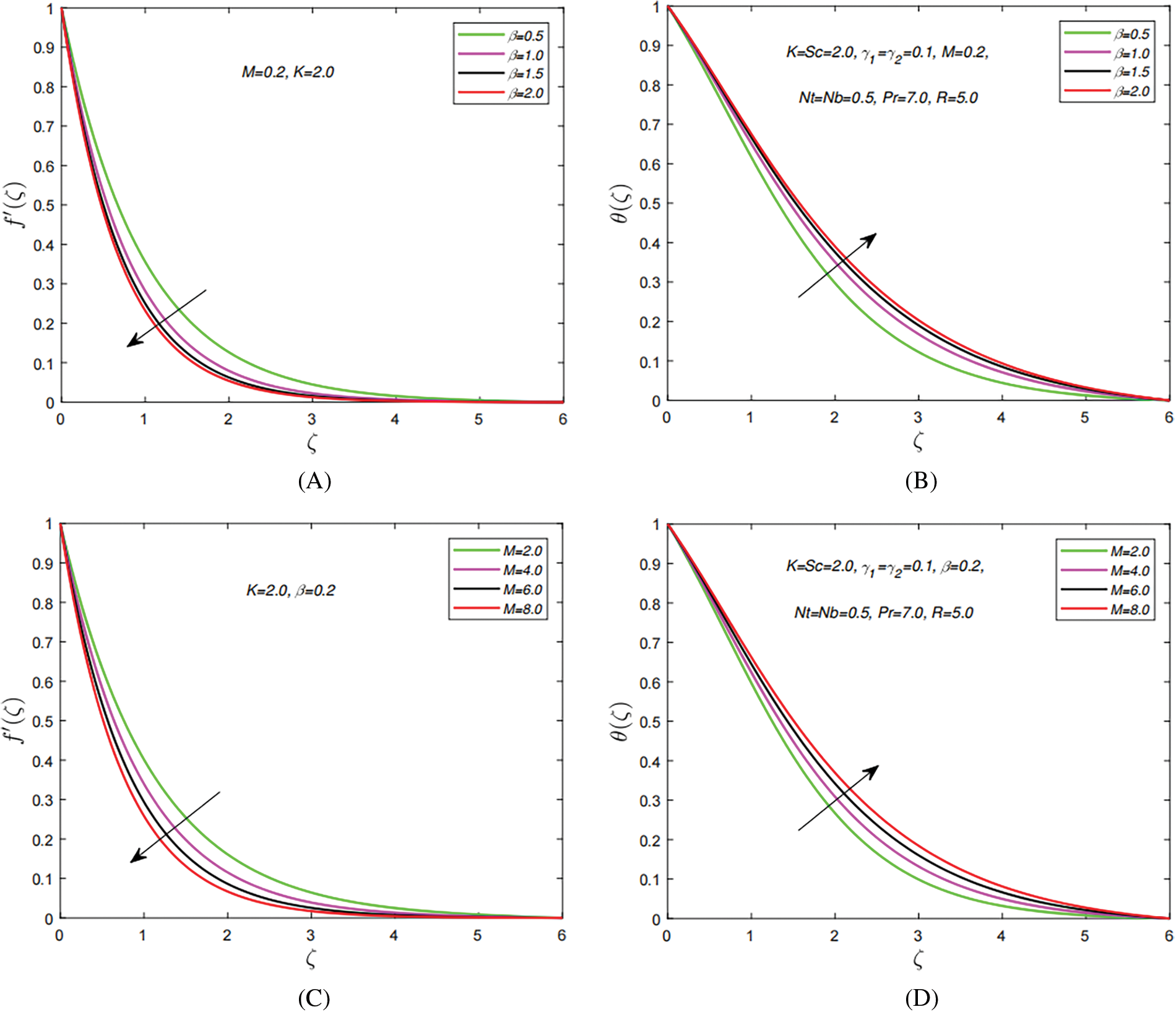
Figure 3: The influence of distinct study parameters on velocity and temperature profiles. (A) Effect of β on velocity profile f(ζ). (B) Influence of β on temperature profile θ(ζ). (C) Impact of M on velocity profile f(ζ). (D) Influence of M on temperature profile θ(ζ)

Fig. 4a,b depicts effects of the permeability parameter K on the temperature distribution and velocity field. These outcomes indicate that when the porosity K of material is raised, the velocity profile drops. This outcome is attributed to the fact that when K is raised, the porous layer is amplified, reducing the thickness of the momentum boundary layer. Similarly, a rise in K improves the boundary layer region’s temperature of the fluid. Darcian’s body force is transferring that heat from the solid wall to the stream zone. Fig. 4c,d indicates the impact of Nb on the dimensionless temperature and concentration distribution. It has been seen that when Nb rises, the temperature field expands while the concentration profile contracts. Brownian motion refers to the movement of particles as a result, the more heat is created and the temperature rises, the more actively the particles move.

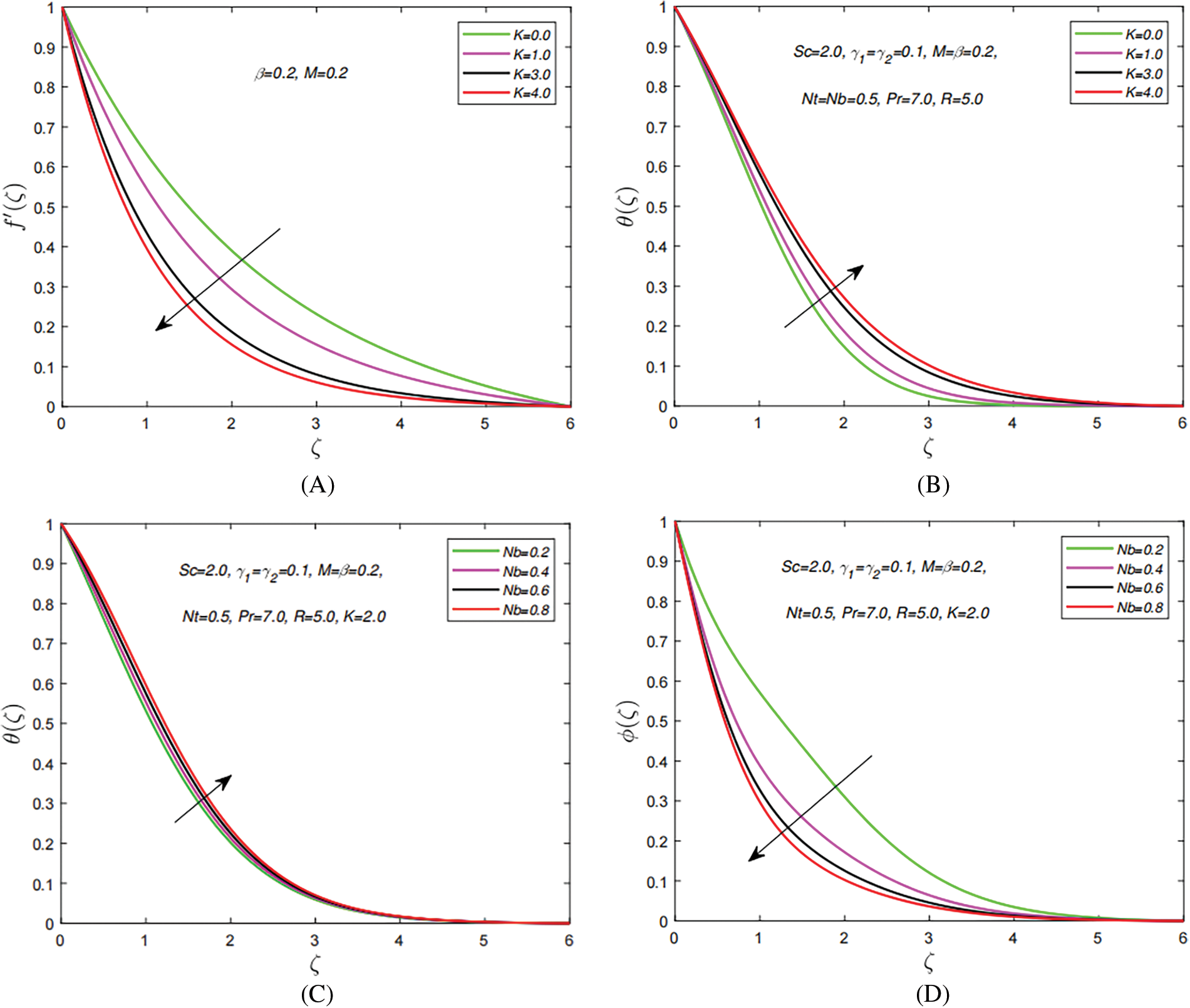
Figure 4: The impact of distinct study parameters on velocity and temperature profiles. (A) Effect of K on velocity profile f(ζ). (B) Influence of K on temperature profile θ(ζ). (C) Impact of Nb on temperature profile θ(ζ). (D) Effect of Nb on concentration profile ϕ(ζ)

Fig. 5a,b represents the impact of thermal radiation R and thermal relaxation time factor γ1 on temperature θ(ζ). In this graph, we observed that on rising values of R, the temperature profile θ(ζ) also increases. The system generates more heat as a result of a high value for the radiation parameter, which ultimately raises the fluid’s temperature and lengthens the thermal boundary layer. It is obvious that the mean absorption coefficient decreases as it rises, which may be the cause of the rising thermal field. Temperature increases are influenced by the magnetic field as well. This demonstrates that for a better cooling process, heat radiation should be kept to a minimum. We find a relationship between temperature and γ1 is inverse. Furthermore, for increasing R, the temperature rises closer to the state of a free stream at shorter levels above the surface. Fig. 5c,d illustrates the impact of Schmidt number and chemical reaction parameter γ2 on concentration profile. Fluid’s concentration exhibits a behavior that is decreasing as Sc achieves greater values. The inverse connection between the Sc and the mass diffusion rate is the source of this behavior. As a consequence, when Sc is increased, the mass diffusivity process decelerates, which results in a fall in concentration as well as a decline in the width of the concentration boundary layer. The concentration gradient is also affected by a chemical reaction factor (γ2) in a similar manner. Raising the value of γ2 causes a decrease in chemical molecule diffusion, which in turn causes the fluid’s concentration to de-escalate and the width of the related concentration boundary layer to decline.

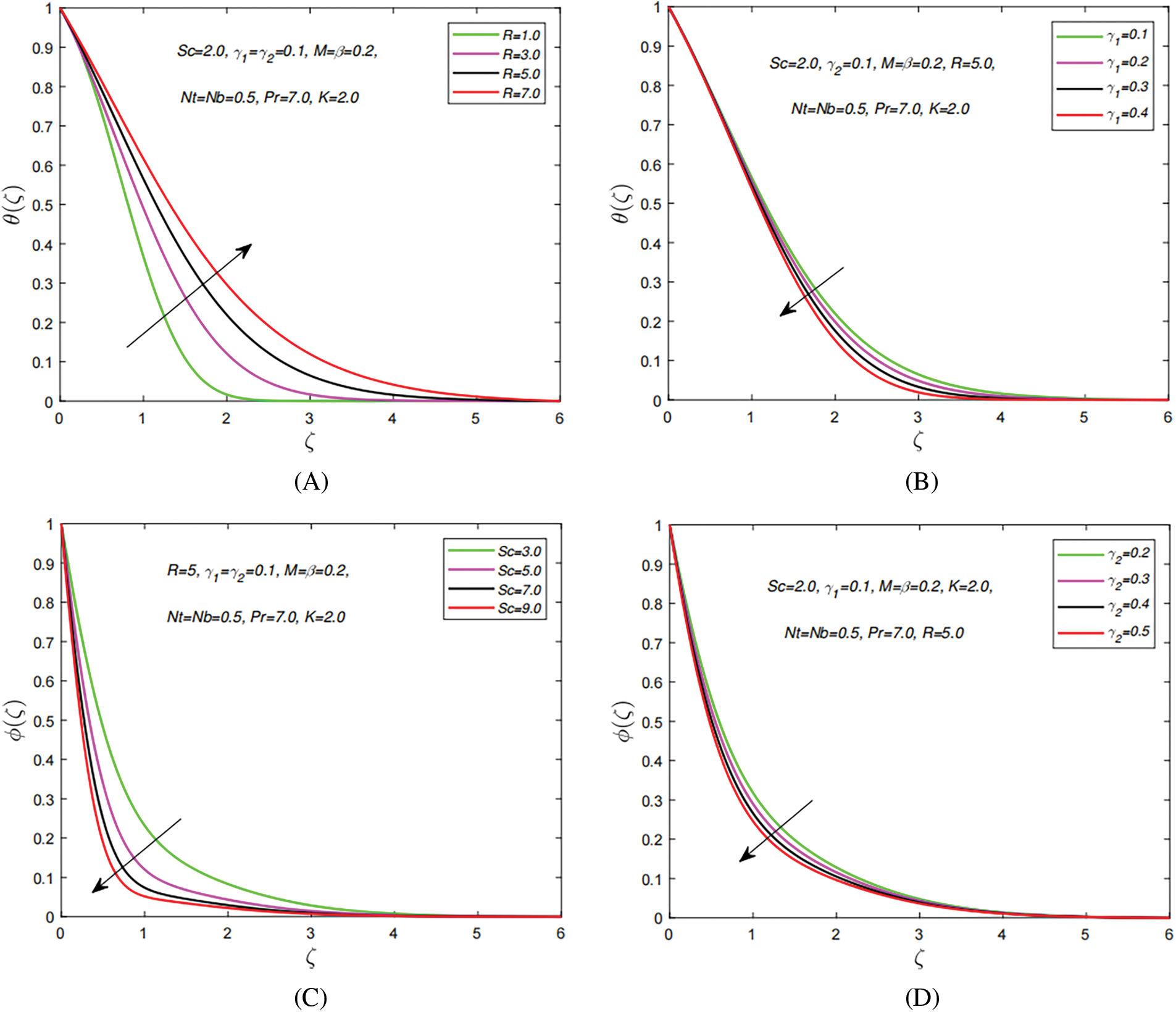
Figure 5: The distinct study parameters vs. temperature and concentration profiles. (A) Effect of R on temperature profile θ(ζ). (B) Impact of γ1 on temperature profile θ(ζ). (C) Effect of Sc on concentration profile ϕ(ζ). (D) Impact of γ2 on concentration profile ϕ(ζ)

4.3 Nusselt Number and Skin Friction

The validation of our results has been presented for the skin friction coefficient in Table 1 under varying effects of magnetization force, a good agreement has been found with already published results and present outcomes. In this section, numerical outcomes of the skin friction coefficient, local Nusselt number, and Sherwood number for the distinct values of parameters namely, magnetization force, Casson fluid parameter, permeability parameter, thermal radiation, and chemical reaction parameter are shown in Tables 2 and 3.

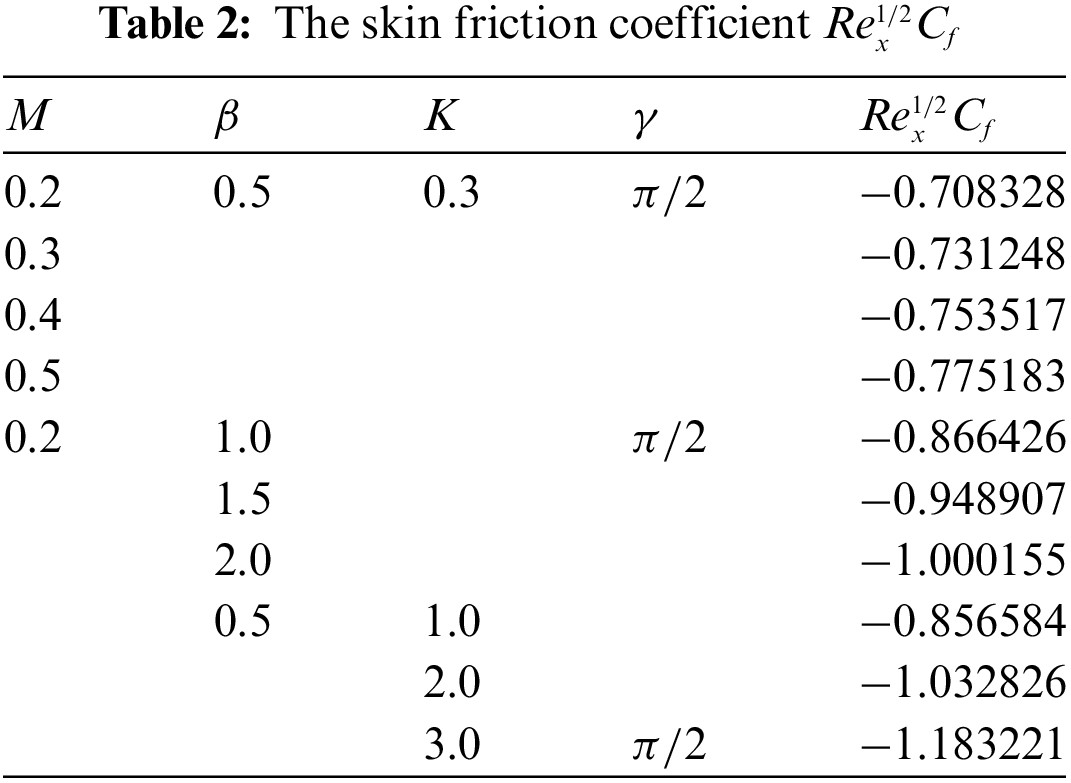
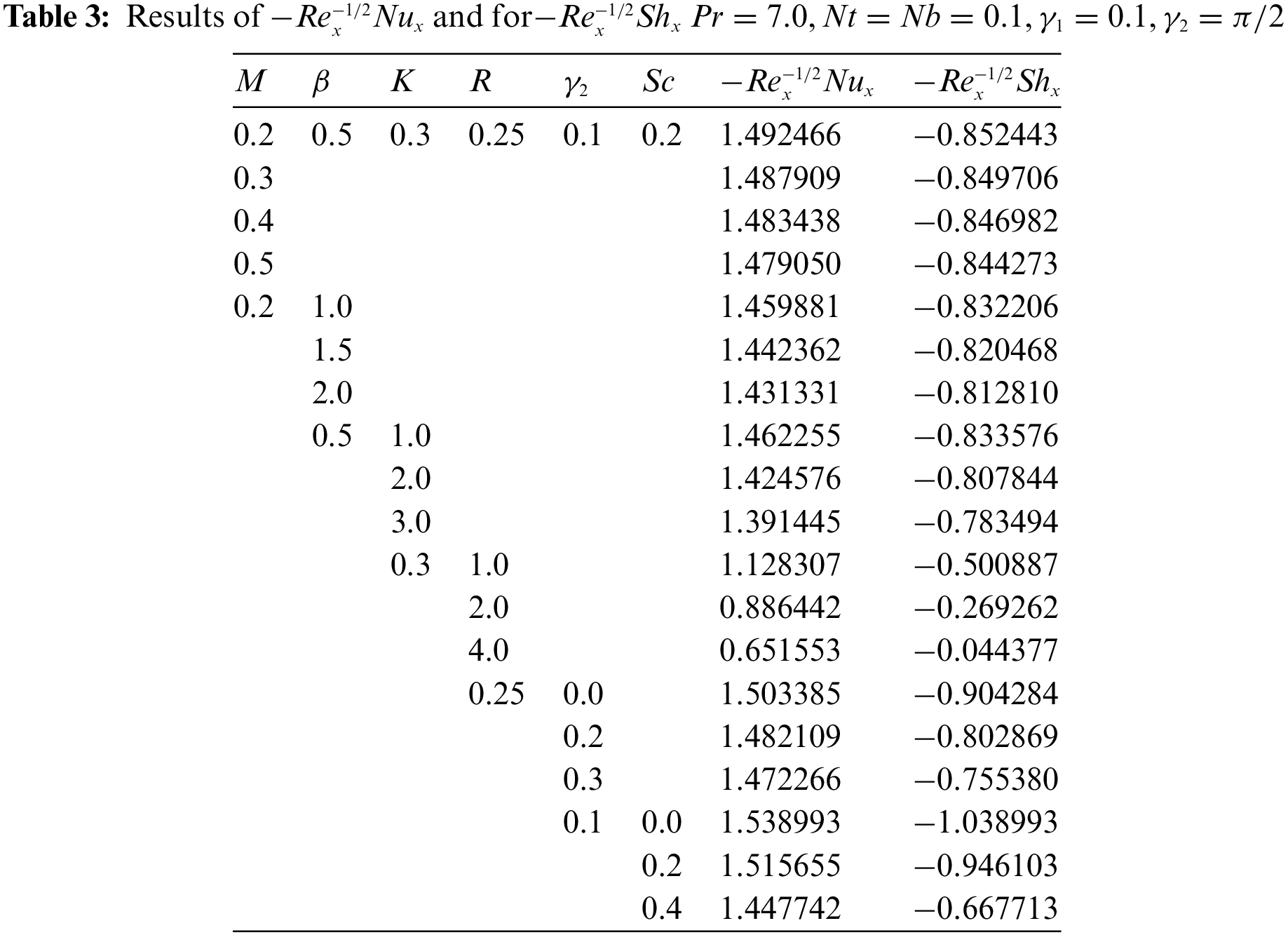
Table 2 shows the numerical outcomes for the skin friction coefficient under the influence of the magnetization force, Casson fluid, and permeability parameters. It can be noted from the outcomes of skin friction that when permeability levels are increased the skin friction is enhanced whereas reduced skin friction rates have been obtained under the varying impact of magnetic field and Casson fluid parameter. Table 3 demonstrates Nusselt number and Sherwood number outcomes under the effect of different varying study parameters. It is worth mentioning here that raising the levels of permeability and chemical reaction decreases the Nusselt number whereas raising the levels of thermal radiation, magnetization force, and Casson fluid parameter enhances the rate of heat transfer coefficient. Moreover, raising the Schmidt number reduce Sherwood’s number as compared to other study parameters.

5  Conclusions

In this paper, two-dimensional Casson nanofluid flow across a stretched sheet under the impact of the inclined magnetic field, Cattaneo-Christov heat flux, and first-order chemical reaction has been investigated numerically using the shooting method in MATLAB. The results of the current investigation can be categorized as follows:

•   The temperature profile of the fluid and its velocity are directly and inversely proportional in Casson fluid, respectively.

•   Magnetization force is inversely proportional to the velocity of the fluid and directly proportional to the fluid temperature.

•   The temperature distribution gets larger with increasing values of thermal radiation.

•   Enhancing the magnetic parameter M results in a rise in the skin friction coefficient.

•   The behavior of the temperature profile decreases as the thermal relaxation time parameter γ1 increases.

•   The Nusselt number decreases as the value of the chemical reaction parameter rises.

•   An increment is noticed in the temperature distribution by raising the values of Brownian motion Nb.

•   The concentration profile can be reduced by raising the values of the chemical reaction parameter γ2.

•   Due to the increasing values of the thermal radiation R, the values of Nux are decreased while Shx is increased.

Acknowledgement: The authors would like to thank the editors and worthy reviewers for the constructive suggestions to enhance the overall presentation of this version of the article.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Mahzad Ahmed, Raja Mussadaq Yousaf; Data collection: Mahzad Ahmed, Raja Mussadaq Yousaf, B. Shankar Goud; Analysis and interpretation of results: Mahzad Ahmed, Raja Mussadaq Yousaf; Draft manuscript preparation: Mahzad Ahmed, Raja Mussadaq Yousaf, B. Shankar Goud; Project administration, Supervision, Sources and writing—review and editing: Ali Hassan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: This research has no unavailable data.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. Argonne, IL, USA: Argonne National Lab. (ANL); 1995. [Google Scholar]

2. Wang XQ, Mujumdar AS. A review on nanofluids–part I: theoretical and numerical investigations. Braz J Chem Eng. 2008;25(4):613–30. doi:10.1590/S0104-66322008000400001. [Google Scholar] [CrossRef]

3. Jahani K, Mohammadi M, Shafii MB, Shiee Z. Promising technology for electronic cooling: nanofluidic micro pulsating heat pipes. J Electron Packag. 2013;135(2):021005. doi:10.1115/1.4023847. [Google Scholar] [CrossRef]

4. Buongiorno J. Convective transport in nanofluids. ASME J Heat Transfer. 2006;128(3):240–50. doi:10.1115/1.2150834. [Google Scholar] [CrossRef]

5. Hussain SM, Sharma R, Seth GS, Mishra MR. Thermal radiation impact on boundary layer dissipative flow of magneto-nanofluid over an exponentially stretching sheet. Int J Heat Technol. 2018;36(4):1163–73. doi:10.18280/ijht.360402. [Google Scholar] [CrossRef]

6. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Transf. 2010;53(11–12):2477–83. doi:10.1016/j.ijheatmasstransfer.2010.01.032. [Google Scholar] [CrossRef]

7. Noghrehabadi A, Saffarian MR, Pourrajab R, Ghalambaz M. Entropy analysis for nanofluid flow over a stretching sheet in the presence of heat generation/absorption and partial slip. J Mech Sci Technol. 2013;27:927–37. [Google Scholar]

8. Hady FM, Ibrahim FS, Abdel-Gaied SM, Eid MR. Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Nanoscale Res Lett. 2012;7(1):1–3. doi:10.1186/1556-276X-7-229. [Google Scholar] [PubMed] [CrossRef]

9. Wang CY. Free convection on a vertical stretching surface. ZAMM. 1989;69(11):418–20. doi:10.1002/zamm.19890691115. [Google Scholar] [CrossRef]

10. Nadeem S, Haq RU, Khan ZH. Numerical solution of non-Newtonian nanofluid flow over a stretching sheet. Appl Nanosci. 2014;4(5):625–31. doi:10.1007/s13204-013-0235-8. [Google Scholar] [CrossRef]

11. Prasannakumara BC, Gireesha BJ, Gorla RS, Krishnamurthy MR. Effects of chemical reaction and nonlinear thermal radiation on Williamson nanofluid slip flow over a stretching sheet embedded in a porous medium. J Aerosp Eng. 2016;29(5):04016019. doi:10.1061/(ASCE)AS.1943-5525.0000578. [Google Scholar] [CrossRef]

12. Danish GA, Imran M, Tahir M, Waqas H, Asjad MI, Akgül A, et al. Effects of non-linear thermal radiation and chemical reaction on time dependent flow of williamson nanofluid with combine electrical MHD and activation energy. J Appl Comput Mech. 2021;7(2):546–58. [Google Scholar]

13. Srinivasulu T, Goud BS. Effect of inclined magnetic field on flow, heat and mass transfer of Williamson nanofluid over a stretching sheet. Case Stud Therm Eng. 2021;23(6):100819. doi:10.1016/j.csite.2020.100819. [Google Scholar] [CrossRef]

14. Zainal NA, Nazar R, Naganthran K, Pop I. MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation. Int J Numer Method H. 2021;31(3):858–79. doi:10.1108/HFF-03-2020-0126. [Google Scholar] [CrossRef]

15. Reddy YD, Goud BS, Nalivela NR, Rao VS. Impact of porosity on two-dimensional unsteady MHD boundary layer heat and mass transfer stagnation point flow with radiation and viscous dissipation. Numer Heat Transf A. 2023;85(8):1172–90. doi:10.1080/10407782.2023.2198739. [Google Scholar] [CrossRef]

16. Mondal H, Goqo SP, Sibanda P, De P. Effect of chemical reaction on mixed convective nanofluid flow on a vertical plate with uniform heat and mass fluxes. Int J Appl Mech. 2019;24(2):329–42. doi:10.2478/ijame-2019-0021. [Google Scholar] [CrossRef]

17. Hassan A, Hussain A, Arshad M, Awrejcewicz J, Pawlowski W, Alharbi FM, et al. Heat and mass transport analysis of MHD rotating hybrid nanofluids conveying silver and molybdenum di-sulfide nano-particles under effect of linear and non-linear radiation. Energies. 2022;15(17):6269. doi:10.3390/en15176269. [Google Scholar] [CrossRef]

18. Shah SAGA, Hassan A, Alsubaie N, Alhushaybari A, Alharbi FM, Galal AM, et al. Convective heat transfer in magneto-hydrodynamic Carreau fluid with temperature dependent viscosity and thermal conductivity. Nanomater. 2022;12(22):4084. doi:10.3390/nano12224084. [Google Scholar] [PubMed] [CrossRef]

19. Arshad M, Hassan A, Haider Q, Alharbi FM, Alsubaie N, Alhushaybari A, et al. Rotating hybrid nanofluid flow with chemical reaction and thermal radiation between parallel plates. Nanomater. 2022;12(23):4177. doi:10.3390/nano12234177. [Google Scholar] [PubMed] [CrossRef]

20. Shah SAGA, Hassan A, Karamti H, Alhushaybari A, Eldin SM, Galal AM. Effect of thermal radiation on convective heat transfer in MHD boundary layer Carreau fluid with chemical reaction. Sci Rep. 2023;13(1):4117. doi:10.1038/s41598-023-31151-4. [Google Scholar] [PubMed] [CrossRef]

21. Gul H, Ramzan M, Chung JD, Chu YM, Kadry S. Multiple slips impact in the MHD hybrid nanofluid flow with Cattaneo-Christov heat flux and autocatalytic chemical reaction. Sci Rep. 2021 Jul 16;11(1):14625. doi:10.1038/s41598-021-94187-4. [Google Scholar] [PubMed] [CrossRef]

22. Pramanik S. Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng J. 2014 Mar 1;5(1):205–12. doi:10.1016/j.asej.2013.05.003. [Google Scholar] [CrossRef]

23. Mahanthesh B, Gireesha BJ, Gorla RS. Nanoparticles effect on 3D flow, heat and mass transfer of nanofluid with nonlinear radiation, thermal-diffusion and diffusion-thermo effects. J Nanofluids. 2016;5(5):669–78. doi:10.1166/jon.2016.1257. [Google Scholar] [CrossRef]

24. Mohyud-Din ST, Usman M, Wang W, Hamid M. A study of heat transfer analysis for squeezing flow of a Casson fluid via differential transform method. Neural Comput Appl. 2018;30(10):3253–64. doi:10.1007/s00521-017-2915-x. [Google Scholar] [CrossRef]

25. Vijayaragavan R, Karthikeyan S. Hall current effect on chemically reacting MHD Casson fluid flow with dufour effect and thermal radiation. Asian J Appl Sci Technol. 2018;2(2):228–45. [Google Scholar]

26. Yousef NS, Megahed AM, Ghoneim NI, Elsafi M, Fares E. Chemical reaction impact on MHD dissipative Casson-Williamson nanofluid flow over a slippery stretching sheet through porous medium. Alex Eng J. 2022;61(12):10161–70. doi:10.1016/j.aej.2022.03.032. [Google Scholar] [CrossRef]

27. Mukhopadhyay S. Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin Phys B. 2013;22(7):074701. doi:10.1088/1674-1056/22/7/074701. [Google Scholar] [CrossRef]

28. Dero S, Mohd Rohni A, Saaban A. Effects of the viscous dissipation and chemical reaction on Casson nanofluid flow over the permeable stretching/shrinking sheet. Heat Transfer. 2020;49(4):1736–55. doi:10.1002/htj.21688. [Google Scholar] [CrossRef]

29. Goud BS, Reddy YD, Rao VS, Khan ZH. Thermal radiation and Joule heating effects on a magnetohydrodynamic Casson nanofluid flow in the presence of chemical reaction through a non-linear inclined porous stretching sheet. J Nav Archit Mar Eng. 2020;17(2):143–64. doi:10.3329/jname.v17i2.49978. [Google Scholar] [CrossRef]

30. Khan MI, Waqas M, Hayat T, Alsaedi A. A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J Colloid Interface Sci. 2017;498:85–90. doi:10.1016/j.jcis.2017.03.024. [Google Scholar] [PubMed] [CrossRef]

31. Hassan A, Hussain A, Arshad M, Gouadria S, Awrejcewicz J, Galal AM, et al. Insight into the significance of viscous dissipation and heat generation/absorption in magneto-hydrodynamic radiative casson fluid flow with first-order chemical reaction. Front Phys. 2022;10:920372. doi:10.3389/fphy.2022.920372. [Google Scholar] [CrossRef]

32. Khan S, Shu W, Ali M, Sultan F, Shahzad M. Numerical simulation for MHD flow of Casson nanofluid by heated surface. Appl Nanosci. 2020;10(12):5391–9. doi:10.1007/s13204-020-01546-0. [Google Scholar] [CrossRef]

33. Mabood F, Khan WA, Ismail AM. MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet: a numerical study. J Magn Magn Mater. 2015;374:569–76. [Google Scholar]

34. Zhang L, Bhatti MM, Shahid A, Ellahi R, Bég OA, Sait SM. Nonlinear nanofluid fluid flow under the consequences of Lorentz forces and Arrhenius kinetics through a permeable surface: a robust spectral approach. J Taiwan Inst Chem Eng. 2021;124:98–105. [Google Scholar]

35. Krishna MV. Chemical reaction, heat absorption and Newtonian heating on MHD free convective Casson hybrid nanofluids past an infinite oscillating vertical porous plate. Int Commun Heat Mass. 2022;138:106327. [Google Scholar]

36. Nadeem S, Ul Haq R. MHD boundary layer flow of a nanofluid passed through a porous shrinking sheet with thermal radiation. J Aerosp Eng. 2015 Mar 1;28(2):04014061. [Google Scholar]

37. Bhatti MM, Arain MB, Zeeshan A, Ellahi R, Doranehgard MH. Swimming of gyrotactic microorganism in MHD Williamson nanofluid flow between rotating circular plates embedded in porous medium: application of thermal energy storage. J Energy Storage. 2022;45:103511. [Google Scholar]

38. Manvi BK, Kerur SB, Tawade JV, Nieto JJ, Sankeshwari SN, Ahmad H, et al. MHD Casson nanofluid boundary layer flow in presence of radiation and non-uniform heat source/sink. Math Model Control. 2023;3:152–67. [Google Scholar]

39. Poply V, Singh P, Yadav AK. Stability analysis of MHD outer velocity flow on a stretching cylinder. Alex Eng J. 2018;57(3):2077–83. [Google Scholar]

40. Chamkha AJ, Aly AM. MHD free convection flow of a nanofluid past a vertical plate in the presence of heat generation or absorption effects. Chem Eng Commun. 2010;198(3):425–41. [Google Scholar]

41. Malik MY, Khan M, Salahuddin T, Khan I. Variable viscosity and MHD flow in Casson fluid with Cattaneo-Christov heat flux model: using Keller box method. Eng Sci Technol Int J. 2016;19(4):1985–92. [Google Scholar]

42. Ganga B, Ansari SM, Ganesh NV, Hakeem AA. MHD radiative boundary layer flow of nanofluid past a vertical plate with internal heat generation/absorption, viscous and ohmic dissipation effects. J Nigerian Math Soc. 2015;34(2):181–94. [Google Scholar]

43. Waheed SE, Moatimid GM, Elfeshawey AS. Unsteady magnetohydrodynamic squeezing darcy-forchheimer flow of Fe3O4 casson nanofluid: impact of heat source/sink and thermal radiation. Partial Differ Equ Appl Math. 2024;10:100666. doi:10.1016/j.padiff.2024.100666. [Google Scholar] [CrossRef]

44. Biswal MM, Swain K, Dash GC, Mishra S. Study of chemically reactive and thermally radiative Casson nanofluid flow past a stretching sheet with a heat source. Heat Transfer. 2023;52(1):333–53. [Google Scholar]

45. Chamkha AJ, Rashad AM. Unsteady heat and mass transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and Soret and Dufour effects. Can J Chem Eng. 2014;92(4):758–67. [Google Scholar]

46. Reddy NN, Rao VS, Reddy BR. Impact of thermal radiation and chemical reaction on MHD heat and mass transfer Casson nanofluid flow past a stretching sheet in presence of heat source/sink. ARPN J Eng Appl Sci. 2006;16:1165–11. [Google Scholar]