Numerical Study of Multi-Factor Coupling Effects on Energy Conversion Performance of Nanofluidic Reverse Electrodialysis

1  Introduction

Salinity Gradient Energy (SGE), a kind of Gibbs free energy that releases naturally from the mixing of solutions with different concentrations, holds immense potential for widespread utilization as a sustainable and eco-friendly energy source. Three prevalent energy conversion methodologies, namely Pressure Retarded Osmosis (PRO), Vapor Pressure Difference (VPD) Energy, and Reverse Electrodialysis (RED), have been extensively researched and implemented for the extraction of SGE [1]. In comparison to PRO and VPD, RED exhibits a significant advantage by directly transforming SGE into electricity solely through the utilization of ion-selective membranes. This approach circumvents the mechanical energy losses encountered in PRO and the heat dissipation associated with VPD, thereby rendering RED a highly efficient and often-termed osmotic energy conversion technique [2,3]. Recently, the rapid advancements in nanotechnology and innovative nanomaterials have ushered in a new era of enhanced RED, commonly known as Nanofluidic Reverse Electrodialysis (NRED) [4,5]. Instead of using conventional ion-selective membranes, this cutting-edge NRED system innovatively incorporates nanofluidic-enabled membranes, which exhibit exceptional capabilities in facilitating mass transfer, thereby propelling the energy conversion efficiency of the SGE to unprecedented heights.

Numerous experimental and numerical studies on the NRED have been carried out from different perspectives [6–11], such as nanochannel geometries [12–15], surface charge densities of nanochannels [16–18], nanochannel materials [19], solute concentrations [20,21], solution temperatures [22], pH values of solutions [23], and their effects on the energy conversion performance of the NRED system. It is found that the geometric configurations of nanochannels play a pivotal role in determining the energy conversion performance of the NRED system Specifically, nanochannels with longer lengths and smaller diameters potentially give rise to high output power [24,25]. However, it is also demonstrated that maximal energy conversion efficiencies could only be achieved at certain optimal nanochannel lengths [26]. Asymmetric nanochannels, such as conical nanochannels [27], bullet-shaped nanochannels [28], asymmetric nano-roughness-featured nanochannels [29], etc., perform differently during the energy conversion processes when coupling with different concentration gradients. In practical applications, the radii of nanochannels often exhibit random variations along their length due to prevalent fabrication imperfections, resulting in an irregular geometry that can significantly impact their performance characteristics. In addition, it is noteworthy to mention that membranes employed in the majority of RED experiments can be equivalently regarded as a cluster of irregularly shaped nanochannels.

Concentration ratio between the two solutions to be mixed is another key parameter in determining the energy conversion performance of NRED. It has been observed that an increment in the concentration ratio, within a relatively low range, results in a corresponding enhancement of the generated potential [25]. However, a subsequent increase in the concentration ratio beyond a certain threshold adversely affects ion selectivity, resulting in a subsequent decline in the generated potential [23]. Thus, it is logically deduced that the potential initially escalates and subsequently decrease as the concentration ratio rises. However, contrasting findings from certain studies reveal a monotonic augmentation of potential with an increment in concentration ratio, which is also related to the nanochannel length [24].

Recent extensive researches have unveiled a pivotal role of solution temperature in governing the intricacies of energy conversion processes [30,31]. This critical parameter influences ion transportations [32,33], modulates currents [34,35], controls potentials and consequently impacts the overall energy conversion efficiency in a complicated manner [36–39]. In particular, asymmetric thermal environments have demonstrated remarkable capabilities in mitigating the ion concentration polarization (ICP) effect at the interface between nanopores and the reservoir, particularly within regions of low solution concentration. This mitigation subsequently enhances the corresponding energy conversion processes [40,41]. Another research has also revealed that the utilization of a NRED device, when coupled with a photothermal condition, significantly enhances the efficiency of harvesting SGE [42]. Furthermore, leveraging temperature effects to enhance the performance of salinity gradient energy can facilitate the recovery and conversion of low-grade thermal energy [43,44]. Moreover, integrating salinity gradient energy with solar power generation can further enhance the efficiency of both energy sources [45,46].

Generally, the performance of the NRED system is intricately influenced by a series of complex factors. Although extensive research works have been carried out on NRED, the majority of them have predominantly focused on isolating and examining the influence of individual characteristics on energy conversion processes. The comprehensive investigations on complex interplay and coupling effects of multiple factors remain scarce. This study aims to examine the complicated multi-factor coupling effects of three pivotal parameters, including the nanochannel geometry, solution temperature, and the solution concentration, on the energy conversion processes of NRED. Particularly, axisymmetric nanochannels with randomly varying wall curvature are going to be innovatively considered. The core performance metrics, which encompass the open-circuit potential, short-circuit current, maximum power output, cation transfer number, and ultimately, the energy conversion efficiency across the nanochannels, will be systematically analyzed under various prescribed conditions.

2  Mathematical Model

2.1 Numerical Model

As depicted in a typical energy conversion system of NRED in Fig. 1a, an axisymmetric nanochannel, featured with varied radii along the axial direction, bridges two reservoirs at each end of the nanochannel. Two KCl solutions, with two different solution concentrations of cH and cL (where cH > cL) and two different solution temperatures of TH and TL, are filled in the reservoirs, respectively. Since the thermal conductivity across the nanochannel membrane is also considered in this study, the computational domain involves both the fluid and the solid components for mass and heat transfer. Fig. 1b illustrates the corresponding computational domain of the energy conversion system. The wall of the nanochannel, consisting of a randomly distributed curve, is controlled by a scaling factor of amplitude, s. When s equals 0, the wall of the nanochannel becomes a straight line and the radius of the nanochannel equals the mean radius, as indicated by the dashed line in green in the figure. When s > 0, the nanochannel wall deviates from a straight line and exhibits random variations. Notably, larger values of s lead to more significant variations in the amplitude of the nanochannel wall. In addition, the gradient direction of the temperature that is opposite to that of the concentration is defined as the negative temperature gradient in this study.

Figure 1: Schematic of a typical energy conversion system of NRED. (a) An energy conversion system of NRED within an electric circuit. (b) The corresponding calculation domain for the numerical study

The steady-state Poisson-Nernst-Planck equation integrated with the Navier-Stokes equation are employed to simulate ion transports in nanochannels where the temperature and concentration gradients exists [21,41]. To facilitate numerical calculations and comparisons, a set of characteristic parameters are defined for scaling the governing equations: length Lref = a; concentration cref = c0 with c0 representing the low solution concentration; temperature Tref = T0; relative permittivity εr,ref = εr,0 with εr,0 representing the dielectric constant at T = T0; diffusion coefficient D1,ref = D1,0, D2,ref = D2,0 with D1,0 and D2,0 respectively representing diffusion coefficients of cations and anions at T = T0; potential ϕref = RTref/F with R and F respectively representing the Universal gas constant and the Faraday constant; electric strength Eref = ϕref/Lref; fluid viscosity μref = μ0; charge density σref = ε0εr,refϕref/Lref with ε0 representing the vacuum dielectric constant; velocity uref = (ε0 εr,ref ϕref/Lref)Eref; pressure pref = μref (uref/Lref); electric current density iref = F uref cref; electric conductivity τref = iref Lref/ϕref. In addition, dimensionless numbers are defined as Reynolds number Re = ρuref Lref/μref with ρ representing the fluid density, Peclet number of cation Pe1 = uref Lref/D1 with D1 representing the diffusion coefficient of the cation K+, Peclet number of anion Pe2 = uref Lref/D2 with D2 representing the diffusion coefficient of the anion Cl−, and PeT = ρurefLrefCp/k with Cp and k respectively representing the specific capacity and thermal conductivity. Consequently, the dimensionless form of the governing equations is achieved as follows [27,47–50]:

∇~ϕ~=−12λ2∑zkc~k(1)

∇~u~=0(2)

∇~c~kuD~k/Pek(∇~2c~k+zk∇~c~k∇~ϕ~+2αk∇~c~k∇~T~/T)=0(3)

Re(u~∇~u~)=−∇~p~+μ~∇~2u~−12∇~ϕ~∑zkc~k−12|−∇~ϕ~|2∇~ε~r=0(4)

PeTu~∇~T~=∇~2T~(5)

where the subscript k is denoted as 1 or 2, representing ionic specie K+ or Cl−, respectively. In addition, zk is the valence of the ionic specie, λ is the scaled Debye length, expressed as λ=[(2c0F2a2)/(ε0εr0RT0)]1/2, αk is the reduced Soret coefficient. Then the electric current density is additionally given as:

i~=u~∑zkc~k−∑D~k/Pek(zk∇~c~k+zk2c~k∇~ϕ~+2zkαkc~k∇~T~/T)(6)

Remarkably, some certain parameters cannot be considered as constants within a calculation domain where the temperature gradient exists. They should be expressed as functions of the temperature [30,42]:

εr=exp⁡(4.4716−4.60128×10−3dT+2.6952×10−7dT2)(7)

where dT = T − 273.15, 0 < dT < 100.

μ=2.414×10−5×10247.8/(T−140)(8)

where 273.15 ≤ T ≤ 643.15.

Di=RTF2[1/|zk|1/τm,k0](9)

where τm,k0 is the limiting molar conductivity of the ith ionic specie. In particular, τm,10 = 40.5017 + 1.2194(dT) + 4.1859 × 10−3(dT)2 and τm,20 = 76.35 + 1.51037(δT) + 4.65 × 10−3(δT)2 – 1.285 × 10−5(δT)3. δT is the temperature difference of the heat source compared to the reference temperature of 298 K (i.e., δT = T – 298). The following performance parameters of the energy conversion process of the NRED are thoroughly investigated in this work, including the open-circuit potential ϕ~oc, short-circuit current I~sc, power P~, maximum power P~max=ϕ~ocI~sc/4, cation transfer number t+=I~+/(I~++|I~−|), and maximum energy conversion efficiency ηmax = (2t+ − 1)2/2.

2.2 Boundary Conditions

Different boundary conditions are used to achieve the open-circuit potential ϕ~oc, short-circuit current I~sc, as well as the potential-current (ϕ~−I~) curve. As depicted in Fig. 1b, the potential at the boundary AC is always set as zero, When the current at the boundary BD, expressed as ∫Ai~ as shown in Table 1, is set as zero, the induced at this boundary is precisely the open-circuit potential ϕ~oc. In contrast, when the potential at the boundary BD is set as zero, the induced current is precisely the short-circuit current I~sc. The corresponding ϕ~−I~ curve can be consequently obtained by setting the potential at the boundary BD as ϕ~=ϕ~0(0<ϕ~0<ϕ~oc). All the other relevant boundary conditions are elaborated in Table 1.

3  Results and Discussion

3.1 Model Validation

A research work reported by Mai et al. [41] is reproduced and compared in this work to validate the proposed theoretical and numerical model. A comprehensive investigation was conducted on a nanochannel, with a focus on its energy conversion behavior under the intricate interplay of temperature and concentration gradients. The radii, length, and surface charge density of the nanochannel were given as 5, 1000 nm, and −5 mC·m−2, respectively. At one end of the nanochannel, the KCl solution was adjusted to a precise concentration of 1 mM, whereas at the opposite end, the concentration was varied systematically, spanning from 1 to 1000 mM, respectively. In addition, on the side with the higher concentration of KCl, the temperature was precisely set at 298 K, whereas on the side featuring a lower concentration, the temperature was adjusted to 323 K, respectively. As illustrated in Fig. 2, the induced potential achieved based on the numerical model applied in this work is compared with the ones numerically and experimentally obtained in literature [41]. The remarkable consistent results validate the feasibility and reliability of the theoretical and numerical model proposed in this study for accurately capturing mass transfer phenomena in nanochannels under conditions of the concentration and temperature gradients.

Figure 2: Validation of the theoretical and numerical model proposed in this work

3.2 Osmotic Energy Conversion

As depicted in Fig. 1b, the dimensionless sizes of the nanochannel and the reservoirs are a~×L~ = 1 × 50 and a~r×L~r = 50 × 50, respectively. Taking the room temperature of T0 = 298 K as the baseline temperature, then the relevant physical parameters at this temperature are given as follows: μ0 = 8.9 × 10−4 Pa·s, D1,0 = 1.957 × 10−9 m2/s, D2,0 = 2.032 × 10−9 m2/s, εr,0 = 78. The characteristic length and the characteristic concentration are set as a = 10 nm and c0 = 1 mM, respectively. In addition, the reduced Soret coefficient and constants are α1(K+) = 0.5, α2(Cl−) = 0.1 [21], F = 9.649 × 104 C·mol−1, R = 8.314 J·K−1·mol−1 and ε0 = 8.854 × 10−12. Then the corresponding characteristic groups are calculated as ϕref = 2.57 × 10−2 V, uref = 4.56 × 10−2 m·s−1, pref = 4.56 × 103 Pa, σref = 1.77 mC·m−2. The numerical model was solved by a finite-element analysis software, COMSOL Multiphysics 6.1, and free triangular meshes were employed in this work. The grid independence test was conducted first. Variations of the open-circuit potential and the short-circuit current with the increment of the number of meshes are drawn in Fig. 3. It is found that the discretization strategy with a total grid number of 26,473 gives rise to relatively stable potential and current when comparing with the other discretization strategies. Therefore, all the following parametric numerical calculations were carried out based on this discretization strategy.

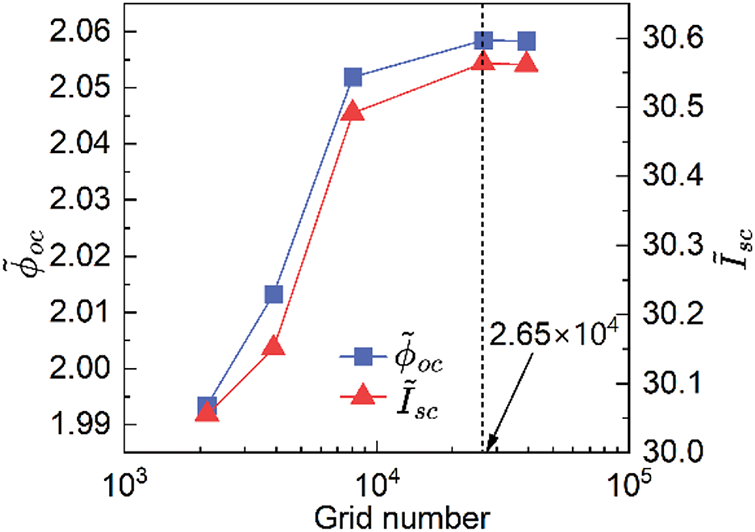
Figure 3: Grid independence test

3.2.1 Effect of Temperature

The general effects of temperature on the osmotic energy conversion happening at given conditions of cH/cL = 50, nanochannel of s = 0.06 are investigated first. As shown in Fig. 4a, four different temperature fields are imposed on the energy conversion system: (I) uniform temperature of 298 K across the nanochannel denoted as T-298 K, (II) uniform temperature of 323 K across the nanochannel denoted as T-323 K, (III) temperature field with temperatures of 298 and 323 K respectively at the left (high-concentration side) and right (low-concentration side) terminals denoted as T-298 K/323 K, (IV) temperature field with temperatures of 323 and 298 K respectively at the left (high-concentration side) and right (low-concentration side) terminals denoted as T-323 K/298 K. In this study, the low-concentration solution is always fixed as 1 at the right terminal of the NRED system and the high-concentration solution is placed at the left side. Therefore, the temperature gradient that has the same direction as that of the concentration gradient is defined as the positive temperature gradient. Otherwise, the temperature gradient that is opposite to the concentration gradient is defined as the negative temperature gradient. Fig. 4b presents variations of the current and the output power with the potential at these four different temperature fields. Generally, linear variations of the current with the potential are observed for all four temperature fields. Thus, the corresponding maximum power occurs at the half of the open-circuit potential, given as P~max=ϕ~ocI~sc/4. It is observed from Fig. 4b,c that the isothermal scenario of T-323 K yields the highest open-circuit potential, short-circuit current, and power, while the isothermal scenario of T-298 K yields the lowest performance of these three parameters. Both the scenarios of T-298 K/323 K and T-323 K/298 K, which exhibit non-uniform temperature distributions yet maintain an identical average temperature, give rise to intermediate results compared to the two isothermal scenarios as mentioned above and, meanwhile, they perform closely with each other. It reasonably proves that high solution temperatures are beneficial to inducing better performance in aspects of the open-circuit potential, short-circuit current, as well as the output power. However, remarkable different variation trend of the effect of the temperature on the cation transfer number t+ is observed in Fig. 4c where the scenarios of T-323 K and T-298 K/323 K yields the lowest and the highest cation transfer numbers, respectively. This special trend will be thoroughly explored in cooperation with all kinds of ion flow rate investigated in the following section. Consequently, based on the theoretical equation ηmax = (2t+ − 1)2/2, it is logically deduced that these temperature conditions of T-323 K and T-298 K/323 K correspondingly result in the lowest and the highest maximum conversion efficiencies. Generally, the Fig. 4 shows that although the high average temperature of a solution can yield better output power, it leads to low energy conversion efficiency. On the contrary, the scenario of T-298 K/323 K gives rise to lowest output power but the highest energy conversion efficiency.

Figure 4: Effects of temperature on the osmotic energy conversion under given conditions of s = 0.06 and cH/cL = 50. (a) Four temperature fields imposed on nanochannel-based the energy conversion system. (b) Variations of the current and the corresponding output power with the potential. (c) Open-circuit potentials, short-circuit currents, maximum powers, and the corresponding cation transfer numbers achieved at these four different temperature fields

All these variations trends above are dominated by ion transportations within the nanochannel which are essentially reflected by the induced currents. As theoretically presented by Eq. (6), current density throughout the nanochannel is simultaneously dominated by mechanisms of convection, diffusion, migration, and thermophoresis, which jointly forms the overall electric current of the NRED system. Since the current density under the short-circuit condition reaches the maximum value and thus can reflect effects of each factor more distinctly. Therefore, as shown in Fig. 5, the contour plot of the current density at the short-circuit scenario and the corresponding current, defined as the surface integration of the current density distributed at a certain cross-section area, varying along the axial direction under conditions of T-298 K/323 K, s = 0.06, and cH/cL = 50, are investigated first. It is found that although the overall current is a constant at around a dimensionless value of 13 throughout the nanochannel, the corresponding variations of each current components along the axial direction are remarkably different with each other. As a result of the selectivity and rectification characteristics of the nanochannel, the ion concentration polarization phenomenon becomes more pronounced [50], particularly at the interface between the nanochannel and its attached reservoirs. Consequently, the diffusion current and migration current undergo notable fluctuations along the axial direction, with peak variations observed at the junction region. in contrast, the convection current and thermophoresis current remain relatively modest and stable throughout. Importantly, the overall current is mainly dominated by the diffusion current and migration current. Furthermore, it is also noticed that the thermophoresis current varies moderately from −800 at the left junction to 0 at the right junction.

Figure 5: Contour plot of current density and variations of the overall current and its components along the axial direction of the nanochannel at the short-circuit scenario under conditions of T-298 K/323 K, s = 0.06, and cH/cL = 50: (a) Contour plot of the overall current density at the short-circuit scenario, (b) Variation of the overall current and each current component at the left junction of the channel, (c) Variation of the overall current and each current component at the middle section of the channel, (d) Variation of the overall current and each current component at the right junction of the channel

The solution temperature significantly influences the transportations of different ion species during the energy conversion process at different levels. Variations of the cation and anion flow rates and the corresponding currents along the axis of the middle region of the nanochannel under conditions of s = 0.06, cH/cL = 50 are summarized in Fig. 6. Fig. 6a–c shows that isothermal scenarios of T-323 K and T-298 K yield the highest and lowest anion/cation flow rates, respectively. The scenarios of T-323 K/298 K and T-298 K/323 K exhibit intermediate effects on the ion flow rates compared to these two isothermal scenarios. In addition, since the ion flow rate induced by thermophoresis is directly related with the temperature, it varies remarkably different with the convection, diffusion, and migration ion flow rates when the temperature field changes within the nanochannel. As for the scenario of T-323 K/298 K, since the temperature gradient has the same direction with the concentration gradient, the direction of the induced thermophoresis ion flow rate is from the high-concentration side to the low-concentration side. Therefore, the scenario of T-323 K/298 K enhance the ion flow rate. Opposite influences occur at the scenario of T-298 K/323 K which eventually weakens the ion flow rate. The isothermal scenarios of T-323 K and T-298 K have negligible impact on the ion flow rate since there is no temperature gradient within the nanochannel. The overall current is thus achieved according to the relationship of I~overall=q~+,overall⋅z1+q~−,overall⋅z2, the variation trends of which along the axial direction are similar with those of the cation/anion flow rate.

Figure 6: Variations of the ion flow rates and the corresponding currents along the axis of the middle region of the nanochannel at different scenarios: (a) Cation flow rate achieved at scenario of P~max, (b) Anion flow rate achieved at scenario of P~max, (c) Current achieved at scenario of P~max, (d) Cation flow rate achieved at scenario of T-298 K/323 K, (e) Anion flow rate achieved at scenario of T-298 K/323 K, (f) Current achieved at scenario of T-298 K/323 K. The other related operation parameters of the NRED system are given as s = 0.06 and cH/cL = 50

Taking the scenario of T-298 K/323 K as an example, variations of ion flow rates and the corresponding currents along the axis of the middle region of the nanochannel are compared in Fig. 6d–f. The variations of all the flow rates contributed by different mechanisms, as shown in Fig. 6d,e, prove that ion transportations within the nanochannel is dominated by mechanisms of the diffusion and the migration. Therefore, as for a NRED system operating under certain concentration and temperature gradients, the ion transportations are only affected by migration for all electric circuit states. Consequently, the cation and anion flow rates only vary with the induced potential of the energy conversion system. As for the open-circuit situation, since the induced potential reaches the maximum, the cation and the anion flow rates reach the maximum and the minimum values, respectively. On the contrary, the cation flow rate and the anion flow rate reach the minimum and the maximum values, respectively, under the short-circuit condition where the induced potential is zero. Finally, the overall currents under the open-circuit, the maximum power, and the short-circuit conditions are estimated at around 0, 7.53, and 14.77, respectively.

As shown in Fig. 4c, the cation transfer number t+ is observed to vary oppositely with the other performance parameters under different temperature fields. Since the energy conversion efficiency, one of the most essential energy conversion parameters, is only a function of the cation transfer number t+, it is necessary to make clear why the cation transfer number varies so differently. The cation transfer number t+ is calculated as t+=I~+/(I~++|I~−|), where I~+=q~+,overall⋅z1 and I~−=q~−,overall⋅z2. Since z1 and z2 respectively are 1 and −1 in this work, the cation transfer number thus can be expressed as a function of ion flow rates, that is t+=q~+,overall/(q~+,overall+q~−,overall). According to calculations, although the cation transfer number fluctuates along the axial direction of the NRED system, it stabilizes at a certain average value throughout the NRED system and it is almost a constant within the reservoir region. Therefore, at the given scenario of the maximum power, s = 0.06, and cH/cL = 50, variations of ion flow rates and the corresponding cation transfer numbers with the temperature gradient, obtained at the right terminal of the reservoir, are investigated as shown in Fig. 7.

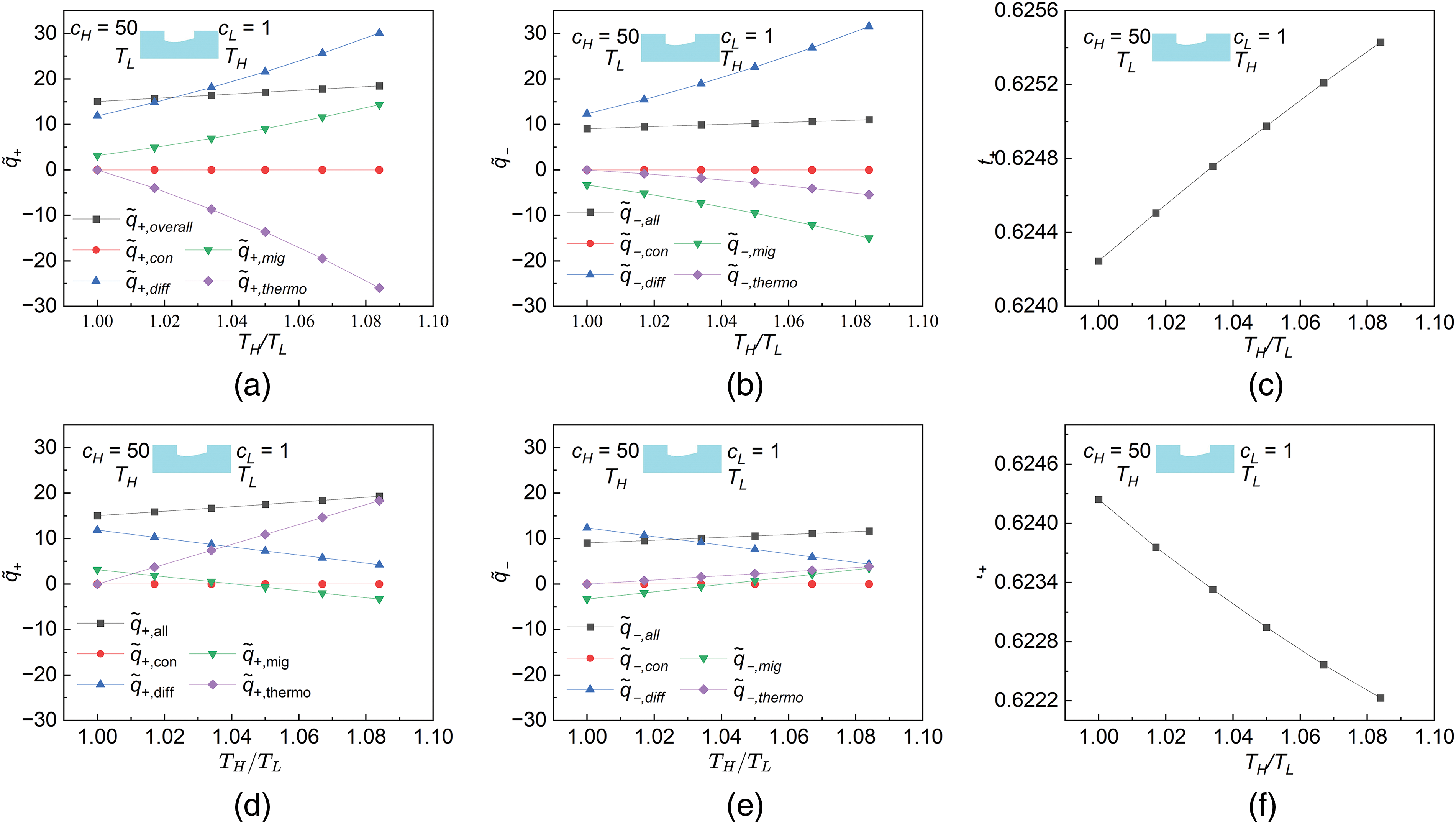
Figure 7: Variations of ion flow rates and the corresponding cation transfer numbers with the temperature gradient at the scenario of the maximum power, s = 0.06, and cH/cL = 50. (a) Cation flow rate under the negative temperature gradient, (b) Anion flow rate under the negative temperature gradient, (c) Cation transfer number under the negative temperature gradient, (d) Cation flow rate under the positive temperature gradient, (e) Anion flow rate under the positive temperature gradient, (f) Cation transfer number under the positive temperature gradient

When a negative temperature gradient is applied to the NRED system as shown in Fig. 7a–c, both the cation and anion flow rates induced by thermophoresis decrease with the increment of the negative temperature gradient. As for the ion flow rates induced by migration at a given negative temperature gradient, the one of cation is enhanced because of the increased temperature but the one of anion is restrained because of the increased potential induced at the right terminal of the reservoir. Therefore, the cation and the anion flow rates induced by migration vary differently with the temperature gradient. In other words, the negative temperature gradient enhances separation of the cations from the anions. Both the cation and anion flow rates induced by diffusion rise with the increment of the negative temperature gradient because of the gradually increased cation and anion diffusivities from the high-concentration side to the low-concentration side. The cation and anion flow rates induced by convection remain unchanged. Finally, the cation transfer number is achieved as an incremental function of the negative temperature gradient by coupling all the factors above. Similarly, when a positive temperature gradient is applied to the NRED system as shown in Fig. 7d–f, both the cation and anion flow rates induced by thermophoresis are enhanced by increasing the positive temperature gradient. Therefore, the separation occurring between the cations and anions is relatively weakened. Variation of cation and anion flow rates induced by migration and convection with the positive temperature gradient are insignificant as for the case of positive temperature gradient. Since both cation and anion diffusivities are gradually decreased from the low-concentration side to the high-concentration side due to the gradually reduced temperature, the ion diffusion from the low-concentration side to the high-concentration side becomes increasingly difficult. Therefore, both the cation and anion flow rates induced by the diffusion decrease with the increment of the positive temperature. The cation transfer number is ultimately achieved as a decremental function of the positive temperature gradient by coupling all the above factors. In generally, compared to the positive temperature gradient, the negative temperature gradient separates the cations from the anions more efficiently.

3.2.2 Effect of Nanochannel Shape

Effects of the nanochannel shape on the energy conversion performance of NRED under conditions of cH/cL = 50 and four typical temperature fields are primarily investigated first as shown in Fig. 8. The open-circuit potentials (Fig. 8a), the maximum powers (Fig. 8c), and the corresponding cation transfer numbers (Fig. 8d) under the condition of s = 0.06 (non-straight nanochannel wall) are generally higher than that under conditions of s = 0 (straight nanochannel wall) at all four temperature fields. On the contrary, the short-circuit currents (Fig. 8b) under the condition of s = 0.06 are slightly lower than that under conditions of s = 0 at all four temperature fields. The temperature field has a more pronounced effect on the energy conversion performance compared to the nanochannel shape.

Figure 8: Effects of the nanochannel shape on key performance parameters of the NRED system under condition of cH/cL = 50 and four different temperature fields. The terms I, II, III, and IV represent temperature fields of T-298 K, T-323 K, T-298 K/323 K, and T-323 K/298 K, respectively. (a) Open-circuit voltage, (b) Short-circuit current, (c) Maximum power, and (d) Cation transfer number

A series of variation trends of the key performance parameters, summarized in Fig. 9 corporately show how the nanochannel shape acting on the energy conversion process of the NRED system thoroughly. The nanochannel wall fluctuates increasingly as the dimensionless amplitude s rises. One the one hand, as shown in Fig. 9a–d, the increasingly fluctuated wall of the nanochannel mainly affects the ion flow rates induced by the diffusion and the convection and has almost no influence on that induced by the migration and thermophoresis at any given temperature fields. Since the magnitude of ion flow rates induced by the convection is remarkably small, the ion diffusion is the predominant contributor to discrepancies of the ion flow rates across various s. The increasing fluctuation in the local radius of the nanochannel leads to a more pronounced overlap of electric double layer and also set more obstacles along the axial direction which eventually restrains the ion diffusion from the high-concentration side to the low-concentration side. Therefore, both the cation and anion overall flow rates achieved at scenario of P~max are reduced when increasing the dimensionless amplitude s at all temperature fields. On the other hand, the surface area and thus the total surface charges of the nanochannel are enlarged accordingly. At the open-circuit situation, relatively more cations are induced to be accumulated at the downstream end of the nanochannel to balance the increased negative surface charges. Therefore, as shown in Fig. 9e,j, the induced open-circuit potentials achieved at both the positive and negative temperature gradients are enhanced with the increment of the dimensionless amplitude s. Based on the impact of s on both anion and cation flow rates, it is evident that the total current, particularly the short-circuit current as shown in Fig. 9f,k, also shows a consistent variation trend with the rising dimensionless amplitude s. Although the induced open-circuit potential and the short-circuit current vary oppositely with the rising s, the maximum power are finally calculated to be slightly enhanced when rising the dimensionless amplitude s for both negative and positive temperature gradients as shown in Fig. 9g,l. When increasing the dimensionless amplitude s at a certain negative or positive temperature gradient, the fluctuation in the local radius of the nanochannel becomes more significant, which thus gives rise to more regions filled with overlapped electric double layer. Consequently, the ion selectivity of the nanochannel is enhanced and thus the corresponding cation transfer number (Fig. 9h,m) and the maximum energy conversion efficiency (Fig. 9i,n) are increased.

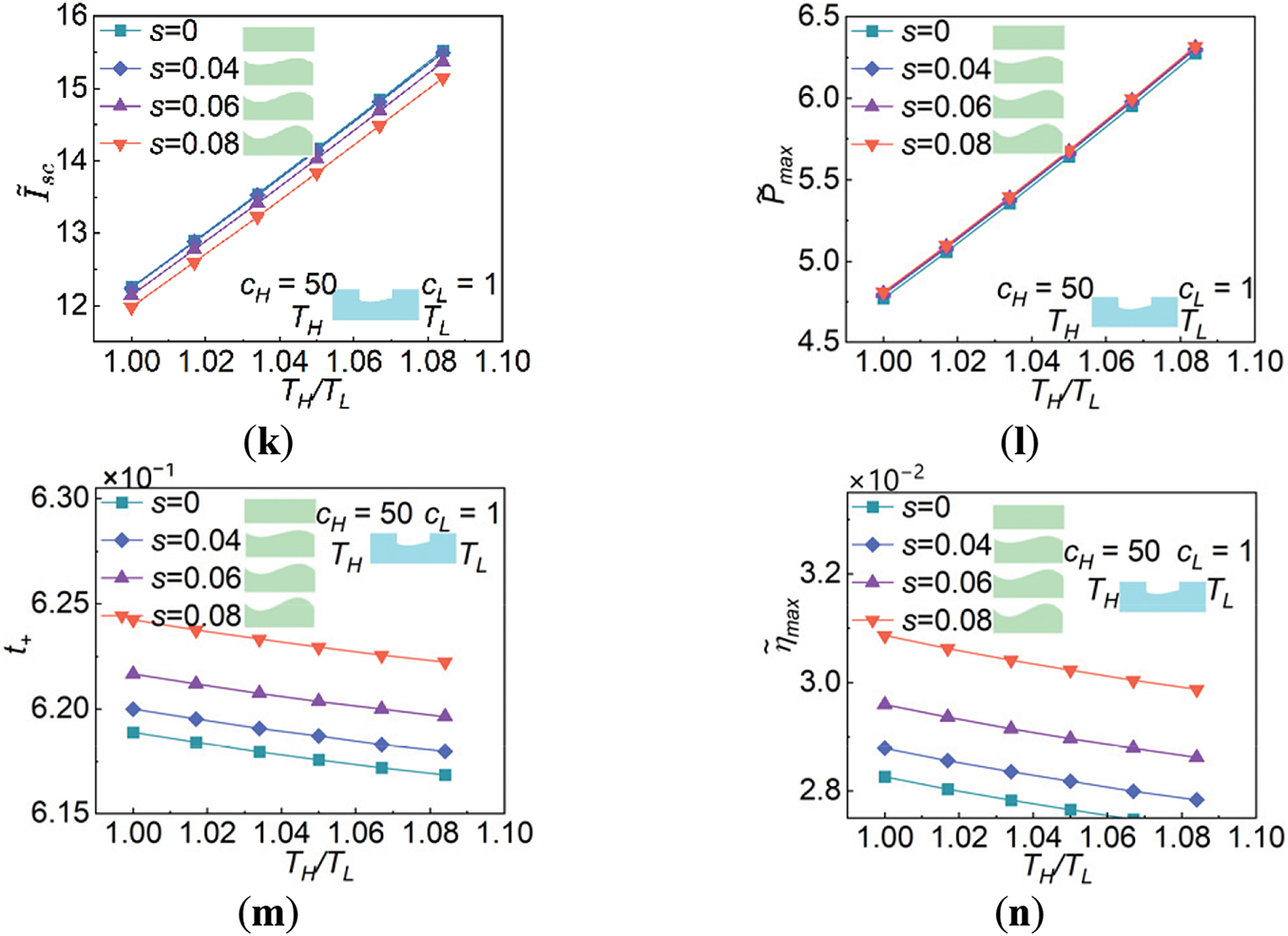
Figure 9: Effects of the nanochannel shape on key performance parameters of the NRED system under condition cH/cL = 50. (a) Cation flow rates achieved at scenario of P~max and the negative temperature gradient, (b) Anion flow rates achieved at scenario of P~max and the negative temperature gradient, (c) Cation flow rates achieved at scenario of P~max and the positive temperature gradient, (d) Anion flow rates achieved at scenario of P~max and the positive temperature gradient, (e) Open-circuit potentials at the negative temperature gradient, (f) Short-circuit currents at the negative temperature gradient, (g) Maximum powers at the negative temperature gradient, (h) Cation transfer numbers at the negative gradient, (i) Maximum energy conversion efficiencies at the negative temperature gradient, (j) Open-circuit potentials at the positive temperature gradient, (k) Short-circuit currents at the positive temperature gradient, (l) Maximum powers at the positive temperature gradient, (m) Cation transfer numbers at the positive gradient, (n) Maximum energy conversion efficiencies at the positive temperature gradient

3.2.3 Effect of Concentration

As the source of driven force for ion transportations, the solution concentration plays an important role in determining the energy conversion performance of the NRED system. However, parameters of the energy conversion performance are not always monotonously enhanced by increasing the concentration difference generated between the two terminals of the NRED system.

As shown in Fig. 10a,b, the ion flow rate induced by diffusion at scenario of the maximum power, s = 0.08, and ΔT = 25 K, is greatly enhanced by the growth of the concentration gradient compared with the other ones induced by convection, migration, and thermophoresis. This eventually leads to the monotonous variation of the overall current with the concentration gradient as shown in Fig. 10c. Similar trends of the short-circuit currents can also be achieved for different temperature differences at the given condition of s = 0.08 (Fig. 10e) and for different dimensionless amplitudes at the given condition of ΔT = 25 K (Fig. 10e).

Figure 10: Effects of the concentration on key performance parameters of the NRED system. (a) Cation flow rate at scenario of P~max, (b) Anion flow rate at scenario of P~max, (c) Current at scenario of P~max, (d) Open-circuit potential under condition of s = 0.08, (e) Short-circuit current under condition of s = 0.08, (f) Maximum power under condition of s = 0.08, (g) Cation transfer number under condition of s = 0.08, (h) Open-circuit potential under condition of ΔT = 25 K, (i) Short-circuit current under condition of ΔT = 25 K, (j) Maximum power under condition of ΔT = 25 K, (k) Cation transfer number under condition of ΔT = 25 K

As for the open-circuit potentials obtained at a relatively large interval of concentration gradient as shown in Fig. 10d,h, they exhibit a slight increase as the concentration ratio rises from 10 to 50, followed by a notable decrease across all varying negative temperature fields (temperature gradient opposite to the concentration gradient) or different dimensionless amplitudes. When the concentration ratio is relatively low, the ion concentration within the NRED system is relatively low which causes the nanochannel being more selective due to the occurrence of the electric double layer. Therefore, a growing number of cations are attracted by the negatively charged nanochannel to accumulate at the downstream terminal, which leads to the increment of open-circuit potential as rising the concentration ratio from 10 to 50. However, when the concentration ratio continues to increase beyond 50, the electric double layer is gradually screened by free ions within the solution, consequently weakening the ability of the negatively charged surface of the nanochannel to attract more counterions at the downstream terminal. Therefore, the open-circuit potentials decrease significantly as the concentration ratio increases from 50 to 1000.

The maximum powers are accordingly achieved as shown in Fig. 10f,j. The optimum concentration ratio that giving rise to the highest power happens at the 100 for all varying negative temperature fields or different dimensionless amplitudes. In addition, the high negative temperature gradient can further improve the maximum power due to the enhanced current.

Finally, the progressively elevated solution concentration gradually diminishes the electric double layer, consequently weakening the selectivity of the nanochannel. Therefore, the cation transfer numbers monotonously decrease with the increment of the concentration ratio as shown in Fig. 10g,k.

3.2.4 Multi-Factor Coupling Effects

Different energy conversion performances of NRED can be achieved by varying parameters such as the dimensionless amplitude s, the concentration ratio cH/cL, and the temperature difference ΔT, either simultaneously or separately, to investigate their multi-factor coupling effects. The baseline operation conditions are set as s = 0, cH/cL = 10, and ΔT = 0 K. Among all the investigated dimensionless amplitudes in this study, the case of s = 0.08 gives the best performance. In addition, the condition where cH/cL = 50 represents the most prevalent concentration ratio found in natural solution sources, such as the ratio of seawater to river water [8]. Furthermore, high temperature difference at a negative temperature field is found to be able to simultaneously enhance all the performance parameter in this work. Therefore, the target operation conditions of s = 0.08, cH/cL = 50, and ΔT = 25 K at the negative temperature field are applied. Table 2 illustrates the various given conditions and their corresponding performance results.

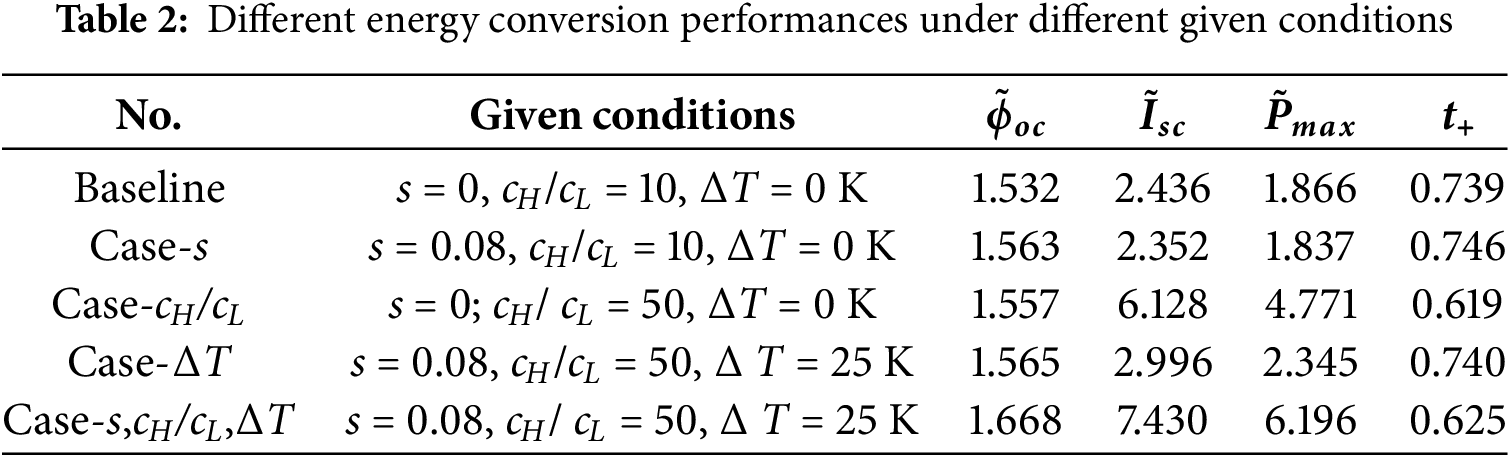
To elucidate the impacts of varying conditions more clearly, the outcomes of enhancement and impediment are concisely consolidated and illustrated Fig. 11. Changes solely in dimensionless amplitude from 0 to 0.08 or temperature difference from 0 to 25 K result in similar relative variations for each performance parameter, while a change in the concentration ratio alone from 10 to 50 leads to larger relative variations for the short-circuit current and the maximum power. The comparative fluctuations in open-circuit potentials observed under these three distinct conditions exhibit a remarkable similarity. When all condition parameters are changed to the target values of s = 0.08, cH/cL = 50, and ΔT = 25 K, the open-circuit potential, the short-circuit current, and the maximum power are simultaneously enhanced by 8.86%, 204.97%, and 232.01%, respectively. However, the cation transfer number is weakened remarkably by 15.37% under this condition.

Figure 11: Relative changes in performance parameters at different conditions compared with the baseline condition

4  Conclusions

4.1 Summary and Main Findings

In this comprehensive study, we undertake a numerical investigation into the intricate multi-factorial coupling influences on the energy conversion performance of NRED including the ion flow rate, the open-circuit potential, the short circuit current, the maximum power, and the cation transfer number. Apart from the pivotal parameter of the concentration ratio, we innovatively incorporate a dimensionless amplitude, denoted as s, to emulate the randomly varied wall structure of nanochannels that inherently occur in practical applications, thereby enhancing the realism and applicability of our analysis. The effects of temperature fields in positive and negative gradients on the energy conversion performance are also comprehensively investigated. Finally, we explore the intricate multi-factor coupling effects of nanochannel geometry, concentration ratio, and temperature difference acting on the energy conversion performance of NRED. Generally, this work presents a comprehensive analysis of multi-factor coupling effect of three pivotal operational parameters, including the nanochannel configuration, the temperature field, and the concentration difference, on the energy conversion performance of NRED and thus establishes a robust foundational research base for advancing its industrial utilization prospects. Key findings of this work are concisely summarized as follows.

(1)   At given dimensionless amplitude and concentration field, although the high average temperature of a solution yields better output power, it gives rise to low energy conversion efficiency. Importantly, in contrast to positive temperature gradients that align congruently with the concentration gradient’s direction, negative temperature gradients significantly enhance the ion selectivity. This enhancement not only boosts the open-circuit voltage and maximum power but also concurrently elevates the energy conversion efficiency, marking a substantial improvement in the overall performance.

(2)   At given temperature and concentration fields, a nanochannel with large dimensionless amplitude s, indicative of large wall fluctuations, exhibits pronounced enhancements in the open-circuit voltage, maximum power, cation transfer number, and energy conversion efficiency. Notably, while the short-circuit current undergoes a marginal decrement with an increase in this dimensionless amplitude, this subtle reduction does not detract from the overarching improvement observed in the maximum power and corresponding energy conversion efficiency.

(3)   Upon escalating the concentration ratio from 10 to 1000, either within a fixed temperature field or at a constant dimensionless amplitude, the maximum power consistently attains its optimal value at a concentration ratio of 100. Conversely, the cation transfer number experiences a monotonic decrease across this entire range of concentration ratios.

(4)   Upon modifying the operational parameters from the baseline condition of s = 0, cH/cL = 10, and ΔT = 0 K to the targeted condition of s = 0.08, cH/cL = 50, and ΔT = 25 K, there is a concerted improvement observed in the open-circuit potential, short-circuit current, and maximum power, with respective increments of 8.86%, 204.97%, and 232.01%. Notably, despite this overall enhancement, the cation transfer number experiences a notable decrease of 15.37%.

4.2 Limitations and Future Work

While our study offers valuable insights into the multifaceted coupling effects on the energy conversion performance of Nanofluidic Reverse Electrodialysis (NRED), it is important to acknowledge the inherent limitations and assumptions of our model.

Firstly, our model operates under the assumption of steady-state conditions, neglecting the transient effects that are prevalent in real-world systems. In practical applications, NRED systems may undergo dynamic changes in solution chemistry, temperature gradients, and ion concentrations, all of which can impact performance over time. To address this, future work could incorporate time-dependent simulations to accurately capture these transient phenomena.

Secondly, the nanochannel geometries in our model are idealized, assuming smooth and axisymmetric walls. However, in reality, nanochannels may exhibit surface roughness, irregularities, and non-uniform charge distributions, which can significantly influence ion transport and selectivity. Experimental validation and the development of more sophisticated models that account for these complexities are essential to refine our understanding.

Furthermore, our model simplifies the solution chemistry by focusing solely on KCl solutions. Different salt types and concentrations can alter ionic strength, viscosity, and diffusion coefficients, all of which play a crucial role in energy conversion efficiency. To enhance the applicability of our model, future work should consider a wider range of electrolyte solutions.

Additionally, the effects of temperature on material properties, such as diffusion coefficients and dielectric constants, are currently approximated using empirical relationships. To improve the predictive capability of our simulations, more accurate material models that capture the temperature dependence at the nanoscale should be incorporated.

In conclusion, while our current model provides a solid foundational understanding, there are numerous opportunities to enhance its realism and applicability by addressing the aforementioned limitations. Future research efforts could focus on developing transient simulations, incorporating more realistic nanochannel geometries, expanding the range of electrolyte solutions considered, and refining material property models. These advancements would help bridge the gap between theoretical predictions and the practical implementation of NRED systems.

Acknowledgement: The authors acknowledge Professor Yi Huang from Beihang University for his insightful discussions and invaluable guidance.

Funding Statement: This research was funded by the National Natural Science Foundation of China [52106246] and the Postgraduate Research & Practice innovation Program of Jiangsu Province [KYCX24_1641].

Author Contributions: Conceptualization, Hao Li, Jun Zhang, Hui Wang, Yugang Zhao and Yanmei Jiao; methodology, Hao Li, Yugang Zhao and Yanmei Jiao; software, Cunlu Zhao; validation, Hao Li and Cunlu Zhao; formal analysis, Hao Li, Jinhui Zhou and Yugang Zhao; data curation, Hao Li and Jinhui Zhou; writing—original draft preparation, Hao Li and Jinhui Zhou; writing—review and editing, Jun Zhang, Yugang Zhao and Yanmei Jiao; visualization, Cunlu Zhao, Yugang Zhao and Yanmei Jiao; supervision, Jun Zhang, Hui Wang and Yanmei Jiao; project administration, Jun Zhang and Hui Wang; funding acquisition, Yanmei Jiao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Long R, Kuang Z, Liu Z, Liu W. Reverse electrodialysis in bilayer nanochannels: salinity gradient-driven power generation. Phys Chem Chem Phys. 2018;20(10):7295–302. doi:10.1039/C7CP08394G. [Google Scholar] [PubMed] [CrossRef]

2. Mahadeva R, Manik G, Verma OP. Modelling and simulation of desalination process using artificial neural network: a review. Desalination Water Treat. 2018;122:351–64. doi:10.5004/dwt.2018.23106. [Google Scholar] [CrossRef]

3. Mei Y, Tang CY. Recent developments and future perspectives of reverse electrodialysis technology: a review. Desalination. 2018;425:156–74. doi:10.1016/j.desal.2017.10.021. [Google Scholar] [CrossRef]

4. Tian H, Wang Y, Pei Y, Crittenden JC. Unique applications and improvements of reverse electrodialysis: a review and outlook. Appl Energy. 2020;262:114482. doi:10.1016/j.apenergy.2019.114482. [Google Scholar] [CrossRef]

5. Nazif A, Karkhanechi H, Saljoughi E, Mousavi SM, Matsuyama H. Recent progress in membrane development, affecting parameters, and applications of reverse electrodialysis: a review. J Water Process Eng. 2022;47(1):102706. doi:10.1016/j.jwpe.2022.102706. [Google Scholar] [CrossRef]

6. Khatibi M, Aminnia A, Ashrafizadeh SN. The role of ionic concentration polarization on the behavior of nanofluidic membranes. Chem Eng Process-Process Intensif. 2024;202:109849. doi:10.1016/j.cep.2024.109849. [Google Scholar] [CrossRef]

7. Luca G, Salvo JL, Cipollina A, Luque GL, Fuoco A, Leiva EPM, et al. Vertically aligned carbon nanotubes for monovalent cation selective membranes designed by in silico experiments. Desalination. 2022;544:116123. doi:10.1016/j.desal.2022.116123. [Google Scholar] [CrossRef]

8. Ma T, Walko M, Lepoitevin M, Janot JM, Balanzat E, Kocer A, et al. Combining light-gated and ph-responsive nanopore based on peg-spiropyran functionalization. Adv Mater Interfaces. 2018;5(2):1701051. doi:10.1002/admi.201701051. [Google Scholar] [CrossRef]

9. Balme S, Picaud F, Lepoitevin M, Bechelany M, Balanzat E, Janot JM. Unexpected ionic transport behavior in hydrophobic and uncharged conical nanopores. Faraday Discuss. 2018;210:69–85. doi:10.1039/c8fd00008e. [Google Scholar] [PubMed] [CrossRef]

10. Zhang Z, Sui X, Li P, Xie GH, Kong XY, Xiao K, et al. Ultrathin and ion-selective janus membranes for high-performance osmotic energy conversion. J Am Chem Soc. 2017;139(26):8905–14. doi:10.1021/jacs.7b02794. [Google Scholar] [PubMed] [CrossRef]

11. Zhang Y, Wu G, Si W, Ma J, Yuan Z, Xie X, et al. Ionic current modulation from DNA translocation through nanopores under high ionic strength and concentration gradients. Nanoscale. 2017;9(2):930–9. doi:10.1039/c6nr08123a. [Google Scholar] [PubMed] [CrossRef]

12. Feng J, Graf M, Liu K, Ovchinnikov D, Dumcenco D, Heiranian M, et al. Single-layer MoS2 nanopores as nanopower generators. Nature. 2016;536(7615):197–200. doi:10.1038/nature18593. [Google Scholar] [PubMed] [CrossRef]

13. Hong S, Ming FW, Shi Y, Li RY, Kim IS, Tang CYY, et al. Two-dimensional Ti3C2Tx mxene membranes as nanofluidic osmotic power generators. Acs Nano. 2019;13(8):8917–25. doi:10.1021/acsnano.9b02579. [Google Scholar] [PubMed] [CrossRef]

14. Yan F, Yao LN, Chen KX, Yang Q, Su B. An ultrathin and highly porous silica nanochannel membrane: toward highly efficient salinity energy conversion. J Mater Chem A. 2019;7(5):2385–91. doi:10.1039/c8ta10848j. [Google Scholar] [CrossRef]

15. Zhang Y, Huang Z, He Y, Miao X. Enhancing the efficiency of energy harvesting from salt gradient with ion-selective nanochannel. Nanotechnology. 2019;30(29):295402. doi:10.1088/1361-6528/ab0ed8. [Google Scholar] [PubMed] [CrossRef]

16. Jiao Y, Song L, Zhao C, An Y, Lu W, He B, et al. Membrane-based indirect power generation technologies for harvesting salinity gradient energy—a review. Desalination. 2022;525:115485. doi:10.1016/j.desal.2021.115485. [Google Scholar] [CrossRef]

17. Yameen B, Ali M, Neumann R, Ensinger W, Knoll W, Azzaroni O. Ionic transport through single solid-state nanopores controlled with thermally nanoactuated macromolecular gates. Small. 2009;5(11):1287–91. doi:10.1002/smll.200801318. [Google Scholar] [PubMed] [CrossRef]

18. Guo W, Cao L, Xia J, Nie FQ, Ma W, Xue J, et al. Energy harvesting with single-ion-selective nanopores: a concentration-gradient-driven nanofluidic power source. Adv Funct Mater. 2010;20(8):1339–44. doi:10.1002/adfm.200902312. [Google Scholar] [CrossRef]

19. Cao L, Guo W, Ma W, Wang L, Xia F, Wang S, et al. Towards understanding the nanofluidic reverse electrodialysis system: well matched charge selectivity and ionic composition. Energy Environ Sci. 2011;4(6):2259. doi:10.1039/c1ee01088c. [Google Scholar] [CrossRef]

20. Kim DK. Numerical study of power generation by reverse electrodialysis in ion-selective nanochannels. J Mech Sci Technol. 2011;25(1):5–10. doi:10.1007/s12206-010-1113-x. [Google Scholar] [CrossRef]

21. Long R, Li M, Chen X, Liu Z, Liu W. Synergy analysis for ion selectivity in nanofluidic salinity gradient energy harvesting. Int J Heat Mass Transf. 2021;171:121126. doi:10.1016/j.ijheatmasstransfer.2021.121126. [Google Scholar] [CrossRef]

22. Ren Q, Cui Q, Chen K, Xie J, Wang P. Salinity-gradient power harvesting using osmotic energy conversion with designed interfacial nanostructures under thermal modulation. Desalination. 2022;535(11):115802. doi:10.1016/j.desal.2022.115802. [Google Scholar] [CrossRef]

23. Hsu JP, Lin SC, Lin CY, Tseng S. Power generation by a ph-regulated conical nanopore through reverse electrodialysis. J Power Sources. 2017;366:169–77. doi:10.1016/j.jpowsour.2017.09.022. [Google Scholar] [CrossRef]

24. Kang BD, Kim HJ, Lee MG, Kim DK. Numerical study on energy harvesting from concentration gradient by reverse electrodialysis in anodic alumina nanopores. Energy. 2015;86(1):525–38. doi:10.1016/j.energy.2015.04.056. [Google Scholar] [CrossRef]

25. Chein R, Liu B. Energy conversion from electrolyte concentration gradient using charged nano-pores. Int J Green Energy. 2016;13(13):1400–11. doi:10.1080/15435075.2016.1206900. [Google Scholar] [CrossRef]

26. Yeh HC, Chang CC, Yang RJ. Reverse electrodialysis in conical-shaped nanopores: salinity gradient-driven power generation. RSC Adv. 2014;4(6):2705–14. doi:10.1039/C3RA45392H. [Google Scholar] [CrossRef]

27. Li C, Liu Z, Wang Y, Ali A, Tian ZQ. Energy harvesting from charged conical nanopore with salinity and temperature gradient. Int J Heat Mass Transf. 2023;200:123509. doi:10.1016/j.ijheatmasstransfer.2022.123509. [Google Scholar] [CrossRef]

28. Laucirica G, Albesa AG, Toimil-Molares ME, Trautmann C, Marmisollé WA, Azzaroni O. Shape matters: enhanced osmotic energy harvesting in bullet-shaped nanochannels. Nano Energy. 2020;71:104612. doi:10.1016/j.nanoen.2020.104612. [Google Scholar] [CrossRef]

29. Zhang X, Qu Z, Wang Q, Iqbal M. Geometry design and mechanism analysis of artificial nanoroughness for enhanced osmotic energy conversion. Energy Convers Manag. 2022;273(7411):116373. doi:10.1016/j.enconman.2022.116373. [Google Scholar] [CrossRef]

30. Zhang Y. Effect of temperature on water transportation in nanochannel. Front Heat Mass Transf. 2017;9:1–4. doi:10.5098/hmt.9.16. [Google Scholar] [CrossRef]

31. Banerjee D, Yu J, Kang SW, Jeon S. Heat transfer measurements for flow of nanofluids in microchannels using temperature nano-sensors. Front Heat Mass Transf. 2012;3(1):1–9. doi:10.5098/hmt.v3.1.3004. [Google Scholar] [CrossRef]

32. Long R, Luo Z, Kuang Z, Liu Z, Liu W. Effects of heat transfer and the membrane thermal conductivity on the thermally nanofluidic salinity gradient energy conversion. Nano Energy. 2020;67:104284. doi:10.1016/j.nanoen.2019.104284. [Google Scholar] [CrossRef]

33. Karimzadeh M, Khatibi M, Ashrafizadeh SN, Mondal PK. Blue energy generation by the temperature-dependent properties in funnel-shaped soft nanochannels. Phys Chem Chem Phys. 2022;24(34):20303–17. doi:10.1039/D2CP01015A. [Google Scholar] [PubMed] [CrossRef]

34. Han J, Ko Y-S, Nam Y, Lee C. Thermally enhanced osmotic power generation from salinity difference. J Membr Sci. 2023;672:121451. doi:10.1016/j.memsci.2023.121451. [Google Scholar] [CrossRef]

35. Song D, Li L, Huang C, Wang K. Synergy between ionic thermoelectric conversion and nanofluidic reverse electrodialysis for high power density generation. Appl Energy. 2023;334:120681. doi:10.1016/j.apenergy.2023.120681. [Google Scholar] [CrossRef]

36. Zheng DC, Hsu JP. Enhancing the osmotic energy conversion of a nanoporous membrane: influence of pore density, ph, and temperature. Phys Chem Chem Phys. 2023;25(8):6089–101. doi:10.1039/D2CP05831F. [Google Scholar] [PubMed] [CrossRef]

37. Qian F, Zhang W, Huang D, Li W, Wang Q, Zhao C. Electrokinetic power generation in conical nanochannels: regulation effects due to conicity. Phys Chem Chem Phys. 2020;22(4):2386–98. doi:10.1039/C9CP05317D. [Google Scholar] [PubMed] [CrossRef]

38. Zhang W, Yan H, Wang Q, Zhao C. An extended teorell-meyer-sievers theory for membrane potential under non-isothermal conditions. J Membr Sci. 2022;643:120073. doi:10.1016/j.memsci.2021.120073. [Google Scholar] [CrossRef]

39. Jiao K, Yan HL, Qian F, Zhang WY, Li HY, Wang QW, et al. Energy harvesting based on water evaporation-induced electrokinetic streaming potential/current in porous carbonized carrots. J Power Sources. 2023;569:233007. doi:10.1016/j.jpowsour.2023.233007. [Google Scholar] [CrossRef]

40. Benneker AM, Klomp J, Lammertink RGH, Wood JA. Influence of temperature gradients on mono and divalent ion transport in electrodialysis at limiting currents. Desalination. 2018;443(3):62–9. doi:10.1016/j.desal.2018.05.005. [Google Scholar] [CrossRef]

41. Mai VP, Yang RJ. Boosting power generation from salinity gradient on high-density nanoporous membrane using thermal effect. Appl Energy. 2020;274:115294. doi:10.1016/j.apenergy.2020.115294. [Google Scholar] [CrossRef]

42. Zhang X, Zhang X, Qu Z, Pu J, Wang Q. Thermal-enhanced nanofluidic osmotic energy conversion with the interfacial photothermal method. Appl Energy. 2022;326(10):120005. doi:10.1016/j.apenergy.2022.120005. [Google Scholar] [CrossRef]

43. Song D, Zhao Z, Zhao C, Wang T, Li L, Wang K, et al. Collaborative optimization of regeneration unit and power generation unit in reverse electrodialysis heat engine for low-grade heat recovery. Energy Convers Manag. 2023;295:117614. doi:10.1016/j.enconman.2023.117614. [Google Scholar] [CrossRef]

44. Liu Z, Lu D, Bai Y, Zhang J, Gong M. Energy and exergy analysis of heat to salinity gradient power conversion in reverse electrodialysis heat engine. Energy Convers Manag. 2022;252(9):115068. doi:10.1016/j.enconman.2021.115068. [Google Scholar] [CrossRef]

45. Liu Q, Zhu H, Qu Z. Experiment and simulation analyses of GOM based salinity gradient osmotic energy conversion with nonsymmetric photothermal effect. Energy Convers Manag. 2023;298(12):117783. doi:10.1016/j.enconman.2023.117783. [Google Scholar] [CrossRef]

46. Cao Y, Dhahad HA, Parikhani T, Anqi AE, Mohamed AM. Thermo-economic evaluation of a combined kalina cycle and humidification-dehumidification (HDH) desalination system integrated with thermoelectric generator and solar pond. Int J Heat Mass Transf. 2021;168(8):120844. doi:10.1016/j.ijheatmasstransfer.2020.120844. [Google Scholar] [CrossRef]

47. Wood JA, Benneker AM, Lammertink RGH. Temperature effects on the electrohydrodynamic and electrokinetic behaviour of ion-selective nanochannels. J Phys-Condens Matter. 2016;28(11):114002. doi:10.1088/0953-8984/28/11/114002. [Google Scholar] [PubMed] [CrossRef]

48. Hsu J-P, Chen Y-C, Chen Y-M, Tseng S. Influence of temperature and electroosmotic flow on the rectification behavior of conical nanochannels. J Taiwan Inst Chem Eng. 2018;93:142–9. doi:10.1016/j.jtice.2018.10.013. [Google Scholar] [CrossRef]

49. Long R, Kuang Z, Liu Z, Liu W. Temperature regulated reverse electrodialysis in charged nanopores. J Membr Sci. 2018;561:1–9. doi:10.1016/j.memsci.2018.05.026. [Google Scholar] [CrossRef]

50. Alinezhad A, Khatibi M, Ashrafizadeh SN. Ionic transfer behavior of bipolar nanochannels resembling PNP nanotransistor. Electrochim Acta. 2023;460:142625. doi:10.1016/j.electacta.2023.142625. [Google Scholar] [CrossRef]