Viscoelastic Flow Analysis with Buongiorno Nanofluid Model over a Nonlinear Stretching Sheet: A Homotopy Approach

1  Introduction

Due to the astounding ability of nanofluids to boost heat and mass transport qualities, which are significantly beyond those of conventional fluids, scientists must seek out the dynamics of nanofluids. In addition to having boosted thermal conductivity, viscosity, and convective heat transfer coefficients, nanofluids, which are nanoparticle suspensions in base fluids, also have improved viscosity. Because of such benefits, they are incredibly well-suited for use in applications involving thermal management, energy systems, the cooling of electronic equipment, and medicinal devices. The exploration of nanofluids stems from the contributions of Choi et al. [1], which incorporated nanometre-scale particles into a base fluid characterized by low-temperature conductivity. Nanoparticles significantly increase nanofluids’ thermal conductivity, enhancing their ability to transmit heat. Bhatti et al. [2] explored non-Newtonian fluids in their perusal of chemical interactions and the effects of thermal radiation on nanoparticles by examining two unique classifications of non-Newtonian fluids: time-dependent and time-independent. Sumathi et al. [3] examined a nanofluid’s magnetohydrodynamic (MHD) flow across an inclined strained sheet and the consequence related to different factors. Elements of the energy formulation include the results of heat production, absorption, and thermal radiation. Shahidian et al. [4] studied the numerical investigation of nanofluid properties of the flow field as well as the temperature distribution in a MHD pump using finite difference techniques. The effect of static radial magnetic field on natural convection heat transfer in a horizontal cylindrical annulus enclosure filled with nanofluid is investigated numerically using the Lattice Boltzmann method was proposed by Ashorynejad et al. [5]. Ghadimi et al. [6] discussed the stability of nanofluids which play a major role in heat transfer enhancement. Many experts [7–10] have looked into nanofluids under multifaceted flow conditions owing to their profound significance and wide-ranging applications in science and technology.

For researchers, comprehending non-Newtonian fluids has become crucial for enhancing operations in polymer manufacturing, biomedical engineering, oil recovery, food processing, and cosmetics production. It facilitates the advancement of more efficient equipment design, enhanced material compositions, and superior control over industrial operations. Furthermore, examining non-Newtonian fluids facilitates progress in theoretical models and computational simulations, which are essential for engineering systems where traditional fluid dynamics inadequately represent real-world complexities. Integrating this comprehension into research fosters more innovative solutions across disciplines, establishing it as a pivotal focus for scientists and engineers striving to advance the frontiers of fluid mechanics and its applications. Sarada et al. [11] developed a computational framework to characterize the structure of a non-Newtonian (Jeffrey and Oldroyd-B) liquid’s mass transfer, flow, and heat transmission over a stretching sheet. Sharma et al. [12] documented the mass and heat transfer in two-dimensional MHD flows associating non-Newtonian fluids subjected to various repercussions. It flows through an expanding domain with varying thicknesses. Under conditions of variable thermal conductivity caused by an exponentially stretched sheet, Anwar et al. [13] addressed the MHD flow of second-grade nanofluids. Elgazery et al. [14] explored multiple strategies for the flow of non-Newtonian Casson nanofluids past a moving, expanding sheet in a porous medium with varying thermal conductivity and nonlinear radiation, considering convective boundary factors.

For researchers, comprehending non-Newtonian fluids has become crucial for enhancing polymer manufacturing and biomedical operations. Exploring features of viscoelastic fluids, a key group of non-Newtonian fluids is paramount for researchers in light of its distinctive capacity to display both viscous and elastic properties, contingent upon the flow circumstances. The dual nature of viscoelastic fluids renders them very pertinent in various applications where conventional Newtonian models inadequately represent the fluid’s behavior. Examining viscoelastic fluids enables researchers to get novel insights into material behavior under dynamic settings, facilitating advancements in material design, process optimization, and energy-efficient technologies. Consequently, research on viscoelastic fluids is essential for progressing both theoretical fluid dynamics and actual engineering applications. Nadeem et al. [15] investigated the two-dimensional Maxwell micropolar fluid flow over a stretching surface. They highlighted the impacts of viscoelasticity to analyze the flow behavior under the assumptions of nanomaterial over a stretching surface. Swain et al. [16] investigated the heat and mass transfer of MHD viscoelastic (Walters’ B’ model) nanofluid flow over a stretching sheet embedded in a saturated porous medium subject to thermal slip and temperature jump. Alrehili [17] examined the significance of velocity slip by employing a computational approach to the flow of viscoelastic fluids over an extended surface. The porous medium is a substance with empty spaces or pores, which can be either connected or separated and arranged in different patterns, whether regular or random. These empty spaces can be filled with various substances, such as air, water, or oil. The ratio of these empty spaces to the entire volume of the substance affects its overall permeability, indicating the substance’s ability to allow fluid to flow through it. The composition of the porous material determines permeability and is typically correlated with the average dimensions of the pores. Multiple research has investigated the attributes and actions of materials with pores. Mahanthesh et al. [18] performed an investigation regarding the subject of non-linear convective motion in a nano Maxwell fluid that included radiation. Hsiao et al. [19] explored the buoyant effect and the electric number E1 coupled with magnetic parameter M to represent the dominance of the electric and magnetic effects and added the specific item of nonuniform heat source/sink. Venkatadri et al. [20] explored heat conduction in non-Newtonian fluids through porous materials. While utilizing nanofluids, Mahdi et al. [21] extensively examined heat transmission and fluid dynamics in porous media. Their analysis centered on multiple characteristics, such as the porous media’s geometry, the nanofluid’s thermophysical properties, various thermal boundary conditions, and the varieties of nanofluids employed. The impact of the porous medium on heat transfer is accounted for by examining the variations in energy dissipation and thermal conductivity affected by the porous structure. Including the dissipative factor in the energy equation signifies the influence of internal friction and heat production resulting from viscous dissipation. This methodology aligns with previous research on heat transmission in porous material, and pertinent references have been included for corroboration. These concepts encapsulate the cumulative impacts of fluid resistance and improved thermal conduction inside the porous structure.

It has been essential to look into fluid flow dynamics across a nonlinear stretching sheet owing to its widespread applicability in industrial processes like metal stretching, paper making, polymer extrusion, fiber spinning, and glass forming. These nonlinear profiles better depict complex physical events in such processes. Consideration of flow over a nonlinear stretching sheet improves heat and mass transfer predictions, boundary layer behavior comprehension, and viscous and thermal models. Ali et al. [22] reported that when radiation and Hall current have been assessed together over a nonlinear stretching sheet, tiny fragments delivering fluid have more potent heat transfer features than separately addressed. Jabeen et al. [23] examined the consequence of viscous and Ohmic dissipation on magnetohydrodynamic flow in porous media under conditions of suction and injection. Khan et al. [24] looked at the characteristics of Sisko nanofluid on a sheet that stretched nonlinearly.

HAM is ideal for solving viscoelastic nanofluid model strongly nonlinear differential equations, including the impacts of nonlinear stretching, viscous dissipation, and thermal radiation. The Homotopy Analysis Method (HAM) offers several advantages over traditional analytical and numerical methods. It provides a flexible framework to construct approximate solutions for nonlinear problems, allowing for the adjustment of convergence via an auxiliary parameter. Unlike perturbation methods, HAM is not limited by small parameters, making it applicable to a broader range of problems. Additionally, HAM ensures high accuracy by controlling series solutions and allows for explicit, analytical forms that are computationally efficient. Its adaptability and robustness make it a powerful tool for solving complex mathematical models. Unlike conventional perturbation methods, HAM has zero reliance on small or linear coefficients. Tricky issues in fluid dynamics, heat transfer, and other applied sciences can be effectively addressed with this method, which generates solutions that converge quickly and precisely. The flexibility and accuracy of HAM have made it a go-to method for nonlinear analysis. Yang et al. [25] exhibited that the degree of precision of the HAM approach outweighs that of the HTR method, with the former’s approximations being significantly more precise than those of the latter in the same order. Masjedi et al. [26] delivered innovative analytical solutions for arbitrary three-dimensional massive deflections of geometrically exact beams. Ibrahim et al. [27] developed a model for the study of heat source on MHD convection flow of Casson nanofluid over a nonlinear stretching sheet by employing HAM method. The repercussion of Joule radiative heating MHD flow of Jeffrey fluid over a stretching sheet with the help of HAM technique was studied by Kumar et al. [28]. Pavan Kumar et al. [29] explored the Homotopy analysis method for investigating the thermal behavior of a porous longitudinal fin under fully wet condition, focusing on the impacts of convection and radiation. Refer to [30–34] for more knowledge addressing the implementation of indicated point procedures.

Three innovative attributes supported our present undertaking. This study primarily aims to simulate and assess the progress of a viscoelastic nanofluid across a porous stretched sheet under various limitations. Earlier studies have inadequately addressed this specific area of the HAM technique. This paper examines this deficiency. As research advances, we may observe other applications for these strategies. Our study uses Buongiorno’s nanofluid model to study the synergistic effects of nonlinear stretching, porous media, heat radiation, and viscous dissipation on viscoelastic nanofluid flow, providing a deep understanding of nanoparticle behavior. The Homotopy Analysis Method (HAM) is innovative, giving an entire analytical framework with convergence control to solve complex coupled equations and overcome numerical approaches’ limitations. This research illuminates critical parameter effects on flow, heat, and mass transfer in viscoelastic nanofluid systems, which can be used to optimize energy and biomedical applications. This study has significant industrial and engineering applications. It is pivotal in optimizing heat and mass transfer processes in industries such as polymer extrusion, thermal management in nanotechnology, and advanced material manufacturing. The analysis aids in designing efficient cooling systems for electronic devices, improving coating technologies, and enhancing energy systems like solar collectors and thermal insulators. By understanding flow dynamics and thermal behavior, the study supports advancements in chemical processing, biomedical engineering, and aerospace engineering.

2  Mathematical Formulation

The primary goal of the ongoing scrutiny is to examine the flow of non-Newtonian viscoelastic nanofluid flow in a porous medium influenced by a variable stretching sheet. We have established a rectangular coordinate system. x-axis and y-axis alongside and orthogonal to the surface. Where u,v are the horizontal and vertical velocity factors, respectively. The fluid motion is achieved by elongating the surface from the slot and facing equal opposite forces along the x-axis. The temperature and concentration are respectively represented as T and C, at the stretching surface Tw and Cw at the surrounding environment T∞ and C∞. The stretching velocity of the sheet is Uw=U0(xl)m, where U0 is a dimensional constant, l is the characteristic length, m is the nonlinear stretching parameter. The characteristic length is the gap. x evaluated from the slot where the stretching velocity Uw=U0. A variable magnetic field B(x)=B0(xm-12lm2) is applied perpendicular to the surface. None of the external forces and pressure gradient are considered. The physical model is given in Fig. 1.

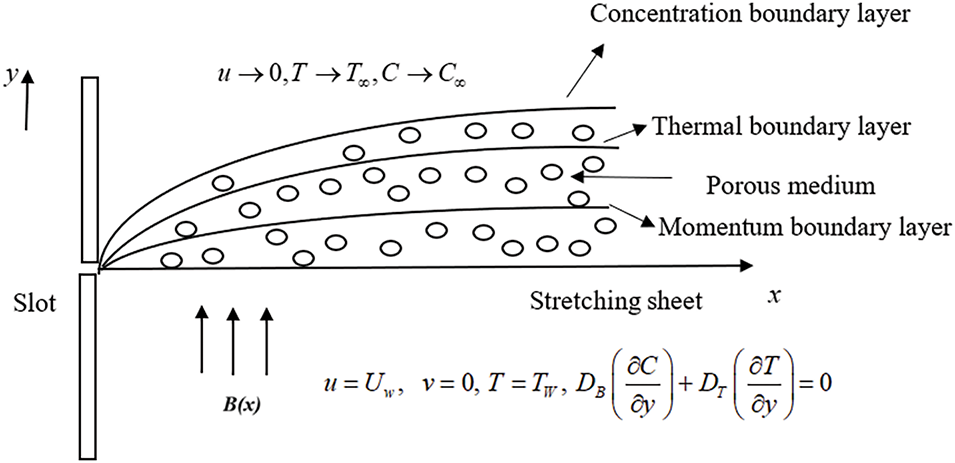
Figure 1: Geometric analysis of a fluid motion problem

Assuming the foregoing, the equations that control the boundary layer are (Nadeem et al. [35])

∂u∂x+∂v∂y=0,(1)

u∂u∂x+v∂u∂y=ν∂2u∂y2+k0ρ(u∂3u∂x∂y2+∂u∂x∂2u∂y2+∂u∂y∂2v∂y2+v∂3u∂y3)−σB(x)2ρu−νK∗u,(2)

u∂T∂x+v∂T∂y=α∂2T∂y2+τ[DB∂C∂y∂T∂y+DTD∞(∂T∂y)2]−1(ρCp)∂qr∂y+νCp(∂u∂y)2,(3)

u∂C∂x+v∂C∂y=DB∂2C∂y2+DTT∞∂2T∂y2,α=k(ρC)f, K∗=K0∗lmxm-1, τ=(ρC)f(ρC)p.(4)

The corresponding boundary constraints are given by

u=Uw,v=0,T=TW,DB(∂C∂y)+DT(∂T∂y)=0aty=0,u→0,v→0,T→T∞,C→C∞asy→∞.(5)

Following Ross eland’s approximation, the radiative heat flux is

qr=−4σ∗∂T43k∗∂y.

Moreover, we infer that the internal temperature difference of the flow is sufficiently significant that T4 is deliberated as a linear function in temperature. Linearizing the temperature term T4 simplifies the equations for analytical or numerical analysis. Due to negligible higher-order terms, it approximates but does not affect accuracy for tiny temperature fluctuations. Simpler solutions may affect outcomes with large heat gradients, so they should be tested against accurate or experimental solutions. Consequently, with the process of expanding T4 in Taylor’s series about T∞ by precluding terms of higher order, we obtain

T4≅4T∞3T−3T∞4.

Here, the nonlinear ordinary differential equations are derived using the stream function.

ψ=ψ(x,y), where

u=∂ψ∂y,v=−∂ψ∂x,(6)

where Eq. (1) is satisfied precisely. The similarity transformations are

ψ=A(x)f(ζ),ζ=Z(x)y,θ(ζ)=T−T∞Tw−T∞,ϕ(ζ)=C−C∞Cw−C∞,A(x)=νRe(xl)m+12,Z(x)=Rel(xl)m−12,Re=U0lν.(7)

By substituting Eq. (7) in Eqs. (2) to (5), we get the following nonlinear ordinary differential equations.

f′′′+(m+12)ff′′−mf′2+k1((3m−1)f′f′′′−(m+12)ff′′′′−(3m−12)f′′2)−(M+K)f′=0,(8)

(1+43R)θ′′+(m+12)Prfθ′+PrNbϕ′θ′+PrNtθ′2+PrEcf′′2=0,(9)

ϕ′′+(m+12)Scfϕ′+NtNbθ′′=0.(10)

The boundary conditions are

f(ζ)=0,f′(ζ)=1,θ(ζ)=1,Nbϕ′(ζ)+Ntθ′(ζ)=0 atζ=0,f′(ζ)→0,θ(ζ)→0,ϕ(ζ)→0 asζ→∞.(11)

where k1=k0Uwμx, M=σB02ρU0, K=νK0∗U0, Nb=τDB(Cw−C∞)ν, Nt=τDT(Tw−T∞)T∞ν, R=4T∞3σ∗kk∗, Ec=Uw2CP(Tw−T∞), Pr=να, Sc=νDB.

The physical parameters have been defined as

Cf=τwρUw2,(12)

is the skin-friction,

Nu=xqwk(Tw−T∞)(13)

is the Nusselt number,

Sh=xqmDB(Cw−C∞)(14)

is the Sherwood number,

where

qm=−DB∂C∂y,qw=−(k+16σ∗T3∞3k∗)∂T∂y,τw=μ(∂u∂y)+k0(u∂2u∂x∂y+v∂2u∂y2−2∂u∂y∂v∂y),aty=0.(15)

Utilizing parameters in Eq. (5), we obtain

Cfx=(1+k1(7m−12))f′′(0),Nux=−(1+4R3)θ′(0),Shx=−ϕ′(0).(16)

3  HAM

We employ the specified initial estimates and linear operators to incorporate the homotopic methodologies to Eqs. (7) to (10). The subsequent procedure is visualized in Fig. 2.

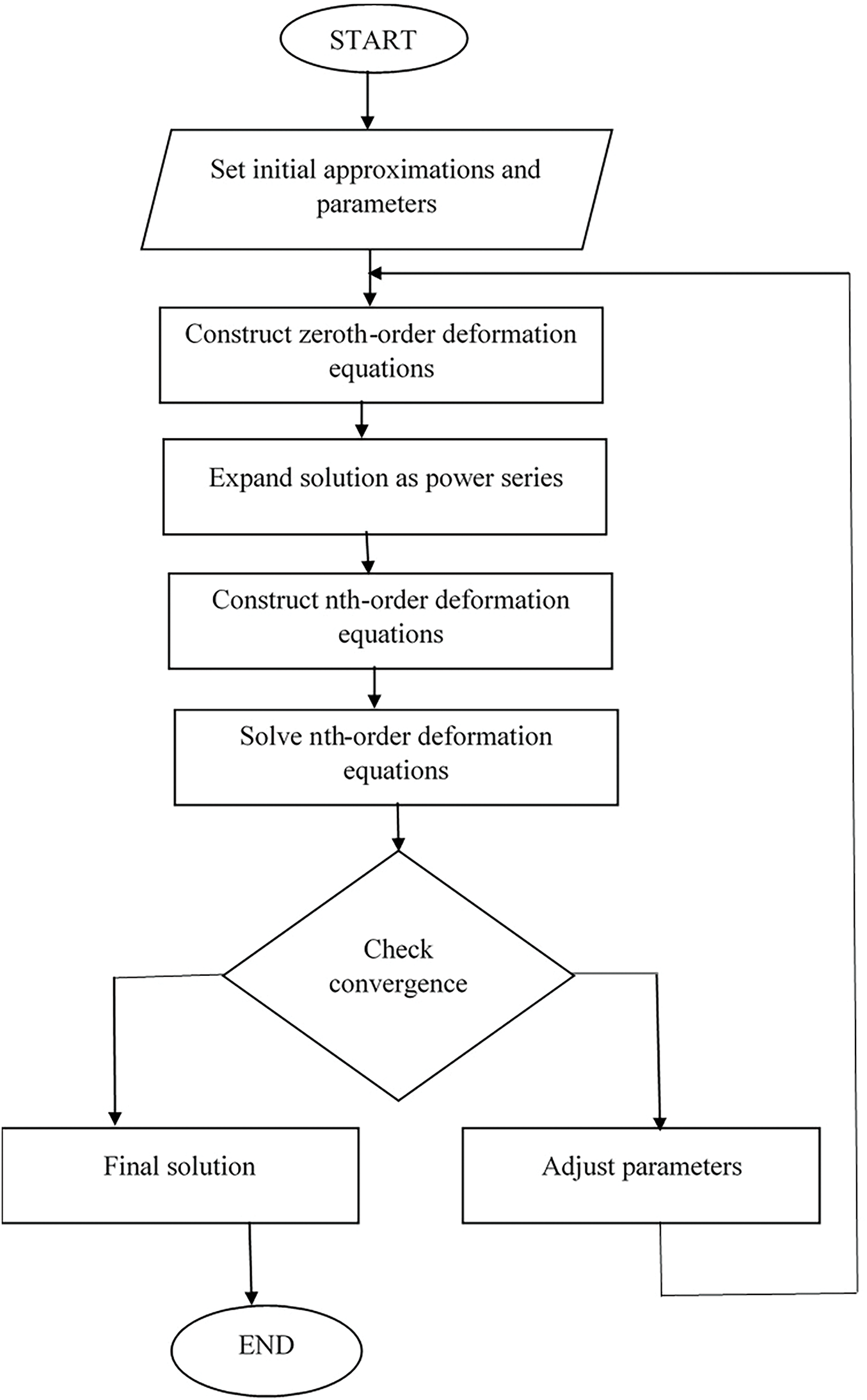
Figure 2: Diagrammatic representation of HAM process

f0(ζ)=1−e−ζ,θ0(ζ)=e−ζ,ϕ0(ζ)=−(NtNb)e−ζ,

L1(f)=f′′′−f′,L2(θ)=θ′′−θ,L3(ϕ)=ϕ′′−ϕ,

with

L1(j1+j2eζ+j3e−ζ)=0,L2(j4eζ+j5e−ζ)=0,L3(j6eζ+j7e−ζ)=0,

where ji(i=1to7) are the arbitrary constants.

We construct the zeroth-order deformation equations.

(1−p)L1(f(ζ;p)−f0(ζ))=pℏ1N1[f(ζ;p)],(17)

(1−p)L2(θ(ζ;p)−θ0(ζ))=pℏ2N2[f(ζ;p),θ(ζ;p),ϕ(ζ;p)],(18)

(1−p)L3(ϕ(ζ;p)−ϕ0(ζ))=pℏ3N3[f(ζ;p),θ(ζ;p),ϕ(ζ;p)],(19)

subject to the boundary conditions

f(0;p)=0,f′(0;p)=1,f′(∞;p)=0,θ(0;p)=1,θ(∞;p)=0,Nbϕ′(0;p)+Ntθ′(0;p)=0,ϕ(∞;p)=0,(20)

N1[f(ζ;p)]=∂3f(ζ;p)∂ζ3+(m+12)f(ζ;p)∂2f(ζ;p)∂ζ2−m(∂f(ζ;p)∂ζ)2+k1((3m−1)∂f(ζ;p)∂ζ∂3f(ζ;p)∂ζ3−(m+12)f(ζ;p)∂4f(ζ;p)∂ζ4−(3m−12)(∂2f(ζ;p)∂ζ2)2)−(M+K)∂f(ζ;p)∂ζ(21)

N2[f(ζ;p),θ(ζ;p),ϕ(ζ;p)]=1Pr(1+43R)∂2θ(ζ;p)∂ζ2+(m+12)(f(ζ;p)∂θ(ζ;p)∂ζ)+Nb∂θ(ζ;p)∂ζ∂ϕ(ζ;p)∂ζ+Nt(∂θ(ζ;p)∂ζ)2+Ec(∂2θ(ζ;p)∂ζ2)2,(22)

N3[f(ζ;p),θ(ζ;p),ϕ(ζ;p)]=∂2ϕ(ζ;p)∂ζ2+Sc(m+12)(f(ζ;p)∂ϕ(ζ;p)∂ζ)+NtNb∂2θ(ζ;p)∂ζ2,(23)

where p∈[0,1] is the embedding parameter, ℏ1,ℏ2 and ℏ3 are non-zero auxiliary parameters and N1,N2 and N3 are nonlinear operators.

The nth-order deformation equations are as follows.

L1(fn(ζ)−χnfn−1(ζ))=ℏ1Rnf(ζ),(24)

L2(θn(ζ)−χnθn−1(ζ))=ℏ2Rnθ(ζ),(25)

L3(ϕn(ζ)−χnϕn−1(ζ))=ℏ3Rnϕ(ζ),(26)

with the following boundary conditions

fn(0)=0,fn′(0)=0,fn′(∞)=0,θn(0)=0,θn(∞)=0,Nbϕn′(0)+Ntθn′=0,ϕn(∞)=0,(27)

where

Rnf(ζ)=fn−1′′′+(m+12)∑i=0m−1fn−1−ifi′′−m∑i=0m−1fn−1−i′fi′+k1((3m−1)∑i=0n−1fn−1−i′fi′′′−(m+12)∑i=0n−1fn−1−ifi′′′′−(3m−12)∑i=0m−1fn−1−i′′fi′′)−(M+K)fn−1′,(28)

Rnθ(ζ)=1Pr(1+4R3)θn−1′′+(m+12)∑i=0n−1fn−1−iθi′+Nb∑i=0n−1θn−1−i′ϕi′+Nt∑i=0n−1θn−1−i′θi′+Ec∑i=0n−1fn−1−i′′fi′′,(29)

Rnϕ(ζ)=ϕn−1′′+(m+12)Sc(∑i=0n−1fn−1−iϕi′)+NtNbθn−1′′,(30)

χn={0,n≤1,1,n>1.

4  Convergence of HAM

The auxiliary factors significantly greatly affect the convergence and interpolation rates of the specific inferences ℏ1,ℏ2&ℏ3. Therefore, in Fig. 3, ℏ curves are recognized as necessary to accomplish the parameter quantities. Based on such an extensive overview, we can figure out that the primary parameter paradigm is all about [−1.5,0.0]. For ℏ1=ℏ2=ℏ3=−0.67, the series solutions are convergent across the whole ζ area. The convergence of the approach is insinuated by Table 1.

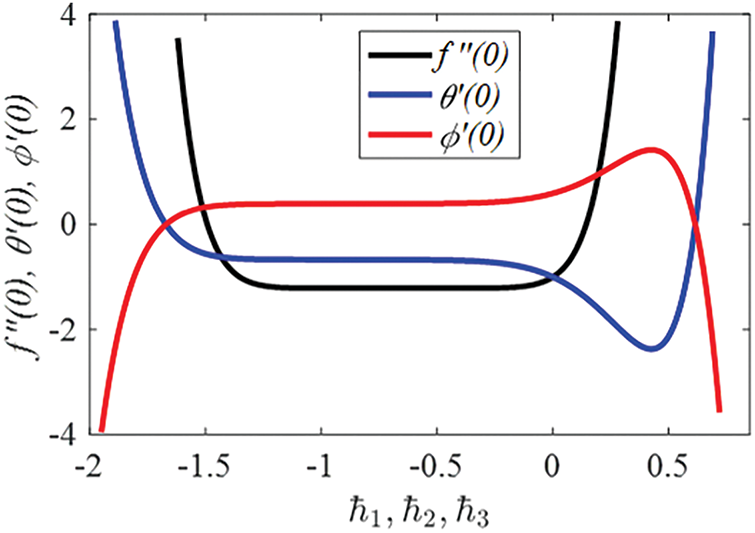
Figure 3: Curves of f′′(0), θ′(0) and ϕ′(0)

5  Results and Discussion

The mathematical frameworks that reflect the features of magnetohydrodynamic (MHD) viscoelastic nanofluids, a category of non-Newtonian fluids, are laid out in this portion of the article. The flow of this fluid through a porous medium over a nonlinearly stretched sheet is the main emphasis. We examine the influence of diverse physical parameters on the distinctive flow features, specifically fluid velocities, thermal profiles, and concentration. The differential equations are transformed via an appropriate similarity transformation and solved analytically using HAM. Fig. 4 describes the problem’s flow chart. Typically, the values of parameters are systematically changed for most figures to study their repercussions while keeping other parameters constant during the simulation, such as:

k1=K=R=Ec=0.1,M=0.2,m=0.5,Nb=0.5,Nt=0.3,Pr=1.5,Sc=1.0.

Figure 4: Analysis of the flow problem

Figs. 5–7 illustrate the repercussion of the viscoelastic parameter on f′(ζ), θ(ζ) and ϕ(ζ). The reason behind the obtained outcomes is that fluid viscosity has a negative correlation with the viscoelastic parameter. Fluids with higher values of the viscoelastic parameter have lower viscosities, enabling the fluid to extend and flow more easily, thereby improving f′(ζ). Because the fluid moves more quickly, there is less time for heat and mass diffusion close to the surface, which might reduce the thickness of the thermal and concentration boundary layers.

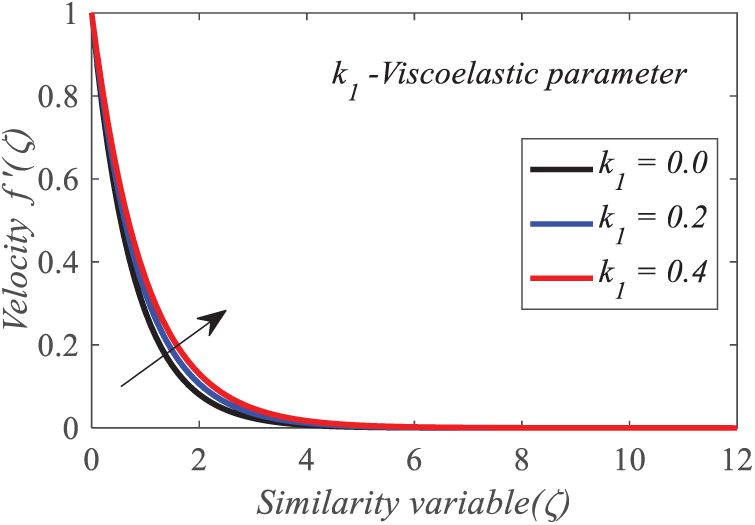
Figure 5: Repercussion of k1 on f′(ζ)

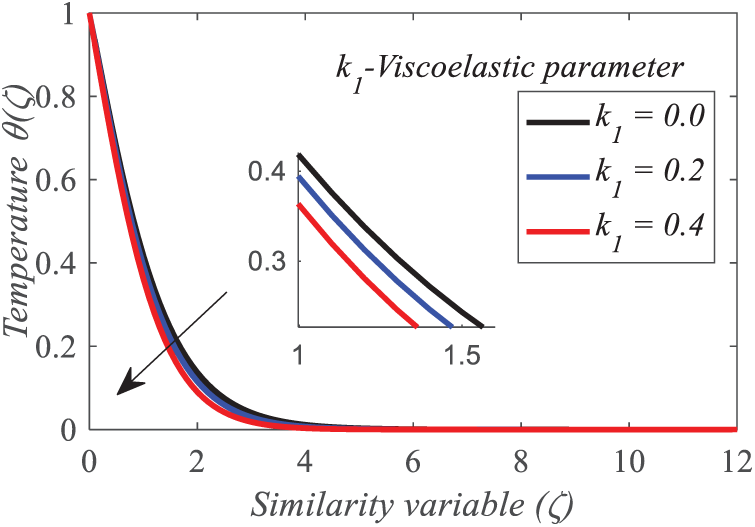
Figure 6: Repercussion of k1 on θ(ζ)

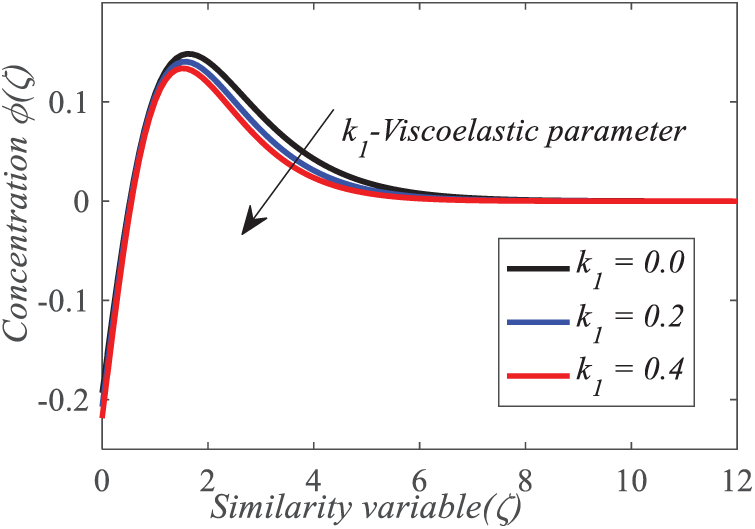
Figure 7: Repercussion of k1 on ϕ(ζ)

f′(ζ), θ(ζ) and ϕ(ζ) all fall as the stretching parameter m elevates, since it is readily apparent that elevated numbers of the parameter thin the boundary layer. This is shown in Figs. 8–10.

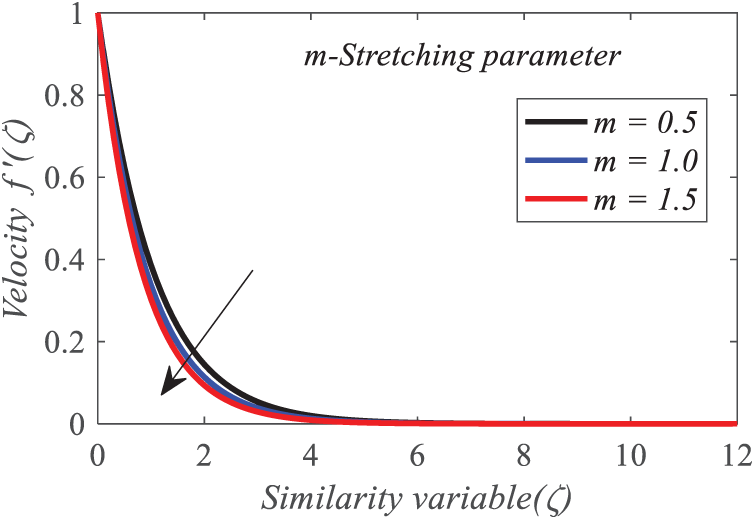
Figure 8: Repercussion of m on f′(ζ)

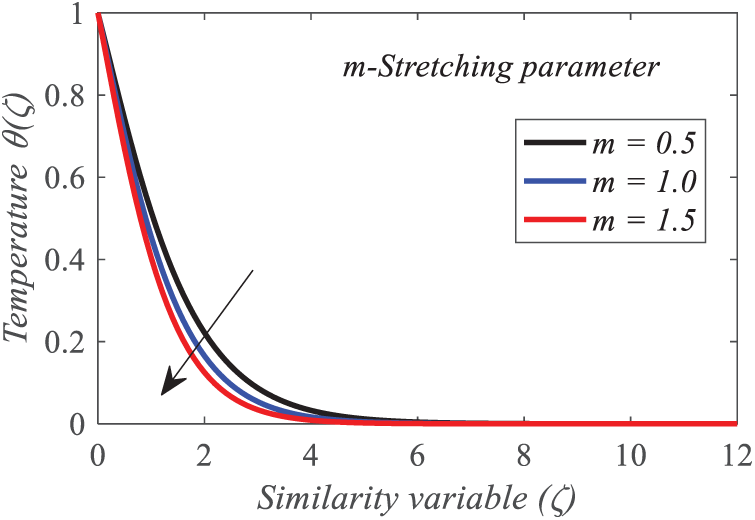
Figure 9: Repercussion of m on θ(ζ)

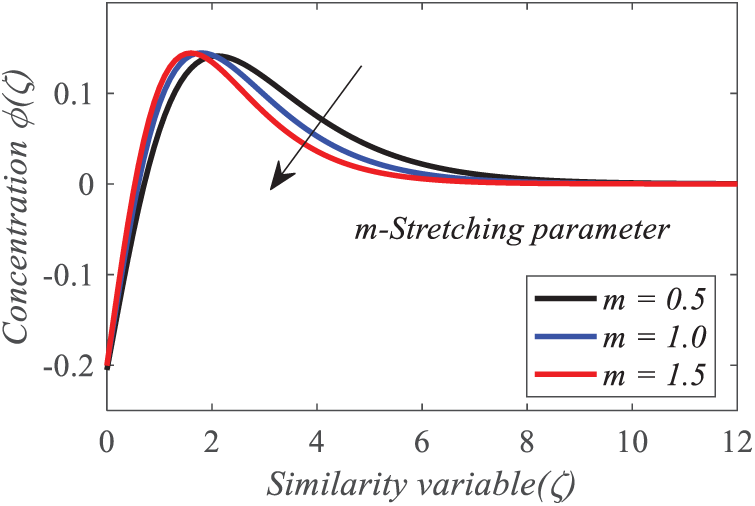
Figure 10: Repercussion of m on ϕ(ζ)

Figs. 11–13 depict the effect of the magnetic parameter M concerning f′(ζ), θ(ζ) and ϕ(ζ). As M grows, f′(ζ) demonstrates a diminishing trend, whereas θ(ζ) and ϕ(ζ) exhibit augmenting trends. This phenomenon arisesowing to the heightened Lorentz force produced through the magnetic field, that provides additional barrier to fluid movement, resulting in its deceleration. The resistance causes an enhancement in θ(ζ) and ϕ(ζ).

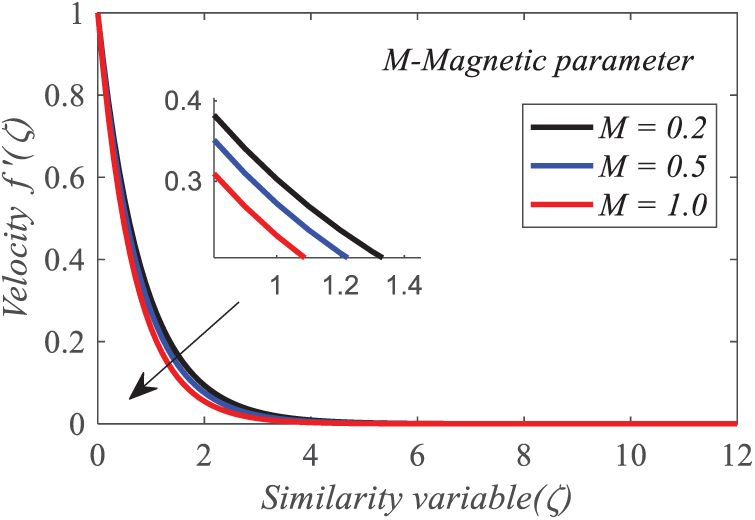
Figure 11: Repercussion of M on f′(ζ)

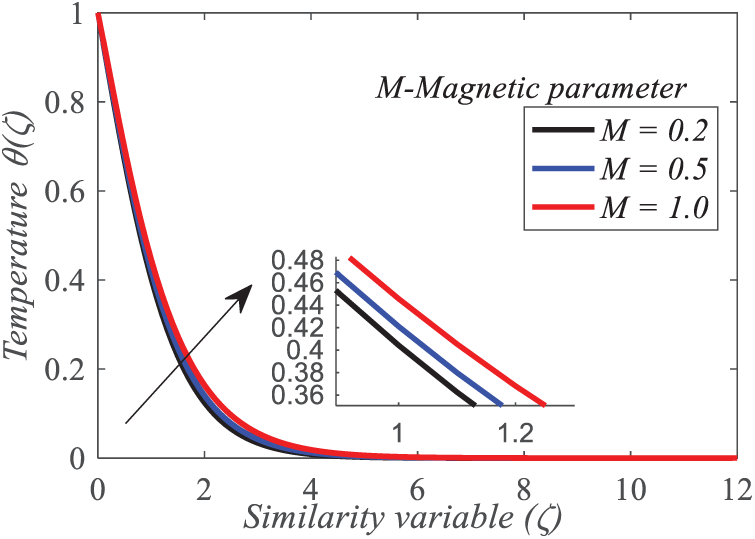
Figure 12: Repercussion of M on θ(ζ)

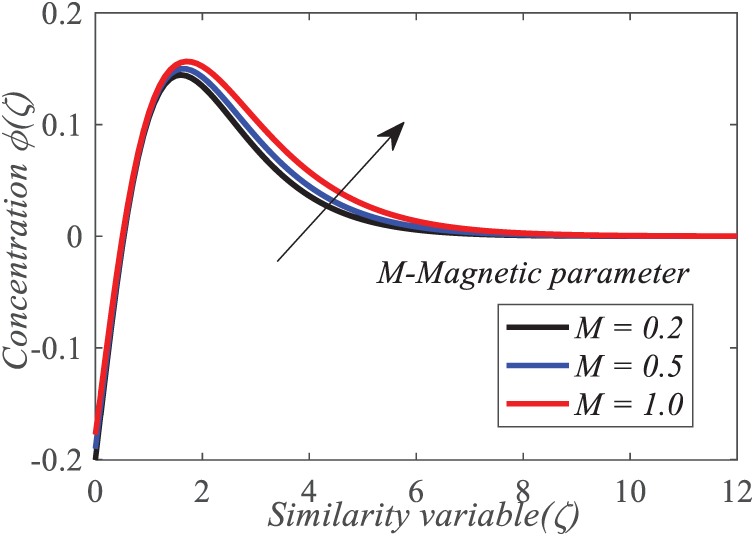
Figure 13: Repercussion of M on ϕ(ζ)

Figs. 14–16 depict the effect of the porous medium parameter K concerning f′(ζ), θ(ζ) and ϕ(ζ). Fluid motion is reduced and f′(ζ) near the stretched sheet is lowered as a result ofenhanced resistance caused by high values of K as shown in Fig. 14. θ(ζ) rises because the boundary layer retains more heat as a result of the reduced f′(ζ) caused by the accelerated resistance. Higher values of K also cause a higher ϕ(ζ)in the boundary layer, as species have more time to accumulate near the surface as shown in Figs. 15 and 16.

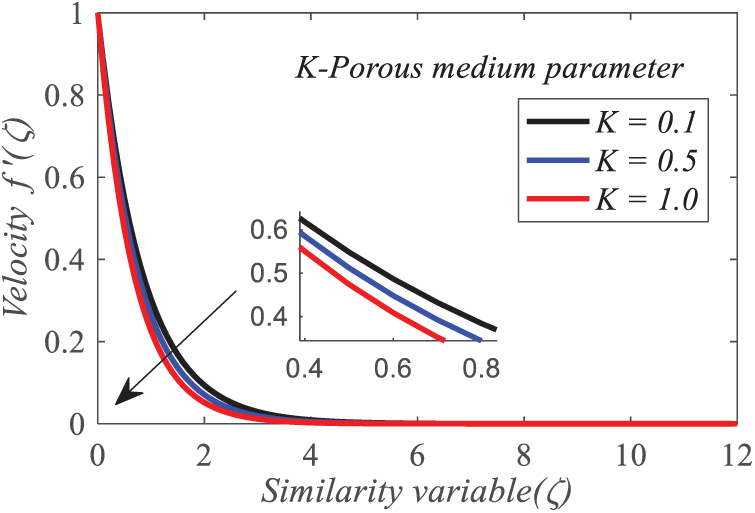
Figure 14: Repercussion of K on f′(ζ)

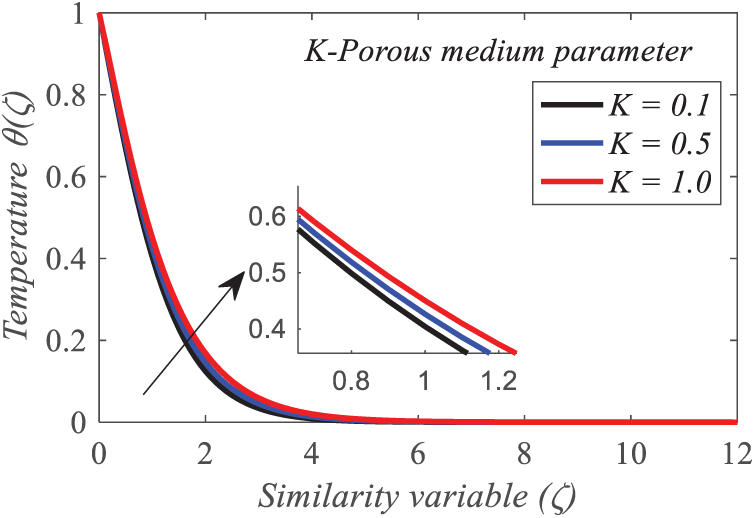
Figure 15: Repercussion of K on θ(ζ)

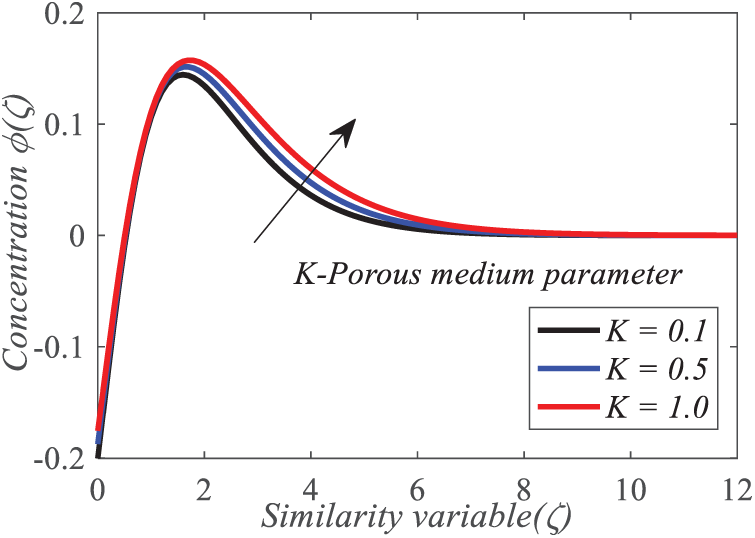
Figure 16: Repercussion of K on ϕ(ζ)

Fig. 17 illustrates that an enhancement in the Prandtl number Pr yields a reduction in θ(ζ). This phenomenon arises owing to a larger Pr is linked to an augmented viscosity and a diminished thermal conductivity.

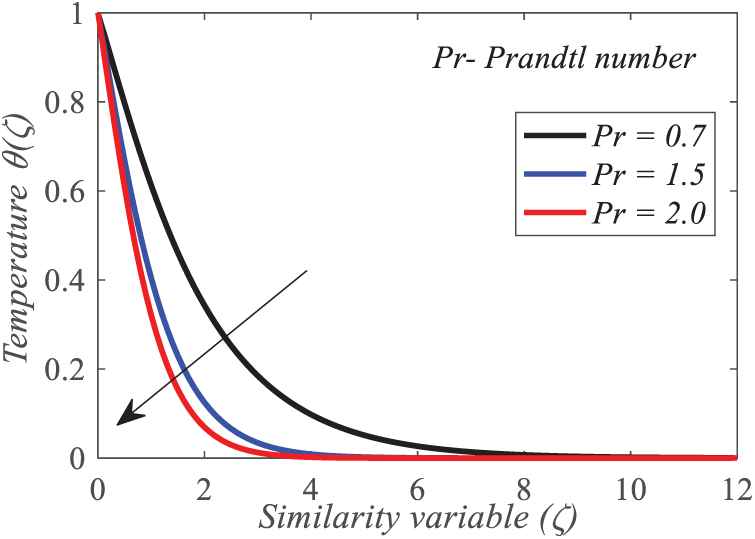
Figure 17: Repercussion of Pr on θ(ζ)

As the radiation parameter R is elevated, θ(ζ) significantly accelerates. Higher R augment thermal radiation inside the fluid, resulting in elevated heat transfer to the fluid. Consequently, the comprehensive θ(ζ) rises. This is depicted in Fig. 18.

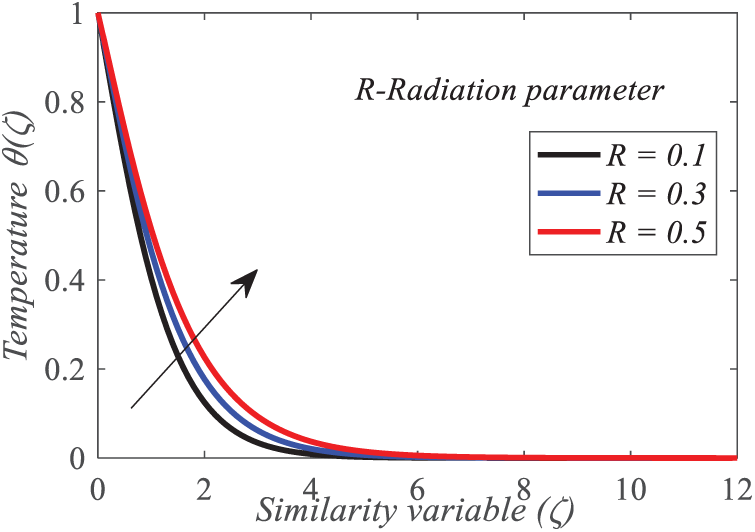
Figure 18: Repercussion of R on θ(ζ)

Conduction transfers thermal energy at low Eckert numbers, with little viscous dissipation. This regime applies to low-velocity, temperature-gradient flows. Viscous dissipation turns flow kinetic energy into thermal energy, causing high Eckert numbers. Viscous heating can substantially alter fluid properties and temperature distributions in high-speed flows. Ec number impacts polymer extrusion viscosity and flow uniformity by affecting viscous dissipation heat generation. Viscous heating elevates surface temperatures to critical levels, compromising aircraft thermal shielding. A larger Eckert number Ec indicates that viscous forces transform more mechanical energy into heat. This results in heightened fluid resistance, necessitating increased energy expenditure to surmount these forces. Consequently, θ(ζ) accelerates due to the dissipation of excess energy. This is depicted in Fig. 19.

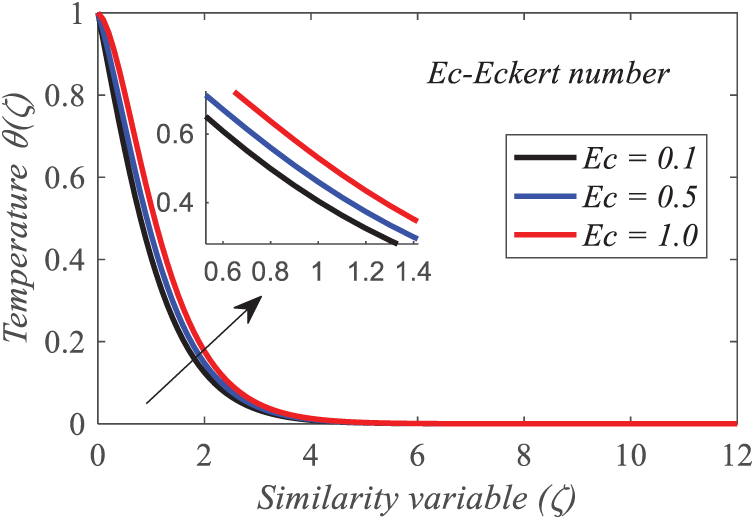
Figure 19: Repercussion of Ec on θ(ζ)

Figs. 20 and 21 illustrate the repercussion of the Brownian motion factor Nb on θ(ζ) and ϕ(ζ) curves. The broader spectrum of Nb enhances nanoparticle kinetic energy, facilitating more particles to surpass the surface, increasing θ(ζ) while diminishing ϕ(ζ). The repercussion of the Brownian motion parameter on temperature is insignificant, as it leads poorly to thermal energy transfer.

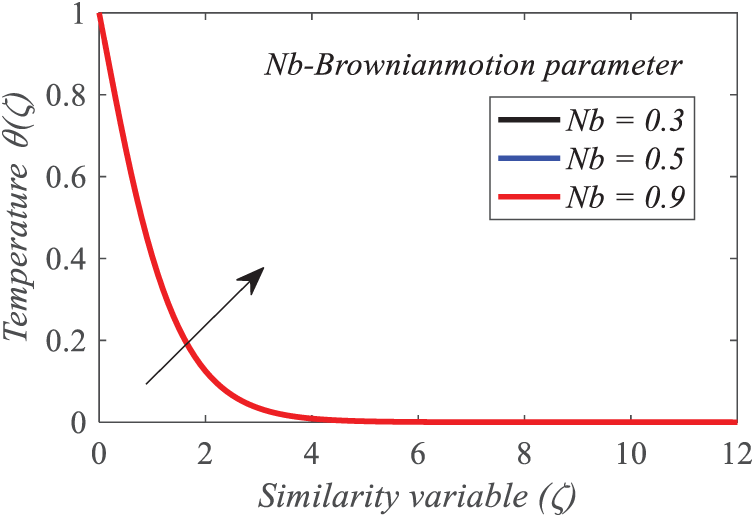
Figure 20: Repercussion of Nb on θ(ζ)

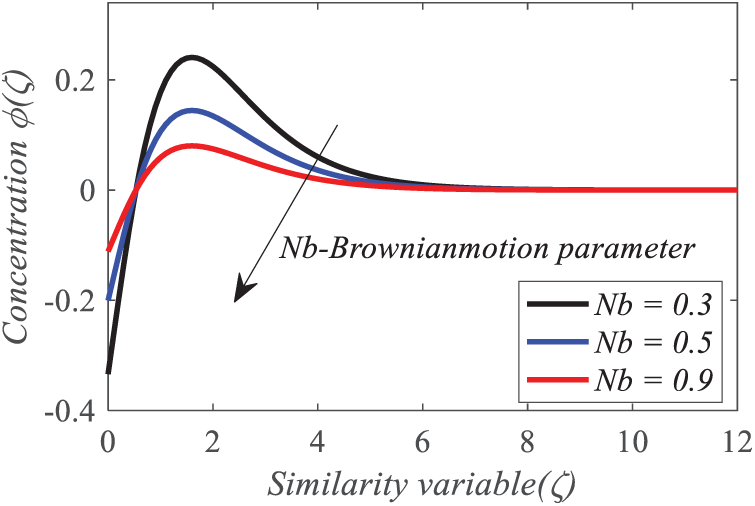
Figure 21: Repercussion of Nb on ϕ(ζ)

The thermophoresis component Nt alters θ(ζ) and ϕ(ζ) distributions in Figs. 22 and 23. The parameter Nt propels nanoparticles from regions of hot to cold, altering the θ(ζ). Additionally, modifies ϕ(ζ) in a comparable manner.

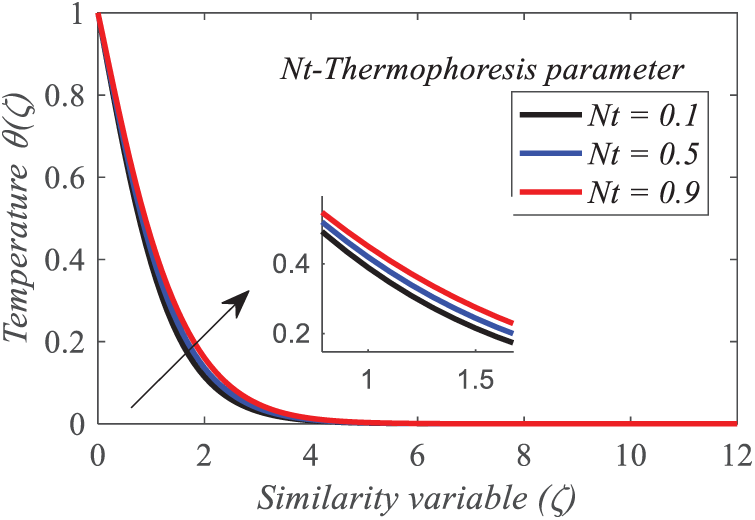
Figure 22: Repercussion of Nt on θ(ζ)

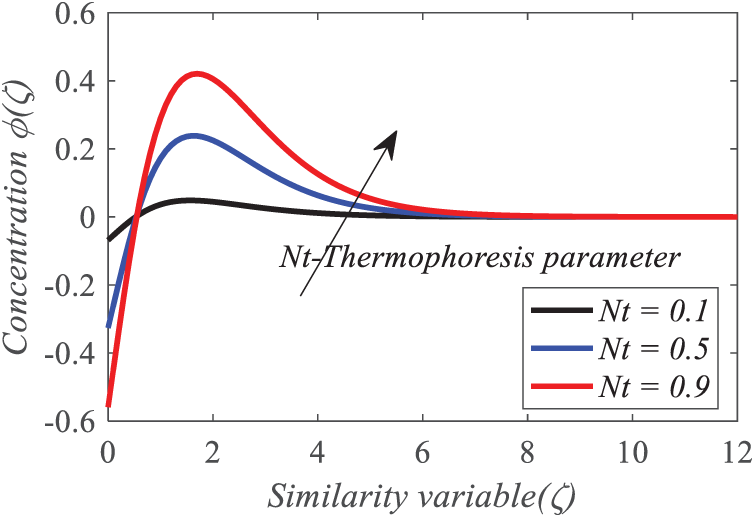
Figure 23: Repercussion of Nt on ϕ(ζ)

Elevated Schmidt number Sc indicate diminished mass diffusivity, hence impeding the transit of species from the surface and resulting in a drop-in ϕ(ζ) in near to the surface as shown in Fig. 24.

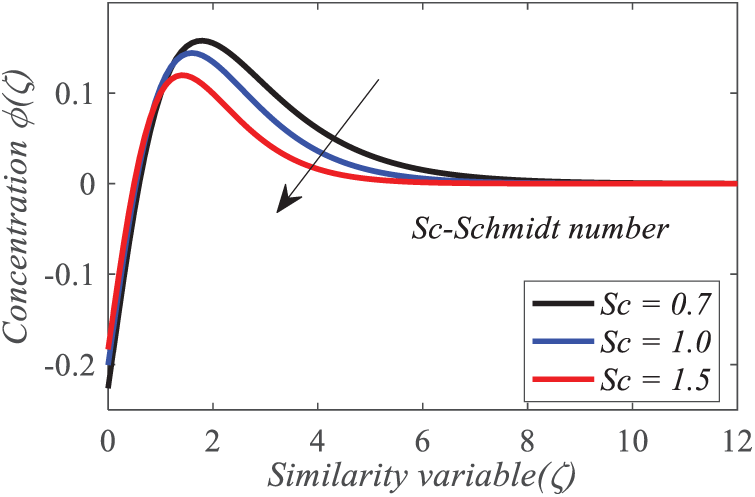
Figure 24: Repercussion of Sc on ϕ(ζ)

From Fig. 25, it is noticed that skin friction coefficient accelerates with the increase of M and k1.

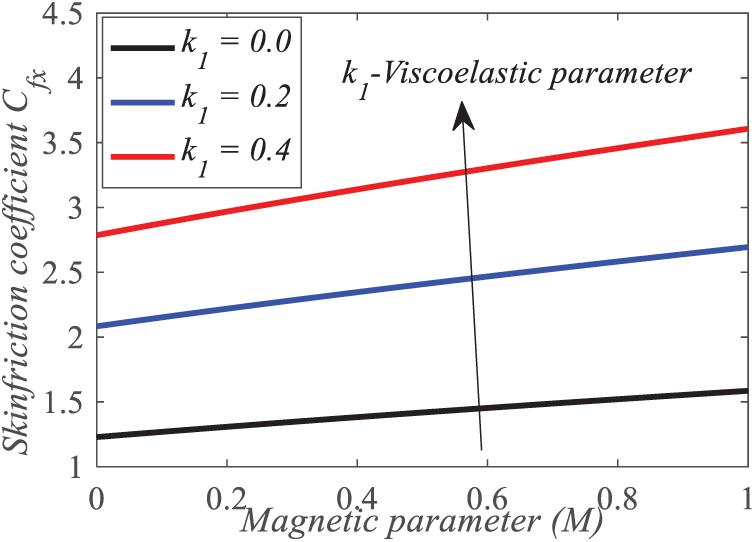
Figure 25: Repercussion of k1 and M on Cfx

Convection over conduction effective surface heat transfer is indicated by a high Nusselt number. Heat exchangers and cooling systems that demand fast heat dispersion benefit from this. Insulating materials or stagnant fluid layers have low Nusselt values, indicating conduction heat transfer. In electrical device thermal management, the Nusselt number reduces overheating by increasing heat dissipation. In contrast, insulating design reduces heat losses with low Nusselt. A declining pattern in the Nusselt number becomes apparent with an upsurge in the Ec and Nt which is given in Fig. 26.

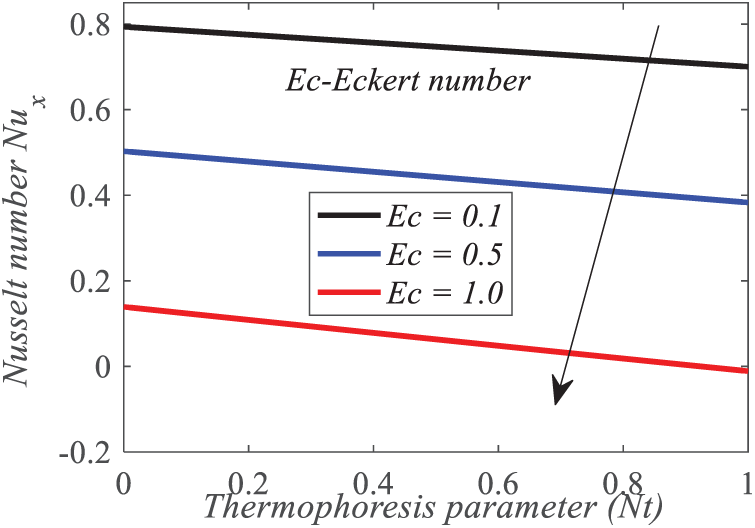
Figure 26: Repercussion of Ec and Nt on Nux

Convective mass transfer is necessary for drying, distillation, and catalytic reactions with high Sherwood numbers. Low Sherwood numbers suggest diffusion-dominated mass movement in stationary or slow diffusion systems. To optimize catalyst surface reactant movement, chemical engineers want high Sherwood numbers in packed bed reactors. Water removal efficiency is seen during drying. The rate of mass transfer rises at the plate in the presence of M and Sc. This is shown in Fig. 27.

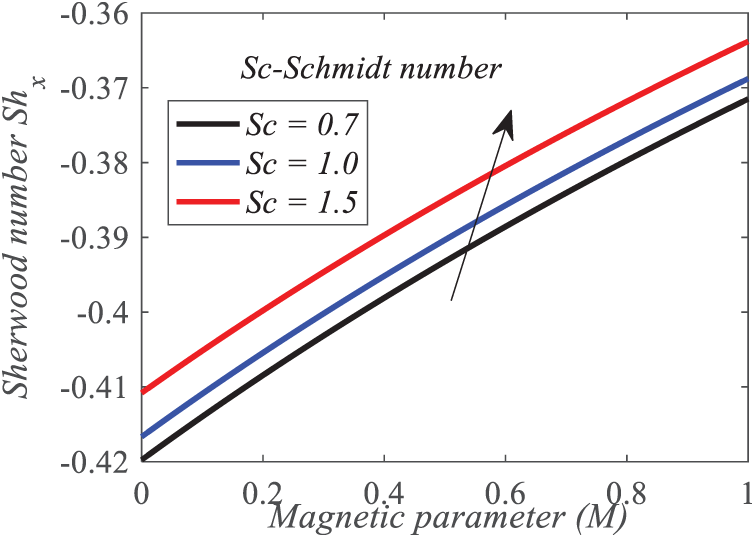
Figure 27: Repercussion of Sc and M on Shx

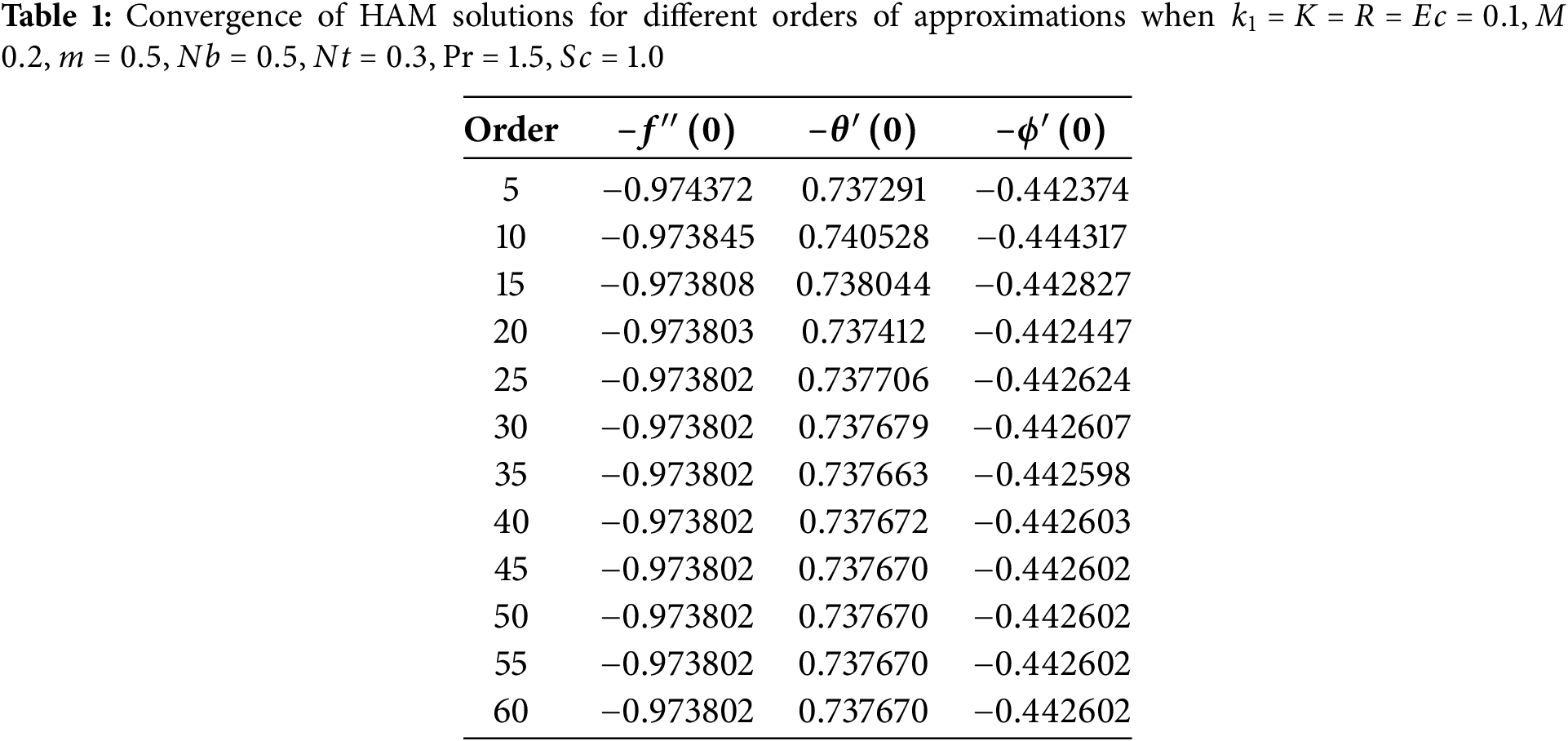
To evaluate the numerical scheme’s accuracy, we assess the most current findings. of −f′′(0)and −θ′(0) with the findings of Nayak et al. [36], Wahid et al. [37] and Goyal et al. [38] in Tables 2 and 3.

6  Conclusions

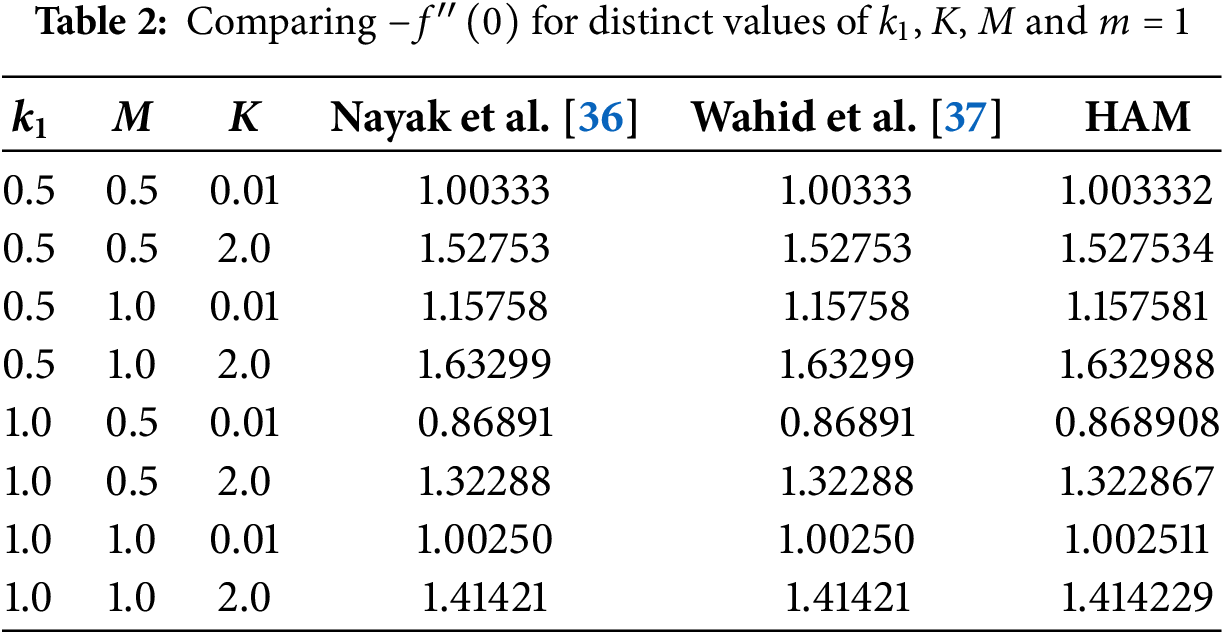
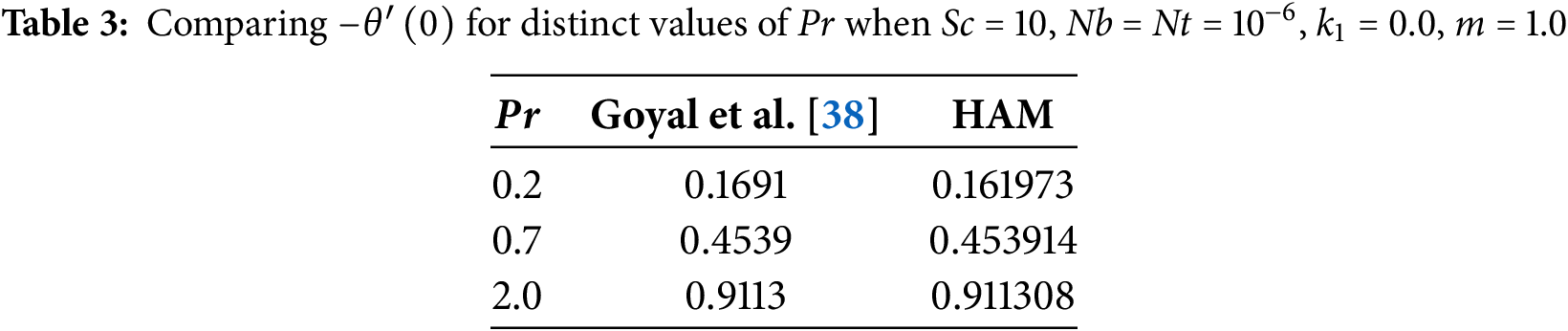
This work examines the mass and heat transfer characteristics of nanofluid flow within a viscoelastic boundary layer over a porous sheet undergoing nonlinear stretching. The analysis, based on Buongiorno’s empirical nanofluid framework, incorporates the effects of viscous dissipation and heat radiation. The governing equations are solved using the Homotopy Analysis Method (HAM), and the results are validated against known research.

•   The fluid’s velocity grows with a rise in the viscoelastic parameter, signifying improved momentum transfer attributable to the fluid’s elasticity, which aids its flow. In contrast, velocity diminishes with increased levels of the magnetic parameter, porous medium parameter, and stretching sheet index. This behavior illustrates the cumulative impact of Lorentz forces, augmented drag inside the porous medium, and resistance due to non-linear stretching, all of which counteract fluid motion. These findings underscore the essential importance of these factors in regulating fluid dynamics in applications such as electromagnetic flow control and filtration in porous media.

•   The temperature profile increases with a rise in the radiation parameter, indicating improved thermal energy transfer from intensified radiative heat flux. Likewise, elevated levels of the Brownian motion and thermophoresis factors enhance temperature, as nanoparticle mobility and thermophoretic effects facilitate heat diffusion. The positive effect of the Eckert number underscores the transformation of kinetic energy into internal energy via viscous dissipation, hence increasing the temperature. These findings highlight the significance of these factors in enhancing thermal management in nanofluid systems for sophisticated heat transfer applications.

•   The concentration profile diminishes as the Brownian motion parameter increases, indicating the augmented dispersion of nanoparticles that lessens concentration gradients. A greater Schmidt number corresponds to a decrease in concentration, indicating less molecular diffusivity, which restricts the transit of solute particles. These results underscore the significant impact of these factors on mass transfer processes, with ramifications for applications like chemical mixing and separation technologies.

•   The skin friction coefficient increases with the elevation of both the magnetic parameter and the viscoelastic parameter. The magnetic parameter intensifies the Lorentz force, augmenting resistance to fluid motion at the surface, whereas the viscoelastic value boosts the elastic properties of the fluid, resulting in elevated surface shear stress. These findings emphasize the impact of electromagnetic forces and fluid elasticity on shear properties, with consequences for the design of systems that incorporate viscoelastic and magnetohydrodynamic flows.

•   An ascending tendency in the Sherwood number is evident with the elevation of Sc and M.

•   The insights gained through HAM align closely with the prior findings.

Acknowledgement: The authors appreciate the valuable feedback from the esteemed reviewers, which contributed to the improvements in this revised article.

Funding Statement: For the purpose of this study, the authors did not receive any specific funding.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Syamala Ramadevu, Parthi Vijaya Kumar; data collection: Shaik Mohammed Ibrahim; analysis and interpretation of results: Kanithi Jyothsna; draft manuscript preparation: Giulio Lorenzini. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Requests for data can be made at any time.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

References

1. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29). Argonne, IL, USA: Argonne National Lab. (ANL); 1995. [Google Scholar]

2. Bhatti MM, Rashidi MM. Entropy generation with nonlinear thermal radiation in MHD boundary layer flow over a permeable shrinking/stretching sheet: numerical solution. J Nanofluids. 2016;5(4):543–8. doi:10.1166/jon.2016.1248. [Google Scholar] [CrossRef]

3. Sumathi MG, Prathi V, Mohammed IS. Numerical analysis study of chemically radiative MHD williamson nanofluid flow over an inclined surface with heat source. CFD Lett. 2024;16(9):126–42. doi:10.37934/cfdl.16.9.126142. [Google Scholar] [CrossRef]

4. Shahidian A, Ghassemi M, Mohammadi R. Effect of nanofluid properties on magnetohydrodynamic pump (MHD). Adv Mater Res. 2011;403–408:663–9. doi:10.4028/www.scientific.net/AMR.403-408.663. [Google Scholar] [CrossRef]

5. Ashorynejad HR, Mohamad AA, Sheikholeslami M. Magnetic field effects on natural convection flow of a nanofluid in a horizontal cylindrical annulus using Lattice Boltzmann method. Int J Therm Sci. 2013;64(10):240–50. doi:10.1016/j.ijthermalsci.2012.08.006. [Google Scholar] [CrossRef]

6. Ghadimi A, Saidur R, Metselaar HSC. A review of nanofluid stability properties and characterization in stationary conditions. Int J Heat Mass Transf. 2011;54(17–18):4051–68. doi:10.1016/j.ijheatmasstransfer.2011.04.014. [Google Scholar] [CrossRef]

7. Khan KA, Javed MF, Ullah MA, Riaz MB. Heat and Mass transport analysis for Williamson MHD nanofluid flow over a stretched sheet. Results Phys. 2023;53(2021):106873. doi:10.1016/j.rinp.2023.106873. [Google Scholar] [CrossRef]

8. Venkata Ramudu AC, Anantha Kumar K, Sugunamma V, Sandeep N. Heat and mass transfer in MHD Casson nanofluid flow past a stretching sheet with thermophoresis and Brownian motion. Heat Trans. 2020;49(8):5020–37. doi:10.1002/htj.21865. [Google Scholar] [CrossRef]

9. Krishna MV, Vijaya Kumar AG. Chemical reaction, slip effects and non-linear thermal radiation on unsteady MHD Jeffreys nanofluid flow over a stretching sheet. Case Stud Therm Eng. 2024;55(3):104129. doi:10.1016/j.csite.2024.104129. [Google Scholar] [CrossRef]

10. Abo-Eldahab EM, Adel R, Mobarak HM, Abdelhakem M. The effects of magnetic field on boundary layer nano-fluid flow over stretching sheet. Appl Math Inf Sci. 2021;15(6):731–41. doi:10.18576/amis/150607. [Google Scholar] [CrossRef]

11. Sarada K, Gowda RJP, Sarris IE, Kumar RN, Prasannakumara BC. Effect of magnetohydrodynamics on heat transfer behaviour of a non-Newtonian fluid flow over a stretching sheet under local thermal non-equilibrium condition. Fluids. 2021;6(8):264. doi:10.3390/fluids6080264. [Google Scholar] [CrossRef]

12. Sharma RP, Shaw S. MHD non-newtonian fluid flow past a stretching sheet under the influence of non-linear radiation and viscous dissipation. J Appl Computat Mech. 2022;8(3):949–61. doi:10.22055/JACM.2021.34993.2533. [Google Scholar] [CrossRef]

13. Anwar MI, Firdous H, Al Zubaidi A, Abbas N, Nadeem S. Computational analysis of induced magnetohydrodynamic non-Newtonian nanofluid flow over nonlinear stretching sheet. Prog React Kinet Mech. 2022;47(2):14686783211072712. doi:10.1177/14686783211072712. [Google Scholar] [CrossRef]

14. Elgazery NS, Elelamy AF. Multiple solutions for non-Newtonian nanofluid flow over a stretching sheet with nonlinear thermal radiation: application in transdermal drug delivery. Pramana. 2020;94(1):68. doi:10.1007/s12043-020-1925-x. [Google Scholar] [CrossRef]

15. Nadeem S, Amin A, Abbas N. On the stagnation point flow of nanomaterial with base viscoelastic micropolar fluid over a stretching surface. Alex Eng J. 2020;59(3):1751–60. doi:10.1016/j.aej.2020.04.041. [Google Scholar] [CrossRef]

16. Swain K, Parida SK, Dash GC. MHD flow of viscoelastic nanofluid over a stretching sheet in a porous medium with heat source and chemical reaction. Ann Chim-Sci Mat. 2018;42(1):7–21. doi:10.3166/acsm.42.7-21. [Google Scholar] [CrossRef]

17. Alrehili M. Viscoelastic thermal nanofluid flow and heat mass transfer due to a stretching sheet with slip velocity phenomenon and convective heating. Int J Thermofluids. 2023;17(10):100281. doi:10.1016/j.ijft.2023.100281. [Google Scholar] [CrossRef]

18. Mahanthesh B, Gireesha B, Thammanna G, Shehzad S, Abbasi F, Gorla R. Nonlinear convection in nano Maxwell fluid with nonlinear thermal radiation: a three-dimensional study. Alex Eng J. 2018;57(3):1927–35. doi:10.1016/j.aej.2017.03.037. [Google Scholar] [CrossRef]

19. Hsiao KL. Viscoelastic fluid over a stretching sheet with electromagnetic effects and nonuniform heat source/sink. Math Probl Eng. 2010;2010(1):740943. doi:10.1155/2010/740943. [Google Scholar] [CrossRef]

20. Venkatadri K, Abdul GS, Rajarajeswari P, Prasad VR, Anwar BO, Hidayathulla KBM. Melting heat transfer analysis of electrically conducting nanofluid flow over an exponentially shrinking/stretching porous sheet with radiative heat flux under a magnetic field. Heat Trans. 2020;49(8):4281–303. doi:10.1002/htj.21827. [Google Scholar] [CrossRef]

21. Abed Mahdi R, Mohammed HA, Munisamy KM, Saeid NH. Review of convection heat transfer and fluid flow in porous media with nanofluid. Renew Sustain Energy Rev. 2015;41(2):715–34. doi:10.1016/j.rser.2014.08.040. [Google Scholar] [CrossRef]

22. Ali MY, Reza-E-Rabbi S, Rasel MMH, Ahmmed SF. Combined impacts of thermoelectric and radiation on hydromagnetic nanofluid flow over a nonlinear stretching sheet. Partial Differ Equ Appl Math. 2023;7(1):100500. doi:10.1016/j.padiff.2023.100500. [Google Scholar] [CrossRef]

23. Jabeen K, Mushtaq M, Akram RM. Analysis of the MHD boundary layer flow over a nonlinear stretching sheet in a porous medium using semianalytical approaches. Math Probl Eng. 2020;2020(5):3012854. doi:10.1155/2020/3012854. [Google Scholar] [CrossRef]

24. Khan M, Malik R, Munir A, Khan WA. Flow and heat transfer to Sisko nanofluid over a nonlinear stretching sheet. PLoS One. 2015;10(5):e0125683. doi:10.1371/journal.pone.0125683. [Google Scholar] [PubMed] [CrossRef]

25. Yang Y, Liao S. Comparison between Homotopy analysis method and Homotopy renormalization method in fluid mechanics. Eur J Mech Fluids. 2023;97(2):187–98. doi:10.1016/j.euromechflu.2022.10.005. [Google Scholar] [CrossRef]

26. Masjedi PK, Weaver PM. Analytical solution for arbitrary large deflection of geometrically exact beams using the Homotopy analysis method. Appl Math Model. 2022;103(2216):516–42. doi:10.1016/j.apm.2021.10.037. [Google Scholar] [CrossRef]

27. Ibrahim SM, Lorenzini G, Vijaya Kumar P, Raju CSK. Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a Casson nanofluid over a nonlinear permeable stretching sheet. Int J Heat Mass Transf. 2017;111:346–55. doi:10.1016/j.ijheatmasstransfer.2017.03.097. [Google Scholar] [CrossRef]

28. Kumar P, Ibrahim S, Lorenzinir G. Impact of thermal radiation and Joule heating on MHD mixed convection flow of a Jeffrey fluid over a stretching sheet using Homotopy analysis method. Int J Heat Technol. 2017;35(4):978–86. doi:10.18280/ijht.350434. [Google Scholar] [CrossRef]

29. Pavan Kumar PL, Gireesha BJ, Venkatesh P. Homotopy analysis method in thermal profiling of porous fin: a comparison of rectangular and triangular configurations. Int Commun Heat Mass Transf. 2024;159(8):108023. doi:10.1016/j.icheatmasstransfer.2024.108023. [Google Scholar] [CrossRef]

30. Saratha SR, Sai Sundara Krishnan G, Bagyalakshmi M. Analysis of a fractional epidemic model by fractional generalised Homotopy analysis method using modified Riemann-Liouville derivative. Appl Math Model. 2021;92(1):525–45. doi:10.1016/j.apm.2020.11.019. [Google Scholar] [CrossRef]

31. Kumar Prathi V, Ibrahim Shaik M, Giulio L. The study of three dimensional radiative MHD Casson nanofluid over an exponential porous stretching sheet with heat source under convective boundary conditions. Int J Heat Technol. 2018;36(1):1–10. doi:10.18280/ijht.360101. [Google Scholar] [CrossRef]

32. Zaheer M, Abbas SZ, Huang N, Elmasry Y. Analysis of buoyancy features on magneto hydrodynamic stagnation point flow of nanofluid using Homotopy analysis method. Int J Heat Mass Transf. 2024;221(2):125045. doi:10.1016/j.ijheatmasstransfer.2023.125045. [Google Scholar] [CrossRef]

33. Jameel AF, Anakira NR, Alomari AK, Man NH. Solution and analysis of the fuzzy Volterra integral equations via Homotopy analysis method. Comput Model Eng Sci. 2021;127(3):875–99. doi:10.32604/cmes.2021.014460. [Google Scholar] [CrossRef]

34. Mohammed Ibrahim S, Vijaya Kumar P, Lorenzini G. Influence of thermophoresis and Brownian motion of nanoparticles on radiative chemically-reacting MHD hiemenz flow over a nonlinear stretching sheet with heat generation. Fluid Dyn Mater Process. 2023;19(4):855–68. doi:10.32604/fdmp.2022.019796. [Google Scholar] [CrossRef]

35. Nadeem S, Wang F, Alharbi FM, Sajid F, Abbas N, El-Shafay AS, et al. Numerical computations for Buongiorno nano fluid model on the boundary layer flow of viscoelastic fluid towards a nonlinear stretching sheet. Alex Eng J. 2022;61(2):1769–78. doi:10.1016/j.aej.2021.11.013. [Google Scholar] [CrossRef]

36. Nayak MK, Dash GC, Singh LP. Heat and mass transfer effects on MHD viscoelastic fluid over a stretching sheet through porous medium in presence of chemical reaction. Propuls Power Res. 2016;5(1):70–80. doi:10.1016/j.jppr.2016.01.006. [Google Scholar] [CrossRef]

37. Wahid NS, Hafidzuddin MEH, Arifin NM, Turkyilmazoglu M, Rahmin NAA. Magnetohydrodynamic (MHD) slip darcy flow of viscoelastic fluid over A stretching sheet and heat transfer with thermal radiation and viscous dissipation. CFD Lett. 2020;12(1):1–12. [Google Scholar]

38. Goyal M, Bhargava R. Boundary layer flow and heat transfer of viscoelastic nanofluids past a stretching sheet with partial slip conditions. Appl Nanosci. 2014;4(6):761–7. doi:10.1007/s13204-013-0254-5. [Google Scholar] [CrossRef]