SRM Simulation of Thermal Convective on MHD Nanofluids across Moving Flat Plate

1  Introduction

Recent studies have explored thermal performance enhancement in thermo-mechanical components, highlighting the growing use of nanofluids for their superior thermal properties and wide-ranging engineering applications. Their integration into technological and industrial systems has significantly increased in recent years. Several commonly used liquids, including ethylene glycol, kerosene oil, engine oil, and water, had minimal heat conductivity prior to the discovery of nanotechnology. One of the many diverse areas where nanofluids have proven useful and functional is heat flow. Technological advancements demand efficient thermal transport methods, and nanofluids offer a more effective solution for transferring heat from one source to another. Nanofluids have a wide range of innovative and efficient applications in various fields, including heat exchangers [1], nuclear reactor cooling [2], chemical and biological engineering [3], liquid electronic devices (LEDs), microelectronics, aerodynamics, artificial intelligence [4], and alternative energy. There have been significant attempts to comprehend the properties and behavior of nanofluids for application [5]. Numerous researchers worldwide have conducted significant studies on nanofluids and their practical applications [6–10].

A novel class of materials called nanofluids contains nanoparticles suspended in more common liquids with low thermal conductivity, such as kerosene, water, or ethylene glycol. Each metal or metal oxide particle increases the conduction and convection coefficients, enhancing heat transfer from the cooling medium to the environment. Sus [11] initially defined the word “nanofluid” as a liquid solution containing tiny particles. The diameter of nanoparticles, such as those made of copper (Cu), silver (Ag), alumina (Al2O3), and titanium (TiO2), varies between 1 to 100 nm [12]. If the base liquid is suspended by an insignificant volumetric fraction (less than 5%) of nanoparticles, its thermal conductivity will improve by 10% to 50% [13–15]. The authors of Kakaç and Pramuanjaroenkij [16] investigated methods to increase the thermal conductivity of fluids that are impervious to heat transfer by floating nano/micro particle materials in that fluid. These fluids include oil, water, and mixtures of ethylene glycol and water. The boundary layer flow over a moving flat surface in a nanofluid, incorporating viscous dissipation, is analyzed by Mohamed et al. [17]. Mousavi et al. [18] established the flow of a nanofluid throughout a permeable shrinking/stretching surface, incorporating second-order slip effects along with an unsteady convective boundary layer. Abd Elazem [19] investigated the impact of MHD nanofluid flow on heat and mass transport past a stretched surface. The impact of radiation, internal heat generation, and viscous dissipation on the convective flow of a viscous fluid through a moving plate is examined theoretically in the work by Ferdows et al. [20]. It is observed that, with a sizeable convective heat volume fraction in the fluid, the heat transfer coefficient is continually enhanced. In their review investigations, Said et al. [21] found that nanofluids display a significantly higher and significantly better temperature-dependent thermal efficiency than conventional fluids.

The presence of a magnetic field in a flow problem plays a significant role in influencing the rate of heat transfer within the system. This effect is particularly evident in conductive fluids such as liquid metals, electrolytes, plasma, and salt water, where the interaction between the magnetic field and the electrically conducting fluid induces magnetohydrodynamic (MHD) effects. These effects can alter the velocity distribution, modify thermal boundary layers, and introduce additional resistive forces, known as the Lorentz force, which can either enhance or suppress heat transfer depending on the flow conditions. As a result, understanding the impact of magnetic fields on heat transfer dynamics is crucial in applications such as nuclear reactors, astrophysical flows, geophysical systems, and advanced cooling technologies. In boundary layer flow involving various fluids, an applied magnetic field is commonly used to regulate heat transfer and momentum [22]. The application of a magnetic field over a heated surface has led to significant advancements in the research of flow and heat transfer in electrically conducting fluids. These applications involve manufacturing procedures like nuclear reactors, thermal insulators, cooling down iron plates, polymer extrusion, MHD pumps, and MHD power generators. Induced magnetism’s impact on the radiated flow of a chemically susceptible nanofluid was researched by Mahanthesh et al. [23]. Ilias et al. [24] examine the effects of a wedge-shaped unsteady aligned MHD free convective heat transfer flow of magnetic nanofluid. Kumar [25] conducted a study on the influence of thermal radiation and an induced magnetic field, incorporating Newtonian heating and cooling boundary conditions, on the magnetohydrodynamic flow occurring between two parallel, non-conducting walls. The study conducted by Sehra et al. [26] explores the unsteady free convective fluid flow of a viscous incompressible fluid influenced by magnetohydrodynamics (MHD). It also examines the impact of chemical molecular diffusivity on a perpendicular plate subjected to arbitrary time-dependent shear stresses and exponential heating phenomena. Al Salman et al. [27] introduced a numerical method to address a two-dimensional Williamson fluid flow model concerning heat and mass transfer in the presence of an induced magnetic field through a moving surface. Diwate et al. [28] investigates the flow and heat transfer of an unsteady laminar boundary layer over a horizontal sheet influenced by radiation and a nonuniform heat source/sink, providing valuable strategies for enhancing heat transfer techniques in engineering applications. Nasir et al. and other researchers have recently made significant advancements in the study of hybrid nanofluids, radiation effects, renewable and sustainable energy applications, and entropy generation in magnetohydrodynamic (MHD) flows [29–33]. The role of energy dissipation, magnetic fields, and viscous dissipation in non-Newtonian fluids is elaborated by Awais et al. and other analysts [34–38], who also look at how these elements impact the heat transfer process in boundary layers. These investigations are particularly helpful in comprehending how changing thermophysical characteristics, including viscosity, affect heat transfer rates and flow characteristics when magnetic fields are present. This knowledge immediately aids in the analysis of MHD flow.

The conversion of mechanical energy into thermal energy is characterized by viscous dissipation. Viscous dissipation is relevant to various applications since it has led to significant temperature increases in polymer manufacturing processes like high-speed extrusion and injection modelling. The dimensionless Eckert number is used widely to describe viscous thermal dissipation of convection, particularly for forced convection [39,40]. It expresses the relationship between the kinetic energy of a flow and the enthalpy difference at the boundary layer. The energy equation is adjusted by adding a factor corresponding to the viscous dissipation effect. Reddy et al. [41] analysed the impact of viscous dissipation on MHD natural convective flow over an oscillating vertical plate. This study by Jafar et al. [42] numerically examined the impact of viscous dissipation in the boundary-layer flow of an electrically conducting viscoelastic fluid over a nonlinear stretching sheet. The steady natural convection flow of an incompressible viscous fluid with varying characteristics was theoretically analyzed by Ajibade et al. [43] in accordance with the effects of boundary plate thickness and viscous dissipation. According to Mishra and Kumar [44], the phenomenon of heat transfer is influenced by elements such as viscous dissipation and Joule heating, which are useful in a variety of technological domains. Viscosity dissipation in connection to nodal as well as saddle points was studied by Gangadhar et al. [45] in 2021. Additionally, Mahesh et al. [46] examined the impact of radiation on a porous sheet, finding that the temperature distribution was significantly influenced by the viscosity parameter values.

The flow of a boundary layer across a moving flat surface in a nanofluid with variable wall temperature and viscous dissipation is studied numerically and reported by Bao et al. [47]. The study by Ajeeb et al. [48] experimentally examines the heat transfer efficiency and thermophysical properties of Al2O3 nanofluids in a compact plate heat exchanger. They found that nanofluid thermal conductivity improved with particle concentration for several base fluid types. Mohana et al.’s [49] work from 2023 provided insight into how various nanoparticle shape parameters affect the flow and heat transfer of a magnetohydrodynamic Cu-water nanofluid over a stretching sheet. Behera et al. [50] used Hamilton-Crosser conductivity, in which the base fluid is combined with the gold nanoparticles, to study the variation of varied shaped nanoparticles. Wang et al. [51] analyzed the transfer of mass and heat when a thin layer of Ag-water flows through a stretching sheet, experiencing thermal and velocity slips. The impacts of MHD, stretching, shrinking, mixed convection, and thermal radiation in a Cu-water-based nanofluid with MHT effects are investigated by Hyder et al. [52]. A two-dimensional mode of MHD extended flow of a second-grade viscoelastic nanofluid on a curved stretching surface is investigated by Hosseinzadeh et al. [53], utilising the curvature parameter and Joule heating to assess the rates of mass and heat transfer. The study reveals that, in contrast to Newtonian fluid, the mass transfer of second-grade fluid is significantly influenced by Schmidt number and chemical reaction parameters. The study by Ali et al. [54] investigate the convective flow of nanoparticles on an exponentially stretching sheet, focusing on the Buongiorno model for Cross nanofluid, and includes a comparative analysis of dissipation and Joule heating effects within the thermal and energy equations. The research reveals that as thermophoresis and random diffusion increase, the temperature field becomes more potent. Rafique et al. [55] investigates heat transfer and entropy production, focusing on the Bejan number at a non-axisymmetric MHD stagnation point with 3D flow, using Al2O3–Cu/H2O hybrid nanofluid. Khan et al. [56] expanded the use of the Buongiorno model to analyse the dynamic interactions of nanoparticle migration across a variable thickness stretching sheet in a mixed convection second-grade fluid. Using a heated horizontal tube arrangement, the thermal performance of water-based hybrid nanofluids with a 50:50 ratio of red mud (RM) and grapheme oxide (GO) nanoparticles under turbulent flow conditions with a constant heat input was effectively assessed by Kanti et al. [57]. A significant improvement in heat transfer coefficient and Nusselt number (Nu) for RM+GO hybrid nanofluid at a maximum concentration of 0.75% is confirmed by the analysis. A vast body of literature shows that Al2O3 has been extensively studied for its use in nanofluids across various applications. Numerous research studies have focused on investigating the thermophysical properties and heat transfer behavior of Al2O3, resulting in the development of various correlations. At different concentrations (0 to 1 vol%) and temperatures (30°C to 60°C), Kanti et al. [58] investigated the thermal conductivity and viscosity of water-based nanofluids including silicon dioxide, graphene oxide, titanium dioxide, and their hybrids. Selvarajoo et al. [59] investigated the thermophysical characteristics of a mono nanofluid made of Al2O3–Go nanoparticles at four distinct volume concentrations using a constant 80:20 ratio. The influence of temperature and volume concentration on Al2O3 and GO–based mono and hybrid nanofluids is investigated, revealing that the thermal conductivity of Al2O3–Go hybrid nanofluid is higher than that of mono nanofluid. With fully developed turbulent flow conditions and an inlet fluid temperature of 60°C, Kanti et al. [60] conducted an extensive study on the synthesis, characterization, thermophysical properties, heat transfer, and fluid flow interactions of water-based nanofluids containing Al2O3, Al2O3–Go (80:20), and Al2O3–Go (50:50) in a horizontal tube.

This article examines the steady flow and heat transfer characteristics, considering the effects of viscous dissipation in a convective, aligned magnetohydrodynamic flow of a water-based nanofluid over a semi-infinite moving flat surface. In this system, the flow velocity and magnetic field vectors remain parallel to each other at a certain distance from the plate. The mathematical model is developed by applying the viscous dissipation effects on the Tiwari and Das [61] model. Four different types of nanoparticles considered are Cu,Ag,Al2O3, and TiO2 using a water-based fluid with Prandtl number Pr=6.2. Due to their expanding applications in various technical and manufacturing processes, the study of these fluid models has become increasingly essential in today’s techno-industrial era. The SRM technique numerically solves the nonlinear coupled partial differential equations. To resolve large algebraic systems of equations, SRM is an iterative approach similar to the Gauss-Seidel relaxation process. Compared to other numerical/analytical techniques, the suggested methodology, SRM, demonstrated that it is accurate, simple to create, convergent, and highly efficient [62–64]. Graphical observations are discussed for the embedded physical parameters for the velocity, temperature, concentration distributions, skin friction, and Nusselt number within the boundary layer. The skin friction coefficient and heat transfer rate have also been studied. The findings have direct applications in cooling systems, electronics, biomedical fields, and magnetically controlled heat transfer processes, making the study highly relevant for modern industries. Considering the mentioned applications the primary goals and novelty of this study are as follows:

(1)   Extends the Tiwari et al. [61] model by including viscous dissipation effects, which significantly influence heat transfer and energy distribution in high-temperature applications.

(2)   Highlight the significance of nanofluid-based MHD flows in technical and manufacturing processes.

(3)   Introduces SRM as an efficient, accurate, and convergent numerical technique for solving nonlinear coupled PDEs, outperforming conventional methods.

(4)   Provide insights into optimizing heat transfer efficiency in engineering applications.

2  Mathematical Model with Flow Configuration

Examine a stable 2D MHD laminar free convective heat and mass transfer flow of a viscous, incompressible, electrically conducting nanofluid with uniform physical properties. This flow originates from a moving flat plate within a magnetic field aligned with the motion. Parallel to the plate, an induced magnetic field with intensity H0 is applied and the velocity of the plate is Uw=εU∞, where ε is the velocity parameter. Fig. 1 shows a schematic illustration and the coordinate system. We also note that both the viscous dissipation and ohmic heating terms are considered in the energy equation. Based on these physical assumptions and employing a boundary-layer approach, the governing equations for the conservation of mass, momentum, and thermal energy are formulated as follows [20,65]:

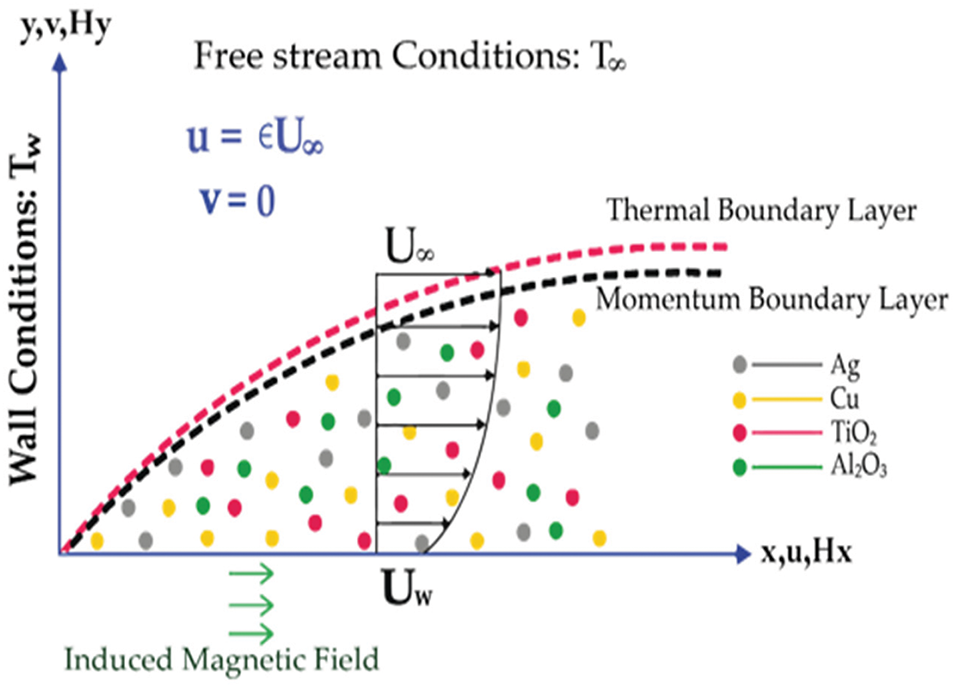
Figure 1: Geometry of flat moving plate

Continuity:

∂u∂x+∂v∂y=0(1)

∂Hx∂x+∂Hy∂y=0(2)

Momentum:

u∂u∂x+v∂u∂y=νnf∂2u∂y2+μeρnf(Hx∂Hx∂x+Hy∂Hx∂y)(3)

Induced magnetic field:

u∂Hx∂x+v∂Hx∂y=Hx∂u∂x+Hy∂u∂y+1μeσnf∂2Hx∂y2(4)

Thermal energy:

u∂T∂x+v∂T∂y=αnf∂2T∂y2+μnf(ρCp)nf(∂u∂y)2+1σnf(ρCp)nf(∂Hx∂y)2(5)

where (u,v) and (Hx,Hy) represent velocity and magnetic components of the nanofluid towards the x and y axes, respectively, μnf and ρnf are the effective dynamic viscosity, and density of the nanofluid, σnf, and Knf signify the electric conductivity and thermal conductivity of the nanofluid. T is the temperature of the nanofluid inside the thermal boundary layer.

The appropriate boundary conditions for the current study are described by:

u=εU∞,v=0,∂Hx∂y=Hy=0,T=Tw At y=0

u→U∞,Hx→H0,T→T∞ At y→∞(6)

The appropriate similarity transformations that convert the governing PDEs into ODEs are as follows:

ψ=(U∞νfx)12f(η),Φ=(νfxU∞)12H0g(η),θ(η)=T−T∞Tw−T∞,η=y2(U∞νfx)12(7)

Using Eq. (7) along with the boundary conditions Eq. (6), the governing Eqs. (3)–(5) are transformed to the following non-dimensional form:

f′′′+ϕ1ff′′−ϕ2Mgg′′=0(8)

g′′′+ϕ3Prm(fg′′−gf′′)=0(9)

ϕ4Prθ″+ϕ5fθ′+Ec4ϕ2(f″)2+MEc4ϕ3Prm(g″)2=0(10)

where:

ϕ1=(1−ϕ)2.5(1−ϕ+ϕρsρf)

ϕ2=(1−ϕ)2.5

ϕ3=σnfσf=1+3((σs/σf)−1)ϕ((σs/σf)+2)−ϕ((σs/σf)−1)

ϕ4=KnfKf=1−ϕ+2ϕKsKs−Kfln⁡Ks+Kf2Kf1−ϕ+2ϕKfKs−Kfln⁡Ks+Kf2Kf

ϕ5=1−ϕ+ϕ(ρCp)s(ρCp)f

The relevant converted boundary conditions are given by:

f(0)=0,f′(0)=2ε,g(0)=g″(0)=0,θ(0)=1 as η=0f′→2,g′→2,θ→0 as η→∞(11)

In the above equations, ε=UwU∞ represents the velocity ratio of the plate, M=μeH02U∞2ρf is the magnetic parameter, Pr=νf(ρCp)fKf is the Prandtl number, Prm=μeνfσf is the magnetic Prandtl number, and Ec=U∞2ΔT(Cp)f is the Eckert number.

The physical quantities of interest are the skin friction coefficient Cf and the local Nusselt number Nux, defined by:

Cf=τwρfU∞2 and Nux=xqwKf(Tw−T∞)(12)

where τw is the surface shear stress or skin friction, and qw is the heat flux from the plate; these are given by:

τw=μnf(∂u∂y)y=0 and  qw=−Knf(∂T∂y)y=0(13)

Substituting Eqs. (7) into (12) and (13), the skin friction coefficient and the local Nusselt number are obtained as:

RexCf=14(1−ϕ)2.5f′′(0) and (Rex2)−12Nux=−12Dθ′(0)(14)

where Rex=U∞xνf is the local Reynolds number.

The dynamic viscosity of the nanofluid, as given by Brinkman (1951), is:

μnf=μf(1−ϕ)2.5

where ϕ is the solid volume fraction of spherical nanoparticles. The effective density and heat capacitance of the nanofluid are defined as:

ρnf=(1−ϕ)ρf+ϕρs

(ρCp)nf=(1−ϕ)(ρCp)f−ϕ(ρCp)s

The effective electrical conductivity of the nanofluid can be approximated, following Maxwell (1881), as:

σnfσf=1+3((σs/σf)−1)ϕ((σs/σf)+2)−ϕ((σs/σf)−1)

The effective thermal conductivity of the nanofluid is expressed by the Maxwell Garnett (1904) model as:

KnfKf=1−ϕ+2ϕKsKs−Kfln⁡Ks+Kf2Kf1−ϕ+2ϕKfKs−Kfln⁡Ks+Kf2Kf

Based on Abu-Nada’s [12] research, Table 1 lists the thermophysical characteristics of the base fluid and the nanoparticles.

3  Solution Procedure with the Spectral Relaxation Method Scheme

The Spectral Relaxation Method (SRM) is widely recognized for solving similarity boundary layer problems with exponentially decaying profiles. There is currently a substantial quantity of literature on the practical application of spectral collocation methods [66–69]. The SRM algorithm can be applied to the problem under study through the following steps:

(1)   Transformation of Equations: Introduce the transformations f′(η)=F(η) and g′(η)=G(η) to reduce the order of the momentum equations, rewriting the original equation in terms of r.

(2)   Iteration Scheme Development: Construct an iterative scheme for the linear terms of F(η) and G(η), represented as Fr+1(η) and Gr+1(η). This is done by assuming that f(η) and g(η), denoted as fr(η) and gr(η), along with all other linear and nonlinear terms, are obtained from previous iterations. Additionally, nonlinear terms in F(η) and G(η) are approximated using values from prior iterations.

(3)   Treatment of Other Governing Variables: The remaining dependent variables in the governing equations are handled using a similar approach.

This structured methodology ensures the efficient application of SRM to solve the given problem.

The SRM iteration scheme can be described as follows:

F″r+1+ϕ1frFr+1′−ϕ2MgrGr′=0(15)

fr+1′=Fr+1(16)

G″r+1+ϕ3Prm(fr+1Gr+1′−grFr+1′)=0(17)

gr+1′=Gr+1(18)

ϕ4Prθ″r+1+ϕ5fr+1θr+1′+Ec4ϕ2(Fr+1′)2+MEc4ϕ3Prm(Gr+1′)2=0(19)

subject to the boundary conditions:

Fr+1(0)=2ε,Fr+1(∞)=2(20)

fr+1(0)=0(21)

Gr+1′(0)=0,Gr+1′(∞)=2(22)

gr+1(0)=0(23)

θr+1(0)=1,θr+1(∞)=0(24)

The Chebyshev spectral collocation method is used to discretize the linear partial differential Eqs. (8)–(10). To implement the spectral procedure, the computational domain [0,L] is converted to the interval [−1,1] using the linear transformation ηL=ζ+12, where L is the scaling parameter used to apply the boundary conditions at infinity. The fundamental principle of the spectral collocation approach is the introduction of a differentiation matrix D, which is utilized to determine the derivatives of the unknown variables at the collocation points [70–74]. The matrix is described in the following form:

dfr+1dη=∑k=0NDikfr(ζk)=Dfr,i=0,1,2,…,N(25)

where N+1 is the number of grid points, D=2DL, and f=[f(ζ0),f(ζ1),…,f(ζN)]T is the vector function at the collocation points. Higher-order derivatives are obtained as powers of D, that is:

f(p)=Dpf(26)

where p is the order of derivatives. The technique Trefethen [72] outlined in the cheb.m Matlab m-file is employed in this study.

Applying the Chebyshev pseudo-spectral approach to Eqs. (15)–(24) yields

A1Fr+1=B1,Fr+1(ζN)=2,Fr+1(ζ0)=2ε(27)

A2fr+1=B2,fr+1(ζN)=0(28)

A3Gr+1=B3,Gr+1(ζN)=2,Gr+1′(ζ0)=0(29)

A4gr+1=B4,gr+1(ζN)=0(30)

A5θr+1=B5,θr+1(ζN)=0,θr+1(ζ0)=1(31)

where:

A1=D2+diag(ϕ1fr)D,B1=ϕ2MgrGr′(32)

A2=D,B2=Fr+1(33)

A3=D2+diag(ϕ3Prmfr+1)D,B3=ϕ3PrmgrFr+1′(34)

A4=D,B4=Gr+1(35)

A5=diag(ϕ4Pr)D2+diag(ϕ5fr+1)D,B5=−Ec4ϕ2(Fr+1′)2−MEc4ϕ3Prm(Gr+1′)2(36)

here, diag denotes a diagonal matrix of size (N+1)×(N+1), where N is the number of grid points and fr(η),gr(η), and θr(η) are the values of the functions f,g, and θ, respectively, when calculated at the grid points, and the subscript r is the number of iterations. The spectral collocation approach can be used to solve Eqs. (27)–(36), which make up the SRM scheme, beginning with the initial conditions listed below, which are selected to fulfil the boundary constraints:

f0(η)=η+2εη−ηe−η,g0(η)=2η−(2+η)e−η,θ0(η)=e−η(37)

4  Computational Results and Physical Interpretation

Numerical computations for the solution of the system of ordinary differential Eqs. (8)–(10) with associated boundary constraints Eq. (11) are carried out using the SRM. The results are attained using N=60 grid points, and the infinity value η∞ is taken as 15. To evaluate the accuracy and convergence of the SRM method, Table 2 compares the outcomes with numerical methods reported to be correct within a specified number of decimal digits. The numerical simulations for dimensionless velocity, temperature, skin friction, Nusselt numbers, and streamlines under the impact of the flow parameters are presented in this section and are displayed in Figs. 2–12. Figs. 2–6 present the results for an Al2O3–water nanofluid.

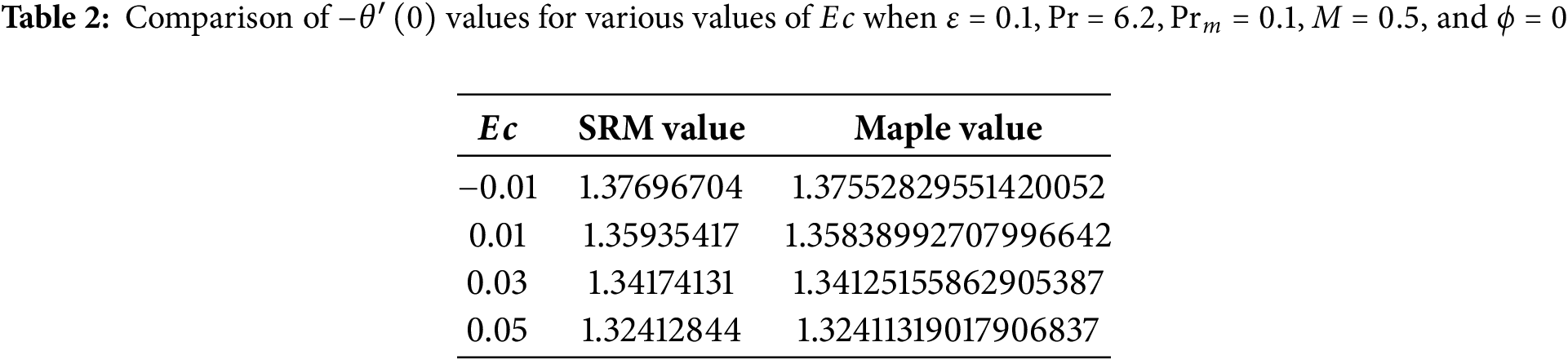
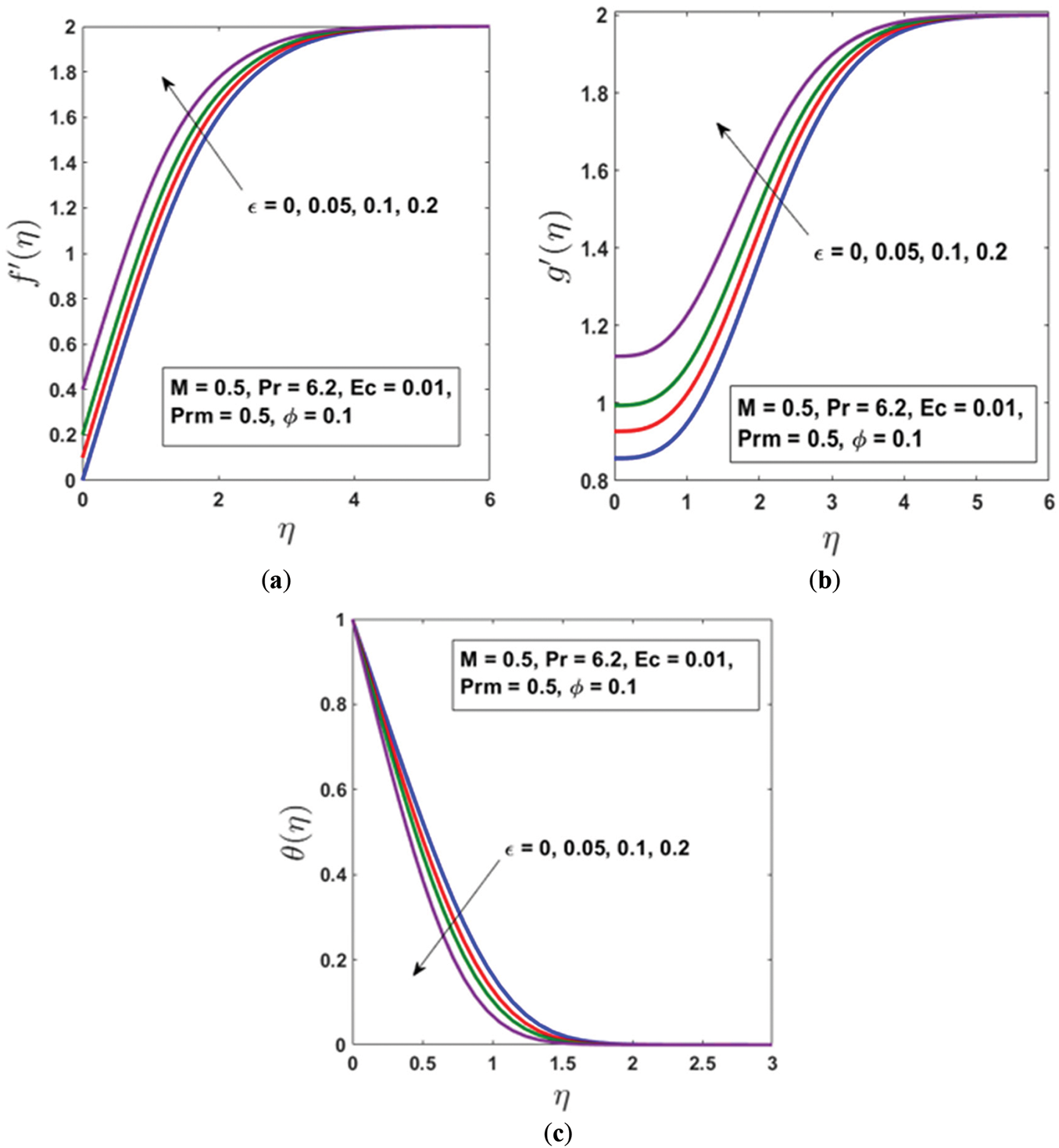
Figure 2: Impact of velocity ratio parameter ε on (a) velocity, (b) induced magnetic field, and (c) temperature

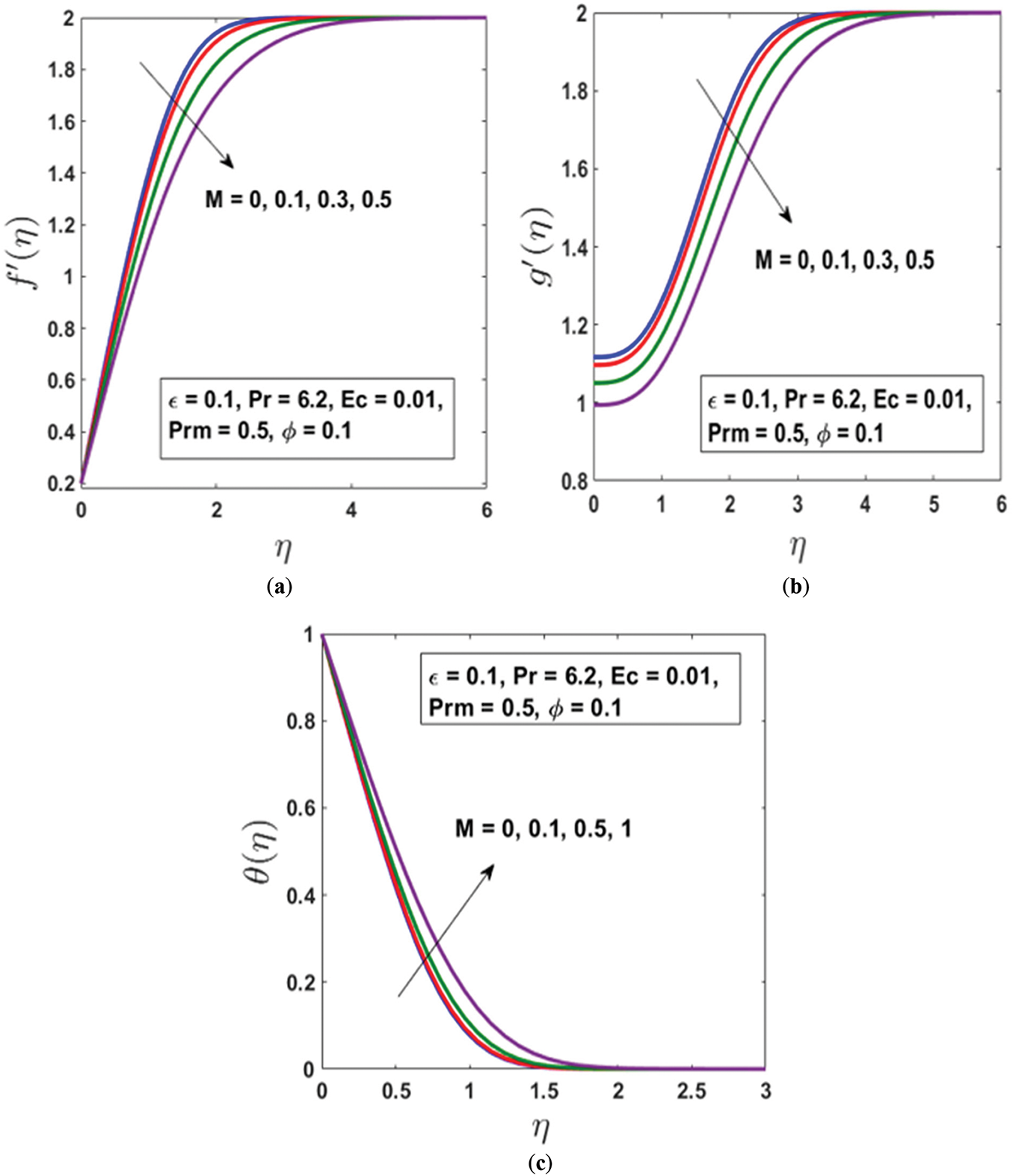
Figure 3: Impact of magnetic parameter M on (a) velocity, (b) induced magnetic field, and (c) temperature

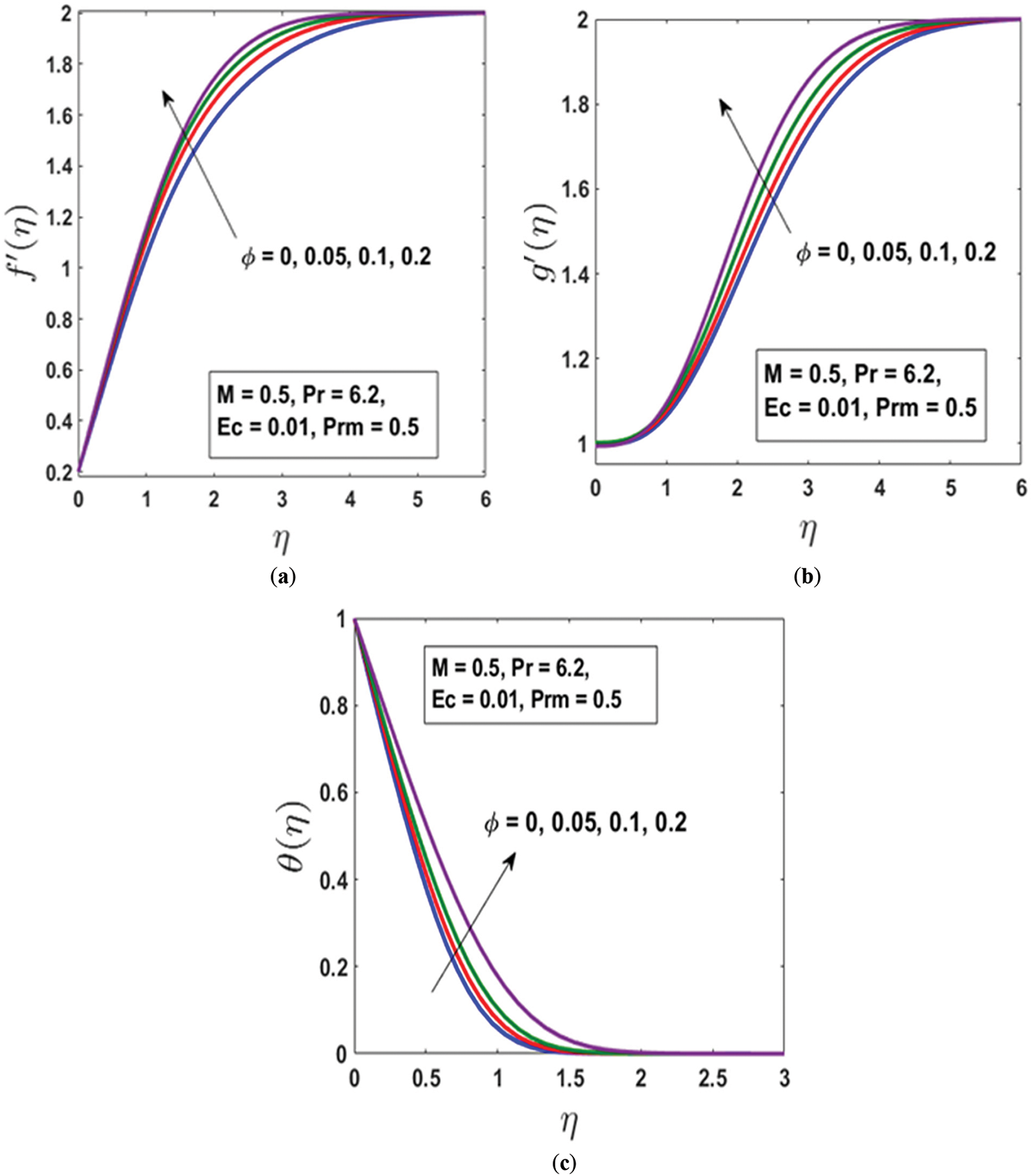
Figure 4: Impact of volume fraction parameter ϕ on (a) velocity, (b) induced magnetic field, and (c) temperature

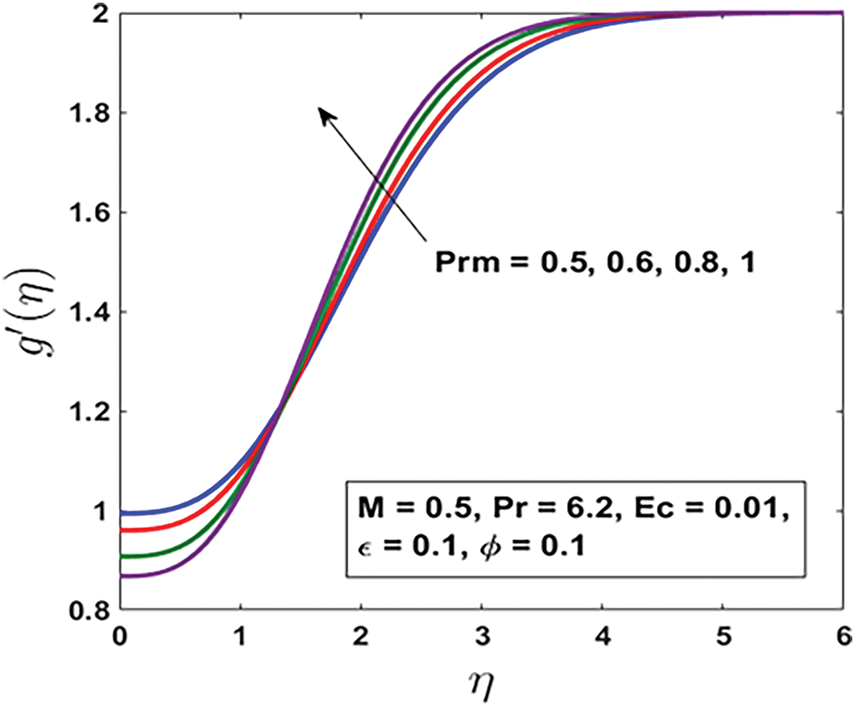
Figure 5: Impact of Prm on induced magnetic field

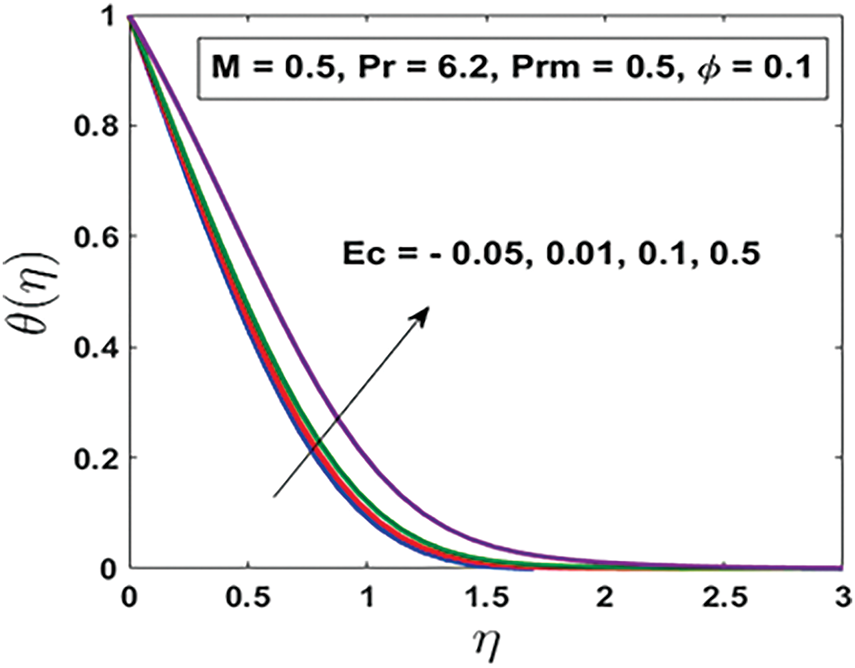
Figure 6: Temperature distributions for different values of Eckert number Ec

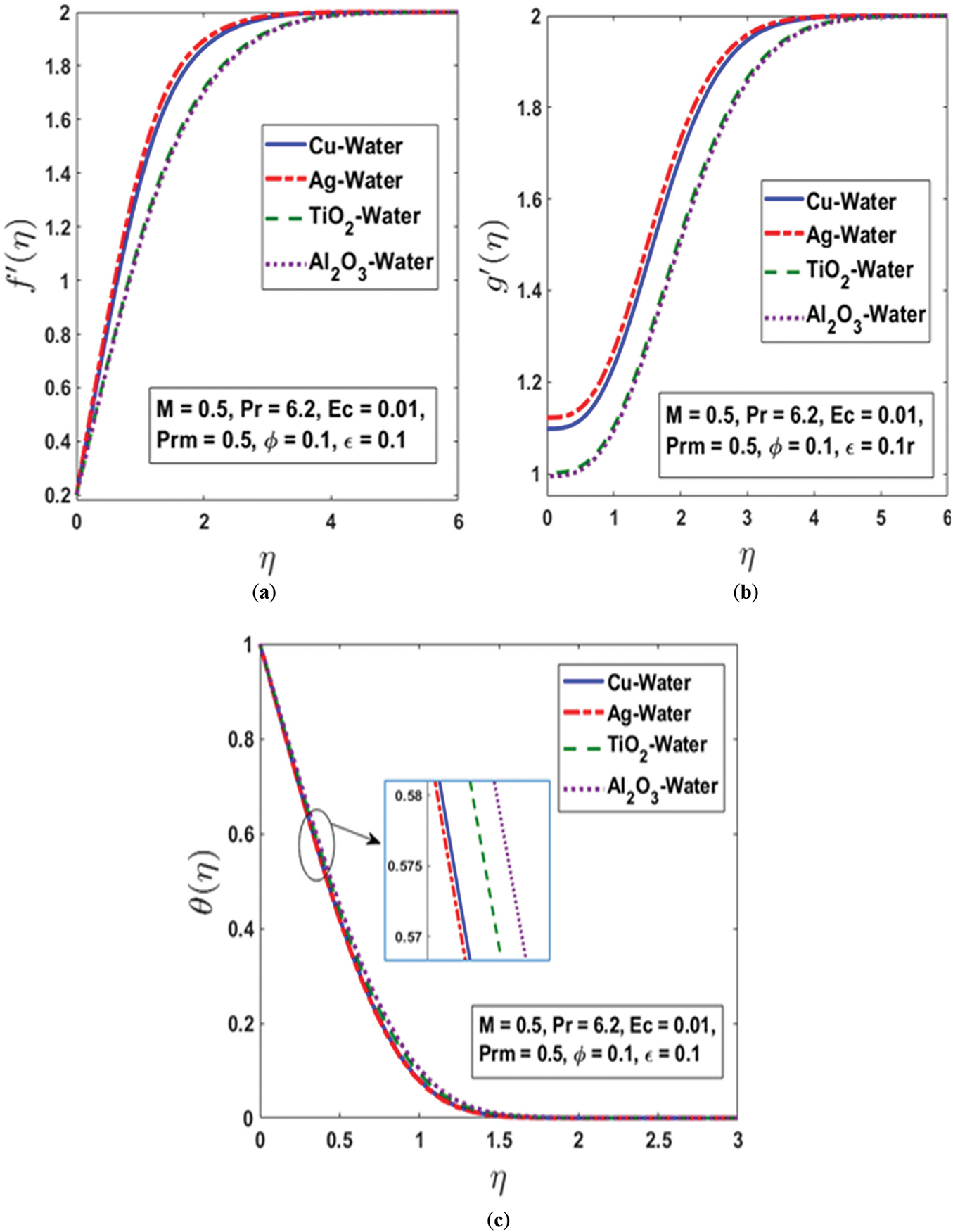
Figure 7: (a) Velocity, (b) induced magnetic field, and (c) temperature distributions for different nanofluids

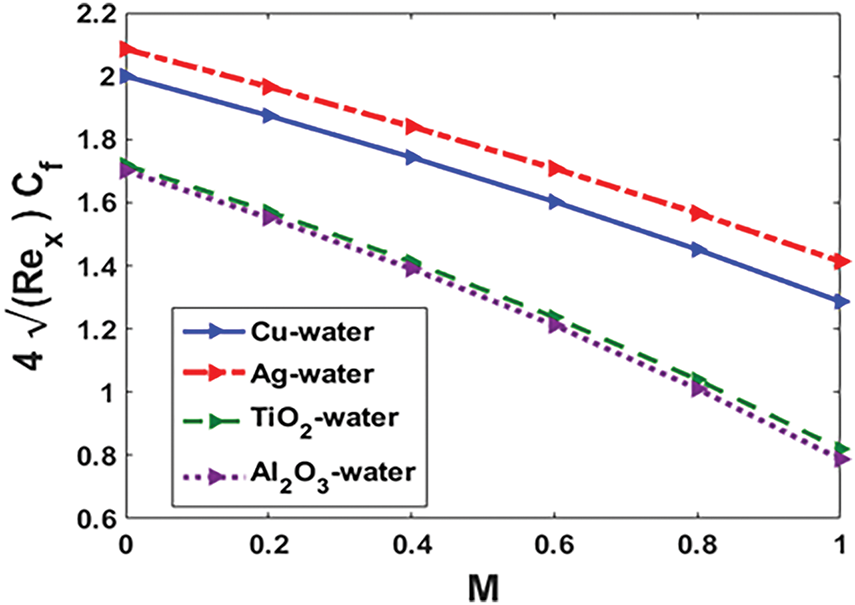
Figure 8: Impact of M on skin friction for different nanofluids

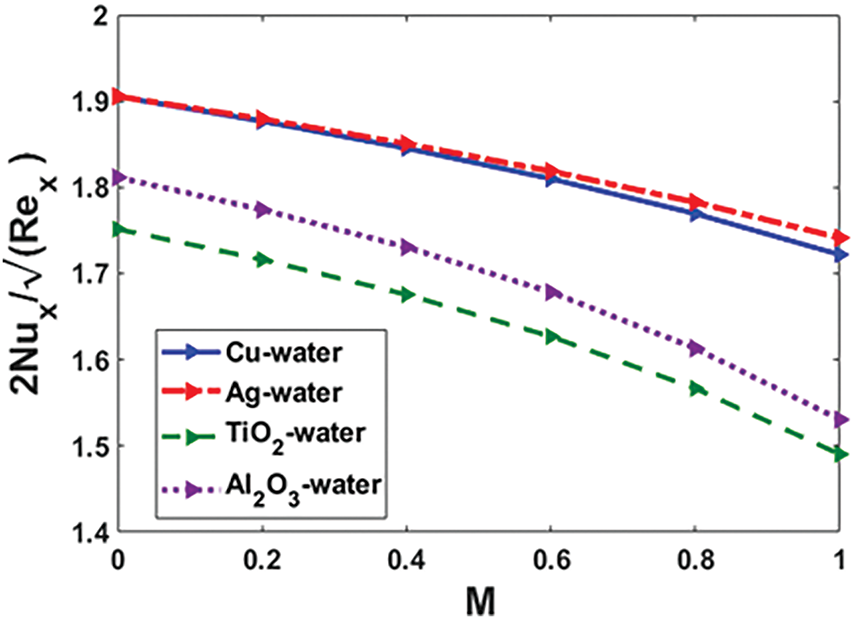
Figure 9: Impact of M on Nusselt number for different nanofluids

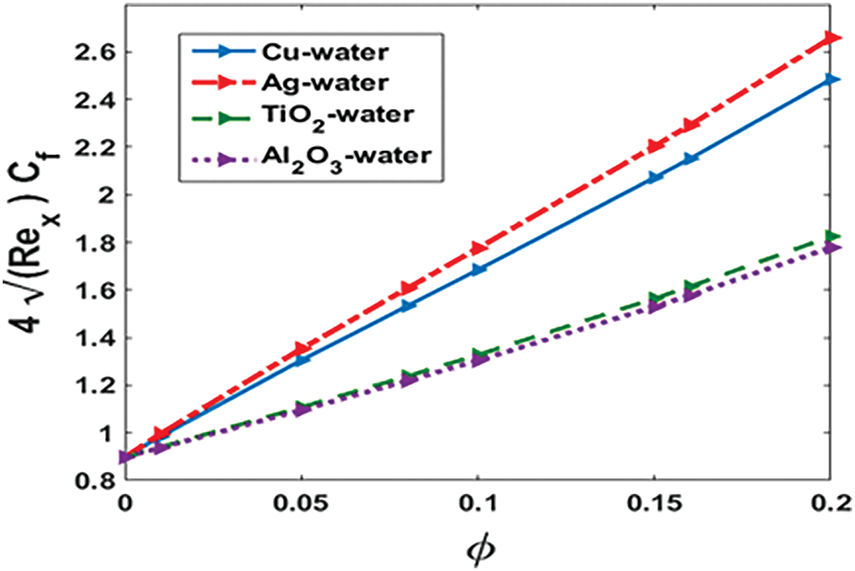
Figure 10: Impact of ϕ on skin friction for different nanofluids

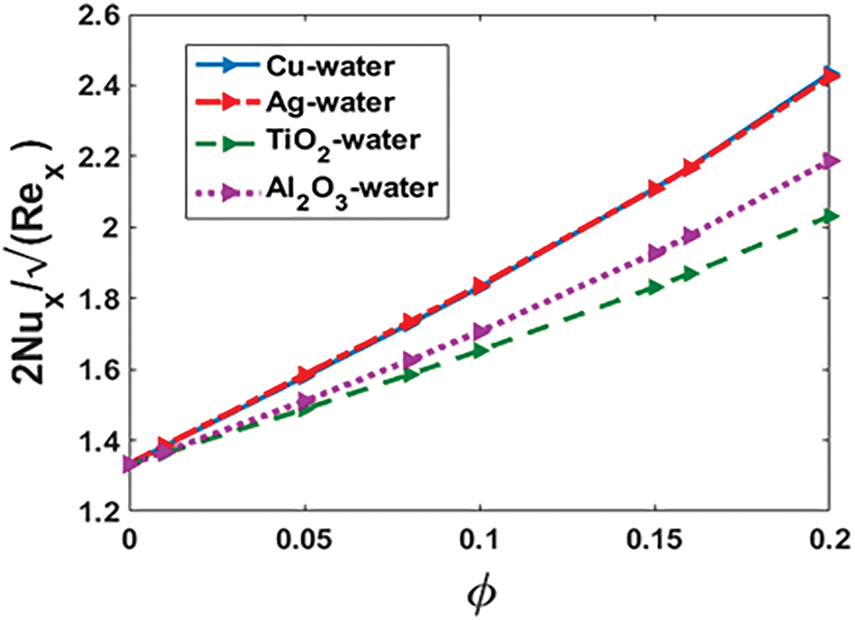
Figure 11: Impact of ϕ on Nusselt number for different nanofluid

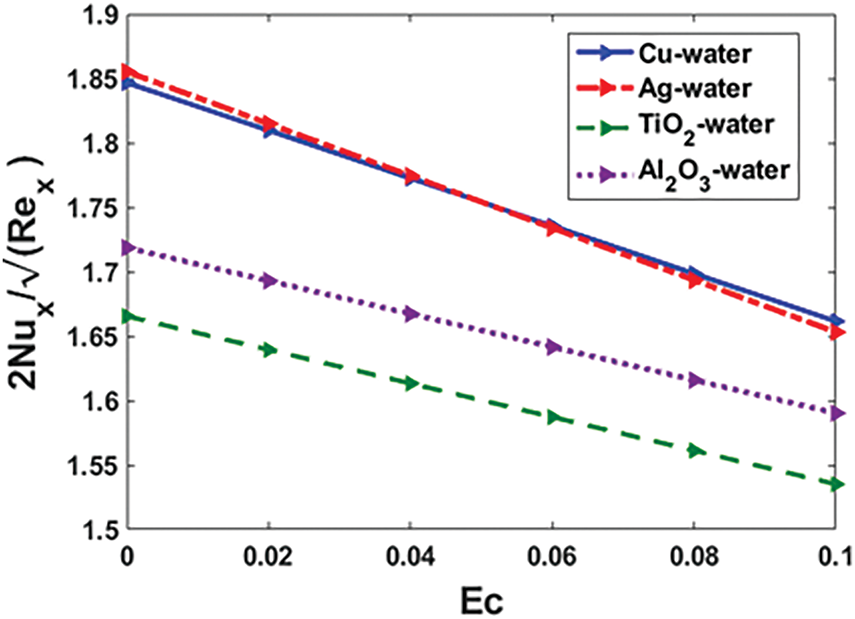
Figure 12: Impact of Ec on Nusselt number for different nanofluids

The trends observed in Fig. 2a–c can be justified based on fundamental principles of fluid dynamics, heat transfer, and magnetohydrodynamics (MHD). The velocity ratio parameter ε plays a significant role in modifying the behavior of the velocity, induced magnetic field, and thermal field. As ε increases, the velocity of the plate relative to the free-stream fluid velocity becomes larger, enhancing the momentum transfer from the plate to the surrounding fluid. This results in a higher velocity profile, as seen in Fig. 2a, where the fluid near the plate experiences an increase in speed. Since the moving plate drags the adjacent fluid layers along with it, the velocity boundary layer develops more efficiently, leading to a more streamlined flow. This increased velocity gradient near the plate also affects the thickness of the boundary layer, causing it to decrease.

Similarly, the induced magnetic field, illustrated in Fig. 2b, also increases with ε. This can be attributed to the fact that a faster-moving electrically conducting fluid interacts more strongly with the applied magnetic field, leading to a more pronounced electromagnetic induction effect. As the velocity of the fluid rises, the stretching and convection of magnetic field lines become more significant, amplifying the induced magnetic field intensity. This effect is particularly relevant in magnetohydrodynamic (MHD) flows, where fluid motion actively influences the magnetic properties of the system. The enhanced induced magnetic field can, in turn, alter the overall flow characteristics, contributing to changes in the velocity and temperature distributions.

Conversely, the thermal field, shown in Fig. 2c, exhibits a decreasing trend with increasing ε. This occurs because as the fluid moves faster, it spends less time in the heated region near the plate, reducing the amount of heat it absorbs from the surface. The dominance of convective heat transport over conductive heat diffusion results in a reduced thermal boundary layer thickness. Essentially, the increased velocity facilitates the removal of heat from the region near the plate, leading to lower overall temperature profiles. As a result, the thickness of the thermal boundary layer decreases, which is a typical characteristic of high-speed convective flows.

The observed reduction in the thermal boundary layer thickness with increasing ε suggests that adjusting the plate velocity can be an effective method for controlling heat dissipation in thermal management systems. The interplay between velocity, induced magnetic field, and temperature fields aligns well with classical boundary layer theory and magnetohydrodynamic flow principles. These findings further confirm the accuracy of the numerical analysis performed using the Spectral Relaxation Method (SRM).

The effects of the applied magnetic field on nanofluid flow, as illustrated in Fig. 3a–c, highlight the influence of the magnetic parameter M, which represents the ratio of electromagnetic to viscous forces and quantifies the strength of the externally applied magnetic field. As shown in Fig. 3a,b, an increase in M results in a reduction in the thickness of the momentum boundary layer. This behavior is attributed to the presence of the Lorentz force, an opposing electromagnetic force generated when a magnetic field interacts with an electrically conducting fluid. The Lorentz force acts as a resistive force against the fluid motion, effectively slowing down the flow and restricting the development of the velocity boundary layer. As M increases, the dominance of this resistive force further suppresses the velocity of the nanofluid, leading to a thinner momentum boundary layer. Additionally, the natural viscous resistance of the fluid further contributes to reducing its velocity, enhancing the damping effects caused by the applied magnetic field. The magnetic field, therefore, plays a crucial role in controlling and modifying the flow characteristics of the nanofluid, which is particularly relevant in magnetohydrodynamic (MHD) applications such as electromagnetic pumps, cooling systems, and energy conversion devices.

In contrast to its effect on velocity, Fig. 3c reveals that the temperature profile increases with M. This phenomenon can be attributed to the influence of viscous heating, which becomes more pronounced in the presence of a magnetic field. As the fluid motion is hindered by the Lorentz force, kinetic energy is converted into internal energy, leading to an overall rise in temperature. The resistive effect of the Lorentz force, which opposes the fluid motion, effectively retards the free convection flow within the boundary layer while simultaneously increasing its thermal energy. This results in an increase in temperature, as the suppressed convective transport limits the dissipation of heat away from the heated surface. The observed trend is consistent with the fundamental principle that an applied magnetic field enhances energy dissipation through Joule heating effects, which further contributes to the rise in temperature. This behavior is particularly significant in MHD-based thermal management applications, where controlling heat transfer and flow characteristics is essential for optimizing system performance. The findings confirm that while the magnetic field suppresses fluid velocity and reduces the boundary layer thickness, it simultaneously enhances thermal energy retention, leading to a rise in temperature within the boundary layer.

An increase in the volumetric fraction ϕ of nanoparticles has a significant influence on various fluid dynamics and thermal characteristics, as illustrated in Fig. 4a–c. As the volume fraction of nanoparticles rises, the velocity profile, magnetic stream function gradient, and temperature field exhibit distinct trends. Specifically, an increase in the volume fraction leads to a reduction in the thicknesses of both the momentum boundary layer and the induced magnetic boundary layer. This reduction occurs due to the enhanced viscosity and altered flow dynamics caused by the suspended nanoparticles, which, in turn, affect the overall velocity distribution. Conversely, the thermal boundary layer exhibits an opposite trend, expanding as the nanoparticle volume fraction increases within the range of 0<ϕ<0.2. This expansion is attributed to the enhanced thermal conductivity of the nanofluid, which allows for more efficient heat conduction within the fluid medium.

From a physical perspective, the boundary layer thickness is influenced by the combined effects of nanoparticle concentration and thermal conductivity. As the nanoparticle volume fraction increases, the nanofluid’s overall thermal conductivity improves, facilitating more effective heat dissipation. This improvement in thermal conductivity is often accompanied by higher thermal diffusivity values, which significantly impact the temperature gradients within the fluid. Higher thermal diffusivity results in reduced temperature gradients, leading to an overall increase in the thermal boundary layer thickness. Essentially, as more nanoparticles are introduced into the fluid, their superior thermal properties enhance heat conduction, thereby altering the thermal boundary layer structure.

Moreover, the characteristics of the nanoparticles—such as their shape, size, volume percentage, and material composition—play a crucial role in determining the efficiency of heat transfer within the nanofluid. By optimizing these factors, the heat transfer process can be enhanced, ensuring better thermal performance. The convective heat transfer efficiency of nanofluids is not solely dependent on thermal conductivity but also on other thermophysical properties, including density, specific heat capacity, and dynamic viscosity. These properties collectively influence the overall heat transfer mechanism and fluid behavior. Furthermore, integrating multiple enhancement techniques—such as optimizing nanoparticle concentration and utilizing high-conductivity materials—can significantly improve the heat transfer rate. By strategically combining these approaches, a substantially higher heat transfer efficiency can be achieved, making nanofluids a promising solution for various thermal management applications.

The impact of the magnetic Prandtl number Prm on the induced magnetic field profiles is clearly depicted in Fig. 5. As Prm increases, the thickness of the induced magnetic boundary layer expands significantly. This phenomenon occurs because a higher magnetic Prandtl number corresponds to an increase in the nanofluid’s magnetic diffusivity. Magnetic diffusivity plays a crucial role in determining how the induced magnetic field interacts with the fluid flow, influencing the overall electromagnetic behavior of the system. When the magnetic diffusivity is high, the magnetic field can penetrate deeper into the fluid, leading to an extended boundary layer thickness.

Physically, the magnetic Prandtl number is defined as the ratio of kinematic viscosity to magnetic diffusivity, indicating the relative dominance of momentum diffusion compared to magnetic field diffusion within the nanofluid. A higher Prm suggests that magnetic diffusion occurs at an enhanced rate, allowing the induced magnetic field to spread more efficiently throughout the flow domain. This, in turn, results in stronger magnetohydrodynamic (MHD) effects, altering the velocity and temperature profiles within the boundary layer. Additionally, as the induced magnetic field grows with increasing Prm, it influences the Lorentz force acting on the fluid, further modifying the flow structure and increasing resistance to motion.

From a practical perspective, understanding and controlling the effects of the magnetic Prandtl number are essential for optimizing MHD-based applications, such as cooling systems, electromagnetic pumps, and energy conversion devices. By carefully adjusting the properties of the nanofluid—such as its electrical conductivity, viscosity, and magnetic permeability—it is possible to regulate the influence of Prm and enhance the efficiency of magnetically controlled fluid systems. Therefore, the manipulation of the magnetic Prandtl number presents a valuable opportunity for improving thermal and fluid flow management in various industrial and engineering applications.

Fig. 6 illustrates the influence of the Eckert number Ec on the temperature profile, revealing a notable increase in temperature and an expansion of the thermal boundary layer thickness as Ec rises. This effect occurs due to the enhancement of temperature dispersion within the boundary layer region. The primary reason for this behavior is frictional heating, which stems from viscous dissipation. As fluid particles experience shear forces and internal friction, mechanical energy is converted into thermal energy, leading to an accumulation of heat within the fluid. Consequently, higher Ec values result in a more pronounced increase in fluid temperature throughout the boundary layer.

Additionally, the presence of ohmic heating further contributes to this temperature rise. When an electrically conducting fluid interacts with a magnetic field, resistive heating occurs due to the induced electric currents. This phenomenon adds to the overall thermal energy within the fluid, thereby reducing the surface temperature gradient. A lower surface temperature gradient implies a reduced rate of heat transfer from the surface to the fluid, leading to a thicker thermal boundary layer. Overall, the combined effects of viscous dissipation and ohmic heating intensify the thermal characteristics of the fluid, reinforcing the direct correlation between Ec and temperature distribution. Understanding this relationship is crucial in applications where thermal energy management plays a key role, such as in MHD cooling systems, heat exchangers, and energy conversion processes.

The impact of different nanoparticles on the nanofluid’s velocity, induced magnetic field, and temperature distribution is illustrated in Fig. 7a–c. It is apparent that the type of nanoparticles significantly influences the behavior of nanofluids, resulting in variations in their velocity. Among the examined nanofluids, Al2O3-based nanofluids demonstrate a faster flow compared to those containing Cu, Ag, or TiO2 nanoparticles. This disparity in flow speed is primarily attributed to the density of the nanoparticles, which plays a critical role in determining the fluid’s motion. Nanoparticles with lower densities, such as Al2O3, contribute to a reduced viscosity and enhanced fluidity, enabling faster movement of the nanofluid.

In contrast, the silver–water nanofluid exhibits a relatively modest flow speed. This behavior can be explained by the higher density of silver compared to other nanoparticles like copper, aluminum oxide, and titanium dioxide. The increased density leads to a higher viscosity and greater resistance to motion, which slows down the flow of the silver-based nanofluid. These findings emphasize the importance of nanoparticle density in controlling the flow characteristics of nanofluids, which is crucial for applications requiring specific flow dynamics.

Fig. 7c provides a comprehensive overview of the influence of nanoparticles on the thermal field when water is used as the base fluid. The thermal conductivity of the nanoparticles plays a significant role in shaping the nanofluid’s temperature distribution. Nanofluids containing nanoparticles with higher thermal conductivity exhibit greater temperatures, as they are more effective in transferring and retaining thermal energy. For instance, the Ag–water nanofluid, due to the superior thermal conductivity of silver, demonstrates a stronger thermal field compared to nanofluids containing lower-thermal-conductivity nanoparticles like TiO2 or Al2O3. These observations highlight the dual impact of nanoparticle properties—density on velocity and thermal conductivity on temperature—on the overall performance of nanofluids in heat transfer and fluid flow applications.

Figs. 8 and 9 provide a comprehensive analysis of how the magnetic field parameter affects both the skin friction coefficient and the heat transfer rate for various nanoparticles. The graphical representations clearly demonstrate that an increase in the magnetic field parameter leads to a rise in the shear stress at the wall, which can be attributed to the influence of the Lorentz force. This force generates resistance in the fluid motion, thereby increasing the drag along the surface. Simultaneously, a reduction in the magnetic field parameter optimizes heat transfer by allowing enhanced thermal conduction and convection mechanisms. Among the different nanofluids examined, Ag–water nanofluids exhibit the highest drag force due to their superior electrical conductivity, which amplifies the Lorentz force effect. Additionally, Ag–water nanofluids also achieve the most significant enhancement in heat transfer efficiency compared to other nanofluids. This can be attributed to the exceptional thermal conductivity of silver nanoparticles, which facilitates more efficient thermal energy transport within the fluid. Consequently, the presence of silver nanoparticles in the base fluid results in a substantial improvement in heat dissipation performance, making Ag–water nanofluids highly effective for thermal management applications.

Figs. 10 and 11 illustrate the variation of the skin friction coefficient and the mean Nusselt number with increasing nanoparticle volume fractions for different nanofluids. The graphical trends indicate that both skin friction and heat transfer rates increase almost monotonically with a rise in nanoparticle concentration across all tested nanofluids. This behavior is primarily attributed to the enhanced viscosity and thermal conductivity resulting from the presence of nanoparticles. Among the nanofluids examined, those containing Ag nanoparticles exhibit the highest drag force. This is due to the significantly higher density of silver compared to other nanoparticles such as Cu, Al2O3, and TiO2. The increased density leads to greater resistance to flow, thereby elevating the skin friction coefficient.

In terms of heat transfer performance, Cu–based nanofluids demonstrate the highest enhancement, surpassing those containing Ag, Al2O3, and TiO2. This superior performance is attributed to the high thermal diffusivity of copper nanoparticles, which facilitates rapid heat dispersion and effectively reduces temperature gradients within the fluid. The improved thermal diffusion ensures more efficient energy transport, making Cu–based nanofluids particularly suitable for applications requiring enhanced heat dissipation.

Conversely, TiO2–based nanofluids exhibit the lowest heat transfer efficiency among the four nanoparticle types. This is because titanium dioxide has a relatively lower thermal conductivity compared to Ag, Cu, and Al2O3, leading to a dominance of conduction over convection as the primary heat transfer mechanism. The limited ability of TiO2 nanoparticles to enhance convective heat transfer results in lower Nusselt numbers, thereby reducing overall thermal performance. However, as the nanoparticle volume fraction increases, the influence of convection becomes more pronounced, leading to a greater disparity in the mean Nusselt number between different nanofluids. This trend highlights the critical role of nanoparticle selection and concentration in optimizing the thermal performance of nanofluids for various industrial and engineering applications.

As the Ec increases, the heat transfer rate, represented by the Nusselt number Nu, decreases for all nanoparticles. This indicates that higher Ec values, which correspond to greater viscous dissipation effects, reduce the efficiency of convective heat transfer. This phenomenon can be attributed to the fact that viscous dissipation generates additional heat within the fluid, counteracting the temperature gradient responsible for driving convective heat transfer. Among the studied nanoparticles in Fig. 12, the TiO2–water nanofluid exhibits the lowest cooling rate, as reflected by its comparatively lower Nusselt number. This suggests that the thermal conductivity of TiO2 nanoparticles, combined with their interaction with the base fluid (water), is less effective in enhancing heat transfer performance relative to other nanofluids. Consequently, the TiO2–water nanofluid is less suitable for applications requiring high cooling rates, particularly under conditions of significant viscous dissipation. This trend underscores the importance of carefully selecting nanofluids based on their thermal properties and compatibility with operational conditions, such as high Ec values, to optimize heat transfer performance.

5  Conclusions

External magnetic fields play a crucial role in controlling nanofluid flow, heat transfer, and thermal properties, with the applied field strength directly influencing thermal conductivity. Motivated by this, a numerical study investigated a water-based nanofluid with various nanoparticles in an unstable aligned MHD boundary layer over a moving surface, focusing on the induced magnetic field’s effects. Key parameters such as the velocity ratio ε, magnetic parameter M, nanoparticle volume fraction ϕ, Eckert number Ec, and magnetic Prandtl number Prm were analyzed in relation to momentum and thermal properties. The study assumed a homogeneous nanofluid model and demonstrated its reliability in capturing the thermal and hydrodynamic behavior of nanofluids. The present study stands out due to its unique combination of viscous dissipation effects, aligned MHD flow, comparative nanoparticle analysis, and the use of SRM for numerical computation. These aspects collectively enhance the understanding of nanofluid-based heat transfer mechanisms, making the work highly relevant for both academic research and industrial applications. Key findings include:

•   Increasing ε enhances velocity and magnetic field changes, while temperature variation follows an inverse trend.

•   Higher M reduces momentum boundary layer thickness but increases thermal boundary layer thickness.

•   Rising Ec accelerates temperature changes in nanofluids.

•   Ag nanofluids exhibit higher drag and a thicker momentum boundary layer, while Al2O3 has a thinner layer and a greater impact on temperature.

•   Ag–water nanofluids achieve the highest heat transfer rates, whereas TiO2–water nanofluids show the lowest cooling efficiency.

The study can be extended to time- or space-dependent magnetic fields, unsteady or turbulent MHD flows, and three-dimensional or non-Newtonian nanofluids for deeper insights into industrial, biomedical, and manufacturing applications. Additionally, future research can explore alternative base fluids (e.g., ethylene glycol, oil, or hybrid nanofluids) to enhance thermal performance. This study highlights the importance of selecting nanoparticles based on specific thermal and flow requirements to optimize performance in MHD-based heat transfer applications. It also demonstrates the diverse engineering and industrial applications of MHD nanofluids in advanced cooling systems, aerospace, automotive, biomedical, energy, and microfluidics. These nanofluids enhance heat dissipation in electronics and industrial heat exchangers, improve thermal protection in spacecraft and vehicles, and enable targeted cancer treatment and precision drug delivery. Additionally, they optimize nuclear reactor cooling, boost solar thermal efficiency, and facilitate lab-on-a-chip diagnostics and soft robotics. By optimizing nanofluid formulations based on specific operational needs, this research enhances their applicability across various high-tech industries.

Acknowledgement: The authors sincerely appreciate the reviewers for their valuable and constructive feedback, which has played a crucial role in improving the quality of this article and aligning it with the journal’s standards.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, methodology, software, validation, formal analysis, writing—original draft preparation: Shahina Akter; writing—review and editing: Mohammad Ferdows; supervision: Muhammad Amer Qureshi and Mohammad Ferdows. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included within this article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Rashidi MM, Mahariq I, Alhuyi NM, Accouche O, Bhatti MM. Comprehensive review on exergy analysis of shell and tube heat exchangers. J Therm Anal Calorim. 2022;147(22):12301–11. doi:10.1007/s10973-022-11478-2. [Google Scholar] [CrossRef]

2. Sayantan M, Shikha E, Chandra MP, Naser A, Paritosh C. A review on pool and flow boiling enhancement using nanofluids: nuclear reactor application. Processes. 2022;10(1):177. [Google Scholar]

3. Qayyum M, Afzal S, Saeed ST, Akgül A, Riaz MB. Unsteady hybrid nanofluid (Cu-UO2/blood) with chemical reaction and non-linear thermal radiation through convective boundaries: an application to bio-medicine. Heliyon. 2023;9(6):e16578. doi:10.1016/j.heliyon.2023.e16578. [Google Scholar] [PubMed] [CrossRef]

4. Basu A, Saha A, Banerjee S, Roy PC, Kundu B. A review of artificial intelligence methods in predicting thermophysical properties of nanofluids for heat transfer applications. Energies. 2024;17(6):1351. doi:10.3390/en17061351. [Google Scholar] [CrossRef]

5. Bani-Fwaz MZ, Mahmood Z, Bilal M, Ei-Zahhar AA, Khan I, Niazai S. Computational investigation of thermal process in radiated nanofluid modulation influenced by nanoparticles (Al2O3) and molecular (H2O) diameters. J Comput Des Eng. 2024;11(2):22–36. doi:10.1093/jcde/qwae011. [Google Scholar] [CrossRef]

6. Khan SA, Hayat T, Alsaedi A, Alhodaly MS. Thermal analysis for radiative flow of Darcy-Forchheimer nanomaterials subject to entropy generation. J Comput Des Eng. 2022;9(5):1756–64. doi:10.1093/jcde/qwac080. [Google Scholar] [CrossRef]

7. Khan SA, Razaq A, Alsaedi A, Hayat T. Modified thermal and solutal fluxes through convective flow of Reiner-Rivlin material. Energy. 2023;283:128516. doi:10.1016/j.energy.2023.128516. [Google Scholar] [CrossRef]

8. Nadeem S, Ishtiaq B, Akkurt N, Eldin SM. Swirling flow analysis of Eyring-Powell fluid between coaxial disks with variable property. J Comput Des Eng. 2023;10(2):632–40. doi:10.1093/jcde/qwad015. [Google Scholar] [CrossRef]

9. Khan ZH, Makinde OD, Usman M, Ahmad R, Khan WA, Huang Z. Inherent irreversibility in unsteady magnetohydrodynamic nanofluid flow past a slippery permeable vertical plate with fractional-order derivative. J Comput Des Eng. 2023;10(5):2049–64. doi:10.1093/jcde/qwad090. [Google Scholar] [CrossRef]

10. Wang F, Sajid T, Katbar NM, Jamshed W, Eid MR, Abd-Elmonem A, et al. Computational examination of non-Darcian flow of radiative ternary hybridity Casson nanoliquid through moving rotary cone. J Comput Des Eng. 2023;10(4):1657–76. doi:10.1093/jcde/qwad057. [Google Scholar] [CrossRef]

11. Sus C. Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows. Am Soc Mech Eng. 1995;231:99–I05. [Google Scholar]

12. Oztop HF, Abu-Nada E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int J Heat Fluid Flow. 2008;29(5):1326–36. doi:10.1016/j.ijheatfluidflow.2008.04.009. [Google Scholar] [CrossRef]

13. Eastman JA, Choi SUS, Li S, Yu W, Thompson LJ. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl Phys Lett. 2001;78(6):718–20. doi:10.1063/1.1341218. [Google Scholar] [CrossRef]

14. Mintsa HA, Roy G, Nguyen CT, Doucet D. New temperature dependent thermal conductivity data for water-based nanofluids. Int J Therm Sci. 2009;48(2):363–71. doi:10.1016/j.ijthermalsci.2008.03.009. [Google Scholar] [CrossRef]

15. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Transf. 2010;53(11–12):2477–83. doi:10.1016/j.ijheatmasstransfer.2010.01.032. [Google Scholar] [CrossRef]

16. Kakaç S, Pramuanjaroenkij A. Review of convective heat transfer enhancement with nanofluids. Int J Heat Mass Transf. 2009;52(13–14):3187–96. doi:10.1016/j.ijheatmasstransfer.2009.02.006. [Google Scholar] [CrossRef]

17. Mohamed M, Md Noar N, Salleh MZ, Ishak A. Boundary layer flow over a moving plate in a nanofluid with viscous dissipation. In: The 3rd International Conference on Computer Engineering and Mathematical Sciences (ICCEMS); 2014 Dec 4–5; Langkawi, Malaysia. [Google Scholar]

18. Mousavi SM, Dinarvand S, Yazdi ME. Generalized second-order slip for unsteady convective flow of a nanofluid: a utilization of Buongiorno’s two-component nonhomogeneous equilibrium model. Nonlinear Eng. 2020;9(1):156–68. doi:10.1515/nleng-2020-0005. [Google Scholar] [CrossRef]

19. Abd Elazem NY. Numerical results for influence the flow of MHD nanofluids on heat and mass transfer past a stretched surface. Nonlinear Eng. 2021;10(1):28–38. doi:10.1515/nleng-2021-0003. [Google Scholar] [CrossRef]

20. Ferdows M, Shamshuddin M, Salawu SO, Zaimi K. Numerical simulation for the steady nanofluid boundary layer flow over a moving plate with suction and heat generation. SN Appl Sci. 2021;3(2):264. doi:10.1007/s42452-021-04224-0. [Google Scholar] [CrossRef]

21. Said Z, Sundar LS, Tiwari AK, Ali HM, Sheikholeslami M, Bellos E, et al. Recent advances on the fundamental physical phenomena behind stability, dynamic motion, thermophysical properties, heat transport, applications, and challenges of nanofluids. Phys Rep. 2022;946(2):1–94. doi:10.1016/j.physrep.2021.07.002. [Google Scholar] [CrossRef]

22. Turkyilmazoglu M. Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids. Chem Eng Sci. 2012;84:182–7. doi:10.1016/j.ces.2012.08.029. [Google Scholar] [CrossRef]

23. Mahanthesh B, Gireesha BJ, Athira PR. Radiated flow of chemically reacting nanoliquid with an induced magnetic field across a permeable vertical plate. Results Phys. 2017;7(4):2375–83. doi:10.1016/j.rinp.2017.07.010. [Google Scholar] [CrossRef]

24. Ilias MR, Rawi NA, Zaki NHM, Shafie S. Aligned MHD magnetic nanofluid flow past a static wedge. Int J Eng Technol. 2018;7:28. doi:10.14419/ijet.v7i3.28.20960. [Google Scholar] [CrossRef]

25. Kumar D. Radiation effect on magnetohydrodynamic flow with induced magnetic field and Newtonian heating/cooling: an analytic approach. Propuls Power Res. 2021;10(3):303–13. doi:10.1016/j.jppr.2021.07.001. [Google Scholar] [CrossRef]

26. Sehra, Haq SU, Shah SI, Nisar KS, Jan SU, Khan I. Convection heat mass transfer and MHD flow over a vertical plate with chemical reaction, arbitrary shear stress and exponential heating. Sci Rep. 2021;11(1):4265. doi:10.1038/s41598-021-81615-8. [Google Scholar] [PubMed] [CrossRef]

27. Al Salman HJ, Nawaz Y, Al Ghafli AA. An implicit finite difference scheme and neural network approach for non-Newtonian nanofluid flow using induced magnetic field. Mathematics. 2023;11(9):2089. doi:10.3390/math11092089. [Google Scholar] [CrossRef]

28. Diwate M, Tawade JV, Janthe PG, Garayev M, El-Meligy M, Kulkarni N, et al. Numerical solutions for unsteady laminar boundary layer flow and heat transfer over a horizontal sheet with radiation and nonuniform heat source/sink. J Radiat Res Appl Sci. 2024;17(4):101196. doi:10.1016/j.jrras.2024.101196. [Google Scholar] [CrossRef]

29. Nasir S, Berrouk AS. Comparative study of computational frameworks for magnetite and carbon nanotube-based nanofluids in enclosure. J Therm Anal Calorim. 2024;149(5):2403–23. doi:10.1007/s10973-023-12811-z. [Google Scholar] [CrossRef]

30. Nasir S, Berrouk AS, Gul T, Zari I. Chemically radioactive unsteady nonlinear convective couple stress Casson hybrid nanofluid flow over a gyrating sphere. J Therm Anal Calorim. 2023;148(22):12583–95. doi:10.1007/s10973-023-12608-0. [Google Scholar] [CrossRef]

31. Nasir S, Berrouk AS, Aamir A. Efficiency analysis of solar radiation on chemical radioactive nanofluid flow over a porous surface with magnetic field. Case Stud Therm Eng. 2024;63(11):105231. doi:10.1016/j.csite.2024.105231. [Google Scholar] [CrossRef]

32. Sulochana G, Prasad CV, Bhatti SK, Venu Madhav VV, Saxena KK, Khan MI, et al. Impact of multi-walled carbon nanotubes (MWCNTs) on hybrid biodiesel blends for cleaner combustion in CI engines. Energy. 2024;303(28):131911. doi:10.1016/j.energy.2024.131911. [Google Scholar] [CrossRef]

33. Teja DH, Muvvala P, Nittala NAP, Bandhu D, Khan MI, Saxena KK, et al. Comparative performance analysis of recuperative helium and supercritical CO2 Brayton cycles for high-temperature energy systems. Energy. 2024;31:133469. doi:10.1016/j.energy.2024.133469. [Google Scholar] [CrossRef]

34. Hamid A, Chu YM, Khan MI, Kumar RN, Gowd RJP, Prasannakumara BC. Critical values in axisymmetric flow of magneto-cross nanomaterial towards a radially shrinking disk. Int J Mod Phys B. 2021;35(7):2150105. doi:10.1142/S0217979221501058. [Google Scholar] [CrossRef]

35. Awais M, Salahuddin T. Natural convection with variable fluid properties of couple stress fluid with Cattaneo-Christov model and enthalpy process. Heliyon. 2023;9(8):e18546. doi:10.1016/j.heliyon.2023.e18546. [Google Scholar] [PubMed] [CrossRef]

36. Awais M, Salahuddin T. Variable thermophysical properties of magnetohydrodynamic cross fluid model with effect of energy dissipation and chemical reaction. Int J Mod Phys B. 2024;38(16):2450197. doi:10.1142/S0217979224501972. [Google Scholar] [CrossRef]

37. Awais M, Salahuddin T, Muhammad S. Evaluating the thermo-physical characteristics of non-Newtonian Casson fluid with enthalpy change. Therm Sci Eng Prog. 2023;42(4):101948. doi:10.1016/j.tsep.2023.101948. [Google Scholar] [CrossRef]

38. Awais M, Salahuddin T, Muhammad S. Effects of viscous dissipation and activation energy for the MHD Eyring-Powell fluid flow with Darcy-Forchheimer and variable fluid properties. Ain Shams Eng J. 2024;15(2):102422. doi:10.1016/j.asej.2023.102422. [Google Scholar] [CrossRef]

39. Eckert ERG, Drake RM. Analysis of heat and mass transfer. New York, NY, USA: McGraw-Hill; 1972. 832 p. doi:10.1002/aic.690180342. [Google Scholar] [CrossRef]

40. Oosthuizen PH, Naylor D. An introduction to convective heat transfer analysis. New York, NY, USA: WCB/McGraw Hill; 1999. [Google Scholar]

41. Reddy GJ, Raju RS, Rao JA. Influence of viscous dissipation on unsteady MHD natural convective flow of Casson fluid over an oscillating vertical plate via FEM. Ain Shams Eng J. 2018;9(4):1907–15. doi:10.1016/j.asej.2016.10.012. [Google Scholar] [CrossRef]

42. Jafar AB, Shafie S, Ullah I. Magnetohydrodynamic boundary layer flow of a viscoelastic fluid past a nonlinear stretching sheet in the presence of viscous dissipation effect. Coatings. 2019;9(8):490. doi:10.3390/coatings9080490. [Google Scholar] [CrossRef]

43. Ajibade AO, Umar AM. Effects of viscous dissipation and boundary wall thickness on steady natural convection Couette flow with variable viscosity and thermal conductivity. Int J Thermofluids. 2020;7:100052. doi:10.1016/j.ijft.2020.100052. [Google Scholar] [CrossRef]

44. Mishra A, Kumar M. Velocity and thermal slip effects on MHD nanofluid flow past a stretching cylinder with viscous dissipation and Joule heating. SN Appl Sci. 2020;2(8):1350. doi:10.1007/s42452-020-3156-7. [Google Scholar] [CrossRef]

45. Gangadhar K, Vijayakumar D, Thangavelu K. Nonlinear radiation on Maxwell fluid in a convective heat transfer with viscous dissipation and activation energy. Heat Transf. 2021;50(7):7363–79. doi:10.1002/htj.22233. [Google Scholar] [CrossRef]

46. Mahesh R, Mahabaleshwar US, Kumar PNV, Öztop HF, Abu-Hamdeh N. Impact of radiation on the MHD couple stress hybrid nanofluid flow over a porous sheet with viscous dissipation. Results Eng. 2023;17(3):100905. doi:10.1016/j.rineng.2023.100905. [Google Scholar] [CrossRef]

47. Bao HX, Arain M, Shaheen S, Khan H, Usman U, Inc M, et al. Boundary-layer flow of heat and mass for Tiwari-Das nanofluid model over a flat plate with variable wall temperature. Therm Sci. 2022;26(Spec. issue 1):39–47. doi:10.2298/tsci22s1039b. [Google Scholar] [CrossRef]

48. Ajeeb W, Silva RRST, Sohel SMM. Experimental investigation of heat transfer performance of Al2O3 nanofluids in a compact plate heat exchanger. Appl Therm Eng. 2023;218:119321. doi:10.1016/j.applthermaleng.2022.119321. [Google Scholar] [CrossRef]

49. Mohana CM, Rushi Kumar B. Nanoparticle shape effects on MHD Cu-water nanofluid flow over a stretching sheet with thermal radiation and heat source/sink. Int J Mod Phys B. 2024;38(10):2450151. doi:10.1142/s0217979224501510. [Google Scholar] [CrossRef]

50. Behera S, Pattnaik PK, Mishra SR, Dash AK. Variation of nanoparticle shapes using the Hamilton-Crosser conductivity model for the gold-water nanofluid through a channel. Mod Phys Lett B. 2023;37(24):2350082. doi:10.1142/s0217984923500823. [Google Scholar] [CrossRef]

51. Wang F, Saeed AM, Puneeth V, Shah NA, Anwar MS, Geudri K, et al. Heat and mass transfer of Ag-H2O nano-thin film flowing over a porous medium: a modified Buongiorno’s model. Chin J Phys. 2023;84:330–42. doi:10.1016/j.cjph.2023.01.001. [Google Scholar] [CrossRef]

52. Hyder A, Lim YJ, Khan I, Shafie S. Unveiling the performance of Cu-water nanofluid flow with melting heat transfer, MHD, and thermal radiation over a stretching/shrinking sheet. ACS Omega. 2023;8(32):29424–36. doi:10.1021/acsomega.3c02949. [Google Scholar] [PubMed] [CrossRef]

53. Hosseinzadeh K, Mardani MR, Paikar M, Hasibi A, Tavangar T, Nimafar M, et al. Investigation of second grade viscoelastic non-Newtonian nanofluid flow on the curve stretching surface in presence of MHD. Results Eng. 2023;17:100838. doi:10.1016/j.rineng.2022.100838. [Google Scholar] [CrossRef]

54. Ali M, Pasha AA, Nawaz R, Khan WA, Irshad K, Algarni S, et al. Innovation modeling and simulation of thermal convective on cross nanofluid flow over exponentially stretchable surface. Heliyon. 2023;9(8):e18672. doi:10.1016/j.heliyon.2023.e18672. [Google Scholar] [PubMed] [CrossRef]

55. Rafique K, Mahmood Z, Adnan Khan U, Muhammad T, El-Rahman MA, Bajri SA. Numerical investigation of entropy generation of Joule heating in non-axisymmetric flow of hybrid nanofluid towards stretching surface. J Comput Des Eng. 2024;11(2):146–60. doi:10.1093/jcde/qwae029. [Google Scholar] [CrossRef]

56. Khan M, Anwar MS, Imran M, Rasheed A. Nanofluid heat transfer in irregular 3D surfaces under magnetohydrodynamics and multi-slip effects. Front Heat Mass Transf. 2024;22(5):1399–419. doi:10.32604/fhmt.2024.056597. [Google Scholar] [CrossRef]

57. Kanti PK, Paramasivam P, Wanatasanappan VV, Dhanasekaran S, Sharma P. Experimental and explainable machine learning approach on thermal conductivity and viscosity of water based graphene oxide based mono and hybrid nanofluids. Sci Rep. 2024;14(1):30967. doi:10.1038/s41598-024-81955-1. [Google Scholar] [PubMed] [CrossRef]

58. Kanti PK, Wanatasanappan VV, Said NM, Sharma KV. Stability, thermophysical properties, forced convective heat transfer, entropy minimization and exergy performance of a novel hybrid nanofluid: experimental study. J Mol Liq. 2024;410:125571. doi:10.1016/j.molliq.2024.125571. [Google Scholar] [CrossRef]

59. Selvarajoo K, Wanatasanappan VV, Luon NY. Experimental measurement of thermal conductivity and viscosity of Al2O3-GO (80:20) hybrid and mono nanofluids: a new correlation. Diam Relat Mater. 2024;144:111018. doi:10.1016/j.diamond.2024.111018. [Google Scholar] [CrossRef]

60. Kanti PK, Wanatasanappan VV, Sharma P, Said NM, Sharma KV. Experimental and machine learning insights on heat transfer and friction factor analysis of novel hybrid nanofluids subjected to constant heat flux at various mixture ratios. Int J Therm Sci. 2025;209:109548. doi:10.1016/j.ijthermalsci.2024.109548. [Google Scholar] [CrossRef]

61. Tiwari RK, Das MK. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Transf. 2007;50(9–10):2002–18. doi:10.1016/j.ijheatmasstransfer.2006.09.034. [Google Scholar] [CrossRef]

62. Motsa S, Makukula Z. On spectral relaxation method approach for steady von Kármán flow of a Reiner-Rivlin fluid with Joule heating, viscous dissipation and suction/injection. Open Phys. 2013;11(3):363–74. doi:10.2478/s11534-013-0182-8. [Google Scholar] [CrossRef]

63. Shateyi S, Marewo GT. A new numerical approach for the laminar boundary layer flow and heat transfer along a stretching cylinder embedded in a porous medium with variable thermal conductivity. J Appl Math. 2013;2013(4):576453. doi:10.1155/2013/576453. [Google Scholar] [CrossRef]

64. Motsa SS. A new spectral relaxation method for similarity variable nonlinear boundary layer flow systems. Chem Eng Commun. 2014;201(2):241–56. doi:10.1080/00986445.2013.766882. [Google Scholar] [CrossRef]

65. Tan CW, Wang CCT. Heat transfer in aligned-field magnetohydrodynamic flow past a flat plate. Int J Heat Mass Transf. 1968;11(2):319–29. doi:10.1016/0017-9310(68)90160-9. [Google Scholar] [CrossRef]

66. Mosayebidorcheh S, Hatami M. Analytical investigation of peristaltic nanofluid flow and heat transfer in an asymmetric wavy wall channel (Part I: straight channel). Int J Heat Mass Transf. 2018;126(3):790–9. doi:10.1016/j.ijheatmasstransfer.2018.05.080. [Google Scholar] [CrossRef]

67. Fakhar MH, Fakhar A, Tabatabaei H. Mathematical modeling of pipes reinforced by agglomerated CNTs conveying turbulent nanofluid and application of semi-analytical method for studying the instable Nusselt number and fluid velocity. J Comput Appl Math. 2020;378(1):112945. doi:10.1016/j.cam.2020.112945. [Google Scholar] [CrossRef]

68. Ghasemi SE, Mohsenian S, Gouran S, Zolfagharian A. A novel spectral relaxation approach for nanofluid flow past a stretching surface in presence of magnetic field and nonlinear radiation. Results Phys. 2022;32(4):105141. doi:10.1016/j.rinp.2021.105141. [Google Scholar] [CrossRef]

69. Rasool G, Shah SZH, Sajid T, Jamshed W, Altamirano GC, Keswani B, et al. Spectral relaxation methodology for chemical and bioconvection processes for cross nanofluid flowing around an oblique cylinder with a slanted magnetic field effect. Coatings. 2022;12(10):1560. doi:10.3390/coatings12101560. [Google Scholar] [CrossRef]

70. Hussaini MY, Zang TA. Spectral methods in fluid dynamics. Preston, UK: ICASE; 1986. [Google Scholar]

71. Don WS, Solomonoff A. Accuracy and speed in computing the Chebyshev collocation derivative. SIAM J Sci Comput. 1995;16(6):1253–68. doi:10.1137/0916073. [Google Scholar] [CrossRef]

72. Trefethen LN. Spectral methods in MATLAB. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics; 2000. [Google Scholar]

73. Weideman JA, Reddy SC. A MATLAB differentiation matrix suite. ACM Trans Math Softw. 2000;26(4):465–519. doi:10.1145/365723.365727. [Google Scholar] [CrossRef]

74. Boyd JP. Chebyshev and Fourier spectral methods. North Chelmsford, MA, USA: Courier Corporation; 2001. [Google Scholar]