Optimum Machine Learning on Gas Extraction and Production for Adaptive Negative Control

1  Introduction

The introduction of the “dual carbon” goal has imposed more stringent requirements on the sustainable development of China’s energy sector. As a predominant energy source, coal necessitates stringent carbon reduction measures and emission controls [1]. As a major contributor to carbon emissions in coal mining, enhancing the efficiency and concentration of gas extraction not only mitigates greenhouse gas emissions but also bolsters clean energy supply, thereby facilitating gas-related carbon reduction [2]. The extraction of coal seam gas relies on negative pressure to induce desorption and facilitate gas migration [3]. Throughout this process, borehole extraction pressure plays a crucial role in governing gas seepage dynamics and desorption efficiency while simultaneously affecting borehole leakage behavior [4,5]. Insufficient negative pressure diminishes gas extraction flow, thereby compromising efficiency, whereas excessive negative pressure exacerbates borehole leakage, leading to a decline in extraction concentration. Thus, optimizing borehole negative pressure regulation is paramount for enhancing coal seam gas extraction efficiency [6]. Accordingly, considering the gas occurrence conditions in coal seams, a comprehensive analysis of gas extraction data characteristics is performed to construct a gas extraction prediction model and an adaptive borehole negative pressure regulation framework. By precisely forecasting gas extraction flow and pressure, the proposed system facilitates adaptive negative pressure regulation, thereby significantly improving gas extraction efficiency.

Numerous scholars have undertaken extensive investigations into gas extraction theories and technologies. Xia et al. examined multiple factors influencing gas extraction and formulated a multi-field coupling model incorporating gas migration, airflow dynamics, and coal deformation mechanisms [7]. Zheng et al. investigated the stress distribution around boreholes and the characteristics of leakage zones, establishing a multi-field coupling model for gas flow [8]. Liu et al. performed a comprehensive analysis of the multiphysics coupling process involved in gas extraction [9]. Cheng et al. developed a gas-solid coupling model of gas migration to study the influence of negative pressure during gas extraction [10]. Pan examined the effects of different extraction pressures on extraction flow rate and concentration [11]. Wang et al. used numerical simulation to model the gas extraction process in coal seam boreholes and investigated the impact of negative pressure variation on borehole permeability [12]. Many scholars have also applied deep neural networks and graph theory to predict and optimize gas extraction parameters based on theoretical research, providing guidance for improving borehole gas concentration and enhancing gas utilization efficiency. Ma et al. utilized a simple recurrent neural network (RNN) to predict gas extraction volumes [13]. Gou and Sun applied the analytic hierarchy process and support vector machines to study gas extraction systems and construct mathematical models [14,15]. Hao et al. used deep neural network models to predict the effective radius of boreholes, providing a scientific basis for optimal borehole layout [16]. Wang integrated the grasshopper optimization algorithm to propose a multi-parameter gas concentration prediction model using long short-term memory (LSTM) networks [17]. Wang investigated the correlation between negative pressure and extraction concentration, proposing an approach to enhance borehole gas extraction concentration by adjusting valve openings [18]. Zhou, Wang, and others systematically optimized pipeline resistance in gas extraction systems using graph theory and multi-objective optimization methods [19–21].

These prior research findings have significantly enhanced gas extraction efficiency in mining operations, particularly during the initial borehole extraction phase, thereby playing a pivotal role in predicting gas extraction concentration and optimizing system performance. However, in continuously extracting gas boreholes, fluctuations in extraction duration and regional geological conditions within the pipeline network result in substantial variations in gas concentrations among boreholes. Many high-gas and gas-outburst mines, after multiple rounds of gas extraction measures, find it difficult to meet the safety and efficiency requirements for mine gas extraction due to reduced borehole extraction purity and concentration. Therefore, it is urgent to propose a method that can predict and enhance gas extraction purity to improve the efficiency of the extraction system. To address this challenge, this study—guided by field data—constructed a gas extraction purity prediction model and, leveraging these predictions, established an adaptive negative pressure control model. This research provides technical support for timely understanding the variation patterns of borehole gas extraction purity and enhancing gas extraction efficiency.

2  Construction of Gas Extraction Pure Volume Prediction Model

Gas extraction parameters exemplify a complex system of multidimensional nonlinear variables. Considering both gas extraction engineering practices and the key determinants of gas occurrence, the primary factors influencing gas extraction purity—within the constraints of current daily monitoring technologies—include extraction negative pressure, extraction concentration, extraction location, and extraction temperature. Accordingly, a multidimensional dataset is constructed based on these determinants. Given the significant interdependencies among parameters, each data dimension encapsulates its intrinsic characteristics while also manifesting interdimensional dependency relationships. For instance, extraction negative pressure directly influences gas concentration, thereby introducing pronounced nonlinear characteristics within the dataset. Moreover, gas extraction efficiency is governed by factors including regional structural distribution, roof and floor lithology, and permeability enhancement strategies, resulting in spatial variations in extraction data correlation characteristics. This study incorporates extraction location characteristic values and employs data dimensionality expansion techniques to encapsulate these variations, thereby enhancing the dataset’s dimensional complexity. Consequently, given the high-dimensional nonlinear nature of gas extraction purity prediction data and the prevalence of anomalies, this study leverages two robust machine learning models-Random Forest (RF) and Support Vector Regression (SVR)-renowned for their efficacy in capturing nonlinear dependencies and processing high-dimensional datasets. Both models effectively capture intrinsic dependencies within multidimensional data and demonstrate strong resilience to missing and anomalous values, rendering them particularly suitable for gas extraction data modeling and analysis.

2.1 Support Vector Regression Prediction Model

Owing to the intricate nature of underground extraction conditions, gas extraction purity is governed by a multitude of interdependent factors. Furthermore, state parameters—such as extraction negative pressure and concentration—are intrinsically interdependent, exerting mutual influence and demonstrating pronounced coupling characteristics alongside nonlinear dynamics. The fundamental principle of Support Vector Regression (SVR) lies in maintaining a predefined tolerance for error while identifying an optimal hyperplane within a high-dimensional space, thereby minimizing the margin between the hyperplane and the support vectors. By mapping input data into a high-dimensional feature space and identifying an optimal linear function, SVR effectively resolves nonlinear complexities present in the original space, thereby enhancing model formulation and predictive accuracy. A schematic representation of its underlying principle is provided in Fig. 1.

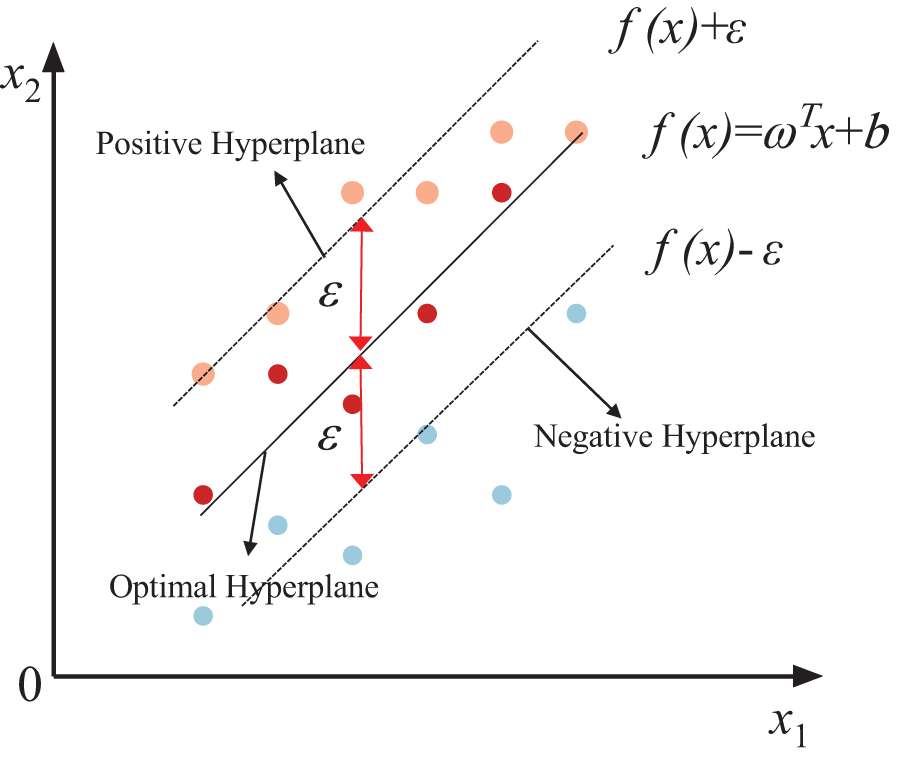
Figure 1: Schematic diagram of the support vector regression (SVR) principle

The hyperplane is mathematically expressed as f(x)=ωTx+b, where ω=(ω1,ω2,ω3,…,ωn) denotes the normal vector, representing the weights of features after mapping to the high-dimensional space. Each component of the normal vector corresponds to a specific feature weight, quantifying its contribution to the predicted value and governing the relative importance of input features within the regression model. The bias term b adjusts the positioning of the regression function, enabling the model to fit the data more accurately by preventing it from being constrained to pass through the origin, thereby accounting for overall data shifts. The primary objective of SVR is to minimize the deviation between the predicted value f(x) and the actual observation y. By introducing the concept of error tolerance ε, this objective can be expressed using Eq. (1).

minω,b12‖ω‖2+C∑i=1mlε(f(xi),yi)(1)

In the equation, ‖ω‖2 represents the regularization term, which controls the complexity of the model; C denotes the penalty coefficient, balancing the trade-off between model complexity and prediction error; and lε is the ε-insensitive loss function of ε, formally defined in Eq. (2).

lε(z)={0,if|z|≤ε|z|−ε,if|z|>ε(2)

In the equation: z=y−f(x), representing the prediction error, is considered zero when the prediction error is less than or equal to the width of the insensitive zone ε. This means that within this range, the prediction error of the model will not be penalized. The loss is only calculated when the prediction error exceeds ε, and the loss value equals the portion exceeding ε, denoted as |y−f(x)|−ε. This allows SVR to ignore errors within a certain range, reducing model complexity while significantly enhancing its robustness to noise.

In the engineering practice of gas drainage, pipeline blockages and leaks frequently occur, leading to noise and outliers in the monitored data. Since SVR attempts to form a predictive model using a function, including all outliers caused by these drainage failures would make the model overly complex and reduce prediction accuracy. To eliminate the influence of drainage failure parameters and enhance model robustness, we first penalize some outlier data points that exceed the insensitive zone to improve model flexibility. This process is achieved by introducing slack variables ξi and ξ^i, where ξi represents the portion where the predicted value is higher than the actual value and exceeds ε, while ξ^i represents the portion where the predicted value is lower than the actual value and exceeds ε.

In summary, Eqs. (1) and (2) can be combined, and slack variables introduced to establish a constrained optimization mathematical model, as shown in Eq. (3). Additionally, the hyperparameters of the SVR model significantly affect its robustness and prediction accuracy. Therefore, this study adopts an ensemble model approach, optimizing its hyperparameters using a genetic algorithm to obtain the most suitable model parameters for gas drainage data.

{minω,b,ξiξ^i12‖ω‖2+C∑i=1m(ξi,ξ^i)f(xi)−yi≤ε+ξiyi−f(xi)≤ε+ξ^iξ≥0i,ξ^i≥0,i=1,2,…,m(3)

The above modeling process is conducted after mapping the input data into a high-dimensional space, where the model is directly built on the vectors of the input parameters in that space. The process of transforming data into a high-dimensional space through nonlinear mapping is achieved using a kernel function. The radial basis function (RBF) kernel is the most commonly chosen option due to its ability to effectively balance model complexity and generalization capability, the support vector regression (SVR) model directly applies the radial basis function (RBF) kernel in its computations. This study also adopts the RBF kernel as the kernel function, as shown in Eq. (4).

K(xi,xj)=exp⁡(−‖xi−xj‖22σ2)(4)

In the equation, xi and yi represent data points in the input space; ‖xi−yi‖ denotes the Euclidean distance between the two data points; and σ is the bandwidth of the kernel function, which controls its range of influence.

2.2 Random Forest Prediction Model

The random forest prediction model constructs multiple decision trees and combines their prediction results using feature random selection and sample resampling techniques, effectively handling high-dimensional gas extraction data, noise, and missing values, thereby predicting gas extraction volume. During prediction, Bootstrap sampling is first performed on the training set, where multiple subsample sets are randomly drawn with replacement from the training data. Each subsample set has the same size as the original training set but contains duplicate data points. A decision tree is trained for each subsample set. At each node split, a subset of all features is randomly selected, and the best feature from this subset is chosen for splitting, minimizing the mean squared error (MSE) between the resulting child nodes. By repeating the above steps, multiple decision trees are generated, each trained on different Bootstrap samples and randomly selected feature subsets. Each decision tree makes independent predictions on new data, and the final prediction value is obtained by averaging the results from all decision trees. The algorithm framework is shown in Fig. 2.

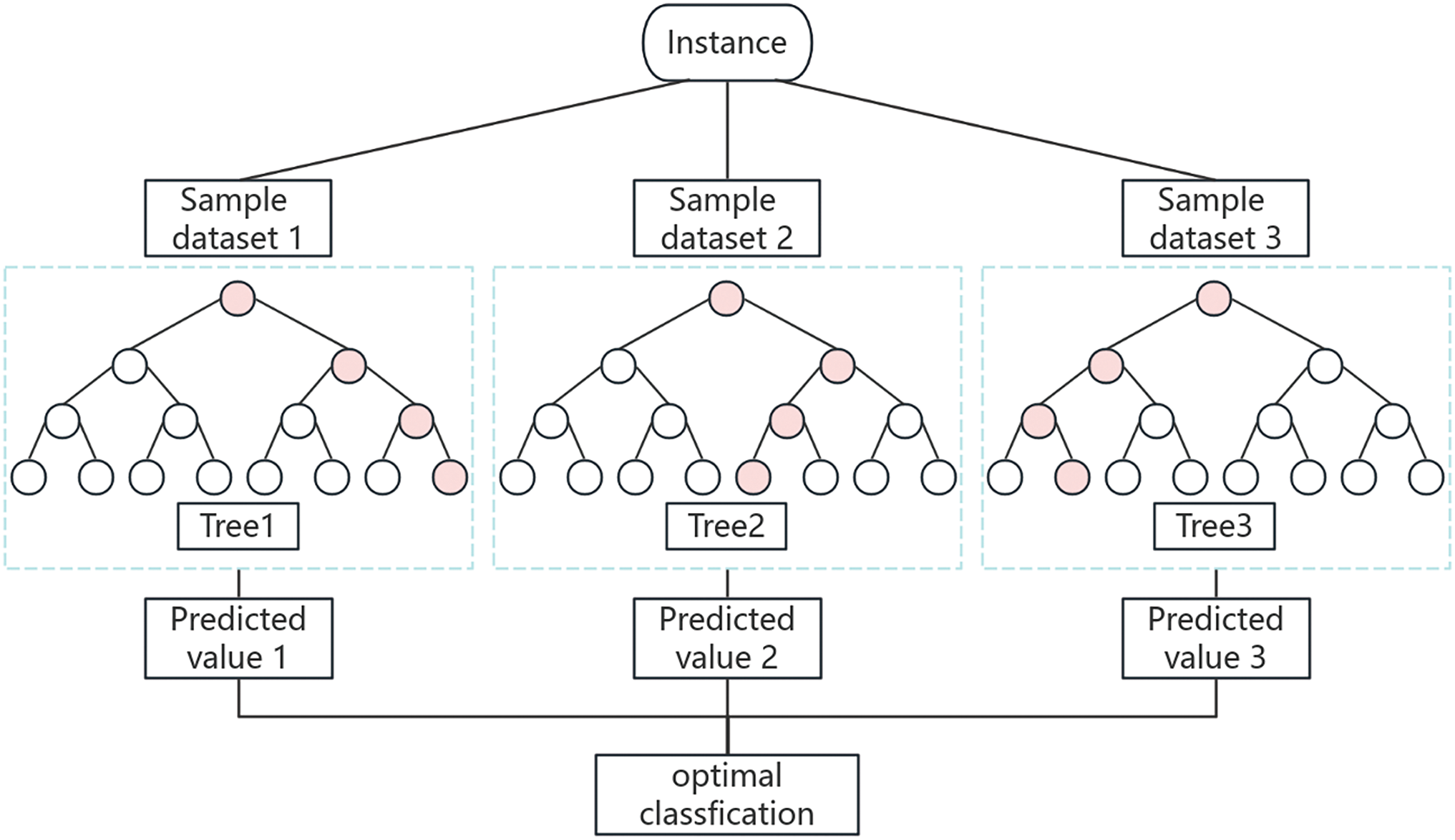
Figure 2: Flowchart of the Random Forest algorithm

2.3 Model Parameter Optimization Based on Genetic Algorithm

Given that genetic algorithms (GA) have strong global search capabilities, high parameter adaptability, robustness, and reliable principles, they are suitable for optimizing the hyperparameters of SVR and RF. This study applies GA to optimize the parameters of SVR and RF prediction models and compares the gas extraction volume prediction performance before and after hyperparameter optimization. The GA-based hyperparameter optimization process begins with the random generation of an initial population, where each hyperparameter combination represents an individual. The performance of each individual in the training set is evaluated based on its mean squared error, with the training-to-testing set ratio set at 1:3. Individuals with higher fitness are further selected as parents for breeding the next generation to preserve favorable genes. In the crossover operation, certain characteristics of parent individuals are randomly combined to form new offspring individuals, introducing new solution space exploration. The mutation operation further increases population diversity by randomly altering the hyperparameter values of individuals to avoid local optima. As generations iterate, individuals with lower fitness in the population are replaced, gradually optimizing toward the best hyperparameter combination. In this study, the genetic algorithm’s hyperparameter optimization process is set to iterate 90 times, with a population size of 8. The genetic algorithm-based optimization process is illustrated in Fig. 3.

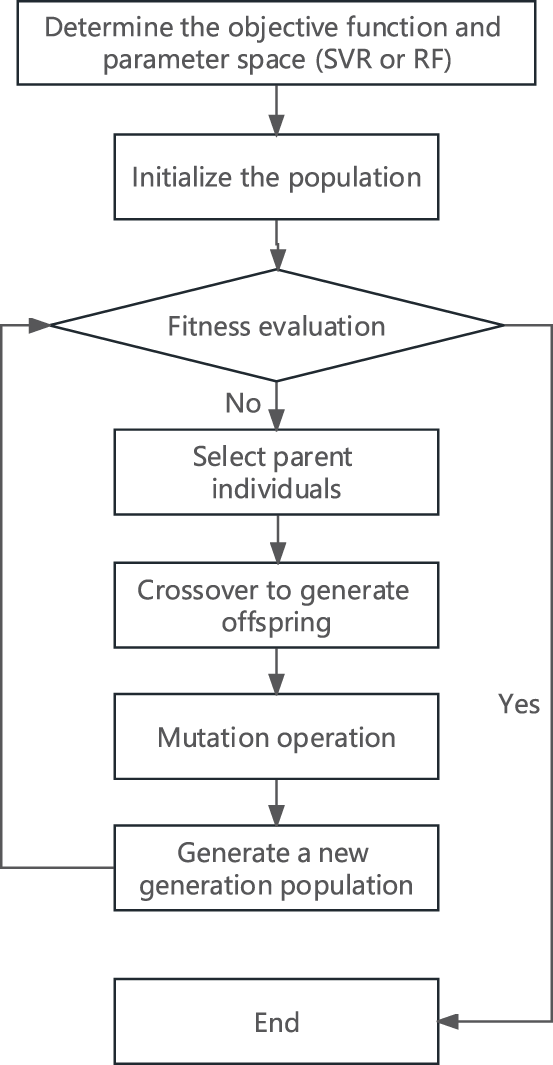
Figure 3: Genetic algorithm-based model parameter optimization process

The hyperparameters to be adjusted in the SVR model include kernel function bandwidth σ, penalty coefficient C, and insensitive zone width ε. The default kernel function bandwidth is 0.1, with an optimization range of [0.1, 0.3] and a gradient of 0.05. The default penalty coefficient is 10, with an optimization range of [10, 100] and a gradient of 10. The default insensitive zone width is 0.1, with a search range of [0.1, 0.3] and a gradient of 0.05. The prediction performance of the RF model is influenced by the number of trees and the maximum depth of each decision tree. The default number of trees is 50, with a range of [50, 500] and a gradient of 50. The default maximum depth starts at 5 and grows until the minimum sample number is reached, with a gradient of 5. The gas extraction volume prediction performance of models constructed with SVR and RF before and after GA parameter optimization is compared.

3  Selection of Gas Extraction Pure Volume Prediction Model

The gas extraction prediction models developed using support vector regression (SVR) and random forest (RF) are fundamentally regression-based. Therefore, it is essential to evaluate the predictive accuracy of these models. By applying appropriate evaluation metrics and leveraging field-acquired data for model training and validation, the predictive performance of each model can be systematically analyzed to identify the most effective model.

3.1 Performance Evaluation Metrics for Prediction Models

To quantify the predictive performance of each model, mean absolute error (MAE), root mean square error (RMSE), and mean absolute percentage error (MAPE) are used to measure the differences between predicted and actual values. MAE reflects the overall magnitude of the error, RMSE represents the deviation between predicted and actual values and is more sensitive to outliers, while MAPE measures the accuracy of the predictions. The calculation methods for these metrics are shown in Eq. (5).

{MAE=1n∑i=0n−1|yi−yi′|RMES=1n∑i=0n−1|yi−yi′|2MAPE=1n∑i=0n−1|yi−yi′yi|×100%(5)

3.2 Data Sources

To simultaneously predict gas extraction for four different locations, a random sampling approach was used to construct the dataset during model development.

Gas extraction data from the 8005 working face of a high-gas coal mine were selected for model training and testing. The mining area covers 69.33 km2 and has an annual production capacity of 1.3 million tons. The targeted coal seam exhibits a thickness of 5.54 m, an average dip angle of 10°, and a gas content ranging from 7 to 20 m3/t. Gas control strategies employed in the mine include surface well extraction, cross-seam drilling, and in-seam drilling. Initially, both gas concentration and pure extraction volume are relatively high during in-seam and cross-seam extraction. However, as extraction proceeds, both parameters decline rapidly. This rapid decline poses challenges in meeting the safety standards required for continuous mining operations.

At the selected working face, gas was extracted sequentially via surface wells, cross-seam drilling from the bottom extraction roadway, and in-seam drilling from the transportation and return air roadways. To evaluate the predictive accuracy of the models under various extraction methods, gas extraction data were collected from cross-seam drilling in the bottom extraction roadway and from in-seam drilling in both the transportation and return air roadways. One dataset was selected each from the bottom extraction and return air roadways, and two datasets from the transportation roadway. Online automated monitoring and data acquisition systems were employed. Monitoring was performed using a CJZ4/50 laser methane multi-parameter detector designed for gas extraction pipelines. This device facilitates automatic metering and real-time monitoring of multiple parameters, including flow rate, pressure, temperature, and gas concentration in the mixed gas extracted from boreholes. Extraction monitoring data for each borehole group are presented in Table 1 and were synchronously collected across different locations. Each location contributed 124 datasets, totaling 496 across all sites. Each dataset comprises five features.

The trend graphs of extraction concentration, negative pressure, temperature, and daily extraction volume for the bottom drainage roadway, return air roadway, and transportation roadways 1 and 2 are shown in Fig. 4. Under similar negative pressure conditions, the bottom drainage roadway has the highest extraction volume. Its extraction volume and concentration are also more sensitive to changes in negative pressure, which is a result of permeability enhancement measures that improved coal seam permeability. The overall increase in permeability offset the variations in gas enrichment conditions caused by local geological structures, reducing abnormal data occurrences and better reflecting the corresponding effects of parameters. The boreholes in the bottom drainage roadway have been extracting for a long period, which explains the relatively low extraction concentration. The extraction systems in the return air and transportation roadways were formed after multiple rounds of extraction, resulting in generally lower extraction volumes. However, a corresponding relationship with extraction negative pressure can still be observed. Due to regional geological structure differences, the correlation between extraction concentration and negative pressure in the boreholes of the return air and transportation roadways is relatively weak, leading to more abnormal data, which is more evident in the return air roadway borehole extraction data. Therefore, these four data sets can represent the parameter variations in a typical extraction network after multiple rounds of extraction.

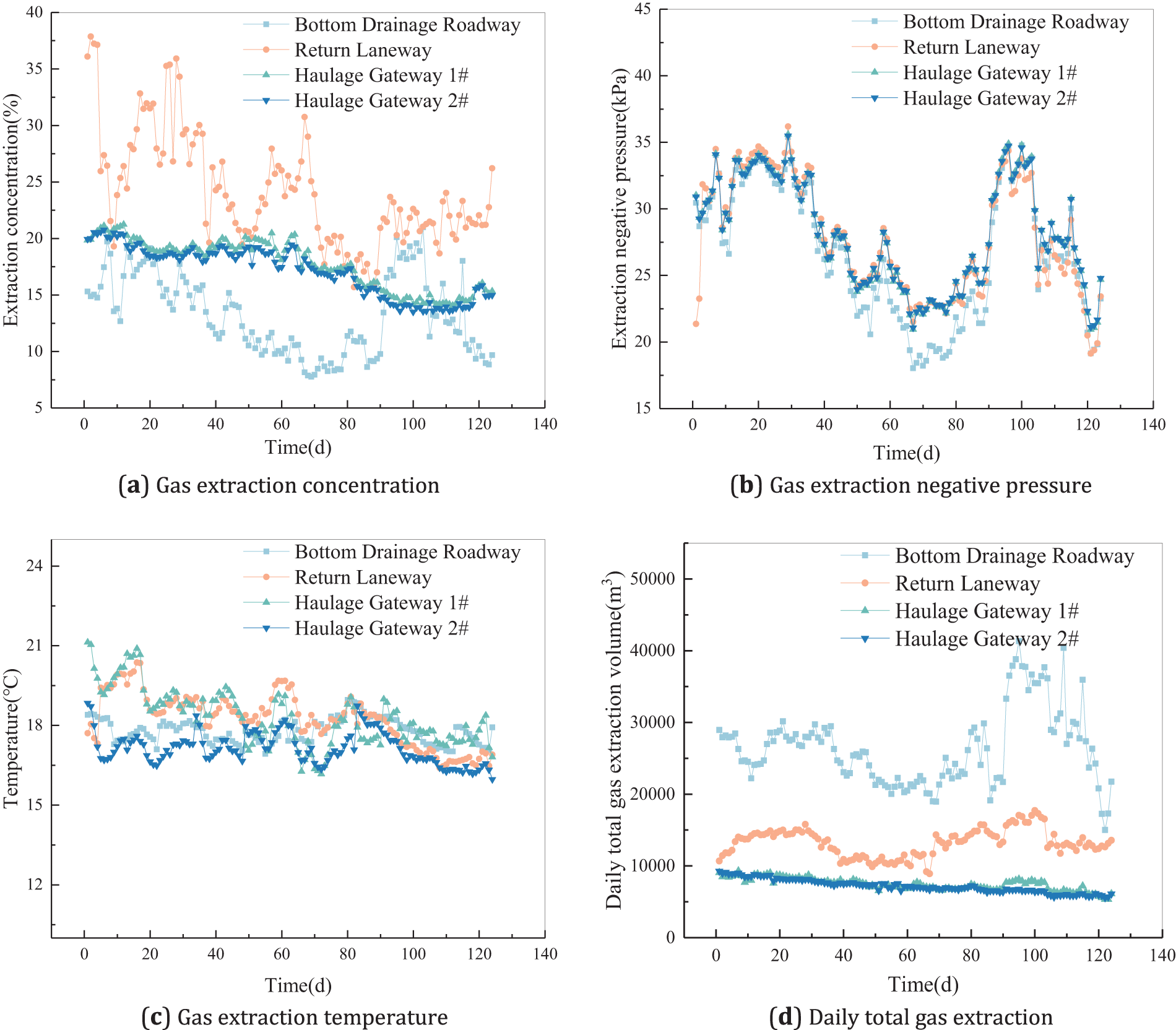
Figure 4: Gas extraction data variation at each testing location in the 8005 working face

3.3 Model Training and Evaluation

To improve the prediction accuracy of the model, data from all four locations were used to create the dataset, with location numbers added for differentiation. The SVR model was trained and tested using random sampling, while the RF model adopted Bootstrap self-sampling. The training set ratio was 0.75 for both models, and their prediction performances are shown in Fig. 5.

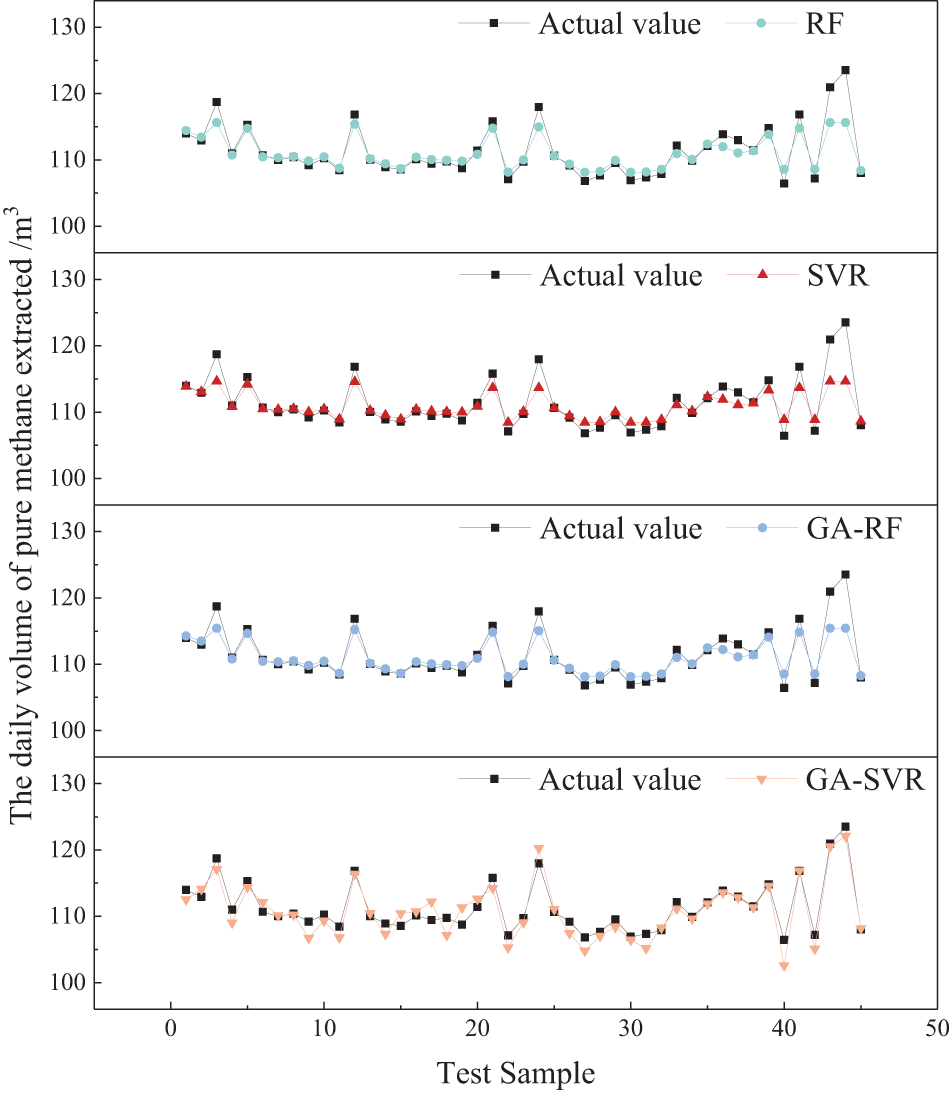
Figure 5: Comparison of prediction performance among different models

The calculated values of MAE, RMSE, and MAPE are presented in Table 2.

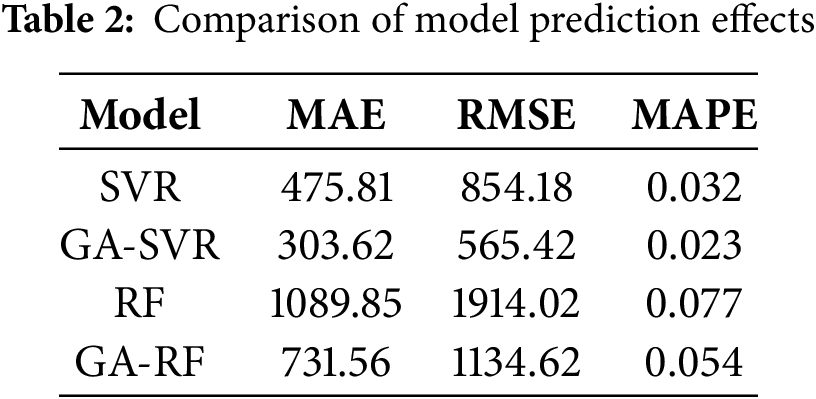
As shown in Table 2, the performance metrics of the SVR and GA-SVR models consistently exceed those of the RF and GA-RF models. This suggests a significant difference in predictive accuracy between the two groups of models. Among all models, the GA-optimized SVR model exhibits the highest predictive performance. It outperforms all other models across all evaluation metrics. Its mean absolute error (MAE) is 303.62. The mean absolute percentage error (MAPE) is merely 0.023. This meets the accuracy requirements for daily gas extraction volume forecasting in the mine.

Fig. 6 also shows that the GA-SVR model has higher stability and accuracy in predicting daily gas extraction volume compared to the other models, with fewer outliers and greater prediction stability.

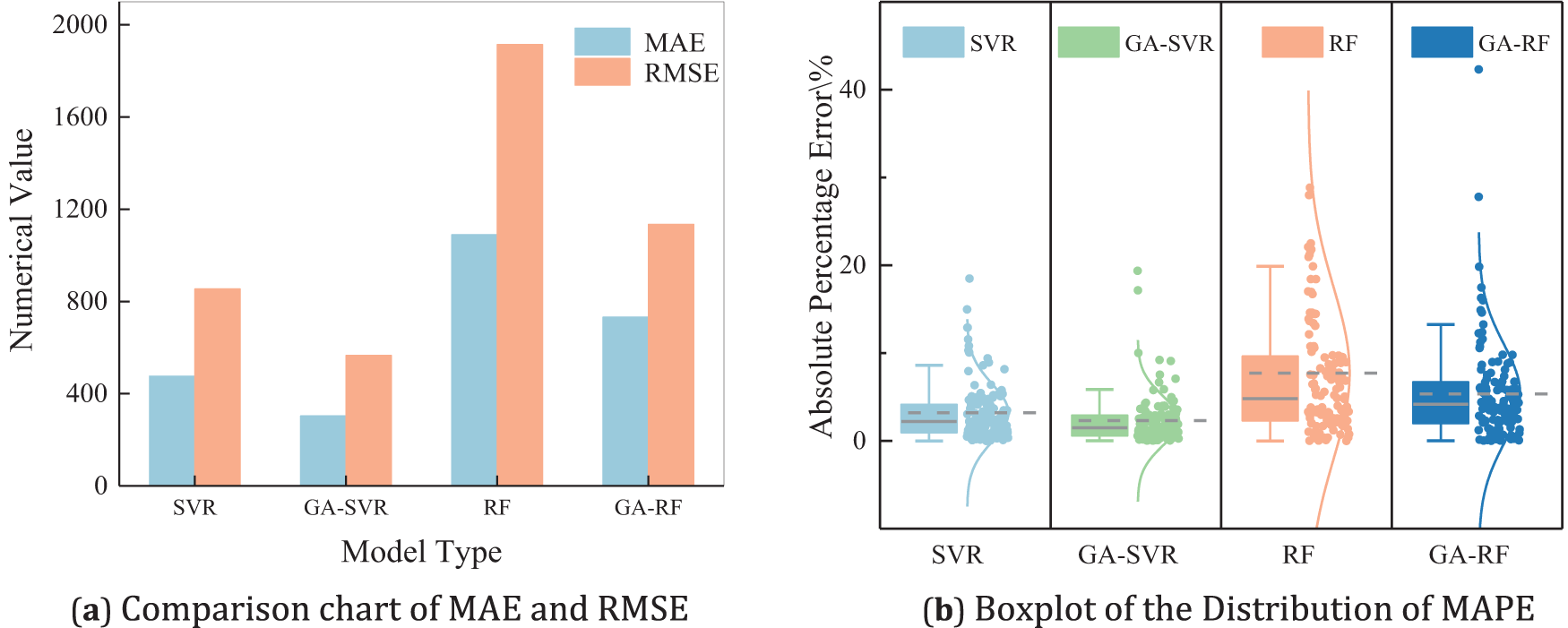
Figure 6: Comparative error analysis of different models

4  Gas Extraction Adaptive Control Technology Based on GA-SVR Model

Numerous factors influence gas volume and concentration during mine extraction. These include extraction negative pressure, location, temperature, and additional operational parameters. Among them, the gas occurrence conditions at different extraction sites are the primary determinant of gas extraction volume, the extraction negative pressure is identified as the second most influential factor. Therefore, maintaining an appropriate negative pressure is critical to ensuring adequate gas extraction.

4.1 Adaptive Control Process for Gas Extraction

Accurate prediction of gas extraction volume not only enhances the efficiency and management of gas extraction in mines but also enables the implementation of adaptive control measures to further increase extraction volume and efficiency. Therefore, this study utilizes the GA-SVR model to predict gas extraction concentration and, based on this, further employs the GA-SVR model to predict the required extraction negative pressure for a target gas extraction volume. Through adaptive regulation of extraction negative pressure, gas extraction volume is further enhanced, as illustrated in the process flow shown in Fig. 7.

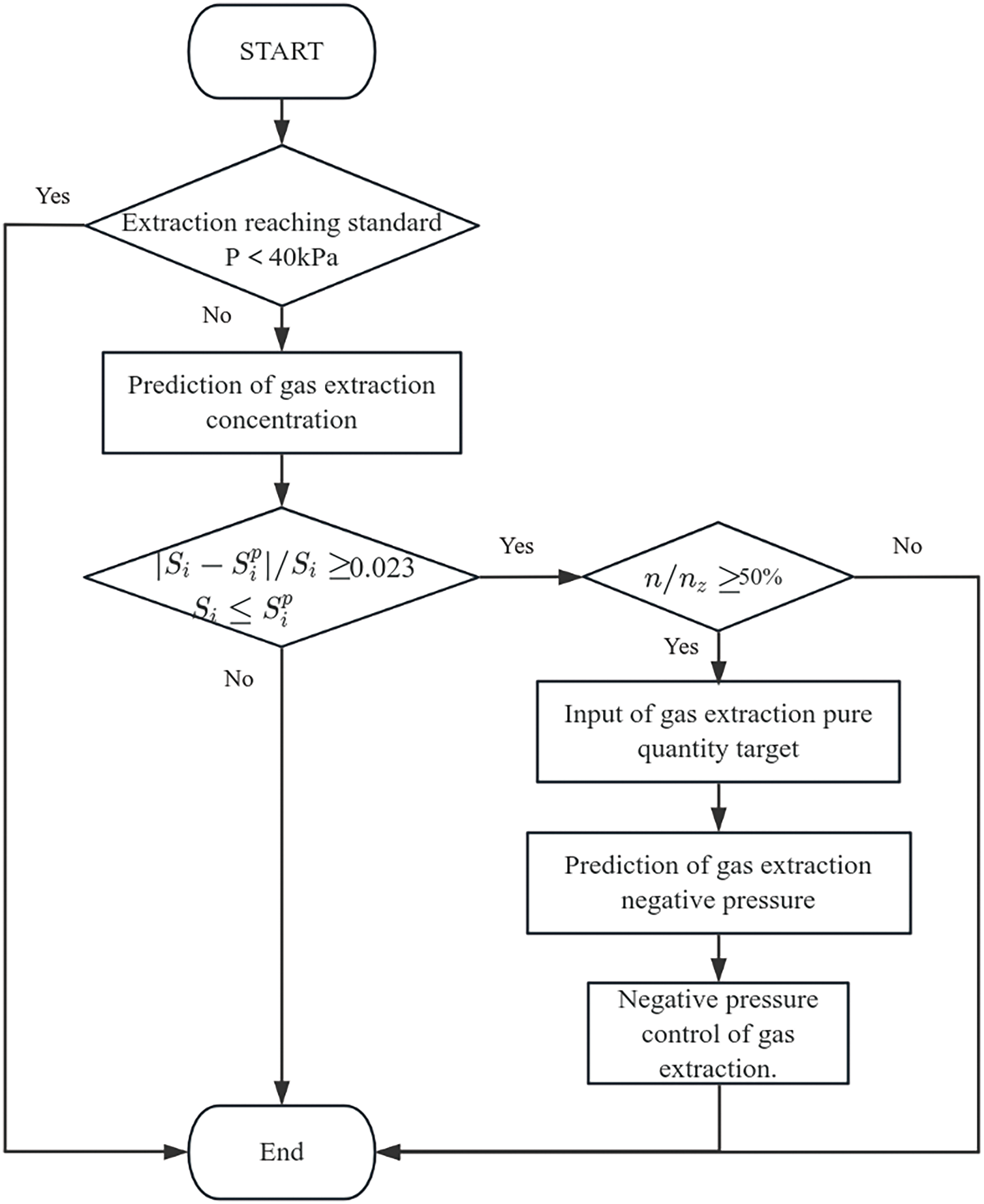
Figure 7: Flowchart of adaptive control for gas extraction

As shown in Fig. 7, under the precondition that the residual gas content in the coal seam has not yet reached the target and the extraction negative pressure is less than 40 kPa, gas extraction parameters are monitored during the extraction process. The GA-SVR model is used to predict the gas extraction volume for the next stage, denoted as Sip. Since the median absolute percentage error of the GA-SVR model is 2.3%, the confidence interval for the prediction model is set at 2.3%. If the error meets conditions |Si−Sip|/Si≥0.023 and Si≤Sip, the extraction volume is considered too low, indicating room for regulation.

Considering the presence of outliers, a tolerance for abnormal occurrences is introduced in the regulation model to enhance robustness. The number of times the extraction volume is deemed too low is recorded as n, while the total number of evaluations is recorded as nz. If n/nz<50\% , the instances of low extraction volume since monitoring began are deemed insufficient to trigger a regulatory action. However, if the number of anomalies accumulates to n/nz≥50\% , it is determined that measures should be taken to increase negative pressure to enhance extraction volume.

Based on the first nz gas extraction volume predictions, a GA-SVR prediction model is established. The monitored gas extraction data is input, with the extraction volume corrected to the predicted value. The model is then trained in reverse with extraction negative pressure as the target. Once training is complete, the model switches to prediction mode to determine the required regulated negative pressure. This value is then used to adjust the negative pressure of the target boreholes, achieving adaptive regulation aimed at maximizing gas extraction flow.

4.2 Assessment of Adaptive Control Effectiveness in Gas Extraction

A 30-day field validation of the proposed adaptive regulation strategy was conducted at the 8005 working face of a high-gas mine. The experimental and control borehole groups were both located in the return airway of the 8005 working face. Before regulation, the extraction negative pressure of both borehole groups was 23.42 kPa. The comparison of gas extraction volumes over the 30-day regulation period is shown in Fig. 8.

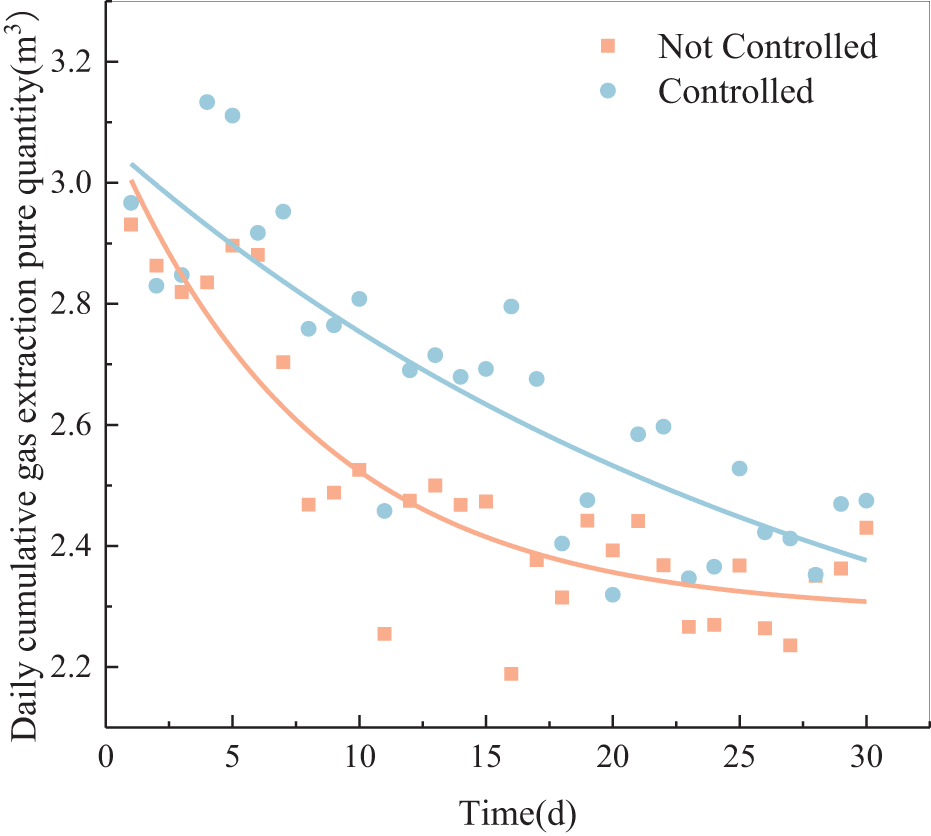
Figure 8: Comparison chart of adaptive control extraction borehole performance

As shown in Fig. 8, the adaptive regulation group demonstrated a noticeable improvement in extraction efficiency compared to the control group. Over the 30-day extraction period, the total average extracted gas volume for the control group was 24,883.75 m3, whereas the regulated group achieved 26,148.95 m3, representing an overall increase of 5.08%. The regulation effect was more pronounced in the first 15 days, with gas extraction volume increasing by 7.15%. This is due to the gradual reduction in gas pressure and concentration within the coal seam as extraction progressed, along with a decrease in coal seam permeability. As extraction continues, the gas pressure in the coal seam gradually decreases, reducing the driving force for gas flow and weakening the regulatory effect. Additionally, pressure reduction causes pore and fracture closure, further diminishing extraction control effectiveness. In conclusion, an adaptive regulation strategy with a 30-day control cycle can effectively enhance gas extraction volume.

5  Discussion

Proper regulation of negative pressure is essential for maintaining safe mining operations. This study proposes an adaptive regulation technology for gas extraction. It integrates historical data with a GA-SVR model to predict gas extraction volumes. Predicted values are compared against actual measurements to assess whether borehole pressure adjustments are necessary. Additionally, historical extraction data are used to train a model with negative pressure as the prediction target. This enables the estimation of the negative pressure required to achieve a desired extraction volume. Subsequently, the borehole group’s negative pressure is adjusted to maximize the gas flow rate. This creates a closed-loop control system for adaptively regulating negative pressure during gas extraction.

Currently, the GA-SVR-based adaptive regulation framework has largely achieved autonomous control of negative pressure in borehole gas extraction. However, several limitations remain. First, the computational efficiency of the genetic algorithm declines significantly with increasing data volume, due to its inherent limitations. This issue is particularly pronounced in large-scale mine gas extraction datasets. Currently, model training and inference are conducted using daily-averaged data. Compared to high-resolution data (e.g., per-minute or per-second), this approach reduces predictive granularity. However, using higher-frequency data substantially increases the volume of input data. This imposes a computational burden and slows down the overall regulatory response. Second, due to constraints imposed by mining schedules, the field experiment for adaptive regulation was limited to a 30-day duration. This duration is relatively insufficient for robust evaluation of the regulation system’s performance. Future research will focus on enhancing the model and further advancing adaptive gas extraction regulation technology. Full-scale gas extraction experiments across the entire working face will be conducted to validate the regulation framework. This will support the robust deployment and broader application of the proposed technology.

6  Conclusions

(1)   Following multiple rounds of gas extraction, the residual gas content in the coal seam decreases significantly, thereby diminishing the influence of extraction negative pressure on both extraction concentration and extracted pure volume. Consequently, during stratified borehole extraction, the influence of negative pressure on concentration weakens, yet it remains correlated with the extracted pure volume. During cross-layer borehole extraction, permeability enhancement measures mitigate variations in gas enrichment conditions induced by local geological structures, thereby minimizing anomalies in gas extraction data. As a result, both extracted pure volume and concentration demonstrate increased sensitivity to variations in negative pressure.

(2)   Given the nonlinear nature of gas extraction data and the necessity for random sampling in multi-region predictive modeling, a GA-SVR model is introduced to forecast the daily cumulative extracted pure volume. Comparative analysis with similar predictive models indicates that the GA-SVR model exhibits superior absolute error metrics and enhanced prediction stability, achieving a median absolute percentage error of just 2.6%.

(3)   The GA-SVR model training results indicate that variations in negative pressure exert the most substantial influence on extracted pure volume at a given location. Consequently, an adaptive negative pressure regulation technique, informed by the GA-SVR predictive model, is proposed. Field experiments demonstrate that, over a 30-day regulation cycle, the adaptive control model enhances the average extracted pure volume in the test borehole group by 5.08% relative to the control group. Furthermore, within the initial 15 days, the extracted pure volume rises by 7.15%, laying a robust foundation for the long-term sustainable and efficient utilization of gas.

Acknowledgement: Not applicable.

Funding Statement: This research is funded by the National Key Research and Development Program of China, grant number: 2023YFF0615404.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Cheng Cheng; methodology, Xuan-Ping Gong; validation, Cheng Cheng, Xiao-Yu Cheng and Lu Xiao; formal analysis, Cheng Cheng; investigation, Xing-Ying Ma; resources, Xiao-Yu Cheng; data curation, Xing-Ying Ma; writing—original draft preparation, Xuan-Ping Gong; writing—review and editing, Cheng Cheng; visualization, Cheng Cheng; supervision, Lu Xiao; project administration, Cheng Cheng; funding acquisition, Xuan-Ping Gong. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Li SG, Zhang JF, Shang JX, Lin HF, Wang SJ, Ding Y. Conception and connotation of coal and gas co-extraction technology system under the goal of carbon peak and carbon neutrality. J China Coal Soc. 2022;47(4):1416–29. doi:10.13225/j.cnki.jccs.2022.0035. [Google Scholar] [CrossRef]

2. Ivanova S, Vesnina A, Fotina N, Fotina N, Prosekov A. An overview of carbon footprint of coal mining to curtail greenhouse gas emissions. Sustainability. 2022;14(22):15135. doi:10.3390/su142215135. [Google Scholar] [CrossRef]

3. Peng SJ, Jia L, Xu J, Chen JR, Dai SJ, Chen YX. Dynamic response characteristics and coupling law of multi physical field parameters in coal seam gas drainage. J China Coal Soc. 2022;47(3):1235–43. [Google Scholar]

4. Zhang J, Liu Y, Ren P, Han H, Zhang S. A fully multifield coupling model of gas extraction and air leakage for in-seam borehole. Energy Rep. 2021;7(3):1293–305. doi:10.1016/j.egyr.2021.02.037. [Google Scholar] [CrossRef]

5. Liu P, Jiang Y, Fu B. A novel approach to characterize gas flow behaviors and air leakage mechanisms in fracture-matrix coal around in-seam drainage borehole. J Nat Gas Sci Eng. 2020;77:103243. doi:10.1016/j.jngse.2020.103243. [Google Scholar] [CrossRef]

6. Zhou F, Wang X, Liu Y. Gas drainage efficiency: an input-output model for evaluating gas drainage projects. Nat Hazards. 2014;74(2):989–1005. doi:10.1007/s11069-014-1224-2. [Google Scholar] [CrossRef]

7. Xia T, Zhou F, Liu J, Gao F. Evaluation of the pre-drained coal seam gas quality. Fuel. 2014;130:296–305. doi:10.1016/j.fuel.2014.04.051. [Google Scholar] [CrossRef]

8. Zheng C, Chen Z, Kizil M, Aminossadati S, Zou Q, Gao P. Characterisation of mechanics and flow fields around in-seam methane gas drainage borehole for preventing ventilation air leakage: a case study. Int J Coal Geol. 2016;162:123–38. doi:10.1016/j.coal.2016.06.008. [Google Scholar] [CrossRef]

9. Liu T, Lin B, Yang W, Liu T, Kong J, Huang Z. Dynamic diffusion-based multifield coupling model for gas drainage. J Nat Gas Sci Eng. 2017;44(5):233–49. doi:10.1016/j.jngse.2017.04.026. [Google Scholar] [CrossRef]

10. Cheng YP, Dong J, Li W, Chen MY, Liu K. Effect of negative pressure on coalbed methane extraction and application in the utilization of methane resource. J China Coal Soc. 2017;6:1466–74. [Google Scholar]

11. Pan R, Cheng Y, Yuan L, Yu M, Dong J. Effect of bedding structural diversity of coal on permeability evolution and gas disasters control with coal mining. Nat Hazards. 2014;73(2):531–46. doi:10.1007/s11069-014-1086-7. [Google Scholar] [CrossRef]

12. Wang DK, Peng M, Fu QC, Qin HJ, Xia YL. Evolution and numerical simulation of coal permeability during gas drainage in coal seams. Chin J Rock Mech Eng. 2016;35(4):704–12. [Google Scholar]

13. Ma L, Shi X, Li S, Lin H, Song S. Research on intelligent control model of gas drainage based on model predictive control. Coal Sci Technol. 2022;50(8):82–90. [Google Scholar]

14. Guo T, Tang S, Sun J, Gong F, Liu X, Qu Z. A coupled thermal-hydraulic-mechanical modeling and evaluation of geothermal extraction in the enhanced geothermal system based on analytic hierarchy process and fuzzy comprehensive evaluation. Appl Energy. 2020;258(32):113981. doi:10.1016/j.apenergy.2019.113981. [Google Scholar] [CrossRef]

15. Sun J, Xiao Q, Wen J, Wang F. Natural gas pipeline small leakage feature extraction and recognition based on LMD envelope spectrum entropy and SVM. Measurement. 2014;55(6):434–43. doi:10.1016/j.measurement.2014.05.012. [Google Scholar] [CrossRef]

16. Hao TX, Chen GY, Zhao LZ, Tang YJ. Quickly determining gas drainage radius based on Adam optimized deep neural network. J Saf Sci Technol. 2022;18(6):52–7. [Google Scholar]

17. Wang YH, Wang SY, Wang ZZ. Multi-parameter gas concentration prediction model based on improved locust algorithm to optimize long and short time memory neural network. Chin J Sens Actuators. 2021;34(9):1196–203. doi:10.1109/icsp58490.2023.10248448. [Google Scholar] [CrossRef]

18. Wang ZF, Zhou Y, Sun YN, Wang YL. Drainage negative pressure optimization based on negative pressure influence factor. Saf Coal Mines. 2015;46(2):12–6. [Google Scholar]

19. Zhou AT, Du CA, Wang K, Fan XH. Research on intelligent control theory and strategy of gas drainage pipe network based on graph theory. Fuel. 2024;357(12):129867. doi:10.1016/j.fuel.2023.129867. [Google Scholar] [CrossRef]

20. Wang X, Zhou F, Xia T, Xu M. A multi-objective optimization model to enhance the comprehensive performance of underground gas drainage system. J Nat Gas Sci Eng. 2016;36(24):852–64. doi:10.1016/j.jngse.2016.11.012. [Google Scholar] [CrossRef]

21. Zhou F, Liu C, Xia T, Liu Y, Sun Y. Intelligent gas extraction and control strategy in coal mine. J China Coal Soc. 2019;8:2377–87. [Google Scholar]