Short-Term Penetration beyond Diffusion Spinodal of a Mixture: Interaction of Liquid-Liquid and Liquid-Vapour Transitions

1  Introduction

Due to the variety of factors and conditions for the manifestation of the liquid-vapor phase transition, as well as its applicability to diverse practical problems [1–5], this phenomenon continues to attract research attention in various fields [6–9]. This interest is also stimulated by the current development of mini- and micro-sized systems [10,11] and the concomitant increase in the heat flux density generated by such systems [12–15]. In particular, the mechanism of explosive boiling-up, which is feasible under the conditions of small characteristic times and sizes [16–19], has found application as a liquid medium mover in engineering devices and advanced medical instruments based on concentrated spatiotemporal boiling-up of various liquids [20–24]. One such current application consists of creating smart technologies for spraying liquids for various purposes [8]. In this connection, we highlight the achievement of conditions for micro-explosive decay of composite droplets (water-in-fuel) with their intensive heating to form a fuel aerosol [25,26].

Boiling-up is preceded by short-term superheating of the liquid concerning the liquid-vapor binodal Ts(p). Here, T is the temperature, p is the pressure, and the “s” index refers to the equilibrium state. In the general case of a multi-component system, the boiling-up conditions are complicated by differences in phase composition. Their quantitative description becomes even more difficult with the growth of differences in the properties of the components, particularly when switching to partially miscible solutions. Under specific conditions, such solutions may exhibit non-equilibrium behavior and metastability of various origins [18,27,28].

In this work, we continue our previous study into the relaxation pattern of a micro-heater/solution system with a lower critical solution temperature (LCST) under a powerful local thermal action, which was initiated to search for a reliable heat carrier for removing significant heat fluxes in mini- and micro-systems [27]. Spontaneous boiling-up [16–19] is studied against the background of a rapid transfer of a homogeneous solution into not fully stable (metastable) and unstable states. As previously, we refer to not fully stable states as those of superheating concerning the liquid-liquid Tll(p) and liquid-vapor Ts(p) binodal lines, whereas unstable states are those of superheating concerning the diffusion (liquid-liquid) spinodal of the solution. Such solutions demonstrate unique relaxation properties in comparison with their analogs comprising fully miscible components. The questions that arise are as follows. How will this circumstance affect the nature of the boiling-up process, in particular its intensity and duration in time? To what depth is the initial solution able to penetrate the region of unstable states ΔT = T(texp) − Tsр? Here the index “sp” refers to the diffusion spinodal, and the index “exp” refers to the duration of observation of the unstable or metastable state. Moreover, is it possible to observe boiling up against the background of the decomposition of the system accompanying heating? The study is based on a systematic change in the heating rate by stepwise changing the heat generation power in the heater—and, as a consequence, by changing the product V·texp (V is the volume of superheated liquid), which is a key parameter in experiments on the attainable superheating of liquids [18,19,25].

In this study, we aim to search for the interaction of phase and relaxation transitions in a pulsed heated micro-volume of an LCST solution across a wide range of changes in the characteristic time (heating rate) and degree of superheating. Examples of similar interactions for other objects can be found in [29–33]. The objectives consist of clarifying the hierarchy of times accompanying this interaction, as well as assessing the prospects for the applicability of this approach to current technological processes associated with the operation of mini- and micro-systems.

A water/PPG-425 solution and its components served as comparison systems. The critical point corresponds to the concentration of PPG-425 in a solution ωcr ≈ 27 wt.% and temperature Tcr ≈ 323 K; a detailed explanation can be found in [34]. The method of pulse heating of a wire probe with the option of controlling the heat release power during the pulse [27,35] was used to maintain the specified heating parameters throughout the entire series of measurements on the same probe, including against the background of structural/phase transformations of the liquid under study. The experiments were carried out mainly at atmospheric pressure. It should be noted that previous experiments [27], which were aimed at observing the phenomenon of spinodal decomposition not disturbed by spontaneous boiling-up, were carried out mainly at near- and supercritical pressures p > pc. Here, the index “c” refers to the liquid-vapor critical point, taking into account the specifics of the supercritical transition in a substantially non-stationary process [35,36]. Before the signs of decomposition appeared, the Ṫ average heating rates ranged from 0.05 × 105 to 2 × 105 K/s. As for spontaneous boiling-up, the T* (texp) temperature and the amplitude of the response signal serve as sensitive indicators of the current state of the system. Hence, the involvement of spontaneous boiling-up is capable of providing additional information on the relaxation of not fully stable and unstable systems.

This paper is structured as follows. In Section 2, the experimental findings of previous experiments with unstable solutions are discussed, the approach to measurements is outlined, and the objective of the current study is formulated. Section 3 is devoted to modeling the decomposition of such a solution against the background of its unstable states. In Section 4, the obtained results are discussed and the hypothesis about the close interaction between spinodal decomposition and spontaneous boiling-up is tested. The results of the study are summarized in Section 5.

2  Background

The preliminary experiments on pulse heating of a solution of near-critical concentration in the mode of constant heat release power P (t) = const [27,35] mentioned in the Introduction were aimed at identifying the response to spinodal decomposition. The sensitive element of the measuring circuit is a wire probe immersed in a liquid under investigation. The probe radius Rp is 1 × 10−5 m, the length is about 1 cm, and the material is platinum. The monitored variable calculated from the primary data (voltage drops across the probe and the “current” resistor over time) consisted in the probe temperature. The conducted experiments [27] yielded unexpected results. When exceeding the spinodal temperature sufficiently (over 150 K), the following effects appeared, which are not typical of solutions with fully miscible components:

–   The observed change in the probe temperature over time T(t) demonstrated a tendency to transition from monotonic heating (Ṫ ≈ 0.74 × 105 K/s), which is caused by the constancy of power and the immobility of the medium, to reaching a plateau (Fig. 1). In this heating mode, the deviation of the curve T(t) downwards from its initial course corresponds to an increase in the heat transfer coefficient from the probe to the liquid;

–   Upon reaching this plateau, a change in the ordinary order of curves T(t) (corresponding to a step-by-step change in pressure) to the opposite, i.e., higher pressure values begin to correspond to lower values of the heat transfer coefficient (Fig. 2).

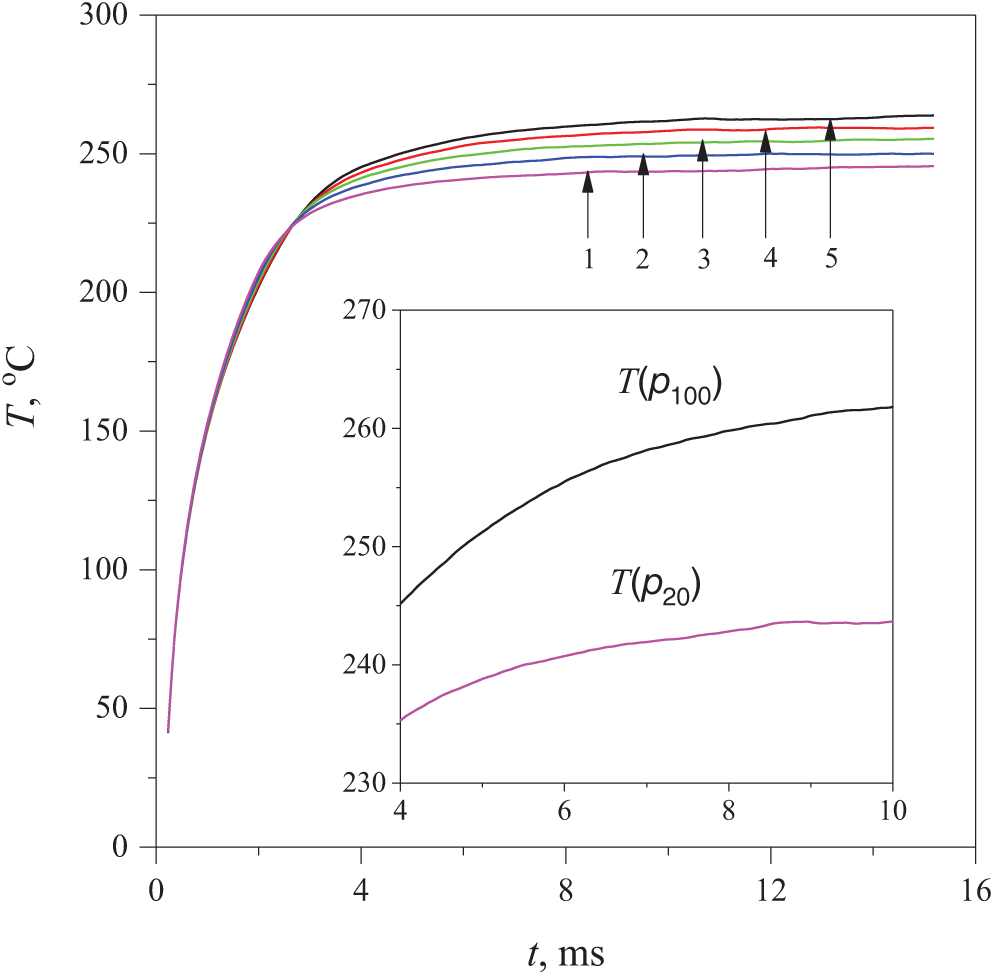
Figure 1: Evolution of the probe temperature in an aqueous solution containing 30 wt.% PPG-425 at given pressure values p, MPa: 20 (curve 1), 40 (curve 2), 60 (curve 3), 80 (curve 4), 100 (curve 5). The insert shows a fragment of the graph T(t) at p100 and p20, where the subscript indicates the pressure value in MPa. Here and in the following figures the results are presented for the mode of constant heat release power P(t) = const

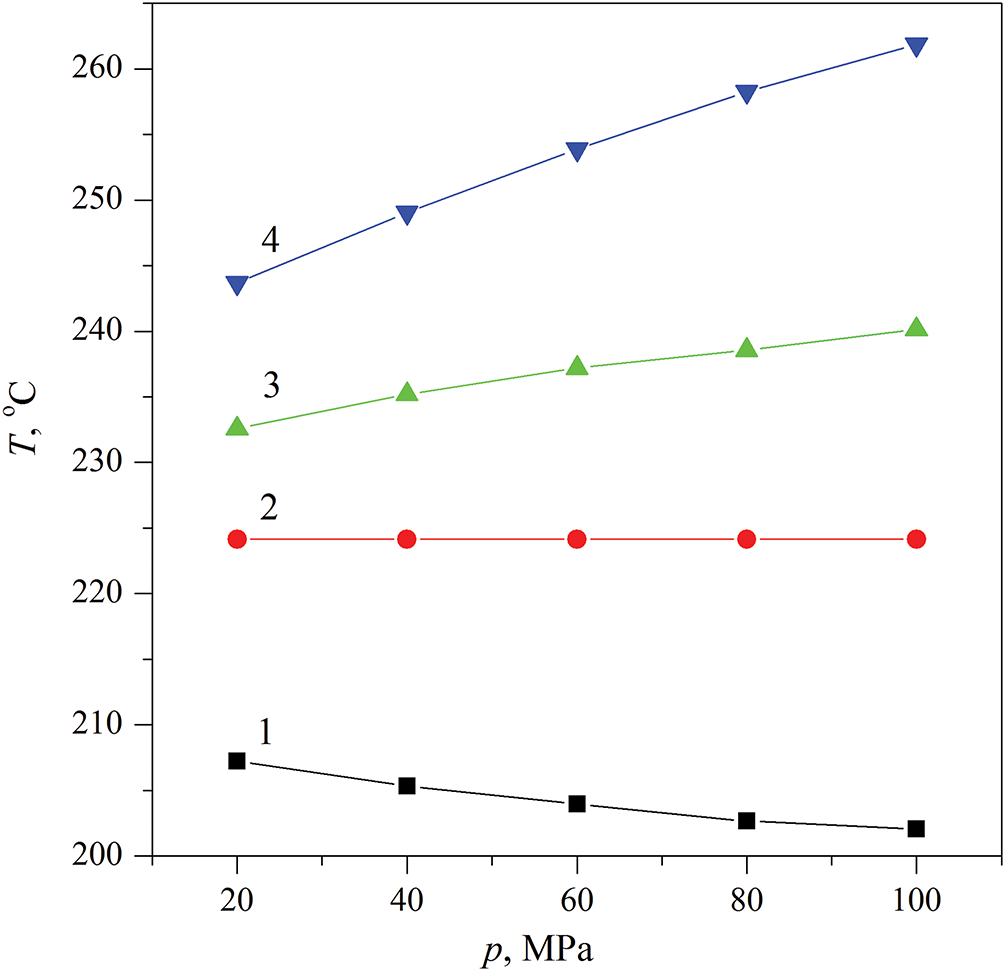
Figure 2: Sampling of probe temperature values depending on pressure according to the data presented in Fig. 1 for different moments of heating, ms: 2.0 (curve 1), 2.66 (curve 2), 3.5 (curve 3), 10 (curve 4)

The authors [27] associate the first effect with the hydrodynamic picture that arises during the spinodal decomposition of the solution—namely, with the activation of the convective mode of heat transfer. The second effect evidently points to the specific influence of pressure on this picture. In particular, the reproducible intersection of the heating curves at one point, see Fig. 2, is a surprising experimental finding. Further, it was revealed that the greatest perturbation of the response curve T(t) accompanies spinodal decomposition and spontaneous boiling-up of the solution. In the current study, experiments involving spontaneous boiling-up are planned at lower reduced pressures p/pc—in particular, at atmospheric pressure.

From the preliminary experiments at different values of heating power, see the results given in Fig. 3, it can be assumed that the first effect can be observed across a limited range of changes in the heating rate. One specific objective of the present study was to test this hypothesis. A more general task consisted in clarifying the spatiotemporal conditions enabling interaction of phase and relaxation transitions in the course of penetration into the region of not fully stable and unstable states of the solution.

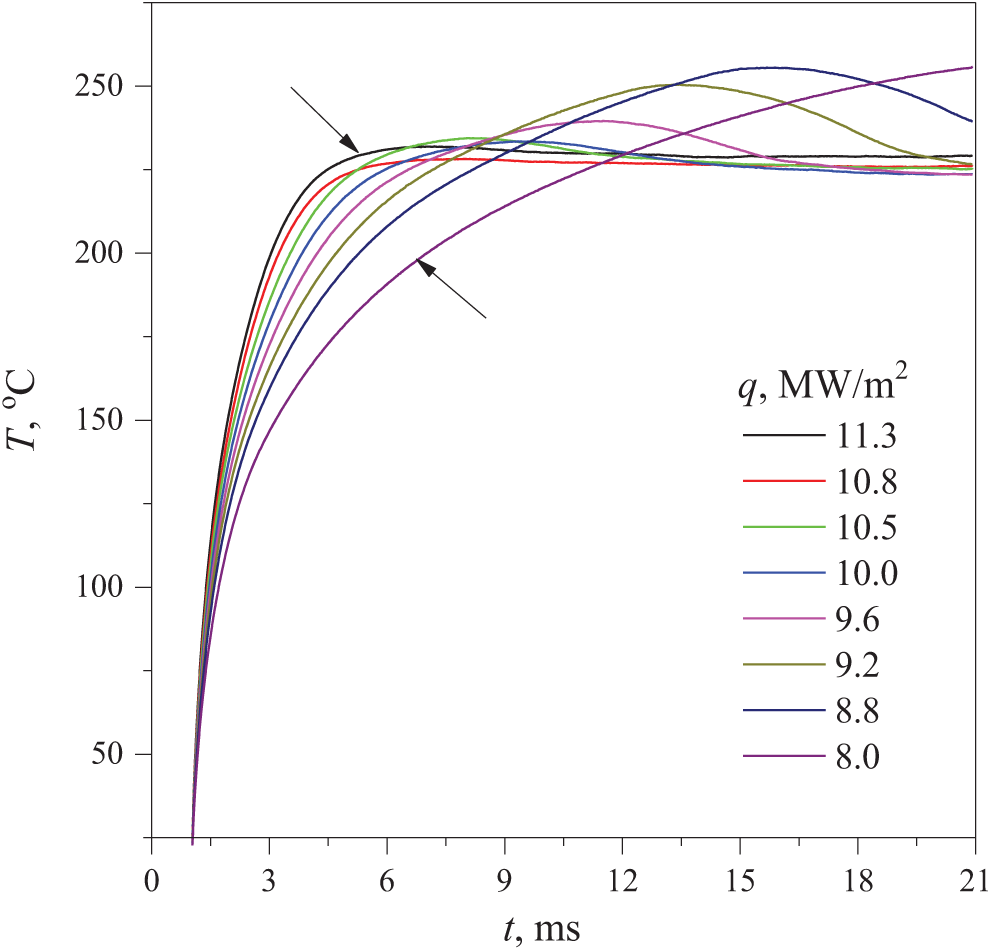
Figure 3: Evolution of the probe temperature in an aqueous solution containing 30 wt.% PPG-425 at a given pressure of 5 MPa. The parameter was the value of the heat flux density q(t) through the probe surface set by the power value. The arrows point to the temperature curves at the lowest value q = 8.0 MW/m2 and at the highest value q = 11.3 MW/m2

To observe the interaction of liquid-liquid and liquid-vapour phase transitions, atmospheric pressure was selected allowing the release of a spontaneous boiling-up signal against the background of a liquid-liquid transition. Similar to the first case, the parameter was the value of P. The experiments were carried out across the entire concentration range corresponding to the region of not fully stable states of the solution—namely, 10–60% PPG in water. The spontaneous boiling-up temperature, denoted as T*(texp), and the amplitude of the corresponding signal (manifested in a sharp disturbance in the course of the heating curve [25]) were monitored depending on the lifetime of the system in this region. These data allow us to indirectly judge the processes that lead to boiling-up—in particular, the current degree of heterogeneity of the system, which breaks down into two liquid phases. Figs. 4–6 show a fragment of the results reflecting the behaviour of the system in the regions near the right branch of the binodal (Fig. 4), the left branch of the binodal (Fig. 5), and the near-critical concentration (Fig. 6) at atmospheric pressure.

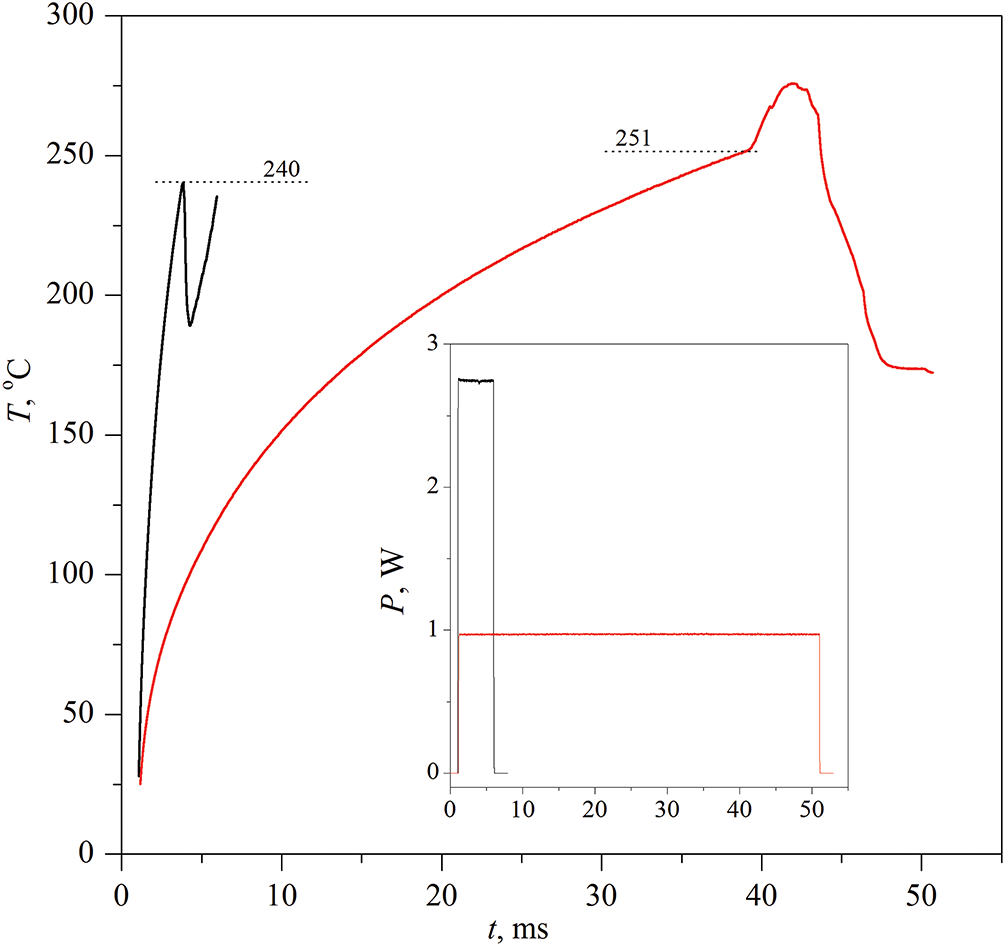
Figure 4: Evolution of the probe temperature in an aqueous solution containing 60 wt.% PPG-425 with pulse durations of 5 and 40 ms. Here and below, the main graph is supplemented by a graph of the specified power values, see the insert, corresponding to the heating curves shown in the main figure

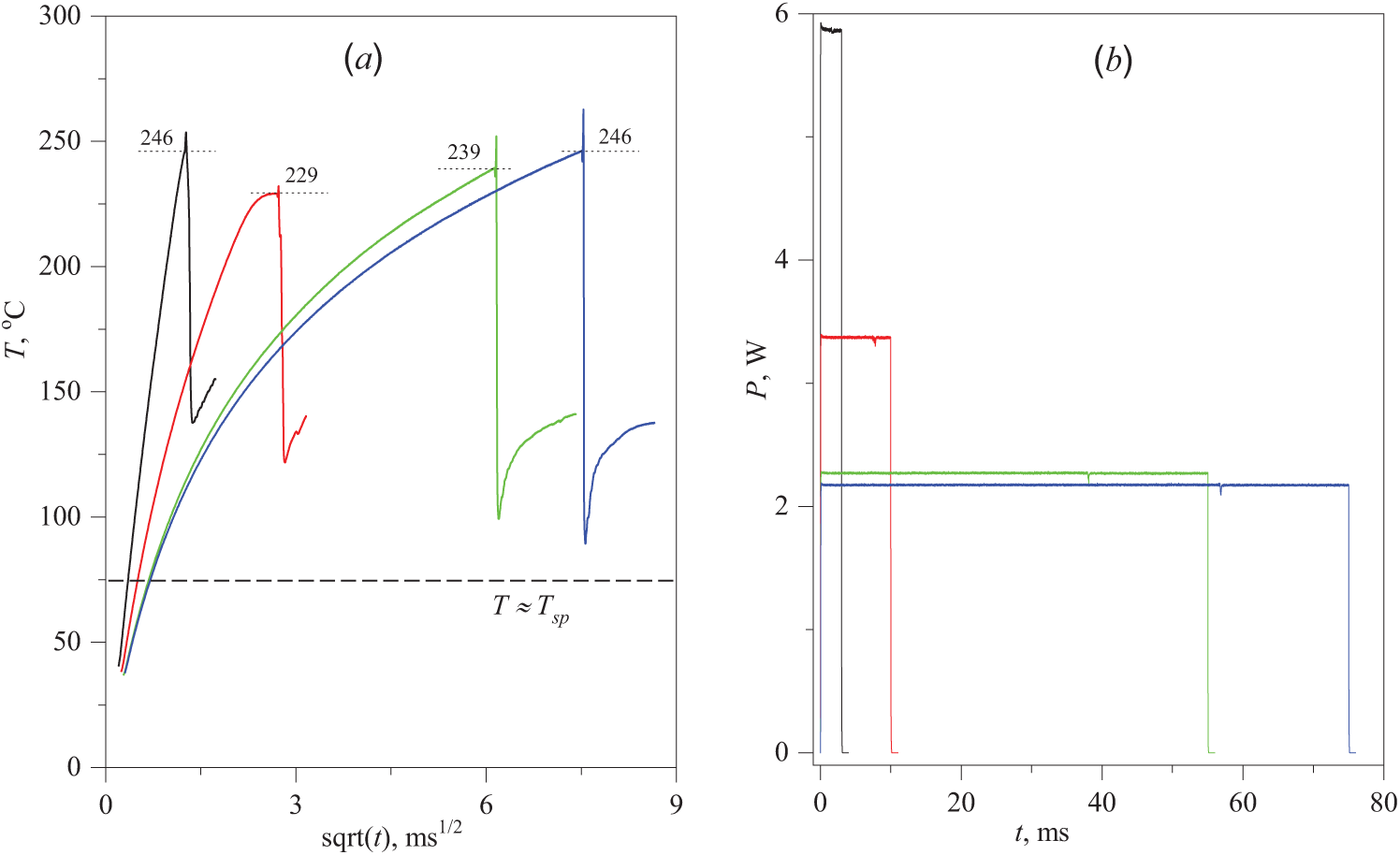
Figure 5: Evolution of the probe temperature in an aqueous solution containing 10 wt.%. PPG-425 with pulse durations of 2, 10, 50 and 70 ms (a) at the corresponding heating power values (b). For clarity of the graph (a), its time scale is taken as the square root of the heating time

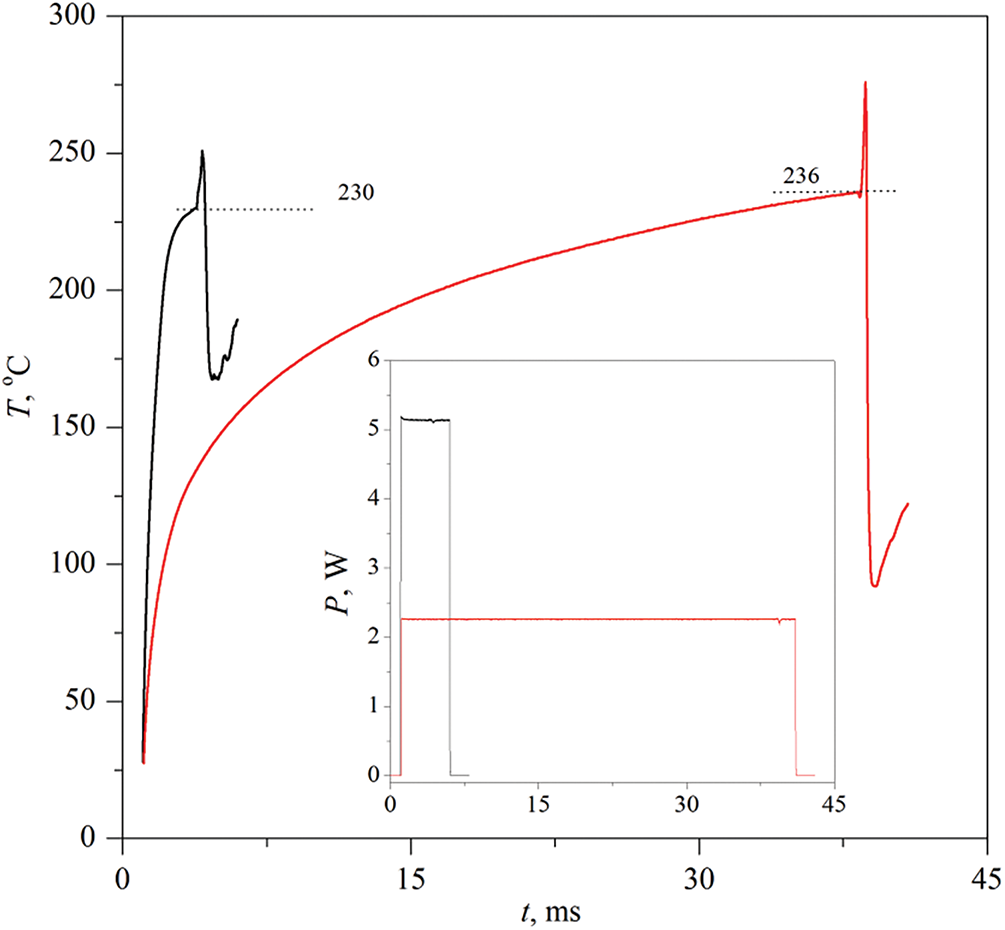
Figure 6: Evolution of the probe temperature in an aqueous solution containing 30 wt.% PPG-425 with pulse durations of 5 and 40 ms

The solution was found to have the lowest temperature T* at heating rates corresponding to the “plateau effect” at near- and supercritical pressures (Fig. 3), namely, Ṫ ~ (0.5–1.0) × 105 K/s. The increase in T* in the regions of greater and lesser heating rates (see Fig. 5 for more information) probably indicates a smaller scale of separation by the liquid-liquid mechanism—and, as a consequence, a lower heterogeneity of the system, see the Discussion section.

3  Model

3.1 Spinodal Decomposition

Spinodal decomposition, which is a consequence of the instability of the solution, leads to its separation into liquid phases of different composition. This process can be described using the language of non-equilibrium thermodynamics. According to classical concepts of thermodynamics of irreversible processes in the linear approximation, the driving force of diffusion is the gradient of chemical potential (μ). The work [37] noted that the expression for the flux density of component 1 (designated by a subscript 1) in a binary mixture can be written as:

j→1=−L(∇→μ1−∇→μ2)(1)

herein, L is the Onsager kinetic coefficient (L11=L22=−L12=L>0), which characterizes the mobility of molecules. As shown in [37], the mutual diffusion coefficient D can be expressed as follows through the coefficient L:

D=Ln∂2φ∂x12(2)

herein, n=n1+n2 is the number of molecules per unit volume, x1 is the molar fraction of the first component, while φ=x1μ1+x2μ2 is the molar Gibbs thermodynamic potential. On this basis, the authors [37] concluded that there is a direct connection between the transfer of matter and the thermodynamic stability parameter ∂2φ∂x12.

Heterogeneity of the solution may manifest itself in the appearance of droplets enriched with one of the components. In the presence of a temperature gradient, these droplets can begin to move (Marangoni effect [38]). Such an effect is described as a crossflow since the force (temperature gradient) causes a flow of mass. Generally speaking, there is a complex relationship between flows and forces. In the presence of local equilibrium, the system of equations includes the Navier–Stokes equation, the energy balance equation, and the continuity equation. Typically, such a system does not have an analytical solution, which encourages the use of simplified approaches.

Such a simplified model of spinodal decomposition of a solution during its pulse heating on the surface of a wire probe was constructed in [27]. The heat balance equation for the probe was obtained as:

dTdt=−(χT−T∞χt)(1+A(T−T∞)t)2Rp+qVρcp(3)

herein, T is the average temperature over the probe volume; T∞—bulk temperature; Rp—radius of the probe; χ—thermal diffusivity; A—constant responsible for the Marangoni effect; qV—source of Joule heat during heating of the probe; ρ—density of the mixture; cp—specific heat capacity of the mixture at constant pressure; t—total (in contrast to the previously entered variable texp) heating duration from the initial value T∞. In dimensionless variables:

dT′dt′=−2(T′−1t′)(1+A′(T′−1)t′)+B(4)

t=Rp2χt′,T=T∞T′,B=qVRp2κT∞,A′=T∞dσdT22τD123ηχRpχ(5)

herein, σ—surface tension and κ—thermal conductivity. As a result, the general dependence of the probe temperature on heating time was obtained; see, e.g., this dependence for the dimensionless case in Fig. 7.

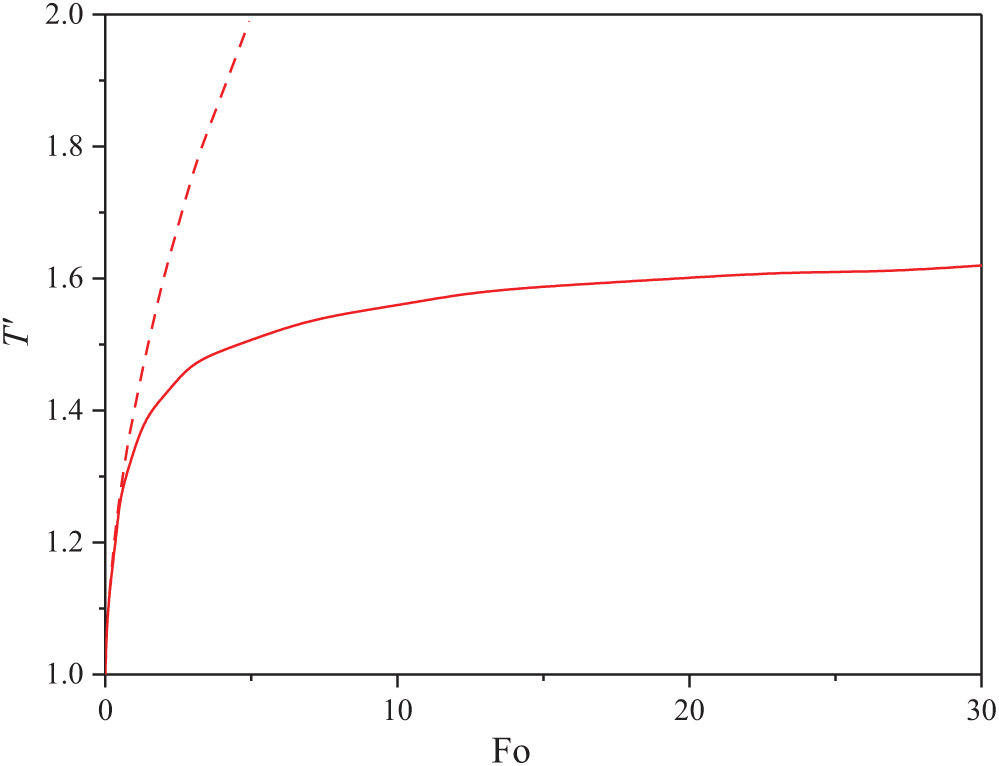
Figure 7: Dependence of dimensionless temperature on dimensionless time (Fourier number) at A′ = 1, B = 1 (solid line) and for A′ = 0, B = 1 (dashed line). The upper curve does not take into account the spinodal decomposition, while the lower curve includes spinodal decomposition and the Marangoni effect

3.2 Exact Solution in the Absence of Motion

Let consider the energy balance equation of the probe, in the absence of movement of drops of liquid phases of the decomposing solution, in a dimensionless form (omitting, for brevity, the primes):

dTdt=−(2T−1t)+B(6)

With the initial condition T(0) = 1, it has a solution:

T(t)=B2t+1−B8(1−exp⁡(−4t))(7)

As an example, the results of calculating the change in probe temperature during its heating by a pulse of constant power are presented in Fig. 8.

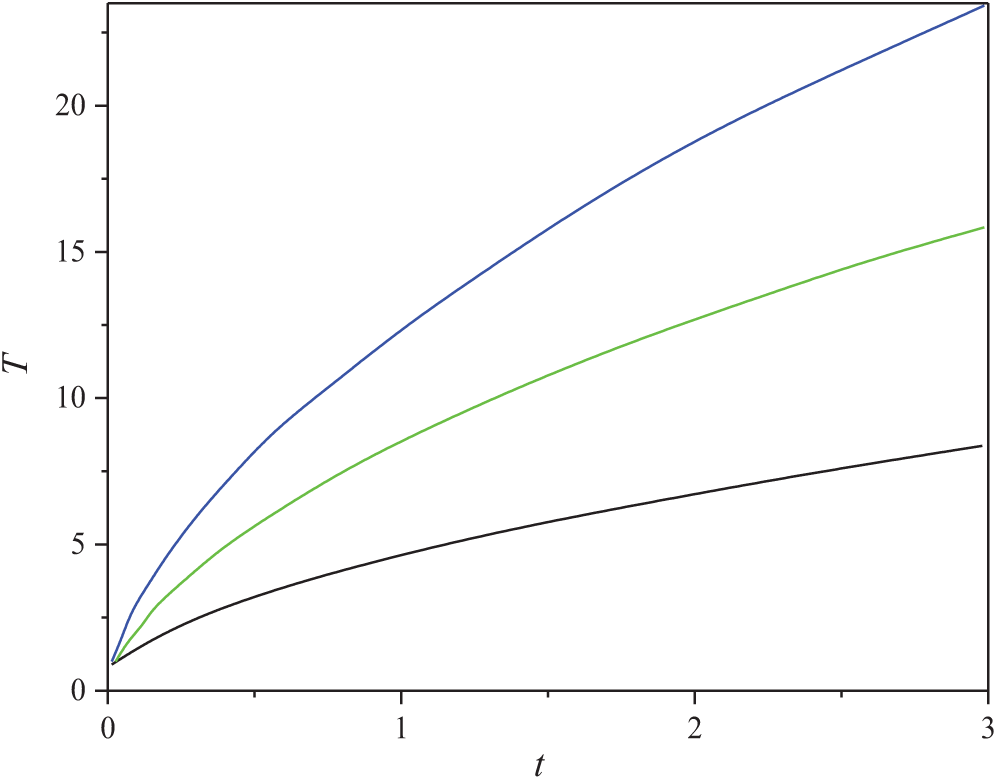
Figure 8: Dependence of the probe temperature on time in dimensionless variables. The parameter is the dimensionless power, from bottom to top: B = 10, 20 and 30

3.3 Distribution of Components near the Probe

Experiments on spontaneous boiling-up of solutions with LCST at different heating rates found a result not typical for pure liquids and solutions with completely miscible components. This is the effect of increasing T* with decreasing the heating rate. It manifests itself at not too high heating rate values, Ṫ < 1 × 105 K/s, see Figs. 4–6. In order to explain this finding, we assume that the distribution patterns of the liquid phases into which the system disintegrates differ significantly in the course of conventionally fast heating (Ṫ > 1 × 105 K/s, typical behaviour) and slow heating (Ṫ < 1 × 105 K/s, unusual behaviour).

The essence of this assumption is as follows. Under the influence of the Marangoni effect, the initial solution is substantially divided with the onset of spinodal decomposition into droplets having a different composition, i.e., enriched predominantly either with water or with PPG. Fig. 9a depicts a hypothetical representation of the droplet distribution near the probe during fast heating. If the probe is wetted by PPG better than by water, then it is the phase near the probe will be the one enriched by PPG. Under slow heating, the drops will have time to merge with one another; however, their movement can be hindered by wettability, as well as an insufficiently large value of the temperature gradient at slow heating. In this case, the water-enriched phase, which has a lower boiling-up point, will be further away from the probe, see Fig. 9b. As a result, the boiling-up temperature recorded in the experiment will increase as the heating rate decreases.

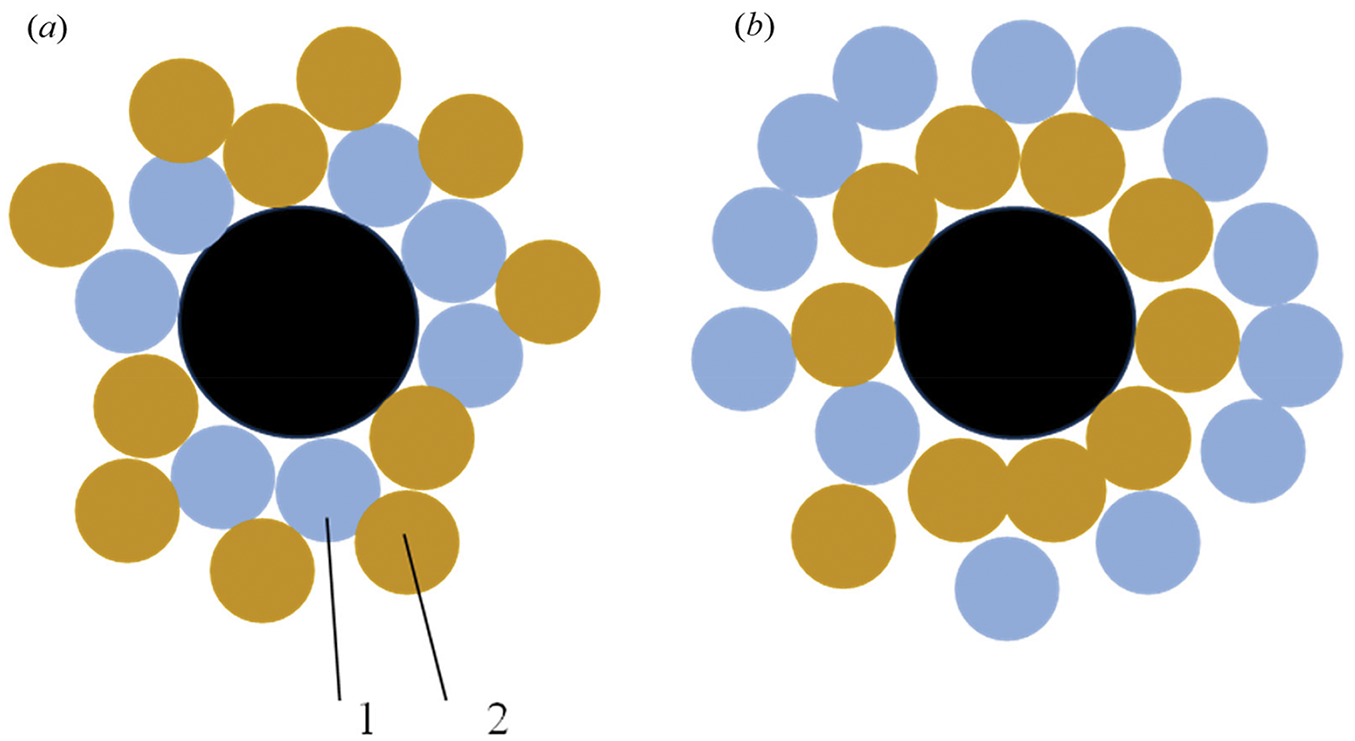
Figure 9: Simplified distribution pattern of liquid phase droplets near the probe during fast (a) and slow (b) heating. 1—phase enriched with water; 2—phase enriched with PPG; the probe cross-section is shown in black

3.4 Estimates of Some Quantities

The thickness of heated layer δ was found from the following relationship:

ρcpΔTπδ2l=Pt(8)

The change in the internal energy of the volume of the mixture layer adjacent to the probe with thickness δ is on the left side of the Eq. (8); on the right is the energy released during time t. Thus, the approximate energy balance at distance δ shows that the thickness of the heated layer is dependent on the power. Let apply this equation for ΔT = 100 К and t = 30 ms under characteristic experimental parameters:

δ=(PtρcpΔTπl)1/2=0.67×10−4=67µm(9)

Fig. 10 shows the dependence of the heated layer thickness (10a) and the radius of the drop (10b) over time for different values of the parameters—P and D, respectively. We assume that all variables during heating to the selected value ΔT retain constant values. In this case, we can use the equation:

δ=67(t30)1/2(10)

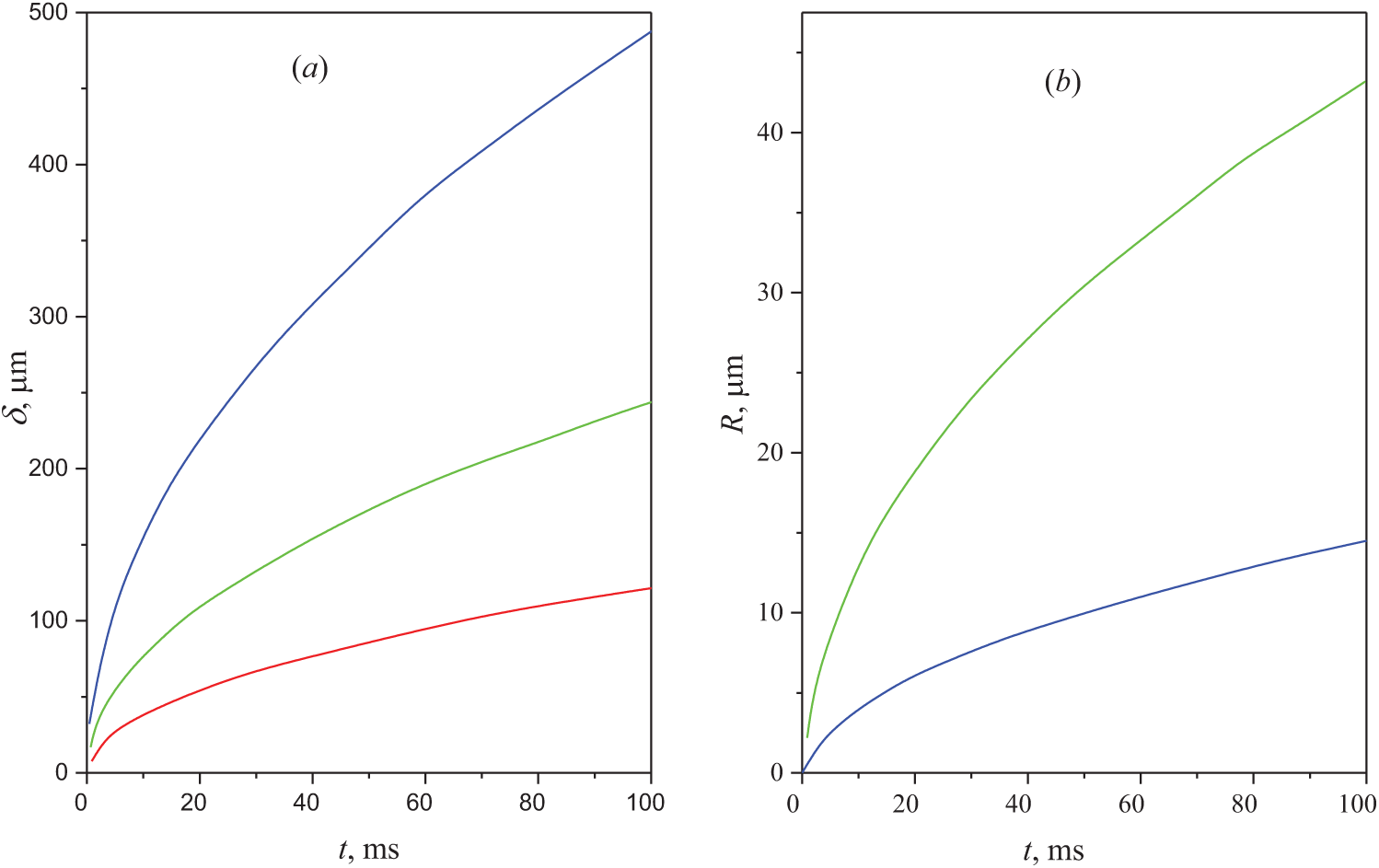
Figure 10: Dependence of the heated layer thickness (in μm) and of the droplet radius (in μm) on the heating duration (in ms). (a) is obtained for different power values, from bottom to top: 2, 4, 16 W. (b) is obtained for two values of the diffusion coefficient: D = 10−8 m2/s at the bottom and D = 10−9 at the top. It is assumed that the initial state of the solution is at the liquid-liquid binodal temperature, Tll = T∞

Drop size:

Let us evaluate the size of a drop that is freely growing due to diffusion: R=2Dt. Fig. 10b shows the change in droplet radius over time for two values of D and a heating duration of 100 ms. These graphs indicate that the size of the drop (provided that the drop exists separately and is not near the probe) is significantly smaller than the thickness of the heated layer. In other words, heating occurs first, and then the droplets grow.

Boiling-up temperature:

Let estimate the boiling-up onset temperature during penetration into the region of not fully stable and unstable states of the solution depending on the heating rate. We will consider an unusual mode that manifests itself at a slow heating rate (Ṫ < 1 × 105 K/s, see Figs. 4–6). At these conditions, spinodal decomposition has already begun, but the liquid does not move essentially, due to, e.g., wetting of the probe or smallness of the temperature gradient. Then the average distance from the probe, at which the water-enriched phase will be located, can be estimated using the equation:

δ=2Dt,orδ=(PtρcpΔTπl)1/2(11)

At this distance, the temperature decrease, compared to its value on the probe surface T(0), will be:

T(δ)=T(0)+δ∂T∂rr=0(12)

Assuming that the onset of boiling-up of the phase Tph is determined mainly by the low-boiling component, i.e., water, we have:

Tph=T∗+ δ∂T∂rr=0(13)

Tph=T∗+(PtρcpΔTπl)1/2∂T∂rr=0(14)

It is obvious that the derivative of temperature with respect to coordinate is negative. This means that the boiling-up temperature of the water-enriched droplet is lower than the experimentally measured probe temperature corresponding to the boiling-up signal (T*). This conclusion, obtained under the assumption presented in Fig. 9b, agrees with the experimental results. Indeed, it follows from Fig. 5 that the smaller Ṫ, the larger the product P·t, and the higher the temperature T*.

Let consider the remaining limiting case, namely, Ṫ > 1 × 105 K/s. In this case, the droplets do not have time to begin moving. In turn, the lower the probability of formation of a critical vapor nucleus, the shorter the time texp = t (T > Ts). Since texp tends to zero, this probability also tends to zero. In an approximation of a uniformly superheated volume of liquid V, we can write the basic relationship for the nucleation rate J (T, p) [16,18] as follows:

J⋅V⋅texp=1(15)

This equation manifests the fact that boiling-up occurs (at least one critical nucleus is formed) and each product V·texp corresponds to each value of the boiling-up temperature. It is evident that, the shorter the time, the greater the nucleation rate and, finally, the temperature T*.

4  Discussion

Let consider the results presented above in the light of previous experiments on studying the spontaneous boiling-up of systems of various origin [19,25,31]. Typically, an increase in the heating duration of superheated liquid texp (decrease in the rate of its heating) is accompanied by a decrease in temperature T*. The decrease is due to an increase in the product V·texp, see (15), which is associated with the probability of boiling-up under the given p-V-t conditions and, less significantly, with an increase in the contribution of end effects inherent in the wire probe method. The scale of this reduction increases in the cases of thermally unstable compounds and gas-saturated liquids [28,39], as well as due to poorly accountable factors inherent in experiments with microheaters [40–44]. Due to this circumstance, the results of the presented experiments on T∗(T˙,T˙<1×105K/s) with unstable solutions, remains unclear.

Let extend the explanation of the nature of the discovered behavior, proposed in the previous section, with an analysis of the situation from the experimental point of view. As a basis for explanation, let find the relationship between temperature T* and the degree of heterogeneity of the system. Experience shows that a violation of the homogeneity of the system due to the introduction of an additional component is generally accompanied by a decrease in temperature T*. As striking examples, the boiling-up of hydrocarbons having traces of moisture [45] and composite water-in-oil droplets [25] can be mentioned. To clarify the generality of this phenomenon, a separate experiment was performed. The influence of the degree of polydispersity d of the solution on its attainable superheating was studied. Polyethylene glycol (PEG) having an average molecular weight of Mn = 1500, which has the narrowest molecular weight distribution d ≈ 1.01 among homologues, was selected as the base sample. The deviation of the d value from unity was changed by selecting the appropriate ratio between the content in the system of the base sample and polymer homologues with larger and smaller values of Mn. The selection was carried out in such a way that the value of Mn remained close to 1500. Homologues with a molecular weight from 100 (diethylene glycol) to 2 × 104 were used in the preparation of the samples. The results of the experiments at a given heating rate (Fig. 11) indicate that an increase in the heterogeneity of the system actually led to a decrease in the temperature of its attainable superheating.

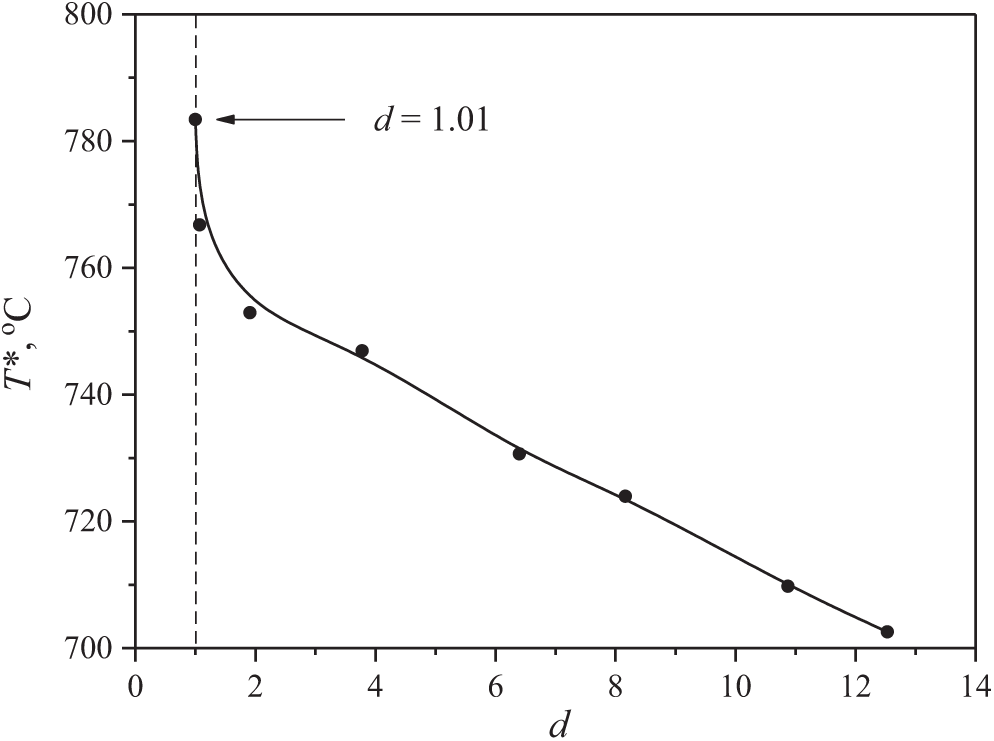
Figure 11: Influence of the polydispersity degree of a mixture of polymer homologues of PEG with Mn ≈ 1500 on its attainable superheating in the course of pulse heating

When penetrating deeper into the region of unstable states, heat transfer is modulated by phase separation according to the liquid-liquid mechanism. In essence, the temperature of the attainable superheating of the solution serves as an indicator of its current microphase state, which is inaccessible to direct observation due to the smallness of the temporal and spatial scales. This circumstance serves as the basis for predicting the details of heat transfer by the discussed solution under given T(texp) conditions. In this connection, let us mention the clarification of the range of heating rates corresponding to the transition of the unstable solution into the intensive mode of heat transfer by a continuous liquid characterised by the “plateau effect”. Indeed, such a mode is feasible in the range of Ṫ ~ (0.5 – 1.0) × 105 K/s as shown in Figs. 1 and 3. Some displacement of the boundaries of this interval depending on the concentration at this stage of the study is not of fundamental importance.

A joint consideration of the results of experiments on the intensity of heat transfer (Figs. 1 and 3) and the temperature of spontaneous boiling-up (Figs. 4–6) provided the basis for the following assumption. In the range of Ṫ ~ (0.5–1.0) × 105 K/s, the relaxing solution has the greatest mobility—and, as a consequence, the greatest degree of heterogeneity. Apparently, with an increase in Ṫ above 1 × 105 K/s, the thickness of the heated layer (~χt)1/2 turns out to be insufficient for the implementation of the spinodal decomposition regime. A similar result was observed when decreasing Ṫ, although for a different reason. When the speed of entry into the region of unstable states decreases, the temperature gradient along the normal to the surface of the heater is likely to become insufficient (to implement movement according to the Marangoni mechanism [38]); for this reason, the decay of the system proceeds mainly according to a much “softer” nucleation scenario. The decrease in the heating rate is accompanied, in turn, by a decrease in the degree of heterogeneity and, obviously, by an “unusual” increase in temperature T*.

In order to verify the hypothesis about a close relation between spinodal decomposition and spontaneous boiling-up in a certain range of heating rates, we performed measurements using small-step changes in the heating power. In these experiments, the response pattern T(texp) was analyzed to test the assumed existence of a maximum of mobility and the degree of heterogeneity in a certain interval of Ṫ, see Fig. 12. The appearance of a dramatic change in the response curve in this figure, accompanying a slight change in the heating rate, indicates that different relaxation mechanisms of the solution are dominant. In the analyzed case, it is the heating rate that turned out to be the key parameter. Our experience suggests that the regime of reaching a “plateau” is characteristic of the liquid-liquid phase separation (curve 1), while the confined (with respect to time and temperature) perturbation of the probe temperature (curves 2 and 3) is associated with spontaneous boiling-up.

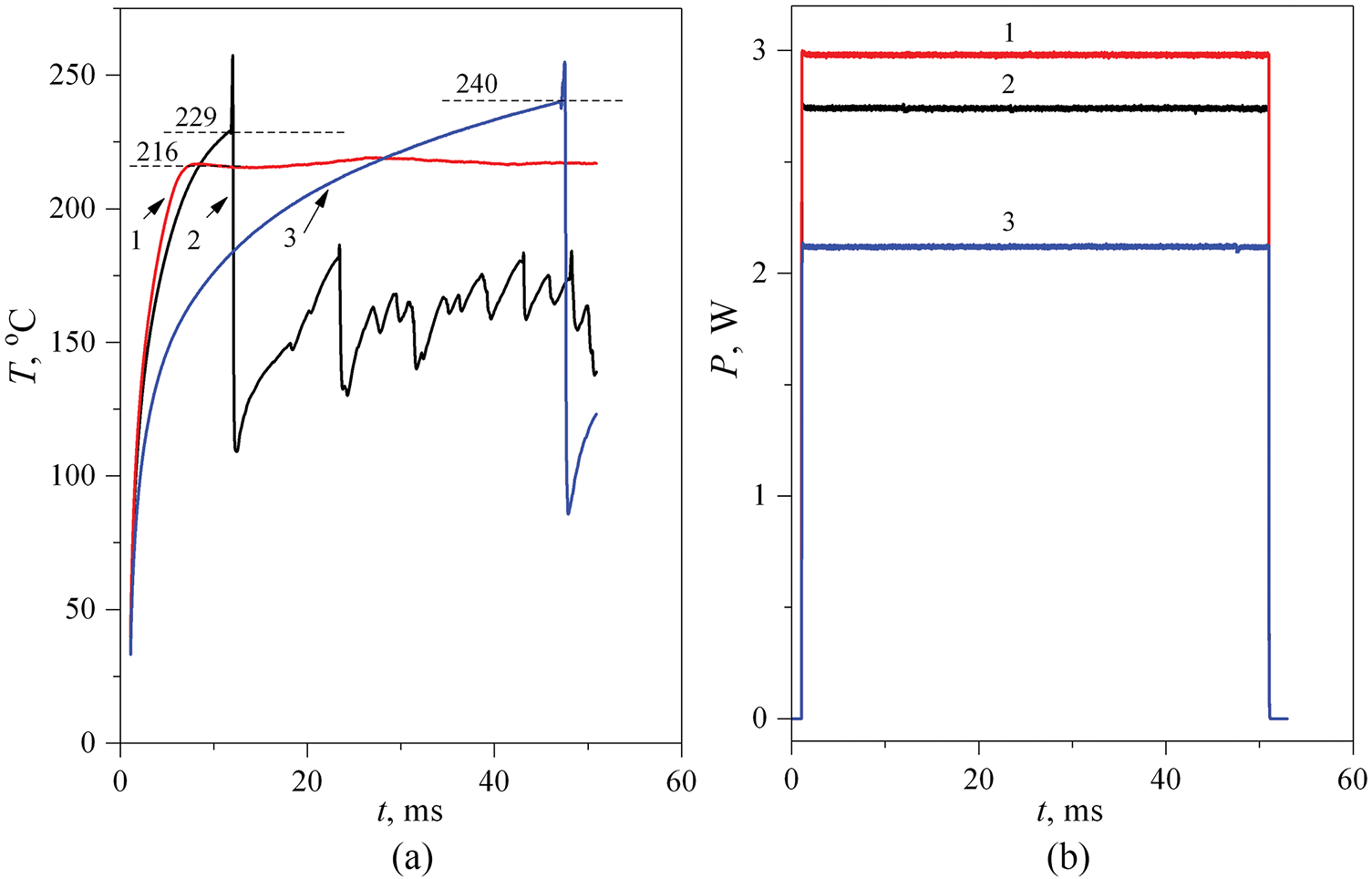
Figure 12: Evolution of the probe temperature in an aqueous solution containing 20 wt.% PPG-425 in the mode P(t) = const at atmospheric pressure (a). The parameter was the power value (b). The average values of Ṫ before the transition were 0.5 × 105 (1), 0.25 × 105 (2) and 0.5 × 104 K/s (3). The curve with T* ≈ 224°C at the highest value Ṫ ≈ 1.5 × 105 K/s is not shown not to complicate the figure

The video frames presented in Fig. 13 generally confirm the assumption about the change in the relaxation mechanism in the course of transition from fast heating (curve 1 in Fig. 12a, Ṫ ≈ 0.5 × 105 K/s) to slow heating (curve 2 in Fig. 12a, Ṫ ≤ 0.25 × 105 K/s), accompanied by an increase in the characteristic response temperature.

Figure 13: Video footage of the probe (diameter 20 µm) in solution (see Fig. 12). The frames in the section (a) refer to curve (1) in Fig. 12a, and those in the section (b) refer to curve (2). The upper frame is the onset of a monotonic heating process, while the lower frame is a certain stage of the developed phase transition

5  Conclusion

A series of experiments was performed to investigate the intensity of heat transfer and the temperature of spontaneous boiling-up of a LCST solution during its rapid transfer to the region of states above the liquid-liquid and liquid-vapour binodals—as well as, for some concentrations, the liquid-liquid spinodal. The experimental parameters were the concentration of the solution and the rate of its heating. The results obtained have confirmed the consistency of the hypothesis about the existence of a limited range of changes in the heating rate corresponding to the regime of intensive liquid-liquid decomposition of the system (spinodal decomposition). The onset temperature of this regime turned out to be somewhat lower than the expected temperature of spontaneous boiling-up of the solution. The developed physical model, which describes a possible scenario of the system response to pulsed heating, is consistent with the experimental data.

The conducted analysis of the results obtained led to the assumption about the maximum mobility in this range, which facilitates the initiation of spinodal decomposition and the consequent maximum degree of heterogeneity of the relaxing solution. Outside this range, a “softer” heat transfer regime is observed, until the temperature of attainable superheating of the liquid is reached. This temperature, which limits the region of existence of the liquid state, can serve as an approximation (from below) for the mechanical spinodal of the solution, including in the region of its unstable states.

The results were further used to clarify the conditions for the feasibility of spinodal decomposition of a solution, representing a poorly studied phase transition against the background of unstable states. The decomposition is accompanied by an increase in the mobility of droplets of fluid phases, manifested in an unusual, plateau-like shape of the response curve, limiting further increase in the heater temperature. This circumstance serves as a practical basis for the development of a theory of boiling-up of not fully miscible mixtures, as well as for assessing the applicability of LCST solutions as heat carriers in processes that allow a powerful local heat release.

Our article has initiated research into the interaction of liquid-liquid and liquid-vapour phase transitions, as well as spinodal decomposition against the background of a rapid transfer of the initially homogeneous solution into not fully stable and unstable states. Future studies will be aimed at clarifying the hierarchy of characteristic response times at finer concentration steps and searching for a general criterion for the possibility of spinodal decomposition under a sufficiently rapid heating of LCST solutions.

Acknowledgement: The authors are grateful to S. Yu. Elina for her help in preparing the manuscript and to N. G. Popova for proofreading the text.

Funding Statement: The investigation has been conducted at the expense of a grant of the Russian Science Foundation (project No. 23-69-10006), https://rscf.ru/project/23-69-10006/ (accessed on 6 May 2025).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Pavel Skripov; methodology, Sergey Rutin; validation, Alexey Melkikh; modeling, Alexey Melkikh and Dmitrii V. Antonov; visualization, Sergey Rutin and Dmitrii V. Antonov; graphical results, Sergey Rutin; interpretation of results and review, Alexey Melkikh; writing—review and editing, Pavel Skripov; supervision, Pavel Skripov. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kenrick FB, Gilbert CS, Wismer KL. By superheating of liquids. J Phys Chem. 1924;28(12):1297–307. doi:10.1021/j150246a009. [Google Scholar] [CrossRef]

2. Volmer M. Kinetik der Phasenbildung. Germany: Dresden-Leipzig; 1939. [Google Scholar]

3. Plesset M, Prosperetti A. Bubble dynamics and cavitation. Annu Rev Fluid Mech. 1977;9(1):145–85. doi:10.1146/annurev.fl.09.010177.001045. [Google Scholar] [CrossRef]

4. Yagov VV. Generic features and puzzles of nucleate boiling. Int J Heat Mass Tran. 2009;52(21–22):5241–9. doi:10.1016/j.ijheatmasstransfer.2009.03.071. [Google Scholar] [CrossRef]

5. Dedov AV. A review of modern methods for enhancing nucleate boiling heat transfer. Therm Eng. 2019;66(12):881–915. doi:10.1134/S0040601519120012. [Google Scholar] [CrossRef]

6. Lamas CP, Vega C, Noya EG, Sanz E. The water cavitation line as predicted by the TIP4P/2005 model. J Chem Phys. 2023;158(12):124504. doi:10.1063/5.0139470. [Google Scholar] [PubMed] [CrossRef]

7. Avdeev AA. Bubble systems. Berlin/Heidelberg, Germany: Springer; 2016. 466 p. [Google Scholar]

8. Sazhin SS. Droplets and sprays: simple models of complex processes. Berlin/Heidelberg, Germany: Springer; 2022. 597 p. [Google Scholar]

9. Moussa O, Tarlet D, Massoli P, Bellettre J. Investigation on the conditions leading to the micro-explosion of emulsified fuel droplet using two colors LIF method. Exp Thermal Fluid Sci. 2020;116(4):110106. doi:10.1016/j.expthermflusci.2020.110106. [Google Scholar] [CrossRef]

10. Nahar MM, Ma B, Guye K, Chau QH, Padilla J, Iyengar M, et al. Microscale evaporative cooling technologies for high heat flux microelectronics devices: background and recent advances. Appl Therm Eng. 2021;194(6):117109. doi:10.1016/j.applthermaleng.2021.117109. [Google Scholar] [CrossRef]

11. Law J, Kong KW, Chan HY, Sun W, Li WJ, Chau EBF, et al. Atomization of high-viscosity fluids for aromatherapy using micro-heaters for heterogeneous bubble nucleation. Sci Rep. 2017;7(1):40289. doi:10.1038/srep40289. [Google Scholar] [PubMed] [CrossRef]

12. Murshed SMS, Nieto de Castro CA. A critical review of traditional and emerging techniques and fluids for electronics cooling. Renew Sustain Energy Rev. 2017;78(1):821–33. doi:10.1016/j.rser.2017.04.112. [Google Scholar] [CrossRef]

13. Pavlenko AN, Kataev AI, Mironova IB. Hysteresis phenomena at boiling in liquid film flowing down the tubes with microarc oxidation coating. J Engin Thermophys. 2024;33(3):445–66. doi:10.1134/S1810232824030019. [Google Scholar] [CrossRef]

14. Lv Y, Chu W, Wang Q. Microscale bubble evolution on microheater during microsecond-pulse heating process. Cell Rep Phys Sci. 2025;6(2):102403. doi:10.1016/j.xcrp.2025.102403. [Google Scholar] [CrossRef]

15. Surtaev A, Malakhov I, Serdyukov V. Explosive vaporization of ethanol on microheater during pulse heating. Heat Transf Eng. 2023;44(6):502–11. doi:10.1080/01457632.2022.2073667. [Google Scholar] [CrossRef]

16. Skripov VP. Metastable liquids. Hoboken, NJ, USA: John Wiley & Sons, Inc.; 1974. 272 p. [Google Scholar]

17. Reid RC. Superheated liquids. Am Sci. 1976;64(2):146–56. [Google Scholar]

18. Skripov VP. Metastable states. J Non-Equilib Thermodyn. 1992;17(3):193–236. doi:10.1515/jnet.1992.17.3.193. [Google Scholar] [CrossRef]

19. Lipnyagov EV, Gurashkin AL, Starostin AA, Skripov PV. Going to spontaneous boiling-up onset. J Eng Thermophys. 2018;27(3):307–18. doi:10.1134/S1810232818030062. [Google Scholar] [CrossRef]

20. Kosyakov VA, Fursenko RV, Chudnovskii VM, Minaev SS. Physical mechanisms controlling a vapor bubble collapse and formation of a liquid jet during a laser-induced subcooled boiling near the end face of a thin waveguide. Int Comm Heat Mass Tran. 2023;148(6):107053. doi:10.1016/j.icheatmasstransfer.2023.107053. [Google Scholar] [CrossRef]

21. Qiao C, Yang D, Mao X, Xie L, Gong L, Peng X, et al. Recent advances in bubble-based technologies: underlying interaction mechanisms and applications. Appl Phys Rev. 2021;8(1):011315. doi:10.1063/5.0040331. [Google Scholar] [CrossRef]

22. Zhou Y, Dai L, Jiao N. Review of bubble applications in microrobotics: propulsion, manipulation, and assembly. Micromachines. 2022;13(7):1068. doi:10.3390/mi13071068. [Google Scholar] [PubMed] [CrossRef]

23. Busov KA. The effect of boiling-up on the shape and droplet size of a jet of superheated water discharged through a semi-cylindrical nozzle. Int Comm Heat Mass Tran. 2022;136(1):106199. doi:10.1016/j.icheatmasstransfer.2022.106199. [Google Scholar] [CrossRef]

24. Kotov AN, Gurashkin AL, Starostin AA, Lukianov KV, Skripov PV. Nucleation of a vapor phase and vapor front dynamics due to boiling-up on a solid surface. Energies. 2023;16(19):6966. doi:10.3390/en16196966. [Google Scholar] [CrossRef]

25. Melkikh AV, Skripov PV. Composite liquids under high-power heating: superheat of water in micro-explosion of water-in-fuel droplets. J Non-Equilib Thermodyn. 2024;49(4):543–54. doi:10.1515/jnet-2024-0017. [Google Scholar] [CrossRef]

26. Shinjo J, Xia J, Ganippa L, Megaritis A. Physics of puffing and microexplosion of emulsion fuel droplets. Phys Fluids. 2014;278(10):103302. doi:10.1063/1.4897918. [Google Scholar] [CrossRef]

27. Skripov PV, Igolnikov AA, Rutin SB, Melkikh AV. Heat transfer by unstable solution having the lower critical solution temperature. Int J Heat Mass Tran. 2022;184(4):122290. doi:10.1016/j.ijheatmasstransfer.2021.122290. [Google Scholar] [CrossRef]

28. Pavlov PA, Skripov PV. Bubble nucleation in polymeric liquids under shock processes. Intern J Thermophys. 1999;20(6):1779–90. doi:10.1023/A:1022618215413. [Google Scholar] [CrossRef]

29. Jennings JH, Middleman S. Homogeneous nucleation of vapor from polymer solutions. Macromolecules. 1987;18(11):2274–76. doi:10.1021/ma00153a037. [Google Scholar] [CrossRef]

30. Henderson SJ, Speedy RJ. Melting temperature of ice at positive and negative pressures. J Phys Chem. 1987;91(11):3069–72. doi:10.1021/j100295a085. [Google Scholar] [CrossRef]

31. Skripov PV, Puchinskis SE. Spontaneous boiling up as a specific relaxation process in polymer-solvent systems. J Appl Polym Sci. 1996;59(11):1659–65. doi:10.1002/(SICI)1097-4628(19960314)59:11<1659::AID-APP1>3.0.CO;2-N. [Google Scholar] [CrossRef]

32. Koverda VP, Skokov VN. The origin of fluctuations and scale transformations of time series at nonequilibrium phase transitions. Phys A Stat Mech Its Appl. 2005;346(3):203–16. doi:10.1016/j.physa.2004.07.042. [Google Scholar] [CrossRef]

33. Zhou S, Du M, Jariyavidyanont K, Zhuravlev E, Zou H, Androsch R, et al. Interplay between chain relaxation time and melt crystallization time in microinjection molding of polyoxymethylene. Macromolecules. 2024;57(12):5780–7. doi:10.1021/acs.macromol.3c02502. [Google Scholar] [CrossRef]

34. Igolnikov AA, Yampol’skiy AD. To the possibility of experimental estimation of the diffusion spinodal position of binary mixture with LCST via pulsed heating method. Chim Tech Acta. 2022;9(4):20229408. doi:10.15826/chimtech.2022.9.4.08. [Google Scholar] [CrossRef]

35. Rutin SB, Lipchak AI. Experimental setup for comprehensive study of non-stationary heat transfer in complex liquid media. Rev Sci Instrum. 2024;95(10):105114. doi:10.1063/5.0222705. [Google Scholar] [PubMed] [CrossRef]

36. Beysens D. A review on transport phenomena near the critical point of fluids under weightlessness. Front Space Technol. 2022;3:876642. doi:10.3389/frspt.2022.876642. [Google Scholar] [CrossRef]

37. Skripov VP, Skripov AV. Spinodal decomposition (phase transitions via unstable states). Sov Phys Usp. 1979;22(6):389–410. doi:10.1070/pu1979v022n06abeh005571. [Google Scholar] [CrossRef]

38. Lamorgese AG, Mauri R. Liquid mixture convection during phase separation in a temperature gradient. Phys Fluids. 2011;23(3):034102. doi:10.1063/1.3545840. [Google Scholar] [CrossRef]

39. Nikitin ED, Pavlov PA, Popov AP. Temperatures of the attainable superheat of some thermally unstable liquids. Int J Thermophys. 2002;23(2):529–41. doi:10.1023/A:1015165620863. [Google Scholar] [CrossRef]

40. Ching EJ, Avedisian CT, Cavicchi RC, Chung DH, Rah KJ, Carrier MJ. Rapid evaporation at the superheat limit of methanol, ethanol, butanol and n-heptane on platinum films supported by low-stress sin membranes. Int J Heat Mass Tran. 2016;101(3):707–18. doi:10.1016/j.ijheatmasstransfer.2016.04.008. [Google Scholar] [PubMed] [CrossRef]

41. Lankry A, Koyfman A, Haustein HD, Nir Y, Ziskind G, Bar-Kohany T. Onset of heterogeneous nucleation in pool boiling of HFE-7100 following rapid heating on a microscale heater. Exp Therm Fluid Sci. 2024;152(2):111125. doi:10.1016/j.expthermflusci.2023.111125. [Google Scholar] [CrossRef]

42. Lv YG, Li X, Chu WX, Wang QW, Li GX. Numerical study on temperature response of microheater and evolution characteristics of superheated zone under fast transient heating. Case Stud Therm Eng. 2024;60:104728. doi:10.1016/j.csite.2024.104728. [Google Scholar] [CrossRef]

43. Abyzov AS, Davydov LN, Schmelzer JWP. Heterogeneous nucleation in solutions on rough solid surfaces: generalized Gibbs approach. Entropy. 2019;21(8):782. doi:10.3390/e21080782. [Google Scholar] [PubMed] [CrossRef]

44. Wang G, Hu ZC. Explosive breakup and evolution of the thermal boundary layer around a pulse-heated microwire in sub-and supercritical CO2. Phys Fluids. 2022;34(8):083318. doi:10.1063/5.0106496. [Google Scholar] [CrossRef]

45. Melkikh AV, Skripov PV. Peculiarity of superheated hydrocarbons: jump in heat transfer due to micro-additives of moisture. Int J Thermophys. 2024;45(9):130. doi:10.1007/s10765-024-03427-y. [Google Scholar] [CrossRef]